ug表达式之详细讲解
UG8.0表达式应用知识讲解

U G8.0表达式应用UG8.0 表达式及应用1、表达式输入:工具----表达式2、执行:插入----曲线----规律曲线----根据方程。
如果没有“规律曲线”命令,用:帮助----命令查找器;查找。
3、“表达式”对话框如下:将方程转换为参数方程时注意:将方程转化为参数方程时,一定要将其转换为以变量t为参数的方程,在 UG中,t的变化范围一定是从0到1。
4、规律曲线命令如下:恒定允许您给整个规律函数定义一个常数值。
系统会提示您只输入一个规律值(即该常数)。
线性用于定义一个从起点到终点的线性变化率。
三次用于定义一个从起点到终点的三次变化率。
沿着样条的值 - 线性使用沿着脊线的两个或多个点来定义线性规律函数。
在选择脊线曲线后,可以沿着这条曲线指出多个点。
系统会提示您在每个点处输入一个值。
沿着样条的值 - 三次的使用沿着脊线的两个或多个点来定义一个三次规律函数。
在选择脊线曲线后,可以沿着该脊线指出多个点。
系统会提示您在每个点处输入一个值。
根据等式使用一个现有表达式及“参数表达式变量”来定义一个规律。
根据规律曲线允许您选择一条由光顺连接的曲线组成的线串来定义一个规律函数。
5、UG 常用内置函数在UG中利用【规律曲线】|【根据方程】绘制各种方程曲线:1、极坐标(或柱坐标r,θ,z)与直角坐标系(x,y,z)的转换关系:x=r*cos(θ);y=r*sin(θ);z=z2、球坐标系(r,θ,φ)与直角坐标系(x,y,z)的转换关系:x=rsinθcosφ;y=rsinθsinφ;z=rcosθ在UG表达式中输入的theta=θ;phi=φ;r=rho【注:所有UG表达式中,必须先在名称栏输入t,公式栏输入0,类型为恒定的,即无单位。
t是UG自带的系统变量,其取值为0~1之间的连续数】1.直线直线的数学方程为y-y0=tan(θ)*(x-x0),若直线经过点(10,20),倾角θ为30°,长度L为40,即UG表达式为:theta=30L=40xt=10+L*cos(theta)*tyt=20+L*sin(theta)*tzt=0效果如图1图1 图22.圆和圆弧圆的数学方程为(x-x0)^2+(y-y0)^2=r^2,若圆心坐标为(50,40),半径r为30,即UG表达式为:r=30theta=t*360xt=50+r*cos(theta)yt=40+r*sin(theta)zt=0效果如图23.椭圆和椭圆弧椭圆的数学方程为(x-x0)^2/a^2+(y-y0)^2/b^2=1,若椭圆中心坐标为(50,40),长半轴a为30(在X 轴上),短半轴b为20,即UG表达式为:a=30b=20theta=t*360xt=50+a*cos(theta)yt=40+b*sin(theta)zt=0效果如图3图3 图44.双曲线双曲线的数学方程为x2/a2-y2/b2=1,若中心坐标为(0,0),实长半轴a为4(在x轴上),虚半轴b 为3,y的取值范围为-5~+5内的一段,即UG表达式为:a=4b=3yt=10*t-5zt=0做出一半后进行镜像复制,效果如图45.抛物线抛物线I的数学方程为y2=2px,若抛物线的顶点为(30,20)焦点到准线的距离p=8,y的取值范围为-25~+25,即UG表达式为:p=8yt=50*t-25+20xt=(yt-20)^2/(2*p)+30zt=0效果如图5-1抛物线II数学参数方程:x=2pt2,y=2pt(其中t为参数)。
UG表达式
重 命
达 式 表
锁 定 表 表 达 打 开 式 式 达 出
输 输 入 表 达 式
几何表达式
几何表达式用来在抽象几何特性的基础上定义变量.
open part exp_geo.prt
表 达 式 . 者 两 象 象 点 间 的 最 小 距 离 而 建 个 或 对 象
个 距 离 表 达 式
立 的 表 达 式 基 于 两 个 线 对 象 边 或 曲 . 基 于 . 式 达 表 长 度
建模工作步骤
8 1 7 5 4 6 3 2
建模几个基本原则
1. 一个零件中只能有一个基本体素 2. 如果是用草图作,只能有一个固定的基准平面及两个固定的基准轴. 3. 尽量用(feature)特征做零件造型,当特征不好造型时再用草图做. 4. 用草图时,曲线要简洁,容易约束. 5. 做草图时,一次性拉伸或旋转用的曲线作在一张草图上.不是在同 一次拉伸或旋转中使用的曲线尽量不要做在一张草图上,可以分别 做在不同的草图上. 6.通过草图到三维图形create的每一个对象是独立的,需要经过布尔运 算得到一个整体模型.
表达式的建立
表达式的建立方法有两种: 1. 系统自动建立的表达式(只要是参数化设计,就会自动生成表达式.) 当用户建立特征,定位特征或草图,标注草图尺寸,建立配对条件等时,系统 自动建立表达式,表达式类型为简单的算术表达式. Open part file exp_part1.prt from the exp subdirectory
expression
hole_h=length/2 //hole horizontal position //表示后面为解释语句
建模工作步骤
1. 2. 3. 4. 5. 6. 7. 8. 建立一个新的 UG部件文件或恢复一个已存的UG部件文 件:File→New… File→Open…(一个标准格式文件) 选择一个应用 : Application→Modeling/Assemblies… 检查 /预设置参数 : Preferences→Object/Modeling/Sketcher… 建立少数关键设计变量:Tools→Expression… 建立对象 : Insert→… 分析对象 : Information → / Analysis→ 修改对象: Edit→… 存贮 UG部件文件: File→Save
ug正弦曲线表达式

ug正弦曲线表达式
【原创实用版】
目录
1.UG 正弦曲线表达式的概念
2.UG 正弦曲线表达式的基本形式
3.UG 正弦曲线表达式的应用
正文
1.UG 正弦曲线表达式的概念
UG 正弦曲线表达式,是指用 UG(一种计算机辅助设计软件)绘制的正弦曲线所对应的数学表达式。
在工程领域,正弦曲线常常用于描述周期性的变化或者振荡现象,而 UG 正弦曲线表达式则可以精确地描述这种变化。
2.UG 正弦曲线表达式的基本形式
UG 正弦曲线表达式的基本形式为 y=Asin(ωx+φ),其中 y 表示曲线上的点的纵坐标,A 表示振幅,ω表示角频率,x 表示曲线上的点的横坐标,φ表示初相位。
这个表达式描述的是一个周期性的波形,其周期为2π/ω。
3.UG 正弦曲线表达式的应用
UG 正弦曲线表达式在工程领域中有广泛的应用,例如在信号处理、通信系统、控制理论等方面都有重要的应用。
在信号处理中,正弦曲线常用于模拟信号的振荡部分,而在通信系统中,正弦曲线则可以用于调制信号,以实现信号的传输。
在控制理论中,正弦曲线则可以用于分析系统的稳定性。
第1页共1页。
UG最全方程式曲线及详细表达式

UG方程式曲线及表达式作者:登科设计在UG中利用【规律曲线】|【根据方程】绘制各种方程曲线:1、极坐标(或柱坐标r,θ,z)与直角坐标系(x,y,z)的转换关系:x=r*cos(θ);y=r*sin(θ);z=z2、球坐标系(r,θ,φ)与直角坐标系(x,y,z)的转换关系:x=rsinθcosφ;y=rsinθsinφ;z=rcosθ在UG表达式中输入的theta=θ;phi=φ;r=rho【注:所有UG表达式中,必须先在名称栏输入t,公式栏输入0,类型为恒定的,即无单位。
t是UG自带的系统变量,其取值为0~1之间的连续数】1.直线直线的数学方程为y-y0=tan(θ)*(x-x0),若直线经过点(10,20),倾角θ为30°,长度L为40,即UG表达式为:theta=30L=40xt=10+L*cos(theta)*tyt=20+L*sin(theta)*tzt=0效果如图1图1 图22.圆和圆弧圆的数学方程为(x-x0)^2+(y-y0)^2=r^2,若圆心坐标为(50,40),半径r为30,即UG 表达式为:r=30theta=t*360xt=50+r*cos(theta)yt=40+r*sin(theta)zt=0效果如图23.椭圆和椭圆弧椭圆的数学方程为(x-x0)^2/a^2+(y-y0)^2/b^2=1,若椭圆中心坐标为(50,40),长半轴a为30(在X轴上),短半轴b为20,即UG表达式为:a=30b=20theta=t*360xt=50+a*cos(theta)yt=40+b*sin(theta)zt=0效果如图3图3 图44.双曲线双曲线的数学方程为x2/a2-y2/b2=1,若中心坐标为(0,0),实长半轴a为4(在x轴上),虚半轴b为3,y的取值范围为-5~+5内的一段,即UG表达式为:a=4b=3yt=10*t-5xt=a/b*sqrt(b^2+yt^2)或xt=-a/b*sqrt(b^2+yt^2)zt=0做出一半后进行镜像复制,效果如图45.抛物线抛物线I的数学方程为y2=2px,若抛物线的顶点为(30,20)焦点到准线的距离p=8,y的取值范围为-25~+25,即UG表达式为:p=8yt=50*t-25+20xt=(yt-20)^2/(2*p)+30zt=0效果如图5-1抛物线II数学参数方程:x=2pt2,y=2pt(其中t为参数)。
的UG方程曲线及详细表达式

在UG中利用【规律曲线】|【根据方程】绘制各种方程曲线:1、极坐标(或柱坐标r,θ,z)与直角坐标系(x,y,z)的转换关系:x=r*cos(θ);y=r*sin(θ);z=z2、球坐标系(r,θ,φ)与直角坐标系(x,y,z)的转换关系:x=rsinθcosφ;y=rsinθsinφ;z=rcosθ在UG表达式中输入的theta=θ;phi=φ;r=rho【注:所有UG表达式中,必须先在名称栏输入t,公式栏输入0,类型为恒定的,即无单位。
t是UG自带的系统变量,其取值为0~1之间的连续数】1.直线直线的数学方程为y-y0=tan(θ)*(x-x0),若直线经过点(10,20),倾角θ为30°,长度L为40,即UG表达式为:theta=30L=40xt=10+L*cos(theta)*tyt=20+L*sin(theta)*tzt=0效果如图1图1 图22.圆和圆弧圆的数学方程为(x-x0)^2+(y-y0)^2=r^2,若圆心坐标为(50,40),半径r为30,即UG 表达式为:r=30theta=t*360xt=50+r*cos(theta)yt=40+r*sin(theta)zt=0效果如图23.椭圆和椭圆弧椭圆的数学方程为(x-x0)^2/a^2+(y-y0)^2/b^2=1,若椭圆中心坐标为(50,40),长半轴a为30(在X轴上),短半轴b为20,即UG表达式为:a=30b=20theta=t*360xt=50+a*cos(theta)yt=40+b*sin(theta)zt=0效果如图3图3 图44.双曲线双曲线的数学方程为x2/a2-y2/b2=1,若中心坐标为(0,0),实长半轴a为4(在x轴上),虚半轴b为3,y的取值范围为-5~+5内的一段,即UG表达式为:a=4b=3yt=10*t-5xt=a/b*sqrt(b^2+yt^2)或xt=-a/b*sqrt(b^2+yt^2)zt=0做出一半后进行镜像复制,效果如图45.抛物线抛物线I的数学方程为y2=2px,若抛物线的顶点为(30,20)焦点到准线的距离p=8,y的取值范围为-25~+25,即UG表达式为:p=8yt=50*t-25+20xt=(yt-20)^2/(2*p)+30zt=0效果如图5-1抛物线II数学参数方程:x=2pt2,y=2pt(其中t为参数)。
UG的表达式讲解

UG的表达式讲解64 UG的设计应用第二章表达式2.1 综述2.1.1 表达式的概念表达式是算术或条件语句,用来控制零件特征。
表达式可以用来定义或控制一个模型的多种尺寸,例如一个特征或一个草图的尺寸。
表达式在参数化设计中是十分有意义的,它可以用来控制同一个零件上的不同特征间的关系或一个装配中的不同零件间的关系。
例如:我们可以用一个表达式来建立一个支架零件的厚度和长度之间的关系。
当支架的长度改变之后,它的厚度自动更新。
图2-1所示为表达式的一个实例。
在创建表达式时必须注意以下几点: ? 表达式左侧必须是一个简单变量,等式右侧是一个数学语句或一条件语句。
? 所有表达式均有一个值(实数或整数),该值被赋给表达式的左侧变量。
表达式等式的右侧可认是含有变量、数字、运算符和符号的组合或常数。
?? 用于表达式等式右侧中的每一个变量,必须作为一个表达式名字出现在某处。
Length=.5+2*Cos(60)图2-1 表达式格式2.1.2 创建表达式的方法1(手工创建表达式?选择下拉菜单Tool?Expression或按快捷键Ctrl+E?改变一个已存在的表达式的名字,可选择下拉菜单Tool?Expression,选取已存在的表达式,然后单击Rename。
?将文本文件中存在的表达式引入到UG中,可选择下拉菜单Tool?Expression?Import。
2. 系统自动建立表达式当用户作下列操作时,系统自动地建立表达式,其名字用一个小写字母p开始。
第二章表达式 65?建立一个特征(Create a Feature)时,系统对特征的每个参数建立一个表达式。
?建立一个草图(Create a Sketch)时,系统对定义草图基准的XC和YC坐标建立两个表达式。
例如:p1_YDATUM_V1=0?标注草图尺寸(Dimension a Sketch)后,系统对草图的每一个尺寸都建立一个相应的表达式。
?定位一个特征或一个草图(Position a feature or sketch)时,系统对每一个定位尺寸都建立一个相应的表达式。
最全的UG方程曲线及详细表达式讲解

在UG中利用【规律曲线】|【根据方程】绘制各种方程曲线:1、极坐标(或柱坐标r,θ,z)与直角坐标系(x,y,z)的转换关系:x=r*cos(θ);y=r*sin(θ);z=z2、球坐标系(r,θ,φ)与直角坐标系(x,y,z)的转换关系:x=rsinθcosφ;y=rsinθsinφ;z=rcosθ在UG表达式中输入的theta=θ;phi=φ;r=rho【注:所有UG表达式中,必须先在名称栏输入t,公式栏输入0,类型为恒定的,即无单位。
t是UG自带的系统变量,其取值为0~1之间的连续数】1.直线直线的数学方程为y-y0=tan(θ)*(x-x0),若直线经过点(10,20),倾角θ为30°,长度L为40,即UG表达式为:theta=30L=40xt=10+L*cos(theta)*tyt=20+L*sin(theta)*tzt=0效果如图1图1 图22.圆和圆弧圆的数学方程为(x-x0)^2+(y-y0)^2=r^2,若圆心坐标为(50,40),半径r为30,即UG 表达式为:r=30theta=t*360xt=50+r*cos(theta)yt=40+r*sin(theta)zt=0效果如图23.椭圆和椭圆弧椭圆的数学方程为(x-x0)^2/a^2+(y-y0)^2/b^2=1,若椭圆中心坐标为(50,40),长半轴a为30(在X轴上),短半轴b为20,即UG表达式为:a=30b=20theta=t*360xt=50+a*cos(theta)yt=40+b*sin(theta)zt=0效果如图3图3 图44.双曲线双曲线的数学方程为x2/a2-y2/b2=1,若中心坐标为(0,0),实长半轴a为4(在x轴上),虚半轴b为3,y的取值范围为-5~+5内的一段,即UG表达式为:a=4b=3yt=10*t-5xt=a/b*sqrt(b^2+yt^2)或xt=-a/b*sqrt(b^2+yt^2)zt=0做出一半后进行镜像复制,效果如图45.抛物线抛物线I的数学方程为y2=2px,若抛物线的顶点为(30,20)焦点到准线的距离p=8,y的取值范围为-25~+25,即UG表达式为:p=8yt=50*t-25+20xt=(yt-20)^2/(2*p)+30zt=0效果如图5-1抛物线II数学参数方程:x=2pt2,y=2pt(其中t为参数)。
全面地UG方程曲线及详细表达式

在UG中利用【规律曲线】|【根据方程】绘制各种方程曲线:1、极坐标(或柱坐标r,θ,z)与直角坐标系(x,y,z)的转换关系:x=r*cos(θ);y=r*sin(θ);z=z2、球坐标系(r,θ,φ)与直角坐标系(x,y,z)的转换关系:x=rsinθcosφ;y=rsinθsinφ;z=rcosθ在UG表达式中输入的theta=θ;phi=φ;r=rho【注:所有UG表达式中,必须先在名称栏输入t,公式栏输入0,类型为恒定的,即无单位。
t是UG自带的系统变量,其取值为0~1之间的连续数】1.直线直线的数学方程为y-y0=tan(θ)*(x-x0),若直线经过点(10,20),倾角θ为30°,长度L为40,即UG表达式为:theta=30L=40xt=10+L*cos(theta)*tyt=20+L*sin(theta)*tzt=0效果如图1图1 图22.圆和圆弧圆的数学方程为(x-x0)^2+(y-y0)^2=r^2,若圆心坐标为(50,40),半径r为30,即UG 表达式为:r=30theta=t*360xt=50+r*cos(theta)yt=40+r*sin(theta)zt=0效果如图23.椭圆和椭圆弧椭圆的数学方程为(x-x0)^2/a^2+(y-y0)^2/b^2=1,若椭圆中心坐标为(50,40),长半轴a为30(在X轴上),短半轴b为20,即UG表达式为:a=30b=20theta=t*360xt=50+a*cos(theta)yt=40+b*sin(theta)zt=0效果如图3图3 图44.双曲线双曲线的数学方程为x2/a2-y2/b2=1,若中心坐标为(0,0),实长半轴a为4(在x轴上),虚半轴b为3,y的取值围为-5~+5的一段,即UG表达式为:a=4b=3yt=10*t-5xt=a/b*sqrt(b^2+yt^2)或xt=-a/b*sqrt(b^2+yt^2)zt=0做出一半后进行镜像复制,效果如图45.抛物线抛物线I的数学方程为y2=2px,若抛物线的顶点为(30,20)焦点到准线的距离p=8,y的取值围为-25~+25,即UG表达式为:p=8yt=50*t-25+20xt=(yt-20)^2/(2*p)+30zt=0效果如图5-1抛物线II数学参数方程:x=2pt2,y=2pt(其中t为参数)。
ug表达式之详细讲解

规律曲线简介:“规律曲线”选项用于使用规律子函数创建样条。
规律样条定义为一组X、Y及Z分量,必须指定每个分量的规律。
要创建规律曲线:使用规律子函数,为X、Y及Z各分量选择并定义一个规律选项。
1.通过定义一个方位和/或基点,或指定一个参考坐标系来控制方位(样条的方位)。
2.选择“确定”或“应用”来创建曲线。
可以通过“信息”→“对象”来显示规律样条的非参数或特征信息。
规律曲线通过X、Y及Z分量的组合来定义一条规律样条。
必须指定每个组件的规律类型,可通过规律子函数进行指定。
可用的选项有:恒定:允许您给整个规律函数定义一个常数值。
系统会提示您只输入一个规律值(即该常数)。
线性:用于定义一个从起点到终点的线性变化率。
三次:用于定义一个从起点到终点的三次变化率。
沿着样条的值-线性:使用沿着脊线的两个或多个点来定义线性规律函数。
在选择脊线曲线后,可以沿着这条曲线指出多个点。
系统会提示您在每个点处输入一个值。
沿着样条的值-三次的:使用沿着脊线的两个或多个点来定义一个三次规律函数。
在选择脊线曲线后,可以沿着该脊线指出多个点。
系统会提示您在每个点处输入一个值。
根据方程:使用一个现有表达式及“参数表达式变量”来定义一个规律。
根据规律曲线:允许您选择一条由光顺连接的曲线组成的线串来定义一个规律函数。
对于所有规律样条,必须组合使用规律子函数选项(即,X分量可能是线性规律,Y分量可能是等式规律,而Z分量可能是常数规律)。
通过组合不同的选项,可控制每个分量以及样条的数学特征。
既可以定义二维规律样条,也可以定义三维规律样条。
例如,二维规律样条要求一个平面具有常数值(即,如果Z分量由某一常数规律定义为值0,则可在Z=0的XC-YC平面上生成一条曲线。
同理,如果X 分量由某一常数规律定义为值100,则在X=100的ZC-YC平面内生成一条曲线)。
规首选项对话框中设置的距离公差和角度公差而近似创建的。
任360度的规律曲线必须使用螺旋线选项或根据方程规律子函数来构建。
UG表达式应用说明

●表达式左侧必须是一个简单变量,等式右侧是一个数学语句或一条件语句。
●所有表达式均有一个值(实数或整数),该值被赋给表达式的左侧变量。
●表达式等式的右侧可认是含有变量、数字、运算符和符号的组合或常数。
●用于表达式等式右侧中的每一个变量,必须作为一个表达式名字出现在某处。
Length=.5+2*Cos(60)图2-1 表达式格式2.1.2 表达式的方法1.手工创建表达式●选择下拉菜单Tool→Expression或按快捷键Ctrl+E●改变一个已存在的表达式的名字,可选择下拉菜单Tool→Expression,选取已存在的表达式,然后单击Rename。
●将文本文件中存在的表达式引入到UG中,可选择下拉菜单Tool→Expression→Import。
2. 系统自动建立表达式当用户作下列操作时,系统自动地建立表达式,其名字用一个小写字母p开始。
●建立一个特征(Create a Feature)时,系统对特征的每个参数建立一个表达式。
●建立一个草图(Create a Sketch)时,系统对定义草图基准的XC和YC坐标建立两个表达式。
例如:p1_YDATUM_V1=0●标注草图尺寸(Dimension a Sketch)后,系统对草图的每一个尺寸都建立一个相应的表达式。
●定位一个特征或一个草图(Position a feature or sketch)时,系统对每一个定位尺寸都建立一个相应的表达式。
●生成一个匹配条件(Create a mating)时,系统会自动建立相应的表达式。
表达式可应用于多个方面,它可以用来控制草图和特征尺寸和约束;可用来定义一个常量,如pi=3.1415926;也可被其它表达式调用,如expression1=expression2+expression3,这对于缩短一个很长的数字表达式十分有效,并且能表达它们之间的关系。
2.1.3 为什么使用表达式表达式是一个功能强大的工具,可以使UG实现参数化设计。
ug表达式

abs 绝对值,abs(x) = |x|arccos 反余弦,acos(x) = arc cos(x),(结果为弧度)arcsin 反正弦,asin(x) = arc sin(x),(结果为弧度)arctan 反正切,atan(x) = arc tan(x),(结果为弧度)arctan2 反正切,atan2(x, y) = arc tan(x / y),(结果为弧度)ceiling 向上取整,ceil(x) = x 是一个实数,函数返回大于或等于x 的最接近的整数,如果a=ceil(.1),a 等于1。
cos 余弦,cos(x) = cos(x),(x 必须为度数)hypcos 双曲余弦,cosh(x) = cosh(x)deg 度数转换,deg(x) 将弧度转换成度数。
exp 指数,exp(x) = exhypot 直角三角形斜边,hypot(x, y) = /x2 + y2log 自然对数,log(x) = ln (x) = loge (x)log10 常用对数,log10(x) = log10(x)rad 弧度转换,rad (x) 将度数转换成弧度sin 正弦,sin(x) = sin(x),(x 必须为度数)hypsin 双曲正弦,sinh(x) = sinh(x)sqrt 平方根,sqrt (x) = /xtan 正切,tan(x) = tan(x),(x 必须为度数)hyptan 双曲正切,tanh(x) = tanh(x)trnc取整,trnc(x) 移去数字x 上的任何小数部分(小数点右边的所有数字)pi() 无自变量,返回pi 的值用于单位转换的内置函数(使用以下函数将测量单位转换为其它单位。
)名称描述cm cm(x) 将x 从厘米转换成部件文件默认的单位。
ft ft(x) 将x 从英尺转换成部件文件默认的单位。
grd grd(x) 将x 从梯度转换成度数。
inch inch(x)将x 从英寸转换成部件文件默认的单位。
ug表达式解释

ABS ABS 绝对值是ARCCOS ARCCOS 反余弦是ACOSH ACOSH 反双曲余弦是ACOT N/A 反余切否ACOTH N/A 反双曲余切否ACSC N/A 反余割否ACSCH N/A 反双曲余割否ASEC N/A 反正割否ASECH N/A 反双曲正割否ARCSIN ARCSIN 反正弦是ASINH ASINH 反双曲正弦是ARCTAN ARCTAN 反正切是ARCTAN2 ARCTAN2 x, y 的反正切是ATANH ATANH 反双曲正切是CEIL (X) CEILING (X,1) 大于等于X 的最小整数是COS COS 余弦是HYPCOS HYPCOS 双曲余弦是COT N/A 余切否COTH N/A 双曲余切否CSC N/A 余割否CSCH N/A 双曲余割否DEGREES DEGREES 将用弧度表示的角度转换为角度是DET MDETERM 矩阵行列式是DOT N/A 矢量点乘否EVEN EVEN 返回下一个更大绝对值的偶数是EXP EXP 指数是FACT FACT 阶乘是FLOOR(X) FLOOR(X,1) 小于等于X 的最大整数是FRAC N/A X 的小数部分NaGAMMA N/A Gamma 函数- 可表示为EXP(GAMMALN(X)) NaGCD GCD 最大公分母是GRAND N/A 高斯随机数否INT INT X 的整数部分是LCM LCM 最小公倍数是LN LN 自然对数是LNGAMMA GAMMALN gamma 函数的自然对数是LOG(X) LOG(X,10) 以10 为底的对数LOG10 LOG10 以10 为底的对数是LOG2(X) LOG(X,2) 以2 为底的对数- LOG(X,2) 是MOD MOD 余数是MODULUS N/A 模数否ODD ODD 返回下一个更大绝对值的奇数是PI PI Pi 值是POLY N/A N 次多项式的值否PRODUCT PRODUCT 参数列表中所有数值的积是RADIANS RADIANS 将用度表示的角度转换为弧度是RAND RAND 0 和1 之间的均匀随机数是ROUND(X,N) ROUND(X,N) X 保留N 位小数是SEC N/A 正割否SECH N/A 双曲正割否SIGMOID N/A Sigmoid 函数值否SIGN SIGN 参数的符号是SIN SIN 正弦是HYPSIN HYPSIN 双曲正弦是SQRT SQRT 平方根是SQRTPI SQRTPI 一个数与Pi 之积的平方根是SUMNEGATIVE N/A 列表中负值之和否SUMPOSITIVE N/A 列表中正值之和否SUMPRODUCT SUMPRODUCT 数组中所有对应元素之积的和是SUMSQ SUMSQ 参数平方之和是SUMXMY2 SUMXMY2 返回两数组对应值之差的平方之和是SUMX2MY2 SUMX2MY2 返回两数组对应值的平方差之和是SUMX2PY2 SUMX2PY2 返回两数组对应值的平方和之和是TAN TAN 正切是HYPTAN HYPTAN 双曲正切是TRANSPOSE N/A 否VECLEN N/A 平方和的平方根- 可表示为SQRT(SUMSQ(...))。
最全的UG方程曲线详细表达式

在UG中利用【规律曲线】|【根据方程】绘制各种方程曲线:1、极坐标(或柱坐标r,θ,z)与直角坐标系(x,y,z)的转换关系:x=r*cos(θ);y=r*sin(θ);z=z2、球坐标系(r,θ,φ)与直角坐标系(x,y,z)的转换关系:x=rsinθcosφ;y=rsinθsinφ;z=rcosθ在UG表达式中输入的theta=θ;phi=φ;r=rho【注:所有UG表达式中,必须先在名称栏输入t,公式栏输入0,类型为恒定的,即无单位。
t是UG自带的系统变量,其取值为0~1之间的连续数】1.直线直线的数学方程为y-y0=tan(θ)*(x-x0),若直线经过点(10,20),倾角θ为30°,长度L为40,即UG表达式为:theta=30L=40xt=10+L*cos(theta)*tyt=20+L*sin(theta)*tzt=0效果如图1图1 图22.圆和圆弧圆的数学方程为(x-x0)^2+(y-y0)^2=r^2,若圆心坐标为(50,40),半径r为30,即UG表达式为:r=30theta=t*360xt=50+r*cos(theta)yt=40+r*sin(theta)zt=0效果如图23.椭圆和椭圆弧椭圆的数学方程为(x-x0)^2/a^2+(y-y0)^2/b^2=1,若椭圆中心坐标为(50,40),长半轴a为30(在X轴上),短半轴b为20,即UG表达式为:a=30b=20theta=t*360xt=50+a*cos(theta)yt=40+b*sin(theta)zt=0效果如图3图3 图44.双曲线双曲线的数学方程为x2/a2-y2/b2=1,若中心坐标为(0,0),实长半轴a为4(在x轴上),虚半轴b为3,y的取值范围为-5~+5内的一段,即UG表达式为:a=4b=3yt=10*t-5xt=a/b*sqrt(b^2+yt^2)或xt=-a/b*sqrt(b^2+yt^2)zt=0做出一半后进行镜像复制,效果如图45.抛物线抛物线I的数学方程为y2=2px,若抛物线的顶点为(30,20)焦点到准线的距离p=8,y的取值范围为-25~+25,即UG表达式为:p=8yt=50*t-25+20xt=(yt-20)^2/(2*p)+30zt=0效果如图5-1抛物线II数学参数方程:x=2pt2,y=2pt(其中t为参数)。
UG表达式应用

反正切(atan2(x,y)为x/y的反正 切)
atan(1,0)(其值为1.5708rad)
向上取整
ceil l(3,12)(其值为4)
向下取整
floor(3,12) (其值为3)
表达式的建立
表达式的建立方法有两种: 一. 系统自动建立的表达式(只要是参数化设计,就会自动生成表达式。)
当用户建立特征、定位特征、定位草图、标注草图尺寸、建立配对条件等时, 系统自动建立表达式,表达式类型为简单的算术表达式。 二. 用户建立的表达式 可以建立较复杂的算术表达式以及条件表达式、几何表达式和部件间相关表达 式。
地对模型进行编辑;同时,通过更改控制某一特定参数的表达式,可以改变一实体模型的特征
尺寸或对其重新定位。使用表达式也可产生一个零件族。通过改变表达式值,可将一个零件转
为一个带有同样拓朴关系的新零件。
Expression 表达式概念
一. 数学表达式,通过数学方法来定义变量。如 P1=5+8*sin45 二. 条件表达式,通过指定不同的条件来定义变量。利用if/else结构建立表达式,其句法为:
UG表达式应用
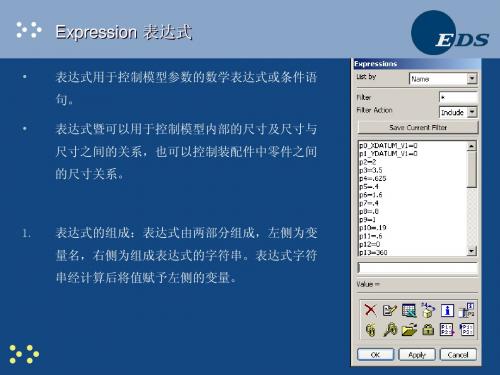
表达式是用于控制模型参数的数学表达式或条件语句。
表达式既可以用于控制模型内部的尺寸及尺寸与尺寸之间的关系,也可以控制装配件中零件之
间的尺寸关系。
表达式的组成:表达式由两部分组成,左侧为变量名,右侧为组成表达式的字符串。表达式字
符串经计算后将值赋予左侧的变量。
表达式在参数化设计中是十分有意义的,可以使UG实现参数化设计。运用表达式,可十分简便
Expression 表达式的类型
表达式语言
一. 变量名:变量名是由字母与数字组成的字符串,其长度小于或等于32个字符。 变量名必须以字母开始,可包含下划线“_”,不能有空格,注意大小写有差 别,如M1与m1代表不同的变量名。
UG表达式概述

1.8 表达式概述表达式是UG的一个工具,是用于控制模型参数的数学表达式或条件语句。
其等式左侧必须是一个简单变量,等式右侧是一个数学语句或一个条件语句。
通过算术和条件表达式,用户可以控制部件的特性,如控制部件中特征或对象的尺寸。
通过表达式不但可以控制部件中特征与特征之间、对象与对象之间、特征与对象之间的相互尺寸与位置关系,而且可以控制装配中的部件与部件之间的尺寸与位置关系。
另外,【信息】菜单下也有关于表达式的查询,如图1-50所示。
图1-50 表达式的菜单1.8.1 表达式概念在UG中,表达式有它自己的语言,它是可以用来控制部件特性的算术或条件语句,可以定义和控制模型的许多尺寸,如特征或草图的尺寸。
表达式在参数化设计中是十分有意义的,它可以用来控制同一个零件上的不同特征之间的关系或者一个装配中不同的零件关系。
例如,一个立方体的高度可以用它与长度的关系来表达,那么它的长度变化时,则其高度也随之自动更新。
表达式是定义关系的语句,它由两部分组成,左侧为变量名,右侧为组成表达式的字符串。
表达式字符串经计算后将值赋予左侧的变量。
一个表达式等式的右侧可以是含有变量、函数、数字、运算符和符号的组合或常数。
用于表达式等式右侧中的每一个变量,必须作为一个表达式名字出现在某处。
1.8.2 表达式的建立方式表达式可以自动建立或手动建立。
系统自动生成开头用p的限定符(p0、p1表示的表达式关系式)。
以下情况会自动建立表达式:(1)创建草图时,用两个表达式定义草图基准XC和YC坐标。
(2)特征或草图定位时,每个定位尺寸用一个表达式表示。
(3)定义草图尺寸约束时,每个定位尺寸用一个表达式表示。
(4)建立特征时,某些特征参数将用相应的表达式表示。
(5)建立装配配对条件时。
用户也可通过手动生成表达式:(1)执行【工具】-【表达式】命令来选择旧的表达式,并选择更名。
(2)从草图生成表达式。
(3)在文本文件中输入表达式,然后选择【工具】-【表达式】-【导入】命令,将它们导入表达式变量表中。
UG表达式应用讲解

64 UG的设计应用第二章表达式2.1 综述2.1.1 表达式的概念表达式是算术或条件语句,用来控制零件特征。
表达式可以用来定义或控制一个模型的多种尺寸,例如一个特征或一个草图的尺寸。
表达式在参数化设计中是十分有意义的,它可以用来控制同一个零件上的不同特征间的关系或一个装配中的不同零件间的关系。
例如:我们可以用一个表达式来建立一个支架零件的厚度和长度之间的关系。
当支架的长度改变之后,它的厚度自动更新。
图2-1所示为表达式的一个实例。
在创建表达式时必须注意以下几点:●表达式左侧必须是一个简单变量,等式右侧是一个数学语句或一条件语句。
●所有表达式均有一个值(实数或整数),该值被赋给表达式的左侧变量。
●表达式等式的右侧可认是含有变量、数字、运算符和符号的组合或常数。
●用于表达式等式右侧中的每一个变量,必须作为一个表达式名字出现在某处。
Length=.5+2*Cos(60)图2-1 表达式格式2.1.2 创建表达式的方法1.手工创建表达式●选择下拉菜单Tool→Expression或按快捷键Ctrl+E●改变一个已存在的表达式的名字,可选择下拉菜单Tool→Expression,选取已存在的表达式,然后单击Rename。
●将文本文件中存在的表达式引入到UG中,可选择下拉菜单Tool→Expression→Import。
2. 系统自动建立表达式当用户作下列操作时,系统自动地建立表达式,其名字用一个小写字母p开始。
第二章表达式65●建立一个特征(Create a Feature)时,系统对特征的每个参数建立一个表达式。
●建立一个草图(Create a Sketch)时,系统对定义草图基准的XC和YC坐标建立两个表达式。
例如:p1_YDATUM_V1=0●标注草图尺寸(Dimension a Sketch)后,系统对草图的每一个尺寸都建立一个相应的表达式。
●定位一个特征或一个草图(Position a feature or sketch)时,系统对每一个定位尺寸都建立一个相应的表达式。
ug正弦曲线表达式

ug正弦曲线表达式
摘要:
1.UG 正弦曲线表达式的概念
2.UG 正弦曲线表达式的基本形式
3.UG 正弦曲线表达式的应用
正文:
1.UG 正弦曲线表达式的概念
UG 正弦曲线表达式,是一种在数学和物理学中常用的表达式,用于描述正弦曲线。
正弦曲线是周期函数的一种图像表现形式,其表达式一般为
y=Asin(ωx+φ)。
在这个表达式中,A 表示振幅,ω表示角频率,x 表示时间,φ表示初相位。
2.UG 正弦曲线表达式的基本形式
UG 正弦曲线表达式的基本形式和一般正弦曲线表达式一样,也是
y=Asin(ωx+φ)。
其中,A 表示振幅,ω表示角频率,x 表示时间,φ表示初相位。
UG 正弦曲线表达式和一般正弦曲线表达式的区别在于,UG 正弦曲线表达式中的A、ω、x、φ都是UG(Universal Geometry)中的向量。
3.UG 正弦曲线表达式的应用
UG 正弦曲线表达式在UG(Universal Geometry)中被广泛应用。
UG 是一种基于几何学的数学理论,它将几何学中的向量和矩阵运算引入到数学和物理学的各个领域,使得数学和物理学的运算更加直观和简单。
在UG 中,正弦曲线表达式y=Asin(ωx+φ) 被用来描述周期函数的图像,这个图像在UG
中被看作是一个向量在时间上的变化。
通过这个表达式,我们可以直观地描述和分析周期函数的性质,如周期、振幅、频率等。
此外,UG 正弦曲线表达式还被广泛应用于信号处理、图像处理、物理学、工程学等领域。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
规律曲线2008-01-15 12:33:30 作者:来源:互联网浏览次数:0 文字大小:【大】【中】【小】简介:“规律曲线”选项用于使用规律子函数创建样条。
规律样条定义为一组X、Y 及Z 分量。
必须指定每个分量的规律。
要创建规律曲线:使用规律子函数,为X、Y 及Z 各分量选择并定义一个规律选项。
(可...“规律曲线”选项用于使用规律子函数创建样条。
规律样条定义为一组X、Y 及Z 分量。
必须指定每个分量的规律。
要创建规律曲线:1.使用规律子函数,为X、Y 及Z 各分量选择并定义一个规律选项。
2.(可选步骤)通过定义一个方位和/或基点,或指定一个参考坐标系来控制方位(样条的方位)。
3.选择“确定”或“应用”来创建曲线。
可以通过“信息”→“对象”来显示规律样条的非参数或特征信息。
X、Y 及Z 分量规律曲线通过X、Y 及Z 分量的组合来定义一条规律样条。
必须指定每个组件的规律类型,可通过规律子函数进行指定。
可用的选项有:恒定允许您给整个规律函数定义一个常数值。
系统会提示您只输入一个规律值(即该常数)。
线性用于定义一个从起点到终点的线性变化率。
三次用于定义一个从起点到终点的三次变化率。
沿着样条的值- 线性使用沿着脊线的两个或多个点来定义线性规律函数。
在选择脊线曲线后,可以沿着这条曲线指出多个点。
系统会提示您在每个点处输入一个值。
沿着样条的值- 三次的使用沿着脊线的两个或多个点来定义一个三次规律函数。
在选择脊线曲线后,可以沿着该脊线指出多个点。
系统会提示您在每个点处输入一个值。
根据等式使用一个现有表达式及“参数表达式变量”来定义一个规律。
根据规律曲线允许您选择一条由光顺连接的曲线组成的线串来定义一个规律函数。
对于所有规律样条,必须组合使用规律子函数选项(即,X 分量可能是线性规律,Y 分量可能是等式规律,而Z 分量可能是常数规律)。
通过组合不同的选项,可控制每个分量以及样条的数学特征。
既可以定义二维规律样条,也可以定义三维规律样条。
例如,二维规律样条要求一个平面具有常数值(即,如果Z 分量由某一常数规律定义为值0,则可在Z=0 的XC-YC 平面上生成一条曲线。
同理,如果X 分量由某一常数规律定义为值100,则在X=100 的ZC-YC 平面内生成一条曲线)。
规律样条是根据建模首选项对话框中设置的距离公差和角度公差而近似创建的。
任何大于360 度的规律曲线必须使用螺旋线选项或根据等式规律子函数来构建。
如果使用“编辑”→“变换”→“比例”或“点拟合”来编辑规律样条,将会移除该样条的创建参数。
如下所述,有两种控制规律曲线方向的方法。
定义方向“定义方向”选项能够通过指定一个局部Z 轴及点(类似于使用坐标系工具中的“Z 轴、X 点”选项)来控制样条的方向。
还可以使用“点构造器”选项定义一个基点。
如果没有定义方向,则使用当前的WCS。
如果不定义基点,则使用当前的XC=0、YC=0 和ZC=0 作为默认基点。
坐标系还可以通过指定坐标系(使用三个基准平面或两个基准平面和一根基准轴)来控制样条的方向。
这种方式的优点是,如果更改基准平面和/或基准轴(通过更改与它们相关联的几何体),则样条会相应更改。
必须在创建样条之前创建参考坐标系的基准平面和基准轴。
要使用坐标系,应先指定X、Y 和Z 规律,然后在“创建坐标系”对话框中选择“指定坐标系参考”,并执行下列步骤(如下图所示):1.选择一个基准平面作为“放置平面”。
局部的Z 轴垂直于该平面,并用箭头矢量表示。
如果该矢量指向了错误的方向,则应选择“反向放置法向”。
如果选择了具有基准坐标系的任意平面,则整个“基准坐标系”用于“规律曲线”,且跳过步骤 2 和步骤3。
2.选择另一个基准平面作为“水平参考”。
局部X 轴的指向沿着两平面的交线,并用箭头矢量指示出来。
如果该矢量指向了错误的方向,则应选择“水平参考反向”。
3.选择第三个基准平面或一根基准轴以建立“原点参考”。
如果选择一个平面,则参考坐标系的原点就是三个平面的交点。
如果选择一个轴,这原点为该轴与第一个选中的平面的交点。
Z 轴与X 轴的矢量积定义了局部Y 轴。
如果删除了定义样条局部坐标系所用的任何基准平面或基准轴,则将删除该样条。
规律曲线示例下图中的示例显示了使用“规律曲线”选项创建的样条,其中X 和Y 分量由创建圆的公式组成,Z 分量由一条规律曲线(由两条直线和两个圆角组成)确定。
使用了一个简单草图来定义规律曲线,该曲线在Z 向创建光顺的过渡,同时创建圆的公式在X 和Y 向创建圆形。
必须在创建样条之前先创建必需的表达式。
“t”变量是一个内部系统变量,“根据公式”规律需要用到该变量。
其在0 到1 之间的变化范围定义了函数的参数空间。
下图显示了两个样条。
虚线的X 分量是从0 到1 的三次规律。
实线的X 分量是从0 到1 的线性规律。
两个样条的Y 分量和Z 分量都是相同的。
Z 分量是值为0 的常数规律(将导致在XC-YC 平面中生成一条平面曲线),Y 分量为公式规律。
最后一个图显示了简单抛物线的一个示例。
X 分量是从0 到1 的线性规律。
Z 分量是一个值为0 的常数规律(会导致生成一条XC-YC 平面内的平面曲线),Y 分量是一个公式规律。
规律子函数可以使用几种方法中的一种来描述一个函数。
这里有几个例子,描述了Modeling 应用模块中使用这一子函数的各种方法:•控制螺旋样条的半径(如下图所示)•控制曲线的形状•控制“面倒圆”的横截面•对扫掠自由曲面特征定义“角度规律”或“面积规律”可以根据数值、等式或图形规律描述函数值。
虽然最常用的函数是常数、线性或三次,但是一个函数也可以是一条现有曲线或一个等式(根据表达式输入)。
如果调用函数支持,则在指定规律对象时可以使用选择意图。
下列规律选项有效:规律控制的子函数选项恒定允许您给整个规律函数定义一个常数值。
系统会提示您只输入一个规律值(即该常数)。
默认值是1(单位是在部件文件创建时指定的度量单位)。
这一选项使用常数规则(规律),以便当系统计算曲面沿着基本曲线线串移动时的延伸曲面时,剖面曲线的长度保持常数值。
线性用于定义一个从起点到终点的线性变化率。
默认的“起始值”和“终止值”都是1(单位是在部件文件生成时指定的度量单位)。
这一选项使用线性规则(规律),以便当系统计算曲面沿着基本曲线线串移动时的延伸曲面时,剖面曲线的长度在基本曲线线串起点的“起始值”和基本曲线线串终点的“终止值”之间作线性变化。
即使已经指定“脊线曲线”避免创建整个曲面,这一变化仍会发生。
在其一端处的长度可以是0,但不能两端都为0。
三次用于定义一个从起点到终点的三次变化率。
默认的“起始值”和“终止值”都是1(单位是在部件文件生成时指定的度量单位)。
这一选项使用三次规则(规律),以便当系统计算曲面沿着基本曲线线串移动时的延伸曲面时,剖面曲线的长度在基本曲线线串起点的“起始值”和基本曲线线串终点的“终止值”之间作非线性变化。
即使已经指定“脊线曲线”避免创建整个曲面,这一变化仍会发生。
在其一端处的长度可以是0,但不能两端都为0。
沿脊线的值- 线性可以用两个或多个沿着一条脊线的点来定义线性规律函数。
在选择脊线曲线后,可以沿着该脊线指出多个点。
系统会提示您在每个点处输入一个值。
沿脊线的值- 三次可以用两个或多个沿着一条脊线的点来定义三次规律函数。
在选择脊线曲线后,可以沿着该脊线指出多个点。
系统会提示您在每个点处输入一个值。
根据等式可以用表达式和“参数表达式变量”来定义规律。
根据规律曲线允许您选择一条由光顺连接的曲线组成的线串来定义一个规律函数。
如何使用函数值取决于使用规律的应用模块(即:对于螺旋线而言,任何点处的规律值都是螺旋半径)。
根据正在创建的几何体,可能需要指定一个、两个或三个规律。
根据等式“根据等式”让用户用表达式和“参数表达式变量”来定义规律。
必须事先使用“工具”→表达式定义了所有变量,并且表达式必须使用参数表达式变量“t”。
使用“根据等式”选项创建一条曲线的一般步骤如下:1.以参数形式使用参数表达式变量t 来定义等式。
2.将参数方程输入到“表达式编辑器”中。
3.选择“根据等式”选项来识别所有的参数表达式并创建曲线。
必须定义希望以参数形式使用的等式。
在这种形式中,点的每个坐标被表示为一个使用参数t 的函数。
系统使用默认的参数表达式变量,标准化范围为0 到1(0<= t <= 1)。
在表达式编辑器中,可以初始化t 为任何值,因为系统使t 在0 和1 之间变化。
为了简单起见,初始化t 为t=0。
例如,考虑标准数学形式中下面的抛物线等式。
y = 2 -0.25 x2可以在表达式编辑器中使用t、xt、yt 和zt 来确定这个等式的参数,如下所示。
t=0 xt = -sqrt(8)*(1-t)+sqrt(8)*t yt = 2-0.25*xt^2 zt = 0使用t、xt、yt 和zt 是因为它们是“根据等式”选项中使用的默认变量名。
请注意有多种方法来确定一个等式的参数。
我们使用了一种标准方法将一个表达式的参数确定在一个线性范围内:a*(1-t)+b*t.其中,a 和 b 是范围的界限。
当t 为零时,表达式的值为a。
当t 为1时,表达式的值为b。
在我们的示例中,范围设置成 a = -sqrt(8) 和b = sqrt(8)。
“根据等式”的基本步骤1.选择“工具”→表达式。
2.输入每个参数确定的表达式。
如果使用上面所示的例子,将是:t=0 xt = -sqrt(8)*(1-t)+sqrt(8)*t yt = 2-0.25*xt^2 zt = 0输入第一个表达式t=0,然后按Enter 键。
继续输入每个表达式,直到将它们全部输入完为止。
3.选择“确定”或“应用”。
现在等式定义完毕,可以用接下来的步骤创建规律曲线。
4.选择“插入”→“曲线”→“规律曲线”。
显示初始的“规律曲线”对话框。
5.选择“根据等式”。
会显示一个包含默认表达式名t 的文本框。
6.选择“确定”。
会显示一个“定义X”对话框,其中包含默认的表达式名称xt。
7.选择“确定”。
再次显示初始的“规律曲线”对话框。
8.选择“根据等式”。
会显示一个包含默认表达式名t 的文本框。
9.选择“确定”。
会显示一个“定义Y”对话框,其中包含默认的表达式名称yt。
10.选择“确定”。
再次显示初始的“规律曲线”对话框。
11.选择“根据等式”。
会显示一个包含默认表达式名t 的文本框。
12.选择“确定”。
会显示一个“定义Z”的对话框,其中包含默认的表达式名称zt。
13.选择“确定”。
会显示一个带有下列选项的“规律曲线”对话框:“定义方向"、“点构造器”和“指定CSYS 参考”。
这些选项可以定义规律曲线的方向和放置。
在这个例子中,我们使用WCS 方向。
