maple 求高等数学问题
Maple软件在高等数学教学中的应用研究6页

Maple软件在高等数学教学中的应用研究《高等数学》是数学学科的一门传统课程。
在当今世界的数学内部学科趋于统一性和数学在其他学科的广泛应用,《高等数学》以其追求内容结构的清晰刻画和作为数学应用的基础,是大学数学各个专业的主干基础课程。
然而高等数学中大量冗长的计算往往使学生望而却步,觉得高等数学这门课麻烦、难学,从而对高等数学失去信心。
在高等数学教学中若能运用一些数学软件来实现数值计算与符号计算的机械化,省去以往繁杂的手工计算,同时也革新教学方法和教学手段,定能充分调动学生学习的积极性,加深对知识的理解,从而获得更好的教学效果。
Maple的出现为高等数学的学习提供了轻松的氛围。
Maple是当今流行的计算机代数系统之一,它是加拿大Keith Geddes和Gaston Gonnot教授于1980年在滑铁卢(Waterloo)大学开始设计开发的用于科研和教育的数学软件,并以加拿大的国树枫叶(Maple)命名。
在赞助者的推动下,大约在1982、1983年左右,Maple被推广到美国和欧洲一些大学,应用的领域扩展到数学、计算机科学、物理、经济和工程等。
Maple的线性代数函数库(linalg),可提供丰富的代数运算指令,几乎完成高等代数中的各种运算,为高等代数的教学和学习提供了强有力的工具。
本文以文献中的一些例子来说明Maple在其教学中的应用。
一、多项式问题一般情况下,辗转相除法来完成最大公因式的求解,在两个多项式的次数较高时,其过程将会非常繁琐,并且极易出错。
同时,推导满足“(f (x),g(x))=u(x)f(x)+v(x)g(x)”中“u(x)”和“v(x)”的过程也会非常复杂。
Maple软件提供了用于求多项式最大公因式的相应函数,其中“gcdex”函数应用得较为广泛。
值得一提的是,“gcdex”函数不仅可以求得最大公因式,还可以同时给出能够满足等式“(f(x),g (x))=u(x)f(x)+v(x)g(x)”的“u(x)”和“v(x)”。
maple在高等代数与解析几何教学中的应用

maple在高等代数与解析几何教学中的应用在当今,Maple在数学教育中应用越来越广泛,其在高等代数与解析几何教学中也获得了许多成就,对学生理解学科知识有很大帮助。
因此,本文将引入Maple在高等代数与解析几何教学中的应用,以期探索Maple在学术教学活动中的价值。
首先,Maple在高等代数与解析几何教学中的主要功能是帮助学生理解数学概念。
Maple具有强大的计算能力,可以帮助学生通过数学模型的建立理解数学概念。
例如,可以用Maple创建对象来表示多元函数,然后用函数运算符计算极值,使学生更容易理解函数的性质。
此外,可以使用Maple的可视化功能,绘制出二维和三维图形,使学生更容易理解几何概念,例如几何体的构造、特征点及结构。
其次,Maple在高等代数与解析几何教学中也可以帮助学生掌握数学技巧。
Maple可以自动执行一些复杂的数学运算,让学生不必费力繁琐地一步步计算,而是能够通过观察自动计算的结果,掌握数学技巧。
此外,Maple中的助教功能也可以帮助学生更快地掌握数学技巧,允许学生在计算过程中添加、删除、修改、查看及执行更多操作,以使学习更有效。
此外,Maple还可以帮助学生更好地掌握数学知识。
Maple可以利用数学思维,一步步让学生分析问题,从而理解数学知识。
同时,Maple还提供了许多教学工具,可以帮助学生在实践中掌握数学知识,使学生通过实践来更深入地理解数学理论。
最后,Maple还可以帮助学生提高学习效率。
Maple拥有完善的知识管理功能,可以帮助学生储存并管理学习资料,这样可以更有效地掌握学习知识,更快地完成教学任务。
此外,Maple还可以通过模拟实验测试学生的学习成果,及时发现学生的学习问题,及时提出解决方案,从而提高学习效率。
总之,Maple在高等代数与解析几何教学中已经具有重要价值,为学生学习理解数学概念、掌握数学技巧、深入理解数学知识、提高学习效率提供了坚实的基础。
因此,Maple应该在高等代数与解析几何教学中得到更广泛的应用,并在学科教学活动中发挥较大作用。
《高等数学》中的数学实验与Maple教学

202016/310《高等数学》中的数学实验与Maple 教学孙宪波韩江峰李成群摘要创新型、复合型和应用型人才培养是我国高等教育的重大战略。
在理工科和财经类高校,加强数学类课程基础教学和应用教学是培养“三型”人才的重要基础,其中加强数学实验和数学软件应用教学是高等院校加强数学基础教学和数学应用教学的重要内容。
关键词高等数学;线性代数;应用教学;数学软件中图分类号:O212文献标识码:ADOI :10.19694/ki.issn2095-2457.2020.16.026孙宪波1986—/男/河南人/博士/副教授/研究方向:应用数学/广西财经学院信息与统计学院(南宁530003)韩江峰广西财经学院信息与统计学院(南宁530003)李成群广西财经学院信息与统计学院(南宁530003)基金项目:本文由广西高等教育本科教改项目(2019JGB344)资助。
0引言加强数学类基础课程和数学应用类课程的教学是理工科和财经类高校培养创新型、复合型、应用型人才的重要内容。
我国在精密制造业等若干“卡脖子”技术落后相关国家的重要基础原因是我国应用数学公关关键技术的薄弱,其深层原因在我国在高等院校的数学类课程的基础教学和应用教学相对落后。
我国高等院校数学类课程教学内容上着重于多种特殊情的定理、原理和结果,在训练上着重难题解决技巧的积累;在课程体系上,非数学专业数学课程相对开设较少,数学专业数学课程着重于古典类基础课程,缺少数学应用类课程;在数学实践上,数学实验和数学软件的教学亟待加强。
本文第二部分分析高等数学中数学软件教学的几个重要内容,最后探讨数学实践教学与数学综合应用课的研发和推广。
1数学软件教学内容目前世界上流行的三大数学软件有Matlab,Maple 和Mathematica。
Matlab 的主要特色是数值计算及工程应用;Maple 的特色是符号计算和动力系统研究应用;Mathe matica 介于两者之间。
多数研究工作者使用Matlab 和Maple。
师大maple考题
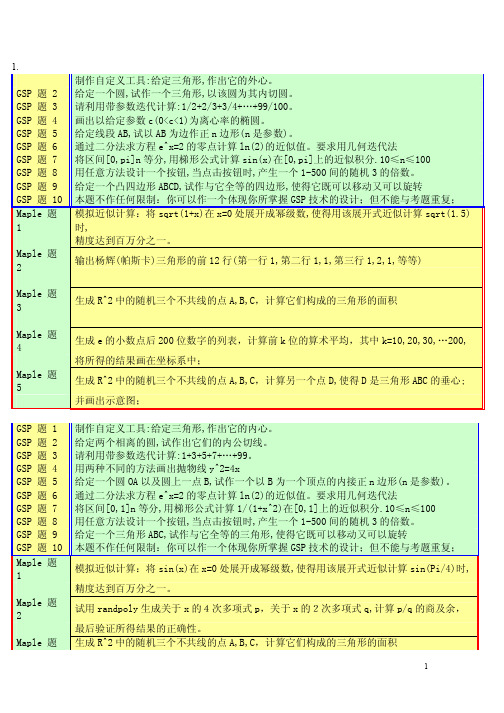
制作自定义工具:给定三角形,作出它的外心。
GSP 题 2 给定一个圆,试作一个三角形,以该圆为其内切圆。
GSP 题 3 请利用带参数迭代计算:1/2+2/3+3/4+…+99/100。
GSP 题 4 画出以给定参数c(0<c<1)为离心率的椭圆。
GSP 题 5 给定线段AB,试以AB为边作正n边形(n是参数)。
GSP 题 6 通过二分法求方程e^x=2的零点计算ln(2)的近似值。
要求用几何迭代法GSP 题 7 将区间[0,pi]n等分,用梯形公式计算sin(x)在[0,pi]上的近似积分.10≤n≤100GSP 题 8 用任意方法设计一个按钮,当点击按钮时,产生一个1-500间的随机3的倍数。
GSP 题 9 给定一个凸四边形ABCD,试作与它全等的四边形,使得它既可以移动又可以旋转GSP 题 10 本题不作任何限制:你可以作一个体现你所掌握GSP技术的设计;但不能与考题重复;Maple 题 1 模拟近似计算:将sqrt(1+x)在x=0处展开成幂级数,使得用该展开式近似计算sqrt(1.5)时,精度达到百万分之一。
Maple 题2输出杨辉(帕斯卡)三角形的前12行(第一行1,第二行1,1,第三行1,2,1,等等)Maple 题3生成R^2中的随机三个不共线的点A,B,C,计算它们构成的三角形的面积Maple 题4生成e的小数点后200位数字的列表,计算前k位的算术平均,其中k=10,20,30,…200,将所得的结果画在坐标系中;Maple 题5生成R^2中的随机三个不共线的点A,B,C,计算另一个点D,使得D是三角形ABC的垂心;并画出示意图;GSP 题 1 制作自定义工具:给定三角形,作出它的内心。
GSP 题 2 给定两个相离的圆,试作出它们的内公切线。
GSP 题 3 请利用带参数迭代计算:1+3+5+7+ (99)GSP 题 4 用两种不同的方法画出抛物线y^2=4xGSP 题 5 给定一个圆OA以及圆上一点B,试作一个以B为一个顶点的内接正n边形(n是参数)。
Maple中微积分与极限的命令介绍

Maple中微积分与极限的命令介绍在使用Maple进行计算时,对于函数的计算是涉及很多的,但是在计算函数的过程中,有很多需要用到高等数学中的微积分与极限。
而这些计算的命令构成了复杂函数的命令。
下面就对Maple微积分和命令和极限的命令做一些基本介绍。
一、极限Limit(f(x),极限点,选项),Limit为极限号(可用value看值)。
选项有:左left、右right,省略则为普通极限。
注:不能对过程函数直接计算。
1.x=a点极限,limit(f(x),x=a)。
2.x趋向无穷极限,limit(f(x),x=infinity)。
3.x趋向正负无穷大极限,在infinity前直接加+、-号即可。
注:函数若由箭头算子、过程、转换法定义,求极限函数要用f(x)形式。
二、导数。
1.diff(f,x1,x2,…) x1,x2,…为各次求混合导数的自变量。
diff(f,x$m,y$n) m,n 分别为对自变量x、y 求导阶数。
Diff 为求导符号,可用value 显示值。
注:不能对过程函数直接使用。
注:函数若由箭头算子、过程、转换法定义,求导函数要用f(x)形式。
2.隐函数导数:diff(方程,自变量及阶数);(1)将方程中函数变量全部写成自变量函数形式(如y(x)),再求导。
(2)用别名命令alias将函数变量先定义为自变量的函数,如alias(y=y(x))再对方程求导。
3.导数算子:D(函数),D[i$m,j$n,…](函数) i,j 整数表示,对第i、第j 个变量求导。
注:只有箭头算子、过程、转换法定义函数,才能使用求导算子。
三、积分1.一元积分int(f,x)不定积分,int(f,x=a..b)定积分,int为积分符号,用value 显示值。
注:不能对过程函数使用。
注:箭头算子、过程、转换法定义函数要用int(f(x),x)。
2.二重积分,int(int(f(x,y),y=y1(x)..y2(x)),x=a..b)以上内容向大家介绍了Maple微积分和极限的一般使用命令,命令格式相对来说比较简单,只需要进行相应的变量输入就可以了,Maple函数包的数量很多,功能非常齐全。
利用Maple计算数学的常见命令

示例:使用微积分面板求表达式4t6+sin(t)的积分。
操作过程:
打开“微积分”面板,然后点击不定积分的模板。一个不定积分模版将出当前工作表中。在占位符处输入被积表达式,完成后,按下回车键计算。
示例:使用表达式面板用于求解函数的极限。
操作过程:将光标移到要工作的位置,点击极限表达式,在占位符中填入表达式,完成后按回车键计算。
提示:可以将经常要用的面板项移到收藏夹中。操作方式是鼠标右击面板按钮,然后选
择添加到收藏夹面板中。
符号和命令补全
符号和命令补全机制帮助用户完成符号和命令的输入。键入符号名称开始的几个字符,按下“Esc”键,从弹出的下拉菜单中选择需要的符号。
示例:对表达式y=ex绘图,使用符号补全方式创建指数e。操作过程:标签
按回车键执行计算返回结果,工作表将自动给出一个方程标签。如果想引用前面的计算
结果,使用“Ctrl+L”,在弹出的对话框中输入标签数字。
示例:用标签(1)引用前面的计算结果乘以x。
以上内容向大家介绍了利用Maple计算数学时常用的命令与操作。这些命令与操作都是在Maple数学计算中经常用到的。如果需要了解更多Maple入门的使用技巧,可以参考Maple中文版教程:介绍Maple入门的一些常见操作。
利用Maple计算数学的常见命令
在进行数学论文撰写时会根据具体的问题来对数学问题进行求解计算。利用Maple面板中数学模板就能够输入数学公式并利用Maple计算数学问题。
更多Maple入门教程、功能介绍请访问Maple中文官网。
面板介绍
Maple工作表左侧的20个面板含有1,000多个符号。用户也可以使用Maple面
Maple区分大小写,X,x表示不同的变量名。
Maple软件在《高等数学》教学中的应用

。
p : a r r a y ( 1 …1 2 ) ; q : a r r a y ( 1 …1 2 ) ;
1
例 3 : 余 弦 函 数 的 泰 勒 展 式 C O S X = 1 一 - 争+ - 手一 手
8 1
篓 一 ! 一 . .
1 0 1 。
> p l o t ( ( 1 + 一) , = 一 1 0 0 …l O O ) > p l o t ( 曼 , 一1 0 0 …1 0 0 )
列通项的解析表达式来 . 说 明 数 列 极 限 的过 程 . 学 生 比 较 难 理 解 。但 是 , 如 果 用 Ma p l e 软件 , 把这个 数列的 图
/
2 Ma p l e软 件在 泰 勒 级 数教 学 中的 应 用
《 高等数学 》 中的泰勒公式是数学 分析中重要 的公
斗 的各阶导
数 确 定 。通 过 Ma p l e 软件绘 图, 能 直 观 地 体 现 出 已知 函
数和函数 的泰勒级数之 间关系 .使学生加深 对泰勒定 理的理解 , 并 由此牢记 泰勒定 理的内容l 引 。
和l i m曼 ! : 1
等数学》 教 学 中来
目前 较 流 行 的 数 学 软 件 主 要 有 四 种 : Ma t h AC D、
的理解往往感到很困难 如果借助 Ma p l e 软件 . 通过作
图能 够 很 形 象 的体 现 极 限 概 念 的 内 涵嘲
例 1 : 验证数列极]  ̄l i m( 1 + 上:
式 之 一 .它 的 基 本 思 想 是 用 多 项 式 来 逼 近 一 个 已知 的
形绘制 出来 . 如图 1 所示 . 学生 们可以非常直 观地可 以
Maple的一个非常实用的功能就是微积分计算它能求导数,作积分,作级数

第3章微积分Maple 的一个非常实用的功能就是微积分计算.它能求导数,作积分,作级数展开,作无穷求和,还有很多很多功能.在这一章,我们关注最基本的功能.极限极限思想是微积分学中最基本的思想,而Maple 知道怎么计算它们.例如,要求lim x →0sin 3x x 的极限值,可以使用Maple 的limit 命令,表达式如下所示:>limit(sin(3*x)/x,x=0);3当然你也可以使用Maple 函数来求解>y:=x->sin(3*x)/x;limit(y(x),x=0);y :=x →sin (3x )x3您可以输入?limit 来查看这条命令的详细说明,但这并不是命令的全部说明.问题3.1尝试着练习这个问题:lim x →0cos (x )−1x 2微分导数相对来说是容易的,所以这一节也一样.Maple 对初等函数和特殊函数的求导是同样容易的,所以这一节只是展示两条Maple 的微分命令,一条用于表达式,一条用于函数.首先,我们对表达式进行微分.我建议你使用下面说明正切函数用法的形式来求一阶导数,二阶导数和三阶导数.你也可以使用diff命令,它直接求出导数,或者Diff和value 命令,给出所求表达式的导数,并计算其值.Diff命令的用途实际上超出你的想像,因为它给你一个机会查看你要Maple 求的导数是不是你所想要的.>diff(tan(x),x);1+tan (x )2>diff(tan(x),x\$2);2tan (x )(1+tan (x )2)>d:=Diff(tan(x),x\$3);>d:=value(d);d :=∂3∂x3tan (x )d :=2(1+tan (x )2)2+4tan (x )2(1+tan (x )2)>d:=simplify(d);d:=2+8tan(x)2+6tan(x)4下面让我们看一下如何对函数进行微分.>f:=x->tan(x)/x;f:=x→tan(x)xDiff命令不能对函数进行微分,因此我们要使用Maple的D命令.这是一条体积小但功能非常强的命令.它能求复合函数的多阶导数(查看所有用法请输入?D),但我们只能对单一函数求一阶导数.求一阶导数是非常容易的fp:=D(f);f p:=x→1+tan(x)2x−tan(x)x2注意,指定D(f)对f p的结果产生函数f p(x).求高阶导数的方法有很多种,这是最通用的一种.>fpp:=D[1$2](f);f pp:=x→2tan(x)(1+tan(x)2x−2(1+tan(x)2)x2+2tan(x)x3方括号里的“1”表示关于参数列表里的第一个变量(这里只有一个)求微分,“$2”表示相当于执行diff命令两次.好了,内容就这么多.这里有一些练习需要训练.问题3.2求下列函数的形式导数.大部分使用表达式形式,(a)和(d)使用函数形式.如果得到混乱的结果,尝试使用simplify命令化简它.你会发现simplify命令对函数无效,为了使结果更好看,用鼠标把你想要化简的混乱结果复制到剪贴板,把它赋给一个新的变量,删除无关的内容,然后再执行化简命令.然后再使用剪切和粘贴命令重建求导函数.Maple的这个组合及编辑是做无错误代数的好方法.(a)∂3∂x3√1+x3(b)∂∂xJ0(x)(c)∂∂xI1(x)(d)∂2∂x2e tan(x)(e)∂∂xΓ(x)(f)∂∂xerf(x)(g)∂∂kK(k)((g)是第一种形式的完全椭圆积分,使用Maple的EllipticK命令.)问题3.3这是一个你在大学里也使用的求最大最小问题.考虑函数ln(x)J0(x)(我用词“函数”是数学意义的,而不是Maple意义的.如果你仅仅使用一个Maple表达式来定义上面的函数,这个问题是很简单的.)(a)首先画出函数在区间[0,10]上的图像.(b)观察图像,找出并估摸函数取得最大最小值时x的值.接着对函数求导,然后使用fsolve 命令求出x的精确值.假若求导后的表达式为f,如果你想求出1.1附近的零点,你可以这样做:fsolve(f,x=1.1);在量子力学中,你会遇到近似我们已经见过的勒让德函数P n (x ).这些新函数叫做联合勒让德函数P m n .对于每一个整数n ,在区间[0..n ]上,函数由m 的值定义,当m =0时,函数等价于P n (x ).这些函数由勒让德函数的导数的项定义:P m n =(−1)m (1−x 2)(m 2),diff (P n (x ),x $m )这个定义对于大多数的计算机语言来说是累赘的,但是Maple 操控它很容易,因为Maple 用符号化代替数值化.这里有个函数评价它>with(orthopoly);[G,H,L,P,T,U ]>Pnm:=(n,m,x)->(-1)^m*(1-x^2)^(m/2)*diff(P(n,x),x$m);P nm:=(n,m,x )→(−1)m (1−x 2)(12m ),diff (P (n,x ),x $m )在做任何花哨的事情之前我们测试它,因此让我们为n,m 和x 输入数字.>Pnm(3,1,.5);Error,(in Pnm)wrong number (or type)of parameters in function diff 好了,我们又遇到麻烦了.这个问题是P (n,x )返回了什么.如同我们在第2章一个节中看到的这个函数,它不返回数字,而是返回多项式.当我们把0.5赋给x 时,它进入到上面定义的函数Pnm ,并代替x ,然后diff命令尝试关于0.5求导数,而这是没有意义的.观察当我们用一个变量而不是数字来代替x 时发生什么.>Pnm(3,1,t);−√1−t 2(152t 2−32)倘若你想要一个数值结果你可以这样做>a:=Pnm(3,1,t);t:=0.5;a;a :=−√1−t 2(152t 2−32)t :=.5−.3247595264这是很烦人的,另一方面,仅仅考虑它;总之,为什么在Maple 里需要一个数字呢?你要画函数图像,微分,求积,在微分方程里使用,等等.有什么事情比得到一个明确的表达式更好呢?Maple 认为这不是一个问题;而是一个特性.而且这个特性为你使用with(orthopoly)想要得到的所有正交函数所享有.这里还有另一个关于函数Pnm 更烦人的事情.观察当我们尝试用m =0执行时发生什么.>Pnm(5,0,x);Error,(in Pnm)wrong number (or type)of parameters in function diff 当m =0时它假想返回Pn(x)的结果,但事与愿违.不工作的原因是因为我们要求它求一个函数的0阶导数,而Maple 的diff命令应付不了.稍后学习程序之后我们返回这个问题并修复它,使得当m =0时也工作.好了,我已经演示怎样做了.现在请你结合P (5,x )作5个联合勒让德函数的图像,例如,n =5及m =1,2,3,4,5.图像从x =−1画到x =1.用不同的颜色把5个图像画在同一轴上,当m 的范围从1变化到n =5时发生了什么.看过图片之后你可能想要重新缩放函数图像使得它们看起来大小相同.在下一节积分中,我们会重新绘制并用一种自然的方式让函数图像接近相同的尺寸.这是下一节积分中引过来的一个电学问题.电势函数z ,电荷球半径为R ,电荷面密度为σ,其中z 上升到半球的对称轴,表达式如下>V:=-1/2*sigma*R*(-sqrt(R^2+z^2)+sqrt((z-R)^2))/(z*e0);V :=−12σR (−√R 2+z 2+√(z −R )2)ze 0其中e 0表示电荷常数ε0.电场分量E z 可以通过电势V 微分得到:E z =−(∂∂zV ).使用Maple 对这个求导可以得到一个关于E z (繁杂)的表达式.化简它.你会看到一个叫csgn 的陌生函数,输入?csgn 查看函数说明以确保你知道它是做什么的.然后令σ=1,R =1及e 0=1,然后从z =−4到z =4同时画V 和E z 的图像.这是一个电磁定律关于跨表面电荷密度,电场区域通过σε0变化.(你可能注意到上面定义的V 我用e 0代替ε0.这是故意的.尽可能是避免变量下标,因为Maple 中的下标引用矩阵元素.)验证你的图像以获得正确的跳跃.在图像中,负z 在半球圆缘的下方,正z 从0到R 在半球内部,且正z 从R 到无穷在圆顶之上.想像你的图像并说服你自己使它有意义.问题3.6这是一类花俏的微分叫做隐式微分,且Maple 可能求解.假设你有一个方程涉及x 和y ,像这个x 2+y 2=3.你想要解出dy dx 而不求解y (x ).这种方式求隐式方程的微分得2x +3y 2(∂∂x y )=0,然后求解dy dx .Maple 知道如何求解,规定你告诉它y 依赖于x ,像这样.>restart;>eq:=x^2+y(x)^3=3;eq :=x 2+y (x )3=3>deq:=diff(eq,x);deq :=2x +3y (x )2(∂∂x y (x ))=0>dydx:=solve(deq,diff(y(x),x));dydx :=−23xy (x )2如果你任何时候都不想输入y (x ),你可以使用Maple 的alias 命令告诉它把y 变为y (x )(只适用Maple 的内部进程)当遇到的时候.>restart;允许我们使用y 代替y (x )>alias(y=y(x));y>eq:=x^2+y^3=3;eq :=x 2+y 3=3>deq:=diff(eq,x);deq :=2x +3y 2(∂∂x y )=0>dydx:=solve(deq,diff(y,x));dydx :=−23xy 2这是一个物理学中的例子.等离子体电磁波的分散关系是ω2=wp 2+k 2c 2,其中wp 是一个频率叫做等离子体频率.波的相对速度由ωk 给出,群速度由dωdk 给出.首先用Maple 求出相对和群速度的公式,在wp ,k 及c 的条件下求解ω(k )并微分.然后在k ,c 及ω的条件下用隐式微分得到群速度.最后,Maple 也知道怎样求解偏导数.考虑关于x 和y 的函数f (x,y )=cos (xy )y .这是关于x ,y ,以及x 和y 的导数,用表达式形式>restart;f:=cos(x*y)/y;f :=cos (xy )y>diff(f,x);diff(f,y);diff(f,x,y);−sin (xy )−sin (xy )x y −cos (xy )y 2−cos (xy )x也可以通过Maple 的符号函数来做相同的事情>restart;f:=(x,y)->cos(x*y)/y;f :=(x,y )→cos (xy )y>D[1](f);D[2](f);D[1,2](f);(x,y )→−sin (xy )(x,y )→−sin (xy )x y −cos (xy )y 2(x,y )→−cos (xy )x问题3.7求出下面这个函数的一阶导数及三个二阶导数(两个x ,两个y 以及xy )K (√4xy (x +y )2)其中K 是完全椭圆积分EllipticK .使用符号表达式并用diff命令求解.尝试使用expand 和simplify 命令清除杂乱的东西以得到结果.积分你使用Maple做得最多的简单事情就是积分.事实上,你没有更多的思想比较积分表和计算尺.大多数都是可以的,因为你很容易获得Maple并且它是不错的.但是它不会做任何事情(就如果你在这一节看到的一些例子一样),所以你需要知道当Maple 失败的时候该怎么做.最好的做法是看一本由Gradshteyn和Ryzhik编写的一本名为《A Table of Series and Integrals》的数学参考书.你可以从图书馆的数学参考书部分找到它,或者在我们系图书室,如果没有教员把它借走.初等积分Maple可以求解你在第一节积分课里遇到的所有积分问题.实现这个功能的命令叫做int,你可以像这样使用表达式>int(sin(x),x);−cos(x)或者>f:=sin(x)*x;int(f,x);f:=sin(x)xsin(x)−x cos(x)注释:不要使用f(x)作为参数如果f是一个表达式.倘若是函数,积分命令这样用:>g:=(x,y)->sin(x*y)*x;g:=(x,y)→sin(xy)x>int(g(x,y),x);sin(xy)−xy cos(xy)y2这有一个int的简化形式,叫做Int,用来显示积分.这个形式你可以用于记录表.尝试这个:>s1:=Int(exp(x),x);s1:=∫e x dx请注意:Int命令只显示,并不做数学运算.也许你会问,“但如果它不做任何事,我为什么要用它呢?”因为它能帮助查看你是否输入正确的积分,Int命令是很有价值的调试工具.当显示形式你看起来对之后,使用value(s1)得到结果.因此正确求解上面的简单积分并取得结果是这样的:>s1:=Int(exp(x),x);>s1:=value(s1);s1:=∫e2dxs1:=e2我建议你总是使用Int和value组合的方式求解积分.这是一个好习惯,可以减少你查看愚蠢错误的时间.当然,你也可以像这样求解定积分:>s2:=Int(tan(x),x=0..1);>s2:=value(s2);s 2:=∫10tan (x )dxs 2:=−ln (cos (1))如果想要求积分值,你可以这样做:>evalf(s2);.6156264703噢,如果你仅仅是想要数值结果而不通过evalf 命令,只需给int 命令浮点极限你就可马上得到结果.>s2:=Int(tan(x),x=0..1.);>value(s2);s 2:=∫10tan (x )dx当然你也知道Maple 可以对无穷极限求积分,但你需要通过assume 命令做一些引导.好了,你要了解的Maple 求解积分的东西就这么多.输入?int 获取更多Maple 提供的积分选项.下面让我们做些练习.问题3.8用Maple 求解下列积分,其中(a)-(d)用表达式符号,(e)-(g)用函数符号.求出(e)和(f)的积分值.求解(g)时你会遇到麻烦,你得到的结果看起来很繁杂,试着用simplify 命令化简.(a )∫ln (x )dx (b )∫√1−x 2dx (c )∫x 1+x 3dx (d )∫cos h (x )dx (e )∫10√1+x 1−x dx (f )∫120x x 3−1dx (尝试使用1/2和1./2.作为积分上限)(g )∫∞e −ax cos (x )dx (不知道如何输入∞,输入?使用联机帮助.)。
积分和微分方程的MAPLE求解

> ans1 := combine(dsolve(sys1 union IC_1,{x(t),y(t)}),trig);
> IC_2 := {x(a)=A,diff(x(a),a)=B}; > ans2 := combine(dsolve(sys1 union IC_2,{x(t),y(t)}),trig);
> Int(exp(t)/t,t)=int(exp(t)/t,t);
定积分
Int(exp(-x),x=a..b);
int(exp(-x),x=a..b);
I1:=Int(exp(-x^2),x=0..1)
=int(exp(-x^2),x=0..1);
> ?erf > evalf(I1); ## 求近似值
微分方程组求通解
> ######## solve the system of ODES
> sys1:= {diff(y(t),t) =-x(t),diff(x(t),t)=y(t)};
> dsolve(sys1, {x(t),y(t)}); sys2 := {diff(f(x),x) = cos(f(x)), diff(g(x),x) = -f(x)^(1/2), diff(h(x),x,x) = g(x)/f(x)};
> dsolve(sys2, {f,g,h});
微分方程组的初值问题求解
> ######### solve the system of ODES with initial value conditions
> IC_1 := {x(a)=A,y(b)=B}; > ans1 := dsolve(sys1 union IC_1,{x(t),y(t)});
如何利用Maple求解偏微分方程

如何利用Maple求解偏微分方程微分方程分有常微分和偏微分方程两种,利用Maple对微分方程求解是Maple的一个核心优势,下面介绍利用Maple求偏微分方程的命令。
求偏微分方程或偏微分方程系统的命令是“Pdsolve”。
调用格式是:pdsolve(PDE, f, HINT = hint, INTEGRATE, build)pdsolve(PDE_system, funcs, HINT, other_options)pdsolve(PDE_or_PDE_system, conds, type=numeric, other_options)其中:PDE:偏微分方程。
f:不定函数或名称;当有很多导函数时需要指定此项。
hint:(可选项)HINT = hint中的右边,其中hint 为“+,“*”之一,关键词strip 或TWS之一,结构TWS(math_function_name),或关于不定函数的任意代数表达式。
INTEGRATE:(可选项)当使用变量分离法求解PDE时发现ODE集合,此选项表明进行自动积分。
Build:(可选项)尝试建立不定函数的显式表达式,不管所得解的一般性。
PDE_system:偏微分方程系统;可包含不等式。
Funcs:(可选项)由不定函数或名称构成的集合或列表。
other_options:当精确求解PDE系统时,casesplit命令接受的所有选项也被pdsolve 接受。
PDE_or_PDE_system:偏微分方程或偏微分方程系统;可包含不等式。
Conds:初始或边界条件。
type=numeric:等式;表明寻找数值解;可使用关键词numeric替代整个等式。
示例:求解热传导方程的数值解、解析解和图形解。
初始条件:为了得到数值解,我们需要定义a和h的值,以及提供第二个边界条件:这个命令创建了一个模块(module,使用方法类似于Maple的函数包),可以看到模块的输出函数是plot,plot3d,animate和value。
几何图形在高等数学中的作用及在Maple下的实现

作者简介 :纪宏伟 ( 97 ,男,江苏南通 人,讲师,硕士,从事数学教赍及信息技术研究.E m i iso u 2. t 17 一) - al uuw @16C l :q O
高 师 理 科 学 刊
第 3 卷 l
观印象 , 深化理解水平 , 这也弥¥ T传统教学的不足 , b 减低 了高等数 学 教与 学 的难度 ,对 教学效果 必将 有 提高作 用 .
t 0=0, t 2=2.
() 2 另一个积分限就是横坐标 的最大值. t= a() 则 t d; 边梯 积S S S, — S  ̄t(t = Yx) )t
i ( *2 t )2 2 t = 一) n ( t 一 3 ( ,t O,得到的结果是 t2 ' ^ — ) 2 O.
第 3 卷 第 4期 1
2 1年 7 月 01
高 师 理 科 学 刊
Ju n l fS in eo e c es Colg n nv ri o ra ce c f a h r o T l ea dU iest e y
V 1 3 N . o. 1 o4
J 1 2 1 u. 0 1
图 5 曲线 图形
S = y (d o t t,即 S= yt ) . 为 了计 算 S= yt )f 在 Mal ) (x(d ) tt (x f , )(d p e命 令 窗 口中输 人 :
Mp al e为基于图形的教学提供 了很好的手段.借助于 M p 绘制的几何图形可以直观 、充分体现高等 al e 数学的概念 、定理 的内涵 , 克服传统教学中讲解内容抽象 ,手工绘图不准确 ,教学内容难以扩展等方面 的 不足 ,使高等数学的教学变得更加形象生动.将 M p 引入高等数学教学 中无疑具有十分积极的意义. al e
maple考试题及答案

maple考试题及答案**Maple考试题及答案**一、选择题(每题5分,共30分)1. Maple中,以下哪个函数用于求解方程?A. solveB. plotC. diffD. int答案:A2. 在Maple中,如何表示无穷大?A. infB. infinityC. ∞D. undef答案:C3. 以下哪个选项是Maple中定义函数的正确语法?A. f(x) := x^2B. f(x) = x^2C. function f(x) = x^2D. f(x) = x^2;答案:A4. Maple中,以下哪个命令用于绘制函数的图像?A. plotB. solveC. diffD. int答案:A5. 在Maple中,如何计算定积分?A. intB. sumC. limitD. evalf答案:A6. Maple中,以下哪个命令用于求导数?A. diffB. intC. limitD. evalf答案:A二、填空题(每题5分,共20分)1. 在Maple中,使用____命令可以求解方程组。
答案:solve2. 若要在Maple中计算函数f(x) = x^3 - 2x + 1在x=2处的导数值,应使用命令____。
答案:diff(f(x), x)(2)3. Maple中,使用____命令可以计算不定积分。
答案:int4. 若要在Maple中绘制函数y = sin(x)的图像,应使用命令____。
答案:plot(sin(x))三、简答题(每题10分,共40分)1. 请解释Maple中solve命令的基本用法。
答案:solve命令在Maple中用于求解方程或方程组。
基本用法是solve(equation, variable),其中equation是待求解的方程,variable是方程中的变量。
例如,求解方程x^2 - 4 = 0,可以使用solve(x^2 - 4 = 0, x)。
2. 描述Maple中diff命令的用途和基本语法。
Maple软件在高等数学定积分教学的应用

Maple软件在高等数学定积分教学的应用摘要:高等数学是每一位大一新生都要面对的一门非常重要的公共基础课,因此如何让学生们能够直观,形象地理解高等数学中的众多定理和计算就成为了我们高等数学任课老师的教学关键所在。
我们都知道,高等数学是研究变量与变量之间关系的一门学科,而定积分则是一元函数微积分中的重点。
Maple一款非常强大的数值计算软件。
因此本文从如何使用Maple对定积分教学进行辅助教学的角度出发,通过两个例子,形象而直观地演示了如何对定积分的定义,面积和体积等内容进行教学的关键。
最后,在总结中,我们给出了在高等数学定积分教学中使用Maple软件的前景和未来的趋势。
关键词:高等数学;定积分;Maple;辅助教学我们都知道,高等数学是研究变量与变量之间关系的一门学科。
其主要内容包括:一元函数微积分,多元函数微积分,无穷级数,向量与空间解析几何以及常微分方程。
简言之,就是微分,积分,级数,向量和方程[1]。
因此,在国外的很多教材中都把高等数学称之为微积分(Calculus)。
从这个意义上来说,积分学无疑在整个高等数学教学中占有非常重要的地位。
而学生们初次接触积分就是不定积分和定积分,从一般意义上讲,定积分应该属于一元函数积分学。
因此,如何让学生们更好的理解并学好定积分就是我们高校老师的重要任务所在。
一高等数学定积分教学的重点与难点很多高数教材在讲解定积分的定义的时候,都会用曲边梯形的面积这个经典例子作为案例引入来开始定积分课程的教学。
但是如何能用最直观的形式教会学生定积分并不是一件容易的事[2]。
首先,定积分的概念的引入一般会有两个:①曲边梯形求面积;②变速直线运动求路程。
这两个问题看似风马牛不相及,但是研究思路却有着异曲同工之处,那就是:分割,近似,求和和取极限。
也就是其和式极限可以写成下面的样子:01lim()niiiAfxλξ→==∑∆。
因此我们可以看到,这里的iii1xxx−∆=−是第i个小区间的长度,()iifξ∆x使用来近似第i…个小区间上的矩形的面积,12max{,,...}nλ=∆x∆x∆x是所有小区间上的间距的最大值。
Maple在高等数学教学中的应用

作者简介 : 王剑侠 ( 1966 - ) , 男 , 讲师 , 硕士 ; 主要研究方向 : 偏微分方程 .
70
广州大学学报 ( 自然科学版) 第1卷
z ( s , t ) ] , s = a. . b , t = c ( s ) . . d ( s ) , opts ) . (3) 函数 spacecurve 用于作空间曲线图形 , 该
( 1) 关于无界量与无穷大量 , 通过图形演示加
( 4) 关于旋转曲面和柱面生成过程的动态演示
例如 : xoz 面上的曲线 y =
1
x
( 0 . 3 < x < 1) 绕 z
以区别 . 例如 :在 x ϖ + ∞ 时 , x sin ( x ) 是无界量 , 而 x + sin ( x ) 是无穷大量 . animatecurve ( x 3 sin ( x ) , x = 0. . 10 3 Pi ) ; animatecurve ( x + sin ( x ) , x = 0. . 40 3 Pi ) ;plot ( x 3 sin ( x ) , x = 0. . infinity) ; plot ( x + sin ( x ) , x = 0. . infinity) . (2) 关于振荡间断点 , 利用 Maple 的动画功能 展示振荡过程 . 例 : x = 0 是 y = sin
a. . b , opts ) : q : = plot ( g ( x ) , x = c. . d , opts ) : dis2
1 Maple 5. 5 使用介绍 [2 ]
Maple 是由加拿大 Waterloo University 发展起来
的一种数学软件 , 它提供了范围广泛的符号计算 、 数值计算 、 函数作图功能 . Maple 的使用相当简单 , 在 Maple 工作区内出现提示符号 “> ” 后 , 输入命 令 ,结尾用分号 “ ;” 或冒号 “ : ” , 并按回车键即可 . 现介绍它在高等数学教学中一些命令的使用格式 . 1. 1 Maple 用于求极限 、 微分 、 积分 、 级数与求和 ( 1) limit 函数求表达式的极限 . x 趋向于 a 时 表达式 f ( x ) 的极限 , 调用格式 : limit ( f ( x ) , x = a ) 和 limit ( f ( x ) , x = a , dir) . dir 为可选项 , 取 left 或
maple求函数的积分

maple求函数的积分函数的积分是数学中常见的求导运算的逆运算。
它在微积分中起着重要的作用,可以用来计算函数下的面积、求解微分方程以及进行函数的逆变换。
在本文中,我们将探讨如何求函数的积分。
首先,我们需要了解函数的积分定义。
函数的积分可以通过求取其原函数(也称为不定积分)来得到。
如果函数f(x)的原函数是F(x),那么函数f(x)的积分可以表示为∫f(x)dx = F(x) + C,其中C是常数。
不定积分可以理解为是对函数f(x)进行求导的逆过程。
在求取函数的不定积分时,我们可以利用一些常用的积分公式和基本积分法则。
以下是一些常见的积分公式:1. ∫kdx = kx + C(k是常数)2. ∫x^n dx = (x^(n+1))/(n+1) + C(n不等于-1)3. ∫e^x dx = e^x + C4. ∫sin(x)dx = -cos(x) + C5. ∫cos(x)dx = sin(x) + C根据这些积分公式,我们可以通过逐步求积分的方法来计算函数的积分。
首先,我们需要将函数进行合理的变换,以便可以应用上述的积分公式。
例如,如果我们要求函数f(x) = 2x^2 + 3x + 1的积分∫f(x)dx,我们可以将其拆分成∫2x^2 dx + ∫3x dx + ∫1 dx。
根据积分公式,我们可以得到(2/3)x^3 + (3/2)x^2 + x + C的积分结果。
除了使用基本积分公式外,还可以使用一些特殊的积分方法来求取一些特定形式的函数积分。
例如,可以使用分部积分法、换元积分法、三角换元和部分分式分解等方法。
分部积分法是一种用于求解乘积函数的积分的方法。
它基于积分的乘法法则,将一个函数的积分化为另一种形式的积分。
具体来说,分部积分法可以表示为∫u dv = uv - ∫v du。
通过选择合适的u和dv,我们可以将整个积分问题转化为一个易于求解的形式。
换元积分法是一种将复杂函数转化为简单函数进行积分的方法。
maple求函数的积分

maple求函数的积分# maple求函数的积分在数学领域中,导数和积分是两个非常重要的概念。
导数可以衡量函数在某一点的变化率,而积分可以计算函数在给定区间上的面积或曲线长度。
Maple是一种强大的数学计算软件,能够帮助我们求解各种复杂的数学问题,包括函数的积分。
下面我们将介绍如何使用Maple来求解函数的积分。
## 1. 定义函数在使用Maple之前,我们首先需要定义我们要求解的函数。
在Maple中,我们可以通过以下方式来定义一个函数:```maplef := x -> x^2 + 2*x + 1;```上述代码定义了一个函数f,它可以计算x的平方加上2x加1的值。
## 2. 求函数的积分求函数的积分在Maple中非常简单。
我们可以使用Maple的内置函数`int`来实现。
下面是求解函数积分的示例代码:```mapleint(f(x), x);```上述代码中,`f(x)`是我们定义的函数,`x`是积分变量。
通过调用`int`函数并传入函数和积分变量,Maple将自动计算函数的积分结果。
## 3. 指定积分区间有时我们需要计算函数在某一给定区间上的积分,而不仅仅是在整个定义域上。
在Maple中,我们可以通过指定积分区间的上下限来进行计算。
下面是一个示例代码:```mapleint(f(x), x = a .. b);```上述代码中,`a`和`b`分别是积分区间的下限和上限。
通过在`int`函数中使用`x = a .. b`来指定积分区间,Maple将计算函数在该区间上的积分结果。
## 4. 解决复杂积分对于一些复杂的积分问题,Maple也提供了强大的功能来解决。
我们可以使用`int`函数的一些参数来指定积分的方法。
例如,我们可以使用参数`numeric`来进行数值积分,或者使用参数`symbolic`来进行符号积分。
下面是一个示例代码:```mapleint(f(x), x = a .. b, numeric);```上述代码中,`numeric`参数告诉Maple使用数值积分方法来计算函数的积分结果。
maple复合函数求导

maple复合函数求导复合函数是由两个或多个函数组合而成的新函数。
在数学中,求复合函数的导数是非常常见的问题。
下面我们来讨论如何求复合函数的导数。
设有两个函数y=f(x)和z=g(y),我们要求复合函数h(x)=g(f(x))的导数。
这里的思路是先求出h(x)对y的导数,再求出y对x的导数,最后将这两个导数相乘即可得到h(x)对x的导数。
首先,我们求出 h(x) 对 y 的导数 (d(h(x))/dy)。
利用链式法则,我们有:d(h(x))(d(h(x))/dy) = ──────── (1)dy/dx其中,dy/dx 是 y 对 x 的导数,也就是 f'(x)。
因此,我们可以将式(1) 改写为:d(h(x))(d(h(x))/dy) = ──────── (2)df(x)/dx接下来,我们求出 y 对 x 的导数 (dy/dx)。
根据题目中的信息,我们可能需要使用到一些常见函数的导数公式。
下面是一些常见函数的导数公式:1. 常数函数的导数:d(c)/dx = 0,其中 c 是一个常数。
2. 幂函数的导数:d(x^n)/dx = nx^(n-1),其中 n 是一个实数。
3. 指数函数的导数:d(e^x)/dx = e^x。
4. 对数函数的导数:d(ln(x))/dx = 1/x。
5. 三角函数的导数:d(sin(x))/dx = cos(x),d(cos(x))/dx = -sin(x),d(tan(x))/dx = sec^2(x)。
根据这些导数公式,我们可以将函数f(x)的公式写成一个组合函数的形式。
然后,我们可以利用链式法则将这个组合函数的导数求出来,从而得到f'(x)。
最后,我们将 d(h(x))/dy 和 f'(x) 相乘即可得到 h(x) 对 x 的导数。
具体的求导步骤可能会有所不同,具体要根据题目给出的函数形式和要求的导数形式来决定。
接下来,我们以一个具体的例子来说明如何求复合函数的导数。
用数学软件Maple计算定积分

用数学软件Maple计算定积分2012/6/15定积分的概念与性质1.(2)f:=x->exp(x):a:=0:b:=1:Integrate(f(x),x=a..b)=integrate(f(x),x=a..b);2(2)f:=x->x:a:=-1:b:=3:Integrate(f(x),x=a..b)=integrate(f(x),x=a..b);(4)f:=x->k*x+m:Integrate(f(x),x=a..b)=integrate(f(x),x=a..b);3(1)例求极限1lim... n n→∞++a:=n->(1/n)*sum((1+k/n)^(1/3),k=1..n);Limit(a(n),n=infinity)=limit(a(n),n=infinity);验证:01lim ...n n →∞++=⎰f:=x->(1+x)^(1/3):a:=0:b:=1:Integrate(f(x),x=a..b)=integrate(f(x),x=a..b);(2)a:=n->(h/n)*sum(sin(a+h*(k-1)/n),k=1..n):Limit(a(n),n=infinity)=limit(a(n),n=infinity);f:=x->sin(x):Integrate(f(x),x=a..a+h)=integrate(f(x),x=a..a+h);7(1)f:=x->x*exp(-x): a:=0.0:b:=2:Integrate(f(x),x=a..b)=integrate(f(x),x=a..b);(2)f:=x->x^x:a:=1/4:b:=1/2:Integrate(f(x),x=a..b)=integrate(f(x),x=a..b); evalf(%);1/4/exp(1)^(1/exp(1));evalf(%); 1/4/sqrt(2);evalf(%); (1/4)^(1/4);evalf(%); solve(D(f)(x)=0,x); plot(f(x),x=1/4..1/2);= d ⎛⎠⎜/14/12x x x d ⎛⎠⎜/14/12x x x = 0.17428542100.1742854210141()e ⎛⎝ ⎫⎭⎪⎪1e0.1730501569280.17677669524()/3440.70710678121e8(1)f:=x->tan(x):a:=Pi/4:b:=Pi/3:Integrate(f(x),x=a..b)=integrate(f(x),x=a..b);evalf(%);evalf(Pi/12);evalf(Pi*sqrt(3)/12);(2)f:=x->sin(x)/x:a:=Pi/4:b:=Pi/2:Integrate(f(x),x=a..b)=integrate(f(x),x=a..b); evalf(%);evalf(sqrt(2)/2);9(1)f:=x->sin(x)^2:a:=0:b:=Pi/4:Integrate(f(x),x=a..b)=integrate(f(x),x=a..b); evalf(%);g:=x->sin(x)^4:a:=0:b:=Pi/4:Integrate(g(x),x=a..b)=integrate(g(x),x=a..b); evalf(%);(2)f:=x->sqrt(5-x):a:=1:b:=2:Integrate(f(x),x=a..b)=integrate(f(x),x=a..b); evalf(%);g:=x->sqrt(x+1):a:=1:b:=2:Integrate(g(x),x=a..b)=integrate(g(x),x=a..b); evalf(%);(3)f:=x->exp(-x):g:=x->exp(-sin(x)):a:=0:b:=Pi/2:Integrate(f(x),x=a..b)=integrate(f(x),x=a..b); evalf(%);Integrate(g(x),x=a..b)=integrate(g(x),x=a..b); evalf(%);13.a:=n->int(x^2/(x^2+a^2),x=n..n+p);Limit(a(n),n=infinity)=limit(a(n),n=infinity);微积分基本公式1(1)f:=x->sin(x^2):F:=Integrate(f(t),t=0..x):Diff(F,x)=diff(F,x);(2)f:=x->sqrt(1+t^2):F:=Integrate(f(t),t=x..2):Diff(F,x)=diff(F,x);(3)f:=x->1/sqrt(1+t^2):F:=Integrate(f(t),t=1..x^3):Diff(F,x)=diff(F,x);(4)f:=x->exp(-t^2):F:=Integrate(f(t),t=cos(x)..sin(x)^2): Diff(F,x)=diff(F,x);2.x:=t->int(sin(u)/u,u=0..t);y:=t->int(cos(u^2),u=t..t^2);Dx:=diff(x(t),t):Dy:=diff(y(t),t):DyDx=Dy/Dx;3F:=(x,y)->int(sin(t^3),t=0..x)+int(exp(-t^2),t=x..y); Fx:=diff(F(x,y),x);Fy:=diff(F(x,y),y);DyDx:=-Fx/Fy;很复杂!4.(1)例求极限222(1)limx txxt e dtxe→∞+⎰。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用Maple求函数极限1. 自变量趋于有限值的极限解输入:f:=x->sin(x)/x;Limit(f(x),x=0);输出:或f:=x->sin(x)/x;limit(f(x),x=0);或f:=x->sin(x)/x:Limit(f(x),x=0)=limit(f(x),x=0);f:=x->(1+x^2/2-sqrt(1+x^2))/((cos(x)-exp(x^2))*sin(x^2)): Limit(f(x),x=0)=limit(f(x),x=0);2. 自变量趋于无穷大的极限f:=x->(1+a/x)^x;Limit(f(x),x=infinity)=limit(f(x),x=infinity);f:=x->x*sin(a/x);Limit(f(x),x=infinity)=limit(f(x),x=infinity);用Maple求单侧极限解输入:f:=x->exp(1/x);Limit(f(x),x=0,left)=limit(f(x),x=0,left);输出:f:=x->exp(1/x);Limit(f(x),x=0,right)=limit(f(x),x=0,right);f:=x->exp(1/x);Limit(f(x),x=0)=limit(f(x),x=0);f:=x->arctan(1/x);Limit(f(x),x=0,right)=limit(f(x),x=0,right);用Maple求分段函数的极限2011-07-29 10:30:50| 分类:Maple应用| 标签:|举报|字号大中小订阅用微信“扫一扫”将文章分享到朋友圈。
用易信“扫一扫”将文章分享到朋友圈。
下载LOFTER客户端g:=x->piecewise(x<3,x^2-6,3<=x,2*x-1);Limit(g(x), x=3,right)=limit(g(x), x=3,right);Limit(g(x), x=3,left)=limit(g(x), x=3,left);Limit(g(x), x=3)=limit(g(x), x=3);Maple求单向极限2011-07-29 10:42:39| 分类:Maple应用| 标签:|举报|字号大中小订阅用微信“扫一扫”将文章分享到朋友圈。
用易信“扫一扫”将文章分享到朋友圈。
下载LOFTER客户端f:=x->arctan(x);Limit(f(x),x=infinity)=limit(f(x),x=infinity);f:=x->arctan(x);Limit(f(x),x=-infinity)=limit(f(x),x=-infinity);用Maple求无穷大的极限2011-07-29 10:47:22| 分类:Maple应用| 标签:|举报|字号大中小订阅用微信“扫一扫”将文章分享到朋友圈。
用易信“扫一扫”将文章分享到朋友圈。
下载LOFTER客户端f:=x->exp(1/x);Limit(f(x),x=0,right)=limit(f(x),x=0,right);用Maple求数列的极限2011-07-29 10:57:11| 分类:Maple应用| 标签:|举报|字号大中小订阅用微信“扫一扫”将文章分享到朋友圈。
用易信“扫一扫”将文章分享到朋友圈。
下载LOFTER客户端f:=n-<(1-1/n)^n;Limit(f(n),n=infinity)=limit(f(n),n=infinity);递归定义的数列的极限x[0]:=0:for n from 1 to 100 dox[n]:=sqrt(2+x[n-1]);od:seq(evalf(x[n]),n=1..20);a:=proc(n)option remember;sqrt(a(n-1)+2);end;a(1):=sqrt(2);plot([seq([n,a(n)],n=1..10)],style=point);seq(evalf(a(n)),n=1..10);limit(a(n),n=infinity);Maple不能求递归定义的数列的极限。
参考:/math/Calculus/labs/215/html%20labs/%5BIndex%20215%5D/Sequences%20215%20problem%2002.html用Maple求显函数的导数2011-07-29 11:03:31| 分类:Maple应用| 标签:|举报|字号大中小订阅用微信“扫一扫”将文章分享到朋友圈。
用易信“扫一扫”将文章分享到朋友圈。
下载LOFTER客户端1. 求导函数f:=x->sin(2*x^2+2);Diff(f(x),x);diff(f(x),x);Diff(f(x),x)=diff(f(x),x);或f:=x->sin(2*x^2+2);D(f);Diff(f(x),x)=D(f)(x);2. 求某一点的导数f:=x->(2*x^2+3)*sin(x);D(f)(x);D(f)(2);3. 用定义求导数f:=x->piecewise(x<0,x,0<=x,sin(x));a:=0:Limit((f(x+a)-f(a))/(x-a),x=a)=limit((f(x+a)-f(a))/(x-a),x=a);用Maple求单侧导数2011-07-29 11:14:07| 分类:Maple应用| 标签:|举报|字号大中小订阅用微信“扫一扫”将文章分享到朋友圈。
用易信“扫一扫”将文章分享到朋友圈。
下载LOFTER客户端用定义求导:f:=x->piecewise(x<0,x,0<=x,sin(2*x));a:=0:Limit((f(x+a)-f(a))/(x-a),x=a,left)=limit((f(x+a)-f(a))/(x-a),x=a,left);Limit((f(x+a)-f(a))/(x-a),x=a,right)=limit((f(x+a)-f(a))/(x-a),x=a,right);用Maple求高阶导数2011-07-29 16:44:50| 分类:Maple应用| 标签:|举报|字号大中小订阅用微信“扫一扫”将文章分享到朋友圈。
用易信“扫一扫”将文章分享到朋友圈。
下载LOFTER客户端二阶导数f:=x->sin(2*x^2+3);diff(f(x),x$2);Diff(f(x),x$2)=diff(f(x),x$2);或f:=x->sin(2*x^2+3);(D@@2)(f)(x);或f:=x->sin(2*x^2+3):Diff(f(x),x$2)=(D@@2)(f)(x);三阶导数f:=x->sin(2*x^2+3);Diff(f(x),x$3)=diff(f(x),x$3);或Diff(f(x),x$3)=(D@@3)(f)(x);求某一点的二阶导数f:=x->exp(x)*cos(2*x^2);(D@@2)(f)(x);(D@@2)(f)(1);f:=x->1/(x+1);seq([Diff(f(x),x$n)=diff(f(x),x$n)],n=1..10);或f:=x->1/(x+1);seq((D@@n)(f)(x),n=1..10);f:=x->1/(x+1);seq((D@@n)(f)(0),n=1..10);用Maple求参数方程的导数2011-07-29 17:06:00| 分类:Maple应用| 标签:|举报|字号大中小订阅用微信“扫一扫”将文章分享到朋友圈。
用易信“扫一扫”将文章分享到朋友圈。
下载LOFTER客户端x:=t->2*t^2;y:=t->sin(t);Dx:=diff(x(t),t);Dy:=diff(y(t),t);DyDx=Dy/Dx;x:=t->exp(t)*sin(t);y:=t->exp(t)*cos(t);Dx:=D(x)(t);Dy:=D(y)(t);DyDx=Dy/Dx;simplify(%);或x:=t->exp(t)*sin(t); y:=t->exp(t)*cos(t);a:=Pi/3:Dx:=D(x)(a);Dy:=D(y)(a);DyDx=Dy/Dx;simplify(%);参数方程的高阶导数x:=t->2*t^2;y:=t->sin(t);Y:=D(y)(t)/D(x)(t);Yi:=t->D(y)(t)/D(x)(t);Er:=D(Yi)(t)/D(x)(t);simplify(%);(用微分记号D)x:=t->2*t^2;y:=t->sin(t);(D(x)(t)*(D@@2)(y)(t)-D(y)(t)*(D@@2)(x)(t))/(D(x)(t))^3;simplify(%);(或用记号diff)x:=t->2*t^2;y:=t->sin(t);(diff(x(t),t)*diff(y(t),t$2)-diff(x(t),t$2)*diff(y(t),t))/diff(x(t),t)^3;simplify(%);x:=t->2*t^2:y:=t->sin(t):Yi:=D(y)(t)/D(x)(t);Yi:=t->D(y)(t)/D(x)(t):Er:=D(Yi)(t)/D(x)(t);Er:=simplify(%); Er:=t->D(Yi)(t)/D(x)(t): San:=D(Er)(t)/D(x)(t);San:=simplify(%);只显示最终结果:x:=t->2*t^2:y:=t->sin(t): Yi:=D(y)(t)/D(x)(t); Yi:=t->D(y)(t)/D(x)(t): Er:=D(Yi)(t)/D(x)(t):Er:=simplify(%); Er:=t->D(Yi)(t)/D(x)(t): San:=D(Er)(t)/D(x)(t):San:=simplify(%);用Maple求隐函数的导数2011-07-29 17:33:45| 分类:Maple应用| 标签:|举报|字号大中小订阅用微信“扫一扫”将文章分享到朋友圈。
用易信“扫一扫”将文章分享到朋友圈。
下载LOFTER客户端F:=(x,y)->1-x*exp(y)-y;Fx:=diff(F(x,y),x);Fy:=diff(F(x,y),y);DyDx:=-Fx/Fy;方法二直接求导eq:=1-x*exp(y(x))=y(x);solve(diff(eq, x), diff(y(x),x));(参考:/~johnson/calcA98/implicit.html)方法三利用命令implicitdiffF:=1-x*exp(y)-y;implicitdiff(F,y,x);隐函数的二阶导数F:=(x,y)->x+sin(y)/2-y;Fx:=diff(F(x,y),x);Fy:=diff(F(x,y),y);Yijie:=-Fx/Fy;Fxx:=diff(F(x,y),x,x);Fxy:=diff(F(x,y),x,y);Fyy:=diff(F(x,y),y,y);Erjie:=-(Fxx*Fy^2-2*Fxy*Fx*Fy+Fyy*Fx^2)/Fy^3;。
