2019最新高等数学(下册)期末考试试题(含答案)YM
2019年高三数学下期末试题附答案
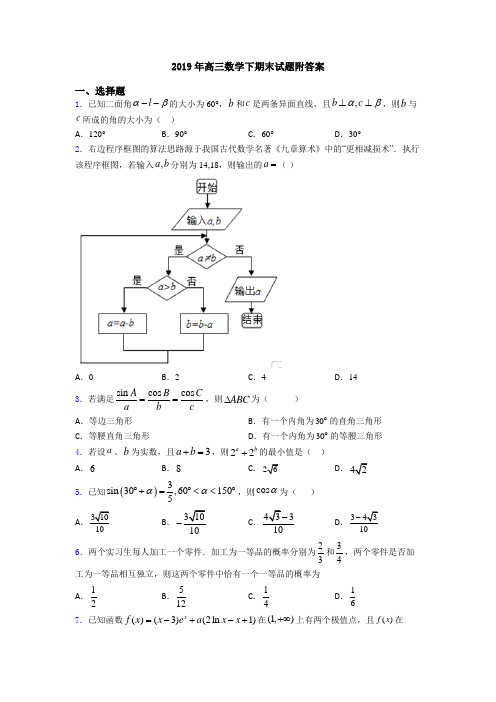
2019年高三数学下期末试题附答案一、选择题1.已知二面角l αβ--的大小为60°,b 和c 是两条异面直线,且,b c αβ⊥⊥,则b 与c 所成的角的大小为( )A .120°B .90°C .60°D .30°2.右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入,a b 分别为14,18,则输出的a =( )A .0B .2C .4D .143.若满足sin cos cos A B Ca b c==,则ABC ∆为( ) A .等边三角形 B .有一个内角为30°的直角三角形 C .等腰直角三角形 D .有一个内角为30°的等腰三角形4.若设a 、b 为实数,且3a b +=,则22a b +的最小值是( )A .6B .8C .26D .425.已知()3sin 30,601505αα︒+=︒<<︒,则cos α为( ) A 310 B .31010-C 433- D 343-6.两个实习生每人加工一个零件.加工为一等品的概率分别为23和34,两个零件是否加工为一等品相互独立,则这两个零件中恰有一个一等品的概率为A .12B .512C .14D .167.已知函数()(3)(2ln 1)xf x x e a x x =-+-+在(1,)+∞上有两个极值点,且()f x 在(1,2)上单调递增,则实数a 的取值范围是( )A .(,)e +∞B .2(,2)e eC .2(2,)e +∞D .22(,2)(2,)e e e +∞U8.已知函数()3sin 2cos 2[0,]2f xx x m π=+-在上有两个零点,则m 的取值范围是A .(1,2)B .[1,2)C .(1,2]D .[l,2]9.设A (3,3,1),B (1,0,5),C (0,1,0),AB 的中点M ,则CM = A .534B .532C .53 D .13 10.由a 2,2﹣a ,4组成一个集合A ,A 中含有3个元素,则实数a 的取值可以是( ) A .1B .﹣2C .6D .211.在等比数列{}n a 中,44a =,则26a a ⋅=( ) A .4B .16C .8D .3212.一个样本a,3,4,5,6的平均数是b ,且不等式x 2-6x +c <0的解集为(a ,b ),则这个样本的标准差是( ) A .1 B .2 C .3D .2二、填空题13.某工厂生产甲、乙、丙、丁四种不同型号的产品,产量分别为200,400,300,100件,为检验产品的质量,现用分层抽样的方法从以上所有的产品中抽取60件进行检验,则应从丙种型号的产品中抽取________ 件.14.一个算法的伪代码如图所示,执行此算法,最后输出的S 的值为________.15.在平行四边形ABCD 中,3A π∠=,边AB ,AD 的长分别为2和1,若M ,N 分别是边BC ,CD 上的点,且满足CN CDBM BC =u u u u v u u u v u u u v u u u v ,则AM AN ⋅u u u u v u u u v 的取值范围是_________. 16.某大学为了解在校本科生对参加某项社会实践活动的意向,拟采用分层抽样的方法,从该校四个年级的本科生中抽取一个容量为300的样本进行调查.已知该校一年级、二年级、三年级、四年级的本科生人数之比为4:5:5:6,则应从一年级本科生中抽取_______名学生.17.若,满足约束条件则的最大值 .18.计算:1726cos()sin 43ππ-+=_____. 19.有三张卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是________.20.ABC △的内角,,A B C 的对边分别为,,a b c .若π6,2,3b ac B ===,则ABC △的面积为__________.三、解答题21.在平面直角坐标系中,直线l 的参数方程为cos sin x t y t αα=⎧⎨=⎩(t 为参数,0≤α<π).以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,曲线C 的极坐标方程为244cos 2sin ρρθρθ-=-.(Ⅰ)写出曲线C 的直角坐标方程;(Ⅱ)若直线l 与曲线C 交于A ,B 两点,且AB 的长度为25,求直线l 的普通方程. 22.已知曲线C :(t 为参数), C :(为参数).(1)化C ,C 的方程为普通方程,并说明它们分别表示什么曲线; (2)若C 上的点P 对应的参数为,Q 为C 上的动点,求中点到直线(t 为参数)距离的最小值.23.为评估设备生产某种零件的性能,从设备生产该零件的流水线上随机抽取100个零件为样本,测量其直径后,整理得到下表:经计算,样本的平均值,标准差,以频率值作为概率的估计值.(I )为评判一台设备的性能,从该设备加工的零件中任意抽取一件,记其直径为,并根据以下不等式进行判定(表示相应事件的概率): ①;②; ③.判定规则为:若同时满足上述三个式子,则设备等级为甲;若仅满足其中两个,则等级为乙,若仅满足其中一个,则等级为丙;若全部都不满足,则等级为了.试判断设备的性能等级.(Ⅱ)将直径尺寸在之外的零件认定为是“次品”.①从设备的生产流水线上随机抽取2个零件,求其中次品个数的数学期望;②从样本中随意抽取2个零件,求其中次品个数的数学期望.24.已知椭圆()2222:10x y C a b a b+=>>的一个焦点为()5,0,离心率为5.(1)求椭圆C 的标准方程;(2)若动点()00,P x y 为椭圆外一点,且点P 到椭圆C 的两条切线相互垂直,求点P 的轨迹方程.25.已知函数()32f x x ax bx c =+++,过曲线()y f x =上的点()()1,1P f 处的切线方程为31y x =+.(1)若函数()f x 在2x =-处有极值,求()f x 的解析式; (2)在(1)的条件下,求函数()y f x =在区间[]3,1-上的最大值. 26.四棱锥P ABCD -中,底面ABCD 是边长为2的菱形,3BAD π∠=,PAD ∆是等边三角形,F 为AD 的中点,PD BF ⊥.(1)求证:AD PB ⊥; (2)若E 在线段BC 上,且14EC BC =,能否在棱PC 上找到一点G ,使平面DEG ⊥平面ABCD ?若存在,求四面体D CEG -的体积.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C解析:C 【解析】 【分析】,b c αβ⊥⊥,直线,b c 的方向向量,b c r r分别是平面,αβ的法向量,根据二面角与法向量的关系,即可求解. 【详解】设直线,b c 的方向向量,b c r r,,b c αβ⊥⊥,所以,b c r r分别是平面,αβ的法向量,二面角l αβ--的大小为60°,,b c r r的夹角为060或0120,因为异面直线所的角为锐角或直角, 所以b 与c 所成的角为060. 故选:C. 【点睛】本题考查二面角与二面角平面的法向量的关系,属于基础题.2.B解析:B 【解析】 【分析】 【详解】由a=14,b=18,a <b , 则b 变为18﹣14=4, 由a >b ,则a 变为14﹣4=10, 由a >b ,则a 变为10﹣4=6, 由a >b ,则a 变为6﹣4=2, 由a <b ,则b 变为4﹣2=2, 由a=b=2, 则输出的a=2. 故选B .3.C解析:C 【解析】 【分析】由正弦定理结合条件可得tan tan 1B C ==,从而得三角形的三个内角,进而得三角形的形状. 【详解】 由正弦定理可知sin sin sin A B Ca b c ==,又sin cos cos A B C a b c==,所以cos sin ,cos sin B B C C ==,有tan tan 1B C ==. 所以45B C ==o .所以180454590A =--=o o o o . 所以ABC ∆为等腰直角三角形. 故选C. 【点睛】本题主要考查了正弦定理解三角形,属于基础题.4.D解析:D 【解析】 【分析】2a b+≤转化为指数运算即可求解。
2019最新高等数学(下册)期末考试试题(含答案)WI

2019最新高等数学(下册)期末考试试题(含答案)一、解答题1.(0 < t < 2π)为何值时,曲线L :x = t -sin t , y =1-cos t , z = 4sin2t在相应点的切线垂直于平面0x y +=,并求相应的切线和法平面方程。
解:1cos ,sin ,2cos2t x t y t z '''=-==, 在t 处切向量为{}1cos ,sin ,2cos 2t T t t =-, 已知平面的法向量为{1,1,2n =.且T ∥n ,故2cos 1cos sin 11tt t-==解得π2t=,相应点的坐标为π2⎛- ⎝.且{1T = 故切线方程为π11211x y -+-==法平面方程为π1102x y z -++--=即 π042x y ⎛⎫+-=+⎪⎝⎭.2.当Σ为xOy 面内的一个闭区域时,曲面积分()d d ,,R x y x y z ∑⎰⎰与二重积分有什么关系?解:因为Σ:z =0,在xOy 面上的投影区域就是Σ故()()d d d d ,,,,0R x y R x y x y z x y ∑∑=±⎰⎰⎰⎰当Σ取的是上侧时为正号,Σ取的是下侧时为负号.3.证明:22d d x x y yx y ++在整个xOy 平面内除y 轴的负半轴及原点外的开区域G 内是某个二元函数的全微分,并求出这样的一个二元函数.证:22x P x y =+,22yQ x y =+,显然G 是单连通的,P 和Q 在G 内具有一阶连续偏导数,并且.()2222∂∂-==∂∂+P Q xy y x x y ,(x ,y )∈G 因此22d d x x y yx y ++在开区域G 内是某个二元函数u (x ,y )的全微分.由()()22222222d d 11ln 22d x y x x y y d x y x y x y ++⎡⎤==+⎢⎥++⎣⎦知()()221ln ,2u x y x y =+.4.验证下列P (x , y )d x +Q (x , y )d y 在整个xOy 面内是某一函数u (x , y )的全微分,并求这样的一个函数u (x , y ): (1)(x +2y )d x +(2x +y )d y ; (2)2xy d x +x 2d y ;(3)(3x 2y +8xy 2)d x +(x 3+8x 2y +12y e y )d y ; (4)(2x cos y +y 2cos x )d x +(2y sin x -x 2sin y )d y . 解:证:(1)P =x +2y ,Q =2x +y .2P Q y x ∂∂==∂∂,所以(x +2y )d x +(2x +y )d y 是某个定义在整个xOy 面内的函数u (x ,y )的全微分. ()()()()()(),0,0022022d d ,22d d 2222222x y xy yu x y x y x y x y x x yx y x y xy x y xy =+++=++⎡⎤=++⎢⎥⎣⎦=++⎰⎰⎰(2)P =2xy ,Q =x 2, 2P Qx y x∂∂==∂∂,故2xy d x +x 2d y 是某个定义在整个xOy 面内的函数u (x ,y )的全微分. ()()(),20,02022d d ,0d d x y xy u xy x x y x y x x yx y=+=+=⎰⎰⎰(3)P =3x 2y +8xy 2,Q =x 3+8x 2y +12y e y,2316∂∂=+=∂∂P Q x xy y x,故(3x 2y +8xy 2)d x +(x 3+8x 2y +12y e y )d y 是某个定义在整个xOy 面内函数u (x ,y )的全微分,()()()()()(),22320,03200322d ,38812e 0d d 812e 412e 12e 12x y y xyy y y u x x y x y x y x x y y x y x x y y x y x y y =++++=+++=++-+⎰⎰⎰(4)P =2x cos y +y 2cos x ,Q =2y sin x -x 2sin y ,2sin 2cos P x y y x y ∂=-+∂,2cos 2sin Qy x x y x∂=-∂, 有P Qy x∂∂=∂∂,故(2x cos y +y 2cos x )d x +(2y sin x -x 2sin y )d y 是某一个定义在整个xOy 面内的函数u (x ,y )的全微分, ()()()()()(),220,020022d d ,2cos cos 2sin sin 2d d 2sin sin sin cos x y xyu x y x y x y y x y x x y x x yy x x y y x x y=++-=+-=+⎰⎰⎰5.求下列线性微分方程的通解:(1)e x y y -'+=;解:由通解公式d de e e e d e ()e e d xx x x x x x y x c x c x c -----⎰⎡⎤⎰⎡⎤==⋅+=+⋅+⎢⎥⎣⎦⎣⎦⎰⎰ 2(2)32xy y x x '+=++;解:方程可化为 123y y x x x'+=++ 由通解公式得11d d 22e (3) e d 12(3)d 132.32x x x x y x x c x x x x c x x c x x x-⎡⎤⎰⎰=++⋅+⎢⎥⎣⎦⎡⎤=++⋅+⎢⎥⎣⎦=+++⎰⎰ sin (3)cos e ;x y y x -'+=解: cos d cos d sin sin e e ().e e d x xx x x x y x c x c ---⎰⎡⎤⎰==+⋅+⎢⎥⎣⎦⎰(4)44y xy x '=+;解: 22(4)d (4)d 22e e 4e d 4e d x xx x x x y x x c x x c ----⎰⎡⎤⎰⎡⎤==++⎢⎥⎣⎦⎣⎦⎰⎰ ()222222e e e 1x x x c c -=-+=-.3(5)(2)2(2)x y y x '-=+-;解:方程可化为2d 12()d 2y y x x x x -=-- 11d d 222ln(2)2ln(2)3e 2(2)e d e 2(2)e d (2)2(2)d (2)(2)x x x x x x y x x c x x c x x x c x c x --------⎰⎡⎤⎰=-+⎢⎥⎣⎦⎡⎤=-+⎣⎦⎡⎤=--+⎣⎦=-+-⎰⎰⎰22(6)(1)24.x y xy x '++=解:方程可化为 2222411x x y y x x '+=++ 222222d d 1123ln(1)224e ed 14e 4d 3(1)xxx x x x x x y x c x x c x x c x -++-+⎡⎤⎰⎰=+⎢⎥+⎣⎦+⎡⎤=+=⎣⎦+⎰⎰6.利用斯托克斯公式,计算下列曲线积分: (1)d d d y x z y x z Γ++⎰,其中Γ为圆周x 2+y 2+z 2= a 2,x +y +z = 0,若从x 轴的正向看去,这圆周是取逆时针的方向; (2)()()()222222d d d x y z y z x y z x Γ++---⎰,其中Γ是用平面32x y z ++=截立方体:0≤x ≤1,0≤y ≤1,0≤z ≤1的表面所得的截痕,若从Ox 轴的正向看去,取逆时针方向; (3)23d d d y x xz y yz z Γ++⎰,其中Γ是圆周x 2+y 2= 2z ,z =2,若从z 轴正向看去,这圆周是取逆时针方向; (4)22d 3d d +-⎰y x x y z z Γ,其中Γ是圆周x 2+y 2+z2= 9,z =0,若从z 轴正向看去,这圆周是取逆时针方向.解:(1)取Σ为平面x +y +z =0被Γ所围成部分的上侧,Σ的面积为πa 2(大圆面积),Σ的单位法向量为{}cos ,cos ,cos n αβγ==. 由斯托克斯公式22d d dcos cos cos ddπy x z y x zR Q Q PP Rsy z x yz xssaaΓ∑∑∑αβγ++⎡∂∂∂∂⎤⎛⎫⎛⎫∂∂⎛⎫--=++-⎪⎢⎥⎪ ⎪∂∂∂∂∂∂⎝⎭⎝⎭⎝⎭⎣⎦====⎰⎰⎰⎰⎰⎰⎰(2)记为Σ为平面32x y z++=被Γ所围成部分的上侧,可求得Σ(是一个边长为2的正六边形);Σ的单位法向量为{}cos,cos,cosαβγ==n.由斯托克斯公式()()()(((()222222d d d2222d22d3d232492x y zy z x yz xy z x y sz xsx y zsΓ∑∑∑++---⎡+----=--⎢⎣=++==⋅=-⎰⎰⎰⎰⎰(3)取Σ:z=2,D xy:x2+y2≤4的上侧,由斯托克斯公式得:()()()2223d d dd d0d d d d3d d35d d5π220π-+=++--+=-+=-=-⨯⨯=-⎰⎰⎰⎰⎰⎰⎰xyDy x xz y yz zy z z x x yzz xx yzx yΓ∑∑(4)圆周x 2+y 2+z 2=9,z =0实际就是xOy 面上的圆x 2+y 2=9,z =0,取Σ:z =0,D xy :x 2+y 2≤9由斯托克斯公式得:()()()222d 3d d d d d d d d 000032d d d d π39π+-=++---===⋅=⎰⎰⎰⎰⎰⎰⎰xyD y x x y z zy z z x x yx yx yΓ∑∑7.计算下列对面积的曲面积分: (1)4d 23s z x y ∑⎛⎫++ ⎪⎝⎭⎰⎰,其中∑为平面1234x y z ++=在第I 卦限中的部分; (2)()2d 22s xy xx z ∑--+⎰⎰,其中∑为平面2x +2y +z =6在第I 卦限中的部分;(3)()d s x y z ∑++⎰⎰,其中∑为球面x 2+y 2+z 2=a 2上z ≥h (0<h <a )的部分; (4)()d s xy yz zx ∑++⎰⎰,其中∑为锥面z =被柱面x 2+y 2=2ax 所截得的有限部分; (5)()222d s R x y ∑--⎰⎰,其中∑为上半球面z =解:(1)4:423z x y ∑=--(如图10-69所示)图10-69d d d s x y x y ==故4d 4d d d d 23331232xy xy D D s x y x y z x y ∑⎛⎫=⋅=++ ⎪⎝⎭=⨯⨯=⎰⎰⎰⎰⎰⎰(2)∑:z =6-2x -2y (如图10-70所示)。
2019高数(下)试题及答案

第二学期期末考试试卷一、 填空题(每空 3 分,共 15 分) 1. 已知向量()1,1,4a =-,()3,4,0b =,则以a ,b为边的平行四边形的面积等于.2. 曲面sin cos z x y =在点1,,442ππ⎛⎫⎪⎝⎭处的切平面方程是.3. 交换积分次序()220,x dx f x y dy =⎰⎰.4. 对于级数11n n a∞=∑(a >0),当a 满足条件时收敛.5. 函数12y x=-展开成x 的幂级数为.二、 单项选择题 (每小题3分,共15分)1. 平面20x z -=的位置是 ( ) (A )通过y 轴 (B )通过x 轴 (C )垂直于y 轴 (D )平行于xoz 平面2. 函数(),z f x y =在点()00,x y 处具有偏导数()00,x f x y ',()00,y f x y ',是函数在该点可微分的( )(A )充要条件 (B )充分但非必要条件 (C )必要但非充分条件 (D )既非充分又非必要条件3. 设()cos sin x z e y x y =+,则10x y dz ===( )(A )e (B )()e dx dy + (C )1()e dx dy -+ (D )()x e dx dy + 4. 若级数()11nn n a x ∞=-∑在1x =-处收敛,则此级数在2x =处( )(A )敛散性不确定 (B )发散 (C )条件收敛 (D )绝对收敛 5. 微分方程y xy x '-=的通解是( ) (A )2121x y e=- (B )2121x y e-=- (C )212x y Ce-= (D )2121x y Ce=-三、(本题满分8分)设平面通过点()3,1,2-,而且通过直线43521x y z-+==, 求该平面方程. 四、(本题满分8分)设(),z f xy x y =+,其中(),f u v 具有二阶连续偏导数, 试求z x ∂∂和2zx y∂∂∂.五、(本题满分8分)计算三重积分y zdxdydz Ω=⎰⎰⎰,其中(){},,01,11,12x y z x y z ≤≤-≤≤≤≤.六、(本题满分8分)计算对弧长的曲线积分L ⎰,其中L 是圆周222x y R +=在第一象限的部分.七、(本题满分9分)计算曲面积分3xdydz zdzdx dxdy ∑++⎰⎰,其中∑是柱面221x y +=与平面0z =和1z =所围成的边界曲面外侧.八、(本题满分9分)求幂级数11n n nx ∞-=∑的收敛域及和函数.九、(本题满分9分)求微分方程4x y y e ''-=的通解.十、(本题满分11分)设L 是上半平面()0y >内的有向分段光滑曲线, 其起点为()1,2,终点为()2,3, 记2221L x I xy dx x y dy y y ⎛⎫⎛⎫=++- ⎪ ⎪⎝⎭⎝⎭⎰1.证明曲线积分I 与路径L 无关; 2.求I 的值.第二学期期末考试试卷及答案一、 填空题(每空 3 分,共 15 分)1. 已知向量()1,1,4a =-,()3,4,0b =,则以a ,b为边的平行四边形的面积等于.2. 曲面sin cos z x y =在点1,,442ππ⎛⎫⎪⎝⎭处的切平面方程是210x y z --+=.3. 交换积分次序()220,x dx f x y dy =⎰⎰()20,ydy f x y dx⎰⎰.4. 对于级数11n n a∞=∑(a >0),当a 满足条件1a >时收敛.5. 函数12y x=-展开成x 的幂级数为()10222n n n x x ∞+=-<<∑.二、 单项选择题 (每小题3分,共15分)1. 平面20x z -=的位置是 ( A ) (A )通过y 轴 (B )通过x 轴 (C )垂直于y 轴 (D )平行于xoz 平面2. 函数(),z f x y =在点()00,x y 处具有偏导数()00,x f x y ',()00,y f x y ',是函数在该点可微分的( C )(A )充要条件 (B )充分但非必要条件 (C )必要但非充分条件 (D )既非充分又非必要条件 3. 设()cos sin x z e y x y =+,则10x y dz ===( B )(A )e (B )()e dx dy + (C )1()e dx dy -+ (D )()x e dx dy + 4. 若级数()11nn n a x ∞=-∑在1x =-处收敛,则此级数在2x =处( D )(A )敛散性不确定 (B )发散 (C )条件收敛 (D )绝对收敛 5. 微分方程y xy x '-=的通解是( D ) (A )2121x y e=- (B )2121x y e-=- (C )212x y Ce-= (D )2121x y Ce=-三、(本题满分8分)设平面通过点()3,1,2-,而且通过直线 43521x y z-+==,求该平面方程. 解: 由于平面通过点()3,1,2A -及直线上的点()4,3,0B -, 因而向量()1,4,2AB →=-平行于该平面。
2019最新高等数学(下册)期末考试试题(含答案)MV

2019最新高等数学(下册)期末考试试题(含答案)一、解答题1.求函数u =xy 2+z 3-xyz 在点(1,1,2)处沿方向角为πππ,,343αβγ===的方向导数。
解:(1,1,2)(1,1,2)(1,1,2)cos cos cos u u u u y l x z αβγ∂∂∂∂=++∂∂∂∂ 22(1,1,2)(1,1,2)(1,1,2)πππcoscos cos 5.(2)()(3)343xy xz y yz z xy =++=---2.求22224428u x y z x y x y z =+++-+-在点,,,1,1,1,1,1,1(000)()()O A B ---的梯度,并求梯度为零的点.解:()()()()54,2,8,2,10,6,10,6,10,3,,42-------3.设()()(),,,,,,w f x y z u g x z v h x y ===,求,,w w w x y z∂∂∂∂∂∂. 解:,w w w v w w u w v w w u x x v x y u y v x z u z∂∂∂∂∂∂∂∂∂∂∂∂=+=+=∂∂∂∂∂∂∂∂∂∂∂∂,4.设质点受力作用,力的反方向指向原点,大小与质点离原点的距离成正比,若质点由(a ,0)沿椭圆移动到B (0,b ),求力所做的功.解:依题意知 F =kxi +kyj ,且L :cos sin x a t y a t=⎧⎨=⎩,t :0→π2 ()()()()π2022π20π222022d d cos sin sin cos d sin 2d 2cos 2222LW kx x ky y ka t t kb t b t tk b a t tk b a t k b a =+=-+⋅⎡⎤⎣⎦-=--⎡⎤=⎢⎥⎣⎦-=⎰⎰⎰(其中k 为比例系数)5.计算下列对坐标的曲线积分:(1)()22d -⎰Lx y x ,其中L 是抛物线y =x 2上从点(0,0)到点(2,4)的一段弧; (2)d L xy x ⎰其中L 为圆周(x -a )2+y 2=a 2(a >0)及x 轴所围成的在第一象限内的区域的整个边界(按逆时针方向绕行);(3)d d L y x x y +⎰,其中L 为圆周x =R cos t ,y =R sin t 上对应t 从0到π2的一段弧; (4)()()22d d L x y x x y y x y +--+⎰,其中L 为圆周x 2+y 2=a 2(按逆时针方向绕行); (5)2d d d x x z y y z Γ+-⎰,其中Γ为曲线x =kθ,y =a cos θ,z =a sin θ上对应θ从0到π的一段弧;(6)()322d 3d d x x zy y x y z Γ++-⎰,其中Γ是从点(3,2,1)到点(0,0,0)的一段直线; (7)d d d L x y y z -+⎰,其中Γ为有向闭拆线ABCA ,这里A ,B ,C 依次为点(1,0,0),(0,1,0),(0,0,1);(8)()()222d 2d Lx xy x y xy y -+-⎰,其中L 是抛物线y =x 2上从点(-1,1)到点(1,1)的段弧. 解:(1)L :y =x 2,x 从0变到2,()()22222435001156d d 3515L x y x x x x x x ⎡⎤-=-=-=-⎢⎥⎣⎦⎰⎰ (2)如图11-1所示,L =L 1+L 2.其中L 1的参数方程为图11-1cos 0πsin x a a t t y a t =+⎧≤≤⎨=⎩ L 2的方程为y =0(0≤x ≤2a )故 ()()()()()12π200π320ππ322003d d d 1+cost sin cos d 0d sin 1cos d sin d sin dsin π2L L L a xy x xy x xy x a a t a a t t x a t t t a t t t t a =+'=⋅++=-+=-+=-⎰⎰⎰⎰⎰⎰⎰⎰。
2019最新高等数学(下册)期末考试试题(含答案)RK

2019最新高等数学(下册)期末考试试题(含答案)一、解答题1.设f (x ,y ) = x +(yf x (x ,1) .解:1(,)1(x f x y y y =+- 则(,1)101x f x =+=.2.证明本章关于梯度的基本性质(1)~(5).证明:略3.设()()(),,,,,,w f x y z u g x z v h x y ===,求,,w w w x y z∂∂∂∂∂∂. 解:,w w w v w w u w v w w u x x v x y u y v x z u z∂∂∂∂∂∂∂∂∂∂∂∂=+=+=∂∂∂∂∂∂∂∂∂∂∂∂,4.求抛物面壳221()(01)2z x y z =+≤≤的质量,此壳的面密度大小为z ρ=. 22221:():22xy z x y D x y ∑=++≤221d d ()d 2xy D M s z s x y x y ∑∑ρ===+⎰⎰⎰⎰⎰⎰12π222001222205322220d (1)d 2π1)(1)(1)2π2π221)(1)(1)21553r r r r r r d r r r θ=+=+-++⎡==+-+⎢⎥⎣⎦⎰5.证明: 本章关于旋度的基本性质(1)~(3)(可应用算符∇解:略。
6.求下列各齐次方程满足所给初始条件的解:220(1)(3)d 2d 0,1x y x y xy x y =-+== ;解: 22d d 3y y x x y x =-⎛⎫- ⎪⎝⎭令y ux =,则得 2d 2d 3u u u xx u +=-- 分离变量,得 233d d u x u u u x-=- 积分得 3ln ln(1)ln(1)ln u u u cx -+-++=即 231ln ln u c u x-= 得方程通解为 223y x cy -=以x =0,y =1代入上式得c =1.故所求特解为 223y x y -=. 1(2),2x x y y y y x='=+= . 解:设y ux =, 则d d d d y u u x x x=+ 原方程可变为 d d x u u x =积分得 21ln ln 2u x c =+. 得方程通解为 222(ln ln )y x x c =+以x =1,y =2代入上式得c =e 2.故所求特解为 222(ln 2)y x x =+.7.把对坐标的曲线积分()()d d ,,LP x Q y x y x y +⎰化成对弧长的曲线积分,其中L 为: (1)在xOy 面内沿直线从点(0,0)到点(1,1);(2)沿抛物线y = x 2从点(0,0)到点(1,1);(3)沿上半圆周x 2+y 2 = 2x 从点(0,0)到点(1,1).解:(1)L的方向余弦πcos cos cos 42αβ===,。
2019最新高等数学(下册)期末考试试题(含答案)VP

2019最新高等数学(下册)期末考试试题(含答案)一、解答题1.求旋转抛物面z = x 2+y 2与平面x +y -z =1之间的最短距离。
解:设P (x ,y ,z )为抛物面上任一点.则点P 到平面的距离的平方为2(1)3x y z d +--=,即求其在条件z = x 2+y 2下的最值。
设F (x ,y ,z )=222(1)()3x y z z x y λ+--+-- 解方程组222(1)2032(1)2032(1)03x y z x y z F x x y z F y x y z F z x yλλλ+--⎧=-=⎪⎪+--⎪=-=⎪⎨⎪-+--=+=⎪⎪⎪=+⎩ 得12x y z ===1==2.求下各微分方程的通解:(1)22e x y y y '''+-=;解: 2210r r +-=1211,2r r ∴=-= 得相应齐次方程的通解为 1212e e x xy c c -=+令特解为*e x y A =,代入原方程得 2e e e 2e x x x x A A A +-=,解得1A =, 故*e x y =,故原方程通解为 212e e e xx x y c c -=++. 2(2)25521y y x x '''+=--;解:2250r r +=1250,2r r ==- 对应齐次方程通解为 5212ex y c c -=+ 令*2()y x ax bx c =++, 代入原方程得222(62)5(32)521ax b ax bx c x x ++++=--比较等式两边系数得137,,3525a b c ==-= 则 *321373525y x x x =-+ 故方程所求通解为 532212137e 3525x y c c x x x -⎛⎫=++-+ ⎪⎝⎭. (3)323e x y y y x -'''++=;解:2320r r ++=121,2r r =-=-,对应齐次方程通解为 212e e x x y c c --=+令*()e xy x Ax B -=+代入原方程得 (22)e 3e x x Ax B A x --++=解得 3,32A B ==- 则 *23e 32x y x x -⎛⎫=-⎪⎝⎭ 故所求通解为 22123e e e 32x x x y c c x x ---⎛⎫=++- ⎪⎝⎭. (4)25e sin 2x y y y x '''-+=;解:2250r r -+=1,212r i =±相应齐次方程的通解为12e (cos 2sin 2)x y c x c x =+令*e (cos 2sin 2)xy x A x B x =+,代入原方程并整理得 4cos24sin 2sin 2B x A x x -=得 1,04A B =-=。
2019最新高等数学(下册)期末考试试题(含答案)SM

曲线在点(x0,y0,z0)处的切向量为 ,故切线方程为
法平面方程为
.
2.求下列函数在所示点的导数:
(1) ,在点 ;
解:
(2) ,在点 ;
解:
(3) ,在点 ;
解:
(4) 在点 .
解:
3.计算下列对坐标的曲面积分:
(1) ,其中Σ是球面x2+y2+z2=R2的下半部分的下侧;
(2) ,其中Σ是柱面x2+y2=1被平面z=0及z=3所截得的在第Ⅰ封限内的部分的前侧;
解:(1)Σ: ,下侧,Σ在xOy面上的投影区域Dxy为:x2+y2≤R2.
(2)Σ如图11-8所示,Σ在xOy面的投影为一段弧,
图11-8
故 ,Σ在yOz面上的投影
Dyz={(y,z)|0≤y≤1,0≤z≤3},此时Σ可表示为:
,(y,z)∈Dyz,
故
Σ在xOz面上的投影为Dxz={(x,z)|0≤x≤1,0≤z≤3},此时Σ可表示为:
证:
10.计算积分
解:由于
而 收敛,
故 收敛,从而,采用极坐标有:
11.解:因为 为一常数,不妨设
则有
从而有
而
故
12.根据二重积分性质,估计下列积分的值:
(1) ;
(2) ;
(3) .
解:(1)因为当 时,有 ,
因而 .
从而
故
即
而 (σ为区域D的面积),由σ=4
得 .
(2)因为 ,从而
故
即
而
所以
(3)因为当 时, 所以
,(x,y)∈G
因此 在开区域G内是某个二元函数u(x,y)的全微分.
由
2019最新高等数学(下册)期末考试试题(含答案)MJ

一、解答题
1.设 ,其中f(u)为可导函数,验证:
.
证明:∵ ,
,
∴
2.设 ,求 .
解:
3.求面密度为 的均匀半球壳x2+y2+z2=a2(z≥0)对于z轴的转动惯量。
解:
4.求抛物面壳 的质量,此壳的面密度大小为 .
5.求由抛物线y=x2及直线y= 1所围成的均匀薄片(面密度为常数 )c对于直线y=-1的转动惯量。
则有
从而有
而
故
10.在第I卦限内作椭球面
的切平面,使切平面与三坐标面所围成的四面体体积最小,求切点坐标。
解:令
∵
∴椭球面上任一点 的切平面方程为
即
切平面在三个坐标轴上的截距分别为 ,因此切平面与三个坐标面所围的四面体的体积为
即求 在约束条件 下的最小值,也即求xyz的最大值问题。
设 ,
解方程组
得 .
故切点为 ,此时最小体积为
11.解:平面 与曲面 在 的切平面的法向量为
从而平面 的方程为:
又 的方向向量为
由 求得
在 上取一点,不妨取 求得
由于 在平面 上,代入平面方程中可求得 .
12.证明:曲面xyz=a3上任一点的切平面与坐标面围成的四面体体积一定。
证明:设F(x,y,z)=xyz-a3.
因为Fx=yz,Fy=xz,Fz=xy,
26.已知a=3i+2j-k,b=i-j+2k,求:
(1)a×b;(2)2a×7b;
(3) 7b×2a; (4)a×a.
解:(1)
(2)
(3)
(4) .
27.已知四点A(1,-2,3),B(4,-4,-3),C(2,4,3),D(8,6,6),求向量 在向量 上的投影.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019最新高等数学(下册)期末考试试题(含答案)一、解答题1.已知过去几年产量和利润的数据如下:解:在直角坐标系下描点,从图可以看出,这些点大致接近一条直线,因此可设f (x )=ax +b ,求[]621()i i i u y ax b ==-+∑的最小值,即求解方程组66621116611,6.i i i i i i i i i i i a x b x y x a x b y=====⎧+=⎪⎪⎨⎪+=⎪⎩∑∑∑∑∑ 把(x i ,y i )代入方程组,得29834402240034026320a b a b +=⎧⎨+=⎩解得 a =0.884, b =-5.894 即 y =0.884x -5.894,当x =120时,y =100.186(310元).2.求下列伯努利方程的通解:2(1)(cos sin );y y y x x '+=-解:令121z yy --==,则有d d (12)(12)(cos sin )sin cos d d z zz x x z x x x x+-=--⇒-=- (1)d (1)d e (sin cos )e d e e (sin cos )d e sin xx x xx z x x x c x x x c c x ----⎰⎡⎤⎰=-+⎢⎥⎣⎦⎡⎤=-+=-⎣⎦⎰⎰1e sin x c x y⇒=- 即为原方程通解.411(2)(12)33y y x y '+=-.解:令3d 21d zz y z x x-=⇒-=-.d de 21e (21)e d x x x z x c x x c -⎰⎡⎤⎰==--+-+⎢⎥⎣⎦⎰ 3(e 21)1x y c x ⇒--=即为原方程通解.3.证明:22d d x x y yx y ++在整个xOy 平面内除y 轴的负半轴及原点外的开区域G 内是某个二元函数的全微分,并求出这样的一个二元函数. 证:22x P x y =+,22yQ x y =+,显然G 是单连通的,P 和Q 在G 内具有一阶连续偏导数,并且.()2222∂∂-==∂∂+P Q xy y x x y ,(x ,y )∈G 因此22d d x x y yx y ++在开区域G 内是某个二元函数u (x ,y )的全微分.由()()22222222d d 11ln 22d x y x x y y d x y x y x y ++⎡⎤==+⎢⎥++⎣⎦知()()221ln ,2u x y x y =+.4.应用格林公式计算下列积分: (1)()()d d 24356+-++-⎰x y x y x y Γ, 其中L 为三顶点分别为(0,0),(3,0)和(3,2)的三角形正向边界; (2)()()222d d cos 2sin e sin 2e x x L x y xy x xy x y x x y ++--⎰,其中L 为正向星形线()2223330x y a a +=>;(3)()()3222d d 2cos 12sin 3+--+⎰L x y xy y x y x x y ,其中L 为抛物线2x =πy 2上由点(0,0)到(π2,1)的一段弧;(4)()()22d d sin L x y x y x y --+⎰,L是圆周y =(0,0)到(1,1)的一段弧; (5)()()d d esin e cos xx Lx y y my y m +--⎰,其中m 为常数,L 为由点(a ,0)到(0,0)经过圆x 2+y 2=ax 上半部分的路线(a 为正数).图11-4解:(1)L 所围区域D 如图11-4所示,P =2x -y +4, Q =3x +5y -6,3Qx∂=∂,1P y ∂=-∂,由格林公式得 ()()d d 24356d d 4d d 4d d 1432212LD DDx yx y x y Q P x y x y x yx y+-++-∂∂⎛⎫-= ⎪∂∂⎝⎭===⨯⨯⨯=⎰⎰⎰⎰⎰⎰⎰(2)P =x 2y cos x +2xy sin x -y 2e x ,Q =x 2sin x -2y e x , 则2cos 2sin 2e x Px x x x y y∂=+-∂, 2cos 2sin 2e x Qx x x x y x∂=+-∂. 从而P Qy x∂∂=∂∂,由格林公式得. ()()222d d cos 2sin e sin 2e d d 0++--∂∂⎛⎫-= ⎪∂∂⎝⎭=⎰⎰⎰x x LD x yxy x xy x y x x y Q P x y x y(3)如图11-5所示,记OA ,AB ,BO 围成的区域为D .(其中BO =-L )图11-5P =2xy 3-y 2cos x ,Q =1-2y sin x +3x 2y 2 262cos P xy y x y ∂=-∂,262cos Q xy y x x∂=-∂ 由格林公式有:d d d d 0L OA AB D Q P P x Q y x y x y -++∂∂⎛⎫-+== ⎪∂∂⎝⎭⎰⎰⎰ 故π21220012202d d d d d d d d ππd d 12sin 3243d 12π4π4++=+=+++⎛⎫=+-+⋅⋅ ⎪⎝⎭⎛⎫=-+ ⎪⎝⎭=⎰⎰⎰⎰⎰⎰⎰LOA AB OA ABP x Q y P x Q yP x Q y P x Q y O x yy y y y y(4)L 、AB 、BO 及D 如图11-6所示.图11-6由格林公式有d d d d ++∂∂⎛⎫-+=- ⎪∂∂⎝⎭⎰⎰⎰L AB BO D Q P P x Q y x y x y 而P =x 2-y ,Q =-(x +sin 2y ).1∂=-∂Py ,1∂=-∂Q x,即,0∂∂-=∂∂Q P x y 于是()d d d d 0+++++=+=⎰⎰⎰⎰LABBOL AB BOP x Q y P x Q y从而()()()()()()()22222211220011300d d d d sin d d d d sin sin d d 1sin 131sin 232471sin 264LLBA OB P x Q y x yx y x y x y x yx y x y x y x y y x x y x y y +=--+=-+--+-+=-++⎡⎤⎡⎤=+-+⎢⎥⎢⎥⎣⎦⎣⎦=-+⎰⎰⎰⎰⎰⎰(5)L ,OA 如图11-7所示.图11-7P =e x sin y -my , Q =e x cos y -m ,e cos x P y m y ∂=-∂,e cos x Q y x∂=∂ 由格林公式得:22d d d d d d d d 1π22π8L OA D DDQ P P x Q y x y x y m x ym x ya m m a +∂∂⎛⎫-+=⎪∂∂⎝⎭==⎛⎫=⋅⋅ ⎪⎝⎭=⎰⎰⎰⎰⎰⎰⎰ 于是:()()[]220202πd d d d 8πd 0e sin 00e cos08π0d 8π8+=-+=-+⋅⋅-⋅⋅-=-=⎰⎰⎰⎰L OA a x x a m a P x Q y P x Q ym a xm m m a xm a5.设L 为xOy 面内x 轴上从点(a ,0)到点(b ,0)的一段直线,证明:()(),d 0d bLaP x y x P x,x =⎰⎰,其中P (x , y )在L 上连续.证:L :0x xa xb y =⎧≤≤⎨=⎩,起点参数为x =a ,终点参数为x =b .故()(),d ,0d bLaP x y x P x x =⎰⎰6.求抛物面壳221()(01)2z x y z =+≤≤的质量,此壳的面密度大小为z ρ=. 22221:():22xy z x y D x y ∑=++≤221d d ()d 2xy D M s z s x y x y ∑∑ρ===+⎰⎰⎰⎰⎰⎰12π222122225322220d (1)d 2π1)(1)(1)2π2π221)(1)(1)21553r r r r r r d r r r θ=+=+-++⎡==+-+⎢⎥⎣⎦⎰7.求下列线性微分方程的通解:(1)e x y y -'+=;解:由通解公式d de e e e d e ()e e d xx x x x x x y x c x c x c -----⎰⎡⎤⎰⎡⎤==⋅+=+⋅+⎢⎥⎣⎦⎣⎦⎰⎰ 2(2)32xy y x x '+=++;解:方程可化为 123y y x x x'+=++ 由通解公式得11d d 22e (3) e d 12(3)d 132.32x x x x y x x c x x x x c x x c x x x-⎡⎤⎰⎰=++⋅+⎢⎥⎣⎦⎡⎤=++⋅+⎢⎥⎣⎦=+++⎰⎰ sin (3)cos e ;x y y x -'+=解: cos d cos d sin sin e e ().e e d x xx x x x y x c x c ---⎰⎡⎤⎰==+⋅+⎢⎥⎣⎦⎰(4)44y xy x '=+;解: 22(4)d (4)d 22e e 4e d 4e d x xx x x x y x x c x x c ----⎰⎡⎤⎰⎡⎤==++⎢⎥⎣⎦⎣⎦⎰⎰()222222e e e 1x x x c c -=-+=-.3(5)(2)2(2)x y y x '-=+-;解:方程可化为2d 12()d 2y y x x x x -=-- 11d d 222ln(2)2ln(2)3e 2(2)e d e 2(2)e d (2)2(2)d (2)(2)x x x x x x y x x c x x c x x x c x c x --------⎰⎡⎤⎰=-+⎢⎥⎣⎦⎡⎤=-+⎣⎦⎡⎤=--+⎣⎦=-+-⎰⎰⎰22(6)(1)24.x y xy x '++=解:方程可化为 2222411x x y y x x '+=++ 222222d d 1123ln(1)224e ed 14e 4d 3(1)xxx x x x x x y x c x x c x x c x -++-+⎡⎤⎰⎰=+⎢⎥+⎣⎦+⎡⎤=+=⎣⎦+⎰⎰8.求下列各微分方程的通解:(1)ln 0xy y y '-=;解:分离变量,得d 1d ln y x y y x= 积分得11d ln d ln y x y x =⎰⎰ln ln ln ln y x c =+ln y cx =得 e cxy =.(2)y '=解:分离变量,得=积分得=⎰得通解:.c -=-(3)(e e )d (e e )d 0x y x x y y x y ++-++=;解:分离变量,得 e e d d 1e 1ey yy xy x =-+积分得 ln(e 1)ln(e 1)ln y xc --=+- 得通解为 (e 1)(e 1)xyc +-=.(4)cos sin d sin cos d 0x y x x y y +=;解:分离变量,得cos cos d d 0sin sin x yx y x y+= 积分得 lnsin lnsin ln y x c += 得通解为 sin sin .y x c ⋅=(5)y xy '=;解:分离变量,得d d yx x y = 积分得 211ln 2y x c =+ 得通解为 2112e(e )x c y c c ==(6)210x y '++=;解: 21y x '=--积分得 (21)d y x x =--⎰得通解为 2y x x c =--+.32(7)4230x x y y '+-=;解:分离变量,得 233d (42)d y y x x x =+ 积分得 342y x x c =++ 即为通解.(8)e x y y +'=.解:分离变量,得 e d e d yxy x -= 积分得 e d e d y x y x -=⎰⎰得通解为: e e y x c --=+.9.计算曲面积分(,,)d f x y z s ∑⎰⎰,其中∑为抛物面z = 2-(x 2+y 2)在xOy 面上方的部分,f (x , y , z )分别如下:(1) f (x , y , z )=1; (2) f (x , y , z )=x 2+y 2; (3) f (x , y , z )=3z .解:抛物面z =2-(x 2+y 2)与xOy 面的交线是xOy 面上的圆x 2+y 2=2,因而曲面∑在xOy 面上的投影区域D xy : x 2+y 2≤2,且d s d d x y x y =故(1)2π0322(,,)d d d d 1312ππ.(14)312xyD f x y z s x y rr ∑θ==⎡==+⎢⎥⎣⎦⎰⎰⎰⎰⎰(2)22(,,)d (d xyD f x y z s x y x y ∑=+⎰⎰⎰⎰2π220312222205322220d d π1)1)16π1)(14)]d(41)16π14922π.(41)(14)163053r rr r r r r r r θ==+-+=+-++⎡==+-+⎢⎥⎣⎦⎰(3)22(,,)d 3d 3d 2()xyD f x y z s z s x y x y ∑∑==⎡-+⎣⎰⎰⎰⎰⎰⎰12π22212222035222203d )(14)d 16π(14)(14)9(14)323π11122π.9(14)(14)161035r r r rr d r r r r θ=-+=⨯++⎤-+⎦⎡==⨯+-+⎢⎥⎣⎦⎰10.设薄片所占的闭区域D 如下,求均匀薄片的重心。
