四年级奥数 找规律 数图形59
按规律画图形小学奥数试题大全

知识要点:把一些图形按照一定的规律排列起来,然后用白纸盖住其中一部分,你想要画出被盖住的部分,就必须仔细观察没盖住的图形,从中寻找规律.观察图形的变化,可从图形的形状、位置、方向、数量、大小、颜色等方面入手,从中找出规律.{例1} 观察下列图形的变化,想一想,按图形变化的规律,在空白处应画什么样的图形?这样思考: 在方向上,图1图2画的是笑脸,只不过是数量上有增减;图2图4所画的虽不相同,但是数量和位置相同.从而我们确定,图3图4画的都是月亮,并且图3位置和数量都与图1相同.答案:{例2}观察下列图形的变化,按照规律补充完整.这样思考: 从左至右黑点的个数依次为4、3、2个,依此推断,第四个圆里只有一个圆点;图1图3斜线的方向相同,那么图2图4斜线的方向相同.答案:{例3} 按顺序观察下列图形的变化,然后按照规律在空白处填上合适的图形。
这样思考:我们把第一幅图的星当作1号, 方形是2号, 三角是3号, 圆是4号.第二幅图星是2号,第三幅图星是3号,依此规律,第4幅图星是4号.其他三个小图形也会发现此规律.答案:{例4}小红在院子里采了许多花,把它们整整齐齐的排列着.下面这个空圈中应摆什么花?这样思考:仔细观察每份花朵的变化规律。
从种类上看有两种花,它们依次交替出现。
从枝数上看,1枝、2枝、2枝依次重复出现。
答案:{例5}观察下面图形的变化,请你接着再画出一幅图来。
这样思考: 观察上面的图发现,横着看最下面一排的骨头每次多一块,第二排的骨头也每次多一块,依次类推。
从形状上看像楼梯,第一幅图是1块,第二幅图是按照1、2的顺序排列,第三幅图是按照1、2、3的顺序来排列。
那么第四幅图就是按照1、2、3、4的顺序排列。
答案:·题目1:有一堵墙上的砖坏了一部分,现在请你仔细观察排列规律,猜一猜要补上多少块同样的砖,才能把墙补好?图1A.AB.B查看答案 如图看不清或变形,可以点击图片放大窗体底部·题目2:仔细观察,寻找规律,在问号处填上合适的图形。
小学四年级奥数第2讲 寻找规律(二)后附答案

第2讲寻找规律(二)一、知识要点对于较复杂的按规律填数的问题,我们可以从以下几个方面来思考:1.对于几列数组成的一组数变化规律的分析,需要我们灵活地思考,没有一成不变的方法,有时需要综合运用其他知识,一种方法不行,就要及时调整思路,换一种方法再分析;2.对于那些分布在某些图中的数,它们之间的变化规律往往与这些数在图形中的特殊位置有关,这是我们解这类题的突破口。
3.对于找到的规律,应该适合这组数中的所有数或这组算式中的所有算式。
二、精讲精练【例题1】根据下表中的排列规律,在空格里填上适当的数。
【思路导航】经仔细观察、分析表格中的数可以发现:12+6=18,8+7=15,即每一横行中间的数等于两边的两个数的和。
依此规律,空格中应填的数为:4+8=12。
练习1:找规律,在空格里填上适当的数。
【答案】(1)13(2)2(3)20【例题2】根据前面图形中的数之间的关系,想一想第三个图形的括号里应填什么数?【思路导航】经仔细观察、分析可以发现前面两个圈中三个数之间有这样的关系:5×12÷10=6 4×20÷10=8根据这一规律,第三个圈中右下角应填的数为:8×30÷10=24.练习2:根据前面图形中数之间的关系,想一想第三个图形的空格里应填什么数。
(1)(2)(3)【答案】(1)15(2)7(3)60,20【例题3】先计算下面一组算式的第一题,然后找出其中的规律,并根据规律直接写出后几题的得数。
12345679×9= 12345679×18= 12345679×54= 12345679×81=【思路导航】题中每个算式的第一个因数都是12345679,它是有趣的“缺8数”,与9相乘,结果是由九个1组成的九位数,即:111111111。
不难发现,这组题得数的规律是:只要看每道算式的第二个因数中包含几个9,乘积中就包含几个111111111。
小学奥数图形找规律四年级

找规律是解决数学问题的一种重要的手段,而规律的找寻既需要敏锐的观察力,又需要严密的逻辑推理能力一般地说,在观察图形变化规律时,应抓住一下几点来考虑问题:⑴图形数量的变化;⑵图形形状的变化;⑶图形大小的变化;⑷图形颜色的变化;⑸图形位置的变化;⑹图形繁简的变化.对于较复杂的图形,也可分为几部分来分别考虑,总而言之,只要全面观察,勤于思考就一定能抓住规律,解决问题•板块一数量规律【例1】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?O0O OO■O△O△△6△△△【解析】横着看,每行圆形的个数一次减少,而三角形的个数依次增加,但每行图形的总个数不变的个数是按4、3、?、1的顺序变化的,显然“?”处应填一个圆形。
【巩固】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?△△△△△△△□△?□□△□□□【解析】(方法一)横着看,每行三角形的个数依次减少,而正方形的个数依次增加,但每行图形的总个数不变•因为三角形的个数是按4、3、?、1的顺序变化的,显然“?”处应填一个三角形△ (方法二)竖着看,三角形由左而右依次减少,而正方形由左而右依次增加,三角形按照4、的顺序变化,也可以看出“?”处应是三角形△ •【例2】观察下面的图形,按规律在“?”处填上适当的图形•因为圆形?、2、1(1)(2)(3)(4)(5)【解析】本题中,几何图形的变化表现在数量关系上,图中黑三角形的个数从左到右依次增多,从( 每一个格比前面一个格多两个黑三角形,所以,第( 4)个方框中应填七个黑三角形【解析】观察发现,乌龟的顺序是:头、身T 一只脚、背上一个点T 两只脚、背上两个点T 两只脚、一条尾、 背上三个点T 三只脚、一条尾、背上四个点,根据这个规律,最后一幅图应该是:宀四只脚、一条 尾、背上五个点•即:【例4】观察图形变化规律,在右边再补上一幅,使它们成为一个完整的系列【解析】第一格有8个圆圈,第二格有 4个圆圈,第三格有2个圆圈,第四格有1个圆圈,第五格有半个圆圈•由此发现,前一格中的图减少一般,正好是后一格的图 即:板块二旋转、轮换型规律相传古时候一位老人留在人间很多宝盒,里面装着世界上最宝贵的财富,但是并不是拥有宝盒都可 以得到这笔财富,在宝盒的上面设置了密码,只有写出密码的人才会真正拥有这笔财富,聪明的你 你能找出密码吗?O□ ☆ △ O □ ☆ △ △O □ ☆ △ O □ ☆ ☆ △O □ ☆ △ O □ () () () () () () () ()【解析】有几种方法可以找出密码:(方法一)后面一排和前面一排比,上排的第一个图形移到最后,其他每个图形都向前移动了一格, 变成了下一排.(方法二)斜着看,每一斜列的图形是一样的 所以密码就是: □☆△。
小学奥数 图形找规律 精选例题练习习题(含知识点拨)
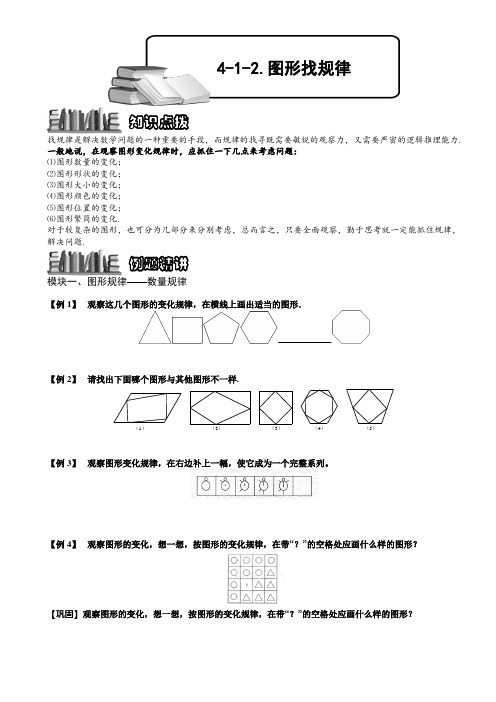
找规律是解决数学问题的一种重要的手段,而规律的找寻既需要敏锐的观察力,又需要严密的逻辑推理能力.一般地说,在观察图形变化规律时,应抓住一下几点来考虑问题: ⑴图形数量的变化; ⑵图形形状的变化; ⑶图形大小的变化; ⑷图形颜色的变化; ⑸图形位置的变化; ⑹图形繁简的变化.对于较复杂的图形,也可分为几部分来分别考虑,总而言之,只要全面观察,勤于思考就一定能抓住规律,解决问题.模块一、图形规律——数量规律【例 1】 观察这几个图形的变化规律,在横线上画出适当的图形.【例 2】 请找出下面哪个图形与其他图形不一样.(1)(2)(3)(4)(5)【例 3】 观察图形变化规律,在右边补上一幅,使它成为一个完整系列。
【例 4】 观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?【巩固】 观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?例题精讲知识点拨4-1-2.图形找规律【巩固】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形??【例5】观察下面的图形,按规律在“?”处填上适当的图形.(4)?【例6】观察图形变化规律,在右边再补上一幅,使它们成为一个完整的系列.【例7】观察下图中的点群,请回答:(1)方框内的点群包含个点;(2)推测第10个点群中包含个点;(3)前10个点群中,所有点的总数是。
【例8】观察下面由点组成的图形(点群),请回答:(1)方框内的点群包含个点;(2)第(10)个点群中包含个点;(3)前十个点群中,所有点的总数是。
【例9】下图表示“宝塔”,它们的层数不同,但都是由一样大的小三角形摆成的.仔细观察后,请回答:(1)五层的“宝塔”的最下层包含多少个小三角形?(2)整个五层“宝塔”一共包含多少个小三角形?【例 10】 在纸上画5条直线,最多可有 个交点。
模块二、图形规律—— 旋转、轮换型规律【例 11】 相传古时候一位老人留在人间很多宝盒,里面装着世界上最宝贵的财富,但是并不是拥有宝盒都可以得到这笔财富,在宝盒的上面设置了密码,只有写出密码的人才会真正拥有这笔财富,聪明的你你能找出密码吗? ○ □ ☆ △ ○ □ ☆ △ △ ○ □ ☆ △ ○ □ ☆ ☆ △ ○ □ ☆ △ ○ □ ()()()()()()()()【例 12】 下面的图形是按一定规律排列的,请仔细观察,并在“?”处填上适当的图形.(1)(2)(3)【例 13】 观察下图的变化规律,画出丙图.甲DA乙BC丙【例 14】 图中的三个图形都是由A 、B 、C 、D (线段或圆)中的两个组合而成,记为A ★B 、C ★D 、A ★D .请你画出表示A ★C 的图形.A★B C★D A★D【例15】(希望杯五年级一试第7题,6分)下列四个图形是由四个简单图形A、B、C、D(线段和正方形)组合(记为*)而成。
四年级奥数找规律

第1讲找规律(一)【例题1】先找出下列数排列的规律,并根据规律在括号里填上适当的数。
1,4,7,10,(),16,19练习1:先找出下列各列数的排列规律,然后在括号里填上适当的数。
(1)2,6,10,14,(),22,26(2)3,6,9,12,(),18,21(3)33,28,23,(),13,(),3(4)55,49,43,(),31,(),19(5)3,6,12,(),48,(),192(6)2,6,18,(),162,()(7)128,64,32,(),8,(),2(8)19,3,17,3,15,3,(),(),11,3..【例题2】先找出下列数排列的规律,然后在括号里填上适当的数。
1,2,4,7,(),16,22练习2:先找出下列数排列的规律,然后在括号里填上适当的数。
(1)10,11,13,16,20,(),31(2)1,4,9,16,25,(),49,64(3)3,2,5,2,7,2,(),(),11,2(4)53,44,36,29,(),18,(),11,9,8(5)81,64,49,36,(),16,(),4,1,0(6)28,1,26,1,24,1,(),(),20,1(7)30,2,26,2,22,2,(),(),14,2【例题3】先找出规律,然后在括号里填上适当的数。
23,4,20,6,17,8,(),(),11,12练习3:先找出规律,然后在括号里填上适当的数。
(1)1,6,5,10,9,14,13,(),()(2)13,2,15,4,17,6,(),()(3)3,29,4,28,6,26,9,23,(),(),18,14(4)21,2,19,5,17,8,(),()(5)32,20,29,18,26,16,(),(),20,12(6)2,9,6,10,18,11,54,(),(),13,486(7)1,5,2,8,4,11,8,14,(),()(8)320,1,160,3,80,9,40,27,(),()(9)1,6,4,8,7,10,(),(),13,14【例题4】在数列1,1,2,3,5,8,13,(),34,55……中,括号里应填什么数练习4:先找出规律,然后在括号里填上适当的数。
四年级下册奥数试题 第1讲 找规律填数(PDF无答案)人教版

先 找 出 下 列 各 列 数 的 排 列 规 律 然 后 在 括 号 里 填 上 合 适 的 数 !##%+!(!+ #$+!!!&#' -!++ $&/!!!% #$ %!$+&!+!& '+'& -&!+%%/$+ !+ %!( +#-/!%#( '%+!(!+ &$%+!(!&
#观察这组数发现第一个数与第三个数和第五个数 有 规 律 第 二 个 数 与 第 四 个 数 和 第 六 个 数 有 规 律 第 一 个 数 加 等 于 第 三 个 数 第 三 个 数 加- 等 于 第 五 个 数 第 二 个 数 加! 等 于第四个数第四个数加!等于第+个数由此后 两 个 数 应 该 是 $-,-*%($,!*%
#
数学四年级
找 规 律 在 括 号 里 填 上 合 适 的 数 !$-!(!#!'!/ ##-!$(#$-$ !这 一 列 数 可 以 把 $- 看 成 一 组 !(!# 看 成 一 组!'!/看成一组来分析组内的数之间相差 #组 与 组 之 间 相 邻 的 数 相 差- 两 个 括 号 可 以 看 成 一 组 两 数 相 差#这 组 第 一 个 数 与 前 组 第 二 个 数 相 差 -即 !/,-*#%#%,#*#+
第一讲找规律填数 +#&+!(!&!#-% !+%&+ '#!# !/ - !' & &$#(!!+($&(/%(#'
小学奥数图形找规律四年级

找规律是解决数学问题的图形找规律一种重要的手段,而规律的找寻既需要敏锐的观察力,又需要严密的逻辑推理能力.一般地说,在观察图形变化规律时,应抓住一下几点来考虑问题:⑴图形数量的变化;⑵图形形状的变化;⑶图形大小的变化;⑷图形颜色的变化;⑸图形位置的变化;⑹图形繁简的变化.对于较复杂的图形,也可分为几部分来分别考虑,总而言之,只要全面观察,勤于思考就一定能抓住规律,解决问题.板块一数量规律【例 1】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?【解析】横着看,每行圆形的个数一次减少,而三角形的个数依次增加,但每行图形的总个数不变.因为圆形的个数是按4、3、?、1的顺序变化的,显然“?”处应填一个圆形。
【巩固】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?【解析】(方法一)横着看,每行三角形的个数依次减少,而正方形的个数依次增加,但每行图形的总个数不变.因为三角形的个数是按4、3、?、1的顺序变化的,显然“?”处应填一个三角形△.(方法二)竖着看,三角形由左而右依次减少,而正方形由左而右依次增加,三角形按照4、?、2、1的顺序变化,也可以看出“?”处应是三角形△.【例 2】观察下面的图形,按规律在“?”处填上适当的图形.【解析】本题中,几何图形的变化表现在数量关系上,图中黑三角形的个数从左到右依次增多,从(2)起,每一个格比前面一个格多两个黑三角形,所以,第(4)个方框中应填七个黑三角形.【例 3】观察图形变化规律,在右边补上一幅,使它成为一个完整系列。
【解析】观察发现,乌龟的顺序是:头、身→一只脚、背上一个点→两只脚、背上两个点→两只脚、一条尾、背上三个点→三只脚、一条尾、背上四个点,根据这个规律,最后一幅图应该是:→四只脚、一条尾、背上五个点.即:【例 4】观察图形变化规律,在右边再补上一幅,使它们成为一个完整的系列.【解析】第一格有8个圆圈,第二格有4个圆圈,第三格有2个圆圈,第四格有1个圆圈,第五格有半个圆圈.由此发现,前一格中的图减少一般,正好是后一格的图.所以第六格的图应该是第五格图的一半,即:板块二旋转、轮换型规律【例 5】相传古时候一位老人留在人间很多宝盒,里面装着世界上最宝贵的财富,但是并不是拥有宝盒都可以得到这笔财富,在宝盒的上面设置了密码,只有写出密码的人才会真正拥有这笔财富,聪明的你你能找出密码吗?○□☆△○□☆△△○□☆△○□☆☆△○□☆△○□()()()()()()()()【解析】有几种方法可以找出密码:(方法一)后面一排和前面一排比,上排的第一个图形移到最后,其他每个图形都向前移动了一格,变成了下一排.(方法二)斜着看,每一斜列的图形是一样的.所以密码就是:□☆△○□☆△○【例 6】观察下图的变化规律,画出丙图.【总结】旋转是数学中的重要概念,掌握好这个概念,可以提高观察能力,加快解题速度,对于许多问题的解决,也有事半而功倍的效果.【例 7】下面各种各样的娃娃头好看吗?认真观察你能找到它们排列的规律吗?根据规律把最后一个画出来.【例 8】观察图中所给出图形的变化规律,然后在空白处填画上所缺的图形.【例 9】琪琪特别喜欢蝴蝶,她用直尺和圆规在纸上画了9幅蝴蝶图,并用剪刀将它们一一剪下来.她将这9只纸蝴蝶摆在桌上,见下图1,她发现这些纸蝴蝶排列挺有规律,突然一阵风来,吹走了3只纸蝴蝶,见下图2.你能找出蝴蝶的排列规律,将图2的3只蝴蝶放入图1的空缺处吗?【解析】从已摆好的第一行和第一列来看,无论横看或竖看,同一行中3只蝴蝶的翅膀形状各不相同,翅膀上的斑点的形状也各不相同.根据这个规律,剩下的3只蝴蝶图案的排列应该是:6号位置放图案C;8号位置放图案B;9号位置放图案A.【例 10】观察下列各组图的变化规律,并在“?”处画出相关的图形.(1)【解析】(1)这四个图形的变化规律是:每一个图形都是由其前一个图形顺时针旋转90°而得到的.见下面左图;(2)甲乙丙丁四个图形变化规律也类似,注意因为图形是由旋转而得到的,所以其中三角形、菱形的方向随旋转而变化,作图的时候要注意到这一点.丁图处的图形应是下面右图:【例 11】请你认真仔细观察,按照下面图形的变化规律,在“?”处画出合适的图形。
小学四年级奥数找规律练习版

小学四年级奥数第五讲找规律(一)一、精讲精练【例题 1】在括号内填上适合的数。
( 1) 3, 6, 9, 12,(),()( 2) 1, 2, 4, 7, 11,(),()( 3) 2, 6, 18,54,(),()练习 1:在括号内填上适合的数。
( 1) 2, 4, 6, 8, 10,(),()( 2) 1, 2, 5, 10,17,(),()( 3) 2, 8, 32,128,(),()( 4) 1, 5, 25,125,(),()( 5) 12,1,10,1,8,1,(),()【例题 2】先找出规律,再在括号里填上适合的数。
( 1) 15,2,12,2,9,2,(),()( 2) 21,4,18,5,15,6,(),()练习 2:按规律填数。
(1)2,1,4,1,6,1,(),()( 2) 3, 2, 9, 2, 27,2,(),()( 3) 18,3,15,4,12,5,(),()( 4) 1, 15,3,13,5,11,(),()( 5) 1, 2, 5, 14,(),()【例题 3】先找出规律,再在括号里填上适合的数。
( 1) 2, 5, 14,41,()(2)252, 124, 60,28,()( 3) 1, 2, 5, 13,34,()(4)1,4,9,16, 25,36,()练习 3:按规律填数。
( 1) 2, 3, 5, 9, 17,(),()(2)2,4,10, 28,82,(),()( 3) 94,46,22, 10,(),()(4)2,3,7,18, 47,(),()【例题 4】依据前方图形里的数的摆列规律,填入适合的数。
( 1)510712914914116131(2)47981681443 249327(3)124363612练习 4:找出摆列规律,在空缺处填上适合的数。
(1)37812121659101414(2)7948286278(3)8416515121683272118321664927【例题 5】按规律填数。
小学四年级奥数-

【练习2】
(1)一只西瓜的重量等于两个菠萝的重量,1个菠萝的重量等于4个苹果 的重量,1个苹果的重量等于两个橘子的重量。1只西瓜的重量等于几个 橘子的重量? (2)一头牛一天吃草的重量和一只兔子9天吃草的重量相等,也和6只羊 一天吃草的重量相等。已知一头牛每天吃青草 18千克,一只兔子和一只 羊一天共吃青草多少千克? (3)一只小猪的重量等于6只鸡的重量,3只鸡的重量等于4只鸭的重量, 两只鸭的重量等于6条鱼的重量。问:两只小猪的重量等于几条鱼的重量?
小学 四年级 举一反三
观察是解决问题的根据。通过观察,得以揭示出事物的 发展和变化规律,在一般情况下,我们可以从以下几个方面 来找规律: 1.根据每组相邻两个数之间的关系,找出规律,推断出所 要填的数; 2.根据相隔的每两个数的关系,找出规律,推断出所要填 的数; 3.要善于从整体上把握数据之间的联系,从而很快找出规 律; 4.数之间的联系往往可以从不同的角度来理解,只要言之 有理,所得出的规律都可以认为是正确的。
(1)(6,9)(7,8)(10,5)(□,)
(2)(1,24)(2,12)(3,8)(4,□) (3)(18,17)(14,10)(10,1)(□,5)
(4)(2,3)(5,9)(7,13)(9,□)
(5)(2,3)(5,7)(7,10)(10,□) (6)(64,62)(48,46)(29,27)(15,□)
(2)根据下面两个算式,求○与□各代表多少?
○+○+○=15 +□=40 ○-△=8
○+○+□+□
(3)根据下面两个算式,求○与△各代表多少?
△+△+△=○
【例题4】根据下面两个算式,求○与△各代表多少?
△-○=2
○+○+△+△+△=56
【思路导航】 由第一个算式可知,△比○多 2 ;如果将第二个算式的○ 都换成△,那么5个△=56+2×2,△=12,再由第一个算式 可知,○=12-2=10.
小学奥数:图形找规律.专项练习及答案解析

找规律是解决数学问题的一种重要的手段,而规律的找寻既需要敏锐的观察力,又需要严密的逻辑推理能力.一般地说,在观察图形变化规律时,应抓住一下几点来考虑问题:⑴图形数量的变化;⑵图形形状的变化;⑶图形大小的变化;⑷图形颜色的变化;⑸图形位置的变化;⑹图形繁简的变化.对于较复杂的图形,也可分为几部分来分别考虑,总而言之,只要全面观察,勤于思考就一定能抓住规律,解决问题.模块一、图形规律——数量规律【例 1】观察这几个图形的变化规律,在横线上画出适当的图形.【考点】图形找规律【难度】1星【题型】填空【解析】几个图形的边数依次增加,因此横线上应为一个七边形.【答案】七边形【例 2】请找出下面哪个图形与其他图形不一样.(1)(2)(3)(4)(5)【考点】图形找规律【难度】1星【题型】填空【解析】这组图形的共同特征是,连接各边上一点,组成一个复合图形.所不同的是,第四个图形是一个六边形,而其它几个都是四边形,这样,只有(4)与其它不一样【答案】(4)【例 3】观察图形变化规律,在右边补上一幅,使它成为一个完整系列。
【考点】图形找规律【难度】2星【题型】填空【解析】观察发现,乌龟的顺序是:头、身→一只脚、背上一个点→两只脚、背上两个点→两只脚、一条尾、背上三个点→三只脚、一条尾、背上四个点,根据这个规律,最后一幅图应该是:→四只脚、一条尾、背上五个点.即:例题精讲知识点拨4-1-2.图形找规律【答案】【例 4】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?【考点】图形找规律【难度】2星【题型】填空【解析】横着看,每行圆形的个数一次减少,而三角形的个数依次增加,但每行图形的总个数不变.因为圆形的个数是按4、3、?、1的顺序变化的,显然“?”处应填一个圆形。
【答案】圆形【巩固】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?【考点】图形找规律【难度】2星【题型】填空【解析】(方法一)横着看,每行圆形的个数一次减少,而三角形的个数依次增加,但每行图形的总个数不变.因为圆形的个数是按5、4、3、?、1的顺序变化的,显然“?”处应填一个圆形.(方法二)竖着看,圆形由左而右依次减少,而三角形由左而右依次增加,圆形按照5、4、?、2、1的顺序变化,也可以看出“?”处应是圆形.【答案】圆形【巩固】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形??【考点】图形找规律【难度】2星【题型】填空【解析】(方法一)横着看,每行三角形的个数依次减少,而正方形的个数依次增加,但每行图形的总个数不变.因为三角形的个数是按4、3、?、1的顺序变化的,显然“?”处应填一个三角形△.(方法二)竖着看,三角形由左而右依次减少,而正方形由左而右依次增加,三角形按照4、?、2、1的顺序变化,也可以看出“?”处应是三角形△.【答案】△【例 5】观察下面的图形,按规律在“?”处填上适当的图形.(5)(4)(3)(2)(1)?【考点】图形找规律【难度】2星【题型】填空【解析】本题中,几何图形的变化表现在数量关系上,图中黑三角形的个数从左到右依次增多,从(2)起,每一个格比前面一个格多两个黑三角形,所以,第(4)个方框中应填七个黑三角形.【答案】七个黑三角形【例 6】观察图形变化规律,在右边再补上一幅,使它们成为一个完整的系列.【考点】图形找规律【难度】2星【题型】填空【解析】第一格有8个圆圈,第二格有4个圆圈,第三格有2个圆圈,第四格有1个圆圈,第五格有半个圆圈.由此发现,前一格中的图减少一般,正好是后一格的图.所以第六格的图应该是第五格图的一半,即:【答案】【例 7】观察下图中的点群,请回答:(1)方框内的点群包含个点;(2)推测第10个点群中包含个点;(3)前10个点群中,所有点的总数是。
图形找规律专项练习60题有答案

图形找规律专项练习60题(有答案)1.按如下方式摆放餐桌和椅子:填表中缺少可坐人数_________ ;_________ .2.观察表中三角形个数的变化规律:图形横截线0 1 2 …n条数6 ??…?三角形个数若三角形的横截线有0条,则三角形的个数是6;若三角形的横截线有n条,则三角形的个数是_________ (用含n的代数式表示).3.如图,在线段AB上,画1个点,可得3条线段;画2个不同点,可得6条线段;画3个不同点,可得10条线段;…照此规律,画10个不同点,可得线段_________ 条.4.如图是由数字组成的三角形,除最顶端的1以外,以下出现的数字都按一定的规律排列.根据它的规律,则最下排数字中x的值是_________ ,y的值是_________ .5.下列图形都是由相同大小的单位正方形构成,依照图中规律,第六个图形中有_________ 个单位正方形.6.如图,用相同的火柴棒拼三角形,依此拼图规律,第7个图形中共有_________ 根火柴棒.7.图1是一个正方形,分别连接这个正方形的对边中点,得到图2;分别连接图2中右下角的小正方形对边中点,得到图3;再分别连接图3中右下角的小正方形对边中点,得到图4;按此方法继续下去,第n个图的所有正方形个数是_________ 个.8.观察下列图案:它们是按照一定规律排列的,依照此规律,第6个图案中共有_________ 个三角形.9.如图,依次连接一个边长为1的正方形各边的中点,得到第二个正方形,再依次连接第二个正方形各边的中点,得到第三个正方形,按此方法继续下去,则第二个正方形的面积是_________ ;第六个正方形的面积是_________ .10.下列各图形中的小正方形是按照一定规律排列的,根据图形所揭示的规律我们可以发现:第1个图形有1个小正方形,第2个图形有3个小正方形,第3个图形有6个小正方形,第4个图形有10个小正方形…,按照这样的规律,则第10个图形有_________ 个小正方形.11.如图,用围棋子按下面的规律摆图形,则摆第n个图形需要围棋子的枚数为_________ .12.为庆祝“六一”儿童节,幼儿园举行用火柴棒摆“金鱼”比赛,如图所示,则摆n条“金鱼”需用火柴棒的根数为_________ .13.如图,两条直线相交只有1个交点,三条直线相交最多有3个交点,四条直线相交最多有6个交点,五条直线相交最多有10个交点,六条直线相交最多有_________ 个交点,二十条直线相交最多有_________ 个交点.14.用火柴棒按如图所示的方式搭图形,按照这样的规律搭下去,填写下表:图形编号(1)(2)(3)…n火柴根数从左到右依次为_________ _________ _________ _________ .15.图(1)是一个黑色的正三角形,顺次连接三边中点,得到如图(2)所示的第2个图形(它的中间为一个白色的正三角形);在图(2)的每个黑色的正三角形中分别重复上述的作法,得到如图(3)所示的第3个图形.如此继续作下去,则在得到的第5个图形中,白色的正三角形的个数是_________ .16.如图,一块圆形烙饼切一刀可以切成2块,若切两刀最多可以切成4块,切三刀最多可以切成7块…通过观察、计算填下表(其中S表示切n刀最多可以切成的块数)后,可探究一圆形烙饼切n刀最多能切成_________ 块(结果用n的代数式表示).n 0 1 2 3 4 5 …n17.如图,是用相同的等腰梯形拼成的等腰梯形图案.第(1)个图案只有1个等腰梯形,其两腰之和为4,上下底之和为3,周长为7;第(2)个图案由3个等腰梯形拼成,其周长为13;…第(n)个图案由(2n﹣1)个等腰梯形拼成,其周长为_________ .(用正整数n表示)18.下列各图均是用有一定规律的点组成的图案,用S表示第n个图案中点的总数,则S= _________ (用含n 的式子表示).19.如图,由若干盆花摆成图案,每个点表示一盆花,几何图形的每条边上(包括两个顶点)都摆有n(n≥3)盆花,每个图案中花盆总数为S,按照图中的规律可以推断S与n(n≥3)的关系是_________ .20.用火柴棍象如图这样搭图形,搭第n个图形需要_________ 根火柴棍.21.现有黑色三角形“”和白色三角形“”共有2011个,按照一定的规律排列如下:则黑色三角形有_________ 个.22.假设有足够多的黑白围棋子,按照一定的规律排成一行:○●●○○●○●●○○●○●●○○●○●●○○●…请问第2011个棋子是黑的还是白的?答:_________ .23.观察下列由等腰梯形组成的图形和所给表中数据的规律后填空:梯形的个数 1 2 3 4 5 …图形的周长 5 8 11 14 17 …当梯形个数为2007个时,这时图形的周长为_________24.如图,下面是一些小正方形组成的图案,第4个图案有_________ 个小正方形组成;第n个图案有_________个小正方形组成.25.如图所示是由火柴棒按一定规律拼出的一系列图形:依照此规律,第7个图形中火柴棒的根数是_________ .26.图中的每个图形都是由若干个棋子围成的正方形图案,图案的每条边(包括两个顶点)上都有n(n≥2)个棋子,每个图案的棋子总数为s,按图的排列规律推断,s与n之间的关系可用式子_________ 表示.27.观察下列图形,它是按一定规律排列的,那么第_________ 个图形中,十字星与五角星的个数和为27个.28.2条直线最多只有1个交点;3条直线最多只有3个交点;4条直线最多只有6个交点;2000条直线最多只有_________ 个交点.29.以下各图分别由一些边长为1的小正方形组成,请填写图2、图3中的周长,并以此推断出图10的周长为_________ .30.如图所示,第1个图案是由黑白两种颜色的正六边形地面砖组成,第2个,第3个图案可以看作是第1个图案经过平移而得,那么设第n个图案中有白色地面砖m块,则m与n的函数关系式是_________ .31.用同样大小的黑色棋子按如图所示的规律摆放:(1)分别写出第6、7两个图形各有多少颗黑色棋子?(2)写出第n个图形黑色棋子的颗数?(3)是否存在某个图形有2012颗黑色棋子?若存在,求出是第几个图形;若不存在,请说明理由.32.如图,给出四个点阵,s表示每个点阵中点的个数,按照图形中的点的个数变化规律,(1)猜想第n个点阵中的点的个数s= _________ .(2)若已知点阵中点的个数为37,问这个点阵是第几个?33.用棋子摆出下列一组图形:(1)填写下表:图形编号 1 2 3 4 5 6图中棋子数 5 8 11 14 17 20(2)照这样的方式摆下去,写出摆第n个图形所需棋子的枚数;(3)其中某一图形可能共有2011枚棋子吗?若不可能,请说明理由;若可能,请你求出是第几个图形.34.观察图中四个顶点的数字规律:(1)数字“30”在_________ 个正方形的_________ ;(2)请你用含有n(n≥1的整数)的式子表示正方形四个顶点的数字规律;(3)数字“2011”应标在什么位置.35.如图,各图表示若干盆花组成的形如三角形的图案,每条边(包括两个顶点)有n(n>1)盆花,每个图案中花盆的总数为S.问:①当每条边有2盆花时,花盆的总数S是多少?②当每条边有3盆花时,花盆的总数S是多少?③当每条边有4盆花时,花盆的总数S是多少?④当每条边有10盆花时,花盆的总数S是多少?⑤按此规律推断,当每条边有n盆花时,花盆的总数S是多少?36.如下图是用棋子摆成的“上”字:如果按照以上规律继续摆下去,那么通过观察,可以发现:(1)第④、第⑤个“上”字分别需用_________ 和_________ 枚棋子;(2)第n个“上”字需用_________ 枚棋子;(3)七(3)班有50名同学,把每一位同学当做一枚棋子,能否让这50枚“棋子”按照以上规律恰好站成一个“上”字?若能,请计算最下一“横”的学生数;若不能,请说明理由.37.下列表格是一张对同一线段上的个数变化及线段总条数的探究统计.线段上点的个数线段的总条数11+2=31+2+3=6……(1)请你完成探究,并把探究结果填在相应的表格里;(2)若在同一线段上有10个点,则线段的总条数为_________ ;若在同一线段上有n个点,则有_________ 条线段(用含n 的式子表示)(3)若你所在的班级有60名学生,20年后参加同学聚会,见面时每两个同学之间握一次手,共握手_________ 次.38.如图是用棋子摆成的“H”字.(1)摆成第一个“H”字需要_________ 个棋子;摆第x个“H”字需要的棋子数可用含x的代数式表示为_________ ;(2)问第几个“H”字棋子数量正好是2012个棋子?39.我们知道,两条直线相交只有一个交点.请你探究:(1)三条直线两两相交,最多有_________ 个交点;(2)四条直线两两相交,最多有_________ 个交点;(3)n条直线两两相交,最多有_________ 个交点(n为正整数,且n≥2).40.如图所示,小王玩游戏:一张纸片,第一次将其撕成四小片,手中共有4张纸片,以后每次都将其中一片撕成更小的四片.如此进行下去,当小王撕到第n次时,手张共有S张纸片.根据上述情况:(1)用含n的代数式表示S;(2)当小王撕到第几次时,他手中共有70张小纸片?41.如图①是一张长方形餐桌,四周可坐6人,2张这样的桌子按图②方式拼接,四周可坐10人.现将若干张这样的餐桌按图③方式拼接起来:(1)三张餐桌按题中的拼接方式,四周可坐_________ 人;(2)n张餐桌按上面的方式拼接,四周可坐_________ 人(用含n的代数式表示).若用餐人数为26人,则这样的餐桌需要_________ 张.42.用棋子摆出下列一组图形:(1)填写下表:图形编号 1 2 3 4 5 6图形中的棋子(2)照这样的方式摆下去,写出摆第n个图形棋子的枚数;(用含n的代数式表示)(3)如果某一图形共有99枚棋子,你知道它是第几个图形吗?43.如图①,图②,图③,图④,…,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律,(1)第5个“广”字中的棋子个数是_________ .(2)第n个“广”字需要多少枚棋子?44.如图,用同样规格黑白两色的正方形瓷砖铺设矩形地面,请观察图形并解答有关问题:(1)在第n个图中共有_________ 块黑瓷砖,_________ 块白瓷砖;(2)是否存在黑瓷砖与白瓷砖块数相等的情形?你能通过计算说明吗?45.用火柴棒按如图的方式搭三角形.照这样搭下去:(1)搭4个这样的三角形要用_________ 根火柴棒;13根火柴棒可以搭_________ 个这样的三角形;46.观察图中的棋子:(1)按照这样的规律摆下去,第4个图形中的棋子个数是多少?(2)用含n的代数式表示第n个图形的棋子个数;(3)求第20个图形需棋子多少个?47.如图,用正方体石墩垒石梯,下图分别表示垒到一、二、三阶梯时的情况.那么照这样垒下去,请你观察规律,并完成下列问题.(1)填出下表中未填的两个空格:阶梯级数一级二级三级四级石墩块数 3 9(2)当垒到第n级阶梯时,共用正方体石墩多少块(用含n的代数式表示)?并求当n=100时,共用正方体石墩多少块?48.有一张厚度为0.05毫米的纸,将它对折1次后,厚度为2×0.05毫米.(1)对折3次后,厚度为多少毫米?(2)对折n次后,厚度为多少毫米?(3)对折n次后,可以得到多少条折痕?49.如图所示,用同样规格正方形瓷砖铺设矩形地面,请观察下图:按此规律,铺设了一矩形地面,共用瓷砖506块,请问这一矩形的每一横行有多少块瓷砖,每一竖列有多少瓷砖?50.找规律:观察下面的星阵图和相应的等式,探究其中的规律.(1)在④、⑤和⑥后面的横线上分别写出相应的等式:①1=12②1+3=22③1+3+5=32④_________ ;⑤_________ ;⑥_________ ;(2)通过猜想,写出第n个星阵图相对应的等式.51.将一张正方形纸片剪成四个大小一样的小正方形,然后将其中的一个正方形再剪成四个小正方形,如此循环下去,如图所示:(1)完成下表:所剪次数n 1 2 3 4 5正方形个数Sn 4(2)剪n次共有S n个正方形,请用含n的代数式表示S n= _________ ;(3)若原正方形的边长为1,则第n次所剪得的正方形边长是_________ (用含n的代数式表示).52.如图是用五角星摆成的三角形图案,每条边上有n(n>1)个点(即五角星),每个图案的总点数(即五角星总数)用S表示.(1)观察图案,当n=6时,S= _________ ;(2)分析上面的一些特例,你能得出怎样的规律?(用n表示S)(3)当n=2008时,求S.53.用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点,叫格点.观察图中每一个正方形(实线)四条边上的格点的个数,请回答下列问题:(1)由里向外第1个正方形(实线)四条边上的格点个数共有_________ 个;由里向外第2个正方形(实线)四条边上的格点个数共有_________ 个;由里向外第3个正方形(实线)四条边上的格点个数共有_________ 个;(2)由里向外第10个正方形(实线)四条边上的格点个数共有_________ 个;(3)由里向外第n个正方形(实线)四条边上的格点个数共有_________ 个.54.下列各图是由若干花盆组成的形如正方形的图案,每条边(包括两个顶点)有n(n>1)个花盆,每个图案花盆总数是S.(1)按要求填表:n 2 3 4 5 …S 4 8 12 …(2)写出当n=10时,S= _________ .(3)写出S与n的关系式:S= _________ .(4)用42个花盆能摆出类似的图案吗?55.如图,用同样规格的黑白两色正方形瓷砖铺设矩形地面,请观察下列图形,探究并解答下列问题.(1)在第1个图中,共有白色瓷砖_________ 块.(2)在第2个图中,共有白色瓷砖_________ 块.(3)在第3个图中,共有白色瓷砖_________ 块.(4)在第10个图中,共有白色瓷砖_________ 块.(5)在第n个图中,共有白色瓷砖_________ 块.56.淮北市为创建文明城市,各种颜色的菊花摆成如下三角形的图案,每条边(包括两个顶点)上有n(n>1)盆花,每个图案花盆的总数为S,当n=2时,S=3;n=3时,S=6;n=4时,S=10.(1)当n=6时,S= _________ ;n=100时,S= _________ .(2)你能得出怎样的规律?用n表示S.57.下面是按照一定规律画出的一系列“树枝”经观察,图(2)比图(1)多出2个“树枝”,图(3)比图(2)多出4个“树枝”,图(4)比图(3)多出8个“树枝”,按此规律:图(5)比图(4)多出_________ 个树枝;图(6)比图(5)多出_________ 个树枝;图(8)比图(7)多出_________ 个树枝;…图(n+1)比图(n)多出_________ 个树枝.58.如图是用棋子成的“T”字图案.从图案中可以出,第一个“T”字图案需要5枚棋子,第二个“T”字图案需要8枚棋子,第三个“T”图案需要11枚棋子.(1)照此规律,摆成第八个图案需要几枚棋子?(2)摆成第n个图案需要几枚棋子?(3)摆成第2010个图案需要几枚棋子?59.用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干图案:(1)当黑砖n=1时,白砖有_________ 块,当黑砖n=2时,白砖有_________ 块,当黑砖n=3时,白砖有_________ 块.(2)第n个图案中,白色地砖共_________ 块.60.下列图案是晋商大院窗格的一部分.其中,“o”代表窗纸上所贴的剪纸.探索并回答下列问题:(1)第6个图案中所贴剪纸“o”的个数是_________ ;(2)第n个图案中所贴剪纸“o”的个数是_________ ;(3)是否存在一个图案,其上所贴剪纸“o”的个数为2012个?若存在,指出是第几个;若不存在,请说明理由.图形找规律60题参考答案:1.结合图形和表格,不难发现:1张桌子座6人,多一张桌子多2人.4张桌子可以座10+2=12.即n张桌子时,共座6+2(n﹣1)=2n+4.2.当横截线有n条时,在6个的基础上多了n个6,即三角形的个数共有6+6n=6(n+1)个.故应填6(n+1)或6n+63.∵画1个点,可得3条线段,2+1=3;画2个点,可得6条线段,3+2+1=6;画3个点,可得10条线段,4+3+2+1=10;…;画n个点,则可得(1+2+3+…+n+n+1)=条线段.所以画10个点,可得=66条线段;4.根据图形可以发现,第七排的第一个数和第二数与第八排的第二个数相等,而第八排的第二个数就是x,所以x=61.另外,由图形可知,x右边的数是2×61=122,y左边的数是2×61+56=178,所以y=178+46=2245.根据题意分析可得:第1个图案中正方形的个数2个,第2个图案中正方形的个数比第1个图案中正方形的个数多4个,第3个图案中正方形的个数比第2个图案中正方形的个数多6个…,依照图中规律,第六个图形中有2+4+6+8+10+12=42个单位正方形6.图形从上到下可以分成几行,第n行中,斜放的火柴有2n根,下面横放的有n根,因而图形中有n排三角形时,火柴的根数是:斜放的是2+4+…+2n=2(1+2+…+n)横放的是:1+2+3+…+n,则每排放n根时总计有火柴数是:3(1+2+…+n)=21)nn3(把n=7代入就可以求出.故第7个图形中共有=84根火柴棒7.图1中,是1个正方形;图2中,是1+4=5个正方形;图3中,是1+4×2=9个正方形;依此类推,第n个图的所有正方形个数是1+4(n﹣1)=4n﹣3.8.∵第1个图案中有2×2+2×1=6个三角形;第2个图案中有2×3+2×2=10个三角形;第3个图案中有2×4+2×3=14个三角形;…∴第6个图案中有2×7+2×6=26个三角形.故答案为269.∵正方形的边长是1,所以它的斜边长是:=,所以第二个正方形的面积是:×=,第三个正方形的面积为=()2,以此类推,第n个正方形的面积为()n﹣1,所以第六个正方形的面积是()6﹣1=;故答案为:,.10.∵第一个有1个小正方形,第二个有1+2个,第三个有1+2+3个,第四个有1+2+3+4,第五个有1+2+3+4+5,∴则第10个图形有1+2+3+4+5+6+7+8+9+10=55个.故答案为:5511.依题意得:(1)摆第1个“小屋子”需要5个点;摆第2个“小屋子”需要11个点;摆第3个“小屋子”需要17个点.当n=n时,需要的点数为(6n﹣1)个.故答案为6n﹣112.由图形可知:第一个金鱼需用火柴棒的根数为:2+6=8;第二个金鱼需用火柴棒的根数为:2+2×6=14;第三个金鱼需用火柴棒的根数为:2+3×6=20;…;第n个金鱼需用火柴棒的根数为:2+n×6=2+6n.故答案为2+6n13.6条直线两两相交,最多有n(n﹣1)=×6×5=15,20条直线两两相交,最多有n(n﹣1)=×20×19=190.故答案为:15,190.14.如表格所示:图形编号(1)(2)(3)…n火柴根数7 12 17 …5n+215.设白三角形x个,黑三角形y个,则:n=1时,x=0,y=1;n=2时,x=0+1=1,y=3;n=3时,x=3+1=4,y=9;n=4时,x=4+9=13,y=27;当n=5时,x=13+27=40,所以白的正三角形个数为:40,故答案为:4016.n=1时,S=1+1=2,n=2时,S=1+1+2=4,n=3时,S=1+1+2+3=7,n=4时,S=1+1+2+3+4=11,…所以当切n刀时,S=1+1+2+3+4+…+n=1+n(n+1)=n2+n+1.故答案为n2+n+117.根据题意得:第(1)个图案只有1个等腰梯形,周长为3×1+4=7;第(2)个图案由3个等腰梯形拼成,其周长为3×3+4=13;第(3)个图案由5个等腰梯形拼成,其周长为3×5+4=19;…第(n)个图案由(2n﹣1)个等腰梯形拼成,其周长为3(2n﹣1)+4=6n+1;故答案为:6n+118.观察发现:第1个图形有S=9×1+1=10个点,第2个图形有S=9×2+1=19个点,第3个图形有S=9×3+1=28个点,…第n个图形有S=9n+1个点.故答案为:9n+119.n=3时,S=6=3×3﹣3=3,n=4时,S=12=4×4﹣4,n=5时,S=20=5×5﹣5,…,依此类推,边数为n数,S=n•n﹣n=n(n﹣1).故答案为:n(n﹣1).20.结合图形,发现:搭第n个三角形,需要3+2(n﹣1)=2n+1(根).故答案为2n+121.因为2011÷6=335…1.余下的1个根据顺序应是黑色三角形,所以共有1+335×3=1006.故答案为:100622.从所给的图中可以看出,每六个棋子为一个循环,∵2011÷6=335…1,∴第2011个棋子是白的.故答案为:白23.依题意可求出梯形个数与图形周长的关系为3n+2=周长,当梯形个数为2007个时,这时图形的周长为3×2007+2=6023.故答案为:6023.24.观察图形知:第一个图形有1=12个小正方形;第二个图形有1+3=4=22个小正方形;第三个图形有1+3+5=9=32个小正方形;…第n个图形共有1+2+3+…+(2n﹣1)=n2个小正方形,当n=4时,有n2=42=16个小正方形.故答案为:16,n225.根据已知图形可以发现:第2个图形中,火柴棒的根数是7;第3个图形中,火柴棒的根数是10;第4个图形中,火柴棒的根数是13;∵每增加一个正方形火柴棒数增加3,∴第n个图形中应有的火柴棒数为:4+3(n﹣1)=3n+1.当n=7时,4+3(n﹣1)=4+3×6=22,故答案为:2226.观察图形发现:当n=2时,s=4,当n=3时,s=9,当n=4时,s=16,当n=5时,s=25,…当n=n时,s=n2,故答案为:s=n227.∵第1个图形中,十字星与五角星的个数和为3×2=6,第2个图形中,十字星与五角星的个数和为3×3=9,第3个图形中,十字星与五角星的个数和为3×4=12,…而27=3×9,∴第8个图形中,十字星与五角星的个数和=3×9=27.故答案为:828.2条直线最多的交点个数为1,3条直线最多的交点个数为1+2=3,4条直线最多的交点个数为1+2+3=6,5条直线最多的交点个数为1+2+3+4=10,…所以2000条直线最多的交点个数为1+2+3+4+…+1999==1999000.故答案为199900029.∵小正方形的边长是1,∴图1的周长是:1×4=4,图2的周长是:2×4=8,图3的周长是3×4=12,…第n个图的周长是4n,∴图10的周长是10×4=40;故答案为:8,12,4030.首先发现:第一个图案中,有白色的是6个,后边是依次多4个.所以第n个图案中,是6+4(n﹣1)=4n+2.∴m与n的函数关系式是m=4n+2.故答案为:4n+2.31.第一个图需棋子6,第二个图需棋子9,第三个图需棋子12,第四个图需棋子15,第五个图需棋子18,…第n个图需棋子3(n+1)枚.(1)当n=6时,3×(6+1)=21;当n=7时,3×(7+1)=24;(2)第n个图需棋子3(n+1)枚.(3)设第n个图形有2012颗黑色棋子,根据(1)得3(n+1)=2012解得n=,所以不存在某个图形有2012颗黑色棋子32.(1)由点阵图形可得它们的点的个数分别为:1,5,9,13,…,并得出以下规律:第一个点数:1=1+4×(1﹣1)第二个点数:5=1+4×(2﹣1)第三个点数:9=1+4×(3﹣1)第四个点数:13=1+4×(4﹣1)…因此可得:第n个点数:1+4×(n﹣1)=4n﹣3.故答案为:4n﹣3;(2)设这个点阵是x个,根据(1)得:1+4×(x﹣1)=37解得:x=10.答:这个点阵是10个33.(1)观察图形,得出枚数分别是,5,8,11,…,每个比前一个多3个,所以图形编号为5,6的棋字子数分别为17,20.故答案为:17和20.(2)由(1)得,图中棋子数是首项为5,公差为3的等差数列,所以摆第n个图形所需棋子的枚数为:5+3(n﹣1)=3n+2.(3)不可能由3n+2=2010,解得:n=669,∵n为整数,∴n=669不合题意故其中某一图形不可能共有2011枚棋子34.(1)由图可知,每个正方形标4个数字,∵30÷4=7…2,∴数字30在第8个正方形的第2个位置,即右上角;故答案为:8,右上角;(2)左下角是4的倍数,按照逆时针顺序依次减1,即正方形左下角顶点数字:4n,正方形左上角顶点数字:4n﹣1,正方形右上角顶点数字:4n﹣2,正方形右下角顶点数字:4n﹣3;(3)2011÷4=502…3,所以,数字“2011”应标第503个正方形的左上角顶点处35.依题意得:①n=2,S=3=3×2﹣3.②n=3,S=6=3×3﹣3.③n=4,S=9=3×4﹣3④n=10,S=27=3×10﹣3.…⑤按此规律推断,当每条边有n盆花时,S=3n﹣3 36.(1)第①个图形中有6个棋子;第②个图形中有6+4=10个棋子;第③个图形中有6+2×4=14个棋子;∴第⑤个图形中有6+3×4=18个棋子;第⑥个图形中有6+4×4=22个棋子.故答案为18、22;(3分)(2)第n个图形中有6+(n﹣1)×4=4n+2.故答案为4n+2.(3分)(3)4n+2=50,解得n=12.最下一横人数为2n+1=25.(4分)37.(1)5个点时,线段的条数:1+2+3+4=10,6个点时,线段的条数:1+2+3+4+5=15;(2)10个点时,线段的条数:1+2+3+4+5+6+7+8+9=45,n个点时,线段的条数:1+2+3+…+(n﹣1)=;(3)60人握手次数==1770.故答案为:(2)45,;(3)1770.38.(1)摆成第一个“H”字需要7个棋子,第二个“H”字需要棋子12个;第三个“H”字需要棋子17个;…第x个图中,有7+5(x﹣1)=5x+2(个).(2)当5x+2=2012时,解得:x=402,故第402个“H”字棋子数量正好是2012个棋子39.(1)如图(1),可得三条直线两两相交,最多有3个交点;(2)如图(2),可得三条直线两两相交,最多有6个交点;(3)由(1)得,=3,由(2)得,=6;∴可得,n 条直线两两相交,最多有个交点(n为正整数,且n≥2).故答案为3;6;.40.(1)由题目中的“每次都将其中﹣片撕成更小的四片”,可知:小王每撕一次,比上一次多增加3张小纸片.∴s=4+3(n﹣1)=3n+1;(2)当s=70时,有3n+1=70,n=23.即小王撕纸23次41.(1)结合图形,发现:每个图中,两端都是坐2人,剩下的两边则是每一张桌子是4人.则三张餐桌按题中的拼接方式,四周可坐3×4+2=14(人);(2)n张餐桌按上面的方式拼接,四周可坐(4n+2)人;若用餐人数为26人,则4n+2=26,解得n=6.故答案为:14;(4n+2),642.(1)如图所示:图形编号1 2 3 4 5 6图形中的棋子6 9 12 15 18 21(2)依题意可得当摆到第n个图形时棋子的枚数应为:6+3(n﹣1)=6+3n﹣3=3n+3;(3)由上题可知此时3n+3=99,∴n=32.答:第32个图形共有99枚棋子13.由题目得:第1个“广”字中的棋子个数是7;第2个“广”字中的棋子个数是7+(2﹣1)×2=9;第3个“广”字中的棋子个数是7+(3﹣1)×2=11;第4个“广”字中的棋子个数是7+(4﹣1)×2=13;发现第5个“广”字中的棋子个数是7+(5﹣1)×2=15…进一步发现规律:第n个“广”字中的棋子个数是7+(n﹣1)×2=2n+5.故答案为:1544.(1)在第n个图形中,需用黑瓷砖4n+6块,白瓷砖n(n+1)块;(2)根据题意得n(n+1)=4n+6,n2﹣3n﹣6=0,此时没有整数解,所以不存在.故答案为:4n+6;n(n+1)45.(1)结合图形,发现:后边每多一个三角形,则需要多2根火柴.则搭4个这样的三角形要用3+2×3=9根火柴棒;13根火柴棒可以搭(13﹣3)÷2+1=6个这样的三角形;(2)根据(1)中的规律,得搭n个这样的三角形要用3+2(n﹣1)=2n+1根火柴棒.故答案为9;6;2n+146.(1)第4个图形中的棋子个数是13;(2)第n个图形的棋子个数是3n+1;(3)当n=20时,3n+1=3×20+1=61∴第20个图形需棋子61个47.(1)第一级台阶中正方体石墩的块数为:=3;第一级台阶中正方体石墩的块数为:=9;第一级台阶中正方体石墩的块数为:;…依此类推,可以发现:第几级台阶中正方体石墩的块数为:3与几的乘积乘以几加1,然后除以2.阶梯级数一级二级三级四级石墩块数 3 9 18 30(2)按照(1)中总结的规律可得:当垒到第n级阶梯时,共用正方体石墩块;当n=100时,∴当n=100时,共用正方体石墩15150块.答:当垒到第n级阶梯时,共用正方体石墩块;当n=100时,共用正方体石墩15150块48.由题意可知:第一次对折后,纸的厚度为2×0.05;可以得到折痕为1条;第二次对折后,纸的厚度为2×2×0.05=22×0.05;可以得到折痕为3=22﹣1条;第三次对折后,纸的厚度为2×2×2×0.05=23×0.05;可以得到折痕为7=23﹣1条;…;第n次对折后,纸的厚度为2×2×2×2× (2)0.05=2n×0.05.可以得到折痕为2n﹣1条.故:(1)对折3次后,厚度为0.4毫米;(2)对折n次后,厚度为2n×0.05毫米;(3)对折n次后,可以得到2n﹣1条折痕49.由图形我们不难看出横行砖数量为n+3,竖行砖数量为n+2,总数量为n2+5n+6;若用瓷砖506块,可以求n2+5n+6=506;所以答案为:(1)n+3,n+2;(2)每一行有23块,每一列有22块50.等号左边是从1开始,连续奇数相加,等号右边是奇数个数也就是n的平方.(1)①1+3+5+7=42;②1+3+5+7+9=52;③1+3+5+7+9+11=62.(2)1+3+5+…+(2n﹣1)=n2(n≥1的正整数)51.(1)依题意得:所剪次数n 1 2 3 4 5正方形个数Sn 4 7 10 13 16 (2)可知剪n次时,S n=3n+1.(3)n=1时,边长=;n=2时,边长=;n=3时,边长=;…;剪n次时,边长=.52.(1)S=15(2)∵n=2时,S=3×(2﹣1)=3;n=3时,S=3×(3﹣1)=6;n=4时,S=3×(4﹣1)=9;…∴S=3×(n﹣1)=3n﹣3.(3)当n=2008时,S=3×2008﹣3=6021.53.第1个正方形四条边上的格点共有4个第2个正方形四条边上的格点个数共有(4+4×1)个第3个正方形四条边上的格点个数共有(4+4×2)个…第10个正方形四条边上的格点个数共有(4+4×9)=40个第n个正方形四条边上的格点个数共有[4+4×(n﹣1)]=4n个54.由图可知,每个图形为边长是n的正方形,因此四条边的花盆数为4n,再减去重复的四个角的花盆数,即S=4n﹣4;(1)将n=5代入S=4n﹣4,得S=16;(2)将n=10入S=4n﹣4,得S=36;(3)S=4n﹣4;(4)将S=42代入S=4n﹣4得,4n﹣4=42解得n=11.5所以用42个花盆不能摆出类似的图案55.(1)在第1个图中,共有白色瓷砖1×(1+1)=2块,(2)在第2个图中,共有白色瓷砖2×(2+1)=6块,(3)在第3个图中,共有白色瓷砖3×(3+1)=12块,(4)在第10个图中,共有白色瓷砖10×(10+1)=110块,(5)在第n个图中,共有白色瓷砖n(n+1)块56.(1)由分析得:当n=6时,s=1+2+3+4+5+6=21;当n=100时,s=1+2+3+…+99+100=5050;(2)用n表示S得:S=57.(1)图(5)比图(4)多出25﹣1=16个;(2)图(6)比图(5)多出26﹣1=32个;(3)图(8)比图(7)多出28﹣1=128个;(4)图(n+1)比图(n)多出2n个.58.(1)首先观察图形,得到前面三个图形的具体个数,不难发现:在5的基础上依次多3枚.即第n个图案需要5+3(n﹣1)=3n+2.那么当n=8时,则有26枚;故摆成第八个图案需要26枚棋子.(2)因为第①个图案有5枚棋子,第②个图案有(5+3×1)枚棋子,第③个图案有(5+3×2)枚棋子,依此规律可得第n个图案需5+3×(n﹣1)=5+3n﹣3=(3n+2)枚棋子.(3)3×2010+2=6032(枚)即第2010个图案需6032枚棋子59.(1)观察图形得:当黑砖n=1时,白砖有6块,当黑砖n=2时,白砖有10块,当黑砖n=3时,白砖有14块;(2)根据题意得:∵每个图形都比其前一个图形多4个白色地砖,∴可得规律为:第n个图形中有白色地砖6+4(n﹣1)=4n+2块.故答案为6,10,14,4n+260.第一个图案为3+2=5个窗花;第二个图案为2×3+2=8个窗花;第三个图案为3×3+2=11个窗花;…从而可以探究:第n个图案所贴窗花数为(3n+2)个.(1)20(2)3n+2(3)存在,令3n+2=2012,则3n=2010 n=670 因此是第670个。
(完整版)小学奥数图形找规律(四年级)

找规律是解决数学问题的一种重要的手段,而规律的找寻既需要敏锐的观察力,又需要严密的逻辑推理能力.一般地说,在观察图形变化规律时,应抓住一下几点来考虑问题:⑴图形数量的变化;⑵图形形状的变化;⑶图形大小的变化;⑷图形颜色的变化;⑸图形位置的变化;⑹图形繁简的变化.对于较复杂的图形,也可分为几部分来分别考虑,总而言之,只要全面观察,勤于思考就一定能抓住规律,解决问题.板块一数量规律【例 1】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?【解析】横着看,每行圆形的个数一次减少,而三角形的个数依次增加,但每行图形的总个数不变.因为圆形的个数是按4、3、?、1的顺序变化的,显然“?”处应填一个圆形。
【巩固】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?丁【解析】(方法一)横着看,每行三角形的个数依次减少,而正方形的个数依次增加,但每行图形的总个数不变.因为三角形的个数是按4、3、?、1的顺序变化的,显然“?”处应填一个三角形△.(方法二)竖着看,三角形由左而右依次减少,而正方形由左而右依次增加,三角形按照4、?、2、1的顺序变化,也可以看出“?”处应是三角形△.【例 2】观察下面的图形,按规律在“?”处填上适当的图形.丁图形找规律【解析】本题中,几何图形的变化表现在数量关系上,图中黑三角形的个数从左到右依次增多,从(2)起,每一个格比前面一个格多两个黑三角形,所以,第(4)个方框中应填七个黑三角形.【例 3】观察图形变化规律,在右边补上一幅,使它成为一个完整系列。
【解析】观察发现,乌龟的顺序是:头、身→一只脚、背上一个点→两只脚、背上两个点→两只脚、一条尾、背上三个点→三只脚、一条尾、背上四个点,根据这个规律,最后一幅图应该是:→四只脚、一条尾、背上五个点.即:【例 4】观察图形变化规律,在右边再补上一幅,使它们成为一个完整的系列.【解析】第一格有8个圆圈,第二格有4个圆圈,第三格有2个圆圈,第四格有1个圆圈,第五格有半个圆圈.由此发现,前一格中的图减少一般,正好是后一格的图.所以第六格的图应该是第五格图的一半,即:板块二 旋转、轮换型规律【例 5】相传古时候一位老人留在人间很多宝盒,里面装着世界上最宝贵的财富,但是并不是拥有宝盒都可以得到这笔财富,在宝盒的上面设置了密码,只有写出密码的人才会真正拥有这笔财富,聪明的你你能找出密码吗?○ □ ☆ △ ○ □ ☆ △ △ ○ □ ☆ △ ○ □ ☆☆ △ ○ □ ☆ △ ○ □()()()()()()()()【解析】有几种方法可以找出密码:(方法一)后面一排和前面一排比,上排的第一个图形移到最后,其他每个图形都向前移动了一格,变成了下一排.(方法二)斜着看,每一斜列的图形是一样的.所以密码就是: □ ☆ △ ○ □ ☆ △ ○【例 6】观察下图的变化规律,画出丙图.丁丁丁A【解析】AC【总结】旋转是数学中的重要概念,掌握好这个概念,可以提高观察能力,加快解题速度,对于许多问题的解决,也有事半而功倍的效果.【例 7】下面各种各样的娃娃头好看吗?认真观察你能找到它们排列的规律吗?根据规律把最后一个画出来.【解析】【例 8】观察图中所给出图形的变化规律,然后在空白处填画上所缺的图形.e an dh e i rb 【解析】【例 9】琪琪特别喜欢蝴蝶,她用直尺和圆规在纸上画了9幅蝴蝶图,并用剪刀将它们一一剪下来.她将这9只纸蝴蝶摆在桌上,见下图1,她发现这些纸蝴蝶排列挺有规律,突然一阵风来,吹走了3只纸蝴蝶,见下图2.你能找出蝴蝶的排列规律,将图2的3只蝴蝶放入图1的空缺处吗?丁1987654321丁2B CA【解析】从已摆好的第一行和第一列来看,无论横看或竖看,同一行中3只蝴蝶的翅膀形状各不相同,翅膀上的斑点的形状也各不相同.根据这个规律,剩下的3只蝴蝶图案的排列应该是:6号位置放图案C ;8号位置放图案B ;9号位置放图案A.【例 10】观察下列各组图的变化规律,并在“?”处画出相关的图形.(1)丁丁丁丁丁【解析】(1)这四个图形的变化规律是:每一个图形都是由其前一个图形顺时针旋转90°而得到的.见下面左图;(2)甲乙丙丁四个图形变化规律也类似,注意因为图形是由旋转而得到的,所以其中三角形、菱形的方向随旋转而变化,作图的时候要注意到这一点.丁图处的图形应是下面右图:丁【例 11】请你认真仔细观察,按照下面图形的变化规律,在“?”处画出合适的图形。
(word完整版)小学四年级奥数找规律(2021年整理)

(word完整版)小学四年级奥数找规律(word版可编辑修改)(word完整版)小学四年级奥数找规律(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((word完整版)小学四年级奥数找规律(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(word完整版)小学四年级奥数找规律(word版可编辑修改)的全部内容。
(word完整版)小学四年级奥数找规律(word版可编辑修改)小学四年级奥数第五讲找规律(一)一、知识要点按照一定次序排列起来的一列数,叫做数列。
如自然数列:1,2,3,4,……双数列:2,4,6,8,……我们研究数列,目的就是为了发现数列中数排列的规律,并依据这个规律来填写空缺的数.按照一定的顺序排列的一列数,只要从连续的几个数中找到规律,那么就可以知道其余所有的数。
寻找数列的排列规律,除了从相邻两数的和、差考虑,有时还要从积、商考虑。
善于发现数列的规律是填数的关键。
二、精讲精练【例题1】在括号内填上合适的数.(1)3,6,9,12,(),()(2)1,2,4,7,11,( ),( )(3)2,6,18,54,( ),()练习1:在括号内填上合适的数。
(1)2,4,6,8,10,( ),()(2)1,2,5,10,17,( ),( )(3)2,8,32,128,( ),()(4)1,5,25,125,(),()(5)12,1,10,1,8,1,(),()【例题2】先找出规律,再在括号里填上合适的数.(1)15,2,12,2,9,2,(),()(2)21,4,18,5,15,6,( ),()练习2:按规律填数。
小学奥数图形找规律(四年级)

找规律是解决数学问题的一种重要的手段,而规律的找寻既需要敏锐的观察力,又需要严密的逻辑推理能力.一般地说,在观察图形变化规律时,应抓住一下几点来考虑问题: ⑴图形数量的变化;⑵图形形状的变化;⑶图形大小的变化; ⑷图形颜色的变化;⑸图形位置的变化;⑹图形繁简的变化.对于较复杂的图形,也可分为几部分来分别考虑,总而言之,只要全面观察,勤于思考就一定能抓住规律,解决问题.板块一 数量规律【例 1】 观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?【解析】 横着看,每行圆形的个数一次减少,而三角形的个数依次增加,但每行图形的总个数不变.因为圆形的个数是按4、3、?、1的顺序变化的,显然“?”处应填一个圆形。
【巩固】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形??【解析】 (方法一)横着看,每行三角形的个数依次减少,而正方形的个数依次增加,但每行图形的总个数不变.因为三角形的个数是按4、3、?、1的顺序变化的,显然“?”处应填一个三角形△. (方法二)竖着看,三角形由左而右依次减少,而正方形由左而右依次增加,三角形按照4、?、2、1的顺序变化,也可以看出 “?”处应是三角形△.【例 2】 观察下面的图形,按规律在“?”处填上适当的图形.(4)(1)?图形找规律【解析】本题中,几何图形的变化表现在数量关系上,图中黑三角形的个数从左到右依次增多,从(2)起,每一个格比前面一个格多两个黑三角形,所以,第(4)个方框中应填七个黑三角形.【例 3】观察图形变化规律,在右边补上一幅,使它成为一个完整系列。
【解析】观察发现,乌龟的顺序是:头、身→一只脚、背上一个点→两只脚、背上两个点→两只脚、一条尾、背上三个点→三只脚、一条尾、背上四个点,根据这个规律,最后一幅图应该是:→四只脚、一条尾、背上五个点.即:【例 4】观察图形变化规律,在右边再补上一幅,使它们成为一个完整的系列.【解析】第一格有8个圆圈,第二格有4个圆圈,第三格有2个圆圈,第四格有1个圆圈,第五格有半个圆圈.由此发现,前一格中的图减少一般,正好是后一格的图.所以第六格的图应该是第五格图的一半,即:板块二旋转、轮换型规律【例5】相传古时候一位老人留在人间很多宝盒,里面装着世界上最宝贵的财富,但是并不是拥有宝盒都可以得到这笔财富,在宝盒的上面设置了密码,只有写出密码的人才会真正拥有这笔财富,聪明的你你能找出密码吗?○□☆△○□☆△△○□☆△○□☆☆△○□☆△○□()()()()()()()()【解析】有几种方法可以找出密码:(方法一)后面一排和前面一排比,上排的第一个图形移到最后,其他每个图形都向前移动了一格,变成了下一排.(方法二)斜着看,每一斜列的图形是一样的.所以密码就是:□☆△○□☆△○【例 6】 观察下图的变化规律,画出丙图.DBA丙乙甲CB A【解析】ACD【总结】旋转是数学中的重要概念,掌握好这个概念,可以提高观察能力,加快解题速度,对于许多问题的解决,也有事半而功倍的效果.【例 7】 下面各种各样的娃娃头好看吗?认真观察你能找到它们排列的规律吗?根据规律把最后一个画出来.【解析】【例 8】 观察图中所给出图形的变化规律,然后在空白处填画上所缺的图形.【解析】【例 9】 琪琪特别喜欢蝴蝶,她用直尺和圆规在纸上画了9幅蝴蝶图,并用剪刀将它们一一剪下来.她将这9只纸蝴蝶摆在桌上,见下图1,她发现这些纸蝴蝶排列挺有规律,突然一阵风来,吹走了3只纸蝴蝶,见下图2.你能找出蝴蝶的排列规律,将图2的3只蝴蝶放入图1的空缺处吗?图1987654321 图2B CA【解析】 从已摆好的第一行和第一列来看,无论横看或竖看,同一行中3只蝴蝶的翅膀形状各不相同,翅膀上的斑点的形状也各不相同.根据这个规律,剩下的3只蝴蝶图案的排列应该是:6号位置放图案C ;8号位置放图案B ;9号位置放图案A.【例 10】 观察下列各组图的变化规律,并在“?”处画出相关的图形.(1)丁丙乙甲?【解析】 (1)这四个图形的变化规律是:每一个图形都是由其前一个图形顺时针旋转90°而得到的.见下面左图;(2)甲乙丙丁四个图形变化规律也类似,注意因为图形是由旋转而得到的,所以其中三角形、菱形的方向随旋转而变化,作图的时候要注意到这一点.丁图处的图形应是下面右图:丁【例 11】 请你认真仔细观察,按照下面图形的变化规律,在“?”处画出合适的图形。
奥数图形找规律教师版
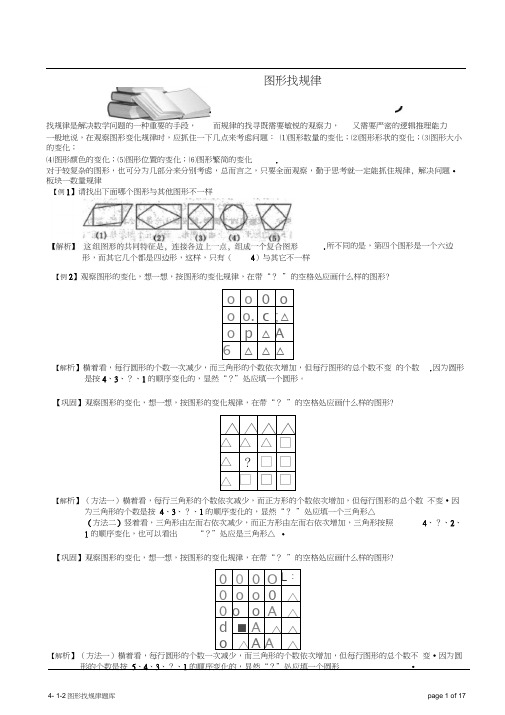
找规律是解决数学问题的一种重要的手段, 而规律的找寻既需要敏锐的观察力, 又需要严密的逻辑推理能力一般地说,在观察图形变化规律时,应抓住一下几点来考虑问题: ⑴图形数量的变化;⑵图形形状的变化;⑶图形大小的变化;⑷图形颜色的变化;⑸图形位置的变化;⑹图形繁简的变化 .对于较复杂的图形,也可分为几部分来分别考虑,总而言之,只要全面观察,勤于思考就一定能抓住规律, 解决问题•【例2】观察图形的变化,想一想,按图形的变化规律,在带“? ”的空格处应画什么样的图形?o o 0 o o o. c ;△ o p △ A 6 △ △ △【解析】横着看,每行圆形的个数一次减少,而三角形的个数依次增加,但每行图形的总个数不变 的个数是按4、3、?、1的顺序变化的,显然“?”处应填一个圆形。
【巩固】观察图形的变化,想一想,按图形的变化规律,在带“? ”的空格处应画什么样的图形?△ △ △ △ △ △ △ □△ ? □ □ △ □ □ □【解析】(方法一)横着看,每行三角形的个数依次减少,而正方形的个数依次增加,但每行图形的总个数 不变•因为三角形的个数是按 4、3、?、1的顺序变化的,显然“? ”处应填一个三角形△(方法二)竖着看,三角形由左而右依次减少,而正方形由左而右依次增加,三角形按照 4、?、2、1的顺序变化,也可以看出 “?”处应是三角形△ •【巩固】观察图形的变化,想一想,按图形的变化规律,在带“? ”的空格处应画什么样的图形?0 0 0 OL : 0 o o 0 △0 o o A △ d ■ A △ △ o △ A A△【解析】(方法一)横着看,每行圆形的个数一次减少,而三角形的个数依次增加,但每行图形的总个数不 变•因为圆形的个数是按 5、4、3、?、1的顺序变化的,显然“?”处应填一个圆形 •图形找规律.所不同的是,第四个图形是一个六边.因为圆形板块一数量规律【例1】请找出下面哪个图形与其他图形不一样形,而其它几个都是四边形,这样,只有(4)与其它不一样(方法二)竖着看,圆形由左而右依次减少,而三角形由左而右依次增加,圆形按照5、4、?、2、1的顺序变化,也可以看出“?”处应是圆形•【例3】观察下面的图形,按规律在“?”处填上适当的图形(1)(2)(3)(4)(5)【解析】本题中,几何图形的变化表现在数量关系上,图中黑三角形的个数从左到右依次增多,从(2)起, 每一个格比前面一个格多两个黑三角形,所以,第(4)个方框中应填七个黑三角形.【例4】观察图形变化规律,在右边补上一幅,使它成为一个完整系列。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
拓展1、下面图形中有多少个正方形,多少个三角形?
有1个正方形。8个三角形。 有1正方形。8个三角形。
拓展2、下面二图形叠加后有多少个正方形,多少个三角形?
+
二图形共有2个正方 形,16个三角形
二图叠加后新增8个正方形,新增三角形:16+12=28个 二图叠加后【例题1】 数出下图中有多少条线段?
_A
_B
_C
_D
请跟我一起来数一数吧!
A
B
C
D
例1、数线段:方法一
31542
共5+4+3+2+1= 15条线段
练习1、数线段
1 23 4
5
67
共 7+6+5+4+3+2+1=28 条线段
方法二:
你能一口报出有多少条线段吗?
A B C D E F GHI J K L 12×11÷2=66(条)
或直接数三角形16+16+8+4=44 8组合 4组合 2组合 单个
拓展20. 数一数,图中有多少个正方形?
6+2+7+2=17个
4+1+4+1=10个
拓展21. 数一数,图中有多少个正方形?
15+6+1= 22个
9+2= 11 个
拓展22. 数一数,图中有多少个正方形? 115
5+11= 16 个
例5.数一数,下图中有多少个三角形?
12 3 4
1 234 5
(4+3+2+1)×2=20 个
(5+4+3+2+1)×3=45 个
【例题6】 数出下图中有多少个长方形?
_A
_B
_C
_D
【思路导航】
数图中有多少个长方形和数三角形的方法一样,长方形是 由长、宽两对线段围成,线段 CD上有3+2+1=6(条)线段,其 中每一条与AC中一条线段对应,分别作为长方形的长和宽,这 里共有6×1=6(个)长方形,而AC上共有2+1=3(条)线段也 就有6×3=18(个)长方形。
拓展24. 数一数,图中有多少个正方形?
51
5+4+1= 10 个
回顾探究的经历
数线段 和角的 个数
先数单一的线 段和角的个数
再数“二合一”线 段和角的个数,然 后数“三合一”线 段和角的个数……, 最后个数相加。
数三角形 的个数
数长方形 的个数
同学们,你想学会数图形的方法吗?要想不重复也不遗漏 地数出线段、角、三角形、长方形……那就必须要有次序、有 条理地数,从中发现规律,以便得到正确的结果。
要正确数出图形的个数,关键是要从基本图形入手。首先
要弄清图形中包含的基本图形是什么,有多少个,然后再数出 由基本图形组成的新的图形,并求出它们的和。
例3.数一数,下图中有多少个角?
1
11
2
3
4
2
4+3+2+1=10 个
例4.数出图中共有多少三角形。
A
三角形个数: 4+3+2+1=10
1 2 34
B C DE F
数三角形有时也可以用数线段的方法;有的图形要用 编号数图形的方法,还有的图形先要分成几部分分别 去数,再考虑几部分拼合起来看看有没有产生新三角 形。
练习1.数一数,下列图形各有多少三角形?
12345
5+4+3+2+1= 15 个 6+5+4+3+2+1= 21个
线段总数=端点数×基本线段数÷2同样适用于数角的个数 角总数=基本射线数×(基本射线数-1)÷2
这两图三角形的总数也可这样计算: 6 ×(6-1) ÷2=15 7×(7-1) ÷2=21
_1
_2
_3
_4
_5
从上图可以看出,第1个同学要与其余4个同学握手共握手
4次;第2个同学还要与其余3个同学握手共握手3次,第3个同
学要与其余2个同学握手共握手2次;第4个同学还要与最后1个
同学握手共握手1次。
所以,一共要握手4+3+2+1=10(次)
【练习5】 (1)银海学校三年级有9个班,每两个班要比赛拔河一次, 这样一共要拔河几次?
线段总数=端点数×基本线段数÷2
【练习1】 (1)数出下图中有多少条线段?
_A
_B
_C
_D
_E
(2)数出下图中有几个长方形?
例2、下面图中有几个长方形?
数一数:
总计: 5+4+3+2+1=15
单个
5
2个组合 4
3个组合 3
4个组合 2
5个组合 1
总计
15
可见,整齐单排长方形个数的算法与线段计算相同。
它的计算公式为: 长方形的总数=长边线段的总数×宽边线段的总数 (3+2+1)×(2+1)=18(个) 答:图中共有18个长方形。
【练习4】
(1)数出下图中有多少个长方形?
_A
_B
_C
_D
(2)数出右图中有多少个正方形?
【例题7】 有5个同学,每两个人握手一次,一共要握手多少次?
【思路导航】
这道题可以用数线段的方法来解答。根据题意,画出线段 图,每一个端点代表一个同学。
(2)有1,2,3,4,5,6,7,8等8个数字,能组成多少个 不同的两位数?
解决问题(二):一年级有六个班,每 两个班之间要进行一场比赛,一共需要 几场比赛?
6×5÷2=15(场)
答:一共需要15场比赛。
解决问题(三):有10个老朋友见面, 每两人要握一次手,一共要握几次手?
10×9÷2=45(次)
