必修四第一章三角函数测试题(含答案)之欧阳数创编
必修四第一章三角函数测试题(含答案)[2]
![必修四第一章三角函数测试题(含答案)[2]](https://img.taocdn.com/s3/m/3c1b605ff121dd36a22d8225.png)
必修四第一章三角函数测试题(含答案)(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(必修四第一章三角函数测试题(含答案)(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为必修四第一章三角函数测试题(含答案)(word版可编辑修改)的全部内容。
必修四第一章三角函数测试题班别姓名分数一、选择题1.已知cos α=错误!,α∈(370°,520°),则α等于( )A.390°B.420°C.450°D.480°2.若sin x·tan x〈0,则角x的终边位于()A.第一、二象限B.第二、三象限 C.第二、四象限D.第三、四象限3.函数y=tan 错误!是( )A.周期为2π的奇函数B.周期为错误!的奇函数C.周期为π的偶函数D.周期为2π的偶函数4.已知函数y=2sin(ωx+φ)(ω〉0)在区间[0,2π]的图象如图,那么ω等于( )A.1 B.2 C.错误! D.错误!5.函数f(x)=cos(3x+φ)的图象关于原点成中心对称,则φ等于( )A.-错误!B.2kπ-错误!(k∈Z) C.kπ(k∈Z)D.kπ+错误!(k∈Z)6.若sin θ+cos θsin θ-cos θ=2,则sin θcos θ的值是( ) A.-错误! B.错误!C.±错误!D。
错误!7.将函数y=sin x的图象上所有的点向右平行移动π10个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是( )A.y=sin错误!B.y=sin错误! C.y=sin错误! D.y=sin错误!8.在同一平面直角坐标系中,函数y=cos错误!(x∈[0,2π])的图象和直线y=错误!的交点个数是 ( )A.0 B.1 C.2 D.49.已知集合M=错误!,N={x|x=错误!+错误!,k∈Z}.则()必修四第一章三角函数测试题(含答案)(word版可编辑修改)A.M=N B.M N C.N M D.M∩N=∅10.设a=sin 错误!,b=cos 错误!,c=tan 错误!,则()A.a〈b<c B.a<c〈b C.b〈c<a D.b<a〈c二、填空题11.已知一扇形的弧所对的圆心角为54°,半径r=20 cm,则扇形的周长为________ cm。
(常考题)北师大版高中数学必修四第一章《三角函数》测试题(包含答案解析)

一、选择题1.函数()sin()0,0,||2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示,将函数()f x 的图象向左平移3π个单位长度后得到()y g x =的图象,则下列说法正确的是( )A .函数()g x 为奇函数B .函数()g x 的最小正周期为2πC .函数()g x 的图象的对称轴为直线()6x k k ππ=+∈ZD .函数()g x 的单调递增区间为5,()1212k k k ππππ⎡⎤-++∈⎢⎥⎣⎦Z2.设函数5()sin 26f x x π⎛⎫=-⎪⎝⎭,将函数()f x 的图象向左平移()0ϕϕ>个单位长度,得到函数()g x 的图象,若()g x 为偶函数,则ϕ的最小值是( ) A .6π B .3π C .23π D .56π 3.函数()sin()(0||)2,f x x πωϕωϕ=+><的部分函数图象如图所示,将函数()f x 的图象先向右平移3π个单位长度,然后向上平移1个单位长度,得到函数()g x 的解析式为( )A .()sin 21g x x =-B .()sin 21g x x =+C .()sin(2)13g x x π=-- D .()sin(2)13g x x π=-+4.已知点,024A π⎛⎫⎪⎝⎭在函数()()()cos 0,0f x x ωϕωϕπ=+><<的图象上,直线6x π=是函数()f x 图象的一条对称轴.若()f x 在区间,63ππ⎛⎫⎪⎝⎭内单调,则ϕ=( ) A .6πB .3π C .23π D .56π 5.如图,一半径为4.8m 的筒车按逆时针方向转动,已知筒车圆心O 距离水面2.4m ,筒车每60s 转动一圈,如果当筒车上点P 从水中浮现时(图中点0P )开始计时,则( )A .点P 第一次到达最高点需要10sB .点P 距离水面的高度h (单位:m )与时间t (单位:s )的函数解析式为4.8sin 2.4306h t ππ⎛⎫=-+ ⎪⎝⎭ C .在筒车转动的一圈内,点P 距离水面的高度不低于4.8m 共有10s 的时间 D .当筒车转动50s 时,点P 在水面下方,距离水面1.2m 6.已知函数sin()0,0,||2y A x b A πωϕωϕ⎛⎫=++>>< ⎪⎝⎭的图象上相邻的一个最大值点与对称中心分别为2,39π⎛⎫ ⎪⎝⎭,,018π⎛⎫⎪⎝⎭,则函数()f x 的单调增区间为( ) A .222,3939k k ππππ⎛⎫-+ ⎪⎝⎭,k Z ∈ B .242,3939k k ππππ⎛⎫--⎪⎝⎭,k Z ∈ C .227,318318k k ππππ⎛⎫++⎪⎝⎭,k Z ∈ D .272,318318k k ππππ⎛⎫--⎪⎝⎭,k Z ∈ 7.已知函数y =f (x )的部分图象如图所示,则其解析式可能是( )A .()sin 2f x x x =B .()||sin 2f x x x =C .()cos 2f x x x =D .()||cos2f x x x =8.675︒用弧度制表示为( ) A .114π B .134π C .154π D .174π 9.现有四个函数:①y =x |sin x |,②y =x 2cos x ,③y =x ·e x ;④1y x x=+的图象(部分)如下,但顺序被打乱,则按照从左到右将图象对应的函数序号安排正确的一组是( )A .①②③④B .①③②④C .②①③④D .③②①④10.已知函数()sin()f x A x ωϕ=+(0A >,0>ω,0ϕπ≤≤)的部分图象如图所示,则()f x 的解析式是( )A .()2sin 6f x x π⎛⎫=+⎪⎝⎭B .()2sin 3f x x π⎛⎫=+⎪⎝⎭C .()2sin 26f x x π⎛⎫=+⎪⎝⎭D .2n 2)3(si f x x π⎛⎫=+⎪⎝⎭11.将函数()2sin (04)6f x x πωω⎛⎫=-<< ⎪⎝⎭的周期为π,则以下说法正确的是( ) A .1ω=B .函数()y f x =图象的一条对称轴为12x π=C .()3f f x π⎛⎫⎪⎝⎭D .函数()y f x =在区间0,2π⎛⎫⎪⎝⎭,上单调递增12.已知函数()()sin 0,0,2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象(如图所示),则下列有关函数()f x 的结论错误的是( )A .图象关于点,012π⎛⎫- ⎪⎝⎭对称 B .最小正周期是π C .在0,6π⎛⎫⎪⎝⎭上单调递减 D .在0,12π⎡⎤⎢⎥⎣⎦3二、填空题13.以下关于函数()()21sin 324f x x x R π⎛⎫=-∈ ⎪⎝⎭的结论: ①()y f x =的图象关于直线2x π=-对称; ②()f x 的最小正周期是4π;③()y f x =在区间[]2,3ππ上是减函数; ④()y f x =的图象关于点,02π⎛⎫- ⎪⎝⎭对称.其中正确的结论是__________________(写出所有正确结论的序号). 14.若将函数()cos 212f x x π⎛⎫=+⎪⎝⎭的图象向左平移8π个单位长度,得到函数()g x 的图象,则下列说法正确的是_________.①()g x 的最小正周期为π ②()g x 在区间0,2π⎡⎤⎢⎥⎣⎦上单调递减 ③12x π=不是函数()g x 图象的对称轴 ④()g x 在,66ππ⎡⎤-⎢⎥⎣⎦上的最小值为12-15.已知函数()()πsin (00)2f x M x M ωϕωϕ=+>><,的部分图象如图所示,其中()23A ,(点A 为图象的一个最高点)502B ⎛⎫- ⎪⎝⎭,,则函数()f x =___________.16.将函数()4cos 2f x x π⎛⎫=⎪⎝⎭与直线()1g x x =-的所有交点从左到右依次记为125,,...,A A A ,若P 点坐标为()0,3,则125...PA PA PA +++=____.17.如图,某公园要在一块圆心角为3π,半径为20m 的扇形草坪OAB 中修建一个内接矩形文化景观区域CDEF ,若//EF AB ,则文化景观区域面积的最大值为______2m .18.将函数()sin 23cos2f x a x x =+的图象向左平移6π个单位长度,若所得图象关于原点对称,则a 的值为_________.19.已知函数()sin f x x =,若对任意的实数(,)46αππ∈--,都存在唯一的实数(0,)m β∈,使()()0f f αβ+=,则实数m 的最大值是____.20.已知函数()sin cos x f x x x =-,23,34x ππ⎡⎤∈⎢⎥⎣⎦,则()f x 的最小值是__________ 三、解答题21.已知函数()()sin (0,)2f x A x πωϕωϕ=+><部分图象如图所示.(1)求ω和ϕ的值;(2)求函数()f x 在[,]-ππ上的单调递增区间;(3)设()1212x f x f x ππϕ⎛⎫⎛⎫=--+ ⎪ ⎪⎝⎭⎝⎭,已知函数2()2()3()21g x x x a ϕϕ=-+-在,62ππ⎡⎤⎢⎥⎣⎦上存在零点,求实数a 的最小值和最大值. 22.在①()f x 的图象关于直线3x π=对称,②()f x 的图象关于点,06π⎛⎫-⎪⎝⎭对称,③()f x 的图象上最高点中,有一个点的横坐标为6π这三个条件中任选一个,补充在下面问题中,并解答.问题:已知函数()()sin 0,0,02f x A x A πωϕωϕ⎛⎫=+>><<⎪⎝⎭的振幅为2,初相为3π,最小正周期不小于...π,且______. (1)求()f x 的解析式;(2)求()f x 在区间[],0π-上的最大值和最小值以及取得最大值和最小值时自变量x 的值.注:如果选择多个条件分别解答,按第一个解答计分.23.已知函数()sin(2)02f x x πϕϕ⎛⎫=+<< ⎪⎝⎭,函数12y f x π⎛⎫=- ⎪⎝⎭为奇函数. (1)求函数()f x 的单调递增区间; (2)将函数()y f x =的图象向右平移6π个单位,然后将所得的图象上各点的横坐标缩小到原来的12倍(纵坐标不变),得到函数()y g x =的图象,证明:当0,4x π⎡⎤∈⎢⎥⎣⎦时,22()()10g x g x --≤.24.已知函数()()sin f x A x =+ωϕ(0A >,0>ω,2πϕ<)的部分图象如图所示.(1)求函数()f x 的解析式; (2)将函数()f x 的图象向右平移3π个单位长度,再将得到的图象上各点的横坐标缩短为原来的12,纵坐标不变,得到函数()g x 的图象,若函数()g x 在[]0,m 上单调递增,当实数m 取最大值时,求函数()f x 在[]0,m 上的最大值.25.函数()sin()f x A x ωϕ=+(0,0,[0,2))A ωϕπ>>∈的图象如图所示:(1)求()f x 的解析式; (2)()f x 向左平移12π个单位后得到函数()g x ,求()g x 的单调递减区间;(3)若,2x ππ⎡⎤∈-⎢⎥⎣⎦且()32f x ≥,求x 的取值范围.26.已知函数()2sin 1f x x =-.(1)求函数f (x )的最大值,并求此时x 的值; (2)写出()0f x >的解集.【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【分析】根据图象得到函数()f x 解析式,将函数()f x 的图象向左平移3π个单位长度后得到()y g x =的图象,可得()y g x =解析式,分别根据正弦函数的奇偶性、单调性、周期性与对称性,对选项中的结论判断,从而可得结论. 【详解】 由图象可知3A =,33253441234ππππω⎛⎫=⋅=--= ⎪⎝⎭T , ∴2ω=,则()3sin(2)f x x ϕ=+. 将点5,312π⎛⎫⎪⎝⎭的坐标代入()3sin(2)f x x ϕ=+中, 整理得5sin 2112πϕ⎛⎫⨯+= ⎪⎝⎭, ∴522,Z 122k k ππϕπ⨯+=+∈, 即2,Z 3k k πϕπ=-∈;||2ϕπ<, ∴3πϕ=-,∴()3sin 23f x x π⎛⎫=-⎪⎝⎭. ∵将函数()f x 的图象向左平移3π个单位长度后得到()y g x =的图象, ∴()3sin 23sin 2,333g x x x x R πππ⎡⎤⎛⎫⎛⎫=+-=+∈ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦. ()()3sin 23sin 233g x x x g x ππ⎛⎫⎛⎫-=-+=--≠- ⎪ ⎪⎝⎭⎝⎭,∴()g x 既不是奇函数也不是偶函数, 故A 错误;∴()g x 的最小正周期22T ππ==, 故B 不正确. 令2,32πππ+=+∈x k k Z ,解得,122k x k Z ππ=+∈, 则函数()g x 图像的对称轴为直线,122k x k Z ππ=+∈. 故C 错误; 由222,232k x k k πππππ-++∈Z ,可得5,1212k x k k ππππ-+∈Z ,∴函数()g x 的单调递增区间为5,,1212k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦. 故D 正确; 故选:D. 【点睛】关键点睛:本题主要考查三角函数的图象与性质,熟记正弦函数的奇偶性、单调区间、最小正周期与对称轴是解决本题的关键.2.A解析:A 【分析】根据题意有()5sin 226g x x ϕπ⎛⎫=+ ⎪⎝⎭-,若()g x 为偶函数则52()62k k Z πππϕ-=+∈,结合0ϕ>可得出答案. 【详解】 解:由题意可得()()55()sin 2sin 2266g x f x x x πϕϕϕπ⎛⎫⎛⎫=+=+-=+ -⎪⎪⎝⎭⎝⎭因为()g x 为偶函数,则52()62k k Z πππϕ-=+∈,即2()32k k Z ππϕ=+∈ 因为0ϕ>,所以当1k =-时ϕ取得最小值6π. 故选:A. 【点睛】应用函数奇偶性可解决的四类问题及解题方法(1)求函数值:将待求值利用奇偶性转化为已知区间上的函数值求解;(2)求解析式:先将待求区间上的自变量转化到已知区间上,再利用奇偶性求解,或充分利用奇偶性构造关于()f x 的方程(组),从而得到()f x 的解析式;(3)求函数解析式中参数的值:利用待定系数法求解,根据()()0f x f x ±-=得到关于待求参数的恒等式,由系数的对等性得参数的值或方程(组),进而得出参数的值; (4)画函数图象和判断单调性:利用奇偶性可画出另一对称区间上的图象及判断另一区间上的单调性.3.D解析:D 【分析】由周期求出ω,由五点法作图求出ϕ的值,可得()f x 的解析式,再根据函数sin()y A x ωϕ=+的图象变换规律,得出结论.【详解】根据函数()sin()(0f x x ωϕω=+>,||)2πϕ<的部分函数图象,1274123πππω⋅=-,2ω∴=. 再根据五点法作图,23πϕπ⨯+=,3πϕ∴=,()sin(2)3f x x π=+.将函数()f x 的图象先向右平移3π个单位长度,可得sin(2)3y x π=-的图象.然后向上平移1个单位长度,得到函数()g x 的解析式为()sin(2)13g x x π=-+,故选:D 【点睛】关键点睛:解答本题的关键在于准确地根据三角函数的图象求出三角函数sin()y A x ωϕ=+的解析式,一般根据周期求出ω的值,根据最值求出A 的值,根据最值点求出ϕ的值.4.B解析:B 【分析】 先由点,024A π⎛⎫⎪⎝⎭在函数()()()cos 0,0f x x ωϕωϕπ=+><<的图象上,直线6x π=是函数()f x 图象的一条对称轴,求出ω的范围,再由()f x 在区间,63ππ⎛⎫⎪⎝⎭内单调求出φ.【详解】 由题意得:62484T πππ-=≥, 得1248ππω⨯≤,所以ω4≥. 又()f x 在区间,63ππ⎛⎫⎪⎝⎭内单调,所以3662T πππ-=≤,得1226ππω⨯≥,所以ω6≤所以ω=4或5或6.当ω=4时, ()()cos 4f x x ϕ=+,有cos 402424460f k ππϕπϕπϕπ⎧⎛⎫⎛⎫=⨯+= ⎪ ⎪⎪⎝⎭⎝⎭⎪⎪⨯+=⎨⎪<<⎪⎪⎩解得3πϕ=.当ω=5时, ()()cos 4f x x ϕ=+,有cos 502424560f k ππϕπϕπϕπ⎧⎛⎫⎛⎫=⨯+= ⎪⎪⎪⎝⎭⎝⎭⎪⎪⨯+=⎨⎪<<⎪⎪⎩无解. 当ω=6时, ()()cos 4f x x ϕ=+,有cos 602424660f k ππϕπϕπϕπ⎧⎛⎫⎛⎫=⨯+= ⎪ ⎪⎪⎝⎭⎝⎭⎪⎪⨯+=⎨⎪<<⎪⎪⎩无解.综上: 3πϕ=.故选:B 【点睛】求三角函数解析式的方法: (1)求A 通常用最大值或最小值; (2)求ω通常用周期;(3)求φ通常利用函数上的点带入即可求解.5.B解析:B 【分析】先建立坐标系,从点0P 开始计时,建立三角函数模型()0sin h A t b ωϕ=++,通过题中条件求出参数0,,,A b ωϕ,再利用函数解析式对选项依次判断正误即可. 【详解】以水面所在直线为t 轴,过O 作OO t '⊥轴,建立坐标系如图:设点P 距离水面的高度h (单位:m )与时间t (单位:s )的函数解析式为()0sin h A t b ωϕ=++.依题意可知, 2.4OO '=, 2.41sin 4.82OPO '∠==,6OPO π'∠=. 高度h 最大值为2.4 4.87.2+=,最小值为2.4 4.8 2.4-=-,故()()7.2 2.47.2 2.44.8, 2.422A b --+-====, 周期60T =s ,则230T ππω==, 0t =时,06πϕ=-,故函数解析式为 4.8sin 2.4306h t ππ⎛⎫=-+⎪⎝⎭,故B 正确;点P 到达最高点时 4.8sin 2.47.2306h t ππ⎛⎫=-+= ⎪⎝⎭,即sin 1306t ππ⎛⎫-= ⎪⎝⎭,故2,3062t k k Z ππππ-=+∈,即2060,t k k Z =+∈,又0t ≥,故第一次到达最高点时,0,20k t ==s ,故A 错误;在筒车转动的一圈内,点P 距离水面的高度不低于4.8m ,即4.8sin 2.4 4.8306h t ππ⎛⎫=-+≥ ⎪⎝⎭,得1sin 3062t ππ⎛⎫-≥ ⎪⎝⎭,故563066t ππππ≤-≤,解得1030t ≤≤,故共有20 s 时间,C 错误;当筒车转动50s 时,即50t =代入 4.8sin 2.4306h t ππ⎛⎫=-+⎪⎝⎭得,34.8sin 50 2.4 4.8sin 2.4 2.43062h πππ⎛⎫=⨯-+=+=- ⎪⎝⎭,故点P 在水面下方,距离水面2.4m ,故D 错误. 故选:B. 【点睛】 关键点点睛:本题解题关键在于按照题意,建立三角函数模型()0sin h A t b ωϕ=++,并解出解析式,才能解决选项中的实际问题,突破难点.6.A解析:A 【分析】由最大值点和对称中心的坐标可以求出()f x 的解析式,利用三角函数的性质,整体代换得出该复合函数的单调增区间. 【详解】图像上相邻的一个最大值点与对称中心分别为2,39π⎛⎫⎪⎝⎭,,018π⎛⎫⎪⎝⎭, 3A ∴=,0b =且124918T ππ=-,可得23T π=, 23Tπω∴==, 3sin(3)y x ϕ∴=+ 将2,39π⎛⎫⎪⎝⎭代入可得3sin(3)3y x ϕ=+=, 可得22,32k k Z ππϕπ+=+∈,且2πϕ<, 6πϕ∴=-,可得()3sin(3)6f x x π=-,令6232,22k x k k Z πππππ-+≤-≤+∈,可得222+9393k x k ππππ-≤≤, 故选:A. 【点睛】方法点睛:根据图像求函数()sin()f x A x k ωϕ=++的解析式,根据最高点和对称中心的纵坐标可求出A 和k ,根据横坐标可求出周期T ,进而求出ω.求该函数的单调区间时,用整体代换的思想,借助正弦函数的单调区间,用解不等式的方法求复合函数的单调区间.7.B解析:B 【分析】利用函数()0f π=排除两个选项,再由奇偶性排除一个后可得正确选项. 【详解】由图象知()0f π=,经验证只有AB 满足,C 中()cos 2f ππππ==,D 中()f ππ=,排除CD ,A 中函数满足()sin(2)sin 2()f x x x x x f x -=--==为偶函数,B 中函数满足()sin(2)sin 2()f x x x x x f x -=--=-=-为奇函数,而图象关于原点对称,函数为奇函数,排除A ,选B . 故选:B . 【点睛】思路点睛:由函数图象选择解析式可从以下方面入手:(1)从图象的左右位置,观察函数的定义域;从图象的上下位置,观察函数的值域; (2)从图象的变化趋势观察函数的单调性; (3)从图象的对称性观察函数的奇偶性; (4)从图象的特殊点,排除不合要求的解析式..8.C解析:C 【分析】根据弧度制与角度制的关系求解即可. 【详解】因为180π︒=弧度, 所以156********4ππ︒=⨯=, 故选:C9.D解析:D 【分析】根据各函数的特征如函数值的正负,单调性、奇偶性,定义域、值域等进行判断. 【详解】左边第一个图象中0x <时,0y <,只有③满足,此时只有D 可选,实际上,左边第二个图象关于y 轴对称,是偶函数,只有②满足,而0x >时,10y x x=+>恒成立,只有最右边的图象满足,由此也可得顺序是③②①④,选D . 故选:D . 【点睛】思路点睛:本题考查由函数解析式选择函数图象,解题时可两者结合,由函数解析式和图象分别确定函数的性质,如奇偶性、单调性、函数值的正负,特殊的函数值,变化趋势等等,两者对照可得结论.10.D解析:D 【分析】结合图象,依次求得,,A ωϕ的值. 【详解】 由图象可知2A =,2,,22362T T πππππωω⎛⎫=--==== ⎪⎝⎭,所以()()2sin 2f x x ϕ=+,依题意0ϕπ≤≤,则2333πππϕ-≤-≤, 2sin 0,0,6333f ππππϕϕϕ⎛⎫⎛⎫-=-+=-+== ⎪ ⎪⎝⎭⎝⎭,所以2n 2)3(si f x x π⎛⎫=+ ⎪⎝⎭.故选:D. 【点睛】方法点睛:根据三角函数()()sin f x A x b ωϕ=++或的部分图象求函数解析式的方法: (1)求A 、()()max min:2f x f x b A -=,()()max min2f x f x b +=;(2)求出函数的最小正周期T ,进而得出2Tπω=; (3)取特殊点代入函数可求得ϕ的值.11.C解析:C 【分析】由周期求出ω,然后由正弦函数的性质判断. 【详解】函数()2sin (04)6f x x πωω⎛⎫=-<< ⎪⎝⎭的周期为π,所以22πωπ==,A 错; 12x π=时,206x π-=,12x π=不是对称轴,B 错;3x π=时,226x ππ-=,即23f π⎛⎫= ⎪⎝⎭为最大值,因此()3f f x π⎛⎫⎪⎝⎭正确,C 正确; 0,2x π⎛⎫∈ ⎪⎝⎭时,52,666x πππ⎛⎫-∈- ⎪⎝⎭,而sin y x =在5,66ππ⎛⎫- ⎪⎝⎭上不单调,D 错; 故选:C . 【点睛】方法点睛:本题考查三角函数的性质,对函数()sin()f x A x ωϕ=+,掌握五点法是解题关键.解题时可由x 的值或范围求得x ωϕ+的值或范围,然后结合正弦函数性质判断.12.C解析:C 【分析】首先根据题中所给的函数图象,从最值、周期和特殊点着手将解析式确定,之后结合函数的性质对选项逐一分析,得到结果. 【详解】根据图象得到:2A =,311341264T πππ=-=,所以T π=, 所以2ππω=,解得2ω=,所以()()2sin 2f x x ϕ=+.将点,26π⎛⎫ ⎪⎝⎭代入,得到2sin 23πϕ⎛⎫+= ⎪⎝⎭,则()232k k Z ππϕπ+=+∈,得()26k k Z πϕπ=+∈,又2πϕ<,所以6π=ϕ, 所以()2sin 26f x x π⎛⎫=+ ⎪⎝⎭. 对于A ,20126ππ⎛⎫⨯-+= ⎪⎝⎭,则函数()f x 关于,012π⎛⎫- ⎪⎝⎭对称,故A 正确; 对于B ,函数的周期22T ππ==,故B 正确; 对于C ,当0,6x π⎛⎫∈ ⎪⎝⎭时,2,662x πππ⎛⎫+∈ ⎪⎝⎭,此时函数()f x 为增函数,故C 错误; 对于D ,当0,12x π⎡⎤∈⎢⎥⎣⎦时,2,663x πππ⎡⎤+∈⎢⎥⎣⎦,则1sin 262x π⎡⎛⎫+∈⎢ ⎪⎝⎭⎣⎦,2sin 26x π⎛⎫⎡+∈ ⎪⎣⎝⎭,故()f x 在0,12π⎡⎤⎢⎥⎣⎦D 正确.故选:C . 【点睛】该题考查的是有关三角函数的问题,涉及到的知识点有根据图象确定函数解析式,正弦型函数的相关性质,属于简单题目.二、填空题13.①②③【分析】利用正弦型函数的对称性可判断①④的正误;利用正弦型函数的周期公式可判断②的正误;利用正弦型函数的单调性可判断③的正误【详解】对于①所以的图象关于直线对称①正确;对于②的最小正周期是②正解析:①②③ 【分析】利用正弦型函数的对称性可判断①④的正误;利用正弦型函数的周期公式可判断②的正误;利用正弦型函数的单调性可判断③的正误. 【详解】 对于①,212sin 232243f πππ⎡⎤⎛⎫⎛⎫-=⨯--=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦, 所以,()y f x =的图象关于直线2x π=-对称,①正确; 对于②,()f x 的最小正周期是2412T ππ==,②正确; 对于③,当23x ππ≤≤时,3154244x πππ≤-≤, 所以,函数()y f x =在区间[]2,3ππ上是减函数,③正确; 对于④,由①可知,④错误. 故答案为:①②③. 【点睛】方法点睛:求较为复杂的三角函数的单调区间时,首先化简成()sin y A ωx φ=+形式,再求()sin y A ωx φ=+的单调区间,只需把x ωϕ+看作一个整体代入sin y x =的相应单调区间内即可,注意要先把ω化为正数.14.①③④【分析】由函数图像的变换可得结合余弦函数的周期性单调性对称轴等即可判断选项得出答案【详解】的最小正周期为选项A 正确;当时时故在上有增有减选项B 错误;故不是图象的一条对称轴选项C 正确;当时且当即解析:①③④ 【分析】由函数图像的变换可得()cos 23π⎛⎫=+ ⎪⎝⎭g x x ,结合余弦函数的周期性、单调性、对称轴等即可判断选项,得出答案. 【详解】()cos 2cos 28123g x x x πππ⎡⎤⎛⎫⎛⎫=++=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦.()g x 的最小正周期为π,选项A 正确;当0,2x π⎡⎤∈⎢⎥⎣⎦时,42,333x πππ⎡⎤+∈⎢⎥⎣⎦ 时,故()g x 在0,2π⎡⎤⎢⎥⎣⎦上有增有减,选项B 错误;012g π⎛⎫= ⎪⎝⎭,故12x π=不是()g x 图象的一条对称轴,选项C 正确;当,66x ππ⎡⎤∈-⎢⎥⎣⎦时,220,33x ππ⎡⎤+∈⎢⎥⎣⎦,且当2233x ππ+=,即6x π=时,()g x 取最小值12-,D 正确. 故答案为:①③④. 【点睛】本题考查了三角函数图像的变换、余弦函数的周期性、单调性和对称轴等基本知识,考查了运算求解能力和逻辑推理能力,属于一般题目.15.【分析】由点的坐标可得的值由图象可求得函数的图象可得该函数的最小正周期可求得的值再将点的坐标代入函数的解析式结合的取值范围可求得的值可得出函数的解析式【详解】由于函数的图象的一个最高点为则由图象可知解析:ππ3sin 36x ⎛⎫- ⎪⎝⎭【分析】由点A 的坐标可得M 的值,由图象可求得函数()y f x =的图象可得该函数的最小正周期,可求得ω的值,再将点A 的坐标代入函数()y f x =的解析式,结合ϕ的取值范围可求得ϕ的值,可得出函数()y f x =的解析式. 【详解】由于函数()y f x =的图象的一个最高点为()2,3A ,则3M =, 由图象可知,函数()y f x =的最小正周期为452632T ⎛⎫=+= ⎪⎝⎭, 23T ππω∴==,()3sin 3x f x πϕ⎛⎫∴=+⎪⎝⎭, 将点A 的坐标代入函数()y f x =的解析式得()223sin 33f πϕ⎛⎫=+=⎪⎝⎭,可得2sin 13πϕ⎛⎫+= ⎪⎝⎭, 22ππϕ-<<,则27636πππϕ<+<,232ππϕ∴+=,解得6πϕ=-,()3sin 36x f x ππ⎛⎫∴=- ⎪⎝⎭故答案为:()3sin 36x f x ππ⎛⎫=- ⎪⎝⎭ 【点睛】本题考查利用三角函数图象求解函数解析式,考查计算能力,属于中等题.16.10【分析】由函数与直线的图象可知它们都关于点中心对称再由向量的加法运算得最后求得向量的模【详解】由函数与直线的图象可知它们都关于点中心对称所以【点睛】本题以三角函数和直线的中心对称为背景与平面向量解析:10 【分析】由函数()4cos 2f x x π⎛⎫=⎪⎝⎭与直线()1g x x =-的图象可知,它们都关于点3(1,0)A 中心对称,再由向量的加法运算得1253...5PA PA PA PA +++=,最后求得向量的模. 【详解】由函数()4cos 2f x x π⎛⎫=⎪⎝⎭与直线()1g x x =-的图象可知, 它们都关于点3(1,0)A 中心对称,所以221253...5||5(01)(30)10PA PA PA PA +++==-+-=. 【点睛】本题以三角函数和直线的中心对称为背景,与平面向量进行交会,考查运用数形结合思想解决问题的能力.17.【分析】取中点连结交于点交于点连结设推导出和从而得出文化景观区域面积利用三角函数的性质解出面积最大值【详解】取中点连结交于点交于点连结设则文化景观区域面积:当即时文化景观区域面积取得最大值为故答案为 解析:()40023-【分析】取DC 中点M ,连结OM ,交EF 于点P ,交CD 于点N ,连结OD ,设DOM ϕ∠=,推导出DC 和CF ,从而得出文化景观区域面积,利用三角函数的性质,解出面积最大值. 【详解】取DC 中点M ,连结OM ,交EF 于点P ,交CD 于点N ,连结OD ,设DOM ϕ∠=,则20sin DN CN ϕ==,40sin DC ϕ∴=,20cos 20cos 203tan 30PFCF DE PN ON OP ϕϕϕ===-=-=-︒,∴文化景观区域面积:()4020203EFCD S sin cos sin ϕϕϕ=-矩形400sin 2cos 2)ϕϕ=--800sin(2)3πϕ=+-∴当232ππϕ+=,即12πϕ=时,文化景观区域面积取得最大值为2400(2)m -.故答案为:400(2-. 【点睛】本题考查文化景观区域面积的最大值的求法,考查扇形、三角函数恒等变换等基础知识,考查运算求解能力,是中档题.18.【分析】求出平移后的函数解析式由新函数图象过原点得出【详解】将函数的图象向左平移个单位长度得解析式为它的图象关于原点对称则即故答案为:【点睛】本题考查三角函数的图象平移变换考查三角函数的对称性注意性解析:【分析】求出平移后的函数解析式,由新函数图象过原点得出a , 【详解】将函数()sin 23cos2f x a x x =+的图象向左平移6π个单位长度,得解析式为()sin 23cos 266g x a x x ππ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭,它的图象关于原点对称,则(0)0g =,即sin3cos033a ππ+=,a =故答案为:. 【点睛】本题考查三角函数的图象平移变换,考查三角函数的对称性,注意性质:函数()sin()f x A x ωϕ=+的图象与x 轴的交点是其对称中心,它的对称中心在函数图象上.19.【分析】利用任意性与存在性原命题可转化为有且仅有一个解然后根据三角函数的性质和图像求解即可【详解】由则存在唯一的实数使即有且仅有一个解作函数图像与直线当两个图像只有一个交点时由图可知故实数的最大值是解析:34π【分析】利用任意性与存在性原命题可转化为()1,,22f k k β⎛=∈ ⎝⎭有且仅有一个解,然后根据三角函数的性质和图像求解即可. 【详解】由()sin f x x =,(,)46αππ∈--,则()21,22f α⎛⎫∈-- ⎪ ⎪⎝⎭,存在唯一的实数(0,)m β∈,使()()0f f αβ+=, 即()12,,22f k k β⎛⎫=∈ ⎪ ⎪⎝⎭有且仅有一个解,作函数图像()y f β=与直线12,,22y k k ⎛=∈ ⎝⎭,当两个图像只有一个交点时,由图可知,344m ππ<≤, 故实数m 的最大值是34π. 故答案为:34π 【点睛】本题主要考查了三角函数的图像与性质,属于较为基础题.20.【分析】计算导数然后构造函数利用导数研究该函数的单调性进而判断原函数的单调性可得结果【详解】由题可知:令则由所以所以则在递减所以又则所以函数在递增所以所以故答案为:【点睛】本题考查函数在区间的最值难 解析:433π-【分析】计算导数,然后构造函数()cos sin h x x x x =+,利用导数研究该函数的单调性进而判断原函数的单调性,可得结果. 【详解】 由题可知:'2cos si ()cos co n s f x x xxx x =-+ 令()cos sin h x x x x =+,则()'sin sin cos cos h x x x x x x x =-++=由23,34x ππ⎡⎤∈⎢⎥⎣⎦,所以cos 0x < 所以()'0h x <,则()h x 在23,34x ππ⎡⎤∈⎢⎥⎣⎦递减 所以()min 3333cos sin 4444h x h ππππ⎛⎫==+⎪⎝⎭()min 31024h x π⎫=->⎪⎝⎭,又cos 0x < 则'2cos sin ()cos 0cos f x x x x xx=-+> 所以函数()f x 在23,34x ππ⎡⎤∈⎢⎥⎣⎦递增 所以min 2223()sin 233cos 3f x f ππππ⎛⎫==- ⎪⎝⎭所以min 243()132f x ππ==--故答案为:43π- 【点睛】本题考查函数在区间的最值,难点在于构造函数二次求导,注意细节,需要通过判断函数在区间的单调情况才能代值计算,考查对问题的分析能力,属中档题.三、解答题21.(1)ω=2,6π=ϕ;(2)5,6ππ⎡⎤--⎢⎥⎣⎦,,36ππ⎡⎤-⎢⎥⎣⎦,2π,π3;.(3)最小值为12,最大值为1716. 【分析】(1)先由函数图象,先得到周期,求出ω,再由最大值点,求出ϕ;(2)由(1)的结果,确定函数解析式,利用正弦函数的单调性,求出函数增区间,再由给定区间,即可得出结果;(3)先化简得到()sin 23x x πϕ⎛⎫=- ⎪⎝⎭,根据函数()g x 在,62ππ⎡⎤⎢⎥⎣⎦上存在零点,得到222sin 23sin 2133ππa x x ⎛⎫⎛⎫=--+-+ ⎪ ⎪⎝⎭⎝⎭在,62ππ⎡⎤⎢⎥⎣⎦上有解,令sin 23t x π⎛⎫=- ⎪⎝⎭,由正弦函数性质,求出,62x ππ⎡⎤⎢⎥⎣⎦时,[]0,1t ∈,再结合二次函数的性质,得到2231y t t =-++的范围,即可得出结果.【详解】(1)由图象可知:22362T πππ=-=,T π=,则22T πω==,又22,62k k Z ππϕπ⨯+=+∈得26k πϕπ=+,又2πϕ<,所以6π=ϕ,(2)()sin 26f x x π⎛⎫+⎝=⎪⎭,由222,262k x k k Z πππππ-≤+≤+∈得,,36k x k k Z ππππ-≤≤+∈,令1k =-,得4536x ππ-≤≤-,因x ππ-≤≤,则56x ππ-≤≤-, 令0k =,得36x ππ-≤≤,令1k =,得2736x ππ≤≤,因x ππ-≤≤,则2ππ3x ,所以()f x 在[,]-ππ上的单调递增区间为5,6ππ⎡⎤--⎢⎥⎣⎦,,36ππ⎡⎤-⎢⎥⎣⎦,2π,π3;. (3)()sin 2sin 21212126126x f x f x x x ππππππϕ⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=--+=-+-++ ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦1sin 2sin 2sin 22sin 2323x x x x x ππ⎛⎫⎛⎫=-+=-=- ⎪ ⎪⎝⎭⎝⎭,2()2sin 23sin 22133g x x x a ππ⎛⎫⎛⎫=---+- ⎪ ⎪⎝⎭⎝⎭,由函数()g x 在,62ππ⎡⎤⎢⎥⎣⎦上存在零点,则222sin 23sin 2133ππa x x ⎛⎫⎛⎫=--+-+ ⎪ ⎪⎝⎭⎝⎭在,62ππ⎡⎤⎢⎥⎣⎦上有解, 令sin 23t x π⎛⎫=-⎪⎝⎭,由,62x ππ⎡⎤∈⎢⎥⎣⎦,则220,33x ππ⎡⎤-∈⎢⎥⎣⎦,即[]0,1t ∈,则223171723121,488y t t t ⎛⎫⎡⎤=-++=--+∈ ⎪⎢⎥⎝⎭⎣⎦,所以17128a ≤≤,即117216a ≤≤, 故a 的最小值为12,最大值为1716. 【点睛】 思路点睛:求解含三角函数的二次式在给定区间上的最值时,一般需要用换元法,将三角函数换成t 来表示,得到关于t 的二次函数,由三角函数的性质,得到t 的范围,再结合二次函数的性质,即可求解.22.(1)见解析(2)见解析 【分析】(1)由题意可知2,3A πϕ==,选择条件①,由正弦函数的对称性求出ω,进而得出解析式;选择条件②,由正弦函数的对称性求出ω,进而得出解析式;选择条件③,由正弦函数的性质求出ω,进而得出解析式;(2)由[],0x π∈-,求出x ωϕ+的范围,再结合正弦函数的性质求出最值. 【详解】(1)由题意可知2,3A πϕ==选择条件①因为()f x 的图象关于直线3x π=对称,所以332k πππωπ+=+,解得13,2k k Z ω=+∈ 由21321302kk k Z ππ⎧≥⎪+⎪⎪⎨⎪+>⎪⎪∈⎩,解得0k =,即12ω=故1()2sin 23f x x π⎛⎫=+ ⎪⎝⎭选择条件②因为()f x 的图象关于点,06π⎛⎫- ⎪⎝⎭对称,所以,26,63k k k Z ππωπω-+==-∈由226260k k k Zππ⎧≥⎪-⎪⎨->⎪⎪∈⎩,解得0k =,即2ω=故()2sin 23f x x π⎛⎫=+ ⎪⎝⎭选择条件③因为()f x 的图象上最高点中,有一个点的横坐标为6π,所以2,632k k Z πππωπ+=+∈,解得112,k k Z ω=+∈由21121120kk k Zππ⎧≥⎪+⎪⎨+>⎪⎪∈⎩,解得0k =,即1ω= 故()2sin 3f x x π⎛⎫=+ ⎪⎝⎭(2)选择条件①1,2363x πππ⎡⎤+∈-⎢⎥⎣⎦当1236x ππ+=-,即x π=-时,min ()2sin 16f x π⎛⎫=-=- ⎪⎝⎭当1233x ππ+=,即0x =时,max ()2sin 3f x π== 选择条件②52,333x πππ⎡⎤+∈-⎢⎥⎣⎦当5233x ππ+=-或233x ππ+=,即x π=-或0x =时,max ()2sin 3f x π==当232x ππ+=-,即512x π=-时,min ()2sin 22f x π⎛⎫=-=- ⎪⎝⎭选择条件③2,333x πππ⎡⎤+∈-⎢⎥⎣⎦当33x ππ+=,即0x =时,max ()2sin3f x π==当32x ππ+=-,即65x π=-时,min ()2sin 22f x π⎛⎫=-=- ⎪⎝⎭【点睛】关键点睛:解决本题的关键是将正弦型函数的问题转化为正弦函数的性质进行求解,利用已知知识解决未知问题.23.(1),(Z)36k k k ππππ⎡⎤-+∈⎢⎥⎣⎦;(2)证明见解析. 【分析】(1)根据sin 2126f x x ππϕ⎛⎫⎛⎫-=+- ⎪ ⎪⎝⎭⎝⎭为奇函数可得6π=ϕ,则()sin 26f x x π⎛⎫=+ ⎪⎝⎭,再由222,Z 262k x k k πππππ-≤+≤+∈可得答案;(2)根据三角函数图象的变换规律可得()sin 46g x x π⎛⎫=-⎪⎝⎭,由0,4x π⎡⎤∈⎢⎥⎣⎦,求出1(),12g x ⎡⎤=-⎢⎥⎣⎦,进而可得结论.【详解】(1)由题意知:sin 2126y f x x ππϕ⎛⎫⎛⎫=-=+- ⎪ ⎪⎝⎭⎝⎭为奇函数 所以()6k k Z πϕπ-=∈,(Z)6k k πϕπ=+∈因为02πϕ<<,所以0k =,6π=ϕ 所以()sin 26f x x π⎛⎫=+ ⎪⎝⎭由222,Z 262k x k k πππππ-≤+≤+∈,解得:,Z 36k x k k ππππ-≤≤+∈, 所以()f x 的单调递增区间为,(Z)36k k k ππππ⎡⎤-+∈⎢⎥⎣⎦;(2)由题知:将()y f x =的图象向右平移6π个单位得sin 266y x ππ⎡⎤⎛⎫=-+ ⎪⎢⎥⎝⎭⎣⎦, 即sin 26y x π⎛⎫=-⎪⎝⎭,再将图象上各点的横坐标缩小到原来的12倍, 得()sin 46g x x π⎛⎫=- ⎪⎝⎭,因为0,4x π⎡⎤∈⎢⎥⎣⎦,所以54,666x πππ⎡⎤-∈-⎢⎥⎣⎦, 因此1()sin 4,162g x x π⎛⎫⎡⎤=-∈- ⎪⎢⎥⎝⎭⎣⎦, 则2()10g x +≥且()10g x -≤,所以22()()1[2()1][()1]0g x g x g x g x --=+-≤ 【点睛】方法点睛:函数sin()y A x ωϕ=+()0,0A ω>>的单调区间的求法:,把x ωϕ+看作是一个整体,由22k x ππωϕ+≤+≤()322k k Z ππ+∈求得函数的减区间;2222k x k πππωϕπ-+≤+≤+求得增区间.24.(1) ())3f x x π=+;【分析】(1)根据函数()f x 的部分图象可得A 及周期T ,再根据周期公式可求出ω,由五点法作图的第三个点可求出ϕ的值,从而可得函数()f x 的解析式;(2)根据平移变换和伸缩变换的规律,可求出()g x 的解析式,再根据函数()g x 在[]0,m 上单调递增,可求出m 的最大值,再根据正弦函数的图象与性质,即可求出函数()f x 在[0,]m 上的最大值.【详解】(1)由已知可得A =52()63πT ππ=-=,所以22=πωT=,所以())f x x ϕ=+,根据五点法作图可得23πϕπ⨯+=,所以=3πϕ,所以())3f x x π=+(2) 将函数()f x 的图象向右平移3π个单位长度,可得22333πππy x x ⎡⎤⎛⎫⎛⎫=-+=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦的图象,再将得到的图象上各点的横坐标缩短为原来的12,纵坐标不变,得到函数()43g x x π⎛⎫=- ⎪⎝⎭的图象,因为函数()g x 在[]0,m 上单调递增,所以432m ππ-≤,所以524m π≤,m 的最大值为524π,由50,24x π⎡⎤∈⎢⎥⎣⎦,可得32,334x πππ⎡⎤+∈⎢⎥⎣⎦,所以当2=32x +ππ时,()f x .故函数()f x 在[]0,m .【点睛】方法点睛:确定()sin()(0,0)f x A x B A ωϕω=++>>的解析式的步骤: (1)求A ,B ,确定函数的最大值M 和最小值m ,则2M mA ,2M mB +=; (2)求ω,确定函数的周期T ,则2Tπω=; (3)求ϕ,常用方法有以下2种方法:①代入法:把图象上的一个已知点代入(此时要注意该点在上升区间上还是在下降区间上)或把图象的最高点或最低点代入;②五点法:确定ϕ值时,往往以寻找“五点法”中的特殊点作为突破口.25.(1)()23f x x π⎛⎫=+⎪⎝⎭;(2),,2πππ⎡⎤+∈⎢⎥⎣⎦k k k Z ;(3){},66πππ⎡⎤-⋃⎢⎥⎣⎦. 【分析】(1)利用题中图象可知A =,44T π=,结合周期公式求得=2ω,再由3x π=代入计算得=3πϕ即得解析式;(2)根据三角函数平移的方法求得()g x ,再利用整体代入法求单调递减区间即可;(3)先由()32fx ≥可得sin 23x π⎛⎫+≥ ⎪⎝⎭,再由,2x ππ⎡⎤∈-⎢⎥⎣⎦得到23x π+的前提范围,结合正弦函数性质得到不等式中23x π+的范围,再计算x 范围即可.【详解】解:(1)由题中图象可知:A =,741234T πππ=-=, 2T ππω∴==,即2ω=,又由图象知,3x π=时,223k πϕππ⋅+=+,即23k πϕπ=+,k Z ∈,又02ϕπ≤<,∴=3πϕ,()23f x x π⎛⎫∴=+ ⎪⎝⎭;(2)()f x 向左平移12π个单位后得到函数()g x ,故()2221232g x x x x πππ⎡⎤⎛⎫⎛⎫=++=+= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,由余弦函数性质知,令222,k x k k Z πππ≤≤+∈,得减区间,,2πππ⎡⎤+∈⎢⎥⎣⎦k k k Z , ∴()g x 的单调递减区间为,,2πππ⎡⎤+∈⎢⎥⎣⎦k k k Z ;(3)由题意知:()3232f x x π⎛⎫=+≥ ⎪⎝⎭,即sin 232x π⎛⎫+≥ ⎪⎝⎭, 由,2x ππ⎡⎤∈-⎢⎥⎣⎦,知[]0,x π∈,2,2333x ππππ⎡⎤+∈+⎢⎥⎣⎦,由正弦函数图象性质可知,22333x πππ≤+≤或2233x πππ+=+ 即06x π≤≤或x =π,又,2x ππ⎡⎤∈-⎢⎥⎣⎦,得x 的取值范围为{},66x πππ⎡⎤∈-⋃⎢⎥⎣⎦.【点睛】 方法点睛:求三角函数()()sin f x A x b ωϕ=++性质问题时,通常利用整体代入法求解单调性、对称性,最值等性质,或者整体法求三角不等式的解. 26.(1)最大值1,2,2x k k Z ππ=+∈;(2)5{|22,}66x k x k k Z ππππ+≤≤+∈. 【分析】(1)当sin 1x =时,函数取最大值得解; (2)根据三角函数的图象解不等式得解集. 【详解】(1)当sin 1x =即2,2x k k Z ππ=+∈时,()2111max f x =⨯-=;(2)由题得1sin 2x >,所以不等式的解集为5{|22,}66x k x k k Z ππππ+≤≤+∈. 【点睛】关键点睛:解答这类题的关键是熟练掌握三角函数的图象和性质,再灵活利用其解题.。
必修四第一章三角函数测试题(2套)(含答案)

11.函数 是( )
A. 上是增函数B. 上是减函数
C. 上是减函数D. 上是减函数
12.函数 的定义域是()
A. B.
C. D.
二、填空题:
13.函数 的最小值是.
14 与 终边相同的最小正角是_______________
15.已知 则 .
16 若集合 , ,
一、选择题:
1.已知A={第一象限角},B={锐角},C={小于90°的角},那么A、B、C关系是()
A.B=A∩CB.B∪C=CC.A CD.A=B=C
2 等于()
A B C D
3.已知 的值为( )
A.-2B.2C. D.-
4.下列函数中,最小正周期为π的偶函数是( )
=sin2x=cos C .sin2x+cos2xD. y=
5 若角 的终边上有一点 ,则 的值是( )
A B C D
6. 要得到函数y=cos( )的图象,只需将y=sin 的图象( )
A.向左平移 个单位B.同右平移 个单位
C.向左平移 个单位D.向右平移 个单位
7.若函数y=f(x)的图象上每一点的纵坐标保持不变,横坐标伸长到原来的2倍,再将整个图象沿轴
二、填空题
13、 14 3 15.略 16.答案:
三、解答题:
17.【解】: ,而 ,则
得 ,则 ,
18.【解】∵
(1)∴ 函数y的最大值为2,最小值为-2,最小正周期
(2)由 ,得
函数y的单调递增区间为:
19.【解】∵ 是方程 的两根,
∴ ,从而可知
故
又
∴
20.【解】(1)由图可知,从4~12的的图像是函数 的三分之二
(完整)必修四第一章三角函数测试题(含答案),推荐文档

9.必修四第一章三角函数测试题、选择题11 .已知 cos a= — a€ (370 ° 520°,则 a 等于2 .若sin x tan x<0,则角x 的终边位于x 口3 .函数y = tan 2是 班别姓名 分数A . 390°B . 420°C . 450°D . 480°A .第一、二象限B .第二、三象限C .第二、四象限D .第三、四象限A .周期为2 n 的奇函数B .周期为扌的奇函数C .周期为n 的偶函数D .周期为 2n 的偶函数已知函数y = 2sin( «x+妨(3>0)在区间[0,2函数 f(x)= cos(3x +Q 的图象关于原点成中心对称,则 0等于nB . 2k n- 2(k € Z)C . k n :k € Z)n D . k n+ 2(k € Z)若sin 0+ cos 0 = 2,贝y sin 0cos B 的值是 sin — cos 0C . ±3oD .37t将函数y = sin x 的图象上所有的点向右平行移动 石个单位长度, 再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是_n- nA . y = sin 2x —石B . y = sin 2x — 5C . y = sinn—10 D . 1 x —x 3 n 在同一平面直角坐标系中,函数y = cos 2+y (x € [0,2n 的图象和直线1y = §的交点个数C . 2的图象如图,那么-亠人k n n已知集合M = x|x= - + 4, k€ Z , N= {x|x=〒+n k€ Z}.则C . N MD . M A N= ? 9.5 n . 2 n 丄 2 n 口订10.设 a = sin —, b = cos —, c = tan —,则二、填空题A . a<b<cB . a<c<bC . b<c<aD . b<a<c11.已知一扇形的弧所对的圆心角为54 °半径r = 20 cm ,则扇形的周长为12.方程sin1秋=4x 的解的个数是13.已知函数 f(x) = 2sin( cox+())的图象如图所示, … 7 n则 f@)=14.已知函数 y = sin ^在区间[0, t ]上至少取得2次最大值,则正整数t 的最小值是3三、解答题15 .已知 f( a =.2sin n — a C OS 2 n — a tan — n+ asin — n+ a t an — a+ 3 n(1)化简 f (a ; 1 n n(2)若 f( a = 8,且 4< o<2,求 cos a — Sin a 的值;cm.⑶若a=—3|n求f(a的值.16. 求函数y = 3—4sin x—4cos2x的最大值和最小值,并写出函数取最值时对应的x的值.n17. 设函数f(x) = sin(2x+ ©( —n<(j)<0), y= f(x)图象的一条对称轴是直线x=⑴求購(2)求函数y= f(x)的单调增区间;⑶画出函数y= f(x)在区间[0,n上的图象.n18. 在已知函数f(x)= Asin(3x+$), x€ R(其中A>0, 3>O,O< 临)的图象与x轴的交点中,相邻两个交点之间的距离为n,且图象上一个最低点为M牛一2.n n(1)求f(x)的解析式;(2)当x€ 12,2时,求f(x)的值域.n19. 如下图所示,函数尸2cos(»+ B)(X€ R , 3>0,0 w ㊁)的图象与丫轴交于点(0,-, 3),且该函数的最小正周期为⑵已知点A(n,0),点P是该函数图象上一点,点Q(X o, y o)是PA的中点,当y o=¥,nx o€【2,n时,求X o的值.必修四第一章三角函数测试题(答案)1、 答案 B2、 答案 B3、 答案 A4、 答案 B2 n 解析 由图象知 2T = 2 n, T = n, ••• — = n, w= 2.w5、 解析 若函数f(x) = cos(3x +妨的图象关于原点成中心对称,贝Uf(0)= cos $= 0,n•- 0= k n+ ^(k € Z).答案 D6、答案 B 解析•/ sin 9+ cos 9=tan 9+ 1= 2 , sin 9— cos 9 tan 9— 1 • sin 6cos 9= sin 9cos 9=盘丄=A. sin 2 9+ cos 2 9 tan 2 9+ 1 107、答案 C.1 n ysin 2x 〔°9、答案 B得M N 选B.z2n时,sin a >cos a • a = sin y>cos ~ = b. 2 n 2 nsin a <tan a • c = tan y>sin 7 = a.「. c>a.「. c>a>b.向右平性希*单位长朋癮坐标仲丧到原来的2倍• --------------------------------- > xy = sin x —三 纵坐标不变解析函数y = sin x 3 n x函数 y = cos + y = sin 2 , x € [0,2,n]1y = 2与该图象有两个交点.7_vl2nx图象如图所示,直线 &答案 C 解析解析 M = x x =牛 n, k € Z , N =x x = x 4k + 2n k € Z比较两集合中分式的分子,知前者为奇数倍n 后者为整数倍n 再根据整数分类关系,10、答案 D 解析. .5 n-a = sin ~ = sin( n — 5 n 2 冗2 n n 7 ) =7.7 —4」28 28 8 n 7 n —二 >0.n 2 n n• ;<y<2.又 a€n又a€ 0, 2时,2 23 n11、答案 6n+ 40 解析 •••圆心角 a= 54° =和,:I =|a|r = 6 n ・「.周长为(6 n 40) cm.13、答案 0将(n 0)代入上式sin(¥+0)= 0.n _n=cos 3 • — sin 312、答案 7解析 在同一坐标系中作出1y = sin <与y = 4X 的图象观察易知两函数图象有7个交点,所以方程有 7个解.解析方法由图可知,|T = 5n — 4= n , 即 T = 2n ,• 3= 2n= 3..・.y = 2sin(3x + 册, •- ¥+(f )= k n, k € Z ,贝U (= k n — 3 n ~4,k € Z. 方法由图可知,3T =5n —n= n,2 n即T =亍.又由正弦图象性质可知,f(X 0)= — f(x ° + T),14、答案 8 解析 T = 6,则 5T < t , • t > 竺,•• t min = 8.15、解(1)f( a=血I""atan a= sin—sin a — ta n aa C OS a1⑵由 f( a = sin a cos a=:可知(cos a — sin 8 2 2 a )2= cos 2 a — 2sin a cos a+ sin 2 a1 3=1 — 2sin a cos a= 1 — 2 x 8= 4.n n又 T 4< a <|, •- cos a <sin a,即 cosa — sin a <0. cos a — sin a=(3) •/ a=— 33-^=— 6X 25 n n +§,31 n~3 = cos31 n3 sin 31 n 3=cos — 6X 2 n+5 n 7 sin5 n 5 n —6X 2 n+ ~ = cos ~ sin5 n~ = cos(2 n — 3) sin(2 7tnn — 3)7 n 3 n=2si n(h + k n — R = °.16、解y= 3—4sin x—4cos2x= 4sin2x—4sin x —1=4 sin x— 2 2- 2,令t = sin x,则—1< t< 1, y= 4 t —2 2—2 (—1< t W 1).1 n 5 n•••当t= 2■,即卩x= 6 + 2k n或x = $+ 2k n(k€ Z)时,y min = —2;3 n当t =—1,即卩x= 2 + 2k 冗(k€ Z)时,y max = 7.n17、解(1)••• x = §是函数y= f(x)的图象的对称轴,n• sin 2 x ~+ $ = ±1.8n n…4 + $= k n+ ^,k€ 乙—n<(j<0 ,⑵由(1)知(=—号5,因此y= sin 2x—乎.由题意得2k n—2x —3j n< 2k n+ 才,k€ Z.3 n n 5 n•函数y = sin 2x —的单调增区间为k n+ ;, k n+ —, k€ Z.4 8 8(3)由y= sin 2x—节,知x0n83n"85 n~87_n~8ny 迄2—1010亚2故函数y = f(x)在区间[0, n上的图象是2 n18、解 ⑴由最低点为 M ㊁,-2得A = 2.n由x 轴上相邻两个交点之间的距离为 2,T n2 n2n得 2= 2,即 T = n ••• 3= T =_T =2. 2 2 I n2 n 2 n 由点M , - 2在图象上得 2si n2 x -3 +$=— 2,4 n, 4 n n即 sin & +=— 1,故—+ $= 2k n-^(k € Z),「小11 n--0= 2k n —百(k € Z).- n n 「 n又 $€ 0, 2 , •- 0= 6,故 f (x) = 2sin 2x + 6 ・n nn 厂⑵••• x € 12 2 , • 2x + 6€当2x + 6 = 2,即x = 6时,f(x)取得最大值2;n 7 n n当2x + 6 = S ,即x = 2时,f(x)取得最小值一1 , 故f(x)的值域为[—1,2].19、解 (1)将 x = 0, y = . 3 代入函数 y = 2cos(®x+ 9 中, 得cos 皓当,因为° w n ,所以9=n2 n 2 n由已知T = n 且3>0,得3=〒==2.I nn⑵因为点AQ , 0), Q(x °, y °)是PA 的中点, y °=¥,所以点P 的坐标为(2x °—n,V 3).nn 又因为点P 在y = 2cos(2x + 6)的图象上,且2^ x o w n,,,.5 n 11 n ,、 5 n 13 n 卄 2 n ,、3 n所以 cos(4x °—5 n 5P= _^3 2 ,且 H 4x ° —19 n 6,n 7 n 3,从而得4x0-石=g,或4x0-石=专,即x°= 7,或x0= 7.11。
(好题)高中数学必修四第一章《三角函数》检测题(包含答案解析)(2)

一、选择题1.函数()()2sin f x x ωϕ=+(0>ω,2πϕ<)的部分图象如图所示,则()fπ=( )A .3-B .3-C .32D .32.函数()()2sin 0,2f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭的部分图像如图所示,则下列结论正确的是( )A .3x π=-是()f x 图像的一条对称轴B .()f x 图像的对称中心为22,0,3k k Z ππ⎛⎫+∈⎪⎝⎭ C .()1f x ≥的解集为44,4,3k k k Z πππ⎡⎤+∈⎢⎥⎣⎦ D .()f x 的单调递减区间为282,2,33k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦ 3.已知实数a ,b 满足0<2a <b <3-2a ,则下列不等关系一定成立的是( ) A .sin sin2ba < B .()2cos >cos 3a b -C .()2sin sin3a b +<D .23cos >sin 2b a ⎛⎫-⎪⎝⎭4.如图,一半径为4.8m 的筒车按逆时针方向转动,已知筒车圆心O 距离水面2.4m ,筒车每60s 转动一圈,如果当筒车上点P 从水中浮现时(图中点0P )开始计时,则( )A .点P 第一次到达最高点需要10sB .点P 距离水面的高度h (单位:m )与时间t (单位:s )的函数解析式为4.8sin 2.4306h t ππ⎛⎫=-+ ⎪⎝⎭ C .在筒车转动的一圈内,点P 距离水面的高度不低于4.8m 共有10s 的时间 D .当筒车转动50s 时,点P 在水面下方,距离水面1.2m5.已知函数()tan()0,02f x x πωϕϕω⎛⎫=+<<<⎪⎝⎭最小正周期为2π,且()f x 的图象过点,03π⎛⎫⎪⎝⎭,则方程()sin 2([0,])3f x x x π⎛⎫=+∈π ⎪⎝⎭所有解的和为( )A .76πB .56π C .2πD .3π 6.对于函数()12sin 3()42f x x x R π⎛⎫=-++∈ ⎪⎝⎭,有以下四种说法: ①函数的最小值是32-②图象的对称轴是直线()312k x k Z ππ=-∈ ③图象的对称中心为,0()312k k Z ππ⎛⎫-∈⎪⎝⎭④函数在区间7,123ππ⎡⎤--⎢⎥⎣⎦上单调递增. 其中正确的说法的个数是( ) A .1B .2C .3D .47.设()sin 24f x x π⎛⎫=+⎪⎝⎭,90,8x π⎡⎤∈⎢⎥⎣⎦,若函数()y f x a =-恰好有三个不同的零点,分别为1x 、2x 、()3123x x x x <<,则1232x x x ++的值为( ) A .πB .34π C .32π D .74π 8.已知1sin 34x π⎛⎫+= ⎪⎝⎭,则22sin sin 36x x ππ⎛⎫⎛⎫-+-=⎪ ⎪⎝⎭⎝⎭( ) A .1B .1514+ C .1916D .349.函数()13cos313xxf x x -=+的图象大致是( ) A . B .C .D .10.函数1cos y x x=+的图象可能是( ) A . B .C .D .11.如图,摩天轮是一种大型转轮状的机械建筑设施,游客坐在摩天轮的座舱里慢慢地往上转,可以从高处俯瞰四周景色.某摩天轮最高点距离地面高度为120m ,转盘直径为110m 设置有48个座舱,开启后按逆时针方向匀速旋转,游客在座舱转到距离地面最近的位置进舱,转一周大约需要20min .游客甲坐上摩天轮的座舱,开始转动t min 后距离地面的高度为H m ,则在转动一周的过程中,高度H 关于时间t 的函数解析式是( )A .()55cos 65020102H t t ππ⎛⎫=-+≤≤ ⎪⎝⎭B .()55sin 65020102H t t ππ⎛⎫=-+≤≤ ⎪⎝⎭C .()55cos 65020102H t t ππ⎛⎫=++≤≤ ⎪⎝⎭D .()55sin 65020102H t t ππ⎛⎫=++≤≤ ⎪⎝⎭12.函数()()sin 0,2f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭的部分图象如图所示,为了得sin 26y x π⎛⎫=- ⎪⎝⎭的图象,只需将()f x 的图象( )A .向右平移3π个单位长度 B .向右平移4π个单位长度 C .向左平移3π个单位长度D .向左平移4π个单位长度 二、填空题13.下列判断正确的是___________(将你认为所有正确的情况的代号填入横线上). ①函数1tan 21tan 2xy x+=-的最小正周期为π;②若函数()lg f x x =,且()()f a f b =,则1ab =; ③若22tan 3tan 2αβ=+,则223sin sin 2αβ-=;④若函数()2221sin 41x xy x ++=+的最大值为M ,最小值为N ,则2M N +=.14.已知函数()22cos f x x ω=-(0>ω)的图象关于点3,04π⎛⎫⎪⎝⎭对称,且()f x 在区间20,3π⎛⎫⎪⎝⎭上单调,则ω的值为______. 15.将函数()2sin 26f x x π⎛⎫=+⎪⎝⎭的图象向左平移12π个单位,再向上平移1个单位,得到()g x 的图象.若()()129g x g x =,且[]12,2,2x x ππ∈-,则122x x -的最大值为_______________.16.圆心角为2弧度的扇形的周长为3,则此扇形的面积为 _____ .17.函数(x)Asin(x )f ωϕ=+ (0A >,0>ω,0ϕπ<< )的部分图象如图所示,则4f π⎛⎫= ⎪⎝⎭________.18.已知函数()()()sin 0,πf x x ωϕωϕ=+><的图像如图所示,则ϕ=__________.19.已知函数()sin f x x =,若对任意的实数(,)46αππ∈--,都存在唯一的实数(0,)m β∈,使()()0f f αβ+=,则实数m 的最大值是____.20.给出下列命题: ①函数()4cos 23f x x π⎛⎫=+⎪⎝⎭的一个对称中心为5,012π⎛⎫-⎪⎝⎭; ②若α,β为第一象限角,且αβ>,则tan tan αβ>;③在ABC ∆中,内角A ,B ,C 所对的边分别为a ,b ,c ,若40a =,20b =,25B =︒,则ABC ∆必有两解.④函数sin 2y x =的图象向左平移4π个单位长度,得到sin 24y x π⎛⎫=+ ⎪⎝⎭的图象.其中正确命题的序号是 _________(把你认为正确的序号都填上).三、解答题21.已知函数()()1sin 226f x x x R π⎛⎫=+∈ ⎪⎝⎭. (1)填写下表,并用“五点法”画出()f x 在[0,]π上的图象;26x π+6π 136πxπ ()f x(2)将()y f x =的图象向上平移1个单位,横坐标缩短为原来的2,再将得到的图象上所有点向右平移4π个单位后,得到()g x 的图象,求()g x 的对称轴方程.22.已知函数2()3sin cos cos (0)f x x x x ωωωω=->周期是2π.(1)求()f x 的解析式,并求()f x 的单调递增区间;(2)将()f x 图像上所有点的横坐标扩大到原来的2倍,再向左平移6π个单位,最后将整个函数图像向上平移32个单位后得到函数()g x 的图像,若263x ππ≤≤时,()2g x m -<恒成立,求m 得取值范围. 23.已知sin(2)cos 2()cos tan()2f ππαααπαπα⎛⎫-+ ⎪⎝⎭=⎛⎫-++ ⎪⎝⎭.(1)化简()f α,并求3f π⎛⎫⎪⎝⎭; (2)若tan 2α=,求224sin 3sin cos 5cos αααα--的值;(3)求函数2()2()12g x f x f x π⎛⎫=-++ ⎪⎝⎭的值域.24.下图是函数()()sin()0,0f x x ωϕωϕπ=+><<的部分图象.(1)求ϕ的值及()f x 单调递增区间.(2)若()f x 的图象横坐标不变,纵坐标扩大为原来的2倍,然后再将所得图象向右平移3π个单位,最后向上平移1个单位,得到函数()g x 的图象,若()g x 在[0,](0)b b >上恰有10个零点,求b 的取值范围.25.已知函数2()3sin 22cos 1f x x x =+-.(I )求函数()f x 的最小正周期; (II )求函数()f x 的单调增区间; (III )当0,2x π⎡⎤∈⎢⎥⎣⎦时,求函数()f x 的最小值. 26.己知函数()sin 3cos (0, 0 )f x A x A x A ωωω=+>>,其部分图象如图所示.(1)求A 和ω的值;(2)求函数()y f x =在[]0,π的单调增区间.【参考答案】***试卷处理标记,请不要删除一、选择题 1.A 解析:A 【分析】由函数()f x 的部分图像得到函数()f x 的最小正周期,求出ω,代入5,212π⎛⎫⎪⎝⎭求出ϕ值,则函数()f x 的解析式可求,取x π=可得()f π的值.【详解】由图像可得函数()f x 的最小正周期为521212T πππ⎡⎤⎛⎫=⨯--= ⎪⎢⎥⎝⎭⎣⎦,则22T πω==. 又5552sin 22sin 212126f πππϕϕ⎛⎫⎛⎫⎛⎫=⨯+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,则5sin 16⎛⎫+= ⎪⎝⎭πϕ, 则5262k ϕπ=π+π+,k Z ∈,则23k πϕπ=-,k Z ∈,22ππϕ-<<,则0k =,3πϕ=-,则()2sin 23f x x π⎛⎫=-⎪⎝⎭, ()2sin 22sin 33f ππππ⎛⎫∴=-=-= ⎪⎝⎭故选:A. 【点睛】方法点睛:根据三角函数()()sin 0,0,2f x A x b A πωϕωϕ⎛⎫=++>>< ⎪⎝⎭的部分图像求函数解析式的方法: (1)求A 、()()max min:2f x f x b A -=,()()max min2f x f x b +=;(2)求出函数的最小正周期T ,进而得出2Tπω=; (3)取特殊点代入函数可求得ϕ的值.2.C解析:C 【分析】结合五点作图法和函数图像可求得函数解析式,采用代入检验法可依次判断各个选项得到结果. 【详解】()10sin 2f ϕ==且2πϕ<,6πϕ∴=,又882sin 233f ππωϕ⎛⎫⎛⎫=+=-⎪ ⎪⎝⎭⎝⎭,由五点作图法可得:83362πππω+=,解得:12ω=, ()12sin 26f x x π⎛⎫∴=+ ⎪⎝⎭.对于A ,当3x π=-时,1026x π+=,,03π⎛⎫∴- ⎪⎝⎭是()f x 的对称中心,A 错误; 对于B ,当223x k ππ=+时,1262x k πππ+=+,223x k ππ∴=+是()f x 的对称轴,B 错误;对于C ,由()1f x ≥得:1in 2612s x π⎛⎫ ⎪⎭≥+⎝,15226266k x k πππππ∴+≤+≤+, 解得:4344k x k πππ≤+≤,C 正确;对于D ,当282,233x k k ππππ⎡⎤∈++⎢⎥⎣⎦时,13,2622x k k πππππ⎡⎤+∈++⎢⎥⎣⎦, 当1k =时,135,2622x πππ⎡⎤+∈⎢⎥⎣⎦,不是()f x 的单调递减区间,D 错误. 故选:C. 【点睛】方法点睛:本题考查正弦型函数()sin y A ωx φ=+的性质的判断,解决此类问题常用的方法有:(1)代入检验法:将所给单调区间、对称轴或对称中心代入x ωϕ+,确定x ωϕ+的值或范围,根据x ωϕ+是否为正弦函数对应的单调区间、对称轴或对称中心来确定正误; (2)整体对应法:根据五点作图法基本原理,将x ωϕ+整体对应正弦函数的单调区间、对称轴或对称中心,从而求得()sin y A ωx φ=+的单调区间、对称轴或对称中心.3.D解析:D 【分析】对各个选项一一验证:对于A.由0<2a <b <3-2a ,可以判断出2ba <,借助于正弦函数的单调性判断; 对于B.由0<2a <b <3-2a ,可以判断出23a b <-,借助于余弦函数的单调性判断; 对于C.由0<2a <b <3-2a ,可以判断出23a b +<,借助于正弦函数的单调性判断; 对于D.先用诱导公式转化为同名三角函数,借助于余弦函数的单调性判断; 【详解】 因为0<2a <b <3-2a 对于A. 有0<2b a <, 若22b a π<<,有sin sin 2b a <;若22b a π<<,有sin sin 2ba >,故A 错; 对于B.有 23ab <-,若232a b π<<-,有()2cos >cos 3a b -,故B 错;对于C. 23a b +<,若232a b π<+<,有()2sin sin 3a b +>,故C 错;对于D. 222333sin cos cos 2222a a a ππ+⎛⎫⎛⎫⎛⎫-=--=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭又因为b <3-2a <3,所以2cos >cos(3)b a - ∵22332a a π+-<-∴()223cos 3cos 2a a π+⎛⎫->-⎪⎝⎭∴()22233cos cos 3cos sin 22a a b a π+⎛⎫⎛⎫>->-=- ⎪ ⎪⎝⎭⎝⎭,故D 对.故选:D. 【点睛】利用函数单调性比较大小,需要在同一个单调区间内.4.B解析:B 【分析】先建立坐标系,从点0P 开始计时,建立三角函数模型()0sin h A t b ωϕ=++,通过题中条件求出参数0,,,A b ωϕ,再利用函数解析式对选项依次判断正误即可. 【详解】以水面所在直线为t 轴,过O 作OO t '⊥轴,建立坐标系如图:设点P 距离水面的高度h (单位:m )与时间t (单位:s )的函数解析式为()0sin h A t b ωϕ=++.依题意可知, 2.4OO '=, 2.41sin 4.82OPO '∠==,6OPO π'∠=. 高度h 最大值为2.4 4.87.2+=,最小值为2.4 4.8 2.4-=-,故()()7.2 2.47.2 2.44.8, 2.422A b --+-====, 周期60T =s ,则230T ππω==, 0t =时,06πϕ=-,故函数解析式为 4.8sin 2.4306h t ππ⎛⎫=-+⎪⎝⎭,故B 正确;点P 到达最高点时 4.8sin 2.47.2306h t ππ⎛⎫=-+=⎪⎝⎭,即sin 1306t ππ⎛⎫-= ⎪⎝⎭,故2,3062t k k Z ππππ-=+∈,即2060,t k k Z =+∈,又0t ≥,故第一次到达最高点时,0,20k t ==s ,故A 错误;在筒车转动的一圈内,点P 距离水面的高度不低于4.8m ,即4.8sin 2.4 4.8306h t ππ⎛⎫=-+≥ ⎪⎝⎭,得1sin 3062t ππ⎛⎫-≥ ⎪⎝⎭,故563066t ππππ≤-≤,解得1030t ≤≤,故共有20 s 时间,C 错误;当筒车转动50s 时,即50t =代入 4.8sin 2.4306h t ππ⎛⎫=-+⎪⎝⎭得,34.8sin 50 2.4 4.8sin 2.4 2.43062h πππ⎛⎫=⨯-+=+=- ⎪⎝⎭,故点P 在水面下方,距离水面2.4m ,故D 错误. 故选:B. 【点睛】 关键点点睛:本题解题关键在于按照题意,建立三角函数模型()0sin h A t b ωϕ=++,并解出解析式,才能解决选项中的实际问题,突破难点.5.A解析:A 【分析】先根据()f x 的最小正周期计算出ω的值,再根据图象过点,03π⎛⎫⎪⎝⎭结合ϕ的范围求解出ϕ的值,再根据条件将方程变形,先确定出tan 23x π⎛⎫+ ⎪⎝⎭的值,然后即可求解出方程的根,由此确定出方程所有解的和. 【详解】因为()f x 的最小正周期为2π,所以22πωπ==,又因为()f x 的图象过点,03π⎛⎫⎪⎝⎭,所以2tan 03πϕ⎛⎫+= ⎪⎝⎭, 所以2,3k k Z ϕππ+=∈,又因为02πϕ<<,所以3πϕ=且此时1k =,所以()sin 23f x x π⎛⎫=+ ⎪⎝⎭,即tan 2sin 233x x ππ⎛⎫⎛⎫+=+ ⎪ ⎪⎝⎭⎝⎭, 即tan 2cos 21033x x ππ⎡⎤⎛⎫⎛⎫++-= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦, 又因为tan 203x π⎛⎫+= ⎪⎝⎭时,sin 203x π⎛⎫+= ⎪⎝⎭,cos 213x π⎛⎫+=± ⎪⎝⎭, 所以tan 2cos 210tan 2=0333x x x πππ⎡⎤⎛⎫⎛⎫⎛⎫++-=⇔+ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,因为[]0,x π∈,所以72,333x πππ⎛⎫⎡⎤+∈ ⎪⎢⎥⎝⎭⎣⎦,当tan 2=03x π⎛⎫+⎪⎝⎭时,23x ππ+=或223x ππ+=,解得3x π=或56x π=, 所以方程()[]()sin 20,3f x x x ππ⎛⎫=+∈ ⎪⎝⎭所有解的和为57366πππ+=. 故选:A. 【点睛】关键点点睛:解答本题的关键是通过分析方程得到tan 2=03x π⎛⎫+ ⎪⎝⎭,此处需要注意不能直接约去tan 23x π⎛⎫+⎪⎝⎭,因为需要考虑tan 2=03x π⎛⎫+⎪⎝⎭的情况. 6.B解析:B 【分析】求出函数的最值,对称中心坐标,对称轴方程,以及函数的单调区间,即可判断正误. 【详解】函数()12sin 3()42f x x x R π⎛⎫=-++∈ ⎪⎝⎭, 当3=42x ππ+时,即=12x π,函数()f x 取得最小值为132122-⨯+=-,故①正确; 当342x k πππ+=+时,即=,123k x k Z ππ+∈,函数()f x 的图象的对称轴是直线=,123k x k Z ππ+∈,故②错误; 当34x k ππ+=时,即,123k x k Z ππ=-+∈,函数()f x 的图象的对称中心为1,,1232k k Z ππ⎛⎫-+∈ ⎪⎝⎭,故③错误; 当3232242k x k πππππ+≤+≤+,即252,123123k k x k Z ππππ+≤≤+∈,函数()f x 的递增区间为252,,123123k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦, 当1k =-时,()f x 的递增区间为7,124ππ⎡⎤--⎢⎥⎣⎦,故④正确. 故选:B 【点睛】关键点点睛:函数()12sin 3()42f x x x R π⎛⎫=-++∈ ⎪⎝⎭的递增区间转化为sin 34y x π⎛⎫=+ ⎪⎝⎭的递减区间.7.C解析:C 【分析】根据三角函数的对称性,先求出函数的对称轴,结合函数与方程的关系转化为两个函数的交点问题,利用数形结合进行求解即可. 【详解】 由()242x k k Z πππ+=+∈,得对称轴()28k x k ππ=+∈Z , 90,8x π⎡⎤∈⎢⎥⎣⎦,由90288k πππ≤+≤,解得124k -≤≤,当0k =时,对称轴8x π=,1k =时,对称轴58x π=. 由()0f x a -=得()f x a =,若函数()y f x a =-恰好有三个不同的零点,等价于函数()y f x =与y a =的图象有三个交点,作出函数()f x 的图象如图,得()20f =,则21a ≤<,由图象可知,点()()11,x f x 、()()22,x f x 关于直线8x π=对称,则124x x π+=, 点()()22,x f x 、()()33,x f x 关于直线58x π=对称,则2354x x π+=, 因此,1231223532442x x x x x x x πππ++=+++=+=. 故选:C . 【点睛】关键点点睛:本题考查正弦型函数的零点之和问题的求解,解题的关键就是分析出正弦型函数图象的对称轴,结合对称性求解.8.C解析:C 【分析】由诱导公式求得cos 6x π⎛⎫- ⎪⎝⎭,然后再由平方关系和诱导公式计算. 【详解】 由已知1cos cos sin 62334x x x ππππ⎡⎤⎛⎫⎛⎫⎛⎫-=-+=+=⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦, 222115sin 1cos 166416x x ππ⎛⎫⎛⎫⎛⎫-=--=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,21sin sin cos 32664x x x ππππ⎛⎫⎛⎫⎛⎫-=+-=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 所以2211519sin sin 3641616x x ππ⎛⎫⎛⎫-+-=+= ⎪ ⎪⎝⎭⎝⎭. 故选:C . 【点睛】关键点点睛:本题考查三角函数的求值.解题关键是确定“已知角”和“未知角”的关系,选用适当的公式进行变形求值.本题中首先利用诱导公式得出cos 6x π⎛⎫-⎪⎝⎭,然后再用诱导公式得出2sin 3x π⎛⎫- ⎪⎝⎭,用平方关系得出2sin 6x π⎛⎫- ⎪⎝⎭,这样求解比较方便. 9.A解析:A 【分析】先判断奇偶性,可排除C ,D ,由特殊值()f π,可排除B ,即可得到答案.【详解】因为()()()1331cos 3cos31331x x xx f x x x f x -----=⋅-=⋅=-++,所以函数()f x 为奇函数,排除C ,D ;又()13cos3013f ππππ-=>+,排除B , 故选:A. 【点睛】函数图象的识辨可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置.(2)从函数的单调性,判断图象的变化趋势.(3)从函数的奇偶性,判断图象的对称性.(4)从函数的特征点,排除不合要求的图象.利用上述方法排除、筛选选项.10.C解析:C 【分析】利用函数的奇偶性和特殊的函数值的正负排除错误选项. 【详解】函数定义域是{|0}x x ≠,关于原点对称,记1()cos f x x x=+,则11()cos()cos f x x x x x -=-+=+-()f x =,是偶函数,排除BD , 11()cos 10f ππππ=+=-+<,排除A .故选:C . 【点睛】思路点睛:函数图象的辨识可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置. (2)从函数的单调性,判断图象的变化趋势; (3)从函数的奇偶性,判断图象的对称性; (4)从函数的特征点,排除不合要求的图象.11.B解析:B 【分析】先判断游客进仓后第一次到达最高点时摩天轮旋转半周,大约需要10min ,结合摩天轮最高点距离地面高度为120m ,可得10t =时,120H =,再利用排除法可得答案. 【详解】因为游客在座舱转到距离地面最近的位置进舱,转一周大约需要20min , 所以游客进仓后第一次到达最高点时摩天轮旋转半周,大约需要10min , 又因为摩天轮最高点距离地面高度为120m , 所以10t =时,120H =,对于A ,10t =时,55cos 106555cos 65651022H πππ⎛⎫=⨯-+=+= ⎪⎝⎭,不合题意;对于B ,10t =时,55sin 106555sin 651201022H πππ⎛⎫=⨯-+=+= ⎪⎝⎭,符合题意;对于C ,10t =时,355cos 106555cos65651022H πππ⎛⎫=⨯++=+= ⎪⎝⎭,不合题意; 对于D ,10t =时,355sin 106555sin65101022H πππ⎛⎫=⨯++=+= ⎪⎝⎭,不合题意; 故选:B. 【点睛】方法点睛:特殊法是“小题小做”的重要策略,排除法解答选择题是高中数学一种常见的解题思路和方法,这种方法即可以提高做题速度和效率,又能提高准确性,这种方法主要适合下列题型: (1)求值问题(可将选项逐个验证);(2)求范围问题(可在选项中取特殊值,逐一排除);(3)图象问题(可以用函数性质及特殊点排除);(4)解方程、求解析式、求通项、求前n 项和公式问题等等.12.B解析:B 【分析】首先根据图象求函数的解析式,再根据左右平移规律判断选项. 【详解】由图象可知37341264T T ππππ⎛⎫=--=⇒= ⎪⎝⎭, 即22ππωω=⇒=,当6x π=-时,22,6k k Z πϕπ⎛⎫⨯-+=∈ ⎪⎝⎭, 解得:2,3k k Z πϕπ=+∈,2πϕ<,3πϕ∴=,()sin 23f x x π⎛⎫∴=+⎪⎝⎭, 22643x x πππ⎛⎫-=-+ ⎪⎝⎭, ∴ 要得到sin 26y x π⎛⎫=- ⎪⎝⎭的图象,只需将()sin 23f x x π⎛⎫=+ ⎪⎝⎭的图象向右平移4π个单位. 故选:B 【点睛】方法点睛:本题考查函数的图象变换,以及()sin y A ωx φ=+的性质,属于中档题型,()sin y A x ϕ=+的横坐标伸长(或缩短)到原来的1ω倍,得到函数的解析式是()sin y A ωx φ=+,若sin y A x ω=向右(或左)平移ϕ(0ϕ>)个单位,得到函数的解析式是()sin y A x ωϕ=-⎡⎤⎣⎦或()sin y A x ωϕ=+⎡⎤⎣⎦.二、填空题13.③④【分析】①化简可得即可求出;②由可能相等可判断;③利用同角三角函数关系可化简求出;④化简可得利用奇函数的性质可得【详解】对①则最小正周期为故①错误;对②若则可能相等故②错误;对③若则即即解析:③④ 【分析】①,化简可得tan 24y x π⎛⎫=+⎪⎝⎭,即可求出;②由,a b 可能相等可判断;③利用同角三角函数关系可化简求出;④化简可得24sin 141x xy x +=++,利用奇函数的性质可得.【详解】对①,tantan 21tan 24tan 21tan 241tan tan 24xx y x x x πππ++⎛⎫===+ ⎪-⎝⎭-⋅,则最小正周期为2π,故①错误;对②,若()()f a f b =,则,a b 可能相等,故②错误;对③,若22tan 3tan 2αβ=+,则2222sin 3sin 2cos cos αβαβ=+,即222222sin cos 3cos sin 2cos cos αβαβαβ=+,即22222222sin cos cos cos 3cos sin 3cos cos αβαβαβαβ+=+,即22cos 3cos βα=,即223sin sin 2αβ-=,故③正确;对④,()22221sin 4sin 14141x xx x y x x +++==+++,令()24sin 41x x g x x =++,则()()g x g x -=,故()g x 是奇函数,()()max min 0g x g x ∴+=,()()max min 112M N g x g x ∴+=+++=,故④正确.故答案为:③④. 【点睛】本题考查正切型函数的周期,考查同角三角函数的关系,考查奇函数的应用,解题的关键是正确利用三角函数的关键进行化简.14.【分析】根据函数图像的对称点得到的表达式根据在区间上单调得到的范围从而得到的范围再得到的值【详解】函数的图像关于点对称所以即得到在区间上单调所以即所以所以而所以故答案为:【点睛】本题考查根据余弦型函解析:23【分析】根据函数图像的对称点,得到ω的表达式,根据()f x 在区间20,3π⎛⎫⎪⎝⎭上单调,得到T 的范围,从而得到ω的范围,再得到ω的值.函数()f x x ω=-的图像关于点3,04π⎛⎫⎪⎝⎭对称,所以304πω⎛⎫-= ⎪⎝⎭,即342k ππωπ=+,k ∈Z ,得到4233k ω=+,k ∈Z , ()f x 在区间20,3π⎛⎫⎪⎝⎭上单调,所以223T π≥,即43T π≥, 所以243ππω≥,所以32ω≤,而0>ω,所以0k =,23ω=. 故答案为:23. 【点睛】本题考查根据余弦型函数的对称中心求参数的值,根据余弦型函数的周期求参数的值,属于中档题.15.【分析】根据图象的平移得出函数再由已知得或要使最大则最大最小可求得取得的最大值【详解】将函数的图象向左平移个单位可得的图象再向上平移1个单位得到的图象则因为所以当得或∵∴要使最大则最大最小则当最大最 解析:5512π【分析】根据图象的平移得出函数()2sin 213g x x π⎛⎫=++ ⎪⎝⎭,再由已知得()()123g x g x ==或()()123g x g x ==-.要使122x x -最大,则123x π+最大,223x π+最小.可求得122x x -取得的最大值. 【详解】将函数()2sin 26f x x π⎛⎫=+⎪⎝⎭的图象向左平移12π个单位,可得2sin 2+2sin 21263y x x πππ⎡⎤⎛⎫⎛⎫=+=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦的图象,再向上平移1个单位,得到()2sin 213g x x π⎛⎫=++ ⎪⎝⎭的图象.则()33g x -≤≤,因为[]12,2,2x x ππ∈-,所以当()()129g x g x =,得()()123g x g x ==或()()123g x g x ==-.∵[]12,2,2x x ππ∈-,∴1211132,2,3333x x ππππ⎡⎤++∈-⎢⎥⎣⎦, 要使122x x -最大,则123x π+最大,223x π+最小.则当17232x ππ+=最大,25232x ππ+=-最小时,即11912x π=,2176x π=-时,122x x -取得最大值为5512π. 故答案为:5512π. 【点睛】本题考查三角函数的图象平移,正弦型函数的最值,属于中档题.16.【分析】根据扇形的周长求出扇形半径再根据扇形面积公式计算即可【详解】设该扇形的半径为r 根据题意有故答案为【点睛】本题主要考查了扇形的面积公式弧长公式属于中档题 解析:916【分析】根据扇形的周长求出扇形半径,再根据扇形面积公式计算即可. 【详解】设该扇形的半径为r ,根据题意,有2l r r α=+,322r r ∴=+,34r ∴=,211992221616S r α∴==⨯⨯=扇形.故答案为916. 【点睛】本题主要考查了扇形的面积公式,弧长公式,属于中档题.17.【分析】观察图象可求得进而可得然后求出的值可得;而后由可求得的值得出最后代值计算即可得解【详解】由图象可知∴∴∴又∴()∴()∵∴∴则故答案为:【点睛】本题重点考查了正弦型三角函数的图象和性质考查逻【分析】观察图象可求得2A =,311341264T πππ=-=,进而可得T π=,然后求出ω的值,可得()()22f x sin x ϕ=+;而后由26f π⎛⎫= ⎪⎝⎭,可求得ϕ的值,得出()2sin 26f x x π⎛⎫=+ ⎪⎝⎭,最后代值计算即可得解. 【详解】由图象可知2A =,311341264T πππ=-=,∴T π=, ∴22πωπ==,∴()()22f x sin x ϕ=+,又26f π⎛⎫= ⎪⎝⎭,∴2262k ππϕπ⨯+=+(k Z ∈), ∴26k πϕπ=+(k Z ∈),∵0ϕπ<<,∴6π=ϕ, ∴()2sin 26f x x π⎛⎫=+ ⎪⎝⎭,则222cos 4466f sin ππππ⎛⎫⎛⎫=⨯+==⎪ ⎪⎝⎭⎝⎭【点睛】本题重点考查了正弦型三角函数的图象和性质,考查逻辑思维能力和计算能力,属于常考题.18.【分析】结合函数图象由解得得到进而得到然后由函数图象过点求解【详解】由图可知:所以所以所以因为函数图象过点所以所以解得又因为解得故答案为:【点睛】本题主要考查三角函数的图象和性质还考查了数形结合的思 解析:9π10【分析】 结合函数图象由352244πππ=-=T ,解得52π=T ,得到45ω=,进而得到()45sin ϕ⎛⎫⎪=+⎝⎭f x x ,然后由函数图象过点()2,1π求解.【详解】 由图可知:352244πππ=-=T , 所以52π=T , 所以245πω==T ,所以()45sin ϕ⎛⎫⎪=+⎝⎭f x x , 因为函数图象过点()2,1π, 所以sin 815πϕ⎛⎫= ⎪⎝⎭+, 所以2825ππϕπ+=+k , 解得11210ϕππ=-k , 又因为π<ϕ,解得910πϕ=. 故答案为:9π10【点睛】本题主要考查三角函数的图象和性质,还考查了数形结合的思想方法,属于中档题.19.【分析】利用任意性与存在性原命题可转化为有且仅有一个解然后根据三角函数的性质和图像求解即可【详解】由则存在唯一的实数使即有且仅有一个解作函数图像与直线当两个图像只有一个交点时由图可知故实数的最大值是解析:34π【分析】利用任意性与存在性原命题可转化为()12,,22f k k β⎛⎫=∈ ⎪ ⎪⎝⎭有且仅有一个解,然后根据三角函数的性质和图像求解即可. 【详解】由()sin f x x =,(,)46αππ∈--,则()12f α⎛⎫∈- ⎪ ⎪⎝⎭,存在唯一的实数(0,)m β∈,使()()0f f αβ+=,即()1,,22f k k β⎛⎫=∈ ⎪ ⎪⎝⎭有且仅有一个解,作函数图像()y fβ=与直线1,,22y k k ⎛=∈ ⎝⎭, 当两个图像只有一个交点时,由图可知,344m ππ<≤, 故实数m 的最大值是34π. 故答案为:34π 【点睛】本题主要考查了三角函数的图像与性质,属于较为基础题.20.①③【分析】分别利用余弦函数的对称性正切函数的单调性正弦定理三角函数图象变换等知识对各个命题判断【详解】①令是函数的一个对称中心①正确;②若它们为第一象限角且但②错;③在中内角所对的边分别为若∵∴∴解析:①③ 【分析】分别利用余弦函数的对称性,正切函数的单调性,正弦定理,三角函数图象变换等知识对各个命题判断. 【详解】 ①,令55()4cos()4cos()012632f ππππ-=-+=-=,5,012π⎛⎫- ⎪⎝⎭是函数()4cos 23f x x π⎛⎫=+ ⎪⎝⎭的一个对称中心,①正确;②若136απ=,3πβ=,它们为第一象限角,且αβ>,但tan tan αβ=<=②错;③在ABC ∆中,内角A ,B ,C 所对的边分别为a ,b ,c ,若40a =,20b =,25B =︒,sin sin 2sin 251a BA b==︒<,∵b a <,∴B A <,∴A 可能为锐角,也可能为钝角,则ABC ∆有两解,③正确;④函数sin 2y x =的图象向左平移4π个单位长度,得到sin 2()sin(2)42y x x ππ=+=+的图象,④错.故答案为:①③. 【点睛】本题考查命题的真假判断,掌握三角函数的图象与性质是解题关键.本题需要掌握余弦函数的对称性,正切函数的单调性,正弦定理,三角函数图象变换等知识,属于中档题.三、解答题21.(1)答案见解析;(2)34k x ππ=+,k Z ∈. 【分析】(1)分别令x 等于0、6π、512π、23π、1112π、π,求得对应的纵坐标,确定点的坐标,列表、描点、作图即可;(2)利用放缩变换与平移变换法则可得到()15sin 4126g x x π⎛⎫=-+ ⎪⎝⎭,再令5462x k k Z πππ-=+∈,可得答案. 【详解】(1)由题意可得表格如下: 26x π+6π 2π π 32π 2π136πx6π 512π 23π 1112ππ()f x141212- 014(2)将()y f x =的图象向上平移1个单位得到1sin 2126y x π⎛⎫=++ ⎪⎝⎭的图象,再横坐标缩短为原来的12可得到1sin 4126y x π⎛⎫=++ ⎪⎝⎭的图象,再向右平移4π个单位可得115sin 41sin 412626y x x πππ⎛⎫⎛⎫=-++=-+ ⎪ ⎪⎝⎭⎝⎭的图象, 即()15sin 4126g x x π⎛⎫=-+ ⎪⎝⎭, 令5462x k πππ-=+,解得34k x k Z ππ=+∈,, 所以()g x 的对称轴方程是34k x ππ=+,k Z ∈. 【点睛】方法点睛:“五点法”作一个周期上的图象,主要把握三处主要位置点:1、区间端点;2、最值点;3、零点. 22.(1)1()sin 462f x x π⎛⎫=-- ⎪⎝⎭,单调递增区间为,21226k k ππππ-+⎡⎤⎢⎥⎣⎦,k Z ∈;(2)()0,2. 【分析】(1)根据正弦和余弦的二倍角公式化简可得1()sin 262f x x πω⎛⎫=-- ⎪⎝⎭,由222T ππω==,解得2ω=,带入正弦函数的递增区间242262k x k πππππ-≤-≤+,化简即可得解; (2)根据三角函数的平移和伸缩变换可得()sin 216g x x π⎛⎫=++ ⎪⎝⎭,根据题意只需要max min [()2][()2]g x m g x -<<+,分别在263x ππ≤≤范围内求出()g x 的最值即可得解. 【详解】(1)2()cos cos f x x x x ωωω=-12(cos 21)2x x ωω=-+ 1sin 262x πω⎛⎫=-- ⎪⎝⎭由222T ππω==,解得2ω= 所以,1()sin 462f x x π⎛⎫=-- ⎪⎝⎭∵242262k x k πππππ-≤-≤+∴224233k x k ππππ-≤≤+∴21226k k x ππππ-≤≤+ ∴()f x 的单调递增区间为,21226k k ππππ-+⎡⎤⎢⎥⎣⎦,k Z ∈ (2)依题意得()sin 216g x x π⎛⎫=++ ⎪⎝⎭因为|()|2g x m -<,所以()2()2g x m g x -<<+因为当2,63x ππ⎡⎤∈⎢⎥⎣⎦时,()2()2g x m g x -<<+恒成立所以只需max min [()2][()2]g x m g x -<<+转化为求()g x 的最大值与最小值当2,63x ππ⎡⎤∈⎢⎥⎣⎦时,()y g x =为单调减函数所以max ()1126g x g π⎛⎫==+=⎪⎝⎭,()min 21103g x g π⎛⎫==-+= ⎪⎝⎭, 从而max [()2]0g x -=,min [()2]2g x +=,即02m << 所以m 的取值范围是()0,2. 【点睛】本题考查了三角函数的单调性和最值,考查了三角函数的辅助角公式和平移伸缩变换,有一定的计算量,属于中档题.本题关键点有: (1)三角函数基本量的理解应用; (2)三角函数图像平移伸缩变换的方法; (3)恒成立思想的理解及转化. 23.(1)()cos f αα=,π132f ;(2)1;(3)250,8⎡⎤⎢⎥⎣⎦. 【分析】(1)由诱导公式化简可得()cos f αα=,进而可得3f π⎛⎫⎪⎝⎭; (2)由平方关系和商数关系可转化条件为224tan 3tan 5tan 1ααα--+,即可得解; (3)转化条件为()21252sin 48g x x ⎛⎫=--+ ⎪⎝⎭,结合二次函数的性质即可得解. 【详解】(1)由题意可得sin(2)cos 2()cos tan()2f ππαααπαπα⎛⎫-+ ⎪⎝⎭=⎛⎫-++ ⎪⎝⎭sin (sin )cos sin tan ααααα-⋅-==⋅, 故1cos 332f ππ⎛⎫== ⎪⎝⎭; (2)∵tan 2α=,故224sin 3sin cos 5cos αααα--22224sin 3sin cos 5cos sin cos αααααα--=+224tan 3tan 51tan 1ααα--==+; (3)因为()cos f αα=,所以22()2cos cos 12cos sin 12g x x x x x π⎛⎫=-++=++ ⎪⎝⎭22sin sin 3x x =-++21252sin 48x ⎛⎫=--+⎪⎝⎭, 因为sin [1,1]x ∈-, 所以当1sin 4x =时,max 25()8g x =,当sin 1x =-时,min ()0g x =所以()g x 的值域为250,8⎡⎤⎢⎥⎣⎦. 【点睛】关键点点睛:解决本题的关键是利用诱导公式、同角三角函数的关系对原式进行合理变形. 24.(1)23ϕπ=,7[,],1212k k k Z ππππ--∈;(2)59671212b ππ≤<. 【分析】(1)依题意求出函数的周期T ,再根据2Tπω=,求出ω,再根据函数过点,06π⎛⎫⎪⎝⎭,求出ϕ,即可求出函数解析式,再令222+2,232k x k k Z πππππ-≤≤+∈,求出x 的取值范围,即可求出函数的单调区间;(2)根据三角函数的变换规则求出()g x 的解析式,令()0g x =即可求出函数的零点,要使()g x 在[0,](0)b b >上恰有10个零点,则b 不小于第10个零点的横坐标,小于第11个零点的横坐标即可,即可得到不等式,解得即可; 【详解】 解:(1)由图易知22362T πππ=-=,则T π=,22T πω==,所以()()sin 2f x x ϕ=+ 因为函数过点,06π⎛⎫⎪⎝⎭所以sin 2066f ππϕ⎛⎫⎛⎫=⨯+= ⎪ ⎪⎝⎭⎝⎭所以2,6k k Z πϕπ⨯+=∈,又0ϕπ<<,故23ϕπ=, 则()2sin(2)3f x x π=+ 令:222+2,232k x k k Z πππππ-≤≤+∈,整理得7,1212k x k k Z ππππ-≤≤-∈, 所以()f x 的单调增区间是7,,1212k k k Z ππππ⎡⎤--∈⎢⎥⎣⎦. (2)若()f x 的图象横坐标不变,纵坐标扩大为原来的2倍,然后再将所得图象向右平移3π个单位,最后向上平移1个单位,得到函数()2sin 21g x x =+ 令()0g x =,得712x k ππ=+或11()12x k k Z ππ=+∈. 所以在[0,]π上恰好有两个零点,若()g x 在[0,]b 上恰有10个零点,则b 不小于第10个零点的横坐标,小于第11个零点的横坐标即可,即b 的范围为:115941212b πππ≥+=.且1111767412121212b ππππππ<++-+= 即59671212b ππ≤< 【点睛】已知f (x )=Asin (ωx +φ)(A >0,ω>0)的部分图象求其解析式时,A 比较容易看图得出,困难的是求待定系数ω和φ,常用如下两种方法:(1)由ω=2Tπ即可求出ω;确定φ时,若能求出离原点最近的右侧图象上升(或下降)的“零点”横坐标x 0,则令ωx 0+φ=0(或ωx 0+φ=π),即可求出φ.(2)代入点的坐标,利用一些已知点(最高点、最低点或“零点”)坐标代入解析式,再结合图形解出ω和φ,若对A ,ω的符号或对φ的范围有要求,则可用诱导公式变换使其符合要求.25.(Ⅰ)最小正周期为π;(Ⅱ),36k k ππππ⎡⎤-++⎢⎥⎣⎦,k Z ∈;(Ⅲ)-1.【分析】(I )先将解析式化为()2sin 26f x x π⎛⎫=+⎪⎝⎭,然后利用正弦型函数的周期公式可计算出该函数的最小正周期;(II )根据正弦函数的单调区间,利用整体法得出222262k x k πππππ-+≤+≤+,k Z ∈,,即可求出该函数的单调增区间;(III )由0,2x π⎡⎤∈⎢⎥⎣⎦可计算出26x π+的取值范围,再根据正弦函数的性质,即可求出函数的最大值和最小值. 【详解】解:(Ⅰ)因为2()22cos 1f x x x =+-,则()2cos2f x x x =+2sin 26x π⎛⎫=+ ⎪⎝⎭, 所以函数()f x 最小正周期为22T ππ==; (Ⅱ)因为222262k x k πππππ-+≤+≤+,k Z ∈,所以36k x k ππππ-+≤≤+,k Z ∈,函数()f x 的单调增区间为,36k k ππππ⎡⎤-++⎢⎥⎣⎦,k Z ∈;(Ⅲ)因为0,2x π⎡⎤∈⎢⎥⎣⎦,所以72666x πππ≤+≤, 而716f π⎛⎫=-⎪⎝⎭,22f π⎛⎫= ⎪⎝⎭,所以12sin 226x π⎛⎫-≤+≤ ⎪⎝⎭,所以()f x 的最小值为1-. 【点睛】关键点点睛:本题考查正弦型函数的最小正周期,利用整体法求正弦型函数的单调增区间,以及正弦型函数在给定区间的最值,熟练掌握正弦函数的图像和性质是解题的关键,属于常考题型.26.(1)1A =,2ω=;(2)0,12π⎡⎤⎢⎥⎣⎦和7,12ππ⎡⎤⎢⎥⎣⎦. 【分析】(1)根据辅助角公式和两角和的正弦公式化简得()2sin 3f x A x πω⎛⎫=+ ⎪⎝⎭,由函数图象可知()f x 的最大值为2,可求出A ,由图象可知43124T πππ=-=,结合2T πω=,即可求出ω的值;(2)由(1)得2n 2)3(si f x x π⎛⎫=+⎪⎝⎭,利用整体代入法并结合正弦函数的单调性,即可求出()y f x =在[]0,π的单调增区间. 【详解】解:(1)由题可知,()sin cos (0,0)f x A x x A ωωω=+>>即1()2sin cos 2sin 223f x A x x A x πωωω⎛⎫⎛⎫=+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭, 由图象可知,()f x 的最大值为2,则22A =,所以1A =, 由图象可知,43124T πππ=-=,则2T ππω==,所以2ω=; (2)由(1)得2n 2)3(si f x x π⎛⎫=+ ⎪⎝⎭, 令222,232k x k k πππ-+π≤+≤+π∈Z , 解得:5,1212k x k k Z ππππ-+≤≤+∈, 又因为[]0,x π∈,所以函数()y f x =在[]0,π的单调增区间为:0,12π⎡⎤⎢⎥⎣⎦和7,12ππ⎡⎤⎢⎥⎣⎦. 【点睛】思路点睛:本题考查由函数()sin y A ωx φ=+的部分图象求解析式,由函数图象的最大值求出A ,由周期2T πω=求出ω,从而可求出函数解析式,再利用整体代入法求正弦型函数的单调性,熟练掌握正弦函数的图象和性质是解题的关键.。
(典型题)高中数学必修四第一章《三角函数》检测卷(包含答案解析)(1)
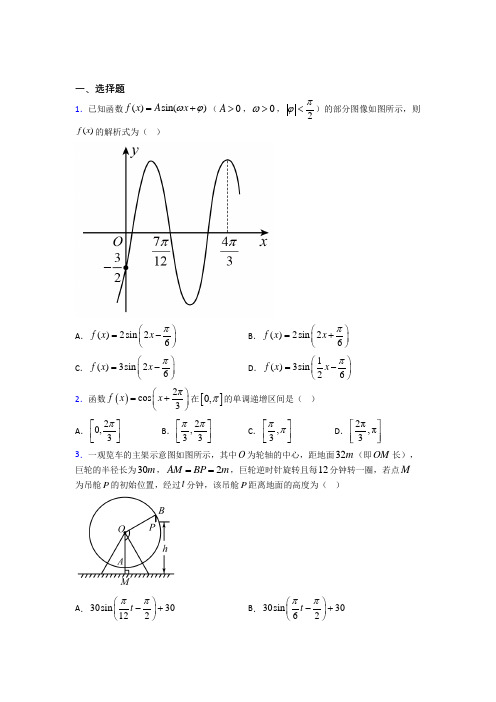
一、选择题1.已知函数()sin()f x A x ωϕ=+(0A >,0>ω,2πϕ<)的部分图像如图所示,则()f x 的解析式为( )A .()2sin 26f x x π⎛⎫=- ⎪⎝⎭B .()2sin 26f x x π⎛⎫=+ ⎪⎝⎭C .()3sin 26f x x π⎛⎫=-⎪⎝⎭D .1()3sin 26f x x π⎛⎫=-⎪⎝⎭ 2.函数()2cos 3⎛⎫=+ ⎪⎝⎭πf x x 在[]0,π的单调递增区间是( ) A .20,3π⎡⎤⎢⎥⎣⎦B .2,33ππ⎡⎤⎢⎥⎣⎦C .,3ππ⎡⎤⎢⎥⎣⎦D .2π,π33.一观览车的主架示意图如图所示,其中O 为轮轴的中心,距地面32m (即OM 长),巨轮的半径长为30m ,2AM BP m ==,巨轮逆时针旋转且每12分钟转一圈,若点M 为吊舱P 的初始位置,经过t 分钟,该吊舱P 距离地面的高度为( )A .30sin 30122t ππ⎛⎫-+⎪⎝⎭B .30sin 3062t ππ⎛⎫-+⎪⎝⎭C .30sin 3262t ππ⎛⎫-+⎪⎝⎭D .30sin 62t ππ⎛⎫-⎪⎝⎭ 4.已知函数()sin 26f x x π⎛⎫=-⎪⎝⎭,若方程()35f x =的解为1x ,2x (120x x π<<<),则()12sin x x -=( )A .35B .45-C .D .5.将函数()sin 25f x x π⎛⎫=+⎪⎝⎭的图象向右平移10π个单位长度后得到函数()y g x =的图象,对于函数()y g x =有以下四个判断: ①该函数的解析式为2sin 210y x π⎛⎫=+ ⎪⎝⎭; ②该函数图象关于点,02π⎛⎫⎪⎝⎭对称; ③该函数在区间,44ππ⎡⎤-⎢⎥⎣⎦上单调递增; ④该函数在区间,42ππ⎡⎤⎢⎥⎣⎦上单调递增. 其中,正确判断的序号是( ) A .②③B .①②C .②④D .③④6.已知函数()()cos f x x ωϕ=+(0>ω,0πϕ-<<)的图象关于点,08π⎛⎫⎪⎝⎭对称,且其相邻对称轴间的距离为23π,将函数()f x 的图象向左平移3π个单位长度后,得到函数()g x 的图象,则下列说法中正确的是( )A .()f x 的最小正周期23T π= B .58πϕ=-C .()317cos 248πx g x ⎛⎫=- ⎪⎝⎭D .()g x 在0,2π⎡⎤⎢⎥⎣⎦上的单调递减区间为,82ππ⎡⎤⎢⎥⎣⎦7.筒车是我国古代发明的一种水利灌溉工具,因其经济又环保,至今还在农业生产中得到使用.假设在水流量稳定的情况下,简车上的每一个盛水筒都做逆时针匀速圆周运动.现将筒车抽象为一个几何图形,如图所示,圆O 的半径为4米,盛水筒M 从点0P 处开始运动,0OP 与水平面的所成角为30,且每分钟恰好转动1圈,则盛水筒M 距离水面的高度H (单位;m )与时间t (单位:s )之间的函数关系式的图象可能是( )A .B .C .D .8.下列结论正确的是( ) A .sin1cos1< B .2317cos cos 54ππ⎛⎫⎛⎫->- ⎪ ⎪⎝⎭⎝⎭C .()()tan 52tan 47->-D .sin sin 1810ππ⎛⎫⎛⎫->- ⎪ ⎪⎝⎭⎝⎭9.使函数()3)cos(2)f x x x θθ=+++是偶函数,且在0,4⎡⎤⎢⎥⎣⎦π上是减函数的θ的一个值是( ) A .6π B .3π C .23π D .56π 10.已知函数()[][]sin cos cos sin f x x x =+,其中[]x 表示不超过实数x 的最大整数,则( )A .()f x 是奇函数B .π2π33f f ⎛⎫⎛⎫<⎪ ⎪⎝⎭⎝⎭C .()f x 的一个周期是πD .()f x 的最小值小于011.如图,摩天轮是一种大型转轮状的机械建筑设施,游客坐在摩天轮的座舱里慢慢地往上转,可以从高处俯瞰四周景色.某摩天轮最高点距离地面高度为120m ,转盘直径为110m 设置有48个座舱,开启后按逆时针方向匀速旋转,游客在座舱转到距离地面最近的位置进舱,转一周大约需要20min .游客甲坐上摩天轮的座舱,开始转动t min 后距离地面的高度为H m ,则在转动一周的过程中,高度H 关于时间t 的函数解析式是( )A .()55cos 65020102H t t ππ⎛⎫=-+≤≤ ⎪⎝⎭B .()55sin 65020102H t t ππ⎛⎫=-+≤≤ ⎪⎝⎭C .()55cos 65020102H t t ππ⎛⎫=++≤≤ ⎪⎝⎭D .()55sin 65020102H t t ππ⎛⎫=++≤≤ ⎪⎝⎭12.已知函数()()()3cos 0g x x ωϕω=+>在7,6ππ⎛⎫ ⎪⎝⎭上具有单调性,且满足04g π⎛⎫= ⎪⎝⎭,()3g π=,则ω的取值共有( ) A .6个B .5个C .4个D .3个二、填空题13.已知3()tan 1f x a x x =+(a ,b 为实数),且3(lg log 10)5f =,则(lglg3)f =____________.14.已知定义在R 上的函数()f x 满足:()()2f x f x π+=,且当[]0,x π∈时,()sin f x x =.若对任意的(],x m ∈-∞,都有()2f x ≤,则实数m 的取值范围是______. 15.如图,某公园要在一块圆心角为3π,半径为20m 的扇形草坪OAB 中修建一个内接矩形文化景观区域CDEF ,若//EF AB ,则文化景观区域面积的最大值为______2m .16.若函数f (x )=2sin(ωx +φ)(ω>0,0<φ<π)的图象经过点,26π⎛⎫⎪⎝⎭,且相邻两条对称轴间的距离为2π,则4f π⎛⎫⎪⎝⎭的值为________. 17.设函数()y f x =的定义域为D ,若对任意的1x ∈D ,总存在2x ∈D ,使得()()121f x f x ⋅=,则称函数()f x 具有性质M .下列结论:①函数3y x x =-具有性质M ; ②函数35x x y =+具有性质M ;③若函数()[]8log 2,0,y x x t =+∈具有性质M ,则510t =; ④若3sin y x a =+具有性质M ,则5a =. 其中正确结论的序号是____________.18.函数251612()sin (0)236x x f x x x x ππ-+⎛⎫=--> ⎪⎝⎭的最小值为_______. 19.关于函数()4sin(2)(),3f x x x R π=+∈有下列命题:①由12()()0f x f x ==可得12x x -必是π的整数倍;②()y f x =的图象关于点(,0)6π-对称;③()y f x =的表达式可改写为4cos(2);6y x π=-④()y f x =的图象关于直线6x π=-对称.其中正确命题的序号是_________.20.将函数()sin (0)f x x ωω=>的图象向右平移6π个单位长度,得到函数()y g x =的图像,若()y g x =是偶函数,则ω的最小值为________.三、解答题21.已知函数()12sin 26x f x π⎛⎫=+⎪⎝⎭,x ∈R .(1)用“五点法”画出函数()f x 一个周期内的图象; (2)求函数()f x 在[],ππ-内的值域; (3)若将函数()f x 的图象向右平移6π个单位长度,得到函数()g x 的图象,求函数()g x 在[],ππ-内的单调增区间.22.函数()sin()f x A x ωϕ=+(0,0,[0,2))A ωϕπ>>∈的图象如图所示:(1)求()f x 的解析式; (2)()f x 向左平移12π个单位后得到函数()g x ,求()g x 的单调递减区间;(3)若,2x ππ⎡⎤∈-⎢⎥⎣⎦且()32f x ≥,求x 的取值范围.23.已知向量a =(cosωx -sinωx ,sinωx),b =(-cosωx -sinωx,2cosωx).设函数f(x)=a b ⋅+λ(x ∈R)的图象关于直线x =π对称,其中ω,λ为常数,且ω∈1,12⎛⎫⎪⎝⎭.(1)求函数f(x)的最小正周期; (2)若y =f(x)的图象经过点,04π⎛⎫⎪⎝⎭,求函数f(x)在区间30,5π⎡⎤⎢⎥⎣⎦上的取值范围 24.已知函数()()()f x g x h x =,其()22g x x =,()h x =_____. (1)写出函数()f x 的一个周期(不用说明理由); (2)当,44x ππ⎡⎤∈-⎢⎥⎣⎦时,求函数()f x 的最大值和最小值. 从①cos 4x π⎛⎫+⎪⎝⎭,②2sin 24x π⎛⎫- ⎪⎝⎭这两个条件中任选一个,补充在上面问题中并作答, 注:如果选择多个条件分别解答.按第一个解答计分. 25.已知sin(3)(),cos x f x x R xπ-=∈(1)若α为第三象限角,且3sin 5α=-,求()f α的值. (2)若,34x ππ⎡⎤∈-⎢⎥⎣⎦,且21()2()1cos g x f x x =++,求函数()g x 的最小值,并求出此时对应的x 的值.26.函数()cos()(0)f x x ωφω=+>的部分图像如图所示.(1)求()f x 的表达式; (2)若[1,2]x ∈,求()f x 的值域;(3)将()f x 的图像向右平移112个单位后,再将所得图像横坐标伸长到原来的2倍,纵坐标不变,得到函数()y g x =的图像,求()g x 的单调递减区间.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】 本题首先可根据33π44T 求出ω,然后根据当43x π=时函数()f x 取最大值求出ϕ,最后代入30,2⎛⎫- ⎪⎝⎭,即可求出A 的值. 【详解】因为4π7π3π3124,所以33π44T ,T π=,因为2T πω=,所以2ω=,()sin(2)f x A x ϕ=+,因为当43x π=时函数()sin(2)f x A x ϕ=+取最大值,所以()42232k k Z ππϕπ⨯+=+∈,()26k k Z πϕπ=-+∈,因为2πϕ<,所以6πϕ=-,()sin 26f x A x π⎛⎫=- ⎪⎝⎭,代入30,2⎛⎫- ⎪⎝⎭,3sin 26A π⎛⎫-=- ⎪⎝⎭,解得3A =,()3sin 26f x x π⎛⎫=- ⎪⎝⎭, 故选:C. 【点睛】关键点点睛:本题考查根据函数图像求函数解析式,对于()sin()f x A x ωϕ=+,可通过周期求出ω,通过最值求出A ,通过代入点坐标求出ϕ,考查数形结合思想,是中档题.2.C解析:C 【分析】先求出函数的单调增区间,再给k 取值即得解. 【详解】 令22223+<+<+ππk πx πk π(k ∈Z ) ∴42233+<<+ππk πx k π(k ∈Z ), 所以函数的单调递增区间为4[2,2]33ππk πk π++(k ∈Z ), 当1k =-时,5233ππx -<<- 当0k =时,433x ππ<<又∵[]0,x π∈, 故选:C 【点睛】方法点睛:求三角函数()cos()f x A wx ϕ=+的单调区间,一般利用复合函数的单调性原理解答:首先是对复合函数进行分解,接着是根据复合函数的单调性原理分析出分解出的函数的单调性,最后根据分解函数的单调性求出复合函数的单调区间.3.B解析:B 【分析】先通过计算得出转动的角速度,然后利用三角函数模型表示在转动的过程中点B 的纵坐标满足的关系式,则吊舱到底面的距离为点B 的纵坐标减2. 【详解】如图所示,以点M 为坐标原点,以水平方向为x 轴,以OM 所在直线为y 轴建立平面直角坐标系.因为巨轮逆时针旋转且每12分钟转一圈,则转动的角速度为6π每分钟, 经过t 分钟之后,转过的角度为6BOA t π∠=,所以,在转动的过程中,点B 的纵坐标满足:3230sin 30sin 322662y t t ππππ⎛⎫⎛⎫=--=-+ ⎪ ⎪⎝⎭⎝⎭则吊舱距离地面的距离30sin 32230sin 306262h t t ππππ⎛⎫⎛⎫=-+-=-+ ⎪ ⎪⎝⎭⎝⎭. 故选:B . 【点睛】建立三角函数模型解决实际问题的一般步骤: (1)审题:审清楚题目条件、要求、理解数学关系; (2)建模:分析题目变化趋势,选择合适的三角函数模型; (3)求解:对所建立的数学模型进行分析研究,从而得到结论.4.B解析:B 【分析】求出函数()f x 在(0,)π上的对称轴,然后由正弦函数性质得1223x x π+=,这样12sin()x x -化为2222sin(2)sin 2cos(2)336x x x πππ⎛⎫-=+=- ⎪⎝⎭,而已知条件为23sin(2)65x π-=,再由正弦函数性质确定226x π-的范围,从而由平方关系求得结论.【详解】函数()sin 26f x x π⎛⎫=-⎪⎝⎭的对称轴满足:()262x k k Z πππ-=+∈,即()23k x k Z ππ=+∈,令0k =可得函数在区间()0,π上的一条对称轴为3x π=,结合三角函数的对称性可知1223x x π+=,则:1223x x π=-,()122222sin sin 2sin 2cos 2336x x x x x πππ⎛⎫⎛⎫⎛⎫-=-=+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,由题意:0πx <<,则112666x πππ-<-<,23sin 265x π⎛⎫-= ⎪⎝⎭,120x x π<<<,则2226x πππ<-<,由同角三角函数基本关系可知:24cos 265x π⎛⎫-=- ⎪⎝⎭, 故选:B . 【点睛】关键点点睛:本题考查正弦函数的性质,考查平方关系.解题时根据自变量的范围求得此范围内函数的对称轴,从而得出两个变量12,x x 的关系,可化双变量为单变量,再根据函数值及函数性质确定出单变量的范围,从而求得结论.注意其中诱导公式的应用,目的是把求值式与已知条件中的角化为一致.5.A解析:A 【分析】根据函数平移变换得sin 2y x =,再根据正弦函数的性质依次讨论即可得答案. 【详解】解:由函数sin 25y x π⎛⎫=+ ⎪⎝⎭的图象平移变换的性质可知: 将sin 25y x π⎛⎫=+⎪⎝⎭的图象向右平移10π个单位长度之后 解析式为sin 2sin 2105y x x ππ⎡⎤⎛⎫=-+= ⎪⎢⎥⎝⎭⎣⎦,选项①错误; 令2x k =π,k Z ∈,求得2k x =π,k Z ∈, 故函数的图象关于点,02k ⎛⎫⎪⎝⎭π对称, 令1k =,故函数的图象关于点,02π⎛⎫⎪⎝⎭对称,选项②正确; 则函数的单调递增区间满足:222()22k x k k Z ππππ-≤≤+∈,即()44k x k k Z ππππ-≤≤+∈,令0k =可得函数的一个单调递增区间为,44ππ⎡⎤-⎢⎥⎣⎦,选项③正确,④错误.故选:A. 【点睛】本题考查三角函数平移变换,正弦型函数的单调区间,对称中心等,考查运算求解能力,解题的易错点在于平移变换时,当1ω≠时,须将ω提出,平移只针对x 进行平移,具体的在本题中,sin 25y x π⎛⎫=+⎪⎝⎭的图象向右平移10π个单位长度之后得sin 2sin 2105y x x ππ⎡⎤⎛⎫=-+= ⎪⎢⎥⎝⎭⎣⎦,而不是sin 2sin 251010y x x πππ⎡⎤⎛⎫⎛⎫=+-=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,是中档题. 6.D解析:D 【分析】首先根据三角函数的性质,可知相邻对称轴间的距离是半个周期,判断A ;再求函数的解析式,判断B ;根据平移规律得到函数()g x ,判断C ;最后根据函数()g x 的解析式,利用整体代入的方法求函数的单调递减区间. 【详解】相邻对称轴间的距离是半个周期,所以周期是43π,故A 不正确; 243T ππω==,解得:32ω=,()f x 的图象关于点,08π⎛⎫⎪⎝⎭对称,3,282k k Z ππϕπ∴⨯+=+∈,解得:5,16k k Z πϕπ=+∈ 0πϕ-<<, 1116πϕ∴=-,故B 不正确; ()311cos 216f x x π⎛⎫=- ⎪⎝⎭,向左平移3π个单位长度后得()31133cos cos 2316216g x x x πππ⎡⎤⎛⎫⎛⎫=+-=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ 故C 不正确; 当02x π≤≤时,3339,2161616x πππ⎡⎤-∈-⎢⎥⎣⎦,当3390,21616x ππ⎡⎤-∈⎢⎥⎣⎦时,函数单调递减,即 ,82x ππ⎡⎤∈⎢⎥⎣⎦,故D 正确. 故选:D 【点睛】关键点点睛:本题的关键是根据三角函数的性质求得函数()f x 的解析式,第四个选项是关键,需根据整体代入的方法,先求33216x π-的范围,再确定函数的单调递减区间. 7.D解析:D 【分析】先根据题意建立坐标系,写出盛水筒M 距离水面的高度H 与时间t 之间的函数关系式,再根据关系式即可判断. 【详解】解:以O 为圆心,过点O 的水平直线为x 轴,建立如图所示的平面直角坐标系:0306xOP π∠==,OP ∴在()t s 内转过的角为:26030t t ππ=, ∴以x 轴正半轴为始边,以OP 为终边的角为:306t ππ-,P ∴点的纵坐标为:4sin 306t ππ⎛⎫-⎪⎝⎭, H ∴与t 之间的函数关系式为:4sin 2306H t ππ⎛⎫=-+⎪⎝⎭, 当sin 1306t ππ⎛⎫-= ⎪⎝⎭时,max 426H =+=, 当sin 1306t ππ⎛⎫-=-⎪⎝⎭时,max 422H =-+=-, 对A ,B ,由图像易知max min H H =-,故A ,B 错误; 对C ,max min H H <-,故C 错误; 对D ,max min H H >-,故D 正确. 故选:D. 【点睛】关键点点睛:本题解题的关键是理解题意,根据题意写出H 与t 之间的函数关系式.8.D解析:D 【分析】利用正弦函数的单调性可判断AD 选项的正误;利用正切函数的单调性可判断C 选项的正误;利用余弦函数的单调性可判断B 选项的正误. 【详解】对于A 选项,因为正弦函数sin y x =在0,2π⎛⎫⎪⎝⎭上单调递增, 且01122ππ<-<<,则sin1sin 1cos12π⎛⎫>-=⎪⎝⎭,A 选项错误; 对于B 选项,因为余弦函数cos y x =在()0,π上为减函数,23233cos cos cos 555πππ⎛⎫-== ⎪⎝⎭,1717cos cos cos 444πππ⎛⎫-== ⎪⎝⎭, 3045πππ<<<,则3cos cos 54ππ<,即2317cos cos 54ππ⎛⎫⎛⎫-<- ⎪ ⎪⎝⎭⎝⎭,B 选项错误; 对于C 选项,当900x -<<时,正切函数tan y x =单调递增, 因为9052470-<-<-<,所以,()()tan 52tan 47-<-,C 选项错误;对于D 选项,因为正弦函数sin y x =在,02π⎛⎫- ⎪⎝⎭上单调递增,因为021018πππ-<-<-<,所以,sin sin 1810ππ⎛⎫⎛⎫->- ⎪ ⎪⎝⎭⎝⎭,D 选项正确. 故选:D. 【点睛】思路点睛:解答比较函数值大小问题,常见的思路有两个: (1)判断各个数值所在的区间; (2)利用函数的单调性直接解答.9.B解析:B 【解析】1())cos(2))cos(2))2sin(2)26f x x x x x x πθθθθθ=+++=+++=++,由于()f x 为偶函数,则(0)2sin()26f πθ=+=±,sin()1,662k πππθθπ+=±+=+,3k πθπ=+,当0k =时,3πθ=,()2sin(2)2sin(2)362f x x x πππ=++=+2cos2x =,当[0,]4x π∈时,2[0,]2x π∈,()2cos2f x x =为减函数,符合题意,所以选B.10.D解析:D 【分析】利用奇函数的性质判断A ,分别求3f π⎛⎫⎪⎝⎭和23f π⎛⎫⎪⎝⎭判断大小,取特殊值验证的方法判断C ,分区间计算一个周期内的最小值,判断选项D 。
(好题)高中数学必修四第一章《三角函数》测试卷(包含答案解析)(1)

一、选择题1.若函数()sin 2f x x =与()2cos g x x =都在区间(),a b 上单调递减,则b a -的最大值是( ) A .π4B .π3C .π2D .2π32.已知函数f (x )=2sinxsin (x+3φ)是奇函数,其中(0,)2πϕ∈ ,则函数g (x )=cos (2x-φ)的图象( ) A .关于点(,0)12π对称 B .关于轴512x π=-对称 C .可由函数f (x )的图象向右平移6π个单位得到 D .可由函数f (x )的图象向左平移3π个单位得到 3.将函数()sin 25f x x π⎛⎫=+⎪⎝⎭的图象向右平移10π个单位长度后得到函数()y g x =的图象,对于函数()y g x =有以下四个判断: ①该函数的解析式为2sin 210y x π⎛⎫=+ ⎪⎝⎭; ②该函数图象关于点,02π⎛⎫⎪⎝⎭对称; ③该函数在区间,44ππ⎡⎤-⎢⎥⎣⎦上单调递增;④该函数在区间,42ππ⎡⎤⎢⎥⎣⎦上单调递增.其中,正确判断的序号是( ) A .②③B .①②C .②④D .③④4.将函数sin()y x ϕ=+的图像上所有点的横坐标缩短到原来的12倍(纵坐标不变),再将所得图像向左平移12π个单位后得到的函数图像关于原点中心对称,则sin 2ϕ=( )A .12-B .12C .D .25.已知函数()cos2sin 2f x x x =-,将()y f x =的图象向左平移a (0a >)个单位长度可以得到一个奇函数的图象,将()y f x =的图象向右平移b (0b >)个单位长度可以得到一个偶函数的图象,则a b -的最小值等于( )A .0B .8π C .4π D .2π 6.声音是由物体振动产生的声波.我们听到的每个音都是由纯音合成的,纯音的数学模型是函数sin y A wt =.音有四要素:音调、响度、音长和音色,它们都与函数sin y A wt =中的参数有关,比如:响度与振幅有关,振幅越大响度越大,振幅越小响度越小;音调与频率有关,频率低的声音低沉,频率高的声音尖利.像我们平时听到乐音不只是一个音在响,而是许多音的结合,称为复合音.我们听到的声音函数是111sin sin 2sin 3sin 4234y x x x x =++++.结合上述材料及所学知识,你认为下列说法中正确的有( ).A .函数1111sin sin 2sin3sin 4sin100234100y x x x x x =+++++不具有奇偶性; B .函数111()sin sin 2sin3sin 4234f x x x x x =+++在区间,1616ππ⎡⎤-⎢⎥⎣⎦上单调递增; C .若某声音甲对应函数近似为111()sin sin 2sin3sin 4234f x x x x x =+++,则声音甲的响度一定比纯音1()sin 22h x x =响度大; D .若某声音甲对应函数近似为1()sin sin 22g x x x =+,则声音甲一定比纯音1()sin33h x x =更低沉.7.下列函数中,既是偶函数,又在(),0-∞上是增函数的是( ) A .()22xxf x -=- B .()23f x x =-C .()2ln =-f x xD .()cos3=f x x x8.设函数()()sin 16f x x N πωω*⎛⎫=-+∈ ⎪⎝⎭在55,126ππ⎡⎤⎢⎥⎣⎦上单调递减,则下述结论: ①()f x 关于,012π⎛⎫⎪⎝⎭中心对称;②()f x 关于直线23x π=轴对称;③()f x 在,2ππ⎡⎤⎢⎥⎣⎦上的值域为30,2⎡⎤⎢⎥⎣⎦;④方程()1f x =在[]0,2π有4个不相同的根. 其中正确结论的编号是( ) A .①②B .②③C .②④D .③④9.已知函数()sin()f x x ωϕ=+,具有以下性质:(1)对任意的x ∈R ,都有()()12()f x f x f x ≤≤,且12x x -的最小值为2π; (2)6f x π⎛⎫+⎪⎝⎭为奇函数;(3)任取12,0,4x x π⎡⎤∈⎢⎥⎣⎦,当12x x ≠时,都有()()()()11222112x f x x f x x f x x f x +>+. 同时满足上述性质的一个函数可以是( ) A .4sin 23y x π⎛⎫=- ⎪⎝⎭ B .sin 23y x π⎛⎫=- ⎪⎝⎭C .2sin 23y x π⎛⎫=+⎪⎝⎭D .sin 26y x π⎛⎫=+⎪⎝⎭10.已知函数()tan()0,2f x x πωϕωϕ⎛⎫=+≠< ⎪⎝⎭,点2,03π⎛⎫⎪⎝⎭和7,06π⎛⎫⎪⎝⎭是其相邻的两个对称中心,且在区间54,63ππ⎛⎫⎪⎝⎭内单调递减,则ϕ=( ) A .6π B .6π-C .3π D .3π-11.函数()sin ln ||f x x x =⋅的部分图象大致为( )A .B .C .D .12.函数22y cos x sinx =- 的最大值与最小值分别为( ) A .3,-1 B .3,-2 C .2,-1D .2,-2二、填空题13.对任意0,4πϕ⎡⎤∈⎢⎥⎣⎦,函数()sin()f x x ωϕ=+在区间,2ππ⎡⎤⎢⎥⎣⎦上单调递增,则实数ω的取值范围是________.14.已知函数()sin()0,0,2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示,关于函数()y f x =有下列结论:①图象关于点,03π⎛⎫⎪⎝⎭对称; ②单调递减区间为2,,63k k k ππππ⎛⎫++∈ ⎪⎝⎭Z ; ③若()f x a =,则cos 32a x πω⎛⎫-= ⎪⎝⎭; ④2()()log g x f x x =-有4个零点. 则其中结论正确的有____________(填上所有正确结论的序号)15.2020年是苏颂诞辰1000周年,苏颂发明的水运仪象台被誉为世界上最早的天文钟.水运仪象台的原动轮叫枢轮,是一个直径约3.4米的水轮,它转一圈需要30分钟.如图,当点P 从枢轮最高处随枢轮开始转动时,退水壶内水面位于枢轮中心下方1.19米处.此时打开退水壶出水口,壶内水位以每分钟0.017米的速度下降,将枢轮转动视为匀速圆周运动,则点P 至少经过______分钟(结果取整数)进入水中.(参考数据:cos0.9815π≈,2cos0.9115π≈,cos 0.815π≈)16.函数()2sin(2),0,32f x x x ππ⎡⎤=-∈⎢⎥⎣⎦的单调减区间___________ 17.已知()()sin 03f x x πωϕω⎛⎫=++> ⎪⎝⎭同时满足下列三个条件:①T π=;②3y f x π⎛⎫=-⎪⎝⎭是奇函数;③()06f f π⎛⎫<⎪⎝⎭.若()f x 在[)0,t 上没有最小值,则实数t 的取值范围是___________.18.某校运动会开幕式上举行升旗仪式,旗杆正好处在坡度15的看台的某一列的正前方,从这一列的第一排和最后一排测得旗杆顶部的仰角分别为60和30,第一排和最后一排的距离为106米(如图所示),旗杆底部与第一排在一个水平面上,若国歌长度约为50秒,升旗手应以__________(米 /秒)的速度匀速升旗.19.已知函数()2sin()(0)f x x ωϕω=+>满足()24f π=,()0f π=,且()f x 在区间(,)43ππ上单调,则ω的值有_________个.20.关于函数()4sin(2)(),3f x x x R π=+∈有下列命题:①由12()()0f x f x ==可得12x x -必是π的整数倍;②()y f x =的图象关于点(,0)6π-对称;③()y f x =的表达式可改写为4cos(2);6y x π=-④()y f x =的图象关于直线6x π=-对称.其中正确命题的序号是_________.三、解答题21.在①将函数f (x )图象向右平移12π个单位所得图象关于y 轴对称:②函数6y f x π⎛⎫=+ ⎪⎝⎭是奇函数;③当712x π=时,函数6y f x π⎛⎫=- ⎪⎝⎭取得最大值.三个中任选一个,补充在题干中的横线处,然后解答问题.题干:已知函数()2sin()f x x ωϕ=+,其中0,||2πωϕ><,其图象相邻的对称中心之间的距离为2π,___________. (1)求函数y =f (x )的解析式;(2)求函数y =f (x )在,22ππ⎡⎤-⎢⎥⎣⎦上的最小值,并写出取得最小值时x 的值. 注:如果选择多个条件分别解答,按第一个解答计分.22.如图,在矩形OABC 中,22OA OC ==,将矩形OABC 绕着顶点O 逆时针旋转,得到矩形OA B C ''',记旋转的角度为θ,0,2πθ⎛⎫∈ ⎪⎝⎭旋转前后两个矩形公共部分的面积为()S θ.(1)求3S π⎛⎫⎪⎝⎭; (2)若()728S θ=,求sin θ. 23.为整治校园环境,设计如图所示的平行四边形绿地ABCD ,在绿地中种植两块相同的扇形花卉景观,两扇形的边(圆心分别为A 和C )均落在平行四边形ABCD 的边上,圆弧均与BD 相切,其中扇形的圆心角为120°,扇形的半径为12米.(1)求两块花卉景观扇形的面积;(2)记BDA θ∠=,求平行四边形绿地ABCD 占地面积S 关于θ的函数解析式,并求面积S 的最小值.24.下图是函数()()sin()0,0f x x ωϕωϕπ=+><<的部分图象.(1)求ϕ的值及()f x 单调递增区间.(2)若()f x 的图象横坐标不变,纵坐标扩大为原来的2倍,然后再将所得图象向右平移3π个单位,最后向上平移1个单位,得到函数()g x 的图象,若()g x 在[0,](0)b b >上恰有10个零点,求b 的取值范围.25.长春某日气温()C y ︒是时间t (024t ≤≤,单位:小时)的函数,下面是某天不同时间的气温预报数据: t (时)3 6 9 12 15 18 21 24 ()C y ︒ 15.714.015.720.024.226.024.220.015.7cos()y A t b ωϕ=++的图象.(1)根据以上数据,试求cos()y A t b ωϕ=++(0A >,0>ω,0ϕπ<<)的表达式; (2)大数据统计显示,某种特殊商品在室外销售可获3倍于室内销售的利润,但对室外温度要求是气温不能低于23C ︒.根据(1)中所得模型,一个24小时营业的商家想获得最大利润,应在什么时间段(用区间表示)将该种商品放在室外销售,单日室外销售时间最长不能超过多长时间?(忽略商品搬运时间及其它非主要因素,理想状态下哦,奥力给!)26.如图,在平面直角坐标系xOy 中,31,22A ⎛⎫⎪ ⎪⎝⎭为单位圆上一点,射线OA 绕点O 按逆时针方向旋转θ后交单位圆于点B ,点B 的纵坐标y 关于θ的函数为()y fθ=.(1)求函数()y f θ=的解析式,并求223f f ππ⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭; (2)若1()3f θ=,求7cos sin 36ππθθ⎛⎫⎛⎫--+⎪ ⎪⎝⎭⎝⎭的值.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】根据题意求出(),()f x g x 原点附近的单调递减区间,根据递减区间分析可得max 3π4b =,min π4a =,相减即可. 【详解】 解:由题意函数()sin 2f x x =在π3π,44⎛⎫⎪⎝⎭上单调递减,函数()2cos g x x =在()0,π上单调递减, 所以则max 3π4b =,min π4a =,所以b a -的最大值为3πππ442-=. 故选:C. 【点睛】求三角函数单调区间的2种方法:(1)代换法:就是将比较复杂的三角函数处理后的整体当作一个角u (或t ),利用基本三角函数的单调性来求所要求的三角函数的单调区间;(2)图象法:函数的单调性表现在图象上是从左到右,图象上升趋势的区间为单调递增区间,图象下降趋势的区间为单调递减区间,画出三角函数的图象,结合图象易求它的单调区间.2.B解析:B 【分析】利用三角函数的奇偶性求得φ,再利用三角函数的图象对称性、函数y=Asin (ωx+φ)的图象变换规律,判断各个选项是否正确,从而得出结论. 【详解】函数f (x )=2sinxsin (x+3φ)是奇函数,其中0,2πϕ⎛⎫∈ ⎪⎝⎭, ∴y=2sinxsin (x+3φ)是奇函数,∴3φ=2π,φ=6π,则函数g (x )=cos (2x ﹣φ)=cos (2x ﹣6π). 当12x π=时,206x π-=,112g π⎛⎫= ⎪⎝⎭,则函数不关于点,012π⎛⎫ ⎪⎝⎭对称,选项A 错误;当512x π=-时,26x ππ-=-,则函数关于直线512x π=-对称,选项B 正确;函数()2sin sin 2sin cos sin 22f x x x x x x π⎛⎫=+== ⎪⎝⎭, 其图像向右平移6π个单位的解析式为sin 2sin 2sin 263y x x x ππ⎡⎤⎛⎫⎛⎫==-=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦, 选项C 错误; 其图像向左平移3π个单位的解析式为2sin 2sin 2sin 233y x x x ππ⎡⎤⎛⎫⎛⎫==+=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦, 选项D 错误; 故选B. 【点睛】本题主要考查三角函数的奇偶性、对称性,函数y=Asin (ωx+φ)的图象变换规律,属于中档题.函数()sin y A x ωϕ=+(A >0,ω>0)的性质:(1)奇偶性:=k ϕπ ,k Z ∈时,函数()sin y A x ωϕ=+为奇函数;=2k πϕπ+,k Z ∈时,函数()sin y A x ωϕ=+为偶函数.;(2)周期性:()sin y A x ωϕ=+存在周期性,其最小正周期为T =2πω;(3)单调性:根据y =sin t 和t =x ωϕ+的单调性来研究,由+22,22k x k k Z πππωϕπ-≤+≤+∈得单调增区间;由3+22,22k x k k Z πππωϕπ≤+≤+∈得单调减区间;(4)对称性:利用y =sin x 的对称中心为()(),0k k Z π∈求解,令()x k k ωϕπ+=∈Z ,求得x ;利用y =sin x 的对称轴为()2x k k Z ππ=+∈求解,令()+2x k k πωϕπ+=∈Z ,得其对称轴.3.A解析:A 【分析】根据函数平移变换得sin 2y x =,再根据正弦函数的性质依次讨论即可得答案. 【详解】解:由函数sin 25y x π⎛⎫=+ ⎪⎝⎭的图象平移变换的性质可知:将sin 25y x π⎛⎫=+⎪⎝⎭的图象向右平移10π个单位长度之后 解析式为sin 2sin 2105y x x ππ⎡⎤⎛⎫=-+= ⎪⎢⎥⎝⎭⎣⎦,选项①错误; 令2x k =π,k Z ∈,求得2k x =π,k Z ∈, 故函数的图象关于点,02k ⎛⎫⎪⎝⎭π对称, 令1k =,故函数的图象关于点,02π⎛⎫⎪⎝⎭对称,选项②正确; 则函数的单调递增区间满足:222()22k x k k Z ππππ-≤≤+∈,即()44k x k k Z ππππ-≤≤+∈,令0k =可得函数的一个单调递增区间为,44ππ⎡⎤-⎢⎥⎣⎦,选项③正确,④错误. 故选:A. 【点睛】本题考查三角函数平移变换,正弦型函数的单调区间,对称中心等,考查运算求解能力,解题的易错点在于平移变换时,当1ω≠时,须将ω提出,平移只针对x 进行平移,具体的在本题中,sin 25y x π⎛⎫=+⎪⎝⎭的图象向右平移10π个单位长度之后得sin 2sin 2105y x x ππ⎡⎤⎛⎫=-+= ⎪⎢⎥⎝⎭⎣⎦,而不是sin 2sin 251010y x x πππ⎡⎤⎛⎫⎛⎫=+-=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,是中档题. 4.C解析:C 【分析】先根据条件写出图像变换后的函数解析式,然后根据图像关于原点中心对称可知函数为奇函数,由此得到ϕ的表示并计算出sin 2ϕ的结果. 【详解】因为变换平移后得到函数sin 26y x πϕ⎛⎫=++ ⎪⎝⎭,由条件可知sin 26y x πϕ⎛⎫=++ ⎪⎝⎭为奇函数,所以6k πϕπ+=,sin 2sin 2sin 332k ππϕπ⎛⎫⎛⎫=-=-=- ⎪ ⎪⎝⎭⎝⎭故选C . 【点睛】本题考查三角函数的图像变换以及根据函数奇偶性判断参数值,难度一般.正弦型函数()()sin f x A x =+ωϕ为奇函数时,k k Z ϕπ=∈,为偶函数时,2k k Z πϕπ=+∈.5.A解析:A 【分析】先整理函数,再根据平移后函数的奇偶性得到a ,b 的值,即可得结果. 【详解】解:函数()cos 2sin 224f x x x x π⎛⎫=-=+ ⎪⎝⎭,函数()24f x x π⎛⎫=+ ⎪⎝⎭的图象向左平移a 个单位得到()224g x x a π⎛⎫=++ ⎪⎝⎭,又因为函数为奇函数,则242a k πππ+=+(k Z ∈),整理得28k a ππ=+(k Z ∈);函数()24f x x π⎛⎫=+ ⎪⎝⎭的图象向右平移b 个单位得到()224h x x b π⎛⎫=-+ ⎪⎝⎭,由于得到的函数的图象为偶函数,2=4b k ππ-+-,=,()82k b k Z ππ+∈;当0k =时,min 0a b -= 故选:A. 【点睛】本题考查了三角函数的平移变换和奇偶性,属于中档题.6.B解析:B 【分析】A.结合奇偶性的定义判断即可B.用正弦型函数的单调性作出判断 CD 可取特值说明 【详解】A. ()1111sin sin 2sin 3sin 4sin100234100f x x x x x x =+++++ ()()()()()()()1111sin sin 2sin 3sin 4sin 100234100f x x x x x x f x -=-+-+-+-++-=-,()f x 为奇函数B. ,1616x ππ⎡⎤∈-⎢⎥⎣⎦时,2,88x ππ⎡⎤∈-⎢⎥⎣⎦,333,1616x ππ⎡⎤∈-⎢⎥⎣⎦,4,44x ππ⎡⎤∈-⎢⎥⎣⎦,故sin ,sin 2,sin 3,sin 4x x x x 在,1616ππ⎡⎤-⎢⎥⎣⎦上均为增函数故111()sin sin 2sin3sin 4234f x x x x x =+++在区间,1616ππ⎡⎤-⎢⎥⎣⎦上单调递增. C. ()()11()sin sin 3sin 434g x f x h x x x x =-=++()()11()sin sin 3sin 434g x f x h x x x x =-=++()()11()sin sin 3sin 4034g f h ππππππ=-=++=故声音甲的响度不一定比纯音1()sin 22h x x =响度大 D. ()11()()sin sin 2sin 323h x g x h x x x x =-=+- ()11()()sin sin 2sin 3023h g h ππππππ=-=+-=甲不一定比纯音1()sin33h x x =更低沉 故选:B 【点睛】“新定义”主要是指即时定义新概念、新公式、新定理、新法则、新运算五种,然后根据此新定义去解决问题,有时还需要用类比的方法去理解新的定义,这样有助于对新定义的透彻理解.但是,透过现象看本质,它们考查的还是基础数学知识,所以说“新题”不一定是“难题”,掌握好三基,以不变应万变才是制胜法宝.7.C解析:C 【分析】利用奇偶性的定义判断函数奇偶性,判断AD 错误,结合常见基本初等函数的单调性判断B 错误,C 正确即可. 【详解】选项A 中,()22xxf x -=-,定义域R ,()()()2222xx x x f x f x ---=-=--=-,则()f x 是奇函数,不符合题意;选项D 中,()cos3=f x x x ,定义域R ,()()()cos 3cos3f x x x x x f x -=--=-=-,则()f x 是奇函数,不符合题意;选项B 中,()23f x x =-,定义域R ,()()()2233x x f x f x -=--=-=,则()f x 是偶函数,但二次函数()23f x x =-在在(),0-∞上是减函数,在()0,∞+上是增函数,故不符合题意;选项C 中,()2ln =-f x x ,定义域为(),0-∞()0,+∞,()()2ln 2ln f x x x f x -=--=-=,则()f x 是偶函数.当()0,x ∈+∞时,()2ln f x x =-是减函数,所以由偶函数图象关于y 轴对称可知,()f x 在(),0-∞上是增函数,故符合题意. 故选:C. 【点睛】 方法点睛:定义法判断函数()f x 奇偶性的方法: (1)确定定义域关于原点对称; (2)计算()f x -;(3)判断()f x -与()f x 的关系,若()()f x f x -=,则()f x 是偶函数;若()()f x f x -=-,则()f x 是奇函数;若两者均不成立,则()f x 是非奇非偶函数.8.D解析:D 【分析】利用题干中的已知条件求得2ω=,可得出()sin 216f x x π⎛⎫=-+ ⎪⎝⎭,利用正弦型函数的对称性可判断①②的正误,利用正弦型函数的值域可判断③的正误,求出方程()1f x =在[]0,2π上的解,可判断④的正误. 【详解】N ω*∈,由55,126x ππ⎡⎤∈⎢⎥⎣⎦可得55126666x πωπππωπω-≤-≤-, 由于函数()()sin 16f x x N πωω*⎛⎫=-+∈ ⎪⎝⎭在55,126ππ⎡⎤⎢⎥⎣⎦上单调递减, 所以,()553,2,21266622k k k Z πωππωπππππ⎡⎤⎡⎤--⊆++∈⎢⎥⎢⎥⎣⎦⎣⎦,所以,521262532662k k ωππππωππππ⎧-≥+⎪⎪⎨⎪-≤+⎪⎩,解得()248121055k k k Z ω++≤≤∈,由248121055k k ++≤,解得16k ≤,N ω*∈且k Z ∈,0k ∴=,可得825ω≤≤,2ω∴=,则()sin 216f x x π⎛⎫=-+ ⎪⎝⎭.对于①,sin 2sin 00126ππ⎛⎫⨯-== ⎪⎝⎭,所以,112f π⎛⎫= ⎪⎝⎭, 所以,函数()f x 的图象关于点,112π⎛⎫⎪⎝⎭成中心对称,①错误; 对于②,271sin 2sin 13662πππ⎛⎫⨯-==-≠± ⎪⎝⎭,②错误;对于③,当,2x ππ⎡⎤∈⎢⎥⎣⎦时,5112,666x πππ⎡⎤-∈⎢⎥⎣⎦,则11sin 262x π⎛⎫-≤-≤ ⎪⎝⎭, 所以,()302f x ≤≤,即()f x 在,2ππ⎡⎤⎢⎥⎣⎦上的值域为30,2⎡⎤⎢⎥⎣⎦,③正确; 对于④,当[]0,2x π∈时,232,666x πππ⎡⎤-∈-⎢⎥⎣⎦, 令()1f x =,可得sin 206x π⎛⎫-= ⎪⎝⎭,206x π∴-=或26x ππ-=或226x ππ-=或236x ππ-=.所以,方程()1f x =在[]0,2π有4个不相同的根,④正确. 故选:D. 【点睛】方法点睛:求函数()()sin f x A x =+ωϕ在区间[],a b 上值域的一般步骤: 第一步:三角函数式的化简,一般化成形如()sin y A x k ωϕ=++的形式或()cos y A x k ωϕ=++的形式;第二步:由x 的取值范围确定x ωϕ+的取值范围,再确定()sin x ωϕ+(或()cos x ωϕ+)的取值范围;第三步:求出所求函数的值域(或最值).9.B解析:B 【分析】根据题设的条件可得正弦型函数的周期、对称中心以及函数在0,4⎡⎤⎢⎥⎣⎦π上的单调性,再逐项检验各选项中的函数是否满足即可得到正确的选项. 【详解】因为对任意的x ∈R ,都有()()12()f x f x f x ≤≤,且12x x -的最小值为2π, 故()f x 的半周期为2π即周期为π,此时A B C D 各选项中的函数均满足. 因为6f x π⎛⎫+⎪⎝⎭为奇函数,故()f x 图象的对称中心为,06π⎛⎫⎪⎝⎭, 对于D 中的函数,因为sin 2166ππ⎛⎫⨯+= ⎪⎝⎭,故,06π⎛⎫⎪⎝⎭不是sin 26y x π⎛⎫=+ ⎪⎝⎭图象的对称中心,故排除D . 因为()()()()11222112x f x x f x x f x x f x +>+等价于()()()12120x x f x f x -->⎡⎤⎣⎦, 故()f x 在0,4⎡⎤⎢⎥⎣⎦π上为增函数, 当0,4x π⎡⎤∈⎢⎥⎣⎦时,4452336x πππ-≤-≤-,而sin y u =在45,36ππ⎡⎤--⎢⎥⎣⎦为减函数, 故4sin 23y x π⎛⎫=-⎪⎝⎭在0,4⎡⎤⎢⎥⎣⎦π为减函数,不合题意,舍; 当0,4x π⎡⎤∈⎢⎥⎣⎦时,2336x πππ-≤-≤,而sin y u =在,36ππ⎡⎤-⎢⎥⎣⎦为增函数, 故sin 23y x π⎛⎫=- ⎪⎝⎭在0,4⎡⎤⎢⎥⎣⎦π为增函数,符合; 当0,4x π⎡⎤∈⎢⎥⎣⎦时,2272336x πππ≤+≤,而sin y u =在27,36ππ⎡⎤⎢⎥⎣⎦为减函数,故2sin 23y x π⎛⎫=+ ⎪⎝⎭在0,4⎡⎤⎢⎥⎣⎦π为减函数,不合题意,舍; 故选:B . 【点睛】方法点睛:已知检验给定的点是否正弦型函数的对称中心,可以用代入检验法,而单调性的研究则需结合“同增异减”的原则来判断.10.A解析:A 【分析】由正切函数的图象性质,得出相邻两个对称中心之间的距离为半个周期,可求出T ,然后由T πω=求出ω,然后再代点讨论满足题意的ϕ,即可得出答案. 【详解】由正切函数图象的性质可知相邻两个对称中心的距离为2T ,得72263T πππ⎛⎫=-= ⎪⎝⎭. 则由1T πω==得1ω=,即得1ω=±. 由2πϕ<,且在区间54,63ππ⎛⎫⎪⎝⎭内单调递减,则可得1ω=-, ∴()()()tan tan f x x x ϕϕ=-+=--. 由2,32k k Z ππϕ-=∈得2,32k k Z ππϕ=-∈,因2πϕ<,可得6π=ϕ或3π-,当3πϕ=-时,()tan +3f x x π⎛⎫=- ⎪⎝⎭,由+,232k x k k Z πππππ-<<+∈,得5,66k x k k Z ππππ-<<+∈, 则函数()f x 的单调减区间为5,,66k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭, 令1k =,由54,63ππ⎛⎫ ⎪⎝⎭7,66ππ⎛⎫ ⎪⎝⎭⊄,得函数()f x 在54,63ππ⎛⎫⎪⎝⎭上不是单调递减, 所以3πϕ=-不满足题意;当6π=ϕ时,()tan 6f x x π⎛⎫=-- ⎪⎝⎭,由,262k x k k Z πππππ-<-<+∈,得2,33k x k k Z ππππ-<<+∈,则函数()f x 的单调减区间为2,,33k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭, 令1k =,由25,3354,63ππππ⎛⎫⊂⎛⎫ ⎪⎝ ⎪⎝⎭⎭,得函数()f x 在54,63ππ⎛⎫⎪⎝⎭上单调递减, 所以6π=ϕ满足题意; 综上可得:6π=ϕ满足题意. 故选:A.【点睛】关键点睛:正切型函数的对称中心和单调性的问题,通常采用代入检验法,注意正切函数的对称中心为0,2k k Z π⎛⎫∈⎪⎝⎭,. 11.D解析:D 【分析】先根据函数的奇偶性,可排除A ,C ,根据当01x <<时,()0f x <即可排除B .得出答案. 【详解】因为()sin ln ||(0)f x x x x =⋅≠,所以()sin()ln ||sin ln ||()f x x x x x f x -=-⋅-=-=-,所以()f x 为奇函数,故排除A ,C .当01x <<时,sin 0x >,ln ||0x <,则()0f x <,故排除B , 故选:D .【点睛】思路点睛:函数图象的辨识可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置. (2)从函数的单调性,判断图象的变化趋势; (3)从函数的奇偶性,判断图象的对称性; (4)从函数的特征点,排除不合要求的图象.12.D解析:D 【解析】分析:将2cos x 化为21sin x -,令()sin 11x t t =-≤≤,可得关于t 的二次函数,根据t 的取值范围,求二次函数的最值即可.详解:利用同角三角函数关系化简,22cos 2sin sin 2sin 1y x x x x =-=--+ 设()sin 11x t t =-≤≤,则()()22211211y t t t t =--+=-++-≤≤,根据二次函数性质当1t =-时,y 取最大值2,当1t =时,y 取最小值2-.故选D.点睛:本题考查三角函数有关的最值问题,此类问题一般分为两类,一种是解析式化为2sin sin y A x B x C =++的形式,用换元法求解;另一种是将解析式化为()sin y A x k ωϕ=++的形式,根据角的范围求解.二、填空题13.【分析】根据题意可得从而可得讨论或再求出的单调递增区间只需是单调递增区间的子集即可求解【详解】由正弦函数的性质的每个增区间的长度为其中函数的最小正周期为函数在区间上单调地藏可得即①当时此时单调递增当解析:130,42⎛⎤⎧⎫⋃-⎨⎬ ⎥⎝⎦⎩⎭【分析】 根据题意可得22T π≥,从而可得2ω≤,讨论0>ω,0ω=或0ω<,再求出()sin()f x x ωϕ=+的单调递增区间,只需,2ππ⎡⎤⎢⎥⎣⎦是单调递增区间的子集即可求解.【详解】()()sin f x x ωϕ=+,0,4πϕ⎡⎤∈⎢⎥⎣⎦,由正弦函数的性质,()f x 的每个增区间的长度为2T,其中函数()f x 的最小正周期为2T ωπ=.函数()f x 在区间,2ππ⎡⎤⎢⎥⎣⎦上单调地藏,可得22T π≥,即2ω≤.①当0>ω时,此时02ω<≤,x ωϕ+单调递增,当2,2,22x k k k Z ππωϕππ⎡⎤+∈-+∈⎢⎥⎣⎦,()f x 单调递增, 解得112,2,22x k k k Z πππϕπϕωω⎡⎤⎛⎫⎛⎫∈--+-∈ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦, 只需11,2,2,222k k k Z πππππϕπϕωω⎡⎤⎡⎤⎛⎫⎛⎫⊆--+-∈ ⎪ ⎪⎢⎥⎢⎥⎣⎦⎝⎭⎝⎭⎣⎦, 从而可得1222,122k k Z k πππϕωπππϕω⎧⎛⎫≥-- ⎪⎪⎪⎝⎭∈⎨⎛⎫⎪≤+- ⎪⎪⎝⎭⎩,解得2141,2,2k k k Z ϕϕωππ⎡⎤∈--+-∈⎢⎥⎣⎦对0,4πϕ⎡⎤∀∈⎢⎥⎣⎦成立, 则21410214k k πωππ--⨯≤≤+-⨯,即141,2,4k k k Z ω⎡⎤∈-+∈⎢⎥⎣⎦,由124141204k k k ⎧+>-⎪⎪⎨⎪+>⎪⎩,解得1588k -<<,k Z ∈,0k ∴=.所以,10,4ω⎛⎤∈ ⎥⎝⎦;②当0ω=时,函数()sin f x ϕ=为常函数,不合乎题意; ③当0ω<时,20ω-≤<,x ωϕ+单调递减, 由322,22k x k k Z πππωϕπ+≤+≤+∈, 解得13122,22k x k k Z πππϕπϕωω⎛⎫⎛⎫+-≤≤+-∈ ⎪ ⎪⎝⎭⎝⎭对0,4πϕ⎡⎤∀∈⎢⎥⎣⎦成立, 可得13222,122k k Z k πππϕωπππϕω⎧⎛⎫≥+- ⎪⎪⎪⎝⎭∈⎨⎛⎫⎪≤+- ⎪⎪⎝⎭⎩,解得122,43,2k k k Z ϕϕωππ⎡⎤∈+-+-∈⎢⎥⎣⎦对0,4πϕ⎡⎤∀∈⎢⎥⎣⎦成立,于是12210434k k πωππ+-⨯≤≤+-⋅,即521,4,2k k k Z ω⎡⎤∈++∈⎢⎥⎣⎦,由5142225402k k k ⎧+≥+⎪⎪⎨⎪+<⎪⎩,解得518k -≤<-,由k Z ∈,1k =-,此时,32ω=-.综上所述,实数ω的取值范围是130,42⎛⎤⎧⎫⋃-⎨⎬ ⎥⎝⎦⎩⎭.故答案为:130,42⎛⎤⎧⎫⋃-⎨⎬ ⎥⎝⎦⎩⎭.【点睛】关键点点睛:本题考查了三角函数的性质,解题的关键是求出函数的单调递增区间,使,2ππ⎡⎤⎢⎥⎣⎦是单调递增区间的子集,考查了分类讨论的思想. 14.②③【分析】先根据图象结合已知条件限制求出的解析式再利用代入验证法判断①错误;利用整体代入法求单调区间判断②正确;解方程并结合诱导公式判断③正确;将函数零点问题转化成函数交点问题数形结合判断④错误即解析:②③ 【分析】先根据图象,结合已知条件限制求出()y f x =的解析式,再利用代入验证法判断①错误;利用整体代入法求单调区间判断②正确;解方程并结合诱导公式判断③正确;将函数零点问题转化成函数交点问题,数形结合判断④错误即可. 【详解】由图象可知,2A =,(0)2sin 1f ϕ==,故1sin 2ϕ=,又2πϕ<,故6π=ϕ,故()2sin 6f x x πω⎛⎫=+ ⎪⎝⎭,又由11112sin 012126f πππω⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭得,112,126k k Z ππωπ+=∈,即224,1111kk Z ω=-+∈, 由题意0>ω,由图知1112T π>,即22411T πω=<,故1k =时2ω=.故()2sin 26f x x π⎛⎫=+ ⎪⎝⎭. ①因为252sin 2sin 103366f ππππ⎛⎫⎛⎫=+==≠⎪ ⎪⎝⎭⎝⎭,故点,03π⎛⎫ ⎪⎝⎭不是()y f x =图象的对称中心,故错误; ②令322,2,622x k k k Z πππππ⎛⎫+∈++∈ ⎪⎝⎭, 解得单调递减区间为2,,63k k k ππππ⎛⎫++∈⎪⎝⎭Z ,故正确;③若()2sin 26f x x a π⎛⎫=+= ⎪⎝⎭,则sin 262a x π⎛⎫+= ⎪⎝⎭,则cos cos 2sin 2sin 2332362a x x x x πππππω⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫-=-=+-=+= ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦,故正确; ④令2()()log 0g x f x x =-=,得方程2()log f x x =的根的问题, 即函数()2sin 26y f x x π⎛⎫==+⎪⎝⎭与函数2log y x =的交点个数问题,如图,令22,62x k k Z πππ+=+∈,则,6x k k Z ππ=+∈时()y f x =取得最大值2.如图,6x π=时,2()log f x x >;76x π=时,746π<,227log log 426π<=2()2log f x x =>;当136x π=时,1346π>,2213log log 426π>=,2()2log f x x =<. 故函数()2sin 26y f x x π⎛⎫==+ ⎪⎝⎭与函数2log y x =有3个交点,即2()()log g x f x x =-有3个零点.故错误. 故答案为:②③. 【点睛】方法点睛:判断函数零点个数的方法(1)直接法:令()0f x =,如果能求出解,那么有几个不同的解就有几个零点; (2)利用函数的零点存在性定理:利用函数的零点存在性定理时,不仅要求函数的图象在区间[],a b 上是连续不断的曲线,并且()()0f a f b ⋅<,还必须结合函数的图象与性质,(如单调性、奇偶性)才能确定函数有多少个零点;(3)图象法:画出函数()f x 的图象,函数()f x 的图象与x 轴交点的个数就是函数()f x 的零点个数;将函数()f x 拆成两个函数,()h x 和()g x 的形式,根据()0f x =等价于()()h x g x =,则函数()f x 的零点个数就是函数()y h x =和()y g x =的图象交点个数;(4)利用函数的性质:若能确定函数的单调性,则其零点个数不难得到,若所考查的函数是周期函数,则需要求出在一个周期内的零点个数,根据周期性则可以得出函数的零点个数.15.【分析】根据题意作出示意图结合枢纽中心到初始水平面的高度水面下降的高度刚进入水面时枢纽中心到水面的高度这三者间的关系列出关于运动时间的方程结合所给数据分析的取值即可【详解】设至少经过分钟进入水中如下 解析:13【分析】根据题意作出示意图,结合枢纽中心到初始水平面的高度、水面下降的高度、P 刚进入水面时枢纽中心到水面的高度这三者间的关系,列出关于运动时间x 的方程,结合所给数据分析x 的取值即可. 【详解】设至少经过x 分钟,P 进入水中,如下图P '为刚好进入水中的位置,由条件可知: 1.7, 1.19OP OA '==,P 转过的角度为23015x x ππ⋅=,所以15xP OB ππ'∠=-,因为OA AB OB +=,所以1.170.017 1.7cos 15x x ππ⎛⎫+=-⎪⎝⎭,所以70100cos 15x x ππ⎛⎫+=- ⎪⎝⎭(*),根据所给数据可知:当12x =时,(*)的左边82=,右边81=,此时左边>右边,说明P 还未进入水中,当13x =时,(*)的左边83=,右边91=,此时左边<右边,说明P 已经进入水中, 当14x =时,(*)的左边84=,右边98=,此时左边<右边,说明P 已经进入水中, 由上可知:x 的取值介于12和13之间,又因为x 的结果取整数,所以13x =, 故答案为:13. 【点睛】关键点点睛:解答本题的关键是通过示意图寻找到枢纽中心到水面的高度与水面下降高度之间的等量关系,通过所给的数据去分析方程的解也是很重要的一步.16.【解析】当时由得所以减区间为解析:5,122ππ⎡⎤⎢⎥⎣⎦【解析】当[0,]2x π∈时,ππ2π2[,]333x -∈-,由22233x πππ≤-≤,得5122x ππ≤≤,所以减区间为5[,]122ππ. 17.【分析】由周期公式可得由三角函数的中心对称可得结合即可得为奇数即可得由可得进而可得即可得解【详解】由可得由是奇函数可得函数的图象关于中心对称所以即又所以所以为奇数由可得因为在上没有最小值所以即故答案解析:511,612ππ⎛⎤⎥⎝⎦【分析】由周期公式可得ω,由三角函数的中心对称可得,3k k Z πϕπ=+∈,结合()06f f π⎛⎫< ⎪⎝⎭即可得k 为奇数,即可得()sin 23πf x x ⎛⎫=- ⎪⎝⎭,由[)0,x t ∈可得2,2333x t πππ⎡⎫-∈--⎪⎢⎣⎭,进而可得432332t πππ<-≤,即可得解. 【详解】由T π=可得22T πω==,()sin 23f x x πϕ⎛⎫=++ ⎪⎝⎭由3y f x π⎛⎫=- ⎪⎝⎭是奇函数可得函数()f x 的图象关于,03π⎛-⎫⎪⎝⎭中心对称, 所以2,33k k Z ππϕπ⎛⎫⨯-++=∈ ⎪⎝⎭,即,3k k Z πϕπ=+∈, 又()06f f π⎛⎫< ⎪⎝⎭,所以2sin sin 33ππϕϕ⎛⎫⎛⎫+<+ ⎪ ⎪⎝⎭⎝⎭, 所以,3k k πϕπ=+为奇数,()sin 2sin 2333f x x k x ππππ⎛⎫⎛⎫=+++=- ⎪ ⎪⎝⎭⎝⎭,由[)0,x t ∈可得2,2333x t πππ⎡⎫-∈--⎪⎢⎣⎭, 因为()f x 在[)0,t 上没有最小值,所以432332t πππ<-≤即511,612t ππ⎛⎤∈⎥⎝⎦. 故答案为:511,612ππ⎛⎤⎥⎝⎦. 【点睛】本题考查了三角函数图象与性质的应用,考查了运算求解能力,牢记知识点是解题关键,属于中档题.18.6【分析】根据题意可求得然后利用正弦定理求得最后在中利用求得答案【详解】在中由正弦定理得;在中(米)所以升旗速度(米/秒)故答案为06【点睛】本题主要考查了解三角形的实际应用此类问题的解决关键是建立解析:6 【分析】根据题意可求得,45BDC ∠=︒,30CBD ∠=︒,CD =BC ,最后在Rt ABC 中利用sin60AB BC =︒求得答案. 【详解】在BCD 中,45BDC ∠=︒,30CBD ∠=︒,CD =由正弦定理,得sin 45sin 30CD BC ︒==︒在Rt ABC 中,sin?6030AB BC =︒==(米). 所以升旗速度300.650t AB v ===(米/秒). 故答案为0.6. 【点睛】本题主要考查了解三角形的实际应用.此类问题的解决关键是建立数学模型,把实际问题转化成数学问题,利用所学知识解决,属于中档题.19.9【分析】由在区间上单调可得故进一步求出范围即可【详解】由知故;又在区间上单调故即18符合条件的的值有9个故答案为:9【点睛】本题考查三角函数的图象与性质考查转化与化归思想考查逻辑推理能力运算求解能解析:9 【分析】 由()f x 在区间(,)43ππ上单调,可得342T ππ-,故6T π,进一步求出ω范围即可. 【详解】由()24f π=,()0f π=知,34244T kT πππ+=-=,k ∈N , 故312T k π=+,2(12)3k ω+=,k ∈N ; 又()f x 在区间(,)43ππ上单调,∴342T ππ-,故6T π,∴212T πω=,即2(12)123k +, ∴172k,k ∈N , 0k ∴=,1,2⋯,8符合条件的ω的值有9个. 故答案为:9. 【点睛】本题考查三角函数的图象与性质,考查转化与化归思想,考查逻辑推理能力、运算求解能力,属中档题.20.②③【分析】根据三角函数的零点性质三角函数对称和三角函数诱导公式依次判断每个选项得到答案【详解】①中是的两个零点即是的整数倍①错误;②中②正确;故④错误;③中③正确;所以正确命题序号是②③故答案为:解析:②③ 【分析】根据三角函数的零点性质,三角函数对称和三角函数诱导公式依次判断每个选项得到答案. 【详解】①中12,x x 是()f x 的两个零点,即12x x -是2π的整数倍,①错误; ②中06f π⎛⎫-= ⎪⎝⎭,②正确;故④错误; ③中4sin 24cos 2cos 23236y x x x ππππ⎛⎫⎛⎫⎛⎫=+=--=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,③正确; 所以正确命题序号是②③. 故答案为:②③. 【点睛】本题考查了三角函数的对称,零点,诱导公式,意在考查学生对于三角函数知识的综合应用.三、解答题21.条件选择见解析;(1)()2sin 23f x x π⎛⎫=- ⎪⎝⎭;(2)12x π=-时,函数f (x )取得最小值,最小值为2-. 【分析】(1)由相邻中心距离得周期,从而可得ω,选择①,写出平移后解析式,由对称性得新函数为偶函数,结合诱导公式求得ϕ,选择②,求出6y f x π⎛⎫=+ ⎪⎝⎭,由函数为奇函数,结合诱导公式求得ϕ,选择③,求出()6y f x π=-,代入712x π=,结合正弦函数最大值可得ω, 从而得函数解析式; (2)()2sin 23f x x π⎛⎫=- ⎪⎝⎭由,求得23x π-的范围,然后由正弦函数性质得最小值.【详解】(1)因为函数f (x )=2sin(ωx +φ)的图象相邻的对称中心之间的距离为2π, 所以周期22T π=,即T =π,所以22T πω==.若选择①,因为函数f (x )图象向右平移12π个单位所得图象关于y 轴对称,所以()2sin 22sin 2126g x x x ππϕϕ⎡⎤⎛⎫⎛⎫=-+=-+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦的图象关于y 轴对称,所以62k ππϕπ-=+,k Z ∈,因为||2ϕπ<,所以3πϕ=-.所以函数y =f (x )的解析式为()2sin 23f x x π⎛⎫=- ⎪⎝⎭.若选择②,因为2sin 22sin 2663y f x x x πππϕϕ⎡⎤⎛⎫⎛⎫⎛⎫=+=++=++ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦是奇函数,所以3k πϕπ+=,k Z ∈,因为||2ϕπ<,所以3πϕ=-.所以函数y =f (x )的解析式为()2sin 23f x x π⎛⎫=- ⎪⎝⎭.若选择③,2sin 22sin 2663y f x x x πππϕϕ⎡⎤⎛⎫⎛⎫⎛⎫=-=⨯-+=-+ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,由题设,当712x π=时,函数6y f x π⎛⎫=- ⎪⎝⎭取得最大值,所以当722()1232k k Z πππϕπ⨯-+=+∈,即2()3k k Z πϕπ=-∈, 因为||2ϕπ<,所以3πϕ=-.所以函数y =f (x )的解析式为()2sin 23f x x π⎛⎫=- ⎪⎝⎭.(2)因为()2sin 23f x x π⎛⎫=-⎪⎝⎭,,22x ππ⎡⎤∈-⎢⎥⎣⎦,所以422,333x πππ⎡⎤-∈-⎢⎥⎣⎦,所以当232x ππ-=-,即12x π=-时,函数f (x )取得最小值,最小值为2-.【点睛】关键点点睛:本题考查由三角函数的图象与性质求解析式,解题关键是掌握正弦函数的图象与性质,解题时注意“五点法”和整体思想的应用.对于奇偶性问题注意诱导公式的应用,由此计算比较方便. 22.(1)336S π⎛⎫= ⎪⎝⎭;(2)1sin 3θ=. 【分析】(1)作出图形,可知公共部分区域为直角三角形,计算出两直角边的长,由此可求得该直角三角形的面积; (2)分6πθ=、06πθ<<、62ππθ<<三种情况讨论,求出()S θ的表达式,结合()72S θ=可求得sin θ的值. 【详解】 (1)当3πθ=时,A '点在矩形OABC 外部,公共部分形状为三角形,设A O BC D '⋂=,则6COD π∠=,3tan6CD CO π==, 则11331322S CD CO π⎛⎫=⨯⨯=⨯⨯=⎪⎝⎭;(2)①当6πθ=时,点A '在线段BC 上,此时,223A C A O OC ''-=11313622S OC A C π⎛⎫'=⨯=⨯=⎪⎝⎭; ②当06πθ<<时,公共部分为四边形,A '点在矩形OABC 内部,过点A '作线段AB 的平行线,分别交线段AO 、BC 于点E 、。
(典型题)高中数学必修四第一章《三角函数》检测(含答案解析)(1)

一、选择题1.若函数()sin 2f x x =与()2cos g x x =都在区间(),a b 上单调递减,则b a -的最大值是( ) A .π4B .π3C .π2D .2π32.函数()sin()(0||)2,f x x πωϕωϕ=+><的部分函数图象如图所示,将函数()f x 的图象先向右平移3π个单位长度,然后向上平移1个单位长度,得到函数()g x 的解析式为( )A .()sin 21g x x =-B .()sin 21g x x =+C .()sin(2)13g x x π=--D .()sin(2)13g x x π=-+3.函数()()sin cos y x =的部分图象大致为( )A .B .C .D .4.如图,一个质点在半径为1的圆O 上以点P 为起始点,沿逆时针方向旋转,每2s 转一圈,由该质点到x 轴的距离y 关于时间t 的函数解析式是( )A .2sin()3y t ππ=+ B .2sin()3y t ππ=- C .2sin()3y t ππ=-D .2sin()3y t ππ=+5.将函数sin()y x ϕ=+的图像上所有点的横坐标缩短到原来的12倍(纵坐标不变),再将所得图像向左平移12π个单位后得到的函数图像关于原点中心对称,则sin 2ϕ=( )A .12-B .12C .3D 36.函数1sin3y x =-的图像与直线3x π=,53x π=及x 轴所围成的图形的面积是( ) A .23π B .πC .43π D .53π 7.已知函数sin()0,0,||2y A x b A πωϕωϕ⎛⎫=++>>< ⎪⎝⎭的图象上相邻的一个最大值点与对称中心分别为2,39π⎛⎫ ⎪⎝⎭,,018π⎛⎫⎪⎝⎭,则函数()f x 的单调增区间为( ) A .222,3939k k ππππ⎛⎫-+ ⎪⎝⎭,k Z ∈ B .242,3939k k ππππ⎛⎫--⎪⎝⎭,k Z ∈ C .227,318318k k ππππ⎛⎫++⎪⎝⎭,k Z ∈ D .272,318318k k ππππ⎛⎫--⎪⎝⎭,k Z ∈ 8.已知函数()tan()0,02f x x πωϕϕω⎛⎫=+<<< ⎪⎝⎭最小正周期为2π,且()f x 的图象过点,03π⎛⎫⎪⎝⎭,则方程()sin 2([0,])3f x x x π⎛⎫=+∈π ⎪⎝⎭所有解的和为( )A .76πB .56π C .2πD .3π 9.函数()()πsin 0,0,2f x A x A ωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图,将()y f x =的图象向右平移π6个单位长得到函数y g x 的图象,则()g x 的单调增区间为( )A .()ππ2π,2π63k k k ⎡⎤-+∈⎢⎥⎣⎦Z B .()π5π2π,2π36k k k ⎡⎤++∈⎢⎥⎣⎦Z C .()πππ,π63k k k ⎡⎤-+∈⎢⎥⎣⎦Z D .()π5ππ,π36k k k ⎡⎤++∈⎢⎥⎣⎦Z 10.已知1sin 34x π⎛⎫+= ⎪⎝⎭,则22sin sin 36x x ππ⎛⎫⎛⎫-+-=⎪ ⎪⎝⎭⎝⎭( ) A .1B 151+C .1916D .3411.下列函数中,既是偶函数,又在(),0-∞上是增函数的是( ) A .()22xxf x -=- B .()23f x x =-C .()2ln =-f x xD .()cos3=f x x x12.已知函数()tan()0,2f x x πωϕωϕ⎛⎫=+≠< ⎪⎝⎭,点2,03π⎛⎫⎪⎝⎭和7,06π⎛⎫⎪⎝⎭是其相邻的两个对称中心,且在区间54,63ππ⎛⎫⎪⎝⎭内单调递减,则ϕ=( ) A .6π B .6π-C .3π D .3π-二、填空题13.若函数()sin (0)4f x x πωωω⎛⎫=-> ⎪⎝⎭取得最值的点到y 轴的最近距离小于6π,且()f x 在711,2020ππ⎛⎫⎪⎝⎭单调递增,则ω的取值范围为_________. 14.关于1()sin sin f x x x=-,有如下四个结论: ①()f x 是奇函数.②()f x 图像关于y 轴对称. ③2x π=是()f x 的一条对称轴.④()f x 有最大值和最小值. 其中说法正确的序号是________.15.已知函数()()3cos g x x ωϕ=+()0ω>满足04g π⎛⎫=⎪⎝⎭,()3g π=,且最小正周期3T π≥,则符合条件的ω的取值个数为___________.16.圆心角为2弧度的扇形的周长为3,则此扇形的面积为 _____ . 17.如图,某公园要在一块圆心角为3π,半径为20m 的扇形草坪OAB 中修建一个内接矩形文化景观区域CDEF ,若//EF AB ,则文化景观区域面积的最大值为______2m .18.设函数()2sin()0,02f x x πωϕωϕ⎛⎫=+><<⎪⎝⎭的图象关于直线23x π=对称,它的周期为π,则下列说法正确是________(填写序号) ①()f x 的图象过点30,2⎛⎫ ⎪⎝⎭; ②()f x 在2,123ππ⎡⎤⎢⎥⎣⎦上单调递减; ③()f x 的一个对称中心是5,012π⎛⎫⎪⎝⎭; ④将()f x 的图象向右平移ϕ个单位长度得到函数2sin 2y x =的图象. 19.若函数f (x )=2sin(ωx +φ)(ω>0,0<φ<π)的图象经过点,26π⎛⎫⎪⎝⎭,且相邻两条对称轴间的距离为2π,则4f π⎛⎫⎪⎝⎭的值为________. 20.如图,游乐场所的摩天轮匀速旋转,每转一周需要l2min ,其中心O 离地面45米,半径40米.如果你从最低处登上摩天轮,那么你与地面的距离将随时间的变化而变化,以你登上摩天轮的时刻开始计时,请问:当你第六次距离地面65米时,用了________分钟?三、解答题21.已知函数()2sin()0,02f x x πωϕωϕ⎛⎫=+><< ⎪⎝⎭的图象与直线2y =的相邻两个交点间的距离为2π,且________.在①函数6f x π⎛⎫+ ⎪⎝⎭为偶函数;②33f π⎛⎫=⎪⎝⎭;③x R ∀∈,()6f x f π⎛⎫≤⎪⎝⎭;这三个条件中任选一个,补充在上面问题中,并解答. (1)求函数()f x 的解析式;(2)求函数()f x 在[]0,π上的单调递增区间.22.如图,一个水轮的半径为4米,水轮圆心O 距离水面2米,已知水轮每分钟逆时针转动1圈,当水轮上点P 从水中浮现时(图中点0P )开始计算时间.(1)将点P 距离水面的距离z (单位:米,在水面以下,则z 为负数)表示为时间t (单位:秒)的函数;(2)在水轮转动1圈内,有多长时间点P 位于水面上方? 23.设函数()3sin (0)4f x x πωω⎛⎫=+> ⎪⎝⎭,且以23π为最小正周期. (1)求函数()f x 的单调递减区间; (2)当,32x ππ⎡⎤∈⎢⎥⎣⎦时,求()f x 的值域. 24.已知向量a =(cosωx -sinωx ,sinωx),b =(-cosωx -sinωx,2cosωx).设函数f(x)=a b⋅+λ(x ∈R)的图象关于直线x =π对称,其中ω,λ为常数,且ω∈1,12⎛⎫ ⎪⎝⎭. (1)求函数f(x)的最小正周期; (2)若y =f(x)的图象经过点,04π⎛⎫⎪⎝⎭,求函数f(x)在区间30,5π⎡⎤⎢⎥⎣⎦上的取值范围 25.己知函数()sin 3cos (0, 0 )f x A x x A ωωω=>>,其部分图象如图所示.(1)求A 和ω的值;(2)求函数()y f x =在[]0,π的单调增区间. 26.已知函数()23,4f x x x R π⎛⎫=+∈ ⎪⎝⎭.(1)求f (x )的最小正周期;(2)求f (x )的单调递增区间和单调递减区间; (3)当0,2x π⎡⎤∈⎢⎥⎣⎦,求f (x )值域.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】根据题意求出(),()f x g x 原点附近的单调递减区间,根据递减区间分析可得max 3π4b =,min π4a =,相减即可. 【详解】 解:由题意函数()sin 2f x x =在π3π,44⎛⎫⎪⎝⎭上单调递减,函数()2cos g x x =在()0,π上单调递减, 所以则max 3π4b =,min π4a =,所以b a -的最大值为3πππ442-=. 故选:C. 【点睛】求三角函数单调区间的2种方法:(1)代换法:就是将比较复杂的三角函数处理后的整体当作一个角u (或t ),利用基本三角函数的单调性来求所要求的三角函数的单调区间;(2)图象法:函数的单调性表现在图象上是从左到右,图象上升趋势的区间为单调递增区间,图象下降趋势的区间为单调递减区间,画出三角函数的图象,结合图象易求它的单调区间.2.D解析:D 【分析】由周期求出ω,由五点法作图求出ϕ的值,可得()f x 的解析式,再根据函数sin()y A x ωϕ=+的图象变换规律,得出结论.【详解】根据函数()sin()(0f x x ωϕω=+>,||)2πϕ<的部分函数图象,1274123πππω⋅=-,2ω∴=. 再根据五点法作图,23πϕπ⨯+=,3πϕ∴=,()sin(2)3f x x π=+.将函数()f x 的图象先向右平移3π个单位长度,可得sin(2)3y x π=-的图象.然后向上平移1个单位长度,得到函数()g x 的解析式为()sin(2)13g x x π=-+,故选:D 【点睛】关键点睛:解答本题的关键在于准确地根据三角函数的图象求出三角函数sin()y A x ωϕ=+的解析式,一般根据周期求出ω的值,根据最值求出A 的值,根据最值点求出ϕ的值.3.A解析:A 【分析】先确定奇偶性,再取特殊值确定函数值可能为负,排除三个选项后得出结论. 【详解】记()()sin cos f x x =,则()()()sin cos()sin cos ()f x x x f x -=-==,为偶函数,排除D , 当23x π=时,21()sin cos sin 032f x π⎛⎫⎛⎫⎛⎫==-< ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,排除B ,C .故选:A . 【点睛】本题考查由解析式先把函数图象,解题方法是排除法,可通过研究函数的性质如奇偶性、单调性等排除一些选项,再由特殊的函数值,函数值的正负,变化趋势等排除一些选项后得出正确结论.4.A解析:A 【分析】首先根据图象理解t 秒后23POx t ππ∠=+,再根据三角函数的定义求点P 的纵坐标和该质点到x 轴的距离y 关于时间t 的函数解析式. 【详解】由题意可知点P 运动的角速度是22ππ=(弧度/秒) 那么点P 运动t 秒后23POx t ππ∠=+, 又三角函数的定义可知,点P 的纵坐标是2sin 3t ππ⎛⎫+⎪⎝⎭, 因此该质点到x 轴的距离y 关于时间t 的函数解析式是2sin 3y t ππ⎛⎫=+ ⎪⎝⎭. 故选:A 【点睛】关键点点睛:本题的关键是理解三角函数的定义,并正确表示点23POx t ππ∠=+,即可表示函数的解析式.5.C解析:C 【分析】先根据条件写出图像变换后的函数解析式,然后根据图像关于原点中心对称可知函数为奇函数,由此得到ϕ的表示并计算出sin 2ϕ的结果. 【详解】因为变换平移后得到函数sin 26y x πϕ⎛⎫=++ ⎪⎝⎭,由条件可知sin 26y x πϕ⎛⎫=++⎪⎝⎭为奇函数,所以6k πϕπ+=,sin 2sin 2sin 33k ππϕπ⎛⎫⎛⎫=-=-= ⎪ ⎪⎝⎭⎝⎭故选C . 【点睛】本题考查三角函数的图像变换以及根据函数奇偶性判断参数值,难度一般.正弦型函数()()sin f x A x =+ωϕ为奇函数时,k k Z ϕπ=∈,为偶函数时,2k k Z πϕπ=+∈.6.C解析:C 【分析】作出函数1sin3y x =-的图像,利用割补法,补成长方形,计算面积即可. 【详解】作出函数1sin3y x =-的图象,如图所示,利用割补法,将23π到π部分的图象与x 轴围成的图形补到图中3π到23π处阴影部分,凑成一个长为3π,宽为2的长方形,后面π到53π,同理;∴1sin3y x =-的图象与直线3x π=,53x π=及x 轴所围成的面积为24233ππ⨯=,故选:C. 【点睛】用“五点法”作()sin y A ωx φ=+的简图,主要是通过变量代换,设z x ωϕ=+,由z 取0,2π,π,32π,2π来求出相应的x ,通过列表,计算得出五点坐标,描点后得出图象. 7.A解析:A 【分析】由最大值点和对称中心的坐标可以求出()f x 的解析式,利用三角函数的性质,整体代换得出该复合函数的单调增区间. 【详解】图像上相邻的一个最大值点与对称中心分别为2,39π⎛⎫⎪⎝⎭,,018π⎛⎫⎪⎝⎭, 3A ∴=,0b =且124918T ππ=-,可得23T π=, 23Tπω∴==, 3sin(3)y x ϕ∴=+将2,39π⎛⎫⎪⎝⎭代入可得3sin(3)3y x ϕ=+=, 可得22,32k k Z ππϕπ+=+∈,且2πϕ<, 6πϕ∴=-,可得()3sin(3)6f x x π=-,令6232,22k x k k Z πππππ-+≤-≤+∈,可得222+9393k x k ππππ-≤≤, 故选:A. 【点睛】方法点睛:根据图像求函数()sin()f x A x k ωϕ=++的解析式,根据最高点和对称中心的纵坐标可求出A 和k ,根据横坐标可求出周期T ,进而求出ω.求该函数的单调区间时,用整体代换的思想,借助正弦函数的单调区间,用解不等式的方法求复合函数的单调区间.8.A解析:A 【分析】先根据()f x 的最小正周期计算出ω的值,再根据图象过点,03π⎛⎫⎪⎝⎭结合ϕ的范围求解出ϕ的值,再根据条件将方程变形,先确定出tan 23x π⎛⎫+ ⎪⎝⎭的值,然后即可求解出方程的根,由此确定出方程所有解的和. 【详解】因为()f x 的最小正周期为2π,所以22πωπ==,又因为()f x 的图象过点,03π⎛⎫⎪⎝⎭,所以2tan 03πϕ⎛⎫+= ⎪⎝⎭, 所以2,3k k Z ϕππ+=∈,又因为02πϕ<<,所以3πϕ=且此时1k =,所以()sin 23f x x π⎛⎫=+ ⎪⎝⎭,即tan 2sin 233x x ππ⎛⎫⎛⎫+=+ ⎪ ⎪⎝⎭⎝⎭, 即tan 2cos 21033x x ππ⎡⎤⎛⎫⎛⎫++-= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,又因为tan 203x π⎛⎫+= ⎪⎝⎭时,sin 203x π⎛⎫+= ⎪⎝⎭,cos 213x π⎛⎫+=± ⎪⎝⎭, 所以tan 2cos 210tan 2=0333x x x πππ⎡⎤⎛⎫⎛⎫⎛⎫++-=⇔+ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦, 因为[]0,x π∈,所以72,333x πππ⎛⎫⎡⎤+∈ ⎪⎢⎥⎝⎭⎣⎦, 当tan 2=03x π⎛⎫+⎪⎝⎭时,23x ππ+=或223x ππ+=,解得3x π=或56x π=, 所以方程()[]()sin 20,3f x x x ππ⎛⎫=+∈ ⎪⎝⎭所有解的和为57366πππ+=. 故选:A. 【点睛】关键点点睛:解答本题的关键是通过分析方程得到tan 2=03x π⎛⎫+⎪⎝⎭,此处需要注意不能直接约去tan 23x π⎛⎫+ ⎪⎝⎭,因为需要考虑tan 2=03x π⎛⎫+ ⎪⎝⎭的情况.9.C解析:C 【分析】根据()f x 的图象,可求出()f x 的解析式,进而根据图象平移变换规律,可得到()g x 的解析式,然后求出单调增区间即可. 【详解】由()f x 的图象,可得1A =,311ππ4126T =-,即πT =,则2ππT ω==,所以2ω=,由π16f ⎛⎫=⎪⎝⎭,可得πsin 216ϕ⎛⎫⨯+= ⎪⎝⎭,所以ππ22π62k ϕ⨯+=+()k ∈Z ,则π2π6k ϕ=+()k ∈Z , 又π2ϕ<,所以π6ϕ=,故()πsin 26f x x ⎛⎫=+ ⎪⎝⎭.将()f x 的图象向右平移π6个单位长得到函数πππsin 22sin 2666y x x ⎛⎫⎛⎫=-⨯+=- ⎪ ⎪⎝⎭⎝⎭,故函数()πsin 26g x x ⎛⎫=- ⎪⎝⎭, 令πππ2π22π262k x k -≤-≤+()k ∈Z ,解得()ππππ63k x k k -≤≤+∈Z ,所以()g x 的单调增区间为()πππ,π63k k k ⎡⎤-+∈⎢⎥⎣⎦Z . 故选:C. 【点睛】本题考查三角函数的图象性质,考查三角函数图象的平移变换,考查三角函数的单调性,考查学生的推理能力与计算求解能力,属于中档题.10.C解析:C 【分析】由诱导公式求得cos 6x π⎛⎫- ⎪⎝⎭,然后再由平方关系和诱导公式计算. 【详解】 由已知1cos cos sin 62334x x x ππππ⎡⎤⎛⎫⎛⎫⎛⎫-=-+=+=⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦, 222115sin 1cos 166416x x ππ⎛⎫⎛⎫⎛⎫-=--=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,21sin sin cos 32664x x x ππππ⎛⎫⎛⎫⎛⎫-=+-=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 所以2211519sin sin 3641616x x ππ⎛⎫⎛⎫-+-=+= ⎪ ⎪⎝⎭⎝⎭. 故选:C . 【点睛】关键点点睛:本题考查三角函数的求值.解题关键是确定“已知角”和“未知角”的关系,选用适当的公式进行变形求值.本题中首先利用诱导公式得出cos 6x π⎛⎫- ⎪⎝⎭,然后再用诱导公式得出2sin 3x π⎛⎫-⎪⎝⎭,用平方关系得出2sin 6x π⎛⎫- ⎪⎝⎭,这样求解比较方便.11.C解析:C 【分析】利用奇偶性的定义判断函数奇偶性,判断AD 错误,结合常见基本初等函数的单调性判断B 错误,C 正确即可. 【详解】选项A 中,()22xxf x -=-,定义域R ,()()()2222xx x x f x f x ---=-=--=-,则()f x 是奇函数,不符合题意;选项D 中,()cos3=f x x x ,定义域R ,()()()cos 3cos3f x x x x x f x -=--=-=-,则()f x 是奇函数,不符合题意;选项B 中,()23f x x =-,定义域R ,()()()2233x x f x f x -=--=-=,则()f x 是偶函数,但二次函数()23f x x =-在在(),0-∞上是减函数,在()0,∞+上是增函数,故不符合题意;选项C 中,()2ln =-f x x ,定义域为(),0-∞()0,+∞,()()2ln 2ln f x x x f x -=--=-=,则()f x 是偶函数.当()0,x ∈+∞时,()2ln f x x =-是减函数,所以由偶函数图象关于y 轴对称可知,()f x 在(),0-∞上是增函数,故符合题意. 故选:C. 【点睛】 方法点睛:定义法判断函数()f x 奇偶性的方法: (1)确定定义域关于原点对称; (2)计算()f x -;(3)判断()f x -与()f x 的关系,若()()f x f x -=,则()f x 是偶函数;若()()f x f x -=-,则()f x 是奇函数;若两者均不成立,则()f x 是非奇非偶函数.12.A解析:A 【分析】由正切函数的图象性质,得出相邻两个对称中心之间的距离为半个周期,可求出T ,然后由T πω=求出ω,然后再代点讨论满足题意的ϕ,即可得出答案. 【详解】由正切函数图象的性质可知相邻两个对称中心的距离为2T ,得72263T πππ⎛⎫=-= ⎪⎝⎭. 则由1T πω==得1ω=,即得1ω=±. 由2πϕ<,且在区间54,63ππ⎛⎫⎪⎝⎭内单调递减,则可得1ω=-, ∴()()()tan tan f x x x ϕϕ=-+=--. 由2,32k k Z ππϕ-=∈得2,32k k Z ππϕ=-∈,因2πϕ<,可得6π=ϕ或3π-,当3πϕ=-时,()tan +3f x x π⎛⎫=- ⎪⎝⎭,由+,232k x k k Z πππππ-<<+∈,得5,66k x k k Z ππππ-<<+∈, 则函数()f x 的单调减区间为5,,66k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭,令1k =,由54,63ππ⎛⎫ ⎪⎝⎭7,66ππ⎛⎫ ⎪⎝⎭⊄,得函数()f x 在54,63ππ⎛⎫⎪⎝⎭上不是单调递减, 所以3πϕ=-不满足题意;当6π=ϕ时,()tan 6f x x π⎛⎫=-- ⎪⎝⎭,由,262k x k k Z πππππ-<-<+∈,得2,33k x k k Z ππππ-<<+∈, 则函数()f x 的单调减区间为2,,33k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭, 令1k =,由25,3354,63ππππ⎛⎫⊂⎛⎫ ⎪⎝ ⎪⎝⎭⎭,得函数()f x 在54,63ππ⎛⎫⎪⎝⎭上单调递减, 所以6π=ϕ满足题意; 综上可得:6π=ϕ满足题意. 故选:A.【点睛】关键点睛:正切型函数的对称中心和单调性的问题,通常采用代入检验法,注意正切函数的对称中心为0,2k k Z π⎛⎫∈⎪⎝⎭,. 二、填空题13.【分析】根据题意可得为的一个零点且且上有且只有一个最值点从而可得再由在单调递增可得解不等式组即可求解【详解】依题意为的一个零点且所以在上有且只有一个最值点可得化简得又则所以解得当时可得又所以故答案为解析:65,53⎛⎤⎥⎝⎦【分析】 根据题意可得,04π⎛⎫⎪⎝⎭为()f x 的一个零点,且45T π≥,且,66ππ⎛⎫- ⎪⎝⎭上有且只有一个最值点,从而可得665ω<<,再由()f x 在711,2020ππ⎛⎫ ⎪⎝⎭单调递增,可得221032210k k ππωπππωπ⎧-+≤⎪⎪⎨⎪+≥⎪⎩,解不等式组即可求解. 【详解】依题意,04π⎛⎫⎪⎝⎭为()f x 的一个零点且117420205T πππ≥-=, 所以在,66ππ⎛⎫- ⎪⎝⎭上有且只有一个最值点, 可得46446T ππππ-<<+,化简得665ω<<, 又711,2020x ππ⎛⎫∈⎪⎝⎭,则3,41010x πωπωπω⎛⎫⎛⎫-∈ ⎪⎪⎝⎭⎝⎭所以221032210k k ππωπππωπ⎧-+≤⎪⎪⎨⎪+≥⎪⎩,解得5520203k k ω-+≤≤+,k Z ∈,当0k =时,可得553ω-≤≤,又665ω<<,所以6553ω<≤. 故答案为:65,53⎛⎤⎥⎝⎦【点睛】关键点点睛:本题考查了三角函数的性质,解题的关键是根据三角函数的最值得665ω<<,以及函数的单调递增区间可得5520203k k ω-+≤≤+,k Z ∈,考查了分析、计算能力.14.①③【分析】借助于的性质对照四个选项一一验证【详解】的定义域对于①:定义域关于原点对称即是奇函数故①正确;是奇函数图像关于原点对称故②错误;对于③:而所以故③正确;对于④:令则无最小值无最大值故④错解析:①③ 【分析】借助于sin y x =的性质,对照四个选项,一一验证. 【详解】1()sin sin f x x x=-的定义域{}|,x x k k Z π≠∈ 对于①:定义域关于原点对称,()()11()sin sin ()sin sin f x x x f x x x ⎛⎫-=--=-+=- ⎪-⎝⎭,即()f x 是奇函数,故①正确;()f x 是奇函数,图像关于原点对称,故②错误;对于③:11()sin cos 22cos sin 2f x x x x x πππ⎛⎫-=--=-⎪⎛⎫⎝⎭- ⎪⎝⎭而11()sin cos 22cos sin 2f x x x x x πππ⎛⎫+=+-=- ⎪⎛⎫⎝⎭+ ⎪⎝⎭, 所以()()22f x f x ππ-=+,故③正确;对于④:令[)(]sin ,1,00,1t x t =∈-,则1y t t=-(),∈-∞+∞, 无最小值,无最大值,故④错误. 故答案为:①③ 【点睛】这是另一种形式的多项选择,多项选择题是2020年高考新题型,需要要对选项一一验证.15.5【分析】是零点是极大值点利用三角函数图像与性质可知它们之间相差可得到的一个关系式由可得到另一个范围解出的范围得到符合条件的的取值个数【详解】因为满足且最小正周期所以得所以解得故的取值共有5个故答案解析:5 【分析】4π是零点,π是极大值点,利用三角函数图像与性质,可知它们之间相差42T nT +,可得到,n ω的一个关系式423n ω+=,由3T π≥可得到ω另一个范围,解出n 的范围,得到符合条件的ω的取值个数. 【详解】因为()g x 满足04g π⎛⎫= ⎪⎝⎭,()3g π=, 且最小正周期3T π≥,所以()()23214422T n T n T n N ππωπππω⎧=≥⎪⎪⎨+⎪-=+=∈⎪⎩,得06ω<≤,423n ω+=, 所以42063n +<≤,解得04n ≤≤.故ω的取值共有5个. 故答案为:5 【点睛】求三角函数的解析式时,由2Tπω=即可表示出ω;确定ϕ时,若能求出离原点最近的右侧图象上升(或下降)的“零点”横坐标0x ,则令00x ωϕ+=或0x ωϕπ+=),即可求出ϕ,否则需要代入点的坐标,利用一些已知点的坐标代入解析式,再结合函数的性质解出ω和ϕ,若对,A ω的符号或对ϕ的范围有要求,则可用诱导公式变换使其符合要求.16.【分析】根据扇形的周长求出扇形半径再根据扇形面积公式计算即可【详解】设该扇形的半径为r 根据题意有故答案为【点睛】本题主要考查了扇形的面积公式弧长公式属于中档题 解析:916【分析】根据扇形的周长求出扇形半径,再根据扇形面积公式计算即可. 【详解】设该扇形的半径为r ,根据题意,有2l r r α=+,322r r ∴=+,34r ∴=,211992221616S r α∴==⨯⨯=扇形.故答案为916. 【点睛】本题主要考查了扇形的面积公式,弧长公式,属于中档题.17.【分析】取中点连结交于点交于点连结设推导出和从而得出文化景观区域面积利用三角函数的性质解出面积最大值【详解】取中点连结交于点交于点连结设则文化景观区域面积:当即时文化景观区域面积取得最大值为故答案为 解析:()40023-【分析】取DC 中点M ,连结OM ,交EF 于点P ,交CD 于点N ,连结OD ,设DOM ϕ∠=,推导出DC 和CF ,从而得出文化景观区域面积,利用三角函数的性质,解出面积最大值. 【详解】取DC 中点M ,连结OM ,交EF 于点P ,交CD 于点N ,连结OD ,设DOM ϕ∠=,则20sin DN CN ϕ==,40sin DC ϕ∴=,20cos 20cos tan 30PFCF DE PN ON OP ϕϕϕ===-=-=-︒,∴文化景观区域面积:()4020EFCD S sin cos ϕϕϕ=-矩形400sin 2cos 2)ϕϕ=--800sin(2)3πϕ=+-∴当232ππϕ+=,即12πϕ=时,文化景观区域面积取得最大值为2400(2)m -.故答案为:400(2-. 【点睛】本题考查文化景观区域面积的最大值的求法,考查扇形、三角函数恒等变换等基础知识,考查运算求解能力,是中档题.18.③【分析】先根据对称轴及最小正周期求得函数的解析式再结合正弦函数的图象与性质判断点是否在函数图象上求得函数的单调区间及对称中心判断选项由平移变换求得变化后的解析式并对比即可【详解】函数的最小正周期是解析:③ 【分析】先根据对称轴及最小正周期,求得函数()f x 的解析式.再结合正弦函数的图象与性质,判断点是否在函数图象上,求得函数的单调区间及对称中心判断选项,由平移变换求得变化后的解析式并对比即可. 【详解】函数()()2sin 0,0,2f x x πωϕωϕ⎛⎫⎛⎫=+>∈ ⎪ ⎪⎝⎭⎝⎭的最小正周期是π,所以22πωπ==,则()()2sin 2f x x ϕ=+,又()()2sin 2f x x ϕ=+图象关于直线23x π=对称, 所以对称轴为2,2x k k Z πϕπ+=+∈,代入可得22,32k k Z ππϕπ⨯+=+∈,解得5,6k k Z πϕπ=-+∈, 因为0,2πϕ⎛⎫∈ ⎪⎝⎭,所以当1k =时, 6π=ϕ,则()2sin 26f x x π⎛⎫=+ ⎪⎝⎭,对于①,当0x =时,()02sin 16f π==,()f x 的图象不过点30,2⎛⎫⎪⎝⎭,所以①不正确;对于②,()2sin 26f x x π⎛⎫=+⎪⎝⎭的单调递减区间为3222,262k x k k Z πππππ+≤+≤+∈,解得2,63k x k k Z ππππ+≤≤+∈, 当0k =时,263x ππ≤≤,又因为126ππ<,则()f x 在2,123ππ⎡⎤⎢⎥⎣⎦上不是减函数,所以②错误;对于③,()2sin 26f x x π⎛⎫=+⎪⎝⎭的对称中心为2,6x k k Z ππ+=∈,解得,122k x k Z ππ=-+∈,当1k =时,512x π=,所以5,012π⎛⎫⎪⎝⎭是()f x 的一个对称中心,所以③正确;对于④,将()2sin 26f x x π⎛⎫=+ ⎪⎝⎭向右平移6π个单位长度,可得2sin 22sin 2666y x x πππ⎡⎤⎛⎫⎛⎫=-+=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,所以不能得到2sin 2y x =的图象,所以④错误.综上可知,正确的为③. 故答案为: ③. 【点睛】本题考查了三角函数解析式的求法,正弦函数的图像与性质的综合应用,属于中档题. 19.【分析】根据函数f (x )的图象与性质求出Tω和φ的值写出f (x )的解析式再求出的值即可【详解】函数f (x )=2sin (ωx+φ)图象相邻两条对称轴间的距离为∴从而得ω=又f(x)=2sin(2x+φ【分析】根据函数f (x )的图象与性质求出T 、ω和φ的值,写出f (x )的解析式,再求出4f π⎛⎫ ⎪⎝⎭的值即可. 【详解】函数f (x )=2sin (ωx +φ)图象相邻两条对称轴间的距离为2π,∴22T π=,从而得ω=222T πππ==, 又f (x )=2sin (2x +φ)的图象经过点,26π⎛⎫⎪⎝⎭,∴2sin 26πϕ⎛⎫⨯+ ⎪⎝⎭=2,即3π+φ=2π+2k π,k ∈Z ,又因为0<φ<π,所以φ=6π,故f (x )=2sin 26x π⎛⎫+ ⎪⎝⎭,∴2sin 2446f πππ⎛⎫⎛⎫=⨯+=⎪ ⎪⎝⎭⎝⎭【点睛】本题考查了正弦型函数的图象与性质的应用问题,属于中档题.20.【分析】根据题意得到化简得到或得到答案【详解】设时间为根据题意:故故或故或故故答案为:【点睛】本题考查了三角函数的应用意在考查学生的应用能力解析:【分析】 根据题意得到40sin 456562t ππ⎛⎫-+= ⎪⎝⎭,化简得到124t k =+或128t k =+,得到答案. 【详解】设时间为t ,0t >,根据题意:40sin 456562t ππ⎛⎫-+= ⎪⎝⎭,故1sin 622t ππ⎛⎫-= ⎪⎝⎭. 故2626t k ππππ-=+或52626t k ππππ-=+,故124t k =+或128t k =+,k Z ∈. 故1234564,8,16,20,28,32t t t t t t ======. 故答案为:32. 【点睛】本题考查了三角函数的应用,意在考查学生的应用能力.三、解答题21.(1)()()2sin f x x ϕ=+;(2)答案见解析. 【分析】由已知得周期从而求得ω, 选①:(1)得出()6f x π+,根据偶函数与诱导公式求得ϕ;(2)求出()f x 的增区间,再与[0,]π求交集可得;选②:(1)解方程3f π⎛⎫= ⎪⎝⎭ϕ; (2)同选① 选③:(1)由6f π⎛⎫⎪⎝⎭是最大值可得ϕ; (2)同选① 【详解】解:∵()f x 的图象与直线2y =的相邻两个交点间的距离为2π, ∴2T π=,即22ππω=,∴1ω=,∴()()2sin f x x ϕ=+. 方案一:选条件① (1)∵2sin 66f x x ππϕ⎛⎫⎛⎫+=++ ⎪ ⎪⎝⎭⎝⎭为偶函数, ∴62k ππϕπ+=+,即3k πϕπ=+,k Z ∈,∵02πϕ<<,∴3πϕ=,∴()2sin 3f x x π⎛⎫=+⎪⎝⎭. (2)令22232k x k πππππ-+≤+≤+,k Z ∈,得:52266k x k ππππ-+≤≤+,k Z ∈, 令0k =,得566x ππ-≤≤, ∴函数()f x 在[]0,π上的单调递增区间为06,π⎡⎤⎢⎥⎣⎦(写成开区间也可得分) 方案二:选条件②(1)方法1:∵2sin 33f ππϕ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭∴sin 32πϕ⎛⎫+= ⎪⎝⎭,∴2k 33ππϕπ+=+或2233k ππϕπ+=+,k Z ∈, ∴2k ϕ=π或23k πϕπ=+,k Z ∈,∵02πϕ<<,∴3πϕ=,∴()2sin 3f x x π⎛⎫=+⎪⎝⎭;方法2:∵2sin 33f ππϕ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭∴sin 32πϕ⎛⎫+= ⎪⎝⎭,∵02πϕ<<,∴5336πππϕ<+<, ∴233ππϕ+=即3πϕ=,∴()2sin 3f x x π⎛⎫=+ ⎪⎝⎭;(2)同方案一. 方案三:选条件③∵x R ∀∈,()6f x f π⎛⎫≤ ⎪⎝⎭,∴6f π⎛⎫⎪⎝⎭为()f x 的最大值, ∴262k ππϕπ+=+,k Z ∈,即23k πϕπ=+,k Z ∈,∵02πϕ<<,∴3πϕ=,∴()2sin 3f x x π⎛⎫=+⎪⎝⎭; (2)同方案一. 【点睛】思路点睛:本题考查三角函数的图象与性质,掌握正弦函数的性质是解题关键.()sin()(0,0)f x A x A ωϕω=+>>,只要把x ωϕ+作为一个整体,用它替换sin y x =中的x 可确定函数的性质如单调性、对称中心、对称轴,最值,也可由()sin()(0,0)f x A x A ωϕω=+>>中x 的范围求出t x ωϕ=+的范围M ,然后考虑sin y x =在x M ∈时的性质得出结论.22.(1)()4sin 20306t z t ππ⎛⎫=-+≥ ⎪⎝⎭;(2)40秒.【分析】(1)以圆心为原点建立平面直角坐标系,根据O 距离水面的高度计算出0P 坐标,再利用三角函数表示出P 点坐标,将P 的纵坐标加2即可得到z 关于t 的函数;(2)根据条件可知0z >,解对应的不等式求解出t 的范围,由此确定出有多长时间点P 位于水面上方. 【详解】(1)建立如图所示平面直角坐标系,由题意可知:()023,2P -,则3tan 3ϕ=,所以6π=ϕ,因为水轮每分钟逆时针转动1圈,所以t 秒可转动的角度为26030tt ππ=,所以P 的坐标为4cos ,4sin 306306t t ππππ⎛⎫⎛⎫⎛⎫--⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,且P 的纵坐标加上2即为P 到水面的距离, 所以()4sin 20306t z t ππ⎛⎫=-+≥⎪⎝⎭; (2)因为[]110,60,,30666t t ππππ⎛⎫⎡⎤∈-∈- ⎪⎢⎥⎝⎭⎣⎦,令4sin 20306t ππ⎛⎫-+> ⎪⎝⎭, 所以1sin 3062t ππ⎛⎫->-⎪⎝⎭,所以763066t ππππ-<-<,所以040t <<, 所以在水轮转动1圈内,有40秒时间点P 位于水面上方 【点睛】关键点点睛:解答本题的关键是通过建立合适平面直角坐标系结合三角函数定义求解出z 关于t 的函数,其中着重去分析P 点的纵坐标值得注意.23.(1)225,,312312k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦;(2)3,2⎡--⎢⎣⎦. 【分析】(1)根据()f x 的最小正周期求解出ω的值,再采用整体替换的方法结合正弦函数的单调递减区间的公式求解出()f x 的单调递减区间;(2)先求解出t x ωϕ=+的范围,然后根据3sin y t =的单调性求解出()f x 的最值,从而()f x 的值域可求. 【详解】 (1)因为2T πω=,所以22323Tππωπ===,所以()3sin 34f x x π⎛⎫=+ ⎪⎝⎭, 令3232,242k x k k Z πππππ+≤+≤+∈,所以225,312312k x k k Z ππππ+≤≤+∈, 所以()f x 的单调递减区间为:225,,312312k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦; (2)因为()3sin 34f x x π⎛⎫=+⎪⎝⎭且,32x ππ⎡⎤∈⎢⎥⎣⎦,所以令573,444t x πππ⎡⎤=+∈⎢⎥⎣⎦, 又因为3sin y t =在5342ππ⎡⎫⎪⎢⎣⎭,上单调递减,在37,24ππ⎛⎤⎥⎝⎦上单调递增, 所以()min 33sin 32f x π==-,此时512x π=,又57sinsin 44ππ==()max53sin 4f x π==,此时3x π=或2π,所以()f x 的值域为:323,2⎡⎤--⎢⎥⎣⎦.【点睛】思路点睛:求解形如()sin y A ωx φ=+的函数在指定区间上的值域或最值的一般步骤如下:(1)先确定t x ωϕ=+这个整体的范围; (2)分析sin y A t =在(1)中范围下的取值情况;(3)根据取值情况确定出值域或最值,并分析对应的x 的取值.24.(1)65π;(2)1222⎡⎤---⎣⎦, . 【解析】 试题分析:(1)整理函数的解析式可得:56ω=,利用最小正周期公式可得函数的最小正周期为65π ; (2)化简三角函数的解析式()52sin 236f x x π⎛⎫=--⎪⎝⎭,结合函数的定义域可得函数的取值范围是12,22⎡⎤---⎣⎦ .试题(1)因为f(x)=sin 2ωx -cos 2ωx +2sinωx·cosωx +λ=-cos2ωx +sin2ωx +λ =2sin+λ.由直线x =π是y =f(x)图象的一条对称轴,可得sin =±1,所以2ωπ-=kπ+ (k ∈Z),即ω=+ (k ∈Z). 又ω∈,k ∈Z ,所以k =1,故ω=.所以f(x)的最小正周期是. (2)由y =f(x)的图象过点,得f =0, 即λ=-2sin =-2sin =-,即λ=-.故f(x)=2sin -,由0≤x≤,有-≤x -≤,所以-≤sin ≤1,得-1-≤2sin x --≤2-.故函数f(x)在上的取值范围为[-1-,2-].25.(1)1A =,2ω=;(2)0,12π⎡⎤⎢⎥⎣⎦和7,12ππ⎡⎤⎢⎥⎣⎦. 【分析】(1)根据辅助角公式和两角和的正弦公式化简得()2sin 3f x A x πω⎛⎫=+ ⎪⎝⎭,由函数图象可知()f x 的最大值为2,可求出A ,由图象可知43124T πππ=-=,结合2T πω=,即可求出ω的值;(2)由(1)得2n 2)3(si f x x π⎛⎫=+⎪⎝⎭,利用整体代入法并结合正弦函数的单调性,即可求出()y f x =在[]0,π的单调增区间. 【详解】解:(1)由题可知,()sin 3cos (0,0)f x A x A x A ωωω=+>>即13()2sin 2sin 23f x A x x A x πωωω⎛⎫⎛⎫=+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭, 由图象可知,()f x 的最大值为2,则22A =,所以1A =, 由图象可知,43124T πππ=-=,则2T ππω==,所以2ω=; (2)由(1)得2n 2)3(si f x x π⎛⎫=+ ⎪⎝⎭, 令222,232k x k k πππ-+π≤+≤+π∈Z , 解得:5,1212k x k k Z ππππ-+≤≤+∈, 又因为[]0,x π∈,所以函数()y f x =在[]0,π的单调增区间为:0,12π⎡⎤⎢⎥⎣⎦和7,12ππ⎡⎤⎢⎥⎣⎦. 【点睛】思路点睛:本题考查由函数()sin y A ωx φ=+的部分图象求解析式,由函数图象的最大值求出A ,由周期2T πω=求出ω,从而可求出函数解析式,再利用整体代入法求正弦型函数的单调性,熟练掌握正弦函数的图象和性质是解题的关键. 26.(1)23π;(2)单调递增区间为22,,34312k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦;单调递减区间为225,,312312k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦;(3)⎡⎣. 【分析】 (1)由公式2T πω=求周期;(2)利用正弦函数的单调性求单调区间; (3)求出34x π+的范围,然后结合正弦函数的性质得值域.【详解】解:(1)由解析式得ω=3, 则函数的最小周期223T ππω==. (2)由232242k x k πππππ-≤+≤+,k ∈Z ,所以2234312k k x ππππ-≤≤+,k ∈Z , 即函数的单调递增区间为22,34312k k ππππ⎡⎤-+⎢⎥⎣⎦,k ∈Z , 由3232242k x k πππππ+≤+≤+k ∈Z , 得225312312k k x ππππ+≤≤+,k ∈Z , 即函数的单调递减区间为225,312312k k ππππ⎡⎤++⎢⎥⎣⎦,k ∈Z . (3)当x ∈[0,2π]时,73,444x πππ⎡⎤+∈⎢⎥⎣⎦,则当3x +4π=2π时,函数f (x )取得最大值,此时f (x 2π=,当3x +342ππ=时,函数f (x )取得最小值,此时f (x 32π=即f (x )值域为[. 【点睛】关键点点睛:本题考查正弦型三角函数的性质.对于()sin()f x A x ωϕ=+(0,0)A ω>>,最小正周期为2T πω=,利用正弦函数sin y x =的性质,把x ωϕ+作为一个整体替换sin x 中的x ,可得()f x 的性质.。
必修四第一章三角函数精选练习题(有答案和解析)

4 ∏1.必修四第一章 、选择题 在0°〜3600的范围内, 330° B . 210° 2. [因为一510°= — 3600 cos 420o 的值为(1 1 32 B. — 2 c. ^2^ [cos 420°= cos(360 3.已知角θ的终边上一点 A .±孑 B . — 2 C . 亠 —1 B [由题意得tan θ==a 所以a 2= 1, 二角函数精选练习题与一510°终边相同的角是()C . 150°D . 30°× 2 + 210° ,因此与一510°终边相同的角是 210 .]5.已知 A .彳Si n + 60o ) = cos 60 1=2故选A.] P(a , — 1)(a ≠ 0),且 tan θ= — a,则 Sin θ的值是( 2 c 1 -Jt- D 一 _2 D . 2 =—a , 所以 Sin θ= a 2+(- 1) 2= 4.一个扇形的弧长与面积的数值都是 6,这个扇形中心角的弧度数是( )A . 1B . 2C . 3D . 4 C [设扇形的半径为r ,中心角为α 1 1 根据扇形面积公式S =步 得6 = 2× 6× r ,所以u 2,6= 3.]所以 CO= = ^ =θ÷ cos θ= 3C .Si n 二 1 + 2sinθosθ∈ 0, R ,则 Sin θ— cos θ 的值为( )FD ∙θ+CoS16θ=~9, 7.∙∙ 2si n fcos ="9,θ=3 θ∈ 0,故 Sin (一 cos A —p (Sin θ-COS θ) 2 =—1 — 2sin θ ∙ cos θ-^32故选 C .]6. C .函数y =tan (sin x )的值域是(∏ π 4,4 [—tan 1, tan 1]√2 √2 2, 2 [T ,1]∏ ∏ ∏ ∏[sin x ∈ [ — 1, 1],又一^<— 1v 1v"2,且 y =tan X 在一㊁,㊁上是增函数,所以 y min = tan(— 1)= — tan 1, y max =tan1.]7.将函数y = Sin x —3的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象向左平移 1A . y = sin^x才个单位,得到的图象对应的解析式为()1 _nB . y = Sin *—"21 πy= Sin 2x —6C BC CD CSI n T tA B Tt CD88 2C T t ∈ 8JlTO 卫I 03π 8' 2 冗π 0 3π°,8 1 π 2x —6 •] ∏ ∏8.函数f(x) = sin 2x — 4在0, 2上的单调递增区间是( )C πA . y = 2sin 2x — 4Sin 2x —π,再将所得的图象向左平移 ∏个单位,得到函数y = Sin g X ^n— ∏ = 冗2 ?3π,又 x ∈ 0,3 π t ..∙∙∙x ∈ 0, §,故选 C.]9.已知函数y= ASin(ωχ+ φ)(A>0, ω>0, |φ IV π的一段图象如图所示,贝U函数的解析式为() L t∏ ∏且 2× — 8 + φp + 2k ∏K ∈Z)∙ φ = 2k ∏+ 34(k ∈ Z),又 τ l φ<π3 π∙ φ =3π故选 C.]10.如图,质点P 在半径为2的圆周上逆时针运动,其初始位置为PoC 2,—. 2),角速度为1,那么点P 到X 轴的距离d 关于时间t 的函数图象大致为( )C ∏D . y = Sin 2x —百 ∏ [函数y = Sin x — 3的图象上所有点的横坐标伸长到原来的 2倍可得y = C ∏ 亠 C 3 π y = 2sin 2x —玄或 y =2sin 2x +43πy= 2sin 2x+~^ C 3π y=2sin2x —匸∏, ∏ 2 ∏口 C[由图可知A = 2, 4θ+8 =匚得ω= 2,C [ V P o ( .2, — 2),[令 2k ∏- 2≤ 2x —∏≤2k ∏+ ∏(k∏ 3 ∏∈ Z)得 kn — 8≤x ≤k ∏+^8(k ∈ Z), k = 0 时,XIwYZπ∠ P 0°xp按逆时针转时间t后得∏∠ PoP o= t, ∠ PoX= t — 4.∏此时P点纵坐标为2sin t—4 ,π.∙∙ d = 2 Sin t—4 .当t= 0时,d= 2,排除A , D;当t= ∏⅛, d= 0,排除 B.]11•设α是第三象限的角,且CoSa = —cog,则2的终边所在的象限是( ) A•第一象限B•第二象限C第三象限D•第四象限B [ V a是第三象限的角,3π.∙∙ ∏+ 2k∏v aV~2 + 2k∏, k∈ Z.π , a 3 π I•石+ k∏<2<才 + k∏, k∈ Z..∙∙ a在第二或第四象限.a a又V COS^ = —cos^,•COSa < o.•a是第二象限的角.]12.化简,1+ 2sin (π- 2)∙COS ∏-2)得()A . Sin 2+ COS 2B . COS 2— Sin 2C. Sin 2 —cos 2 D . ± cos 2— Sin 2C 1 + 2sin ( ∏—2) ∙COS ∏-2)=1 + 2sin 2 •(—cos 2)= (Sin 2—cos 2) 2,πV2< 2< ∏ • Sin 2— cos 2>0.•原式=Sin 2—cos 2.]13.同时具有下列性质的函数可以是( )①对任意x∈ R, f(x+ ∏ = f(x)恒成立;②图象关于直线X=3对称;∏ ∏③在—吞3上是增函数.X πA.f(x) = sin ㊁ + 6C ∏B.f(x) = Sin 2x—石C ∏C.f(x) = cos 2x+~3πD . f(x) = cos 2x—石B [依题意知,满足条件的函数的周期是∏图象以直线x=∏为对称轴,且在∏ π—6, 3上是增函数.对于A选项,函数周期为4π,因此A选项不符合;对于C选∏ ∏ ∏项,f^3 =—1,但该函数在—石,勺上不是增函数,因此C选项不符合;对于D选∏ ∏项,f 3 ≠± 1,即函数图象不以直线X =3为对称轴,因此D 选项不符合.综上可知, 应选B.]π14. 已知函数f(x)= — 2tan(2x + φ)(∣ φv∏ )若f 花=—2,贝U f(x)的一个单调递 减区间是()3π 11 π π 9 π 3 π 5 ππ 5 πA . 16,76 B. 16,16 C . —16,16 D . 16,16, ∏ ,r ∏A [由 fψ6 = — 2 得—2tan § + φ= — 2, ∏所以 tan 8 + Φ = 1,又 I ΦV ∏ ∏ ∏所以 Φ= 8,f(x) = — 2tan 2x + g , 令 kn — ∏V 2x+ ∏V k∏+ ~,k∈ Z 得k∏ 5 π k∏ 3 π 厂 2—16VX V 刁+16, k ∈L可得f(x)的单调递减区间是k ∏— 1n ,k ∏+1∏,k ∈ Z ,3 π 11 π令k = 1,可得f(x)的一个单调递减区间是36,,16π.]二、填空题315.__________________________________________________ 对于锐角a ,若tan ■ 则 cos 2 α+ 2sin 2 a= _______________________________________ .2642COS a+ 4sin OCOS a 1 + 4tan a 64[由题意可得:COS 2 a+ 2sin 2a= 2 2 = 厂=.]25cos 2 a+ sιn 2 a 1 + tan 2 a 25 J116. 已知sin a=空,且a 是第二象限角,那么cos(3 — a 的值为仃.函数y=U — tan X 的定义域是 ____________ .冗冗tk n — 2, k ∏+ 3 (k ∈ Z)[作出三角数线如图,由函数可知.3 — tan x ≥ 0中tan X ≤√3,而√3对应角为才 由图中阴影部分可得定义域为 kn —才,k ∏+扌(k ∈Z).]∏18. ____________________________________ 函数y = tan 2x —N 的定义域为 . 3 π k nπ π 3 π k nX x ≠+ ~2 , k ∈ Z[2x — 4≠2+ kn, 即 x ≠^8 +^2, k ∈ Z.]19. 若函数y = Sin(ωX φ(ω>0)的部分图象如图所示,贝U ω= ___________ .∕Γ‰I i4 [观察图象可知[cos(3 — a = — COs a= — 2晋] (—∖,i 1 —sin 2a =n 函数y= Sin(ω汁φ的半个周期为-,2n n _所以—=^2, ω= 4.]ω 24 [由条件可知,图象变换后的解析式分别为 y = Sin ω汁^^3 + Φ和y =Sin ωχ- 6 + φ ,由于两图象重合,所以 3 + Φ=— 6 + Φ+ 2k ∏ K ∈ Z).即 ω= 4K(K∈ Z),由 ω>0, ∙°∙ ωmin = 4.]C — 121. 一扇形的圆心角为2弧度,记此扇形的周长为C ,面积为S ,则可的最大 值为 4 1 2 + cos X≤ 2— COS x ≤ 4,由此可得3≤ y ≤ 3,于是函数y = 2 — cos χ(x ∈ R)的最大值为3.]Sin X , Sin x ≤ COS X ,24•对于函数f(x)=给出下列四个命题:cos X , Sin x > cos X ,① 该函数是以π为最小正周期的周期函数;② 当且仅当X = π+ K ∏K ∈ Z)时,该函数取得最小值—1;5 ∏③ 该函数的图象关于X =^4 + 2K π K ∈ Z)对称;4 [由已知可得弧长 1I = 2r ,周长 C = 4r ,面积 S =㊁× Ir = r 2, C — 1 4r — 1 S = r 2 =④当且仅当 2K∏VXv ∏+ 2K ∏K ∈ Z)时,Ovf(x)≤今. -和 4 =- 1-22+ 4, 其中正确命题的序号是22.已知角 α终边C — 1故S 的最大值为4.]③④[作出函数f(x)的图象如图所示:点P 的坐标为sin"5?,, coS 5Π ,贝蛹的最小正值是5?[角α终边上一点P 的坐标为sin^5∏t , coS 5∏ ,即1 ,—弩, -逅―2tan α= —1 — =— 3 ,且α为第四象限角,2所以角α的最小正值是竽]由图象可知f(x)为周期函数,T = 2 ∏①错误;当X = 2K π+ π或X = 2K π+时, 取最小值—1 ,故②错误;x =∏+ 2K ∏K ∈ Z)和X =5∏+ 2K ∏K ∈ Z)都是该图象的对称轴,故③正确; ∏当 2k∏vXV - + 2K∏K∈ Z)时,∏20.已知函数f(x)= Sin(ω汁φ)( ω> 0),若将f(x)的图象向左平移空个单位长度所 得的图象与将f(x)的2+ cos X23•函数y= ------- (x ∈ R)的最大值为2— cos X43 [由题意有 y =2 — cos X — 1,因为一1 ≤ cos x ≤ 1,所以 1 ≤ 2 — cos2 .• r = |OP|= 5, X = 4, y = — 3,⑵ V α终边过点 P(4a , — 3a)(a ≠ 0),2• ∙ 2si n α+ cos α= 5. 宀 2、2 综上,2sin α+ cos a=—5或5.4 0 •丄 2Cos a= — 5, 2Sin a+ CoS a= 5;xf 2故0v f(x)≤三.故④正确.] • Sin α= y=3X 4 5, cos a=^r = 5 3 4 • 2s in a+ cos a= 2× —"5 +^5 = 25.25.已知 sin( —α ∙ C o —(8 冗一 α=π,求 Sin α与 cos α 的值.∙°∙ r = IoPl = 5∣a∣, X= 4a , y = — 3a.[解]由已知条件可得Sin CCOS a= 169,当 a>0 时,r = 5a , Si ny OC== r 3 5,2^120 289• ∙ (Sin a+ cos 0) = 1 + 2sin OCOS O= 1 +169=169,X 4cos a= r = 5 2 , C ∙. 120 49 (Sin a — cos 0 = 1 — 2s In CCOS a= 1 —169=169"∙ 2si n α+ cosα=25;π Vx∈ 4,当 a<0 时,r = — 5a , ∙ SinO=∙ Sin α> COS α, X 4cos a= ~r = — 512 5解方程组得 Sin C= 13, cos a= 13.⑶当点P 在第一象限时,Sin3α= 5,26. (1)已知角α的终边经过点P(4,— 3),求2sin α+ cos α的值; (2)已知角α的终边经过点P(4a ,— 3a)(a ≠0),求2sin α+ cos α的值; 4 .cos α= 5, 2sin α+ cos α= 2;(3)已知角α终边上一点P 到X 轴的距离与到y 轴的距离之比为3 : 4,求2sin α当点P 在第二象限时,Sin α= 35,f(x)图象在X 轴上方且f(x) max三、解答题17Sin α+ cos a=ZSin a — cos a=+ cos α的值.[解](1) V α终边过点P(4, — 3),4 c • 2COS α=匚,2sin (Ur COS C=^-.5 527.是否存在角a, β, α∈ —2’ 2 , β∈ (0, ∏)使等式Sin(3 —O =2COS~2—β , J3cos(- O = -ΛJ2COS(r β同时成立?若存在,求出a, β的值;若不存在,请说明理由.[解]假设存在角a , β满足条件,则{Sin a= 12sin β , ① 3cos a= . 2cos β , ②由①2+②2得sin2 a+ 3CO$ a= 2.π28.已知函数f(x)= 2sin 2x+^ + 1.(1)求函数f(x)的最大值,并求取得最大值时X的值;(2)求函数f(x)的单调递增区间.[解](1)当2x+ 3= 2k∏+∏,则X= k∏+ 1∏(k∈ Z)时,f(x)max= 3.⑵当2k∏-∏≤2X+3≤2k∏+ ∏,即k∏-5∏≤ x≤ k∏+ W时,函数f(x)为增函数.5∏∏故函数f(x)的单调递增区间是kn—p , k∏+p(k∈ Z).当点P在第二象限时,Sin C=3 5,COS (O=4.,2sin Crr COS U=- 2;5当点P在第四象限时,Sin U=35,'T Ov β< ∏∏∙∙∙β= 6 ,此时代入①式不成立,故舍去..∙.存在a=4 β=^6满足条件.• COS a= 2y.29.如图是函数y= ASin(ωχ+φ+ k(A>0 ,∏ω>0 , φ |<"2)的一段图象.∙.∙a∈当O= 4时,代入②得:COS β= ,T Ov β< ∏∏.∙. β= 6,代入①可知成立;当a=- π∏时,代入②得COS β=^23 , (1)求此函数解析式;(2)分析一下该函数是如何通过y= Sin X变换得来的?(1)由图象知A=.∙∙ coS2O= 2'1 3—2+ — 2k= 2 =_ 1,2 π πT=2× J-6 二∏2π 1.∙. ω= T = 2..∙∙ y=qsin(2x+ φ— 1.π π ππ当X= 6, 2× 6+ φ= 2,■ ■ φ = 6*1 ∏•••所求函数解析式为y=^sin 2x+6 —1.∏ ∏(2)把y= Sin X向左平移舌个单位得到y= sin x+石,然后纵坐标保持不变、横坐标缩短为原来的2倍,得到y=sin 2x+ 6 ,再横坐标保持不变,纵坐标变为原来的舟倍,1 ∏ 1 ∏得到y=^sin 2x+ 6 ,最后把函数y=2sin 2x+6的图象向下平移1个单位,得到y1 ∏=2sin 2x+6 — 1 的图象•∏30.已知函数f(x) = ASi n( ωX (D A> 0, ω> 0, ∣φ IV㊁的图象在y轴上的截距为1,它在y轴右侧的第一个最大值点和最小值点分别为(x o, 2)和(x o+ 3∏ —2).(1)求f(x)的解析式;1⑵将f(x)的图象上的所有点的横坐标缩短到原来的3倍(纵坐标不变),然后再将所得的图象向右平移∏个单位,得到函数g(x)的图象,写出函数g(x)的解析式,并用五点作图的方法画出g(x)在长度为一个周期的闭区间上的图象.[解](1)由f(x) = ASin(ω汁D)在y轴上的截距为1,最大值为2,得1 = 2sin D,1 ∏ ∏ 所以Sin D = 2.又IDVq,所以由题意易知T = 2[(x o + 3 π —x o] = 6 ∏2 ∏ 1 所以ω=亍=3X ∏ 所以f(x) = 2sin 3+6 .⑵将f(x)的图象上的所有点的横坐标缩短到原来的£倍(纵坐标不变),得到y=∏ ∏ ∏ ∏2sin x+6的图象;再把所得图象向右平移§个单位,得到g(x) = 2sin x—§+石=冗2sin x—石的图象.列表:描点画图:。
(压轴题)高中数学必修四第一章《三角函数》测试(答案解析)

一、选择题1.已知函数()sin()(f x A x A ωϕ=+,ω,ϕ是常数,0A >,0>ω,0)2πϕ<<的部分图象如图所示.为了得到函数()f x 的图象,可以将函数2sin y x =的图象( )A .先向右平移6π个单位长度,再将所得图象的横坐标缩短为原来的12,纵坐标不变 B .先向左平移6π个单位长度,再将所得图象的横坐标伸长为原来的2倍,纵坐标不变 C .先向左平移3π个单位长度,再将所得图象的横坐标伸长为原来的2倍,纵坐标不变 D .先向左平移3π个单位长度,再将所得图象的横坐标缩短为原来的12,纵坐标不变2.函数()sin()(0||)2,f x x πωϕωϕ=+><的部分函数图象如图所示,将函数()f x 的图象先向右平移3π个单位长度,然后向上平移1个单位长度,得到函数()g x 的解析式为( )A .()sin 21g x x =-B .()sin 21g x x =+C .()sin(2)13g x x π=--D .()sin(2)13g x x π=-+3.已知关于x 的方程2cos ||2sin ||20(0)+-+=≠a x x a a 在(2,2)x ππ∈-有四个不同的实数解,则实数a 的取值范围为( ) A .(,0)(2,)-∞+∞ B .(4,)+∞ C .(0,2)D .(0,4)4.已知函数()sin 26f x x π⎛⎫=- ⎪⎝⎭,若方程()35f x =的解为1x ,2x (120x x π<<<),则()12sin x x -=( ) A .35B .45-C .23-D .3-5.如图,一个质点在半径为1的圆O 上以点P 为起始点,沿逆时针方向旋转,每2s 转一圈,由该质点到x 轴的距离y 关于时间t 的函数解析式是( )A .2sin()3y t ππ=+ B .2sin()3y t ππ=- C .2sin()3y t ππ=-D .2sin()3y t ππ=+6.将函数sin()y x ϕ=+的图像上所有点的横坐标缩短到原来的12倍(纵坐标不变),再将所得图像向左平移12π个单位后得到的函数图像关于原点中心对称,则sin 2ϕ=( )A .12-B .12C .3D 37.函数1sin3y x =-的图像与直线3x π=,53x π=及x 轴所围成的图形的面积是( ) A .23π B .πC .43π D .53π 8.函数()3sin 22xf x x =-的部分图象大致为( )A .B .C .D .9.已知奇函数()f x 满足()(2)f x f x =+,当(0,1)x ∈时,函数()2x f x =,则12log 23f ⎛⎫= ⎪⎝⎭( ) A .1623-B .2316-C .1623D .231610.已知1sin 34x π⎛⎫+= ⎪⎝⎭,则22sin sin 36x x ππ⎛⎫⎛⎫-+-=⎪ ⎪⎝⎭⎝⎭( ) A .1B 151+C .1916D .3411.有以下四种变换方式: ①向左平移12π个单位长度,再将每个点的横坐标伸长为原来的2倍;②向左平移6π个单位长度,再将每个点的横坐标伸长为原来的2倍; ③再将每个点的横坐标伸长为原来的2倍,再向左平移6π个单位长度; ④再将每个点的横坐标伸长为原来的2倍,再向右平移6π个单位长度; 其中能将函数sin 26y x π⎛⎫=- ⎪⎝⎭的图象变为函数sin y x =图象的是( ) A .①③B .②③C .①④D .②④12.已知函数()tan()0,2f x x πωϕωϕ⎛⎫=+≠< ⎪⎝⎭,点2,03π⎛⎫⎪⎝⎭和7,06π⎛⎫⎪⎝⎭是其相邻的两个对称中心,且在区间54,63ππ⎛⎫⎪⎝⎭内单调递减,则ϕ=( )A .6π B .6π-C .3π D .3π-二、填空题13.将函数()sin 24f x x π⎛⎫=-⎪⎝⎭的图像先向右平移8π个单位,再将横坐标缩短到原来的一半(纵坐标不变)后,得到函数()g x 的图像,则函数()g x 的解析式为_________. 14.已知函数()22cos f x x ω=-(0>ω)的图象关于点3,04π⎛⎫⎪⎝⎭对称,且()f x 在区间20,3π⎛⎫⎪⎝⎭上单调,则ω的值为______. 15.已知sin 78a =︒,cos10b =︒,tan55c =︒,则a ,b ,c 的大小关系为______. 16.函数y =的定义域为________.17.若函数()cos()(0)4f x wx w π=+>在[]0,π的值域为21⎡⎤-⎢⎥⎣⎦,,则w 的取值范围是______18.已知函数()3sin(2)cos(2)(||)2f x x x πϕϕϕ=---<的图象关于y 轴对称,则()f x 在区[6π-,5]12π上的最大值为__.19.奇函数()f x 对任意实数x 都有(2)()f x f x +=-成立,且01x 时,()21x f x =-,则()2log 11f =______.20.函数()()0,0,2(f x Asin x A πωϕωϕ=+>><)的部分图像如图所示.则()f x 的解析式是_____.三、解答题21.已知函数()()1sin 226f x x x R π⎛⎫=+∈ ⎪⎝⎭. (1)填写下表,并用“五点法”画出()f x 在[0,]π上的图象;26x π+6π 136πxπ ()f x(2)将()y f x =的图象向上平移1个单位,横坐标缩短为原来的2,再将得到的图象上所有点向右平移4π个单位后,得到()g x 的图象,求()g x 的对称轴方程. 22.某同学用“五点法”画函数()() sin ωϕ=++f x A x B (其中A >0,0>0,||)2πϕ<在某一个周期内的图象时,列表并填入部分数据,如表: ωx +φπ2 π3π22π xπ35π6A sin(ωx +φ)+B3-1f (x )的解析式; (2)若定义在区间,44ππ⎡⎤-⎢⎥⎣⎦上的函数g (x )=af (x )+b 的最大值为7,最小值为1,求实数a ,b 的值.23.把()cos()(0,||)2f x x πωϕωϕ=+><的图象纵坐标保持不变,横坐标变为原来的2倍得()g x 的图象,已知()g x 图象如图所示(1)求函数()f x 的解析式; (2)若()()2()6h x f x g x π=-+,求()h x 在0,2π⎡⎤⎢⎥⎣⎦上的值域. 24.已知函数()()sin 0,2f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭的部分图象如图所示:(1)求()f x 的解析式;(2)将()f x 的图象上所有的点横坐标缩短到原来的12,纵坐标不变,得到函数()g x 的图象求方程()12g x =在[]0,π的实数解. 25.已知函数()2sin(2)(0)6f x x πωω=+>.(1)若点5(,0)8π是函数()f x 图像的一个对称中心,且(0,1)ω∈,求函数()f x 在3[0,]4π上的值域; (2)若函数()f x 在(,)33π2π上单调递增,求实数ω的取值范围.26.海水受日月的引力,在一定的时候发生涨落的现象叫潮,一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋.下面是某港口在某季节每天的时间与水深关系表: 时刻 0:00 1:00 2:00 3:00 4:00 5:00 水深 5.000 6.250 7.165 7.500 7.165 6.250 时刻6:007:008:009:0010:0011:00(1)这个港口的水深与时间的关系可用函数(,)近似描述,试求出这个函数解析式;(2)一条货船的吃水深度(船底与水面的距离)为5米,安全条例规定至少要有1.25米的安全间隙(船底与洋底的距离),利用(1)中的函数计算,该船何时能进入港口?在港口最多能呆多久?【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【分析】先根据函数图象求出函数()f x 的解析式,由三角函数图象的变换即可求解. 【详解】 由图可知,1741234A T πππ==-=,, 所以T π=,即2ππω=,解得2ω=.当712x π=时,73π22π,122k k Z πϕ⨯+=+∈, 所以 2,3k k Z πϕπ=+∈又2πϕ<,所以3πϕ=.所以()23f x x π⎛⎫=+ ⎪⎝⎭.将y x =的图象先向左平移3π个单位长度,得到)3y x π=+,.再将所得图象的横坐标缩短为原来的12,纵坐标不变,得到())3f x x π=+.故选:D 【点睛】易错点点睛:图象变换的两种方法的区别,由sin y x =的图象,利用图象变换作函数()()()sin 0,0y A x A x R ωϕω=+>>∈的图象,要特别注意:当周期变换和相位变换的先后顺序不同时,原图象沿x 轴的伸缩量的区别.先平移变换再周期变换(伸缩变换),平移的量是|φ|个单位,而先周期变换(伸缩变换)再平移变换,平移的量是ϕω个单位. 2.D解析:D 【分析】由周期求出ω,由五点法作图求出ϕ的值,可得()f x 的解析式,再根据函数sin()y A x ωϕ=+的图象变换规律,得出结论.【详解】根据函数()sin()(0f x x ωϕω=+>,||)2πϕ<的部分函数图象,1274123πππω⋅=-,2ω∴=. 再根据五点法作图,23πϕπ⨯+=,3πϕ∴=,()sin(2)3f x x π=+.将函数()f x 的图象先向右平移3π个单位长度,可得sin(2)3y x π=-的图象.然后向上平移1个单位长度,得到函数()g x 的解析式为()sin(2)13g x x π=-+,故选:D 【点睛】关键点睛:解答本题的关键在于准确地根据三角函数的图象求出三角函数sin()y A x ωϕ=+的解析式,一般根据周期求出ω的值,根据最值求出A 的值,根据最值点求出ϕ的值.3.D解析:D 【分析】令2()cos ||2sin ||2(0)=+-+≠f x a x x a a ,易知函数()f x 是偶函数,将问题转化为研究当(0,2)x π∈时,2()cos 2sin 2=+-+f x a x x a 有两个零点,令sin t x =,则转化为2()22(0)=--≠h t at t a 有一个根(1,1)t ∈-求解.【详解】当(2,2)x ππ∈-,2()cos ||2sin ||2(0)=+-+≠f x a x x a a ,则()()f x f x -=,函数()f x 是偶函数,由偶函数的对称性,只需研究当(0,2)x π∈时,2()cos 2sin 2=+-+f x a x x a 有两个零点,设sin t x =,则2()22(0)=--≠h t at t a 有一个根(1,1)t ∈- ①当0a <时,2()22=--h t at t 是开口向下,对称轴为10t a=<的二次函数, (0)20h =-<则(1)0->=h a ,这与0a <矛盾,舍去;②当0a >时,2()22=--h t at t 是开口向上,对称轴为10t a=>的二次函数, 因为(0)20h =-<,(1)220-=+->=h a a , 则存在(1,0)t ∈-,只需(1)220=--<h a ,解得4a <, 所以04a <<.综上,非零实数a 的取值范围为04a <<. 故选:D . 【点睛】方法点睛:已知函数有零点(方程有根)求参数值(取值范围)常用的方法: (1)直接法:直接求解方程得到方程的根,再通过解不等式确定参数范围; (2)分离参数法:先将参数分离,转化成求函数的值域问题加以解决;(3)数形结合法:先对解析式变形,进而构造两个函数,然后在同一平面直角坐标系中画出函数的图象,利用数形结合的方法求解4.B解析:B 【分析】求出函数()f x 在(0,)π上的对称轴,然后由正弦函数性质得1223x x π+=,这样12sin()x x -化为2222sin(2)sin 2cos(2)336x x x πππ⎛⎫-=+=- ⎪⎝⎭,而已知条件为23sin(2)65x π-=,再由正弦函数性质确定226x π-的范围,从而由平方关系求得结论.【详解】函数()sin 26f x x π⎛⎫=-⎪⎝⎭的对称轴满足:()262x k k Z πππ-=+∈,即()23k x k Z ππ=+∈,令0k =可得函数在区间()0,π上的一条对称轴为3x π=,结合三角函数的对称性可知1223x x π+=,则:1223x x π=-,()122222sin sin 2sin 2cos 2336x x x x x πππ⎛⎫⎛⎫⎛⎫-=-=+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,由题意:0πx <<,则112666x πππ-<-<,23sin 265x π⎛⎫-= ⎪⎝⎭,120x x π<<<,则2226x πππ<-<,由同角三角函数基本关系可知:24cos 265x π⎛⎫-=- ⎪⎝⎭, 故选:B . 【点睛】关键点点睛:本题考查正弦函数的性质,考查平方关系.解题时根据自变量的范围求得此范围内函数的对称轴,从而得出两个变量12,x x 的关系,可化双变量为单变量,再根据函数值及函数性质确定出单变量的范围,从而求得结论.注意其中诱导公式的应用,目的是把求值式与已知条件中的角化为一致.5.A解析:A 【分析】首先根据图象理解t 秒后23POx t ππ∠=+,再根据三角函数的定义求点P 的纵坐标和该质点到x 轴的距离y 关于时间t 的函数解析式. 【详解】由题意可知点P 运动的角速度是22ππ=(弧度/秒) 那么点P 运动t 秒后23POx t ππ∠=+, 又三角函数的定义可知,点P 的纵坐标是2sin 3t ππ⎛⎫+ ⎪⎝⎭,因此该质点到x 轴的距离y 关于时间t 的函数解析式是2sin 3y t ππ⎛⎫=+ ⎪⎝⎭. 故选:A 【点睛】关键点点睛:本题的关键是理解三角函数的定义,并正确表示点23POx t ππ∠=+,即可表示函数的解析式.6.C解析:C 【分析】先根据条件写出图像变换后的函数解析式,然后根据图像关于原点中心对称可知函数为奇函数,由此得到ϕ的表示并计算出sin 2ϕ的结果. 【详解】因为变换平移后得到函数sin 26y x πϕ⎛⎫=++ ⎪⎝⎭,由条件可知sin 26y x πϕ⎛⎫=++ ⎪⎝⎭为奇函数,所以6k πϕπ+=,3sin 2sin 2sin 33k ππϕπ⎛⎫⎛⎫=-=-=- ⎪ ⎪⎝⎭⎝⎭.故选C . 【点睛】本题考查三角函数的图像变换以及根据函数奇偶性判断参数值,难度一般.正弦型函数()()sin f x A x =+ωϕ为奇函数时,k k Z ϕπ=∈,为偶函数时,2k k Z πϕπ=+∈.7.C解析:C 【分析】作出函数1sin3y x =-的图像,利用割补法,补成长方形,计算面积即可. 【详解】作出函数1sin3y x =-的图象,如图所示,利用割补法,将23π到π部分的图象与x 轴围成的图形补到图中3π到23π处阴影部分,凑成一个长为3π,宽为2的长方形,后面π到53π,同理;∴1sin3y x =-的图象与直线3x π=,53x π=及x 轴所围成的面积为24233ππ⨯=,故选:C. 【点睛】用“五点法”作()sin y A ωx φ=+的简图,主要是通过变量代换,设z x ωϕ=+,由z 取0,2π,π,32π,2π来求出相应的x ,通过列表,计算得出五点坐标,描点后得出图象. 8.A解析:A 【分析】求得函数()y f x =的定义域,分析函数()y f x =的奇偶性,结合2f π⎛⎫⎪⎝⎭的值以及排除法可得出合适的选项. 【详解】对于函数()3sin 22xf x x =-,20x -≠,得2x ≠±,所以,函数()y f x =的定义域为{}2x x ≠±.()()()sin 2sin 222x xf x f x x x --==-=----,函数()y f x =为奇函数,图象关于原点对称,排除B 、D 选项;又02f ⎛⎫= ⎪⎝⎭π,排除C 选项. 故选:A. 【点睛】本题考查利用函数的解析式选择图象,一般分析函数的定义域、奇偶性、单调性、零点以及函数值符号,考查分析问题和解决问题的能力,属于中等题.9.B解析:B 【分析】由已知得到(2)()f x f x +=,即得函数的周期是2,把12(log 23)f 进行变形得到223()16f log -, 由223(0,1)16log ∈满足()2x f x =,求出即可. 【详解】(2)()f x f x +=,所以函数的周期是2.根据对数函数的图象可知12log 230<,且122log 23log 23=-;奇函数()f x 满足(2)()f x f x +=和()()f x f x -=-则2312222223(log 23)(log )(log 23)(log 234)()16f f f f f log =-=-=--=-, 因为223(0,1)16log ∈ 2231622323()21616log f log ∴-=-=-,故选:B . 【点睛】考查学生应用函数奇偶性的能力,函数的周期性的掌握能力,以及运用对数的运算性质能力.10.C解析:C 【分析】由诱导公式求得cos 6x π⎛⎫- ⎪⎝⎭,然后再由平方关系和诱导公式计算. 【详解】由已知1cos cos sin 62334x x x ππππ⎡⎤⎛⎫⎛⎫⎛⎫-=-+=+= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦, 222115sin 1cos 166416x x ππ⎛⎫⎛⎫⎛⎫-=--=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,21sin sin cos 32664x x x ππππ⎛⎫⎛⎫⎛⎫-=+-=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 所以2211519sin sin 3641616x x ππ⎛⎫⎛⎫-+-=+= ⎪ ⎪⎝⎭⎝⎭. 故选:C . 【点睛】关键点点睛:本题考查三角函数的求值.解题关键是确定“已知角”和“未知角”的关系,选用适当的公式进行变形求值.本题中首先利用诱导公式得出cos 6x π⎛⎫- ⎪⎝⎭,然后再用诱导公式得出2sin 3x π⎛⎫-⎪⎝⎭,用平方关系得出2sin 6x π⎛⎫- ⎪⎝⎭,这样求解比较方便.11.A解析:A 【分析】直接利用三角函数图像的平移变换和伸缩变换求出结果. 【详解】对于①:sin 26y x π⎛⎫=-⎪⎝⎭向左平移12π个单位长度得到sin 2+=sin2126y x x ππ⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭,再将每个点的横坐标伸长为原来的2倍,得到sin y x =;故①正确;对于②:sin 26y x π⎛⎫=-⎪⎝⎭向左平移6π个单位长度得到sin 2+=sin 2+666y x x πππ⎛⎫⎛⎫⎛⎫=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,再将每个点的横坐标伸长为原来的2倍,得到sin 6y x π⎛⎫=+ ⎪⎝⎭;故②错误;对于③:sin 26y x π⎛⎫=-⎪⎝⎭将每个点的横坐标伸长为原来的2倍,得到sin 6y x π⎛⎫=-⎪⎝⎭,再向左平移6π个单位长度,得到sin sin 66y x x ππ⎛⎫=+-= ⎪⎝⎭;故③正确; 对于③:sin 26y x π⎛⎫=- ⎪⎝⎭将每个点的横坐标伸长为原来的2倍,得到sin 6y x π⎛⎫=-⎪⎝⎭,再向右平移6π个单位长度,得到sin sin()663y x x πππ⎛⎫=--=- ⎪⎝⎭;故④错误; 故选:A 【点睛】关于三角函数图像平移伸缩变换:先平移的话,如果平移a 个单位长度那么相位就会改变ωa ;而先伸缩势必会改变ω大小,这时再平移要使相位改变值仍为ωa ,那么平移长度不等于a .12.A解析:A 【分析】由正切函数的图象性质,得出相邻两个对称中心之间的距离为半个周期,可求出T ,然后由T πω=求出ω,然后再代点讨论满足题意的ϕ,即可得出答案. 【详解】由正切函数图象的性质可知相邻两个对称中心的距离为2T ,得72263T πππ⎛⎫=-= ⎪⎝⎭. 则由1T πω==得1ω=,即得1ω=±. 由2πϕ<,且在区间54,63ππ⎛⎫⎪⎝⎭内单调递减,则可得1ω=-, ∴()()()tan tan f x x x ϕϕ=-+=--. 由2,32k k Z ππϕ-=∈得2,32k k Z ππϕ=-∈,因2πϕ<,可得6π=ϕ或3π-,当3πϕ=-时,()tan +3f x x π⎛⎫=- ⎪⎝⎭,由+,232k x k k Z πππππ-<<+∈,得5,66k x k k Z ππππ-<<+∈, 则函数()f x 的单调减区间为5,,66k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭, 令1k =,由54,63ππ⎛⎫ ⎪⎝⎭7,66ππ⎛⎫ ⎪⎝⎭⊄,得函数()f x 在54,63ππ⎛⎫⎪⎝⎭上不是单调递减, 所以3πϕ=-不满足题意;当6π=ϕ时,()tan 6f x x π⎛⎫=-- ⎪⎝⎭,由,262k x k k Z πππππ-<-<+∈,得2,33k x k k Z ππππ-<<+∈, 则函数()f x 的单调减区间为2,,33k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭, 令1k =,由25,3354,63ππππ⎛⎫⊂⎛⎫ ⎪⎝ ⎪⎝⎭⎭,得函数()f x 在54,63ππ⎛⎫⎪⎝⎭上单调递减, 所以6π=ϕ满足题意; 综上可得:6π=ϕ满足题意. 故选:A.【点睛】关键点睛:正切型函数的对称中心和单调性的问题,通常采用代入检验法,注意正切函数的对称中心为0,2k k Z π⎛⎫∈⎪⎝⎭,. 二、填空题13.【分析】利用函数的图象变换规律即可得到的解析式【详解】函数的图像先向右平移个单位后解析式变为:再将横坐标缩短到原来的一半(纵坐标不变)后解析式变为:所以故答案为:【点睛】方法点睛:函数的图像与函数的 解析:cos4x -【分析】利用函数()()sin f x A x =+ωϕ的图象变换规律,即可得到()g x 的解析式. 【详解】函数()sin 24f x x π⎛⎫=-⎪⎝⎭的图像先向右平移8π个单位后解析式变为: sin 2sin 2co 288s 2y x x x πππ⎡⎤⎛⎫⎛⎫=--=-=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,再将横坐标缩短到原来的一半(纵坐标不变)后解析式变为:()cos 22x y -=⨯,所以()cos 4g x x =-. 故答案为:cos4x -. 【点睛】方法点睛:函数sin ωφf xA xB 的图像与函数sin y x =的图像两者之间可以通过变化A ,ω,φ,B 来相互转化,A 、ω影响图像的形状,φ、B 影响图像与x 轴交点的位置,由A 引起的变换称为振幅变换,由ω引起的变换称为周期变换,它们都是伸缩变换;由φ引起的变换称为相位变换,由B 引起的变换称为上下平移变换,它们都是平移变换.三角函数图像变换的两种方法为先平移后伸缩和先伸缩后平移.14.【分析】根据函数图像的对称点得到的表达式根据在区间上单调得到的范围从而得到的范围再得到的值【详解】函数的图像关于点对称所以即得到在区间上单调所以即所以所以而所以故答案为:【点睛】本题考查根据余弦型函解析:23【分析】根据函数图像的对称点,得到ω的表达式,根据()f x 在区间20,3π⎛⎫⎪⎝⎭上单调,得到T 的范围,从而得到ω的范围,再得到ω的值. 【详解】函数()f x x ω=-的图像关于点3,04π⎛⎫⎪⎝⎭对称,所以304πω⎛⎫-= ⎪⎝⎭,即342k ππωπ=+,k ∈Z ,得到4233k ω=+,k ∈Z , ()f x 在区间20,3π⎛⎫⎪⎝⎭上单调, 所以223T π≥,即43T π≥, 所以243ππω≥,所以32ω≤,而0>ω,所以0k =,23ω=.故答案为:23.【点睛】本题考查根据余弦型函数的对称中心求参数的值,根据余弦型函数的周期求参数的值,属于中档题.15.【分析】同角三角函数关系知又由的区间单调性知根据的区间单调性知即可知的大小关系【详解】而∴故答案为:【点睛】本题考查了比较三角函数值的大小根据正弦函数正切函数的区间单调性及正弦函数的值域范围比较函数 解析:c b a >>【分析】同角三角函数关系知sin80b =︒,又由sin y x =的区间单调性知b a >,根据tan y x =的区间单调性知1c>,即可知a,b,c的大小关系【详解】cos10cos(9080)sin80sin78b a=︒=︒-︒=︒>=︒,而tan55tan451c=︒>︒=∴c b a>>故答案为:c b a>>【点睛】本题考查了比较三角函数值的大小,根据正弦函数、正切函数的区间单调性及正弦函数的值域范围,比较函数值的大小16.(k∈Z)【分析】解不等式2cosx-1≥0即得函数的定义域【详解】∵2cosx-1≥0∴cosx≥由三角函数线画出x满足条件的终边的范围(如图阴影所示)∴x∈(k∈Z)故答案为(k∈Z)【点睛】(解析: (k∈Z)【分析】解不等式2cos x-1≥0即得函数的定义域.【详解】∵2cos x-1≥0,∴cos x≥.由三角函数线画出x满足条件的终边的范围(如图阴影所示).∴x∈ (k∈Z).故答案为 (k∈Z)【点睛】(1)本题主要考查三角函数线和解三角不等式,意在考查学生对这些知识的掌握水平和分析推理能力.(2)三角函数线是解三角不等式较好的工具,要理解掌握并灵活运用. 17.【分析】先根据题意计算出的范围再根据函数的单调性结合值域列出不等式即可求得【详解】因为且故可得因为在区间单调递减在单调递增且故要满足题意只需解得故答案为:【点睛】本题考查由余弦型函数在区间上的值域求解析:33 42⎡⎤⎢⎥⎣⎦,【分析】先根据题意计算出4wx π+的范围,再根据函数的单调性,结合值域,列出不等式,即可求得. 【详解】因为[]0,x π∈,且0w >, 故可得1,444wx w πππ⎡⎤⎛⎫+∈+ ⎪⎢⎥⎝⎭⎣⎦, 因为y cosx =在区间,4ππ⎡⎤⎢⎥⎣⎦单调递减,在7,4ππ⎡⎤⎢⎥⎣⎦单调递增,且7coscos424ππ==,1cos π=-, 故要满足题意,只需1744w πππ⎛⎫≤+≤ ⎪⎝⎭ 解得33,42w ⎡⎤∈⎢⎥⎣⎦. 故答案为:3342⎡⎤⎢⎥⎣⎦,.【点睛】本题考查由余弦型函数在区间上的值域,求参数范围的问题,属中档题.18.【分析】利用辅助角公式化简可得再根据图象关于轴对称可求得再结合余弦函数的图像求出最值即可【详解】因为函数的图象关于轴对称所以即又则即又因为所以则当即时取得最大值故答案为:【点睛】判定三角函数的奇偶性【分析】利用辅助角公式化简可得()2sin(2)6f x x πϕ=--,再根据图象关于y 轴对称可求得()2cos2f x x =-,再结合余弦函数的图像求出最值即可.【详解】因为函数()()()2cos 2f x x x ϕϕ=---2sin(2)6x πϕ=--的图象关于y 轴对称,所以πππ62k ϕ--=+,即()2ππ,3k k Z ϕ=--∈. 又2πϕ<,则π3ϕ=,即()2sin(2)2cos22f x x x π=-=-.又因为π5π612x -≤≤,所以π5π236x -≤≤,则当5π26x =,即5π12x =时,()f x 取得最大值5π2cos6-=.【点睛】判定三角函数的奇偶性时,往往与诱导公式进行结合,如: 若()sin y x ωϕ=+为奇函数,则π,Z k k ϕ=∈;若()sin y x ωϕ=+为偶函数,则ππ+,Z 2k k ϕ=∈; 若()cos y x ωϕ=+为偶函数,则π,Z k k ϕ=∈;若()cos y x ωϕ=+为奇函数,则ππ+,Z 2k k ϕ=∈. 19.【分析】易得函数周期为4则结合函数为奇函数可得再由时即可求解【详解】则又则故答案为:【点睛】本题考查函数奇偶性与周期性的综合应用具体函数值的求法属于中档题 解析:511-【分析】易得函数周期为4,则()()22211log 11log 114log 16f f f ⎛⎫=-= ⎪⎝⎭,结合函数为奇函数可得222111616log log log 161111f f f⎛⎫⎛⎫⎛⎫=-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,再由01x 时,()21xf x =-即可求解 【详解】()()(2)()4(2)4f x f x f x f x f x T +=-⇒+=-+=⇒=,则()()22211log 11log 114log 16f f f ⎛⎫=-= ⎪⎝⎭, 又222111616log log log 161111f f f ⎛⎫⎛⎫⎛⎫=-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,[]216log 0,111∈, 则216log 112165log 211111f ⎛⎫⎛⎫-=--=- ⎪ ⎪⎝⎭⎝⎭故答案为:511- 【点睛】本题考查函数奇偶性与周期性的综合应用,具体函数值的求法,属于中档题20.【分析】由图像对应横坐标可求再将代入可进一步求解由图像过点可求进而求解【详解】由解得又函数过所以解得又图像过可得解得故故答案为:【点睛】本题考查由三角函数图像求解析式属于中档题解析:()2sin 26f x πx ⎛⎫+ ⎝=⎪⎭【分析】由34T 图像对应横坐标可求ω,再将6x π=代入可进一步求解ϕ,由图像过()0,1点可求A ,进而求解 【详解】由1132312644T πππω-==⋅,解得2ω=,又函数过()max ,6f x π⎛⎫⎪⎝⎭, 所以63A f Asin ππϕ⎛⎫⎛⎫=⎪ ⎪⎝⎝⎭+⎭=,解得6π=ϕ,又图像过()0,1可得()106f Asin π==,解得2A =,故()2sin 26f x πx ⎛⎫+ ⎝=⎪⎭故答案为:()2sin 26f x πx ⎛⎫+ ⎝=⎪⎭【点睛】本题考查由三角函数图像求解析式,属于中档题三、解答题21.(1)答案见解析;(2)34k x ππ=+,k Z ∈. 【分析】(1)分别令x 等于0、6π、512π、23π、1112π、π,求得对应的纵坐标,确定点的坐标,列表、描点、作图即可;(2)利用放缩变换与平移变换法则可得到()15sin 4126g x x π⎛⎫=-+ ⎪⎝⎭,再令5462x k k Z πππ-=+∈,可得答案. 【详解】(1)由题意可得表格如下:()f x141212- 014(2)将()y f x =的图象向上平移1个单位得到1sin 2126y x π⎛⎫=++ ⎪⎝⎭的图象,再横坐标缩短为原来的12可得到1sin 4126y x π⎛⎫=++ ⎪⎝⎭的图象,再向右平移4π个单位可得115sin 41sin 412626y x x πππ⎛⎫⎛⎫=-++=-+ ⎪ ⎪⎝⎭⎝⎭的图象, 即()15sin 4126g x x π⎛⎫=-+ ⎪⎝⎭, 令5462x k πππ-=+,解得34k x k Z ππ=+∈,, 所以()g x 的对称轴方程是34k x ππ=+,k Z ∈. 【点睛】方法点睛:“五点法”作一个周期上的图象,主要把握三处主要位置点:1、区间端点;2、最值点;3、零点.22.(1)()2sin 213f x x π⎛⎫=++ ⎪⎝⎭;(2)2,1a b ==或2,7a b =-=.【分析】(1)由表中数据可得周期及A 、B 、ϕ的值; (2)()2sin 23g x a x a b π⎛⎫=+++ ⎪⎝⎭,讨论a 的正负,根据()g x 的最大值、最小值可得答案. 【详解】(1)由题,函数()f x 的周期5263T πππ⎛⎫=⨯-= ⎪⎝⎭, 所以22Tπω==, 由31A B A B +=⎧⎨-+=-⎩,得21A B =⎧⎨=⎩,故()2sin(2)1f x x ϕ=++,由表可知,23πϕπ⨯+=,得3πϕ=,所以()2sin 213f x x π⎛⎫=++ ⎪⎝⎭. (2)由(1)可知()2sin 23g x a x a b π⎛⎫=+++ ⎪⎝⎭, 由44x ππ-≤≤,得52636x πππ-≤+≤,所以1sin 2123x π⎛⎫-≤+≤ ⎪⎝⎭;当0a >时,()g x 的最大值是37a b +=,最小值是1b =, 解得2,1a b ==;当0a <时,()g x 的最大值是7b =,最小值是31a b +=, 解得2,7a b =-=,综上,2,1a b ==;或2,7a b =-=. 【点睛】本题考查了由三角函数图象上的点求解析式及利用单调性参数的问题,要正确分析表中数据,熟练掌握三角函数的性质是解题的关键,考查了学生的计算能力. 23.(1)1()cos(2)3f x x π=-;(2)3,12⎡⎤--⎢⎥⎣⎦. 【分析】(1)由伸缩变换得1()cos()2g x x ωϕ=+,由()g x 的图像的周期为54()263T πππ=-=,解得2ω=,由()g x 图像过点(,1)3π,求得ϕ,进而得到()g x ,()f x 的解析式.(2)易得()22cos ()2cos()166h x x x ππ=----,令cos()6t x π=-,利用二次函数的性质求解. 【详解】(1)由题意1()cos()2g x x ωϕ=+, 由()g x 的图像可得:函数()g x 的周期为54()263T πππ=-=, 解得2ω=,∴()cos )(g x x ϕ=+, 由图知()g x 图像过点(,1)3π,所以cos()13πϕ+=,则23k πϕπ=-+,k Z ∈,因为||2ϕπ<,取0k =得3πϕ=-,所以()cos()3g x x π=-,从而函数()f x 的解析式为()cos(2)3f x x π=-.(2)()()2()cos(2)2cos()636h x f x g x x x πππ=-+=---, 22cos ()2cos()166x x ππ=----,令cos()6t x π=-,由0,2x π⎡⎤∈⎢⎥⎣⎦,得,663x πππ⎡⎤-∈-⎢⎥⎣⎦, 所以1,12t ⎡⎤∈⎢⎥⎣⎦,则22132212()22y t t t =--=--,1,12t ⎡⎤∈⎢⎥⎣⎦, 当12t =时,y 有最小值32-,此时,1cos()62x π-=,63x ππ-=,即2x π=,当1t =时有最大值1-,此时cos()16x π-=,06x π-=,即6x π=.所以函数()h x 的值域为3,12⎡⎤--⎢⎥⎣⎦. 【点睛】方法点睛:求解三角函数的值域(最值)常见到以下几种类型:①形如y =a sin x +b cos x +c 的三角函数化为y =A sin(ωx +φ)+k 的形式,再求最值(值域);②形如y =a sin 2x +b sin x +c 的三角函数,可先设sin x =t ,化为关于t 的二次函数求值域(最值);③形如y =a sin x cos x +b (sin x ±cos x )+c 的三角函数,可先设t =sin x ±cos x ,化为关于t 的二次函数求值域(最值). 24.(1)()sin 6f x x π⎛⎫=+ ⎪⎝⎭;(2)0或3π或π. 【分析】(1)先根据函数图象确定出()f x 的最小正周期,再根据最小正周期的计算公式2T ωπ=求解出ω的值,然后代入点,13π⎛⎫⎪⎝⎭结合ϕ的范围求解出ϕ的值,从而()f x 的解析式可求;(2)先根据图象变换求解出()g x 的解析式,然后根据()12g x =得到关于x 的方程,结合[]0,x π∈,求解出x 的值即为方程的实数解. 【详解】(1)因为由图象可知4362T πππ⎛⎫=--= ⎪⎝⎭,所以22T ππω==且0>ω,所以1ω=, 所以()()sin f x x ϕ=+,代入点,13π⎛⎫⎪⎝⎭,所以sin 13πϕ⎛⎫+= ⎪⎝⎭且2πϕ<,所以6π=ϕ,所以()sin 6f x x π⎛⎫=+ ⎪⎝⎭;(2)()f x 的图象上所有的点横坐标缩短到原来的12后得到的函数解析式为:()sin 26g x x π⎛⎫=+ ⎪⎝⎭,因为[]0,x π∈,所以132,666x πππ⎛⎫⎡⎤+∈ ⎪⎢⎥⎝⎭⎣⎦,又因为()12g x =,所以1sin 262x π⎛⎫+= ⎪⎝⎭,所以266x ππ+=或56π或136π,所以0x =或3π或π, 所以方程()12g x =在[]0,π的实数解为:0或3π或π. 【点睛】思路点睛:根据()sin y A ωx φ=+的图象求解函数解析式的步骤: (1)根据图象的最高点可直接确定出A 的值;(2)根据图象的对称轴、对称中心确定出函数的最小正周期,再利用最小正周期的计算公式求解出ω的值;(3)代入图象中非平衡位置的点,结合ϕ的范围求解出ϕ,则函数解析式可求. 25.(1)[1,2]-; (2)1(0,]4. 【分析】(1)由5·,46k k Z ππωπ+=∈,可得4156k ω⎛⎫=- ⎪⎝⎭,k Z ∈,结合()0,1ω∈,得23ω=,所以()42sin 22sin 636f x x x ππω⎛⎫⎛⎫=+=+ ⎪ ⎪⎝⎭⎝⎭,由30,4x π⎡⎤∈⎢⎥⎣⎦,利用正弦定理的单调性可得函数()f x 在30,4π⎡⎤⎢⎥⎣⎦上的值域;(2)令222,262k x k k Z ππππωπ-+≤+≤+∈,解得36k k x ππππωωωω-≤≤+, 由函数()f x 在2,33ππ⎛⎫ ⎪⎝⎭上单调递增,可得002,,3336k k ππππππωωωω⎛⎫⎛⎫⊆-+ ⎪ ⎪⎝⎭⎝⎭,列不等式求解即可. 【详解】(1)由题意得:5·,46k k Z ππωπ+=∈,∴4156k ω⎛⎫=- ⎪⎝⎭,k Z ∈,∵()0,1ω∈,∴23ω=,∴()42sin 22sin 636f x x x ππω⎛⎫⎛⎫=+=+ ⎪ ⎪⎝⎭⎝⎭,∵30,4x π⎡⎤∈⎢⎥⎣⎦,∴47,3666x πππ⎡⎤+∈⎢⎥⎣⎦,∴41sin ,1362x π⎛⎫⎡⎤+∈- ⎪⎢⎥⎝⎭⎣⎦, 故函数()f x 在30,4π⎡⎤⎢⎥⎣⎦上的值域为[]1,2-. (2)令222,262k x k k Z ππππωπ-+≤+≤+∈,解得36k k x ππππωωωω-≤≤+,∵函数()f x 在2,33ππ⎛⎫ ⎪⎝⎭上单调递增,∴002,,3336k k ππππππωωωω⎛⎫⎛⎫⊆-+ ⎪⎪⎝⎭⎝⎭,0k Z ∈,∴0033263k k πππωωπππωω⎧-≤⎪⎪⎨⎪+≥⎪⎩,即0031614k k ωω≤+⎧⎨+≥⎩,又212·3322πππω-≤,∴302ω<≤,∴01566k -<≤,∴00k =, ∴104ω<≤,即ω的取值范围为10,4⎛⎤⎥⎝⎦. 【点睛】本题主要考查三角函数的单调性、三角函数的图象对称性,属于中档题.函数sin()y A x ωϕ=+的单调区间的求法:(1) 代换法:①若0,0A ω>>,把x ωϕ+看作是一个整体,由22k x ππωϕ+≤+≤()322k k Z ππ+∈求得函数的减区间,2222k x k πππωϕπ-+≤+≤+求得增区间;②若0,0A ω><,则利用诱导公式先将ω的符号化为正,再利用①的方法,或根据复合函数的单调性规律进行求解;(2) 图象法:画出三角函数图象,利用图象求函数的单调区间. 26.(1) 2.5sin()56y x π=+;(2)该船1:00至5:00和13:00至17:00期间可以进港,在港口最多能呆4个小时. 【分析】(1)由表格中数据可得, 2.5,5,12A B T ===,26T ππω==,取3x =代入可得2,k k Z ϕπ=∈,则解析式可得;(2)由(1)得计算2.5sin()5 6.256x π+≥解x 范围即可得结果.【详解】解:(1)由表格中数据可得, 2.5,5,12A B T ===. 因为0>ω,所以22126T πππω===. 因为3x =时y 取得最大值,所以32,62k k Z ππϕπ⨯+=+∈,解得2,k k Z ϕπ=∈.所以这个函数解析式为 2.5sin()56y x π=+(2)因为货船的吃水深度为5米,安全间隙至少要有1.25米, 所以2.5sin()5 6.256x π+≥,即1sin()562x π+≥, 所以522,666m x m m N πππππ+≤≤+∈,解得112512,m x m m N +≤≤+∈.取0,1,m m ==得15,1317x x ≤≤≤≤.答:该船1:00至5:00和13:00至17:00期间可以进港,在港口最多能呆4个小时. 【点睛】已知f (x )=Asin (ωx +φ)(A >0,ω>0)的部分图象求其解析式时,A 比较容易看图得出,困难的是求待定系数ω和φ,常用如下两种方法:(1)由ω=2T即可求出ω;确定φ时,若能求出离原点最近的右侧图象上升(或下降)的“零点”横坐标x0,则令ωx0+φ=0(或ωx0+φ=π),即可求出φ.(2)代入点的坐标,利用一些已知点(最高点、最低点或“零点”)坐标代入解析式,再结合图形解出ω和φ,若对A,ω的符号或对φ的范围有要求,则可用诱导公式变换使其符合要求.。
(典型题)高中数学必修四第一章《三角函数》测试(含答案解析)

一、选择题1.设函数5()sin 26f x x π⎛⎫=-⎪⎝⎭,将函数()f x 的图象向左平移()0ϕϕ>个单位长度,得到函数()g x 的图象,若()g x 为偶函数,则ϕ的最小值是( ) A .6π B .3π C .23π D .56π 2.已知函数()cos 2y x ϕ=+()πϕπ-≤<的图象向右平移2π个单位后,与函数sin 23y x π⎛⎫=+ ⎪⎝⎭的图象重合,则ϕ的值为( )A .56πB .56π-C .6π D .6π-3.将函数()sin 2f x x =的图象向右平移ϕ(02πϕ<≤)个单位,得到函数()g x 的图象.在同一坐标系中,这两个函数的部分图象如图所示,则ϕ=( )A .6π B .4π C .3π D .2π 4.函数()()12cos 20211f x x x π=++⎡⎤⎣⎦-在区间[]3,5-上所有零点的和等于( ) A .2B .4C .6D .85.设函数()sin()f x A x ωϕ=+(,,A ωϕ是常数,0,0A ω>>).若()f x 在区间[,]32ππ上具有单调性,且()(),23f f ππ=-2()()23f f ππ=,则ω=( ) A .6 B .3 C .2D .16.设函数()3sin()10,2f x x πωϕωϕ⎛⎫=++>< ⎪⎝⎭的最小正周期为π,其图象关于直线3x π=对称,则下列说法正确是( )A .()f x 的图象过点30,2⎛⎫ ⎪⎝⎭; B .()f x 在2,123ππ⎡⎤⎢⎥⎣⎦上单调递减; C .()f x 的一个对称中心是7,012π⎛⎫⎪⎝⎭; D .将()f x 的图象向左平移12ϕ个单位长度得到函数3sin 21y x =+ 的图象. 7.己知函数()sin()(0,||)2f x x πωϕωϕ=+><的最小正周期为π,且图象向右平移12π个单位后得到的函数为偶函数,则下列说法错误的有( ) A .()f x 关于点5(,0)12π对称 B .()f x 关于直线6x π=对称C .()f x 在,]1212π5π[-单调递增 D .()f x 在7[,]1212ππ单调递减8.已知函数()sin 0,2y x πωϕωϕ⎛⎫=+><⎪⎝⎭的部分图象如图所示,则( )A .1ω=,6π=ϕ B .1ω=,6πϕ=-C .2ω=,6π=ϕ D .2ω=,6πϕ=-9.已知曲线1C :sin y x =,2C :cos 23y x π⎛⎫=-⎪⎝⎭,则下面结论正确的是( ) A .把1C 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移3π个单位长度,得到曲线2CB .把1C 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移23π个单位长度,得到曲线2CC .把1C 上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向左平移12π个单位长度,得到曲线2CD .把1C 上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向右平移12π个单位长度,得到曲线2C10.已知1sin 34x π⎛⎫+= ⎪⎝⎭,则22sin sin 36x x ππ⎛⎫⎛⎫-+-=⎪ ⎪⎝⎭⎝⎭( )A .1B C .1916D .3411.已知函数2()[sin()])cos()f x x x x ωωω=+(0)>ω在[0,]π上有且只有四个零点,则实数ω的取值范围是( ) A .5[,2]3B .5(,2)3C .5[,2)3D .5(,2]312.已知函数11()sin sin sin sin f x x x x x ⎛⎫⎛⎫=+- ⎪⎪⎝⎭⎝⎭,现有命题:①()f x 的最大值为0; ②()f x 是偶函数; ③()f x 的周期为π; ④()f x 的图象关于直线2x π=对称.其中真命题的个数是( ) A .4B .3C .2D .1二、填空题13.下列判断正确的是___________(将你认为所有正确的情况的代号填入横线上). ①函数1tan 21tan 2xy x+=-的最小正周期为π;②若函数()lg f x x =,且()()f a f b =,则1ab =; ③若22tan 3tan 2αβ=+,则223sin sin 2αβ-=;④若函数()2221sin 41x xy x ++=+的最大值为M ,最小值为N ,则2M N +=.14.已知()tan 1f x a x =+(a ,b 为实数),且3(lg log 10)5f =,则(lglg3)f =____________.15.将函数()sin (0)f x x ωω=>的图象向右平移12π个单位长度得到函数()y g x =的图象,若函数()g x 在区间0,2π⎡⎤⎢⎥⎣⎦上是单调递增函数,则实数ω的取值范围是__________.16.若函数()()()4sin 0f x x ωϕω=+>对任意的x 都有()3f x f x π⎛⎫+=- ⎪⎝⎭,则6f π⎛⎫⎪⎝⎭的值是___________. 17.若函数π()sin()cos()3f x x x ωω=++的一个周期是π,则常数ω的一个取值可以为__________.18.已知函数()()π5sin 24f x x x ⎛⎫=-∈ ⎪⎝⎭R ,对于下列说法:①要得到()5sin 2g x x =的图象,只需将()f x 的图象向左平移4π个单位长度即可;②()y f x =的图象关于直线3π8x =对称:③()y f x =在[]π,π-内的单调递减区间为3π7π,88⎡⎤⎢⎥⎣⎦;④5π8y f x ⎛⎫=+⎪⎝⎭为奇函数.则上述说法正确的是________(填入所有正确说法的序号). 19.已知()()sin 03f x x πωϕω⎛⎫=++> ⎪⎝⎭同时满足下列三个条件:①T π=;②3y f x π⎛⎫=-⎪⎝⎭是奇函数;③()06f f π⎛⎫<⎪⎝⎭.若()f x 在[)0,t 上没有最小值,则实数t 的取值范围是___________.20.已知函数()()()sin 0,0,f x A x A ωϕωπϕπ=+>>-<<的部分图象如下图所示,则ϕ=________.三、解答题21.已知函数27()sin cos 2sin 632x f x x x ππ⎛⎫⎛⎫=-+--⎪ ⎪⎝⎭⎝⎭.(1)求函数()f x 的单调递增区间; (2)求使()0f x <成立的实数x 的取值集合.22.函数()cos()0,02f x x πωϕωϕ⎛⎫=+><<⎪⎝⎭的部分图象如图所示.(1)写出()f x 的解析式; (2)将函数()f x 的图象向右平移12π个单位后得到函数()g x 的图象,讨论关于x 的方程()3()0f x g x m -=(11)m -<≤在区间,2ππ⎡⎤-⎢⎥⎣⎦上的实数解的个数.23.已知()442sin cos cossin f x x x x x ωωωω=+-(其中ω>0).(1)若()f x 的最小正周期是π,求ω的值及此时()f x 的对称中心; (2)若将()y f x =的图像向左平移4π个单位,再将所得的图像纵坐标不变,横坐标缩小为原来的12,得到()g x 的图像,若y g x 在0,8π⎡⎤⎢⎥⎣⎦上单调递减,求ω的取值范围.24.已知函数()()2sin f x x ωϕ=+(0>ω,0ϕπ<<)的最大值和最小正周期相同,()f x 的图象过点(3,且在区间10,12⎡⎤⎢⎥⎣⎦上为增函数.(1)求函数()f x 的解析式;(2)若函数()()1g x f x =+在区间()0,b 上只有4个零点,求b 的最大值. 25.已知函数()231cos 2f x x x =-+. (1)当π02x ⎡⎤∈⎢⎥⎣⎦,时,求函数()f x 的取值范围;(2)将()f x 的图象向左平移π6个单位得到函数()g x 的图象,求()g x 的单调递增区间. 26.已知函数()sin()(0,0,||)f x A x A ωϕωϕπ=+>><的部分图象如下图所示.(1)求函数()f x 的解析式,并写出函数()f x 的单调递增区间; (2)将函数()f x 图象上所有点的横坐标缩短到原来的14(纵坐标不变),再将所得的函数图象上所有点向左平移02m m π⎛⎫<< ⎪⎝⎭个单位长度,得到函数()g x 的图象.若函数()g x 的图象关于直线512x π=对称,求函数()g x 在区间7,1212ππ⎡⎤⎢⎥⎣⎦上的值域.【参考答案】***试卷处理标记,请不要删除一、选择题 1.A 解析:A 【分析】根据题意有()5sin 226g x x ϕπ⎛⎫=+ ⎪⎝⎭-,若()g x 为偶函数则52()62k k Z πππϕ-=+∈,结合0ϕ>可得出答案. 【详解】 解:由题意可得()()55()sin 2sin 2266g x f x x x πϕϕϕπ⎛⎫⎛⎫=+=+-=+ -⎪ ⎪⎝⎭⎝⎭因为()g x 为偶函数,则52()62k k Z πππϕ-=+∈,即2()32k k Z ππϕ=+∈ 因为0ϕ>,所以当1k =-时ϕ取得最小值6π. 故选:A. 【点睛】应用函数奇偶性可解决的四类问题及解题方法(1)求函数值:将待求值利用奇偶性转化为已知区间上的函数值求解;(2)求解析式:先将待求区间上的自变量转化到已知区间上,再利用奇偶性求解,或充分利用奇偶性构造关于()f x 的方程(组),从而得到()f x 的解析式;(3)求函数解析式中参数的值:利用待定系数法求解,根据()()0f x f x ±-=得到关于待求参数的恒等式,由系数的对等性得参数的值或方程(组),进而得出参数的值; (4)画函数图象和判断单调性:利用奇偶性可画出另一对称区间上的图象及判断另一区间上的单调性.2.A解析:A 【分析】根据三角函数的平移变换得到cos(2)y x ϕπ=+-后,再根据诱导公式变为sin(2)2y x πϕ=+-,然后利用图象重合列式可得结果.【详解】函数()cos 2y x ϕ=+()πϕπ-≤<的图象向右平移2π个单位后,得到cos[2()]cos(2)2y x x πϕϕπ=-+=+-sin(2)2x πϕπ=+-+sin(2)2x πϕ=+-,依题意可得223k ππϕπ-=+()k ∈Z ,所以526k πϕπ=+()k ∈Z 因为πϕπ-≤≤,所以0k =,56πϕ=. 故选:A. 【点睛】关键点点睛;经过平移变换后,利用诱导公式化为同名函数是解题关键,属于中档题. 3.C解析:C 【分析】由图可知,17248g f ππ⎛⎫⎛⎫==⎪ ⎪⎝⎭⎝⎭()()sin 2x g x ϕ=-,于是推出1717sin 224242g ππϕ⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭,即1722124k ππϕπ-=+或324k ππ+,k Z ∈,再结合02πϕ<≤,解之即可得ϕ的值.【详解】由图可知,17sin 224882g f πππ⎛⎫⎛⎫⎛⎫==⨯=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,因为()f x 的图象向右平移ϕ个单位,得到函数()g x 的图象,所以()()sin 2x g x ϕ=-,所以171717sin 2sin 22424122g πππϕϕ⎛⎫⎛⎫⎛⎫=-=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 所以1722124k ππϕπ-=+或17322124k ππϕπ-=+,k Z ∈, 解得712k πϕπ=-或3k πϕπ=-,k Z ∈,因为02πϕ<≤,所以3πϕ=.故选:C 【点睛】本小题主要考查三角函数图象变换,属于中档题.4.D解析:D 【分析】由图可得函数的零点就是11y x =-和2cos y x π=交点的横坐标,画出函数图象,可得出()f x 在[]3,5-有8个零点,且关于1x =对称,即可求出.【详解】()()112cos 20212cos 11f x x x x x ππ=++=-⎡⎤⎣⎦--, 令()0f x =,则12cos 1x x π=-, 则函数的零点就是11y x =-和2cos y x π=交点的横坐标, 可得11y x =-和2cos y x π=的函数图象都关于1x =对称,则交点也关于1x =对称, 画出两个函数的图象,观察图象可知,11y x =-和2cos y x π=在[]3,5-有8个交点, 即()f x 有8个零点,且关于1x =对称,故所有零点的和为428⨯=. 故选:D. 【点睛】本题考查求函数的零点之和,解题的关键是将题目化为找11y x =-和2cos y x π=交点的横坐标,从而通过函数图象求解.5.B解析:B 【分析】 由2()()23f f ππ=求出函数的一条对称轴,结合()f x 在区间[,]32ππ上具有单调性,且()()23f f ππ=-,可得函数的四分之一周期,即可求出ω的值.【详解】解:由2()()23f f ππ=,可知函数()f x 的一条对称轴为2723212x πππ+==, 则2x π=离最近对称轴距离为712212πππ-=. 又()()23f f ππ=-,则()f x 有对称中心5,012π⎛⎫⎪⎝⎭, 由于()f x 在区间,32ππ⎡⎤⎢⎥⎣⎦上具有单调性, 则1232T ππ-,所以3T π≥,从而7512124T ππ-=,所以23T π=,因为2T πω=,所以3ω=.故选:B【点睛】本题考查()sin()f x A x ωϕ=+型函数图象的应用,考查了学生灵活处理问题和解决问题的能力.6.D解析:D 【分析】先根据对称轴及最小正周期,求得函数()f x 的解析式,再结合正弦函数的图象与性质,判断点是否在函数图象上可判断A ,求得函数的单调区间及对称中心即可判断选项BC ,由平移变换求得变化后的解析式并对比即可判断D. 【详解】函数()3sin()10,2f x x πωϕωϕ⎛⎫=++>< ⎪⎝⎭的最小正周期是π 所以22πωπ==,则()()3sin 21f x x ϕ=++,()()3sin 21f x x ϕ=++图象关于直线3x π=对称,对称轴为2,2x k k Z πϕπ+=+∈,代入可得2,32k k Z ππϕπ⨯+=+∈,解得,6k k Z πϕπ=-+∈,因为,22ππϕ⎛⎫∈- ⎪⎝⎭,所以当0k =时, 6πϕ=-, 则()3sin 216f x x π⎛⎫=-+ ⎪⎝⎭,对于A,当0x =时,()3103sin 11622f π=-+=-+=- ,所以错误; 对于B,()3sin 216f x x π⎛⎫=-+ ⎪⎝⎭的单调递减区间为3222,262k x k k πππππ+-+∈Z ≤≤, 解得5,36k x k k Z ππππ+≤≤+∈,因为123ππ<,则()f x 在2,123ππ⎡⎤⎢⎥⎣⎦上不是减函数,所以错误; 对于C ,773sin 213sin 11012126f ππππ⎛⎫⎛⎫=⨯-+=+=≠⎪ ⎪⎝⎭⎝⎭,所以7,012π⎛⎫ ⎪⎝⎭不是()f x 的一个对称中心,所以错误; 对于D ,1212πϕ=,将()3sin 216f x x π⎛⎫=-+ ⎪⎝⎭的图象向左平移12π个单位长度得到可得3sin 213sin 21126y x x ππ⎡⎤⎛⎫=-++=+ ⎪⎢⎥⎝⎭⎣⎦,所以能得到3sin 21y x =+的图象,所以正确. 故选: D. 【点睛】本题考查了正弦函数的图象与性质的综合应用,关键点是根据已知条件先求出正弦函数的解析式,还要熟练掌握三角函数的性质才能正确的解题,属于中档题.7.A解析:ABD 【分析】由周期可求出ω,再由平移后为偶函数求出ϕ,即得()sin 23πf x x ⎛⎫=-⎪⎝⎭,求出512f π⎛⎫⎪⎝⎭可判断A ;求出6f π⎛⎫⎪⎝⎭可判断B ;令222,232k x k k Z πππππ-+≤-≤+∈求出单调递增区间可判断C ;由C 选项可判断D. 【详解】()f x 的最小正周期为π,22πωπ∴==,()sin(2)f x x ϕ=+,向右平移12π个单位后得到sin 26y x πϕ⎛⎫=-+ ⎪⎝⎭为偶函数, ,62k k Z ππϕπ∴-=+∈,即2,3k k Z πϕπ=+∈, ||2πϕ<,3ϕπ∴=-,()sin 23f x x π⎛⎫∴=- ⎪⎝⎭, 对于A ,55sin 2sin 10121232f ππππ⎛⎫⎛⎫=⨯-==≠ ⎪ ⎪⎝⎭⎝⎭,故()f x 不关于点5(,0)12π对称,故A 错误; 对于B ,sin 2sin 001663f πππ⎛⎫⎛⎫=⨯-==≠± ⎪ ⎪⎝⎭⎝⎭,故B 错误;对于C ,令222,232k x k k Z πππππ-+≤-≤+∈,解得5,1212k x k k Z ππππ-+≤≤+∈, 当0k =时,51212x ππ-≤≤,故()f x 在,]1212π5π[-单调递增,故C 正确; 对于D ,由C 选项可知,()f x 在5[,]1212ππ单调递增,故D 错误.故选:ABD.本题考查正弦型函数的性质,可通过代入验证的方法判断对称轴和对称中心,利用整体换元可求单调区间.8.D解析:D 【分析】根据函数的图象求出函数的周期,然后可以求出ω,通过函数经过的最大值点求出ϕ值,即可得到结果. 【详解】由函数的图象可知:74123T πππ⎛⎫=-⨯= ⎪⎝⎭,22T πω∴==. 当3x π=,函数取得最大值1,所以sin 213πϕ⎛⎫⨯+= ⎪⎝⎭,2232k k Z ππϕπ+=+∈,, ||,02k πϕ<∴=,6πϕ∴=-,故选:D. 【点睛】本题主要考查了由三角函数的图象求解析式,通过周期求ω的值,通过最值点求ϕ的值是解题的关键,属于基础题.9.C解析:C 【分析】由题意利用诱导公式得1sin cos :2C y x x π⎛⎫==- ⎪⎝⎭,根据函数()cos y A x ωϕ=+的图象变换规律,得出结论. 【详解】已知曲线1sin cos :2C y x x π⎛⎫==- ⎪⎝⎭,2cos 23:C y x π⎛⎫=- ⎪⎝⎭,∴把1C 上各点的横坐标缩短到原来的12倍,纵坐标不变,可得cos 22y x π⎛⎫=- ⎪⎝⎭的图象,再把得到的曲线向左平移 12π个单位长度,得到曲线2cos 2cos 263:2C x x πππ⎛⎫⎛⎫+-=- ⎪ ⎪⎝⎭⎝⎭的图象,故选C .【点睛】本题主要考查函数()cos y A x ωϕ=+的图象变换规律,属于基础题.10.C【分析】由诱导公式求得cos 6x π⎛⎫- ⎪⎝⎭,然后再由平方关系和诱导公式计算. 【详解】 由已知1cos cos sin 62334x x x ππππ⎡⎤⎛⎫⎛⎫⎛⎫-=-+=+=⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦, 222115sin 1cos 166416x x ππ⎛⎫⎛⎫⎛⎫-=--=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,21sin sin cos 32664x x x ππππ⎛⎫⎛⎫⎛⎫-=+-=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 所以2211519sin sin 3641616x x ππ⎛⎫⎛⎫-+-=+= ⎪ ⎪⎝⎭⎝⎭. 故选:C . 【点睛】关键点点睛:本题考查三角函数的求值.解题关键是确定“已知角”和“未知角”的关系,选用适当的公式进行变形求值.本题中首先利用诱导公式得出cos 6x π⎛⎫- ⎪⎝⎭,然后再用诱导公式得出2sin 3x π⎛⎫-⎪⎝⎭,用平方关系得出2sin 6x π⎛⎫- ⎪⎝⎭,这样求解比较方便.11.C解析:C 【分析】先化简函数的解析式,然后利用x 的范围求出26x πω⎛⎫-⎪⎝⎭的范围,根据题意列不等式求解ω.【详解】221cos 21()[sin()])cos()2sin(2)2262ωπωωωωω-=+=+=-+x f x x x x x x ,因为[0,]x π∈,得2,2666πππωωπ⎛⎫⎡⎤-∈-- ⎪⎢⎥⎝⎭⎣⎦x ,因为函数在[0,]π有且只有四个零点,则19232666πππωπ≤-<,解得523ω≤<. 故选:C. 【点睛】关于三角函数中求解ω的取值范围问题,一般要先求解出整体的范围,即x ωϕ+的范围,然后根据题意,分析x ωϕ+范围所在的区间,列不等式求解,即可求出ω.12.A【分析】先求函数的定义域,再根据函数奇偶性定义,周期函数的定义可判断②③的正误,再根据函数解析的特征可判断④的正误,最后利用换元法可求判断①的正误. 【详解】22111()sin sin sin sin sin sin f x x x x x x x ⎛⎫⎛⎫=+-=- ⎪⎪⎝⎭⎝⎭, 由sin 0x ≠可得,x k k Z π≠∈,故函数的定义域为{}|,x x k k Z π≠∈, 所以函数的定义域关于原点对称.又()()()222211()sin sin sin sin f x x x f x x x-=--=-=-,故()f x 为偶函数, 故②正确.又()()()221()sin sin f x x f x x πππ+=+-=+, 故()f x 是周期函数且周期为π,故③正确.又()()()221()sin sin f x x f x x πππ-=--=-,故()f x 的图象关于直线2x π=对称,故④正确.令2sin t x =,则(]0,1t ∈且()1f x t t=-,因为1y t t=-为(]0,1上的增函数,故()max 0f x =,故①正确. 故选:A. 【点睛】思路点睛:对于复杂函数的性质的研究,注意先研究函数的定义域,再研究函数的奇偶性或周期性,最后再研究函数的单调性,讨论函数图象的对称性,注意根据()()f a x f x -=来讨论. 二、填空题13.③④【分析】①化简可得即可求出;②由可能相等可判断;③利用同角三角函数关系可化简求出;④化简可得利用奇函数的性质可得【详解】对①则最小正周期为故①错误;对②若则可能相等故②错误;对③若则即即即即故③解析:③④ 【分析】①,化简可得tan 24y x π⎛⎫=+⎪⎝⎭,即可求出;②由,a b 可能相等可判断;③利用同角三角函数关系可化简求出;④化简可得24sin 141x xy x +=++,利用奇函数的性质可得.【详解】对①,tantan 21tan 24tan 21tan 241tan tan 24xx y x x x πππ++⎛⎫===+ ⎪-⎝⎭-⋅,则最小正周期为2π,故①错误;对②,若()()f a f b =,则,a b 可能相等,故②错误;对③,若22tan 3tan 2αβ=+,则2222sin 3sin 2cos cos αβαβ=+,即222222sin cos 3cos sin 2cos cos αβαβαβ=+,即22222222sin cos cos cos 3cos sin 3cos cos αβαβαβαβ+=+,即22cos 3cos βα=,即223sin sin 2αβ-=,故③正确;对④,()22221sin 4sin 14141x xx x y x x +++==+++,令()24sin 41x x g x x =++,则()()g x g x -=,故()g x 是奇函数,()()max min 0g x g x ∴+=,()()max min 112M N g x g x ∴+=+++=,故④正确.故答案为:③④. 【点睛】本题考查正切型函数的周期,考查同角三角函数的关系,考查奇函数的应用,解题的关键是正确利用三角函数的关键进行化简.14.【分析】令可知为奇函数根据与为相反数即可求解【详解】令定义域关于原点对称且所以为奇函数则所以由奇函数性质可得所以故答案为:【点睛】关键点点睛:首先要观察出中的部分为奇函数其次要能利用换底公式对数的运 解析:3-【分析】令tan ()a x g x =+,可知()g x 为奇函数,根据3lg log 10与lg lg3为相反数即可求解. 【详解】令tan ()a x g x =+,,2x k k Z ππ≠+∈,定义域关于原点对称,且()tan ()g x a x g x -=--=-, 所以()g x 为奇函数,则31(lg log 10)(lg)(lg lg 3)(lg lg 3)15lg 3f f fg ==-=-+=, 所以(lg lg3)514g -=-=, 由奇函数性质可得(lg lg3)4g =-, 所以(lglg3)(lglg3)1413f g =+=-+=-, 故答案为:3- 【点睛】关键点点睛:首先要观察出()f x中的部分tan ()a x g x =+为奇函数,其次要能利用换底公式,对数的运算性质找到3lg log 10与lg lg3为相反数,借助奇函数的性质求解.15.【分析】先求出由可求出利用单调性可得结合即可求解【详解】将函数的图象向右平移个单位长度得到函数因为所以因为函数在区间上是单调递增函数所以解得:因为所以故答案为:【点睛】关键点点睛:本题解题的关键点是解析:60,5⎛⎤⎥⎝⎦【分析】先求出()sin 12g x x πω⎛⎫=-⎪⎝⎭,由0,2x π⎡⎤∈⎢⎥⎣⎦可求出5121212x πππωωω⎛⎫-≤-≤ ⎪⎝⎭,利用单调性可得1225122ππωππω⎧-≥-⎪⎪⎨⎪≤⎪⎩,结合0>ω即可求解.【详解】将函数()sin (0)f x x ωω=>的图象向右平移12π个单位长度得到函数()sin 12g x x πω⎛⎫=- ⎪⎝⎭,因为02x π≤≤,所以5121212x πππωωω⎛⎫-≤-≤⎪⎝⎭, 因为函数()g x 在区间0,2π⎡⎤⎢⎥⎣⎦上是单调递增函数, 所以1225122ππωππω⎧-≥-⎪⎪⎨⎪≤⎪⎩,解得:665ωω≤⎧⎪⎨≤⎪⎩,因为0>ω,所以605ω<≤, 故答案为:60,5⎛⎤ ⎥⎝⎦【点睛】关键点点睛:本题解题的关键点是由x 的范围求出12x πω⎛⎫-⎪⎝⎭的范围,将12x πω⎛⎫-⎪⎝⎭看成一个整体让其满足正弦函数的单调递增区间,即可得其满足的条件.16.4或-4【分析】由题意可得故函数的周期为求得;在中令求得从而求得的值【详解】∵函数对任意的都有∴故函数的周期为∴所以∴在中令可得:即∴则故答案为:4或-4【点睛】求三角函数解析式的方法:(1)求A 通解析:4或-4. 【分析】 由题意可得()23f x f x π⎛⎫+= ⎪⎝⎭,故函数()f x 的周期为23π,求得=3ω;在()3f x f x π⎛⎫+=- ⎪⎝⎭中,令=0x ,求得sin 0ϕ=,从而求得6f π⎛⎫⎪⎝⎭的值. 【详解】∵函数()()()4sin 0f x x ωϕω=+>对任意的x 都有()3f x f x π⎛⎫+=- ⎪⎝⎭, ∴()23f x f x π⎛⎫+= ⎪⎝⎭,故函数()f x 的周期为23π, ∴22=3ππω,所以=3ω. ∴()()4sin 3f x x ϕ=+. 在()3f x f x π⎛⎫+=- ⎪⎝⎭中,令=0x ,可得:()03f f π⎛⎫= ⎪⎝⎭, 即()4sin =4sin πϕϕ+,∴sin =0ϕ. 则=4sin()4cos 462f ππϕϕ⎛⎫+==±⎪⎝⎭. 故答案为: 4或-4. 【点睛】求三角函数解析式的方法: (1)求A 通常用最大值或最小值; (2)求ω通常用周期;()求φ通常利用函数上的点带入即可求解.17.2(答案不唯一)【分析】把函数化为一个角的一个三角函数形式然后利用正弦函数的周期求解注意题中已知条件是函数的一个周期是并没有说是最小正周期因此只要函数的最小正周期是除以一个正整数都可满足题意【详解】解析:2(答案不唯一) 【分析】把函数化为一个角的一个三角函数形式,然后利用正弦函数的周期求解,注意题中已知条件是函数的一个周期是π,并没有说π是最小正周期.因此只要函数的最小正周期是π除以一个正整数,都可满足题意. 【详解】1()sin cos cossin sin(1cos 332f x x x x x x ππωωωωω=+-=-+,令cosϕ=sin ϕ=,且ϕ为锐角,则()sin()f x x ωϕ=+,由2T ππω==,得2ω=,实际上,由2T ππω==得2ω=±,或者2kππω=(k Z ∈且0k ≠),2k ω=(k Z ∈且0k ≠),ω可为任意一个非零点的偶数. 故答案为:2.(填任一非0的偶数都可以). 【点睛】关键点点睛:本题考查三角函数的周期,求解三角函数周期,一般是把函数化为一个角的一个三角函数形式,然后利用正弦函数的周期性求解.而我们一般说周期通常是求最值正周期,若题中强调某个数是函数的一个周期,则这个周期不一定是最小正周期.18.②④【分析】结合三角函数的图象与性质对四个结论逐个分析即可得出答案【详解】①要得到的图象应将的图象向左平移个单位长度所以①错误;②令解得所以直线是的一条对称轴故②正确;③令解得因为所以在定义域内的单解析:②④ 【分析】结合三角函数的图象与性质对四个结论逐个分析即可得出答案. 【详解】①要得到()5sin 2g x x =的图象,应将()ππ5sin 25sin 248f x x x ⎡⎤⎛⎫⎛⎫=-=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦的图象向左平移π8个单位长度,所以①错误;②令ππ2π42x k -=+,k ∈Z ,解得3ππ82k x =+,k ∈Z ,所以直线3π8x =是()y f x =的一条对称轴,故②正确;③令ππ3π22π42π22k k x ≤+≤-+,k ∈Z ,解得3π7πππ88k x k +≤≤+,k ∈Z ,因为[]π,πx ∈-,所以()f x 在定义域内的单调递减区间为3π7π,88⎡⎤⎢⎥⎣⎦和5ππ,88⎡⎤--⎢⎥⎣⎦,所以③错误;④5π5ππ5sin 25sin 2884y f x x x ⎡⎤⎛⎫⎛⎫=+=+-=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦是奇函数,所以该说法正确. 【点睛】本题考查了正弦型函数的对称轴、单调性、奇偶性与平移变换,考查了学生对()sin y A ωx φ=+的图象与性质的掌握,属于中档题.19.【分析】由周期公式可得由三角函数的中心对称可得结合即可得为奇数即可得由可得进而可得即可得解【详解】由可得由是奇函数可得函数的图象关于中心对称所以即又所以所以为奇数由可得因为在上没有最小值所以即故答案解析:511,612ππ⎛⎤⎥⎝⎦【分析】由周期公式可得ω,由三角函数的中心对称可得,3k k Z πϕπ=+∈,结合()06f f π⎛⎫< ⎪⎝⎭即可得k 为奇数,即可得()sin 23πf x x ⎛⎫=-⎪⎝⎭,由[)0,x t ∈可得2,2333x t πππ⎡⎫-∈--⎪⎢⎣⎭,进而可得432332t πππ<-≤,即可得解. 【详解】 由T π=可得22T πω==,()sin 23f x x πϕ⎛⎫=++ ⎪⎝⎭由3y f x π⎛⎫=- ⎪⎝⎭是奇函数可得函数()f x 的图象关于,03π⎛-⎫⎪⎝⎭中心对称, 所以2,33k k Z ππϕπ⎛⎫⨯-++=∈ ⎪⎝⎭,即,3k k Z πϕπ=+∈, 又()06f f π⎛⎫< ⎪⎝⎭,所以2sin sin 33ππϕϕ⎛⎫⎛⎫+<+ ⎪ ⎪⎝⎭⎝⎭, 所以,3k k πϕπ=+为奇数,()sin 2sin 2333f x x k x ππππ⎛⎫⎛⎫=+++=- ⎪ ⎪⎝⎭⎝⎭,由[)0,x t ∈可得2,2333x t πππ⎡⎫-∈--⎪⎢⎣⎭, 因为()f x 在[)0,t 上没有最小值,所以432332t πππ<-≤即511,612t ππ⎛⎤∈ ⎥⎝⎦. 故答案为:511,612ππ⎛⎤⎥⎝⎦. 【点睛】本题考查了三角函数图象与性质的应用,考查了运算求解能力,牢记知识点是解题关键,属于中档题.20.【分析】根据图象得出函数的最小正周期可得出的值再将点代入函数解析式结合的取值范围可求出的值【详解】由图象可知函数的最小正周期则将点代入函数解析式得即因为函数在附近单调递减则得故答案为:【点睛】本题考 解析:6π【分析】根据图象得出函数()y f x =的最小正周期T ,可得出ω的值,再将点5,012π⎛⎫⎪⎝⎭代入函数解析式,结合ϕ的取值范围,可求出ϕ的值. 【详解】由图象可知,函数()y f x =的最小正周期11521212T πππ⎛⎫=⨯-=⎪⎝⎭,222T ππωπ∴===, 则()()sin 2f x A x ϕ=+, 将点5,012π⎛⎫⎪⎝⎭代入函数解析式得55sin 201212f A ππϕ⎛⎫⎛⎫=⨯+= ⎪ ⎪⎝⎭⎝⎭,即5sin 06πϕ⎛⎫+= ⎪⎝⎭, 因为函数()y f x =在512x π=附近单调递减,则()526k k Z πϕππ+=+∈, 得()26k k Z πϕπ=+∈,πϕπ-<<,0k ∴=,6π=ϕ. 故答案为:6π. 【点睛】本题考查利用图象求三角函数解析式中的参数,考查分析问题和解决问题的能力,属于中等题.三、解答题21.(1)22,2,33k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦;(2)422,3x k x k k Z πππ⎧⎫-+<<∈⎨⎬⎩⎭∣.【分析】(1)化简()f x ,应用整体思想,结合正弦函数的递增区间,即可得出结论; (2)应用整体思想,运用正弦函数图像,建立不等式,即可求解. 【详解】()sin cos cos sincoscos sinsin cos 16633f x x x x x x ππππ=-+++-11cos cos cos 1cos 122x x x x x x x =-++-=+-12cos 12sin 126x x x π⎫⎛⎫=+-=+-⎪ ⎪⎪⎝⎭⎝⎭. (1)由22,262k x k k Z πππππ-+++∈,解得222,33k x k k Z ππππ-++∈, 所以()f x 的单调递增区间为22,2,33k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦.(2)由(1)知()2sin 16f x x π⎛⎫=+- ⎪⎝⎭.因为()0f x <,即2sin 106x π⎛⎫+-< ⎪⎝⎭.所以1sin 62x π⎛⎫+< ⎪⎝⎭, 所以7+2++2,666k x k k Z πππππ-<<∈. 所以422,3k x k k Z πππ-+<<∈, 所以使()0f x <成立的x 的取值集合为422,3xk x k k Z πππ⎧⎫-+<<∈⎨⎬⎩⎭∣. 【点睛】方法点睛:解决正弦型函数的单调性和不等式的相关问题,运用整体思想,先由三角函数恒等变换,化简解析式为同一角同一三角函数的形式,再运用三角函数的性质以及建立三角不等式求解.22.(1)()cos(2)6f x x π=+;(2)见解析.【分析】(1)根据图象求出周期,再根据最低点可求ϕ,从而得到函数解析式. (2)求出()g x 的解析式,故方程可化为cos 206m x π⎛⎫---= ⎪⎝⎭,可通过直线y m =-与cos 26y x π⎛⎫=- ⎪⎝⎭ 的图象的交点的个数解决方程的解的个数.【详解】(1)由函数的图象可得()f x 的周期为2236πππ⎛⎫⨯-=⎪⎝⎭,故22πωπ==,又26312fππ⎛⎫+⎪=- ⎪⎪⎝⎭,故5cos2+112πϕ⎛⎫⨯=-⎪⎝⎭,所以526kπϕππ+=+即2,6k k Zπϕπ=+∈,因为02πϕ<<,故6π=ϕ,所以()cos(2)6f x xπ=+.(2)()cos(2)cos266g x x xππ=-+=,故()3()cos(2)3cos26f xg x m x x mπ-⋅-=+--cos2cos sin2sin3cos2cos2666x x x m m xπππ⎛⎫=---=---⎪⎝⎭故方程在区间,2ππ⎡⎤-⎢⎥⎣⎦上的实数解的个数即为y m=-与cos26y xπ⎛⎫=-⎪⎝⎭图象交点的个数,cos26y xπ⎛⎫=-⎪⎝⎭在,2ππ⎡⎤-⎢⎥⎣⎦上的图象如图所示,由图象可得:当1m-=-31m<-<即1m=或31m-<<时,方程有2个不同的解;当31m-<-≤31m≤<时,方程有4个不同的解;当3322m-<-≤即3322m-≤<时,方程有3个不同的解;【点睛】方法点睛:(1)平移变换有“左加右减”(水平方向的平移),注意是对自变量x做加减.(2)与余弦型函数有关的方程的解的个数的讨论,一般可转化为动直线与确定函数的图象的交点个数来讨论.23.(1)=1ω,对称中心是(,0),82k k Z ππ-+∈,(2)1524ω≤≤【分析】(1)先对函数化简变形得(2+4f x x πω(),由函数的周期为π,得=1ω,再由2+=4x k ππ,可求出对称中心的横坐标,进而可得对称中心;(2)由题意得到())24g x x ωππω=++,由0,8x π⎡⎤∈⎢⎥⎣⎦可得424244x ωππωπππωωπ⎡⎤++∈++⎢⎥⎣⎦,,而y g x 在0,8π⎡⎤⎢⎥⎣⎦上单调递减,所以可得322,24422k k k Z ωπππππωπππ⎡⎤⎡⎤++⊆++∈⎢⎥⎢⎥⎣⎦⎣⎦,,,从而可求出ω的取值范围 【详解】解:(1)()sin 2+cos 22+4f x x x x πωωω=(),()f x 的最小正周期是π,2==12ππωω∴∴,此时()2+4f x x π=(),令2+=4x k ππ,得,82k x k Z ππ=-+∈ ()f x ∴的对称中心是(,0),82k k Z ππ-+∈. (2)由题知())24g x x ωππω=++, 0,4824244x x πωππωπππωωπ⎡⎤⎡⎤∈∴++∈++⎢⎥⎢⎥⎣⎦⎣⎦,,,又()y g x =在08π⎡⎤⎢⎥⎣⎦,上单调递减,322,24422k k k Z ωπππππωπππ⎡⎤⎡⎤∴++⊆++∈⎢⎥⎢⎥⎣⎦⎣⎦,,,即32154242,242242k k k k Z k ππωππωωππππ⎧+≤+⎪⎪⇒+≤≤+∈⎨⎪+≥+⎪⎩, 150,24ωω>∴≤≤【点睛】关键点点睛:此题考查三角函数的恒等变换,考查三角函数的图像和性质,第2问解题的关键是求出424244x ωππωπππωωπ⎡⎤++∈++⎢⎥⎣⎦,,再由y g x 在0,8π⎡⎤⎢⎥⎣⎦上单调递减,可得322,24422k k k Z ωπππππωπππ⎡⎤⎡⎤++⊆++∈⎢⎥⎢⎥⎣⎦⎣⎦,,,从而可求出ω的取值范围,属于中档题 24.()2sin 3f x x ππ⎛⎫=+ ⎪⎝⎭;(2)296【分析】(1)根据条件先求ω,再根据()0f =ϕ,最后再验证ϕ值,确定函数的解析式;(2)根据条件求函数的零点,确定b 的最大值应是第5个零点. 【详解】 (1)函数的最大值是2,∴,函数的周期2T =,即22πωπω=⇒=,()02sin f ϕ==,且0ϕπ<<,3πϕ∴=或23π, 当3πϕ=时,()2sin 3f x x ππ⎛⎫=+⎪⎝⎭,当10,12x ⎡⎤∈⎢⎥⎣⎦时,5,3312x ππππ⎡⎤+∈⎢⎥⎣⎦ 0,2π⎡⎤⎢⎥⎣⎦,满足条件; 当23ϕπ=时,()22sin 3f x x ππ⎛⎫=+⎪⎝⎭,当10,12x ⎡⎤∈⎢⎥⎣⎦时,223,334x ππππ⎡⎤+∈⎢⎥⎣⎦ 3,22ππ⎡⎤⎢⎥⎣⎦,所以函数在区间10,12⎡⎤⎢⎥⎣⎦上为减函数,所以舍去, 所以函数()2sin 3f x x ππ⎛⎫=+⎪⎝⎭; (2)()2sin 103g x x ππ⎛⎫=++= ⎪⎝⎭,得1sin 32x ππ⎛⎫+=- ⎪⎝⎭, 72,36x k k Z ππππ+=+∈,解得:52,6x k k Z =+∈, 或112,36x k k Z ππππ+=+∈,解得:32,2x k k Z =+∈, 函数()()1g x f x =+在区间()0,b 上只有4个零点,∴这四个零点应是56,32,176,72,那么b 的最大值应是第5个零点,即296,所以b 的最大值是296. 【点睛】关键点点睛:本题第一问注意求出两个ϕ 后需验证是否满足条件,第二个关键点是,注意()0,b 是开区间,开区间内只有四个零点,则b 的最大值是第5个零点.25.(1)112⎡⎤-⎢⎥⎣⎦,;(2)ππππ36k k ⎡⎤-+⎢⎥⎣⎦,,k Z ∈. 【分析】(1)根据余弦的二倍角公式、辅助角公式化简()f x ,得到()πsin 26f x x ⎛⎫=- ⎪⎝⎭,再利用正弦函数的性质确定当π02x ⎡⎤∈⎢⎥⎣⎦,时,()f x 的取值范围; (2)根据图象的平移得到()πsin 26g x x ⎛⎫=+ ⎪⎝⎭,再利用正弦函数的性质可求得()g x 得单调递增区间. 【详解】(1)()211πcos cos2sin 2226f x x x x x x ⎛⎫=-+=-=- ⎪⎝⎭,π02x ⎡⎤∈⎢⎥⎣⎦,,ππ5π2666x ⎡⎤∴-∈-⎢⎥⎣⎦,, π1sin 2162x ⎛⎫⎡⎤∴-∈- ⎪⎢⎥⎝⎭⎣⎦,.∴函数()f x 的取值范围为112⎡⎤-⎢⎥⎣⎦,.(2)由题意知:()ππππsin 2sin 26666g x f x x x ⎡⎤⎛⎫⎛⎫⎛⎫=+=+-=+ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦, 令πππ2π22π262k x k -≤+≤+,k Z ∈, 解得πππ2π.36k k k Z -≤≤+∈, ∴()g x 的单调递增区间为ππππ36k k ⎡⎤-+⎢⎥⎣⎦,,k Z ∈. 【点睛】本题考查了三角函数的性质,根据二倍角的余弦公式、辅助角公式化简函数,并求函数在区间上的最值,及函数的单调区间,考查学生的运算能力,属于中档题. 26.(1)12()2sin 23f x x π⎛⎫=- ⎪⎝⎭,递增区间为74,4,33k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦; (2)[]1,2-. 【分析】(1)由三角函数的图象,求得函数的解析式12()2sin 23f x x π⎛⎫=- ⎪⎝⎭,结合三角函数的性质,即可求解.(2)由三角函数的图象变换,求得2()2sin 223g x x m π⎛⎫=-+ ⎪⎝⎭,根据()g x 的图象关于直线512x π=对称,求得m 的值,得到()2sin 23g x x π⎛⎫=- ⎪⎝⎭,结合三角函数的性质,即可求解. 【详解】(1)由图象可知2A =,422433T πππ⎡⎤⎛⎫=--= ⎪⎢⎥⎝⎭⎣⎦, 所以212T πω==,所以1()2sin 2f x x ϕ⎛⎫=+ ⎪⎝⎭, 由图可求出最低点的坐标为,23π⎛⎫- ⎪⎝⎭,所以2sin 236f ππϕ⎛⎫⎛⎫=+=- ⎪ ⎪⎝⎭⎝⎭, 所以262k ππϕπ+=-+,所以22,3k k Z πϕπ=-+∈, 因为||ϕπ<,所以23πϕ=-,所以12()2sin 23f x x π⎛⎫=- ⎪⎝⎭,由1222,2232k x k k Z πππππ-+≤-≤+∈,可得744,33k x k k Z ππππ+≤≤+∈. 所以函数()f x 的单调递增区间为74,4,33k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦. (2)由题意知,函数22()2sin 2()2sin 2233g x x m x m ππ⎡⎤⎛⎫=+-=-+ ⎪⎢⎥⎣⎦⎝⎭, 因为()g x 的图象关于直线512x π=对称, 所以5222,1232m k k Z ππππ⨯-+=+∈,即,62k m k Z ππ=+∈, 因为02m π<<,所以6m π=,所以()2sin 23g x x π⎛⎫=-⎪⎝⎭. 当7,1212x ππ⎡⎤∈⎢⎥⎣⎦时,52,366x πππ⎡⎤-∈-⎢⎥⎣⎦,可得1sin 2,132x π⎛⎫⎡⎤-∈- ⎪⎢⎥⎝⎭⎣⎦,所以2sin 2[1,2]3x π⎛⎫-∈- ⎪⎝⎭,即函数()g x 的值域为[]1,2-.【点睛】解答三角函数的图象与性质的基本方法:1、根据已知条件化简得出三角函数的解析式为sin()y A wx ϕ=+的形式;2、熟练应用三角函数的图象与性质,结合数形结合法的思想研究函数的性质(如:单调性、奇偶性、对称性、周期性与最值等),进而加深理解函数的极值点、最值点、零点及有界性等概念与性质,但解答中主要角的范围的判定,防止错解.。
(好题)高中数学必修四第一章《三角函数》测试题(含答案解析)(4)

一、选择题1.若函数()sin 2f x x =与()2cos g x x =都在区间(),a b 上单调递减,则b a -的最大值是( ) A .π4B .π3C .π2D .2π32.函数()sin()(0||)2,f x x πωϕωϕ=+><的部分函数图象如图所示,将函数()f x 的图象先向右平移3π个单位长度,然后向上平移1个单位长度,得到函数()g x 的解析式为( )A .()sin 21g x x =-B .()sin 21g x x =+C .()sin(2)13g x x π=--D .()sin(2)13g x x π=-+3.在平面直角坐标系中,AB 是单位圆上的一段弧(如右图),点P 是圆弧AB 上的动点,角α以Ox 为始边,OP 为终边.以下结论正确的是( )A .tan α<cos α<sin αB .cos α<tan α<sin αC .sin α<cos α<tan αD .以上答案都不对4.函数()2cos 3⎛⎫=+⎪⎝⎭πf x x 在[]0,π的单调递增区间是( ) A .20,3π⎡⎤⎢⎥⎣⎦B .2,33ππ⎡⎤⎢⎥⎣⎦C .,3ππ⎡⎤⎢⎥⎣⎦D .2π,π35.已知函数()sin 26f x x π⎛⎫=-⎪⎝⎭,若方程()35f x =的解为1x ,2x (120x x π<<<),则()12sin x x -=( ) A .35B .45-C .23-D .33-6.将函数()sin 2f x x =的图象向右平移ϕ(02πϕ<≤)个单位,得到函数()g x 的图象.在同一坐标系中,这两个函数的部分图象如图所示,则ϕ=( )A .6π B .4π C .3π D .2π 7.已知函数f (x )=2sinxsin (x+3φ)是奇函数,其中(0,)2πϕ∈ ,则函数g (x )=cos (2x-φ)的图象( ) A .关于点(,0)12π对称 B .关于轴512x π=-对称 C .可由函数f (x )的图象向右平移6π个单位得到 D .可由函数f (x )的图象向左平移3π个单位得到 8.《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验方式为:弧田面积12=(弦⨯矢+矢2),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有弧AB 长为83π,半径等于4米的弧田,按照上述经验公式计算所得弧田面积约是( )(3 1.73≈)A .6平方米B .9平方米C .12平方米D .15平方米9.如图,一个摩天轮的半径为10m ,轮子的最低处距离地面2m .如果此摩天轮按逆时针匀速转动,每30分钟转一圈,且当摩天轮上某人经过点P (点P 与摩天轮天轮中心O 的高度相同)时开始计时,在摩天轮转动的一圈内,此人相对于地面的高度不小于17m 的时间大约是( )A .8分钟B .10分钟C .12分钟D .14分钟10.已知函数y =f (x )的部分图象如图所示,则其解析式可能是( )A .()sin 2f x x x =B .()||sin 2f x x x =C .()cos 2f x x x =D .()||cos2f x x x =11.设函数()tan 3f x x π=-,()sin 3g x x π⎛⎫=-⎪⎝⎭,则函数()()()h x f x g x =-在区间[]2,2ππ-上的零点个数是( ) A .4B .5C .12D .1312.已知函数()sin()f x A x ωϕ=+(0A >,0>ω,0ϕπ≤≤)的部分图象如图所示,则()f x 的解析式是( )A .()2sin 6f x x π⎛⎫=+⎪⎝⎭B .()2sin 3f x x π⎛⎫=+⎪⎝⎭C .()2sin 26f x x π⎛⎫=+⎪⎝⎭D .2n 2)3(si f x x π⎛⎫=+⎪⎝⎭二、填空题13.sin 75=______.14.函数(x)Asin(x )f ωϕ=+ (0A >,0>ω,0ϕπ<< )的部分图象如图所示,则4f π⎛⎫= ⎪⎝⎭________.15.某校运动会开幕式上举行升旗仪式,旗杆正好处在坡度15的看台的某一列的正前方,从这一列的第一排和最后一排测得旗杆顶部的仰角分别为60和30,第一排和最后一排的距离为106米(如图所示),旗杆底部与第一排在一个水平面上,若国歌长度约为50秒,升旗手应以__________(米 /秒)的速度匀速升旗.16.已知函数()2sin()(0)f x x ωϕω=+>满足()24f π=,()0f π=,且()f x 在区间(,)43ππ上单调,则ω的值有_________个. 17.关于函数()()4sin 23f x x x π⎛⎫=-∈ ⎪⎝⎭R ,有下列命题:①43y f x π⎛⎫=+⎪⎝⎭为偶函数; ②方程()2f x =的解集为,4x x k k Z ππ⎧⎫=+∈⎨⎬⎩⎭; ③()y f x =的图象关于点,03π⎛-⎫⎪⎝⎭对称; ④()y f x =在[]0,2π内的增区间为50,12π⎡⎤⎢⎥⎣⎦和11,212ππ⎡⎤⎢⎥⎣⎦; ⑤()y f x =的振幅为4,频率为1π,初相为3π-. 其中真命题的序号为______.18.关于函数()sin |||sin |f x x x =+有下述四个结论: ①()f x 是偶函数;②()f x 在区间,2ππ⎛⎫⎪⎝⎭单调递增; ③()f x 在[],ππ-有4个零点;④()f x 的最大值为2; 其中所有正确结论的编号是_________.19.函数251612()sin (0)236x x f x x x x ππ-+⎛⎫=--> ⎪⎝⎭的最小值为_______. 20.某城市一年中12个月的平均气温与月份的关系可近似地用三角函数()()cos[6]1,2,...,126y A x B x π=-+=来表示.已知6月份的平均气温最高,为28℃,12月份的月平均气温最低,为18℃,则10月份的平均气温为______℃.三、解答题21.函数()cos()0,02f x x πωϕωϕ⎛⎫=+><<⎪⎝⎭的部分图象如图所示.(1)写出()f x 的解析式; (2)将函数()f x 的图象向右平移12π个单位后得到函数()g x 的图象,讨论关于x 的方程()3()0f x g x m -=(11)m -<≤在区间,2ππ⎡⎤-⎢⎥⎣⎦上的实数解的个数.22.如图,某公园摩天轮的半径为40m ,圆心O 距地面的高度为50m ,摩天轮做匀速转动,每3min 转一圈,摩天轮上的点P 的起始位置在距地面最近处.(1)已知在(min)t 时点P 距离地面的高度为()sin()0,0,||2f t A t h A πωϕωϕ⎛⎫=++>>≤ ⎪⎝⎭,求2020t =时,点P 距离地面的高度;(2)当离地面(503)m +以上时,可以看到公园的全貌,求转一圈中在点P 处有多少时间可以看到公园的全貌.23.已知函数()sin()f x x ωϕ=+,其中π0,(0,)2ωϕ>∈.从条件①、条件②、条件③这三个条件中选择两个作为已知条件,求: (Ⅰ)()f x 的单调递增区间; (Ⅱ)()f x 在区间[0,]2π的最大值和最小值.条件①:函数()f x 最小正周期为π; 条件②:函数()f x 图象关于点π(,0)6-对称; 条件③: 函数()f x 图象关于π12x =对称. 24.已知函数()2sin(2)f x x ϕ=+.(1)当,0,62x ππϕ⎡⎤=∈⎢⎥⎣⎦时,求()f x 的值域和单调减区间; (2)若()f x 关于3x π=对称,且(0,)ϕπ∈,求ϕ的值.25.设函数()3sin (0)4f x x πωω⎛⎫=+> ⎪⎝⎭,且以23π为最小正周期. (1)求函数()f x 的单调递减区间; (2)当,32x ππ⎡⎤∈⎢⎥⎣⎦时,求()f x 的值域. 26.已知sin(3)(),cos x f x x R xπ-=∈(1)若α为第三象限角,且3sin 5α=-,求()f α的值.(2)若,34x ππ⎡⎤∈-⎢⎥⎣⎦,且21()2()1cos g x f x x =++,求函数()g x 的最小值,并求出此时对应的x 的值.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】根据题意求出(),()f x g x 原点附近的单调递减区间,根据递减区间分析可得max 3π4b =,min π4a =,相减即可. 【详解】 解:由题意函数()sin 2f x x =在π3π,44⎛⎫⎪⎝⎭上单调递减,函数()2cos g x x =在()0,π上单调递减, 所以则max 3π4b =,min π4a =,所以b a -的最大值为3πππ442-=. 故选:C. 【点睛】求三角函数单调区间的2种方法:(1)代换法:就是将比较复杂的三角函数处理后的整体当作一个角u (或t ),利用基本三角函数的单调性来求所要求的三角函数的单调区间;(2)图象法:函数的单调性表现在图象上是从左到右,图象上升趋势的区间为单调递增区间,图象下降趋势的区间为单调递减区间,画出三角函数的图象,结合图象易求它的单调区间.2.D解析:D 【分析】由周期求出ω,由五点法作图求出ϕ的值,可得()f x 的解析式,再根据函数sin()y A x ωϕ=+的图象变换规律,得出结论.【详解】根据函数()sin()(0f x x ωϕω=+>,||)2πϕ<的部分函数图象,1274123πππω⋅=-,2ω∴=. 再根据五点法作图,23πϕπ⨯+=,3πϕ∴=,()sin(2)3f x x π=+.将函数()f x 的图象先向右平移3π个单位长度,可得sin(2)3y x π=-的图象.然后向上平移1个单位长度,得到函数()g x 的解析式为()sin(2)13g x x π=-+,故选:D 【点睛】关键点睛:解答本题的关键在于准确地根据三角函数的图象求出三角函数sin()y A x ωϕ=+的解析式,一般根据周期求出ω的值,根据最值求出A 的值,根据最值点求出ϕ的值.3.D解析:D 【分析】根据三者的符号可得sin cos ,sin tan αααα>>,利用作差法可得tan ,cos αα大小关系不确定,从而可得正确的选项. 【详解】由题设可得AB 上的动点P 的坐标为()cos ,sin αα且()()1122cos ,sin ,cos ,sin A B θθθθ,其中122πθαθπ<<<<,12324ππθθπ<<<<, 注意到当13,4παθ⎛⎤∈ ⎥⎝⎦,tan 1α≤-,故按如下分类讨论: 若1324ππθα<<≤,则sin 0,cos 1,tan 1ααα>>-≤-, 故sin cos tan ααα>>.若234παθ<≤,则sin 0,cos 0,tan 0ααα><<,且20sin sin 2θα<≤<所以22221sin sin 1sin sin 12θθαα+-≤+-<,因为234πθπ<<,故20sin 2θ<<,故22211sin sin 12θθ-<+-<, 所以222sin sin 1θθ+-有正有负,所以2sin sin 1αα+-有正有负,而2sin sin 1tan cos cos ααααα+--=,cos 0α<,故tan cos αα-有正有负,故tan ,cos αα大小关系不确定.故选:D. 【点睛】方法点睛:三角函数式的大小比较,可先依据终边的位置判断出它们的符号,也可以利用作差作商法来讨论,注意根据三角函数值的范围确定代数式的符号.4.C解析:C 【分析】先求出函数的单调增区间,再给k 取值即得解. 【详解】 令22223+<+<+ππk πx πk π(k ∈Z ) ∴42233+<<+ππk πx k π(k ∈Z ), 所以函数的单调递增区间为4[2,2]33ππk πk π++(k ∈Z ), 当1k =-时,5233ππx -<<- 当0k =时,433x ππ<<又∵[]0,x π∈, 故选:C 【点睛】方法点睛:求三角函数()cos()f x A wx ϕ=+的单调区间,一般利用复合函数的单调性原理解答:首先是对复合函数进行分解,接着是根据复合函数的单调性原理分析出分解出的函数的单调性,最后根据分解函数的单调性求出复合函数的单调区间.5.B解析:B 【分析】求出函数()f x 在(0,)π上的对称轴,然后由正弦函数性质得1223x x π+=,这样12sin()x x -化为2222sin(2)sin 2cos(2)336x x x πππ⎛⎫-=+=- ⎪⎝⎭,而已知条件为23sin(2)65x π-=,再由正弦函数性质确定226x π-的范围,从而由平方关系求得结论.【详解】函数()sin 26f x x π⎛⎫=-⎪⎝⎭的对称轴满足:()262x k k Z πππ-=+∈,即()23k x k Z ππ=+∈,令0k =可得函数在区间()0,π上的一条对称轴为3x π=,结合三角函数的对称性可知1223x x π+=,则:1223x x π=-,()122222sin sin 2sin 2cos 2336x x x x x πππ⎛⎫⎛⎫⎛⎫-=-=+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,由题意:0πx <<,则112666x πππ-<-<,23sin 265x π⎛⎫-= ⎪⎝⎭,120x x π<<<,则2226x πππ<-<,由同角三角函数基本关系可知:24cos 265x π⎛⎫-=- ⎪⎝⎭, 故选:B . 【点睛】关键点点睛:本题考查正弦函数的性质,考查平方关系.解题时根据自变量的范围求得此范围内函数的对称轴,从而得出两个变量12,x x 的关系,可化双变量为单变量,再根据函数值及函数性质确定出单变量的范围,从而求得结论.注意其中诱导公式的应用,目的是把求值式与已知条件中的角化为一致.6.C解析:C 【分析】由图可知,172482g f ππ⎛⎫⎛⎫==⎪ ⎪⎝⎭⎝⎭,根据函数图象的平移变化法则可知()()sin 2x g x ϕ=-,于是推出1717sin 224242g ππϕ⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭,即1722124k ππϕπ-=+或324k ππ+,k Z ∈,再结合02πϕ<≤,解之即可得ϕ的值.【详解】由图可知,17sin 224882g f πππ⎛⎫⎛⎫⎛⎫==⨯=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 因为()f x 的图象向右平移ϕ个单位,得到函数()g x 的图象,所以()()sin 2x g x ϕ=-,所以171717sin 2sin 22424122g πππϕϕ⎛⎫⎛⎫⎛⎫=-=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 所以1722124k ππϕπ-=+或17322124k ππϕπ-=+,k Z ∈, 解得712k πϕπ=-或3k πϕπ=-,k Z ∈,因为02πϕ<≤,所以3πϕ=.故选:C 【点睛】本小题主要考查三角函数图象变换,属于中档题.7.B解析:B 【分析】利用三角函数的奇偶性求得φ,再利用三角函数的图象对称性、函数y=Asin (ωx+φ)的图象变换规律,判断各个选项是否正确,从而得出结论. 【详解】函数f (x )=2sinxsin (x+3φ)是奇函数,其中0,2πϕ⎛⎫∈ ⎪⎝⎭, ∴y=2sinxsin (x+3φ)是奇函数,∴3φ=2π,φ=6π,则函数g (x )=cos (2x ﹣φ)=cos (2x ﹣6π). 当12x π=时,206x π-=,112g π⎛⎫= ⎪⎝⎭,则函数不关于点,012π⎛⎫⎪⎝⎭对称,选项A 错误; 当512x π=-时,26x ππ-=-,则函数关于直线512x π=-对称,选项B 正确;函数()2sin sin 2sin cos sin 22f x x x x x x π⎛⎫=+== ⎪⎝⎭, 其图像向右平移6π个单位的解析式为sin 2sin 2sin 263y x x x ππ⎡⎤⎛⎫⎛⎫==-=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦, 选项C 错误; 其图像向左平移3π个单位的解析式为2sin 2sin 2sin 233y x x x ππ⎡⎤⎛⎫⎛⎫==+=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦, 选项D 错误; 故选B. 【点睛】本题主要考查三角函数的奇偶性、对称性,函数y=Asin (ωx+φ)的图象变换规律,属于中档题.函数()sin y A x ωϕ=+(A >0,ω>0)的性质:(1)奇偶性:=k ϕπ ,k Z ∈时,函数()sin y A x ωϕ=+为奇函数;=2k πϕπ+,k Z ∈时,函数()sin y A x ωϕ=+为偶函数.;(2)周期性:()sin y A x ωϕ=+存在周期性,其最小正周期为T =2πω;(3)单调性:根据y =sin t 和t =x ωϕ+的单调性来研究,由+22,22k x k k Z πππωϕπ-≤+≤+∈得单调增区间;由3+22,22k x k k Z πππωϕπ≤+≤+∈得单调减区间;(4)对称性:利用y =sin x 的对称中心为()(),0k k Z π∈求解,令()x k k ωϕπ+=∈Z ,求得x ;利用y =sin x 的对称轴为()2x k k Z ππ=+∈求解,令()+2x k k πωϕπ+=∈Z ,得其对称轴.8.B解析:B 【分析】根据已知求出矢2=,弦2AD ==. 【详解】由题意可得:823=43AOB ππ∠=,4OA =,在Rt AOD 中,可得:3AOD π∠=,6DAO π∠=,114222OD AO ==⨯=, 可得:矢422=-=,由sin43AD AO π===可得:弦2AD ==所以:弧田面积12=(弦⨯矢+矢221)22)292=+=≈平方米.故选:B 【点睛】方法点睛:有关扇形的计算,一般是利用弧长公式l r α=、扇形面积公式12S lr =及直角三角函数求解.9.B解析:B 【分析】由题可得此人相对于地面的高度h 与时间t 的关系是()10sin1203015h t t π=+≤≤,再令10sin121715t π+≥求出t 的范围即可得出. 【详解】设时间为t 时,此人相对于地面的高度为h , 则由题可得当0t =时,12h =,在时间t 时,此人转过的角为23015t t ππ=, 此时此人相对于地面的高度()10sin 1203015h t t π=+≤≤,令10sin 121715t π+≥,则1sin 152t π≥, 所以56156t πππ≤≤,解得52522t ≤≤, 故在摩天轮转动的一圈内,此人相对于地面的高度不小于17m 的时间大约是()25510min 22-=. 故选:B. 【点睛】本题考查三角函数的实际应用,解题的关键是得出高度与时间的关系()10sin1203015h t t π=+≤≤,再解三角函数不等式即可.10.B解析:B 【分析】利用函数()0f π=排除两个选项,再由奇偶性排除一个后可得正确选项. 【详解】由图象知()0f π=,经验证只有AB 满足,C 中()cos 2f ππππ==,D 中()f ππ=,排除CD ,A 中函数满足()sin(2)sin 2()f x x x x x f x -=--==为偶函数,B 中函数满足()sin(2)sin 2()f x x x x x f x -=--=-=-为奇函数,而图象关于原点对称,函数为奇函数,排除A ,选B . 故选:B . 【点睛】思路点睛:由函数图象选择解析式可从以下方面入手:(1)从图象的左右位置,观察函数的定义域;从图象的上下位置,观察函数的值域; (2)从图象的变化趋势观察函数的单调性; (3)从图象的对称性观察函数的奇偶性; (4)从图象的特殊点,排除不合要求的解析式..11.A解析:A 【分析】由题意知函数()()()h x f x g x =-在区间[]2,2ππ-上的零点个数等价于函数()tan 3f x x π=-与()sin 3g x x π⎛⎫=-⎪⎝⎭图象在区间[]2,2ππ-上交点的个数,作出两个函数图象,数形结合即可求解. 【详解】令()()()0h x f x g x =-=可得()()f x g x =,所以函数()()()h x f x g x =-在区间[]2,2ππ-上的零点个数等价于 函数()tan 3f x x π=-与()sin 3g x x π⎛⎫=-⎪⎝⎭图象在区间[]2,2ππ-上交点的个数. 分别作出()tan 3f x x π=-与()sin 3g x x π⎛⎫=-⎪⎝⎭图象,由图知两个函数图象在区间[]2,2ππ-上有4个交点,所以函数()()()h x f x g x =-在区间[]2,2ππ-上的零点个数是4, 故选:A 【点睛】方法点睛:判断函数零点个数的方法(1)直接法:令()0f x =,如果能求出解,那么有几个不同的解就有几个零点; (2)利用函数的零点存在性定理:利用函数的零点存在性定理时,不仅要求函数的图象在区间[],a b 上是连续不断的曲线,并且()()0f a f b ⋅<,还必须结合函数的图象与性质,(如单调性、奇偶性)才能确定函数有多少个零点;(3)图象法:画出函数()f x 的图象,函数()f x 的图象与x 轴交点的个数就是函数()f x 的零点个数;将函数()f x 拆成两个函数,()h x 和()g x 的形式,根据()()()0f x h x g x =⇔=,则函数()f x 的零点个数就是函数()y h x =和()y g x =的图象交点个数;(4)利用函数的性质:若能确定函数的单调性,则其零点个数不难得到,若所考查的函数是周期函数,则需要求出在一个周期内的零点个数,根据周期性则可以得出函数的零点个数.12.D解析:D 【分析】结合图象,依次求得,,A ωϕ的值. 【详解】 由图象可知2A =,2,,22362T T πππππωω⎛⎫=--==== ⎪⎝⎭,所以()()2sin 2f x x ϕ=+,依题意0ϕπ≤≤,则2333πππϕ-≤-≤, 2sin 0,0,6333f ππππϕϕϕ⎛⎫⎛⎫-=-+=-+== ⎪ ⎪⎝⎭⎝⎭,所以2n 2)3(si f x x π⎛⎫=+ ⎪⎝⎭.故选:D. 【点睛】方法点睛:根据三角函数()()sin f x A x b ωϕ=++或的部分图象求函数解析式的方法: (1)求A 、()()max min:2f x f x b A -=,()()max min2f x f x b +=;(2)求出函数的最小正周期T ,进而得出2Tπω=; (3)取特殊点代入函数可求得ϕ的值.二、填空题13.【解析】试题分析:将非特殊角化为特殊角的和与差是求三角函数值的一个有效方法考点:两角和的正弦 解析:【解析】 试题分析:232162sin 75sin(4530)sin 45cos30cos 45sin 302︒︒︒︒︒︒︒+=+=+==将非特殊角化为特殊角的和与差,是求三角函数值的一个有效方法. 考点:两角和的正弦14.【分析】观察图象可求得进而可得然后求出的值可得;而后由可求得的值得出最后代值计算即可得解【详解】由图象可知∴∴∴又∴()∴()∵∴∴则故答案为:【点睛】本题重点考查了正弦型三角函数的图象和性质考查逻 3【分析】观察图象可求得2A =,311341264T πππ=-=,进而可得T π=,然后求出ω的值,可得()()22f x sin x ϕ=+;而后由26f π⎛⎫= ⎪⎝⎭,可求得ϕ的值,得出()2sin 26f x x π⎛⎫=+ ⎪⎝⎭,最后代值计算即可得解. 【详解】由图象可知2A =,311341264T πππ=-=,∴T π=, ∴22πωπ==,∴()()22f x sin x ϕ=+,又26f π⎛⎫= ⎪⎝⎭,∴2262k ππϕπ⨯+=+(k Z ∈), ∴26k πϕπ=+(k Z ∈),∵0ϕπ<<,∴6π=ϕ, ∴()2sin 26f x x π⎛⎫=+ ⎪⎝⎭,则222cos 4466f sin ππππ⎛⎫⎛⎫=⨯+==⎪ ⎪⎝⎭⎝⎭【点睛】本题重点考查了正弦型三角函数的图象和性质,考查逻辑思维能力和计算能力,属于常考题.15.6【分析】根据题意可求得然后利用正弦定理求得最后在中利用求得答案【详解】在中由正弦定理得;在中(米)所以升旗速度(米/秒)故答案为06【点睛】本题主要考查了解三角形的实际应用此类问题的解决关键是建立解析:6 【分析】根据题意可求得,45BDC ∠=︒,30CBD ∠=︒,CD =BC ,最后在Rt ABC 中利用sin60AB BC =︒求得答案.【详解】在BCD 中,45BDC ∠=︒,30CBD ∠=︒,CD =由正弦定理,得sin 45sin 30CD BC ︒==︒在Rt ABC 中,sin?60302AB BC =︒==(米). 所以升旗速度300.650t AB v ===(米/秒). 故答案为0.6. 【点睛】本题主要考查了解三角形的实际应用.此类问题的解决关键是建立数学模型,把实际问题转化成数学问题,利用所学知识解决,属于中档题.16.9【分析】由在区间上单调可得故进一步求出范围即可【详解】由知故;又在区间上单调故即18符合条件的的值有9个故答案为:9【点睛】本题考查三角函数的图象与性质考查转化与化归思想考查逻辑推理能力运算求解能解析:9 【分析】 由()f x 在区间(,)43ππ上单调,可得342T ππ-,故6T π,进一步求出ω范围即可. 【详解】由()24f π=,()0f π=知,34244T kT πππ+=-=,k ∈N , 故312T k π=+,2(12)3k ω+=,k ∈N ; 又()f x 在区间(,)43ππ上单调,∴342T ππ-,故6T π, ∴212T πω=,即2(12)123k +, ∴172k,k ∈N , 0k ∴=,1,2⋯,8符合条件的ω的值有9个. 故答案为:9. 【点睛】本题考查三角函数的图象与性质,考查转化与化归思想,考查逻辑推理能力、运算求解能力,属中档题.17.③⑤【分析】①利用三角函数的奇偶性判断真假;②解三角方程来判断真假;③利用代入法判断真假;④利用单调性的知识判断真假;⑤根据的有关概念判断真假【详解】①依题意令则所以①错误②由得当即时但所以②错误③解析:③⑤【分析】①利用三角函数的奇偶性判断真假;②解三角方程来判断真假;③利用代入法判断真假;④利用单调性的知识判断真假;⑤根据()sin y A ωx φ=+的有关概念判断真假. 【详解】 ①,依题意4474sin 24sin 24sin 233333y f x x x x πππππ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=+=+-=+=+ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦,令()4sin 23g x x π⎛⎫+ ⎝=⎪⎭,则()4sin 24sin 233g x x x ππ⎛⎫⎛⎫-=-+≠+ ⎪ ⎪⎝⎭⎝⎭,所以①错误.②,由()4sin 223f x x π⎛⎫=-= ⎪⎝⎭得1sin 232x π⎛⎫-= ⎪⎝⎭.当5236x ππ-=,即712x π=时,1sin 232x π⎛⎫-= ⎪⎝⎭,但7,124x x x k k Z πππ⎧⎫=∉=+∈⎨⎬⎩⎭,所以②错误.③,()24sin 4sin 0333f ππππ⎛⎫⎛⎫-=--=-= ⎪ ⎪⎝⎭⎝⎭,所以()y f x =的图象关于点,03π⎛-⎫⎪⎝⎭对称,即③正确. ④,由于5104sin 4sin 30333f ππππ⎛⎫⎛⎫=-==⎪⎪⎝⎭⎝⎭,()24sin 44sin 4332f ππππ⎛⎛⎫⎛⎫=-=-=⨯-=- ⎪ ⎪ ⎝⎭⎝⎭⎝⎭所以11,212ππ⎡⎤⎢⎥⎣⎦不是()f x 的增区间,所以④错误. ⑤,()y f x =的振幅为4,周期22T ππ==,频率为11T π=,初相为3π-,所以⑤正确. 故答案为:③⑤ 【点睛】本小题主要考查三角函数的奇偶性、对称性、单调性、和三角函数的概念,属于中档题.18.①④【分析】结合题意得出函数的奇偶性根据奇偶性研究函数在时的性质对结论逐一判断即可【详解】解:∵定义域为∴∴函数是偶函数故①对;当时∴由正弦函数的单调性可知函数在区间上单调递减故②错;当时由得根据偶解析:①④ 【分析】结合题意,得出函数的奇偶性,根据奇偶性研究函数在0x >时的性质对结论逐一判断即可. 【详解】解:∵()sin |||sin |f x x x =+,定义域为R ,∴()()sin |||sin |f x x x -=-+-sin sin ()x x f x =+=, ∴函数()f x 是偶函数,故①对;当[]0,x π∈时,()sin |||sin |f x x x =+sin sin 2sin x x x =+=, ∴由正弦函数的单调性可知,函数()f x 在区间,2ππ⎛⎫⎪⎝⎭上单调递减,故②错; 当[]0,x π∈时,由()2sin 0f x x ==得0x =,x π=,根据偶函数的图象和性质可得,()f x 在[),0π-上有1个零点x π=- , ∴()f x 在[],ππ-有3个零点,故③错;当0x ≥时,()sin |||sin |f x x x =+sin sin x x =+2sin ,sin 00,sin 0x x x ≥⎧=⎨<⎩,根据奇偶性可得函数()f x 的图象如图,∴当sin 1x =时,函数()f x 有最大值()max 2f x =,故④对; 故答案为:①④. 【点睛】本题主要考查与三角函数有关的命题的真假判断,结合绝对值的应用以及利用三角函数的性质是解决本题的关键,属于中档题.19.【分析】可拆分理解构造由对勾函数可得时取得最小值又当时也取到最小值即可求解【详解】令由对勾函数性质可知当时;因为当时所以当时取到最小值所以故答案为:【点睛】本题考查函数最值的求解拆分构造函数是解题关解析:52【分析】可拆分理解,构造251616()5x x g x x x x-+==+-,由对勾函数可得4x =时取得最小值,又当4x =时,12sin 236x ππ⎛⎫-- ⎪⎝⎭也取到最小值,即可求解 【详解】令251616()5x x g x x x x-+==+-,由对勾函数性质可知当4x =时,min ()3g x =;因为121sin 2362x ππ⎛⎫--- ⎪⎝⎭,当4x =时,121sin 2362x ππ⎛⎫--=-⎪⎝⎭,所以当4x =时,()f x 取到最小值,5(4)2f =,所以min 5()2f x =. 故答案为:52【点睛】本题考查函数最值的求解,拆分构造函数是解题关键,属于中档题20.【分析】根据题意列出方程组求出求出年中12个月的平均气温与月份的三角函数关系将代入求出10月份的平均气温值【详解】据题意得解得所以令得故答案为:205【点睛】本题考查通过待定系数法求出三角函数的解析 解析:20.5【分析】根据题意列出方程组,求出,A B ,求出年中12个月的平均气温与月份的三角函数关系,将10x =代入求出10月份的平均气温值. 【详解】据题意得28A B =+,18A B =-+ 解得5A =,23B = 所以235cos[(6)]6y x π=+-令10x =得2235cos[(106)]235cos20.563y ππ=+-=+=. 故答案为:20.5 【点睛】本题考查通过待定系数法求出三角函数的解析式,根据解析式求函数值,意在考查学生对这些知识的理解掌握水平.三、解答题21.(1)()cos(2)6f x x π=+;(2)见解析.【分析】(1)根据图象求出周期,再根据最低点可求ϕ,从而得到函数解析式.(2)求出()g x 的解析式,故方程可化为cos 206m x π⎛⎫---= ⎪⎝⎭,可通过直线y m =-与cos 26y x π⎛⎫=- ⎪⎝⎭ 的图象的交点的个数解决方程的解的个数.【详解】(1)由函数的图象可得()f x 的周期为2236πππ⎛⎫⨯-=⎪⎝⎭,故22πωπ==, 又26312f ππ⎛⎫+ ⎪=- ⎪ ⎪⎝⎭,故5cos 2+112πϕ⎛⎫⨯=- ⎪⎝⎭, 所以526k πϕππ+=+即2,6k k Z πϕπ=+∈, 因为02πϕ<<,故6π=ϕ,所以()cos(2)6f x x π=+. (2)()cos(2)cos 266g x x x ππ=-+=, 故()3()cos(2)3cos 26f xg x m x x m π-⋅-=+--cos 2cossin 2sin3cos 2cos 2666x x x m m x πππ⎛⎫=---=--- ⎪⎝⎭ 故方程在区间,2ππ⎡⎤-⎢⎥⎣⎦上的实数解的个数即为y m =-与cos 26y x π⎛⎫=- ⎪⎝⎭图象交点的个数,cos 26y x π⎛⎫=- ⎪⎝⎭在,2ππ⎡⎤-⎢⎥⎣⎦上的图象如图所示,由图象可得: 当1m -=-或312m <-<即1m =或312m -<<-时,方程有2个不同的解; 当31m -<-≤31m ≤<时,方程有4个不同的解;当22m -<-≤即22m -≤<时,方程有3个不同的解; 【点睛】 方法点睛:(1)平移变换有“左加右减”(水平方向的平移),注意是对自变量x 做加减.(2)与余弦型函数有关的方程的解的个数的讨论,一般可转化为动直线与确定函数的图象的交点个数来讨论.22.(1)70m ;(2)0.5min . 【分析】(1)根据题意,确定()sin()f t A t h ωϕ=++的表达式,代入2020t =运算即可;(2)要求()50f t >+2cos 32t π<,解不等式即可. 【详解】(1)依题意,40A =,50h =,3T =, 由23πω=得23πω=,所以2()40sin 503f t t πϕ⎛⎫=++⎪⎝⎭. 因为(0)10f =,所以sin 1ϕ=-,又||2πϕ≤,所以2πϕ=-.所以2()40sin 50(0)32f t t t ππ⎛⎫=-+≥⎪⎝⎭, 所以2(2020)40sin 2020507032f ππ⎛⎫=⨯-+=⎪⎝⎭.即2020t =时点P 距离地面的高度为70m . (2)由(1)知22()40sin 505040cos (0)323f t t t t πππ⎛⎫=-+=-≥ ⎪⎝⎭.令()50f t >+2cos 32t π<-, 从而()*52722N 636k t k k πππππ+<<+∈, ∴()*5733N 44k t k k +<<+∈. ∵()*751330.5N 442k k k ⎛⎫+-+==∈ ⎪⎝⎭, ∴转一圈中在点P 处有0.5min 的时间可以看到公园的全貌. 【点睛】本题考查了已知三角函数模型的应用问题,解答本题的关键是能根据题目条件,得出相应的函数模型,作出正确的示意图,然后再由三角函数中的相关知识进行求解,解题时要注意综合利用所学知识与题中的条件,是中档题.23.答案见解析. 【分析】若选择条件①②,(Ⅰ)根据最小正周期求出ω,根据对称中心求出ϕ,根据正弦函数的单调递增区间可求出函数()f x 的单调区间;(Ⅱ)根据正弦函数的图象可求得结果. 若选择条件①③,(Ⅰ)根据最小正周期求出ω,根据对称轴求出ϕ,根据正弦函数的单调递增区间可求出函数()f x 的单调区间;(Ⅱ)根据正弦函数的图象可求得结果.若选择②③,不能确定函数最小正周期,无法确定ω,所以无法确定函数解析式. 【详解】若选择条件①②,(Ⅰ)由函数()f x 最小正周期2π=πT ω=,得2ω=.因为()f x 图象关于点π(,0)6-对称,所以πsin[2()]06ϕ⨯-+=, 所以3k πϕπ-=,k Z ∈,所以3k πϕπ=+,k Z ∈,又已知π(0,)2ϕ∈,故π3ϕ=. 因此π()sin(2)3f x x =+. πππ2π22π,232k x k k -+≤+≤+∈Z 由,解得5,1212k x k ππππ-+≤≤+k Z ∈. 所以()f x 的单调递增区间为5ππ[π,π]()1212k k k -++∈Z . (Ⅱ)因为02x π≤≤,所以ππ4π2333x ≤+≤.当ππ2=32x +,即π12x =时,()f x 取得最大值1;当π4π2=33x +,即π2x =时,()f x 取得最小值.若选择条件①③,(Ⅰ)由函数()f x 最小正周期2π=πT ω=,得2ω=. 又函数()f x 图象关于π12x =对称,所以有πsin(2)112ϕ⨯+=±,所以62k ππϕπ+=+,k Z ∈,即3k πϕπ=+,k Z ∈,又已知π(0,)2ϕ∈,故π3ϕ=. 因此π()sin(2)3f x x =+. πππ2π22π,232k x k k -+≤+≤+∈Z 由,解得5,1212k x k ππππ-+≤≤+k Z ∈. 所以()f x 的单调递增区间为5ππ[π,π]()1212k k k -++∈Z . (Ⅱ)因为02x π≤≤,所以ππ4π2333x ≤+≤.当ππ2=32x +,即π12x =时,()f x 取得最大值1;当π4π2=33x +,即π2x =时,()f x 取得最小值.若选择②③,不能确定函数最小正周期,无法确定ω,所以无法确定函数解析式.【点睛】关键点点睛:根据函数性质确定函数解析式是解题关键.24.(1)()f x 的值域为[]1,2-,单调减区间为62ππ⎡⎤⎢⎥⎣⎦, ;(2)56πϕ=【分析】(1)由条件可得72666x πππ⎡⎤+∈⎢⎥⎣⎦,,则1sin 2162x π⎛⎫⎡⎤+∈- ⎪⎢⎥⎝⎭⎣⎦,可得值域,由3222,262k x k k Z πππππ+≤+≤+∈可得答案. (2)由()f x 关于3x π=对称,则2,32k k Z ππϕπ+=+∈⨯可得答案.【详解】 (1)当6π=ϕ时,()2sin(2)6f x x π=+ 当0,2x π⎡⎤∈⎢⎥⎣⎦时,72666x πππ⎡⎤+∈⎢⎥⎣⎦,,则1sin 2162x π⎛⎫⎡⎤+∈- ⎪⎢⎥⎝⎭⎣⎦, 所以[]()1,2f x ∈- 由3222,262k x k k Z πππππ+≤+≤+∈ 4222,33k x k k Z ππππ+≤≤+∈ 所以2,63k x k k Z ππππ+≤≤+∈由0,2x π⎡⎤∈⎢⎥⎣⎦,则0k =时,263x ππ⎡⎤∈⎢⎥⎣⎦,,即此时减区间为62ππ⎡⎤⎢⎥⎣⎦, 所以当,0,62x ππϕ⎡⎤=∈⎢⎥⎣⎦时,()f x 的值域为[]1,2-,单调减区间为62ππ⎡⎤⎢⎥⎣⎦,; (2)由()f x 关于3x π=对称,则2,32k k Z ππϕπ+=+∈⨯即,6k k Z πϕπ=-∈,又(0,)ϕπ∈,所以56πϕ=【点睛】关键点睛:本题考查三角函数的值域、单调性和对称性等性质,解答本题的关键是由72666x πππ⎡⎤+∈⎢⎥⎣⎦,,得出1sin 2162x π⎛⎫⎡⎤+∈- ⎪⎢⎥⎝⎭⎣⎦,,根据()f x 关于3x π=对称,得到2,32k k Z ππϕπ+=+∈⨯,属于中档题.25.(1)225,,312312k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦;(2)3,2⎡--⎢⎣⎦.【分析】(1)根据()f x 的最小正周期求解出ω的值,再采用整体替换的方法结合正弦函数的单调递减区间的公式求解出()f x 的单调递减区间;(2)先求解出t x ωϕ=+的范围,然后根据3sin y t =的单调性求解出()f x 的最值,从而()f x 的值域可求. 【详解】 (1)因为2T πω=,所以22323T ππωπ===,所以()3sin 34f x x π⎛⎫=+ ⎪⎝⎭, 令3232,242k x k k Z πππππ+≤+≤+∈,所以225,312312k x k k Z ππππ+≤≤+∈, 所以()f x 的单调递减区间为:225,,312312k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦; (2)因为()3sin 34f x x π⎛⎫=+ ⎪⎝⎭且,32x ππ⎡⎤∈⎢⎥⎣⎦,所以令573,444t x πππ⎡⎤=+∈⎢⎥⎣⎦, 又因为3sin y t =在5342ππ⎡⎫⎪⎢⎣⎭,上单调递减,在37,24ππ⎛⎤⎥⎝⎦上单调递增, 所以()min 33sin32f x π==-,此时512x π=,又57sinsin 442ππ==-()max 53sin 42f x π==-,此时3x π=或2π,所以()f x 的值域为:3,2⎡--⎢⎣⎦.【点睛】思路点睛:求解形如()sin y A ωx φ=+的函数在指定区间上的值域或最值的一般步骤如下:(1)先确定t x ωϕ=+这个整体的范围; (2)分析sin y A t =在(1)中范围下的取值情况;(3)根据取值情况确定出值域或最值,并分析对应的x 的取值. 26.(1) 34- (2) 函数()g x 的最小值为1,此时4x π= 【分析】(1)先化简函数解析式得()tan f x x =-,则由条件可得3tan 4α=,得出答案.(2)由条件可得()2tan 2tan 2g x x x =-+,则由,34x ππ⎡⎤∈-⎢⎥⎣⎦,设tan t x ⎡⎤=∈⎣⎦,根据二次函数()222211y t t t =-+=-+即可得出答案. 【详解】 由已知有sin(3)sin(3)sin ()tan cos cos cos x x xf x x x x xππ---===-=-(1)若α为第三象限角,且3sin 5α=-,则4cos 5α=-,则3tan 4α= ()3tan 4f αα=-=-(2)()()2222cos sin 21tan 2tan 2cos x xg x f x x x x +=++=-+,34x ππ⎡⎤∈-⎢⎥⎣⎦,设tan t x ⎡⎤=∈⎣⎦ 即()222211y t t t =-+=-+,当1t =,即4x π= 时,有最小值1所以当4x π=时,函数()g x 有最小值1.【点睛】关键点睛:本题考查根据三角函数求值和将函数化为tan α的二次式求最值,解答本题的关键是由()()2222cos sin 21tan 2tan 2cos x x g x f x x x x+=++=-+将函数化为二次式,根∈求最小值,属于中档题.据tanα⎡⎤⎣⎦。
(压轴题)高中数学必修四第一章《三角函数》测试(含答案解析)

一、选择题1.将函数()sin 2f x x =的图象向右平移ϕ(02πϕ<≤)个单位,得到函数()g x 的图象.在同一坐标系中,这两个函数的部分图象如图所示,则ϕ=( )A .6π B .4π C .3π D .2π 2.函数()()12cos 20211f x x x π=++⎡⎤⎣⎦-在区间[]3,5-上所有零点的和等于( ) A .2B .4C .6D .83.筒车是我国古代发明的一种水利灌溉工具,因其经济又环保,至今还在农业生产中得到使用.假设在水流量稳定的情况下,简车上的每一个盛水筒都做逆时针匀速圆周运动.现将筒车抽象为一个几何图形,如图所示,圆O 的半径为4米,盛水筒M 从点0P 处开始运动,0OP 与水平面的所成角为30,且每分钟恰好转动1圈,则盛水筒M 距离水面的高度H (单位;m )与时间t (单位:s )之间的函数关系式的图象可能是( )A .B .C .D .4.下列结论正确的是( ) A .sin1cos1< B .2317cos cos 54ππ⎛⎫⎛⎫->- ⎪ ⎪⎝⎭⎝⎭C .()()tan 52tan 47->-D .sin sin 1810ππ⎛⎫⎛⎫->- ⎪ ⎪⎝⎭⎝⎭5.平面直角坐标系xOy 中,点()00,P x y 在单位圆O 上,设xOP α∠=,若5,36ππα⎛⎫∈ ⎪⎝⎭,且3sin 65πα⎛⎫+= ⎪⎝⎭,则0x 的值为A .3310- B .3310+ C .3310D .43310- 6.已知曲线1C :sin y x =,2C :cos 23y x π⎛⎫=-⎪⎝⎭,则下面结论正确的是( ) A .把1C 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移3π个单位长度,得到曲线2CB .把1C 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移23π个单位长度,得到曲线2CC .把1C 上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向左平移12π个单位长度,得到曲线2CD .把1C 上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向右平移12π个单位长度,得到曲线2C7.已知函数y =f (x )的部分图象如图所示,则其解析式可能是( )A .()sin 2f x x x =B .()||sin 2f x x x =C .()cos 2f x x x =D .()||cos2f x x x =8.《九章算术》中《方田》章有弧田面积计算问题,术日:以弦乘矢,矢又自乘,并之,二而一.其大意是弧田面积计算公式为:弧田面积12=(弦×矢+矢×矢).弧田是由圆弧(弧田弧)及圆弧两端点的弦(弧田弦)围成的平面图形,公式中的“弦”指的是弧田弦的长,“矢”指的是弧田所在圆的半径与圆心到孤田弦的距离之差,现有一弧田,其矢长等于8米,若用上述弧田面积计算公式算得该弧田的面积为128平方米,则其弧田弧所对圆心角的正弦值为( ) A .60169B .120169C .119169D .591699.设函数()()sin 16f x x N πωω*⎛⎫=-+∈ ⎪⎝⎭在55,126ππ⎡⎤⎢⎥⎣⎦上单调递减,则下述结论: ①()f x 关于,012π⎛⎫⎪⎝⎭中心对称;②()f x 关于直线23x π=轴对称;③()f x 在,2ππ⎡⎤⎢⎥⎣⎦上的值域为30,2⎡⎤⎢⎥⎣⎦;④方程()1f x =在[]0,2π有4个不相同的根. 其中正确结论的编号是( ) A .①②B .②③C .②④D .③④10.设函数()tan 3f x x π=-,()sin 3g x x π⎛⎫=-⎪⎝⎭,则函数()()()h x f x g x =-在区间[]2,2ππ-上的零点个数是( ) A .4B .5C .12D .1311.已知函数11()sin sin sin sin f x x x x x ⎛⎫⎛⎫=+- ⎪⎪⎝⎭⎝⎭,现有命题:①()f x 的最大值为0; ②()f x 是偶函数; ③()f x 的周期为π; ④()f x 的图象关于直线2x π=对称.其中真命题的个数是( ) A .4B .3C .2D .112.若函数()22()sin 23cos sin f x x x x =+-的图像为E ,则下列结论正确的是( ) A .()f x 的最小正周期为2π B .对任意的x ∈R ,都有()()3f x f x π=-C .()f x 在7(,)1212ππ上是减函数 D .由2sin 2y x =的图像向左平移3π个单位长度可以得到图像E 二、填空题13.“一湾如月弦初上,半壁澄波镜比明”描述的是敦煌八景之一的月牙泉.如图所示,月牙泉由两段在同一平面内的圆弧形岸连接围成.两岸连接点间距离为603米.其中外岸为半圆形,内岸圆弧所在圆的半径为60米.某游客绕着月牙泉的岸边步行一周,则该游客步行的路程为_______米.14.设函数()3sin 23f x x π⎛⎫=-⎪⎝⎭的图象为C ,给出下列命题:①图象C 关于直线1112π=x 对称;②函数()f x 在区间5,1212ππ⎛⎫- ⎪⎝⎭内是减函数;③函数()f x 是奇函数;④图象C 关于点,03π⎛⎫⎪⎝⎭对称.其中,错误命题的是______.15.已知函数()()2sin 0f x x ωω=>在区间,34ππ⎡⎤-⎢⎥⎣⎦上的最小值是-2,则ω的最小值等于__________.16.已知M 是函数()()238sin f x x x x R π=--∈的所有零点之和.则M 的值为_____. 17.给出下列4个命题:①函数2cos 32y x π⎛⎫=+ ⎪⎝⎭是奇函数;②函数y =sin (2x +3π)的图象关于点(12π,0)成中心对称; ③x =8π是函数y =sin (2x +54π)的一条对称轴方程;④存在实数α,使得32sin 42πα⎛⎫+= ⎪⎝⎭.把你认为正确命题的序号都填在横线上____. 18.关于函数()4sin(2)(),3f x x x R π=+∈有下列命题:①由12()()0f x f x ==可得12x x -必是π的整数倍;②()y f x =的图象关于点(,0)6π-对称;③()y f x =的表达式可改写为4cos(2);6y x π=-④()y f x =的图象关于直线6x π=-对称.其中正确命题的序号是_________.19.已知将函数()sin()(06,)22f x x ππωθωθ=+<<-<<的图象向右平移3π个单位长度得到画()g x 的图象,若()f x 和()g x 的图象都关于4x π=对称,则ωθ⋅=________.20.函数()()0,0,2(f x Asin x A πωϕωϕ=+>><)的部分图像如图所示.则()f x 的解析式是_____.三、解答题21.已知函数()()2sin 0,22x f x ωϕωπϕ=≥<⎛⎫+ ⎪⎝⎭的图像向右平移6π个单位长度得到()g x 的图像, ()g x 图像关于原点对称,()f x 的相邻两条对称轴的距离是2π. (1)求()f x 在[]0,π上的增区间; (2)若()230f x m -=+在0,2x π⎡⎤∈⎢⎥⎣⎦上有两解,求实数m 的取值范围.22.已知函数2()3sin cos cos (0)f x x x x ωωωω=->周期是2π. (1)求()f x 的解析式,并求()f x 的单调递增区间;(2)将()f x 图像上所有点的横坐标扩大到原来的2倍,再向左平移6π个单位,最后将整个函数图像向上平移32个单位后得到函数()g x 的图像,若263x ππ≤≤时,()2g x m -<恒成立,求m 得取值范围.23.如图所示,摩天轮的半径为50m ,最高点距离地面高度为110m ,摩天轮的圆周上均匀地安装着24个座舱,并且运行时按逆时针匀速旋转,转一周大约需要12min .甲,乙两游客分别坐在P ,Q 两个座舱里,且他们之间间隔2个座舱(本题中将座舱视为圆周上的点).(1)求劣弧PQ 的弧长l (单位:m );(2)设游客丙从最低点M 处进舱,开始转动min t 后距离地面的高度为m H ,求在转动一周的过程中,H 关于时间t 的函数解析式;(3)若游客在距离地面至少85m 的高度能够获得最佳视觉效果,请问摩天轮转动一周能有多长时间使甲,乙两位游客都有最佳视觉效果.24.游客乘坐位于长沙贺龙体育场的摩天轮可近观长沙中心城区城市美景,远眺岳麓山,俯瞰橘子洲,饱览湘江风光.据工作人员介绍,该摩天轮直径约100米,摩天轮的最低处P 与地面的距离为20米,设有60个座舱,游客先乘坐直升电梯到入口(人口在摩天轮距地面的最低处)处等待,当座舱到达最低处P 时有序进入座舱,摩天轮逆时针方向匀速运行一周约需20分钟.以摩天轮的圆心为坐标原点,水平线为x 轴建立如图所示的平面直角坐标系.(1)试将游客甲离地面的距离()h t (单位:米)表示为其坐上摩天轮的时间t (单位:分钟)的函数;(2)若游客乙在甲后的5分钟也在点P 处坐上摩天轮,求在乙坐上摩天轮后的多少分钟时甲乙的离地面距离之差首次达到最大.25.已知函数()()()2cos 0,0f x x ωϕωϕπ=+><<的部分图象如图所示.(1)求函数()f x 的解析式;(2)将函数()f x 图象上每个点的横坐标变为原来的2倍(纵坐标不变),再将得到的图象向右平移4个单位长度,所得图象的函数为()g x ,若不等式()0g x m -≤在[]0,6x ∈恒成立,求实数m 的取值范围.26.己知函数()sin 3cos (0, 0 )f x A x A x A ωωω=+>>,其部分图象如图所示.(1)求A 和ω的值;(2)求函数()y f x =在[]0,π的单调增区间.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】由图可知,172482g f ππ⎛⎫⎛⎫==⎪ ⎪⎝⎭⎝⎭,根据函数图象的平移变化法则可知()()sin 2x g x ϕ=-,于是推出1717sin 224242g ππϕ⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭,即1722124k ππϕπ-=+或324k ππ+,k Z ∈,再结合02πϕ<≤,解之即可得ϕ的值.【详解】由图可知,17sin 224882g f πππ⎛⎫⎛⎫⎛⎫==⨯=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 因为()f x 的图象向右平移ϕ个单位,得到函数()g x 的图象,所以()()sin 2x g x ϕ=-,所以171717sin 2sin 22424122g πππϕϕ⎛⎫⎛⎫⎛⎫=-=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 所以1722124k ππϕπ-=+或17322124k ππϕπ-=+,k Z ∈, 解得712k πϕπ=-或3k πϕπ=-,k Z ∈, 因为02πϕ<≤,所以3πϕ=.故选:C 【点睛】本小题主要考查三角函数图象变换,属于中档题.2.D解析:D 【分析】由图可得函数的零点就是11y x =-和2cos y x π=交点的横坐标,画出函数图象,可得出()f x 在[]3,5-有8个零点,且关于1x =对称,即可求出.【详解】()()112cos 20212cos 11f x x x x x ππ=++=-⎡⎤⎣⎦--, 令()0f x =,则12cos 1x x π=-, 则函数的零点就是11y x =-和2cos y x π=交点的横坐标,可得11y x =-和2cos y x π=的函数图象都关于1x =对称,则交点也关于1x =对称, 画出两个函数的图象,观察图象可知,11y x =-和2cos y x π=在[]3,5-有8个交点, 即()f x 有8个零点,且关于1x =对称,故所有零点的和为428⨯=. 故选:D. 【点睛】本题考查求函数的零点之和,解题的关键是将题目化为找11y x =-和2cos y x π=交点的横坐标,从而通过函数图象求解.3.D解析:D 【分析】先根据题意建立坐标系,写出盛水筒M 距离水面的高度H 与时间t 之间的函数关系式,再根据关系式即可判断. 【详解】解:以O 为圆心,过点O 的水平直线为x 轴,建立如图所示的平面直角坐标系:0306xOP π∠==,OP ∴在()t s 内转过的角为:26030t t ππ=, ∴以x 轴正半轴为始边,以OP 为终边的角为:306t ππ-,P ∴点的纵坐标为:4sin 306t ππ⎛⎫-⎪⎝⎭, H ∴与t 之间的函数关系式为:4sin 2306H t ππ⎛⎫=-+⎪⎝⎭, 当sin 1306t ππ⎛⎫-= ⎪⎝⎭时,max 426H =+=, 当sin 1306t ππ⎛⎫-=-⎪⎝⎭时,max 422H =-+=-, 对A ,B ,由图像易知max min H H =-,故A ,B 错误; 对C ,max min H H <-,故C 错误; 对D ,max min H H >-,故D 正确. 故选:D. 【点睛】关键点点睛:本题解题的关键是理解题意,根据题意写出H 与t 之间的函数关系式.4.D解析:D 【分析】利用正弦函数的单调性可判断AD 选项的正误;利用正切函数的单调性可判断C 选项的正误;利用余弦函数的单调性可判断B 选项的正误. 【详解】对于A 选项,因为正弦函数sin y x =在0,2π⎛⎫⎪⎝⎭上单调递增, 且01122ππ<-<<,则sin1sin 1cos12π⎛⎫>-=⎪⎝⎭,A 选项错误; 对于B 选项,因为余弦函数cos y x =在()0,π上为减函数,23233cos cos cos 555πππ⎛⎫-== ⎪⎝⎭,1717cos cos cos 444πππ⎛⎫-== ⎪⎝⎭, 3045πππ<<<,则3cos cos 54ππ<,即2317cos cos 54ππ⎛⎫⎛⎫-<- ⎪ ⎪⎝⎭⎝⎭,B 选项错误; 对于C 选项,当900x -<<时,正切函数tan y x =单调递增,因为9052470-<-<-<,所以,()()tan 52tan 47-<-,C 选项错误;对于D 选项,因为正弦函数sin y x =在,02π⎛⎫- ⎪⎝⎭上单调递增,因为021018πππ-<-<-<,所以,sin sin 1810ππ⎛⎫⎛⎫->- ⎪ ⎪⎝⎭⎝⎭,D 选项正确. 故选:D. 【点睛】思路点睛:解答比较函数值大小问题,常见的思路有两个: (1)判断各个数值所在的区间; (2)利用函数的单调性直接解答.5.A解析:A 【分析】由题意根据三角函数定义可知0x cos α=,先根据角α的取值范围求出6πα⎛⎫+⎪⎝⎭的取值范围继而求出4cos 65πα⎛⎫+=- ⎪⎝⎭,再通过凑角求cos α. 【详解】5,36ππα⎛⎫∈ ⎪⎝⎭,则26ππαπ<+<,则由3sin 65πα⎛⎫+= ⎪⎝⎭,得4cos 65πα⎛⎫+=- ⎪⎝⎭.由点()00,P x y 在单位圆O 上,设xOP α∠=,则0x cos α=. 又cos αcos 66ππα⎡⎤⎛⎫=+-⎪⎢⎥⎝⎭⎣⎦cos sin 6666cos sin ππππαα⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭431552=-+⨯310-=故0x =.选A. 【点睛】本题考查三角函数定义及三角恒等变换的简单应用.解题中注意所求角的取值范围.由配凑法根据已知角构造所求角进行求解是三角恒等变换中常用的解题技巧.6.C解析:C 【分析】由题意利用诱导公式得1sin cos :2C y x x π⎛⎫==- ⎪⎝⎭,根据函数()cos y A x ωϕ=+的图象变换规律,得出结论. 【详解】已知曲线1sin cos :2C y x x π⎛⎫==-⎪⎝⎭,2cos 23:C y x π⎛⎫=-⎪⎝⎭, ∴把1C 上各点的横坐标缩短到原来的12倍,纵坐标不变,可得cos 22y x π⎛⎫=- ⎪⎝⎭的图象,再把得到的曲线向左平移 12π个单位长度,得到曲线2cos 2cos 263:2C x x πππ⎛⎫⎛⎫+-=- ⎪ ⎪⎝⎭⎝⎭的图象,故选C .【点睛】本题主要考查函数()cos y A x ωϕ=+的图象变换规律,属于基础题.7.B解析:B 【分析】利用函数()0f π=排除两个选项,再由奇偶性排除一个后可得正确选项. 【详解】由图象知()0f π=,经验证只有AB 满足,C 中()cos 2f ππππ==,D 中()f ππ=,排除CD ,A 中函数满足()sin(2)sin 2()f x x x x x f x -=--==为偶函数,B 中函数满足()sin(2)sin 2()f x x x x x f x -=--=-=-为奇函数,而图象关于原点对称,函数为奇函数,排除A ,选B . 故选:B . 【点睛】思路点睛:由函数图象选择解析式可从以下方面入手:(1)从图象的左右位置,观察函数的定义域;从图象的上下位置,观察函数的值域; (2)从图象的变化趋势观察函数的单调性; (3)从图象的对称性观察函数的奇偶性; (4)从图象的特殊点,排除不合要求的解析式..8.B解析:B 【分析】求出弦长,再求出圆的半径,然后利用三角形面积求解. 【详解】如图,由题意8CD =,弓琖ACB 的面积为128,1(8)81282AB ⨯+⨯=,24AB =, 设所在圆半径为R ,即OA OB R ==,则22224(8)2R R ⎛⎫=-+ ⎪⎝⎭,解得13R =, 5OD =,由211sin 22AB OD OA AOB ⨯=∠得 2245120sin 13169AOB ⨯∠==. 故选:B .【点睛】关键点点睛:本题考查扇形与弓形的的有关计算问题,解题关键是读懂题意,在读懂题意基础上求出弦长AB ,然后求得半径R ,从而可解决扇形中的所有问题.9.D解析:D 【分析】利用题干中的已知条件求得2ω=,可得出()sin 216f x x π⎛⎫=-+ ⎪⎝⎭,利用正弦型函数的对称性可判断①②的正误,利用正弦型函数的值域可判断③的正误,求出方程()1f x =在[]0,2π上的解,可判断④的正误. 【详解】N ω*∈,由55,126x ππ⎡⎤∈⎢⎥⎣⎦可得55126666x πωπππωπω-≤-≤-, 由于函数()()sin 16f x x N πωω*⎛⎫=-+∈ ⎪⎝⎭在55,126ππ⎡⎤⎢⎥⎣⎦上单调递减, 所以,()553,2,21266622k k k Z πωππωπππππ⎡⎤⎡⎤--⊆++∈⎢⎥⎢⎥⎣⎦⎣⎦,所以,521262532662k k ωππππωππππ⎧-≥+⎪⎪⎨⎪-≤+⎪⎩,解得()248121055k k k Z ω++≤≤∈,由248121055k k ++≤,解得16k ≤,N ω*∈且k Z ∈,0k ∴=,可得825ω≤≤,2ω∴=,则()sin 216f x x π⎛⎫=-+ ⎪⎝⎭.对于①,sin 2sin 00126ππ⎛⎫⨯-==⎪⎝⎭,所以,112f π⎛⎫= ⎪⎝⎭, 所以,函数()f x 的图象关于点,112π⎛⎫⎪⎝⎭成中心对称,①错误; 对于②,271sin 2sin 13662πππ⎛⎫⨯-==-≠± ⎪⎝⎭,②错误;对于③,当,2x ππ⎡⎤∈⎢⎥⎣⎦时,5112,666x πππ⎡⎤-∈⎢⎥⎣⎦,则11sin 262x π⎛⎫-≤-≤ ⎪⎝⎭, 所以,()302f x ≤≤,即()f x 在,2ππ⎡⎤⎢⎥⎣⎦上的值域为30,2⎡⎤⎢⎥⎣⎦,③正确; 对于④,当[]0,2x π∈时,232,666x πππ⎡⎤-∈-⎢⎥⎣⎦, 令()1f x =,可得sin 206x π⎛⎫-= ⎪⎝⎭,206x π∴-=或26x ππ-=或226x ππ-=或236x ππ-=.所以,方程()1f x =在[]0,2π有4个不相同的根,④正确. 故选:D. 【点睛】方法点睛:求函数()()sin f x A x =+ωϕ在区间[],a b 上值域的一般步骤: 第一步:三角函数式的化简,一般化成形如()sin y A x k ωϕ=++的形式或()cos y A x k ωϕ=++的形式;第二步:由x 的取值范围确定x ωϕ+的取值范围,再确定()sin x ωϕ+(或()cos x ωϕ+)的取值范围;第三步:求出所求函数的值域(或最值).10.A解析:A 【分析】由题意知函数()()()h x f x g x =-在区间[]2,2ππ-上的零点个数等价于函数()tan 3f x x π=-与()sin 3g x x π⎛⎫=-⎪⎝⎭图象在区间[]2,2ππ-上交点的个数,作出两个函数图象,数形结合即可求解. 【详解】令()()()0h x f x g x =-=可得()()f x g x =,所以函数()()()h x f x g x =-在区间[]2,2ππ-上的零点个数等价于 函数()tan 3f x x π=-与()sin 3g x x π⎛⎫=-⎪⎝⎭图象在区间[]2,2ππ-上交点的个数. 分别作出()tan 3f x x π=-与()sin 3g x x π⎛⎫=-⎪⎝⎭图象,由图知两个函数图象在区间[]2,2ππ-上有4个交点,所以函数()()()h x f x g x =-在区间[]2,2ππ-上的零点个数是4, 故选:A 【点睛】方法点睛:判断函数零点个数的方法(1)直接法:令()0f x =,如果能求出解,那么有几个不同的解就有几个零点; (2)利用函数的零点存在性定理:利用函数的零点存在性定理时,不仅要求函数的图象在区间[],a b 上是连续不断的曲线,并且()()0f a f b ⋅<,还必须结合函数的图象与性质,(如单调性、奇偶性)才能确定函数有多少个零点;(3)图象法:画出函数()f x 的图象,函数()f x 的图象与x 轴交点的个数就是函数()f x 的零点个数;将函数()f x 拆成两个函数,()h x 和()g x 的形式,根据()()()0f x h x g x =⇔=,则函数()f x 的零点个数就是函数()y h x =和()y g x =的图象交点个数;(4)利用函数的性质:若能确定函数的单调性,则其零点个数不难得到,若所考查的函数是周期函数,则需要求出在一个周期内的零点个数,根据周期性则可以得出函数的零点个数.11.A解析:A 【分析】先求函数的定义域,再根据函数奇偶性定义,周期函数的定义可判断②③的正误,再根据函数解析的特征可判断④的正误,最后利用换元法可求判断①的正误. 【详解】22111()sin sin sin sin sin sin f x x x x x x x ⎛⎫⎛⎫=+-=- ⎪⎪⎝⎭⎝⎭, 由sin 0x ≠可得,x k k Z π≠∈,故函数的定义域为{}|,x x k k Z π≠∈, 所以函数的定义域关于原点对称.又()()()222211()sin sin sin sin f x x x f x x x-=--=-=-,故()f x 为偶函数, 故②正确.又()()()221()sin sin f x x f x x πππ+=+-=+,故()f x 是周期函数且周期为π,故③正确. 又()()()221()sin sin f x x f x x πππ-=--=-,故()f x 的图象关于直线2x π=对称,故④正确.令2sin t x =,则(]0,1t ∈且()1f x t t=-,因为1y t t=-为(]0,1上的增函数,故()max 0f x =,故①正确. 故选:A. 【点睛】思路点睛:对于复杂函数的性质的研究,注意先研究函数的定义域,再研究函数的奇偶性或周期性,最后再研究函数的单调性,讨论函数图象的对称性,注意根据()()f a x f x -=来讨论. 12.C解析:C 【分析】利用二倍角和辅助角公式化简函数为()2sin(2+)3f x x π=;根据正弦型函数的性质验证选项得解 【详解】()sin 222sin(2+)3f x x x x π==()f x 最小正周期22T ππ==,A 错误; ()2sin[2()+]2sin(2)2sin 2333f x x x x ππππ-=-=-=,B 错误; 当7(,)1212x ππ∈时,32(,)322x πππ+∈ ()f x ∴在7(,)1212ππ上是减函数,C 正确; 将2sin 2y x =向左平移3π个单位长度得到22sin[2()]2sin(2)33y x x ππ=-=-,D 错误. 故选:C 【点睛】本题考查正弦型函数性质的相关命题的辨析,涉及到二倍角和辅助角公式化简三角函数、正弦型函数的周期性、对称性和单调区间的求解、三角函数平移变换的应用等知识;关键是能够熟练掌握整体对应的方法,通过代入检验,结合正弦函数图象可确定正弦型函数的性质.二、填空题13.【分析】如图作出月牙湖的示意图由题意可得可求的值进而由图利用扇形的弧长公式可计算得解【详解】如图是月牙湖的示意图是的中点连结可得由条件可知所以所以所以月牙泉的周长故答案为:【点睛】关键点点睛:本题的 解析:(40303)π+【分析】如图,作出月牙湖的示意图,由题意可得3sin QPO ∠=,可求,QPO QPT ∠∠的值,进而由图利用扇形的弧长公式可计算得解. 【详解】如图,是月牙湖的示意图,O 是QT 的中点,连结PO ,可得PO QT ⊥,由条件可知603QT =,60PQ = 所以3sin 2QPO ∠=,所以3QPO π∠=,23QPT π∠=,所以月牙泉的周长(260303403033l πππ=⨯+⨯=+.故答案为:(40π+ 【点睛】关键点点睛:本题的关键是根据实际问题抽象出图象,再根据数形结合分析问题.14.②③④【分析】根据函数的图象与性质分析函数的对称性奇偶性与单调性即可得出结论【详解】解:①由得令直线为函数图象的对称轴故图象C 关于直线对称故①正确;由得令得函数在区间内是增函数故②错误;故函数不是奇解析:②③④ 【分析】根据函数()3sin 23f x x π⎛⎫=- ⎪⎝⎭的图象与性质,分析函数的对称性,奇偶性与单调性,即可得出结论. 【详解】 解:①由232x k πππ-=+,Z k ∈,得25121x k ππ=+,Z k ∈, 令1k =,直线1112π=x 为函数图象的对称轴, 故图象C 关于直线1112π=x 对称,故①正确; 由222232k x k πππππ-+≤-≤+,k Z ∈,得5,1212x k k ππππ⎡⎤∈-++⎢⎥⎣⎦,k Z ∈, 令0k =,得函数()f x 在区间5,1212ππ⎛⎫-⎪⎝⎭内是增函数,故②错误; ()00f ≠,故函数()f x 不是奇函数,故③错误;由23x k ππ-=,k Z ∈,得612x k ππ=+,k Z ∈,图象C 不关于点,03π⎛⎫ ⎪⎝⎭对称,故④错误.故答案为:②③④. 【点睛】本题考查正弦函数的图象与性质,考查函数与方程思想、转化与化归思想,考查逻辑推理能力、运算求解能力.15.【分析】先根据函数在区间上的最小值是确定的取值范围进而可得到或求出的范围得到答案【详解】函数在区间上的最小值是则的取值范围是当时函数有最小值或或的最小值等于故答案为:【点睛】本题主要考查正弦函数的最解析:32【分析】先根据函数在区间[,]34ππ-上的最小值是2-确定x ω的取值范围,进而可得到32ωππ--或342ωππ,求出ω的范围得到答案. 【详解】函数()2sin (0)f x x ωω=>在区间[,]34ππ-上的最小值是2-, 则x ω的取值范围是[,]34ωπωπ-,当22x k πωπ=-+,k Z ∈时,函数有最小值2-,32ωππ∴--,或342ωππ,k Z ∈, ∴32ω≥,或6ω,k Z ∈, 0ω>,ω∴的最小值等于32.故答案为:32. 【点睛】本题主要考查正弦函数的最值的应用.考查基础知识的运用能力.三角函数式高考的重要考点,一定要强化复习.16.【分析】根据和的函数图像的对称点和交点个数得出答案【详解】令可得作出和的函数图像如图所示:由图像可知两函数图像有个交点又两函数图像均关于直线对称的个零点之和为故答案为:【点睛】本题考查了函数零点之和 解析:12【分析】根据8sin y x π=和23y x =-的函数图像的对称点和交点个数得出答案. 【详解】令()0f x =可得8sin 23x x π=-,作出8sin y x π=和23y x =-的函数图像如图所示:由图像可知两函数图像有8个交点, 又两函数图像均关于直线32x =对称, ∴()f x 的8个零点之和为324122⨯⨯=.故答案为:12 【点睛】本题考查了函数零点之和,考查了转化与化归、数形结合的思想,属于基础题.17.①③【分析】根据三角函数的奇偶性对称中心对称轴和最值对四个命题逐一分析由此确定正确命题的序号【详解】①为奇函数所以①正确②由于所以②错误③由于所以③正确④由于的最大值为所以④错误故答案为:①③【点睛解析:①③ 【分析】根据三角函数的奇偶性、对称中心、对称轴和最值对四个命题逐一分析,由此确定正确命题的序号. 【详解】①,22cos sin 323y x x π⎛⎫=+=- ⎪⎝⎭为奇函数,所以①正确.②,由于sin 2sin 11232πππ⎛⎫⨯+== ⎪⎝⎭,所以②错误. ③,由于53sin 2sin 1842πππ⎛⎫⨯+==- ⎪⎝⎭,所以③正确. ④24πα⎛⎫+ ⎪⎝⎭2322<,所以④错误.故答案为:①③ 【点睛】本小题主要考查三角函数的奇偶性、对称性、最值以及诱导公式,属于中档题.18.②③【分析】根据三角函数的零点性质三角函数对称和三角函数诱导公式依次判断每个选项得到答案【详解】①中是的两个零点即是的整数倍①错误;②中②正确;故④错误;③中③正确;所以正确命题序号是②③故答案为:解析:②③ 【分析】根据三角函数的零点性质,三角函数对称和三角函数诱导公式依次判断每个选项得到答案. 【详解】①中12,x x 是()f x 的两个零点,即12x x -是2π的整数倍,①错误; ②中06f π⎛⎫-= ⎪⎝⎭,②正确;故④错误; ③中4sin 24cos 2cos 23236y x x x ππππ⎛⎫⎛⎫⎛⎫=+=--=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,③正确; 所以正确命题序号是②③. 故答案为:②③. 【点睛】本题考查了三角函数的对称,零点,诱导公式,意在考查学生对于三角函数知识的综合应用.19.【分析】和的图象都关于对称所以①②由①②结合即可得到答案【详解】由题意因为和的图象都关于对称所以①②由①②得又所以将代入①得注意到所以所以故答案为:【点睛】本题考查正弦型函数的性质涉及到函数图象的平解析:34π-【分析】()f x 和()g x 的图象都关于4x π=对称,所以11,42k k Z ππωθπ+=+∈①,22,432k k Z πππωωθπ-+=+∈②,由①②结合06,22ππωθ<<-<<即可得到答案.【详解】由题意,()()sin()33g x f x x ππωωθ=-=-+,因为()f x 和()g x 的图象都关于4x π=对 称,所以11,42k k Z ππωθπ+=+∈①,22,432k k Z πππωωθπ-+=+∈②,由①②,得12123(),,k k k k Z ω=-∈,又06ω<<,所以3ω=,将3ω=代入①,得11,4k k Z πθπ=-∈,注意到22ππθ-<<,所以4πθ=-,所以34ωθπ⋅=-.故答案为:34π- 【点睛】本题考查正弦型函数的性质,涉及到函数图象的平移、函数的对称性,考查学生的运算求解能力,是一道中档题.20.【分析】由图像对应横坐标可求再将代入可进一步求解由图像过点可求进而求解【详解】由解得又函数过所以解得又图像过可得解得故故答案为:【点睛】本题考查由三角函数图像求解析式属于中档题解析:()2sin 26f x πx ⎛⎫+ ⎝=⎪⎭【分析】由34T 图像对应横坐标可求ω,再将6x π=代入可进一步求解ϕ,由图像过()0,1点可求A ,进而求解 【详解】由1132312644T πππω-==⋅,解得2ω=,又函数过()max ,6f x π⎛⎫⎪⎝⎭, 所以63A f Asin ππϕ⎛⎫⎛⎫=⎪ ⎪⎝⎝⎭+⎭=,解得6π=ϕ,又图像过()0,1可得()106f Asin π==,解得2A =,故()2sin 26f x πx ⎛⎫+ ⎝=⎪⎭故答案为:()2sin 26f x πx ⎛⎫+ ⎝=⎪⎭【点睛】本题考查由三角函数图像求解析式,属于中档题三、解答题21.(1)70,,,1212ππ⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦;(2)12⎛ ⎝⎦. 【分析】(1)由()f x 的相邻两条对称轴的距离是2π,可得函数的周期,从而得出ω的值,由平移得出()g x 的解析式,根据()g x 图像关于原点对称,可求出ϕ的值,从而可求()f x 单调增区间,得出答案.(2)令23t x π=+则4,33t ππ⎡⎤∈⎢⎥⎣⎦,则[2s n 2]i t ∈,根据()230f x m -=+有两解,即2sin 32t m =-有两解,从而可得答案. 【详解】解:由()f x 的相邻两条对称轴的距离是2π,则22T ππω==,1,ω∴= ()()2sin 2f x x ϕ∴=+()2sin 2sin 2326x g x x ππϕϕ⎡⎤⎛⎫-+ ⎪⎢⎛⎫==-+ ⎪⎝⎥⎝⎣⎦⎭⎭函数()g x 的图像关于原点对称,3k πϕπ-+=,,2πϕ<所以3πϕ=()2sin 23f x x π⎛⎫∴=+ ⎪⎝⎭(1)由222232k x k πππππ-≤+≤+,k Z ∈得51212k x k ππππ-≤≤+,k Z ∈ 令0k =得51212x ππ-≤≤ 1k =得7131212x ππ≤≤ ()f x ∴在[]0,π增区间是70,,,1212ππ⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦()2令23t x π=+,0,,2x π⎡⎤∈⎢⎥⎣⎦则4,33t ππ⎡⎤∴∈⎢⎥⎣⎦所以[2s n 2]i t ∈若()230f x m -=+有两解,即2sin 32t m =-在4,33t ππ⎡⎤∈⎢⎥⎣⎦上有两解,由2sin y t =322m -<,即123m <≤12m ∴<≤m ∴的取值范围是12⎛ ⎝⎦【点睛】关键点睛:本题考查求正弦型函数的单调增区间和根据方程的解个数求参数的范围问题,解答本题的关键是设23t x π=+,由0,,2x π⎡⎤∈⎢⎥⎣⎦则4,33t ππ⎡⎤∈⎢⎥⎣⎦所以[2s n ,2]i 3t ∈-若()230f x m -=+有两解,即2sin 32t m =-在4,33t ππ⎡⎤∈⎢⎥⎣⎦上有两解,然后数形结合求解,属于中档题.22.(1)1()sin 462f x x π⎛⎫=-- ⎪⎝⎭,单调递增区间为,21226k k ππππ-+⎡⎤⎢⎥⎣⎦,k Z ∈;(2)()0,2. 【分析】(1)根据正弦和余弦的二倍角公式化简可得1()sin 262f x x πω⎛⎫=-- ⎪⎝⎭,由222T ππω==,解得2ω=,带入正弦函数的递增区间242262k x k πππππ-≤-≤+,化简即可得解; (2)根据三角函数的平移和伸缩变换可得()sin 216g x x π⎛⎫=++ ⎪⎝⎭,根据题意只需要max min [()2][()2]g x m g x -<<+,分别在263x ππ≤≤范围内求出()g x 的最值即可得解. 【详解】(1)2()3cos cos f x x x x ωωω=-312(cos 21)22x x ωω=-+ 1sin 262x πω⎛⎫=-- ⎪⎝⎭由222T ππω==,解得2ω=所以,1()sin 462f x x π⎛⎫=-- ⎪⎝⎭ ∵242262k x k πππππ-≤-≤+∴224233k x k ππππ-≤≤+∴21226k k x ππππ-≤≤+ ∴()f x 的单调递增区间为,21226k k ππππ-+⎡⎤⎢⎥⎣⎦,k Z ∈ (2)依题意得()sin 216g x x π⎛⎫=++ ⎪⎝⎭因为|()|2g x m -<,所以()2()2g x m g x -<<+因为当2,63x ππ⎡⎤∈⎢⎥⎣⎦时,()2()2g x m g x -<<+恒成立所以只需max min [()2][()2]g x m g x -<<+转化为求()g x 的最大值与最小值当2,63x ππ⎡⎤∈⎢⎥⎣⎦时,()y g x =为单调减函数所以max ()1126g x g π⎛⎫==+= ⎪⎝⎭,()min21103g x g π⎛⎫==-+= ⎪⎝⎭, 从而max [()2]0g x -=,min [()2]2g x +=,即02m <<所以m 的取值范围是()0,2. 【点睛】本题考查了三角函数的单调性和最值,考查了三角函数的辅助角公式和平移伸缩变换,有一定的计算量,属于中档题.本题关键点有: (1)三角函数基本量的理解应用; (2)三角函数图像平移伸缩变换的方法; (3)恒成立思想的理解及转化. 23.(1)252m π;(2)50sin()6062H x ππ=-+,其中012t ≤≤;(3)5min 2. 【分析】(1)根据弧长的计算公式可求PQ 的长度.(2)建立如图所示的平面直角坐标系,利用三角函数的定义可求H 关于时间t 的函数解析式.(3)利用(2)中所得的解析式并令85H ≥,求出不等式的解后可得甲,乙两位游客都有最佳视觉效果的时间长度. 【详解】(1)因为摩天轮的圆周上均匀地安装着24个座舱,故每个座舱与中心连线所成的扇形的圆心角为22412ππ=, 故25350122lm ππ. (2)建立如图所示的平面直角坐标系,设sin()H A wx B ϕ=++, 由题意知,12T =,所以26w T ππ==, 又由50,1105060A r B ===-=,所以50sin()606H x πϕ=++,当0x =时,可得sin 1ϕ=-,所以2πϕ=-,故H 关于时间t 的函数解析式为50sin()6062H x ππ=-+,其中012t ≤≤.(3)令50sin()608562H x ππ=-+≥,即1sin()622x ππ-≥, 令522,6626k x k k Z ππππππ+≤-≤+∈,解得412812,k x k k Z +≤≤+∈, 因为甲乙两人相差3312min 242⨯=, 又由354min 22-=,所以有5min 2甲乙都有最佳视觉效果. 【点睛】三角函数实际应用问题的处理策略: 1、已知函数模型求解数学问题;2、把实际问题抽象转化成数学问题,利用三角函数的有关知识解决问题;3、根据实际问题转化为已知条件转化为三角函数的解析式和图象,然后在根据数形结合思想研究三角函数的性质,进而加深理解函数的性质. 24.(1)()50sin 707050cos ,010210h t t t t πππ⎛⎫=-+=-≥ ⎪⎝⎭;(2)52分钟. 【分析】(1)根据题意分析游客甲绕原点作匀速圆周运动,根据三角函数定义可把他离地面的距离()h t 表示出来;(2)先求出游客乙离地面距离的函数()g t ,则()()h h t g t =-△即为甲乙的离地面距离之差,利用函数求最值. 【详解】(1)法1:据题意,游客甲绕原点按逆时针方向作角速度为22010ππ=弧度/分钟的匀速圆周运动,设经过t 分钟后甲到达Q ,则以OP 为始边,OQ 为终边的角的大小是10t π, 因为圆的半径为50r =米,由三角函数定义知点Q 的纵坐标为50sin 102y t ππ⎛⎫=-⎪⎝⎭, 则其离地面的距离为:()()205050sin 7050cos 010210h t t t t πππ⎛⎫=++-=-≥⎪⎝⎭. 法2:因为摩天轮是作匀速圆周运动,故可设()()()sin 0,0h t A t b A ωϕω=++>>,据题意有12050,2070,A b A A b b ⎧+==⎧⇒⎨⎨-+==⎩⎩又周期20T =,所以10πω=,由在最低点入舱得01022πππϕϕ⋅+=-⇒=-,故得()50sin 707050cos ,010210h t t t t πππ⎛⎫=-+=-≥ ⎪⎝⎭. (2)由(1)可知游客乙离地面的距离:()()7050cos 57050sin 1010g t t t ππ⎡⎤=--=-⎢⎥⎣⎦,其中时间t 表示游客甲坐上摩天轮的时间,则甲乙的离地面距离之差为:()()50sin cos 1010104h h t g t t t t ππππ⎛⎫⎛⎫=-=-=- ⎪ ⎪⎝⎭⎝⎭△,当()21042t k k ππππ-=+∈Z ,即()15202t k k =+∈Z 时,甲乙离地面距离之差达到最大,所以152t =,即游客乙坐上摩天轮552t -=分钟后,甲乙的离地面距离之差首次达到最大. 【点睛】数学建模是高中数学六大核心素养之一,在高中数学中,应用题是常见考查形式:(1)求解应用性问题时,首先要弄清题意,分清条件和结论,抓住关键词和量,理顺数量关系,然后将文字语言转化成数学语言,建立相应的数学模型;。
完整版)高中三角函数测试题及答案

完整版)高中三角函数测试题及答案高一数学必修4第一章三角函数单元测试班级:__________ 姓名:__________ 座号:__________评分:__________一、选择题:共12小题,在每小题给出的四个选项中,只有一项是符合题目要求的。
(48分)1、已知$A=\{\text{第一象限角}\}$,$B=\{\text{锐角}\}$,$C=\{\text{小于90°的角}\}$,那么$A$、$B$、$C$ 关系是()A.$B=A\cap C$B.$B\cup C=C$C.$A\cap D$D.$A=B=C$2、将分针拨慢5分钟,则分钟转过的弧度数是A。
$\frac{\pi}{3}\sin\alpha-\frac{2}{3}\cos\alpha$ B。
$-\frac{\pi}{3}$C。
$\frac{\pi}{6}$D。
$-\frac{\pi}{6}$3、已知 $\tan\alpha=-5$,那么 $\tan\alpha$ 的值为A。
2B。
$\frac{1}{6164}$C。
$-\frac{1}{6164}$D。
$-\frac{2}{3}$4、已知角 $\alpha$ 的余弦线是单位长度的有向线段,那么角 $\alpha$ 的终边()A。
在 $x$ 轴上B。
在直线 $y=x$ 上C。
在 $y$ 轴上D。
在直线 $y=x$ 或 $y=-x$ 上5、若 $f(\cos x)=\cos 2x$,则 $f(\sin 15^\circ)$ 等于()A。
$-\frac{2}{3}$B。
$\frac{3}{2}$C。
$\frac{1}{2}$D。
$-\frac{1}{2}$6、要得到 $y=3\sin(2x+\frac{\pi}{4})$ 的图象只需将$y=3\sin 2x$ 的图象A。
向左平移 $\frac{\pi}{4}$ 个单位B。
向右平移 $\frac{\pi}{4}$ 个单位C。
新课标数学必修4第1章三角函数练习(含答案)

1.1.1任意角一、情景导入: 1.角的概念的推广(1)任意角的形成:角可以看成是由一条射线绕着它的端点旋转而成的,射线的端点叫做角的顶点,旋转开始时的射线叫做角的始边,终止时的射线叫做角的终边.(2)正角、负角和零角:按逆时针方向旋转而成的角叫做正角.按顺时针方向旋转而成的角叫做负角.当射线没有作任何旋转时,形成的角叫做零角.(3)象限角:角的顶点与坐标原点重合,角的始边与x 轴的正半轴重合,角的终边落在第几象限,就把这个角称为第几象限的角.如果角的终边落在坐标轴上,则称这个角称为轴上角. 2.象限角及终边相同的角:所有与角α终边相同的角,连同角α在内,可构成一个集合{|360,}S k k Z ββα==+⋅︒∈,即任一与角α终边相同的角,都可以表示成角α与整数个周角的和; 二、感受理解: 1.设{}90E =︒小于的角,{}F =锐角,{}G =第一象限的角,{}90M =︒︒小于的角,但不小于0的角 ,你能分清这几个有关角的集合之间的包含关系吗?2.在 ~间,求出与下列各角终边相同的角,并判定它们分别是哪一个象限的角.(1);(2).3.分别写出: ①终边在轴负半轴上的角的集合; ②终边在 轴上的角的集合;③终边在第一、三象限角平分线上的角的集合; ④终边在四象限角平分线上的角的集合.4.如图,终边落在 位置时的角的集合是____________;线边落在位置,且在[]360,360-︒︒内的角的集合是_________;终边落在阴影部分(含边界)的角的集合是______________.5.探究等分角所在的象限我们都知道,60︒是锐角,60︒角的一半30︒也是锐角.60360k ︒+⋅︒,k Z ∈是第一象限角,它的一半30180,k k Z ︒+⋅︒∈是否仍在第一象限呢?三、迁移拓展:6.下列命题中,正确的是( ).A .始边和终边都相同的两个角一定相等B . 是第二象限的角C .若,则4α是第一象限角 D .相等的两个角终边一定相同7.在“①160°②480°③-960°④-1600°”这四个角中,属于第二象限的角是( )A .①B .①②C .①②③D .①②③④8.经过3小时35分钟,时针与分针转过的度数之差是( ).A .B .C .D .9.下列结论中正确的是( )A.小于90°的角是锐角B.第二象限的角是钝角C.相等的角终边一定相同D.终边相同的角一定相等10.若α是第一象限的角,则-2α是( )A.第一象限的角B.第一或第四象限的角C.第二或第三象限的角D.第二或第四象限的角11.与终边相同的角的集合是___________,它们是第____________象限的角,其中最小的正角是___________,最大负角是___________.12.已知 的终边在 轴上的上方,那么是第__________象限的角.13.设,,,则相等的角集合为____________.14.若角与 的终边关于轴对称,则与的关系是__________;若角与的终边互相垂直,则与的关系是___________.提示:可结合图形分析 15.给出下列命题:①和的角的终边方向相反; ②和的角的终边相同;③第一象限的角和锐角终边相同; ④ (21)180k α=+⋅︒与(41)180,()k k Z β=±⋅︒∈终边相同; 其中所有正确命题的序号是______________.16.求所有与所给角终边相同的角的集合,并求出其中的最小正角,最大负角:(1) ;(2).17.已知{}9036045360,90360225360,A k k k k k Z ααα=-︒+⋅︒<<︒+⋅︒︒+⋅︒<<︒+⋅︒∈或{}360150360,B k k k Z ββ=⋅︒<<︒+⋅︒∈,求与提示:可根据图形分析两集合间的关系18.如图所示,写出图中阴影部分(包括边界)的角的集合,并指出 是否是该集合中的角.19.已知 是第二象限的角,你能结合图示分别找到以下问题的答案吗?(1)2α角所在的象限 (2) 角所在的象限20.若角 的终边经过点 ,试写出角的集合,并求出集合中绝对值最小的角.四、实践应用:21.α是一个任意角,则α与-α的终边是( )A .关于坐标原点对称B .关于x 轴对称C .关于直线y=x 对称D .关于y 轴对称 22.若α与β的终边互为反向延长线,则有( )A .α=β+180°B .α=β-180°C .α=-βD .α=β+(2k+1)180°,k∈Z参考答案: 1.1.1任意角 二、感受理解 1.略2.(1),三(2),三3.①;② ;③;④.4.{}120k k Zαα=︒+⋅︒∈;{}45,315-︒︒{}45360120360,k k k Z ββ-︒+⋅︒≤≤︒+⋅︒∈.5. 一、三三、迁移拓展:6.D 7.C 8.C 9.C 10.D11. ,三,,12.一、三13.,14.(21)180,k k Z αβ+=+⋅︒∈,90360,k k Z αβ-=±︒+⋅︒∈15.②、④16.(1){}120360,k k Z αα=-︒+⋅︒∈, ,;(2),31523'︒,4437'-︒.17. {}90360150360,36045360,A B k k k k k Z ααα=︒+⋅︒<<︒+⋅︒⋅︒<<︒+⋅︒∈或 {}90360225360,A B k k k Z αα=︒+⋅︒<<︒+⋅︒∈-18.,是19.(1)一、三,(2)三,四,或轴负半轴上的角20.,.四、实践应用: 21.B 22.D1.1.2弧度制一、情景导入:1. 弧度制(1)1弧度的角:等于半径长的圆弧所对的圆心角叫做1弧度的角,这种用弧度来度量的制度称弧度制(2)正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为零,任一已知角α的弧度数都满足lr α=,其中l 为以角α作为圆心角时所对圆弧的长,r 为圆的半径.2.度数与弧度数的换算:180rad π︒=10.01745180rad rad π︒=≈, 1801()57.35718'rad π=︒≈︒=︒请写出下列特殊角的弧度数与角度数.3.相关计算公式(1)圆心角α,半径r ,弧长l 之间的关系:l r α==180n r π(2)扇形面积公式:221122360n r S r lr πα===二、感受理解:1.请你用弧度制表示下列特殊位置的角,这些内容对今后的学习很重要.(1)终边在x 轴上的角 (2)终边在y 轴上的角 (3)终边在坐标轴上的角(4)终边在第一、三象限角平分线上的角。
必修4第一章三角函数单元基础测试题及答案

1
A. 5
1
B. 4
13
C. 18
13
D. 22
11.sin1,cos1,tan1 的大小关系是(
)
A.tan1>sin1>cos1
B.tan1>cos1>sin1
C。cos1>sin1>tan1
D.sin1〉cos1>tan1
12.已知函数 f (x)=f (x),且当 x( , ) 时,f (x)=x+sinx,设 a=f (1),b=f
4 3
3、已知 cosθ=cos30°,则θ等于( )
A. 30°
B. k·360°+30°(k∈Z)
C。 k·360°±30°(k∈Z)
D. k·180°+30°(k∈Z)
4、若 cos 0,且sin 2 0,则角 的终边所在象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限( )
18.解、∵ tan 3 ∴ cos 0
(4sin 2 cos ) 1∴Fra bibliotek式=cos
(5cos 3sin ) 1
cos
= 4 tan 2
5 3 tan
= 432
5 33
=5
7
19. 解: f (x) 2 cos x(sin x cos x) 1 sin 2x cos 2x 2 sin(2x )
5、函数
的递增区间是(
)
y 5sin(2x )
6、函数
6 图象的一条对称轴方程是( )
( A)
x
12
;
(B) x 0;
(C)
x
6
;
(D)
x
(必考题)高中数学必修四第一章《三角函数》测试卷(含答案解析)(1)

一、选择题1.设函数5()sin 26f x x π⎛⎫=-⎪⎝⎭,将函数()f x 的图象向左平移()0ϕϕ>个单位长度,得到函数()g x 的图象,若()g x 为偶函数,则ϕ的最小值是( ) A .6π B .3πC .23π D .56π 2.将函数sin()y x ϕ=+的图像上所有点的横坐标缩短到原来的12倍(纵坐标不变),再将所得图像向左平移12π个单位后得到的函数图像关于原点中心对称,则sin 2ϕ=( )A .12-B .12C .3-D .3 3.已知函数()f x 是定义在R 上的增函数,()0,1A -,()3,1B 是其图象上的两点,那么|(2sin 1)|1f x +≤ 的解集为( )A .,33xk x k k ππππ⎧⎫-≤≤+∈⎨⎬⎩⎭Z ∣ B .722,66xk x k k ππππ⎧⎫+≤≤+∈⎨⎬⎩⎭Z ∣ C .,63x k x k k ππππ⎧⎫-≤≤+∈⎨⎬⎩⎭Z ∣ D .722,66x k x k k ππππ⎧⎫-≤≤+∈⎨⎬⎩⎭Z ∣ 4.函数()()12cos 20211f x x x π=++⎡⎤⎣⎦-在区间[]3,5-上所有零点的和等于( ) A .2B .4C .6D .85.《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验方式为:弧田面积12=(弦⨯矢+矢2),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有弧AB 长为83π,半径等于4米的弧田,按照上述经验公式计算所得弧田面积约是( )(3 1.73≈)A .6平方米B .9平方米C .12平方米D .15平方米6.函数1sin3y x =-的图像与直线3x π=,53x π=及x 轴所围成的图形的面积是( ) A .23π B .πC .43π D .53π 7.已知函数()sin 213f x x π⎛⎫=++ ⎪⎝⎭,下列说法错误的是( )A .3π是函数()f x 的一个周期B .函数()f x 的图象关于,13π⎛⎫⎪⎝⎭成中心对称C .函数的一条对称轴为712x π= D .函数图象向左平移6π个单位后关于y 轴对称8.使函数())cos(2)f x x x θθ+++是偶函数,且在0,4⎡⎤⎢⎥⎣⎦π上是减函数的θ的一个值是( ) A .6π B .3π C .23π D .56π9.《九章算术》中《方田》章有弧田面积计算问题,术日:以弦乘矢,矢又自乘,并之,二而一.其大意是弧田面积计算公式为:弧田面积12=(弦×矢+矢×矢).弧田是由圆弧(弧田弧)及圆弧两端点的弦(弧田弦)围成的平面图形,公式中的“弦”指的是弧田弦的长,“矢”指的是弧田所在圆的半径与圆心到孤田弦的距离之差,现有一弧田,其矢长等于8米,若用上述弧田面积计算公式算得该弧田的面积为128平方米,则其弧田弧所对圆心角的正弦值为( ) A .60169B .120169C .119169D .5916910.设函数()()sin 16f x x N πωω*⎛⎫=-+∈ ⎪⎝⎭在55,126ππ⎡⎤⎢⎥⎣⎦上单调递减,则下述结论: ①()f x 关于,012π⎛⎫⎪⎝⎭中心对称;②()f x 关于直线23x π=轴对称; ③()f x 在,2ππ⎡⎤⎢⎥⎣⎦上的值域为30,2⎡⎤⎢⎥⎣⎦;④方程()1f x =在[]0,2π有4个不相同的根. 其中正确结论的编号是( ) A .①② B .②③C .②④D .③④11.当5,2,2παβπ⎛⎫∈ ⎪⎝⎭时,若αβ>,则以下不正确的是( ) A .sin sin tan tan αββα->-B .cos tan cos tan αββα+<+C .sin tan sin tan αββα> D .tan sin tan sin αββα<12.函数()sin ln ||f x x x =⋅的部分图象大致为( )A .B .C .D .二、填空题13.以下关于函数()()21sin 324f x x x R π⎛⎫=-∈ ⎪⎝⎭的结论: ①()y f x =的图象关于直线2x π=-对称; ②()f x 的最小正周期是4π;③()y f x =在区间[]2,3ππ上是减函数; ④()y f x =的图象关于点,02π⎛⎫- ⎪⎝⎭对称.其中正确的结论是__________________(写出所有正确结论的序号). 14.将函数()sin 24f x x π⎛⎫=-⎪⎝⎭的图像先向右平移8π个单位,再将横坐标缩短到原来的一半(纵坐标不变)后,得到函数()g x 的图像,则函数()g x 的解析式为_________. 15.已知函数()sin()0,0,2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示,关于函数()y f x =有下列结论:①图象关于点,03π⎛⎫ ⎪⎝⎭对称; ②单调递减区间为2,,63k k k ππππ⎛⎫++∈ ⎪⎝⎭Z ;③若()f x a =,则cos 32a x πω⎛⎫-= ⎪⎝⎭; ④2()()log g x f x x =-有4个零点. 则其中结论正确的有____________(填上所有正确结论的序号)16.已知sin 78a =︒,cos10b =︒,tan 55c =︒,则a ,b ,c 的大小关系为______.17.函数f (x )=A sin(ωx +φ)(00)2A πωϕ>><,,的部分图象如图所示,则f (0)的值为___________.18.如图,某公园要在一块圆心角为3π,半径为20m 的扇形草坪OAB 中修建一个内接矩形文化景观区域CDEF ,若//EF AB ,则文化景观区域面积的最大值为______2m .19.已知函数()sin()f x A x ωϕ=+(其中0A >,0,0ωϕπ><<)的图象关于点M 5(,0)12π成中心对称,且与点M 相邻的一个最低点为2(,3)3π-,则对于下列判断: ①直线2x π=是函数()f x 图象的一条对称轴;②函数()3y f x π=-为偶函数;③函数1y =与35()()1212y f x x ππ=-≤≤的图象的所有交点的横坐标之和为7π. 其中正确的判断是__________________.(写出所有正确判断的序号) 20.设函数()y f x =的定义域为D ,若对任意的1x ∈D ,总存在2x ∈D ,使得()()121f x f x ⋅=,则称函数()f x 具有性质M .下列结论:①函数3y x x =-具有性质M ; ②函数35x x y =+具有性质M ;③若函数()[]8log 2,0,y x x t =+∈具有性质M ,则510t =; ④若3sin y x a =+具有性质M ,则5a =. 其中正确结论的序号是____________.三、解答题21.广东省清远市美林湖摩天轮是国内最大的屋顶摩天轮,该摩天轮直径为84米,摩天轮的最高点距地面101米,摩天轮匀速转动,每转动一圈需要t 分钟,若小明从摩天轮的最低点处登上摩天轮,从小明登上摩天轮的时刻开始计时.(1)求小明与地面的距离y (米)与时间x (分钟)的函数关系式;(2)在摩天轮转动一圈过程中,小明的高度在距地面80米以上的时间不少于5分钟,求t 的最小值.22.已知函数()()sin (0,)2f x A x πωϕωϕ=+><部分图象如图所示.(1)求ω和ϕ的值;(2)求函数()f x 在[,]-ππ上的单调递增区间;(3)设()1212x f x f x ππϕ⎛⎫⎛⎫=--+ ⎪ ⎪⎝⎭⎝⎭,已知函数2()2()3()21g x x x a ϕϕ=-+-在,62ππ⎡⎤⎢⎥⎣⎦上存在零点,求实数a 的最小值和最大值. 23.在①()f x 的图象关于直线3x π=对称,②()f x 的图象关于点,06π⎛⎫-⎪⎝⎭对称,③()f x 的图象上最高点中,有一个点的横坐标为6π这三个条件中任选一个,补充在下面问题中,并解答.问题:已知函数()()sin 0,0,02f x A x A πωϕωϕ⎛⎫=+>><<⎪⎝⎭的振幅为2,初相为3π,最小正周期不小于...π,且______.(1)求()f x 的解析式;(2)求()f x 在区间[],0π-上的最大值和最小值以及取得最大值和最小值时自变量x 的值.注:如果选择多个条件分别解答,按第一个解答计分.24.定义行列式运算法则为:12142334a aa a a aa a=-,已知函数()2cos cos2sin23x xf xx=.(1)求()f x的最小正周期;(2)若函数()()02g x f x m mπ⎛⎫=+<<⎪⎝⎭是偶函数,求不等式()0g x≤的解集. 25.已知函数()()sin0,2f x xπωϕωϕ⎛⎫=+><⎪⎝⎭的部分图象如图所示:(1)求()f x的解析式;(2)将()f x的图象上所有的点横坐标缩短到原来的12,纵坐标不变,得到函数()g x的图象求方程()12g x=在[]0,π的实数解.26.设函数()3sin(0)4f x xπωω⎛⎫=+>⎪⎝⎭,且以23π为最小正周期.(1)求函数()f x的单调递减区间;(2)当,32xππ⎡⎤∈⎢⎥⎣⎦时,求()f x的值域.【参考答案】***试卷处理标记,请不要删除一、选择题1.A解析:A【分析】根据题意有()5sin226g x xϕπ⎛⎫=+⎪⎝⎭-,若()g x为偶函数则52()62k k Zπππϕ-=+∈,结合0ϕ>可得出答案.【详解】解:由题意可得()()55()sin 2sin 2266g x f x x x πϕϕϕπ⎛⎫⎛⎫=+=+-=+ -⎪⎪⎝⎭⎝⎭因为()g x 为偶函数,则52()62k k Z πππϕ-=+∈,即2()32k k Z ππϕ=+∈ 因为0ϕ>,所以当1k =-时ϕ取得最小值6π. 故选:A. 【点睛】应用函数奇偶性可解决的四类问题及解题方法(1)求函数值:将待求值利用奇偶性转化为已知区间上的函数值求解;(2)求解析式:先将待求区间上的自变量转化到已知区间上,再利用奇偶性求解,或充分利用奇偶性构造关于()f x 的方程(组),从而得到()f x 的解析式;(3)求函数解析式中参数的值:利用待定系数法求解,根据()()0f x f x ±-=得到关于待求参数的恒等式,由系数的对等性得参数的值或方程(组),进而得出参数的值; (4)画函数图象和判断单调性:利用奇偶性可画出另一对称区间上的图象及判断另一区间上的单调性.2.C解析:C 【分析】先根据条件写出图像变换后的函数解析式,然后根据图像关于原点中心对称可知函数为奇函数,由此得到ϕ的表示并计算出sin 2ϕ的结果. 【详解】因为变换平移后得到函数sin 26y x πϕ⎛⎫=++ ⎪⎝⎭,由条件可知sin 26y x πϕ⎛⎫=++ ⎪⎝⎭为奇函数,所以6k πϕπ+=,sin 2sin 2sin 33k ππϕπ⎛⎫⎛⎫=-=-= ⎪ ⎪⎝⎭⎝⎭故选C . 【点睛】本题考查三角函数的图像变换以及根据函数奇偶性判断参数值,难度一般.正弦型函数()()sin f x A x =+ωϕ为奇函数时,k k Z ϕπ=∈,为偶函数时,2k k Z πϕπ=+∈.3.D解析:D 【分析】由题意可得()01f =-,()31f =,所要解的不等式等价于()()0(2sin 1)3f f x f ≤+≤,再利用单调性脱掉f ,可得02sin 13x ≤+≤,再结合正弦函数的图象即可求解. 【详解】由|(2sin 1)|1f x +≤可得1(2sin 1)1f x -≤+≤, 因为()0,1A -,()3,1B 是函数()f x 图象上的两点,所以()01f =-,()31f =,所以()()0(2sin 1)3f f x f ≤+≤, 因为()f x 是定义在R 上的增函数, 可得02sin 13x ≤+≤,解得:1sin 12x -≤≤, 由正弦函数的性质可得722,66k x k k Z ππππ-+≤≤+∈, 所以原不等式的解集为722,66xk x k k ππππ⎧⎫-≤≤+∈⎨⎬⎩⎭Z ∣, 故选:D 【点睛】关键点点睛:本题解题的关键点是将要解得不等式转化为()()0(2sin 1)3f f x f ≤+≤利用单调性可得02sin 13x ≤+≤.4.D解析:D 【分析】由图可得函数的零点就是11y x =-和2cos y x π=交点的横坐标,画出函数图象,可得出()f x 在[]3,5-有8个零点,且关于1x =对称,即可求出.【详解】()()112cos 20212cos 11f x x x x x ππ=++=-⎡⎤⎣⎦--, 令()0f x =,则12cos 1x x π=-, 则函数的零点就是11y x =-和2cos y x π=交点的横坐标, 可得11y x =-和2cos y x π=的函数图象都关于1x =对称,则交点也关于1x =对称, 画出两个函数的图象,观察图象可知,11y x =-和2cos y x π=在[]3,5-有8个交点, 即()f x 有8个零点,且关于1x =对称,故所有零点的和为428⨯=. 故选:D. 【点睛】本题考查求函数的零点之和,解题的关键是将题目化为找11y x =-和2cos y x π=交点的横坐标,从而通过函数图象求解.5.B解析:B 【分析】根据已知求出矢2=,弦243AD ==. 【详解】由题意可得:823=43AOB ππ∠=,4OA =,在Rt AOD 中,可得:3AOD π∠=,6DAO π∠=,114222OD AO ==⨯=, 可得:矢422=-=, 由3sin433AD AO π=== 可得:弦243AD == 所以:弧田面积12=(弦⨯矢+矢221)(4322)43292=+=≈平方米.故选:B 【点睛】方法点睛:有关扇形的计算,一般是利用弧长公式l r α=、扇形面积公式12S lr =及直角三角函数求解.6.C解析:C 【分析】作出函数1sin3y x =-的图像,利用割补法,补成长方形,计算面积即可. 【详解】作出函数1sin3y x =-的图象,如图所示,利用割补法,将23π到π部分的图象与x 轴围成的图形补到图中3π到23π处阴影部分,凑成一个长为3π,宽为2的长方形,后面π到53π,同理;∴1sin3y x =-的图象与直线3x π=,53x π=及x 轴所围成的面积为24233ππ⨯=,故选:C. 【点睛】用“五点法”作()sin y A ωx φ=+的简图,主要是通过变量代换,设z x ωϕ=+,由z 取0,2π,π,32π,2π来求出相应的x ,通过列表,计算得出五点坐标,描点后得出图象. 7.D解析:D 【分析】根据正弦函数性质周期,对称性,图象变换判断各选项. 【详解】函数()f x 的最小正周期为π,故3π是函数()f x 的一个周期,A 正确; 当3x π=时,sin 203x π⎛⎫+= ⎪⎝⎭,故B 正确; 当712x π=时,函数()f x 取得最小值,712x π=为对称轴,C 正确; 函数图象向左平移6π个单位后函数解析式为sin 2163y x ππ⎡⎤⎛⎫=+++ ⎪⎢⎥⎝⎭⎣⎦,即2sin 213y x π⎛⎫=++ ⎪⎝⎭,不是偶函数,图象不关于y 轴对称,D 错误.故选:D. 【点睛】本题考查正弦型函数的性质,考查周期的概念,对称轴与对称中心、奇偶性等性质,属于基础题.8.B解析:B 【解析】31()3sin(2)cos(2)2(sin(2)cos(2))2sin(2)226f x x x x x x πθθθθθ=+++=+++=++,由于()f x 为偶函数,则(0)2sin()26f πθ=+=±,sin()1,662k πππθθπ+=±+=+,3k πθπ=+,当0k =时,3πθ=,()2sin(2)2sin(2)362f x x x πππ=++=+2cos 2x =,当[0,]4x π∈时,2[0,]2x π∈,()2cos 2f x x =为减函数,符合题意,所以选B.9.B解析:B 【分析】求出弦长,再求出圆的半径,然后利用三角形面积求解. 【详解】如图,由题意8CD =,弓琖ACB 的面积为128,1(8)81282AB ⨯+⨯=,24AB =, 设所在圆半径为R ,即OA OB R ==,则22224(8)2R R ⎛⎫=-+ ⎪⎝⎭,解得13R =, 5OD =,由211sin 22AB OD OA AOB ⨯=∠得 2245120sin 13169AOB ⨯∠==. 故选:B .【点睛】关键点点睛:本题考查扇形与弓形的的有关计算问题,解题关键是读懂题意,在读懂题意基础上求出弦长AB ,然后求得半径R ,从而可解决扇形中的所有问题.10.D解析:D 【分析】利用题干中的已知条件求得2ω=,可得出()sin 216f x x π⎛⎫=-+ ⎪⎝⎭,利用正弦型函数的对称性可判断①②的正误,利用正弦型函数的值域可判断③的正误,求出方程()1f x =在[]0,2π上的解,可判断④的正误. 【详解】N ω*∈,由55,126x ππ⎡⎤∈⎢⎥⎣⎦可得55126666x πωπππωπω-≤-≤-, 由于函数()()sin 16f x x N πωω*⎛⎫=-+∈ ⎪⎝⎭在55,126ππ⎡⎤⎢⎥⎣⎦上单调递减, 所以,()553,2,21266622k k k Z πωππωπππππ⎡⎤⎡⎤--⊆++∈⎢⎥⎢⎥⎣⎦⎣⎦,所以,521262532662k k ωππππωππππ⎧-≥+⎪⎪⎨⎪-≤+⎪⎩,解得()248121055k k k Z ω++≤≤∈,由248121055k k ++≤,解得16k ≤,N ω*∈且k Z ∈,0k ∴=,可得825ω≤≤,2ω∴=,则()sin 216f x x π⎛⎫=-+ ⎪⎝⎭.对于①,sin 2sin 00126ππ⎛⎫⨯-== ⎪⎝⎭,所以,112f π⎛⎫= ⎪⎝⎭, 所以,函数()f x 的图象关于点,112π⎛⎫⎪⎝⎭成中心对称,①错误; 对于②,271sin 2sin 13662πππ⎛⎫⨯-==-≠± ⎪⎝⎭,②错误;对于③,当,2x ππ⎡⎤∈⎢⎥⎣⎦时,5112,666x πππ⎡⎤-∈⎢⎥⎣⎦,则11sin 262x π⎛⎫-≤-≤ ⎪⎝⎭, 所以,()302f x ≤≤,即()f x 在,2ππ⎡⎤⎢⎥⎣⎦上的值域为30,2⎡⎤⎢⎥⎣⎦,③正确; 对于④,当[]0,2x π∈时,232,666x πππ⎡⎤-∈-⎢⎥⎣⎦, 令()1f x =,可得sin 206x π⎛⎫-= ⎪⎝⎭,206x π∴-=或26x ππ-=或226x ππ-=或236x ππ-=.所以,方程()1f x =在[]0,2π有4个不相同的根,④正确. 故选:D. 【点睛】方法点睛:求函数()()sin f x A x =+ωϕ在区间[],a b 上值域的一般步骤: 第一步:三角函数式的化简,一般化成形如()sin y A x k ωϕ=++的形式或()cos y A x k ωϕ=++的形式;第二步:由x 的取值范围确定x ωϕ+的取值范围,再确定()sin x ωϕ+(或()cos x ωϕ+)的取值范围;第三步:求出所求函数的值域(或最值).11.D解析:D 【分析】对A ,由()sin tan f x x x =+在52,2ππ⎛⎫⎪⎝⎭上单调递增可判断;对B ,由()cos tan f x x x =-在52,2ππ⎛⎫ ⎪⎝⎭上单调递减可判断;对C ,由()sin tan f x x x =在52,2ππ⎛⎫⎪⎝⎭上单调递增可判断;对D ,由tan ()sin x f x x =在52,2ππ⎛⎫⎪⎝⎭上单调递增可判断. 【详解】A .设()sin tan f x x x =+,则()f x 在52,2ππ⎛⎫⎪⎝⎭上单调递增, 因为αβ>,所以()()f αf β>,所以sin tan sin tan ααββ+>+,所以sin sin tan tan αββα->-,所以A 对,不符合题意;B .设()cos tan f x x x =-,则()f x 在52,2ππ⎛⎫⎪⎝⎭上单调递减, 因为αβ>,所以()()f f αβ<,所以cos tan cos tan ααββ-<-, 所以cos tan cos tan αββα+<+,所以B 对,不符合题意; C .设()sin tan f x x x =,因为sin ,tan x x 在52,2ππ⎛⎫⎪⎝⎭都为正数,且都单调递增, 所以()sin tan f x x x =在52,2ππ⎛⎫⎪⎝⎭上单调递增, 因为αβ>,所以()()f αf β>,所以sin tan sin tan ααββ>,所以sin tan sin tan αββα>,所以C 对,不符合题意; D .设tan ()sin x f x x =,则tan 1()sin cos x f x x x ==在52,2ππ⎛⎫⎪⎝⎭上单调递增, 因为αβ>,所以()()f αf β>,所以tan tan sin sin αβαβ>, 所以tan sin tan sin αββα>,所以D 错,符合题意. 故选:D. 【点睛】本题考查利用三角函数的单调性比较大小,解题的关键是恰当构造函数,判断函数的单调性,利用单调性判断大小.12.D解析:D 【分析】先根据函数的奇偶性,可排除A ,C ,根据当01x <<时,()0f x <即可排除B .得出答案. 【详解】因为()sin ln ||(0)f x x x x =⋅≠,所以()sin()ln ||sin ln ||()f x x x x x f x -=-⋅-=-=-,所以()f x 为奇函数,故排除A ,C .当01x <<时,sin 0x >,ln ||0x <,则()0f x <,故排除B , 故选:D .【点睛】思路点睛:函数图象的辨识可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置. (2)从函数的单调性,判断图象的变化趋势; (3)从函数的奇偶性,判断图象的对称性; (4)从函数的特征点,排除不合要求的图象.二、填空题13.①②③【分析】利用正弦型函数的对称性可判断①④的正误;利用正弦型函数的周期公式可判断②的正误;利用正弦型函数的单调性可判断③的正误【详解】对于①所以的图象关于直线对称①正确;对于②的最小正周期是②正解析:①②③ 【分析】利用正弦型函数的对称性可判断①④的正误;利用正弦型函数的周期公式可判断②的正误;利用正弦型函数的单调性可判断③的正误. 【详解】 对于①,212sin 232243f πππ⎡⎤⎛⎫⎛⎫-=⨯--=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦, 所以,()y f x =的图象关于直线2x π=-对称,①正确; 对于②,()f x 的最小正周期是2412T ππ==,②正确; 对于③,当23x ππ≤≤时,3154244x πππ≤-≤, 所以,函数()y f x =在区间[]2,3ππ上是减函数,③正确; 对于④,由①可知,④错误. 故答案为:①②③. 【点睛】方法点睛:求较为复杂的三角函数的单调区间时,首先化简成()sin y A ωx φ=+形式,再求()sin y A ωx φ=+的单调区间,只需把x ωϕ+看作一个整体代入sin y x =的相应单调区间内即可,注意要先把ω化为正数.14.【分析】利用函数的图象变换规律即可得到的解析式【详解】函数的图像先向右平移个单位后解析式变为:再将横坐标缩短到原来的一半(纵坐标不变)后解析式变为:所以故答案为:【点睛】方法点睛:函数的图像与函数的 解析:cos 4x -【分析】利用函数()()sin f x A x =+ωϕ的图象变换规律,即可得到()g x 的解析式. 【详解】函数()sin 24f x x π⎛⎫=-⎪⎝⎭的图像先向右平移8π个单位后解析式变为: sin 2sin 2co 288s 2y x x x πππ⎡⎤⎛⎫⎛⎫=--=-=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,再将横坐标缩短到原来的一半(纵坐标不变)后解析式变为:()cos 22x y -=⨯,所以()cos 4g x x =-. 故答案为:cos 4x -. 【点睛】方法点睛:函数sin ωφf xA xB 的图像与函数sin y x =的图像两者之间可以通过变化A ,ω,φ,B 来相互转化,A 、ω影响图像的形状,φ、B 影响图像与x 轴交点的位置,由A 引起的变换称为振幅变换,由ω引起的变换称为周期变换,它们都是伸缩变换;由φ引起的变换称为相位变换,由B 引起的变换称为上下平移变换,它们都是平移变换.三角函数图像变换的两种方法为先平移后伸缩和先伸缩后平移.15.②③【分析】先根据图象结合已知条件限制求出的解析式再利用代入验证法判断①错误;利用整体代入法求单调区间判断②正确;解方程并结合诱导公式判断③正确;将函数零点问题转化成函数交点问题数形结合判断④错误即解析:②③ 【分析】先根据图象,结合已知条件限制求出()y f x =的解析式,再利用代入验证法判断①错误;利用整体代入法求单调区间判断②正确;解方程并结合诱导公式判断③正确;将函数零点问题转化成函数交点问题,数形结合判断④错误即可. 【详解】由图象可知,2A =,(0)2sin 1f ϕ==,故1sin 2ϕ=,又2πϕ<,故6π=ϕ,故()2sin 6f x x πω⎛⎫=+⎪⎝⎭,又由11112sin 012126f πππω⎛⎫⎛⎫=+=⎪ ⎪⎝⎭⎝⎭得,112,126k k Z ππωπ+=∈,即224,1111kk Z ω=-+∈, 由题意0>ω,由图知1112T π>,即22411T πω=<,故1k =时2ω=.故()2sin 26f x x π⎛⎫=+ ⎪⎝⎭.①因为252sin 2sin 103366f ππππ⎛⎫⎛⎫=+==≠⎪ ⎪⎝⎭⎝⎭,故点,03π⎛⎫ ⎪⎝⎭不是()y f x =图象的对称中心,故错误; ②令322,2,622x k k k Z πππππ⎛⎫+∈++∈ ⎪⎝⎭, 解得单调递减区间为2,,63k k k ππππ⎛⎫++∈⎪⎝⎭Z ,故正确;③若()2sin 26f x x a π⎛⎫=+= ⎪⎝⎭,则sin 262a x π⎛⎫+= ⎪⎝⎭, 则cos cos 2sin 2sin 2332362a x x x x πππππω⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫-=-=+-=+= ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦,故正确; ④令2()()log 0g x f x x =-=,得方程2()log f x x =的根的问题,即函数()2sin 26y f x x π⎛⎫==+ ⎪⎝⎭与函数2log y x =的交点个数问题,如图,令22,62x k k Z πππ+=+∈,则,6x k k Z ππ=+∈时()y f x =取得最大值2.如图,6x π=时,2()log f x x >;76x π=时,746π<,227log log 426π<=2()2log f x x =>;当136x π=时,1346π>,2213log log 426π>=,2()2log f x x =<. 故函数()2sin 26y f x x π⎛⎫==+ ⎪⎝⎭与函数2log y x =有3个交点,即2()()log g x f x x =-有3个零点.故错误. 故答案为:②③. 【点睛】方法点睛:判断函数零点个数的方法(1)直接法:令()0f x =,如果能求出解,那么有几个不同的解就有几个零点; (2)利用函数的零点存在性定理:利用函数的零点存在性定理时,不仅要求函数的图象在区间[],a b 上是连续不断的曲线,并且()()0f a f b ⋅<,还必须结合函数的图象与性质,(如单调性、奇偶性)才能确定函数有多少个零点;(3)图象法:画出函数()f x 的图象,函数()f x 的图象与x 轴交点的个数就是函数()f x 的零点个数;将函数()f x 拆成两个函数,()h x 和()g x 的形式,根据()0f x =等价于()()h x g x =,则函数()f x 的零点个数就是函数()y h x =和()y g x =的图象交点个数;(4)利用函数的性质:若能确定函数的单调性,则其零点个数不难得到,若所考查的函数是周期函数,则需要求出在一个周期内的零点个数,根据周期性则可以得出函数的零点个数.16.【分析】同角三角函数关系知又由的区间单调性知根据的区间单调性知即可知的大小关系【详解】而∴故答案为:【点睛】本题考查了比较三角函数值的大小根据正弦函数正切函数的区间单调性及正弦函数的值域范围比较函数 解析:c b a >>【分析】同角三角函数关系知sin 80b =︒,又由sin y x =的区间单调性知b a >,根据tan y x =的区间单调性知1c >,即可知a ,b ,c 的大小关系 【详解】cos10cos(9080)sin80sin 78b a =︒=︒-︒=︒>=︒,而tan 55tan 451c =︒>︒=∴c b a >> 故答案为:c b a >> 【点睛】本题考查了比较三角函数值的大小,根据正弦函数、正切函数的区间单调性及正弦函数的值域范围,比较函数值的大小17.【分析】由图可得的周期振幅即可得再将代入可解得进一步求得解析式及【详解】由图可得所以即又即又故所以故答案为:【点睛】本题考查由图象求解析式及函数值考查学生识图计算等能力是一道中档题解析: 【分析】由图可得()f x 的周期、振幅,即可得,A ω,再将(,0)6π代入可解得ϕ,进一步求得解析式及()0f . 【详解】由图可得2A =,1()46124T πππ=--=,所以2T ππω==,即2ω=,又()06f π=,即2sin(2)06πϕ⨯+=,,3k k Z πϕπ+=∈,又||2ϕπ<,故3πϕ=-,所以()sin()f x x π=-223,(0)2sin()3f π=-=故答案为: 【点睛】本题考查由图象求解析式及函数值,考查学生识图、计算等能力,是一道中档题.18.【分析】取中点连结交于点交于点连结设推导出和从而得出文化景观区域面积利用三角函数的性质解出面积最大值【详解】取中点连结交于点交于点连结设则文化景观区域面积:当即时文化景观区域面积取得最大值为故答案为解析:(4002【分析】取DC 中点M ,连结OM ,交EF 于点P ,交CD 于点N ,连结OD ,设DOM ϕ∠=,推导出DC 和CF ,从而得出文化景观区域面积,利用三角函数的性质,解出面积最大值. 【详解】取DC 中点M ,连结OM ,交EF 于点P ,交CD 于点N ,连结OD ,设DOM ϕ∠=,则20sin DN CN ϕ==,40sin DC ϕ∴=,20cos 20cos 203tan 30PFCF DE PN ON OP ϕϕϕ===-=-=-︒,∴文化景观区域面积:()4020203EFCD S sin cos sin ϕϕϕ=-矩形400sin 24003(1cos2)ϕϕ=-- 800sin(2)40033πϕ=+-∴当232ππϕ+=,即12πϕ=时,文化景观区域面积取得最大值为2400(23)()m .故答案为:400(23). 【点睛】本题考查文化景观区域面积的最大值的求法,考查扇形、三角函数恒等变换等基础知识,考查运算求解能力,是中档题.19.②③【分析】根据已知条件确定函数的解析式进一步利用整体思想确定函数的对称轴方程对称中心及各个交点的特点进一步确定答案【详解】函数(其中)的图象关于点成中心对称且与点相邻的一个最低点为则:所以进一步解解析:②③ 【分析】根据已知条件确定函数的解析式,进一步利用整体思想确定函数的对称轴方程,对称中心及各个交点的特点,进一步确定答案. 【详解】函数()()sin f x A x ωϕ=+(其中0A >,0,0ωϕπ><<)的图象关于点M 5,012π⎛⎫⎪⎝⎭成中心对称,且与点M 相邻的一个最低点为2,33π⎛⎫- ⎪⎝⎭,, 则:2543124T πππ-== , 所以T π=: ,326f x sin x π⎛⎫=+ ⎪⎝⎭().进一步解得:223A πωπ===, 由于()()sin f x A x ωϕ=+(其中0A >,0,0ωϕπ><<)的图象关于点M 5,012π⎛⎫⎪⎝⎭成中心对称,,所以:5212k k Z πϕπ⋅+∈=(), 解得:5,6k k Z πϕπ-∈= ,由于0ϕπ<<, 所以:当1k = 时,6πϕ=.所以: ①当2x π=时,33262f sin πππ⎛⎫=+=- ⎪⎝⎭().故错误. ②3232633f x sin x cos x πππ⎡⎤⎛⎫⎛⎫--+=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦=. 则3y f x π⎛⎫=- ⎪⎝⎭为偶函数,故正确. ③由于:351212x ππ-≤≤, 则:0266x ππ≤+≤,所以函数()f x 的图象与1y =有6个交点. 根据函数的交点设横坐标为123456x x x x x x 、、、、、, 根据函数的图象所有交点的横标和为7π.故正确. 故答案为②③ 【点睛】本题考查的知识要点:正弦型函数的解析式的求法,主要确定A ,ω、φ的值,三角函数诱导公式的变换,及相关性质得应用,属于基础题型.20.②③【分析】根据函数性质的定义结合每个选项中具体函数的定义即可判断【详解】①当时显然不存在是的故①错误;②是单调增函数其值域为对任意的总存在使得故②正确;③函数在上是单调增函数其值域为要使得其具有性解析:②③【分析】根据函数性质M 的定义,结合每个选项中具体函数的定义,即可判断. 【详解】①当10x =时,显然不存在2x ,是的()()121f x f x =,故①错误; ②35x x y =+是单调增函数,其值域为()0,∞+,对任意的1x ∈D ,总存在2x ∈D ,使得()()121f x f x ⋅=,故②正确; ③函数()8log 2y x =+在[]0,t 上是单调增函数,其值域为()88log 2,log 2t ⎡⎤+⎣⎦要使得其具有M 性质,则88881log 2log (2)1log (2)log 2t t ⎧≤⎪+⎪⎨⎪+≤⎪⎩,即()88log 2log 21t ⨯+=,解得()328t +=,故510t =.故③正确;④若函数3y sinx a =+具有性质M ,一方面函数值不可能为零,也即30sinx a +≠对任意的x 恒成立, 解得3a >或3a <-,在此条件下, 另一方面,13y sinx a=+的值域是3y sinx a =+值域的子集.3y sinx a =+的值域为[]3,3a a -+, 13y sinx a =+的值域为11,33a a ⎡⎤⎢⎥+-⎣⎦要满足题意,只需113,333a a a a ≥-≤++-, 解得291a -=,故a =故④错误. 综上所述,正确的是②③. 故答案为:②③ 【点睛】本题考查函数新定义问题,涉及正弦函数值域的求解,对数函数值域的求解,属综合中档题.三、解答题21.(1)242cos 59y x tπ⎛⎫=-+ ⎪⎝⎭(0x ,t 为参数);(2)15. 【分析】(1)以摩天轮最低点为原点,最低点的切线为x 轴建立直角坐标系,设sin()y A x b ωϕ=++,根据最高点和最低点的距离,求得,A b 的值,进而求得,ωϕ的值,即可求解.(2)由80y ≥,得到21cos 2x t π⎛⎫≤- ⎪⎝⎭,得到2533t t -≥,即可求解.【详解】(1)如图所示,以摩天轮最低点为原点,最低点的切线为x 轴建立直角坐标系, 由题意可设sin()(0,0,0)y A x b A b ωϕω=++>>因为摩天轮的最高点距地面101m ,最低点距地面1018417(m)-=,所以101,17,A b A b +=⎧⎨-+=⎩解得42,59A b ==,又函数周期为t ,可得2t πω=,所以242sin 59(0)y x x t πϕ⎛⎫=++⎪⎝⎭. 又0x =时,17y =,所以21742sin 059t πϕ⎛⎫=⨯++⎪⎝⎭,即sin 1,ϕϕ=-可取2π-,所以2242sin 5942cos 592y x x t tπππ⎛⎫⎛⎫=-+=-+ ⎪⎪⎝⎭⎝⎭(0x ≥,t 为参数). (2)依题意,可知242cos 5980y x t π⎛⎫=-+≥ ⎪⎝⎭,即21cos 2x tπ⎛⎫≤- ⎪⎝⎭,不妨取第一圈,可得2242,3333t tx x t πππ≤≤≤≤, 所以持续时间为2533t t-≥,即15t ≥,所以t 的最小值为15.【点睛】三角函数实际应用问题的处理策略: 1、已知函数模型求解数学问题;2、把实际问题抽象转化成数学问题,利用三角函数的有关知识解决问题;3、根据实际问题转化为已知条件转化为三角函数的解析式和图象,然后在根据数形结合思想研究三角函数的性质,进而加深理解函数的性质. 22.(1)ω=2,6π=ϕ;(2)5,6ππ⎡⎤--⎢⎥⎣⎦,,36ππ⎡⎤-⎢⎥⎣⎦,2π,π3;.(3)最小值为12,最大值为1716. 【分析】(1)先由函数图象,先得到周期,求出ω,再由最大值点,求出ϕ;(2)由(1)的结果,确定函数解析式,利用正弦函数的单调性,求出函数增区间,再由给定区间,即可得出结果;(3)先化简得到()sin 23x x πϕ⎛⎫=- ⎪⎝⎭,根据函数()g x 在,62ππ⎡⎤⎢⎥⎣⎦上存在零点,得到222sin 23sin 2133ππa x x ⎛⎫⎛⎫=--+-+ ⎪ ⎪⎝⎭⎝⎭在,62ππ⎡⎤⎢⎥⎣⎦上有解,令sin 23t x π⎛⎫=- ⎪⎝⎭,由正弦函数性质,求出,62x ππ⎡⎤⎢⎥⎣⎦时,[]0,1t ∈,再结合二次函数的性质,得到2231y t t =-++的范围,即可得出结果.【详解】 (1)由图象可知:22362T πππ=-=,T π=,则22Tπω==, 又22,62k k Z ππϕπ⨯+=+∈得26k πϕπ=+,又2πϕ<,所以6π=ϕ, (2)()sin 26f x x π⎛⎫+⎝=⎪⎭,由222,262k x k k Z πππππ-≤+≤+∈得,,36k x k k Z ππππ-≤≤+∈,令1k =-,得4536x ππ-≤≤-,因x ππ-≤≤,则56x ππ-≤≤-, 令0k =,得36x ππ-≤≤,令1k =,得2736x ππ≤≤,因x ππ-≤≤,则2ππ3x ,所以()f x 在[,]-ππ上的单调递增区间为5,6ππ⎡⎤--⎢⎥⎣⎦,,36ππ⎡⎤-⎢⎥⎣⎦,2π,π3;. (3)()sin 2sin 21212126126x f x f x x x ππππππϕ⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=--+=-+-++ ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦1sin 2sin 2sin 22sin 2323x x x x x ππ⎛⎫⎛⎫=-+==- ⎪ ⎪⎝⎭⎝⎭,2()2sin 23sin 22133g x x x a ππ⎛⎫⎛⎫=---+- ⎪ ⎪⎝⎭⎝⎭,由函数()g x 在,62ππ⎡⎤⎢⎥⎣⎦上存在零点,则222sin 23sin 2133ππa x x ⎛⎫⎛⎫=--+-+ ⎪ ⎪⎝⎭⎝⎭在,62ππ⎡⎤⎢⎥⎣⎦上有解, 令sin 23t x π⎛⎫=-⎪⎝⎭,由,62x ππ⎡⎤∈⎢⎥⎣⎦,则220,33x ππ⎡⎤-∈⎢⎥⎣⎦,即[]0,1t ∈,则223171723121,488y t t t ⎛⎫⎡⎤=-++=--+∈ ⎪⎢⎥⎝⎭⎣⎦, 所以17128a ≤≤,即117216a ≤≤, 故a 的最小值为12,最大值为1716. 【点睛】 思路点睛:求解含三角函数的二次式在给定区间上的最值时,一般需要用换元法,将三角函数换成t 来表示,得到关于t 的二次函数,由三角函数的性质,得到t 的范围,再结合二次函数的性质,即可求解.23.(1)见解析(2)见解析 【分析】(1)由题意可知2,3A πϕ==,选择条件①,由正弦函数的对称性求出ω,进而得出解析式;选择条件②,由正弦函数的对称性求出ω,进而得出解析式;选择条件③,由正弦函数的性质求出ω,进而得出解析式;(2)由[],0x π∈-,求出x ωϕ+的范围,再结合正弦函数的性质求出最值. 【详解】(1)由题意可知2,3A πϕ==选择条件①因为()f x 的图象关于直线3x π=对称,所以332k πππωπ+=+,解得13,2k k Z ω=+∈ 由21321302k k k Zππ⎧≥⎪+⎪⎪⎨⎪+>⎪⎪∈⎩,解得0k =,即12ω=故1()2sin 23f x x π⎛⎫=+ ⎪⎝⎭选择条件②因为()f x 的图象关于点,06π⎛⎫-⎪⎝⎭对称,所以,26,63k k k Z ππωπω-+==-∈由226260k k k Zππ⎧≥⎪-⎪⎨->⎪⎪∈⎩,解得0k =,即2ω=故()2sin 23f x x π⎛⎫=+ ⎪⎝⎭选择条件③因为()f x 的图象上最高点中,有一个点的横坐标为6π,所以2,632k k Z πππωπ+=+∈,解得112,k k Z ω=+∈由21121120kk k Zππ⎧≥⎪+⎪⎨+>⎪⎪∈⎩,解得0k =,即1ω= 故()2sin 3f x x π⎛⎫=+ ⎪⎝⎭(2)选择条件①1,2363x πππ⎡⎤+∈-⎢⎥⎣⎦当1236x ππ+=-,即x π=-时,min ()2sin 16f x π⎛⎫=-=- ⎪⎝⎭当1233x ππ+=,即0x =时,max ()2sin 3f x π==选择条件②52,333x πππ⎡⎤+∈-⎢⎥⎣⎦当5233x ππ+=-或233x ππ+=,即x π=-或0x =时,max ()2sin 3f x π==当232x ππ+=-,即512x π=-时,min ()2sin 22f x π⎛⎫=-=- ⎪⎝⎭选择条件③2,333x πππ⎡⎤+∈-⎢⎥⎣⎦当33x ππ+=,即0x =时,max ()2sin3f x π==当32x ππ+=-,即65x π=-时,min ()2sin 22f x π⎛⎫=-=- ⎪⎝⎭【点睛】关键点睛:解决本题的关键是将正弦型函数的问题转化为正弦函数的性质进行求解,利用已知知识解决未知问题. 24.(1)π;(2),,1212k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦.【分析】(1)先利用题中定义计算化简行列式,再利用周期的公式计算即可;(2)先利用()g x 是偶函数计算参数m ,再结合余弦函数图象与性质解不等式即可. 【详解】解:(1)依题意得,()22cos 2sin cos 2sin x f x x x x x==-sin 2x x =-2cos 26x π⎛⎫=++ ⎪⎝⎭故()f x 的最小正周期为:22T ππ==; (2)函数()()2cos 22cos 2266g x x m x m ππ⎡⎤⎛⎫=++=++ ⎪⎢⎥⎣⎦⎝⎭ 故2,6m k k Z ππ+=∈,即,122k m k Z ππ=-+∈, 又02m π<<可知,1k =时512m π=,故5()2cos 222cos 2126g x x x ππ⎛⎫=+⋅+=- ⎪⎝⎭. 故不等式()0g x ≤,即2cos20x -≤,即cos 22x ≥, 结合余弦函数图象与性质可知,222,66k x k k Z ππππ-+≤≤+∈,解得,1212k x k k Z ππππ-+≤≤+∈.故不等式的解集为,,1212k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦.【点睛】 关键点点睛:本题解题关键在于读懂新定义中行列式的计算法则,才能结合三角函数的图象与性质突破难点.25.(1)()sin 6f x x π⎛⎫=+ ⎪⎝⎭;(2)0或3π或π.【分析】(1)先根据函数图象确定出()f x 的最小正周期,再根据最小正周期的计算公式2T ωπ=求解出ω的值,然后代入点,13π⎛⎫⎪⎝⎭结合ϕ的范围求解出ϕ的值,从而()f x 的解析式可求;(2)先根据图象变换求解出()g x 的解析式,然后根据()12g x =得到关于x 的方程,结合[]0,x π∈,求解出x 的值即为方程的实数解. 【详解】(1)因为由图象可知4362T πππ⎛⎫=--= ⎪⎝⎭,所以22T ππω==且0>ω,所以1ω=, 所以()()sin f x x ϕ=+,代入点,13π⎛⎫ ⎪⎝⎭,所以sin 13πϕ⎛⎫+= ⎪⎝⎭且2πϕ<,所以6π=ϕ,所以()sin 6f x x π⎛⎫=+⎪⎝⎭; (2)()f x 的图象上所有的点横坐标缩短到原来的12后得到的函数解析式为:()sin 26g x x π⎛⎫=+ ⎪⎝⎭,因为[]0,x π∈,所以132,666x πππ⎛⎫⎡⎤+∈ ⎪⎢⎥⎝⎭⎣⎦,又因为()12g x =,所以1sin 262x π⎛⎫+= ⎪⎝⎭,所以266x ππ+=或56π或136π,所以0x =或3π或π, 所以方程()12g x =在[]0,π的实数解为:0或3π或π. 【点睛】思路点睛:根据()sin y A ωx φ=+的图象求解函数解析式的步骤: (1)根据图象的最高点可直接确定出A 的值;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
必修四第一章三角函数测试题班别 姓名 分数一、选择题1.已知cosα=12,α∈(370°,520°),则α等于( )A .390°B.420°C.450°D.480° 2.若sinx·tanx<0,则角x 的终边位于( )A .第一、二象限B .第二、三象限C .第二、四象限D .第三、四象限3.函数y =tan x2是( )A .周期为2π的奇函数B .周期为π2的奇函数C .周期为π的偶函数D .周期为2π的偶函数4.已知函数y =2sin(ωx+φ)(ω>0)在区间[0,2π]的图象如图,那么ω等于( )A .1B .2C.12D.135.函数f(x)=cos(3x +φ)的图象关于原点成中心对称,则φ等于( )A .-π2B .2kπ-π2(k∈Z)C.kπ(k∈Z)D.kπ+π2(k∈Z)6.若sinθ+cosθsinθ-cosθ=2,则sinθcosθ的值是( )A .-310B.310C .±310D.347.将函数y =sinx 的图象上所有的点向右平行移动π10个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是( )A .y =sin ⎝ ⎛⎭⎪⎪⎫2x -π10B .y =sin ⎝ ⎛⎭⎪⎪⎫2x -π5C .y =sin ⎝⎛⎭⎪⎪⎫12x -π10D .y =sin ⎝⎛⎭⎪⎪⎫12x -π20 8.在同一平面直角坐标系中,函数y =cos ⎝ ⎛⎭⎪⎪⎫x 2+3π2(x∈[0,2π])的图象和直线y =12的交点个数是( )A .0B .1C .2D .4 9.已知集合M =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x|x =kπ2+π4,k∈Z ,N ={x|x =kπ4+π2,k∈Z}.则( )A .M =NB .M NC .NMD .M∩N=∅10.设a =sin 5π7,b =cos 2π7,c =tan 2π7,则( )A .a<b<cB .a<c<bC .b<c<aD .b<a<c 二、填空题11.已知一扇形的弧所对的圆心角为54°,半径r =20cm ,则扇形的周长为________cm.12.方程sinπx=14x 的解的个数是________.13.已知函数f(x)=2sin(ωx+φ)的图象如图所示,则f(7π12)=________.14.已知函数y =sin πx3在区间[0,t]上至少取得2次最大值,则正整数t 的最小值是________. 三、解答题 15.已知f(α)=sin2π-α·cos 2π-α·tan -π+αsin -π+α·tan -α+3π.(1)化简f(α);(2)若f(α)=18,且π4<α<π2,求cosα-sinα的值;(3)若α=-31π3,求f(α)的值.16.求函数y =3-4sinx -4cos2x 的最大值和最小值,并写出函数取最值时对应的x 的值.17.设函数f(x)=sin(2x +φ)(-π<φ<0),y =f(x)图象的一条对称轴是直线x =π8.(1)求φ;(2)求函数y =f(x)的单调增区间; (3)画出函数y =f(x)在区间[0,π]上的图象.18.在已知函数f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,0<φ<π2)的图象与x 轴的交点中,相邻两个交点之间的距离为π2,且图象上一个最低点为M ⎝⎛⎭⎪⎪⎫2π3,-2. (1)求f(x)的解析式;(2)当x∈⎣⎢⎢⎡⎦⎥⎥⎤π12,π2时,求f(x)的值域.19.如下图所示,函数y =2cos(ωx +θ)(x∈R ,ω>0,0≤θ≤π2)的图象与y 轴交于点(0,3),且该函数的最小正周期为π. (1)求θ和ω的值;(2)已知点A(π2,0),点P 是该函数图象上一点,点Q(x0,y0)是PA 的中点,当y0=32,x0∈[π2,π]时,求x0的值.必修四第一章三角函数测试题(答案) 1、答案B 2、答案B 3、答案A 4、答案B解析由图象知2T =2π,T =π,∴2πω=π,ω=2.5、解析若函数f(x)=cos(3x +φ)的图象关于原点成中心对称,则f(0)=cosφ=0,∴φ=kπ+π2(k∈Z).答案D6、答案B 解析∵sinθ+cosθsinθ-cosθ=tanθ+1tanθ-1=2,∴tanθ=3.∴sinθcosθ=sinθcosθsin2θ+cos2θ=tanθtan2θ+1=310.7、答案C解析函数y =sinxy =sin ⎝⎛⎭⎪⎪⎫x -π10y =sin ⎝⎛⎭⎪⎪⎫12x -π10. 8、答案C 解析函数y =cos ⎝ ⎛⎭⎪⎪⎫x 2+3π2=sin x 2,x∈[0,2π],图象如图所示,直线y =12与该图象有两个交点.9、答案B 解析M =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪⎪x =2k +14π,k∈Z,N =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪⎪x =k +24π,k∈Z. 比较两集合中分式的分子,知前者为奇数倍π,后者为整数倍π.再根据整数分类关系,得M N.选B.10、答案D 解析∵a =sin 5π7=sin(π-5π7)=sin 2π7.2π7-π4=8π28-7π28>0.∴π4<2π7<π2.又α∈⎝ ⎛⎭⎪⎪⎫π4,π2时,sinα>cosα.∴a=sin 2π7>cos 2π7=b.又α∈⎝ ⎛⎭⎪⎪⎫0,π2时,sinα<tanα.∴c=tan 2π7>sin2π7=a.∴c>a.∴c>a>b.11、答案6π+40解析∵圆心角α=54°=3π10,∴l=|α|·r=6π.∴周长为(6π+40) cm.12、答案7解析在同一坐标系中作出y =sinπx 与y =14x 的图象观察易知两函数图象有7个交点,所以方程有7个解.13、答案0解析方法一由图可知,32T =5π4-π4=π,即T =2π3,∴ω=2πT=3.∴y=2sin(3x +φ),将(π4,0)代入上式sin(3π4+φ)=0.∴3π4+φ=kπ,k∈Z,则φ=kπ-3π4,k∈Z.∴f(7π12)=2sin(7π4+kπ-3π4)=0.方法二由图可知,32T =5π4-π4=π,即T =2π3.又由正弦图象性质可知,f(x0)=-f(x0+T2),∴f(7π12)=f(π4+π3)=-f(π4)=0.14、答案8解析T =6,则5T 4≤t,∴t≥152,∴tmin=8.15、解(1)f(α)=sin2α·cosα·tanα-sinα-tanα=sinα·cosα.(2)由f(α)=sinαcosα=18可知(cosα-sinα)2=cos2α-2sinαcosα+sin2α=1-2sinαcosα=1-2×18=34.又∵π4<α<π2,∴cosα<sinα,即cosα-sinα<0.∴cosα-sinα=-32.(3)∵α=-31π3=-6×2π+5π3,∴f ⎝⎛⎭⎪⎪⎫-31π3=cos ⎝ ⎛⎭⎪⎪⎫-31π3·sin ⎝ ⎛⎭⎪⎪⎫-31π3 =cos⎝ ⎛⎭⎪⎪⎫-6×2π+5π3·sin⎝ ⎛⎭⎪⎪⎫-6×2π+5π3=cos5π3·sin 5π3=cos(2π-π3)·sin(2π-π3) =cos π3·⎝ ⎛⎭⎪⎪⎫-sin π3=12·⎝⎛⎭⎪⎪⎫-32=-34.16、解y =3-4sinx -4cos2x =4sin2x -4sinx -1=4⎝⎛⎭⎪⎪⎫sinx -122-2,令t =sinx ,则-1≤t≤1,∴y=4⎝⎛⎭⎪⎪⎫t -122-2 (-1≤t≤1). ∴当t =12,即x =π6+2kπ或x =5π6+2kπ(k∈Z)时,ymin =-2;当t =-1,即x =3π2+2kπ (k∈Z)时,ymax =7.17、解(1)∵x=π8是函数y =f(x)的图象的对称轴,∴sin ⎝⎛⎭⎪⎪⎫2×π8+φ=±1. ∴π4+φ=kπ+π2,k∈Z.∵-π<φ<0,∴φ=-3π4.(2)由(1)知φ=-3π4,因此y =sin ⎝⎛⎭⎪⎪⎫2x -3π4. 由题意得2kπ-π2≤2x-3π4≤2kπ+π2,k∈Z.∴函数y =sin⎝ ⎛⎭⎪⎪⎫2x -3π4的单调增区间为⎣⎢⎢⎡⎦⎥⎥⎤kπ+π8,kπ+5π8,k∈Z. (3)由y =sin ⎝⎛⎭⎪⎪⎫2x -3π4,知18、解(1)由最低点为M ⎝⎛⎭⎪⎪⎫2π3,-2得A =2.由x 轴上相邻两个交点之间的距离为π2,得T 2=π2,即T =π,∴ω=2πT =2ππ=2. 由点M ⎝⎛⎭⎪⎪⎫2π3,-2在图象上得2sin ⎝⎛⎭⎪⎪⎫2×2π3+φ=-2, 即sin ⎝ ⎛⎭⎪⎪⎫4π3+φ=-1,故4π3+φ=2kπ-π2(k∈Z), ∴φ=2kπ-11π6(k∈Z).又φ∈⎝⎛⎭⎪⎪⎫0,π2,∴φ=π6,故f(x)=2sin ⎝⎛⎭⎪⎪⎫2x +π6. (2)∵x∈⎣⎢⎢⎡⎦⎥⎥⎤π12,π2,∴2x+π6∈⎣⎢⎢⎡⎦⎥⎥⎤π3,7π6,当2x +π6=π2,即x =π6时,f(x)取得最大值2;当2x +π6=7π6,即x =π2时,f(x)取得最小值-1,故f(x)的值域为[-1,2].19、解(1)将x =0,y =3代入函数y =2cos (ωx+θ)中,得cosθ=32,因为0≤θ≤π2,所以θ=π6.由已知T =π,且ω>0,得ω=2πT =2ππ=2.(2)因为点A(π2,0),Q(x0,y0)是PA 的中点,y0=32,所以点P 的坐标为(2x0-π2,3).又因为点P 在y =2cos(2x +π6)的图象上,且π2≤x0≤π,所以cos(4x0-5π6)=32,且7π6≤4x0-5π6≤19π6,从而得4x0-5π6=11π6,或4x0-5π6=13π6,即x0=欧阳数创编欧阳数创编 2π3,或x0=3π4.。
