最新初二数学下册四边形综合测试题及答案
八年级数学(下册)四边形综合测试题和答案

八年级数学〔下册〕四边形综合测试题和答案八年级数学下册四边形综合测试题〔一〕(时间45分钟.共100分)姓名:___________ 班级:_____________ 得分:_______________一、选择题〔每题5分.共30分〕°° C、1620° D、1800° 2、能判定四边形ABCD为平行四边形的题设是〔〕.〔A〕AB∥CD.AD=BC; 〔B〕∠A=∠B.∠C=∠D; 〔C〕AB=CD.AD=BC; 〔D〕AB=AD.CB=CD 3、以下图案中既是轴对称图形又是中心对称图形的是( ).(A) (B) (C) (D)4、菱形ABCD的对角线长分别为6cm和8cm.那么菱形的面积为〔〕 A.12.B.24C.36D.48 5.以下说法不正确的选项是〔〕⊥AB.E为垂足.如果∠∠BCE?〔〕A.55B.35C.25D.30二、填空题〔每题5分.共30分〕BD相交于点O.过点O的直线分别交AD和BC于点E、F.AB?2,BC?3.那么图中阴影局部的面积为.□ABCD与□EBCF关于BC所在直线对称.∠ABE=90°.那么∠F =°. .10、如图4.把一张矩形纸片ABCD沿EF折叠后.点C,D分别落在C?,D?的位置上.EC?交AD于点G.那么△EFG形状为∥BC,?B?45?,?C?90?,AD?1,BC?411、如图那么AB=∠⊥AC交AC于点F.假设BE=2.那么CF长为三、解答题〔每题10分.共40分〕13、〔10分〕:如图7.E、F是平行四边行ABCD的对角线AC上的两点.AE=CF。
求证:∠CDF=∠ABE14、〔10分〕如图8.把正方形ABCD绕着点A.按顺时针方向旋转得到正方形AEFG.边FG与BC交于点H.求证:HC=HF.. .△⊥△AB外角∠⊥AN.垂足为点E.猜测四边形ADCE的形状.并给予证明.′E.求证:四边形CDC′E是菱形.“拓展创新〞时间30分钟.共50分.一、选择及填空题〔每题5分.共10分〕 1、如图11.在菱形ABCD中.∠BAD =80°∠CDE=_________度. .AECF是等腰梯形.以下结论中不一定正确...的是〔〕.〔A〕AE=FC 〔B〕AD=BC 〔C〕∠AEB=∠CFD 〔D〕BE=AF 二、填空题〔每题5分.共10分〕 3、如图13.:平行四边形ABCD中.?BCD的平分线CE交边AD于EG=_______ cm .4、将矩形纸片ABCD按如图14所示的方式折叠.得到菱形AECF.假设AB=9.那么AC的长为 _________三、解答题〔每题15分.共30分〕“任画一个△△△ABC与它的中心对称图形拼成了一个什么形状的特殊四边形?并说明理由.〞于是大家讨论开了.小亮说:“拼成的是平行四边形〞;小华说:“拼成的是矩形〞;小强说:“拼成的是菱形〞;小红说:“拼成的是正方形〞;其他同学也说出了自己的看法……你赞同他们中的谁的观点?为什么?假设都不赞同.请说出你的观点〔画出图形〕.并说明理由. .⊥AD交BC于F,通过一番研究之后得出两条重要结论:〔1〕S?APB?S?CPD?S?APD?S?BPC.〔2)PA2?PC2?PB2?PD2; 1〕请你写出小东探究的过程.2〕当P在矩形外时.如图15-2.上述两个结论是否仍成立?假设成立.请说明理由;假设不成立.请写出你猜测的结论〔不必证明〕. .。
八年级数学下册四边形测试题及详细答案(新人教版)(20201124001305)

八年级数学四边形测试题姓名(考试时间:90分钟 满分:100分)一、填空:(每小题2分,共24分)1、对角线 ________ 平行四边形是矩形。
__ cm 。
5、 已知菱形的一条对角线长为 12cm ,面积为30cm 2,则这个菱形的另一条对角线长为___________ c m 。
6、 _______________________________________________________________ 菱形ABCD 中,/ A = 60。
,对角线BD 长为7cm ,则此菱形周长 __________________ cm 。
7、如果一个正方形的对角线长为 2,那么它的面积 ___________ 。
&如图(2)矩形ABCD 的两条对角线相交于 O,/AOB = 60o ,AB = 8,则矩形对 角线的长_____ 。
9、 如图(3),等腰梯形 ABCD 中,AD // BC , AB // DE , BC = 8, AB = 6, AD=5则厶CDE 周长 ______ 。
10、 正方形的对称轴有 ___ 条11、 如图(4), BD 是口 ABCD 的对角线,点E 、F 在BD 上,要使四边形AECF 是平行四边形,还需增加的一个条件是 ___________2、如图⑴已知 O 是平行四边形ABCD 的对角线交点,AC = 24, BD = 38, AD =14,那么△ OBC3、 在平行四边形ABCD 中,/ C =Z B+ / D,则/ A =,/ D =4、 一个平行四边形的周长为 70cm ,两边的差是10cm ,则平行四边形各边长为 的周长等于.COC⑷12、要从一张长为40cm,宽为20cm的矩形纸片中,剪出长为18cm,宽为12cm 的矩形纸片,最多能剪出_____________ 张。
二、选择题:(每小题3分,共18分)13、在平行四边形ABCD中,/ A :/ B:/ C :/ D的值可以是()A、1: 2: 3: 4B、1: 2: 2: 1C、2: 2: 1: 1D、2: 1: 2: 114、菱形和矩形一定都具有的性质是()A、对角线相等B、对角线互相垂直C、对角线互相平分D、对角线互相平分且相等15、下列命题中的假命题是()A、等腰梯形在同一底边上的两个底角相等B、对角线相等的四边形是等腰梯形C、等腰梯形是轴对称图形D、等腰梯形的对角线相等16、四边形ABCD的对角线AC、BD交于点O,能判定它是正方形的是()A、AO = OC , OB = ODC、AO = OC , OB = OD , AC 丄BD17、给出下列四个命题⑴一组对边平行的四边形是平行四边形边形是菱形⑶两条对角线互相垂直的矩形是正方形边形是等腰梯形。
八年级数学(下册)四边形综合测试题和答案

八年级数学(下册)四边形综合测试题和答案八年级数学下册四边形综合测试题(一)(时间45分钟.共100分)姓名:___________ 班级:_____________ 得分:_______________一、选择题(每题5分.共30分)1、十二边形的内角和为() A.1080° B.1360° C、1620° D、1800°2、能判定四边形ABCD为平行四边形的题设是().(A)AB∥CD.AD=BC; (B)∠A=∠B.∠C=∠D; (C)AB=CD.AD=BC; (D)AB=AD.CB=CD 3、下列图案中既是轴对称图形又是中心对称图形的是( ).(A) (B) (C) (D)4、菱形ABCD的对角线长分别为6cm和8cm.则菱形的面积为() A.12.B.24C.36D.48 5.下列说法不正确的是()(A)对角线相等且互相平分的四边形是矩形;(B)对角线互相垂直平分的四边形是菱形; (C)对角线垂直的菱形是正方形;(D)底边上的两角相等的梯形是等腰梯形 6、如图1.在平行四边形ABCD中.CE⊥AB.E为垂足.如果∠A?125.则∠BCE?()A.55B.35C.25D.30二、填空题(每题5分.共30分)7、顺次连结任意四边形各边中点所得到的四边形一定是__ ___. 8、如图2.矩形ABCD的对角线AC和BD相交于点O.过点O的直线分别交AD和BC于点E、F.AB?2,BC?3.则图中阴影部分的面积为.9、如图3.若□ABCD与□EBCF关于BC所在直线对称.∠ABE=90°.则∠F =°. .10、如图4.把一张矩形纸片ABCD沿EF折叠后.点C,D分别落在C?,D?的位置上.EC?交AD于点G.则△EFG形状为ABCD中.AD∥BC,?B?45?,?C?90?,AD?1,BC?411、如图5.在梯形则AB=12.如图6.AC是正方形ABCD的对角线.AE平分∠BAC.EF⊥AC交AC于点F.若BE=2.则CF长为三、解答题(每题10分.共40分)(10分)已知:如图7.E、F是平行四边行ABCD的对角线AC上的两点.AE=CF。
八年级数学下册四边形综合测试题及答案(20200703014259)
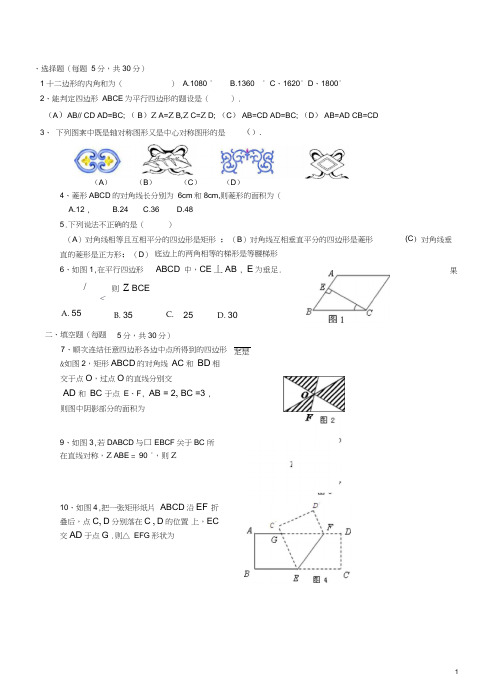
、选择题(每题 5分,共30分) 1 十二边形的内角和为() A.1080 °B.1360 ° C 、1620° D 、1800° 2、 能判定四边形 ABCE 为平行四边形的题设是().(A )AB// CD AD=BC; ( B )Z A=Z B ,Z C=Z D; (C ) AB=CD AD=BC; (D ) AB=AD CB=CD3、 下列图案中既是轴对称图形又是中心对称图形的是().A.12 ,5.下列说法不正确的是()(A )对角线相等且互相平分的四边形是矩形 ;(B )对角线互相垂直平分的四边形是菱形 直的菱形是正方形;(D ) B.24C.36D.48 底边上的两角相等的梯形是等腰梯形 (C ) 6、如图1,在平行四边形ABCD 中,CE 丄AB , E 为垂足./<则 Z BCEA. 55B. 35C. 25D. 30对角线垂果二、填空题(每题 7、顺次连结任意四边形各边中点所得到的四边形 &如图2,矩形ABCD 的对角线 AC 和 BD 相交于点O ,过点O 的直线分别交AD 和 BC 于点 E 、F , AB = 2, BC =3 ,则图中阴影部分的面积为5分,共30分)心曰 定是 9、如图3,若DABCD 与口EBCF 关于BC 所在直线对称,Z ABE = 90 °,则Z10、如图4,把一张矩形纸片 ABCD 沿EF 折叠后,点C , D 分别落在C , D 的位置 上,EC 交AD 于点G .则△ EFG 形状为(A )(B ) (C ) (D )4、菱形ABCD 的对角线长分别为 6cm 和8cm,则菱形的面积为(B =45 ,C =90 , AD =1, BC = 4 贝y AB=11、如图5 ,在梯形ABCD中,AD// B ,C12. 如图6, AC 是正方形 ABCD 勺对角线, AE 平分/ BACEF 丄AC 交AC 于点F,若BE=2 则CF 长为 ________三、解答题(每题10分,共40分)13、( 10分)已知:如图 7,E 、F 是平行四边行 ABCD 勺对角线AC 上的两点,AE=CF求证:/ CDF =Z ABE14、( 10分)如图8,把正方形ABCD 绕着点A ,按顺时针方向旋转得到正方形AEFG ,边FG 与BC交于点H •求证:HC=HF.垂足为15、(10 分)已知:如图9,在△ ABC 中,AB=AC, AD丄BC,点D , AN是厶AB外角/ CAM的平分线,CE丄AN,垂足为点E,猜想四边形ADCE的形状,并给予证明16、(10 分)如图10,在梯形纸片ABCD 中,AD//BC , AD>CD ,沿过点D的直线折叠,使点C落在AD上的点C处,折痕DE 于点E,连结C E求证:四边形CDC E是菱形.“拓展创新”一、选择及填空题(每题5分,共10分)1、如图11,在菱形ABCD 中,/ BAD =80°, AB的垂直平分线交对角线AC于点E,交AB于点F, F为垂足,连接DE, 则/ CDE= _________________ 度时间30分钟,共50分,2. 如图12,四边形ABCD是矩形,F是AD上一点,E是CB延长线上一点,且四边形AECF是等腰梯形.下列结论中不一定正确刈” Q的是().(A )AE=FC (B)AD=BC(C)ZAEB =Z CFD (D)BE=AF二、填空题(每题5分,共10分)3、如图13,已知:平行四边形ABCD 中,BCD的平分线CE交边AD于E , /ABC的平分线BG 交CE于F,交AD 于G .若AB=4cm , AD=6cm ,则EG= cm .4、将矩形纸片ABCD按如图14所示的方式折叠, 得到菱形AECF .若AB = 9,则AC的长为将纸片交BC三、解答题(每题15分,共30 分)5、一次数学活动课上,老师留下了这样一道题“任画一个△ ABC ,以BC的中点0为对称中心,作厶ABC 的中心对称图形,问△ ABC与它的中心对称图形拼成了一个什么形状的特殊四边形?并说明理由•”于是大家讨论开了,小亮说:“拼成的是平行四边形”;小华说:“拼成的是矩形”;小强说:“拼成的是菱形”;小红说:“拼成的是正方形”;其他同学也说出了自己的看法……你赞同他们中的谁的观点?为什么?若都不赞同,请说出你的观点(画出图形),并说明理由6、如图15-1,已知点P是矩形ABCD内一点,PA、PB、PC、PD把矩形分割成四个三角形,小东对该图形进行了研究。
初二八年级下册数学四边形测试题及试卷答案

所在直线对称,/ABE=90°,则/
F=°
匡]3
10、如图4,把一张矩形纸片ABCD沿EF折叠后,点C,D分别落在C,D的位置 上,EC交AD于点G.则△EFG形状为
込D
14、(10分)
边FG与BC交于点H•求证:HC=HF.
15、(10分)已知:如图9,在△ABC中,
B.1360
).
(C)AB=CD AD=BC;(D)AB=AD CB=CD
().
)
4、 菱形ABCD的对角线长分别为6cm和8cm,则菱形的面积为(
A.12,B.24C.36D.48
5、 下列说法不正确的是()
(A)对角线相等且互相平分的四边形是矩形;(B)对角线互相垂直平分的四边形是菱形
(C)对角线垂直的菱形是正方形;(D)底边上的两角相等的梯形是等腰梯形
6、如图1,在平行四边形ABCD中,CE丄AB,
果/A 125o,则/BCE()
A.55o
B.35o
C.25o
D.30o
二、填空题(每题5分,共30分)
7、顺次连结任意四边形各边中点所得到的四边形一定是 &如图2,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交
AD和BC于点E、F,AB2,BC3, 则图中阴Fra bibliotek部分的面积为.
垂足为点D,AN是厶AB外角/CAM的平分线,CE丄AN,垂足
为点E,猜想四边形ADCE的形状,并给予证明
姓名:
初二八年级下册数学四边形测试题及试卷答案
班级:
得分:
、选择题(每题5分,共30分)
1、十二边形的内角和为(
2、能判定四边形ABCE为平行四边形的题设是(
八年级数学下册四边形测试题含答案5

八年级数学下册精品同步练习四边形单元测试班级 姓名 座号 评分一、选择题(每小题3分,共24分)1.下列图形不是轴对称图形的是( )(A )平行四边形 (B )矩形 (C )菱形 (D )等腰梯形2.若O 是四边形ABCD 对角线的交点且OA=OB=OC=OD ,则四边形ABCD 是( )(A )平行四边形 (B )矩形 (C )正方形 (D )菱形3.%¡ABCD 的周长为40cm ,△ABC 的周长为25cm ,则对角线AC 的长为( )(A )6cm (B )15cm (C )5cm (D )16cm4.如图,梯形ABCD 中A D ∥BC ,AB=CD,延长CB 至E ,使EB=AD ,连接AE ,则下列结论不成立的是( )(A )BC=CA (B )EA=AC (C )∠DAC=∠E (D )∠ABE=∠D5.已知菱形的两条对角线长分别是4cm 和8cm ,则与此菱形同面积的正方形的边长是( )(A )8cm (B )24cm (C )22cm (D )4cm6.已知一组邻边的长,能作出确定的图形是( )(A )梯形 (B )平行四边形 (C )矩形 (D )菱形7.用两个全等的直角三角形拼下列图形:①平行四边形②矩形③菱形④正方形⑤等腰三角⑥等边三角形,一定可以拼成的是( )(A )①④⑤ (B )②⑤⑥ (C )①②③ (D )①②⑤8.如图,在Rt △ABC 中,∠BAC=90°,D 、E 分别是AB 、BC 的中点,F 在CA 延长线上,∠FDA=∠B ,AC=6,AB=8,则四边形AEDF 的周长为( )(A )16 (B )20 (C )18 (D )22二、填空题(每小题3分,共24分)9.四边形ABCD 中,AB ∥DC ,AD ∥BC ,如果∠B=50°,则∠C=10.已知等腰梯形ABCD 的中位线EF 的长为6,腰AD 的长为5,则该等腰梯形的周长为11.如图,在正方形ABCD 内取一点M ,使△MAB 是等边三角形,那么∠DMC 的度数是12.如图,在正方形ABCD 中,E 是对角线BD 上任意一点,过E 作EF ⊥BC 于F ,作EG ⊥CD 于G ,若正方形ABCD 的周长为m ,则四边形EFCG 的周长为13.如图,用8块相同的小矩形地砖拼成一个大矩形,则每个小矩形的面积是14.如图,在等腰梯形ABCD中,对角线AC=BC+AD,则∠ACB 的度数是15.已知如图,矩形ABCD中,AB=3cm,BC=4cm,E是边AD上一点,且BE = ED,P是对角线上任意一点,P F⊥BE,PG⊥AD,垂足分别为F、G。
八年级数学下册四边形测试题含答案3

八年级数学下册精品同步练习第十九章四边形单元测试题一、选择题(每小题3分,共30分)1、能够判定一个四边形是平行四边形的条件是 ( )A 、一组对角相等B 、两条对角线互相平分C 、两条对角线互相垂直D 、一对邻角的和为180°2、中,的值可以是( )A .1:2:3:4B .1:2:2:1C .2:2:1:1D .2:1:2:13、对角线互相垂直平分的四边形是 ( )A 、平行四边形B 、矩形C 、菱形D 、梯形4、已知:如图,在矩形ABCD 中,E 、F 、G 、H 分别为边AB 、BC 、CD 、DA 的中点.若AB =2,AD =4,则图中阴影部分的面积为 ( )A .8B .6C .4D .35、如图,□ABCD 中,对角线AC 、BD 交于点O ,点E 是BC 的中点.若OE=3 cm ,则AB 的长为 ( )A .3 cmB .6 cmC .9 cmD .12 cm6、如图,□ABCD 中,∠C=108°,BE 平分∠ABC,则∠ABE 等于( )A.18°B.36°C.72°D.108°7、下列四个命题中,假命题是( ).A 等腰梯形的两条对角线相等B 顺次连结四边形的各边中点所得的四边形是平行四边形C 菱形的对角线平分一组对角D 两条对角线互相垂直且相等的四边形是正方形8、等腰梯形的腰长为13cm ,两底差为10cm ,则高为 ( )A 、69cmB 、12cmC 、69cmD 、144cm9、已知四边形ABCD 的对角线相交于O ,给出下列5个条件①AB ∥CD ②AD ∥BC ③AB=CD④∠BAD=∠DCB ,从以上4个条件中任选 2个条件为一组,能推出四边形ABCD 为平行四边形的有( )A 6组 B.5组 C.4组 D.3组10、某校计划修建一座既是中心对称图形又是轴对称图形的花坛, 从学生中征集到设计方案有等腰三角形、正三角形、等腰梯形、菱形等四种图案,你认为符合条件的是( ).A .等腰三角形B .正三角形C .等腰梯形 D.菱形E D C B A二.填空题: (每小题3分,共24分)1.在%¡ABCD 中,∠A +∠C =270°,则∠B =______,∠C =______.2.平行四边形的周长等于56 cm ,两邻边长的比为3∶1,那么这个平行四边形较长的边长为_______.3.平行四边形ABCD ,加一个条件__________________,它就是菱形.4.如图,长方形ABCD 是篮球场地的简图,长是28m ,宽是15m , 则它的对角线长约为________m .(精确到1m )5 如图,在正方形ABCD 的外侧,作等边△ADE ,则∠AEB=_______.6.如图,在梯形ABCD 中,AD ∥BC ,DE ∥AB ,△DEC 的周长为10cm ,BE=5cm ,则该梯形的周长为 。
八年级数学下册四边形测试题及详细答案(新人教版)

八年级数学四边形测试题 姓名之杨若古兰创作(考试时间:90分钟 满分:100分)一、填空:(每小题2分,共24分)1、对角线_____平行四边形是矩形.2、如图⑴已知O 是平行四边形ABCD 的对角线交点,AC =24,BD =38,AD =14,那么△OBC 的周长等于_____.3、在平行四边形ABCD 中,∠C=∠B+∠D,则∠A=___,∠D =___.4、一个平行四边形的周长为70cm ,两边的差是10cm ,则平行四边形各边长为____cm.5、已知菱形的一条对角线长为12cm ,面积为30cm2,则这个菱形的另一条对角线长为__________cm.6、菱形ABCD 中,∠A=60o ,对角线BD 长为7cm ,则此菱形周长_____cm.7、如果一个正方形的对角线长为,那么它的面积______.8、如图(2)矩形ABCD 的两条对角线订交于O,∠AOB=60o,AB =8,则矩形对角线的长___.9、如图(3),等腰梯形ABCD 中,AD∥BC,AB∥DE,BC =8,AB =6,AD =5则△CDE 周长___.10、正方形的对称轴有___条11、如图(4),BD 是□ABCD 的对角线,点E 、F 在BD 上,要使四边形AECF 是平行四边形,还需添加的一个条件是______12、要从一张长为40cm ,宽为20cm 的矩形纸片中,剪出长为AB C O ⑴ A B CO ⑵ A BD ⑶ A D B CF E ⑷18cm,宽为12cm的矩形纸片,最多能剪出______张.二、选择题:(每小题3分,共18分)13、在平行四边形ABCD中,∠A:∠B:∠C:∠D的值可所以()A、1:2:3:4B、1:2:2:1C、2:2:1:1D、2:1:2:114、菱形和矩形必定都具有的性质是()A、对角线相等B、对角线互相垂直C、对角线互相平分D、对角线互相平分且相等15、以下命题中的假命题是()A、等腰梯形在同一底边上的两个底角相等B、对角线相等的四边形是等腰梯形C、等腰梯形是轴对称图形D、等腰梯形的对角线相等16、四边形ABCD的对角线AC、BD交于点O,能判定它是正方形的是()A、AO=OC,OB=ODB、AO=BO=CO=DO,AC⊥BDC、AO=OC,OB=OD,AC⊥BDD、AO=OC=OB=OD17、给出以下四个命题⑴一组对边平行的四边形是平行四边形⑵一条对角线平分一个内角的平行四边形是菱形⑶两条对角线互相垂直的矩形是正方形⑷顺次连接等腰梯形四边中点所得四边形是等腰梯形.其中准确命题的个数为()A、1个B、2个C、3个D、4个18、以下矩形中按虚线剪开后,能拼成平行四边形,又能拼成直角三角形的是()C D三、解答题(58分)19、(8分)如图:在□ABCD中,∠BAD的平分线AE交DC于E,若∠DAE=25o,求∠C、∠B的度数.ABCD中,AD∥BC,AB=DC,∠D=120o,对角线CA平分∠BCD,且梯形的周长20,求AC.ABCD中,E为CD边上的一点,F为BC的耽误线上一点,CE=CF.⑴△BCE与△DCF全等吗?说明理由;⑵若∠BEC=60o,求∠EFD.22、证实题:(8分)如图,△ABC中∠ACB=90o,点D、E分别是AC,AB的中点,点F在BC的耽误线上,且∠CDF=∠A.求证:四边形DECF是平行四边形.中点ABDCFE60oABDCFE23、(8分)已知:如图所示,△ABC 中,E 、F 、D 分别是AB 、AC 、BC 上的点,且DE∥AC,DF∥AB,要使四边形AEDF 是菱形,在不改变图形的前提下,你需添加的一个条件是_______________试证实:这个多边形是菱形.24、利用题(8分)某村要挖一条长1500米的水渠,渠道的横断面为等腰梯形,渠道深0.8米,渠底宽为1.2米,腰与渠底的夹角为135o ,问挖此渠需挖出土多少方?25、(10分)观察下图⑴正方形A 中含有_____个小方格,即A 的面积为____个单位面积.⑵正方形B 中含有_____个小方格,即B 的面积为____个单位面积.⑶正方形C 中含有_____个小方格,即C 的面积为____个单位面积.⑷你从中得到的规律是:_______________________.25、附加题(10已知:如图,在直角梯形ABCD AD =24cm ,BC =26cm ,动点P 从A 点开始沿动,动点Q 从C 点开始沿CB 边向B 以、Q 分别AB DC F E从A 、C 同时出发,当其一点到端点时,另一点也随之停止活动,设活动时间为t 秒,t 分别为什么值时,四边形PQCD 是平行四边形?等腰梯形?八年级数学单元测试答案 一、⑴相等;⑵45;⑶∠A=120o ,∠D=60o ;⑷22.5,12.5;⑸5;⑹28;⑺1;⑻16;⑼15;⑽4;⑾略;⑿3.二、⒀D;⒁C;⒂B;⒃B;⒄B;⒅B19、解:∠BAD=2∠DAE=2×25o=50o (2分)又∵□ABCD ∴∠C=∠BAD=50o (4分)∴AD∥BC∴∠B=180o -∠BAD (6分)=180o -50o =130o (8分) 20、解:∵AD∥BC ∴∠1=∠2 又∠2=∠3 ∴∠1=∠3 AD =DC (2分)又AB =DC 得AB =AD =DC =在△ADC 中∵∠D=120o∠1=∠3=又∠BCD=2∠3=60o∴∠B=∠BCD=60o (4分)∠BAD=180o -∠B-∠2=90o∠2=30o则BC =2AB =2x (6分)AB =4 BC =8 在Rt△ABC 中AC =(8分)21、⑴△BCE≌△DCF (1分) 理由:由于四边形ABCD 是正方形∴BC=CD ,∠BCD=90o A P DD Q C A DB 1 2 3∴∠BCE =∠DCF又CE =CF ∴△BCE≌△DCF(4分) ⑵∵CE =CF∴∠CEF =∠CFE∵∠FCE =90o∴∠CFE =又∵△BCE≌△DCF ∴∠CFD=∠BEC=60o (6分) ∴∠EFD=∠CFD-∠CFE=60o -45o =15o (8分)22、证实:∵D、E 分别是AC 、AB 的中点 ∴DE∥BC (1分) ∵∠ACB=90o∴CE=AB =AE (3分)∵∠A=∠ECA ∴∠CDF=∠A (4分)∴∠CDF=∠ECA ∴DF∥CE (7分)∴四边形DECF 是平行四边形 (8分)23、答条件AE =AF (或AD 平分角BAC ,等) (3分) 证实:∵DE∥AC DF∥AB∴四边形AEDF 是平行四边形 (6分)又AE =AF∴四边形AEDF 是菱形(8分)24、如图所示设等腰梯形ABCD 为渠道横断面,分别作DE⊥AB,CF⊥AB (2分)垂足为E 、F 则CD =1.2米,DE =CF =0.8米∠ADC=∠BCD =135o (4分)AB∥CD ∠A+∠ADC=180o∴∠A=45o =∠B 又DE⊥AB CF⊥AB ∴∠EDA=∠A ∠BCF=∠B又∵四边形CDEF 是矩形 ∴EF=CD =1.2米 (6分)A D C E FS梯形ABCD=∴所挖土方为1.6×1500=2400(立方米)(8分)(解析:解决本题的关键是数学建模,求梯形面积时,留意作辅助线,把梯形成绩向三角形和矩形转化)25、①4,4 (2分)②9,9 (4分)③13,13 (6分)④在直角三角形中两直角边的平方和等于斜边的平方(10分)26、解由于AD∥BC,所以,只需QC=PD,则四边形PQCD就是平行四边形,此时有3t=24-t.(3分)解之,得t=6(秒)(4分)当t=6秒时,四边形PQCD平行四边形. (5分)同理,只需PQ=CD,PD≠QC,四边形PQCD为等腰梯形.过P、D分别作BC的垂线交BC于E、F,则由等腰梯形的性质可知,EF=PD,QE=FC=26-24=2,所以2,解得.(10分)所以当t=7秒时,四边形PQCD是等腰梯形.。
初二八年级下册数学四边形测试题及试卷答案

2、能判定四边形ABCD 为平行四边形的题设是( ).(A )AB ∥CD ,AD=BC; (B )∠A=∠B ,∠C=∠D; (C )AB=CD ,AD=BC; (D )AB=AD ,CB=CD4、菱形ABCD 的对角线长分别为6cm 和8cm ,则菱形的面积为( )A.12,B.24C.36D.485.下列说法不正确的是( )(A )对角线相等且互相平分的四边形是矩形;(B )对角线互相垂直平分的四边形是菱形;(C )对角线垂直的菱形是正方形;(D )底边上的两角相等的梯形是等腰梯形6、如图1,在平行四边形ABCD 中,CE AB ⊥,E 为垂足.如果125A =∠,则BCE =∠( )A.55 B.35 C.25 D.30二、填空题(每题5分,共30分)7、顺次连结任意四边形各边中点所得到的四边形一定是__10、如图4,把一张矩形纸片ABCD 沿EF折叠后,点C D ,分别落在C D '',的位置上,EC '交AD 于点G .则△EFG 形状为12.如图6,AC 是正方形ABCD 的对角线,AE 平分∠BAC ,EF ⊥AC 交AC 于点F ,若BE=2,则CF 长为三、解答题(每题10分,共40分)13、(10分)已知:如图7,E 、F 是平行四边行ABCD 的对角线AC 上的两点,AE=CF 。
求证:∠CDF =∠ABE14、(10分)如图8,把正方形ABCD绕着点A,按顺时针方向旋转得到正方形AEFG,边FG与BC交于点H.求证:HC=HF.15、(10分)已知:如图9,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△AB外角∠CAM的平分线,CE⊥AN,垂足为点E,猜想四边形ADCE的形状,并给予证明.16、(10分)如图10,在梯形纸片ABCD中,AD//BC,AD>CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C处,折痕DE交BC于点E,连结C′E.求证:四边形CDC′E是菱形,一.选择及填空题(每题5分,共10分)1、如图11,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点E,交AB于点F,F为垂足,连接DE,则∠CDE=_________度2.如图12,四边形ABCD是矩形,F是AD上一点,E是CB延长线上一点,且四边形AECF是等腰梯形.下列结论中不一定...正确的是().(A)AE=FC(B)AD=BC (C)∠AEB=∠CFD(D)BE=AF二、填空题(每题5分,共10分)3、如图13,已知:平行四边形ABCD中,∠的平分线CE交边AD于E,BCD∠的平分线BG交CE于F,交AD ABC于G.若AB=4cm,AD=6cm,则EG=_______ cm .4、将矩形纸片ABCD 按如图14所示的方式折叠,得到菱形AECF .若AB =9,则AC 的长为 _________《“四边形”综合测试题(一)》参考答案基础巩固一、选择题1、D2、C3、A4、B5、C.6、B二、填空题7、平行四边形 8、3. 9、45° 10、等腰三角形 11、23 12.2三、解答题13、证明:(1)∵ ABCD 是平行四边形,∴DC=AB ,DC ∥AB,∴∠DCF=∠BAE ,∵ AE=CF , ∴△ADF ≌△CBE ,∴∠CDF =∠ABE14、如图8,把正方形ABCD 绕着点A ,按顺时针方向旋转得到正方形AEFG ,边FG 与BC 交于点H .求证:HC=HF.解:证明:连结AH ,∵四边形ABCD ,AEFG 都是正方形.∴90B G ∠=∠=°,AG AB =,BC=GF ,又AH AH =.Rt Rt ()AGH ABH HL ∴△≌△,HG HB =∴,∴HC=HF.15、解:猜想四边形ADCE 是矩形。
八年级数学下册四边形测试题含答案18

图10DC B A八年级数学下册精品同步练习章节测试题第十九章《四边形》一、选择题(本大题10个小题,每小题3分,共30分)1.能判定四边形ABCD 为平行四边形的题设是( ).A 、AB ∥CD ,AD=BC; B 、∠A=∠B ,∠C=∠D;C 、AB=CD ,AD=BC; D 、AB=AD ,CB=CD用两块完全相同的直角三角形拼下列图形:①平行四边形 ②矩形 ③菱形 2、④ 正方形 ⑤等腰三角形 ⑥等边三角形,一定能拼成的图形是( )A 、①④⑤B 、②⑤⑥C 、①②③D 、①②⑤3、顺次连结任意四边形四边中点所得的四边形一定是( ) A 、平行四边形 B 、矩形 C 、菱形 D 、正方形4、如图,平行四边形ABCD 中,∠A 的平分线AE 交CD 于E ,AB=5,BC=3,则EC 的长( )A 、1 B 、1.5 C 、2D 、3等腰梯形的两底之差等于腰长,则腰与下底的5、夹角为( )A 、120°B 、60°C 、45°D 、50°6、如图10,在梯形ABCD 中,AD∥BC ,AB=CD ,那么它的四个内角按一定顺序的度数比可能为( ) A 、3:4:5:6 B 、4:5:4:5C 、2:3:3:2D 、2:4:3:3四边形ABCD 的对角线AC 、BD 交于点O ,设有以下论断:①AB =BC ;②7、∠DAB =90°;③BO =DO ;AO =CO ;④矩形ABCD ;⑤菱形ABCD ;⑥正方形ABCD ,则在下列推理中 不正确的是( )8、一组对边平行,并且对角线互相垂直且相等的四边形可能是( ) A 、菱形或矩形 B 、正方形或等腰梯形 C 、矩形或等腰梯形 D 、菱形或直角梯形9、小明和小亮在做一道习题,若四边形ABCD 是平行四边形,请补充条件 ,使得四边形ABCD 是菱形。
小明补充的条件是AB=BC ;小亮补充的条件是AC=BD ,你认为下列说法正确的是( ) A 、小明、小亮都正确 B 、小明正确,小亮错误 C 、小明错误,小亮正确 D 、小明、小亮都错误如图,在一个由4×4个小正方形组成的正方形网格10、中, 阴影部分面积与正方形ABCD 的面积比是( ) A 、3:4 B 、5:8 C 、9:16 D 、1:2二、填空题(本大题6个小题,每空3分,共24分)11、ABCD 中,∠A=50°,则∠B=_________,∠C=_________。
八年级数学(下册)四边形测试题及详细答案(新人版)

八年级数学四边形测试题 班级(考试时间:90分钟 满分:100分)一、填空:(每小题2分,共24分)1、对角线_____平行四边形是矩形。
2、如图⑴已知O 是□ABCD 的对角线交点,AC =24,BD =38,AD =14,那么△OBC 的周长等于_____。
3、在平行四边形ABCD 中,∠C =∠B+∠D,则∠A =___,∠D =___。
4、一个平行四边形的周长为70cm,两边的差是10cm ,则平行四边形各边长为____cm 。
5、已知菱形的一条对角线长为12cm ,面积为30cm 2,则这个菱形的另一条对角线长为__________cm 。
6、菱形ABCD 中,∠A =60o ,对角线BD 长为7cm ,则此菱形周长_____cm 。
7,那么它的面积______。
8、如图2矩形ABCD 的两条对角线相交于O,∠AOB =60o ,AB =8,则矩形对角线的长___。
10、正方形的对称轴有___条11、如图4,BD 是□ABCD 的对角线,点E 、F 在BD 上,要使四边形AECF 是平行四边形,还需增加的一个条件是______12、要从一长为40cm ,宽为20cm 的矩形纸片中,剪出长为18cm ,宽为12cm 的矩形纸片,最多能剪出______。
二、选择题:(每小题3分,共18分)⑴⑵⑶ ⑷13、在□ABCD 中,∠A :∠B :∠C :∠D 的值可以是( )A 、1:2:3:4B 、1:2:2:1C 、2:2:1:1D 、2:1:2:1 14、菱形和矩形一定都具有的性质是( ) A 、对角线相等 B 、对角线互相垂直 C 、对角线互相平分 D 、对角线互相平分且相等16、四边形ABCD 的对角线AC 、BD 交于点O ,能判定它是正方形的是( ) A 、AO =OC ,OB =OD B 、AO =BO =CO =DO ,AC ⊥BD C 、AO =OC ,OB =OD ,AC ⊥BD D 、AO =OC =OB =OD18、下列矩形中按虚线剪开后,能拼成平行四边形,又能拼成直角三角形的是( )三、解答题(58分)19、(8分)如图:在□ABCD 中,∠BAD 的平分线AE 交DC 于E ,若∠DAE =25o ,求∠C 、∠B 的度数。
初二数学下册四边形综合测试题及答案(K12教育文档)

(直打版)初二数学下册四边形综合测试题及答案(word版可编辑修改) 编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((直打版)初二数学下册四边形综合测试题及答案(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(直打版)初二数学下册四边形综合测试题及答案(word版可编辑修改)的全部内容。
一、选择题(每题5分,共30分)1、十二边形的内角和为() A。
1080° B。
1360° C、1620° D、1800°2、能判定四边形ABCD为平行四边形的题设是().(A)AB∥CD,AD=BC;(B)∠A=∠B,∠C=∠D;(C)AB=CD,AD=BC; (D)AB=AD,CB=CD3、下列图案中既是轴对称图形又是中心对称图形的是( )。
(A) (B) (C) (D)4、菱形ABCD的对角线长分别为6cm和8cm,则菱形的面积为()A.12,B.24 C。
36 D。
485.下列说法不正确的是()(A)对角线相等且互相平分的四边形是矩形;(B)对角线互相垂直平分的四边形是菱形; (C)对角线垂直的菱形是正方形;(D)底边上的两角相等的梯形是等腰梯形6、如图1,在平行四边形ABCD中,CE AB⊥,E为垂足.如果125∠,则BCE=A=∠()A.55B.35C.25D.30二、填空题(每题5分,共30分)7、顺次连结任意四边形各边中点所得到的四边形一定是__ ___.8、如图2,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,23,,则图中阴影部分的面积为.==AB BC9、如图3,若□ABCD 与□EBCF 关于BC 所在直线对称,∠ABE =90°,则∠F = °10、如图4,把一张矩形纸片ABCD 沿EF 折叠后,点C D ,分别落在C D '',的位置上,EC '交AD于点G .则△EFG 形状为11、如图5,在梯形ABCD 中,AD BC ∥,419045==︒=∠︒=∠BC AD C B ,,,则AB=12.如图6,AC 是正方形ABCD 的对角线,AE 平分∠BAC ,EF ⊥AC 交AC 于点F,若BE=2,则CF 长为三、解答题(每题10分,共40分)13、(10分)已知:如图7,E、F是平行四边行ABCD的对角线AC上的两点,AE=CF。
八年级数学下册四边形测试题及详细答案(新人教版)

八年级数学四边形测试题 姓名(测验时光:90分钟 满分:100分)一.填空:(每小题2分,共24分)1.对角线_____平行四边形是矩形.2.如图⑴已知O 是平行四边形ABCD 的对角线交点,AC =24,BD =38,AD =14,那么△OBC 的周长等于_____.CA. ____cm.5.已知菱形的一条对角线长为12cm,面积为30cm 2,则这个菱形的另一条对角线长为__________cm.6.菱形ABCD 中,∠A =60o,对角线BD 长为7cm,则此菱形周长_____cm. 7.,那么它的面积______.8.如图(2)矩形ABCD 的两条对角线订交于O,∠AOB =60o,AB =8,则矩形对角线的长___.9.如图(3),等腰梯形ABCD 中,AD ∥BC,AB ∥DE,BC =8,AB =6,AD =5则△CDE 周长___.10.正方形的对称轴有___条11.如图(4),BD 是□ABCD 的对角线,点E.F 在BD 上,要使四边形AECF 是平行四边形,还需增长的一个前提是______12.要从一张长为40cm,宽为20cm 的矩形纸片中,剪出长为18cm,宽为12cm 的矩形纸片,最多能剪出______张.二.选择题:(每小题3分,共18分)⑴ ⑵ ⑶⑷13.在平行四边形ABCD 中,∠A :∠B :∠C :∠D 的值可所以( ) A.1:2:3:4 B.1:2:2:1 C.2:2:1:1 D.2:1:2:1 14.菱形和矩形一建都具有的性质是( ) A.对角线相等 B.对角线互相垂直 C.对角线互相等分 D.对角线互相等分且相等 15.下列命题中的假命题是( ) A.等腰梯形在统一底边上的两个底角相等 B.对角线相等的四边形是等腰梯形 C.等腰梯形是轴对称图形 D.等腰梯形的对角线相等16.四边形ABCD 的对角线AC.BD 交于点O,能剖断它是正方形的是( ) A.AO =OC,OB =OD B.AO =BO =CO =DO,AC ⊥BD C.AO =OC,OB =OD,AC ⊥BD D.AO =OC =OB =OD 17.给出下列四个命题⑴一组对边平行的四边形是平行四边形 ⑵一条对角线等分一个内角的平行四边形是菱形⑶两条对角线互相垂直的矩形是正方形 ⑷按序衔接等腰梯形四边中点所得四边形是等腰梯形.个中准确命题的个数为( ) A.1个 B.2个 C.3个 D.4个18.下列矩形中按虚线剪开后,能拼成平行四边形,又能拼成直角三角形的是( )D中点三.解答题(58分)19.(8分)如图:在□ABCD 中,∠BAD 的等分线AE 交DC 于E,若∠DAE =25o,求∠C.∠B 的度数.20.(8分)已知在梯形ABCD 中,AD ∥BC,AB =DC,∠D =120o,对角线CA 等分∠BCD,且梯形的周长20,求AC.ABCD 中,E 为CD 边上的一点,F 为BC 的延伸线上一点,CE =CF.⑴△BCE 与△DCF 全等吗?解释来由; ⑵若∠BEC =60o,求∠EFD.22.证实题:(8分)如图,△ABC 中∠ACB =90o,点D.E 分离是AC,AB 的中点,点F 在BC 的延伸线上,且∠CDF =∠A.求证:四边形DECF 是平行四边形.23.(8分)已知:如图所示,△ABC 中,E.F.D 分离是AB.AC.BC 上的点,且DE∥AC,DF ∥AB,要使四边形AEDF 是菱形,在不转变图形的前提下,你需添加的一个前提是_______________试证实:这个多边形是菱形.24.8分)A BD CFE60oA B DCF EABDCF E某村要挖一条长1500米的沟渠,渠道的横断面为等腰梯形,渠道深0.8米,渠底宽为1.2米,腰与渠底的夹角为135o,问挖此渠需挖出土若干方?25.(10分)不雅察下图⑴正方形A中含有_____个小方格,即A的面积为____个单位面积.⑵正方形B中含有_____个小方格,即B的面积为____个单位面积.⑶正方形C中含有_____个小方格,即C的面积为____个单位面积.⑷你从中得到的纪律是:_______________________.25.附加题(10分)(计入总分,已知:如图,在直角梯形ABCD中,∠B==26cm,动点P从A点开端沿AD边向D以1cm/CB边向B以3cm/秒的速度活动,P.Q分离从A.C,另一点也随之停滞活动,设活动时光为t秒,t分离为何值时,四边形PQCD是平行四边形?等腰梯形?八年级数学单元测试答案45;⑶∠A=120o,∠D=60o;⑷22.5,12.5;⑸5;⑹28;⑺1;⑻16;3.二.⒀D;⒁C;⒂B;⒃B;⒄B;⒅B19.解:∠BAD=2∠DAE=2×25o=50o(2分)又∵□ABCD ∴∠C=∠BAD=50o(4分)∴AD∥BC∴∠B=180o-∠BAD (6分)=180o-50o=130o(8分)20.解:∵AD∥BC ∴∠1=∠2 又∠2=∠3∴∠1=∠3 AD=DC (2分)又AB=DC 得AB=AD=DC=x在△ADC中∵∠D=120o∠1=∠3=180120302o oo-=又∠BCD=2∠3=60o∴∠B=∠BCD=60o(4分)∠BAD=180o-∠B-∠2=90o∠2=30o则BC=2AB=2x (6分)AB=4 BC=8 在Rt△ABC中AC===(8分)21.⑴△BCE≌△DCF (1分)来由:因为四边形ABCD是正方形∴BC =CD,∠BCD=90o∴∠BCE=∠DCF 又CE=CF ∴△BCE≌△DCF (4分)⑵∵CE=CF∴∠CEF=∠CFE ∵∠FCE=90o∴∠CFE=1(18090)45 2o o o-=又∵△BCE≌△DCF ∴∠CFD=∠BEC=60o(6分)∴∠EFD=∠CFD-∠CFE=60o-45o=15o(8分)22.证实:∵D.E分离是AC.AB的中点∴DE∥BC (1分)∵∠ACB=90o∴CE=12AB=AE (3分)∵∠A=∠ECA ∴∠CDF=∠A (4分)∴∠CDF=∠ECA ∴DF∥CE (7分)∴四边形DECF是平行四边形(8分)23.答前提AE=AF(或AD等分角BAC,等)(3分)证实:∵DE∥AC DF∥AB∴四边形AEDF是平行四边形(6分)又AE=AF∴四边形AEDF是菱形(8分)24.如图所示设等腰梯形ABCD为渠道横断面,分离作DE⊥AB,CF⊥AB (2分)∠ADC=∠BCD=135o(4分)AB∥CD ∠A+∠ADC=180o∴∠A=45o又DE⊥AB CF⊥AB ∴∠EDA=∠A ∠∴又∵四边形CDEF是矩形∴EF=CD=1.2米(6分)S梯形ABCD=11()(1.20.82 1.2)0.8 1.6 22AB CD DE+⋅=+⨯+⨯=∴×1500=2400(立方米)(8分)(解析:解决本题的症结是数学建模,求梯形面积时,留意作帮助线,把梯形问题向三角形和矩形转化)25.①4,4 (2分)②9,9 (4分)③13,13 (6分)④在直角三角形中两直角边的平方和等于斜边的平方(10分)26.解因为AD∥BC,所以,只要QC=PD,则四边形PQCD就是平行四边形,此时有3t=24-t.(3分)解之,得t=6(秒)(4分)当t=6秒时,四边形PQCD平行四边形. (5分)同理,只要PQ=CD,PD≠QC,四边形PQCD为等腰梯形.过P.D分离作BC的垂线交BC于E.F,则由等腰梯形的性质可知,EF=PD,QE=FC=26-24=2,所以23(24)2t t--=,解得7()t=秒.(10分)所以当t=7秒时,四边形PQCD是等腰梯形.。
八年级数学下册第四边形测试题及详细答案

八年级数学四边形测试题班级_____ 姓名___ 成绩________一.填空题(每小题3分,共30分)1.平行四边形ABCD中,∠A=500,AB=30cm,则∠B=____,DC=____ cm。
2.平行四边形ABCD的周长为20cm,对角线AC、BD相交于点O,若△BOC的周长比△AOB的周长大2cm,则CD= cm。
3.若边长为4cm的菱形的两邻角度数之比为1∶2,则该菱形的面积为cm2。
4.如图2,△ABC中,EF是它的中位线,M、N分别是EB、CF的中点,若BC=8cm,那么EF= cm,MN= cm;5.若矩形的对角线长为8cm,两条对角线的一个交角为600,则该矩形的面积为 cm2。
6.如右图,若梯形的两底长分别为4cm和9cm,两条对角线长分别为5cm和12cm,则该梯形的面积为 cm2。
7.在□ABCD 中,若添加一个条件________,则四边形ABCD是矩形;若添加一个条件_______,则四边形ABCD是菱形.8.菱形的两条对角线分别是6cm,8cm,则菱形的边长为_____ cm,面积为______ cm2.9.在等腰梯形ABCD中,AD∥BC,•AD=•6cm,•BC=•8cm,•∠B=•60•°,•则AB=_______cm.10.梯形的上底长为2,下底长为5,一腰为4,则另一腰m的范围是。
二.单选题(每小题3分,共30分)11.菱形具有而矩形不具有的性质是()A.对角线互相平分; B.四条边都相等; C.对角相等; D.邻角互补12.关于四边形ABCD ①两组对边分别平行;②两组对边分别相等;③有一组对边平行且相等;④对角线AC和BD相等;以上四个条件中可以判定四边形ABCD是平行四边形的有()。
(A) 1个(B)2个(C)3个(D)4个13.能够判定一个四边形是菱形的条件是()。
(A)对角线相等且互相平分(B)对角线互相垂直且互相平分(C)对角线相等且互相垂直(D)对角线互相垂直14.矩形、菱形、正方形都具有的性质是()A、对角线相等B、对角线互相平分C、对角线互相垂直D、对角线平分对角15.三角形的重心是三角形三条()的交点A.中线 B.高 C.角平分线D.垂直平分线16.若顺次连结四边形ABCD各边中点所得四边形是矩形,则四边形ABCD必定是()A、菱形B、对角线相互垂直的四边形C、正方形D、对角线相等的四边形17.下列命题中,真命题是()A、有两边相等的平行四边形是菱形B、有一个角是直角的四边形是矩形C、四个角相等的菱形是正方形D、两条对角线互相垂直且相等的四边形是正方形18.如右图,在梯形ABCD中,AD∥BC,AB=DC,∠C=60°,BD平分∠ABC.如果这个梯形的周长为30,则AB的长为().(A)4 (B)5(C)6 (D)719.下列说法中,不正确的是().(A)有三个角是直角的四边形是矩形;(B)对角线相等的四边形是矩形(C)对角线互相垂直的矩形是正方形;(D)对角线互相垂直的平行四边形是菱形20.如图,矩形ABCD中,DE⊥AC于E,且∠ADE:∠EDC=3:2,则∠BDE的度数为()A、36oB、9oC、27oD、18o三.解答题:(21、22每小题5分,23、24、25每小题6分共28分)21.如图:已知在△ABC中,AB=AC,D为BC上任意一点,DE∥AC交AB于E,DF∥AB交AC于F,求证:DE+DF=ACBCADO22. 已知:如图, □ABCD 各角的平分线分别相交于点E ,F ,G ,•H , •求证:•四边形EFGH 是矩形.23.如图,在菱形ABCD 中,∠ABC 与∠BAD 的度数比为1:2,周长是48cm .求:(1)两条对角线的长度;(2)菱形的面积.24.如图,梯形ABCD 中,AD ∥BC ,M 、N 、P 、Q 分别为AD 、BC 、BD 、AC 的中点。
八年级数学下册四边形测试题含答案6

八年级数学下册精品同步练习第十九章 四边形测试题(B )一、选择题(每小题4分,共40分)1、下列哪组条件能判别四边形ABCD 是平行四边形?( )A :AB ∥CD ,AD =BC B :AB =CD ,AD =BCC :∠A =∠B ,∠C =∠D D :AB =AD ,CB =CD2、如图,□ABCD 中,对角线AC 、BD 交于点O ,点E 是BC 的中点.若OE=3 cm ,则AB 的长为 ( )A :3 cmB :6 cmC :9 cmD :12 cm3、已知:如图,在矩形ABCD 中,E 、F 、G 、H 分别为边AB 、BC 、CD 、DA 的中点.若AB =2,AD =4,则图中阴影部分的面积为 ( )A :8 B :6 C :4 D :34、对角线互相垂直平分的四边形是( )A :平行四边形B :矩形C :菱形D :梯形5、下列四个命题中,假命题是( )A :等腰梯形的两条对角线相等B :顺次连结四边形的各边中点所得的四边形是平行四边形C :菱形的对角线平分一组对角D :两条对角线互相垂直且相等的四边形是正方形6、顺次连结任意四边形四边中点所得的四边形一定是( )A :平行四边形B :矩形C :菱形D :正方形7、用两块完全相同的直角三角形拼下列图形:①平行四边形 ②矩形 ③菱形 ④正方形 ⑤等腰三角形 ⑥等边三角形,一定能拼成的图形是( )A :①④⑤B :②⑤⑥C :①②③D :①②⑤8、如图,已知矩形ABCD ,R 、P 分别是DC 、BC 上的点,E 、F 分别是AP 、RP 的中点,当P 在BC 上从B 向C 移动而R 不动时,那么下列结论成立的是( )A :线段EF 的长逐渐增大。
B :线段EF 的长逐渐减少。
姓名 班级 D CB A RP FED C B AC :线段EF 的长不变。
D :线段EF 的长不能确定。
9、如图,在梯形ABCD 中,AD ∥BC ,对角线AC ⊥BD ,且AC =12,BD =9,则该梯形的面积是( )A :30B :15C :7.5D :5410、三角形的重心是三角形的( )A :三条角平分线的交点B :一条边的中线与另一边的高的交点C :三条高的交点D :三条中线的交点二、填空题(每小题4分,共40分)11、在□ABCD 中,∠A+∠C=270°,则∠B=______,∠C=______。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级数学下册四边形综合测试题(一)(时间45分钟,共100分)姓名:___________ 班级:_____________ 得分:_______________一、选择题(每题5分,共30分)1、十二边形的内角和为( ) A.1080° B.1360° C 、1620° D 、1800°2、能判定四边形ABCD 为平行四边形的题设是( ).(A )AB ∥CD ,AD=BC; (B )∠A=∠B ,∠C=∠D; (C )AB=CD ,AD=BC; (D )AB=AD ,CB=CD3、下列图案中既是轴对称图形又是中心对称图形的是( ).(A) (B) (C) (D)4、菱形ABCD 的对角线长分别为6cm 和8cm ,则菱形的面积为( )A.12,B.24C.36D.485.下列说法不正确的是( )(A )对角线相等且互相平分的四边形是矩形;(B )对角线互相垂直平分的四边形是菱形;(C )对角线垂直的菱形是正方形;(D )底边上的两角相等的梯形是等腰梯形6、如图1,在平行四边形ABCD 中,CE AB ⊥,E 为垂足.如果125A =∠,则BCE =∠( )A.55 B.35 C.25 D.30二、填空题(每题5分,共30分)7、顺次连结任意四边形各边中点所得到的四边形一定是__ ___.8、如图2,矩形ABCD 的对角线AC 和BD 相交于点O ,过点O 的直线分别交AD 和BC 于点E 、F ,23AB BC ==,,则图中阴影部分的面积为 .9、如图3,若□ABCD 与□EBCF 关于BC所在直线对称,∠ABE =90°,则∠F = °10、如图4,把一张矩形纸片ABCD 沿EF折叠后,点C D ,分别落在C D '',的位置上,EC '交AD 于点G .则△EFG 形状为11、如图5,在梯形ABCD 中,AD BC ∥,419045==︒=∠︒=∠BC AD C B ,,,则AB=12.如图6,AC 是正方形ABCD 的对角线,AE 平分∠BAC ,EF ⊥AC 交AC 于点F ,若BE=2,则CF 长为 三、解答题(每题10分,共40分)13、(10分)已知:如图7,E 、F 是平行四边行ABCD 的对角线AC 上的两点,AE=CF 。
求证:∠CDF =∠ABE14、(10分)如图8,把正方形ABCD 绕着点A ,按顺时针方向旋转得到正方形AEFG ,边FG 与BC 交于点H .求证:HC=HF.15、(10分)已知:如图9,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△AB 外角∠CAM的平分线,CE⊥AN,垂足为点E,猜想四边形ADCE的形状,并给予证明.16、(10分)如图10,在梯形纸片ABCD中,AD//BC,AD>CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C处,折痕DE交BC于点E,连结C′E.求证:四边形CDC′E是菱形.“拓展创新”时间30分钟,共50分,一、选择及填空题(每题5分,共10分)1、如图11,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点E,交AB于点F,F为垂足,连接DE,则∠CDE=_________度2.如图12,四边形ABCD是矩形,F是AD上一点,E是CB延长线上一点,且四边形AECF是等腰梯形.下列结论中不一定...正确的是().(A)AE=FC(B)AD=BC(C)∠AEB=∠CFD(D)BE=AF二、填空题(每题5分,共10分)3、如图13,已知:平行四边形ABCD中,∠的平分线CE交边AD于E,BCD∠的平分线BG交CE于F,交ABCAD于G.若AB=4cm,AD=6cm,则EG=_______ cm .4、将矩形纸片ABCD按如图14所示的方式折叠,得到菱形AECF.若AB=9,则AC的长为_________三、解答题(每题15分,共30分)5、一次数学活动课上,老师留下了这样一道题“任画一个△ABC,以BC的中点O为对称中心,作△ABC的中心对称图形,问△ABC与它的中心对称图形拼成了一个什么形状的特殊四边形?并说明理由.”于是大家讨论开了,小亮说:“拼成的是平行四边形”;小华说:“拼成的是矩形”;小强说:“拼成的是菱形”;小红说:“拼成的是正方形”;其他同学也说出了自己的看法……你赞同他们中的谁的观点?为什么?若都不赞同,请说出你的观点(画出图形),并说明理由6、如图15-1 ,已知点P 是矩形ABCD 内一点,PA 、PB 、PC 、PD 把矩形分割成四个三角形,小东对该图形进行了研究。
为了探究的需要,小东过点P 作PE ⊥AD 交BC 于F,通过一番研究之后得出两条重要结论:(1)BPC APD CPD APB S S S S ∆∆∆∆+=+,(2)2222PD PB PC PA +=+;1)请你写出小东探究的过程.2)当P 在矩形外时,如图15-2,上述两个结论是否仍成立?若成立,请说明理由;若不成立,请写出你猜想的结论(不必证明)《“四边形”综合测试题(一)》参考答案基础巩固一、选择题1、D2、C3、A4、B5、C.6、B二、填空题7、平行四边形 8、3. 9、45° 10、等腰三角形 11、23 12.2三、解答题13、证明:(1)∵ ABCD 是平行四边形,∴DC=AB ,DC ∥AB,∴∠DCF=∠BAE ,∵ AE=CF , ∴△ADF ≌△CBE ,∴∠CDF =∠ABE14、如图8,把正方形ABCD 绕着点A ,按顺时针方向旋转得到正方形AEFG ,边FG 与BC 交于点H .求证:HC=HF.解:证明:连结AH ,∵四边形ABCD ,AEFG 都是正方形.∴90B G ∠=∠=°,AG AB =,BC=GF ,又AH AH =.Rt Rt ()AGH ABH HL ∴△≌△,HG HB =∴,∴HC=HF.15、解:猜想四边形ADCE 是矩形。
证明:在△A BC 中, AB =AC ,AD ⊥BC . ∴ ∠BAD =∠DA C .∵ AN 是△ABC 外角∠CAM的平分线,∴MAE CAE ∠=∠.∴ ∠DAE =∠DAC +∠CAE =⨯21180°=90°.又 ∵ AD ⊥BC ,CE ⊥AN ,∴ ADC CEA ∠=∠=90°,∴ 四边形ADCE为矩形.16、证明:根据题意可知 DE C CDE 'ΔΔ≅则 '''CD C D C DE CDE CE C E =∠=∠=,,∵AD//BC ∴∠C ′DE=∠CED ,∴∠CDE=∠CED ∴CD=CE∴CD=C ′D=C ′E=CE∴四边形CDC ′E 为菱形“拓展创新”,二、选择题1、60°2、D三、填空题 3、2cm 4、36三、解答题5、解:不赞同他们的观点,因为△ABC 形状不确定,所以应分情况讨论.(1)若△ABC 中,AC AB ≠且︒≠∠90BAC 时,如图1、图2. △ABC 与它的中心对称图形拼成了一个平行四边形.理由:∵B 与C 、A 与D 关于O 对称,∴OA=OD ,OB=OC ,∴四边形ABDC 是平行四边形.(2)若△ABC 中,AC AB =且︒≠∠90BAC 时,如图3、图4. △ABC 与它的中心对称图形拼成一个菱形.理由:∵B 与C 、A 与D 关于O 对称,∴OA=OD ,OB=OC ,∵AC AB =∴四边形ABDC 是菱形.(3)若△ABC 中,AC AB ≠且︒=∠90BAC 时,如图5,△ABC 与它的中心对称图形拼成一个矩形.理由:∵B 与C 、A 与D 关于O 对称,∴OA=OD ,OB=OC ,∵AC AB ≠︒=∠90BAC ,∴四边形ABDC 是矩形.(4)若△ABC 中,AC AB =且︒=∠90BAC 时,如图6,△ABC 与它的中心对称图形拼成一个正方形.理由:∵B 与C 、A 与D 关于O 对称,∴OA=OD ,OB=OC ,∵AC AB =,︒=∠90BAC ,∴四边形ABDC 是正方形..6、1)证明:(1)∵矩形ABCD 中,PE ⊥AD ,∴四边形ABFE 和四边形CDEF 都是矩形,CDEF CPD ABFE APB S S S S 矩形矩形,2121==∆∆,∴ABCD CPD APB S S S 矩形21=+∆∆,∴BPC APD CPD APB S S S S ∆∆∆∆+=+。
(2)∵矩形ABCD 中,PE ⊥AD ,∴由勾股定理,得222222222222,DE PE PD PF BF PB FC PF PC PE AE PA +=+=+=+=,,; ∴+++=++++=+22222222222PE PF BF PD PB FC PF PE AE PC PA ; 2DE .四边形ABFE 和四边形CDEF 都是矩形,∴CF DE BF AE ==,,∴2222PD PB PC PA +=+2). 当P 在矩形外时,结论(1)不成立;应为结论PAD BPC CPD APB S S S S ∆∆∆∆-=+ 结论(2)仍然成立.理由:同1)中证明(2).1.A2.C3.B4.举例说明教学准确性、有效性、美感三者的关系。
准确,就是指教师所讲知识是科学的,无误的、清晰明确的,正如足球可以准确地踢进球门(科学性)。
有效,就是教师讲授的知识学生听明白了,理解了,达到了预设的教学目标;高效就是用了很少时间,学生就听明白的了,理解了,达到了预设教学目标甚至实现了超标发展,正如开场不久很快足球就踢进了球门,而且还不断进球(技术性)。
美感,就是在准确、有效基础上,教师讲得形象生动;学生感觉轻松,愉悦,思维活跃,情绪饱满,兴趣盎然;这正如踢足球过程中的哪些艺术的观赏性很强的动作、人物、甚至服饰、发型、足球宝贝等等。
在教学实践中出现的准确、有效和美感三者处理不当问题,在理论上其实是对教学科学性、技术性与艺术性三者关系认识不清,对新课程倡导的三个维度:知识、能力(包含过程与方法)、情感态度价值观之间关系认知不清的表现。
那么,科学知识、能力、情感态度价值观三者,或这三个维度是什么关系呢?科学知识是基础,能力是知识的迁移和行为转化;情感态度价值观是知识的感召与观念沉淀。
知识是学生所有发展的基石;而科学知识是最具概括性的知识,其最基本形态就是概念。
基本知识(概念)没讲清楚、没听明白(缺乏科学有效性),能力就无从形成,有形象也没有真正感动,就无法积淀成积极情感态度态度价值观。
例如,共产主义理想信念,是一种很崇高的情感态度价值观,这种情感态度价值观,或者理想信念,如果没有对“共产主义”这个概念和相关知识的深透理解,可能形成吗?即使形成了一些,也是盲目的,难以上升到自我觉醒的最高境界。
