Matlab第5章数据处理与多项式计算
matlab第一讲

·
1.2 MATLAB 集成开发环境
如果一个命令行很长,一个物理行之内写不下,可以在第1个物理行之 后加上3个小黑点并按下回车键,然后接着下一个物理行继续写命令的 其他部分。3个小黑点称为续行符,即把下面的物理行看作该行的“逻 辑”继续。 例如:
z=1+1/(1*2)+(1*2*3)+1/(1*2*3*4)+…
系统科学研究所
1.2 MATLAB 集成开发环境
MATLAB的工具栏提供了一些命令按钮和一个当前路径列表框。
2.命令窗口
一般来说,在命令编辑区的一个命令行输入一条命令,命令行以回车 结束。但一个命令行可以输入若干条命令,各命令之间以逗号分隔, 若前一命令后带有分号,则逗号可以省略。例如:
x=720,y=68 x= 720 y=86 x=720;y=86 y=86
1.3MATLAB 的帮助功能
1.3.1帮助界面
进入MATLAB帮助界面可以通过以下3种方法。 单击MATLAB主窗口工具栏中的Help按钮。
在命令窗口中输入”helpwin”、”helpdesk”或“doc”命令。
选择Help菜单中的”MATLAB Help”选项。 1.3.2帮助命令
1.help命令
系统科学研究所
1.2 MATLAB 集成开发环境
检查该命令是否为MATLAB 搜索路径中其他目录下的M文件。 2.设置搜索路径
用户可以将自己的工作目录列入MATLAB搜索路径,从而将用户目录
纳入MATLAB系统统一管理。 (1)用path命令设置搜索路径 (2)用对话框设置搜索路径
·
系统科学研究所
统程序设计语言一样进行程序设计,而且结合MATLAB的数值计算和
MATLAB语言基础与应用(第二版)第5章 习题答案

第5章习题与答案5.1用矩阵三角分解方法解方程组123123123214453186920x x x x x x x x x +-=⎧⎪-+=⎨⎪+-=⎩ 解答:>>A=[2 1 -1;4 -1 3;6 9 -1] A =2 1 -1 4 -13 6 9 -1 >>b=[14 18 20]; b =14 18 20 >> [L, U, P]=lu(A) L =1.0000 0 0 0.6667 1.0000 0 0.3333 0.2857 1.0000 U =6.0000 9.0000 -1.0000 0 -7.0000 3.6667 0 0 -1.7143 P =0 0 1 0 1 0 1 0 0 >> y=backsub(L,P*b’) y =20.0000 4.6667 6.0000 >> x=backsub(U,y) x =6.5000 -2.5000 -3.5000 5.2 Cholesky 分解方法解方程组123121332352233127x x x x x x x ++=⎧⎪+=⎨⎪+=⎩ 解答:>> A=[3 2 3;2 2 0;3 0 12] A =3 2 32 2 03 0 12>> b=[5;3;7]b =537>> L=chol(A)L =1.7321 1.1547 1.73210 0.8165 -2.44950 0 1.7321>> y=backsub(L,b)y =-11.6871 15.7986 4.0415>> x=backsub(L',y)x =-6.7475 28.8917 49.93995.3解答:观察数据点图形>> x=0:0.5:2.5x =0 0.5000 1.0000 1.5000 2.0000 2.5000 >> y=[2.0 1.1 0.9 0.6 0.4 0.3]y =2.0000 1.1000 0.9000 0.6000 0.4000 0.3000 >> plot(x,y)图5.1 离散点分布示意图从图5.1观察数据点分布,用二次曲线拟合。
第六讲 MATLAB数值计算

5.2.4 矩阵的秩
求矩阵秩的函数: rank(A)。
例如,求例 5.7 中方程组系数矩阵 D 的秩,命令是:
D=[2, 2, -1, 1; 4, 3, -1, 2; 8, 5, -3, 4; 3, 3, -2, 2]; r=rank(D) r= 4
说明D是一个满秩矩阵。
5.2.5 向量和矩阵的范数
第五讲 MATLAB数值计算
5.1 5.2 5.3 5.4 5.5 5.6 5.7 5.8 5.9 特殊矩阵 矩阵分析 矩阵分解与线性方程组求解 数据处理与多项式计算 傅立叶分析 数值微积分 常微分方程的数值求解 非线性方程的数值求解 稀疏矩阵
5.1 特殊矩阵
5.1.1 对角阵与三角阵
1. 矩阵的对角元素 (1)提取矩阵的对角线元素 设 A 为 m×n 矩阵, diag(A) 函数用于提取矩阵 A主对 角线元素产生一个具有min(m,n)个元素的列向量。 (2)构造对角矩阵
2. 矩阵的伪逆
对奇异方阵和长方阵,求矩阵伪逆的函数是 pinv(A)。
例5.5 求A的伪逆,并将结果送B。 A=[3,1,1,1; 1,3,1,1; 1,1,3,1]; B=pinv(A) 例5.6 求矩阵A的伪逆。 A=[0,0,0; 0,1,0; 0,0,1]; pinv(A)
5.2.3 方阵的行列式
函数A = pascal(n)生成一个n阶的帕斯卡矩阵。
1 1 3 4 6 10 10 20 15 35
1 5 15 35 70
5.2 矩阵分析
5.2.1 矩阵结构变换
1. 矩阵的转置
转置运算符是单撇号(')。
2. 矩阵的旋转
矩阵的旋转利用函数 rot90(A,k) ,功能是将矩阵 A旋 转90º 的k倍,当k为1时可省略。
MATLAB中的数据处理

四、使用输入函数 对于大量的数据,或者格式更加复杂的数据文件,以上方法就不 太方便,此时针对不同格式的数据文件,可以采用相应的输入函数导 入数据。 1、load 函数 装载 Matlab 格式的数据文件(.mat)和文本格式的定界符为空格的 矩形文件。 例:载入文件“data02.txt”中的数据 2、dlmread 函数 将带有定界字符的 ASCII 数字数据读入矩阵 常用格式: M=dlmread(‘filename’) 是默认定界符。 M=dlmread(‘filename’,delimiter),指定定界符。 M=dlmread(‘filename’,delimiter,R,C),从矩形数据的左上角 R 行、C 列的位置开始读入。 注意:矩形数据的开始位置是 0 行 0 列。 M=dlmread(‘filename’,delimiter,range) ,读取用 range 指定范围的数 据,range=[R1 C1 R2 C2],R1C1 是左上角的行列号,R2C2 是右下角 的行列号;range 也可以用如下表示法:range=’A1..B7’。 例:对于 data02.txt 中的数据 >> dlmread('d:\data\data02.txt') %读全部数据 %Matlab 从文件格式中推断定界符,逗号
num = xlsread(filename, -1) %将在 Excel 窗口打开 filename 文件, 可以交互选择工作区中的数据文件; num = xlsread(filename, sheet) %选择工作表 sheet,默认为第一 个工作表; num = xlsread(filename, range) %指定工作表中的数据范围, 如’A4:B5’ num = xlsread(filename, sheet, range) 例:将电子表格 data01.xls 中的数据载入到 Matlab 工作区 >> xlsread('d:\data\data01')
MATLAB_数值计算

b31 b32 b33
对于编程语言,矩阵就是二维的数组
2.1 MATLAB的基本计算
数学计算分为数值计算与符号计算,前者 不允许出现未定义变量,后者允许。(Eg 2-1) 常用的基本数学函数表。 (Eg 2-2)
Eg 2-1
三角函数
函数
sin sinh asin cos acos
说明
正弦函数 双曲正弦函数 反正弦函数 余弦函数 反余弦函数
MATLAB数值计算
2.1 MATLAB的基本计算 2.2 MATLAB矩阵和数组 2.3 关系和逻辑运算 2.4 多项式 2.5 稀疏矩阵 2.6 数据分析函数 2.7 数值分析
概述
在M语言中最常用的数据类型表现手段和形
式就是变量和常量
M语言的基本处理单位是数值矩阵或者数值
Eg 2-14 低维数组合成高维数组
建立3阶魔方及帕斯卡数组
将A、B串联成三维数组
cat(1,A,B)=[A;B]
cat(2,A,B)=[A,B]
>> A=eye(4) A= 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 >> A(:,:,2)=eye(4)*10; >> A(:,:,3)=eye(4)*100 A(:,:,1) = 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 A(:,:,2) = 10 0 0 0 0 10 0 0 0 0 10 0 0 0 0 10 A(:,:,3) = 100 0 0 0 0 100 0 0 0 0 100 0 0 0 0 100
复数运算函数
函数
abs
பைடு நூலகம்
说明
求复数的模,若参数为实数则求绝对值
matlab多项式与特征方程

MATLAB是一种常用的数学软件,它在科学计算领域有着广泛的应用。
在MATLAB中,多项式和特征方程是两个非常重要的概念。
本文将首先介绍多项式的相关知识,然后深入探讨多项式在MATLAB中的应用。
接着会详细介绍特征方程及其在MATLAB中的应用。
希望本文对读者能有所帮助。
一、多项式1. 多项式的定义多项式是代数学中的基本概念之一。
它是由若干个数与字母的乘积相加而成的代数式。
一般地,多项式的形式可以表示为:P(x) = a0 + a1x + a2x^2 + ... + anx^n其中,P(x)为多项式,x为自变量,a0, a1, ..., an为系数,n为多项式的次数。
2. MATLAB中的多项式表示在MATLAB中,可以使用polyval函数来计算多项式的值,使用polyfit函数来拟合数据得到多项式方程。
给定一组数据点(x, y),可以使用polyfit函数拟合出最佳拟合多项式,并使用polyval函数计算出对应x值时的多项式函数值。
3. MATLAB中的多项式运算MATLAB提供了丰富的多项式运算函数,例如polyadd、polymul、polyder、polyint等。
通过这些函数,可以方便地进行多项式的加法、乘法、求导、积分等运算。
二、特征方程1. 特征方程的定义特征方程是矩阵论中的一个重要概念。
对于一个n阶方阵A,其特征方程可以表示为:det(A - λI) = 0其中,det表示矩阵的行列式,λ是特征值,I为单位矩阵。
特征方程的解即为矩阵A的特征值。
2. MATLAB中的特征方程求解在MATLAB中,可以使用eig函数来求解特征方程。
eig函数可以计算出矩阵的所有特征值和对应的特征向量。
这对于解决线性代数中的特征值和特征向量相关问题非常有用。
3. 特征方程的应用特征方程在科学计算领域有着广泛的应用,例如在控制系统、信号处理、结构力学等方面都有重要作用。
通过求解特征方程,可以分析和预测系统的稳定性、自由振动特性等。
第5讲MATLAB多项式及插值

第5讲MATLAB多项式及插值
5.1.2 求和与求积
数据序列求和与求积的函数是sum和prod,其使用方 法类似。设X是一个向量,A是一个矩阵,函数的调用格 式为:
sum(X):返回向量X各元素的和。 prod(X):返回向量X各元素的乘积。 sum(A):返回一个行向量,其第i个元素是A的第i列的元素和。 prod(A):返回一个行向量,其第i个元素是A的第i列的元素乘积。 sum(A,dim):当dim为1时,该函数等同于sum(A);当dim为2时, 返回一个列向量,其第i个元素是A的第i行的各元素之和。 prod(A,dim):当dim为1时,该函数等同于prod(A);当dim为2时, 返回一个列向量,其第i个元素是A的第i行的各元素乘积。
为解决Rung问题,引入分段插值。 第5讲MATLAB多项式及插值
算法分析:所谓分段插值就是通过插值点用折线或低次曲线 连接起来逼近原曲线。
MATLAB实现 可调用内部函数。 ➢ 命令 interp1
功能 : 一维数据插值(表格查找)。该命令对数据点之 间计算内插值。它找出一元函数f(x)在中间点的数值。其 中函数f(x)由所给数据决定。
t = 1900:10:1990; p = [75.995 91.972 105.711 123.203 131.669...
150.697 179.323 203.212 226.505 249.633]; 对应于美国从1900年到1990年的每10年的人口数,求 1975年的人口。由此推断美国1900年到2000年每一年的 人口数,并画出图形。
k1
j1
xxj ) xk xj
jk
MATLAB中没有直接实现拉格朗日算法的函数,我们已经介 绍过该函数的书写:
MATLAB基础及应用课件(下)第5-8章

图5-5 拟合曲线
第5章 MATLAB数值计算
第5章 MATLAB数值计算
5.4.4 图形窗口的拟合和统计工具
第5章 MATLAB数值计算
在图5-6中的“绘制拟合图”中选择拟合方 法(可同时选多种);
“显示方程”复核框可以选择是否在图形上 显示拟合多项式;
“绘制残差图”复核框选中时会产生第二幅 图形,该图形显示了每一个数据点与计算出来的 拟合曲线之间的距离。
例如选择“线性”和“三次方”拟合方法, 同时选中两个复核框,产生图形如图5-7所示。
MATLAB的图形窗口中提供了简单方便的数 据拟合和基本统计工具。
数据拟合工具可以对所绘制的曲线使用多种 方法进行拟合;
基本统计工具可提供最小值、最大值、平均 值、中位值、标准差、数据范围等统计运算。
1.数据拟合工具
第5章 MATLAB数值计算
使用数据拟合工具首先需要创建一幅图形,在 命令行窗口输入以下程序:
两个矩阵x和y的相关系 数
第5章 MATLAB数值计算
5.2 数值运算 一、 多项式
名称
创建多项 式
求根
求值
多项式乘 法
多项式除 法
多项式求 导
函数格式 P=[ a0 a1 a2 …an-1
an] P=poly(A) roots(P) polyval(P,A)
polyvalm(P,m)
说明
P为多项式(以下各函数中P均为多项式),a0 a1 a2 … an-1 an为按降幂顺序排列的多项式系数 A为向量。创建以向量A中元素为根的多项式
matlab在科学计算中的应用5多项式插值与数据拟合

>> x=[-5:1:5]; y=1./(1+x.^2); x0=[-5:0.1:5]; >> y0=lagrange(x,y,x0); >> y1=1./(1+x0.^2); %绘制图形 >> plot(x0,y0,'--r') %插值曲线 >> hold on >> plot(x0,y1,‘-b') %原曲线
5.1 关于多项式MATLAB命令
• 一个多项式的幂级数形式可表示为:
y c1xn c2 xn1 cn x cn1
• 也可表为嵌套形式
y ( ((c1x c2 )x c3)x cn )x cn1
• 或因子形式
y c1(x r1)(x r2 ) (x rn )
N阶多项式n个根,其中包含重根和复根。若多 项式所有系数均为实数,则全部复根都将以共轭对 的形式出现
cn 2
x2
cn1x cn2
多项式微分:
y c1xn c2 xn1
cn x cn1
y' nc1xn1 (n 1)c2 xn2 cn
• Polyder: 求多项式一阶导数的系数。 调用格式为: b=polyder(c ) c为多项式y的系数,b是微分后的系数,
其值为:
[nc1, (n 1)c2 , , cn ]
23.8125 76.0000
• polyfit:给定n+1个点将可以唯一确定一个n阶多项式。利 用命令polyfit可容易确定多项式的系数。 例:
>> x=[1.1,2.3,3.9,5.1]; >> y=[3.887,4.276,4.651,2.117]; >> a=polyfit(x,y,length(x)-1) a=
Matlab中的数据处理

Matlab中的数据处理Matlab中的各种工具箱最主要是以矩阵或数组作为处理对象,因此首先必须将原始数据以矩阵形式加载到Matlab的工作空间,然后对矩阵进行相关操作。
第一部分数据输入在Matlab中创建一个矩阵可以有如下几种途径:一、在Matlab命令窗口直接输入矩阵例如:>> A=[1 3 0;2 4 3;-3 4 9]说明:矩阵或数组的标识符都是[ ],矩阵同一行之间的元素用空格或逗号分隔,不同行之间用分号或回车符分隔。
二、利用workspace(工作空间)创建或修改矩阵在工作空间中新建一个空矩阵,然后双击该矩阵名,可以像Office 中的Excel电子表格一样进行输入和编辑数据,也可以双击已经存在于工作空间中的变量名,对其进行修改编辑。
例如:>> B=[];三、采用复制、粘贴的方式构造矩阵对于存在于外部文件中的比较规范的数据(排列成矩阵形式),可以先将数据块复制到剪贴板上,然后在Matlab中粘贴到相应变量。
举例:1、将data01.xls中的数据粘贴到Matlab工作空间中的变量C 中。
2、将data02.txt中的数据输入到Matlab工作空间中的变量D中。
四、使用输入函数对于大量的数据,或者格式更加复杂的数据文件,以上方法就不太方便,此时针对不同格式的数据文件,可以采用相应的输入函数导入数据。
1、load函数装载Matlab格式的数据文件(.mat)和文本格式的定界符为空格的矩形文件。
例:载入文件“data02.txt”中的数据2、dlmread函数将带有定界字符的ASCII数字数据读入矩阵常用格式:M=dlmread(‘filename’) %Matlab 从文件格式中推断定界符,逗号是默认定界符。
M=dlmread(‘filename’,delimiter),指定定界符。
M=dlmread(‘filename’,delimiter,R,C),从矩形数据的左上角R行、C 列的位置开始读入。
第6章 MATLAB数据分析与多项式计算_习题答案教学提纲

第6章M A T L A B数据分析与多项式计算_习题答案精品资料第6章 MATLAB数据分析与多项式计算习题6一、选择题1.设A=[1,2,3,4,5;3,4,5,6,7],则min(max(A))的值是()。
BA.1 B.3 C.5 D.72.已知a为3×3矩阵,则运行mean(a)命令是()。
BA.计算a每行的平均值 B.计算a每列的平均值C.a增加一行平均值 D.a增加一列平均值3.在MATLAB命令行窗口输入下列命令:>> x=[1,2,3,4];>> y=polyval(x,1);则y的值为()。
DA.5 B.8 C.24 D.104.设P是多项式系数向量,A为方阵,则函数polyval(P,A)与函数polyvalm(P,A)的值()。
DA.一个是标量,一个是方阵 B.都是标量C.值相等 D.值不相等5.在MATLAB命令行窗口输入下列命令:>> A=[1,0,-2];>> x=roots(A);则x(1)的值为()。
CA.1 B.-2 C.1.4142 D.-1.41426.关于数据插值与曲线拟合,下列说法不正确的是()。
AA.3次样条方法的插值结果肯定比线性插值方法精度高。
B.插值函数是必须满足原始数据点坐标,而拟合函数则是整体最接近原始数据点,而不一定要必须经过原始数据点。
C.曲线拟合常常采用最小二乘原理,即要求拟合函数与原始数据的均方误差达到极小。
D.插值和拟合都是通过已知数据集来求取未知点的函数值。
二、填空题1.设A=[1,2,3;10 20 30;4 5 6],则sum(A)= ,median(A)= 。
[15 27 39],[4 5 6[2.向量[2,0,-1]所代表的多项式是。
2x2-1仅供学习与交流,如有侵权请联系网站删除谢谢2精品资料3.为了求ax2+bx+c=0的根,相应的命令是(假定a、b、c已经赋值)。
Matlab使用方法

solve('x^2+3x-6') solve('-x^2*y+3*x-6','x+y^2-1')
求方程的符号解
solve (eq1,eq2,…eqn) 求方程组的符号解
2.方程(组)的数值解 fzero (fun,x0) 用数值方法求方程根
七、积分变换 1. Fourier积分变换
返回a、b的并集,即c = a∪b 返回向量a、b的公共部分,即c= a∩b
差:setdiff
返回属于a但不属于b的不同元素的集合,C = a-b
交集的非: setxor
检测集合中的元素: ismember
4. 除法运算
A/B
5. 矩阵乘方
exp(A) :EA 6. 矩阵函数 expm logm sqrtm
五. 拟合和插值 1. 多项式拟合: 2. 插值: polyfit ( x, y , n)
a. interp1( X,Y,xi,method) method 可取下列值:
linear spline cubic 线性插值
一维数据插值
b. interp2( X,Y,Z,xi, yi,method) 二维数据插值
注: M文件的调用以文件名为准。
%为Matlab的注释符,其后的语句 不执行(只对当前行有效)。
二、Matlab语言
1.逻辑判断符 >= <= > isequal函数 2.逻辑运算符 & | ~
<
==
~=
3.条件语句 ① if-else语句
② switch-case语句
4.循环语句
Matlab原理与工程应用第二版第五章(函数)

14
非线性方程数值求解
函数fzero()求一元函数的零点,其具体使用方法如下:
x = fzero(@fun,x0,options,p1,p2,…) , 在 x0 点 附 x = fzero(@fun,[x0,x1]) ,在 [x0,x1] 区间内寻找函
近寻找函数的零点;
数的零点;
x = fzero(@fun,x0,options) ,用 options 指定寻找零
subplot(1,3,1); plot(x,y,'ro',xi,yi_nearest,'b-'); title(‘最邻近插值'); subplot(1,3,2); plot(x,y,'ro',xi,yi_linear,'b-'); title(‘线性插值'); subplot(1,3,3); plot(x,y,'ro',xi,yi_spline,'b-'); title(‘三次样条插值');
23
8.1.2 数值积分的实现方法 1.变步长辛普生法 基于变步长辛普生法,MATLAB给出了quad函数来求定积 分。该函数的调用格式为: [I,n]=quad('fname',a,b,tol,trace) 其中fname是被积函数名。a和b分别是定积分的下限和 上限。tol用来控制积分精度,缺省时取tol=0.001。 trace控制是否展现积分过程,若取非0则展现积分过程, 取0则不展现,缺省时取trace=0。返回参数I即定积分 值,n为被积函数的调用次数。
19
将求得的解代回原方程,可以检验结果是否正确, 命令如下: q=myfun(x) q = 1.0e-009 * 0.2375 0.2957 可见得到了较高精度的结果。
MATLAB基础教程 第5章 符号运算

第五章 符号运算
5.1 符号运算基础
2. 符号表达式的转换
(2)expand:该函数用于符号表达式的展开。其操作对象可以是多种类型,如多项 式、三角函数、指数函数等。
例5-6 符号表达式的展开。 >>syms x y; >>f=(x+y)^3; >>expand(f) ans= x^3+3*x^2*y+3*x*y^2+y^3 >>expand(sin(x+y)) ans= sin(x)*cos(y)+cos(x)*sin(y) >>expand(exp(x+y)) ans= exp(x)*exp(y)
第五章 符号运算
5.1 符号运算基础
例5-2 符号运算和数值运算之间的差别 >>sym(2)/sym(5) ans= 2/5 >>2/5+1/3 ans=0.7333 >>sym(2)/sym(5)+sym(1)/sym(3) ans= 11/15 >>double(sym(2)/sym(5)+sym(1)/sym(3)) ans= 0.7333 由上例可以看出,当进行数值运算时,得到的结果为double型数据;采用符号进 行运算时,输出的结果为分数形式。
第五章 符号运算
5.1 符号运算基础
2. 符号表达式的转换
(4)simplify:该函数实现表达式的化简。 例5-8 simplify函数的应用。 >>simplify(sin(x)^2+cos(x)^2) ans= 1 >>syms a b c; >>simplify(exp(c*log(sqrt(a+b)))) ans= (a+b)^(1/2*c) >>S=[(x^2+5*x+6)/(x+2),sqrt(16)]; >>R=simplify(S) R= [3+x, 4]
刘卫国版MATLAB程序设计与应用课后实验六八九
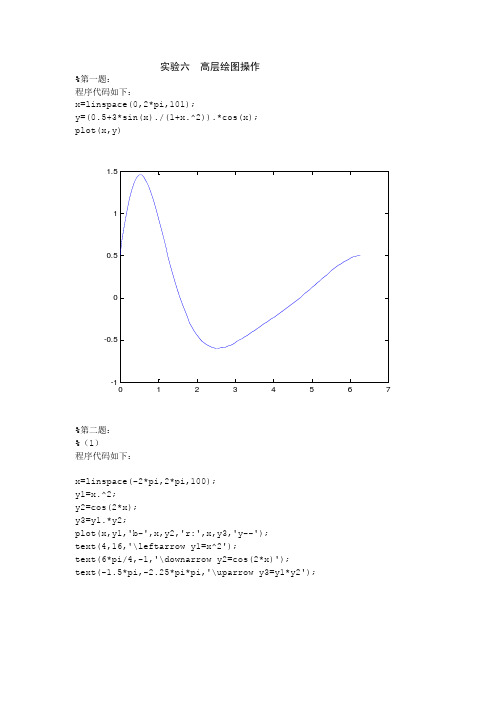
实验六 高层绘图操作%第一题:程序代码如下:x=linspace(0,2*pi,101);y=(0.5+3*sin(x)./(1+x.^2)).*cos(x); plot(x,y)01234567-1-0.50.511.5%第二题: %(1)程序代码如下:x=linspace(-2*pi,2*pi,100); y1=x.^2;y2=cos(2*x); y3=y1.*y2;plot(x,y1,'b-',x,y2,'r:',x,y3,'y--'); text(4,16,'\leftarrow y1=x^2');text(6*pi/4,-1,'\downarrow y2=cos(2*x)');text(-1.5*pi,-2.25*pi*pi,'\uparrow y3=y1*y2');-8-6-4-22468-30-20-1010203040%(2)程序代码如下:x=linspace(-2*pi,2*pi,100); y1=x.^2;y2=cos(2*x); y3=y1.*y2;subplot(1,3,1);%分区 plot(x,y1);title('y1=x^2');%设置标题 subplot(1,3,2); plot(x,y2);title('y2=cos(2*x)'); subplot(1,3,3); plot(x,y3);title('y3=x^2*cos(2*x)');-10100510152025303540y1=x 2-1010-1-0.8-0.6-0.4-0.200.20.40.60.81y2=cos(2*x)-1010-30-20-1010203040y3=x 2*cos(2*x)%(3)程序代码如下:x=linspace(-2*pi,2*pi,20); y1=x.^2;subplot(2,2,1);%分区 bar(x,y1);title('y1=x^2的条形图');%设置标题 subplot(2,2,2); stairs(x,y1);title('y1=x^2的阶梯图'); subplot(2,2,3); stem(x,y1);title('y1=x^2的杆图'); subplot(2,2,4);fill(x,y1,'r');%如果少了'r'则会出错 title('y1=x^2的填充图'); %其他的函数照样做。
matlab多项式

matlab多项式10.1 根找出多项式的根,即多项式为零的值,可能是许多学科共同的问题,。
MA TLAB求解这个问题,并提供其它的多项式操作工具。
在MA TLAB里,多项式由一个行向量表示,它的系数是按降序排列。
例如,输入多项式x4-12x3+0x2+25x+116» p=[1-12025116]p =1-12025116注意,必须包括具有零系数的项。
除非特别地辨认,MA TLAB无法知道哪一项为零。
给出这种形式,用函数roots找出一个多项式的根。
» r=roots(p)r =11.74732.7028-1.2251 + 1.4672i-1.2251 - 1.4672i因为在MA TLAB中,无论是一个多项式,还是它的根,都是向量,MA TLAB按惯例规定,多项式是行向量,根是列向量。
给出一» pp=poly(r)pp =1.0e+002 *Columns 1 through 40.0100-0.12000.00000.2500Column 51.1600 + 0.0000i» pp=real(pp) %throw away spurious imaginary partpp =1.0000-12.00000.000025.0000116.0000因为MA TLAB无隙地处理复数,当用根重组多项式时,如果一些根有虚部,由于截断误差,则poly的结果有一些小的虚部,这是很普通的。
消除虚假的虚部,如上所示,只要使用函数real抽取实部。
10.2 乘法函数conv支持多项式乘法(执行两个数组的卷积)。
考虑两个多项式a(x)=x3+2x2+3x+4和b(x)= x3+4x2+9x+16的乘积:» a=[1234] ;b=[14916];» c=conv(a , b)c =162050758464结果是c(x)=x6+6x5+20x4+50x3+75x2+84x+64。
matlab求解多项式展开系数

文章主题:如何使用MATLAB求解多项式展开系数在数学和工程领域中,多项式展开是一个经常出现的问题,它们在数据逼近、信号处理、微积分、代数等各个领域都有着广泛的应用。
而在使用MATLAB进行多项式展开系数的求解时,可以借助其强大的数值计算和符号计算功能,从而方便快捷地完成复杂的计算工作。
下面,我们将从简单到复杂地讨论如何使用MATLAB求解多项式展开系数。
1. 简单情况下的多项式展开系数求解在MATLAB中,可以使用polyfit函数来求解简单情况下的多项式展开系数。
对于一组已知的数据点(x,y),我们可以使用polyfit函数来拟合这些数据点,从而得到多项式展开系数。
具体函数调用如下:```matlabp = polyfit(x,y,n);```其中,x和y分别为已知的数据点,n为所需要拟合的多项式的阶数。
通过调用polyfit函数,即可得到多项式展开系数p。
2. 复杂情况下的多项式展开系数求解在实际应用中,经常会遇到复杂情况下的多项式展开系数求解问题,比如变量的多重指数、高次多项式的展开等。
针对这些情况,MATLAB提供了符号计算工具箱,可以使用符号变量来表示和处理这些复杂的数学表达式。
对于一个复杂的多项式展开问题,我们可以使用符号计算工具箱中的函数进行求解。
具体步骤如下:- 定义符号变量:```matlabsyms x```- 构建复杂的多项式表达式:```matlabf = x^2 + 3*x + 1;```- 求解多项式展开系数:```matlabc = coeffs(f,x);```通过上述步骤,即可得到复杂多项式的展开系数c。
3. 总结与回顾在本文中,我们从简单到复杂地讨论了如何使用MATLAB求解多项式展开系数。
在简单情况下,可以使用polyfit函数进行求解;在复杂情况下,可以借助符号计算工具箱进行求解。
通过MATLAB强大的数值计算和符号计算功能,我们能够方便快捷地完成多项式展开系数的求解工作。
MATLAB实验报告

MATLAB实践报告2016/2017学年第一学期专业:电气工程及其自动化班级:学号:姓名:2017年 2 月目录第1章绪论 (1)1.1 Matlab简介 (1)1.2 Matlab语言特点及优势 (1)1.2.1 语言特点 (1)1.2.2 优势 (2)1.3 Matlab的功能 (5)第2章Matlab实践任务 (6)2.1实验一Matlab环境语法、基本运算及绘图 (6)2.1.1实验目的 (6)2.1.2实验原理 (6)2.1.3实验内容 (6)2.2实验二Matlab数值运算 (10)2.2.1实验目的 (10)2.2.2实验原理 (10)2.2.3实验内容 (10)2.3实验三Matlab的符号计算 (19)2.3.1实验目的 (19)2.3.2实验内容 (19)2.4实验四Matlab基本编程方法 (23)2.4.1实验目的 (23)2.4.2实验内容 (23)第3章小结 (27)参考文献 (28)第1章绪论1.1 Matlab简介Matlab是“Matrix Laboratory”的缩写,意为“矩阵实验室”,是当今美国很流行的科学计算软件.信息技术、计算机技术发展到今天,科学计算在各个领域得到了广泛的应用.在许多诸如控制论、时间序列分析、系统仿真、图像信号处理等方面产生了大量的矩阵及其相应的计算问题.自己去编写大量的繁复的计算程序,不仅会消耗大量的时间和精力,减缓工作进程,而且往往质量不高.美国Mathwork软件公司推出的Matlab软件就是为了给人们提供一个方便的数值计算平台而设计的.Matlab是一个交互式的系统,它的基本运算单元是不需指定维数的矩阵,按照IEEE的数值计算标准(能正确处理无穷数Inf(Infinity)、无定义数NaN(not-a-number)及其运算)进行计算。
系统提供了大量的矩阵及其它运算函数,可以方便地进行一些很复杂的计算,而且运算效率极高。
Matlab命令和数学中的符号、公式非常接近,可读性强,容易掌握,还可利用它所提供的编程语言进行编程完成特定的工作。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【例5.9】表5.3所示为我国0~6个月婴儿的体重、身 长参考标准,用3次样条插值分别求得婴儿出生后半 个月到5个半月每隔1个月的身长、体重参考值。
表5.3 我国婴儿体重、身长计量表
出生 身长(cm) 50.6 体重(kg) 3.27 1月 56.5 4.97 2月 59.6 5.95 3月 62.3 6.73 4月 64.6 7.32 5月 65.9 7.70 6月 68.1 8.22
2.相关系数
相关系数用来衡量两组数据之间的线性相关程度。 corrcoef函数用于求数据的相关系数矩阵。 ● corrcoef(X,Y):求向量X和Y的相关系数。 ● corrcoef(X):返回从矩阵X形成的一个相关系 数矩阵。它把矩阵X的每列作为一个变量,然后 求它们的相关系数。
【例5.7】随机抽取15名健康成人,测定血液的凝血 酶浓度及凝血时间,分析凝血酶浓度与凝血时间之间 的相关性。 命令如下: X=[1.1,1.2,1.0,0.9,1.2,1.1,0.9,0.6,1.0,0.9,1.1,0.9,1.1, 1,0.7]'; Y=[14,13,15,15,13,14,16,17,14,16,15,16,14,15,17]'; R=corrcoef(X,Y) R= 1.0000 -0.9265 -0.9265 1.0000 求得的R说明凝血酶浓度与凝血时间之间的相关程度较 高。
5.1.3 平均值和中值
数据序列的平均值指的是算术平均值。中值是指在数据序列中 其值的大小恰好处在中间的元素。例如: 数据序列 2,5,7,9,12的中值为7 如果数据为偶数个,则中值等于中间的两项之平均值。例如, 数据序列 2,5,6,7,9,12中,处于中间的数是6和7,故 其中值为此两数之平均值6.5。 求数据序列平均值的函数是mean,mean函数的调用格式如下。 ● mean(A):如果A是一个向量,则返回向量的算术平均值。如 果A是一个矩阵,则返回一个行向量,其第i个元素是A的第i列 的算术平均值。 ● mean(A,dim):当dim为1时,该函数等同于mean(A);当dim 为2时,返回一个列向量,其第i个元素是A的第i行的算术平均 值。 求数据序列中值的函数是median,其用法和mean完全相同。
【例5.2】已知 , 求矩阵x、y所有同一位置上的较大元素构成的 新矩阵p。
45 73 34 84
443 x 67
43 43
65 y 61
34 326
x=[443,45,43;67,34,-43]; y=[65,73,34;61,84,326]; p=max(x,y) p= 443 73 43 67 84 326
5.1.6 排序
MATLAB提供了对向量X进行排序的函数sort(X), 函数返回一个对X中的元素按升序排列的新向量。 sort函数也可以对矩阵A的各列或各行重新排序, 其调用格式为 [Y,I]=sort(A,dim,mode) 其中Y是排序后的矩阵,而I记录Y中的元素在A中 的位置。dim指明对A的列还是行进行排序,若 dim = 1,则按列排;若dim = 2,则按行排。 mode指明按升序还是降序排序,'ascend'为升序, 'descend'为降序。dim默认取1,mode默认取 'ascend'。
2
32
64
5.1.5 标准方差与相关系数
1.求标准方差 方差描述了一组数据波动的大小,方差越小,数据波 动越小。在MATLAB中,提供了计算数据序列的标 准方差的函数std。对于向量X,std(X)返回一个标准 方差。对于矩阵A,std(A)返回一个行向量,它的各 个元素便是矩阵A各列或各行的标准方差。std函数的 一般调用格式为: Y=std(A,flag,dim) 其中flag取0或1,当flag = 0时,按σ1所列公式计算 标准方差;当flag = 1时,按σ2所列公式计算标准方 差。dim取1或2,当dim = 1时,求各列元素的标准 方差;当dim = 2时,则求各行元素的标准方差。默 认flag = 0,dim = 1。
【例5.6】某次射击选拔比赛中小明与小华的10次射击 成绩(单位:环)记录在矩阵a中,试比较两人的成绩。
a=[7,4,9,8,10,7,8,7,8,7;7,6,10,5,9,8,10,9,5,6]'; mean(a) ans = 7.5000 7.5000 std(a) ans = 1.5811 1.9579 两人成绩的平均值相同,但小明的成绩的标准方差较小, 说明小明的成绩波动较小,成绩更稳定。
2 10 s 1 2 2 ... 2 【例5.5】求
的值。
命令如下: x=[1,ones(1,10)*2] x= 1 2 2 2 2 2 2 2 2 2 y=cumprod(x) y= Columns 1 through 7 1 2 4 8 16 Columns 8 through 11 128 256 512 1024 s=sum(y) s= 2047
【例5.8】对二维矩阵 1
命令如下: A=[1,-8,5;4,12,6;13,7,-13]; sort(A,2,‘descend’) %对A的每行按降序排序 Ans= 5 1 -8 12 6 4 13 7 -13 [X,I]=sort(A) %对A按列排序,并将每个元素所在行号送矩阵I X= I= 1 -8 -13 1 1 3 4 7 5 2 3 1 13 12 6 3 2 2
数据序列求积的函数是prod,其用法和sum完全 相同。
【例5.3】已知 ,求矩阵A的每 行元素的成绩和全部元素的乘积。
10 11
1 A 5 9
2 6
3 7
4 8 12
A=[1:4;5:8;9:12]; S=prod(A,2) %求每行元素的乘积 S= 24 1680 11880 P=prod(S) %求全部元素的乘积,即12! P= 479001600
第5章 数据处理与多项式计算
Hale Waihona Puke 【本章学习目标】● ● ● ● 掌握数据统计和分析的方法。 掌握数值插值与曲线拟合的方法及其应用。 掌握快速傅立叶变换的应用方法。 掌握多项式的常用运算。
5.1 数据统计处理
5.1.1 最大值和最小值 1.求最大值和最小值 ● max(A):如果A是向量,则返回向量A的最大值。如果A 中包含复数元素,则按模取最大值。如果A是矩阵,则返 回一个行向量,向量的第i个元素是矩阵A的第i列上的最大 值。 ● [Y,U] = max(A):如果A是向量,则返回向量A的最大值存 入Y,最大值的序号存入U。如果A中包含复数元素,则按 模取最大值。如果A是矩阵,则Y向量记录A的每列的最大 值,U向量记录每列最大值的行号。 ● max(A,[],dim):仅用于矩阵。dim取1或2。dim取1时, 该函数和max(A)完全相同;dim取2时,该函数返回一个 列向量,其第i个元素是A矩阵的第i行上的最大值。
【例5.1】分别求矩阵 54 90 列和各行元素中的最大值。 23
86 32 12
453 64 71
45 54 18
中各
x=[54,86,453,45;90,32,64,54;-23,12,71,18]; [y,l]=max(x) %求矩阵x中各列元素的最大值及其这些元素的行下标 y= 90 86 453 54 l= 2 1 1 2 y=max(x,[ ],2) %命令中dim=2,故查找操作在各行中进行 y= 453 90 71
5.2.1 一维数据插值
若已知的数据集是平面上的一组离散点集,即被插值函数是一个单变 量函数,则数值插值问题称为一维插值。在MATLAB中,实现插值的 函数是interp1,其调用格式为 Y1=interp1(X,Y,X1,'method') 函数根据X、Y的值,计算函数在X1处的值。X、Y是两个等长的已知 向量,分别描述采样点和样本值,X1是一个向量或标量,描述欲插值 的点,Y1是一个与X1等长的插值结果。method是插值方法,允许的 取值如下: ● 'linear':线性插值。线性插值是默认的插值方法。它是把与插值点靠 近的两个数据点用直线连接,然后在直线上选取对应插值点的数据。 ● 'nearest':最近点插值。根据已知插值点与已知数据点的远近程度进 行插值。插值点优先选择较近的数据点进行插值操作。 ● 'cubic':3次多项式插值。根据已知数据求出一个3次多项式,然后根 据该多项式进行插值。 ● 'spline':3次样条插值。所谓3次样条插值,是指在每个分段(子区 间)内构造一个3次多项式,使其插值函数除满足插值条件外,还要 求在各节点处具有光滑的条件。
% 偶数个元素
5.1.4 累加和与累乘积
所谓累加和或累乘积,是指从数据序列的第1元素开始直 到当前元素进行累加或累乘,作为结果序列的当前元素值。 在MATLAB中,使用cumsum和cumprod函数求得向量 和矩阵元素的累加和与累乘积向量。cumsum函数的调用 格式如下。 ● cumsum(A):如果A是一个向量,则返回向量的累加和。 如果A是一个矩阵,则返回一个矩阵,其第i列是A的第i列 的累加和向量。 ● cumsum(A,dim):当dim为1时,该函数等同于 cumsum(A);当dim为2时,返回一个矩阵,其第i行是A 的第i行的累加和向量。 求累乘积的函数是cumprod,其用法和cumsum完全相 同。
5.1.2 求和与求积
数据序列求和的函数是sum。sum函数的调用格 式如下。
–● sum(A):如果A是一个向量,则返回向量各元 素的和。如果A是一个矩阵,则返回一个行向量,其第i 个元素是A的第i列的元素和。 –● sum(A,dim):当dim为1时,该函数等同于 sum(A);当dim为2时,返回一个列向量,其第i个元 素是A的第i行的各元素之和。
