数学建模-模型-大全
数学建模—函数模型及其应用

(k为常数,k≠0);
(4)指数型函数模型:f(x)=abx+c(a,b,c为常数,a≠0,b>0,b≠1);
(5)对数型函数模型:f(x)=mlogax+n(m,n,a为常数,m≠0,a>0,a≠1);
(6)幂型函数模型:f(x)=axn+b(a,b,n为常数,a≠0);
1 (),∈1 ,
了该车相邻两次加油时的情况.
加油时间
2020年5月1日
2020年5月15日
加油量(升)
12
48
加油时的累计里程(千米)
35 000
35 600
注:“累计里程”指汽车从出厂开始累计行驶的路程.
在这段时间内,该车每100千米平均耗油量为(
A.6升 B.8升
C.10升 D.12升
)
答案 B
解析 因为第一次油箱加满,所以第二次的加油量即为该段时间内的耗油量,
3
log 4 8 + = 1,
+ = 1,
解析依题意得
即 2
解得 a=2,b=-2.则
log 4 64 + = 4,
3 + = 4.
y=2log4x-2,当 y=8 时,即 2log4x-2=8,解得 x=1 024.
关键能力 学案突破
考点1
利用函数图像刻画实际问题
【例1】 (2020北京东城一模,10)
故耗油量V=48升.而这段时间内行驶的里程数S=35 600-35 000=600千米.
所以这段时间内,该车每100千米平均耗油量为
48
×100=8升,故选B.
600
3.(2020北京平谷二模,9)溶液酸碱度是通过pH计算的,pH的计算公式为
数学建模常用算法和模型全集

数学建模常用算法和模型全集数学建模是一种将现实世界的问题转化为数学问题,并通过建立数学模型来求解的方法。
在数学建模中,常常会用到各种算法和模型,下面是一些常用的算法和模型的全集。
一、算法1.线性规划算法:用于求解线性规划问题,例如单纯形法、内点法等。
2.非线性规划算法:用于求解非线性规划问题,例如牛顿法、梯度下降法等。
3.整数规划算法:用于求解整数规划问题,例如分支定界法、割平面法等。
4.动态规划算法:用于求解具有最优子结构性质的问题,例如背包问题、最短路径问题等。
5.遗传算法:模拟生物进化过程,用于求解优化问题,例如遗传算法、粒子群算法等。
6.蚁群算法:模拟蚂蚁寻找食物的行为,用于求解优化问题,例如蚁群算法、人工鱼群算法等。
7.模拟退火算法:模拟固体退火过程,用于求解优化问题,例如模拟退火算法、蒙特卡罗模拟等。
8.蒙特卡罗算法:通过随机抽样的方法求解问题,例如蒙特卡罗模拟、马尔科夫链蒙特卡罗等。
9.人工神经网络:模拟人脑神经元的工作原理,用于模式识别和函数逼近等问题,例如感知机、多层感知机等。
10.支持向量机:用于分类和回归问题,通过构造最大间隔超平面实现分类或回归的算法,例如支持向量机、核函数方法等。
二、模型1.线性模型:假设模型的输出与输入之间是线性关系,例如线性回归模型、线性分类模型等。
2.非线性模型:假设模型的输出与输入之间是非线性关系,例如多项式回归模型、神经网络模型等。
3.高斯模型:假设模型的输出服从高斯分布,例如线性回归模型、高斯朴素贝叶斯模型等。
4.时间序列模型:用于对时间序列数据进行建模和预测,例如AR模型、MA模型、ARMA模型等。
5.最优化模型:用于求解优化问题,例如线性规划模型、整数规划模型等。
6.图论模型:用于处理图结构数据的问题,例如最短路径模型、旅行商问题模型等。
7.神经网络模型:用于模式识别和函数逼近等问题,例如感知机模型、多层感知机模型等。
8.隐马尔可夫模型:用于对具有隐藏状态的序列进行建模,例如语音识别、自然语言处理等。
数学建模 模型 大全
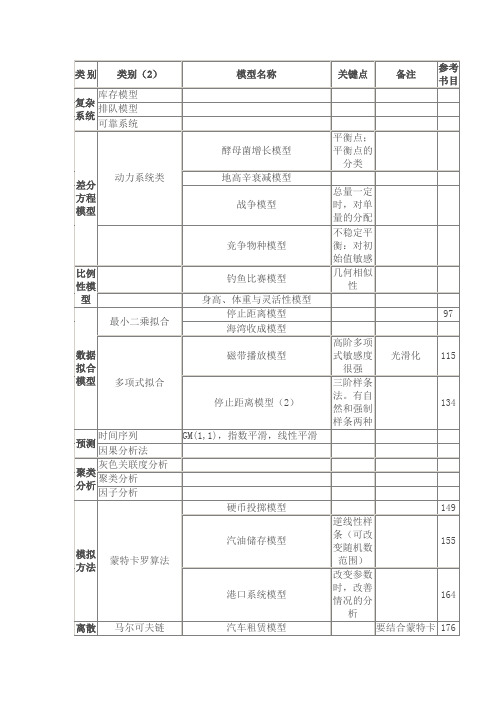
Scheafer微分方程模型
Lanchester战斗模型
350
SIR模型
军备竞赛的经济模型
355
混沌与分形模型
连续优化问题
Steiner树
库存模型
制造模型
最陡上升梯度方法
375
石油转运模型
Lagrange乘子法
注意里面涉及到的经济学概念和意义
381
航天飞机的水箱模型
渔业模型
注意各种“最优”的意义
155
港口系统模型
改变参数时,改善情况的分析
164
离散概率模型
马尔可夫链
汽车租赁模型
要结合蒙特卡罗算法
176
投票趋势模型
177
Markov决策
串联和并联系统模型
178
线性规划模型
无约束类
生产计划模型
192
取整数类
载货模型
194
动态规划类
1Hale Waihona Puke 7多目标规划类投资问题
有时须对目标进行取舍。可采取加权
系统层次分析
97
海湾收成模型
多项式拟合
磁带播放模型
高阶多项式敏感度很强
光滑化
115
停止距离模型(2)
三阶样条法。有自然和强制样条两种
134
预测
时间序列
GM(1,1),指数平滑,线性平滑
因果分析法
聚类分析
灰色关联度分析
聚类分析
因子分析
模拟方法
蒙特卡罗算法
硬币投掷模型
149
汽油储存模型
逆线性样条(可改变随机数范围)
图标模型
军备竞赛模型
民防、移动发射台、多弹头
数学建模中的常见模型

数学建模中的常见模型数学建模综合评价模型是一种通过对各个评价指标进行量化,并将它们按照权重进行加权,最终得到一个综合评价值的方法。
这个模型可以应用于多指标决策问题,用于对被评价对象进行排名或分类。
常见的数学建模综合评价模型包括模糊综合评价模型、灰色关联分析模型、Topsis(理想解法)、线性加权综合评价模型、熵值法和秩和比法等。
模糊综合评价模型是一种基于模糊数学理论的方法,它将评价指标的模糊程度考虑在内,得到一个模糊评价结果。
该模型的步骤包括确定评价指标及其权重、构建模糊评价矩阵、进行模糊运算、得到模糊评价结果。
灰色关联分析模型是一种用于分析指标间关联性的方法,它可以帮助我们确定各个指标对被评价对象的影响程度。
该模型的步骤包括确定关联度计算方法、计算各个指标的关联度、得到综合关联度。
Topsis(理想解法)是一种基于距离的方法,它通过计算每个评价对象与理想解的距离,得到一个综合评价值。
该模型的步骤包括确定正负理想解、计算距离、得到综合评价值。
线性加权综合评价模型是一种常用的多指标决策方法,它将各个评价指标的权重与指标值线性组合起来,得到一个综合评价值。
该模型的优点是简单易操作,计算方便,可以对各个指标的重要性进行量化,并将其考虑在评价中。
但是,该模型的权重确定较为主观,且假设指标之间相互独立,不考虑相关性。
熵值法是一种基于信息熵理论的方法,它通过计算每个指标的熵值,得到一个综合评价值。
该模型的步骤包括计算指标的熵值、计算权重、得到综合评价值。
秩和比法是一种用于处理多指标决策问题的方法,它通过计算指标的秩和比,得到一个综合评价值。
该模型的步骤包括编秩、计算秩和比、得到综合评价值。
根据具体的评价需求和问题特点,我们可以选择合适的数学建模综合评价模型来进行评价。
每个模型都有其优点和缺点,需要根据具体情况进行选择和应用。
<span class="em">1</span><spanclass="em">2</span><span class="em">3</span> #### 引用[.reference_title] - *1* *2* *3* [数学建模——评价模型]()[target="_blank" data-report-click={"spm":"1018.2226.3001.9630","extra":{"utm_sourc e":"vip_chatgpt_mon_search_pc_result","utm_medium":"di stribute.pc_search_result.none-task-cask-2~all~insert_cask~default-1-null.142^v93^chatsearchT3_1"}}] [.reference_itemstyle="max-width: 100%"] [ .reference_list ]。
数学建模图论模型

任意两点均有通路的图称为连通图。
连通而无圈的图称为树,常用T=<V,E>表示树。
若图G’是图 G 的生成子图,且G’又是一棵树, 则称G’是图G 的生成树。
例 Ramsey问题
图1
图2
并且常记: V = v1, v2, … , vn, |V | = n ; E = {e1, e2, … , em}ek=vivj , |E | = m
称点vi , vj为边vivj的端点 在有向图中, 称点vi , vj分别为边vivj的 始点和终点. 该图称为n,m图
8
对于一个图G = V, E , 人们常用图形来表示它, 称其 为图解 凡是有向边, 在图解上都用箭头标明其方向.
4、P'代替P,T'代替T,重复步骤2,3
定理2 设 T为V的子集,P=V-T,设 (1)对P中的任一点p,存在一条从a到p的最短路径,这条路径仅有P中的
点构成, (2)对于每一点t,它关于P的指标为l(t),令x为最小指标所在的点, 即:
l(x)mli(tn )} t{ ,T
(3)令P’=P Ux,T’=T-{x},l’(t)表示T'中结点t关于P'的指标,则
解:用四维01向量表示人,狼,羊,菜例在过河西河岸问的题状态(在
岸则分量取1;否则取0),共有24 =16 种状态; 在河东岸 态类似记作。
由题设,状态(0,1,1,0),(0,0,1,1),(0,1,1,1)是不允许的
其对应状态:(1,0,0,1), (1,1,0,0),(1,0,0,0)也是不允许
数学建模系列-常用模型

A1, A2 , A3, A4 , A5
分别表示 景色、费用、 居住、饮食、 旅途。
由上表,可得成对比较矩阵
1
2
1 2 1
4 7
3 5
3
5
A
1 4Βιβλιοθήκη 1 711 1 2 3
1 3
1 3
1 5
1 5
2 3
1 1
1
1
旅游问题的成对比较矩阵共有6个(一个5阶,5个3阶)。
问题:两两进行比较后,怎样才能知道,下层各因素对上 层某因素的影响程度的排序结果呢?
3 层次单排序及一致性检验
层次单排序:确定下层各因素对上层某因素影响程度的过程。 用权值表示影响程度,先从一个简单的例子看如何确定权值。
例如 一块石头重量记为1,打碎分成 n各小块,各块的重量
分别记为:w1, w2, , wn
则可得成对比较矩阵 由右面矩阵可以看出,
wi wi wk
wj
wk w j
决策层对总目标的权向量为: 0.3, 0.246, 0.456
又 CR (0.263 0.003 0.475 0.001 0.055 0 0.099 0.005 0.110 0) / 0.58 0.015 0.1
故,层次总排序通过一致性检验。
0.3, 0.246, 0.456 可作为最后的决策依据。
率 CR 较大的成对比较矩阵。
三 层次分析法建模举例
1 旅游问题 (1)建模
Z
A1
A2 A3
B1
B2
A4 A5
B3
A1, A2 , A3, A4 , A5
分别分别表示景色、费用、 居住、饮食、旅途。
B1, B2 , B3
数学建模常用模型及代码

数学建模常用模型及代码
一.规划模型
1.线性规划
线性规划与非线性规划问题一般都是求最大值和最小值,都是利用最小的有限资源来求最大利益等,一般都利用lingo工具进行求解。
点击进入传送门
2.整数规划
求解方式类似于线性规划,但是其决策变量x1,x2等限定都是整数的最优化问题。
传送门
3. 0-1规划
决策变量只能为0或者为1的一类特殊的整数规划。
n个人指派n项工作的问题。
传送门
4.非线性规划
目标函数或者存在约束条件函数是决策变量的非线性函数的最优化问题。
传送门
5.多目标规划
研究多于一个的目标函数在给定区域上的最优化。
把求一个单目标,在此单目标最优的情况下将其作为约束条件再求另外一个目标。
传送门
6.动态规划
运筹学的一个分支。
求解决策过程最优化的过程。
传送门
二. 层次分析法
是一种将定性和定量相结合的,系统化的,层次化的分析方法,主要有机理分析法和统计分析法。
传送门
三.主成分分析
指标之间的相关性比较高,不利于建立指标遵循的独立性原则,指标之间应该互相独立,彼此之间不存在联系。
传送门。
数学建模 模型 大全

冲突目标
Minmax与maxmin
机会约束
约束满足概率性>P
矛盾约束
约束相互矛盾
单纯形法
木匠生产模型
注意步骤性。
215
组合模型
参数模型
动态规划
决策法
背包问题
排序问题
多步骤形的规划
数值搜索法
工业流程优化
黄金分割搜索法
还有二分搜索法
233
网络流
最大树络计划
布点问题
中心问题
重心问题
384
最优化
模拟退火法
神经网络
遗传算法
分治算法
差分进化
蚁行算法
粒子群
不确定
模型
灰色系统
数理统计
模糊数学
聚类分析
模型名称
所在目录
1, 国有企业业绩分化的数学模型
2, 打假问题的机理数学分析
3, 足球比赛排名问题
4, 大象群落的稳定性分析
5, 火车便餐最有价格方案
6, 影院最优设计方案
7, 国有企业业绩分化的数学模型
运输问题
分配问题
匈牙利方法
最大匹配
最优匹配
旅行推销问题
中国邮递员问题
非线性规划
分式规划
目标是分式
凸规划
几何规划
对策
2人0种对策
鞍点对策
混合对策
合作
量纲分析模型
单摆模型
通过实验选择最终模型
253
爆炸模型
函数随爆炸威力上升改变
258
烤火鸡模型
262
阻力模型
使用相似性、比例性。
注意它额外定义的物理量。
268
类别
数学建模模型常用的四大模型及对应算法原理总结

数学建模模型常用的四大模型及对应算法原理总结四大模型对应算法原理及案例使用教程:一、优化模型线性规划线性回归是利用数理统计中回归分析,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法,在线性回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。
如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。
案例实操非线性规划如果目标函数或者约束条件中至少有一个是非线性函数时的最优化问题叫非线性规划问题,是求解目标函数或约束条件中有一个或几个非线性函数的最优化问题的方法。
建立非线性规划模型首先要选定适当的目标变量和决策变量,并建立起目标变量与决策变量之间的函数关系,即目标函数。
然后将各种限制条件加以抽象,得出决策变量应满足的一些等式或不等式,即约束条件。
整数规划整数规划分为两类:一类为纯整数规划,记为PIP,它要求问题中的全部变量都取整数;另一类是混合整数规划,记之为MIP,它的某些变量只能取整数,而其他变量则为连续变量。
整数规划的特殊情况是0-1规划,其变量只取0或者1。
多目标规划求解多目标规划的方法大体上有以下几种:一种是化多为少的方法,即把多目标化为比较容易求解的单目标,如主要目标法、线性加权法、理想点法等;另一种叫分层序列法,即把目标按其重要性给出一个序列,每次都在前一目标最优解集内求下一个目标最优解,直到求出共同的最优解。
目标规划目标规划是一种用来进行含有单目标和多目标的决策分析的数学规划方法,是线性规划的特殊类型。
目标规划的一般模型如下:设xj是目标规划的决策变量,共有m个约束条件是刚性约束,可能是等式约束,也可能是不等式约束。
设有l个柔性目标约束条件,其目标规划约束的偏差为d+, d-。
设有q个优先级别,分别为P1, P2, …, Pq。
在同一个优先级Pk中,有不同的权重,分别记为[插图], [插图](j=1,2, …, l)。
数学建模_四大模型总结

数学建模_四大模型总结四类基本模型1 优化模型1.1 数学规划模型线性规划、整数线性规划、非线性规划、多目标规划、动态规划。
1.2 微分方程组模型阻滞增长模型、SARS 传播模型。
1.3 图论与网络优化问题最短路径问题、网络最大流问题、最小费用最大流问题、最小生成树问题(MST)、旅行商问题(TSP)、图的着色问题。
1.4 概率模型决策模型、随机存储模型、随机人口模型、报童问题、Markov 链模型。
1.5 组合优化经典问题● 多维背包问题(MKP)背包问题:n 个物品,对物品i ,体积为i w ,背包容量为W 。
如何将尽可能多的物品装入背包。
多维背包问题:n 个物品,对物品i ,价值为i p ,体积为i w ,背包容量为W 。
如何选取物品装入背包,是背包中物品的总价值最大。
多维背包问题在实际中的应用有:资源分配、货物装载和存储分配等问题。
该问题属于NP 难问题。
● 二维指派问题(QAP)工作指派问题:n 个工作可以由n 个工人分别完成。
工人i 完成工作j 的时间为ij d 。
如何安排使总工作时间最小。
二维指派问题(常以机器布局问题为例):n 台机器要布置在n 个地方,机器i 与k 之间的物流量为ik f ,位置j 与l 之间的距离为jl d ,如何布置使费用最小。
二维指派问题在实际中的应用有:校园建筑物的布局、医院科室的安排、成组技术中加工中心的组成问题等。
● 旅行商问题(TSP)旅行商问题:有n 个城市,城市i 与j 之间的距离为ij d ,找一条经过n 个城市的巡回(每个城市经过且只经过一次,最后回到出发点),使得总路程最小。
● 车辆路径问题(VRP)车辆路径问题(也称车辆计划):已知n 个客户的位置坐标和货物需求,在可供使用车辆数量及运载能力条件的约束下,每辆车都从起点出发,完成若干客户点的运送任务后再回到起点,要求以最少的车辆数、最小的车辆总行程完成货物的派送任务。
TSP 问题是VRP 问题的特例。
数学建模分类方法大全
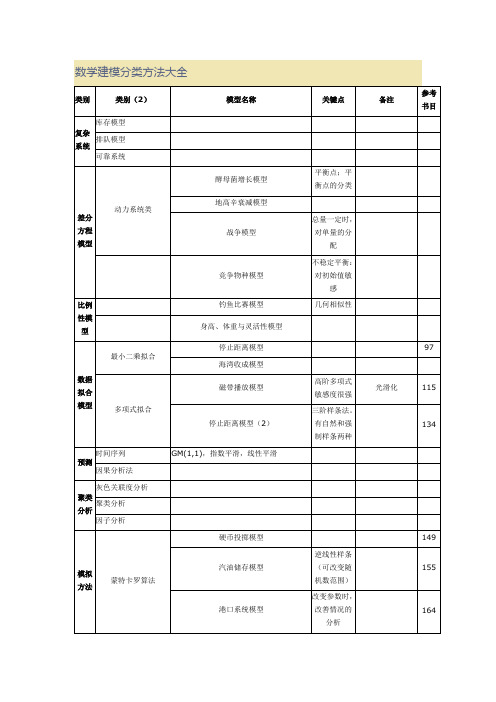
汽车租赁模型要结合蒙特卡罗算法176投票趋势模型177马尔可夫链Markov 决策离散概率模型串联和并联系统模型178无约束类生产计划模型192取整数类载货模型194动态规划类197多目标规划类投资问题有时须对目标进行取舍。
可采取加权系统层次分析196冲突目标Minmax 与maxmin机会约束约束满足概率性>P 矛盾约束约束相互矛盾单纯形法木匠生产模型注意步骤性。
215组合模型参数模型动态规划决策法背包问题排序问题多步骤形的规划线性规划模型数值搜索法工业流程优化黄金分割搜索法还有二分搜索法233最大树最大流最短路关键路线法网络计划布点问题中心问题重心问题运输问题网络流分配问题匈牙利方法最大匹配最优匹配旅行推销问题中国邮递员问题分式规划目标是分式凸规划非线性规划几何规划2人0种对策鞍点对策混合对策对策合作单摆模型通过实验选择最终模型253爆炸模型函数随爆炸威力上升改变258烤火鸡模型262量纲分析模型阻力模型使用相似性、比例性。
注意它额外定义的物理量。
268军备竞赛模型民防、移动发射台、多弹头271税收-能源危机模型参考经济学书籍!288图标模型税收归宿模型税收-汽油短缺模型马尔萨斯人口模型无限增长299人口模型有限增长模型可推广到其它生物的增长301用药模型储蓄模型关注Euler 法的使用(该法并不精确)326竞争捕猎模型363页:相应的Euler 法使用生物关系模型捕食者-食饵模型Scheafer 微分方程模型Lanchester 战斗模型350SIR 模型军备竞赛的经济模型355微分方程模型混沌与分形模型连续Steiner 树模型名称所在目录1,国有企业业绩分化的数学模型2,打假问题的机理数学分析3,足球比赛排名问题4,大象群落的稳定性分析5,火车便餐最有价格方案6,影院最优设计方案7,国有企业业绩分化的数学模型8,打假问题的机理数学分析9,足球比赛排名问题10,大象群落的稳定性分析11,火车便餐最有价格方案12,施肥效果分析13,迷宫问题14,锁具装箱问题15,密码问题16,席位分配模型初等模型17,双重玻璃窗功效模型18,储存模型优化模型19,森林救火模型20,消费者均衡模型21,加工奶制品模型数学规划模型22,自来水输送模型23,混合泳接力模型24,投入产出模型25,三级火箭模型26,糖尿病模型27,传染病模型28,生物种群模型29,人口模型30,分子模型31,扫雪模型32,商人过河问题。
数学建模c题常用模型

数学建模c题常用模型第一种常用模型是线性规划模型。
线性规划模型是一种优化模型,可以用于解决最大化或最小化的问题。
该模型的目标函数和约束条件都是线性的,可以通过线性规划算法求解。
线性规划模型广泛应用于生产调度、资源分配、运输问题等领域。
例如,在生产调度中,可以利用线性规划模型确定最优的生产计划,以最大化产量或最小化成本。
第二种常用模型是整数规划模型。
整数规划模型是在线性规划模型的基础上加上了整数变量的限制条件,即决策变量必须取整数值。
整数规划模型适用于需要做出离散决策的问题,如旅行商问题、装箱问题等。
例如,在旅行商问题中,整数规划模型可以用于确定旅行商的最短路径,以便在有限的时间内访问所有城市。
第三种常用模型是动态规划模型。
动态规划模型适用于具有重叠子问题和最优子结构特征的问题。
通过将问题分解为多个子问题,并保存子问题的解,可以避免重复计算,提高求解效率。
动态规划模型广泛应用于路径规划、资源分配、序列比对等问题。
例如,在路径规划中,可以利用动态规划模型确定最短路径或最优路径。
第四种常用模型是随机模型。
随机模型是一种考虑不确定性因素的模型,可以用于分析风险和制定决策策略。
随机模型通常使用概率分布描述不确定性,并通过概率方法进行求解。
随机模型广泛应用于金融风险管理、供应链管理、环境管理等领域。
例如,在金融风险管理中,可以利用随机模型对投资组合的风险进行评估和优化。
第五种常用模型是图论模型。
图论模型是一种用图来表示和解决问题的模型。
通过将问题抽象为图的结构和关系,可以利用图论算法求解最优解或最优路径。
图论模型广泛应用于网络优化、社交网络分析、物流路径规划等领域。
例如,在网络优化中,可以利用图论模型确定最短路径、最小生成树等问题。
以上是数学建模中常用的几种模型,每种模型都有其独特的应用场景和解决问题的方法。
在实际应用中,可以根据具体问题的特点选择合适的模型,并利用数学建模的方法进行求解。
数学建模模型的使用不仅能够提高问题的求解效率和准确性,还可以帮助分析问题的本质和规律,为决策提供科学依据。
数学建模系列-常用模型

性能,并根据评估结果进行模型优化或调整。
03
CATALOGUE
支持向量机模型
模型定义
线性分类器
支持向量机是一种线性分类器,通过找到一个超平面来分隔两个类 别的数据点。
核函数
支持向量机使用核函数将输入空间映射到一个高维特征空间,使得 线性分类器在高维空间中更容易找到分隔超平面。
间隔最大化
支持向量机旨在最大化间隔,即最小化分类错误的距离,以提高分类 器的泛化能力。
模型建立
数据预处理
对数据进行标准化或归一化处理,以确保不同特征的尺度不会影 响模型的性能。
核函数选择
选择合适的核函数,如线性核、多项式核、径向基函数等,以适 应不同的数据分布和问题类型。
参数调整
调整模型参数,如惩罚系数和核函数的参数,以获得最佳的分类 效果。
模型应用
二分类问题
支持向量机适用于解决二分类问题,如垃圾邮件分类、人脸识别 等。
05
CATALOGUE
主成分分析模型
模型定义
主成分分析(PCA)是一种常用的多 元统计分析方法,它通过线性变换将 多个相关变量转化为少数几个不相关 的变量,这些不相关的变量称为主成 分。
主成分分析旨在减少数据集的维度同 时保留数据集中的主要变化模式,以 便更好地理解数据的结构和关系。
模型建立
确定数据集
模型应用
总结词
K-均值聚类模型广泛应用于数据挖掘、模式识别、图 像处理等领域,可以用于市场细分、异常检测、分类 问题等。
详细描述
K-均值聚类模型的应用非常广泛,例如在市场细分中 ,可以将消费者按照购买行为、偏好等特征进行分类 ,帮助企业更好地理解客户需求和市场趋势。在异常 检测中,可以通过观察聚类结果中的离群点,发现数 据中的异常值。在图像处理中,可以将图像分割成不 同的区域,对每个区域进行特征提取和分析。此外, K-均值聚类模型还可以用于分类问题中,将数据点划 分为不同的类别。
数学建模30种经典模型matlab

一、概述数学建模是数学与实际问题相结合的产物,通过建立数学模型来解决现实生活中的复杂问题。
Matlab作为一个强大的数学计算工具,在数学建模中具有重要的应用价值。
本文将介绍30种经典的数学建模模型,以及如何利用Matlab对这些模型进行建模和求解。
二、线性规划模型1. 线性规划是数学建模中常用的一种模型,用于寻找最优化的解决方案。
在Matlab中,可以使用linprog函数对线性规划模型进行建模和求解。
2. 举例:假设有一家工厂生产两种产品,分别为A和B,要求最大化利润。
产品A的利润为$5,产品B的利润为$8,而生产每单位产品A 和B分别需要8个单位的原料X和10个单位的原料Y。
此时,可以建立线性规划模型,使用Matlab求解最大化利润。
三、非线性规划模型3. 非线性规划是一类更加复杂的规划问题,其中目标函数或约束条件存在非线性关系。
在Matlab中,可以使用fmincon函数对非线性规划模型进行建模和求解。
4. 举例:考虑一个有约束条件的目标函数,可以使用fmincon函数在Matlab中进行建模和求解。
四、整数规划模型5. 整数规划是一种特殊的线性规划问题,其中决策变量被限制为整数。
在Matlab中,可以使用intlinprog函数对整数规划模型进行建模和求解。
6. 举例:假设有一家工厂需要决定购物哪种机器设备,以最大化利润。
设备的成本、维护费用和每台设备能生产的产品数量均为已知条件。
可以使用Matlab的intlinprog函数对该整数规划模型进行建模和求解。
五、动态规划模型7. 动态规划是一种数学优化方法,常用于多阶段决策问题。
在Matlab 中,可以使用dynamic programming toolbox对动态规划模型进行建模和求解。
8. 举例:考虑一个多阶段生产问题,在每个阶段都需要做出决策以最大化总利润。
可以使用Matlab的dynamic programming toolbox对该动态规划模型进行建模和求解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
港口系统模型
改变参数时,改善情况的分析
164
离散概率模型
马尔可夫链
汽车租赁模型
要结合蒙特卡罗算法
176
投票趋势模型
177
Markov决策
串联和并联系统模型
178
线性规划模型
无约束类
生产计划模型
192
取整数类
载货模型
194
动态规划类
197
多目标规划类
投资问题
有时须对目标进行取舍。可采取加权
系统层次分析
运输问题
分配问题
匈牙利方法
最大匹配
最优匹配
旅行推销问题
中国邮递员问题
非线性规划
分式规划
目标是分式
凸规划
几何规划
对策
2人0种对策
鞍点对策
混合对策
合作
量纲分析模型
单摆模型
通过实验选择最终模型
253
爆炸模型
函数随爆炸威力上升改变
258
烤火鸡模型
262
阻力模型
使用相似性、比例性。
注意它额外定义的物理量。
268
类别
类别(2)
模型名称
关键点
备注
参考书目
复杂系统
库存模型
排队模型
可靠系统
差分方程模型
动力系统类
酵母菌增长模型
平衡点;平衡点的分类
地高辛衰减模型
战争模型
总量一定时,对单量的分配
竞争物种模型
不稳定平衡:对初始值敏感
比例性模型
钓鱼比赛模型
几何相似性
身高、体重与灵活性模型
数据拟合模型
最小二乘拟合
停止距离模型
196
冲突目标
Minmax与maxmin
机会约束
约束满足概率性>P
矛盾约束
约束相互矛盾
单纯形法
木匠生产模型
注意步骤性。
215
组合模型
参数模型
动态规划
决策法
背包问题
排序问题
多步骤形的规划
数值搜索法
工业流程优化
黄金分割搜索法
还有二分搜索法
233
网络流
最大树
最大流
最短路
关键路线法
网络计划
布点问题
中心问题
重心问题
图标模型
军备竞赛模型
民防、移动发射台、多弹头
271
税收归宿模型
税收-能源危机模型
参考经济学书籍!
288
税收-汽油短缺模型
微分方程模型
人口模型
马尔萨斯人口模型
无限增长
299
有限增长模型
可推广到其它生物的增长
301
用药模型
储蓄模型
关注Euler法的使用(该法并不精确)
326
生物关系模型
竞争捕猎模型
363页:相应的Euler法使用
97
海湾收成模型
多项式拟合
磁带播放模型
高阶多项式敏感度很强
光滑化
115
停止距离模型(2)
三阶样条法。有自然和强制样条两种
134
预测
时间序列
GM(1,1),指数平滑,线性平滑
因果分析法
聚类分析
灰色关联度分析
聚类分析
因子分析
模拟方法
蒙特卡罗算法
硬币投掷模型
149
汽油储存模型
逆线性样条(可改变随机数范围)
8, 打假问题的机理数学分析
9, 足球比赛排名问题
10, 大象群落的稳定性分析
11, 火车便餐最有价格方案
12, 施肥效果分析
13, 迷宫问题
14, 锁具装箱问题
15, 密码问题
16, 席位分配模型
初等模型
17, 双重玻璃窗功效模型
18, 储存模型
优化模型
19, 森林救火模型
20, 消费者均衡模型
21, 加工奶制品模型
384
最优化
模拟退火法
神经网络
遗传算法
分治算法
差分进化
蚁行算法
粒子群
不确定
模型
灰色系统
数理统计
模糊数学
聚类分析
模型名称
所在目录
1, 国有企业业绩分化的数学模型
2, 打假问题的机理数学分析
3, 足球比赛排名问题
4, 大象群落的稳定性分析
5, 火车便餐最有价格方案
6, 影院最优设计方案
7, 国有企业业绩分化的数学模型
பைடு நூலகம்捕食者-食饵模型
Scheafer微分方程模型
Lanchester战斗模型
350
SIR模型
军备竞赛的经济模型
355
混沌与分形模型
连续优化问题
Steiner树
库存模型
制造模型
最陡上升梯度方法
375
石油转运模型
Lagrange乘子法
注意里面涉及到的经济学概念和意义
381
航天飞机的水箱模型
渔业模型
注意各种“最优”的意义
数学规划模型
22, 自来水输送模型
23, 混合泳接力模型
24, 投入产出模型
25, 三级火箭模型
26, 糖尿病模型
27, 传染病模型
28, 生物种群模型
29, 人口模型
30, 分子模型
31, 扫雪模型
32, 商人过河问题
