人教版初三数学圆练习题汇总
人教版九年级数学圆练习题

人教版九年级数学圆练习题圆是平面几何中的一个重要概念,它由平面上所有与给定点(圆心)距离相等的点组成。
这个距离称为半径。
圆的性质和定理在数学中有着广泛的应用。
以下是一些适合九年级学生的圆的练习题:一、选择题1. 圆的半径为5,圆心到圆上任意一点的距离是:A. 6B. 4C. 5D. 22. 如果一个圆的直径是10,那么它的半径是:A. 5B. 10C. 15D. 203. 一个圆的周长是16π,那么它的半径是:A. 4B. 8C. 16D. 32二、填空题4. 圆的周长公式是 ________ 。
5. 如果圆的半径为r,那么它的面积公式是 ________ 。
6. 一个圆的直径是12cm,那么它的周长是 ________ cm。
三、判断题7. 圆的直径是半径的两倍。
()8. 圆的周长与半径成正比。
()9. 圆的面积与半径的平方成正比。
()四、简答题10. 已知圆的半径为7cm,求圆的周长和面积。
11. 如果一个圆的周长是44cm,求它的半径。
五、计算题12. 一个圆的半径为10cm,求圆的直径、周长和面积。
13. 一个圆的周长是圆的直径的π倍,求这个圆的半径。
六、证明题14. 证明:在一个圆中,任意两点之间的线段中,直径是最长的。
15. 证明:圆周角定理,即圆周上任意两点所对的圆心角是圆周角的两倍。
七、应用题16. 一个圆形花坛的半径是15米,如果绕花坛周围铺设一条1米宽的小路,求小路的面积。
17. 一个圆的半径是10cm,圆内有一个正方形,正方形的对角线等于圆的直径,求正方形的面积。
八、开放性问题18. 假设你有一个圆的周长,如何利用这个信息来设计一个简单的几何证明,证明圆的周长与半径的关系?19. 圆的面积公式是如何推导出来的?请给出推导过程。
通过这些练习题,学生可以加深对圆的基本概念、性质和公式的理解,同时也能够锻炼解决实际问题的能力。
希望这些练习题能够帮助学生更好地掌握圆的相关知识。
初三人教版圆的性质练习题

初三人教版圆的性质练习题圆是初中数学中的一个基本几何图形,对圆的性质的理解和掌握是提高数学能力的关键。
本文将为大家提供一些关于圆的性质的练习题,帮助大家巩固对圆的认识和应用。
练习题一:判断题1. 半径相等的两个圆一定是同心圆。
()2. 圆的直径等于其半径的两倍。
()3. 圆的周长是它的直径的两倍。
()4. 圆的面积与其半径的平方成正比。
()5. 切线是与圆相切且过圆心的直线。
()练习题二:填空题1. 圆的一个扇形的弧长是5cm,圆心角为60°,则这个圆的半径为_________。
2. 已知圆的周长为24π cm,则其半径为_________。
3. 圆的直径是10cm,那么它的面积是_________。
4. 圆的周长是8π cm,则它的直径为_________。
练习题三:应用题1. 一个圆的半径为7cm,一只蚂蚁从圆的某一点出发,顺着圆的边界行走,最后回到出发点所经过的距离是多少?2. 一个球的直径为18cm,求该球的表面积和体积。
解答:练习题一:判断题1. 正确。
同心圆是指有同一个圆心的两个或多个圆。
2. 错误。
直径等于半径的两倍,即直径=2×半径。
3. 错误。
圆的周长是其直径的π倍,即周长=π×直径。
4. 正确。
圆的面积等于半径的平方乘以π,即面积=π×半径²。
5. 错误。
切线与圆只有一个交点,并且与圆相切。
练习题二:填空题1. 该圆的半径为5cm。
由圆心角的定义可知,弧长的长度等于圆心角的弧度数(单位为弧度)乘以圆的半径。
2. 该圆的半径为6cm。
已知圆的周长为2πr,其中r为半径。
3. 该圆的面积为75π cm²。
圆的面积等于半径的平方乘以π。
4. 该圆的直径为8cm。
圆的周长等于直径的π倍。
练习题三:应用题1. 蚂蚁行走的距离等于圆的周长,即2π×半径=2π×7=14π cm。
2. 该球的表面积为4π×半径²=4π×9²=36π cm²,体积为(4/3)π×半径³=(4/3)π×9³=972π cm³。
人教版九年级数学上册《24.1.1圆》同步测试题带答案
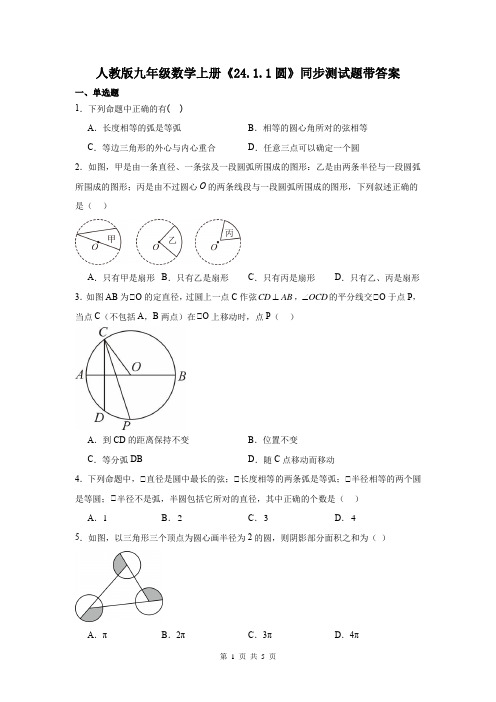
人教版九年级数学上册《24.1.1圆》同步测试题带答案一、单选题1.下列命题中正确的有( ) A .长度相等的弧是等弧 B .相等的圆心角所对的弦相等 C .等边三角形的外心与内心重合D .任意三点可以确定一个圆2.如图,甲是由一条直径、一条弦及一段圆弧所围成的图形:乙是由两条半径与一段圆弧所围成的图形;丙是由不过圆心O 的两条线段与一段圆弧所围成的图形,下列叙述正确的是( )A .只有甲是扇形B .只有乙是扇形C .只有丙是扇形D .只有乙、丙是扇形3.如图AB 为⊙O 的定直径,过圆上一点C 作弦CD AB ⊥,OCD ∠的平分线交⊙O 于点P ,当点C (不包括A ,B 两点)在⊙O 上移动时,点P ( )A .到CD 的距离保持不变B .位置不变C .等分弧DBD .随C 点移动而移动4.下列命题中,⊙直径是圆中最长的弦;⊙长度相等的两条弧是等弧;⊙半径相等的两个圆是等圆;⊙半径不是弧,半圆包括它所对的直径,其中正确的个数是( ) A .1B .2C .3D .45.如图,以三角形三个顶点为圆心画半径为2的圆,则阴影部分面积之和为( )A .πB .2πC .3πD .4π6.如图,在Rt ⊙ABC 中,⊙ACB =90°, AC =3,以点C 为圆心、CA 为半径的圆与AB 交于点D ,若点D 巧好为线段AB 的中点,则AB 的长度为( )A .32B .3C . 6D .9二、填空题7.到点O 的距离等于7cm 的点的集合是 .8.下图中,点O 是( ),线段OA 是圆的( ),线段BC 是圆的( ).9.已知,如图AB ,AD 是O 的弦 30B ∠=︒,点C 在弦AB 上,连结CO 并延长交O 于点D ,35D ∠=︒则BAD ∠的度数是 .10.如图,半径为r 的O 沿着边长为a 的正方形ABCD 的边作无滑动地滚动一周回到原来的位置,O 自身转动的圈数是 .(用含a r ,的代数式表示)11.下列说法:⊙直径是弦;⊙弦是直径;⊙大于半圆的弧是优弧;⊙长度相等的弧是等弧,其中正确的是 .12.顶点在圆外,并且两边都和圆相交的角叫做圆外角.圆外角的两边所夹的两条弧的度数与该角的度数之间的数量关系是:圆外角的度数等于 .三、解答题13.如图,O 的弦,AB CD 的延长线交于点P ,连接OP ,且OP 平分APC ∠.求证:PA PC =.14.如图,点O 是同心圆的圆心,大圆半径OA ,OB 分别交小圆于点C ,D ,求证:AB CD ∥.15.如图所示,AB 为O 的直径,CD 是O 的弦,AB CD ,的延长线交于点E ,已知220AB DE AEC =∠=︒,.求AOC ∠的度数.16.如图,O 的半径5cm OA =,AB 是弦,C 是AB 上一点,且OC OA ⊥,OC BC =求A ∠的度数.17.如图,破残的圆形轮片上,弦AB 的垂直平分线交弧AB 于C,交弦AB 于D .(1)求作此残片所在的圆的圆心(不写作法,保留作图痕迹); (2)若AB=8cm,CD=2cm,求(1)中所作圆的半径.18.如图,在O 中,AB 是直径,CD 是弦,延长AB ,CD 相交于点P ,且2AB DP = 18P ∠=︒ 求AOC ∠的度数.题号 1 2 3 4 5 6 答案CBBCD C7.以点O 为圆心,7cm 为半径的圆 8. 圆心 半径 直径 9.65︒ 10.21a r π+/21arπ+ 11.①③/③①12.两条弧度数差值的绝对值的一半 15.60AOC ∠=︒ 16.30︒17.(2) 圆的半径为5cm. 18.54。
人教版九年级数学上册第24章《圆》单元练习题(含答案)

人教版九年级数学上册第24章《圆》单元练习题(含答案)一、单选题1.如图,一个油桶靠在直立的墙边,量得0.8m,BC =并且,AB BC ⊥则这个油桶的底面半径是( )A .1.6mB .1.2mC .0.8mD .0.4m 2.在O 中,AB ,CD 为两条弦,下列说法:①若AB CD =,则AB CD =;②若AB CD =,则2AB CD =;③若2AB CD =,则弧AB=2弧CD ;④若2AOB COD ∠=∠,则2AB CD =.其中正确的有( )A .1个B .2个C .3个D .4个3.如图,点A 、B 、C 在⊙O 上,且∠ACB=100o ,则∠α度数为( )A .160oB .120oC .100oD .80o4.如图,在⊙O 中,CD 是直径,AB 是弦,AB ⊥CD 于E ,AB =8,OD =5,则CE 的长为( )A .4B .2C 2D .15.如图,ABC 内接于O ,CD 是O 的直径,40ACD ∠=︒,则B ∠=( )A .70°B .60°C .50°D .40°6.如图,AB 为⊙O 的直径,点 D 是弧 AC 的中点,过点 D 作 DE ⊥AB 于点 E ,延长 DE 交⊙O 于点 F ,若 AC =12,AE =3,则⊙O 的直径长为( )A .7.5B .15C .16D .187.如图,已知AB 、AD 是O 的弦,30B ∠=︒,点C 在弦AB 上,连接CO 并延长CO 交于O 于点D ,20D ∠=︒,则BAD ∠的度数是( )A .30°B .40°C .50°D .60°8.将量角器按如图所示的方式放置在三角形纸板上,使点C 在半圆上.点A ,B 的读数分别为86°,30°,则∠ACB 的度数是( )A .28°B .30°C .36°D .56°9.如图,⊙O 是△ABC 的外接圆,将△ABC 绕点C 顺时针旋转至△EDC ,使点E 在⊙O 上,再将△EDC 沿CD 翻折,点E 恰好与点A 重合,已知∠BAC =36°,则∠DCE 的度数是( )A.24 B.27 C.30 D.3310.下列说法正确的是()①近似数2⨯精确到十分位;32.610--中,最小的是38-;②在2,2,38-,2③如图所示,在数轴上点P所表示的数为15-+;④用反证法证明命题“一个三角形最多有一个钝角”时,首先应假设“这个三角形中有两个钝角”;⑤如图,在ABC内一点P到这三条边的距离相等,则点P是三个角平分线的交点.A.1 B.2 C.3 D.4二、填空题11.某圆的周长是12.56米,那么它的半径是______________,面积是__________.OA=,12.如图,A、B、C是O上的点,OC AB⊥,垂足为点D,且D为OC的中点,若7则BC的长为___________.13.如图,AB 、AC 是O 的弦,过点A 的切线交CB 的延长线于点D ,若35BAD ∠=︒,则C ∠=___________°.14.如图,在正五边形ABCDE 中,连结AC ,以点A 为圆心,AB 为半径画圆弧交AC 于点F ,连接DF .则∠FDC 的度数是 _____.15.如图,A 、B 是⊙O 上的两点,AC 是过A 点的一条直线,如果∠AOB =120°,那么当∠CAB 的度数等于________度时,AC 才能成为⊙O 的切线.16.如图,ABC 是O 的内接三角形.若=45ABC ∠︒,2AC =,则O 的半径是______.三、解答题17.如图,在菱形ABCD 中,90BAD ∠>︒,P 为AC ,BD 的交点,O 经过A ,B ,P 三点.(1)求证:AB 为O 的直径.(2)请用无刻度的直尺在圆上找一点Q ,使得BP =PQ (不写作法,保留作图痕迹).18.请用圆规、直尺作图,不写作法,但要保留作图痕迹.已知:如图,Rt △ABC 中,∠C =90°.求作:一个⊙O ,使⊙O 与AB 、BC 所在直线都相切,且圆心O 在边AC 上.19.如图所示,AB 为⊙O 的直径,在△ABC 中,AB =BC ,AC 交⊙O 于点D ,过点D 作DE ⊥BC ,垂足为点E .(1)证明DE 是⊙O 的切线;(2)AD =8,P 为⊙O 上一点,P 到弦AD 的最大距离为8.①尺规作图作出此时的P 点,保留作图痕迹;②求DE 的长.20.如图,在Rt ABC △中,90ACB ∠=︒,延长CA 到点D ,以AD 为直径作O ,交BA 的延长线于点E ,延长BC 到点F ,使BF EF =.(1)求证:EF 是O 的切线;(2)若9OC =,4AC =,8AE =,求BE 的长.21.如图,点A ,B ,C ,D 在⊙O 上,AB =CD .求证:AC =BD ;<),点E是线段OP的中点.在22.如图,点P是O的直径AB延长线上的一点(PB OB=.求证:PC是O的切线.直径AB上方的圆上作一点C,使得EC EP23.如图,四边形ABCD内接于120,,,求证:ABC是等边三角形.O AB AC ADC=∠=︒24.如图,四边形ABCD是菱形,以AB为直径作⊙O,交CB于点F,点E在CD上,且CE=CF,连接AE.(1)求证:AE是⊙O的切线;(2)连接AC交⊙O于点P,若3AP ,BF=1,求⊙O的半径.25.如图,⊙O是以△ABC的边AC为直径的外接圆,∠ACB=54°,如图所示,D为⊙O上与点B关于AC的对称点,F为劣弧BC上的一点,DF交AC于N点,BD交AC于M点.(1)求∠DBC的度数;(2)若F为弧BC的中点,求MN ON.26.已知P为⊙O上一点,过点P作不过圆心的弦PQ,在劣弧PQ和优弧PQ上分别有点A、B(不与P、Q重合),连接AP、BP,若∠APQ=∠BPQ(1)如图1,当∠APQ=45°,AP=1,2⊙O的半径。
初中数学人教版九年级上册 第二十四章 圆单元测试卷(含答案)

人教版数学九上圆一、单选题1.下列语句中正确的是( )A.长度相等的两条弧是等弧B.圆上一条弧所对的圆心角等于它所对圆周角的一半C.垂直于圆的半径的直线是圆的切线D.三角形有且只有一个外接圆2.如图,OA,OC是⊙O的半径,点B在⊙O上,若AB∥OC,∠BCO=21°,则∠AOC的度数是( )A.42°B.21°C.84°D.60°3.如图,在矩形ABCD中,AD=8,以AD的中点O为圆心,以OA长为半径画弧与BC相切于点E,则阴影部分的面积为( )A.8―4πB.16―4πC.32―4πD.32―8π4.如图,⊙O的半径OD⊥弦AB于点C,连接BO并延长交⊙O于点E,连接CE,若AB=4,CD=1,则CE的长为( )A.13B.4C.10D.155.如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线l,与⊙O过A点的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )A.B.C.D.6.如图.将扇形AOB翻折,使点A与圆心O重合,展开后折痕所在直线l与AB交于点C,连接AC.若OA=2,则图中阴影部分的面积是( )A.2π3―32B.2π3―3C.π3―32D.π37.如图,⊙O是正△ABC的外接圆,△DOE是顶角为120°的等腰三角形,点O与圆心重合,点D,E 分别在圆弧上,若⊙O的半径是6,则图中阴影部分的面积是( )A.4πB.12π―9 3C.12π―923D.24π―9 38.如图,在正方形ABCD中,点E,F分别是边BC和CD上的动点(不与端点重合),∠EAF=45°,AF、AE分别与对角线BD交于点G和点H,连接EG.以下四个结论:(1)BE+DF=EF;(2)△AGE是等腰直角三角形;(3)S△AGH:S△AEF=1:2;(4)AB+BE=2BG,其中正确结论的个数是( )A.1B.2C.3D.49.【情境】如图是某数学项目学习小组设计的“鱼跃龙门”徽章图案,已知A,B,C,D,E是圆的5个等分点,连结BD,CE交于点F.设鱼头部分的四边形ABFE的面积为S1,鱼尾部分的△CDF的面积为S2.【问知】设S1:S2=n:1,则n的值为( )A.43―1B.3+5C.1+25D.35―110.如图,半径为5的圆中有一个内接矩形ABCD,AB>BC,点M是ABC的中点,MN⊥AB于点N,若矩形ABCD的面积为30,则线段MN的长为()A.10B.522C.702D.210二、填空题11.如图,在⊙O的内接五边形ABCDE中,∠EBD=31°,则∠A+∠C= °.12.如图,在半径为10cm的圆形铁片上切下一块高为4cm的弓形铁片,则弓形弦AB的长为 cm.13.如图,⊙O是△ABC的外接圆,∠A=45°,BC=2,则⊙O的直径为 .14.如图,将扇形AOB翻折,使点A与圆心O重合,展开后折痕所在直线l与AB交于点C,若OA=2,则OC的长为 .15.如图,半径为5的⊙O与y轴相交于A点,B为⊙O在x轴上方的一个动点(不与点A重合),C 为y轴上一点且∠OCB=60°,I为△BCO的内心,则△AIO的外接圆的半径的取值(或取值范围)为 .16.如图,已知△ABC是⊙O的内接三角形,⊙O的半径为2,将劣弧AC沿AC折叠后刚好经过弦BC的中点D.若∠ACB=60°,则弦AC的长为 .三、解答题17.如图,直径为1m的圆柱形水管有积水(阴影部分),水面的宽度AB为0.8m,求水的最大深度CD.18.如图,在⊙O中,半径OA⊥OB,∠B=28°,求∠BOC的度数.19.如图,△ABC是⊙O的内接三角形,AB为⊙O的直径,AB=6,AD平分∠BAC,交BC于点E,交⊙O于点D,连结BD.(1)求证:∠BAD=∠CBD.(2)若∠AEB=125°,求BD的长.(结果保留π)20.如图,AB为⊙O的直径,弦CD⊥AB于E,连接AC,过A作AF⊥AC,交⊙O于点F,连接DF,过B作BG⊥DF,交DF的延长线于点G.(1)求证:BG是⊙O的切线:(2)若∠DFA=30°,DF=4,求阴影部分的面积.21.在直角坐标系中,以M(3,0)为圆心的⊙M交x轴负半轴于A,交x轴正半轴于B,交y轴于C、D.其中C点坐标为(0,4).(1)求点A坐标.(2)如图,过C作⊙M的切线CE,过A作AN⊥CE于F,交⊙M于N,求AN的长度.(3)在⊙M上,若∠CPM=45°,求出点P的坐标.22.圆内接四边形若有一组邻边相等,则称之为等邻边圆内接四边形.(1)如图1,四边形ABCD为等邻边圆内接四边形,AD=CD,∠ADC=60°,直接写出∠ABD的度数;(2)如图2,四边形ADBC内接于⊙O,AB为⊙O的直径,AB=10,AC=6,若四边形ADBC为等邻边圆内接四边形,AD=BD,求CD的长.(3)如图3,四边形ABCD为等邻边圆内接四边形,BC=CD,AB为⊙O的直径,且AB=48.设BC= x,四边形ABCD的周长为y,试确定y与x的函数关系式,并求出y的最大值.答案解析部分1.【答案】D2.【答案】A3.【答案】D4.【答案】A5.【答案】D6.【答案】B7.【答案】B8.【答案】D9.【答案】B10.【答案】A11.【答案】21112.【答案】1613.【答案】2214.【答案】2π315.【答案】53316.【答案】621717.【答案】解:∵⊙O的直径为1m,∴OA=OD=0.5m.∵OD⊥AB,AB=0.8m,∴AC=0.4m,∴OC=OA2―AC2=0.52―0.42=0.3m,∴CD=OD―OC=0.5―0.3=0.2m.答:水的最大深度为0.2m.18.【答案】解:∵OA⊥OB,∴∠AOB=90°,∴∠A=90°﹣∠B=90°﹣28°=62°,∵OA=OC,∴∠ACO=∠A=62°,而∠ACO=∠BOC+∠B,∴∠BOC=62°﹣28°=34°.19.【答案】(1)证明:∵AD平分∠BAC,∴∠CAD=∠BAD.∵∠CAD=∠CBD,∴∠BAD=∠CBD;(2)解:如图,连结OD.∵∠AEB= 125°,∴∠AEC= 55°.∵AB为⊙O的直径,∴∠ACE=90°,∴∠CAE= 35°,∴∠DAB=∠CAE=35°,∴∠BOD=2∠BAD=70°,∴BD的长为70×π×3180=7 6π.20.【答案】(1)证明:∵C,A,D,F在⊙O上,AF⊥AC,∴∠D=∠CAF=90°,∵AB⊥CD,BG⊥DF,∴∠BED=∠G=90°,∴四边形BEDG中,∠ABG=90°,∴半径OB⊥BG,∴BG是⊙O的切线;(2)解:连接CF,∵∠CAF=90°,∴CF是⊙O的直径,∴OC=OF,∵直径AB⊥CD于E,∴CE=DE,∴OE是△CDF的中位线,∴OE=12DF=2,∵∠AFD=30°,∴∠ACD=∠AFD=30°,∴∠CAE=90°―∠ACE=60°,∵OA=OC,∴△AOC是等边三角形,∵CE⊥AB,∴E为AO的中点,∴OA=2OE=4,OB=4,AE=2,∴BE=OB+OE=6,DE=CE=23,∵∠BED=∠D=∠G=90°,∴四边形BEDG是矩形,∴S阴影=S矩形BEDG―S梯形OEDF―S扇形BOF=6×23―12×(2+4)×23―60π⋅42360=63―83π.21.【答案】(1)解:连接CM,∵M(3,0),C(0,4),∴OM=3,OC=4,∴CM=5,即⊙M的半径为5,∴MA=5,∴AO=AM-OM=2,∴A(―2,0);(2)连接CM,作MH⊥AN于H,∵CE为⊙M的切线,∴MC⊥EC,即∠MCE=90°.∵AN⊥CE于F,即∠AFC=90°.又∵MH⊥AN于H,即∠MHA=90°.∴在四边形FHMC中,∠CMH=90°=∠CMO+∠AMH.∵在Rt△AHM中,∠HAM+∠AMH=90°,∴∠HAM=∠CMO.∵在Rt△COM中,∠CMO+∠OCM=90°,∴∠OCM=∠AMH.∵在△AMH与△MCO中,{∠HAM=∠CMOMC=MA∠OCM=∠AMH∴△AMH≌△MCO(ASA),故AH=MO=3.即AN=HN+AH=3+3=6;(3)解:结合题意,可知PM=CM,△CMP为等腰三角形,同时因为∠CPM=45°=∠PCM,因此△CMP也是等腰直角三角形,即∠CMP=90°且CM=PM=5.①当P在CM右侧时,作PE垂直x轴于E.∵∠CMP=90°,∴∠CMO+∠PME=90°.又∵在Rt△PEM中,∠PME+∠MPE=90°,∴∠CMO=∠MPE.∴同理可得∠MCO=∠PME.在△MCO与△PME中,{∠CMO=∠MPECM=PM∠MCO=∠PME∴△MCO≌△PME(ASA)∴OM=PE=3,ME=OC=4,即存在P1(7,3);②当P在CM左侧时(设为P2),作PF垂直x轴于F.根据圆的对称性,结合①的结论,易证:△MCO≌△PMF,∴OM=PF=3,FM=OC=4,即存在P2(―1,―3).22.【答案】(1)解:60°(2)解:连接CD,过点A作AH⊥CD,交CD于点H.如图:在Rt△AHC中,∵∠ACH=∠ABD=45°,AC=6,∴CH=AH=32,此时△ADB为等腰直角三角形,AD=BD=52,在Rt△AHD中,∵AH=32,AD=52,∴DH=42,∴CD=CH+DH=72.(3)解:如图,连接OC,BD.∵BC=CD,OB=OD,∴OC垂直平分BD,∵O为AB中点,∴OF为△BDA的中位线,有OF=12AD,OF//AD,设OF=t,则CF=24―t,AD=2t,y=48+x+x+2t=2t+2x+48,在Rt△BFC中,B F2=B C2―C F2=x2―(24―t)2,在Rt△BFO中,B F2=B O2―O F2=242―t2,于是有:x2―(24―t)2=242―t2,整理得,t=―148x2+24,∴y=―124x 2+2x+96=―124(x―24)2+120,当x=24时,y max=120。
人教版数学九年级上册第二十四章《圆》知识点及练习题(附答案)

《圆》章节知识点复习和练习附参考答案一、圆的概念集合形式的概念: 1、 圆可以看作是到定点的距离等于定长的点的集合; 2、圆的外部:可以看作是到定点的距离大于定长的点的集合; 3、圆的内部:可以看作是到定点的距离小于定长的点的集合 轨迹形式的概念:1、圆:到定点的距离等于定长的点的轨迹就是以定点为圆心,定长为半径的圆;(补充)2、垂直平分线:到线段两端距离相等的点的轨迹是这条线段的垂直平分线(也叫中垂线); 3、角的平分线:到角两边距离相等的点的轨迹是这个角的平分线;4、到直线的距离相等的点的轨迹是:平行于这条直线且到这条直线的距离等于定长的两条直线;5、到两条平行线距离相等的点的轨迹是:平行于这两条平行线且到两条直线距离都相等的一条直线。
二、点与圆的位置关系1、点在圆内 ⇒ d r < ⇒ 点C 在圆内;2、点在圆上 ⇒ d r = ⇒ 点B 在圆上;3、点在圆外 ⇒ d r > ⇒ 点A 在圆外; 三、直线与圆的位置关系1、直线与圆相离 ⇒ d r > ⇒ 无交点;2、直线与圆相切 ⇒ d r = ⇒ 有一个交点;3、直线与圆相交 ⇒ d r < ⇒ 有两个交点;四、圆与圆的位置关系外离(图1)⇒ 无交点 ⇒ d R r >+; 外切(图2)⇒ 有一个交点 ⇒ d R r =+; 相交(图3)⇒ 有两个交点 ⇒ R r d R r -<<+; 内切(图4)⇒ 有一个交点 ⇒ d R r =-; 内含(图5)⇒ 无交点 ⇒ d R r <-;A五、垂径定理垂径定理:垂直于弦的直径平分弦且平分弦所对的弧。
推论1:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧; (2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;(3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧以上共4个定理,简称2推3定理:此定理中共5个结论中,只要知道其中2个即可推出其它3个结论,即:①AB 是直径 ②AB CD ⊥ ③CE DE = ④ 弧BC =弧BD ⑤ 弧AC =弧AD中任意2个条件推出其他3个结论。
圆的切线的判定练习题2024~2025学年人教版数学九年级上册++
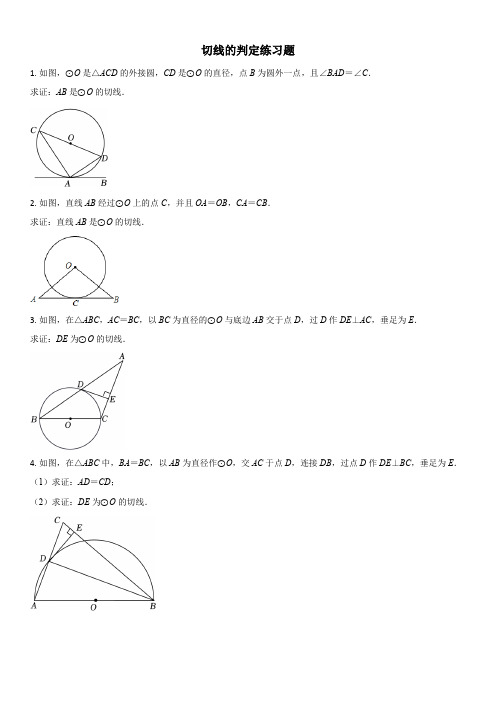
切线的判定练习题1.如图,⊙O是△ACD的外接圆,CD是⊙O的直径,点B为圆外一点,且∠BAD=∠C.求证:AB是⊙O的切线.2.如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB.求证:直线AB是⊙O的切线.3.如图,在△ABC,AC=BC,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.求证:DE为⊙O的切线.4.如图,在△ABC中,BA=BC,以AB为直径作⊙O,交AC于点D,连接DB,过点D作DE⊥BC,垂足为E.(1)求证:AD=CD;(2)求证:DE为⊙O的切线.5.如图,AB为⊙O的直径,点C,D在⊙O上,AĈ=CD̂=DB̂,DE⊥AC.求证:DE是⊙O的切线.6.如图,AB为⊙O的直径,AC平分∠BAD交⊙O于点C,CD⊥AD,垂足为点D.求证:CD是⊙O的切线.7.如图△ABC中,∠ABC=90°,CD平分∠ACB交AB于点D,以点D为圆心,BD为半径作⊙D交AB于点E.(1)求证:⊙D与AC相切;(2)若AC=5,BC=3,试求AE的长.8.如图,在△ABC中,AB=BC,以AB为直径的⊙O与AC交于点D,过D作DF⊥BC,交AB的延长线于E,垂足为F.求证:直线DE是⊙O的切线.9.如图,在△ABC中,CA=CB,O为AB上一点.以O为圆心,OB长为半径的⊙O过点C,交AB于另一点D.若D是OA的中点,求证:AC是⊙O的切线.10.如图所示,AB为半圆O的直径,C是半圆上一点,AD平分∠CAB交半圆于点D,过点D作DE⊥AC,DE交AC的延长线于点E.(1)求证:DE是⊙O的切线;(2)若⊙O的半径为2,DE=√3,求线段AC的长.11.如图,在△ABC中,AB=AC,D为AC上一点,以CD为直径的⊙O交BC于点F,FG⊥AB,垂足为G,求证:FG是⊙O的切线.12.如图,已知AB=AC,以AB为直径的圆O交边BC于点D,过点D作DE⊥AC,垂足为点E.(1)求证:DE是圆O的切线;(2)如果∠BAC=120°,求证:DE=14BC.13.如图,已知AB是⊙O的直径,D是⊙O上一点,且∠A=∠CDB=∠COB.求证:CB是⊙O的切线.14.如图,在Rt△ABC中,∠ABC=90°,AC=10,BC=6,∠ACB的平分线CO交AB于点O,以OB为半径作⊙O.(1)请判断AC与⊙O的位置关系,并说明理由;(2)求⊙O的半径.。
【单元练】人教版初中九年级数学上册第二十四章《圆》经典练习题(含答案解析)

一、选择题1.如图,,AB AC 分别是O 的直径和弦,OD AC ⊥于点,D 连接,BD BC .若10,8AB AC ==,则BD 的长是( )A .25B .4C .213D .245C 解析:C【分析】 先根据圆周角定理得∠ACB=90°,则利用勾股定理计算出BC=6,再根据垂径定理得到CD=AD=12AC=4,然后利用勾股定理计算BD 的长. 【详解】解:∵AB 为直径,∴∠ACB=90°,∴22221086BC AB AC =-=-=,∵OD ⊥AC , ∴CD=AD=12AC=4, 在Rt △CBD 中,222246213BD BC CD =+=+=.故选:C .【点睛】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了垂径定理.2.如图,四个水平放置正方形的边长都为4,顶点A 、B 、C 是圆上的点,则此圆的面积为( )A .72πB .85πC .100πD .104πB解析:B【分析】连接BC,作AB,BC的垂直平分线,交点为点O,连接OB,OC,根据垂直平分线可得AE=BE=2,DE=4×4=16,DC=4+2=6,设OD=x,则OE=16-x,再根据OB=OC即可列出方程求得x=7,最后再根据圆的面积公式计算即可.【详解】解:如图,连接BC,作AB,BC的垂直平分线,交点为点O,连接OB,OC,则OB=OC,AE=BE=2,DE=4×4=16,DC=4+2=6,设OD=x,则OE=16-x,∵OB=OC,∴OB2=OC2,∴22+(16-x) 2=62+x2,解得x=7,∴r2=OB2=22+92=85,∴圆的面积S=πr2=85π,故选:B.【点睛】本题考查了作三角形的外心,垂径定理的应用,圆的面积公式,熟练掌握垂径定理是解决本题的关键.3.如图,分别以AB,AC为直径的两个半圆,其中AC是半圆O的一条弦,E是弧AEC中点,D是半圆ADC中点.若DE=2,AB=12,且AC˃6,则AC长为()A.2B.2C.2D.2D解析:D【分析】连接OE,交AC于点F,由勾股定理结合垂径定理求出AF的长,即可得到结论.【详解】解:连接OE ,交AC 于点F ,∵E 为AEC 的中点,∴OE AC ⊥,F 为AC 的中点,∵12AB =∴6OE AO ==设EF x =,则6OF x =-∵F 为AC 的中点,D 为半圆ADC 的中点,∴DF AC ⊥,DF AF =∵2DE =,∴2DF x AF =+=在Rt △AOF 中,222OA OF AF =+即2226(6)(2)x x =-++, ∴122x =+,222x =-∴2(2)822AC x =+=+或822-∵6AC >∴822AC =+故选:D【点睛】本题考查了垂径定理,熟练掌握垂径定理,运用勾股定理求出AF 是解题的关键. 4.为落实好扶贫工作,某村驻村干部帮助村民修建了一个粮仓,该粮仓的屋顶是一个圆锥,为了合理购买、不浪费原材料,需要进行计算1个屋顶的侧面积大小,该圆锥母线长为5m ,底面圆周长为8m π,则1个屋顶的侧面积等于( )2m .(结果保留π)A .40πB .20πC .16πD .80πB解析:B【分析】 先根据底面周长可求得底面圆的半径,再根据圆锥的侧面积公式计算即可求解.【详解】解:∵2πr=8π,∴r=4,又∵母线l=5,∴圆锥的侧面积=πrl =π×4×5=20π.故选:B .【点睛】本题考查了圆锥的侧面积计算方法,牢记有关圆锥和扇形之间的对应关系是解决本题的关键.5.如图,在三角形ABC 中,AB=22,∠B=30°,∠C=45°,以A 为圆心,以AC 长为半径作弧与AB 相交于点E ,与BC 相交于点F ,则弧EF 的长为( )A .6πB .2πC .23πD .πA解析:A【分析】过A 作AD ⊥BC ,连接AF ,求出∠FAE ,再利用弧长计算公式计算EF 的长即可.【详解】解:过A 作AD 垂直BC ,连接AF ,如图,∵2,30,45AB B C =∠=︒∠=︒,可得2∴AC=2,∵AC=AF∴∠AFC=∠C=45°,∴∠FAE=∠AFC-∠B=45°-30°=15°∴EF 的长为:152180π⨯=6π 故选:A【点睛】此题主要考查了弧长的计算,关键是掌握弧长计算公式.6.已知⊙O ,如图,(1)作⊙O 的直径AB ;(2)以点A 为圆心,AO 长为半径画弧,交⊙O 于C ,D 两点;(3)连接CD 交AB 于点E ,连接AC ,BC .根据以上作图过程及所作图形,有下面三个推断:①CE DE =;②3BE AE =;③2BC CE =.其中正确的推断的个数是( )A .0个B .1个C .2个D .3个D解析:D【分析】 ①根据作图过程可得AC AD =,根据垂径定理可判断;②连接OC ,根据作图过程可证得△AOC 为等边三角形,由等边三角形的性质即可判断; ③根据直角三角形中30°角所对的直角边等于斜边的一半即可判断.【详解】解:①∵以点A 为圆心,AO 长为半径画弧,交⊙O 于C ,D 两点,∴AC AD =,根据垂径定理可知,AB ⊥CE ,CE=DE ,∴①正确;②连接OC ,∵AC=OA=OC ,∴△AOC 为直角三角形,∵AB ⊥CE ,∴AE=OE ,∴BE=BO+OE=3AE ,∴②正确;③∵AB 为直径,∴∠ACB=90°,∵∠CAB=60°,∴∠ABC=30°,∴BC=2CE ,∴③正确,故选:D .【点睛】本题考查了垂径定理、圆周角定理、等边三角形的判定与性质、含30°角的直角三角形的性质,理解基本作图知识,熟练掌握各基本性质和综合运用是解答的关键.7.如图,在⊙O 中,AB 是直径,弦AC=5,∠BAC=∠D .则AB 的长为( )A .5B .10C .52D .102解析:C【分析】 根据圆周角定理得出∠D=∠B ,得出△ABC 是等腰直角三角形,进而解答即可.【详解】∵AC=AC ,∴∠D=∠B ,∵∠BAC=∠D ,∴∠B=∠BAC ,∴△ABC 是等腰三角形,∵AB 是直径,∴△ABC 是等腰直角三角形,∵AC=5,∴AB=52故选:C .【点睛】本题考查了圆周角定理,等腰直角三角形的判定和性质,勾股定理的应用,关键是根据圆周角定理得出∠D=∠B .8.如图,AB 为O 的弦,半径OC 交AB 于点D ,AD DB =,5OC =,3OD =,则AB 的长为( )A.8 B.6 C.4 D.2A解析:A【分析】连接OB,根据⊙O的半径为5,CD=2得出OD的长,再由垂径定理的推论得出OC⊥AB,由勾股定理求出BD的长,进而可得出结论.【详解】解:连接OB,如图所示:∵⊙O的半径为5,OD=3,∵AD=DB,∴OC⊥AB,∴∠ODB=90°,∴2222=-=-=,BD OB OD.534∴AB=2BD=8.故选:A.【点睛】本题考查的是垂径定理以及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.9.如图,四边形ABCD内接于⊙O,AB为⊙O的直径,点C为BD的中点.若∠=︒,则B的度数是()A50A.50︒B.55︒C.60︒D.65︒D解析:D【分析】连接AC,根据圆心角、弧、弦的关系求出∠BAC,根据圆周角定理求出∠ACB=90°,根据三角形内角和定理计算即可.【详解】解:连接AC ,∵点C 为BD 的中点,∴∠BAC=12∠BAD=25°, ∵AB 为⊙O 的直径,∴∠ACB=90°,∴∠B=90°-∠BAC=65°,故选:D .【点睛】本题考查的是圆心角、弧、弦的关系、圆周角定理的应用,掌握圆心角、弧、弦的关系定理和圆周角定理是解题的关键.10.如图,在平行四边形ABCO 中,45C ∠=︒,点A ,B 在O 上,点D 在ADB 上,DA DB =,则AOD ∠的度数为( )A .112.5°B .120°C .135°D .150°C解析:C【分析】 延长DO 交AB 于点H ,连接OB ,证明△△AOD BOD ≅,OD 是AOB ∠的角平分线,求得290345∠=︒-∠=︒,进行求解即可;【详解】延长DO 交AB 于点H ,连接OB ,∵四边形ABCD 是平行四边形,45C ∠=︒,∴345∠=︒,∵DA DB =,OA OB =,∴△△AOD BOD ≅,∴OD 是AOB ∠的角平分线,又∵AO BO =,∴DH AB ⊥,∴290345∠=︒-∠=︒,又∵221∠=∠,∴18045135AOD ∠=︒-︒=︒.故选:C .【点睛】本题主要考查了与圆有关的计算,结合全等三角形的性质和角平分线的性质计算即可.二、填空题11.已知正方形MNKO 和正六边形ABCDEF 边长均为1,把正方形放在正六边形外边,使OK 边与AB 边重合,如图所示,按下列步骤操作:将正方形在正六边形外绕点B 顺时针旋转,使KN 边与BC 边重合,完成第一次旋转;再绕点C 顺时针旋转,使NM 边与CD 边重合,完成第二次旋转;…在这样连续的旋转过程中,第一次点M 在图中直角坐标系中的坐标是_______,第6次点M 的坐标是_______.【分析】先将正方形旋转六次的图形画出确定六次旋转之后点的位置然后通过添加辅助线构造出直角三角形进而利用含角的直角三角形的性质求得再根据勾股定理求得再根据正六边形的性质线段的和差即可求得即可得解【详解 解析:13,12⎛+ ⎝⎭332⎛ ⎝⎭【分析】先将正方形旋转六次的图形画出,确定六次旋转之后点M 的位置,然后通过添加辅助线构造出直角三角形,进而利用30含角的直角三角形的性质求得12FH =、12CJ =,再根据勾股定理求得632JM =,再根据正六边形的性质、线段的和差即可求得32JF =,即可得解.【详解】解:经历六次旋转后点M 落在点6M 处,过M 作MH x ⊥于点H ,过6M 作6M J x ⊥于点J ,连接6IM ,如图:∵在Rt AFH 中,1AF =,60AFH ∠=︒,30FAH ∠=︒∴1122FH AF == ∵已知点M 的纵坐标是312+,即312MH =+ ∴点M 的坐标是:13,12⎛ ⎝⎭; ∵在6Rt CJM 中,61CM =,660JCM ∠=︒,630CM J ∠=︒∴61122CJ CM ==,226632JM CM CJ =-= ∵点I 是正六边形的中心∴1IC IF ==∴32JF IF IC CJ =+-=∴点6M 的坐标是:33,22⎛⎫ ⎪ ⎪⎝⎭. 故答案是:13,122⎛⎫+ ⎪ ⎪⎝⎭;33,22⎛⎫ ⎪ ⎪⎝⎭【点睛】本题考查了正多边形、旋转变换、含30角的直角三角形、勾股定理、线段的和差以及坐标系中的图形与坐标,体现了数形结合的数学思想.12.如图,在平面直角坐标系xOy 中,点,,A B C 的坐标分别是(0,),(22,0),()4,0,M是ABC ∆的外接圆,则圆心M 的坐标为__________________,M 的半径为_______________________. 【分析】M 点为BC 和AB 的垂直平分线的交点利用点ABC 坐标易得BC 的垂直平分线为直线x=3AB 的垂直平分线为直线y=x 从而得到M 点的坐标然后计算MB 得到⊙M 的半径【详解】解:∵点ABC 的坐标分别是(解析:()3,310【分析】M 点为BC 和AB 的垂直平分线的交点,利用点A 、B 、C 坐标易得BC 的垂直平分线为直线x=3,AB 的垂直平分线为直线y=x ,从而得到M 点的坐标,然后计算MB 得到⊙M 的半径.【详解】解:∵点A ,B ,C 的坐标分别是(0,2),(2,0),(4,0),∴BC 的垂直平分线为直线x=3,∵OA=OB ,∴△OAB 为等腰直角三角形,∴AB 的垂直平分线为第一、三象限的角平分线,即直线y=x ,∵直线x=3与直线y=x 的交点为M 点,∴M 点的坐标为(3,3),∵22(32)310MB =-+=∴⊙M 10.故答案为(3,3),10.【点睛】本题考查了三角形的外接圆与外心:三角形外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心.也考查了坐标与图形的性质.13.如图,等腰直角△ABC中,∠BAC=90°,AB=AC=4.平面内的直线l经过点A,作CE⊥l 于点E,连接BE.则当直线l绕着点A转动时,线段BE长度的最大值是________.【分析】以AC为直径作圆O连接BO并延长交圆O于点可得BO+O>B从而可得BO+OE>B即BE为最大值再由勾股定理求出BO 的长即可解决问题【详解】解:由题意知CE⊥l于点E∴以AC为直径作圆O∵CE解析:225+【分析】以AC为直径作圆O,连接BO,并延长交圆O于点E',可得BO+O E'>B E',从而可得BO+OE>B E',即BE为最大值,再由勾股定理求出BO的长即可解决问题.【详解】解:由题意知,CE⊥l于点E,∴以AC为直径作圆O,∵CE⊥AE,∴点E在圆O上运动,连接BO,并延长交圆O于点E',如图,∴BO+O E'>B E',∵OE=O E',∴BO+OE>B E',∴BE的长为最大值,∵AO=OC=OE,且AB=AC=4,∴122OE AC==又∵∠BAC=90°∴22222BO AO AB=+=+=4220∴25BO=∴BE=252+=+BO OE+故答案为:225【点睛】此题主要考查了求线段的最大值,构造出△ACE的外接贺是解答本题的关键.14.如图,点A,B,C在O上,顺次连接A,B,C,O.若四边形ABCO为平行∠=________︒.四边形,则AOC120【分析】连接OB先证明四边形ABCD是菱形然后再说明△AOB△OBC为等边三角形最后根据等边三角形的性质即可解答【详解】解:如图:连接OB∵点在上∴OA=OC=OB∵四边形为平行四边形∴四边形解析:120【分析】连接OB,先证明四边形ABCD是菱形,然后再说明△AOB、△OBC为等边三角形,最后根据等边三角形的性质即可解答.【详解】解:如图:连接OB∵点A,B,C在O上∴OA=OC=OB∵四边形ABCO为平行四边形∴四边形ABCO是菱形∴OA=OC=OB=AB=BC∴△AOB、△OBC为等边三角形∴∠AOB=∠BOC=60°∴∠AOC=120°.故答案为120.【点睛】本题主要考查了圆的性质和等边三角形的性质,根据题意证得△AOB 、△OBC 为等边三角形是解答本题的关键.15.如图,在平面直角坐标系中,点()3,4A ,()3,0B ,以A 为圆心,2为半径作A ,点P 为A 上一动点,M 为OP 的中点,连接BM ,设BM 的最大值为m ,最小值为n ,则m n -的值为_________.2【分析】方法一:在轴上取一点连接可求由可得由点在上运动可知共线时可以取得最大值或最小值最大值最小值由最大值与最小值求出即可;方法二:连接取中点连接利用三角形三边关系有可得作差计算即可【详解】解:方解析:2【分析】方法一:在x 轴上取一点()6,0E ,连接PE ,可求3OB BE ==,22345AE +=,由OM PM =,OB BE =,可得12BM PE =,由点P 在A 上运动,可知P 、A 、B 共线时,可以取得最大值或最小值,最大值'527EP ==+=,最小值''523EP =-=,由最大值与最小值求出72m =,32n =即可;方法二:连接PA 、OA ,取OA 中点N ,连接MN 、BN ,利用三角形三边关系有BN MN BM BN MN -≤≤+,可得m BN MN =+,n BN MN =-,作差计算22m n MN PA -===即可.【详解】解:方法一:在x 轴上取一点()6,0E ,连接PE ,∵()3,0B ,()3,4A ,∴3OB BE ==,22345AE =+=,∵OM PM =,OB BE =,∴12BM PE =, ∵点P 在A 上运动, ∴P 、A 、B 共线时,可以取得最大值或最小值,最大值'527EP ==+=,最小值''523EP =-=,∴72m =,32n =, ∴2m n -=, 故答案为2.方法二:连接PA 、OA ,取OA 中点N ,连接MN 、BN ,BN MN BM BN MN -≤≤+,m BN MN =+,n BN MN =-,22m n MN PA -===.故答案为:2.【点睛】本题考查三角形的中位线,勾股定理,三角形三边关系,线段和差,掌握三角形的中位线,勾股定理,三角形三边关系,线段和差,引辅助线构造准确图形是解题关键. 16.如图,已知点C 是半圆О上一点,将弧BC 沿弦BC 折叠后恰好经过点,O 若半圆O 的半径是2,则图中阴影部分的面积是________________________.【分析】过点O 作OD ⊥BC 于E 交半圆O 于D 点连接CD如图根据垂径定理由OD ⊥BC 得BE =CE 再根据折叠的性质得到ED =EO 则OE =OB 则可根据含30度的直角三角形三边的关系得∠OBC =30°即∠AB 解析:23π 【分析】过点O 作OD ⊥BC 于E ,交半圆O 于D 点,连接CD ,如图,根据垂径定理由OD ⊥BC 得BE =CE ,再根据折叠的性质得到ED =EO ,则OE =12OB ,则可根据含30度的直角三角形三边的关系得∠OBC =30°,即∠ABC =30°则∠AOC=60°,由于OC =OB ,则弓形OC 的面积=弓形OB 的面积,然后根据扇形的面积公式及S 阴影部分=S 扇形OAC 即可得到阴影部分的面积.【详解】如图:过点O 作OD ⊥BC 于E ,交半圆O 于D 点,连接CD ,∵OD ⊥BC ,∴BE =CE ,∵半圆O 沿BC 所在的直线折叠,圆弧BC 恰好过圆心O ,∴ED =EO ,∴OE =12OB , ∴∠OBC =30°,即∠ABC =30°,∴∠AOC=60°;∵OC =OB ,∴弓形OC 的面积=弓形OB 的面积,∴S 阴影部分=S 扇形OAC =260223603ππ⋅= . 【点睛】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了垂定定理、圆周角定理和扇形的面积公式.17.如图,在圆O 的内接五边形ABCDE 中,40CAD ∠=︒,则B E ∠+∠=_______°.220【分析】连接CE根据圆内接四边形对角互补可得∠B+∠AEC=180°再根据同弧所对的圆周角相等可得∠CED=∠CAD然后求解即可【详解】解析:220【分析】连接CE,根据圆内接四边形对角互补可得∠B+∠AEC=180°,再根据同弧所对的圆周角相等可得∠CED=∠CAD,然后求解即可.【详解】连接CE,∵五边形ABCDE是⊙O的内接五边形,∴四边形ABCE是⊙O的内接四边形,∴∠B+∠AEC=180°,∵∠CED=∠CAD=40°,∴∠B+∠AED=180°+40°=220°【点睛】本题考查圆内接四边形的性质,同弧所对的圆周角相等的性质,熟记性质并作辅助线构造出圆内接四边形是解题关键.BC=,若点P是矩形ABCD上一动点,要使得18.在矩形ABCD中,43AB=6∠=︒,则AP的长为__________.或4或8【分析】取CD中点P1连接60APBAP1BP1由勾股定理可求AP1=BP1=4即可证△AP1B是等边三角形可得∠AP1B =60°过点A点P1点B作圆与ADBC各有一个交点即这样的P点一共3个再运用勾解析:434或8.【分析】取CD中点P1,连接AP1,BP1,由勾股定理可求AP1=BP1=3△AP1B是等边三角形,可得∠AP1B=60°,过点A,点P1,点B作圆与AD,BC各有一个交点,即这样的P 点一共3个.再运用勾股定理求解即可.【详解】解:如图,取CD 中点P 1,连接AP 1,BP 1,如图1,∵四边形ABCD 是矩形∴AB =CD =43,AD =BC =6,∠D =∠C =90°∵点P 1是CD 中点∴CP =DP 1=23∴AP 1=221AD DP +=43, BP 1=221BC CP +=43 ∴AP 1=P 1B =AB∴△APB 是等边三角形∴∠AP 1B =60°,过点A ,点P 1,点B 作圆与AD ,BC 的相交,∴这样的P 点一共有3个当点P 2在AD 上时,如图2,∵四边形ABCD 是矩形,∴3,43,90AB A CD AD =∠===︒∵260,AP B ∠=︒∴221,2P A P B = 即222,P B P A =在2Rt P AB ∆中,22222,P B P A AB -=∴222222(43),P A P A -=∴24AP =;当点P 3在BC 上时,如图3,∵四边形ABCD 是矩形,∴∠B=90°∵∠360,AP B =︒∴∠3390906030,P AB AP B =︒-∠=︒-︒=︒ ∴331,2BP AP = 在3Rt ABP ∆中,22233,AP BP AB -=222331()(43),2AP AP -= 23348,4AP = ∴8,AP =综上所述,AP 的长为:43或4或8.故答案为:43或4或8.【点睛】本题考查了矩形的性质,勾股定理,等边三角形的判定和性质,灵活运用这些性质进行推理是本题的关键.19.如图,半径为10的扇形AOB 中,∠AOB=90°,C 为AB 上一点,CD ⊥OA ,CE ⊥OB ,垂足分别为D 、E .若∠CDE=36°,则图中阴影部分的面积为____.10π【分析】连接OC 易得△ODE ≌△ECO 所以扇形OBC 的面积就是图中阴影部分的面积因此求得扇形OBC 的面积即可【详解】解:如下图连接OC ∵∠AOB=90°CD ⊥OACE ⊥OB ∴四边形ODCE 为矩解析:10π【分析】连接OC ,易得△ODE ≌△ECO ,所以扇形OBC 的面积就是图中阴影部分的面积,因此求得扇形OBC 的面积即可.【详解】解:如下图连接OC ,∵∠AOB=90°、CD ⊥OA 、CE ⊥OB∴四边形ODCE 为矩形∴OD=CE ,OE 为公共边∴△ODE ≌△ECO∴△ODE 的面积=△ECO 的面积∴图中阴影部分的面积=2236361010360360O BC SOB πππ-==⨯=. 故答案为:10π.【点睛】本题考查扇形面积的计算和矩形的性质.其关键是用矩形性质对阴影部分进行等积变换,发现△ODE 的面积=△ECO 的面积.20.湖州南浔镇河流密如蛛网,民间有“千步一桥”之说.如图,某圆弧形桥拱的跨度AB =12米,拱高CD =4米,则该拱桥的半径为____米. 65【分析】根据垂径定理的推论此圆的圆心在CD 所在的直线上设圆心是O 连接OA 根据垂径定理和勾股定理求解【详解】根据垂径定理的推论知此圆的圆心在CD 所在的直线上设圆心是O 连接OA 拱桥的跨度AB=12m解析:6.5【分析】根据垂径定理的推论,此圆的圆心在CD 所在的直线上,设圆心是O .连接OA .根据垂径定理和勾股定理求解.【详解】根据垂径定理的推论,知此圆的圆心在CD 所在的直线上,设圆心是O ,连接OA . 拱桥的跨度AB =12m ,拱高CD =4m ,根据垂径定理,得AD=6 m ,利用勾股定理可得:()22264AO AO =--,解得:AO =6.5m .即圆弧半径为6.5米,故答案为:6.5.【点睛】本题综合运用了勾股定理以及垂径定理.注意由半径、半弦、弦心距构造的直角三角形进行有关的计算. 三、解答题21.如图,AB 是⊙O 的直径,点C 在⊙O 上,BD 平分ABC ∠交⊙O 于点D ,过点D 作DE BC ⊥,垂足为E .(1)求证:DE 与⊙O 相切;(2)若10AB =,6AD =,求DE 的长.解析:(1)见解析;(2)245 【分析】(1)连接OD ,由BD 为角平分线得到OBD CBD ∠=∠,再由OB=OD ,利用等边对等角得到ODB OBD ∠=∠,从而得出ODB CBD ∠=∠,利用内错角相等两直线平行得到OD 与BE 平行,由DE 垂直于BE 得到OD 垂直于DE ,即可得证;(2)过D 作DH AB ⊥于H ,根据HL 得出△≌△Rt ADH Rt CDE ,得出AH CE =,再根据勾股定理得出22221068BD AB AD -=-=,再利用等积法即可得出DE 的长.【详解】(1)证明:连接OD .∵OD OB =,∴ODB OBD ∠=∠.∵BD 平分ABC ∠,∴OBD CBD ∠=∠.∴ODB CBD ∠=∠,∴//OD BE .∴180BED ODE ∠+∠=︒.∵BE DE ⊥,∴90BED ∠=︒.∴90ODE ∠=︒.∴OD DE ⊥.∴DE 与O 相切;(2)过D 作DH AB ⊥于H .∵BD 平分ABC ∠,DE BE ⊥,∴DH DE =.∵AD CD =,∴AD CD =.∴()Rt ADH Rt CDE HL △≌△,∴AH CE =.∵AB 是O 的直径,∴90ADB ∠=︒. ∵10AB =,6AD =, ∴22221068BD AB AD =-=-=. ∵1122AB DH AD BD ⋅=⋅,∴245DH =. ∴245DE =. 【点睛】 此题考查了切线的判定,角平分线的性质、圆周角定理、平行线的判定与性质等知识,熟练掌握切线的判定方法是解本题的关键,属于中考常考题型.22.如图,AB 是圆的直径,且AD//OC ,求证:CD BC =.解析:证明见解析.【分析】主要是根据弧相等只需要证明弧所对的圆周角相等或者弧所对的圆心角相等即可证明.连接AC 或者OD 都可以证明.【详解】解:连接ACAD//OC∴∠DAC=∠OCAOA=OC∴∠BAC=∠ACO∴∠DAC=∠BAC∴CD BC =.【点睛】主要是考察学生对圆周角定理的内容的掌握.同时角相等和弧相等之间的转化. 23.如图,已知直线PT 与⊙O 相交于点T ,直线PO 与⊙O 相交于A 、B 两点,已知PTA B ∠=∠.(1)求证:PT 是⊙O 的切线;(2)若3PT BT ==解析:(1)证明见解析;(2)364π- 【分析】 (1)先根据圆周角定理得:∠ATB=90°,则∠B+∠OAT=90°,根据同圆的半径相等和等腰三角形的性质得:∠OAT=∠2,从而得∠PTA+∠2=90°,即∠OTP=90°,所以直线PT 与⊙O 相切;(2)利用TP=TB 得到∠P=∠B ,而∠OAT=2∠P ,所以∠OAT=2∠B ,则利用∠ATB=90°可计算出∠B=30°,∠POT=60°,利用含30度的直角三角形三边的关系得到AT=12AB ,△AOT 为等边三角形,然后根据扇形的面积公式和图中阴影部分的面积=S 扇形OAT -S △AOT 进行计算.【详解】(1)证明:连接OT ,∵AB 是⊙O 的直径,∴∠ATB=90°,∴∠B+∠OAT=90°,∵OA=OT ,∴∠OAT=∠2,∵∠PTA=∠B ,∴∠PTA+∠2=90°,即∠OTP=90°,∴直线PT 与⊙O 相切;(2)∵3PT BT ==∴∠P=∠B=∠PTA ,∵∠TAB=∠P+∠PTA ,∴∠TAB=2∠B ,∵∠TAB+∠B=90°,∴∠TAB=60°,∠B=30°,在Rt △ABT 中,设AT=a ,则AB=2AT=2a ,∴a 232=(2a)2,解得:a=1,∴AT=1,∵OA=OT ,∠TAO=60°,∴△AOT 为等边三角形, 13312AOT S ∴=⨯=. ∴阴影部分的面积2Δ 60133360464AOT AOTS S ππ⨯=-=-=-扇形. 【点睛】本题考查了切线的判定、勾股定理,此类题常与方程结合,列方程求圆的半径和线段的长,也考查了扇形的面积公式.24.如图,已知AB 是O 的直径,四边形AODE 是平行四边形,请用无刻度直尺按下列要求作图.(1)如图1,当点D 在圆上时,作BAC ∠的平分线;(2)如图2,当点D 不在圆上时,作BAC ∠的平分线.解析:(1)见解析;(2)见解析.【分析】(1)由四边形AODE 是平行四边形,结合圆的 半径相等,可知四边形AODE 是菱形,利用菱形的性质即可做出BAC ∠的平分线;(2)延长OD 交于圆一点,连接该点与点A ,由此即可作出C BA ∠的平分线.【详解】解:(1)如图①:AD 即为所求.∵四边形AODE 是平行四边形点D 在圆上∴四边形AODE 是菱形∴AD 平分BAC ∠;(2)如图②:延长OD 交于圆一点P ,连接AP ,同理可证AP 即为所求.【点睛】此题考查尺规作图,关键是掌握圆的相关知识及角平分线的判定方法.25.如图1是某人荡秋千的情形,简化成图2所示,起始状态下秋千顶端O 与座板A 的距离为2m (此时OA 垂直于地面),现一人荡秋千时,座板到达点B (OA 不弯曲).(1)当BOA 30∠=时,求AB 弧的长度(保留π);(2)当从点C 荡至点B ,且BC 与地面平行,3m BC =时,若点A 离地面0.4m ,求点B 到地面的距离(保号根号).解析:(1)3m π;(2)127()52m -. 【分析】(1)利用弧长公式计算,得到答案;(2)根据等腰三角形的性质求出BD ,根据勾股定理求出OD ,结合图形计算即可.【详解】解:(1)AB 弧线的长度=302()1803m ππ⨯=; (2)如图,∵OB=OC ,OD ⊥BC ,∴1322BD BC ==, 在Rt △OBD 中,OD 2+BD 2=OB 2, ∴2222372()2OD OB BD =-=-=, ∴点B 到地面的距离=712720.4252-+=-, 答:点B 到地面的距离为127(5m -. 【点睛】本题考查的是解直角三角形的应用、弧长的计算、勾股定理,掌握弧长公式是解题的关键.26.如图,已知AB 是⊙O 的直径,点C 、D 在⊙O 上,点E 在⊙O 外,∠CAE=∠ADC .(1)求证:AE 是⊙O 的切线;(2)若⊙O 的半径为2,∠B=60°,求图中阴影部分的面积.(结果保留根号和π) 解析:(1)见解析;(2)433π- 【分析】(1)根据AB 是直径得到∠ACB=90°,根据已知条件得到∠BAE =90°,即可得到结果; (2)作OM ⊥AC ,垂足为M ,求得AM=3,根据扇形的面积计算公式计算即可;【详解】(1)证明:∵AB 是⊙O 的直径,∴∠ACB=90°,∴∠B+∠BAC=90°,∵∠B=∠ADC=∠CAE ,∴∠BAE=∠BAC+∠EAC=∠BAC+∠B=90°,∴ BA ⊥AE ,∴AE 是⊙O 的切线.(2)解:作OM ⊥AC ,垂足为M .∵∠B=60°,∴∠AOC=2∠B=120°,∴∠AOM=∠COM=60°, ∴OM=12AO=1, ∴3 ∴AC=2AM=23∴S 阴=S 扇形AOC -S △AOC =120414-231336023ππ. 【点睛】本题主要考查了切线的证明和扇形的面积计算,准确分析计算是解题的关键. 27.如图,ABC 内接于O ,60BAC ∠=︒,点D 是BC 的中点.BC ,AB 边上的高AE ,CF 相交于点H .试证明:(1)FAH CAO ∠=∠;(2)四边形AHDO 是菱形.解析:(1)见详解;(2)见详解【分析】(1)连接AD ,根据题意易得,BAD CAD OD BC ∠=∠⊥,则有∠DAE=∠ODA ,∠DAO=∠ODA ,然后根据角的等量关系可求解;(2)过点O 作OM ⊥AC 于M ,由题意易得AC=2AM ,AC=2AF ,进而可证△AFH ≌△AMO ,然后可得四边形AHDO 是平行四边形,最后问题可证.【详解】证明:(1)连接AD ,如图所示:∵点D 是BC 的中点,∴,BAD CAD OD BC ∠=∠⊥,∵AE ⊥BC ,∴AE ∥OD ,∴∠DAE=∠ODA ,∵OA=OD ,∴∠DAO=∠ODA ,∴∠BAD-∠DAE=∠CAD-∠DAO ,∴∠FAH=∠CAO ;(2)过点O 作OM ⊥AC 于M ,∴AC=2AM ,∵CF ⊥AB ,∠BAC=60°,∴AC=2AF ,∴AF=AM ,∵∠AFH=∠AMO=90°,∠FAH=∠OAM ,∴△AFH ≌△AMO (ASA ),∴AH=AO ,∵OA=OD ,∴AH //CD ,∴四边形AHDO 是平行四边形,∵OA=OD ,∴四边形AHDO 是菱形.【点睛】本题主要考查圆周角定理、垂径定理及菱形的判定,熟练掌握圆周角定理、垂径定理及菱形的判定是解题的关键.28.已知PA 、PB 分别与O 相切于点A ,B 两点,76APB ∠=︒ ,C 为O 上一点. (1)如图,求ACB ∠的大小; (2)如图,AE 为O 的直径,AE 与BC 相交于点D ,若AB AD =,求EAC ∠的大小.解析:(1)52︒;(2)19︒【分析】(1)连接OA 、OB ,根据切线的性质得到90OAP OBP ∠=∠=︒,可以求出AOB ∠的度数,再根据圆周角定理得到ACB ∠的度数;(2)连接CE ,根据(1)的结论,先求出BCE ∠的度数,再由圆周角定理得到BAE BCE ∠=∠,再等腰三角形ABD 中求出底角ADB ∠的度数,再由外角和定理就可以求出EAC ∠的度数.【详解】解:(1)如图,连接OA 、OB ,∵PA 、PB 是O 的切线,∴90OAP OBP ∠=∠=︒,∴360909076104AOB ∠=︒-︒-︒-︒=︒,根据圆周角定理,1522ACB AOB ∠=∠=︒;(2)如图,连接CE , ∵AE 是O 的直径, ∴90ACE ∠=︒, ∵52ACB ∠=︒, ∴905238BCE ∠=︒-︒=︒, ∴38BAE BCE ∠=∠=︒, ∵AB AD =, ∴71ABD ADB ∠=∠=︒, ∴19EAC ADB ACB ∠=∠-∠=︒.【点睛】本题考查圆周角定理和切线的性质,解题的关键是掌握这些性质定理进行求解.。
人教版初中数学圆的专项训练及答案

人教版初中数学圆的专项训练及答案(总17页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--人教版初中数学圆的专项训练及答案一、选择题1.如图,3个正方形在⊙O直径的同侧,顶点B、C、G、H都在⊙O的直径上,正方形ABCD的顶点A在⊙O上,顶点D在PC上,正方形EFGH的顶点E在⊙O上、顶点F在QG上,正方形PCGQ的顶点P也在⊙O上.若BC=1,GH=2,则CG的长为()A.125B.6C.21+D.22【答案】B【解析】【分析】【详解】解:连接AO、PO、EO,设⊙O的半径为r,OC=x,OG=y,由勾股定理可知:22222222211{22r xr x x yr y=++=++=++()①()②()③,②﹣③得到:x2+(x+y)2﹣(y+2)2﹣22=0,∴(x+y)2﹣22=(y+2)2﹣x2,∴(x+y+2)(x+y﹣2)=(y+2+x)(y+2﹣x).∵x+y+2≠0,∴x+y﹣2=y+2﹣x,∴x=2,代入①得到r2=10,代入②得到:10=4+(x+y)2,∴(x+y)2=6.∵x+y>0,∴x+y=6,∴CG=x+y=6.故选B.点睛:本题考查了正方形的性质、圆、勾股定理等知识,解题的关键是设未知数列方程组解决问题,难点是解方程组,利用因式分解法巧妙求出x的值,学会把问题转化为方程组,用方程组的思想去思考问题.2.如图,已知AB是⊙O的直径,点C在⊙O上,过点C的切线与AB的延长线交于点P,连接AC,若∠A=30°,PC=3,则⊙O的半径为()A.3B.23C.32D.233【答案】A【解析】连接OC,∵OA=OC,∠A=30°,∴∠OCA=∠A=30°,∴∠COB=∠A+∠ACO=60°,∵PC是⊙O切线,∴∠PCO=90°,∠P=30°,∵PC=3,∴OC=PC•tan30°=3,故选A3.如图,正方形ABCD内接于⊙O,AB=22,则AB的长是()A.πB.32πC.2πD.12π【答案】A【解析】【分析】连接OA、OB,求出∠AOB=90°,根据勾股定理求出AO,根据弧长公式求出即可.【详解】连接OA、OB,∵正方形ABCD内接于⊙O,∴AB=BC=DC=AD,∴AB BC CD DA===,∴∠AOB=14×360°=90°,在Rt△AOB中,由勾股定理得:2AO2=(22)2,解得:AO=2,∴AB的长为902 180π=π,故选A.【点睛】本题考查了弧长公式和正方形的性质,求出∠AOB的度数和OA的长是解此题的关键.4.如图,在平面直角坐标系中,点P是以C(﹣2,7)为圆心,1为半径的⊙C上的一个动点,已知A(﹣1,0),B(1,0),连接PA,PB,则PA2+PB2的最小值是()A.6 B.8 C.10 D.12【答案】C【解析】【分析】设点P(x,y),表示出PA2+PB2的值,从而转化为求OP的最值,画出图形后可直观得出OP的最值,代入求解即可.【详解】设P(x,y),∵PA2=(x+1)2+y2,PB2=(x﹣1)2+y2,∴PA2+PB2=2x2+2y2+2=2(x2+y2)+2,∵OP2=x2+y2,∴PA 2+PB 2=2OP 2+2,当点P 处于OC 与圆的交点上时,OP 取得最值,∴OP 的最小值为CO ﹣CP =3﹣1=2,∴PA 2+PB 2最小值为2×22+2=10.故选:C .【点睛】本题考查了圆的综合,解答本题的关键是设出点P 坐标,将所求代数式的值转化为求解OP 的最小值,难度较大.5.下列命题中,是假命题的是( )A .任意多边形的外角和为360B .在ABC 和'''A B C 中,若''AB A B =,''BC B C =,'90C C ∠=∠=,则ABC ≌'''A B CC .在一个三角形中,任意两边之差小于第三边D .同弧所对的圆周角和圆心角相等【答案】D【解析】【分析】根据相关的知识点逐个分析.【详解】解:A. 任意多边形的外角和为360,是真命题;B. 在ABC 和'''A B C 中,若''AB A B =,''BC B C =,'90C C ∠=∠=,则ABC ≌'''A B C ,根据HL ,是真命题;C. 在一个三角形中,任意两边之差小于第三边,是真命题;D. 同弧所对的圆周角等于圆心角的一半,本选项是假命题.故选D .【点睛】本题考核知识点:判断命题的真假. 解题关键点:熟记相关性质或定义.6.如图,AC BC ⊥,8AC BC ==,以BC 为直径作半圆,圆心为点O ;以点C 为圆心,BC 为半径作AB ,过点O 作AC 的平行线交两弧于点D 、E ,则图中阴影部分的面积是( )A.20833π-B.20833π+C.20833π-D.20433π+【答案】A【解析】【分析】如图,连接CE.图中S阴影=S扇形BCE−S扇形BOD−S△OCE.根据已知条件易求得OB=OC=OD =4,BC=CE=8,∠ECB=60°,OE=43,所以由扇形面积公式、三角形面积公式进行解答即可.【详解】解:如图,连接CE.∵AC⊥BC,AC=BC=8,以BC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作弧AB,∴∠ACB=90°,OB=OC=OD=4,BC=CE=8.又∵OE∥AC,∴∠ACB=∠COE=90°.∴在Rt△OEC中,OC=4,CE=8,∴∠CEO=30°,∠ECB=60°,OE=3∴S阴影=S扇形BCE−S扇形BOD−S△OCE=2260811-4-443 36042ππ⨯⨯⨯⨯=20-83 3π故选:A.【点睛】本题考查了扇形面积的计算.不规则图形的面积一定要注意分割成规则图形的面积进行计算.7.已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作PQ,交射线OB于点D,连接CD;(2)分别以点C,D为圆心,CD长为半径作弧,交PQ于点M,N;(3)连接OM,MN.根据以上作图过程及所作图形,下列结论中错误的是()A.∠COM=∠COD B.若OM=MN,则∠AOB=20°C.MN∥CD D.MN=3CD【答案】D【解析】【分析】由作图知CM=CD=DN,再利用圆周角定理、圆心角定理逐一判断可得.【详解】解:由作图知CM=CD=DN,∴∠COM=∠COD,故A选项正确;∵OM=ON=MN,∴△OMN是等边三角形,∴∠MON=60°,∵CM=CD=DN,∴∠MOA=∠AOB=∠BON=13∠MON=20°,故B选项正确;∵∠MOA=∠AOB=∠BON=20°,∴∠OCD=∠OCM=80°,∴∠MCD=160°,又∠CMN=12∠AON=20°,∴∠MCD+∠CMN=180°,∴MN∥CD,故C选项正确;∵MC+CD+DN>MN,且CM=CD=DN,∴3CD>MN,故D选项错误;故选:D.【点睛】本题主要考查作图-复杂作图,解题的关键是掌握圆心角定理和圆周角定理等知识点.8.如图,四边形ABCD为⊙O的内接四边形.延长AB与DC相交于点G,AO⊥CD,垂足为E,连接BD,∠GBC=50°,则∠DBC的度数为()A.50°B.60°C.80°D.90°【答案】C【解析】【分析】根据圆内接四边形的性质得:∠GBC=∠ADC=50°,由垂径定理得:CM DM=,则∠DBC=2∠EAD=80°.【详解】如图,∵四边形ABCD为⊙O的内接四边形,∴∠GBC=∠ADC=50°.∵AE⊥CD,∴∠AED=90°,∴∠EAD=90°﹣50°=40°,延长AE交⊙O于点M.∵AO⊥CD,∴CM DM=,∴∠DBC=2∠EAD=80°.故选C.【点睛】本题考查了圆内接四边形的性质:圆内接四边形的任意一个外角等于它的内对角,还考查了垂径定理的应用,属于基础题.9.从下列直角三角板与圆弧的位置关系中,可判断圆弧为半圆的是( )A .B .C .D .【答案】B【解析】【分析】根据圆周角定理(直径所对的圆周角是直角)求解,即可求得答案.【详解】∵直径所对的圆周角等于直角,∴从直角三角板与圆弧的位置关系中,可判断圆弧为半圆的是B .故选B .【点睛】本题考查了圆周角定理.此题比较简单,注意掌握数形结合思想的应用.10.如图,ABC ∆是一块绿化带,将阴影部分修建为花圃.已知15AB =,9AC =,12BC =,阴影部分是ABC ∆的内切圆,一只自由飞翔的小鸟将随机落在这块绿化带上,则小鸟落在花圃上的概率为( ).A .16B .6πC .8πD .5π 【答案】B【解析】【分析】由AB=5,BC=4,AC=3,得到AB 2=BC 2+AC 2,根据勾股定理的逆定理得到△ABC 为直角三角形,于是得到△ABC 的内切圆半径=4+3-52=1,求得直角三角形的面积和圆的面积,即可得到结论.【详解】解:∵AB=5,BC=4,AC=3,∴AB 2=BC 2+AC 2,∴△ABC 为直角三角形,∴△ABC 的内切圆半径=4+3-52=1, ∴S △ABC =12AC•BC=12×4×3=6, S 圆=π,∴小鸟落在花圃上的概率=6π , 故选B .【点睛】本题考查几何概率,直角三角形内切圆的半径等于两直角边的和与斜边差的一半及勾股定理的逆定理,解题关键是熟练掌握公式.11.如图,⊙O 的直径CD =10cm ,AB 是⊙O 的弦,AB ⊥CD ,垂足为M ,OM :OC =3:5,则AB 的长为( )A 91B .8cmC .6cmD .4cm【答案】B【解析】【分析】由于⊙O的直径CD=10cm,则⊙O的半径为5cm,又已知OM:OC=3:5,则可以求出OM=3,OC=5,连接OA,根据勾股定理和垂径定理可求得AB.【详解】解:如图所示,连接OA.⊙O的直径CD=10cm,则⊙O的半径为5cm,即OA=OC=5,又∵OM:OC=3:5,所以OM=3,∵AB⊥CD,垂足为M,OC过圆心∴AM=BM,在Rt△AOM中,22AM=5-3=4,∴AB=2AM=2×4=8.故选:B.【点睛】本题考查了垂径定理和勾股定理的应用,构造以半径、弦心距和弦长的一半为三边的直角三角形,是解题的关键.12.如图,点I是Rt△ABC的内心,∠C=90°,AC=3,BC=4,将∠ACB平移使其顶点C 与I重合,两边分别交AB于D、E,则△IDE的周长为()A.3 B.4 C.5 D.7【答案】C【解析】【分析】连接AI、BI,根据三角形的内心的性质可得∠CAI=∠BAI,再根据平移的性质得到∠CAI=∠AID,AD=DI,同理得到BE=EI,即可解答.【详解】连接AI、BI,∵∠C=90°,AC=3,BC=4,∴AB=22+=5AC BC∵点I为△ABC的内心,∴AI平分∠CAB,∴∠CAI=∠BAI,由平移得:AC∥DI,∴∠CAI=∠AID,∴∠BAI=∠AID,∴AD=DI,同理可得:BE=EI,∴△DIE的周长=DE+DI+EI=DE+AD+BE=AB=5故选C.【点睛】此题考查了平移的性质和三角形内心的性质,解题关键在于作出辅助线13.如图,在边长为8的菱形ABCD中,∠DAB=60°,以点D为圆心,菱形的高DF为半径画弧,交AD于点E,交CD于点G,则图中阴影部分的面积是()-B.183πC.32316πD.39πA.183π【答案】C【解析】【分析】由菱形的性质得出AD=AB=8,∠ADC=120°,由三角函数求出菱形的高DF,图中阴影部分的面积=菱形ABCD的面积-扇形DEFG的面积,根据面积公式计算即可.【详解】解:∵四边形ABCD是菱形,∠DAB=60°,∴AD=AB=8,∠ADC=180°-60°=120°,∵DF是菱形的高,∴DF⊥AB,∴DF=AD•sin60°=38432⨯=, ∴图中阴影部分的面积=菱形ABCD 的面积-扇形DEFG 的面积 =2120(43)84332316360ππ⨯⨯-=-. 故选:C.【点睛】本题考查了菱形的性质、三角函数、菱形和扇形面积的计算;由三角函数求出菱形的高是解决问题的关键.14.如图,AB 是⊙O 的直径,弦CD ⊥AB 于E 点,若AD CD23.则BC 的长为( )A .3πB .23πC .33πD .233π 【答案】B【解析】【分析】根据垂径定理得到3CE DE ==,BC BD = ,∠A=30°,再利用三角函数求出OD=2,即可利用弧长公式计算解答. 【详解】如图:连接OD ,∵AB 是⊙O 的直径,弦CD ⊥AB 于E 点,AD CD23 ∴3CE DE ==BC BD = ,∠A=30°, ∴∠DOE=60°,∴OD=2sin 60DE =, ∴BC 的长=BD 的长=60221803ππ⨯=, 故选:B.【点睛】此题考查垂径定理,三角函数,弧长公式,圆周角定理,是一道圆的综合题.15.如图,点A、B、C、D、E、F等分⊙O,分别以点B、D、F为圆心,AF的长为半径画弧,形成美丽的“三叶轮”图案.已知⊙O的半径为1,那么“三叶轮”图案的面积为()A.π+33B.π-33C.33π+D.33π-【答案】B【解析】【分析】连接OA、OB、AB,作OH⊥AB于H,根据正多边形的中心角的求法求出∠AOB,根据扇形面积公式计算.【详解】连接OA、OB、AB,作OH⊥AB于H,∵点A、B、C、D、E、F是⊙O的等分点,∴∠AOB=60°,又OA=OB,∴△AOB是等边三角形,∴AB=OB=1,∠ABO=60°,∴OH=2211()2-=32, ∴“三叶轮”图案的面积=(2601360π⨯⨯-12×1×3)×6=π-332, 故选B .【点睛】本题考查的是正多边形和圆、扇形面积的计算,掌握正多边形的中心角的求法、扇形面积公式是解题的关键.16.若正六边形的半径长为4,则它的边长等于( )A .4B .2C .23D .43【答案】A【解析】试题分析:正六边形的中心角为360°÷6=60°,那么外接圆的半径和正六边形的边长将组成一个等边三角形,故正六边形的半径等于4,则正六边形的边长是4.故选A . 考点:正多边形和圆.17.如图,四边形ABCD 内接于⊙O ,F 是CD 上一点,且DF BC =,连接CF 并延长交AD 的延长线于点E ,连接AC .若∠ABC=105°,∠BAC=25°,则∠E 的度数为( )A .45°B .50°C .55°D .60°【答案】B【解析】【分析】 先根据圆内接四边形的性质求出∠ADC 的度数,再由圆周角定理得出∠DCE 的度数,根据三角形外角的性质即可得出结论.【详解】∵四边形ABCD 内接于⊙O ,∠ABC=105°,∴∠ADC=180°﹣∠ABC=180°﹣105°=75°.∵DF BC =,∠BAC=25°,∴∠DCE=∠BAC=25°,∴∠E=∠ADC﹣∠DCE=75°﹣25°=50°.【点睛】本题考查圆内接四边形的性质,圆周角定理.圆内接四边形对角互补.在同圆或等圆中,同弧或等弧所对的圆心角相等,而同弧所对的圆周角等于圆心角的一半,所以在同圆或等圆中,同弧或等弧所对的圆周角相等.18.如图,AB是⊙O的直径,弦CD⊥AB于点M,若CD=8 cm,MB=2 cm,则直径AB 的长为()A.9 cm B.10 cm C.11 cm D.12 cm【答案】B【解析】【分析】由CD⊥AB,可得DM=4.设半径OD=Rcm,则可求得OM的长,连接OD,在直角三角形DMO中,由勾股定理可求得OD的长,继而求得答案.【详解】解:连接OD,设⊙O半径OD为R,∵AB是⊙O的直径,弦CD⊥AB于点M,∴DM=12CD=4cm,OM=R-2,在RT△OMD中,OD²=DM²+OM²即R²=4²+(R-2)²,解得:R=5,∴直径AB的长为:2×5=10cm.故选B.【点睛】本题考查了垂径定理以及勾股定理.注意掌握辅助线的作法及数形结合思想的应用.19.我们研究过的图形中,圆的任何一对平行切线的距离总是相等的,所以圆是“等宽曲线”.除了圆以外,还有一些几何图形也是“等宽曲线”,如勒洛三角形(如图1),它是分别以等边三角形的每个顶点为圆心,以边长为半径,在另两个顶点间画一段圆弧,三段圆弧围成的曲边三角形. 图2是等宽的勒洛三角形和圆形滚木的截面图.图1图2有如下四个结论:①勒洛三角形是中心对称图形②图1中,点A到BC上任意一点的距离都相等③图2中,勒洛三角形的周长与圆的周长相等④使用截面是勒洛三角形的滚木来搬运东西,会发生上下抖动上述结论中,所有正确结论的序号是()A.①②B.②③C.②④D.③④【答案】B【解析】【分析】逐一对选项进行分析即可.【详解】①勒洛三角形不是中心对称图形,故①错误;②图1中,点A到BC上任意一点的距离都相等,故②正确;③图2中,设圆的半径为r∴勒洛三角形的周长=12032180rrππ⨯=圆的周长为2rπ∴勒洛三角形的周长与圆的周长相等,故③正确;④使用截面是勒洛三角形的滚木来搬运东西,不会发生上下抖动,故④错误故选B【点睛】本题主要考查中心对称图形,弧长公式等,掌握中心对称图形和弧长公式是解题的关键. 20.已知圆锥的三视图如图所示,则这个圆锥的侧面展开图的面积为()A.60πcm2B.65πcm2C.120πcm2D.130πcm2【答案】B【解析】【分析】先利用三视图得到底面圆的半径为5cm,圆锥的高为12cm,再根据勾股定理计算出母线长为13cm,然后根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式计算.【详解】根据三视图得到圆锥的底面圆的直径为10cm,即底面圆的半径为5cm,圆锥的高为12cm,所以圆锥的母线长225+12,所以这个圆锥的侧面积=12×2π×5×13=65π(cm2).故选B.【点睛】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.也考查了三视图.。
人教版九年级数学中考圆的综合专项练习及参考答案

人教版九年级数学中考圆的综合专项练习类型一 与全等结合1. 如图,⊙O 的直径AB =4,C 为⊙O 上一点,AC =2.过点C 作⊙O 的切线DC ,P 点为优弧CBA ︵上一动点(不与A 、C 重合). (1)求∠APC 与∠ACD 的度数;(2)当点P 移动到劣弧CB ︵的中点时,求证:四边形OBPC 是菱形; (3)当PC 为⊙O 的直径时,求证:△APC 与△ABC 全等.第1题图(1)解:∵AC =2,OA =OB =OC =12AB =2,∴AC =OA =OC , ∴△ACO 为等边三角形, ∴∠AOC =∠ACO =∠OAC =60°, ∴∠APC =12∠AOC =30°,又∵DC 与⊙O 相切于点C , ∴OC ⊥DC , ∴∠DCO =90°,∴∠ACD =∠DCO -∠ACO =90°-60°=30°;第1题解图(2)证明:如解图,连接PB ,OP ,∵AB 为直径,∠AOC =60°, ∴∠COB =120°,当点P 移动到CB ︵的中点时,∠COP =∠POB =60°, ∴△COP 和△BOP 都为等边三角形, ∴OC =CP =OB =PB , ∴四边形OBPC 为菱形;(3)证明:∵CP 与AB 都为⊙O 的直径,∴∠CAP =∠ACB =90°, 在Rt △ABC 与Rt △CPA 中,⎩⎪⎨⎪⎧AB =CP AC =AC , ∴Rt △ABC ≌Rt △CPA (HL).2. 如图,AB 为⊙O 的直径,CA 、CD 分别切⊙O 于点A 、D ,CO 的延长线交⊙O 于点M ,连接BD 、DM . (1)求证:AC =DC ; (2)求证:BD ∥CM ;(3)若sin B =45,求cos ∠BDM 的值.第2题图(1)证明:如解图,连接OD ,∵CA 、CD 分别与⊙O 相切于点A 、D , ∴OA ⊥AC ,OD ⊥CD , 在Rt △OAC 和Rt △ODC 中,⎩⎪⎨⎪⎧OA =OD OC =OC,∴Rt△OAC≌Rt△ODC(HL),∴AC=DC;(2)证明:由(1)知,△OAC≌△ODC,∴∠AOC=∠DOC,∴∠AOD=2∠AOC,∵∠AOD=2∠OBD,∴∠AOC=∠OBD,∴BD∥CM;(3)解:∵BD∥CM,∴∠BDM=∠M,∠DOC=∠ODB,∠AOC=∠B,∵OD=OB=OM,∴∠ODM=∠OMD,∠ODB=∠B=∠DOC,∵∠DOC=2∠DMO,∴∠DOC=2∠BDM,∴∠B=2∠BDM,如解图,作OE平分∠AOC,交AC于点E,作EF⊥OC于点F,第2题解图∴EF =AE ,在Rt △EAO 和Rt △EFO 中,∵⎩⎪⎨⎪⎧OE =OE AE =EF , ∴Rt △EAO ≌Rt △EFO (HL), ∴OA =OF ,∠AOE =12∠AOC ,∴点F 在⊙O 上,又∵∠AOC =∠B =2∠BDM , ∴∠AOE =∠BDM , 设AE =EF =y , ∵sin B =45,∴在Rt △AOC 中,sin ∠AOC =AC OC =45,∴设AC =4x ,OC =5x ,则OA =3x ,在Rt △EFC 中,EC 2=EF 2+CF 2, ∵EC =4x -y ,CF =5x -3x =2x , ∴(4x -y )2=y 2+(2x )2, 解得y =32x ,∴在Rt △OAE 中,OE =OA 2+AE 2=(3x )2+(32x )2=352x ,∴cos ∠BDM =cos ∠AOE =OA OE =3x 352x=255.3. 如图,⊙O 是△ABC 的外接圆,AC 为直径,AB ︵=BD ︵,BE ⊥DC 交DC 的延长线于点E . (1)求证:∠1=∠BCE ; (2)求证:BE 是⊙O 的切线; (3)若EC =1,CD =3,求cos ∠DBA .第3题图(1)证明:如解图,过点B 作BF ⊥AC 于点F ,∵AB ︵=BD ︵, ∴AB =BD在△ABF 与△DBE 中, ⎩⎪⎨⎪⎧∠BAF =∠BDE ∠AFB =∠DEB AB =DB, ∴△ABF ≌△DBE (AAS), ∴BF =BE , ∵BE ⊥DC ,BF ⊥AC , ∴∠1=∠BCE ; (2)证明:如解图,连接OB ,∵AC 是⊙O 的直径,∴∠ABC =90°,即∠1+∠BAC =90°, ∵∠BCE +∠EBC =90°,且∠1=∠BCE , ∴∠BAC =∠EBC , ∵OA =OB , ∴∠BAC =∠OBA ,∴∠EBC =∠OBA ,∴∠EBC +∠CBO =∠OBA +∠CBO =90°, ∴∠EBO =90°, 又∵OB 为⊙O 的半径, ∴BE 是⊙O 的切线;第3题解图(3)解:在△EBC 与△FBC 中,⎩⎪⎨⎪⎧∠BEC =∠CFB ,∠ECB =∠FCB ,BC =BC ,∴△EBC ≌△FBC (AAS), ∴CE =CF =1.由(1)可知:AF =DE =1+3=4, ∴AC =CF +AF =1+4=5,∴cos ∠DBA =cos ∠DCA =CD CA =35.类型二 与相似结合4. 如图,△ABC 内接于⊙O ,AB =AC ,∠BAC =36°,过点A 作AD ∥BC ,与∠ABC 的平分线交于点D ,BD 与AC 交于点E ,与⊙O 交于点F .(1)求∠DAF 的度数; (2)求证:AE 2=EF ·ED ; (3)求证:AD 是⊙O 的切线.第4题图(1)解:∵AB =AC ,∠BAC =36°,∴∠ABC =∠ACB =12(180°-36°)=72°,∴∠AFB =∠ACB =72°, ∵BD 平分∠ABC , ∴∠DBC =36°, ∵AD ∥BC ,∴∠D =∠DBC =36°,∴∠DAF =∠AFB -∠D =72°-36°=36°;(2)证明:∵∠EAF =∠FBC =∠D ,∠AEF =∠AED ,∴△EAF ∽△EDA ,∴AE DE =EF EA, ∴AE 2=EF ·ED ;(3)证明:如解图,过点A 作BC 的垂线,G 为垂足,∵AB =AC , ∴AG 垂直平分BC , ∴AG 过圆心O , ∵AD ∥BC , ∴AD ⊥AG , ∴AD 是⊙O 的切线.第4题解图5. 如图,AB 为半圆的直径,O 为圆心,OC ⊥AB ,D 为BC ︵的中点,连接DA 、DB 、DC ,过点C 作DC 的垂线交DA 于点E ,DA 交OC 于点F .(1)求证:∠CED =45°;(2)求证:AE =BD ;(3)求AO OF的值.第5题图(1)证明:∵∠CDA =12∠COA =12×90°=45°, 又∵CE ⊥DC ,∴∠DCE =90°,∴∠CED =180°-90°-45°=45°;(2)解:如解图,连接AC ,∵D 为BC ︵的中点,∴∠BAD =∠CAD =12×45°=22.5°, 而∠CED =∠CAE +∠ACE =45°,∴∠CAE =∠ACE =22.5°,∴AE =CE ,∵∠ECD =90°,∠CED =45°,∴CE =CD ,又∵CD ︵=BD ︵,∴CD =BD ,∴AE =CE =CD =BD ,∴AE =BD ;第5题解图(3)解:设BD =CD =x ,∴AE =CE =x ,由勾股定理得,DE =2x ,则AD =x +2x ,又∵AB 是直径,则∠ADB =90°,∴△AOF ∽△ADB ,∴AO OF =AD DB =x +2x x=1+ 2. 6. 如图,AB 为⊙O 的直径,P 点为半径OA 上异于点O 和点A 的一个点,过P 点作与直径AB 垂直的弦CD ,连接AD ,作BE ⊥AB ,OE //AD 交BE 于E 点,连接AE 、DE ,AE 交CD 于点F .(1)求证:DE 为⊙O 的切线;(2)若⊙O 的半径为3,sin ∠ADP =13,求AD ; (3)请猜想PF 与FD 的数量关系,并加以证明.第6题图(1)证明:如解图,连接OD ,∵OA =OD ,∴∠OAD =∠ODA ,∵OE ∥AD ,∴∠OAD =∠BOE ,∠DOE =∠ODA ,∴∠BOE =∠DOE ,在△BOE 和△DOE 中,⎩⎪⎨⎪⎧OB =OD ∠BOE =∠DOE OE =OE,∴△BOE ≌△DOE (SAS),∴∠ODE =∠OBE ,∵BE ⊥AB ,∴∠OBE =90°,∴∠ODE =90°,∵OD 为⊙O 的半径,∴DE 为⊙O 的切线;(2)解:如解图,连接BD ,∵AB 为⊙O 的直径,∴∠ADB =90°,∴∠ABD +∠BAD =90°,∵AB ⊥CD ,∴∠ADP +∠BAD =90°,∴∠ABD =∠ADP ,∴sin ∠ABD =AD AB =sin ∠ADP =13, ∵⊙O 的半径为3,∴AB =6,∴AD =13AB =2;第6题解图(3)解:猜想PF =FD ,证明:∵CD ⊥AB ,BE ⊥AB ,∴CD ∥BE ,∴△APF ∽△ABE ,∴PF BE =AP AB ,∴PF =AP ·BE AB ,在△APD 和△OBE 中,⎩⎪⎨⎪⎧∠APD =∠OBE∠PAD =∠BOE ,∴△APD ∽△OBE ,∴PD BE =AP OB ,∴PD =AP ·BE OB ,∵AB =2OB ,∴PF =12PD , ∴PF =FD .7. 如图①,⊙O 是△ABC 的外接圆,AB 是⊙O 的直径,OD ∥AC ,OD 交⊙O 于点E ,且∠CBD =∠COD .(1)求证:BD 是⊙O 的切线;(2)若点E 为线段OD 的中点,求证:四边形OACE 是菱形.(3)如图②,作CF ⊥AB 于点F ,连接AD 交CF 于点G ,求FG FC的值.第7题图(1)证明:∵AB 是⊙O 的直径,∴∠BCA =90°,∴∠ABC +∠BAC =90°,∵OD ∥AC ,∴∠ACO =∠COD .∵OA=OC,∴∠BAC=∠ACO,又∵∠COD=∠CBD,∴∠CBD=∠BAC,∴∠ABC+∠CBD=90°,∴∠ABD=90°,即OB⊥BD,又∵OB是⊙O的半径,∴BD是⊙O的切线;(2)证明:如解图,连接CE、BE,∵OE=ED,∠OBD=90°,∴BE=OE=ED,∴△OBE为等边三角形,∴∠BOE=60°,又∵AC∥OD,∴∠OAC=60°,又∵OA=OC,∴△OAC为等边三角形,∴AC=OA=OE,∴AC∥OE且AC=OE,∴四边形OACE是平行四边形,而OA=OE,∴四边形OACE是菱形;第7题解图(3)解:∵CF⊥AB,∴∠AFC=∠OBD=90°,而AC∥OD,∴∠CAF=∠DOB,∴Rt△AFC∽Rt△OBD,∴FCBD=AFOB,即FC=BD·AFOB,又∵FG∥BD,∴△AFG∽△ABD,∴FGBD=AFAB,即FG=BD·AFAB,∴FC FG =AB OB=2, ∴FG FC =12. 8. 如图,AB 是⊙O 的直径,点E 为线段OB 上一点(不与O 、B 重合),作EC ⊥OB 交⊙O 于点C ,作直径CD 过点C 的切线交DB 的延长线于点P ,作AF ⊥PC 于点F ,连接CB .(1)求证:AC 平分∠FAB ;(2)求证:BC 2=CE ·CP ;(3)当AB =43且CF CP =34时,求劣弧BD ︵的长度.第8题图(1)证明:∵PF 切⊙O 于点C ,CD 是⊙O 的直径,∴CD ⊥PF ,又∵AF ⊥PC ,∴AF ∥CD ,∴∠OCA =∠CAF ,∵OA=OC,∴∠OAC=∠OCA,∴∠CAF=∠OAC,∴AC平分∠FAB;(2)证明:∵AB是⊙O的直径,∴∠ACB=90°,∵∠DCP=90°,∴∠ACB=∠DCP=90°,又∵∠BAC=∠D,∴△ACB∽△DCP,∴∠EBC=∠P,∵CE⊥AB,∴∠BEC=90°,∵CD是⊙O的直径,∴∠DBC=90°,∴∠CBP=90°,∴∠BEC=∠CBP,∴△CBE ∽△CPB ,∴BC PC =CE CB, ∴BC 2=CE ·CP ;(3)解:∵AC 平分∠FAB ,CF ⊥AF ,CE ⊥AB ,∴CF =CE ,∵CF CP =34, ∴CE CP =34, 设CE =3k ,则CP =4k ,∴BC 2=3k ·4k =12k 2,∴BC =23k ,在Rt △BEC 中,∵sin ∠EBC =CE BC =3k 23k =32, ∴∠EBC =60°,∴△OBC 是等边三角形,∴∠DOB =120°,∴BD ︵=120π·23180=43π3.类型三 与全等相似结合9. 如图,四边形ABCD 内接于圆O ,∠BAD =90°,AC 为直径,过点A 作圆O 的切线交CB 的延长线于点E ,过AC 的三等分点F (靠近点C )作CE 的平行线交AB 于点G ,连接CG .(1)求证:AB =CD ;(2)求证:CD 2=BE ·BC ;(3)当CG =3,BE =92,求CD 的长.第9题图(1)证明:∵AC 为直径,∴∠ABC =∠ADC =90°,∴∠ABC =∠BAD =90°,∴BC ∥AD ,∴∠BCA =∠CAD ,又∵AC=CA,∴△ABC≌△CDA(AAS),∴AB=CD;(2)证明:∵AE为⊙O的切线且O为圆心,∴OA⊥AE,即CA⊥AE,∴∠EAB+∠BAC=90°,而∠BAC+∠BCA=90°,∴∠EAB=∠BCA,而∠EBA=∠ABC,∴△EBA∽△ABC,∴EBAB=BABC,∴AB2=BE·BC,由(1)知AB=CD,∴CD2=BE·BC;(3)解:由(2)知CD2=BE·BC,即CD 2=92BC ①, ∵FG ∥BC 且点F 为AC 的三等分点,∴G 为AB 的三等分点,即CD =AB =3BG ,在Rt △CBG 中,CG 2=BG 2+BC 2,即3=(13CD )2+BC 2②, 将①代入②,消去CD 得,BC 2+12BC -3=0, 即2BC 2+BC -6=0,解得BC =32或BC =-2(舍)③, 将③代入①得,CD =332. 10.如图,AB 为⊙O 的直径,C 为圆外一点,AC 交⊙O 于点D ,BC 2=CD ·CA ,ED ︵=BD ︵,BE 交AC 于点F .(1)求证:BC 为⊙O 的切线;(2)判断△BCF 的形状并说明理由;(3)已知BC =15,CD =9,∠BAC =36°,求BD ︵的长度(结果保留π).第10题图 (1)证明:∵BC 2=CD ·CA ,∴BC CA =CD BC ,∵∠C =∠C ,∴△CBD ∽△CAB ,∴∠CBD =∠BAC ,又∵AB 为⊙O 的直径,∴∠ADB =90°,即∠BAC +∠ABD =90°,∴∠ABD +∠CBD =90°,即AB ⊥BC ,又∵AB 为⊙O 的直径,∴BC 为⊙O 的切线;(2)解:△BCF 为等腰三角形.证明如下:∵ED ︵=BD ︵,∴∠DAE =∠BAC ,又∵△CBD ∽△CAB ,∴∠BAC =∠CBD ,∴∠CBD =∠DAE ,∵∠DAE =∠DBF ,∴∠DBF =∠CBD ,∵∠BDF =90°,∴∠BDC =∠BDF =90°,∵BD =BD ,∴△BDF ≌△BDC ,∴BF =BC ,∴△BCF 为等腰三角形;(3)解:由(1)知,BC 为⊙O 的切线,∴∠ABC =90°∵BC 2=CD ·CA ,∴AC =BC 2CD =1529=25,由勾股定理得AB =AC 2-BC 2=252-152=20,∴⊙O 的半径为r =AB 2=10,∵∠BAC =36°, ∴BD ︵所对圆心角为72°.则BD ︵=72×π×10180=4π.。
人教版2023年中考数学专题复习练习圆的性质

第26 讲圆的性质一.圆周角定理(共11小题)1.(2021•阜新)如图,A,B,C是⊙O上的三点,若∠O=70°,则∠C的度数是()A.40°B.35°C.30°D.25°2.(2022•阜新)如图,A,B,C是⊙O上的三点,若∠C=35°,则∠ABO的度数是()A.35°B.55°C.60°D.70°3.(2022•朝阳)如图,在⊙O中,点A是BĈ的中点,∠ADC=24°,则∠AOB的度数是()A.24°B.26°C.48°D.66°4.(2022•营口)如图,点A,B,C,D在⊙O上,AC⊥BC,AC=4,∠ADC=30°,则BC的长为()A.4√3B.8C.4√2D.4 5.(2021•营口)如图,⊙O中,点C为弦AB中点,连接OC,OB,∠COB=56°,点D̂上任意一点,则∠ADB度数为()是ABA.112°B.124°C.122°D.134°6.(2021•鞍山)如图,AB为⊙O的直径,C,D为⊙O上的两点,若∠ABD=54°,则∠C的度数为()A.34°B.36°C.46°D.54°7.(2021•辽宁)如图,在⊙O中,弦CD与直径AB相交于点E,连接OC,BD.若∠ABD =20°,∠AED=80°,则∠COB的度数为()A.80°B.100°C.120°D.140°8.(2020•阜新)如图,AB为⊙O的直径,C,D是圆周上的两点,若∠ABC=38°,则锐角∠BDC的度数为()A.57°B.52°C.38°D.26°9.(2021•盘锦)如图,在平面直角坐标系xOy中,点A在x轴负半轴上,点B在y轴正半轴上,⊙D经过A,B,O,C四点,∠ACO=120°,AB=4,则圆心点D的坐标是.10.(2021•朝阳)已知⊙O的半径是7,AB是⊙O的弦,且AB的长为7√3,则弦AB所对的圆周角的度数为.11.(2021•辽宁)如图,由边长为1的小正方形组成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C和点D,则tan∠ADC=.二.圆内接四边形的性质(共1小题)12.(2022•锦州)如图,四边形ABCD内接于⊙O,AB为⊙O的直径,∠ADC=130°,连接AC,则∠BAC的度数为.三.三角形的外接圆与外心(共2小题)13.(2021•沈阳)如图,△ABC是⊙O的内接三角形,AB=2√3,∠ACB=60°,连接OA,̂的长是()OB,则ABA .π3B .2π3C .πD .4π314.(2020•锦州)如图,⊙O 是△ABC 的外接圆,∠ABC =30°,AC =6,则AĈ的长为 .四.圆与解直角三角形(共1小题)15.(2022•丹东)如图,AB 是⊙O 的直径,点E 在⊙O 上,连接AE 和BE ,BC 平分∠ABE交⊙O 于点C ,过点C 作CD ⊥BE ,交BE 的延长线于点D ,连接CE .(1)请判断直线CD 与⊙O 的位置关系,并说明理由;(2)若sin ∠ECD =35,CE =5,求⊙O 的半径.五.圆与相似三角形(共6小题)16.(2021•锦州)如图,△ABC 内接于⊙O ,AB 为⊙O 的直径,D 为⊙O 上一点(位于AB下方),CD 交AB 于点E ,若∠BDC =45°,BC =6√2,CE =2DE ,则CE 的长为( )A.2√6B.4√2C.3√5D.4√3 17.(2022•朝阳)如图,AC是⊙O的直径,弦BD交AC于点E,点F为BD延长线上一点,∠DAF=∠B.(1)求证:AF是⊙O的切线;(2)若⊙O的半径为5,AD是△AEF的中线,且AD=6,求AE的长.18.(2022•辽宁)如图,在Rt△ABC中,∠ACB=90°,▱ODEF的顶点O,D在斜边AB 上,顶点E,F分别在边BC,AC上,以点O为圆心,OA长为半径的⊙O恰好经过点D 和点E.(1)求证:BC与⊙O相切;(2)若sin∠BAC=35,CE=6,求OF的长.19.(2022•营口)如图,在△ABC中,AB=AC,以AB为直径作⊙O与AC交于点E,过点A作⊙O的切线交BC的延长线于点D.(1)求证:∠D=∠EBC;(2)若CD=2BC,AE=3,求⊙O的半径.̂=CD̂,连接AC,20.(2021•营口)如图,AB是⊙O直径,点C,D为⊙O上的两点,且AD BD交于点E,⊙O的切线AF与BD延长线相交于点F,A为切点.(1)求证:AF=AE;(2)若AB=8,BC=2,求AF的长.21.(2021•丹东)如图,⊙O是△ABC的外接圆,点D是BĈ的中点,过点D作EF∥BC分别交AB、AC的延长线于点E和点F,连接AD、BD,∠ABC的平分线BM交AD于点M.(1)求证:EF是⊙O的切线;(2)若AB:BE=5:2,AD=√14,求线段DM的长.第 26 讲 圆的性质参考答案一.圆周角定理(共11小题)1.B ; 2.B ; 3.C ; 4.A ; 5.B ; 6.B ; 7.C ; 8.B ; 9.(−√3,1); 10.60°或120°; 11.32; 二.圆内接四边形的性质(共1小题)12.40°;三.三角形的外接圆与外心(共2小题)13.D ; 14.2π;四.圆与解直角三角形(共1小题)15.(1)结论:CD 是⊙O 的切线,证明见解析部分;(2)256.;五.圆与相似三角形(共6小题)16.D ; 17.(1)见解析;(2)365.; 18.(1)见解析;(2)2√10.;19. ; 20.(1)证明见解答过程; (2)8√155.; 21.(1)见详解;(2)2.;。
人教版初三圆测试题及答案

人教版初三圆测试题及答案一、选择题(每题2分,共10分)1. 半径为2的圆的面积是多少?A. 4πB. 6πC. 8πD. 12π2. 圆的周长公式是:A. C = πrB. C = 2πrC. C = 4πrD. C = 8πr3. 若圆的半径是3,圆心角为60°,那么这个弧长是多少?A. πB. 3πC. 6πD. 9π4. 点P到圆心O的距离是5,圆的半径是3,那么点P与圆的位置关系是:A. 在圆上B. 在圆内C. 在圆外D. 无法确定5. 圆的切线与半径垂直,且切点到圆心的距离等于:A. 半径B. 直径C. 周长的一半D. 面积的平方根二、填空题(每题2分,共10分)6. 半径为4的圆的面积是_________。
7. 若圆的周长为12π,那么圆的半径是_________。
8. 圆心角为120°的弧所对的圆心角是_________。
9. 点P到圆心O的距离是2,圆的半径是4,点P与圆的位置关系是_________。
10. 圆的切线与半径垂直,切点到圆心的距离是_________。
三、计算题(每题5分,共20分)11. 已知圆的半径为5,求圆的周长和面积。
12. 已知圆的周长为16π,求圆的半径。
13. 若圆的半径为7,圆心角为45°,求该弧长。
14. 已知点P到圆心O的距离为10,圆的半径为8,求点P与圆的位置关系。
四、解答题(每题10分,共20分)15. 某圆的半径为6,圆心角为30°,求该弧所对的圆心角和弧长。
16. 已知圆的切线在点M处与圆相切,OM=6,半径为4,求切线PM的长度。
五、综合题(15分)17. 某工厂需要在一块半径为10米的圆形场地上安装一个直径为4米的圆形水池,水池的中心与场地的中心重合。
求水池的半径占场地半径的比例,以及水池的面积占整个场地面积的比例。
六、结束语本测试题覆盖了圆的基本概念、公式和计算方法,旨在帮助学生巩固和检验对圆的相关知识的掌握。
人教版初三圆试题及答案

人教版初三圆试题及答案一、选择题1. 已知圆的半径为5,圆心到直线的距离为3,那么直线与圆的位置关系是什么?A. 相交B. 相切B. 相离D. 无法确定2. 圆的周长是圆的直径的几倍?A. π倍B. 2倍C. 3倍D. 4倍3. 已知点A到圆心O的距离为6,点B到圆心O的距离为4,那么点A 和点B在圆上的位置关系是什么?A. 都在圆上B. 点A在圆外,点B在圆内C. 点A在圆内,点B在圆上D. 点A和点B都不在圆上二、填空题1. 圆的面积公式为__________。
2. 已知圆的半径为r,圆的直径为d,则d=__________。
3. 圆的切线与半径垂直,且切线的长度等于__________。
三、解答题1. 已知圆的半径为7,求圆的周长和面积。
解:圆的周长公式为C=2πr,代入r=7,得C=2×π×7=14π。
圆的面积公式为A=πr²,代入r=7,得A=π×7²=49π。
2. 已知点P在圆O上,OP=10,PA=6,求圆O的半径。
解:根据勾股定理,PA²+r²=OP²,即6²+r²=10²,解得r²=10²-6²=64,所以r=8。
四、应用题1. 某圆形花坛的周长为628厘米,求花坛的直径。
解:根据圆的周长公式C=πd,代入C=628,得d=628/π。
2. 一个圆的半径为8厘米,求这个圆的面积。
解:根据圆的面积公式A=πr²,代入r=8,得A=π×8²=64π。
结束语:本次试题涵盖了圆的基本性质和公式,通过选择题、填空题、解答题和应用题的形式,全面考察了学生对圆的理解和应用能力。
希望同学们能够通过练习,加深对圆的理解和掌握,提高解题技巧。
人教版初三数学圆练习题

人教版初三数学圆练习题练习一:判断题1. 两个相交圆的公共弦又叫做两个圆的公共切线。
(错)2. 弦的中点到圆心的距离等于弦长的一半。
(对)3. 半径相等的两个圆一定相切。
(对)4. 两个互相交于一点的圆是外离的。
(错)5. 两个内切于同一个圆的圆是内切的。
(错)练习二:选择题1. 在下图中,已知⊙O的半径为3cm,⊙O与⊙Q内切,若⊙Q的半径是4cm,则∠BOC的度数是()。
[图略]A. 30°B. 45°C. 60°D. 90°答案:C2. 直径为10cm的圆上,一条弧的长为12cm,则该弧所对圆心角的度数是()。
A. 216°B. 144°C. 120°D. 72°答案:B3. 已知⊙O的半径为2cm,⊙O与⊙P相外切于点A,切点B连接线段OA,若OA=6cm,则OB=()。
A. 6cmB. 7cmC. 8cmD. 9cm答案:D练习三:计算题1. 如图所示,⊙O的直径AB的长为8cm,圆内一条弦CD的长为6cm,求弦CD所对的圆心角的度数。
[图略]解:由于圆的直径是弦的最长弦,所以AC>CD,所以这是一个小弧。
设圆心角的度数为x°,则根据圆的性质,弦CD所对的圆心角和弦AC所对的圆心角的度数相等。
∴弦AC所对的圆心角的度数为x°。
∵在三角形ADC中,根据余弦定理有:AC²=AD²+CD²。
代入已知数据,得:AD²+6²=8²。
解得:AD=√20。
∴根据正弦定理有:sin(A/2)=CD/2AD,代入已知数据,得:sin(x/2)=6/2√20=3/√20。
∵ sin(x/2)=3/√20=3/2√5/2=3√5/10∴ sin(x/2)=3√5/10。
根据x=2arcsin(3√5/10)。
计算得:x≈109.47°。
∴弦CD所对的圆心角的度数约为109.47°。
人教版九年级数学上册圆的练习题

人教版九年级数学上册圆的练习题练一一、选择题1.若⊙O的半径为5㎝,点A到圆心O的距离为4㎝,那么点A与圆心O的位置关系是()A。
点A在圆外B。
点A在圆上C。
点A在圆内D。
不能确定2.在⊙O中,已知弦AB的长为8㎝,AB的弦心距为3㎝,则⊙O的半径为()A。
7㎝B。
5㎝C。
7㎝D。
3㎝3.如图,半径为10的⊙O中,弦AB的长为16,则这条弦的弦心距为()A。
6B。
8C。
10D。
124.下列命题中,①圆是轴对称图形;②圆是中心对称图形;③圆既是轴对称图形,又是中心对称图形;④圆是轴对称图形,对称轴是直径;⑤圆是中心对称图形,对称中心是圆心。
其中正确的命题是()A。
①②③B。
①②⑤C。
①②③⑤D。
②③④⑤5.如图所示,正方形ABCD内接于⊙O,P是劣弧AD上任意一点,则∠ABP+∠DCP=()A。
90°B。
60°C。
45°D。
30°6.以已知点O为圆心作圆,可以作()圆A。
1个B。
2个C。
3个D。
无数个7.若圆心角∠PCB=60°,则弧PCB所对的圆周角等于()A。
30°B。
40°C。
60°D。
80°8.如图,A、B、C是⊙O上的三点,∠AOC=100°则∠ABC的度数是()A。
30°B。
45°C。
50°D。
60°9.如图,AB为⊙O的直径,点C在⊙O上,若∠A=40°,则∠B等于()A。
80°B。
60°C。
50°D。
40°二、填空题11.已知⊙O的半径为4cm,A为线段OP的中点,当OP=5 cm时,点A在⊙O 上;当OP=8cm时,点A在⊙O 上;当OP=10 cm时,点A在⊙O 外。
12.如图,弓形的弦长AB为23cm,高CD为1cm,则弓形所在圆的半径为12cm。
13.一条弦把圆心分成1:3两部分,则劣弧所对的圆心角为120°。
人教版数学九年级上册《圆》测试题及答案

r 180 , n°的圆心角所对的弧长
nr 为 180 ,弧长公式为 l
nr 180
n 为圆心角的度数上为圆半径
).
2. 圆的面积为
π r 2 , 1°的圆心角所在的扇形面积为
r2 360
, n°的圆心角所在
n 的扇形面积为 S= 360
R2 =
1 rl 2
(n 为圆心角的度数 ,R 为圆的半径) .
3. 圆柱的侧面积公式: S= 2 r l(其中 r 为 底面圆 的半径 ,l 为 圆柱 的高 . )
4. 圆锥的侧面积公式: S= r l (其中 r 为 底面 的半径 , l 为 母线 的长 . )
圆锥的侧面积与底面积之和称为圆锥的全面积
一、选择题(每小题 3 分,共 45 分)
A组
1.在△ ABC中,∠ C=90°, AB= 3cm, BC= 2cm,以点 A 为圆心,以 2.5cm 为半径作圆,则点
C 和⊙ A 的位置关系是(
)。
A. C在⊙ A 上
B. C在⊙ A 外
C. C在⊙ A 内
D. C在⊙ A 位置不能确定。
2.一个点到圆的最大距离为 11cm,最小距离为 5cm, 则圆的半径为(
)。
A. 16cm或 6cm
B. 3cm或 8cm
C .3cm
D. 8cm
3. AB是⊙ O的弦,∠ AOB= 80°则弦 AB所对的圆周角是(
1.两圆相切,圆心距为 9 cm,已知其中一圆半径为 5 cm,另一圆半径为 _____.
2.两个同心圆,小圆的切线被大圆截得的部分为
6,则两圆围成的环形面积为 _________。
3.边长为 6 的正三角形的外接圆和内切圆的周长分别为 _________。
人教版九年级圆专题卷(有答案)

人教版九年级圆专题卷(有答案)一、单选题(共10题;共20分)1.已知两圆的半径分别是3和4,圆心距的长为1,则两圆的位置关系为:()A. 外离B. 相交C. 内切D. 外切2.如图,AB为⊙O的直径,弦DC垂直AB于点E,∠DCB=30°,EB=3,则弦AC的长度为()A. 3B.C.D.3.如图,线段AB是圆O的直径,弦CD⊥AB,如果∠BOC=70°,那么∠BAD等于()A. 20°B. 30°C. 35°D. 70°4.边长为1的正六边形的内切圆的半径为()A. 2B. 1C.D.5.点A、O、D与点B、O、C分别在同一直线上,图中弦的条数为()6.(2017•台湾)如图,O为锐角三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,判断下列叙述何者正确()A. O是△AEB的外心,O是△AED的外心B. O是△AEB的外心,O不是△AED的外心C. O不是△AEB的外心,O是△AED的外心D. O不是△AEB的外心,O不是△AED的外心7.如图,⊙O1、⊙O2内切于点A,其半径分别是6和3,将⊙O2沿直线O1O2平移至两圆外切时,则点O2移动的长度是()A. 3B. 6C. 12D. 6或128.如图,已知AB为⊙O的直径,C为⊙O上一点,CD⊥AB于D,AD=9,BD=4,以C为圆心,CD为半径的圆与⊙O相交于P,Q两点,弦PQ交CD于E,则PE•EQ的值是()A. 24B. 9C. 36D. 279.如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为S1,正八边形外侧八个扇形(阴影部分)面积之和为S2,则=()A. B. C. D. 110.如图,在中,,以的中点为圆心分别与,相切于,两点,则的长为()二、填空题(共8题;共18分)11.已知,如图,⊙O是△ABC的外接圆,OD⊥AC交圆于D,连接AD,CD,BD,∠ABD=50°.则∠DBC=________.12.(2016•呼和浩特)在周长为26π的⊙O中,CD是⊙O的一条弦,AB是⊙O的切线,且AB∥CD,若AB 和CD之间的距离为18,则弦CD的长为________.13.如图,在正方形ABCD中,对角线BD的长为。
24.1圆的有关性质练习卷人教版数学九年级上册

人教版九年级上册《24.1圆的有关性质》同步练习卷 一、选择题 1. 下列说法中错误的是( )A .半圆是弧B .半径相等的圆是等圆C .过圆心的线段是直径D .弓形是弦及弦所对的弧组成的图形2. 在以AB=8cm 为直径的圆上,到AB 的距离为4cm 的点有( )A .无数个B .1个C .2个D .4个3. 下列命题中是真命题的有( )①两个端点能够重合的弧是等弧;②圆的任意一条弦把圆分成优弧和劣弧两部分;③长度相等的弧是等弧;④半径相等的圆是等圆;⑤直径是最大的弦;⑥半圆所对的弦是直径.A .3个B .4个C .5个D .6个4. 如图,BC 是半圆O 的直径,D ,E 是BC ―上两点,连接BD ,CE 并延长交于点A ,连接OD ,OE ,如果∠DOE=40°,那么∠A 的度数为( )A .35°B .40°C .60°D .70°5.若⊙O所在平面内一点P到⊙O上的点的最大距离为7,最小距离为3,则此圆的半径为()A.5 B.2 C.10或4 D.5或2 二、填空题6.若四边形的四个顶点在同一个圆上,则这个四边形可能是______ .7.如图,AB是⊙O的弦,AB=5,点C是⊙O上的一个动点,且∠ACB=45°,若点M、N分别是AB、AC的中点,则MN长的最大值是 ______ .8.如图,在△ABC中,∠B=60°,∠C=70°,若AC与以AB为直径的⊙O相交于点D,则∠BOD的度数是 ______ 度.9.如图,OB、OC是⊙O的半径,A是⊙O上一点,若∠B=20°,∠C=30°,则∠BOC= ______ .10.如图,在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ,OP⊥AB,则PQ的长是 ______ .三、解答题11.如图,AC是⊙O的直径,点B在圆上(不与点A,C重合),点D在AC的延长线上,连接BD交⊙O于点E,∠AOB=3∠ADB.求证:DE= 1AC.212.如图,A、B、C为⊙O上三点,∠ACB=20〇,求∠BAO的度数.13.如图,AB、AC为⊙O的弦,连接CO、BO并延长分别交弦AB、AC于点E、F,∠B=∠C.问:线段CE和线段BF相等吗?请说明理由.14.如图,AB为⊙O的直径,点C在⊙O上.(1)尺规作图:作∠BAC的平分线,与⊙O交于点D;连接OD,交BC于点E(不写作法,只保留作图痕迹,且用黑色墨水笔将作图痕迹加黑);(2)探究OE与AC的位置及数量关系,并证明你的结论.15.如图a,直线l经过⊙O的圆心O,且与⊙O交于A,B两点,点C在⊙O上,且∠AOC=30°,点P是直线l上的一个动点(与圆心O不重合),直线CP与⊙O相交于点Q.(1)如图b,当点P在半径OA上时,若QP=QO,求∠OCP的度数.(2)当点P在直线l上其他位置时,是否还存在∠OCP使得QP=QO?若存在,请求出∠OCP的度数;若不存在,请说明理由.。
人教版初三数学圆练习题汇总

圆练习题1.如图,已知线段OA 交⊙O 于点B ,且OB =AB ,点P 是⊙O 上的一个动点,那么∠OAP 的最大值是( )A. 30°B. 45°C. 60°D. 90°2.如图,已知AB 是⊙O 的直径,AD 切⊙O 于点A ,点C 是EB ︵的中点,则下列结论不成立的是( )A. OC ∥AEB. EC =BCC. ∠DAE =∠ABED. AC ⊥OE3. 如图,在平面直角坐标系xOy 中,半径为2的⊙P 的圆心P 的坐标为(-3,0),将⊙P 沿x 轴正方向平移,使⊙P 与y 轴相切,则平移的距离为( )A. 1B. 1或5C. 3D. 54.若正方形的边长为6,则其外接圆半径与内切圆半径的大小分别为( )A. 6,3 2B. 32,3C. 6,3D. 62,3 25.已知⊙O 1和⊙O 2的半径分别为2 cm 和3 cm ,若O 1O 2=7 cm ,则⊙O 1和⊙O 2的位置关系是( )A. 外离B. 外切C. 内切D. 相交6在同一平面直角坐标系中有5个点:A(1,1),B(-3,-1),C(-3,1),D(-2,-2), E(0,-3).(1)画出△ABC 的外接圆⊙P ,并指出点D 与⊙P 的位置关系.(2)若直线l 经过点D(-2,-2),E(0,-3),判断直线l 与⊙P 的位置关系.7如图,AB 是⊙O 的直径,CD 是⊙O 的切线,切点为D ,CD 与AB 的延长线交于点C ,∠A =30°,给出下面3个结论:①AD =CD ;②BD =BC ;③AB =2BC ,其中正确结论的个数是( )A. 3B. 2C. 1D. 08如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于D点,连接CD.(1)求证:∠A=∠BCD.(2)若M为线段BC上一点,试问当点M在什么位置时,直线DM与⊙O相切?并说明理由.9如图,AB是⊙O的切线,B为切点,AO与⊙O交于点C,若∠BAO=40°,则∠OCB 的度数为()A. 40°B. 50°C. 65°D. 75°10如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于D,且CO=CD,则∠PCA等于()A. 30°B. 45°C. 60°D. 67.5°11如图,⊙O的半径为3,P是CB延长线上一点,PO=5,PA切⊙O于A点,则PA=________.12如图,⊙O的半径为4 cm,直线l与⊙O相交于A,B两点,AB=4 3 cm,P为直线l 上一动点,以1 cm为半径的⊙P与⊙O没有公共点,设PO=d cm,则d的范围是________.13若⊙O1,⊙O2的半径分别是r1=2,r2=4,圆心距d=5,则这两个圆的位置关系是()A. 内切B. 相交C. 外切D. 外离14如图,以O为圆心的两个同心圆中,大圆和小圆的半径分别为3 cm和1 cm.若⊙P与这两个圆都相切,则⊙P的半径为________cm.15已知两圆的半径是3和7,且它们有唯一的公共点,则两圆的圆心距d 为( )A. 4B. 10C. 4或10D. 无法确定16如图所示,已知OC 平分∠AOB ,D 是OC 上任意一点,过D 作圆,使⊙D 与OA 相切于点E.求证:OB 与⊙D 相切.17已知:如图,在△ABC 中,AB=AC,以AB为直径的⊙O 交BC 于点D ,作DE ⊥AC 于点E 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人教版初三数学圆练习题汇总检验日期圆练习题1.如图,已知线段OA 交⊙O 于点B ,且OB =AB ,点P 是⊙O 上的一个动点,那么∠OAP 的最大值是( )A. 30°B. 45°C. 60°D. 90°2.如图,已知AB 是⊙O 的直径,AD 切⊙O 于点A ,点C 是EB ︵的中点,则下列结论不成立的是( )A. OC ∥AEB. EC =BCC. ∠DAE =∠ABED. AC ⊥OE3. 如图,在平面直角坐标系xOy 中,半径为2的⊙P 的圆心P 的坐标为(-3,0),将⊙P 沿x 轴正方向平移,使⊙P 与y 轴相切,则平移的距离为( )A. 1B. 1或5C. 3D. 54.若正方形的边长为6,则其外接圆半径与内切圆半径的大小分别为( )A. 6,3 2B. 32,3C. 6,3D. 62,3 25.已知⊙O 1和⊙O 2的半径分别为2 cm 和3 cm ,若O 1O 2=7 cm ,则⊙O 1和⊙O 2的位置关系是( )A. 外离B. 外切C. 内切D. 相交6在同一平面直角坐标系中有5个点:A(1,1),B(-3,-1),C(-3,1),D(-2,-2), E(0,-3).(1)画出△ABC 的外接圆⊙P ,并指出点D 与⊙P 的位置关系.(2)若直线l 经过点D(-2,-2),E(0,-3),判断直线l 与⊙P 的位置关系.7如图,AB 是⊙O 的直径,CD 是⊙O 的切线,切点为D ,CD 与AB 的延长线交于点C ,∠A =30°,给出下面3个结论:①AD =CD ;②BD =BC ;③AB =2BC ,其中正确结论的个数是( )A. 3B. 2C. 1D. 08如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于D点,连接CD.(1)求证:∠A=∠BCD.(2)若M为线段BC上一点,试问当点M在什么位置时,直线DM与⊙O相切?并说明理由.9如图,AB是⊙O的切线,B为切点,AO与⊙O交于点C,若∠BAO=40°,则∠OCB 的度数为( )A. 40°B. 50°C. 65°D. 75°10如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于D,且CO=CD,则∠PCA等于( )A. 30°B. 45°C. 60°D. 67.5°11如图,⊙O的半径为3,P是CB延长线上一点,PO=5,PA切⊙O于A点,则PA=________.12如图,⊙O的半径为4 cm,直线l与⊙O相交于A,B两点,AB=4 3 cm,P为直线l上一动点,以1 cm为半径的⊙P与⊙O没有公共点,设PO=d cm,则d的范围是________.13若⊙O1,⊙O2的半径分别是r1=2,r2=4,圆心距d=5,则这两个圆的位置关系是( )A. 内切B. 相交C. 外切D. 外离14如图,以O为圆心的两个同心圆中,大圆和小圆的半径分别为3 cm和1 cm.若⊙P与这两个圆都相切,则⊙P的半径为________cm.15已知两圆的半径是3和7,且它们有唯一的公共点,则两圆的圆心距d为( )A. 4B. 10C. 4或10D. 无法确定16如图所示,已知OC平分∠AOB,D是OC上任意一点,过D作圆,使⊙D与OA相切于点E.求证:OB与⊙D相切.17已知:如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,作DE⊥AC于点E。
求证:DE是⊙O的切线。
18已知:如图∠PAC=30°,在射线AC上顺次截取AD=3cm,DB=10cm,以DB为直径作⊙O交射线AP于E、F两点,求圆心O到AP的距离及EF的长.19如图所示,AB是⊙O的直径,AD是弦,∠DAB=22.5°,延长AB到点C,使得∠ACD=45°.(1)求证:CD是⊙O的切线;(2)若AB=22,求BC的长.20如图,PA,PB是⊙O的切线,点A、B为切点,AC是⊙O的直径,∠ACB=70°,求∠P的度数。
OAB CDEFP●●ABCDO●AOBCPABCDEO21如图,在Rt△ABC中,∠ACB=90°,AC=5,CB=12,AD是△ABC的角平分线。
过A、D、C三点的圆与斜边AB交于点E,连接DE。
(1)求证:AC=AE(2)求△ACD的外接圆的半径。
22如图,A城气象台测得台风中心在A城正西方向300千米的B处,并以每小时107千米的速度向北偏东60°的BF方向移动,距台风中心200千米的范围受台风影响.(1) A城是否会受到这次台风的影响?为什么?(2) 若A城受到这次台风的影响,试计算A城遭受这次台风影响的时间有多长?1.如图,AB,CD是⊙O的两条互相垂直的直径,点O1,O2,O3,O4分别为OA,OB,OC,OD的中点,若⊙O的半径是2,则阴影部分的面积为( )A. 8B. 4C. 4π+4D. 4π-42. 在学校组织的实践活动中,小新同学用纸板制作了一个圆锥模型,它的底面半径为1,高为22,则这个圆锥的侧面积是( )A. 4πB. 3πC. 22πD. 2π3已知圆柱体的底面半径为3 cm,髙为4 cm,则圆柱体的侧面积为( )A. 24π cm2B. 36π cm2C. 12 cm2D. 24 cm24在△ABC中,∠C为锐角,分别以AB,AC为直径作半圆,过点B,A,C作BAC︵,如图所示,若AB=4,AC=2,S1-S2=π4,则S3-S4的值是( )A.29π4B.23π4C.11π4D.5π45如图是一个几何体的三视图,则这个几何体的侧面积是( )A. 12π cm2B. 8π cm2C. 6π cm2D. 3π cm2ABC DE6如图,某厂生产横截面直径为7 cm的圆柱形罐头,需将“蘑菇罐头”字样贴在罐头侧面,为了获得较佳视觉效果,字样在罐头侧面所形成的弧的度数为90°,则“蘑菇罐头”字样的长度为( )A. π4cm B.7π4cm C.7π2cm D. 7π cm7如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2,将△ABC绕直角顶点C 逆时针旋转60°得△A′B′C,则点B转过的路径长为( )A. π3B.3π3C.2π3D. π8如图,在边长为1的正方形组成的网格中,△ABC的顶点都在格点上,将△ABC绕点C 顺时针旋转60°,则顶点A所经过的路径长为( )A. 10πB. 103C.103π D. π9如图,扇形AOB的半径为1,∠AOB=90°,以AB为直径画半圆,则图中的阴影部分的面积为( )A. 14π B. π-12C.12D.14π+1210如图,在直角坐标系中放置一个边长为1的正方形ABCD,将正方形ABCD沿x轴的正方向无滑动的在x轴上滚动,当点A离开原点后第一次落在x轴上时,点A运动的路径线与x轴围成图形的面积为( )A. π2+12B.π2+1 C. π+1 D. π+1211如图,已知正方形的边长为1,若圆与正方形的四条边都相切,则阴影部分的面积与下列各数最接近的是( )A. 0.1B. 0.2C. 0.3D. 0.412如图,一块边长为8 cm 的正方形木板ABCD,在水平桌面上绕点A按逆时针方向旋转至A′B′C′D′的位置,则顶点C从开始到结束所经过的路径长为( )A. 16 cmB. 16 2 cmC. 8π cmD. 42π cm13如图,圆锥的侧面展开图是半径为3,圆心角为90°的扇形,则该圆锥的底面周长为( )A. 34π B.32π C.34D. 错误!14如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10。
(1)求此圆的半径;(2)求图中阴影部分的面积。
15如图,在△ABC 中,∠ABC =900,O 是AB 上一点,以O 为圆心,OB 为半径的圆与AB 交于点E ,与AC 切于点D ,AD =2,AE =1,求BCD S ∆。
16如图,在梯形ABCD 中,AB ∥CD ,⊙O 为内切圆,E 为切点。
(1) 求∠AOD 的度数 (2) 若AO=8cm ,DO=6cm,求OE的长.•O D E C B AC D OE。
