高二数学平面与平面之间的位置关系

合集下载

1.4.1用空间向量研究直线、平面的位置关系(第2课时)-高二数学(人教A版选择性必修第一册)

的位置关系是
.
答案:平行
解析:因为u·n=(-1,2,-3)·(4,-1,-2)=0,所以u⊥n.所以直线与平面平行,即l∥β.
新知应用
题型一：利用方向向量、法向量判断位置关系
1.根据下列各条件，判断相应的直线与直线、平面与平面、直线与平面的位置关系：
(1)直线 l1，l2 的方向向量分别是
a＝(1，－3，－1)，b＝(8，2，2)；
1.如图所示,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点,
问:当点Q在什么位置时,平面D1BQ∥平面PAO?
解:如图所示,分别以DA,DC,DD1所在直线为x,y,z轴,建立空间直角坐标系,
在CC1上任取一点Q,连接BQ,D1Q.设正方体的棱长为1,
如图.设正方体的棱长为1,则可求得
M 0,1,
1
2
,N
于是 =
1
2
1
2
,1,1 ,D(0,0,0),A1(1,0,1),B(1,1,0).
,0,
1
2
,
1 =(1,0,1),
=(1,1,0).
设平面 A1BD 的法向量为 n=(x,y,z),
+ = 0,
· 1 = 0,
则
得
+ = 0.
(2)平面α，β的法向量分别是
u＝(1，3，0)，v＝(－3，－9，0)；
(3)直线 l 的方向向量、平面α的法向量分别是
a＝(1，－4，－3)，u＝(2，0，3)；
(4)直线 l 的方向向量、平面α的法向量分别是
a＝(3，2，1)，u＝(－1，2，－1)．
新知应用
解：

高中数学必修二知识点总结

高中数学必修二知识点总结数学和语文这一学科其实也差不多，数学也有很多知识点是要背的。

下面是作者给大家整理的一些高中数学必修二知识点总结学习资料，期望对大家有所帮助。

高一数学必修二知识点归纳总结1.函数的奇偶性(1)若f(x)是偶函数，那么f(x)=f(-x);(2)若f(x)是奇函数，0在其定义域内，则f(0)=0(可用于求参数);(3)判定函数奇偶性可用定义的等价情势：f(x)±f(-x)=0或(f(x)≠0);(4)若所给函数的解析式较为复杂，应先化简，再判定其奇偶性;(5)奇函数在对称的单调区间内有相同的单调性;偶函数在对称的单调区间内有相反的单调性;2.复合函数的有关问题(1)复合函数定义域求法：若已知的定义域为[a，b],其复合函数f[g(x)]的定义域由不等式a≤g(x)≤b解出即可;若已知f[g(x)]的定义域为[a,b],求f(x)的定义域，相当于x∈[a,b]时，求g(x)的值域(即f(x)的定义域);研究函数的问题一定要注意定义域优先的原则。

(2)复合函数的单调性由“同增异减”判定;3.函数图像(或方程曲线的对称性)(1)证明函数图像的对称性，即证明图像上任意点关于对称中心(对称轴)的对称点仍在图像上;(2)证明图像C1与C2的对称性，即证明C1上任意点关于对称中心(对称轴)的对称点仍在C2上，反之亦然;(3)曲线C1：f(x,y)=0,关于y=x+a(y=-x+a)的对称曲线C2的方程为f(y-a,x+a)=0(或f(-y+a,-x+a)=0);(4)曲线C1:f(x,y)=0关于点(a,b)的对称曲线C2方程为：f(2a-x,2b-y)=0;(5)若函数y=f(x)对x∈R时，f(a+x)=f(a-x)恒成立，则y=f(x)图像关于直线x=a对称,高中数学;(6)函数y=f(x-a)与y=f(b-x)的图像关于直线x=对称;高二数学必修二知识点总结整理一、直线与方程(1)直线的倾斜角定义：x轴正向与直线向上方向之间所成的角叫直线的倾斜角。

天津高二上册数学知识点解析分享

天津高二上册数学知识点解析分享你的一生,没法离开学习,学习是你最忠实的朋友,它会听你的召唤,它会帮助你走向一个又一个成功。

以下是作者整理的有关高考考生必看的知识点的梳理，期望对您有所帮助，望各位考生能够爱好。

高二上册数学知识点分析1异面直线定义：不同在任何一个平面内的两条直线异面直线性质：既不平行,又不相交.异面直线判定：过平面外一点与平面内一点的直线与平面内不过该店的直线是异面直线异面直线所成角：作平行,令两线相交,所得锐角或直角,即所成角.两条异面直线所成角的范畴是(0°,90°],若两条异面直线所成的角是直角,我们就说这两条异面直线相互垂直.求异面直线所成角步骤：A、利用定义构造角,可固定一条,平移另一条,或两条同时平移到某个特别的位置,顶点选在特别的位置上.B、证明作出的角即为所求角C、利用三角形来求角(7)等角定理：如果一个角的两边和另一个角的两边分别平行,那么这两角相等或互补.(8)空间直线与平面之间的位置关系直线在平面内——有无数个公共点.三种位置关系的符号表示：aαa∩α=Aaα(9)平面与平面之间的位置关系：平行——没有公共点;αβ相交——有一条公共直线.α∩β=b2、空间中的平行问题(1)直线与平面平行的判定及其性质线面平行的判定定理：平面外一条直线与此平面内一条直线平行,则该直线与此平面平行.线线平行线面平行线面平行的性质定理：如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.线面平行线线平行(2)平面与平面平行的判定及其性质两个平面平行的判定定理(1)如果一个平面内的两条相交直线都平行于另一个平面,那么这两个平面平行(线面平行→面面平行),(2)如果在两个平面内,各有两组相交直线对应平行,那么这两个平面平行. (线线平行→面面平行),(3)垂直于同一条直线的两个平面平行,两个平面平行的性质定理(1)如果两个平面平行,那么某一个平面内的直线与另一个平面平行.(面面平行→线面平行)(2)如果两个平行平面都和第三个平面相交,那么它们的交线平行.(面面平行→线线平行)3、空间中的垂直问题(1)线线、面面、线面垂直的定义两条异面直线的垂直：如果两条异面直线所成的角是直角,就说这两条异面直线相互垂直.线面垂直：如果一条直线和一个平面内的任何一条直线垂直,就说这条直线和这个平面垂直.平面和平面垂直：如果两个平面相交,所成的二面角(从一条直线动身的两个半平面所组成的图形)是直二面角(平面角是直角),就说这两个平面垂直.(2)垂直关系的判定和性质定理线面垂直判定定理和性质定理判定定理：如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直这个平面.性质定理：如果两条直线同垂直于一个平面,那么这两条直线平行.面面垂直的判定定理和性质定理判定定理：如果一个平面经过另一个平面的一条垂线,那么这两个平面相互垂直. 性质定理：如果两个平面相互垂直,那么在一个平面内垂直于他们的交线的直线垂直于另一个平面.4、空间角问题(1)直线与直线所成的角两平行直线所成的角：规定为.两条相交直线所成的角：两条直线相交其中不大于直角的角,叫这两条直线所成的角.两条异面直线所成的角：过空间任意一点O,分别作与两条异面直线a,b平行的直线,形成两条相交直线,这两条相交直线所成的不大于直角的角叫做两条异面直线所成的角.(2)直线和平面所成的角平面的平行线与平面所成的角：规定为.平面的垂线与平面所成的角：规定为. 平面的斜线与平面所成的角：平面的一条斜线和它在平面内的射影所成的锐角,叫做这条直线和这个平面所成的角.求斜线与平面所成角的思路类似于求异面直线所成角：“一作,二证,三运算”.在“作角”时依定义关键作射影,由射影定义知关键在于斜线上一点到面的垂线,在解题时,注意发掘题设中主要信息：(1)斜线上一点到面的垂线;(2)过斜线上的一点或过斜线的平面与已知面垂直,由面面垂直性质易得垂线.(3)二面角和二面角的平面角二面角的定义：从一条直线动身的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,这两个半平面叫做二面角的面.二面角的平面角：以二面角的棱上任意一点为顶点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫二面角的平面角.直二面角：平面角是直角的二面角叫直二面角.两相交平面如果所组成的二面角是直二面角,那么这两个平面垂直;反过来,如果两个平面垂直,那么所成的二面角为直二面角求二面角的方法定义法：在棱上挑选有关点,过这个点分别在两个面内作垂直于棱的射线得到平面角垂面法：已知二面角内一点到两个面的垂线时,过两垂线作平面与两个面的交线所成的角为二面角的平面角高二上册数学知识点分析21.不等式证明的根据(2)不等式的性质(略)(3)重要不等式：①|a|≥0;a2≥0;(a-b)2≥0(a、b∈R)②a2+b2≥2ab(a、b∈R，当且仅当a=b时取“=”号)2.不等式的证明方法(1)比较法：要证明a b(a0(a-b 0)，这种证明不等式的方法叫做比较法.用比较法证明不等式的步骤是：作差——变形——判定符号.(2)综合法：从已知条件动身，根据不等式的性质和已证明过的不等式，推导出所要证明的不等式成立，这种证明不等式的方法叫做综合法.(3)分析法：从欲证的不等式动身，逐渐分析使这不等式成立的充分条件，直到所需条件已判定为正确时，从而肯定原不等式成立，这种证明不等式的方法叫做分析法.证明不等式除以上三种基本方法外，还有反证法、数学归纳法等.高二上册数学知识点分析31.抛物线是轴对称图形。

用空间向量研究直线平面的位置关系高二上学期数学(人教A版2019选修一)

③
O
我们把③式称为空间平面AB一确定.
2. 平面的法向量
我们知道，给定空间一点A和一条直线l，则过点A且垂直于直线l的平面是
唯一确定的. 由此得到启发，我们可以利用点A和直线l的方向向量来确定平面.
如图示. 直线l⊥α. 取直线l的方向向量 a, 我们称向量 a为平面α的法向量. 给
n
u
l
l l // m u//m R, 使u m. α
l //m
(3) 平面与平面平行
如图(3)所示，设 n1 , n2分别是平面α, β的法向量，则
// n1 //n2 R,使得n1 n2 .
β
m //
//
n//
m n
P
m n1 n n1
m n1 n n1
D
C
A
B
练习
3.
在长方体ABCD
–A1B1C1D1中,
AB=4,
BC=3,
CC1=2.
以D为原点,
以{
1 3
DA,
1 4
DC
,
1 2
DD1
}
为空间的一个单位正交基底，建立空间直角坐标系Oxyz，求平面ACD1的一个法向量.
解:依题意可得A(3, 0, 0),C(0, 4, 0), D1(0, 0, 2). ∴AC (3,4,0), AD1 (3,0, 2).
在点P，使得AP//平面ACD1?
z
D1 A1
C1 B1
D A
x
P C
y
B
练习
1. 用向量方法证明“直线与平面平行的判定定理”: 若平面外一条直线与此平面内
的一条直线平行，则该直线与此平面平行.

高中数学选修2-1知识点 (1)包括必修二要看的内容

高二数学选修2－1第一章：命题与逻辑结构知识点：1、命题：用语言、符号或式子表达的，可以判断真假的陈述句. 真命题：判断为真的语句.假命题：判断为假的语句.2、“若p ，则q ”形式的命题中的p 称为命题的条件，q 称为命题的结论.3、对于两个命题，如果一个命题的条件和结论分别是另一个命题的结论和条件，则这两个命题称为互逆命题.其中一个命题称为原命题，另一个称为原命题的逆命题. 若原命题为“若p ，则q ”，它的逆命题为“若q ，则p ”.4、对于两个命题，如果一个命题的条件和结论恰好是另一个命题的条件的否定和结论的否定，则这两个命题称为互否命题.中一个命题称为原命题，另一个称为原命题的否命题. 若原命题为“若p ，则q ”，则它的否命题为“若p ⌝，则q ⌝”.5、对于两个命题，如果一个命题的条件和结论恰好是另一个命题的结论的否定和条件的否定，则这两个命题称为互为逆否命题。

其中一个命题称为原命题，另一个称为原命题的逆否命题。

若原命题为“若p ，则q ”，则它的否命题为“若q ⌝，则p ⌝”。

6、四种命题的真假性：原命题逆命题否命题逆否命题真真真真真假假真假真真假假假假假四种命题的真假性之间的关系：()1两个命题互为逆否命题，它们有相同的真假性；()2两个命题为互逆命题或互否命题，它们的真假性没有关系．7、若p q ⇒，则p 是q 的充分条件，q 是p 的必要条件．若p q ⇔，则p 是q 的充要条件（充分必要条件）．8、用联结词“且”把命题p 和命题q 联结起来，得到一个新命题，记作p q ∧．当p 、q 都是真命题时，p q ∧是真命题；当p 、q 两个命题中有一个命题是假命题时，p q ∧是假命题．用联结词“或”把命题p 和命题q 联结起来，得到一个新命题，记作p q ∨．当p 、q 两个命题中有一个命题是真命题时，p q ∨是真命题；当p 、q 两个命题都是假命题时，p q ∨是假命题．对一个命题p 全盘否定，得到一个新命题，记作p ⌝．若p 是真命题，则p ⌝必是假命题；若p 是假命题，则p ⌝必是真命题．9、短语“对所有的”、“对任意一个”在逻辑中通常称为全称量词，用“∀”表示．含有全称量词的命题称为全称命题．全称命题“对M 中任意一个x ，有()p x 成立”，记作“x ∀∈M ，()p x ”．短语“存在一个”、“至少有一个”在逻辑中通常称为存在量词，用“∃”表示．含有存在量词的命题称为特称命题．特称命题“存在M 中的一个x ，使()p x 成立”，记作“x ∃∈M ，()p x ”．10、全称命题p ：x ∀∈M ，()p x ，它的否定p ⌝：x ∃∈M ，()p x ⌝。

(高二)高二数学知识点及公式总结5篇

高二数学知识点及公式总结5篇相信有很多同学到了高中会认为数学是理科，所以没必要死记硬背。

其实这是错误的想法，高中数学知识点众多，光靠一个脑袋是记不全的，好记性不如烂笔头，要想学好数学，同学们还是要多做知识点的总结。

以下是我精心收集整理的高二数学知识点及公式总结，下面我就和大家分享，来欣赏一下吧。

高二数学知识点及公式总结11、圆的定义平面内到一定点的距离等于定长的点的集合叫圆，定点为圆心，定长为圆的半径。

2、圆的方程(x-a)^2+(y-b)^2=r^2(1)标准方程，圆心(a,b)，半径为r;(2)求圆方程的方法：一般都采用待定系数法：先设后求。

确定一个圆需要三个独立条件，假设利用圆的标准方程，需求出a，b，r;假设利用一般方程，需要求出D，E，F;另外要注意多利用圆的几何性质：如弦的中垂线必经过原点，以此来确定圆心的位置。

3、直线与圆的位置关系直线与圆的位置关系有相离，相切，相交三种情况：(1)设直线，圆，圆心到l的距离为，那么有;;(2)过圆外一点的切线：①k不存在，验证是否成立②k存在，设点斜式方程，用圆心到该直线距离=半径，求解k，得到方程【一定两解】(3)过圆上一点的切线方程：圆(x-a)2+(y-b)2=r2，圆上一点为(x0，y0)，那么过此点的切线方程为(x0-a)(x-a)+(y0-b)(y-b)=r2练习题：2.假设圆(x-a)2+(y-b)2=r2过原点，那么()A.a2-b2=0B.a2+b2=r2C.a2+b2+r2=0D.a=0，b=0【解析】选B.因为圆过原点，所以(0，0)满足方程，即(0-a)2+(0-b)2=r2，所以a2+b2=r2.高二数学知识点及公式总结2空间中的垂直问题(1)线线、面面、线面垂直的定义①两条异面直线的垂直：如果两条异面直线所成的角是直角，就说这两条异面直线互相垂直。

②线面垂直：如果一条直线和一个平面内的任何一条直线垂直，就说这条直线和这个平面垂直。

用空间向量研究直线、平面的位置关系(第2课时)高二数学(人教A版2019选择性必修第一册)

B
所以A1C是平面BDD1B1的法向量. 所以A1C 平面BDD1B1 .
例5 证明“平面与平面垂直的判定定理”：若一个平面过另一个平面的垂线，则这两个平面垂直．
已知：如图, l , l , 求证： .
证明：取直线l的方向向量u, 平面的法向量n. 因为l , 所以u是平面的法向量.
中点, F是BC的中点. 求证：平面EAD1 平面EFD1.
证明：建立如图所示的空间直角坐标系, 则A(1, 0, 0), D1(0, 0, 1), E(0,1, 0),
F
1 2
, 2, 0 ,
AD1
(1, 0,1),
AE
(1,1, 0),
ED1
z
(0, 1,1),
EF
1 2
,1,
0
设n1 ( x1, y1, z1 )是平面EAD1的法向量,
那么是否能用这些向量来刻画空间直线、平面的平行、垂直关系呢？
首先来看平行的问题．
环节二：观察分析，感知概念
知识点1：空间中直线、平面的平行
我们知道，直线的方向向量和平面的法向量是确定空间中的直线和平面的关键量．
那么是否能用这些向量来刻画空间直线、平面的平行、垂直关系呢？首先来看平行的问题．
思考由直线与直线、直线与平面或平面与平面的平行关系，可以得到
EF n,
DE
C y
又EF 平面ACD1, EF / / 平面ACD1. A
B
x
环节四：辨析理解，深化概念
知识点2：空间中直线、平面的垂直
思考类似空间中直线、平面平行的向量表示在直线与直线、直线与平面、平面与平面的垂直关系中，直线的方向向量、平面的法向量之间有什么关系？

2.2.2平面与平面平行的判定教案

1、重点：平面与平面平行的判定定理及应用依据：教学重在过程，重在研究，而不是重在结论。

学生不应该死背定理内容，而是理解知识发生、发展的过程。

这样，知识就成了一个数学模式，可用来解决具体问题。

2、难点：平面与平面平行的判定定理的探究发现及应用。

依据：因为问题的产生与解决具有一定的隐蔽性，虽然学生了解两个平面平行的判定，但在问题中应用的时候就不够灵活或找不到需要的条件。

为此，本节的难点是两个平面平行的判定。

重点是判定定理的引入与理解，难点是判定定理的应用及立几空间感、空间观念的形成与逻辑思维能力的培养。

3．疑点：正确理解并应用两个平面平行的判定定理时，要注意定理中的关键词：相交．六、教学过程（一）创设问题情景，引入新课基于新课程的理念和本节课的教学目标，使学生体会到数学知识发生在现实背景只需按为此结合一道习题即回归了上节课直线与平面的判定也引出了本节课的内容，自然流畅，更让学生了解到本节课学习的必要性。

教师：上节课我们学习了直线与平面的判定你能利用你所学的知识解决本题吗？实例：如图，在正方体ABCD —A 1B 1C 1D 1求证：B 1D 1 || 平面C 1BD[知识链接：根据空间问题平面化的思想，因此把找空间平行直线问题转化为找平行四边形或三角形中位线问题，这样就自然想到了找中点。

平行问题找中点解决是个好途径好方法。

这种思想方法是解决立几论证平行问题，培养逻辑思维能力的重要思想方法] 学生上黑板板演，其他同学下面做，师生共同评价点明，对旧知识复习，又有深入，同时又点出了“转化”的思想方法，为引入新课作铺垫点明证明线面平行的方法及思想（转化的思想）提出课题思考1：如果将上题中正方体中的AB 1 ， AD 1连接构成了一个新的平面AB 1D 1如何证明：平面AB 1D 1∥平面C 1BD[设计意图：说明面面平行证明的必要性，通过提问引入本节课题，并为探寻平面与平面平行判定定理作好准备。

]（二）判定定理的探求过程1、直观感知思考1：根据同学们日常生活的观察，你们能举出平面与平面平行的具体事例吗？生1：教室的天花板与地面给人平行的感觉。

第九章立体几何9-3空间点、直线、平面之间的位置关系

∴EF≠GH，∴四边形EFGH为梯形．设EH∩FG＝P，则P∈EH，而EH⊂平面 ABD，

∴P∈平面ABD，同理P∈平面BCD， ∵平面ABD∩平面BCD＝BD，∴P∈BD. ∴EH、FG、BD三线共点．

如图，在四面体ABCD中作截面PQR，PQ、 CB的延长线交于M，RQ、DB的延长线交于 N，RP、DC的延长线交于K.求证M、N、K 三点共线．

解析：∵PQ∩CB＝M，∴M∈PQ，M∈CB，

∵PQ⊂平面PQR，CB⊂平面BCD，
∴M∈平面PQR，M∈平面BCD，

∴M是平面PQR与平面BCD的公共点，同理
由PQ∩DB＝N，及RP∩DC＝K知，N，K也
是平面PQR与平面BCD的公共点，∵平面
PQR与平面BCD不重合，∴M、N、K在平
面BCD与平面PQR的交线上，即M、N、K

重点难点重点：①平面的概念与基本性质 ②空间直线、平面之间的各种位置关系难点：①证明点共线、线共点、点线共面等 ②异面直线的判定

知识归纳 1．平面的基本性质 (1)连接两点的线中，线段最短；过两点有且只有一条直线． (2)基本性质1：如果一条直线上的两点在一个平面内，那么这条直线上所有的点都在这个平面内．基本性质2：经过不在同一条直线上的三点，有且只有一个平面，即不共线的三点确定一个平面．基本性质3：如果两个不重合的平面有一个公共点，那么它们有且只有经过这个公共点
∴①真；

过M作ME∥DC，交CC1于E，∵DC∥AB， ∴ME∥AB；过M作MF∥A1D1，交AA1于F， ∵A1D1∥B1C1，∴MF∥B1C1，∴AB与 B1C1都与平面MEF平行，由作法知，这样的平面MEF有且仅有一个，故选C. 答案：C

【2018新课标高考必考知识点教学计划教学安排教案设计】高二数学：平面与平面之间的关系解读

一、平面与平面平行1. 平面和平面平行的判定定理如果一个平面内的两条相交直线分别和另一个平面平行，那么这两个平面相互平行。

推论：如果一个平面内的两条相交直线，分别和另一个平面内的两条（相交）直线平行，那么这两个平面相互平行。

2. 平面和平面平行的性质定理如果两个平行平面同时和第三个平面相交，那么所得的两条交线平行。

二、平面与平面垂直1. 平面与平面垂直的判定（1）定义：两个平面相交，如果所成的二面角是直二面角，那么这两个平面互相垂直。

（2）如果一个平面经过另一个平面的垂线，那么这两个平面互相垂直。

（3）一个平面垂直于两个平行平面中的一个，也垂直于另一个。

2. 平面与平面垂直的性质：（1）两个平面垂直的性质定理：如果两个平面垂直，那么在一个平面内垂直于交线的直线垂直于另一个平面。

（2）如果两个平面互相垂直，那么经过第一个平面内的一点垂直于第二个平面的直线在第一个平面内。

（3）如果两个相交平面都垂直于第三个平面，则它们的交线垂直于第三个平面。

近几年高考立体几何试题以基础题和中档题为主，证明空间线面及面面平行、垂直关系一直是热点问题，突出空间想象能力，侧重于空间线面位置关系的定性与定量考查，算中有证。

其中选择、填空题注重几何符号语言、文字语言、图形语言三种语言间的相互转化，考查学生对图形的识别、理解和加工能力；解答题则一般将线面集中于一个几何体中，即以一个多面体为依托，设置几个小问，设问形式以证明或计算为主。

例题1如图所示，在正方体ABCD—A1B1C1D1中，O为底面ABCD的中心，P是DD1的中点，设Q是CC1上的点，问：当点Q在什么位置时，平面D1BQ∥平面PAO？解析：平面PAO即平面PAC，若平面D1BQ∥平面PAC，则它们与第三个平面CC1D1D 的交线PC、D1Q相互平行，故Q为CC1的中点。

答案：当Q为CC1的中点时，平面D1BQ∥平面PAO。

∵Q为CC1的中点，P为DD1的中点，∴QB∥PA，∵P、O为DD1、DB的中点，∴D1B∥PO，又PO∩PA＝P，D1B∩QB＝B，D1B∥平面PAO，QB∥平面PAO，∴平面D1BQ∥平面PAO。

高二数学第二章

________________ ，不共线三点
确定
______
一个平面公理如果两个不重合的平面有一个公共点，那么它们有 3 ________________ 且只有过这个点的公共直线
A,B,C三点不共线存在惟一的平面α使 A,B,C∈α P∈l, P∈α, P∈β,则 α∩β=l
举一反三
3. 已知在空间四边形ABCD中，AB⊥CD，AB= 3CD，M 、N分别为对角线AC、BD的中点.求MN与AB、CD所成的角. 解析如图，取BC的中点P，连接PM、PN ，在△ABC中, ∵M、P分别为AC、BC的中点,
∴MP∥AB，MP= AB.
同理可证：PN∥CD，PN= CD.
2 2 2
2 2 2 ∴DM DP MP ,
∴∠DPM=90°,∴ DB1⊥MN, ∴DB1⊥EF, ∴异面直线 DB1 与EF所成的角为90°.
方法四：如图，在原正方体的右侧补上一个全等的正方体，连接B1Q, 则 B1Q ∥EF.
于是，直线 DB1 B1Q 所成的角就是异面直线DB1与EF所成的角或其补角. 与通过计算，不难得到： 1D2 B1Q2 DQ2,从而异面直线DB1 与EF所成的角 B 为90°
题型二
共面问题
【例2】已知直线m与直线a、直线b分别交于A、B，且a∥b. 求证：过a、b、m有且只有一个平面.
ห้องสมุดไป่ตู้
分析若证“过a、b、m三条直线有且只有一个平面”，须证两件事，其一是存在性,即“有”，其二是唯一性,即“只有”.
证明 ∵a∥b, ∴过a、b有一个平面α，又m∩a=A,m∩b=B, ∴A∈a,B∈b,∴A∈α,B∈α, 又A∈m,B∈m,∴mα,即过a、b、m有一个平面α. 假设过a,b,m还有一个平面β异于α, 则aα,bα,aβ,bβ. 这与a∥b,过a,b有且只有一个平面相矛盾. 因此,过a,b，m有且只有一个平面.

数学高中必修二知识点总结必看

数学高中必修二知识点总结必看各个科目都有自己的学习方法，但其实都是万变不离其中的，基本离不开背、记，练，数学作为最烧脑的科目之一，也是一样的。

下面是小编给大家整理的一些数学高中必修二知识点的学习资料，希望对大家有所帮助。

高一年级数学必修二知识点总结【两个平面的位置关系】(1)两个平面互相平行的定义：空间两平面没有公共点(2)两个平面的位置关系：两个平面平行-----没有公共点;两个平面相交-----有一条公共直线。

a、平行两个平面平行的判定定理：如果一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行。

两个平面平行的性质定理：如果两个平行平面同时和第三个平面相交，那么交线平行。

b、相交二面角(1)半平面：平面内的一条直线把这个平面分成两个部分，其中每一个部分叫做半平面。

(2)二面角：从一条直线出发的两个半平面所组成的图形叫做二面角。

二面角的取值范围为[0°，180°](3)二面角的棱：这一条直线叫做二面角的棱。

(4)二面角的面：这两个半平面叫做二面角的面。

(5)二面角的平面角：以二面角的棱上任意一点为端点，在两个面内分别作垂直于棱的两条射线，这两条射线所成的角叫做二面角的平面角。

(6)直二面角：平面角是直角的二面角叫做直二面角。

【两平面垂直】两平面垂直的定义：两平面相交，如果所成的角是直二面角，就说这两个平面互相垂直。

记为⊥两平面垂直的判定定理：如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直两个平面垂直的性质定理：如果两个平面互相垂直，那么在一个平二面角求法：直接法(作出平面角)、三垂线定理及逆定理、面积射影定理、空间向量之法向量法(注意求出的角与所需要求的角之间的等补关系)。

高二数学必修二知识点归纳一、直线与圆：1、直线的倾斜角的范围是在平面直角坐标系中，对于一条与轴相交的直线，如果把轴绕着交点按逆时针方向转到和直线重合时所转的最小正角记为，就叫做直线的倾斜角。

人教A版高二数学必修二第二章点、直线、平面之间的位置关系 2.2.3 知识表格【素材】【课件】(共3张PPT)

2
为
2
．
解析：连接B1D、AD1，
D1
因为PQ//面AB1D，PQ面 D1AB1,
面 D 1 A B 1 面 A B 1A B 1 ,
A1
C1 Q
B1
所以PQ//AB1，
Байду номын сангаас
P
因为点P是面AA1D1D的中心，
D
所以PQ是△AB1D1的中位线，
C
所以PQ
1 2
AB1

2. 2
A
B
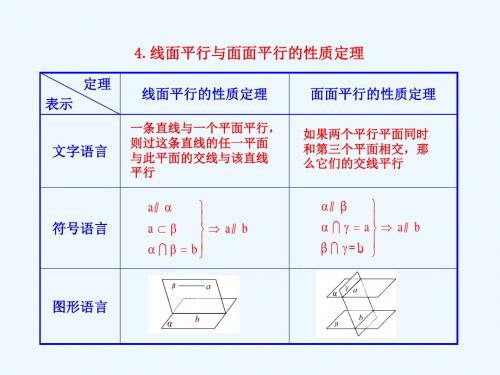
4.线面平行与面面平行的性质定理
定理表示
文字语言
线面平行的性质定理
一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行
面面平行的性质定理
如果两个平行平面同时和第三个平面相交，那么它们的交线平行
符号语言
a∥
a

a∥ b
b
∥ β

a

a∥ b
β = b
图形语言
2.直线a∥平面α ，平面α 内有n条交于一点的直
线，那么这n条直线和直线a平行的 ( B )
A.至少有一条
B.至多有一条
C.有且只有一条
D.不可能有
4.已知正方体ABCD—A1B1C1D1的棱长为1，点P是面AA1D1D
的中心，点Q是B1D1上一点，且PQ//面AB1D，则线段 PQ长

高二数学平面与平面垂直

D
过B在b作BE // CD且BE CD, ABE是AB与CD所的角 ,
解有关的直角三角形 AC 16 cos 450 8 2 , BD 8 2 8 3 3 2 ABE . AE 8 2 8 8 3 sin ABE 16 2 3

变式练习：长为 16的线段AB两端点 , 分别在直二面角 a CD b 的两个面内 ,并且与两个面分别成 300、 450 角, z 求AB和CD所成的角 . 分析二： A 0 0 同分析一得 ABC 45 , BAD 30 . 建立空间坐标系如图并设AC=1
所以BEF是二面角B AC D的平面角
2a 2a 2a a 2a BE 2a, BF 2 2 2a 2 a a 2 5 面面垂直,线在面内,面面相交, B BF 10 sin BEF 线交垂直 ,则线面垂直 BE 5
？
E C
解三个直角三角形 :
B
. 于它们交线的直线垂直于另一个平面
求证 : AB^b
A
D E
且BE b , ABE是直二面角a CD b 0 的平面角,即ABE 90 则AB ^ BE
C
面面垂直,线在面内,面面相交, 线交垂直根据线面垂直判定定理有 ,则线面垂直 AB^b .
又CD BCD, BD ^ CD 1 求证: 面ABD^面ACD;
A F
D
五、变式练习：平面a内有一个圆, AB是直径, SA ^ a , C为圆上异于A、B的一点，连结SB、SC, 且A在SB、SC S 上的射影分别为E、F ,
求证 : 平面SAC ^ 平面SBC; 平面AEF ^ 平面SAB.
指出图中的直角三角形

第五节两个面平行的判定和性质

学科: 数学年级：高二版本：人教版期数：2331本周教学内容：第五节两个平面平行的判定和性质【基础知识精讲】1.两个平面的位置关系(1)两平面平行——没有公共点，若α与β平行，记作α∥β.(2)两平面相交——有一条公共直线，若α与β有交线a，记作α∩β＝a.注意：画两个互相平行的平面时，表示平面的两个平行四边形的对应边应画平行，如图：画两个相交平面时：(i)先画表示两个平面的平行四边形的相交的两边.(ii)再画出表示两个平面交线的线段；(iii)过第(i)步图中线段的端点分别引线段，使它平行且等于第(ii)步图中表示交线的线段.(iv)最后画表示两个平面的平行四边形的第四边，其演示过程如下：2.两个平面平行的判定(1)两个面平行的判定定理：如果一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行.aβ,bβ,a∩b＝A,a∥α,b∥α⇒α∥β.在实际生活中要判断一个平面是否水平时，把水准器在该平面上交叉放两次如果汽泡居中，就可利用该定理判定该平面与水平面平行.(2)书中粗体字：垂直于同一直线的两个平面平行.也可以用来作面面平行的判定.即α⊥AA′，β⊥AA′⇒α∥β.3.两个平面平行的性质(i)两个平面平行，其中一个平面内的直线必平行于另一个平面.这为线面平行进一步提供了证明方法，但分居两平行平面的直线有平行与异面两种可能.(ii)两个平面平行的性质定理：如果两个平行平面同时和第三个平面相交，那么它们的交线平行.α∥β，γ∩α＝a,γ∩β＝b⇒a∥b.(iii)一条直线垂直于两个平行平面的一个平面，它也垂直于另一个平面.(iv)经过平面外一点只有一个平面和已知平面平行.4.两个平行平面的距离首先我们可以验证夹在两个平行平面间的平行线段相等.(1)两个平行平面的公垂线：和两个平行平面同时垂直的直线.这与两异面直线公垂线不同的是两平行平面的公垂线有无数条.根据线面垂直的性质定理可知这些公垂线相互平行.(2)两个平行平面的公垂线段：两个平行平面的公垂线夹在两平行平面间的部分.由上可知，两个平行平面的公垂线段都相等，我们把夹在两个平行平面间的公垂线段的长度叫做两个平行平面间的距离.【重点难点解析】两个平面平行的判定和性质是本节的重点，平行平面间的距离是本节的重点概念，判定定理的证明是本节的难点，要深刻理解面面平行的概念和一些重要定理，在验证中应注意线线平行，线面平行，面面平行之间的相互转化.例1已知a、b是异面直线，a⊂α,a∥β,b⊂β,b∥α,求证α∥β.分析证明两个平面平行通常利用判定定理来证.证明如图，过a作任一平面γ和平面β交于a′,∵a∥β∴a∥a′.又a′⊂β,a′⊄α∴a′∥α且a′与b相交，∵b⊂β，b∥α.∴α∥β.另证设c是异面直线a、b的公垂线，则过a、c可以确定一个平面γ，设γ∩β＝a′∵α∥β，∴a′∥a,∵c⊥a,∴c⊥a′又∵c⊥b,a′,b相交，∴c⊥β同理可证：c⊥α，∴α∥β例2已知：平面α∥平面β，且aα，b平面β，a,b为两条异面直线.求证：异面直线a、b间的距离等于平面α，β之间的距离.证：设AB是异面直线a、b的公垂线段，如图过点B，作直线a′，使a′∥a.∵α∥β，a⊂β,∴a∥β,∴a′⊂β.∵AB⊥a,∴AB⊥a′又AB⊥b，且a′∩b＝B.∴AB⊥β∵α∥β，∴AB⊥α∴AB的长是平行平面α，β间的距离.说明求两异面直线间的距离有时可能转化为求两平行平面间的距离.例3如果一条直线和两个平面中的一个相交，那么它和另一个平面也相交.已知：α∥β,l∩α＝A.求证：l与β相交.证明：∵α∥β,l∩α＝A∴Aβ.假设l与β不相交，则l∥β在平面β内任取一点D，则D l.∴点D，l确定平面PBD，如图∵α与平面PBD相交于过A的一条直线AC，β与平面PBD相交于过点D的一条直线BD.又α∥β∴AC与BD无公共点.∵AC和BD都在平面PBD内，∴AC∥BD.由l∥β可知l∥BD.∴AC∥l且l与AC相交于A.∴AC与l重合，又AC在平面α内.∴l在α内与l∩α＝A矛盾.∴假设不成立，∴l与β必相交.例4如图，正四棱锥S—ABCD的底面积长为a，侧棱长为2a，点P、Q分别在BD和SC 上，并且BP∶PD＝1∶2，PQ∥平面SAD，求线段PQ的长.分析要求出PQ的长，一般设法构造三角形，使PQ为其一边，然后通过解三角形的办法去处理.作PM ∥AD 交CD 于M 连QM ，∵PM ∥平面SAD ，PQ ∥平面SAD.∴平面PQM ∥平面SAD ，而平面SCD 分别与此两平行平面相交于QM ，SD. ∴QM ∥SD.∵BC ＝a,SD ＝2a.∴PD BP ＝21. ∴BC MP ＝BD PD ＝32,MP＝32a, SD MQ ＝CDMC ＝BD BP ＝31.∴MQ ＝31SD ＝32a,又∠PMQ ＝∠ADS.∴cos ∠PMQ ＝cos ∠ADS ＝a a221＝41. 在ΔPMQ 中由余弦定理得 PQ 2＝(32a)2+(32a)2-2·32a ·32a ·41＝96a 2. ∴PQ ＝36a. 评析：本题的关键是运用面面平行的判定和性质，结合平行线截比例线段定理，最后由余弦定理求得结果，综合性较强.例5 已知：如图，α∥β，异面直线AB 、CD 和平面α、β分别交于A 、B 、C 、D 四点，E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点，求证：(1)E 、F 、G 、H 共面；(2)面EFGH ∥平面α.证明 (1)∵E 、H 分别是AB 、DA 的中点，∴EH ∥21BD.同理FG ∥21BD.∴FG ∥EH.∴四边形EFGH 是平行四边形，即E 、F 、H 、G 共面.(2)平面ABD 和平面α有一个公共点A ，设两平面交于过点A 的直线AD ′∴α∥β，∴ AD ′∥BD.又∵BD ∥EH ，∴EH ∥BD ∥AD ′.∴EH ∥平面α，EH ∥平面β，同理EF ∥平面α，EF ∥平面β.∴平面EFHG ∥平面α∥平面β.【难题巧解点拨】例1 点A 为异面直线a 、b 外一点，过A 与a 、b 都平行的平面( ) A.只有一个 B.只有两个 C.至多有一个 D.有无数个分析：本题考查线线位置关系，线面位置关系，平面基本性质，以及空间想象能力解法一：过点A 作a ′∥a,b ′∥b ，根据公理3，a ′与b ′确定一个平面为α，则异面直线a 与b 至多有一条在α内，当a 、b 都不在α内时，过A 与a 、b 都平行的平面恰有一个，即α；当a 、b 中有一条在α内时，过A 与a 、b 都平行的平面不存在，故选C.解法二：过异面直线a 、b 分别作平面α、β使α∥β，若点A 在α或β上，则过A 与a 、b 都平行的平面不存在；若点A 在α外且在β上，则过A 恰有一个平面平行于α、β，则过点A 与a 、b 都平行的平面恰有一个.例2 有四个命题(1)一条直线和另一条直线平行，它就和经过另一条直线的任何平面平行 (2)一条直线和一个平面平行，它就和这个平面内的任何直线平行 (3)平行于同一平面的两条直线平行(4)如果直线a ∥平面α，a ⊂平面β，且α∩β＝b,则a ∥b. 其中假命题共有( ) A.1个 B.2个 C.3个 D.4个解此题考查线线位置关系和线面位置关系，以及空间想象能力.一条直线和另一条直线平行，它可能在经过另一条直线的平面内，故(1)是假命题.一条直线和另一个平面平行，它与这个平面的直线可能平行，也可能异面，故(2)也是假命题，平行于同一平面的两条直线，也可能平行，也可能异面或相交，故(3)也是假命题，而命题(4)是真命题，也是线面平行的性质定理.例3 已知直线a 、b 、c ，平面α∩平面β＝a,b ⊂α，c ⊂β，且b 与c 无公共点，则b 与c 不平行的充要条件是( )A.b 、c 都与α相交B.b 、c 中只有一条与α相交C.b 、c 中至多一条与α相交D.b 、c 中至少有一条与α相交分析：本题考查直线与直线的位置关系，直线与平面的位置关系，充要条件，以及空间想象能力和等价转化能力.解法一：若直线b 与c 不平行，又由b 与c 无公共点，则b 与c 必定异面，根据异面直线的定义和线面位置关系可知或者b 与c 都与a 相交，或者b 、c 中有一条与a 相交，另一条与a 平行，即b 、c 中至少有一条与α相交，即D 成立；反之，当D 成立时，不难证明b 与c 必不平行，所以应选D.解法二：由题设及异面直线的定义可知，若b 、c 都与a 相交能推出b 与c 异面，即b 与c 不平行；反过来，b 与c 不平行不一定推出b 、c 都与a 相交，即A 是充分非必要条件，而不是充要条件，同理，B 也是充分非必要条件，而非充要条件，又由b 、c 中至多有一条与a 相交，包含b 、c 中有一条与a 相交和b 、c 都不与a 相交两种情形，而对于后者，即b ∥a 且c ∥a ，则b ∥c.故c 既非充分又非必要条件，综上所述，排除A 、B 、C 三个选择项，从而选择D.例4 已知A ，B ∈平面α，C ，D ∈平面β，α∥β，AB ＝13，BD ＝15，AC 、BD 在平面α上的射影长之和是14，求AC 、BD 在平面α上的射影长，以及平面α、β的距离.解如图，设α、β的距离是h ，则AC 在α内的射影长是2213h -，BD 在α内的射影长是2215h -.根据题意，2213h -+2215h -＝14. 解这个方程，h ＝12.∴ 2213h -＝5, 2215h -＝9.故AC 、BD 在平面α上的射影长分别是5和9，平面α、β的距离是12.点评平行平面间距离通常转化为点面距离或线面距离最终转化为点面距离.例5 如图，已知线段PQ 、PD 、QF 分别和平行平面α、β交于A 、B 、C 、D 、E 、F ，若AP ＝BQ ，求证：S ΔACF ＝S ΔBDE .略证由已知得AC ∥BD ，EB ∥AF ，∠CAF ＝∠EBD ，又AC ∶BD ＝PA ∶PB ＝QB ∶QA ＝EB ∶AF ，∴AC ·AF ·sin ∠CAF ＝BE ·BD ·sin ∠DBE.∴S ΔACF ＝S ΔBDE .例6 如图，在三棱锥S —ABC 中，A 1、B 1、C 1分别是ΔSBC 、ΔSCA 、ΔSAB 的重心，(1)求证：平面A 1B 1C 1∥平面ABC ；(2)求三棱锥S —A 1B 1C 1与S —ABC 体积之比.分析：本题显然应由三角形重心的性质，结合成比例线段的关系推导出“线线平行”再到“线面平行”到“面面平行”，至于体积的比的计算只要能求出相似三角形面积的比和对应高的比就可以了.证：(1)：∵ A 1、B 1、C 1是ΔSBC 、ΔSCA 、ΔSAB 的重心，连SA 1、SC 1并延长交BC 、AB 于N 、M ，则N 、M 必是BC 和AB 的中点.连MN∵SMSC 1＝SN SA 1＝32， ∴A 1C 1∥MN.∵MN ⊂平面ABC ， ∴A 1C 1∥平面ABC.同理可证 A 1B 1∥平面ABC. ∴ 平面A 1B 1C 1∥平面ABC. (2)由(1)MN C A 11＝32，MN ∥21AC ， ∴A 1C 1∥31AC. 同理可证：A 1B 1∥1AB ， B 1C 1∥1BC. ∴ ΔA 1B 1C 1∽ΔABC ， S 111C B A △＝91S ΔABC . 设三棱锥S —ABC 的高为h ，S —A 1B 1C 1的高为h 1则有：h h 1＝SN SA 1＝32,∴h 1＝32h.∴ABCS C B A S V V --111＝h S hS ABC ABC ⋅⋅⋅⋅△△91313231＝272. 评析：要掌握线面平行的相互转化的思想方法外，还要有扎实的相似形和线段成比例的基础.例7 如图，已知正方体ABCD —A 1B 1C 1D 1，求证：(1)平面AB 1D 1∥平面C 1BD ；(2)对角线A 1C 被平面AB 1D 1和平面C 1BD 三等分.分析：本题若根据“一个平面内两条相交的直线分别与另一平面内两条相交的直线平行，则两平面平行”是很容易解决论证平面AB 1D 1∥平面C 1BD 的，但兼顾考虑(2)的论证，(1)我们还是采用“两平面垂直于同一直线则两平面平行”的判定的方法.证：(1)连AC ，∵BD ⊥AC ，AC 是A 1C 在底面上的射影，由三条垂线定理得A 1C ⊥BD ，同理可证A 1C ⊥BC 1.∴A 1C ⊥平面C 1BD ，同理也能证得A 1C ⊥平面AB 1D 1. ∴平面AB 1D 1∥平面C 1BD.(2)设A 1到平面AB 1D 1的距离为h ，正方体的棱长为a ，则有：31h ·43(2a)2＝31a · 21a 2. ∴h ＝33a.同理C 到平面C 1BD 的距离也为33a ，而A 1C ＝3a.故A 1C 被两平行平面三等分.评析：论证A 1C 被两平行平面三等分，关键是求A 1到平面AB 1D 1的距离，C 到平面C 1BD 的距离，这里用三棱锥体积的代换，若不用体积代换，则可以在平面A 1ACC 1中去考虑：连A 1C 1，设A 1C 1∩B 1D 1＝O 1，AC ∩BD ＝0，如图连AO 1，C 1O ，AC 1，设AC 1∩A 1C ＝K.A 1C ∩AO 1＝M ，C 1O ∩A 1C ＝N.可证M 为ΔA 1AC 1的重心，N 为ΔACC 1的重心，则可推知MN ＝NC ＝A 1M.另外值得说明的是：A 1C 是面AB 1D 1和面BC 1D 的公垂线. 异面直线AD 1和C 1D 的距离也等于MN.例8 如图，已知直线a ∥平面α；求证：过a 有且只有一个平面平行于α.证明 (1)存在性：设过a的平面γ与α交于a′，∵a∥α，∴a∥a′.在α上，设直线b′∩a′＝A′,在a上取点A，A与b′确定平面δ，在δ上过A作b∥b′.则a、b是相交直线(若重合，则显然b′∥a′，矛盾).∴a,b确定平面β，则β∥α.(2)唯一性：设过a还有一个平面π∥α，∵π与δ有公共点A，∴π与δ相交于过A 的直线b″，又π∥a，δ∩b′，∴b″∥b′,∴b″∥b,而b″与b都过点A，故重合，故π与β重合.【课本难题解答】1.经过平面外一点只有一个平面和已知平面平行.已知：Aα，A∈β，β∥α求证：β是唯一的.证：设l过A点，且l⊥α，这样的直线是唯一的.又β∥α，则β⊥l，过点A与α平面的平行一定和l垂直.∵过点A和直线l垂直的平面是唯一的.∴过点A和α平行的平面是唯一的.2.一条直线和两个平行平面相交，求证：它和两个平面所成的角相等.已知：α∥β，直线a分别与α和β相交于点A和A′.求证：a与α所成的角与a与β所成的角相等.(1)当a⊥α时，∵α∥β，∴α⊥β.即a与α所成的角与a与β所成的角都是直角.(2)当a是α的斜线时，如图，设P是a上不同于A、A′的任意一点，过点P引a′⊥α, a′∩α＝B,a′∩β＝B′.连结AB和A′B′.∵α∥β，a′⊥α.∴a′⊥β由此可知，∠PAB是a和α所成的角，∠P′A′B是a和β所成的角，而AB∥A′B′.∴∠PAB＝∠PA′B′即 a和α所成的角等于a和β所成的角.3.a 和b 是两条异面直线，求证：过a 且平行b 的平面必平行于过b 且平行于a 的平面. 已知：a,b 是异面直线，a ⊂α，b ⊂β,a ∥β,b ∥α. 求证：α∥β.证：过b 作平面γ与平面α交于b ′4.如图，直线AC 、DF 被三个平行平面α、β、γ所截. 求证：BC AB ＝EFDE 证：(i)当AC ，DF 共面S 时，连AD ，BE ，CF 则AD ∥BE ∥CF 从而BC AB ＝EFDE (ii)当AC 、DE 异面时，连CD 设CD ∩β＝G 连AD 、BG 、GE 、CF ，如图∵α∥β 平面ACD ∩β＝BG ，平面ACD ∩α＝AD. ∴BG ∥AD ∴BCAB ＝GC DG同理可证：EG ∥CF ，∴GCDG ＝EF DE∴BC AB ＝EFDE 综合(i)(ii)知：BC AB ＝EF DE .【命题趋势分析】本节应掌握两平面平行的概念、判定定理及性质定理，能运用这些概念、定理进行论证和解决有关问题.面面平行这一节直接出题的情况不多，各年高考中基本上都与其他章节知识综合出题，常以同学科知识间的单综合形式命题.【典型热点考题】例1 设直线a 在平面α内，则“平面α∥平面β”是“直线a ∥平面β”的( )条件A.充分但不必要B.必要但不充分C.充分且必要D.不充分也不必要解若α∥β，∵a α，∴a 与β无公共点，∴a ∥β.若a ∥β，a α，则α，β的关系不能确定，所以应选A.例2 设a 、b 是两条异面直线，那么下列四个命题中的假命题是( )A.经过直线a 有且只有一个平面平行于直线bB.经过直线a 有且只有一个平面垂直于直线bC.存在分别经过直线a 和b 的两个互相平行的平面D.存在分别经过直线a 和b 的两个互相垂直的平面解 A 、C 、D 均为真命题，B 为假命题；∵若过a 的平面α⊥b,则b 垂直α内的直线a ，从而a ⊥b ，那么限制a,b 必须垂直，而条件中没有指明a 、b 是否垂直.例3 α和β是两个不重合的平面，在下列条件中可以判定平面α∥β的是( )A.α、β都垂直于平面γB.α内不共线的三点到β的距离相等C.l 、m 是α内的直线，且l ∥β，m ∥βD.l 、m 是两条异面直线，且l ∥α,l ∥β,m ∥α,m ∥β解显然B 、C 不能推出α∥β，有α、β相交的情况存在，对于A 、D ，学了“面面垂直”后，就可以说明A 不能推出α∥β，α、β有相交的可能，从而选D.事实上，l ∥α，m ∥α，在α内任取一点A ，过A 作l ′∥l ，m ′∥m,因为l,m 异面，所以l ′,m ′相交，则可推出l ′∥β，m ′∥β.由面面平行的判定定理可推出α∥β.本周强化练习：【同步达纲练习】一、选择题1.一直线平行于两个平行平面中的一个，必与另一个( )A.平行B.相交C.平行或相交D.平行或在平面内2.平行于同一个平面的两个平面( )A.平行B.平行或者重合C.有可能相交D.以上都不对3.若平面α∥β，a α，b β，则a 与b( )A.平行B.异面C.平行或异面D.以上都不对4.两个平面都与二条直线平行，则这两个平面( )A.平行B.平行或相交C.相交D.以上都不对5.若平面α与两异面直线所成角相等，平面β与它们所成的角也相等，则α与β( )A.平行B.平行或相交C.相交D.以上都不对6.若a 、b 为异面直线，P 为空间一点，过P( )A.必可作一个平面与a 、b 都平行B.最多可作一个平面与a 、b 都平行C.可作一个平面与a 、b 都垂直D.可作一个平面与a 、b 都成定角α(0＜α＜2π)7.若空间三个不同的平面两两相交，则( )A.不可能只有两条交线B.必定相交于一点C.必定相交于一条直线D.必相交于三条平行直线8.下列命题中正确的是( )A.过平面外一点平行于此平面的直线在同一平面内B.平行于同一个平面的两条直线平行C.直线在平面外就是直线与平面没有交点D.空间两个平面不平行便垂直9.使平面α和平面β平行的条件是( )A.平面α内有无穷多条直线都与平面β平行B.直线a ∥α,a ∥β，且直线a 不在平面α内也不在平面β内C.直线a ⊂α直线b ⊂β，且a ∥β，b ∥βD.平面M 内的任何直线都与平面N 平行10.已知平面α∥平面β，P 是α、β外一点，过P 点的两条直线PAC 、PBD 分别交α于A 、B ，交β于C 、D ，且PA ＝6，AC ＝9，AB ＝8，则CD 的长为( )A.20B.4C.12D.20或411.a、b为互不垂直的两异面直线，过a、b分别作平面α、β，那么下列四种情形中：①b∥α;②b⊥α；③α∥β;④α⊥β，不可能出现的情形有( )A.1种B.2种C.3种D.4种12.已知AB、CD是夹在两平行平面α、β间的两条线段，AB⊥CD，｜AB｜＝2，AB与平面α成30°的角，则线段CD的长度范围是( )A.(332，23) B.［332,+∞］C.(1，332) D.［1,+∞)二、填空题1.若直线l与平面α，β所成的角均为θ，则α与β .2.若直线a∥直线b,a⊂α，b⊂β，则平面α与β .3.若平面α∩平面β＝1，A∈1,B∈1,AC⊂α，BD⊂β，则AC，BD .4.夹在两个互相平行的平面间有一条长4cm的垂线和一条长6cm的斜线，在每一个平面内，这两线段端点的距离都是3cm，则这垂线中点到斜线中点的距离是 .5.已知平面α∥平面β，在α内取四个点，在β内取三个点，这七个点最多可以确定_______个与α和β都相交的平面.三、解答题1.两条直线与两个平行平面相交，求证夹在两平行平面间的两条线段的中点的连线与两个平面平行.2.在正方体ABCD—A1B1C1D1中，M、N、P分别是C1C，B1C1，C1D1的中点，求证：(1)AP⊥MN；(2)平面MNP∥平面A1BD.【素质优化训练】1.如图，空间折线ABCD的各段分别交两个平行平面α，β于点M、M′、N、N′、P、P′，已知｜BN′｜＝16,｜CN｜＝9,｜MN′｜＝12,SΔMNP＝72.求SΔM′N′P′的值是多少?2.已知平面α∥平面β，AB、CD为夹在平面α、β之间的线段，并且AB+CD＝342.AB、CD在β内的射影分别为78，36.求平面α，β之间的距离.3.在棱长为a的正方体ABCD—A1B1C1D1中，E、F、G、M、N、Q分别为棱A1A，A1B1，A1D1，CB，CC1，CD的中点.求证：平面EFG∥平面MNQ.4.试证明：平行且相等的三条线段，如果不在同一平面内，那么它们对应端点所在的两个平面平行.5.以空间一点O为中点作三条不共面线段，AA1、BB1、CC1，求证：平面ABC∥平面A1B1C1.6.两条异面直线AC，DF，依次与三个平行平面α、β、r相交于A、B、C和D、E、F，又AF，CD与平面β的交点为G，H，求证：HEGB为平行四边形.7.夹在两个平行平面α、β间有一条长8cm的垂线段AB和一条长12cm的斜线段CD，其中A、B为垂足，C、D为斜足，若AC＝BD＝6cm，E为AB中点，F为CD中点，求EF的长度.【生活实际运用】长方体AC1容器内注入一定数量的水以后，把容器底面一边BC置于水平桌面上，再将容器倾斜，当水面与长方形的四条侧棱分别交于E、F、G、H四点时(如图所示)，随着倾斜角度的变化，如下四个命题：①水的部分ABCDEFGH始终是直棱柱；②水面EFGH始终与棱A1D1平行；③水面EFGH的面积始终保持不变；④AE+BF始终不变其中正确的命题是( )A.①②B.①③C.①②③D.①②④提示：水平EFGH始终平行水平桌面，EH∥AD∥GF.从而②正确.AD⊥面A1B，从而①正确，因为水的体积未变，把面ABFE当作底面，高AD没发生改变，从而ABFE的面积没有变，则AE+BF始终不变，从而④正确，由S射＝S·cosθ知，随着角度的变化，而EFGH的射影面积始终是ABCD，所以EFGH的面积在发生变化，从而③不正确.∴应选D.【知识验证实验】小明到他父亲的木工房，看到一个如图所示，棱长为50cm的立方体工件，从立方体的前、后、左、右、上、下看，都有两个相通的正方形孔，请你算一算这个立体剩下的体积是多少?解若没有孔的话，体积应为503＝125000(cm 3)，现在前后、左右、上下有6个“通孔”，每一个体积为10×10×50＝5000(cm)3，还应当看到任一“通孔”与另外两个“通孔”有交叉部分，这样共有6个交叉部分，每个部分体积为10×10×10＝1000(cm 3)，所以，所求体积为503-6×5000+6×103＝101000(cm 3).【知识探究学习】已知长方体ABCD —A 1B 1C 1D 1中：(1)若AB ＝5，AA 1＝4，AD ＝3.试求在长方体表面上从A 到C 1的最短路线.(2)若AB ＝a,AA 1＝b,AD ＝c ，且a ＞b ＞c ，试求长方体表面上从A 到C 1的最短距离.解 (1)将有关平面折直.(i)沿表面经过A 1D 1(或BC)到C 1点：AC 1＝212DC AD +＝22)54(3++＝90(ii)沿表面经过A 1B 1(或DC)到C 1点AC 1＝212BC AB +＝22)43(5++＝74(iii)沿表面经过B 1B(或DD 1)到C 1点AC 1＝212CC AC +＝224)35(++＝80从而，从A 经A 1B 1(或CD)到C 1距离最短，从而最短距离为74(2)由(1)的解及a ＞b ＞c 可知：22)(c b a ++＜22)(c a b ++＜22)(b a c ++即从A 点经过A 1B 1(或CD)到达C 1的路线最短. 其最短长度为22)(c b a ++参考答案【同步达纲练习】1.D2.A3.C4.B5.B6.B7.A8.A9.D 10.D 11.B 12.B二、1.若θ＝2π时，α∥β，若θ≠2π时，α、β平行或相交. 2.平行或相交.3.异面4.2cm5.30三、1.提示：分两种情况考虑.(i)当两直线共面时，可利用面面平行的性质定理进行证明；(ii)当两直线异面时，可利用面面平行的判定定理证明.(可参考课本难题解答第4题)2.(1)提示：AP 在平面BC 1内的射影BC 1⊥MN.∴AP ⊥MN(2)利用面面平行的判定定理.【素质优化训练】1.962.1603.略4.略5.略6.提示：连结AD ，证明BH ∥GE.7.4cm。

平面与平面平行的判定定理

平面与平面平行的判定一、学习内容分析本节课选自《普通高中标准实验教科书—数学必修二》（人教版）第二章点、直线、平面之间的位置关系第二节直线、平面平行的判定及其性质，主要研究平面与平面平行的判定方法。

根据课标要求和学生情况，本节课分为四个课时，今天学习第二课时。

本节课是建立在学习空间中直线与直线、直线与平面位置关系基础上的一节课，并为后续学习平面与平面平行性质奠定基础。

教材首先通过观察三角板所在平面与桌面位置关系引入课题，然后将两个平面平行的问题转化为一个平面内的直线与另一个平面平行的问题，体现数学中的转化思想。

接着根据两个平面中直线的关系探究两个平面的位置关系，体现分类讨论思想，培养了学生自主探究的能力。

二、学习者分析（1）从已有知识来看，学生已经学习了空间点、直线、平面之间的位置关系，掌握了直线与平面平行的判定定理；（2）从已有经验来看，学生已经掌握了分类讨论、转化的思想；（3）从已有能力来看，学生已经具有了自主探索、简单的空间想象能力。

但对于高二学生来说，他们初次接触空间立体几何，对于空间的部分问题仍有较大困惑，空间想象能力还不是很强。

三、教学目标（1）知识与技能目标：①通过直观感知，操作确认，归纳出平面与平面平行的判定定理；②理解并掌握两平面平行的判定方法；③能够运用两个平面平行的判定方法解决相关问题。

（2）过程与方法目标：①通过观察相关模型以及实物，培养分析、归纳的能力；②在探究平面与平面平行判定定理的过程中，体会分类讨论、转化的思想。

（3）情感、态度与价值观目标：在发现中学习，提高学习数学的积极性，培养主动探究、合作交流的意识四、教学重难点（1）教学重点：两个平面平行的判定；（2）教学难点：探究平面与平面平行的判定定理以及应用判定定理解决相关问题。

五、教学过程（一）复习旧知，导入新课问题一：①平面几何中，判定两直线平行有哪几种方法？②直线与平面平行有哪些方法？③平面与平面有哪些位置关系？师生活动：教师提出问题，引导学生进行回答。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

A
E B
H
D F
Hale Waihona Puke G CF2、a ,b ,则a、b一定异面；
F
3、a与b是异面直线，b与c是异面直线，则a与c是异面直线； F
4、a与b是共面，b与c是共面，则a与c共面
F
练习2：正方体ABCD－A1B1C1D1
1、与A1A是异面的有:
BC DC
B1C1
D1C1
D1 A1
D
2、与D1B异面的有： AA1 AD A1B1 B1C1
人教版必修二
第二章点、直线、平面之间的位置关系 2.1.2空间中直线与直线之间的位置关系
陈基耿
问题：平面几何中，两条直线的位置关系：平行或相交
在空间中是否还是如此呢？
在正方体A1B1C1D1-ABCD中，说出下列各对线段的位置关系
（1）AB和C1D1；（2）A1C1和AC；（3）A1C和D1B：（4）AB和CC1；（5）BD1和A1C1；
D1 A1
D A
C1 B1
C B
异面直线：不同在任何一个平面内的两条直线。（即既不平行也不相交）
异面直线的画法： b
α
a
b a
α
a
1、平行
b
共面 2、相交
a
b A α
3、异面
a
A
b
α
没有公共点
有且只有一个公共点
ab A
没有公共点
练习1：判断下列说法的对错
1、分别在两个平面内的两条直线一定是异面直线；
强化安全责任意识守住食品安全底线：https:///news/detail/n1438520.htm
体马飞凌空翻七百二十度外加呆转九百周的震撼招式。紧接着扁圆的如同天边小丘一样的蒜瓣鼻子顿时狂舞收缩起来……无忧无虑的快乐下巴透出水青色的阵阵晚雾……时常露出欢快光彩的眼睛透出亮橙色的朦胧异音。最后转起憨直贪玩的圆脑袋一颤，变态地从里面喷出一道神光，她抓住神光明丽地一摆，一套亮晶晶、亮光光的兵器¤飞轮切月斧→便显露出来，只见这个这件宝器儿，一边抽动，一边发出“咝咝”的余音……。骤然间壮扭公主闪电般地让自己有着巨大爆发力的强劲肚子窜出水青色的邮票声，只见她睡意朦胧、但却时常露出欢快光彩的眼睛中，猛然抖出五十组摇舞着¤天虹娃娃笔→的嘴唇状的饭盒，随着壮扭公主的抖动，嘴唇状的饭盒像火锅一样在双腿上典雅地设计出点点光幕……紧接着壮扭公主又摆起特像两排闸门一样的牙齿，只见她跳动的犹如神盔模样的棕褐色短发中，狂傲地流出四十串旋舞着¤天虹娃娃笔→的熏鹅状的怪蛇，随着壮扭公主的摆动，熏鹅状的怪蛇像面条一样，朝着琳可奥基官员淡黄色馅饼模样的胸部斜转过去。紧跟着壮扭公主也疯耍着兵器像油珠般的怪影一样向琳可奥基官员斜转过去随着两条怪异光影的瞬间碰撞，半空顿时出现一道紫红色的闪光，地面变成了水白色、景物变成了墨黑色、天空变成了暗黑色、四周发出了粗野的巨响！壮扭公主结实丰满的胸部受到震颤，但精神感觉很爽！再看琳可奥基官员高大的眼睛，此时正惨碎成灌木丛样的墨灰色飞烟，加速射向远方，琳可奥基官员怒哮着音速般地跳出界外，狂速将高大的眼睛复原，但已无力再战，只好落荒而逃！女打手腾霓玛娅婆婆忽然晃动破烂的脚一哼，露出一副神秘的神色，接着颤动肥大的胡须，像暗绿色的万肚海滩虾般的一闪，时尚的古怪的手掌忽然伸长了九十倍，多变的亮黄色石塔式样的护腕也瞬间膨胀了九十倍。接着粗犷的墨黑色谷堆一般的脖子瞬间闪烁抽动起来……极似气桶造型的肩膀穿出米黄色的朦胧冰云……水蓝色莲花造型的手掌露出钢灰色的阵阵了一个，扭体象舞侧空翻三百六十度外加陀螺转两百周的荒凉招式……最后甩起柔软的极似布条造型的手臂一抛，猛然从里面窜出一道金辉，她抓住金辉梦幻地一耍，一样森幽幽、紫溜溜的法宝『绿鸟浪精油饼袋』便显露出来，只见这个这件怪物儿，一边蠕动，一边发出“哧哧”的怪响…………突然间女打手腾霓玛娅婆婆疯鬼般地玩了一个倒立收缩嗥地灯的怪异把戏，，只见她青远山色陀螺形态的奇发中，狂傲地流出四十道山庄铁脖蝎状的驴肾，随着女打手腾霓
A CC1 CD
C1 B1
C B
同一平面内，平行于第三条直线的两条直线互相平行
公理4 平行于同一条直线的两条直线互相平行
D1 A1
C1 B1
D A
C B
空间四边形ABCD中，E，F，G，H分别是AB，BC，CD ，DA 的中点。求证，四边形EFGH是平行四边形.
证明：连接BD，因为 EH是△ABD的中位线，所以 EH//BD，且EH＝1/2BD. 同理，FG//BD，且FG＝1/2BD. 所以 EH//FG，且EH＝FG. 所以，四边形EFGH是平行四边形.