回转体相贯线的投影
回旋体表面相贯线的画法.

例 2:圆柱与圆锥相贯,求其相贯线的投影。
●
●
●
P
●
假想用水平面P截切立体,P面与圆柱 体的截交线为两条直线,与圆锥面的交线 为圆,圆与两直线的交点即为交线上的点。
例 2:圆柱与圆锥相贯,求其相贯线的投影。
● ●
● ●
●
●
●
●
●
●
●
●
●
解题步骤:
★ 求特殊点 ★ 用辅助平面法求
中间点 ★ 光滑连接各点
例4:求俯视图
●
●
●
●
●
●
● ●●
●
●●
●● ●
●
●●
例4:求俯视图
●
1
●
例3:补全主视图
三面共点
●
●
●
作图时要抓住 一个关键点,相贯 线汇交于这一点。
五、不完全形体相交
小结
一、本章的基本内容
⒈ 立体表面相贯线的概念
相贯线的性质:表面性 共有性 封闭性
⒉ 求相贯线的基本方法
利用积聚性面上找点法,辅助平面法,辅助球面法
二、解题过程
⒈ 交线分析
⑴ 空间分析: 分析相交两立体的表面形状, 形体大小及相
2.相贯线的主要性质
★ 表面性
相贯线位于两立体的表面上。
★ 封闭性
相贯线一般是封闭的空间折线(通 常由直线和曲线组成)或空间曲线。
★ 共有性
相贯线是两立体表面的共有线。
其作图实质是找出相贯的两立 体表面的若干共有点的投影。
7.2 平面体与回转体相贯
1.相贯线的性质
相贯线是由若干段平面曲 线(或直线)所组成的空间折 线,每一段是平面体的棱面与 回转体表面的交线。
3-3、 回转体相贯线
画立体投影图,应 画出所有表面交线 (相贯线)的投影
两内表面相交 的相贯线
内外表面相交 的相贯线
例3 两圆筒正交相贯(共有四条相贯线)
选择该物体正确的侧面投影小 Nhomakorabea试三、特殊相贯线
1、两回转面共轴相贯
相贯线为圆(二者共有的纬圆)
共轴相贯的其它实例(一)
过圆球球心钻一个圆孔
● ●
相切处无线
1 2
3 4
本节内容结束
适用于:辅助平面与两个回转面的交线是直线或圆
辅助球面法
利用辅助球面与两个回转面的交线投影求解相贯线。
适用于:两回转面轴线平行于某一投影面且相交
例2 完成两正交圆柱面交线的投影
交线分析 投影分析 投影作图
交线总是弯向直径大的圆柱的轴线
几何性质、相对位置相同,相对大小不同产生交线形状不同
例2 求两圆柱体的交线
表面取点法
讨论
圆柱变成圆柱筒将如何?
有虚线
无线
内表面为四棱柱孔
交线不变
分别求四棱柱孔与圆柱 外表面、内表面的交线
归纳
相交形式
外表面与外表面相交 外表面与内表面相交 内表面与内表面相交
交线相同 求交线的实质相同 求交线的方法相同
需解决 的问题
如何画出下列立体的投影图?
一、两回转面相贯线的性质
共有性 相贯线是两相交表面的共有线(所有共有点的轨迹)。
例4 多形体相交
2
3
有虚线
3
2
a'
c'
e' b'(f')
(c") a"
f"
e" b"
第3章 回转体的三视图及表面交线

R
3.3.3 相贯线的特殊情况 3.3.3.1 相贯线为圆 当两个具有公共轴线的回转体相贯时,相贯线为垂直于轴线的 圆,该圆在平行于轴线的投影面上的投影积聚为直线,在垂直 于轴线的投影面上的投影反映实形。
3.3.3.2 相贯线为椭圆
当两圆柱(或圆孔)直径相等且轴线垂直相交时,相贯线为椭圆, 该椭圆在平行于两圆柱(或圆孔)轴线的投影面上的投影积聚为 直线。
§3-2
回转体的截交线
在很多机械零件的表面,常常会出现一些平面与回转体表 面相交的情况,当平面与回转体表面相交时,在回转体的 表面上形成的交线称为截交线。
3.2.1 截交线的性质和求法
概念:
截切——用一个与立体相
交的平面, 截去立体的一部分。
截平面——用以截切立体的
平面。 截交线——截平面与立体表 面的交线。 截断面——因截平面的截切, 在立体上形成的平面。
图3-12
(1)先把完整圆柱的左视图做出来。 (2)先求出截交线上特殊位置点。 (3)求一般点。 (4)分析求出这些点的可见性, 将求出的各点的侧面投影光 2' c'(d')• 滑地连接起来。 d"• 3'(4') • a'(b') • (5)判断圆柱哪部分被 4"• • b"• 截走了,擦去多余图线, 1' • 将剩余图线描粗整理即 可。 4 b• • •d 1• a• • 3 •2
b' (b) 1 a 2
b"
3.1.4 组合回转体
组合回转体是由若干个基本回转体组成,作图时首先要分析 各部分的曲面性质,区分出各自是什么回转体、轴线的相对位 置,依次分别划出每个回转体的投影即可。
已知在组合回转体表面上有M、N两点的正面投影m'和n', 求M、N水平投影m、n和侧面投影m"、n",并判断可见性。
回转体的投影

C
d”
a’ c’d’ A
X
a
d
C
a”b” c”
b c
Y
圆柱的三面投影图
a’
c’(d’) b’ d’
a”(b”) c’ (1) 先绘出圆柱的对称线、
回转轴线。 (2)绘出圆柱的顶面和底面 。 (3)画出正面转向轮廓线和 侧面转向轮廓线。 Z
圆柱投影图的绘制:
a’
c’(d’) d
b’d’
a”(b”)
c’
1.求特殊位置点 2.求一般位置点 3.判断可见性,光滑
连接各点 4.整理图线,完成图形
例:已知联轴节的正投影和水平投影,求侧面投影。 联轴节的主体是圆筒,其上端用两个左、右对称并平行于轴线的 侧平面P及垂直于轴线的水平面Q截切。其下端用两个左、右对称并 平行于轴线的侧平面S及垂直于轴线的水平面R截切。
回转体的投影
二、曲面立体的投影及表面取点
回转体由回转面或回转面与平面围成。回转面是由母线(直线或 曲线)绕某一轴线旋转而形成的。常见的回转体有: 圆柱 转向轮 廓线
圆锥
圆球
圆环
素线
纬线
母线的任一位置称为素线,母线上各点的运动轨迹都是垂直于轴 线的圆,称为纬线或纬圆。根据这一性质可在回转面上作素线、纬线 取点。 回转面上的转向轮廓素线,就是在某一投影方向观察曲面立体时 可见与不可见部分的分界素线。
圆柱表面由圆柱 面和顶面、底面所组 成。圆柱面是由一直 母线绕与之平行的轴 线回转而成。
Z
b’ c’d’ V a’ D A d” a”b” B c” W
如图所示,圆柱 的轴线垂直于H面, 其上下底圆为水平面 ,水平投影反映实形 ,其正面和侧面投影 重影为一直线。而圆 柱面则用曲面投影的 转向轮廓线表示。
两回转体表面的交线—相贯线
辅助平面法
作图分析: 在适当位置作一辅助平面截切 两相交立体,便会在两立体的表 面上产生截交线。因两截交线共 面,其交点便为两立体表面的共 有点,即为相贯线上的点。 按此方法作出若干辅助平面便 可得到相贯线上的一系列点,依 次连接各点就可作出相贯线的投 影。
三、相贯线的特殊情况 一般情况下相贯线为封闭的空间曲线,而特殊情况的相 贯线则为平面曲线或直线。 图中两圆柱轴线相交并与V面平行,故相贯线为垂直于V 面的两椭圆。即主视图中两相交直线。
相贯线的特殊情况
两曲面立体相交,一般情况下相贯线为空间曲线, 但特殊情况下可能是平面曲线或直线。
2.两同轴回转体的相贯线是垂直于轴线的圆。 图中圆球与圆柱同轴且轴线平行于V面,
2’,(4’)
3’
4 (4;
d" b"
QW
4"
2"
PW
c"
a"
RW
3"
注:圆柱与球相贯
当圆球与圆柱同轴且轴线平行于V面, 则相贯线圆在V面上的投影积聚为直线。
如是圆球开孔,相贯线同前面分析相同。 圆球与圆锥相交,其相贯线同前 面分析的情况相同。
例、求圆柱与半球相贯线主俯视图
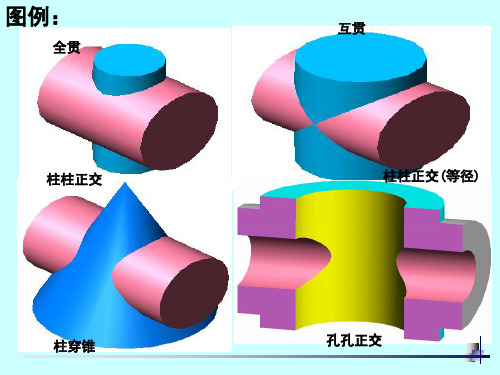
图例:
全贯 柱柱正交
柱穿锥
互贯 柱柱正交(等径)
孔孔正交
1.相贯线的主要性质
★ 表面性
相贯线位于两立体的表面上。
★ 封闭性
相贯线一般是封闭的空间折线(通常 由直线和曲线组成)或空间曲线。
回转体轴线相交且表面内切于公共球的相贯线
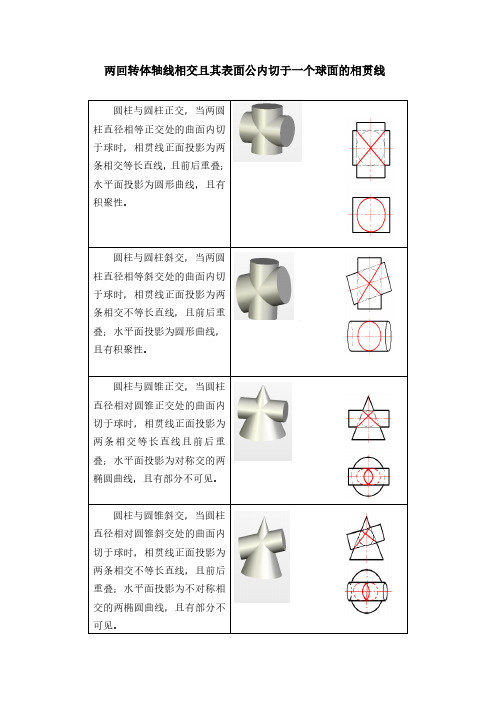
两回转体轴线相交且其表面公内切于一个球面的相贯线
圆柱与圆柱斜交,当两圆
柱直径相等斜交处的曲面内切
于球时,相贯线正面投影为两
条相交不等长直线,且前后重
叠;水平面投影为圆形曲线,
圆柱与圆锥正交,当圆柱
直径相对圆锥正交处的曲面内
切于球时,相贯线正面投影为
两条相交等长直线且前后重
叠;水平面投影为对称交的两
圆柱与圆锥斜交,当圆柱
直径相对圆锥斜交处的曲面内
切于球时,相贯线正面投影为
两条相交不等长直线,且前后
重叠;水平面投影为不对称相
交的两椭圆曲线,且有部分不。
03 - 回转体相贯线

求解思路
轴线垂直于投影面的圆柱 面,其投影具有积聚性。 相贯线是相交两者共有线, 所以柱面积聚性等于相贯 线的一面投影已知。
求相贯线的其余投影,实 质就是根据这一已知投影 在另一回转面的表面取点。
例1 完成圆锥面与圆柱面交线的投影
例2 完成圆柱面与圆柱面交线的投影
分析: 根据圆柱面积聚性, 相贯线的水平投影 和侧面投影已知。 只需求作其正面投影
ห้องสมุดไป่ตู้
侧平半圆
水平圆
两内孔的 相贯线
两个正垂椭圆
空间形状?
水平孔与柱 面的相贯线
空间曲线
例2 完成多形体相贯立体的投影(答案)
多形体相贯的其它实例(一)
多形体相贯的其它实例(二)
本节内容结束
该相贯线既在球面 上,也在锥面上。
相贯线是直线
封闭空间曲线
相贯线的形状取决相交两者的几何性质、相对大小、相对位置
几何性质、相对位置相同,相对大小不同产生交线形状不同
几何性质、相对大小相同,但相对位置不同产生交线形状不同
二、两回转面相贯线的求法
利用圆柱面的积聚性求解相贯线。
适用于:两回转面之一为圆柱面,且该柱面与投影面垂直
§4-5
需解决 的问题
回转面与回转体相交
如何画出下列回转体的投影图?
两立体相交称为相贯,两立体表面的交线称为相贯线。 常见的立体相贯分为三种:
a. 平面立体与平面立体相贯
用平面体截交线知识求解
b. 平面立体与曲面立体(回转体)相贯
用回转体截交线知识求解
c. 曲面立体(回转体)与曲面立体(回转体)相贯
3、相贯线为直线
两圆柱面轴线平行相贯
两圆锥面共锥顶相贯
四、多形体相贯
两回转体相贯线的投影作图

两回转体相贯线的投影作图山东电子职业技术学院教案第十讲两回转体相贯线的投影作图计划课程名称机械制图与CAD 2 课时教学课题两回转体相贯线的投影作图两回转体相交~最常见的是圆柱与圆柱相交~圆锥与圆柱相交及圆柱课前思考与圆球相交~其相交线为相贯线~相贯线的形状取决于两回转体各自的形状、大小和相对位置。
1. 掌握相贯线的投影特点、相贯线的作图方法教学目标2. 相贯线的特殊情况教学重点相贯线投影图的画法教学难点求相贯线的作图方法、圆柱体与圆锥体相交教学方法通过课件多媒体教学和在黑板上画图讲解相结合本讲主题两回转体相贯线的投影作图1. 圆柱与圆柱相交2. 圆锥与圆柱相交3. 相贯线的特殊情况山东电子职业技术学院教案3.4 两回转体相贯线的投影作图一、相贯线1.定义:两回转体表面的交线称为相贯线,如图3-18所示。
2.相贯线的一般性质如下:(1) 相贯线是两回转体表面的共有线,也是两相交立体的分界线。
相贯线上的所有点都是两回转体表面的共有点。
(2) 由于立体的表面是封闭的,因此相贯线在一般情况下是封闭的线框。
(3) 相贯线的形状决定于回转体的形状、大小以及两回转体之间的相对位置。
作图时,首先作出相贯线上一些特殊点的投影,如回转体投影的转向轮廓线上的点。
对称的相贯线在其对称面上的点,以及最高、最低、最左、最右、最前、最后这些确定相贯线形状和范围的点,然后再求作一般点,从而作出相贯线的投影,最后连接各点的同面投影。
要注意的是一段相贯线只有同时位于两个立体的可见表面上时,这段相贯线才是可见的。
具体作图采用两种方法。
二、表面取点法两回转体相交,如果其中有一个是轴线垂直于投影面的圆柱,则相贯线在该投影面上的投影就积聚在圆柱面的积聚投影圆周上。
这样就可以在相贯线上取一些点,按回转体表面取点的方法作出相贯线的其他投影,如图3-17所示。
例 1 如图3—17所示(已知两圆柱的三面投影,求作它们的相贯线。
山东电子职业技术学院教案三、辅助平面法求两回转体相贯线比较普遍的方法是辅助平面法。
第3章 回转体的三视图及表面交线

3.1 回转体的投影及其表面取点
3.2 回转体的截交线
3.3 回转体的相贯线 本章小节
§3-1回转体的投影及其表面取点
常见的回转体
回转体——一动线绕一定直线旋转而成的曲面,称为回
转面。由回转面或回转面与平面所围成的立体称为回转体。
3.1.1 圆柱体
3.1.1.1 圆柱体的形成
圆的正面投1'2',然
s
k
后作出水平投影k在此 圆周上,由k' 求出k,
最后求出k"。
3.1.3 圆球
3.1.3.1 圆球面的形成 • 球是圆母线绕其直径回转轴旋转而成的。 • 球的三面投影均为圆,且与球的直径相等。
例:已知A、B两点在球面上,并知a和b‘的投影,求A、B两 点的另两个投影。 解: 利用辅助纬圆作图。 a' (a") 作图:过a作直线∥OX得水平 投影12,正面投影为直径为 12的圆,a'必在此圆周上。 因a可见,位于上半球,求得 a',由a、a' 求出a",因a 在右半球,所以a"不可见。 因为b'处于正面投影外形轮 廓线上,可由b'直接求得b、 b"。
图3-13 开槽圆柱的三视图
5'(6') 6" • • 1'(2') • 2" • • • 3'(4') 4"
•
5"
• • 1" 3"
2
• •64
• • 5 1 3
完成后的投影图
3.2.2.1 圆锥体的截交线
根据截平面与圆锥轴线的相对位置不同,圆锥的截交线有圆、椭圆、抛物线 与直线围成的平面图形、双曲线与直线围成的平面图形和三角形五种,见表 3-2。
第五章 回转体表面相贯线画法

第五章回转体表面相贯线画法平面体与回转体相贯回转体与回转体相贯多体相贯概述1.相贯的形式两立体相交叫作相贯,其表面产生的交线叫做相贯线。
本章主要讨论常用不同立体相交时其表面相贯线的投影特性及画法。
2.相贯线的主要性质★表面性相贯线位于两立体的表面上。
★封闭性相贯线一般是封闭的空间折线(通常由直线和曲线组成)或空间曲线。
★共有性相贯线是两立体表面的共有线。
其作图实质是找出相贯的两立体表面的若干共有点的投影。
平面体与回转体相贯1.相贯线的性质相贯线是由若干段平面曲线(或直线)所组成的空间折线,每一段是平面体的棱面与回转体表面的交线。
2.作图方法求交线的实质是求各棱面与回转面的截交线。
∙分析各棱面与回转体表面的相对位置,从而确定交线的形状。
∙求出各棱面与回转体表面的截交线。
∙连接各段交线,并判断可见性。
空间分析:四棱柱的四个棱面分别与圆柱面相交,前后两棱面与圆柱轴线平行,截交线为两段直线;左右两棱面与圆柱轴线垂直,截交线为两段圆弧。
投影分析:由于相贯线是两立体表面的共有线,所以相贯线的侧面投影积聚在一段圆弧上,水平投影积聚在矩形上。
例2:求作主视图例2:求作主视图1. 相贯线的性质相贯线一般为光滑封闭的空间曲线,它是两回转体表面的共有线。
回转体与回转体相贯2.作图方法∙利用投影的积聚性直接找点。
∙用辅助平面法。
∙先找特殊点。
⒊作图过程∙补充中间点。
确定交线的弯曲趋势确定交线的范围例1 :圆柱与圆柱相贯,求其相贯线。
●●●●●●●●●空间及投影分析:小圆柱轴线垂直于H面,水平投影积聚为圆,根据相贯线的共有性,相贯线的水平投影即为该圆。
大圆柱轴线垂直于W面,侧面投影积聚为圆,相贯线的侧面投影在该圆上。
求相贯线的投影:利用积聚性,采用表面取点法。
☆找特殊点☆补充中间点☆光滑连接当圆柱直径变化时,相贯线的变化趋势。
交线向大圆柱一侧弯交线为两条平面曲线(椭圆)●●●●●●●●●●●●●●●●●●●★外形交线◆两外表面相贯◆一内表面和一外表面相贯★内形交线◆两内表面相贯无轮是两外表面相贯,还是一内表面和一外表面相贯,或者两内表面相贯,求相贯线的方法和思路是一样的。
CHAPTER8-两回转体表面相交-相贯线

正 交
2 大圆柱
交线
擦除多余的作图线后的结 果
[例题十五] 补全图中所缺的交线 作图步骤 形体分析
1. 求小圆柱与圆台的交线; 该模型由两个圆
PV
PW
2. 求两圆柱的交线。 。其中大圆柱与圆
台同轴,小圆柱与 圆台的轴线垂直。
柱和一个圆台组成
y
圆台
圆柱
y
圆柱
擦除多余的作图线后的结 果
[例题] 补全图中所缺的交线
★ 求特殊点 ★ 用辅助平面 法求中间点 ★ 光滑连接各点, 注意投影的可见性
求解方法 辅助平面法
★ 补全轮廓线 的投影
小
重点掌握:
结
★ 截交线的特点,求截交线的方法与步骤。 ★ 平面与平面体截交线的画法。 ★ 平面与圆柱的截交线的画法。
习
题
P25 P26:7,9 P27; P28;5,6,8,9
例题补全视图形体分析分析组成模型的基本几何形体及其相互位置关系判断哪些表面之间圆柱和与之相切的平面立体求大小两圆柱的交线224多形体表面相交和不完整形体表面相交擦除多余的作图线后的结形体分析该模型由两个圆柱和一个圆台组成
2.2.3 两回转体表面相交
两立体相交叫作相贯,其表面产生的交线叫做相贯线。 本章主要讨论立体相交时其表面相贯线的投影特性及画法。
2.2.4 多形体表面相交和不完整形体表面相交
[例题] 补全视图
作图步骤 形体分析
1. 画出基本体的投影 分析组成模型 2. 的基本几何形体及 求大圆柱与形体3的交线
其相互位置关系, 判断哪些表面之间 4. 有交线,并分析交 求大小两圆柱的交线 线趋势。
1 小圆柱
3. 求形体3与小圆柱的交线
3 圆柱和与 之相切的平 面立体
两回转体表面的交线—相贯线

可编辑ppt
10
第四章 第三节 两回转体表面的交线—相贯线
例:求圆柱与圆台的相贯线。
注 意:在连接各点时,应注意判别相贯线的可 见性,只有两相交立体都可见表面上的相贯线才 可见。
作图步骤:
可编辑ppt
11
第四章 第三节 两回转体表面的交线—相贯线
例2:求圆台与半球的相贯线。
作图分析: 由于两立体的三个投影都没有积聚性,故需补出相贯线的三面 投影。 可过圆台轴线作一侧平面辅助面求得两特殊点,另作一水平面 辅助面求得相贯线的中间点。
两相交圆柱相贯线的常见情况:
在生产实际中,两圆柱轴线垂直相交的情况较为常见,其相贯线有 以下三种形式
1.两实心圆柱相交 相贯线为上下对称的两条封闭的空间曲线。
可编辑ppt
6
第四章 第三节 两回转体表面的交线—相贯线
两相交圆柱相贯线的常见情况:
2.圆柱孔与实心圆柱相交
圆柱开孔会在其表面上产生与两圆柱相交形状相同的相贯线, 因形状相同故求作方法也相同。
§4 — 3 两回转体表面的交线—相贯线
一般将相交的立体称为相贯体,而相交立体的表面交线则称为相贯线。
图中显示了几种不同类型的相贯体。
绘制相交立体的投影图一定要掌握相贯线的画法。
可编辑ppt
1
第四章 第三节 两回转体表面的交线—相贯线
相贯线的性质以及求作方法 1.相贯线的性质
虽然相交立体的形状、位置等不尽相同,但相贯线都具有以下两点 共性:
例:完成相贯体的正面投影和侧面投影。
作图步骤:
可编辑ppt
21
第四章 第三节 两回转体表面的交线—相贯线
四、综合相贯
例:完成相贯体的正面投影和侧面投影。 作图分析: 该立体由半球、小圆柱、大圆柱以及长圆形凸台组成。 长圆形凸台与半球和小圆柱左边部分的相贯线为特殊情况,右边 与大小圆柱间的相贯线为空间曲线。并与大圆柱左端面相交产生两条 平行线。
回转体相贯线的投影

轴线相交且平行于同一投影面的圆柱与圆柱、圆柱与圆锥、圆锥与圆锥相交,若它们能共切一个球(等径相贯),则它们的相贯线是 垂直于这个投影面的椭圆 选择辅助平面的原则:一般选用投影面的平行面,并使它与两曲面立体截交线的投影为直素线或圆
轴线相交且平行于同一投影面的圆柱与圆柱、圆柱与圆锥、圆锥与圆锥相交,若它们能共切一个球(等径相贯),则它们的相贯线是 垂直于这个投影面的椭圆 参加相贯的几何体分别是什么形体 利用同时交于(或切于)两曲面立体的辅助平面切割两个立体,两组截交线的交点(或切点),是两曲面立体和辅助平面的三面共点, 即为相贯线上的点。 共顶两圆锥面相交的交线是直线
利用同时交于(或切于)两曲面立体的辅助平面切割两个立体,两组截交线的交点(或切点),是两曲面立体和辅助平面的三面共点, 即为相贯线上的点。
例题3:
工程中常见的两圆柱正贯:
两外表面
内外表面
两内表面
ii. 辅助平面法
• 适用于相贯体中任意两形体相贯的 情况下
• 利用同时交于(或切于)两曲面立 体的辅助平面切割两个立体,两组 截交线的交点(或切点),是两曲 面立体和辅助平面的三面共点,即 为相贯线上的点。用一系列的辅助 平面求出诸多点,依次连接就可求 出相贯线的投影
利用同时交于(或切于)两曲面立体的辅助平面切割两个立体,两组截交线的交点(或切点),是两曲面立体和辅助平面的三面共点, 即为相贯线上的点。
3-3回转体投影
(二)圆锥
1. 圆锥的投影 圆锥表面由圆锥面和底圆组成。它是 一母线绕与它相交的轴线回转而成。 如图所示,圆锥轴线垂直 H面,底面为水平面,它 的水平投影反映实形,正 面和侧面投影由外形线形 成直线。 X
侧面外形线
a s’ V b’ a’ 正面外形线 c’d’ s” S d” Ba” (b”) C b c” W
3 . 球的截交线
平面与球的截交线是圆,圆的直径大小与截平面到 球心的距离有关。截交线圆的投影与截平面对投影 面的相对位置有关。
例 求投影为部分圆弧,侧 面椭圆积聚为直线。
两个侧平面截切圆球,截 交线侧面投影为部分圆弧,水 平投影积聚为直线。
(2)圆环的三视图
(1) 先绘出圆环的 对称线、回转轴线、 母线圆心位置、母线 圆心轨迹。 (2)画正面投影和侧 面投影
(3)
画水平投影
(3)圆环表面取点
给题
圆环表面取点
m'
(n')
( n)
m
圆环表面取点
回转体表面取点、取线
回转体表面取点取线与平面体表面取点取线方法相同
1判断点在立体的哪一个表面 有积聚性,利用积聚性直接求
2 常见回转面
与轴线平行的直 母线绕轴线旋转 形成圆柱面
与轴线相交的直 母线绕轴线旋转 形成圆锥面
圆心在轴线上的 圆弧绕轴线旋转 形成圆球面
轴线
轴线
母线
母线
圆心不在轴线 上的圆弧绕轴 线旋转形成圆 环面
组合线段绕轴 线旋转形成组 合回转面
二、回转体的投影及其表面取点;
(一) 圆柱
圆柱表面由圆柱面和顶面、底 面所组成。圆柱面是由一直母 线绕与之平行的轴线回转而成。
m
(n ) (n )
两回转体相贯线的投影

《两回转体相贯线投影的作图》教案一、知识目标:1.了解相贯线的概念和性质。
2、学会相贯线投影的分析,重点掌握应用表面取点法求作相贯线。
二、能力目标:会画垂直相交两圆柱体的相贯线。
三、素质目标:通过学习相贯线,培养空间的想象能力。
【学习的重点和难点】重点:相贯线的投影分析及基本作图方法。
难点:相贯线的空间分析和想象。
【教学设计及方法】教学中强调相贯线的三个投影,结合具体示例讲解相贯线的画图规律,特别是等直径圆柱相贯的情况。
(讲练发)教学中让学生先看教具、模型,然后将动画和黑板画图结合起来介绍基本概念和作图方法。
(演示法)(归纳法)【课前准备】准备模型、教具,熟悉教学内容和要使用的教学课件。
【课时】1课时【学习过程】(一)复习回顾(5分钟)思考问题:、1、什么是截交线?平面截切立体,在其表面形成的交线称为截交线。
2、截交线的作图步骤?•*求出全部特殊点;•*根据情况求若干一般点;•*光滑地用细线连线;•*判别截交线的可见性;•*修整轮廓线。
导入新课:简述本节内容、要点、作用和地位,导出教学目标。
新课教学:(35分钟)一、观察实物和模型,理解定义相贯线:两回转体相交,在其表面形成的交线称为相贯线。
二、对照模型了解相贯线的性质(1)相贯线一般为闭合的空间曲线,特殊情况为平面曲线或直线。
(2)相贯线是两曲面立体的共有线,也是两曲面立体的分界线;相贯线上的点是两曲面立体的共有点。
根据相贯线的性质,相贯线的画法可归结为求相贯线上一系列共有点的问题。
三、相贯线的作图方法表面取点法:当相交两立体之一表面的投影具有积聚时,相贯线的这面的投影也在积聚性投影上。
可利用表面上取点法作图。
利用曲面的积聚投影法求相贯线例题:求垂直相交两圆柱的相贯线解:分析——两圆柱体轴线垂直相交,其轴线分别为铅垂线和侧垂线,因此小圆柱的水平投影和大圆柱的侧面投影都具有积聚性。
相贯线的水平投影积聚在圆周上,侧面投影积聚于圆周的一部分。
作图步骤:(1)求特殊点 a'、b'是两圆柱表面共有点的正面投影,也是相贯线的最高点、最左点和最右点。
