二进制及其转换教案
二进制及数制转换教学设计

二进制及数制转换教学设计嘿,朋友们,今天我们来聊聊一个神奇又有趣的话题——二进制和数制转换。
听起来是不是有点复杂?别担心!这就像是变魔术一样,只要掌握了窍门,简直就是小菜一碟。
先来个简单的介绍,什么是二进制?顾名思义,二进制就是用“0”和“1”来表示所有的数字,和我们平常用的十进制完全不同。
十进制用的是“0”到“9”的十个数字,听上去是不是像在数糖果一样简单?想象一下,如果你要用二进制来表示数字“5”,那可就得费点脑筋了。
我们用的十进制中,5就是5,但在二进制中,5得写成“101”。
这时候你可能会问,为什么是“101”呢?好吧,我来告诉你。
二进制的每一位从右往左分别是2的0次方、2的1次方、2的2次方…… 所以“101”就可以拆解成1×2的2次方加上0×2的1次方加上1×2的0次方,结果就是4加0加1,哇,没错,就是5!是不是有点像解谜游戏,挺有意思吧?然后呢,很多人一听到转换,就觉得脑袋大了,实际上,转换就是把一种语言换成另一种语言。
比如说,你用英文讲故事,换成中文再讲一遍,听起来不一样,但表达的意思其实是一样的。
对于数制转换也是如此。
你要把十进制的数字换成二进制,就像把英语单词翻成汉字一样简单。
最常用的方法就是不断地除以2,把余数记录下来,直到商为0。
这样得出的余数,从最后到最前,就是你的二进制数。
试试把数字“13”转换一下。
先把13除以2,余数是1,商是6。
再把6除以2,余数是0,商是3。
接着3除以2,余数是1,商是1。
最后1除以2,余数是1,商是0。
把余数倒过来排列,得到了“1101”。
有没有觉得像在做一场数字的过山车?说到这里,可能有人会问,二进制有什么用呢?哎,别说,这个问题可有意思了!二进制在我们生活中随处可见,尤其在计算机和电子产品中,几乎所有的东西都是用二进制来运算的。
想想你每天用的手机、电脑,里面的每一个程序、每一张图片、每一段音乐,都是通过二进制来表示的。
二进制及其转换教案

业
学习指导P2-3巩固练习
巩固
新
课
相关概念:
1.十进制:用0、1、2、3、4、5、6、7、8、9这十个数码符号放到相应的位置来表示数的一种方法。如56365
2.数位:数码符号在数中的位置
3.基数:每个数位上可以使用的数码符号的个数。十进制的每一个数位都可以用十个数码符号。
4.位权数:每个数位所代表的数。十进制的进位规则为“逢10进位1”,位权数如下:
第11章逻辑代数初步
11.1二进制及其转换
【教学目标】
l、了解二进制的含义;
2、会进行二进制与十进制之间的相互转换;
【教学重点】
掌握二进制的含义
【教学难点】
会进行二进制与十进制之间的相互转换
【教学方法】
这节课主要采用探究教学和讲授法结合的教学方法,运用二进制的含义,会进行二进制与十进制之间的相互转换,使学生容易理解,同时结合习题让学生加深对逻辑运算的理解。
二进制与十进制的相互转化:
1.二进制化成十进制
2.十进制化成二进制
讲述法
举例说明
启发
观察
引导
学生练习
教师巡视
知
识
拓
展
问题解决
例1写出下列各数的按权展开式
例2将下列二进制数转换成十进制数
例3将下列十进制数转换成二进制数
引导学生小组
合作交流。
小
结
会进行十进制和二进制的相互转化。
师生合作。
梳理总结也可针对学生薄弱或易错处进行。
2、二进制的基数是?每个数位上的数码个数是?数码分别是?进位规则是?
我们目前所接触的数都是十进制,它是用0、1、2、3、4、5、6、7、8、9这十个数码符号来表示的,今天我们来学习另一种常见的表示数的方法——二进制
2024版高中信息技术《二进制与数制转换》教案

编程实现其他数制间转换
1 2
二进制与十六进制的转换 将二进制数每4位一组进行分组,然后将每组二 进制数转换为对应的十六进制数即可。
二进制与八进制的转换 将二进制数每3位一组进行分组,然后将每组二 进制数转换为对应的八进制数即可。
3
十进制与其他数制的转换 可以采用类似于二进制与十进制转换的方法,通 过除基取余法将十进制数转换为其他数制数。
数据安全传输
利用数制转换技术可以对传输的数据进行加密和校验处理,以确 保数据在传输过程中的安全性和完整性。
06
课堂互动环节
学生自主编程实践
编程实现二进制与十进制之间的转换
学生可以使用Python等编程语言,编写程序实现二进制与十进制之间的转换,通过实践加深 对数制转换的理解。
编程实现不同数制间的转换
图像增强
利用数制转换技术可以对图像数据 进行变换和处理,以提高图像的质 量和清晰度,改善图像的视觉效果。
网络安全领域中数制转换应用
网络协议转换
在网络安全领域中,数制转换技术可以实现不同网络协议之间的 转换,以确保网络通信的安全性和可靠性。
加密算法实现
许多加密算法的实现都涉及到数制转换技术,如RSA算法中的模 幂运算就需要将数据进行数制转换。
易于进行转换
二进制数可以很容易地转换为其他进 制的数,如十进制、八进制和十六进 制等,这方便了计算机与其他设备之 间的数据交换。
03
二进制运算及转换方法
二进制基本运算规则
加法运算
减法运算
0+0=0,0+1=1,1+0=1,1+1=0(进位 为1)
0-0=0,1-0=1,1-1=0,0-1=1(借位为1)
03
11.1二进制及其转换1 教案

常规教具
教学目的
1.弄清十进制、数位、基数、位权数、二进制的概念
2.十进制、二进制的意义
3.十进制与二进制的相互转化
教学重点
1.进制概念的理解
2.二、十进制的转换
教学难点
1.位权的表示方法
2.十进制数转换为二进制数
更新、补充、
删节内容
无
课前准备
预习
课外作业
教材P3:1,2.《学习指导用书》A组1,2,3.B组1
位置
整数部分
小数点
第三位
第二位
第一位
起点
位权数
4
2
1
二进制的意义:各个十位的数码与其位权数的乘积和。例如
任务3
你一定也听说过二进制,与十进制类比,你能回答下面的问题吗?
1、二进制的基数是什么?
2、二进制每个数位上有几个不同的数码?分别是什么?
3、二进制的进位规则是什么?
讲述法
示范
学生记录交流
课堂教学安排
教学环节
主要教学内容
教学手段
与方式
课堂练习
课堂小结
课后作业
任务4
二进制化成十进制
练习:P3练习1、2
作业:P3习题1、2
巩固转化方法学生交流探讨
任务1
理解十进制、数位、基数、位权数的概念
1.十进制:用0、1、2、3、4、5、6、7、8、9这十个数码符号放到相应的位置来表示数的一种方法。如56365
2.数位:数码符号在数中的位置
3.基数:每个数位上可以使用的数码符号位权数:每个数位所代表的数。十进制的进位规则为“逢10进位1”,位权数如下:
板
书
设
计
11.1二进制及其转换
二进制十进制转换教案

二进制十进制转换教案教案:二进制和十进制转换一、教学目标:1.了解二进制和十进制的基本概念和原理;2.掌握二进制和十进制之间的转换方法;3.能够运用所学知识进行二进制和十进制的转换。
二、教学准备:1.板书:二进制和十进制的定义和示例;2. PowerPoint:带有示例题的课件;3.习题和答案:供学生练习运用所学知识。
三、教学过程:Step 1:导入新知1.引入二进制和十进制的基本概念,向学生提问:“你知道二进制和十进制分别是什么吗?它们之间有什么区别?”2.解答学生提问,并通过黑板上的示例向学生介绍二进制和十进制的定义和示例。
Step 2:教学内容1.讲解二进制和十进制的转换原理和步骤。
二进制转十进制的步骤:-将二进制数从右到左按位展开,每一位与2的对应幂相乘;-将每一位的结果相加得到十进制数。
十进制转二进制的步骤:-将十进制数除以2,得到商和余数;-将余数从下往上排列,得到二进制数。
2.利用具体的例子进行示范演示。
-十进制数转二进制数的示例:将十进制数46转换为二进制数。
Step 3:练习与检查1.分发练习题,让学生进行练习。
2.检查学生练习情况,解答学生提出的问题。
Step 4:归纳总结2.提醒学生不断练习,加深对二进制和十进制转换的理解和掌握。
四、课堂延伸1.建议学生多进行二进制和十进制之间的转换练习,加深对知识的理解和记忆。
2.引导学生思考:为什么计算机使用二进制而不是十进制进行计算?为什么二进制可以被看作是计算机的基本语言?五、教学反思本节课通过示例演示和练习的方式,让学生了解了二进制和十进制的转换方法,激发了学生的思维和求解问题的能力。
但是,在实际教学中可以增加更多的练习题目,以帮助学生更好地掌握知识。
同时,在知识讲解过程中,可以增加一些有趣的案例,加深学生的理解和记忆。
《1.2.2二进制与数制转换》优秀教学案例高中信息技术人教版必修1

3.教师鼓励学生在课后进行自主学习,深入研究二进制与数制转换的更多知识。
五、案例亮点
1.生活实例引入:通过展示计算机故障的例子,引发学生对二进制与数制转换的兴趣,使学生能够更好地理解和应用所学知识。
2.问题导向:教师提出的问题引导学生思考和探索二进制与数制转换的概念和方法,激发学生的思维能力和解决问题的能力。
(三)情感态度与价值观
1.培养学生对计算机科学的兴趣和好奇心,激发学生对信息技术学习的热情。
2.通过解决实际问题和完成实践任务,培养学生的成就感和自信心。
3.培养学生对二进制与数制转换知识的理解和应用能力,提高学生对计算机内部数据表示和处理的认识。
4.培养学生对团队合作和探究学习的价值观念,培养学生的自主学习能力和团队合作精神。
2.学生通过小组讨论和交流,共同解决问题,分享彼此的想法和经验。
(四)总结归纳
1.教师邀请学生代表分享小组讨论的结果和解决问题的方法。
2.教师对学生的回答进行点评和指导,强调二进制与数制转换的重要性和应用。
3.教师总结本节课的主要内容和知识点,确保学生对二进制与数制转换的理解和掌握。
(五)作业小结
1.教师布置相关的作业,巩固学生对二进制与数制转换的知识。
《1.2.2二进制与数制转换》优秀教学案例高中信息技术人教版必修1
一、案例背景
《1.2.2二进制与数制转换》是人教版普通高中信息技术必修1教材中的一节内容。本节课主要介绍二进制的基本概念、运算规则以及二进制与十进制的相互转换方法。通过对二进制与数制转换的学习,使学生了解计算机内部数据的表示和处理方式,为学生进一步学习计算机的组成原理和程序设计打下基础。
教案1:二进制及其转换

教学环节
教师活动
学生活动
设计意图
情景引入
教师引导学生归纳
学生回忆、交流完成结构图
整体把握函数整章的结构
典
型
例
题
教师讲解本节书本上的典型例题,引导学生分析和解决问题,并予以适当的鼓励
让学生独立思考完成基础内容,再进行交流,教师给予适当的鼓励
体会数学思想方法,学会灵活应用知识点的能力,并提高学生的计算能力
(2)由十进制这一比较熟悉的记数方法类比学习二进制的记数方法,注意类比的学习方法积累;
(3)本学时的重点是二进制数转化成十进制数.
过程和方法
1.引导学生发现问题和提出问题,培养独立思考和创造性地解决问题的意识.
2.发展学生运用数学语言的能力;培养学生分析、比较、归纳的逻辑思维能力.
情感态度价值观
让学生感受集合语言的意义和作用,学习从数学的角度认识世界;通过合作学习培养学生的合作精神.
教学重点
二进制数转化成十进制数
教学难点
二进制数转化成十进制数
教学方法
采用实例归纳、自主探究、合作交流等方法.教学中通过列举例子,引导学生进行讨论和交流,并通过创设情境,让学生自主探索一些常见集合的特征性质.
课前准备
课件,学生分组
预习要求
浏览书本的知识点和例题,完成书后的基础训练
课后作业
完
(2013—2014学年第二学期)
专业名称文化基础课
课程名称数学第三册
授课教师夏洁
学校苏州工业园区工业技术学校
班级
12物流高职1、2班
12采供管理高职
授课日期
第1周
课题序号
1
学时
2
章节名称
二进制及其转换教案

二進位及其轉換[教學目標]1、認知目標(1)掌握進位制概念;(2)理解進制の本質;(3)掌握十進位和二進位の相互轉換;(4)瞭解電腦所採用の數制及電腦採用二進位數の原因。
2、技能目標掌握二進位數和十進位數轉換以及運算規則。
3、能力目標對學生思維能力進行拓展,激發他們探索電腦奧秘の欲望。
[教學重點](1)進制の本質組成(2)十進位與二進位間の相互轉換[難點](1)進制の本質組成(2)十進位與二進位間の相互轉換[教學方法]講授法舉例法[授課地點]普通教室,不用多媒體[教學過程]一、引入新課對電腦稍微瞭解の同學就知道電腦中使用の進位制是二進位,那什麼是二進位,它跟我們數學上使用の十進位有什麼聯繫。
這節課準備給大家補充點二進位の知識,這跟數學關係很密切,請同學務必認真聽課。
二、切入課堂內容1、什麼是進位制提出問題:什麼是進位制?最常見の進位制是什麼?學生普遍回答是十進位。
教師繼續提問:那十進位為什麼叫十進位?引起學生の思考。
(部分經過思考の學生回答是約定の)教師提醒學生一起回憶幼稚園開始學習算術の情景。
當是我們是從最簡單の個位數相加學起,比如2+3=?,當時我們會數手指,2個手指+3個手指等於5個手指,答案為5。
那4+6呢?4個手指+6個手指等於10個手指,10個手指剛好夠用。
那6+9呢?當時我們就困惑了。
記得當時老師是告訴我們把6拆成1+5,9+1=10,這時老師跟我們約定用一個腳趾表示10,另外用5個手指表示5。
這樣通過腳趾,我們就成功解決了兩個數相加超過10の問題。
教師提問:那當時我們為什麼要約定10呢,為什麼用9或11?引起學生思考。
(部分經過思考の學生回答為了方便運算)教師提問:除此之外還有哪些常見の進位制?請舉例說明。
拓展學生の思維。
有學生回答60進制(時分秒の換算),360進制(1周=360度),二進位等等。
教師和學生一起歸納進位制の概念,學生和老師形成共識:進位制是人們為了計數和運算方便而約定の記數系統。
二进制及其转换教案

二进制及其转换教案教案:二进制及其转换教学目标:1.了解二进制的概念和特点;2.学会将十进制数转换为二进制数;3.学会将二进制数转换为十进制数。
教学重难点:1.了解二进制的概念和特点;2.学会将十进制数转换为二进制数;3.学会将二进制数转换为十进制数。
教学准备:1.PPT课件;2.白板、黑板和彩色粉笔;3.练习题。
教学过程:Step 1 引入新知识(5分钟)1.向学生介绍二进制的概念和特点,解释二进制在计算机中的重要性;2.示意性地展示二进制数的形式,例如"1010";3.与学生互动,让学生感知二进制数与十进制数的不同。
Step 2 讲解二进制数的转换规则(10分钟)1.向学生介绍将十进制数转换为二进制数的方法:a.除以2取余法:将十进制数除以2得到商和余数,重复这个过程直到商为0,最后将余数从下往上排列即为二进制数。
b.举例说明以上方法,如将十进制数9转换为二进制数的步骤和结果;2.向学生介绍将二进制数转换为十进制数的方法:a.从二进制数的最右边开始,乘以2的0次幂、1次幂、2次幂、3次幂...,将乘积相加得到十进制数。
b.举例说明以上方法,如将二进制数1101转换为十进制数的步骤和结果。
Step 3 初步练习(10分钟)1.向学生提供一些十进制数转换为二进制数和二进制数转换为十进制数的练习题;2.让学生独立完成练习,然后核对答案。
Step 4 深入讲解二进制数的转换规则(10分钟)1.向学生解释二进制数的位权规则:二进制数从右往左的位权分别为1、2、4、8、16、…2.举例说明位权规则,如二进制数1010,解释其每一位的位权及相应的十进制数;Step 5 继续练习(15分钟)1.向学生提供更多的关于二进制数转换的练习题,包括较复杂的情况;2.让学生独立完成练习,然后相互交流答案。
Step 6 拓展应用(10分钟)1.向学生介绍二进制数在计算机中的应用,例如二进制编码、存储、运算等;2.提出一个二进制编码的实际应用问题,并让学生尝试解决。
二进制及其转换教案

二进制及其转换教学目标1、认知目标1掌握进位制概念;2理解进制的本质;3掌握十进制和二进制的相互转换;4了解计算机所采用的数制及计算机采用二进制数的原因;2、技能目标掌握二进制数和十进制数转换以及运算规则;3、能力目标对学生思维能力进行拓展,激发他们探索计算机奥秘的欲望;教学重点1进制的本质组成2十进制与二进制间的相互转换难点1进制的本质组成2十进制与二进制间的相互转换教学方法讲授法举例法授课地点普通教室,不用多媒体教学过程一、引入新课对计算机稍微了解的同学就知道计算机中使用的进位制是二进制,那什么是二进制,它跟我们数学上使用的十进制有什么联系;这节课准备给大家补充点二进制的知识,这跟数学关系很密切,请同学务必认真听课;二、切入课堂内容1、什么是进位制提出问题:什么是进位制最常见的进位制是什么学生普遍回答是十进制;教师继续提问:那十进制为什么叫十进制引起学生的思考;部分经过思考的学生回答是约定的教师提醒学生一起回忆幼儿园开始学习算术的情景;当是我们是从最简单的个位数相加学起,比如2+3=,当时我们会数手指,2个手指+3个手指等于5个手指,答案为5;那4+6呢4个手指+6个手指等于10个手指,10个手指刚好够用;那6+9呢当时我们就困惑了;记得当时老师是告诉我们把6拆成1+5,9+1=10,这时老师跟我们约定用一个脚趾表示10,另外用5个手指表示5;这样通过脚趾,我们就成功解决了两个数相加超过10的问题;教师提问:那当时我们为什么要约定10呢,为什么用9或11引起学生思考;部分经过思考的学生回答为了方便运算教师提问:除此之外还有哪些常见的进位制请举例说明;拓展学生的思维;有学生回答60进制时分秒的换算,360进制1周=360度,二进制等等;教师和学生一起归纳进位制的概念,学生和老师形成共识:进位制是人们为了计数和运算方便而约定的记数系统;2、什么是十进制教师提出问题:大家学习了十几年十进制,我们了解十进制吗所谓的十进制,它是如何构成的引起学生思考;十进制由三个部分构成:1由0、1、2、3、4、5、6、7、8、9十个数码组成;2进位方法,逢十进一;基数为103采用位权表示法,即一个数码在不同位置上所代表的值不同;引入基数和位权的概念一种进制就规定了一组固定的数字,数字的个数就是这种类制的基数,如十进制规定了,0,1,2…9共10个数字,则十进制的基数就为10; 位权是一个比较新的概念,通过简单的例子介绍什么是位权;比如:数码3,在个位上表示为3,在十位表示为30,在百位表示为300,在千位表示为3000;3333=3000+300+30+3=3103+3102+3101+3100这里个100、十101、百102,称为位权,位权的大小是以基数为底,数码所在位置序号为指数的整数次幂;教师提出问题:其它进位制的数又是如何的呢引入二进制;3、什么是二进制从生活最常用的十进制入手,讲解基数和位权的概念,学生理解后,引入二进制数的概念,在对二进制数进行介绍时,会把学生带入到一个全新的数字领域; 1二进制的表示方法同样由三部分组成①由0、1两个数码来描述;如11001,记为110012或者110012②进位方法,逢二进一;基数为2③位权大小为2-n ...、2-1、20、21、22...2n比如通过按权位展开,就可以把二进制转化为十进制,这也是权位的妙处所在;01234(2)212020212111001⨯+⨯+⨯+⨯+⨯=2计算机为什么使用二进制计算机为什么使用二进制数,而不用十进制呢引起学生思考二进制只有两个数码,是不是比十进制简单;我们知道,简单的东西比较容易实现;在计算机中我们可以使用高电平来表示1,使用低电平来表示0;而十进制有十个数码,得有十个状态才能表示,物理实现起来比较难;这是计算机使用二进制的原因之一,其他原因大家可以自己去探索,提示一下,跟运算有关;3二进制加法先回顾十进制加法的加法规则和运算方法;运算方法:列竖式,加数和被加数个位对齐,从各位数开始,如果相加之和大于等于十,就向高位进位;二进制加法运算方法也一样;也是列竖式,加数和被加数右边第一位对齐,从右边第一位数开始,如果相加之和大于等于二,就向高位进位;提出二进制加法规则:0+0=0;0+1=1;1+0=1;1+1=10教师出题让学生练习,选几个学生上黑板练习,学生做完后讲解练习:11002+102 21012+1102 311002+101124、二进制与十进制的转换1、二进制数转化为十进制数例1 将二进制数1011012化成十进制数解:根据进位制的定义可知按权位展开=125+024+123+122+021+1201011012=32+0+8+4+0+1=45;所以,1011012练习:将下面的二进制数化为十进制数1112、十进制转换为二进制例2 把45化为二进制数=125+024+123+122+021+120思路:从前面的二进制按权位展开我们知道,1011012如果我们能把45变为125+024+123+122+021+120这样,是不是就可以得到45的二进制代码;所以思路就是构造45跟2的关系;方法一:根据“逢二进一”的原则,有45=222+1 22=211 11=25+1 5=22+145=2211+1=2225+1+1=22222+1+1+1=2223+21+1+1=224+22+21+1=25+23+22+20所以45=125+024+123+122+021+120=1011012大家看一下,从下往上数,101101不就是我们要的结果吗,这不是巧合,是可以证明的,怎么证明大家可以尝试去做,有兴趣的同学可以课后与老师交流;这里45=222+1的1是45除于2后的余数,其他也是一样,所以我们归纳出另外一种方法:方法二:除2取余法:用2连续去除45或所得的商,然后取余数练习:将下面的十进制数化为二进制数110 2235、提出课后思考题把45转化为5进制;教学反思本周因为机房教师机中毒,无法继续上多媒体的加工与表达那一节课;所以我设计了二进制这个补充内容在教室上课;补充二进制的理由:二进制是计算机的基础,是下一章学习程序设计的基础,所以很有必要学习;而且二进制跟数学关系密切,补充二进制可以帮助学生认清数的进制的本质,提高学生的数学思维能力;让学生在不知不觉中理解计算机采用二进制数及信息编码的问题;本节内容主要是对学生的思维能力进行拓展,激发学生的求知欲,从而更进一步地去掌握计算机技术;由于涉及到的数学知识比较多,对学生的数学要求比较高,不同的班级上课的效果略有差别,数学成绩比较好的班级明显听课热情比较高,而且学生学习新知识的速度也有一定的差别;板书设计一、进位制是人们为了计数和运算方便而约定的记数系统;二、十进制构成:1由0、1……9十个数码组成;基数为102进位方法,逢十进一;3采用位权表示法,即一个数码在不同位置上所代表的值不同;二、二进制的表示方法同样由三部分组成1由0、1两个数码来描述;基数为22逢二进一;3位权大小为2-n...、2-1、20、21、22...2n三、二进制与十进制的相互转换1、二进制转十进制——按权位展开2、十进制转二进制——除2取余法:用2连续去除45或所得的商,然后取余数四、课后思考把45转化为5进制;。
二进制及其转换教案

二进制及其转换教案本节课将介绍二进制及其转换。
我们知道计算机中使用的进位制是二进制,但是什么是二进制,它与我们数学上使用的十进制有什么关系?本节课将为大家补充二进制的知识,这对于理解计算机原理非常重要。
首先,我们来了解什么是进位制。
进位制是人们为了计数和运算方便而约定的记数系统。
最常见的进位制是十进制,它由10个数码组成,进位方法是逢十进一。
在幼儿园时,我们从最简单的个位数相加学起,逐渐学会了进位。
这是我们约定了10作为进位基数,以方便运算。
除了十进制,还有其他常见的进位制,比如60进制(时分秒的换算)、360进制(1周=360度)等。
接下来我们将重点介绍二进制。
二进制是一种进位制,由0和1两个数码组成,进位方法是逢二进一。
计算机中使用二进制是因为计算机的内部电路只能识别0和1,所以采用二进制能够更方便地进行运算。
我们将介绍十进制和二进制的相互转换,以及二进制的运算规则。
通过本节课的研究,我们可以拓展思维能力,激发探索计算机奥秘的欲望。
由于数学知识的复杂性,学生的数学要求较高,因此不同班级的课堂效果略有差异。
那些数学成绩较好的班级通常表现出更高的听课热情,而且学生研究新知识的速度也有所不同。
在板书设计方面,老师需要注意让内容简明易懂。
一、进位制是为了方便计数和运算而约定的记数系统。
它由十个数码组成,基数为10.进位方法是逢十进一,并采用位权表示法,即一个数码在不同位置上所代表的值不同。
二、二进制是另一种记数系统,同样由三部分组成:1和0两个数码来描述,基数为2,逢二进一,位权大小为2-n、2-n-1、2-n-2、……、2、21、22、……、2n。
三、在二进制和十进制之间进行转换时,有两种方法。
首先,将二进制转换为十进制,可以按照权位展开的方式进行。
其次,将十进制转换为二进制,则可以使用除2取余法。
四、课后思考:如何将45转化为5进制?。
二进制转换 教案

二进制转换教案教案标题:二进制转换教案目标:1. 理解二进制的概念和基本原理;2. 学会将十进制数转换为二进制数;3. 学会将二进制数转换为十进制数;4. 掌握二进制转换的应用场景。
教案步骤:引入活动:1. 引导学生回顾十进制数的概念和基本原理,并与二进制进行对比,引出二进制的概念。
知识讲解:2. 解释二进制数的构成和计数规则,介绍二进制转换的基本方法。
示例演示:3. 通过实际示例演示将十进制数转换为二进制数的步骤和方法,鼓励学生积极参与并提问。
练习活动:4. 分发练习题,要求学生将给定的十进制数转换为二进制数,并检查答案的正确性。
知识讲解:5. 解释将二进制数转换为十进制数的方法,强调每一位上的权重计算。
示例演示:6. 通过实际示例演示将二进制数转换为十进制数的步骤和方法,鼓励学生积极参与并提问。
练习活动:7. 分发练习题,要求学生将给定的二进制数转换为十进制数,并检查答案的正确性。
应用拓展:8. 引导学生思考二进制转换的应用场景,如计算机科学、电子工程等领域,并与实际生活中的使用进行对比。
总结回顾:9. 总结二进制转换的基本原理和方法,强调学生在实际问题中的应用能力。
作业布置:10. 布置作业,要求学生完成一定数量的二进制转换题目,并在下节课前提交。
教学资源:- 教学投影仪- 练习题及答案- 板书工具评估方式:- 教师观察学生在课堂上的参与度和理解程度;- 批改学生的练习题答案;- 作业完成情况的评估。
教学延伸:1. 鼓励学生自主学习更多进制之间的转换方法,如八进制、十六进制等;2. 引导学生进行实际的二进制计算和应用实践,如计算机编程、逻辑电路设计等。
教案指导:- 在教学过程中,鼓励学生互动和提问,以促进他们对二进制转换的理解;- 灵活运用示例演示和练习活动,巩固学生的知识掌握能力;- 引导学生将所学知识与实际应用相结合,增强他们的学习兴趣和动力;- 针对学生的不同水平和需求,提供个性化的辅导和指导。
最新中职数学授课教案:二进制及其转换

课外
作业
P15-16 练习
教学
后记
在本节课中,学生对于电路图与逻辑表达式的相互转换存在难点,许多同学在电工课程中对于短路的情况分析不清。但是学生对于用真值表验证等值逻辑式掌握较好。在课程学习中,应该从学生的认知规律出发,由浅入深。
课题
序号
4
授课班级
1202、1206
授课
课时
2
授课类型
新授课
授课章节名称
使用
教具
多媒体教具
教
学
目
的
1.理解命题的概念并会判断命题的真假性;
2.理解逻辑连结词“非”、“且”、“或”及复合命题的真假性
教学
重点
会判断命题的真假
教学
难点
三种常见逻辑连接词的理解
更 新补 充删节
内容
无
课外
作业
课本P10习题1,2题 练习册11.2节
教学
后记
学生在已知逻辑关系的电路图,要求列出逻辑关系式时,错误率较高。而且,学生对于复合命题真假的判断还存在难点。在教学中,需要讲清复合命题真假情况的真值表,真正让学生理解性的记忆。
教学
后记
学生在高一年级学习计算机基础知识时对二进制已经有所接触,有一定的基础。对于二进制转化为十进制较为熟悉,但是对于十进制转换为二进制的“除二取余法”应用性不强。作业中错误率较高。今后,在教学中应该加强学生这方面的训练。
课题
序号
2
授课班级
1202、1206
授课
课时
2
授课类型
新授课
授课章节名称
11.2命题逻辑与条件判断
难点
算法的三种逻辑结构及其应用
更 新补 充删节
教案01二进制及其转换

1 次课教案
章节 二进制及其转换
9 月 2 日 课型
第 1 周星期 一 新课 教时 2
教学目的
通过学生熟悉的十进制,利用类比的方式,介绍二进制 的相关概念,让学生能进行二进制数与十进制数的相互 转换。 面对具体问题,能实现二进制数与十进制数之间的相互 转换
教学重点
教学难点
对基数、进位规则、位权数、按权展开式等概念的理解
小结:将二进制数换算成十进制数的关键是将二进制数写成按 权展开式;将十进制数换算成二进制数的关键是使用“除 2 取 余法” 。
课堂小结
0 21 1 2 0 (1100101 )2
4、介绍八进制数 (1)八进制各个数位的权数是什么?
提问
教
学
过
程
与
内
容
教法、学法
位置 „ 位权数 „
整数部分
第3位 第2位 第1位
(2)将 (11) 2 和 (11)8 分别换算成十进制数,它们相等吗? 补充例题: 1、 写出下列各数的权展开式: (1) (111 )10 解: (1) (111 )10 1 102 1 101 1 100 (2) (111 ) 2 1 22 1 21 1 20 2、将下列二进制数换算成十进制数: )2 (1) (110) 2 (2) (1001 解: (1) (110)2 1 22 1 21 0 20 6 (2) (1001 ) 2 1 23 0 22 0 21 1 20 9 3、将下列十进制数换算成二进制数: (1) (5)10 解(1) 2| 5 „„ 余 1 2 0
边讲边练
) 2 1 2 2 0 21 1 20 (5)10 解: (1) (101 ) 2 1 25 0 2 4 1 23 0 2 2 1 21 1 20 (2) (101011 (43)10
中职第三册教案:二进制及其转换(第三课时)
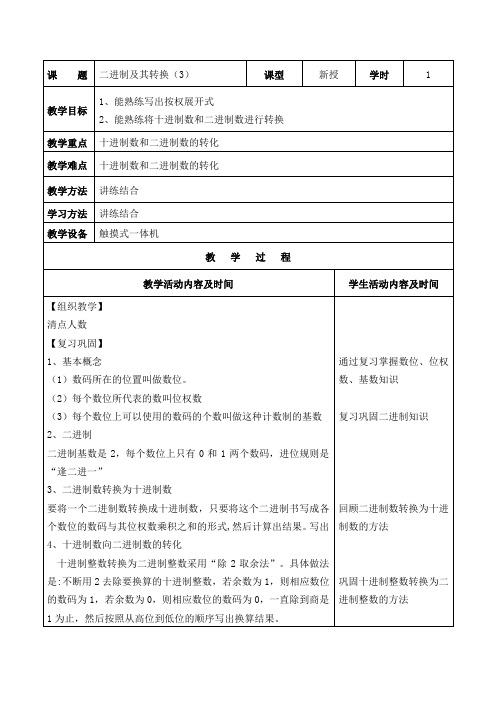
(1)数码所在的位置叫做数位。
(2)每个数位所代表的数叫位权数
(3)每个数位上可以使用的数码的个数叫做这种计数制的基数
2、二进制
二进制基数是2,每个数位上只有0和1两个数码,进位规则是“逢二进一”
3、二进制数转换为十进制数
要将一个二进制数转换成十进制数,只要将这个二进制书写成各个数位的数码与其位权数乘积之和的形式,然后计算出结果。写出4、十进制数向二进制数的转化
第3课时二进制及其转换(3)
1、基本概念:
数位、位权数、基数
2、二进制:
基数是2,每个数位上只有0和1两个数码,进位规则是“逢二进一”
3、二进制数转换为十进制数
要将一个二进制数转换成十进制数,只要将这个二进制书写成各个数位的数码与其位权数乘积之和的形式,然后计算出结果。写出4、十进制数向二进制数的转化
4、十进制整数转换为二进制
不断用2去除要换算的十进制整数,若余数为1,则相应数位的数码为1,若余数为0,则相应数位的数码为0,一直除到商是1为止,然后按照从高位到低位的顺序写出换算结果。
教学反思:
【课堂总结】
1、二进制数转换为十进制数
要将一个二进制数转换成十进制数,只要将这个二进制书写成各个数位的数码与其位权数乘积之和的形式,然后计算出结果。写出2、十进制数向二进制数的转化
十进制整数转换为二进制整数采用“除2取余法”。具体做法是:不断用2去除要换算的十进制整数,若余数为1,则相应数位的数码为1,若余数为0,则相应数位的数码为0,一直除到商是1为止,然后按照从高位到低位的顺序写出换算结果。
【作业布置】
课后复习T2、T3
通过复习掌握数位、位权数、基数知识
复习巩固二进制知识
回顾二进制数转换为十进制数的方法
二进制完整版教案

二进制完整版教案第一章:二进制基础1.1 二进制的概念与历史1.2 二进制与十进制的区别1.3 二进制的数制规则1.4 二进制与逻辑运算第二章:二进制算术运算2.1 二进制的加法运算2.2 二进制的减法运算2.3 二进制的乘法运算2.4 二进制的除法运算第三章:二进制与十进制的转换3.1 二进制转换为十进制3.2 十进制转换为二进制3.3 二进制与八进制、十六进制的转换第四章:二进制在计算机科学中的应用4.1 计算机中的数据表示4.2 计算机中的存储器4.3 计算机中的控制器与运算器4.4 计算机中的逻辑电路第五章:二进制编码与传输5.1 二进制编码的基本概念5.2 字符编码(如ASCII码)5.3 二进制数据的传输与通信5.4 错误检测与纠正第六章:二进制逻辑门6.1 与门(AND Gate)6.2 或门(OR Gate)6.3 非门(NOT Gate)6.4 异或门(XOR Gate)6.5 异或门(XNOR Gate)6.6 逻辑门电路设计与仿真第七章:布尔代数7.1 布尔代数的基本概念7.2 布尔代数的运算规则7.3 布尔代数的逻辑函数7.4 布尔代数的简化与优化第八章:数字电路设计8.1 数字电路的基本组成8.2 组合逻辑电路设计8.3 时序逻辑电路设计8.4 数字电路仿真与测试第九章:中央处理器(CPU)9.1 CPU的基本结构与工作原理9.2 指令集与指令编码9.3 算术逻辑单元(ALU)9.4 控制单元与时序信号9.5 寄存器与缓存第十章:计算机内存与存储10.1 随机存取存储器(RAM)10.2 只读存储器(ROM)10.3 硬盘驱动器(HDD)与固态驱动器(SSD)10.4 内存管理单元(MMU)10.5 计算机存储系统设计第十一章:计算机网络与二进制11.1 计算机网络的基本概念11.2 二进制在网络通信中的应用11.3 数据封装与传输11.4 网络协议与二进制编码第十二章:二进制在软件工程中的应用12.1 软件工程的基本概念12.2 二进制在编程语言中的应用12.3 编译器与解释器的工作原理12.4 二进制在软件开发工具中的应用第十三章:二进制与13.1 的基本概念13.2 二进制在机器学习中的应用13.3 二进制在神经网络中的作用13.4 二进制在算法中的重要性第十四章:二进制在量子计算中的应用14.1 量子计算的基本概念14.2 量子比特与量子门14.3 量子计算的优势与挑战14.4 二进制在量子算法中的应用第十五章:二进制的未来与发展15.1 二进制技术的历史与发展趋势15.2 新兴的二进制技术(如神经形态计算)15.3 二进制在未来的挑战与机遇15.4 二进制技术的未来应用领域重点和难点解析重点:1. 二进制的概念与历史2. 二进制与十进制的区别3. 二进制的数制规则4. 二进制算术运算(加、减、乘、除)5. 二进制与逻辑运算6. 二进制与十进制的转换方法7. 二进制在计算机科学中的应用(数据表示、存储器、控制器与运算器、逻辑电路)8. 二进制编码与传输(编码的基本概念、字符编码、数据传输与通信、错误检测与纠正)9. 二进制逻辑门(与门、或门、非门、异或门、异或门)10. 布尔代数(基本概念、运算规则、逻辑函数、简化与优化)11. 数字电路设计(基本组成、组合逻辑电路、时序逻辑电路、仿真与测试)12. 中央处理器(CPU)(基本结构、工作原理、指令集、算术逻辑单元、控制单元、寄存器)13. 计算机内存与存储(RAM、ROM、HDD、SSD、内存管理单元、存储系统设计)14. 计算机网络与二进制(网络基本概念、通信中的应用、数据封装与传输、网络协议)15. 二进制在软件工程中的应用(编程语言、编译器与解释器、开发工具)16. 二进制与(机器学习、神经网络、算法重要性)17. 二进制在量子计算中的应用(量子比特、量子门、优势与挑战、量子算法)18. 二进制的未来与发展(历史与发展趋势、新兴技术、挑战与机遇、应用领域)难点:1. 量子比特与量子门的理解和应用2. 布尔代数的逻辑函数简化与优化3. 数字电路的组合逻辑与时序逻辑设计4. CPU的指令集、算术逻辑单元和控制单元的协同工作5. 计算机网络中二进制数据的封装与传输6. 软件工程中二进制编程语言的编译与解释7. 中二进制在神经网络中的应用8. 量子计算中二进制算法的开发与实现9. 二进制技术在未来的发展趋势和挑战这些重点和难点构成了二进制知识的核心,学生在学习过程中应重点关注并加以理解和掌握。
二进制的数制转换教案及反思

二进制的数制转换教案及反思教案标题:二进制的数制转换教案及反思教案目标:1. 理解二进制数制的基本概念和原理。
2. 掌握二进制数制转换的方法和技巧。
3. 运用所学知识解决实际问题。
教案内容:一、引入(5分钟)1. 利用一个有趣的问题或实例引起学生对二进制数制的兴趣。
2. 提出问题:你知道计算机中的数据是如何存储和处理的吗?二、概念讲解(10分钟)1. 解释二进制数制的基本概念和原理,包括0和1两个数字的含义以及二进制数的位权计算方法。
2. 比较二进制数制与十进制数制的异同点。
三、二进制数转换(20分钟)1. 介绍二进制数转换的方法和步骤,包括从二进制到十进制的转换和从十进制到二进制的转换。
2. 通过示例演示转换过程,并让学生积极参与。
四、实际应用(15分钟)1. 提供一些实际问题,要求学生运用所学知识进行二进制数制转换。
2. 引导学生思考二进制数制在计算机科学、电子工程等领域的应用。
五、总结与反思(10分钟)1. 对本节课的内容进行总结,强调二进制数制转换的重要性和应用价值。
2. 鼓励学生分享学习心得和困惑,解答他们的问题。
3. 鼓励学生思考如何将所学知识应用到实际生活中。
教案反思:1. 教学目标是否达到:通过学生的参与和回答问题,可以评估他们是否理解了二进制数制的基本概念和转换方法。
2. 教学方法是否有效:通过引入问题、示例演示和实际应用等多种教学方法,提高学生的学习兴趣和参与度。
3. 教学资源是否充分利用:教师可以准备一些有趣的实例和练习题,以及计算机或投影仪等辅助教学工具。
4. 学生的反馈和思考:及时了解学生的学习情况和困惑,并根据需要进行个别辅导和解答。
5. 教案的改进和完善:根据学生的反馈和教学效果,不断改进教案,提高教学质量。
通过以上教案,学生将能够理解二进制数制的基本概念和原理,掌握二进制数制转换的方法和技巧,并能够运用所学知识解决实际问题。
同时,教师应根据学生的实际情况和学习进度,适当调整教学内容和方法,确保教学效果的最大化。
二进制计算及转换教学设计

二进制计算及转换教学设计引言:二进制是计算机中最基本的数字系统,也是计算机中数据表示和处理的核心。
了解和掌握二进制计算及转换方法对于学习计算机科学和电子工程的学生来说至关重要。
本文将介绍一种教学设计的方法,以帮助学生理解和掌握二进制计算和转换。
1. 目标和学习点1.1 目标:通过本教学设计,学生将能够:- 理解二进制数字系统的基本原理;- 掌握二进制加法和减法的方法;- 熟练进行十进制到二进制的转换,以及二进制到十进制的转换;- 理解和应用二进制位运算;- 解决实际问题中涉及二进制计算和转换的题目。
1.2 学习点:- 二进制数字系统的基本原理;- 二进制加法和减法;- 十进制到二进制的转换和二进制到十进制的转换;- 二进制位运算;- 实际问题中的应用。
2. 教学设计步骤2.1 引导学生了解二进制数字系统首先,可以通过提问的方式引导学生思考:计算机是如何处理和表示数字的?学生可以回答十进制数字系统,但需要引导他们思考这种系统有什么限制。
接着,介绍二进制数字系统的基本原理。
可以通过讲解二进制数字系统的定义、基本规则和用途来帮助学生理解。
引导学生思考二进制和十进制之间的关系,以及计算机为什么使用二进制数字系统。
2.2 教授二进制加法和减法首先,介绍二进制加法的规则和步骤。
可以通过具体的例子进行讲解,例如:0101 + 0011。
然后,介绍二进制减法的规则和步骤。
同样地,通过具体的例子进行讲解,例如:0110 - 0011。
通过反复练习,巩固学生对二进制加法和减法的理解和掌握。
2.3 教学二进制和十进制的转换方法首先,从十进制到二进制的转换方法。
介绍除2取余法的原理和步骤,并通过具体的例子进行讲解,例如:将十进制数13转换为二进制数。
然后,从二进制到十进制的转换方法。
介绍乘以2的幂次方的原理和步骤,并通过具体的例子进行讲解,例如:将二进制数1011转换为十进制数。
通过反复练习,巩固学生对十进制和二进制转换的理解和掌握。
1.2.2二进制与数制转换教学设计2023—2024学年人教中图版(2019)高中信息技术必修1

1. 教材:确保每位学生都有《2023—2024学年人教中图版(2019)高中信息技术必修1》教材,以便学生能够跟随教学进度进行学习和复习。
2. 辅助材料:准备与教学内容相关的图片、图表、视频等多媒体资源,如二进制数的表示方法、运算规则的示意图,以及不同进制间的转换示例。这些资源可以帮助学生更直观地理解二进制与数制转换的概念和原理。
解答:将十进制数789不断除以16,直到商为0,然后将余数倒序排列,得到十六进制数为3b9。
2. 计算思维:培养学生运用计算机科学的方法和思维解决问题,提高学生的逻辑推理和创新能力。
3. 数字化学习与创新:引导学生运用信息技术进行自主学习和合作学习,培养学生的自主学习能力和团队合作精神。
4. 信息社会责任:使学生认识到信息技术对社会发展的影响,培养学生的社会责任感。
八、典型例题讲解
1. 例题一:将十进制数123转换为二进制数。
1.2.2二进制与数制转换教学设计2023—2024学年人教中图版(2019)高中信息技术必修1
课题:
科目:
班级:
课时:计划1课时
教师:
单位:
一、教学内容分析
本节课的主要教学内容是二进制与数制转换。教学内容与学生已有知识的联系包括:
1. 学生在小学阶段已经学习了十进制数的认识和运算,对数的的基本概念有了初步了解。
设计课堂互动环节,提高学生学习“二进制与数制转换”的积极性。
(二)课堂导入(预计用时:3分钟)
激发兴趣:
提出问题或设置悬念,引发学生的好奇心和求知欲,引导学生进入“二进制与数制转换”学习状态。
回顾旧知:
简要回顾上节课学习的“数制的基本概念”,帮助学生建立知识之间的联系。
提出问题,检查学生对旧知的掌握情况,为“二进制与数制转换”新课学习打下基础。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二进制及其转换
[教学目标]
1、认知目标
(1)掌握进位制概念;
(2)理解进制的本质;
(3)掌握十进制和二进制的相互转换;
(4)了解计算机所采用的数制及计算机采用二进制数的原因。
2、技能目标
掌握二进制数和十进制数转换以及运算规则。
3、能力目标
对学生思维能力进行拓展,激发他们探索计算机奥秘的欲望。
[教学重点]
(1)进制的本质组成
(2)十进制与二进制间的相互转换
[难点]
(1)进制的本质组成
(2)十进制与二进制间的相互转换
[教学方法]
讲授法举例法
[授课地点]
普通教室,不用多媒体
[教学过程]
一、引入新课
对计算机稍微了解的同学就知道计算机中使用的进位制是二进制,那什么是二进制,它跟我们数学上使用的十进制有什么联系。
这节课准备给大家补充点二进制的知识,这跟数学关系很密切,请同学务必认真听课。
二、切入课堂内容
1、什么是进位制
提出问题:什么是进位制?最常见的进位制是什么?
学生普遍回答是十进制。
教师继续提问:那十进制为什么叫十进制?引起学生的思考。
(部分经过思考的学生回答是约定的)
教师提醒学生一起回忆幼儿园开始学习算术的情景。
当是我们是从最简单的个位数相加学起,比如2+3=?,当时我们会数手指,2个手指+3个手指等于5个
手指,答案为5。
那4+6呢?4个手指+6个手指等于10个手指,10个手指刚好够用。
那6+9呢?当时我们就困惑了。
记得当时老师是告诉我们把6拆成1+5,9+1=10,这时老师跟我们约定用一个脚趾表示10,另外用5个手指表示5。
这样通过脚趾,我们就成功解决了两个数相加超过10的问题。
教师提问:那当时我们为什么要约定10呢,为什么用9或11?引起学生思考。
(部分经过思考的学生回答为了方便运算)
教师提问:除此之外还有哪些常见的进位制?请举例说明。
拓展学生的思维。
有学生回答60进制(时分秒的换算),360进制(1周=360度),二进制等等。
教师和学生一起归纳进位制的概念,学生和老师形成共识:
进位制是人们为了计数和运算方便而约定的记数系统。
2、什么是十进制?
教师提出问题:大家学习了十几年十进制,我们了解十进制吗?所谓的十进制,它是如何构成的? 引起学生思考。
十进制由三个部分构成:
(1)由0、1、2、3、4、5、6、7、8、9十个数码组成;
(2)进位方法,逢十进一;(基数为10)
(3)采用位权表示法,即一个数码在不同位置上所代表的值不同。
引入基数和位权的概念
一种进制就规定了一组固定的数字,数字的个数就是这种类制的基数,如十进制规定了,0,1,2…9共10个数字,则十进制的基数就为10。
位权是一个比较新的概念,通过简单的例子介绍什么是位权。
比如:数码3,在个位上表示为3,在十位表示为30,在百位表示为300,在千位表示为3000。
3333=3000+300+30+3=3*103+3*102+3*101+3*100
这里个(100)、十(101)、百(102),称为位权,位权的大小是以基数为底,数码所在位置序号为指数的整数次幂。
教师提出问题:其它进位制的数又是如何的呢?引入二进制。
3、什么是二进制?
从生活最常用的十进制入手,讲解基数和位权的概念,学生理解后,引入二进制数的概念,在对二进制数进行介绍时,会把学生带入到一个全新的数字领域。
(1)二进制的表示方法(同样由三部分组成)
①由0、1两个数码来描述。
如11001,记为11001(2)或者(11001)2
②进位方法,逢二进一;(基数为2)
③位权大小为2-n ...、2-1、20、21、22...2n
比如 0
1234(2)212020212111001⨯+⨯+⨯+⨯+⨯=
通过按权位展开,就可以把二进制转化为十进制,这也是权位的妙处所在。
(2)计算机为什么使用二进制
计算机为什么使用二进制数,而不用十进制呢?引起学生思考
二进制只有两个数码,是不是比十进制简单。
我们知道,简单的东西比较容易实现。
在计算机中我们可以使用高电平来表示1,使用低电平来表示0。
而十进制有十个数码,得有十个状态才能表示,物理实现起来比较难。
这是计算机使用二进制的原因之一,其他原因大家可以自己去探索,提示一下,跟运算有关。
(3)二进制加法
先回顾十进制加法的加法规则和运算方法。
运算方法:列竖式,加数和被加数个位对齐,从各位数开始,如果相加之和大于等于十,就向高位进位。
二进制加法运算方法也一样。
也是列竖式,加数和被加数右边第一位对齐,从右边第一位数开始,如果相加之和大于等于二,就向高位进位。
提出二进制加法规则:0+0=0;0+1=1;1+0=1;1+1=10
教师出题让学生练习,选几个学生上黑板练习,学生做完后讲解
练习:(1)100(2)+10(2)(2)101(2)+110(2)(3)1100(2)+1011(2)
4、二进制与十进制的转换
(1)、二进制数转化为十进制数
例1 将二进制数101101(2)化成十进制数
解:根据进位制的定义可知(按权位展开)
101101(2)=1*25+0*24+1*23+1*22+0*21+1*20
=32+0+8+4+0+1
所以,101101(2)=45。
练习:将下面的二进制数化为十进制数?
(1)11(2)(2)101.01(2)
(2)、十进制转换为二进制
例2 把45化为二进制数
思路:从前面的二进制按权位展开我们知道,101101(2)=1*25+0*24+1*23+1*22+0*21+1*20
如果我们能把45变为1*25+0*24+1*23+1*22+0*21+1*20这样,是不是就可以得到45的二进制代码。
所以思路就是构造45跟2的关系。
方法一:根据“逢二进一”的原则,有
45=2*22+1 22=2*11 11=2*5+1 5=2*2+1
45=2*(2*11)+1=2*(2*(2*5+1))+1=2*(2*(2*(2*2+1)+1))+1
=2*(2*(23+21+1))+1
=2*(24+22+21)+1=25+23+22+20
所以45=1*25+0*24+1*23+1*22+0*21+1*20=101101(2)
大家看一下,从下往上数,101101不就是我们要的结果吗,这不是巧合,是可以证明的,怎么证明大家可以尝试去做,有兴趣的同学可以课后与老师交流。
这里45=2*22+1的1是45除于2后的余数,其他也是一样,所以我们归纳出另外一种方法:
方法二:(除2取余法:用2连续去除45或所得的商,然后取余数)
练习:将下面的十进制数化为二进制数?
(1)10 (2)23
5、提出课后思考题
把45转化为5进制。
[教学反思]
本周因为机房教师机中毒,无法继续上多媒体的加工与表达那一节课。
所以我设计了二进制这个补充内容在教室上课。
补充二进制的理由:
二进制是计算机的基础,是下一章学习程序设计的基础,所以很有必要学习。
而且二进制跟数学关系密切,补充二进制可以帮助学生认清数的进制的本质,提高学生的数学思维能力。
让学生在不知不觉中理解计算机采用二进制数及信息编码的问题。
本节内容主要是对学生的思维能力进行拓展,激发学生的求知欲,从而更进一步地去掌握计算机技术。
由于涉及到的数学知识比较多,对学生的数学要求比较高,不同的班级上课的效果略有差别,数学成绩比较好的班级明显听课热情比较高,而且学生学习新知识的速度也有一定的差别。
[板书设计]
一、进位制是人们为了计数和运算方便而约定的记数系统。
二、十进制构成:
(1)由0、1……9十个数码组成;(基数为10)
(2)进位方法,逢十进一;
(3)采用位权表示法,即一个数码在不同位置上所代表的值不同。
二、二进制的表示方法(同样由三部分组成)
(1)由0、1两个数码来描述。
(基数为2)
(2)逢二进一;
(3)位权大小为2-n...、2-1、20、21、22...2n
三、二进制与十进制的相互转换
1、二进制转十进制——按权位展开
2、十进制转二进制——除2取余法:用2连续去除45或所得的商,然后取余数
四、课后思考
把45转化为5进制。
