有穷自动机在字符串匹配中的应用
编译原理课程教学的几点思考

编译原理课程教学的几点思考摘要:针对编译原理课程在计算机本科教学中难讲、难学的特点,从理论教学、教学方法、实践能力培养等方面进行了探索,提出了相应的解决方法。
关键词:编译原理;教学方法;实践能力编译原理课程是计算机科学与技术学科下各专业的核心专业课程,其教学目标是通过教学实践训练学生的抽象思维能力和动手能力,旨在使学生掌握程序设计语言的形式化描述和编译的基本理论、原理和技术,并对编译程序有较为具体的认识。
使学生能运用所学过的基本知识、着手开发系统程序,为今后的工作(理论研究和技术开发)打下基础。
但由于其内容具有较强的理论性和实践性,学生在学习过程中感到内容抽象、算法复杂、难于理解,因此“编译原理”被普遍看作是计算机本科教学中最难讲解、最难学习的课程。
针对这种情况,如何提高这门课程的教学效果,是一个值得探讨的问题。
笔者近年来一直从事“编译原理”课程的教学,对如何改进教学方法和提高教学效果做了一些研究和探索。
1 明确教学目标,增强学习兴趣对于编译原理这门课程,普通高校本科的教学目标是:通过编程语言实现技术的学习,提高学习编程语言及在程序开发中应用编程语言的能力,具体解释如下:提高学习、理解和使用编程语言的能力;提高程序排错的能力,即快速理解、定位和解决在程序开发与程序运行中遇到的问题的能力;提高编写高质量代码的能力。
另外,由于编译程序,由于编译程序作为系统软件在性能上具有严格的要求,这使得它所使用的算法经典、高效,而这些算法、思想和实现技术也可广泛地应用于一般软件的设计实现。
如正规式和有穷自动机在文本编辑器中的广泛应用,有穷自动机在字符串查找中的运用,必经节点算法在网络中的运用,由文法来定义网络协议等。
在教学中,可以鼓励学生尝试将编译程序中的各种算法和技术应用到各个应用领域,从而激发学生的创造性思维,培养学生的创新能力,为今后的学习打下坚实的基础。
2 运用多种教学方法,提高教学效果“编译原理”课程具有很多概念和定理,再加上大量复杂的算法,抽象程度很高,因此要想获得良好的教学效果,必须借助形象化教学手段,使抽象的理论具体化。
第三章有穷自动机

例:将图示的DFA M最小化。
a
b
6
4
a
a
a
b
a
1
ab
5a
7
b3
b
b
2 b
1、将M状态分为两个子集: P0=({1,2,3,4},{5,6,7})
2、{1,2,3,4}读入a后划为: P1=({1,2},{3,4},{5,6,7})
3、进一步划分: P2=({1,2},{3},{4},{5,6,7})
对M的状态集S进行划分的步骤:
①把S的终态与非终态分开,分成两个子集, 形成基本划分,属于这两个不同子集的 状态是可区别的。
②假定某个时候已含m个子集,记={I(1) , I(2) , …,I(m) }且属于不同子集的状态是可 区别的,再检查中的每个I能否进一步划 分,对于某个I(i) ,令I(i) ={S1,S2,…,Sk}, 若存在一个输入字符使得move(I(i) ,a)不包 含在现行的某一子集I(i)中,则将I(i)一分 为二。
若M的某些结既是初态结,又是终态结,
或者存在一条从某个初态结到某个终态结 的道路,则空字可为M所接受。
例: NFA M=({0,1,2,3,4},{a,b},f,{0},{2,4})
f(0,a)={0,3} f(2,b)={2} f(0,b)={0,1}
f(3,a)={4} f(1,b)={2} f(4,a)={4}
M’=(K, ,f,S,Z)
一个含有m个状态和n个输入字符的NFA 可表示为一张状态转换图,该图含有m个 状态结,每个结可射出若干条 箭弧与别的 结点相连接,每条弧用*中的一个字(不 一定要不同的字,且可以为空字)作标记 (称输入字),整个图至少含有一个初态 结以及若干个终态结。
从正规文法构造有穷状态自动机

课程名称: 从正规文法构造有穷状态自动机年级/专业/班: 11级计算机类(二)班姓名: 徐勇兵学号: E01114278从正规文法构造有穷状态自动机输入:任意的正规文法输出:相应的有穷状态自动机要求:识别有穷状态自动机是确定的还是非确定的,生成相应的五元组形式。
说明:应检查输入的是否正规文法。
实验截图:测试一:测试二:*************************************************************************** 测试三:import java.util.Vector;import javax.swing.JOptionPane;class Tools{public Vector<String> protection(Vector<String> vs){Vector<String> newvector=new Vector<String>();for(int i=0;i<vs.size();i++)newvector.add(vs.get(i));return newvector;}public Vector<Vector<String>> doubleprotection(Vector<Vector<String>> vs){ Vector<Vector<String>> newvector=new Vector<Vector<String>>();for(int i=0;i<vs.size();i++){Vector<String> produce=(Vector<String>)vs.get(i);Vector<String> temp=new Vector<String>();for(int j=0;j<produce.size();j++){temp.add((String)produce.get(j));}//for jnewvector.add(temp);}//for ireturn newvector;}public Vector<String> addElements(Vector<String> vs,Vector<String>temp){ for(int i=0;i<temp.size();i++){//if(!vs.contains(temp.get(i)))vs.add(temp.get(i));}//forreturn vs;}//public Vector<String> addElements(Vector<String> vs,Vector<String>temp){ }//class toolsclass Elements{Vector<String> end=new Vector<String>();//表示终结符Vector<String> noend=new Vector<String>();//表示非终结符Vector<Vector<String>> produce=new Vector<Vector<String>>();//产生式public void setend(){//终结符元素添加while(true){String s=JOptionPane.showInputDialog(null,"请输入终结符");if(s==null){ return;}//ifend.add(s);}//while}//public void addend(){//元素添加public void setnoend(){//非终结符元素添加while(true){String s=JOptionPane.showInputDialog(null,"非请输入终结符");if(s==null){ return;}//ifnoend.add(s);}//while}//public void addnoend(){//public void setproduce(){while(true){String s=JOptionPane.showInputDialog(null,"请输入产生式,->隔开");if(s==null)return;Vector<String> temp=new Vector<String>();temp.add(s.split("->")[0]);temp.add(s.split("->")[1]);produce.add(temp);}//while}//public void addproduce()public Vector<String> getend(){return end;}public Vector<String> getnoend(){return noend;}public Vector<Vector<String>> getproduce(){return this.produce;}public void run(){/*************************TEST********************************/ end.add("a");end.add("b");noend.add("S");noend.add("A");noend.add("B");Vector<String> temp=new Vector<String>();temp.add("S");temp.add("aA");produce.add(temp);/*************************/Vector<String> temp1=new Vector<String>();temp1.add("S");temp1.add("bB");produce.add(temp1);/*************************/Vector<String> temp2=new Vector<String>();temp2.add("S");temp2.add("e");produce.add(temp2);/*************************/Vector<String> temp3=new Vector<String>();temp3.add("A");temp3.add("aB");produce.add(temp3);/*************************/Vector<String> temp4=new Vector<String>();temp4.add("A");temp4.add("bA");produce.add(temp4);/*************************/Vector<String> temp5=new Vector<String>();temp5.add("B");temp5.add("aS");produce.add(temp5);/*************************/Vector<String> temp6=new Vector<String>();temp6.add("B");temp6.add("bA");produce.add(temp6);/*************************/Vector<String> temp7=new Vector<String>();temp7.add("B");temp7.add("e");produce.add(temp7);/*************************/Vector<String> temp8=new Vector<String>();temp8.add("S");temp8.add("aB");produce.add(temp8);/* Vector<String> temp9=new Vector<String>();temp9.add("S");temp9.add("aAA");produce.add(temp9);*/// System.out.println("produce.size()="+produce.size());/***********************TEST**********************************///this.setend();//this.setnoend();//this.setproduce();}public boolean Iscontainend(String s)//正则表达式判断s1是否在END的闭包里面正则忘了怎么写了{int length=s.length();for(int i=0;i<length;i++){String a=""+s.charAt(i);if(end.contains(a))continue;else return false;}//forreturn true;}//public boolean isRGPcontain(String s)public boolean IsNoENd(String s){String ss=""+s.charAt(0);if(! Iscontainend(ss))//如果不含有终结符,则为非终结符return true;return false;}// public booleanpublic void show(){System.out.print("终结符输出如下:");for(int i=0;i<end.size();i++){System.out.print((String)end.get(i)+", ");}System.out.println(" ");System.out.print("非终结符输出如下:");for(int i=0;i<noend.size();i++){System.out.print((String)noend.get(i)+", ");}System.out.println(" ");System.out.print("产生式输出如下:");for(int i=0;i<produce.size();i++){System.out.println(" ");Vector<String> temp=(Vector<String>)produce.get(i);System.out.print((String)temp.get(0)+"->"+(String)temp.get(1));}System.out.println(" ");}}//class Elementspublic class Test {Elements elements;Tools tools=new Tools();Vector<String> end=new Vector<String>();//表示终结符Vector<String> noend=new Vector<String>();//表示非终结符Vector<String> inputTable=new Vector<String>();//表示输入符号的集合即又穷字母表Vector<String> statusTable=new Vector<String>();//状态表Vector<Vector<String>> produce=new Vector<Vector<String>>();//产生式Vector<Vector<String>> newproduce=new Vector<Vector<String>>();//转换函数String start="S";//初态String last="Z";//终态public void firststep(){if(elements.Iscontainend("aA")==true)System.out.println("yes");for(int i=0;i<produce.size();i++){Vector<String> temp=produce.get(i);String left=temp.get(0);String right=temp.get(1);if(right.length()!=1){//S->aA形式String one=""+right.charAt(0);String two=""+right.charAt(1);Vector<String> temp1=new Vector<String>();temp1.add(left);temp1.add(one);temp1.add(two);newproduce.add(temp1);}//ifelse{//S->a形式String one=""+right.charAt(0);Vector<String> temp1=new Vector<String>();temp1.add(left);temp1.add(one);temp1.add(last);newproduce.add(temp1);}}}public boolean iszhenggui(){for(int i=0;i<produce.size();i++){Vector<String> temp=produce.get(i);String left=temp.get(0);String right=temp.get(1);if(right.length()>2)return false;if(right.length()==1){if(elements.IsNoENd(right)==false)//S->A 不满足return false;}if(right.length()==2){String one=""+right.charAt(0);String two=""+right.charAt(1);if(elements.Iscontainend(one)==false)//return false;if(elements.IsNoENd(two)==false)//return false;}}return true;}public void FA(){//构造自动机}public void setstatusTable(){//状态表for(int i=0;i<noend.size();i++){statusTable.add(noend.get(i));}statusTable.add(last);}public void setinputTable(){//状态表for(int i=0;i<end.size();i++){inputTable.add(end.get(i));}}public void show(){System.out.print("状态表输出如下:");for(int i=0;i<statusTable.size();i++){System.out.print((String)statusTable.get(i)+", ");}System.out.println(" ");System.out.print("字母表输出如下:");for(int i=0;i<inputTable.size();i++){System.out.print((String)inputTable.get(i)+", ");}System.out.println(" ");System.out.print("转换函数输出如下:");for(int i=0;i<newproduce.size();i++){System.out.println(" ");Vector<String> temp=(Vector<String>)newproduce.get(i);System.out.print((String)temp.get(0)+" "+(String)temp.get(1)+" "+(String)temp.get(2));}System.out.println(" ");System.out.println("初态是"+start);System.out.println("终态是"+last);}public boolean judge(){boolean flag=true;Vector<Vector<String>> vs=new Vector<Vector<String>>();//Vector<String> vv=new Vector<String>();for(int i=0;i<newproduce.size();i++){Vector<String> temp=newproduce.get(i);String left=temp.get(0);String midle=temp.get(1);if(vs.isEmpty()){//如果是第一次放入数据Vector<String> temp2=new Vector<String>();temp2.add(left);temp2.add(midle);vs.add(temp2);}else{//System.out.println("11");Vector<String> temp2=new Vector<String>();temp2.add(left);temp2.add(midle);//System.out.println("left="+left+" midle="+midle);if(vs.contains(temp2))return false;elsevs.add(temp2);}}return true;}public Test(){elements=new Elements();elements.run();this.end=elements.getend();this.noend=elements.getnoend();this.produce=elements.getproduce();elements.show();实用标准文档文案大全boolean tag1=iszhenggui();if(tag1)System.out.println("是正规式");else{System.out.println("不是正规式");System.out.println("程序结束");return;}firststep();setstatusTable();setinputTable();this.show();Boolean tag=judge();if(tag)System.out.println("是DFA");elseSystem.out.println("不是NFA");}//public static void main(String[] args) { Test app=new Test();}}。
有穷状态自动机

有穷状态自动机
实验内容: 实验内容:
输入:任意的正则文法和待识别的字符串。 输入:任意的正则文法和待识别的字符串。 输出: 对输入的字符串运行相应有穷状态 输出 自动机过程。 自动机过程。 要求: 对任意的输入字符串给出运行过程,最后 入字符串是否为所输入 给出识别结论 输入字符串是否为所输入 文法的句子)。 文法的句子 。
有穷状态自动机
有穷状态自动机很容易用程序实现, 有穷状态自动机很容易用程序实现,这只 需让每个状态对应一小段程序。 需让每个状态对应一小段程序。当一个节 点有不止一条的弧自它射出时, 点有不止一条的弧自它射出时,表明将有 不止一种的情况出现,因此让它对应于if语 不止一种的情况出现,因此让它对应于 语 句和goto语句配合组成的程序段。终止状 语句配合组成的程序段。 句和 语句配合组成的程序段 态一般对应于出口或返回语句。 态一般对应于出口或返回语句。
例
字母或数字
s
字母
1
其他
s E
可有如下程序: 可有如下程序:
例
STATES: Getchar(); if(letter()) goto STATES; else goto FALURE; STATES1: Getchar(); while(letter()||digit()) Getchar(); STATEE: return; FALURE: 出错处理; 出错处理;
有穷自动机在词法分析器建模中的应用研究

界符= l 1 I , ; . (I) 其中l 示 a 表 —— z中 的 任 何 一 个 字 母 , 示 d表 9中的任何一 个数 字 。 e*也 都 是 正 规 式 , 们 所 表 示 的 正 规 集 分 别 为 l 它 关 键字 也 是一 种单 词 ,关 键 字集 合是 标 识符集 合 Le) (1ULe) (1・(2, (1 ; (1Le) (2, e)Le)Le) , L ( ) 的子集 , 关键字 与标 识符 的构 词原则 相 同。 ()仅 由有 限次 使 用上 述 三个 步骤 而 定 义 的表 达 4 式才 是 ∑上 的正 规式 , 由这些 正 规式 所 表示 的字 集 仅 整数 前 面 的正 负 号 在 词 法 分 析 中可看 作 运 算 符 , 因此 只定 义无 符号 整数 的词法 。 才是 ∑上 的正 规集 。[ 1 1 - . 正 规式 可 用 来 描述 符 号 串所 遵从 的规则 ,用 正规 232将词法 转化 为有穷 自动机形 式 的词法模 型
2 1 年第 1 0 1 1期
福 建 电
脑
9 5
有 穷 自动机在词 法分 析器建模 中的应 用研究
罗 海 丽
(内 蒙古科技 大 学 信息工程 学院 内蒙古 包头 0 4 1 1 0 0)
【 摘 要】 :有 穷自动机可用于描述语言的词法模型,有穷自动机形式的词法模型与特定的控制程序 相 配合 可构 成语 言 的词 法分析 器 。介 绍 了利 用有 穷 自动机 建 立语 言的词 法模 型及 以此 词 法模 型为基础 构 建词 法分析 器的过程 。实例 证 明 , 方 法构造 的词 法 分析 器正确 、 该 有效 。 【 关键词】 :有穷 自 动机; 正规文法; 控制程序; 词法模型; 词法分析器
DFA的实现与应用

DFA的实现与应用自动机(Automaton)是计算机科学中的重要概念之一,它是基于形式化逻辑的数学模型,能够接收输入并根据预先定义的规则进行状态转移。
确定有穷自动机(Deterministic Finite Automaton,简称DFA)是自动机的一种常见形式,其实现和应用已经得到广泛应用。
一、DFA的定义与原理DFA可以被定义为一个五元组(M, Σ, S, δ, F),其中:- M代表一个有限状态集合;- Σ代表一个有限输入字符集合;- S代表DFA的初始状态;- δ代表一个状态转移函数,将状态和输入映射到下一个状态;- F代表一个终止状态集合,用于标识DFA的接受状态。
DFA的实现流程如下:1. 定义状态集合M和输入字符集合Σ,并确定初始状态S;2. 设计状态转移函数δ,规定在接收到某个输入字符时,DFA应该如何从当前状态转移到下一个状态;3. 确定终止状态集合F,标识DFA的接受状态;4. 根据定义的五元组构建DFA,并进行状态转移,直到遇到终止状态。
二、DFA的应用领域1. 词法分析器DFA在编程语言中的词法分析阶段起着重要作用。
通过构建对应编程语言的DFA,可以将代码文本分解为各种语法单元,如标识符、关键字、运算符等。
这为编译器的下一步处理提供了基础。
2. 字符串匹配在文本处理和模式匹配中,DFA被广泛用于字符串匹配。
可以使用DFA在目标文本中搜索是否存在某个特定的字符串,并且可以在匹配时进行一些后续操作,如替换、提取等。
3. 自然语言处理DFA可以应用于自然语言处理,用于分析文本并识别其中的不同语法结构。
例如,可以使用DFA来识别句子、词组和词性等。
这对于机器翻译、文本分类和信息提取等任务非常有用。
4. 网络安全DFA的应用还可见于网络安全领域。
通过构建用于检测网络流量中的恶意行为的DFA模型,可以有效识别并阻止入侵、垃圾邮件、网络欺诈等网络安全威胁。
5. 语音识别在语音识别中,DFA可以用于根据输入音频信号的频谱特征识别出不同的音素或字母。
一种字符串模式匹配算法的实现

J r 2 0 uL 0 7
文章编 号 : 1 7 —9 5 2 0 ) 32 20 6 39 6 ( 0 7 0 —7 —2
一
种 字符 串模 式 匹配 算 法 的实现
陈 芳 ,沈 虹 ,张 霞
( 西安工业大学 计算机科学与工程学院 , 西安 7 0 3 ) 10 2
摘
Байду номын сангаас
要 : 为 寻求更有 效的 字符 串搜 索 方法 , 用有 穷 自动机 的定 义 , 析 KMP算 法 以及 自 利 分
模式 匹配搜 索算 法. 此算 法 的基 本 思想 是 : 模式 把 串和 目标 串匹配 的过 程 理解 为 不 断 的 向 自动 机 内
输 入 目标 串的过程 , 利用 有穷 自动 机状 态转换规 律
输入
…
样本 PE , , ] > 0 , 本 TE , 1… ( )文 1
进行模式匹配. 自动机最初都处于初始状态, 当状 态 变为终 止状 态 时 , 为 完 成 了 一 次 模 式 匹 配 过 认 程. 自动机返 回初始状 态 准备下一 次匹 配.
q i i 即输入字符后移一位. J ,— +1 + 否则当前状态 变为 q () … ()为 z z … 从 两端计 算 的 .q z
,
]Net1 … , . , xE , ]
输 出 样 本 P在 文 本 T 中出现 的次 数 cu t o n
值. 如果 没有 匹配 的样本 串时 , cu t 即 o n 值为零 .
KMP算 法 的时间 复杂度 为 O( m+ ) 阶.
1 有穷 自动机定义 。
一
台有穷 自动机 包括 以下几个 部分 : 一个状 态
维普资讯
有穷自动机的应用

在设备管理系统中的ຫໍສະໝຸດ 用所谓“有穷自动机”是什么?
第一丶 为什么要用有穷自动机
“设备管理系统”是对设备从购入→报废整个使用 过程进行全面管理的计算机信息管理系统。设备在 其使用过程的状态不断发生改变,因而使设备管理 具有很强的动态化特征。如果在系统分析阶段不能 对设备生命周期的状态变换过程做出准确、清晰的 描述,将会导致运行阶段非法操作的出现,甚至会 引起管理过程中的混乱,造成设备信息的破坏。因 此,成功开发设备管理系统的关健在于对设备管理 的全过程做出正确的分析和描述。
第二丶怎么用自动机管理设备
(1)将设备管理全过程作为一个有穷自动机,记为M (2)将设备在其整个使用周期中可能其有的各种现状作为M的状态集K; K={“在用”,“待修”,“待废”,......} (3)将现有设备管理有关的业务处理作为M的输入字母表∑(括号中的 字母为该业务处理的代号): ∑={“待修处理(a)”,“待废申请(b),“报失处理(k)”....} (4)将设备状态“在用”作为设备开始状态q0={“在用”}; (5)将设备的“报废”、“丢失”、“调出”、“退库”状态作为M 的终止状态集F. F= {“报废”,“丢失”,“调出”,“退库”} (6)把各项业务处理及引起的设备状态变化原则作为M的从K ×∑—〉 K的映射δ(δ描述中,业务处理用相应的字母代号表示),δ定义如下: δ(“在用”,a ) =“待修” δ(“在用”,b ) =“待废”......
大家有什么问题?
制作人:陈沐豪 罗超靖 制作人:陈沐豪 罗超靖
有限自动机在模式匹配中的应用与研究

件 下 能 压 缩 自动 机 的规 模 ,从 而 提 高 模 式 匹配 的 速 度 . 反 向 有 限 自动 机 算 法 与 BM 算 法 相 将
结 合 , 用 当前 获 取 信 息 进 一 步 增 大 匹配 过 程 中 的 跳 跃 距 离 , 进 一 步 提 高模 式 匹配 的 速 度 . 利 可
2 反 向有 限 自动机 匹配算 法 的思想 有 限 自动机 的构造 过程 是将模 式 串集 合变换 成 由转 向 函数 、失 效 函数 和输 出 函数 所组 成 的有 限 自动 机 . 正 向有 限 自动 机 的构 造 中 , 式 串的字 符是从 前 到后 依次 加到树 型 有 限 自动 机 中的 , 在 模 匹配 过程 也 是 按照从 前到后 的次 序 . 而在反 向有 限 自动机 的构 造 中 , 个模式 串的字符 是从 后 到前 , 每 加到树 型 自动机 中 , 同时在匹配 过程 中 , 目标 串 的输 入也 是从后 往前 的顺 序 , 即逆 向扫描 . , 例: 以模式 串集合 {em , , eae} 例 , 造 的反 向 自动 机如 图 1 示 . 图 1 知 反 向有 限 自动 h , er s ,r 为 e h 构 所 由 可
[ 收稿 日期 ]0 0 1 2 2 1—1— 2
[ 作者简介 ] 左金平(9 5 , , 17 一)女 山西长治人 , 中学院计算机科 学与技 术学院, 师, 士, 晋 讲 硕 研究方向: 计算机软件
・
6 ・ 4
左金 平
有 限 自动 机在 模 式 匹配 中的 应 用与 研 究
[ e s ] h
实现有穷状态自动机

#include <stdio.h>#include <string.h>#define STATE_NUMBER 4 //状态数目#define CHAR_NUMBER 2 //输入字符的种类: d 和 .#define DIGIT 0 //输入数字在状态表中位于第0列#define DOT 1 //小数点位于状态表的第1列//State[][]为状态表,以整数组形式存放,0,1,2,3表示状态,-1表示没有此状态int State[STATE_NUMBER][CHAR_NUMBER]= {{1,-1},{1,2},{3,-1},{3,-1}};int Q[STATE_NUMBER] = {0,1,0,1}; //终态标志:0非终态,1终态。
//缓冲区://输入缓冲区:由专门函数操作(ReadALine(),GetChar())#define BUFFER_SIZE 1000 //表达式缓冲区大小char Buffer[BUFFER_SIZE]; //表达式缓冲区,以'\0'表示结束int ipBuffer = 0; //表达式缓冲区当前位置序号char ch; //存放取得的一个字符//*****************************************************//函数声明:bool Run(); //对存储在缓冲区的一行字符串(以'#'结束)进行运行void Init(); //全局初始化bool ReadALine(); //从键盘读一行(没有空格),存于表达式缓冲区Buffer[]中char GetChar(); //从缓冲区取一个字符,返回该字符的同时将它存于全局变量ch中//*****************************************************//主程序:void main(){Init();while(ReadALine()) //读一行成功,对它进行判断{if(Run()) //对该行进行运行,看是否能被接受?printf("接受\n\n");elseprintf("不接受\n\n");}}//对存储在缓冲区的一行字符串(以'#'结束)进行运行//返回:如果是无符号定点实数,返回true;否则返回:falsebool Run(){int S=0; //S存放运行时的当前状态,目前为初态while(GetChar()!='#'){if(ch >= '0' && ch <= '9') //数字S = State[S][DIGIT]; //将状态转换成输入数字后的状态else if(ch == '.') //小数点S = State[S][DOT]; //将状态转换成输入小数点后的状态else //其他都为非法字符return false;if(S == -1) //处于非法状态return false;}//运行结束,判断S是否为终态if(Q[S] == 1) //终态return true;else //非终态return false;}//全局初始化void Init(){//好像无需初始化printf("程序功能:输入一个字符串,判断它是否是无符号定点实数。
dfa可行性报告

DFA可行性报告1. 引言在信息技术发展迅猛的时代背景下,各行各业都在积极探索利用新技术来提高工作效率和降低成本。
面对日益复杂的业务需求,许多公司开始关注自动化技术的应用。
本报告旨在评估确定一种叫做确定有穷自动机(DFA)的自动化技术在我们公司中的可行性。
2. 背景确定有穷自动机是一种数学模型,用于描述和处理各种抽象的计算问题。
它由一组状态、输入符号和状态转移函数组成,能够根据输入符号的序列来改变状态。
DFA被广泛用于自动化领域,例如编译器设计、字符串匹配和网络协议分析等。
3. 目标我们公司希望通过引入DFA技术来改善我们的业务流程,提高工作效率和准确性。
具体目标如下:-实现自动化的任务处理,减少人工干预的需求。
-提高业务处理的速度和准确性。
-降低人力成本和错误率。
4. 方法为了评估DFA技术在我们公司的可行性,我们将采取以下方法:4.1 研究现有流程首先,我们将详细了解当前的业务流程,包括各个环节、涉及的人员和资源等。
通过对现有流程的研究,我们可以确定哪些任务适合自动化处理,并找出可能的问题和挑战。
4.2 识别可自动化的任务基于对现有流程的研究,我们将识别出适合使用DFA技术自动化的任务。
这些任务通常是重复性的、规则性的,并且可以通过定义状态和输入符号来描述。
4.3 设计DFA模型针对识别出的可自动化任务,我们将设计相应的DFA模型。
这包括确定状态集合、输入符号集合和状态转移函数。
通过合理的设计,我们可以实现自动化任务的准确和高效处理。
4.4 开发和测试在设计完成后,我们将进行DFA模型的开发和测试。
开发阶段将涉及编写代码、实现状态转移函数和输入符号的处理逻辑等。
测试阶段将验证DFA模型的正确性和性能,确保其能够满足我们的需求。
4.5 部署和评估经过测试验证后,我们将在公司内部部署DFA技术,并进行实际应用和评估。
我们将关注DFA技术在业务流程中的表现,包括处理速度、准确性和成本效益等方面的评估。
有穷自动机的原理及应用-old

汇合状态(Confluence State):有多个前驱 状态的状态 需要克隆从汇合状态开始的路径 加入当前串之后,在当前串的路径上从后往 前执行最小化 每加入一个串,整个自动机是完全最小化的
ADFA 与字典序号
我们大多数情况下需要一个Map<string, Data>
可行的策略:
Waiting Set
可以任意次序进出 栈式的Waiting Set可使算法运行得更快
ADFA最小化的基本原理
ADFA最小化的实用算法
注册表
按右语言等价的定义,实现一个 map<TargetSet, StateID>
TargetSet 是 StateID 标识的状态的转移:pair(Char,Target) 的有序集合
标红中,扩展的全匹配
源代码
代码使用了 C++11
需要gcc-4.7以上版本 其他C++11编译器还没有测试过 /p/febird/source/brow se/trunk/febird/src/febird/automata /p/febird/source/brow se/trunk/febird/netbeans-cygwin/automata
根据新的输入(字符串)和当前状态构造一个 TargetSet 作为Key,用 该Key查找map,如果找到,则用找到的状态替换当前状态 替换时,使用深度优先,后序遍历(从深往浅)
为什么该算法不能用在非ADFA上?
数学归纳法必须有初始条件
有穷自动机

有几个输入符号 都导致从q到p的转 移.
§2.2 确定型有穷自动机(DFA)
其转移表(函数)为:
3、 转移函数的扩充(处理串)
ˆ : Q Q
称为扩展转移函数。
描述从任何转态开始读任何输入序列时所发生的事情。 接受状态q和串w, 返回状态p。
§2.2 确定型有穷自动机(DFA)
⑷ 用标有Start的箭头指出的DFA的初始状态。
定义2.2.3 转移表,就是列出δ函数的表格,隐含地说明状态 集合和输入字母表。
§2.2 确定型有穷自动机(DFA)
例2 设计一个DFA满足如下情况:
Q q0 , q1, q2 , 0,1, F q1
(q0 ,0) q2 , (q1,0) q1, (q2 ,0) q2 , (q0 ,1) q0 , (q1,1) q1, (q2 ,1) q1,
对(q,a)∈Q×∑,δ(q,a)= {p1,p2,…,pm}表示A在状态q读入字符a, 可以选择地将状态变成p1、或者p2、…、或者pm ,并将读头向右移动一个带
方格而指向输入字符串的下一个字符。
§2.3 非确定型有穷自动机(NFA)
FA的状态转移图、FA的状态对应的等价类对NFA都有效。
读入0时,引导A到达下一个状态的字符串为x0, x0=2*(3*n+2)=3*2*n+4=3*(2*n+1)+1。所以δ(q2,0)= q1;
读入1时,引导A到达下一个状态的字符串为x1,
x1=2*(3*n+2)+1=3*2*n+4+1=3*(2*n+1)+2。所以,δ(q2,1)= q2 。
有限自动机的应用

有限自动机可以分为确定性有限自动 机和不确定性有限自动机,其中确定 性有限自动机又可以分为有限状态机 和下推自动机。
有限自动机的状态转换
状态转换函数
有限自动机的状态转换函数定义了当前状态和输入字符的组合所引发的状态转 移。
状态转换图
状态转换图是有限自动机的可视化表示,通过图形方式展示状态之间的转换关 系。
3
药物设计
有限自动机可以用于药物设计,如用于寻找与目 标分子结合的小分子抑制剂或激活剂。
有限自动机在物理学中的应用
量子计算模拟
有限自动机可以用于模拟量子计算的过程和结果,有助于理解量 子力学中的现象和计算复杂性。
物理系统ቤተ መጻሕፍቲ ባይዱ拟
有限自动机可以用于模拟物理系统的行为和演化,如流体动力学、 电磁学和热力学等领域的模拟。
词法分析
有限自动机可以用于识别和分割 文本中的单词、短语等语言单位, 为后续的句法分析和语义分析提 供基础。
词性标注
有限自动机可以用于标注文本中 每个单词的词性,例如名词、动 词、形容词等,有助于理解句子 的语法结构和语义。
分词
有限自动机可以用于将连续的自 然语言文本切分成独立的词语或 符号,是自然语言处理中的基础 任务之一。
有限自动机的应用
目录
CONTENTS
• 有限自动机的基本概念 • 有限自动机在计算机科学中的应用 • 有限自动机在通信领域的应用 • 有限自动机在人工智能领域的应用 • 有限自动机在其他领域的应用
01
CHAPTER
有限自动机的基本概念
定义与分类
定义
有限自动机是一种抽象计算模型,用 于描述字符串的识别和转换过程。
有限自动机在密码学中的应用
加密算法
形式语言与自动机有穷自动机讲述
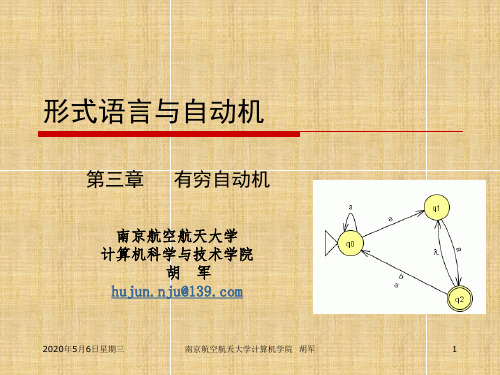
NFA:可以进行猜测选择
0, 1 q0 1 q1 0 q2 1 q3
q3 没有任何转换出来; q3 上如果读入0,1, NFA也运行进入死状态。
2019年1月2日星期三
南京航空航天大学计算机学院 胡军
21
NFA: 猜测的能力
猜测是否已经到了最后三位字符的 位置了?
0, 1
q0
1
q1
0
q2
δ(q3,0)= q1 。
2019年1月2日星期三
南京航空航天大学计算机学院 胡军
12
有穷自动机的基本定义
ˆ 的扩充是很自然的,δ就是 d ˆ 的特例(当 从δ到 d |x|=1时)。 ˆ 这种写法, 今后在提到FA的转移函数时,不再强调 d
一律用δ表示,即δ的第二个变元既可以是单个字符也 可以是一个字符串。
δ(q0,1)= q1 δ(q1,1)= q0 δ(q2,1)= q3 δ(q3,1)= q2 δ(q0,0)= q2 δ(q1,0)= q3 δ(q2,0)= q0 δ(q3,0)= q1
→ *
2019年1月2日星期三
南京航空航天大学计算机学院 胡军
11
有穷自动机的扩充定义
定义3.2 对于有穷自动机M =(Q,∑,δ,q0,F),它的扩充转 ˆ ,是从Q×∑*到Q的映射,其具体定义如下: 移函数 d
提示:DFA得记住 读入字符串的最后两位。
qe
q0 0
1
0 1
DFA 例子
设计一个DFA(字母表为{0,1}),接受所有结尾 是101的字符串。
2019年1月2日星期三
南京航空航天大学计算机学院 胡军
10
DFA 例子
例3.1 给出一个有穷自动机 M=({q0,q1,q2,q3},{0,1},δ,q0,{q0}) 其中:转移函数δ具体定义如下:
DFA和NFA的区别

DFA和NFA的区别正则表达式引擎分成两类,⼀类称为DFA(确定性有穷⾃动机),另⼀类称为NFA(⾮确定性有穷⾃动机)。
两类引擎要顺利⼯作,都必须有⼀个正则式和⼀个⽂本串,⼀个捏在⼿⾥,⼀个吃下去。
DFA捏着⽂本串去⽐较正则式,看到⼀个⼦正则式,就把可能的匹配串全标注出来,然后再看正则式的下⼀个部分,根据新的匹配结果更新标注。
⽽NFA是捏着正则式去⽐⽂本,吃掉⼀个字符,就把它跟正则式⽐较,匹配就记下来:“某年某⽉某⽇在某处匹配上了!”,然后接着往下⼲。
⼀旦不匹配,就把刚吃的这个字符吐出来,⼀个个的吐,直到回到上⼀次匹配的地⽅。
DFA与NFA机制上的不同带来5个影响:1. DFA对于⽂本串⾥的每⼀个字符只需扫描⼀次,⽐较快,但特性较少;NFA要翻来覆去吃字符、吐字符,速度慢,但是特性丰富,所以反⽽应⽤⼴泛,当今主要的正则表达式引擎,如Perl、Ruby、Python的re模块、Java和.NET的regex库,都是NFA的。
2. 只有NFA才⽀持lazy和backreference等特性;3. NFA急于邀功请赏,所以最左⼦正则式优先匹配成功,因此偶尔会错过最佳匹配结果;DFA则是“最长的左⼦正则式优先匹配成功”。
4. NFA缺省采⽤greedy量词(见item 4);5. NFA可能会陷⼊递归调⽤的陷阱⽽表现得性能极差。
例如⽤正则式/perl|perlman/来匹配⽂本 ‘perlman book’。
如果是NFA,则以正则式为导向,⼿⾥捏着正则式,眼睛看着⽂本,⼀个字符⼀个字符的吃,吃完 ‘perl’ 以后,跟第⼀个⼦正则式/perl/已经匹配上了,于是记录在案,往下再看,吃进⼀个 ‘m’,这下糟了,跟⼦式/perl/不匹配了,于是把m吐出来,向上汇报说成功匹配 ‘perl’,不再关⼼其他,也不尝试后⾯那个⼦正则式/perlman/,⾃然也就看不到那个更好的答案了。
如果是DFA,它是以⽂本为导向,⼿⾥捏着⽂本,眼睛看着正则式,⼀⼝⼀⼝的吃。
基于Mealy机的汉字输入有穷自动机及其应用

基于Mealy机的汉字输入有穷自动机及其应用
任磊;谷文祥
【期刊名称】《计算机应用研究》
【年(卷),期】2003(020)004
【摘要】从自动机理论的角度对汉字输入模型的建立进行了一定的研究,并相应地建立了一个基于Mealy有穷自动机的汉字输入有穷自动机模型,在这种模型中对自动机的输入进行了刻画,同时也对自动机的输出进行了相应地刻画,较之以前的汉字输入模型更全面.根据这种模型的特点还介绍了它在汉字GB码与BIG5码转换中的应用.
【总页数】3页(P15-17)
【作者】任磊;谷文祥
【作者单位】东北师范大学,计算机科学系,吉林,长春,130024;东北师范大学,计算机科学系,吉林,长春,130024
【正文语种】中文
【中图分类】TP391.14;TP301.1
【相关文献】
1.基于 Mealy 机的藏文字构件分解 [J], 才让卓玛;李永明;才智杰
2.基于Mealy型状态机的莫尔条纹细分和辨向技术 [J], 邱葭华;胡毅
3.一种基于Mealy!机的语义程序验证方法 [J], 胡罗凯;柴新;许庆炜;应时
4.基于Mealy机精化关系的验证算法 [J], 梁虹;金乃咏
5.基于Mealy机的航空电子组件仿真模型 [J], 刘家学;李蒙阳
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.2 多模式串匹配的情况
图结构进行设计,结构较为简单,随意,实现方 便。针对多模式串匹配的特点,我们可以采用树的数 据结构。同样的,在这里,我们把 DFA 的每个状态当 做是树结构中的每个节点,把 DFA 中输入对应的状态 跳转当做是树结构中的边[3]。
树形结构的构造特点,做一些改进: 1. 每条边都会指向确定的一个节点。 2. 不会存在同一个节点同样的输入对应两个或
4. 复杂度分析
由于树形结构的应用是比较广泛的,在这里只讨 论树形结构构造的算法复杂度。
通过复杂度的计算,可以看出将 n 个模式串插入 到一棵这样的树中的时间复杂度为 O(∑length(i)), length(i)表示第 i 个模式串的长度。创建这树的效 率还是很高的[6]。
而母串在树形结构上遍历的效率就更高了,最好 情况是每个模式串第一个就出现匹配错误复杂度是 O(n),最坏情况也是 O(log(n))[5]。由此可见,此技 术运用在字符串匹配上还是很可行的。
一个确定的有穷自动机 M 是一个五元组[1]:M=
DOI:10.7544/issn1000-1239.2014.20121044 51(1):1-16,2014
(K,Σ,f,S,Z)其中
1. K:有穷非空的状态集合; 2. Σ:有穷非空的输入符号字母表; 3. f:转换函数,是在 K×Σ→K 上的映像,即,
找到合适的低成本,高效率的字符串匹配算法也 不容易。在 Fischer 和 Paterson 于 1974 年将通配符* 引入模式匹配问题之后,如何将通配符与传统的模式 匹配有效结合是研究的重点。带有通配符的串匹配进 入了人们的视野。
比较常用的是 KMP 算法。KMP 算法是通过分析 模式串,预先计算每个位置发生不匹配的时候,所需 GOTO 的下一个比较位置,整理出来一个 next 数组, 然后在上面的算法中使用。
两个以上的边。 3. 允许一条边的起点和终点是一个节点的情
况。 4. 允许没有输出的节点,此节点即为终结节点。 5. 只允许出现一个没有输入的节点,该节点是
根节点。 6. 只允许根节点没有相应的数值。 7. 每个节点可以有只能有一个输入,但可以有
多个输出。 按照如下方式构造自动机: 1. 初始节点对应子字符串的 start。 2. 先按照 3.1 中的方法构造第一个模式串,第
DOI:10.7544/issn1000-1239.2014.20121044 51(1):1-16,2014
6. 直至创建完所有的模式串。 如图 2 所示,举两个例子[4],构造两个多模式串 的树状结构。
4个模式串 b ab aab aaa
a
b
a
b
a
b
模式串
abcd abc abe ae bc be bce
3. 用有穷自动机构造图、树结构进行字符串 匹配
3.1 单模式串匹配的情况
DFA 可以看成是一个图的数据结构,可以按照图 的思想构造出节点和边。在这里,我们把 DFA 的每个 状态当成是图结构中的每个节点,把 DFA 中输入对应 的状态跳转当成是图结构中的边。
由于 DFA 存在着状态的确定性,此图具有以下特 点:
The Application of Deterministic Finite Automata in String Matching
Hou Dan1
1 (School of Information Science & Technology, Beijing Forestry University, Beijing 100083)
Key words DFA; compiler; tree; string matching
摘要 字符串匹配是计算机科学领域内热门的课题,其效率影响着搜索等多个领域,很有必要研发一款时间、 空间复杂度高,有简单实用的算法。基于自动机的思想,将确定有穷自动机应用于字符串匹配上,用树和图的 数据结构进行实现,能一定程度上解决这个问题。而且还避免比较中的冗余的提高空间。
如 f(ki,a)=kj,(ki∈K,kj∈K)就意味着,当前状 态为 ki,输入符为 a 时,将转换为下一个状 态 kj,我们把 kj 称作 ki 的一个后继状态; 4. S∈K 是唯一的一个初态;
5. Z K 是非空的终态集合。
用 DFA 的思想描述程序中的一些状态,具有形 象、严密、清晰地优点。DFA 可以用状态转换图、状 态矩阵等方式表示,并且有严格的逻辑语言的限制。 在应用于字符串匹配中,能够清晰地分出不同的匹配 状态,能减少很多不必要的浪费。
计算机研究与发展 Journal of Computer Research and Development
有穷自动机在字符串匹配中的应用
DOI:10.7544/issn1000-1239.2014.20121044 51(1):1-16,2014
侯丹 1
1 北京林业大学信息学院,北京 100083 (Heidi_0727@)
传统的串匹配算法和技术还有许多,可以概括为 前缀搜索、后缀搜索、子串搜索。代表算法有 KMP, Shift-And,Shift-Or,BM,Horspool,BNDM,BOM 等。所用到的技术包括滑动窗口、位并行、自动机、 后缀树等。
2. 确定有穷自动机相关知识的介绍
有穷自动机,或有穷状态的机器,是描述(或“机 器”)特定类型算法的数学方法。特别地,有穷自动 机可用作描述在输入串中识别模式的过程,因此也能 用作构造扫描程序。DFA(英文全称:Deterministic Finite Automaton)是专指确定型的有穷自动机,在其 输入确定的情况下,相对应的输出是确定的。
的自动机[2]。
n
other
start
empty
n
n
n
a
na
other
other
other
a any
n
ቤተ መጻሕፍቲ ባይዱ
nan
a
nano
图 1 终结状态为“nano”的自动机
此自动机构造好之后,母串的字符串,可以通过 此自动机“跑”一遍,如果依次输入各字符,在自动 机上走一遍,依次经过各状态最终跳转至终结状态, 则该模式串与母串字符串匹配成功,母串包含相应的 模式串,否则,匹配失败。
1. 每条边都会指向确定的一个节点。 2. 不会存在同一个节点同样的输入对应两个或
两个以上的边。 3. 允许一条边的起点和终点是一个节点的情
况。 4. 允许没有输出的节点,此节点即为终结节点。 5. 允许节点没有对应的数值 6. 只允许出现一个没有输入的节点,该节点是
起始节点。 7. 每个节点可以有多个输入,也可以有多个输
一个模式串的输入接在 start 之下。 3. 把模式串每个字符当做一个输入,依次排出
各个输入字符,每输入一个字符跳到下一个 状态。直至跳转到最后一个状态,最后一个 状态为终结状态。 4. 判断是否有下一个模式串,如果有,按照 5 的方法再构造下一个模式串。 5. 把本模式串当做输入,从 start 开始,依次 读入各个字符,当遇到模式串中的字符在树 中没有输入与之对应时,从此节点新建一个 分支,继续 3 的步骤,创建下面的树枝。
Abstract The string match is one of the main research issues in the field of computer science. Its efficiency has influence on a number of areas. For instance, online information search. So that, it is necessary to develop a algorithm with high time complexity and high space complexity .Also the algorithm is simple and practical. Based on the idea of automatic machines, The article will describe the application of determinant finite automatic in string matching. The technology is implemented with structures of tree and graph data. It can solve this problem in some extent. Also, it can avoid redundant space.
1. 字符串匹配相关研究介绍
串匹配算法虽然发展了几十年,然而非常实用的 算法是今年才发现。串匹配问题的研究存在理论研究 和实际应用的脱节。在字符串匹配这个领域,潜心研
收稿日期:2015-06-20 基金项目:如有国家或省部级基金资助,请写上正确基金项目名称和编号
计算机研究与发展 Journal of Computer Research and Development
出。 按照如下方式构造自动机: 1. 初始节点对应子字符串的 start 2. 把模式串每个字符当做一个输入,依次排出
各个输入字符,每输入一个字符跳到下一个 状态。 3. 以此类推,直至跳转到最后一个状态,最后 一个状态为终结状态。 如图所示,本图给出了一个终结状态为“nano”
计算机研究与发展 Journal of Computer Research and Development
关键词 确定的有穷自动机;编译原理;树;字符串匹配
中图法分类号 TP391
字符串匹配是计算机科学中最古老、研究最广泛 的问题之一。一个字符串是一个定义在有限字母表∑ 上的字符序列。例如,ATCTAGAGA 是字母表∑ = {A,C,G,T}上的一个字符串。字符串匹配问题就是在 一个大的字符串 T 中搜索某个字符串 P(子字符串) 的所有出现位置。其中,T 称为文本,P 称为模式, T 和 P 都定义在同一个字母表∑上。
