第2章3节 动量与角动量
合集下载
第3动量与角动量

i t1 t1 i
写成:
t2 Fidt F外dt t2 i t1 t1
将所有的外力 共点力相加 F 2 F
c F3
1
17
t2 ( Fidt f idt ) t2 i t1 t1
(Pi Pi 0 )
i
再看内力冲量之和
I P
积分形式
6
I x Fx dt mv2 x mv1x
分量表示
t2
I y Fy dt mv2 y mv1 y I z Fz dt mv2 z mv1z
t1 t1 t2
t1 t2
说明 某方向受到冲量,该方向上动量就增加.
7
讨论
I P
x
mv1
O
mv2
y
11
解
由动量定理得:
Fx t mv2 x mv1x x mv cos (mv cos ) mv2 2mv cos Fy t mv2 y mv1 y y mv sin mv sin 0 2mv cos F Fx 14.1 N t 方向与 Ox 轴正向相同. F' F
(2) ft mv mv 0 4.7 N s (设v 0 反响为正方向) 负号表示冲量方向与 相反
v0
25
2.静水中停着两条质量均为M的小船,当第一条船中的一个质量为m的人以水平速 v 度 (相对于地面)跳上第二条船后,两船运动的速度各多大?(忽略水对船的阻 力). 解:以人与第一条船为系统,因水平方向合外力为零。所以水平方向动量守恒, 则有: Mv1 +mv =0 v1 =-mv/M 再以人与第二条船为系统,因水平方向合外力为零。所以水平方向动量守恒, 则有:mv = (m+M)v2 v2 =mv/(M+m)
写成:
t2 Fidt F外dt t2 i t1 t1
将所有的外力 共点力相加 F 2 F
c F3
1
17
t2 ( Fidt f idt ) t2 i t1 t1
(Pi Pi 0 )
i
再看内力冲量之和
I P
积分形式
6
I x Fx dt mv2 x mv1x
分量表示
t2
I y Fy dt mv2 y mv1 y I z Fz dt mv2 z mv1z
t1 t1 t2
t1 t2
说明 某方向受到冲量,该方向上动量就增加.
7
讨论
I P
x
mv1
O
mv2
y
11
解
由动量定理得:
Fx t mv2 x mv1x x mv cos (mv cos ) mv2 2mv cos Fy t mv2 y mv1 y y mv sin mv sin 0 2mv cos F Fx 14.1 N t 方向与 Ox 轴正向相同. F' F
(2) ft mv mv 0 4.7 N s (设v 0 反响为正方向) 负号表示冲量方向与 相反
v0
25
2.静水中停着两条质量均为M的小船,当第一条船中的一个质量为m的人以水平速 v 度 (相对于地面)跳上第二条船后,两船运动的速度各多大?(忽略水对船的阻 力). 解:以人与第一条船为系统,因水平方向合外力为零。所以水平方向动量守恒, 则有: Mv1 +mv =0 v1 =-mv/M 再以人与第二条船为系统,因水平方向合外力为零。所以水平方向动量守恒, 则有:mv = (m+M)v2 v2 =mv/(M+m)
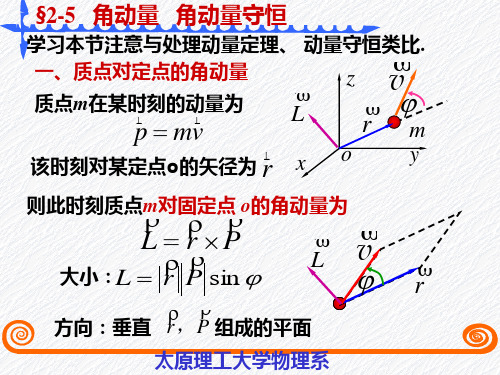
§2-5角动量定理 角动量守恒定律
太原理工大学物理系
L r P
在直角坐标系中
L ( xi yj zk ) ( Px i Py j Pz k )
L x y z
i j k p x p y p z
太原理工大学物理系
L
v
方向:垂直 r ,P 组成的平面
太原理工大学物理系
r
讨论: 1) 同一质点相对于不同的点,角动量不同。 2) 在说明质点的角动量时,必须指明是对哪个 点而言的。
3)质点以角速度作半径为r的圆运动,相对 圆心的角动量
L = mvr
L
p
mr J
2
o r
2)在具体的坐标系中,角动量在各坐标轴的分 量称作对轴的角动量。力矩在各坐标轴的分量, 称作对轴的力矩。
L Lx i Ly j Lz k L 是质点对o点的角动量
Lx Ly Lz
分别是质点对x、y、z轴的角动量.
M M x i M y j M z k M 是力对o点的力矩
三、质点的角动量定理 dP 由牛顿第二定律 F dt
dP 两边用位矢叉乘 r F r dt dp d dr r (r p) p dt dt dt
dr 由速度定义 v dt
v p 0 dL dp d r (r p) dt dt dt
i
ri fi 质点系受到的内力矩的矢量和
i
矩
太原理工大学物理系
可以证明:内力对定点的力矩之和为零,即
ri fi 0
i
质点系内的重要结论之三
动量与角动量

r p
得 即 质点 对某定点 的
r p
mv
p
角动量的时间变化率 称为质点的
所受的合外力矩
角动量定理
的微分形式
质点的角动量定理也可用积分形式表达
由微分形式
积分形式
即
称为 冲量矩 这就是质点的
角动量的增量
角动量定理
的积分形式
冲量矩的单位是
牛顿 · 米 · 秒 ( N · m · s )
质点的动量矩定理表明,合外力矩是引起角动量变化的原因。 合外力矩的时间积累效果(冲量矩)可用动量矩的增量来量度。 动量矩定理也只有在惯性系中才适用。
凡例
再用三角 公式算出
原子系统衰变,内力远大于外力(重力) 。 系统动量守恒。 选实验室坐标系
例p.49
动量
剩 余 核 中微子静止 放射性原子核 电子
发生衰变
1
动量
设 剩余核 反冲动量为 则 即 大小
。
= 6.4×10 -23 kg · m · s 1
= 1.2×10 -22 kg · m · s -
重力
本题的合外力是向心力
由a到b 绕行半周 的 冲量 的 冲量
对应的冲量式为 方向 可用 于是 待求 已求 标识 然后合成 求出 的 大小和方向
3.2
质点系
系动量定理
p.47例 人车之间的作用为
内力,不影响系统 建立坐标系:
质点系:人,车
系统受
外力: 重 力 支持力 側向力
跳车后车速 轨车侧向力 应用质点系 的动量定理
喷出燃料
主体质量不断减少
变质量问题的牛顿定律可用
运行装料
主体质量不断增加
此类问题并非惯性质量随 速度而变,而是物质的流动 称为质量的流动问题。
力学3动量角动量

0t Mdt Lt L0
((注21意))或:是ML普遍rr规FP律0,宏恒观矢Fr、量//微F—0,观—均r角适动0用量。守力恒F心定r律F r
(3)有心力:运动质点所受的力总是通过一个固定点。
质点对力心的角动量守恒。 r / / F
(4)质点对某点的角动量守恒, 对另一点不一定守恒.
(5)角动量守恒, 不见得动量守恒. 如:匀速圆周运动.
今用手提起链的一端使之以匀速v 铅直上升。
求: 从一端离地到全链离地,手的拉力的冲量?
F
v
y
பைடு நூலகம்
解: t时刻铁链的动量为:
P0 yv
t+dt时刻铁链的动量为:
P y dyv
l
动量的变化为:
gy
dP P P0 vdy
dt时间内合外力的冲量为:
根据动量定理:
dI F gydt
dI dP F gydt vdy
u
u
v
dv
m
dm u
dt时间内系统动量增量 dP (m dm)(v dv) mv mdv dmv
(
dm)v
'
mv
dmdv dmv
'
地面
mv
m dv vdm v'dm
由动量定理 F合外dt dP F合外
F合 外
d(mv )
dt
v'
dm dt
dP dt
m
dv
dm
P mv dv ?
v gL
P m + dmv dv
dt时间内动量的变化:
dP P P0
m + dmv dv mv
mdv + vdm dmv
第二章 动量、角动量守恒-2

β
( )
' 2
= 0.32 m/ s
(
2
)
2 a' = an + at2 = 0.51 m 2 s
a
an
合加速度的方向与轮缘切线方向夹角
an β = arctan = 38.70 at
6
4、转动动能: 、转动动能
1 2 Ek = mv 2 i 刚体是有许多质点组成的,第 刚体是有许多质点组成的 第
2
2、刚体运动的角量描述: 、刚体运动的角量描述
角位置: 角位置 角位移: 角位移
θ1
θ2
p
'
∆θ = θ2 − θ1
0
∆θ
p
角位移是矢量 角速度: 角速度 平均角速度: 平均角速度 瞬时角速度 角加速度: 角加速度
θ1
x
∆θ ω = = t2 − t1 ∆t
θ2 − θ1
dθ ω= dr t r 2 r dω d θ = 2 α= r
( 2 m 1 + m / 2 )m 2 g T2 = m1 + m 2 + m / 2
(m1 − m2 )g a= m1 +m2 +m / 2
15
2.不计滑轮质量 m=0 不计滑轮质量
T1 =
2 m 2 m1 g + m1 M f / R m1 + m 2
a= (m1 − m2 )g − M f / R m1 +m2
J=
∑
i =1
n
∆mi ri2
如果刚体是连续分布的质点系
J = r dm
2
∫
例1、计算质量为 m , 长为 l 的均匀细杆的转动惯量 、 (1) 假定转轴通过杆中心并与杆垂直 假定转轴通过杆中心并与杆垂直; (2) 假定转轴通过杆的端点与杆垂直。 解: dm = m dx
( )
' 2
= 0.32 m/ s
(
2
)
2 a' = an + at2 = 0.51 m 2 s
a
an
合加速度的方向与轮缘切线方向夹角
an β = arctan = 38.70 at
6
4、转动动能: 、转动动能
1 2 Ek = mv 2 i 刚体是有许多质点组成的,第 刚体是有许多质点组成的 第
2
2、刚体运动的角量描述: 、刚体运动的角量描述
角位置: 角位置 角位移: 角位移
θ1
θ2
p
'
∆θ = θ2 − θ1
0
∆θ
p
角位移是矢量 角速度: 角速度 平均角速度: 平均角速度 瞬时角速度 角加速度: 角加速度
θ1
x
∆θ ω = = t2 − t1 ∆t
θ2 − θ1
dθ ω= dr t r 2 r dω d θ = 2 α= r
( 2 m 1 + m / 2 )m 2 g T2 = m1 + m 2 + m / 2
(m1 − m2 )g a= m1 +m2 +m / 2
15
2.不计滑轮质量 m=0 不计滑轮质量
T1 =
2 m 2 m1 g + m1 M f / R m1 + m 2
a= (m1 − m2 )g − M f / R m1 +m2
J=
∑
i =1
n
∆mi ri2
如果刚体是连续分布的质点系
J = r dm
2
∫
例1、计算质量为 m , 长为 l 的均匀细杆的转动惯量 、 (1) 假定转轴通过杆中心并与杆垂直 假定转轴通过杆中心并与杆垂直; (2) 假定转轴通过杆的端点与杆垂直。 解: dm = m dx
02_动量角动量3

瞬时功率:
A dA P lim dt t 0 t dA F dr F v P dt dt
i 1
i 1
b A lim Fi ri F dr
n r 0 i 1
F1
F2
a
b A F dr a
a
r1
1
2
功和能
合力的功:
A
L
F dr F1 F2 Fn dr
动量与角动量
一、质点的角动量 angular momentum
定义:
L r P r mv
——质点对O点的 角动量
L
z
O
x
mv
y
L rmv sin L Lx i Ly j Lz k
单位:kg · m2· s-1
动量与角动量
地球在椭圆的一个焦点上,则
(1)卫星的动量是否守恒? (2)卫星的角动量是否守恒?
m
(3)卫星的动能是否守恒?
(4)开普勒面积定律的实质是什么?
动量与角动量
Example 质量为 m 小球系在绳子的一端,绳穿过铅 直套管,使小球限制在一光滑水平面上运动。先使小 球一速度 v0 绕管心作半径为 r0 的圆周运动,然后向下 拉绳子,使小球运动半径变为 r1 。求小球的速度.
• 对质点系
dLi F2 M i外 M i内 dt f2 dLi (M i外 M i内 ) f1 d t i i d( L) dL F 1 M外 m1 dt dt t t0 M 外 dt L L0 t ——外力矩的冲量矩 M d t 外
动量角动量

I = ∑ f i ∆t i
i =1
n
f1∆ t1
f2∆t2
f3∆t3
若力的变 化连续
I =
t + ∆tI Nhomakorabeaf4∆t4
∫
t
fd t
矢量 冲量 过程量
二、质点运动的动量定理 由牛顿第 二定律
dP F= dt
t
微分形式
( Fd t = d P )
∫ Fdt = ∫ dP
t0 P
P + ∆P
质点运动的 动量定理
∑ Fi x = 0 ,
∑ Fi y = 0 ,
∑ mi vi x = ∑ mi vi 0 x
∑ mi vi y = ∑ mi vi 0 y
动量守恒定律在微观高速范围仍适用。 4. 动量守恒定律在微观高速范围仍适用。
例1:如图所示 大炮在发射时炮身会发生反冲现 :如图所示, 设炮身的仰角为θ, 炮弹和炮身的质量分别为m 象。设炮身的仰角为 炮弹和炮身的质量分别为 炮弹在离开炮口时的速率为v, 和M, 炮弹在离开炮口时的速率为 若忽略炮身反冲 时与地面的摩擦力, 求炮身的反冲速率。 时与地面的摩擦力 求炮身的反冲速率。 轴沿水平向右, 解:设x轴沿水平向右 轴沿水平向右 根据动量守恒定律得
由于内力成对出现, 由于内力成对出现,根据牛顿第三定律得
∑∑ f
j ≠i
n
ij
=0
d n 所以 微分形式) ∑Fi = dt (∑mivi ) (微分形式) i=1 i=1 n n 两边积分得 t n 积分形式) ∫ ∑Fi dt = ∑mivi − ∑mivi0(积分形式)
t0 i=1 i=1 i=1
y
M 2 gh
动量与角动量

2mv 2 0.58 6.26 2 F 3.82 10 N t 0.019
例2:质量为m的质点做圆锥摆运动,质点的速 率为v,圆半径为R。圆锥母线与轴线之间的夹 角为 ,计算质点所受的拉力在一周内的冲量。
演示
逆风行舟
F进 风
F风对帆
F横
1 1 2
帆
Δ
2
F帆对风 Δ
×
i c i
x 质心位置是质点位置 以质量为权重的平均值。
二、几种系统的质心 ● 两质点系统 m1
·r
z
C
1
×
m2 r2
·
m1 r1 = m2 r2
● 连续体
dm ×C rc m y
r
0
r dm rC m
xdm xC m
x
……
●均匀杆、圆盘圆环、球,质心为其几何中心。 ●“小”线度物体的质心和重心是重合的。 求挖掉小圆盘后系统的质心坐标。 [例6]如图示, 解: 由对称性分析,质心C应在x轴上。 y 令 为圆盘的面密度, 均质圆盘 R
L r p
·
于是有
dL M dt
质点角动量定理 (微分形式)
或
d L M dt
积分
t2 M t1
d t L2 L1
质点角动量定理 (积分形式)
t2 M t1
d t 称冲量矩 ——力矩对时间的积累作用。
力矩的量纲是ML2T-2,单位是N.m
可认为动量近似守恒。
6、动量守恒定律是比牛顿定律更普遍、更基本 的定律,它在宏观和微观领域均适用。 7、用守恒定律作题,应注意分析过程、系统和 条件。
例4:一个有1/4圆弧滑槽的大物体的质量为M, 停在光滑的水平面上,另一质量为m的小物体自 圆弧顶端由静止下滑。求当小物体m滑到底时, 大物体M在水平面上移动的距离。
例2:质量为m的质点做圆锥摆运动,质点的速 率为v,圆半径为R。圆锥母线与轴线之间的夹 角为 ,计算质点所受的拉力在一周内的冲量。
演示
逆风行舟
F进 风
F风对帆
F横
1 1 2
帆
Δ
2
F帆对风 Δ
×
i c i
x 质心位置是质点位置 以质量为权重的平均值。
二、几种系统的质心 ● 两质点系统 m1
·r
z
C
1
×
m2 r2
·
m1 r1 = m2 r2
● 连续体
dm ×C rc m y
r
0
r dm rC m
xdm xC m
x
……
●均匀杆、圆盘圆环、球,质心为其几何中心。 ●“小”线度物体的质心和重心是重合的。 求挖掉小圆盘后系统的质心坐标。 [例6]如图示, 解: 由对称性分析,质心C应在x轴上。 y 令 为圆盘的面密度, 均质圆盘 R
L r p
·
于是有
dL M dt
质点角动量定理 (微分形式)
或
d L M dt
积分
t2 M t1
d t L2 L1
质点角动量定理 (积分形式)
t2 M t1
d t 称冲量矩 ——力矩对时间的积累作用。
力矩的量纲是ML2T-2,单位是N.m
可认为动量近似守恒。
6、动量守恒定律是比牛顿定律更普遍、更基本 的定律,它在宏观和微观领域均适用。 7、用守恒定律作题,应注意分析过程、系统和 条件。
例4:一个有1/4圆弧滑槽的大物体的质量为M, 停在光滑的水平面上,另一质量为m的小物体自 圆弧顶端由静止下滑。求当小物体m滑到底时, 大物体M在水平面上移动的距离。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
t1
Fx
Fx 0
t
t
5.可解变质量问题。 如洒水车、火箭发射过程
6.分量式,即:
I y Fy dt mv 2 y mv1 y
7.由牛二定律推导得,只适用于惯性系
I x Fx dt mv 2 x mv1x
三、质点的动量守恒定律 1. 若 F 0, 即 P 常矢量 则 P 0,
注意:
1、动量守恒定律只适用于惯性系。
2、系统动量守恒,但每个质点的动量可能变化。
例4. 在水平冰面上以一定速度向东行驶的炮车,向东 南(斜向上)方向发射一炮弹,对于炮车和炮弹这一 系统,在此过程中(忽略冰面摩擦力及空气阻力)
(A)总动量守恒。 (B)总动量在任何方向的分量均不守恒。 (C)总动量在水平面上任意方向的分量守恒, 竖直方向分量不守恒。 [C]
t2
m1
m2
m v m v ( F f ) dt P 1 12 1 11 1 21 t1 1 t2 t1 (F2 f12 )dt P2 m2v22 -m2v21 t2 (F1 F2 )dt P 1 P 2
mAvA0 mBvB0 mAvA mBvB
EKA EKB 1 mAv 2 A 2 1 2 mB v B 2
vA 2 vB
2
例6、质量为 m1 20g的子弹以 v 400m s 的速率沿与 30 竖直方向呈 角的方向射入原来静止的摆球中,小 球质量为 m2 980 g,摆线不伸缩,不计质量,子弹 射入小球后与小球一起运动,求一起运动的速率。 解: 以水平向右为x轴正方向,竖直向下为y轴正方向
r
M b
1 2 ˆ gt 0 mgb k 2 0 mg 0
iˆ
ˆ j
ˆ k
y
ˆ mg j
M 力 力臂 m gb
M rmg sin 大小:
方向:右手螺旋
例 4 、哈雷彗星绕太阳的轨道是以太阳为一个焦点的 作椭圆,它离太阳中心的最近距离 l1 8.751010 m , 4 此时它的速率v1 5.4610 m / s。离太阳中心的最远时 2 v 9 . 08 10 m / s ,求它离太阳中心最远距离 的速率 2 为多少?
t1
f 21
F1 f 31 f13
f 32
f12
F3
f 23
m3
3)、n个质点的系统
t2
内力矢量和为零: F内 0
( Fi )dt ( Pi )
t1 i i
质点系的动量定理:
系统受合外力的冲量 = 系统总动量的增量
动量定理
分量形式
t2 I dI Fdt
t1
二、质点的动量定理
dP F dt
I
P2
P 1
t1
t2 Fdt dP
t2
Fdt =P mv2 - mv1
t
P2 P 1
I
1
质点所受合外力的冲量,等于该质点动量的增量。 说明
若合外力为0,则动量守恒
则 Px 0, 即 Px 常矢量 2. 若 Fx 0,
若某方向合外力为0,则在这个方向上动量守恒
例1. 在一次物理竞赛中,赛题是从桌角A处向B发 射一个乒乓球,让竞赛者在桌边B处用一只吹管将 球吹进球门C(见本题图),看谁最先成功。某生 将吹管对准C拼命吹,但球总是不进球门。试分析 该生失败的原因。
t1
t 2 t1
M 1 M 21 dt L12 L11
O
r1
f 21
m1
F2
f12
r2
m2
系统t 2
t1
M 1 M 2 M 21 M 12 dt
0
L12 L22 L11 L21
2
Fdt 6t 3dt
2
t1
2
0
(2)动量定理: I
mv2 - mv 1
0
v2 18 m / s
作业P62:2.9(2), 2.13, 2.14
四、质点系的动量定理
1、质点系的动量定理
动量守恒定律
1)、两个质点的质点系 m1 : 外力 F1 内力 f 21 m2 : 外力 F2 内力 f12
1.
I
大小:
t2
t1
Fdt =动量增量的大小
矢量
方向: 由力的性质决定, 动量增量方向
2. 单位:Ns
3.
I 是过程量
和整个过程力的性质有关, 不能由某一时刻的力决定。
4.可以求冲力的平均值。
t2 I Fdt mv2 - mv1
I P F t t
t2
Mdt dL L2 L1
t1
L1
L2
积分形式
合力矩的冲量 =质点对该参考点角动量的增量 冲量矩 与质点的动量定理地位相当 质点的角动量定理
3、质点系的角动量定理
(1)两个质点的质点系
t2
F1
质点1
质点2 M 2 M 12 dt L L 22 21
t2
t1
Fdt P mx dt Fy dt
m v
i i 2x
m v
i i 1x
t1
m v
i i2y
m v
i
i i1y
2、质点系动量守恒定律
即 P Pi mi vi 常矢量 1) 若 F 0 , 则 P 0 , 合
系统受合外力矩的冲量 =系统总角动量的增量
三、角动量守恒定律
若对于某一固定点,质点所受的合外力矩为零,则 此质点对该固定点的角动量矢量保持不变。
dL 如果M 0, 则 0 即L=常矢量 dt
dL M dt
如:匀速直线运动 F 0时,M 0 质点: 力的作用点是参考点 r 0时, M 0 力和位矢方向共线, 有心力 r F 0时, M 0 如:天体问题 质点系: M1 M 2 M n 0 如:刚体
F1
m1 f 21
t2
M 1 M 2 dt
t1
r1
L12 L22 L11 L21
O
r2
F2
f12 m2
(2)n个质点的系统 t2 ( M i )dt ( Li )
t1 i i
内力矩的矢量和为0
质点系的角动量定理:
t1
F1
mn f 21
m1
F2
f12
m1v12 m2v22 - m1v11 m2v21
m2
2)、三个质点的系统 t2 m1 1 f 21 f31 )dt P 1 m 1v12 -m 1v11 t1t (F 2 F2 ( F f f ) dt P m v m v 2 12 32 2 2 22 2 21 t1t 2 m2 ( F f f ) dt P m v m v 3 3 32 3 31 t1 3 13 23 t2 (F1 F2 F3 )dt P1 P2 P3
例5. A、B两木块质量分别为mA、mB ,且 mB 2mA, 两者用一轻弹簧连接后静止于光滑水平桌面上,如 图所示,若用外力将两木块压近使弹簧被压缩,然 后将外力撤去,则此后两木块运动速度之比 vA vB 2 ,两木块运动动能之比 EKA / EKB = 2 解: A B F合 0 动量守恒
r
L m b
0
iˆ
ˆ j 1 2 gt 2 gt
ˆ k
ˆ 0 mgbt k
0
y L rmv sin 大小:
b gt m r = r = mgbt
v
方向: z轴正向
例2、判断正误
(1)质点系的总动量为0,总角动量一定为0
(2)一质点做变速直线运动,角动量一定为0 (3)一做直线运动的质点,角动量一定不变 (4)一质点做匀速圆周运动,动量方向不断 变化,角动量方向也不断变化。
§2.3 动量和角动量
§2.3.1 动量和冲量 动量定理 质点系的动量定理 动量守恒定律
§2.3.2
质点的角动量
角动量定理和角动量守恒定律
§2.3.3
质心 质心运动定律
§2.3.1 动量
一、冲量 1.恒力的冲量
动量定理 动量守恒
I Ft
2.变力的冲量
dI Fdt
力的元冲量
二、角动量定理
1、角动量定理
由 LrP dL d dr dP (r P) 得: P r dt d t dt dt mv v F
dL v mv r F dt
彗星在运动中仅受太阳的引力(其他引力比此力小得多,可 忽略),该引力始终指向太阳中心O,因而对O的外力矩为零, 所以彗星对O的角动量守恒。
2、单位:kgm2/s
L r P r mv
定义质点对点O的角动量 L
P mv
v
r
O
r
O
3、 L 与参考点有关
L的方向
4、 L 方向垂直于 r 和 P 的平面
O
L
r
L
θ
P
5、作圆周运动的质点对圆心的 角动量大小
Fx
Fx 0
t
t
5.可解变质量问题。 如洒水车、火箭发射过程
6.分量式,即:
I y Fy dt mv 2 y mv1 y
7.由牛二定律推导得,只适用于惯性系
I x Fx dt mv 2 x mv1x
三、质点的动量守恒定律 1. 若 F 0, 即 P 常矢量 则 P 0,
注意:
1、动量守恒定律只适用于惯性系。
2、系统动量守恒,但每个质点的动量可能变化。
例4. 在水平冰面上以一定速度向东行驶的炮车,向东 南(斜向上)方向发射一炮弹,对于炮车和炮弹这一 系统,在此过程中(忽略冰面摩擦力及空气阻力)
(A)总动量守恒。 (B)总动量在任何方向的分量均不守恒。 (C)总动量在水平面上任意方向的分量守恒, 竖直方向分量不守恒。 [C]
t2
m1
m2
m v m v ( F f ) dt P 1 12 1 11 1 21 t1 1 t2 t1 (F2 f12 )dt P2 m2v22 -m2v21 t2 (F1 F2 )dt P 1 P 2
mAvA0 mBvB0 mAvA mBvB
EKA EKB 1 mAv 2 A 2 1 2 mB v B 2
vA 2 vB
2
例6、质量为 m1 20g的子弹以 v 400m s 的速率沿与 30 竖直方向呈 角的方向射入原来静止的摆球中,小 球质量为 m2 980 g,摆线不伸缩,不计质量,子弹 射入小球后与小球一起运动,求一起运动的速率。 解: 以水平向右为x轴正方向,竖直向下为y轴正方向
r
M b
1 2 ˆ gt 0 mgb k 2 0 mg 0
iˆ
ˆ j
ˆ k
y
ˆ mg j
M 力 力臂 m gb
M rmg sin 大小:
方向:右手螺旋
例 4 、哈雷彗星绕太阳的轨道是以太阳为一个焦点的 作椭圆,它离太阳中心的最近距离 l1 8.751010 m , 4 此时它的速率v1 5.4610 m / s。离太阳中心的最远时 2 v 9 . 08 10 m / s ,求它离太阳中心最远距离 的速率 2 为多少?
t1
f 21
F1 f 31 f13
f 32
f12
F3
f 23
m3
3)、n个质点的系统
t2
内力矢量和为零: F内 0
( Fi )dt ( Pi )
t1 i i
质点系的动量定理:
系统受合外力的冲量 = 系统总动量的增量
动量定理
分量形式
t2 I dI Fdt
t1
二、质点的动量定理
dP F dt
I
P2
P 1
t1
t2 Fdt dP
t2
Fdt =P mv2 - mv1
t
P2 P 1
I
1
质点所受合外力的冲量,等于该质点动量的增量。 说明
若合外力为0,则动量守恒
则 Px 0, 即 Px 常矢量 2. 若 Fx 0,
若某方向合外力为0,则在这个方向上动量守恒
例1. 在一次物理竞赛中,赛题是从桌角A处向B发 射一个乒乓球,让竞赛者在桌边B处用一只吹管将 球吹进球门C(见本题图),看谁最先成功。某生 将吹管对准C拼命吹,但球总是不进球门。试分析 该生失败的原因。
t1
t 2 t1
M 1 M 21 dt L12 L11
O
r1
f 21
m1
F2
f12
r2
m2
系统t 2
t1
M 1 M 2 M 21 M 12 dt
0
L12 L22 L11 L21
2
Fdt 6t 3dt
2
t1
2
0
(2)动量定理: I
mv2 - mv 1
0
v2 18 m / s
作业P62:2.9(2), 2.13, 2.14
四、质点系的动量定理
1、质点系的动量定理
动量守恒定律
1)、两个质点的质点系 m1 : 外力 F1 内力 f 21 m2 : 外力 F2 内力 f12
1.
I
大小:
t2
t1
Fdt =动量增量的大小
矢量
方向: 由力的性质决定, 动量增量方向
2. 单位:Ns
3.
I 是过程量
和整个过程力的性质有关, 不能由某一时刻的力决定。
4.可以求冲力的平均值。
t2 I Fdt mv2 - mv1
I P F t t
t2
Mdt dL L2 L1
t1
L1
L2
积分形式
合力矩的冲量 =质点对该参考点角动量的增量 冲量矩 与质点的动量定理地位相当 质点的角动量定理
3、质点系的角动量定理
(1)两个质点的质点系
t2
F1
质点1
质点2 M 2 M 12 dt L L 22 21
t2
t1
Fdt P mx dt Fy dt
m v
i i 2x
m v
i i 1x
t1
m v
i i2y
m v
i
i i1y
2、质点系动量守恒定律
即 P Pi mi vi 常矢量 1) 若 F 0 , 则 P 0 , 合
系统受合外力矩的冲量 =系统总角动量的增量
三、角动量守恒定律
若对于某一固定点,质点所受的合外力矩为零,则 此质点对该固定点的角动量矢量保持不变。
dL 如果M 0, 则 0 即L=常矢量 dt
dL M dt
如:匀速直线运动 F 0时,M 0 质点: 力的作用点是参考点 r 0时, M 0 力和位矢方向共线, 有心力 r F 0时, M 0 如:天体问题 质点系: M1 M 2 M n 0 如:刚体
F1
m1 f 21
t2
M 1 M 2 dt
t1
r1
L12 L22 L11 L21
O
r2
F2
f12 m2
(2)n个质点的系统 t2 ( M i )dt ( Li )
t1 i i
内力矩的矢量和为0
质点系的角动量定理:
t1
F1
mn f 21
m1
F2
f12
m1v12 m2v22 - m1v11 m2v21
m2
2)、三个质点的系统 t2 m1 1 f 21 f31 )dt P 1 m 1v12 -m 1v11 t1t (F 2 F2 ( F f f ) dt P m v m v 2 12 32 2 2 22 2 21 t1t 2 m2 ( F f f ) dt P m v m v 3 3 32 3 31 t1 3 13 23 t2 (F1 F2 F3 )dt P1 P2 P3
例5. A、B两木块质量分别为mA、mB ,且 mB 2mA, 两者用一轻弹簧连接后静止于光滑水平桌面上,如 图所示,若用外力将两木块压近使弹簧被压缩,然 后将外力撤去,则此后两木块运动速度之比 vA vB 2 ,两木块运动动能之比 EKA / EKB = 2 解: A B F合 0 动量守恒
r
L m b
0
iˆ
ˆ j 1 2 gt 2 gt
ˆ k
ˆ 0 mgbt k
0
y L rmv sin 大小:
b gt m r = r = mgbt
v
方向: z轴正向
例2、判断正误
(1)质点系的总动量为0,总角动量一定为0
(2)一质点做变速直线运动,角动量一定为0 (3)一做直线运动的质点,角动量一定不变 (4)一质点做匀速圆周运动,动量方向不断 变化,角动量方向也不断变化。
§2.3 动量和角动量
§2.3.1 动量和冲量 动量定理 质点系的动量定理 动量守恒定律
§2.3.2
质点的角动量
角动量定理和角动量守恒定律
§2.3.3
质心 质心运动定律
§2.3.1 动量
一、冲量 1.恒力的冲量
动量定理 动量守恒
I Ft
2.变力的冲量
dI Fdt
力的元冲量
二、角动量定理
1、角动量定理
由 LrP dL d dr dP (r P) 得: P r dt d t dt dt mv v F
dL v mv r F dt
彗星在运动中仅受太阳的引力(其他引力比此力小得多,可 忽略),该引力始终指向太阳中心O,因而对O的外力矩为零, 所以彗星对O的角动量守恒。
2、单位:kgm2/s
L r P r mv
定义质点对点O的角动量 L
P mv
v
r
O
r
O
3、 L 与参考点有关
L的方向
4、 L 方向垂直于 r 和 P 的平面
O
L
r
L
θ
P
5、作圆周运动的质点对圆心的 角动量大小
