fdm有限差分法不能求解的方程
有限差分法的基本原理

f (x) ≈
2h
中心二阶差商
′′
f (x+h)−2f (x)+f (x−h)
f (x) ≈
h2
O(h) O(h)
2
O(h )
2
O(h )
其中,h表示网格间距,O(hn)表示截断误差与hn成正比。可以看出,中心差商比前向或后向差商具有更高的精度。
误差分析
有限差分法求得的数值解与真实解之间存在误差,这些误差主要来源于以下几个方面:
常用差分格式
有限差分法中最重要的步骤是构造合适的差分格式来近似微分项。根据泰勒展开式,可以得到以下常用的一阶和二阶差分格式:
差分格式
表达式
截断误差
前向一阶差商
′
f (x+h)−f (x)
f (x) ≈
h
后向一阶差商
′
f (x)−f (x−h)
f (x) ≈
h
中心一阶差商
′
f (x+h)−f (x−h)
截断误差:由于使用有限项级数来近似无穷级数而产生的误差; 舍入误差:由于计算机对小数进行四舍五入而产生的误差;
离散误差:由于对连续区域进行离散化而产生的误差; 稳定性误差:由于数值格式的稳定性不足而导致误差的累积或放大。
为了减小误差,一般可以采取以下措施:
选择更高阶或更精确的差分格式; 减小网格间距或时间步长; 选择合适的初始条件和边界条件; 选择稳定且收敛的数值格式。
+
。 2
h)
为了验证上述方法的正确性,我们取M = 10, N = 100,则原问题可以写为如下形式:
则该问题对应的递推关系式为:
⎧ut (x, t) − uxx (x, t) = 0,
复杂介质地震波正演模拟方法及优化

复杂介质地震波正演模拟方法及优化摘要本文旨在探讨复杂介质地震波正演模拟方法及其优化。
我们将介绍地震波正演模拟的基本原理,同时介绍目前常用的模拟方法,并针对复杂介质中的挑战提出了一些优化措施。
通过本文的学习,读者将能够更好地理解复杂介质中地震波的正演模拟,并了解如何优化模拟结果。
1.引言地震波正演模拟是地震学中的重要研究方法,通过模拟地震波在地下介质中的传播过程,可以帮助我们解决很多实际问题,如地震勘探、地震灾害预测等。
然而,由于地下介质的复杂性,正演模拟在复杂介质中存在着一些挑战,如速度模型不准确、界面反射等问题。
因此,本文将介绍一些常用的地震波正演模拟方法,并提出一些优化措施,以改善正演模拟结果的准确性和可靠性。
2.地震波正演模拟方法地震波正演模拟方法可以分为有限差分法(F DM)、有限元法(F EM)和谱元法(S EM)等。
下面将逐一介绍它们的基本原理和适用范围。
2.1有限差分法(FD M)有限差分法是一种常用的地震波正演模拟方法,它将介质离散化为网格,通过有限差分的方式,近似求解地震波动方程。
有限差分法简单易行,适用范围广,但在复杂介质中存在一些限制,如对较大的速度变化不敏感。
2.2有限元法(F E M)有限元法是一种基于变分原理的地震波正演模拟方法。
它将介质离散化为小单元,并利用插值函数表示波场的变化。
有限元法相对于有限差分法更加灵活,适用于处理复杂介质中的问题。
然而,有限元法的计算量较大,在大规模模拟中可能存在困难。
2.3谱元法(S E M)谱元法是一种将频率域方法与网格法相结合的地震波正演模拟方法。
它首先利用傅里叶变换将地震波动方程转换为频率域方程,然后在空间域上进行离散化求解。
谱元法具有较高的精度和稳定性,适用于处理复杂介质中的地震波传播问题。
3.优化方法为了改善复杂介质中地震波正演模拟的精度和可靠性,我们提出了以下优化方法:3.1速度模型优化在复杂介质中,速度模型的准确性对地震波正演模拟结果具有重要影响。
微分方程数值求解——有限差分法
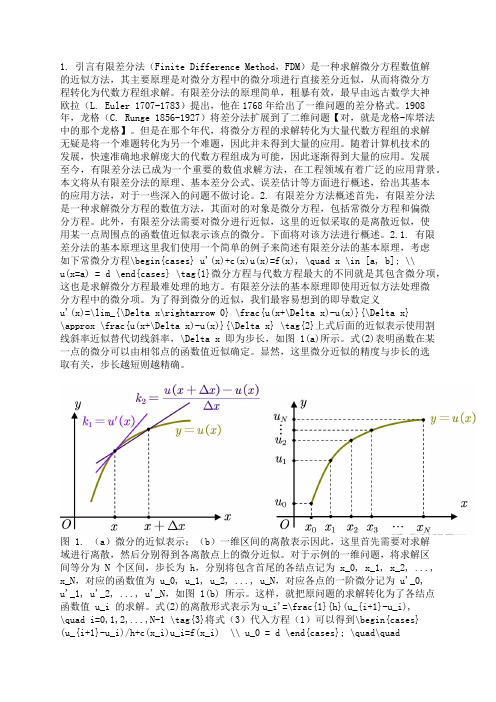
1. 引言有限差分法(Finite Difference Method,FDM)是一种求解微分方程数值解的近似方法,其主要原理是对微分方程中的微分项进行直接差分近似,从而将微分方程转化为代数方程组求解。
有限差分法的原理简单,粗暴有效,最早由远古数学大神欧拉(L. Euler 1707-1783)提出,他在1768年给出了一维问题的差分格式。
1908年,龙格(C. Runge 1856-1927)将差分法扩展到了二维问题【对,就是龙格-库塔法中的那个龙格】。
但是在那个年代,将微分方程的求解转化为大量代数方程组的求解无疑是将一个难题转化为另一个难题,因此并未得到大量的应用。
随着计算机技术的发展,快速准确地求解庞大的代数方程组成为可能,因此逐渐得到大量的应用。
发展至今,有限差分法已成为一个重要的数值求解方法,在工程领域有着广泛的应用背景。
本文将从有限差分法的原理、基本差分公式、误差估计等方面进行概述,给出其基本的应用方法,对于一些深入的问题不做讨论。
2. 有限差分方法概述首先,有限差分法是一种求解微分方程的数值方法,其面对的对象是微分方程,包括常微分方程和偏微分方程。
此外,有限差分法需要对微分进行近似,这里的近似采取的是离散近似,使用某一点周围点的函数值近似表示该点的微分。
下面将对该方法进行概述。
2.1. 有限差分法的基本原理这里我们使用一个简单的例子来简述有限差分法的基本原理,考虑如下常微分方程\begin{cases} u'(x)+c(x)u(x)=f(x), \quad x \in [a, b]; \\u(x=a) = d \end{cases} \tag{1}微分方程与代数方程最大的不同就是其包含微分项,这也是求解微分方程最难处理的地方。
有限差分法的基本原理即使用近似方法处理微分方程中的微分项。
为了得到微分的近似,我们最容易想到的即导数定义u'(x)=\lim_{\Delta x\rightarrow 0} \frac{u(x+\Delta x)-u(x)}{\Delta x}\approx \frac{u(x+\Delta x)-u(x)}{\Delta x} \tag{2}上式后面的近似表示使用割线斜率近似替代切线斜率,\Delta x 即为步长,如图 1(a)所示。
计算流体力学有限差分法

计算流体力学有限差分法流体力学有限差分法(Finite Difference Method,FDM)是一种常用的计算流体力学的方法。
它是基于流体力学基本方程对系统求解压力、速度和位置变化的一种近似数值方法,这些方程可以使用有限差分法求解得到准确结果。
一、流体力学有限差分法的概念1、端点条件:端点条件是差分方程组确定变量的边界条件,主要有边界条件和内部条件。
2、场变量定义:流动的物质可以用速度、压力和密度来描述,这种变量称为场变量。
3、有限差分法:有限差分法试图使描述精度在最小情况下得到一个可以接受的结果。
它将待求解区域划分为若干个小块,并且计算每一个小块上的变量。
4、边界条件:边界条件是用来描述物理事件发生的时候的物理量,如压力、流动量等。
二、流体力学有限差分法的基本步骤1、数学模型:开发有限差分方程,用来描述流体力学问题,这种模型可以由流体力学的基本方程得到。
2、网格划分:将区域网格划分成更小的网格,为了更准确的解决流体力学问题。
3、空间离散:将每一个网格按照有限差分公式空间离散,获得离散的压力方程式。
4、时间离散:在解决大规模动态流体力学问题时,通过一个更小的时间步骤进行求解。
5、求解:用适当的方法和算法求解有限差分方程式,获得求解结果。
三、流体力学有限差分法的优势1、高精度:使用此法,可以获得较高数值精度,从而准确描述流体力学过程。
2、计算效率:该方法可以快速找出有效的解决方案,并且计算效率更高。
3、计算能力:此方法可以处理复杂的物理问题,而且没有太多的硬件限制。
4、收敛性:当求解复杂的物理问题时,有限差分法不太容易出现"收敛"的情况。
5、可靠性:此方法可以快速、准确的求解出可靠的结果,相对于其他求解方法,其精度更高。
四、总结流体力学有限差分法是一种常用的计算流体力学的方法。
它易于实施,并且可以获得较高数值精度,从而准确描述流体力学过程。
处理复杂的物理问题时,它可以提供较快、较准确的结果,更能可靠性和可靠性更好。
电磁计算方法

电磁计算方法是用于解决电磁场问题的数值计算方法。
在电磁学中,常见的电磁计算方法包括有限差分法(Finite Difference Method, FDM)、有限元法(Finite Element Method, FEM)、边界元法(Boundary Element Method, BEM)、时域积分法(Time Domain Integral Method, TDIM)和频域积分法(Frequency Domain Integral Method, FDIM)等。
这些方法的基本思想是将连续的电磁场分割成离散的小单元,然后通过数值近似方法求解每个小单元内的电磁场分布,最终得到整个电磁场的近似解。
下面对每种方法进行简要介绍:
1.有限差分法:将空间区域划分为网格,通过有限差分近似来逼近偏微分方程,从而得到
电场和磁场的数值解。
2.有限元法:将物体或区域划分为有限数量的几何元素,通过建立节点和元素之间的关系,
利用一组适当的形状函数来近似解析解,从而求解电磁场分布。
3.边界元法:将问题转化为求解边界上的积分方程,将边界上的电磁场表示为边界积分的
形式,通过求解边界上的积分方程获得电磁场分布。
4.时域积分法:将时域Maxwell方程组转化为积分形式,在时间上进行离散,通过时间步
进方法求解电磁场的时变行为。
5.频域积分法:将频域Maxwell方程组转化为积分形式,在频域上进行离散,通过迭代方
法求解电磁场的稳态或周期性行为。
每种计算方法都有其适用范围和特点,选择合适的方法取决于具体的问题和计算需求。
此外,还需要考虑边界条件、材料特性以及计算资源等因素。
数值模拟偏微分方程的三种方法:FDM、FEM及FVM

数值模拟偏微分方程的三种方法:FDM、FEM及FVM偏微分方程数值模拟常用的方法主要有三种:有限差分方法(FDM)、有限元方法(FEM)、有限体积方法(FVM),本文将对这三种方法进行简单的介绍和比较。
有限差分方法有限差分方法(Finite Difference Methods)是数值模拟偏微分方程最早采用的方法,至今仍被广泛运用。
该方法包括区域剖分和差商代替导数两个过程。
具体地,首先将求解区域划分为差分网格,用有限个网格节点代替连续的求解区域。
其次,利用Taylor级数展开等方法将偏微分方程中的导数项在网格节点上用函数值的差商代替来进行离散,从而建立以网格节点上的值为未知量的代数方程组。
该方法是一种直接将微分问题变为代数问题的近似数值解法,数学概念直观,表达简单,是发展较早且比较成熟的数值方法。
差商代替导数后的格式称为有限差分格式,从格式的精度来考虑,有一阶格式、二阶格式和高阶格式。
从差分的空间离散形式来考虑,有中心格式和迎风格式。
对于瞬态方程,考虑时间方向的离散,有显格式、隐格式、交替显隐格式等。
目前常见的差分格式,主要是以上几种格式的组合,不同的组合构成不同的差分格式。
差分方法主要适用于结构网格,网格的步长一般根据问题模型和Courant稳定条件来决定。
请输入标题有限元方法(Finite Element Methods)的基础是变分原理和分片多项式插值。
该方法的构造过程包括以下三个步骤。
首先,利用变分原理得到偏微分方程的弱形式(利用泛函分析的知识将求解空间扩大)。
其次,将计算区域划分为有限个互不重叠的单元(三角形、四边形、四面体、六面体等)。
再次,在每个单元内选择合适的节点作为求解函数的插值点,将偏微分方程中的变量改写成由各变量或其导数的节点值与所选用的分片插值基函数组成的线性表达式,得到微分方程的离散形式。
利用插值函数的局部支集性质及数值积分可以得到未知量的代数方程组。
有限元方法有较完善的理论基础,具有求解区域灵活(复杂区域)、单元类型灵活(适于结构网格和非结构网格)、程序代码通用(数值模拟软件多数基于有限元方法)等特点。
有限差分法求解扩散方程的步骤

有限差分法求解扩散方程的步骤有限差分法是求解扩散方程的一种有效方法,简称FDM,有限差分法能够解决复杂的扩散方程,可以看作数值计算在扩散方程中的一个应用。
一般情况下,有限差分法求解扩散方程是通过将扩散方程分解为两部分:非线性问题和线性问题,分别用不同的求解方法解决。
在这篇文章中,我们将讨论使用有限差分法求解扩散方程的步骤,帮助读者更好地理解有限差分法。
第一步:建立数值解模型。
有限差分法求解扩散方程,首先要建立数值解模型。
可以将扩散方程的区域划分为若干个小矩形,用每个小矩形的中心的值代表这一区域的大致状态,然后计算每一部分的有限差分,从而建立起数值解模型。
第二步:求解线性问题。
这一步用来求解扩散方程中的线性部分,包括:首先,对离散点的值进行定义;其次,在离散点之间建立差分关系;最后,根据上述关系,求解离散点的值。
第三步:求解非线性问题。
有限差分法还可以求解扩散方程中的非线性部分。
可以先将非线性部分转化为线性部分,然后求解,也可以使用迭代法求解。
第四步:检查模型的正确性。
有限差分法求解扩散方程后,需要检查模型的正确性,可以使用数值积分方法、定性方法或定量分析等方法来检查求解结果的正确性。
总之,有限差分法求解扩散方程的五个步骤是:建立数值解模型,求解线性问题,求解非线性问题,进行模型校正以及检查模型的正确性。
在这五个步骤中,第一步特别重要,因为它是整个有限差分法求解过程的基础,如果第一步建立的模型不合理,就不可能得到准确的结果。
有限差分法的运用不仅当前广泛,而且在未来也有很大的发展前景。
由于有限差分法求解扩散方程的步骤具有一定的复杂性,因此有必要在深入研究有限差分法求解扩散方程之前,充分理解这一步骤。
综上所述,有限差分法求解扩散方程的步骤是:建立数值解模型,求解线性问题,求解非线性问题,进行模型校正以及检查模型的正确性。
有限差分法在求解扩散问题方面具有一定的优势,适用范围也较广,此外还有很大的发展前景。
FDM 有限差分法
z
2 3
(
h (1 0 ) h (3 0 ) )0 x h1h3 (h1 h3 )
2 3 2 1
h3
h2 h4
4
h1
1
h4 (2 0 ) h2 (4 0 ) 2 ( 2 )0 2 y h2 h4 (h2 h4 )
r0
r
0 (
Ab1 Ab 2 R( Aa 3 Aa 4 ) 2(1 R) A0
( 1 ) [(1) (2)] 2
(1)
1 2 Rh Wa 0 2
(2)
1 1 Ab1 Ab 2 (1 R)( A3 A4 ) (3 R) A0 Rh 2Wa 0 2 4
有限差分(FDM)
在电磁散射计算方法中,有限差分法自上世纪 五十年代以来得到了广泛的应用,该方法概念清晰 ,方法简单,直观。虽然其与变分法相结合所形成 的有限元法更有效,但有限差分还是以其固有特点 在数值计算中有其重要地位。
为求解由偏微分方程定解问题所构造的数 学模型,有限差分法是将定解区域(场区)离 散化为网格离散节点的集合。并以各离散点上 函数的差商来近似该点的偏导数,使待求的偏 微分方程定解问题转化为一组相应的差分方程 。根据差分方程组解出各离散点处的待求函数 值—离散解。
2 2 2 2 2 0 r z
★★
1 3
整个场域内点的差分格式共有两种!
60 2 4 41
边界条件的处理
• 1、不同介质平面分界面的情形
2
h2
3
0
1
h3
A有源
B无源
1
h4
4
2
h1
a1 a 2 a3 a 4 4a0 h2Wa 0
化学催化反应动力学的数学建模方法

化学催化反应动力学的数学建模方法化学催化反应是一个重要的研究领域,涉及到很多实际问题和实验。
它是指一个化学反应在催化剂的作用下发生,而催化剂本身并不参与反应,只是起到了促进反应速率的作用。
在化学催化反应中,动力学过程是一个非常重要的方面,因为它涉及到反应速率、反应机制等方面,而这些都是影响反应活性的关键因素。
因此,为了更好地理解化学催化反应中的动力学过程,科学家们开发出了数学模型来描述化学反应动力学过程。
化学催化反应动力学的数学建模方法就是这样一个数学模型,本文将对其进行介绍。
化学催化反应动力学的数学模型主要涉及到化学反应的速率常数、反应机理、反应物浓度和温度等因素。
其中,速率常数是指化学反应速率与反应物浓度的乘积之间的关系。
反应机理则是指反应物之间的相互作用和化学键的破裂和形成等过程。
在化学反应动力学方面,最常用的模型是基于Arrhenius公式的模型,这个公式描述了温度和反应速率之间的关系。
当温度升高,反应速率会增加,而温度降低则会使反应速率减慢。
因此,这个公式非常重要,因为它使我们能够预测化学反应的速率和反应条件。
另一方面,反应机理也是非常重要的。
反应机理描述了反应物之间的相互作用和化学键的破裂和形成等过程。
在化学反应中,反应物之间的相互作用是决定反应速率的关键因素。
因此,建立反应机理模型是非常重要的。
为了描述化学反应动力学过程,科学家们开发了一些数学模型和方法。
其中,最常用的是微分方程模型。
微分方程模型是对反应动力学过程进行描述的数学模型。
它能够准确描述反应物和产物的浓度随时间的变化,从而揭示化学反应的特性和机理。
但是,微分方程模型也存在一些问题,其中最常见的是难以求解。
对于大多数化学反应动力学模型,由于它们复杂的数学形式和缺乏数值算法的问题,它们往往难以求解。
因此,一些科学家提出了不同的数值方法来解决这些问题。
其中,流行的解决方案包括有限元法( FEM)和有限差分法( FDM)等。
这些方法可以将反应过程分为许多小时间段,然后通过数值近似来计算反应物浓度随时间的变化。
分数阶脉冲时滞微分方程

分数阶脉冲时滞微分方程英文回答:Fractional order impulsive delay differential equations (FOIDDEs) are a class of differential equations that arisein various fields of science and engineering, such as viscoelasticity, electrochemistry, and population dynamics. Due to their complex nature, developing efficient and accurate numerical methods for solving FOIDDEs is a challenging task.In this paper, we propose a novel numerical method for solving FOIDDEs based on the finite difference method (FDM). The proposed method utilizes the Caputo fractionalderivative and employs a backward difference scheme to approximate the time derivative. The delay term is handled by introducing a delay operator. The resulting system of equations is then solved using a suitable linear solver.To demonstrate the accuracy and efficiency of theproposed method, we conduct numerical experiments on several FOIDDEs with different fractional orders and delay times. The numerical results show that the proposed method is able to obtain accurate solutions with high order of accuracy. Moreover, the method is efficient and can handle problems with large delay times.In summary, the proposed numerical method provides a powerful tool for solving FOIDDEs. The method is easy to implement and can be applied to a wide range of problems.中文回答:分数阶脉冲时滞微分方程 (FOIDDEs) 是一类在粘弹性、电化学和种群动力学等各个科学和工程领域中广泛应用的微分方程。
有限差分法

有 限 差 分 法流体运动的控制方程多为偏微分方程,在复杂的情况下不存在解析解。
但是对于一些简单的情况存在解析解,偏微分方程的解析解可用精确的数学表达式表示,该表达式给出了因变量在整个定义域中的连续变化状况。
有限差分法(Finite Difference Method ,FDM )是数值计算中比较经典的方法,由于其计算格式直观且计算简便,因此被广泛地应用在计算流体力学中。
有限差分法首先将求解区域划分为差分网格,变量信息存储在网格节点上,然后将偏微分方程的导数用差商代替,代入微分方程的边界条件,推导出关于网格节点变量的代数方程组,通过求解代数方程组,获得偏微分方程的近似解。
偏微分方程被包含离散点未知量的代数方程所替代,这个代数方程能求出离散节点处的变量,这种离散方法叫做有限差分法。
2.1有 限 差 分 逼 近2.1.1 有限差分网格 由于有限差分法求解的是网格节点上的未知量值,因此首先介绍有限差分网格。
图2.1 – 1是x-y 平面上的矩形差分网格示意图。
在x 轴方向的网格间距为△x ,在y 轴方向的网格间距为△y ,网格的交点称为节点,计算变量定义在网格节点上。
称△x 和△y 为空间步长,△x 一般不等于△y ,且△x 和△y 也可以不为常数。
取各方向等距离的网格,可以大大简化数学模型推导过程,并且经常会取得更加精确的数值解。
本章作为计算流体力学入门知识,假设沿坐标轴的各个方向网格间距分别相等,但是并不要求各方向的网格间距一致。
例如假设△x 和△y 是定值,但是不要求△x 等于△y 。
在图2.1 - 1中,网格节点在x 方向用i 表示,在y 方向用j 表示。
因此,假如(i ,j )是点P 在图2.1 – 1中的坐标,那么,点P 右边的第一个点的就可以用(i+1,j )表示;在P 左边的第一个点的就可以用(i —1,j )表示;点P 上边的第一个点的就可以用(i ,j+1)表示;点P 下边的第一个点的就可以用(i ,j —1)表示。
pinn求解burger方程代码

pinn求解burger方程代码为了解决Burger方程,我们可以使用多种数值方法。
在这篇文章中,我将介绍使用有限差分法(Finite Difference Method,FDM)求解Burger方程的代码。
Burger方程是一维非线性对流方程,可以表示为:∂u/∂t + u * ∂u/∂x = ν * ∂²u/∂x²其中,u是守恒变量,t是时间,x是空间,ν是粘性系数。
首先,我们需要在代码中定义一些参数。
这些参数包括网格大小,时间步长,粘性系数,以及求解域的起始和结束位置。
```#定义参数nx = 100 #网格数量nt = 100 #时间步长数量nu = 0.07 #粘性系数dx = 2 * np.pi / (nx - 1) #网格步长dt = dx * nu #根据CFL条件计算时间步长x = np.linspace(0, 2 * np.pi, nx) #定义求解域u = np.sin(x) #初始化u```接下来,我们需要在代码中定义一个函数来更新u的值。
我们可以使用向前差分方法(Forward Difference Method)来数值计算Burger方程。
```#定义更新函数def update_u(u, nu, dt, dx):un = u.copy() #创建u的副本for i in range(1, nx - 1):u[i] = un[i] - un[i] * dt / dx * (un[i] - un[i-1]) + nu * dt / dx**2 * (un[i+1] - 2 * un[i] + un[i-1])return u```在主程序中,我们可以循环调用更新函数来计算u的值,并将结果可视化。
```#循环调用更新函数for n in range(nt):u = update_u(u, nu, dt, dx)#可视化结果plt.plot(x, u)plt.xlabel('x')plt.ylabel('u')plt.show()```通过以上代码,我们可以得到关于时间的一维Burger方程的数值解。
fdm微分方程

FDM,全称为有限差分法,是一种数值求解偏微分方程的方法。
在FDM中,微分方程中的导数被离散化为差分,从而将原微分方程转化为差分方程。
差分方程可以在计算机上迭代求解,从而得到微分方程的近似解。
FDM在处理偏微分方程时具有简单、易实现等优点,特别适合处理离散化后能够方便求解的微分方程。
然而,FDM也存在一些局限性,如数值稳定性和精度等问题。
此外,FDM在处理复杂边界条件和奇异点等问题时也可能遇到困难。
如需更多关于FDM微分方程的信息,建议查阅相关学术文献或咨询数学专业人士。
导管架式海洋平台地震响应研究

导管架式海洋平台地震响应研究一、概览随着全球经济的快速发展,海洋资源的开发利用日益受到重视。
海洋平台作为海上油气生产和输送的重要设施,其安全性和稳定性对于保障能源供应具有重要意义。
然而海洋平台所面临的地震风险也日益凸显,近年来我国沿海地区的地震活动频发,给海洋平台的安全稳定带来了严重威胁。
因此研究海洋平台在地震作用下的响应特性,对于提高海洋平台的抗震能力具有重要的现实意义。
导管架式海洋平台是一种典型的海洋石油钻采设施,其结构特点决定了其在地震作用下的响应特性。
导管架式海洋平台主要由上部结构、下部结构和平台本体三部分组成,其中上部结构主要包括桅杆、横桁、纵桁等构件;下部结构主要包括基础、桩腿等构件;平台本体主要包括平台主体结构、设备安装等。
在地震作用下,导管架式海洋平台的各个构件将受到不同程度的振动作用,从而产生各种形式的位移、变形和破坏。
为了更好地了解导管架式海洋平台在地震作用下的响应特性,本文首先对导管架式海洋平台的结构特点进行了分析,然后根据地震波传播规律,采用数值模拟方法对导管架式海洋平台在不同震级、震源距离和水平地震作用下的响应进行了研究。
通过对比分析不同工况下的响应结果,揭示了导管架式海洋平台在地震作用下的动态响应特性,为优化设计、提高抗震能力提供了理论依据。
1. 研究背景及意义导管架式海洋平台是一种典型的高耸结构,其主要由钢管组成的导管架和平台上的各种设备组成。
在地震作用下,导管架式海洋平台的结构体系将受到强烈的振动和变形作用,这可能导致结构的破坏甚至倒塌。
因此研究导管架式海洋平台在地震作用下的响应特性,有助于揭示其结构体系在地震中的动态行为,为优化结构设计、提高结构抗震性能提供理论依据。
此外导管架式海洋平台在地震作用下的响应特性还与海洋环境因素密切相关。
海洋环境中的波浪、潮流等因素可能对导管架式海洋平台产生附加的动力荷载,从而影响到结构的振动特性。
因此研究导管架式海洋平台在地震作用下的响应特性,有助于揭示其在复杂海洋环境下的工作性能,为提高海洋平台的适应性提供科学依据。
有限差分法

一阶导数
第4章 有限差分法
即是无限小的微分
除以无限小的微分
应用差分,显然,它可近似地表达为
的商,
即有限小的差分Δf(x)除以有限小的差分Δx 的商,称为差商。同理,一阶导数
f ' (x) 还可近似表达为
第4章 有限差分法
式(4-2)、 式(4-3)和式(4-4)分别称为一阶向前、 向后和中心差商。 如图 4-1 所示, 对应于点 P 的一阶向前、 向后和中心差商,在几何意义上 可分别表征为弧线 PB、 AP 和 AB的斜率,而在理论上它们对于该点一阶导 数的逼近度则分别可从以下泰勒公式的展开式中得知,即由
第4章 有限差分法
对于场域内典型的内节点 o (xi,yj), 如图 4-2 所示, 它与周围相邻的节 点 1、 2、 3 和 4构成一个所谓对称的星形。今采用双下标(i,j)的识别方法, 设在这些离散节点上的待求位函数 u 的 近 似 值 分 别 记 作 uo = u(i,j)、 u1 = u(i+1,j)、 u2 = u(i,j+1)、 u3 = u(i-1,j) 和u4 = u(i,j-1), 则参照式 (4-7),二维泊松方程(4-8)可近似离散化表示为
同样,相应的二阶偏导数可以近似表达为
第4章 有限差分法
4.3 差分格式的构造
现以二维静态电、 磁场泊松方程的第一类边值问题为例, 来具体阐明有 限差分法的应用。设具有平行平面场特征的电磁场场域 D, 如图 4-2 所示, 为一由闭合边界 L 所界定的平面域,其定解问题可表述为
4.3.1 偏微分方程的离散化—五点差分格式
对于包括电磁场在内的各种物理场,应用有限差分法进行数值计算的 步骤通常是:
1)采用一定的网格剖分方式离散化场域;
有限差分法及其应用

有限差分法及其应用1有限差分法简介有限差分法(FDM)是计算机数值模拟最早采用的方法,至今仍被广泛运用。
该方程将解域划分为差分网格,用有限个网络节点代替连续的求解域。
有限差分法通过泰勒级数展开等方法,把控制方程中的导数用网格节点上的函数值得差商代替进行离散,从而建立以网格节点上的值为未知数的代数方程组。
该方法是一种直接将微分问题变为代数问题的近似值解法,数学概念直观,表达简单,是发展较早且比较成熟的数值方法。
2有限差分法的数学基础有限差分法的数学基础是用差分代替微分,用差商代替微商而用差商代替微商的意义是用函数在某区域内的平均变化率来代替函数的真是变化率。
而根据泰勒级数展开可以看出,用差商代替微商必然会带来阶段误差,相应的用差分方程代替微分方程也会带来误差,因此,在应用有限差分法进行计算的时候,必须注意差分方程的形式,建立方法及由此产生的误差。
3有限差分解题基本步骤有限差分法的主要解题步骤如下:1)建立微分方程根据问题的性质选择计算区域,建立微分方程式,写出初始条件和边界条件。
2)构建差分格式首先对求解域进行离散化,确定计算节点,选择网格布局,差分形式和步长;然后以有限差分代替无线微分,以差商代替微商,以差分方程代替微分方程及边界条件。
3)求解差分方程差分方程通常是一组数量较多的线性代数方程,其求解方法主要包括两种:精确法和近似法。
其中精确法又称直接发,主要包括矩阵法,高斯消元法及主元素消元法等;近似法又称间接法,以迭代法为主,主要包括直接迭代法,间接迭代法以及超松弛迭代法。
4)精度分析和检验对所得到的数值进行精度与收敛性分析和检验。
4商用有限差分软件简介商用有限差分软件主要包括FLAC、UDEC/3DEC和PFC程序,其中,FLAC是一个基于显式有限差分法的连续介质程序,主要用来进行土质、岩石和其他材料的三维结构受力特性模拟和塑性流动分析;UDEC/3DEC是针对岩体不连续问题开发,用于模拟非连续介质在静,动态载荷作用下的反应;PFC是利用显式差分算法和离散元理论开发的微、细观力学程序,它是从介质的基本粒子结构的角度考虑介质的基本力学特性,并认为给定介质在不同应力条件下的基本特征主要取决于粒子之间接粗状态的变化,适用于研究粒状集合体的破裂和破裂发展问题,以及颗粒的流动(大位移)问题。
用matlab求解超越方程的方法

用matlab求解超越方程的方法Matlab作为一款强大的数学软件,可以帮助我们比较轻松地解决超越方程,提供了一个快速、灵活且可靠的求解超越方程的方法。
Matlab是一种流行的计算机软件,它拥有强大的数值分析能力。
它经常用来求解复杂的函数方程,特别是有关超越方程的计算。
本文介绍使用Matlab求解超越方程的几种方法:一、用数值方法求解1、采用有限差分法(Finite Difference Method)Finite Difference Method(FDM)是以在离散的网格上对变量的数值求解来实现的。
FDM可以有效的求解多维、非线性的超越方程。
通过在网格上求解多次,可以找出方程的根。
2、采用拉格朗日插值法(Lagrange Interpolation)Lagrange Interpolation是一种数学插值方法,可以有效地解决超越方程中多维非线性方程组。
其运算速度快、精度高,且可以有效求解实际问题中出现的复杂超越方程。
二、用几何方法求解1、采用图像法(Graphics Method)使用图像法可以可视化超越方程。
当然,由于超越方程具有多个变量,因此采用图像法进行求解的难度较大。
但由于图像简单明了,它仍然是一种有效的计算方法。
2、采用微分几何(Differential Geometry)Differential Geometry是一种在曲面上进行计算的数学方法。
它有助于求解超越方程,尤其是表达形式为系统多元不等式的超越方程。
总结:Matlab是一种强大的计算软件,可以用来求解超越方程。
它有许多方法可以用于求解超越方程,包括:用数值方法求解、用几何方法求解等。
它能帮助我们解决复杂的科学问题,因此得到了广泛的应用。
二、有限差分法

∆t ≤
µε
1 1 + 2 (∆x ) (∆y )2
=
1 1 1 c + 2 (∆x ) (∆y )2
作业:独立完成稳定条件的推导。
二、有限差分法(FDM)
2-3-2 频域分析
v ∂ v v ∇× E = − B ∇•D = ρ ∂t v v ∂D v v v ∇× H = + σE + J i ∇ • B = 0 ∂t v v v & = − jωµH & & =ρ ∇× E ∇•D &
二、有限差分法(FDM)
v v ∂ v ∂ v 2 ∇ (∇ • E ) − ∇ E + µ σE + µ J i = 0 ∂t ∂t v ∂ v ∂ v − ∇ E + µ σE + µ J i = 0 ∂t ∂t
2
v E
v J i 只有z方向分量,只与x坐标有关,
∂ 2 Ez ∂ ∂ − µσ E z = µ J zi 2 ∂t ∂t ∂x
前向差分公式二有限差分法fdm更好的离散方案二有限差分法fdmtc二有限差分法fdm2二维吸收边界条件sincosaejkcosjk二有限差分法fdm证明jkrefraeaejkraejkaejkraeaejkraejkaejkrerecoscoscoscos二有限差分法fdm无限长接地导电槽二维问题静电场问题边值方程边界条件静电场举例一二有限差分法fdm二有限差分法fdm应用matlab软件编程求解各网格点的电场位设定初值及利用超松弛迭代方法求各网格电位显示计算结果1迭代顺序2迭代过程3迭代结束条件两次迭代之差小于某一给定值迭代次数超过某一给定的值二有限差分法fdmsin100作业
& g = jωµJ z
块中心有限差分方法的概述

块中心有限差分方法的概述
块中心有限差分(FDM)方法是一种数值求解偏微分方程的方法。
它将求解域划分成多个网格,并在网格上使用中心差分格式来逼近偏微分方程中的微分项。
块中心有限差分方法不考虑离散的边界,因此它比其他方法更容易分析和实现。
这种方法的基本思想是将偏微分方程中的微分算子离散化成有限差分格式,并用这些离散化的算子在网格节点上逼近偏微分方程的解。
具体来说,块中心有限差分方法计算网格节点上的函数值,即节点函数值,而不是像有限差分方法一样计算网格边界上的函数值。
因此,块中心有限差分方法要求在节点值处使用更高级别的数值方法,如牛顿法、拟牛顿法或线性多步法。
块中心有限差分方法具有高精度、高效率和均衡适应性的优点,并在流体力学、固体力学、地球物理学、电磁学、热传导等多个领域得到了广泛应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有限差分法(Finite Difference Method, FDM)是一种常见的数值方法,用于求解偏微分方程。
然而,并非所有的方程都可以通过有限差
分法来求解。
本文将讨论有限差分法不能求解的方程,并探讨其原因。
一、有限差分法求解的方程类型
有限差分法主要用于求解偏微分方程,尤其是常见的热传导方程、扩
散方程和波动方程等。
这些方程通常可以通过有限差分法离散化空间
和时间,从而转化为代数方程组,再通过迭代等方法求解。
二、有限差分法不能求解的方程类型
然而,并非所有的偏微分方程都适合用有限差分法求解。
以下是一些
有限差分法不能求解的方程类型:
1. 非线性偏微分方程:有限差分法主要适用于线性偏微分方程,对于
非线性偏微分方程,由于其复杂的性质和解的多样性,有限差分法往
往难以适用。
2. 高阶偏微分方程:有限差分法通常只适用于一阶和二阶偏微分方程,对于高阶偏微分方程,需要进行更复杂的离散化处理,难以直接通过
有限差分法求解。
3. 变系数偏微分方程:对于系数随空间或时间变化的偏微分方程,有
限差分法往往难以准确描述其变化规律,因此难以求解。
4. 非线性边值问题:对于带有非线性边值条件的偏微分方程,有限差分法的稳定性和收敛性难以保证,因此难以求解。
三、原因分析
有限差分法不能求解某些偏微分方程的原因主要包括以下几点:
1. 离散化处理困难:一些复杂的方程很难通过简单的差分离散化处理转化为代数方程组,从而难以应用有限差分法求解。
2. 解的多样性:对于非线性偏微分方程和非线性边值条件,解的多样性导致有限差分法往往无法准确描述其解的特性。
3. 稳定性和收敛性难以保证:对于一些特殊的偏微分方程,由于有限差分法的稳定性和收敛性难以保证,因此难以求解。
四、解决方法
针对有限差分法不能求解的方程,可以考虑以下解决方法:
1. 使用其他数值方法:对于非线性偏微分方程和高阶偏微分方程,可以考虑使用有限元法、有限体积法等其他数值方法进行求解。
2. 手工推导精确解:对于一些特殊的偏微分方程,可以尝试手工推导
其解析解,从而获得准确的解。
3. 寻求数值计算软件的帮助:一些专业的数值计算软件如MATLAB、COMSOL等提供了丰富的数值求解工具和方法,可以尝试使用这些软件进行求解。
五、结论
有限差分法是一种常见的数值方法,用于求解偏微分方程,然而,并非所有的方程都适合通过有限差分法求解。
对于那些不能通过有限差分法求解的方程,可以尝试使用其他数值方法、手工推导精确解或寻求数值计算软件的帮助进行求解。
通过这些方法的尝试和实践,可以更好地理解有限差分法的应用范围和局限性。
有限差分法(Finite Difference Method, FDM)是一种广泛应用的数值方法,可以对偏微分方程进行离散化处理,并转化为代数方程组进行求解。
然而,并非所有的偏微分方程都适合用有限差分法求解。
在前文中,我们已经讨论了有限差分法不能求解的方程类型和原因分析,本文将继续扩展对于这些方程类型的概括,并提出更多的解决方法。
---
六、有限差分法不能求解的方程类型的进一步概括
除了前文提到的非线性偏微分方程、高阶偏微分方程、变系数偏微分方程和非线性边值问题之外,还有一些其他类型的偏微分方程也不适
合用有限差分法求解:
5. 变分问题:对于变分问题(variational problems),例如变分方
程(variational equations)、泛函方程(functional equations)等,有限差分法求解困难,因为这些问题需要借助变分法等数学工具进行
求解。
6. 混合偏微分方程:对于混合偏微分方程,即同时包含椭圆型、抛物
型和双曲型部分的偏微分方程,有限差分法的适用性也受到限制,因
为不同类型部分的求解方法不同,很难同时进行简单的离散化处理。
7. 积分-微分方程:对于包含积分和微分操作的积分-微分方程,如泛
函微分方程(functional differential equations)、微分积分方程(differential integral equations)等,有限差分法也面临困难,因
为它需要对积分进行离散化处理,难以直接应用有限差分法。
这些类型的偏微分方程因其特殊的性质和求解难度,使得有限差分法
难以直接求解,需要考虑其他数值方法进行求解。
---
七、更多解决方法的探讨
除了前文提到的使用其他数值方法、手工推导精确解和寻求数值计算
软件的帮助之外,还可以探讨更多的解决方法:
4. 应用特殊的离散化处理方法:对于一些特殊的偏微分方程,可以尝试使用特殊的离散化处理方法,如有限元法的高阶元素、有限差分法的特殊差分格式等,从而提高对这些方程的求解能力。
5. 利用对称性和简化条件:对于一些有特殊对称性或简化条件的偏微分方程,可以利用这些特性,对方程进行简化,再尝试使用有限差分法进行求解。
6. 结合数值算法:有些复杂的偏微分方程求解问题可能需要结合数值分析中的其他算法和技术,如迭代法、插值方法等,从而获得更有效的求解结果。
7. 进行合理的参数选择和网格剖分:对于一些难以求解的偏微分方程问题,合理选择参数和网格剖分,优化求解的条件,有时也可以提高有限差分法的适用性。
8. 深入研究偏微分方程的特性:对于特定的偏微分方程问题,深入研究其特性和解的结构,可以为选择合适的数值方法提供更多的依据和指导。
上述方法的尝试和实践,有助于进一步扩展对于有限差分法不能求解
的方程的认识,同时也促进对于其他数值方法的研究和应用,为更广泛的偏微分方程求解问题提供更多的选择和思路。
---
八、结语
在实际的科学与工程问题中,有限差分法作为一种数值方法,可以很好地应用于求解许多偏微分方程。
然而,并非所有的方程都适合用有限差分法求解。
对于那些不能通过有限差分法求解的方程,在选择其他数值方法进行求解时,需要根据问题的具体特点和数值方法的特性进行合理的选择和权衡,以获得准确和可靠的数值解。
在今后的研究和实践中,我们希望能够通过对于这些方法的不断探索和尝试,为更广泛的偏微分方程求解问题提供更多的解决途径和思路。
通过上述对于有限差分法不能求解的方程类型和解决方法的扩展和探讨,进一步加深了对于这一问题的理解,也为未来的研究和应用提供了更多的启示。
我们相信,通过不断的努力和实践,将能够更好地发挥数值方法在偏微分方程求解中的作用,为科学与工程领域的发展做出更多的贡献。
