第18章分析力学基础动力学普遍方程拉格朗日方程.ppt
合集下载
理论力学(Ⅱ)—拉格朗日方程
角 度加为速a 。度假为想1 加、上 2，惯轮性B力质，心如的图加。速
C
yC
M
g B
ma g 2
其中
M
g A
1 2
mR21
FBg ma
M
g B
1 2
mR2 2
此系统具有两个自由度，取轮A、轮B的转
角1、 2 为广义坐标。给系统一组虚位移，如图。
1
yC R 1 R 2 (1)
N
miri
k 1
ri qk
qk
Nn
(
k 1 i1
mi
ri
ri qk
)qk
ri
N k 1
ri qk
qk
n
i 1
Fi
δ
n
ri
i1
miai
δ
ri
N
(Qk
k 1
n i1
miri
ห้องสมุดไป่ตู้
ri qk
)qk
0
Qk
n i 1
xA l cos yA l sin xB l cos
O1
x1
rA
l l rB
FIA A m1g l
rC l
B
m1g
FIB
C
yB l sin
m2g
yC 2l sin
y1
2m1lsin2lcos 2m1glsin 2m2glsin 0
sin
1 g
(a1cos
3 2
ar
)
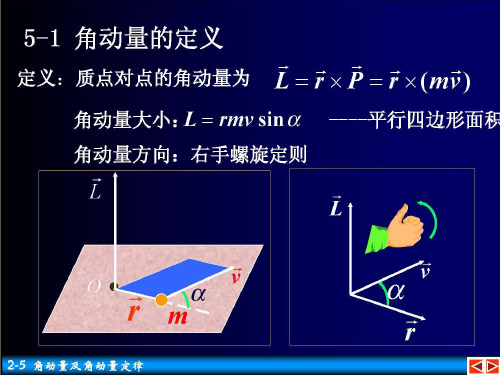
C
yC
M
g B
ma g 2
其中
M
g A
1 2
mR21
FBg ma
M
g B
1 2
mR2 2
此系统具有两个自由度，取轮A、轮B的转
角1、 2 为广义坐标。给系统一组虚位移，如图。
1
yC R 1 R 2 (1)
N
miri
k 1
ri qk
qk
Nn
(
k 1 i1
mi
ri
ri qk
)qk
ri
N k 1
ri qk
qk
n
i 1
Fi
δ
n
ri
i1
miai
δ
ri
N
(Qk
k 1
n i1
miri
ห้องสมุดไป่ตู้
ri qk
)qk
0
Qk
n i 1
xA l cos yA l sin xB l cos
O1
x1
rA
l l rB
FIA A m1g l
rC l
B
m1g
FIB
C
yB l sin
m2g
yC 2l sin
y1
2m1lsin2lcos 2m1glsin 2m2glsin 0
sin
1 g
(a1cos
3 2
ar
)
分析力学基础-拉格朗日方程
支持。
其他应用领域
要点一
机器人学
在机器人学中，拉格朗日方程被用于描述机器人的运动规 律。通过建立机器人运动的拉格朗日方程，可以求解出机 器人的关节角度和速度，为机器人的运动控制提供理论依 据。
要点二
生物力学
在生物力学中，拉格朗日方程也被应用于描述生物体的运 动规律。例如，在分析动物的运动行为或人体姿势控制时 ，可以使用拉格朗日方程来描述生物体的运动状态和变化 规律。
解析解法的优缺点分析
优点
解析解法可以得到系统的精确解，适用 于简单模型和特定条件下的复杂模型。
VS
缺点
对于复杂模型，解析解法可能非常困难甚 至无法求解，需要借助数值方法或其他近 似方法。
04
拉格朗日方程的数值解法
数值解法的概念和步骤
概念
数值解法是一种通过数学计算来求解数学问 题的方法，它通过将问题离散化，将连续的 问题转化为离散的问题，然后使用计算机进 行计算求解。
步骤
1.建立数学模型：根据实际问题建立数学模 型，将实际问题转化为数学问题。2.离散化 ：将连续的问题离散化，将连续的时间和空 间划分为若干个小的单元，每个单元称为一 个网格点或节点。3.求解离散化后的方程： 使用数值方法求解离散化后的方程，得到每 个网格点的数值解。4.后处理：对计算结果 进行后处理，提取所需的信息，并进行分析
分析力学基础-拉格 朗日方程
目录
• 引言 • 拉格朗日方程的推导 • 拉格朗日方程的解析解法 • 拉格朗日方程的数值解法 • 拉格朗日方程的应用领域
01
引言
拉格朗日方程的背景和重要性
背景
拉格朗日方程是分析力学中的基 本方程，它描述了系统的运动规 律。
重要性
拉格朗日方程在理论物理、工程 技术和科学研究等领域有着广泛 的应用，是理解和研究复杂系统 运动行为的关键工具。
其他应用领域
要点一
机器人学
在机器人学中，拉格朗日方程被用于描述机器人的运动规 律。通过建立机器人运动的拉格朗日方程，可以求解出机 器人的关节角度和速度，为机器人的运动控制提供理论依 据。
要点二
生物力学
在生物力学中，拉格朗日方程也被应用于描述生物体的运 动规律。例如，在分析动物的运动行为或人体姿势控制时 ，可以使用拉格朗日方程来描述生物体的运动状态和变化 规律。
解析解法的优缺点分析
优点
解析解法可以得到系统的精确解，适用 于简单模型和特定条件下的复杂模型。
VS
缺点
对于复杂模型，解析解法可能非常困难甚 至无法求解，需要借助数值方法或其他近 似方法。
04
拉格朗日方程的数值解法
数值解法的概念和步骤
概念
数值解法是一种通过数学计算来求解数学问 题的方法，它通过将问题离散化，将连续的 问题转化为离散的问题，然后使用计算机进 行计算求解。
步骤
1.建立数学模型：根据实际问题建立数学模 型，将实际问题转化为数学问题。2.离散化 ：将连续的问题离散化，将连续的时间和空 间划分为若干个小的单元，每个单元称为一 个网格点或节点。3.求解离散化后的方程： 使用数值方法求解离散化后的方程，得到每 个网格点的数值解。4.后处理：对计算结果 进行后处理，提取所需的信息，并进行分析
分析力学基础-拉格 朗日方程
目录
• 引言 • 拉格朗日方程的推导 • 拉格朗日方程的解析解法 • 拉格朗日方程的数值解法 • 拉格朗日方程的应用领域
01
引言
拉格朗日方程的背景和重要性
背景
拉格朗日方程是分析力学中的基 本方程，它描述了系统的运动规 律。
重要性
拉格朗日方程在理论物理、工程 技术和科学研究等领域有着广泛 的应用，是理解和研究复杂系统 运动行为的关键工具。
2_拉格朗日方程
O
(x1,y1)
A
P1
(x2,y2) B(x3,y3)
P2
F
(1)
由已知条件可得
x1
1 2
l1 sin 1 l 2 sin (2)
x 2 l1 sin
2 y 3 l1 cos l 2 cos
把(2) 式代入(1) 式得
P1 (
1 2
l1 sin ) P2 ( l1 sin
x i x i ( q1 , q 2 , , q s , t ) y i y i ( q1 , q 2 , , q s , t ) z i z i ( q1 , q 2 , , q s , t )
或 式中
( i 1, 2 , , n , s 3 n )
ri ri ( q 1 , q 2 , , q s , t )
以上分量式若改用s 个独立广义坐标表示，然后令s 个独立的 虚位移前的乘数等于零，则可得出所求的平衡条件。 若求约束力，则要利用拉格朗日未定乘数。 广义坐标下 ri 的虚位移为
ri
n
s
ri
由此得广义坐标下的平衡方程是
W
Q
1
q
q 0
s
F
i 1 s
n
i n
i 1
虚功原理：受理想约束的力学体系平衡的充要条件是此力学 体系的诸主动力在任意虚位移中所做的元功之和为零。这就 是虚功原理，也叫虚位移原理。是1717年伯努利首先发现。 对于理想约束体系，利用虚功原理可以方便的求出主动力满 足的平衡条件，但无法求出约束反力。 由于约束，3n 个坐标不独立，即作用在任一质点上的合外 力在虚位移方向上的投影，一般不会全令之为零。否则就可 能变成n 个自由质点的平衡方程。
动力学普遍方程和拉格朗日方程
(i 1,2,......... .n)
对这n个式子求和
(25.2)
iq
(F N F
i 1 i i
n
) r i 0
(25.3)
若为理想约束，由虚位移和理想约束的条件知
N r
i 1 i
n
i
0
上式变为：
(F F
i 1 i
n
iq
) r i 0或者 （F i mi ai ) r i 0 (25.4)
s
k 2 2 i i i s j 1 j s j s k i i j 1 j s j s
即
v q
r
i s
r d ( ri ) dt q
s
也可以写为
v q
r
i j
r d ri ( ) dt q
j
n
或
r q
r
i j
r d ri ( ) dt q
j
j
( j 1,2...k )
r 在任意瞬时,加速度为a
i
根据达朗伯原理，在其上加达朗伯惯性力
r r mi ai F iq
则
约束反力的合力
r rr F N F
i i
0
iq
(i 1,2,......... .n)
(25.1)
达朗伯惯性力
作用于此质点上 的主动力的合力
点积虚位移 ri
( F i N i F iq) r i 0
对时间求导
得到
q
vi
j
q
ri
j
或
q ri
j
( j 1,2...k )
最新理论力学-拉格朗日方程教学讲义ppt
m2g
此为一个自由度质点系，选角α为
广义坐标。
y
第七章 拉格朗日方程
§7-1 动力学普遍方程
例题 7-1
δrB F*B B
m1g δrC
d
O
α
x
ω dα
δrA A F*A
m1g
C
m2g
各质点的虚位移可用广义坐标的
变分表示
xA(dlsi n), xAlcos
yAlcos
yAlsin
xB(dlsi n),xBlcos
yBlcos,
yBlsin
yC2lcos, yC2lsin
y
第七章 拉格朗日方程
δrB F*B B
m1g δrC
§7-1 动力学普遍方程
例题 7-1
F A * x A F B * x B m 1 g y A m 1 g y B m 2 g y C 0(a)
d
O
α
x
ω dα
δrA A F*A
理论力学-拉格朗日方程
动力学
第 七
§7– 1 动力学普遍方程
章
拉
格
§7–2 拉格郎日方程
郎
日
方
程
§7–3 拉格郎日方程的第一积分
目录
第七章 拉格朗日方程
§7-1 动力学普遍方程
第七章 拉格朗日方程
第七章 拉格朗日方程
第七章 拉格朗日方程
第七章 拉格朗日方程
§7-1 动力学普遍方程
n
(Fi Fi*)ri 0
m1g
C
m2g
y
代入式（a）得
2m 1(dlsi n)2lcos2 m 1gsli n 2m 2gsli n 0
动力学普遍方程及拉格朗日方程
C
O1
x1
δα
l α α l
A
− FIA ⋅ δxA + FIB ⋅ δxB + m1g ⋅ δyA + m1g ⋅ δyB + m2 g ⋅ δyC = 0
根据几何关系，有 根据几何关系，
ωB
δrC
δrB FIB
l m1g
xA = −lsinα yA = lcosα xB = lsinα yB = lcosα yC = 2lcosα
由动力学普遍方程， 由动力学普遍方程，得
∑F ⋅ δr −∑m a ⋅ δr
i =1 i i i =1 i i
n j j
N
N
i
=0
∑F ⋅ δr = ∑Q δ q
i =1 i i j =1
N
Q j ——广义力
n N ∂ri ∂r && ⋅ ∑ δ qj = ∑(∑mi && ⋅ i )δ qj ri ∑miai ⋅ δr i = ∑miri j=1 ∂qj ∂qj i =1 j =1 i =1 i =1
MI2 = J2 α2
J2 = 1 m2 R2 2
α
m2 g
B
x
m1g
ar = Rα2
m2 gsinα ⋅ Rδϕ + FI2ecosα ⋅ Rδϕ − FI2r ⋅ Rδϕ－J2α2 ⋅ δϕ = 0
1 3 sinα ⋅ + (a1cosα − ar ) = 0 g 2
解：4、应用动力学普遍方程 令： δ x ≠ 0，δ ϕ = 0
i i i i i
(i = 1,2, ⋅⋅⋅, N)
动力学普遍方程的直角坐标形式
∑[(F
O1
x1
δα
l α α l
A
− FIA ⋅ δxA + FIB ⋅ δxB + m1g ⋅ δyA + m1g ⋅ δyB + m2 g ⋅ δyC = 0
根据几何关系，有 根据几何关系，
ωB
δrC
δrB FIB
l m1g
xA = −lsinα yA = lcosα xB = lsinα yB = lcosα yC = 2lcosα
由动力学普遍方程， 由动力学普遍方程，得
∑F ⋅ δr −∑m a ⋅ δr
i =1 i i i =1 i i
n j j
N
N
i
=0
∑F ⋅ δr = ∑Q δ q
i =1 i i j =1
N
Q j ——广义力
n N ∂ri ∂r && ⋅ ∑ δ qj = ∑(∑mi && ⋅ i )δ qj ri ∑miai ⋅ δr i = ∑miri j=1 ∂qj ∂qj i =1 j =1 i =1 i =1
MI2 = J2 α2
J2 = 1 m2 R2 2
α
m2 g
B
x
m1g
ar = Rα2
m2 gsinα ⋅ Rδϕ + FI2ecosα ⋅ Rδϕ − FI2r ⋅ Rδϕ－J2α2 ⋅ δϕ = 0
1 3 sinα ⋅ + (a1cosα − ar ) = 0 g 2
解：4、应用动力学普遍方程 令： δ x ≠ 0，δ ϕ = 0
i i i i i
(i = 1,2, ⋅⋅⋅, N)
动力学普遍方程的直角坐标形式
∑[(F
分析力学拉格朗日方程
分析力学拉格朗日方程分析力学是物理学中的一个重要分支，它主要研究物体的运动规律和力学系统的宏观性质。
拉格朗日力学是分析力学的基础，是分析力学发展过程中的一个重要理论。
它由意大利数学家拉格朗日于18世纪发展而来，利用广义坐标和拉格朗日方程来描述物体的运动学和动力学。
在拉格朗日力学中，系统的运动由极值原理来决定。
这个极值原理是“达朗贝尔原理”，即系统的运动满足使作用量(S)是极值的路径。
作用量是拉格朗日力学中的一个重要概念，它表示物体在运动过程中所受到的所有力的作用。
具体来说，作用量可以表示为：S = ∫ (L - T) dt其中，L是拉格朗日函数，表示系统的动能和势能之差；T是系统的动能，表示物体的运动能量。
积分表示对整个运动过程的积分求和。
根据达朗贝尔原理，系统的运动满足作用量的极值条件，即δS=0。
为了使作用量的变分δS等于零，我们可以通过拉格朗日方程来推导系统的运动方程。
假设系统有n个自由度，我们引入广义坐标q1, q2, ..., qn来描述系统的位置。
每个广义坐标都是关于时间的函数，即q(t)。
拉格朗日函数L也是广义坐标的函数，即L(q, dq/dt, t)。
其中dq/dt表示广义坐标的时间导数。
利用拉格朗日函数，我们可以定义拉格朗日方程：d/dt (∂L/∂(dq/dt)) - ∂L/∂q = 0这个方程就是拉格朗日方程。
其中∂L/∂(dq/dt)表示拉格朗日函数对广义速度的偏导数，∂L/∂q表示拉格朗日函数对广义坐标的偏导数。
该方程描述了系统在广义坐标下的运动规律。
拉格朗日方程的推导过程是基于变分法和哈密顿原理的。
通过对作用量进行变分，我们可以得到极值的条件，即达朗贝尔原理。
然后利用这个极值条件，我们可以推导出拉格朗日方程。
拉格朗日方程在物理学中有着广泛的应用，不仅可以用来描述质点的运动，还可以用来描述刚体的运动、连续介质的运动、以及相对论力学等。
它提供了一种统一的描述物体运动的方法，同时也为我们研究物体的宏观性质提供了一个有力的工具。
大学物理优质课件精选——分析力学拉格朗日方程课件
在其名著分析力学中把数学分析应用于质点和刚体力学提出了运用于静力学和动力学的普遍方程引进广义坐标的概念建立了拉格朗日方程把力学体系的运动方程从以力为基本概念的牛顿形式改变为以能量为基本概念的分析力学形式奠定了分析力学的基础为把力学理论推广应用到物理学其他领域开辟了道路哈密顿hamiltonwilliamrowan18051865爱尔兰人他的研究工作涉及不少领域成果最大的是光学力学和四元数
系统自由度数目：3N-(3N-S)=S →力学体系只有S个独立变量。
约束的分类
1. 约束方程 2. 约束方程
中不含时间t ——稳定约束 中含时间t ——不稳定约束
约束另外的分类1：可解约束与不可解约束
1. 由不等式表示的约束——可解约束: 质点在某一方 向上能脱离的那种约束
2. 由等式表示的约束——不可解约束: 质点始终不能 脱离的那种约束
分析力学
教材：理论物理基础教程
——分析力学部分
绪论
Ⅰ 分析力学是怎样的一门学科？
Ⅱ 怎样学好分析力学？
Ⅰ 分析力学是怎样的一门学科？
力学：主要指牛顿力学
普通物理
光学 热学
感性认识 建立在实验的基础上
大
电磁学
学
物
原子物理学
理
理论力学：核心是分析力学
理论物理 (四大力学)
热力学与统计物理
电动力学 量子力学
4. 正则共轭坐标（第6章）
坐标概念的第三次飞跃
§1.1.1 无约束质点的拉格朗日方程
推导拉格朗日方程的方法之一：从牛顿方程出发推导 两种情况：1．不受约束的质点；
2．受约束的质点。（两种情况均在保守力场中） 注意：约束的概念、约束性质（限制物体相互位置的
性质）、保守力场的概念 约束:在一个力学体系中，存在着一些限制各质点自由运动 的条件，我们把这些条件叫做约束。
系统自由度数目：3N-(3N-S)=S →力学体系只有S个独立变量。
约束的分类
1. 约束方程 2. 约束方程
中不含时间t ——稳定约束 中含时间t ——不稳定约束
约束另外的分类1：可解约束与不可解约束
1. 由不等式表示的约束——可解约束: 质点在某一方 向上能脱离的那种约束
2. 由等式表示的约束——不可解约束: 质点始终不能 脱离的那种约束
分析力学
教材：理论物理基础教程
——分析力学部分
绪论
Ⅰ 分析力学是怎样的一门学科？
Ⅱ 怎样学好分析力学？
Ⅰ 分析力学是怎样的一门学科？
力学：主要指牛顿力学
普通物理
光学 热学
感性认识 建立在实验的基础上
大
电磁学
学
物
原子物理学
理
理论力学：核心是分析力学
理论物理 (四大力学)
热力学与统计物理
电动力学 量子力学
4. 正则共轭坐标（第6章）
坐标概念的第三次飞跃
§1.1.1 无约束质点的拉格朗日方程
推导拉格朗日方程的方法之一：从牛顿方程出发推导 两种情况：1．不受约束的质点；
2．受约束的质点。（两种情况均在保守力场中） 注意：约束的概念、约束性质（限制物体相互位置的
性质）、保守力场的概念 约束:在一个力学体系中，存在着一些限制各质点自由运动 的条件，我们把这些条件叫做约束。
拉格朗日方程
统的自由度数目，选取合适的广义坐标。
2、分析系统的运动，写出用广义坐标及广义速 度表示的系统的动能。（速度及角速度均为绝对的）
d L L ( ) 0 (k 1,2, , N ) k dt q qk
1.2
拉 T T d T 或 L L d L ( ) ( ) 格 q q j k dt q k dt q k q k q k k 朗 5、写出拉格朗日方程并加以整理，得到N个二 日 阶常微分方程。由2 N个初始条件，解得运动方程。 方 程
1.2
d T T Q ，得 由 ( ) dt 1 2 M (2Q 9 P)(r R) 6g
拉 6Mg 即 格 (2Q 9 P)(r R) 2 朗 积分得曲柄的运动方程为 日 3Mg 2 0t 0 t 方 2 (2Q 9 P)(r R) 程 0分别为初始转角和初始角速度。 式中， 0 、
1.2
拉 格 朗 日 方 程
例4 如图轮A的质量为 m1，在水平面上只滚动不 滑动，定滑轮B的质量为 m2，两轮均为均质圆盘，半 m3 径均为R，重物C的质量为 ，弹簧的弹性系数为 ， k 试求系统的运动微分方程。 k AR 解：以系统为研究对象， B R 系统具有一个自由度。取 x x C 为广义坐标，x 从重物的平衡 位置量起。系统的动能为 2 1 1 2 1 1 3 x x 2 2 2 T ( m1 R )( ) ( m2 R )( ) m3 x 2 2 2R 2 2 R 2 1 2 (3m1 4m2 8m3 ) x 16 设系统平衡时弹簧的静伸长为 st ，则有关系式
整理后得 3 1 1 2 2 1 2 2 2 2 T m1 x m2 ( x L Lx cos ) m2 L 4 2 4 24
2、分析系统的运动，写出用广义坐标及广义速 度表示的系统的动能。（速度及角速度均为绝对的）
d L L ( ) 0 (k 1,2, , N ) k dt q qk
1.2
拉 T T d T 或 L L d L ( ) ( ) 格 q q j k dt q k dt q k q k q k k 朗 5、写出拉格朗日方程并加以整理，得到N个二 日 阶常微分方程。由2 N个初始条件，解得运动方程。 方 程
1.2
d T T Q ，得 由 ( ) dt 1 2 M (2Q 9 P)(r R) 6g
拉 6Mg 即 格 (2Q 9 P)(r R) 2 朗 积分得曲柄的运动方程为 日 3Mg 2 0t 0 t 方 2 (2Q 9 P)(r R) 程 0分别为初始转角和初始角速度。 式中， 0 、
1.2
拉 格 朗 日 方 程
例4 如图轮A的质量为 m1，在水平面上只滚动不 滑动，定滑轮B的质量为 m2，两轮均为均质圆盘，半 m3 径均为R，重物C的质量为 ，弹簧的弹性系数为 ， k 试求系统的运动微分方程。 k AR 解：以系统为研究对象， B R 系统具有一个自由度。取 x x C 为广义坐标，x 从重物的平衡 位置量起。系统的动能为 2 1 1 2 1 1 3 x x 2 2 2 T ( m1 R )( ) ( m2 R )( ) m3 x 2 2 2R 2 2 R 2 1 2 (3m1 4m2 8m3 ) x 16 设系统平衡时弹簧的静伸长为 st ，则有关系式
整理后得 3 1 1 2 2 1 2 2 2 2 T m1 x m2 ( x L Lx cos ) m2 L 4 2 4 24
理论力学—拉格朗日方程PPT
m2 cos
a1
3(m1
m2 gsin2 m2 )－2m2cos2
ar
2gsin (m1 m2 ) 3(m1 m2 )－2m2cos2
15
§18-2 拉格朗日(Lagrange)方程
由n个质点所 组成的质点系
主动力 虚位移
广义坐标 第i个质 点的位矢
F (F1, F2,, Fn )
r (r1,r2,,rn )
O1
x1
l
l
rA
rB
xA l cos yA l sin
FIA
A B FIB
m1g l
rC l m1g
xB l cos
C
yB l sin
m2g
yC 2l sin
y1
2m1lsin2lcos 2m1glsin 2m2glsin 0
2 (m1 m2 )g
m1lcos
10
例题3 质量为m1的三棱柱ABC
FIA
A B FIB
m1g l
rC l m1g
根据几何关系，有
C
m2g
xA lsin yA lcos
xA l cos
yA l sin
y1
xB lsin
xB l cos
yB lcos
yB l sin
yC 2lcos
yC 2l sin
9
3、应用动力学普遍方程
FIA δxA FIB δxB m1g δyA m1g δyB m2 g δyC 0
其次，要确定系统的自由度，选择合适的广义坐标。 按照所选择的广义坐标，写出系统的动能、势能或广 义力。
将动能或拉格朗日函数、广义力代入拉格朗日方程。
23
a1
3(m1
m2 gsin2 m2 )－2m2cos2
ar
2gsin (m1 m2 ) 3(m1 m2 )－2m2cos2
15
§18-2 拉格朗日(Lagrange)方程
由n个质点所 组成的质点系
主动力 虚位移
广义坐标 第i个质 点的位矢
F (F1, F2,, Fn )
r (r1,r2,,rn )
O1
x1
l
l
rA
rB
xA l cos yA l sin
FIA
A B FIB
m1g l
rC l m1g
xB l cos
C
yB l sin
m2g
yC 2l sin
y1
2m1lsin2lcos 2m1glsin 2m2glsin 0
2 (m1 m2 )g
m1lcos
10
例题3 质量为m1的三棱柱ABC
FIA
A B FIB
m1g l
rC l m1g
根据几何关系，有
C
m2g
xA lsin yA lcos
xA l cos
yA l sin
y1
xB lsin
xB l cos
yB lcos
yB l sin
yC 2lcos
yC 2l sin
9
3、应用动力学普遍方程
FIA δxA FIB δxB m1g δyA m1g δyB m2 g δyC 0
其次，要确定系统的自由度，选择合适的广义坐标。 按照所选择的广义坐标，写出系统的动能、势能或广 义力。
将动能或拉格朗日函数、广义力代入拉格朗日方程。
23
分析力学动力学普遍方程和拉格朗日方程实用课件
圆柱的角速度为 O (设圆柱o的半径为r)
m(l
R )2,
d dt
L
2mR (l
R) 2
m(l
R ) 2
L mR(l R) 2 mg (l R)sin
已求得
d dt
L
2mR (l
R) 2
m(l
R ) 2
L mR(l R) 2 mg (l R)sin
将式上式代入保守系统的拉氏方程
d dt
L
L
0
得摆的运动微分方程
(l R) R 2 g sin 0
M v
P
R'=－R=－ ma
此力是摆锤被迫作非惯性运动时产生的“反作用力”， 称为惯性力。
结论：质点在作非惯性运动的任意瞬时，对于施力于它的物 体会作用一个惯性力，该力的大小等于其质量与加速度的乘 积，方向与其加速度方向相反。
若用Fg表示惯性力，则有 Fg =－ ma
说明： 1.此力是不是真实的力！ 2.此力作用于施力给质点的物体上！ 3.此力又称为牛顿惯性力！
拉格朗日
1736 — 1813,法籍 意大利人，数学家、 力学家、天文学家， 十九岁成为数学教 授，与欧拉共同创 立变分法，是十八 世纪继欧拉后伟大 的数学家。
设质点系由n个质点组成，具有s个完整理想约束，则有 N=3n-s个自由度（广义坐标）。
用q1，q2，…qN表示系统的广义坐标，第i个质点质量为mi， 矢径为ri。则
i 1
n
或 (Fi miai ) δri 0 i 1
动力学普遍方程
表明：在理想约束条件下，在任意瞬时，作用于质点系上 的主动力和惯性力在质点系的任意虚位移上所做虚功之和 等于零。
若 Fi X ii Yi j Zik, ai xii yi j zik,
第18章分析力学基础动力学普遍方程拉格朗日方程.ppt
Q2
3 i 1
Xi
xi
2
Yi
yi
2
Zi
zi
2
(P cos2
W2 2
sin 2 )l2
5
解2：（几何法）选1、2为广义坐标，对应虚位移为1、2。
① 先令1≠0、2＝0，如图（a）。所
有力在此虚位移上的虚功为
ΣWF
mO (W1)1
注：由于使用动力学普遍方程较麻烦，通常不用其直接求
解动力学问题。其意义在于导出拉格朗日方程。
作业：选做18-5（试用动力学普遍方程求。注意为2自由度问题） 11
§18-3 拉格朗日方程（简介）
简称拉氏方程。拉格朗日推导出两种形式的拉氏方程，即第一类拉格朗日 方程和第二类拉格朗日方程。第一类方程使用直角坐标及约束方程（用待 定乘子法），因而方程组中的方程很多；第二类方程使用广义坐标、广义 力及动能的概念，使方程组中的方程数大大减少（为广义坐标数或自由度 数）。一般（此处亦如此）的拉格朗日方程均指第二类方程。
Q g
vC2
1 2
1 2
Q g
r 2 2
s
P 2Q v2 P 2Q s2
2g
2g
A C
设系统起始位置为0势能位置，系统 势能为：
vC aC
Q
V Ps Q s sin
OB
Q va
P
s
则拉格朗日函数： 拉格朗日方程：
L T V P 2Q s2 Ps Qssin
WF
n
Wi
i 1
n i 1
(
动力学方程 拉格朗日方程
ri ri (q1, q2 , , qs , t)
则
ri
ri q1
q1
ri q2
q2
ri qs
qs
s
ri
1 q
q
代入达朗伯－拉格朗日方程
n
i 1
(
miri
Fi )
s a 1
由
ri
ri
,
d
ri
ri
q q
dt q q
P
d dt
n i 1miFra bibliotekri
ri q
n i1
mi
ri
ri q
d dt
n i 1
q
现在我们从达朗伯－拉格朗日方程出发，把各并不彼此 独立的坐标 ri 用各彼此独立的广义坐标 q ( 1,2, , s)
重新表述，从而导出适用于受理想约束的完整力学系所遵守的 动力学方程—拉格朗日方程。
设n个质点受k个约束，因是完整约束，体系的自由度数 应为 s＝3n－k。以广义坐标 ri 表出
一、达朗伯－拉格朗日方程
设受完整约束的力学体系有n个质点，体系中每一个质点都
服从如下形式的牛顿运动定律，设第i个质点受主动力，受约束
反力，则
mi ri
Fi
Ri , i
1,
2,
,
n
miri
mi
ri
Fi
18拉格朗日方程与哈密顿原理
主讲 贾启芬
第18章 拉格朗日方程与哈密顿原理 18章
18.1 第二类拉格朗日方程
Theoretical Mechanics
返回首页
18.1 第二类拉格朗日方程 设质点系有n个质点， 个完整约束且系统所受 设质点系有 个质点，受s个完整约束且系统所受 个质点 的约束是理想约束， 的约束是理想约束，自由度 k=3n- s 。 质点 mi , ri 。若取系统的一组广义坐标 为 q1 , q2 ,⋯ qk ，则
经推导得
d ∂T ∂T − =Q j ɺ dt ∂ q j ∂ q j
( j = 1,2, ⋯ ,k )
拉格朗日第二类动力学方程，简称拉格朗日方程。 拉格朗日第二类动力学方程，简称拉格朗日方程。
Theoretical Mechanics
18.1 第二类拉格朗日方程 如果作用于质点系的力是有势力， 如果作用于质点系的力是有势力，则广义力 Q j 可 用质点系的势能来表达。 用质点系的势能来表达。
若主动力为有势力，须将势能U表示为广义坐 若主动力为有势力，须将势能 表示为广义坐 标的函数。 标的函数。 建立拉氏方程并加以整理，得出k个二阶常微分 4. 建立拉氏方程并加以整理，得出 个二阶常微分 方程。 方程。 求出上述一组微分方程的积分。 5. 求出上述一组微分方程的积分。
Theoretical Mechanics
保守系统的拉格朗日方程。 保守系统的拉格朗日方程。
Theoretical Mechanics
18.1 第二类拉格朗日方程 应用拉氏方程解题的步骤： 应用拉氏方程解题的步骤： 判定质点系的自由度k， 1. 判定质点系的自由度 ，选取适宜的广义坐 必须注意：不能遗漏独立的坐标， 标。必须注意：不能遗漏独立的坐标，也不能有 多余的（不独立）坐标。 多余的（不独立）坐标。 计算质点系的动能T， 2. 计算质点系的动能 ，表示为广义速度和 广义坐标的函数。 广义坐标的函数。
理论力学第十八章 拉格朗日方程 教学PPT
q t
h
h
j
h
（2）
ri ri (q1, q2 ,...qk ; t) 对任 qh求偏导，再对时间t求导得
d
dt
( ri ) qh
k j1 q j
(
ri qh
)qj
2 ri tqh
k 2r
i
j1 q q
q j
2r i
tq
j
h
h
（3）
式（3）右边与式（2）右边比较可得关系式
i 1
以上二式称为动力学普遍方程 或 达朗贝尔——拉格朗日方程。
n
Fi miai δ ri 0
i 1
n
Fix mi xi δ xi Fiy mi yi δ yi Fiz mizi δ zi 0
i 1
动力学普遍方程
但是，如果改用广义坐标，来描述系统的运动，将动力 学普遍方程表达成广义坐标的形式，就可得到与广义坐标 数目相同的一组独立的运动微分方程，这就是著名的拉格 朗日方程，用它求解较复杂的非自由质点系的动力学问题 常很方便。
拉格朗日方程的推导
设由 n 个质点组成的质点系，受到 s 个理想、完整约束，因此该系统 具有k= 3m- s个自由度，可用 k 个广义坐标 q1 , q2 , … , qk 来确定该系统的 位形。
动力学普遍方程－例题1
动力学普遍方程－例题1
δrB F*B B
m1g δrC
解： 球简化为质点，除主动力外，图上画出了
d
O α δ x
ω dα
δrA A F*A
m1g
飞球的惯性力F*A和F*B，两力大小相等，方 向相反。
h
h
j
h
（2）
ri ri (q1, q2 ,...qk ; t) 对任 qh求偏导，再对时间t求导得
d
dt
( ri ) qh
k j1 q j
(
ri qh
)qj
2 ri tqh
k 2r
i
j1 q q
q j
2r i
tq
j
h
h
（3）
式（3）右边与式（2）右边比较可得关系式
i 1
以上二式称为动力学普遍方程 或 达朗贝尔——拉格朗日方程。
n
Fi miai δ ri 0
i 1
n
Fix mi xi δ xi Fiy mi yi δ yi Fiz mizi δ zi 0
i 1
动力学普遍方程
但是，如果改用广义坐标，来描述系统的运动，将动力 学普遍方程表达成广义坐标的形式，就可得到与广义坐标 数目相同的一组独立的运动微分方程，这就是著名的拉格 朗日方程，用它求解较复杂的非自由质点系的动力学问题 常很方便。
拉格朗日方程的推导
设由 n 个质点组成的质点系，受到 s 个理想、完整约束，因此该系统 具有k= 3m- s个自由度，可用 k 个广义坐标 q1 , q2 , … , qk 来确定该系统的 位形。
动力学普遍方程－例题1
动力学普遍方程－例题1
δrB F*B B
m1g δrC
解： 球简化为质点，除主动力外，图上画出了
d
O α δ x
ω dα
δrA A F*A
m1g
飞球的惯性力F*A和F*B，两力大小相等，方 向相反。
课件：拉格朗日方程
7
第二类拉格朗日方程 几种形式
d dt
T q j
T q j
Qj
( j 1,2,, k)
1、当主动力均为有势力时
Qj
V (q1,,qk ) q j
d T dt q j
T q j
V
q j
设：L＝T-V
（拉格朗日函数）
d dt
T q j
(T V q j
)
0
2、当主动力部分为有势力时
m2g x2 x1 m1g
解： 2个自由度，取广义坐标（x1, x2） 系统的动能：
b
T
1 2
m1x12
1 2
m2 x22
1 2
J C 2
T
12（m1
m2）x12
m2 x22
x2
m2 x2 x1
r
x1
系统的势能： 以x1 =x2 =0处为零势能位置
V m1gx1 sin m2gx2 sin b
拉格朗日函数： L T V 18
3、求非有势主动力的广义力
I
vC
21
例、车厢质量为m，质心C，转动惯量 JC m，2 弹簧刚度如图 所示。水平位置为静平衡位置，建立运动微分方程。
解：系统自由度 2
广义坐标： z 静平衡位置为坐标原点
该系统外力均为有势力，
选取零势能位置：静平衡位置
系统动能： T 1 mz2 1 m 2 2
系统势能： 2
)
L z
0
mz k1(z l1 ) k2 (z l2) 0
23
mg
l 2
k 0b
0)
衡位置的伸长量有关。
拉格朗日函数: L 1 (1 ml 2 ) 2 k 2b2
力学竞赛之拉格朗日方程-PPT课件
N
如令
x y z i i i Q ( F F F k 1 ， 2 ， ， N ) k xi yi zi )( q q q k k k i 1
n
称为与广义坐标 q k 相对应的广义力 。
δW Q qk 0 F kδ
k 1
N
由于广义坐标的独立性
例：一单摆在空间摆动，摆长为l。
O
x
约束方程为
fx (, y ,) z x y z l
2 2 2
2
自由度数为2。
y
z
x，y为独立变量
2 2 2 zxy (, ) l x y x xxy ( , ) x y yxy ( , ) y z
, （单摆在xy面上的投影与x轴夹角）为独立变量。 xx (, ) l s i n c o s y y (, ) l s i n s i n
δ q k 可以为任一值
Q Q Q 0 1 2 N
质点系的平衡条件是系统所有的广义力都等于零。
——用广义坐标表示的质点系的平衡条件
求广义力的两种方法 1.直接计算法（解析法）
x y z i i i Q ( F F F k 1 ， 2 ， ， N ) k xi yi zi )( q q q k k k i 1
z z (, ) l c o s
思考：导弹在追踪飞机的情况下，广义坐标的数目和自由度
数目的关系如何？ 描述导弹的位置： 质心的位置
xC , yC
导弹的纵轴和x 轴的夹角 独立的广义坐标数目为3 导弹的速度方向要对准飞机的质心 约束方程
yC yP yC xC xP xC
如令
x y z i i i Q ( F F F k 1 ， 2 ， ， N ) k xi yi zi )( q q q k k k i 1
n
称为与广义坐标 q k 相对应的广义力 。
δW Q qk 0 F kδ
k 1
N
由于广义坐标的独立性
例：一单摆在空间摆动，摆长为l。
O
x
约束方程为
fx (, y ,) z x y z l
2 2 2
2
自由度数为2。
y
z
x，y为独立变量
2 2 2 zxy (, ) l x y x xxy ( , ) x y yxy ( , ) y z
, （单摆在xy面上的投影与x轴夹角）为独立变量。 xx (, ) l s i n c o s y y (, ) l s i n s i n
δ q k 可以为任一值
Q Q Q 0 1 2 N
质点系的平衡条件是系统所有的广义力都等于零。
——用广义坐标表示的质点系的平衡条件
求广义力的两种方法 1.直接计算法（解析法）
x y z i i i Q ( F F F k 1 ， 2 ， ， N ) k xi yi zi )( q q q k k k i 1
z z (, ) l c o s
思考：导弹在追踪飞机的情况下，广义坐标的数目和自由度
数目的关系如何？ 描述导弹的位置： 质心的位置
xC , yC
导弹的纵轴和x 轴的夹角 独立的广义坐标数目为3 导弹的速度方向要对准飞机的质心 约束方程
yC yP yC xC xP xC
拉格朗日方程
对i求和并移项得
∂ri d ∂ 1 ∂ 1 2 2 mi v i • = ∑[ ( mi vi ) − ( mi vi )] ∑ • ∂qs dt ∂ q 2 ∂qs 2 i i s
•
引入系统动能
T =
∑
i
1 2 m i vi 2
s = 1, 2, • • •, n
dvi ∂ri Qs − ∑ mi • =0 dt ∂qs i
若全部主动力均为有势力,设势能函数为 V(xi,yi,zi),则有
∂V ∂V ∂V ∂V = −( Fi = − i+ j+ k) ∂ri ∂xi ∂ yi ∂zi
∂ri Qs = ∑ Fi • ∂qs i =1
N
s=1,2, …,n 上式即为主动力有势时的广义力表达式。
∂V ∂ri • = −∑ ∂qs i =1 ∂r i
ri = ri(q1, q2, …, qn,t)
i=1,2, … ,N
于是用广义坐标的独立变分表示的虚位移为
δ ri =
∑
s =1
n
∂ ri δqs ∂qs
i
i=1,2, …,N
δW = ∑ Fi • δri
n N ∂ri ∂ri δW = ∑ Fi • ( ∑ δqs ) = ∑ ( ∑ Fi • )δqs ∂qs i =1 s =1 ∂qs s =1 i =1
m φ1 φ2
m
ϕ1 + ϕ 2 2 mr 2 • 2 • 2 cr 2 L= (ϕ1 + ϕ 2 ) − (1 − 2 cos ) 2 2 2
mr 2 • 2 • 2 cr 2 ϕ1 + ϕ 2 2 L= (ϕ1 + ϕ 2 ) − (1 − 2 cos ) 2 2 2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
W2
r2
P
r2
W1
l1 2
sin
11
W2r2
sin
1
Pr3
c
os1
P
c os1
(W1 2
W2
) sin
1 l11
C1
r1
rA
W1
r2
r3
C2
P
W2
(a)
所以，对应1的广义力为
Q1 W1 2
W2 ) sin 1l1
6
② 再令2≠0、1＝0，如图(b)。 所有力在此虚位移上的虚功为： WF mA (W2 ) 2 mA (P) 2
W2
l2 2
sin2 2
Pl2 2
cos2
C1
(P
cos2
W2 2
i 1
n
(Fi Ni FIi ) ri 0
i 1
理想约束：
n
Ni
ri
0
i 1
(1)
n
或
[( X i mxi ) xi (Yi myi ) yi (Zi mzi ) zi ] 0 (2)
i 1
或
ΣWF ΣWFI 0
Q2
3 i 1
Xi
xi
2
Yi
yi
2
Zi
zi
2
(P cos2
W2 2
sin 2 )l2
5
解2：（几何法）选1、2为广义坐标，对应虚位移为1、2。
① 先令1≠0、2＝0，如图（a）。所
有力在此虚位移上的虚功为
ΣWF
mO (W1)1
一、广义力的概念
§18-1 广义力
质点系任一质点坐标可用广义坐标 qh ( h = 1,2,…,k) 表示：
ri
ri
(q1,
q2
,,
qk
)
i 1,2,, n
求变分，得用广义坐标 变分表示的虚位移：
ri
k h1
ri qh
qh
i 1,2,, n
对应第 h 个广义坐
该质点上的力所作虚功：
标的广义
Wi
Fi
ri
Fi
k
(
h1
ri qh
qh )
k h1
Fi
ri qh
qh
力 i 1,2,, n
整个质点系上所有（主 动）力所作虚功：
Qh
n i 1
Fi
ri qh
h 1,2,, k
(3)
即，对动力学问题，给系统加上惯性力，再应用虚位移原理即可解题。
注：①上式中不一定指质点，而一般可理解为力或力偶个数；
②当质点系静止时（静平衡），ΣWFI 0 ，退化为虚功方程：
WF 0
8
解题步骤： (一)研究整体（若求反力，需先去其约束，画上约束力）； (二)画主动力，并加惯性力（偶），画运动图；给系统虚位移； (三)列解方程。
WF
n
Wi
i 1
n i 1
(
k h1
Fi
ri qh
qh
)
k h1
(
n i 1
Fi
ri qh
)qh
k
Qhqh
h1
3
二、广义力的求法
1. 解析法——由各力及其作用点求
Qh
n i 1
Fi
ri qh
Qh
WF qh
4
例1 （书上例17-10）
计算双摆的广义力，已知摆长各为l1、l2，
重量各为W1、W2，力P。（2自由度）
C1
解1：（解析法）建立坐标系如图。选1、
2为广义坐标。
C2
各力在坐标轴上的投影为
W1
P
X1 W1, X 2 W2 , Y3 P
W2
各力作用点坐标为
x O
即，一个变分方程可对 应几个独立的代数方程： 独立代数方程数 ＝ 广
x y ——广义坐标的变分
义坐标数
X , Y , mC (F ) ——虚功表达式中广义坐标的
变分的系数，称为广义力Qi
可见，虚功方程等价于 Qi = 0 (i = 1, 2, ... , k)
1
注1：
sin 2
)l2
2
所以，对应2的广义力为
Q2
WF 2
(P
cos2
W2 2
sin2
)l2
W1
r2
r3
C2
P
W2
(b)
§18-2 动力学普遍方程
回到动力学问题上来。
达朗贝尔原理 虚位移原理
动力学普遍方程
拉格朗日方程
拉格朗日是分析力学的创始人。 分析力学的基础
7
动力学普遍方程的思想是： 对n个质点的质点系：
达朗贝尔原理
虚位移原理
动力学问题
形式上的平衡问题
动力学普遍方程
n
(Fi Ni ) 0
i 1
n
(Fi Ni FIi ) 0
i 1
n
(Fi
FIi )
ri
0
i 1
n
(Fi mai ) ri 0
对单个自由刚体，该组方程等同于平衡方程；对非自由质点系， 该组方程不同于平衡方程（见后面例1）。
注2：
①对应每一个广义坐标，有一个广义力； ②广义力是代数量而非矢量； ③广义力不作用在某个物体上，故也无法画出。 在以下（拉格朗日方程）的讲解中，会用到广义力的概念，故下面首 先介绍广义力。
2
第18章 动力学普遍方程 拉格朗日方程
x1
l1 2
c
os1,
x2
l1
cos1
l2 2
c os 2 ,
y3 l1 sin 1 l2 sin 2
代入广义力公式（过程略，你可以再详细些），得
Q1
3 i 1
Xi
xi
1
Yi
yi
1
Zi
zi
1
Pcos1
(W1 2
W2 ) sin 1l1
用虚功方程解决过若干问题， WF 0
问题：用虚功方程可解几个代数未知量？
y
y
看例子——平面平衡自由刚体 几个自由度？
C
x
给刚体虚位移： x y 对应平动
对应转动
WF X x Y y mC (F) 0
X 0, Y 0, mC (F) 0
用直角坐标表示：
h 1,2,, k
Qh
n i 1
(Xi
xi qh
Yi
yi qh
Zi
zi ) qh
h 1,2,, k
2. 几何法——由虚功求
k
质点系虚功： WF Qhqh h 1
若只给定第h个广义坐标的虚位移，其余广义坐标的虚位移为0，则
WF Qhqh