数据、模型与决策(第10章线性规划原理与应用)
自考数据、模型与决策

高纲1396江苏省高等教育自学考试大纲30447 数据、模型与决策南京大学编江苏省高等教育自学考试委员会办公室I 课程性质、设置目的与要求一、《数据、模型与决策》课程的性质随着社会信息化水平的提高和科学管理意识的普遍增强,人们对如何从数据资料角度进行认识显示出越来越多的兴趣。
数据资料本身并没有什么意义,关键是采用合适的方法对其进行分析和处理,只有这样才能探索客观现象发展变化的内在规律,从而更好地服务于管理决策的需要。
《数据、模型与决策》属于数量性质的课程,侧重于讲解数据资料的搜集、描述、分析和解释,以及管理决策方法和技术方面的知识。
管理决策分为两类,一类是理性决策一类是行为决策。
数据分析与决策模型中,不论是以不确定性为特征的统计决策,还是以确定性为特征的管理科学优化决策,和以策略互动为特征的博弈决策,都可以把它们归结为理性决策范畴。
既然是理性决策,必然会要求建立某种决策准则,然后在既定的准则下通过度量来选择决策方案。
这一过程一方面要对研究的问题进行结构化处理,另一方面也需要有相应的数据资料。
前者是为了能够建立决策模型,后者则是帮助实现计算。
有鉴于此,数据与模型在决策分析中的重要意义不言而喻。
数据与模型除了共同服务于决策分析以外,两者之间也存在密切的关系。
从应用的角度,统计方法比较强调实证性做法,统计分析与决策中,没有大量的、客观准确的数据资料,统计决策分析只能停留在纯理论的状态,无法形成具体的分析结论。
管理运筹优化和博弈决策分析中,虽然不像统计分析那样,需要拥有充足的数据,但是必要的不可控因素比如模型中的有关参数,其数值资料就必须事先给以确定。
尽管现在的企业一般都积累了大量的可供开发利用的数据资料,不过由于这样那样的原因,数据资料本身总会存在不系统、不充分、不完备的情况。
因此,对于背景数据必须经过科学的编辑、处理、汇总和提炼,然后才能用于决策分析。
对此,模型起着重要的转化作用,通过模型化处理,不仅能对数据的价值结构进行改造,而且还能对决策赋以深层次的分析。
数据,模型,与决策

第一章(管理科学简介)P5(1)管理科学介绍管理科学本质:是对与定量因素有关的管理问题通过应用科学的方法进行辅助管理决策制定的一门学科.管理科学发展过程:快速发展开始于20世纪四五十年代起初的动力来自于第二次世界大战另一个里程碑是1947年丹捷格发明单纯形罚更大的推动作用的是计算机革命的爆发管理决策:管理者考虑管理科学对定量因素进行分析得出的结果后,再考虑管理科学以外的众多无形因素,然后根据其最佳判断做出决策管理科学小组系统和考察时步骤:定义问题与收集数据——构件数学模型——从模型中形成对于一个问题进行求解的基于计算机的程序——测试模型并在必要时进行修正——应用模型分析问题以及提出管理建议——帮助实施被管理者采纳的小组建议课后问题:1.管理科学什么时候有了快速发展?快速发展开始于20世纪四五十年代2.商学院以外还广泛使用的对管理科学学科的叫法:运筹学3.管理科学研究提供给管理者什么?对问题涉及的定量因素进行分析并向开明的管理者提出建议4.管理科学以哪些领域作为基础?科学领域:数学,计算机社会领域:经济学5.什么是决策支持系统?辅助管理决策制定的交互式基于计算机的系统6.与管理问题有关的一般定量因素有哪些?生产数量,收入,成本,资源P11(2)一个例子:盈亏平衡分析步骤:分析问题——建立模型——敏感性分析,电子表格模型提供上述三者了方便的途径如果预测销售数量<盈亏平衡点,Q=0预测销售数量>盈亏平衡点,Q=预测销售数量敏感性分析目的:研究如果一个估计值发生了变化,将会给模型带来什么样的变化Min(a,b):取a,b中的最小值If(A,b,c):如果表达式A为真,则值为b,否则为c第二章(线性规划:基本概念)P31(3)在电子表格上建立恩德公司问题的模型1.开始在电子表格上建立线性规划模型时需要回答的三个问题:要做出的决策是什么?在做出这些决策上有哪些约束条件?这些决策的全部绩效测度是什么?2.以下各个单元格的作用数据单元格:显示数据的单元格可变单元格:需要做出决策的单元格输出单元格:依赖于可变单元格的输出结果的单元格目标单元格:在生产率做出决策时目标值定为尽可能大的特殊单元格3.该案例中每个输出单元格(包括目标单元格)的Excel等式的形式:可以表达为一个SUMPRODUCT函数,这里的每一项是一个数据单元格和可变单元格的乘积P33(4)电子表格的数学模型1.电子表格模型与代数模型相同的初始步骤:收集相关数据确定要做出的决策确定对这些决策的约束条件确定为这些决策的完全绩效测度把约束条件和绩效测度的口头描述转化为数据和决策表示的定量表达式2.用代数形式建立线性规划模型时,模型中需要引入代数符号来表示哪几类数量?用来表示绩效测度与决策4.模型的一个可行解是什么意思?决策变量的任何一个取值P41(5)求两问题变量的图解法1.图解法能用来求解带有几个决策变量的线性规划问题?只有两个2.什么是约束边界线?形成一个约束条件所允许的边界的直线什么是约束边界方程?形成一个约束条件所允许的边界的直线的方程可行域?比所有约束边界线更靠近原点的那些点成为可行解,可行解所在的区域成为可行域会作图求解P44(6)应用Excel求解线性规划问题(solver)1.用来输入目标单元格和可变单元格地址的对话框是什么?目标单元格:set target cell 可变单元格:by changing cells2.具体化模型的函数约束的对话框是什么?subjecttotheConstraints3.在solver中,哪些选项一般需要选定以求得一个线性规划模型?采用线性模型,假定非负P48(7)一个最小化的例子——利博公司广告组合问题3. 利博公司的目标?在达到市场份额的前提下,确定最低的总成本并决定要在每种媒体上做多少钱的广告4.在电子表格中设置目标单元格和可变单元格的基本原理是什么?目标单元格:?可变单元格:?P50(8)管理视角的线性规划1.管理部门一般对线性规划研究的技术细节设计深么?不深,没有必要2.一般问题有两个以上决策变量看,那么研究两个决策变量问题的图解法的意义?实际意义中没有价值,但对于传达线性规划设计确定约束边界和使目标值往尽可能大的这一方向移动的这一基本观念有很大价值3.开明的管理者关于线性规划应该知道哪些事项?需要知道线性规划是什么的一个良好直觉对线性规划的适用性和作用有一个正确的评价使得在合适的时候鼓励应用能够区分能胜任和以次充好的线性规划研究理解如何解释研究成果第三章(电子表格建模的艺术)(多简答和选择)P76(2)电子表格建模程序的概述1.当你不知道从哪里开始时,帮助你开始建立电子表格模型的方法是什么?设想一下的目标手工进行一些计算建立一个小的电子表格2.手工计算可从那两方面帮助你?首先,它能帮助理清输出单元格公式的形式其次,它可以帮助检验表格3.描述一下组织和编排电子表格的一个有用方法计划设想一下你的目标手工进行一些计算建立一个电子表格建模先建立一个小模型测试利用不同的测试数据分析模型的逻辑关系,将模型扩展为完整的模型分析评估建议的解和/或利用solver优化4.哪些数值应被输入数据单元格以测试模型?试着输入一些我知道输出单元格结果的数值5.单元格绝对坐标:当被填入其它单元格时,坐标不会改变的坐标,如&E&11单元格相对坐标:公式中单元格或者范围的坐标通常是基于他们相对含有公式的单元格的位置P81(3)建立一个好的电子表格模型的几个原则1.模型的哪个部分最先输入电子表格?在建立电子表格之前,先输入和仔细编排所有数据2.数据应包含在公式中,还是被单独输入数据单元格?单独3.区域名称是如何使公式和模型在Solver对话框中更易于理解?如何选择区域名称??1:用区域名称取代单元格地址写入公式中,使得公式更容易说明?2:选择“插入”菜单中“名称/定义”,然后输入一个名称,获得区域名称4.区分数据单元格,可变单元格,输出单元格,目标单元格有哪些方法?对不同类型的单元格使用不同的边框,单元格阴影5.在电子表格中完整的表达一个约束条件需要多少单元格?3P86(4)调试电子表格模型1.调试电子表格模型的第一个步骤是什么?在你预知输出单元格正确结果的情况下,将不同的数值输入可变单元格,然后观察模型的计算结果是否和预期结果一致2.如何输出单元格在数值和公式中的切换?pc上同时按control和~键(Mac上同时按Command和~键)3.对于一个给定的单元格,哪一个Excel工具可以用来追踪其从属单元格或引用单元格?“工具”——“审核/追踪从属单元格”,会显示出箭头,以观察单元格之间的联系建立一个好的电子表格所需原则:●首先输入数据●组织和清楚标识数据●每个数据输入唯一的单元格●将数据与公式分离●保持简单化●使用区域名称●使用相对和绝对坐标简化公式的复制●使用边框、阴影和颜色来区分单元格类型●在电子表格中显示整个模型第四章(线性规划:建模与应用)P97(1)案例研究——超级食品公司的广告混合问题4.在评价使用线性规划来表示该实际问题的准确性时,要做出的假设条件有哪些?允许有分数解包括目标单元格和可变单元格都可以用SUMPRODUCT函数以数据单元格和可变单元格表示(有时候只是可变单元格的加总)P106(2)资源分配问题1.资源分配问题的共性在线性规划模型中每一个函数限制均为资源限制,并且,每一种资源都可以表现为如下的形式:使用的资源数量<=可用的资源数量2.资源限制的形式如何?使用的数量<=可获得的数量3.为解决资源分配问题,必须收集哪三类数据?每种资源的可供量每一种活动所需要的各种资源的数量,对于每一种资源约活动的组合,单位活动所消耗的资源量必须首先估计出来每一种活动对总的绩效测度的单位贡献P113(3)成本收益平衡问题1.资源分配问题与成本收益平衡问题在管理目标上的差异是什么?资源分配问题:各种资源是受限制的因素(包括财务资源),问题的目标是(根据特定的总绩效测度)最有效的利用各种资源成本收益问题:管理层采取更为主动的姿态,他们指定哪些收益必须实现(不管如何使用资源),并且要以最低的成本实现所指明的收益2.成本收益平衡问题的共性是什么?所有的函数约束均为收益约束,并具有如下的形式:完成的水平>=最低可接受的水平3.收益限制的形式如何?完成的水平>=最低可接受的水平4.为解决成本收益平衡问题必须收集的三类数据包括哪些?每种收益的最低可接受水平(管理决策)每一种活动对每一种收益的贡献(单位活动的贡献)每种活动的单位成本P117(4)网络配送问题1.为什么这类问题为网络配送问题?这类问题通过配送网络能以最小的成本完成货物的配送,所以称之为网络配送问题2.网络配送问题的共性是什么?确定需求的约束,提供的数量=需要的数量3.确定需求的约束与资源约束和收益约束的区别是什么?确定需求的约束:提供的数量=需要的数量资源约束:使用的资源数量<=可用的资源数量收益约束:完成的水平>=最低可接受的水平P129(7)管理视角的建模1.为什么what-if分析是线性规划的研究中非常重要的一个组成部分?尽管可能使用许多变异的模型,但是对于一个特定版本的模型,一次只能求得一个解,但是在求得一个解以后,管理层会有很多问题:如果模型的参数估计有误怎么办?如果做出不同的似是而非的假设,问题的将会如何变化?如果管理方面所要求的某一选项没有被考虑在内,会产生怎样的结果?What-if分析有助于解决上述等相关问题P131(8)线性规划应用经典回顾1.比较三种线性规划的应用,注意各种类型的问题应该使用哪一类型的线性规划模型(资源分配、成本收益平衡、网络配送以及混合问题)第五章(线性规划的What-if分析)P158(3)只有一个目标函数系数变动1.目标函数系数允许变化范围的含义是什么?能使最优解保持不变的目标函数系数的变化范围称为目标函数系数允许变化范围2.如果目标系数的估计值不是实际值,并且不在允许变化范围之内,会有怎样的影响?最优解不正确3.在Excel的灵敏度分析报告中,目标函数系数一栏该如何解释?允许增加值和允许减少值一栏又该如何解释?目标函数系数一栏:目标函数系数的现值允许增加值和允许减少值一栏:是这些系数在最优的范围内,允许增加和减少的量(1E+30):10的三十次方的缩写,表示无穷大P165(4)目标函数系数同时变动的影响1.目标系数变动百分比法则中,变动的百分比指什么?各个变动系数占该系数允许变化范围允许变动量的百分比之和(有方向)2.在百分百法则中,如果变动的百分比之和不超过100%,最初的最优解将如何?不会改变3.在百分百法则中,如果变动的百分比之和超过100%,是否就意味着最初的最优解已经不再是最优解?不能确定最优解是否改变P172(5)单个约束条件变化的影响1.为什么要研究函数的约束条件的变化带来的影响?因为在建模时,还不能得到模型的这些参数的精确值更重要的是:这些常数往往不是由外界决定而是由管理层的政策决策决定的2.为什么函数约束的右端值可能改变?这些常数往往不是由外界决定而是由管理层的政策决策决定的,因此,在建模并求解之后管理者想要知道如果改变这些决策是否会提高最终的收益3.影子价格的含义是什么?约束常数增加微小的量1,使得目标函数增加的量4.用电子表格如何找到影子价格?用Solver表格呢?用灵敏度报告呢?电子表格:改变某一约束条件的值,重新按下Solver键,尝试在约束条件变化范围内找出每单位约束条件变化引起的目标函数值的变化即为影子价格Solver表格:?灵敏度报告:Shadow price栏5.为什么管理者会对影子价格感兴趣?管理者可以用影子价格评价,在影子价格的有效域内幅度不大的改变工作时间的各种决策6.影子价格是否也同样适用于减少函数约束右端值的数值的情况?是7.影子价格0对管理者来说是什么意思?该影子价格对应的约束条件在其变化范围内对目前的最优解没有影响8.为什么管理层会对可行域感兴趣??176(6)约束右端值同时变动的情形1.为什么要研究约束条件同时发生变化的情况?经常会出现需要我们考虑约束条件同时变动的情况。
线性规划:建模与应用

什么是线性规划模型
线性规划模型的一般形式
4
线性规划问题的分类
资源分配问题(resource-allocation):资源 约束。伟恩德玻璃制品公司产品组合问题
成本收益平衡问题(cost-benefit-trade-off): 收益约束。利博公司广告组合问题,大沼 泽地金色年代公司的现金流问题
网络配送问题(distribution-network):确 定需求约束。
混合问题(mix):多种约束。
5
主要内容
Super Grain Corp. Advertising-Mix Problem (Section 4.1)(超级食品公司的广告 组合问题)
Resource Allocation Problems & Think-Big Capital Budgeting (Section 4.2)(资源分配问 题和梦大发展公司的资金预算问题)
Question: At what level should they advertise Crunchy Start in each of the three media?
确定各种媒介的广
告力度以获得最有 效的广告组合?
11
Algebraic Formulation (数学模型)
Let (设定) TV = Number of commercials for separate spots on television (电视上的广告时段数目) M = Number of advertisements in magazines. (杂志上的广告数目) SS = Number of advertisements in Sunday supplements. (星期天增刊上的广告数目)
管理科学-数据模型与决策简介

Introduction to Management Science 管理科学简介
What is Data, Model and Decisions 数据模型与决策是什么
管理者 信息提供 模型
结论
决策
执行
反馈
结果
管理者在组织内制定决策,数据、模型与决策的目的 是在科学、符合逻辑和合理的基础上制定决策。内容 主要是管理科学和统计学。
Fixed Cost = $50,000 (if Q > 0) Variable Cost = $400 Q Total Cost =
0, if Q = 0 $50,000 + $400 Q, if Q > 0
Profit:
Profit = Total revenue – Total cost
为管理科学实践者颁发的最负盛名的奖项是 弗兰茨·厄德曼(Franz Edelman) 奖。这些奖项授予全世界年度 管理科学的最佳应用。评奖活动由国际运筹学会、管理科学协会 、管理科学实践学会联合发起。
Theory of Quantitative Analysis 管理定量分析理论
解决方法
线性规划 整数规划 非线性规划 多目标规划 预测 网络分析 决策分析 库存模型 模拟
实际问题
Many real world examples 许多实际问题举例
▪ Breakeven point Analysis 盈亏平衡分析 ▪ Optimum loan plan of the bank银行的最优贷 款计划 ▪Portfolio selection 投资方案的选择 ▪ Optimal payback plan for the investment 最优 还款计划
数据、模型与决策第九章到十章

追求至善 凭技术 开拓市 场,凭 管理增 创效益 ,凭服 务树立 形象。2 020年1 1月4日 星期三 下午5 时33分5 7秒17: 33:572 0.11.4
专业精神 和专业 素养, 进一步 提升离 退休工 作的质 量和水 平。202 0年11 月下午5 时33分 20.11. 417:33 Novemb er 4, 2020
第三节 控制图的制作与识别
第三节 控制图的制作与识别
第三节 控制图的制作与识别
第三节 控制图的制作与识别
第三节 控制图的制作与识别
第三节 控制图的制作与识别
第三节 控制图的制作与识别
第三节 控制图的制作与识别
第四节 工序能力分析
工序能力指数是产品质量规定的变化范围与产品质量实际变化范围相比较 的结果。通常,我们就是依据Cp判断工序实际能力
第三节 控制图的制作与识别
控制图是质量过程监测的重要工具,统计过程控制实质上 是指运用控制图对产品生产过程中发生的质量波动实施实 时观察,并在这个基础上决定是否需要对生产过程进行调 整。控制图是贝尔实验室工程师休哈特博士发明滴,故又 称为哈特控制图,它是运用统计方法确定管理界限,并用 于管理监控的一种图表
3 控制图制作与识别
4 工序能力分析
第一节 质量因素与质量数据
质量管理是指确定质量方针、质量目标和质量职责,并在 质量体系中贯彻质量策划、质量控制、质量保证和质量改 进,从而使全部管理职能能得到有效实施的各种活动。
第一节 质量因素与质量数据
第一节 质量因素与质量数据
第二节 质量分析的一般方法
人生不是 自发的 自我发 展,而 是一长 串机缘 。事件 和决定 ,这些 机缘、 事件和 决定在 它们实 现的当 时是取 决于我 们的意 志的。2 020年1 1月4日 星期三 5时33 分57秒W ednesd ay, No vember 04, 2 020
MBA数据模型与决策考卷及答案

MBA数据模型与决策考卷及答案一、选择题(每题1分,共5分)A. 线性回归模型B. 决策树模型C. 主成分分析模型D. 聚类分析模型A. 信息增益B. 均方误差C. 相关系数D. F值A. 加权评分模型B. 层次分析法C. 数据包络分析法D. 逻辑回归分析法A. 目标函数线性B. 约束条件线性C. 变量非负D. 变量连续A. SPSSB. ExcelC. SASD. MATLAB二、判断题(每题1分,共5分)1. 数据模型可以用来描述现实世界中的数据关系和规律。
(√)2. 在决策分析中,只需要关注定量数据,无需考虑定性数据。
(×)3. 熵值法可以用于评估决策树的节点纯度。
(√)4. 线性规划问题中,目标函数和约束条件都必须是线性的。
(√)5. 数据挖掘就是从大量数据中提取有价值信息的过程。
(√)三、填空题(每题1分,共5分)1. 在决策树中,用于分割节点的属性称为______属性。
2. 多属性决策方法中,加权评分模型的核心是确定各属性的______。
3. 线性规划问题中,目标函数的取值称为______。
4. 在数据挖掘过程中,将原始数据转换为适合挖掘的格式的过程称为______。
5. ______是一种基于样本相似度的分类方法。
四、简答题(每题2分,共10分)1. 简述决策树的基本原理。
2. 什么是线性规划?它有哪些应用场景?3. 简述主成分分析的基本步骤。
4. 聚类分析的主要目的是什么?5. 请列举三种常用的多属性决策方法。
五、应用题(每题2分,共10分)1. 某企业拟投资两个项目,项目A的预期收益为100万元,风险系数为0.6;项目B的预期收益为150万元,风险系数为0.8。
请使用加权评分模型为企业选择投资项目。
2. 某公司生产两种产品,产品1的单件利润为10元,产品2的单件利润为15元。
生产一件产品1需要2小时,生产一件产品2需要3小时。
公司每月最多生产100件产品,且生产时间不超过240小时。
线性规划

M1 : 目标函数: max z c 1 x 1 c 2 x 2 c n x n a 11 x 1 a 12 x 2 a 1 n x n b1 a x a 22 x 2 a 2 n x n b 2 21 1 约束条件: a x a x a x b m2 2 mn n n m1 1 x 1 , x 2 , , x n 0
24
第2节 应用举例
最终计算表(第3次计算)
c j→ CB 0.1 -0.3 0 XB x2 x4 x1 c j -z j b 10 50 30 0 x1 0 0 1 0 0.1 x2 1 0 0 0 0.2 x3 -1 1 1 0 0.3 x4 0 1 0 0 0.8 x5 -9/10 1/3 13/10 -0.74 -M x6 3/5 0 -1/5 -M + 0.06 -M x7 -3/10 1/3 1/10 -M + 0.12 -M x8 -1/5 0 2/5 -M -0.02 θ
27
第2节 应用举例
表1-7表明这些原材料供应数量的限额。加入到产品A、 B、D的原材料C总量每天不超过100kg,P的总量不超过 100kg,H总量不超过60kg。
表1-7
原材料名称 C P H 每 天 最 多 供 应 量 ( kg) 100 100 60 单 价 /(元 /kg) 65 25 35
29
第2节 应用举例
约束条件可表示为:
1 2 1 4 x1 x1 1 2 3 4 x2 x2 1 2 1 4 x3 x3 x1 x2 x3 x1 , , x 9 0 3 4 1 2 x4 x4 1 4 1 2 x5 x5 1 4 1 2 x6 x6 x7 x5 x6 x8 0 0 0 0 100 100 x 9 60
《数据、模型与决策》教学大纲.doc

《数据、模型与决策》教学大纲一、课程主要内容简介本课程作为MBA的一门必修课程。
各行各业的管理者都必需具备数字信息处理能力,利用数据信息得出正确的结论,并在诸多的策略中选取最优的策略。
数据分析、模型建立、策略选择是一个完整的过程。
对管理者而言,在处理问题时往往首先遇到的是数据,必须科学地、合理地在这些数据中提取他所需要的信息,或建立相应的模型,最后作出决策。
本课程是一门系统、完整、整体结构严谨、各部分紧密关联、理论与实际并重的课程,因此采用以基本理论为本、实用为主的教学指导思想。
既要求学生了解理论的内涵,掌握方法;也要求学生能学以致用,解决实际问题。
以基本理论为本,讲清来龙去脉,讲清应用背景,讲清内容要点以及使用条件,而略去比较烦难的推导证明。
以实用为主,是选择一些典型的案例或例子,运用基本理论知识给予解决。
本课程是一门理论性与实践性都比较强的课程,教学中注意循序渐进、由浅入深,理论讲解与案例讲解交叉进行。
既要避免在课堂上进行枯燥的、不完整的、不必要的数学论证,也要避免漫无目的、不得要领地去讨论实际问题。
案例讨论是本课程教学的重要部分。
选择一些有代表性的、能清晰说明一个原理或一种方法的案例,使学生能理解原理的内涵或方法的效用,同时选择一些涉及多种原理、方法和计算技巧的案例,它们可以被用来综合学生的知识,加强彼此联络,使学生学到的东西系统化、一体化。
第1章数据、模型与决策简介《数据、模型与决策》是应用分析、试验、量化的方法,对经济管理系统中人力、物力、财力等资源进行统筹安排,为决策者提供有依据的最优化方案,以实现最有效的管理。
本章主要介绍《数据、模型与决策》的学习内容和学习方法等。
第2章线性规划首先通过对大量实际问题的介绍,引入线性规划模型。
然后介绍微软的Solver在建模和求解这些问题中的作用,再讨论建立线性规划模型的用处和一些不足。
本章的主要目标是要使得学员用电子表格建立线性规划模型对实际问题进行分析的能力。
线性规划问题的数学模型

式中所有非基变量的系数均是负数,意味着目标函数值不 可能再增加,故此时的基本可行解就是最优解,最优值为8
2.最优性检验
由标准形等式约束条件得
代入目标函数进行简单的运算后,用非基变量表示目标函数为
某工厂生产A 、B两种产品,现有资源数、生产每单位产品所需原 材料数以及每单位产品可得利润如下表所示。问如何制定生产计划使两 种产品总利润最大?
单位产品
产品
耗用资源
资源
铜(吨)
电力(千瓦)
劳动日(个)
单位利润 (万元/公斤)
A(公斤)
9 4 3 7
B(公斤)
4 5 10 12
现有资源
360 200 300
解 : x2
例4 若把例3改为使的目标函数的值最 大,从图可看出目标函数无上界,因此 无最优解
X1+2x2=0
X1-x2=1
2X1+2x2=16
x1 0
2X1+2x2=6 2X1+2x2=10
2X1+2x2=2 最优解 X1=1,x2=0, 目标函数最小值 s=2
例5 求x1、x2的值,使它们满足 并且使目标函数s=2 x1+2x2的值最小。
3. 单纯形表
用表格的形式来表示上面求解线性规划问题的单纯形法的计算过程可以 使计算和检验更加简便。具体方法如下:
将目标函数式改写为-f+ c1 x1 + c2 x2 +…+ cnxn =0 且作为等式约束方程 组的第m+1个方程,得
数据、模型与决策第十讲案例分析

二、农户种植计划的优化问题
设选择种植第一、第二、第三、第四、第五、第六种作物的
份数(1份对应于获得100元收入所需要的亩数)分别为x1、x2、 x3、x4、x5、x6,则可建立该问题的线性规划模型如下: 目标函数 max z =
100x1+100x2+100x3+100x4+100x5+100x6
四、产品结构优化问题
在以上技术状态约束下,经测算,提供给甲客户产品的单 套利润为48万元,提供给乙客户产品的单套利润为46万元 ,提供给丙客户产品的单套利润为36万元。
经生产能力平衡测算,各种部件产品的年生产能力上限分 别为:A1部件年产624个,A2部件年产920个,B1部件年 产412个,B2部件年产770个,B3部件年产350个。
约束条件 0.4x1 +0.2x3+0.18x4
≤10
0.3x1+0.25x2+0.15x3+0.1x4
≤8
0.4x3 +0.15x5+0.1x6≤5
x1,x2,x3,x4,x5,x6≥0
解得:
x1*=0,x2*=9.777778,x3*=0,x4*=55.55556,x5*=0,x6*=50。 全部的5亩水田都用来种植第六种作物;在旱地中拿出2.45
约束条件
x1
≤1
x1 + x2 ≤2.5
x1 + x2 + x3 ≤3.5
x1,x2,x3 ≥0
解得:x1*=1,x2*=1.5,x3*=1,z*=2.25。
显然,最优的选择是自然科学类选修课自修时间与当前自
修时间的比值为1.5,即下午和晚上各增加半个小时。三类
数据模型与决策试题及参考答案

《数据模型与决策》复习(附参考答案)2018.9一、填空题(五题共15分)1.已知成年男子的身高服从正态分布N(167.48,6.092),随机调查100位成年男子的身高,那么,这100位男子身高的平均数服从的分布是①。
解:N(167.48,0.609)考查知识点:已知总体服从正态分布,求样本均值的分布。
2.某高校想了解大学生每个月的消费情况,随机抽取了100名大学生,算得平均月消费额为1488元,标准差是2240元。
根据正态分布的“68-95-99”法则,该高校大学生每个月的消费额的95%估计区间为②。
解:[1040,1936]考查知识点:区间估计的求法。
正态总体均值的区间估计是[X-Z上,X + Z与] 1-a n'n1-a nn 其中X是样本平均数,s是样本的标准差,n是样本数。
详解:直接带公式得:区间估计是— s _ s2240 2240[X—Z -=, X + Z ,]= [1488 —2^^,1488 + 2^^] 山nn山.nn x100 * 100=[1040,1936]3.从遗传规律看,一个产妇生男生女的概率是一样的,都是50%,但也有个人的特殊情况。
假设某人前一胎是女孩,那么她的下一胎也是女孩的概率为0.55;如果某人前一胎是男孩,那么她的下一胎还是男孩的概率为0.48。
已知小李第一胎是女孩,那么她的第三胎生男孩的概率是③。
解p=0.4653考查知识点:离散概率计算方法。
详解:假设B1二第1胎生男孩,B2二第2胎生男孩,B3二第3胎生男孩G1二第1胎生女孩,G2=第2胎生女孩,G3=第3胎生女孩P(B3)二P(B3B2)+P(B3G2)(直观解释是:第二胎生男孩的情况下第三胎生男孩,第二胎生女孩的情况下第三胎生男孩,两个概率之和为P(B3))= P(B3|B2)P(B2)+P(B3|G2)P(G2)=0.48 义(1-0.55) + (1-0.55)义 0.55=0.46534.调查发现,一个刚参加工作的MBA毕业生在顶级管理咨询公司的初始年薪可以用均值为9万美元和标准差是2万美元的正态分布来表示,那么一个这样的毕业生初始年薪超过9万美元的概率是④。
线性规划的实际应用

密封线线性规划的实际应用摘要线性规划模型是科学与工程领域广泛应用的数学模型。
本文应用线性规划模型,以某水库输水管的选择为研究对象,以实现输水管的选择既能保证供水,又能使造价最低为目标,根据水库的特点和实际运行情况,分析了其输水管选择过程中线性规划模型的建立方法,并分别通过单纯形法和MATLAB软件进行求解。
关键词线性规划模型单纯形法 MATLAB一、专著背景简介《最优化方法》介绍最优化模型的理论与计算方法,其中理论包括对偶理论、非线性规划的最优性理论、非线性半定规划的最优性理论、非线性二阶锥优化的最优性理论;计算方法包括无约束优化的线搜索方法、线性规划的单纯形方法和内点方法、非线性规划的序列二次规划方法、非线性规划的增广Lagrange方法、非线性半定规划的增广Lagrange方法、非线性二阶锥优化的增广Lagrange方法以及整数规划的Lagrange松弛方法。
《最优化方法》注重知识的准确性、系统性和算法论述的完整性,是学习最优化方法的一本入门书。
最优化方法(也称做运筹学方法)是近几十年形成的,它主要运用数学方法研究各种系统的优化途径及方案,为决策者提供科学决策的依据。
最优化方法的主要研究对象是各种有组织系统的管理问题及其生产经营活动。
最优化方法的目的在于针对所研究的系统,求得一个合理运用人力、物力和财力的最佳方案,发挥和提高系统的效能及效益,最终达到系统的最优目标。
实践表明,随着科学技术的日益进步和生产经营的日益发展,最优化方法已成为现代管理科学的重要理论基础和不可缺少的方法,被人们广泛地应用到公共管理、经济管理、工程建设、国防等各个领域,发挥着越来越重要的作用。
本章将介绍最优化方法的研究对象、特点,以及最优化方法模型的建立和模型的分析、求解、应用。
主要是线性规划问题的模型、求解(线性规划问题的单纯形解法)及其应用-运输问题;以及动态规划的模型、求解、应用-资源分配问题。
二、专著的主要结构内容《最优化方法》是一本着重实际应用又有一定理论深度的最优化方法教材,内容包括线密封线性规划、运输问题、整数规划、目标规划、非线性规划(无约束最优化与约束最优化)、动态规划等最基本、应用最广又最有代表性的最优化方法。
线性规划模型

(1)模型中常数数据不精确
(2)模型中常数数据可能发生变化
价值变动
min z cx s.t. Ax b x0
11/43
资源总量变动
敏感性分析
max z 60d 30t 20c 8d + 6t + c <=48 4d + 2t + 1.5c <= 20 d + 1.5t + 0.5c <=8 t <= 5
mn
满足约束条件的解称为可行解,所有可行解的集合 称为可行域 ,满足最优目标的解称为最优解 决策变量为整数时,称为整数线性规划
决策变量取0或1时,称为0-1线性规划
7/43
线性规划问题的解
线性规划问题的可行域是一个凸多边形;
线性规划问题如果存在最优解,则最优解必在可行域的
顶点处达到。
单纯形法:
约束条件右端变化一个单位时目标函数变化量,只对紧约 决策变量改变一个单位时目标函数的改变量,只有非基变 量有值 束有值
12/43
敏感性分析
Objective Coefficient Ranges Current Allowable Allowable Coefficient Increase Decrease 60.00000 0.0 8.000000 30.00000 60.00000 0.0 20.00000 2.500000 INFINITY Righthand Side Ranges Current Allowable Allowable RHS Increase Decrease 48.00000 INFINITY 2.000000 20.00000 1.333333 8.000000 8.000000 1.000000 3.000000 5.000000 INFINITY 2.000000
《数据模型与决策》练习题及答案
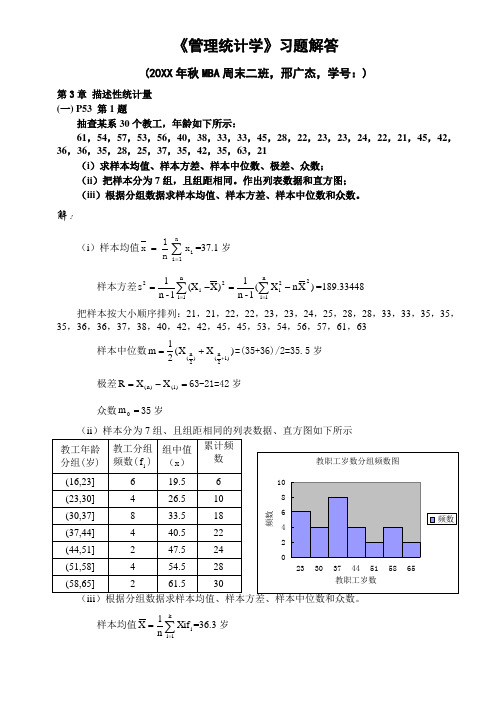
《管理统计学》习题解答(20XX 年秋MBA 周末二班,邢广杰,学号:)第3章 描述性统计量 (一) P53 第1题抽查某系30个教工,年龄如下所示:61,54,57,53,56,40,38,33,33,45,28,22,23,23,24,22,21,45,42,36,36,35,28,25,37,35,42,35,63,21(i )求样本均值、样本方差、样本中位数、极差、众数;(ii )把样本分为7组,且组距相同。
作出列表数据和直方图; (iii )根据分组数据求样本均值、样本方差、样本中位数和众数。
解:(i )样本均值∑==n1i ixn1x =37.1岁样本方差)X n X (1-n 1)X (X 1-n 1s 2n 1i 2i2n 1i i 2-=-=∑∑===189.33448 把样本按大小顺序排列:21,21,22,22,23,23,24,25,28,28,33,33,35,35,35,36,36,37,38,40,42,42,45,45,53,54,56,57,61,63样本中位数)X X (21m 1)2n ()2n (++==(35+36)/2=35.5岁极差=-=1)()n (X X R 63-21=42岁 众数=0m 35岁(ii )样本分为7组、且组距相同的列表数据、直方图如下所示样本均值i k1i f Xi n 1X ∑===36.3岁样本方差)X n f X (1-n 1f )X (X 1-n 1s 2k 1i i 2i i2k 1i i 2-=-=∑∑===174.3724 样本中位数810230730f F 2n i I m -+=-+==34.375岁 众数=--⨯-+=---+=+448248730f f 2f f f iI m 1m 1-m m 1-m m 033.5岁(二)P53 第2题某单位统计了不同级别的员工的月工资水平资料如下:解:样本均值i k1i f Xi n 1X ∑===1566.667元样本标准差)X n f X (1-n 1f )X (X 1-n 1s 2k 1i i2i i 2k 1i i -=-=∑∑===398.1751元 样本中位数在累计74人的那一组,m=1500元; 众数1500m 0=元。
《数据、模型与决策》第2部分_线性规划理论_学生

a21 x1 + a22 x2 + ···+ a2nxn = b2
s.t
······
am1x1 + am2x2 + ···+amn xn = bm
x i ≥ 0 i = 1······n
要求右端项 bj ≥0 j = 1······m
线性规划模型的标准形式
模型的矩阵表示:
决策变量 X =(x1, x2 , ······, xn ) T (列向量)
目标系数 c = ( c1, c2 , ······, cn ) T (列向量)
右端项 b = ( b1 , b2 , ······, bm )T (列向量)
系数矩阵
a11 a12 ···a1n
A = a21 a22 ···a2n = ( a i j ) m × n
a···m1
a
···
m2
···a···mn
• 若设计变量要求只取 ( 0, 1 ), —— 0 -1规划
• 若函数中引入时间参数,
—— 动态规划
另:若目标有多个,
—— 多目标规划/
北京科技大学 经济管理学院
8
线性与非线性的区别:
f(x1)
2维(一元)
x1
3维(二元)
x2
f(x1 , x2) x1
• 不是线性的函数,均称为非线性函数。
例如: 2 x12 + 3 x1x2
x i ≥ 0 i =1······5
Max Z = 20 x 1 + 30 x 2
1 40
x1 +
1 56
1 600
x1 +
1 380
x2 ≤ 120 x2 ≤ 10
线性规划原理

线性规划原理
线性规划(linear programming)是一种数学建模方法,用于求解含有一组线性约束条件的最优化问题。
它的目标是找到使得线性目标函数取得最大(或最小)值的最优决策变量的组合。
线性规划的基本原理可以概括为以下几个步骤:
1. 建立数学模型:根据实际问题确定决策变量、约束条件和目标函数。
决策变量通常表示决策的选择或分配方案,约束条件指定了这些变量的取值范围或关系,目标函数则衡量了决策的优劣程度。
2. 确定可行解的集合:根据约束条件,找到满足所有条件的决策变量的取值范围。
这个集合被称为可行解集,其中的每个解都满足所有约束条件。
3. 确定最优解:通过在可行解集中搜索,找到使得目标函数取得最大(或最小)值的解。
这个解被称为最优解,它代表了在所有可行解中最优的决策方案。
4. 验证最优性:对于找到的最优解,需要验证它是否确实是最优的。
这可以通过检查满足条件的附加条件、使用灵敏度分析等方法来进行。
线性规划方法的关键在于将实际问题抽象为数学模型,并利用线性关系进行求解。
它在许多领域都有广泛的应用,如生产计
划、资源优化、供应链管理等。
通过线性规划,可以做出高效而优化的决策,达到最大化利益或最小化成本的目的。
MBA数据模型与决策考试复习资料要点

MBA数据模型与决策考试复习资料要点数据模型与决策考试复习资料⼀、简答题1.数据、模型与决策的本质是什么?根据⽬标〔管理问题〕,确定影响⽬标的关键要素,采集相关的数据,构建相应模型,应⽤定量分析⽅法,进⾏辅助决策的科学(即管理科学)2.数据、模型与决策的基本流程是什么?确定⽬标→分析类型→确定因素→收集数据→整理信息→分析建模→预测决策3.数据、模型与决策的基本框架是什么?4.举例说明数据模型与决策的作⽤抄⼀实例:解决⽣产计划的线性规划问题。
例某企业⽣产A、B两种产品为畅销产品,已知,所需的资源总量和单耗如下表1,并调查知2004-2008年该企业⽣产A、B两种产品的单位售价分别为A:2、3、4、5、6千元,B:3、4、5、6、7千元,试问:2009年该企业A、B两种产品的⽣产计划是是什么?5.图与⽹络的概念是什么?图:由点和边组成的集合⽹络:带有某种数量指标的图(即赋权图)称为⽹络6.⽹络的基本特征是什么?1)三要素:点、边、权2)⼀般将研究“对象”作为“点”,“对象”之间的关系作为“边”,“对象”之间的关系程度作为“权”7.什么是树?什么是最⼩树?树:⽆圈连通图;最⼩树:权重之和最⼩的树8.什么情况下⽤破圈法,什么情况下⽤避圈法?破圈法适⽤于⽹络图已存在的问题,基本思路:对于⽹络图中每⼀个圈都破掉其最长边,直⾄⽹络图中不存在圈为⽌。
避圈法适⽤于⽹络图不存在的问题,基本思路:对⽹络图中在不构成圈的条件下,每次连接距离最短的边,直⾄⽹络图中各点连通为⽌。
9.什么是最短路?在⼀⽹络中,求给定⼀初始点⾄⼀终点的⼀条路长最短的路(即路的各边权数之和最⼩)。
10.什么是线性规划?线性规划是求⼀个线性函数在满⾜⼀组线性等式或不等式⽅程条件下的极值问题的统称。
11.线性规划问题的组成1)决策变量构成反映决策者⽬标的线性⽬标函数2)决策变量的线性等式或不等式构成约束⽅程3)限制决策变量取值范围的⾮负结束12.线性规划的基本特征1)⽬标函数是线性的2)约束条件是线性的13.线性规则的三要素决策变量、⽬标、约束14.线性规划建⽴模型的基本步骤1)根据问题确定⽬标2)根据⽬标设计决策变量3)根据⽬标与决策变量设计⽬标函数4)根据影响⽬标因素的关系与限制设计约束条件15.线性规划基本求解⽅法1)图解法;2)单纯形法;3)计算机解法16.数据的概念数据是字母、数字、下划线和符号等,⽤于表达事件和它们的形态,并根据正式的规则和惯例加以组织的状态(形式)17.数据收集的基本要素,基本流程基本要素:“⼈、财、物”基本流程:根据问题→明确⽬标→确定指标→准备要素→选择渠道→选⽤⽅式→运⽤⽅法→实施活动18.模型有⼏类?数学模型、⽹络模型、计算机模型、图表模型19.常⽤的统计调查⽅法定期统计报表制度、普查、典型调查、重点调查和抽样调查。
《数据模型与决策》复习题及参考答案

《数据模型与决策》复习题及参考答案第一章绪言一、填空题1.运筹学的主要研究对象是各种有组织系统的管理问题,经营活动。
2.运筹学的核心是运用数学方法研究各种系统的优化途径及方案,为决策者提供科学决策的依据。
3.模型是一件实际事物或现实情况的代表或抽象。
4、通常对问题中变量值的限制称为约束条件,它可以表示成一个等式或不等式的集合。
5.运筹学研究和解决问题的基础是最优化技术,并强调系统整体优化功能。
运筹学研究和解决问题的效果具有连续性。
6.运筹学用系统的观点研究功能之间的关系。
7.运筹学研究和解决问题的优势是应用各学科交叉的方法,具有典型综合应用特性。
8.运筹学的发展趋势是进一步依赖于_计算机的应用和发展。
9.运筹学解决问题时首先要观察待决策问题所处的环境。
10.用运筹学分析与解决问题,是一个科学决策的过程。
11.运筹学的主要目的在于求得一个合理运用人力、物力和财力的最佳方案。
12.运筹学中所使用的模型是数学模型。
用运筹学解决问题的核心是建立数学模型,并对模型求解。
13用运筹学解决问题时,要分析,定议待决策的问题。
14.运筹学的系统特征之一是用系统的观点研究功能关系。
15.数学模型中,“s·t”表示约束。
16.建立数学模型时,需要回答的问题有性能的客观量度,可控制因素,不可控因素。
17.运筹学的主要研究对象是各种有组织系统的管理问题及经营活动。
二、单选题1.建立数学模型时,考虑可以由决策者控制的因素是( A )A.销售数量 B.销售价格 C.顾客的需求 D.竞争价格2.我们可以通过( C )来验证模型最优解。
A.观察 B.应用 C.实验 D.调查3.建立运筹学模型的过程不包括( A )阶段。
A.观察环境 B.数据分析 C.模型设计 D.模型实施4.建立模型的一个基本理由是去揭晓那些重要的或有关的( B )A数量 B变量 C 约束条件 D 目标函数5.模型中要求变量取值( D )A可正 B可负 C非正 D非负6.运筹学研究和解决问题的效果具有( A )A 连续性B 整体性C 阶段性D 再生性7.运筹学运用数学方法分析与解决问题,以达到系统的最优目标。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
am1x1+am2x2+…+amnxn≥(=、≤)bm x1,x2, …,xn ≥0
2021/2/20
6
第10章线性规划原理与应用
三、线性规划的应用
(1)配料问题
配料问题线性规划的一般性数学提法:假设 有n种原料,已知每种原料都含有m种成分,又 已知每种原料的单位成分含量为aij(i=1,2, …,m, j=1,2, …,n)。现欲用这n种原料配制成一种产 品,要求单位产品的各种成分的含量为bi ,如果 每种原料的单价为cj。问如何配料,才能使产品 的生产成本最低
第10章线性规划原理与应用
本讲的主要内容: 一、背景介绍 二、线性规划基本模型 三、线性规划的应用 四、电子表格求解
2021/2/20
1
第10章线性规划原理与应用
一、背景介绍 在现有的资源条件下,如何充分利用资
源,使任务或目标完成得最好。 在给定目标下,如何以最少的资源消耗,
实现这个目标。
2021/2/20
到的 A2 c21 c22 … c2n
b2
毛坯 …
…
…
…
…
…
数量 Am cm1 cm2 … cmn bm
2021/2/20
9
第10章线性规划原理与应用
四、电子表格求解 电子表格模型建立及求解过程为:
➢第一步,在EXCEL工作表中,对模型中的参数
资料进行编辑;
➢第二步,编辑建立函数关系; ➢第三步,点击“数据”,打开右上方的“规
个压制工时。使用的原料是巴西木和美国云杉,由于进口
方面的限制,每周从市场上最多能获得巴西木2500立方米,
美国云杉2000立方米,单位板材对巴西木的需要量分别为
50,40,30,40,对美国云杉需要量为20,30,50,
20。另外,每种产品的单位利润是:40,110,75,35。
2021/2/20
的利润最大。
2021/2/20
8
第10章线性规划原理与应用
三、线性规划的应用
(3)截料问题。截料问题的一般性提法:用某种材 料切割m种毛坯,根据经验,单位材料上有n种不 同的下料方案,每种下料方案可得各种毛坯数量 及每种毛坯的需求量为:
截料方法
需要量
B1 B2 … Bn
可得 A1 c11 c12 … c1n b1
一个子对话框,将约束条件计算部分所在的区域输
入到“单元格引用”,从中间的等式符合中选定想
要的不等号,将资源总量所在的区域输入到“约束
”中。
2021/2/20
11
3
第10章线性规划原理与应用
一、背景介绍 例2:人员安排问题
物资因条件限制只能在A1 、A2 、 A3 三个地方生产,生产出来的物资需要 运到B1、B2、B3、B4四个地方销售,产 地产量、销地销售量,以及从产地运到 销地单位运费见下表。
2021/2/20
4
第10章线性规划原理与应用
单位
运费
B1
划求解”,得到一个对话框;
2021/2/20
10
第10章线性规划原理与应用
四、电子表格求解
➢ 第四步,根据要求进行相应的设置。
(1)在“设置目标”中输入目标函数值所在单位格。
(2)选定“最大值”还是“最小值”。
(3)在“通过更改可变单元格”中,输入决策变量所 在的区域。
(4)在“遵守约束”对话组中,点击“添加”,得到
2
第10章线性规划原理与应用
一、背景介绍
例1:生产计划问题
一家企业专门为钢琴制造商生产密质板材,产品有古典
型、现代型、豪华型和实用型。生产这些产品需要经过切
割抛光、压制定型两道工序,每种产品一个批次需要切割
抛光的工时为1,1,2,2,需要压制定型的工时1,4,3,
2。现有的生产条件下,每周只能提供80个切割工时和100
A1
20
产地
BBA124123
A2
5
A3
18
需要量
3
销地
B2
B3
11 8
9 10
74
3 12
B4
生产量
6
5
2
10
1
15
12 30
2021/2/20
5
第10章线性规划原理与应用
二、线性规划基本模型 线性规划模型的一般形式:
Max(Min) z=c1x1+c2x2+…+cnxn s.t. a11x1+a12x2+…+a1nxn≥(=、≤)b1
2021/2/20
7
第10章线性规划原理与应用
三、线性规划的应用
(2)资源利用问题
资源利用线性规划问题的一般性数学提法: 生产n种产品,每种产品都要经过m道工序,其中, 第j种产品在第i道工序上加工所需要的工时为aij (i=1,2, …,m,j=1,2,,…,n),第i道工 序可提供的工时最多为bi ,第j种产品的单位利润 为cj 。问如何规划各种产品的数量,才能使获得
