中考数学新定义题型专题复习(最新整理)
专题2.4新定义的四种题型与真题训练-中考数学考前30天迅速提分复习方案(上海专用)(解析版)

专题2.4新定义的四种题型与真题训练题型一:函数中新定义问题1.(2022青浦一模18)如图,一次函数y =ax +b (a <0,b >0)的图象与x 轴,y 轴分别相交于点A ,点B ,将它绕点O 逆时针旋转90°后,与x 轴相交于点C ,我们将图象过点A ,B ,C 的二次函数叫做与这个一次函数关联的二次函数.如果一次函数y =﹣kx +k (k >0)的关联二次函数是y =mx 2+2mx +c (m ≠0),那么这个一次函数的解析式为.【解答】解:对y =﹣kx +k ,当x =0时,y =k ,当y =0时,x =1,∴A (1,0),B (0,k ),∴C (﹣k ,0),将A 、B 、C 的坐标代入y =mx 2+2mx +c 得,,解得:或或,∵m ≠0,k >0,∴m =﹣1,k =3,c =3,∴一次函数的解析式为y =﹣3x +3,故答案为:y =﹣3x +3.2.(2022黄埔一模18)若抛物线2111y ax b x c =++的顶点为A ,抛物线2222y ax b x c =-++的顶点为B ,且满足顶点A 在抛物线2y 上,顶点B 在抛物线1y 上,则称抛物线1y 与抛物线2y 互为“关联抛物线”,已知顶点为M 的抛物线()223y x =-+与顶点为N 的抛物线互为“关联抛物线”,直线MN 与x 轴正半轴交于点D ,如果3tan 4MDO ∠=,那么顶点为N 的抛物线的表达式为_________【详解】设顶点为N 的抛物线顶点坐标N 为(a ,b )已知抛物线()223y x =-+的顶点坐标M 为(2,3)∵3tan 4MDO ∠=,∴34M M N y x x =-,即3324Dx =-,解得24D x =±∵直线MN 与x 轴正半轴交于点D,∴D 点坐标为(6,0)则直线MD 解析式为3(6)4y x =--N 点在直线MD 3(6)4y x =--上,N 点也在抛物线()223y x =-+故有()23(6)423b a b a ⎧=--⎪⎨⎪=-+⎩,化简得2394247b a b a a ⎧=-+⎪⎨⎪=-+⎩联立得2394742a a a --=-+,化简得2135042a a -+=解得a =54或a =2(舍),将a =54代入3942b a =-有359157257442161616b =-⨯+=-+=解得545716a b ⎧=⎪⎪⎨⎪=⎪⎩,故N 点坐标为(54,5716)则顶点为N 的抛物线的表达式为2557()416y a x =-+将(2,3)代入2557()416y a x =-+有,25573(2416a =-+化简得95731616a =+,解得a =-1故顶点为N 的抛物线的表达式为2557(416y x =--+故答案为:2557()416y x =--+.3.(2020杨浦二模)定义:对于函数y =f (x ),如果当a ≤x ≤b 时,m ≤y ≤n ,且满足n ﹣m =k (b ﹣a )(k 是常数),那么称此函数为“k 级函数”.如:正比例函数y =﹣3x ,当1≤x ≤3时,﹣9≤y ≤﹣3,则﹣3﹣(﹣9)=k (3﹣1),求得k =3,所以函数y =﹣3x 为“3级函数”.如果一次函数y =2x ﹣1(1≤x ≤5)为“k 级函数”,那么k 的值是.【分析】根据一次函数y =2x ﹣1(1≤x ≤5)为“k 级函数”解答即可.【解答】解:因为一次函数y=2x﹣1(1≤x≤5)为“k级函数”,可得:k=2,故答案为:2.题型二:三角形中的新定义1.(2022嘉定一模18)如图,在△ABC中,∠C=90°,BC=2,,点D在边AC上,CD:AD=1:3,联结BD,点E在线段BD上,如果∠BCE=∠A,那么CE=.【解答】解:过点E作EF⊥BC,垂足为F,∵∠ACB=90°,BC=2,,∴AC===4,∵CD:AD=1:3,∴CD=1,∵∠BCE=∠A,∠ACB=∠CFE=90°,∴△ABC∽△CEF,∴===2,∴设EF为a,则CF为2a,BF为2﹣2a,∵∠ACB=∠BFE=90°,∠CBD=∠FBE,∴△BFE∽△BCD,∴=,∴=,∴a=,∴EF=,CF=1,∴CE===,故答案为:.2、(2022杨浦一模17)新定义:已知三条平行直线,相邻两条平行线间的距离相等,我们把三个顶点分别在这样的三条平行线上的三角形称为格线三角形.如图,已知等腰Rt△ABC为“格线三角形”,且∠BAC=90°,那么直线BC与直线c的夹角α的余切值为.【解答】解:过B 作BE ⊥直线a 于E ,延长EB 交直线c 于F ,过C 作CD ⊥直线a 于D ,则∠CDA =∠AEB =90°,∵直线a ∥直线b ∥直线c ,相邻两条平行线间的距离相等(设为d ),∴BF ⊥直线c ,CD =2d ,∴BE =BF =d ,∵∠CAB =90°,∠CDA =90°,∴∠DCA +∠DAC =90°,∠EAB +∠DAC =90°,∴∠DCA =∠EAB ,在△CDA 和△AEB 中,,∴△CDA ≌△AEB (AAS ),∴AE =CD =2d ,AD =BE =d ,∴CF =DE =AE +AD =2d +d =3d ,∵BF =d ,∴cotα===3,故答案为:3.3.(2022长宁一模17)定义:在△A 中,点D 和点E 分别在AB 边、AC 边上,且DE //BC ,点D 、点E 之间距离与直线DE 与直线BC 间的距离之比称为DE 关于BC 的横纵比.已知,在△A 中,4,BC BC =上的高长为3,DE 关于BC 的横纵比为2:3,则DE =_______.【详解】如图,AF BC ⊥于F ,交DE 于点G ,//DE BC ,ADE ABC ∴△△∽,AG DE ⊥,DE AGBC AF∴=,3AF = DE 关于BC 的横纵比为2:3,4BC =,23DE GF ∴=设2DE a =,则3GF a =,33AG AF GF a∴=-=-23343a a -∴=,解得23a =,43DE ∴=,故答案为:434.(2022虹口一模17)在网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形称为“格点三角形”.如图,在4×4的网格中,△ABC 是一个格点三角形,如果△DEF 也是该网格中的一个格点三角形,它与△ABC 相似且面积最大,那么△DEF 与△ABC 相似比的值是.【解答】解:由表格可得:AB =,BC =2,AC =,如图所示:作△DEF ,DE =,DF =,EF =5,∵===,∴△DEF ∽△ABC ,则△DEF 与△ABC 相似比的值是.故答案为:.5.(2020松江二模)如果一个三角形中有一个内角的度数是另外两个内角度数差的2倍,我们就称这个三角形为“奇巧三角形”.已知一个直角三角形是“奇巧三角形”,那么该三角形的最小内角等于度.【分析】设直角三角形的最小内角为x ,另一个内角为y ,根据三角形的内角和列方程组即可得到结论.【解答】解:设直角三角形的最小内角为x ,另一个内角为y ,由题意得,,解得:,答:该三角形的最小内角等于22.5°,故答案为:22.5.6.(2020嘉定二模)定义:如果三角形的两个内角∠α与∠β满足∠α=2∠β,那么,我们将这样的三角形称为“倍角三角形”,如果一个等腰三角形是“倍角三角形”,那么这个等腰三角形的腰长与底边长的比值为【考查内容】新定义题型,黄金三角形【评析】中等【解析】当∠α为底角时,用内角和公式求得∠β= 36,此时为黄金三角形,腰长与底边长的比值215+;当当∠α为顶角时,用内角和公式求得∠β= 45,此时为等腰直角三角形,腰长与底边长的比值22。
2024年九年级中考数学压轴题-圆中的新定义问题(解析版)
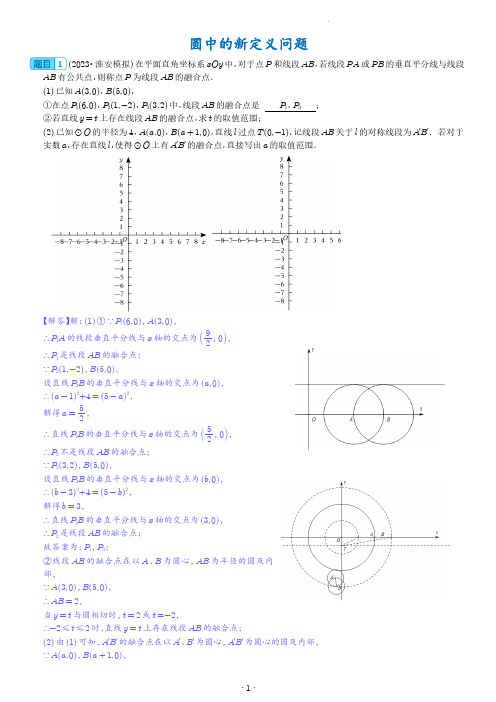
圆中的新定义问题1(2023•淮安模拟)在平面直角坐标系xOy 中,对于点P 和线段AB ,若线段PA 或PB 的垂直平分线与线段AB 有公共点,则称点P 为线段AB 的融合点.(1)已知A (3,0),B (5,0),①在点P 1(6,0),P 2(1,-2),P 3(3,2)中,线段AB 的融合点是 P 1,P 3 ;②若直线y =t 上存在线段AB 的融合点,求t 的取值范围;(2)已知⊙O 的半径为4,A (a ,0),B (a +1,0),直线l 过点T (0,-1),记线段AB 关于l 的对称线段为A B .若对于实数a ,存在直线l ,使得⊙O 上有A B 的融合点,直接写出a 的取值范围.【解答】解:(1)①∵P 1(6,0),A (3,0),∴P 1A 的线段垂直平分线与x 轴的交点为92,0,∴P 1是线段AB 的融合点;∵P 2(1,-2),B (5,0),设直线P 2B 的垂直平分线与x 轴的交点为(a ,0),∴(a -1)2+4=(5-a )2,解得a =52,∴直线P 2B 的垂直平分线与x 轴的交点为52,0,∴P 2不是线段AB 的融合点;∵P 3(3,2),B (5,0),设直线P 3B 的垂直平分线与x 轴的交点为(b ,0),∴(b -3)2+4=(5-b )2,解得b =3,∴直线P 3B 的垂直平分线与x 轴的交点为(3,0),∴P 3是线段AB 的融合点;故答案为:P 1,P 3;②线段AB 的融合点在以A 、B 为圆心,AB 为半径的圆及内部,∵A (3,0),B (5,0),∴AB =2,当y =t 与圆相切时,t =2或t =-2,∴-2≤t ≤2时,直线y =t 上存在线段AB 的融合点;(2)由(1)可知,A B 的融合点在以A 、B 为圆心,A B 为圆心的圆及内部,∵A (a ,0),B (a +1,0),∴AB =A B =1,∵⊙O 上有A B 的融合点,∴圆O 与圆A 、B 有交点,∴圆O 与圆A 、圆B 的公共区域为以O 为圆心2为半径,以O 为圆心6为半径的圆环及内部区域,当a >0时,a 的最大值为62-12=35,最小值为22-12-1=3-1,∴3-1≤a ≤35;当a <0时,a 的最大值为-22-12=-3,最小值为-62-12-1=-35-1,∴-35-1≤a ≤-3;综上所述:a 的取值范围为3-1≤a ≤35或-35-1≤a ≤-3.2(2023•西城区校级模拟)在平面内,C 为线段AB 外的一点,若以点A ,B ,C 为顶点的三角形为直角三角形,则称C 为线段AB 的直角点.特别地,当该三角形为等腰直角三角形时,称C 为线段AB 的等腰直角点.(1)如图1,在平面直角坐标系xOy 中,点M 的坐标为(-1,0),点N 的坐标为(1,0),在点P 1(2,1),P 2(-1,2),P 332,12 中,线段MN 的直角点是 P 2、P 3 ;(2)在平面直角坐标系xOy 中,点A ,B 的坐标分别为(t ,0),(0,4).①若t =4,如图2所示,若C 是线段AB 的直角点,且点C 在直线y =-x +8上,求点C 的坐标;②如图3,点D 的坐标为(m ,-2),⊙D 的半径为1,若⊙D 上存在线段AB 的等腰直角点,求出m 的取值范围.【解答】解:(1)∵P 2(-1,2),M (-1,0),∴P 2M ⊥MN ,∴P 2是线段MN 的直角点;∵M (-1,0),N (1,0),∴MN =2,∵P 332,12,∴P 3O =1,∴P 3在以O 为圆心,MN 为直径的圆上,∴∠MP 3N =90°,∴P 3是线段MN 的直角点;故答案为:P 2、P 3;(2)①∵A (4,0),B (0,4),∴OA =OB =4,∴∠OAB =∠OBA =45°.根据题意,若点C 为线段AB 的直角点,则需要分三种情况:当点B 为直角顶点,过点B 作BC 1⊥AB 于点C 1,过点C 1作C 1M ⊥y 轴于点M ,∴∠C 1BM =45°,∴C 1M =BM ,设C 1M =BM =a ,∴C 1(a ,a +4),∴-a +8=a +4,解得a =2,∴C 1(2,6);当点A 为直角顶点,过点A 作AC 2⊥AB 于点C 2,过点C 2作C 2N ⊥x 轴于点N ,∴∠C 2AN =45°,∴C 2N =AN ,设C 2N =AN =b ,∴C 2(b +4,b ),∴-(b +4)+8=b ,解得b =2,∴C 2(6,2);当点C 为直角顶点,取AB 的中点P ,则P (2,2),设C 3的横坐标为t ,则C 3(t ,-t +8),由直角三角形的性质可知,C 3P =BP =AP =22,∴(t -2)2+(-t +6)2=(22)2,解得t =4,∴C3(4,4),综上,点C的坐标为(2,6)或(6,2)或(4,4).②如图,以AB为边向下作正方形ABC1C2,连接AC1,BC2交于点C3,则C1,C2,C3是线段AB的等腰直角点.根据点A的运动可知,点C1在直线l1:x=-4上运动,C2在直线l2:y=-x-4上运动,C3在直线l3:y=-x上运动.设l2与y=-2相交于点K,l3与y=-2相交于点L,∴K(2,-2),L(2,-2).由此可得出临界情况如图:如图3(1)中,当⊙D与l1相切时,m=-5;如图3(2)中,当⊙D与l2相切时,点F为切点,连接DF,则ΔDFK为等腰直角三角形,且DF=1,∴DK=2;∴D(-2+2,-2),即m=-2+2;如图3(3)中,当⊙D与l3相切时,点G为切点,连接DG,则ΔDGL为等腰直角三角形,且DG=1,∴DL=2;∴D(2-2,-2),即m=2-2;如图3(4)中,当⊙D与l3相切时,点H为切点,连接DH,则ΔDHL为等腰直角三角形,且DH=1,∴DL=2;∴D(2+2,-2),即m=2+2;综上,符合题意的m的取值范围:-5≤m≤-2+2或2-2≤m≤2+2.3(2023•秀洲区校级二模)婆罗摩芨多是公元7世纪古印度伟大的数学家,他在三角形、四边形、零和负数的运算规则,二次方程等方面均有建树,他也研究过对角线互相垂直的圆内接四边形,我们把这类对角线互相垂直的圆内接四边形称为“婆氏四边形”;(1)若平行四边形ABCD是“婆氏四边形”,则四边形ABCD是③.(填序号)①矩形②菱形③正方形(2)如图1,RtΔABC中,∠BAC=90°,以AB为弦的⊙O交AC于D,交BC于E,连接DE、AE、BD,AB=6,sin C=35,若四边形ABED是“婆氏四边形”,求DE的长;(3)如图2,四边形ABCD为⊙O的内接四边形,连接AC,BD,OA,OB,OC,OD,已知∠BOC+∠AOD= 180°,①求证:四边形ABCD是“婆氏四边形”;②当AD+BC=4时,求⊙O半径的最小值.【解答】(1)解:∵平行四边形ABCD为⊙O的内接四边形,∴∠ABC=∠ADC,∠ABC+∠ADC=180°,∴∠ABC=∠ADC=90°,∴平行四边形ABCD是矩形,∵四边形ABCD是“婆氏四边形”,∴AC⊥BD,∴矩形ABCD是正方形,故答案为:③;(2)解:∵∠BAC=90°,AB=6,sin C=35,∴BC=10,AC=8,∴BD为直径,∴∠BED =∠DEC =90°,∵四边形ABED 是“婆氏四边形”,∴AE ⊥BD ,∴AD =DE ,AB =BE =6,设AD =DE =m ,则CD =8-m ,EC =4,在Rt ΔEDC 中,m 2+42=(8-m )2,解得m =3,∴DE =3;(3)①证明:如图2,设AC ,BD 相交于点E ,∵∠DCA =12∠AOD ,∠BDC =12∠BOC ,∠BOC +∠AOD =180°,∴∠DCA +∠BDC =12(∠AOD +∠BOC )=12×180°=90°,∴∠CED =90°,∴AC ⊥BD ,∵四边形ABCD 是⊙O 的内接四边形,∴四边形ABCD 是“婆氏四边形”;②解:过点O 作OM ⊥AD 交于M ,过O 作ON ⊥BC 交于N ,∴AM =12AD ,BN =12BC ,∠AMO =∠BNO =90°,∴∠AOM +∠OAM =90°,∵OA =BO =CO =DO ,∴∠AOM =12∠AOD ,∠BON =12∠BOC ,∵∠BOC +∠AOD =180°,∴∠AOM =∠OBN ,∴ΔOAM ≅ΔBON (AAS ),∴ON =AM =12AD ,∵AD +BC =4,设ON =AM =n ,则AD =2n ,BC =4-2n ,BN =2-n ,在Rt ΔBON 中,BO =n 2+(2-n )2=2(n -1)2+2,当n =1时,BO 有最小值2,∴⊙O 半径的最小值为2.4(2022秋•西城区期末)给定图形W 和点P ,Q ,若图形W 上存在两个不重合的点M ,N ,使得点P 关于点M 的对称点与点Q 关于点N 的对称点重合,则称点P 与点Q 关于图形W 双对合.在平面直角坐标系xOy 中,已知点A (-1,-2),B (5,-2),C (-1,4).(1)在点D (-4,0),E (2,2),F (6,0)中,与点O 关于线段AB 双对合的点是 D ,F ;(2)点K 是x 轴上一动点,⊙K 的直径为1,①若点A 与点T (0,t )关于⊙K 双对合,求t 的取值范围;②当点K 运动时,若ΔABC 上存在一点与⊙K 上任意一点关于⊙K 双对合,直接写出点K 的横坐标k 的取值范围.【解答】解:(1)当A 点是D 点的中点时,对应点为(2,-4);当B 点是D 点的中点时,对应点为(14,-4);当A 点是E 点的中点时,对应点为(-4,-6);当B 点是E 点的中点时,对应点为(8,-6);当A 点是F 点的中点时,对应点为(-8,-4);当B 点是F 点的中点时,对应点为(4,-4);当A 点是O 点的中点时,对应点为(-2,-4);当B 点是O 点的中点时,对应点为(10,-4);∴D 、F 与点O 关于线段AB 双对合,故答案为:D 、F ;(2)①设K(k,0),∵A(-1,-2),T(0,t),∴A点关于K点对称点G为(2k+1,2),T点关于K点对称点H为(2k,-t),∵点A与点T(0,t)关于⊙K双对合,∴A点关于点K的对称点在以G为圆心,∵⊙K的直径为1,∴点A关于点K的对称点在以G点为圆心,1为半径的圆上,点T关于点K的对称点在以H为圆心,1为半径的圆上,如图所示,∵点A与点T(0,t)关于⊙K双对合,∴当圆G与圆H有交点,∵GH=1+(t+2)2,∴1+(t+2)2≤2,解得-2-3≤t≤-2+3;②∵A(-1,-2),B(5,-2),C(-1,4),K(k,0),∴A点关于K点的对称点F(2k+1,2),B点关于K点的对称点E(2k-5,2),C点关于K点的对称点G(2k+1, -4),∴ΔABC上任意一点关于K点对称点在阴影区域,∵ΔABC上存在一点与⊙K上任意一点关于⊙K双对合,∴阴影区域与圆K有公共交点,∵阴影部分是由ΔEGF边上任意一点为圆心,1为半径的圆构成的区域,如图1时,k-(2k+1)=12+1,解得k=-52;如图2时,2k+1-k=12+1,解得k=12;∴-52≤k≤12时,ΔABC上存在一点与⊙K上任意一点关于⊙K双对合;过点K作KN⊥EG交于N,直线EG交x轴于点M,设直线EG的解析式为y=k x+b,∴(2k-5)k +b=2 (2k+1)k +b=-4 ,解得k =-1b=2k-3 ,∴y=-x+2k-3,∴M(2k-3,0),∵直线y=-x与y=-x+2k-3平行,∴∠KMN=45°,∴KM=2KN=322,如图3时,k-(2k-3)=322,解得k=3-322,如图4时,2k-3-k=322,解得k=3+322,∴3-322≤k≤3+322时,ΔABC上存在一点与⊙K上任意一点关于⊙K双对合;综上所述:-52≤k≤12或3-322≤k≤3+322时,ΔABC上存在一点与⊙K上任意一点关于⊙K双对合.5(2022•钟楼区模拟)概念认识:平面内,M为图形T上任意一点,N为⊙O上任意一点,将M、N两点间距离的最小值称为图形T到⊙O的“最近距离”,记作d(T-⊙O).例:如图1,在直线l上有A、C、O三点,以AC为对角线作正方形ABCD,以点O为圆心作圆,与l交于E、F两点,若将正方形ABCD记为图形T,则C、E两点间的距离称为图形T到⊙的“最近距离”.数学理解:(1)在平面内有A、B两点,以点A为圆心,5为半径作⊙A,将点B记为图形T,若d(T-⊙A)=2,则AB= 3或7.(2)如图2,在平面直角坐标系中,以O(0,0)为圆心,半径为2作圆.①将点C(4,3)记为图形T,则d(T-⊙O)=.②将一次函数y=kx+22的图记为图形T,若d(T-⊙)>0,求k的取值范围.推广运用:(3)在平面直角坐标系中,P的坐标为(t,0),⊙P的半径为2,D、E两点的坐标分别为(5,5)、(5,-5),将ΔDOE记为图形T,若d(T-⊙P)=1,则t=.【解答】解:(1)如图1中,∵d(T-⊙A)=2,∴CB=CB′=2,∵AC=5,∴AB′=5-2=3,AB=5+2=7.故答案为:3或7.(2)①如图2中,连接OC交⊙O于E.∵C(4,3),∴OC=42+32=5,∵OE=2,∴EC=3,∴d(T-⊙O)=3.故答案为:3.②如图,设直线y=kx+22与⊙O相切于E,K.连接OK,OE.∵OE⊥DE,OK⊥DK,OD=22,OE=OK=2,∴DK=OD2?OK2=(22)2-22=2,DE=OD2?OE2=(22)2-22=2,∴DE=OE=DK=OK,∴四边形DEOK是菱形,∵∠DKO=∠DEO=90°,∴四边形DEOK是正方形,∴∠ODE=∠ODK=45°,∴直线DE的解析式为y=-x+22,直线DK的解析式为y=x+22,∵d(T-⊙O)>0,∴观察图象可知满足条件的k的值为-1<k<1且k≠0.(3)如图3-1中,当点P在DE的右边时.∵D(5,5),∴∠DOP=45°,∵d(T-⊙P)=1,∴OP=5+1+2=8∴t=8.如图3-2中,当点P在∠DOE的外侧时,由题意可知OM=1,OP=1+2=3,t=-3.综上所述,满足条件的t的值为8或-3.6(2022秋•昌平区期末)已知:对于平面直角坐标系xOy中的点P和⊙O,⊙O的半径为4,交x轴于点A,B,对于点P给出如下定义:过点C的直线与⊙O交于点M,N,点P为线段MN的中点,我们把这样的点P叫做关于MN的“折弦点”.(1)若C(-2,0).①点P1(0,0),P2(-1,1),P3(2,2)中是关于MN的“折弦点”的是 P1,P2 ;②若直线y=kx+3(k≠0).上只存在一个关于MN的“折弦点”,求k的值;(2)点C在线段AB上,直线y=x+b上存在关于MN的“折弦点”,直接写出b的取值范围.【解答】解:(1)①连接OP,∵P点是弦MN的中点,∴OP⊥MN,∴∠CPO=90°,∴P点在以CO为直径的圆上,∵C(-2,0),∴P点在以(-1,0)为圆心,1为半径的圆上,∵点P1(0,0),P2(-1,1)在该圆上,∴点P1(0,0),P2(-1,1)是关于MN的“折弦点”,故答案为:P1,P2;②由①可知,P点在以(-1,0)为圆心,1为半径的圆上,设圆心D(-1,0),∵直线y=kx+3(k≠0)上只存在一个关于MN的“折弦点”,∴直线y=kx+3(k≠0)与圆D相切,过点D作DF垂直直线y=kx+3交于点F,∵直线y=kx+3与x轴交于点E-3k,0,与y轴交于点G(0,3),∴DE=-1+3k,OF=3k,OG=3,∵∠DFE=∠EOG=90°,∴ΔEGO∽ΔEFD,∴DF GO =ED EG,∴13=3k-13+3k2,解得k=3 3;(2)由(1)可知,P点在以OC为直径的圆上,∵直线y=x+b上存在关于MN的“折弦点”,∴直线y=x+b与圆D相交或相切,过D点作DF垂直直线y=x+b交于点F,∵直线y=x+b与x轴交于点(-b,0),与y轴交于点(0,b),当C点与A点重合时,b有最大值,此时D(-2,0),∴(-2+b)2=8,解得b=22+2或b=22+2(舍);当C点与B点重合时,b有最小值,此时D(2,0),∴(-b-2)2=8,解得b=22-2(舍)或b=-22-2;∴-22-2≤b≤22+2时,直线y=x+b上存在关于MN的“折弦点”.7(2022秋•东城区校级月考)如图,在平面直角坐标系xOy中,过⊙T外一点P引它的两条切线,切点分别为M,N,若60°<∠MPN<180°,则称P为⊙T的环绕点.(1)当⊙O半径为1时,①在P1(2,2),P2(2,0),P3(2,1)中,⊙O的环绕点是 P1 ;②直线y=3x+b与x轴交于点A,y轴交于点B,若线段AB上存在⊙O的环绕点,求b的取值范围;(2)⊙T的半径为2,圆心为(0,t),以-m,33m(m>0)为圆心,33m为半径的所有圆构成图形H,若在图形H上存在⊙T的环绕点,直接写出t的取值范围.【解答】解:(1)①如图,PM,PN是⊙T的两条切线,M,N为切点,连接TM,TN,当∠MPN=60°时,∵PT平分∠MPN,∴∠TPN=∠MPT=30°,∵TM⊥PM,TN⊥PN,∴∠TNP=∠PMT=90°,∴TP =2TM =2,以T 为圆心,TP 为半径作⊙T .观察图象可知:当60°<∠MPN <180°时,⊙T 的环绕点在图中的圆环内部(包括大圆上的点不包括小圆上的点),故答案为:P 1;②如图中,设小圆交y 轴的正半轴于F ,当直线y =3x +b 经过点F 时,b =1,当直线y =3x +b 与大圆相切于K (在第二象限)时,连接OK ,由题意B (0,b ),A -b 3,0,所以OB =b ,OA =b 3,AB =103b ,∵OK =2,12×AB ×OK =12×OA ×OB ,∴b =210,观察图象可知,当1<b <210时,线段AB 上存在⊙的环绕点,根据对称怀可知:当-210<b <-1时,线段AB 上存在⊙的环绕点,综上所述,满足条件的b 的值为1<b <210或-210<b <-1;(2)如图中,不妨设E -m ,33m (m >0),则点E 直线y =-33x 上,∵m >0,∴点E 在射线OE 上运动,作EM ⊥x 轴;∵E -m ,33m (m >0),∴OM =m ,EM =33m ,以E -m ,33m (m >0)为圆心,33m 为半径的⊙E 与x 轴相切,作⊙E 的切线ON ,观察图象可知:以E -m ,33m (m >0)为圆心,33m 为半径的所有圆构成图形H ,图形H 即为∠MON 的内部,包括射线OM ,ON 上,当⊙T 的圆心在y 轴的正半轴上时,假设以T 为圆心,4为半径的圆与射线ON 相切于D ,连接TD ,∵tan ∠EOM =EM OM=33,∴∠EOM =30°,∵OM ,ON 是⊙E 的切线,∴∠EON =∠EOM =30°.∴∠TOD =30°,∴OT =2DT =8,∴T (0,8),当⊙T 的圆心在y 轴的负半轴上时,且经过点O (0.0)时,T (0,-4),观察图象可知,当-4<t <8时,在图象上存在⊙T 的环绕点.8(2022秋•海淀区校级月考)对于平面直角坐标系中的线段AB 和点P (点P 不在线段AB 上),给出如下定义:当PA =PB 时,过点A (或点B )向直线PB (或PA )作垂线段,则称此垂线段为点P 关于线段AB 的“测度线段”,垂足称为点P 关于线段AB 的“测度点”.如图所示,线段AD 和BC 为点P 关于线段AB 的“测度线段”,点C 与点D为点P关于线段AB的“测度点”.(1)如图,点M(0,4)、N(2,0),①点P的坐标为(5,4),直接写出点P关于线段MN的“测度线段”的长度4;②点H为平面直角坐标系中的一点,且HM=HN,则下列四个点:Q1(0,0),Q2(3,3),Q3(1,0),Q4(0,4)中,是点H 关于线段MN的“测度点”的是;(2)直线y=-34x+6与x轴、y轴分别交于点A与点B,①点G为平面直角坐标系中一点,且GA=GB,若一次函数y=kx-14k+3上存在点G关于线段AB的“测度点”,直接写出k的取值范围为;②⊙O的半径为r,点C与点D均在⊙O上,且线段CD=65r.点K与点O位于线段CD的异侧,且KC=KD,若在线段AB上存在点K关于线段CD的“测度点”,直接写出r的取值范围为.【解答】解:(1)①∵M(0,4)、P(5,4),∴MP⎳x轴,∴点P关于线段MN的“测度线段”的长度为4,故答案为:4;②∵过点N作NF⊥MH交于F点,过点M作MG⊥NH交于点G,∵∠MFN=∠MGN=90°,∴F、G点在以MN为直径的圆上,设MN的中点为E,∵点M(0,4)、N(2,0),∴E(1,2),MN=25,∴点H关于线段MN的“测度点”在以E为圆心,5为半径的圆上,且不与M、N重合,∵Q1(0,0),Q2(3,3),Q3(1,0),Q4(0,4)中,Q1E=5,Q2E=5,Q3E=2,Q4E=5,∴Q1,Q2是点H关于线段MN的“测度点”,故答案为:Q1,Q2;(2)①当x=0时,y=6,∴B(0,6),当y=0时,x=8,∴A(8,0),∴AB的中点F(4,3),AB=10,由(1)可知,点G关于线段AB的“测度点”在以F为圆心,5为半径的圆上,且不与A、B点重合,∵一次函数y=kx-14k+3上存在点G关于线段AB的“测度点”,∴直线y=kx-14k+3与圆F相切或相交,过点F作FK垂直直线y=kx-14k+3交于点K,直线与y轴的交点为T,过点F作FL⎳KT交于交y轴于点L,过点L作SL⊥KT交于点S,∴LS =FK =5,∴LF 的直线解析式为y =kx -4k +3,∴L (0,-4k +3),T (0,-14k +3),∴TL =-10k ,∵sin ∠LTS =5-10k =11+k 2,∴k =±33,∴-33≤k ≤33时,一次函数y =kx -14k +3上存在点G 关于线段AB 的“测度点”,故答案为:-33≤k ≤33;②由(1)可知,K 点关于线段CD 的“测度点”在以CD 为直角的半圆上,且不与C 、D 重合,当CD ⎳AB ,且AB 与圆P 相切时,r 有最小值,由①可得,45=35r 6-r ,解得r =247,当CD 在AB 上时,r 有最大值,r =6,∴247≤r <6时,线段AB 上存在点K 关于线段CD 的“测度点”,故答案为:247≤r <6.9(2022•盐城一模)对于平面内的两点K 、L ,作出如下定义:若点Q 是点L 绕点K 旋转所得到的点,则称点Q 是点L 关于点K 的旋转点;若旋转角小于90°,则称点Q 是点L 关于点K 的锐角旋转点.如图1,点Q 是点L 关于点K 的锐角旋转点.(1)已知点A (4,0),在点Q 1(0,4),Q 2(2,23),Q 3(-2,23),Q 4(22,-22)中,是点A 关于点O 的锐角旋转点的是 Q 2,Q 4 .(2)已知点B (5,0),点C 在直线y =2x +b 上,若点C 是点B 关于点O 的锐角旋转点,求实数b 的取值范围.(3)点D 是x 轴上的动点,D (t ,0),E (t -3,0),点F (m ,n )是以D 为圆心,3为半径的圆上一个动点,且满足n ≥0.若直线y =2x +6上存在点F 关于点E 的锐角旋转点,请直接写出t 的取值范围.【解答】解:(1)如图,∵A (4,0),Q 1(0,4),∴OA =OQ 1=4,∠AOQ 1=90°,∴点Q 1不是点A 关于点O 的锐角旋转点;∵Q 2(2,23),作Q 2F ⊥x 轴于点F ,∴OQ 2=OF 2+Q 2F 2=22+(23)2=4=OA ,∵tan ∠Q 2OF =232=3,∴∠Q 2OF =60°,∴点Q 2是点A 关于点O 的锐角旋转点;∵Q 3(-2,23),作Q 3G ⊥x 轴于点G ,则tan ∠Q 3OG =Q 3G OG=232=3,∴∠Q3OG =60°,∴OQ 3=OG cos ∠Q 3OG =2cos60°=4=OA ,∵∠AOQ 3=180°-60°=120°,∴Q 3不是点A 关于点O 的锐角旋转点;∵Q 4(22,-22),作Q 4H ⊥x 轴于点H ,则tan ∠Q 4OH =Q 4H OH =2222=1,∴∠Q 4OH =45°,∵OQ 4=OH cos ∠Q 4OH =22cos45°=4=OA ,∴Q 4是点A 关于点O 的锐角旋转点;综上所述,在点Q 1,Q 2,Q 3,Q 4中,是点A 关于点O 的锐角旋转点的是Q 2,Q 4,故答案为:Q 2,Q 4.(2)在y 轴上取点P (0,5),当直线y =2x +b 经过点P 时,可得b =5,当直线y =2x +b 经过点B 时,则2×5+b =0,解得:b =-10,∴当-10<b <5时,OB 绕点O 逆时针旋转锐角时,点C 一定可以落在某条直线y =2x +b 上,过点O 作OG ⊥直线y =2x +b ,垂足G 在第四象限时,如图,则OT =-b ,OS =-12b ,∴ST =OS 2+OT 2=-12b 2+(-b )2=-52b ,当OG =5时,b 取得最小值,∵5×-52b =-b ×-12b ,∴b =-55,∴-55≤b <5.(3)根据题意,点F 关于点E 的锐角旋转点在半圆E 上,设点P 在半圆S 上,点Q 在半圆T 上(将半圆D 绕点E 旋转),如图3(1),半圆扫过的区域为图3(1)中阴影部分,如图3(2)中,阴影部分与直线y =2x +6相切于点G ,tan ∠EMG =2,SG =3,过点G 作GI ⊥x 轴于点I ,过点S 作SJ ⊥GI 于点J ,∴∠SGJ =∠EMG ,∴tan ∠SGJ =tan ∠EMG =2,∴GJ =355,SJ =655,∴GI =GJ +JI =3+355,∴MI =12GI =32+3510,∴OE =IE +MI -OM =352-32,即x E =t -3=352-32,解得t =352+32,如图3(3)中,阴影部分与HK 相切于点G ,tan ∠OMK =tan ∠EMH =2,EH =6,则MH =3,EM =35,∴x E =t -3=-3-35,解得t =-35,观察图象可知,-35≤t <3+352+32.10(2022秋•姜堰区期中)如图1,在平面内,过⊙T 外一点P 画它的两条切线,切点分别为M 、N ,若∠MPN ≥90°,则称点P 为⊙T 的“限角点”.(1)在平面直角坐标系xOy 中,当⊙O 半径为1时,在①P 1(1,0),②P 2-1,12,③P 3(-1,-1),④P 4(2,-1)中,⊙O 的“限角点”是②④;(填写序号)(2)如图2,⊙A 的半径为2,圆心为(0,2),直线l :y =-34x +b 交坐标轴于点B 、C ,若直线l 上有且只有一个⊙A 的“限角点”,求b 的值.(3)如图3,E (2,3)、F (1,2)、G (3,2),⊙D 的半径为2,圆心D 从原点O 出发,以2个单位/s 的速度沿直线l :y =x 向上运动,若ΔEFG 三边上存在⊙D 的“限角点”,请直接写出运动的时间t (s )的取值范围.【解答】解:(1)∵⊙O 半径为1,∴当P 为圆O 的“限角点”时,1<OP ≤2,∵OP 1=1,OP 2=52,OP 3=2,OP 4=5,∴⊙O 的“限角点”是P 2,P 3,故答案为:②③;(2)∵⊙A 的半径为2,∴当P 为圆A 的“限角点”时,2<AP ≤2,设直线l 上有且只有一个⊙O 的“限角点”P m ,-34m +b ,∴PA =2,此时AP ⊥BC ,令x =0,则y =b ,∴C (0,b ),令y =0,则x =43b ,∴B 43b ,0 ,∴tan ∠OCB =OB OC =43=AP CP ,∴CP =32,∴AC =52,∴|b -2|=52,∴b =92或b =-12;(3)∵圆心D 从原点O 出发,以2个单位/s 的速度沿直线l 移动,∴圆沿x 轴正方向移动t 个单位,沿y 轴正方向移动t 个单位,∴移动后D 点坐标为(t ,t ),设ΔEFG 边上的点P 是圆D 的“限角点”,则2<PD ≤2,在圆D 移动的过程中,当DF =2时,(t -1)2+(t -2)2=4,解得t =3-72或t =3+72,当t =3-72时,ΔEFG 边上开始出现⊙D 的“限角点”,当圆D 移动到E 点在圆上时,DE =2,(t -2)2+(t -3)2=2,解得t =5+32或t =5-32,∴3-72≤t <5-32时,ΔEFG 边上存在⊙D 的“限角点”,当圆D 再次移动到点F 在圆上时,DF =2,(t -2)2+(t -1)2=2,解得t =3+32或t 3-32,当t =3+32时,ΔEFG 三边上开始又要出现⊙D 的“限角点”;设直线EG 的解析式为y =kx +b ,直线y =x 与直线EG 的交点设为点H ,∴2k +b =33k +b=2 ,解得k =-1b =5 ,解得y =-x +5,联立方程组y =-x +5y =x,解得x =52y =52,∴H 52,52,当DH =2时,2t -52 2=4,解得t =2+52或t =-2+52,∴当t =2+52,ΔEFG 边上存在⊙D 的“限角点”,∴3+32<t ≤2+52时,ΔEFG 边上存在⊙D 的“限角点”;综上所述:3-72≤t <5-32或3+32<t ≤2+52时,ΔEFG 边上存在⊙D 的“限角点”.11(2022秋•西城区校级期中)在平面直角坐标系xOy中,已知点M(a,b),N.对于点P给出如下定义:将点P绕点M逆时针旋转90°,得到点P ,点P 关于点N的对称点为Q,称点Q为点P的“对应点”.(1)如图1,若点M在坐标原点,点N(1,1),①点P(-2,0)的“对应点”Q的坐标为 (2,0) ;②若点P的“对应点”Q的坐标为(-1,3),则点P的坐标为;(2)如图2,已知⊙O的半径为1,M是⊙O上一点,点N(0,2),若P(m,0)(m>1)为⊙O外一点,点Q为点P的“对应点”,连接PQ.①当点M(a,b)在第一象限时,求点Q的坐标(用含a,b,m的式子表示);②当点M在⊙O 上运动时,直接写出PQ长的最大值与最小值的积为.(用含m的式子表示)【解答】解:(1)①∵P(-2,0),∴P点绕点M逆时针旋转90°得到点P (0,-2),∵点P 关于点N的对称点为Q,∴Q(2,0);故答案为:(2,0);②∵Q的坐标为(-1,3),∴Q点关于N(1,1)的对称点为P (3,-1),将P 绕M点顺时针旋转90°得到点P,过P 作P F⊥x轴于点F,过点P作PE⊥x轴于点E,∵∠P OP=90°,∴∠POE+∠FOP =90°,∵∠EPO+∠EOP=90°,∴∠FOP =∠EPO,∵OP=OP ,∴ΔPOE≅△OP F(AAS),∴EO=P F=1,PE=OF=3,∴P(-1.-3),故答案为:(-1,-3);(2)①过点M作EF⊥x轴于点F,过点P 作P E⊥EF交于点E,由(1)可得ΔMPF≅△P ME(AAS),∴MF=EP ,FP=ME,∵M(a,b),P(m,0),∴EF=b+m-a,EP =b,∴P (a+b,b+m-a),∵点N(0,2),∴Q(-a-b,4-b-m+a);②P点绕O点逆时针旋转90°后得到点G,∴G(0,m),∵P (a+b,b+m-a),∴GP =2(a 2+b 2),∵M (a ,b )在圆O 上,∴a 2+b 2=1,∴GP =2,∴P 在以G 为圆心,2为半径的圆上,设G 点关于N 点的对称点为H ,则H (0,4-m ),∴QH =2(a 2+b 2)=2,∴Q 点在以H 为圆心2为半径的圆上,∴PQ 的最大值为PH +2,PQ 的最小值为PH -2,∴PQ 长的最大值与最小值的积为(PH +2)(PH -2)=2m 2-8m +14,故答案为:2m 2-8m +14.12(2022•秦淮区二模)【概念认识】与矩形一边相切(切点不是顶点)且经过矩形的两个顶点的圆叫做矩形的第Ⅰ类圆;与矩形两边相切(切点都不是顶点)且经过矩形的一个顶点的圆叫做矩形的第Ⅱ类圆.【初步理解】(1)如图①~③,四边形ABCD 是矩形,⊙O 1和⊙O 2都与边AD 相切,⊙O 2与边AB 相切,⊙O 1和⊙O 3都经过点B ,⊙O 3经过点D ,3个圆都经过点C .在这3个圆中,是矩形ABCD 的第Ⅰ类圆的是①,是矩形ABCD 的第Ⅱ类圆的是.【计算求解】(2)已知一个矩形的相邻两边的长分别为4和6,直接写出它的第Ⅰ类圆和第Ⅱ类圆的半径长.【深入研究】(3)如图④,已知矩形ABCD ,用直尺和圆规作图.(保留作图痕迹,并写出必要的文字说明)①作它的1个第Ⅰ类圆;②作它的1个第Ⅱ类圆.【解答】解:(1)由定义可得,①的矩形有一条边AD 与⊙O 1相切,点B 、C 在圆上,∴①是第Ⅰ类圆;②的矩形有两条边AD 、AB 与⊙O 2相切,点C 在圆上,∴②是第Ⅱ类圆;故答案为:①,②;(2)如图1,设AD =6,AB =4,切点为E ,过点O 作EF ⊥BC 交BC 于F ,交AD 于E ,连接BO ,设BO =r ,则OE =r ,OF =4-r ,由垂径定理可得,BF =CF =3,在Rt ΔBOF 中,r 2=(4-r )2+32,解得r =258;如图2,设AD =4,BC =6,切点为E ,过点O 作EF ⊥BC 交BC 于F ,交AD 于E ,连接BO ,设BO =r ,则OE =r ,OF =6-r ,由垂径定理可得,BF =CF =2,在Rt ΔBOF 中,r 2=(6-r )2+22,解得r =103;综上所述:第Ⅰ类圆的半径是258或103;如图3,AD =6,AB =4,过点O 作MN ⊥AD 交于点M ,交BC 于点N ,连接OC ,设AB 边与⊙O 的切点为G ,连接OG ,∴GO ⊥AB ,设OM =r ,则OC =r ,则ON =4-r ,∵OG =r ,∴BN =r ,∴NC =6-r ,在Rt ΔOCN 中,r 2=(4-r )2+(6-r )2,解得r =10-43,∴第Ⅱ类圆的半径是10-43;(3)①如图4,第一步,作线段AD 的垂直平分线交AD 于点E ,第二步,连接EC ,第三步,作EC 的垂直平分线交EF 于点O ,第四步,以O 为圆心,EO 为半径作圆,∴⊙O 即为所求第Ⅰ类圆;②如图5,第一步:作∠BAD 的平分线;第二步:在角平分线上任取点E ,过点E 作EF ⊥AD ,垂足为点F ;第三步:以点E 为圆心,EF 为半径作圆E ,交AC 于点G ,连接FG ;第四步:过点C 作CH ⎳FG ,CH 交AD 于点H ;第五步:过点H 作AD 的垂线,交∠BAD 的平分线于点O ;第六步:以点O 为圆心,OH 为半径的圆,⊙O 即为所求第Ⅱ类圆.13(2021秋•海淀区校级期末)新定义:在平面直角坐标系xOy 中,若几何图形G 与⊙A 有公共点,则称几何图形G 的叫⊙A 的关联图形,特别地,若⊙A 的关联图形G 为直线,则称该直线为⊙A 的关联直线.如图,∠M 为⊙A 的关联图形,直线l 为⊙A 的关联直线.(1)已知⊙O 是以原点为圆心,2为半径的圆,下列图形:①直线y =2x +2;②直线y =-x +3;③双曲线y =2x,是⊙O 的关联图形的是①③(请直接写出正确的序号).(2)如图1,⊙T 的圆心为T (1,0),半径为1,直线l :y =-x +b 与x 轴交于点N ,若直线l 是⊙T 的关联直线,求点N 的横坐标的取值范围.(3)如图2,已知点B (0,2),C (2,0),D (0,-2),⊙I 经过点C ,⊙I 的关联直线HB 经过点B ,与⊙I 的一个交点为P ;⊙I 的关联直线HD 经过点D ,与⊙I 的一个交点为Q ;直线HB ,HD 交于点H ,若线段PQ 在直线x =6上且恰为⊙I 的直径,请直接写出点H 横坐标h 的取值范围.【解答】解:(1)由题意①③是⊙O的关联图形,故答案为①③.(2)如图1中,∵直线l1y=-x+b是⊙T的关联直线,∴直线l的临界状态是和⊙T相切的两条直线l1和l2,当临界状态为l1时,连接TM(M为切点),∴TM=1,TM⊥MB,且∠MNO=45°,∴ΔTMN是等腰直角三角形,∴TN=2,OT=1,∴N(1+2,0),把N(1+2,0)代入y=-x+b中,得到b=1+2,同法可得当直线l2是临界状态时,b=-2+1,∴点N的横坐标的取值范围为-2+1≤N x≤2+1.(3)如图3-1中,当点Q在点P是上方时,连接BQ,PD交于点H,当圆心I在x轴上时,点H与点C重合,此时H(2,0),得到h的最大值为2,如图3-2中,当点P在点Q是上方时,直线PB,QD交于点H,当圆心I在x轴上时,点H(-6,0)得到h的最小值为-6,综上所述,-6≤h<0,0<h≤2.14(2022春•海淀区校级月考)定义:P、Q分别是两条线段a和b上任意一点,线段PQ长度的最小值叫做线段a与线段b的“冰雪距离”.已知O(0,0),A(1,1),B(m,n),C(m,n+2)是平面直角坐标系中四点.(1)根据上述定义,完成下面的问题:①当m=2,n=1时,如图1,线段BC与线段OA的“冰雪距离”是1.②当m=2时,线段BC与线段OA的“冰雪距离”是1,则n的取值范围是.(2)如图2,若点B落在圆心为A,半径为1的圆上,当n≥1时,线段BC与线段OA的“冰雪距离”记为d,结合图象,求d的最小值;(3)当m的值变化时,动线段BC与线段OA的“冰雪距离”始终为1,线段BC的中点为M.求点M随线段BC运动所走过的路径长.【解答】解:(1)①当m=2,n=1时,B(2,1),C(2,3).线段BC与线段OA的冰雪距离为AB=1.故答案为:1.②当m=2时,点A到直线BC的距离为1.若线段BC与线段OA的冰雪距离是1,则点A到BC的垂线的垂足在线段BC上,∴n≤1≤n+2,即-1≤n≤1.故答案为:-1≤n ≤1.(2)如图,B 2(0,1)为圆A 与y 轴的切点,B 11-22,1+22满足∠B 1AO =90°.当B 在B 1右侧时,冰雪距离d ≥B 1A =22.当B 在弧B 1B 2上时,冰雪距离d 为点B 到OA 的距离,结合图象可知,当且仅当B 处在点B 2时,d 取最小值22.(3)如图,当点B 位于图中弧DI 、线段IH 、弧HG 时,线段BC 与线段OA 的“冰雪距离”始终为1.当点C 位于图中弧DE 、线段EF 、弧FG 时,线段BC 与线段OA 的“冰雪距离”始终为1.当线段BC 由图中B 1D 向上平移到DC 3时,或由B 2G 向上平移到GC 4时,线段BC 与线段OA 的“冰雪距离”始终为1.对应中点M 所走过的路线长为:2π+4+22.15(2022•东城区校级开学)对于⊙C 和⊙C 上的一点A ,若平面内的点P 满足:射线AP 与⊙C 交于点Q (点Q 可以与点P 重合),且1≤PAQA ≤2,则点P 称为点A 关于⊙C 的“生长点”.已知点O 为坐标原点,⊙O 的半径为1,点A (-1,0).(1)若点P 是点A 关于⊙O 的“生长点”,且点P 在x 轴上,请写出一个符合条件的点P 的坐标 (2,0)(答案不唯一);(2)若点B 是点A 关于⊙O 的“生长点”,且满足∠BAO =30°,求点B 的纵坐标t 的取值范围;(3)直线y =3x +b 与x 轴交于点M ,且与y 轴交于点N ,若线段MN 上存在点A 关于⊙O 的“生长点”,直接写出b 的取值范围是.【解答】解:(1)根据“生长点”定义,点P 的坐标可以是(2,0),故答案为:(2,0)(答案不唯一);(2)如图,在x 轴上方作射线AM ,与⊙O 交于M ,使得∠OAM =30°,并在射线AM 上取点N ,使AM =MN ,并由对称性,将MN 关于x 轴对称,得M N ,则由题意,线段MN 和M N 上的点是满足条件的点B .作MH ⊥x 轴于H ,连接MC ,∴∠MHA =90°,即∠OAM +∠AMH =90°.∵AC 是⊙O 的直径,∴∠AMC =90°,即∠AMH +∠HMC =90°.∴∠OAM =∠HMC =30°.∴tan30°=MH AH=HC MH =33,设MH=y,则AH=3y,CH=33y,∴AC=AH+CH=433y=2,解得y=32,即点M的纵坐标为32.又由AN=2AM,A为(-1,0),可得点N的纵坐标为3,故在线段MN上,点B的纵坐标t满足:32≤t≤3,由对称性,在线段M N 上,点B的纵坐标t满足:?3≤t≤?3 2,∴点B的纵坐标t的取值范围是:32≤t≤3或?3≤t≤?32.(3)如图,Q是⊙O上异于点A的任意一点,延长AQ到P,使得PA=2AQ,∵Q的轨迹是以O为圆心,1为半径的圆,∴点P的运动轨迹是以K(1,0)为圆心,2为半径的圆,当直线MN与⊙K相切于点R时,连接KR,在RtΔKMR中,∠KRM=90°,∵直线y=3x+b与x轴夹角为60°,∴∠KMR=60°,KR=2,∴KM=2÷sin60°=433,∴OM=1+433,∴ON=3OM=4+3,∴b=-4-3,当直线MN经过G(0,-1)时,满足条件,此时b=-1,观察图象可知:当-4-3≤b≤-1时,线段MN上存在点A关于⊙O的“生长点”,根据对称性,同法可得当1≤b≤4-3时,也满足条件.故答案为:-4-3≤b≤-1或1≤b≤4-3.16(2022•东城区校级开学)在平面直角坐标系xOy中,给出如下定义:若点P在图形M上,点Q在图形N 上,称线段PQ长度的最小值为图形M,N的“近距离”,记为d(M,N).特别地,若图形M,N有公共点,规定d(M,N)=0,如图,点A(-23,0),B(0,2).(1)如果⊙O的半径为2,那么d(A,⊙O)= 23-2 ,d(B,⊙O)=;(2)如果⊙O的半径为r,且d(⊙O,AB)>0,求r的取值范围;(3)如果C(0,m)是y轴上的动点,⊙C的半径为1,使d(⊙C,AB)<1,直接写出m的取值范围为.【解答】解:(1)∵⊙O的半径为2,A(-23,0),B(0,2),∴OB=2,OA=23>2,∴点A在⊙O外,点B在⊙O上,∴d(A,⊙O)=23-2,d(B,⊙O)=0,故答案为:23-2;0;(2)如图1,过点O 作OD ⊥AB 于点D ,在Rt ΔAOB 中,∵tan ∠BAO =OB OA =223=33,∴∠BAO =30°.在Rt ΔADO 中,sin ∠BAO =DO OA =12=DO23,∴DO =3,∵d (⊙O ,AB )=0,∴r 的取值范围是0<r <3或r >23;(3)如图2,过点C 作CN ⊥AB 于点N ,由(2)知,∠BAO =30°.∵C (m ,0),当点C 在点B 的上边时,m >2,此时,d (⊙C ,AB )=BC ,∴BC ≤1,即m -2≤1,解得m ≤3;当点C 与点B 重合时,m =2,此时d (⊙C ,AB )=0,当点C 在点B 的下边时,m <2,∴BC =2-m ,∴CN =BC ⋅sin ∠OBA =32(2-m ).∵d (⊙C ,AB )<1,⊙C 的半径为1,∴0<32(2-m )<1.∴2-233<m <2.综上所述:2-233<m ≤3.故答案为:2-233<m ≤3.17(2021秋•润州区校级月考)在平面直角坐标系xOy 中,⊙C 的半径为r ,P 是与圆心C 不重合的点,点P 关于⊙C 的反称点的定义如下:若在射线CP 上存在一点P ′,满足CP +CP ′=2r ,则称P ′为点P 关于⊙C 的反称点,如图为点P 及其关于⊙C 的反称点P ′的示意图.(1)当⊙O 的半径为1时,①分别判断点M (3,1),N 32,0,T (-1,3)关于⊙O 的反称点是否存在?若存在,直接求其坐标;②将⊙O 沿x 轴水平向右平移1个单位为⊙O ′,点P 在直线y =-x +1上,若点P 关于⊙O ′的反称点P ′存在,且点P ′不在坐标轴上,则点P 的横坐标的取值范围 1-2≤x ≤1+2且x ≠2-2 ;(2)⊙C 的圆心在x 轴上,半径为1,直线y =-x +12与x 轴,y 轴分别交于点A 、B ,点E 与点D 分别在点A 与点B 的右侧2个单位,线段AE 、线段BD 都是水平的,若四边形ABDE 四边上存在点P ,使得点P 关于⊙C 的反称点P ′在⊙C 的内部,直接写出圆心C 的横坐标的取值范围.。
2024年九年级中考数学专题复习:新定义型问题与二次函数相关的问题含参考答案
2024年九年级中考数学专题复习:新定义型问题与二次函数相关的问题一、单选题1在R 上定义运算⊗:x ⊗y =x (1-y ),若不等式(x -a )⊗x +a <1对任意实数x 成立,则实数a 的取值范围()A.-1<a <1B.0<a <2C.-12<a <32D.-32<a <122我们定义一种新函数:形如y =ax 2+bx +c a ≠0,b 2-4ac >0 的函数叫做“鹊桥”函数.数学兴趣小组画出一个“鹊桥”函数y =x 2+bx +c 的图象如图所示,则下列结论正确的是()A.bc <0B.当x =1时,函数的最大值是4C.当直线y =x +m 与该图象恰有三个公共点时,则m =1D.关于x 的方程x 2+bx +c =3的所有实数根的和为43我们定义:若点A 在某一个函数的图象上,且点A 的横纵坐标相等,我们称点A 为这个函数的“好点”.若关于x 的二次函数y =ax 2+tx -3t 对于任意的常数t ,恒有两个“好点”,则a 的取值范围为()A.0<a <13B.0<a <12C.13<a <12D.12<a <14对于实数a ,b ,定义符号min a ,b ,其意义为:min a ,b =ba ≥baa <b .例如:min =2,-1 =-1,若关于x 的函数y =min 2x -1,-x +3,x 2-ax 则使该函数的最大值小于0时a 的范围是()A.a >2B.-1<a <0C.1<a <2D.a >35定义:两个不相交的函数图象在平行于y 轴方向上的最短距离称为这两个函数的“完美距离”.抛物线y =2x 2-5x +3与直线y =-2x -1的“完美距离”为()A.238B.3C.278D.2186定义运算“※”为:a ※b =ab 2(b >0)-ab2b ≤0,如:1※-2 =-1×(-2)2=-4,则函数y =2※x 的图象大致是()A. B.C. D.7新定义:若一个点的纵坐标是横坐标的2倍,则称这个点为二倍点.若二次函数y=x2-x+c(c为常数)在-2<x<4的图象上存在两个二倍点,则c的取值范围是()A.-2<c<14B.-2<c<94C.-4<c<14D.-4<c<948对于任意实数a和b,定义新运算,a#b=a2-ab a≥bb2-ab a<b有下列四个结论,其中正确的结论个数为()①2#-1的运算结果为6;②方程3x#x-2=0的解为x1=0,x2=-1;③当x<5时,函数y=2#x-3的图像经过第一、二、四象限;④函数y=2x#x-1的图像不经过第二、四象限.A.1个B.2个C.3个D.4个二、填空题9定义:两个不相交的函数图象在竖直方向上的最短距离,叫做这两个函数的“向心值”.则抛物线y =x2-2x+3与直线y=x-2的“向心值”为.10定义一种新的运算“早”,运算规则如下:(1)当a≥b时,a♀b=a;(2)当a<b时,a♀b=b2.那么当-2≤x≤2时,1♀x♀x-2♀x的最大值是.11对于实数a,b,定义运算:“☆”为a☆b=a2-ab-2a,如:2☆3=22-2×3-2×2=-6,若m,n 是二次函数y=x2-2x-3的图象与x轴的交点的横坐标,则m☆n=.12定义新运算:对于任意实数a,b,都有a⊗b=ab-a+b,例如 2⊗=2×3-2+3=1.若y关于x的函数y=kx+1⊗x-1的图象与x轴仅有一个公共点,则实数k的值为.13新定义:若一个点的纵坐标是横坐标的2倍,则称这个点为二倍点.若二次函数y=x2-x+c(c(c 为常数)在-2<x<4的图象上存在两个二倍点,则c的取值范围是.14新定义:任意两数m,n,按规定y=mn-m+n得到一个新数y,称所得新数y为数m,n的“愉悦数”.则当m=2x+1,n=x-1,且m,n的“愉悦数”y为正整数时,正整数x的值是.15定义:在平面直角坐标系中,若点A满足横、纵坐标都为整数,则把点A叫做“整点”.如:B3,0、C-1,3都是“整点”.抛物线y=ax2+2ax+a-2a>0与x轴交于点M,N两点,若该抛物线在M、N 之间的部分与线段MN所围的区域(包括边界)恰有5个整点,则a的取值范围是.16定义:对角线互相垂直的四边形为垂美四边形.已知垂美四边形ABCD的对角线AC、BD满足AC+BD=12,则当AC=时,四边形ABCD的面积最大.三、解答题17新定义:[a,b,c]为二次函数y=ax2+bx+c(a≠0,a,b,c为实数)的“图象数”,如:y=-x2+2x+ 3的“图象数”为[-1,2,3].(1)图像数为[1,-1,0]的二次函数表达式为.(2)求证:“图象数”为[1,m+3,m]的二次函数的图象与x轴恒有两个交点.18定义:若x,y满足x2=4y+t,y2=4x+t且x≠y(t为常数),则称点M(x,y)为“和谐点”.(1)请直接判断点(1,-5)是否为“和谐点”;(2)P(2,m)是“和谐点”,求m值;(-3<x<-1)的图象上存在“和谐点”,求k的取值范围.(3)若双曲线y=kx19某网店有(万件)商品,计划在元旦旺季售出商品x(万件),经市场调查测算,花费t(万元)进行促销后,商品的剩余量3-x与促销费t之间的关系为3-x=kt+1(其中k为常数),如果不搞促销活动,只能售出1(万件)商品.(1)要使促销后商品的剩余量不大于0.1(万件),促销费t至少为多少(万元)?(2)已知商品的进价为32(元/件),另有固定成本3(万元),定义每件售出商品的平均成本为32+3x(元),若将商品售价为:“每件售出商品平均成本的1.5倍”与“每件售出商品平均促销费的一半”之和,则当促销费t为多少(万元)时,该网店售出商品的总利润最大?此时商品的剩余量为多少?20我们定义一种新函数:形如y=ax2+bx+ca≠0,b2-4ac>0的函数叫作“华为”函数.如图,小丽同学画出了“华为”函数y=x2-2x-3的图像,根据该图像解答下列问题:(1)求该函数图像与x轴和y轴的交点坐标.(2)当函数值y随x值的增大而减小时,求自变量x的取值范围.2024年九年级中考数学专题复习:新定义型问题与二次函数相关的问题一、单选题1在R 上定义运算⊗:x ⊗y =x (1-y ),若不等式(x -a )⊗x +a <1对任意实数x 成立,则实数a 的取值范围()A.-1<a <1B.0<a <2C.-12<a <32D.-32<a <12【答案】C【分析】本题的考点是函数恒成立问题,主要考查了函数恒成立问题,关键是理解新定义的运算,掌握将不等式转化为二次不等式,解决恒成立问题转化成图象恒在x 轴上方,从而有△<0,解△<0即可.【详解】根据运算法则得x -a ⊗x +a =x -a 1-x -a <1化简得:x 2-x -a 2+a +1>0在R 上恒成立,即Δ<0,1-4-a ²+a +1 <0,即4a 2-4a -3<0,解得-12<a <32,故选:C .2我们定义一种新函数:形如y =ax 2+bx +c a ≠0,b 2-4ac >0 的函数叫做“鹊桥”函数.数学兴趣小组画出一个“鹊桥”函数y =x 2+bx +c 的图象如图所示,则下列结论正确的是()A.bc <0B.当x =1时,函数的最大值是4C.当直线y =x +m 与该图象恰有三个公共点时,则m =1D.关于x 的方程x 2+bx +c =3的所有实数根的和为4【答案】D【分析】本题考查二次函数的应用、新定义、二次函数的性质,由-1,0 ,3,0 是函数图象和x 轴的交点,利用待定系数法求得b 、c 的值可判断A 错误;根据图象可判断B 错误;由图象可判断C 错误;由题意可得x 2-2x -3=3或x 2-2x -3=-3,利用根与系数的关系可判断D 正确.利用数形结合的思想解答是解题的关键.【详解】解:∵-1,0 ,3,0 是函数图象和x 轴的交点,∴1-b +c =09+3b +c =0,解得:b =-2c =-3 ,∴bc =-2 ×-3 =6>0,故A 错误;由图象可得,函数没有最大值,故B 错误;如图,当直线y =x +m 与该图象恰有三个公共点时,应该有2条直线,故C 错误;关于x 的方程x 2+bx +c =3,即x 2-2x -3=3或x 2-2x -3=-3,当x 2-2x -3=3时,x 1+x 2=--21=2,当x 2-2x -3=-3时,x 3+x 4=--21=2,∴关于x 的方程x 2+bx +c =3的所有实数根的和为2+2=4,故D 正确,故选:D .3我们定义:若点A 在某一个函数的图象上,且点A 的横纵坐标相等,我们称点A 为这个函数的“好点”.若关于x 的二次函数y =ax 2+tx -3t 对于任意的常数t ,恒有两个“好点”,则a 的取值范围为()A.0<a <13B.0<a <12C.13<a <12D.12<a <1【答案】A【分析】“好点”A 的横纵坐标相等,即:x =y =ax 2+tx -3t a ≠0 ,Δ=(t -1)2+12at >0,整理得:t 2-2-12a t +1=0,△1=(2-12a )2-4<0,即可求解.【详解】解:“好点”A 的横纵坐标相等,∴x =y =ax 2+tx -3t a ≠0 ,∴ax 2+t -1 x -3t =0,Δ=b 2-4ac =(t -1)2+12at >0,整理得:t 2-2-12a t +1>0,∵1>0,故当Δ<0时,抛物线开口向上,且与x 轴没有交点,故上式成立,△1=(2-12a )2-4<0,解得:0<a <13,故选:A .【点睛】本题考查的是二次函数图象与系数的关系,要求学生熟悉函数的基本性质,能熟练求解函数与坐标轴的交点及顶点的坐标等.4对于实数a ,b ,定义符号min a ,b ,其意义为:min a ,b =ba ≥baa <b .例如:min =2,-1 =-1,若关于x 的函数y =min 2x -1,-x +3,x 2-ax 则使该函数的最大值小于0时a 的范围是()A.a >2B.-1<a <0C.1<a <2D.a >3【答案】D【分析】画出y =2x -1,y =-x +3,y =x 2-ax 的函数图象,根据题意,最大值小于0时,结合函数图象,即可求解.【详解】解:如图所示,y =min 2x -1,-x +3,x 2-ax 即为函数图象的红色部分,由y=x2-ax,令y=0,则x2-ax=0解得:x1=0,x2=a∵y=x2-ax经过原点,y=-x+3与x轴的交点为3,0,∴当y=min2x-1,-x+3,x2-ax最大值小于0时,则y=x2-ax与x轴的交点在3,0的右侧,∴a>3故选:D【点睛】本题考查了新定义、一元一次不等式以及二次函数、一次函数的交点问题,认真阅读理解其意义,并利用数形结合的思想解决函数的最值问题.5定义:两个不相交的函数图象在平行于y轴方向上的最短距离称为这两个函数的“完美距离”.抛物线y=2x2-5x+3与直线y=-2x-1的“完美距离”为()A.238B.3 C.278D.218【答案】A【分析】先判断抛物线与直线无交点,再根据定义和二次函数的性质求解即可.【详解】解:由2x2-5x+3=-2x-1得2x2-3x+4=0,∵Δ=-32-4×2×4=-23<0,∴方程2x2-3x+4=0没有实数根,∴抛物线y=2x2-5x+3与直线y=-2x-1不相交,设w=2x2-5x+3--2x-1=2x2-3x+4=2x-342+238,∵2>0,∴当x=34时,w有最小值为23 8,即抛物线y=2x2-5x+3与直线y=-2x-1的“完美距离”为23 8,故选:A.【点睛】本题考查二次函数的性质、一元二次方程根的判别式,理解题中定义,熟练掌握二次函数的性质是解答的关键.6定义运算“※”为:a※b=ab2(b>0)-ab2b≤0,如:1※-2 =-1×(-2)2=-4,则函数y=2※x的图象大致是()A. B.C. D.【答案】D【分析】根据定义运算“※”为:a※b=ab2(b>0)-ab2b≤0,可得y=2※x的函数解析式,根据函数解析式,可得函数图象.【详解】解:y=2※x=2x2(x>0) -2x2x≤0,x>0时,图象是y=2x2对称轴右侧的部分;x≤0时,图象是y=-2x2对称轴左侧的部分,故选:D.【点睛】本题考查了二次函数的图象,利用定义运算“※”为:a※b=ab2(b>0)-ab2b≤0得出分段函数是解题关键.7新定义:若一个点的纵坐标是横坐标的2倍,则称这个点为二倍点.若二次函数y=x2-x+c(c为常数)在-2<x<4的图象上存在两个二倍点,则c的取值范围是()A.-2<c<14B.-2<c<94C.-4<c<14D.-4<c<94【答案】D【分析】由点的纵坐标是横坐标的2倍可得二倍点在直线y=2x上,由-2<x<4可得二倍点所在线段AB的端点坐标,结合图象,通过求抛物线与线段交点求解.【详解】解:由题意可得二倍点所在直线为y=2x,将x=-2代入y=2x得y=-4,将x=4代入y=2x得y=8,设A(-2,-4),B(4,8),如图,联立方程x2-x+c=2x,当△>0时,抛物线与直线y=2x有两个交点,即9-4c>0,解得c<9 4,此时,直线x=-2和直线x=4与抛物线交点在点A,B上方时,抛物线与线段AB有两个交点,把x=-2代入y=x2-x+c得y=6+c,把x=4代入y=x2-x+c得y=12+c,∴6+c>-4 12+c>8 ,解得c>-4,∴-4<c<94满足题意.故选:D.【点睛】本题考查二次函数图象与系数的关系,解题关键掌握函数与方程及不等式的关系,将代数问题转化为图形问题求解.8对于任意实数a和b,定义新运算,a#b=a2-ab a≥bb2-ab a<b有下列四个结论,其中正确的结论个数为()①2#-1的运算结果为6;②方程3x#x-2=0的解为x1=0,x2=-1;③当x<5时,函数y=2#x-3的图像经过第一、二、四象限;④函数y=2x#x-1的图像不经过第二、四象限.A.1个B.2个C.3个D.4个【答案】C【分析】本题主要考查了实数的运算,解一元二次方程,二次函数的性质,熟练掌握解一元二次方程的方法以及二次函数的性质是解题的关键.根据新定义的运算即可判断①;分两种情况讨论得到一元二次方程,解方程即可判断②;根据二次函数的性质即可判断③;利用二次函数的图像即可判断④.【详解】解:①∵2>-1,∴2#-1=22-2×-1=6,故正确;②当3x≥x-2时,即x≥-1时,方程为9x2-3x x-2=0,整理得6x2+6x=0,解得x1=0,x2=-1,当3x <x -2时,即x <-1时,方程为x -2 2-3x x -2 =0,整理得x 2-x -2=0,解得x =2或x =-1(不符合题意,舍去),∴方程3x #x -2 =0的解为x 1=0,x 2=-1,故正确;③∵当x <5时,函数y =2#x -3 =4-2x -3 =-2x +10,∴函数y =2#x -3 的图像经过第一、二象限,故错误;④当2x ≥x -1时,即x ≥-1时,函数为y =4x 2-2x x -1 =2x +12 2-12,当2x <x -1时,即x <-1时,函数为y =x -1 2-2x x -1 =-x 2+1,画出函数图像如下:由图可知函数图像不经过第二、四象限,故正确;故选:C .二、填空题9定义:两个不相交的函数图象在竖直方向上的最短距离,叫做这两个函数的“向心值”.则抛物线y =x 2-2x +3与直线y =x -2的“向心值”为.【答案】114【分析】此题考查了一次函数,二次函数的性质以及新定义问题,解题的关键是熟练掌握正确分析“向心值”的概念.根据“向心值”的概念让两个表达式相减,然后求解得到的二次函数最小值即可.【详解】解:∵两个不相交的函数图象在竖直方向上的最短距离为这两个函数的“向心值”,∴设“向心值”为w ,∴w =x 2-2x +3-x -2 =x 2-3x +5=x -322+114,∴w 的最小值为114.故答案为:114.10定义一种新的运算“早”,运算规则如下:(1)当a ≥b 时,a ♀b =a ;(2)当a <b 时,a ♀b =b 2.那么当-2≤x ≤2时,1♀x ♀x -2♀x 的最大值是.【答案】2【分析】本题主要考查了新运算法则、二次函数的性质等知识点,掌握分类讨论思想是解题的关键.分-2≤x ≤1和1≤x ≤2两种情况,分别根据新运算法则求出最值,然后进行比较即可解答.【详解】解:当-2≤x ≤1时,1♀x ♀x -2♀x =1♀x -2=1-2=-1;当1≤x≤2时,1♀x=x2♀x-2=x2-2;♀x-2♀x∵a=1>0,对称轴为x=0,1≤x≤2,∴当x=2时,x2-2有最大值,22-2=2,∴1♀x的最大值是2.♀x-2♀x故答案为:2.11对于实数a,b,定义运算:“☆”为a☆b=a2-ab-2a,如:2☆3=22-2×3-2×2=-6,若m,n 是二次函数y=x2-2x-3的图象与x轴的交点的横坐标,则m☆n=.【答案】6【分析】本题考查了二次函数与一元二次方程的关系,新定义下的实数运算.熟练掌握二次函数与一元二次方程的关系是解题的关键.由题意知,m,n是x2-2x-3=0的两个根,解得x=-1或x=3,分当m=-1,n=3时;当m=3,n=-1时两种情况计算求解即可.【详解】解:由题意知,m,n是x2-2x-3=0的两个根,x+1=0,x-3∴x+1=0或x-3=0,解得x=-1或x=3,当m=-1,n=3时,m☆n=m2-mn-2m=m m-n-2=-1×-1-3-2=6;当m=3,n=-1时,m☆n=m2-mn-2m=m m-n-2=6;=3×3+1-2故答案为:6.12定义新运算:对于任意实数a,b,都有a⊗b=ab-a+b=1.若y关,例如 2⊗=2×3-2+3于x的函数y=kx+1的图象与x轴仅有一个公共点,则实数k的值为.⊗x-1【答案】-1或0/0或-1【分析】由定义的新运算求得y关于x的函数为:y=-x2+kx+k,再由y关于x函数的图象与x轴仅有一个公共点得到,求解即可.【详解】解:∵a⊗b=ab-a+b,∴y=kx+1⊗x-1=kx+1+x-1-kx+1x-1=kx2-2kx-1即y=kx2-2kx-1,∵y=kx2-2kx-1的图象与x轴仅有一个公共点,令y=0,得kx2-2kx-1=0,∴Δ=b2-4ac=4k2+4k=0,∴k2+k=0,解得:k=0或k=-1.故答案为:-1或0.【点睛】本题主要考查了一元二次方程的根与二次函数图像和x轴交点坐标的关系,解题关键是熟记:一元二次方程有两个根,说明二次函数图像和x轴的横坐标有两个交点;一元二次方程有一个根,说明二次函数图像和x轴的横坐标有一个交点;一元二次方程(在实数范围)无解,说明二次函数图像和x轴的横坐标没有交点.13新定义:若一个点的纵坐标是横坐标的2倍,则称这个点为二倍点.若二次函数y=x2-x+c(c(c 为常数)在-2<x<4的图象上存在两个二倍点,则c的取值范围是.【答案】-4<c <94【分析】由点的纵坐标是横坐标的2倍可得二倍点在直线y =2x 上,由-2<x <4可得二倍点所在线段AB 的端点坐标,结合图象,通过求抛物线与线段交点求解.【详解】解:由题意可得二倍点所在直线为y =2x ,将x =-2代入y =2x 得y =-4,将x =4代入y =2x 得y =8,设A (-2,-4),B (4,8),如图,联立方程x 2-x +c =2x ,当∆>0时,抛物线与直线y =2x 有两个交点,即9-4c >0,解得c <94,此时,直线x =-2和直线x =4与抛物线交点在点A ,B 上方时,抛物线与线段AB 有两个交点,把x =-2代入y =x 2-x +c 得y =6+c ,把x =4代入y =x 2-x +c 得y =12+c ,∴6+c >-412+c >8 ,解得c >-4,∴-4<c <94满足题意.故答案为:-4<c <94.【点睛】本题考查二次函数图象与系数的关系,解题关键掌握函数与方程及不等式的关系,将代数问题转化为图形问题求解.14新定义:任意两数m ,n ,按规定y =m n-m +n 得到一个新数y ,称所得新数y 为数m ,n 的“愉悦数”.则当m =2x +1,n =x -1,且m ,n 的“愉悦数”y 为正整数时,正整数x 的值是.【答案】2【分析】根据“愉悦数”的定义,将m 、n 代入y =m n -m +n 得到一个关于x 的方程,然后再求解即可.【详解】解:当m =2x +1,n =x -1,且m ,n 的“愉悦数”y =2x +1x -1-2x +1 +x -1 >0化简得:-x 2+x +3x -1>0∵x 是正整数∴x -1>0即:x -1>0-x 2+x +3>0解得:1<x <1+132∵x 是正整数∴x =2.故答案是2.【点睛】本题主要考查运用二次函数解不等式、分式的混合运算等知识点,正确运用二次函数解不等式成为解答本题的关键.15定义:在平面直角坐标系中,若点A 满足横、纵坐标都为整数,则把点A 叫做“整点”.如:B 3,0 、C -1,3 都是“整点”.抛物线y =ax 2+2ax +a -2a >0 与x 轴交于点M ,N 两点,若该抛物线在M 、N 之间的部分与线段MN 所围的区域(包括边界)恰有5个整点,则a 的取值范围是.【答案】1<a ≤2【分析】画出图象,找到该抛物线在M 、N 之间的部分与线段MN 所围的区域(包括边界)恰有5个整点的边界,利用与y 交点位置可得a 的取值范围.【详解】解:抛物线y =ax 2+2ax +a -2(a >0)化为顶点式为y =a (x +1)2-2,∴函数的对称轴:x =-1,顶点坐标为(-1,-2),∴M 和N 两点关于x =-1对称,根据题意,抛物线在M 、N 之间的部分与线段MN 所围的区域(包括边界)恰有5个整点,这些整点是(0,0),(-1,0),(-1,-1),(-1,-2),(-2,0),如图所示:∵当x =0时,y =a -2,∴-1<a -2≤0,当x =1时,y =4a -2>0,即:-1<a -2≤04a -2>0,解得1<a ≤2,故答案为:1<a ≤2.【点睛】本题考查抛物线与x 轴的交点、配方法确定顶点坐标、待定系数法等知识,利用函数图象确定与y 轴交点位置是本题的关键.16定义:对角线互相垂直的四边形为垂美四边形.已知垂美四边形ABCD 的对角线AC 、BD 满足AC +BD =12,则当AC =时,四边形ABCD 的面积最大.【答案】6【分析】根据垂美四边形的性质列出函数解析式,进行求解即可.【详解】解:∵四边形ABCD 的对角线互相垂直,∴S ABCD =12AC ∙BD ,∵AC +BD =12,∴BD =12-AC ,∴S 四边形ABCD =12AC ∙BD =12AC 12-AC =-12AC 2+6AC ,∵-12<0且0<AC <12,当AC =-62×-12=6时,函数有最大值,∴AC =6时,面积有最大值;故答案是6.【点睛】本题主要考查了二次函数的应用,准确分析计算是解题的关键.三、解答题17新定义:[a ,b ,c ]为二次函数y =ax 2+bx +c (a ≠0,a ,b ,c 为实数)的“图象数”,如:y =-x 2+2x +3的“图象数”为[-1,2,3].(1)图像数为[1,-1,0]的二次函数表达式为.(2)求证:“图象数”为[1,m +3,m ]的二次函数的图象与x 轴恒有两个交点.【答案】(1)y =x 2-x(2)见详解【分析】本题考查了抛物线与轴的交点:(1)根据新定义得到二次函数的解析式即可;(2)根据新定义得到二次函数的解析式为y =x 2+m +3 x +m ,然后根据判别式的意义得到Δ=m +3 2-4m =m +1 2+8>0,从而求证.【详解】(1)解:图像数为[1,-1,0]的二次函数表达式为:y =x 2-x .(2)解:“图象数”为[1,m +3,m ]的二次函数表达式为:y =x 2+m +3 x +m .当y =0时,x 2+m +3 x +m =0Δ=m +3 2-4m =m +1 2+8>0∴该一元二次方程有两个不相等的实数根,即“图象数”为[1,m +3,m ]的二次函数的图象与x 轴恒有两个交点.18定义:若x ,y 满足x 2=4y +t ,y 2=4x +t 且x ≠y (t 为常数),则称点M (x ,y )为“和谐点”.(1)请直接判断点(1,-5)是否为“和谐点”;(2)P (2,m )是“和谐点”,求m 值;(3)若双曲线y =k x(-3<x <-1)的图象上存在“和谐点”,求k 的取值范围.【答案】(1)点1,-5 是“和谐点”(2)m =-6(3)k 的取值范围为3<k ≤4【分析】(1)由题意得,x 2-4y =y 2-4x ,由12-4×-5 =-5 2-4×1,可得点1,-5 是“和谐点”;(2)由题意知,22-4m =m 2-8,即m 2+4m -12=0,计算求出满足要求的解即可;(3)设点a,b为双曲线y=kx(-3<x<-1)上的“和谐点”,则a2=4b+t,b2=4a+t,b=ka(-3<a<-1),即a-ba+b+4=0,可得b=-a-4,由b=ka,可得k=ab=a-a-4=-a2-4a=-a+22+4,且-3<a<-1,然后利用二次函数的图象与性质求取值范围即可.【详解】(1)解:∵x2=4y+t,y2=4x+t,∴x2-4y=t,y2-4x=t,∴x2-4y=y2-4x,∵12-4×-5=-52-4×1,∴点1,-5是“和谐点”;(2)解:∵P2,m是“和谐点”,∴22=4m+t,m2=4×2+t,∴22-4m=t,m2-8=t,∴22-4m=m2-8,即m2+4m-12=0,解得m1=-6,m2=2(不合题意,舍去)∴m=-6;(3)解:设点a,b为双曲线y=kx(-3<x<-1)上的“和谐点”,∴a2=4b+t,b2=4a+t,b=ka(-3<a<-1),∴a2-4b=b2-4a,即a2-b2+4a-4b=0,∴a-ba+b+4=0,∵a≠b,∴a+b+4=0,即b=-a-4,∵b=ka(-3<a<-1),∴k=ab=a-a-4=-a2-4a=-a+22+4,且-3<a<-1,∵-1<0,∴图象开口向下,当a=-2时,k max=4,当a=-1时,k=--1+22+4=3;当a=-3时,k=--3+22+4=3;∴k的取值范围为3<k≤4.【点睛】本题考查了新定义下的实数运算,因式分解法解一元二次方程,二次函数的图象与性质,平方差公式,二次函数的最值,反比例函数解析式等知识.理解题意,熟练掌握因式分解法解一元二次方程,平方差公式,二次函数的图象与性质是解题的关键.19某网店有(万件)商品,计划在元旦旺季售出商品x(万件),经市场调查测算,花费t(万元)进行促销后,商品的剩余量3-x与促销费t之间的关系为3-x=kt+1(其中k为常数),如果不搞促销活动,只能售出1(万件)商品.(1)要使促销后商品的剩余量不大于0.1(万件),促销费t至少为多少(万元)?(2)已知商品的进价为32(元/件),另有固定成本3(万元),定义每件售出商品的平均成本为32+3x(元),若将商品售价为:“每件售出商品平均成本的1.5倍”与“每件售出商品平均促销费的一半”之和,则当促销费t为多少(万元)时,该网店售出商品的总利润最大?此时商品的剩余量为多少?【答案】(1)至少为19万元(2)当促销费为7万元时,网店利润最大为42万元,此时商品的剩余量为0.25万件【分析】题目主要考查不等式的应用及函数的应用,(1)根据题意得出k=2,代入原不等式求解即可;(2)设网店的利润y(万元),根据题意得出相应的函数关系式,然后再由其性质求解即可;理解题意列出相应的函数关系式是解题关键.【详解】(1)解:∵3-x=kt+1,当t=0时,x=1,∴k=2,∴3-x=2t+1,∵2t+1≤0.1,解得:t≥19;(2)设网店的利润y(万元),根据题意得:y=x3+32xx×1.5+t2x-3+32x+t=992-32t+1-t2=50-32t+1+t+12≤50-232t+1×t+12=42,当且仅当32t+1=t+12即t=7时,等号成立,此时3-x=0.25,当促销费为7万元时,网店利润最大为42万元,此时商品的剩余量为0.25万件.20我们定义一种新函数:形如y=ax2+bx+ca≠0,b2-4ac>0的函数叫作“华为”函数.如图,小丽同学画出了“华为”函数y=x2-2x-3的图像,根据该图像解答下列问题:(1)求该函数图像与x轴和y轴的交点坐标.(2)当函数值y随x值的增大而减小时,求自变量x的取值范围.【答案】(1)与x轴交点坐标-1,0,3,0,与y轴交点坐标0,3(2)x≤-1或1≤x≤3【分析】(1)分别令y=0和x=0,然后求解,即可获得答案;(2)首先确定该函数图像的对称轴,然后结合图像,即可获得答案.【详解】(1)解:令y=0,即x2-2x-3=0,可得x2-2x-3=0,∴x+1x-3=0,解得x1=-1,x2=3,∴函数图像与x轴的交点坐标为-1,0和3,0,令x=0,则y=x2-2x-3=-3=3,∴函数图像与y轴的交点坐标为0,3;(2)该图像具有对称性,对称轴是直线x=-b=1,2a函数图像与x轴的交点坐标为-1,0,和3,0观察图像可知,当x≤-1或1≤x≤3时,函数值y随x值的增大而减小.【点睛】本题主要考查了二次函数图像与x轴交点、二次函数图像与y轴交点、解一元二方程、二次函数图像与性质等知识,解题关键是运用数形结合的思想分析问题.。
中考数学专题复习

中考数学专题复习附答案1. 定义新运算“a∗b”:对于任意实数a,b,都有a∗b=(a+b)(a−b)−1,其中等式右边是通常的加法、减法、乘法运算,例4∗3=(4+3)(4−3)−1=7−1=6.若x∗k=x(k为实数)是关于x的方程,则它的根的情况为( )A.有一个实数根B.有两个相等的实数根C.有两个不相等的实数根D.没有实数根2. 定义运算:若a m=b,则log a b=m(a>0),例如23=8,则log28= 3.运用以上定义,计算:log5125−log381=()A.−1B.2C.1D.443. 定义a※b=a(b+1),例如2※3=2×(3+1)=2×4=8.则(x−1)※x的结果为________.4. 对于任意两个不相等的数a,b,定义一种新运算“⊕”如下:a⊕b=√a+b √a−b ,如:3⊕2=√3+2√3−2=√5,那么12⊕4=________.5. 规定:如果一个四边形有一组对边平行,一组邻边相等,那么称此四边形为广义菱形.根据规定判断下面四个结论:①正方形和菱形都是广义菱形;②平行四边形是广义菱形;③对角线互相垂直,且两组邻边分别相等的四边形是广义菱形;④若M、N的坐标分别为(0, 1),(0, −1),P是二次函数y=14x2的图象上在第一象限内的任意一点,PQ垂直直线y=−1于点Q,则四边形PMNQ是广义菱形.其中正确的是________.(填序号)6. 定义:有一组对角互余的四边形叫做对余四边形.理解:(1)若四边形ABCD是对余四边形,则∠A与∠C的度数之和为________;证明:(2)如图1,MN是⊙O的直径,点A,B,C在⊙O上,AM,CN相交于点D.求证:四边形ABCD是对余四边形;探究:(3)如图2,在对余四边形ABCD中,AB=BC,∠ABC=60∘,探究线段AD,CD和BD之间有怎样的数量关系?写出猜想,并说明理由.7. 用※定义一种新运算:对于任意实数m和n,规定m※n=m2n−mn−3n,如:1※2=12×2−1×2−3×2=−6.(1)求(−2)※√3;(2)若3※m≥−6,求m的取值范围,并在所给的数轴上表示出解集.8. 阅读下面的材料:对于实数a,b,我们定义符号min{a, b}的意义为:当a<b时,min{a, b}= a;当a≥b时,min{a, b}=b,如:min{4, −2}=−2,min{5, 5}=5.根据上面的材料回答下列问题:(1)min{−1, 3}=________;(2)当min{2x−32,x+23}=x+23时,求x的取值范围.9. 阅读理解:材料一:若三个非零实数x,y,z满足:只要其中一个数的倒数等于另外两个数的倒数的和,则称这三个实数x,y,z构成“和谐三数组”.材料二:若关于x的一元二次方程ax2+bx+c=0(a≠0)的两根分别为x1,x2,则有x1+x2=−ba ,x1⋅x2=ca.问题解决:(1)请你写出三个能构成“和谐三数组”的实数________;(2)若x1,x2是关于x的方程ax2+bx+c=0(a,b,c均不为0)的两根,x3是关于x的方程bx+c=0(b,c均不为0)的解.求证:x1,x2,x3可以构成“和谐三数组”;(3)若A(m, y1),B(m+1, y2),C(m+3, y3)三个点均在反比例函数y=4x的图象上,且三点的纵坐标恰好构成“和谐三数组”,求实数m的值.10. 在整数的除法运算中,只有能整除与不能整除两种情况,当不能整除时,就会产生余数,现在我们利用整数的除法运算来研究一种数--“差一定义:对于一个自然数,如果这个数除以5余数为4,且除以3余数为2,则称这个数为“差一数”.例如:14÷5=2...4,14÷3=4...2,所以14是“差一数”;19÷5=3...4,但19÷3=6...1,所以19不是“差一数”.(1)判断49和74是否为“差一数”?请说明理由;(2)求大于300且小于400的所有“差一数”.参考答案与试题解析中考专题复习(新型定义题型)一、选择题(本题共计 2 小题,每题 3 分,共计6分)1.【答案】C2.【答案】A二、填空题(本题共计 3 小题,每题 3 分,共计9分)3.【答案】x2−14.【答案】√25.【答案】①④三、解答题(本题共计 5 小题,每题 10 分,共计50分)6.【答案】90∘或270∘(2)证明:∵MN是⊙O的直径,点A,B,C在⊙O上,∴∠BAM+∠BCN=90∘,即∠BAD+∠BCD=90∘,∴四边形ABCD是对余四边形.(3)解:线段AD,CD和BD之间数量关系为:AD2+CD2=BD2,理由如下:∵对余四边形ABCD中,∠ABC=60∘,∴∠ADC=30∘,∵AB=BC,∴将△BCD绕点B逆时针旋转60∘,得到△BAF,连接FD,如图3所示:∴△BCD≅△BAF,∠FBD=60∘,∴BF=BD,AF=CD,∠BDC=∠BFA,∴△BFD是等边三角形,∴BF=BD=DF,∵∠ADC=30∘,∴∠ADB+∠BDC=30∘,∴∠BFA+∠ADB=30∘,∵∠FBD+∠BFA+∠ADB+∠AFD+∠ADF=180∘,∴60∘+30∘+∠AFD+∠ADF=180∘,∴∠AFD+∠ADF=90∘,∴∠FAD=90∘,∴AD2+AF2=DF2,∴AD2+CD2=BD2.7.【答案】解:(1)(−2)※√3=(−2)2×√3−(−2)×√3−3√3=4√3+2√3−3√3=3√3.(2)3※m≥−6,则9m−3m−3m≥−6,解得:m≥−2,将解集表示在数轴上如下:8.【答案】−1(2)由题意得:2x−32≥x+23,3(2x−3)≥2(x+2),6x−9≥2x+4,x ≥134,∴ x 的取值范围为x ≥134.9.【答案】如12,13,15 (2)证明: x 1,x 2是关于x 的方程ax 2+bx +c =0(a,b,c 均不为0)的两根,∴ x 1+x 2=−b a ,x 1⋅x 2=c a ,1x 1+1x 2=x 1+x 2x 1x 2=−b c , ∵ x 3是关于x 的方程bx +c =0(b,c 均不为0)的解,∴ x 3=−c b ,∴1x 3=−b c , ∴ 1x 1+1x 2=1x 3,∴ x 1,x 2,x 3可以构成“和谐三数组”.(3)A (m,y 1),B (m +1,y 2), C (m +3,y 3)三个点均在反比例函数y =4x 的图象上, y 1=4m ,y 2=4m+1,y 3=4m+3, ∴ 1y 1=m 4,1y 2=m+14,1y 3=m+34,∵ A (m,y 1),B (m +1,y 2), C (m +3,y 3)三点的纵坐标恰好构成“和谐三数组”, ∴ ①1y 1+1y 2=1y 3, ∴ m 4+m+14=m+34, ∴ m =2. ②1y 2+1y 3=1y 1, m+14+m+34=m 4, m =−4.③1y 3+1y 1=1y 2, ∴ m+34+m 4=m+14,m =−2,即满足条件的实数m 的值为2或−4或−2.10.解:(1)49÷5=9...4,但49÷3=16...1,所以49不是“差一数”;74÷5=14...4,74÷3=24...2,所以74是“差一数”.(2)大于300且小于400的数除以5余数为4的有304,309,314,319,324,329,334,339,344,349,354,359,364,369,374,379,384,389,394,399,其中除以3余数为2的有314,329,344,359,374,389.故大于300且小于400的所有“差一数”有314,329,344,359,374,389.。
专题八 新定义问题__2023届中考数学热点题型突破(含答案)

专题八新定义问题——2023届中考数学热点题型突破1.对任意两个实数a,b定义两种运算:并且定义运算顺序仍然是先做括号内的,例如,,,那么等于( )A. B.3 C.6 D.2.我们知道, 如果直角三角形的三边的长都是正整数, 这样的三个正整数就叫做一组勾股数. 定义: 如果一个正整数m能表示为两个正整数a,b的平方和, 即, 那么称m 为广义勾股数. 下面的结论:① 7 不是广义勾股数;②13 是广义勾股数;③两个广义勾股数的和是广义勾股数;④两个广义勾股数的积是广义勾股数;⑤若,,, 其中x,y,z,m,n 均为正整数, 则x,y,z 为一组勾股数;⑥一个正奇数 (除 1 外) 与两个和等于此正奇数的平方的连续正整数是一组勾股数.正确的是( )A.①②⑤⑥B.①③④⑤C.②④⑥D.②④⑤⑥3.对x,y定义一种新运算T,规定:(其中a,b均为非零常数),这里等式右边是通常的四则运算,例如:,若,,则结论正确的个数为( )(1),;(2)若,则;(3)若,m,n均取整数,则或或;(4)若,当n取s,t时,m对应的值为c,d,当时,;(5)若对任意有理数x,y都成立(这里和T均有意义),则A.2个B.3个C.4个D.5个4.阅读材料:定义:如果一个数的平方等于,记为,这个数i叫做虚数单位,把形如为实数)的数叫做复数,其中a叫这个复数的实部,b叫这个复数的虚部.它的加、减、乘法运算与整式的加、减、乘法运算类似:例如计算:;;;.根据以上信息,完成下面的计算:__________.5.定义:在平面直角坐标系xOy中,如果将点绕点旋转得到点Q,那么称线段PQ为“拓展带”,点Q为点P的“拓展带”.(1)当时,点的“拓展带”坐标为__________.(2)如果,当点的“拓展带”N在函数的图象上时,t的值为__________.6.新定义:在平面直角坐标系中,对于点和点,若满足时,;时,,则称点是点的限变点.例如:点的限变点是,则点的限变点是____________.若点在二次函数的图象上,则当时,其限变点的纵坐标的取值范围是____________.7.阅读以下材料:指数与对数之间有密切的联系,它们之间可以互化.对数的定义:一般地,若(且),那么x叫做以a为底N的对数,记作,比如指数式可以转化为对数式,对数式,可以转化为指数式.我们根据对数的定义可得到对数的一个性质:(,,,),理由如下:设,,则,,,由对数的定义得又,.请解决以下问题:(1)将指数式转化为对数式__________;(2)求证:(,,,);(3)拓展运用:计算__________.8.定义如果一个正整数等于两个连续偶数的平方差, 那么称这个正整数为 “奇巧数”.发现数28,32,36 中, 是 “奇巧数” 的是探究已知正奇数的 4 倍一定是 “奇巧数”, 设一个正奇数为 (n为正整数), 请你论证这个结论.9.已知一个三位自然数N, 若满足十位数字与个位数字之和减去百位数字为 0 , 则称这个数为“雪花数”, 并把其十位数字与个位数字的乘积记为. 定义为 “雪花数”, m,n为常数),已知,. 例如: 945,,945是 “雪花数”, ,634,,634不是 “雪花数”.(1)请填空: 817 _______“雪花数”, 527______ “雪花数” (填“是”或“不是”);(2)求出常数m,n的值;(3)已知s 是个位数字不为 1 的 “雪花数”, 其十位数字为, 个位数字为b, 将s的个位数字移到十位上,十位数字移到百位上, 百位数字移到个位上, 得到一个新数, 若s 与的差能被17整除, 求出所有满足条件的s及由这些s两两组合形成的P 的值.答案以及解析1.答案:A解析:,故选A.2.答案:A解析:7 不能表示为两个正整数的平方和, 7不是广义勾股数,故结论①正确., 13是广义勾股数,故结论②正确. 两个广义勾股数的和不一定是广义勾股数, 如 5 和 10 是广义勾股数, 但是它们的和 15 不是广义勾股数, 故结论③错误 . 两个广义勾股数的积不一定是广义勾股数, 如 2 和 2 是广义勾股数, 但,4 不是广义勾股数, 故结论④错误. , 即. 又x,y,z均为正整数, 故结论⑤正确. 设正奇数为 (k为正整数), 2 个连续正整数为p,, 由题意得,,,. 又,p,都是正整数, 结论⑥正确. 综上, 正确结论有①②⑤⑥.故选 A.3.答案:C解析:由题意可知,,,即,解得,故(1)正确;,;,,则;故(2)正确m,n均取整数,,的取值为,,,1,2,4;当,即时,;当,即时,;当,即时,;当,即时,;当,即时,;当,即时,;故(3)不正确,,,,当时,;故(4)正确;,,,,,,对任意有理数x,y都成立(这里和均有意义),则故(5)正确故选C4.答案:解析:.5.答案:①.②.2解析:(1)根据“拓展带”的定义,互为“拓展带”的两点关于点成中心对称,互为“拓展带”的两点的横坐标互为相反数,纵坐标的平均数等于t,点的“拓展带”坐标为.(2)根据“拓展带”的定义,点M和点N关于点成中心对称,设N点坐标为,则,,解得,,在函数的图象上,,解得.6.答案:①.②.解析:,,,点的限变点是,点在二次函数的图象上,当时,,,当时,,当时,,综上,当时,其限变点的纵坐标n'的取值范围是,故答案为:,.7.答案:(1)(2)证明见解析(3)2解析:(1)解:根据指数与对数关系得:.故答案为:;(2)解:设,,则,,,..(3)解:.故答案为:2.8.答案:见解析解析:发现 28,36,,32不是两个连续偶数的平方差,28,36 是“奇巧数”.探究正奇数的 4 倍为.总能表示为两个连续偶数的平方差,正奇数的 4 倍一定是“奇巧数”.9.答案: (1) 是,不是(2)(3)见解析解析:817,, 817 是“雪花数”;527,,527不是 “雪花数”.(2),,,①,,,,②联立①②得解得(3) 由 “雪花数” 的定义可知, 由题意可知, s与的差能被 17 整除,能被 17 整除,为 17 的倍数.s为“雪花数”, 且个位数字不为 1 ,,且,,34,51,68 或 85 .若, 则不符合题意;若, 则符合题意;若, 则符合题意;若, 则此时, 不符合题意;若, 则此时, 不符合题意.综上可得或 615 .。
完整版)北京中考数学新定义题目汇总

完整版)北京中考数学新定义题目汇总28.对于平面内的圆C和圆C外一点Q,定义如下:若过点Q的直线与圆C存在公共点,记为点A、B,设$k=\frac{AQ+BQ}{CQ}$,则称点A(或点B)是圆C的“k相关依附点”。
特别地,当点A和点B重合时,规定$AQ=BQ$,$k=\frac{2AQ^2}{CQ^2}$。
已知在平面直角坐标系$xOy$中,$Q(-1,0)$,$C(1,0)$,圆C的半径为$r$。
1) 当$r=2$时。
①若$A_1(0,1)$是圆C的“k相关依附点”,则$k$的值为$\frac{3}{2}$。
② $A_2(3,0)$是否为圆C的“2相关依附点”:否。
2) 若圆C上存在“k相关依附点”点M。
①当$r=1$,直线QM与圆C相切时,$k$的值为$2$。
②当$k=3$时,$r$的取值范围为$[\sqrt{\frac{3}{2}},2]$。
3) 若存在$r$的值使得直线$y=-3x+b$与圆C有公共点,且公共点是圆C的“3相关依附点”,则$b$的取值范围为$[-2\sqrt{2},2\sqrt{2}]$。
28.在平面直角坐标系$xOy$中,点M的坐标为$(x_1,y_1)$,点N的坐标为$(x_2,y_2)$,且$x_1\neq x_2$,$y_1\neq y_2$,以MN为边构造菱形,若该菱形的两条对角线分别平行于$x$轴,$y$轴,则称该菱形为边的“坐标菱形”。
1) 已知点$A(2,0)$,$B(0,23)$,则以AB为边的“坐标菱形”的最小内角为$60^\circ$。
2) 若点$C(1,2)$,点$D$在直线$y=5$上,以CD为边的“坐标菱形”为正方形,则直线$CD$的表达式为$y=5$。
3) 圆O的半径为2,点$P(m,1)$。
若在圆O上存在一点Q,使得以QP为边的“坐标菱形”为正方形,则$m$的取值范围为$[-1,3]$。
28.对于平面上两点A、B,定义如下:以点A或B为圆心,AB长为半径的圆称为点A、B的“确定圆”。
中考数学最新代数新定义

代数新定义(一)1.在平面直角坐标系中,如果一个点的横坐标与纵坐标相等,则称该点为“实验点”.例如(1,1),(2021,2021)…都是“实验点”.(1)求函数y=﹣2x+1图象上的“实验点”坐标;(2)函数y=kx﹣2(k是常数)的图象上存在“实验点”吗?若存在,请求出“实验点”的坐标;2.已知y是x的函数,若函数图象上存在一点P(a,b),满足b﹣a=2,则称点P为函数图象上“梦幻点”.例如:直线y=2x+1上存在的“梦幻点”P(1,3).(1)求直线上的“梦幻点”的坐标;(2)若二次函数的图象上存在唯一的梦幻点,且﹣2≤m≤3时,n的最小值为t,求t的值.3.定义:若一个函数图象上存在横、纵坐标相等的点,称该点为这个函数图象的“等值点”,该函数称为“等值函数”.例如:“等值函数”y=x+,其图象上的“等值点”为(1,1).(1)在下列关于x的函数中,是“等值函数”的,请在相应题目后面的横线上打“√”.①y=x﹣2 ;②y=x2﹣2x.(2)若点A,点B是“等值函数”y=x2﹣(2m+1)x+(m﹣1)2(其中m>0)上的“等值点”,且8≤AB≤10,求m的取值范围;(3)若“等值函数”y=x2+(m﹣k+2)x+n+k﹣1的图象上存在唯一的一个“等值点”,且当﹣1≤m≤3时,n的最小值为k,求k的值.4.定义:若实数x,y满足x2=y+t,y2=x+t,且x≠y,t为常数,则称点(x,y)为“轮换点”.例如,点(1,﹣2)满足:12=﹣2+3,(﹣2)2=1+3,则点(1,﹣2)是“轮换点”.已知:在直角坐标系xOy中,点A(m,n).(1)A1(3,﹣2)和A2(2,﹣3)两点中,点是“轮换点”;(2)在直角坐标系xOy中,点A(m,n).是“轮换点”求出m与n之间的关系(3)若二次函数上有且仅有一个“轮换点”,且满足:①当x=1时,y=8,②b2﹣4ac=1,求二次函数解析式;(4)若点A是“轮换点”,用含t的代数式表示m•n,并求t的取值范围.5.若实数m、n满足m+n=mn且n≠0时,就称点P(m,)为“完美点”(1)判断点A(2,1),B(1,2)是不是“完美点”;(2)一次函数y=2px+q(p,q为常数)的图象上存在“完美点”吗?若存在,请求出“完美点”的坐标,若不存在,说明理由.(3)直线l:y=﹣x+b的图象经过“完美点”(﹣,t),且直线l与二次函数y=x2﹣kx+k2+3k 有交点C,D(C,D可以重合),设C,D两点的横坐标分别为x1,x2,求x12+x22的最大值.6.在平面直角坐标系中,若点P的纵坐标比横坐标多3,则称点P为“梅花点”,例如点(﹣3,0),(2,5),(,+3),…都是“梅花点”(1)函数y=kx+1(k为常数,且k≠0)的图象上存在“梅花点”吗?若存在,请求出“梅花点”的坐标(用含k的代数式表示);若不存在,请说明理由;(2)若二次函数y=ax2+bx+4(a,b是常数,a>0)的图象上有且只有一个“梅花点”,令s=(2﹣t)b+4a,当0≤b≤2时,试求s的最小值(用含t的代数式表示)7.在平面直角坐标系中,我们不妨把纵坐标的值与横坐标的值的平方相等的点称为“雅心点”,例如点(﹣1,1),(0,0),(,2),…都是“雅心点”,显然,这样的“雅心点”有无数个.(1)求一次函数y=x+2上的所有“雅心点”的坐标为;(2)若过点(1,﹣3)的直线上恰好只有一个“雅心点”,请求出符合要求的直线解析式;8.若二次函数y=ax2+bx+c(a≠0)图象的顶点在一次函数y=kx+t(k≠0)的图象上,则称y=ax2+bx+c(a≠0)为y=kx+t(k≠0)的立信抛物线,y=kx+t(k≠0)为y=ax2+bx+c(a ≠0)的立信直线,如:y=x2是y=x的立信抛物线,y=x是y=x2的立信直线.(1)若y=x2﹣4是y=﹣x+p的立信抛物线,求直线y=﹣x+p与两坐标轴围成的三角形的面积;(2)若直线y=mx﹣3(m≠0)与其立信抛物线y=x2+2x+n的两个交点间的距离为,求m,n的值.代数新定义(二)1.我们不妨约定:在平面直角坐标系中,若某函数图象上至少存在不同的两点关于直线x=n(n为常数)对称,则把该函数称之为“X(n)函数”.(1)在下列关于x的函数中,是“X(n)函数”的是(填序号);①y=|4x|;②y=x2﹣2x﹣5.(2)若关于x的“X(n)函数”y=ax2+bx+4(a,b为常数)经过点(﹣1,1),且n=1,当t﹣1≤x≤t时,函数的最大值为y1,最小值为y2,且y1﹣y2=,求t的值.2.在平面直角坐标系中,我们把横坐标与纵坐标相等的点(a,a)叫做“至善点”,显然,这样的“至善点”有无数个,两个“至善点”(x1,x1),(x2,x2)之间的距离d=,叫做“至美距离”.(1)求函数y=x2﹣2x+2的图象的“至善点”,并求出“至美距离”;(2)求函数y=x2+mx﹣m上两个“至善点”之间的“至美距离”的最小值;(3)若二次函数y=ax2+bx+1(a,b是常数,a>0)的图象上存在两个不同的“至善点”A (x1,x1)、B(x2,x2),且满足﹣2≤x1≤2,且A、B两点之间的“至美距离”为2,求代数式b2﹣2b+5的取值范围.3.定义:在平面直角坐标系中,图形G上的点P(x,y)的横坐标x和纵坐标y的和x+y称为点P的“横纵和”,而图形G上所有点的“横纵和”中最小的值称为图形的“极小和”.(1)抛物线y=x2﹣2x﹣2的图象上点P(1,﹣3)的“横纵和”是;该抛物线的“极小和”是.(2)记抛物线y=x2﹣(2m+1)x﹣2的“极小和”为s,若﹣2021≤s≤﹣2020,求m 的取值范围.(3)已知二次函数y=x2+bx+c(c≠0)的图象上的点A(,2c)和点C(0,c)的“横纵和”相等,求该二次函数的“极小和”.这个“极小和”是否有最大值?如果有,请求出这个最大值;如果没有,请说明理由.4.定义:若x0=ax02+bx0+c成立,则称点(x0,x0)为抛物线y=ax2+bx+c(a≠0)上的不动点,设抛物线C的解析式为:y=ax2+(b+1)x+b﹣1(a≠0)(1)当a=1,b=4时,判断M(﹣1,﹣1),N(﹣2,﹣2),P(﹣3,﹣3)是否是C 上的不动点.(2)若抛物线C过点(0,﹣3),且抛物线C上有一个不动点(1,1),求抛物线上的另一个不动点.(3)对于任意实数b,抛物线C上总有两个不同的不动点,令S=,求S的取值范围.5.如果一个函数的图象与直线y=3x+4有交点,则称该函数为“三高四新函数”,交点为该函数的“新高点”.(1)判断下列函数是不是“三高四新函数”,是“三高四新函数”的请在相应题目后面的括号中打“√”,不是“三高四新函数”的打“×”.①y=3x﹣4 ;②y=﹣x2+x+3 .(2)若关于x的二次函数y=ax2+(2b+3)x+(c+4)有两个不同的“新高点”,不妨将这两个点设为A(x1,y1),B(x2,y2),且二次函数还满足以下三个条件:①开口向上;②a+b+c=0;③a>2b>3c.求|y1﹣y2|的取值范围?6.我们不妨约定:若某一函数图象经过点P(x0,x0),则点P(x0,x0)称为该函数的“不动点”,两个“不动点”之间的距离称为“不动长度”L.特别地,若函数只有一个“不动点”,则规定“不动长度”L=0.例如:函数y=x2图象上存在两个“不动点”A(0,0)、B(1,1),则其“不动长度”L=|AB|=.(1)一次函数y=3x﹣1的“不动点”是;(2)若二次函数y=x2﹣mx+m的“不动长度”L=6,求m的值;(3)若关于x的函数y=ax2+(2b+1)x+c存在两个“不动点”并且同时满足:①a+b+c =0,②a>b>c,求“不动长度”L的取值范围.7.在平面直角坐标系内,已知任意两点的坐标A(x1,y1),B(x2,y2),我们把|x1﹣x2|称为A、B两点的“云距离”,记作=|x1﹣x2|.例如:A(3,4),B(0,1),则=|3﹣0|=3.(1)①若A(1,2),B(3,4),则=.②若点A(x1,2),B(x2,﹣6),当A、B都在函数y=2x的函数图象上时,=(2)若抛物线y=ax2+bx+c(a≠0)与直线y=﹣2bx﹣3c(b≠0)在同一坐标平面内交于A (x1,y1),B(x2,y2),且满足下列两个条件:①a>2b>3c,②抛物线过(1,0),试求的取值范围8.我们不妨约定:若某函数图象上至少存在不同的两点关于原点对称,则把该函数称之为“D函数”,其图象上关于原点对称的两点叫做一对“D点”根据该约定,完成下列各题.(1)在下列关于x的函数中,是“D函数”的,请在相应题目后面的括号中打“√”,不是“D函数”的打“x,y=3x﹣1();y=2x();(2)若点A(1,m)与点B(n,﹣4)是关于x的“D函数”y=ax2+bx+c(a≠0)的一对“D点”,且该函数的对称轴始终位于直线x=1的右侧,求a,b,c的值或取值范围;(3)若关于x的“D函数”y=ax2+2bx+3c(a,b,c是常数)同时满足下列两个条件:①a+b+c=0;②(2c+b﹣a)(2c+b+3a)<0.求该“D函数”截x轴得到的线段长度的取值范围.代数新定义(三)1.定义:与坐标轴不重合的直线交坐标轴于A、B两点(A、B不重合),若抛物线L过点A,点B,则称此抛物线为直线的“友谊线”(1)若抛物线L为直线y=﹣x+3的“友谊线”,且过点(﹣1,0),求此抛物线的解析式;(2)若有直线y=mx+n,且m+n=1,对任意的实数a,一定存在其“友谊线”为抛物线L:y=ax2+bx+c,求b的取值范围.2.在平面直角坐标系中,将一点(横坐标与纵坐标不相等)横坐标与纵坐标互换后得到的点叫这一点的“H点”,如(2,﹣3)与(﹣3,2)是一对“H点”.(1)点(m,n)和它的“H点“均在直线y=kx+a上,求k的值;(2)已知A(m,n)(m<n),B为抛物线y=ax2+bx+c上的一对“H点”,且满足:m+n =2,mn=﹣3,点P为抛物线上一动点,若该抛物线上有且仅存在3个点P满足△P AB 的面积为16,求a+b+c的值.3.规定:我们把直线l:y=ax+b叫做抛物线L:y=ax2+bx的“温暖直线”.若该直线与该抛物线的图象还有两个不同的交点,则两个交点叫做“幸福点”,并且称直线l与抛物线L 具备“温暖而幸福关系”,否则称直线l与抛物线L不具备“温暖而幸福关系”.(1)已知直线l:y=ax﹣4是抛物线L:y=2x2+bx的“温暖直线”,请判断直线l与抛物线L是否具备“温暖而幸福关系”,若具备,请求出“幸福点”的坐标,若不具备,请说明理由;(2)已知直线l:y=ax+b与抛物线L:y=ax2+bx不具备“温暖而幸福关系”,当0≤x ≤2时,抛物线L:y=ax2+bx的最小值是﹣6,求直线l的解析式;4.若将函数F的图象沿直线l对折,与函数G的图象重合,则称函数F与G互为“轴对称函数”,直线l叫作函数F与函数G的“轴直线”.如函数y=2x关于直线y轴的轴对称函数是y=﹣2x.(1)若轴直线为x轴,求函数y=x+1的关于x轴的轴对称函数的解析式;(2)若函数F:y=﹣x2+9,轴直线为x=1,函数F的轴对称函数是G,求函数G的解析式5.如果一个函数y=f(x)图象上存在点A(a,b)(a≠0),且3a=4b,那么我们称该函数y =f(x)为“三高四新”函数,把点A(a,b)叫做该函数的“三高四新”焦点.(1)判断函数y=2x﹣1是否为“三高四新”函数,如果是,请求出“三高四新”焦点,如果不是,请说明理由;(2)已知函数y=x2+(k﹣1)x+1是“三高四新”函数,且有唯一的“三高四新”焦点,求函数y=x2+(k﹣1)x+1的“三高四新”焦点;(3)已知二次函数y=ax2+bx+c(a≠0)的两个“三高四新”焦点M、N(M点在N点左侧),一次函数y=bx+(b≠0)的“三高四新”焦点P,且满足①a+b+c=0;②4a﹣4b+3≠0;③MN=;④焦点M、N关于P点对称,求“三高四新”函数y=ax2+bx+c(a≠0)的焦点.6.定义:在平面直角坐标系中,对于任意两点A(x1,y1),B(x2,y2),如果点C(x,y)满足x=x1﹣x2,y=y1﹣y2,那么称点C是点A,B的“双减点”.例如:A(3,2),B(﹣1,5),当点C(x,y)满足x=3﹣(﹣1)=4,y=2﹣5=﹣3,则称点C(4,﹣3)是点A,B的“双减点”.(1)写出点A(﹣1,2),B(2,﹣4)的“双减点”C的坐标,并且判断点C是否在直线AB上;(2)点E(t,y1),F(t+1,y2),点G(x,y)是点E,F的“双减点”,是否存在非零实数k,使得点E,F,G均在函数y=的图象上,若存在,求实数k的值,若不存在,请说明理由;(3)已知二次函数y=ax2+2bx﹣2(a>b>0)的图象经过点(2,6),且与x轴交于点M(x1,0),N(x2,0),若点P为M,N的“双减点”,求点P与原点O的距离OP的取值范围.7.若一次函数y=kx+m的图象经过二次函数y=ax2+bx+c的顶点,我们则称这两个函数为“丘比特函数组”(1)请判断一次函数y=﹣3x+5和二次函数y=x2﹣4x+5是否为“丘比特函数组”,并说明理由.(2)若一次函数y=x+2和二次函数y=ax2+bx+c为“丘比特函数组”,已知二次函数y =ax2+bx+c顶点在二次函数y=2x2﹣3x﹣4图象上并且二次函数y=ax2+bx+c经过一次函数y=x+2与y轴的交点,求二次函数y=ax2+bx+c的解析式;(3)当﹣3≤x≤﹣1时,二次函数y=x2﹣2x﹣4的最小值为a,若“丘比特函数组”中的一次函数y=2x+3和二次函数y=ax2+bx+c(b、c为参数)相交于PQ两点请问PQ的长度为定值吗?若是,请求出该定值;若不是,请说明理由.代数新定义(四)1.已知两个函数,如果对于任意的自变量x,这两个函数对应的函数值记为y1,y2,都有点(x,y1)、(x,y2)关于点(x,x)对称,则称这两个函数为关于y=x的对称函数,例如,y1=x和y2=x为关于y=x的对称函数.(1)判断:①y1=3x和y2=﹣x;②y1=x+1和y2=x﹣1;③y1=x2+1和y2=x2﹣1,其中为关于y=x的对称函数的是(填序号)(2)若y1=3x+2和y2=kx+b(k≠0)为关于y=x的对称函数.①求k、b的值.②对于任意的实数x,满足x>m时,y1>y2恒成立,则m满足的条件为.(3)若y1=ax2+bx+c(a≠0)和y2=x2+n为关于y=x的对称函数,且对于任意的实数x,都有y1<y2,请结合函数的图象,求n的取值范围.2.定义:在平面直角坐标系xOy中,称两个不同的点P(m,n)和点Q(﹣n,﹣m)为“云对称点”.如:点(﹣3,1)和(﹣1,3)是一对“云对称点”.(1)下列函数中,其图象上至少存在一对“云对称点”的,请在相应题目后面的横线上打“√”,不存在的打“×”.①y=2x;②y=﹣x+4 ;(2)抛物线y=x2+9x上是否存在一对“云对称点”?如果存在,请求出这一对“云对称点”所连线段的中点坐标;如果不存在,请说明理由.3.在y关于x的函数中,对于实数a,b(b>a),当a≤x≤b时,函数y有最大值y max,满足y max=2(b﹣a),则称函数为“倍增函数”.(1)当a=1,b=3时,判断下列函数是否为“倍增函数”?如果是,请在对应_____内画“√”,如果不是,请在对应_____内画“×”;①y=2x;②y=﹣2x+2 ;③.(2)已知二次函数y=x2﹣bx+a2+2a﹣1是“倍增函数”,且y有最大值4,求实数a的值.4.设a、b是任意两个不等实数,我们规定:①不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].②对于一个函数,它的自变量x的取值范围叫做函数的定义域,函数y的取值范围叫做函数的值域.函数y=2x定义域为[1,2]时,其值域为[2,4].(1)若一次函数y=﹣x+3,定义域为[﹣6,2]时,求这个函数的值域.(2)若一次函数y=kx+b(k≠0),定义域为[2,3]时,它的值域为[3,5],求这个一次函数解析式.(3)若二次函数y=x2﹣2mx+n,其定义域为[2,6]时,其值域为[﹣2,7],求m,n的值.5.设a、b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m ≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m,n]上的“闭函数”.(1)正比例函数y=x是闭区间[1,2021]上的“闭函数”吗?请判断并说明理由;(2)若一次函数y=kx+3(k≠0)是闭区间[m,n]上的“闭函数”,求此函数的解析式;(3)若二次函数y=(x﹣h)2+k是闭区间[2,3]上的“闭函数”,求实数h,k的值.6.我们把函数图象上横坐标与纵坐标互为相反数的点定义为这个函数图象上的“互反点”.例如在二次函数y=x2的图象上,存在一点P(﹣1,1),则点P为二次函数y=x2图象上的“互反点”.(1)求一次函数y=﹣2x﹣3的“互反点”.(2)若二次函数y=x2﹣(2a+1)x+a只有一个“互反点”,且与y轴交于正半轴,求当1≤x≤3时,y的取值范围.(3)若对于任意的实数n,在二次函数y=(m+1)x2+nx+n﹣1的图象上,恒有两个相异的“互反点”,求m的取值范围.7.在平面直角坐标系xOy中,对于点P(a,b)和Q(a,b'),给出如下定义:若b'=,则称点Q为点P关于m的值变点.例如:点(2,3)关于1的值变点的坐标是(2,3),点(﹣2,5)关于1的值变点的坐标是(﹣2,﹣5).(1)点(﹣3,1)关于﹣1的值变点坐标是;(2)若点P在函数y=﹣2x+3的图象上,其关于0的值变点Q的纵坐标b'=﹣4,求值变点Q的横坐标;(3)已知点M(﹣3,1),N(1,﹣3),若点P在关于x的二次函数y=x2+2x+t2﹣t的图象上,当且仅当存在两个点P使其关于﹣2的值变点Q在线段MN上,求t的取值范围.8.若三个非零实数x,y,z满足:只要其中一个数的倒数等于另外两个数的倒数的和,则称这三个实数x,y,z构成“和谐三组数”.(1)实数1,2,3可以构成“和谐三组数”吗?请说明理由;(2)若M(t,y1),N(t+1,y2),R(t+3,y3)三点均在函数y=(k为常数,k≠0)的图象上,且这三点的纵坐标y1,y2,y3构成“和谐三组数”,求实数t的值;(3)若直线y=2bx+2c(bc≠0)与x轴交于点A(x1,0),与抛物线y=ax2+3bx+3c(a ≠0)交于B(x2,y2),C(x3,y3)两点.①求证:A,B,C三点的横坐标x1,x2,x3构成“和谐三组数”;②若a>2b>3c,x2=1,求点P(,)与原点O的距离OP的取值范围.9.定义:用函数的最值来判定参数的取值范围,这种方法称为“最值判定法”.例如:当﹣1≤x≤2时,x+a≤0恒成立,求a的取值范围.可令y=x+a,因为y随x的增大而增大,所以当x取最大值2时,对应的y取最大值2+a,由2+a≤0,得a≤﹣2.(1)若当﹣1≤x≤1时,不等式﹣x2+ax﹣3≤x恒成立,求实数a的取值范围.(2)若当﹣1≤x≤1时,二次函数y=﹣x2+(a﹣1)x﹣3有最大值a,求实数a的值.10.设a为任意的一个实数,我们规定,满足不等式a≤x≤a+2的实数x的所有取值的全体叫做和谐区间,表示为[a,a+2],对于一个函数,如果它的自变量x与函数值y满足:当a≤x≤a+2时,有y≥a+2,我们就称此函数是和谐区间[a,a+2]上的“和谐函数”(1)当a=1时,反比例函数y=是和谐区间[a,a+2]上的“和谐函数”吗?请判断并说明理由;(2)当a=k时,若关于x的一次函数y=kx+2(k≠0)是和谐区间[a,a+2]上的“和谐函数”,求k的取值范围.(3)若关于x的二次函数y=x2+mx+3﹣m是和谐区间[0,2]上的“和谐函数”,求m的取值范围.11.若“子函数”y1、y2满足y=y1+y2,则称函数y是“子函数”y1、y2的“母函数”.例如,“子函数”分别为一次函数y1=x+1和二次函数y2=x2+2x﹣3,则“子函数”y1、y2的“母函数”为y=y1+y2=x2+3x﹣2.(1)“子函数”分别为反比例函数y1=和一次函数y2=kx﹣1,它们的“母函数”过点(1,5),求k的值;(2)若“子函数”y1=ax2+bx+c为二次函数,且a+b+c=3,在x=t时取得最值,“子函数”y2是一次函数,且“母函数”为y=x2+2x﹣3,当﹣2≤x≤3时,求“子函数”y1的最小值(用含t的式子表示);(3)“子函数”分别为二次函数y1=ax2+bx+c与一次函数y2=﹣ax﹣b,其中a+b+c=0且a>b>c,若它们的“母函数”与x轴交点为A(x1,0)、B(x2,0),求|x1﹣x2|的取值范围.。
中考数学新定义题型专题复习(最新整理)

考点三:探索题型中的新定义3 + 2(一)专题诠释新定义型专题所谓“新定义”型问题,主要是指在问题中定义了中学数学中没有学过的一些概念、新运算、 新符号,要求学生读懂题意并结合已有知识、能力进行理解,根据新定义进行运算、推理、迁移的一种题型.“新定义”型问题成为近年来中考数学压轴题的新亮点.在复习中应重视学生应用新的知识解决问题的能力(二)解题策略和解法精讲“新定义型专题”关键要把握两点:一是掌握问题原型的特点及其问题解决的思想方法; 二是根据问题情景的变化,通过认真思考,合理进行思想方法的迁移.(三)考点精讲考点一:规律题型中的新定义例 1.定义:a 是不为 1 的有理数,我们把 1 1- a 称为 a 的差倒数.如:2 的差倒数是 11- 2= -1,-1 1 11 的差倒数是 = .已知 a 1=- ,a2 是 a 1 的差倒数,a3 是 a 2 的差倒数,a 41- (-1) 2 3是 a 3 的差倒数,…,依此类推,a 2009=.考点二:运算题型中的新定义例 2.对于两个不相等的实数 a 、b ,定义一种新的运算如下, a *b = a + ba +b >0),如:( a ﹣b3* 2 = = 3﹣2,那么 6*(5*4)=.ab 例 3.我们定义 cd = ad - bc ,例如23=2×5﹣3×4=10﹣12=﹣2,若 x ,y 均为整数,且满足 1<1x <45y 43,则 x+y 的值是 .5例4.定义:到凸四边形一组对边距离相等,到另一组对边距离也相等的点叫凸四边形的准内点.如图1,PH=PJ,PI=PG,则点P 就是四边形ABCD 的准内点.(1)如图2,∠AFD 与∠DEC 的角平分线FP,EP 相交于点P.求证:点P 是四边形ABCD 的准内点.(2)分别画出图3 平行四边形和图4 梯形的准内点.(作图工具不限,不写作法,但要有必要的说明)(3)判断下列命题的真假,在括号内填“真”或“假”.①任意凸四边形一定存在准内点.()②任意凸四边形一定只有一个准内点.()③若P 是任意凸四边形ABCD 的准内点,则PA+PB=PC+PD 或PA+PC=PB+PD.()考点四:阅读材料题型中的新定义阅读材料我们经常通过认识一个事物的局部或其特殊类型,来逐步认识这个事物;比如我们通过学习两类特殊的四边形,即平行四边形和梯形(继续学习它们的特殊类型如矩形、等腰梯形等)来逐步认识四边形;我们对课本里特殊四边形的学习,一般先学习图形的定义,再探索发现其性质和判定方法,然后通过解决简单的问题巩固所学知识;请解决以下问题:如图,我们把满足AB=AD、CB=CD 且AB≠BC 的四边形ABCD 叫做“筝形”;(1)写出筝形的两个性质(定义除外);(2)写出筝形的两个判定方法(定义除外),并选出一个进行证明.真题演练1.定义运算a ⊗b=a(1﹣b),下列给出了关于这种运算的几点结论:①2 ⊗(﹣2)=6;②a ⊗b=b ⊗a;③若a+b=0,则(a ⊗b)+(b ⊗a)=2ab;④若a ⊗b=0,则a=0.其中正确结论序号是.(把在横线上填上你认为所有正确结论的序号)2.如果一条直线把一个平面图形的面积分成相等的两部分,我们把这条直线称为这个平面图形的一条面积等分线,例如平行四边形的一条对角线所在的直线就是平行四边形的一条面积等分线.(1)三角形的中线、高线、角平分线分别所在的直线一定是三角形的面积等分线的有;(2)如图,梯形ABCD 中,AB∥DC,如果延长DC 到E,使CE=AB,连接AE,那么有S梯形ABCD=S△ADE.请你给出这个结论成立的理由,并过点A 作出梯形ABCD 的面积等分线(不写作法,保留作图痕迹);(3)如图,四边形ABCD 中,AB 与CD 不平行,S△ADC>S△ABC,过点A 能否作出四边形ABCD 的面积等分线?若能,请画出面积等分线,并给出证明;若不能,说明理由.3.如图,六边形ABCDEF 是正六边形,曲线FK1K2K3K4K5K6K7……叫做“正六边形的渐开线”,其中 F K 1 , K 1K 2 , K 2 K 3 , K 3 K 4 , K 4 K 5 , K 5 K 6,……的圆心依次按点 A ,B , C ,D ,E ,F 循环,其弧长分别记为 l 1,l 2,l 3,l 4,l 5,l 6,…….当 AB =1 时,l 2 011等于( )A.2011 2B.2011 3C.2011 4D.2011 6K 5K 6K 4D ECF B A K 1 K 3K 2 (第 12 题图)一、选择题1 11、定义一种运算☆,其规则为 a ☆b = + ,根据这个规则,计算 2☆3 的值是()A. 56B. 1 5 a bC.5D.62.在快速计算法中,法国的“小九九”从“一一得一”到“五五二十五”和我国的“小九九”算法是完全一样的,而后面“六到九”的运算就改用手势了.如计算 8×9 时,左手伸出 3 根手指,右手伸出 4 根手指,两只手伸出手指数的和为 7, 未伸出手指数的积为 2,则 8×9=10×7+2=72.那么在计算 6×7 时,左、右手伸出的手指数应该分别为( )A 、1,2B 、1,3C 、4,2D 、4,33.(2010 浙江杭州,10,3 分)定义[ a , b , c ]为函数 y = a x 2+ bx c 的特征数,下面给出特征数为[2m ,1﹣m ,﹣1﹣m]的函数的一些结论:①当 m =﹣3 时,函数图象的顶点坐标是( 1 , 8);3 3②当 m >0 时,函数图象截 x 轴所得的线段长度大于 3;2③当 m <0 时,函数在 x > 1时, y 随 x 的增大而减小;4 ④当 m≠0 时,函数图象经过同一个点. 其中正确的结论有()A 、①②③④B 、①②④C 、①③④D 、②④二、填空题4.通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的K 7( ) ( ) 比值相互唯一确定,因此边长与角的大小之间可以相互转化。
2024中考数学新定义及探究题专题 《二次函数及新定义》 (含解析)

2024中考数学新定义及探究题专题《二次函数及新定义》(学生版)【类型1二次函数问题中的新定义问题】1.(2023春·山东济南·九年级统考期末)新定义:若一个点的纵坐标是横坐标的2倍,则称这个点为二倍点.若二次函数(c为常数)在的图象上存在两个二倍点,则c的取值范围是()A.B.C.D.2.(2023春·湖北咸宁·九年级统考期中)定义:我们将顶点的横坐标和纵坐标互为相反数的二次函数称为“互异二次函数”.若互异二次函数的对称轴为直线x=1且图象经过点(﹣1,0),则这个互异二次函数的二次项系数是()A.B.C.1D.﹣13.(2023春·广西南宁·九年级统考期中)新定义:在平面直角坐标系中,对于点P(m,n)和点P′(m,n′),若满足m≥0时,n′=n-4;m<0时,n′=-n,则称点P′(m,n′)是点P(m,n)的限变点.例如:点P1(2,5)的限变点是P1′(2,1),点P2(-2,3)的限变点是P2′(-2,-3).若点P(m,n)在二次函数y=-x2+4x+2的图象上,则当-1≤m≤3时,其限变点P′的纵坐标n'的取值范围是()A.B.C.D.4.(2023春·湖南长沙·九年级长沙市开福区青竹湖湘一外国语学校校考期末)定义:我们不妨把纵坐标是横坐标2倍的点称为“青竹点”.例如:点、……都是“青竹点”.显然,函数的图象上有两个“青竹点”:和.(1)下列函数中,函数图象上存在“青竹点”的,请在横线上打“√”,不存在“青竹点”的,请打“×”.①________;②________;③________.(2)若抛物线(m为常数)上存在两个不同的“青竹点”,求m的取值范围;(3)若函数的图象上存在唯一的一个“青竹点”,且当时,a的最小值为c,求c的值.5.(2023春·江苏泰州·九年级统考期中)定义:两个二次项系数之和为,对称轴相同,且图像与轴交点也相同的二次函数互为友好同轴二次函数.例如:的友好同轴二次函数为.(1)函数的友好同轴二次函数为.(2)当时,函数的友好同轴二次函数有最大值为,求的值.(3)已知点分别在二次函数及其友好同轴二次函数的图像上,比较的大小,并说明理由.6.(2023春·浙江金华·九年级校考期中)定义:若抛物线y=ax2+bx+c与x轴两交点间的距离为4,称此抛物线为定弦抛物线.(1)判断抛物线y=x2+2x﹣3是否是定弦抛物线,请说明理由;(2)当一定弦抛物线的对称轴为直线x=1,且它的图像与坐标轴的交点间的连线所围成的图形是直角三角形,求该抛物线的表达式;(3)若定弦抛物线y=x2+bx+c(b<0)与x轴交于A、B两点(A在B左边),当2≤x≤4时,该抛物线的最大值与最小值之差等于OB之间的距离,求b的值.7.(2023春·浙江·九年级期末)定义:若抛物线与抛物线.同时满足且,则称这两条抛物线是一对“共轭抛物线”.(1)已知抛物线与是一对共轭抛物线,求的解析式;(2)如图1,将一副边长为的正方形七巧板拼成图2的形式,若以BC中点为原点,直线BC为x轴建立平面直角坐标系,设经过点A,E,D的抛物线为,经过A、B、C的抛物线为,请立接写出、的解析式并判断它们是否为一对共轭抛物线.8.(2023春·湖南长沙·九年级校联考期末)定义:如果抛物线与轴交于点,,那么我们把线段叫做雅礼弦,两点之间的距离称为抛物线的雅礼弦长.(1)求抛物线的雅礼弦长;(2)求抛物线的雅礼弦长的取值范围;(3)设,为正整数,且,抛物线的雅礼弦长为,抛物线的雅礼弦长为,,试求出与之间的函数关系式,若不论为何值,恒成立,求,的值.9.(2023春·河南濮阳·九年级统考期中)小明在课外学习时遇到这样一个问题:定义:如果二次函数y=a1x2+b1x+c1(a1≠0)与y=a2x2+b2x+c2(a2≠0)满足a1+a2=0,b1=b2,c1+c2=0,则称这两个函数互为“旋转函数”.求函数y=x2-3x-2的“旋转函数”.小明是这样思考的:由函数y=x2-3x-2可知,a1=1,b1=-3,c1=-2,根据a1+a2=0,b1=b2,c1+c2=0,求出a2,b2,c2,就能确定这个函数的“旋转函数”.请参考小明的方法解决下面问题:(1)直接写出函数y=x2-3x-2的“旋转函数”;(2)若函数与y=x2-2nx+n互为“旋转函数”,求(m+n)2020的值;(3)已知函数的图象与x轴交于点A、B两点(A在B的左边),与y轴交于点C,点A、B、C关于原点的对称点分别是A1,B1,C1,试证明经过点A1,B1,C1的二次函数与函数互为“旋转函数”10.(2023春·山西大同·九年级统考期中)请阅读下列材料,并完成相应的任务:定义:我们把自变量为的二次函数与(,)称为一对“亲密函数”,如的“亲密函数”是.任务:(1)写出二次函数的“亲密函数”:______;(2)二次函数的图像与轴交点的横坐标为1和,它的“亲密函数”的图像与轴交点的横坐标为______,猜想二次函数()的图像与轴交点的横坐标与其“亲密函数”的图像与轴交点的横坐标之间的关系是______;(3)二次函数的图像与轴交点的横坐标为1和,请利用(2)中的结论直接写出二次函数的图像与轴交点的横坐标.【类型2二次函数与一次函数综合问题中的新定义问题】1.(2023春·九年级课时练习)定义:由a,b构造的二次函数叫做一次函数y=ax+b的“滋生函数”,一次函数y=ax+b叫做二次函数的“本源函数”(a,b为常数,且).若一次函数y=ax+b的“滋生函数”是,那么二次函数的“本源函数”是.2.(2023春·浙江湖州·九年级统考期中)定义:如果函数图象上存在横、纵坐标相等的点,则称该点为函数的不动点.例如,点是函数的不动点.已知二次函数(是实数).(1)若点是该二次函数的一个不动点,求的值;(2)若该二次函数始终存在不动点,求的取值范围.3.(2023·安徽·模拟预测)已知函数与函数,定义“和函数”.(1)若,则“和函数”;(2)若“和函数”为,则,;(3)若该“和函数”的顶点在直线上,求.4.(2023·北京·模拟预测)城市的许多街道是相互垂直或平行的,因此,往往不能沿直线行走到达目的地,只能按直角拐弯的方式行走.可以按照街道的垂直和平行方向建立平面直角坐标系,对两点和,用以下方式定义两点间距离:.(1)①已知点,则______.②函数的图象如图①所示,是图象上一点,,求点的坐标.(2)函数的图象如图②所示,是图象上一点,求的最小值及对应的点的坐标.5.(2023春·上海·九年级上海市民办新复兴初级中学校考期中)我们定义【,,】为函数的“特征数”,如:函数的“特征数”是【2,,5】,函数的“特征数”是【0,1,2】(1)若一个函数的“特征数”是【1,,1】,将此函数图像先向左平移2个单位,再向上平移1个单位,得到一个图像对应的函数“特征数”是______;(2)将“特征数”是【0,,】的图像向上平移2个单位,得到一个新函数,这个函数的解析式是______;(3)在(2)中,平移前后的两个函数图像分别与轴交于A、两点,与直线分别交于、两点,在给出的平面直角坐标系中画出图形,并求出以A、、、四点为顶点的四边形的面积;(4)若(3)中的四边形与“特征数”是【1,,】的函数图像有交点,求满足条件的实数的取值范围.6.(2023春·福建龙岩·九年级校考期末)定义:对于给定的两个函数,任取自变量x的一个值,当x<0时,它们对应的函数值互为相反数;当x≥0时,它们对应的函数值相等.我们称这样的两个函数互为相关函数.例如:一次函数,它的相关函数为(1)已知点A(-2,1)在一次函数的相关函数的图象上时,求a的值.(2)已知二次函数.当点B(m,)在这个函数的相关函数的图象上时,求m的值.7.(2023春·江苏南通·九年级统考期末)定义:若图形与图形有且只有两个公共点,则称图形与图形互为“双联图形”,即图形是图形的“双联图形”,图形是图形的“双联图形”.(1)若直线与抛物线互为“双联图形”,且直线不是双曲线的“双联图形”,求实数的取值范围;(2)如图2,已知,,三点.若二次函数的图象与互为“双联图形”,直接写出的取值范围.8.(2023春·北京·九年级北京市第三中学校考期中)定义:在平面直角坐标系中,图形G 上点P(x,y)的纵坐标y与其横坐标x的差y﹣x称为P点的“坐标差”,而图形G上所有点的“坐标差”中的最大值称为图形G的“特征值”.(1)①点A(1,3)的“坐标差”为;②抛物线y=﹣x2+3x+3的“特征值”为;(2)某二次函数y=﹣x2+bx+c(c≠0)的“特征值”为1,点B(m,0)与点C分别是此二次函数的图象与x轴和y轴的交点,且点B与点C的“坐标差”相等.①直接写出m=;(用含c的式子表示)②求b的值.9.(2023春·北京·九年级人大附中校考期中)对某一个函数给出如下定义:若存在实数,对于任意的函数值,都满足,则称这个函数是有界函数,在所有满足条件的中,其最小值称为这个函数的边界值.例如,如图中的函数是有界函数,其边界值是.(1)直接写出有界函数的边界值;(2)已知函数是有界函数,且边界值为3,直接写出的最大值;(3)将函数的图象向下平移个单位,得到的函数的边界值是,直接写出的取值范围,使得.10.(2023春·湖南长沙·九年级校考期中)若定义:若一个函数图像上存在纵坐标是横坐标2倍的点,则把该函数称为“明德函数”,该点称为“明德点”,例如:“明德函数”,其“明德点”为(1,2).(1)①判断:函数__________“明德函数”(填“是”或“不是”);②函数的图像上的明德点是___________;(2)若抛物线上有两个“明德点”,求m的取值范围;(3)若函数的图像上存在唯一的一个“明德点”,且当时,的最小值为,求的值.【类型3二次函数与几何图形综合问题中的新定义问题】1.(2023春·四川绵阳·九年级统考期末)定义:我们将顶点的横坐标和纵坐标互为相反数的二次函数称为“互异二次函数”.如图,在正方形中,点,点,则互异二次函数与正方形有交点时的最大值和最小值分别是()A.4,-1B.,-1C.4,0D.,-1 2.(2023春·山东济南·九年级统考期末)定义:关于x轴对称且对称轴相同的两条抛物线叫作“同轴对称抛物线”.例如:y1=(x﹣1)2﹣2的“同轴对称抛物线”为y2=﹣(x﹣1)2+2.(1)请写出抛物线y1=(x﹣1)2﹣2的顶点坐标;及其“同轴对称抛物线”y2=﹣(x﹣1)2+2的顶点坐标;(2)求抛物线y=﹣2x2+4x+3的“同轴对称抛物线”的解析式.(3)如图,在平面直角坐标系中,点B是抛物线L:y=ax2﹣4ax+1上一点,点B的横坐标为1,过点B作x轴的垂线,交抛物线L的“同轴对称抛物线”于点C,分别作点B、C关于抛物线对称轴对称的点、,连接BC、、、.①当四边形为正方形时,求a的值.②当抛物线L与其“同轴对称抛物线”围成的封闭区域内(不包括边界)共有11个横、纵坐标均为整数的点时,直接写出a的取值范围.3.(2023春·北京门头沟·九年级大峪中学校考期中)定义:对于平面直角坐标系上的点和抛物线,我们称是抛物线的相伴点,抛物线是点的相伴抛物线.如图,已知点,,.(1)点的相伴抛物线的解析式为______;过,两点的抛物线的相伴点坐标为______;(2)设点在直线上运动:①点的相伴抛物线的顶点都在同一条抛物线上,求抛物线的解析式.②当点的相伴抛物线的顶点落在内部时,请直接写出的取值范围.4.(2023春·浙江绍兴·九年级校联考期中)定义:如图1,抛物线与x轴交于A,B两点,点P在该抛物线上(P点与A.B两点不重合),如果△ABP中PA与PB两条边的三边满足其中一边是另一边倍,则称点P为抛物线的“好”点.(1)命题:P(0,3)是抛物线的“好”点.该命题是_____(真或假)命题.(2)如图2,已知抛物线C:与轴交于A,B两点,点P(1,2)是抛物线C的“好”点,求抛物线C的函数表达式.=S△AB P的Q点(异于点P)的(3)在(2)的条件下,点Q在抛物线C上,求满足条件S△ABQ坐标.5.(2023·安徽安庆·九年级统考期末)在平面直角坐标系中,我们定义直线y=ax-a为抛物线y=ax2+bx+c(a、b、c为常数,a≠0)的“梦想直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.已知抛物线y=-与其“梦想直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.(1)填空:该抛物线的“梦想直线”的解析式为______,点A的坐标为______,点B的坐标为______.(2)如图,点M为线段CB上一动点,将△ACM以AM所在直线为对称轴翻折,点C的对称点为N,若△AMN为该抛物线的“梦想三角形”,求点M的坐标.6.(2023春·湖南长沙·九年级统考期中)定义:在线段MN上存在点P、Q将线段MN分为相等的三部分,则称P、Q为线段MN的三等分点.已知一次函数y=﹣x+3的图象与x、y轴分别交于点M、N,且A、C为线段MN的三等分点(点A在点C的左边).(1)直接写出点A、C的坐标;(2)①二次函数的图象恰好经过点O、A、C,试求此二次函数的解析式;②过点A、C分别作AB、CD垂直x轴于B、D两点,在此抛物线O、C之间取一点P(点P不与O、C重合)作PF⊥x轴于点F,PF交OC于点E,是否存在点P使得AP=BE?若存在,求出点P的坐标?若不存在,试说明理由;(3)在(2)的条件下,将△OAB沿AC方向移动到△O'A'B'(点A'在线段AC上,且不与C重合),△O'A'B'与△OCD重叠部分的面积为S,试求当S=时点A'的坐标.7.(2023春·安徽合肥·九年级统考期中)定义:在平面直角坐标系中,图形G上点P(x,y)的纵坐标y与其横坐标x的差y﹣x称为点P的“坐标差”,而图形G上所有点的“坐标差”中的最大值称为图形G的“特征值”.(1)求点A(2,1)的“坐标差”和抛物线y=﹣x2+3x+4的“特征值”.(2)某二次函数=﹣x2+bx+c(c≠0)的“特征值”为﹣1,点B与点C分别是此二次函数的图象与x轴和y轴的交点,且点B与点C的“坐标差”相等,求此二次函数的解析式.(3)如图所示,二次函数y=﹣x2+px+q的图象顶点在“坐标差”为2的一次函数的图象上,四边形DEFO是矩形,点E的坐标为(7,3),点O为坐标原点,点D在x轴上,当二次函数y=﹣x2+px+q的图象与矩形的边有四个交点时,求p的取值范围.8.(2023·浙江杭州·九年级统考期中)新定义:我们把两个面积相等但不全等的三角形叫做偏等积三角形.(1)初步尝试如图1,已知等腰直角△ABC,∠ACB=90°,请将它分成两个三角形,使它们成为偏等积三角形.(2)理解运用如图2,已知△ACD为直角三角形,∠ADC=90°,以AC,AD为边向外作正方向ACFB和正方形ADGE,连接BE,求证:△ACD与△ABE为偏等积三角形.(3)综合探究如图3,二次函数y=x2–x–5的图象与x轴交于A,B两点,与y轴交于点C,在二次函数的图象上是否存在一点D,使△ABC与△ABD是偏等积三角形?若存在,请求出点D的坐标;若不存在,请说明理由.9.(2023春·江西赣州·九年级统考期末)我们给出如下定义:在平面直角坐标系xOy中,如果一条抛物线平移后得到的抛物线经过原抛物线的顶点,那么这条抛物线叫做原抛物线的过顶抛物线.如下图,抛物线F2都是抛物线F1的过顶抛物线,设F1的顶点为A,F2的对称轴分别交F1、F2于点D、B,点C是点A关于直线BD的对称点.(1)如图1,如果抛物线y=x2的过顶抛物线为y=ax2+bx,C(2,0),那么①a=,b=.②如果顺次连接A、B、C、D四点,那么四边形ABCD为()A.平行四边形B.矩形C.菱形D.正方形(2)如图2,抛物线y=ax2+c的过顶抛物线为F2,B(2,c-1).求四边形ABCD的面积.(3)如果抛物线的过顶抛物线是F2,四边形ABCD的面积为,请直接写出点B的坐标.10.(2023春·江西赣州·九年级校考期末)定义:在平面直角坐标系中,抛物线y=a+bx+c (a≠0)与直线y=m交于点A、C(点C在点A右边)将抛物线y=a+bx+c沿直线y=m翻折,翻折前后两抛物线的顶点分别为点B、D.我们将两抛物线之间形成的封闭图形称为惊喜线,四边形ABCD称为惊喜四边形,对角线BD与AC之比称为惊喜度(Degreeofsurprise),记作|D|=.(1)图①是抛物线y=﹣2x﹣3沿直线y=0翻折后得到惊喜线.则点A坐标,点B 坐标,惊喜四边形ABCD属于所学过的哪种特殊平行四边形,|D|为.(2)如果抛物线y=m﹣6m(m>0)沿直线y=m翻折后所得惊喜线的惊喜度为1,求m的值.(3)如果抛物线y=﹣6m沿直线y=m翻折后所得的惊喜线在m﹣1≤x≤m+3时,其最高点的纵坐标为16,求m的值并直接写出惊喜度|D|2024中考数学新定义及探究题专题《二次函数及新定义》(解析版)【类型1二次函数问题中的新定义问题】1.(2023春·山东济南·九年级统考期末)新定义:若一个点的纵坐标是横坐标的2倍,则称这个点为二倍点.若二次函数(c为常数)在的图象上存在两个二倍点,则c的取值范围是()A.B.C.D.【答案】D【分析】由点的纵坐标是横坐标的2倍可得二倍点在直线上,由可得二倍点所在线段的端点坐标,结合图象,通过求抛物线与线段的交点求解.【详解】解:由题意可得二倍点所在直线为,将代入得,将代入得,设,,如图,联立与,得方程,即抛物线与直线有两个交点,,解得,当直线和直线与抛物线交点在点A,上方时,抛物线与线段有两个交点,把代入,得,把代入得,,解得,.故选D.【点睛】本题考查二次函数图象与正比例函数图象的交点问题,解题关键掌握函数与方程及不等式的关系,将代数问题转化为图形问题求解.2.(2023春·湖北咸宁·九年级统考期中)定义:我们将顶点的横坐标和纵坐标互为相反数的二次函数称为“互异二次函数”.若互异二次函数的对称轴为直线x=1且图象经过点(﹣1,0),则这个互异二次函数的二次项系数是()A.B.C.1D.﹣1【答案】B【分析】根据函数的对称轴和互异二次函数的特点计算即可;【详解】由题可知:此函数的横坐标与纵坐标互为相反数,且对称轴为直线x=1且图象经过点(﹣1,0),设此函数为,∴,解得:,∴此函数的二次项系数为;故选B.【点睛】本题主要考查了二次函数的性质,准确计算是解题的关键.3.(2023春·广西南宁·九年级统考期中)新定义:在平面直角坐标系中,对于点P(m,n)和点P′(m,n′),若满足m≥0时,n′=n-4;m<0时,n′=-n,则称点P′(m,n′)是点P(m,n)的限变点.例如:点P1(2,5)的限变点是P1′(2,1),点P2(-2,3)的限变点是P2′(-2,-3).若点P(m,n)在二次函数y=-x2+4x+2的图象上,则当-1≤m≤3时,其限变点P′的纵坐标n'的取值范围是()A.B.C.D.【答案】D【分析】根据新定义得到当m≥0时,n′=-m2+4m+2-4=-(m-2)2+2,在0≤m≤3时,得到-2≤n′≤2;当m<0时,n′=m2-4m-2=(m-2)2-6,在-1≤m<0时,得到-2≤n′≤3,即可得到限变点P′的纵坐标n'的取值范围是-2≤n′≤3.【详解】解:由题意可知,当m≥0时,n′=-m2+4m+2-4=-(m-2)2+2,∴当0≤m≤3时,-2≤n′≤2,当m<0时,n′=m2-4m-2=(m-2)2-6,∴当-1≤m<0时,-2<n′≤3,综上,当-1≤m≤3时,其限变点P′的纵坐标n'的取值范围是-2≤n′≤3,故选:D.【点睛】本题主要考查了二次函数图象上点的坐标特征,解题的关键是根据限变点的定义得到n′关于m的函数.4.(2023春·湖南长沙·九年级长沙市开福区青竹湖湘一外国语学校校考期末)定义:我们不妨把纵坐标是横坐标2倍的点称为“青竹点”.例如:点、……都是“青竹点”.显然,函数的图象上有两个“青竹点”:和.(1)下列函数中,函数图象上存在“青竹点”的,请在横线上打“√”,不存在“青竹点”的,请打“×”.①________;②________;③________.(2)若抛物线(m为常数)上存在两个不同的“青竹点”,求m的取值范围;(3)若函数的图象上存在唯一的一个“青竹点”,且当时,a的最小值为c,求c的值.【答案】(1)×;√;×(2)(3)【分析】(1)根据“青一函数”的定义直接判断即可;(2)根据题意得出关于的一元二次方程,再根据根的判别式得出关于m的不等式,即可求解;(3)根据题意得出关于的一元二次方程,再根据根的判别式得出关于a的二次函数,利用二次函数最值求解即可.【详解】(1)解:①令,方程无解,∴函数图像上不存在“青竹点”,故答案为:×;②令,解得:,,∴函数图像上存在“青竹点”和,故答案为:√;③令,方程无解,∴函数图像上不存在“青竹点”,故答案为:×;(2)解:由题意得,整理,得,∵抛物线(m为常数)上存在两个不同的“青竹点”,∴,解得;(3)解:由题意得整理,得∵函数的图像上存在唯一的一个“青竹点”,∴整理,得∴当时,a的最小值为,∵当时,a的最小值为c,∴∴,【点睛】本题属于函数背景下新定义问题,主要考查二次函数的性质,二次函数与一元二次方程的关系,解题关键是掌握二次函数图象与系数的关系,掌握二次函数与方程的关系,一元二次方程根的判别式.5.(2023春·江苏泰州·九年级统考期中)定义:两个二次项系数之和为,对称轴相同,且图像与轴交点也相同的二次函数互为友好同轴二次函数.例如:的友好同轴二次函数为.(1)函数的友好同轴二次函数为.(2)当时,函数的友好同轴二次函数有最大值为,求的值.(3)已知点分别在二次函数及其友好同轴二次函数的图像上,比较的大小,并说明理由.【答案】(1);(2);(3)当时,;当时,;当时,【分析】(1)根据友好同轴二次函数的定义,找出的友好同轴二次函数即可;(2)根据友好同轴二次函数的定义,找出的友好同轴二次函数,判断函数图像开口方向,利用函数的对称轴和自变量范围进行最大值讨论;(3)先根据友好同轴二次函数的定义,找出的友好同轴二次函数,再把两点代入,作差后比较大小,为含参数的二次不等式,求解的范围即可.【详解】(1)设友好同轴二次函数为,由函数可知,对称轴为直线,与轴交点为,,,对称轴为直线,,友好同轴二次函数为;(2)由函数可求得,该函数的友好同轴二次函数为;①当时,时,,解得:;②当时,时,,解得:;综上所述,;(3)由函数可求得,该函数的友好同轴二次函数为,把分别代入可得,,,则,,,①当时,,即,,解得:;②当时,,即,,解得:;③当时,,即,,解得:;综上所述,当时,;当时,;当时,.【点睛】本题考查二次函数的性质以及新定义问题,掌握二次函数的基本性质以及研究手段,准确根据题意求出符合要求的友好同轴二次函数是解题关键.6.(2023春·浙江金华·九年级校考期中)定义:若抛物线y=ax2+bx+c与x轴两交点间的距离为4,称此抛物线为定弦抛物线.(1)判断抛物线y=x2+2x﹣3是否是定弦抛物线,请说明理由;(2)当一定弦抛物线的对称轴为直线x=1,且它的图像与坐标轴的交点间的连线所围成的图形是直角三角形,求该抛物线的表达式;(3)若定弦抛物线y=x2+bx+c(b<0)与x轴交于A、B两点(A在B左边),当2≤x≤4时,该抛物线的最大值与最小值之差等于OB之间的距离,求b的值.【答案】(1)是定弦抛物线,理由见解析(2)或(3)b=﹣4或【分析】(1)令y=0,求出与x轴的交点坐标,可判断;(2)分开口向上向下讨论,利用定弦抛物线的定义和对称轴可求出与x轴交点坐标,用相似求出与y轴交点坐标,代入可得答案;(3)根据对称轴和所给范围分情况讨论即可.【详解】(1)解:当y=0时,x2+2x﹣3=0,解得:x1=1,x2=﹣3,则|x1-x2|=4,即该抛物线是定弦抛物线;(2):当该抛物线开口向下时,如图所示.∵该定弦抛物线的对称轴为直线x=1,设则解得:∴C(﹣1,0),D(3,0),∵△CED为直角三角形∴由题意可得∠CED=90°,∵EO⊥CD,∴△CEO∽△EDO,∴OE2=OC·OD=3,∴E(0,)设该定弦抛物线表达式为,把E(0,)代入求得∴该定弦抛物线表达式为,当该抛物线开口向上时,同理可得该定弦抛物线表达式为,∴综上所述,该定弦抛物线表达式为或;(3)解:若≤2,则在2≤x≤4中,当x=4时该定弦抛物线取最大值,当x=2时该定弦抛物线取最小值.∴l6+4b+c-(4+2b+c)=+2,解得:b=﹣4,∵≤2,∴b≥﹣4,即b=﹣4,若≤3,则在2≤x≤4中,当x=4时该定弦抛物线取最大值,当x=时该定弦抛物线取最小值.∴16+4b+c﹣=+2,解得:b1=﹣4,b2=﹣14,∵2≤≤3,∴﹣6≤b≤﹣4,∴b1=﹣4,b2=﹣14(舍去),若≤4,则在2≤x≤4中,当x=2时该定弦抛物线取最大值,当x=时该定弦抛物线取最小值.∴4+2b+c﹣=+2,解得:b=﹣5,∵≤4,∴﹣8≤b<﹣6,∴b=﹣5不合题意,舍去,若>4,则在2≤x≤4中,当x=2时该定弦抛物线取最大值,当x=4时该定弦抛物线取最小值.∴4+2b+c-(16+4b+c)=+2,解得:b=-,∵>4,∴b<﹣8,∴b=﹣,∴综上所述b=﹣4或.【点睛】本题考查了二次函数的综合性质,包括与x轴交点问题,最值问题,以及和相似的结合,准确地理解定弦抛物线的定义以及分类讨论是解决本题的关键.7.(2023春·浙江·九年级期末)定义:若抛物线与抛物线.同时满足且,则称这两条抛物线是一对“共轭抛物线”.(1)已知抛物线与是一对共轭抛物线,求的解析式;(2)如图1,将一副边长为的正方形七巧板拼成图2的形式,若以BC中点为原点,直线BC为x轴建立平面直角坐标系,设经过点A,E,D的抛物线为,经过A、B、C的抛物线为,请立接写出、的解析式并判断它们是否为一对共轭抛物线.【答案】(1)(2),,、是一对共轭抛物线【分析】(1)将化作顶点式,可求出,和的值,根据“共轭抛物线”的定义可求出,和的值,进而求出的解析式;(2)根据七巧板各个图形之间的关系可求出各个图形的边长,进而可表示点,,,,的坐标,分别求出和的解析式,再根据“共轭抛物线”的定义可求解.【详解】(1)解:,∴,,,∵抛物线与是一对共轭抛物线,∴,且,.(2)解:如图,由题意得,,则,,,,,∵点为的中点,∴,∴,,,,,∴可设抛物线,与抛物线,∴,,解得:,,∴抛物线,抛物线,∴,,,,,,∵,,∴满足且,∴、是一对共轭抛物线.【点睛】本题属于二次函数的新定义类问题,主要考查利用待定系数法求函数表达式,二次函数的顶点式,一般式及交点式三种方式的变换,熟知相关运算是解题关键.8.(2023春·湖南长沙·九年级校联考期末)定义:如果抛物线与轴交于点,,那么我们把线段叫做雅礼弦,两点之间的距离称为抛物线。
2024年中考数学复习重难点(全国通用版):专题20 新定义型二次函数问题(重点突围)(解析版)

专题20新定义型二次函数问题【中考考向导航】目录【直击中考】 (1)【考向一新定义型二次函数问题】 (1)【直击中考】【考向一新定义型二次函数问题】求解体验:(1)已知抛物线23y x bx 经过点 1,0 成中心对称的抛物线表达式是.抽象感悟:我们定义:对于抛物线 2y ax bx c a 抛物线,则我们又称抛物线为抛物线y 的(2)已知抛物线225y x x 关于点 0,m②若抛物线y 关于点 20,1k 的衍生抛物线为1y ,其顶点为1A ;关于点 20,2k 的衍生抛物线为2y ,其顶点为2A ;…;关于点 20,k n 的衍生抛物线为n y ,其顶点为n A ,…(n 为正整数).求1n n A A 的长(用含n 的式子表示).【答案】(1)4 ; 2,1 ;245y x x ;(2)5m (3)①33a b;衍生中心的坐标为 0,6;②42n 【分析】(1)把 10 ,代入23y x bx 即可求出4b ,然后把抛物线解析式变为顶点式即可求得抛物线的顶点坐标,继而可得顶点关于 0,1的对称点,从而可写出原抛物线关于点 0,1成中心对称的抛物线的表达式;(2)先求出抛物线225y x x 的顶点是 1,6 ,从而求出1,6 关于 0m ,的对称点是 126m ,,得 2'126y x m ,根据两抛物线有交点,可以确定方程 2216126x x m 有解,继而求得m 的取值范围即可;(3)①先求出抛物线 220y ax ax b a 以及抛物线y 的衍生抛物线为 2220y bx bx a b ,的顶点坐标,根据两抛物线有两个交点,且恰好是它们的顶点,求a b ,的值及再根据中点坐标公式即可求出衍生中心的坐标;②根据中心对称,由题意得出12B B ,23B B …1n n B B 分别是12AA A ,23AA A …1n n AA A 的中位线,继而可得12122A A B B ,23232A A B B ,…112n n n n A A B B ,再根据点的坐标即可求得1n n A A 的长,即可求解.【详解】(1)解:把 10 ,代入23y x bx ,得4b ,∴ 224321y x x x ,∴顶点坐标是 2,1 ,∵ 2,1 关于 0,1的对称点 2,1,∴成中心对称的抛物线表达式是: 221y x ,即245y x x ,故答案为:4 , 2,1 ,245y x x ;(2)∵ 222516y x x x ,∴顶点是1,6 ∵ 1,6 关于 0m ,的对称点是 126m ,,∴ 2'126y x m ,∵两抛物线有交点,∴ 2216126x x m 有解,∴25x m 有解,∴50m ,∴5m ;(3)①∵22y ax ax b 21a x a b ,∴顶点 1,a b ,代入222y bx bx a 得:22b b a a b ①∵ 222221y bx bx a b x a b ,∴顶点 21,a b ,代入22y ax ax b 得:22a a b a b ②由①②得224030a a b a a,∵0a ,0b ,∴33a b,∴两顶点坐标分别是 1,0 , 1,12,由中点坐标公式得“衍生中心”的坐标是 06,;②如图,设1AA ,2AA …n AA ,1n AA 与y 轴分别相于1B ,2B …n B ,1n B ,则1A A ,,2,A A ,…,n A A ,1,n A A 分别关于1B ,2B …n B ,1n B 中心对称,∴12B B ,23B B …1n n B B 分别是12AA A ,23AA A …1n n AA A 的中位线,∴12122A A B B ,23232A A B B ,…112n n n n A A B B ,∵ 20n B k n ,,2101n B k n ,,∴112n n n n A A B B2221k n k n42n .【点睛】本题考查了二次函数的图像和性质,理解题意,画出符合题意的图形借助数形结合思想解决问题是关键.【变式训练】(1)请将点Q “去隐”,得到该抛物线表达式;(2)记(1)中抛物线为W (如图),W 与x 轴交于点A ,B (A 在B 的左侧)移,平移后的抛物线W 始终过点A ,点C 的对应点为C .ⅰ)试确定点C 运动路径所对应的函数表达式;ⅱ)在直线2x 的左侧,是否存在点C ,使ACC △为等腰三角形?若存在,求出点请说明理由.【答案】(1)213y x x ;【点睛】本题考查二次函数的图像及性质,熟练掌握二次函数的图像及性质,理解定义,将所求问题转化:y(1)求抛物线C2的解析式和点G的坐标.(2)点M是x轴下方抛物线C1上的点,过点M作MN⊥x轴于点N,交抛物线DM的长度的比值.(3)如图②,点E是点H关于抛物线对称轴的对称点,连接EG,在x轴上是否存在点EG为腰的等腰三角形?若存在,请求出点F的坐标;若不存在,请说明理由.【答案】(1)y=13x2+23x﹣1,G(0,﹣3)(2)32【答案】(1)假(2)221y x x (3)见解析(4)①真;②见解析;③见解析【分析】(1)根据题意举反例验证求解即可;(2) 224521y x x x ,则“反顶伴侣二次函数”为 212y a x ,再将(2,1)代入求出a 值,即可得出解析式;(3)根据题意,分别表示出过顶点坐标的函数解析式,进行相加化简即可得出结果;(4)①由旋转的性质,找到对称中心M ,可知对于任意二次函数都有“反顶旋转二次函数”;②利用A ,B 坐标求出中点M 的坐标,进而得出结论;③根据矩形的性质和平行的性质,得出AB ∥y 轴,进而得出A ,B 点的坐标均为(h ,h ),最后得出结论.【详解】(1)解:令1C 的顶点坐标A 为(1,4),开口向上,则2C 的顶点坐标B 为(4,1),此时C 1不经过B (4,1),∴所有二次函数都有“反顶伴侣二次函数”是假命题.故答案为:假.(2)解: 224521y x x x ,则“反顶伴侣二次函数”为 212y a x ,由题意,得将(2,1)代入 212y a x ,得21212a ,解得a =-1,∴245y x x 的“反顶伴侣二次函数”为 221221y x x x .(3)解:∵二次函数 211:C y a x h k 经过2C 的顶点B ,且 222:C y a x k h 经过1C 的顶点A ,∴ 211:C h a k h k ①,222:C k a h k h ②,①+②,得 2120a a h k ,②∵M 为A ,B 的中点,∴M 的坐标为22h k h k,,的长,再利用同高的三角形的面积比等于底的比即可得出结∴如图,整点个数有(1,1),【点睛】本题考查二次函数的图象和性质,正方形的性质,两点的距离公式.解题的关键是读懂题意理解“镜像抛物线”和“整点”的概念.。
中考数学复习专项练习卷_新定义型问题(含答案解析)

中考数学二轮复习精品资料附参考答案新定义型问题一、中考专题诠释所谓“新定义”型问题,主要是指在问题中定义了中学数学中没有学过的一些概念、新运算、新符号,要求学生读懂题意并结合已有知识、能力进行理解,根据新定义进行运算、推理、迁移的一种题型.“新定义”型问题成为近年来中考数学压轴题的新亮点.在复习中应重视学生应用新的知识解决问题的能力二、解题策略和解法精讲“新定义型专题”关键要把握两点:一是掌握问题原型的特点及其问题解决的思想方法;二是根据问题情景的变化,通过认真思考,合理进行思想方法的迁移.三、中考典例剖析考点一:规律题型中的新定义例2 (2013•河北)定义新运算:对于任意实数a,b,都有a⊕b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算,比如:2⊕5=2×(2-5)+1=2×(-3)+1=-6+1==-5。
(1)求(-2)⊕3的值;(2)若3⊕x的值小于13,求x的取值范围,并在图所示的数轴上表示出来.思路分析:(1)按照定义新运算a⊕b=a(a-b)+1,求解即可;(2)先按照定义新运算a⊕b=a(a-b)+1,得出3⊕x,再令其小于13,得到一元一次不等式,解不等式求出x的取值范围,即可在数轴上表示.解:(1)∵a⊕b=a(a-b)+1,∴(-2)⊕3=-2(-2-3)+1=10+1=11;(2)∵3⊕x<13,∴3(3-x)+1<13,9-3x+1<13,-3x<3,x>-1.在数轴上表示如下:例3 (2013•钦州)定义:直线l1与l2相交于点O,对于平面内任意一点M,点M到直线l1、l2的距离分别为p、q,则称有序实数对(p,q)是点M的“距离坐标”,根据上述定义,“距离坐标”是(1,2)的点的个数是()A.2 B.3 C.4 D.5思路分析:“距离坐标”是(1,2)的点表示的含义是该点到直线l1、l2的距离分别为1、2.由于到直线l1的距离是1的点在与直线l1平行且与l1的距离是1的两条平行线a1、a2上,到直线l2的距离是2的点在与直线l2平行且与l2的距离是2的两条平行线b1、b2上,它们有4个交点,即为所求.解:如图,∵到直线l1的距离是1的点在与直线l1平行且与l1的距离是1的两条平行线a1、a2上,到直线l2的距离是2的点在与直线l2平行且与l2的距离是2的两条平行线b1、b2上,∴“距离坐标”是(1,2)的点是M1、M2、M3、M4,一共4个.故选C.点评:本题考查了点到直线的距离,两平行线之间的距离的定义,理解新定义,掌握到一条直线的距离等于定长k的点在与已知直线相距k的两条平行线上是解题的关键.-CE PC PC a s2考点四:开放题型中的新定义例4 (2013•宁波)若一个四边形的一条对角线把四边形分成两个等腰三角形,我们把这条对角线叫这个四边形的和谐线,这个四边形叫做和谐四边形.如菱形就是和谐四边形.(1)如图1,在梯形ABCD中,AD∥BC,∠BAD=120°,∠C=75°,BD平分∠ABC.求证:BD是梯形ABCD的和谐线;(2)如图2,在12×16的网格图上(每个小正方形的边长为1)有一个扇形BAC,点A.B.C 均在格点上,请在答题卷给出的两个网格图上各找一个点D,使得以A、B、C、D为顶点的四边形的两条对角线都是和谐线,并画出相应的和谐四边形;(3)四边形ABCD中,AB=AD=BC,∠BAD=90°,AC是四边形ABCD的和谐线,求∠BCD的度数.思路分析:(1)要证明BD是四边形ABCD的和谐线,只需要证明△ABD和△BDC是等腰三角形就可以;»BC上任意一点构成的四边形(2)根据扇形的性质弧上的点到顶点的距离相等,只要D在ABDC就是和谐四边形;连接BC,在△BAC外作一个以AC为腰的等腰三角形ACD,构成的四边形ABCD就是和谐四边形,(3)由AC是四边形ABCD的和谐线,可以得出△ACD是等腰三角形,从图4,图5,图6三种情况运用等边三角形的性质,正方形的性质和30°的直角三角形性质就可以求出∠BCD 的度数.解:(1)∵AD∥BC,∴∠ABC+∠BAD=180°,∠ADB=∠DBC.∵∠BAD=120°,∴∠ABC=60°.∵BD平分∠ABC,∴∠ABD=∠DBC=30°,∴∠ABD=∠ADB,∴△ADB是等腰三角形.在△BCD中,∠C=75°,∠DBC=30°,∴∠BDC=∠C=75°,∴△BCD为等腰三角形,∴BD是梯形ABCD的和谐线;(2)由题意作图为:图2,图3(3)∵AC是四边形ABCD的和谐线,∴△ACD是等腰三角形.∵AB=AD=BC,如图4,当AD=AC时,A.在同一条直线上B.在同一条抛物线上C.在同一反比例函数图象上D.是同一个正方形的四个顶点思路分析:如果设C(x3,y3),D(x4,y4),E(x5,y5),F(x6,y6),先根据新定义运算得出(x3+x4)+(y3+y4)=(x4+x5)+(y4+y5)=(x5+x6)+(y5+y6)=(x4+x6)+(y4+y6),则x3+y3=x4+y4=x5+y5=x6+y6,若令x3+y3=x4+y4=x5+y5=x6+y6=k,则C(x3,y3),D(x4,y4),E(x5,y5),F(x6,y6)都在直线y=-x+k上.解:∵对于点A(x1,y1),B(x2,y2),A⊕B=(x1+x2)+(y1+y2),如果设C(x3,y3),D(x4,y4),E(x5,y5),F(x6,y6),那么C⊕D=(x3+x4)+(y3+y4),D⊕E=(x4+x5)+(y4+y5),E⊕F=(x5+x6)+(y5+y6),F⊕D=(x4+x6)+(y4+y6),又∵C⊕D=D⊕E=E⊕F=F⊕D,∴(x3+x4)+(y3+y4)=(x4+x5)+(y4+y5)=(x5+x6)+(y5+y6)=(x4+x6)+(y4+y6),∴x3+y3=x4+y4=x5+y5=x6+y6,令x3+y3=x4+y4=x5+y5=x6+y6=k,则C(x3,y3),D(x4,y4),E(x5,y5),F(x6,y6)都在直线y=-x+k上,∴互不重合的四点C,D,E,F在同一条直线上.故选A.点评:本题考查了一次函数图象上点的坐标特征,以及学生的阅读理解能力,有一定难度.对应训练5.(2013•天门)一张矩形纸片,剪下一个正方形,剩下一个矩形,称为第一次操作;在剩下的矩形纸片中再剪下一个正方形,剩下一个矩形,称为第二次操作;…;若在第n次操作后,剩下的矩形为正方形,则称原矩形为n阶奇异矩形.如图1,矩形ABCD中,若AB=2,BC=6,则称矩形ABCD为2阶奇异矩形.(1)判断与操作:如图2,矩形ABCD长为5,宽为2,它是奇异矩形吗?如果是,请写出它是几阶奇异矩形,并在图中画出裁剪线;如果不是,请说明理由.(2)探究与计算:已知矩形ABCD的一边长为20,另一边长为a(a<20),且它是3阶奇异矩形,请画出矩形四、中考真题演练一、选择题1.(2013•成都)在平面直角坐标系中,下列函数的图象经过原点的是()A.y=-x+3 B.y= 5xC.y=2x D.y=-2x2+x-71.C2.(2013•绍兴)若圆锥的轴截图为等边三角形,则称此圆锥为正圆锥,则正圆锥的侧面展开图的圆心角是()A.90°B.120°C.150°D.180°2.DA.40 B.45 C.51 D.563.C4.(2013•乌鲁木齐)对平面上任意一点(a,b),定义f,g两种变换:f(a,b)=(a,-b).如f(1,2)=(1,-2);g(a,b)=(b,a).如g(1,2)=(2,1).据此得g(f(5,-9))=()A.(5,-9)B.(-9,-5)C.(5,9)D.(9,5)4.D5.(2013•常德)连接一个几何图形上任意两点间的线段中,最长的线段称为这个几何图形的直径,根据此定义,图(扇形、菱形、直角梯形、红十字图标)中“直径”最小的是()A.B.C.D.5.C二、填空题6.(2013•上海)当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的“特征角”为100°,那么这个“特征三角形”的最小内角的度数为.6.30°7.(2013•宜宾)如图,△ABC是正三角形,曲线CDEF叫做正三角形的渐开线,其中弧CD、弧DE、弧EF的圆心依次是A、B、C,如果AB=1,那么曲线CDEF的长是.三、解答题10.(2013•莆田)定义:如图1,点C在线段AB上,若满足AC2=BC•AB,则称点C为线段AB的黄金分割点.(3)作EF ⊥AB 于F ,EG ⊥AD 于G ,EH ⊥CD 于H ,∴∠BFE =∠CHE =90°.∵AE 平分∠BAD ,DE 平分∠ADC ,∴EF =EG =EH ,在Rt △EFB 和Rt △EHC 中BE CE EF EH=⎧⎨=⎩, ∴Rt △EFB ≌Rt △EHC (HL ),∴∠3=∠4.∵BE =CE ,∴∠1=∠2.∴∠1+∠3=∠2+∠4即∠ABC =∠DCB ,∵ABCD 为AD 截某三角形所得,且AD 不平行BC ,∴ABCD 是“准等腰梯形”.当点E 不在四边形ABCD 的内部时,有两种情况:如图4,当点E 在BC 边上时,同理可以证明△EFB ≌△EHC ,∴∠B =∠C ,∴ABCD 是“准等腰梯形”.如图5,当点E 在四边形ABCD 的外部时,同理可以证明△EFB ≌△EHC ,∴∠EBF =∠ECH .∵BE =CE ,∴∠3=∠4,∴∠EBF -∠3=∠ECH -∠4,即∠1=∠2,。
中考数学专题复习新定义问题【含解析】

新定义问题【专题点拨】新定义运算、新概念问题一般是介绍新定义、新概念,然后利用新定义、新概念解题,其解题步骤一般都可分为以下几步:1.阅读定义或概念,并理解;2.总结信息,建立数模;3.解决数模,回顾检查.“新概念”试题,其设计新颖,构思独特,思维容量大,既能考查学生的阅读、分析、推理、概括等能力,又能考查学生知识迁移的能力和数学素养,同时还兼具了区分选拔的功能 .【解题策略】具体分析新颖问题→弄清问题题意→向已知知识点转化→利用相关联知识查验→转化问题思路解决【典例解析】类型一:规律题型中的新定义例题1:(2015•永州,第10题3分)定义[x]为不超过x的最大整数,如[3.6]=3,[0.6]=0,[﹣3.6]=﹣4.对于任意实数x,下列式子中错误的是()A.[x]=x(x为整数) B.0≤x﹣[x]<1C.[x+y]≤[x]+[y]D.[n+x]=n+[x](n为整数)【解析】:根据“定义[x]为不超过x的最大整数”进行计算【解答】:解:A、∵[x]为不超过x的最大整数,∴当x是整数时,[x]=x,成立;B、∵[x]为不超过x的最大整数,∴0≤x﹣[x]<1,成立;C、例如,[﹣5.4﹣3.2]=[﹣8.6]=﹣9,[﹣5.4]+[﹣3.2]=﹣6+(﹣4)=﹣10,∵﹣9>﹣10,∴[﹣5.4﹣3.2]>[﹣5.4]+[﹣3.2],∴[x+y]≤[x]+[y]不成立,D、[n+x]=n+[x](n为整数),成立;故选:C.【点评】本题考查了一元一次不等式组的应用,解决本题的关键是理解新定义.新定义解题是近几年中考常考的题型.变式训练1:(2015•山东潍坊,第12题3分)如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2014次变换后,正方形ABCD的对角线交点M的坐标变为( )A.(—2012,2) B.(一2012,一2)C. (—2013,—2)D. (—2013,2)类型二:运算题型中的新定义例题2:(2016·四川宜宾)规定:log a b(a>0,a≠1,b>0)表示a,b之间的一种运算.现有如下的运算法则:log n a n=n.log N M=(a>0,a≠1,N>0,N≠1,M>0).例如:log223=3,log25=,则log1001000= .【解析】实数的运算.先根据log N M=(a>0,a≠1,N>0,N≠1,M>0)将所求式子化成以10为底的对数形式,再利用公式进行计算.【解答】解:log1001000===.故答案为:.变式训练2:(2016四川省乐山市第16题)在直角坐标系xOy 中,对于点P (x ,y )和Q (x ,y′),给出如下定义:若(0)(0)y x y y x ≥⎧'=⎨-<⎩,则称点Q 为点P 的“可控变点”.例如:点(1,2)的“可控变点”为点(1,2),点(﹣1,3)的“可控变点”为点(﹣1,﹣3).(1)若点(﹣1,﹣2)是一次函数3y x =+图象上点M 的“可控变点”,则点M 的坐标为 ;(2)若点P 在函数216y x =-+(5x a -≤≤)的图象上,其“可控变点”Q 的纵坐标y′的取值范围是1616y '-≤≤,则实数a 的取值范围是 .类型三: 探索题型中的新定义例题3:(2016山西省第10题)宽与长的比是21-5(约为0.618)的矩形叫做黄金矩形.黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:作正方形ABCD ,分别取AD ,BC 的中点E ,F ,连接EF ;以点F 为圆心,以FD 为半径画弧,交BC 的延长线与点G ;作AD GH ⊥,交AD 的延长线于点H .则图中下列矩形是黄金矩形的是( )A .矩形ABFEB .矩形EFCDC .矩形EFGHD .矩形DCGH【解析】考点:黄金分割的识别【解答】:由作图方法可知DF=5CF ,所以CG=CF )15(-,且GH=CD=2CF ,从而得出黄金矩形CG=CF )15(-,GH=2CF ∴2152)15(-=-=CF CF GH CG ∴矩形DCGH 是黄金矩形。
2023年中考数学专题《 函数中的新定义问题》试卷含答案解析

考点1 一次函数新定义问题【例1】.定义:我们把一次函数y =kx +b (k ≠0)与正比例函数y =x 的交点称为一次函数y =kx +b (k ≠0)的“不动点”.例如求y =2x ﹣1的“不动点”:联立方程,解得,则y =2x ﹣1的“不动点”为(1,1).(1)由定义可知,一次函数y =3x +2的“不动点”为 (﹣1,﹣1) ;(2)若一次函数y =mx +n 的“不动点”为(2,n ﹣1),求m 、n 的值;(3)若直线y =kx ﹣3(k ≠0)与x 轴交于点A ,与y 轴交于点B ,且直线y =kx ﹣3上没有“不动点”,若P 点为x 轴上一个动点,使得S △ABP =3S △ABO ,求满足条件的P 点坐标.解:(1)联立,解得,∴一次函数y =3x +2的“不动点”为(﹣1,﹣1),故答案为:(﹣1,﹣1);(2)∵一次函数y =mx +n 的“不动点”为(2,n ﹣1),∴n ﹣1=2,∴n =3,∴“不动点”为(2,2),∴2=2m +3,解得m =﹣;(3)∵直线y =kx ﹣3上没有“不动点”,∴直线y =kx ﹣3与直线y =x 平行,∴k =1,例题精讲∴y=x﹣3,∴A(3,0),B(0,﹣3),设P(t,0),∴AP=|3﹣t|,∴S△ABP=×|t﹣3|×3,S△ABO=×3×3,∵S△ABP=3S△ABO,∴|t﹣3|=9,∴t=12或t=﹣6,∴P(﹣6,0)或P(12,0).变式训练【变1-1】.在初中阶段的函数学习中,我们经历了“确定函数的表达式一一利用函数图象研究其性质一一运用函数解决问题”的学习过程.在画函数图象时,我们通过描点或平移的方法画出了所学的函数图象.同时,我们也学习了绝对值的意义.结合上面经历的学习过程,现在来解决下面的问题:在函数y=|kx﹣3|+b中,当x=2时,y=﹣4;当x=0时,y=﹣1.(1)求这个函数的表达式;(2)在给出的平面直角坐标系中,请用你喜欢的方法画出这个函数的图象,并写出这个函数的一条性质;(3)已知函数的图象如图所示,结合你所画的函数图象,直接写出不等式的解集.(4)若方程|x2﹣6x|﹣a=0有四个不相等的实数根,则实数a的取值范围是 0<a<9 .解:(1)∵在函数y=|kx﹣3|+b中,当x=2时,y=﹣4;当x=0时,y=﹣1,∴,解得,∴这个函数的表达式是y=|﹣3|﹣4;(2)∵y=|﹣3|﹣4,∴,∴函数y=x﹣7过点(2,﹣4)和点(4,﹣1);函数y=﹣x﹣1过点(0,﹣1)和点(﹣2,2),该函数的图象如图所示,性质:当x>2时,y的值随x的增大而增大;(3)由函数的图象可得,不等式的解集是:1≤x≤4;(4)由|x2﹣6x|﹣a=0得a=|x2﹣6x|,作出y=|x2﹣6x|的图象,由图象可知,要使方程|x2﹣6x|﹣a=0有四个不相等实数根,则0<a<9,故答案为:0<a<9.考点2 反比例函数新定义问题【例2】.探究函数性质时,我们经历了列表、描点、连线画函数图象,观察分析图象特征,概括函数性质的过程,以下是我们研究函数y=x+|﹣2x+6|+m性质及其应用的部分过程,请按要求完成下列各小题.x…﹣2﹣1012345…y…654a21b7…(1)写出函数关系式中m及表格中a,b的值;m= ﹣2 ,a= 3 ,b= 4 ;(2)根据表格中的数据在所给的平面直角坐标系中画出该函数的图象;(3)已知函数y=﹣(x﹣2)2+8的图象如图所示,结合你所画的函数图象,不等式x+|﹣2x+6|+m>﹣(x﹣2)2+8的解集为 x<0或x>4. .解:(1)由表格可知,点(3,1)在该函数图象上,∴将点(3,1)代入函数解析式可得:1=3+|﹣2×3+6|+m,解得:m=﹣2,∴原函数的解析式为:y=x+|﹣2x+6|﹣2;当x=1时,y=3;当x=4时,y=4;∴m=﹣2,a=3,b=4,故答案为:﹣2,3,4;(2)通过列表—描点—连线的方法作图,如图所示;(3)要求不等式x+|﹣2x+6|+m>﹣(x﹣2)2+8的解集,实际上求出函数y=x+|﹣2x+6|+m的图象位于函数y=﹣(x﹣2)2+8图象上方的自变量的范围,∴由图象可知,当x<0或x>4时,满足条件,故答案为:x<0或x>4.变式训练【定义】在平面内,把一个图形上任意一点与另一个图形上任意一点之间的距离的最小值,称为这两个图形之间的距离,即A,B分别是图形M和图形N上任意一点,当AB的长最小时,称这个最小值为图形M与图形N之间的距离.例如,如图1,AB⊥l1,线段AB的长度称为点A与直线l1之间的距离,当l2∥l1时,线段AB 的长度也是l1与l2之间的距离.【应用】(1)如图2,在等腰Rt△BAC中,∠A=90°,AB=AC,点D为AB边上一点,过点D作DE∥BC交AC于点E.若AB=6,AD=4,则DE与BC之间的距离是 ;(2)如图3,已知直线l3:y=﹣x+4与双曲线C1:y=(x>0)交于A(1,m)与B两点,点A与点B之间的距离是 2 ,点O与双曲线C1之间的距离是 ;【拓展】(3)按规定,住宅小区的外延到高速路的距离不超过80m时,需要在高速路旁修建与高速路相同走向的隔音屏障(如图4).有一条“东南﹣西北”走向的笔直高速路,路旁某住宅小区建筑外延呈双曲线的形状,它们之间的距离小于80m.现以高速路上某一合适位置为坐标原点,建立如图5所示的直角坐标系,此时高速路所在直线l4的函数表达式为y=﹣x,小区外延所在双曲线C2的函数表达式为y=(x>0),那么需要在高速路旁修建隔音屏障的长度是多少?解:(1)如图,过点D作DH⊥BC于点H,∵∠A=90°,AB=AC,∴∠B=45°,∵DH⊥BC,∴△BDH是等腰直角三角形,∴DH=BD,∵AB=6,AD=4,∴BD=AB﹣AD=6﹣4=2,∴DH=×2=;故答案为:;(2)把A(1,m)代入y=﹣x+4中,得:m=﹣1+4=3,∴A(1,3),把A(1,3)代入y=,得:3=,∴k=3,∴双曲线C1的解析式为y=,联立,得:﹣x+4=,即x2﹣4x+3=0,解得:x1=1,x2=3,∴B(3,1),∴AB==2;如图,作FG∥AB,且FG与双曲线y=只有一个交点,设直线FG的解析式为y=﹣x+b,则﹣x+b=,整理得:x2﹣bx+3=0,∴Δ=(﹣b)2﹣4×1×3=b2﹣12=0,∴b=2或b=﹣2(不符合题意,舍去),∴直线FG的解析式为y=﹣x+2,由﹣x+2=,解得:x1=x2=,∴K(,),∴OK==;故答案为:2,;(3)如图,设点S(a,b)是双曲线y=(x>0)上任意一点,且a<b,以点S 为圆心,80为半径作⊙S交l4于E,过点S作SF⊥直线l4于F,交y轴于W,SH⊥x轴于H,SG⊥y轴于G,则SG=a,SH=b,ab=2400,∵直线y=﹣x平分第二、四象限角,∴∠FOW=45°,∵∠OFW=∠SGW=90°,∴∠OWF=90°﹣45°=45°,∴∠SWG=∠OWF=45°,∴△WOF 和△SWG 是等腰直角三角形,∴SW =SG ,WF =OW ,∴SF =SW +WF =SG +OW =a +(b ﹣a )=(a +b ),∵EF====,∵OF =OW =(b ﹣a ),∴OE =(b ﹣a )+,设b ﹣a =m (m >0),则OE =m +≤=40,∴需要在高速路旁修建隔音屏障的长度=2OE =2×40=80,答:需要在高速路旁修建隔音屏障的长度是80米.考点3 二次函数新定义问题【例3】.小爱同学学习二次函数后,对函数y =﹣(|x |﹣1)2进行了探究.在经历列表、描点、连线步骤后,得到如图的函数图象.请根据函数图象,回答下列问题:(1)观察探究:①写出该函数的一条性质: 函数图象关于y轴对称 ;②方程﹣(|x|﹣1)2=﹣1的解为: x=﹣2或x=0或x=2 ;③若方程﹣(|x|﹣1)2=m有四个实数根,则m的取值范围是 ﹣1<m<0 .(2)延伸思考:将函数y=﹣(|x|﹣1)2的图象经过怎样的平移可得到函数y1=﹣(|x﹣1|﹣1)2+2的图象?写出平移过程,并直接写出当1<y1≤2时,自变量x的取值范围.解:(1)观察探究:①该函数的一条性质为:函数图象关于y轴对称;②方程﹣(|x|﹣1)2=﹣1的解为:x=﹣2或x=0或x=2;③若方程﹣(|x|﹣1)2=m有四个实数根,则a的取值范围是﹣1<m<0.故答案为:函数图象关于y轴对称;x=﹣2或x=0或x=2;﹣1<m<0.(2)将函数y=﹣(|x|﹣1)2的图象向右平移1个单位,向上平移2个单位可得到函数y1=﹣(|x﹣1|﹣1)2+2的图象,当1<y1≤2时,自变量x的取值范围是﹣1<x<3且x≠1,变式训练【变3-1】.我们定义一种新函数:形如y=|ax2+bx+c|(a≠0,b2﹣4ac>0)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|ax2+bx+c|的图象(如图所示),下列结论正确的是( )A.图象具有对称性,对称轴是直线x=1.5B.有且只有﹣1≤x≤1时,函数值y随x值的增大而增大C.若a<0,则8a+c>0D.若a<0,则a+b≥m(am+b)(m为任意实数)解:由图象可得,图象具有对称性,对称轴是直线x==1,故选项A错误,不符合题意;当﹣1≤x≤1或x>3时,函数值y随x值的增大而增大,故选项B错误,不符合题意;∵﹣=1,∴b=﹣2a,当x=﹣2时,y=4a﹣2b+c<0,∴4a﹣2b+c=4a﹣2×(﹣2a)+c=4a+4a+c=8a+c<0,故选项C错误,不符合题意;∵y=ax2+bx+c开口向下,对称轴为直线x=1,∴a+b+c≥am2+bm+c(m为任意实数),∴a+b≥m(am+b)+c,故选项D正确,符合题意;故选:D.【变3-2】.已知抛物线y=ax2+c过点A(﹣2,0)和D(﹣1,3)两点,交x轴于另一点B.(1)求抛物线解析式;(2)如图1,点P是BD上方抛物线上一点,连接AD,BD,PD,当BD平分∠ADP时,求P点坐标;(3)将抛物线图象绕原点O顺时针旋转90°形成如图2的“心形”图案,其中点M,N 分别是旋转前后抛物线的顶点,点E、F是旋转前后抛物线的交点.①直线EF的解析式是 y=x ;②点G、H是“心形”图案上两点且关于EF对称,则线段GH的最大值是 .解:(1)∵抛物线y=ax2+c过点A(﹣2,0)和D(﹣1,3)两点,∴,解得,∴抛物线解析式为y=﹣x2+4;(2)过点B作BE⊥x轴交DP延长线于点E,过D作DF⊥x于点F,由y=﹣x2+4,令y=0,则﹣x2+4=0,解得:x1=﹣2,x2=2,则B(2,0),∵DF=3,BF=2﹣(﹣1)=3,∴DF=BF,∴∠DBF=45°,∴∠DBE=45°,又∵DB=DB,BD平分∠ADP,∴△DAB≌△DEB(ASA),∴BA=BE,∵B(2,0),∴E(2,4),设直线DE的解析式为y=kx+b,则,解得,∴直线DE的解析式为y=x+,联立,解得或,则P(,);(3)①∵抛物线关于y轴对称,所以旋转后图形关于x轴对称,∴对于抛物线上任意一点P(a,b)关于原点旋转90°后对应点为P1(b,﹣a)在旋转后图形上,P1(b,﹣a)关于x轴对称的点P2(b,a)在旋转后图形上,∵P(a,b)与P2(b,a)关于y=x对称,∴图形2关于y=x对称,∴直线EF的解析式为y=x,故答案为:y=x;②如图,连接GH,交EF与点K,则GH=2GK,过点G作x轴的垂线,交EF于点I,∴当GK最大时,△GFE面积最大,又∵S△GFE=GI•(x E﹣x F),设G(m,﹣m2+4),则I(m,m),∴GI=y G﹣y I=﹣m2+4﹣m=﹣(m+)2+,∴当m=﹣时,△GFE面积最大,∴G(﹣,),由①可知G(﹣,)关于y=x的对称点H(,﹣),∴K(,),∴GK==,∴GH=2GK=,∴GH的最大值为,故答案为:.1.对于实数a,b,定义符号max|a,b|,其意义为:当a≥b时,max|a,b|=a,当a<b时,max|a,b|=b.例如max|2,﹣1|=2,若关于x的函数y=max|2x﹣1,﹣x+5|,则该函数的最小值为( )A.B.1C.D.3解:当2x﹣1≥﹣x+5时,即x≥2,y=max|2x﹣1,﹣x+5|=2x﹣1,此时x=2时,y有最小值,最小值为2×2﹣1=3;当2x﹣1≤﹣x+5时,即x≤2,y=max|2x﹣1,﹣x+5|=﹣x+5,此时x=2时,y有最小值,最小值为﹣2+5=3;综上所述,该函数的最小值为3.故选:D.2.在平面直角坐标系xOy中,对于点P(a,b),若点P′的坐标为(ka+b,a+)(其中k为常数且k≠0),则称点P′为点P的“k关联点”.已知点A在反比例函数y=的图象上运动,且点A是点B的“关联点”,当线段OB最短时,点B的坐标为 (,)或(﹣,﹣) .解:设B(x,y),∵点A是点B的“关联点”,∴A(x+y,x+)∵点A在函数y=(x>0)的图象上,∴(x+y)(x+)=,即:x+y=或x+y=﹣,当点B在直线y=﹣x+上时,设直线y=﹣x+与x轴、y轴相交于点M、N,则M(1,0)、N(0,),当OB⊥MN时,线段OB最短,此时OB==,由∠NMO=60°,可得点B(,);设直线y=﹣x﹣时,同理可得点B(﹣,﹣);故答案为:(,)或(﹣,﹣).3.定义:由a,b构造的二次函数y=ax2+(a+b)x+b叫做一次函数y=ax+b的“滋生函数”,一次函数y=ax+b叫做二次函数y=ax2+(a+b)x+b的“本源函数”(a,b为常数,且a≠0).若一次函数y=ax+b的“滋生函数”是y=ax2﹣3x+a+1,那么二次函数y=ax2﹣3x+a+1的“本源函数”是 y=﹣2x﹣1 .解:∵y=ax+b的“滋生函数”是y=ax2﹣3x+a+1,∴ax2﹣3x+a+1=ax2+(a+b)x+b,即,解得,∴y=ax2﹣3x+a+1的“本源函数”是y=﹣2x﹣1,故答案为:y=﹣2x﹣1.4.在平面直角坐标系中,如果一个点的横坐标与纵坐标相等,则称该点为“不动点”.例如(﹣3,﹣3)、(1,1)、(2023,2023)都是“不动点”.已知双曲线.(1)下列说法不正确的是 C .A.直线y=x的图象上有无数个“不动点”B.函数的图象上没有“不动点”C.直线y=x+1的图象上有无数个“不动点”D.函数y=x2的图象上有两个“不动点”(2)求双曲线上的“不动点”;。
圆中新定义问题 2023年九年级数学中考复习

圆中新定义问题 2023九年级数学中考复习1.在平面直角坐标系xOy 中,O 的半径为1,1AB =,且A ,B 两点中至少有一点在O 外.给出如下定义:平移线段AB ,得到线段(A B A ''',B '分别为点A ,B 的对应点),若线段A B ''上所有的点都在O 的内部或O 上,则线段AA '长度的最小值称为线段AB 到O 的“平移距离”.(1)如图1,点1A ,1B 的坐标分别为(3,0)-,(2,0)-,线段11A B 到O 的“平移距离”为 ,点2A ,2B 的坐标分别为1(2-3),1(23),线段22A B 到O 的“平移距离”为 ; (2)若点A ,B 都在直线33y x =+上,记线段AB 到O 的“平移距离”为d ,求d 的最小值;(3)如图2,若点A 坐标为3),线段AB 到O 的“平移距离”为1,画图并说明所有满足条件的点B 形成的图形(不需证明).2.所谓“新定义”试题指给出一个从未接触过的新规定,源于中学数学内容但又是学生没有遇到过的新信息,它可以是新的概念、新的运算、新的符号、新的图形、新的定理或新的操作规则与程序等.在解决它们的过程中又可产生了许多新方法、新观念,增强了学生创新意识.主要包括以下类型:①概念的“新定义”;②运算的“新定义”;③新规则的“新定义”;④实验操作的“新定义”;⑤几何图形的新定义.如果我们新定义一种四边形:有两个内角分别是它们对角的一半的四边形叫做半对角四边形.(1)如图1,在半对角四边形ABCD中,12B D∠=∠,12C A∠=∠,请你利用所学知识求出B∠与C∠的度数之和;(2)如图2,锐角ABC∆内接于O,若边AB上存在一点D,使得BD BO=.OBA∠的平分线交OA于点E,连接DE并延长交AC于点F,若2AFE EAF∠=∠.请你判断四边形DBCF是不是半对角四边形?并说明理由.3.如图1,在平面直角坐标系xOy 中,点A 的坐标为1(x ,1)y ,点B 的坐标为2(x ,2)y ,且12x x ≠,12y y =.给出如下定义:若平面上存在一点P ,使APB ∆是以线段AB 为斜边的直角三角形,则称点P 为点A 、点B 的“直角点”.(1)已知点A 的坐标为(1,0).①若点B 的坐标为(5,0),在点1(4,3)P 、2(3,2)P 和3(2,3)P -中,是点A 、点B 的“直角点”的是;②点B 在x 轴的正半轴上,且42AB =当直线y x b =-+上存在点A 、点B 的“直角点”时,求b 的取值范围;(2)O 的半径为r ,点(0,4)D 为点(1,2)E -、点(,2)F m 的“直角点”,若使得DEF ∆的边与O 有交点,直接写出半径r 的取值范围.4.对于C与C上一点A,若平面内的点P满足:射线AP与C交于点Q,且2PA QA=,则称点P为点A关于C的“倍距点”.已知平面直角坐标系xOy中,点A的坐标是(3,0).(1)如图1,点O为坐标原点,O3P是点A关于O的“倍距点”.①若点P在x轴正半轴上,直接写出点P的坐标是;②若点P在第一象限,且30PAO∠=︒,求点P的坐标;(2)设点(,0)T t,以点T为圆心,TA长为半径作T,一次函数34y x=+的图象分别与x轴、y轴交于D、E,若一次函数34y=+的图象上存在唯一一点P,使点P是点A关于T的“倍距点”,求t的值.5.新定义:我们把一个方程解的范围定义为“安全域”.(1)已知关于x的方程32x b+=,安全域为13x<<,请求出此时b的取值范围;(2)一次函数2y x m=-+与反比例函数23(0)my mx-=≠交于两个点,此时两交点的横坐标所在的方程中有一解的安全域是12x<<,请求出此时m的取值范围;(3)如图在边长为2的等边OAB∆中,以边AB为直径作D,AO与D交于点F,以O 为圆心OA长为半径作圆O,点C在弧FB上且不与F、B重合的一动点,射线AC交于点E,BC a=,AC b=,求关于x的方程2233x ax b ab=+的安全域.6.定义:三角形一边上的点将该边分为两条线段,且这两条线段的积等于这个点到该边所对顶点连线的平方,则称这个点为三角形该边的“好点”.如图1,ABC∆中,点D是BC边上一点,连接AD,若2AD BD CD=⋅,则称点D是ABC∆中BC边上的“好点”.(1)如图2,ABC∆的顶点是43⨯网格图的格点,请仅用直尺画出AB边上的一个“好点”.(2)ABC∆中,9BC=,4tan3B=,2tan3C=,点D是BC边上的“好点”,求线段BD的长.(3)如图3,ABC∆是O的内接三角形,OH AB⊥于点H,连接CH并延长交O于点D.①求证:点H是BCD∆中CD边上的“好点”.②若O的半径为9,90ABD∠=︒,6OH=,请直接写出CHDH的值.7.在平面直角坐标系xOy 中,对于点P 和图形W ,如果线段OP 与图形W 无公共点,则称点P 为关于图形W 的“无关点”;如果线段OP 与图形W 有公共点,则称点P 为关于图形W 的“阳光点”.(1)如图1,已知点(1,3)A -,(1,1)B -,连接AB .①在1(1,2)P -,2(1,4)P -,3(2,1)P -,4(2,3)P -这四个点中,关于线段AB 的“无关点”是 ; ②线段11//A B AB ,11A B 上的所有点都是关于线段AB 的“阳光点”,且当线段11A B 向上或向下平移时,都会有11A B 上的点成为关于线段AB 的“无关点“,若11A B 的长为4,且点1A 在1B 的上方,求点1A 的坐标.(2)如图2,已知点(3)C -,C 与y 轴相切于点D ,若E 的半径为32,圆心E 在直线:33l y x =+E 的所有点都是关于C 的“阳光点”,求点E 的横坐标E x 的取值范围;(3)如图3,M 的半径为3,点M 到原点的距离为5,点N 是M 上到原点距离最近的点,点Q 和T 是坐标平面内的两个动点,且M 上的所有点都是关于NQT ∆的“阳光点”,直接写出NQT ∆的周长的最小值 .8.如图,在平面直角坐标系xOy中,过T外一点P引它的两条切线,切点分别为M,N,若60180MPN︒<∠<︒,则称P为T的环绕点.(1)当O半径为1时,①在1(2P2),2(2,0)P,3(2,1)P中,O的环绕点是;②直线3y x b=+与x轴交于点A,y轴交于点B,若线段AB上存在O的环绕点,求b的取值范围;(2)T的半径为2,圆心为(0,)t,以(m-3)(0)m>3为半径的所有圆构成图形H,若在图形H上存在T的环绕点,直接写出t的取值范围.9.定义:把经过三角形的一个顶点并与其对边所在直线相切的圆叫做三角形的“切接圆”,根据上述定义解决下列问题:在Rt ABC ∆中,90C ∠=︒,6AC =,8BC =.(1)如图1,点D 在AB 边上,D 过点A 且与BC 相切于点E ,则D 是Rt ABC ∆的一个“切接圆”,求该圆的半径DE ;(2)过点A 的Rt ABC ∆的“切接圆”中,是否存在半径的最小值,若存在请求出最小值,若不存在请说明理由;(3)如图2,把Rt ABC ∆放在平面直角坐标系中,使点B 与原点O 重合,点C 落在x 轴正半轴上.求证:以抛物线21(8)312y x =-+上任意一点为圆心都可以作过点A 的Rt ABC ∆的“切接圆”.10.一般地,关于x ,y 的二元一次方程(ax by c a +=,b ,c 为常数,0)ab ≠,都可以改写成(y mx n m =+,n 是常数,0)m ≠的形式,所以每个这样的方程都对应一个一次函数,于是也对应一条直线.这条直线上每个点的坐标(,)x y 都是这个二元一次方程的解. 类似的,在平面直角坐标系中,满足x ,y 的不等式(ax by c a +,b ,c 为常数,0)ab ≠的解也可以用坐标(,)x y 表示,以该不等式的解为坐标的点的全体叫做该不等式的解集,所有这些点构成的图形记为G .若点(,)P x y 在图形G 内,我们称点P 被不等式ax by c +所覆盖;对于任意图形W ,若该图形上的所有点都在图形G 内,那么我们就称图形W 被ax by c +所覆盖. 结合以上信息,回答下列问题:(1)以下三个点:(1,1)A -,(3,3)B ,(0,2)C 其中被不等式0x y -覆盖的点有 ;(2)已知(2,1)D ,(4,2)E ,(3,)F m ,若DEF ∆被不等式30x y -覆盖,求m 的取值范围;(3)如图1,图形W 是以(3,2)P 为圆心,半径为2的圆,要使图形W 被不等式2x y c +(其中c 为常数)所覆盖,求c 的最大值.11.在平面直角坐标系xOy中,圆O的半径为1,对于ABC∆和直线l给出如下定义:若ABC∆是圆∆的一条边关于直线l的对称线段PQ,且P、Q两点均在圆O上,则称ABCO的关于直线l的“关联三角形”,直线l是“关联轴”.(1)如图1,若ABC∆是圆O的关于直线l的“关联三角形”,请画出ABC∆与圆O的“关联轴l”(至少画两条);(2)如图2,若ABC∆中,点A坐标为(2,3),点B坐标为(4,1),点C在直线l上,存在“关联轴l”使ABC∆是圆O的关联三角形,写出点C横坐标的取值范围:;A1),将点A向上平移2个单位得到点M,以M为圆心MA为半径画圆,(3)已知(3AB=(点B在点A右侧),若ABCB,C为圆M上的两点,且2∆与圆O的关联轴至少有两条,直接写出OC的最小值和最大值,以及最大时AC的长.OC的最小值为;OC的最大值为,OC的最大时,AC的长为.12.在平面直角坐标系xOy 中,点P 的坐标为1(x ,1)y ,点Q 的坐标为2(x ,2)y ,且12x x ≠,12y y ≠,若P ,Q 为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P ,Q 的“相关矩形”,如图为点P ,Q 的“相关矩形”示意图. (1)已知点A 的坐标为(1,0),①若点B 的坐标为(4,1),求点A ,B 的“相关矩形”的面积;②点C 在直线4x =上,若点A ,C 的“相关矩形”为正方形,求直线AC 的表达式. (2)O 2,点M 的坐标为(,4)m ,若在O 上存在一点N ,使得点M 、N 的“相关矩形”为正方形,求m 的取值范围.13.对于平面内点P 和G ,给出如下定义:T 是G 上任意一点,点P 绕点T 旋转180︒后得到点P ',则称点P '为点P 关于G 的旋转点.如图为点P 及其关于G 的旋转点P '的示意图.在平面直角坐标系xOy 中,O 的半径为1,点(0,2)P -.(1)在点(1,0)A -,(0,4)B ,(2,2)C 中,是点P 关于O 的旋转点的是 ; (2)若在直线y x b =+上存在点P 关于O 的旋转点,求b 的取值范围; (3)若点D 在O 上,D 的半径为1,点P 关于D 的旋转点为点P ',请直接写出点P '的横坐标P x '的取值范围.14.在平面直角坐标系xOy 中,有不重合的两个点1(Q x ,1)y 与2(P x ,2)y .若Q ,P 为某个直角三角形的两个锐角顶点,且该直角三角形的直角边均与x 轴或y 轴平行(或重合),则我们将该直角三角形的两条直角边的边长之和称为点Q 与点P 之间的“折距”,记做PQ D .特别地,当PQ 与某条坐标轴平行(或重合)时,线段PQ 的长即点Q 与点P 之间的“折距”.例如,在图1中,点(1,1)P -,点(3,2)Q -,此时点Q 与点P 之间的“折距” 3PQ D =. (1)①已知O 为坐标原点,点(3,2)A -,(1,0)B -,则AO D = ,BO D = . ②点C 在直线4y x =-+上,请你求出CO D 的最小值.(2)点E 是以原点O 为圆心,1为半径的圆上的一个动点,点F 是直线36y x =+上以动点.请你直接写出点E 与点F 之间“折距” EF D 的最小值.答案版: 1.【解答】解:(1)根据“平移距离”的定义可得:线段11A B 到O 的“平移距离”为2, 如图1,设22A B 与y 轴交于E ,线段22A B 向下平移得到O 的弦22A B '',线段22A B ''与y 轴交于点F , 则212A F '=,21OA '=,3OE = 3OF ∴=, 22333A A EF OE OF ∴'==-=, ∴线段22A B 到O 3, 故答案为:23; (2)如图2中,作等边OEF ∆,点E 在x 轴上,1OE EF OF ===, 设直线323y x =+交x 轴于M ,交y 轴于N .则(2,0)M -,(0N ,23), 过点E 作EH MN ⊥于H ,2OM =,23ON =, tan 3NMO ∴∠=60NMO ∴∠=︒, 3sin 60EH EM ∴=⋅︒=观察图象可知,线段AB 到O 的“平移距离”为1d 3. (3)如图3,连接OA ,交O 于点A ', 则221(3)2OA +,OA ∴到O 任意一点距离的最小值为11OA OA '=-=,∴点1(2A '3, 设平移后圆上另一点为B ',由题意得:1A B ''=, 有三种情况:①点B '与点O 重合,则点B 的坐标为1(23;②点B '与点(1,0)重合,则点B 的坐标为3(23;③点B '与点1(2-3重合,则点B 的坐标为3);如图可知所有满足条件的点B 形成的图形是以A 为圆心圆心角为120︒的132B B B .2.【解答】(1)解:在半对角四边形ABCD 中,12B D ∠=∠,12C A ∠=∠.360A B C D ∠+∠+∠+∠=︒, 33360B C ∴∠+∠=︒. 120B C ∴∠+∠=︒.即B ∠与C ∠的度数之和120︒. (2)证明:在BED ∆和BEO ∆中, BD BOEBD EBO BE BB =⎧⎪∠=∠⎨⎪=⎩. ()BED BEO SAS ∴∆≅∆.BDE BOE ∴∠=∠. 又12BCF BOE ∠=∠.12BCF BDE ∴∠=∠.如图2,连接OC ,设EAF α∠=,则22AFE EAF α∠=∠=.1801802EFC AFE α∴∠=︒-∠=︒-. OA OC =,OAC OCA α∴∠=∠=.1801802AOC OAC OCA α∴∠=︒-∠-∠=︒-, 则AOC EFC ∠=∠, 又12ABC AOC ∠=∠,1122ABC AOC EFC ∴∠=∠=∠.∴四边形DBCF 是半对角四边形.3.【解答】解:(1)①点A 的坐标为(1,0),点B 的坐标为(5,0),点1(4,3)P ,22(51)16AB ∴=-=,2221(41)(30)18AP =-+-=,2221(54)310BP =-+=,22211AB AP BP ≠+,1P ∴不是点A 、B 的“直角点”; 同理得,2P 、3P 是点A 、点B 的“直角点”, 故答案为:2P 、3P ;②由题意知,AB 的中点C 为(122+,0),∴点A 、B 的“直角点”在以C 为圆心,22为半径的C 上,当直线y x b =-+与C 相切于点D ,如图,连接CD ,45OMN ∠=︒,22CD =,4∴=,CMOM OC CM∴=+=+=+1224522∴===+,b ON OM522同理:当直线y x b=-+与C相切于E时,4CH=,4(122)322∴=-+=-OHb∴=,223b+综上:223522(2)如图,由题意知,2DH=,90∠=︒,EDF∴∠=∠,EDH DFHEDH DFH∴∠=∠,tan tan∴==,FH DH2422∴=+=,2425OF∆的边与O有交点,DEF∴.r2254.【解答】解:(1)①P在x轴正半轴时,如图1,设点Q为O与x轴正半轴的交点,点O为坐标原点,O3P是点A关于O的“倍距点”,23AQ ∴=,23PA QA ==∴点P 离开原点O 的距离43333== ∴点P 的坐标是(33,0),故答案为:(330);②若30PAO ∠=︒时,如图2,作QM x ⊥轴于M ,PN x ⊥轴于N ,连接OQ , 90QMA PNA ∴∠=∠=︒,PAO PAO ∠=∠, AQM APN ∴∆∆∽,∴AM QM AQAN PN AP==, 点O 为坐标原点,O 3P 是点A 关于O 的“倍距点”, 2PA QA =, 3OA OQ ∴==12AQ AP =, 30AQO PAO ∴∠=∠=︒, 60QOM ∴∠=︒, 30OQM ∴∠=︒,在Rt OQM ∆中,3OQ 30OQM ∠=︒,3cos 3cos302QM OQ OQM ∴=⋅∠=︒=,3sin 3sin30OM OQ OQM =⋅∠︒=,33AM OA OM ∴=+=, ∴由比例式12AM QM AQ AN PN AP ===得:33AN =3PN =,33323ON AN AO ∴=-==(23P ∴,3);(2)存在符合条件的点P .如图3, 一次函数34y x =+的图象分别与x 轴、y 轴交于D 、E , ∴令0y =340+=,令0x =,则4y =, 解得43x =-(3D ∴-,0),(0,4)E , 43OD ∴=,4OE =,y 轴x ⊥轴,90EOD ∴∠=︒, 3tan 43OE EDO OD ∴∠== 30EDO ∴∠=︒, 取AD 的中点53(G 0),过点G 作//GH DE 交y 轴于点H , 则直线GH 的解析式为352y =+, 当T 与直线GH 相切时,一次函数34y =+的图象上存在唯一一点P ,使点P 是点A 关于T 的“倍距点”,设切点为1L 或2L ,连接11T L ,22T L , 则112290GLT GL T ∠=∠=︒,//GH DE ,30OGH EDO ∴∠=∠=︒,111112AT LT GT ∴==,22212L T GT =,222AT L T =, 13AT t =,23AT t =+,153GT t =253GT t =, 1533(2t t ∴-=⨯+或1533()2t t +=⨯,解得:33t =3.5.【解答】解:(1)由32x b +=得:1(2)3x b =--, 13x <<,即11(2)33b <--<, 解得:71b -<<-;(2)联立2y x m =-+和23m y x -=得:232m x m x--+=, 解得:3x m =或m -, 102x <<, 当3x m =时,则1032m <<,解得106m <<; 当x m =-时,则102m <-<,解得102m -<<; 故答案为106m <<或102m -<<;(3)连接BE ,OAB ∆为等边三角形,60AOB ∴∠=︒,30AEB ∴∠=︒,AB 为直径,90ACB BCE ∴∠=∠=︒,BC a =,2BE a ∴=,3CE a =,AC b =,3AE b a ∴=;过点C 作CH AB ⊥于H ,在Rt ABC ∆中,BC a =,AC b =,2AB =, 224a b ∴+=,1122ABC S AC BC AB CH ∆=⋅=⋅, AC BC AB CH ∴⋅=⋅,即2ab CH =,当点C 在OD 上时,CH 取得最大值,即CH AD <,222()242444444428a b a b ab ab CH AB CH AD AB ∴+=++=+=+⋅=++=+=, 22a b ∴+,a b ∴+的最大值为222233x ax b ab +=,()()3()0x b x b a x b ∴+--=,()(3)0x b x b a ∴-+=, x b ∴=或(3)x b a =-+,设m 是方程的一个根,当m b =时,2m b AC AB ==<=,02m ∴<<,当(3)m b a =-时,AE m =-, 又24AB AE AO <<=,24m ∴<-<,42m ∴-<<-,x ∴的取值范围为02x <<或42x -<<-.6.【解答】解:(1)如答图1,当CD AB ⊥或点D 是AB 的中点是,2CD AD BD =⋅;(2)作AE BC⊥于点E,由4tan3B=,2tan3C=可设4AE x=,则3BE x=,6CE x=,99BC x∴==,1x∴=,3BE∴=,6CE=,4AE=,设DE a=,①如答图2,若点D在点E左侧,由点D是BC边上的“好点”知,2AD BD CD=⋅,224(3)(6)a a a∴+=-+,即22320a a+-=,解得11 2a=,22a=-(舍去),∴153322 BD a=-=-=.②如答图3,若点D在点E右侧,由点D是BC边上的“好点”知,2AD BD CD=⋅,224(3)(6)a a a∴+=+-,即22320a a--=,解得12a=,21 2a=-(舍去)3325BD a ∴=+=+=. ∴52BD =或5. 方法二、设BD y =,则22(9)4(3)y y y -=+-,解得:5y =或52, ∴52BD =或5.(3)①如答图4,连接AD ,BD ,CHA BHD ∠=∠,ACH DBH ∠=∠AHC DHB ∴∆∆∽, ∴AH CH DH BH=,即AH BH CH DH ⋅=⋅, OH AB ⊥,AH BH ∴=,2BH CH DH ∴=⋅∴点H 是BCD ∆中CD 边上的“好点”. ②521CH DH =. 理由如下:如答图4,90ABD ∠=︒,AD ∴是直径,18AD ∴=.又OH AB ⊥,//OH BD ∴.点O 是线段AD 的中点,OH ∴是ABD ∆的中位线,212BD OH ∴==.在直角ABD ∆中,由勾股定理知:2222181265AB AD BD -- ∴由垂径定理得到:1352BH AB == 在直角BDH ∆中,由勾股定理知:2245144321DH BH BD =+=+= 又由①知,2BH CH DH =⋅,即45321CH =,则521CH = ∴5215721321CH DH =,即521CH DH =. 7.【解答】解(1)①线段OP 与图形W 无公共点,则称点P 为关于图形W 的“无关点”, 1OP 与线段AB 有公共点(1,2)-,2OP 与线段AB 没有公共点,3OP 与线段AB 没有公共点,4OP 与线段AB 有公共点3(1,)2-,如图1, ∴关于线段AB 的“阳光点”是2P ,3P ,故答案为:2P ,3P ;②11//A B AB , ∴1112142OA AB OA A B ===, 点1A 在1B 的上方,1(2,6)A ∴-.(2)情况一:当E 与y 轴相切时,设切点为F ,连接EF , E 与y 轴相切于点F ,EF y ∴⊥轴, E 的半径为32, 32EF ∴=,∴此时点E 的横坐标32E x =-, 情况二:如图2,设直线l 分别与x 轴,y 轴交于点G ,H ,连接CD ,CO ,过点O 作C 的另一条切线OI ,切点为I ,直线OI 与直线l 交于点J ,当E '与直线OI 相切时,过点E '作E F y ''⊥轴于点F ', C 与y 轴相切于点D ,CD y ∴⊥轴,点C 的坐标(3)-,3tan COD ∴∠= 30COD ∴∠=︒, C 与OI 相切于点I ,30COI COD ∴∠=∠=︒60HOJ COI COD ∴∠=∠+∠=︒, 直线:33l y x =+x 轴,y 轴交于点G ,H ,∴点(4,0)G -,(0H ,43),3tan OHG ∴∠, 30OHG ∴∠=︒,18090OJH HOJ OHJ ∴∠=︒-∠-∠=︒,HG OJ ∴⊥,E '与直线OJ 相切,∴切点为点J ,32E J ∴'=, 在Rt OHJ ∆中,cos 43cos306HJ OH OHJ =⨯∠=︒=,39622HE HJ E J ''∴=-=-=, 1924E F HE '∴''==, ∴此时点E 的横坐标为94-;可知,点E 在直线l 上,从情况一中的位置运动到情况二中的位置时,都满足题意, 所以点E 的横坐标的取值范围为9342E x -. (3)如图3: 连接OM ,交圆于N ,OA 与OB 分别于M 相切,则N 点在OA 与OB 上对称点分别为N '与N '',连接NN '、NN '',NN ''交OB 于点D ,连接N N '''交OA 于T ,交OB 于Q ,交OM 于C ,连接NT 、NQ ,NTQ ∆的周长l TN TQ QN TN TQ QN '''=++=++;只有当N '、T 、Q 、N ''共线时,l 取得最小值N N ''',此时的T 与Q 即为所求;由辅助线知,90MHO NDO ∠=∠=︒,2NN DN ''=,3sin 5MH DN MOH OM ON ∠===, ∴352DN =, 65DN ∴=, 1225NN DN ∴''==, 90N DQN ''''∠+∠=︒,90CQO COQ ∠+∠=︒,N MOH ∴∠''=∠,3sin 5N ∴''=, 4cos 5CN N NN ''∴''=='', 4825CN ∴''=, 96225N N CN '∴''=''=, NQT ∴∆的周长最小值9625l N N '=''=, 故答案为:9625.8.【解答】解:(1)①如图,PM ,PN 是T 的两条切线,M ,N 为切点,连接TM ,TN ,当60MPN ∠=︒时, PT 平分MPN ∠,30TPN MPT ∴∠=∠=︒,TM PM ⊥,TN PN ⊥,90TNP PMT ∴∠=∠=︒,22TP TM ∴==,以T 为圆心,TP 为半径作T .观察图象可知:当60180MPN ︒<∠<︒时,T 的环绕点在图中的圆环内部(包括大圆上的点不包括小圆上的点),故答案为:1P ;②如图中,设小圆交y 轴的正半轴于F ,当直线3y x b =+经过点F 时,1b =,当直线3y x b =+与大圆相切于K (在第二象限)时,连接OK ,由题意(0,)B b ,(3b A -,0), 所以OB b =,3b OA =,10AB =, 2OK =,1122AB OK OA OB ⨯⨯=⨯⨯, 210b ∴= 观察图象可知,当1210b <<时,线段AB 上存在的环绕点, 根据对称怀可知:当2101b -<-时,线段AB 上存在的环绕点,综上所述,满足条件的b 的值为1210b <<或2101b -<-;(2)如图中,不妨设(E m -3)(0)m >,则点E 直线3y x =上, 0m >,∴点E 在射线OE 上运动,作EM x ⊥轴;(E m -,3)(0)m >, OM m ∴=,3EM =, 以(E m -3)(0)m >3为半径的E 与x 轴相切,作E 的切线ON , 观察图象可知:以(E m -3)(0)m >3为半径的所有圆构成图形H ,图形H 即为MON ∠的内部,包括射线OM ,ON 上,当T 的圆心在y 轴的正半轴上时,假设以T 为圆心,4为半径的圆与射线ON 相切于D ,连接TD ,3tan EM EOM OM ∠==, 30EOM ∴∠=︒, OM ,ON 是E 的切线,30EON EOM ∴∠=∠=︒.30TOD ∴∠=︒,28OT DT ∴==,(0,8)T ∴,当T 的圆心在y 轴的负半轴上时,且经过点(0.0)O 时,(0,4)T -, 观察图象可知,当48t -<<时,在图象上存在T 的环绕点.9.【解答】(1)解:连接DE .设AD DE x ==. D 与BC 相切于点E ,DE CB ∴⊥,90DEB C ∴∠=∠=︒,//DE AC ∴, ∴BD DE AB AC=, 6AC =,8BC =,22226810AB AC BC ∴=++=, ∴10106x x -=, 154x ∴=, 154DE ∴=;(2)解:存在.当AC 是D 的直径时,D 的半径最小,最小值为3;(3)证明:设抛物线21(8)312y x =-+上任意一点为(,)P x y , 3y ∴, 设P 到x 轴的距离为h ,(8,6)A ,22222211(8)(6)(8)[(8)36](8)31212PA x y x x x h ∴=-+--+-+--+=,∴抛物线21(8)312y x =-+上任意一点为圆心都可以作都可以作过点A 的Rt ABC ∆的“切接圆”.10.【解答】解:(1)被不等式0x y -覆盖的点在直线y x =的上方或直线y x =上, 故点C ,B 被不等式0x y -覆盖,故答案为:B ,C ;(2)如图,不等式30x y -的覆盖点值直线3y x =的下方,或直线3y x =上,当3x =时,9y =,(3,9)N ∴,观察图象可知满足条件的点F 在点N 的下方,且不在线段DE 上, 9m ∴且32m ≠; (3)设直线2y x c =-+,圆P 上的点满足222(3)(2)2x y -+-=,把2y x c =-+代入222(3)(2)2x y -+-=,得到22269444844x x x c cx x c -++++-+-=, 225(24)940x c x c c ∴+-+-+=,当△0=时,22(24)45(94)0c c c --⨯⨯-+=, 216440c c ∴-+=,825c ∴=+(85)-,观察图象可知满足条件的c 的最大值为825- 11.【解答】解:(1)如图,直线1l ,直线2l 即为所求;(2)由题意可知,点C 横坐标x 的取值范围是04x ;(3)如图,连接OM ,AM ,由题意(3M ,3),223(3)23OM ∴=+=当点C 在线段OM 上时,OC 的值最小,且符合题意, OC ∴的最小值为232,当2BC =时,符合题意,此时OC 的值最大, 连接BM ,CM ,此时ABM ∆,MBC ∆都是等边三角形, 2AM CM BC AB ∴====,∴四边形AMCB 是菱形,(23C ∴4),OC ∴的最大值22(23)427=+AC 的长为23故答案为:32,27312.【解答】解:(1)①如图:(1,0)A ,(4,1)B ,四边形ACBD 是矩形,3AC ∴=,1BC =,∴点A ,B 的“相关矩形”的面积为313⨯=; ②如图:由定义可知:AC 是点A ,C 的“相关矩形”的对角线, 点A ,C 的“相关矩形”为正方形,(1,0)A ,C 在直线4x =上, ∴直线AC 与x 轴的夹角为45︒,(4,3)C 或(4,3)-, 设直线AC 的解析为:y kx b =+,把A ,C 坐标分别代入得:034k b k b =+⎧⎨=+⎩或034k b k b =+⎧⎨-=+⎩, 解得:11k b =⎧⎨=-⎩或11k b =-⎧⎨=⎩, 综上所述,若点A ,C 的“相关矩形”为正方形,直线AC 的表达式为1y x =-或1y x =-+;(2)点M ,N 的“相关矩形”为正方形,∴由定义可知:直线MN 与x 轴的夹角为45︒, ∴直线MN 与直线y x =或直线y x =-平行, ①当直线MN 与直线y x =平行时,设直线MN 的解析式为y x b =+, 将(,4)M m 代入y x b =+得:4m b =+,解得4b m =-, ∴直线MN 的解析式为4y x m =+-, ∴直线MN 与y 轴交点纵坐标为4m -, 平移直线y x =,使平移后的直线AD 、BC 与O 相切,其中A 、B 是切点,切线与y 轴分别交于D 、C ,如图:O 22OA OB ∴== AD 、BC 与直线y x =平行, AOD ∴∆和BOC ∆均是等腰直角三角形, 2OD OC ∴==,∴当242m --时,直线MN 与O 有交点,且点M ,N 的“相关矩形”为正方形, 26m ∴,②当直线MN 与直线y x =-平行时,设直线MN 的解析式为y x c =-+, 将(,4)M m 代入y x c =-+得:4m c =-+,解得4c m =+, ∴直线MN 的解析式为4y x m =++, ∴直线MN 与y 轴交点纵坐标为4m +, 平移直线y x =,使平移后的直线EH 、FG 与O 相切,其中E 、F 是切点,切线与y 轴分别交于H 、G ,如图:O 22OE OF ∴== EH 、FG 与直线y x =-平行, EOH ∴∆和FOG ∆均是等腰直角三角形, 2OH OG ∴==,∴当242m -+时,直线MN 与O 有交点,且点M ,N 的“相关矩形”为正方形, 62m ∴--,综上所述,当点M ,N 的“相关矩形”为正方形时,m 的取值范围是:26m 或62m --.13.【解答】解:(1)连接AP 、BP 、CP ,分别取AP 、BP 、CP 的中点为D 、E 、F ,如图:(0,2)P -,(1,0)A -,(0,4)B ,(2,2)C ,1(2D ∴-,1)-、(0,1)E 、(1,0)F ,5OD ∴=1OE =,1OF =, D ∴不在O 上,而E 、F 在O 上, D 、E 、F 分别是AP 、BP 、CP 的中点, ∴点P 绕点D 旋转180︒后得到点A ,点P 绕点E 旋转180︒后得到点B ,点P 绕点F 旋转180︒后得到点C ,根据旋转点的定义,P 关于O 的旋转点为B 、C ; 故答案为:B 、C .(2)设直线y x b =+上点M 是P 关于O 的旋转点,连接PM ,作PM 中点N ,如图:设(,)M x x b +,则(2x N ,2)2x b +-, 根据旋转点定义,N 在O 上,即1ON =, ∴222()()122xx b +-+=, ∴22(2)144x x b +-+=,方程变形为:2222(2)40x b x b b +-+-=, 在直线y x b =+上存在点P 关于O 的旋转点, 2222(2)40x b x b b ∴+-+-=总有实数解, ∴△0,即224(2)8(4)0b b b ---, 解得222222b -+;(3)当D 运动到(1,0)-时,P x '有最小值,连接PP ',作PP '中点H ,如图:设(,)P m n ',则(2m H ,2)2n -, 根据旋转点定义,1HD =, ∴222(1)()122m n -++, ∴2211144m n m n +++-+=,变形为224440n n m m -+++=, P '是P 关于D 的旋转点, ∴关于n 的方程224440n n m m -+++=有实数解, ∴△0,即22(4)4(44)0m m --++, 解得40m -,即40P x '-, 当D 运动到(1,0)时,P x '有最大值,如图:同理可得04P x ',综上所述,点P 关于D 的旋转点为点P ',则点P '的横坐标P x '的取值范围是44P x '-. 14.【解答】解:(1)①|30||20|5AO D =-+--=,同理1BO D =,故答案为:5,1;②设点(,4)C m m -,则|||4|CO D m m =+-,当04m 时,CO D 最小,最小值为4;(2)如图2,过点E 分别作x 、y 轴的平行线交直线36y x =+于1F 、2F , 则1EF 是“折距” EF D 的最小值,即求1EF 的最小值即可, 当点E 在y 轴左侧于平行于直线36y x =+上相切时,1EF 最小,如图3,将直线36y x =+向右平移与圆相切于点E ,平移后的直线与x 轴交于点G ,连接OE ,设原直线与x 、y 轴交于点M 、N ,则点M 、N 的坐标分别为(2,0)-、点(0,6)N , 则210MN =则MON GEO ∆∆∽, 则MN ON GO OE=21061=, 则10GO =, 1106102EF MG -===。
中考数学最全“新定义”汇总

中考数学最全“新定义”汇总新定义【⽅法说明】1、点①在矩形ABCD的内部(不含边界),把横、纵坐标都是整数的点称为“好点”.②对于平⾯直⾓坐标系xOy中的点P和⊙C,给出如下的定义:若⊙C上存在两个点A、B,使得∠APB=60°,则称P为⊙C的关联点.③在平⾯直⾓坐标系中,我们不妨把横坐标和纵坐标相等的点叫“梦之点”,例如点(1,1),(-2,-2),…都是“梦之点”.④如图①,在四边形ABCD的边AB上任取⼀点E(点E不与A、B重合),分别连接ED、EC,可以把四边形ABCD分成三个三⾓形,如果其中有两个三⾓形相似,我们就把E叫做四边形ABCD的边AB上的“相似点”;如果这三个三⾓形都相似,我们就把E叫做四边形ABCD的边AB上的“强相似点”.图①图②2、线①如果⼀条直线把⼀个平⾯的图形的⾯积分成相等的两部分,我们把这条直线称为这个平⾯图形的⼀条⾯积等分线.②如果两条线段将⼀个三⾓形分成3个等腰三⾓形,我们把这两条线段叫做这个三⾓形的三分线.③我们常见的炒菜锅和锅盖都是抛物线⾯,经过锅⼼和盖⼼的纵断⾯是两端抛物线组合⽽成的封闭图形,不妨简称为“锅线”④如图,在平⾯直⾓坐标系中,A、B为轴上两点,C、D为轴上的两点,经过点A、C、B的抛物线的⼀部分C1与经过点A、D、B的抛物线的⼀部分C2组合成⼀条封闭曲线,我们把这条封闭曲线称为“蛋线”.⑤若两个⼆次函数图象的顶点,开⼝⽅向都相同,则称这两个⼆次函数为“同簇⼆次函数”.⑥如图,抛物线y=ax2+2ax(a<0)位于x轴上⽅的图象记为F1,它与x轴交于P1、O两点,图象F2与F1关于原点O对称,F2与x轴的另⼀个交点为P2,将F1与F2同时沿x轴向右平移P1P2的长度即可得到F3与F4;再将F3与F4同时沿x轴向右平移P1P2的长度即可得到F5与F6;…;按这样的⽅式⼀直平移下去即可得到⼀系列图象F1,F2,…,F n.我们把这组图象称为“波浪抛物线”.⑦如图,抛物线y=ax2+bx+c(a>0)的顶点为M,直线y=m与x轴平⾏,且与抛物线交于点A,B,若△AMB为等腰直⾓三⾓形,我们把抛物线上A,B两点之间的部分与线段AB围成的图形称为该抛物线对应的准蝶形,线段AB称为碟宽,顶点M称为碟顶,点M到线段AB的距离称为碟⾼.准蝶形AMB3、三⾓形①如果⼀条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三⾓形称为这条抛物线的“抛物线三⾓形”.②新定义⼀种三⾓形,两边平⽅和等于第三边平⽅的2倍的三⾓形叫做奇异三⾓形.③如果三⾓形有⼀边上的中线长恰好等于这边的长,那么称这个三⾓形为“好玩三⾓形”.④若△HNK满⾜HN=2HK,则称△HNK为以H为顶点的倍边三⾓形.⑤我们把三⾓形被⼀边中线分成的两个三⾓形叫做“友好三⾓形”.4、多边形①若⼀个四边形的⼀条对⾓线把四边形分成两个等腰三⾓形,我们把这条对⾓线叫做这个四边形的和谐线,这个四边形叫做和谐四边形.②类⽐梯形的定义,我们定义:有⼀组对⾓相等⽽另⼀组对⾓不相等的凸四边形叫做“等对⾓四边形”.③若⼀个四边形中存在相邻两边的平⽅和等于⼀条对⾓线的平⽅,则称该四边形为勾股四边形.④如图,我们把满⾜AB=AD、CB=CD且AB≠BC的四边形ABCD叫做“筝形”.⑤邻边不相等的平⾏四边形纸⽚,剪去⼀个菱形,余下⼀个四边形,称为第⼀次操作;在余下的四边形纸⽚中再剪去⼀个菱形,⼜剩下⼀个四边形,称为第⼆次操作;…依此类推,若第n次操作余下的四边形是菱形,则称原平⾏四边形为n阶准菱形.如图1,□ABCD中,若AB=1,BC=2,则□ABCD为1阶准菱形.⑥我们把由不平⾏于底的直线截等腰三⾓形的两腰所得的四边形称为“准等腰梯形”.如图1,四边形ABCD即为“准等腰梯形”.其中∠B=∠C.⑦六个内⾓相等的六边形叫等⾓六边形.7、其他①对于两个相似三⾓形,如果沿周界按对应点顺序环绕的⽅向相同,那么称这两个三⾓形互为顺相似;如果沿周界按对应点顺序环绕的⽅向相反,那么称这两个三⾓形互为逆相似.①②②在平⾯直⾓坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“⾮常距离”,给出如下定义:若|x1-x2|≥|y1-y2|,则点P1与点P2的“⾮常距离”为|x1-x2|;若|x1-x2|<|y1-y2|,则点与点的“⾮常距离”为|y1-y2|.【典型例题】1.(13宁波)若⼀个四边形的⼀条对⾓线把四边形分成两个等腰三⾓形,我们把这条对⾓线叫做这个四边形的和谐线,这个四边形叫做和谐四边形。
2024中考数学新定义及探究题专题 《三角函数及新定义(一)》 (含解析)

2024中考数学新定义及探究题专题《三角函数及新定义(一)》(学生版)【知识储备】模型1、新定义模型此类模型主要包含高中数学中的三角函数和解三角形的相关定理(公式),而这些定理(公式)也可利用初中数学知识证明。
若无特殊说明,一般认为△ABC 的3个角∠A 、∠B 、∠C ,分别对应边a 、b 、c ;1)正弦定理:如图1,R Cc B b A a 2sin sin sin ===(其中R 是三角形外接圆的半径)。
图1图22)余弦定理:如图2,2222cos a b c bc A =+-2222cos b a c ac B=+-2222cos c a b ab C =+-.3)正弦面积公式:如图2,B ac A bc C ab S sin 21sin 21sin 21===∆.4)同角三角函数的基本关系式:221sin cos θθ+=,sin tan cos θθθ=。
5)和(差)、二倍角角公式:()sin sin cos cos sin αβαβαβ±=±;22sin sin cos ααα=.()cos cos cos sin sin αβαβαβ±=;222222112cos cos sin cos sin ααααα=-=-=-.()1tan tan tan tan tan αβαβαβ±±=2221tan tan tan ααα=-.广东九年级课时练习)我们知道,直角三角形的边角关系可用三角函数来描九年级校考开学考试)设一个三角形的三边长分别为a,b,c,例7.(2022·山东济南·统考模拟预测)通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad ).如果ABC 中,AB AC =,那么顶角A 的正对记作sad A ,这时sad A =BC AB=底边腰.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,填空:如果A ∠的正弦函数值为35,那么sad A 的值为___________.如图1:2211sin sin A B ∠∠+=,如图2:2222sin sin A B ∠∠+=,如图2233sin sin A B =∠∠+①观察上述等式,猜想:如图4,在Rt ABC △中,=90C ∠︒,都有2sin A ∠②如图4,在Rt ABC △中,=90C ∠︒,A ∠,B ∠,C ∠的对边分别是a ,(1)若90180α︒<<︒,则角α的三角函数值sin α、cos α、tan α,其中取正值的是(2)若角α的终边与直线2y x =重合,则sin cos αα+的值;(3)若角α是钝角,其终边上一点(,2)P x ,且1cos =3x α,求tan α的值;(4)若090α︒<≤︒,则sin cos αα+的取值范围是.专项训练(一)2.(2022·广东东莞·校考一模)关于三角函数有如下的公式:()sin sin cos cos sin αβαβαβ-=-,由该公式可求得sin15︒的值是()A .4B .4C .4D .12-(1)sad90︒=________.(2)对于0180A <<︒︒,(3)如图②,已知3sin 5A =,其中A ∠为锐角,试求(1)试仿照例题,求出cos 75的准确值;(2)我们知道:sin tan cos αα=,试求出tan75的准确值;15.(2023.广东九年级期中)阅读:△ABC 中,a ,b ,c 分别是∠A ,∠B ,∠C 的对边,△ABC 的边角有如下性质:①正弦定理:==②余弦定理:a 2=b 2+c 2﹣2bc cos A ,b 2=a 2+c 2﹣2ac cos B ,c 2=a 2+b 2﹣2ab cos C .③S △ABC =ab sin C =bc sin A =ac sin B请你根据上述结论求解下列问题:在锐角△ABC 中,a ,b ,c 分别是∠A ,∠B ,∠C 的对边,且2a sin B =b .(1)求角A 的大小;(2)若a =6,b +c =8,求△ABC 的面积.2024中考数学新定义及探究题专题《三角函数及新定义(一)》(解析版)【类型1二次函数问题中的新定义问题】1.(2023春·山东济南·九年级统考期末)新定义:若一个点的纵坐标是横坐标的2倍,则称这个点为二倍点.若二次函数(c为常数)在的图象上存在两个二倍点,则c的取值范围是()A.B.C.D.【答案】D【分析】由点的纵坐标是横坐标的2倍可得二倍点在直线上,由可得二倍点所在线段的端点坐标,结合图象,通过求抛物线与线段的交点求解.【详解】解:由题意可得二倍点所在直线为,将代入得,将代入得,设,,如图,联立与,得方程,即抛物线与直线有两个交点,,解得,当直线和直线与抛物线交点在点A,上方时,抛物线与线段有两个交点,把代入,得,把代入得,,解得,.故选D.【点睛】本题考查二次函数图象与正比例函数图象的交点问题,解题关键掌握函数与方程及不等式的关系,将代数问题转化为图形问题求解.2.(2023春·湖北咸宁·九年级统考期中)定义:我们将顶点的横坐标和纵坐标互为相反数的二次函数称为“互异二次函数”.若互异二次函数的对称轴为直线x=1且图象经过点(﹣1,0),则这个互异二次函数的二次项系数是()A.B.C.1D.﹣1【答案】B【分析】根据函数的对称轴和互异二次函数的特点计算即可;【详解】由题可知:此函数的横坐标与纵坐标互为相反数,且对称轴为直线x=1且图象经过点(﹣1,0),设此函数为,∴,解得:,∴此函数的二次项系数为;故选B.【点睛】本题主要考查了二次函数的性质,准确计算是解题的关键.3.(2023春·广西南宁·九年级统考期中)新定义:在平面直角坐标系中,对于点P(m,n)和点P′(m,n′),若满足m≥0时,n′=n-4;m<0时,n′=-n,则称点P′(m,n′)是点P(m,n)的限变点.例如:点P1(2,5)的限变点是P1′(2,1),点P2(-2,3)的限变点是P2′(-2,-3).若点P(m,n)在二次函数y=-x2+4x+2的图象上,则当-1≤m≤3时,其限变点P′的纵坐标n'的取值范围是()A.B.C.D.【答案】D【分析】根据新定义得到当m≥0时,n′=-m2+4m+2-4=-(m-2)2+2,在0≤m≤3时,得到-2≤n′≤2;当m<0时,n′=m2-4m-2=(m-2)2-6,在-1≤m<0时,得到-2≤n′≤3,即可得到限变点P′的纵坐标n'的取值范围是-2≤n′≤3.【详解】解:由题意可知,当m≥0时,n′=-m2+4m+2-4=-(m-2)2+2,∴当0≤m≤3时,-2≤n′≤2,当m<0时,n′=m2-4m-2=(m-2)2-6,∴当-1≤m<0时,-2<n′≤3,综上,当-1≤m≤3时,其限变点P′的纵坐标n'的取值范围是-2≤n′≤3,故选:D.【点睛】本题主要考查了二次函数图象上点的坐标特征,解题的关键是根据限变点的定义得到n′关于m的函数.4.(2023春·湖南长沙·九年级长沙市开福区青竹湖湘一外国语学校校考期末)定义:我们不妨把纵坐标是横坐标2倍的点称为“青竹点”.例如:点、……都是“青竹点”.显然,函数的图象上有两个“青竹点”:和.(1)下列函数中,函数图象上存在“青竹点”的,请在横线上打“√”,不存在“青竹点”的,请打“×”.①________;②________;③________.(2)若抛物线(m为常数)上存在两个不同的“青竹点”,求m的取值范围;(3)若函数的图象上存在唯一的一个“青竹点”,且当时,a的最小值为c,求c的值.【答案】(1)×;√;×(2)(3)【分析】(1)根据“青一函数”的定义直接判断即可;(2)根据题意得出关于的一元二次方程,再根据根的判别式得出关于m的不等式,即可求解;(3)根据题意得出关于的一元二次方程,再根据根的判别式得出关于a的二次函数,利用二次函数最值求解即可.【详解】(1)解:①令,方程无解,∴函数图像上不存在“青竹点”,故答案为:×;②令,解得:,,∴函数图像上存在“青竹点”和,故答案为:√;③令,方程无解,∴函数图像上不存在“青竹点”,故答案为:×;(2)解:由题意得,整理,得,∵抛物线(m为常数)上存在两个不同的“青竹点”,∴,解得;(3)解:由题意得整理,得∵函数的图像上存在唯一的一个“青竹点”,∴整理,得∴当时,a的最小值为,∵当时,a的最小值为c,∴∴,【点睛】本题属于函数背景下新定义问题,主要考查二次函数的性质,二次函数与一元二次方程的关系,解题关键是掌握二次函数图象与系数的关系,掌握二次函数与方程的关系,一元二次方程根的判别式.5.(2023春·江苏泰州·九年级统考期中)定义:两个二次项系数之和为,对称轴相同,且图像与轴交点也相同的二次函数互为友好同轴二次函数.例如:的友好同轴二次函数为.(1)函数的友好同轴二次函数为.(2)当时,函数的友好同轴二次函数有最大值为,求的值.(3)已知点分别在二次函数及其友好同轴二次函数的图像上,比较的大小,并说明理由.【答案】(1);(2);(3)当时,;当时,;当时,【分析】(1)根据友好同轴二次函数的定义,找出的友好同轴二次函数即可;(2)根据友好同轴二次函数的定义,找出的友好同轴二次函数,判断函数图像开口方向,利用函数的对称轴和自变量范围进行最大值讨论;(3)先根据友好同轴二次函数的定义,找出的友好同轴二次函数,再把两点代入,作差后比较大小,为含参数的二次不等式,求解的范围即可.【详解】(1)设友好同轴二次函数为,由函数可知,对称轴为直线,与轴交点为,,,对称轴为直线,,友好同轴二次函数为;(2)由函数可求得,该函数的友好同轴二次函数为;①当时,时,,解得:;②当时,时,,解得:;综上所述,;(3)由函数可求得,该函数的友好同轴二次函数为,把分别代入可得,,,则,,,①当时,,即,,解得:;②当时,,即,,解得:;③当时,,即,,解得:;综上所述,当时,;当时,;当时,.【点睛】本题考查二次函数的性质以及新定义问题,掌握二次函数的基本性质以及研究手段,准确根据题意求出符合要求的友好同轴二次函数是解题关键.6.(2023春·浙江金华·九年级校考期中)定义:若抛物线y=ax2+bx+c与x轴两交点间的距离为4,称此抛物线为定弦抛物线.(1)判断抛物线y=x2+2x﹣3是否是定弦抛物线,请说明理由;(2)当一定弦抛物线的对称轴为直线x=1,且它的图像与坐标轴的交点间的连线所围成的图形是直角三角形,求该抛物线的表达式;(3)若定弦抛物线y=x2+bx+c(b<0)与x轴交于A、B两点(A在B左边),当2≤x≤4时,该抛物线的最大值与最小值之差等于OB之间的距离,求b的值.【答案】(1)是定弦抛物线,理由见解析(2)或(3)b=﹣4或【分析】(1)令y=0,求出与x轴的交点坐标,可判断;(2)分开口向上向下讨论,利用定弦抛物线的定义和对称轴可求出与x轴交点坐标,用相似求出与y轴交点坐标,代入可得答案;(3)根据对称轴和所给范围分情况讨论即可.【详解】(1)解:当y=0时,x2+2x﹣3=0,解得:x1=1,x2=﹣3,则|x1-x2|=4,即该抛物线是定弦抛物线;(2):当该抛物线开口向下时,如图所示.∵该定弦抛物线的对称轴为直线x=1,设则解得:∴C(﹣1,0),D(3,0),∵△CED为直角三角形∴由题意可得∠CED=90°,∵EO⊥CD,∴△CEO∽△EDO,∴OE2=OC·OD=3,∴E(0,)设该定弦抛物线表达式为,把E(0,)代入求得∴该定弦抛物线表达式为,当该抛物线开口向上时,同理可得该定弦抛物线表达式为,∴综上所述,该定弦抛物线表达式为或;(3)解:若≤2,则在2≤x≤4中,当x=4时该定弦抛物线取最大值,当x=2时该定弦抛物线取最小值.∴l6+4b+c-(4+2b+c)=+2,解得:b=﹣4,∵≤2,∴b≥﹣4,即b=﹣4,若≤3,则在2≤x≤4中,当x=4时该定弦抛物线取最大值,当x=时该定弦抛物线取最小值.∴16+4b+c﹣=+2,解得:b1=﹣4,b2=﹣14,∵2≤≤3,∴﹣6≤b≤﹣4,∴b1=﹣4,b2=﹣14(舍去),若≤4,则在2≤x≤4中,当x=2时该定弦抛物线取最大值,当x=时该定弦抛物线取最小值.∴4+2b+c﹣=+2,解得:b=﹣5,∵≤4,∴﹣8≤b<﹣6,∴b=﹣5不合题意,舍去,若>4,则在2≤x≤4中,当x=2时该定弦抛物线取最大值,当x=4时该定弦抛物线取最小值.∴4+2b+c-(16+4b+c)=+2,解得:b=-,∵>4,∴b<﹣8,∴b=﹣,∴综上所述b=﹣4或.【点睛】本题考查了二次函数的综合性质,包括与x轴交点问题,最值问题,以及和相似的结合,准确地理解定弦抛物线的定义以及分类讨论是解决本题的关键.7.(2023春·浙江·九年级期末)定义:若抛物线与抛物线.同时满足且,则称这两条抛物线是一对“共轭抛物线”.(1)已知抛物线与是一对共轭抛物线,求的解析式;(2)如图1,将一副边长为的正方形七巧板拼成图2的形式,若以BC中点为原点,直线BC为x轴建立平面直角坐标系,设经过点A,E,D的抛物线为,经过A、B、C的抛物线为,请立接写出、的解析式并判断它们是否为一对共轭抛物线.【答案】(1)(2),,、是一对共轭抛物线【分析】(1)将化作顶点式,可求出,和的值,根据“共轭抛物线”的定义可求出,和的值,进而求出的解析式;(2)根据七巧板各个图形之间的关系可求出各个图形的边长,进而可表示点,,,,的坐标,分别求出和的解析式,再根据“共轭抛物线”的定义可求解.【详解】(1)解:,∴,,,∵抛物线与是一对共轭抛物线,∴,且,.(2)解:如图,由题意得,,则,,,,,∵点为的中点,∴,∴,,,,,∴可设抛物线,与抛物线,∴,,解得:,,∴抛物线,抛物线,∴,,,,,,∵,,∴满足且,∴、是一对共轭抛物线.【点睛】本题属于二次函数的新定义类问题,主要考查利用待定系数法求函数表达式,二次函数的顶点式,一般式及交点式三种方式的变换,熟知相关运算是解题关键.8.(2023春·湖南长沙·九年级校联考期末)定义:如果抛物线与轴交于点,,那么我们把线段叫做雅礼弦,两点之间的距离称为抛物线的雅礼弦长.(1)求抛物线的雅礼弦长;(2)求抛物线的雅礼弦长的取值范围;(3)设,为正整数,且,抛物线的雅礼弦长为,抛物线的雅礼弦长为,,试求出与之间的函数关系式,若不论为何值,恒成立,求,的值.【答案】(1)4(2)(3),或,【分析】(1)根据定义求得抛物线与x轴的交点坐标即可求解;(2)根据(1)的方法求得,根据的范围,即可求解.(3)根据题意,分别求得,根据,求得出与之间的函数关系式,根据恒成立,可得,根据,为正整数,且,即可求解.【详解】(1)解:,,,,雅礼弦长;(2),,,,,,,当时,最小值为,当时,最大值小于,;(3)由题意,令,,,则,同理,,,要不论为何值,恒成立,即:恒成立,由题意得:,,解得:,,为正整数,且,则,或,.【点睛】本题考查了抛物线与坐标轴交点问题,一元二次方程根与系数的关系,综合运用以上知识是解题的关键.9.(2023春·河南濮阳·九年级统考期中)小明在课外学习时遇到这样一个问题:定义:如果二次函数y=a1x2+b1x+c1(a1≠0)与y=a2x2+b2x+c2(a2≠0)满足a1+a2=0,b1=b2,c1+c2=0,则称这两个函数互为“旋转函数”.求函数y=x2-3x-2的“旋转函数”.小明是这样思考的:由函数y=x2-3x-2可知,a1=1,b1=-3,c1=-2,根据a1+a2=0,b1=b2,c1+c2=0,求出a2,b2,c2,就能确定这个函数的“旋转函数”.请参考小明的方法解决下面问题:(1)直接写出函数y=x2-3x-2的“旋转函数”;(2)若函数与y=x2-2nx+n互为“旋转函数”,求(m+n)2020的值;(3)已知函数的图象与x轴交于点A、B两点(A在B的左边),与y轴交于点C,点A、B、C关于原点的对称点分别是A1,B1,C1,试证明经过点A1,B1,C1的二次函数与函数互为“旋转函数”【答案】(1)y=-x2-3x+2;(2)1(3)见解析【分析】(1)根据y=a1x2+b1x+c1(a1≠0,a1,b1,c1是常数)与y=a2x2+b2x+c2(a2≠0,a2,b2,c2是常数)满足a1+a2=0,b1=b2,c1+c2=0,则称这两个函数互为“旋转函数”,可得a2,b2,c2,可得旋转函数;(2)根据y=a1x2+b1x+c1(a1≠0,a1,b1,c1是常数)与y=a2x2+b2x+c2(a2≠0,a2,b2,c2是常数)满足a1+a2=0,b1=b2,c1+c2=0,则称这两个函数互为“旋转函数”,可得a2,b2,c2,根据负数奇数次幂是负数,可得答案;(3)根据自变量与函数值的对应关系,可得A、B、C的坐标,根据关于原点对称的点横坐标互为相反数,纵坐标互为相反数,可得A1,B1,C1,根据待定系数法,可得函数解析式;根据y=a1x2+b1x+c1(a1≠0,a1,b1,c1是常数)与y=a2x2+b2x+c2(a2≠0,a2,b2,c2是常数)满足a1+a2=0,b1=b2,c1+c2=0,则称这两个函数互为“旋转函数”,可得a2,b2,c2,可得旋转函数.【详解】(1)解:由y=x2-3x-2函数可知a1=1,b1=-3,c1=−2.由a1+a2=0,b1=b2,c1+c2=0,得a2=-1,b2=-3,c2=2.函数y=x2+3x−2的“旋转函数”为y=-x2-3x+2;(2)由与y=x2−2nx+n互为“旋转函数“,得−2n=,−2+n=0.解得n=2,m=−3.当m=2,n=−3时,(m+n)2020=(2−3)2020=(−1)2020=1;(3)∵当y=0时,,解得x=−1,x=4,∴A(−1,0),B(4,0).当x=0时,y=×(−4)=-2,即C(0,-2).由点A,B,C关于原点的对称点分别是A1,B1,C1,得A1(1,0),B1(−4,0),C1(0,2).设过点A1,B1,C1的二次函数y=a,将C1(0,2)代入,解得,∴过点A1,B1,C1的二次函数而∴a1+a2=0,b1=b2,c1+c2=0,∴经过点A1、B1、C1的二次函数与函数互为“旋转函数”.【点睛】本题考查了二次函数的综合题:熟练掌握关于原点对称的两点的坐标特征;会求二次函数图象与坐标轴的交点和待定系数法求二次函数解析式;对新定义的理解能力.10.(2023春·山西大同·九年级统考期中)请阅读下列材料,并完成相应的任务:定义:我们把自变量为的二次函数与(,)称为一对“亲密函数”,如的“亲密函数”是.任务:(1)写出二次函数的“亲密函数”:______;(2)二次函数的图像与轴交点的横坐标为1和,它的“亲密函数”的图像与轴交点的横坐标为______,猜想二次函数()的图像与轴交点的横坐标与其“亲密函数”的图像与轴交点的横坐标之间的关系是______;(3)二次函数的图像与轴交点的横坐标为1和,请利用(2)中的结论直接写出二次函数的图像与轴交点的横坐标.【答案】(1);(2)4和-1;互为相反数;(3)二次函数的图像与轴交点的横坐标为和【分析】(1)根据二次函数的“亲密函数”定义把一次项系数变为相反数即可;(2)利用“亲密函数”建立y=0时方程,解方程,得出“亲密函数”与x轴交点横坐标,与原函数与x轴交点横坐标比较,得出规律即可;(3)先将函数变形,发现与“亲密函数”类似,根据原函数与x轴交点横坐标得出“亲密函数”与x轴交点横坐标,利用2x等于交点横坐标,求出x得出所求函数与x轴的交点横坐标即可.【详解】解:(1)二次函数的“亲密函数”为,故答案为:;(2),解得,它的“亲密函数”的图像与轴交点的横坐标为4和-1,∴二次函数()的图像与轴交点的横坐标与其“亲密函数”的图像与轴交点的横坐标之间的关系是互为相反数;故答案为4和-1;互为相反数;(3),∵二次函数的图像与轴交点的横坐标为1和,∴二次函数的图像与轴交点的横坐标为-1和,∴图像与轴交点的横坐标为-1和,∴2x=-1,2x=2021,∴,,∴二次函数的图像与轴交点的横坐标为和.【点睛】本题考查新定义函数,仔细阅读题目,抓住实质,抛物线与x轴交点横坐标和一元二次方程的根,利用“亲密函数”变形得出新函数图像与x轴的交点横坐标是解题关键.【类型2二次函数与一次函数综合问题中的新定义问题】1.(2023春·九年级课时练习)定义:由a,b构造的二次函数叫做一次函数y=ax+b的“滋生函数”,一次函数y=ax+b叫做二次函数的“本源函数”(a,b为常数,且).若一次函数y=ax+b的“滋生函数”是,那么二次函数的“本源函数”是.【答案】【分析】由“滋生函数”和“本源函数”的定义,运用待定系数法求出函数的本源函数.【详解】解:由题意得解得∴函数的本源函数是.故答案为:.【点睛】本题考查新定义运算下的一次函数和二次函数的应用,解题关键是充分理解新定义“本源函数”.2.(2023春·浙江湖州·九年级统考期中)定义:如果函数图象上存在横、纵坐标相等的点,则称该点为函数的不动点.例如,点是函数的不动点.已知二次函数(是实数).(1)若点是该二次函数的一个不动点,求的值;(2)若该二次函数始终存在不动点,求的取值范围.【答案】(1)或(2)【分析】(1)根据“不动点”定义,建立方程求解即可;(2)根据不动点的定义求出函数,再根据判别式计算即可.【详解】(1)解:依题意把点代入解析式,得,化简得:,解得:;(2)解:设点是函数的一个不动点,则有,化简得,,关于的方程有实数解,,解得:.【点睛】本题考查了二次函数与新定义“不动点”应用,涉及解一元二次方程、一元二次方程根的情况与判别式等知识,解题的关键是理解并利用新定义解决问题.3.(2023·安徽·模拟预测)已知函数与函数,定义“和函数”.(1)若,则“和函数”;(2)若“和函数”为,则,;(3)若该“和函数”的顶点在直线上,求.【答案】(1).(2),.(3)或.【分析】(1)将代入函数中得出函数,再利用即可得出结论;(2)的解析式为,又,利用两者相等即可得出结论;(3)先得出和函数,进而根据顶点在直线上得出,即可得出结论.【详解】(1)解:当时,,∵函数,此时和函数,∴,故答案为:.(2)解:∵函数与函数,和函数,∴和函数的解析式为,∵和函数的解析式为,∴,,∴,,故答案为:,.(3)解:由题意得和函数为,,∴和函数的顶点为,∵和函数的顶点在上,∴,整理得,解得,.故答案为:或.【点睛】此题主要考查了待定系数法求二次函数解析式、二次函数的顶点坐标、二次函数的性质,熟练掌握二次函数的性质是解本题的关键.4.(2023·北京·模拟预测)城市的许多街道是相互垂直或平行的,因此,往往不能沿直线行走到达目的地,只能按直角拐弯的方式行走.可以按照街道的垂直和平行方向建立平面直角坐标系,对两点和,用以下方式定义两点间距离:.(1)①已知点,则______.②函数的图象如图①所示,是图象上一点,,求点的坐标.(2)函数的图象如图②所示,是图象上一点,求的最小值及对应的点的坐标.【答案】(1)①,②(2),【分析】(1)①根据公式直接计算即可;②根据函数的图象上的点的横纵坐标均非负,可得,,,再根据,可得,即有,进而可得,解方程即可求解;(2)函数化为顶点式为:,即可得,,根据点是图象上一点,可得,,,则有,即可得,问题随之得解.【详解】(1)①∵,,∴,故答案为:;②∵点B是函数的图象点,∵函数的图象上的点的横纵坐标均非负,∴,,,∵,∴,∴,∵,∴,解得:,∴B点坐标为:,(2)函数化为顶点式为:,∴,∵,点是图象上一点,∴,,,∴,∴,∴,∴当时,有最小值,最小值为,∴,∴D点坐标为:,即最小值为3,D点坐标为.【点睛】本题主要考查了二次函数的图象与性质,充分理解定义的两点间距离:,是解答本题的关键.5.(2023春·上海·九年级上海市民办新复兴初级中学校考期中)我们定义【,,】为函数的“特征数”,如:函数的“特征数”是【2,,5】,函数的“特征数”是【0,1,2】(1)若一个函数的“特征数”是【1,,1】,将此函数图像先向左平移2个单位,再向上平移1个单位,得到一个图像对应的函数“特征数”是______;(2)将“特征数”是【0,,】的图像向上平移2个单位,得到一个新函数,这个函数的解析式是______;(3)在(2)中,平移前后的两个函数图像分别与轴交于A、两点,与直线分别交于、两点,在给出的平面直角坐标系中画出图形,并求出以A、、、四点为顶点的四边形的面积;(4)若(3)中的四边形与“特征数”是【1,,】的函数图像有交点,求满足条件的实数的取值范围.【答案】(1)【1,0,】(2)(3)图见解析;面积为(4)【分析】(1)由已知可知,平移后的函数为,则可求“特征数”;(2)由已知可知函数为,平移后函数为;(3)令,求出,令,求出,,则,又由,可判断四边形是菱形;然后结合图形求面积即可;(4)由已知可得,则函数与AD边无交点,只能与BC 边有交点,将代入函数,将代入函数求解即可得出结果.【详解】(1)解:∵函数的特征数是【1,,1】,∴函数为,将函数向左平移2个单位,再向上平移1个单位得到,∴函数的“特征数”是【1,0,】.故答案为:【1,0,】.(2)∵函数的“特征数”是【0,,】,∴,∵函数图象向上平移2个单位,∴平移后函数为.故答案为:.(3)解:令,则,∴,令,则,,∴,,∵,,∴四边形是平行四边形,∵,∴四边形是菱形.;(4)∵函数的“特征数”是【1,,】,∴,∴由函数图象得:函数与AD边无交点,∴函数与BC边有交点,将代入函数得:,将代入函数得:,∴.【点睛】本题考查二次函数的综合、新定义,函数的平移,理解定义,能将定义与所学函数知识结合是解题的关键.6.(2023春·福建龙岩·九年级校考期末)定义:对于给定的两个函数,任取自变量x的一个值,当x<0时,它们对应的函数值互为相反数;当x≥0时,它们对应的函数值相等.我们称这样的两个函数互为相关函数.例如:一次函数,它的相关函数为(1)已知点A(-2,1)在一次函数的相关函数的图象上时,求a的值.(2)已知二次函数.当点B(m,)在这个函数的相关函数的图象上时,求m的值.【答案】(1)a=-1;(2)m=2-或m=3或m=1.【分析】(1)函数y=ax-3的相关函数为y=,将点A(-2,1)代入y=-ax+3即可求解;(2)当m<0时,将B(m,)代入y=x2-4x+得m2-4m+=,可求得m的值;当m≥0时,将B(m,)代入y=-x2+4x-得:-m2+4m-=,可求得m的值.(1)解:函数y=ax-3的相关函数为y=,将点A(-2,1)代入y=-ax+3得:2a+3=1,解得:a=-1;(2)解:二次函数y=-x2+4x-的相关函数为y=,①当m<0时,将B(m,)代入y=x2-4x+得m2-4m+=,解得:m=2+(舍去)或m=2-;②当m≥0时,将B(m,)代入y=-x2+4x-得:-m2+4m-=,解得:m=3或m=1.综上所述:m=2-或m=3或m=1.【点睛】本题主要考查的是二次函数的综合应用,解答本题主要应用了二次函数的图象和性质、函数图象上点的坐标与函数解析式的关系,理解互为相关函数的概念是解题的关键.7.(2023春·江苏南通·九年级统考期末)定义:若图形与图形有且只有两个公共点,则称图形与图形互为“双联图形”,即图形是图形的“双联图形”,图形是图形的“双联图形”.(1)若直线与抛物线互为“双联图形”,且直线不是双曲线的“双联图形”,求实数的取值范围;(2)如图2,已知,,三点.若二次函数的图象与互为“双联图形”,直接写出的取值范围.【答案】(1)的取值范围是(2)或【分析】(1)已知直线与抛物线有且只有两个公共点,∴将代入抛物线中,得,配方得,∵方程有实数解,∴即又直线不是双曲线的“双联图形”,∴直线与双曲线最多有一个公共点,即当时,代入得,,即,∴实数的取值范围是;(2)∵是二次函数,∴∵二次函数的顶点坐标为(-1,3),且对称轴为直线x=-1,∴当时,二次函数的图象与的图象没有交点,∴不成立;当时,二次函数的图象开口向下,为使它与互为双联图形,即有且只有两个公共点,∴①当抛物线与AC和AB相交时,设直线BC的解析式为y=mx+n,把C(1,4),B(4,0)代入,得,∴,∴y=-x+4,∵抛物线与BC不想交,∴,即ax2+(2a+1)x+a-1=0无实数根,∴(2a+1)2-4a(a-1)<0,解得a<,又当时,要满足,相当于,所以;∴;②当抛物线与AC和BC相交时,当x=4时,要满足,相当于,所以,,∴;综上,a的取值范围为:或8.(2023春·北京·九年级北京市第三中学校考期中)定义:在平面直角坐标系中,图形G上点P(x,y)的纵坐标y与其横坐标x的差y﹣x称为P点的“坐标差”,而图形G上所有点的“坐标差”中的最大值称为图形G的“特征值”.(1)①点A(1,3)的“坐标差”为;②抛物线y=﹣x2+3x+3的“特征值”为;(2)某二次函数y=﹣x2+bx+c(c≠0)的“特征值”为1,点B(m,0)与点C分别是此二次函数的图象与x轴和y轴的交点,且点B与点C的“坐标差”相等.①直接写出m=;(用含c的式子表示)②求b的值.【答案】(1)①2;②5;(2)①m=-c;②或.【分析】(1)①由题中所给“坐标差”的定义即可得到点A(1,3)的坐标差.②由坐标差的定义可得:二次函数y=-x2+3x+4图象上点的坐标差为:y-x=-x2+3x +4-x=-x2+2x+4,将此关系式配方即可求得y-x的最大值,从而得到抛物线y=-x2+3x+4的“特征值”.(2)①由题意可得:0-m=c-0,由此可得:m=-c.②由m=-c可得点B的坐标为(-c,0),把点B的坐标代入y=x2+bx+c(c≠0)中可得c(c-b+1)=0,由c≠0可得c-b+1=0,即b=c+1,再由y-x=-x2+(b-1)x+c.(c≠0)的特征值为1可得:=1,两者即可解得b和c的值.【详解】解:(1)①根据图形G上点P(x,y)的纵坐标y与其横坐标x的差y﹣x称为P点的“坐标差”,点A(1,3)的“坐标差”为3-1=2,故答案为2;②抛物线y=﹣x2+3x+4的“特征值”为-x2+3x+4-x-x2+3x+4-x=-x2+2x+4=-(x2-2x+1-1)+4=-(x-1)2+5,所以抛物线y=﹣x2+3x+4的“特征值”为5.故答案为5;(2)①∵点C是此二次函数的图象与y轴的交点,∴C(0,c),∵B(m,0),点B与点C的“坐标差”相等.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
④当 m≠0 时,函数图象经过同一个点.
其中正确的结论有( )
A、①②③④
B、①②④ C、①③④ D、②④
二、填空题 4.通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的
比值相互唯一确定,因此边长与角的大小之间可以相互转化。类似的,可以在等
8.阅读下面的材料: 在平面几何中,我们学过两条直线平行的定义.下面就两个一次函数的图象所
确定的两条直线,给出它们平行的定义:设一次函数 y k1x b1(k1 0) 的图象
为直线 l1 ,一次函数 y k2 x b2 (k2 0) 的图象为直线 l2 ,若 k1 k2 ,且 b1 b2 ,
-2
2 4 6x
且交 x 轴于点 C ,求出△ ABC 的面积 S 关于 t
的函数表达式.
(第 23 题)
3﹣2
ab
23
1x
例 3.我们定义 ad bc ,例如 =2×5﹣3×4=10﹣12=﹣2,若 x,y 均为整数,且满足 1< <
cd
45
y4
3,则 x+y 的值是 .
考点三:探索题型中的新定义
例 4.定义:到凸四边形一组对边距离相等,到另一组对边距离也相等的点叫凸四边形的准内
点.如图 1,PH=PJ,PI=PG,则点 P 就是四边形 ABCD 的准内点.
新定义型专题
(一)专题诠释
所谓“新定义”型问题,主要是指在问题中定义了中学数学中没有学过的一些概念、新运算、
新符号,要求学生读懂题意并结合已有知识、能力进行理解,根据新定义进行运算、推理、
迁移的一种题型.“新定义”型问题成为近年来中考数学压轴题的新亮点.在复习中应重视学生应
用新的知识解决问题的能力
(二)解题策略和解法精讲
112 2
2
)表示当
x=
1
时
y
的值,即
f(
1
)=
(f 1)
(1 )2 2
1 ;…;则 f(1)+f(2)+f(
2
2
2 1(1)2 5
2
(f 1)
(1 )2 2
1 )+f(3)+f( 1 )+…+f(2011)+f(
1
)=
2 1(1)2 5
3
2011
2
.
三、解答题
7.在平面直角坐标系中.过一点分別作坐标轴的垂线,若与坐标轴围成矩形的周 长与面积相等,则这个点叫做和谐点.例如.图中过点 P 分別作 x 轴,y 轴的垂 线.与坐标轴围成矩形 OAPB 的周长与面积相等,则点 P 是和谐点. (1)判断点 M(l,2),N(4,4)是否为和谐点,并说明理由; (2)若和谐点 P(a,3)在直线 y=﹣x+b(b 为常数)上,求 a,b 的值.
腰三角形中建立边角之间的联系。我们定义:等腰三角形中底边与腰的比叫做顶
角的正对(sad).如图①在△ABC 中,AB=AC,顶角 A 的正对记作 sadA,这时 sadA
底边 BC .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据
腰 AB
上述角的正对定义,解下列问题:
(1)sad60°=
.
(2)对于 0°<A<180°,∠A 的正对值 sadA 的取值范围
是
.
(3)如图②,已知 sinA 3 ,其中∠A 为锐角,试求 sadA 的值. 5
A
B
B
C
CALeabharlann 图①图②5、若记 y=f(x)= x2 ,其中 f(1)表示当 x=1 时 y 的值,即 f(1)= 12 = 1 ;f( 1
1 x2
3. 如图,六边形 ABCDEF 是正六边形,曲线 FK1K2K3K4K5K6K7……叫做“正六边形的
渐开线”,其中 FAK1 , KA1K2 , KA2K3 , KA3K4 , KA4K5 , KA5K6 ,……的圆心依次按点 A,B,
C,D,E,F 循环,其弧长分别记为 l1,l2,l3,l4,l5,l6,…….当 AB=1 时,l2 011 等于( )
真题演练
1.定义运算 a b=a(1﹣b),下列给出了关于这种运算的几点结论: ①2 (﹣2)=6;②a b=b a;③若 a+b=0,则(a b)+(b a)=2ab;④若 a b=0,
则 a=0. 其中正确结论序号是 .(把在横线上填上你认为所有正确结论的序号)
2.如果一条直线把一个平面图形的面积分成相等的两部分,我们把这条直线称为这个平面图
(1)如图 2,∠AFD 与∠DEC 的角平分线 FP,EP 相交于点 P.求证:点 P 是四边形 ABCD 的准内点.
(2)分别画出图 3 平行四边形和图 4 梯形的准内点.(作图工具不限,不写作法,但要有必 要的说明)
(3)判断下列命题的真假,在括号内填“真”或“假”. ①任意凸四边形一定存在准内点.( ) ②任意凸四边形一定只有一个准内点.( ) ③若 P 是任意凸四边形 ABCD 的准内点,则 PA+PB=PC+PD 或 PA+PC=PB+PD.( )
我们就称直线 l1 与直线 l2 互相平行.
解答下面的问题:
y
(1)求过点 P(1, 4) 且与已知直线 y 2x 1平
6
行的直线 l 的函数表达式,并画出直线 l 的图
4
象;
(2)设直线 l 分别与 y 轴、 x 轴交于点 A 、 B
2
,如果直线 m : y kx t(t 0) 与直线 l 平行 -2
“新定义型专题”关键要把握两点:一是掌握问题原型的特点及其问题解决的思想方法;
二是根据问题情景的变化,通过认真思考,合理进行思想方法的迁移.
(三)考点精讲
考点一:规律题型中的新定义
例 1.定义:a 是不为 1 的有理数,我们把 1 称为 a 的差倒数.如:2 的差倒数是 1 1,-
1 a
1 2
1
的差倒数是
的“小九九”算法是完全一样的,而后面“六到九”的运算就改用手势了.如计
算 8×9 时,左手伸出 3 根手指,右手伸出 4 根手指,两只手伸出手指数的和为 7,
未伸出手指数的积为 2,则 8×9=10×7+2=72.那么在计算 6×7 时,左、右手伸
出的手指数应该分别为( )
A、1,2
B、1,3
C、4,2 D、4,3
A. 2011
2
B. 2011
3
C. 2011
4
D. 2011
6
K5
K6
K4
DE
C
F
B A K1
K7
K3
K2
(第 12 题图)
一、选择题
11 1、定义一种运算☆,其规则为 a☆b= + ,根据这个规则,计算 2☆3 的值是( )
ab
A. 5
B. 1
C.5
D.6
6
5
2.在快速计算法中,法国的“小九九”从“一一得一”到“五五二十五”和我国
形的一条面积等分线,例如平行四边形的一条对角线所在的直线就是平行四边形的一条面积 等分线. (1)三角形的中线、高线、角平分线分别所在的直线一定是三角形的面积等分线的有 ; (2)如图,梯形 ABCD 中,AB∥DC,如果延长 DC 到 E,使 CE=AB,连接 AE,那么有 S 梯形 ABCD=S△ADE.请你给出这个结论成立的理由,并过点 A 作出梯形 ABCD 的面积等分线(不 写作法,保留作图痕迹); (3)如图,四边形 ABCD 中,AB 与 CD 不平行,S△ADC>S△ABC,过点 A 能否作出四边形 ABCD 的面积等分线?若能,请画出面积等分线,并给出证明;若不能,说明理由.
1
1 (1)
1 2
.已知
a1=-
1 3
,a2
是
a1
的差倒数,a3
是
a2
的差倒数,a4
是 a3 的差倒数,…,依此类推,a2009= .
考点二:运算题型中的新定义 例 2.对于两个不相等的实数 a、b,定义一种新的运算如下, a *b a b(a b>0),如:
a﹣b 3* 2 3 2 5 ,那么 6*(5*4)= .
考点四:阅读材料题型中的新定义
阅读材料 我们经常通过认识一个事物的局部或其特殊类型,来逐步认识这个事物; 比如我们通过学习两类特殊的四边形,即平行四边形和梯形(继续学习它们的特殊类型如矩 形、等腰梯形等)来逐步认识四边形;
我们对课本里特殊四边形的学习,一般先学习图形的定义,再探索发现其性质和判定方法, 然后通过解决简单的问题巩固所学知识; 请解决以下问题: 如图,我们把满足 AB=AD、CB=CD 且 AB≠BC 的四边形 ABCD 叫做“筝形”; (1)写出筝形的两个性质(定义除外); (2)写出筝形的两个判定方法(定义除外),并选出一个进行证明.
3.(2010 浙江杭州,10,3 分)定义[ a , b , c ]为函数 y = a x 2+ bx c 的特征数,
下面给出特征数为[2m,1﹣m,﹣1﹣m]的函数的一些结论:
①当 m=﹣3 时,函数图象的顶点坐标是( 1 , 8 ); 33
②当 m>0 时,函数图象截 x 轴所得的线段长度大于 3 ; 2
