钢结构基本原理习题参考解答第五章
钢结构基本原理(沈祖炎)课后习题答案完全版之欧阳治创编

第二章2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
图2-34 σε-图(a )理想弹性-塑性 (b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅ 非弹性阶段:y f σ=(应力不随应变的增大而变化)(2)弹性阶段:tan E σεαε==⋅非弹性阶段:'()tan '()tan yyy y f f f E f E σεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610yf E ε===⨯卸载后残余应变:0c ε=可恢复弹性应变:0.00114y c εεε=-=(2)B 点:卸载前应变:0.025F εε== 卸载后残余应变:0.02386yc f E εε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点: 卸载前应变:0.0250.0350.06'c yF f E σεε-=-=+= 卸载后残余应变:0.05869c c Eσεε=-= 可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
钢结构U5课后答案

一平台的梁格布置如图所示,铺板为预制钢筋混凝土板,焊于次梁上。
设平台恒荷载的标准值(不包括梁自重)为2/kN m 。
试选择次梁截面,钢材为Q345钢。
解:1、普通工字形钢34I45a143332241x x W cm I cm ==选3、验算:1)强度 63410.410272.82951.05143310x a x x M Mpa f Mp r W σ⨯====⨯⨯p 2)挠度445455666000384384 2.0610322411016.77[]15k q l v EIx mm v mm⨯=⋅=⋅⨯⨯⨯==f重选I50a444544647255666000384384 2.06104647210x k X I cm q l v EI =⋅⨯=⋅=⋅⨯⨯⨯ 3)整稳:不必计算。
4)局稳:因为是型钢,不必验算。
解:图(a )所示的简支梁,其截面为不对称工字形[图(b )],材料为Q235B 钢;梁的中点和梁端均有侧向支承;在集中荷载(未包括梁自重)F=160kN (设计值)的作用下,梁能否保证其整体稳定性?2422max 132301800.81011041041076.980.8/0.812160121.2497.384842800.840.5101810.533.2301800.810110.880(82/233.2)80012G X A cm q kN mql Pl M kN m y cm I γ-⎡⎤⎣⎦=⨯+⨯+⨯==⨯⨯=⨯⨯=+=⨯+=⋅⎡⎤⎣⎦⨯⨯+⨯⨯=+=⨯+⨯+⨯=⨯⨯+-⨯⨯1、计算梁自重、计算中和轴位置2243133413112.8301(33.20.5)101(48.80.5)9344093440281033.23 3.1 1.751(130110)2330124.7/600/4.7127.7(130)/12/()0.9623300X X b b y y y y b b cm I W cm y I cm i cm l i I I I ϕβλαη+⨯⨯-+⨯⨯-====⎡⎤⎣⎦⇒==⨯⨯+⨯=======⨯=+===、求查附表22'.8(21)0.8(20.961)0.7443202354320104822351.750.74127.728102352.50.60.2820.2821.07 1.070.9572.5b b b b y X y b b Ah W f αϕβηλϕϕ-=⨯⨯-=⎤⎥=⨯⨯⨯⨯⎥⎦⎤⨯⎥=⨯⨯⨯⨯⎥⎦==-=-=f 4、梁整63497.310184.9215()0.957281010b X M Mpa f Mpa W ϕ⎡⎤⎣⎦⨯===⨯⨯p 体稳定计算满足解:设计习题的中间主梁(焊接组合梁),包括选择截面、计算翼缘焊缝、确定腹板加劲肋的间距。
钢结构基本原理-同济第二版沈祖炎重点习题课后答案
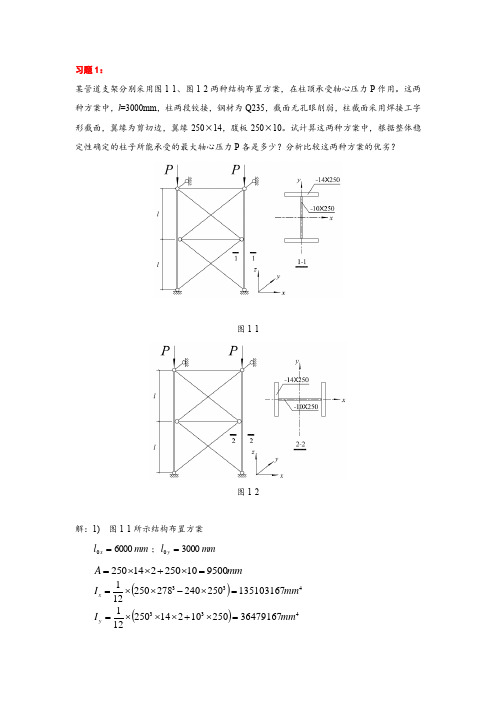
习题1:某管道支架分别采用图1-1、图1-2两种结构布置方案,在柱顶承受轴心压力P 作用。
这两种方案中,l =3000mm ,柱两段铰接,钢材为Q235,截面无孔眼削弱,柱截面采用焊接工字形截面,翼缘为剪切边,翼缘-250×14,腹板-250×10。
试计算这两种方案中,根据整体稳定性确定的柱子所能承受的最大轴心压力P 各是多少?分析比较这两种方案的优劣?图1-1图1-2解:1) 图1-1所示结构布置方案mm l x 60000=;mm l y 30000=mm A 950010250214250=⨯+⨯⨯=()433135103167250240278250121mm I x =⨯-⨯⨯=()4333647916725010214250121mm I y =⨯+⨯⨯⨯=mm A I i x x 3.1199500135103167===;mm AI i y y 0.62950036479167===3.503.11960000===x x x i l λ;4.480.6230000===y y y i l λ此截面对x 轴为b 类,对y 轴为c 类,查表得855.0=x ϕ(附表4-4);785.0=y ϕ(附表4-5)应根据y ϕ确定柱子整体稳定的承载力kN Af P d y 16032159500785.0max =⨯⨯==ϕ2) 图1-2所示结构布置方案mm l x 60000=;mm l y 30000=mm A 9500=;mm i x 0.62=;mm i y 3.119= 8.960.6260000===x x x i l λ;1.253.11930000===y y y i l λ此截面对x 轴为c 类,对y 轴为b 类,查表得478.0=x ϕ(附表4-5);953.0=y ϕ(附表4-4)应根据x ϕ确定柱子整体稳定的承载力kN Af P d x 9762159500478.0max =⨯⨯==ϕ3) 分析比较两种结构布置方案所使用的材料完全相同,但是图1-1所示方案(为下文表述的方便,以后简称方案A )的承载力为1603kN ,而图1-2所示方案(为下文表述的方便,以后简称方案B )的承载力仅为976kN 。
钢结构基本原理(沈祖炎)课后习题答案完全版

钢结构基本原理(沈祖炎)课后习题答案完全版钢结构基本原理(沈祖炎)课后习题答案完全版第⼆章2.1 如图2-34所⽰钢材在单向拉伸状态下的应⼒-应变曲线,请写出弹性阶段和⾮弹性阶段的σε-关系式。
图2-34 σε-图(a )理想弹性-塑性(b )理想弹性强化解:(1)弹性阶段:tan E σεαε==?⾮弹性阶段:y f σ=(应⼒不随应变的增⼤⽽变化)(2)弹性阶段:tan E σεαε==?⾮弹性阶段:'()tan '()tan y yy y f f f E f E σεαεα=+-=+-2.2如图2-35所⽰的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载⾄零,则在三种情况下,卸载前应变ε、卸载后残余应变cε及可恢复的弹性应变yε各是多少?2235/y f N mm = 2270/c N mm σ= 0.025F ε=522.0610/E N mm =?2'1000/E N mm =tgα'=E'f y 0f ytgα=E答:钢材σε-曲线与反复应⼒⼤⼩和作⽤时间关系:当构件反复⼒yf σ≤时,即材料处于弹性阶段时,反复应⼒作⽤下钢材材性⽆变化,不存在残余变形,钢材σε-曲线基本⽆变化;当yf σ>时,即材料处于弹塑性阶段,反复应⼒会引起残余变形,但若加载-卸载连续进⾏,钢材σε-曲线也基本⽆变化;若加载-卸载具有⼀定时间间隔,会使钢材屈服点、极限强度提⾼,⽽塑性韧性降低(时效现象)。
钢材σε-曲线会相对更⾼⽽更短。
另外,载⼀定作⽤⼒下,作⽤时间越快,钢材强度会提⾼、⽽变形能⼒减弱,钢材σε-曲线也会更⾼⽽更短。
钢材疲劳强度与反复⼒⼤⼩和作⽤时间关系:反复应⼒⼤⼩对钢材疲劳强度的影响以应⼒⽐或应⼒幅(焊接结构)来量度。
⼀般来说,应⼒⽐或应⼒幅越⼤,疲劳强度越低;⽽作⽤时间越长(指次数多),疲劳强度也越低。
2.4试述导致钢材发⽣脆性破坏的各种原因。
钢结构原理习题答案第五章精品文档9页

第五章 轴心受力构件5.1 验算由2635L ⨯组成的水平放置的轴心拉杆的强度和长细比。
轴心拉力的设计值为270KN ,只承受静力作用,计算长度为3m 。
杆端有一排直径为20mm 的孔眼,钢材为Q235钢。
如截面尺寸不够,应改用什么角钢?注:计算时忽略连接偏心和杆件自重的影响。
解:查型钢表2635L ⨯角钢,221.94, 2.82,215/,6.142x y i cm i cm f N mm A cm ====⨯ 确定危险截面如图1—1截面净截面面积2(6.1420.5)210.28n A cm =-⨯⨯=验算强度: 322227010262.65/215/10.2810n N N mm f N mm A ⨯==>=⨯ (说明截面尺寸不够) 验算长细比:[]0300154.63501.94x x l i λλ===<= 所以,刚度满足要求需用净截面面积322701012.56215n N A cm f ⨯≥== 改用2755L ⨯角钢,22.32,3.29,7.412x y i cm i cm A cm ===⨯此时净截面面积22(7.4120.5)212.8212.56n A cm cm =-⨯⨯=> (满足强度要求)[]030091.183503.29y y l i λλ===<= (满足刚度要求) 5.2 一块—400×20的钢板用两块拼接板—400×12进行拼接。
螺栓孔径为22mm ,排列如图5.30所示。
钢板轴心受拉,N =135KN (设计值)。
钢材为Q235钢,解答下列问题:(1)钢板1-1截面的强度够否? (2)是否还需要验算2—2截面的强度?假定N 力在13个螺栓中平均分配,2—2截面应如何验算?(3)拼接板的强度够否? 解:(1)验算钢板1—1截面的强度:A n =40×2-3×2.2×2=66.8cm 2(2)2-2截面虽受力较小,但截面消弱较多,尚应进行验算。
钢结构第5章(带答案)

第5章 受弯构件1 梁截面高度的确定应考虑三种参考高度,是指由建筑确定的最大梁高;由刚度确定的最小梁高 ;由用料最省确定的经济梁高 。
2 梁腹板中,设置横向加劲肋对防止剪力引起的局部失稳有效,设置纵向加劲肋对防止弯矩引起的局部失稳有效。
3 梁整体稳定判别式11b l 中,1l 是受压翼缘自由长度,1b 是受压翼缘梁宽。
4 当w t h 0大于80y f 235但小于120y f 235时,应在梁的腹板上配置横向向加劲肋。
5 在工字形梁弯矩、剪力都比较大的截面中,除了要验算正应力和剪应力外,还要在翼缘与腹板相交处验算折算应力。
6 对无集中荷载作用的焊接工字形截面梁,当其腹板高厚比:80y f 235≤w t h 0≤120y f 235时,腹板将在剪力作用下失去局部稳定。
7 受均布荷载作用的简支梁,如要改变截面,应在距支座约六分之一梁长处改变截面较为经济。
8 组合梁当w t h 0大于150时,除配置横向加劲肋外,在弯矩大的受压区应配置纵向加劲肋。
9 梁的正应力计算公式为:nxx X W M γ≤f ,式中:x γ是截面塑性发展系数,nx W 是净截面抗弯模量。
10 对承受静力荷载或间接承受动力荷载的钢梁,允许考虑部分截面发展塑性变形,在计算中引入塑性发展系数。
11 按构造要求,组合梁腹板横向加劲肋间距不得小于0.5h0。
12 组合梁腹板的纵向加劲肋与受压翼缘的距离应在0.2~0.25ho 之间。
13 当组合梁腹板高厚比w t h 0≤80y f 235时,对一般梁可不配置加劲肋。
14 提高梁整体稳定的措施主要有1.增加受压翼缘的宽度;2在受压翼缘设置侧向支撑 。
15 焊接工字形等截面简支梁的b ϕ为:yb y x y b b f h t W Ah 235])4.4(1[4320212⨯++=ηλλβϕ,b β考虑的是等效临界弯矩系数,b η考虑的是不对称系数。
16 影响梁弯扭屈曲临界弯矩的主要因素有侧向抗弯刚度、抗扭刚度;梁的支座情况 ;荷载作用种类;荷载作用位置;受压翼缘的自由长度。
同济大学版钢结构基本原理(第二版)习题参考解答第五章

5.1 影响轴心受压稳定极限承载力的初始缺陷有哪些?在钢结构设计中应如何考虑?5.2 某车间工作平台柱高2.6m,轴心受压,两端铰接.材料用I16,Q235钢,钢材的强度设计值2215/d f N mm =.求轴心受压稳定系数ϕ及其稳定临界荷载.如改用Q345钢2310/d f N mm =,则各为多少?解答:查P335附表3-6,知I16截面特性,26.57, 1.89,26.11x y i cm i cm A cm === 柱子两端较接, 1.0x y μμ== 故柱子长细比为 1.0260039.665.7x x xli μλ⨯===,2600 1.0137.618.9y y y l i μλ⨯===因为x y λλ<,故对于Q235钢相对长细比为137.61.48λπ=== 钢柱轧制, /0.8b h ≤.对y 轴查P106表5-4(a)知为不b 类截面。
故由式5-34b得()223212ϕααλλλ⎡=++⎢⎣ ()2210.9650.300 1.48 1.482 1.48⎡=+⨯+⎢⎣⨯ 0.354=(或计算137.6λ=,再由附表4-4查得0.354ϕ=)故得到稳定临界荷载为20.35426.1110215198.7crd d N Af kN ϕ==⨯⨯⨯=当改用Q365钢时,同理可求得 1.792λ=。
由式5-34b 计算得0.257ϕ= (或由166.7λ=,查表得0.257ϕ=)故稳定临界荷载为20.25726.1110310208.0crd d N Af kN ϕ==⨯⨯⨯=5.3 图5-25所示为一轴心受压构件,两端铰接,截面形式为十字形.设在弹塑性范围内/E G 值保持常数,问在什么条件下,扭转屈曲临界力低于弯曲屈曲临界力,钢材为Q235.5.4 截面由钢板组成的轴心受压构件,其局部稳定计算公式是按什么准则进行推导得出的.5.5 两端铰接的轴心受压柱,高10m,截面为三块钢板焊接而成,翼缘为剪切边,材料为Q235,强度设计值2205/d f N mm =,承受轴心压力设计值3000kN (包括自重).如采用图5-26所示的两种截面,计算两种情况下柱是否安全.图5-26 题5.5解答:截面特性计算: 对a)截面:32394112(5002020500260)8500 1.436101212x I mm =⨯⨯⨯+⨯⨯+⨯⨯=⨯ 3384112205005008 4.167101212y I mm =⨯⨯⨯+⨯⨯=⨯ 2250020500824000A mm =⨯⨯+⨯=244.6x i mm ==131.8y i mm==对b)截面:32384112(4002540025212.5)104009.575101212x I mm =⨯⨯⨯+⨯⨯+⨯⨯=⨯ 33841122540040010 2.667101212y I mm =⨯⨯⨯+⨯⨯=⨯ 24002524001024000A mm =⨯⨯+⨯=199.7x i mm ==105.4y i mm==整体稳定系数的计算:钢柱两端铰接,计算长度10000ox oy l l mm == 对a)截面: 1000040.88244.6ox x x l i λ=== 1000075.87131.8ox y y l i λ=== 对b)截面: 1000050.08199.7kx x x l i λ=== 1000094.88105.4ox y y l i λ=== 根据题意,查P106表5-4(a),知钢柱对x 轴为b 类截面,对y 轴为c 类截面.对a)截面:对x 轴:40.880.440x λπ===()223212x x x x ϕααλλλ⎡=++⎢⎣()2210.9650.30.440.4420.44⎡=⨯+⨯+-⎢⨯⎣0.895=(或计算40.88λ=,再由附表4-4查得0.896xϕ)对y 轴:25.870.816y λπ===()223212y y y y ϕααλλλ⎡=++⎢⎣()2210.9060.5950.8160.81620.816⎡=⨯+⨯+⎢⨯⎣0.604=(或计算75.87λ=,再由附表4-5查得0.604yϕ)故取该柱的整体稳定系数为0.604ϕ=对b)截面,同理可求得0.852x ϕ=,0.489y ϕ=,故取该柱截面整体稳定系数为0.489ϕ= 整体稳定验算:对a)截面 0.604240002052971.68 3000 crd d N Af kN kN ϕ==⨯⨯=<不满足。
钢结构基本原理课后习题与答案完全版电子教案

钢结构基本原理课后习题与答案完全版2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
tgα'=E'f y 0f y 0tgα=E图2-34 σε-图(a )理想弹性-塑性 (b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化)(2)弹性阶段:tan E σεαε==⋅非弹性阶段:'()tan '()tan yyy y f f f E f E σεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f y 0σF图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610y f E ε===⨯卸载后残余应变:0c ε= 可恢复弹性应变:0.00114y c εεε=-=(2)B 点:卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f E εε=-= 可恢复弹性应变:0.00114y c εεε=-=(3)C 点:卸载前应变:0.0250.0350.06'c y F f E σεε-=-=+= 卸载后残余应变:0.05869c c E σεε=-=可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
钢结构设计原理章节习题及答案

第一章绪论1.选择题(1)在结构设计中,失效概率P f与可靠指标β的关系为。
A. P f越大,β越大,结构可靠性越差B. P f越大,β越小,结构可靠性越差C. P f越大,β越小,结构越可靠D. P f越大,β越大,结构越可靠(2)按承载力极限状态设计钢结构时,应考虑。
A. 荷载效应的基本组合B. 荷载效应的标准组合C. 荷载效应的基本组合,必要时尚应考虑荷载效应的偶然组合D. 荷载效应的频遇组合2.填空题(1)某构件当其可靠指标 减小时,相应失效概率将随之。
(2)承载能力极限状态为结构或构件达到或达到不适于继续承载的变形时的极限状态。
(3)在对结构或构件进行极限状态验算时,应采用永久荷载和可变荷载的标准值。
3.简答题(1)钢结构和其他建筑材料结构相比的特点。
(2)钢结构的设计方法。
第二章钢结构的材料1.选择题(1)钢材的设计强度是根据确定的。
A. 比例极限B. 弹性极限C. 屈服点D. 极限强度(2)钢结构设计中钢材的设计强度为。
A. 强度标准值B. 钢材屈服点C. 强度极限值D. 钢材的强度标准值除以抗力分项系数(3)钢材是理想的体。
A. 弹性B. 塑性C. 弹塑性D. 非弹性(4)钢结构中使用钢材的塑性指标,目前最主要用表示。
A. 流幅B. 冲击韧性C. 可焊性D. 伸长率(5)钢材的伸长率 用来反映材料的。
A. 承载能力B. 弹性变形能力C. 塑性变形能力D. 抗冲击荷载能力(6)建筑钢材的伸长率与标准拉伸试件标距间长度的伸长值有关。
A. 达到屈服应力时B. 达到极限应力时C. 试件塑性变形后D. 试件断裂后(7)钢材的三项主要力学性能为。
A. 抗拉强度、屈服强度、伸长率B. 抗拉强度、屈服强度、冷弯性能C. 抗拉强度、冷弯性能、伸长率D. 冷弯性能、屈服强度、伸长率(8)钢材的剪切模量数值钢材的弹性模量数值。
A. 高于B. 低于C. 相等于D. 近似于(9)在构件发生断裂破坏前,有明显先兆的情况是的典型特征。
钢结构习题5-6章参考答案

第5章 受弯构件14. 一简支梁,梁跨为7m,焊接组合工字形对称截面150mm 450mm 18mm 12mm ×××(图5-57),梁上作用有均布恒载(标准值,未含梁自重)17.1kN/m ,均布活荷载6.8kN/m ,距梁端2.5m 处,尚有集中恒荷载标准值60kN ,支承长度200mm ,荷载作用面距离钢梁顶面为120mm ,钢材抗拉强度设计值为2215N/mm ,抗剪强度设计值为2125N/mm ,荷载分项系数对恒载取1.2,对活载取1.4。
试验算钢梁截面是否满足强度要求(不考虑疲劳)。
解:截面积2A=1501824141210368mm ××+×=334150450138414323046144mm 1212××=−=x I3x W 1440000mm 2==xI h梁自重 32-67850kg/m 10368mm 10=81.4kg/m=0.814kN/m ××简支梁承受的均布恒载荷载标准值k (0.814+17.1)kN/m=17.9kN/m q =均布线荷载设计值y 1.217.9+1.4 6.8=31kN/m q =××集中荷载设计值y 1.26072kN p =×=(1)验算该简支梁的抗弯强度按y xx nx y ny+γW γW M M f ≤计算,取y 0M =。
集中恒荷载作用处有2x 317 4.512.572 2.531 2.5290.1kN m 272M ×=×+××−××=⋅ 跨中处2x 317 4.513.572 3.531 3.5721279.9kN m 272M ×=×+××−××−×=⋅受压翼缘的宽厚比:w 1b-t b 15012= 3.8t 2t 36−==取x 1.05γ=截面模量6y 22xx nx y ny 290.110+192.3N/mm 215N/mm 1.051440000γγ×==<=×M M f W W (满足) (2)验算抗剪强度 支座处剪力最大且317 4.572108.546.3154.8kN 27V ×=+×=+= 320715018(2079)20712840294mm 2S =××++××=322v w 154.810840294=33.5N/mm 125N/mm 32304614412VS f It τ××==<=×(满足) (3)局部承压强度集中力沿腹板平面作用于梁上翼缘,该荷载作用处未加加劲肋,应验算该处腹板计算高度上边缘的局部承压强度。
钢结构基本原理(沈祖炎)课后习题答案完全版

第二章2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
图2-34 σε-图(a )理想弹性-塑性(b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化) (2)弹性阶段:tan E σεαε==⋅ 非弹性阶段:'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =图2-35 理想化的σε-图解:tgα'=E'f y 0f y 0tgα=E σf yCσF(1)A 点: 卸载前应变:52350.001142.0610y f Eε===⨯卸载后残余应变:0c ε=可恢复弹性应变:0.00114y c εεε=-=(2)B 点: 卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f Eεε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点: 卸载前应变:0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变:0.05869cc Eσεε=-=可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
钢结构基本原理课后习题解答.pptx

第78页/共88页
第79页/共88页
第80页/共88页
第81页/共88页
第82页/共88页
第83页/共88页
第84页/共88页
第85页/共88页
第86页/共88页
第87页/共88页
感谢您的观看。
第88页/共88页
第48页/共88页
第49页/共88页
第50页/共88页
第51页/共88页
第52页/共88页
第53页/共88页
第54页/共88页
第55页/共88页
第56页/共88页
第57页/共88页
第58页/共88页
第59页/共88页
第60页/共88页
第61页/共88页
第62页/共88页
第63页/共88页
第64页/共88页
第65页/共88页
第66页/共88页
第67页/共88页
第68页/共88页
第69页/共88页
第70页/共88页
第71页/共88页
第72页/共88页
第73页/共88页
第74页/共88页
第75页/共88页
第76页/共88页
第77页/共88页
第18页/共88页
第19页/共88页
第20页/共88页
第21页/共88页
第22页/共88页
第23页/共88页
第24页/共88页
第25页/共88页
第26页/共88页
第27页/共88页
第2ห้องสมุดไป่ตู้页/共88页
第29页/共88页
第30页/共88页
第31页/共88页
第32页/共88页
第33页/共88页
第34页/共88页
第35页/共88页
钢结构基本原理课后习题标准答案完全版
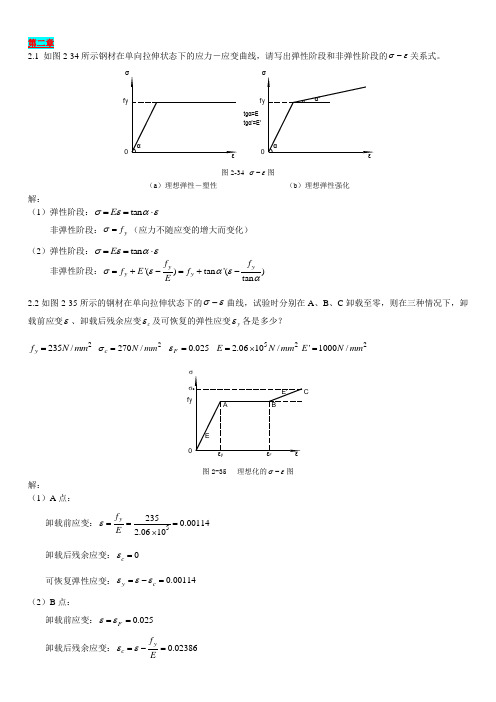
2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
tgα'=E'f y0f y 0tgα=E图2-34 σε-图(a )理想弹性-塑性 (b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化)(2)弹性阶段:tan E σεαε==⋅非弹性阶段:'()tan '()tan yyy y f f f E f E σεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f y 0σ图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610yf E ε===⨯卸载后残余应变:0c ε= 可恢复弹性应变:0.00114y c εεε=-=(2)B 点:卸载前应变:0.025F εε== 卸载后残余应变:0.02386yc f E εε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点:卸载前应变:0.0250.0350.06'c y F f E σεε-=-=+= 卸载后残余应变:0.05869c c E σεε=-= 可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
第三版钢结构 课后题答案第五章

5.1一平台的梁格布置如图5.53所示,铺板为预制钢筋混凝土板,焊于次梁上,设平台恒荷载的标准值(不包括梁自重)为 2.0kN/m 2,活荷载的标准值为20kN/m 2。
试选择次梁截面,钢材为Q345钢。
解:平台板与次梁连牢,所以不必计算整体稳定。
假设次梁自重为m kN 1,次梁间距为3m ,故次梁承受的线荷载标准值为:()mm N 67m kN 67320130.2k ==⨯++⨯=q 线荷载设计值为:[可以判定是活载起控制作用,故恒载分项系数为1.2,活载分项系数为1.3]: ()m kN 4.863.13202.1130.2=⨯⨯+⨯+⨯=q 最大弯矩设计值:m kN 8.38864.86818122x ⋅=⨯⨯==ql M 根据抗弯强度选择截面,需要的截面模量为: 36x x nx cm1194)31005.1/(108.388)/(=⨯⨯==f r M W 选用HN 446199812⨯⨯⨯,3x 1217cm W =验算强度: 跨中无孔眼削弱,此nx W 大于3nx cm 1194=W 。
由于型钢的腹板较厚,一般不必验算抗剪强度;若将次梁连于主梁的加劲肋上也不必验算次梁支座处的局部承压强度。
其他截面特性:4X 27146cm I =,自重65.1㎏/m=0.651kN m ,小于假设自重,不必重新计算抗弯强度。
由附表2,验算刚度:()k 2.030.65120366.651kN m 66.651N mm q =⨯++⨯==在全部荷载标准值作用下:()[]33T k 34x T 66.65160005538438420610271001011294250v q l l EI v l ⨯=⋅=⨯⨯⨯⨯=<=在可变荷载标准值作用下:Q Q 12031129466.651323300v v l l ⎡⎤⨯⎣⎦=⨯=<= 5.3 图5.54(a)所示的简支梁,其截面为不对称工字型[图5.54(b)],材料为Q235-B 钢;梁的中点和两端均有侧向支撑;在集中荷载(未包括梁自重)F =160kN (设计值)的作用下,梁能否保证稳定性?解:该简支梁的稳定性系数b ϕ应按附3.1计算y b 21y x 2y b b 2354.41.4320f h t W Ah ⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫ ⎝⎛+=ηλλβϕ该梁的跨度中点有侧向支撑m 61=l ,且主要承受集中荷载的作用,查附表3.1,得75.1b =β;()()4333y cm 8.23361018.080301121=⨯+⨯+⨯=I 2cm 1048.080110130=⨯+⨯+⨯=Acm 74.41048.2336y y ===A I i 6.12674.4600y 1y ===i l λ 964.0101121301121301121333211b =⨯⨯+⨯⨯⨯⨯=+=I I I α截面不对称影响系数b η(加强受压翼缘)()()7424.01964.028.0128.0b b =-⨯⨯=-=αη求形心,设形心到上翼缘外边缘的距离为d ,则: d⨯=⨯⨯+⨯⨯+⨯⨯1045.81110418.0805.0130cm 2.33=∴d ()()()4232323x cm934405.0811*******1418.080808.01215.0130130121=+-⨯⨯+⨯⨯+-⨯⨯+⨯⨯+-⨯⨯+⨯⨯=d d d I 上翼缘:3x 1x cm 28102.3393440===d I W 下翼缘:x13X x2cm 8.19148.489344082W d I W <==-=()2352356.05.27424.0824.416.12612810821046.126432075.12354.41.432022yb 1y x12y b b >=⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯⨯⨯=⎥⎦⎤⎢⎣⎡+⎪⎪⎭⎫ ⎝⎛+=f h t W Ah ηλλβϕ得:由bb 282.007.1ϕϕ-='∴0.1957.05.2282.007.1b <=-='ϕ 梁单位长度自重标准值(钢材重量集度为 77kN/m 3): m kN 8.010104774k =⨯⨯==-A q ρmkN 3.4971216041122.18.081418122x ⋅=⨯⨯+⨯⨯⨯=+=Fl ql M236x1b x N/mm 9.184102810957.0103.497=⨯⨯⨯='W M ϕ2mm N 215=<f故梁可以保证其整体稳定性。
