等腰三角形和等边三角形练习题
专题17 等腰(等边)三角形问题(学生版)

备考2024中考二轮数学《高频考点冲刺》(全国通用)专题17 等腰(等边)三角形问题考点扫描☆聚焦中考等腰(等边)三角形问题近几年各地中考主要以填空题或选择题考查,也有解答题出现,难度系数小,较简单,属于低档题;考查的知识点主要有:等腰三角形的性质与判定、等边三角形的性质与判定、线段的垂直平分线的性质;考查热点主要有:等腰三角形性质与判定、等边三角形性质与判定、线段垂直平分线的性质.考点剖析☆典型例题(2023•宿迁)若等腰三角形有一个内角为110°,则这个等腰三角形的底角是()A.70°B.45°C.35°D.50°2020•青海)已知a,b,c为△ABC的三边长.b,c满足(b﹣2)2+|c﹣3|=0,且a为方程|x ﹣4|=2的解,则△ABC的形状为三角形.2023•益阳)如图,AB∥CD,直线MN与AB,CD分别交于点E,F,CD上有一点G且GE =GF,∠1=122°,求∠2的度数.例4(2023•绵阳)如图,在等边△ABC中,BD是AC边上的中线,延长BC至点E,使CE=CD,若DE=,则AB=()A.B.6C.8D.例5(2021•宁夏)如图,在▱ABCD中,AD=4,对角线BD=8,分别以点A、B为圆心,以大于AB 的长为半径画弧,两弧相交于点E和点F,作直线EF,交对角线BD于点G,连接GA,GA恰好垂直于边AD,则GA的长是()A.2B.3C.4D.5考点过关☆专项突破类型一等腰三角形的性质与判定1.(2023•南京)若一个等腰三角形的腰长为3,则它的周长可能是()A.5B.10C.15D.202.(2023•眉山)如图,△ABC中,AB=AC,∠A=40°,则∠ACD的度数为()A.70°B.100°C.110°D.140°3.(2023•内蒙古)如图,直线a∥b,直线l与直线a,b分别相交于点A,B,点C在直线b上,且CA=CB.若∠1=32°,则∠2的度数为()A.32°B.58°C.74°D.75°4.(2023•菏泽)△ABC的三边长a,b,c满足(a﹣b)2++|c﹣3|=0,则△ABC是()A.等腰三角形B.直角三角形C.锐角三角形D.等腰直角三角形5.(2022•宁波)如图,在Rt△ABC中,D为斜边AC的中点,E为BD上一点,F为CE中点.若AE=AD,DF=2,则BD的长为()A.2B.3C.2D.46.(2023•重庆)如图,在△ABC中,AB=AC,AD是BC边的中线,若AB=5,BC=6,则AD的长度为.7.(2023•西宁)在△ABC中,AB=AC,∠BAC=100°,点D在BC边上,连接AD,若△ABD为直角三角形,则∠ADB的度数是.8.(2023•山西)如图,在四边形ABCD中,∠BCD=90°,对角线AC,BD相交于点O.若AB=AC=5,BC=6,∠ADB=2∠CBD,则AD的长为.9.(2022•温州)如图,BD是△ABC的角平分线,DE∥BC,交AB于点E.(1)求证:∠EBD=∠EDB.(2)当AB=AC时,请判断CD与ED的大小关系,并说明理由.10.(2023•烟台)如图,点C为线段AB上一点,分别以AC,BC为等腰三角形的底边,在AB的同侧作等腰△ACD和等腰△BCE,且∠A=∠CBE.在线段EC上取一点F,使EF=AD,连接BF,DE.(1)如图1,求证:DE=BF;(2)如图2,若AD=2,BF的延长线恰好经过DE的中点G,求BE的长.类型二等边三角形的性质与判定1.(2023•金昌)如图,BD是等边△ABC的边AC上的高,以点D为圆心,DB长为半径作弧交BC 的延长线于点E,则∠DEC=()A.20°B.25°C.30°D.35°2.(2022•绵阳)下列关于等边三角形的描述不正确的是()A.是轴对称图形B.对称轴的交点是其重心C.是中心对称图形D.绕重心顺时针旋转120°能与自身重合3.(2022•鞍山)如图,直线a∥b,等边三角形ABC的顶点C在直线b上,∠2=40°,则∠1的度数为()A.80°B.70°C.60°D.50°4.(2023•滨州)已知点P是等边△ABC的边BC上的一点,若∠APC=104°,则在以线段AP,BP,CP为边的三角形中,最小内角的大小为()A.14°B.16°C.24°D.26°5.(2019•铜仁市)如图,四边形ABCD为菱形,AB=2,∠DAB=60°,点E、F分别在边DC、BC上,且CE=CD,CF=CB,则S△CEF=()A.B.C.D.6.(2022•张家界)如图,点O是等边三角形ABC内一点,OA=2,OB=1,OC=,则△AOB 与△BOC的面积之和为()A.B.C.D.7.(2020•台州)如图,等边三角形纸片ABC的边长为6,E,F是边BC上的三等分点.分别过点E,F沿着平行于BA,CA方向各剪一刀,则剪下的△DEF的周长是.8.(2023•雅安)如图,四边形ABCD中,AB=AD,BC=DC,∠C=60°,AE∥CD交BC于点E,BC=8,AE=6,则AB的长为.9.(2023•凉山州)如图,边长为2的等边△ABC的两个顶点A、B分别在两条射线OM、ON上滑动,若OM⊥ON,则OC的最大值是.10.(2023•武汉)如图,DE平分等边△ABC的面积,折叠△BDE得到△FDE,AC分别与DF,EF 相交于G,H两点.若DG=m,EH=n,用含m,n的式子表示GH的长是.类型三线段垂直平分线的性质1.(2023•青海)如图,在△ABC中,DE是BC的垂直平分线.若AB=5,AC=8,则△ABD的周长是.2.(2023•丽水)如图,在△ABC中,AC的垂直平分线交BC于点D,交AC于点E,∠B=∠ADB.若AB=4,则DC的长是.3.(2022•青海)如图,在Rt△ABC中,∠ABC=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E,∠BAE=10°,则∠C的度数是.4.(2021•淮安)如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,连接AE,若AE=4,EC=2,则BC的长是()A.2B.4C.6D.85.(2022•宜昌)如图,在△ABC中,分别以点B和点C为圆心,大于BC长为半径画弧,两弧相交于点M,N.作直线MN,交AC于点D,交BC于点E,连接BD.若AB=7,AC=12,BC=6,则△ABD的周长为()A.25B.22C.19D.186.(2022•湖北)如图,在矩形ABCD中,AB<BC,连接AC,分别以点A,C为圆心,大于AC 的长为半径画弧,两弧交于点M,N,直线MN分别交AD,BC于点E,F.下列结论:①四边形AECF是菱形;②∠AFB=2∠ACB;③AC•EF=CF•CD;④若AF平分∠BAC,则CF=2BF.其中正确结论的个数是()A.4B.3C.2D.17.(2021•河北)如图,直线l,m相交于点O.P为这两直线外一点,且OP=2.8.若点P关于直线l,m的对称点分别是点P1,P2,则P1,P2之间的距离可能是()A.0B.5C.6D.78.(2021•长沙)如图,在△ABC中,AD⊥BC,垂足为D,BD=CD,延长BC至E,使得CE=CA,连接AE.(1)求证:∠B=∠ACB;(2)若AB=5,AD=4,求△ABE的周长和面积.。
等腰三角形与等边三角形的综合练习题

等腰三角形与等边三角形的综合练习题在几何学中,等腰三角形和等边三角形是两个基本的三角形类型。
虽然它们具有一些共同点,但也有一些不同之处。
本文将为您提供一些相关的综合练习题,以帮助您更好地理解和应用这两种三角形。
练习题1:等边三角形的性质和相关计算题目:已知一个等边三角形ABC,边长为a。
请计算以下内容:1. 三角形ABC的内角和是多少?2. 计算三角形ABC的高和面积。
3. 求三角形ABC的外接圆半径。
4. 若等边三角形ABC的周长为15cm,求边长a的值。
解答:1. 由于等边三角形的三个内角相等,所以三角形ABC的内角和为180°。
2. 等边三角形ABC的高等于边长,因此三角形ABC的高为a。
根据三角形面积公式,三角形ABC的面积S = 1/2 * a * a * sin60°= a² * √3 / 4。
3. 由于等边三角形的外接圆半径等于边长的一半,所以三角形ABC 的外接圆半径为a / 2。
4. 根据等边三角形的性质,边长a乘以3即为等边三角形的周长。
所以3a = 15,解得a = 5。
练习题2:等腰三角形的性质和相关计算题目:已知一个等腰三角形DEF,底边DE = 8cm,等腰边DF = EF = 6cm。
请计算以下内容:1. 三角形DEF的内角和是多少?2. 求三角形DEF的高和面积。
3. 已知等腰三角形DEF的底边DE = 8cm,求EF的值,使得三角形DEF的面积为12平方厘米。
解答:1. 由于等腰三角形的两个底角相等,所以三角形DEF的内角和为180°。
2. 等腰三角形DEF的高可以通过勾股定理计算,即高h = √(DF² - (DE/2)²) = √(6² - (8/2)²) = √16 = 4。
根据三角形面积公式,三角形DEF的面积S = 1/2 * DE * h = 1/2 * 8 * 4 = 16 平方厘米。
等腰三角形和等边三角形练习题

等腰三角形和等边三角形练习题
1. 如图,等边△ABC 的边长为 3,P 为 BC 上一点,且 BP=1,D 为 AC 上一点,
若∠APD=60°,则 CD 的长为( )
A. 3 2
A
B. 2 3
C. 1 2
D. 3 4
60° D
BP
C
2.如图,△ABC 中,D、E 分别是 BC、AC 的中点,BF 平分∠ABC,交 DE 于点 F,若 BC=6,则 DF
A
第 8 题图
A.6
B.7
C.8
D.9
17.已知等腰三角形的一个角为 70°,则另外两个角的度数是( )
A.55°,55° B.70°,40° C.55°,55°或 70°,40° D.以上都不对
18.已知:一等腰三角形的两边长
x、y
满足方程组
2x 3x
-y 2y
3, 8,
则此等腰三角形的周长为(
连接 BD.若 BD 平分∠ABC,则下列结论错误的是
A
E
D
B
A.BC=2BE B.∠A=∠EDA
C.BC=2AD
D.BD⊥AC
C
16.如图所示的正方形网格中,网格线的交点称为格点.已知 A 、B 是两格点,如果 C 也是图中
的格点,且使得 ABC 为等.腰.三.角.形.,则点 C 的个数是
.
.
B
A. 0 x 3
B. x 3 C. 3 x 6
D. x 6
22.如图,吴伯伯家有一块等边三角形的空地 ABC,已知点 E、F 分别是边 AB、AC 的中点,量得
.
.
EF=5 米,他想把四边形 BCFE 用篱笆围成一圈放养小鸡,则需用篱笆的长是
一年级数学三角形分类练习题

一年级数学三角形分类练习题在学习数学的过程中,三角形是一个非常重要且基础的概念。
它们有着不同的性质和分类标准。
今天,我们将一起来进行一年级数学的三角形分类练习题。
通过这些练习题,我们可以巩固对三角形分类的理解,提高数学运算能力。
1. 根据三边长度分类练习题一:下列三角形中,哪些是等边三角形,哪些是等腰三角形,哪些是普通三角形?1)边长为3cm、3cm、3cm2)边长为5cm、5cm、4cm3)边长为6cm、7cm、8cm4)边长为2cm、2cm、1cm解答:1)边长为3cm、3cm、3cm是等边三角形。
2)边长为5cm、5cm、4cm是等腰三角形。
3)边长为6cm、7cm、8cm是普通三角形。
4)边长为2cm、2cm、1cm是等腰三角形。
2. 根据角度大小分类练习题二:下列三角形中,哪些是锐角三角形,哪些是直角三角形,哪些是钝角三角形?1)角A = 60°,角B = 60°,角C = 60°2)角A = 30°,角B = 90°,角C = 60°3)角A = 100°,角B = 40°,角C = 40°4)角A = 90°,角B = 45°,角C = 45°解答:1)角A = 60°,角B = 60°,角C = 60°是锐角三角形。
2)角A = 30°,角B = 90°,角C = 60°是直角三角形。
3)角A = 100°,角B = 40°,角C = 40°是钝角三角形。
4)角A = 90°,角B = 45°,角C = 45°是直角三角形。
3. 根据边长和角度共同分类练习题三:下列三角形中,哪些是等腰锐角三角形,哪些是等腰直角三角形,哪些是等腰钝角三角形?1)边长为3cm、3cm、4cm,角A = 60°,角C = 60°2)边长为5cm、5cm、6cm,角A = 45°,角C = 45°3)边长为8cm、8cm、8cm,角A = 90°,角C = 90°4)边长为7cm、7cm、10cm,角A = 120°,角C = 120°解答:1)边长为3cm、3cm、4cm,角A = 60°,角C = 60°是等腰锐角三角形。
(完整)等腰三角形和等边三角形习题例题
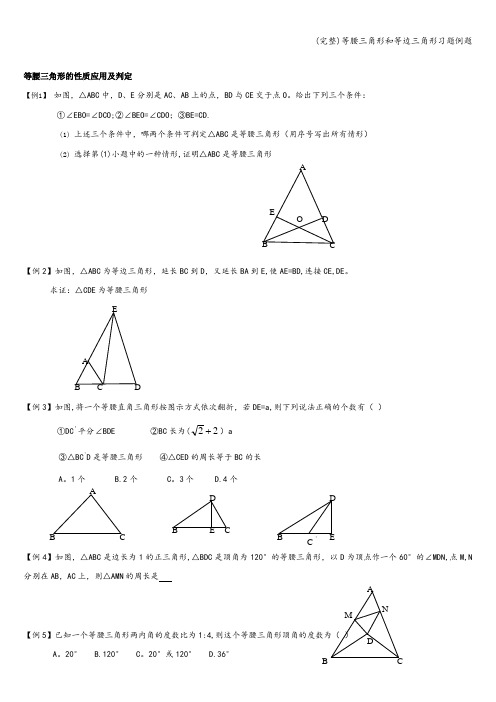
等腰三角形的性质应用及判定【例1】 如图,△ABC 中,D 、E 分别是AC 、AB 上的点,BD 与CE 交于点O 。
给出下列三个条件:①∠EBO=∠DCO;②∠BEO=∠CDO ;③BE=CD.(1) 上述三个条件中,哪两个条件可判定△ABC 是等腰三角形(用序号写出所有情形) (2) 选择第(1)小题中的一种情形,证明△ABC 是等腰三角形【例2】如图,△ABC 为等边三角形,延长BC 到D ,又延长BA 到E,使AE=BD,连接CE,DE 。
求证:△CDE 为等腰三角形【例3】如图,将一个等腰直角三角形按图示方式依次翻折,若DE=a,则下列说法正确的个数有( ) ①DC '平分∠BDE②BC 长为(22 )a③△BC 'D 是等腰三角形 ④△CED 的周长等于BC 的长 A 。
1个 B.2个 C 。
3个 D.4个【例4】如图,△ABC 是边长为1的正三角形,△BDC 是顶角为120°的等腰三角形,以D 为顶点作一个60°的∠MDN,点M,N分别在AB ,AC 上,则△AMN 的周长是【例5】已知一个等腰三角形两内角的度数比为1:4,则这个等腰三角形顶角的度数为( ) A 。
20° B.120° C 。
20°或120° D.36°AEBCO D EA BCDD BE CDBC '. E ACB A MNDBC【例6】等腰三角形两边长分别为4和9,则第三边长为【例7】如图,点O 事等边△ABC 内一点,∠AOB=110°,∠BOC=α,将△BOC 绕点C 按顺时针方向旋转60°得△ADC ,连接OD ,则△COD 是等边三角形;(1)当α为多少度时,△AOD 是等腰三角形?(2)求证:△COD 是等边三角形(3)当α=150°时,试判断△AOD 的形状,并说明理由等边三角形的性质应用及判定【例8】如图,在等边△ABC 中,点D ,E 分别在边BC ,AB 上,BD=AE,AD 与CE 交于点F.求证:(1)AD=CE;(2)求∠DFC 的度数。
专题19等腰三角形、等边三角形、直角三角形(基础巩固练习)解析版

2021年中考数学专题19 等腰、等边三角形、直角三角形(基础巩固练习,共50个小题)一、选择题(共20小题):1.(2020•毕节市)已知等腰三角形两边的长分别为3和7,则此等腰三角形的周长为()A.13 B.17 C.13或17 D.13或10【答案】B【解析】解:①当腰是3,底边是7时,不满足三角形的三边关系,因此舍去.②当底边是3,腰长是7时,能构成三角形,则其周长=3+7+7=17.故选:B.2.(2020•福建)如图,AD是等腰三角形ABC的顶角平分线,BD=5,则CD等于()A.10 B.5 C.4 D.3【答案】B【解析】解:∵AD是等腰三角形ABC的顶角平分线,BD=5,∴CD=5.故选:B.3.(2020•呼伦贝尔)如图,AB=AC,AB的垂直平分线MN交AC于点D,若∠C=65°,则∠DBC的度数是()A.25°B.20°C.30°D.15°【解析】解:∵AB=AC,∠C=∠ABC=65°,∴∠A=180°﹣65°×2=50°,∵MN垂直平分AB,∴AD=BD,∴∠A=∠ABD=50°,∴∠DBC=∠ABC﹣∠ABD=15°,故选:D.4.(2020•兰州)如图,在△ABC中,AB=AC,点D在CA的延长线上,DE⊥BC于点E,∠BAC=100°,则∠D=()A.40°B.50°C.60°D.80°【答案】B【解析】解:∵AB=AC,∠BAC=100°,∴∠C=∠B=40°,∵DE⊥BC于点E,∴∠D=90°﹣∠C=50°,故选:B.5.(2020•青海)等腰三角形的一个内角为70°,则另外两个内角的度数分别是()A.55°,55°B.70°,40°或70°,55°C.70°,40°D.55°,55°或70°,40°【解析】解:分情况讨论:(1)若等腰三角形的顶角为70°时,底角=(180°﹣70°)÷2=55°;(2)若等腰三角形的底角为70°时,顶角为180°﹣70°﹣70°=40°.故选:D.6.(2020•临沂)如图,在△ABC中,AB=AC,∠A=40°,CD∥AB,则∠BCD=()A.40°B.50°C.60°D.70°【答案】D【解析】解:∵在△ABC中,AB=AC,∠A=40°,∴∠ACB=70°,∵CD∥AB,∴∠ACD=180°﹣∠A=140°,∴∠BCD=∠ACD﹣∠ACB=70°.故选:D.7.(2020•自贡)如图,在Rt△ABC中,∠ACB=90°,∠A=50°,以点B为圆心,BC长为半径画弧,交AB于点D,连接CD,则∠ACD的度数是()A.50°B.40°C.30°D.20°【答案】D【解析】解:∵在Rt△ABC中,∠ACB=90°,∠A=50°,∴∠B=40°,∵BC=BD,∴∠BCD=∠BDC=1(180°﹣40°)=70°,2∴∠ACD=90°﹣70°=20°,故选:D.8.(2020•巴中)如图,在△ABC中,∠BAC=120°,AD平分∠BAC,DE∥AB,AD=3,CE=5,则AC的长为()A.9 B.8 C.6 D.7【答案】B【解析】解:∵∠BAC=120°,AD平分∠BAC,∴∠BAD=∠CAD=1∠BAC=60°,2∵DE∥AB,∴∠BAD=∠ADE=60°,∠DEC=∠BAC=120°,∴∠AED=60°,∴∠ADE=∠AED,∴△ADE是等边三角形,∴AE=AD=3,∴AC=AE+CE=3+5=8,故选:B.9.(2020•铜仁市)已知等边三角形一边上的高为2√3,则它的边长为()A.2 B.3 C.4 D.4√3【答案】C【解析】解:根据等边三角形:三线合一,)2+(2√3)2,设它的边长为x,可得:x2=(x2解得:x=4,x=﹣4(舍去),故选:C.10.(2019•天水)如图,等边△OAB的边长为2,则点B的坐标为()A.(1,1)B.(1,√3)C.(√3,1)D.(√3,√3)【答案】B【解析】解:过点B 作BH ⊥AO 于H 点,∵△OAB 是等边三角形,∴OH =1,BH =√3.∴点B 的坐标为(1,√3).故选:B .11.(2019•铜仁市)如图,四边形ABCD 为菱形,AB =2,∠DAB =60°,点E 、F 分别在边DC 、BC 上,且CE =13CD ,CF =13CB ,则S △CEF =( )A .√32B .√33C .√34D .√39 【答案】D【解析】解:∵四边形ABCD 为菱形,AB =2,∠DAB =60°∴AB =BC =CD =2,∠DCB =60°∵CE =13CD ,CF =13CB∴CE =CF =23∴△CEF 为等边三角形∴S △CEF =√34×(23)2=√39故选:D .12.(2018•扬州)在Rt△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACD交AB于E,则下列结论一定成立的是()A.BC=EC B.EC=BE C.BC=BE D.AE=EC【答案】C【解析】解:∵∠ACB=90°,CD⊥AB,∴∠ACD+∠BCD=90°,∠ACD+∠A=90°,∴∠BCD=∠A.∵CE平分∠ACD,∴∠ACE=∠DCE.又∵∠BEC=∠A+∠ACE,∠BCE=∠BCD+∠DCE,∴∠BEC=∠BCE,∴BC=BE.故选:C.13.(2020•常州)如图,AB是⊙O的弦,点C是优弧AB上的动点(C不与A、B重合),CH⊥AB,垂足为H,点M是BC的中点.若⊙O的半径是3,则MH长的最大值是()A.3 B.4 C.5 D.6【答案】A【解析】解:∵CH⊥AB,垂足为H,∴∠CHB=90°,∵点M是BC的中点.BC,∴MH=12∵BC的最大值是直径的长,⊙O的半径是3,∴MH的最大值为3,故选:A.14.(2019•陕西)如图,在△ABC中,∠ABC=90°,∠C=52°,BE为AC边上的中线,AD平分∠BAC,交BC边于点D,过点B作BF⊥AD,垂足为F,则∠EBF的度数为()A.19°B.33°C.34°D.43°【答案】B【解析】解:∵∠ABC=90°,BE为AC边上的中线,AC=AE,∴∠BAC=90°﹣∠C=90°﹣52°=38°,BE=12∴∠BAC=∠ABE=38°,∵AD平分∠BAC,∴∠BAF=1∠BAC=19°,2∴∠BOF =∠BAD+∠ABE =19°+38°=57°,∵BF ⊥AD ,∴∠BFO =90°,∴∠EBF =90°﹣∠BOF =90°﹣57°=33°;故选:B .15.(2020•赤峰)如图,Rt △ABC 中,∠ACB =90°,AB =5,AC =3,把Rt △ABC 沿直线BC 向右平移3个单位长度得到△A'B'C',则四边形ABC'A'的面积是( )A .15B .18C .20D .22【答案】A【解析】解:∵把Rt △ABC 沿直线BC 向右平移3个单位长度得到△A'B'C', ∴A ′A =CC ′=3,AA ′∥BC ′,在Rt △ABC 中,∵AB =5,AC =3,∴BC =√52−32=4,∵AA ′∥BC ′,∴四边形ABC ′A ′是梯形,∴四边形ABC'A'的面积=12(AA ′+BC ′)•AC =12×(3+4+3)×3=15,故选:A .16.(2020•绵阳)如图,在四边形ABCD 中,∠A =∠C =90°,DF ∥BC ,∠ABC 的平分线BE交DF于点G,GH⊥DF,点E恰好为DH的中点,若AE=3,CD=2,则GH=()A.1 B.2 C.3 D.4【答案】B【解析】解:过E作EM⊥BC,交FD于点N,∵DF∥BC,∴EN⊥DF,∴EN∥HG,∴∠DEN=∠DHG,∠END=∠HGD,∴△END∽△HGD,∴ENHG =EDHD,∵E为HD中点,∴EDHD =12,∴ENHG =12,即HG=2EN,∴∠DNM=∠NMC=∠C=90°,∴四边形NMCD为矩形,∴MN=DC=2,∵BE 平分∠ABC ,EA ⊥AB ,EM ⊥BC ,∴EM =AE =3,∴EN =EM ﹣MN =3﹣2=1,则HG =2EN =2.故选:B .17.(2020•包头)如图,在Rt △ABC 中,∠ACB =90°,D 是AB 的中点,BE ⊥CD ,交CD 的延长线于点E .若AC =2,BC =2√2,则BE 的长为( )A .2√63B .√62C .√3D .√2【答案】A【解析】解:方法1:在Rt △ABC 中,∠ACB =90°,AC =2,BC =2√2,由勾股定理得AB =√AC 2+BC 2=√22+(2√2)2=2√3,∵D 是AB 的中点,∴BD =CD =√3,设DE =x ,由勾股定理得(√3)2﹣x 2=(2√2)2﹣(√3+x )2,解得x =√33, ∴在Rt △BED 中,BE =2−DE 2=√(√3)2−(√33)2=2√63.方法2:三角形ABC 的面积=12×AC ×BC =12×2×2√2=2√2,∵D 是AB 中点,∴△BCD 的面积=△ABC 面积×12=√2,Rt △ABC 中,∠ACB =90°,AC =2,BC =2√2,由勾股定理得AB =√AC 2+BC 2=√22+(2√2)2=2√3,∵D 是AB 的中点,∴CD =√3,∴BE =√2×2÷2×2÷√3=2√63.故选:A . 18.(2020•陕西)如图,在3×3的网格中,每个小正方形的边长均为1,点A ,B ,C 都在格点上,若BD 是△ABC 的高,则BD 的长为( )A .1013√13B .913√13C .813√13D .713√13 【答案】D【解析】解:由勾股定理得:AC =2+32=√13,∵S △ABC =3×3−12×1×2−12×1×3−12×2×3=3.5,∴12AC ⋅BD =72,∴√13⋅BD =7,∴BD=7√13,故选:D.1319.(2020•德阳)已知:等腰直角三角形ABC的腰长为4,点M在斜边AB上,点P为该平面内一动点,且满足PC=2,则PM的最小值为()A.2 B.2√2−2 C.2√2+2 D.2√2【答案】B【解析】解:∵等腰直角三角形ABC的腰长为4,∴斜边AB=4√2,∵点P为该平面内一动点,且满足PC=2,∴点P在以C为圆心,PC为半径的圆上,当点P在斜边AB的中线上时,PM的值最小,∵△ABC是等腰直角三角形,AB=2√2,∴CM=12∵PC=2,∴PM=CM﹣CP=2√2−2,故选:B.20.(2020•威海)七巧板是大家熟悉的一种益智玩具.用七巧板能拼出许多有趣的图案.小李将一块等腰直角三角形硬纸板(如图①)切割七块,正好制成一副七巧板(如图②).已知AB=40cm,则图中阴影部分的面积为()A.25cm2B.100cm2C.50cm2D.75cm23【答案】C【解析】解:如图:设OF=EF=FG=x(cm),∴OE=OH=2x,在Rt△EOH中,EH=2√2x,由题意EH=20cm,∴20=2√2x,∴x=5√2,∴阴影部分的面积=(5√2)2=50(cm2)故选:C.二、填空题(共16小题):21.(2020•齐齐哈尔)等腰三角形的两条边长分别为3和4,则这个等腰三角形的周长是.【答案】10或11【解析】解:①3是腰长时,三角形的三边分别为3、3、4,∵此时能组成三角形,∴周长=3+3+4=10;②3是底边长时,三角形的三边分别为3、4、4,此时能组成三角形,所以周长=3+4+4=11.综上所述,这个等腰三角形的周长是10或11.故答案为:10或11.22.(2020•眉山)如图,等腰△ABC 中,AB =AC =10,边AC 的垂直平分线交BC 于点D ,交AC 于点E .若△ABD 的周长为26,则DE 的长为 .【答案】154【解析】解:作AM ⊥BC 于M ,∵边AC 的垂直平分线交BC 于点D ,交AC 于点E ,∴∠AED =90°,AE =CE =12AC =12×10=5,AD =CD ,∴∠DAC =∠C ,∵△ABD 的周长为26,∴AB+BD+AD =AB+BD+CD =AB+BC =26,∵AB =AC =10,∴BC =16,∠B =∠C ,∴∠B =∠DAC ,∵∠ACB =∠DCA ,∴△ABC ∽△DAC ,∴AM DE =BC AC ,∵AB =AC ,∴BM=12BC=8,∴AM=√AB2−BM2=√102−82=6,∴6DE =1610,∴DE=154,故答案为154.23.(2020•滨州)在等腰△ABC中,AB=AC,∠B=50°,则∠A的大小为.【答案】80°【解析】解:∵AB=AC,∠B=50°,∴∠C=∠B=50°,∴∠A=180°﹣2×50°=80°.故答案为:80°.24.(2020•恩施州)如图,直线l1∥l2,点A在直线l1上,点B在直线l2上,AB=BC,∠C=30°,∠1=80°,则∠2=.【答案】40°【解析】解:如图,延长CB交l1于点D,∵AB=BC,∠C=30°,∴∠C=∠4=30°,∵l1∥l2,∠1=80°,∴∠1=∠3=80°,∵∠C+∠3+∠2+∠4=180°,即30°+80°+∠2+30°=180°,∴∠2=40°.故答案为:40°.25.(2020•黄冈)已知:如图,在△ABC中,点D在边BC上,AB=AD=DC,∠C=35°,则∠BAD=度.【答案】40°【解析】解:∵AD=DC,∴∠DAC=∠C=35°,∴∠ADB=∠DAC+∠C=70°.∵AB=AD,∴∠B=∠ADB=70°,∴∠BAD=180°﹣∠B﹣∠ADB=180°﹣70°﹣70°=40°.故答案为:40.26.(2020•常州)如图,在△ABC中,BC的垂直平分线分别交BC、AB于点E、F.若△AFC是等边三角形,则∠B=°.【答案】30【解析】解:∵EF垂直平分BC,∴BF=CF,∴∠B=∠BCF,∵△ACF为等边三角形,∴∠AFC=60°,∴∠B=∠BCF=30°.故答案为:30.27.(2019•哈尔滨)如图,在四边形ABCD中,AB=AD,BC=DC,∠A=60°,点E为AD边上一点,连接BD、CE,CE与BD交于点F,且CE∥AB,若AB=8,CE=6,则BC的长为.【答案】2√7【解析】解:如图,连接AC交BD于点O∵AB=AD,BC=DC,∠A=60°,∴AC垂直平分BD,△ABD是等边三角形∴∠BAO=∠DAO=30°,AB=AD=BD=8,BO=OD=4∵CE∥AB∴∠BAO=∠ACE=30°,∠CED=∠BAD=60°∴∠DAO=∠ACE=30°∴AE=CE=6∴DE=AD﹣AE=2∵∠CED=∠ADB=60°∴△EDF是等边三角形∴DE=EF=DF=2∴CF=CE﹣EF=4,OF=OD﹣DF=2∴OC=√CF2−OF2=2√3∴BC=√BO2+OC2=2√728.(2020•岳阳)如图,在Rt△ABC中,CD是斜边AB上的中线,∠A=20°,则∠BCD=°.【答案】70【解析】解:在Rt△ABC中,∵∠A=20°,∴∠B=90°﹣∠A=70°,∵CD是斜边AB上的中线,∴BD=CD,∴∠BCD=∠B=70°,故答案为70.29.(2020•绵阳)如图,四边形ABCD中,AB∥CD,∠ABC=60°,AD=BC=CD=4,点M是四边形ABCD内的一个动点,满足∠AMD=90°,则点M到直线BC的距离的最小值为.【答案】3√3−2【解析】解:取AD的中点O,连接OM,过点M作ME⊥BC交BC的延长线于E,过点O 作OF⊥BC于F,交CD于G,则OM+ME≥OF.∵∠AMD=90°,AD=4,OA=OD,AD=2,∴OM=12∵AB∥CD,∴∠GCF=∠B=60°,∴∠DGO=∠CGF=30°,∵AD=BC,∴∠DAB=∠B=60°,∴∠ADC=∠BCD=120°,∴∠DOG=30°=∠DGO,∴DG=DO=2,∵CD=4,∴CG=2,∴OG=2√3,GF=√3,OF=3√3,∴ME≥OF﹣OM=3√3−2,∴当O,M,E共线时,ME的值最小,最小值为3√3−2.30.(2020•宿迁)如图,在△ABC中,AB=AC,∠BAC的平分线AD交BC于点D,E为AB的中点,若BC=12,AD=8,则DE的长为.【答案】5【解析】解:∵AB=AC,AD平分∠BAC,∴AD⊥BC,BD=CD=6,∴∠ADB=90°,∴AB=√AD2+BD2=√82+62=10,∵AE=EB,∴DE=1AB=5,2故答案为5.31.(2020•雅安)对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形ABCD,对角线AC、BD交于点O.若AD=2,BC=4,则AB2+CD2=.【答案】20【解析】解:∵AC⊥BD,∴∠AOD=∠AOB=∠BOC=∠COD=90°,由勾股定理得,AB2+CD2=AO2+BO2+CO2+DO2,AD2+BC2=AO2+DO2+BO2+CO2,∴AB2+CD2=AD2+BC2,∵AD=2,BC=4,∴AB2+CD2=22+42=20.故答案为:20.32.(2020•苏州)如图,在△ABC中,已知AB=2,AD⊥BC,垂足为D,BD=2CD.若E是AD的中点,则EC=.【答案】1【解析】解:设AE=ED=x,CD=y,∴BD=2y,∵AD⊥BC,∴∠ADB=∠ADC=90°,在Rt△ABD中,∴AB2=4x2+4y2,∴x2+y2=1,在Rt△CDE中,∴EC2=x2+y2=1∵EC>0∴EC=1.另解:依据AD⊥BC,BD=2CD,E是AD的中点,即可得判定△CDE∽△BDA,且相似比为1:2,∴CEAB =12,即CE=1.故答案为:133.(2020•安顺)如图,△ABC中,点E在边AC上,EB=EA,∠A=2∠CBE,CD垂直于BE的延长线于点D,BD=8,AC=11,则边BC的长为.【答案】4√5【解析】解:延长BD到F,使得DF=BD,∵CD⊥BF,∴△BCF是等腰三角形,∴BC=CF,过点C作CH∥AB,交BF于点H∴∠ABD=∠CHD=2∠CBD=2∠F,∴HF=HC,∵CH∥AB,∴∠ABE=∠CHE,∠BAE=∠ECH,∴EH=CE,∵EA=EB,∴AC=BH,∵BD=8,AC=11,∴DH=BH﹣BD=AC﹣BD=3,∴HF=HC=8﹣3=5,在Rt△CDH,∴由勾股定理可知:CD=4,在Rt△BCD中,∴BC=√82+42=4√5,故答案为:4√534.(2020•丹东)如图,在四边形ABCD中,AB⊥BC,AD⊥AC,AD=AC,∠BAD=105°,点E和点F分别是AC和CD的中点,连接BE,EF,BF,若CD=8,则△BEF的面积是.【答案】2√3【解析】解:过点E作EH⊥BF于H.∵AD=AC,∠DAC=90°,CD=8,∴AD=AC=4√2,∵DF=FC,AE=EC,AD=2√2,EF∥AD,∴EF=12∴∠FEC=∠DAC=90°,∵∠ABC=90°,AE=EC,∴BE=AE=EC=2√2,∴EF=BE=2√2,∵∠BAD=105°,∠DAC=90°,∴∠BAE=105°﹣90°=15°,∴∠EAB=∠EBA=15°,∴∠CEB=∠EAB+∠EBA=30°,∴∠FEB=90°+30°=120°,∴∠EFB=∠EBF=30°,∵EH⊥BF,∴EH=12EF=√2,FH=√3EH=√6,∴BF=2FH=2√6,∴S△EFB =12•BF•EH=12×2√6×√2=2√3.故答案为2√3.35.(2020•十堰)如图,在△ABC中,DE是AC的垂直平分线.若AE=3,△ABD的周长为13,则△ABC的周长为.【答案】19【解析】解:∵DE是AC的垂直平分线,AE=3,∴AC=2AE=6,AD=DC,∵AB+BD+AD=13,∴△ABC的周长=AB+BC+AC=AB+BD+AD+AC=13+6=19.故答案为:19.36.(2020•青海)如图,△ABC中,AB=AC=14cm,AB的垂直平分线MN交AC于点D,且△DBC的周长是24cm,则BC=cm.【答案】10=24cm,【解析】解:∵C△DBC∴BD+DC+BC=24cm①,又∵MN垂直平分AB,∴AD=BD②,将②代入①得:AD+DC+BC=24cm,即AC+BC=24cm,又∵AC=14cm,∴BC=24﹣14=10cm.故填10.三、解答题(共14小题):37.(2020•衡阳)如图,在△ABC中,∠B=∠C,过BC的中点D作DE⊥AB,DF⊥AC,垂足分别为点E、F.(1)求证:DE =DF ;(2)若∠BDE =40°,求∠BAC 的度数.【答案】(1)见解析;(2)80°.【解析】(1)证明:∵DE ⊥AB ,DF ⊥AC ,∴∠BED =∠CFD =90°,∵D 是BC 的中点,∴BD =CD ,在△BED 与△CFD 中,{∠BED =∠CFD∠B =∠C BD =CD,∴△BED ≌△CFD (AAS ),∴DE =DF ;(2)解:∵∠BDE =40°,∴∠B =50°,∴∠C =50°,∴∠BAC =80°.38.(2019•攀枝花)如图,在△ABC 中,CD 是AB 边上的高,BE 是AC 边上的中线,且BD =CE .求证:(1)点D 在BE 的垂直平分线上;(2)∠BEC =3∠ABE .【答案】(1)见解析;(2)见解析.【解析】解:(1)连接DE,∵CD是AB边上的高,∴∠ADC=∠BDC=90°,∵BE是AC边上的中线,∴AE=CE,∴DE=CE,∵BD=CE,∴BD=DE,∴点D在BE的垂直平分线上;(2)∵DE=AE,∴∠A=∠ADE,∵∠ADE=∠DBE+∠DEB,∵BD=DE,∴∠DBE=∠DEB,∴∠A=∠ADE=2∠ABE,∵∠BEC=∠A+∠ABE,∴∠BEC=3∠ABE.39.(2019•重庆)如图,在△ABC中,AB=AC,AD⊥BC于点D.(1)若∠C=42°,求∠BAD的度数;(2)若点E在边AB上,EF∥AC交AD的延长线于点F.求证:AE=FE.【答案】(1)48°;(2)见解析.【解析】解:(1)∵AB=AC,AD⊥BC于点D,∴∠BAD=∠CAD,∠ADC=90°,又∠C=42°,∴∠BAD=∠CAD=90°﹣42°=48°;(2)∵AB=AC,AD⊥BC于点D,∴∠BAD=∠CAD,∵EF∥AC,∴∠F=∠CAD,∴∠BAD=∠F,∴AE=FE.40.(2019•重庆)如图,在△ABC中,AB=AC,D是BC边上的中点,连结AD,BE平分∠ABC交AC于点E,过点E作EF∥BC交AB于点F.(1)若∠C=36°,求∠BAD的度数;【答案】(1)54°;(2)见解析.【解析】(1)解:∵AB=AC,∴∠C=∠ABC,∵∠C=36°,∴∠ABC=36°,∵BD=CD,AB=AC,∴AD⊥BC,∴∠ADB=90°,∴∠BAD=90°﹣36°=54°.(2)证明:∵BE平分∠ABC,∴∠ABE=∠CBE=1∠ABC,2∵EF∥BC,∴∠FEB=∠CBE,∴∠FBE=∠FEB,∴FB=FE.41.(2020秋•河北区期末)如图,在等边△ABC中,点D,E分别在边BC,AC上,DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.(1)求∠F的度数.【答案】(1)30°;(2)见解析.【解析】(1)解:∵△ABC是等边三角形,∴∠B=60°,∵DE∥AB,∴∠B=∠EDC=60°,∵DE⊥EF,∴∠DEF=90°,∴∠F=90°﹣60°=30°.(2)证明:∵△ABC是等边三角形,∴∠B=∠C=60°,∵DE∥AB,∴∠B=∠EDC=60°,∴∠EDC=∠ECD=∠DEC=60°,∴△DEC是等边三角形,∴CE=CD,∵∠ECD=∠F+∠CEF,∠F=30°,∴∠CEF=∠F=30°,∴EC=CF,42.(2020秋•道外区期中)如图1,已知等边△ABC中,D、E分别是AB、AC上的点,连接DE.(1)若DE∥BC,求证:△ADE是等边三角形;(2)如图2,若D、E分别为AB、AC中点,连接CD、BE,CD与BE相交于点F,请直接写出图中所有等腰三角形.(△ADE与△ABC除外)【答案】(1)见解析;(2)△DEF和△BFC都为等腰三角形.【解析】(1)证明:∵△ABC是等边三角形,∴∠A=∠B=∠C,∵DE∥BC,∴∠ADE=∠B,∠AED=∠C,∴∠A=∠ADE=∠AED,∴△ADE是等边三角形.(2)解:△BDE,△DEC,△DEF和△BFC为等腰三角形.由(1)可知,AB=AC,∠=60°,∵D、E分别为AB、AC中点,∴AD=12AB,AE=12AC,∴△ADE为等边三角形,AB,∴AD=DE=12∴BD=DE,即△BDE为等腰三角形,同理△DEC为等腰三角形.∵AB=BC,E为AC的中点,∴∠ABE=∠CBE=30°,∵∠ADE=∠ABC=60°,∴DE∥BC,∴∠EBC=∠DEB=30°,同理∠BCD=∠EDC=30°,∴FB=FC,DF=EF.即△DEF和△BFC都为等腰三角形.43.(2020•海淀区一模)如图,在▱ABCD中,∠ABC=60°,∠BAD的平分线交CD于点E,交BC的延长线于点F,连接DF.(1)求证:△ABF是等边三角形;(2)若∠CDF=45°,CF=2,求AB的长度.【答案】(1)见解析;(2)√3+.【解析】(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,∴∠DAB+∠ABC=180°,∵∠ABC=60°,∴∠DAB=120°,∵AF平分∠DAB,∴∠FAB=60°,∴∠FAB=∠ABF=60°,∴∠FAB=∠ABF=∠AFB=60°,∴△ABF是等边三角形;(2)作FG⊥DC于点G,∵四边形ABCD是平行四边形,∠ABC=60°,∴DC∥AB,DC=AB,∴∠FCG=∠ABC=60°,∴∠GFC=30°,∵CF=2,∠FGC=90°,∴CG=1,FG=√3,∵∠FDG=45°,∠FGD=90°,∴∠FDG=∠DFG=45°,∴DG=FG=√3,∴DC=DG+CG=√3+1,∴AB=√3+1,即AB的长度是√3+1.44.(2018•无锡)如图,在△ABC中,∠ACB=90°,AC=m,BC=n,m>n,点P是边AB上一点,连结CP,将△ACP沿CP翻折得到△QCP.(1)若m=4,n=3,且PQ⊥AB,求BP的长;(2)连结BQ,若四边形BCPQ是平行四边形,求m与n之间的关系式.【答案】(1)PB=125+95=215;(2)m=√3n.【解析】解:(1)如图,作CH⊥AB于H.由翻折的性质可知:∠APC=∠QPC,∵PQ⊥PA,∴∠APQ=90°,∴∠APC=∠QPC=135°,∵∠QPB =90°,∴∠BPC =45°,∵CH ⊥AB ,∴CH =PH ,在Rt △ABC 中,AB =2+BC 2=√32+42=5,∵12•AB •CH =12•AC •BC ,∴CH =125,BH =2−CH 2=95, ∴PB =PH+BH =125+95=215.(2)如图2中,连接BQ .由翻折不变性可知:PA =PQ ,∠QPC =∠APC ,∵四边形BCPQ 是平行四边形,∴PQ =BC =PA =n ,PQ ∥BC ,∴∠QPC+∠PCB =180°,∴∠PCB=∠BPC,∴PB=BC=n,∴AP=PB=n,AB=2n,在Rt△ABC中,则有(2n)2=m2+n2,∴m2=3n2,∵m>0.n>0,∴m=√3n.45.(2020秋•齐河县期末)如图,在△ABC中,∠ACB=90°,∠B=30°,CE垂直于AB于点E,D是AB的中点.(1)求证:AE=ED;(2)若AC=2,求DE的长.【答案】(1)见解析;(2)1.【解析】(1)证明:在△ABC中,∠ACB=90°,D是AB的中点,AB,∴CD=AD=BD=12∴∠DCB=∠B,∵∠B=30°,∠ACB=90°,∴∠DCB=30°,∠A=180°﹣90°﹣30°=60°,∴∠A=∠ADC,∴AC=DC,∵CE垂直于AB于点E,∴AE=ED;(2)解:∵CE⊥AB,∴∠AEC=90°,∵∠A=60°,∴∠ACE=30°,AC,∴AE=12∵AC=2,AE=DE,∴DE=AE=1.46.(2020秋•农安县期末)如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.(1)求证:CE=CF;(2)若CD=2,求DF的长.【答案】(1)见解析;(2)4.【解析】证明:(1)∵△ABC是等边三角形,∵DE∥AB,∴∠B=EDC=60°,∠A=∠CED=60°,∴∠EDC=∠ECD=∠DEC=60°,∵EF⊥ED,∴∠DEF=90°,∴∠F=30°∵∠F+∠FEC=∠ECD=60°,∴∠F=∠FEC=30°,∴CE=CF.(2)由(1)可知∠EDC=∠ECD=∠DEC=60°,∴CE=DC=2.又∵CE=CF,∴CF=2.∴DF=DC+CF=2+2=4.47.(2020秋•松江区期末)如图,已知四边形ABCD中,∠ABC=∠ADC=90°,点E是AC中点,点F是BD中点.(1)求证:EF⊥BD;(2)过点D作DH⊥AC于H点,如果BD平分∠HDE,求证:BA=BC.【答案】(1)见解析;(2)见解析.【解析】(1)证明:∵∠ABC =∠ADC =90°,点E 是AC 中点,∴DE =12AC ,BE =12AC ,∴DE =BE ,∵点F 是BD 中点,∴EF ⊥BD ;(2)证明:设AC ,BD 交于点O ,∵DH ⊥AC ,EF ⊥BD ,∴∠DHO =∠EFO =90°,∵∠DOH =∠BOE ,∴∠HDF =∠OEF ,∵DE =BE ,∴∠EDO =∠EBO ,∵BD 平分∠HDE ,∴∠HDF =∠BDE ,∴∠OEF =∠OBE ,∵∠OEF+∠EOF=90°,∴∠EOF+∠EBO=90°,∴∠BEO=90°,∴BE⊥AC,∴BA=BC.48.(2020秋•南海区期末)在△ABC中,(1)如图1,AC=15,AD=9,CD=12,BC=20,求△ABC的面积;(2)如图2,AC=13,BC=20,AB=11,求△ABC的面积.【答案】(1)S△ABC =150;(2)S△ABC=42.1575.【解析】解:(1)∵CD2+AD2=144+81=225,AC2=225,∴CD2+AD2=CA2,∴△△ADC是直角三角形,∴∠ADC=90°,∴CD⊥AB,∴∠ADC=90°,∴BD=√BC2−CD2=16,∴AB=AD+DB=16+9=25,∴S△ABC =12×25×12=150;(2)过C作CD⊥BA的延长线于点D,∵CD⊥AB,∴∠CDB=90°,设AD为x,DB=(x+11),由勾股定理得:CD2=AC2﹣AD2,CD2=BC2﹣DB2,即AC2﹣AD2=BC2﹣DB2,则132﹣x2=202﹣(x+11)2,解得:x=10.5,∴CD=2−AD2=√132−10.52≈7.665,∴S△ABC =12AB⋅CD=12×11×7.665=42.1575.49.(2020春•米东区期末)如图1,∠BAC=∠ACD=90°,∠ABC=∠ADC,CE⊥AD,且BE平分∠ABC.(1)求证:∠ACE=∠ABC;(2)求证:∠ECD+∠EBC=∠BEC;(3)求证:∠CEF=∠CFE.【答案】(1)见解析;(2)见解析;(3)见解析. 【解析】证明:(1)∵CE⊥AD,∠ACD=90°,∵∠ACE+∠ECD=∠D+∠ECD=90°,∴∠ACE=∠D.∵∠D=∠ABC,∴∠ACE=∠ABC;(2)∵∠BAC=∠ACD=90°,∠ABC=∠ADC,∴∠ACB=∠DAC,∴AD∥BC,∵CE⊥AD,∴CE⊥BC,∴∠BEC+∠EBC=90°,∵∠D+∠ECD=90°,∠D=∠ABC,∴∠ABC+∠ECD=90°,∵BE平分∠ABC,∴∠ABC=2∠EBC∴2∠EBC+∠ECD=90°,∴2∠EBC+∠ECD=∠BEC+∠EBC,即∠EBC+∠ECD=∠BEC;(3)∵∠ABF+∠AFB=90°,∠AFB=∠CFE,∴∠ABF+∠CFE=90°,∵∠CBE+∠CEF=90°,∠ABF=∠CAE,∴∠CEF=CFE.50.(2020秋•锦江区校级期末)如图1,已知Rt△ABC中,∠BAC=90°,点D是AB上一点,且AC=8,∠DCA=45°,AE⊥BC于点E,交CD于点F.(1)如图1,若AB=2AC,求AE的长;(2)如图2,若∠B=30°,求△CEF的面积;(3)如图3,点P是BA延长线上一点,且AP=BD,连接PF,求证:PF+AF=BC【答案】(1)AE=8√5=16√55;(2)S△ECF=8(2−√3);(3)见解析.【解析】(1)解:如图1中,∵AB=2AC,AC=8,∴AB=16,∵∠BAC=90°,∴BC=√AC2+AB2=√82+162=8√5,∵AE⊥BC,∴S△ABC =12•BC•AE=12•AC•AB,∴AE=8√5=16√55.(2)解:如图2中,在CE上取一点T,使得FJ=CJ,连接FJ.∵∠BAC=90°,∠B=30°,∴∠ACE=90°﹣30°=60°,∵AE⊥BC,AC=8,∴CE=AC•cos60°=4,∵∠DCA=45°,∴∠FCE=∠ACE﹣∠ACD=15°,∵JF=JC,∴∠JFC=∠JCF=15°,∴∠EJF=∠JFC+∠JCF=30°,设EF=m,则FJ=JC=2m,EJ=√3m,∴√3m+2m=4,∴m=4(2−√3),∴EF=4(2−√3),∴S△ECF =12×4×4(2−√3)=8(2−√3).(3)证明:如图3中,过A点作AM⊥CD于点M,与BC交于点N,连接DN.∵∠BAC=90°,AC=AD,∴AM⊥CD,AM=DM=CM,∠DAM=∠CAM=∠ADM=∠ACD=45°,∴DN=CN,∴∠NDM=∠NCM,∵AE⊥BC,∴∠ECF+∠EFC=∠MAF+∠AFM=90°,∵∠AFM=∠EFC,∴∠MAF=∠ECF,∴∠MAF=∠MDN,∵∠AMF=∠AMN,∴△AMF≌△DMN(ASA),∴AF=DN=CN,∵∠BAC=90°,AC=AD,∴∠DAM=∠CAM=∠ADM=∠ACD=45°,∴∠NAP=∠CDB=135°,∵∠MAF=∠MDN,∴∠PAF=∠BDN,∵AP=DB,∴△APF≌△DBN(SAS),∴PF=BN,∵AF=CN,∴PF+AF=CN+BN,即PF+AF=BC.。
初中数学特殊三角形(等腰三角形、等边三角形、30°直角三角形)常考题及答案解析

特殊三角形(等腰三角形、等边三角形、30°直角三角形)常考题及答案解析1.(2020秋•喀什地区期末)下列说法错误的是()A.等腰三角形的两个底角相等B.等腰三角形的高、中线、角平分线互相重合C.三角形两边的垂直平分线的交点到三个顶点距离相等D.等腰三角形顶角的外角是其底角的2倍2.(2020秋•顺城区期末)已知等腰三角形的周长为17cm,一边长为4cm,则它的腰长为()A.4cm B.6.5cm C.6.5cm或9cm D.4cm或6.5cm 3.(2017•海南)已知△ABC的三边长分别为4、4、6,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画()条.A.3B.4C.5D.6 4.(2019•白银)定义:等腰三角形的顶角与其一个底角的度数的比值k称为这个等腰三角形的“特征值”.若等腰△ABC中,∠A=80°,则它的特征值k=.5.(2013•凉山州)已知实数x,y满足,则以x,y的值为两边长的等腰三角形的周长是.6.(2020秋•五常市期末)如图,点D、E在△ABC的边BC上,AD=AE,BD=CE.(1)求证:AB=AC;(2)若∠BAC=108°,∠DAE=36°,直接写出图中除△ABC与△ADE外所有的等腰三角形.7.(2019秋•龙岩期末)如图,AB=AC,AE=EC=CD,∠A=60°,若EF=2,则DF=()A.3B.4C.5D.6 8.(2006•烟台)如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于()A.25°B.30°C.45°D.60°9.(2020秋•慈溪市期中)已知:如图,AB=BC,∠A=∠C.求证:AD=CD.10.(2014秋•青山区期中)已知:如图,在等边三角形ABC的三边上,分别取点D,E,F,使AD=BE=CF.求证:△DEF是等边三角形.11.(2018秋•六合区期中)如图,△ABC为等边三角形,BD平分∠ABC交AC于点D,DE ∥BC交AB于点E.(1)求证:△ADE是等边三角形.(2)求证:AE=AB.12.(2017•裕华区校级模拟)已知,如图,△ABC是正三角形,D,E,F分别是各边上的一点,且AD=BE=CF.请你说明△DEF是正三角形.13.(2012秋•姜堰市校级期中)如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC =α,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.(1)△COD是什么三角形?说明理由;(2)若AO=n2+1,AD=n2﹣1,OD=2n(n为大于1的整数),求α的度数;(3)当α为多少度时,△AOD是等腰三角形?14.(2000•内蒙古)如图,已知△ABC为等边三角形,延长BC到D,延长BA到E,并且使AE=BD,连接CE,DE.求证:EC=ED.15.(2020秋•连山区期末)如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,∠A=60°,AD=2,则BD=()A.2B.4C.6D.816.(2020秋•肇州县期末)如图,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,AE=6cm,则AC=()A.6cm B.5cm C.4cm D.3cm 17.(2020秋•朝阳县期末)如图,在△ABC中,AB=AC=11,∠BAC=120°,AD是△ABC 的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,则DF的长为()A.4.5B.5C.5.5D.618.(2020秋•抚顺县期末)右图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=7.4m,∠A=30°,则DE长为.19.(2020秋•宽城区期中)如图,△ABC中,∠C=90°,∠A=30°,AB的垂直平分线交AC于D,交AB于E,CD=2,则AD等于()A.10B.8C.6D.420.(2020秋•无棣县期中)如图,在△ABC中,∠C=90°,AC=3,∠B=30°,点P是BC边上一动点,连接AP,则AP的长度不可能是()A.4B.4.5C.5D.721.(2020秋•云县期中)如图,点D是AB的中点,DE⊥AC,AB=7.2,∠A=30°,则DE=()A.1.8B.2.4C.3.6D.4.822.(2020秋•北碚区校级期中)如图,已知∠AOB=60°,P在边OA上,OP=8,点M,N在边OB上,PM=PN,若MN=5,则ON的长度是()A.9B.6.5C.6D.5.523.(2020秋•天宁区校级期中)如图,△ABC中,∠ACB=90°,∠CAB=60°,动点P 在斜边AB所在的直线m上运动,连结PC,那点P在直线m上运动时,能使图中出现等腰三角形的点P的位置有()A.6个B.5个C.4个D.3个24.(2020秋•连江县期中)如图,等边△ABC中,AB=4,点P在边AB上,PD⊥BC,DE ⊥AC,垂足分别为D、E,设PA=x,若用含x的式子表示AE的长,正确的是()A.2﹣x B.3﹣x C.1D.2+x 25.(2020秋•赣榆区期中)如图,在△ABC中,AB=AC=6,∠BAC=120°,AD是△ABC 的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,则DF的长是()A.5B.2C.4D.326.(2019秋•勃利县期末)如图,在△ABC中,∠ACB=90°,D是AB上的点,过点D 作DE⊥AB交BC于点F,交AC的延长线于点E,连接CD,∠DCA=∠DAC,则下列结论正确的有()①∠DCB=∠B;②CD=AB;③△ADC是等边三角形;④若∠E=30°,则DE=EF+CF.A.①②③B.①②④C.②③④D.①②③④27.(2019春•秦淮区期末)如图,△ABC是等边三角形,P是三角形内任意一点,D、E、F分别是AC、AB、BC边上的三点,且PF∥AB,PD∥BC,PE∥AC.若PF+PD+PE=a,则△ABC的边长为()A.a B.a C.a D.a28.下列说法中,正确的个数是()①三条边都相等的三角形是等边三角形;②有一个角为60°的等腰三角形是等边三角形;③有两个角为60°的三角形是等边三角形;④底角的角平分线所在的直线是这等腰三角形的对称轴,则这个三角形是等边三角形A.1个B.2个C.3个D.4个29.(2020•和平区三模)如图,在边长为2的等边三角形ABC中,D为边BC上一点,且BD=CD.点E,F分别在边AB,AC上,且∠EDF=90°,M为边EF的中点,连接CM交DF于点N.若DF∥AB,则CM的长为()A.B.C.D.30.(2020秋•天心区期中)下列说法错误的是()A.有一个角是60°的等腰三角形是等边三角形B.如果一个三角形有两个角相等,那么这两个角所对的边相等C.等腰三角形的角平分线,中线,高相互重合D.三个角都相等的三角形是等边三角形.31.(2019春•杏花岭区校级期中)关于等边三角形,下列说法中错误的是()A.等边三角形中,各边都相等B.等腰三角形是特殊的等边三角形C.两个角都等于60°的三角形是等边三角形D.有一个角为60°的等腰三角形是等边三角形32.(2019•城步县模拟)一个六边形的六个内角都是120°(如图),连续四条边的长依次为1,3,3,2,则这个六边形的周长是()A.13B.14C.15D.16 33.(2018•柳州一模)如图,在四边形ABCD中,∠A=∠B=60°,∠D=90°,AB=2,则CD长的取值范围是()A.<CD<B.CD>2C.1<CD<2D.0<CD<34.(2018秋•罗庄区期中)如图,以点O为圆心,任意长为半径画弧,与射线OM交于点A,再以点A为圆心,AO长为半径画弧,两弧交于点B,画出射线OB,则∠AOB=()A.30°B.45°C.60°D.90°参考答案与试题解析1.【考点】线段垂直平分线的性质;等腰三角形的性质.【专题】线段、角、相交线与平行线;三角形;推理能力.【分析】根据等腰三角形的性质即可判断A;根据三角形的高、角平分线、中线的定义和等腰三角形的性质即可判断B;根据角平分线的性质即可判断C;根据三角形的外角性质和等腰三角形的性质即可判断D.【解答】解:A.等腰三角形的两底角相等,故本选项不符合题意;B.等腰三角形的两个底角的高、角平分线和中线不一定互相重合,故本选项符合题意;C.过O作OM⊥AB于M,OQ⊥AC于Q,ON⊥BC于N,∵O是∠ABC和∠ACB的角平分线的交点,∴OM=ON,ON=OQ,∴OM=ON=OQ,即三角形的两边的垂直平分线的交点到三个顶点的距离相等,故本选项不符合题意;D.∵AB=AC,∴∠B=∠C,∵∠EAC=∠B+∠C,∴∠EAC=2∠B,即等腰三角形顶角的外角是其底角的2倍,故本选项不符合题意;故选:B.【点评】本题考查了角平分线的性质,等腰三角形的性质,三角形的外角性质等知识点,能灵活运用知识点进行推理是解此题的关键.2.【考点】三角形三边关系;等腰三角形的性质.【专题】等腰三角形与直角三角形.【分析】分两种情况讨论:当4cm为腰长时,当4cm为底边时,分别判断是否符合三角形三边关系即可.【解答】解:①若4cm是腰长,则底边长为:20﹣4﹣4=12(cm),∵4+4<12,不能组成三角形,舍去;②若4cm是底边长,则腰长为:=6.5(cm).则腰长为6.5cm.故选:B.【点评】此题考查等腰三角形的性质与三角形的三边关系.此题难度不大,注意掌握分类讨论思想的应用是解此题的关键.3.【考点】等腰三角形的判定.【专题】三角形.【分析】根据等腰三角形的性质,利用4作为腰或底边长,得出符合题意的图形即可.【解答】解:如图所示:当AC=CD,AB=BG,AF=CF,AE=BE时,都能得到符合题意的等腰三角形(AD,AE,AF,AG分别为分割线).故选:B.【点评】此题主要考查了等腰三角形的判定以及应用设计与作图等知识,正确利用图形分类讨论得出是解题关键.4.【考点】等腰三角形的性质.【专题】等腰三角形与直角三角形.【分析】可知等腰三角形的两底角相等,则可求得底角的度数.从而可求解.【解答】解:①当∠A为顶角时,等腰三角形两底角的度数为:=50°∴特征值k==②当∠A为底角时,顶角的度数为:180°﹣80°﹣80°=20°∴特征值k==综上所述,特征值k为或故答案为或【点评】本题主要考查等腰三角形的性质,熟记等腰三角形的性质是解题的关键,要注意到本题中,已知∠A的度数,要分∠A是顶角和底角两种情况,以免造成答案的遗漏.5.【考点】非负数的性质:绝对值;非负数的性质:算术平方根;三角形三边关系;等腰三角形的性质.【专题】压轴题;分类讨论.【分析】先根据非负数的性质列式求出x、y的值,再分4是腰长与底边两种情况讨论求解.【解答】解:根据题意得,x﹣4=0,y﹣8=0,解得x=4,y=8,①4是腰长时,三角形的三边分别为4、4、8,∵4+4=8,∴不能组成三角形,②4是底边时,三角形的三边分别为4、8、8,能组成三角形,周长=4+8+8=20,所以,三角形的周长为20.故答案为:20.【点评】本题考查了等腰三角形的性质,绝对值非负数,算术平方根非负数的性质,根据几个非负数的和等于0,则每一个算式都等于0求出x、y的值是解题的关键,难点在于要分情况讨论并且利用三角形的三边关系进行判断.6.【考点】等腰三角形的判定.【专题】几何图形.【分析】(1)首先过点A作AF⊥BC于点F,由AD=AE,根据三线合一的性质,可得DF=EF,又由BD=CE,可得BF=CF,然后由线段垂直平分线的性质,可证得AB=AC.(2)根据等腰三角形的判定解答即可.【解答】证明:(1)过点A作AF⊥BC于点F,∵AD=AE,∴DF=EF,∵BD=CE,∴BF=CF,∴AB=AC.(2)∵∠B=∠BAD,∠C=∠EAC,∠BAE=∠BEA,∠ADC=∠DAC,∴除△ABC与△ADE外所有的等腰三角形为:△ABD、△AEC、△ABE、△ADC,【点评】此题考查了等腰三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.7.【考点】等边三角形的判定与性质.【专题】数形结合;三角形;等腰三角形与直角三角形;运算能力;推理能力.【分析】过点E作EG⊥BC,交BC于点G,先证明△ABC是等边三角形,再证明∠AFE =90°,然后利用等腰三角形的“三线合一”性质及角平分线的性质定理求得EG的长,随后利用含30度角的直角三角形的性质求得DE的长,最后将EF与DE相加即可.【解答】解:如图,过点E作EG⊥BC,交BC于点G∵AB=AC,∠A=60°,∴△ABC是等边三角形,∴∠ACB=60°,∵EC=CD,∴∠CED=∠CDE=∠ACB=30°,∴∠AEF=30°,∴∠AFE=90°,即EF⊥AB,∵△ABC是等边三角形,AE=CE,∴BE平分∠ABC,∴EG=EF=2,在Rt△DEG中,DE=2EG=4,∴DF=EF+DE=2+4=6;方法二、∵AB=AC,∠A=60°,∴△ABC是等边三角形,∴∠ACB=60°,∵EC=CD,∴∠CED=∠CDE=∠ACB=30°,∵△ABC是等边三角形,AE=CE,∴BE平分∠ABC,∴∠ABE=∠CBE=30°=∠CDE,∴BE=DE,∠BFD=90°,∴BE=2EF=4=DE,∴DF=DE+EF=6;故选:D.【点评】本题考查了等边三角形的判定与性质、等腰三角形的“三线合一”性质及含30度角的直角三角形的性质,熟练掌握相关性质及定理是解题的关键.8.【考点】等边三角形的判定与性质.【分析】先根据图形折叠的性质得出BC=CE,再由直角三角形斜边的中线等于斜边的一半即可得出CE=AE=BE,进而可判断出△BEC是等边三角形,由等边三角形的性质及直角三角形两锐角互补的性质即可得出结论.【解答】解:△ABC沿CD折叠B与E重合,则BC=CE,∵E为AB中点,△ABC是直角三角形,∴CE=BE=AE,∴△BEC是等边三角形.∴∠B=60°,∴∠A=30°,故选:B.【点评】考查直角三角形的性质,等边三角形的判定及图形折叠等知识的综合应用能力及推理能力.9.【考点】等腰三角形的判定与性质.【专题】几何图形.【分析】连接AC,根据等边对等角得到∠BAC=∠BCA,因为∠A=∠C,则可以得到∠CAD=∠ACD,根据等角对等边可得到AD=DC.【解答】证明:连接AC,∵AB=BC,∴∠BAC=∠BCA.∵∠BAD=∠BCD,∴∠CAD=∠ACD.∴AD=CD.【点评】重点考查了等腰三角形的判定方法,即:如果一个三角形有两个角相等,那么这两个角所对的边也相等.10.【考点】全等三角形的判定与性质;等边三角形的判定与性质.【专题】证明题.【分析】由△ABC是等边三角形,AD=BE=CF,易证得△ADF≌△BED,即可得DF=DE,同理可得DF=EF,即可证得:△DEF是等边三角形.【解答】证明:∵△ABC是等边三角形,∴AB=BC=AC,∵AD=BE=CF,∴AF=BD,在△ADF和△BED中,,∴△ADF≌△BED(SAS),∴DF=DE,同理DE=EF,∴DE=DF=EF.∴△DEF是等边三角形.【点评】此题考查了等边三角形的判定与性质以及全等三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.11.【考点】平行线的性质;等腰三角形的判定与性质;等边三角形的判定与性质.【专题】几何图形.【分析】(1)根据等边三角形的性质和平行线的性质证明即可.(2)根据等边三角形的性质解答即可.【解答】证明:(1)∵△ABC为等边三角形,∴∠A=∠ABC=∠C=60°.∵DE∥BC,∴∠AED=∠ABC=60°,∠ADE=∠C=60°.∴△ADE是等边三角形.(2)∵△ABC为等边三角形,∴AB=BC=AC.∵BD平分∠ABC,∴AD=AC.∵△ADE是等边三角形,∴AE=AD.∴AE=AB.【点评】此题考查等边三角形的判定和性质,关键是根据等边三角形的性质和平行线的性质解答.12.【考点】全等三角形的判定与性质;等边三角形的判定与性质.【专题】证明题.【分析】根据等边△ABC中AD=BE=CF,证得△ADE≌△BEF≌△CFD即可得出△DEF 是等边三角形.【解答】解:∵△ABC为等边三角形,且AD=BE=CF,∴AE=BF=CD,又∵∠A=∠B=∠C=60°,∴△ADE≌△BEF≌△CFD(SAS),∴DE=EF=FD,∴△DEF是等边三角形.【点评】本题主要考查了等边三角形的判定与性质和全等三角形判定,根据已知得出△ADE≌△BEF≌△CFD是解答此题的关键.13.【考点】全等三角形的判定与性质;等边三角形的判定与性质.【专题】分类讨论.【分析】(1)根据旋转的性质可得CO=CD,∠OCD=60°,根据有一个角是60°的等腰三角形是等边三角形解答;(2)利用勾股定理逆定理判定△AOD是直角三角形,并且∠ADO=90°,从而求出∠ADC=150°,再根据旋转变换只改变图形的位置不改变图形的形状与大小可得α=∠ADC;(3)根据周角为360°用α表示出∠AOD,再根据旋转的性质表示出∠ADO,然后利用三角形的内角和定理表示出∠DAO,再分∠AOD=∠ADO,∠AOD=∠DAO,∠ADO=∠DAO三种情况讨论求解.【解答】解:(1)△COD是等边三角形.理由如下:∵△BOC绕点C按顺时针方向旋转60°得△ADC,∴CO=CD,∠OCD=60°,∴△COD是等边三角形;(2)∵AD2+OD2=(n2﹣1)2+(2n)2=n4﹣2n2+1+4n2=n4+2n2+1=(n2+1)2=AO2,∴△AOD是直角三角形,且∠ADO=90°,∵△COD是等边三角形,∴∠CDO=60°,∴∠ADC=∠ADO+∠CDO=90°+60°=150°,根据旋转的性质,α=∠ADC=150;(3)∵α=∠ADC,∠CDO=60°,∴∠ADO=α﹣60°,又∵∠AOD=360°﹣110°﹣α﹣60°=190°﹣α,∴∠DAO=180°﹣(190°﹣α)﹣(α﹣60°)=180°﹣190°+α﹣α+60°=50°,∵△AOD是等腰三角形,∴①∠AOD=∠ADO时,190°﹣α=α﹣60°,解得α=125°,②∠AOD=∠DAO时,190°﹣α=50°,解得α=140°,③∠ADO=∠DAO时,α﹣60°=50°,解得α=110°,综上所述,α为125°或140°或110°时,△AOD是等腰三角形.【点评】本题考查了等边三角形的判定与性质,旋转变换只改变图形的位置不改变图形的形状与大小的性质,勾股定理逆定理,等腰三角形的性质,(3)用α表示出△AOD的各个内角是解题的关键,注意要分情况讨论.14.【考点】全等三角形的判定与性质;等边三角形的判定与性质.【专题】证明题;压轴题.【分析】首先延长BD至F,使DF=BC,连接EF,得出△BEF为等边三角形,进而求出△ECB≌△EDF,从而得出EC=DE.【解答】证明:延长BD至F,使DF=BC,连接EF,∵AE=BD,△ABC为等边三角形,∴BE=BF,∠B=60°,∴△BEF为等边三角形,∴∠F=60°,在△ECB和△EDF中∴△ECB≌△EDF(SAS),∴EC=ED.【点评】此题主要考查了等边三角形的性质与判定以及全等三角形的判定等知识,作出辅助线是解决问题的关键.15.【考点】含30度角的直角三角形.【专题】计算题;等腰三角形与直角三角形;运算能力;推理能力.【分析】根据同角的余角相等求出∠BCD=∠A=60°,再根据30°角所对的直角边等于斜边的一半求出AC、AB的长,然后根据BD=AB﹣AD计算即可得解.【解答】解:∵∠ACB=90°,CD⊥AB,∴∠BCD+∠ACD=90°,∠A+∠ACD=90°,∴∠BCD=∠A=60°,∴∠ACD=∠B=30°,∵AD=2,∴AC=2AD=4,∴AB=2AC=8,∴BD=AB﹣AD=8﹣2=6.故选:C.【点评】本题主要考查了直角三角形30°角所对的直角边等于斜边的一半的性质,同角的余角相等的性质,熟记性质是解题的关键.16.【考点】线段垂直平分线的性质;含30度角的直角三角形.【专题】等腰三角形与直角三角形.【分析】根据线段垂直平分线的性质得到EB=EA,根据等腰三角形的性质得到∠EAB=∠B=15°,根据三角形的外角的性质求出∠AEC=30°,根据直角三角形的性质计算.【解答】解:∵DE垂直平分AB,∴EB=EA,∴∠EAB=∠B=15°,∴∠AEC=30°,∴AC=AE=3(cm),故选:D.【点评】本题考查的是线段垂直平分线的性质,直角三角形的性质,在直角三角形中,30°角所对的直角边等于斜边的一半.17.【考点】等腰三角形的性质;含30度角的直角三角形.【分析】根据等腰三角形三线合一的性质可得到AD⊥BC,∠BAD=∠CAD,从而可得到∠BAD=60°,∠ADB=90°,再根据角平分线的性质即可得到∠DAE=∠EAB=30°,从而可推出AD=DF,根据直角三角形30度角的性质即可求得AD的长,即得到了DF 的长.【解答】解:∵△ABC是等腰三角形,D为底边的中点,∴AD⊥BC,∠BAD=∠CAD,∵∠BAC=120°,∴∠BAD=60°,∠ADB=90°,∵AE是∠BAD的角平分线,∴∠DAE=∠EAB=30°.∵DF∥AB,∴∠F=∠BAE=30°.∴∠DAF=∠F=30°,∴AD=DF.∵AB=11,∠B=30°,∴AD=5.5,∴DF=5.5故选:C.【点评】本题考查了含30°角的直角三角形,等腰三角形的判定与性质,平行线的性质等知识点,能求出AD=DF是解此题的关键.18.【考点】含30度角的直角三角形.【专题】推理填空题.【分析】根据直角三角形的性质求出BC,根据三角形中位线定理计算即可.【解答】解:∵∠A=30°,BC⊥AC,∴BC=AB=3.7,∵DE⊥AC,BC⊥AC,∴DE∥BC,∵点D是斜梁AB的中点,∴DE=BC=1.85m,故答案为:1.85m.【点评】本题考查的是直角三角形的性质,掌握在直角三角形中,30°角所对的直角边等于斜边的一半是解题的关键.19.【考点】线段垂直平分线的性质;含30度角的直角三角形.【专题】计算题;等腰三角形与直角三角形;运算能力;推理能力.【分析】先由直角三角形的性质求出∠ABC的度数,由AB的垂直平分线交AC于D,交AB于E,垂足为E,可得BD=AD,由∠A=30°可知∠ABD=30°,故可得出∠DBC =30°,根据CD=2可得出BD的长,进而得出AD的长.【解答】解:连接BD,∵在△ABC中,∠C=90°,∠A=30°,∴∠ABC=60°.∵AB的垂直平分线交AC于D,交AB于E,∴AD=BD,DE⊥AB,∴∠ABD=∠A=30°,∴∠DBC=30°,∵CD=2,∴BD=2CD=4,∴AD=4.故选:D.【点评】此题考查了线段垂直平分线的性质以及含30°角的直角三角形的性质.熟练掌握直角三角形的性质是解题的关键.20.【考点】垂线段最短;含30度角的直角三角形.【专题】解直角三角形及其应用;推理能力.【分析】在Rt△ABC中,利用“在直角三角形中,30°角所对的直角边等于斜边的一半”可求出AB的长,由点P是BC边上一动点结合AC,AB的长,即可得出AP长的取值范围,再对照四个选项即可得出结论.【解答】解:在Rt△ABC中,∠C=90°,∠B=30°,AC=3,∴AB=2AC=6.∵点P是BC边上一动点,∴AC≤AP≤AB,即3≤AP≤6.故选:D.【点评】本题考查了含30度角的直角三角形以及垂线段最短,通过解含30度角的直角三角形,求出AB的长是解题的关键.21.【考点】含30度角的直角三角形.【专题】等腰三角形与直角三角形;运算能力.【分析】求出AD的长,再根据含30°角的直角三角形的性质得出DE=AD,即可求出答案.【解答】解:∵点D是AB的中点,AB=7.2,∴AD=AB=3.6,∵DE⊥AC,∴∠DEA=90°,∵∠A=30°,∴DE=AD=1.8,故选:A.【点评】本题考查了含30°角的直角三角形的性质,能根据含30°角的直角三角形的性质得出DE=AD是解此题的关键.22.【考点】等腰三角形的性质;含30度角的直角三角形.【专题】等腰三角形与直角三角形;推理能力.【分析】过P作PC⊥MN于C,先由等腰三角形的性质得CM=CN=2.5,再由含30°角的直角三角形的性质求出OC的长,然后由OC+CM求出ON的长即可.【解答】解:过P作PC⊥MN于C,如图所示:∵PM=PN,MN=5,∴CM=NC=MN=2.5,在Rt△OPC中,∠AOB=60°,∴∠OPC=30°,∴OC=OP=4,则ON=OC+CM=4+2.5=6.5,故选:B.【点评】本题考查的是含30°角的直角三角形的性质、等腰三角形的性质等知识;熟练掌握含30°角的直角三角形的性质和等腰三角形的性质是解题的关键.23.【考点】三角形内角和定理;等腰三角形的判定;含30度角的直角三角形.【专题】等腰三角形与直角三角形;几何直观.【分析】根据等腰三角形的判定和含30°的直角三角形的性质解答即可.【解答】解:如图所示:以B为圆心,BC长为半径画弧,交直线m于点P4,P2,以A为圆心,AC长为半径画弧,交直线m于点P1,P3,边AC和BC的垂直平分线都交于点P3位置,因此出现等腰三角形的点P的位置有4个,故选:C.【点评】此题考查等腰三角形的判定,关键是根据等腰三角形的判定和含30°的直角三角形的性质解答.24.【考点】列代数式;等边三角形的性质;含30度角的直角三角形.【专题】等腰三角形与直角三角形;推理能力.【分析】利用等边三角形的性质可得AB=BC=AC=4,∠B=∠C=60°,再利用含30度角的直角三角形的性质进行计算即可.【解答】解:∵△ABC是等边三角形,∴AB=BC=AC=4,∠B=∠C=60°,∵PD⊥BC,DE⊥AC,∴BD=PB,CE=CD,∵P A=x,∴BP=4﹣x,∴BD=PB=2﹣x,∴CD=4﹣(2﹣x)=2+x,∴CE=1+x,∴AE=4﹣(1+x)=3﹣x,故选:B.【点评】此题主要考查了等边三角形的性质和含30度角的直角三角形的性质,关键是掌握在直角三角形中,30°角所对的直角边等于斜边的一半.25.【考点】平行线的性质;等腰三角形的性质;含30度角的直角三角形.【专题】等腰三角形与直角三角形;推理能力.【分析】根据等腰三角形三线合一的性质可得到AD⊥BC,∠BAD=∠CAD,从而可得到∠BAD=60°,∠ADB=90°,再根据角平分线的性质即可得到∠DAE=∠EAB=30°,从而可推出AD=DF,根据直角三角形30度角的性质即可求得AD的长,即得到了DF 的长.【解答】解:∵△ABC是等腰三角形,D为底边的中点,∴AD⊥BC,∠BAD=∠CAD,∵∠BAC=120°,∴∠BAD=60°,∠ADB=90°,∵AE是∠BAD的角平分线,∴∠DAE=∠EAB=30°,∵DF∥AB,∴∠F=∠BAE=30°,∴∠DAF=∠F=30°,∴AD=DF,∵AB=6,∠B=30°,∴AD=AB=3,∴DF=3,故选:D.【点评】本题考查了含30°角的直角三角形,等腰三角形的判定与性质,平行线的性质等知识点,能求出AD=DF是解此题的关键.26.【考点】等边三角形的判定与性质.【专题】等腰三角形与直角三角形.【分析】由在△ABC中,∠ACB=90°,DE⊥AB,易证得∠DCA=∠DAC,继而可得①∠DCB=∠B正确;由①可证得AD=BD=CD,即可得②CD=AB正确;易得③△ADC是等腰三角形,但不能证得△ADC是等边三角形;由若∠E=30°,易求得∠FDC=∠FCD=30°,则可证得DF=CF,继而证得DE=EF+CF.【解答】解:∵在△ABC中,∠ACB=90°,DE⊥AB,∴∠ADE=∠ACB=90°,∴∠A+∠B=90°,∠ACD+∠DCB=90°,∵∠DCA=∠DAC,∴AD=CD,∠DCB=∠B;故①正确;∴CD=BD,∵AD=CD,∴CD=AB;故②正确;∠DCA=∠DAC,∴AD=CD,但不能判定△ADC是等边三角形;故③错误;∵若∠E=30°,∴∠A=60°,∴△ACD是等边三角形,∴∠ADC=60°,∵∠ADE=∠ACB=90°,∴∠EDC=∠BCD=∠B=30°,∴CF=DF,∴DE=EF+DF=EF+CF.故④正确.故选:B.【点评】此题考查了等腰三角形的性质与判定以及直角三角形的性质.注意证得D是AB 的中点是解此题的关键.27.【考点】平行线的性质;等边三角形的判定与性质.【专题】等腰三角形与直角三角形;多边形与平行四边形.【分析】延长EP交BC于点G,延长FP交AC于点H,证出四边形AEPH、四边形PDCG 均为平行四边形,得出PE=AH,PG=CD.证出△FGP和△HPD也是等边三角形,得出PF=PG=CD,PD=DH,得出PE+PD+PF=AH+DH+CD=AC即可.【解答】解:延长EP交BC于点G,延长FP交AC于点H,如图所示:∵PF∥AB,PD∥BC,PE∥AC,∴四边形AEPH、四边形PDCG均为平行四边形,∴PE=AH,PG=CD.又∵△ABC为等边三角形,∴△FGP和△HPD也是等边三角形,∴PF=PG=CD,PD=DH,∴PE+PD+PF=AH+DH+CD=AC,∴AC=a;故选:D.【点评】本题考查了平行四边形的判定与性质,熟练掌握性质定理和判定定理是解题的关键.平行四边形的五种判定方法与平行四边形的性质相呼应,每种方法都对应着一种性质,在应用时应注意它们的区别与联系.28.【考点】等腰三角形的判定与性质;等边三角形的判定与性质.【专题】三角形.【分析】根据等边三角形的判定、轴对称的性质即可判断;【解答】解:①三条边都相等的三角形是等边三角形;正确.②有一个角为60°的等腰三角形是等边三角形;正确.③有两个角为60°的三角形是等边三角形;正确.④底角的角平分线所在的直线是这等腰三角形的对称轴,则这个三角形是等边三角形;正确.故选:D.【点评】本题考查等边三角形的判定和性质、等腰三角形的判定和性质、轴对称等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.29.【考点】平行线的性质;等边三角形的判定与性质.【专题】等腰三角形与直角三角形;推理能力.【分析】根据等边三角形边长为2,在Rt△BDE中求得DE的长,再根据CM垂直平分DF,在Rt△CDN中求得CN,最后根据线段和可得CM的长.【解答】解:∵等边三角形边长为2,BD=CD,∴BD=,CD=,∵等边三角形ABC中,DF∥AB,∴∠FDC=∠B=60°,∵∠EDF=90°,∴∠BDE=30°,∴DE⊥BE,∴BE=BD=,DE=,如图,连接DM,则Rt△DEF中,DM=EF=FM,∵∠FDC=∠FCD=60°,∴△CDF是等边三角形,∴CD=CF=,∴CM垂直平分DF,∴∠DCN=30°,DN=FN,∴Rt△CDN中,DN=,CN=,∵M为EF的中点,∴MN=DE=,∴CM=CN+MN=+=,故选:C.【点评】本题主要考查了三角形的综合应用,解决问题的关键是掌握等边三角形的性质、平行线的性质、线段垂直平分线的判定等.熟练掌握这些性质是解题的关键.30.【考点】等腰三角形的性质;等边三角形的判定与性质.【专题】等腰三角形与直角三角形;推理能力.【分析】根据等腰三角形的性质和等边三角形的性质和判定逐个进行分析判断,即可得到答案.【解答】解:A.有一个角为60°的等腰三角形是等边三角形,故本选项不合题意;B.如果一个三角形有两个角相等,那么这两个角所对的边相等,故本选项不合题意;C.等腰三角形顶角的角平分线,底边的中线,高相互重合,说法错误,故本选项符合题意;D.三个角都相等的三角形是等边三角形,故本选项不合题意;故选:C.【点评】本题考查了等边三角形的判定和性质,等腰三角形的性质,熟练掌握等边三角形的判定和性质定理是解题的关键.31.【考点】等腰三角形的性质;等边三角形的判定与性质.【专题】等腰三角形与直角三角形;推理能力.。
等腰三角形与等边三角形专项练习(精品测试卷)(2022年最新)

6.若式子 有意义,则一次函数 的图象可能是()
A. B. C. D.
7.要使直线y=(2m-3)x+(3n+1)的图象经过一、二、四象限,则m与n的取值为( )
A.m> ,n> B.m>3,n>-3
C.m< ,n< D.m< ,n>
8.为了节省空间,家里的饭碗一般是摞起来存放的.如果6只饭碗摞起来的高度为15cm,9只饭碗摞起来的高度为20cm,那么11只饭碗摞起来的高度更接近()
13.如果直线y=2x+m不经过第二象限,那么实数m的取值范围是___.
14.表格描述的是y与x之间的函数关系:
x
…
-2
0
2
4
…
y=kx+b
…
3
-1
m
n
…
则m与n的大小关系是____________.
15.如图,直线y=kx+b经过A(-2,-1)和B(-3,0)两点,则不等式-3≤-2x-5<kx+b的解集是_______________.
18.(2020秋•杨浦区校级期中)如图,AD是△ABC的高,∠B=2∠C,BD=5,BC=25,求AB的长.
19.(2020秋•朝阳区校级期中)如图,在△ABC中,∠B=2∠C,AD⊥BC,垂足为D,判断AB、CD和BD这三条线段的数量关系(用等式表示),并证明.
20.(2020春•延庆区期中)已知:在△ABC中,AB=AC,DE∥AB,DF∥AC.
25.(2020秋•慈溪市期中)已知:如图,AB=BC,∠A=∠C.求证:AD=CD.
26.(2020秋•泰兴市期中)已知:如图,AB=AD,∠ABC=∠ADC.求证:BC=DC.
27.(2020春•渭南期中)已知:如图,△ABO是等边三角形,CD∥AB,分别交AO、BO的延长线于点C、D.求证:△OCD是等边三角形.
等腰三角形与等边三角形(优选真题60道)三年(2021-2023)中考数学真题分项汇编(全国通用)

三年(2021-2023)中考数学真题分项汇编(全国通用)等腰三角形与等边三角形(优选真题60道)一.选择题(共30小题)1.(2023•贵州)5月26日,“2023中国国际大数据产业博览会”在贵阳开幕,在“自动化立体库”中有许多几何元素,其中有一个等腰三角形模型(示意图如图所示),它的顶角为120°,腰长为12m,则底边上的高是()A.4m B.6m C.10m D.12m【分析】作AD⊥BC于点D,根据等腰三角形的性质和三角形内角和定理可得∠B=∠C=12(180°﹣∠BAC)=30°,再根据含30度角的直角三角形的性质即可得出答案.【解答】解:如图,作AD⊥BC于点D,在△ABC中,∠BAC=120°,AB=AC,∴∠B=∠C=12(180°﹣∠BAC30°,又∵AD⊥BC,∴AD=12AB=12×12=6(m),故选:B.【点评】本题考查等腰三角形的性质,三角形内角和定理,含30度角的直角三角形的性质等,解题关键是掌握30度角所对的直角边是斜边的一半.2.(2023•内蒙古)如图,直线a∥b,直线l与直线a,b分别相交于点A,B,点C在直线b上,且CA=CB.若∠1=32°,则∠2的度数为()A.32°B.58°C.74°D.75°【分析】由CA =CB 可得△ABC 是等腰三角形,从而可求∠CBA 的大小,再结合平行线的性质即可解答.【解答】解:∵CA =CB ,∴△ABC 是等腰三角形,∴∠CBA =∠CAB =(180°﹣32°)÷2=74°,∵a ∥b ,∴∠2=∠CBA =74°.故选:C .【点评】本题考查等腰三角形的性质和平行线的性质,熟练掌握性质是解题关键.3.(2023•菏泽)△ABC 的三边长a ,b ,c 满足(a ﹣b )2+√2a −b −3+|c ﹣3√2|=0,则△ABC 是( )A .等腰三角形B .直角三角形C .锐角三角形D .等腰直角三角形【分析】由等式可分别得到关于a 、b 、c 的等式,从而分别计算得到a 、b 、c 的值,再由 a 2+b 2=c 2 的关系,可推导得到△ABC 为直角三角形.【解答】解:由题意得{a −b =02a −b −3=0c −3√2=0,解得{a =3b =3c =3√2,∵a 2+b 2=c 2,且a =b ,∴△ABC 为等腰直角三角形,故选:D .【点评】本题考查了非负性和勾股定理逆定理的知识,求解的关键是熟练掌握非负数的和为0,每一个非负 数均为0,和勾股定理逆定理.4.(2023•河北)在△ABC 和△A 'B 'C ′中,∠B =∠B '=30°,AB =A 'B '=6,AC =A 'C ′=4,已知∠C =n °,则∠C ′=( )A .30°B .n °C .n °或180°﹣n °D .30°或150°【分析】分两种情况讨论,当BC =B ′C ′时,则△ABC ≌△A ′B ′C ′,得出∠C ′=∠C =n °,当BC ≠B ′C ′时,如图,利用等腰三角形的性质求得∠A ′C ″C ′=∠C ′=n °,从而求得∠A ′C ″B ′=180°﹣n °.【解答】解:当BC =B ′C ′时,△ABC ≌△A ′B ′C ′(SSS ),∴∠C ′=∠C =n °,当BC≠B′C′时,如图,∵A′C′=A′C″,∴∠A′C″C′=∠C′=n°,∴∠A′C″B′=180°﹣n°,∴∠C′=n°或180°﹣n°,故选:C.【点评】本题考查了等腰三角形的性质,三角形全等的性质,熟练掌握等腰三角形两底角相等是解题的关键.5.(2023•滨州)已知点P是等边△ABC的边BC上的一点,若∠APC=104°,则在以线段AP,BP,CP 为边的三角形中,最小内角的大小为()A.14°B.16°C.24°D.26°【分析】过点P作PD∥AB交AC于点D,过点PE∥AC交AB于点E,四边形AEPD为平行四边形,根据平行线的性质易得△CDP为等边三角形,△BEP为等边三角形,则CP=DP=AE,BP=EP,因此△AEP 就是以线段AP,BP,CP AEP的三个内角即可求解.【解答】解:如图,过点P作PD∥AB交AC于点D,过点PE∥AC交AB于点E,则四边形AEPD为平行四边形,∴DP=AE,∵△ABC为等边三角形,∴∠B=∠C=∠BAC=60°,∵PD∥AB,∴∠CPD=∠B=60°,∠CDP=∠BAC=60°,∴△CDP为等边三角形,∴CP=DP=CD,∴CP=DP=AE,∵PE∥AC,∴∠BEP=∠BAC=60°,∠BPE=∠C=60°,∴△BEP为等边三角形,∴BP=EP=BE,∴△AEP就是以线段AP,BP,CP为边的三角形,∵∠APC=104°,∴∠APB=180°﹣∠APC=76°,∴∠APE=∠APB﹣∠BPE=16°,∠P AE=∠APC﹣∠B=44°,∠AEP=180°﹣∠BEP=120°,∴以线段AP,BP,CP为边的三角形的三个内角分别为16°、44°、120°,∴最小内角的大小为16°.故选:B.角性质,根据题意正确画出图形,推理论证得到△AEP就是以线段AP,BP,CP为边的三角形是解题关键.6.(2023•河北)四边形ABCD的边长如图所示,对角线AC的长度随四边形形状的改变而变化.当△ABC 为等腰三角形时,对角线AC的长为()A.2B.3C.4D.5【分析】分两种情况,由三角形的三边关系定理:三角形两边的和大于第三边,即可解决问题.【解答】解:∵△ABC为等腰三角形,∴AB=AC或AC=BC,当AC=BC=4时,AD+CD=AC=4,此时不满足三角形三边关系定理,当AC=AB=3时.满足三角形三边关系定理,∴AC=3.故选:B.【点评】本题考查等腰三角形的性质,三角形的三边关系定理,关键是掌握三角形的三边关系定理.7.(2023•金昌)如图,BD是等边△ABC的边AC上的高,以点D为圆心,DB长为半径作弧交BC的延长线于点E,则∠DEC=()A.20°B.25°C.30°D.35°【分析】根据等边三角形的性质可得∠ABC=60°,根据等边三角形三线合一可得∠CBD=30°,再根据作图可知BD=ED,进一步可得∠DEC的度数.【解答】解:在等边△ABC中,∠ABC=60°,∵BD是AC边上的高,∴BD平分∠ABC,∴∠CBD=12∠ABC=30°,∵BD=ED,∴∠DEC=∠CBD=30°,故选:C.【点评】本题考查了等边三角形的性质,等腰三角形的性质,熟练掌握这些性质是解题的关键.8.(2023•眉山)如图,△ABC中,AB=AC,∠A=40°,则∠ACD的度数为()A.70°B.100°C.110°D.140°【分析】根据等边对等角得到∠B=∠ACB,利用三角形内角和定理求出∠B的度数,再根据三角形外角的性质即可求出∠ACD的度数.【解答】解:∵AB=AC,∴∠B=∠ACB,∵∠A=40°,∴∠B=∠ACB=180°−∠A2=180°−40°2=70°,∵∠ACD是△ABC的一个外角,∴∠ACD=∠A+∠B=40°+70°=110°,故选:C.【点评】本题主要考查了等腰三角形的性质,三角形内角和定理,三角形外角的性质,掌握等腰三角形的性质:等边对等角.9.(2022•泰安)如图,l1∥l2,点A在直线l1上,点B在直线l2上,AB=BC,∠C=25°,∠1=60°.则∠2的度数是()A.70°B.65°C.60°D.55°【分析】利用等腰三角形的性质得到∠C=∠BAC=25°,利用平行线的性质得到∠BEA=95°,再根据三角形外角的性质即可求解.【解答】解:如图,∵AB=BC,∠C=25°,∴∠C=∠BAC=25°,∵l1∥l2,∠1=60°,∴∠BEA=180°﹣60°﹣25°=95°,∵∠BEA=∠C+∠2,∴∠2=95°﹣25°=70°.故选:A.【点评】本题考查了等腰三角形的性质,平行线的性质以及三角形外角的性质,解决问题的关键是注意运用两直线平行,同旁内角互补.10.(2022•淄博)某城市几条道路的位置关系如图所示,道路AB∥CD,道路AB与AE的夹角∠BAE=50°.城市规划部门想新修一条道路CE,要求CF=EF,则∠E的度数为()A.23°B.25°C.27°D.30°【分析】先根据平行线的性质,由AB∥CD得到∠DFE=∠BAE=50°,根据等腰三角形的性质得出∠C =∠E,再根据三角形外角性质计算∠E的度数.【解答】解:∵AB∥CD,∴∠DFE=∠BAE=50°,∵CF=EF,∴∠C=∠E,∵∠DFE=∠C+∠E,∴∠C=12∠DFE=12×50°=25°,故选:B.【点评】本题考查了等腰三角形的性质、平行线的性质,熟记等腰三角形的性质、平行线的性质是解题的关键.11.(2022•台湾)如图,△ABC中,D点在AB上,E点在BC上,DE为AB的中垂线.若∠B=∠C,且∠EAC>90°,则根据图中标示的角,判断下列叙述何者正确?()A.∠1=∠2,∠1<∠3B.∠1=∠2,∠1>∠3C.∠1≠∠2,∠1<∠3D.∠1≠∠2,∠1>∠3【分析】根据线段垂直平分线的性质,等腰三角形的性质解答即可.【解答】解:∵DE为AB的中垂线,∴∠BDE=∠ADE,BE=AE,∴∠B=∠BAE,∴∠1=∠2,∵∠EAC>90°,∴∠3+∠C<90°,∵∠B+∠1=90°,∠B=∠C,∴∠1>∠3,∴∠1=∠2,∠1>∠3,故选:B.本题的关键.12.(2022•荆州)如图,直线l1∥l2,AB=AC,∠BAC=40°,则∠1+∠2的度数是()A.60°B.70°C.80°D.90°【分析】过点C作CD∥l1,利用平行线的性质可得∠1+∠2=∠ACB,再由等腰三角形的性质可得∠ACB =∠ABC,从而可求解.【解答】解:过点C作CD∥l1,如图,∵l1∥l2,∴l1∥l2∥CD,∴∠1=∠BCD,∠2=∠ACD,∴∠1+∠2=∠BCD+∠ACD=∠ACB,∵AB=AC,∴∠ACB=∠ABC,∵∠BAC=40°,∴∠ACB=12(180°﹣∠BAC)=70°,∴∠1+∠2=70°.故选:B.【点评】本题主要考查等腰三角形的性质,平行线的性质,解答的关键是由平行线的性质得∠1+∠2=∠ACB.13.(2022•宿迁)若等腰三角形的两边长分别是3cm和5cm,则这个等腰三角形的周长是()A.8cm B.13cm C.8cm或13cm D.11cm或13cm【分析】题目给出等腰三角形有两条边长为3cm和5cm,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.【解答】解:当3cm,3,5能组成三角形,当5cm是腰长时,5,5,3能够组成三角形.则三角形的周长为11cm或13cm.故选:D.【点评】本题考查等腰三角形的性质及三角形三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.14.(2022•天津)如图,△OAB的顶点O(0,0),顶点A,B分别在第一、四象限,且AB⊥x轴,若AB =6,OA=OB=5,则点A的坐标是()A.(5,4)B.(3,4)C.(5,3)D.(4,3)【分析】根据等腰三角形的性质求出AC,根据勾股定理求出OC,根据坐标与图形性质写出点A的坐标.【解答】解:设AB与x轴交于点C,∵OA=OB,OC⊥AB,AB=6,∴AC=12AB=3,由勾股定理得:OC=√OA2−AC2=√52−32=4,∴点A的坐标为(4,3),故选:D.【点评】本题考查的是等腰三角形的性质、坐标与图形性质,掌握等腰三角形的三线合一是解题的关键.15.(2022•海南)如图,直线m∥n,△ABC是等边三角形,顶点B在直线n上,直线m交AB于点E,交AC于点F,若∠1=140°,则∠2的度数是()A.80°B.100°C.120°D.140°【分析】先根据等边三角形的性质可得∠A=∠B=∠C=60°,由三角形外角的性质可得∠AEF的度数,由平行线的性质可得同旁内角互补,可得结论.【解答】解:∵△ABC是等边三角形,∴∠A=60°.对于△AEF,∵∠1=∠A+∠AEF=140°,∴∠AEF=140°﹣60°=80°,∴∠DEB=∠AEF=80°,∵m∥n,∴∠2+∠DEB=180°,∴∠2=180°﹣80°=100°,故选:B.【点评】本题主要考查了等边三角形的性质,平行线的性质,三角形外角的性质,题目比较基础,熟练掌握性质是解题的关键.16.(2022•鞍山)如图,在△ABC中,AB=AC,∠BAC=24°,延长BC到点D,使CD=AC,连接AD,则∠D的度数为()A.39°B.40°C.49°D.51°【分析】利用等边对等角求得∠B=∠ACB=78°,然后利用三角形外角的性质求得答案即可.【解答】解:∵AB=AC,∠BAC=24°,∴∠B=∠ACB=78°.∵CD=AC,∠ACB=78°,∠ACB=∠D+∠CAD,∴∠D=∠CAD=12∠ACB=39°.故选:A.【点评】本题考查了等腰三角形的性质,解题的关键是了解“等边对等角”的性质,难度不大.17.(2022•自贡)等腰三角形顶角度数比一个底角度数的2倍多20°,则这个底角的度数是( )A .30°B .40°C .50°D .60°【分析】设底角的度数是x °,则顶角的度数为(2x +20)°,根据三角形内角和是180°列出方程,解方程即可得出答案.【解答】解:设底角的度数是x °,则顶角的度数为(2x +20)°,根据题意得:x +x +2x +20=180,解得:x =40,故选:B .【点评】本题考查了等腰三角形的性质,考查了方程思想,掌握等腰三角形两个底角相等是解题的关键.18.(2021•青海)已知a ,b 是等腰三角形的两边长,且a ,b 满足√2a −3b +5+(2a +3b ﹣13)2=0,则此等腰三角形的周长为( )A .8B .6或8C .7D .7或8【分析】首先根据√2a −3b +5+(2a +3b ﹣13)2=0,并根据非负数的性质列方程组求得a 、b 的值,然后求得等腰三角形的周长即可.【解答】解:∵√2a −3b +5+(2a +3b ﹣13)2=0,∴{2a −3b +5=02a +3b −13=0,解得:{a =2b =3, 当b ,2,3,周长为7;当a 为底时,三角形的三边长为2,3,3,则周长为8,∴等腰三角形的周长为7或8.故选:D .【点评】本题考查了等腰三角形的性质,三角形三边关系定理、二元一次方程方程组,关键是根据2,3分别作为腰,由三边关系定理,分类讨论.19.(2021•赤峰)如图,AB ∥CD ,点E 在线段BC 上,CD =CE .若∠ABC =30°,则∠D 的度数为( )A .85°B .75°C .65°D .30°【分析】先由AB∥CD,得∠C=∠ABC=30°,CD=CE,得∠D=∠CED,再根据三角形内角和定理得,∠C+∠D+∠CED=180°,即30°+2∠D=180°,从而求出∠D.【解答】解:∵AB∥CD,∴∠C=∠ABC=30°,又∵CD=CE,∴∠D=∠CED,∵∠C+∠D+∠CED=180°,即30°+2∠D=180°,∴∠D=75°.故选:B.【点评】此题考查的是平行线的性质及三角形内角和定理,解题的关键是先根据平行线的性质求出∠C,再由CD=CE得出∠D=∠CED,由三角形内角和定理求出∠D.20.(2021•广西)如图,⊙O的半径OB为4,OC⊥AB于点D,∠BAC=30°,则OD的长是()A.√2B.√3C.2D.3【分析】连接OA,证明△【解答】解:连接OA,∵OC⊥AB,∴∠ADC=90°,∴∠DAC+∠ACD=90°,∵∠BAC=30°,∴∠ACO=60°,∵OA=OC,∴△AOC为等边三角形,∵OC⊥AB,∴OD=12OC=2,故选:C.【点评】本题考查的是垂径定理、等边三角形的判定和性质,掌握等腰三角形的三线合一是解题的关键.21.(2021•辽宁)如图,在△ABC中,AB=BC,由图中的尺规作图痕迹得到的射线BD与AC交于点E,点F为BC的中点,连接EF,若BE=AC=2,则△CEF的周长为()A.√3+1B.√5+3C.√5+1D.4【分析】由题意得BE是∠ABC的平分线,再由等腰三角形的性质得BE⊥AC,AE=CE=12AC=1,由勾股定理得BC=√5,然后由直角三角形斜边上的中线性质得EF=12BC=BF=CF,求解即可.【解答】解:由图中的尺规作图得:BE是∠ABC的平分线,∵AB=BC,∴BE⊥AC,AE=CE=12AC=1,∴∠BEC=90°,∴BC=√BE2+CE2=√22+12=√5,∵点F为BC的中点,∴EF=12BC=BF=CF,∴△CEF的周长=CF+EF+CE=CF+BF+CE=BC+CE=√5+1,故选:C.【点评】本题考查了等腰三角形的性质、直角三角形斜边上的中线性质、勾股定理、尺规作图等知识;熟练掌握尺规作图和等腰三角形的性质,证出EF=12BC=BF=CF是解题的关键.22.(2021•益阳)如图,AB∥CD,△ACE为等边三角形,∠DCE=40°,则∠EAB等于()A.40°B.30°C.20°D.15°【分析】根据平行线的性质可得∠DCA+∠CAB=180°,即∠DCE+∠ECA+∠EAC+∠EAB=180°,由△ACE为等边三角形得∠ECA=∠EAC=60°,即可得出∠EAB的度数.【解答】解:∵AB∥CD,∴∠DCA+∠CAB=180°,即∠DCE+∠ECA+∠EAC+∠EAB=180°,∵△ACE为等边三角形,∴∠ECA=∠EAC=60°,∴∠EAB=180°﹣40°﹣60°﹣60°=20°.故选:C.【点评】本题考查等边三角形的性质,平行线的性质,根据等边三角形的性质得出∠ECA=∠EAC=60°是解题的关键.23.(2022•鞍山)如图,直线a∥b,等边三角形ABC的顶点C在直线b上,∠2=40°,则∠1的度数为()A.80°B.70°C.60°D.50°【分析】先根据等边三角形的性质得到∠A=60°,再根据三角形内角和定理计算出∠3=80°,然后根据平行线的性质得到∠1的度数.【解答】解:∵△ABC为等边三角形,∴∠A=60°,∵∠A+∠3+∠2=180°,∴∠3=180°﹣40°﹣60°=80°,∵a∥b,∴∠1=∠3=80°.故选:A.【点评】本题考查了等边三角形的性质:等边三角形的三个内角都相等,且都等于60°.也考查了平行线的性质.24.(2022•绵阳)下列关于等边三角形的描述不正确的是()A.是轴对称图形B.对称轴的交点是其重心C.是中心对称图形D.绕重心顺时针旋转120°能与自身重合【分析】根据等边三角形的性质,轴对称图形的定义,中心对称图形的定义进行判断即可.【解答】解:等边三角形是轴对称图形,每条边的高线所在的直线是其对称轴,故A选项不符合题意;三条高线的交点为等边三角形的重心,∴对称轴的交点是其重心,故B选项不符合题意;等边三角形不是中心对称图形,故C选项符合题意;等边三角形绕重心顺时针旋转120°能与自身重合,故D选项不符合题意,故选:C.【点评】本题考查了等边三角形的性质,轴对称图形,中心对称图形等,熟练掌握这些知识是解题的关键.25.(2023•台湾)如图,△ABC 中,D 点在BC 上,且BD 的中垂线与AB 相交于E 点,CD 的中垂线与AC 相交于F 点,已知△ABC 的三个内角皆不相等,根据图中标示的角,判断下列叙述何者正确( )A .∠1=∠3,∠2=∠4B .∠1=∠3,∠2≠∠4C .∠1≠∠3,∠2=∠4D .∠1≠∠3,∠2≠∠4【分析】根据线段的垂直平分线的性质得到EB =ED ,FD =FC ,得到∠B =∠EDB ,∠FDC =∠C ,根据三角形的外角性质、三角形内角和定理计算即可.【解答】解:∵BD 的中垂线与AB 相交于E 点,CD 的中垂线与AC 相交于F 点,∴EB =ED ,FD =FC ,∴∠B =∠EDB ,∠FDC =∠C ,∵∠1=∠B +∠EDB ,∠3=∠FDC +∠C ,∠B ≠∠C ,∴∠1≠∠3,∵∠4=180°﹣∠B ﹣∠C ,∠2=180°﹣∠EDB +∠FDC ,∴∠2=∠4,综上所述:∠1≠∠3,∠2=∠故选:C .【点评】本题考查的是线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.26.(2022•宜昌)如图,在△ABC 中,分别以点B 和点C 为圆心,大于12BC 长为半径画弧,两弧相交于点M ,N .作直线MN ,交AC 于点D ,交BC 于点E ,连接BD .若AB =7,AC =12,BC =6,则△ABD 的周长为( )A .25B .22C .19D .18【分析】根据题意可知MN 垂直平分BC ,即可得到DB =DC ,然后即可得到AB +BD +AD =AB +DC +AD =AB +AC ,从而可以求得△ABD 的周长.【解答】解:由题意可得,MN 垂直平分BC ,∴DB =DC ,∵△ABD 的周长是AB +BD +AD ,∴AB +BD +AD =AB +DC +AD =AB +AC ,∵AB =7,AC =12,∴AB +AC =19,∴△ABD 的周长是19,故选:C .【点评】本题考查线段垂直平分线的性质,三角形的周长,解答本题的关键是明确题意,利用数形结合的思想解答.27.(2022•湖北)如图,在矩形ABCD 中,AB <BC ,连接AC ,分别以点A ,C 为圆心,大于12AC 的长为半径画弧,两弧交于点M ,N ,直线MN 分别交AD ,BC 于点E ,F .下列结论:①四边形AECF 是菱形;②∠AFB =2∠ACB ;③AC •EF =CF •CD ;④若AF 平分∠BAC ,则CF =2BF .其中正确结论的个数是( )A .4B .3C .2D .1【分析】根据题意分别证明各个结论来判断即可.【解答】解:根据题意知,EF 垂直平分AC ,在△AOE 和△COF 中,{∠EAO =∠FCOAO =CO ∠AOE =∠COF =90°,∴△AOE ≌△COF (ASA ),∴OE =OF ,∴AE =AF =CF =CE ,即四边形AECF 是菱形,故①结论正确;∵∠AFB =∠F AO +∠ACB ,AF =FC ,∴∠F AO =∠ACB ,∴∠AFB =2∠ACB ,故②结论正确;∵S 四边形AECF =CF •CD =12AC •OE ×2=12AC •EF ,故③结论不正确;若AF 平分∠BAC ,则∠BAF =∠F AC =∠CAD =13×90°=30°,∴AF =2BF ,∵CF =AF ,∴CF =2BF ,故④结论正确;故选:B .【点评】本题主要考查长方形的综合题,熟练掌握长方形的性质,基本作图,菱形的判定和性质,全等三角形的判定和性质等知识是解题的关键.28.(2021•梧州)如图,DE是△ABC的边BC的垂直平分线,分别交边AB,BC于点D,E,且AB=9,AC=6,则△ACD的周长是()A.10.5B.12C.15D.18【分析】由DE是△ABC的边BC的垂直平分线,可得DB=DC,则所求△ACD的周长=AB+AC,再将已知代入即可.【解答】解:∵DE是△ABC的边BC的垂直平分线,∴DB=DC,∴△ACD的周长=AD+AC+CD=AD+BD+AC=AB+AC,∵AB=9,AC=6,∴△ACD的周长=9+6=15,故选:C.【点评】本题考查线段垂直平分线的性质,熟练掌握线段垂直平分线的性质是解题的关键.29.(2021•河北)如图,直线l,m相交于点O.P为这两直线外一点,且OP=2.8.若点P关于直线l,m 的对称点分别是点P1,P2,则1,P2之间的距离可能是()A.0B.5C.6D.7【分析】由对称得OP1=OP=2.8,OP=OP2=2.8,再根据三角形任意两边之和大于第三边,即可得出结果.【解答】解:连接OP1,OP2,P1P2,∵点P关于直线l,m的对称点分别是点P1,P2,∴OP1=OP=2.8,OP=OP2=2.8,OP1+OP2>P1P2,0<P 1P 2<5.6,故选:B .【点评】本题考查线段垂直平分线的性质,解本题的关键熟练掌握对称性和三角形边长的关系.30.(2021•淮安)如图,在△ABC 中,AB 的垂直平分线分别交AB 、BC 于点D 、E ,连接AE ,若AE =4,EC =2,则BC 的长是( )A .2B .4C .6D .8【分析】根据线段的垂直平分线的性质得到EB =EA =4,结合图形计算,得到答案.【解答】解:∵DE 是AB 的垂直平分线,AE =4,∴EB =EA =4,∴BC =EB +EC =4+2=6,故选:C .【点评】本题考查的是线段的垂直平分线的性质,解题的关键是掌握线段的垂直平分线上的点到线段的两个端点的距离相等.二.填空题(共23小题)31.(2023•吉林)如图,在△ABC 中,AB =AC .分别以点B 和点C 为圆心,大于12BC 的长为半径作弧,两弧交于点D ,作直线AD 交BC 于点E .若∠BAC =110°,则∠BAE 的大小为 度.【分析】根据尺规作图可得AE 是BC 的垂直平分线,再根据等腰三角形三线合一的性质可得AE 是∠BAC 的角平分线,从而可求∠BAE 得大小.【解答】解:∵AB =AC .∴△ABC 是等腰三角形,∵分别以点B 和点C 为圆心,大于12BC 的长为半径作弧,两弧交于点D ,作直线AD 交BC 于点E . ∴AE 垂直平分BC ,∴AE 是∠BAC 的平分线,∴∠BAE =12∠BAC =55°.故答案为:55°.【点评】本题考查等腰三角形的性质和尺规作图,熟练掌握垂直平分线的作法是解题关键.32.(2023•江西)将含30°角的直角三角板和直尺按如图所示的方式放置,已知∠α=60°,点B ,C 表示的刻度分别为1cm ,3cm ,则线段AB 的长为 cm .【分析】先由平行线的性质可得∠ACB 的度数,根据等边三角形的判定和性质定理可得AB =BC ,则可得出AB 的长.【解答】解:∵直尺的两对边相互平行,∴∠ACB =∠α=60°,∵∠A =60°,∴∠ABC =180°﹣∠ACB ﹣∠A =180°﹣60°﹣60°=60°,∴∠A =∠ABC =∠ACB ,∴△ABC 是等边三角形,∴AB =BC =3﹣1=2(cm ).故答案为:2.【点评】此题主要是考查了等边三角形的判定和性质,平行线的性质,能够得出AB=BC是解答此题的关键.33.(2023•新疆)如图,在△ABC中,若AB=AC,AD=BD,∠CAD=24°,则∠C=°.【分析】由等腰三角形的性质可知∠C=∠B=∠BAD,利用三角形内角和定理得出180°﹣2∠C=24°+∠C,解得∠C=52°.【解答】解:∵AB=AC,AD=BD,∴∠B=∠C,∠B=∠BAD,∴∠BAC=180°﹣∠B﹣∠C=∠CAD+∠BAD,∴180°﹣2∠C=24°+∠C,∴∠C=52°,故答案为:52.【点评】本题考查了等腰三角形的性质,三角形内角和定理,熟练掌握等腰三角形的性质是解题的关键.34.(2023•重庆)如图,在△ABC中,AB=AC,AD是BC边的中线,若AB=5,BC=6,则AD的长度为.【分析】根据等腰三角形的性质可得AD⊥BC,在Rt△ABD中,根据勾股定理即可求出AD的长.【解答】解:∵AB=AC,AD是BC边的中线,∴AD⊥BC,∴∠ADB=90°,∵AB=5,BC=6,∴BD=CD=3,在Rt△ABD中,根据勾股定理,得AD=√AB2−BD2=√52−32=4,故答案为:4.【点评】本题考查了等腰三角形的性质,涉及勾股定理,熟练掌握等腰三角形的性质是解题的关键.35.(2023•凉山州)如图,边长为2的等边△ABC的两个顶点A、B分别在两条射线OM、ON上滑动,若OM⊥ON,则OC的最大值是.【分析】取AB的中点D,连接OD及DC,根据三角形的三边关系得到OC小于等于OD+DC,只有当O、D及C共线时,OC取得最大值,最大值为OD+CD,由等边三角形的边长为2,根据D为AB中点,得到BD为1,根据三线合一得到CD垂直于AB,在直角三角形BCD中,根据勾股定理求出CD的长,在直角三角形AOB中,OD为斜边AB上的中线,根据直角三角形斜边上的中线等于斜边的一半可得OD 等于AB的一半,由AB的长求出OD的长,进而求出DC+OD,即为OC的最大值.【解答】解:取AB中点D,连OD,DC,∴OC≤OD+DC,当O、D、C共线时,OC有最大值,最大值是OD+CD,∵△ABC为等边三角形,D为AB中点,∴BD=1,BC=2,∴CD=√BC2−BD2=√3,∵△AOB为直角三角形,D为斜边AB的中点,∴OD=12AB=1,∴OD +CD =1+√3,即OC 的最大值为1+√3.故答案为:1+√3.【点评】本题考查了等边三角形的性质,涉及直角三角形斜边上的中线等于斜边的一半,勾股定理,其中找出OC 最大时的长为CD +OD 是解本题的关键.36.(2023•沙依巴克区模拟)已知:一等腰三角形的两边长x 、y 满足方程组{2x −y =33x +2y =8,则此等腰三角形的周长为 .【分析】先解二元一次方程组,然后讨论腰长的大小,再根据三角形三边关系即可得出答案.【解答】解:解方程组 {2x −y =33x +2y =8得 {x =2y =1. 所以,等腰三角形的两边长为2,1.若腰长为1,底边长为2,由1+1=2知,这样的三角形不存在.若腰长为2,底边长为1,则三角形的周长为5.所以这个等腰三角形的周长为5.故答案为:5.【点评】本题考查了等腰三角形的性质及解二元一次方程组,难度一般,关键是掌握分类讨论的思想解题.37.(2022•云南)已知△ABC 是等腰三角形.若∠A =40°,则△ABC 的顶角度数是 .【分析】分∠A 是顶角和底角两种情况讨论,即可解答.【解答】解:当∠A 是顶角时,△ABC 的顶角度数是40°;当∠A 是底角时,则△ABC 的顶角度数为180°﹣2×40°=100°;综上,△ABC 的顶角度数是40°或100°.故答案为:40°或100°.【点评】本题考查了等腰三角形的性质,此类题目,难点在于要分情况讨论.38.(2022•广安)若(a ﹣3)2+√b −5=0,则以a 、b 为边长的等腰三角形的周长为 .【分析】先求a ,b .再求第三边c 即可.【解答】解:∵(a ﹣3)2+√b −5=0,(a ﹣3)2≥0,√b −5≥0,∴a ﹣3=0,b ﹣5=0,∴a =3,b =5,设三角形的第三边为c ,当a=c=3时,三角形的周长=a+b+c=3+5+3=11,当b=c=5时,三角形的周长=3+5+5=13,故答案为:11或13.【点评】本题考查等腰三角形周长计算,求出a,b后确定腰和底是求解本题的关键.39.(2022•苏州)定义:一个三角形的一边长是另一边长的2倍,这样的三角形叫做“倍长三角形”.若等腰△ABC是“倍长三角形”,底边BC的长为3,则腰AB的长为.【分析】由等腰△ABC是“倍长三角形”,可知AB=2BC或BC=2AB,若AB=2BC=6,可得AB的长为6;若BC=3=2AB,因1.5+1.5=3,故此时不能构成三角形,这种情况不存在;即可得答案.【解答】解:∵等腰△ABC是“倍长三角形”,∴AB=2BC或BC=2AB,若AB=2BC=6,则△ABC三边分别是6,6,3,符合题意,∴腰AB的长为6;若BC=3=2AB,则AB=1.5,△ABC三边分别是1.5,1.5,3,∵1.5+1.5=3,∴此时不能构成三角形,这种情况不存在;综上所述,腰AB的长是6,故答案为:6.的和大于第三边.40.(2022•滨州)如图,屋顶钢架外框是等腰三角形,其中AB=AC,立柱AD⊥BC,且顶角∠BAC=120°,则∠C的大小为.【分析】根据等腰三角形的性质和三角形内角和得到∠B=∠C=30°.【解答】解:∵AB=AC且∠BAC=120°,∴∠B=∠C=12(180°﹣∠BAC)=12×60°=30°.故答案为:30°.【点评】本题考查了等腰三角形的性质,熟练掌握等腰三角形的两个底角相等的性质是解题的关键.41.(2022•鄂州)如图,在边长为6的等边△ABC 中,D 、E 分别为边BC 、AC 上的点,AD 与BE 相交于点P ,若BD =CE =2,则△ABP 的周长为 .【分析】根据SAS 证△ABD ≌△BCE ,得出∠APB =120°,在CB 上取一点F 使CF =CE =2,则BF =BC ﹣CF =4,证△APB ∽△BFE ,根据比例关系设BP =x ,则AP =2x ,作BH ⊥AD 延长线于H ,利用勾股定理列方程求解即可得出BP 和AP 的长.【解答】解:∵△ABC 是等边三角形,∴AB =BC ,∠ABD =∠C =60°,在△ABD 和△BCE 中,{AB =BC∠ABD =∠C BD =CE∴△ABD ≌△BCE (SAS ),∴∠BAD =∠CBE ,∴∠APE =∠ABP +∠BAD =∠ABP +∠CBE =∠ABD =60°,∴∠APB =120°,在CB 上取一点F 使CF =CE =2,则BF =BC ﹣CF =4,∴∠C =60°,∴△CEF 是等边三角形,∴∠BFE =120°,即∠APB =∠BFE ,∴△APB ∽△BFE ,∴AP BP =BF EF =42=2,设BP =x ,则AP =2x ,作BH ⊥AD 延长线于H ,∵∠BPD=∠APE=60°,∴∠PBH=30°,∴PH=x2,BH=√32x,∴AH=AP+PH=2x+x2=52x,在Rt△ABH中,AH2+BH2=AB2,即(52x)2+(√32x)2=62,解得x=6√77或−6√77(舍去),∴AP=12√77,BP=6√77,∴△ABP的周长为AB+AP+BP=6+12√77+6√77=6+18√77=42+18√77,故答案为:42+18√77.【点评】本题主要考查全等三角形的判定和性质,相似三角形的判定和性质,勾股定理,解直角三角形等知识,熟练掌握这些基础知识是解题的关键.42.(2021•苏州)如图,在Rt△ABC中,∠C=90°,AF=EF.若∠CFE=72°,则∠B=°.【分析】根据等边对等角可得∠A=∠AEF,再根据∠A+∠AEF=∠CFE=72°,求出∠A的度数,最后根据在Rt△ABC中,∠C=90°,即可求出∠B的度数.【解答】解:∵AF=EF,∴∠A=∠AEF,∵∠A+∠AEF=∠CFE=72°,∴∠A=12×72°=36°,在Rt△ABC中,∠A=36°,∴∠B=90°﹣36°=54°.故答案为:54.【点评】本题主要考查了等腰三角形的性质.解题的关键是熟练掌握等腰三角形的性质:等腰三角形的两个底角相等,即:等边对等角.43.(2021•绍兴)如图,在△ABC中,AB=AC,∠B=70°,以点C为圆心,CA长为半径作弧,交直线BC于点P,连结AP,则∠BAP的度数是.【分析】根据等腰三角形的性质可以得到△ABC各内角的关系,然后根据题意,画出图形,利用分类讨论的方法求出∠BAP的度数即可.【解答】解:如右图所示,当点P在点B的左侧时,∵AB=AC,∠ABC=70°,∴∠ACB=∠ABC=70°,∴∠BAC=180°﹣∠ACB﹣∠ABC=180°﹣70°﹣70°=40°,∵CA=CP1,∴∠CAP1=∠CP1A=180°−∠ACP12=180°−70°2=55°,∴∠BAP1=∠CAP1﹣∠CAB=55°﹣40°=15°;当点P在点C的右侧时,∵AB=AC,∠ABC=70°,∴∠ACB=∠ABC=70°,∴∠BAC=180°﹣∠ACB﹣∠ABC=180°﹣70°﹣70°=40°,∵CA=CP2,∴∠CAP2=∠CP2A=∠ACB2=70°2=35°,∴∠BAP2=∠CAP2+∠CAB=35°+40°=75°;由上可得,∠BAP的度数是15°或75°,故答案为:15°或75°.【点评】本题考查等腰三角形的性质、圆的性质,解答本题的关键是画出合适的辅助线,利用分类讨论的方法解答.44.(2021•朝阳)如图,在平面直角坐标系中,点A的坐标为(5,0),点M的坐标为(0,4),过点M作MN∥x轴,点P在射线MN MAP为等腰三角形,则点P的坐标为.【分析】分三种情况:①PM=P A,②MP=MA,③AM=AP,分别画图,根据等腰三角形的性质和两点的距离公式,即可求解.【解答】解:设点P的坐标为(x,4),分三种情况:①PM=P A,∵点A 的坐标为(5,0),点M 的坐标为(0,4),∴PM =x ,P A =√42+(5−x)2,∵PM =P A ,∴x =√42+(5−x)2,解得:x =4110, ∴点P 的坐标为(4110,4); ②MP =MA ,∵点A 的坐标为(5,0),点M 的坐标为(0,4),∴MP =x ,MA =√42+52=√41,∵MP =MA ,∴x =√41,∴点P 的坐标为(√41,4);③AM =AP ,∵点A 的坐标为(5,0),点M 的坐标为(0,4),∴AP =√42+(x −5)2,MA =√42+52=√41,∵AM =AP ,∴√42+(x −5)2=√41,解得:x 1=10,x 2=0(舍去),∴点P 的坐标为(10,4);综上,点P 的坐标为(4110,4)或(√41,4)或(10,4). 故答案为:(4110,4)或(√41,4)或(10,4).【点评】本题考查了等腰三角形的性质和坐标与图形的性质,熟练掌握坐标与图形特征,利用坐标特征和勾股定理求线段的长是解题的关键.45.(2021•陕西)如图,在Rt △ABC 中,∠C =90°,∠B =30°,AB =8.若E 、F 是BC 边上的两个动点,以EF 为边的等边△EFP 的顶点P 在△ABC 内部或边上,则等边△EFP 的周长的最大值为 .【分析】当点F 与C 重合时,△EFP 的边长最长,周长也最长,根据30°角所对的直角边是斜边的一半可得AC =4,AP =2,再由勾股定理可得答案.【解答】解:如图,当点F 与C 重合时,△EFP 的边长最长,周长也最长,∵∠ACB =90°,∠PFE =60°,∴∠PCA =30°,∵∠A =60°,∴∠APC =90°,△ABC 中,AC =12AB =4,△ACP 中,AP =12AC =2,∴PC =√AC 2−AP 2=√42−22=2√3,∴周长为2√3×3=6√3.故答案为:6√3.【点评】本题考查含30°角的直角三角形的性质,运用勾股定理是解题关键.46.(2021•牡丹江)过等腰三角形顶角顶点的一条直线,将该等腰三角形分成的两个三角形均为等腰三角形,则原等腰三角形的底角度数为.【分析】首先根据题意画出符合题意的所有图形,然后利用等腰三角形求解即可求得答案.【解答】解:(1)如图.∵AB=AC,BD=AD,AC=CD,∴∠ABC=∠C=∠BAD,∠CDA=∠CAD,∵∠CDA=2∠ABC,∴∠CAB=3∠ABC,∵∠BAC+∠B+∠C=180°,∴5∠ABC=180°,∴∠ABC=36°,(2)如图.∵AB=AC,AD=BD=CD,∴∠B=∠C=∠DAC=∠DAB∴∠BAC=2∠ABC,∵∠BAC+∠B+∠C=180°,∴4∠ABC=180°,∴∠ABC=45°,故答案为:36°或45°.【点评】此题主要考查等腰三角形的性质,三角形外角的性质及三角形内角和定理的综合运用.注意分类讨论思想的应用是解此题的关键.。
等边三角形练习题(共10篇)

等边三角形练习题(共10篇)等边三角形练习题(一): 等边三角形、等腰三角形练习题急求关于等边三角形、等腰三角形的练习题,稍微难一点,八年级上学期的, 稍微再提高点难度就好了!1.等腰三角形ABC,D为内部一点,AB=BC,角ABC=80,角DAC=30,角DCA=40,求角ADB延长CD交AB于E,延长AD交BC于F,过A作AG垂直BF于G因为 AB=BC,角ABC=80度所以角BCA=角BAC=50度因为角DCA=40度,角DAC=30度所以角CEA=90度,角EDA=角DCA+角DAC=70度因为角BCA=角BAC=50度,角DCA=40度,角DAC=30度所以角BCE=角BCA-角DCA=10度,角BAF=20度因为角ABC=80度所以角BFA=180-80-20=80度所以角ABC=角BFA所以 AB=AF因为 AG垂直BF所以 BG=GF=1/2BF,角BAG=角FAG=1/2角BAF=10度因为角CEA=90度,BC=BA,角BCE=角BAG=10度所以三角形BCE全等于三角形BAG所以 BE=BG=1/2BF以下是假设和验证的过程:假设 BD=BF要使假设成立,则三角形BDE是直角三角形,即Sin角BDE=BE/BD因为 BD=BF,角BFA=80度所以角CBD=20度因为角BCE=10度所以角BDE=角CBD+角BCE=30度因为 BE=1/2BF,BD=BF所以 Sin角BDE=1/2,BE/BD=1/2所以假设成立所以角BDE=30度成立因为角EDA=70度所以角ADB=角EDA+角BDE=70+30=100度2.已知AB=AC,D是AB上一点,DE⊥BC于E,ED的延长线于F,那么△ADF是等腰三角形么为什么△ADF是等腰三角形,理由如下:证明:∵AB=AC∴∠B=∠C(等边对等角)又∵DE⊥BC∴∠B+∠BDE=90° ∠F+∠C=90° (直角三角形的两个锐角互余)∴∠BDE=∠C(等角的余角相等)又∵∠BDE=∠ADF(对顶角相等)∴∠BDE=∠ADF∴AD=AF(等角对等边)∴△ADF是等腰三角形(有两边相等的三角形叫做等腰三角形)等边三角形练习题(二): 等边三角形试题如图,在等边三角形ABC中,M、N分别是边AB、AC的中点,D为MN上任意一点,BD、CD的延长线分别交AC、AB于点F、E.若1/CE+1/BF=6,则三角形ABC的边长为特殊值法:设边长为a令点D与点E重合,则CE=AC=a,BF=BE=二分之根号3倍的a所以由条件1/CE+1/BF=6得a=(2倍根号3 +3)/18算错的话请见谅...等边三角形练习题(三): 等边三角形试题已知:如图,△ABC中,AB=AC,D是三角形外一点,且∠ABD=60°,∠ACD=60°.试说明BD+DC=AB选自《朗曼全息题解》106页第3题D点在线段BC下方【等边三角形练习题】要做辅助线延长DC于N(任意一点)使CN=AB我帮你的就这么多等边三角形练习题(四): 人教版八年级数学上册习题11.1第6. 6.一个等腰三角形的一边为6cm,周长人教版八年级数学上册习题11.1第6.6.一个等腰三角形的一边为6cm,周长为20cm,求其他两边的长.7.(1)已知等腰三角形的一边长等于5,一边长等于6,求它的周长;(2)已知等腰三角形的一边长等于4,一边长等于9,求它的周长.【等边三角形练习题】当底边为6厘米时,腰长为(20-6)÷2=7厘米.即其他两边长都为7厘米.当腰长为6厘米时,另外一边为腰长6厘米,底边围20-6-6=8厘米.祝您在新的一年一帆风顺,二龙腾飞,三羊开泰,四季平安,五福临门,六六大顺,七星高照,八方来财,九九同心,十全十美.等边三角形练习题(五): 等边三角形练习1.已知△ABC中,AB=AC,点E是AB上一点,点F是AC延长线上一点,且BE=CF,EF交BC于O,求证:EO=OF.2.在等腰三角形ABC中,AB=AC,CD为腰上的高,若2BD÷BA为整数,试判定△ABC的形状.会哪道就写哪道.急用,1.过点E做辅助线EG‖AC交BC与点G因为EG‖AC所以∠EGB=∠ACB因为AB=AC所以∠B=∠ACB所以∠B=∠EGB所以EG=EB所以EG=CF在三角形EGO和三角形FCO中EG=CF,角EOG=角FOC(对顶角),角EGO=角FCO(EG和AC平行)所以三角形EGO≌三角形FCO所以OE=OF2.三角形为等腰直角三角形.角A为直角.腰上的高CD其实就是CA(点D与点A重合)2BD/AB=2AB/AB=2 为整数所以这个等腰三角形为等腰直角三角形(45度,45度,90度)等边三角形练习题(六): 等腰三角形习题等腰三角形ABC中,点D在AB上,点E在AC上,且BD=AE,CD和BE相交于点0,DF⊥BE,垂足为F,求∠ CDF 的度数(图可以根据题目画出来)用等边三角形假设我也会,30度.你假设它是等边三角行,假设D.E都是中点.就算出来了.这样的题就得这样,算的快还准等边三角形练习题(七): 等腰三角形练习题等腰三角形中AB=AC,O为BC上非中点的一点,过O的直线l平分等腰三角形ABC的面积,问l与三角形的交点位于哪里用相似三角形做过O做直线与AB平行,交AC于M设B0:OC=1:X则OC:BC=X/(1+x)则S三角形AMO:S三角形ABC=X^2/(1+X)^2四边形OMAB=(1+X)^2-X^2=X^2解出x即可等边三角形练习题(八): 全等三角形的练习题帮出几道练习题 8道填空题 5道证明题全都是有关全等的!难度中等可以的话有追加看题如何回答者: 5154225 - 魔法学徒一级 7-29 15:371 过两点有且只有一条直线2 两点之间线段最短3 同角或等角的补角相等 \x1d4 同角或等角的余角相等5 过一点有且只有一条直线和已知直线垂直6 直线外一点与直线上各点连接的所有线段中,垂线段最短7 平行公理经过直线外一点,有且只有一条直线与这条直线平行8 如果两条直线都和第三条直线平行,这两条直线也互相平行9 同位角相等,两直线平行10 内错角相等,两直线平行11 同旁内角互补,两直线平行12两直线平行,同位角相等13 两直线平行,内错角相等14 两直线平行,同旁内角互补15 定理三角形两边的和大于第三边16 推论三角形两边的差小于第三边17 三角形内角和定理三角形三个内角的和等于180°18 推论1 直角三角形的两个锐角互余19 推论2 三角形的一个外角等于和它不相邻的两个内角的和20 推论3 三角形的一个外角大于任何一个和它不相邻的内角21 全等三角形的对应边、对应角相等22边角边公理(SAS) 有两边和它们的夹角对应相等的两个三角形全等23 角边角公理( ASA)有两角和它们的夹边对应相等的两个三角形全等24 推论(AAS) 有两角和其中一角的对边对应相等的两个三角形全等25 边边边公理(SSS) 有三边对应相等的两个三角形全等26 斜边、直角边公理(HL) 有斜边和一条直角边对应相等的两个直角三角形全等27 定理1 在角的平分线上的点到这个角的两边的距离相等28 定理2 到一个角的两边的距离相同的点,在这个角的平分线上29 角的平分线是到角的两边距离相等的所有点的集合30 等腰三角形的性质定理等腰三角形的两个底角相等 (即等边对等角)31 推论1 等腰三角形顶角的平分线平分底边并且垂直于底边32 等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合33 推论3 等边三角形的各角都相等,并且每一个角都等于60°34 等腰三角形的判定定理如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边)35 推论1 三个角都相等的三角形是等边三角形36 推论 2 有一个角等于60°的等腰三角形是等边三角形37 在直角三角形中,如果一个锐角等于30°那么它所对的直角边等于斜边的一半38 直角三角形斜边上的中线等于斜边上的一半39 定理线段垂直平分线上的点和这条线段两个端点的距离相等40 逆定理和一条线段两个端点距离相等的点,在这条线段的垂直平分线上41 线段的垂直平分线可看作和线段两端点距离相等的所有点的集合42 定理1 关于某条直线对称的两个图形是全等形43 定理 2 如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线44定理3 两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上45逆定理如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称46勾股定理直角三角形两直角边a、b的平方和、等于斜边c的平方,即a^2+b^2=c^247勾股定理的逆定理如果三角形的三边长a、b、c有关系a^2+b^2=c^2 ,那么这个三角形是直角三角形48定理四边形的内角和等于360°49四边形的外角和等于360°50多边形内角和定理 n边形的内角的和等于(n-2)×180°51推论任意多边的外角和等于360°52平行四边形性质定理1 平行四边形的对角相等53平行四边形性质定理2 平行四边形的对边相等54推论夹在两条平行线间的平行线段相等55平行四边形性质定理3 平行四边形的对角线互相平分56平行四边形判定定理1 两组对角分别相等的四边形是平行四边形57平行四边形判定定理2 两组对边分别相等的四边形是平行四边形58平行四边形判定定理3 对角线互相平分的四边形是平行四边形59平行四边形判定定理4 一组对边平行相等的四边形是平行四边形60矩形性质定理1 矩形的四个角都是直角61矩形性质定理2 矩形的对角线相等62矩形判定定理1 有三个角是直角的四边形是矩形63矩形判定定理2 对角线相等的平行四边形是矩形64菱形性质定理1 菱形的四条边都相等65菱形性质定理2 菱形的对角线互相垂直,并且每一条对角线平分一组对角 66菱形面积=对角线乘积的一半,即S=(a×b)÷267菱形判定定理1 四边都相等的四边形是菱形68菱形判定定理2 对角线互相垂直的平行四边形是菱形69正方形性质定理1 正方形的四个角都是直角,四条边都相等70正方形性质定理2正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角71定理1 关于中心对称的两个图形是全等的72定理2 关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分73逆定理如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称74等腰梯形性质定理等腰梯形在同一底上的两个角相等75等腰梯形的两条对角线相等76等腰梯形判定定理在同一底上的两个角相等的梯形是等腰梯形77对角线相等的梯形是等腰梯形78平行线等分线段定理如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等79 推论1 经过梯形一腰的中点与底平行的直线,必平分另一腰80 推论2 经过三角形一边的中点与另一边平行的直线,必平分第三边81 三角形中位线定理三角形的中位线平行于第三边,并且等于它的一半82 梯形中位线定理梯形的中位线平行于两底,并且等于两底和的一半 L=(a+b)÷2 S=L×h83 (1)比例的基本性质如果a:b=c:d,那么ad=bc如果ad=bc,那么a:b=c:d wc呁/S∕\x1e84 (2)合比性质如果a/b=c/d,那么(a±b)/b=(c±d)/d85 (3)等比性质如果a/b=c/d=…=m/n(b+d+…+n≠0),那么(a+c+…+m)/(b+d+…+n)=a/b86 平行线分线段成比例定理三条平行线截两条直线,所得的对应线段成比例87 推论平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例88 定理如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边89 平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形三边对应成比例90 定理平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似91 相似三角形判定定理1 两角对应相等,两三角形相似(ASA)92 直角三角形被斜边上的高分成的两个直角三角形和原三角形相似93 判定定理2 两边对应成比例且夹角相等,两三角形相似(SAS)94 判定定理3 三边对应成比例,两三角形相似(SSS)等边三角形练习题(九): 圆的周长练习题一、填一填.(1)等边三角形的边长为3.5分泌,它的周长是()分米.(2)一个等腰梯形上底长4.5厘米,下底长6厘米,腰长3厘米,这个等腰梯形的周长是()厘米.(3)圆的()除以()的商是一个固定的数,通常叫做(),它大约等于().二、对号入座.(1)想要求圆的周长,就必须知道().A.圆周率B.直径和半径C.直径或半径(2)π是一个()小数A.有限B.无限循环C.无限不循环三、应用题.1.校园里有一个圆形花圃,它的直径是4.5m,这个花圃的周长是多少米2.小强每天绕直径为20m的花坛跑15圈,则小强每天要跑多少米一、填一填.(1)等边三角形的边长为3.5分泌,它的周长是( 10.5 )分米.(2)一个等腰梯形上底长4.5厘米,下底长6厘米,腰长3厘米,这个等腰梯形的周长是( 16.5 )厘米.(3)圆的(周长)除以(直径)...等边三角形练习题(十): 全等三角形练习题八年级数学三角形全等测试题一、填空(3分×10=30分)1、如果△ABC≌△DEF,△DEF周长是32cm,DE=9cm,EF=13cm.∠E=∠B,则AC=________.2、如图,某人把一块三角形的玻璃打碎成了三块,现在你要到玻璃店去配一块完全一样的玻璃,则应带哪块玻璃去__________(填上玻璃序号).3、已知△ABC中,∠BAC=60°,将△ABC绕着点A顺时针旋转40°,如图所示,则△BAC′的度数为______.4、如图,点D、E、F、B在同一直线上,AB‖CD、AE‖CF,且AE=CF,若BD=10,BF=2,则EF=____________.5、△ABC中,AC=4,中线AD=6,则AB边的取值范围是______________.6、已知如图,CD⊥AB,BE⊥AC,垂足分别为D、E、BE、CD相交于O点,∠1=∠2,图中全等的三角形共有________对.7、如图,在△ABC中,∠C=90°,AD平分∠BAC,BC=10cm,BD=6cm,则点D到AB的距离为_________.8、如图,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.其中正确的结论是________(填序号).9、如图,已知铁路上A、B两站(视为线上两点)相距45km,C、D为铁路同旁的两个村庄(视为两点),DA⊥AB于A,CB⊥AB于B,DA=25km,CB=20km,现在要在铁路AB上建一个收购站E,使C、D两村庄到E站的距离相等,则E站应建在距A 站_______km处.10、如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BD于D,DE⊥AB于E,且AB=10,则△DEB周长为_______.二、选择题(3分×10=30分)11、如图△ABC≌△BAD,点A和点B,点C和点D是对应点,若AB=6cm,BD=5cm,AD=4cm,则BC长为()A、4cmB、5cmC、6cmD、无法确定12、如图△ABE≌△ACD,AB=AC,BE=CD,∠B=50°,∠AEC=120°,则∠DAC的度数等于()A、120°B、70°C、60°D、50°13、在△ABC和△A′B′C′中,已知∠A=∠A′,AB=A′B′,在下面判断中错误的是()A、若添加条件AC=A′C′,则△ABC≌△A′B′C′B、若添加条件BC=B′C′,则△ABC≌△A′B′C′C、若添加条件∠B=∠B′,则△ABC≌△A′B′C′D、若添加条件∠C=∠C′,则△ABC≌△A′B′C′14、工人师傅常用角尺平分一个任意角,做法是:如图在∠AOB的边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合,得到∠AOB的平分线OP,做法中用到三角形全等的判定方法是()A、SSSB、SASC、ASAD、HL15、下列命题错误的是()A、全等三角形的对应线段相等B、全等三角形的面积相等C、一个锐角和相邻的直角边对应相等的两个直角三角形全等D、两角对应相等的两个三角形全等16、不能确定两三角形全等的条件是()A、三条边对应相等B、两条边及其夹角对应相等C、两角和一条边对应相等D、两条边和一条边所对应的角对应相等17、在△ABC和△A′B′C′中,①AB=A′B′;②BC=B′C′;③AC=A′C′;④∠A=∠A′;⑤∠B=∠B′;⑥∠C=∠C′,则下列哪组条件不能保证△ABC≌△A′B′C′()A、①②③B、①②⑤C、①⑤⑥D、①②④18、如图△ABC中,∠C=90°,AB=2BC,D为AB中点过点D作DE⊥AB交AC于点E,下列结论:①CE=DE;②AE=BC;③∠B=2∠A;④∠A=30°中正确个数为()A、1个B、2个C、3个D、4个19、如图,在△ABC中,AB=AC,BF=CD,BD=CE,∠FDE=α ,则下列结论正确的是()A、2 α+∠A=180°B、α +∠A=90°C、2α +∠A=90°D、α+∠A=180°20、如图,已知△ABC中,AQ=PQ,PR=PS,PR⊥AB于R,RS⊥AC于S,则三个结论:①AS=AR;②QP‖AR;③△BRP≌△QSP()A、全部正确B、仅①和②正确C、仅①正确D、仅①和③正确三、解答题21、已知:△DEF≌△MNP,且EF=NP,∠F=∠P,∠D=58°,∠E=62°,MN=10cm,求∠P的度数及DE的长.(5分)22、如图,D是AB上一点,DF交AC于点E,AE=CE,FC‖AB,求证:DE=EF.(5分)23、如图,△ABC为等边三角形,点M、N,分别在BC、AC上,且BM=CN,AM与BN 交于Q点,求∠AQN的度数.(6分24、如图,点E在△ABC的外部,点D在BC边上,DE交AC于点F,若∠1=∠2 =∠3,AC=AE,求证:AB=AD.(6分)25、如图,在正方形ABCD中,E是AD中点,F是BA延长线上一点,AF= AB,则线段BE与DF大小,位置有什么关系并证明你的结论.(7分)26、如图,AB‖CD,BE平分∠ABC,点E为AD中点,且BC=AB+CD,求证:CE平分∠BCD.(7分)27、如图,已知△ABC中,AB=AC,∠BAC=90°,分别过B、C向过A的直线作垂线,垂足分别为E、F.(1)如图,①过A的直线与斜边BC不相交时,求证:EF=BE+CF(4分)(2)如图,②过A的直线与斜边BC相交时,其他条件不变,若BE=10,CF=3,试求:FE长.(4分)28、在直角坐标系xOy中,O为坐标原点直线AB平行直线:y = x,且与x轴交于点A(-3,0),与y轴交于B点,点M、N在x轴上,(点M在点N的左边),点N在原点的右边作MP⊥BN,垂足为P(点P在线段BN上,且点P与点B 不重合)直线MP与y轴交于点G,MG=BN.(1)求直线AB的解析式及B点坐标;(4分)(2)求点M的坐标;(4分)(3)设ON=t,△MOG的面积为S,求S与t的函数关系式,并写出自变量t的取值范围;(4分)(4)若以A为锐角顶点,直角顶点D在x轴上的直角三角形ADF与以A、O、B为顶点的直角三角形全等,设F(a、b),求a、b值(只需写出结果,不必写出解答过程).(4分)。
等腰三角形和等边三角形练习题

等腰三角形和等边三角形练习题一、选择题1、等腰三角形的一个角是 80°,则它顶角的度数是()A 80°B 80°或 20°C 80°或 50°D 20°解析:分两种情况讨论。
若 80°角是顶角,则顶角就是 80°;若 80°角是底角,则顶角为 180° 80°×2 = 20°。
所以顶角的度数为 80°或 20°,答案选 B。
2、等腰三角形的两边长分别为 3 和 6,则这个等腰三角形的周长为()A 12B 15C 12 或 15D 18解析:因为等腰三角形两腰长度相等,当腰长为3 时,3 +3 =6,不能构成三角形;当腰长为 6 时,周长为 6 + 6 + 3 = 15。
所以答案选 B。
3、下列说法正确的是()A 等边三角形是等腰三角形B 等腰三角形是等边三角形C 等腰三角形的两角相等D 等边三角形的三个角不相等解析:等边三角形是特殊的等腰三角形,A 选项正确;等腰三角形不一定是等边三角形,B 选项错误;等腰三角形两底角相等,C 选项说法不全面;等边三角形的三个角都相等,D 选项错误。
所以答案选A。
4、若一个等腰三角形的一个外角为 100°,则这个等腰三角形的底角为()A 50°B 80°C 50°或 80°D 40°或 80°解析:若外角 100°是顶角的外角,则顶角为 80°,底角为(180°80°)÷2 = 50°;若外角 100°是底角的外角,则底角为 80°。
所以答案选 C。
5、等腰三角形一腰上的高与另一腰的夹角为 45°,则这个等腰三角形的顶角为()A 45°B 135°C 45°或 675°D 45°或 135°解析:分两种情况。
等腰和等边三角形的性质习题
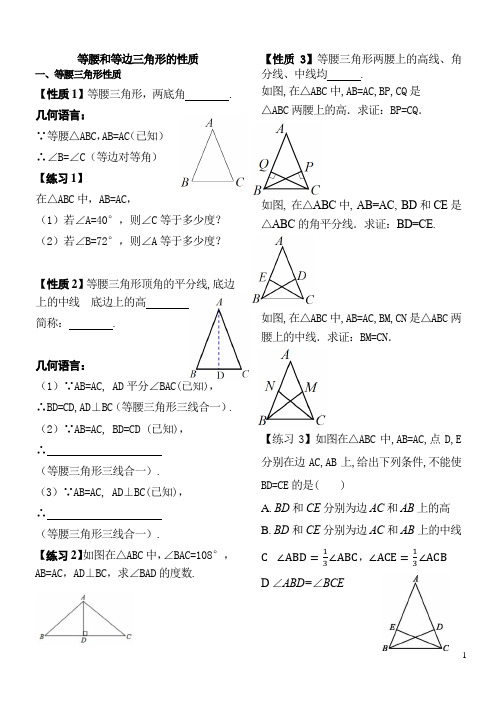
等腰和等边三角形的性质一、等腰三角形性质【性质1】等腰三角形,两底角 .几何语言:∵等腰△ABC ,AB=AC (已知)∴∠B=∠C(等边对等角)【练习1】在△ABC中,AB=AC,(1)若∠A=40°,则∠C等于多少度?(2)若∠B=72°,则∠A等于多少度?【性质2】等腰三角形顶角的平分线,底边上的中线底边上的高 .简称: .几何语言:(1)∵AB=AC, AD平分∠BAC(已知),∴BD=CD,AD⊥BC(等腰三角形三线合一). (2)∵AB=AC, BD=CD (已知),∴(等腰三角形三线合一).(3)∵AB=AC, AD⊥BC(已知),∴(等腰三角形三线合一).【练习2】如图在△ABC中,∠BAC=108°,AB=AC,AD⊥BC,求∠BAD的度数.【性质3】【性质3】等腰三角形两腰上的高线、角分线、中线均 .如图,在△ABC中,AB=AC,BP,CQ是△ABC两腰上的高.求证:BP=CQ.如图, 在△ABC中, AB=AC, BD和CE是△ABC的角平分线.求证:BD=CE.如图,在△ABC中,AB=AC,BM,CN是△ABC两腰上的中线.求证:BM=CN.【练习3】【练习3】如图在△ABC中,AB=AC,点D,E 分别在边AC,AB上,给出下列条件,不能使BD=CE的是( )A.BD和CE分别为边AC和AB上的高B.BD和CE分别为边AC和AB上的中线C ∠ABD=13∠ABC,∠ACE=13∠ACBD ∠ABD=∠BCE二、等边三角形性质【性质1】等边三角形的三个内角都 .并且每个角都等于 .几何语言:∵等边△ABC (已知)∴∠A∠B=∠C=60°(等边三角形三个内角都相等)【练习4】(1)如图,在△ABC中,D,E是BC的三等分点,且△ADE是等边三角形,求∠BAC的度数.(2)等边三角形ABC中,BE和CD分别是AC和AB边上的高,且相交于点F,则∠BFC的度数为【性质2】等边三角形每条边上的角分线、中线、高线都是 .(共有条.)等边△ABC中,若AD⊥BC,求证:BD=CD,AD⊥BC 【练习5】如图,在等边三角形ABC中,BD⊥AC于点D,若AB=8,则AD=.【性质3】等边△ABC中,三条三线合一的线段长度.等边△ABC中,若AD、BE、CF分别为三边中线,求证:AD=BE=CF三、当堂检测1、如图在△ABC中,AD⊥BC于点D,D为BC的中点,则下列结论不正确的是() A.△ABD≌△ACD B.∠B=∠CC.AD平分∠BACD.△ABC是等边三角形1题图2题图2、如图在等边三角形ABC中,AD⊥BC于点D,E为AD上一点,若∠CED=50°,则∠ABE等于()3、等腰三角形的一个外角等于100°,则与它不相邻的两个内角的度数分别为() A.40°,40° B.80°,20°C.50°,50°D.50°,50°或80°,20°作业(一)[等腰和等边△性质]一、选择题1、如图,BE⊥AC于点D,且AB=BC,BD=ED,若∠ABC=54°,则∠E的度数为() A.27° B.36° C.40° D.54°1题图 2题图2、如图,等边△ABC,AD是角平分线,△ADE 是等边三角形,下列结论不正确的是()A.AD⊥BCB.EF=FDC.BE=BDD.AE=AC二、填空题3、如图△ABC的周长为18,且AB=AC,AD⊥BC于点D,△ACD的周长为12,那么AD的长为.3题图 4题图4、如图,点B在AC上,点D在CE,AD=BD=BC,∠ACE=25°,则∠ADE= °.5、如图,△ABC为等边三角形,以边AC为腰作等腰三角形ACD,使AC=CD,连接BD,若∠ABD=32°,则∠CAD= °.5题图6题图三、解答题6、如图,在△ABC中,AB=AC,D是BC的中点,E,F分别是AB,AC边上的点,且AE=AF.求证:DE=DF.7.如图,已知在等边三角形ABC中,点D,E 分别在边BC,AC上,且BD=CE,连接BE,AD 交于点F.求证:∠AFE=60°.。
等腰三角形和等边三角形大题

师生共用导学稿年级:八年级 学科:数学 执笔:张艳芹 审核:内容:十二章轴对称(2) 课型: 复习 时间:10年12月 日 复习目标:等腰三角形与等边三角形性质,判定的综合应用1.如图所等边三示,在ABC △中,D E ,分别是AC 和AB 上的一点,BD 与CE 交于点O ,给出下列四个条件:①EBO DCO ∠=∠;②BEO CDO ∠=∠;③BE CD =;④OB OC =.(1)上述四个条件中,哪两个条件可以判定ABC △是等腰三角形(用序号写出所有的情形);(2)选择(1)小题中的一种情形,证明ABC △是等腰三角形.2. (2006 聊城课改)如图,在等腰Rt ABC △中,P 是斜边BC 的中点,以P 为顶点的直角的两边分别与边AB ,AC 交于点E ,F ,连接EF .当EPF ∠绕顶点P 旋转时(点E 不与A ,B 重合),PEF △也始终是等腰直角三角形,请你说明理由.3. (2007重庆,3分)已知:如图,在平面直角坐标系中,O 为坐标原点,四边形OABC 是矩形,点A C ,的坐标分别为(100)A ,,(04)C ,,点D 是OA 的中点,点P 在BC 边上运动.当ODP △是腰长为5的等腰三角形时,点P 的坐标为 .CPBA xD OyC D E A BOAF EBP C4. (2007湖南邵阳课改,6分)如图,ABC △中,90ACB ∠=°,将ABC △沿着一条直线折叠后,使点A 与点C 重合(图②).(1)在图①中画出折痕所在的直线l .设直线l 与AB AC ,分别相交于点D E ,,连结CD .(画图工具不限,不要求写画法) (2)请你找出完成问题(1)后所得到的图形中的等腰三角形.(不要求证明)5. (2008河南省,9分)复习“全等三角形”的知识时,老师布置了一道作业题:“如图①,已知,在ABC △中,AB AC =,P 是ABC △内任意一点,将AP 绕点A 顺时针旋转至AQ ,使QAP BAC ∠=∠,连结BQ CP ,,则BQ CP =.” 小亮是个爱动脑筋的同学,他通过对图①的分析,证明了ABQ ACP △≌△,从而证得BQ CP =.之后,他将点P 移到等腰三角形ABC 之外,原题中其它条件不变,发现“BQ CP =”仍然成立,请你就图②给出证明.6. (2008浙江省绍兴市,12分)学完“几何的回顾”一章后,老师布置了一道思考题:① A B②B折叠后 图① Q P CB A A QB PC 图②如图,点M N ,分别在正三角形ABC 的BC CA ,边上, 且BM CN =,AM BN ,交于点Q .求证:60BQM =∠. (1)请你完成这道思考题;(2)做完(1)后,同学们在老师的启发下进行了反思,提出 了许多问题,如:①若将题中“BM CN =”与“60BQM =∠”的位置交换,得到的是否仍是真命题? ②若将题中的点M N ,分别移动到BC CA ,的延长线上,是否仍能得到60BQM =∠? ③若将题中的条件“点M N ,分别在正三角形ABC 的BC CA ,边上”改为“点M N ,分别在正方形ABCD 的BC CD ,边上”,是否仍能得到60BQM =∠?……请你作出判断,在下列横线上填写“是”或“否”:① ;② ;③ .并对②,③的判断,选择一个给出证明..7。
等腰、等边三角形的性质(练习课)

2 B
1 C E
拓展4
将不全等的两个等边三角形△ABC和等边三角形△DEF任意摆放, 请你画出不少于5种的摆放示意图,使得AE=CF,同时满足在重合的 一条直线上C有且只有三个顶点(重合的顶点算C一个),并说明理由.
E
E
A
B
F
A
B
F
C
A
B
F
在一个三角形中,如果两条边 不相等,那么它们所对的角是否相 等呢?
1:在一个三角形中,如果两条边不相等,那 么它们所对的角也不相等,大边所对的角较大, 小边所对的角较小。
A 已知:△ABC中,AB>AC
求证:∠ACB> ∠ B
D1 2
B
C
证明:在AB 上截取AD,使AD=AC,连结DC
在△ABC中:
FE
MN
A
B
C
(1)AE与CD相等吗?说明理由.
(1)AE与CD相等吗?说明理由. D
证明: ∵△ABD和△BCE为等边三角形
FE
∴DB=AB BC=BE
∠ABD=∠EBC= 60°
A
∴∠ABD+DBE=∠DBE+∠EBC
MN
B
C
即∠ABE=∠DBC
在△ABE和△DBC中
{AB=DB (已证) ∠ ABE= ∠ DBC (已证)
BE=BC (已证)
∴△ABE≌△DBC ∴AE=CD
∴∠MAB=∠FDM
已知: A、B、C三点在一条直线上,分别以
AB 、 BC为边在AC的同侧作等边△ ABD D
和△ BCE,连接AE 、CD交于F,交BD于M, 交BE于N.
FE MN
A
B
C
等腰和等边三角形专项练习80题(有答案)

等腰三角形和等边三角形专项练习60题(有答案)1.已知,如图,△ABC中,AB=AC,DE是AB的中垂线,点D在AB上,点E在AC上,若△ABC的周长为25cm,△EBC的周长为16cm,则AC的长度为()A.16cm B.9cm C.8cm D.7cm2.如图,在△ABC中,∠B=∠C,点F为AC上一点,FD⊥BC于D,过D点作DE⊥AB于E.若∠AFD=158°,则∠EDF 的度数为()A.90°B.80°C.68°D.60°3.如图所示,在△ABC中,点D是BC上一点,∠BAD=80°,AB=AD=DC,则∠C的大小为()A.50°B.40°C.20°D.25°4.下列说法正确的是()A.等腰三角形的两条高相等B.等腰三角形一定是锐角三角形C.有一个角是60°的锐角三角形是等边三角形D.三角形三条角平分线的交点到三边的距离相等5.已知等腰三角形ABC,∠A是顶角,且∠A等于∠C的一半,BD是△ABC的角平分线,则该图中共有等腰三角形的个数是()A.4个B.3个C.2个D.1个6.边长为2的等边三角形的面积是()A.B.C.3D.67.如图,在等边△ABC中,∠BAD=20°,AE=AD,则∠CDE的度数是()A.10°B.12.5°C.15°D.20°8.如图,在△ABC中,∠C=90°,∠ABC=15°,点D、E分别在BC、AB上,且DE垂直平分AB,BD=3,则DC等于()A.B.C.3D.9.如图,等边△ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点,若AE=2,当EF+CF取得最小值时,则∠ECF的度数为()A.15°B.22.5°C.30°D.45°10.如图,钢架中∠A=16°,焊上等长的钢条P1P2,P2P3,P3P4…来加固钢架,若AP1=P1P2,则这样的钢条至多需要()根.A.4B.5C.6D.711.如图,已知等边△ABC的周长为6,BD是AC边的中线,E为BC延长线上一点,CD=CE,那么△BDE的周长是()A.5+2B.5+C.3+2D.3+12.以下关于等边三角形的判定:①三条边相等的三角形是等边三角形;②有一个角是60°的等腰三角形是等边三角形;③有两个角为60°的三角形是等边三角形④三个角相等的三角形是等边三角形其中正确的是()A.只有①②③B.只有①②④C.只有①③④D.①②③④13.如图,△ABC为边长是5的等边三角形,点E在AC边上,点F在AB边上,ED⊥BC,且ED=AE,DF=AF,则CE的长是()A.B.C.20+10D.20﹣1014.已知△ABC是等腰三角形,BC边上的高恰好等于BC的一半,则∠BAC的度数是()A.75°B.90°或75°或25° C.75°或15°D.90°或75°或15°15.如图,已知∠AOB=40°,点P关于OA、OB的对称点分别为C、D,CD交OA、OB于M、N两点,则∠MPN 的度数是()A.70°B.80°C.90°D.100°16.在△ABC中,∠A和∠B的度数如下,能判定△ABC是等腰三角形的是()A.∠A=50°,∠B=70°B.∠A=70°,∠B=40°C.∠A=30°,∠B=90°D.∠A=80°,∠B=60°17.如图∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=10,则PD等于()A.10 B.C.5D.2.518.等腰三角形的一边长为4,另一边长为9,则它的周长为()A.13 B.17 C.17或者22 D.2219.如图所示,共有等腰三角形()A.4个B.5个C.3个D.2个20.如图,AD⊥BC,D为BC的中点,以下结论正确的有几个?()①△ABD≌△ACD;②AB=AC;③∠B=∠C;④AD是△ABC的角平分线.A.1B.2C.3D.421.如图,已知△ABC是等边三角形,点O是BC上任意一点,OE,OF分别于两边垂直,等边三角形的高为2,则OE+OF的值为()A.1B.3C.2D.422.如图,在Rt△ABC中,已知,∠ACB=90°,∠B=15°,AB边的垂直平分线交AB于E,交BC于D,且BD=13cm,则AC的长是()A.13cm B.6.5cm C.30cm D.6cm23.如图所示,AB=AD,∠ABC=∠ADC=90°,则①AC平分∠BAD;②CA平分∠BCD;③AC垂直平分BD;④BD平分∠ABC,其中正确的结论有()A.①②B.①②③C.①②③④D.②③24.已知a,b,c是△ABC的三边,且a2+b2+c2=ab+ac+bc,则△ABC是()A.等腰三角形B.直角三角形C.等边三角形D.等腰直角三角形25.如图,△ABC中,AB=BC=AD,D在BC的延长线上,则角α和β的关系是()A.α+β=180°B.3α+2β=180°C.3α+β=180°D.2β=α26.如图,等边三角形ABC内有一点P,过点P向三边作垂线,垂足分别为S、Q、R,且PQ=6,PR=8,PS=10,则△ABC的面积等于()A.190B.192C.194D.19627.在边长为1的等边三角形内任意放一些点,要使得至少存在2个点之间的距离不超过,那么至少应该放几个点()A.n2+1 B.2n+1 C.2n D.n+128.如图所示,△ABC为正三角形,P是BC上的一点,PM⊥AB,PN⊥AC,设四边形AMPN,△ABC的周长分别为m、n,则有()A.B.C.D.29.如图,D,E,F为等边三角形ABC三边中点,AE、BF、CD交于O,DE,EF,FD为三条中位线,则图中能数出不同的直角三角形的个数是()A.36 B.32 C.30 D.2830.等腰△ABC中,∠B=50°,那么另外两个角的度数分别是_________.31.如图,已知:AB=AC=AD,∠BAC=50°,∠DAC=30°,则∠BDC=_________.32.如图,在△ABC中,∠BAC=135°,AD⊥BC于D,且AB+BD=DC,那么∠C=_________°.33.如图,Rt△ABC中,∠C=90°,BD=2CD,AD是∠BAC的角平分线,则∠B=_________度.34.若一腰上的中线把一个等腰三角形的周长分为12cm和21cm两部分,则其底边长为_________cm.35.等腰三角形顶角80°,一腰上的高与底边的夹角的度数是_________.36.如果一个三角形三边长为a、b、c,且满足(a+b+c)(a﹣c)=0,则该三角形的形状是_________.37.边长为a的等边三角形的面积为_________.38.如图,△ABC中,AB=AC,点P、Q分别在AC、AB上,且AP=PQ=QC=BC,则∠A的大小是_________.39.如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交AB于E,交BC于D,BD=8,则AC=_________.40.如右图,以等边△OAB的高OC为边向逆时针方向作等边△OCD,CD交OB于点E,再以OE为边向逆时针方向作等边△OEF,EF交OD于点G,再以OG为边向逆时针方向作等边△OGH,…,按此方法操作,最终得到△OMN,此时ON在OA上.若AB=1,则ON=_________.41.如图,在△ABC中,∠ACD=90°,CA=CB,AD是△ABC的角平分线,点E在AB上,如果DE=2CD,那么∠ADE= _________度.42.等腰三角形的周长为24,腰长为x,则x的取值范围是_________.43.如图,点C、E和点B、D、F分别在∠GAH的两边上,且AB=BC=CD=DE=EF,若∠A=12°,则∠GEF=_________度.44.如图,AB=AC,∠BAC=120°,点D在BC上,DB=DA=4,那么BC=_________.45.如图,D是等边△ABC的AC边上的中点,点E在BC的延长线上,DE=DB,△ABC的周长是9,则∠E=_________°,CE=_________.46.如图,在△ABC中,AB=AC=5,BC=6,AD=4,点E、F是中线AD上的两点,则图中阴影部分的面积是_________.47.如果一个三角形一边上的中线和这边上的高重合,那么这个三角形是_________三角形.48.△ABC是等腰三角形,AB=AC,分别以两腰为边向外作等边△ADB和等边△ACE,若∠DAE=∠DBC,则∠BAC的度数为_________.49.如图,等边△RST的顶点R、S、T分别在等腰△ABC的边AB、BC、CA上,设∠ART=x度,∠RSB=y度,∠STC=z 度,用含y、z的代数式表示x是:_________.50.等腰三角形一腰上的高与另一腰的夹角为30°,腰长为2,则其底边的高为_________.51.如图所示,△ABC是等边三角形,点是AC的中点,过D点作DM⊥BE,垂足是MD;延长BC到E,使CE=CD,求证:BM=EM.52.如图,△ABC中,AB=AC,DE是AB的垂直平分线,D为垂足,交AC于E.若AD=5cm,△ABC的周长为27cm,求△BCE的周长.53.小明在找等边三角形ABC一边的三等分点时,他是这样做的,先做∠ABC、∠ACB的角平分线并且相交于点O,然后做线段BO、CO的垂直平分线,分别交BC于E、F,他说:“E、F就是BC边的三等分点.”你同意他的说法吗?请说明你的理由.54.如图,已知:等边三角形ABC,点D是AB的中点,过点D作DF⊥AC,垂足为F,过点F作FE⊥BC,垂足为E,若三角形ABC的边长为4.求:(1)线段AF的长度;(2)线段BE的长度.55.如图AF是△ABC的角平分线,BD⊥AF,交AF的延长线于D,DE∥AC交AB于E,求证:AE=BE.56.已知如图,△ABC中,AB=AC,D是AB的中点,DE⊥AB交AC于E,(1)若BE平分∠ABC,求∠A的度数.(2)若△ABC的周长为10,△BCE的周长为6,求BC的长度.57.如图,在△ABC中,∠B=45°,AD是∠BAC的角平分线,EF垂直平分AD,交BC的延长线于点F.求∠FAC的大小.58.如图,在△ABC中,AB=AC,CD平分∠ACB交加于D点,AE∥DC交BC的延长线于点E,已知∠E=36°,求∠B 的度数.59.已知:如图,∠ACB=90°,D、E是AB上的两点,且AE=AC,BD=BC,EF⊥CD于F,求证:CF=EF.60.已知:如图,Rt△ABC中,∠ACB=90°,边AC的垂直平分线DE交AB于点D,交AC于E,连接DC.求证:DA=DC=DB.61.如图,点B,D在射线AM上,点C,E在射线AN上,且AB=BC=CD=DE,已知∠EDM=84°,求∠A的度数.62.等腰三角形中,一边与另一边之比为3:2,该三角形周长为56,求腰长是多少?63.如图:△ABC中,∠B=2∠C,AD是BC边上的高.求证:AB+BD=DC.64.如图,在△ABC中,AB=BC=AC,BD是中线,延长BC到E,使CE=CD.(1)已知CD=3,求BE的长;(2)求证:BD=ED;(3)若点F是BE边的中点,试判断DF与BE的位置关系并简要说明理由.65.如图所示,在△ABC中,∠C=90°,BD平分∠ABC交AC于点D,过点D作DE∥BC交AB于点E,过点D作DF⊥AB于点F,说明:BC=DE+EF成立的理由.66.如图,△ABC为等边三角形,D为BC上一点,∠ADE=60°,DE交∠ACB外角平分线于E.(1)AB与CE平行吗?请说明理由.(2)请说明∠BAD=∠EDC的理由.67.如图,在等腰△ABC中,∠A=80°,∠B和∠C的平分线相交于点O(1)连接OA,求∠OAC的度数;(2)求:∠BOC.68.如图,AD是△ABC的角平分线,过点D作直线DF∥BA,交△ABC的外角平分线AF于点F,DF与AC交于点E.求证:DE=EF.69.如图,在△ABC中,AB=AC=10,点D为BC上一点,过点D分别作DE∥AB交AC于点E,DE∥AC交AB于点F.求四边形AFDE的周长.70.如图,AD是△ABC的角平分线,且∠B=∠ADB,过点C作AD的延长线的垂线,垂足为M.(1)若∠DCM=α,试用α表示∠BAD;(2)求证:AB+AC=2AM.71.王宏和张新是同学,他们两家和学校正好构成一个等腰三角形,而且王宏家距学校2千米,张新家距学校4千米,你知道王宏与张新两家的距离吗?如果王宏家与学校相距2千米,而张新家与学校相距3千米,其他条件不变,王宏与张新两家相距多少千米?72.已知:如图,在△ABC中,∠B=∠C,点D、E、F分别是边BC、AB、AC上的点,BE=CD,连接DE、DF,有∠EDF=∠C,那么DE和DF相等吗?试说明理由.73.如图,在等腰△ABC中,AB=AC,点D在BC上,且AD=AE.(1)若∠BAC=90°,∠BAD=30°,求∠EDC的度数?(2)若∠BAC=a(a>30°),∠BAD=30°,求∠EDC的度数?(3)猜想∠EDC与∠BAD的数量关系?(不必证明)74.已知一个等腰三角形的周长为18cm.(1)如果腰长是底边的2倍,那么各边的长是多少?(2)如果一腰上的中线将该等腰三角形的周长分为1:2两部分,那么各边的长为多少?75.△ABC中,∠B=40°,过点A的直线将这个三角形分成2个等腰三角形,试确定∠C的度数.76.已知一个等腰三角形的两个内角分别为(2x﹣2)°和(3x﹣5)°,求这个等腰三角形各内角的度数.77.如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.(1)求∠ECD的度数;(2)若CE=5,求BC长.78.如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°,∠DAB=45°.(1)求∠DAC的度数;(2)求证:DC=AB.79.如图,在△ABC中,AB=AC,D是BC上任意一点,过D分别向AB,AC引垂线,垂足分别为E,F,CG是AB边上的高.(1)DE,DF,CG的长之间存在着怎样的等量关系?并加以证明;(2)若D在底边的延长线上,(1)中的结论还成立吗?若不成立,又存在怎样的关系?请说明理由.80.如图,已知在△ABC中,AB=AC,D是AB上一点,DE⊥BC,E是垂足,ED的延长线交CA的延长线于点F,求证:AD=AF.参考答案:1.∵DE是AB的垂直平分线,∴AE=BE,∵△ABC的周长为25cm,△EBC的周长为16cm,AC=AB,∴2AC+BC=25cm,BE+CE+BC=AE+EC+BC=AC+BC=16cm,即,解得:AC=9cm,故选B.2.∵AB=AC∴∠B=∠C∵FD⊥BC于D,DE⊥AB于E∴∠BED=∠FDC=90°∵∠AFD=158°∴∠EDB=∠CFD=180°﹣158°=22°∴∠EDF=90°﹣∠EDB=90°﹣22°=68°.故选C3.∵AB=AD,∴∠B=∠ADB,由∠BAD=80°得∠B==50°=∠ADB,∵AD=DC,∴∠C=∠ACD,∴∠C=∠ADB=25°故选D.4.A、等腰三角形两腰上的高相等,故错误;B、等腰三角形不一定是锐角三角形,故错误;C、有一个角是60°的等腰三角形是等边三角形,故错误;D、三角形三条角平分线的交点到三边的距离相等,故正确,故选D5.∵AB=AC,∴△ABC是等腰三角形,∵∠A是顶角,且∠A等于∠C的一半,∴∠A+∠C+∠ABC=∠A+2∠A+2∠A=180°,∴∠A=36°,∠C=∠ABC=72°,BD平分∠ABC交AC于D,∴∠ABD=∠DBC=36°,∵∠A=∠ABD=36°,∴△ABD是等腰三角形.∠BDC=∠A+∠ABD=36°+36°=72°=∠C,∴△BDC是等腰三角形.∴共有3个等腰三角形.6.AB=2,∵等边三角形高线即中点,∴BD=CD=1,在Rt△ABD中,AB=2,BD=1,∴AD==,∴等边△ABC 的面积为BC•AD=×2×=,故选:B.7.∵△ABC是等边三角形,∴∠B=∠BAC=60°,∵∠BAD=20°,∴∠DAE=∠BAC﹣∠BAD=40°,∵AD=AE,∴∠ADE=∠AED,∵∠ADE+∠AED+∠DAE=180°,∴∠ADE=∠AED=×(180°﹣40°)=70°,∵∠ADC=∠B+∠BAD=60°+20°=80°,∴∠CDE=∠CDA﹣∠ADE=80°﹣70°=10°.故选A8.连接AD.∵DE垂直平分AB,BD=3,∴BD=AD=3;∴∠B=∠BAD(等边对等角);又∵∠ABC=15°,∴∠BAC=15°;∴∠ADC=2∠BAC=30°(外角定理),∴=cos∠ADC,∴DC=AD•cos30°=.故选A.9.过E作EM∥BC,交AD于N,∵AC=4,AE=2,∴EC=2=AE,∴AM=BM=2,∴AM=AE,∵AD是BC边上的中线,△ABC是等边三角形,∴AD⊥BC,∵EM∥BC,∴AD⊥EM,∵AM=AE,∴E和M关于AD对称,连接CM交AD于F,连接EF,则此时EF+CF的值最小,∵△ABC是等边三角形,∴∠ACB=60°,AC=BC,∵AM=BM,∴∠ECF=∠ACB=30°,故选C.10.∵∠A=∠P1P2A=16°∴∠P2P1P3=32°,∠P1P3P2=32°∴∠P1P2P3=116°∴∠P3P2P4=48°∴∠P3P2P4=48°∴∠P2P3P4=96°∴∠P4P3P5=52°∴∠P3P5P4=52°∴∠P3P4P5=52°∴∠P5P4P6=76°∴∠P4P6P5=76°∴∠P4P5P6=28°∴∠P6P5P7=86°,此时就不能在往上焊接了,综上所述总共可焊上5条.故选B.11.△ABC的周长为6,∴AB=BC=AC=2,DC=CE=1,又∵∠ACB=∠CDE+∠CED ∴BD+DE+BE=2+2+1=3+2.故选C12.①三条边相等的三角形是等边三角形符合等边三角形的定义,故正确;②有一个角是60°的等腰三角形是等边三角形,正确;③有两个角为60°的三角形是等边三角形,正确;④三个角相等的三角形是等边三角形,正确.故选D13.∵ED⊥BC,∠C=60°,∴∠CED=30°,设DE=x,则AE=x,且CE=x,又∵AE+CE=5,∴x+x=5,解得x=10﹣15,∴CE=5﹣(10﹣15)=20﹣10.故选D14.①BC边为底边时,AD=BC=BD=CD,所以△ABD和△ADC为等腰直角三角形,∠BAC=∠BAD+∠CAD=90°.②BC 边为腰时可分为和两种情况,垂足在三角形内部时,AD==AC,所以∠C=30°,又因为AC=BC,所以∠BAC=∠ABC=(180°﹣∠C)=75°.垂足落在三角形外时,由图知AD=AB,所以∠ABD=30°,所以∠BAC=∠C=∠ABD=15°.故答案为D15.∵P关于OA、OB的对称∴OA垂直平分PC,OB垂直平分PD∴CM=PM,PN=DN∴在四边形OTPR中,∴∠CPD+∠O=180°,∴∠CPD=180°﹣40°=140°∴∠C+∠D=40°∴∠MPN=180°﹣40°×2=100°故选D16.当顶角为∠A=50°时,∠B=65°,当顶角为∠B=70°时,∠A=55°所以A选项错误.当顶角为∠B=40°时,∠A=70°,所以B选项正确.当顶角为∠A=30°时,∠B=75°,当顶角为∠B=90°时,∠A=45°所以C选项错误.当顶角为∠A=80°时,∠B=50°,当顶角为∠B=60°时,∠A=60°所以D选项错误.故选B17.∵PC∥OA,∴∠CPO=∠POA,∵∠AOP=∠BOP=15°,∴∠AOP=∠BOP=∠CPO=15°,过点P作∠OPE=∠CPO交于AO于点E,则△OCP≌△OEP,∴PE=PC=10,∵∠PEA=∠OPE+∠POE=30°,∴PD=10×=5.故选C.18.4是腰长时,三角形的三边分别为4、4、9,∵4+4=8<9,∴不能组成三角形,4是底边时,三角形的三边分别为4、9、9,能组成三角形,周长=4+9+9=22,综上所述,该等腰三角形的周长为22.19.根据三角形的内角和定理,得:∠ABO=∠DCO=36°,根据三角形的外角的性质,得∠AOB=∠COD=72°.再根据等角对等边,得等腰三角形有△AOB,△COD,△ABC,△CBD和△BOC.故选B20.∵AD⊥BC,D为BC的中点,∴∠ADB=∠ADC=90°,BD=BC,AD为公共边,∴△ABD≌△ACD,∴AB=AC,∠B=∠C,∠BAD=∠CAD,即AD是△ABC的角平分线.故选D21.∵△ABC是等边三角形,∴AB=BC=AC,∠A=∠B=∠C=60°又∵OE⊥AB,OF⊥AC,∠B=∠C=60°,∴OE=OB•sin60°=OB,同理OF=OC.∴OE+OF=(OB+OC)=BC.在等边△ABC中,高h=AB=BC.∴OE+OF=h.又∵等边三角形的高为2,∴OE+OF=2,故选C22.∵AB边的垂直平分线交AB于E,交BC于D(已知)∴AD=BD(线段垂直平分线的性质)∴∠DAE=∠B=15°且AD=BD=13cm(等腰三角形的性质)∴∠ADC=30°(外角性质)∴AC=AD=6.5cm.故选B23.在Rt△ABC和Rt△ADC中,AB=AD,AC=AC,所以Rt△ABC≌Rt△ADC(HL).所以∠ACB=∠ACD,∠BAC=∠DAC,即AC平分∠BAD,CA平分∠BCD.故①②正确;在△ABD中,AB=AD,∠BAO=∠DAO,所以BO=DO,AO⊥BD,即AC垂直平分BD.故③正确;不能推出∠ABO=∠CBO,故④不正确.故选B24.原式可化为2a2+2b2+2c2=2ab+2ac+2bc,即a2+b2+c2+a2+b2+c2﹣2ab﹣2ac﹣2bc=0;由非负数的性质,可知:a﹣b=0,c﹣a=0,b﹣c=0;即:a=b=c.所以△ABC是等边三角形.故选C.25.∵AB=AD,∴∠B=∠D=α,∵AB=BC∴∠BAC=∠BCA,∵∠ACB=α+β∴在等腰三角形ABC中,2(α+β)+α=180°∴3α+2β=180°,故选B26.连接AP、BP、CP,过点A作AD⊥BC于D,等边三角形面积S=BC•(PQ+PR+PS)=BC•AD故PQ+PR+PS=AD,∴AD=6+8+10=24,∵∠ABC=60°∴AB=24×=16,∴△ABC的面积S=BC•AD=×24×16=192,故选B.27.把三角形每条边分成n份,相应点之间连线,可以把三角形分成n2个边长为的小三角形,至少n2+1个点可以保证至少有两个点落在同一个小三角形内,所以那两个点的距离是不超过的.故选A28.设BM=x,CN=y则BP=2x,PC=2y,PM=x,PN=yAM+AN=2BC﹣(BM+CN)=3(x+y),故==≈0.7887.故选D.∴EF AB,ED AC,∴四边形CEDF是菱形,∴EF⊥CD,∴在菱形CEDF中有6个不同的直角三角形:Rt△CEG、Rt△CFG、Rt△DGE、Rt△DFG、Rt△EOG、Rt△FOG;同理,在菱形ADEF、菱形BEFD中各有6个不同的直角三角形;②∵D为等边三角形ABC三边中点,∴CD⊥AB,∴△ADC、△BDC、AOD、△BOD是直角三角形;同理,以BF、AE为直角边的三角形各有4个;综上所述,图中能数出的直角三角形由6×3+4×3=30(个);故选C30. 当∠B=50°为顶角时,此时∠A=∠C==65°;当∠B=50°为底角时,此时另一底角为50°,顶角为80°,故答案为:50°,80°或65°,65°31.根据题意,可以以点A为圆心,以AB为半径作圆,即可得出点B、C、D均在圆周上,故有∠BAC=2∠BDC=50°,即∠BDC=25°.故答案为:25°32.在DC上截取DE=BD,连接AE,∵AD⊥BC,∴∠ADB=∠ADE=90°,∵AD=AD,∴△ADB≌△ADE,∴∠B=∠AED,AE=AB,∵AB+BD=DC,DE+EC=DC,∴AE=AB=EC,∴∠AEB=2∠EAC=2∠C,∴∠B=2∠C,∵∠BAC=135°,∠B+∠C+∠BAC=180°,∴3∠C=45°,∴∠C=15°.故答案为:1533.过D作DE⊥AB于E,∵AD是∠BAC的角平分线,∠C=90°,DE⊥AB,∴BD=2DE,∵∠BED=90°,∴∠B=30°.故答案为:3034.设等腰三角形的腰长是xcm,底边是ycm.根据题意,得:或,解得或.再根据三角形的三边关系,知:8,8,17不能组成三角形,应舍去.所以它的底边是5cm.故答案为:535.如图:△ABC中,AB=AC,BD是边AC上的高.∵∠A=80°,且AB=AC,∴∠ABC=∠C=(180°﹣80°)÷2=50°;在Rt△BDC中,∠BDC=90°,∠C=50°;∴∠DBC=90°﹣50°=40°.故答案为:40°36.∵(a+b+c)(a﹣c)=0,∴a+b+c=0或a﹣c=0,∵a、b、c,为三角形三边,∴a+b+c=0(舍去),∴a=c∴该三角形为等腰三角形,故答案为:等腰三角形37.如图作AD⊥BC于点D.∵△ABC为等边三角形,∴∠B=60°,∴AD=AB×sin∠B=a,2故答案为:a238.∵AB=AC,AP=PQ,QP=QC,QC=BC,∴∠ABC=∠ACB,∠A=∠AQP,∠QPC=∠QCP,∠BQC=∠B(等边对等角),设∠A=x°,则∠AQP=x°,∵在△AQP中,∠QPB是外角,∴∠QPC=∠A+∠AQP=2x°(三角形的一个外角等于和它不相邻的两个内角的和),∵在△BCQ中,∠BQC是外角,∴∠BQC=∠ACQ+∠A(三角形的一个外角等于和它不相邻的两个内角的和),∴∠BQC=3x°,∴∠B=3x°,∴∠ABC=3x°,∵在△ABC中,∠A+∠ACB+∠B=180°,∴x°+3x°+3x°=180°(三角形三个内角的和等于180°),解得x=()°,∴∠A=()°.39.∵△ABC中,∠C=90°,∠B=15°,∴∠BAC=180°﹣∠C﹣∠B=180°﹣90°﹣15°=75°.连接AD.∵ED是AB的垂直平分线,∴AD=BD=8,∠B=∠1=15°,∴∠2=∠BAC﹣∠1=75°﹣15°=60°.在Rt△ACD中,∠2=60°,∠C=90°,∴∠3=180°﹣∠C﹣∠2=180°﹣90°﹣60°=30°.∴AC=AD=BD=×8=4.40.∵OC为等边三角形的高,且等边三角形的边长为1,∴NC=,∵△OCD为等边三角形,∴∠OCD=60°,∴OE⊥CD,2∴ON 的长为()10,故答案为()1041.作DF⊥AB于点F∵△ABC中,∠ACD=90°,CA=CB,∴∠CAB=∠B=45°,∵AD是△ABC的角平分线,∴DF=DC,∠DAB=22.5°,∵DE=2CD,∴DE=2DF,∴∠DEB=30°,∴∠ADE=∠DEB=﹣∠DAB=30°﹣22.5°=7.5°,故答案为7.5°.42.底边是24﹣2x,根据三角形的三边关系:两边之和大于第三边,两边之差小于第三边.得:0<24﹣2x<2x.解得6<x<12.故填6<x<1243.∵∠A=12°,AB=BC,∴∠A=∠ACB=12°,∠CBD=∠A+∠ACB=12°+12°=24°;∵BC=CD,∴∠CBD=∠CDB=24°,∴∠ECD=∠A+∠CDA=36°(外角定理);∵CD=DE,∴∠DCE=∠DEC=36°,∴∠EDF=∠A+∠AED=48°;又∵DE=EF,∴∠EDF=∠EFD=48°,∴∠GEF=∠A+∠EFD=12°+48°=60°.故答案是:6044.∵AB=AC,∠BAC=120°,∴∠B═∠C=(180°﹣∠A)=30°,∵DB=DA=4,∴∠B=∠BAD=30°,∴∠ADC=∠B+∠BAD=60°,∴∠DAC=180°﹣∠C﹣∠ADC=90°,∵∠C=30°,∴DC=2AD=2×4=8,∴BC=BD+DC=4+8=12,故答案为:12即∠DBE=30°,又DE=DB,∴∠E=∠DBE=30°,∵等边△ABC的周长为9,∴AC=3,且∠ACB=60°,∴∠CDE=∠ACB﹣∠E=30°,即∠CDE=∠E,∴CD=CE=AC=.故答案为:30;46.∵AB=AC,BC=6,AD是△ABC的中线,∴BD=DC=BC=3,AD⊥BC,∴△ABC关于直线AD对称,∴B、C关于直线AD对称,∴△CEF和△BEF关于直线AD对称,∴S△BEF=S△CEF,∵△ABC 的面积是:×BC×AD=×6×4=12,∴图中阴影部分的面积是S△ABC=6.故答案为:647.∵BD=CD,AD⊥BC,∴AB=AC,即三角形是等腰三角形.故填等腰.48.∵AB=AC,∴∠ABC=∠ACB,故2∠ABC+∠BAC=180°,∵等边三角形各内角为60°,∠DAE=∠DBC,∴120°+∠BAC=60°+∠ABC,又∵2∠ABC+∠BAC=180°,∴∠BAC=20°.故答案为:20°49.∵∠BRS+y=∠TSC+z,∴∠BRS﹣∠TSC=z﹣y,又∠BRS+x=y+∠TSC=120°,∴∠BRS﹣∠TSC=y﹣x,故答案为:x=2y﹣z.50.①如图1,已知AB=AC=2,BD为腰AC上的高,可知∠ABD=30°,可得∠A=60°,即证△ABC为正三角形,即可得出底边AC 上的高等于腰上的高等于.②如图2,AB=AC=2,CD⊥BA交BA是延长线于点D,且∠CAD=30°,可得AD=1,CD=,可得BC=2,即BE=,在Rt△ABE中,AB=2,BE=,即AE=1.故答案为:1或.51.∵△ABC是等边三角形,D是AC的中点,∴BD平分∠ABC(三线合一),∴∠ABC=2∠DBE;∵CE=CD,∴∠CED=∠CDE.又∵∠ACB=∠CED+∠CDE,∴∠ACB=2∠E;又∵∠ABC=∠ACB,∴2∠DBC=2∠E,∴∠DBC=∠E,∴BD=DE.又∵DM⊥BE,∴BM=EM.52.∵DE是AB的垂直平分线.∴AB=2AD,EA=EB.∵AD=5cm,∴AB=10cm.∵△ABC的周长为27cm,∴AC+BC+AB=2cm7,AC+BC=17cm即AE+EC+BC=17cm.∴EB+EC+BC=17.即△BCE的周长为17cm53.E,F是BC的三等分点.理由:连接OE,OF,∵DE垂直平分OB∴BE=OE(线段垂直平分线上的点到线段两端点距离相等),同理OF=CF,∴∠EBO=∠BOE,∠FCO=∠FOC,∵等边三角形ABC中,∴∠ABC=∠ACB=60°(等边三角形各角相等且为60°)∵BO平分∠ABC,CO平分∠ACB∴∠EBO=∠ABC=30°,∠FCO=∠ACB=30°∴∠BOE=∠EBO=30°,∠FOC=∠FCO=30°∴∠OEF=∠BOE+∠EBO=60°,∠OFE=∠FOC+∠FCO=60°,∴△OEF是等边三角形(有两个内角60°的三角形是等边三角形)∴OE=OF=EF(等边三角形各边相等)∴BE=EF=FC,即E,F是BC的三等分点54.(1)∵D是AB的中点,∴AD==2,∵等边三角形ABC中∠A=∠C=60°,且DF⊥AC,∴∠ADF=180°﹣90°﹣60°=30°,在Rt△ADF中,AF==1;(2)FC=AC﹣AF=4﹣1=3,同理,在Rt△FEC中,EC==1.5,∴BE=BC﹣EC=4﹣1.5=2.5.故答案为:AF=1,BE=2.555.∵AF平分∠BAC,∴∠BAD=∠CAD,∵DE∥AC,∴∠EDA=∠CAD=∠BAD,∴AE=ED,∵∠EDB+∠ADE=90°,∴∠BDE+∠BAD=90°,∵∠EBD+∠BAD=90°,∴∠BDE=∠EBD,∴BE=ED,∴AE=BE.56.(1)∵D是AB的中点,DE⊥AB交AC于E,∴EB=EA,∴∠A=∠ABE,∵BE平分∠ABC,∴∠ABE=∠CBE,∵AB=AC,∴∠C=∠ABC=2∠ABE=2∠A,∵∠A+∠ABC+∠C=180°,即:5∠A=180°∴∠A=36°;(2)∵△ABC的周长为10,∴AB+AC+BC=10,∵△BCE的周长为6,∴BE+EC+BC=AE+EC+BC=AC+BC=6,∴AB=AC=4.∴BC=257.∵EF垂直平分AD,∴FA=FD,∴∠ADF=∠DAF,又∵∠ADF=∠B+∠BAD,∠DAF=∠FAC+∠DAC,∵∠BAD=∠DAC,∴∠FAC=∠B=45°.58.∵AE∥DC,∴∠BCD=∠E=36°,又∵CD平分∠ACB,∴∠ACB=2∠BCD=72°,∵AB=AC,∴∠B=∠ACD=72°.答:∠B的度数为72°.59.连接CE.∵AE=AC,∴∠1+∠2=∠AEC=∠3+∠B.①同理,∠2+∠3=∠1+∠A.②①+②得2∠2=∠A+∠B.∵∠ACB=90°,∴∠A+∠B=90°.∴∠2=45°.∵EF⊥CD,∴∠CFE=90°.∴∠CEF=45°=∠2,∴EF=CF.60.∵AC的垂直平分线DE,∴AD=DC,∴∠A=∠ACD,∵∠ACB=90°,∴∠A+∠B=90°,∠ACD+∠BCD=90°,∴∠B=∠BCD,∴DC=BD,∴DA=DC=DB61.∵AB=BC=CD=DE,∴∠A=∠BCA,∠CBD=∠BDC,∠ECD=∠CED,根据三角形的外角性质,∠A+∠BCA=∠CBD,∠A+∠CDB=∠ECD,∠A+∠CED=∠EDM,又∵∠EDM=84°,∴∠A+3∠A=84°,解得:∠A=21°62.∵等腰三角形中,一边与另一边之比为3:2,∴设两边分别为3x,2x,根据题意得:3x+3x+2x=56或3x+2x+2x=56解得:x=7,此时腰长3x=21,或x=8,此时腰长2x=16,所以腰长为21或1663.在线段DC上取一点E,使DE=DB,连接AE,∵AD⊥BC,∴AD垂直平分BE,∴AB=AE,∴∠AEB=∠B,∵∠B=2∠C,∴∠AEB=2∠C,∴∠EAC=∠AEB﹣∠C=2∠C﹣∠C=∠C,∴AE=CE,∴CE=AE=AB,∴DC=DE+CE=AB+BD,∴AB+BD=DC.64.(1)∵AB=BC=AC,BD是中线,∴BC=AC=2CD∵CD=3,∴BC=2CD=6,CE=CD=3∴BE=BC+CE=6+3=9(2)∵△ABC是等边三角形,BD是中线,∴∠ABC=∠ACB=60°.∠DBC=30°(等腰三角形三线合一).又∵CE=CD,∴∠CDE=∠CED.又∵∠BCD=∠CDE+∠CED,∴∠CDE=∠CED=∠BCD=30°.∴∠DBC=∠DEC.∴DB=DE(等角对等边).(3)∵点F是BE边的中点,∴DF是BE边的中线,∵BD=ED∴DF⊥BE65.∵BD平分∠ABC,DF⊥AB,∠C是直角,∴CD=DF,∠DBC=∠DBE,∠DFB=∠C,∴△BCD≌△BFD,∴BC=BF,∵DE∥BC,∴∠DBC=∠EDB,即∠DBC=∠DBE,∴△BDE是等腰三角形,∴BE=DE,∴BF=BC=DE+EF66.(1)∵等边三角形各内角为60°∴∠ACF=180°﹣60°=120°,CE为∠ACF的角平分线,∴∠ECF=60°,∵∠ABC=60°∴EC∥AB.(2)∵∠EDC+∠ADE+∠ADB=180°,∴∠EDC+∠ADB=120°,∵∠ABD+∠BAD+∠ADB=180°,∴∠BAD+∠ADB=120°,∴∠BAD=∠EDC.67.(1)连接AO,∵在等腰△ABC中,∠B和∠C的平分线相交于点O,∴等腰△ABC关于线段AO所在的直线对称,∵∠A=80°,∴∠OAC=40°(2)∵BO、CO分别平分∠ABC和∠ACB,∴∠OBC=∠ABC,∠OCB=∠ACB,∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣(∠ABC+∠ACB)=180°﹣(∠ABC+∠ACB)=180°﹣(180°﹣∠A)=90°+∠A.∴当∠A=80°时,=130°.68.证明:∵AD是△ABC的角平分线,AF平分△ABC的外角,∴∠1=∠2,∠3=∠4,∵DF∥BA,∴∠4=∠ADE,∠1=∠F∴∠3=∠ADE,∠2=∠F∴DE=EA EF=EA∴DE=EF69.∵AB=AC=10,∴∠B=∠C,由DF∥AC,得∠FDB=∠C=∠B,∴FD=FB,同理,得DE=EC.∴四边形AFDE的周长=AF+AE+FD+DE=AF+FB+AE+EC=AB+AC=10+10=20.∴四边形AFDE的周长为2070.(1)∵CM⊥AM,∠DCM=α,∴∠CDM=∠ADB=∠B=90°﹣α,∴∠BAD=180°﹣2∠ABD=180°﹣2(90°﹣α)=2α;(2)延长AM到F使MF=AM,则有AC=CF∵AD平分∠CAB∴∠CAF=∠BAF=∠F∴CF∥AB∴∠FCD=∠ABD=∠ADB=∠CDF∴CF=DF∵AD+DF=2MA∴AB+AC=2MA71.∵王宏和张新他们两家和学校正好构成一个等腰三角形,而且王宏家距学校2千米,张新家距学校4千米,∴此等腰三角形的底边长为2,两腰均为4,∴王宏与张新两家的距离是4千米;当王宏家与学校相距2千米,而张新家与学校相距3千米时,王宏与张新两家相距可能是2千米也可能是3千米72.DE=DF.证明:∵∠CDF+∠EDF+∠BDE=180°,∠CDF+∠C+∠CFD=180°∴∠BDE=∠CFD在△EBD和△DCF中∠BDE=∠CFDBE=CD∠B=∠C∴△EBD≌△DCF∴DE=DF73.(1)解:∵∠BAC=90°,AB=AC,∴∠B=∠C=(180°﹣∠BAC)=45°,∴∠ADC=∠B+∠BAD=45°+30°=75°,∵∠DAC=∠BAC﹣∠BAD=90°﹣30°=60°,∵AD=AE,∴∠ADE=∠AED=(180°﹣∠DAC)=60°,∴∠EDC=∠ADC﹣∠ADE=75°﹣60°=15°,答:∠EDC的度数是15°.(2)解:与(1)类似:∠B=∠C=(180°﹣∠BAC)=90°﹣α,∴∠ADC=∠B+∠BAD=90°﹣α+30°=120°﹣α,∵∠DAC=∠BAC﹣∠BAD=α﹣30°,∴∠ADE=∠AED=(180°﹣∠DAC)=105°﹣α,∴∠EDC=∠ADC﹣∠ADE=(120°﹣α)﹣(105°﹣α)=15°,答:∠EDC的度数是15°.(3)∠EDC与∠BAD的数量关系是∠EDC=∠BAD.74.(1)解:设底边BC=acm,则AC=AB=2acm,∵三角形的周长是18cm,∴2a+2a+a=18,∴a=,2a=,答:等腰三角形的三边长是cm ,cm ,cm.(2)解:设BC=acm,AB=AC=2bcm,∵中线BD将△ABC的周长分为1:2两部分,18×=12,18×=6,∴2b+b=6,b+a=12或2b+b=12,b+a=6,解得:a=10,b=2或b=4,a=2,∴①三角形三边长是10cm,4cm,4cm,因为4+4<10,不符合三角形三边关系定理,∴此种情况舍去,②三角形的三边长是2cm,8cm,8cm,符合三角形的三边关系定理,综合上述:符合条件的三角形三边长是8cm,8cm,2cm,答:等腰三角形的边长是8cm,8cm,2cm.75.分成两类进行研究:(1)∠B为△ABD的底角,如果∠BAD=40°,那么∠ADC=80°;如果∠ADC为△ACD的底角,那么∠C=80°或20°;如果∠ADC为△ACD的顶角,那么∠C=50°;如果∠ADB=70°,那么∠ADC=140°,所以∠C=20°(2)∠B为△ABD的顶角,这时∠ADB=70°,∠ADC=110°,所以∠C=35°;综上所述,∠C的值为20°或35°或50°或80°76.①当(2x﹣2)°和(3x﹣5)°是两个底角时,2x﹣2=3x ﹣5,x=3°,∴三个内角分别是4°,4°,172°;②当2x﹣2是顶角时,2x﹣2+2(3x﹣5)=180°,解得x=24°,∴三个内角分别是46°,67°,67°;③当3x﹣5是顶角时,3x﹣5+2(2x﹣2)=180°,解得x=27°,∴三个内角分别是76°52°,52°77.(1)∵DE垂直平分AC,∴CE=AE,∴∠ECD=∠A=36°;(2)∵AB=AC,∠A=36°,∴∠B=∠ACB=72°,∴∠BEC=∠A+∠ECD=72°,∴∠BEC=∠B,∴BC=EC=5.答:(1)∠ECD的度数是36°;(2)BC 长是5 78.1)解:∵AB=AC , ∴∠B=∠C=30°, ∵∠C+∠BAC+∠B=180°, ∴∠BAC=180°﹣30°﹣30°=120°, ∵∠DAB=45°, ∴∠DAC=∠BAC ﹣∠DAB=120°﹣45°=75°;(2)证明:∵∠DAB=45°, ∴∠ADC=∠B+∠DAB=75°, ∴∠DAC=∠ADC , ∴DC=AC , ∴DC=AB79.(1)DE+DF=CG . 证明:连接AD ,则S △ABC =S △ABD +S △ACD,即AB •CG=AB •DE+AC •DF ,∵AB=AC , ∴CG=DE+DF .(2)当点D 在BC 延长线上时,(1)中的结论不成立,但有DE ﹣DF=CG .理由:连接AD ,则S △ABD =S △ABC +S △ACD , 即AB •DE=AB •CG+AC •DF∵AB=AC , ∴DE=CG+DF , 即DE ﹣DF=CG .同理当D 点在CB 的延长线上时,则有DE ﹣DF=CG ,说明方法同上.80.证明:∵AB=AC , ∴∠B=∠C , ∵DE ⊥BC ,∴∠C+∠F=90°,∠B+∠BDE=90°, ∵∠ADF=∠BDE , ∴∠F=∠ADF , ∴AD=AF。
八年级数学下----等腰三角形和等边三角形培优练习题

八年级数学下----等腰三角形和等边三角形培优练习题一、填空选择题:1.如下图1,等边△ABC 的边长为3,P 为BC 上一点,且BP =1,D 为AC 上一点,若∠APD =60°,则CD 的长为( ) A .32B .23C .12D .342.如上图2,△ABC 中,D 、E 分别是BC 、AC 的中点,BF 平分∠ABC ,交DE 于点F ,若BC =6, 则DF 的长是( )(A )2 (B )3 (C )25(D )4 3.如上图3,点A 的坐标是(2,2),若点P 在x 轴上,且△APO 是等腰三角形,则点P 的坐标 不可能...是( )A .(4,0) B .(1.0) C .(-22,0) D .(2,0)4.如上图1,AB =AC,BD =BC ,若∠A =40°,则∠ABD 的度数是( ) A .20B .30C .35D .405.如上图2,△ABC 中,AB =AC =6,BC =8,AE 平分么BAC 交BC 于点E ,点D 为AB 的中点,连结DE ,则△BDE 的周长是( ) A .7+5 B .10 C .4+25 D .126.如上图3,在△ABC 中,AB =AC ,∠A =36°,BD 、CE 分别是△ABC 、△BCD 的角平分线, 则图中的等腰三角形有 ( ) (A)5个 (B)4个 (C)3个 (D)2个7.在等腰ABC △中,AB AC ,一边上的中线BD 将这个三角形的周长分为15和12两个部分,则这个等腰三角形的底边长为( )A .7B .11C .7或11D .7或108.等腰三角形一腰上的高与另一腰的夹角为30º,腰长为4 cm ,则其腰上的高为 cm . 9.已知等腰ABC △的周长为10,若设腰长为x ,则x 的取值范围是 . 10.在△A BC 中,AB =AC ,AB 的垂直平分线与AC 所在的直线相交所得到锐角为50°,AD PB60° ED CBA(第6题)BA DC1 2 3 4-1 12xy A则∠B 等于_ 度.11.如下图1,过边长为1的等边△ABC 的边AB 上一点P ,作PE ⊥AC 于E ,Q 为BC 延长线上一点,当PA=CQ 时,连PQ 交AC 边于D ,则DE 的长为( )A .13 B .12 C .23D .不能确定12.如下图2,等腰△ ABC 中,AB=AC ,∠A=20°。
等腰三角形和等边三角形

等腰三角形和等边三角形一、等腰三角形的定义和性质1.1 等腰三角形的定义:等腰三角形是指有两边相等的三角形。
1.2 等腰三角形的性质:(1)等腰三角形的两腰相等。
(2)等腰三角形的底角相等。
(3)等腰三角形的底边垂直平分线也是高线、中线和角平分线。
(4)等腰三角形的底角小于或等于顶角。
二、等边三角形的定义和性质2.1 等边三角形的定义:等边三角形是指三边都相等的三角形。
2.2 等边三角形的性质:(1)等边三角形的三边相等。
(2)等边三角形的三角相等,都是60度。
(3)等边三角形的各边垂直平分线也是高线、中线和角平分线。
(4)等边三角形的面积计算公式为:(S = a^2),其中a为边长。
3.1 等腰三角形的判定:(1)如果一个三角形有两边相等,那么这个三角形是等腰三角形。
(2)如果一个三角形的两个角相等,那么这个三角形是等腰三角形。
3.2 等边三角形的判定:(1)如果一个三角形三边都相等,那么这个三角形是等边三角形。
(2)如果一个三角形的三角都相等,都是60度,那么这个三角形是等边三角形。
四、等腰三角形和等边三角形在实际生活中的应用4.1 等腰三角形的应用:(1)建筑物的设计中,等腰三角形的结构稳定性较好,常用于设计桥梁、塔架等。
(2)几何画板或者绘图工具中,等腰三角形可以用来制作对称图案。
4.2 等边三角形的应用:(1)装饰品设计中,等边三角形的对称性美观,常用于设计各种图案。
(2)几何学中,等边三角形是研究三角形性质的基本模型。
五、等腰三角形和等边三角形的相关定理5.1 等腰三角形的定理:(1)角平分线定理:等腰三角形的角平分线、中线和底边垂直平分线是同一条线。
(2)面积定理:等腰三角形的面积等于底边乘以高线除以2。
5.2 等边三角形的定理:(1)面积定理:等边三角形的面积计算公式为:(S = a^2)。
(2)内切圆定理:等边三角形的内切圆半径等于边长乘以根号3除以6。
六、等腰三角形和等边三角形的相关问题6.1 等腰三角形的问题:(1)已知等腰三角形的一边长和一角大小,求其它两边的长度和角度大小。
等腰三角形和等边三角形选择填空专项练习80题(有答案)ok

等腰三角形和等边三角形专项练习60题(有答案)1.已知,如图,△ABC中,AB=AC,DE是AB的中垂线,点D在AB上,点E在AC上,若△ABC的周长为25cm,△EBC的周长为16cm,则AC的长度为()A.16cm B.9cm C.8cm D.7cm2.如图,在△ABC中,∠B=∠C,点F为AC上一点,FD⊥BC于D,过D点作DE⊥AB于E.若∠AFD=158°,则∠EDF的度数为()A.90°B.80°C.68°D.60°3.如图所示,在△ABC中,点D是BC上一点,∠BAD=80°,AB=AD=DC,则∠C的大小为()A.50°B.40°C.20°D.25°4.下列说法正确的是()A.等腰三角形的两条高相等B.等腰三角形一定是锐角三角形C.有一个角是60°的锐角三角形是等边三角形D.三角形三条角平分线的交点到三边的距离相等5.已知等腰三角形ABC,∠A是顶角,且∠A等于∠C的一半,BD是△ABC的角平分线,则该图中共有等腰三角形的个数是()A.4个B.3个C.2个D.1个6.边长为2的等边三角形的面积是()A.B.C.3D.67.如图,在等边△ABC中,∠BAD=20°,AE=AD,则∠CDE的度数是()A.10°B.12.5°C.15°D.20°8.如图,在△ABC中,∠C=90°,∠ABC=15°,点D、E分别在BC、AB上,且DE垂直平分AB,BD=3,则DC 等于()A.B.C.3D.9.如图,等边△ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点,若AE=2,当EF+CF取得最小值时,则∠ECF的度数为()A.15°B.22.5°C.30°D.45°10.如图,钢架中∠A=16°,焊上等长的钢条P1P2,P2P3,P3P4…来加固钢架,若AP1=P1P2,则这样的钢条至多需要()根.A.4B.5C.6D.711.如图,已知等边△ABC的周长为6,BD是AC边的中线,E为BC延长线上一点,CD=CE,那么△BDE的周长是()A.5+2B.5+C.3+2D.3+12.以下关于等边三角形的判定:①三条边相等的三角形是等边三角形;②有一个角是60°的等腰三角形是等边三角形;③有两个角为60°的三角形是等边三角形④三个角相等的三角形是等边三角形其中正确的是()A.只有①②③B.只有①②④C.只有①③④D.①②③④13.如图,△ABC为边长是5的等边三角形,点E在AC边上,点F在AB边上,ED⊥BC,且ED=AE,DF=AF,则CE的长是()A.B.C.20+10D.20﹣1014.已知△ABC是等腰三角形,BC边上的高恰好等于BC的一半,则∠BAC的度数是()A.75°B.90°或75°或25°C.75°或15°D.90°或75°或15°15.如图,已知∠AOB=40°,点P关于OA、OB的对称点分别为C、D,CD交OA、OB于M、N两点,则∠MPN 的度数是()A.70°B.80°C.90°D.100°16.在△ABC中,∠A和∠B的度数如下,能判定△ABC是等腰三角形的是()A.∠A=50°,∠B=70°B.∠A=70°,∠B=40°C.∠A=30°,∠B=90°D.∠A=80°,∠B=60°17.如图∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=10,则PD等于()A.10B.C.5D.2.518.等腰三角形的一边长为4,另一边长为9,则它的周长为()A.13B.17C.17或者22D.2219.如图所示,共有等腰三角形()A.4个B.5个C.3个D.2个20.如图,AD⊥BC,D为BC的中点,以下结论正确的有几个?()①△ABD≌△ACD;②AB=AC;③∠B=∠C;④AD是△ABC的角平分线.A.1B.2C.3D.421.如图,已知△ABC是等边三角形,点O是BC上任意一点,OE,OF分别于两边垂直,等边三角形的高为2,则OE+OF的值为()A.1B.3C.2D.422.如图,在Rt△ABC中,已知,∠ACB=90°,∠B=15°,AB边的垂直平分线交AB于E,交BC于D,且BD=13cm,则AC的长是()A.13cm B.6.5cm C.30cm D.6cm23.如图所示,AB=AD,∠ABC=∠ADC=90°,则①AC平分∠BAD;②CA平分∠BCD;③AC垂直平分BD;④BD平分∠ABC,其中正确的结论有()A.①②B.①②③C.①②③④D.②③24.已知a,b,c是△ABC的三边,且a2+b2+c2=ab+ac+bc,则△ABC是()A.等腰三角形B.直角三角形C.等边三角形D.等腰直角三角形25.如图,△ABC中,AB=BC=AD,D在BC的延长线上,则角α和β的关系是()A.α+β=180°B.3α+2β=180°C.3α+β=180°D.2β=α26.如图,等边三角形ABC内有一点P,过点P向三边作垂线,垂足分别为S、Q、R,且PQ=6,PR=8,PS=10,则△ABC的面积等于()A.190B.192C.194D.19627.在边长为1的等边三角形内任意放一些点,要使得至少存在2个点之间的距离不超过,那么至少应该放几个点()A.n2+1B.2n+1C.2n D.n+128.如图所示,△ABC为正三角形,P是BC上的一点,PM⊥AB,PN⊥AC,设四边形AMPN,△ABC的周长分别为m、n,则有()A.B.C.D.29.如图,D,E,F为等边三角形ABC三边中点,AE、BF、CD交于O,DE,EF,FD为三条中位线,则图中能数出不同的直角三角形的个数是()A.36B.32C.30D.2830.等腰△ABC中,∠B=50°,那么另外两个角的度数分别是_________.31.如图,已知:AB=AC=AD,∠BAC=50°,∠DAC=30°,则∠BDC=_________.32.如图,在△ABC中,∠BAC=135°,AD⊥BC于D,且AB+BD=DC,那么∠C=_________°.33.如图,Rt△ABC中,∠C=90°,BD=2CD,AD是∠BAC的角平分线,则∠B=_________度.34.若一腰上的中线把一个等腰三角形的周长分为12cm和21cm两部分,则其底边长为_________cm.35.等腰三角形顶角80°,一腰上的高与底边的夹角的度数是_________.36.如果一个三角形三边长为a、b、c,且满足(a+b+c)(a﹣c)=0,则该三角形的形状是_________.37.边长为a的等边三角形的面积为_________.38.如图,△ABC中,AB=AC,点P、Q分别在AC、AB上,且AP=PQ=QC=BC,则∠A的大小是_________.39.如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交AB于E,交BC于D,BD=8,则AC=_________.40.如右图,以等边△OAB的高OC为边向逆时针方向作等边△OCD,CD交OB于点E,再以OE为边向逆时针方向作等边△OEF,EF交OD于点G,再以OG为边向逆时针方向作等边△OGH,…,按此方法操作,最终得到△OMN,此时ON在OA上.若AB=1,则ON=_________.41.如图,在△ABC中,∠ACD=90°,CA=CB,AD是△ABC的角平分线,点E在AB上,如果DE=2CD,那么∠ADE=_________度.42.等腰三角形的周长为24,腰长为x,则x的取值范围是_________.43.如图,点C、E和点B、D、F分别在∠GAH的两边上,且AB=BC=CD=DE=EF,若∠A=12°,则∠GEF=_________度.44.如图,AB=AC,∠BAC=120°,点D在BC上,DB=DA=4,那么BC=_________.45.如图,D是等边△ABC的AC边上的中点,点E在BC的延长线上,DE=DB,△ABC的周长是9,则∠E= _________°,CE=_________.46.如图,在△ABC中,AB=AC=5,BC=6,AD=4,点E、F是中线AD上的两点,则图中阴影部分的面积是_________.47.如果一个三角形一边上的中线和这边上的高重合,那么这个三角形是_________三角形.48.△ABC是等腰三角形,AB=AC,分别以两腰为边向外作等边△ADB和等边△ACE,若∠DAE=∠DBC,则∠BAC 的度数为_________.49.如图,等边△RST的顶点R、S、T分别在等腰△ABC的边AB、BC、CA上,设∠ART=x度,∠RSB=y度,∠STC=z度,用含y、z的代数式表示x是:_________.50.等腰三角形一腰上的高与另一腰的夹角为30°,腰长为2,则其底边的高为_________.51.如图所示,△ABC是等边三角形,点是AC的中点,过D点作DM⊥BE,垂足是MD;延长BC到E,使CE=CD,求证:BM=EM.52.如图,△ABC中,AB=AC,DE是AB的垂直平分线,D为垂足,交AC于E.若AD=5cm,△ABC的周长为27cm,求△BCE的周长.53.小明在找等边三角形ABC一边的三等分点时,他是这样做的,先做∠ABC、∠ACB的角平分线并且相交于点O,然后做线段BO、CO的垂直平分线,分别交BC于E、F,他说:“E、F就是BC边的三等分点.”你同意他的说法吗?请说明你的理由.54.如图,已知:等边三角形ABC,点D是AB的中点,过点D作DF⊥AC,垂足为F,过点F作FE⊥BC,垂足为E,若三角形ABC的边长为4.求:(1)线段AF的长度;(2)线段BE的长度.55.如图AF是△ABC的角平分线,BD⊥AF,交AF的延长线于D,DE∥AC交AB于E,求证:AE=BE.56.已知如图,△ABC中,AB=AC,D是AB的中点,DE⊥AB交AC于E,(1)若BE平分∠ABC,求∠A的度数.(2)若△ABC的周长为10,△BCE的周长为6,求BC的长度.57.如图,在△ABC中,∠B=45°,AD是∠BAC的角平分线,EF垂直平分AD,交BC的延长线于点F.求∠FAC 的大小.58.如图,在△ABC中,AB=AC,CD平分∠ACB交加于D点,AE∥DC交BC的延长线于点E,已知∠E=36°,求∠B的度数.59.已知:如图,∠ACB=90°,D、E是AB上的两点,且AE=AC,BD=BC,EF⊥CD于F,求证:CF=EF.60.已知:如图,Rt△ABC中,∠ACB=90°,边AC的垂直平分线DE交AB于点D,交AC于E,连接DC.求证:DA=DC=DB.61.如图,点B,D在射线AM上,点C,E在射线AN上,且AB=BC=CD=DE,已知∠EDM=84°,求∠A的度数.62.等腰三角形中,一边与另一边之比为3:2,该三角形周长为56,求腰长是多少?63.如图:△ABC中,∠B=2∠C,AD是BC边上的高.求证:AB+BD=DC.64.如图,在△ABC中,AB=BC=AC,BD是中线,延长BC到E,使CE=CD.(1)已知CD=3,求BE的长;(2)求证:BD=ED;(3)若点F是BE边的中点,试判断DF与BE的位置关系并简要说明理由.65.如图所示,在△ABC中,∠C=90°,BD平分∠ABC交AC于点D,过点D作DE∥BC交AB于点E,过点D 作DF⊥AB于点F,说明:BC=DE+EF成立的理由.66.如图,△ABC为等边三角形,D为BC上一点,∠ADE=60°,DE交∠ACB外角平分线于E.(1)AB与CE平行吗?请说明理由.(2)请说明∠BAD=∠EDC的理由.67.如图,在等腰△ABC中,∠A=80°,∠B和∠C的平分线相交于点O(1)连接OA,求∠OAC的度数;(2)求:∠BOC.68.如图,AD是△ABC的角平分线,过点D作直线DF∥BA,交△ABC的外角平分线AF于点F,DF与AC交于点E.求证:DE=EF.69.如图,在△ABC中,AB=AC=10,点D为BC上一点,过点D分别作DE∥AB交AC于点E,DE∥AC交AB 于点F.求四边形AFDE的周长.70.如图,AD是△ABC的角平分线,且∠B=∠ADB,过点C作AD的延长线的垂线,垂足为M.(1)若∠DCM=α,试用α表示∠BAD;(2)求证:AB+AC=2AM.71.王宏和张新是同学,他们两家和学校正好构成一个等腰三角形,而且王宏家距学校2千米,张新家距学校4千米,你知道王宏与张新两家的距离吗?如果王宏家与学校相距2千米,而张新家与学校相距3千米,其他条件不变,王宏与张新两家相距多少千米?72.已知:如图,在△ABC中,∠B=∠C,点D、E、F分别是边BC、AB、AC上的点,BE=CD,连接DE、DF,有∠EDF=∠C,那么DE和DF相等吗?试说明理由.73.如图,在等腰△ABC中,AB=AC,点D在BC上,且AD=AE.(1)若∠BAC=90°,∠BAD=30°,求∠EDC的度数?(2)若∠BAC=a(a>30°),∠BAD=30°,求∠EDC的度数?(3)猜想∠EDC与∠BAD的数量关系?(不必证明)74.已知一个等腰三角形的周长为18cm.(1)如果腰长是底边的2倍,那么各边的长是多少?(2)如果一腰上的中线将该等腰三角形的周长分为1:2两部分,那么各边的长为多少?75.△ABC中,∠B=40°,过点A的直线将这个三角形分成2个等腰三角形,试确定∠C的度数.76.已知一个等腰三角形的两个内角分别为(2x﹣2)°和(3x﹣5)°,求这个等腰三角形各内角的度数.77.如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.(1)求∠ECD的度数;(2)若CE=5,求BC长.78.如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°,∠DAB=45°.(1)求∠DAC的度数;(2)求证:DC=AB.79.如图,在△ABC中,AB=AC,D是BC上任意一点,过D分别向AB,AC引垂线,垂足分别为E,F,CG是AB边上的高.(1)DE,DF,CG的长之间存在着怎样的等量关系?并加以证明;(2)若D在底边的延长线上,(1)中的结论还成立吗?若不成立,又存在怎样的关系?请说明理由.80.如图,已知在△ABC中,AB=AC,D是AB上一点,DE⊥BC,E是垂足,ED的延长线交CA的延长线于点F,求证:AD=AF.参考答案:1.∵DE是AB的垂直平分线,∴AE=BE,∵△ABC的周长为25cm,△EBC的周长为16cm,AC=AB,∴2AC+BC=25cm,BE+CE+BC=AE+EC+BC=AC+BC=16cm,即,解得:AC=9cm,故选B.2.∵AB=AC∴∠B=∠C∵FD⊥BC于D,DE⊥AB于E∴∠BED=∠FDC=90°∵∠AFD=158°∴∠EDB=∠CFD=180°﹣158°=22°∴∠EDF=90°﹣∠EDB=90°﹣22°=68°.故选C3.∵AB=AD,∴∠B=∠ADB,由∠BAD=80°得∠B==50°=∠ADB,∵AD=DC,∴∠C=∠ACD,∴∠C=∠ADB=25°故选D.4.A、等腰三角形两腰上的高相等,故错误;B、等腰三角形不一定是锐角三角形,故错误;C、有一个角是60°的等腰三角形是等边三角形,故错误;D、三角形三条角平分线的交点到三边的距离相等,故正确,故选D5.∵AB=AC,∴△ABC是等腰三角形,∵∠A是顶角,且∠A等于∠C的一半,∴∠A+∠C+∠ABC=∠A+2∠A+2∠A=180°,∴∠A=36°,∠C=∠ABC=72°,BD平分∠ABC交AC于D,∴∠ABD=∠DBC=36°,∵∠A=∠ABD=36°,∴△ABD是等腰三角形.∠BDC=∠A+∠ABD=36°+36°=72°=∠C,∴△BDC是等腰三角形.∴共有3个等腰三角形.故选B.6.AB=2,∵等边三角形高线即中点,∴BD=CD=1,在Rt△ABD中,AB=2,BD=1,∴AD==,∴等边△ABC 的面积为BC•AD=×2×=,故选:B.7.∵△ABC是等边三角形,∴∠B=∠BAC=60°,∵∠BAD=20°,∴∠DAE=∠BAC﹣∠BAD=40°,∵AD=AE,∴∠ADE=∠AED,∵∠ADE+∠AED+∠DAE=180°,∴∠ADE=∠AED=×(180°﹣40°)=70°,∵∠ADC=∠B+∠BAD=60°+20°=80°,∴∠CDE=∠CDA﹣∠ADE=80°﹣70°=10°.故选A8.连接AD.∵DE垂直平分AB,BD=3,∴BD=AD=3;∴∠B=∠BAD(等边对等角);又∵∠ABC=15°,∴∠BAC=15°;∴∠ADC=2∠BAC=30°(外角定理),∴=cos∠ADC,∴DC=AD•cos30°=.故选A.9.过E作EM∥BC,交AD于N,∵AC=4,AE=2,∴EC=2=AE,∴AM=BM=2,∴AM=AE,∵AD是BC边上的中线,△ABC是等边三角形,∴AD⊥BC,∵EM∥BC,∴AD⊥EM,∵AM=AE,∴E和M关于AD对称,连接CM交AD于F,连接EF,则此时EF+CF的值最小,∵△ABC是等边三角形,∴∠ACB=60°,AC=BC,∵AM=BM,∴∠ECF=∠ACB=30°,故选C.10.∵∠A=∠P1P2A=16°∴∠P2P1P3=32°,∠P1P3P2=32°∴∠P1P2P3=116°∴∠P3P2P4=48°∴∠P3P2P4=48°∴∠P2P3P4=96°∴∠P4P3P5=52°∴∠P3P5P4=52°∴∠P3P4P5=52°∴∠P5P4P6=76°∴∠P4P6P5=76°∴∠P4P5P6=28°∴∠P6P5P7=86°,此时就不能在往上焊接了,综上所述总共可焊上5条.故选B.11.△ABC的周长为6,∴AB=BC=AC=2,DC=CE=1,又∵∠ACB=∠CDE+∠CED∴∠CED=30°,△BDE为等腰三角形,DE=BD=∴BD+DE+BE=2+2+1=3+2.故选C12.①三条边相等的三角形是等边三角形符合等边三角形的定义,故正确;②有一个角是60°的等腰三角形是等边三角形,正确;③有两个角为60°的三角形是等边三角形,正确;④三个角相等的三角形是等边三角形,正确.故选D13.∵ED⊥BC,∠C=60°,∴∠CED=30°,设DE=x,则AE=x,且CE=x,又∵AE+CE=5,∴x+x=5,解得x=10﹣15,∴CE=5﹣(10﹣15)=20﹣10.故选D14.①BC边为底边时,AD=BC=BD=CD,所以△ABD和△ADC为等腰直角三角形,∠BAC=∠BAD+∠CAD=90°.②BC 边为腰时可分为和两种情况,垂足在三角形内部时,AD==AC,所以∠C=30°,又因为AC=BC,所以∠BAC=∠ABC=(180°﹣∠C)=75°.垂足落在三角形外时,由图知AD=AB,所以∠ABD=30°,所以∠BAC=∠C=∠ABD=15°.故答案为D15.∵P关于OA、OB的对称∴OA垂直平分PC,OB垂直平分PD∴CM=PM,PN=DN∴∠PMN=2∠C,∠PNM=2∠D,∵∠PRM=∠PTN=90°,∴在四边形OTPR中,∴∠CPD+∠O=180°,∴∠CPD=180°﹣40°=140°∴∠C+∠D=40°∴∠MPN=180°﹣40°×2=100°故选D16.当顶角为∠A=50°时,∠B=65°,当顶角为∠B=70°时,∠A=55°所以A选项错误.当顶角为∠B=40°时,∠A=70°,所以B选项正确.当顶角为∠A=30°时,∠B=75°,当顶角为∠B=90°时,∠A=45°所以C选项错误.当顶角为∠A=80°时,∠B=50°,当顶角为∠B=60°时,∠A=60°所以D选项错误.故选B17.∵PC∥OA,∴∠CPO=∠POA,∵∠AOP=∠BOP=15°,∴∠AOP=∠BOP=∠CPO=15°,过点P作∠OPE=∠CPO交于AO于点E,则△OCP≌△OEP,∴PE=PC=10,∵∠PEA=∠OPE+∠POE=30°,∴PD=10×=5.故选C.18.4是腰长时,三角形的三边分别为4、4、9,∵4+4=8<9,∴不能组成三角形,4是底边时,三角形的三边分别为4、9、9,能组成三角形,周长=4+9+9=22,综上所述,该等腰三角形的周长为22.故选D 19.根据三角形的内角和定理,得:∠ABO=∠DCO=36°,根据三角形的外角的性质,得∠AOB=∠COD=72°.再根据等角对等边,得等腰三角形有△AOB,△COD,△ABC,△CBD和△BOC.故选B20.∵AD⊥BC,D为BC的中点,∴∠ADB=∠ADC=90°,BD=BC,AD为公共边,∴△ABD≌△ACD,∴AB=AC,∠B=∠C,∠BAD=∠CAD,即AD是△ABC的角平分线.故选D21.∵△ABC是等边三角形,∴AB=BC=AC,∠A=∠B=∠C=60°又∵OE⊥AB,OF⊥AC,∠B=∠C=60°,∴OE=OB•sin60°=OB,同理OF=OC.∴OE+OF=(OB+OC)=BC.在等边△ABC中,高h=AB=BC.∴OE+OF=h.又∵等边三角形的高为2,∴OE+OF=2,故选C22.∵AB边的垂直平分线交AB于E,交BC于D(已知)∴AD=BD(线段垂直平分线的性质)∴∠DAE=∠B=15°且AD=BD=13cm(等腰三角形的性质)∴∠ADC=30°(外角性质)∴AC=AD=6.5cm.故选B23.在Rt△ABC和Rt△ADC中,AB=AD,AC=AC,所以Rt△ABC≌Rt△ADC(HL).所以∠ACB=∠ACD,∠BAC=∠DAC,即AC平分∠BAD,CA平分∠BCD.故①②正确;在△ABD中,AB=AD,∠BAO=∠DAO,所以BO=DO,AO⊥BD,即AC垂直平分BD.故③正确;不能推出∠ABO=∠CBO,故④不正确.故选B24.原式可化为2a2+2b2+2c2=2ab+2ac+2bc,即a2+b2+c2+a2+b2+c2﹣2ab﹣2ac﹣2bc=0;根据完全平方公式,得:(a﹣b)2+(c﹣a)2+(b﹣c)2=0;由非负数的性质,可知:a﹣b=0,c﹣a=0,b﹣c=0;即:a=b=c.所以△ABC是等边三角形.故选C.25.∵AB=AD,∴∠B=∠D=α,∵AB=BC∴∠BAC=∠BCA,∵∠ACB=α+β∴在等腰三角形ABC中,2(α+β)+α=180°∴3α+2β=180°,故选B26.连接AP、BP、CP,过点A作AD⊥BC于D,等边三角形面积S=BC•(PQ+PR+PS)=BC•AD故PQ+PR+PS=AD,∴AD=6+8+10=24,∵∠ABC=60°∴AB=24×=16,∴△ABC的面积S=BC•AD=×24×16=192,故选B.27.把三角形每条边分成n份,相应点之间连线,可以把三角形分成n2个边长为的小三角形,至少n2+1个点可以保证至少有两个点落在同一个小三角形内,所以那两个点的距离是不超过的.故选A28.设BM=x,CN=y则BP=2x,PC=2y,PM=x,PN=yAM+AN=2BC﹣(BM+CN)=3(x+y),故==≈0.7887.故选D.29.①∵DE,EF,FD为等边△ABC三条中位线,∴AB=AC=BC,∴EF AB,ED AC,∴四边形CEDF是菱形,∴EF⊥CD,∴在菱形CEDF中有6个不同的直角三角形:Rt△CEG、Rt△CFG、Rt△DGE、Rt△DFG、Rt△EOG、Rt△FOG;同理,在菱形ADEF、菱形BEFD中各有6个不同的直角三角形;②∵D为等边三角形ABC三边中点,∴CD⊥AB,∴△ADC、△BDC、AOD、△BOD是直角三角形;同理,以BF、AE为直角边的三角形各有4个;综上所述,图中能数出的直角三角形由6×3+4×3=30(个);故选C30.当∠B=50°为顶角时,此时∠A=∠C==65°;当∠B=50°为底角时,此时另一底角为50°,顶角为80°,故答案为:50°,80°或65°,65°31.根据题意,可以以点A为圆心,以AB为半径作圆,即可得出点B、C、D均在圆周上,故有∠BAC=2∠BDC=50°,即∠BDC=25°.故答案为:25°32.在DC上截取DE=BD,连接AE,∵AD⊥BC,∴∠ADB=∠ADE=90°,∵AD=AD,∴△ADB≌△ADE,∴∠B=∠AED,AE=AB,∵AB+BD=DC,DE+EC=DC,∴AE=AB=EC,∴∠AEB=2∠EAC=2∠C,∴∠B=2∠C,∵∠BAC=135°,∠B+∠C+∠BAC=180°,∴3∠C=45°,∴∠C=15°.故答案为:1533.过D作DE⊥AB于E,∵AD是∠BAC的角平分线,∠C=90°,DE⊥AB,∴CD=DE,∵BD=2CD,∴BD=2DE,∵∠BED=90°,∴∠B=30°.故答案为:3034.设等腰三角形的腰长是xcm,底边是ycm.根据题意,得:或,解得或.再根据三角形的三边关系,知:8,8,17不能组成三角形,应舍去.所以它的底边是5cm.故答案为:535.如图:△ABC中,AB=AC,BD是边AC上的高.∵∠A=80°,且AB=AC,∴∠ABC=∠C=(180°﹣80°)÷2=50°;在Rt△BDC中,∠BDC=90°,∠C=50°;∴∠DBC=90°﹣50°=40°.故答案为:40°36.∵(a+b+c)(a﹣c)=0,∴a+b+c=0或a﹣c=0,∵a、b、c,为三角形三边,∴a+b+c=0(舍去),∴a=c∴该三角形为等腰三角形,故答案为:等腰三角形37.如图作AD⊥BC于点D.∵△ABC为等边三角形,∴∠B=60°,∴AD=AB×sin∠B=a,∴边长为a 的等边三角形的面积为×a ×a=a2,故答案为:a238.∵AB=AC,AP=PQ,QP=QC,QC=BC,∴∠ABC=∠ACB,∠A=∠AQP,∠QPC=∠QCP,∠BQC=∠B(等边对等角),设∠A=x°,则∠AQP=x°,∵在△AQP中,∠QPB是外角,∴∠QPC=∠A+∠AQP=2x°(三角形的一个外角等于和它不相邻的两个内角的和),∵在△BCQ中,∠BQC是外角,∴∠BQC=∠ACQ+∠A(三角形的一个外角等于和它不相邻的两个内角的和),∴∠BQC=3x°,∴∠B=3x°,∴∠ABC=3x°,∵在△ABC中,∠A+∠ACB+∠B=180°,∴x°+3x°+3x°=180°(三角形三个内角的和等于180°),解得x=()°,∴∠A=()°.39.∵△ABC中,∠C=90°,∠B=15°,∴∠BAC=180°﹣∠C﹣∠B=180°﹣90°﹣15°=75°.连接AD.∵ED是AB的垂直平分线,∴AD=BD=8,∠B=∠1=15°,∴∠2=∠BAC﹣∠1=75°﹣15°=60°.在Rt△ACD中,∠2=60°,∠C=90°,∴∠3=180°﹣∠C﹣∠2=180°﹣90°﹣60°=30°.∴AC=AD=BD=×8=4.40.∵OC为等边三角形的高,且等边三角形的边长为1,∴NC=,∵△OCD为等边三角形,∴∠OCD=60°,∴OE⊥CD,∴OE==()2,以此类推,当ON与OA重合时,一共旋转了10次,∴ON 的长为()10,故答案为()1041.作DF⊥AB于点F∵△ABC中,∠ACD=90°,CA=CB,∴∠CAB=∠B=45°,∵AD是△ABC的角平分线,∴DF=DC,∠DAB=22.5°,∵DE=2CD,∴DE=2DF,∴∠DEB=30°,∴∠ADE=∠DEB=﹣∠DAB=30°﹣22.5°=7.5°,故答案为7.5°.42.底边是24﹣2x,根据三角形的三边关系:两边之和大于第三边,两边之差小于第三边.得:0<24﹣2x<2x.解得6<x<12.故填6<x<1243.∵∠A=12°,AB=BC,∴∠A=∠ACB=12°,∠CBD=∠A+∠ACB=12°+12°=24°;∵BC=CD,∴∠CBD=∠CDB=24°,∴∠ECD=∠A+∠CDA=36°(外角定理);∵CD=DE,∴∠DCE=∠DEC=36°,∴∠EDF=∠A+∠AED=48°;又∵DE=EF,∴∠EDF=∠EFD=48°,∴∠GEF=∠A+∠EFD=12°+48°=60°.故答案是:6044.∵AB=AC,∠BAC=120°,∴∠B═∠C=(180°﹣∠A)=30°,∵DB=DA=4,∴∠B=∠BAD=30°,∴∠ADC=∠B+∠BAD=60°,∴∠DAC=180°﹣∠C﹣∠ADC=90°,∵∠C=30°,∴DC=2AD=2×4=8,∴BC=BD+DC=4+8=12,故答案为:1245.∵△ABC为等边三角形,D为AC边上的中点,∴BD为∠ABC的平分线,且∠ABC=60°,即∠DBE=30°,又DE=DB,∴∠E=∠DBE=30°,∵等边△ABC的周长为9,∴AC=3,且∠ACB=60°,∴∠CDE=∠ACB﹣∠E=30°,即∠CDE=∠E,∴CD=CE=AC=.故答案为:30;46.∵AB=AC,BC=6,AD是△ABC的中线,∴BD=DC=BC=3,AD⊥BC,∴△ABC关于直线AD对称,∴B、C关于直线AD对称,∴△CEF和△BEF关于直线AD对称,∴S△BEF=S△CEF,∵△ABC 的面积是:×BC×AD=×6×4=12,∴图中阴影部分的面积是S△ABC=6.故答案为:647.∵BD=CD,AD⊥BC,∴AB=AC,即三角形是等腰三角形.故填等腰.48.∵AB=AC,∴∠ABC=∠ACB,故2∠ABC+∠BAC=180°,∵等边三角形各内角为60°,∠DAE=∠DBC,∴120°+∠BAC=60°+∠ABC,又∵2∠ABC+∠BAC=180°,∴∠BAC=20°.故答案为:20°49.∵∠BRS+y=∠TSC+z,∴∠BRS﹣∠TSC=z﹣y,又∠BRS+x=y+∠TSC=120°,∴∠BRS﹣∠TSC=y﹣x,∴z﹣y=y﹣x,∴x=2y﹣z.故答案为:x=2y﹣z.50.①如图1,已知AB=AC=2,BD为腰AC上的高,可知∠ABD=30°,可得∠A=60°,即证△ABC为正三角形,即可得出底边AC 上的高等于腰上的高等于.②如图2,AB=AC=2,CD⊥BA交BA是延长线于点D,且∠CAD=30°,可得AD=1,CD=,可得BC=2,即BE=,在Rt△ABE中,AB=2,BE=,即AE=1.故答案为:1或.51.∵△ABC是等边三角形,D是AC的中点,∴BD平分∠ABC(三线合一),∴∠ABC=2∠DBE;∵CE=CD,∴∠CED=∠CDE.又∵∠ACB=∠CED+∠CDE,∴∠ACB=2∠E;又∵∠ABC=∠ACB,∴2∠DBC=2∠E,∴∠DBC=∠E,∴BD=DE.又∵DM⊥BE,∴BM=EM.52.∵DE是AB的垂直平分线.∴AB=2AD,EA=EB.∵AD=5cm,∴AB=10cm.∵△ABC的周长为27cm,∴AC+BC+AB=2cm7,AC+BC=17cm即AE+EC+BC=17cm.∴EB+EC+BC=17.即△BCE的周长为17cm53.E,F是BC的三等分点.理由:连接OE,OF,∵DE垂直平分OB∴BE=OE(线段垂直平分线上的点到线段两端点距离相等),同理OF=CF,∴∠EBO=∠BOE,∠FCO=∠FOC,∵等边三角形ABC中,∴∠ABC=∠ACB=60°(等边三角形各角相等且为60°)∵BO平分∠ABC,CO平分∠ACB∴∠EBO=∠ABC=30°,∠FCO=∠ACB=30°∴∠BOE=∠EBO=30°,∠FOC=∠FCO=30°∴∠OEF=∠BOE+∠EBO=60°,∠OFE=∠FOC+∠FCO=60°,∴△OEF是等边三角形(有两个内角60°的三角形是等边三角形)∴OE=OF=EF(等边三角形各边相等)∴BE=EF=FC,即E,F是BC的三等分点54.(1)∵D是AB的中点,∴AD==2,∵等边三角形ABC中∠A=∠C=60°,且DF⊥AC,∴∠ADF=180°﹣90°﹣60°=30°,在Rt△ADF中,AF==1;(2)FC=AC﹣AF=4﹣1=3,同理,在Rt△FEC中,EC==1.5,∴BE=BC﹣EC=4﹣1.5=2.5.故答案为:AF=1,BE=2.555.∵AF平分∠BAC,∴∠BAD=∠CAD,∵DE∥AC,∴∠EDA=∠CAD=∠BAD,∴AE=ED,∵∠EDB+∠ADE=90°,∴∠BDE+∠BAD=90°,∵∠EBD+∠BAD=90°,∴∠BDE=∠EBD,∴BE=ED,∴AE=BE.56.(1)∵D是AB的中点,DE⊥AB交AC于E,∴EB=EA,∴∠A=∠ABE,∵BE平分∠ABC,∴∠ABE=∠CBE,∵AB=AC,∴∠C=∠ABC=2∠ABE=2∠A,∵∠A+∠ABC+∠C=180°,即:5∠A=180°∴∠A=36°;(2)∵△ABC的周长为10,∴AB+AC+BC=10,∵△BCE的周长为6,∴BE+EC+BC=AE+EC+BC=AC+BC=6,∴AB=AC=4.∴BC=257.∵EF垂直平分AD,∴FA=FD,∴∠ADF=∠DAF,又∵∠ADF=∠B+∠BAD,∠DAF=∠FAC+∠DAC,∵∠BAD=∠DAC,∴∠FAC=∠B=45°.58.∵AE∥DC,∴∠BCD=∠E=36°,又∵CD平分∠ACB,∴∠ACB=2∠BCD=72°,∵AB=AC,∴∠B=∠ACD=72°.答:∠B的度数为72°.59.连接CE.∵AE=AC,∴∠1+∠2=∠AEC=∠3+∠B.①同理,∠2+∠3=∠1+∠A.②①+②得2∠2=∠A+∠B.∵∠ACB=90°,∴∠A+∠B=90°.∴∠2=45°.∵EF⊥CD,∴∠CFE=90°.∴∠CEF=45°=∠2,∴EF=CF.60.∵AC的垂直平分线DE,∴AD=DC,∴∠A=∠ACD,∵∠ACB=90°,∴∠A+∠B=90°,∠ACD+∠BCD=90°,∴∠B=∠BCD,∴DC=BD,∴DA=DC=DB61.∵AB=BC=CD=DE,∴∠A=∠BCA,∠CBD=∠BDC,∠ECD=∠CED,根据三角形的外角性质,∠A+∠BCA=∠CBD,∠A+∠CDB=∠ECD,∠A+∠CED=∠EDM,又∵∠EDM=84°,∴∠A+3∠A=84°,解得:∠A=21°62.∵等腰三角形中,一边与另一边之比为3:2,∴设两边分别为3x,2x,根据题意得:3x+3x+2x=56或3x+2x+2x=56解得:x=7,此时腰长3x=21,或x=8,此时腰长2x=16,所以腰长为21或1663.在线段DC上取一点E,使DE=DB,连接AE,∵AD⊥BC,∴AD垂直平分BE,∴AB=AE,∴∠AEB=∠B,∵∠B=2∠C,∴∠AEB=2∠C,∴∠EAC=∠AEB﹣∠C=2∠C﹣∠C=∠C,∴AE=CE,∴CE=AE=AB,∴DC=DE+CE=AB+BD,∴AB+BD=DC.64.(1)∵AB=BC=AC,BD是中线,∴BC=AC=2CD∵CD=3,∴BC=2CD=6,CE=CD=3∴BE=BC+CE=6+3=9(2)∵△ABC是等边三角形,BD是中线,∴∠ABC=∠ACB=60°.∠DBC=30°(等腰三角形三线合一).又∵CE=CD,∴∠CDE=∠CED.又∵∠BCD=∠CDE+∠CED,∴∠CDE=∠CED=∠BCD=30°.∴∠DBC=∠DEC.∴DB=DE(等角对等边).(3)∵点F是BE边的中点,∴DF是BE边的中线,∵BD=ED∴DF⊥BE65.∵BD平分∠ABC,DF⊥AB,∠C是直角,∴CD=DF,∠DBC=∠DBE,∠DFB=∠C,∴△BCD≌△BFD,∴BC=BF,∵DE∥BC,∴∠DBC=∠EDB,即∠DBC=∠DBE,∴△BDE是等腰三角形,∴BE=DE,∴BF=BC=DE+EF66.(1)∵等边三角形各内角为60°∴∠ACF=180°﹣60°=120°,CE为∠ACF的角平分线,∴∠ECF=60°,∵∠ABC=60°∴EC∥AB.(2)∵∠EDC+∠ADE+∠ADB=180°,∴∠EDC+∠ADB=120°,∵∠ABD+∠BAD+∠ADB=180°,∴∠BAD+∠ADB=120°,∴∠BAD=∠EDC.67.(1)连接AO,∵在等腰△ABC中,∠B和∠C的平分线相交于点O,∴等腰△ABC关于线段AO所在的直线对称,∵∠A=80°,∴∠OAC=40°(2)∵BO、CO分别平分∠ABC和∠ACB,∴∠OBC=∠ABC,∠OCB=∠ACB,∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣(∠ABC+∠ACB)=180°﹣(∠ABC+∠ACB)=180°﹣(180°﹣∠A)=90°+∠A.∴当∠A=80°时,=130°.68.证明:∵AD是△ABC的角平分线,AF平分△ABC 的外角,∴∠1=∠2,∠3=∠4,∵DF∥BA,∴∠4=∠ADE,∠1=∠F∴∠3=∠ADE,∠2=∠F∴DE=EA EF=EA∴DE=EF69.∵AB=AC=10,∴∠B=∠C,由DF∥AC,得∠FDB=∠C=∠B,∴FD=FB,同理,得DE=EC.∴四边形AFDE的周长=AF+AE+FD+DE=AF+FB+AE+EC=AB+AC=10+10=20.∴四边形AFDE的周长为2070.(1)∵CM⊥AM,∠DCM=α,∴∠CDM=∠ADB=∠B=90°﹣α,∴∠BAD=180°﹣2∠ABD=180°﹣2(90°﹣α)=2α;(2)延长AM到F使MF=AM,则有AC=CF∵AD平分∠CAB∴∠CAF=∠BAF=∠F∴CF∥AB∴∠FCD=∠ABD=∠ADB=∠CDF∴CF=DF∵AD+DF=2MA∴AB+AC=2MA71.∵王宏和张新他们两家和学校正好构成一个等腰三角形,而且王宏家距学校2千米,张新家距学校4千米,∴此等腰三角形的底边长为2,两腰均为4,∴王宏与张新两家的距离是4千米;当王宏家与学校相距2千米,而张新家与学校相距3千米时,王宏与张新两家相距可能是2千米也可能是3千米72.DE=DF.证明:∵∠CDF+∠EDF+∠BDE=180°,∠CDF+∠C+∠CFD=180°∴∠BDE=∠CFD在△EBD和△DCF中∠BDE=∠CFDBE=CD∠B=∠C∴△EBD≌△DCF∴DE=DF73.(1)解:∵∠BAC=90°,AB=AC,∴∠B=∠C=(180°﹣∠BAC)=45°,∴∠ADC=∠B+∠BAD=45°+30°=75°,∵∠DAC=∠BAC﹣∠BAD=90°﹣30°=60°,∵AD=AE,∴∠ADE=∠AED=(180°﹣∠DAC)=60°,∴∠EDC=∠ADC﹣∠ADE=75°﹣60°=15°,答:∠EDC的度数是15°.(2)解:与(1)类似:∠B=∠C=(180°﹣∠BAC)=90°﹣α,∴∠ADC=∠B+∠BAD=90°﹣α+30°=120°﹣α,∵∠DAC=∠BAC﹣∠BAD=α﹣30°,∴∠ADE=∠AED=(180°﹣∠DAC)=105°﹣α,∴∠EDC=∠ADC﹣∠ADE=(120°﹣α)﹣(105°﹣α)=15°,答:∠EDC的度数是15°.(3)∠EDC与∠BAD的数量关系是∠EDC=∠BAD.74.(1)解:设底边BC=acm,则AC=AB=2acm,∵三角形的周长是18cm,∴2a+2a+a=18,∴a=,2a=,答:等腰三角形的三边长是cm ,cm ,cm.(2)解:设BC=acm,AB=AC=2bcm,∵中线BD将△ABC的周长分为1:2两部分,18×=12,18×=6,∴2b+b=6,b+a=12或2b+b=12,b+a=6,解得:a=10,b=2或b=4,a=2,∴①三角形三边长是10cm,4cm,4cm,因为4+4<10,不符合三角形三边关系定理,∴此种情况舍去,②三角形的三边长是2cm,8cm,8cm,符合三角形的三边关系定理,综合上述:符合条件的三角形三边长是8cm,8cm,2cm,答:等腰三角形的边长是8cm,8cm,2cm.75.分成两类进行研究:(1)∠B为△ABD的底角,如果∠BAD=40°,那么∠ADC=80°;如果∠ADC为△ACD的底角,那么∠C=80°或20°;如果∠ADC为△ACD的顶角,那么∠C=50°;如果∠ADB=70°,那么∠ADC=140°,所以∠C=20°(2)∠B为△ABD的顶角,这时∠ADB=70°,∠ADC=110°,所以∠C=35°;综上所述,∠C的值为20°或35°或50°或80°76.①当(2x﹣2)°和(3x﹣5)°是两个底角时,2x﹣2=3x﹣5,x=3°,∴三个内角分别是4°,4°,172°;②当2x﹣2是顶角时,2x﹣2+2(3x﹣5)=180°,解得x=24°,∴三个内角分别是46°,67°,67°;③当3x﹣5是顶角时,3x﹣5+2(2x﹣2)=180°,解得x=27°,∴三个内角分别是76°52°,52°77.(1)∵DE垂直平分AC,∴CE=AE,∴∠ECD=∠A=36°;(2)∵AB=AC,∠A=36°,∴∠B=∠ACB=72°,∴∠BEC=∠A+∠ECD=72°,∴∠BEC=∠B ,∴BC=EC=5.答:(1)∠ECD 的度数是36°;(2)BC 长是578.1)解:∵AB=AC ,∴∠B=∠C=30°,∵∠C+∠BAC+∠B=180°,∴∠BAC=180°﹣30°﹣30°=120°,∵∠DAB=45°,∴∠DAC=∠BAC ﹣∠DAB=120°﹣45°=75°;(2)证明:∵∠DAB=45°,∴∠ADC=∠B+∠DAB=75°,∴∠DAC=∠ADC ,∴DC=AC ,∴DC=AB 79.(1)DE+DF=CG .证明:连接AD ,则S △ABC =S △ABD +S △ACD ,即AB •CG=AB •DE+AC •DF ,∵AB=AC ,∴CG=DE+DF .(2)当点D 在BC 延长线上时,(1)中的结论不成立,但有DE ﹣DF=CG .理由:连接AD ,则S △ABD =S △ABC +S △ACD ,即AB •DE=AB •CG+AC •DF∵AB=AC ,∴DE=CG+DF ,即DE ﹣DF=CG .同理当D 点在CB 的延长线上时,则有DE ﹣DF=CG ,说明方法同上.80.证明:∵AB=AC ,∴∠B=∠C ,∵DE ⊥BC ,∴∠C+∠F=90°,∠B+∠BDE=90°,∵∠ADF=∠BDE ,∴∠F=∠ADF ,∴AD=AF。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
.等腰三角形和等边三角形练习题1.如图,等边△ABC 的边长为3,P 为BC 上一点,且BP=1,D 为AC 上一点,若∠APD=60°,则CD 的长为()A.32B.23C.12D.34 AD60°CBP2.如图,△ABC 中,D、E 分别是 BC、AC 的中点,BF 平分∠ABC,交 DE 于点 F,若 BC=6,则DF 的长是(A)2 (B)3 (C)52(D)43.如图,点A 的坐标是(2,2) ,若点 P 在x 轴上,且△APO 是等腰三角形,则点P 的坐标不.可.能.是()A.(4,0) B.(1.0)C.(-2 2 ,0)D.(2,0)yByA21-1 0 1 2 3 4 x A DC4.如图, AB=AC,BD=BC,若∠A=40°,则∠ABD 的度数是()A.20 B.30 C.35 D.405.如图,△ABC 中,AB=AC=6,BC=8,AE 平分么 BAC 交BC 于点E,点D 为 AB 的中点,连结DE,则△BDE 的周长是( )A.7+ 5 B.10 C.4+2 5 D.12..6.在等腰△ABC中,AB AC ,一边上的中线BD 将这个三角形的周长分为15 和12 两个部分,则这个等腰三角形的底边长为()A.7 B.11 C.7 或11 D.7 或107 .等腰三角形一腰上的高与另一腰的夹角为30 o,腰长为 4 cm ,则其腰上的高为cm .8.已知等腰△ABC的周长为10,若设腰长为x ,则x 的取值范围是.9.在△ABC 中,AB=AC,AB 的垂直平分线与AC 所在的直线相交所得到锐角为50°,则∠B 等于__________度_ .10.如图,在△ABC 中,AB= AC,∠A =36 °,BD、CE分别是△ABC、△BCD 的角平分线,则图中的等腰三角形有(A)5 个(B)4 个(C)3 个(D)2 个ADEB C(第 10 题)11.(2010 黄冈)如图,过边长为 1 的等边△ABC 的边 AB 上一点 P,作 PE⊥AC 于E,Q 为1 BC 延长线上一点,当PA=CQ 时,连 PQ 交AC 边于D ,则DE 的长为()A.31 B.2C.23D.不能确定12.如图,等腰△ ABC 中,AB=AC ,∠A=20 °。
线段AB 的垂直平分线交AB 于D,交 AC 于E,连接 BE,则∠CBE 等A、80 °B、70°C、60°D、50°..13.已知等腰三角形的两条边长分别是7 和3,则下列四个数中,第三条边的长是( ) A.8 B.7 C.4 D.314.如图,△ABC 内有一点D,且 DA=DB=DC ,若∠DAB=20 °,∠DAC=30 °,则∠BDC 的大小是()ADCB A.100 ° B.80° C.70° D.50°15.如图,在△ABC 中,D,E分别是边 AC,AB 的中点,连接 BD.若 BD 平分∠ABC,则下列结论错误的是AEDBA.BC=2BE B.∠A=∠EDA C.BC=2AD D.BD⊥ACC16.如图所示的正方形网格中,网格线的交点称为格点.已知A、B 是两格点,如果C 也是图中的格点,且使得ABC为等.腰.三.角.形.,则点C 的个数是.BA第 8 题图A.6 B.7 C.8 D.917.已知等腰三角形的一个内角为70°,则另外两个内角的度数是()A.55 °,55°B.70°,40°C.55°,55°或 70°,40°D.以上都不对18.已知:一等腰三角形的两边长x、y 满足方程组2x- y 3,则此等腰三角形的周长为()3x 2y8,A.5 B.4 C.3 D.5 或 419.如图,点C 是线段 AB 上的一个动点,△ACD 和△BCE是在 AB 同侧的两个等边三角形, DM ,EN 分别是△ACD 和△BCE 的高,点 C 在线段 AB 上沿着从点A 向点 B 的方向移动(不与点 A,B 重合),连接 DE,得到四边形DMNE .这个四边形的面积变化情况为()(A)逐渐增大(B) 逐渐减小(C) 始终不变(D) 先增大后变小20.如图,把等腰直角△ABC 沿BD 折叠,使点 A 落在边 BC 上的点 E处.下面结论错误的是()A.AB=BE B.AD =DC C.AD =DE D.AD =EC21.已知:△ABC中,AB=AC= x ,BC=6 ,则腰长 x 的取值范围是()A.0 x 3 B.x 3 C.3 x 6 D.x 6.22.如图,吴伯伯家有一块等边三角形的空地 ABC,已知点E、F 分别是边AB、AC 的中点,量得EF=5 米,他想把四边形BCFE用篱笆围成一圈放养小鸡,则需用篱笆的长是AE FB C(第5题图 )A、15 米B、20 米C、25 米D、30 米23.如图1,△ABC 中, AC=AD=BD ,∠DAC=80 °。
则∠B 的度数是A.40 °B.35°C.25°D.20°24.如图,小红作出了边长为1 的第1 个正△A1B1C1,算出了正△A1B1C1 的面积,然后分别取△A1 B1C1 三边的中点A2,B2,C2,作出了第 2 个正△A2B2C2,算出了正△A2B2C2 的面积,用同样的方法,作出了第 3 个正△A3B3C3,算出了正△A3B3C3 的面积⋯⋯,由此可得,第8 个正△A8 B8C8 的面积是()A.3 17( )4 2B.3 18( )4 2C.3 17( )4 4D .3 18( )4 425.等腰三角形的两边长为4、9,则它的周长是A.17 B.17 或22 C.20 D.2226.如图所示,已知△ABC 和△DCE 均是等边三角形,点B、C、E 在同一条直线上,AE 与 BD 交于点O,AE 与 CD 交于点G,AC 与 BD 交于点F,连结O C、FG,则下列结论:①AE=.BD ②AG=BF ③FG∥BE ④∠ BOC=∠EOC,其中正确结论的个数()A.1 个B.2 个C.3 个D.4 个27.如图,△ABC 中, DE 垂直平分AC 交AB 于E,∠A=30 °,∠ACB =80 °,则∠BCE= ▲°.CDABE(第16 题)28.如图,将第一个图(图①)所示的正三角形连结各边中点进行分割,得到第二个图(图②);再将第二个图中最中间的小正三角形按同样的方式进行分割,得到第三个图(图③);再将第三个图中最中间的小正三角形按同样的方式进行分割,⋯⋯,则得到的第五个图中,共有_______个_正三角形.⋯⋯图①图②图③29.(2010 山东滨州)如图,等边△ABC 的边长为6,AD 是BC 边上的中线,M 是 AD 上的动点 ,E 是 AC 边上一点 .若AE=2,EM+CM 的最小值为..30.如图,在△ABC 中,AB=AC=13 ,BC=10 ,D 是AB 的中点,过点D 作DE⊥AC 于点 E,则DE 的长是。
31.如图,等腰三角形ABC 中,已知 AB=AC,∠A=30°,AB 的垂直平分线交AC 于D,则∠CBD 的度数为.7.如果一个等腰三角形的两边长分别是5cm 和6cm ,那么此三角形的周长是A.15cm B.16cm C.17cm D .16cm 或17cm 8.如图,在△ABC 中,AB AC 13,BC 10,点D 为BC 的中点, DE DE AB ,垂足为点E ,则DE 等于()A.1013B.1513C.6013D.75139.边长为 6cm 的等边三角形中,其一边上高的长度为________.10.等腰三角形的周长为14,其一边长为4,那么,它的底边为.12.在等腰Rt△ABC 中,∠C=90 °,AC=1,过点 C 作直线 l∥AB,F 是l 上的一点,且AB=AF,则点 F 到直线 BC 的距离为.13.已知等边△ABC 中,点 D,E分别在边AB,BC 上,把△BDE 沿直线 DE 翻折,使点B 落在点Bˊ处,DBˊ,EBˊ分别交边 AC 于点 F,G,若∠ADF=80 o ,则∠EGC的度数为10.如图,等边三角形ABC 中,D、E 分别为AB、BC 边上的两个动点,且总使AD=BE ,AE与CD 交于点 F,AG⊥CD 于点G,则F GAF.CEFGAD第15 题B11.如图 6,在△ABC 中,AB=AC ,∠BAC 的角平分线交BC 边于点 D,AB=5 ,BC=6 ,则AD=__________________.解答题11.如图,已知点 D 为等腰直角△ABC 内一点,∠CAD =∠CBD=15°,E 为AD 延长线上的一点,且CE=CA.(1)求证:DE 平分∠BDC;(2)若点 M 在DE 上,且 DC=DM ,求证:ME=BD .12.如图,在等腰三角形ABC 中,∠ABC=90 °,D 为AC 边上中点,过D 点作DE⊥DF,交 AB 于E,交 BC 于F,若AE=4 ,FC=3 ,求 EF长.ADEB F C13.如图 1,在等边△ABC 中,点 D 是边 AC 的中点,点P 是线段 DC 上的动点(点P 与点 C 不重合),连结 BP. 将△ABP 绕点 P 按顺时针方向旋转α角(0°<α<180 °),得到△A1B1P,连结AA 1,射线 AA1 分别交射线PB、射线 B1B 于点 E、F.(1)如图1,当 0°<α<60°时,在α角变化过程中,△BEF与△AEP 始终存在▲关系(填“相似”或“全等”),并说明理由;(2)如图2,设∠ABP= β. 当60°<α<180 °时,在α角变化过程中,是否存在△BEF与△AEP 全等?若存在,求出α与β之间的数量关系;若不存在,请说明理由;(3)如图 3,当α=60 °时,点 E、F 与点B 重合. 已知AB =4 ,设 DP= x,△A1BB1 的面积为S,求S 关于 x 的函数关系E BBFMA1A1B B1EFMB1A1CA D CA D PPA DPCB1图 1 图2 图314.如图,△ABC 中,AB=AC ,∠A=36 °,AC 的垂直平分线交AB 于E,D 为垂足,连结E C.(1)求∠ECD 的度数;(2)若CE=5 ,求BC 长.5.如图,等边△ABC 中,AO 是∠BAC 的角平分线, D 为AO 上一点,以CD 为一边且在CD 下方作等边△CDE,连结B E.(1) 求证:△ACD≌△BCE;(2) 延长BE 至 Q, P 为BQ 上一点,连结CP、CQ 使CP=CQ=5, 若 BC=8 时,求PQ 的长.12.已知:如图,锐角△ABC 的两条高BD、CE 相交于点O,且OB=OC ,(1)求证:△ABC 是等腰三角形;(2)判断点O 是否在∠BAC 的角平分线上,并说明理由。
