2018届二轮复习关联速度问题学案(全国通用)

合集下载

2018届高三二轮复习教学设计

注意：对象、受力图、合理性；
考向二、整体法、隔离法
案例二、（2013•北京）倾角为α、质量为M的斜面体静止在水平桌面上，质量为m的木块静止在斜面体上．下列结论正确的是（） A．木块受到的摩擦力大小是mgcosα B．木块对斜两体的压力大小是mgsinα C．桌面对斜面体的摩擦力大小是mgsinαcosα D．桌面对斜面体的支持力大小是（M+m）g
专题一、（1课时）力与平衡；专题二、（2课时）直线运动类运动学问题；力与直线运动综合动力学问题；专题三、（2课时）力与平抛及圆周等曲线运动；万有引力与航天；专题四、（2课时）功和功率、动能定理运用；能量守恒与功能关系；专题五、（2课时）带电粒子在电磁场中的加速与偏转类；专题六、（2课时）电磁感应和电路分析；电磁感应电与动力学能量的综合；专题七、电学实验（2课时仅1班---详见教案）专题八、压轴题预测性讲练（2课时仅1班）
注意：
1、过程划分； 2、过程分析； 3、过程联系； 4、分类求解；
专题三、力与曲线运动；
条件
抛体运动
曲线运动
处理方法圆周运动
专题三、力与曲线运动；
平抛曲线运动抛体运动
类平抛匀速圆周变速圆周
运动合成分解规律、推论
圆周运动
天体运动
考向一、运动合成与分解；
（2011海南）如图，水平地面上有一个坑，其竖直截面为半圆。ab为沿水平方向的直径。若在a点以初速度沿ab 方向抛出一小球，小球会击中坑壁上的c点。已知c点与水平地面的距离为圆半径的一半，求圆的半径。
力的效果
力的分类
相互作用
力的计算共点力平衡
平衡条件：F合=0；正交分解时： Fx=0且 Fy=0

2018学高考理科数学通用版练酷专题二轮复习教学案：第一板块求准度提速度

小题押题16—1⎪⎪集合、常用逻辑用语考查点一集合1．(2017·全国卷Ⅲ)已知集合A＝{(x，y)|x2＋y2＝1}，B＝{(x，y)|y＝x}，则A∩B中元素的个数为()A．3B．2C．1 D．0解析：选B因为A表示圆x2＋y2＝1上的点的集合，B表示直线y＝x上的点的集合，直线y＝x与圆x2＋y2＝1有两个交点，所以A∩B中元素的个数为2.2．(2016·全国卷Ⅱ)已知集合A＝{1,2,3}，B＝{x|(x＋1)·(x－2)<0，x∈Z}，则A∪B＝() A．{1} B．{1,2}C．{0,1,2,3} D．{－1,0,1,2,3}解析：选C因为B＝{x|(x＋1)(x－2)<0，x∈Z}＝{x|－1<x<2，x∈Z}＝{0,1}，A＝{1,2,3}，所以A∪B＝{0,1,2,3}．3．(2015·全国卷Ⅰ)已知集合A＝{x|x＝3n＋2，n∈N}，B＝{6,8,10,12,14}，则集合A∩B 中元素的个数为()A ．5B ．4C ．3D ．2解析：选D 集合A 中元素满足x ＝3n ＋2，n ∈N ，即被3除余2，而集合B 中满足这一要求的元素只有8和14.故选D.4．(2016·全国卷Ⅰ)设集合A ＝{x |x 2－4x ＋3<0}，B ＝{x |2x －3>0}，则A ∩B ＝( ) A.⎝⎛⎭⎫－3，－32 B.⎝⎛⎭⎫－3，32 C.⎝⎛⎭⎫1，32 D.⎝⎛⎭⎫32，3解析：选D ∵x 2－4x ＋3<0，∴1<x <3， ∴A ＝{x |1<x <3}．∵2x －3>0，∴x >32，∴B ＝⎩⎨⎧⎭⎬⎫x ⎪⎪x >32. ∴A ∩B ＝{x |1<x <3}∩⎩⎨⎧⎭⎬⎫x ⎪⎪x >32＝⎝⎛⎭⎫32，3. 考查点二命题及其真假的判断5．(2017·山东高考)已知命题p ：∀x >0，ln(x ＋1)>0；命题q ：若a >b ，则a 2>b 2.下列命题为真命题的是( )A ．p ∧qB ．p ∧綈qC ．綈p ∧qD ．綈p ∧綈q解析：选B 当x >0时，x ＋1>1，因此ln(x ＋1)>0，即p 为真命题；取a ＝1，b ＝－2，这时满足a >b ，显然a 2>b 2不成立，因此q 为假命题．由复合命题的真假性，知B 为真命题．6．(2015·全国卷Ⅰ)设命题p ：∃n ∈N ，n 2>2n ，则綈p 为( ) A ．∀n ∈N ，n 2>2n B ．∃n ∈N ，n 2≤2n C ．∀n ∈N ，n 2≤2nD ．∃n ∈N ，n 2＝2n解析：选C 因为“∃x ∈M ，p (x )”的否定是“∀x ∈M ，綈p (x )”，所以命题p 的否定是“∀n ∈N ，n 2≤2n ”．7．(2014·湖南高考)已知命题p ：若x >y ，则－x <－y ；命题q ：若x >y ，则x 2>y 2，在命题①p ∧q ；②p ∨q ；③p ∧(綈q )；④(綈p )∨q 中，真命题是( )A ．①③B ．①④C ．②③D ．②④解析：选C 由不等式的性质可知，命题p 是真命题，命题q 为假命题，故①p ∧q 为假命题，②p ∨q 为真命题，③綈q 为真命题，则p ∧(綈q )为真命题，④綈p 为假命题，则(綈p )∨q 为假命题，故选C.考查点三充分、必要条件的判断8．(2017·天津高考)设θ∈R ，则“⎪⎪⎪⎪θ－π12<π12”是“sin θ<12”的( ) A ．充分而不必要条件 B ．必要而不充分条件 C ．充要条件D ．既不充分也不必要条件解析：选A 法一：由⎪⎪⎪⎪θ－π12<π12，得0<θ<π6，故sin θ<12.由sin θ<12，得－7π6＋2k π<θ<π6＋2k π，k ∈Z ，推不出“⎪⎪⎪⎪θ－π12<π12”．故“⎪⎪⎪⎪θ－π12<π12”是“sin θ<12”的充分而不必要条件．法二：⎪⎪⎪⎪θ－π12<π12⇒0<θ<π6⇒sin θ<12，而当sin θ<12时，取θ＝－π6，⎪⎪⎪⎪－π6－π12＝π4>π12. 故“⎪⎪⎪⎪θ－π12<π12”是“sin θ<12”的充分而不必要条件． 9．(2016·山东高考)已知直线a ，b 分别在两个不同的平面α，β内，则“直线a 和直线b 相交”是“平面α和平面β相交”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件解析：选A 由题意知a ⊂α，b ⊂β，若a ，b 相交，则a ，b 有公共点，从而α，β有公共点，可得出α，β相交；反之，若α，β相交，则a ，b 的位置关系可能为平行、相交或异面．因此“直线a 和直线b 相交”是“平面α和平面β相交”的充分不必要条件．10．(2015·陕西高考)“sin α＝cos α”是“cos 2α＝0”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件D ．既不充分也不必要条件解析：选A cos 2α＝0等价于cos 2α－sin 2α＝0，即cos α＝±sin α.由sin α＝cos α可得到cos 2α＝0，反之不成立，故选A.11．(2014·全国卷Ⅱ)函数f (x ) 在x ＝x 0 处导数存在．若p ：f ′(x 0)＝0；q ：x ＝x 0是f (x )的极值点，则( )A ．p 是q 的充分必要条件B ．p 是q 的充分条件，但不是q 的必要条件C ．p 是q 的必要条件，但不是q 的充分条件D ．p 既不是q 的充分条件，也不是q 的必要条件解析：选C 设f (x )＝x 3，f ′(0)＝0，但是f (x )是单调增函数，在x ＝0处不存在极值，故若p 则q 是一个假命题，由极值的定义可得若q 则p 是一个真命题．故选C.集合——重点突破2个常考点(一)集合的运算1．(2017·福州模拟)已知集合A ＝{x |x 2－4x ＋3＜0}，B ＝{x |1＜2x ≤4，x ∈N}，则A ∩B ＝( )A ．∅B ．(1,2]C ．{2}D ．{1,2}解析：选C 因为A ＝{x |x 2－4x ＋3＜0}＝{x |1＜x ＜3}，B ＝{x |1＜2x ≤4，x ∈N}＝{1,2}，所以A ∩B ＝{2}．2．(2018届高三·西安八校联考)已知集合M ＝⎩⎨⎧⎭⎬⎫x ⎪⎪2x≥1，N ＝{y |y ＝1－x 2}，则M ∩N ＝( )A ．(－∞，2]B ．(0,1]C ．[0,1]D ．(0,2]解析：选B 由2x ≥1得x －2x ≤0，解得0＜x ≤2，则M ＝{x |0＜x ≤2}；函数y ＝1－x 2的值域是(－∞，1]，则N ＝{y |y ≤1}，因此M ∩N ＝{x |0＜x ≤1}＝(0,1]．3．已知集合A ＝{(x ，y )|x ＋y －1＝0，x ，y ∈R}，B ＝{(x ，y )|x 2＋y 2＝1，x ，y ∈R}，则A ∩B 的元素个数为( )A ．0B ．1C ．2D ．3解析：选C 集合A ∩B 的元素个数即为方程组⎩⎪⎨⎪⎧x ＋y －1＝0，x 2＋y 2＝1解的个数，解方程组得⎩⎪⎨⎪⎧ x ＝0，y ＝1或⎩⎪⎨⎪⎧x ＝1，y ＝0，故选C. 4．(2017·全国卷Ⅰ)已知集合A ＝{x |x <1}，B ＝{x |3x <1}，则( ) A ．A ∩B ＝{x |x <0} B ．A ∪B ＝R C ．A ∪B ＝{x |x >1}D ．A ∩B ＝∅解析：选A ∵集合A ＝{x |x <1}，B ＝{x |x <0}， ∴A ∩B ＝{x |x <0}，A ∪B ＝{x |x <1}，故选A.5．(2018届高三·江西七校联考)已知集合A ＝{x |y ＝lg(x －x 2)}，B ＝{x |x 2－cx ＜0，c ＞0}，若A ∩B ＝A ，则实数c 的取值范围是( )A ．(0,1]B ．[1，＋∞)C ．(0,1)D ．(1，＋∞)解析：选B A ＝{x |y ＝lg(x －x 2)}＝{x |x －x 2＞0}＝{x |0＜x ＜1}，B ＝{x |x 2－cx ＜0，c ＞0}＝{x |0＜x ＜c }，又A ∩B ＝A ，即A ⊆B ，所以c ≥1.[解题方略]破解集合运算需掌握2招第1招，化简各个集合，即明确集合中元素的性质，化简集合；第2招，借形解题，即与不等式有关的无限集之间的运算常借助数轴、有限集之间的运算常用Venn 图(或直接计算)，与函数的图象有关的点集之间的运算常借助坐标轴等，再根据集合的交集、并集、补集的定义进行基本运算．(二)集合的创新问题以集合为背景的创新性问题是命题的一个热点，这类题目常以问题为核心，考查学生探究、发现的能力，常见的命题形式有：新定义、新运算与新性质等．[题组突破]1．(2017·河北衡水中学月考)设A ，B 是两个非空集合，定义运算A ×B ＝{x |x ∈(A ∪B )且x ∉(A ∩B )}，已知A ＝{x |y ＝2x －x 2}，B ＝{y |y ＝2x ，x ＞0}，则A ×B ＝( )A ．[0,1]∪(2，＋∞)B ．[0,1)∪[2，＋∞)C ．[0,1]D ．[0,2]解析：选A 由题意得A ＝{x |2x －x 2≥0}＝{x |0≤x ≤2}，B ＝{y |y ＞1}，所以A ∪B ＝[0，＋∞)，A ∩B ＝(1,2]，所以A ×B ＝[0,1]∪(2，＋∞)．2．用C (A )表示非空集合A 中的元素个数，定义|A －B |＝⎩⎪⎨⎪⎧C (A )－C (B )，C (A )＞C (B )，C (B )－C (A )，C (A )＜C (B ).若A ＝{1,2}，B ＝{x ||x 2＋2x －3|＝a }，且|A －B |＝1，则a ＝________.解析：由于|x 2＋2x －3|＝a 的根可能有2个，3个，4个，而|A －B |＝1，故|x 2＋2x －3|＝a 只有3个根，故a ＝4.答案：4常用逻辑用语——从2方面强化完善(一)把握充分、必要条件判断的3种方法充分、必要条件的3种判断方法利用定义判断直接判断“若p ，则q ”，“若q ，则p ”的真假从集合的角度判断若A ⊆B ，则“x ∈A ”是“x ∈B ”的充分条件或“x ∈B ”是“x ∈A ”的必要条件；若A ＝B ，则“x ∈A ”是“x ∈B ”的充要条件利用等价转化法判条件和结论带有否定性词语的命题，常转化为其逆否命题来判断真假断[典例] 若命题A ：“log 2a <1”，命题B ：“关于x 的二次方程x 2＋(a ＋1)x ＋a －2＝0的一个根大于零，另一个根小于零”，则A 是B 的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件[解析] 法一：由log 2a <1，解得0<a <2；而方程x 2＋(a ＋1)x ＋a －2＝0的一个根大于零，另一个根小于零的充要条件是a －2<0，解得a <2.因为命题：“若0<a <2，则a <2”是真命题；而“若a <2，则0<a <2”是假命题，所以“0<a <2”是“a <2”的充分不必要条件，所以A 是B 充分不必要条件．法二：由法一可知，满足条件A 的参数a 的取值集合为M ＝{a |0<a <2}，满足条件B 的参数a 的取值集合为N ＝{a |a <2}，显然M N ，所以A 是B 充分不必要条件．[答案] A [解题方略]解决充分、必要条件问题的策略(1)准确化简条件，也就是求出每个条件对应的充要条件；(2)注意问题的形式，看清“p 是q 的……”还是“p 的……是q ”，如果是第二种形式，要先转化为第一种形式，再判断；(3)灵活利用各种方法判断两个条件之间的关系，充要条件的判断常通过“⇔”来判断，即转化为两个命题的判断．当遇到比较难于判断的问题时，可借助两个集合之间的关系来判断．[针对训练]1．设0＜x ＜π2，则“x sin 2x ＜1”是“x sin x ＜1”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件解析：选B 因为0＜x ＜π2，所以0＜sin x ＜1.不等式x sin x ＜1两边同乘以sin x 可得x sin 2x ＜sin x ，所以x sin 2x ＜sin x ＜1，即x sin x ＜1⇒x sin 2x ＜1；不等式x sin 2x ＜1两边同除以sin x 可得x sin x ＜1sin x ，而由0＜sin x ＜1知1sin x ＞1，故x sin x ＜1不一定成立，即x sin 2x＜1⇒ / x sin x ＜1.由以上可知，“x sin 2x ＜1”是“x sin x ＜1”的必要不充分条件．2．(2018届高三·皖南八校联考)“a ＝－2”是“直线l 1：ax －y ＋3＝0与l 2：2x －(a ＋1)y ＋4＝0互相平行”的( )A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件解析：选A当a＝－2时，直线l1：2x＋y－3＝0，l2：2x＋y＋4＝0，所以直线l1∥l2；若l1∥l2，则－a(a＋1)＋2＝0，解得a＝－2或a＝1.所以“a＝－2”是“直线l1：ax－y＋3＝0与l2：2x－(a＋1)y＋4＝0互相平行”的充分不必要条件．(二)警惕命题及命题真假判断的3个易错点1．判断含有一个量词的命题的否定常忽视量词的否定，而直接对结论进行否定，导致结果出错[练1](2017·西安质检)已知命题p：∃x0∈R，log2(3x0＋1)≤0，则()A．p是假命题；綈p：∀x∈R，log2(3x＋1)≤0B．p是假命题；綈p：∀x∈R，log2(3x＋1)>0C．p是真命题；綈p：∀x∈R，log2(3x＋1)≤0D．p是真命题；綈p：∀x∈R，log2(3x＋1)>0解析：选B∵3x>0，∴3x＋1>1，则log2(3x＋1)>0，∴p是假命题；綈p：∀x∈R，log2(3x＋1)>0.[练2]已知命题p：∀x∈R,2x＝5，则綈p为()A．∀x∉R,2x＝5 B．∀x∈R,2x≠5C．∃x0∈R,2x0＝5 D．∃x0∈R,2x0≠5解析：选D结合全称命题的含义及其否定的格式可得綈p为“∃x0∈R,2x0≠5”，所以选D.2．命题的否定与否命题的易错点命题的“否定”与“否命题”是两个不同的概念，命题p的否定是否定命题所作的判断，而“否命题”是对“若p，则q”形式的命题而言，既要否定条件也要否定结论.[练3]命题“若xy＝1，则x，y互为倒数”的否命题为________；命题的否定为________．答案：若xy≠1，则x，y不互为倒数若xy＝1，则x，y不互为倒数3．含逻辑联结词的命题的真假判断易错点(1)对构成它的命题p ，q 的真假判断出错；(2)对构成它的命题p ，q 的真假判断正确，但将含有逻辑联结词的命题的真值表中的“且”与“或”搞混，对“p ∧q ”是全真才真，一假必假；对“p ∨q ”是一真就真，全假才假，应注意识别.[练4] 若命题p ：函数y ＝x 2－2x 的单调递增区间是[1，＋∞)，命题q ：函数y ＝x －1x的单调递增区间是[1，＋∞)，则( )A ．p ∧q 是真命题B ．p ∨q 是假命题C ．綈p 是真命题D ．綈q 是真命题解析：选D 因为函数y ＝x 2－2x 的单调递增区间是[1，＋∞)，所以p 是真命题；因为函数y ＝x －1x 的单调递增区间是(－∞，0)和(0，＋∞)，所以q 是假命题．所以p ∧q 为假命题，p ∨q 为真命题，綈p 为假命题，綈q 为真命题，故选D.[练5] (2018届高三·腾冲调研)给出下列3个命题： p 1：函数y ＝a x ＋x (a ＞0，且a ≠1)在R 上为增函数；p 2：∃a 0，b 0∈R ，a 20－a 0b 0＋b 20＜0；p 3：cos α＝cos β成立的一个充分不必要条件是α＝2k π＋β(k ∈Z)．则下列命题中的真命题为( ) A ．p 1∨p 2 B ．p 2∨綈p 3 C ．p 1∨綈p 3D ．綈p 2∧p 3解析：选D 对于p 1，令f (x )＝a x ＋x (a ＞0，且a ≠1)，当a ＝12时，f (0)＝⎝⎛⎭⎫120＋0＝1，f (－1)＝⎝⎛⎭⎫12－1－1＝1，所以p 1为假命题；对于p 2，因为a 2－ab ＋b 2＝⎝⎛⎭⎫a －12b 2＋34b 2≥0，所以p 2为假命题；对于p 3，因为cos α＝cos β⇔α＝2k π±β(k ∈Z)，所以p 3为真命题，所以綈p 2∧p 3为真命题，故选D.1．(2017·全国卷Ⅱ)设集合A ＝{1,2,4}，B ＝{x |x 2－4x ＋m ＝0}．若A ∩B ＝{1}，则B ＝( )A ．{1，－3}B ．{1,0}C ．{1,3}D ．{1,5}解析：选C 因为A ∩B ＝{1}，所以1∈B ，所以1是方程x 2－4x ＋m ＝0的根，所以1－4＋m ＝0，m ＝3，方程为x 2－4x ＋3＝0，解得x ＝1或x ＝3，所以B ＝{1,3}．2．(2017·山东高考)设函数y＝4－x2的定义域为A，函数y＝ln(1－x)的定义域为B，则A∩B＝()A．(1,2) B．(1,2]C．(－2,1) D．[－2,1)解析：选D由题意可知A＝{x|－2≤x≤2}，B＝{x|x<1}，故A∩B＝{x|－2≤x<1}．3．(2017·合肥模拟)已知命题q：∀x∈R，x2＞0，则()A．命题綈q：∀x∈R，x2≤0为假命题B．命题綈q：∀x∈R，x2≤0为真命题C．命题綈q：∃x0∈R，x20≤0为假命题D．命题綈q：∃x0∈R，x20≤0为真命题解析：选D全称命题的否定是将“∀”改为“∃”，然后再否定结论．又当x＝0时，x2≤0成立，所以綈q为真命题．4．(2018届高三·郑州四校联考)命题“若a＞b，则a＋c＞b＋c”的否命题是() A．若a≤b，则a＋c≤b＋c B．若a＋c≤b＋c，则a≤bC．若a＋c＞b＋c，则a＞b D．若a＞b，则a＋c≤b＋c解析：选A命题的否命题是将原命题的条件和结论均否定，所以题中命题的否命题为“若a≤b，则a＋c≤b＋c”，故选A.5．(2017·石家庄模拟)“x＞1”是“x2＋2x＞0”的()A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件解析：选A由x2＋2x＞0，得x＞0或x＜－2，所以“x＞1”是“x2＋2x＞0”的充分不必要条件．6．已知集合A＝{x|x2≥4}，B＝{m}．若A∪B＝A，则m的取值范围是()A．(－∞，－2) B．[2，＋∞)C．[－2,2] D．(－∞，－2]∪[2，＋∞)解析：选D因为A∪B＝A，所以B⊆A，即m∈A，得m2≥4，所以m≥2或m≤－2.7.(2017·唐山模拟)已知集合A＝{x|x2－5x－6<0}，B＝{x|2x<1}，则图中阴影部分表示的集合是()A．{x|2<x<3} B．{x|－1<x≤0}C．{x|0≤x<6} D．{x|x<－1}解析：选C由x2－5x－6<0，解得－1<x<6，所以A＝{x|－1<x<6}．由2x<1，解得x<0，所以B ＝{x |x <0}．又图中阴影部分表示的集合为(∁U B )∩A ，因为∁U B ＝{x |x ≥0}，所以(∁U B )∩A ＝{x |0≤x <6}．8．(2018届高三·河北五校联考)已知命题p ：∃x 0∈(－∞，0)，2x 0<3x 0；命题q ：∀x ∈⎝⎛⎭⎫0，π2，tan x >sin x ，则下列命题为真命题的是( ) A ．p ∧q B ．p ∨(綈q ) C ．(綈p )∧qD ．p ∧(綈q )解析：选C 根据指数函数的图象与性质知命题p 是假命题，綈p 是真命题；∵x ∈⎝⎛⎭⎫0，π2，且tan x ＝sin x cos x， ∴0<cos x <1，tan x >sin x ， ∴q 为真命题，选C.9．(2017·合肥模拟)祖暅原理：“幂势既同，则积不容异”，它是中国古代一个涉及几何体体积的问题，意思是两个同高的几何体，如果在等高处的截面积恒相等，那么体积相等．设A ，B 为两个同高的几何体，p ：A ，B 的体积不相等，q ：A ，B 在等高处的截面积不恒相等，根据祖暅原理可知，p 是q 的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件解析：选A 根据祖暅原理，“A ，B 在等高处的截面积恒相等”是“A ，B 的体积相等”的充分不必要条件，即綈q 是綈p 的充分不必要条件，即命题“若綈q ，则綈p ”为真，逆命题为假，故逆否命题“若p ，则q ”为真，否命题“若q ，则p ”为假，即p 是q 的充分不必要条件，选A.10．设P 和Q 是两个集合，定义集合P －Q ＝{x |x ∈P ，且x ∉Q }，若P ＝{x |log 2x <1}，Q ＝{x ||x －2|<1}，则P －Q ＝( )A ．{x |0<x <1}B ．{x |0<x ≤1}C ．{x |1≤x <2}D ．{x |2≤x <3}解析：选B 由log 2x <1，得0<x <2，所以P ＝{x |0<x <2}．由|x －2|<1，得1<x <3，所以Q ＝{x |1<x <3}．由题意，得P －Q ＝{x |0<x ≤1}．11．(2018届高三·广西五校联考)命题p ：“∃x 0∈R ，使得x 20＋mx 0＋2m ＋5＜0”，命题q ：“关于x 的方程2x －m ＝0有正实数解”，若“p 或q ”为真，“p 且q ”为假，则实数m 的取值范围是( )A ．[1,10]B ．(－∞，－2)∪(1,10]C ．[－2,10]D ．(－∞，－2]∪(0,10]解析：选B 若命题p ：“∃x 0∈R ，使得x 20＋mx 0＋2m ＋5＜0”为真命题，则Δ＝m 2－8m －20＞0，∴m ＜－2或m ＞10；若命题q 为真命题，则关于x 的方程m ＝2x 有正实数解，因为当x ＞0时，2x ＞1，所以m ＞1.因为“p 或q ”为真，“p 且q ”为假，故p 真q 假或p 假q 真，所以⎩⎪⎨⎪⎧m ＜－2或m ＞10，m ≤1或⎩⎪⎨⎪⎧－2≤m ≤10，m ＞1，所以m ＜－2或1＜m ≤10.12．(2017·石家庄模拟)下列选项中，说法正确的是( ) A ．若a ＞b ＞0，则ln a ＜ln bB ．向量a ＝(1，m )与b ＝(m,2m －1)(m ∈R)垂直的充要条件是m ＝1C ．命题“∀n ∈N *,3n ＞(n ＋2)·2n －1”的否定是“∀n ∈N *,3n ≥(n ＋2)·2n －1”D ．已知函数f (x )在区间[a ，b ]上的图象是连续不断的，则命题“若f (a )·f (b )＜0，则f (x )在区间(a ，b )内至少有一个零点”的逆命题为假命题解析：选D A 中，因为函数y ＝ln x (x ＞0)是增函数，所以若a ＞b ＞0，则ln a ＞ln b ，故A 错；B 中，若a ⊥b ，则m ＋m (2m －1)＝0，解得m ＝0，故B 错；C 中，命题“∀n ∈N *,3n ＞(n ＋2)·2n －1”的否定是“∃n 0∈N *，3n 0≤(n 0＋2)·2n 0－1”，故C 错；D 中，原命题的逆命题是“若f (x )在区间(a ，b )内至少有一个零点，则f (a )·f (b )＜0”，是假命题，如函数f (x )＝x 2－2x －3在区间[－2,4]上的图象是连续不断的，且在区间(－2,4)内有两个零点，但f (－2)·f (4)＞0，故D 正确．13．(2018届高三·辽宁师大附中调研)若集合A ＝{x |(a －1)x 2＋3x －2＝0}有且仅有两个子集，则实数a 的值为________．解析：由题意知，集合A 有且仅有两个子集，则集合A 中只有一个元素．当a －1＝0，即a ＝1时，A ＝⎩⎨⎧⎭⎬⎫23，满足题意；当a －1≠0，即a ≠1时，要使集合A 中只有一个元素，需Δ＝9＋8(a －1)＝0，解得a ＝－18.综上可知，实数a 的值为1或－18.答案：1或－1814．已知集合A ＝⎩⎨⎧⎭⎬⎫x ⎪⎪12<2x <8，x ∈R ，B ＝{x |－1<x <m ＋1，x ∈R}，若x ∈B 成立的一个充分不必要的条件是x ∈A ，则实数m 的取值范围是________．解析：A ＝⎩⎨⎧⎭⎬⎫x ⎪⎪12<2x <8，x ∈R ＝{x |－1<x <3}， ∵x ∈B 成立的一个充分不必要条件是x ∈A ， ∴A B ，∴m ＋1>3，即m >2. 答案：(2，＋∞)15．(2017·广东中山一中模拟)已知非空集合A ，B 满足下列四个条件： ①A ∪B ＝{1,2,3,4,5,6,7}； ②A ∩B ＝∅；③A 中的元素个数不是A 中的元素； ④B 中的元素个数不是B 中的元素．(1)如果集合A 中只有1个元素，那么A ＝________； (2)有序集合对(A ，B )的个数是________．解析：(1)若集合A 中只有1个元素，则集合B 中有6个元素，6∉B ，故A ＝{6}． (2)当集合A 中有1个元素时，A ＝{6}，B ＝{1,2,3,4,5,7}，此时有序集合对(A ，B )有1个；当集合A 中有2个元素时，5∉B,2∉A ，此时有序集合对(A ，B )有5个；当集合A 中有3个元素时，4∉B,3∉A ，此时有序集合对(A ，B )有10个；当集合A 中有4个元素时，3∉B,4∉A ，此时有序集合对(A ，B )有10个；当集合A 中有5个元素时，2∉B,5∉A ，此时有序集合对(A ，B )有5个；当集合A 中有6个元素时，A ＝{1,2,3,4,5,7}，B ＝{6}，此时有序集合对(A ，B )有1个．综上可知，有序集合对(A ，B )的个数是1＋5＋10＋10＋5＋1＝32. 答案：(1){6} (2)3216．(2017·张掖模拟)下列说法中不正确的是________．(填序号) ①若a ∈R ，则“1a ＜1”是“a ＞1”的必要不充分条件； ②“p ∧q 为真命题”是“p ∨q 为真命题”的必要不充分条件； ③若命题p ：“∀x ∈R ，sin x ＋cos x ≤2”，则p 是真命题；④命题“∃x 0∈R ，x 20＋2x 0＋3＜0”的否定是“∀x ∈R ，x 2＋2x ＋3＞0”．解析：由1a ＜1，得a ＜0或a ＞1，反之，由a ＞1，得1a ＜1，∴“1a ＜1”是“a ＞1”的必要不充分条件，故①正确；由p ∧q 为真命题，知p ，q 均为真命题，所以p ∨q 为真命题，反之，由p ∨q 为真命题，得p ，q 至少有一个为真命题，所以p ∧q 不一定为真命题，所以“p ∧q 为真命题”是“p ∨q 为真命题”的充分不必要条件，故②不正确；∵sin x ＋cos x ＝2sin ⎝⎛⎭⎫x ＋π4≤2， ∴命题p 为真命题，③正确；命题“∃x 0∈R ，x 20＋2x 0＋3＜0”的否定是“∀x ∈R ，x 2＋2x ＋3≥0”，故④不正确．答案：②④小题押题16—2⎪⎪平面向量与复数卷Ⅰ题，考查平面向量的模、数量积的运算、线性运算等，难度较低；另一方面会与三角函数、解析几何等其他知识综合命题，难度中等．选择题第2题复数相等及模的运算 2015选择题第7题平面向量的线性运算选择题第1题复数的基本运算、复数的模2017选择题第12题平面向量的坐标表示、向量的数量积选择题第1题复数的除法运算考查点一平面向量的线性运算及坐标运算1．(2015·全国卷Ⅰ)设D 为△ABC 所在平面内一点，BC ―→＝3CD ―→，则( ) A ．AD ―→＝－13AB ―→＋43AC ―→B ．AD ―→＝13AB ―→－43AC ―→C ．AD ―→＝43AB ―→＋13AC ―→D ．AD ―→＝43AB ―→－13AC ―→解析：选A AD ―→＝AC ―→＋CD ―→＝AC ―→＋13BC ―→＝AC ―→＋13(AC ―→－AB ―→)＝43AC ―→－13AB ―→＝－13AB ―→＋43AC ―→.2．(2016·全国卷Ⅱ)已知向量a ＝(m,4)，b ＝(3，－2)，且a ∥b ，则m ＝________. 解析：∵a ＝(m,4)，b ＝(3，－2)，a ∥b ， ∴－2m －4×3＝0，∴m ＝－6. 答案：－63．(2015·全国卷Ⅱ)设向量a ，b 不平行，向量λa ＋b 与a ＋2b 平行，则实数λ＝________. 解析：∵λa ＋b 与a ＋2b 平行， ∴λa ＋b ＝t (a ＋2b )，即λa ＋b ＝ta ＋2tb ，∴⎩⎪⎨⎪⎧λ＝t ，1＝2t ，解得⎩⎨⎧λ＝12，t ＝12.答案：12考查点二平面向量的数量积及应用4．(2016·全国卷Ⅱ)已知向量a ＝(1，m )，b ＝(3，－2)，且(a ＋b )⊥b ，则m ＝( ) A ．－8 B ．－6 C ．6D ．8解析：选D 法一：因为a ＝(1，m )，b ＝(3，－2)，所以a ＋b ＝(4，m －2)．因为(a ＋b )⊥b ，所以(a ＋b )·b ＝0，所以12－2(m －2)＝0，解得m ＝8.法二：因为(a ＋b )⊥b ，所以(a ＋b )·b ＝0，即a ·b ＋b 2＝3－2m ＋32＋(－2)2＝16－2m ＝0，解得m ＝8.5．(2016·全国卷Ⅲ)已知向量BA ―→＝⎝⎛⎭⎫12，32，BC ―→＝⎝⎛⎭⎫32，12，则∠ABC ＝( ) A ．30° B ．45° C ．60°D ．120°解析：选A 因为BA ―→＝⎝⎛⎭⎫12，32，BC ―→＝⎝⎛⎭⎫32，12，所以BA ―→·BC ―→＝34＋34＝32.又因为BA ―→·BC ―→＝|BA ―→||BC ―→|cos ∠ABC ＝1×1×cos ∠ABC ＝32，所以cos ∠ABC ＝32. 又0°≤∠ABC ≤180°，所以∠ABC ＝30°.6．(2016·全国卷Ⅰ)设向量a ＝(m,1)，b ＝(1,2)，且|a ＋b |2＝|a |2＋|b |2，则m ＝________. 解析：∵|a ＋b |2＝|a |2＋|b |2＋2a ·b ＝|a |2＋|b |2， ∴a ·b ＝0.又a ＝(m,1)，b ＝(1,2)，∴m ＋2＝0，∴m ＝－2. 答案：－27．(2017·全国卷Ⅰ)已知向量a ，b 的夹角为60°，|a |＝2，|b |＝1，则|a ＋2b |＝________. 解析：法一：易知|a ＋2b |＝|a |2＋4a ·b ＋4|b |2＝4＋4×2×1×12＋4＝2 3.法二：(数形结合法)由|a |＝|2b |＝2，知以a 与2b 为邻边可作出边长为2的菱形OACB ，如图，则|a ＋2b |＝|OC ―→|.又∠AOB ＝60°，所以|a ＋2b |＝2 3.答案：2 3考查点三复数8．(2017·全国卷Ⅰ)设有下面四个命题： p 1：若复数z 满足1z ∈R ，则z ∈R ； p 2：若复数z 满足z 2∈R ，则z ∈R ； p 3：若复数z 1，z 2满足z 1z 2∈R ，则z 1＝z 2； p 4：若复数z ∈R ，则z ∈R. 其中的真命题为( ) A ．p 1，p 3 B ．p 1，p 4 C ．p 2，p 3D ．p 2，p 4解析：选B 设复数z ＝a ＋b i(a ，b ∈R)，对于p 1，∵1z ＝1a ＋b i ＝a －b i a 2＋b 2∈R ，∴b ＝0，∴z ∈R ，∴p 1是真命题；对于p 2，∵z 2＝(a ＋b i)2＝a 2－b 2＋2ab i ∈R ，∴ab ＝0，∴a ＝0或b ＝0，∴p 2不是真命题；对于p 3，设z 1＝x ＋y i(x ，y ∈R)，z 2＝c ＋d i(c ，d ∈R)，则z 1z 2＝(x ＋y i)(c ＋d i)＝cx －dy ＋(dx ＋cy )i ∈R ， ∴dx ＋cy ＝0，取z 1＝1＋2i ，z 2＝－1＋2i ，z 1≠z 2， ∴p 3不是真命题；对于p 4，∵z ＝a ＋b i ∈R ，∴b ＝0，∴z ＝a －b i ＝a ∈R ， ∴p 4是真命题．9．(2016·全国卷Ⅱ)已知z ＝(m ＋3)＋(m －1)i 在复平面内对应的点在第四象限，则实数m 的取值范围是( )A ．(－3,1)B ．(－1,3)C ．(1，＋∞)D ．(－∞，－3)解析：选A 由题意知⎩⎪⎨⎪⎧m ＋3>0，m －1<0，即－3<m <1，故实数m 的取值范围为(－3,1)．10．(2016·全国卷Ⅲ)若z ＝1＋2i ，则4iz z －1＝( )A ．1B ．－1C ．iD ．－i解析：选C 因为z ＝1＋2i ，则z ＝1－2i ，所以z z ＝(1＋2i)(1－2i)＝5，则4iz z －1＝4i 4＝i. 11．(2016·全国卷Ⅰ)设(1＋i)x ＝1＋y i ，其中x ，y 是实数，则|x ＋y i|＝( ) A ．1 B. 2 C. 3D ．2解析：选B ∵(1＋i)x ＝1＋y i ，∴x ＋x i ＝1＋y i. 又∵x ，y ∈R ，∴x ＝1，y ＝1. ∴|x ＋y i|＝|1＋i|＝ 2.平面向量——重点突破2个常考点考法(一) 平面向量数量积的运算及应用[题组突破]1．(2018届高三·珠海摸底)已知|a |＝|b |，且|a ＋b |＝3|a －b |，则向量a 与b 的夹角为( ) A ．30° B ．45° C ．60° D ．120° 解析：选C 设a 与b 的夹角为θ，由已知可得a 2＋2a·b ＋b 2＝3(a 2－2a·b ＋b 2)，即4a·b ＝a 2＋b 2.因为|a|＝|b|，所以a·b ＝12a 2，所以cos θ＝a·b |a|·|b|＝12，θ＝60°.2.如图，△AOB 为直角三角形，OA ＝1，OB ＝2，C 为斜边AB 的中点，P 为线段OC 的中点，则AP ―→·OP ―→＝( )A ．1 B.116 C.14D ．－12解析：选B 法一：因为△AOB 为直角三角形，OA ＝1，OB ＝2，C 为斜边AB 的中点，所以OC ―→＝12OA ―→＋12OB ―→，所以OP ―→＝12OC ―→＝14(OA ―→＋OB ―→)，则AP ―→＝OP ―→－OA ―→＝14OB ―→－34OA ―→，所以AP ―→·OP ―→＝14(OB ―→－3 OA ―→)·14(OA ―→＋OB ―→)＝116(OB ―→2－3OA ―→2)＝116.法二：以O 为坐标原点，OB ―→的方向为x 轴正方向，OA ―→的方向为y 轴正方向建立平面直角坐标系(如图)，则A (0,1)，B (2,0)，C ⎝⎛⎭⎫1，12，P ⎝⎛⎭⎫12，14，所以OP ―→＝⎝⎛⎭⎫12，14， AP ―→＝⎝⎛⎭⎫12，－34，故AP ―→·OP ―→＝12×12－34×14＝116.3．(2017·云南模拟)平面向量a 与b 的夹角为45°，a ＝(1,1)，|b |＝2，则|3a ＋b |＝( ) A ．13＋6 2 B ．2 5 C.30D.34解析：选D 依题意得a 2＝2，a·b ＝2×2×cos 45°＝2，所以|3a ＋b |＝(3a ＋b )2＝9a 2＋6a·b ＋b 2 ＝18＋12＋4＝34.考法(二) 平面向量数量积的范围问题平面向量数量积的应用中，常考查向量的模或数量积的最值或范围问题，能力要求较高，综合性强．题型1 平面向量模的最值或范围问题[典例] (1)(2017·河北衡水中学调研)已知向量a ，b ，c 满足|a |＝|b |＝a·b ＝2，(a －c )·(b －2c )＝0，则|b －c |的最小值为( )A.7－32B.3－12 C.32 D.72[解析] 由|a |＝|b |＝a·b ＝2，知a ，b 的夹角为π3，可设a ＝(2,0)，b ＝(1，3)，c ＝(x ，y )， ∵(a －c )·(b －2c )＝0，∴(2－x ，－y )·(1－2x ，3－2y )＝0，即2x 2＋2y 2－5x －3y ＋2＝0.方程2x 2＋2y 2－5x －3y ＋2＝0表示圆心为⎝⎛⎭⎫54，34，半径为32的圆，|b －c |＝(x －1)2＋(y －3)2表示圆2x 2＋2y 2－5x －3y ＋2＝0上的点到点(1，3)的距离，所以|b －c |的最小值为⎝⎛⎭⎫54－12＋⎝⎛⎭⎫34－32－32＝7－32. [答案] A(2)(2017·全国卷Ⅱ)已知△ABC 是边长为2的等边三角形，P 为平面ABC 内一点，则PA ―→·(PB ―→＋PC ―→)的最小值是( )A ．－2B ．－32C ．－43D ．－1[解析] 如图，以等边三角形ABC 的底边BC 所在直线为x 轴，以BC 的垂直平分线为y 轴建立平面直角坐标系，则A (0，3)，B (－1，0)，C (1,0)，设P (x ，y )，则PA ―→＝(－x, 3－y )，PB ―→＝(－1－x ，－y )，PC ―→＝(1－x ，－y )，所以PA ―→·(PB ―→＋PC ―→)＝(－x ，3－y )·(－2x ，－2y )＝2x 2＋2⎝⎛⎭⎫y －322－32，当x ＝0，y ＝32时，PA ―→·(PB ―→＋PC ―→)取得最小值，为－32.[答案] B [解题方略]求向量模的最值(范围)的2种方法(1)代数法：把所求的模表示成某个变量的函数，再用求最值的方法求解．(2)几何法(数形结合法)：弄清所求的模表示的几何意义，结合动点表示的图形求解．[针对训练]1．(2017·抚州二模)已知a ，b 是两个互相垂直的单位向量，且c ·a ＝1，c ·b ＝1，|c |＝2，则对任意的正实数t ，⎪⎪⎪⎪c ＋ta ＋1t b 的最小值是( ) A ．2 B ．2 2 C ．4D ．4 2解析：选B ⎪⎪⎪⎪c ＋ta ＋1t b 2＝c 2＋t 2a 2＋1t 2b 2＋2ta ·c ＋2t c ·b ＋2a ·b ＝2＋t 2＋1t 2＋2t ＋2t ≥2＋2t 2·1t2＋22t ·2t ＝8(t ＞0)，当且仅当t 2＝1t2，2t ＝2t ，即t ＝1时等号成立，∴⎪⎪⎪⎪c ＋ta ＋1t b 的最小值为2 2.2．(2017·泰安二模)已知平面向量a ，b 满足|b |＝1，且a 与b －a 的夹角为120°，则|a |的取值范围为________．解析：在△ABC 中，设AB ―→＝a ，AC ―→＝b ，则b －a ＝AC ―→－AB ―→＝BC ―→， ∵a 与b －a 的夹角为120°， ∴∠B ＝60°，由正弦定理得1sin 60°＝|a |sin C，∴|a |＝sin C sin 60°＝233sin C ，∵0°＜C ＜120°，∴sin C ∈(0,1]，∴|a |∈⎝⎛⎦⎤0，233. 答案：⎝⎛⎦⎤0，233题型2 数量积的最值或范围问题[典例] (1)(2018届高三·南昌调研)如图，在直角梯形ABCD 中，DA ＝AB ＝1，BC ＝2，点P 在阴影区域(含边界)中运动，则PA ―→·BD ―→的取值范围是( )A.⎣⎡⎦⎤－12，1 B.⎣⎡⎦⎤－1，12 C ．[－1,1] D ．[－1,0][解析]∵在直角梯形ABCD 中，DA ＝AB ＝1，BC ＝2，∴BD ＝ 2.如图所示，过点A 作AO ⊥BD ，垂足为O ，则PA ―→＝PO ―→＋OA ―→，OA ―→·BD ―→＝0，∴PA ―→·BD ―→＝(PO ―→＋OA ―→)·BD ―→＝PO ―→·BD ―→. ∴当点P 与点B 重合时，PA ―→·BD ―→取得最大值，即PA ―→·BD ―→＝PO ―→·BD ―→＝12×2×2＝1；当点P 与点D 重合时，PA ―→·BD ―→取得最小值，即PA ―→·BD ―→＝－12×2×2＝－1.∴PA ―→·BD ―→的取值范围是[－1,1]． [答案] C(2)(2017·宝鸡模拟)在等腰直角△ABC 中，∠ABC ＝90°，AB ＝BC ＝2，M ，N (不与A ，C 重合)为AC 边上的两个动点，且满足|MN ―→|＝2，则BM ―→·BN ―→的取值范围为( )A.⎣⎡⎦⎤32，2 B.⎝⎛⎭⎫32，2 C.⎣⎡⎭⎫32，2D.⎣⎡⎭⎫32，＋∞ [解析] 以等腰直角三角形的直角边BC 所在直线为x 轴，BA 所在直线为y 轴，建立平面直角坐标系如图所示，则B (0,0)，直线AC 的方程为x ＋y ＝2.设M (a,2－a )，则0＜a ＜1，N (a ＋1,1－a )，∴BM ―→＝(a,2－a )，BN ―→＝(a ＋1,1－a )，∴BM ―→·BN ―→＝a (a ＋1)＋(2－a )(1－a )＝2a 2－2a ＋2， ∵0＜a ＜1，∴当a ＝12时，BM ―→·BN ―→取得最小值32，又BM ―→·BN ―→＜2，故BM ―→·BN ―→的取值范围为⎣⎡⎭⎫32，2.[答案] C[解题方略]数量积的最值或范围问题的2种求解方法(1)临界分析法：结合图形，确定临界位置的动态分析求出范围．(2)目标函数法：将数量积表示为某一个变量或两个变量的函数，建立函数关系式，再利用三角函数有界性、二次函数或基本不等式求最值或范围．[针对训练]1．(2017·湖南一模)在等腰三角形ABC 中，AB ＝AC ＝1，∠BAC ＝90°，点E 为斜边BC 的中点，点M 在线段AB 上运动，则ME ―→·MC ―→的取值范围是( )A.⎣⎡⎦⎤716，12 B.⎣⎡⎦⎤716，1 C.⎣⎡⎦⎤12，1D ．[0,1]解析：选B 如图，以A 为坐标原点，AC ，AB 所在直线分别为x 轴，y 轴建立平面直角坐标系，则A (0,0)，B (0,1)，C (1,0)，E ⎝⎛⎭⎫12，12.设M (0，m )(0≤m ≤1)，则ME ―→＝⎝⎛⎭⎫12，12－m ，MC ―→＝(1，－m )． ME ―→·MC ―→＝12－m ⎝⎛⎭⎫12－m ＝m 2－12m ＋12＝⎝⎛⎭⎫m －142＋716，由于m ∈[0,1]，则当m ＝14时，ME ―→·MC ―→取得最小值716；当m ＝1时，ME ―→·MC ―→取得最大值1. 所以ME ―→·MC ―→的取值范围是⎣⎡⎦⎤716，1.2．若a ，b ，c 是单位向量，且a ·b ＝0，则(a －c )·(b －c )的最大值为________．解析：依题意可设a ＝(1,0)，b ＝(0,1)，c ＝(cos θ，sin θ)，则(a －c )·(b －c )＝1－(sin θ＋cos θ)＝1－2sin ⎝⎛⎭⎫θ＋π4，所以(a －c )·(b －c )的最大值为1＋ 2. 答案：1＋ 2复数——警惕3个易错点1．混淆复数z ＝a ＋b i 的实部与虚部或误认为虚部为b i [练1] (2017·贵阳模拟)复数(i －1－i)3的虚部为( )A ．8iB ．－8iC ．8D ．－8解析：选C 依题意得，复数(i －1－i)3＝(－i －i)3＝－8i 3＝8i 的虚部为8. 2．忽视复数a ＋b i 为纯虚数时，b ≠0这一条件[练2] (2017·张掖模拟)若复数a ＋3i 1＋i (a ∈R ，i 为虚数单位)是纯虚数，则实数a 的值为( )A ．－6B ．－3C ．3D ．6解析：选Ba ＋3i 1＋i ＝(a ＋3i )(1－i )(1＋i )(1－i )＝(a ＋3)＋(3－a )i2，∵⎩⎪⎨⎪⎧a ＋3＝0，3－a ≠0，∴a ＝－3. 3．记不清共轭复数的概念，误认为z ＝a ＋b i 的共轭复数为z ＝－(a ＋b i)[练3] 已知复数z ＝x ＋4i(x ∈R)(i 是虚数单位)在复平面内对应的点在第二象限，且|z |＝5，则z 1＋i的共轭复数为( )A.72＋12iB.72－12iC.12－72i D.12＋72i 解析：选C 由题意知x ＜0，且x 2＋42＝52，解得x ＝－3， ∴z 1＋i ＝－3＋4i 1＋i ＝(－3＋4i )(1－i )(1＋i )(1－i )＝12＋72i ，故其共轭复数为12－72i.1．(2017·全国卷Ⅲ)复平面内表示复数z ＝i(－2＋i)的点位于( ) A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限解析：选C z ＝i(－2＋i)＝－2i ＋i 2＝－1－2i ，故复平面内表示复数z ＝i(－2＋i)的点位于第三象限．2．(2017·全国卷Ⅲ)设复数z 满足(1＋i)z ＝2i ，则|z |＝( )A.12B.22 C. 2 D ．2解析：选C 因为z ＝2i1＋i ＝2i (1－i )(1＋i )(1－i )＝i(1－i)＝1＋i ，所以|z |＝ 2.3．(2017·沈阳模拟)已知平面向量a ＝(3,4)，b ＝⎝⎛⎭⎫x ，12，若a ∥b ，则实数x 的值为( ) A ．－23 B.23 C.38 D ．－38解析：选C ∵a ∥b ，∴3×12＝4x ，解得x ＝38.4．(2018届高三·西安摸底)已知非零单位向量a ，b 满足|a ＋b |＝|a －b |，则a 与b －a 的夹角是( )A.π6B.π3C.π4D.3π4解析：选D 由|a ＋b |＝|a －b |可得(a ＋b )2＝(a －b )2，即a ·b ＝0，而a ·(b －a )＝a ·b －a 2＝－|a |2＜0，即a 与b －a 的夹角为钝角，结合选项知选D.5．(2017·湘中模拟)已知向量a ＝(x ，3)，b ＝(x ，－3)，若(2a ＋b )⊥b ，则|a |＝( ) A ．1 B. 2 C. 3 D ．2解析：选D 因为(2a ＋b )⊥b ，所以(2a ＋b )·b ＝0，即(3x ，3)·(x ，－3)＝3x 2－3＝0，解得x ＝±1，所以a ＝(±1，3)，|a |＝(±1)2＋(3)2＝2.6．(2017·广西五校联考)设D 是△ABC 所在平面内一点，AB ―→＝2DC ―→，则( ) A ．BD ―→＝AC ―→－32AB ―→B ．BD ―→＝32AC ―→－AB ―→C ．BD ―→＝12AC ―→－AB ―→D ．BD ―→＝AC ―→－12AB ―→解析：选A BD ―→＝BC ―→＋CD ―→＝BC ―→－DC ―→＝AC ―→－AB ―→－12AB ―→＝AC ―→－32AB ―→.7．(2018届高三·云南调研)在▱ABCD 中，|AB ―→|＝8，|AD ―→|＝6，N 为DC 的中点，BM ―→＝2MC ―→，则AM ―→·NM ―→＝( )A ．48B ．36C ．24D ．12解析：选C AM ―→·NM ―→＝(AB ―→＋BM ―→)·(NC ―→＋CM ―→)＝⎝⎛⎭⎫AB ―→＋23 AD ―→ ·⎝⎛⎭⎫12 AB ―→－13 AD ―→ ＝12AB ―→2－29AD ―→2＝12×82－29×62＝24. 8．(2018届高三·广西五校联考)已知a 为实数，若复数z ＝(a 2－1)＋(a ＋1)i 为纯虚数，则a ＋i 2 0171－i＝( )A ．1B ．0C ．iD ．1－i解析：选C 因为z ＝(a 2－1)＋(a ＋1)i 为纯虚数，所以⎩⎪⎨⎪⎧a 2－1＝0，a ＋1≠0，得a ＝1，则有1＋i 2 0171－i ＝1＋i 1－i ＝(1＋i )2(1＋i )(1－i )＝i.9．已知点A (－1,1)，B (1,2)，C (－2，－1)，D (3,4)，则向量CD ―→ 在BA ―→方向上的投影是( )A ．－3 5B ．－322 C ．3 5 D.322解析：选A 依题意得，BA ―→＝(－2，－1)，CD ―→＝(5,5)，BA ―→ ·CD ―→＝(－2，－1)·(5,5)＝－15，|BA ―→|＝5，因此向量CD ―→在BA ―→方向上的投影是BA ―→·CD ―→|BA ―→|＝－155＝－3 5.10．(2018届高三·湖南五校联考)△ABC 是边长为2的等边三角形，向量a ，b 满足AB ―→＝2a ，AC ―→＝2a ＋b ，则向量a ，b 的夹角为( )A ．30°B ．60°C ．120°D ．150°解析：选C 法一：设向量a ，b 的夹角为θ，BC ―→＝AC ―→－AB ―→＝2a ＋b －2a ＝b ，∴|BC ―→|＝|b |＝2，|AB ―→|＝2|a |＝2，∴|a |＝1，AC ―→2＝(2a ＋b )2＝4a 2＋4a ·b ＋b 2＝8＋8cos θ＝4，∴cos θ＝－12，θ＝120°.法二：BC ―→＝AC ―→－AB ―→＝2a ＋b －2a ＝b ，则向量a ，b 的夹角为向量AB ―→与BC ―→的夹角，故向量a ，b 的夹角为120°.11．(2017·长春模拟)在△ABC 中，D 为△ABC 所在平面内一点，且AD ―→＝13AB ―→＋12AC ―→，则S △BCDS △ABD＝( ) A.16 B.13 C.12 D.23解析：选B 如图，由已知得，点D 在△ABC 中与AB 平行的中位线上，且在靠近BC 边的三等分点处，从而有S △ABD ＝12S △ABC ，S △ACD ＝13S △ABC ，S △BCD ＝⎝⎛⎭⎫1－12－13S △ABC ＝16S △ABC ，所以S △BCD S △ABD ＝13.12．(2017·全国卷Ⅲ)在矩形ABCD 中，AB ＝1，AD ＝2，动点P 在以点C 为圆心且与BD 相切的圆上．若AP ―→＝λAB ―→＋μAD ―→，则λ＋μ的最大值为( )A ．3B ．2 2 C. 5 D ．2 解析：选A 以A 为坐标原点，AB ，AD 所在直线分别为x 轴，y 轴建立如图所示的平面直角坐标系，则A (0,0)，B (1,0)，C (1,2)，D (0,2)，可得直线BD 的方程为2x ＋y －2＝0，点C 到直线BD 的距离为222＋12＝25，所以圆C ：(x －1)2＋(y －2)2＝45. 因为P 在圆C 上，所以P ⎝⎛⎭⎫1＋255cos θ，2＋255sin θ.又AB ―→＝(1,0)，AD ―→＝(0,2)，AP ―→＝λAB ―→＋μAD ―→＝(λ，2μ)，所以⎩⎨⎧1＋255cos θ＝λ，2＋255sin θ＝2μ，λ＋μ＝2＋255cos θ＋55sin θ＝2＋sin(θ＋φ)≤3(其中tan φ＝2)，当且仅当θ＝π2＋2k π－φ，k ∈Z 时，λ＋μ取得最大值3.13．(2017·成都模拟)若复数z ＝a i1＋i(其中a ∈R ，i 为虚数单位)的虚部为－1，则a ＝________.解析：因为z ＝a i 1＋i ＝a i·(1－i )(1＋i )(1－i )＝a 2＋a 2i 的虚部为－1，所以a2＝－1，解得a ＝－2.答案：－214．(2017·兰州诊断)已知向量OA ―→＝(3,1)，OB ―→＝(－1,3)，OC ―→＝m OA ―→－n OB ―→(m ＞0，n ＞0)，若m ＋n ＝1，则|OC ―→|的最小值为________．解析：由OA ―→＝(3,1)，OB ―→＝(－1,3)，得OC ―→＝m OA ―→－n OB ―→＝(3m ＋n ，m －3n )，因为m ＋n ＝1(m ＞0，n ＞0)，所以n ＝1－m 且0＜m ＜1，所以OC ―→＝(1＋2m,4m －3)，则|OC ―→|＝(1＋2m )2＋(4m －3)2＝20m 2－20m ＋10＝20⎝⎛⎭⎫m －122＋5(0＜m ＜1)，所以当m ＝12时，|OC ―→|min ＝ 5.答案： 515．(2018届高三·石家庄调研)非零向量m ，n 的夹角为π3，且满足|n |＝λ|m |(λ＞0)，向量组x 1，x 2，x 3由一个m 和两个n 排列而成，向量组y 1，y 2，y 3由两个m 和一个n 排列而成，若x 1·y 1＋x 2·y 2＋x 3·y 3所有可能值中的最小值为4m 2，则λ＝________.解析：由题意：x 1·y 1＋x 2·y 2＋x 3·y 3的运算结果有以下两种可能：①m 2＋m ·n ＋n 2＝m 2＋λ|m ||m |cos π3＋λ2m 2＝⎝⎛⎭⎫λ2＋λ2＋1m 2；②m ·n ＋m ·n ＋m ·n ＝3λ|m ||m |cos π3＝3λ2m 2.又λ2＋λ2＋1－3λ2＝λ2－λ＋1＝⎝⎛⎭⎫λ－122＋34＞0，所以3λ2m 2＝4m 2，即3λ2＝4，解得λ＝83. 答案：8316.如图所示，已知正方形ABCD 的边长为1，点E 从点D 出发，按字母顺序D →A →B →C 沿线段DA ，AB ，BC 运动到点C ，在此过程中DE ―→·CD ―→的取值范围为________．解析：以BC ，BA 所在的直线为x 轴，y 轴，建立平面直角坐标系如图所示，可得A (0,1)，B (0,0)，C (1,0)，D (1,1)．当E 在DA 上时，设E (x,1)，其中0≤x ≤1，∵DE ―→＝(x －1,0)，CD ―→＝(0,1)， ∴DE ―→·CD ―→＝0；当E 在AB 上时，设E (0，y )，其中0≤y ≤1，∵DE ―→＝(－1，y －1)，CD ―→＝(0,1)，∴DE ―→·CD ―→＝y －1(0≤y ≤1)，此时DE ―→·CD ―→的取值范围为[－1,0]；当E 在BC 上时，设E (x,0)，其中0≤x ≤1， ∵DE ―→＝(x －1，－1)，CD ―→＝(0,1)， ∴DE ―→·CD ―→＝－1.综上所述，DE ―→·CD ―→的取值范围为[－1,0]．答案：[－1,0]小题押题16—3⎪⎪不等式考查点一不等式的解法及应用1．(2014·全国卷Ⅰ)已知集合A ＝{x |x 2－2x －3≥0}，B ＝{x |－2≤x ＜2}，则A ∩B ＝( ) A ．[－2，－1] B ．[－1,2) C ．[－1,1]D ．[1,2)解析：选A A ＝{x |x ≤－1或x ≥3}，故A ∩B ＝[－2，－1]．2．(2014·大纲卷)不等式组⎩⎪⎨⎪⎧x (x ＋2)>0，|x |<1的解集为( )A ．{x |－2<x <－1}B ．{x |－1<x <0}C ．{x |0<x <1}D ．{x |x >1}解析：选C 由x (x ＋2)>0，得x <－2或x >0；由|x |<1，得－1<x <1.所以不等式组的解集为两个不等式解集的交集，即{x |0<x <1}．考查点二简单的线性规划及应用3．(2017·全国卷Ⅱ)设x ，y 满足约束条件⎩⎪⎨⎪⎧2x ＋3y －3≤0，2x －3y ＋3≥0，y ＋3≥0，则z ＝2x ＋y 的最小值是( )A ．－15B ．－9C ．1D ．9解析：选A 法一：作出不等式组表示的可行域如图中阴影部分所示．易求得可行域的顶点A (0，1)，B (－6，－3)，C (6，－3)，当直线z ＝2x ＋y 过点B (－6，－3)时，z 取得最小值，z min ＝2×(－6)－3＝－15.法二：易求可行域顶点A (0,1)，B (－6，－3)，C (6，－3)，分别代入目标函数，求出对应的z 的值依次为1，－15,9，故最小值为－15.4．(2016·全国卷Ⅲ)若x ，y 满足约束条件⎩⎪⎨⎪⎧x －y ＋1≥0，x －2y ≤0，x ＋2y －2≤0，则z ＝x ＋y 的最大值为________．解析：作出不等式组表示的可行域如图中阴影部分所示．平移直线x ＋y ＝0，当直线经过A 点时，z 取得最大值，由⎩⎪⎨⎪⎧x －2y ＝0，x ＋2y －2＝0得A ⎝⎛⎭⎫1，12，z max ＝1＋12＝32. 答案：325．(2015·全国卷Ⅰ)若x ，y 满足约束条件⎩⎪⎨⎪⎧x －1≥0，x －y ≤0，x ＋y －4≤0，则yx 的最大值为________．解析：作出不等式组表示的可行域如图中阴影部分所示，∵yx 表示过点(x ，y )与原点(0,0)的直线的斜率， ∴点(x ，y )在点A 处时yx 最大．。

【通用版】2018年高考理科数学二轮复习：教学案全集(含答案)

[全国卷3年考情分析][题点·考法·全练]1．(2017·全国卷Ⅱ)设集合A＝{1,2,4}，B＝{x|x2－4x＋m＝0}．若A∩B＝{1}，则B＝()A．{1，－3}B．{1,0}C ．{1,3}D ．{1,5}解析：选C 因为A ∩B ＝{1}，所以1∈B ，所以1是方程x 2－4x ＋m ＝0的根，所以1－4＋m ＝0，m ＝3，方程为x 2－4x ＋3＝0，解得x ＝1或x ＝3，所以B ＝{1,3}．2．(2018届高三·安徽名校阶段测试)设A ＝{x |x 2－4x ＋3≤0}，B ＝{x |ln(3－2x )<0}，则图中阴影部分表示的集合为( )A.⎩⎨⎧⎭⎬⎫x ⎪⎪ x <32B.⎩⎨⎧⎭⎬⎫x ⎪⎪1<x <32 C.⎩⎨⎧⎭⎬⎫x ⎪⎪ 1≤x <32 D.⎩⎨⎧⎭⎬⎫x ⎪⎪32<x ≤3 解析：选B A ＝{x |x 2－4x ＋3≤0}＝{x |1≤x ≤3}，B ＝{x |ln(3－2x )<0}＝{x |0<3－2x <1}＝⎩⎨⎧⎭⎬⎫x ⎪⎪ 1<x <32，结合Venn 图知，图中阴影部分表示的集合为A ∩B ＝⎩⎨⎧⎭⎬⎫x ⎪⎪1<x <32. 3．(2017·全国卷Ⅲ)已知集合A ＝{(x ，y )|x 2＋y 2＝1}，B ＝{(x ，y )|y ＝x }，则A ∩B 中元素的个数为( )A ．3B ．2C ．1D ．0解析：选B 因为A 表示圆x 2＋y 2＝1上的点的集合，B 表示直线y ＝x 上的点的集合，直线y ＝x 与圆x 2＋y 2＝1有两个交点，所以A ∩B 中元素的个数为2.4．已知集合P ＝{n |n ＝2k －1，k ∈N *，k ≤50}，Q ＝{2,3,5}，则集合T ＝{xy |x ∈P ，y ∈Q }中元素的个数为( )A ．147B ．140C ．130D ．117解析：选B 由题意得，y 的取值一共有3种情况，当y ＝2时，xy 是偶数，与y ＝3，y ＝5时，没有相同的元素，当y ＝3，x ＝5,15,25，…，95时，与y ＝5，x ＝3,9,15，…，57时有相同的元素，共10个，故所求元素个数为3×50－10＝140.5．已知集合A ＝⎩⎨⎧⎭⎬⎫－1，12，B ＝{x |mx －1＝0，m ∈R}，若A ∩B ＝B ，则所有符合条件的实数m 组成的集合是( )A ．{－1,0,2} B.⎩⎨⎧⎭⎬⎫－12，0，1 C ．{－1,2}D.⎩⎨⎧⎭⎬⎫－1，0，12解析：选A 因为A ∩B ＝B ，所以B ⊆A .若B 为∅，则m ＝0；若B ≠∅，则－m －1＝0或12m －1＝0，解得m ＝－1或2.综上，m ∈{－1,0,2}． [准解·快解·悟通][题点·考法·全练] 1．(2017·天津高考)设x∈R，则“2－x≥0”是“|x－1|≤1”的() A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件解析：选B由2－x≥0，得x≤2，由|x－1|≤1，得0≤x≤2.∵0≤x≤2⇒x≤2，x≤2⇒/ 0≤x≤2，故“2－x ≥0”是“|x －1|≤1”的必要而不充分条件．2．(2017·惠州三调)设函数y ＝f (x )，x ∈R ，“y ＝|f (x )|是偶函数”是“y ＝f (x )的图象关于原点对称”的( )A ．充分不必要条件B ．充要条件C ．必要不充分条件D ．既不充分也不必要条件解析：选C 设f (x )＝x 2，y ＝|f (x )|是偶函数，但是不能推出y ＝f (x )的图象关于原点对称．反之，若y ＝f (x )的图象关于原点对称，则y ＝f (x )是奇函数，这时y ＝|f (x )|是偶函数，故选C.3．(2017·浙江高考)已知等差数列{a n }的公差为d ，前n 项和为S n ，则“d >0”是“S 4＋S 6>2S 5”的( )A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件解析：选C 因为{a n }为等差数列，所以S 4＋S 6＝4a 1＋6d ＋6a 1＋15d ＝10a 1＋21d,2S 5＝10a 1＋20d ，S 4＋S 6－2S 5＝d ，所以d >0⇔S 4＋S 6>2S 5.4．已知“x >k ”是“3x ＋1<1”的充分不必要条件，则k 的取值范围是( ) A ．[2，＋∞) B ．[1，＋∞) C ．(2，＋∞)D ．(－∞，－1]解析：选A 由3x ＋1<1，可得3x ＋1－1＝－x ＋2x ＋1<0，所以x <－1或x >2，因为“x >k ”是“3x ＋1<1”的充分不必要条件，所以k ≥2. 5．已知条件p ：x ＋y ≠－2，条件q ：x ，y 不都是－1，则p 是q 的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件解析：选A 因为p ：x ＋y ≠－2，q ：x ≠－1或y ≠－1，所以綈p ：x ＋y ＝－2，綈q ：x ＝－1且y ＝－1，因为綈q ⇒綈p 但綈p ⇒/綈q ，所以綈q 是綈p 的充分不必要条件，即p 是q 的充分不必要条件．[准解·快解·悟通][题点·考法·全练]1．下列命题中为真命题的是( ) A ．命题“若x ＞1，则x 2＞1”的否命题 B ．命题“若x ＞y ，则x ＞|y |”的逆命题 C ．命题“若x ＝1，则x 2＋x －2＝0”的否命题 D ．命题“若tan x ＝3，则x ＝π3”的逆否命题解析：选B 对于选项A ，命题“若x ＞1，则x 2＞1”的否命题为“若x ≤1，则x 2≤1”，易知当x ＝－2时，x 2＝4＞1，故选项A 为假命题；对于选项B ，命题“若x ＞y ，则x ＞|y |”的逆命题为“若x ＞|y |，则x ＞y ”，分析可知选项B 为真命题；对于选项C ，命题“若x ＝1，则x 2＋x －2＝0”的否命题为“若x ≠1，则x 2＋x －2≠0”，易知当x ＝－2时，x 2＋x －2＝0，故选项C 为假命题；对于选项D ，命题“若tan x ＝3，则x ＝π3”为假命题，故其逆否命题为假命题，综上可知，选B.2．(2015·全国卷Ⅰ)设命题p ：∃n ∈N ，n 2>2n ，则綈p 为( ) A ．∀n ∈N ，n 2>2n B ．∃n ∈N ，n 2≤2n C ．∀n ∈N ，n 2≤2nD ．∃n ∈N ，n 2＝2n解析：选C 因为“∃x ∈M ，p (x )”的否定是“∀x ∈M ，綈p (x )”，所以命题“∃n ∈N ，n 2>2n ”的否定是“∀n ∈N ，n 2≤2n ”．3．(2017·山东高考)已知命题p ：∀x >0，ln(x ＋1)>0；命题q ：若a >b ，则a 2>b 2.下列命题为真命题的是( )A ．p ∧qB ．p ∧綈qC ．綈p ∧qD ．綈p ∧綈q解析：选B 当x >0时，x ＋1>1，因此ln(x ＋1)>0，即p 为真命题；取a ＝1，b ＝－2，这时满足a >b ，显然a 2>b 2不成立，因此q 为假命题．由复合命题的真假性，知B 为真命题．[准解·快解·悟通][专题过关检测]一、选择题1．(2016·全国卷Ⅱ)已知集合A＝{1,2,3}，B＝{x|(x＋1)·(x－2)<0，x∈Z}，则A∪B＝() A．{1}B．{1,2}C．{0,1,2,3} D．{－1,0,1,2,3}解析：选C因为B＝{x|(x＋1)(x－2)<0，x∈Z}＝{x|－1<x<2，x∈Z}＝{0,1}，A＝{1,2,3}，所以A∪B＝{0,1,2,3}．2．(2017·成都一诊)命题“若a>b，则a＋c>b＋c”的否命题是()A．若a≤b，则a＋c≤b＋c B．若a＋c≤b＋c，则a≤bC．若a＋c>b＋c，则a>b D．若a>b，则a＋c≤b＋c解析：选A命题的否命题是将原命题的条件和结论均否定，所以题中命题的否命题为“若a≤b，则a＋c≤b＋c”．3．(2017·广西三市第一次联考)设集合A＝{x|8＋2x－x2>0}，集合B＝{x|x＝2n－1，n ∈N*}，则A∩B等于()A．{－1,1} B．{－1,3}C．{1,3} D．{3,1，－1}解析：选C∵A＝{x|－2<x<4}，B＝{1,3,5，…}，∴A ∩B ＝{1,3}．4．(2017·郑州第二次质量预测)已知集合A ＝{x |log 2x ≤1}，B ＝⎩⎨⎧⎭⎬⎫x ⎪⎪1x>1，则A ∩(∁R B )＝( )A ．(－∞，2]B ．(0,1]C ．[1,2]D ．(2，＋∞)解析：选C 因为A ＝{x |0<x ≤2}，B ＝{x |0<x <1}，所以A ∩(∁R B )＝{x |0<x ≤2}∩{x |x ≤0或x ≥1}＝{x |1≤x ≤2}．5．(2017·北京高考)设m ，n 为非零向量，则“存在负数λ，使得m ＝λn ”是“m ·n <0”的( )A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件解析：选A ∵m ＝λn ，∴m ·n ＝λn ·n ＝λ|n |2. ∴当λ<0，n ≠0时，m ·n <0.反之，由m ·n ＝|m ||n |cos 〈m ，n 〉<0⇔cos 〈m ，n 〉<0⇔〈m ，n 〉∈⎝⎛⎦⎤π2，π，当〈m ，n 〉∈⎝⎛⎭⎫π2，π时，m ，n 不共线．故“存在负数λ，使得m ＝λn ”是“m ·n <0”的充分而不必要条件．6．(2018届高三·湘中名校联考)已知集合A ＝{x |x 2－11x －12＜0}，B ＝{x |x ＝2(3n ＋1)，n ∈Z}，则A ∩B 等于( )A ．{2}B ．{2,8}C ．{4,10}D ．{2,4,8,10}解析：选B 因为集合A ＝{x |x 2－11x －12＜0}＝{x |－1＜x ＜12}，集合B 为被6整除余数为2的数．又集合A 中的整数有0,1,2,3,4,5,6,7,8,9,10,11，故被6整除余数为2的数有2和8，所以A ∩B ＝{2,8}．7．(2017·石家庄调研)设全集U ＝R ，集合A ＝{x |x ≥1}，B ＝{x |(x ＋2)(x －1)<0}，则( ) A ．A ∩B ＝∅ B ．A ∪B ＝U C ．∁U B ⊆AD ．∁U A ⊆B解析：选A 由(x ＋2)(x －1)<0，解得－2<x <1，所以B ＝{x |－2<x <1}，则A ∩B ＝∅，A ∪B ＝{x |x >－2}，∁U B ＝{x |x ≥1或x ≤－2}，A ⊆∁U B ，∁U A ＝{x |x <1}，B ⊆∁U A ，故选A.8．若x ∈A ，则1x ∈A ，就称A 是伙伴关系集合，集合M ＝⎩⎨⎧⎭⎬⎫－1，0，13，12，1，2，3，4的所有非空子集中，具有伙伴关系的集合的个数为( )A ．15B ．16C ．28D ．25解析：选A 本题关键看清－1和1本身也具备这种运算，这样所求集合即由－1,1,3和13，2和12这“四大”元素所能组成的集合．所以满足条件的集合的个数为24－1＝15. 9．(2017·郑州第一次质量预测)已知命题p ：1a >14，命题q ：∀x ∈R ，ax 2＋ax ＋1>0，则p 成立是q 成立的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件解析：选A 命题p 等价于0<a <4.命题q ，对∀x ∈R ，ax 2＋ax ＋1>0，必有a ＝0或⎩⎪⎨⎪⎧a >0，a 2－4a <0，则0≤a <4，所以命题p 是命题q 的充分不必要条件． 10．已知f (x )＝3sin x －πx ，命题p ：∀x ∈⎝⎛⎭⎫0，π2，f (x )<0，则( ) A ．p 是假命题，綈p ：∀x ∈⎝⎛⎭⎫0，π2，f (x )≥0 B ．p 是假命题，綈p ：∃x 0∈⎝⎛⎭⎫0，π2，f (x 0)≥0 C ．p 是真命题，綈p ：∃x 0∈⎝⎛⎭⎫0，π2，f (x 0)≥0 D ．p 是真命题，綈p ：∀x ∈⎝⎛⎭⎫0，π2，f (x )>0 解析：选C 因为f ′(x )＝3cos x －π，所以当x ∈⎝⎛⎭⎫0，π2 时，f ′(x )<0，函数f (x )单调递减，即对∀x ∈⎝⎛⎭⎫0，π2，f (x )<f (0)＝0恒成立，所以p 是真命题．而p 的否定为∃x 0∈⎝⎛⎭⎫0，π2，f (x 0)≥0，故选C. 11．已知命题p ：函数f (x )＝2ax 2－x －1在(0,1)内恰有一个零点；命题q ：函数y ＝x 2－a在(0，＋∞)上是减函数．若p 且綈q 为真命题，则实数a 的取值范围是( )A ．(1，＋∞)B ．(－∞，2]C ．(1,2]D ．(－∞，1]∪(2，＋∞)解析：选C 由题意可得，对命题p ，令f (0)·f (1)<0，即－1·(2a －2)<0，得a >1；对命题q ，令2－a <0，即a >2，则綈q 对应的a 的范围是(－∞，2]．因为p 且綈q 为真命题，所以实数a 的取值范围是(1,2]．12．在下列结论中，正确的个数是( )①命题p ：“∃x 0∈R ，x 20－2≥0”的否定形式为綈p ：“∀x ∈R ，x 2－2<0”；②O 是△ABC 所在平面上一点，若OA ―→·OB ―→＝OB ―→·OC ―→＝OC ―→·OA ―→，则O 是△ABC 的垂心；③“M >N ”是“⎝⎛⎭⎫23M >⎝⎛⎭⎫23N”的充分不必要条件；④命题“若x 2－3x －4＝0，则x ＝4”的逆否命题为“若x ≠4，则x 2－3x －4≠0”． A ．1 B ．2 C ．3D ．4解析：选C 由特称(存在性)命题与全称命题的关系可知①正确． ∵OA ―→·OB ―→＝OB ―→·OC ―→，∴OB ―→·(OA ―→－OC ―→)＝0，即OB ―→·CA ―→＝0， ∴OB ―→⊥CA ―→.同理可知OA ―→⊥BC ―→，OC ―→⊥BA ―→，故点O 是△ABC 的垂心，∴②正确． ∵y ＝⎝⎛⎭⎫23x是减函数，∴当M >N 时，⎝⎛⎭⎫23M <⎝⎛⎭⎫23N ，当⎝⎛⎭⎫23M >⎝⎛⎭⎫23N 时，M <N . ∴“M >N ”是“⎝⎛⎭⎫23M >⎝⎛⎭⎫23N ”的既不充分也不必要条件，∴③错误．由逆否命题的写法可知，④正确． ∴正确的结论有3个．二、填空题13．设命题p ：∀a >0，a ≠1，函数f (x )＝a x －x －a 有零点，则綈p ：________________________.解析：全称命题的否定为特称(存在性)命题，綈p ：∃a 0>0，a 0≠1，函数f (x )＝a x 0－x－a 0没有零点．答案：∃a 0>0，a 0≠1，函数f (x )＝a x 0－x －a 0没有零点14．设全集U ＝{(x ，y )|x ∈R ，y ∈R}，集合M ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫(x ，y )⎪⎪⎪ y －3x －2＝1，P ＝{(x ，y )|y ≠x ＋1}，则∁U (M ∪P )＝________.解析：集合M ＝{(x ，y )|y ＝x ＋1，且x ≠2，y ≠3}，所以M ∪P ＝{(x ，y )|x ∈R ，y ∈R ，且x ≠2，y ≠3}．则∁U (M ∪P )＝{(2,3)}．答案：{(2,3)}15．已知命题p ：不等式xx －1＜0的解集为{x |0＜x ＜1}；命题q ：在△ABC 中，“A ＞B ”是“sin A ＞sin B ”成立的必要不充分条件．有下列四个结论：①p 真q 假；②“p ∧q ”为真；③“p ∨q ”为真；④p 假q 真，其中正确结论的序号是________．解析：解不等式知，命题p是真命题，在△ABC中，“A＞B”是“sin A＞sin B”的充要条件，所以命题q是假命题，所以①③正确．答案：①③16．a，b，c为三个人，命题A：“如果b的年龄不是最大，那么a的年龄最小”和命题B：“如果c不是年龄最小，那么a的年龄最大”都是真命题，则a，b，c的年龄由小到大依次是________．解析：显然命题A和B的原命题的结论是矛盾的，因此我们应该从它们的逆否命题来看．由命题A可知，当b不是最大时，则a是最小，所以c最大，即c>b>a；而它的逆否命题也为真，即“若a的年龄不是最小，则b的年龄是最大”为真，即b>a>c.同理，由命题B为真可得a>c>b或b>a>c.故由A与B均为真可知b>a>c，所以a，b，c三人的年龄大小顺序是：b最大，a次之，c最小．答案：c，a，b送分专题(二)函数的图象与性质[全国卷3年考情分析][题点·考法·全练]1．(2017·广州综合测试)已知函数f (x )＝⎩⎪⎨⎪⎧2x ＋1，x ≤0，1－log 2x ，x >0，则f (f (－3))＝( ) A.43B ．23C ．－43D ．3解析：选D 因为f (－3)＝2－2＝14，所以f (f (－3))＝f ⎝⎛⎭⎫14＝1－log 214＝3. 2．函数y ＝1－x 22x 2－3x －2的定义域为( )A ．(－∞，1]B ．[－1,1]C ．[1,2)∪(2，＋∞)D.⎣⎡⎭⎫－1，－12∪⎝⎛⎦⎤－12，1 解析：选D 要使函数y ＝1－x 22x 2－3x －2有意义，则⎩⎪⎨⎪⎧1－x 2≥0，2x 2－3x －2≠0，解得⎩⎪⎨⎪⎧－1≤x ≤1，x ≠2且x ≠－12，即－1≤x ≤1且x ≠－12，所以该函数的定义域为⎣⎡⎭⎫－1，－12∪⎝⎛⎦⎤－12，1. 3．(2017·全国卷Ⅲ)设函数f (x )＝⎩⎪⎨⎪⎧x ＋1，x ≤0，2x ，x >0，则满足f (x )＋f ⎝⎛⎭⎫x －12>1的x 的取值范围是________．解析：由题意知，可对不等式分x ≤0,0<x ≤12，x >12讨论．当x ≤0时，原不等式为x ＋1＋x ＋12>1，解得x >－14，∴－14<x ≤0.当0<x ≤12时，原不等式为2x ＋x ＋12>1，显然成立．当x >12时，原不等式为2x ＋2x －12>1，显然成立．综上可知，x 的取值范围是⎝⎛⎭⎫－14，＋∞.答案：⎝⎛⎭⎫－14，＋∞ 4．若函数f (x )＝(x ＋a )(bx ＋2a )(常数a ，b ∈R)是偶函数，且它的值域为(－∞，2]，则该函数的解析式为________．解析：由题意知：a ≠0，f (x )＝(x ＋a )(bx ＋2a )＝bx 2＋(2a ＋ab )x ＋2a 2是偶函数，则其图象关于y 轴对称，所以2a ＋ab ＝0，b ＝－2.所以f (x )＝－2x 2＋2a 2，因为它的值域为(－∞，2]，所以2a 2＝2.所以f (x )＝－2x 2＋2.答案：f (x )＝－2x 2＋25．已知函数f (x )＝⎩⎪⎨⎪⎧(1－2a )x ＋3a ，x <1，2x －1，x ≥1的值域为R ，则实数a 的取值范围是________．解析：当x ≥1时，f (x )＝2x －1≥1，∵函数f (x )＝⎩⎪⎨⎪⎧(1－2a )x ＋3a ，x <1，2x －1，x ≥1的值域为R ，∴当x <1时，y ＝(1－2a )x ＋3a 必须取遍(－∞，1]内的所有实数，则⎩⎪⎨⎪⎧1－2a >0，1－2a ＋3a ≥1，解得0≤a ＜12.答案：⎣⎡⎭⎫0，12 [准解·快解·悟通][题点·考法·全练]1．(2018届高三·安徽名校阶段性测试)函数y ＝x 2ln|x ||x |的图象大致是( )解析：选D 易知函数y ＝x 2ln|x ||x |是偶函数，可排除B ，当x >0时，y ＝x ln x ，y ′＝ln x＋1，令y ′>0，得x >e －1，所以当x >0时，函数在(e －1，＋∞)上单调递增，结合图象可知D正确，故选D.2．已知函数f (x －1)是定义在R 上的奇函数，且在[0，＋∞)上是增函数，则函数f (x )的图象可能是( )解析：选B 函数f (x －1)的图象向左平移1个单位，即可得到函数f (x )的图象，因为函数f (x －1)是定义在R 上的奇函数，所以函数f (x －1)的图象关于原点对称，所以函数f (x )的图象关于点(－1,0)对称，排除A 、C 、D ，选B.3．设函数f (x )＝⎩⎪⎨⎪⎧m ＋x 2，|x |≥1，x ，|x |<1的图象过点(1,1)，函数g (x )是二次函数，若函数f (g (x ))的值域是[0，＋∞)，则函数g (x )的值域是( )A ．(－∞，－1]∪[1，＋∞)B ．(－∞，－1]∪[0，＋∞)C ．[0，＋∞)D ．[1，＋∞)解析：选C 因为函数f (x )＝⎩⎪⎨⎪⎧m ＋x 2，|x |≥1，x ，|x |<1的图象过点(1,1)，所以m ＋1＝1，解得m ＝0，所以f (x )＝⎩⎪⎨⎪⎧x 2，|x |≥1，x ，|x |<1.画出函数y ＝f (x )的图象(如图所示)，由于函数g (x )是二次函数，值域不会是选项A 、B ，易知，当g (x )的值域是[0，＋∞)时，f (g (x ))的值域是[0，＋∞)．[准解·快解·悟通][题点·考法·全练]1．下列函数中，满足“∀x1，x2∈(0，＋∞)，且x1≠x2，(x1－x2)[f(x1)－f(x2)]<0”的是()A．f(x)＝1x－x B．f(x)＝x3C．f(x)＝ln x D．f(x)＝2x解析：选A“∀x1，x2∈(0，＋∞)，且x1≠x2，(x1－x2)·[f(x1)－f(x2)]<0”等价于f(x)在(0，＋∞)上为减函数，易判断f(x)＝1x－x满足条件．2．(2017·广西三市第一次联考)已知f(x)是定义在R上的偶函数，且在区间(－∞，0]上单调递增，若实数a满足f(2log3a)>f(－2)，则a的取值范围是()A．(－∞，3) B．(0，3)C．(3，＋∞) D．(1，3)解析：选B∵f(x)是定义在R上的偶函数，且在区间(－∞，0]上单调递增，∴f(x)在区间[0，＋∞)上单调递减．根据函数的对称性，可得f(－2)＝f(2)，∴f(2log3a)>f(2)．∵2log 3a >0，f (x )在区间[0，＋∞)上单调递减，∴0<2log 3a <2⇒log 3a <12⇒0<a < 3.3．(2017·山东高考)已知f (x )是定义在R 上的偶函数，且f (x ＋4)＝f (x －2)．若当x ∈[－3,0]时，f (x )＝6－x ，则f (919)＝________.解析：∵f (x ＋4)＝f (x －2)，∴f (x ＋6)＝f (x )， ∴f (x )的周期为6，∵919＝153×6＋1，∴f (919)＝f (1)．又f (x )为偶函数，∴f (919)＝f (1)＝f (－1)＝6. 答案：64．(2017·福建普通高中质量检测)已知函数f (x )＝x 2(2x －2－x )，则不等式f (2x ＋1)＋f (1)≥0的解集是________．解析：因为f (－x )＝(－x )2(2－x －2x )＝－x 2(2x －2－x )＝－f (x )，所以函数f (x )是奇函数．不等式f (2x ＋1)＋f (1)≥0等价于f (2x ＋1)≥f (－1)．易知，当x >0时，函数f (x )为增函数，所以函数f (x )在R 上为增函数，所以f (2x ＋1)≥f (－1)等价于2x ＋1≥－1，解得x ≥－1.答案：{x |x ≥－1}[准解·快解·悟通][专题过关检测]一、选择题 1．函数f (x )＝1x －1＋x 的定义域为( ) A ．[0，＋∞) B ．(1，＋∞) C ．[0,1)∪(1，＋∞)D ．[0,1)解析：选C 由题意知⎩⎪⎨⎪⎧x －1≠0，x ≥0，∴f (x )的定义域为[0,1)∪(1，＋∞)．2．下列函数中，既是偶函数又在区间(0，＋∞)上单调递增的是( ) A ．y ＝1xB ．y ＝|x |－1C ．y ＝lg xD ．y ＝⎝⎛⎭⎫12|x |解析：选B A 中函数y ＝1x 不是偶函数且在(0，＋∞)上单调递减，故A 错误；B 中函数满足题意，故B 正确；C 中函数不是偶函数，故C 错误；D 中函数不满足在(0，＋∞)上单调递增，故选B.3．已知函数f (x )＝2×4x －a2x的图象关于原点对称，g (x )＝ln(e x ＋1)－bx 是偶函数，则log a b ＝( )A ．1B ．－1C ．－12D ．14解析：选B 由题意得f (0)＝0，∴a ＝2. ∵g (1)＝g (－1)，∴ln(e ＋1)－b ＝ln ⎝⎛⎭⎫1e ＋1＋b ， ∴b ＝12，∴log 212＝－1.4．若函数f (x )＝⎩⎪⎨⎪⎧ax ＋b ，x <－1，ln (x ＋a )，x ≥－1的图象如图所示，则f (－3)等于( )A ．－12B ．－54C ．－1D ．－2解析：选C 由图象可得a (－1)＋b ＝3，ln(－1＋a )＝0，∴a ＝2，b ＝5，∴f (x )＝⎩⎪⎨⎪⎧2x ＋5，x <－1，ln (x ＋2)，x ≥－1，故f (－3)＝2×(－3)＋5＝－1.5．已知函数f (x )的定义域为(－∞，＋∞)，若f (x ＋2 017)＝⎩⎨⎧2sin x ，x ≥0，lg (－x )，x <0，则f ⎝⎛⎭⎫2 017＋π4·f (－7 983)＝( ) A ．2 016 B.14C ．4 D.12 016解析：选C 由题意得，f ⎝⎛⎭⎫2 017＋π4＝2sin π4＝1， f (－7 983)＝f (2 017－10 000)＝lg 10 000＝4， ∴f ⎝⎛⎭⎫2 017＋π4·f (－7 983)＝4. 6．函数y ＝sin xx ，x ∈(－π，0)∪(0，π)的图象大致是( )解析：选A 函数y ＝sin xx ，x ∈(－π，0)∪(0，π)为偶函数，所以图象关于y 轴对称，排除B 、C ，又当x 趋近于π时，y ＝sin xx 趋近于0，故选A.7．(2016·山东高考)已知函数f (x )的定义域为R.当x ＜0时，f (x )＝x 3－1；当－1≤x ≤1时，f (－x )＝－f (x )；当x ＞12时，f ⎝⎛⎭⎫x ＋12＝f ⎝⎛⎭⎫x －12，则f (6)＝( ) A ．－2 B ．－1 C ．0D ．2解析：选D 由题意知，当x ＞12时，f ⎝⎛⎭⎫x ＋12＝fx －12，则f (x ＋1)＝f (x )．又当－1≤x ≤1时，f (－x )＝－f (x )， ∴f (6)＝f (1)＝－f (－1)．又当x ＜0时，f (x )＝x 3－1， ∴f (－1)＝－2，∴f (6)＝2.8．如图，动点P 在正方体ABCD -A 1B 1C 1D 1的体对角线BD 1上．过点P 作垂直于平面BB 1D 1D 的直线，与正方体的表面相交于M ，N 两点．设BP ＝x ，MN ＝y ，则函数y ＝f (x )的图象大致是( )解析：选B 设正方体的棱长为1，显然，当P 移动到体对角线BD 1的中点E 时，函数y ＝MN ＝AC ＝2取得唯一的最大值，所以排除A 、C ；当P 在BE 上时，分别过M ，N ，P 作底面的垂线，垂足分别为M 1，N 1，P 1，则y ＝MN ＝M 1N 1＝2BP 1＝2x cos ∠D 1BD ＝263x ，是一次函数，所以排除D.故选B.9．(2017·贵阳模拟)定义新运算⊕：当a ≥b 时，a ⊕b ＝a ；当a ＜b 时，a ⊕b ＝b 2，则函数f (x )＝(1⊕x )x －(2⊕x )，x ∈[－2,2]的最大值等于( )A ．－1B ．1C ．6D ．12解析：选C 由已知得当－2≤x ≤1时，f (x )＝x －2，当1＜x ≤2时，f (x )＝x 3－2.∵f (x )＝x －2，f (x )＝x 3－2在定义域内都为增函数． ∴f (x )的最大值为f (2)＝23－2＝6. 10．函数f (x )＝ax ＋b(x ＋c )2的图象如图所示，则下列结论成立的是( )A ．a >0，b >0，c <0B ．a <0，b >0，c >0C ．a <0，b >0，c <0D ．a <0，b <0，c <0 解析：选C ∵f (x )＝ax ＋b(x ＋c )2的图象与x 轴，y 轴分别交于N ，M ，且点M 的纵坐标与点N 的横坐标均为正，∴x ＝－b a >0，y ＝bc 2>0，故a <0，b >0，又函数图象间断点的横坐标为正，∴－c >0，c <0，故选C.11．定义在R 上的函数f (x )对任意0<x 2<x 1都有f (x 1)－f (x 2)x 1－x 2<1，且函数y ＝f (x )的图象关于原点对称，若f (2)＝2，则不等式f (x )－x >0的解集是( )A ．(－2,0)∪(0,2)B ．(－∞，－2)∪(2，＋∞)C ．(－∞，－2)∪(0,2)D ．(－2,0)∪(2，＋∞)解析：选C (转化法)由f (x 1)－f (x 2)x 1－x 2<1，可得[f (x 1)－x 1]－[f (x 2)－x 2]x 1－x 2<0.令F (x )＝f (x )－x ，由题意知F (x )在(－∞，0)，(0，＋∞)上是减函数，且是奇函数，F (2)＝0，F (－2)＝0，所以结合图象，令F (x )>0，得x <－2或0<x <2.12．已知函数f (x )＝2x －1，g (x )＝1－x 2，规定：当|f (x )|≥g (x )时，h (x )＝|f (x )|；当|f (x )|<g (x )时，h (x )＝－g (x )，则h (x )( )A ．有最小值－1，最大值1B ．有最大值1，无最小值C ．有最小值－1，无最大值D ．有最大值－1，无最小值解析：选C 作出函数g (x )＝1－x 2和函数|f (x )|＝|2x －1|的图象如图①所示，得到函数h (x )的图象如图②所示，由图象得函数h (x )有最小值－1，无最大值．二、填空题13．函数f (x )＝ln 1|x |＋1的值域是________．解析：因为|x |≥0，所以|x |＋1≥1. 所以0＜1|x |＋1≤1.所以ln 1|x |＋1≤0，即f (x )＝ln1|x |＋1的值域为(－∞，0]．答案：(－∞，0]14．(2018届高三·安徽名校阶段性测试)已知f (x )是定义在R 上的奇函数，且当x <0时，f (x )＝2x ，则f (log 49)＝________.解析：因为log 49＝log 23>0，又f (x )是定义在R 上的奇函数，且当x <0时，f (x )＝2x ，所以f (log 49)＝f (log 23)＝－2－log 23＝－2log 213＝－13.答案：－1315．若当x ∈(1,2)时，函数y ＝(x －1)2的图象始终在函数y ＝log a x 的图象的下方，则实数a 的取值范围是________．解析：如图，在同一平面直角坐标系中画出函数y ＝(x －1)2和y ＝log a x 的图象，由于当x ∈(1,2)时，函数y ＝(x －1)2的图象恒在函数y ＝log a x 的图象的下方，则⎩⎪⎨⎪⎧a >1，log a 2≥1，解得1<a ≤2.答案：(1,2]16．(2017·惠州三调)已知定义在R 上的函数y ＝f (x )满足条件f ⎝⎛⎭⎫x ＋32＝－f (x )，且函数y ＝f ⎝⎛⎭⎫x －34为奇函数，给出以下四个命题： ①函数f (x )是周期函数；②函数f (x )的图象关于点⎝⎛⎭⎫－34，0对称； ③函数f (x )为R 上的偶函数； ④函数f (x )为R 上的单调函数．其中真命题的序号为____________．解析：f (x ＋3)＝f ⎣⎡⎦⎤⎝⎛⎭⎫x ＋32＋32＝－f ⎝⎛⎭⎫x ＋32＝f (x )，所以f (x )是周期为3的周期函数，①正确；函数f ⎝⎛⎭⎫x －34是奇函数，其图象关于点(0,0)对称，则f (x )的图象关于点⎝⎛⎭⎫－34，0对称，②正确；因为f (x )的图象关于点⎝⎛⎭⎫－34，0对称，－34＝－x ＋⎝⎛⎭⎫－32＋x 2，所以f (－x )＝－f ⎝⎛⎭⎫－32＋x ，又f ⎝⎛⎭⎫－32＋x ＝－f ⎝⎛⎭⎫－32＋x ＋32＝－f (x )，所以f (－x )＝f (x )，③正确；f (x )是周期函数在R 上不可能是单调函数，④错误．故真命题的序号为①②③. 答案：①②③送分专题(三) 平面向量[全国卷3年考情分析][题点·考法·全练]1．(2017·贵州适应性考试)已知向量e 1与e 2不共线，且向量AB ―→＝e 1＋me 2，AC ―→＝ne 1＋e 2，若A ，B ，C 三点共线，则实数m ，n 满足的条件是( )A ．mn ＝1B ．mn ＝－1C ．m ＋n ＝1D ．m ＋n ＝－1解析：选A 法一：因为A ，B ，C 三点共线，所以一定存在一个确定的实数λ，使得AB―→＝λAC ―→，所以有e 1＋me 2＝nλe 1＋λe 2，由此可得⎩⎪⎨⎪⎧1＝nλ，m ＝λ，所以mn ＝1.法二：因为A ，B ，C 三点共线，所以必有1n ＝m1，所以mn ＝1.2.如图所示，下列结论正确的是( )①PQ ―→＝32a ＋32b ；②PT ―→＝32a －b ；③PS ―→＝32a －12b ；④PR ―→＝32a ＋b .A ．①②B ．③④C ．①③D ．②④解析：选C ①根据向量的加法法则，得PQ ―→＝32a ＋32b ，故①正确；②根据向量的减法法则，得PT ―→＝32a －32b ，故②错误；③PS ―→＝PQ ―→＋QS ―→＝32a ＋32b －2b ＝32a －12b ，故③正确；④PR ―→＝PQ ―→＋QR ―→＝32a ＋32b －b ＝32a ＋12b ，故④错误．故正确命题的结论为①③.3．已知平面内不共线的四点O ，A ，B ，C ，若OA ―→－3OB ―→＋2OC ―→＝0，则|AB ―→||BC ―→|＝________.解析：由已知得OA ―→－OB ―→＝2(OB ―→－OC ―→)，即BA ―→＝2CB ―→， ∴|BA ―→|＝2|CB ―→|，∴|AB ―→||BC ―→|＝2.答案：24．已知e 1，e 2是不共线向量，a ＝me 1＋2e 2，b ＝ne 1－e 2，且mn ≠0，若a ∥b ，则mn 等于________．解析：∵a ∥b ，∴a ＝λb ，即me 1＋2e 2＝λ(ne 1－e 2)，则⎩⎪⎨⎪⎧λn ＝m ，－λ＝2，解得m n ＝－2.答案：－2[准解·快解·悟通][题点·考法·全练]1．已知向量m ＝(t ＋1,1)，n ＝(t ＋2,2)，若(m ＋n )⊥(m －n )，则t ＝( ) A ．0 B ．－3 C ．3D ．－1解析：选B 法一：由(m ＋n )⊥(m －n )可得(m ＋n )·(m －n )＝0，即m 2＝n 2，故(t ＋1)2＋1＝(t ＋2)2＋4，解得t ＝－3.法二：m ＋n ＝(2t ＋3,3)，m －n ＝(－1，－1)，∵(m ＋n )⊥(m －n )，∴－(2t ＋3)－3＝0，解得t ＝－3.2．(2017·洛阳统考)已知向量a ＝(1,0)，|b |＝2，a 与b 的夹角为45°，若c ＝a ＋b ，d ＝a －b ，则c 在d 方向上的投影为( )A.55B ．－55C ．1D ．－1解析：选D 依题意得|a |＝1，a ·b ＝1×2×cos 45°＝1，|d |＝(a －b )2＝a 2＋b 2－2a ·b ＝1，c ·d ＝a 2－b 2＝－1，因此c 在d 方向上的投影等于c ·d|d |＝－1. 3．已知向量a ＝(2,1)，b ＝(1，k )，且a 与b 的夹角为锐角，则实数k 的取值范围是( ) A.⎝⎛⎭⎫－2，12 B.⎝⎛⎭⎫－2，12∪⎝⎛⎭⎫12，＋∞ C ．(－2，＋∞)D ．[－2，＋∞)解析：选B 当a ，b 共线时，2k －1＝0，k ＝12，此时a ，b 方向相同，夹角为0，所以要使a 与b 的夹角为锐角，则有a·b >0且a ，b 不共线．由a·b ＝2＋k >0得k >－2，又k ≠12，即实数k 的取值范围是⎝⎛⎭⎫－2，12∪⎝⎛⎭⎫12，＋∞，选B. 4．(2017·全国卷Ⅰ)已知向量a ，b 的夹角为60°，|a |＝2，|b |＝1，则|a ＋2b |＝________. 解析：法一：易知|a ＋2b |＝|a |2＋4a ·b ＋4|b |2＝4＋4×2×1×12＋4＝2 3.法二：(数形结合法)由|a |＝|2b |＝2，知以a 与2b 为邻边可作出边长为2的菱形OACB ，如图，则|a ＋2b |＝|OC ―→|.又∠AOB ＝60°，所以|a ＋2b |＝2 3.答案：2 35．(2017·山东高考)已知e 1，e 2是互相垂直的单位向量．若3e 1－e 2与e 1＋λe 2的夹角为60°，则实数λ的值是________．解析：因为(3e 1－e 2)·(e 1＋λe 2)|3e 1－e 2|·|e 1＋λe 2|＝3－λ21＋λ2，故3－λ21＋λ2＝12，解得λ＝33.答案：33[准解·快解·悟通][题点·考法·全练]1．在△ABC 中，∠ABC ＝90°，AB ＝6，点D 在边AC 上，且2AD ―→＝DC ―→，则BA ―→·BD ―→的值是( )A ．48B ．24C ．12D ．6解析：选B 法一：由题意得，BA ―→·BC ―→＝0，BA ―→·CA ―→＝BA ―→·(BA ―→－BC ―→)＝|BA ―→|2＝36，∴BA ―→·BD ―→＝BA ―→·(BC ―→＋CD ―→)＝BA ―→·⎝⎛⎭⎫BC ―→＋23 CA ―→ ＝0＋23×36＝24. 法二：(特例法)若△ABC 为等腰直角三角形，建立如图所示的平面直角坐标系，则A (6,0)，C (0,6)．由2AD ―→＝DC ―→，得D (4,2)．∴BA ―→·BD ―→＝(6,0)·(4,2)＝24.2.如图所示，已知点G 是△ABC 的重心，过点G 作直线与AB ，AC 两边分别交于M ，N 两点，且AM ―→＝x AB ―→，AN ―→＝y AC ―→，则x ＋2y 的最小值为( )A ．2 B.13 C.3＋223D.34解析：选C 由已知可得AG ―→＝23×12(AB ―→＋AC ―→)＝13AB ―→＋13AC ―→＝13x AM ―→＋13y AN ―→，又M ，G ，N 三点共线，故13x ＋13y＝1，∴1x ＋1y ＝3，则x ＋2y ＝(x ＋2y )·⎝⎛⎭⎫1x ＋1y ·13＝13⎝⎛⎭⎫3＋2y x ＋x y ≥3＋223(当且仅当x ＝2y 时取等号)．3．(2017·全国卷Ⅱ)已知△ABC 是边长为2的等边三角形，P 为平面ABC 内一点，则PA ―→·(PB ―→＋PC ―→)的最小值是( )A ．－2B ．－32C ．－43D ．－1解析：选B 如图，以等边三角形ABC 的底边BC 所在直线为x轴，以BC 的垂直平分线为y 轴建立平面直角坐标系，则A (0，3)，B (－1,0)，C (1,0)，设P (x ，y )，则PA ―→＝(－x, 3－y )，PB ―→＝(－1－x ，－y )，PC ―→＝(1－x ，－y )，所以PA ―→·(PB ―→＋PC ―→)＝(－x ，3－y )·(－2x ，－2y )＝2x 2＋2⎝⎛⎭⎫y －322－32，当x ＝0，y ＝32时，PA ―→·(PB ―→＋PC ―→)取得最小值，为－32.4．如图，已知△ABC 中，∠BAC ＝90°，∠B ＝30°，点P 在线段BC 上运动，且满足CP ―→＝λCB ―→，当PA ―→·PC ―→取到最小值时，λ的值为( )A.14 B.15 C.16D.18解析：选D 如图所示，建立平面直角坐标系．不妨设BC ＝4，P (x,0)(0≤x ≤4)，则A (3，3)，C (4,0)，∴PA ―→·PC ―→＝(3－x ，3)·(4－x,0)＝(3－x )(4－x )＝x 2－7x ＋12＝⎝⎛⎭⎫x －722－14.当x ＝72时，PA ―→·PC ―→取得最小值－14.∵CP ―→＝λCB ―→，∴⎝⎛⎭⎫－12，0＝λ(－4,0)， ∴－4λ＝－12，解得λ＝18.故选D.5.如图，在平行四边形ABCD 中，已知AB ＝8，AD ＝5，CP ―→＝3PD ―→，AP ―→·BP ―→＝2，则AB ―→·AD ―→的值是________．解析：因为AP ―→＝AD ―→＋DP ―→＝AD ―→＋14AB ―→，BP ―→＝BC ―→＋CP ―→＝AD ―→－34AB ―→，所以AP ―→·BP ―→＝⎝⎛⎭⎫AD ―→＋14AB ―→·⎝⎛⎭⎫AD ―→－34AB ―→＝ |AD ―→|2－316|AB ―→|2－12AD ―→·AB ―→＝2，将AB ＝8，AD ＝5代入解得AB ―→·AD ―→＝22. 答案：22[准解·快解·悟通][专题过关检测]一、选择题1．设a ＝(1,2)，b ＝(1,1)，c ＝a ＋kb .若b ⊥c ，则实数k 的值等于( ) A ．－32B ．－53C.53D ．32解析：选A 因为c ＝a ＋kb ＝(1＋k,2＋k )，又b ⊥c ，所以1×(1＋k )＋1×(2＋k )＝0，解得k ＝－32.2．(2017·贵州适应性考试)已知向量a ＝(2,4)，b ＝(－1，1)，c ＝(2,3)，若a ＋λb 与c 共线，则实数λ＝( )A.25 B ．－25C.35D ．－35解析：选B 法一：a ＋λb ＝(2－λ，4＋λ)，c ＝(2,3)，因为a ＋λb 与c 共线，所以必定存在唯一实数μ，使得a ＋λb ＝μc ，所以⎩⎪⎨⎪⎧2－λ＝2μ，4＋λ＝3μ，解得⎩⎨⎧μ＝65，λ＝－25.法二：a ＋λb ＝(2－λ，4＋λ)，c ＝(2,3)，由a ＋λb 与c 共线可知2－λ2＝4＋λ3，解得λ＝－25. 3．(2018届高三·云南11校跨区调研)已知平面向量a 与b 的夹角为45°，a ＝(1,1)，|b |＝2，则|3a ＋b |等于( )A ．13＋6 2B ．2 5 C.30D ．34解析：选D 依题意得a 2＝2，a ·b ＝2×2×cos 45°＝2，|3a ＋b |＝(3a ＋b )2＝9a 2＋6a ·b ＋b 2＝18＋12＋4＝34.4．在等腰梯形ABCD 中，AB ―→＝－2CD ―→CD ―→，M 为BC 的中点，则AM ―→＝( ) A.12AB ―→＋12AD ―→ B.34AB ―→＋12AD ―→ C.34AB ―→＋14AD ―→ D.12AB ―→＋34AD ―→ 解析：选B 因为AB ―→＝－2CD ―→，所以AB ―→＝2DC ―→.又M 是BC 的中点，所以AM ―→＝12(AB―→＋AC ―→)＝12(AB ―→＋AD ―→＋DC ―→)＝12⎝⎛⎭⎫AB ―→＋AD ―→＋12AB ―→＝34AB ―→＋12AD ―→.5．(2017·成都二诊)已知平面向量a ，b 的夹角为π3，且|a |＝1，|b |＝12，则a ＋2b 与b 的夹角是( )A.π6 B.5π6 C.π4D.3π4解析：选A 法一：因为|a ＋2b |2＝|a |2＋4|b |2＋4a ·b ＝1＋1＋4×1×12×cos π3＝3，所以|a ＋2b |＝3，又(a ＋2b )·b ＝a ·b ＋2|b |2＝1×12×cos π3＋2×14＝14＋12＝34，所以cos 〈a ＋2b ，b 〉＝(a ＋2b )·b|a ＋2b ||b |＝343×12＝32，所以a ＋2b 与b 的夹角为π6.法二：(特例法)设a ＝(1,0)，b ＝⎝⎛⎭⎫12cos π3，12sin π3＝⎝⎛⎭⎫14，34，则(a ＋2b )·b ＝⎝⎛⎭⎫32，32·⎝⎛⎭⎫14，34＝34，|a ＋2b |＝⎝⎛⎭⎫322＋⎝⎛⎭⎫322＝3，所以cos 〈a ＋2b ，b 〉＝(a ＋2b )·b |a ＋2b ||b |＝343×12＝32，所以a ＋2b 与b 的夹角为π6. 6．已知点A (－1,1)，B (1,2)，C (－2，－1)，D (3,4)，则向量AB ―→在CD ―→方向上的投影为( ) A.322B ．3152C ．－322D ．－3152解析：选A 由题意知AB ―→＝(2,1)，CD ―→＝(5,5)，则AB ―→在CD ―→方向上的投影为|AB ―→|·cos 〈AB ―→，CD ―→〉＝AB ―→·CD ―→|CD ―→|＝322.7．(2017·安徽二校联考)在边长为1的正三角形ABC 中，D ，E 是边BC 的两个三等分点(D 靠近点B )，则AD ―→·AE ―→等于( )A.16B.29C.1318D.13解析：选C 法一：因为D ，E 是边BC 的两个三等分点，所以BD ＝DE ＝CE ＝13，在△ABD 中，AD 2＝BD 2＋AB 2－2BD ·AB ·cos 60° ＝⎝⎛⎭⎫132＋12－2×13×1×12＝79，即AD ＝73，同理可得AE ＝73，在△ADE 中，由余弦定理得 cos ∠DAE ＝AD 2＋AE 2－DE 22AD ·AE＝79＋79－⎝⎛⎭⎫1322×73×73＝1314，所以AD ―→·AE ―→＝|AD ―→|·|AE ―→|cos ∠DAE ＝73×73×1314＝1318. 法二：如图，建立平面直角坐标系，由正三角形的性质易得A ⎝⎛⎭⎫0，32，D ⎝⎛⎭⎫－16，0，E ⎝⎛⎭⎫16，0，所以AD ―→＝⎝⎛⎭⎫－16，－32，AE ―→＝⎝⎛⎭⎫16，－32，所以AD ―→·AE ―→＝⎝⎛⎭⎫－16，－32·⎝⎛⎭⎫16，－32＝－136＋34＝1318.8．(2017·东北四市模拟)已知向量OA ―→＝(3,1)，OB ―→＝(－1,3)，OC ―→＝m OA ―→－n OB ―→(m >0，n >0)，若m ＋n ＝1，则|OC ―→|的最小值为( )A.52B.102C. 5D.10解析：选C 由OA ―→＝(3,1)，OB ―→＝(－1,3)，得OC ―→＝m OA ―→－n OB ―→＝(3m ＋n ，m －3n )，因为m ＋n ＝1(m >0，n >0)，所以n ＝1－m 且0<m <1，所以OC ―→＝(1＋2m,4m －3)，则|OC ―→|＝(1＋2m )2＋(4m －3)2＝20m 2－20m ＋10 ＝20⎝⎛⎭⎫m －122＋5(0<m <1)，所以当m ＝12时，|OC ―→|min ＝ 5.9．已知向量m ，n 的模分别为2，2，且m ，n 的夹角为45°.在△ABC 中，AB ―→＝2m ＋2n ，AC ―→＝2m －6n ，BC ―→＝2BD ―→，则|AD ―→|＝( )A ．2B ．2 2C ．4D ．8解析：选B 因为BC ―→＝2BD ―→，所以点D 为边BC 的中点，所以AD ―→＝12(AB ―→＋AC ―→)＝2m －2n ，所以|AD ―→|＝2|m －n |＝2(m －n )2＝22＋4－2×2×2×22＝2 2. 10．(2018届高三·湘中名校联考)若点P 是△ABC 的外心，且PA ―→＋PB ―→＋λPC ―→＝0，C ＝120°，则实数λ的值为( )A.12 B ．－12C ．－1D ．1解析：选C 设AB 中点为D ，则PA ―→＋PB ―→＝2PD ―→PD ―→. 因为PA ―→＋PB ―→＋λPC ―→＝0，所以2PD ―→＋λPC ―→＝0，所以向量PD ―→，PC ―→共线．又P 是△ABC 的外心，所以PA ＝PB ，所以PD ⊥AB ，所以CD ⊥AB .因为∠ACB ＝120°，所以∠APB ＝120°，所以四边形APBC 是菱形，从而PA ―→＋PB ―→＝2PD ―→＝PC ―→，所以2PD ―→＋λPC ―→＝PC ―→＋λPC ―→＝0，所以λ＝－1.11．已知Rt △AOB 的面积为1，O 为直角顶点，设向量a ＝OA ―→|OA ―→|，b ＝OB ―→|OB ―→|，OP ―→＝a ＋2b ，则PA ―→·PB ―→的最大值为( )A ．1B ．2C ．3D ．4解析：选A 如图，设A (m,0)，B (0，n )，∴mn ＝2，则a ＝(1,0)，b ＝(0,1)，OP ―→＝a ＋2b ＝(1,2)，PA ―→＝(m －1，－2)，PB ―→＝(－1，n －2)，PA ―→·PB ―→＝5－(m ＋2n )≤5－22nm ＝1，当且仅当m ＝2n ，即m ＝2，n ＝1时，等号成立．12．已知△ABC 是边长为1的等边三角形，点D ，E 分别是边AB ，BC 的中点，连接DE 并延长到点F ，使得DE ＝2EF ，则AF ―→·BC ―→的值为( )A ．－58B.18 C.14D.118解析：选B 如图所示， AF ―→＝AD ―→＋DF ―→.又D ，E 分别为AB ，BC 的中点，且DE ＝2EF ，所以AD ―→＝12AB ―→，DF ―→＝12AC ―→＋14AC ―→＝34AC ―→，所以AF ―→＝12AB ―→＋34AC ―→.又BC ―→＝AC ―→－AB ―→，则AF ―→·BC ―→＝⎝⎛⎭⎫12AB ―→＋34AC ―→·(AC ―→－AB ―→)＝12AB ―→·AC ―→－12AB ―→2＋34AC ―→2－34AC ―→·AB ―→ ＝34AC ―→2－12AB ―→2－14AC ―→·AB ―→. 又|AB ―→|＝|AC ―→|＝1，∠BAC ＝60°，故AF ―→·BC ―→＝34－12－14×1×1×12＝18.二、填空题13．在△ABC 中，点O 在线段BC 的延长线上，且||BO ―→＝3||CO―→，当AO ―→＝x AB ―→＋y AC ―→时，则x －y ＝________.解析：∵AO ―→＝AB ―→＋BO ―→＝AB ―→＋32BC ―→＝AB ―→＋32(AC ―→－AB ―→)＝－12AB ―→＋32AC ―→，∴x －y ＝－2.答案：－214．已知a ，b 是非零向量，f (x )＝(ax ＋b )·(bx －a )的图象是一条直线，|a ＋b |＝2，|a |＝1，则f (x )＝________.解析：由f (x )＝a ·bx 2－(a 2－b 2)x －a ·b 的图象是一条直线，可得a ·b ＝0.因为|a ＋b |＝2，所以a 2＋b 2＝4.因为|a |＝1，所以a 2＝1，b 2＝3，所以f (x )＝2x . 答案：2x15．(2017·天津高考)在△ABC 中，∠A ＝60°，AB ＝3，AC ＝2.若BD ―→＝2DC ―→，AE ―→＝λAC ―→－AB ―→ (λ∈R)，且AD ―→·AE ―→＝－4，则λ的值为________．解析：法一：AD ―→＝AB ―→＋BD ―→＝AB ―→＋23BC ―→＝AB ―→＋23(AC ―→－AB ―→)＝13AB ―→＋23AC ―→.又AB ―→·AC ―→＝3×2×12＝3，所以AD ―→·AE ―→＝⎝⎛⎭⎫13AB ―→＋23AC ―→·(－AB ―→＋λAC ―→) ＝－13AB ―→2＋⎝⎛⎭⎫13λ－23AB ―→·AC ―→＋23λAC ―→2 ＝－3＋3⎝⎛⎭⎫13λ－23＋23λ×4＝113λ－5＝－4，解得λ＝311.法二：以点A 为坐标原点，AB ―→的方向为x 轴正方向，建立平面直角坐标系，不妨假设点C 在第一象限，则A (0,0)，B (3,0)，C (1，3)．由BD ―→＝2DC ―→，得D ⎝⎛⎭⎫53，233，由AE ―→＝λAC ―→－AB ―→，得E (λ－3，3λ)，则AD ―→·AE ―→＝⎝⎛⎭⎫53，233·(λ－3，3λ)＝53(λ－3)＋233×3λ＝113λ－5＝－4，解得λ＝311.答案：31116．定义平面向量的一种运算a ⊙b ＝|a ＋b |·|a －b |·sin 〈a ，b 〉，其中〈a ，b 〉是a 与b 的夹角，给出下列命题：①若〈a ，b 〉＝90°，则a ⊙b ＝a 2＋b 2；②若|a |＝|b |，则(a ＋b )⊙(a －b )＝4a ·b ；③若|a |＝|b |，则a ⊙b ≤2|a |2；④若a ＝(1,2)，b ＝(－2,2)，则(a ＋b )⊙b ＝10.其中真命题的序号是________．解析：①中，因为〈a ，b 〉＝90°，则a ⊙b ＝|a ＋b |·|a －b |＝a 2＋b 2，所以①成立；②中，因为|a |＝|b |，所以〈(a ＋b )，(a －b )〉＝90°，所以(a ＋b )⊙(a －b )＝|2a |·|2b |＝4|a ||b |，所以②不成立；③中，因为|a |＝|b |，所以a ⊙b ＝|a ＋b |·|a －b |·sin 〈a ，b 〉≤|a ＋b |·|a －b |≤|a ＋b |2＋|a －b |22＝2|a |2，所以③成立；④中，因为a ＝(1,2)，b ＝(－2,2)，所以a ＋b ＝(－1,4)，sin 〈(a ＋b )，b 〉＝33434，所以(a ＋b )⊙b ＝35×5×33434＝453434，所以④不成立．故①③正确．答案：①③送分专题(四) 不等式[全国卷3年考情分析][题点·考法·全练]1．已知关于x 的不等式(ax －1)(x ＋1)<0的解集是(－∞，－1)∪⎝⎛⎭⎫－12，＋∞，则a ＝( )A ．2B ．－2C ．－12D ．12解析：选B 根据一元二次不等式与之对应方程的关系知－1，－12是一元二次方程ax 2＋(a －1)x －1＝0的两个根，所以－1×⎝⎛⎭⎫－12＝－1a，所以a ＝－2. 2．若x >y >0，m >n ，则下列不等式正确的是( ) A ．xm >ymB ．x －m ≥y －nC.x n >y mD ．x >xy解析：选D A 不正确，因为同向同正不等式相乘，不等号方向不变，m 可能为0或负数；B 不正确，因为同向不等式相减，不等号方向不确定；C 不正确，因为m ，n 的正负不确定．故选D.3．(2017·云南第一次统一检测)已知函数f (x )＝⎩⎪⎨⎪⎧2x －1－2，x ≥1，21－x －2，x <1，则不等式f (x －1)≤0的解集为( )A ．{x |0≤x ≤2}B ．{x |0≤x ≤3}C ．{x |1≤x ≤2}D ．{x |1≤x ≤3}解析：选D 由题意，得f (x －1)＝⎩⎪⎨⎪⎧2x －2－2，x ≥2，22－x －2，x <2.当x ≥2时，由2x －2－2≤0，解得2≤x ≤3；当x <2时，由22－x －2≤0，解得1≤x <2.综上所述，不等式f (x －1)≤0的解集为{x |1≤x ≤3}．4．已知x ∈(－∞，1]，不等式1＋2x ＋(a －a 2)·4x >0恒成立，则实数a 的取值范围为( ) A.⎝⎛⎭⎫－2，14 B ．⎝⎛⎦⎤－∞，14 C.⎝⎛⎭⎫－12，32 D ．(－∞，6]解析：选C 根据题意，由于1＋2x ＋(a －a 2)·4x >0对于一切的x ∈(－∞，1]恒成立，令2x ＝t (0<t ≤2)，则可知1＋t ＋(a －a 2)t 2>0⇔a －a 2>－1＋t t 2，故只要求解h (t )＝－1＋tt2(0＜t ≤2)的最大值即可，h (t )＝－1t 2－1t ＝－⎝⎛⎭⎫1t ＋122＋14，又1t ≥12，结合二次函数图象知，当1t ＝12，即t ＝2时，h (x )取得最大值－34，即a －a 2>－34，所以4a 2－4a －3<0，解得－12<a <32，故实数a的取值范围为⎝⎛⎭⎫－12，32. [准解·快解·悟通]。

高考物理计算题复习《关联速度问题》(解析版)

《关联速度》一、计算题1.如图所示，竖直平面内放一直角杆，杆的各部分均光滑，水平部分套有质量为m A=3kg的小球A，竖直部分套有质量为m B=2kg的小球B，A、B之间用不可伸长的轻绳相连。

在水平外力F的作用下，系统处于静止状态，且OA=3m，OB=4m，重力加速度g=10m/s2．(1)求水平拉力F的大小和水平杆对小球A弹力F N的大小；(2)若改变水平力F大小，使小球A由静止开始，向右做加速度大小为4.5m/s2的匀拉力F所做的功。

加速直线运动，求经过23s2.如图所示，某人用绳通过定滑轮拉小船，绳某时刻与水平方向夹角为α.求：(1)若人匀速拉绳的速度为v o，则此时刻小船的水平速度v x为多少？(2)若使小船匀速靠岸，则通过运算分析拉绳的速度变化情况？3.如图，足够长光滑斜面的倾角为θ=30°，竖直的光滑细杆到定滑轮的距离为a=3m，斜面上的物体M和穿过细杆的m通过跨过定滑轮的轻绳相连，开始保持两物体静止，连接m的轻绳处于水平状态，放手后两物体从静止开始运动，已知M=5.5kg，m=3.6kg，g=10m/s2．(1)求m下降b=4m时两物体的速度大小各是多大？(2)若m下降b=4m时恰绳子断了，从此时算起M最多还可以上升的高度是多大？4.如图所示，水平光滑长杆上套有一个质量为m A的小物块A，细线跨过O点的轻小光滑定滑轮一端连接小物块A，另一端悬挂质量为m B的小物块B，C为O点正下方杆上一点，滑轮到杆的距离OC=ℎ.开始时小物块A受到水平向左的拉力静止于P 点，PO与水平方向的夹角为30°．(1)求小物块A受到的水平拉力大小；(2)撤去水平拉力，求：①当PO与水平方向的夹角为45°时，物块A的速率是物块B的速率的几倍？②物块A在运动过程中的最大速度．5.如图所示，左侧为一个半径为R的半球形的碗固定在水平桌面上，碗口水平，O点为球心，碗的内表面及碗口光滑。

【配套K12】2018版高考物理二轮复习专题十一鸭部分教学案选修3_4

专题十一选修3－4考情分析命题解读本专题13个考点，皆为Ⅰ要求。

从三年命题情况看，命题特点为：(1)注重基础。

如2013年的“共振”、2014年的“光谱”、2015年与2016年和2017年的“多普勒效应”“相对论”等都较好的考查了学生的理解能力。

(2)联系实际。

2013年的“单反照相机”、2014年的“蝴蝶的翅膀”、2015年的“眼镜片”、2017年的“人的眼球聚光”等都是STS 问题，体现了学以致用的课标理念。

整体难度中等，命题指数★★★★★，复习目标是达B 必会。

1．(2016·江苏高考)(1)一艘太空飞船静止时的长度为30 m ，他以0.6c (c 为光速)的速度沿长度方向飞行越过地球，下列说法正确的是________。

A ．飞船上的观测者测得该飞船的长度小于30 m B ．地球上的观测者测得该飞船的长度小于30 m C ．飞船上的观测者测得地球上发来的光信号速度小于c D ．地球上的观测者测得飞船上发来的光信号速度小于c(2)杨氏干涉实验证明光的确是一种波，一束单色光投射在两条相距很近的狭缝上，两狭缝就成了两个光源，它们发出的光波满足干涉的必要条件，则两列光的________相同。

如图1所示，在这两列光波相遇的区域中，实线表示波峰，虚线表示波谷，如果放置光屏，在________(选填“A ”“B ”或“C ”)点会出现暗条纹。

图1(3)在上述杨氏干涉实验中，若单色光的波长λ＝5.8910－7m ，双缝间的距离d ＝1 mm ，双缝到屏的距离l ＝2 m 。

求第1个亮条纹到第11个亮条纹的中心间距。

解析 (1)飞船上的观察者测得飞船的长度不变，仍为30 m ，由l ＝l 01－⎝ ⎛⎭⎪⎫v c 2＜l 0可知，地球上的观察者测得该飞船的长度小于30 m ，A 错误，B 正确；由光速不变原理可知C 、D 错误。

(2)从两狭缝发出的光，它们的频率相同，是干涉光，在波峰与波谷相遇的区域中，振动相互抵消，会出现暗条纹，即在C 点出现暗条纹。

2018版高考物理二轮复习小题提速练14 含解析精品

小题提速练(十四)(时间：20分钟分值：48分)选择题(本题共8小题，每小题6分，共48分．在每小题给出的四个选项中，第14～18题只有一项符合题目要求，第19～21题有多项符合题目要求．全部选对的得6分，选对但不全的得3分，有选错的得0分．)14．(2018·郑州三模)在人类对微观世界进行探索的过程中，科学实验起到了非常重要的作用．下列说法符合历史事实的是( )A．普朗克通过对光电效应实验的研究，确定了光的粒子性B．汤姆孙通过阴极射线在电、磁场中偏转的实验，发现了原子内部存在电子C．贝可勒尔通过对天然放射现象的研究，发现了原子中存在原子核D．卢瑟福通过α粒子轰击氮核的实验，证实了在原子核内部存在中子B[爱因斯坦的光子学说成功的解释了光电效应实验的规律，确定了光的粒子性，A 错误；汤姆孙通过阴极射线在电、磁场中偏转的实验，测出了这些粒子的荷质比，发现了原子内部存在电子，B正确；贝可勒尔发现了天然放射现象，说明了原子核可以再分，C错误；卢瑟福通过α粒子轰击氮核的实验，发现了质子，D错误．] 15．如图1所示，斜面体置于粗糙水平面上，斜面光滑．小球被轻质细线系住放在斜面上．细线另一端跨过定滑轮，用力拉细线使小球沿斜面缓慢移动一段距离，斜面体始终静止．移动过程中( )【导学号：19624251】图1A．细线对小球的拉力变大B．斜面对小球的支持力变大C．斜面对地面的压力变大D．地面对斜面的摩擦力变大A[如图，根据矢量三角形可知：当小球沿斜面缓慢向上移动一段距离时，β减小，绳子拉力增大，斜面对小球支持力减小；根据牛顿第三定律，小球对斜面体压力减小，将该力沿水平方向和竖直方向分解可知：两个方向的力都减小，所以地面对斜面的支持力和摩擦力都减小．综上所述，A正确．]16．光滑平行金属导轨轨道平面与水平面的夹角为θ，导轨上端接一阻值为R 的电阻，导轨所在空间有垂直导轨平面向上的匀强磁场，有一质量为m 、电阻为r 的金属棒ab ，放在导轨上，其余部分电阻不计．要使金属棒始终处于平衡状态，则磁场随时间变化的图象可能是( )图2A B C DD [杆ab 始终处于平衡状态，感应电流为b →a ，则穿过闭合回路的磁通量应该是增加的，故选项C 错误；根据平衡条件：mg sin θ＝BIL ，I ＝ΔBS Δt R ＋r，杆ab 始终处于平衡状态，则当B 变大时，电流应该减小，故电动势应该减小，故ΔB Δt应该减小，故选项D 正确．]17．(2018·临川一中模拟)北京的纬度约为39.6度，计算时用角度θ表示．已知地球半径为R ，重力加速度为g ，自转周期为T ，光速为c ，则地球同步卫星发射的电磁波到北京的最短时间为( ) A.3R 2T 2g 4π2/c B.⎝ ⎛⎭⎪⎫3R 2T 2g 4π2－R /c C.r 2＋R 2＋2Rr cos θ/c ，其中r ＝3R 2T 2g 4π2 D.r 2＋R 2－2Rr cos θ/c ，其中r ＝3R 2T 2g 4π2D [根据万有引力提供向心力，有GMm r 2＝m 4π2T 2·r ，GM ＝gR 2，得r ＝3gR 2T 24π2，地球同步卫星发射的电磁波到北京的最短路程s ＝r 2＋R 2－2Rr cos θ，电磁波的传播速度为c ，故最短时间t ＝s c ＝r 2＋R 2－2rR cos θc ，其中r ＝3gR 2T 24π2，D 正确，A 、B 、C 均错误．]18．(2018·全国百所名校示范卷)如图3甲所示，在粗糙的水平面上，一质量m ＝1 kg 可视为质点的滑块压缩一轻弹簧并被锁定，滑块与弹簧不相连，解除锁定前滑块处于P 处，t ＝0时解除锁定，计算机通过传感器描绘出滑块的速度－时间图象如图乙所示，其中Oab 段为曲线，bc 段为直线，在t 1＝1 s 时滑块已经在水平面上滑行s ＝4 m 的距离．在滑块运动方向上与P 相距7 m 的Q 处有一竖直挡板，若滑块与挡板碰撞被弹回时无能量损失，g 取10 m/s 2，弹簧的劲度系数为0.8 N/m ，则下列正确的是( )【导学号：19624252】图3A ．滑块与水平面间动摩擦因数为0.2B ．弹簧锁定时具有的弹性势能为1.6 JC ．若水平面光滑，则在滑块向右运动的过程中，滑块的机械能守恒D ．当滑块从P 点向右运动2.5 m 时，滑块具有最大的动能A [从图象可知，滑块脱离弹簧后的加速度为：a 1＝v c －vb Δt ＝2－42－1m/s ＝－2 m/s 2 由牛顿第二定律有：－μmg ＝－ma 1得：μ＝0.2，故A 正确；t 1＝1 s 时滑块已经在水平面上滑行s ＝4 m 的距离，设弹簧对滑块做功为W ，由动能定理知：W －μmgs ＝12mv 2b代入数据得：W ＝16 J由图可知此时弹簧已经恢复原长，弹性势能已经全部释放，所以弹性势能E p ＝W ＝16 J ，故B 错误；若水平面光滑，则在滑块向右运动的过程中，滑块和弹簧组成的系统机械能守恒，但滑块的机械能不守恒，故C 错误；当弹簧弹力等于滑动摩擦力时，滑块的动能最大，则有：k Δx ＝μmg ，解得：Δx ＝0.2×100.8m ＝2.5 m ，则当滑块从P 点向右运动的位移x ＝4 m －2.5 m ＝1.5 m ，故D 错误．]19．如图4所示，质量为M 的三角形滑块置于水平光滑的地面上，斜面亦光滑，当质量为m 的滑块沿斜面下滑的过程中，M 与m 组成的系统( )图4A ．由于不受摩擦力，系统动量守恒B ．由于地面对系统的支持力大小不等于系统所受重力大小，故系统动量不守恒C ．系统水平方向不受外力，故系统水平方向动量守恒D ．M 对m 作用有水平方向分力，故系统水平方向动量也不守恒BC [水平方向不受外力，所以系统水平方向动量守恒，C 正确；竖直方向受重力和支持力，系统竖直方向动量不守恒，B 正确．]20．如图5是自耦变压器的示意图，负载变化时输入电压不会有大的波动，输电线的电阻用R 0表示．如果变压器上的能量损失可以忽略，以下说法正确的是( )图5A ．开关S 1接a ，闭合开关S 后，电压表V 示数减小，电流表A 示数增大B ．开关S 1接a ，闭合开关S 后，原线圈输入功率减小C ．断开开关S ，开关S 1接a 时电流表的示数为I 1，开关S 1接b 时电流表的示数为I 2，则I 1>I 2D ．断开开关S ，开关S 1接a 时原线圈输入功率为P 1，开关S 1接b 时原线圈输入功率为P 2，则P 1<P 2AD [开关S 1接a ，闭合开关S 后，副线圈的电阻R 减小，电流增大，A 的示数增大，R 0上的电压增大，电压表的示数减小，所以选项A 正确；由P 1＝P 2＝U 2副R知，原线圈的输入功率增大，B 错误；断开开关S ，开关S 1接a 时，副线圈两端的电压为U 1，S 1接b 时，副线圈两端的电压为U 2，则U 2>U 1，由I ＝U R可知，I 1<I 2，选项C 错误；由P ＝UI 可知，P 1<P 2，选项D 正确．]21．(2018·哈尔滨九中二模)如图6所示，空间同时存在竖直向上的匀强磁场和匀强电场，磁感应强度为B ，电场强度为E .一质量为m ，电量为q 的带正电小球恰好处于静止状态，现在将磁场方向顺时针旋转30°，同时给小球一个垂直磁场方向斜向下的速度v ，则关于小球的运动，下列说法正确的是( )【导学号：19624253】图6A ．小球做匀速圆周运动B ．小球运动过程中机械能守恒C ．小球运动到最低点时电势能增加了mgv3BqD ．小球第一次运动到最低点历时πm 2qBAD [小球在复合电磁场中处于静止状态，只受两个力作用，即重力和电场力且两者平衡．当把磁场顺时针方向倾斜30°，且给小球一个垂直磁场方向的速度v ，则小球受到的合力就是洛伦兹力，且与速度方向垂直，所以带电小球将做匀速圆周运动，选项A 正确．由于带电小球垂直于纸面的倾斜平面内做匀速圆周运动过程中受到电场力要做功，所以机械能不守恒，选项B 错误．小球从开始到最低点克服电场力做功为W ＝EqR sin 30°＝mg ×mv Bq ×12＝m 2gv 2Bq ，所以电势能的增加量为m 2gv 2Bq，选项C 错误．小球第一次运动到最低点的时间为14T ＝πm 2Bq，所以选项D 正确．]。

2018版高考物理二轮复习小题提速练1 含解析精品

小题提速练(一)(时间：20分钟分值：48分)选择题(本题共8小题，每小题6分，共48分．在每小题给出的四个选项中，第14～18题只有一项符合题目要求，第19～21题有多项符合题目要求．全部选对的得6分，选对但不全的得3分，有选错的得0分．)14．(2018·沧州一中月考)甲、乙两车在同一条直道上行驶，它们运动的位移s 随时间t 变化的关系如图1所示，已知乙车做匀变速直线运动，其图线与t 轴相切于10 s 处，则下列说法正确的是( )图1A ．甲车的初速度为零B ．乙车的初位置在s 0 ＝ 60 m 处C ．乙车的加速度大小为1.6 m/s 2D ．5 s 时两车相遇，此时甲车速度较大C [位移－时间图象的斜率等于速度，则知甲车的速度不变，做匀速直线运动，初速度不为零，选项A 错误；乙车做匀变速直线运动，其图线与t 轴相切于10 s 处，则t ＝10 s 时，速度为零，反过来看成初速度为0的匀加速直线运动，则s ＝12at 2，根据图象可知，s 0＝12a ·100,20＝12a ·25，解得：a ＝1.6 m/s 2，s 0＝80 m ，选项C 正确，B 错误；5 s 时两车相遇，此时甲的速度v 甲＝205 m/s ＝4 m/s ，乙的速度为v 乙＝at＝1.6×5 m/s＝8 m/s ，选项D 错误．]图215．(2018·衡阳市二模)半圆柱体P 放在粗糙的水平面上，有一挡板MN ，其延长线总是过半圆柱体的轴心O ，但挡板与半圆柱体不接触，在P 和MN 之间放有一个光滑均匀的小圆柱体Q (P 的截面半径远大于Q 的截面半径)，整个装置处于静止状态，如图乙是这个装置的截面图，若用外力使MN 绕O 点缓慢地逆时针转动，在Q 到达最高位置前，发现P 始终保持静止，在此过程中，下列说法正确的是( )【导学号：19624215】A ．MN 对Q 的弹力大小逐渐增大B ．P 、Q 间的弹力先增大后减小C ．桌面对P 的摩擦力先增大后减小D ．P 所受桌面的支持力保持不变C [以小圆柱为研究对象，受力分析如图，可得：F 1＝mg cos α，F 2＝mg sin α，随α增大，F 1减小，F 2增大，A 、B 均错误；对半圆柱P 受力分析如图所示．由平衡条件可得：N ＝Mg ＋F 2sin α＝Mg ＋mg sin 2 α， f ＝F 2cos α＝mg sin αcos α，当α由0增大到90°的过程中，N 逐渐增大，f 先增大后减小，故C 正确，D 错误．] 16．(2018·吉林大学附中模拟)如图3所示，空间中存在与等边三角形ABC 所在平面平行的匀强电场．其中电势φA ＝φB ＝0，φC ＝φ.保持该电场的大小和方向不变，让等边三角形以AB 为轴转过60°，则此时C 点的电势为( )图3A.32φ B.12φ C ．－32φ D ．－12φB [因为A 、B 点等势，所以电场方向水平向左，设等边三角形的边长为L ，则C 点到AB 的垂线长度为32L ，所以匀强电场E ＝φ32L ，让等边三角形以AB 为轴转过60°，则C 点在平面上的投影点到AB 的距离为d ＝32L ·cos 60°＝34L ，故此时C 点的电势为φ′＝Ed ＝φ32L ×34L ＝12φ，B 正确．] 17．(2018·虎林市摸底考试)在足够大的匀强磁场中，静止的钠的同位素2411Na 发生衰变，沿与磁场垂直的方向释放出一个粒子后，变为一个新核，新核与放出粒子在磁场中运动的轨迹均为圆，如图4所示，下列说法正确的是( )【导学号：19624216】图4A ．新核为2412MgB ．轨迹2是释放出的粒子的径迹 C.2411Na 发生的是α衰变 D ．新核沿顺时针方向旋转A [由运动轨迹为相内切圆可知，新粒子应带负电，2411Na 的衰变应为β衰变，核反应方程为2411Na ―→ 0－1e ＋2412Mg ，故新核是2412Mg ，A 正确，C 错误；由r ＝mvqB，由动量守恒定律可知，新核与 0－1e 的动量大小相等，因此，新核的半径较小，轨迹2是新核的轨迹，B 错误；根据洛伦兹力提供向心力，由左手定则可判断，新核应沿逆时针方向旋转，故D 错误．]18．(2018·虎林市摸底考试)如图5所示为研究某种带电粒子的装置示意图，粒子源射出的粒子束以一定的初速度沿直线射到荧光屏上的O 点，出现一个光斑．在垂直于纸面向里的方向上加一磁感应强度为B 的匀强磁场后，粒子束发生偏转，沿半径为r 的圆弧运动，打在荧光屏上的P 点，然后在磁场区域再加一竖直向下，场强大小为E 的匀强电场，光斑从P 点又回到O 点，关于该粒子(不计重力)，下列说法正确的是( )图5A ．粒子带负电B ．初速度为v ＝B EC ．比荷为q m ＝B 2rED ．比荷为q m ＝EB 2rD [加上垂直于纸面向里的磁场后，粒子打在屏上P 点，说明粒子在磁场中所受洛伦兹力方向向上，由左手定则可以判断粒子带正电，A 错误；由于电场和磁场同时存在时，粒子不发生偏转，可得：qvB ＝Eq ，解得v ＝EB ，B 错误；由r ＝mv qB ，可得q m ＝v rB＝ErB 2，可知D 正确，C 错误．] 16套小题提速练物理·特色专项考前增分集训19.(2018·中卫市一模)如图6是创意物理实验设计作品《小熊荡秋千》．两根彼此靠近且相互绝缘的金属棒C 、D 固定在铁架台上，与两个铜线圈P 、Q 组成一闭合回路，两个磁性很强的条形磁铁如图放置，当用手左右摆动线圈P 时，线圈Q 也会跟着摆动，仿佛小熊在荡秋千．以下说法正确的是( )【导学号：19624217】图6A ．P 向右摆动的过程中，P 中的电流方向为顺时针方向(从右向左看)B ．P 向右摆动的过程中，Q 也会向右摆动C ．P 向右摆动的过程中，Q 会向左摆动D ．若用手左右摆动Q ，P 会始终保持静止AB [P 向右摆动的过程中，穿过P 的磁通量减小，根据楞次定律，P 中有顺时针方向的电流(从右向左看)，故A 正确．P 向右摆的过程中，P 中的电流方向为顺时针方向，则Q 下端的电流方向向外，根据左手定则知，下端所受的安培力向右，则Q 向右摆动．同理，用手左右摆动Q ，P 会左右摆动，故B 正确，C 错误，D 也错误．]20．(2018·高三第一次全国大联考(新课标卷Ⅲ))如图甲7所示，一理想变压器原线圈匝数为n 1＝1 000匝，副线圈匝数为n 2＝150匝，变压器输入端的正弦交变电压如图乙所示，定值电阻的阻值为11 Ω，总阻值为22 Ω的滑动变阻器滑片为P .下列说法中正确的是( )图7A ．变压器副线圈输出电压的频率为50 HzB ．滑片P 向右滑动时，电阻R 两端的电压不变C ．滑片P 滑到最右端时，通过电阻R 的电流为6 AD ．滑片P 滑到最左端时，变压器的输入功率为66 WAC [原、副线圈的周期T ＝0.02 s ，频率f ＝1T＝50 Hz ，选项A 正确；滑动变阻器的滑片P 向右滑动时，电阻R 两端的电压变大，选项B 错误；原线圈电压的有效值U 1＝U m2＝440 V ，根据U 1U 2＝n 1n 2可得副线圈的电压U 2＝66 V ，滑动变阻器的滑片P 滑到最右端时，通过电阻R 的电流为I 2＝U 2R＝6 A ，选项C 正确；滑动变阻器的滑片P 滑到最左端时，理想变压器的输入功率为P 2＝U 22R ＋R P＝132 W ，选项D 错误．]21．(2018·江苏高考)如图8所示，三个小球A 、B 、C 的质量均为m ，A 与B 、C 间通过铰链用轻杆连接，杆长为L .B 、C 置于水平地面上，用一轻质弹簧连接，弹簧处于原长．现A 由静止释放下降到最低点，两轻杆间夹角α由60°变为120°.A 、B 、C 在同一竖直平面内运动，弹簧在弹性限度内，忽略一切摩擦，重力加速度为g .则此下降过程中( )【导学号：19624218】图8A ．A 的动能达到最大前，B 受到地面的支持力小于32mgB ．A 的动能最大时，B 受到地面的支持力等于32mgC ．弹簧的弹性势能最大时，A 的加速度方向竖直向下D ．弹簧的弹性势能最大值为32mgLAB [A 对：取A 、B 、C 整体研究，三个小球皆静止时，地面对B 、C 球的弹力各为32mg .当A 球下降时，只要A 球未达最大速度，有竖直向下的加速度，A 球就处于失重状态，地面对B 球的支持力小于32mg .B 对：A 球的动能最大时，a A ＝0，系统在竖直方向上F 合＝0，则地面对B 球的弹力为32mg . C 错：弹簧的弹性势能最大时，对应着弹簧伸长量最大，A 球运动到最低点，此时v A ＝0，但a A ≠0，加速度方向竖直向上．D 错：两杆间夹角由60°变为120°，A 球下落的距离h ＝L sin 60°－L sin 30°＝3－12L ，A 球重力势能的减少量为ΔE p ＝3－12mgL .由能量转化知，弹簧的弹性势能最大值为3－12mgL .]。

课题：关联速度导学案(无答案)-河北省涞水波峰中学高三物理复习

波峰中学高三物理学案年级：高二学科：物理导学案编号： 3号编写人：李源审核人：卢超姓名：闲事闲话闲思是学习的大敌。

课题：关联速度问题一、知识回顾1.问题特点沿绳(或杆)方向的速度分量大小相等。

2．思路与方法(1)明确研究对象绳(或杆)连接的物体，或绳(或杆)的端点。

(2)明确合运动与分运动合速度→物体的实际运动速度v分速度→⎩⎨⎧其一：沿绳(或杆)的分速度v 1其二：与绳(或杆)垂直的分速度v 2 遵循的法则：v 的分解(或v 1与v 2的合成)遵循平行四边形定则。

(3)明确等量关系沿绳(或杆)方向的分速度大小相等。

3、关联速度问题常见模型把物体的实际速度分解为垂直于绳(杆)和平行于绳(杆)的两个分量，根据沿绳(杆)方向的分速度大小相等求解。

常见的模型如图所示。

拓展：若两物体运动过程中不是通过绳或杆连接，而是直接接触，则两物体在垂直接触面方向的分速度相等。

也可以将这种情况看做两物体在接触处有一根极短的杆或绳。

二、巩固练习1、如图所示，悬线一端固定在天花板上的O点，另一端穿过一张CD光盘的中央小孔后拴着一个橡胶球，橡胶球静止时，竖直悬线刚好挨着水平桌面的边缘。

现将CD光盘按在桌面上，并沿桌面边缘以速度v匀速移动，移动过程中，CD 光盘中央小孔始终紧挨桌面边缘，当悬线与竖直方向的夹角为θ时，小球移动的速度大小为()A．v1＋sin2θ B.v sinθC．v tanθ D.v tanθ2、一轻杆两端分别固定质量为m A和m B的两个小球A和B(可视为质点)，将其放在一个光滑球形容器中从位置1开始下滑，如图所示，当轻杆到达位置2时，球A与球形容器球心等高，其速度大小为v1，已知此时轻杆与水平方向成θ＝30°角，球B的速度大小为v2，则()A．v2＝12v1 B.v2＝2v1 C．v2＝v1 D.v2＝3v13、如图所示，将楔形木块B放在光滑水平面上靠墙边处并用手扶着，然后在木块和墙面之间放入一个小球A，楔形木块的倾角为θ，放手让小球和木块同时由静止开始运动，某时刻二者速度分别为v A和v B，则()A．v A∶v B＝1∶1 B.v A∶v B＝sinθ∶cosθC．v A∶v B＝cosθ∶sinθ D.v A∶v B＝sinθ∶tanθ4、如图所示，帆板在海面上以速度v朝正西方向运动，帆船以速度v朝正北方向航行。

【配套K12】2018版高考物理二轮复习第一部分专题十一力学实验学案

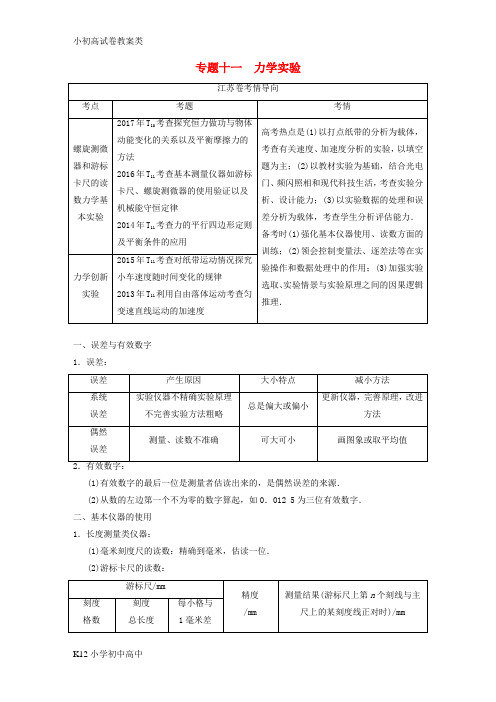
专题十一力学实验一、误差与有效数字1．误差：(1)有效数字的最后一位是测量者估读出来的，是偶然误差的来源．(2)从数的左边第一个不为零的数字算起，如0．012 5为三位有效数字．二、基本仪器的使用1．长度测量类仪器：(1)毫米刻度尺的读数：精确到毫米，估读一位．(2)游标卡尺的读数：读)×0．01 mm．2．时间测量类仪器：(1)打点计时器：每打两个点的时间间隔为0．02 s，一般每五个点取一个计数点，则时间间隔为Δt＝0．02×5 s＝0．1 s．(2)频闪照相机：用等时间间隔获取图象信息的方法将物体在不同时刻的位置记录下来．(3)光电计时器：记录遮光时间．三、两类力学实验1．验证性实验：验证力的平行四边形定则，验证牛顿运动定律，验证机械能守恒定律．2．探究性实验：探究弹力与弹簧伸长的关系，探究动能定理．3．两种实验过程的比较：1．列表法：在记录和处理数据时，为了简单而明显地表示出有关物理量之间的关系，可将数据填写在适当的表格中，即为列表法．2．平均值法：把在同一状态下测定的同一个物理量的若干组数据相加求和，然后除以测量次数．3．作图法：用作图法处理数据的优点是直观、简便，有取平均值的效果．由图线的斜率、截距、包围的面积等可以研究物理量之间的关系．考点1| 螺旋测微器和游标卡尺的读数难度：低档题题型：实验题(对应学生用书第57页)1．螺旋测微器读数时要估读，以毫米为单位，小数点后必须为3位，同时注意固定刻度上的半刻度是否露出，如第1题中图丁半刻度线露出，图甲、乙、丙没露出．2．游标卡尺不估读，以毫米为单位，10分度卡尺，小数点后只有1位；20分度和50分度卡尺，小数点后有2位．3．注意题目要求的单位是否为mm，若不是则要先以mm为单位读数，然后再转变为题目要求的单位．第1、2题中毫米和厘米各半．●考向1 螺旋测微器的读数1．(2017·成都检测)用螺旋测微器测不同规格的金属丝的直径，示数如图111所示．由图可读出金属丝的直径为图甲________mm 图乙________cm图丙________mm 图丁________cm．【导学号：17214176】甲乙丙丁图111【解析】根据螺旋测微器的读数方法：螺旋测微器的读数值＝固定刻度值＋可动刻度×0．01 mm，读出甲、乙、丙、丁四图的读数值分别是10．002(1～3) mm、0．536 5(4～6) cm、9．205(4～6) mm、0．570 0 cm【答案】10．002 0．536 5 9．205 0．570 0●考向2 游标卡尺的读数2．某同学用游标卡尺游标卡尺测定四个不同规格金属杆的直径，示数如图112甲、乙、丙、丁所示，则该金属杆直径分别为甲图：________mm 乙图：________cm丙图：________cm 丁图：________mm．甲乙丙丁图112【解析】根据游标卡尺的读数方法：游标卡尺的读数值＝主尺整毫米数值＋对齐格数×精度(mm)，读出甲、乙、丙、丁四图的读数值分别是甲图：d＝4 mm＋10×0．02 mm＝4．20 mm乙图：d＝12 mm＋4×0．05 mm＝12．20 mm＝1．220 cm丙图：d＝11 mm＋5×0．1 mm＝11．5 mm＝1．15 cm丁图：d＝5 mm＋5×0．05 mm＝5．25 mm．【答案】4．20 mm 1．220 cm 1．15 cm 5．25 mm考点2| 力学基本实验难度：中低档题型：实验题五年3考(对应学生用书第57页)1．(2016·江苏高考T11)某同学用如图113所示的装置验证机械能守恒定律．一根细线系住钢球，悬挂在铁架台上，钢球静止于A点．光电门固定在A的正下方，在钢球底部竖直地粘住一片宽度为d的遮光条．将钢球拉至不同位置由静止释放，遮光条经过光电门的挡光时间t 可由计时器测出，取v ＝d t作为钢球经过A 点时的速度．记录钢球每次下落的高度h 和计时器示数t ，计算并比较钢球在释放点和A 点之间的势能变化大小ΔE p 与动能变化大小ΔE k ，就能验证机械能是否守恒．图113(1)用ΔE p ＝mgh 计算钢球重力势能变化的大小，式中钢球下落高度h 应测量释放时的钢球球心到________之间的竖直距离． A ．钢球在A 点时的顶端 B ．钢球在A 点时的球心 C ．钢球在A 点时的底端(2)用ΔE k ＝12mv 2计算钢球动能变化的大小．用刻度尺测量遮光条宽度，示数如图114所示，其读数为________cm ．某次测量中，计时器的示数为0．010 0 s ．则钢球的速度为v ＝________ m/s ．图114(3)下表为该同学的实验结果：p k 的观点？请说明理由．(4)请你提出一条减小上述差异的改进建议．【解题关键】解答本题应注意以下三点：(1)小球下落的高度h 可以由释放时的钢球球心测到钢球在A 点时的球心，也可以是释放时的钢球顶端测到钢球在A 点时的顶端．(2)空气阻力造成机械能减少，应有ΔE p >ΔE k 的结果． (3)改进建议应从造成误差的原因角度思考．【解析】 (1)高度变化要比较钢球球心的高度变化．(2)毫米刻度尺读数时要估读到毫米下一位，由v ＝dt代入数据可计算出相应速度．(3)从表中数据可知ΔE k ＞ΔE p ，若有空气阻力，则应为ΔE k ＜ΔE p ，所以不同意他的观点． (4)实验中遮光条经过光电门时的速度大于钢球经过A 点时的速度，因此由ΔE k ＝12mv 2计算得到的ΔE k 偏大，要减小ΔE p 与ΔE k 的差异可考虑将遮光条的速度折算为钢球的速度．【答案】 (1)B (2)1．50(1．49～1．51都算对) 1．50(1．49～1．51都算对) (3)不同意，因为空气阻力会造成ΔE k 小于ΔE p ，但表中ΔE k 大于ΔE p (4)分别测出光电门和球心到悬点的长度L 和l ，计算ΔE k 时，将v 折算成钢球的速度v ′＝l Lv 2．(2014·江苏高考T 11)小明通过实验验证力的平行四边形定则．图115(1)实验记录纸如图115所示，O 点为橡皮筋被拉伸后伸长到的位置，两弹簧测力计共同作用时，拉力F 1和F 2的方向分别过P 1和P 2点；一个弹簧测力计拉橡皮筋时，拉力F 3的方向过P 3点．三个力的大小分别为：F 1＝3．30 N 、F 2＝3．85 N 和F 3＝4．25 N ．请根据图中给出的标度作图求出F 1和F 2的合力．(2)仔细分析实验，小明怀疑实验中的橡皮筋被多次拉伸后弹性发生了变化，影响实验结果．他用弹簧测力计先后两次将橡皮筋拉伸到相同长度，发现读数不相同，于是进一步探究了拉伸过程对橡皮筋弹性的影响．实验装置如图116甲所示，将一张白纸固定在竖直放置的木板上，橡皮筋的上端固定于O 点，下端N 挂一重物．用与白纸平行的水平力缓慢地移动N ，在白纸上记录下N 的轨迹．重复上述过程，再次记录下N 的轨迹．甲乙图116两次实验记录的轨迹如图116乙所示．过O 点作一条直线与轨迹交于a 、b 两点，则实验中橡皮筋分别被拉伸到a 和b 时所受拉力F a 、F b 的大小关系为________． (3)根据(2)中的实验，可以得出的实验结果有________．(填写选项前的字母) A ．橡皮筋的长度与受到的拉力成正比B ．两次受到的拉力相同时，橡皮筋第2次的长度较长C ．两次被拉伸到相同长度时，橡皮筋第2次受到的拉力较大D ．两次受到的拉力相同时，拉力越大，橡皮筋两次的长度之差越大(4)根据小明的上述实验探究，请对验证力的平行四边形定则实验提出两点注意事项．【解题关键】解答此题应注意以下三点：(1)拉力F 1和F 2的方向分别过P 1、P 2两点，但OP 1→、OP 2→并不代表F 1和F 2． (2)由平行四边形定则求出的合力并不一定与F 3相等．(3)重物重力一定和橡皮筋拉力与水平拉力方向一定时，橡皮筋拉力大小也是一定的．【解析】根据力的合成法则及平衡条件解题． (1)作出的图示如图所示．(2)重物受力情况如图所示，由于重力不变，两次实验时，橡皮筋拉力T 的方向相同，故水平拉力F 大小相等，即F a ＝F b ．(3)根据题图乙可知，选项B 、D 正确，选项A 、C 错误． (4)橡皮筋拉伸不宜过长，选用新橡皮筋等可减小误差．【答案】 (1)如解析图所示(F 合＝4．6～4．9 N 都算对) (2)F a ＝F b (3)BD(4)橡皮筋拉伸不宜过长；选用新橡皮筋．(或：拉力不宜过大；选用弹性好的橡皮筋；换用弹性好的弹簧)．3．(2017·江苏高考T 10)利用如图117所示的实验装置探究恒力做功与物体动能变化的关系．小车的质量为M ＝200．0 g ，钩码的质量为m ＝10．0 g ，打点计时器的电源为50 Hz 的交流电．【导学号：17214177】图117(1)挂钩码前，为了消除摩擦力的影响，应调节木板右侧的高度，直至向左轻推小车观察到________．(2)挂上钩码，按实验要求打出的一条纸带如图118所示，选择某一点为O ，依次每隔4个计时点取一个计数点．用刻度尺量出相邻计数点间的距离Δx ，记录在纸带上．计算打出各计数点时小车的速度v ，其中打出计数点“1”时小车的速度v 1＝________m/s ．图118(3)将钩码的重力视为小车受到的拉力，取g ＝9．80 m/s 2，利用W ＝mg Δx 算出拉力对小车做的功W ．利用E k ＝12Mv 2算出小车动能，并求出动能的变化量ΔE k ．计算结果见下表．请根据表中的数据，在图119中作出ΔE k W 图象．图119(4)实验结果表明，ΔE k 总是略小于W ．某同学猜想是由于小车所受拉力小于钩码重力造成的．用题中小车和钩码质量的数据可算出小车受到的实际拉力F ＝________N ．【解析】 (1)完全平衡摩擦力的标志是轻推小车，小车做匀速运动． (2)两计数点间的时间间隔T ＝5×0．02 s ＝0．1 sv 1＝x 022T ＝．06＋2．．012×0．1m/s ＝0．228 m/s ．(3)确定标度，根据给出数据描点．作图如图所示．(4)从图线上取两个点(4．5，4．24)，(2．15，2．0) 图线的斜率是k ＝4．24－2．04．5－2．15≈0．953①又有k ＝ΔE k ΔW ＝Mv22mg Δx ②根据运动学公式有v 2＝2a Δx ③ 根据牛顿第二定律有F ＝Ma ④由①②③④式解得F ≈0．093 N ．【答案】 (1)小车做匀速运动 (2)0．228 (3)见解析图 (4)0．093纸带的三大应用 (1)确定时间要区别打点计时器打出的点与人为选取的计数点之间的区别与联系，为便于测量和计算，一般每五个点(或每隔四个点)取一个计数点，这样时间间隔为Δt ＝0．02×5 s＝0．1 s ． (2)求瞬时速度做匀变速运动的物体在一段时间内的平均速度等于中间时刻的瞬时速度．如图1110a 所示，求纸带上某一点的瞬时速度，只需在这一点的前后各取相同时间间隔T 的两段位移x n 和x n ＋1，则打n 点时的速度v n ＝x n ＋x n ＋12T．ab 图1110(3)求加速度①利用a ＝ΔxT2求解：在已经判断出物体做匀变速直线运动的情况下，可利用Δx ＝x n ＋1－x n ＝aT 2求加速度a ． ②逐差法：a ＝a 1＋a 2＋a 33＝x 4＋x 5＋x 6－x 1－x 2－x 39T③两段法：把图1110b 中x 1、x 2、x 3、x 4、x 5、x 6分成时间相等(均为3T )的两大段，则由x Ⅱ－x Ⅰ＝aT 2得：(x 4＋x 5＋x 6)－(x 1＋x 2＋x 3)＝a (3T )2，解出的a 与上面逐差法结果相等，但却要简单得多． ④图象法： a ．由v n ＝x n ＋x n ＋12T，求出相应点的速度． b ．确定各计数点的坐标值(v 1，T )、(v 2，2T )、…(v n ，nT )． c ．画出v t 图象，图线的斜率为物体做匀变速直线运动的加速度．●考向1 “纸带”类实验3．(2017·南京一模)(1)用游标卡尺测量小球的直径如图1111甲、乙所示．测量方法正确的是________(选填“甲”或“乙”)．甲乙丙图1111(2)用螺旋测微器测量合金丝的直径，此示数为______mm ．(3)在“用打点计时器测速度”的实验中，交流电源频率为50 Hz ，打出一段纸带如图1112所示．纸带经过2号计数点时，测得的瞬时速度v ＝________m/s ．若实验时交流电源频率大于50 Hz ，则纸带经过2号点的实际速度________(选填“大于”“小于”“等于”)测量速度．图1112【解析】 (1)游标卡尺测量小球的直径时，应将小球卡在外爪的刀口上，故选甲；(2)螺旋测微器的固定刻度为6．5 mm ，可动刻度为：20．0×0．01 mm ＝0．200 mm ，所以最终读数为：6．5 mm ＋0．200 mm ＝6．700 mm ．(3)从0点开始每5个点取一个计数点，所以相邻计数点间的时间间隔为0．02×5 s＝0．1 s 根据匀变速直线运动中时间中点的速度等于该过程中的平均速度，可以求出打纸带上2点时小车的瞬时速度大小．小车到计数点2时的瞬时速度v 2＝x 132T ＝3．68＋3．522×0．1×10－2 m/s ＝0．36 m/s ，如果在某次实验中，交流电的频率大于50 Hz ，那么实际打点周期变小，据v ＝x t 可知，测出的速度数值将比真实值偏小．【答案】 (1)甲 (2)6．700 (3)0．36；大于●考向2 “弹簧”“橡皮条”类实验4．(2017·镇江一模)在“探究求合力的方法”的实验中，某同学用两把弹簧秤将橡皮筋的端点拉到点O，作出这两个拉力F1、F2的图示(图1113甲)，然后用一把弹簧秤将橡皮筋的端点仍然拉到O，弹簧秤示数F如图乙所示．【导学号：17214178】甲乙图1113(1)弹簧秤的示数F＝________N；(2)请帮他在图甲中画出力F的图示(图中a为记录F方向时所记录的一点)；(3)该同学用虚线把F的箭头末端分别与F1、F2的箭头末端连起来．他观察图形后受到了启发．你认为他紧接着应进行的两个实验步骤是________．(A) 整理实验器材(B) 提出求合力方法的猜想(C) 改变F1、F2的大小和方向，重复上述实验(D) 与同学交流讨论实验结果，得出结论【解析】(1)弹簧秤的最小刻度为0．2 N，可知弹簧秤的示数F＝2．8 N．(2)根据图示法作出F的图示，如图所示．(3)用虚线把F的箭头末端分别与F1、F2的箭头末端连起来．观察图形后受到了启发．提出求合力方法的猜想，然后改变F1、F2的大小和方向，重复上述实验，故BC正确．【答案】(1)2．8 (2)见解析(3)BC5．(2017·徐州期末)如图1114甲所示，在“探究功与速度变化的关系”的实验中，主要过程如下：A．设法让橡皮筋对小车做的功分别为W、2W、3W、…；B．分析纸带，求出橡皮筋做功使小车获得的速度v1、v2、v3、…；C．作出Wv图象；D．分析Wv图象．如果Wv图象是一条直线，表明W∝v；如果不是直线，可考虑是否存在W∝v2、W∝v3、W∝v等关系．(1)实验中得到的一条如图乙所示的纸带，求小车获得的速度应选________(选填“AB”或“CD”)段来计算．甲乙图1114(2)关于该实验，下列说法正确的有( )A．通过增加橡皮筋的条数可以使橡皮筋对小车做的功成整数倍增加B．通过改变小车质量可以改变橡皮筋对小车做的功C．每次实验中，橡皮筋拉伸的长度必须保持一致D．先接通电源，再让小车在橡皮筋的作用下弹出(3)在该实验中，打点计时器正常工作，纸带足够长，点迹清晰的纸带上并没有出现一段等间距的点，造成这种情况的原因可能是________．(写出一条即可)【解析】(1)由图知：在AB之间，由于相邻计数间的距离不断增大，而打点计时器每隔0．02 s打一个点，所以小车做加速运动．在CD之间相邻计数点间距相等，说明小车离开橡皮筋后做匀速运动，应选用CD段纸带来计算小车的速度v．求小车获得的速度应选CD段来计算．(2)该实验中利用相同橡皮筋形变量相同时对小车做功相同，通过增加橡皮筋的条数可以使橡皮筋对小车做的功成整数倍增加，故A正确，B错误；为保证每根橡皮条对小车做功一样多，每次实验中，橡皮筋拉伸的长度必须保持一致，故C正确；用打点计时器测量时间时，为有效利用纸带，总是先接通电源后释放纸带，故D正确．(3)在该实验中，打点计时器正常工作，纸带足够长，点迹清晰的纸带上并没有出现一段等间距的点，造成这种情况的原因可能是没有平衡摩擦力或木板的倾角过大或过小．【答案】(1)CD(2)ACD (3)没有平衡摩擦力或木板的倾角过大或过小●考向3 应用图象法处理实验数据6．(2017·苏州一模)为了探究物体的加速度与物体所受外力、物体质量间的关系，某小组安装了如图1115甲所示的实验装置并开始实验．已知小车以及车上的砝码质量用M表示，盘以及盘中砝码质量用m表示，当地重力加速度为g．【导学号：17214179】甲乙图1115(1)假如已经平衡摩擦力，则在小车做匀加速直线运动的过程中，绳子拉力F T＝________；只有当M 与m 的大小关系满足________时，F T ＝mg 才能成立．(2)该小组同学先保持盘及盘中的砝码质量m 不变，探究加速度a 与质量M 的关系，其具体操作步骤如下，则下列做法正确的是________．(填合适选项前面的符号)A ．平衡摩擦力时，应将盘及盘中的砝码用细绳通过定滑轮系在小车上B ．每次改变小车的质量时，需要重新平衡摩擦力C ．实验时，先接通打点计时器的电源，再放开小车D ．用天平测出m 以及M ，小车运动的加速度直接用公式a ＝mg M 求出(3)该小组同学后来又保持小车以及车上砝码质量M 一定，探究加速度a 与所受外力F 的关系，由于他们操作不当，这组同学得到的a F 关系图象如图乙所示，则：图线不过原点的原因是______________________________；图线上端发生弯曲的原因是________________________________．【解析】 (1)该实验的研究对象是小车，采用控制变量法研究．当质量一定时，研究小车的加速度和小车所受合力的关系．那么小车的合力怎么改变和测量呢？为消除摩擦力对实验的影响，可以把木板的右端适当垫高，以使小车的重力沿斜面的分力和摩擦力抵消，那么小车的合力就是绳子的拉力．根据牛顿第二定律得：对m ：mg －T ＝ma对M ：T ＝Ma解得：T ＝Mmg M ＋m当M ≫m 时，即当砝码和盘的总重力要远小于小车的重力，绳子的拉力近似等于砝码和盘的总重力．(2)平衡摩擦力时，应将绳从小车上拿去，轻轻推动小车，使小车沿木板运动，通过打点计时器打出来的纸带判断小车是否匀速运动，故A 错误．每次改变小车的质量时，小车的重力沿斜面的分力和摩擦力仍能抵消，不需要重新平衡摩擦力，故B 错误．实验时，若先放开小车，再接通打点计时器电源，由于小车运动较快，可能会使打出来的点很少，不利于数据的采集和处理，故C 正确．小车运动的加速度是利用打点计时器打点测量并计算，如果用天平测出m 以及小车质量M ，直接用公式求出，这是在直接运用牛顿第二定律计算的，而我们实验的目的就是在探究加速度与物体所受合外力和质量间的关系，故D 错误．(4)当F ≠0时，a ＝0．也就是说当绳子上有拉力时小车的加速度还为0，说明小车的摩擦力与绳子的拉力抵消了．该组同学实验操作中遗漏了平衡摩擦力或平衡摩擦力不足这个步骤；随着F 的增大，即盘和盘中砝码质量的增大，不再满足盘和盘中砝码远小于小车的质量，因此曲线上部出现弯曲现象．【答案】 (1)Mmg M ＋mM ≫m (2)C (3)遗漏了平衡摩擦力或平衡摩擦力不足；不满足盘和盘中砝码远小于小车的质量，因此曲线上部出现弯曲现象7．(2017·无锡一模)某同学用如图1116甲所示的装置验证机械能守恒定律，他将两物块A 和B 用轻质细绳连接并跨过轻质定滑轮，B 下端连接纸带，纸带穿过固定的打点计时器．用天平测出A 、B 两物块的质量m A ＝300 g 、m B ＝100 g ，m A 从高处由静止开始下落，m B 拖着的纸带打出一系列的点，对纸带上的点迹进行测量，即可验证机械能守恒定律．图乙给出的是实验中获取的一条纸带：0是打下的第一个点，每相邻两计数点间还有4个点(图中未标出)，计数点间的距离如图所示．已知打点计时器计时周期为T ＝0．02 s ，则：(1)在打点0～5过程中系统动能的增量ΔE k ＝________J ，系统势能的减小量ΔE p ＝________J ，由此得出的结论是________________________________；(重力加速度g 取9．8 m/s 2，结果保留三位有效数字)(2)用v 表示物块A 的速度，h 表示物块A 下落的高度．若某同学作出v 22h 图象如图丙，可求出当地的重力加速度g ＝________ m/s 2．【导学号：17214180】甲乙丙图1116【解析】 (1)计数点5的瞬时速度v 5＝x 462T ＝．60＋26．－20．2 m/s ＝2．4 m/s ；则系统动能的增加量ΔE k ＝12(m A ＋m B )v 25＝12×0．4×2．42 J ＝1．15 J ．系统重力势能的减小量ΔE p ＝(m A －m B )gx ＝0．2×9．8×(38．4＋21．6)×10－2 J ＝1．18 J ．在误差允许的范围内，m A 、m B 组成的系统机械能守恒．(2)根据系统机械能守恒定律得，(m A －m B )gh ＝12(m A ＋m B )v 2，解得12v 2＝m A －m B m A ＋m Bgh 图线的斜率k ＝m A －m B m A ＋m B g ＝5．821．20代入数据得，g ＝9．7 m/s 2．【答案】 (1)1．15 1．18 在误差允许的范围内，m A 、m B 组成的系统机械能守恒 (2)9．7考点3| 力学创新实验难度：低档中档高档题型：实验填空题五年2考(对应学生用书第61页)4．(2015·江苏高考T 11)某同学探究小磁铁在铜管中下落时受电磁阻尼作用的运动规律．实验装置如图1117a 所示，打点计时器的电源为50 Hz 的交流电．a(1)下列实验操作中，不正确的有________________．A ．将铜管竖直地固定在限位孔的正下方B ．纸带穿过限位孔，压在复写纸下面C ．用手捏紧磁铁保持静止，然后轻轻地松开让磁铁下落D ．在磁铁下落的同时接通打点计时器的电源b图1117(2)该同学按正确的步骤进行实验(记为“实验①”)，将磁铁从管口处释放，打出一条纸带，取开始下落的一段，确定一合适的点为O 点，每隔一个计时点取一个计数点，标为1，2，…，8．用刻度尺量出各计数点的相邻两计时点到O 点的距离，记录在纸带上，如图b 所示．计算相邻计时点间的平均速度v －，粗略地表示各计数点的速度，抄入下表．请将表中的数据补充完整．_____________；磁铁受到阻尼作用的变化情况是_______________．(4)该同学将装置中的铜管更换为相同尺寸的塑料管，重复上述实验操作(记为“实验②”)，结果表明磁铁下落的运动规律与自由落体运动规律几乎相同．请问实验②是为了说明什么？对比实验①和②的结果可得到什么结论？【解题关键】解此题应注意以下三点：(1)为减小纸带与限位孔之间的阻力，实验时应保持纸带竖直．(2)实验时应先接通打点计时器的电源，再释放纸带．(3)每隔一个计时点取一个计数点，则两计数点之间的计时间隔为0．04 s．【解析】(1)为了探究小磁铁在铜管中下落时受电磁阻尼作用的运动规律，应让铜管竖直地固定在限位孔正下方，避免小磁铁下落时与铜管发生碰撞，选项A正确；纸带穿过限位孔，要压在复写纸下面，使打点计时器工作时纸带上点迹清晰，选项B正确；用手只捏住磁铁，不能使纸带保持竖直，磁铁下落时纸带与打点计时器间有较大阻力，故应捏住纸带的上端，让磁铁从静止释放，选项C不正确；应先接通打点计时器的电源再松开纸带，选项D不正确．(2)计数点“4”的速度用它两侧计时点之间的平均速度来表示，故v4＝5．60－4．040．04cm/s＝39．0 cm/s．(3)由各计数点速度表可以看出，磁铁运动的速度逐渐增大到39．8 cm/s，表明磁铁受到的阻尼作用也是逐渐增大的，最后和重力平衡．(4)实验②中磁铁在塑料管中下落的运动规律与自由落体规律几乎相同，说明磁铁在塑料管中下落几乎不受阻尼作用．对比实验①和②，可以看出磁铁在铜管中受到的阻尼作用主要是电磁阻尼作用．【答案】(1)CD (2)39．0 (3)逐渐增大到39．8 cm/s 逐渐增大到等于重力(4)为了说明磁铁在塑料管中几乎不受阻尼作用．磁铁在铜管中受到的阻尼作用主要是电磁阻尼作用5．(2013·江苏高考T11)某兴趣小组利用自由落体运动测定重力加速度，实验装置如图1118所示．倾斜的球槽中放有若干个小铁球，闭合开关K，电磁铁吸住第1个小球．手动敲击弹性金属片M，M与触头瞬间分开，第1个小球开始下落，M迅速恢复，电磁铁又吸住第2个小球．当第1个小球撞击M时，M与触头分开，第2个小球开始下落……这样，就可测出多个小球下落的总时间．图1118(1)在实验中，下列做法正确的有________．A ．电路中的电源只能选用交流电源B ．实验前应将M 调整到电磁铁的正下方C ．用直尺测量电磁铁下端到M 的竖直距离作为小球下落的高度D ．手动敲击M 的同时按下秒表开始计时(2)实验测得小球下落的高度H ＝1．980 m ，10个小球下落的总时间T ＝6．5 s ．可求出重力加速度g ＝________m/s 2．(结果保留两位有效数字)(3)在不增加实验器材的情况下，请提出减小实验误差的两个办法．(4)某同学考虑到电磁铁在每次断电后需要时间Δt 磁性才消失，因此，每个小球的实际下落时间与它的测量时间相差Δt ，这导致实验误差．为此，他分别取高度H 1和H 2，测量n 个小球下落的总时间T 1和T 2．他是否可以利用这两组数据消除Δt 对实验结果的影响？请推导说明．【解析】根据自由落体运动的规律h ＝12gt 2解决问题． (1)若电源选用直流电源，电磁铁可正常工作，选项A 错误；实验时小球要撞击M 断开电源，因此M 应在电磁铁的正下方，选项B 正确；小球下落的高度为电磁铁下端到M 的竖直距离与小球直径的差，选项C 错误；根据H ＝12gt 2，t 可利用累积法，即从手动敲击M 的同时开始计时，测量出落下n 个小球的时间T ，则一个小球下落时间t ＝T n，选项D 正确．(2)根据H ＝12gt 2和t ＝T n，解得 g ＝2H t 2＝2n 2H T 2＝2×102×1．9806．52 m/s 2≈9．4 m/s 2． (3)要减小实验误差，可以适当增大小球下落的高度，并多次测量取平均值． (4)根据题意，小球从H 1、H 2高处落下需要的时间t 1＝T 1n －Δt 和t 2＝T 2n －Δt ，根据H ＝12gt 2得H 1＝12g (T 1n －Δt )2和H 2＝12g (T 2n－Δt )2 解得g ＝2n 2H 1－H 22T 1－T 22，因此可以消除Δt 的影响．【答案】 (1)BD (2)9．4 (3)增加小球下落的高度；多次重复实验，结果取平均值．(其他答案只要合理也可)(4)可以消除Δt 对实验结果的影响，推导过程见解析。

2018版高考物理二轮复习小题提速练2 含解析精品

小题提速练(二)(时间：20分钟分值：48分)选择题(本题共8小题，每小题6分，共48分．在每小题给出的四个选项中，第14～18题只有一项符合题目要求，第19～21题有多项符合题目要求．全部选对的得6分，选对但不全的得3分，有选错的得0分．)14．(2018·高三第一次全国大联考(新课标卷Ⅰ))A、B两个物体在同一条直线上做直线运动，它们at图象如图1所示，规定水平向右为正方向．已知在t＝0时，两物体的速度均为零，且A在B的左边1.75 m处，则A追上B的时间是( )图1A．t＝0.5 s B．t＝1.5 sC．t＝2.5 s D．t＝3.5 sD[很显然，在前2 s内两个物体运动规律是一样的，不可能追上，故A、B错误；在t＝2.5 s时，A的位移是1.125 m，B的位移是0.875 m，两位移之差为0.25 m，小于1.75 m，故C错误；t＝3.5 s时，A的位移是1.875 m，B的位移是0.125 m，两位移之差等于1.75 m，故D正确．]15．(2018·辽宁省部分重点中学协作体5月模拟)如图2所示，一根不可伸长的轻质细绳两端分别连接在固定框架上的A、B两点，细绳绕过光滑的轻小滑轮，重物悬挂于滑轮下，处于静止状态，若缓慢移动细绳的端点，则绳中拉力大小的变化情况是( )【导学号：19624219】图2A．只将绳的左端移向A′点，拉力变小B．只将绳的左端移向A′点，拉力变大C．只将绳的右端移向B′点，拉力变大D．只将绳的右端移向B′点，拉力不变C[设细绳总长度为L，OA段长度为l1，OB段长度为l2，由对称性可知，OA、OB与竖直方向间夹角相等，设为α，两悬点间的水平距离设为d ，则由l 1sin α＋l 2sin α＝d ，l 1＋l 2＝L 可得sin α＝d L ，只将绳的左端移向A ′点的过程中，d 不变，α不变，由2F cos α＝G 可知，F 不变，A 、B 均错误；只将绳的右端移向B ′点的过程中，d 增大，α增大，F 增大，C 正确，D 错误．]16．(2018·沈阳三模)以无穷远处的电势为零，在电荷量为q 的点电荷周围某点的电势可用φ＝kq r计算，式中r 为该点到点电荷的距离，k 为静电力常量．两电荷量大小均为Q 的异种点电荷固定在相距为L 的两点，如图3所示．现将一质子(电荷量为e )从两点电荷连线上的A 点沿以电荷＋Q 为圆心、半径为R 的半圆形轨迹ABC 移到C 点，质子从A 移到C 的过程中电势能的变化情况为( )图3A ．增加2kQe L 2－R 2B ．增加2kQeR L 2－R 2 C ．减少2kQeR L 2＋R 2 D ．减少2kQe L 2＋R 2B [根据题中φ＝kq r公式和叠加原理可知，φA ＝k －Q L －R ＋k Q R .C 点的电势φC ＝k －Q L ＋R ＋k Q R .故U AC ＝φA －φC ＝－2kQR L 2－R 2，质子由A 移到C 的过程中电场力做功W AC ＝U AC e ＝－2kQeR L 2－R 2，是负功，故质子电势能增加2kQeR L 2－R 2，B 项正确．] 17．(2018·新余市一中七模)放射性物质碘131的衰变方程为131 53I→13154Xe ＋Y ＋γ.根据有关放射性知识，下列说法正确的是( )A ．生成的131 54Xe 处于激发态，放射γ射线．γ射线的穿透能力最强，电离能力也最强B ．若131 53I 的半衰期大约是8天，取4个碘原子核，经16天就只剩下1个碘原子核了C ．Y 粒子为β粒子D.131 53I 中有53个质子和132个核子C [γ射线的穿透能力最强，电离能力最弱，故A 错误．半衰期具有统计规律，对大量的原子核适用，对少数的原子核不适用，故B 错误．根据电荷数守恒、质量数守恒知，Y 粒子的电荷数为－1，质量数为0，可知Y 粒子为β粒子，故C 正确．电荷数等于质子数，可知131 53I 中有53个质子，质量数等于核子数，则有131个核子，故D错误．故选C.]18．(2018·虎林市摸底考试)2018年2月11日，美国科学家宣布探测到引力波，证实了爱因斯坦100年前的预测，弥补了爱因斯坦广义相对论中最后一块缺失的“拼图”，双星的运动是产生引力波的来源之一，假设宇宙中有一双星系统由a 、b 两颗星体组成，这两颗星绕它们的连线的某一点在万有引力作用下做匀速圆周运动，测得a 星的周期为T ，a 、b 两颗星的距离为l ，a 、b 两颗星的轨道半径之差为Δr ，已知a 星的轨道半径大于b 星的轨道半径，则( )【导学号：19624220】A ．b 星的周期为l －Δr l ＋ΔrT B ．a 星的线速度大小为πl －Δr TC ．a 、b 两颗星的半径之比为l ＋Δr l －ΔrD ．a 、b 两颗星的质量之比为l ＋Δr l －Δr C [双星系统中两颗星的周期和角速度均相等，A 错误；由r a ＋r b ＝l ，r a －r b ＝Δr 可知r a ＝l ＋Δr 2，r b ＝l －Δr 2，r a r b ＝l ＋Δr l －Δr ，由m a ω2r a ＝m b ω2r b 可得：m a m b ＝r b r a ＝l －Δr l ＋Δr，C 正确，D 错误；由v a ＝2πr a T 可得：v a ＝πl ＋Δr T ，B 错误．] 19．(2018·Ⅱ卷)某同学自制的简易电动机示意图如图4所示．矩形线圈由一根漆包线绕制而成，漆包线的两端分别从线圈的一组对边的中间位置引出，并作为线圈的转轴．将线圈架在两个金属支架之间，线圈平面位于竖直面内，永磁铁置于线圈下方．为了使电池与两金属支架连接后线圈能连续转动起来，该同学应将( )图4A ．左、右转轴下侧的绝缘漆都刮掉B ．左、右转轴上下两侧的绝缘漆都刮掉C ．左转轴上侧的绝缘漆刮掉，右转轴下侧的绝缘漆刮掉D ．左转轴上下两侧的绝缘漆都刮掉，右转轴下侧的绝缘漆刮掉AD [装置平面示意图如图所示．如图所示的状态，磁感线方向向上，若形成通路，线圈下边导线中电流方向向左，受垂直纸面向里的安培力，同理，上边导线中电流受安培力垂直纸面向外，使线圈转动．当线圈上边导线转到下边时，若仍通路，线圈上、下边中电流方向与图示方向相比均反向，受安培力反向，阻碍线圈转动．若要线圈连续转动，要求左、右转轴只能上一侧或下一侧形成通路，另一侧断路．故选A 、D.]20．(2018·沈阳铁路实验中学模拟)水平面上有两个质量不相等的物体a 和b ，它们分别在水平推力F 1和F 2作用下开始运动，分别运动一段时间后撤去推力，两个物体都将运动一段时间后停下．物体的v t 图线如图5所示，图中线段AC ∥BD .则以下说法正确的是( )图5①水平推力大小F 1>F 2②水平推力大小F 1<F 2③物体a 所受到的摩擦力的冲量大于物体b 所受到的摩擦力的冲量④物体a 所受到的摩擦力的冲量小于物体b 所受到的摩擦力的冲量⑤物体a 克服摩擦力做功大于物体b 克服摩擦力做功⑥物体a 克服摩擦力做功小于物体b 克服摩擦力做功A ．若物体a 的质量大于物体b 的质量，由图可知，①⑤都正确B ．若物体a 的质量大于物体b 的质量，由图可知，④⑥都正确C ．若物体a 的质量小于物体b 的质量，由图可知，②③都正确D ．若物体a 的质量小于物体b 的质量，由图可知，只有④正确AD [根据v t 图象，由于AC ∥BD ，可见撤去外力后，两物体的加速度相等，故两物体与水平面间的动摩擦因数相同．由图可知撤去外力之前，物体a 的加速度大于物体b 的加速度，由牛顿第二定律可知F 1－μm a g m a ＞F 2－μm b g m b ，解得：F 1m a ＞F 2m b，若m a ＞m b 则F 1＞F 2，若m a ＜m b ，则无法比较水平推力F 1和F 2的大小．克服摩擦力做功W f ＝μmgx ，所受到的摩擦力的冲量大小I f ＝μmgt .由图可知：物体b 运动的时间更长，物体a 的位移更大，若m a ＞m b 则物体a 克服摩擦力做功大于物体b 克服摩擦力做功，但无法比较两者所受到的摩擦力的冲量大小，若m a ＜m b ，物体a 所受到的摩擦力的冲量小于物体b所受摩擦力的冲量，但无法比较两者克服摩擦力的做功大小，故A、D正确，B、C错误．]21．(2018·辽宁省部分重点中学协作体5月模拟)如图6所示为某住宅区的应急供电系统，由交流发电机和副线圈匝数可调的理想降压变压器组成，发电机中矩形线圈所围的面积为S，匝数为N，电阻不计，它可绕水平轴OO′在磁感应强度为B的水平匀强磁场中以角速度ω匀速转动，矩形线圈通过滑环连接降压变压器，滑动触头P上下移动时可改变输出电压，R0表示输电线的电阻，以线圈平面与磁场平行时为计时起点，下列判断正确的是( )【导学号：19624221】图6A．若发电机线圈某时刻处于图示位置，变压器原线圈的电流瞬时值为最大B．发电机线圈感应电动势的瞬时值表达式为e＝NBSωcos ωtC．当滑动触头P向下移动时，变压器原线圈两端电压将升高D．当用户功率增加时，为使用户电压保持不变，滑动触头P应向上滑动ABD[从线圈在如图示位置开始计时，电动势的瞬时值表达式为e＝NBSωcos ωt，此时变压器原线圈中的电流值最大，A、B均正确；当滑动触头向下移动时，影响变压器的输出电压，而不影响变压器的输入电压，C错误；当用户功率增加时，因R0的降压作用，用户得到的电压降低，为使用户电压保持不变，应使副线圈匝数增多，即滑动触头P应该向上滑动，故D正确．]。

2018届二轮复习高考物理秘诀学案 (全国通用)

题型1直线运动问题题型概述：直线运动问题是高考的热点，可以单独考查，也可以与其他知识综合考查.单独考查若出现在选择题中，则重在考查基本概念，且常与图像结合;在计算题中常出现在第一个小题，难度为中等，常见形式为单体多过程问题和追及相遇问题.思维模板：解图像类问题关键在于将图像与物理过程对应起来，通过图像的坐标轴、关键点、斜率、面积等信息，对运动过程进行分析，从而解决问题;对单体多过程问题和追及相遇问题应按顺序逐步分析，再根据前后过程之间、两个物体之间的联系列出相应的方程，从而分析求解，前后过程的联系主要是速度关系，两个物体间的联系主要是位移关系.题型2物体的动态平衡问题题型概述：物体的动态平衡问题是指物体始终处于平衡状态，但受力不断发生变化的问题.物体的动态平衡问题一般是三个力作用下的平衡问题，但有时也可将分析三力平衡的方法推广到四个力作用下的动态平衡问题.思维模板：常用的思维方法有两种.(1)解析法：解决此类问题可以根据平衡条件列出方程，由所列方程分析受力变化;(2)图解法：根据平衡条件画出力的合成或分解图，根据图像分析力的变化.题型3运动的合成与分解问题题型概述：运动的合成与分解问题常见的模型有两类.一是绳(杆)末端速度分解的问题，二是小船过河的问题，两类问题的关键都在于速度的合成与分解.思维模板：(1)在绳(杆)末端速度分解问题中，要注意物体的实际速度一定是合速度，分解时两个分速度的方向应取绳(杆)的方向和垂直绳(杆)的方向;如果有两个物体通过绳(杆)相连，则两个物体沿绳(杆)方向速度相等.(2)小船过河时，同时参与两个运动，一是小船相对于水的运动，二是小船随着水一起运动，分析时可以用平行四边形定则，也可以用正交分解法，有些问题可以用解析法分析，有些问题则需要用图解法分析.题型4抛体运动问题题型概述：抛体运动包括平抛运动和斜抛运动，不管是平抛运动还是斜抛运动，研究方法都是采用正交分解法，一般是将速度分解到水平和竖直两个方向上.思维模板：(1)平抛运动物体在水平方向做匀速直线运动，在竖直方向做匀加速直线运动，其位移满足x=v0t,y=gt2/2，速度满足vx=v0,vy=gt;(2)斜抛运动物体在竖直方向上做上抛(或下抛)运动，在水平方向做匀速直线运动，在两个方向上分别列相应的运动方程求解题型5圆周运动问题题型概述：圆周运动问题按照受力情况可分为水平面内的圆周运动和竖直面内的圆周运动，按其运动性质可分为匀速圆周运动和变速圆周运动.水平面内的圆周运动多为匀速圆周运动，竖直面内的圆周运动一般为变速圆周运动.对水平面内的圆周运动重在考查向心力的供求关系及临界问题，而竖直面内的圆周运动则重在考查最高点的受力情况.思维模板：(1)对圆周运动，应先分析物体是否做匀速圆周运动，若是，则物体所受的合外力等于向心力，由F合=mv2/r=mrω2列方程求解即可;若物体的运动不是匀速圆周运动，则应将物体所受的力进行正交分解，物体在指向圆心方向上的合力等于向心力.(2)竖直面内的圆周运动可以分为三个模型：①绳模型：只能对物体提供指向圆心的弹力，能通过最高点的临界态为重力等于向心力;②杆模型：可以提供指向圆心或背离圆心的力，能通过最高点的临界态是速度为零;③外轨模型：只能提供背离圆心方向的力，物体在最高点时，若v<(gR)1/2，沿轨道做圆周运动，若v≥(gR)1/2，离开轨道做抛体运动.题型6牛顿运动定律的综合应用问题题型概述：牛顿运动定律是高考重点考查的内容，每年在高考中都会出现，牛顿运动定律可将力学与运动学结合起来，与直线运动的综合应用问题常见的模型有连接体、传送带等，一般为多过程问题，也可以考查临界问题、周期性问题等内容，综合性较强.天体运动类题目是牛顿运动定律与万有引力定律及圆周运动的综合性题目，近几年来考查频率极高.思维模板：以牛顿第二定律为桥梁，将力和运动联系起来，可以根据力来分析运动情况，也可以根据运动情况来分析力.对于多过程问题一般应根据物体的受力一步一步分析物体的运动情况，直到求出结果或找出规律.对天体运动类问题，应紧抓两个公式：GMm/r2=mv2/r=mrω2=mr4π2/T2①。

(新课标版)备战2018高考数学二轮复习方法3.3解答题的解法教学案

5
（ 2）求这 50 名学生成绩在 80,100 内的人数；
（ 3）现从该校 50名考生成绩在 80,100 的学生中随机抽取两人，该两人成绩排名（从高到低）在全市前 26
名的人数记为 X ，求 X 的分布列和数学期望 .
参考数据：若 X ~ N , 2 ，则 p(
X
) 0.6826 ， p( 2 X
7
【规律总结】答题模板第一步：根据条件合理转化．第二步：写出推证平行或垂直所需的条件，条件要充分．第三步：写出所证明的结论．第四步：建立空间直角坐标系，写出特殊点坐标．第五步：求 ( 或找 ) 两个半平面的法向量．
第六步：求法向量 n1,n2 的夹角或 cos n1, n2 ( 若为锐二面角则求 cos n1, n2 ) ．
3
模板三离散型随机变量的分布列、期望与方差
试题特点：主要考查古典概型、几何概型，等可能事件的概率计算公式，互斥事件的概率加法公式，对立
事件的概率减法公式，相互独立事件的概率乘法公式，事件在
n 次独立重复试验中恰好发生 k 次的概率计
算公式等五个基本公式的应用及离散型随机变量的分布列和数学期望、方差等内容．
2y 0
y0
uuur 由（ 1）可知 PA 平面 CDE ，所以 AP 0 ，1 ， 3 为平面 CDE 的一个法向量 . 所以
uuur r cos AP ，n
uuur r AP n uuur r
AP n
43 2 19
2 57 . 所以二面角 A DE C 的余弦值为
2 57 .
19
19
3 ，0 ， 4 .
B1GE 所成角的正弦值 .
8
（ 2）连结 AO . 因为 AA1

2018年高考数学(文)二轮复习练习：小题提速练4 Word版含答案

小题提速练(四) “12选择＋4填空”80分练 (时间：45分钟分值：80分)一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．函数y ＝ln ⎝ ⎛⎭⎪⎫1x－1的定义域为( )【导学号：04024184】A ．(－∞，0]B ．(0,1)C ．(1，＋∞)D ．(－∞，0)∪(1，＋∞)B [由已知得1x －1＞0，x ≠0，所以1－x x ＞0，x ≠0，所以x －1x＜0，x ≠0，所以0＜x ＜1.故选B.]2．复数(1－i)(2＋2i)＝( )A ．4B ．－4C ．2D ．－2A [(1－i)(2＋2i)＝2＋2i －2i ＋2＝4.]3．已知等比数列{a n }的公比为－12，则a 1＋a 3＋a 5a 2＋a 4＋a 6的值是( )A ．－2B ．－12C.12 D ．2A [a 1＋a 3＋a 5a 2＋a 4＋a 6＝a 1＋a 3＋a 5－12a 1＋a 3＋a 5＝－2.]4．若m ＝6，n ＝4，则运行如图1所示的程序框图后，输出的结果是( )图1A.1100B ．100C ．10D ．1D [因为m ＞n ，所以y ＝lg(m ＋n )＝lg(6＋4)＝1.故选D.]5．设α，β，γ为不重合的平面，m ，n 为不同的直线，则m ⊥β的一个充分条件是( )【导学号：04024185】A ．α⊥β，α∩β＝n ，m ⊥nB ．α∩γ＝m ，α⊥γ，β⊥γC ．α⊥γ，β⊥γ，m ⊥αD ．n ⊥α，n ⊥β，m ⊥αD [因为n ⊥α，m ⊥α，所以m ∥n ，又n ⊥β，所以m ⊥β，故选D.]6．若实数x ，y 满足条件⎩⎨⎧3x －y ≤0，x －3y ＋2≥0，y ≥0，则3x ＋y 的最大值为( )A ．0 B. 3 C ．2 3D.233C [如图所示，画出不等式组表示的平面区域，作直线l ：3x ＋y ＝0，平移直线l ，当直线l 经过点A (1，3)时，3x ＋y 取得最大值，即(3x ＋y )max ＝23，故选C.]7．在△ABC 中，若点D 满足BD →＝2DC →，则AD →＝( )A.13AC →＋23AB →B.53AB →－23AC →C.23AC →－13AB →D.23AC →＋13AB → D [根据题意画出图形如图所示．因为BD →＝2DC →，所以AD →－AB →＝2(AC →－AD →)，所以3AD →＝AB →＋2AC →，所以AD →＝13AB →＋23AC →.]8．一个几何体的三视图如图2所示，则该几何体的体积等于( )图2A ．5π B.556π C.1256π D.716π D [由三视图可知，该几何体为直径为5的球中挖去一个底面直径是3，高是4的圆柱后剩余的几何体，所以该几何体的体积为43π·⎝ ⎛⎭⎪⎫523－π·⎝ ⎛⎭⎪⎫322×4＝716π.]9．将函数f (x )＝－cos 2x 的图象向右平移π4个单位长度后得到函数g (x )的图象，则函数g (x )( )A ．最大值为1，图象关于直线x ＝π2对称B ．在⎝ ⎛⎭⎪⎫0，π4上单调递减，为奇函数C ．在⎝ ⎛⎭⎪⎫－3π8，π8上单调递增，为偶函数D ．周期为π，图象关于点⎝⎛⎭⎪⎫3π8，0对称B [依题意有g (x )＝－cos 2⎝ ⎛⎭⎪⎫x －π4＝－cos ⎝ ⎛⎭⎪⎫2x －π2＝－sin 2x ，显然g (x )在⎝ ⎛⎭⎪⎫0，π4上单调递减，为奇函数．故选B.]10．在平面直角坐标系xOy 中，动点P 到圆(x －2)2＋y 2＝1上的点的最小距离与其到直线x ＝－1的距离相等，则P 点的轨迹方程是( )【导学号：04024186】A ．y 2＝8x B ．x 2＝8y C ．y 2＝4xD ．x 2＝4yA [由题意知点P 在直线x ＝－1的右侧，且点P 在圆的外部，故可将条件等价转化为“P 点到定点(2,0)的距离与其到定直线x ＝－2的距离相等”．根据抛物线的定义知，P 点的轨迹方程为y 2＝8x .] 11．若函数f (x )＝－m xx 2＋m的图象如图3所示，则m 的取值范围为( )图3A ．(－∞，－1)B ．(－1,2)C ．(0,2)D ．(1,2)D [由图可知，函数图象过原点，即f (0)＝0，所以m ≠0.当x >0时，f (x )>0，所以2－m >0，即m <2.函数f (x )在[－1,1]上单调递增，所以f ′(x )>0在[－1,1]上恒成立，因为f ′(x )＝－mx 2＋m －2x －m x x 2＋m 2＝m －x 2－m x 2＋m2，且m －2<0，所以x 2－m <0在[－1,1]上恒成立，所以m >1.综上得1<m <2.故选D. ]12．已知直角三角形ABC 的两直角边AB ，AC 的长分别为方程x 2－2(1＋3)x ＋43＝0的两根，且AB ＜AC ，斜边BC 上有异于端点B ，C 的两点E ，F ，且EF ＝1，设∠EAF ＝θ，则tan θ的取值范围为( ) A.⎝ ⎛⎦⎥⎤239，6311 B.⎝ ⎛⎦⎥⎤39，2311 C.⎝ ⎛⎦⎥⎤39，4311 D.⎝⎛⎦⎥⎤439，16311C [由已知得，AB ＝2，AC ＝23，BC ＝AB 2＋AC 2＝4，建立如图所示的直角坐标系，可得A (0,0)，B (2,0)，C (0,23)．设BF →＝λBC →⎝⎛⎭⎪⎫λ∈⎝⎛⎭⎪⎫0，34，BE →＝⎝⎛⎭⎪⎫λ＋14BC →，则F (2－2λ，23λ)，E ⎝ ⎛⎭⎪⎫32－2λ，23λ＋32，所以AE →·AF →＝3－4λ－3λ＋4λ2＋12λ2＋3λ＝16λ2－4λ＋3＝16·⎝ ⎛⎭⎪⎫λ－182＋114∈⎣⎢⎡⎭⎪⎫114，9.而点A 到BC 的距离d ＝AB ·AC BC ＝3，则S △AEF ＝12EF ·3＝32，所以S △AEF AE →·AF →＝12|AE →||AF →|sin θ|AE →||AF →|cos θ，所以tan θ＝2S △AEF AE →·AF →＝3AE →·AF→∈⎝ ⎛⎦⎥⎤39，4311.]二、填空题(本大题共4小题，每小题5分，共20分．把答案填在题中横线上)13．已知函数f (x )＝ln x －ax 2，且函数f (x )的图象在点(2，f (2))处的切线的斜率是－32，则a＝________.[解析] 由题意知，f ′(2)＝－32，又f ′(x )＝1x －2ax ，所以－32＝12－2a ×2，得a ＝12.[答案] 1214．在距离某晚会直播不到20天的时候，某媒体报道，由两位明星合演的小品节目被毙，为此，某网站针对“是否支持该节目上晚会”对网民进行调查，得到如下数据：为________．[解析] 由分层抽样法的特点得，从持“支持”态度的网民中抽取的人数为48×8 0008 000＋6 000＋10 000＝48×13＝16.[答案] 1615．已知三棱锥P ABC 中，PA ，PB ，PC 两两垂直，且PA ＝2，PB ＝PC ＝1，则三棱锥P ABC 的外接球的体积为________．[解析] 三棱锥P ABC 的三条侧棱PA ，PB ，PC 两两垂直，且PA ＝2，PB ＝PC ＝1，则该三棱锥的外接球就是三棱锥扩展成的长方体的外接球．易得长方体的体对角线长为12＋12＋22＝6，所以该三棱锥的外接球的半径为62，所以三棱锥P ABC 的外接球的体积为4π3×⎝ ⎛⎭⎪⎫623＝6π.[答案]6π16．在△ABC 中，b cos C ＋c cos B ＝a cos C ＋c cos A ＝2，且a cos C ＋3a sin C ＝a ＋b ，则△ABC 的面积为________．【导学号：04024187】[解析] 由已知条件与余弦定理，得b ·a 2＋b 2－c 22ab ＋c ·a 2＋c 2－b 22ac ＝2，a ·a 2＋b 2－c 22ab ＋c ·b 2＋c 2－a 22bc＝2，解得a ＝2，b ＝2.又a cos C ＋3a sin C ＝a ＋b ，即2cos C ＋23sin C＝4，得sin ⎝ ⎛⎭⎪⎫C ＋π6＝1，所以C ＋π6＝π2，得C ＝π3，所以△ABC 的面积S ＝12×2×2sin π3＝3. [答案] 3。

高考物理最新教案-2018届高考物理二轮复习资料C 精品

009届高考物理二轮精品复习资料专题一运动和力参考答案典型例题[例1] 解析：对系统进行整体分析，受力分析如图1—2：由平衡条件有：cos30F f︒=sin 30()N F M m g +︒=+由此解得f =()sin 30135N N M m g F =+-︒=[例2] 解析：（1）设t 1、t 2为声源S 发出两个信号的时刻，12、t t ''为观察者接收到两个信号的时刻．则第一个信号经过11()t t '-时间被观察者A 接收到，第二个信号经过（22t t '-）时刻被观察者A 接收到，且 2121t t t t t t '''∆=-∆=-设声源发出第一个信号时，S 、A 两点间的距离为L ，两个声信号从声源传播到观察者的过程中，它们的运动的距离关系如图所示，可得11112221()()()()P A P A S v t t L v t t v t t L v t t v t ''''-=+--=+--∆ 由以上各式解得P SP Av v t t v v -'∆=∆-（2）设声源发出声波的振动周期为T ，这样，由以上结论，观察者接收到的声波振动的周期T ′,P SP A v v T T v v -'=-．由此可得，观察者接收到的声波频率与声源发出声波频率间的关系为P AP Sv v f f v v -'=-．[例3] 解答：根据题意作图1—4．对这两个天体而言，它们的运动方程分别为212112m m Gm r rω= ①212222m m Gm r r ω= ②以及12r r r += ③由以上三式解得21121212;m m r r r r m m m m ==++．将r 1和r 2的表达式分别代①和②式，f图1—2t v t 't vt t 'S m可得ω=112222v r m v r m T ωωππω====== [例4] 解答：（1）A 、B 两球以相同的初速度v 0，从同一点水平抛出，可以肯定它们沿同一轨道运动．作细线刚被拉直时刻A 、B 球位置示意图1—5．根据题意可知：0 4.50.8 3.6(m) 4.8(m)x v t y ∆=∆=⨯=∆==设A 球运动时间为t ，则B 球运动时间为t －0.8，由于A 、B 球在竖直方向上均作自由落体运动，所以有2211(0.8)22y gt g t ∆=--．由此解得t =1s ．（2）细线刚被拉直时，A 、B 球的水平位移分别为004.5m (0.8)0.9m A B x v t x v t ===-=[例5] 解答：（1）A 球通过最低点时，作用于环形圆管的压力竖直向下，根据牛顿第三定律，A 球受到竖直向上的支持力N 1，由牛顿第二定律，有：2111v N m g m g-= ①由题意知，A 球通过最低点时，B 球恰好通过最高点，而且该时刻A 、B 两球作用于圆管的合力为零；可见B 球作用于圆管的压力肯定竖直向上，根据牛顿第三定律，圆管对B 球的反作用力N 2竖直向下；假设B 球通过最高点时的速度为v ，则B 球在该时刻的运动方程为2222v N m g m R+= ②由题意N 1=N 2 ③∴2210212m v m v m g m g R R+=-④ 对B 球运用机械能守恒定律22202211222m v m v m gR =+ ⑤ 解得2204v v gR =- ⑥⑥式代入④式可得：21212(5)()0v m m g m m R++-=．[例6] 解答：火箭上升到最高点的运动分为两个阶段：匀加速上升阶段和竖直上抛阶段．地面上的摆钟对两个阶段的计时为140(s)t ===xy图1—51218320(s)at t t g=== 即总的读数（计时）为t =t 1＋t 2=360（s ）放在火箭中的摆钟也分两个阶段计时．第一阶段匀加速上升，a =8g ，钟摆周期112233T T '== 其钟面指示时间113120s t t '== 第二阶段竖直上抛，为匀减速直线运动，加速度竖直向下，a =g ，完全失重，摆钟不“走”，计时20t '=．可见放在火箭中的摆钟总计时为12120s t t t '''=+=．综上所述，火箭中的摆钟比地面上的摆钟读数少了240s t t t '∆=-=．[例7] 解答：在情形（1）中，滑块相对于桌面以速度v 0=0.1m/s 向右做匀速运动，放手后，木板由静止开始向右做匀加速运动．20.02m/s mga Mμ==经时间t ，木板的速度增大到v 0=0.1m/s ，05s v t a==．在5s 内滑块相对于桌面向右的位移大小为S 1=v 0t =0.5m ．而木板向右相对于桌面的位移为2210.25m 2S at ==．可见，滑块在木板上向右只滑行了S 1－S 2=0.25m ，即达到相对静止状态，随后，它们一起以共同速度v 0向右做匀速直线运动．只要线足够长，桌上的柱子不阻挡它们运动，滑块就到不了木板的右端．在情形（2）中，滑块与木板组成一个系统，放手后滑块相树于木板的速度仍为v 0，滑块到达木板右端历时05s lt v '==． [例8] 解答：以m 表示球的质量，F 表示两球相互作用的恒定斥力，l 表示两球间的原始距离．A 球作初速度为v 0的匀减速运动，B 球作初速度为零的匀加速运动．在两球间距由l 先减小，到又恢复到l 的过程中，A 球的运动路程为l 1，B 球运动路程为l 2，间距恢复到l 时，A 球速度为v 1，B 球速度为v 2．由动量守恒，有012mv mv mv =+ 由功能关系：A 球221011122Fl mv mv =- B 球：22212Fl mv = 根据题意可知l 1=l 2，由上三式可得22222220120220022()22v v v v v v v v v v =+=-+=-+ 得v 2=v 0、v 1=0 即两球交换速度．当两球速度相同时，两球间距最小，设两球速度相等时的速度为v ，则00(),2v mv m m v v =+= B 球的速度由02v v =增加到v 0花时间t 0，即00002vv v at at =+=+ 得02v a t =．解二：用牛顿第二定律和运动学公式．（略）跟踪练习1．C 提示：利用平衡条件．2．（1）重物先向下做加速运动，后做减速运动，当重物速度为零时，下降的距离最大，设下降的最大距离为h ，由机械能守恒定律得2sin )Mgh mg R θ=解得h ．（2）系统处于平衡状态时，两小环的可能位置为 a ．两小环同时位于大圆环的底端 b ．两小环同时位于大圆环的顶端c ．两小环一个位于大圆环的顶端，另一个位于大圆环的底端d ．除上述三种情况外，根据对称性可知，系统如能平衡，则小圆环的位置一定关于大圆环竖直对称轴对称．设平衡时，两小圆环在大圆环竖直对称轴两侧α角的位置上（如图）．对于重物m ，受绳的拉力T 与重力mg 作用，有T =mg ．对于小圆环，受到三个力的作用，水平绳的拉力T ，竖直绳的拉力T ，大圆环的支持力N ．两绳的拉力沿大圆环切向的分力大小相等，方向相反sin sin T T αα'=．得,90,45ααααα''=+=︒=︒而∴．3．设测速仪扫描速度为v ′，因P 1、P 2在标尺上对应间隔为30小格，所以3030v t'==∆格/s ．测速仪发出超声波信号P 1到接收P 1的反射信号n 1．从图B 上可以看出，测速仪扫描12小格，所以测速仪从发出信号P 1到接收其反射信号n 1所经历时间120.4s t v'=='．汽车接收到P 1信号时与测速仪相距1168m 2t S v ==声．同理，测速仪从发出信号P 2到接收到其反射信号n 2，测速仪扫描9小格，故所经历时间290.3s t v =='．汽车在接收到P 2信号时与测速仪相距2251m 2t S v ==声．所以，汽车在接收到P 1、P 2两个信号的时间内前进的距离△S =S 1－S 2=17m ．从图B 可以看出，n 1与P 2之间有18小格，所以，测速仪从接收反射信号n 1到超声信号P 2的时间间隔3180.6s t v =='．所以汽车接收P 1、P 2两个信号之间的时间间隔为1230.95s 22t tt t ∆=++=． ∴汽车速度17.9Sv t∆==∆m/s ． 4．从B 发出第一个超声波开始计时，经2T被C 车接收．故C 车第一次接收超声波时与B 距离102T S v =．第二个超声波从发出至接收，经T ＋△T 时间，C 车第二车接收超声波时距B 为202T TS v +∆=，C 车从接收第一个超声波到接收第二个超声波内前进S 2－S 1，接收第一个超声波时刻12Tt =，接收第二个超声波时刻为202T Tt T +∆=+． TααNαm 1mT所以接收第一和第二个超声波的时间间距为2102Tt t t T ∆∆=-=+．故车速0021002222C v TTv S S v T T tT T ∆∆-===+∆∆+∆．车向右运动． 5．ACD6．（1）根据动能定理，可求出卫星由近地点到远地点运动过程中，地球引力对卫星的功为22211122W mv mv =-．（2）由牛顿第二定律知1222112()()GM GM a a R h R h ==++ ∴21212()R h a a R h +=+ 7．（1）建立如图所示坐标系，将v 0与g 进行正交分解．0000cos ,sin sin ,cos x y x y v v v v g g g g θθθθ====-在x 方向，小球以0x v 为初速度作匀加速运动．在y 方向，小球以0y v 为初速度，作类竖直上抛运动．当y 方向的速度为零时，小球离斜面最远，由运动学公式02220sin |2|2cos y y v v H g g θθ==．小球经时间t 上升到最大高度，由0y y v g t =得000sin tan cos g yv v v t g g gθθθ===．（2）02220000221sin 1sin 2(2)2cos sin 42cos 2cos ABx x v v Sv t g t v v g g θθθθθθ=+=+ 2202sin (1tan )v gθθ=+8．（1）设滑雪者质量为m ，斜面与水平面夹角为θ，滑雪者滑行过程中克服摩擦力做功cos (cos )W mgS mg L S mgL μθμθμ=+-= ①由动能定理21()2mg H h mgLmv μ--=② 离开B 点时的速度v③ （2）设滑雪者离开B 点后落在台阶上2111122h gt S vt ==<可解得1S =④此时必须满足2H L h μ-< ⑤当2H L h μ->时，滑雪者直接落到地面上，222221,2h gt S v t ==， y可解得2S = 9．AC10．摆球先后以正方形的顶点为圆心，半径分别为R 1=4a ，R 2=3a ，R 3=2a ，R 4=a 为半径各作四分之一圆周的圆运动．当摆球从P 点开始，沿半径R 1=4a 运动到最低点时的速度v 1，根据动量定理221011422mv mv mga -= ① 当摆球开始以v 1绕B 点以半径R 2=3a 作圆周运动时，摆线拉力最大，为T max =7mg ，这时摆球的运动方程为21max3mv T mg a-= ②由此求得v 0的最大许可值为0v当摆球绕C 点以半径R 3=2a 运动到最高点时，为确保沿圆周运动，到达最高点时的速度3v由动能定理223001122mv mv mga v -=-得0v 11．B12．由题意知，周期为42s 63T ==．波速40320m/s 23v T λ===．P 、Q 两点距离相差9(6)4-次全振动所需时间即9235(6)4s.4322t ∆=-⨯=-= ∴50m PQ v t =∆=．13．ABC 开始时小车上的物体受弹簧水平向右的拉力为6N ，水平向左的静摩擦力也为6N ，合力为零．沿水平向右方向对小车施加以作用力，小车向右做加速运动时，车上的物体沿水平向右方向上的合力（F =ma ）逐渐增大到8N 后恒定．在此过程中向左的静摩擦力先减小，改变方向后逐渐增大到（向右的）2N 而保持恒定；弹簧的拉力（大小、方向）始终没有变，物体与小车保持相对静止，小车上的物体不受摩擦力作用时，向右的加速度由弹簧的拉力提供：260.75m/s 8T a m ===． 14．（1）设物体与板的位移分别为S 物、S 板，则由题意有2LS S -=物板 ① 212S S vt a t =物板板∶∶ ② 解得：,2L S L S ==物板．（2）由22112,,mgMv v a S a M mgLμμ===板板板得．212,21,,2,(),2S S L S S S L S L mg M m g Ma v a S μμ''''''-===='''-+==物板物板板物板板板∶∶得由得222()Mv M m gL μ=+，故板与桌面之间的动摩擦因数222()Mv M m gLμ+≥．15．在0～10s 内，物体的加速度210.8m/s va t∆==∆（正向）在10～14s 内，物体的加速度222m/s va t∆==∆ （反向）由牛顿第二定律1F mg ma μ-= ① 23Fm g m a μ-=- ② 由此解得F =8.4Nμ=0.3416．（1）依题意得1B v =0，设小滑块在水平面上运动的加速度大小为a ，由牛顿第二定律，f mg ma μ==，由运动学公式202v gS μ=，解得0.09μ=．（2）滑块在水平面上运动时间为t 1，由01110, 3.3s 23v S t t ===得．在斜面上运动的时间2120.8s 4.1s t t t t ==+=∴（3）若滑块在A 点速度为v 1=5m/s ，则运动到B 点的速度4m/s B v =．即运动到B 点后，小滑块将做平抛运动．假设小滑块不会落到斜面上，则经过30.4s t =落到水平面上，则水平位移3 1.67m tan30B hx v t ==>︒．所以假设正确，即小滑块从A 点运动到地面所需时间为312 1.5s BSt t v v '=+=+．专题二动量与机械能典型例题[例1] D解析：本题辨析一对平衡力和一对作用力和反作用力的功、冲量．因为，一对平衡力大小相等、方向相反，作用在同一物体上，所以，同一段时间内，它们的冲量大小相等、方向相反，故不是相同的冲量，则①错误．如果在同一段时间内，一对平衡力做功，要么均为零（静止），要么大小相等符号相反（正功与负功），故②正确．至于一对作用力与反作用力，虽然两者大小相等，方向相反，但分别作用在两个不同物体上（对方物体），所以，即使在同样时间内，力的作用点的位移不是一定相等的（子弹穿木块中的一对摩擦力），则做功大小不一定相等．而且作功的正负号也不一定相反（点电荷间相互作用力、磁体间相互作用力的做功，都是同时做正功，或同时做负功．）因此③错误，④正确．综上所述，选项D 正确．【例2】解析：（1）飞机达到最大速度时牵引力F 与其所受阻力f 大小相等，由P =Fv 得mmP P fv f v ==（2）航空母舰上飞机跑道的最小长度为s ，由动能定理得22022m mv mv Pt fs -=-220()22mmv mv Pt s f +-= 将m P f v =代入上式得220()22m m mv mv Pt v s P +-=或220()[]2m m m v v s t v P-=+ 【例3】解析：解法1（程序法）：选物体为研究对象，在t 1时间内其受力情况如图①所示，选F 的方向为正方向，根据牛顿第二定律，物体运动的加速度为22180.2210m/s 2m/s 2F mg a m μ--⨯⨯===．撤去F 时物体的速度为v 1=a 1t 1=2×6m/s=12m/s撤去F 后，物体做匀减速运动，其受力情况如图②所示，根据牛顿第二定律，其运动的加速度为2220.210m/s 2m/s mga g mμμ-==-=-⨯=-．物体开始碰撞时的速度为v 2=v 1＋a 2t 2=[12＋(－2)×2]m/s=8m/s ．再研究物体碰撞的过程，设竖直墙对物体的平均作用力为F ，其方向水平向左．若选水平向左为正方向，根据动量定理有32()Ft mv m v '=--．解得123()2(68)N 280N 0.1m v v F t '+⨯+===．解法2（全程考虑）：取从物体开始运动到碰撞后反向弹回的全过程应用动量定理，并取F 的方向为正方向，则1123()F t mg t t F t mv μ'-+-=-所以1123()86(0.2)210(62)26280N 0.1F t mg t t mv F t μ'-++⨯⨯-⨯⨯⨯++⨯===点评：比较上述两种方法看出，当物体所受各力的作用时间不相同且间断作用时，应用动量定理解题对全程列式较简单，这时定理中的合外力的冲量可理解为整个运动过程中各力冲量的矢量和．此题应用牛顿第二定律和运动学公式较繁琐．另外有些变力作用或曲线运动的题目用牛顿定律难以解决，应用动量定理解决可化难为易．【例4】解析：该题用守恒观点和转化观点分别解答如下：解法一：（守恒观点）选小球为研究对象，设小球沿半径为R 的轨道做匀速圆周运动的线速度为v 0，根据牛顿第二定律有212()v m m g M R+= ①当剪断两物体之间的轻线后，轻线对小球的拉力减小，不足以维持小球在半径为R 的轨道上继续做匀速圆周运动，于是小球沿切线方向逐渐偏离原来的轨道，同时轻线下端的物体m 1逐渐上升，且小球的线速度逐渐减小．假设物体m 1上升高度为h ，小球的线速度减为v 时，小球在半径为（R ＋h ）的轨道上再次做N F μmg FN F①N F μmg N F②匀速圆周运动，根据牛顿第二定律有21v m g M R h=+ ②再选小球M 、物体m 1与地球组所的系统为研究对象，研究两物体间的轻线剪断后物体m 1上升的过程，由于只有重力做功，所以系统的机械能守恒．选小球做匀速圆周运动的水平面为零势面，设小球沿半径为R 的轨道做匀速圆周运动时m 1到水平板的距离为H ，根据机械能守恒定律有2201111()22Mv m gH Mv m g H h -=-- ③以上三式联立解得 v =解法二：（转化观点）与解法一相同，首先列出①②两式，然后再选小球、物体m 1与地球组成的系统为研究对象，研究两物体间的轻线剪断后物体m 1上升的过程，由于系统的机械能守恒，所以小球动能的减少量等于物体m 1重力势能的增加量．即22011122Mv Mv m gh -= ④①、②、④式联立解得 v =点评：比较上述两种解法可以看出，根据机械能守恒定律应用守恒观点列方程时，需要选零势面和找出物体与零势面的高度差，比较麻烦；如果应用转化观点列方程，则无需选零势面，往往显得简捷．【例5】解析：（1）第一颗子弹射入木块过程中动量守恒011mv MV mu MV '-=+ ①解得：1v '=3m/s ② 木块向右作减速运动加速度5Mga g Mμμ===m/s 2 ③木块速度减小为零所用时间11v t a'= ④ 解得t 1 =0.6s<1s ⑤所以木块在被第二颗子弹击中前向右运动离A 点最远时，速度为零，移动距离为2112v s a'=解得s 1=0.9m ． ⑥（2）在第二颗子弹射中木块前，木块再向左作加速运动，时间t 2=1s －0.6s=0.4s ⑦ 速度增大为v 2=at 2=2m/s （恰与传送带同速） ⑧ 向左移动的位移为22210.4m 2s at == ⑨ 所以两颗子弹射中木块的时间间隔内，木块总位移S 0=S 1－S 2=0.5m 方向向右 ⑩ 第16颗子弹击中前，木块向右移动的位移为150.57.5m s =⨯= ○11第16颗子弹击中后，木块将会再向右先移动0.9m ，总位移为0.9m ＋7.5=8.4m>8.3m 木块将从B 端落下．所以木块在传送带上最多能被16颗子弹击中．（3）第一颗子弹击穿木块过程中产生的热量为2222101111112222Q mv MV mu MV '=+-- ○12 木块向右减速运动过程中板对传送带的位移为111S v t s '=+ ○13 产生的热量为Q 2=MgS μ' ○14木块向左加速运动过程中相对传送带的位移为122S V t s ''=- ○15 产生的热量为3Q Mgs μ''= ○16第16颗子弹射入后木块滑行时间为t 3有213310.82v t at '-= ○17 解得t 3=0.4s ○18木块与传送带的相对位移为S =v 1t 3＋0.8 ○19 产生的热量为Q 4=Mgs μ ○20全过程中产生的热量为Q =15(Q 1＋Q 2＋Q 3)＋Q 1＋Q 4 解得Q =14155.5J ○21【例6】解析：运动分析：当小车被挡住时，物体落在小车上沿曲面向下滑动，对小车有斜向下方的压力，由于P 的作用小车处于静止状态，物体离开小车时速度为v 1，最终平抛落地，当去掉挡板，由于物对车的作用，小车将向左加速运动，动能增大，物体相对车滑动的同时，随车一起向左移动，整个过程机械能守恒，物体滑离小车时的动能将比在前一种情况下小，最终平抛落地，小车同时向前运动，所求距离是物体平抛过程中的水平位移与小车位移的和．求出此种情况下，物体离开车时的速度v 2，及此时车的速度2v '以及相应运动的时间是关键，由于在物体与小车相互作用过程中水平方向动量守恒这是解决v 2、2v '间关系的具体方法．（1）挡住小车时，求物体滑落时的速度v 1，物体从最高点下落至滑离小车时机械能守恒，设车尾部（右端）离地面高为h ，则有211()2mg H h mv -=， ① 由平抛运动的规律s 0=v 1t ②212h gt =． ③ （2）设去掉挡板时物体离开小车时速度为v 2，小车速度为2v '，物体从最高点至离开小车之时系统机械能守恒222211()22mg H h mv Mv '-=+ ④ 物体与小车相互作用过程中水平方向动量守恒220Mv mv '-=． ⑤ 此式不仅给出了v 2与2v '大小的关系，同时也说明了v 2是向右的．物体离开车后对地平抛 22s v t '= ⑥212h gt '=⑦ 车在t '时间内向前的位移22s v t '''= ⑧比较式⑦、③，得,t t '=解式①、④、⑤，得2122,mv v v M'==．此种情况下落地点距车右端的距离222221()(1)m s s s v v t v t t s M ''=+=+=+==点评：此题解题过程运用了机械能守恒、动量守恒及平抛运动的知识，另外根据动量守恒判断m 离车时速度的方向及速度间的关系也是特别重要的．【例7】解析：（1）设第一次碰墙壁后，平板车向左移动s ，速度为0．由于体系总动量向右，平板车速度为零时，滑块还在向右滑行．由动能定理20102MgS mv μ-=-① 202mv s Mgμ= ②代入数据得22210.33m 20.43103s ⨯===⨯⨯⨯ ③ （3）假如平板车在第二次碰撞前还未和滑块相对静止，那么其速度的大小肯定还是2m/s ，滑块的速度则大于2m/s ，方向均向右．这样就违反动量守恒．所以平板车在第二次碰撞前肯定已和滑块具有共同速度v ．此即平板车碰墙前瞬间的速度．00()Mv mv M m v -=+ ④∴0M mv v M m-=+ ⑤代入数据得010.4m/s 5v v == ⑥ （3）平板车与墙壁第一次碰撞后到滑块与平板又达到共同速度v 前的过程，可用图（a ）（b ）（c ）表示．（a ）为平板车与墙壁撞后瞬间滑块与平板车的位置，图（b ）为平板车到达最左端时两者的位置，图（c ）为平板车与滑块再次达到共同速度为两者的位置．在此过程中滑块板车动能减少等于动能减少等于摩擦力对滑块所做功Mgs μ'，平到A 再回到B 的过程摩擦力对平板车所做功Mgs μ''（平板车从B 中摩擦力做功为零），其中s '、s ''分别为滑块和平板车的位移．滑块和平板车动能总减少为1,Mgl μ其中1l ss '''=+为滑块相对平板车的位移．此后，平板车与墙壁发生多次碰撞，每次情况与此类似，最后停在墙边．设滑块相对平板车总位移为l ，则有201()2M m v Mgl μ+= ⑦ 20()2M m v l Mgμ+= ⑧代入数据得25250.833m 20.43106l ⨯===⨯⨯⨯ ⑨ l 即为平板车的最短长度．【例8】解析：本题应用动量守恒，机械能守恒及能量守恒定律联合求解。

2018届高考物理三轮冲刺学案：曲线运动、平抛运动、圆周运动“关联”速度问题

三轮冲刺---曲线运动、平抛运动、圆周运动“关联”速度问题考点剖析1．“关联”速度绳、杆等有长度的物体，在运动过程中，如果两端点的速度方向不在绳、杆所在直线上，两端的速度通常是不一样的，但两端点的速度是有联系的，称之为“关联”速度。

由于高中研究的绳都是不可伸长的，杆都是不可伸长和压缩的，即绳或杆的长度不会改变，所以解题的原则是把物体的实际速度分解为垂直于绳（杆）和平行于绳（杆）两个分量，根据沿绳（杆）方向的分速度大小相同求解。

2．分析“关联”速度的基本步骤a．确定研究对象，绳杆、物接触点b．确定合运动方向，即物体实际运动的方向c．分析这个合运动所产生的实际效果，使绳或杆伸缩的效果使绳或杆转动的效果d．确定两个分速度的方向，沿绳或杆方向的分速度垂直于绳或杆方向的分速度3、规律总结: 绳（或杆）端速度分解方法a．确定绳（或杆）端的定点。

绳（或杆）两端物体运动时，绳（或杆）在转动，若绳（或杆）的一端不动，另一端运动，则不动的一端为定点；若绳（或杆）的两端均在运动，则欲分解的速度对应的物体端为动点，另一端为等效定点。

本例中滑轮右侧这段绳的上端为定点，与B相连的下端为动点。

b．速度分解的方向。

确定定点之后，动点（研究对象）的速度可分解为沿绳（或杆）伸长（或缩短）的方向和垂直绳（或杆）使绳（或杆）绕定点转动的方向。

牢牢记住实际速度是合速度。

c．绳（或杆）两端物体均在运动，则沿绳（或杆）的方向（弹力方向）速度相等。

典例精析1、如图所示，物体A和B的质量均为m，且分别用轻绳连接并跨过定滑轮（不计绳子与滑轮、滑轮与轴之间的摩擦）。

在用水平变力F拉物体B沿水平方向向右做匀速直线运动的过程中A．物体A也做匀速直线运动B．绳子的拉力始终大于物体A所受的重力C．物体A的速度小于物体B的速度D．地面对物体B的支持力逐渐增大【答案】BCD【解析】将B的运动沿绳子方向和垂直于绳子方向分解，沿绳子方向上的分速度等于A物体的速度，根据平行四边形定则求出A的速度与B的速度的关系。

2018版高考物理二轮小题提速练8 含解析精品

小题提速练(八)(时间：20分钟分值：48分)选择题(本题共8小题，每小题6分，共48分．在每小题给出的四个选项中，第14～18题只有一项符合题目要求，第19～21题有多项符合题目要求．全部选对的得6分，选对但不全的得3分，有选错的得0分．) 14．(2018·鞍山一中最后一模)如图1所示，质量分别为m A＝3.0 kg，m B＝1.0 kg 的A、B两物体置于粗糙的水平面上，A、B与水平面间的动摩擦因数均为0.25.A、B与水平面间的最大静摩擦力可以认为等于滑动摩擦力．一不可伸长的绳子将A、B连接，轻绳恰好处于伸直状态，且与水平方向的夹角为θ＝53°，现以水平向右的力作用于物体A，若B恰好离开水平面，则此时所施加的水平力F等于()图1A．40 N B．45 NC．50 N D．55 NA[B恰好离开地面时有：mg＝T·sin θ，ma＝T cos θ.可解得a＝7.5 m/s2.对A、B组成的整体，由牛顿第二定律可得：F－μ(m A＋m B)g＝(m A＋m B)a 可解得F＝40 N，故A正确．]15．(2018·天津市红桥区期末)为探究理想变压器原、副线圈电压、电流的关系，将原线圈接到电压有效值不变的正弦交流电源上，副线圈连接相同的灯泡L1、L2，交流电压表V1、V2和电流表A1、A2均为理想电表，导线电阻不计．当开关S闭合后()【导学号：19624237】图2A．A1示数变大，A1与A2示数的比值不变B．A1示数变大，A1与A2示数的比值变大C．V2示数变小，V1与V2示数的比值变大D．V2示数变小，V1与V2示数的比值不变A[由于理想变压器原线圈接到电压有效值不变的正弦交流电源上，则副线圈电压不变，V2示数不变，V1与V2示数的比值不变，C、D错误．开关S闭合后，变压器副线圈的负载电阻减小，V2不变，由欧姆定律可得A1示数变大，由于理想变压器P2＝P1，V1与V2示数的比值不变，所以A1与A2示数的比值不变，B错误．所以只有A正确．故选A.]16．如图3所示为磁流体发电机的原理图．金属板M、N之间的距离为d＝20 cm，磁场的磁感应强度大小为B＝5 T，方向垂直纸面向里．现将一束等离子体(即高温下电离的气体，含有大量带正电和带负电的微粒，整体呈中性)从左侧喷射入磁场，发现在M、N两板间接入的额定功率为P＝100 W的灯泡正常发光，且此时灯泡电阻为R＝100 Ω，不计离子重力和发电机内阻，且认为离子均为一价离子，则下列说法中正确的是()图3A．金属板M上聚集负离子，金属板N上聚集正离子B．该发电机的电动势为100 VC．离子从左侧喷射入磁场的初速度大小为118 m/sD．每秒钟有6.25×1018个离子打在金属板N上B[由左手定则可知，射入的等离子体中正离子将向金属板M偏转，负离子将向金属板N偏转，选项A错误；由于不考虑发电机的内阻，由闭合电路欧姆定律可知，电源的电动势等于电源的路端电压，所以E＝U＝PR＝100 V，选项B正确；由Bq v＝q Ud可得v＝UBd＝100 m/s，选项C错误；每秒钟经过灯泡L的电荷量Q＝It，而I＝PR＝1 A，所以Q＝1 C，由于离子为一价离子，所以每秒钟打在金属板N上的离子个数为n＝12×Qe＝12× 1 C 1.6×10－19 C＝3.125×1018个，选项D 错误．] 17．(2018·衡阳市二模)质量m ＝2 kg 的物块放在粗糙水平面上，在水平拉力的作用下由静止开始运动，物块动能E k 与其位移x 之间的关系如图4所示．已知物块与水平面间的动摩擦因数μ＝0.2，重力加速度g 取10 m/s 2，则下列说法正确的是( )图4A ．x ＝1 m 时物块的速度大小为2 m/sB ．x ＝3 m 时物块的加速度大小为2.5 m/s 2C ．在前4 m 位移过程中拉力对物块做的功为9 JD ．在前2 m 位移过程中物块所经历的时间为2 sD [由图象可知x ＝1 m 时E k ＝2 J ，由E k ＝12m v 2可得此时物块速度v ＝ 2m/s ，A 错误；x 1＝2 m 时物块动能为4 J ，对应速度v 2＝2 m/s ，x 2＝4 m 时物块动能为9 J ，对应速度v 4＝3 m/s ，由v 24－v 22＝2a (x 2－x 1)可得2～4 m 范围内物块的加速度a ＝1.25 m/s 2，故B 错误；由W F －μmgx ＝E k －0可求得前4 m 位移过程中拉力做功为W F ＝25 J ，C 错误；由x 1＝v 22t 1可得在前2 m位移过程中物块经历的时间t 1＝2 s ，D 正确．]18．(2018·沧州一中月考)如图5所示，竖直平面内有一段圆弧MN ，小球从圆心O 处水平抛出；若初速度为v a ，将落在圆弧上的a 点；若初速度为v b ，将落在圆弧上的b 点；已知Oa 、Ob 与竖直方向的夹角分别为α、β，不计空气阻力，则( )图5A.v a v b ＝sin αsin BB.v a v b ＝cos βcos αC.v a v b ＝cos βcos αsin αsin β D.v a v b＝sin αsin β cos βcos α D [对a ，根据R cos α＝12gt 21得，t 1＝2R cos αg ，则v a ＝R sin αt 1＝R sin αg 2R cos α，对b ，根据R cos β＝12gt 22得，t 2＝2R cos βg ，则v b ＝R sin βt 2＝R sin βg 2R cos β，解得v a v b ＝sin αsin β cos βcos α.答案为D.]19．(2018·衡水中学二模)如图6所示，两等量异种电荷在同一水平线上，它们连线的中点为O ，竖直面内的半圆弧光滑绝缘轨道的直径AB 水平，圆心在O 点，圆弧的半径为R ，C 为圆弧上的一点，OC 与竖直方向的夹角为37°，一电荷量为＋q ，质量为m 的带电小球从轨道的A 端由静止释放，沿轨道滚动到最低点时，速度v ＝2gR ，g 为重力加速度，取无穷远处电势为零，则下列说法正确的是( )【导学号：19624238】图6A ．电场中A 点的电势为mgR qB ．电场中B 点的电势为－2mgR qC ．小球运动到B 点时的动能为2mgRD ．小球运动到C 点时，其动能与电势能的和为1.6mgRAC [取无穷远处电势为零，则最低点处电势为0，小球从A 点运动到最低点过程中，由动能定理可得mgR ＋qU AO ＝12m v 2，解得U AO ＝mgR q ，而U AO＝φA －0，所以φA ＝mgR q ，A 正确；由对称性可知U AO ＝U OB ，即φA －0＝0－φB ，故φB ＝－mgR q ，B 错误；小球从A 点运动到B 点过程中，由动能定理得E k ＝qU AB ＝2mgR ，C 正确；小球在最低点处的动能和电势能的总和为E 1＝12m v 2＋0＝2mgR ，由最低点运动到C 点过程中，动能、电势能、重力势能的总量守恒，而重力势能增加量ΔE p ＝mgR (1－cos 37°)＝0.2mgR ，故动能、电势能的总和减少了0.2mgR ，所以小球在C 点的动能和电势能的总和为E 2＝E 1－0.2mgR ＝1.8mgR ，D 错误．]20．(2018·郑州三模)2018年4月10日，三名宇航员在国际空间站停留173天后，乘坐“联盟MS-02”飞船从国际空间站成功返回，并在哈萨克斯坦杰兹卡兹甘附近着陆．设国际空间站在离地面高度约400 km 的轨道上绕地球做匀速圆周运动，已知地球同步卫星轨道高度约36 000 km ，地球半径约6 400 km.下列说法正确的是( )A ．飞船在返回地球的过程中机械能守恒B ．经估算，国际空间站的运行周期约为90 minC ．国际空间站的速度小于地球的第一宇宙速度D ．返回时，需先让飞船与国际空间站脱离，然后点火加速，即可下降 BC [飞船在返回地球的过程中需要控制速度，机械能不守恒，A 错误；根据万有引力提供向心力，GMm r 2＝m 4π2T 2r ，T ＝4π2r 3GM 可知，T 1T 2＝r 31r 32，国际空间站的轨道半径约为6 800 km ，地球同步卫星的轨道半径为42 400 km ；地球同步卫星的周期为24 h ，可得国际空间站的运行周期约为90 min ，B 正确；地球的第一宇宙速度是所有地球卫星的最大环绕速度，所以国际空间站的速度小于地球的第一宇宙速度，C 正确；返回时，需先让飞船与国际空间站脱离，然后减速，即可下降，D 错误．]21．(2018·沈阳铁路实验中学模拟)如图7所示，电阻不计间距为L 的光滑平行金属导轨水平放置，导轨左端接有阻值为R 的电阻，以导轨的左端为原点，沿导轨方向建立x 轴，导轨处于竖直向下的磁感应强度大小为B 的匀强磁场中．一根电阻也为R ，质量为m 的金属杆垂直于导轨放置于x 0处，不计金属杆与轨道间的接触电阻，现给金属杆沿x 轴正方向的初速度v 0，金属杆刚好能运动到2x 0处，在金属杆运动过程中( )【导学号：19624239】图7A ．通过电阻R 的电荷量BLx 02RB ．金属杆克服安培力所做的功为12m v 20C ．金属杆上产生的焦耳热为12m v 20D ．金属杆运动到1.5x 0处的速度大小为v 02ABD [由q ＝It ＝ΔΦ2R ＝BLx 02R 可知，选项A 正确；整个过程中回路产生的焦耳热为12m v 20，所以金属杆上产生的焦耳热为12×12m v 20＝14m v 20，C 错误；金属杆在运动过程中克服安培力所做的功等于金属杆动能的减少量12m v 20，B正确；设金属杆速度由v 0减为v 02经过的时间为t 1，通过的位移为x 1，速度由v 02减为0经历的时间为t 2，通过的位移为x 2，由动量定理可得：－B I 1Lt 1＝12m v 0－m v 0，－B I 2Lt 2＝0－12m v 0，又I 1＝BL v 12R I 2＝BL v 22R ，x 1＝v1t 1 x 2＝v 2t 2可得出：B 2L 2x 12R ＝12m v 0 B 2L 2x 22R ＝12m v 0，故x 1＝x 2，又x 1＋x 2＝x 0，所以x 1＝x 2＝x 02，故金属杆运动到1.5x 0处的速度大小为v 02，D 正确．]。

2018届高考二轮复习人教版专题10唯物论和认识论教案(教材必背一站清)(全国)

专题十唯物论和认识论(探索世界与追求真理)■核心知识·巧整合·[核心考点一物质和意识]1．如何理解世界的真正统一性在于它的物质性？(1)自然界的物质性：自然界中的事物都是统一的物质世界的组成部分，按照自身所固有的规律形成和发展，不以人的意志为转移。

(2)人类社会的物质性：从产生过程看，人类社会是物质世界长期发展的产物；从存在的基础看，构成社会物质生活条件的地理环境、人口因素和生产方式等基本要素都是客观的物质的要素，这集中体现了人类社会的客观性。

(3)人的意识一开始就是社会的产物，它是在劳动中伴随着人和人类社会一起产生的。

2．如何理解意识的本质？(1)起源角度：意识是物质世界长期发展的产物。

意识是自然界长期发展的产物，而且是社会发展的产物。

(2)生理基础角度：意识是人脑的机能；人脑是意识活动的物质器官；人脑结构的复杂性和组织的严密性，决定了它具有产生意识的生理基础。

(3)内容角度：意识是客观存在的主观映象，是对客观存在的反映；是客观存在通过生活和实践的环节进入人脑、并在人脑中加工改造的结果。

总体结论：上述内容表明，物质是本原的，意识是派生的，物质决定意识。

3．如何理解人类意识活动的特点？(1)意识活动具有目的性，人们在反映客观世界的时候，总是抱有一定的目地，在行动之前还要确定目标、行动方式和行动步骤等。

(2)意识活动具有主动创造性，不仅能反映事物的外部现象，而且能够把握事物的本质和规律；不仅能够“复制”当前的对象，而且能够追溯过去和推测未来。

(3)意识活动具有自觉选择性，意识反映物质是主动的、有选择的，不同人可以进行不同的反映。

4．如何理解意识的反作用？(1)原理①意识对改造客观世界具有指导作用，人类在意识指导下能动地改造世界，即通过实践把意识中的东西变成现实的东西；正确的意识促进客观事物的发展；错误的意识阻碍客观事物的发展。

②意识对于人体生理活动具有调节和控制作用。

高昂的精神可以催人向上，使人奋进；萎靡的精神则会使人悲观、消沉，丧失斗志。

2018年高考数学(文)二轮复习练习：小题提速练6 Word版含答案

小题提速练(六) “12选择＋4填空”80分练 (时间：45分钟分值：80分)一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．(2016·江西上饶中学月考)若集合A ＝{x |x 2－7x ＜0，x ∈N *}，则B ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫y ⎪⎪⎪4y∈N *，y ∈A中元素的个数为( )A ．3B ．2C ．1D ．0[答案] A2．若等差数列{a n }的前n 项和为S n ，且a 3＋a 8＝13，S 7＝35，则a 8等于( )【导学号：04024192】A ．8B ．9C ．10D ．11 [答案] B3．将某选手的9个得分去掉1个最高分，去掉1个最低分，7个剩余分数的平均分为91.现场作的9个分数的茎叶图后来有1个数据模糊，无法辨认，在图1中以x 表示：则7个剩余分数的方差为( ) A.1169B.367 C ．36 D.677[答案] B4．“m ＝1”是“直线x －y ＝0和直线x ＋my ＝0互相垂直”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件[答案] C5．(2016·全国卷Ⅰ)如图2，某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径．若该几何体的体积是28π3，则它的表面积是( )图2A ．17πB ．18πC ．20πD ．28π[答案] A6．已知sin 2α＝13，则cos 2⎝⎛⎭⎪⎫α－π4等于( ) 【导学号：04024193】A ．－13B ．－23C.13D.23 [答案] D7．(2015·全国卷Ⅱ)下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入的a ，b 分别为14,18，则输出的a 等于( )图3A ．0B ．2C ．4D ．14[答案] B8．若将一个质点随机投入如图4所示的长方形ABCD 中，其中AB ＝2，BC ＝1，则质点落在以AB 为直径的半圆内的概率是( )图4A.π2B.π4C.π6D.π8[答案] B9．已知A (2,5)，B (4,1)，若点P (x ，y )在线段AB 上，则2x －y 的最大值为( )A ．－1B ．3C ．7D ．8[答案] C10．已知函数f (x )＝x 2＋2x ＋1－2x，则y ＝f (x )的图象大致为( )【导学号：04024194】[答案] A11．已知函数f (x )＝A tan(ωx ＋φ)⎝ ⎛⎭⎪⎫ω＞0，|φ|＜π2，y ＝f (x )的部分图象如图5所示，则f ⎝ ⎛⎭⎪⎫π24等于( )图5A ．2＋ 3B. 3C.33D ．2－ 3[答案] B12．(2016·全国卷Ⅲ)已知O 为坐标原点，F 是椭圆C ：x 2a 2＋y 2b2＝1(a ＞b ＞0)的左焦点，A ，B 分别为C 的左、右顶点．P 为C 上一点，且PF ⊥x 轴．过点A 的直线l 与线段PF 交于点M ，与y 轴交于点E .若直线BM 经过OE 的中点，则C 的离心率为( )A.13B.12C.23D.34[答案] A二、填空题(本大题共4小题，每小题5分，共20分．把答案填在题中横线上) 13．圆x 2＋y 2＋x －2y －20＝0与圆x 2＋y 2＝25相交所得的公共弦长为________．[解析] 公共弦的方程为(x 2＋y 2＋x －2y －20)－(x 2＋y 2－25)＝0，即x －2y ＋5＝0，圆x 2＋y 2＝25的圆心到公共弦的距离d ＝|0－2×0＋5|5＝5，而半径为5，故公共弦长为252－52＝4 5.[答案] 4 514．已知函数f (x )＝e x－2x ＋a 有零点，则a 的取值范围是________.【导学号：04024195】[解析] f ′(x )＝e x －2，可得f ′(x )＝0的根为x 0＝ln 2.当x ＜ln 2时，f ′(x )＜0，可得函数在区间(－∞，ln 2)上为减函数，当x ＞ln 2时，f ′(x )＞0，可得函数在区间(ln 2，＋∞)上为增函数，∴函数y ＝f (x )在x ＝ln 2处取得极小值f (ln 2)＝2－2ln 2＋a ，并且这个极小值也是函数的最小值．由题设知函数y ＝f (x )的最小值要小于或等于零，即2－2ln 2＋a ≤0，可得a ≤2ln 2－2，故答案为(－∞，2ln 2－2]． [答案] (－∞，2ln 2－2)15．已知△PAD 所在平面与矩形ABCD 所在平面互相垂直，PA ＝PD ＝AB ＝2，∠APD ＝90°，若点P 、A 、B 、C 、D 都在同一球面上，则此球的表面积等于________．[解析] 如图在Rt △PAD 中，AD ＝4＋4＝22，过△PAD 的外心M 作垂直于平面PAD 的直线l ，过四边形ABCD 的外心O 作垂直于平面ABCD 的直线m ，两线交于点O ，则点O 为四棱锥P ABCD 的外接球球心，2R ＝AC ＝4＋8＝23(R 为四棱锥P ABCD 外接球的半径)，即R ＝3，∴四棱锥P ABCD 外接球的表面积S ＝4πR 2＝12π. [答案] 12π16．已知△ABC 中的内角为A ，B ，C ，重心为G ，若2sin A ·GA →＋3sin B ·GB →＋3sin C ·GC →＝0，则cos B ＝________.[解析] 设a ，b ，c 分别为角A ，B ，C 所对的边，由正弦定理得2aGA →＋3bGB →＋3cGC →＝0，则2aGA →＋3bGB →＝－3cGC → ＝－3c (－GA →－GB →)，即(2a －3c )GA →＋(3b －3c )GB →＝0，又因为GA →，GB →不共线，则2a －3c ＝0，3b －3c ＝0，即2a ＝3b ＝3c ，所以a ＝3b 2，c ＝3b 3， ∴cos B ＝a 2＋c 2－b 22ac ＝112.[答案] 112。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

4.关联速度问题
两个运动的物体通过定滑轮、绳子、轻杆连接，两物体的运动有一定关联，这类问题称为关联速度问题。

关联速度问题是运动合成与分解的较高程度的应用。

一、基础知识
1．问题特点：沿绳(或杆)方向的速度分量大小相等．
2．思路与原则
(1)思路
①明确合速度→物体的实际运动速度v；
(2)原则：v1与v2的合成遵循平行四边形定则．
3．解题方法
把物体的实际速度分解为垂直于绳(杆)和平行于绳(杆)两个分量，根据沿绳(杆)方向的分速度大小相等求解．常见的模型如图所示．
二、典型例题
例题1．在距河面高度h＝20 m的岸上有人用长绳拴住一条小船，开始时绳与水面的夹角为30°.人以恒定的速率v＝3 m/s拉绳，使小船靠岸，那么( ) A．5 s时绳与水面的夹角为60°
B．5 s后小船前进了15 m
C．5 s时小船的速率为4 m/s
D．5 s时小船到岸边的距离为15 m
解析：选D.设开始时小船距岸边为L，则L＝
h
tan 30°
＝20 3 m，5 s后
绳端沿岸位移为x＝vt＝3×5 m＝15 m，设5 s后小船前进了x′，绳与水平面
的夹角为θ，由几何关系得sin θ＝
h
2h－x
＝
20
2×20－15
＝0.8，解得θ＝53°，
选项A错误；由tan θ＝
h
L－x′
，解得x′＝19.64 m，选项B错误；由v船cos
θ＝v可得此时小船的速率为v
船
＝5 m/s，选项C错误；5 s时小船到岸边的距离为L－x′＝20 3 m－19.64 m＝15 m，选项D正确．
例题2. 如图所示，物体A、B经无摩擦的定滑轮用细线连在一起，A物体受水平向右的力F的作用，此时B匀速下降，A水平向左运动，可知( ) A．物体A做匀速运动
B．物体A做加速运动
C．物体A所受摩擦力逐渐增大
D．物体A所受摩擦力不变
解析：选B.设系在A上的细线与水平方向夹角为θ，物体B的速度为v B，
大小不变，细线的拉力为F T，则物体A的速度v A＝
v
B
cos θ
，F f A＝μ(mg－F T sin θ)，
因物体下降，θ增大，故v A增大，物体A做加速运动，A错误，B正确；物体B 匀速下降，F T不变，故随θ增大，F f A减小，C、D均错误．
例题3．如图所示，长为L的直棒一端可绕固定轴O转动，另一端搁在升降平台上，平台以速度v匀速上升，当棒与竖直方向的夹角为α时，棒的角速度为( )
A.v sin α
L
B．
v
L sin α
C.v cos α
L
D.
v
L cos α
解析：选B.棒与平台接触点的实际运动即合运动的速度方向是垂直于棒指向左上方，合速度沿竖直向上方向上的速度分量等于v，即ωL sin α＝v，所以
ω＝
v
L sin α
.
例题4．如图所示，套在竖直细杆上的环A由跨过定滑轮的不可伸长的轻绳与重物B相连．由于B的质量较大，故在释放B后，A将沿杆上升，当A环上升至与定滑轮的连线水平时，其上升速度v1≠0，若这时B的速度为v2，则( )
A．v2＝0 B．v2＞v1
C．v2≠0 D．v2＝v1
解析：选A.环A在虚线位置时，环A的速度沿虚线方向的分速度为零，故物体B的速度v2＝0，A正确．
例题5. 如图所示，A、B两物体系在跨过光滑定滑轮的一根轻绳的两端，当A物体以速度v向左运动时，系A、B的绳分别与水平方向成α、β角，此时B 物体的速度大小为( )
A．v sin α/sin βB．v cos α/sin β
C．v sin α/cos βD．v cos α/cos β
解析：选D.根据A、B两物体的运动情况，将两物体此时的速度v和v B分别分解为两个分速度v1(沿绳的分量)和v2(垂直绳的分量)以及v B1(沿绳的分量)和
v
B2
(垂直绳的分量)，由于两物体沿绳的速度分量相等，v1＝v B1，即v cos α＝v B cos
β，则B物体的速度方向水平向右，其大小为v
B ＝
cos α
cos β
v，D正确．
三、方法总结
关联速度问题，关键找到物体实际运动速度是合速度，分解的就是合速度，一般向两个方向分解，一个沿着绳子或杆的方向，另一个是垂直于绳子或杆的方向，沿着绳子或杆方向的分速度相等。