《同轴谐振腔》课件
合集下载
同轴线谐振腔资料
(4-73) 二端面上的损耗 (4-74)
侧壁上的损耗 当ι=λr/2时，
1 Q0 1 1 a b 8 b r ln a
2
在谐振频率一定时，Q0与同轴线谐振腔的横截面尺寸a、b有关.
用求极值的方法可以得到，当b/a≈3.6时，Q0有极大值。
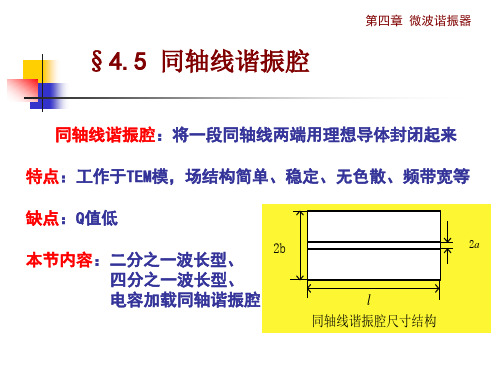
第四章 微波谐振器
§4.5 同轴线谐振腔
b l ln 2 a Q0 l 1 1 2 ln b a b a
(4-77)
当ι=λr/4时，
b ln 2 a Q0 1 1 8 ln b a b r a
故
l 2 p 1
2 ( p 1,2,3)
l 2 p 1
r
4
( p 1,2,3)
(4-75)
可见，当ι等于λr/4或它的奇数倍时，腔产生谐振. 故称：四分之一波长型同轴线谐振腔，多谐性.
第四章 微波谐振器
§4.5 同轴线谐振腔
2.固有品质因数 (1)可用公式计算，参考二分之一波长型同轴线谐振腔的计 算方法; (2)直接利用二分之一波长型同轴线谐振腔的结论 由于缺少一块短路板，则短路板上的损耗是二分之一波 长型同轴线谐振腔的一半，于是，Q0可写为
(4-78)
第四章 微波谐振器
§4.5 同轴线谐振腔
4.5.3 电容加载同轴线谐振腔
内导体端面与短路板间平板电容为 a 2
C t
2a
A
2b l
t
考虑边缘电容后的修正式
4a 2 36.8t b a 12 C 6.94 1 lg 10 t 4a t F
谐振腔构造
A
第五章 谐振腔
0
2al
a2 l2
它为最低谐振模。
四、圆柱谐振腔 圆柱谐振腔是由一段长度为l，两端短路的圆波导构成，其圆柱腔 半径为R。圆柱腔中场分布分析方法和谐振波长的计算与矩形腔相同。
特性：1.Q值高 2.场沿角向无变化，无极化简并模式 用途：
(二) 模式图
对于圆柱腔TEmnp谐振模，有
(二) /4型同轴谐振腔
谐振时应满足：
4l 0 2n 1
~ ~ B1 B2
l 2n 1
谐振波长0与腔体长度l的关系为
或
0
4
由于这类同轴腔内导体长度为 0/4的奇数倍，故称为四分之一 波长型同轴谐振腔。
/4型同轴谐振腔
(三) 电容加载型同轴谐振腔
电容加载型同轴谐振腔 如右图所示。
矩形谐振腔谐振波长计算公式
0
1 1 p 2l c
2 2
式中c为波导中相应模式的截止波长。此式也适用于圆柱谐振腔。 对于矩形腔有
0
2 m n p a b l
2 2 2
TE101模的谐振波长为
2 两端开路的/2微带谐振器可等效为下图所示的电路。
l 2 l n
开路微带边缘电容的存在，而使微带谐振器的实际长度l 缩短。用微带线中计算边缘电容的方法可求得 l 的近似 计算公式为 0.3 W h 0.246 l 0.412h e e 0.258 W h 0.8 类似地，/4微带谐振器的谐振条件为 l l 2n 1 n 1,2,3
(一) 谐振模式及其场分布
矩形波导中传输的电磁波模式有TE模和TM模，相应谐振腔中同样 有TE谐振模和TM谐振模，分别以TEmnp和TMmnp表示，其中下标m、n 和p分别表示场分量沿波导宽壁、窄壁和腔长度方向上分布的驻 波数。在众多谐振模中，TE101为最低谐振模。
光学谐振腔基本概念43页PPT
1、不要轻言放弃，否则对不起自己。
2、要冒一次险!整个生命就是一场冒险。走得最远的人，常是愿意 去做，并愿意去冒险的人。“稳妥”之船，从未能从岸边走远。-戴尔．卡耐基。
梦 境
3、人生就像一杯没有加糖的咖啡，喝起来是苦涩的，回味起来却有 久久不会退去的余香。
光学谐振腔基本概念4、守业的最好办法就是不断的发展。 5、当爱不能完美，我宁愿选择无悔，不管来生多么美丽，我不愿失 去今生对你的记忆，我不求天长地久的美景，我加强。 ——德 谟克利 特 67、今天应做的事没有做，明天再早也 是耽误 了。——裴斯 泰洛齐 68、决定一个人的一生，以及整个命运 的，只 是一瞬 之间。 ——歌 德 69、懒人无法享受休息之乐。——拉布 克 70、浪费时间是一桩大罪过。——卢梭
2、要冒一次险!整个生命就是一场冒险。走得最远的人，常是愿意 去做，并愿意去冒险的人。“稳妥”之船，从未能从岸边走远。-戴尔．卡耐基。
梦 境
3、人生就像一杯没有加糖的咖啡，喝起来是苦涩的，回味起来却有 久久不会退去的余香。
光学谐振腔基本概念4、守业的最好办法就是不断的发展。 5、当爱不能完美，我宁愿选择无悔，不管来生多么美丽，我不愿失 去今生对你的记忆，我不求天长地久的美景，我加强。 ——德 谟克利 特 67、今天应做的事没有做，明天再早也 是耽误 了。——裴斯 泰洛齐 68、决定一个人的一生，以及整个命运 的，只 是一瞬 之间。 ——歌 德 69、懒人无法享受休息之乐。——拉布 克 70、浪费时间是一桩大罪过。——卢梭
同轴谐振腔微波技术基础课件PPT
B
多谐性
p 0,1,2,...
调谐:
▪ 电容调谐（改变d）
▪ 电感调谐（改变l）
/4
O l2
又称缩短电容同轴线谐振腔
ቤተ መጻሕፍቲ ባይዱ
2frC2 2frC1 l
§5－4 同轴谐振腔
由同轴线构成，主模：TEM模 优点：
▪ 场结构简单、稳定、 ▪ 无色散、无频率下限，工作频率范围宽
缺点：Q0低
基本振荡模式有三种
❖ /2型同轴线谐振腔 ❖ /4型同轴线谐振腔 ❖ 电容加载同轴线谐振腔
§5－4 同轴谐振腔
一、 /2型同轴线谐振腔
l=pr /2
腔长 l p r p 1,2,3,...
2
多谐性 调谐
波长计结构简图
§5－4 同轴谐振腔
二、 /4型同轴线谐振腔
l=(2p-1)r/4
腔长 l (2 p 1) r p 1,2,3,...
4
多谐性
调谐
波长计结构简图
§5－4 同轴谐振腔
三、 电容加载同轴线谐振腔
l
d
内导体长 l＝r arctan 1 p r
2
2frCZc 2
腔长：l d
电动力学课件 4.4 谐振腔
k B 0
B
k E
2．有界空间中的电磁波
金属一般为良导体，电磁波几乎全部被反射。因此，若空间中 的良导体构成电磁波存在的边界，金属边界制约管内电磁波的存 在形式。在这种情况下， Helmholtz方程的解不再是平面波解而 受到导体界面边界条件的束缚。
3
二．理想导体边界条件
实际导体虽然不是理想导体，但是象银或铜等金属导体，对无线 电波来说，透入其内而损耗的电磁能量一般很小，接近于理想导体。 在一定频率的电磁波情形，两不同介质（包括导体）界面上的 边值关系可以归结为
E z A 3 s in k x x s in k y y c o11 sk z z
表明 A1、 A2、 A3中只有两个是独立的
3．谐振波型
（ 1）电场强度
E x , t E x e i t
E x E y E z m L1
m n A1 cos x sin y sin L1 L2 m n A2 sin x cos y sin L1 L2 m n A3 sin x sin y cos L1 L2 n p A1 A2 A3 0 L2 L3
0
C3 0
C
z
O
因此
E x A1 co s k x x sin k y y sin k z z
A1 C 1 D 2 D 3
L3
B
Ex
D
（ 2）考虑 x L 1 E x 有 x L1 0 x
sin k x L 1 0
L2
A
k x A1 sin k x x sin k y y sin k z z
光学谐振腔
1
谐振腔是在微波频率下工作的谐振元件，它是一个任意形状的 由导电壁包围的，并能在其中形成电磁振荡的介质区域，它具 有储存电磁能及选择一定频率信号的特性. 根据不同用途，微波谐振腔的种类是多种多样的：矩形腔、圆 柱形腔、球形腔。
2.1光学谐振腔结构与稳定性ppt课件
➢平行平面腔，对应图中的A点。只有与腔轴平行的光线才能在腔内往返g1=1，g2=1 ➢共心腔， 满足条件R1＋R2＝L，对应图中第一象限的g1g2＝1的双曲线。 ➢半共心腔，由一个平面镜和一个凹面镜组成，对应图中C点和D点。 g1=1，g2=0
(3) 非稳腔 :g1 g2＞1 或 g1 g2＜0 ➢对应图中阴影部分的光学谐振腔都是非稳腔。
f ——透镜焦距
2.光腔的稳定条件:
(1)条件:使傍轴模(即近轴光线)在腔内往返无限多次不逸 出腔外的条件, 即近轴光线几何光学损耗为零, 其 数学表达式为
0g1g21
(2)据稳定条件的数学形式,
稳定腔:
0g1g21
非稳腔: 临界腔:
g1g或2 1
g1g2 0
g1g或2 g11 g2=0
2.1.2 共轴球面谐振腔的稳定图及其分类
稳定腔 (光腔中存在着伴轴模,它可在腔内多次传播而不逸出腔外) 光腔 临界腔 (几何光学损耗介乎上二者之间)
非稳腔 (伴轴模在腔内经有限数往返必定由侧面逸出腔外,有很高的几
何光学损耗)
2.1.1共轴球面谐振腔的稳定性条件
一.光腔稳定条件:
球面
1.描述光腔稳定性的g参量,定义:
R1
g1
1
L R1
g2
L
4.共心腔—— 两个球面反射镜的曲率中心重合的共轴球
面腔
实共心腔——双凹腔 g1＜ 0 ，g2＜ 0
虚共心腔——凹凸腔 g1＞ 0 ，g2＞ 0
都有 R1+R2= L g1 g2 =1
（临界腔）
R1
R2
o
o
虚
光线即有简并的，也有非简并的
0g1g21
二.稳定图: 稳定条件的图示 0g1g21
(3) 非稳腔 :g1 g2＞1 或 g1 g2＜0 ➢对应图中阴影部分的光学谐振腔都是非稳腔。
f ——透镜焦距
2.光腔的稳定条件:
(1)条件:使傍轴模(即近轴光线)在腔内往返无限多次不逸 出腔外的条件, 即近轴光线几何光学损耗为零, 其 数学表达式为
0g1g21
(2)据稳定条件的数学形式,
稳定腔:
0g1g21
非稳腔: 临界腔:
g1g或2 1
g1g2 0
g1g或2 g11 g2=0
2.1.2 共轴球面谐振腔的稳定图及其分类
稳定腔 (光腔中存在着伴轴模,它可在腔内多次传播而不逸出腔外) 光腔 临界腔 (几何光学损耗介乎上二者之间)
非稳腔 (伴轴模在腔内经有限数往返必定由侧面逸出腔外,有很高的几
何光学损耗)
2.1.1共轴球面谐振腔的稳定性条件
一.光腔稳定条件:
球面
1.描述光腔稳定性的g参量,定义:
R1
g1
1
L R1
g2
L
4.共心腔—— 两个球面反射镜的曲率中心重合的共轴球
面腔
实共心腔——双凹腔 g1＜ 0 ，g2＜ 0
虚共心腔——凹凸腔 g1＞ 0 ，g2＞ 0
都有 R1+R2= L g1 g2 =1
（临界腔）
R1
R2
o
o
虚
光线即有简并的，也有非简并的
0g1g21
二.稳定图: 稳定条件的图示 0g1g21
同轴微波谐振腔
同轴微波谐振腔同轴微波谐振腔是一种重要的微波元器件，广泛应用于通信、雷达、卫星通信等领域。
它具有频率选择性好、工作稳定性高、功率传输损耗小等优点，在微波技术中起着重要的作用。
同轴微波谐振腔由内外两个金属圆筒组成，内圆筒为中心导体，外圆筒为外导体。
两圆筒之间通过绝缘材料隔离开来，形成同轴结构。
谐振腔内部的介质通常为空气或真空，以降低传输损耗。
同轴微波谐振腔的谐振频率与其尺寸有关，通常由谐振腔的长度、内外导体的半径等因素决定。
当谐振腔的尺寸满足一定的条件时，可以使特定频率的微波信号在腔内得到放大或传输。
同轴微波谐振腔有多种谐振模式，其中最常见的是基模TE_01模式。
在TE_01模式下，电磁场集中在同轴腔的中心区域，电场和磁场方向都与谐振腔的轴线垂直。
这种谐振模式具有较高的品质因子，能够实现较高的频率选择性。
谐振频率是同轴微波谐振腔设计中的重要参数，频率的选择需要考虑到具体应用的需求以及其他系统的限制。
根据谐振频率的要求，可以通过调整谐振腔的尺寸和结构参数来实现。
在实际应用中，为了提高谐振腔的性能，通常会采取一些优化措施。
例如，在腔体内部添加吸波材料，以减少反射损耗；优化腔体的结构，减少电磁波在谐振腔内的损耗；合理设计腔体的输入输出端口，以提高功率传输效率等。
同轴微波谐振腔在通信系统中的应用十分广泛。
例如，在微波通信系统中，可以将微波信号输入到同轴谐振腔中进行放大，然后再输出到天线进行传输。
谐振腔可以起到滤波和放大的作用，提高系统的传输效率和抗干扰能力。
除了通信系统，同轴微波谐振腔还被广泛应用于雷达系统中。
在雷达系统中，同轴谐振腔可以用于信号的发射和接收。
通过调整谐振腔的谐振频率，可以实现对特定频率的信号的选择性放大和传输，从而提高雷达系统的性能。
同轴微波谐振腔是一种重要的微波元器件，具有频率选择性好、工作稳定性高、功率传输损耗小等优点。
它在通信、雷达等领域中发挥着重要的作用。
通过合理设计和优化，可以实现对特定频率的微波信号的放大和传输，提高系统的性能和稳定性。
4-1.2同轴线谐振腔解析
而
ˆ H Js n
2
s
s
s
(4-15)
J s H
第四章 微波谐振器
§4.2 谐振腔的主要特性参数
2 1 故 P Rs H dS 2 s 所以固有品质因数可写为
Q0 2
V
H H
2
dV
S
2
(4-16)
dS
这里δ为趋肤深度:
1 f
腔本身的损耗功率
外界负载上损耗的功率
第四章 微波谐振器
§4.2 谐振腔的主要特性参数
有载品质因数还可以写成
1 Pi Pc Pi Pc 1 1 QL rW rW rW Q0 Qc
(4-21)
固有品质因数
耦合品质因数
Qc
若腔体和外界负载之间的耦合程度定义一个量 k Q0 (4-22)
1.场解法 分析规则波导时，用场解法. 求解波动方程,中间过程 得到关于K的特征方程.
求谐振腔的谐振频率方法类似
边界 条件 ˆE 0 n ˆH 0 n
2 H K 2 H 0
特征值Kc (无穷多个)
截止波长 截止频率 不同之处：特 征值Kr，不仅 与横向参量有 关，也与纵向 参量有关。
e e,max
反之，当磁场最大时，电场为零，且此时总储能为 2 * H H dV H dV (4-13) W Wm Wm ,max 2Βιβλιοθήκη 2v
2
v
v
2
v
谐振腔的耗能包括导体和介质损耗，假定介质是无耗的， 2 则腔内损耗功率为 1 (4-14) P R J dS
第4章微波谐振腔-PPT文档资料
为P谐R 振腔自身损耗功率
代表谐振腔本身质量的优劣，值大表明腔本身功耗小， 自身质量优良。
第四章 微波谐振腔
2. 外部品质因数Q e ：
Qe 0
Wm We PL
式中 P L 为与谐振腔相连接的外部负载消耗的功率
代表谐振腔向外部负载提供能量的效率高低。
3. 有载品质因数QL ：
2l
4. 固有品质因数（TEM模
下）
Q 021b1aln b8a0lnba
当(b/a)=3.6时，
同轴腔的品质因
数Q0达最大。
第四章 微波谐振腔
(二) /4型同轴谐振腔
1. 结构
/4型同轴谐振腔由一端短路，另一端开路的一段长度为 l的同轴线构成，长度l 比/2的整数倍多/4 。
第四章 微波谐振腔
二.主要技术指标
1. 谐振频率 f0 或谐振波长0 ：
指谐振腔中该模式的场量发生谐振时的频率，它是描 述谐振器中电磁能量振荡规律的参量。 2. 谐振模式 3. 品质因数
4-2 微波谐振腔的品质因数
一.品质因数定义
品质因数Q是微波谐振器的一个主要参量，它描述了谐振 器选择性的优劣和能量损耗的大小，其定义为
第四章 微波谐振腔
为了使谐振腔正常工作，就必须合理选择工作方框，使工 作方框内不出现或少出现不需要的干扰模式。工作方框是以
工作模式的调谐直线为对角线，由最大和最小的(f0D)2和相 对应(D/l)2所确定的区域。设计谐振腔时，对所选的工作模式
都可确定其相应的工作方框，方框的中心位置由固有品质因 数来确定。方框的高度由工作频带来确定，在工作方框中任 何非对角线模式，都是不需要的干扰模式。这些干扰模会影 响谐振腔正常工作。因此，选择工作方框时，应尽量避免干 扰模进入工作方框。
代表谐振腔本身质量的优劣，值大表明腔本身功耗小， 自身质量优良。
第四章 微波谐振腔
2. 外部品质因数Q e ：
Qe 0
Wm We PL
式中 P L 为与谐振腔相连接的外部负载消耗的功率
代表谐振腔向外部负载提供能量的效率高低。
3. 有载品质因数QL ：
2l
4. 固有品质因数（TEM模
下）
Q 021b1aln b8a0lnba
当(b/a)=3.6时，
同轴腔的品质因
数Q0达最大。
第四章 微波谐振腔
(二) /4型同轴谐振腔
1. 结构
/4型同轴谐振腔由一端短路，另一端开路的一段长度为 l的同轴线构成，长度l 比/2的整数倍多/4 。
第四章 微波谐振腔
二.主要技术指标
1. 谐振频率 f0 或谐振波长0 ：
指谐振腔中该模式的场量发生谐振时的频率，它是描 述谐振器中电磁能量振荡规律的参量。 2. 谐振模式 3. 品质因数
4-2 微波谐振腔的品质因数
一.品质因数定义
品质因数Q是微波谐振器的一个主要参量，它描述了谐振 器选择性的优劣和能量损耗的大小，其定义为
第四章 微波谐振腔
为了使谐振腔正常工作，就必须合理选择工作方框，使工 作方框内不出现或少出现不需要的干扰模式。工作方框是以
工作模式的调谐直线为对角线，由最大和最小的(f0D)2和相 对应(D/l)2所确定的区域。设计谐振腔时，对所选的工作模式
都可确定其相应的工作方框，方框的中心位置由固有品质因 数来确定。方框的高度由工作频带来确定，在工作方框中任 何非对角线模式，都是不需要的干扰模式。这些干扰模会影 响谐振腔正常工作。因此，选择工作方框时，应尽量避免干 扰模进入工作方框。
光学谐振腔ppt课件PPT课件
第9页/共11页
增益系数
用M1、M2表示两块反射镜，其间距为L，透射率 和折射率分别为T1、R2和T2、R2。假设所有损耗 都包含在折射率T1、T2中。 当z=0时，光强为 I0(v)，经过整个长度为的工作物 质到达第二块反射镜M2时，光强为 I(v,l) I0(v)e(v)l 其中 (v) 称为工作物质的增益系数
光线重合。这样，平行于轴
C
向的光线将始终不会逸出腔
外 第6页/共11页
M
B M
D
典型的开放式光学谐振腔
广义共焦腔
A M'
C F'
B M
C' F
D
E
A-B-D-B-A-E-A
此外，还有平凹腔、平凸腔、凹凸腔等
A
B
C
F
图一
G
F'
E
D
A-B-C-D-E-G-A
半共焦腔，半共焦腔的性质与共焦腔的类似，衍射损耗低，易于装置，而且由于 采用了一块平面镜，成本更低。大多数氦氖激光器都采用这种谐振腔
第7页/共11页
g1
R1
R2
L 2
共焦腔
R1R2L 2来自共心腔(R1 R2 ) 平行平面腔
g2
稳定谐振腔的条件
0
1
L R1
1
L R2
1
图中（0<g1g2<1）区域是 满足稳定性条件的区域
第8页/共11页
光腔损耗 • 有了稳定的光学谐振腔，有了能实现粒子束反转的工作物质，还不一定能
一起受激辐射的光振荡而产生激光。因为工作物质在光学谐振腔内虽然能 够引起光放大，但是在光学谐振腔内还存在许多损耗因素 • 反射镜的吸收、透射和衍射工作物质不均与造成的折射或散射 • 这些损耗中，只有通过部分反射镜而透射出的才是我们需要的，其他一切 损耗都应尽量避免 • 如果由于损耗，使得工作物质的放大作用抵偿不了损耗，就不可能在谐振 腔内形成雪崩式的光放大过程，就不能得到激光输出。因此要产生激光振 荡，对于光放大必须满足一定的条件---阈值条件
增益系数
用M1、M2表示两块反射镜，其间距为L，透射率 和折射率分别为T1、R2和T2、R2。假设所有损耗 都包含在折射率T1、T2中。 当z=0时，光强为 I0(v)，经过整个长度为的工作物 质到达第二块反射镜M2时，光强为 I(v,l) I0(v)e(v)l 其中 (v) 称为工作物质的增益系数
光线重合。这样，平行于轴
C
向的光线将始终不会逸出腔
外 第6页/共11页
M
B M
D
典型的开放式光学谐振腔
广义共焦腔
A M'
C F'
B M
C' F
D
E
A-B-D-B-A-E-A
此外，还有平凹腔、平凸腔、凹凸腔等
A
B
C
F
图一
G
F'
E
D
A-B-C-D-E-G-A
半共焦腔，半共焦腔的性质与共焦腔的类似，衍射损耗低，易于装置，而且由于 采用了一块平面镜，成本更低。大多数氦氖激光器都采用这种谐振腔
第7页/共11页
g1
R1
R2
L 2
共焦腔
R1R2L 2来自共心腔(R1 R2 ) 平行平面腔
g2
稳定谐振腔的条件
0
1
L R1
1
L R2
1
图中（0<g1g2<1）区域是 满足稳定性条件的区域
第8页/共11页
光腔损耗 • 有了稳定的光学谐振腔，有了能实现粒子束反转的工作物质，还不一定能
一起受激辐射的光振荡而产生激光。因为工作物质在光学谐振腔内虽然能 够引起光放大，但是在光学谐振腔内还存在许多损耗因素 • 反射镜的吸收、透射和衍射工作物质不均与造成的折射或散射 • 这些损耗中，只有通过部分反射镜而透射出的才是我们需要的，其他一切 损耗都应尽量避免 • 如果由于损耗，使得工作物质的放大作用抵偿不了损耗，就不可能在谐振 腔内形成雪崩式的光放大过程，就不能得到激光输出。因此要产生激光振 荡，对于光放大必须满足一定的条件---阈值条件
同轴谐振腔2
) 。
因此， /4 同轴线谐振腔的谐振波长为 4l 0 = 2p 1
/4 同轴线谐振腔的品质因数为 0 1 Q0 = 4 l 1 (D d)
D ln( D d )
/4 同轴线谐振腔与 /2
同轴线谐振腔的差别仅在于它 图 5.5-2 /4 同轴线谐振腔 少一个端面的导体损耗。
图 5.5-3
电容加载同轴腔
图 5.5-4
电容加载同轴腔的等效电路
1 cot( l ) 0C = 0 Z0 等效电路中集中参数的电容 C 由两部分组成：一部分 是由内导体端面与端壁构成的平板电容，另一部分是由内 导体侧面与端壁构成的边缘电容。 图 5.5-5 给出了内导体端面与端壁之间电容的示意图。 作为定性分析，假设图 5.5-5 中 边缘电场线为 1/4 圆弧。
/2 和 /4 同轴线谐振腔的横向尺寸的选择应由下列条
件确定： (1)为保证同轴线谐振腔工作于 TEM 模而不出现高次 模要求
(d D)/2 < 0min 即 (a b) < 0min (2)为保证同轴线谐振腔有较高的 Q0 值，应取
2 (D/d) 6
即
2 (b/a) 6
一段两端短路的同轴线构成 的，如图 5.5-1 所示。 图中 D = 2b 为同轴腔的外导体的 内直径，d = 2a 为同轴腔的 内导体直径。
图 5.5-1
/2 同轴线谐振腔
为了满足腔的两端面为纯驻波电压波节点的边界条件，
在谐振时其腔长应等于 0 /2 的整数倍，即 l = p 0/2(p = 1， 因此， /2 同轴线谐振腔的谐振波长为 2，3，)。 2l 0 = p 1) 当腔长 l 一定时，相应于 不同的 p 值存在许多个谐 振波长 0， 这种特性称为 多谐性；
高二物理竞赛光学谐振腔的作用PPT(课件)
kc §6 激光的特性和应用
由2nL k ，c 可知 纵模： 引起的受激辐射的方向也是随机的。
2）造成激光谱线增宽的因素
c 2nL 维持稳定了。
定义：由发射波列的持续时间决定的谱线宽度
纵模间隔： 故多普勒展宽的线型与麦克斯韦分布
§6 激光的特性和应用
（4）阈值条件和阈值增益
2nL 为纵模序数，通常略去不写。
由时间相干反比公式可知： 1
因此，自然线宽： 1kHz（数量级） ，
甚至更小。
（2）碰撞展宽
定义：粒子间碰撞引起的辐射谱线加宽
粒子间的碰撞可加速跃迁， 从而缩短了能级的寿命 粒子碰撞的频率越大， 碰撞展宽也越大。
He Ne激光器的碰撞展宽：
100 ~ 200MHz
（3）多普勒展宽 定义：由多普勒频移效应引起的谱线展宽
粒子间的碰撞可加速跃迁， 的量值约 数量级，
谐振腔内光的 2）激光器谐振腔的选频作用
故多普勒展宽的线型与麦克斯韦分布 粒子间的碰撞可加速跃迁，
I1 I4
I2
增益与损耗
I5
I3
M1
M2
I2 I1eGL , I3 R2 I 2 R2 I1eGL
I4
I5
I 3eGL
R1I 4
RR12RI21eI12eGL2GL
的量值约 106数量级，
满足阈值条件。
好的可高达10 ~ 10 的数量级。 1）定义：谐振腔内与轴向垂直的
（2）实际增益随光强 的增大下降
10
13
而目前大功率激光器输出亮度可达
2）高定向性 测40万公里的地月距离误差不超过数米。
不断增强。
定向连锁放大作用
光束沿空间极小的立体角范围（一般为 （3）一部分激光穿透部分反射镜输出，
由2nL k ，c 可知 纵模： 引起的受激辐射的方向也是随机的。
2）造成激光谱线增宽的因素
c 2nL 维持稳定了。
定义：由发射波列的持续时间决定的谱线宽度
纵模间隔： 故多普勒展宽的线型与麦克斯韦分布
§6 激光的特性和应用
（4）阈值条件和阈值增益
2nL 为纵模序数，通常略去不写。
由时间相干反比公式可知： 1
因此，自然线宽： 1kHz（数量级） ，
甚至更小。
（2）碰撞展宽
定义：粒子间碰撞引起的辐射谱线加宽
粒子间的碰撞可加速跃迁， 从而缩短了能级的寿命 粒子碰撞的频率越大， 碰撞展宽也越大。
He Ne激光器的碰撞展宽：
100 ~ 200MHz
（3）多普勒展宽 定义：由多普勒频移效应引起的谱线展宽
粒子间的碰撞可加速跃迁， 的量值约 数量级，
谐振腔内光的 2）激光器谐振腔的选频作用
故多普勒展宽的线型与麦克斯韦分布 粒子间的碰撞可加速跃迁，
I1 I4
I2
增益与损耗
I5
I3
M1
M2
I2 I1eGL , I3 R2 I 2 R2 I1eGL
I4
I5
I 3eGL
R1I 4
RR12RI21eI12eGL2GL
的量值约 106数量级，
满足阈值条件。
好的可高达10 ~ 10 的数量级。 1）定义：谐振腔内与轴向垂直的
（2）实际增益随光强 的增大下降
10
13
而目前大功率激光器输出亮度可达
2）高定向性 测40万公里的地月距离误差不超过数米。
不断增强。
定向连锁放大作用
光束沿空间极小的立体角范围（一般为 （3）一部分激光穿透部分反射镜输出，