1_高考专题空间角和距离的计算
专题6 向量法求空间角与距离(课件)高考数学二轮复习(新高考地区专用)

=|cos 〈u,n〉|=
·
=
·
.
例1 [2023·河北沧州模拟]如图,在三棱锥P - ABC中,AB是△ABC外
接圆的直径,△PAC是边长为2的等边三角形,E,F分别是PC,PB的
中点,PB=AB,BC=4.
(1)求证:平面PAC⊥平面ABC;
(2)求直线AB与平面AEF所成角的正弦值.
A.直线BC1与DA1所成的角为90°
B.直线BC1与CA1所成的角为90°
C.直线BC1与平面BB1D1D所成的角为45°
D.直线BC1与平面ABCD所成的角为45°
答案:ABD
)
2.[2022·新高考Ⅰ卷 ]如 图,直三棱柱ABC - A1B1C1 的体积为4 ,
△A1BC的面积为2 2.
(1)求A到平面A1BC的距离;
=2.
(1)证明:BD⊥EA.
(2)求平面EDCF与平面EAB夹角的余弦值.
题型三 (空间距离)点到平面的距离
已知平面α的法向量为n,A是平面α内的定点,P是平面α外一点.过
点P作平面α的垂线l,交平面α于点Q,则n是直线l的方向向量,且点P
到平面α的距离就是AP到直线l上的投影向量QP的长度.因此PQ=
(1)证明:A1C⊥AB1;
(2)若三棱锥B1 -
2 2
A1AC的体积为 ,求二面角A1
3
- B1C - A的大小.
题后师说
用法向量求二面角的关键是正确写出点的坐标和法向量,再利用两
个平面的夹角公式求解.
巩固训练2
[2023·河南安阳模拟]在多面体EF - ABCD中,平面EDCF⊥平面
ABCD,EDCF是面积为 3的矩形,CD∥AB,AD=DC=CB=1,AB
空间向量的应用求空间角与距离

空间向量的应用----求空间角与距离一、考点梳理1.自新教材实施以来,近几年高考的立体几何大题,在考察常规解题方法的同时,更多地关注向量法〔基向量法、坐标法〕在解题中的应用。
坐标法〔法向量的应用〕,以其问题〔数量关系:空间角、空间距离〕处理的简单化,而成为高考热点问题。
可以预测到,今后的高考中,还会继续表达法向量的应用价值。
2.利用法向量求空间角和空间距离,其常用技巧与方法总结如下:1)求直线和直线所成的角假设直线AB 、CD 所成的角是α,cos α=|,cos |><CD AB ||||||CD AB CD AB •=2).利用法向量求线面角设θ为直线l 与平面α所成的角,ϕ为直线l 的方向向量v 与平面α的法向量n 之间的夹角,那么有2πϕθ=-或2πϕθ=+。
特别地0ϕ=时, 2πθ=,l α⊥;2πϕ=时,0θ=,l α⊂或l α。
计算公式为:||sin cos ||||v n v n θϕ==或||sin sin()cos (0)2||||||||v n v n v n v n v n πθϕϕ=-=-=-=<3).利用法向量求二面角设1n 、2n 分别为平面α、β的法向量,二面角l αβ--的大小为θ,向量1n 、2n 的夹角为ϕ,那么有θϕπ+=或θϕ=。
计算公式为:1212cos cos ||||n n n n θϕ=-=1212cos cos ||||n n n n θϕ==4).利用法向量求点面距离如图点P 为平面外一点,点A 为平面内的任一点,平面的法向量为n ,过点P 作平面α的垂线PO ,记∠OPA=θ,那么点P 到平面的距离θcos ||||PA PO d ==||||||||||||n PA PA n PA n PA n •=⊗•=5).法向量在距离方面除应用于点到平面的距离外,还能处理异面直线间的距离,线面间的距离,以及平行平面间的距离等。
其一,这三类距离都可以转化为点面间的距离;其二,异面直线间的距离可用如下方法操作:在异面直线上各取一点A 、B ,AB 在n 上的射影长即为所求。
高三数学空间角与空间距离的计算通用版知识精讲

高三数学空间角与空间距离的计算通用版【本讲主要内容】空间角与空间距离的计算 空间直线与直线、直线与平面、平面与平面所成角的大小,直线与直线、直线与平面、平面与平面间的距离的求解【知识掌握】 【知识点精析】空间的角和距离是空间图形中最基本的数量关系,空间的角主要研究射影以及与射影有关的定理、空间两直线所成的角、直线和平面所成的角、以及二面角和二面角的平面角等.解这类问题的基本思路是把空间问题转化为平面问题去解决. 1. 空间的角的概念及计算方法(1)空间角概念——空间的角,是对由点、直线、平面所组成的空间图形中各种元素间的位置关系进行定量分析的一个重要概念,由它们的定义,可得其取值X 围,如①两异面直线所成的角θ∈(0,2π) ②直线与平面所成的角θ∈[0,2π] ③二面角的大小,可用它们的平面角来度量,其平面角θ∈(0,π).说明:对于空间角的计算,总是通过一定的手段将其转化为一个平面内的角,并把它置于一个平面图形,而且是一个三角形的内角来解决,而这种转化就是利用直线与平面的平行与垂直来实现的,因此求这些角的过程也是直线、平面的平行与垂直的重要应用.通过空间角的计算和应用进一步提高运算能力、逻辑推理能力及空间想象能力.(2)空间的角的计算方法①求异面直线所成的角常用平移法(转化为相交直线);②求直线与平面所成的角常利用射影转化为相交直线所成的角; ③求二面角α-l -β的平面角(记作θ)通常有以下几种方法: (ⅰ)根据定义; (ⅱ)过棱l 上任一点O 作棱l 的垂面γ,设γ∩α=OA ,γ∩β=OB ,则∠AOB =θ(图1);(ⅲ)利用三垂线定理或逆定理,过一个半平面α内一点A ,分别作另一个平面β的垂线AB (垂足为B ),或棱l 的垂线AC (垂足为C ),连结AC ,则∠ACB =θ或∠ACB =π-θ(图2);(ⅳ)设A 为平面α外任一点,AB ⊥α,垂足为B ,AC ⊥β,垂足为C ,则∠BAC =θ或∠BAC =π-θ(图3);(ⅴ)利用面积射影定理,设平面α内的平面图形F 的面积为S ,F 在平面β内的射影图形的面积为S ‘,则cos θ=SS '.2. 空间的距离问题 (1)空间各种距离是对点、线、面组成的空间图形位置关系进行定量分析的重要概念.空间距离是指两点间距离、点线距离、点面距离、线线距离、线面距离以及面面距离等,距离都要转化为两点间距离即线段长来计算,在实际题型中,这六种距离的重点和难点是求点到平面的距离,因线线距离、线面距离和面面距离除用定义能直接计算出结果的外,都要转化为求点到平面的距离进行计算.(2)空间的距离问题主要是:求空间两点之间、点到直线、点到平面、两条异面直线之间(限于给出公垂线段的)、平面和它的平行直线、以及两个平行平面之间的距离.(3)求距离的一般方法和步骤是: 一作——作出表示距离的线段;二证——证明它就是所要求的距离;三算——计算其值. 此外,我们还常用体积法或向量法求点到平面的距离.【解题方法指导】例1. 三棱锥P-ABC 中,∠ABC =90,PA =1,AB =3,AC =2,PA ⊥平面ABC.(1)求直线AB 与直线PC 所成的角; (2)求PC 和面ABC 所成的角; (3)求二面角A-PC-B 的大小.PA BC解:(1)作矩形ABCD.∴AB 和PC 所成角即为CD 和PC 所成角,且CD ⊥PD .CD =3,AD =1,PD =2,tanPCD =3632=.故AB 和PC 所成角为arctan 36(2)∵PA ⊥面ABC ,PC 和面ABC 所成角即为∠ACP ,求得tanACP =21, ∴∠ACP =arctan21 (3)∵PA ⊥面ABC ,∴面PAC ⊥面ABC ,过B 作BG ⊥AC 于G ,则BG ⊥面PAC.过G 作GH ⊥PC 于H ,连接BH ,则BH ⊥PC . ∴∠BHG 为二面角A-PC-B 的平面角. 在Rt △ABC 与Rt △PBC 中,PB =2,BC =1,AC =2,AB =3∴PC =5∴BH =52,BG =23. ∴sinBHG =4155223==BH BG ∴∠BHG =arcsin 45.故二面角A-PC-B 的大小为arcsin 45.例2. 在正三棱柱111C B A ABC -中,各棱长都等于a ,D 、E 分别是1AC 、1BB 的中点, (1)求证:DE 是异面直线1AC 与1BB 的公垂线段,并求其长度;(2)求二面角C AC E --1的大小; (3)求点1C 到平面AEC 的距离.解:(1)取AC 中点F ,连接DF .∵ D 是1AC 的中点,F∴DF ∥1CC ,且121CC DF =.又11//CC BB ,E 是1BB 的中点, ∴DF ∥BE ,DF =BE ,∴四边形BEDF 是平行四边形, ∴DE ∥BF ,DE =BF .∵1BB ⊥面ABC ,⊂BF 面ABC ,∴1BB ⊥BF .又∵F 是AC 的中点,△ABC 是正三角形,∴BF ⊥AC ,a BF 23=. ∵1BB ⊥BF ,1BB ∥1CC ,∴BF ⊥1CC ,∴BF ⊥面11A ACC , 又∵⊂1AC 面11A ACC ,∴BF ⊥1AC , ∵DE ∥BF ,∴DE ⊥1AC ,DE ⊥1BB ,∴DE 是异面直线1AC 与1BB 的公垂线段,且a DE 23=. (2)∵11//CC BB ,DE ⊥1BB , ∴DE ⊥1CC , 又∵为DE ⊥1AC ,∴DE ⊥面11A ACC . 又⊂DE 面1AEC ,∴面1AEC ⊥面1ACC , ∴二面角C AC E --1的大小为90°.(3)连接CE ,则三棱锥1CEC A -的底面面积为221a S CEC =∆,高a h 23=.所以32123232311a a a V CEC A ==⋅⋅-.在三棱锥AEC C -1中,底面△AEC 中,a CE AE 25==,则其高为a ,所以22a S AEC =∆.设点1C 到平面AEC 的距离为d ,由AEC C CEC A V V --=11得32123231a a d =⋅, 所以a d 23=,即点1C 到平面AEC 的距离为a 23【考点突破】【考点指要】空间角是立体几何中的一个重要概念.它是空间图形中的一个突出的量化指标,是空间图形位置关系的具体体现,故它以高频率的姿态出现在历届高考试题中,可以在填空题或选择题中出现,更多的在解答题中出现.空间中各种距离都是高考中的重点内容,可以和多种知识相结合,是诸多知识的交汇点,考查题型多以选择题、填空题为主,有时渗透于解答题中,所以复习时应引起重视.【典型例题分析】例1. (2003全国卷文)如图,已知正四棱柱2,1,11111==-AA AB D C B A ABCD ,点E 为1CC 中点,点F 为1BD 中点.(1)证明EF 为BD 1与CC 1的公垂线;(2)求点1D 到平面BDE 的距离.解法1:(1)连结AC 交BD 于点O ,则点O 为BD 中点,连OF ,则可证OCEF 为矩形, 故EF ⊥CC 1 ,EF ∥AC .又可证AC ⊥平面BD 1 ∴AC ⊥BD 1,∴EF ⊥BD 1, 故 EF 为BD 1与CC 1的公垂线.O(2)连结D 1E ,则有三棱锥D1-DBE 的高d 即为点1D 到平面BDE 的距离. 由已知可证三角形DBE 为边长为2的正三角形,故2331311⋅⋅=⋅⋅=∆-d S d V DBE DBE D ; 又31311111=⋅===∆---DBD DBD C DBD E DBE D S CO V V V∴3123=d ∴332=d , 即1D 到平面BDE 的距离为332解法2:解(1)以D 为原点,建立如图所示的直角坐标系,则 )0,0,0(D ,)2,0,0(1D)0,1,1(B ,)0,1,0(C ,)2,1,0(1C ,)1,1,0(E ,)1,21,21(F ,∴)0,21,21(-=EF ,)2,1,1(1--=BD ,)2,0,0(1=CC∴01=⋅BD EF ,01=⋅CC EF ;∴1BD EF ⊥,1BD EF ⊥ 又EF 与CC 1、BD 1分别交于E 、F ,故EF 为BD 1与CC 1的公垂线. (2)由(1))0,1,1(--=BD ,)1,0,1(-=BE ,)2,1,1(1--BD , 设 平面BDE 的法向量为 ),,(z y x n =,则BD n ⊥,BE n ⊥,∴⎪⎩⎪⎨⎧=⋅=⋅00BE n BD n , ∴⎩⎨⎧=+-=--00z x y x , 即 ⎩⎨⎧=-=z x y x ,∴ 不妨设 )1,1,1(-=n ,则点1D 到平面BDE 的距离为33232||1===n n BD d , 即为所求.例2. (2006全国卷Ⅲ文20)如图,12l l ,是互相垂直的异面直线,MN 是它们的公垂线段.点A B ,在1l 上,C 在2l 上,AM MB MN ==.(Ⅰ)证明AC NB ⊥;(Ⅱ)若60ACB ∠=,求NB 与平面ABC 所成角的余弦值.C1l2解法一:(Ⅰ)由已知221l MN l l ⊥⊥,,1MNl M =,可得2l ⊥平面ABN .由已知1MN l AM MB MN ⊥==,,可知AN NB =且AN NB ⊥. 又AN 为AC 在平面ABN 内的射影, AC NB ∴⊥.(Ⅱ)Rt Rt CNA CNB △≌△,AC BC ∴=,又已知60ACB ∠=︒,因此ABC △为正三角形. Rt Rt ANB CNB △≌△,NC NA NB ∴==,因此N 在平面ABC 内的射影H 是正三角形ABC 的中心, 连结BH ,NBH ∠为NB 与平面ABC 所成的角.在Rt NHB △中,cos 3ABHB NBH NB ∠===.N1l l解法二:如图,建立空间直角坐标系M xyz -.1l令1MN =,则有(100)(100)(010)A B N -,,,,,,,,.(Ⅰ)MN 是12l l ,的公垂线,21l l ⊥, 2l ∴⊥平面ABN .2l ∴平行于z 轴.故可设(01)C m ,,.于是(11)(110)AC m NB ==-,,,,,, ∵0011=+-=⋅NB AC AC NB ∴⊥. (Ⅱ)(11)AC m =,,,(11)BC m =-,,,AC BC ∴=.又已知60ACB ∠=︒,ABC ∴△为正三角形,2AC BC AB ===. 在Rt CNB △中,NB =NC =(0C . 连结MC ,作NH MC ⊥于H ,设(0)(0)H λλ>,.(012)(01HN MC λλ∴=--=,,,,,.∵021=--=⋅λλMC HN ,∴31=λ1033H ⎛⎫∴ ⎪ ⎪⎝⎭,,,可得2033HN ⎛⎫=- ⎪ ⎪⎝⎭,,, 连结BH ,则1133BH ⎛⎫=- ⎪ ⎪⎝⎭,,,∵092920=-+=⋅BH HN ,HN BH ∴⊥,又MC BH H =, HN ∴⊥平面ABC ,NBH ∠为NB 与平面ABC 所成的角.又(110)BN =-,,, ∴3623234cos =⨯=⋅=∠BN BH BN BH NBH【综合测试】一、选择题1、已知AB 是异面直线a 、b 的公垂线段,AB =2,a 与b 成30°,在直线a 上取AP =4,则点P 到直线b 的距离是( )A 、22B 、25C 、142D 、5 2、将锐角为60°,边长为a 的菱形ABCD 沿较短的对角线BD 折成60°的二面角,则AC 与BD 的距离为( )A 、a 43B 、a 43C 、a 23 D 、64a 3、正方体ABCD-A 1B 1C 1D 1中,M 是DD 1的中点,O 为正方形A 1B 1C 1D 1的中心,P 是棱AB 上的垂足,则直线A 1M 与OP 所成的角( ).A 、30oB 、45oC 、60oD 、90o 4、二面角α-AB-β大小为θ(0°≤θ≤90°),AC ⊂α,∠CAB =45o ,AC 与平面β所成角为30o ,则θ角等于( ).A 、30oB 、45oC 、60oD 、90o 5、(2005某某卷文4)如图,正方体ABCD -A 1B 1C 1D 1的棱长为1,E 是A 1B 1的中点,则E 到平面AB C 1D 1的距离为( )A 、23 B 、22C 、21 D 、336、已知直线a 及平面α,a 与α间的距离为d .a 在平面α内的射影为a ',l 为平面α内与a '相交的任一直线,则a 与l 间的距离的取值X 围为( )A 、[),d +∞B 、(),d +∞C 、(]0,dD 、{}d二、填空题 7、(2005某某卷理12)如图,PA ⊥平面ABC ,∠ACB =90°且PA =AC =BC =a ,则异面直线PB 与AC 所成角的正切值等于____________.8、已知∠60o ,则以OC三、解答题:9. C 点到AB 1ABC DA 1E B 1C10.(2006理17)如图,在底面为平行四边形的四棱锥P ABCD -中,AB AC ⊥,PA ⊥平面ABCD ,且PA AB =,点E 是PD 的中点.(Ⅰ)求证:AC PB ⊥;(Ⅱ)求证:PB ∥平面AEC ; (Ⅲ)求二面角E AC B --的大小.B[参考答案]一、选择题1. 选A 提示:过P 做直线b 的垂线2. 选A 提示:用异面直线距离公式求解3. 选D 提示:过A 1做OP 的平行线4. 选B 提示:过C 做平面β的垂线5. 选B. 提示:转化为求B 1到平面AB C 1D 1的距离6. 选D 提示:转化为a 与α间的距离 二、填空题7.2. 提示:将三角形ABC 补成正方形ACBD. 8. 33- 提示:利用直线与直线所成角的大小求出边长,再求二面角平面角的大小三、解答题:9. 解:由CD ⊥平面A 1B 1BA ∴CD ⊥DE ∵AB 1⊥平面CDE ∴DE ⊥AB 1,∴DE 是异面直线AB 1与CD 的公垂线段∵CE =23,AC =1 ,∴CD =.22∴21)()(22=-=CD CE DEABC DA 1E B 1C 110. 解法一:(Ⅰ)(Ⅱ)(略 解见第45讲【达标测试】第9题)(Ⅲ)过O 作FG AB ∥,交AD 于F ,交BC 于G ,则F 为AD 的中点.CDAB AC ⊥,OG AC ∴⊥. 又由(Ⅰ),(Ⅱ)知,AC PB EO PB ,⊥∥,AC EO ∴⊥. EOG ∴∠是二面角E AC B --的平面角.连接EF ,在EFO △中,1122EF PA FO AB ==,,word11 / 11 又PA AB EF FO =,⊥,45135EOF EOG ∴∠=∠=,,∴二面角E AC B --的大小为135.解法二:(Ⅰ)建立空间直角坐标系A xyz -,如图.y 设AC a PA b ==,,则有(000)(00)(00)(00)A B b C a P b ,,,,,,,,,,,,(00)(0)AC a PB b b ∴==-,,,,,,从而0=⋅PB AC ,AC PB ∴⊥.(Ⅱ)连接BD ,与AC 相交于O ,连接EO .由已知得(0)D a b -,,,002222ab b a E O ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭,,,,,, 022b b EO ⎛⎫∴=- ⎪⎝⎭,,,又(0)PB b b =-,,, 2PB EO ∴=,PB EO ∴∥,又PB ⊄平面AEC EO ,⊂平面AEC , PB ∴∥平面AEC .(Ⅲ)取BC 中点G .连接OG ,则点G 的坐标为000222a b b OG ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭,,,,,, 又0(00)22b b OE AC a ⎛⎫=-= ⎪⎝⎭,,,,,,00=⋅=⋅∴AC OG AC OE ,.OE AC OG AC ∴,⊥⊥.EOG ∴∠是二面角E AC B --的平面角.22cos -=⋅<OGOE OG OE .135EOG ∴∠=. ∴二面角E AC B --的大小为135.。
专题8.3 立体几何综合问题(原卷版)文科生

【考点1】空间角,距离的求法 【备考知识梳理】 1.空间的角(1)异面直线所成的角:如图,已知两条异面直线,a b ,经过空间任一点O 作直线','a a b b .则把'a 与'b 所成的锐角(或直角)叫做异面直线与所成的角(或夹角).异面直线所成的角的范围是0,2π⎛⎤⎥⎝⎦. (2)平面的一条斜线和它在平面内的射影所成的锐角,叫做这条直线和这个平面所成的角.①直线垂直于平面,则它们所成的角是直角;②直线和平面平行,或在平面内,则它们所成的角是0︒的角.直线与平面所成角的范围是0,2π⎡⎤⎢⎥⎣⎦.(3)二面角的平面角:如图在二面角l αβ--的棱上任取一点O ,以点O 为垂足,在半平面α和β内分别作垂直于棱的射线OA 和OB ,则AOB ∠叫做二面角的平面角.二面角的范围是[]0,π.(4)等角定理:如果一个角的两边和另一个角的两边分别平行,并且方向相同,那么这两个角相等. 推论:如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等. 3.空间距离:(1)两条异面直线的距离:两条异面直线的公垂线在这两条异面直线间的线段的长度,叫做两条异面直线的距离;常有求法①先证线段AB 为异面直线b a ,的公垂线段,然后求出AB 的长即可.②找或作出过且与平行的平面,则直线到平面的距离就是异面直线b a ,间的距离.③找或作出分别过b a ,且与,分别平行的平面,则这两平面间的距离就是异面直线b a ,间的距离.(2)点到平面的距离:点P到直线的距离为点P到直线的垂线段的长,常先找或作直线所在平面的垂线,得垂足为A,过A作的垂线,垂足为B连PB,则由三垂线定理可得线段PB即为点P到直线的距离.在直角三角形PAB中求出PB的长即可.常用求法①作出点P到平面的垂线后求出垂线段的长;②转移法,如果平面α的斜线上两点A,B到斜足C的距离AB,AC的比为n m :,则点A,B到平面α的距离之比也为n m :.特别地,AB=AC时,点A,B到平面α的距离相等;③体积法(3)直线与平面的距离:一条直线和一个平面平行,这条直线上任意一点到平面的距离,叫做这条直线和平面的距离;(4)平行平面间的距离:两个平行平面的公垂线段的长度,叫做两个平行平面的距离. 【规律方法技巧】1.空间中各种角包括:异面直线所成的角、直线与平面所成的角以及二面角. (1)异面直线所成的角的范围是]2,0(π.求两条异面直线所成的角的大小一般方法是通过平行移动直线,把异面问题转化为共面问题来解决具体步骤如下:①利用定义构造角,可固定一条,平移另一条,或两条同时平移到某个特殊的位置,顶点选择在特殊的位置上;②证明作出的角即为所求的角;③利用三角形来求角; ④补形法:将空间图形补成熟悉的、完整的几何体,这样有利于找到两条异面直线所成的角θ. (2)直线与平面所成的角的范围是]2,0[π.求线面角方法:①利用面面垂直性质定理,巧定垂足:由面面垂直的性质定理,可以得到线面垂直,这就为线面角中的垂足的确定提供了捷径. ②利用三棱锥的等体积,省去垂足,在构成线面角的直角三角形中,其中垂线段尤为关键.确定垂足,是常规方法.可是如果垂足位置不好确定,此时可以利用求点面距常用方法---等体积法.从而不用确定垂足的位置,照样可以求出线面角.因为垂线段的长度实际就是点面距h,利用三棱锥的等体积,只需求出h ,然后利用斜线段长h =θsin 进行求解.③妙用公式,直接得到线面角 课本习题出现过这个公式:21cos cos cos θθθ=,如图所示:21,,θθθ=∠=∠=∠OBC ABO ABC .其中1θ为直线AB 与平面所成的线面角.这个公式在求解一些选择填空题时,可直接应用.但是一定要注意三个角的位置,不能张冠李戴.(3)确定点的射影位置有以下几种方法:①斜线上任意一点在平面上的射影必在斜线在平面的射影上;②如果一个角所在的平面外一点到角的两边距离相等,那么这一点在平面上的射影在这个角的平分线上;如果一条直线与一个角的两边的夹角相等,那么这一条直线在平面上的射影在这个角的平分线上;③两个平面相互垂直,一个平面上的点在另一个平面上的射影一定落在这两个平面的交线上;④利用某些特殊三棱锥的有关性质,确定顶点在底面上的射影的位置:a.如果侧棱相等或侧棱与底面所成的角相等,那么顶点落在底面上的射影是底面三角形的外心;b. 如果顶点到底面各边距离相等或侧面与底面所成的角相等,那么顶点落在底面上的射影是底面三角形的内心(或旁心);c. 如果侧棱两两垂直或各组对棱互相垂直,那么顶点落在底面上的射影是底面三角形的垂心;(4)二面角的范围[]0,π,解题时要注意图形的位置和题目的要求.求二面角的方法:①直接法.直接法求二面角大小的步骤是:一作(找)、二证、三计算.即先作(找)出表示二面角大小的平面角,并证明这个角就是所求二面角的平面角,然后再计算这个角的大小. 用直接法求二面角的大小,其关键是确定表示二面角大小的平面角.而确定其平面角,可从以下几个方面着手:①利用三垂线定理(或三垂线定理的逆定理)确定平面角,自二面角的一个面上一点向另一面引垂线,再由垂足向棱作垂线得到棱上的点(即垂足),斜足与面上一点连线和斜足与垂足连线所夹的角,即为二面角的平面角;;②利用与二面角的棱垂直的平面确定平面角, 自空间一点作与棱垂直的平面,截二面角得两条射线,这两条射线所成的角就是二面角的平面角;③利用定义确定平面角, 在棱上任取一点,过这点在两个平面内分别引棱的垂线,这两条射线所成的角,就是二面角的平面角;DBA Cα②射影面积法.利用射影面积公式cos θ=S S';此方法常用于无棱二面角大小的计算;对于无棱二面角问题还有一条途径是设法作出它的棱,作法有“平移法”“延伸平面法”等. 【考点针对训练】1. .【2016高考浙江文数】如图,在三棱台ABC-DEF 中,平面BCFE ⊥平面ABC ,∠ACB =90°,BE=EF=FC =1,BC =2,AC =3.(I )求证:BF ⊥平面ACFD ;(II )求直线BD 与平面ACFD 所成角的余弦值.2. 【2016届湖北省武汉市武昌区高三5月调研】如图,PA 垂直圆O 所在的平面,C 是圆O 上的点,Q 是PA 的中点,G 为AOC ∆的重心,AB 是圆O 的直径,且22AB AC ==.(1)求证://QG 平面PBC ; (2)求G 到平面PAC 的距离. 【考点2】立体几何综合问题 【备考知识梳理】空间线、面的平行与垂直的综合考查一直是高考必考热点.归纳起来常见的命题角度有: 以多面体为载体综合考查平行与垂直的证明. 探索性问题中的平行与垂直问题. 折叠问题中的平行与垂直问题. 【考点针对训练】1. 【2016届宁夏高三三轮冲刺】如图,在三棱锥P ABC -中,平面PAC ⊥平面ABC ,PA AC ⊥,AB BC ⊥.设,D E 分别为,PA AC 中点.(1)求证://DE 平面PBC ; (2)求证:BC ⊥平面PAB ;(3)试问在线段AB 上是否存在点F ,使得过三点D ,,E F 的平面内的任一条直线都与平面PBC 平行?若存在,指出点F 的位置并证明;若不存在,请说明理由.2. 【2016届四川南充高中高三4月模拟三】如图,在正方形ABCD 中,点,E F 分别是,AB BC 的中点,将,AED DCF ∆∆分别沿DE 、DF 折起, 使,A C 两点重合于P .(Ⅰ)求证:平面PBD ⊥平面BFDE ; (Ⅱ)求四棱锥P BFDE -的体积. 【应试技巧点拨】 1.如何求线面角(1)利用面面垂直性质定理,巧定垂足:由面面垂直的性质定理,可以得到线面垂直,这就为线面角中的垂足的确定提供了捷径. (2)利用三棱锥的等体积,省去垂足在构成线面角的直角三角形中,其中垂线段尤为关键.确定垂足,是常规方法.可是如果垂足位置不好确定,此时可以利用求点面距常用方法---等体积法.从而不用确定垂足的位置,照样可以求出线面角.因为垂线段的长度实际就是点面距h !利用三棱锥的等体积,只需求出h ,然后利用斜线段长h=θsin 进行求解.(3)妙用公式,直接得到线面角 课本习题出现过这个公式:21cos cos cos θθθ=,如图所示:21,,θθθ=∠=∠=∠OBC ABO ABC .其中1θ为直线AB 与平面所成的线面角.这个公式在求解一些选择填空题时,可直接应用.但是一定要注意三个角的位置,不能张冠李戴. 2.如何求二面角(1)直接法.直接法求二面角大小的步骤是:一作(找)、二证、三计算.即先作(找)出表示二面角大小的平面角,并证明这个角就是所求二面角的平面角,然后再计算这个角的大小. 用直接法求二面角的大小,其关键是确定表示二面角大小的平面角.而确定其平面角,可从以下几个方面着手:①利用三垂线定理(或三垂线定理的逆定理)确定平面角;②利用与二面角的棱垂直的平面确定平面角;③利用定义确定平面角;(2)射影面积法.利用射影面积公式cos θ=S S';此方法常用于无棱二面角大小的计算;对于无棱二面角问题还有一条途径是设法作出它的棱,作法有“平移法”“延伸平面法”等. 3.探索性问题探求某些点的具体位置,使得线面满足平行或垂直关系,是一类逆向思维的题目.一般可采用两个方法:一是先假设存在,再去推理,下结论;二是运用推理证明计算得出结论,或先利用条件特例得出结论,然后再根据条件给出证明或计算.4.在推证线面平行时,一定要强调直线不在平面内,否则,会出现错误.5.在解决直线与平面垂直的问题过程中,要注意直线与平面垂直定义,判定定理和性质定理的联合交替使用,即注意线线垂直和线面垂直的互相转化.6.面面垂直的性质定理是作辅助线的一个重要依据.我们要作一个平面的一条垂线,通常是先找这个平面的一个垂面,在这个垂面中,作交线的垂线即可. 【三年高考】1. 【2016高考新课标1文数】平面α过正文体ABCD —A 1B 1C 1D 1的顶点A ,11//CB D α平面,ABCD m α=平面,11ABB A n α=平面,则m ,n 所成角的正弦值为( )(A )2 (B )2 (C )3(D )132. 【2016高考浙江文数】如图,已知平面四边形ABCD ,AB =BC =3,CD =1,AD ADC =90°.沿直线AC 将△ACD 翻折成△CD 'A ,直线AC 与D 'B 所成角的余弦的最大值是______.3. 【2016高考北京文数】如图,在四棱锥ABCD P -中,⊥PC 平面ABCD ,,AB DC DC AC ⊥∥(I )求证:DC PAC ⊥平面; (II )求证:PAB PAC ⊥平面平面;(III )设点E 为AB 的中点,在棱PB 上是否存在点F ,使得//PA 平面C F E ?说明理由.4. 【2016高考天津文数】如图,四边形ABCD 是平行四边形,平面AED ⊥平面ABCD ,EF||AB ,AB=2,BC=EF=1,DE=3,∠BAD=60º,G 为BC 的中点.(Ⅰ)求证://FG 平面BED ;(Ⅱ)求证:平面BED ⊥平面AED ;(Ⅲ)求直线EF 与平面BED 所成角的正弦值.5. 【2016高考新课标1文数】如图,在已知正三棱锥P -ABC 的侧面是直角三角形,PA =6,顶点P 在平面ABC 内的正投影为点E ,连接PE 并延长交AB 于点G . (I )证明G 是AB 的中点;(II )在答题卡第(18)题图中作出点E 在平面PAC 内的正投影F (说明作法及理由),并求四面体PDEF 的体积.PABD CGE6. 【2015高考浙江,文7】如图,斜线段AB 与平面α所成的角为60,B 为斜足,平面α上的动点P 满足30∠PAB =,则点P 的轨迹是( )A .直线B .抛物线C .椭圆D .双曲线的一支7.【2015高考福建,文20】如图,AB 是圆O 的直径,点C 是圆O 上异于,A B 的点,PO 垂直于圆O 所在的平面,且1PO =OB =.(Ⅰ)若D 为线段AC 的中点,求证C A ⊥平面D P O ; (Ⅱ)求三棱锥P ABC -体积的最大值;(Ⅲ)若BC =E 在线段PB 上,求CE OE +的最小值.8.【2015高考四川,文18】一个正方体的平面展开图及该正方体的直观图的示意图如图所示. (Ⅰ)请按字母F ,G ,H 标记在正方体相应地顶点处(不需要说明理由) (Ⅱ)判断平面BEG 与平面ACH 的位置关系.并说明你的结论. (Ⅲ)证明:直线DF ⊥平面BEGAB FHED C G CD EAB9.【2015高考重庆,文20】如题(20)图,三棱锥P-ABC 中,平面PAC ⊥平面ABC ,∠ABC=2π,点D 、E 在线段AC 上,且AD=DE=EC=2,PD=PC=4,点F 在线段AB 上,且EF//BC. (Ⅰ)证明:AB ⊥平面PFE.(Ⅱ)若四棱锥P-DFBC 的体积为7,求线段BC 的长.题(20)图AC10. 【2014高考重庆文第20题】如题(20)图,四棱锥P ABCD -中,底面是以O 为中心的菱形,PO ⊥底面ABCD ,2,3AB BAD π=∠=,M 为BC 上一点,且12BM=. (Ⅰ)证明:BC⊥平面POM ;(Ⅱ)若MP AP ⊥,求四棱锥P ABMO -的体积.11. 【2014高考全国1文第19题】如图,三棱柱111C B A ABC -中,侧面C C BB 11为菱形,C B 1的中点为O ,且⊥AO 平面C C BB 11. (1)证明:;1AB C B ⊥(2)若1AB AC ⊥,,1,601==∠BC CBB求三棱柱111C B A ABC -的高.12.【2014高考江西文第19题】如图,三棱柱111C B A ABC -中,111,BB B A BC AA ⊥⊥. (1)求证:111CC C A ⊥;(2)若7,3,2===BC AC AB ,问1AA 为何值时,三棱柱111C B A ABC -体积最大,并求此最大值.【一年原创真预测】1.已知AB ⊥平面ACD ,DE ⊥平面ACD ,ACD ∆为等边三角形,22AD DE AB ===,F 为CD 的中点.(Ⅰ)求证:平面平面BCE DCE ⊥; (Ⅱ)求B CDE 点到平面的距离.2.如图,直三棱柱111ABC A B C -中,底面ABC △是等腰直角三角形,且AB CB ==,且AA 1=3,D 为11AC 的中点,F 在线段1AA 上,设11A F tAA =(102t <<),设11=B C BC M .MFDC 1B 1A 1CBA(Ⅰ)当取何值时,CF ⊥平面1B DF ;(Ⅱ)在(Ⅰ)的条件下,求四面体1F B DM -的体积.3.如图,三棱锥P ABC -中,BC ⊥平面PAB ,PA PB AB BC 6====,点M ,N 分别为PB,BC 的中点.(I )求证:AM ⊥平面PBC ; (Ⅱ)E 是线段AC 上的点,且AM 平面PNE .①确定点E 的位置;②求直线PE 与平面PAB 所成角的正切值.4.如图,在直角三角形ABC 中,∠BAC=60°,点F 在斜边AB 上,且AB=4AF ,D ,E 是平面ABC 同一侧的两点,AD ⊥平面ABC ,BE ⊥平面ABC ,AD=3,AC=BE=4.(Ⅰ)求证:CD ⊥EF ;(Ⅱ)若点M 是线段BC 的中点,求点M 到平面EFC 的距离.5. 如图所示,在边长为12的正方形11ADD A 中,点,B C 在线段AD 上,且3,4AB BC ==,作11//BB AA ,分别交111,A D AD 于点1B ,P .作11//CC AA ,分别交111,A D AD 于点1C ,Q .将该正方形沿11,BB CC 折叠,使得1DD 与1AA 重合,构成如图的三棱柱111ABC A B C -.(1)求证:AB ⊥平面11BCC B ; (2)求四棱锥A BCQP -的体积.【考点1针对训练】 1.2.【考点2针对训练】 1.又因为EF ⊄平面PBC ,BC ⊂平面PBC ,所以//EF PBC .又因为DE EF E =,所以平面//DEF 平面PBC ,所以平面DEF 内的任一条直线都与平面PBC 平行.2.【三年高考】 1. 【答案】A//',//'m m n n ,则,m n 所成的角等于','m n 所成的角.延长AD ,过1D 作11//D E B C ,连接11,CE B D ,则CE 为'm ,同理11B F 为'n ,而111//,//BD CE B F A B ,则','m n 所成的角即为1,A B BD 所成的角,即为60 ,故,m n所成角的正弦值为2,故选A. 2.3. 【解析】(I )因为C P ⊥平面CD AB ,所以C DC P ⊥.又因为DC C ⊥A ,所以DC ⊥平面C PA . (II )因为//DC AB ,DC C ⊥A ,所以C AB ⊥A .因为C P ⊥平面CD AB ,所以C P ⊥AB .所以AB ⊥平面C PA .所以平面PAB ⊥平面C PA .(III )棱PB 上存在点,使得//PA 平面C F E .证明如下:取PB 中点,连结F E ,C E ,CF .又因为E 为AB 的中点,所以F//E PA .又因为PA ⊄平面CF E ,所以//PA 平面C F E .4.5.6. 【答案】C【解析】由题可知,当点运动时,在空间中,满足条件的AP绕AB旋转形成一个圆锥,用一个与圆锥高成60角的平面截圆锥,所得图形为椭圆.故选C.7.解法二:(I)、(II)同解法一.8.【解析】(Ⅰ)点F ,G ,H 的位置如图所示9.【解析】如题(20)图.由,DE EC PD PC ==知,E 为等腰PDC D 中DC 边的中点,故PE AC ^,又平面PAC ⊥平面ABC ,平面PAC 平面ABC AC =,PE Ì平面PAC ,PE AC ^,所以PE ^平面ABC ,从而PE AB ^.因ABC=,,AB EF 2EF BC p衈故. 从而AB 与平面PFE 内两条相交直线PE ,EF 都垂直,所以AB ^平面PFE .(2)解:设BC=x ,则在直角ABC D中,从而11S AB BC=22ABC D =?由EFBC ,知23AF AE AB AC ==,得AEF ABC DD ,故224()S 39AEF ABC S D D ==,即4S 9AEF ABC S D D =.FCDEAB GHO由1AD=2AE ,11421S S =S S 22999AFB AFE ABC ABC D D D D =?=从而四边形DFBC 的面积为DFBC11S S -=29ABC ADF S D D =718=(1)知,PE PE ^平面ABC ,所以PE 为四棱锥P-DFBC 的高.在直角PEC D 中,=体积DFBC 117S 73318P DFBC V PE -=鬃=?,故得42362430x x -+=,解得2297x x ==或,由于0x >,可得3x x ==或.所以3BC =或BC =10.11.12.【解析】(1)证明:由1AA BC ⊥知1BB BC ⊥,又11BB A B ⊥,故1BB ⊥平面1,BCA 即11BB AC ⊥,又11//BB CC ,所以11.AC CC ⊥(2)设1,AA x =在11Rt A BB ∆中1BA同理1AC 在1A BC ∆中,2222111111cos 2A B AC BC BAC BAC A B AC +-∠==∠=⋅11111sin 2A BCS A B A C BA C ∆=⋅∠=从而三棱柱111ABC A B C -的体积为11133A BC V BB S ∆=⨯⨯=因=故当x =时,即1AA =时,体积V取到最大值【一年原创真预测】1.【解析】(Ⅰ)DE ⊥平面ACD ,F A ⊂平面CD A ∴DE AF ⊥,又等边三角形ACD 中AF CD ⊥, D CD D E =,D E ⊂平面CD E ,CD ⊂平面CD E ,∴平面AF ECD ⊥,取CE 的中点M ,连接BM,MF ,则MF 为△CDE 的中位线,故1////,2MF DE AB MF DE AB ==,所以四边形ABMF 为平行四边形,即MB//AF,MB⊂平面C B E ,F A ⊄平面C B E ,//BCE 平面AF ∴,平面平面BCE DCE ∴⊥.(Ⅱ)因为AB ⊥平面ACD ,DE ⊥平面ACD ,所以AB //DE ,故AB //平面DCE ,B CDE 点到平面的距离h 等于A CDE 点到平面的距离d ,由体积相等A DCE E ACD V V --=得,1133DCE ADC S d S DE ∆∆⋅=⨯,011112222sin 6023232d ⋅⨯⨯⋅=⨯⨯⨯⨯,解得h d ==.2.(Ⅱ)由已知得111111==22F B DM M B DF C B DF B CDF V V V V ----=,因为FD FC 1=22CDF S DF FC ⋅=△,由(Ⅰ)得1B D ⊥平面DFC ,故112=21=33B CDF V -⨯⨯,故1F B DM -的体积为13.3.②作EH AB ⊥于H ,则EH //BC ,∴EH ⊥平面PAB ,∴EPH ∠是直线PE 与平面PAB 所成的角.∵1AH AB 23==,π6=3PA PAH =∠, ∴PH ==1EH BC 23==,∴EH tan EPH PH 7∠==,即直线PE 与平面PAB 所成角的正切值为7.4.5.。
空间角和空间距离

空间角和空间距离一、空间角:(1)异面直线所成的角:过空间任一点分别引两异面直线的平行线,则此两相交直线所成的锐角(或直角)叫做两异面直线所成的角.异面直线所成角的范围 .(2)直线与平面所成的角:①当α//l 或α⊂l 时,l 与α所成的角为 0;②当α⊥l 时, l 与α所成的角为 90;③当l 与α斜交时,l 与α所成的角是指l 与l 在面α上的射影'l 所成的锐角.线面角的范围: .(3)二面角的平面角须具有以下三个特点:①顶点在棱上;②角的两边分别在两个半平面内; ③角的两边与棱都垂直.二面角的范围: .方法总结:1、求异面直线所成角的方法:主要通过平移转化法来作出异面直线所成的角,然后利用三角形的边角关系(正、余弦定理)求角的大小,要注意角的范围.2、求线面角的一般过程是:(1)在斜线上找到一个合适的点P ,过P 作面α的垂线(注意垂足/P 的确定),垂足/P 和斜足A 的连线即为斜线PA 在平面α上的射影,则/PAP ∠即为所求;(2)将/PAP ∠放到/PAP ∆或其它包含此角的三角形中去求. 说明:关于线线角和线面角,下面的结论经常用到:①“爪角定理”:如图9-4-1,已知,AB AO 分别是面α在面α内过斜足O 任意引一直线OC ,设12,AOB BOC θθ∠=∠=,AOC θ∠=,则:21cos cos cos θθθ⋅=;② 经过一个角的顶点作这个角所在平面的斜线,如果斜线和这个角两边的夹角相等,那么斜线在平面上的射影是这个角的平分线所在的直线.说明:在解题过程中,我们会发现求角问题难在作角,其中又难在过平面外一点,作平面的垂线后,垂足位置的确定.复习过程中应注意对常用的找垂足的方法进行归纳总结. 上面的②及下面的几个结论是找垂足的有力工具:(ⅰ)若P 为ABC ∆所在平面 外一点, O 是点P 在 内的射影,则:①若PA PB PC ==或PA 、PB 、PC 与 所成角均相等, 则O 为ABC ∆的外心;②若P 到ABC ∆的三边的距离相等, 则O 为ABC ∆△ABC 的内心;③若PA 、PB 、PC 两两互相垂直, 或,PA BC PB AC ⊥⊥则O 为ABC ∆的垂心.(ⅱ)面面垂直的性质定理:如果两个平面垂直,则在一个平面内垂直于交线的直线垂直于另一个平面;(ⅲ)三垂线定理及其逆定理.3、求二面角的平面角的一般方法:如何作出(或找出)二面角的平面角是解题的关键,常用以下方法:①定义法:直接在二面角的棱上取一点(特殊点),分别在两个半平面中作棱的垂线,得出平面角,用定义法时应认真观察图形的特性;②三垂线法(比较常用):已知二面角其中一个面内一点P 到另一个面的垂线(垂足为/P ),则只需过P (或/P )作棱的垂线(垂足为O ),由三垂线定理或其逆定理知/POP ∠即为所求(关键是从题中找到适当的点P );③垂面法:已知二面角内一点到两个面的垂线时,过两垂线作平面与两个半平面的交线所成的角即为平面角(由此知,二面角的平面角所在的平面与棱垂直);④面积投影法:此法最大的优点在于不用作出平面角θ,常用于“无棱二面角”(即在图中没有画出棱);如果α上某一平面图形的面积为斜S ,它在β上的射影的面积为射S ,则射斜S S =θcos 。
2025高考数学一轮复习-7.6-利用空间向量求空间角、距离【课件】

(3)平面与平面的夹角 如图,平面 α 与平面 β 相交,形成四个二面角,我们把四个二面角中不大于 90°的二 面角称为平面 α 与平面 β 的夹角.
若平面 α,β 的法向量分别是 n1 和 n2,则平面 α 与平面 β 的夹角即为向量 n1 和 n2 的 |n1·n2|
夹角或其补角.设平面 α 与平面 β 的夹角为 θ,则 cosθ=|cos n1,n2 |=_____|n_1_||n__2|___.
设平面 CDP 的法向量为 n=(x,y,z),
则nn··PP→→DC==00 ⇒n=(0,1,1).
平面 PAB 的法向量 m=(0,1,0)
cos〈m,n〉=|mm|·|nn|=
2 2.
又∵平面 ABP 与平面 CDP 所成的二面角为锐二面角,∴所求二面角为 45°.
易错点睛:(1)误认为直线的方向向量和平面的法向量所成的角就是线面角出错. (2)不能结合图形准确判定二面角出错.
4.正三棱柱(底面是正三角形的直棱柱)ABC-A1B1C1 的底面边长为 2,侧棱长为 2 2,
π 则 AC1 与侧面 ABB1A1 所成的角为___6_____.
【解析】 以 C 为原点建立坐标系,得下列坐标:A(2,0,0),C1(0,0,2 2).点 C1 在
侧 面 ABB1A1 内 的 射 影 为 点
提醒:(1)利用公式与二面角的平面角时,要注意 n1,n2 与二面角大小的关系,是
相等还是互补,需要结合图形进行判断. (2)注意二面角与两个平面的夹角的区别与联系,二面角的范围为[0,π],两个平面的
夹角的范围为0,π2.
2.空间距离(1)点 P 到直线 l 的距离 设A→P=a,u 是直线 l 的单位方向向量,则向量A→P在直线 l 上的投影向量A→Q=(a·u)u. 在 Rt△APQ 中,由勾股定理,得 PQ= |A→P|2-|A→Q|2=___a_2-___a_·u__2__.
高考理科第一轮课件(7.9利用空间向量求空间角和距离)

) (C) 1
2
(B) 2
4
(D) 3
3
【解析】选B.方法一:E为AD1的中点,过点O作OF∥A1E,交 C1E于点F. ∵E为AD1的中点, ∴EA1⊥AD1. 又BA⊥平面AD1, ∴BA⊥EA1,
∴E1, ∴FO⊥平面ABC1D1,
∴FO= 1 EA1= 2 .
设AD=2,由CD=AD,∠CAD=30°,易知点A,C,D的坐标分 别为A(0,- 3 ,0),C(0, 3 ,0),D(0,0,1),
则 AD 0, 3,1 .
显然向量k=(0,0,1)是平面ABC的一个法向量. 已知平面CAB与平面DAB的夹角为60°,故可取平面ABD的单 位法向量t=(l,m,n),使得〈t,k〉=60°,从而 n 1 .
4 2
MD MA 2 AD 2 2, cosMDP
所以AB与MD的夹角的大小为 .
3
DP 1 ,MDC MDP , MD 2 3
【拓展提升】 1.异面直线夹角的求法 利用空间向量求异面直线的夹角可利用直线的方向向量, 转化成向量的夹角. 2.合理建立空间直角坐标系 (1)①一般来说,如果已知的空间几何体中含有两两垂直且 交于一点的三条直线时,就以这三条直线为坐标轴建立空 间直角坐标系;
图1
在Rt△ABC中,因AC=2AF= 2 3,AB=2BC,
由勾股定理易知BC= 2 15 , AB= 4 15 .
5 5
故四面体ABCD的体积V= 1 ABC DF S
3
1 1 4 15 2 15 4 1 . 3 2 5 5 5
(2)如图2,设F为AC的中点,连接DF, 过F作FM⊥AC,交AB于M,已知AD=CD,平面ABC⊥平面ACD, 易知FC,FD,FM两两垂直,以F为原点,射线FM,FC,FD分 别为x轴,y轴,z轴的正半轴,建立空间直角坐标系.
课件2:8.7 立体几何中的向量方法(二)——求空间角和距离

【规律方法】
1.平面法向量的求法
若要求出一个平面的法向量的坐标,一般要建立空间直角坐标系,
然后用待定系数法求解,一般步骤如下:
设平面的法向量为n=(x,y,z).
(1)找出(求出)平面内的两个不共线的向量a=(a1,b1,c1),b=(a2,b2,c2).
(2)根据法向量的定义建立关于x,y,z的方程组
的距离为 | BO |=| AB || cos〈AB,n〉| =
| AB n | |n|
.
3. (1)常用方法:利用向量求异面直线所成角、线面角、二面角及空间距 离的方法. (2)数学思想:转化与化归、数形结合、函数与方程.
考点1 向量法求异面直线所成的角
【典例1】(1)(2015·上饶模拟)如图所示,已知三棱
考点3 向量法计算与应用二面角的大小 知·考情
利用空间向量计算与应用二面角大小,是高考考查空间角的一个 热点考向,常与线线、线面、面面位置关系等知识综合以解答题第(2) 或(3)问的形式出现.
明·角度 命题角度1:计算二面角的大小 【典例3】(2014·山东高考)如图,在四棱柱 ABCD-A1B1C1D1中,底面ABCD是等腰梯形, ∠DAB=60°,AB=2CD=2,M是线段AB的中点. (1)求证:C1M∥平面A1ADD1. (2)若CD1垂直于平面ABCD且CD1= 3,求平面C1D1M和平面ABCD所成 的角(锐角)的余弦值.
22
所以 AD 0, 3,0 ,AE (0, 3 , 1),AC (m, 3,0). 22
设平面ADE的法向量为n1=(x1,y1,z1), 则n1 AD 0,n1 AE 0, 解得一个n1=(1,0,0). 同理设平面ACE的法向量为n2=(x2,y2,z2), 则 n2 AC 0,n2 AE 0, 解得一个 n2 ( 3,m, 3m).
专题+立体几何中的向量方法(二)—求空间角和距离年领军高考数学一轮复习(文理通用)

专题45立体几何中的向量方法(二)——求空间角和距离 最新考纲1.能用向量方法解决直线与直线、直线与平面、平面与平面所成角的计算问题.2.了解向量方法在研究立体几何问题中的应用.基础知识融会贯通1.两条异面直线所成角的求法设a ,b 分别是两异面直线l 1,l 2的方向向量,则l 1与l 2所成的角θa 与b 的夹角β范围 ⎝⎛⎦⎤0,π2 [0,π] 求法cos θ=|a ·b ||a ||b |cos β=a ·b|a ||b |2.直线与平面所成角的求法设直线l 的方向向量为a ,平面α的法向量为n ,直线l 与平面α所成的角为θ,a 与n 的夹角为β,则sin θ=|cos β|=|a ·n ||a ||n |.3.求二面角的大小(1)如图①,AB ,CD 分别是二面角α-l -β的两个面内与棱l 垂直的直线,则二面角的大小θ=〈AB →,CD →〉.(2)如图②③,n 1,n 2分别是二面角α-l -β的两个半平面α,β的法向量,则二面角的大小θ满足|cos θ|=|cos 〈n 1,n 2〉|,二面角的平面角大小是向量n 1与n 2的夹角(或其补角). 【知识拓展】利用空间向量求距离(供选用) (1)两点间的距离设点A (x 1,y 1,z 1),点B (x 2,y 2,z 2),则|AB |=|AB →|=x 1-x 22+y 1-y 22+z 1-z 22.(2)点到平面的距离如图所示,已知AB 为平面α的一条斜线段,n 为平面α的法向量,则B 到平面α的距离为|BO →|=|AB →·n ||n |.重点难点突破【题型一】求异面直线所成的角【典型例题】如图,直棱柱(侧棱垂直于底面的棱柱) ABC ﹣A 1B 1C 1,在底面ABC 中,CA =CB =1,∠BCA =90°,棱AA 1=2,M ,N 分别为A 1B 1,A 1A 的中点. (1)求的值;(2)求证:BN ⊥平面C 1MN .【解答】解:以C 为原点,CA ,CB ,CC 1所在直线分别为x 轴,y 轴,z 轴,建立如图所示的坐标系C ﹣xyz , (1)依题意,A 1(1,0,2),C (0,0,0),B 1(0,1,2),B (0,1,0), ∴(1,﹣1,2),(0,1,2),∴•1×0+(﹣1)×1+2×2=3, 又||,||,∴cos,6分证明:(2)A1(1,0,2),C1(0,0,2),B1(0,1,2),N(1,0,1),∴M(,,2),∴(,,2),(1,0,﹣1),(1,﹣1,1),∴•1(﹣1)+1×0=0,同理可求•0,∴⊥,⊥,C1M∩C1N=C1,∴BN⊥平面C1MN…12分.【再练一题】如图,BC=2,原点O是BC的中点,点A的坐标为(,,0),点D在平面yOx上,且∠BDC=90°,∠DCB=30°.(1)求向量的坐标.(2)求与的夹角的余弦值.【解答】解:(1)过D作DE⊥BC于E,则DE=CD•sin30°,OE=OB﹣BD cos60°=1,∴D的坐标为D(0,,,又∵C(0,1,0),∴(0,,).(2)依题设有A点坐标为A(,,0),∴(),(0,2,0),则与的夹角的余弦值:cos.思维升华用向量法求异面直线所成角的一般步骤(1)选择三条两两垂直的直线建立空间直角坐标系;(2)确定异面直线上两个点的坐标,从而确定异面直线的方向向量;(3)利用向量的夹角公式求出向量夹角的余弦值;(4)两异面直线所成角的余弦值等于两向量夹角余弦值的绝对值.【题型二】求直线与平面所成的角【典型例题】如图所示,在直角梯形ABCD中,已知BC∥AD,AB⊥AD,BC=BA AD=m,VA⊥平面ABCD.(1)求证:CD⊥平面VAC;(2)若VA m,求CV与平面VAD所成角的大小.【解答】(1)证明:连结AC,∵AB=BC,∠ABC=90°,∴∠CAB=∠ACB=45°,取AD中点G,连CG,因为BC∥AD,所以四边形ABCG为正方形.所以CG=GD,∠CGD=90°,∴∠DCG=45°,∴∠DCA=90°……………………所以CD⊥CA,又VA⊥平面ABCD,所以CD⊥VA,CD⊥平面VAC………………(2)解:法1:连VG由⇒CG⊥面VAD,∴∠CVG是CV与平面VAD所成的角………………VC2m;CG=m,∴∠CVG=30°∴CV与平面VAD所成角为30°………………法2:以A为原点,射线AB,AD,AV所在直线为x,y,z轴正半轴,建立空间直角坐标系,则平面VAD 法向量(m,0,0),又,设向量与夹角为θ,则cosθ,θ,CV与平面VAD所成的角为.【再练一题】如图,四棱锥P﹣ABCD中,底面为直角梯形,AB∥CD,∠BAD=90°,AB=2CD=4,P A⊥CD,在锐角△P AD 中,E是边PD上一点,且AD=PD=3ED.(1)求证:PB∥平面ACE;(2)当P A的长为何值时,AC与平面PCD所成的角为30°?【解答】(1)证明:连接BD交AC于O,∵AB∥CD,∴△OCD∽△OAB,∴,又,∴OE∥PB,又OE⊂平面ACE,PB⊄平面ACE,∴PB∥平面ACE.(2)解:过A作AF⊥PD,垂足为F,连接CF,∵CD⊥AD,CD⊥P A,P A∩AD=A,∴CD⊥平面P AD,∴CD⊥AF,又AF⊥PD,PD∩CD=D,∴AF⊥平面PCD,∴∠ACF为AC与平面PCD所成的角,即∠ACF=30°.AC,∴AF AC,∴sin∠ADF,cos∠ADF,∴P A.∴当P A时,AC与平面PCD所成的角为30°.思维升华利用向量法求线面角的方法(1)分别求出斜线和它在平面内的射影直线的方向向量,转化为求两个方向向量的夹角(或其补角);(2)通过平面的法向量来求,即求出斜线的方向向量与平面的法向量所夹的锐角,取其余角就是斜线和平面所成的角.【题型三】求二面角【典型例题】四棱锥P﹣ABCD中,平面PCD⊥平面ABCD,四边形ABCD为矩形,AB=4,AD=3,∠P AB=90°.(1)求证:PD⊥平面ABCD;(2)若直线BD与平面P AB所成角的正弦值为,求二面角C﹣P A﹣D的余弦值.【解答】证明:(1)因为平面PCD⊥平面ABCD,且∠BCD=90°.所以BC⊥平面PCD,所以PD⊥BC.又因为AB⊥P A,AB⊥AD,所以AB⊥平面P AD,所以PD⊥AB.又因为PD⊥BC,所以PD⊥平面ABCD.解:(2)以D为原点,DA,DP,DC方向分别为x轴,y轴,z轴正方向建立如图空间直角坐标系.作DE⊥P A于E,连接BE,因为平面P AD⊥平面P AB,所以DE⊥平面P AB,∠DBE即为直线BD与平面P AB所成的角,故,所以DE.Rt△P AD中,令PD=x,则x•3•,解得x=3,故A(3,0,0),P(0,3,0),C(0,0,4).(﹣3,3,0),(﹣3,0,4),设平面P AC的一个法向量为(a,b,c),则,取(4,4,3).又因为平面P AD的一个法向量为(0,0,4),故cos.综合图形可知,所求二面角的余弦值为.【再练一题】如图在直角△ABC中,B为直角,AB=2BC,E,F分别为AB,AC的中点,将△AEF沿EF折起,使点A到达点D的位置,连接BD,CD,M为CD的中点.(Ⅰ)证明:MF⊥面BCD;(Ⅱ)若DE⊥BE,求二面角E﹣MF﹣C的余弦值.【解答】证明:(Ⅰ)取DB中点N,连结MN、EN,∵MN,EF,∴四边形EFMN是平行四边形,∵EF⊥BE,EF⊥DE,BE∩EF=E,∴EF⊥平面BDE,∴EF⊥EN,∴MF⊥MN,在△DFC中,DF=FC,又∵M为CD的中点,∴MF⊥CD,又∵MF∩MN=M,∴MF⊥平面BCD.解:(Ⅱ)∵DE⊥BE,DE⊥EF,BE∩EF=E,∴DE⊥平面BEF,以E为原点,BE、EF、ED所在直线分别为x,y,z轴,建立空间直角坐标系,设BC=2,则E(0,0,0),F(0,1,0),C(﹣2,2,0),M(﹣1,1,1),∴(0,1,0),(﹣1,0,1),(2,﹣1,0),设面EMF的法向量(x,y,z),则,取x=1,得(1,0,1),同理,得平面CMF的法向量(1,2,1),设二面角E﹣MF﹣C的平面角为θ,则cosθ,∴二面角E﹣MF﹣C的余弦值为.思维升华利用向量法计算二面角大小的常用方法(1)找法向量法:分别求出二面角的两个半平面所在平面的法向量,然后通过两个平面的法向量的夹角得到二面角的大小,但要注意结合实际图形判断所求角的大小.(2)找与棱垂直的方向向量法:分别在二面角的两个半平面内找到与棱垂直且以垂足为起点的两个向量,则这两个向量的夹角的大小就是二面角的大小.【题型四】求空间距离【典型例题】四棱锥P﹣ABCD中,底面ABCD是菱形,∠BAD=60°,P A=PB=PD.(1)求证:PD⊥AB;(2)若AB=6,PC=8,E是BD的中点,求点E到平面PCD的距离.【解答】(1)证明:由于四边形ABCD是菱形,∠BAD=60°,所以△ABD是正三角形.设AB的中点为K,连接PK,DK,如图所示,则AB⊥DK,又P A=PB,所以AB⊥PK.又PK,DK相交于K,所以AB⊥平面PKD.又PD⊂平面PKD,所以AB⊥PD.(2)解:由(1)可知,AB⊥平面PKD.又AB∥CD,所以CD⊥平面PKD.又CD⊂平面PDC,所以平面PDC⊥平面PKD,设点E到平面PCD的距离为h,则由于BD=2ED,得点B到平面PCD的距离为2h.由于KB∥平面PCD,所以K,B两点到平面PCD的距离均为2h.所以点K到直线PD的距离就是2h.设△ABD的中心为H,则PH⊥平面ABD.HC=4HE=4,在rt△PHC中,PH4,在Rt△PHD中,PH=4,DH=2,所以PD2.由DH=2HK,得点H到直线PD的距离为,即,得h.所以点E到平面PCD的距离为.【再练一题】如图,P A⊥平面ABCD,四边形ABCD是正方形,P A=AD=2,M、N分别是A B.PC的中点.(1)求证:平面MND⊥平面PCD;(2)求点P到平面MND的距离.【解答】解:(1)∵P A⊥平面ABCD,AB⊥AD,∴AB、AD、AP两两互相垂直,如图所示,分别以AB、AD、AP所在直线为x轴、y轴和z轴建立空间直角坐标系,可得A(0,0,0),B (2,0,0),C(2,2,0),D(0,2,0),P(0,0,2),M(1,0,0),N(1,1,1),∴(0,1,1),(﹣1,1,﹣1),(0,2,﹣2)设(x,y,z)是平面MND的一个法向量,可得,取y=﹣1,得x=﹣2,z=1,∴(﹣2,﹣1,1)是平面MND的一个法向量,同理可得(0,1,1)是平面PCD的一个法向量,∵•2×0+(﹣1)×1+1×1=0,∴,即平面MND的法向量与平面PCD的法向量互相垂直,可得平面MND⊥平面PCD;(2)由(1)得(﹣2,﹣1,1)是平面MND的一个法向量,∵(0,2,﹣2),得•0×(﹣2)+2×(﹣1)+(﹣2)×1=﹣4,∴点P 到平面MND 的距离d .思维升华 求点面距一般有以下三种方法:(1)作点到面的垂线,点到垂足的距离即为点到平面的距离. (2)等体积法.(3)向量法.其中向量法在易建立空间直角坐标系的规则图形中较简便.基础知识训练1.【天津市部分区2019届高三联考一模】在如图所示的几何体中,四边形ABCD 是正方形,四边形ADPQ 是梯形,PD ∥QA ,2PDA π∠=,平面ADPQ ⊥平面ABCD ,且22AD PD QA ===.(Ⅰ)求证:QB ∥平面PDC ; (Ⅱ)求二面角C PB Q --的大小;(Ⅲ)已知点H 在棱PD 上,且异面直线AH 与PB,求线段DH 的长. 【答案】(1)证明见解析;(2)56π;(3)32. 【解析】 (1)平面ADPQ ⊥平面ABCD ,平面ADPQ ⋂平面ABCD AD =,PD ADPQ ⊂平面,PD AD ⊥,∴直线PD ⊥平面ABCD .由题意,以点D 为原点,分别以,,DA DC DP 的方向为x 轴,y 轴,z 轴的正向建立如图空间直角坐标系, 则可得:()()()0,0,0,2,2,0,0,2,0D B C ,()()()2,0,0,2,0,1,0,0,2A Q P .依题意,易证:()2,0,0AD =-是平面PDC 的一个法向量, 又()0,2,1QB =-,∴ 0QB AD ⋅=, 又直线QB ⊄平面PDC ,∴ //QB PDC 平面. (2)()()2,2,2,=0,22PB PC =--,.设()1111,,n x y z =为平面PBC 的法向量, 则1100n PB n PC ⎧⋅=⎪⎨⋅=⎪⎩,即111112220220x y z y z +-=⎧⎨-=⎩. 不妨设11z =,可得()10,1,1n =.设()2222,,n x y z =为平面PBQ 的法向量, 又()()2,2,2,2,0,1PB PQ =-=-,则220n PB n PQ ⎧⋅=⎪⎨⋅=⎪⎩,即22222202220x z x y z -=⎧⎨+-=⎩. 不妨设22z =,可得()21,1,2n =,∴ 1212123cos<,nn n n n n ⋅>==⋅, 又二面角C PB Q --为钝二面角,∴二面角C PB Q --的大小为56π. (3)设()()0,0,02H h h ≤≤,则()2,0,AH h =-,又()2,2,2PB =-,又73cos<,15PB AH >=,即24273234h h--=⋅+,∴ 2625240h h -+=,解得32h =或83h =(舍去). 故所求线段DH 的长为32.2.【山东省淄博市部分学校2019届高三5月阶段性检测(三模)】已知正方形的边长为4,,E F 分别为,AD BC 的中点,以EF 为棱将正方形ABCD 折成如图所示的60的二面角,点M 在线段AB 上.(1)若M 为AB 的中点,且直线MF ,由,,A D E 三点所确定平面的交点为O ,试确定点O 的位置,并证明直线//OD 平面EMC ;(2)是否存在点M ,使得直线DE 与平面EMC 所成的角为60;若存在,求此时二面角M EC F --的余弦值,若不存在,说明理由.【答案】(1)证明见解析;(2)10,4±. 【解析】(1)因为直线MF ⊂平面ABFE , 故点O 在平面ABFE 内也在平面ADE 内,所以点O 在平面ABFE 与平面ADE 的交线上(如图所示)因为AOBF ,M 为AB 的中点,所以OAM MBF ∆≅∆,所以OM MF =,AO BF =,所以点O 在EA 的延长线上,且2AO = 连结DF 交EC 于N ,因为四边形CDEF 为矩形,所以N 是EC 的中点 连结MN ,因为MN 为DOF ∆的中位线,所以MN OD ,又因为MN ⊂平面EMC ,所以直线OD平面EMC .(2)由已知可得,EF AE ⊥,EF DE ⊥,所以EF ⊥平面ADE ,所以平面ABEF ⊥平面ODE ,取AE 的中点H 为坐标原点,建立如图所示的空间直角坐标系,所以(1,0,0)E -,3)D ,(0,3)C ,(1,4,0)F -, 所以3)ED =,(1,3)EC =, 设(1,,0)(04)M t t ≤≤,则(2,,0)EM t =,设平面EMC 的法向量(,,)m x y z =,则2000430x ty m EM m EC x y z ⎧+=⎧⋅=⎪⎪⇒⎨⎨⋅=++=⎪⎪⎩⎩, 取2y =-,则x t =,3z =,所以8,2,3t m t -⎛=- ⎪⎝⎭, DE 与平面EMC 所成的角为60,所以2232(8)243t t =-++,所以22332419t t =-+,所以2430t t -+=,解得1t =或3t =, 所以存在点M ,使得直线DE 与平面EMC 所成的角为60,取ED 的中点Q ,则QA 为平面CEF 的法向量,因为13,0,2Q ⎛⎫- ⎪ ⎪⎝⎭,所以33,0,22QA ⎛⎫=- ⎪ ⎪⎝⎭,,2,3m t ⎛=- ⎪⎝⎭, 设二面角M EC F --的大小为θ,所以222|||cos |||||(8)419343QA m QA m t t t t θ⋅===⋅--+++,因为当2t =时,cos 0θ=,平面EMC ⊥平面CDEF , 所以当1t =时,θ为钝角,所以1cos 4θ=-. 当3t =时,θ为锐角,所以1cos 4θ=. 3.【陕西省汉中市2019届高三全真模拟考试】如图,四边形ABCD 为矩形,平面ABEF ⊥平面ABCD ,//EF AB ,90BAF ∠=︒,2AD =,1AB AF ==,点P 在线段DF 上.(1)求证:AF ⊥平面ABCD ;(2)若二面角D AP C --的余弦值为6,求PF 的长度. 【答案】(1)见解析;(2)5【解析】(1)证明:∵90BAF ∠=︒,∴AB AF ⊥, 又平面ABEF ⊥平面ABCD ,平面ABEF 平面ABCD AB =,AF ⊂平面ABEF ,∴AF ⊥平面ABCD .(2)以A 为原点,以AB ,AD ,AF 为x ,y ,z 轴建立如图所示的空间直角坐标系, 则()0,0,0A ,()1,0,0B ,()1,2,0C ,()0,2,0D,()0,0,1F ,∴()0,2,1FD =-,()1,2,0AC =,()1,0,0AB = 由题知,AB ⊥平面ADF ,∴()1,0,0AB =为平面ADF 的一个法向量,设()01FP FD λλ=≤<,则()0,2,1P λλ-,∴()0,2,1AP λλ=-,设平面APC 的一个法向量为(),,x y z =m ,则0m AP m AC ⎧⋅=⎨⋅=⎩, ∴()21020y z x y λλ⎧+-=⎨+=⎩,令1y =,可得22,1,1m λλ⎛⎫=- ⎪-⎝⎭, ∴26cos ,21411m AB m AB m ABλλ⋅===⎛⎫⋅++ ⎪-⎝⎭,得13λ=或1λ=-(舍去), ∴5PF =.4.【河南省八市重点高中联盟“领军考试”2019届高三第五次测评】如图,三棱柱111ABC A B C -中,平面11ACC A ⊥平面ABC ,12AA AC CB ==,90ACB ∠=︒.(1)求证:平面11AB C ⊥平面11A B C ;(2)若1A A 与平面ABC 所成的线面角为60︒,求二面角11C AB C --的余弦值.【答案】(1)详见解析;(23【解析】(1)因为平面11ACC A ⊥平面ABC ,平面11ACC A 平面ABC AC =,BC ⊂平面ABC ,90ACB ∠=︒,所以BC ⊥平面11ACC A ,因为1AC ⊂平面11ACC A ,所以1BC A C ⊥. 因为11B C BC ∥,所以111AC B C ⊥. 因为11ACC A 是平行四边形,且1AA AC =,所以11ACC A 是菱形,11A C AC ⊥. 因为1111AC B C C ⋂=,所以1A C ⊥平面11AB C .又1AC ⊂平面11A B C ,所以平面11AB C ⊥平面11A B C . (2)取AC 的中点M ,连接1A M ,因为11ACC A 是菱形,160A AC ∠=︒, 所以1ACA ∆是正三角形,所以1A M AC ⊥,且13A M AC =. 令122AA AC CB ===,则13A M =所以以C 为原点,以CA 所在直线为x 轴,CB 所在直线为y 轴,过点C 且平行于1A M 的直线为z 轴,建立如图所示的空间直角坐标系.则()0,0,0C ,()2,0,0A ,()11,0,3C -,()0,1,0B,()11,0,3A ,()2,0,0CA =,()()111111,0,30,1,0CB CC CB CC CB =+=+=-+()1,1,3=-,()11,0,3CA =. 设平面1ACB 的一个法向量为(),,n x y z =,则10n CA n CB ⎧=⎪⎨=⎪⎩,所以2030x x y z =⎧⎪⎨-++=⎪⎩,得0x =,令1z =,则3y =-,所以()0,3,1n =-.由(1)知1A C ⊥平面11A B C ,所以()11,0,3CA =是平面11A B C 的一个法向量, 所以111cos ,CA n CA n CA n⋅<>=⋅3341331==+⋅+. 所以二面角11C AB C --的余弦值为3.5.【辽宁省葫芦岛市普通高中2019届高三第二次模拟考试】如图,在多面体ABCDEF 中,平面ADEF ⊥平面ABCD .四边形ADEF 为正方形,四边形ABCD 为梯形,且//AD BC ,ABD ∆是边长为1的等边三角形,M 为线段BD 中点,3BC =.(1)求证:AF BD ⊥;(2)求直线MF 与平面CDE 所成角的正弦值;(3)线段BD 上是否存在点N ,使得直线//CE 平面AFN ?若存在,求BNBD的值;若不存在,请说明理由.【答案】(1)见解析(2)3(3)线段BD 上存在点N,使得直线//CE 平面AFN ,且2=3BN BD ,详见解析. 【解析】(1)证明:因为ADEF 为正方形, 所以AF AD ⊥.又因为平面ADEF ⊥平面ABCD , 且平面ADEF ⋂平面ABCD AD =, 所以AF ⊥平面ABCD .所以AF BD ⊥.(2)取AD 中点O,EF 中点K ,连接OB ,OK.于是在△ABD 中,OB OD ⊥,在正方ADEF 中OK OD ⊥,又平面ADEF ⊥平面ABCD ,故OB ⊥平面AFEF ,进而0B OK ⊥, 即OB, OD, OK 两两垂直. 分别以,,OB OD OK 为x 轴,y 轴,z 轴 建立空间直角坐标系(如图).于是,3B ⎫⎪⎪⎝⎭,10,,02D ⎛⎫ ⎪⎝⎭,3C ⎫⎪⎪⎝⎭,1E 0,,12⎛⎫⋅ ⎪⎝⎭,311M ,0,F 0,,142⎫⎛⎫-⎪ ⎪⎪⎝⎭⎝⎭ 所以3335,,1,,,0,(0,0,1)4422MF CD DE ⎛⎫⎛⎫=-=-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭设平面CDE 的一个法向量为(,,)n x y z =,则00CD n DE n ⎧⋅=⎪⎨⋅=⎪⎩ 即35020x y z ⎧-⋅-⋅=⎪⎨⎪=⎩令5x =-,则3y =,则(5,3,0)n =-.设直线MF 与平面CDE 所成角为θ,||3sin |cos ,|14||||MF n MF n MF n θ⋅=<>==(3) 要使直线//CE 平面AFN ,只需AN //CD ,设,[0,1]BN BD λλ=∈,则331,,,,02n n n x y z λ⎛⎫⎛⎫-=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,331,,02n n n x y z λλ=-==, 331,,02N λλ⎛⎫- ⎪ ⎪⎝⎭,所以3311,,022AN λλ⎛⎫=-+ ⎪ ⎪⎝⎭, 又 35(,,0)2CD =--,由//AN CD 得33112222 5322λλ-+=--解得2=[0,1]3λ∈所以线段BD 上存在点N,使得直线//CE 平面AFN ,且2=3BN BD . 6.【山东省安丘市、诸城市、五莲县、兰山区2019届高三5月校级联合考试】如图所示的多面体是由一个直平行六面体被平面AEFG 所截后得到的,其中45BAE GAD ∠=∠=︒,22AB AD ==,60BAD ∠=︒.(1)求证:平面BDG ⊥平面ADG ; (2)求直线GB 与平面AEFG 所成角的正弦值. 【答案】(1)见解析(221【解析】(1)证明:在BAD ∆中,因为22AB AD ==,60BAD ∠=︒. 由余弦定理得,2222cos60BD AD AB AB AD =+-⋅︒, 解得3BD =, ∴222AB AD DB =+,∴AD DB ⊥, 在直平行六面体中,GD ⊥平面ABCD ,DB ⊂平面ABCD , ∴GD DB ⊥ 又AD GD D ⋂=, ∴BD ⊥平面ADG ,∴平面BDG ⊥平面ADG . (2)解:如图以D 为原点建立空间直角坐标系D xyz -,因为45BAE GAD ∠=∠=︒,22AB AD ==,所以()1,0,0A ,()3,0B ,()3,2E ,()0,0,1G ,()3,2AE →=-,()1,0,1AG →=-,()3,1GB →=-.设平面AEFG 的法向量(),,n x y z →=,3200n AE x z n AG x z ⎧⋅=-++=⎪⎨⋅=-+=⎪⎩, 令1x =,得33y -=,1z =,∴31,,13n→⎛⎫=-⎪⎪⎝⎭.设直线GB和平面AEFG的夹角为θ,所以()()30,3,11,,1321sin cos,730,3,11,,13GB nGB nGB nθ→→→→→→⎛⎫-⋅-⎪⋅⎝⎭====⎛⎫⋅-⋅-⎪⎝⎭,所以直线GB与平面AEFG所成角的正弦值为217.7.【西藏拉萨市2019届高三第三次模拟考试】如图,等边三角形PAC所在平面与梯形ABCD所在平面互相垂直,且有AD BC∥,2AB AD DC===,4BC=.(1)证明:平面PAB⊥平面PAC;(2)求二面角B PC D--的余弦值.【答案】(1)详见解析;(2)513.【解析】(1)证明:取BC中点M,连接AM,则四边形AMCD为菱形,即有12AM MC BC==,所以AB AC⊥.又AB平面ABCD,平面ABCD⊥平面PAC,平面ABCD平面PAC AC=,∴AB⊥平面PAC,又AB平面PAB,∴平面PAB⊥平面PAC.(2)由(1)可得23AC =,取AC 中点O ,连接PO ,则PO AC ⊥,3PO =, 又PO ⊂平面PAC , 平面PAC ⊥平面ABCD , 平面PAC平面ABCD AC =,∴PO ⊥平面ABCD .以A 为原点建系如图,则()2,0,0B ,()3,3P ,()0,23,0C ,()3,0D -,()2,23,0BC =-,()3,3PC =-,()1,3,0CD =--,设平面BPC 的法向量为()1,,n x y z =,则2230330x z ⎧-+=⎪-=,取1z =,得()13,3,1n =. 设平面PCD 的法向量为()2,,n x y z =,则30330x y z ⎧--=⎪⎨-=⎪⎩,取1z =,()23,1n =-,1212125cos ,131313n n n n n n ⋅<>===-⨯.∴二面角B PC D --的余弦值为513.8.【内蒙古呼伦贝尔市2019届高三模拟统一考试(一)】如图,在直三棱柱111ABC A B C -中,D 、E 、F 、G 分别是BC 、11B C 、1AA 、1CC 中点.且22AB AC ==,14BC AA ==.(1)求证:BC ⊥平面ADE ; (2)求二面角1G EF B --的余弦值.【答案】(1)见解析;(2)6- 【解析】(1)∵22AB AC ==,4BC =,∴AB AC ⊥. ∵D 是BC 的中点,∴AD BC ⊥,∵111ABC A B C -为直三棱柱,D ,E 为BC ,11B C 中点, ∴DE ⊥平面ABC ,∴DE BC ⊥,∴BC ⊥平面ADE .(2)由(1)知建系如图,且()002F ,,,()122,0,0B ,()2,2,0E ,()0,22,2G ,∴()2,2,2EF =--,()12,2,0B E =-,()0,22,0FG =.设平面1B EF 的法向量为(),,m x y z =,由100m EF m B E ⎧⋅=⎪⎨⋅=⎪⎩,得2220220x y z xy ⎧--+=⎪⎨-+=⎪⎩. 取()1,1,2m =,同理得平面EFG 的法向量()2,0,1n =.∴226cos ,323m n <>==,而二面角1G EF B --为钝二面角, ∴二面角1G EF B --的余弦值为6-. 9.【广东省肇庆市2019届高中毕业班第三次统一检测】如图,在三棱柱111ABC A B C -中,侧面11ABB A 是菱形,160BAA ∠=︒,E 是棱1BB 的中点,CA CB =,F 在线段AC 上,且2AFFC .(1)证明:1//CB 面1A EF ;(2)若CA CB ⊥,面CAB ⊥面11ABB A ,求二面角1F A E A --的余弦值.【答案】(1)详见解析;(2)52929. 【解析】解:(1)连接1AB 交1A E 于点G ,连接FG . 因为11AGA B GE ∆∆,所以1112AA AG GB EB ==,又因为2AF FC =,所以1AF AG FC GB =,所以1//FG CB ,又1CB ⊄面1A EF ,FG ⊂面1A EF ,所以1//CB 面1A EF .(2)过C 作CO AB ⊥于O ,因为CA CB =,所以O 是线段AB 的中点. 因为面CAB ⊥面11ABB A ,面CAB面11ABB A AB =,所以CO ⊥面1ABA .连接1OA ,因为1ABA ∆是等边三角形,O 是线段AB 的中点,所以1OA AB ⊥.如图以O 为原点,OA ,1OA ,OC 分别为x 轴,y 轴,z 轴的正方向建立空间直角坐标,不妨设2AB =,则(1,0,0)A ,1(0,3,0)A ,(0,0,1)C ,(1,0,0)B -,12(,0,)33F, 由11AA BB =,得(2,3,0)B -,1BB的中点33(,,0)2E -,133(,,0)2A E =--,112(,3,)33A F =--. 设面1A FE 的一个法向量为1111(,,)n x y z =,则111100A E n A F n ⎧⋅=⎪⎨⋅=⎪⎩,即1111230333302x y z x y ⎧-+=⎪⎪⎨⎪--=⎪⎩,得方程的一组解为111135x y z =-⎧⎪=⎨⎪=⎩,即1(1,3,5)n =-.面1ABA 的一个法向量为2(0,0,1)n =,则121212529cos ,n n n n n n ⋅<>==, 所以二面角1F A E A --的余弦值为52929.10.【广东省潮州市2019届高三第二次模拟考试】如图,菱形ABCD 与正三角形BCE 的边长均为2,它们所在平面互相垂直,FD ⊥平面ABCD ,EF 平面ABCD .(1)求证:平面ACF ⊥平面BDF ;(2)若60CBA ∠=︒,求二面角A BC F --的大小. 【答案】(1)见证明;(2) 4π【解析】(1)∵菱形ABCD ,∴AC BD ⊥, ∵FD ⊥平面ABCD ,∴FD AC ⊥, ∵BD FD D ⋂=,∴AC ⊥平面BDF , ∵AC ⊂平面ACF ,∴平面ACF ⊥平面BDF . (2)设ACBD O =,以O 为原点,OB 为x 轴,OA 为y 轴,过O 作平面ABCD 的垂线为z 轴,建立空间直角坐标系,则3,0,0)B ,()0,1,0C -,(3,0,3)F ,(3,1,0)BC =--,(3,0,3)BF =-,设平面BCF 的法向量(,,)n x y z =,则302330n BC y n BF x z ⎧⋅=--=⎪⎨⋅=-=⎪⎩,取1x =,得(1,3,2)n =-, 平面ABC 的法向量(0,0,1)m =, 设二面角A BC F --的大小为θ, 则||2cos ||||28m n m n θ⋅===⋅, ∴4πθ=.∴二面角A BC F --的大小为4π. 11.【山东省栖霞市2019届高三高考模拟卷】如图,在三棱锥V ABC -中,,90,2VC AB ABC AB BC ︒<∠===,侧面ACV ⊥底面ABC ,45ACV ︒∠=,D 为线段AB 上一点,且满足AD CV =.(1)若E 为AC 的中点,求证:BE CV ⊥; (2)当DV 最小时,求二面角A BC V --的余弦值. 【答案】(1)见证明;(2) 33【解析】(1)在ABC ∆,因为90ABC ∠=,AB BC =,E 为AC 的中点,所以BE AC ⊥,因为面ACV ⊥面ABC ,面ACV 面ABCAC =,所以BE ⊥面ACV ,又VC ⊂面ACV ,BE VC ⊥(2)以B 为坐标原点,分别以射线,BC BA 和垂直于面ABC 向上的方向为,,x y z 轴,建立空间直角坐标系-B xyz ,设BD t =,则有(0,0,0),(2,0,0),(0,,0)B C D t ,因为侧面ACV ⊥底面ABC ,45ACV ∠=, 所以(1,1222t t V +-, 所以222232(1)(1)()344222tt t DV t t -=++-+=-+ 当2(0,2)3t =∈时,DV 最小, 此时2(0,,0)3D ,4222(,33V ,4222(2,0,0),(,33BC BV ==设(,,)x y z =n 为平面VBC 的一个法向量,则有0,0BC BV ==n n ,所以204222033xx y z =⎧⎪⎨++=⎪⎩,令2z =,则(0,2,2)=-n , 而平面ABC 的一个法向量为(0,0,1)=m , 所以23cos ,16n m <>==⋅, 故二面角A BC V --的余弦值为33. 12.【河南省百校联盟2019届高三考前仿真试卷】如图,在几何体1111ACD A B C D -中,四边形1111ADD A CDD C ,为矩形,平面11ADD A ⊥平面11CDD C ,11B A ⊥平面11ADD A ,1111,2AD CD AA A B ====,E 为棱1AA 的中点.(Ⅰ)证明:11B C ⊥平面1CC E ;(Ⅱ)求直线11B C 与平面1B CE 所成角的正弦值.【答案】(Ⅰ)证明见解析;(Ⅱ)277. 【解析】(Ⅰ)因为11B A ⊥平面11ADD A , 所以111B A DD ⊥,又11111111DD D A B A D A A ⊥⋂=,,所以1DD ⊥平面1111D C B A ,又因为11//DD CC ,所以1CC ⊥平面1111D C B A ,11B C ⊂平面1111D C B A ,所以111CC B C ⊥,因为平面11ADD A ⊥平面11CDD C ,平面11ADD A ⋂平面111CDD C DD =,111C D DD ⊥,所以11C D ⊥平面11ADD A , 经计算可得1111523B E BC EC ===,,, 从而2221111B E B C EC =+,所以在11B EC 中,111B C C E ⊥,又11CC C E ⊂,平面1111CC E CC C E C ⋂=,,所以11B C ⊥平面1CC E .(Ⅱ)如图,以点A 为原点建立空间直角坐标系,依题意得()()()10001,0,00,2,2A C B ,,,,, ()()11,2,10,1,0C E ,.∵1(1,1,1)(1,2,1)CE B C =--=--,,设平面1B CE 的一个法向量(,,)m x y z =则100m B C m CE ⎧⋅=⎨⋅=⎩,,即200x y z x y z --=⎧⎨-+-=⎩,,消去x 得20y z +=,不妨设1z =,可得()3,2,1m =--,又()111,0,1B C =-,设直线11B C 与平面1B CE 所成角为θ, 于是111111427sin cos ,7142||m B C m B C m B C θ⋅-====⨯⋅, 故直线11B C 与平面1B CE 所成角的正弦值为277. 13.【江西省上饶市横峰中学2019届高三考前模拟考试】如图,在三棱锥P ABC -中,20{28x x ->-≥,2AB BC =,D 为线段AB 上一点,且3AD DB =,PD ⊥平面ABC ,PA 与平面ABC 所成的角为45.(1)求证:平面PAB ⊥平面PCD ;(2)求二面角P AC D --的平面角的余弦值。
2025届高考数学一轮复习讲义立体几何与空间向量之 空间角和空间距离

形,则在正四棱柱 ABCD - A 1 B 1 C 1 D 1中,异面直线 AK 和 LM 所成的角的大小为
(
D )
A. 30°
B. 45°
C. 60°
D. 90°
[解析] 根据题意还原正四棱柱的直观图,如图所示,取 AA 1的中点 G ,连接 KG ,
则有 KG ∥ LM ,所以∠ AKG 或其补角为异面直线 AK 和 LM 所成的角.由题知 AG =
A 1 C 1=5, BC 1=4 2 ,所以 cos
52 +52 −(4 2)2
9
1
∠ BA 1 C 1=
= < ,所以60°<
2×5×5
25
2
∠ BA 1 C 1<90°,则过点 D 1作直线 l ,与直线 A 1 B , AC 所成的角均为60°,即过一
点作直线,使之与同一平面上夹角大于60°的锐角的两边所在直线所成的角均成
2 z -1=0的交线,试写出直线 l 的一个方向向量 (2,2,1)
的余弦值为
65
9
.
,直线 l 与平面α所成角
[解析] 由平面α的方程为 x +2 y -2 z +1=0,可得平面α的一个法向量为 n =(1,
⑫ [0, ] ,二面角的
2
n1,n2>|.
范围是⑬
[0,π] .
易错警示
1. 线面角θ与向量夹角< a , n >的关系
π
2
π
2
如图1(1),θ=< a , n >- ;如图1(2),θ= -< a , n >.
图1
2. 二面角θ与两平面法向量夹角< n 1, n 2>的关系
图2(2)(4)中θ=π-< n 1, n 2>;图2(1)(3)中θ=< n 1, n 2>.
空间几何中的角和距离的计算
空间角和距离的计算(1)一 线线角1.直三棱柱A 1B 1C 1-ABC ,∠BCA=900,点D 1,F 1分别是A 1B 1和A 1C 1的中点,若BC=CA=CC 1,求BD 1与AF 1所成角的余弦值.2.在四棱锥P-ABCD 中,底面ABCD 是直角梯形,∠BAD=900,AD ∥BC ,AB=BC=a ,AD=2a ,且PA ⊥面ABCD ,PD 与底面成300角.(1)若AE ⊥PD ,E 为垂足,求证:BE ⊥PD ;(2)若AE ⊥PD ,求异面直线AE 与CD 所成角的大小.二.线面角1.正方体ABCD-A 1B 1C 1D 1中,E ,F 分别为BB 1、CD 的中点,且正方体的棱长为2.(1)求直线D 1F 和AB 和所成的角;(2)求D 1F 与平面AED 所成的角.B 1D12.在三棱柱A 1B 1C 1-ABC 中,四边形AA 1B 1B 是菱形,四边形BCC 1B 1是矩形,C 1B 1⊥AB ,AB=4,C 1B 1=3,∠ABB 1=600,求AC 1与平面BCC 1B 1所成角的大小.三.二面角1.已知A 1B 1C 1-ABC 是正三棱柱,D 是AC 中点.(1)证明AB 1∥平面DBC 1;(2)设AB 1⊥BC 1,求以BC 1为棱,DBC 1与CBC 1为面的二面角的大小.2.ABCD 是直角梯形,∠ABC=900,SA ⊥面ABCD ,SA=AB=BC=1,AD=0.5.(1)求面SCD 与面SBA 所成的二面角的大小;(2)求SC 与面ABCD 所成的角.3.已知A 1B 1C 1-ABC 是三棱柱,底面是正三角形,∠A 1AC=600,∠A 1AB=450,求二面角B —AA 1—C 的大小.B1B 1BC1空间角和距离的计算(2)四 空间距离计算(点到点、异面直线间距离)1.在棱长为a 的正方体ABCD-A 1B 1C 1D 1中,P 是BC 的中点,DP 交AC 于M ,B 1P 交BC 1于N .(1)求证:MN 上异面直线AC 和BC 1的公垂线; (2)求异面直线AC 和BC 1间的距离.(点到线,点到面的距离)2.点P 为矩形 ABCD 所在平面外一点,PA ⊥面ABCD ,Q 为线段AP 的中点,AB=3,CB=4,PA=2,求:(1)点Q 到直线BD 的距离;(2)点P 到平面BDQ 的距离.3.边长为a 的菱形ABCD 中,∠ABC=600,PC ⊥平面ABCD ,E 是PA 的中点,求E 到平面PBC 的距离.C1A(线到面、面到面的距离)4. 已知斜三棱柱A 1B 1C 1-ABC 的侧面A 1ACC 1与底面ABC 垂直,∠ABC=900,BC=2,AC=23,且AA 1⊥A 1C ,AA 1=A 1C . (1)求侧棱AA 1与底面ABC 所成角的大小;(2)求侧面A 1ABB 1与底面ABC 所成二面角的大小; (3)求侧棱B 1B 和侧面A 1ACC 1距离.5.正方形ABCD 和正方形ABEF 的边长都是1,且平面ABCD 、ABFE 互相垂直,点M 在AC 上移动,点N 在BF 上移动,若CM=NB=a (20<<a ).(1)求MN 的长;(2)当a 为何值时,MN 的长最小.1。
数学新高考第6节 利用空间向量求空间角和距离

《高考特训营》 ·数学 返 回
2.[知识拓展]解空间角最值问题时往往会用到最小角定理 cos θ=cos θ1cos θ2. 如图,若 OA 为平面 α 的一条斜线,O 为斜足,OB 为 OA 在平面 α 内的射影, OC 为平面 α 内的一条直线,其中 θ 为 OA 与 OC 所成的角,θ1 为 OA 与 OB 所成的角,即线面角,θ2 为 OB 与 OC 所成的角,那么 cos θ=cos θ1cos θ2.
《高考特训营》 ·数学 返 回
01
知识特训
知识必记 拓展链接 对点训练
4
利用空间向量求空间角和距离
《高考特训营》 ·数学 返 回
1.两条异面直线所成角的求法
设 a,b 分别是两异面直线 l1,l2 的方向向量,则
l1 与 l2 所成的角 θ
a 与 b 的夹角 β
范围 求法
_____0_,__π2_ ___ cos θ=||aa|·|bb||
9
利用空间向量求空间角和距离
《高考特训营》 ·数学 返 回
4.利用空间向量求距离 (1)两点间的距离 设点 A(x1,y1,z1),点 B(x2,y2,z2),则|AB|=|A→B|= __(__x_1_-__x2_)__2_+__(__y_1-__y_2_)__2+__(__z_1_-__z_2)__2__. (2)点到平面的距离 如图所示,已知 AB 为平面 α 外的一条斜线段,n 为平面 α 的法向量,则 B 到平面 α 的距离为|B→O|=|A→|Bn·|n|.
13
利用空间向量求空间角和距离
《高考特训营》 ·数学 返 回
3.[知识外延]利用空间向量求直线与平面所成的角的两种方法 (1)通过平面的法向量来求,即求出斜线的方向向量与平面的法向量所夹的锐 角,取其余角就是斜线和平面所成的角; (2)分别求出斜线和它在平面内的射影的方向向量,再转化为求这两个方向向 量的夹角(或其补角). [注意] 直线与平面所成角的取值范围是0,π2.
空间角与距离的计算

由△PAD 为等腰直角三角形得 PN⊥AD. 由 DC⊥AD,BC∥AD,BC=12AD,N 是 AD 的中点得 BN⊥AD.所以 AD⊥平面 PBN. 由 BC∥AD 得 BC⊥平面 PBN, 则平面 PBC⊥平面 PBN. 过点 Q 作 PB 的垂线, 垂足为 H,连接 MH,易知 QH⊥平面 PBC, 所以 MH 是 MQ 在平面 PBC 上的射影, 所以∠QMH 是直线 CE 与平面 PBC 所成的角.
令 y=1,则 n=(0,1,-1),
BF=1,EPPF=2,所以 EP=233,设 D 到面 PEA 的距离为 d,
因为 VA-EDP=VD-AEP,即13·AD·S△EDP=13·d·S△AEP,所以 d=
AD·S△EDP= S△AEP
1×
3 3
=
33× 2
2 2.
【通法指导】 诚如上文所说,求点面距问题可以采用等积转换和向量 法求解,除此之外个别问题也可采用垂面法(利用面面垂直性 质定理)和等价转移法(利用线面平行)求解.当然,一些求几 何体体积问题,也是对点面距问题的相应考查.
因为A→P=-1,2
3
3,1,A→E=(-1,0,1)
,
所以xy==z0,, 令 z=1,则 n=(1,0,1). 因为D→A=(1,0,0),
所以
D
到面
APE
的距离为
d=|D→|An·|n|=
|1| = 2
2 2.
解法二:由(1)知,AD⊥平面 BFED,所以 AD⊥EP,
AD⊥ED.又因为 EP⊥ED,所以 EP⊥平面 ADE.BD= 3,
【题型分析】 如图,在梯形 ABCD 中,AB∥CD,AD=DC=CB=1, ∠BCD=120°,四边形 BFED 为矩形,平面 BFED⊥平面 ABCD,BF=1.
高中数学中的立体几何空间角与空间距离计算方法

高中数学中的立体几何空间角与空间距离计算方法立体几何是数学中的一个分支,其重点研究的是三维空间中点、线、面和体之间的关系。
在立体几何中,空间角和空间距离是非常关键的概念。
本文将详细探讨高中数学中的立体几何空间角与空间距离计算方法。
一、空间角的概念与计算方法1. 空间角的概念空间角指的是由两个非共面向量所张成的角度,在立体几何中具有重要的意义。
空间角的大小是依据两个向量的夹角计算得来的。
2. 空间角的计算方法在计算空间角时,我们首先需要求出两个向量的点积。
设向量a=(a1,a2,a3)和向量b=(b1,b2,b3),则它们的点积为a*b=a1b1+a2b2+a3b3。
接下来,我们可以利用余弦定理来计算角度,即cosθ=(a*b)/(|a||b|),其中|a|和|b|分别表示向量a和向量b的模长,θ表示向量a和向量b之间的夹角。
二、空间距离的概念与计算方法1. 空间距离的概念空间距离指的是三维空间中两个点之间的距离,也是立体几何中经常涉及到的一个概念。
2. 空间距离的计算方法我们可以借助勾股定理来计算空间距离。
设点A(x1,y1,z1)和点B(x2,y2,z2)是三维空间中的两个点,它们之间的距离为d,则d=sqrt((x2-x1)^2+(y2-y1)^2+(z2-z1)^2)。
三、空间角和空间距离的应用空间角和空间距离在立体几何中的应用非常广泛,例如在计算棱台的侧面积、计算四面体内切圆半径、求解圆锥截面面积等问题中,我们都需要用到空间角和空间距离的知识。
比如,在计算棱台的侧面积时,我们需要首先求出两条棱所在的平面之间的空间角,然后根据棱长和计算出的角度,就可以快速计算出棱台的侧面积。
在计算四面体内切圆半径时,我们需要先计算出四面体各面的法线向量,然后根据法线向量计算面上的角度,最后用勾股定理求出四面体内切圆的半径。
在求解圆锥截面面积时,我们需要用到空间角和空间距离的知识,以找出圆锥截面的边界和计算截面的面积。
高考数学专题—立体几何(空间向量求空间角与空间距离)

高考数学专题——立体几何(空间向量求角与距离)一、空间向量常考形式与计算方法设直线l,m 的方向向量分别为l ⃗,m ⃗⃗⃗⃗,平面α,β的法向量分别为n ⃗⃗1,n 2⃗⃗⃗⃗⃗. (1)线线角:(正负问题):用向量算取绝对值(因为线线角只能是锐角)直线l,m 所成的角为θ,则0≤θ≤π2,计算方法:cos θ=l⃗⋅m ⃗⃗⃗⃗|l⃗|⋅|m ⃗⃗⃗⃗|; (2)线面角:正常考你正弦值,因为算出来的是角的余角的余弦值 非正常考你余弦值,需要再算一步。
直线l 与平面α所成的角为θ,则0≤θ≤π2,计算方法:sin θ=|l ⃗⋅n 1⃗⃗⃗⃗⃗⃗||l⃗|⋅|n ⃗⃗|; (3)二面角:同进同出为补角;一进一出为原角。
注意:考试从图中观察,若为钝角就取负值,若为锐角就取正值。
平面α,β所成的二面角为θ,则0≤θ≤π,如图①,AB ,CD 是二面角α-l -β的两个面内与棱l 垂直的直线,则二面角的大小θ=⟨AB⃗⃗⃗⃗⃗⃗,CD ⃗⃗⃗⃗⃗⃗⟩.如图②③,n ⃗⃗1,n 2⃗⃗⃗⃗⃗分别是二面角α-l -β的两个半平面α,β的法向量,则二面角的大小θ满足|cos θ|=|n⃗⃗1⋅n 2⃗⃗⃗⃗⃗⃗|n⃗⃗1|⋅|n2⃗⃗⃗⃗⃗⃗||,二面角的平面角大小是向量n 1与n 2的夹角(或其补角). (4)空间距离额计算:通常包含点到平面距离,异面直线间距离。
二、空间向量基本步骤空间向量求余弦值或正弦值四步法(1)建系:三垂直,尽量多点在轴上;左右下建系,建成墙角系;锥体顶点在轴上;对称面建系。
一定要注明怎样建成的坐标系(2)写点坐标(3)写向量:向量最好在面上或者轴上(可简化计算量) (4)法向量的简化计算直线的方向向量和平面的法向量(1)直线的方向向量就是指和这条直线平行(或共线)的向量,记作,显然一条直线的方向向量可以有无数个.(2)若直线l ⊥α,则该直线的方向向量即为该平面的法向量,平面的法向量记作,有无数多个,任意两个都是共线向量.平面法向量的求法:设平面的法向量为α⃗=(x,y,z ).在平面内找出(或求出)两个不共线的向量a ⃗=(x 1,y 1,z 1),b ⃗⃗=(x 2,y 2,z 2),根据定义建立方程组,得到{α⃗×a ⃗=0α⃗×b ⃗⃗=0,通过赋值,取其中一组解,得到平面的法向量.三、空间向量求距离向量方法求异面直线距离:先求两异面直线的公共法向量,再求两异面直线上任意两点的连结线段在公共法向量上的射影长。
高考数学一轮复习利用空间向量求空间角与距离

1 + 1
2
3 31 +
· = 0,
则൝
即ቐ
· = 0,
4 31 = 0,
= 0,
令z1=2,则m=(0,-3,2).
目录
所以|cos<n,m>|=
·
||·||
4 3
= .
13
设二面角C-AE-B的大小为θ,则sin θ= 1−
11
即二面角C-AE-B的正弦值为 .
13
因为AP=PB,所以PD⊥AB.
因为PO为三棱锥P-ABC的高,所以PO⊥平面ABC,
因为AB⊂平面ABC,所以PO⊥AB.
又PO,PD⊂平面POD,且PO∩PD=P,所以AB⊥平面POD.
因为OD⊂平面POD,所以AB⊥OD,
又AB⊥AC,所以OD∥AC,因为OD⊄平面PAC,AC⊂平面APC,所以OD∥
||
|AP·|
| |
;
(3)两异面直线间的距离:即两条异面直线公垂线段的长度.
目录
=
1.判断正误.(正确的画“√”,错误的画“×”)
(1)两直线的方向向量所成的角就是两条直线所成的角.
(
)
答案:(1)×
(2)直线的方向向量和平面的法向量所成的角就是直线与平面所成的角.
(
)
答案:(2)×
目录
弦值.
解 (2)连接OA,因为PO⊥平面ABC,OA,OB⊂平面ABC,所以
PO⊥OA,PO⊥OB,
所以OA=OB= 2 −2 = 52 −32 =4.
1
易得在△AOB中,∠OAB=∠ABO=30°,所以OD=OAsin 30°=4× =2,
3
2
高三复习专题:向量方法求空间角和距离

高三复习专题:向量方法求空间角肖冠承在高考的立体几何试卷中,求角与距离是常考查的问题,其传统的“三步曲”解法:“作图、证明、解三角形”,作辅助线多、技巧性强,是教案和学习的难点.向量进入高中教材,为立体几何增添了活力,新思想、新方法与时俱进,本专题将运用向量方法简捷地解决这些问题.b5E2RGbCAP1求空间角问题空间的角主要有:异面直线所成的角;直线和平面所成的角;二面角.<1)求异面直线所成的角设、分别为异面直线a、b的方向向量,则两异面直线所成的角=<2)求线面角设是斜线l的方向向量,是平面的法向量,则斜线l与平面所成的角=<3)求二面角法一、在内,在内,其方向如图,则二面角的平面角=法二、设是二面角的两个半平面的法向量,其方向一个指向内侧,另一个指向外侧,则二面角的平面角=例1.如图,在棱长为2的正方体中,E、F分别是棱的中点.<Ⅰ)求异面直线所成的角;<II)求和面EFBD所成的角;解:<Ⅰ)记异面直线所成的角为,则等于向量的夹角或其补角,<II)如图建立空间坐标系,则,设面的法向量为由得又记和面EFBD所成的角为则∴和面EFBD所成的角为.设计说明:1.作为本专题的例1,首先选择以一个容易建立空间直角坐标系的多面体―――正方体为载体,来说明空间角的向量求法易于学生理解.p1EanqFDPw2.解决(1>后,可让学生进一步求这两条异面直线的距离,并让学生体会一下:如果用传统方法恐怕很难<不必多讲,高考对公垂线的作法不作要求).DXDiTa9E3d3.完成这2道小题后,总结:对于易建立空间直角坐标系的立几题,无论求角、距离还是证明平行、垂直<是前者的特殊情况),都可用向量方法来解决,RTCrpUDGiT向量方法可以人人学会,它程序化,不需技巧.例2.如图,三棱柱中,已知A BCD是边长为1的正方形,四边形是矩形,<Ⅰ)若=1,求直线AB到面的距离.<II)试问:当的长度为多少时,二面角的大小为解:<Ⅰ)如图建立空间坐标系,则设面的法向量为则得直线AB到面的距离d就等于点A到面的距离,也等于向量在面的法向量上的投影的绝对值,<II)易得面的法向量向量的夹角为由得当=1时,二面角的大小为.设计说明:1.通过<Ⅰ),复习线面距离转化为点面距离再转化为一向量在一向量<法向量)投影的绝对值的解题思路与方法.5PCzVD7HxA2.通过<II),复习面面角转化为两向量的夹角或其补角的方法,也可借此机会说明为什么这两个角相等或互补,就没有其他情况.jLBHrnAILg通过上面的例子,我们看到向量方法<更确切地讲,是用公式:)解决空间角和距离的作用,当然,以上所举例子,用传统方法去做,也是可行的,甚至有的<例2)还较为简单,用向量法的好处在于克服传统立几以纯几何解决问题带来的高度的技巧性和随机性.向量法可操作性强―――运算过程公式化、程序化,有效地突破了立体几何教案和学习中的难点,是解决立体几何问题的重要工具.充分体现出新教材新思想、新方法的优越性.这是继解读几何后用又一次用代数的方法研究几何形体的一块好内容,数形结合,在这里得到淋漓尽致地体现.xHAQX74J0X申明:所有资料为本人收集整理,仅限个人学习使用,勿做商业用途。
高考数学复习:利用向量求空间角和距离

(2)方法一:不存在,证明如下:当面B′OA⊥面AOC时,三
棱锥B′ -AOC的体积最大,因为面B′OA∩面AOC=AO,
B′O⊥AO,所以B′O⊥面AOC,所以OC⊥OB′,又因为
OC⊥OA,所以OC⊥平面AOB′,在直角三角形CPO中,
CO=1,COP ,sinCPO 所以6 POCC=, ,所以 6
令x1=1,得n1=(1,-1,0).
设平面PBC的一个法向量为n2=(x2,y2,z2),
由n2·PC=0,n2· B=C 0得
y2x2
z2 0,
0,?
令y2=1得n2=(0,1,1), 设二面角C -PB -D的大小为θ,则cos θ= 所以θ=60°.
| n1 n2 | 1 , | n1 || n2 | 2
D. 4 15
【解析】选A.以D为原点,DA为x轴,DC为y轴,DD1为z 轴,建立空间直角坐标系,
设正方体ABCD-A1B1C1D1的棱长为2,则N(1,2,2), D(0,0,0),C(0,2,0),M(2,2,1),则 C=M(2,0,1), DN=(1,2,2),设异面直线所成角为θ, 则cos θ= | CM DN | 4所以 4异5面,直线CM与
( 2,0,0) ( 2,0, 2),
所以
cos〈A1F,D1E〉
|
A1F A1F |
D1E | D1E
|
2
2 2 1
解得 1 ( 1 舍去).
3
3
答案: 1
3
3 2, 5 10
【规律方法】利用向量求线线角的解题策略 (1)向量法求异面直线所成的角的方法有两种 ①基向量法:利用线性运算; ②坐标法:利用坐标运算.
D. 10 10
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
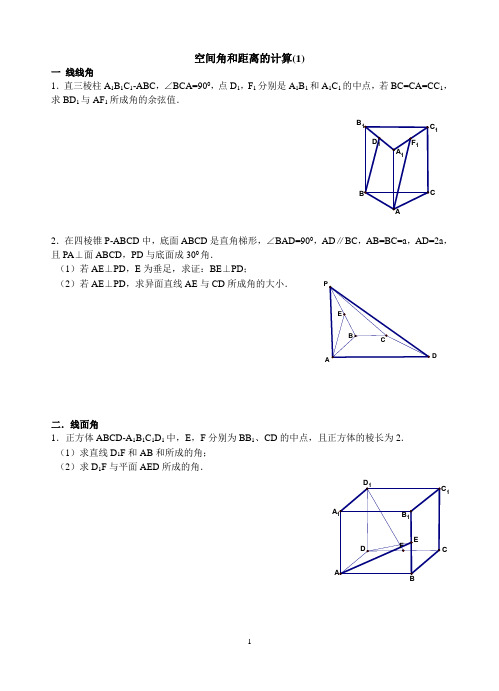
高考专题:空间角和空间距离的求法一. 直线和平面所成的角1.定义:直线和平面所成的角,应分三种情况(1)直线与平面斜交时,直线和平面所成的角是指这条直线和它在平面上的射影所成的锐角;(2)直线和平面垂直时,直线和平面所成的角为。
90(3)直线和平面平行或在平面内时,直线和平面所成的角为。
由此可知,直线和平面所成角的范围是]2,0[π,斜线和平面所成的角的范围是]2,0π( 2.求斜线和平面所成角的方法方法一:定义法或几何法: 斜线和平面所成的角是一个直角三角形的锐角,它的三边分别是平面的垂线、斜线和斜线在平面上的射影,通过斜线上的某个点作出平面的垂线、垂足和斜足的连线是斜线在平面上的射影,这里引平面的垂线,确定垂足的位置是产生线面角的关键。
常借助以下两个方法确定垂足:A: 借助面面垂直的性质:若两个平面垂直,则在第一个平面内的一点在第二个平面内射影在两平面的交线上且垂直于交线。
B :用二面角的平面角的性质:平面角的一边上任意一点到另一边的距离都垂直于第二边所在的平面;方法二:三弦公式法:如图,已知PA 与PB 分别是平面α的垂线和斜线,在平面α内过斜足B 任意引一直线BC ,设θθθ=∠=∠=∠PBC ABC PBA ,,21,有21cos cos cos θθθ⋅=。
方法三:虚拟高法:不需要做出所求线面角,而是先确定出斜线上的某点到斜足的距离L,再求出该点到已知平面的距离d (可用转化法或向量法求得);设斜线与平面所成的角为θ,则Sin θ=Ld.一般的当线面角不易做出时常用该法。
方法四:空间向量法:建立恰当的空间直角坐标系,设直线的方向向量为,平面的法向量为,所求线面角为θ;则=θsin二. 二面角1.定义: 从一条直线出发的两个半平面所组成的图形叫二面角,二面角的大小是通过其平面角来度量的,而二面角的平面角需要具有以下三个特点: (1)顶点在棱上;(2)两边分别在两个面内;(3)角的两边都与棱垂直。
一般认为二面角的范围是]180,0[。
2.求二面角的方法方法一:几何法:即,根据二面角平面角的定义直接找出或做出二面角的平面角,再求解。
常见的二面角平面角的几何作法有:① 定义法:在棱上任取一点,过这点在两个面内分别引棱的垂线,这两条射线所成的角,就是二面角的平面角。
② 三垂线定理:自二面角的一个面上一点向另一面引垂线,再由垂足向棱作垂线得到棱上的点(即斜足),这点和斜足的连线和斜足与垂足连线所夹的角,即为二面角的平面角。
③ 垂面法:自空间一点作与棱垂直的平面,截二面角得两射线,这两条射线所成的角就是二面角的平面角。
方法二:面积射影公式法:若二面角的一个面的面积为S ,它在另一个面上的射影面积为S',两平面的夹角为θ,则有ss 'cos =θ,然后再根据图形确定二面角的大小;当作二面角的平面角有困难时,可考虑利用面积射影公式求出二面角的大小。
方法三:间接转化法:两个平面的垂线的夹角即为两平面的夹角;然后再根据图形确定二面角的大小。
方法四:空间向量法:设,分别是两平面的法向量,则两法向量的夹角或其补角就是两平面的夹角;然后再根据图形确定二面角的大小。
三.空间距离的定义及求解方法:1、点到直线的距离:利用已知条件作出点到直线的垂线段。
一般应用三垂线定理或线面垂直等找到垂线段,垂线段长就为所求。
2、点到平面的距离:从平面外一点引这个平面的垂线,这个点和垂足间的距离叫做这个点到平面的距离。
点到平面的距离是有关距离的问题的重点,它主要由三种方法求得:方法一:用定义,直接作出这段距离,经论证再计算,即确定其在平面内的位置; 常用以下结论确定垂足的位置:A: 借助面面垂直的性质:若两个平面垂直,则在第一个平面内的一点在第二个平面内射影在两平面的交线上且垂直于交线。
B: 三棱锥的三条侧棱两两相等或侧棱与底面所成的角均相等,则顶点在底面上的射影为底面三角形的外心。
C: 三棱锥的顶点到底面三角形三边所在直线的距离相等或侧面与底面所成的二面角均相等,则顶点在底面上的射影为底面三角形的内心或旁心;D: 三棱锥的三侧棱两两垂直或对棱垂直或三侧面两两垂直,则顶点在底面上的射影为底面三角形的垂心; E:AOB ∠所在平面外一点P 到AOB ∠的两边距离相等或OP 与OA 及OB 所成的角相等,则P 在AOB ∠所在平面内的射影在AOB ∠的角平分线上。
F:用二面角的平面角的性质:平面角的一边上任意一点到另一边的距离都垂直于第二边所在的平面;方法二:转化为锥体的高,用等体积法求解。
方法三:空间向量法:若求O到平面α的距离,可在平面内任选一点A,求出OA 及平面的法向量。
则距离d3、直线到它的平行平面的距离的求法:转化为直线上一个特殊点到平面的距离。
即转化为点面距离。
4、两平行平面的距离:在一个平面内任取一点,作它到另一个平面的垂线段,该垂线段的长即为所求。
实际上也是点面距。
5、两异面直线的距离:注意与两直线“都垂直相交”。
常有直接法和转化法,向量法三种:① 直接法:做出两异面直线的公垂线段,求解。
常见图形一般为正方体、长方体、正 四面体、正三棱锥中异面直线间的距离。
② 转化法:把两异面直线分别置于两平行平面,两平行平面间距离即为所求。
③ 空间向量法:在两条异面直线上各取一点A,B,求出AB 及和两条异面直线均垂直的一个向量,则距离d.6、球面上两点间的距离的求法:球面上两点间的最短距离,是经过这两点的大圆在这两点间的一段劣弧的长。
公式:R L ⋅=θ(AOB ∠=θ,O 为球心,即θ为球心角,R 为球半径)。
7、任意几何体表面上两点间的最短距离问题:把该几何体沿某些线剪开后,铺平置于一个平面;此时两点间所连的线段长就是所求最短距离。
难点是需分析出该几何体所有可能的展开情形。
四. 专题突破训练:1.(2019咸阳二模)如图,在直三棱柱CB A ABC 111-中,90,ο=∠=ACB BC AC ,D 是CC 1的中点。
(1)求证:平面⊥DB A 1平面A B AB 11; (2)若异面直线B A 11与BC 1所成的角为60ο,求平面DB A 1与平面ABC 夹角的余弦值.法四:过A 做AH ⊥B A 1交B A 1于H. 则,由(1)可得BD AH A 1平面⊥又因为ABC A A 平面⊥1,所以AH A ∠1就是平面DB A 1与平面ABC 的夹角。
显然BA AH A A 11∠=∠.又由异面直线B A 11与BC 1所成的角为60ο得=∠C AB160ο由BC AC =得A B C C 11=,所以C AB 1∆为正三角形;即,B A AB C C 11==所以AC C C =1.假设AC=BC=2则22,21==AB A A , 所以321=B A所以,363222cos 11cos ==∠=∠BA AH A A 所以平面DB A 1与平面ABC 的夹角的余弦值为36。
2.(2010陕西)如图,在四棱锥P-ABC中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB=2,BC=22,E,F分别是AD,PC的中点。
(1)证明:PC⊥平面BEF (2)求平面BEF与平面BAP夹角的大小。
3.(2019全国1卷理科)如图,直四棱柱ABCD –A 1B 1C 1D 1的底面是菱形,AA 1=4,AB =2,∠BAD =60°,E ,M ,N 分别是BC ,BB 1,A 1D 的中点.(1)证明:MN ∥平面C 1DE ; (2)求二面角A-MA 1-N 的正弦值.4.(2019全国2卷理科)如图,长方体ABCD–A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.(1)证明:BE⊥平面EB1C1;(2)若AE=A1E,求二面角B–EC–C1的正弦值.5.(2019全国3卷理科)图1是由矩形ADEB,Rt△ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°,将其沿AB,BC折起使得BE与BF重合,连结DG,如图2.(1)证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;(2)求图2中的二面角B−CG−A的大小.6.(2018全国1卷理科).如图,四边形ABCD为正方形,E,F分别为AD,BC的中点,以DF为折痕把△DFC折起,使点C 到达点P的位置,且PF⊥BF.(1)证明:平面PEF⊥平面ABFD;(2)求DP与平面ABFD所成角的正弦值.由已知可得,BF⊥PF,BF⊥EF,所以BF⊥平面PEF.又BF ⊂平面ABFD ,所以平面PEF ⊥平面ABFD.(2)作PH ⊥EF ,垂足为H.由(1)得,PH ⊥平面ABFD.以H 为坐标原点,HF⃗⃗⃗⃗⃗ 的方向为y 轴正方向,|BF⃗⃗⃗⃗⃗ |为单位长,建立如图所示的空间直角坐标系H-xyz.由(1)可得,DE ⊥PE.又DP=2,DE=1,所以PE=√3. 又PF=1,EF=2,故PE ⊥PF .可得PH=√32,EH=32.则H (0,0,0),P (0,0,√32),D (-1,-32,0), DP ⃗⃗⃗⃗⃗ =1,32,√32,HP⃗⃗⃗⃗⃗⃗ =(0,0,√32)为平面ABFD 的法向量.设DP 与平面ABFD 所成角为θ, 则sin θ=|HP ⃗⃗⃗⃗⃗⃗ ·DP⃗⃗⃗⃗⃗⃗ |HP ⃗⃗⃗⃗⃗⃗||DP ⃗⃗⃗⃗⃗⃗||=34√3=√34.所以DP 与平面ABFD 所成角的正弦值为√34. 7.(2018全国2卷文科).如图,在三棱锥P ABC -中,AB BC ==4PA PB PC AC ====,O 为AC 的中点.(1)证明:PO ⊥平面ABC ;(2)若点M 在棱BC 上,且2MC MB =,求点C 到平面POM 的距离.8.(2018全国2卷理科)如图,在三棱锥P ABC -中,AB BC ==4PA PB PC AC ====,O 为AC 的中点.(1)证明:PO ⊥平面ABC ;(2)若点M 在棱BC 上,且二面角M PA C --为30︒,求PC 与平面PAM 所成角的正弦值.9.(2018全国3卷理科)如图,边长为2的正方形所在的平面与半圆弧所在平面垂直,是弧上异于,的点.(1)证明:平面平面;(2)当三棱锥体积最大时,求面与面所成二面角的正弦值.CABCD »CD M »CD C D AMD ⊥BMC M ABC -MAB MCD10.(2017全国2卷理科)如图,四棱锥P -ABCD 中, 侧面P AD 为等边三角形且垂直于底面ABCD ,AB =BC=12AD ,∠BAD =∠ABC =90°,E 是PD 的中点. (1)证明:直线CE ∥平面P AB ;(2)点M 在棱PC 上,且直线BM 与底面ABCD 所成角为45°,求二面角M -AB -D 的余弦值.11.如图,平面α内有ABC Rt ∆,。
