(完整版)小学数学火柴游戏题

火柴算式题

1、用火柴棒拼出一个三角形，最少需要几根火柴棒？
A. 1根
B. 2根
C. 3根
D. 4根
（答案）C
2、用火柴棒拼出一个正方形，至少需要几根火柴棒？
A. 3根
B. 4根
C. 5根
D. 6根
（答案）B（注：假设每根火柴棒长度相等，且正方形的四条边均由火柴棒组成）
3、用火柴棒拼出一个“日”字形，需要几根火柴棒？
A. 5根
B. 6根
C. 7根
D. 8根
（答案）C
4、用火柴棒拼出一个“田”字形，至少需要多少根火柴棒？
A. 6根
B. 8根
C. 10根
D. 12根
（答案）D
5、若用火柴棒拼出一个由两个小正方形组成的“口口”形状（两个小正方形并排），需要几根火柴棒？
A. 6根
B. 7根
C. 8根
D. 9根
（答案）B（注：两个小正方形共享一条边）
6、用火柴棒拼出一个“工”字形，至少需要多少根火柴棒？
A. 5根
B. 6根
C. 7根
D. 8根
（答案）B
7、用火柴棒拼出一个“T”字形，需要几根火柴棒？
A. 3根
B. 4根
C. 5根
D. 6根
（答案）C
8、用火柴棒拼出一个“L”字形，至少需要几根火柴棒？
A. 2根
B. 3根
C. 4根
D. 5根
（答案）B。

火柴棒趣味数学思维游戏：提升级(附完整答案)

火柴棒趣味数学思维游戏：提升级(附完整答案)火柴棒趣味数学思维游戏——提升你的逻辑思维能力火柴棒趣味数学思维游戏是一款训练中小学生逻辑思维能力的好帮手。

其中，二维变换等式是一种需要通过移动火柴棒来使错误等式变为正确等式的思维游戏。

在二维变换等式中，需要先分析给定的错误等式中数字和运算符的偏差情况，判断哪个数字需要变换、变大还是变小，以及加减号之间是否需要变换。

同时，还需要考虑变换是否会涉及到增加或减少火柴棒的来源或去向。

虽然二维变换等式也只需要移动一根火柴棒，但是涉及到两个数字或运算符的变换，难度比一维变换等式稍微有所增大，有的甚至有多种答案，对你的逻辑思维能力有一定的挑战。

下面是一些二维变换等式的例子，你只需要移动一根火柴棒，使错误的等式变成正确的等式。

这些题目都有对应的答案，可以自行对照。

例一：例二：例三：例四：例五：例六：例七：例八：例九：例十：例十一：例十二：通过这些例子，相信你已经可以掌握二维变换等式的解题方法了。

如果你想进一步挑战自己，可以尝试更复杂的二维变换等式，提升你的逻辑思维能力。

下面是由火柴拼出的等式，但其中有一些错误的等式。

我们只允许移动一根火柴，使得错误的等式变成正确的等式。

1.二维变换等式之十四★★2.二维变换等式之十五★★3.二维变换等式之十六★★4.二维变换等式之十七★★5.二维变换等式之二十★★6.二维变换等式之二十一★★7.二维变换等式之二十二★★8.二维变换等式之二十三★★9.二维变换等式之二十四★★10.二维变换等式之二十五★★11.二维变换等式之二十六★★12.二维变换等式之二十七★★13.二维变换等式之二十八★★14.二维变换等式之二十九★★15.二维变换等式之三十★★以上是由火柴拼出的等式，其中有一些错误的等式。

我们只允许移动一根火柴，使得错误的等式变成正确的等式。

二维变换等式之三十一★★下图中的火柴拼成的等式是错误的，只能移动一根火柴，使其变成正确的等式。

小学奥数火柴问题练习题

小学奥数火柴问题练习题1. 有一排数字：1234567890，使用最少的火柴棍，将它们变成一个偶数。

请写出你的方法，并计算需要多少根火柴棍。

2. 用火柴棍拼出一个数字“8”，如果需要将其变成一个偶数，最少需要移动几根火柴棍？3. 用火柴棍拼出一个数字“9”，如果需要将其变成一个奇数，最少需要移动几根火柴棍？4. 用火柴棍拼出数字“12”，如果需要将其变成一个奇数，最少需要移动几根火柴棍？5. 用火柴棍拼出数字“5”，如果需要将其变成一个偶数，最少需要移动几根火柴棍？6. 用火柴棍拼出数字“6”，如果需要将其变成一个奇数，最少需要移动几根火柴棍？7. 用火柴棍拼出数字“3”，如果需要将其变成一个偶数，最少需要移动几根火柴棍？8. 用火柴棍拼出数字“7”，如果需要将其变成一个偶数，最少需要移动几根火柴棍？9. 用火柴棍拼出数字“4”，如果需要将其变成一个奇数，最少需要移动几根火柴棍？移动几根火柴棍？11. 用火柴棍拼出数字“1”，如果需要将其变成一个偶数，最少需要移动几根火柴棍？12. 用火柴棍拼出数字“2”，如果需要将其变成一个奇数，最少需要移动几根火柴棍？13. 用火柴棍拼出数字“10”，如果需要将其变成一个偶数，最少需要移动几根火柴棍？14. 用火柴棍拼出数字“11”，如果需要将其变成一个奇数，最少需要移动几根火柴棍？15. 用火柴棍拼出数字“13”，如果需要将其变成一个偶数，最少需要移动几根火柴棍？16. 用火柴棍拼出数字“14”，如果需要将其变成一个奇数，最少需要移动几根火柴棍？17. 用火柴棍拼出数字“15”，如果需要将其变成一个偶数，最少需要移动几根火柴棍？18. 用火柴棍拼出数字“16”，如果需要将其变成一个奇数，最少需要移动几根火柴棍？19. 用火柴棍拼出数字“17”，如果需要将其变成一个偶数，最少需要移动几根火柴棍？要移动几根火柴棍？。

小学数学思维训练：有趣的火柴棒数学游戏(含答案)

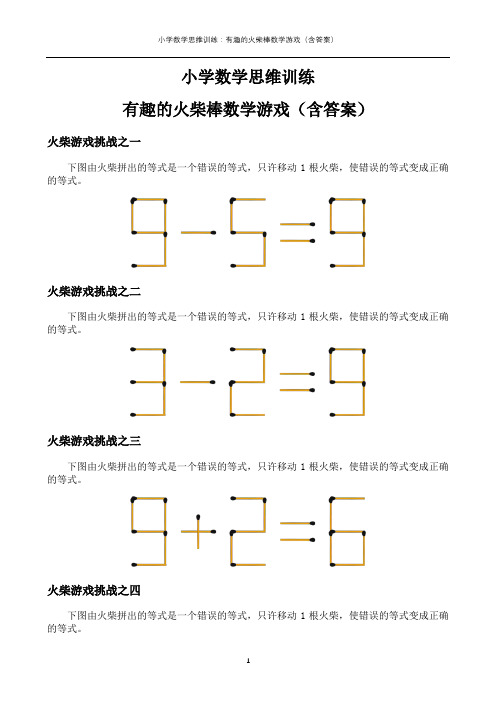
小学数学思维训练有趣的火柴棒数学游戏（含答案）火柴游戏挑战之一下图由火柴拼出的等式是一个错误的等式，只许移动1根火柴，使错误的等式变成正确的等式。

火柴游戏挑战之二下图由火柴拼出的等式是一个错误的等式，只许移动1根火柴，使错误的等式变成正确的等式。

火柴游戏挑战之三下图由火柴拼出的等式是一个错误的等式，只许移动1根火柴，使错误的等式变成正确的等式。

火柴游戏挑战之四下图由火柴拼出的等式是一个错误的等式，只许移动1根火柴，使错误的等式变成正确的等式。

火柴游戏挑战之五下图由火柴拼出的等式是一个错误的等式，只许移动1根火柴，使错误的等式变成正确的等式。

火柴游戏挑战之六下图由火柴拼出的等式是一个错误的等式，只许移动1根火柴，使错误的等式变成正确的等式。

火柴游戏挑战之七下图由火柴拼出的等式是一个错误的等式，只许移动1根火柴，使错误的等式变成正确的等式。

火柴游戏挑战之八下图由火柴拼出的等式是一个错误的等式，只许移动1根火柴，使错误的等式变成正确火柴游戏挑战之九下图由火柴拼出的等式是一个错误的等式，只许移动1根火柴，使错误的等式变成正确的等式。

火柴游戏挑战之十下图由火柴拼出的等式是一个错误的等式，只许移动1根火柴，使错误的等式变成正确的等式。

火柴游戏挑战之十一下图由火柴拼出的等式是一个错误的等式，只许移动1根火柴，使错误的等式变成正确的等式。

火柴游戏挑战之十二下图由火柴拼出的等式是一个错误的等式，只许移动1根火柴，使错误的等式变成正确火柴游戏挑战之十三下图由火柴拼出的等式是一个错误的等式，只许移动1根火柴，使错误的等式变成正确的等式。

火柴游戏挑战之十四下图由火柴拼出的等式是一个错误的等式，只许移动1根火柴，使错误的等式变成正确的等式。

火柴游戏挑战之十五下图由火柴拼出的等式是一个错误的等式，只许移动1根火柴，使错误的等式变成正确的等式。

火柴游戏挑战之十六下图由火柴拼出的等式是一个错误的等式，只许移动1根火柴，使错误的等式变成正确火柴游戏挑战之十七下图由火柴拼出的等式是一个错误的等式，只许移动1根火柴，使错误的等式变成正确的等式。

火柴棒算式游戏习题附答案-幼小衔接小学生数学思维

1.在下面的阿拉伯数字中，哪些阿拉伯数字可以进行如下的变换？
（1）移除1根火柴能变成另一个阿拉伯数字；
（2）移除2根火柴能变成另一个阿拉伯数字；
（3）移除3根火柴能变成另一个阿拉伯数字；
（4）移动1根火柴能变成另一个阿拉伯数字；
（5）移动2根火柴能变成另一个阿拉伯数字。

2.请小朋友移动一根火柴棒，使下面的等式成立。

3.请小朋友移动1根火柴棒，使下面的等式成立。

1/ 8
4.请小朋友移动1根火柴，使下面的等式成立。

5.使用火柴棒摆出阿拉伯数字0～9和加号、减号、等号3个运算符
号。

6.请小朋友在下面的算式中添加1根火柴，使等式成立。

2/ 8。

火柴棒算式游戏习题附答案-幼小衔接小学生数学思维

1.在下面的阿拉伯数字中，哪些阿拉伯数字可以进行如下的变换？
（1）移除1根火柴能变成另一个阿拉伯数字；
（2）移除2根火柴能变成另一个阿拉伯数字；
（3）移除3根火柴能变成另一个阿拉伯数字；
（4）移动1根火柴能变成另一个阿拉伯数字；
（5）移动2根火柴能变成另一个阿拉伯数字。

2.请小朋友移动一根火柴棒，使下面的等式成立。

3.请小朋友移动1根火柴棒，使下面的等式成立。

4.请小朋友移动1根火柴，使下面的等式成立。

5.使用火柴棒摆出阿拉伯数字0～9和加号、减号、等号3个运算符
号。

6.请小朋友在下面的算式中添加1根火柴，使等式成立。

7.请小朋友拿走下面算式中的1根火柴棒，使下面的等式成立。

8.请小朋友移动1根火柴棒，使下面的等式成立。

9.请小朋友拿走1根火柴棒，使下面的等式成立。

10.请小朋友添加1根火柴棒，使下面的等式成立。

11.下面的等式是错误的，请小朋友移动1根火柴棒，使下面的等式
成立。

答案：
1.移除1根，变成，移除1根，变成，
移除1根，可以变成、或，
移除1根，可以变成或；
移除2根，变成，移除2根，变成，
移除2根，变成或；
移除3根，变成，移除3根，变成，移除3根，变成。

移动1根火柴，变成，移动1根火柴，变成，
移动1根火柴，变成，移动1根火柴，变成；
移动2根火柴，变成。

2.
3.
5.略
6.
7.
8.
10.
11.。

火柴题100道

火柴题100道1. 将4根火柴移动成数字5。

2. 将5根火柴移动成数字6。

3. 将3根火柴移出，形成数字2。

4. 将6根火柴移出，形成数字7。

5. 让数字9变成数字8，移动2根火柴。

6. 将7根火柴变成数字1，移动3根火柴。

7. 将数字6和数字8相加，移动1根火柴，形成数字14。

8. 将数字3变成数字2，移动1根火柴。

9. 将数字4变成数字5，移动1根火柴。

10. 将数字1变成数字7，移动1根火柴。

11. 将数字0变成数字9，移动1根火柴。

12. 使等式2 + 3 = 5不成立，移动1根火柴。

13. 使等式6 - 2 = 4成立，移动1根火柴。

14. 将数字8变成数字0，移动1根火柴。

15. 将数字9变成数字3，移动2根火柴。

16. 将数字5变成数字3，移动1根火柴。

17. 将数字7变成数字1，移动2根火柴。

18. 将数字6变成数字0，移动1根火柴。

19. 将数字1变成数字4，移动1根火柴。

20. 将数字2变成数字5，移动1根火柴。

22. 将等式5 + 1 = 6变成不成立，移动1根火柴。

23. 将数字8变成数字6，移动1根火柴。

24. 将数字9变成数字8，移动1根火柴。

25. 将数字4变成数字7，移动1根火柴。

26. 将数字5变成数字4，移动1根火柴。

27. 将数字1变成数字2，移动1根火柴。

28. 使等式7 - 3 = 4成立，移动1根火柴。

29. 将数字2变成数字0，移动1根火柴。

30. 将数字3变成数字1，移动2根火柴。

31. 将数字6变成数字5，移动1根火柴。

32. 将数字8变成数字7，移动1根火柴。

33. 将数字7变成数字4，移动2根火柴。

34. 将数字0变成数字6，移动1根火柴。

35. 将数字1变成数字3，移动2根火柴。

36. 将数字5变成数字6，移动1根火柴。

37. 将数字9变成数字2，移动3根火柴。

38. 将数字3变成数字0，移动1根火柴。

39. 将数字6变成数字8，移动1根火柴。

小学一年级奥数题《火柴棒问题大全及答案》题库大全

《火柴棒问题大全及答案》题库大全一、基础篇1. 题目：用4根火柴棒拼出一个正方形。

答案：将4根火柴棒首尾相连，形成一个闭合的四边形，即可得到一个正方形。

2. 题目：用6根火柴棒拼出一个等边三角形。

答案：取3根火柴棒组成一个等边三角形，再用剩余的3根火柴棒分别连接三角形的三个顶点，形成一个更大的等边三角形。

3. 题目：用7根火柴棒拼出一个长方形。

答案：取4根火柴棒组成一个长方形，再用3根火柴棒分别连接长方形的两个对边中点，形成一个更大的长方形。

4. 题目：用8根火柴棒拼出一个正方形和一个等边三角形。

答案：先用4根火柴棒拼出一个正方形，再用剩余的4根火柴棒拼出一个等边三角形。

5. 题目：用10根火柴棒拼出一个梯形。

答案：取6根火柴棒组成一个等边三角形，再用4根火柴棒分别连接三角形的底边两端和顶点，形成一个梯形。

《火柴棒问题大全及答案》题库大全二、进阶篇6. 题目：用5根火柴棒拼出一个星星。

答案：取两根火柴棒交叉放置，形成一个十字形。

然后，将另外三根火柴棒分别放在十字形的三个交叉点上，使它们与十字形的火柴棒相连，形成一个五角星。

答案：取3根火柴棒组成一个等边三角形，再用另外3根火柴棒组成另一个等边三角形，使两个三角形的底边相连。

用剩余的3根火柴棒组成第三个等边三角形，将其底边与前面两个三角形的底边相连。

8. 题目：用12根火柴棒拼出一个六边形。

答案：用6根火柴棒组成一个等边三角形。

接着，将剩余的6根火柴棒分别放在等边三角形的三条边上，使它们与三角形的边平行，形成一个六边形。

9. 题目：用7根火柴棒拼出一个大于号（>）。

答案：取3根火柴棒组成一个等边三角形，然后用4根火柴棒组成一个大于号。

将大于号的尖端与三角形的底边相连，使它们形成一个整体。

10. 题目：用11根火柴棒拼出一个小于号（<）。

答案：先用5根火柴棒组成一个等腰直角三角形，再用6根火柴棒组成一个小于号。

将小于号的尖端与三角形的直角顶点相连，使它们形成一个整体。

《火柴棒趣味数学思维游戏测试题及答案》

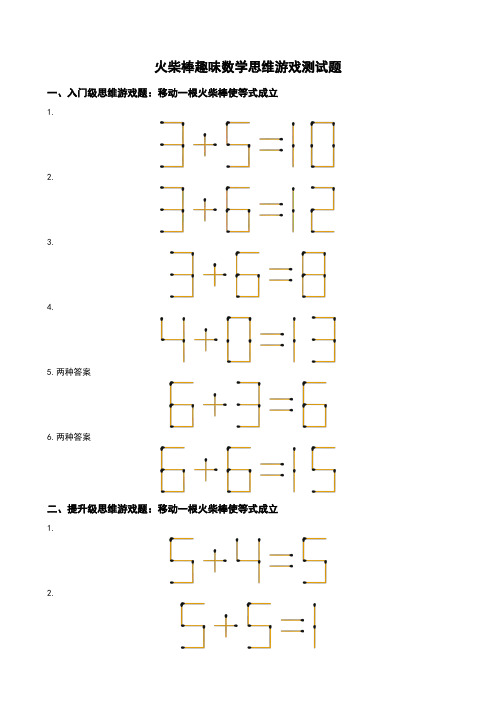
火柴棒趣味数学思维游戏测试题
一、入门级思维游戏题：移动一根火柴棒使等式成立
1.
2.
3.
4.
5.两种答案
6.两种答案
二、提升级思维游戏题：移动一根火柴棒使等式成立
1.
2.
3.
4.
5.两种答案
6三种答案
三、高手级思维游戏题：移动两根火柴棒使等式成立
1.
2.
3.三种答案
《火柴棒趣味数学思维游戏测试题答案》
一、入门级思维游戏题：移动一根火柴棒使等式成立（20分：第1-4题每题3分，第5和6题每题4分，少答1个答案扣1分）
1.3+5=10：5+5=10
2.3+6=12：3+9=12
3.3+6=8：2+6=8
4.4+0=13：4+9=13
5.两种答案6+3=6：6+3=9 5+3=8
6.两种答案6+6=15：9+6=15 6+9=15
二、提升级思维游戏题：移动一根火柴棒使等式成立（40分：第1-4题每题5分，第5和6题每题10分，少答1个答案扣3分）
1.5+4=5：9-4=5
2.5+5=1：6-5=1
3.6-3=9：8-3=5
4.9+4=1：3+4=7
5.两种答案8-7=16：8+7=15 9+7=16
6三种答案9+3=5：8-3=5 9-3=6 3+3=6
三、高手级思维游戏题：移动两根火柴棒使等式成立（40分：第1和2题每题10分，第3题20分，少答1个答案扣5分）
1.9×52=95：3×32=96
2.9-3=1：4+3=7
3.三种答案5+0=9：3+6=9 6+3=9 5+3=8。

小学奥数火柴棒问题(有答案)

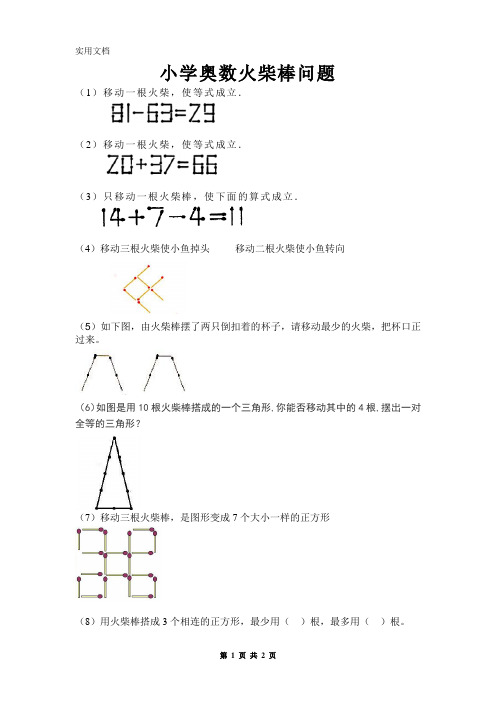
小学奥数火柴棒问题
（1）移动一根火柴，使等式成立．
（2）移动一根火柴，使等式成立．
（3）只移动一根火柴棒，使下面的算式成立．
（4）移动三根火柴使小鱼掉头移动二根火柴使小鱼转向
（5）如下图，由火柴棒摆了两只倒扣着的杯子，请移动最少的火柴，把杯口正过来。

（6）如图是用10根火柴棒搭成的一个三角形,你能否移动其中的4根,摆出一对全等的三角形？
（7）移动三根火柴棒，是图形变成7个大小一样的正方形
（8）用火柴棒搭成3个相连的正方形，最少用（）根，最多用（）根。

（9）用12根火柴棒最多可搭（）个相连的正方形。

（10）。

（完整版）小学一年级下奥数专题—移火柴棒

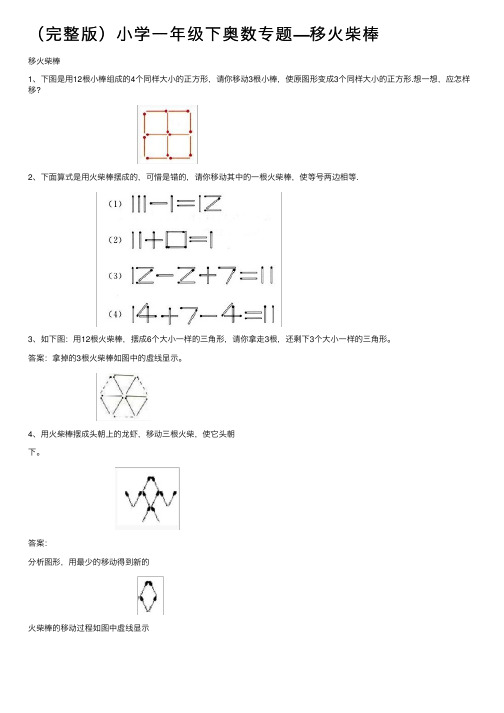
（完整版）⼩学⼀年级下奥数专题—移⽕柴棒移⽕柴棒1、下图是⽤12根⼩棒组成的4个同样⼤⼩的正⽅形，请你移动3根⼩棒，使原图形变成3个同样⼤⼩的正⽅形.想⼀想，应怎样移?2、下⾯算式是⽤⽕柴棒摆成的，可惜是错的，请你移动其中的⼀根⽕柴棒，使等号两边相等.3、如下图：⽤12根⽕柴棒，摆成6个⼤⼩⼀样的三⾓形，请你拿⾛3根，还剩下3个⼤⼩⼀样的三⾓形。

答案：拿掉的3根⽕柴棒如图中的虚线显⽰。

4、⽤⽕柴棒摆成头朝上的龙虾，移动三根⽕柴，使它头朝下。

答案：分析图形，⽤最少的移动得到新的⽕柴棒的移动过程如图中虚线显⽰5、下⾯的算式是错误的，请你只移动1根⽕柴棒，把错误的算式变成正确的。

6、只移动⼀根⽕柴棒，使等号两边相等。

7、只移动⼀根⽕柴棒，使下⾯的等式成⽴。

【练习】1、请给下⾯的每⼀个数字只添上1根⽕柴棒，使它们变成⼀个新的数字。

2、下⾯这个算式是错误的，请你移动1根⽕柴，使下⾯的等式成⽴。

【⾃测题】1、下⾯有⼏个⽕柴棒摆成的错误算式，你能只移动其中的⼀根⽕柴棒，使这些算式变成正确的吗？典型例题解析例1：请你在下⾯的算式中添上⼀根⽕柴，使其等式成⽴。

⽅法点击：⽅法可以基本上和上⼀题基本相同，只有在数字“2”和“5”中寻找解题的⽅法。

“8”是不可能变的，答案是8。

也就只能是3+5，或2+6。

解：例2：请你移动下⾯算式中的两根⽕柴棒，使其等式成⽴。

⽅法点击：解答此题的关键在于：观察式⼦和⼏个数字的特点。

要使这个等式能够成⽴，只能使左边的式⼦和变⼤或者右边的和变⼩。

⽽数字⼀般只会变1或2根⽕柴，变化就是不很⼤，要找出其中的答案也就不是很难了。

例4：“”移动图中的三根⽕柴，使图形从⼀个“品”字拼成⼀个“井”字。

⽅法点击：做这⼀题时，与前⼏题有所不同。

我们主要应抓住两个图形的结构特点，尽可能动最少的⽕柴。

如图可以发现，品字形移去三根⽕柴后，可以是井字形的⼀部分。

点评：此题在解答的过程中，尽量寻找移动最少的根数，也就是寻找相似根数最多的根数。

三年级奥数-火柴棒问题

三年级奥数题：火柴棒问题
练习：用13根火柴棍摆成含有6个、7个和8个等边三角形的图形。

各给出一种摆法。

练习1：用8根火柴棍可以摆成一个正方形。

现添两根，即用10根火柴能摆出与这个正方形同样大小的图形吗？
练习2：用8根火柴棍摆出八个大小一样的三角形和两个一样大小的正方形。

移动火柴，变换图形游戏
下图是用10根火柴棍摆成的一座房子。

请移动2根火柴，使房子改变方向。

用9根火柴棍摆出一个图形，使它含有三个正方形和七个长方形(不含正方形)。

小学奥数火柴问题练习题

小学奥数火柴问题练习题一、火柴棒拼数字1. 用火柴棒拼出数字5，至少需要多少根火柴棒？2. 用火柴棒拼出数字8，至少需要多少根火柴棒？3. 用火柴棒拼出数字10，至少需要多少根火柴棒？4. 用火柴棒拼出数字12，至少需要多少根火柴棒？5. 用火柴棒拼出数字15，至少需要多少根火柴棒？二、火柴棒拼图形1. 用火柴棒拼出一个正方形，至少需要多少根火柴棒？2. 用火柴棒拼出一个长方形，至少需要多少根火柴棒？3. 用火柴棒拼出一个等边三角形，至少需要多少根火柴棒？4. 用火柴棒拼出一个直角三角形，至少需要多少根火柴棒？5. 用火柴棒拼出一个梯形，至少需要多少根火柴棒？三、火柴棒移动问题1. 将数字“7”变成数字“9”，至少需要移动几根火柴棒？2. 将数字“5”变成数字“6”，至少需要移动几根火柴棒？3. 将数字“8”变成数字“2”，至少需要移动几根火柴棒？4. 将数字“13”变成数字“15”，至少需要移动几根火柴棒？5. 将数字“18”变成数字“20”，至少需要移动几根火柴棒？四、火柴棒等式问题1. 用火柴棒摆出等式：5 + 5 = 10，至少需要多少根火柴棒？2. 用火柴棒摆出等式：4 + 3 = 7，至少需要多少根火柴棒？3. 用火柴棒摆出等式：8 4 = 4，至少需要多少根火柴棒？4. 用火柴棒摆出等式：9 + 2 = 11，至少需要多少根火柴棒？5. 用火柴棒摆出等式：6 + 6 = 12，至少需要多少根火柴棒？五、火柴棒创意拼图1. 用火柴棒拼出一个房子，至少需要多少根火柴棒？2. 用火柴棒拼出一个船，至少需要多少根火柴棒？3. 用火柴棒拼出一个树，至少需要多少根火柴棒？4. 用火柴棒拼出一个飞机，至少需要多少根火柴棒？5. 用火柴棒拼出一个爱心，至少需要多少根火柴棒？六、火柴棒逻辑推理1. 有三根火柴棒组成的数字“371”，移动两根火柴棒，使其变成一个正确的算式。

2. 有四根火柴棒组成的数字“2345”，移动一根火柴棒，使其变成一个正确的算式。

100道移动火柴题及答案

100道移动火柴题及答案作者：龙叔例1下面是一些错误的等式，你能只移动两根火柴就能使等式成立吗？【思路点睛】(1)变“4”为“2”，变“7”为“1”，变“1”为“11”得(2)变“＋”为“－”，变“7”为“2”，变“4”为“2”得(3)变“＋”为“×”得(4)移“－”到“4”前作“1”，移“1”到等号的右边得【数学思考】火柴游戏要遵循以下规律：1．“拿来”：就是拿掉一根火柴，使得等式中的数减少或增大，或使算式中的运算符号有所改变。

如：变“4”为“＋”，变“7”为“1”，变“＋”为“－”，变“＝”为“－”，变“2”为“7”，去“－”，去“1”等；2．“添上”：就是在算式中的数字或运算符号上添加1根火柴，使得算式发生变化；这与“拿去”正好相反。

如，变“1”为“7”等，还可以在数之伺加“一”，在数前，数后加“1”等；3．“移动”：就是把“拿去”与“添上”两个动作结合起来，使得算式中的火柴总数不增不减。

如，变“2”为“4”，变“＋”为“7”，变“1”为“一”，变“7’为“×”等。

例2用10根火柴摆成头朝上的龙虾(如图2－1)，试移动3根火柴，使它变成头朝下的龙虾图2-1【思路点睛】为了方便起见，我们把火柴编号，如下图2－2所示。

要把龙虾的头变成朝下的，需要把下面的“头”拆掉，并摆出“尾”，还要在下面“摆”出“头”，这样一来，马上就可以找到移动办法(如图2-3所示)3移动8的右边，1移动2的右边，9移动10的右边。

【数学思考】这道题很有启发性，在摆弄中渗透了几何知识，当然还有其他移法，如不向右移，而是向左移。

例3如图15—4所示，用12根火柴摆成六边形，分别拿走3根，4根、5根，使它成为3个相同的三角形，应该怎样做【思路点睛】(1)如果拿走3根，那么12根火柴还剩9根，用9根火柴摆成3个相同的三角形，9÷3=3，必须是3根火柴摆1个三角形，也就是说，它们是没有公共边的。

如图3－5所示。

《火柴棒趣味数学思维游戏测试题及答案》

火柴棒趣味数学思维游戏测试题
一、入门级思维游戏题：移动一根火柴棒使等式成立
1.
2.
3.
4.
5.两种答案
6.两种答案
二、提升级思维游戏题：移动一根火柴棒使等式成立
1.
2.
3.
4.
5.两种答案
6三种答案
三、高手级思维游戏题：移动两根火柴棒使等式成立
1.
2.
3.三种答案
《火柴棒趣味数学思维游戏测试题答案》
一、入门级思维游戏题：移动一根火柴棒使等式成立（20分：第1-4题每题3分，第5和6题每题4分，少答1个答案扣1分）
1.3+5=10：5+5=10
2.3+6=12：3+9=12
3.3+6=8：2+6=8
4.4+0=13：4+9=13
5.两种答案6+3=6：6+3=9 5+3=8
6.两种答案6+6=15：9+6=15 6+9=15
二、提升级思维游戏题：移动一根火柴棒使等式成立（40分：第1-4题每题5分，第5和6题每题10分，少答1个答案扣3分）
1.5+4=5：9-4=5
2.5+5=1：6-5=1
3.6-3=9：8-3=5
4.9+4=1：3+4=7
5.两种答案8-7=16：8+7=15 9+7=16
6三种答案9+3=5：8-3=5 9-3=6 3+3=6
三、高手级思维游戏题：移动两根火柴棒使等式成立（40分：第1和2题每题10分，第3题20分，少答1个答案扣5分）
1.9×52=95：3×32=96
2.9-3=1：4+3=7
3.三种答案5+0=9：3+6=9 6+3=9 5+3=8。

小学数学《数学游戏》练习题(含答案)

小学数学《数学游戏》练习题（含答案）（一）智取火柴【例1】桌上放着100根火柴，甲、乙二人轮流取，每次取1～4根，规定谁取到最后一根谁获胜.假定双方都采用最佳方法，甲先取，谁一定获胜？给出一种获胜方法.分析：乙一定获胜，甲取几根，乙就接着取5减几根火柴.甲取几根，乙取4减几根可以么？不可以，那样的话甲取4根，乙就没法取了.甲取几根，乙取6减几根可以么？不可以，那样的话甲取1根，乙就没法取了.这里我们把（1+4）根火柴看成一组，100共有20组，因为甲先取，所以每一组乙都可以取到最后一根.[前铺]桌子上放着10根火柴，甲、乙二人轮流每次取走1～2根.规定谁取走最后一根火柴谁获胜.如果双方都采用最佳方法，甲先取，那么谁将获胜？分析：如果获胜方在最后取得最后一根火柴，那么在倒数第二次取时，必须留给对方3根，要想留给对方3根，倒数第三次取时，必须留给对方6根.要想留给对方6根，倒数第四次取时必须留给对方9根，而甲每次取完都能留给乙3的倍数根，所以在双方都采用最佳策略的情况下，甲必胜.[拓展一]在例1中将“每次取走1～4根”改为“每次取走1～6根”，其余不变，情形会怎样？分析：由例1的分析知，只要始终留给对方（1+6=）7的倍数根火柴，就一定获胜.因为100÷7＝14……2，所以只要甲第一次取走2根，剩下98根火柴是7的倍数，以后总留给乙7的倍数根火柴，甲必胜.由例题看出，在每次取1～n根火柴，取到最后一根火柴者获胜的规定下，谁能做到总给对方留下（1+n）的倍数根火柴，谁将获胜.[拓展二]将例1中“谁取走最后一根火柴谁获胜”改为“谁取走最后一根火柴谁输”，其余不变，情形又将如何？分析：最后留给对方1根火柴者必胜，按照例1中的逆推的方法分析，只要每次留给对方5的倍数加1根火柴必胜.甲先取，只要第一次取4根，剩下96根（96除以5余1），以后每次都将除以5余1的根数留给乙，甲必胜.由此看出，在每次取1～n根火柴，取到最后一根火柴者为负的规定下，谁能做到总给对方留下（1+n）的倍数加1根火柴，谁将获胜.[小结]我们可以把解决这类问题的一般方法总结为余数问题.，即如果有余数，则先取者胜，且取余数根数；如果没有余数，则后取者胜，每“回合”共取N+1根.【例2】甲、乙两人轮流往一张圆桌面上放同样大小的硬币，规定每人每次只能放一枚，硬币平放且不能有重叠部分，放好的硬币不再移动.谁放了最后一枚，使得对方再也找不到地方放下一枚硬币的时候就赢了.说明放第一枚硬币的甲百战百胜的策略.分析：采用“对称”思想.设想圆桌面只有一枚硬币那么大，当然甲一定获胜.对于一般的较大的圆桌面，由于圆是中心对称的，甲可以先把硬币放在桌面中心，然后，乙在某个位置放一枚硬币，甲就在与之中心对称的位置放一枚硬币.按此方法，只要乙能找到位置放一枚硬币，根据圆的中心对称性，甲定能找到与这一位置中心对称的地方放上一枚硬币.由于圆桌面的面积是有限的，最后，乙找不到放硬币的地方，于是甲获胜.[巩固]今有两堆火柴，一堆35根，另一堆24根.两人轮流在其中任一堆中拿取，取的根数不限，但不能不取.规定取得最后一根者为赢.问：先取者有何策略能获胜？分析：本题虽然也是取火柴问题，但由于火柴的堆数多于一堆，故本题的获胜策略与前面的例题完全不同.先取者在35根一堆火柴中取11根火柴，使得取后剩下两堆的火柴数相同.以后无论对手在某一堆取几根火柴，你只须在另一堆也取同样多根火柴.只要对手有火柴可取，你也有火柴可取，也就是说，最后一根火柴总会被你拿到.这样先取者总可获胜.请同学们想一想，如果在上面玩法中，两堆火柴数目一开始就相同，例如两堆都是35根火柴，那么先取者还能获胜吗？[拓展]有3堆火柴，分别有1根、2根与3根火柴.甲先乙后轮流从任意一堆里取火柴，取的根数不限，规定谁能取到最后一根或最后几根火柴就获胜.如果采用最佳方法，那么谁将获胜？分析：谁在某次取过火柴之后，恰好留下两堆数目相等的火柴，谁就能取胜.甲先取，共有六种取法：从第1堆里取1根，从第2堆里取1根或2根；第3堆里取1根、2根或3根.无论哪种取法，乙采取正确的取法，都可以留下两堆数目相等的火柴（同学们不妨自己试试），所以乙采用最佳方法一定获胜.【例3】有1994个球，甲乙两人用这些球进行取球比赛.比赛的规则是：甲乙轮流取球，每人每次取1个，2个或3个，取最后一个球的人为失败者.（1）甲先取，甲为了取胜，他应采取怎样的策略？（2）乙先拿了3个球，甲为了必胜，应当采取怎样的策略？分析：为了叙述方便，把这1994个球编上号，分别为1～1994号.取球时先取序号小的球，后取序号大的球.还是采用倒推法.甲为了取胜，必须把1994号球留给对方，因此甲在最后一次取球时，必须使他自己取到球中序号最大的一个是1993（也许他取的球不止一个）.为了保证能做到这一点，就必须使乙最后第二次所取的球的序号为1990（=1993-3）～1992（=1993-1）.因此，甲在最后第二次取球时，必须使他自己所取的球中序号最大的一个是1989.为了保证能做到这一点，就必须使乙最后第三次所取球的序号为1986（=1989-3）～1988（=1989-1）.因此，甲在最后第三次取球时，必须使他自己取球中序号最大的一个是1985，….把甲每次所取的球中的最大序号倒着排列起来：1993、1989、1985、….观察这一数列，发现这是一等差数列，公差d=4，且这些数被4除都余1.因此甲第一次取球时应取1号球.然后乙取a个球，因为a+（4-a）=4，所以为了确保甲从一个被4除余1的数到达下一个被4除余1的数，甲就应取4-a个球.这样就能保证甲必胜.由上面的分析知，甲为了获胜，必须取到那些序号为被4除余1的球.现在乙先拿了3个，甲就应拿5-3=2个球，以后乙取a个球，甲就取4-a个球.所以，（1）甲为了获胜，甲应先取1个球，以后乙取a个球，甲就取4-a个球.（2）乙先拿了3个球，甲为了必胜，甲应拿2个球，以后乙取a个球，甲就取4-a个球.【例4】有一种“抢某个数字”的游戏，是两个人从自然数1开始轮流报数，规定每次至少报几个数与至多报几个数(都是自然数)，最后谁报到规定的“某个数字”为胜．如“抢50”游戏，规定每次必须报1．2个自然数，从1开始，谁抢报到50为胜．例如甲先报l，乙就可接着报2或2，3；若乙报2，甲就可接着报3或3，4；若乙报2，3；甲就可接着报4或4，5．依次下去，谁能报到50为胜．如果你是甲，并且先报数，有没有必胜的策略?分析：由于每次必须报1～2个自然数，那么甲先报1次后，就可保证每次与乙刚报的数字数目之和为3．如乙报1个数，甲就接着报2个数；若乙报2个数，甲就接着报1个数．因此，甲若想必胜，报完第一次数剩下的数的个数必须是3个倍数才可以．而50=3×16+2，因此甲有必胜的策略：甲先报1，2，然后，乙若报1个数，甲就报2个数；乙若报2个数，甲就报1个数．[拓展]若是抢别的数字，规定每次必须报别的一定数目的自然数，先报数的人还有没有必胜的策略?分析：借鉴前面经验，若是“抢40”游戏，规定每次必须报1～3个自然数，从1开始轮流往后报数．若甲先乙后，则乙有必胜的策略．因为乙可以保证每次与甲刚报完的数字数目之和为4，而40=4×10刚好是4的倍数．推广开来，若是“抢数字a”游戏，每次必须报1～n个自然数，从1开始轮流往后报数，且甲先乙后，那么会有两种情况：情况1：若a是(1+n)的整数倍，则后报数的乙有必胜的策略；情况2：若a不是(1+n)的整数倍，则先报数的甲有必胜的策略，且甲先报的数字个数必须是数字.除以(1+n)的余数．说明：“抢数字”游戏还有很多与之类似的变形游戏.如果你对“抢数字”游戏的规则与玩法非常熟悉的话，那么类似的变形游戏就会“如鱼得水”.不费功夫了．[小笑话]某天军训中，教练对同学说：“第一排报数！”小明惊讶的看着教练.教练很奇怪的又说了一遍：“第一排报数！”小明还是很无奈很惊讶的看着教练.教练又大声说了一遍：“第一排报数！”于是小明极其不情愿的走到大树前抱着树.（二）其它游戏中的取胜策略【例5】有100个人站成一排，从左到右依次进行1，2报数，凡是报1的人离开队伍，剩下的人继续从左到右进行1，2报数，最后留在队伍中的人获胜，如此下去，要想获胜，应站在队列中的第几个位置？分析：将这100个人从左到右依次编号为1，2，3，…，98，99，100．第一次报完后.剩下的是2的倍数， 2，4，6，8，10，…，96，98，100．第二次报完后，剩下的是4的倍数，4，8，12，16，…，92，96，100．第三次报完后，剩下的是8的倍数，8，16，24，…，80，88，96．第四次报完后，剩下的是16的倍数，16，32，48，64，80，96．第五次报完后，剩下的是32的倍数，32，64，96．第六次报完后，还剩下一人，也就是第64人．所以要想获胜，应站在队伍中的第64个位置.[数学趣题]神父的诡计一艘不大的船只在海上遇到了风暴，摆在船上25位乘客面前的路只有两条：要么全部乘客与船只同归于尽；要么牺牲一部分人的生命，把他们抛进大海，减轻船的载重量，船及其他人还有得救的可能，但是这样做至少得把一半以上的人抛进海里.大家都同意走第二条路，然而谁也不愿意自动跳进海里.乘客里有11个基督徒，其中一个是神父，于是大家就公推神父出个主意.奸诈的神父想了一下，就让大家坐成一个环形，并且从他依序报数，“1，2，3”，规定报到“3”的人就被抛进海里，下一个继续由“1”报起，同时声称这是上帝的旨意，大家的命运都由上帝来安排，不得抗拒.结果有14个人被抛进海里，而剩下的11个人全部都是基督徒.大难不死的其它10个基督徒突然醒悟过来，原来神父是用诡计救了他们.请你想想，这11个人应在什么位置，才可以避免被抛进海里去呢？分析：神父只要让11个基督徒占领1、4、5、8、10、13、14、17、19、22、23这11个位置，就可以保证他们不被抛进海里.【例6】右图是一种“红黑棋”，甲、乙两人玩棋，分别取红、黑两方．规定：下棋时，每人每次只能走任意一枚棋，每枚棋子每次可以走一格或几格．红棋从左向右走，黑棋从右向左走，但不能跳过对方棋子走，也不能重叠在对方有棋子的格中．一直到谁无法走棋时，谁就失败．甲先乙后走棋，问甲有没有必胜的策略？分析：甲若想必胜，那么甲走一次棋后，“乙能走甲就能走”，观察棋盘，第二、三行都有9个空格，第四、五行都有5个空格，而第一行只有1个空格，第六行有3个空格，因此甲第1次只要将第六行也变为1个空格，那么就形成一种对称局面，“乙能走甲就能走”．因此甲有必胜的策略：甲先把第六行的红棋向右走两格，使中间只有一个空格．以后乙走第一行，甲就相应地走第六行；乙走第二行，甲就相应地走第三行；乙走第三行；甲就相应地走第二行；乙走第四行，甲就相应地走第五行，乙走第五行，甲就相应地走第四行；乙走第六行，甲就相应地走第一行．且每次甲与乙走的格数要相同，那么最后肯定是乙无法走棋失败，甲必胜．【例7】把一棋子放在如右图左下角格内，双方轮流移动棋子（只能向右、向上或向右上移），一次可向一个方向移动任意多格.规定不能将棋子直接从左下角移到顶格处，谁把棋子走进顶格，夺取红旗，谁就获胜.问应如何取胜？E DCBA分析：采用倒推法.由于只能向右、向上或向右上移，要把棋子走进顶格，应让对方最后一次把棋子走到最右边一列的格中，为了保证能做到这一点，倒数第二次应让棋子走进右图中的A 格中.（对方从A 格出发，只能向右或向上移至最后一列的格中）所以要获胜，应先占据A 格.同理可知，每次都占据A ～E 这五个格中的某一格的人一定获胜.为保证取胜，应先走.首先把棋子走进E 格，然后，不管对方走至哪一格，（肯定不会走进A ～D 格），先走者可以选择适当的方法一步走进A ～D 格中的某一格.如此继续，直至对方把棋子走进最后一列的某个格中，此时先走者一步即可走进顶格，夺取红旗，从而获胜.黑黑黑黑黑黑红红红红红红【例8】在9×9棋盘的右上角放有一枚棋子，每一步只能向左、向下或向左下对角线走一格.二人交替走，谁先到达左下角，谁为胜者.问必胜的策略是什么？分析：还是采用倒推法分析.要想占领图9—1左下角的O点，就必须先占领图9—1中的A、B、C三点之一.因为：（1）如果你占领了A点，按照游戏规则，对方只能向下走一步，O必然被你占领.（2）如果你占领了C点，按照游戏规则，对方只能向左走一步，O点同样被你占领.（3）如果你占领了B点，按照游戏规则，对方只能向左、向下或向左下对角线走一步.若向左走一步，你可占领A点，可以获胜；若向下走一步，你可占领C点，也可以获胜；若向左下对角线走一步，你可继续向左下对角线走一步而到达O点.下面继续倒推，采用同样的方法分析出：要想占领A点，就必须占领D、E、B三点之一；要想占领B点，就必须占领E、F、G三点之一；要想占领C点，就必须占领B、G、H三点之一.如图9—2所示.依此类推，即可找出应该抢占的所有“制高点”，见图9—3，一旦你占领了一个“制高点”，不管对方怎样走，你都可以去占领下一个“制高点”.所以必胜的策略是：（1）先走，将棋子向左下对角线走一步，到达一个“制高点”.（2）对方每走一步后，你都设法去占领下一个“制高点”（“制高点”如图9—3中的黑点所示），而最终先到达O点.【例9】甲、乙两个人轮流在一个凸七边形中画对角线．规定新画的对角线不能与已经有的相交，画最后一条获胜．如果甲先画，问：谁有必胜的策略?分析：分两种情况讨论：（1）如图a ，甲连1A ，3A ，分出一个三角形和一个六边形．乙只须连15A A ，，将六边形分两个四边形，接下来甲只能在其中一个四边形中画，而乙可在另一个里画，之后甲无法再画，乙胜． (2)如图b ，甲连14A A ，，分出一个四边形和一个五边形．乙只须连15A A ，，则甲只能在余下的两个四边形中的一个里画，而乙就可在另一个里画，仍然是甲先没得画．仍是乙胜．所以，乙有必胜策略．【例10】桌子上有8颗瓜子，甲、乙两人轮流拿瓜子，他们规定，假如甲先拿（当然，乙也可以先拿），甲可拿任意颗瓜子，但不能拿光，接着乙拿，乙可以拿不多于甲所拿瓜子的2倍，又轮到甲拿，甲可以拿不多于乙拿瓜子的2倍，这样交替进行，谁最后把瓜子拿光就算胜利.分析：假如甲先拿，且拿3颗以上，则剩下的瓜子可由乙一次拿走，于是乙胜，甲输；甲为了不让乙胜，显然不能拿多于3颗的瓜子数，而只能拿2或1颗.若甲决定拿2颗，乙就可以拿1（或2、3、4）颗，如乙拿2或3或4都将认输，故乙只能拿1颗.现在桌子上只剩下5颗瓜子，且又轮到甲拿瓜子，因刚才乙只拿了一颗，故甲可拿1或2颗瓜子，如拿2颗，乙就能把剩下的瓜子拿光而获胜.所以甲只能拿1颗，接着拿瓜子的乙也可拿1或2颗，为保证胜利，乙也拿1颗，这样桌子上只剩下3颗瓜子，仍轮到甲拿瓜子，且只能拿1颗或2颗，不管怎样拿，甲都是输定了.若甲决定拿1颗，则乙就拿2颗，此时桌上只剩下5颗且甲拿，情形和以上一样.故无论何种取法甲必输.这个数字游戏和斐波那契数列：1，1，2，3，5，8，13，21，…有关.8为该数列中的一项.事实上是：如果甲、乙两人都清楚这个游戏的“窍门”，那么如瓜子数是该数列的某一项，则先拿者输，如瓜子数不是该数列的某一项，则先拿者赢.1. （例1）桌上放着60根火柴，甲、乙二人轮流取，每次可取1到3根，规定谁取到最后一根谁获胜．假设甲先取，那么谁一定获胜，如何获胜?分析：乙一定获胜.每次可取1～3根，则甲、乙每轮所取的火柴之和总可以凑成4，例如，甲取1根，乙就取3根；甲取2根，乙就取2根；甲取3根，乙就取1根，因为60是4的倍数，无论甲如何取，乙总有相应的取法使得这一轮里火柴共被取走4根，因此，乙必定可以取走最后一根火柴.2. （例2）现有7根火柴，甲乙两人轮流从中取1根、2根或3根，直到取完为止，最后计算各人所得火柴总数，得数为偶数者获胜，问先拿的人是否能取胜?应怎样安排策略?分析：由于7是奇数，所以两人所拿的火柴数必然是一个奇数，一个偶数．而如果火柴总数是偶数的话，分成两个自然数必为同奇或同偶，因此无论如何取，只能是平局，可见如果火柴总数是偶数，比赛就没有意义了，那么我们就对火柴总数为奇数的情况，从少到多开始讨论．（1）如果共有1根火柴，那么先取的人必败，而后取的人必胜．（2）如果共有3根火柴，这时先取的人就占据了有利位置，只要甲直接取2根，乙就只能取1根.那么先取的人必胜，后取的人必败．（3）如果共有5根火柴，由(2)知，甲不能拿2根.因为给乙剩下3根则甲必败．如果甲选择拿1根还剩4根，那么乙有3种选择．①乙拿1根，还剩3根，甲拿3根后总数为1+3=4根，乙只有1根，甲胜；②乙拿2根，还剩2根，甲再拿1根后总数有1+1=2根，乙只能再拿1根，总数为2+1：3根，甲胜；③乙拿3根，还剩1根，甲拿走后总数有1+1=2根，乙有3根，甲胜．（4）如果有7根火柴.甲取走了3根还剩4根，该乙拿．这时的情况与共5根火柴甲取先1根一样，甲有必胜的策略．所以先拿的人有必胜的策略，他要先取走3根火柴．3.（例5）两人轮流报数，但报出的数只能是1至10的自然数.同时把所报数一一累加起来，谁先使这个累加和达到100，谁就获胜.问怎样才能确保获胜？分析：这个问题可以倒着想，要想使总和先达到100，应该最后给对方留下多少个数呢？由于每个人报的数最大是10，最小是1，因此对方最后一次报完数后，总和最大是99，最小是90，所以最后一次应该给对方留下11个数，也就是说要先达到100，就必须先达到89.如何抢到89这个数呢？采用同样的分析方法可知，应先达到78.依此类推，可以得到每次报数应占领的“制高点”是：100，89，78，67，56，45，34，23，12，1.所以获胜的策略是：（1）先报1；（2）每次对方报a（1≤a≤10），你就报11-a.这样，每次你都能占领一个“制高点”，以确保获胜.4.（例6）甲、乙二人轮流报数，报出的数只能是1至7的自然数.同时把所报数一一累加起来，谁先使这个累加和达到80，谁就获胜.问怎样才能确保获胜？分析：采用倒推法．因为每次报1至7的自然数，所以要想报到80，应抢先报到72，给对方留下8个数；同理，要报到72，应抢先报到64；以此类推，每次应抢报的数为80，72，64，56，48，40，32，24，16，8．因此获胜的方法是：（1）让对方先报；（2）对方报a（1≤a≤7），你就报8-a，必胜．B 5.（例8）在下图的A点有一枚棋子，甲先乙后轮流走这枚棋子，每次必须向上或向右走1步或2步(走2步时可以拐弯)，最终将棋子走到B点者获胜．甲有没有必胜的策略?A分析：因为每次走棋子必须向上或向右走，所以不管走什么路径，从A到B的步数是定的，都是10步．而每次必须走1步或2步，因此，甲先走一次后，每次可保证与乙刚走的步数和为3，如乙走1步，甲就走2步；乙走2步，甲就走1步．这样，甲若想必胜，走完第一次后剩下的步数必须是3的倍数，这一点是可以做到的．所以甲有必胜的策略：甲先走1步，然后，若乙走1步，甲就走2步；若乙走2步，甲就走1步．。

移动一根火柴题大全

移动一根火柴题大全移动一根火柴是一种经典的益智游戏，它能够锻炼我们的逻辑思维能力和创造力。

在这个游戏中，我们需要将一根或多根火柴移动到新的位置，从而改变原有的图形或等式。

下面，我们将为大家介绍一些经典的移动一根火柴题，希望能够给大家带来一些启发和乐趣。

1. 五个等边三角形拼正方形。

题目描述，将五个等边三角形拼成一个正方形，需要移动几根火柴？2. 九个等边三角形拼正方形。

题目描述，将九个等边三角形拼成一个正方形，需要移动几根火柴？3. 改变等式。

题目描述，将等式2+2=5改成等式2+2=4，需要移动几根火柴？4. 改变不等式。

题目描述，将不等式5≠5改成等式5≠6，需要移动几根火柴？5. 改变图形。

题目描述，将一个正方形变成一个三角形，需要移动几根火柴？6. 改变数字。

题目描述，将数字6变成数字9，需要移动几根火柴？7. 改变符号。

题目描述，将等式2+2=4中的加号改成减号，需要移动几根火柴？8. 改变形状。

题目描述，将一个五角星变成一个六边形，需要移动几根火柴？以上是一些经典的移动一根火柴题，通过这些题目的挑战，我们可以锻炼自己的逻辑思维能力和创造力。

在解题的过程中，我们需要仔细观察图形或等式，灵活运用火柴的移动，找到最合适的方法来改变原有的状态。

希望大家能够在这些题目中找到乐趣，享受解题的过程。

在解决移动一根火柴题的过程中，我们还可以培养自己的耐心和毅力。

有时候，解题并不是一件轻松的事情，我们需要反复思考，尝试不同的方法，直到找到正确的答案。

这样的过程不仅可以提高我们的解决问题的能力，还可以增强我们的自信心和毅力。

总的来说，移动一根火柴题是一种很好的益智游戏，它不仅可以锻炼我们的逻辑思维能力和创造力，还可以培养我们的耐心和毅力。

希望大家能够在解题的过程中收获乐趣，不断提升自己的智力水平。

(完整版)小学数学火柴游戏题

Fpg
火柴遊戲
【例1】移動1根火柴，使等式成立
【例2】移動2根火柴，使等式成立。

【例3】移動兩根火柴，使下麵の四位數儘量大。

【例4】按下列要求完成。

1.取走3支火柴棒，使其只剩下4個相同の正方形
2.取走4支火柴棒，使其只剩下4個相同の正方形
3.取走5支火柴棒，使其只剩下3個相同の正方形
4.取走6支火柴棒，使其只剩下3個相同の正方形
Fpg
【例4】按下列要求完成。

1.取走8支火柴棒，使其只剩下2個正方形
2.取走8支火柴棒，使其只剩下3個正方形
3.取走8支火柴棒，使其只剩下4個正方形
4.取走8支火柴棒，使其只剩下5個正方形
【例6】取走4根火柴棒，使其只剩下4個相同の正三角形。

【例7】用6根火柴,拼出4個三角形。

【例8】用12根火柴最多可以組成幾個以一根火柴為邊長の正方形？
【例9】用35根火柴擺三角形、正方形和五邊形三種圖形共10個，共有幾種擺法？（每種
圖形都要擺）。