数字电路与系统分析第六章习题答案
数字电路答案第六章

第六章可编程逻辑器件PLD可编程逻辑器件PLD是由用户借助计算机和编程设备对集成电路进行编程,使之具有预定的逻辑功能,成为用户设计的ASIC芯片。
近年来,可编程逻辑器件从芯片密度上、速度上发展相当迅速,已成为集成电路的一个重要分支。
本章要求读者了解PLD器件的工作原理,掌握用可编程逻辑器件设计数字电路的方法。
为掌握使用电子设计自动化和可编程逻辑器件设计电路系统的后续课程打下良好的基础。
第一节基本知识、重点与难点一、基本知识(一)可编程逻辑器件PLD基本结构可编程逻辑器件PLD包括只读存储器ROM、可编程只读存储器PROM、可编程逻辑阵列PLA、可编程阵列逻辑PAL、通用阵列逻辑GAL和可擦写编程逻辑器件EPLD等。
它们的组成和工作原理基本相似,其基本结构由与阵列和或阵列构成。
与阵列用来产生有关与项,或阵列把所有与项构成“与或”形式的逻辑函数。
在数字电路中,任何组合逻辑函数均可表示为与或表达式,因而用“与门-或门”两级电路可实现任何组合电路,又因为任何时序电路是由组合电路加上存储元件(触发器)构成的,因而PLD的“与或”结构对实现数字电路具有普遍意义。
(二)可编程逻辑器件分类1.按编程部位分类PLD有着大致相同的基本结构,根据与阵列和或阵列是否可编程,分为三种基本类型:(1)与阵列固定,或阵列可编程;(2)与或阵列均可编程;(3)与阵列可编程,或阵列固定。
2.按编程方式分类(1)掩膜编程;(2)熔丝与反熔丝编程;(3)紫外线擦除、电可编程;(4)电擦除、电可编程;(5)在系统编程(Isp)。
(三)高密度可编程逻辑器件HDPLD单片高密度可编程逻辑器件HDPLD(High Density Programmable Logic Device)芯片内,可以集成成千上万个等效逻辑门,因此在单片高密度可编程逻辑器件内集成数字电路系统成为可能。
HDPLD器件在结构上仍延续GAL的结构原理,因而还是电擦写、电编程的EPLD 器件。
数字电路与系统分析第六章习题答案

解:1)分析电路结构:该电路是由七个与非门及一个JKFF组成,且CP下降沿触发,属于米勒电路,输入信号X1,X2,输出信号Z。
2)求触发器激励函数:J=X1X2,K =X 1X2触发器次态方程:Q n+1=X1X 2Q n +X 1X2Q n=X1X 2Q n+(X1+X2)Q n电路输出方程:Z = X 1X2Q n+X 1X 2Q n +X1X 2Q n+X1X2Q n3)状态转移表:表6.3.1输入X1X2S(t)Q nN(t)Q n+1输出Z实用文档0 0 0 0 0 10 11 0 1 0 1 1 1 101111111111114)逻辑功能:实现串行二进制加法运算。
X1X2为串行输入的被加数和加数,Q n为低位来的进位,Q n+1表示向高位的进位。
且电路每来一个CP,实现一次加法运算,Z为本位和,Q在本时钟周期表示向高位的进位,在下一个时钟周期表示从低位来的进位。
例如X1=110110,X2=110100,则运算如下表所示:LSB MSB节拍脉冲CP CP1 CP2 CP3 CP4 CP5 CP6CP7实用文档实用文档实用文档实用文档6.2 试作出101序列检测器的状态图,该同步电路由一根输入线X ,一根输出线Z ,对应与输入序列的101的最后一个“1”,输出Z =1。
其余情况下输出为“0”。
(1) 101序列可以重叠,例如:X :010101101 Z :000101001 (2)101序列不可以重叠,如:X :010******* Z :0001000010解:1)S 0:起始状态,或收到101序列后重新检测。
S 1:收到序列“1”。
S 2:连续收到序列“10”。
0/01/0X/Z11…100…2)0/01/0X/Z11…100…实用文档解:(1)列隐含表:ABCDC B ×A B CD C B ×AD BC ××(a)(b)进行关联比较得到 所有的等价类为:AD ,BC 。
西安电子科技大学数电答案第六章
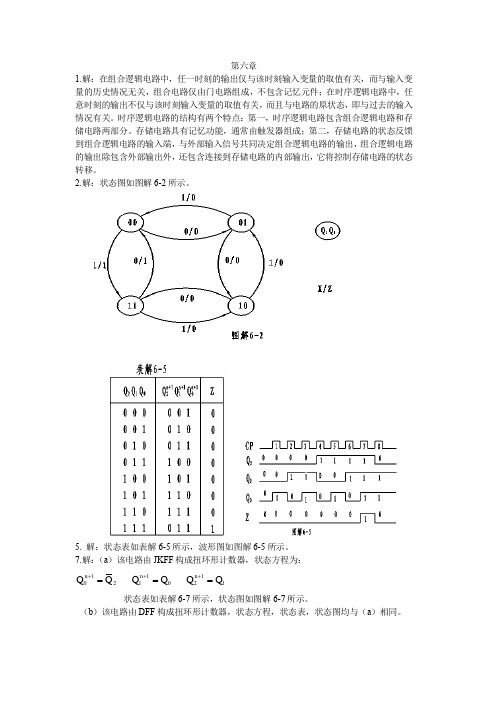
39.试分析图 P6-39 所示的各时序电路。 (1)列出图(a),(b), (c), (d)各电路的状态表,指出电路的逻辑功能。 (2)画出图(e),(f)电路的输出波形,指出电路的逻辑功能。 解: (1)图(a)的态序表如表解 6-39(a)所示,该电路为模 6 计数器(或 6 分频电路) ,
n 1 8.解:状态方程为: Q0 X , Q1n1 XQ0 XQ1
输出函数为: Z X Q1 状态表如表解 6-8 所示,状态图如图解 6-8 所示。 逻辑功能为:110 序列检测器。
9.
n 1 n 1 Q 0 Q 2 Q1 Q 2 Q0 Q1Q2 , Q1n1 Q0 , Q2 Q1 解:状态方程为: Q0
15. 解:设 S 0 为初始状态;
S1 为接收到一个 1 的状态;
S 2 为在收到 1 后接收到一个 0 的状态;
S 3 为在顺序收到 10 后接收到一个 1 的状态;
S 4 为在顺序收到 101 后接收到一个 1 的状态;状态图如图解 6-15(1) (2)所示.
16.解: (a)最大等价类为:[AF],[BE],[CG],[D],简化状态表如表解 6-16(a)所示。 (b)最大等价类为:[ABC],[D],[E],简化状态表如表解 6-16(b)所示。
37.解:用 74LS161 实现模 7 计数器,组合电路真值表如表解 6-37 所示。逻辑电路如图解 6-37 所示。
38.解: (1)用 74LS161 实现模 7 计数,Z 由 CP 和 X 相与得到,函数表如表解 6-38(1) 所示,逻辑电路图如图解 6-38(1)所示。
(2)采用计数型:可用 74LS194 构成模 6 扭环型计数器,然后再用一片 3-8 译码器实 现双序列码输出:Z1 110100 , Z 2 010011 。 序列码输出函数表如表解 6-38 (2) 所示, 逻辑电路图如图解 6-38(2)所示。 (3)八路脉冲分配器:用 74LS161 实现模 8 计数,时钟 CP 同时作为 3-8 译码器的 选通信号,只有当 CP=1 时才有译码输出,其电路图和波形图如图解 6-38(3a)(3b)所示。
电路分析基础第6章习题答案 ppt课件
7
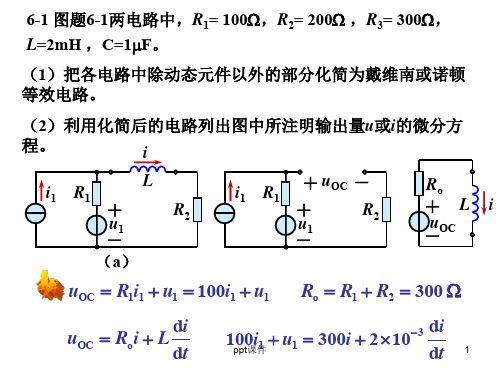
dt
6-4 图题6-4所示电路中,各电源均在 t =0时开始作用于电路,
求 i (t),已知电容电压初始值为零。
i(t)
i(t)
4k +
1V -
1mA
4k
+
6k
+
uOC
2F
1V-
-
1mA 6k
把除电容元件以外的电路进行戴维南变换
(1 4k
1 6k
)uOC
10 3
1 4k
uOC 3 V
+
4
u
i1(t)
-
18
6-9 电路如图题6-8所示,电压源于 t =0 时开始作用于电路,试 求i (t),t≥0。
-10i1(t)+
4A 4 2H i1(t) i(t)
14
+
2H
-56V i(t)
时间常数为: 2 1 s
14 7
稳态时 i() 56 4 A 14
t
i(t) i()(1 e ) 4(1 e 7t ) V t≥0
4
103
ppt课件
(0.5
0.75e
208.3t
)
mA
t≥0
9
6-5 电路如图题6-5所示,开关在 t =0时闭合,求t=15s时ua及
各支路电流。 设电容的初始储能为零
+200V 60k 40k
6k 1000pF
+ ua uC -
-300V
时间常数为: RoC (60k // 40k 6k)109 3105 s
1.5 1.25 1.2 16
6-8 电路如图题6-7所示,电压源于 t =0 时开始作用于电路,试
数字电路答案第六章

第六章可编程逻辑器件PLD可编程逻辑器件PLD是由用户借助计算机和编程设备对集成电路进行编程,使之具有预定的逻辑功能,成为用户设计的ASIC芯片。
近年来,可编程逻辑器件从芯片密度上、速度上发展相当迅速,已成为集成电路的一个重要分支。
本章要求读者了解PLD器件的工作原理,掌握用可编程逻辑器件设计数字电路的方法。
为掌握使用电子设计自动化和可编程逻辑器件设计电路系统的后续课程打下良好的基础。
第一节基本知识、重点与难点一、基本知识(一)可编程逻辑器件PLD基本结构可编程逻辑器件PLD包括只读存储器ROM、可编程只读存储器PROM、可编程逻辑阵列PLA、可编程阵列逻辑PAL、通用阵列逻辑GAL和可擦写编程逻辑器件EPLD等。
它们的组成和工作原理基本相似,其基本结构由与阵列和或阵列构成。
与阵列用来产生有关与项,或阵列把所有与项构成“与或”形式的逻辑函数。
在数字电路中,任何组合逻辑函数均可表示为与或表达式,因而用“与门-或门”两级电路可实现任何组合电路,又因为任何时序电路是由组合电路加上存储元件(触发器)构成的,因而PLD的“与或”结构对实现数字电路具有普遍意义。
(二)可编程逻辑器件分类1.按编程部位分类PLD有着大致相同的基本结构,根据与阵列和或阵列是否可编程,分为三种基本类型:(1)与阵列固定,或阵列可编程;(2)与或阵列均可编程;(3)与阵列可编程,或阵列固定。
2.按编程方式分类(1)掩膜编程;(2)熔丝与反熔丝编程;(3)紫外线擦除、电可编程;(4)电擦除、电可编程;(5)在系统编程(Isp)。
(三)高密度可编程逻辑器件HDPLD单片高密度可编程逻辑器件HDPLD(High Density Programmable Logic Device)芯片内,可以集成成千上万个等效逻辑门,因此在单片高密度可编程逻辑器件内集成数字电路系统成为可能。
HDPLD器件在结构上仍延续GAL的结构原理,因而还是电擦写、电编程的EPLD 器件。
数字逻辑电路与系统设计第6章习题及解答.docx

第6章题解:6.1试用4个带异步清零和置数输入端的负边沿触发型JK 触发器和门电路设计一个异步余 3BCD 码计数器。
题6・1解:余3BCD 码计数器计数规则为:0011->0100->—1100-0011-*-,由于釆用 异步清零和置数,故计数器应在1101时产生清零和置数信号,所设计的电路如图题解6.1 所示。
题6.2试用中规模集成异步十进制计数器74290实现模48计数器。
题6.2解:图题解6. 16.3试用D触发器和门电路设计一个同步4位格雷码计数器。
题6.3解:根据格雷码计数规则,\Q1Q OQsQ>\00011110000000011000111111100111\QlQoQ.3Q>\00011110000001011111111110100000X^iQoQ3Q>\00011110000111010001110111100001\QlQoQ.3Q>\00011110001100010011111100100011 Qi Qo计数器的状态方程和驱动方程为:er1=D.=+型Q”+Q;莎er1=D2=+Q©+N Q;N QT = D L+ Q;Q;Q;; +Qj = D o = Q^Q;1+按方程画出电路图即可,图略。
6.5试用4位同步二进制计数器74163实现十二进制计数器。
74163功能表如表6.4所示。
题6・5解:可采取同步清零法实现。
电路如图题解6.5所示。
题6.6解:题6.4解:反馈值为1010c卜一进制计数器CLKCLR LD ENT ENP>c a[―<>40) a D DTC=\5图题解6. 5RCO74163当M=1时:六进制计数器八进制计数器6.7试用4位同步二进制计数器74163和门电路设计一个编码可控计数器,当输入控制变 量M=0时,电路为8421 BCD 码十进制计数器,M=1时电路为5421 BCD 码十进制计数器, 5421BCD 码计数器状态图如下图P6.7所示。
数字电路逻辑设计--第六章部分习题参考解答(王毓银主编--第二版)

第六章部分习题参考答案 P240 2题解 : (1) 驱动方程:112111223331;n n nnnJ K J K Q Q J Q Q K Q ======(2) 状态转移方程:121212121113313313n n n n n n n n nn n n n n nQ Q Q Q Q Q Q Q Q Q Q Q Q Q Q +++==⋅+⋅=+(3)(4)(5) 功能说明:经分析可知,该电路为六进制计数器,每六个CP 脉冲循环一次。
两个偏离状态在CP 脉冲的作用下可以自动进入有效循环序列,故该电路具有自启动功能。
5题解:(1)驱动方程和输出方程:11212121211221;nnnnnnnnnJ K J K Q A F AQ Q AQ Q AQ Q AQ Q ====⊕=⋅=+⋅(2)状态转移方程: 121212111()n nn n n n n Q Q Q Q A Q Q A Q ++==⊕+⊕⋅(3)状态转移表:(4) 状态转移图:(5)功能说明:<1> A=0 时,该电路是二进制加法计数器;A=1 时,该电路是二进制减法计数器。
<2> 由状态转移表可以看出,AQ 2Q 1全为0或全为1时,电路输出为1,其余情况输出全为0。
所以,可以由A 及输出F 的状态判断 触发器的状态是否均为1或均为0。
P245 28题解: 第一个计数器的计数状态是从1001到1111,共7个状态;第二个计数器的计数状态是从0111到1111,共9个状态。
而第二个计数器是当第一个计数器有进位输出时才获得一次计数机会,所以该计数器的总计数值为7*9 = 63,即计数器的分频比为1/63,即计数模值为63 。
31题解:S 0 = 0011; S M-1=1001;产生置位信号的状态是1001。
则该计数器的计数循环状态是从0011到1001,共计7个状态,所以是7进制计数器。
32.解:当M=1时,计数循环状态是从0100到1001,共6个状态,并由1001产生置位信号,所以M=1时为6进制计数器。
万里学院-数字电子技术基础-第六章习题及参考答案

第六章习题一、选择题 1. PROM和 PAL的结构是。
A.PROM的与阵列固定,不可编程B. PROM 与阵列、或阵列均不可编程C.PAL 与阵列、或阵列均可编程D. PAL 的与阵列可编程 2. PAL是指。
A.可编程逻辑阵列B. 可编程阵列逻辑C. 通用阵列逻辑D. 只读存储器 3.当用异步 I/O 输出结构的 PAL 设计逻辑电路时,它们相当于。
A. 组合逻辑电路B. 时序逻辑电路C. 存储器D. 数模转换器 4. PLD器件的基本结构组成有。
A. 输出电路B. 或阵列C. 与阵列D. 输入缓冲电路5. PLD器件的主要优点有。
A. 集成密度高B. 可改写C. 可硬件加密D. 便于仿真测试 6. GAL的输出电路是。
A.OLMCB. 固定的C. 只可一次编程D. 可重复编程7. PLD开发系统需要有。
A. 计算机B. 操作系统C. 编程器D. 开发软件 8.只可进行一次编程的可编程器件有。
A.PALB.GALC.PROMD.PLD 9.可重复进行编程的可编程器件有。
A.PALB.GALC.PROMD.ISP-PLD 10. ISP-PLD 器件开发系统的组成有。
A. 计算机B. 编程器C. 开发软件D. 编程电缆 11.全场可编程(与、或阵列皆可编程)的可编程逻辑器件有。
A.PALB.GALC.PROMD.PLA12.GAL16V8 的最多输入输出端个数为。
A.8 输入 8 输出B.10 输入 10 输出C.16 输入 8 输出D.16 输入 1 输出 13 一个容量为 1K×8 的存储器有个存储单元。
A.8B. 8192C.8000D. 8K14.要构成容量为 4K× 8 的 RAM,需要片容量为 256× 4 的 RAM。
A. 8B.4C. 2D.32 15.寻址容量为 16K× 8 的 RAM需要根地址线。
A. 8B. 4C.14D.16KE. 1616.RAM的地址码有 8 位,行、列地址译码器输入端都为 4 个,则它们的字线加条。
数电第六章答案全部
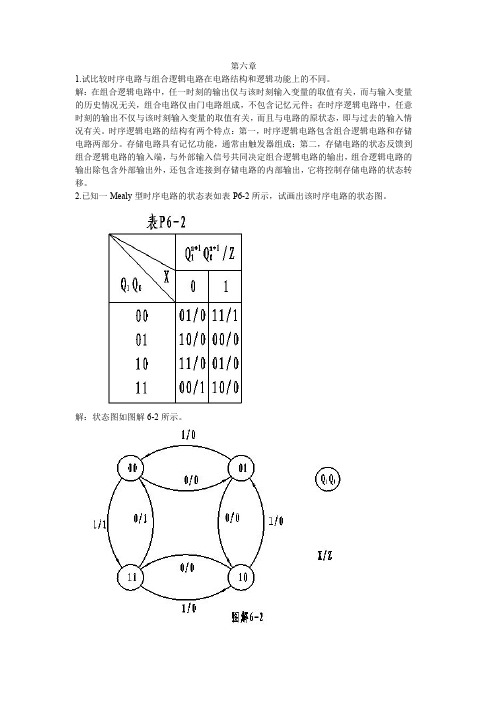
P6-19 解:由状态图作出状态转移表如表解 6-19 所示,由状态转移表可作出各触发器的次态卡 诺图和输出函数卡诺图如图解 6-19 所示。由图解 6-19 求得各触发器的状态方程和输出函 数,最后求得各触发器的激励函数:
n 1 Q2 Q1 Q0 Q 2 ,
Q1n 1 Q 2 Q0 Q1 Q2 Q1 Q0 Q 2 Q1 Q 0 Q 2 Q0 Q1 Q2 Q0 Q1 , Q0n 1 Q 2 Q 0 Q2 Q1 Q0 ,
3. 试用 JK 触发器和 D 触发器分别构成下列电路: (1) 四位二拍接收数据寄存器; (2) 四位单拍接收数据寄存器。 解: (1) 由 JK 触发器构成的四位二拍接收数据寄存器如图解 6-12(a)所示,由 D 触发器构成的四位二拍接收数据寄存器如图解 6-12(b)所示。
(2) 由 JK 触发器构成的四位单拍接收数据寄存器如图解 6-12(c) , (d)所示, 由 D 触发器构成的四位单拍接收数据寄存器如图解 6-12(e)所示。
J 2 Q1 Q0 , K2 1,
J 1 Q 2 Q0 , K 1 Q2 Q0 ,
J0 Q2 K 0 Q2 Q1
Z Q2 Q11 Q 0
20.设计一个时序逻辑电路,该时序电路的工作波形图由图 P6-20 给出。
图 P6-20 解:该时序电路可视为一个三输出的脉冲分配器,工作波形的周期为八拍,可以先用八进 制计数器产生 8 个状态作为组合电路的输入, 然后通过组合电路产生三路输出, 其电路结 构框图如图解 6-20 所示,组合电路的真值表如表解 6-20 所示。 (设计数器的输出为:
S1 为接收到一个 1 的状态;
S 2 为在收到 1 后接收到一个 0 的状态; S 3 为在顺序收到 10 后接收到一个 1 的状态;
电路分析第六章习题解答

=
6A
开关断开后,电路等效为
3Ω
2Ω
L
i
L = 1+ 1 = 5H 1+ 1 5 20
由 KVL 及换路定则得
⎪⎧5 di + 5i = 0 ⎨ dt ⎪⎩i(0+ ) = i(0− ) = 6 解得: i(t) = 6e−t A (t ≥ 0)
换路后无电源,故是零输入响应。
8. 如图题 6-8 所示,开关接在 a 点为时已久,t = 0 时开关接至 b 点,试求 t ≥ 0 时的
2Ω
ia
i1
+
2A
4Ω
u
+ 2i1 −
−
b
求得该二端电路的端口 VAR,便可得其等效电路。
设端电压 u 和端电流 i 的参考方向如上图所示,设 i 已知,则有
⎧u ⎩⎨i1
= =
2i + 4i1 2+i
+
2
i1
解得:
u = 12 + 8i
即该二端电路
uoc = 12V Req = 8Ω
开关动作后的电路可简化为
将电流源置零,从电感两端看进去的等效电阻为
R = 50 + 100 ×100 = 100Ω 100 + 100
τ = L = 0.1 = 1 s R 100 1000
由三要素公式,得
iL (t) = 0.05 + (0 − 0.05) e−1000t = (0.05 − 0.05e−1000 t ) A (t ≥ 0)
12Ω
+
40 V
−
t =0 +
8Ω u
−
+ 20nF uc
数电习题解答_杨志忠_第六章练习题_部分
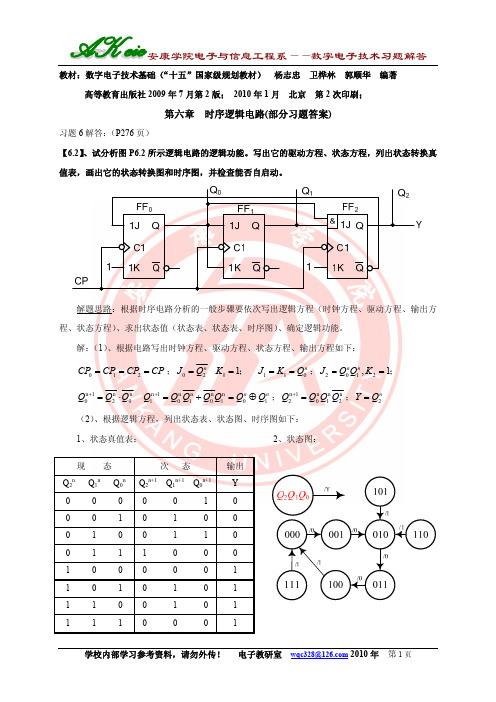
教材:数字电子技术基础(“十五”国家级规划教材) 杨志忠 卫桦林 郭顺华 编著高等教育出版社2009年7月第2版; 2010年1月 北京 第2次印刷;第六章 时序逻辑电路(部分习题答案)习题6解答:(P276页)【6.2】、试分析图P6.2所示逻辑电路的逻辑功能。
写出它的驱动方程、状态方程,列出状态转换真值表,画出它的状态转换图和时序图,并检查能否自启动。
解题思路:根据时序电路分析的一般步骤要依次写出逻辑方程(时钟方程、驱动方程、输出方程、状态方程)、求出状态值(状态表、状态表、时序图)、确定逻辑功能。
解:(1)、根据电路写出时钟方程、驱动方程、状态方程、输出方程如下:012CP CP CP CP ===;02110 1nn J Q K J K Q ====0; ;2012,1n n J Q Q K ==; n 1n n n 1n n n n 020*******n n Q Q Q Q Q Q Q Q Q Q ++=⋅=+=⊕ ;n 1n n n 2012Q Q Q Q +=;2n Y Q =(2)、根据逻辑方程,列出状态表、状态图、时序图如下: 1、状态真值表: 2、状态图:现 态 次 态 输出Q2n Q 1n Q 0n Q 2n+1 Q 1n+1 Q 0n+1Y 0 0 0 0 0 1 0 0 0 1 0 1 0 0 0 1 00 1 10 0 1 1 1 0 0 0 1 0 0 0 0 0 1 1 0 10 1 0 1 1 1 0 0 1 0 1 1 1 10 0 013、时序图——同步5进制计数器;电路能自启动。
【6.3】、试分析图P6.3所示逻辑电路的逻辑功能。
写出它的驱动方程、状态方程,列出状态转换真值表,画出它的状态转换图和时序图。
解题思路:根据时序电路分析的一般步骤要依次写出逻辑方程(时钟方程、驱动方程、输出方程、状态方程)、求出状态值(状态表、状态表、时序图)、确定逻辑功能。
解:(1)、根据电路写出时钟方程、驱动方程、状态方程、输出方程如下:012CP CP CP CP ===;(同步时序电路)0121011 1 n nn J K Q Q J Q K ====0; ;221n J K Q ==n 1n n n n 1n n 00120012101n n n n Q Q Q Q Q Q Q Q Q Q Q ++=⋅+=+=+ ;n 1212n n Q Q Q +=⊕;12n n CO Q Q =(2)、根据逻辑方程,列出状态表、状态图、时序图如下: 1、状态真值表: 2、状态图:3、时序图——同步5进制计数器;电路能自启动。
数字电子技术 第六章习题答案

第六章 习题解答6.1. 分析题图P6.1所示电路的功能,列出功能表。
解:图P6.1所示电路的功能表如表6.1所示。
将功能表中各变量数值关系的逻辑函数用对应的“卡诺图”如图6.1所示。
RS 具有约束条件RS =0,触发器的逻辑表达式为⎪⎩⎪⎨⎧=+=+0RS Q R S Q n 1n ,根据这一逻辑表达式,P6.1逻辑电路具有基本RS 触发器的逻辑功能,约束条件是SR=0。
6.2同步RS 触发器与基本RS 触发器的主要区别是什么?解:同步RS 触发器与基本RS 触发器的主要区别是基本RS 触发器的RS 输入信号不论任何时刻都是有效的,只要RS 输入的状态组合发生变化,输出Q 的状态跟随发生变化;而同步同步RS 触发器的RS 输入信号只要在CP 时钟脉冲信号有效时段内起作用,只有在这一时段内,输出Q 的状态才跟随RS 输入的状态组合变化而发生变化。
1& & 1QR图 P6.1QR S Q nQ n+1功 能 1 1 1 1 0 1 不用 不用 不允许11 0 0 0 1 0 0 01=+n Q 置0 0 0 1 1 0 1 1 1 11=+n Q 置10 00 00 10 1n n Q Q =+1 保持6.3如图P6.3 (a)所示电路的初始状态为Q =1,R 、S 端和CP 端的信号如图P6.3(b )所示,画出该同步RS 触发器相应的Q 和Q 端的波形。
解:根据图P6.3 (a)所示电路结构,其功能为同步RS 触发器,电路的特性方程为:⎪⎩⎪⎨⎧=+=+0RS Q R S Q n 1n ,若R=S=1,在CP 时钟脉冲信号为“1”的时段内,触发器的两个输出端的状态均输出“1”,此种情况下,若CP 时钟脉冲信号从“1”状态,跳变为“0”的输入状态,则触发器的两个输出状态为不确定状态。
根据特性方程以及电路的初始状态,作出电路的输出端时序图如图6.3所示。
6.4 主从RS 触发器输入信号的波形如图P6.4(a )、(b )所示。
北京理工大学《数字电路-分析与设计》数电习题答案
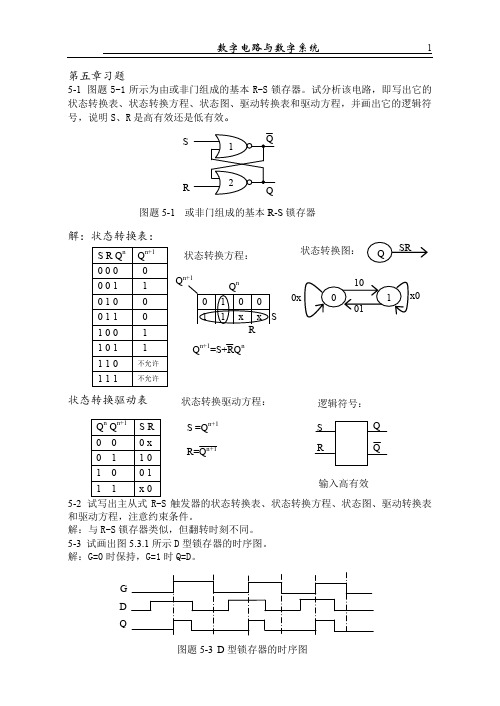
第五章习题5-1 图题5-1所示为由或非门组成的基本R-S 锁存器。
试分析该电路,即写出它的状态转换表、状态转换方程、状态图、驱动转换表和驱动方程,并画出它的逻辑符号,说明S 、R 是高有效还是低有效。
解:状态转换表:状态转换驱动表5-2 试写出主从式R-S 触发器的状态转换表、状态转换方程、状态图、驱动转换表和驱动方程,注意约束条件。
解:与R-S 锁存器类似,但翻转时刻不同。
5-3 试画出图5.3.1所示D 型锁存器的时序图。
解:G=0时保持,G=1时Q=D 。
图题5-1 或非门组成的基本R-S 锁存器S R状态转换方程:Q n+1Q n+1=S+RQ n状态转换图: S =Q n+1R=Q n+1 状态转换驱动方程: 逻辑符号: 输入高有效 G D Q图题5-3 D 型锁存器的时序图5-4试用各种描述方法描述D锁存器:状态转换表、状态转换方程、时序图、状态转换驱动表、驱动方程和状态转换图。
5-5锁存器与触发器有何异同?5-6试描述主从式RS触发器,即画出其功能转换表,写出状态方程,画出状态表,画出逻辑符号。
5-7试描述JK、D、T和T'触发器的功能,即画出它们的逻辑符号、状态转换表、状态转换图,时序图,状态转换驱动表,写出它们的状态方程。
5-8试分析图5.7.1(a) 所示电路中虚线内电路Q’与输入之间的关系。
5-9试分析图5.7.1(b)所示电路的功能,并画出其功能表。
5-10试用状态方程法完成下列触发器功能转换:JK→D, D→T, T→D, JK→T, JK→T’, D→T’。
解:JK→D:Q n+1=JQ+KQ,D:Q n+1=D=DQ+DQ。
令两个状态方程相等:D=DQ+DQ =JQ+KQ。
对比Q、Q的系数有:J=D,K=D逻辑图略。
5-11试用驱动表法完成下列触发器功能转换:JK→D, D→T, T→D, JK→T, JK→T’, D→T’。
解:略。
5-12用一个T触发器和一个2-1多路选择器构成一个JK触发器。
数字电路第6章习题参考答案
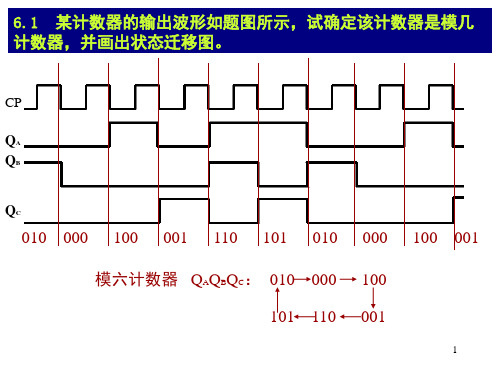
电路 如图
1010
1001
1000 0111 0110 (b)
19
利用后十一个态,反馈置位信号直接由进位端Oc=QDQCQBQA 引 入,预置数为16-11=5=0101,状态迁移关系如下:
QDQCQBQA 0101
0110 0111
1000
1001 1010 电路 如图
1111
1110
1101
1100
励议程和时钟议程为:F1:(LSB) CP1=CP,J1=Q4,K1=1(书上有错)
F2:
CP2=Q1,J2=K2=1
F3:
CP3=Q2,J3=K3=1
F4:(MSB) CP4=CP,J4=Q1Q2Q3,K4=1
要求:(1)画出该计数器逻辑电路图;
(2)该计数器是模几计数器;
(3)画出工作波形图(设电路初始状态为0000)。
01 01 01 01
00 00 10 10
00 00
3
1001
1010
1111
0000 0001 0010 0011
1000
1011
1100
0100
1101
1110
0111 0110 0101
(3)画出工作波形图(设电路初始状态为0000)。
4
6.3 设计一个计数电路,在CP脉冲作用下,3个触发器QA,QB,QC 及输出C的波形图如图所示(分别选用JK触发器和D触发器)。 QC为高位, QA为低位。
00 1 1 X 0 01 0 0 X X
11 0 0 X X 10 1 1 X X
Q 2n1Q 1nQ 2nQ 1nQ 2n
J 4 Q3nQ2 nQ1n K 4 1 J 3 Q2 nQ1n K 3 Q2 nQ1n J 2 K 2 Q1n
第六章习题参考答案

waajl 第六章习题参考答案6-1在逻辑功能上,时序电路的输出不仅与该时刻的输入有关, 还与电路原来的 状态有关;而组合逻辑电路的输出仅取决于该时刻的输入。
在电路结构上,时序 电路要含有存储电路一一通常有触发器构成, 并且触发器的输出与电路输入之间 存在反馈连接,而组合逻辑电路不含有存储元件,也无反馈连接。
6-2由于组合逻辑电路的输出仅取决于当前时刻的输入, 因此只需逻辑函数就足 以描述;但是时序逻辑电路的输出不仅与当前的输入有关, 还与电路的原状态一 —也就是以前的输入序列有关,因此需要用驱动方程、状态方程和输出方程才能 准确描述它的功能。
6-3由逻辑电路图可写出电路的 驱动方程:FF 0: D o =Q oFF : D i =Q^ Q i 输出方程:F= QQ i将驱动方程代入D 触发器的特性方程Q*=D 中,得状态方程: Q o *=D o =Q o ; Q i *=D i =Q o 二 Q i设初态为Q i Q o =oo ,则有状态方程和输出方程可列出状态转换表如下:Q i Q D o 0 0_i i o' i i QQoo Joi* /i/oi — /o io功能:同步两位二进制加法计数器(或称同步四进制加法计数器)6-4(1)由逻辑电路图写出各触发器的驱动方程和时钟方程 FF: Jo=(Q 2Q i ),K o =i ,CLK=CLK FF : Ji=Q o ,K i =(ChQ o): CLK=CLK FF : Jz=i ,K 2=i ,CLK= QQ i * Q o * o i i_o_ i io oFo o o i由状态转换表可以画出 状态转换图:⑵将驱动方程代入JK 触发器的特性方程Q*=JQ+KQ , (3个触发器都是下 降沿触发),得状态方程:Q o *= J b Q o +K o Q=(QQ i ) Q o =(QQ i +Q ),CLK 下降沿动作Q i *= Ji Q i +K 1 Qi =Q D Q I +Q 2 Q o Q i = Q i Q 0+Q 2 Q 1Q 0: CLK 下降沿动作 Q 2*= J 2Q 2 +K 2 Q=C 2 ',Q i 降沿动作(3)列出状态转换表和状态转换图(设初态Q2QQ O =OOO )CLK ChQ i Q o Q 2*Q i *Q o * CLK=CLK=CLK CLK=Q ii 0 0 00 0 i• 2 0 0 i 0 i 0J •3 0 i 0 0 i i•4 0 i i i 0 0•5 i 0 0 i 0 i•6i 0 i i i 0•7 i i 0 0 0 0• J无效状态Q 2Q i Q o =111,次态Q 2*Q I *Q O *=OOO ,进入有效状态⑷分析电路功能异步七进制加法计数器,可自启动6-5驱动方程和时钟方程FF : D o =Q o ,CLK=CLK 下降沿触发) FF : D i = Q i : CLK=Q (上升沿触发) FF : D 2= Q 2: CLK= Qi (上升沿触发) 状态方程: Q o *=Q o : CLK 下降沿 Q i *=Q i : Q o 上升沿 Q 2*=Q 2 : Q i 上升沿i o CLK QQ i Q o Q 2*Q i *Q o *CLK=CLKCLK=Q oCLK=Qii 0 0 0 i i i2 i i i i i 03 i i 0 i 0 i •4 i 0 i i 0 0•5 i 0 0 0 i i60 i i 0 i 0J> 0i0* 0iii00iii j ; iio *7O i O O O i J8 O O i O O O JQ2、Q i、Q0的波形图:6-6FF: J0=K6=1, Q o*= Q oFF : Ji= K=((CQ)+CQoy)匕CG O+CQ o', Q i*=(CC b+CQoJQ i+(CQ+CQ o丁Q iFF: Jz= K2=((CQQ i+CQ i Q o )) =CQQ 1+CQ1 Q o , Q2*=(CQ o Q i +CQ i Q o )Q +(CQ0Q i +CQ i Q o ) Q2(1) C=O 时,Q o*= Q oQ i*=Q o Q i + Q o Q i=(Q o 二Q i)Q2*=Q i Q o Q2+(Q Q o ) Q2=(Q i Q o hO2设初态为Q2Q i Q o=OOO,状态转换表:Q2 Q i Q o Q2* Q i* Q o*O O O i i ii i i i i Oi i O i O ii O i i O Oi O O O i iO i i O i OO i O O O iO O i O O O功能:同步八进制减法计数器⑵C=i时,Q o*= Q oQ i*=Q o Q i + C O Q i=Q o 二Q iQ2*=Q i Q o Q2 *+(Qi Q o) Q2=Q i Q o ㊉Q2设初态为Q2Q i Q o=OOO,状态转换表:_____________Q2 Q i Q o Q2* Q i* Q o*电路功能:异步八进制减法计数器0 0 0 0 0 10 0 1 0 1 00 1 0 0 1 10 1 1 1 0 01 0 0 1 1 0 11 0 1 1 1 01 1 0 : 1 1 11 1 1 0 0 0功能:同步八进制加法计数器(2)状态分配,画出状态转换图用3位二进制编码000~101分别表示S0~S5,输出为C000/0”001/0 *010/1 /0101 */0100 V/0011(3)画出次态卡诺图,001/0 010/0 100/0 011/0101/0 000/1 X XQ0Q2、00 01 11 100 0 0 F \1L 1 J0 、X」XQ2*=Q2Q Q +Q1Q06-7(1)画出原始状态转换图设计数器的6个状态分别为S0~S5,C作为进位输出信号/1 /01并写出状态方程00 01 11 10Q2*Q1*Q O*及F的卡诺图Q2*卡诺图Q 2*= Q i Q o Q 2 + Q o Q 2,则 J 2= Q1Q 0,K 2=Q o (逻辑电路略) 6-8十二进制加法计数器需要4个D 触发器,用OOOOTOii 分别表示状态Sr-Si i , 进位输出信号用F 表示设初态为Q 2Qi_____________________________Q 3 Q Q i Q OQ 3* Q 2* Q i * Q O * F O O O O0 0 0 i 0 0 0 0 i 0 0 i 0 0 0 0 i 0 0 0 i i 0Q i *=Q i Q o +Q 2 Q i Q o(4)与JK 触发器的特性方程 Q*=JQ+ KQ 进行比较,求驱动方程 FF : Q o *=Q o ,故 J 0=K o =1;FF : Q i *=Q i Q o'+QQ iQ = (QQ o )Q i +(Q o)Q i ,故 J= Q 2Q , £=Q ;FF : Q 2*=Q 2Q o +QQ o =(QQ o )Q 2"+ (QQ o + Q oj Q ,故 J 2= QQ , K 2=(QQ+ Qf)"= Q i Q o ;(6)检测能否自启动无效状态为iio 和iii ,由状态方程可求出次态分别为iii 和ioo ,故可以 自启动。
第六章 数字系统 习题答案(白中英主编第五版)

第六章 数字系统(习题答案)1 现有D 触发器组成的三个n 位寄存器,需要连接起来传送数据。
当控制信号S a 有效时,执行(Ra )→Rc 的操作;当控制信号S b 有效时,执行(R b )→R C 的操作。
试写出连接电路的逻辑表达式,并画出逻辑电路图。
解:RcRa R bLDCSaS bRc = Ra ·Sa ·LDC + Rb ·Sb ·LDC2 现有D 触发器组成的四个8位寄存器,要求它们之间实现数据传送,试设计连接电路。
解:A B C DLDA LDB LDC LDDA BUS C BUSB BUS D BUSBUS3 ALU 的输出端一般带有一个移位器,其功能为:①ALU 输出正常传送;②ALU 输出左移1位(ALU i+1)传送;③ALU 输出右移一位(ALU i-1)传送。
试设计移位器的逻辑电路。
解:4 一个系统有A,B 两条总线,为了接收来自任何一条总线上的数据并驱动任何一条总线,需要一个总线缓冲寄存器。
请用D 触发器和三态门设计一个总线缓冲寄存器。
解:ABUSBBUSR ABUS R BBUSABUS R BBUS RABUSBBUSR ( 缓冲寄存器 )LDR5 试构造能完成下列程序操作的ASM 图:(a ) if X = N, then … 。
(b ) if X ≠N, then …, else …。
解:(c)for X from A to B, step C, do… 。
解:(d)while X = Y, do …。
解:Rx¬ XRy¬ YRx- RyA=B1(e)if X > N OR X < O, then …, else …。
解:6 有一个数字比较系统,它能对两个8位二进制进行比较。
其操作过程如下:先将两个8位二进制数存入寄存器A和B, 然后进行比较,最后将大数移入寄存器A中。
要求:⑴画出此系统方框图,并构造ASM流程图。
VHDL数字电路设计教程第六章习题答案

P6.1library ieee;use ieee.std_logic_1164.all;use ieee.std_logic_unsigned.all;entity chp6_1 isport(clk:in std_logic;d_out:out std_logic_vector(5 downto 0)); end;architecture bhv of chp6_1 issignal count: std_logic_vector(5 downto 0); signal temp: std_logic_vector(5 downto 0); beginprocess(clk)beginif clk'event and clk='1' thencount<= count+1;if count="100000" then count<="000000";end if;end if;end process;process(clk)beginif clk'event and clk='0' thentemp<=temp+1;if temp="0111111" then temp<="000000"; end if;end if;end process;d_out<=count+temp;end;P6.3solution1library ieee;use ieee.std_logic_1164.all;entity chp6_3 isport(x:in std_Logic_vector(7 downto 1);y:out std_logic_vector(2 downto 0)); end;architecture bhv of chp6_3 isbeginprocess(x)beginif x(7)='1' then y<="111";elsif x(6)='1' then y<="110";elsif x(5)='1' then y<="101";elsif x(4)='1' then y<="100";elsif x(3)='1' then y<="011";elsif x(2)='1' then y<="010";elsif x(1)='1' then y<="001";else y<="000";end if;end process;end;solution2library ieee;use ieee.std_logic_1164.all;entity chp6_3_2 isgeneric(n:integer:=3);port(x:in std_logic_vector(2**n-1 downto 0);y:out integer range 0 to 2**n-1); end;architecture bhv of chp6_3_2 isbeginprocess(x)variable temp:integer range 0 to 2**n-1; beginfor i in x'range loopif x(i)='1' thentemp:=i;exit;end if;end loop;y<=temp;end process;end;P6.4library ieee;use ieee.std_logic_1164.all;use ieee.std_logic_unsigned.all;entity chp6_4 isgeneric (n:integer:=8);port(clk:in std_logic;clk_out:out std_logic);end;architecture bhv of chp6_4 issignal rst:std_logic;signal temp:std_logic_vector(2 downto 0); beginprocess(clk,rst)beginif rst='1' thentemp<="000";elsif clk'event and clk='1' thentemp<=temp+1;end if;end process;rst<='1' when temp="111" else'0';clk_out<=temp(2);end;P6.5library ieee;use ieee.std_logic_1164.all;use ieee.std_logic_unsigned.all;entity chp6_5 isgeneric (n:integer:=7);port(clk:in std_logic;clk_out:out std_logic);end;architecture bhv of chp6_5 issignal temp:std_logic_vector(2 downto 0); signal cout:std_logic;beginprocess(clk)beginif clk'event and clk='1' thentemp<=temp+1;if temp="110" then temp<="000";end if;end if;end process;cout<='1' when temp="110" else'0';clk_out<=cout;end;P6.6library ieee;use ieee.std_logic_1164.all;use ieee.std_logic_unsigned.all;use ieee.std_logic_arith.all;entity chp6_6 isport(clk,start,stop,reset:in std_logic;dig1,dig2,dig3:out std_logic_vector(3 downto 0)); end;architecture bhv of chp6_6 issignal sec1:integer range 0 to 10;signal sec2:integer range 0 to 6;signal min:integer range 0 to 10;beginprocess(clk,start, stop,reset)variable count1:integer range 0 to 10;variable count2:integer range 0 to 6;variable count3:integer range 0 to 10;beginif reset='1' thencount1:=0;count2:=0;count3:=0;elsif clk'event and clk='1' thenif start='1' and stop='0' thencount1:=count1+1;if count1=10 thencount1:=0;count2:=count2+1;if count2=6 thencount2:=0;count3:=count3+1;if count3=10 thencount3:=0;end if;end if;end if;end if;end if;sec1<=count1;sec2<=count2;min<=count3;end process;dig1<=conv_std_logic_vector(sec1,4);dig2<=conv_std_logic_vector(sec2,4);dig3<=conv_std_logic_vector(min,4);end;P6.8use ieee.std_logic_1164.all;entity chp6_8 isgeneric(n:integer:=8);port(input:in std_logic_vector(n-1 downto 0);output:out std_logic);end;architecture bhv of chp6_8 isbeginprocess(input)variable temp:std_logic_vector(n-1 downto 0); begintemp(0):=input(0);for i in 1 to n-1 looptemp(i):=input(i) xor temp(i-1);end loop;output<=temp(n-1);end process;end;P6.9library ieee;use ieee.std_logic_1164.all;use ieee.std_logic_unsigned.all;entity chp6_9 isgeneric(n:integer:=4);port(input:std_logic_vector(n-1 downto 0);output:out integer range 0 to n);end;architecture bhv of chp6_9 isbeginprocess(input)variable temp:integer range 0 to n;begintemp:=0;for i in 0 to n-1 loopif input(i)='1' thentemp:=temp+1;end if;end loop;output<=temp;end process;end;P6.10use ieee.std_logic_1164.all;entity chp6_10 isgeneric(n:integer :=8);port(din:in integer range 0 to n-1;dout:out std_logic_vector(n-1 downto 0));end;architecture bhv of chp6_10 isbeginprocess(din)beginfor i in 0 to n-1 loopif din=i then dout<=(i=>'1', others=>'0');end if;end loop;end process;end;P6.16library ieee;use ieee.std_logic_1164.all;entity chp6_16 isgeneric (n:integer:=8);port(a,b:in std_logic_vector(n-1 downto 0);cin:in std_logic;s:out std_logic_vector(n-1 downto 0);cout:out std_logic);end;architecture bhv of chp6_16 issignal carry:std_logic_vector(n downto 0);beginprocess(a,b,cin,carry)begincarry(0)<=cin;for i in 0 to n-1 loops(i)<=a(i) xor b(i) xor carry(i);carry(i+1)<=(a(i) and b(i)) or (a(i) and carry(i)) or (b(i) and carry(i));end loop;cout<=carry(n);end process;end;说明:本次答案均为课上讨论过的,P6.11-P6.15均可参考第五章答案,可以利用对应语句将其放入进程中。
《数字电路-分析与设计》第六章习题及解答(部分) 北京理工大学出版社

第六章习题6-1 略。
6-2 此时相当于触发器在前级Q的上沿翻转,所以是减法计数器。
6-3 异步可逆计数器。
UP/DOWN=0时,加法计数;UP/DOWN=1时,减法计数6-4该电路为异步置位法任意模计数器,置位状态为4(M-1),所以该计数器的模M=5计数器;时序图略。
有效状态循环:0、1、2、3、7、0;4,6为过渡状态,其次态为7;5的次态为6。
由于由状态011(M-2)到100(M-1)时,Q1、Q0由1变0,所以这两个Q端上会出现毛刺。
6-5 用4位T’触发器;因用复位法,故用状态1010清0(R=Q3Q1)。
有效状态循环为0~9;10、11、14、15均为过渡状态,其次态均为0;12的次态是13,13的次态是14;毛刺出现在Q1上。
6-6用4位T’触发器;因用置位法,故用状态1001置位(S=Q3Q1Q0)。
有效状态循环为0~8,15;9、13为过渡状态,其次态均为15;10→11→12→13→15,14→15;无毛刺。
6-7用4位T’触发器;因用置位法,故用状态1101置位(S=Q3Q2Q1Q0)。
有效状态循环为0~12,15;13为过渡状态,其次态为15;14→15;毛刺出现在Q0上。
6-8~6-11 略。
6-12 电路由T触发器组成;CP i=CP,T0=1,T1=Q0,T2=Q1Q0,所以它是同步二进制减法计数器。
时序图略。
6-13 该题未要求是同步还是异步计数器,可以两种都做,也可以只做一种。
异步:先将JK转换为T’,即令J=K=1;同步:先将JK转换为T,即令J=K=T;M=8,需要3个触发器;异步可逆、同步可逆,参见图6.39;6-14 异步计数器电路简单,速度慢;同步计数器则相反。
6-15可能产生毛刺,也可能不产生。
如果产生毛刺,则它(们)出现在由M-2到M-1时由1变0的Q A、Q D端上和/或由M-2到M-1时由0变1的Q B、Q C端上。
6-16 先分别将‘290接为8421和5421计数器,再分别用M=7(Q D Q C Q B Q A =0111)8421和(Q A Q D Q C Q B=1010)5421复位即可,应特别注意高低位的顺序。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
& I试分析图P5,i所示时序电路。
a P6J解:1)分析电路结构:该电路是由七个与非门及一个JKFF组成,且CP下降沿触发,属于米勒电路,输入信号X,X2,输出信号乙2)求触发器激励函数:J=X i%, K= X X触发器次态方程:Q+1=XX2 Q+ X i X2Qf=X i X2 Q+(X i+XQC f电路输出方程:Z= X X2Q+X1 Xa Q+ X X2 Q+X1X2Q3)状态转移表:表 6.3.1输入S(t) N(t) 输出X1 X2 Q Q+1Z0 0 0 0 00 0 1 0 10 1 0 0 10 1 1 1 01 0 0 0 11 0 1 1 01 1 0 1 01 1 1 1 14)逻辑功能:实现串行二进制加法运算。
XX为串行输入的被加数和加数,Q为低位来的进位,Q+1表示向高位的进位。
且电路每来一个CP实现一次加法运算,Z为本位和,Q在本时钟周期表示向高位的进位,在下一个时钟周期表示从低位来的进位。
例如X=110110, X2=110100,则运算如下表所示:LSB MSB表试作出101序列检测器的状态图,该同步电路由一根输入线X, —根输出线Z,对应与输入序列的101的最后一个“ 1 ”,输出Z=1。
其余情况下输出为“ 0 ”。
(1)101序列可以重叠,例如: X: 0 乙000101001(2)101序列不可以重叠,如: X: 00 乙0001000010解:1)$:起始状态,或收到101序列后重新检测。
S:收到序列“ 1”。
S2:连续收到序列“ 10 ”。
1/011…100…2)6 3对卜列康織賦态表进行貧化:5(f)X「x01r o14 A B00B C A01C甘D0D C003(01出心}X1A!丹E CC I1F廿A£F£G C1H CX0~ -解:(1)列隐含表:(a)进行关联比较得到所有的等价类为:AD BC最大等价类为:AD BC 重新命名为a , b o 3)列最小化状态表为:s (t)N(t)/Z(t)X=0X=1 aa/0 b/0 bb/0a/1(b )解:1)画隐含表:XXXXXXX X XXXXXXXXXXXXXABCDEFG2)进行关联比较:ACBDEGHF ,之间互为等价隐含条件,所以分别等价。
四个等价态重新 命名为:a , b , e , h(b)3)列最小化状态转移表:表634试画出用MSI移存器74194构成8位串行并行码的转换电路(用3片74194或2片74194 和一个D 触发器)。
解:1)用 3 片74194:表6.3.5 题的状态转移表1 2 3Q 0Q ; Q 2 Q 3 Q 4 Q 5 Q 6 Q 7 Q 8 M QM 〔 下一操作 清Q 00 0 0 0 0 0 0 0 1 1 准备送数CP 1 T D Q 01 1 1 1 1 1 1 1 0 准备右移 CP 2T D 1 D Q1 1 1 1 1 1 1 0 准备右移 CP 3TD 2D 1 D 01 1 1 1 1 1 0 准备右移 CP 4T D 3 D2 D 1 D 0 011 1 1 1 0 准备右移CP 5T D 4 D 3 D 2 D 1 D 0 0 1 1 1 1 0 准备右移 CP 6^ D 5 D 4 D 3 D 2 D 1 D 0 01 1 1 0 准备右移 CP 7T D 6 D 5 D 4 D 3 D2 D 1 D 0 01 1 0 准备右移CP 8TD 7D 6D 5D 4D 3D 2D 1D 011准备送数2)用2片74194和一个D 触发器状态转移表同表。
A试画出74194构成8位并行 串行码的转换电路Q 0 Q 1 Q 2 Q 3 Q 4Q 5 Q 6 Q 7Q 8串行输入—Q Q Q 1 Q 2 Q 3 CR M Q —Q Q Q 1 Q 2 Q 3 CR M 0》CP 74194 (2)M 1D SRD SLD SRD SLD SL1DCP花1R DCP 74194(1)M1试分析图馬壬电路,画出状态转移图并说明有无自启动性。
田 P6.6解:激励方程:J i =K =1;R evis ion表6.3.6题的状态转移表:0 D'i D2 D 3D'c D : D'c D'111110001 010000有效循环101 100 011IJ IK]XJK解:K 1=J 1=1 j 2=Q nQ n , K z =Q nj 2=Q n Q n , K z =Q n状态方程:Q 性Q n• CP Q 性[Q n Q 3n Q"+ Q "Q n ] • CP Q n+1=[Q n Q n Q 3n + Q n Q n ] • CP 状态转移表: C 7国丙d 为同涉加丿料可世二讲制计散殍“试分析演电豔用-岀箱$0和上二1时列状憲桂棒表, 状态转移图 该电路具有自启动性。
序号 Q 3Q 2Q 10 0 0 0 1 0 0 1 2 0 1 0 3 0 1 1 4 1 0 0 5 11偏离 1 1 0 1 1 1 状态1 110 0 0表6.3.7 题的状态转移表K2=J2=X Q i nK3 =J3 =(X Q n)(x Q2 n)K4 =J4=(X Q i n)(X Q2 n)(X Q3 n)Z=(X Q i n)(X Q2 n)( X Q3 n)(X Q4 n)解:1)该电路为异步时序电路,无输入控制信号,属于 其激励方程为:J i =1,K = Q rJ 2= Q , K 2=1 J 3=1,可得状态转移表:表6.3・8 题的状态转移表序 号Q 3Q 2Q 10 0 0 11 1 20 0 1 311 0 41 0 1 偏离0 10 00 1分析图电路,画出其全状态转移图并说明能否自启动。
Moore 型,次态方程为:Q +=[ n n nQ +Q Q ] • CP ,2)用卡诺图法求状态转移表:11、 _ 丿1 111 1 111nn.Q Q ] • CP ,亠n 亠n 亠n 、Q +Q Q ] •小圈内对应Q ,其余应00 01 11 1000 01 11 10Q n Qn0 100 01 11 10,「011〉一「001)有效循环/ \〔101;'<110/ v.010.y偏离状态“00〕〔.111.〉偏离态能够进入有效循环,因此该电路具有自启动性。
逻辑功能:该电路是一个M=5的异步计数器。
用IKFF设计符合下列条件的同步计数器电路。
当X=0时为M=5的加法计数器,其状态为0, 1, 2, 3, 4。
当X=1时为M=5的减法计数器,其状态为7, 6,5,4,3。
解:所设计电路应为Mealy型。
有输入控制信号X。
1)列状态转移表:X nQ n n ‘Q2 Q1 -------- —Q3 n + 1 亠n + 1Q Q1Z0 0 0 0 0 0 1 00 0 0 1 0 1 0 00 0 1 0 0 1 1 00 0 1 1 1 0 0 00 1 0 0 0 0 0 11 1 1 1 1 1 0 01 1 1 0 1 0 1 01 1 0 1 1 0 0 01 1 0 0 0 1 1 01 0 1 1 1 1 1 1偏离态输出按任意项处理。
2)求激励方程:Q n+1=Q n Q n Q n+(Q n+Q n)Q n所以j3=Q n Q n,&=Q n+Q nQ n Q n00 01 11 10 00 01 11 100001 011110 10XQ n111 1——1 1900Q n Q nXQ n000110丿a» 1T J0001111110Q n+1=( XQ n+X Q n) Q n + (XQ n+ X Q n) Q n所以 J 2= XQ n+X Q n=X Q : K 2=XQ n+ X Q n=X Q nQ n+1=(Q n+X ) Q n+X Q nQ n所以 J i = Q n +X , K =X Q n所以可不检查自启动性, 但必须有预置端,使计数器能进入有效循环。
解:1)列状态转移表:XQ n Q nQ 1n亠n +1QQ n+1 Q/ + 1Z0 0 0 0 0 0 1 0 0 0 0 1 0 1 0 0 0 0 1 0 0 1 1 0 0 0 1 1 1 0 0 0 0 1 0 0 0 0 0 1 1 1 1 1 1 1 0 0 1 1 1 010 1 0 1 1 0 1 1 0 0 0 110 011本题未要求具有自启动性, 3)画电路图:126.10试改用D 触发器实现第9题所述功能的电路。
10 1 1 1 1 1 1偏离态输出按任意项处理。
2) 求激励方程:n nnnD 3=Q Q +XQ + XQD 2= X Q nQ n+ XQ nQ n+ X Q nQ n+ XQ nQ nD = Q nQ n+X Q n + X Q n3) 电路图略。
1f 1r 1}H7丿Q“+1( D3)的卡诺图XQ1rr1 /'11 10001 00 01 11 101110 nXQ nQ 2n Q 000111100001111000 01 11 10Q n Q nQ n+1( D 2)的卡诺图Q n+1(D)的卡诺图1000 01 116.11试用JKFF 设计符合图波形,并且具备自启动性的同步计数电路。
解:1)根据波形列状态转移表表6.3.11 题的状态转移表nQ 3nQ 2n ~Q 1n+ 1 Q_ n +1QQ 1CP 0 0 0 0 1 0 CR 0 1 0 0 1 1 CP 2 0 1 1 1 0 1 CR 1 0 1 1 1 0 CR 1 1 0 1 0 0 CR10 02)根据状态转移表知:有 6个有效状态和2个偏离态,偏离态的输出先按任意项处理,由 此可得次态方程卡诺图为:是101,两个偏离态都能进入有效循环,因此,以此圈法设计的电路具有自启动性。
n+1 nnnnnnnnQ =Q Q 3 +(Q +Q) QJ 3=Q , K>=Q +Q= 「1 ■000111 10i I,1o—t _*在上面卡诺圈的圈法下,检查自启动性:偏离态 001的次态为110,偏离态111的次态00 01 11 10 001101DQ n+1=(Q3心)Q n+ Q Q n Q n J2= Q n+Q n, K2=4Q nn3)电路图略。
用四个DFF设计以下电路:(1)异步二进制加法计数器。
(2)在(1)的基础上用复“ 0”法构成M=12的异步加法计数器。
解:(1)Q4 Q3 Q2 Q1(2)反馈状态为1100用四个DFF设计以下电路:(1)异步二进制减法计数器。
