对数频率特性(Bede)
合集下载
自动控制原理-第五章
2.高频段 在T>>1(或>>1/T)的区段,可以近似地认为
渐近特性和准确特性相比,存在误差:越靠近转折频率,误差越大,如在转折频率这一点,误差最大,精确值为 L(=1/T)=-20lg21/2=-3dB 这说明,在转折频率处,精确值应为用渐近线绘制的对数幅值减去3dB。
为简化对数频率特性曲线的绘制,常常使用渐近对数幅频特性曲线(特别是在初步设计阶段)。同时,如需由渐近对数幅频特性曲线获取精确曲线,只须分别在低于或高于转折频率的一个十倍频程范围内对渐近对数幅频特性曲线进行修正就足够了。
而求渐近线时可先绘出构成系统的各串联典型环节的对数幅频特性的渐近线,再由各环节的对数幅频特性的纵坐标值相加而得到。
绘制开环系统的对数相频特性可根据其表达式计算、描点而得到,也可以由各环节的相频特性相加而得。
实际上,与开环奈氏图的绘制相同,当系统全由除延迟环节以外的典型环节构成时(开环传递函数全为左极点与左零点),开环波德图的绘制也具有一定的规律,可以大大简化曲线的绘制过程。
比例环节的相频特性仍为()=0,与无关,为相频特性图的横轴,如图5-29所示。 K的变化只影响对数幅频特性曲线的升降,不改变其形状与对数相频特性。
二、积分环节 积分环节的频率特性为 幅频特性 为A()=1/ 其对数幅频特性为 L()=20lgA()=20lg(1/)=-20lg 绘出对数幅频特性曲线上的几个点: 当=0.1时,L(0.1)=+20dB ; 当=1时,L(1)=0dB; 当=10时, L(10)=-20dB。
容易看出各环节的单独作用,便于对系统的分析设计。
01
可以用分段的直线(渐近线)来代替典型环节的准确的对数幅频特性,而且稍加修正就可得到精确的曲线。
02
渐近特性和准确特性相比,存在误差:越靠近转折频率,误差越大,如在转折频率这一点,误差最大,精确值为 L(=1/T)=-20lg21/2=-3dB 这说明,在转折频率处,精确值应为用渐近线绘制的对数幅值减去3dB。
为简化对数频率特性曲线的绘制,常常使用渐近对数幅频特性曲线(特别是在初步设计阶段)。同时,如需由渐近对数幅频特性曲线获取精确曲线,只须分别在低于或高于转折频率的一个十倍频程范围内对渐近对数幅频特性曲线进行修正就足够了。
而求渐近线时可先绘出构成系统的各串联典型环节的对数幅频特性的渐近线,再由各环节的对数幅频特性的纵坐标值相加而得到。
绘制开环系统的对数相频特性可根据其表达式计算、描点而得到,也可以由各环节的相频特性相加而得。
实际上,与开环奈氏图的绘制相同,当系统全由除延迟环节以外的典型环节构成时(开环传递函数全为左极点与左零点),开环波德图的绘制也具有一定的规律,可以大大简化曲线的绘制过程。
比例环节的相频特性仍为()=0,与无关,为相频特性图的横轴,如图5-29所示。 K的变化只影响对数幅频特性曲线的升降,不改变其形状与对数相频特性。
二、积分环节 积分环节的频率特性为 幅频特性 为A()=1/ 其对数幅频特性为 L()=20lgA()=20lg(1/)=-20lg 绘出对数幅频特性曲线上的几个点: 当=0.1时,L(0.1)=+20dB ; 当=1时,L(1)=0dB; 当=10时, L(10)=-20dB。
容易看出各环节的单独作用,便于对系统的分析设计。
01
可以用分段的直线(渐近线)来代替典型环节的准确的对数幅频特性,而且稍加修正就可得到精确的曲线。
02
自动控制原理3第三节典型环节的频率特性

左图是不同阻尼系数情况下的 对数幅频特性和对数相频特性 图。上图是不同阻尼系数情况 下的对数幅频特性实际曲线与 渐近线之间的误差曲线。
1 2T 1 T 2 T 5 T 10 T
1 5T
Saturday, November 05, 2016
15
微分环节的频率特性
⒌ 微分环节的频率特性: 微分环节有三种:纯微分、一阶微分和二阶微分。传递函 数分别为: G( s) s
05, 2016
12
振荡环节的波德图
2 T ( ) tg 相频特性: 1 T 2 2
1
几个特征点: 0, ( ) 0;
1 , ( ) ; , ( ) 。 T 2
由图可见:
K 10, T 1, 0.3 10 G ( j ) 2 s 0.6s 1 1 o T
1
幅频特性为: 相频特性为:
A( )
(1 T 2 2 )2 (2T )2 2 T ( ) tg 1 1 T 2 2
L( ) 20 log A( ) 20 log (1 T 2 2 ) 2 (2 T ) 2 对数幅频特性为:
低频段渐近线: T 1时,L( ) 0 高频段渐近线: T 1时, L( ) 20 log (T 2 2 ) 2 40 log T 1 两渐进线的交点 o 称为转折频率。斜率为-40dB/Dec。 T Saturday, November
1 2
T
时,无谐振峰值。当
M p A( p )
1 2
1 0.707时, p 0 。 2
时,有谐振峰值。
1 2 1 2
1 当 0 , A(0 ) , 。 L ( ) 20 lg 2 0 2
开关电源频域的对数频率特性

开关电源频域的对数频率特性对数频率特性又称波特(Bode)图,是描述开环或闭环控制系统复数增益(Gain)的方法,也是设计开关电源闭环系统的有力工具。
按频率响应G(jω)幅值,相位与频率的关系,分别给出幅频特性(用对数计算)和相频特性。
幅频特性描述增益|G(jω)|与ω的函数关系:201g|G(jω)|-lgω。
以分贝值(dB)为单位,其斜率用dB/dec 表示(dec 即decade 的缩写,十倍频程),如-20dB/dec,-40dB/dec 等。
为了介绍方便,有时也用-1 代表- 20dB/dec,用-2 代表40dB/dec 等。
相频特性描述相位G(jω)与ω的函数关系:G(jω)-lgω。
某一频率的相位与幅频特性变化率有关,相频特性斜率用°/dec表示,如-45°/dec、-90°/dec 等。
有了各个环节(元器件)的Bode 图,计算开环系统的Bode 图就比较简单,对于系统等效控制框图中的串联环节,只要将各环节(元器件)的幅频特性、相频特性直接相加。
Bode 曲线可以近似用直线(渐近线,asymptote)表示,使作图简化,其最大误差幅频为3dB,相频为5.7°。
图1 表示二阶系统的对数频率特性曲线族,横坐标为ω/ωno。
ω/ωn>1 时,幅频特性斜率为-40 dB/dec,相位总滞后为-180°;在ω/ωn=1,阻尼比ζ<0.707 时,幅频特性出现谐振峰值。
阻尼比ζ越小,谐振峰值越大。
由图2、图1 可知,阻尼比ζ是控制系统的一个重要参数,对时域和频域响应都有很大的影响。
图1 典型二阶系统的对数幅频及相频特性曲线族图2 线性时不变自动调节系统的典型阶跃响应曲线y(t)。
自动控制原理 第五章第四节对数频率特性(上)

⑹ 振荡环节
G ( j )
=
1−
2 n2
1 + j2
n
L() = −20lg [1 − 2 ]2 + [2 ]2
2 n
n
( ) =
−
arctan
2
n
1
-2Βιβλιοθήκη 2 n−360
+
arctan 2
n
1
-
2
2 n
1
L( ) 0
n
( ) 0 − 3 6 0
1
n
L() −40lg( n )
( ) −180
5.4 对数频率特性(Bode图)(上)
⑺ 二阶复合微分
G ( j )
=
1−
2
2 n
+
j2
n
L( ) = 20lg
[1
−
2
2 n
]2
+
[2
n
]2
( ) =
2
arctan
n 2
1
-
2 n
2
360 − arctan
n 2
1
-
2 n
5.4 对数频率特性(Bode图)(上) ⑻ 延迟环节 G(j ) = e−j
G(j) = j
L( ) = 20 lg ( ) = 90
G(j) = 1 j
L( ) = −20lg ( ) = −90
5.4 对数频率特性(Bode图)(上)
⑷ 惯性环节
G(j) = 1 +1 + jT
L( ) = −20lg 1 + 2T2
− arctanT
( ) = − 180 + arctan T
2第二节对数频率特性

第二节 对数频率特性
1-Apr-21
1
一、对数频率特性曲线(波德图,Bode图)
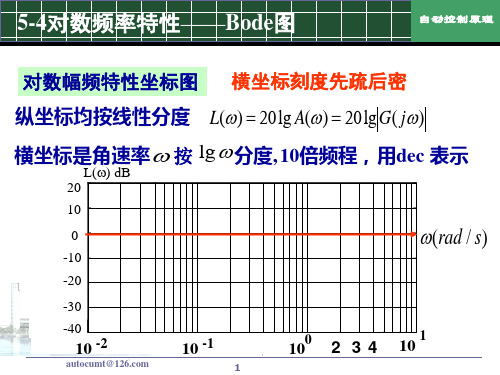
Bode图由对数幅频特性和对数相频特性两条曲线组成。 ⒈波德图坐标(横坐标是频率,纵坐标是幅值和相角)的分度:
横坐标(称为频率轴)分度:它是以频率w 的对数值 logw 进行 线性分度的。但为了便于观察仍标以w 的值,因此对w 而言是 非线性刻度。w 每变化十倍,横坐标变化一个单位长度,称为 十倍频程(或十倍频),用dec表示。类似地,频率w 的数值变化
w L(w )
2 20 log
A(w )
20 log
K
w
40
K 10
20log K 20log w,
20
w 当K 1时,w 1, L(w) 0;
20 40
j (w)
1 10 100 K 1 w
当w 10时,L(w) 20 可见斜率为-20/dec 当K 1时,w 1, L(w) 20log K;
0.3
-120° 0.5
-150° 0.7
1.0
-180°
1
1
10T 5T
1
1
2
2T
T
T
对数幅频特性和对数相频特性
图。上图是不同阻尼系数情况
下的对数幅频特性实际曲线与
渐近线之间的误差曲线。
5 T
10 T
当0.3<<0.8,误差约为±4.5dB
1-Apr-21
16
振荡环节的波德图
相频特性:j
1-Apr-21
6
比例环节的bode图
二、典型环节的波德图 ⒈ 比例环节: G(s) K ;
G( jw) K
幅频特性:A(w) K;相频特性:j(w) 0
1-Apr-21
1
一、对数频率特性曲线(波德图,Bode图)
Bode图由对数幅频特性和对数相频特性两条曲线组成。 ⒈波德图坐标(横坐标是频率,纵坐标是幅值和相角)的分度:
横坐标(称为频率轴)分度:它是以频率w 的对数值 logw 进行 线性分度的。但为了便于观察仍标以w 的值,因此对w 而言是 非线性刻度。w 每变化十倍,横坐标变化一个单位长度,称为 十倍频程(或十倍频),用dec表示。类似地,频率w 的数值变化
w L(w )
2 20 log
A(w )
20 log
K
w
40
K 10
20log K 20log w,
20
w 当K 1时,w 1, L(w) 0;
20 40
j (w)
1 10 100 K 1 w
当w 10时,L(w) 20 可见斜率为-20/dec 当K 1时,w 1, L(w) 20log K;
0.3
-120° 0.5
-150° 0.7
1.0
-180°
1
1
10T 5T
1
1
2
2T
T
T
对数幅频特性和对数相频特性
图。上图是不同阻尼系数情况
下的对数幅频特性实际曲线与
渐近线之间的误差曲线。
5 T
10 T
当0.3<<0.8,误差约为±4.5dB
1-Apr-21
16
振荡环节的波德图
相频特性:j
1-Apr-21
6
比例环节的bode图
二、典型环节的波德图 ⒈ 比例环节: G(s) K ;
G( jw) K
幅频特性:A(w) K;相频特性:j(w) 0
对数频率特性

( ) ~ 为系统的相频特性。
RC网络的幅频特性
和相频特性
1 G( j ) 1 jT
1 A( ) 1 2T 2 ( ) arctgT
RC网络的幅频特性和相频特性
RC网络的幅相特性
1 G( s) Ts 1
G ( j ) G ( s ) s j 1 1 jT 1 j tan 1 T e 2 2 1 T
2
)
C s (t) ( j ) Ar cos( t ( j )
2
)
令 Cs (t ) Ac sin(t )
Ac ( j ) Ar ,
( j )
由此可见,线性定常系统,在正弦信号作用下,
输出稳态分量是与输入同频率的正弦信号。
4、频率分析法还可以推广应用于某些非线性控制系统。
3-1 频率特性
一、频率特性
1、RC电路的正弦稳态输出
G( s) U o (s) 1 , U i ( s) Ts 1 T RC
线性定常系统,输入信号为正弦信号时,稳态输出信号仍 为同频率的正弦信号,只是相位和振幅不同,且相位和振幅与 传递函数的参数有关。 当 ui A sin t 时,初值为0
拉氏反变换
c( t ) C i e si t ( Be j t Be j t )
i 1 n
n
ct ( t ) c s ( t )
其中
Ar ( s j ) s j 2 2 s Ar j [ ( j ) ] ( j ) 2 ( j ) Ar e 2j 2 B ( s)
RC网络的幅相特性曲线
对数频率特性讲解

? 关系
deg -100
-120
-140
-160
-180
-1
10
Phase of 2-order factor
? ? 0.1
0
1
10
10
0
-20
-40
-60
相频特性与 -80
? 关系
deg -100
-120
?
20log ? ?
2
2 n
?
?40log ? ?n
dB
高频时的对数幅频特性曲线是一条斜率为-40分贝/十倍频程的直线
由于在
? ??n
时
? 40 log ? ? ?40 log1 ? 0 dB ?n
所以高频渐近线与低频渐近线在
? ? ? n 处相交。这个频率就是上述二阶因子的转角频率。
20
10
0
幅频特性与
请看下页
Asymptote 渐近线
0
Corner frequency
Bode Diagram of G(jw )=1/(jw T+1) T=0.1
-5
(dB) agnitude
-10 -15
M
-20
精确曲线 Exact curve
-25 0
Asymptote 渐近线
(deg) Phase
-45
精确曲线 Exact curve
? (? ) ? arctg (? T )
0
0
1
2
10
10
10
Frequency (rad/sec)
图: 一阶因子的对数频率特性曲线
L(? ) ? 20 log [1 ? (? T )2] ? 20 log ? T (dB)
第5章4——Bode图
2
1 2 n
2
n
2 arc tg n 2 1 2 n
0 0 ( ) 90 n 180
autocumt@ 22
振荡环节L()
L()dB 40 20 0dB -20
(rad / s)
10 -2
10 -1
1
10
0
2 3 4
10
1
autocumt@
自动控制原理
对数分度:
lg 2 0.301
lg 3 0.4771 lg 4 2lg 2 0.602 lg 5 0.699 lg 6 lg 3 lg 2 0.778
lg 7 0.845 lg 8 3 lg 2 0.903 lg 9 2 lg 3 0.954
()º
(rad / s)
10 -2
autocumt@
10 -1
3
100
10
1
20 10 0
自动控制原理
L() dB -10
-20 -30 -40 900 450
( )
00 0 -450 -900
-1350
完 整 图 二 合 一
-1800
10 -2
autocumt@
[-20] 0.1 0.2
1
2
10 20
[-20]
100
16
5-4 对数频率特性——Bode图
(5)一次微分环节
传递函数: G(S) TS+ 1 频率特性: G ( j ) Tj 1
0 0 1 相频特性 ( ) arctanT 45 T 90
《对数频率特性》课件

表示信号在传输过程中产生的相位偏移。
带宽参数则表示系统能够处理的信号频率范围,这些参数对于
03
理解和优化系统性能至关重要。
数学模型的适用范围
01
对数频率特性数学模型适用于 描述和分析各种类型的电子系 统和信号处理系统,如音频处 理、通信、雷达等。
02
该模型尤其适用于分析具有非 线性或非平坦频率响应的系统 ,这些系统在常规的线性频率 坐标系下难以准确描述。
优缺点对比分析
• 对数频率特性的优点主要在于其能够 提供较大的动态范围和接近人耳的感 知特性,使得音频信号的还原更加真 实和平衡。然而,其缺点在于可能会 产生非线性失真,不易于控制,并且 可能不适合所有应用场景。在选择使 用对数频率特性时,需要根据实际需 求进行权衡和考虑。
05 对数频率特性的未来发展
分析该对数频率特性,可以发现系统在低频段增益较高,而 在高频段增益迅速下降,具有良好的低通滤波器特性。
02
03
动态范围大
对数频率特性能够提供较 大的动态范围,使得音频 信号在低频和高频之间的 变化更加平滑。
接近人耳感知
对数频率特性与人耳的感 知特性较为接近,因此能 够更好地还原声音的真实 感。
计算步骤
01
确定系统的频率响应函数$H(f )$。
02 对$H(f)$取对数,得到对数频率特性$L(f)$。
03 分析$L(f)$的特性,如最大值、最小值、转折点 等,以了解系统在不同频率下的性能。
计算实例
假设一个系统的频率响应函数为$H(f) = 10 times frac{1}{10^3 + f^2}$,则其对应的对数频率特性为$L(f) = log(10 times frac{1}{10^3 + f^2})$。
对数频率特性图
对数频率特性图 (Bode图)
1
2
3
4
5 6 7 891
2
3
4 5 6 7891
2
3
4 5 6 7891
单对数坐标纸
比例环节
G(jω)=K , 20lg| G(jω)|=20lgK , G(jω)=0°
20lg | G( j ) |
20lgK
G ( j )
积分环节
20lg | G( j ) |
dB 0.1 14 0.2 8 0.3 4.4 0.4 2 0.5 0 0.6 -1.6 0.7 -3 0.8 -4 0.9 -6
延迟环节
G( s ) e
r (t )
s
s
r(t)
e
c(t )
0 c(t)
t
—延迟时间
t 0
延迟环节Bode图
20lg | G( j) | 20lg1 0 G( j) 57.3
第四象限
振荡环节Bode图(n=1)
0.1 0.5
0.9
40dB / dec
振荡环节Bode图的修正
1 在 = n T 处,准确值
1 T
20 lg (1 2T 2 ) 2 (2T ) 2 |
20 lg 2
振荡环节在n处幅频特性误差修正表
-20dB/dec
G ( j )
惯性环节Bode图
20lg|G(j)| 0dB -20dB -20dB/dec
-40dB
G ( j )
0° -45°
-90°
0.1 T
1.0 T
பைடு நூலகம்
10 T
惯性环节渐近幅频特性的修正
1
2
3
4
5 6 7 891
2
3
4 5 6 7891
2
3
4 5 6 7891
单对数坐标纸
比例环节
G(jω)=K , 20lg| G(jω)|=20lgK , G(jω)=0°
20lg | G( j ) |
20lgK
G ( j )
积分环节
20lg | G( j ) |
dB 0.1 14 0.2 8 0.3 4.4 0.4 2 0.5 0 0.6 -1.6 0.7 -3 0.8 -4 0.9 -6
延迟环节
G( s ) e
r (t )
s
s
r(t)
e
c(t )
0 c(t)
t
—延迟时间
t 0
延迟环节Bode图
20lg | G( j) | 20lg1 0 G( j) 57.3
第四象限
振荡环节Bode图(n=1)
0.1 0.5
0.9
40dB / dec
振荡环节Bode图的修正
1 在 = n T 处,准确值
1 T
20 lg (1 2T 2 ) 2 (2T ) 2 |
20 lg 2
振荡环节在n处幅频特性误差修正表
-20dB/dec
G ( j )
惯性环节Bode图
20lg|G(j)| 0dB -20dB -20dB/dec
-40dB
G ( j )
0° -45°
-90°
0.1 T
1.0 T
பைடு நூலகம்
10 T
惯性环节渐近幅频特性的修正
自动控制原理5第二节对数频率特性

19
② 一阶微分: A(w) 1 T 2w2,(w) tg1Tw
一阶微分环节的波德图
L(w) 20lg 1 T 2w2 对数幅频特性(用渐近线近似):
低频段渐近线:当Tw 1时,A(w) 1, 20 log A(w) 0 高频段渐近线:当Tw 1时,A(w) Tw,L(w) 20 log Tw
第二节 对数频率特性
1
一、对数频率特性曲线(波德图,Bode图)
Bode图由对数幅频特性和对数相频特性两条曲线组成。 ⒈波德图坐标(横坐标是频率,纵坐标是幅值和相角)的分度:
横坐标(称为频率轴)分度:它是以频率w 的对数值 logw 进行 线性分度的。但为了便于观察仍标以w 的值,因此对w 而言是 非线性刻度。w 每变化十倍,横坐标变化一个单位长度,称为 十倍频程(或十倍频),用dec表示。类似地,频率w 的数值变化
来计算只能求出±90°之间的值(tg-1函数的主值范围),也就是
说当 w ( 1 , ) 时,用计算器计算的结果要经过转换才能得到 。 即当 w (T1 , ) 时,用计算器计算的结果要减180°才能得到 。
T
或用下式计算
(w) tg1 Tw 1 2 tg1 Tw 1 2
17
微分环节的频率特性
(w) K
0 180
K 0 K 0
180
7
K 0
⒉ 积分环节的频率特性:G(s) K
s
频率特性:
G( jw )
K
j
K
K
e2
jw w w
积分环节的Bode图
L(w) / dB
40 20w ) tg1( K 0)
w
2
L(w) 20log A(w) 20log K
对数频率特性Bede讲解
§5.3.2 系统开环对数频率特性 ( Bode) (3)
基准点 (? ? 1, L (1) ? 20 lg K ) 斜率 ? 20 ?v dB dec
??0.2 惯性环节 -20 ??0.5 一阶复合微分 +20 ??1 振荡环节 -40
⑸ 修正 ① 两惯性环节转折频率很接近时 ② 振荡环节 ? ? (0.38, 0.8) 时
⑹ 检查
① L(? ) 最右端曲线斜率=-20(n-m) dB/dec ② 转折点数=(惯性)+(一阶复合微分)+(振荡)+(二阶复合微分) ③ ?(?) ? -90°(n-m)
课程小结(1)
典型环节的频率特性
-1? j? T
j?
?2
?
1?
?
2 n
?
j 2? ?
n
e-? ?
1
?2
?
1?
?
2 n
?
j 2? ?n
? ?n
????
????1
-
? ?
2
2 n
???????
? ?? 1
L(? ) ? 0
?n
? (? ) ? 0? ? 360?
? ?? 1
?n
L(? ) ? ? 40 lg(? ? n )
? (? ) ? ? 180?
§5.3 对数频率特性 ( Bode) (7)
⑺ 二阶复合微分 G(s) ? ( s )2 ? 2? s ? 1
?
?
2 n
G(
j?
)
?
1?
? ?
2
2 n
1 ?
j 2?
? ?n
[1 [ L(? ) ? ? 20 lg
5.3 对数频率特性(Bode图)

172
图 5-27 振荡环节的 Bode 图
图 5-28 振荡环节的误差修正曲线 173
7.二阶复合微分环节
二阶复合微分环节 G(s) = ( s )2 + 2ξ s +1 的对数幅频特性和对数相频特性表达式
ωn
ωn
分别为
⎧ ⎪⎪L(ω) = 20 lg ⎨
⎡ ⎢1 ⎣
−
ω ( ωn
)2
⎤ ⎥ ⎦
2
+
(2ξ
ω ωn
)2
⎪⎪ϕ (ω ) ⎩
=
arctan
2ξω 1− (ω
ωn ωn )2
(5-56)
二阶复合微分环节与振荡环节成倒数关系,两者的 Bode 图关于频率轴对称。
8.延迟环节
延迟环节 G(s) = e−τs 的对数幅频特性和对数相频特性
表达式分别为
⎧⎪L(ω) = 20 lg G( jω) = 0 ⎨⎪⎩ϕ(ω) = −τω
171
振荡环节 G(s) = (
s
1 )2 + 2ξ
s
的对数幅频特性和对数相频特性表达式分别为
+1
ωn
ωn
⎧ ⎪L(ω) = −20 lg ⎪ ⎨
⎡ ⎢1
−
⎣
ω ( ωn
)2
⎤2 ⎥ ⎦
+
(2ξ
ω ωn
)2
⎪⎪ϕ (ω ) ⎩
=
−
arctan
2ξω 1− (ω
ωn ωn )2
(5-55)
当 ω << 1时,略去式(5-55)中 L(ω ) 的 ( ω )2 和 2ξ ω 项,有
(1)将开环传递函数写成尾 1 标准形式:
对数 频率特性

相频特性曲线的纵坐标以度或弧度为单位进行线性分度。
一般将幅频特性和相频特性画在一张图上,使用同一个横 坐标(频率轴)。
当幅制特性值用分贝值表示时,通常将它称为增益。幅值 和增益的关系为:增益 20 log(幅值)
幅值A()
1.0 0
1.2 6
1.5 6
2.0 0
2.5 1
3.1 6
5.6 2
10. 0
Dec Dec Dec Dec
log
... 2 1 0 1 2
0
0.01 0.1
1
10 100
由于 以对数分度,所以零频率线在-∞处。
Thursday, September
10, 2020
2
更详细的刻度如下图所示
1
2
3 4 5 6 7 8 910
20
一倍频程 一倍频程 一倍频程
一倍频程
30 40 50 60 80 100 一倍频程
十倍频程 十倍频程
十倍频程
一倍频程 十倍频程
lg
0
1
2
ω 1 2 3 4 5 6 7 8 9 10
lgω
0.00 0
0.30 1
0.47 7
0.60 2
0.69 9
0.77 8
0.84 5
0.90 3
0.95 4
1.00 0
Thursday, September
10, 2020
3
纵坐标分度:对数幅频特性曲线的纵坐标以 L() 20log A() 表 示。其单位为分贝(dB)。直接将 20log A()值标注在纵坐标上。
第三节 对数频率特性
Thursday, September
10, 2020
一般将幅频特性和相频特性画在一张图上,使用同一个横 坐标(频率轴)。
当幅制特性值用分贝值表示时,通常将它称为增益。幅值 和增益的关系为:增益 20 log(幅值)
幅值A()
1.0 0
1.2 6
1.5 6
2.0 0
2.5 1
3.1 6
5.6 2
10. 0
Dec Dec Dec Dec
log
... 2 1 0 1 2
0
0.01 0.1
1
10 100
由于 以对数分度,所以零频率线在-∞处。
Thursday, September
10, 2020
2
更详细的刻度如下图所示
1
2
3 4 5 6 7 8 910
20
一倍频程 一倍频程 一倍频程
一倍频程
30 40 50 60 80 100 一倍频程
十倍频程 十倍频程
十倍频程
一倍频程 十倍频程
lg
0
1
2
ω 1 2 3 4 5 6 7 8 9 10
lgω
0.00 0
0.30 1
0.47 7
0.60 2
0.69 9
0.77 8
0.84 5
0.90 3
0.95 4
1.00 0
Thursday, September
10, 2020
3
纵坐标分度:对数幅频特性曲线的纵坐标以 L() 20log A() 表 示。其单位为分贝(dB)。直接将 20log A()值标注在纵坐标上。
第三节 对数频率特性
Thursday, September
10, 2020
自动控制原理第12讲(对数频率特性)

10 -2
10 -1
10
0
2 34
10
1
3
Bode图的坐标形式(对数幅频特性)
相频特性坐标图
纵坐标均按线性分度
横坐标刻度先疏后密
( ) i ( )
i 1
N
横坐标是角速率 按 lg 分度 10倍频程,用dec 表示
()0
900 450 00 -450 -900 -1350 -1800
高频时的对数幅频特性曲线是一条斜率为-40dB/dec的直线
20
幅频特性 与 关系
=0.1
10
=0.2 =0.3 =0.5 =0.7 =1.0
0
2 0 0.707 2 r n
dB
-10
r n 122
Mr 1 2 12
-20
-30
1 A( n ) 2
精确曲线
-45
() = -tg-1
-90
1 1 T
10
0
10-1
惯性环节的对数频率特性曲线
Frequency (rad/sec)
1 10
14
惯性环节对数幅频特性误差曲线(左右各十倍频程)
0 -0.5 -1 -1.5 -2
-2.5
-3 10 -1
转 角 处 误 差 最 大 3 分 贝
100
n 1 jtg 2 1 2 n
2
27
2 2 2 (1 2 ) ( 2 ) n n
1 2 10 20
100
-40
②低频0分贝线重合?转角频率?
19
(6)振荡环节
传递函数:
2 n
T
1
n
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
⑴ 化G(s)为尾1标准型 ⑵ 顺序列出转折频率 ⑶ 确定基准线
基准点 ( 1, L(1) 20l g K ) 斜率 20 v dB de c
第一转折频率之左 的特性及其延长线
惯性环节 -20dB/dec 一阶 复合微分 +20dB/dec ⑷ 叠加作图 振荡环节 -40dB/dec 二阶 复合微分 +40dB/dec
1 jT1 1 jTn-v
v
20lg K 20lg1 j 1 20lg1 j m
20v lg 20lg1 jT1 20lg1 jTn- v
( ) G arctan 1 arctan m 90v arctanT1 arctanTn- v
c
2
c
c 2 101.5 63.2 rad s
§5.3
对数频率特性 ( Bode) (10)
K s2
例2 根据Bode图确定系统传递函数。
解. 依图有 G ( s )
20 lg K 20
20 lg M r 20 lg
2 n
2
s
n
1
K 10
1 2 1
§5.3
对数频率特性 ( Bode) (8)
⑻ 延迟环节
G( s) e
s
j
G( j ) e
L( ) 20lg1 0
( ) 57.3
§5.3
对数频率特性 ( Bode) (9)
K Ts 1
例1 根据Bode图确定系统传递函数。 解. 依图有 G ( s )
s
⑺ 二阶复合微分 G( s ) (
2 G( j ) 1 2 j 2 n n
n
)2 2
s
n
1
2 2 2 L( ) 20 l g [1 2 ] [2 ] n n 2 n arctan 2 1- 2 n ( ) 2 n 360 arctan 2 1- 2 n
⑸ 修正 ① 两惯性环节转折频率很接近时 ② 振荡环节 (0.38, 0.8) 时
① L() 最右端曲线斜率=-20(n-m) dB/dec ⑹ 检查 ② 转折点数=(惯性)+(一阶复合微分)+(振荡)+(二阶复合微分) ③ () -90°(n-m)
Pc Pc lg (贝 尔) 10lg (分 贝) Pr Pr
⑴ 幅值相乘 = 对数相加,便于叠加作图;
坐标特点
纵轴
特点
⑵ 可在大范围内表示频率特性;
⑶ 利用实验数据容易确定 L(),进而确定G(s)。
§5.3
对数频率特性 ( Bode) (3)
L( ) 20lg K ( ) 0 L( ) 20lg
2 1 2 j 2 n n 2 2 2 L( ) 20 l g [1 2 ] [2 ] n n
arctan 2 n 2 1- 2 n
( )
1 n 1 n
360 arctan 2 n
L( ) 0 ( ) 0 360 L( ) 40lg( n ) ( ) 180
2 1- 2 n
§5.3
对数频率特性 ( Bode) (7)
0.2 惯性环节 -20 0.5 一阶复合微分 +20 1 振荡环节 -40
§5.3.2 系统开环对数频率特性 ( Bode) (3)
基准点 ( 1, 斜率
L(1) 20l g K )
20 v dB dec
0.2 惯性环节 -20 0.5 一阶复合微分 +20 1 振荡环节 -40
§5.3
对数频率特性 ( Bode) (4)
( ) arctan T
惯性环节对数相频特性() 关于(1/T, 45) 点对称
1 G( j ) , 1 jT
1 K ) ( ) 90 TK T
( 证明:
设
1 arctan K K K ( ) arctan(T ) T T
自动控制原理
( 3)
§5.3 对数频率特性(Bode图)
§5.3
对数频率特性 ( Bode )(1)
Bode图介绍
§5.3
对数频率特性 ( Bode)(2)
Bode图介绍
横轴
按 lg 刻度,dec “十倍频程” 或 “旬 距” 按 标定,等距等比
L( ) 20lgG( j ) dB “分贝”
1 jT
e-j
K
2 ⑹ G( j ) 1 1 2 j 2 n n
1 1 j T
1 1 j T
2 G ( j ) 1 j 2 ⑺ 2 n n
⑻ G( j ) e
j
2 1 2 j 2 n n
§5.3
对数频率特性 ( Bode) (12)
典型环节的频率特性
1 1
- 1 jT
j
2 1 2 j 2 n n
j 2 2 n n
2
1 jT
e -
1 1 j T
1 1 j T
K
2 1 2 j 2 n n
1
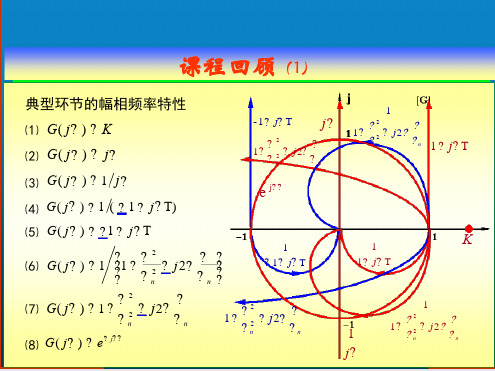
课程回顾(1)
典型环节的幅相频率特性
⑴ G( j ) K ⑵ G ( j ) j ⑶ G( j ) 1 j ⑷ G( j ) 1 ( 1 jT) ⑸ G( j ) 1 jT
- 1 jT
j
1
2 1 2 j 2 n n
2 1 2 j 2 n n
- 1 jT
j
2 1 2 j 2 n n
j 2 2 n n
2
1 jT
e -
1 1 j T
1 1 j T
K
2 1 2 j 2 n n
1
1 j
1
j 2 2 n n
2
课程小结(2)
绘制系统开环Bode图的步骤
20 lg K 30
30 20
转折频率 2 1 T
T 0.5
K 10 31.6 31.6 G( s) s 1 2
• Bode图与Nyquist图之间的对应关系:
• 截止频率c:
G( jc ) 1
30dB 20( lg c lg 2) 20 lg 30 lg 1.5 2 20
⑵ 顺序列出转折频率
最小转折频率之左 ⑶ 确定基准线 的特性及其延长线
惯性环节 -20dB/dec 复合微分 +20dB/dec ⑷ 叠加作图 振荡环节 -40dB/dec 二阶 复合微分 +40dB/dec 一阶
基准点 ( 1, 斜率
L(1) 20l g K )
20 v dB de c
⑸ 一阶复合微分
G( s ) Ts 1
G( j ) 1 jT
L( ) 20lg 1 T
2
2
( )
arctan T
180 arctan T
§5.3
G ( j )
对数频率特性 ( Bode) (6)
1
2 n ⑹ 振荡环节 G( s ) 2 2 s 2n s n
1
1 j
1
j 2 2 n n
2
课程回顾(2) §5.2 幅相频率特性(Nyquist图)
典型环节的幅相特性曲线 系统的开环幅相特性曲线
§5.2.1 §5.2.2
(1)确定幅相曲线的起点G(j0) 和终点 G(j∞); (2)幅相曲线的中间段由s平面零、极点矢量随 s=j的变化规律概略绘制; (3)必要时可以求出G(j) 与实/虚 轴的交点。
1 1 ( ) arctan ( T ) TK TK
1 K tan tan tan( ) K 1 1 tan tan 1 K K
arctan K
90
§5.3
对数频率特性 ( Bode) (5)
1 j
1
j 2 2 n n
2
§5.3.2 系统开环对数频率特性 ( Bode) (1)
§5.3.2 系统的开环Bode图
K ( τ1 s 1)( τ m s 1) G( s ) v s (T1 s 1)(Tn v s 1)
L( ) 20 lg G 20 lg K 1 j 1 1 j m
自动控制原理
( 3)
§5. 线性系统的频域分析
§5.1 §5.2 §5.3 §5.4 §5.5 §5.6 §5.7 §5.8 频率特性的基本概念 幅相频率特性(Nyquist图) 对数频率特性(Bode图) 频域稳定判据 稳定裕度 利用开环频率特性分析系统的性能 闭环频率特性曲线的绘制 利用闭环频率特性分析系统的性能
§5.3.2 系统开环对数频率特性 ( Bode) (2)
绘制系统开环Bode图的步骤
⑴ 化G(s)为尾1标准型
40( s 0.5) 例1 G ( s ) s( s 0.2)(s 2 s 1)
G( s ) 100( s( s 1)(s 2 s 1) 0.2 0.2 惯性环节 0.5 一阶复合微分 1 振荡环节 s 1) 0.5
8 20
2
8 dB
r n 1 2 2 28.77
2 1 2 10
4 2
n
r
1 2
2
30
基准点 ( 1, L(1) 20l g K ) 斜率 20 v dB de c
第一转折频率之左 的特性及其延长线
惯性环节 -20dB/dec 一阶 复合微分 +20dB/dec ⑷ 叠加作图 振荡环节 -40dB/dec 二阶 复合微分 +40dB/dec
1 jT1 1 jTn-v
v
20lg K 20lg1 j 1 20lg1 j m
20v lg 20lg1 jT1 20lg1 jTn- v
( ) G arctan 1 arctan m 90v arctanT1 arctanTn- v
c
2
c
c 2 101.5 63.2 rad s
§5.3
对数频率特性 ( Bode) (10)
K s2
例2 根据Bode图确定系统传递函数。
解. 依图有 G ( s )
20 lg K 20
20 lg M r 20 lg
2 n
2
s
n
1
K 10
1 2 1
§5.3
对数频率特性 ( Bode) (8)
⑻ 延迟环节
G( s) e
s
j
G( j ) e
L( ) 20lg1 0
( ) 57.3
§5.3
对数频率特性 ( Bode) (9)
K Ts 1
例1 根据Bode图确定系统传递函数。 解. 依图有 G ( s )
s
⑺ 二阶复合微分 G( s ) (
2 G( j ) 1 2 j 2 n n
n
)2 2
s
n
1
2 2 2 L( ) 20 l g [1 2 ] [2 ] n n 2 n arctan 2 1- 2 n ( ) 2 n 360 arctan 2 1- 2 n
⑸ 修正 ① 两惯性环节转折频率很接近时 ② 振荡环节 (0.38, 0.8) 时
① L() 最右端曲线斜率=-20(n-m) dB/dec ⑹ 检查 ② 转折点数=(惯性)+(一阶复合微分)+(振荡)+(二阶复合微分) ③ () -90°(n-m)
Pc Pc lg (贝 尔) 10lg (分 贝) Pr Pr
⑴ 幅值相乘 = 对数相加,便于叠加作图;
坐标特点
纵轴
特点
⑵ 可在大范围内表示频率特性;
⑶ 利用实验数据容易确定 L(),进而确定G(s)。
§5.3
对数频率特性 ( Bode) (3)
L( ) 20lg K ( ) 0 L( ) 20lg
2 1 2 j 2 n n 2 2 2 L( ) 20 l g [1 2 ] [2 ] n n
arctan 2 n 2 1- 2 n
( )
1 n 1 n
360 arctan 2 n
L( ) 0 ( ) 0 360 L( ) 40lg( n ) ( ) 180
2 1- 2 n
§5.3
对数频率特性 ( Bode) (7)
0.2 惯性环节 -20 0.5 一阶复合微分 +20 1 振荡环节 -40
§5.3.2 系统开环对数频率特性 ( Bode) (3)
基准点 ( 1, 斜率
L(1) 20l g K )
20 v dB dec
0.2 惯性环节 -20 0.5 一阶复合微分 +20 1 振荡环节 -40
§5.3
对数频率特性 ( Bode) (4)
( ) arctan T
惯性环节对数相频特性() 关于(1/T, 45) 点对称
1 G( j ) , 1 jT
1 K ) ( ) 90 TK T
( 证明:
设
1 arctan K K K ( ) arctan(T ) T T
自动控制原理
( 3)
§5.3 对数频率特性(Bode图)
§5.3
对数频率特性 ( Bode )(1)
Bode图介绍
§5.3
对数频率特性 ( Bode)(2)
Bode图介绍
横轴
按 lg 刻度,dec “十倍频程” 或 “旬 距” 按 标定,等距等比
L( ) 20lgG( j ) dB “分贝”
1 jT
e-j
K
2 ⑹ G( j ) 1 1 2 j 2 n n
1 1 j T
1 1 j T
2 G ( j ) 1 j 2 ⑺ 2 n n
⑻ G( j ) e
j
2 1 2 j 2 n n
§5.3
对数频率特性 ( Bode) (12)
典型环节的频率特性
1 1
- 1 jT
j
2 1 2 j 2 n n
j 2 2 n n
2
1 jT
e -
1 1 j T
1 1 j T
K
2 1 2 j 2 n n
1
课程回顾(1)
典型环节的幅相频率特性
⑴ G( j ) K ⑵ G ( j ) j ⑶ G( j ) 1 j ⑷ G( j ) 1 ( 1 jT) ⑸ G( j ) 1 jT
- 1 jT
j
1
2 1 2 j 2 n n
2 1 2 j 2 n n
- 1 jT
j
2 1 2 j 2 n n
j 2 2 n n
2
1 jT
e -
1 1 j T
1 1 j T
K
2 1 2 j 2 n n
1
1 j
1
j 2 2 n n
2
课程小结(2)
绘制系统开环Bode图的步骤
20 lg K 30
30 20
转折频率 2 1 T
T 0.5
K 10 31.6 31.6 G( s) s 1 2
• Bode图与Nyquist图之间的对应关系:
• 截止频率c:
G( jc ) 1
30dB 20( lg c lg 2) 20 lg 30 lg 1.5 2 20
⑵ 顺序列出转折频率
最小转折频率之左 ⑶ 确定基准线 的特性及其延长线
惯性环节 -20dB/dec 复合微分 +20dB/dec ⑷ 叠加作图 振荡环节 -40dB/dec 二阶 复合微分 +40dB/dec 一阶
基准点 ( 1, 斜率
L(1) 20l g K )
20 v dB de c
⑸ 一阶复合微分
G( s ) Ts 1
G( j ) 1 jT
L( ) 20lg 1 T
2
2
( )
arctan T
180 arctan T
§5.3
G ( j )
对数频率特性 ( Bode) (6)
1
2 n ⑹ 振荡环节 G( s ) 2 2 s 2n s n
1
1 j
1
j 2 2 n n
2
课程回顾(2) §5.2 幅相频率特性(Nyquist图)
典型环节的幅相特性曲线 系统的开环幅相特性曲线
§5.2.1 §5.2.2
(1)确定幅相曲线的起点G(j0) 和终点 G(j∞); (2)幅相曲线的中间段由s平面零、极点矢量随 s=j的变化规律概略绘制; (3)必要时可以求出G(j) 与实/虚 轴的交点。
1 1 ( ) arctan ( T ) TK TK
1 K tan tan tan( ) K 1 1 tan tan 1 K K
arctan K
90
§5.3
对数频率特性 ( Bode) (5)
1 j
1
j 2 2 n n
2
§5.3.2 系统开环对数频率特性 ( Bode) (1)
§5.3.2 系统的开环Bode图
K ( τ1 s 1)( τ m s 1) G( s ) v s (T1 s 1)(Tn v s 1)
L( ) 20 lg G 20 lg K 1 j 1 1 j m
自动控制原理
( 3)
§5. 线性系统的频域分析
§5.1 §5.2 §5.3 §5.4 §5.5 §5.6 §5.7 §5.8 频率特性的基本概念 幅相频率特性(Nyquist图) 对数频率特性(Bode图) 频域稳定判据 稳定裕度 利用开环频率特性分析系统的性能 闭环频率特性曲线的绘制 利用闭环频率特性分析系统的性能
§5.3.2 系统开环对数频率特性 ( Bode) (2)
绘制系统开环Bode图的步骤
⑴ 化G(s)为尾1标准型
40( s 0.5) 例1 G ( s ) s( s 0.2)(s 2 s 1)
G( s ) 100( s( s 1)(s 2 s 1) 0.2 0.2 惯性环节 0.5 一阶复合微分 1 振荡环节 s 1) 0.5
8 20
2
8 dB
r n 1 2 2 28.77
2 1 2 10
4 2
n
r
1 2
2
30
