第八章晶体内部结构的微观对称和空间群2015
晶体对称和极射投影ppt课件

晶体中的宏观对称元素
2,3,4,6次轴和平面点阵的结合
五种平面点阵分别属于下表的四种平面 晶系
对于二维晶体仅有垂直于晶面的1,2, 3,4,6轴和对称心,互相组合只能形 成10种二维晶体学点群
二、晶体对称元素的基本原理:对称性要与晶体内部点阵结构 的周期性相适应。
原理:1、在晶体的空间点阵结构中,任何对称轴都必与一组 直线点阵平行;任何对称面都必与一组平面点阵平行,而与 一组直线点阵垂直。
空间群符号LS1S2S3
运用以下规则,可以从对称元素获得H-M空间群符号。 1. 第一字母(L)是点阵描述符号,指明点阵带心类型: P, I, F, C, A, B。 2. 其于三个符号(S1S2S3)表示在特定方向(对每种晶系分别规定)上的对称元
素。 3. 如果没有二义性可能,常用符号的省略形式 (如Pm,而不用写成P1m1)。 4. * 由于不同的晶轴选择和标记,同一个空间群可能有几种不同的符号。如
对称元素的图示和印刷符号(1)
对称元素的图示和印刷符号(2)
了解Herman-Mauguin空间群符号
空间群是经常用简略Herman-Mauguin符号(即 Pnma、I4/mmm等)来指定。 在简略符号中包含 能产生所有其余对称元素所必需的最少对称元素。
从简略H-M符号,我们可以确定晶系、Bravais点 阵、点群和某些对称元素的存在和取向(反之亦 然)。
立方晶系 六方晶系
四方晶系
三方晶系 正交晶系 单斜晶系 三斜晶系
三个 4 或四个 3 一个 6 或 6
一个 4 或 4
一个 3 或 3
三个 2 一个 2
无(仅有i )
O,Oh,T,Th,Td
C6 ,C6h ,C3h ,C6v D6 ,D6h ,D3h C4 ,S4 ,C4h ,C4V D4 , D4h , D2d
晶体内部结构的微观对称

利用晶体对称性,可以设计具有特定催化性能的 催化剂,提高化学反应的效率和选择性。
3
药物合成与筛选
通过研究药物分子与晶体之间的相互作用,可以 优化药物分子的设计和合成,提高药物的疗效和 降低副作用。
06
晶体内部结构对称性的研 究方法
X射线晶体学
总结词
X射线晶体学是研究晶体内部结构的主要方法之一,通过分析X射线在晶体中的衍射现象,可以获得晶体中原子的 排列方式和晶格结构等信息。
晶体内部结构的微观对 称
目录 CONTENT
• 晶体微观对称的概念 • 晶体微观对称的几何基础 • 晶体内部结构的对称元素 • 晶体内部结构的对称操作 • 晶体内部结构对称性的应用 • 晶体内部结构对称性的研究方法
01
晶体微观对称的概念
定义与特性
定义
晶体内部结构的微观对称是指晶体内 部原子或分子的排列方式具有的对称 性。
空间群对称
晶体内部原子或分子的排列具 有空间群对称性,如立方晶系
的点群对称。
02
晶体微观对称的几何基础
点群
定义
点群是指晶体中由一个或多个对 称元素组成的集合,这些对称元 素在晶体中所有可能的取向中保
持不变。
分类
点群可以分为一维、二维和三维点 群,分别对应于一维、二维和三维 晶体结构。
应用
点群是晶体结构分类的基础,通过 点群可以确定晶体的对称性,进而 确定晶体的物理和化学性质。
总结词
旋转轴是晶体内部结构中的一种对称元素,能够使晶体内部结构在旋转一定角度后恢复到原始状态。
详细描述
旋转轴在晶体内部结构中起着重要的作用,不同的旋转轴会导致晶体具有不同的对称性,从而影响晶体 的物理性质和化学性质。例如,在矿物学中,许多矿物具有特定的对称性,可以通过观察其晶体形态和 内部结构来确定其对称元素。
晶体的对称性

晶体学点群的对称元素方向及国际符号
晶系
第一位
第二位
第三位
点群(32个)
可能对称 元素
三斜 1,`1 单斜 2,m,2/m 正交 2,m
方向 可能对称 元素
任意 无
Y无 X 2,m
方向 可能对称 元素
无 无 Y 2,m
方向 Z
1,`1 2,m,2/m 222,mm2,mmm
比如:单斜空间群Pm 仅有垂直于b轴的二个镜面。 一 个在y = 0,另一个在y = ½位置。
通过镜面操作,在x, y, z的原子 --〉在x, - y, z 第二个原子。如果我们安置原子在其中一个镜面(它的Y座标将
必须是0或½),镜面反射操作就不会产生第二个原子。
Wyckoff位置 (2)
多重性( multiplicity ):告诉我们如果安置一个特定原子在该位置,经过空间 群的所有对称操作,总共会产生多少个原子。
P21/m, Imm2, Ccca, I422, P4/mmm, R3, P3212, P63mc, Fd-3, Im-3m 6. 什么是等效点系,特殊等效点系有什么特点? 7. 什么是wyscoff 晶位,如何表示? 8. 原子参数中的占有率指的是什么? 9. 一般晶体结构数据描述中的Z值指的是什么? 10.完整描述晶体结构的要素有哪些?
记号( letter )是从高对称性位置开始按英文字母顺序指定的位置标记。 对称( symmetry )告诉我们原子所在之处具有的对称元素。
Pm空间群的 Wyckoff位置
多重性 Wyckoff记号 点对称
坐标
2
c
1
(1) x, y, z
(2) x, - y, z
晶体的对称性

点群的Schönflies符号:
主轴:Cn、Dn、Sn、T和O Cn:n次旋转轴; Sn : n次旋转-反映轴; Dn:n次旋转轴加上一个与之垂直的二次轴 T: 四面体群; O: 八面体群。
脚标:h、v、d h:垂直于n次轴(主轴)的水平面为对称面; v:含n次轴(主轴)在内的竖直对称面; d:垂直于主轴的两个二次轴的平分面为对称面。
用的几何变换(旋转和反射)都是正交变换——保持
两点距离不变的变换: ⎛ x ' ⎞ ⎛ a11 a12 a13 ⎞ ⎛ x ⎞
数学上可以写作:
⎜ ⎜⎜⎝
y z
' '
⎟ ⎟⎟⎠
=
⎜ ⎜⎜⎝
a21 a31
a22 a32
a23 a33
⎟⎟⎟⎠i⎜⎜⎜⎝
y z
⎟ ⎟⎟⎠
其中 Aij 为正交矩阵
从解析几何知道,符合正交 变换的是:绕固定轴的转动 (Rotation about an axis)
准晶态结构特点:具有长程取向序,没有长程平移对 称性。
其实准晶可以看作是具有平移对称性的六维超空间在三维真实 空间的投影
黄昆书 47-48 陈长乐书 20-22
1974年Penrose提出的数学游戏
五次对称的黄金分割无理数
边长有两种取值:1, 1+ 5 = 1.618
2
二十面体AlPdMn表面的STM图像
D2、C2V、D2h
C3、S6、D3 C3V、D3d
C4、S4、C4h、D4 C4V、D2d、D4h C6、C3h、C6h、 D6、C6V、D3h、
D6h T、Th、Td
O、Oh
P、C P、C、I、
F R P、I
H
材料分析方法-李晓娜-3 微观对称性-空间群-实际晶体结构
Cu3Au, simple cubic
36
常用晶体学手册及软件介绍
1. 晶体学手册-Pearson’s Handbook (皮尔森手册)介绍
37
2. CaRIne Crystallography 程序简介
3. 晶体结构立体模型 建构软件-Diamond
常用的晶体学软件还有Mercury,Chemdraw,Olex,Atoms……等等,
4
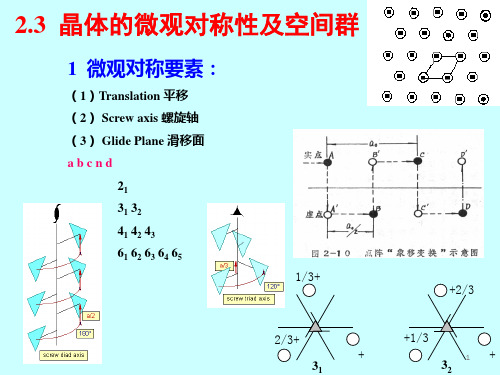
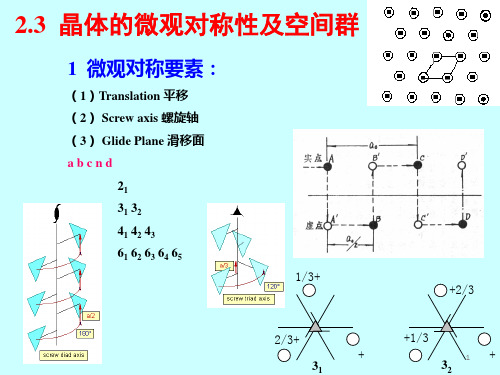
螺旋轴: 旋转+平移
5
6
对称变 换中所 有的轴 对称素
7
滑移面
反映+平移
滑移面可以垂直纸面放置,如左图中虚线表示垂直于纸面的b滑移面的投
影,也可以平行于纸面放置或直接与纸面重合,如右图中右上角的标记表示
n滑移面与纸面重合,所以在图中起始在纸面上方的点,滑移一次后到纸面
下方,用点旁边的正负号分别表示其在纸面上或下,也可由空心圆圈中的点
从高到低用字母a、b、c、d、e、f等表示,称其为乌科夫(
Wyckoff)符号。具有同一个乌科夫符号的位置,属于同一 个等效点系。同乌科夫符号在一起的数字就是它所代表的等 效点系的点数,也就是由空间群对称性联系起来的对称相关 位置数。
17
晶体对称性小结
晶体宏观对称要素:5个旋转轴,5个旋转反轴
按规定组合在一点
40
2. 画出四种平面点阵(它是无限大的)除平移外的所有对称 元素及其所在位置(在有限个阵点画出就可以了)。
41
42
3. 某正交晶系单胞中,在如下位置有单原子存在:①(0, 1/2, 0),(1/2, 0, 1/2)两种位置都是同类原子;②([1/2, 0,0]), (0, 1/2, 1/2)上是A 原子,(0, 0, 1/2),(1/2, 1/2, 0)是B 原子。 问上两种晶胞各属于哪一种布喇菲点阵?
晶体的微观对称性

对称动作只有点动作
无限的晶体结构中的对称性
实际存在的、本质的
不仅考虑方向,还考虑对称元 素的相互位置关系 对称元素不须交于一点,在三 维空间无限分布 包括点动作与空间动作
点阵(平移轴):对应的对称操作为平移。
点阵反映了晶体结构的周期性,这种周期性也就是点阵的平 移复原的特性。对于点阵,连接任意两个阵点的位置矢量: R = ma + nb + pc,进行平移可以使点阵复原,表现在晶体 结构上就是使在三维空间无限伸展的相同部分得以重复。R 可以定义为晶体微观结构平移的方向矢量。
推论:两个平行滑移面的连续操作相当于一个平移对称操作,并 且该平移对称操作垂直于滑移面的分量也是一个平移对称操作。
NaCl结构沿c方向的投影
定理二:平移T及垂直于平移的反映面的连续操作相 当于与该反映面相距T /2处的一个反映面的反映操作。
推论:平移T及垂直于平移的滑移面的连续操作相当于与该 反映面相距T /2处的一个滑移面的反映平移复合操作。
• 布拉威法则: 1、划分出来的平行六面体单位必须充分地反映晶体的固
有对称性。
2、在不违背晶体固有对称性的条件下,平行六面体单位 的棱间直角数尽量多。
3、在满足条件1和2的前提下,平行六面体单位的体积 应为最小。
• 十四种空间格子 1)三斜格子:P 点阵点群:Ci 晶格参数:abc, 90o
• 点阵格子的对称性(点阵点群)
三斜格子:Ci / C 单斜格子:C2h / L2 PC 正交格子:D2h / 3L2 3PC 四方格子:D4h / L4 4L2 5PC 三方格子:D3d / L3 3L2 3PC 六方格子:D6h / L6 6L2 7PC 立方格子:Oh / 3L4 4L3 6L2 9PC 属于某一晶系的晶体,其点阵格子具有该晶系全对称 类型的对称性。
第八章晶体结构内部对称

2.螺旋轴
• 螺旋轴为晶体结构中一条假想的直线,当 结构围绕此直线旋转一定角度,并平行此 直线移动一定距离后,结构中的每一质点 都和与其相同的质点重合,整个结构自相 重合。
• 螺旋轴据其轴次和螺距可分为 21, 31, 32, 41, 42, 43, 61, 62, 63, 64, 65,共11种。
第八章晶体结构内部对称
22
第八章晶体结构内部对称
23
第八章晶体结构内部对称
24
第八章晶体结构内部对称
25
第八章晶体结构内部对称
26
3.滑移面
• 滑移面是晶体结构中一假想的平面,当结 构对此平面反映,并平行此平面移动一定 距离后,构造中的每一个点与其相同的点 重合,整个构造自相重合。
• 滑移面按其滑移的方向和距离可分为a、b、 c、d、n五种。其中a、b、c为轴向滑移,d 为对角线滑移,n为金刚石型滑移。
第八章晶体结构内部对称
27
第八章晶体结构内部对称
28
第八章晶体结构内部对称
29
第八章晶体结构内部对称
30
四、空间群
• 晶体外形为有限图形,其对称要素有对称轴、对称面、 对称中心、旋转反伸轴和旋转反映轴,其相应的对称操 作只有旋转、反映、反伸,而无平移。对称要素相交于 一点(晶体中心)。在进行这样的对称操作时,至少一个 点是不动的,故这些对称操作属于点操作。点操作对称 要素的组合称为点群,共有32种,即前述的32种对称型。
二、空间格子中的行列和面网的符号பைடு நூலகம்点的坐标
• 空间格子中,其结点、行列和面网可以进行 指标。即通过一定的方法以一定的符号形式 把它们的位置或方位表示出来。这与晶面、 晶棱(晶轴、晶带轴)符号的表示方法相同但又 有区别。
晶体的微观对称操作

晶体的微观对称操作首先,晶体的微观对称操作可以分为平移、旋转、镜面反射和反演等几种基本操作。
平移操作是指将晶体中的每个原子或离子沿着某个方向移动相同的距离。
旋转操作是指将晶体中的每个原子或离子绕着某个轴旋转一定的角度。
镜面反射操作是指将晶体中的每个原子或离子关于一个平面进行镜面对称。
反演操作是指将晶体中的每个原子或离子关于一个点进行对称。
其次,晶体的微观对称操作可以用对称元素来描述。
对称元素包括平移矢量、旋转轴和镜面反射面等。
平移矢量描述了晶体中的平移操作,它可以用一个矢量来表示。
旋转轴描述了晶体中的旋转操作,它可以用一个轴线和一个旋转角度来表示。
镜面反射面描述了晶体中的镜面反射操作,它可以用一个平面来表示。
这些对称元素可以组合形成晶体的对称群。
此外,晶体的微观对称操作还可以用空间群来描述。
空间群是指晶体中所有微观对称操作的集合。
空间群包括平移操作和点群操作。
平移操作是指晶体中的平移矢量,它描述了晶体中的周期性重复。
点群操作是指晶体中的旋转操作、镜面反射操作和反演操作,它们描述了晶体中的局部对称性质。
最后,晶体的微观对称操作对晶体的物理性质和化学性质都有重要影响。
对称操作可以决定晶体的晶体系统、晶胞参数和晶体结构。
晶体的对称性决定了晶体的光学性质、电学性质和磁学性质等。
晶体的微观对称操作也对晶体的生长、相变和缺陷行为等有重要影响。
综上所述,晶体的微观对称操作是描述晶体内部对称性质和晶体结构变化的重要概念。
它可以通过对称元素、空间群和物理性质等多个角度来理解和描述。
晶体的微观对称操作对于理解晶体的性质和应用具有重要意义。
材料分析方法-3 微观对称性-空间群-实际晶体结构
•
LiFeO2(Li1/2Fe1/2) O
•
CaF2结构:
•
NaYF4 (Na1/2Y1/2)F2
(Li1/2Fe1/2) O
33
(2)多元化合物的原子有序-无序转变:
离子排列的有序化,产生离子位置的分离,简单的结构类 型变成复杂的晶体结构
• 阳离子配置图:Na+离子占据CaF2 结构一半的顶角位置(棱上)和 5/6的面心位置 ;U5+离子占据其 余1/6的面心位置(体心)和1/2的 顶角位置。
32点群:点对称操作群
根据特征对称要素归属为7种晶系
7种晶系
晶格类型P,I,F,A,B,C,R
14种布拉菲点阵
32个点群+平移操作(螺旋轴,滑移面)
230空间群
2.4 实际晶体结构
1,铁素体铁-Fe:体心立方点阵,空间群:Im3m(229号),每个 单胞包括2个阵点:(0,0,0)点群 m3m;(1/2,1/2,1/2)。
• 有序化,四方体心结构,晶胞参数 沿c轴较CaF2结构增大一倍。
34
黄铜矿(Cu1/2Fe1/2)S
• 立方硫化锌结构。 • 有序化,Fe原子占据立方硫化锌
结构1/2的顶角位置,1/2面心位 置(体心),Cu原子占据立方硫 化锌结构其余1/2的顶角位置(棱 上),1/2面心位置(底心) • 四方体心结构,晶胞参数沿c轴较 ZnS结构增大一倍。
重复点数:一套等效点系在一个单位晶胞中所拥有的等效 点系的数目。重复点数与原始点在晶胞中所处的位置有关, 该点的对称称为点位置的对称性。如原始点处在某个(些) 对称要素位置上,则得到的等效点系位置被称为特殊等效点 系位置;反之,处在一般位置上(点对称为1),则称为一 般等效点系位置。
晶体的微观对称

13
表示面网的通用符号为 (hkl)。 以下为几例特殊面网:
(010)
(020)
(030)
14
(100)
(200)
(111)
15
2.2.2 面网间距 (distance of nets) 定义:
40
2.4.2 国际符号的书写原则:
沿某方位,有对称要素就写出来,无就空着或 写为‘1’。 ① //某方位只有对称轴n,记作 n;⊥某方位只有对
称面m,记作 m。 ②某方位有 n + m⊥,记作 n/m (2/m可简化为m)。 ③ 单斜晶系的空间群通常按3位来写,其中两个位
置为1,只有一个位置有对称要素,如P1211(4)、 P1121(4)、P1121/m(11),这时,3位分别代表晶 体的a、b、c方向。
2.1.1 空间格子的要素
节点、行列、面网、平行六面体
Cs Cl
2
平行六面体的描述:用a0,b0,c0,α、β、γ六个 参数决定,即晶格常数或晶胞常数(参数)。
3
2.1.2 空间格子类型
原始格子 P (Primative):结点分布在平行六面 体的角顶,结点坐标为(0,0,0): (对三方菱面体格子,符号为R (rhombehedral)
25
§2.3 晶体的微观对称要素
2.3.1 螺旋轴(screw rotation axis) 晶体外部对称中的对称轴,在晶体内部可以体
现为对称轴,亦可以体现为螺旋轴。 螺旋轴是指:旋转+平移。 对称轴有:2,3,4,6 螺旋轴有:21; 31、32; 41、42、43; 61、62、63、64、65 共11种螺旋轴。
第八章 晶体点阵结构

1/r:1/s:1/t = 1/3:1/3:1/5= 5:5:3=h:k:l
晶体外形的晶面的指标化
四面体4个面的指标:(111)(1,-1, 1) (-1, 1,1) (1,1-1) 八面体的8个面的指标:(111)(1,-1, 1) (-1, 1,1) (1,1-1) (-1,-1,-1)(1,-1,-1) (-1, -1,1) (-1,1-1)
4.平面间距d(hkl) 平面点阵族(hkl)中相邻2个平面的间距。 晶系 立方晶系 六方晶系 正交晶系 计算公式 d(hkl)=a (h2 + k2 + l2) -1/2 d(hkl)=[(4/3) (h2 + hk + k2) a-2 + l2c-2] -1/2 d(hkl)=[ (h2 / a2+ k2 / b2 + l2 / c2] -1/2
晶体的对称性与空间群

晶体的对称性与空间群3.1 晶格与非晶态物质不同,晶体中分子、离子或原子团在空间按照一定的规律排列而形成的固体物质。
也就是说,在晶体内部,分子、离子或原子团在三维空间以某种结构基元(structural motif)(即重复单位)的形式周期性的排列。
只要知道其中最简单的结构基元,以及他们在空间平移(translation)的向量长度与方向,就可以得到原子或者分子在晶体中的排部的情况。
结构基元可以是一个或者多个原子(离子),也可以是一个或者多个原子(离子),也可以是一个或者多个分子,每个结构基元的化学组成及原子的空间排列完全相同。
如果将结构基元抽象为一个点,晶体中分子或原子的排列就可以看成点阵(lattice)。
也就是说,晶体的结构=结构基元+点阵。
单晶体都属于三维点阵,为了直观,这里采用简化的二维点阵来说明。
图 3.1(a)显示[Cu2(ophen)2]分子[1]在晶胞中二维平面上的排列,其中每个结构基元一个[Cu2(ophen)2]分子,可以抽象为一个点阵点,从而形成一个点阵,如图3.1(b)所示。
显然,每个点阵点按在空间排列而成的平面,点阵的单位向量平移,就与另一个点阵点(即分子)完全重叠。
可以用三个互相不平行的单位向量a, b 和c描述点阵点在空间的平移,通过这个向量的操作,可以得到整个点阵。
点阵中任意点可以用向量r表示。
r=n1a+n2b+n3c(3.1)其中n1, n2和n3为整数。
点阵是抽象的数学概念,其原点可以任意选定。
需要指出的是,晶体学上的坐标系均采用右手定则,即食指代表x轴,中指代表y轴,大拇指代表z轴。
3.1.1晶胞参数晶体的空间点阵可以选择三个互相不平行的单位向量a,b和c,用它们可以画出一个六面体单位,称为点阵单位。
相应地,按照晶体结构的周期性所划分的六面体单位就叫晶胞(cell).三个单位向量的长度a,b和c以及它们之间的夹角α,β,γ就叫晶胞参数(unit cell parameters)其中,α是b和c的夹角,β是a和c的夹角,γ是a和b的夹角(图3.2)。
第八章晶体内部结构的微观对称和空间群2015讲解

十四种空间格子
3.各晶系平行六面体的形状和大小
平行六面体的形状和大小用它的三根棱长(轴长)a、 b、c及棱间的夹角(轴角)、、表征。这组参数 (a、b、c;、、)即为晶胞参数。
在晶体宏观形态中我们可以得到各晶系的晶体常数特 点,是根据晶轴对称特点得出的。 宏观上的晶体常 数与微观的晶胞参数是对应的,但微观的晶体结构中 我们可以得到晶胞参数的具体数值。
斜方
四 方
C=P
F=I
与本晶系对称
三 方
不符
I=F
F=P
六
与本晶系对称
与空间格子
与空间格子方不符条件不符条件不符
等 轴
与本晶系对称 不符
十四种空间格子
请判断CsCl的格子类型 举例:金红石和石盐晶体模型
十四种空间格子
上述画格子的条件实质上与前面所讲的晶体定向的原则 是一致的(回忆晶体定向原则?),也就是说,我们在宏观 晶体上选出的晶轴就是内部晶体结构中空间格子三个方向的
空间格子中,结点、行列和面网可进行指 标。即通过一定的符号形式把它们的位置 或方法表示出来。
点的坐标 行列符号 面网符号
8.3 空间格子中点的坐标、行列及面网符号
① 空间格子中坐标系的建立 Z
坐标轴 单位平行六面体三条棱的方向。
坐标原点 单位平行六面体的角顶。
c
b
a
Y
坐标轴度量单位
一个空间群可看成是由两部分组成的,一部分是晶体结构中 所有平移轴的集合,称为平移群;另一部分就是点群, 即晶 体宏观对称要素的集合。
空间群是从对称型(点群)中推导出来的,每一对称型(点 群)可产生多个空间群,所以32个对称型(点群)可产生 230种空间群。
3 晶体内部结构的微观对称和空间群

14
10种二维点群的极射赤平投影
15
5种二维点阵类型
mp
op
oc
tp
hp
16
17种二维空间群
晶系和 点阵符号 单斜 p 点群符号 1 2 m 正交 p, c 2mm
四方 p
4 4mm 3
六方 p
3m 6 6mm
二维空间群国际符号 完全的 简短的 p1 p1 p211 p2 p1m1 pm p1g1 Pg c1m1 cm p2mm pmm p2mg pmg p2gg pgg c2mm cmm p4 p4 p4mm p4m p4gm p4g p3 p3 p3m1 p3m1 p31m p31m p6 p6 p6mm p6m
29空间群方解石方解石cacocacospacegroupspacegroup3c3c在单胞内含有在单胞内含有3030个原子个原子caca占据占据66aa位置位置0c占据占据66bb位置位置0o占据占据1818ee位置位置x其他其他2727个原子的位置个原子的位置空间群的对称性使得原本复杂的事物描述起来是如空间群的对称性使得原本复杂的事物描述起来是如此简单此简单30空间群空间群的表达方式空间群的表达方式晶体学国际表晶体学国际表internationaltablescrystallographyinternationaltables空间群和相应点群的序号和符号空间群和相应点群的序号和符号对称元素和一般等效位置配置图对称元素和一般等效位置配置图原点的对称性原点的对称性通过原点的对称元素通过原点的对称元素不对称单元不对称单元等效点系等效点系31国际表中的空间群p232p233p2c的图示34空间群分布73个symmorphi157个nonsymmorphi35从空间群符号辨认晶系如
如果没有二义性可能,常用符号的省略形式 (如Pm,而不用写成 P1m1)。
晶体学基础8-晶体内部结构的微观对称和空间群

第七章 晶体内部的微观对称和空间 群
平移轴
螺旋轴
滑移面
透明 单层铁强度的100倍
1平方米的石墨烯 (0.77mg)可承重4KG
透光率97%以上
Geim和Novoselov 2010 诺贝尔物理学奖
学习要求
掌握晶体内部的微观对称元素的对称特点和规 律,掌握平移轴、螺旋轴和滑移面的具体含义。 了解晶体二维空间群的对称元素、点群类型、 点阵类型。
滑移面
是一假想的平面,当结构对此平面反映,并平行此平面移 动一定距离后,结构中的每一个点与其相同的点重合。 滑移面按其滑移的方向和距离可分为a、b、c、n、d五种。 其中a、b、c为轴向滑移,移距分别为 1/2a, 1/2b,1/2c。 n为对角线滑移,移距为1/2(a+b)or 1/2(b+c)等。 d为金刚石型滑移,移距为 1/4(a+b)等。
1,2
1m, 2mm 4,4mm 3,3m,6,6mm
3/4
41
43
规定: 41为右旋,43则为左旋。但43右旋时 移距应为3/4T。
即螺旋轴的国际符号ns是以右旋为准的。
凡0<s<n/2者,为右旋螺旋轴(包括31、 41、61、62);凡n/2<s<n者,为左旋螺 旋轴(包括32、43、64、65);而s=n/2 者,为中性螺旋轴(包括21、42、63)。
阵点平面投影的符号表示 阵点
+
,
在纸面上方
在纸面下方 手性的变换 对称面相关的阵点
- , +
对称面平行纸面
二维空间群
10种二维点群
1 2 3 4 6 / m 2mm 3m 4mm 6mm
4种二维晶系
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1)原始格子( primitive, P):结点分布于平行六面体的八个角顶。
2)底心格子( end-centered, C、A、B):结点分布于平行六面体
的角顶及某一对面的中心。 3)体心格子( body-centered, I):结点分布于平行六面体的角顶和
体中心。 4)面心格子( face-centered, F):结点分布于平行六面体的角顶和
行列。
十四种空间格子
3.各晶系平行六面体的形状和大小
➢ 平行六面体的形状和大小用它的三根棱长(轴长)a、 b、c及棱间的夹角(轴角)、、表征。这组参数 (a、b、c;、、)即为晶胞参数。
➢ 在晶体宏观形态中我们可以得到各晶系的晶体常数特 点,是根据晶轴对称特点得出的。 宏观上的晶体常 数与微观的晶胞参数是对应的,但微观的晶体结构中 我们可以得到晶胞参数的具体数值。
Rhombohedral
= = 90o = 120o = = 90o
a1 = a2 c
a1 = a2 = a3
a1
P
a2
F
I
Isometric
= = = 90o a1 = a2 = a3
二、空间格子中结点、 行列和面网的指标
➢ 空间格子中,结点、行列和面网可进行指 标。即通过一定的符号形式把它们的位置 或方法表示出来。
十四种空间格子
例1:四方底心格子 = 四方原始格子
十四种空间格子
例2:立方底心格子不符合等轴晶系对称 思考:立方底心格子符合什么晶系的对称?
三斜面心→三斜原始格子
三斜I=三斜P
三斜C=三斜P
单斜体心→单斜底心
单斜底心→单斜原始
单斜B心格子转变为单斜原始格子
单斜面心格子转变 为单斜的底心格子
平移轴(translation axis) 螺旋轴(screw axis): 滑移面(glide plane)
晶体微观对称元素
• 平移轴(translation axis)
为一直线方向,相应的对称操作为沿此直线方向平移一 定的距离。对于具有平移轴的图形,当施行上述对称操 作后,可使图形相同部分重复。在平移这一对称变换中, 能够使图形复原的最小平移距离,称为平移轴的移距。
第八章 晶体内部结构的微观对称和空间群
➢ 十四种空间格子 ➢ 空间点阵中结点、行列和面网的指标 ➢ 晶体内部结构的对称要素 ➢ 空间群 ➢ 等效点系
一、十四种空间格子
1.平行六面体的选择
对于每一种晶体结构而言,其结点的分布是客 观平行六面体的选择原则:
[111]
Y
X
[001] [100]
[101] [010]
[011]
[110]
[ 201]
④面网符号
(111) (210)
(110)
(020)
(010)
面网符号
平行于(010)晶面的几组面网的符号
三、晶体内部结构的对称要素
研究空间格子仅仅是研究了晶体结构的平移对称性,除了 平移对称外,晶体结构还有与宏观形态上一样的旋转、反映 对称。并且这些旋转、反映操作与平移操作复合起来就会产 生内部结构特有的一些对称要素:
所选取的平行六面体应能反映结点分 布固有的对称性;
在上述前提下,所选取的平行六面体 棱与棱之间的直角力求最多;
在满足以上两条件的基础上,所选取 的平行六面体的体积力求最小。
十四种空间格子
空间格子的划分
➢ 划分7种平行六面体
对应于7个晶系 形状及参数?
4mm
十四种空间格子
十四种空间格子
c
a
b
P
Triclinic
abc
c
c
c
b
b
aP
aC
Monoclinic
= = 90o
abc
b
aP
C
F
I
Orthorhombic
= = = 90o a b c
c
c
a1
P
a2
I
Tetragonal
= = = 90o a1 = a2 c
a3
a2
a1
P
Hexagonal
R
单斜体心格子转变 为单斜的底心格子
四方底心→四方原始格子
四方面心格子转变为体心格子
三方体心转变为三方原始格子
菱面体面心格子重组为原始格子
空间格子的划分
Why not 7 × 4 = 28 ??
原始格子(P) 底心格子(C) 体心格子(I)
面心格子(F)
三斜
C=I
I=F
F=P
单斜
I=F
F=C
三对面的中心。
十四种空间格子
总结: 在四种格子类型当中,其中底心、
体心、面心格子称带心的格子,这是因为有 些晶体结构在符合其对称的前提下不能画出 原始格子,只能画出带心的格子。
十四种空间格子
➢ 七个晶系—七套晶体常数—七种平行六面体种形状。 ➢ 每种形状有四种类型,那么就有7×4=28种空间格子? ➢ 但在这28种中,某些类型的格子彼此重复并可转换,还有 一些不符合某晶系的对称特点而不能在该晶系中存在,因 此,只有14种空间格子,也叫14种布拉维格子。(A.Bravis 于1848年最先推导出来的) 举例说明: 1、四方底心格子可转变为体积更小的四方原始格子 ; 2、在等轴晶系中,若在立方格子中的一对面的中心安置结点, 则完全不符合等轴晶系具有4L3的对称特点,故不可能存在立 方底心格子。
X
Z 0,0,1
c 0,0,1/2 0,0,0 b
a
1/2,1/2,0 1,0,0,
Y 0,1,0,
③行列(晶向)符号(Crystal directions)
表示行列方向的符号,[x y z]
Z
若行列经过坐标原点,
把该行列上距原点最近 的结点坐标x,y,z放在 “[ ]”内,
[xyz]即为该行列的行 列符号。
➢ 点的坐标 ➢ 行列符号 ➢ 面网符号
8.3 空间格子中点的坐标、行列及面网符号
① 空间格子中坐标系的建立 Z
➢ 坐标轴 单位平行六面体三条棱的方向。
➢ 坐标原点 单位平行六面体的角顶。
c
b
a
Y
➢ 坐标轴度量单位
X
单位平行六面体的棱长a、b、c 。
②空间格子中点的坐标
x,y,z
用单位平行六面体的 棱长a、b、c作为坐标 轴度量单位时的坐标系 数。
斜方
四 方
C=P
F=I
与本晶系对称
三 方
不符
I=F
F=P
六
与本晶系对称
与空间格子
与空间格子
方
不符
条件不符
条件不符
等 轴
与本晶系对称 不符
十四种空间格子
请判断CsCl的格子类型 举例:金红石和石盐晶体模型
十四种空间格子
上述画格子的条件实质上与前面所讲的晶体定向的原则 是一致的(回忆晶体定向原则?),也就是说,我们在宏观 晶体上选出的晶轴就是内部晶体结构中空间格子三个方向的
