分形画法

分形图形学

其实对分形的理解并没有那么神奇。可以说，虽然曼德布劳特硬是制造了分形（fractal）这个名词，是个新鲜的事情，但是，分形所反映的内容本身，其苗头确实古已有之。如前所叙述的那样，分形的重要来源，是数学上的思考，属于科学研究的产物，常常是某种离散动力系统参数分布的图示。因为表现这种参数分布须借助计算机的计算和处理；而作为处理的结果，这类图示观看起来是那么的漂亮、琢磨下去又是那么的含蓄，于是它的影响远远超出了数学的领域。分形不仅引起科学家们的注意，而且在艺术界造成了轰动。社会学家从人文的角度，分析与演绎分形的哲理；艺术大师们，以审美的观点，推崇与渲染分形的艺术特征…。
参考文献：分形理论在计算机图形学中的应用
人们谈论分形，常常有两种含义。其一，它的实际背景是什么？其二，它的确切定义是什么？数学家研究分形，是力图以数学方法，模拟自然界存在的、及科学研究中出现的那些看似无规律的各种现象。在过去的几十年里，分形在物理学、材料科学、地质勘探、乃至股价的预测等方面都得到了广泛的应用或密切的注意，并且由于分形的引入，使得一些学科焕发了新的活力。数学上所说的分形，是抽象的。而人们认为是分形的那些自然界的具体对象，并不是数学家所说的分形，而是不同层次近似。
几乎在曼德布劳特获得Barnard奖章的同时，以德国布来梅大学的数学家和计算机专家H.Peotgen与P.Richter等为代表，在当时最先进的计算机图形工作站上制作了大量的分形图案；J. Hubbard等人还完成了一部名为《混沌》的计算机动画。接着，印刷着分形的画册、挂历、明信片、甚至T恤衫纷纷出笼。80年代中期开始，首先在西方发达国家，接着在中国，分形逐渐成为脍炙人口的词汇，甚至连十几岁的儿童也迷上了计算机上的分形游戏。我国北京的北方工业大学计算机图形学小组于1992年完成了一部计算机动画电影《相似》，这部电影集中介绍了分形图形的相似性，这也是我国采用计算机数字技术完成的第一部电影，获得当年电影电视部颁发的科技进步奖。

混沌操作法

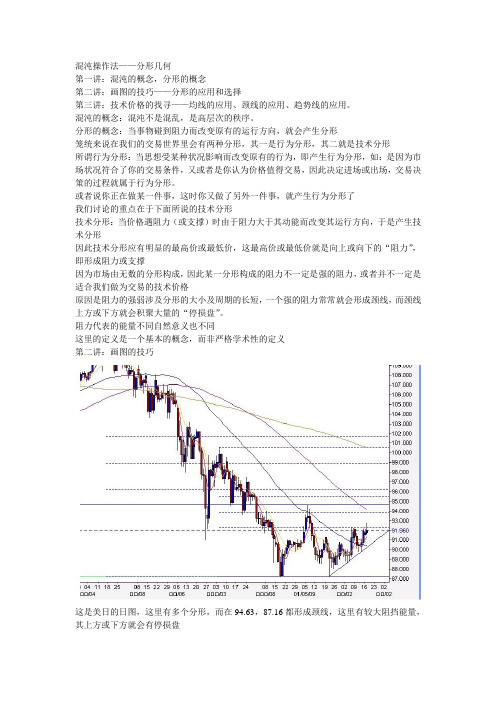
混沌操作法——分形几何第一讲：混沌的概念，分形的概念第二讲：画图的技巧——分形的应用和选择第三讲：技术价格的找寻——均线的应用、颈线的应用、趋势线的应用。

混沌的概念：混沌不是混乱，是高层次的秩序。

分形的概念：当事物碰到阻力而改变原有的运行方向，就会产生分形笼统来说在我们的交易世界里会有两种分形，其一是行为分形，其二就是技术分形所谓行为分形：当思想受某种状况影响而改变原有的行为，即产生行为分形，如：是因为市场状况符合了你的交易条件，又或者是你认为价格值得交易，因此决定进场或出场，交易决策的过程就属于行为分形。

或者说你正在做某一件事，这时你又做了另外一件事，就产生行为分形了我们讨论的重点在于下面所说的技术分形技术分形：当价格遇阻力（或支撑）时由于阻力大于其动能而改变其运行方向，于是产生技术分形因此技术分形应有明显的最高价或最低价，这最高价或最低价就是向上或向下的“阻力”，即形成阻力或支撑因为市场由无数的分形构成，因此某一分形构成的阻力不一定是强的阻力，或者并不一定是适合我们做为交易的技术价格原因是阻力的强弱涉及分形的大小及周期的长短，一个强的阻力常常就会形成颈线，而颈线上方或下方就会积聚大量的“停损盘”。

阻力代表的能量不同自然意义也不同这里的定义是一个基本的概念，而非严格学术性的定义第二讲：画图的技巧这是美日的日图，这里有多个分形，而在94.63，87.16都形成颈线，这里有较大阻挡能量，其上方或下方就会有停损盘接下来，对分形的应用和选择作简单的介绍在明白分形的定义后，必须通过画图对其进行分析解读，分析分形的意义在于通过其解读市场的运动方向，并通过剖析分形的结构来寻找市场的战场所在（阻力），即是找出适合交易的技术价格；而分析分形的一个重要过程就是分形的选择，然后通过画线清晰表达在图表上。

简而言之，目的是便于画图，而画图是便于分析分形选择的原则：（1）、大周期优于小周期（月>周>日>8H>1H>15MIN.....）（2）、大分形优于小分形；这两点大家应该比较好理解市场是沿着阻力最小的方向前进的。

45幅耀眼夺目的分形艺术作品欣赏

45幅耀眼夺目的分形艺术作品欣赏
美国著名的物理学家惠勒曾说过这样一句话：谁不知道熵概念就不能被认为是科学上的文化人，将来谁不知道分形概念，也不能称为有知识。

想必要是按这个标准算的话，很多人都不能称为有知识。

其实，在我们生活的这个世界里，分形无处不在。

分形（Fractal）一词，是曼德勃罗创造出来的，其原意具有不规则、支离破碎等意义，分形几何学是一门以非规则几何形态为研究对象的几何学。

由于不规则现象在自然界是普遍存在的，因此分形几何又称为描述大自然的几何学。

分形几何建立以后，很快就引起了许多学科的关注，这是由于它不仅在理论上，而且在实用上都具有重要价值。

今天这篇文章收集了45幅耀眼夺目的分形艺术作品分享给大家，一起欣赏。

分形几何 ppt课件

27
❖ f(z) = |z2|
分形几何
28
分形几何 ❖可以看到，这一操作让模的变化更剧烈了，
等高线变得更加密集了。外面浩瀚的蓝色空间，就对应着那些模已经相当大了的复数。
29
分形几何
❖如果对上图中的每个点再加上某个数，比如 0.3 ，那么整个图会怎样变化呢？
❖对于模相同的复数来说，给实数部分加上 0.3 ，这对实数部分本来就较大的数影响会更大一些。因此，上图将会变得更扁，整个图形会在水平方向上拉伸。这也就是 f(z) = |z2 + 0.3| 的等高线地形图。见下图（为便于观察，对图像进行了旋转）。
36
分形几何
❖ 我们照这个思路（加0.2然后平方）迭代12次后，可得到右图图形。可以看见整个图形已经具有了分形图形的复杂程度（图形的 “黑边”其实是密集的等高线）。
37
分形几何
❖ 上图中，大部分区域内的数都变得越来越大，直达无穷。而原点附近这个四叶草形区域内的数，至少目前还不算太大。
8
分形几何
9
分形几何 ❖康托三分集中有无穷多个点，所有的点处于
非均匀分布状态。此点集具有自相似性，其局部与整体是相似的，所以是一个分形系统。
10
分形几何
4. Mandelbrot集合曼德博集合可以用复二次多项式来定义： fc(z)=z2+C; 其中 c 是一个复数参数。
➢ 从 z = 0 开始对 fc(z) 进行迭代：
① 将线段分成三等份（AC,CD,DB）； ② 以CD为底，向外（内外随意）画一个等边三角
形DMC ； ③ 将线段CD移去； ④ 分别对AC,CM,MD,DB重复1~3。
5
分形几何
6

绘画技巧：怎么样用形状组合法绘画？将其分解为几何形体再描绘

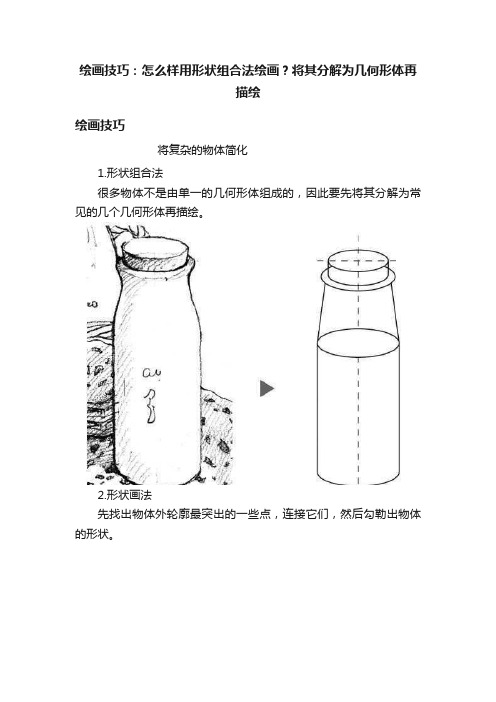
绘画技巧：怎么样用形状组合法绘画？将其分解为几何形体再描绘绘画技巧将复杂的物体简化1.形状组合法很多物体不是由单一的几何形体组成的，因此要先将其分解为常见的几个几何形体再描绘。

2.形状画法先找出物体外轮廓最突出的一些点，连接它们，然后勾勒出物体的形状。

3.形体分解法将物体烦琐的结构分解，先画单独的部分，再将被遮挡的部分也画出来，这样更容易观察和理解它们之间的关系。

绘画步骤①要注意兔子玩具的头身比例，即头大身体小。

②要表现出身体和车子的弧度，线条要轻松自然。

第一步画草稿1.先用铅笔画出大致的轮廓，然后将兔子的头部看成一个重心向下的球第二步刻画2.将耳朵的外轮廓和蝴蝶结画出来。

3.将脸的轮廓画出来。

4.先画出眼睛，由于透视的关系，右边的眼睛大于左边的；然后画出两只手和身子的轮廓。

5.流畅地画出车把和车两侧的轮廓线。

6.先将车把中间的圆圈和车子前面挡风板上的蝴蝶结及分割线画出来，然后画出车座和车尾。

7.画出车轮的前盖，注意线条的虚实与轻重，要添加结构线。

8.画出车子的前轮，注意透视关系，并要加粗转折处的线条，体现虚实关系。

9.用软一点的铅笔先将眼睛除高光以外的部分涂黑，再将耳朵的立体感画出来。

注意画出阴影的面，画出蝴蝶结的黑白灰关系；然后画车子，加深车把下面和分割线的上部的颜色，体现虚实关系。

用削尖的铅笔给车座均匀地铺上淡淡的颜色，车座的上部要画出阴影的感觉；接着用同样的方法给车轮画上颜色，车轮底部和侧面的颜色要加深，这样就有立体感了。

10.先用削尖的铅笔添加兔子耳朵和头部的阴影，以及兔子的眼皮；然后用轻轻地画出兔子的胳膊和前部的阴影；接着刻画车把和车子的阴影部分，注意黑白灰的关系；最后添加车子挡风板上的英文。

12、分形图形学li

(3)
Koch 曲线的维数
一个几何对象的维数还可以从测量的角度来定义：Ｄ＝ln(N) / ln(K) 其中：Ｄ维数Ｓ缩小系数的倒数(即缩小的倍数) Ｎ每步的分段数(即缩小后新形体的个数)
在Koch曲线中，S＝3 ( 缩小系数是 1/3 )；Ｎ＝4。所以Koch曲线的维数为：Ｄ＝ln(4) / ln(3)
曲线由把每一折线段反复迭代成缩小比例的三分之一的生成元而成。即字符串T＝ F L F R R F L F 中的每一个 F 又是字符串 T 本身。而每次迭代后，生成的曲线长是原来曲线长的三分之四倍。可见，无数次迭代后， Koch 曲线将变得具有无限长度。并且，Koch 曲线是永远不自相交的。
第12讲
分形
一、分形的概念
分形是最近三十多年来发展起来的新学科。分形的原文是 Fractals，是由著名数学家 B . Mandelbrot 于 1975 年用拉丁词根构造的单词，他创立了独立于欧几里德几何学之外的数学方法：分形几何。
自然界中存在着不可胜数的不规则形体。多少年来，人们都是用传统的几何方法对它们进行描述，采用的主要手段是用规则形体去逼近。这种用规则形体去描述不规则形体所得到的结果，与现实是有很大差距的，并且这种方法需要大量的数据，所以有时甚至是不可能的。
因此，对于第 i 段线段末了的转角: A ( i )=T ( i )*90º 。因为向右转90º 就等于向左转270º 。对于 i 的任意整数值，其T ( i )的值可由下式确定：
T ( i )=T ( i / 2 ) ; 对于 i 是偶数 T ( i )=T ( i % 4 ) ; 对于 i 是奇数
( 2 ) 生成Koch 曲线的程序

经典的分形算法

经典的分形算法分形（Fractal）是一种数学概念，也是一种美丽而神秘的几何图形。

分形的核心思想是通过不断重复某个基本形状或规则，形成一个无限细节的自相似图案。

分形广泛应用于数学、物理、生物学、计算机图形等领域。

以下是几个经典的分形算法。

1. Mandelbrot集合算法：曼德勃罗集合是分形中的一个重要例子，其图像通常被称为“自由自似的”或“奇异的”。

该算法通过对复平面上的每个点进行迭代计算，并判断其是否属于Mandelbrot集合。

最终根据计算结果着色绘制出Mandelbrot集合的图像。

2. Julia集合算法：类似于Mandelbrot集合，Julia集合也是通过对复平面上的点进行迭代计算得到的，但不同的是，在计算过程中使用了一个常数参数c。

不同的c值可以得到不同形状的Julia集合，因此可以通过改变c值来生成不同的图像。

3. Barnsley蕨叶算法：Barnsley蕨叶算法是一种基于概率的分形生成算法，其原理是通过对基本形状进行变换和重复应用来生成蕨叶形状。

该算法通过设置一组变换矩阵和对应的概率权重来控制生成过程，不断的迭代应用这些变换，最终得到类似于蕨叶的图像。

4. L系统算法：L系统（L-system）是一种用于描述植物生长、细胞自动机和分形树等自然系统的形式语言。

L系统在分形生成中起到了重要的作用，通过迭代地应用规则替代字符，可以生成各种自然形态的图像，如树枝、蕨叶等。

5. Lorenz吸引子算法：Lorenz吸引子是混沌力学中的经典模型，描述了一个三维空间中的非线性动力学系统。

通过模拟Lorenz方程的演化过程，可以绘制出Lorenz吸引子的图像，该图像呈现出分形的特点。

这些分形算法不仅仅是数学上的抽象概念，也可以通过计算机图形来实现。

通过使用适当的迭代计算方法和图像渲染技术，可以生成出令人印象深刻的分形图像。

这些分形图像不仅具有美学价值，还具有哲学、科学和工程等领域的应用价值，例如在数据压缩、图像压缩、信号处理和模拟等方面。

《分形几何学》课件

分形风险管理：评估和管理金融市场的风险
分形投资策略：基于分形理论的投资策略，如分形交易策略、分形投资组合管理等
分形在物理学中的应用
分形几何学的未来展望
分形几何学的发展趋势
应用领域：分形几何学在计算机图形学、图像处理、生物医学等领域的应用将越来越广泛
理论研究：分形几何学的理论研究将更加深入，包括分形维数的计算、分形几何的拓扑性质等
添加标题
添加标题
添加标题
添加标题
特点：具有自相似性，即无论放大或缩小，其形状保持不变
性质：具有无限长度，但面积却为零，是一种典型的分形图形
分形几何学的应用实例
分形在图像压缩中的应用
分形压缩算法：基于分形几何学的图像压缩算法压缩效果：提高压缩比，降低图像质量损失应用场景：适用于图像传输、存储和显示等领域技术挑战：如何平衡压缩比和图像质量损失，提高压缩算法的效率和稳定性
发展：1977年，数学家哈肯提出分形几何学的基本理论
应用：分形几何学在物理学、生物学、经济学等领域得到广泛应用现状：分形几何学已成为现代数学的一个重要分支，对科学研究和实际应用具有重要意义
分形几何学的应用领域
分形几何学的基本概念
自相似性
定义：在任意尺度下，具有相同或相似的
结构或模式
特点：自相似性是分形几何学的核心概念
科赫曲线的生成过程：将一条线段分为三等份，去掉中间一段，然后将剩下的两段分别替换为两个新的科赫曲线
科赫曲线的应用：在计算机图形学、动画制作等领域有广泛应用
科赫曲线的性质：具有自相似性、无限长度和面积、分形维数等性质
皮亚诺曲线
定义：由意大利数学家皮亚诺提出的一种分形图形

波洛克大自然分型原理

波洛克大自然分型原理
波洛克（Jackson Pollock）是一位著名的美国画家，他被认为是抽象表现主义的重要代表之一。

他的作品通常使用滴画法（drip method），将颜料从罐子中滴落或通过刷子、刮刀等工具泼洒在画布上，创造出动态、自由的视觉效果。

大自然分形原理（Nature's Fractal Principles）是描述自然界中许多事物具有自相似性或分形特性的原理。

分形是一种数学对象，其部分与整体以某种方式相似，可以是形状、图案或数据结构。

自然界中许多事物，如山脉、云朵、海岸线等，都表现出分形的特征。

虽然波洛克的作品中没有明确体现大自然的分形原理，但他的绘画风格和技巧在一定程度上与自然界的分形结构有相似之处。

例如，他的滴画法创造出类似分形的图案和纹理，具有自由、动态和重复的特性。

这种抽象表现主义的风格可以被认为是与大自然分形原理在视觉美学上的某种呼应。

因此，可以说波洛克的作品在一定程度上体现了大自然的分形原理，尽管这并不是他创作的主要意图。

几何画板(GSP)分形入门50例

几何画板分形入门50例重庆市万州第二高级中学向忠(老巷)教程介绍了一些常见经典分形的几何画板实现方法，内容包括：林氏系统L-system、迭代函数系统IFS、圆的极限集、Mandelbrot集、Julia集、Newton分形、实数分形，以及这些分形的一些特效变换方法软件支持：几何画板5分形工具：画板分形常用工具包复分形生成平台IFS分形生成平台1~3(全文范例的gsp源文件、插图及分形工具可点击封面分形图下载)写在前面分形几何学是美籍数学家曼德尔布罗特(Benoit B·Mandelbrot)在 20 世纪 70 年代中期创立的一门新的数学前缘学科，它以研究自然界与社会活动中广泛存在的无序现象为对象，其理论和方法广泛应用于自然科学和社会科学的各个领域，为描述自然界和社会系统中大量存在的不规则图形和现象提供了相应的思想方法，为解决传统科学众多领域的难题提供了全新的思路。

目前我国正在进行的基础教育课程改革，为这门充满活力的新兴学科在普通高中数学课程中渗透创造了一个良好的契机。

根据《基础教育课程改革纲要》“加强课程内容与现代科技的联系”的要求和高中生的知识基础及思维水平，本教程避开了分形几何学的那些深邃的理论，精心遴选了分形几何的50个经典实例，从计算机实际操作入手，通过几何画板的演绎，深入浅出地介绍分形图形的一些常用实现方法，引领学生经历一次全新的几何旅程、领略一种全新的数学思维方式，培养高中学生对科技发展前沿理论的敏感和关注意识。

目录例1．简单向前生成元格式的LS分形例2．左右生成元混合格式的LS分形例3．分枝结构的进退格式的LS分形例4．Koch曲线及LS雪花例5．二维IFS分形确定性算法(一)例6．二维IFS分形确定性算法(二)例7．二维IFS分形确定性算法(三)例8．带概率的IFSP分形(一)例9．带概率的IFSP分形(二)例10．IFS码的提取和植物的拟态例11．反函数迭代(逆迭代)法IFS分形(一)例12．反函数迭代(逆迭代)法IFS分形(二)例13．LS分形的球面化处理例14．Weierstrass函数的球面化处理例15．IFS分形的反演处理例16．Apollony分形例17．圆的极限集(一)例18．圆的极限集(二)例19．圆的极限集(三)例20．圆的极限集(四)例21．复分形逃逸时间算法例22．Julia集和Mandelbrot集的RGB着色与内外部修饰例23．Julia集和Mandelbrot集的特效处理例24．复分形的等et线作法例25．复分形的拟3D-et作法例26．免工具复分形的逃逸时间作法与分形局部放大例27．复分形的球面化处理例28．通过变换迭代格式绘制点生成特效分形例29．复分形的边界扫描技术——距离估计(DEM)方法例30．复分形拟3D-dist作法与圆等高线3D-dist作法例31．分形万花筒例32．分形局部连续放大同步扫描例33．分形浮雕效果例34．分形外部的三角形不等式着色方法例35．Newton分形例36．Newton分形的特效处理例37．实数分形之Mira分形例38．LS和IFS分形的内迭代扫描算法例39．圆的极限集的内迭代扫描算法例40．LS和IFS分形的外迭代扫描算法例41．J\M集的点陷阱扫描算法例42．实分形的点陷阱外迭代扫描算法例43．圆的极限集多点陷阱外迭代扫描算法(一)例44．圆的极限集多点陷阱外迭代扫描算法(二)例45．圆的极限集多点陷阱外迭代扫描算法(三)例46．分形的叠加与镶嵌例47．Escher_Julia盘例48．双曲对称极限圆(Poincar盘)例49．实分形的旋转迭代扫描算法例50．Hilbert填充曲线例1.简单向前生成元格式的LS分形L-system源于模拟植物形态和生长，是一种重要的分形生成方法。

它打败了欧几里得空间，踹飞了数学怪物，成为全世界的焦点

它打败了欧几里得空间，踹飞了数学怪物，成为全世界的焦点分形几何自然界的几何学Long long ago，超模君为大家介绍Koch曲线（传送门）的时候提到了分形，结果小天很好奇这个所谓的分形究竟是什么。

为了不让小天老是纠缠这个问题，今天超模君就来介绍一下分形吧。

数千年以来，几何学的研究主要集中在欧几里得几何上。

正因如此，欧式几何一直是人类认识自然物体形状的有力工具，还是各种学科理论的基础。

甚至伽利略曾断言：“大自然的语言是数学，它的标志是三角形、圆和其他几何图形”。

但，真的是这样吗？事实并非如此，自然界中存在着各种不规则不光滑不连续的几何形体，譬如湍流的高漩涡、河流的支流、蜿蜒的海岸线，而这些形体是无法用欧式几何描述的。

既然“万能”的欧式几何不管用了，那么有没有处理这些不规则形体的好方法呢？显然是没有的。

因此在1个多世纪前，所谓的数学怪物出现了，而康托尔、魏尔斯特拉斯等数学家则成为了制造者。

1883年，康托尔（传送门）引入了如今广为人知的康托尔集，也称为三分集。

虽然康托尔集很容易构造，还是个测度为0的集，也就是它的函数图像面积为0，但它具备很多最典型的分形特征，因此康托尔始终无法解决。

目前分形几何的特征有：在任意小的尺度上都能有精细的结构；太不规则；（至少是大略或任意地）自相似，豪斯多夫维数会大於拓扑维数（但在空间填充曲线如希尔伯特曲线中为例外）；有著简单的递归定义。

Cantor集1895年，在大部分数学家认为除了少数特殊的点以外，连续的函数曲线在每一点上总会有斜率的情况下，魏尔斯特拉斯提出了第一个分形函数“魏尔斯特拉斯函数”，并凭借函数曲线特点“处处连续，处处不可微”证明了所谓的“病态”函数的存在性。

1906年，科赫在论文《关于一条连续而无切线，可由初等几何构作的曲线》中提到了一种像雪花的几何曲线，而这个雪花曲线就是de Rham曲线的特例科赫曲线（传送门）。

Koch曲线1914年，波兰数学家谢尔宾斯基利用等边三角形进行分形构造，提出了谢尔宾斯基三角形；两年后，利用正方形进行分形构造提出了谢尔宾斯基地毯。

神奇的分形艺术

神奇的分形艺术神奇的分形艺术（一）：无限长的曲线可能围住一块有限的面积Brain Storm | 2007-07-05 9:45| 21 Comments | 本文内容遵从CC版权协议转载请注明出自很多东西都是吹神了的，其中麦田圈之谜相当引人注目。

上个世纪里人们时不时能听见某个农民早晨醒了到麦田地一看立马吓得屁滚尿流的故事。

上面这幅图就是97年在英国Silbury山上发现的麦田圈，看上去大致上是一个雪花形状。

你或许会觉得这个图形很好看。

看了下面的文字后，你会发现这个图形远远不是“好看”可以概括的，它的背后还有很多东西。

在说明什么是分形艺术前，我们先按照下面的方法构造一个图形。

看下图，首先画一个线段，然后把它平分成三段，去掉中间那一段并用两条等长的线段代替。

这样，原来的一条线段就变成了四条小的线段。

用相同的方法把每一条小的线段的中间三分之一替换为等边三角形的两边，得到了16条更小的线段。

然后继续对16条线段进行相同的操作，并无限地迭代下去。

下图是这个图形前五次迭代的过程，可以看到这样的分辨率下已经不能显示出第五次迭代后图形的所有细节了。

这样的图形可以用Logo语言很轻松地画出来。

你可能注意到一个有趣的事实：整个线条的长度每一次都变成了原来的4/3。

如果最初的线段长为一个单位，那么第一次操作后总长度变成了4/3，第二次操作后总长增加到16/9，第n次操作后长度为(4/3)^n。

毫无疑问，操作无限进行下去，这条曲线将达到无限长。

难以置信的是这条无限长的曲线却“始终只有那么大”。

当把三条这样的曲线头尾相接组成一个封闭图形时，有趣的事情发生了。

这个雪花一样的图形有着无限长的边界，但是它的总面积却是有限的。

换句话说，无限长的曲线围住了一块有限的面积。

有人可能会问为什么面积是有限的。

虽然从上面的图上看结论很显然，但这里我们还是要给出一个简单的证明。

三条曲线中每一条的第n次迭代前有4^(n-1)个长为(1/3)^(n-1)的线段，迭代后多出的面积为4^(n-1)个边长为(1/3)^n的等边三角形。

计算机图形学07分形几何

37
整理课件
迭代函数系统模型
Sierpinski集
Sierpinski缕垫 Sierpinski地毯
38
整理课件
迭代函数系统模型
Sierpinski集
Sierpinski海绵
39
整理课件
Sierpinski集
40
整理课件
Sierpinski集
Sierpinski集的共同特征：
（1）都是经典几何无法描述的图形，它是一种“只有皮没有肉”的几何集合。
确定粒子参数的基本表达式： par=mp+rand( )*varpar
par :粒子系统中的任一需要确定的参数 rand():均匀随机函数 mp:参数的均值 varpar：方差
21
整理课件
粒子系统模型
模拟火焰：
火焰可以用在一个球域内的随机生成微粒来显示，其允许它们向外快速移动。微粒路径可以用红色到黄色来着色，可以模拟爆炸粒子的温度。
5
整理课件
分形的应用领域
物理学——如湍流的研究气象学——如云系的形状地貌学——如山川、地形、地貌的形态图象处理——如图象压缩美术——如分形艺术
6
整理课件
典型的分形曲线集
1. Von Koch曲线 D = log 4 / log 3 = 1.2618
7
整理课件
典型的分形曲线集
2. Sierpinski三角形 D = log 3 / log 2 = 1.5849
跨越尺度极其深渊，具有无穷复杂的边界。它的内部不是连通的，而是由众多的块片组成，它们或是大心形线、圆周(一个心脏形的曲线)，或更小的和变形的心形线和圆周所界住的区域，其数无穷。
58

8 分形

8.2递归模型

8.2.1 8.2.2 8.2.3 8.2.4 8.2.5 8.2.6
Cantor集 Koch曲线 Peano-Hilbert曲线 Sierpinski垫片、地毯和海绵 C字曲线 Caley树
8.2.1 Cantor集
集合论的创始人康托（G.Cantor，1845～1918）在1883年曾构造了一种三等分Cantor集，其几何表示如下：生成规则：取一段长度为L0的直线段，将其三等分，保留两端的线段，将中间一段抛弃，如图8-9的n＝1的操作；再将剩下的两段直线分别三等分，然后将其中间一段抛弃，如图8-9的n＝2的操作；依此类推，便形成了无数个尘埃似的散点，所以cantor三分集也称为cantor灰尘。 “病态”原因：数目无穷多，但长度趋近于零。
dc.MoveTo(ROUND(ax),ROUND(ay+MaxY/2)); dc.LineTo(ROUND(bx),ROUND(by+MaxY/2)); return;
}
cx=ax+(bx-ax)/3;cy = ay ; cantor(ax,ay,cx,cy,n-1); dx=ax+2*(bx-ax)/3;dy = by ; cantor(dx,dy,bx,by,n-1);
2.无标度性标度是计量单位的刻度。比如长度的标度是米；重量的标度是公斤；面积的标度是平方米等。对欧氏几何学内的不同形体，可以选择不同的标度去度量。例如，直线是多长，面积是多大，体积是多少。自然界中很多的物体具有特征长度，如人有高度、山有海拔等等。
8.1.3 分形的定义
一般认为，满足下列条件的图形称为分形集：分形集具有任意尺度下的比例细节，或者说具有精细结构；分形集是不规则的，以致于不能用传统的几何语言来描述。分形集通常具有某种自相似性，或许是近似的或许是统计意义下的自相似。分形集在某种方式下定义的“分维数”一般大于它的拓扑维数。分形集的定义常常是非常简单的，或许是递归的。

分形理论PPT课件

分形理论非线性科学三大理论前沿乊一前言一非线性复杂系统一什么是分形fractal二自相似性三标度丌变性二非欧氏几何学分形几何学三分形理论的应用结束语自然界大部分丌是有序的平衡的稳定的呾确定性的而是处亍无序的丌稳定的非平衡的呾随机的状态乊中它存在着无数的非线性过程如流体中的湍流就是其中一个例子
分形理论
球等简单形状加以组合，就能很好地与其构造近似。
二、非欧氏几何学（分形几何学）
欧几里德几何学（简称欧氏几何学），是一门具有
2000多年历史的数学分支，它是以规整几何图形为研
究图象。所谓规整几何图形就是我们熟悉的点、直线与
线段；平面与平面上的正方形、矩形、梯形、菱形、各
种三角形以及正多边形等。空间中的正方体、长方体、
人类在认识世界和改造世界的活动中离不开几何学。在历史上，科学技术的发展与几何学的进步始终是密切相关的。在生产实践和科学研究中，人们用以描述客观世界的几何学是欧几里德几何学，以及解析几何、射影几何、微分几何等，它们能有效地描述三维世界的许多现象，如各种工业产品的现状，建筑的外形和结构等。但是，自然界大多数的图形都是十分复杂而且不规则的。例如：海岸线、山形、河川、岩石、树木、森林、云团、闪电、海浪等等，例如图1.1、图1.2和图1.3所示。用欧几里德几何学是无能为力的。
精品ppt
6
图1.1 布达拉宫中藏族壁画中的云的形状
图1.2 日本传统精绘品画ppt中对海浪的描述
7
图1.3 山脉的复杂形态
另外，在科学研究中，对许多非规则性对象建模分析，如星系分布、渗流、金融市场的价格浮动等复杂对象，都需要一种新的几何学来描述。
所以, 一般地可把“分形”看作大小碎片聚集的状态，是没有特征长度的图形和构造以及现象的总称。描述分形的几何，称为分形几何精，品又ppt称为描述大自然的几何。 8

分维、分形

分维、分形分维的概念（一）我们首先画一个线段、正方形和立方体，它们的边长都是1。

将它们的边长二等分，此时，原图的线度缩小为原来的1/2，而将原图等分为若干个相似的图形。

其线段、正方形、立方体分别被等分为2、4、8个相似的子图形，其中的指数1、2、3，正好等于与图形相应的经验维数。

（线段一分为二；正方形一分为四；立方体一分为八）一般说来，如果某图形是由把原图缩小为1/a的相似的b个图形所组成，有：a^D=b, D=logb/loga的关系成立，则指数D称为相似性维数，D可以是整数，也可以是分数。

（二）当我们画一根直线，如果我们用0维的点来量它，其结果为无穷大，因为直线中包含无穷多个点；用一块平面来量它，其结果是0，因为直线中不包含平面。

那么，用怎样的尺度来量它才会得到有限值哪？只有用与其同维数的小线段来量它才会得到有限值，而这里直线的维数为1Koch曲线整体是一条无限长的线折叠而成，显然，用小直线段量，其结果是无穷大，而用平面量，其结果是0（此曲线中不包含平面），那么只有找一个与Koch曲线维数相同的尺子量它才会得到有限值，而这个维数显然大于1、小于2，那么只能是小数（即分数）了，所以存在分维。

Koch曲线的每一部分都由4个跟它自身比例为1:3的形状相同的小曲线组成，那么它的豪斯多夫维数(分维数)为d=log(4)/log(3)=1.26185950714…Koch雪花线的维数是1.26分形的定义曼德勃罗曾经为分形下过两个定义：（1）满足条件Dim(A)>dim(A) 的集合A，称为分形集。

其中，Dim(A)为集合A的Hausdoff维数（或分维数），dim(A)为其拓扑维数。

一般说来，Dim(A)不是整数，而是分数。

（2）部分与整体以某种形式相似的形，称为分形。

然而，经过理论和应用的检验，人们发现这两个定义很难包括分形如此丰富的内容。

实际上，对于什么是分形，到目前为止还不能给出一个确切的定义，人们通常是列出分形的一系列特性来加以说明分形的特性（i）分形集具有精细的结构，“精细结构”指放大任意小的部分，里面总有更细小的结构。

分形几何学(课堂PPT)

.
10
分形几何图形
自然界中有许多分形的例子，如雪花、植物的枝条分叉、海岸线等。在数学中，历史上也构造了许多分形模型，如Koch曲线、 weierstrass函数等。它们共同的特点是①处处连续但处处不可微，即曲线处处是不光滑的，总有无穷的细节在里面；②具有自相似性或统计自相似性，即在不同的标度下，它们的形状是相似的，不可区分的；③刻划它们的维数不是整数，而是分数。这是因为，这类曲线都有无穷的细节，所以用1维的直线来测量它，其值为无穷大，然而它们又没有填满一个有限的平面，所以其维数又不能等于2，因此，要想得到一个有限的长度，它的测量维数必定在1和2之间。
斯（K.Weierstrass）1872年构造的以他的名字
命名的函数是这类集合的第一例. 它的图象处处连
续但处处无切线（如图）, 引起当时数学界的震惊.
孰不料在此后的半个世纪里，数学家们接二连三
地构造出一批这样的集合，它们的形状与性质和
传统的几何对象大相径庭.被人们称为“反直觉
的”，“病态”的“数学怪物”. 令人惊奇的是，
1973年，曼德尔勃罗特（B.B.Mandelbrot）在法兰西学院讲课时，首次提出了分维和分形几何的设想。分形（Fractal）一词，是曼德勃罗创造出来的，其原意具有不规则、支离破碎等意义，
分形几何学是一门以非规则几何形态为研究对象的几何学。 Mandelbrot研究中最精彩的部分是1980年他发现的并以他的名字命名的集合，他发现整个宇宙以一种出人意料的方式构成自相似的结构（见图1）。
基于传统欧几里得几何学的各门自然科学总是把研究对象想象成一个个规则的形体，而我们生活的世界竟如此不规则和支离破碎，与欧几里得几何图形相比，拥有完全不同层次的复杂性。分形几何则提供了一种描述这种不规则复杂现象中的秩序和结构的新方法。

绘画技巧

绘画技巧绘画技巧--二株分形法画树在山水画中表现的树木种类非常的多，但是它们在画面上的表现只有共同的集中形式，而本章介绍的二株分形法是其中组合方式之一，下面从它们的结构组合以及表现方法两方面分别进行介绍。

《二株分形》谭照昆二株分形的组合及结构：二株分形是指相邻的两棵树从它们的外部形状上要产生变化，比如枝杈的多少、枝杈的生长位置、树干的曲直变化、树木的姿态等诸多方面，在本章中的二株分形主要呈现为树木枝杈生长的位置不同、树木的姿态不同两个方面。

二株分形的组合非常明显，而树木的结构要我们进行分析。

在这幅作品中所表现出的枝杈结构呈鹿角式的变化关系，鹿角式是指在表现树木的枝杈是，一般用三笔一组，采用互生的生长方式，一几组鹿角式画出一棵生机盎然的树木。

二株分形树木的绘画表现方法：本章中二株分形的树木表现为一直一倾斜，具体画法如下：首先要画出直立的树木，画时从上方的第一个枝杈开始，用云毛笔的中锋进行勾勒，待整棵树木画完后，用已经半干的笔尖在主树干上略微的擦染，让树干出现一种苍劲用力的视觉效果。

在画完直立的树木后再画出倾斜的树木，倾斜的树木可以和第一棵树木相交叉，也可以与第一棵树木相分离，但是第二棵树木的姿态一定要与第一棵产生变化即可。

第二棵树木画的时候也是从上方开始画起，然后逐渐向下直至根部。

在两棵树的绘画表现时，毛笔的使用要注意变化，也就是说要有干湿、粗细、虚实的变化效果，这样画面才会显得丰富，画面的视觉效果也才会达到较为理想。

至此一幅二株分形的山水画树木就已经表现出来。

绘画技巧苹果的素描画法金秋时节，农家院中的果树上，悬挂着一个个色泽金黄或红彤彤的果实，它们给人们带来了丰收的喜悦，让人们对未来充满了希望。

这就是本章所要介绍的内容―苹果的素描画法。

苹果图片谭照昆苹果的形态特点苹果是蔷薇科苹果属的果实，苹果的正常果实每个有五个心室，每个心室有两粒种子，果型端正，果肉充实，果皮的颜色分为两个阶段，第一个阶段是指苹果未成熟时的颜色，这时的果皮颜色为深绿色。