真空中静电场习题详解
《真空中的静电场》选择题解答与分析

12 真空中的静电场 12.1电荷、场强公式1. 如图所示,在直角三角形ABC 的A 点处,有点电荷q 1 = 1.8×10-9C ,B 点处有点电荷q 2 = -4.8×10-9C ,AC = 3cm ,BC = 4cm ,则C 点的场强的大小为(A) 4.5104(N C -1). (B) 3.25104(N C -1). 答案:(B)参考解答:根据点电荷的场强大小的公式,点电荷q 1在C 点产生的场强大小为)C (N 108.1)(4142011-⋅⨯==AC q E πε,方向向下.点电荷q 2在C 点产生的场强大小为)C (N 107.2)(4142022-⋅⨯==AC q E πε,方向向右.C 处的总场强大小为:),C (N 1025.3142221-⋅⨯=+=E E E总场强与分场强E 2的夹角为.69.33arctan 021==E E θ对于错误选择,给出下面的分析:答案(A)不对。
你将)C (N 105.410)7.28.1(14421-⋅⨯=⨯+=+=E E E 作为解答。
错误是没有考虑场强的叠加,是矢量的叠加,应该用),C (N 1025.3142221-⋅⨯=+=E E E进入下一题:2. 真空中点电荷q 的静电场场强大小为2041r qE πε=式中r 为场点离点电荷的距离.当r →0时,E →∞,这一推论显然是没有物理意义的,应如何解释?参考解答:点电荷的场强公式仅适用于点电荷,当r →0时,任何带电体都不能视为点电荷,所以点电荷场强公式已不适用.若仍用此式求场强E ,其结论必然是错误的.当r →0时,需要具体考虑带电体的大小和电荷分布,这样求得的E就有确定值.进入下一题: 12.2高斯定理1. 根据高斯定理的数学表达式⎰∑⋅=Sq S E 0/d ε可知下述各种说法中,正确的是: (A) 闭合面内的电荷代数和为零时,闭合面上各点场强一定为零.(B) 闭合面内的电荷代数和为零时,闭合面上各点场强不一定处处为零.(C) 闭合面上各点场强均为零时,闭合面内一定处处无电荷.答案:(B) 参考解答:高斯定理的表达式:∑⎰==⋅ni i q s E 101d ε .它表明:在真空中的静电场内,通过任意闭合曲面的电通量等于该闭合面所包围的电荷电量代数和的0/1ε倍。
3-1电磁-真空中的静电场 大学物理作业习题解答

dE
zdq 40(z2 r2 )3/2
R cos.ds 40R3
sin cosd 20
d R o
x
故球心o处总场强为:
E
dE
/ 2 sin cos d
0
20
40
4
1-6 均匀带电的无限长细线,弯成如图所示的形状,若点电荷的线
密度为λ,半圆处半径为R,求o点处的电场强度.
解:o电场强是由三部分电荷产生的:
解:作一半径为r的同心球面为高斯面。
当r<R1
当 R1<r<R2
E4r2 0, E 0
R1
r 2r2 sindrdd
E 4r2 R1 0 0
R2
0
1
r
2
A r sindrdd
0 R1 0 0
E
A
r2 R12 20r2
同理,当r>R2
E4r2 1 R2 2 Arsindrdd
0
20
9
1-10 两个无限长的共轴圆柱面,半径分别为R1和R2,面上都均
匀带电,沿轴线单位长度的电量分别为 1和 2 ,求: (1)场强分布;(2)若 1 2,情况如何?画出E-r曲线。
解:由圆柱面的对称性,E的方向为垂直柱面, r
故作一共轴圆柱面为高斯面,由高斯定律得:
R1
高 斯
当
r<R1, 当R1<r<R2 ,
1-12 将q=1.7×10-8库仑的点电荷从电场中的A点移到B点,外力需 做功5.0×10-8焦耳,问A,B俩点间的电势差是多少?哪点电势高?若 设B点的电势为零,A点的电势为多大?
解:(1) AAB=q(VA-VB), WAB=- AAB=+5.0×10-8
真空中的静电场习题详解

习题一一、选择题1.如图所示,半径为R 的圆环开有一小空隙而形成一圆弧,弧长为L ,电荷Q -均匀分布其上。
空隙长为()L L R ∆∆<<,则圆弧中心O 点的电场强度和电势分别为 [ ] (A)200,44Q L Qi R L R πεπε-∆-; (B)2200,84Q L Qi R L R πεπε-∆-; (C)200,44Q L Qi R L Rπεπε∆; (D)200,44Q L Q Li R L RLπεπε-∆-∆。
答案:A解:闭合圆环中心场强为0,则圆弧产生的场强与空隙在圆心处产生的场强之和为0。
由于空隙 ∆l 非常小,可视为点电荷,设它与圆弧电荷密度相同,则所带电荷为/Q L L -∆,产生的场强为204Q L i R L πε∆,所以圆弧产生的场强为204OQ LE i R Lπε-∆=;又根据电势叠加原理可得04O Q U Rπε-= .2.有两个电荷都是+q 的点电荷,相距为2a 。
今以左边的点电荷所在处为球心,以a 为半径作一球形高斯面。
在球面上取两块相等的小面积S 1和S 2,其位置如图所示。
设通过S 1和S 2的电场强度通量分别为1Φ和2Φ,通过整个球面的电场强度通量为S Φ,则[ ] (A )120, /S q εΦ>ΦΦ=; (B )120, 2/S q εΦ<ΦΦ=;(C )120, /S q εΦ=ΦΦ=; (D )120, /S q εΦ<ΦΦ=。
答案:D解:由高斯定理知0Φ=S q ε。
由于面积S 1和S 2相等且很小,场强可视为均匀。
根据场强叠加原理,120,0E E =<,所以12Φ0,Φ0=>。
3.半径为R 的均匀带电球体的静电场中各点的电场强度的大小E 与距球心的距离r 的关系曲线为 [ ]答案:B2∝2∝rRrR解:由高斯定理知均匀带电球体的场强分布为()302041 ()4qrr R R E q r R r πεπε⎧<⎪⎪=⎨⎪>⎪⎩,所以选(B )。
习题讲解1:真空中的静电场习题讲解

解: (1)取圆环ds 2rdr, dq ds, 则 dE dqx 4 r x
2
3 2 2
E
0
R
2rdrx
4 r 2 x
3 2 2
x (1 ) 2 2 2 R x
E
0
R
2rdrx
4 r 2 x
3 2 2
x (1 ) 2 R2 x2
1 求均匀带电细棒中垂线上距O为y点的场强。 设棒长为 l , 电荷线密度为 解:由对称性可知,选用如图所示的坐标系,中垂面上 一点的场强沿y 方向,在x方向抵消。 y dx
4 0 r l 2 cos dx E y ( p) dE y 2 l 2 4 0 r
解:dq dl q q ad d a 0 0
0
a
dE
1 dq 1 q dE d 2 2 4 0 a 4 0 a 0
根据对称性, O处的电场强度方向向下
0
2
O
d E
d E d E
dE y dE cos E y dE y 1 q
S 上
计算无限大均匀带电平板(厚度为d、密度为 )的电场。
4
其中
下
E cos dS E cos dS E cos dS
前 后
上
左
E cos dS E cos dS
右
前 E cos dS 后 E cos dS 0 2
解
V0 0 q q VD 4 0 (3l ) 4 0l
C +q A
大学物理第6章真空中的静电场课后习题与答案

第6章真空中的静电场习题及答案1.电荷为q 和2q 的两个点电荷分别置于x1m 和x1m 处。
一试验电荷置于x 轴上何处,它受到的合力等于零?解:根据两个点电荷对试验电荷的库仑力的大小及方向可以断定,只有试验电荷 q 位于点电荷 0q 的右侧,它受到的合力才可能为0,所以2qqqq00224(x 1)4(x1) ππ 00故x3222.电量都是q 的三个点电荷,分别放在正三角形的三个顶点。
试问:(1)在这三角形的中心放 一个什么样的电荷,就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑力之和都 为零)?(2)这种平衡与三角形的边长有无关系?解:(1)以A 处点电荷为研究对象,由力平衡知,q 为负电荷,所以2 4 1 π 0 q a 22 cos304 1 π 0 ( q 33qa 2 )3故qq3(2)与三角形边长无关。
3.如图所示,半径为R 、电荷线密度为1的一个均匀带电圆环,在其轴线上放一长为l 、电荷线密度为2的均匀带电直线段,该线段的一端处于圆环中心处。
求该直线段受到的电场力。
解:先求均匀带电圆环在其轴线上产生的场强。
在带电圆环上取dqdl 1,dq 在带电圆环轴 线上x 处产生的场强大小为 dE 4 dq20(xRy2 )根据电荷分布的对称性知,yE0E zdEdEcos x41xdq 1R 3 22 2O(xR) 02xl式中:为dq 到场点的连线与x 轴负向的夹角。
E x4x 220(xR) 3 2dqzx21R R 1 x4x 2R2()3 2 2xR 2( 02 )3 2下面求直线段受到的电场力。
在直线段上取dqdx2,dq受到的电场力大小为Rx12dFxdxEdq32222(xR)0方向沿x轴正方向。
直线段受到的电场力大小为Rlx12FdxdF3202220xR)(11R1121/22R22lR方向沿x轴正方向。
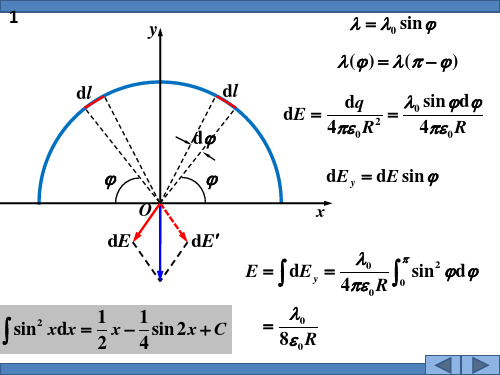
4.一个半径为R的均匀带电半圆环,电荷线密度为。
求:(1)圆心处O点的场强;(2)将此带电半圆环弯成一个整圆后,圆心处O点场强。
第九章 真空中的静电场(答案)

一. 选择题[ B ] 1(基础训练1) 图中所示为一沿x 轴放置的“无限长”分段均匀带电直线,电荷线密度分别为+λ(x <0)和-λ(x >0),则Oxy 坐标平面上点(0,a )处的场强E为(A) 0. (B) i a 02ελπ. (C) i a 04ελπ. (D)()j i a+π04ελ. 【提示】左侧与右侧半无限长带电直线在(0,a )处产生的场强大小E +、E -大小为:E E +-==矢量叠加后,合场强大小为:02E aλπε=合,方向如图。
[ B ] 2(基础训练2) 半径为R 的“无限长”均匀带电圆柱体的静电场中各点的电场强度的大小E 与距轴线的距离r 的关系曲线为:【提示】由场分布的轴对称性,作闭合圆柱面(半径为r ,高度为L )为高斯面。
据Guass 定理:SE dS=iiq ε∑⎰r R ≤时,有:()22012rL=r E L R λππεπ⎛⎫ ⎪⎝⎭,即:20r =2E R λπε r R >时,有:()012rL=E L πλε ,即:0=2rE λπε [ C ] 3(基础训练3) 如图所示,一个电荷为q 的点电荷位于立方体的A 角上,则通过侧面abcd 的电场强度通量等于: (A)06εq . (B) 012εq. (C) 024εq . (D) 048εq .【提示】添加7个与如图相同的小立方体构成一个大立方体,使A 处于大立方体的中心。
则大立方体的外表面构成一个闭合的高斯面。
由Gauss 定理知,通过该高斯面的电通量为qε。
另一方面,该高斯面可看成由24个面积与侧面abcd 相等的面组成,且具有对称性。
所以,通过侧面abcd 的电场强度通量等于24εq [ D ] 4(基础训练6) 在点电荷+q 的电场中,若取图中P 点处为电势零点 , 则M 点的电势为 (A) a q 04επ. (B) a q 08επ. (C) a q 04επ-. (D) a q 08επ-.【提示】200248P a M M aq qU E dl dr r a πεπε-===⎰⎰[ B ] 5(自测提高6)如图所示,两个同心的均匀带电球面,内球面半径为R 1、带电荷Q 1,外球面半径为R 2、带有电荷Q 2.设无穷远处为电势零点,则在内球面之内、距离球心为r 处的P 点的电势U 为:(A)rQ Q 0214επ+. (B) 20210144R Q R Q εεπ+π. (C) 0. (D) 1014R Q επ. 【提示】根据带电球面在球内外所激发电势的公式,以及电势叠加原理即可知结果。
大学大学物理习题解答参考答案-一、真空中的静电场

20XX年复习资料大学复习资料专业:班级:科目老师:一、日期:真空中的静电场一、 选择题:1.下列几个说法哪一个是正确的?(A ) 电场中某点场强的方向,就是将点电荷放在该点所受电场力的方向。
(B ) 在以点电荷为中心的球面上,由该点电荷所产生的场强处处相同。
(C ) 场强方向可由/F E =q 定出,其中q 为试验电荷的电量,q 可正可负,F 为试验电荷所受的电场力。
(D ) 以上说法都不正确。
[ ]2.关于静电场中某点电势值的正负,下列说法中正确的是:(A ) 电势值的正负取决于置于该点的试验电荷的正负。
(B ) 电势值的正负取决于电场力对试验电荷作功的正负。
(C ) 电势值的正负取决于电势零点的选取。
(D ) 电势值的正负取决于产生电场的电荷的正负。
[ ]3、某电场的电力线分布情况如图所示。
一负电荷从M 点移到N 点。
有人根据这个图作出下列几点结论,其中哪点是正确的?(A ) 电场强度N M E E <。
(B )电势N M U U <。
(C )电势能N M W W <。
(D )电场力的功A>0。
[ ]4、将一个试验电荷q 0 (正电荷)放在带有负电荷的大导体附近P 点处,测得它所受的力为F .若考虑到电量q 0不是足够小,则(A)F /q 0 比P 点处原先的场强数值大.(B)F /q 0 比P 点处原先的场强数值小.(C)F /q 0 等于原先P 点处场强的数值.(D)F /q 0 P 点处场强数值关系无法确定,[ ]5、一电偶极子放在均匀电场中,当电偶极矩的方向与场强方向不一致时,其所受的合力F 和合力矩M 为:(A) F =0,M =0, (B) F =0,M ≠0,(C) F ≠0,M =0, (D) F ≠0,M ≠0, [ ]6、已知一高斯面所包围的体积内电量代数和∑i q =0,则可肯定:(A ) 高斯面上各点场强均为零。
(B ) 穿过高斯面上每一面元的电通量均为零。
真空中的静电场(1、3)习题难点讲解
d 4 0a
指向 dq
消。故所有电荷在O点 产生的场强为零。
4. 电荷密度为 Ar 的球体的电场 解:(1)高斯面为同心球面:
4 r E
2
q
0
(i)当 r R 时,
R
dr r
O
q dV
r
r
0
2 Ar 4 r dr
O
r
P
1. 当半径从r1变到r2时,电能变化为
Q 1 1 1 2 1 2 0 r11 8 0 r2 8 0 r1 8 0 r2 r1 r2 r1 5 108 J Q
2
Q
2
2
2.
r EP E面 E洞 1 2 2 2 0 2 0 R r r 2 0 R 2 r 2
Ar 4
4 r E1
2
1
故
0
Ar 4
Ar 2 E1 er 4 0
(ii)当 r R 时,
R
q dV AR
4
Ar 4 r 2dr 0
R
dr r
O
r
4 r E2
2 r 4 0 r
dq dl ad
ad d dE 2 4 0a 4 0a
指向 dq
rd sin 这一对线元在O点的元 1 rd d dE 2 4 0 r sin 4 0 r sin 场强等值反向,相互抵 dq dl
E2 y (sin 2 sin 1 ) 4 0a 1 , 2
E2 y E2 4 0a 2 0a
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
方向沿 方向,即水平向左。
3.图示为一个均匀带电的球层,其电荷体密度为,球层内表面半径为R1,外表面半径为R2。设无穷远处为电势零点,求该带电系统的场强分布和空腔内任一点的电势。
答案:
(1) , , ;
(2) 。
解:(1)根据电场分布的球对称性,可以选以O为球心、半径为r的球面作高斯面,根据高斯定理即可求出: 。
(A) ;(B) ;
(C) ;(D) 。
答案:C
解:由高斯定理知内圆柱面里面各点E=0,两圆柱面之间 ,则P点的电势为
5.在边长为a的正方体中心处放置一点电荷Q,设无穷远处为电势零点,则在正方体顶角处的电势为
(A) ;(B) ;(C) ;(D) 。
答案:B
解:正方体中心到顶角处的距离 ,由点电荷的电势公式得
答案:
解:设内球上所带电荷为Q,则两球间的电场强度的大小为
( )
两球的电势差
所以
5.一平面圆环,内外半径分别为R1,R2,均匀带电且电荷面密度为 。(1)求圆环轴线上离环心O为x处的P点的电势;(2)再应用场强和电势梯度的关系求P点的场强;(3)若令 ,则P点的场强又为多少?
答案:(1) ;
(2) ;
总场强
方向沿x轴,即杆的延长线方向。
2.如图所示,一半径为R的半圆环,右半部均匀带电 ,左半部均匀带电 。问半圆环中心O点的电场强度大小为多少?方向如何?
答案: ,方向水平向左。
解:本题运用点电荷公式对电荷连续分布的带电体在空间产生的电场进行计算。
如图所示,取电荷元 ,则电荷元在中心O点产生的场强为
3.半径为R的均匀带电球体的静电场中各点的电场强度的大小E与距球心的距离r的关系曲线为[ ]
答案:B
解:由高斯定理知均匀带电球体的场强分布为 ,所以选(B)。
4.如图所示,一半径为a的“无限长”圆柱面上均匀带电,其电荷线密度为。在它外面同轴地套一半径为b的薄金属圆筒,圆筒原先不带电,但与地连接。设地的电势为零,则在内圆柱面里面、距离轴线为r的P点的场强大小和电势分别为[ ]
习题一
一、选择题
1.如图所示,半径为R的圆环开有一小空隙而形成一圆弧,弧长为L,电荷 均匀分布其上。空隙长为 ,则圆弧中心O点的电场强度和电势分别为[]
(A) ;(B) ;
(C) ;(D) 。
答案:A
解:闭合圆环中心场强为0,则圆弧产生的场强与空隙在圆心处产生的场强之和为0。由于空隙l非常小,可视为点电荷,设它与圆弧电荷密度相同,则所带电荷为 ,产生的场强为 ,所以圆弧产生的场强为 ;又根据电势叠加原理可得
答案: ; 。
解:电场力做功与路径无关。
(1) , ,
(2)
4.如图所示,两同心带电球面,内球面半径为 ,带电荷 ;外球面半径为 ,带电荷 。设无穷远处电势为零,则在两球面间另一电势为零的球面半径 __________。
答案:10cm
解:半径为R的均匀带电球面的电势分布为 。所以,当 时, 。令 ,得 。
(3)当 , 。
解:(1)把圆环分成许多小圆环。对半径为y,宽为dy的小圆环,其电量为 ,该带电小圆环在P点产生的电势为
整个园环上的电荷在P点产生的电势
(2) ,方向沿x正向;
(3)相距为2a。今以左边的点电荷所在处为球心,以a为半径作一球形高斯面。在球面上取两块相等的小面积S1和S2,其位置如图所示。设通过S1和S2的电场强度通量分别为 和 ,通过整个球面的电场强度通量为 ,则[]
(A) ;(B) ;
(C) ;(D) 。
答案:D
解:由高斯定理知 。由于面积S1和S2相等且很小,场强可视为均匀。根据场强叠加原理, ,所以 。
在空腔内( ): ,所以
在带电球层内( ): ,
在带电球层外( ): ,
(2)空腔内任一点的电势为
还可用电势叠加法求空腔内任一点的电势。在球层内取半径为 的薄球层,其电量为
在球心处产生的电势为
整个带电球层在球心处产生的电势为
因为空腔内为等势区( ),所以空腔内任一点的电势U为
4.两个带等量异号电荷的均匀带电同心球面,半径分别为 和 。已知两者的电势差为450 V,求内球面上所带的电荷。
5.已知某静电场的电势分布为 ,则场强分布
_______________________________________。
答案:
解:电场强度与电势梯度的关系为 。由此可求得
三、计算题
1.如图所示,真空中一长为L的均匀带电细直杆,总电荷为q,试求在直杆延长线上距杆的一端为d的P点的电场强度。
答案:
解:带电直杆的电荷线密度为 。设坐标原点O在杆的左端,在x处取一电荷元 ,它在P点的场强为
二、填空题
1.真空中两平行的无限长均匀带电直线,电荷线密度分别为 和 ,点P1和P2与两带电线共面,位置如图,取向右为坐标正方向,则P1和P2两点的场强分别
为和。
答案: ; 。
解:无限长均匀带电直线,在空间某点产生的场强 ,方向垂直于带电直线沿径向向外( )。式中a为该点到带电直线的距离。
由场强叠加原理,P1,P2点的场强为两直线产生的场强的矢量和。在P1点,两场强方向相同,均沿x轴正向;在P2点,两场强方向相反,所以
;
2.一半径为R,长为L的均匀带电圆柱面,其单位长度带有。在带电圆柱的中垂面上有一点P,它到轴线距离为 ,则P点的电场强度的大小:当 时, _____________;当 时, _____________。
答案: ; 。
解:当 时,带电体可视为无限长均匀带电圆柱面;当 时,带电体可视为点电荷。
3.如图,A点与B点间距离为2l,OCD是以B为中心,以l为半径的半圆路径。A、B两处各放有一点电荷,电量分别为+q和-q。若把单位正电荷从O点沿OCD移到D点,则电场力所做的功为______________;把单位负电荷从D点沿AB延长线移到无穷远,电场力所做的功为_______________。
