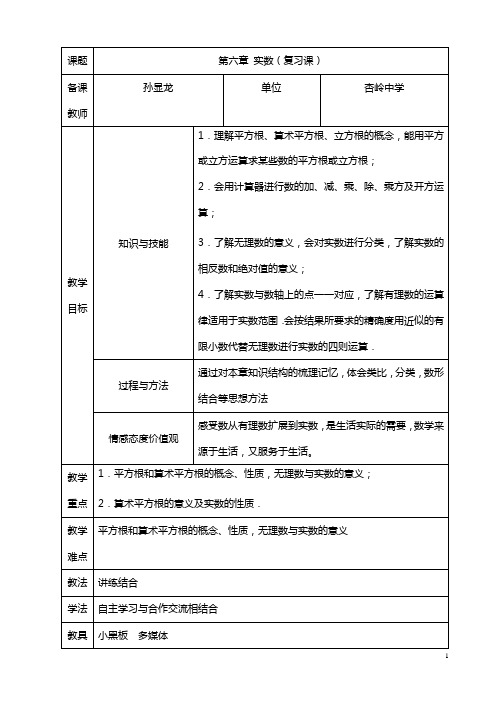
第六章 实数 复习课
合集下载
七年级下总复习第六章实数复习优质课公开课课件
数学·人教版（RJ）
第六章 | 复习
训练题
[2012·毕节] 实数 a，b 在数轴上的位置如图 6－3 所示，下
列式子错误的是( C )
A．a＜b C．－a＜－b
图 6－3
B．|a|＞|b| D．b－a＞0
数学·人教版（RJ）
第六章 | 复习
训练题
[2012·义乌] 一个正方形的面积是 15，估计它的边长大小
数学·人教版（RJ）
数学·人教版（RJ）
第六章 | 复习
进行．正实数和零都能进行开方运算，而负实数只能开立方，不 能开平方．
[说明] (1)有理数的一切运算性质和运算律都适用于实数运 算．
(2)实数的运算顺序：先算乘方、开方，再算乘除，最后算 加减，有括号的要先算括号内的，若没有括号，在同一级运算中， 要从左至右依次进行运算．
12321＝111；…；
由此猜想 12345678987654321＝1_1_1_1_1_1_1_1_1．
2．用计算器计算3 0.000064，3 0.064，3 64，3 64000，你能发 现什么规律？
解：被开方数的小数点每向右(或向左)移动3位，其立方根 的小数点相应地向右(或向左)移动一位．
方法技巧
（1）常见的非负数的形式： a , a2 , a
（2）非负数的性质：几个非负数之和为0，则每一个非 负数都为0.
数学·人教版（RJ）
第六章 | 复习
►考点五 实数的运算
例 6 计算： 36× 1－3 64－ 1 × 121.
4
11
解： 原式＝6×1－4－ 1 ×11＝3－4－1＝－2. 2 11
第六章 实数
（七年级下册总复习）
数学·人教版（RJ）
实数的复习课件(共38张PPT)
零
你知道算术平方根、平方根、立方根联系和区别吗？
算术平方根
平方根
立方根
表示方法
a 的取值
性 正数
0
质
负数
a
a
3a
a≥ 0
a≥ 0
a 是任何数
正数（一个） 互为相反数（两个） 正数（一个）
0
0
0
没有
没有
负数（一个）
开方
求一个数的平方根 求一个数的立方根 的运算叫开平方 的运算叫开立方
是本身
0,1
0
律
则3 5250的值是 17.38
1.已知 x 和 a 2 的和为0,则x的范围是为( B )
A.任意实数 B.非正实数 C .非负实数 D. 0
2.若- 3 m
=
7
3
8
,则m的值是
(B )
A 7
7 B
7
C
8
8
8
D
343 512
3. 若 (x 2)2 2 x成立,则x的取值范围是( A )
5.已知满足 3 a a 4 a ,求a的值
6、a、b互为相反数，c与d互为倒数，则a+1+b+
cd= 2
。
8、已知 a - 2 b 3 0,
则（a b)2 25 ;
9、计算： 1- x x 1 x2 1 0 ;
10、计算： 5 5 2 33
二.已知实数a、b、c，在数轴上的位置如下图所示， 试化简：
a
b0 c
（1） a2－ |a－b|+|c－a|+ (b c)2
（2）|a+b－c|+|b－2c|+ (b a)2 －2 a2
你知道算术平方根、平方根、立方根联系和区别吗？
算术平方根
平方根
立方根
表示方法
a 的取值
性 正数
0
质
负数
a
a
3a
a≥ 0
a≥ 0
a 是任何数
正数（一个） 互为相反数（两个） 正数（一个）
0
0
0
没有
没有
负数（一个）
开方
求一个数的平方根 求一个数的立方根 的运算叫开平方 的运算叫开立方
是本身
0,1
0
律
则3 5250的值是 17.38
1.已知 x 和 a 2 的和为0,则x的范围是为( B )
A.任意实数 B.非正实数 C .非负实数 D. 0
2.若- 3 m
=
7
3
8
,则m的值是
(B )
A 7
7 B
7
C
8
8
8
D
343 512
3. 若 (x 2)2 2 x成立,则x的取值范围是( A )
5.已知满足 3 a a 4 a ,求a的值
6、a、b互为相反数，c与d互为倒数，则a+1+b+
cd= 2
。
8、已知 a - 2 b 3 0,
则（a b)2 25 ;
9、计算： 1- x x 1 x2 1 0 ;
10、计算： 5 5 2 33
二.已知实数a、b、c，在数轴上的位置如下图所示， 试化简：
a
b0 c
（1） a2－ |a－b|+|c－a|+ (b c)2
（2）|a+b－c|+|b－2c|+ (b a)2 －2 a2
第六章实数复习(公开课)ppt课件
金融
在金融领域，实数被用来表示各种数据，例如，股票价格、 汇率等。
统计
在统计学中，实数被用来表示各种数据，例如，平均值、中 位数、众数等。
05
实数的扩展知识
实数的连续性
实数的连续性定义
实数连续性的性质
实数具有连续性，即任意两个实数之 间都存在无数个其他实数。
实数的连续性是实数的基本性质之一 ，它在数学分析中有着广泛的应用， 如极限的定义、函数的连续性等。
实数连续性的几何意义
在数轴上，任意两个不同的实数之间 都存在一个线段，这个线段上包含无 数个点，这些点都是实数。
无理数的性质和证明
无理数的定义
无理数是不能表示为两个整数的 比的数，如π和√2。
无理数的性质
无理数具有无限不循环小数表示的 特性，它们既不是整数也不是分数 。
无理数的证明
无理数的存在可以通过反证法或构 造法等方式进行证明，例如通过反 证法证明√2是无理数。
体积
实数可以用来表示三维物 体的体积，例如，圆柱体 的体积可以用实数表示。
科学计算和工程计算
科学计算
实数在科学计算中有着广泛的应用， 例如，物理、化学、生物等学科中的 计算都需要用到实数。
工程计算
在工程领域，实数被广泛应用于各种 计算中，例如，建筑设计、机械制造 、航空航天等。
金融和统计中的数据表示
第六章实数复习( 公开课)ppt课件
汇报人：可编辑 2023-12-22
目录
• 实数的定义与性质 • 实数的运算 • 实数的分类 • 实数的应用 • 实数的扩展知识
01
实数的定义与性质
实数的定义
实数是有理数和无理数的总称，即既包括有理数又包括无理数的数。实 数可以用来表示长度、重量、时间等实际量，也可以表示数学中的概念 和运算结果。
在金融领域，实数被用来表示各种数据，例如，股票价格、 汇率等。
统计
在统计学中，实数被用来表示各种数据，例如，平均值、中 位数、众数等。
05
实数的扩展知识
实数的连续性
实数的连续性定义
实数连续性的性质
实数具有连续性，即任意两个实数之 间都存在无数个其他实数。
实数的连续性是实数的基本性质之一 ，它在数学分析中有着广泛的应用， 如极限的定义、函数的连续性等。
实数连续性的几何意义
在数轴上，任意两个不同的实数之间 都存在一个线段，这个线段上包含无 数个点，这些点都是实数。
无理数的性质和证明
无理数的定义
无理数是不能表示为两个整数的 比的数，如π和√2。
无理数的性质
无理数具有无限不循环小数表示的 特性，它们既不是整数也不是分数 。
无理数的证明
无理数的存在可以通过反证法或构 造法等方式进行证明，例如通过反 证法证明√2是无理数。
体积
实数可以用来表示三维物 体的体积，例如，圆柱体 的体积可以用实数表示。
科学计算和工程计算
科学计算
实数在科学计算中有着广泛的应用， 例如，物理、化学、生物等学科中的 计算都需要用到实数。
工程计算
在工程领域，实数被广泛应用于各种 计算中，例如，建筑设计、机械制造 、航空航天等。
金融和统计中的数据表示
第六章实数复习( 公开课)ppt课件
汇报人：可编辑 2023-12-22
目录
• 实数的定义与性质 • 实数的运算 • 实数的分类 • 实数的应用 • 实数的扩展知识
01
实数的定义与性质
实数的定义
实数是有理数和无理数的总称，即既包括有理数又包括无理数的数。实 数可以用来表示长度、重量、时间等实际量，也可以表示数学中的概念 和运算结果。
第六章 实数 复习课
5 2 2 3 7 （精确到 0.01） ．
6．计算：
1 7．在实数 2 、0.31 、 3 、 7 、0.80108 中，无理数的个数为
个．
1．通过今天的探究学习，你们有哪些收获？ 归 纳 2．非负数的和等于零的条件是：当且仅当每个非负数的值都等于零．此性质在 小结 解题时经常会被用到． 3．对于本章的内容你还有那些疑问？ 1．教科书第 61 页复习题 6 作 业 2．自编练习题 布置 3．第七章综合测试题。
1
一、知识疏理,形成体系。 本章的主要内容是开方运算．从定义出发解题是解本章有关题目 的基本方法，我们注意掌握用计算器进行数的计算的方法的同时， 还必须注意区分清楚有理数与无理数的概念，掌握实数的四则运算． 平方根、算术平方根、立方根的定义、性质也都非常重要．总 结如下：
定义 一个正数有两个平方 平方根 根, 们互为相反数 : 性质 0的平方根是 0; 开平方 负数没有平方根 . 定义 算术平方根 正数a的正的平方根 ; 互为逆运算 乘方 开方 性质0的算术平方根是 0 定义 正数有一个正的立 ___ 方根; 开立方 立方根 性质负数有一个负的立 方根; 0的立方根是 0.
板书 设计
正有理数 有理数 0 负有理数 实数 无理数 正无理数 负无理数
4
2
9
5
2
3．x 取何值时，下列各式有意义． （1） 2 x ； （2） x 2 1 ．
知识 运用，掌 对于 a ，必须满足 a≥0，它才有意义，所以被开方数必须是非负 握各种题 数． 型的解法 4．求下列各数的值： 技巧，进 一步巩固 3 2 ； 新知。 如何化简 a 2 呢？ 首先应考虑 a 2 中 a 的范围．
6．计算：
1 7．在实数 2 、0.31 、 3 、 7 、0.80108 中，无理数的个数为
个．
1．通过今天的探究学习，你们有哪些收获？ 归 纳 2．非负数的和等于零的条件是：当且仅当每个非负数的值都等于零．此性质在 小结 解题时经常会被用到． 3．对于本章的内容你还有那些疑问？ 1．教科书第 61 页复习题 6 作 业 2．自编练习题 布置 3．第七章综合测试题。
1
一、知识疏理,形成体系。 本章的主要内容是开方运算．从定义出发解题是解本章有关题目 的基本方法，我们注意掌握用计算器进行数的计算的方法的同时， 还必须注意区分清楚有理数与无理数的概念，掌握实数的四则运算． 平方根、算术平方根、立方根的定义、性质也都非常重要．总 结如下：
定义 一个正数有两个平方 平方根 根, 们互为相反数 : 性质 0的平方根是 0; 开平方 负数没有平方根 . 定义 算术平方根 正数a的正的平方根 ; 互为逆运算 乘方 开方 性质0的算术平方根是 0 定义 正数有一个正的立 ___ 方根; 开立方 立方根 性质负数有一个负的立 方根; 0的立方根是 0.
板书 设计
正有理数 有理数 0 负有理数 实数 无理数 正无理数 负无理数
4
2
9
5
2
3．x 取何值时，下列各式有意义． （1） 2 x ； （2） x 2 1 ．
知识 运用，掌 对于 a ，必须满足 a≥0，它才有意义，所以被开方数必须是非负 握各种题 数． 型的解法 4．求下列各数的值： 技巧，进 一步巩固 3 2 ； 新知。 如何化简 a 2 呢？ 首先应考虑 a 2 中 a 的范围．
最新人教版初中数学七年级下册第六章《实数》复习教案
最新人教版初中数学七年级下册第六章《实数》复习教案第六章《实数》复习课教学设计一、教学目标1、理解平方根、算数平方根、立方根的概念；理解乘方与开方互为逆运算。
2、理解无理数及实数的有关概念；知道实数与数轴上的点一一对应；理解实数的分类。
3、学生能运用开方运算求复杂算式的平方根或立方根。
4、学生能利用已知平方根立方根求值。
5、学生能利用数形结合解决问题。
二、教学重、难点1、平方根和算术平方根、立方根的概念、性质，无理数与实数的意义理解与应用;2、对数即是形，形也是数的认识与理解。
3、灵活运用已学知识解决问题。
三、教学准备多媒体课件、视频、学案四、教学过程二、课中环节一：组内互助，答疑解惑1、小组内合作交流：解决自主学习过程中遇到的疑难问题。
2、小组代表提出问题。
3、小组之间交流合作：小组无法解决的问题，组与组之间进行解决，教师实时点拨。
4、课前学习达标检测（1）:若121x的值为（）（2）：下列说法中，正确的有（）①任何实数的平方根都有两个，且他们互为相反数；②无理数就是带根号的数；③数轴上的所有点都表示实数；④负数的立方根仍为负数。
环节二：巩固提高，归纳提升1、概括提升学案中不易解决的几种问题的类型，形成本节课学习目标并展示学习目标。
2、展示疑难问题一，利用开方运算求复杂算式的平方根和立方根①的算术平方根是_____②的立方根_____③|-0.64|的平方根是_______3、展示疑难问题二，利用已知平方根立方根求值。
①已知3x-4是25的算术平方根，求x的值_____=16-,求x的1、学生组内交流，集思广益，互帮互助，解决自主学习过程中遇到的疑难问题。
2、学生归纳提出疑难问题。
3、组间学生交流答疑解惑4、各层级学生独立完成，各尽其能学生了解本节课的学习目标学生解决问题，完成后提交展示，学生交流解题思路。
小组合作交流，学生点评，分析讲解方法和思路。
所有同学完成后提交展示弄清解析过程，存在困难。
第六章 实数(复习课件)七年级数学下册(人教版)
举一反三
【7-2】如图，用两个边长为 18cm的小正方形纸片拼成一个大的正方形纸
片，沿着大正方形纸片的边的方向截出一个长方形纸片，能否使截得的长
方形纸片长宽之比为3:2，且面积为30cm2?请说明理由.
解:不能.理由如下：因为大正方形纸片的面
积为( 18)2+( 18)2=36(cm2) ，
高频考点
高频考点七 实数的综合运用
(3)如果2+ 5的整数部分是a，小数部分是b，求出a-b的值.
(3)因为 4< 5< 9，即2< 5<3，
所以4<2+ 5<5，
所以2+ 5的整数部分为4，小数部分为2+ 5-4= 5-2，即a=4，b= 5-2，
所以a-b=4-( 5-2)= 6- 5.
举一反三
【7-1】若 2的整数部分为x，小数部分为y，则 2x-y的值是( C )
A.2 2-2
B.2
C.1
D. 2
【7-2】如图，用两个边长为 18cm的小正方形纸片拼成一个大的正方形纸
片，沿着大正方形纸片的边的方向截出一个长方形纸片，能否使截得的长
方形纸片长宽之比为3:2，且面积为30cm2?请说明理由.
0
一个，为负数
3
a
可以为任何数
知识梳理
四、实数及其运算
有理数包括整数和分数，它们都可以写成有限小数或者无限循环小数的形
式.
5 3 27 11 9
, , , , .
2 5 4 9 11
5
2.5
2
3
0.6
5
27
6.75
4
.
11
第六章实数复习(公开课)ppt课件
在几何图形中，我们也需要使用在绘制函数图像时，我们需要使用实 数。例如，绘制一次函数、二次函数 、三角函数等图像时都需要用到实数 。
科学问题中的实数应用
物理测量
在物理学中，许多物理量都是用 实数来表示的。例如，物体的速 度、加速度、力等都需要用到实
总结词
实数减法的运算律
详细描述
实数减法具有一些重要的运算律，如差不变性质、减法结 合律和减法交换律等。这些运算律可以帮助我们简化复杂 的减法计算，提高计算的准确性和效率。
实数的乘法
总结词
实数乘法的定义与性质
详细描述
实数乘法是数学中的基本运算之一，它具有结合律、交换 律和分配律等性质。实数乘法可以用来解决许多实际问题 ，如计算面积、解决概率问题等。
根式的化简
化简根式是指将根式化简为一个最简 形式的过程。例如，√8=2√2，因为8 可以分解为4×2，而4的平方根是2， 所以√8=2√2。
Part
05
实数的应用
生活中的实数应用
长度测量
在日常生活中，我们经常需要测 量物体的长度、宽度和高度等， 这些都需要用到实数。例如，测 量房间的尺寸、家具的大小等。
总结词
实数乘法的几何意义
详细描述
实数乘法的几何意义可以理解为将数轴上的点进行拉伸或 压缩。在数轴上，一个数乘以另一个数的结果等于一个数 覆盖另一个数的长度。
总结词
实数乘法的运算律
详细描述
实数乘法具有结合律、交换律和分配律。结合律是指 (ab)c=a(bc)；交换律是指ab=ba；分配律是指 a(b+c)=ab+ac。这些运算律可以帮助我们简化复杂的乘 法计算，提高计算的准确性和效率。
在数轴上进行乘法运算时，将数 轴上的每个点乘以一个正数或负 数，长度会相应地扩大或缩小。
第六章实数复习(公开课)ppt课件
19世纪
数学家逐步完善实数理论 ，形成了完备的实数体系 ，为数学分析、连续函数 等研究奠定了基础。
减法运算
总结词
减法运算的基本性质
详细描述
实数的减法运算可以转化为加法运算，即a-b=a+(-b)。
总结词
减法运算的运算律
详细描述
减法运算同样满足交换律和结合律，即a-b=b-a和(ab)-c=a-(b+c)。
总结词
减法运算的运算性质
详细描述
减法的可逆性也是减法的一个重要性质，每一个数都有 唯一的相反数；另外，0是减法的单位元，任何数与0 相减都等于它本身。
总结词
加法运算的运算律
详细描述
加法运算还有一些特殊的运算律，例如，任何数与0相加 都等于它本身，即a+0=a；相反数相加等于0，即a+(a)=0。
总结词
加法运算的运算性质
详细描述
加法运算还有一些重要的运算性质，例如，加法的可逆性 ，即每一个数都有加法逆元，与它相加等于0；加法的单 位元，即有一个特殊的数0，任何数与它相加都等于它本 身。
实数在几何学中有着广泛的应用，例如在计算长度 、面积和体积时，需要使用实数表示测量值。
函数定义域与值域
实数可以用来定义各种数学函数，包括代数函数、 三角函数、指数函数和对数函数等，同时函数的值 域也由实数构成。
数学分析基础
实数对于数学分析来说是必不可少的基础，极限、 连续性和可微性的定义都离不开实数。
在物理中的应用
80%
测量与计算
在物理学中，实数常被用于表示 和计算各种物理量，如长度、时 间、质量、电荷等。
100%
物理定律的数学表达
许多物理定律可以用实数表示的 数学公式来描述，例如牛顿第二 定律 F=ma。
第六章实数复习(公开课)ppt课件
$a times (b + c) = a times b + a times c$
。
特别注意
乘法中负负得正，即负 数乘以负数结果为正。
除法运算规则
除数为0的情况
任何数除以0都是无意义的，结果不确定。
被除数为0的情况
0除以任何非零数都等于0。
特别注意
在除法中，负负得正，即负数除以负数结果为正 。
03
3完备性Βιβλιοθήκη 实数集具有完备性，即任何实数域上的柯西序列 都收敛于一个实数，这保证了数学分析的严密性 。
无理数和有理数在解决实际问题中应用
几何应用
物理应用
在几何学中，无理数常常出现，如√2代表 对角线长度与边长之比为√2的等腰直角三 角形的边长。
在物理学中，许多常数都是无理数，如圆 周率π和自然对数的底e等，这些常数在描 述自然现象时具有重要作用。
开方运算应用
开方运算在数学、物理、工程等领域有广泛应用，如求解方程、计算面积和体积等。
05
无理数和有理数在实数范 围内地位和作用
无理数和有理数定义及分类
有理数定义
01
可以表示为两个整数之比的数，包括整数、有限小数和无限循
环小数。
无理数定义
02
无法表示为两个整数之比的数，即无限不循环小数。
分类
03
数值大小与结果
正数减去正数结果可能为 正也可能为负，负数减去 负数结果为正，正数减去 负数结果为正。
特别注意
减法没有交换律，即$ab$和$b-a$的结果不同。
乘法运算规则
乘法交换律
$a times b = b times a$。
乘法结合律
乘法分配律
$(a times b) times c = a times (b times c)$。
第六章《实数》总复习课件
2、如果一个正数的平方根是a＋3和2a－15，求这个数的立方 根。
3、计算：
(1) 2 2 2 (2)
3 3
2 2 (1
2)
(3)、 2 9 2
5 2
谢谢指导！ 再见！
(4)、 点A在数轴上表示的数为3 5，
点B在数轴上对应的数为 5， 则A，B两点的距离为
实数与数轴上的点
4 5
是一一对应的
(5)、3
2 （ 2 2 - 3）
5 2 -2 3
在进行实数的运算时，有理数的运算法则及 运算性质同样适用。
三、典例赏析
例1：计算
（1） 1.44 0.16 3 1 3 8
32 2
2 3
2 3
2 2 3
3 2
解原式 2 2 3 2 3 （ 3 2）
2 2 3 2 3 3 2 2 2 2 2 3 3 3
4 2 3ຫໍສະໝຸດ 三、典例赏析1 3 (1).( 2 x 1) 4 0 ( 2). ( x 3) 4 0 2 2
4、 5 的整数部分是 ，则它的小数部分是 ；
5、已知实数a、b在数轴上对应点的位置如图所示。 化简：a b (a b) 2
b
a
o
6、 | x 3 | y 2 0， 则x - y
x
五、达标检测
4、解答题：
1、若M＝a b 2 a＋8是（a＋8）的算术平方根， N＝2 a b 4 b 3是（b 3）的立方根，求： M N的值.
二、诊断回顾
2、填空
几个基本公式：（注意字母的取值范围）
3、计算：
(1) 2 2 2 (2)
3 3
2 2 (1
2)
(3)、 2 9 2
5 2
谢谢指导！ 再见！
(4)、 点A在数轴上表示的数为3 5，
点B在数轴上对应的数为 5， 则A，B两点的距离为
实数与数轴上的点
4 5
是一一对应的
(5)、3
2 （ 2 2 - 3）
5 2 -2 3
在进行实数的运算时，有理数的运算法则及 运算性质同样适用。
三、典例赏析
例1：计算
（1） 1.44 0.16 3 1 3 8
32 2
2 3
2 3
2 2 3
3 2
解原式 2 2 3 2 3 （ 3 2）
2 2 3 2 3 3 2 2 2 2 2 3 3 3
4 2 3ຫໍສະໝຸດ 三、典例赏析1 3 (1).( 2 x 1) 4 0 ( 2). ( x 3) 4 0 2 2
4、 5 的整数部分是 ，则它的小数部分是 ；
5、已知实数a、b在数轴上对应点的位置如图所示。 化简：a b (a b) 2
b
a
o
6、 | x 3 | y 2 0， 则x - y
x
五、达标检测
4、解答题：
1、若M＝a b 2 a＋8是（a＋8）的算术平方根， N＝2 a b 4 b 3是（b 3）的立方根，求： M N的值.
二、诊断回顾
2、填空
几个基本公式：（注意字母的取值范围）
最新人教版七年级数学下册第6章《实数》优质复习课件
1、下列各数中，最小的实数是（ C）
A. -
3；
B.- 1
2
；
C.-2；
D. 1
3
2、 3.14 的值是（C ）
A.0 B. 3.14- C.п-3.14 D.0.14
广东省怀集县大岗镇大岗中学 石迎伦
六、课堂小结
正___有__理__数
__有__理__数 0
_有__限___小__数__或__无___限__循__环___小__数
、27
无理数的个数是
( C)
A.1 B.2 C.3 D.4
2、如图,在数轴上表示实数 15 的点
可能是( C )
A.点P B.点Q C.点M D.点N
广东省怀集县大岗镇大岗中学 石迎伦
三、强化训练
3、3 7 的相反数是 3 7 ， 绝对值等于 3 的数是 3 ．
4、已知 a 2 b 3 0，则(a-b)2=
实数
负___有__理__数
_无__理____数
正__无___理__数 负___无__理__数
__无__限__不___循__环__小___数___
七、课后练习
1.完成课本P61页复习题第6、7、8题； 2.完成《学考精练》P36页习题第1、3、 4、7、10、12、13、14题。
课堂小结
25 ；
广东省怀集县大岗镇大岗中学 石迎伦
三、强化训练 5、比较大小：
（1） 3 _<___ 5 （2）- 5 __>__ - 26 （3）3 2 __>__2 3
广东省怀集县大岗镇大岗中学 石迎伦
三、强化训练
6、计算：
（1）2 2 3 2 2 解：原式 （2+3-1） 2 4 2
第六章实数小结与复习课件人教版数学七年级下册
解：∵(-2+ 5 )-(-2+ 3)= -2+ 5 +2- 3 = 5 - 3 ＞0 ∴-2+ 5＞-2+ 3
另解：直接由正负决定-2+ 5 ＞-2+ 3
查漏补缺
当堂训练
实数
6.若|3a+4|+(4b-3)2=0,求-ab的平方根.
解：∵|3a+4|≥0且(4b-3)2≥0
而|3a+4|+(4b-3)2=0
∴|3a+4|=0且(4b-3)2=0
∴a= 4 ， 3 .
3
∴-ab=-(
4
4 ×
3
)=1
,
34
∴1的平方根是±1.
查漏补缺
当堂训练
7.计算：
(1) 0.36 1 2016 3 8;
解：原式=3.6；
(2)
1
1
2
3
64.
16 2
解：原式=-4.
实数
查漏补缺
算术平方根.
知识点一
开方运算
【迁移应用1】求下列各式的值：
① 400 ; ② 16
81
③ 49 ④ 3 1 63
100
64
答案：①
20；
② 94
；
③
7 10
；
④
1 4
.
基础训练
01
开方运算
知识要点
02
实数的有关概念
03 实数的估算及与数轴的结合
精讲精练
04
实数的运算
知识点二
实数的有关概念
0.15
典例精讲
B
【归纳拓展】对实数进行分类不能只看表面形式，应先化简，再根据结 果去判断.
第六章《实数》总复习课件
从数的发展和数的研
究两个方面对本节课
进行小结，让学生感
悟数学的发展经历了
漫长的历史，是数学
家们智慧的结晶。同
时，通过回顾本章的
内容，感受学习实数
的过程同样遵循并体
现了学习一类数的方
式方法。
6
教学反思
1.本节课从实数的存在、概念、分类、表示、比较大小、运算几个角
度展开复习，帮助学生头脑中形成研究数的逻辑和方法。
0
0
负数
开立方
开平方
问题4 在数轴上能找到数
吗？
0
实数
1
一一对应
22
3
数轴上的点
表示的点
问题5
2有多大？
追问 我们是怎么得到 2的近似值的？
. . . . . . . . .
1.21 1.44 1.69 1.96 2.25 2.56 2.89 3.24 3.61
了数的范围，但有
理数的相关概念及
运算同样适用于实
数。利用数轴，我
们建立起了数与形
的桥梁。
5
教学过程设计
数的大小是研究数的重要
方面，该环节通过再现学
生之前的学习经验，复习
用夹逼的方式估计无理数
的大小，学以致用，根据
该方法解决更实际更复杂
的问题。另外，借用华罗
庚的故事也能激发学生的
学习积极性。
5
教学过程设计
.
1.9881
.
2.0164
.
2.0449
.
2.0736
.
2.1025
.
.
.
.
.
1.993744 1.996569 1.999396 2.002225 2.005056
第六章实数复习课
绝对值
二、知识点分解－－数
每个实数都可以用数轴上的一个点来表示；反过 来，数轴上的每一个点都表示一个实数。即实数和数
轴上点是一一对应的。
性质：在数轴上，右边的点表示的数比左边的点表示 的数大.
牛刀三试
填空
5 5 1、 5 的相反数是_____, 绝对值是_____; 没有倒数的实数是_____. 0
即：若x3 = a,则x =
3
a
开平方:求一个数的平方根的运算，叫做开平方。 开立方:求一个数的立方根的运算，叫做开立方。
二、知识点分解－－三种根的对比
算术平方根
平方根
立方根
3
表示方法
a
a0
a
a0
a
a 的取 值
性 质 正数 0 负数
a 为任意数
正数（一个） 互为相反数（两个） 正数（一个）
3 (6) 3 (3)3 _____.
三、知识点应用
计算题：
(1) 144 16 1 8
3 3
(2)2 2 3( 3 2)
(3) (2)
2
2 1 ( 2 1)
四、课堂小结
1、请同学们谈谈这节课你们收获了什么？
2、请同学们谈谈这节课你们有什么疑惑？
实 数
无理数
正无理数 , 2, 3 3,0.010010001 负无理数 , 2, 3 3, 0.010010001
无限不循环小数
牛刀二试
填空：将下列各数分别填入下列的集合括号中
3
9,
7,
4 , 9
3
5 , 7
2,
1 , 3
16, 5,
3
人教版七年级下册第6章 实数整理和复习课件共22张
没有
负数（一个）
开方
求一个数的平方根 求一个数的立方根 的运算叫开平方 的运算叫开立方
是本身
0,1
0
0,1,-1
题型一 开方运算
习题：
1、求下列各数的平方根：
解解：：32?651的285平的方立根方根是是? 3
25
8
?
-31625
??
5
2
-65
2、求下列各数的立方根：
06.0142的7的平立方方根根是是?
题型二 实数的有关概念及分类
2、在- ，0.618， ， ，
中，负有理数的个
数是（ B ）
A. 1个
B. 2个
C.3个
D.4个
3、下列实数 ， , ,3.1415， ， 中，正分
数的个数是（ B ）
A. 1个
B. 2个
C.3个
D.4个
【注意】 ， 不属于分数，而是无理数.
题型二 实数的有关概念及分类
实数ɑ 的绝对值记作：
题型三 实数的相反数和绝对值
习题:
2
2
3 ? 2 ? ?( 3 ? 2) ? ? 3 ? 2
题型三 实数的相反数和绝对值
习题:
8或－6
题型三 实数的相反数和绝对值
其中：
题型三 实数的相反数和绝对值
（5）如图所示，数轴上与1， 对应的点分
别是为 A、B，点 B关于点 A的对称点为 C,设点C
3
2045.0?27?
5
2?
0.3
(?11?0)72的平立方根根是是
?3
1（- 7-
1?0）32 1?
??
1
10
8
8 82
第6章实数复习-人教版七年级数学下册课件(共17张PPT)
解：(1)点 B 表示的数是 5－2. (2)点 C 表示的数是 2－ 5. (3)由题可知，点 A 表示 5，点 B 表示 5－2，点 C 表示 2－ 5， ∴OA＝ 5，OB＝ 5－2，OC＝|2－ 5|＝ 5－2，∴OA＋OB＋OC ＝ 5＋ 5－2＋ 5－2＝3 5－4.
互为逆运算
乘方
开方
2、填空
（1）因为 4 的立方是64，所以64的立方根是 4 ， -27的立方根是 -3 。
（2） 0 的平方根是它本身， 1和0 的算术平方根是它本 身， 1和0 的立方根是它本身。
（3）下列说法中：① 3 都是27的立方根，
② 3 y 3 y， ③ 64 的立方根是2， ④ 3 82 4 ⑤两数互为相反数，则这两数的立方 根也互为相反数，正确的有 ②③⑤（填序号）。
3
9
0,
5, 3 8,
0.3737737773 （相邻两个3之间的7的个数逐次加1）
1 , 5 , 42
4, 9
0,
3 8,
有理数集合
3 2, 7, , 2, 20 , 3
5, 0.3737737773
无理数集合
3、填一填
(1)
2 2
的相反数是
2 2
， 7 3 3
7 ， 的倒数是
1
（1）按定义分
整数
有理数：
有限小数或无限循环小数
实
分数
数
无理数： 无限不循环小数
含开方开不尽的数
π 含有 的数
有规律但不循环的小数
【例2】在-7.5，
, 4,
,
gg
,0.15 ,
中，无理数
的个数是（ B ）
A. 1个 B. 2个 C.3个 D.4个
互为逆运算
乘方
开方
2、填空
（1）因为 4 的立方是64，所以64的立方根是 4 ， -27的立方根是 -3 。
（2） 0 的平方根是它本身， 1和0 的算术平方根是它本 身， 1和0 的立方根是它本身。
（3）下列说法中：① 3 都是27的立方根，
② 3 y 3 y， ③ 64 的立方根是2， ④ 3 82 4 ⑤两数互为相反数，则这两数的立方 根也互为相反数，正确的有 ②③⑤（填序号）。
3
9
0,
5, 3 8,
0.3737737773 （相邻两个3之间的7的个数逐次加1）
1 , 5 , 42
4, 9
0,
3 8,
有理数集合
3 2, 7, , 2, 20 , 3
5, 0.3737737773
无理数集合
3、填一填
(1)
2 2
的相反数是
2 2
， 7 3 3
7 ， 的倒数是
1
（1）按定义分
整数
有理数：
有限小数或无限循环小数
实
分数
数
无理数： 无限不循环小数
含开方开不尽的数
π 含有 的数
有规律但不循环的小数
【例2】在-7.5，
, 4,
,
gg
,0.15 ,
中，无理数
的个数是（ B ）
A. 1个 B. 2个 C.3个 D.4个
人教版七年级数学下册 第六章 实数 复习课 课程教学设计
《实数复习课》教学设计教学目标：一、知识与技能目标1.进一步巩固实数的定义性质及其运算规律2．能运用实数的运算解决简单的实际问题，提高对知识的应用能力。
二、过程与方法目标自主探索出各知识点间的关系,总结出实数在实际问题中的解题步骤.三、情感态度与价值观目标联系实际,生活中常见的问题,培养并提高学生归纳,•对比及分析问题,解决问题的能力,激发学生的学习兴趣,养成勤于思考的好习惯.教学重难点：重点：无理数、平方根，算术平方根，立方根及实数的意义与性质，以及实数的运算法则。
难点：利用平方根、算术平方根、立方根及实数运算法则的进行有关计算题目，特别是平方根与算术平方根的不同之处。
教学设计：活动一 平方根和开平方知识梳理：（1）如果2(0)x a a =≥，那么x 叫做a 的平方根．a 的平方根记作 。
若x ≥0，则x叫a 的算术平方根，记作 。
注：a 有双重非负性：①被开方数a 是非负数，即a 0.②a 本身是非负数，。
互逆（2）求一个数平方根的运算叫开平方。
开平方平方（3）一个正数有 平方根,它们 ；0的平方根是 ；负数 平方根. 设计说明：通过知识点的呈现,加深学生对所学知识的理解,进一步提升学生的认知能力。
练习：（1）求下列各数的算术平方根：① 900 ； ② 1 ； ③ ;6449 ④ 14 .（2） 求下列各数的平方根：① 11 ② 49121③ 0.0004 ④ ()225- （3）25的算术平方根是 ；3的平方根是 ；16的平方根是 。
（4）计算: ①44.1-21.1; ②256481-+;设计说明：通过简单题型的训练，加强学生对所学知识升华，体验数学源于生活又高于生活的内涵。
活动二 立方根和开立方知识梳理：(1)如果x 3=a ，那么x 叫做a 的立方根．a 的立方根记作 。
互逆(2)求一个数立方根的运算叫开立方。
开立方 立方(3)正数有 个 的立方根，负数有 个 的立方根，0的立方根为 . 设计说明：通过知识点的呈现,加深学生对所学知识的理解,进一步提升学生的认知能力。
人教版初中七年级(下册)数学《第六章实数复习课》ppt课件
C） 的 值 是 （ ( A )1 ( B )5
( C )2 5
( D )不 能 确 定
三、知识点应用
选择题：
2 2 3 、 已 知 x 2 y 80 , 则 x 2 x y y
的 值 是 ( C)
( A )6 ( C )1 0
( B ) 1 0 ( D )不 能 确 定
4、下列运算正确的是（ A ）
唯一对应
数轴上一个点
性质：在数轴上，右边的点表示的数比左边的点表示
的数大.
二、知识点分解－－实数的性质
在实数范围内，相反数、倒数、绝对值的 意义和有理数的相反数、倒数、绝对值的意义 完全一样。即
a a
相反数 倒数
a
1 (a 0) a , a0 a | a | 0 , a0 a , a0
(× 10)任何数都有平方根
( 11 ) a 一定没有平方根 ×
2
三、知识点应用
填空：将下列各数分别填入下列的集合括号中
3
9,
1 , 4
7,
4 , 9
3
5 , 7
2,
1 , 3
16 ,
1 , 3 1 , 4
3
8 ,
0 .
…｝
,
9,
5, 5,
4 , 9
无理数集合：｛
7,
16 ,
3
2 , ,
三、知识点应用
1、a、b互为相反数，c与d互为倒数，则a＋1＋b＋cd
＝ 2 。
2、实数a,b,c,d在数轴上的对应点如图所示，则 （1）它们从小到大的顺序是 （ 2 ） a b a +b c<d<b<a 。
( C )2 5
( D )不 能 确 定
三、知识点应用
选择题：
2 2 3 、 已 知 x 2 y 80 , 则 x 2 x y y
的 值 是 ( C)
( A )6 ( C )1 0
( B ) 1 0 ( D )不 能 确 定
4、下列运算正确的是（ A ）
唯一对应
数轴上一个点
性质：在数轴上，右边的点表示的数比左边的点表示
的数大.
二、知识点分解－－实数的性质
在实数范围内，相反数、倒数、绝对值的 意义和有理数的相反数、倒数、绝对值的意义 完全一样。即
a a
相反数 倒数
a
1 (a 0) a , a0 a | a | 0 , a0 a , a0
(× 10)任何数都有平方根
( 11 ) a 一定没有平方根 ×
2
三、知识点应用
填空：将下列各数分别填入下列的集合括号中
3
9,
1 , 4
7,
4 , 9
3
5 , 7
2,
1 , 3
16 ,
1 , 3 1 , 4
3
8 ,
0 .
…｝
,
9,
5, 5,
4 , 9
无理数集合：｛
7,
16 ,
3
2 , ,
三、知识点应用
1、a、b互为相反数，c与d互为倒数，则a＋1＋b＋cd
＝ 2 。
2、实数a,b,c,d在数轴上的对应点如图所示，则 （1）它们从小到大的顺序是 （ 2 ） a b a +b c<d<b<a 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
考点讲练
例6
计算：
2 2
2 3
2 4
5 2 = 12 .
【归纳拓展】开立方运算时要注意小数点的变化规 律，开立方是三位与一位的关系，开平方是二位与 一位的关系.
【迁移应用4】计算： （1） 7 +π；（精确到0.01） （2） 6g 5 （精确到0.01）
（1）5.79；（2）5.48
解：∵(-2+ 5 )-(-2+ 3)= -2+ 5 +2- 3 = 5 - 3 ＞0 ∴-2+ 5 ＞-2+ 3
另解：直接由正负决定-2+ 5 ＞-2+ 3
随堂即练
6.若 3a 4 (4b 3)2 0, 求-ab 的平方根.
解：∵｜3a+4｜≥0且(4b-3)2≥0
而｜3a+4｜+(4b-3)2=0
考点讲练
课堂小结
1.通过对本章内容的复习，你认为平方根和立方根之 间有怎么样的区别与联系？
2.什么是实数？ 3.实数的运算法则与有理数的运算法则有什么联系？
课后训练
随堂即练
1.写出两个大于1小于4的无理数___2_、_π___.
2. 10 的整数部分为__3__,小数部分为_ 10 __3__.
CAB
0
1
2
考点4 实数的运算
例4 （1）3 24 45 200；
60
考点讲练
（2）3 （y 1)3 .
y-1
考点讲练
例5 已知 3 0.539 0.8138, 3 53.9 3.777, 3 5.39 1.753,则3 0.000539 0.08138 ，3 53900 37.77 .
RJ七(下) 教学课件
第六章 实数
复习课
互为逆运算
乘方
开方
知识梳理
实数
平方根 正
算术平方根
立方根
有理数
无理数
运算
考点1 开方运算
考点讲练
例1 1.求下列各数的平方根：
(1) 25 ; (2) 6 1 ; (3) (10)2
36
4
2.求下列各数的立方根：
(1)
-
8 ；（2）0.027；（3）1125
4；③
9
7 10
；④ 1
4
.
考点讲练
考点讲练
考点2 实数的有关概念
例2
在-7.5， 15 , 4, 3 8 , π
gg
,0.15
,
2
中，无理
3
数的个数是（ B ）
A. 1个 B. 2个 C.3个 D.4个
【归纳拓展】对实数进行分类不能只看表面形式， 应先化简，再根据结果去判断.
考点讲练
【迁移应用2】（1）在-
3.一个立方体的棱长是4cm，如果把它体积扩大为 原来的8倍,则扩大后的立方体的表面积是_3_8_4_c_m_2_.
4.求下列各式中的x. （1） (x-1)2=64；
(x=9或-7 )
随堂即练
(2)( x)3 729 0. 2
(x=-18)
随堂即练
5.比较大小： 2 5 与 2 3 .
∴｜3a+4｜=0且(4b-3)2=0
∴ ∴a-=ab=43-(， b43=×3434
. )=1
,
∴ 1 的平方根是±1.
7.计算：
(1) 0.36 1 2018 3 8;
解：原式=3.6；
(2)
1
1
2
3
64.
16 2
解：原式=-4.
随堂即练
23 7
，0.618，π
，3 8
，3
2
中，
负有理数的个数是（ A ）
A. 1个 B. 2个 C.3个 D.4个
43 （2）下列实数 7
，3,
2
,3.14159，（
3
7）2，
9中，
正分数的个数是（ B ）
A. 1个 B. 2个 C.3个 D.4个
【注意】 3 ， 等不属于分数，而是无理数.
23
考点3 实数的估算及与数轴的结合
7 8
(1) 5 ; (2) 5 ;
6
2
(1) 2 ; (2) 0.3; 5
(3) 10. (3) 1 .
2
【归纳拓展】解题时，要注意题目的要求，是求平方 根、立方根还是求算术平方根.
【迁移应用1】求下列各式的值：
① 400 ;
③ 49 100
② 16 81
④ 3 1 63 64
①
20；②
考点讲练
例3 (1) 20 位于整数 4 和 5 之间.
(2)实数a,b在数轴上的位置如图所示，化简
a b (b a)2 -2a .
a 0b
【归纳拓展】
1.实数与数轴上的点是一一对应的关系； 2.在数轴上表示的数，右边的数总是比左边的数大.
考点讲练
【迁移应用3】如图所示，数轴上与1， 2 对应的点分 别是为A、B，点B关于点A的对称点为C,设点C表示的 数为x,则 x 2 = 2 2 2 .