传输原理-第十二章 对流换热的基本方程和分析解
传热学12 对流换热的基本方程和分析解

此式称为傅里叶-克希荷夫导热微分方程,适用于无内 热源不可压缩流体的对流换热分析。 a 2/s。 称为导温系数,单位是 m CP
式中,Ψ为壁面的几何因素。
12.2 对流换热微分方程 (1) 换热微分方程
由于在贴壁处流体受到黏性的作用,没有相
T 式中, y
对于壁面的流动,因此被称为贴壁处的无滑移 边界条件。将傅里叶定律应用于贴壁流体层, 与牛顿冷却公式联系,得换热微分方程: T T y y 0
由换热微分方程得:
x 0.332
L Re Pr
1/2 L 1/3
x x Nu x 0.332 Rex1/ 2 Pr1/ 3
对宽为W、长为L的平板上的平均对流传热系数α,可用 L αx沿全板长从0到L积分: 1 x dx L0 1/2 1/3 2 x 对上式积分可得: 0.664 ReL Pr L x Nu 0.664 Rex1/2 Pr1/3 Nu 2Nux
对于不可压缩流体,不存 在体积功,只有黏性力作功 产生摩擦热。 微元体获得的热能有:一 是通过微元体界面从外界以 对流和导热方式得到;二是 由微元体的内热源产生。
12.2 对流换热微分方程
对于不可压缩流体,不存在体积功,只有黏性 力作功产生摩擦热。 微元体获得的热能:一是由微元体界面从外界 以对流和导热方式得到;二是由微元体的内热 源产生。 微元体在热量传输过程的热力学第一定律为:
y 0
12.4 对流换热边界层微分方程组的分析解
df ' d
y 0
d{2[(T Tw ) / (T Tw )]} d[(y / 2x) Rex ]
对流换热能量方程

对流换热能量方程一、概述对流换热是指通过流体的运动将热量从高温区域传递到低温区域的过程。
对流换热能量方程是描述这一过程的数学表达式。
本文将详细介绍对流换热能量方程的含义、推导过程和应用。
二、对流换热能量方程含义对流换热能量方程描述了在某一时刻,单位时间内通过流体的运动传递到单位面积上的热量。
它可以表示为:q = hA(Ts - Tf)其中,q是单位时间内通过单位面积传递的热量,h是对流换热系数,A是传热面积,Ts和Tf分别是固体表面温度和流体温度。
三、对流换热系数对于不同的情况,对流换热系数也会有所不同。
例如,在自然对流中,h通常非常小;而在强制对流中,h则会比较大。
此外,在液态介质中和气态介质中,h也会有很大差别。
四、推导过程为了得到上述公式,我们需要做出以下假设:1. 流体速度与距离无关;2. 流体温度与距离无关;3. 流体是定常的。
在这些假设下,我们可以通过质量守恒和能量守恒来推导出对流换热能量方程。
首先,考虑单位时间内通过单位面积的热量传递。
根据热传导定律,这个值可以表示为:q = -k(dT/dx)其中,k是热导率,dT/dx是温度梯度。
但是,在对流换热中,温度梯度并不是一个固定值,因为它随着流体的运动而发生变化。
因此,我们需要将上述公式进行修正。
假设在距离x处的流体速度为v(x),温度为T(x),则单位时间内通过单位面积的热量传递可以表示为:q = -k(dT/dx) + pvCp(Ts - T)其中,p是密度,Cp是比热容,Ts是固体表面温度。
第一项表示由于温度梯度引起的传热;第二项表示由于流体运动引起的传热。
接下来,我们需要确定对流换热系数h。
根据牛顿冷却定律:q = hA(Ts - Tf)我们可以将上述公式中的q和Ts替换成上述修正后的公式,得到:h = pvCp(v/x)最终,我们将上述公式代入修正后的热传导定律中,即可得到对流换热能量方程。
五、应用对流换热能量方程在工程领域中有着广泛的应用。
对流换热基本方程课件

相似理论与量纲分析
相似理论
相似理论是研究两个或多个物理现象之间相似性的理论。在对流换热问题中,如 果两个物理现象的相似准则数相等,则它们之间的对流换热过程具有相似性。
量纲分析
量纲分析是一种通过比较不同物理量之间的量纲关系来研究物理现象的方法。在 对流换热问题中,可以利用量纲分析来确定影响对流换热的无量纲参数,从而简 化对流换热问题的研究。
THANKS FOR WATCHING
感谢您的观看
对流换热基本方程课件
目 录
• 引言 • 对流换热基本概念 • 对流换热基本方程推导 • 对流换热基本方程求解方法 • 对流换热强化技术及应用案例 • 总结与展望
01 引言
对流换热现象
01
02
03
定义
对流换热是指流体与固体 壁面之间由于温度差异引 起的热量传递过程。
分类
对流换热可分为自然对流 和强制对流两种形式。
对流换热研究有助于降低设备能耗、 减少废热排放,对于环境保护和可持 续发展具有积极作用。
对流换热基本方程重要性
描述对流换热过程
对流换热基本方程是描述对流换 热过程中热量传递、流体流动及 物性参数变化等规律的基础工具
。
指导工程实践
掌握对流换热基本方程有助于工程 师在设计、优化和运行工程设备时 做出合理决策,提高设备性能和经 济性。
推动理论研究
对流换热基本方程是研究对流换热 机理、探索新现象和新规律的基础 ,对于推动传热学及相关领域理论 研究具有重要意义。
02 对流换热基本概念
对流换热定义及分类
对流换热定义
对流换热是指流体与固体表面之间的 热量传递过程,其中流体可以是气体 或液体,固体表面可以是各种形状和 材料的壁面。
对流方程及其解法

对流方程及其解法对流方程是描述流体运动的最基本方程之一,涉及热、动量、物质等的传递现象,对于各种物理问题的研究都具有重要意义。
本文将从对流方程的基本形式和意义出发,探讨其常见解法及相关应用。
一、对流方程的基本形式与意义对流方程是描述流体中质量、热量和动量传递的方程,其基本形式可以写作:$$ \frac{\partial\phi}{\partial t} + (\mathbf{v}\cdot\nabla)\phi =\nabla\cdot(\Gamma\nabla\phi) $$其中,$\phi$为描述流体量的变量,如温度、密度、浓度等;$\mathbf{v}$为流体的流速,$\Gamma$为扩散系数。
对该方程的解析求解较为困难,故通常采用数值方法进行求解。
下面介绍几种常见的数值解法。
二、有限差分法有限差分法是在连续方程的基础上,利用有限差分代替导数,将微分方程变为代数方程组,从而利用计算机求解的方法。
其基本思想是将求解区域划分为有限个网格,对每个网格内的量用差分代替导数,从而得到有限差分方程。
以简单的二维对流扩散为例,其对流方程为:$$ \frac{\partial\phi}{\partial t} + u\frac{\partial\phi}{\partial x} + v\frac{\partial\phi}{\partial y} = \Gamma\frac{\partial^2\phi}{\partial x^2} + \Gamma\frac{\partial^2\phi}{\partial y^2} $$其中,$u$和$v$分别代表$x$和$y$方向的流速。
对该方程进行离散,假设$\phi_{i,j}$为$x=i\Delta x$,$y=j\Delta y$处的$\phi$值,则可以得到:$$ \frac{\phi^{k+1}_{i,j} - \phi^k_{i,j}}{\Delta t} +u\frac{\phi^k_{i+1,j} - \phi^k_{i-1,j}}{2\Delta x} +v\frac{\phi^k_{i,j+1} - \phi^k_{i,j-1}}{2\Delta y} $$$$ = \frac{\Gamma\Delta t}{(\Delta x)^2}(\phi^k_{i+1,j} -2\phi^k_{i,j} + \phi^k_{i-1,j}) + \frac{\Gamma\Delta t}{(\Deltay)^2}(\phi^k_{i,j+1} - 2\phi^k_{i,j} + \phi^k_{i,j-1}) $$其中,$k$为时刻,$\Delta x$和$\Delta y$分别为$x$和$y$方向的网格间距。
对流换热部分解析

cp
t )dy
c p
y
(vt)dV
对流
c
p[
(ut) x
(vt) y
]dV
c
p
(
u x
t
t x
u
v y
t
t y
v)dV
c p [t (
u x
v y
)
u
t x
v
t y
]dV
c
p
(u
t x
v
t y
)dV
华北电力大学
梁秀俊
高等传热学
导热
(
2t x2
2t y 2
)dV
对流
c
p
(u
t x
v
t y
u v 0 x y
(u
u x
v
u y
)
Fx
p x
(
2u x 2
2u y 2
)
(u
v x
v
v ) y
Fy
p y
(
2v x 2
2v y 2
)
cp u
t x
v t y
2t x 2
2t y 2
hx
tw
t
t y
y0,x
华北电力大学
5个方程,5个未知量 — 理论上可解
梁秀俊
高等传热学
理论求解对流换热思路
hx
tw
t
t y
y0,x
特别是壁面 附近的温度 温度场 分布
温度场 受到流场的影响
流场
连续性方程 质量守恒定律 动量方程 动量守恒定律
温度场 能量方程 能量守恒定律
对流换热微分方程式
传输原理对流换热课件

有限差分法基于泰勒级数展开,将微 分问题转化为差分问题,通过迭代求 解离散点上的值,最终得到近似解。 该方法简单直观,适用于规则区域。
有限元法
总结词
一种将连续域离散化为有限个小的子 域(或单元),再将每个子域(或单 元)的解用近似函数表示,最后将所 有子域(或单元)的解组合起来形成 原问题的近似解的方法。
详细描述
对流换热是流体流动过程中,流体的热量通过壁面的导热和 对流作用传递给壁面的过程。这种热量传递方式在自然界和 工程领域中广泛存在,如空气与物体的对流换热、液体与管 道的对流换热等。
对流换热分类
总结词
根据流动状态和流体物性,对流换热可以分为层流换热、湍流换热、凝结换热、沸腾换热等。
详细描述
层流换热是指流体在层流状态下进行的热量传递过程,湍流换热是指流体在湍流状态下进行的热量传递过程;凝 结换热是指水蒸气在冷壁上凝结时释放的潜热传递给壁面的过程;沸腾换热是指液体在沸腾状态下,通过汽化作 用将热量传递给壁面的过程。
详细描述
在建筑环境中,对流换热是实现室内温度和湿度控制 的主要方式之一。通过对流换热,室内空气可以与外 界空气进行交换,以保持室内环境的舒适度。建筑环 境中的对流换热可以通过自然对流、机械通风等方式 实现,同时需要考虑建筑物的朝向、窗户设计等因素 的影响。
THANKS
谢谢
传输原理对流换热课件
目录
CONTENTS
• 对流换热基础 • 传输原理在热对流中的应用 • 传输原理在热对流中的数学描述 • 对流换热的数值模拟方法 • 对流换热实验研究方法 • 对流换热在工程中的应用实例
01
CHAPTER
对流换热基础
对流换热定义
总结词
对流换热是指流体与固体壁面之间由于温差而引起的热量传 递过程。
对流传热分析和计算

对流传热分析和计算传热是物质内部或不同物体之间热量传递的过程,对流传热是其中一种重要形式。
通过对流传热的分析和计算,我们可以更好地理解和应用这一过程,以满足需求和优化能源利用等方面的目标。
本文将介绍对流传热的基本原理、分析方法和计算模型。
一、对流传热的基本原理对流传热是指通过流体(如气体或液体)的运动,将热量从一个物体传递到另一个物体的过程。
在对流传热中,流体既可以通过自然对流(由密度和温度梯度引起的流动),也可以通过强制对流(通过外部装置引起的流动)来实现热量的传递。
对流传热的基本原理可以通过牛顿冷却定律来描述,即传热速率与温度差成正比。
牛顿冷却定律的一般表达式如下:q = h * A * (T1 - T2)其中,q表示单位时间内传递给或从物体中传出的热量;h为对流传热系数,代表了对流传热的特性;A为接触面积;T1和T2分别为两个物体的温度。
二、对流传热的分析方法对流传热的分析方法主要包括实验分析和数值模拟两种。
1. 实验分析实验分析是通过实际测量和观察来研究对流传热的过程和特性。
常用的实验方法包括热电偶测温法、平板法、圆管法等。
通过实验,我们可以获取到对流传热系数、传热速率等重要参数,为其他工程和研究提供参考和依据。
2. 数值模拟数值模拟是利用计算机和数值方法对对流传热进行模拟和计算。
通过建立数学模型、采用数值算法和边界条件,我们可以通过计算得到对流传热的各种参数和特性。
常用的数值模拟方法有有限元法、有限体积法和计算流体力学(CFD)等。
三、对流传热的计算模型对流传热的计算模型是通过数学方程和物理模型来描述和计算对流传热的过程。
在对流传热的计算模型中,需要考虑流体的性质、流动的速度和流动的特性等因素。
1. 粘性流体模型在粘性流体模型中,对流传热的计算将考虑流体的黏性和流速的分布等因素。
一般来说,黏性流体模型适用于流速较低、流动较平稳的情况。
2. 湍流模型湍流模型适用于流速较高、流动较复杂的情况。
对流换热

工学院机电工程教研室
传输原理
y
t∞
u∞
qw
tw
x
工学院机电工程教研室
传输原理
◆
特点 • (1) 导热与热对流同时存在的复杂热传递 过程 • (2) 必须有直接接触(流体与壁面)和宏 观运动;也必须有温差 y t
∞
u∞
qw
工学院机电工程教研室
tw
x
传输原理
对流换热的基本计算式
牛顿冷却公式:
y t∞ u∞
• t w :壁温
t :流体温度
工学院机电工程教研室
传输原理
壁面形状
水平圆管 d<0.2m 垂直管或板 l<1m
特征尺寸
外径 d 高度 l
C
1.09 0.53 0.13 1.36 0.59 0.10
N
1/5 1/4 1/3 1/5 1/4 1/3
(GrPr)范围
1-104 104-109 109-1012 <104 104-109 109-1012
6 105 f 1 Re1.8
3.圆形直管内强制层流时的对流传热系数 (1)只有在小管径、水平管、壁面与流体之间的温差比
较小时、流速比较低的情况下才有严格的层流传热。在 4 其他情况下往往伴有自然对流传热。当 Gr < 2.5 × 10 1 d 0.14 3 时,自然对流影响可忽略 Nu 1.86(Re Pr ) ( ) l w
Φ hA(t w t )
qw
twபைடு நூலகம்
x
q Φ A h (t w t )
工学院机电工程教研室
传输原理
表面传热系数(对流换热系数)
Φ h At w t
传热学12 对流换热的基本方程和分析解PPT文档31页

41、俯仰终宇宙,不乐复何如。 42、夏日长抱饥,寒夜无被眠。 43、不戚戚于贫贱,不汲汲于富贵。 44、欲言无予和,挥杯劝孤影。 45、盛年不重来,一日难再晨。及时 当勉励 ,岁月 不待人 。
Байду номын сангаас
61、奢侈是舒适的,否则就不是奢侈 。——CocoCha nel 62、少而好学,如日出之阳;壮而好学 ,如日 中之光 ;志而 好学, 如炳烛 之光。 ——刘 向 63、三军可夺帅也,匹夫不可夺志也。 ——孔 丘 64、人生就是学校。在那里,与其说好 的教师 是幸福 ,不如 说好的 教师是 不幸。 ——海 贝尔 65、接受挑战,就可以享受胜利的喜悦 。——杰纳勒 尔·乔治·S·巴顿
谢谢!
对流换热公式汇总与分析精品

对流换热公式汇总与分析【摘要】流体与固体壁直接接触时所发生的热量传递过程,称为对流换热,它已不是基本传热方式。
本文尝试对对流换热进行简单分类并对无相变对流换热公式简单汇总与分析。
【关键词】对流换热类型公式适用范围对流换热的基本计算形式一一牛顿冷却公式:q=h(t w-t f) (W/m2)或Am2上热流量门二h(t w -t f) (W)上式中表面传热系数h最为关键,表面传热系数是众多因素的函数,即h = f(u,t w,t f, ■ ,C p,匚:,fl)综上所述,由于影响对流换热的因素很多,因此对流换热的分析与计算将分类进行,本文所涉及的典型换热类型如表 1所示。
表1典型换热类型1.1内部流动1.1.1圆管内受迫对流换热(1)层流换热公式西德和塔特提出的常壁温层流换热关联式为Nu =1.86Re73 Pr;/3(g)1/3( -)0.14f f f Iw或写成NU f =1.86(Pe f d)1/3(>)0.14f I (J.w式中引用了几何参数准则d,以考虑进口段的影响。
[1适用范围:0.48 ::: Pr <16700,0.0044 ::(」厂:9.75。
—w定性温度取全管长流体的平均温度,定性尺寸为管内径d。
如果管子较长,以致[(Re 卩芒)1/3(土)0.14]乞 2lw则NU f可作为常数处理,采用下式计算表面传热系数。
常物性流体在热充分发展段的 Nu是NU f =4.36(q=co nsl)NU f =3.66(t w =c onst)(2)过渡流换热公式对于气体,0.6 ::: Pr f :: 1.5, 0.5 ::匚::1.5,2300 :: Re f :: 104。
0.8 0.4 d、2/3 Tf、0.45NU f =0.0214(Re f -100)Pr f [1 (一)]()l T wPr对于液体,1.5 :: Pr f ::: 500,0.05 —:: 20,2300 :: Re f :: 104。
对流传热的基本概念及传热方程讲解

23
13). 热焓的变化: x y z [( ρH )t+ t– ( ρH )t]
y ·z ·t [ qx–q x+ x ] + z ·x ·t [ qy–q y+ y ] + x ·y ·t [ qz–q z+ z ] + y ·z ·t [( ρVxH )x–( ρVxH )x+ x] + z ·x ·t [( ρVyH )y–( ρVyH )y+ y] + x ·y ·t [( ρVzH )z–( ρVzH )z+ z] = x y z [( ρH )t+ t– ( ρH )t]
q导
T y
|y0
18
而 q导 应该等于(9-2)式中的 q,即:
q导Ty|y0h(TTs)
从而得到(9-3)公式:
hTy|y0 (TTs)
19
9.2 、热量传输方程 -傅立叶-克希荷夫导热微分方程
本节将用微元体法导出含有对流条件下的流体中的 热量传出方程。 做下列假设: 1) 没有内热源(如化学反应热效应)产生 2) 流体流速不高,由粘性引起的耗散热可忽
热扩散系数; 2 T
x 2
项可忽略。
34
说明: ▪ 上式(9-9)中,考虑了 Vx和Vy对流传热的影响; ▪ 方程右端为扩散项,对于沿平板流动流体与板间的对
流传热,以垂直平板方向传热为主,在靠近平板处 (V≈0),以导热为主; ▪ 在 x方向上,由于对流,温度分布近于均匀әT/әx=0 , 所以在(9-9)式中忽略了ә2T/әx2 项。
此式称为傅立叶-克希荷夫导热微方程 适用:一切传导、对流的稳定和不稳定传热
对流换热部分资料

(2) 特点:边界层厚度δ是比壁面尺度L 小一个数量 级以上的小量。 δ << L
如:20℃空气在平板上以16m/s 的速度流动, 在1m处边界层的厚度约为5mm。
5
边4
界
层3
0.5
厚2
2
度1
8 16
0
0 10 20 30 40 50 60 70 80 90 100 110
空气沿平板流动时边界层厚度变化的情况
华北电力大学
梁秀俊
高等传热学
分析:求解该题的思路是首先建立坐标,写出对流传 热微分方程组,然后根据该问题涉及的流动与传热的 特点,将方程组中的各方程进行简化求解。 ① 库埃特流是稳态层流,因此其微分方程组中各非
稳态项均为零; ② 在图中所建立坐标情况下,流体只在x方向有流速
u,在y方向流速υ为0; ③ 任何特性沿x方向不变; ④ 忽略体积力。
高等传热学
为便于分析,推导时作下列假设: • 流动是二维的。 • 流体为不可压缩的牛顿型流体。 • 流体物性为常数、无内热源。 • 粘性耗散产生的耗散热可以忽略不计。
华北电力大学
梁秀俊
高等传热学
2. 运动流体能量微分方程
导热引起净热量 +热对流引起的净热量 =微元体内能的增量
华北电力大学
梁秀俊
高等传热学
华北电力大学
梁秀俊
高等传热学
2u 0 y 2
2t y 2
0
y 0: u 0, t tw1
y b: u U , t tw2
u yU, b
t
tw1
y b
tw2
tw1
华北电力大学
梁秀俊
高等传热学
练习:推导三维常物性不可压缩流动能量方程。
对流换热微分方程

(二)、描述对流换热过程的相似准数
1、动力相似准数
运用相似理论,根据 连续微分方程: 运动微分方程:
div( w) 0
Dw g grad( p) 2 w D
可以得到如下准数
1)、均时性准数 2)、弗鲁德准数
w Ho l gl Fr w2
3)、欧拉准数
即:
div(w) 0
(四)、流体的运动微分方程
[不可压缩流体的纳维尔——斯托克斯(Navier-Stokes)方程]
Dwx 1 p 2 wx 2 wx 2 wx Fx ( 2 ) 2 2 D x x y z Dwy 1 p wy wy wy Fy ( 2 ) 2 2 D y x y z
3、对流换热系数α的分析
物理意义 因为: 所以:
Q Ft
Q Ft
物理意义:表示对流换热能力大小的参数。 在数值上等于单位表面积,单位时间内、流体 与固体表面温差相差1℃时对流换热所传递的热量。 单位:W/(m 2 ℃)
影响因素:
f (, l1, l2 , l3 , tw , t f , w, , c p , , )
系数C与n则取决于乘机(GrPr)b,参 见有关表2-6。
2、 有限空间的自然对流换热准数方程
指换热空间相对换热表面很小,流体的自然对流受到空间限制 有限空间的自然对流换热可按导热方式进行 以两个平板间的导热为例: 导热方程: 对流换热: 所以:
2)、流体流动的状态的影响
3)、流体的物理性质的影响 影响流动速度、状态的物性参数等,都会影响对流换热。 如: 流体的密度ρ(kg/m3)、 动力粘度μ(kg/m.s)或运动粘度υ(=μ/ρ), 比热容cp(kJ/kg· ℃)、 导热系数λ(W/m·℃) 导温系数a=λ/(cpρ)(m2/s)。 4)相变的影响 流体的相变:凝结——凝结换热 沸腾——沸腾换热
对流换热知识点总结

对流换热知识点总结导言对流换热是热传递的一种方式。
在许多实际问题中,流体和固体之间都会发生对流换热现象。
对流换热是指热能通过流体传输到物体表面上,然后再通过固体的传热机制传递到物体内部。
对流换热的基本原理是通过流体的流动将热能传送到物体之间,并在传热过程中通过流体对物体表面的冷却来达到等温条件。
本文将会围绕对流换热知识点进行总结,着重讨论对流换热的基本原理、传热系数计算、传热器设计、流动形式以及一些应用等方面。
一、对流换热的基本原理对流换热的基本原理是通过流体的流动将热能传送到物体之间,并在传热过程中通过流体对物体表面的冷却来达到等温条件。
对流换热是通过流体对物体表面进行冲刷,从而带走物体表面的热量。
对流换热的基本原理可以用纽塔尔方程来描述,该方程为:Q = h*A*ΔT其中Q表示热交换量,h表示传热系数,A表示传热面积,ΔT表示传热温差。
传热系数h是对流换热的特性参数,它描述了在单位面积上对流换热所需要的热传导率。
当流体在物体表面上流动时,会形成一层相对静止的边界层,边界层中的流体速度较低,温度较高,因此会对物体表面带走较多的热量,进而提高传热系数h。
二、传热系数的计算传热系数是描述对流换热的特性参数,它有多种计算方法,其中常用的方法有理论计算和实验测定两种。
理论计算方法一般包括:经验公式法、边界层理论法、流体力学法和数值模拟法。
而实验测定则通过对流体在传热器上的温度和流速进行测定,进而得到传热系数。
对于复杂的情况,常常需要采用复杂的数学模型和计算方法来精确求解传热系数。
在一些工程问题中,传热系数的计算是非常重要的,它直接影响到传热器的设计和使用效果。
三、传热器的设计传热器是用来加热或冷却流体的设备,它包括热交换管、冷凝器、蒸发器、换热管、加热器和冷却器等。
传热器的设计是通过传热系数的计算和流体的流动特性来确定的。
在传热器的设计过程中,需要考虑传热器的结构形式、材料选用、传热系数、流体流动参数等因素。
对流换热
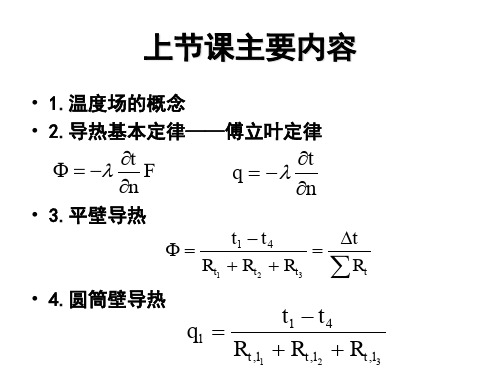
上节课主要内容
• 1.温度场的概念
• 2.导热基本定律——傅立叶定律
(2)流体的物理性质 流体的物理性质主要指流体的导热系数、比热、密度、粘度等,它们对对流换热影响较 大。 流体的导热系数大,层流层的热阻小,对流换热增强;比热和密度大,说明单位体积能 携带更多的能量,故以对流作用转移热量的能力也大;粘性大的流体,粘性剪应力大,边界 层增厚,对流换热效果降低。但是,流体的物理性质对对流换热的影响不是单一的结果而是 综合的结果。 (3)放热表面的几何尺寸、形状和位置 由于壁面的几何因素会影响边界层的形成和发展以及温度场、速度场的状况,从而影响 了对流换热。
对于垂直夹层,如 P53 图 2-14 所示。由于靠近热壁的气体向上流动和靠近冷壁的气体向 下流动,冷热两流股的流动边界层将相互结合,在一段距离内形成环流,在整个夹层内可能 有若干个这样的环流。但当夹层的厚度 δ 与高度 h 之比较大(>0.3)时,则冷热两壁的自由 流动边界层将不会互相干扰,环流不会出现,此时夹层可按无限空间自由运动换热计算。此 外如果两壁面温差和高度都很小,以致 Gr <2000,可以认为夹层内没有流动发生,则通过 夹层的热量应按纯导热计算。
无限空间流体自由运动换热时,相似准数之间的关系可表示为:
Num C(Gr Pr)mn ………………………………….(1)
准数的角码 m 表示取流体与壁面的平均温度作为定性温度 tm
tf
tw 2
。式中常数 C 及 n
对流换热原理

Nu f = 0.023 Re f
λf
Pr
0.4 f
(1.1× 105)0.8 × 5.42 0.4 = 678.96 = 0.023 ×
0.618 h= Nu f = × 678.96 = 13986.5w / m 2 ⋅ k d 0.03
(
)
φ = hA(t w − t f ) = 13986.5 × 0.03 × 3π (50 − 30 ) = 79051.6 w
Pr = 0.7 ~ 120
l d ≥ 60
加热流体时n=0.4,冷却流体时n=0.3。饱和水的热物理性质表
t ℃ 0 10 20 30 40 50 P*10-2 Pa 0.0611 0.01227 0.02338 0.04241 0.07375 0.12335 ρ kg/m3 999.9 999.7 998.2 995.7 992.2 988.1 Cp
W
W /m 2
对流换热系数
q α= ∆t W
(m K )
2
热流密度,约定取正值; 固体壁面温度tW与流体温度tf温差的绝对值; 对流换热系数,简称换热系数,单位为W/(m2·K)。
局部换热系数和平均换热系数
1.局部换热系数
qx αx = ∆t x
换热壁面上x处的局部热流密度;
x处的局部温差 该处的局部对流换热系数
流体的热物理性质: 流体的热物理性质: 热导率 比热容
λ [W (m⋅ C)]
3 密度 ρ [kg m ]
c [J (kg⋅ C)]
2 动力粘度 η [N ⋅ s m ]
2 运动粘度ν =η ρ [m s] 体胀系数 α [1 K]
牛顿冷却公式:
Q =αA(t w − t f )
对流换热基本方程

dcQ on v
x
y
z
dxdydz
2 通过导热在界面导入的净能量
x方向净导入能量是
q x dydz
(qx
qx x
dx)dydz
之差
考虑傅立叶定律
qx
T x
x方向净导入能量可写为
(T)dxdydz x x
类似y,z方向净导入能量为
(T)dxdydz y y
(T)dxdydz z z
单位时间内通过界面净导入控制体的能量为
消去控制体体积xy,得到
(xu)(yv)0
三维流动,类似可以得到
(xu)(yv)(zw )0
这就是流体的连续性方程式,并且是守恒形式
(xu)(yv)(zw )0
用矢量形式表示,则为
di(vV)0 div(V)= (u)(v)(w)
x y z
局部的质量守恒表达式也可以写为
uxvywz(
u v w)=0 x y z
e U1(u2v2w2) 2
x方向流体携入控制体的净能量为
uedydz与 uedydz(u x e)dxdyd
之差 (ue) dxdydz x
类似可以得到y,z方向流体净携入的能量
(ve) dxdydz y
(we) dxdydz z
单位时间内流体通过界面净携入控制体的能量
(ue ) (ve) (w)e
对流换热是指流动的流体与固体壁面或其它界面之间 的换热:
q=h(tw-tf)
6.1 质量守恒和连续性方程(参见图6-1)
研究对象取控制体, 则有
Mcv
.
m
.
m
t
in
o ut
控制体为xy,点(x,y)处的速度为u和v。控制体内 质量为xy,上式应用在该控制体中,得到
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Q1为单位时间内通过对流传入微元体净热量; Q2为单位时间内通过导热传入微元体的净热量; Q3为单位时间内微元体内热源生成的热量; Q4为单位时间里外界对微元体作黏性功产生的摩擦热; Q5为单位时里内微元体内能的增加量。单位都是J/s。
12.2 对流换热微分方程
T y
z
T z
qv
DU Dt
T qv
对于不可压缩流体(或固体),可认为dU=cVdT,并且 cV≈cP,于是:
cP
T t
cP
x
T x
y
T y
z
T z
对流换热是流体的导热和对流共同作用 的结果,其影响因素主要有:
① 流体流动的起因 ② 流体有无相变 ③ 流体的 流动状态 ④ 流体的物理性质 ⑤ 换热表面(指固 体)的几何因素
综合以上分析,可将对流换热系数α与各
影响因素写成如下函数关系:
f (v, , cP , ,Tw,Tf , L, )
微元体获得的热能有:一 是通过微元体界面从外界以 对流和导热方式得到;二是 由微元体的内热源产生。
12.2 对流换热微分方程
对于不可压缩流体,不存在体积功,只有黏性 力作功产生摩擦热。
微元体获得的热能:一是由微元体界面从外界 以对流和导热方式得到;二是由微元体的内热 源产生。
微元体在热量传输过程的热力学第一定律为:
U
x
x
y
y
z
z
dxdydz
12.2 对流换热微分方程
由动量传输可知,对于不可压缩流体,其连续性方程
为
x y z 0
x y z
Q1
在x x方向Ux,单位时间内y对流U传y入微元体的z净热量U为z
x
T x
y
T y
z
T z
qv
cP
DT Dt
T qv
12.2 对流换热微分方程
方程中最后一项耗散热是流体黏度和剪切应变率的函
数,对一般工程问题可忽略不计。于是可变为:
cP
式中,Ψ为壁面的几何因素。
12.2 对流换热微分方程
(1) 换热微分方程
由于在贴壁处流体受到黏性的作用,没有相 对于壁面的流动,因此被称为贴壁处的无滑移 边界条件。将傅里叶定律应用于贴壁流体层, 与牛顿冷却公式联系,得换热微分方程:
T
T
T y y0
式中,
y
为贴壁处流体的法向温度变化率,℃/m;
Q4 dxdydz
单位时间内,微元体内能的增加量为:
Q5
U t
dxdydz
12.2 对流换热微分方程
代入原式,消去dxdydz,整理后可得:
U t
x
U x
y
U y
z
U z
x
T x
y
为计算微元体内热源产生的热量,定义单位时间、单
位体积所生成的热量为内热源强度,用qv 表示。于是 单位时间内微元体内热源生成的热量为:
Q3 qvdxdydz
外界流体对微元体所做黏性功的推导比较复杂,令单 位体积流体由于黏性力作用产生的摩擦热速率为Φ,称 为耗散热。则为单位时间内黏性功产生的热能量为:
DT Dt
T qv
如果流体的导热系数λ为常数,且流体无内热源,即
qv=0,则可进一步简化为: DT a2T Dt
T t
x
T x
y
T y
z
T z
a
2T x2
2T y 2
2T z 2
此式称为傅里叶-克希荷夫导热微分方程,适用于无内
y0
λ为流体的导热系数,W/(m·℃);△T为传热面上的平均温度
差,℃,α为对流换热系数,W/(m2·℃)。
12.2 对流换热微分方程
(2) 热量传输微分方程
推导依据是能量守恒定律,采用微元体分析法
,假定流体不可压缩,微元体只有内能发生变化 ,忽略位能、动能的变化。
对于不可压缩流体,不存 在体积功,只有黏性力作功 产生摩擦热。
在x方向,由于流体流动,单位时间内从EFGH面对流
传入和从ABCD面对流传出的热量分别为(U为每千克
流体的内能 ):
Q1,x xUdydz
Q1, x dx
Q1,x
Q1,x x
dx
在x方向,单位在x时方向间,单内位时对间内流对流传传入入微元微体的元净热体量为的净热量为:
Q1,x
Q1,xdx
Q1,x x
dx
xU
x
dxdydz
U
x
x
x
U x
dxdydz
同理,可写出y和z方向在单位时间内对流传入微元体
的净热量。因此,单位时间内对流净传入微元体的总热
量为:
Q1
x
U x
y
U y
z
U z
流体与不同温度的固体壁面接触时,因相对运
动而发生的热量传递过程称为对流换热。
对流换热与热对流的区别:
① 热对流是传热的三种基本方式之一,但 对流换热不是;
② 对流换热是导热和对流这两种基本传热 方式的综合;
③ 对流换热必然涉及流体与不同温度的固 体壁面(或液面)之间的相对运动。
12.1 对流换热概述
dxdydz
导热传入微元体的热量可按傅里叶定律计算,在λ
不为常数的情况下,单位时间内通过导热传入微元体的
净热量为:
Q2
x
T x
y
T y
z
T z
dxdydz
12.2 对流换热微分方程
第十二章 对流换热的基本 方程和分析解
第12章 对流换热的基本方程和分析解 12.1 对流换热概述 12.2 对流换热微分方程组 12.3 对流换热边界层微分方程组 12.4 对流换热边界层微分方程组的分析解 12.5 对流换热边界层积分方程近似解 12.6 小结
12.1 对流换热概述
