自由电子论1讲解
合集下载
固体物理-第三章 金属自由电子论讲解
N=I0G(EF)+ I1G’(EF)+ I2G’’(EF)+….. 其中, I0=- (-f/E) dE, I1=-(E-EF)(-f/E)dE,
3.1.量子自由电子理论
I2=(1/2!)-(E-EF)2(-f/E) dE 不难算出, I0=1(d-函数积分), I1=0 (根据d-函数的性质） 为了计算I2, 而令h=(E-EF)/kBT,于是, I2=[(kBT)2/2]-{h2/[(eh+1)(e-h+1)] }dh=(pkBT)2/6
波长)，可见k为电子的波矢, 是3 维空间矢量. r:电 子的位置矢量。
由波函数的归一化性质:vy*(r) y(r)d(r)=1, v:金属体积, 假设为立方体,边长为L，把3.1.1.3式 代入归一化式子, 得: A=L-3/2=V-1/2, 所以
y(r)= V-1/2eik•r 3.1.1.4， 此即自由电子的本征态。 由周期性边界条件, y(x,y,z)= y(x+L,y,z) = y(x,y+L,z) = y(x,y,z+L)
一状态的电子具有确定的动量ħk和能量ħ2k2/(2m)，因而 具有确定的速度,v=ħk/m,故一个k全面反映了自由电子 的一个状态，简称态。
2. k-空间
以kx, ky , kz 为坐标轴建立的 波矢空间叫k-空间。电子的 本征态可以用该空间的一点
来代表。点的坐标由3.1.1.5 式确定。
3.1.量子自由电子理论
T>0K的费米能EF 把3.1.2.2和3.1.3.1代入3.1.3.2, 分步积分, 得:
N= (-2C/3) 0 E3/2(f/E) dE 3.1.3.3 令G(E)= 2C E3/2/3, 3.1.3.3.式化简为 N= 0G(E) (-f/E) dE 3.1.3.4 (-f/E)函数具有类似d函数的特性,仅仅在EF附近kBT范 围内才有显著的值，且为E-EF偶函数. 由于(-f/E)函数 具有这些性质,把G(E)在EF附近展开为泰勒级数, 且积分 下限写成 -,不会影响积分值. 3.1.3.4化为:
3.1.量子自由电子理论
I2=(1/2!)-(E-EF)2(-f/E) dE 不难算出, I0=1(d-函数积分), I1=0 (根据d-函数的性质） 为了计算I2, 而令h=(E-EF)/kBT,于是, I2=[(kBT)2/2]-{h2/[(eh+1)(e-h+1)] }dh=(pkBT)2/6
波长)，可见k为电子的波矢, 是3 维空间矢量. r:电 子的位置矢量。
由波函数的归一化性质:vy*(r) y(r)d(r)=1, v:金属体积, 假设为立方体,边长为L，把3.1.1.3式 代入归一化式子, 得: A=L-3/2=V-1/2, 所以
y(r)= V-1/2eik•r 3.1.1.4， 此即自由电子的本征态。 由周期性边界条件, y(x,y,z)= y(x+L,y,z) = y(x,y+L,z) = y(x,y,z+L)
一状态的电子具有确定的动量ħk和能量ħ2k2/(2m)，因而 具有确定的速度,v=ħk/m,故一个k全面反映了自由电子 的一个状态，简称态。
2. k-空间
以kx, ky , kz 为坐标轴建立的 波矢空间叫k-空间。电子的 本征态可以用该空间的一点
来代表。点的坐标由3.1.1.5 式确定。
3.1.量子自由电子理论
T>0K的费米能EF 把3.1.2.2和3.1.3.1代入3.1.3.2, 分步积分, 得:
N= (-2C/3) 0 E3/2(f/E) dE 3.1.3.3 令G(E)= 2C E3/2/3, 3.1.3.3.式化简为 N= 0G(E) (-f/E) dE 3.1.3.4 (-f/E)函数具有类似d函数的特性,仅仅在EF附近kBT范 围内才有显著的值，且为E-EF偶函数. 由于(-f/E)函数 具有这些性质,把G(E)在EF附近展开为泰勒级数, 且积分 下限写成 -,不会影响积分值. 3.1.3.4化为:
清华大学固体物理：第一章 自由电子论
1 金属中自由电子的量子态
金属中的传导电子好比理想气体，相互之间没有相互作用，各自独立地在平均势场中运动，通常取
平均势场为能量零点。要使自由电子逸出体外，必须克服电子的脱出功，因此金属中自由电子的能态，
可以从在一定深度的势阱中运动的粒子能态估算，通常设势阱深度是无限的，设金属中自由电子的平均
势能为零，金属外电子的平均势能为无穷大，则金属中自由电子的薛定谔方程为：
(1) 在两次碰撞间隙，忽略给定电子和其它电子及离子的相互作用。没有外加电磁场时，电子作匀速直 线运动，在有外加电磁场时，电子受电磁力，运动遵从牛顿运动定律。忽略其它电子和离子产生的复杂 的附加场。在两次碰撞间隙，忽略电子－电子之间的相互作用称为独立电子近似；忽略电子－离子之间 的相互作用称为自由电子近似。
x21 x y22 y
0 0
d
2 3 z
dz 2
k z2 3
z
0
(1.2.4)
这样问题简化为三个一维无限深势阱中粒子的量子态。设金属体是边长为 L 的立方体，周期性边界条件
为：
x L, y, z x, y, z x, y L, z x, y, z x, y, z L x, y, z
i
0
0 1
2
2
(1.1.26)
介质的复数折射率定义为：
n~ ~r12 n i
(1.1.27)
这里 n 是通常的折射率， 是消光系数。在光学实验中，通常不直接测量 n 和 ，而是测量反射率 R 和
吸收系数。它们之间的关系为：
R
n n
12 12
2 2
(1.1.28)
低频时 1 ， ~r i r " ，因此：
H Ex
《自由电子论》课件
自由电子的散射和碰撞
自由电子在固体中的运动受到晶格 振动的影响，会发生散射和碰撞
散射和碰撞也会影响自由电子的传 输和输运性质
添加标题
添加标题
添加标题
添加标题
散射和碰撞会导致自由电子的能级 发生变化，影响其分布
散射和碰撞是自由电子论中重要的 物理过程，对理解固体中的电子行 为具有重要意义
Part Four
金属导电的应用： 金属导电广泛应 用于电力传输、 电子设备等领域
自由电子的应用前景
半导体材料：自由 电子在半导体材料 中的运动和相互作 用，是半导体器件 工作的基础。
超导材料：自由电 子在超导材料中的 运动和相互作用， 是超导现象的基础。
磁性材料：自由电 子在磁性材料中的 运动和相互作用， 是磁性现象的基础 。
子云
自由电子的浓度和能量分布
自由电子的浓度：在金属中，自由电子的浓度与温度和压力有关，温度越高，浓度越大。 自由电子的能量分布：自由电子的能量分布遵循费米-狄拉克分布，能量越高，电子数越少。 自由电子的能级：自由电子的能级由电子的波长和能量决定，能级越高，电子的波长越短。 自由电子的散射：自由电子在金属中会发生散射，散射会导致电子的能级和浓度发生变化。
自由电子在电磁场 中的行为
自由电子在电场中的行为
自由电子在电场中受到电场力的作用，产生加速度，从而改变运动方向和 速度。
自由电子在电场中运动时，会与电磁波相互作用，产生能量交换和散射等 现象。
自由电子在电场中可以表现出波动性和粒子性，其行为与经典粒子不同， 需要用量子力学描述。
自由电子在电场中的行为与材料性质、温度、电磁波频率等因素有关，可 以用于研究物质的光电性质和电子输运等问题。
Part Three
自由电子论
ne2 1 0 ' i " m 1 i 1 i
0
ne2
m
其中 0 是直流电导率。以上推导见阎守胜书 p22
'
1
0 2
2
,
"
0 1 2
2
,
实数部分体现了与电压同位相的电流，也就是产生焦耳热
的那个电流，而虚部则体现的是与电压有 2 位相差的电流， 也就是感应电流。
—— Richardson－Dushman公式
其中
A
mekB2
2 2 3
W V0 EF0
在上面的推导中，用到两个积分公式：
exp
mv
2 y
2kBT
dvy
exp
mvz2 2kBT
dvz
2 kBT
i t
H
0
i
E t
故相对介电常数为：r
0
1
i
0
将上面求出的交流电导率代入该式，有：
r r ' ir " 1 0
0 1 2 2
i
0
0 1 2 2
示为： Ey E0 exp i qx t
运动方程的稳态解为：
e 1 v y m 1 it E y
电流密度 jy n e vy
ne2 1 0 ' i " m 1 i 1 i
自由电子论1课件
固体物理章节安排可能有多种方式，它体现了作者的认识和意图，我 们在学习具体内容的过程中，也要注意从整体上把握好各部分内容之间的 链接，他们之间的相互关系等。
4.2 量子自由电子论（Sommerfeld） ：
一. 金属中自由电子的运动状态 二. 能态密度 三. 基态能量 四. T>0K 时电子的分布和能量
0.983 1.833 15%
Cu：fcc a 3.61
金属中 r 1.28
离子实占体积的 75%
数据取自Kittel书
哪里有电子的自由?! 所以当时是大胆假设
电磁学中曾给出按Drude自由电子模型导出了电导率表达 式，解释了欧姆定律：
ne2 l
2mv
这里， l 是平均自由程，即两次碰撞之间的平均行程，
说明：
★ Blakemore: Solid State Physics (1985) 一书在晶体结构、晶格振 动之后，以金属中的电子为第3章标题，统一平等的论述了：金属的特征； 经典自由电子论；量子自由电子论；固体的能带；电子运动动力学；超导 等6节。突出了自由电子论在解释金属性质上的历史作用和现实意义，把能 带论和它的关系讲的比较清晰，有利于理解。
既然Drude 模型在定性方面是正确的，那么问题的来源就是 不能把电子气看作是经典粒子，不应服从 Maxwell-Boltzman 经 典统计规律，而应该服从量子统计规律。1927年，Sommerfeld 应用量子力学重新建立了自由电子论，正确地解释了金属的大多 数性质，使自由电子论成为解释金属物理性质的一个方便而直观 的模型。虽然以后能带论以更加严格的数学处理得到了更加完美 的理论结果，但在很多情形下，我们仍然乐于方便地使用自由电 子论来讨论金属问题。
这个无法调和的矛盾在量子力学诞生后才得以正确解决。服 从量子规律的自由电子即可以同时和谐的解释上述性质。
4.2 量子自由电子论（Sommerfeld） ：
一. 金属中自由电子的运动状态 二. 能态密度 三. 基态能量 四. T>0K 时电子的分布和能量
0.983 1.833 15%
Cu：fcc a 3.61
金属中 r 1.28
离子实占体积的 75%
数据取自Kittel书
哪里有电子的自由?! 所以当时是大胆假设
电磁学中曾给出按Drude自由电子模型导出了电导率表达 式，解释了欧姆定律：
ne2 l
2mv
这里， l 是平均自由程，即两次碰撞之间的平均行程，
说明：
★ Blakemore: Solid State Physics (1985) 一书在晶体结构、晶格振 动之后，以金属中的电子为第3章标题，统一平等的论述了：金属的特征； 经典自由电子论；量子自由电子论；固体的能带；电子运动动力学；超导 等6节。突出了自由电子论在解释金属性质上的历史作用和现实意义，把能 带论和它的关系讲的比较清晰，有利于理解。
既然Drude 模型在定性方面是正确的，那么问题的来源就是 不能把电子气看作是经典粒子，不应服从 Maxwell-Boltzman 经 典统计规律，而应该服从量子统计规律。1927年，Sommerfeld 应用量子力学重新建立了自由电子论，正确地解释了金属的大多 数性质，使自由电子论成为解释金属物理性质的一个方便而直观 的模型。虽然以后能带论以更加严格的数学处理得到了更加完美 的理论结果，但在很多情形下，我们仍然乐于方便地使用自由电 子论来讨论金属问题。
这个无法调和的矛盾在量子力学诞生后才得以正确解决。服 从量子规律的自由电子即可以同时和谐的解释上述性质。
第五章 金属自由电子论
∞ 0
N = ∫ f ( E ) N ( E ) dE
T＝0
0 EF
∫
0
3 2 0 N ( E ) dE = ∫ CE dE = C ( EF ) 2 3 0 1 2
3 2
0 EF
V ( 2m ) = 3π 2 3
2
3 2
(E )
0 F
2 3
2 2N 2 0 2 ∴ EF = 3π = (3π n ) 3 2m V 2m
3 4 3 V 4 ( 2m ) 2 Z ( E ) = 2 ρ (k ) π k = 2 3 π E 3 3 8π 3
3 2
3 V ( 2m ) 2 = E 2 3 3π 3 2
定义：能态密度
1 1 dZ V ( 2m ) N (E) = = E 2 = CE 2 dE 2π 2 3
2. Pauli顺磁 这里只考虑T →0的极端情况。
E
当B=0时，由于电子 自旋方向相反的两种 取向的几率相等，所 以，整个系统不显示 磁性，即M=0。 当B ≠ 0时，自旋磁矩 在磁场中的取向能：
B=0 -B EF
0
B
N(E)/2
0
N(E)/2
B平行于B： －BB； B反平行于B： ＋ BB
导致两种自旋电子的能级图发生移动，相应的费米 能相差2 BB。因此，电子的填充情况要重新调整， 即有一部分电子从自旋磁矩反平行于B转到平行于B 的方向，最后使两边的费米能相等。
(E ) f ( E ) ≈ exp = exp k T k BT B
E exp k BT
这时，Fermi－Dirac分布过渡到经典的Boltzmann分布。 且f(E)随E的增大而迅速趋于零。这表明， E－ >几个 kBT的能态是没有电子占据的空态。
N = ∫ f ( E ) N ( E ) dE
T＝0
0 EF
∫
0
3 2 0 N ( E ) dE = ∫ CE dE = C ( EF ) 2 3 0 1 2
3 2
0 EF
V ( 2m ) = 3π 2 3
2
3 2
(E )
0 F
2 3
2 2N 2 0 2 ∴ EF = 3π = (3π n ) 3 2m V 2m
3 4 3 V 4 ( 2m ) 2 Z ( E ) = 2 ρ (k ) π k = 2 3 π E 3 3 8π 3
3 2
3 V ( 2m ) 2 = E 2 3 3π 3 2
定义：能态密度
1 1 dZ V ( 2m ) N (E) = = E 2 = CE 2 dE 2π 2 3
2. Pauli顺磁 这里只考虑T →0的极端情况。
E
当B=0时，由于电子 自旋方向相反的两种 取向的几率相等，所 以，整个系统不显示 磁性，即M=0。 当B ≠ 0时，自旋磁矩 在磁场中的取向能：
B=0 -B EF
0
B
N(E)/2
0
N(E)/2
B平行于B： －BB； B反平行于B： ＋ BB
导致两种自旋电子的能级图发生移动，相应的费米 能相差2 BB。因此，电子的填充情况要重新调整， 即有一部分电子从自旋磁矩反平行于B转到平行于B 的方向，最后使两边的费米能相等。
(E ) f ( E ) ≈ exp = exp k T k BT B
E exp k BT
这时，Fermi－Dirac分布过渡到经典的Boltzmann分布。 且f(E)随E的增大而迅速趋于零。这表明， E－ >几个 kBT的能态是没有电子占据的空态。
经典自由电子论
2 m
2 T eΒιβλιοθήκη 2 3k Bne 2 2m
3.1.3 Drude模型的局限
Drude模型最成功之处在于解释了维德曼-弗兰茨定律。 与很多更精致、更复杂的理论得出的值相差不多。 但后来固体物理证明，Drude模型关于维德曼-弗兰茨 定律的证明是建立在两个大错误的互相抵消上，即室 温下的电子比热容高估了100倍，而电子的平均速度 低估了100倍。 电子热容问题：比热和温度无关，结果过大（100倍） 电导率与温度的关系T1/2（实际上T） 不能解释一、二价金属的导电能力的问题。
第2章 金属电子理论 （固体电子理论）
3.1 经典自由电子论
引言
为什么研究固体从金属开始？ 自然界最基本的物质状态之一，元素周期表中 有2/3的元素属于金属。应用广泛（电导、热 导、光泽、延展），当时对金属的了解比其它 固体多。
当时人们对金属的了解有多少？ 有良好的导电，导热性能 有较好的延展性和可塑性 维德曼-弗兰茨定律（Wiedemann-Franz law）
1 j nvx T x vx T x vx 2 d dT d 1 nvx x 2vx dT dx dx 2 d 3 dT 2 cv nvx cv kB dT 2 dx
1 1 eE vd vd a 2 2 2m
电流密度——单位时间内通过单位面积的电荷量。
ne 2 E nevd 2m 2 ne j E, 2m
电导率
其中，n为单位体积内的电子数（电子浓度），m为电子 质量，e为电子电荷量。 欧姆定律
固体物理第二章金属自由电子论
u为平均附加速度: v
v :电场附加给电子的平均速度(平均附加速度)。?? 10
考虑某一个电子，从上次碰撞发生起，有t时间的行 程。如果无外电场，其速度为v0。根据特鲁德模型德假 设，碰撞后电子出现的方向是随机的，因此v0将对总体 的电子平均速度毫无影响，即：
v0 0
但在外电场存在条件下，在上一次碰撞后立即附加
上一个速度：
eEt vt m
(E为外加电场，m为电子质量)。因此电子平均速度 只是由各电子的附加速度取平均获得。
vv0vt
eE
m
t2 t1
11
欧姆定律E=j ，其中E为外加电场强度、为电阻率、j 为电流密度。
成功用微观量解释了宏观量！
12
特鲁德模型的其他成功之处
Nat. Photon. 1, 641, 2007
EF0 ~ 几个eV
定义 Fermi 温度：
TF
E
0 F
kB
物理意义：设想将EF0转换成热振动能，相当于多高温度 下的振动能。
金属：TF： 104 ~ 105 K 36
一些金属元素费米能与费米温度的计算值
元素
Li Na K Rb Cs Cu Ag Au Be
EF0 (eV) 4.72 3.23 2.12 1.85 1.58 7.00 5.48 5.51 14.14
怎么求dN！ 接下来问题就来了！ dU EdN
Here comes the problem U EdN
16
§2.2 Sommerfeld的自由电子论
核心问题
怎么求dN！
对于理想气体貌似有某个方法 对于dV范围内的分子数为： dN=dV内分子密度×dV
对于dE范围内的：
第4章 金属自由电子论
Z
Ae
L
K为波矢，A由归一化条件决定。 3 1 2 A L V 决定这一状态的能量为：
L L
Y
X
2K 2 2 2 2 2 E kx k y kz 2m 2m
11
《固体物理学》 微电子与固体电子学院
4.2 量子自由电子论
Z
由周期性边界条件：
L
(0, y, z ) ( L, y, z ) ( x, o, z ) ( x, L, z ) ( x, y , o ) ( x, y , L)
《固体物理学》 微电子与固体电子学院
28
4.2 量子自由电子论
电子平均能量为:
K BT 3 0 2 E EF K BT 0 E 5 4 F
第一项为绝对零度时的电子平均能 量;第二项为热激发能.每个电子获 得的热能为KBT 。
《固体物理学》 微电子与固体电子学院
2
2 (r ) [ E V (r )] (r ) 0 2m
《固体物理学》 微电子与固体电子学院 9
4.2 量子自由电子论
用近自由电子近似来处理金属电子，作为零级近似，可以
把金属看成是一个边长为L的立方体，根据金属自由电子理
论的基本观点。由于电子被限定在金属中，所以，可以认 为金属中的电子是在一个无限深方势井中运动,势能函数为：
29
4.2 量子自由电子论
4.2.4 费米面
k空间中，能量为EF ，即半径为
面，kF就是费米半径。 T = 0 时，费米面内，都被电子填满。面外为空态；T ＞ 0 时， 有部分电子从 EF内 kT范围激发到EF外 kT 范围内。
3/ 2
《固体物理学》 微电子与固体电子学院
金属自由电子理论.ppt
二、金属的热容
低温下，由德拜模型得到晶格热容为：
5cT ( J mol K )
1 2 V
4
T 12 3 c Nk bT V B 5 D
4 3
3
2
1
KCl
低温下金属总的比热容为:
3 c c c T bT V V V e c
C
u
3.2 自由电子的量子理论
一、波函数与能级
薛定谔方程： 平面波形式的解 :
2 2 E 2 m
i k r ( r ) e 0
其中 r 为电子的位置矢量， k 为波矢量.
2k 2 E 2m
p k
上面讨论的是无任何限制的自由电子的性质，它的动量具有确定值，速度与波的 群速度一致，而坐标不受任何限制，电子在空间各电出现的几率相等.在金属的 自由电子论中，电子的势能为零，但它不完全自由，它的位置受金属边界的限制.
将周期性边界条件（1）式与金属电子的波动方程联立得：
e
ikxLx
1
同理有：
能级
2 2 2 n n 2 2 n y x E (2 2 z ) 2 m L L L x y z
2 k n ,n 0 , 1 , 2 , x x x L x 2 k n ,n 0 , 1 , 2 , y y y L y 2 k n n 0 , 1 , 2 , z z, z L z 2
1 E EF 1 f (E) E EF 2 0 E EF
c . k T 2 . 5 B
1 E E F 1 f (E) E EF 2 0 E E F
kBT 0
kBT 1 k T2 .5 B
低温下，由德拜模型得到晶格热容为：
5cT ( J mol K )
1 2 V
4
T 12 3 c Nk bT V B 5 D
4 3
3
2
1
KCl
低温下金属总的比热容为:
3 c c c T bT V V V e c
C
u
3.2 自由电子的量子理论
一、波函数与能级
薛定谔方程： 平面波形式的解 :
2 2 E 2 m
i k r ( r ) e 0
其中 r 为电子的位置矢量， k 为波矢量.
2k 2 E 2m
p k
上面讨论的是无任何限制的自由电子的性质，它的动量具有确定值，速度与波的 群速度一致，而坐标不受任何限制，电子在空间各电出现的几率相等.在金属的 自由电子论中，电子的势能为零，但它不完全自由，它的位置受金属边界的限制.
将周期性边界条件（1）式与金属电子的波动方程联立得：
e
ikxLx
1
同理有：
能级
2 2 2 n n 2 2 n y x E (2 2 z ) 2 m L L L x y z
2 k n ,n 0 , 1 , 2 , x x x L x 2 k n ,n 0 , 1 , 2 , y y y L y 2 k n n 0 , 1 , 2 , z z, z L z 2
1 E EF 1 f (E) E EF 2 0 E EF
c . k T 2 . 5 B
1 E E F 1 f (E) E EF 2 0 E E F
kBT 0
kBT 1 k T2 .5 B
自由电子理论g
即：一个能量为E、动量为p的粒子，同时也具有波 性，其
德布罗意波长
h h
p mv
E
h
1927 年 美 国 的 戴 维 孙 电子
和革末实验证实了实物 粒子波动性
枪
探测 器
观察到在晶体表面电子 的衍射现象与x射线的衍 射现象相类似
----电子具有波动性
加
速 电 镍极单 晶
实物粒子波动性实验
同年，小汤姆逊的电子束穿过多晶 薄膜后的衍射实验，得到了与x射线 实验极其相似的衍射图样
NE dN
dE
dN为能量从E ~ E dE能量范围内总的状态数
dN应该是能量为E和E dE的两个等能面之间的 空间中包含的（边界条件所允许的）代表电子状
的点的数目！
dN
V
2
3
4k
2dk
ky
dk
E 2k2 2m
k2
2mE 2
dk
kx
dN
V
4
2
2m 2
3/
2
E1/
2dE
k空间的等能面示意图
1.1 金属的电子理论
原子最外层活跃的价电子的运动规律
金属的电子论大致划分为三个阶段： 1. 古典自由电子理论
连续能量分布的价电子在均匀势场中的运动
2. 量子自由电子理论
不连续能量分布的价电子在均匀势场中的运动
3. 能带理论
不连续能量分布的价电子在周期性势场中的运动
1.1.1.古典自由电子理论（量子理论发展前）
应！（光的发射和吸收现象）
• 1900年，普朗克提出（谐振子）能量量子化假说
• 1905年爱因斯坦受普朗克量子假定启发，提出光由
“光量子（光子）”组成假说并成功解释了光电效 应。
自由电子论PPT课件
电子束加工
自由电子还可以用于电子束加工中， 如电子束焊接、电子束切割等，具 有高精度、高效率的特点。
半导体技术领域的应用
集成电路
在半导体技术领域中，自 由电子是集成电路制造的 基础，通过控制自由电子 的运动实现电路的功能。
太阳能电池
自由电子在太阳能电池中 起到重要作用，通过光电 效应将太阳能转化为电能。
绝缘体的特性
03
由于缺乏自由电子，绝缘体通常表现出较高的电阻其他粒子的相 互作用
自由电子与光子的相互作用
光电效应
当光子与自由电子相互作用时，光子 的能量可以被电子吸收，使电子从金 属表面逸出，产生光电流。
康普顿散射
当光子与自由电子发生碰撞时，光子 的能量会部分传递给电子，导致光子 散射，散射光子的能量低于入射光子 。
它涉及到电子在固体 材料中的运动、散射 和输运等物理过程。
研究背景与意义
随着科技的发展，人们对电子器 件的性能要求越来越高，需要深
入理解电子在材料中的行为。
自由电子论为理解电子在物质中 的行为提供了理论基础，对于发 展新型电子器件和优化现有器件
性能具有重要意义。
自由电子论在半导体技术、集成 电路、光电子器件等领域有广泛 应用，对于推动科技进步和经济
自由电子在电场的作用下， 受到电场力作用，其运动 状态满足牛顿第二定律。
波尔兹曼方程
描述了自由电子在热平衡 状态下的分布情况，是统 计物理中的重要方程。
狄拉克方程
描述了相对论条件下的自 由电子运动规律，预言了 相对论性电子的存在。
03 自由电子在固体中的行为
自由电子在金属中的行为
金属中的自由电子
发展具有重要意义。
02 自由电子理论概述
自由电子的定义与特性
自由电子还可以用于电子束加工中， 如电子束焊接、电子束切割等，具 有高精度、高效率的特点。
半导体技术领域的应用
集成电路
在半导体技术领域中，自 由电子是集成电路制造的 基础，通过控制自由电子 的运动实现电路的功能。
太阳能电池
自由电子在太阳能电池中 起到重要作用，通过光电 效应将太阳能转化为电能。
绝缘体的特性
03
由于缺乏自由电子，绝缘体通常表现出较高的电阻其他粒子的相 互作用
自由电子与光子的相互作用
光电效应
当光子与自由电子相互作用时，光子 的能量可以被电子吸收，使电子从金 属表面逸出，产生光电流。
康普顿散射
当光子与自由电子发生碰撞时，光子 的能量会部分传递给电子，导致光子 散射，散射光子的能量低于入射光子 。
它涉及到电子在固体 材料中的运动、散射 和输运等物理过程。
研究背景与意义
随着科技的发展，人们对电子器 件的性能要求越来越高，需要深
入理解电子在材料中的行为。
自由电子论为理解电子在物质中 的行为提供了理论基础，对于发 展新型电子器件和优化现有器件
性能具有重要意义。
自由电子论在半导体技术、集成 电路、光电子器件等领域有广泛 应用，对于推动科技进步和经济
自由电子在电场的作用下， 受到电场力作用，其运动 状态满足牛顿第二定律。
波尔兹曼方程
描述了自由电子在热平衡 状态下的分布情况，是统 计物理中的重要方程。
狄拉克方程
描述了相对论条件下的自 由电子运动规律，预言了 相对论性电子的存在。
03 自由电子在固体中的行为
自由电子在金属中的行为
金属中的自由电子
发展具有重要意义。
02 自由电子理论概述
自由电子的定义与特性
兰州大学固体物理第6章自由电子论ppt课件
温度的变化很小。
总电子数：
N 0 D( )
f (.T ) dε=常数
（不随温度变化）
N T 0
F N 0 F D( )
f (.T ) dε=常数
即： F N T 0
或
0 F
D( )
f T
d 0
又
cel 0 D( )
f T
d
再加上一项等于零的积分对Cel无影响 则：
cel 0 D( )
sω
dsω Kω
相应的电子气的轨道密度的一般表达式为：
D(ε)
V 4π 3
sε
dsε k ε
(由于自旋×2)
总电子数与费米能的关系：
N
V
3
2
(
2m
2
F
3
)2
在波式空间中能量为的等能面所包围
的轨道数为：
N
V
3
2
(2m
3
2) 2
下面推导此式：
k
2m
2
在波矢空间，波矢为k的球的球体体积为：
4/3πk3，每个k值占的体积为(2π/L)3，每
2 z
)
=恒常
在波矢空间是一球面方程，不同能量的等 能面是一系列同心球面。
电子在T=0k时所能填充到的最高 等能面称为费米面，我们知道自由电 子的等能面是球面，在T=0k时，费米 面把电子填充过的轨道与电子未填充 过的轨道完全分开了，即费米面内所 有的轨道都被填充，费米面外边都是 空轨道，这一点对金属是非常主要的， 因为只有费米面附近的电子才能决定 金属的动力学性质。
电子气的轨道密度为抛物线关系，费米分 布函数为：
在T=0时，轨道全占满，但当温度T上升 时，费米面附近的电子可能激发到高轨道上 去，在温度T时能受热激发的电子数(只看到 数量级)大约为：（kBT/εF）N，则在温度T 时电子气热能的增加为：
第二章 金属的自由电子论
d (1 e ) f e I0 d d (1 e ) 2 (1 e ) 2 1 此为 I0 | 0 (1) 1 奇函 此为 偶函 (1 e ) 数
I1
kx
2 ky ny L 2 kz nz L
2 nx L
( nx 0, 1, 2, )
( ny 0, 1, 2, ) ( nz 0, 1, 2, )
h
注： 由于德布洛意关系 P 所以 k 空间也称为动量空间。
，即 P k
，
上式告诉我们，沿 k 空间的每个坐标轴方向， 2 电子的相邻两个状态点之间的距离都是 L 。 2 所以三维 k 空间每个点所占的体积是 L 。
0
f dE E
f I1 ( E EF ) dE 0 E 2 f 1 I 2 ( E EF ) dE 0 2! E
f (E) e
1
E EF 1 k BT
E EF 1 令f ( ) , , e 1 k BT E 0, k BT EF时， f ( ) e , 2 (1 e ) E , E EF k BT f dE f ( ) d E 积分限发生变化
eBT ) 2
I g (E)
2
6
(k BT ) 2 g '' ( E )
3 2 g ( E ) CE 2 3 1 2 3 1 g ' (E) C E 2 C E 2 3 2 1 1 C 1 g '' ( E ) C E 2 E 2 2 2
固体物理学6自由电子论
第六章 自由电子论和电子的输运性质6-1电子气的费米能和热容量自由电子气(自由电子费米气体)：自由的、无相互作用的 、遵从泡利原理的电子气。
一 费米能量1.模型(索末菲)(1)金属中的价电子彼此之间无相互作用；(2)金属内部势场为恒定势场(价电子各自在势能等于平均势能的势场中运动)； (3)价电子速度服从费米—狄拉克分布。
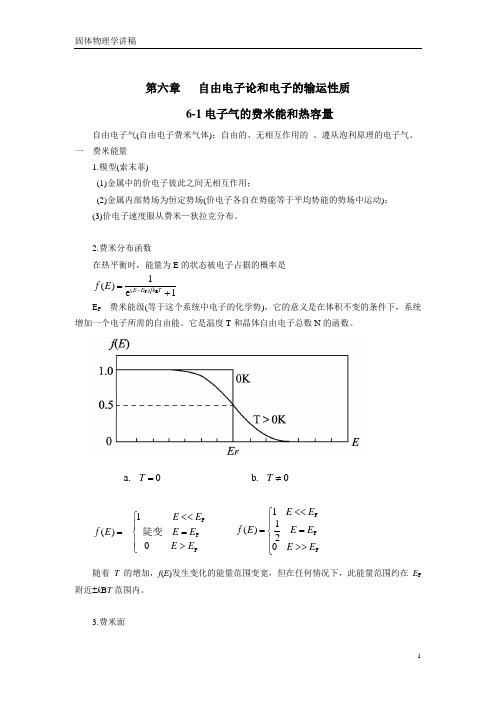
2.费米分布函数在热平衡时，能量为E 的状态被电子占据的概率是1e 1)(B F )(+=-T k E E E fE F ---费米能级(等于这个系统中电子的化学势)，它的意义是在体积不变的条件下，系统增加一个电子所需的自由能。
它是温度T 和晶体自由电子总数N的函数。
随着T 的增加，f (E )发生变化的能量范围变宽，但在任何情况下，此能量范围约在E F附近±k B T 范围内。
3.费米面0.a =T ⎪⎩⎪⎨⎧>=<<=F FF 01)(E E E E E E E f 陡变0.b ≠T ⎪⎩⎪⎨⎧>>=<<=FFF0211)(E E E E E E E fE=EF 的等能面称为费米面。
在绝对零度时，费米面以内的状态都被电子占据，球外没有电子。
T ≠0时，费米球面的半径k F 比绝对零度时费米面半径小，此时费米面以内能量离EF 约k B T 范围的能级上的电子被激发到EF 之上约k B T 范围的能级。
4.求EF 的表达式E~E+dE 间的电子状态数：E E N )d ( E~E+dE 间的电子数：E E N E f )d ()( 系统总的电子数：⎰∞=０E E N E f N )d ()(分两种情况讨论：(1)在T=0K 时，上式变成：⎰=0)d (FE E E N N ０将自由电子密度N(E)=CE 1/2代入得：()23021032d ⎰==FE FE C E CE N ０其中23222π2⎪⎭⎫⎝⎛= m V C c()23023222π232FE m V N ⎪⎭⎫ ⎝⎛=令n=N/V ，代表系统的价电子浓度()32220π32n mE F=金属中一般 n~1028m-3，电子质量m=9×10-31kg ， 自由电子气系统中每个电子的平均能量由下式计算NN E E ⎰d ＝０⎰=0023d FE E E NC053F E =由上式可以看出即使在绝对零度时电子仍有相当大的平均能量，这与经典的结果是截然不同的。
高二物理竞赛自由电子论课件
不同金属间的接触电势来自不同的金属具有不同 的费米能。
六、自由电子的输运问题（推导过程不要求）
导电率： s ne 2t F m
2
Wiegrmann－Franz定律：
T
2
Lorenz数： L
const.
许多金属的实验结果证实了Wiedemann－Franz定律 的正确性。
Hall效应： RH
对金属，由于其费米能很高，EF0>>kBT （TF>>T），所以，尽管金属中有大量的自由电子， 但对金属性质有贡献的仅是费米面附近的一小部分电 子， 而能量比费米能低得较多的电子不能吸收外界的 能量而跃迁到高能态，而仍保持原来T＝0时的状态， 对金属的性质没有贡献。
来自晶格的周期性 来自晶体的宏观对称性 来自时间反演对称性
NE
2r k 2dk 维
NE 维
E1/2 三 二
E 1/2 一
四、Fermi －Dirac统计
{ vT=0时 f E
0 F 0
F
费米球、费米面、费米能EF0 、费米半径kF 、费米速
度VF和费米温度TF等概念。
自由电子总数： N f E N E dE 0
T=0
EF0
N E dE
0
0 3 /2
C EF
七、自由电子论的成功与局限性
v成功：电子热容量； Pauli顺磁； 热电子发射与接触电势； Wiedemann－Franz定律等。
v困难：一价金属的导电率比二价、三价金属高 ； 有些金属的Hall系数大于零； 电子的平均自由程远大于原子间距； 固体材料分为导体、半导体和绝缘体； 实际金属的费米面基本上都不是球面。
E = m时
fm
当E-m>几个kBT时 f E exp
六、自由电子的输运问题（推导过程不要求）
导电率： s ne 2t F m
2
Wiegrmann－Franz定律：
T
2
Lorenz数： L
const.
许多金属的实验结果证实了Wiedemann－Franz定律 的正确性。
Hall效应： RH
对金属，由于其费米能很高，EF0>>kBT （TF>>T），所以，尽管金属中有大量的自由电子， 但对金属性质有贡献的仅是费米面附近的一小部分电 子， 而能量比费米能低得较多的电子不能吸收外界的 能量而跃迁到高能态，而仍保持原来T＝0时的状态， 对金属的性质没有贡献。
来自晶格的周期性 来自晶体的宏观对称性 来自时间反演对称性
NE
2r k 2dk 维
NE 维
E1/2 三 二
E 1/2 一
四、Fermi －Dirac统计
{ vT=0时 f E
0 F 0
F
费米球、费米面、费米能EF0 、费米半径kF 、费米速
度VF和费米温度TF等概念。
自由电子总数： N f E N E dE 0
T=0
EF0
N E dE
0
0 3 /2
C EF
七、自由电子论的成功与局限性
v成功：电子热容量； Pauli顺磁； 热电子发射与接触电势； Wiedemann－Franz定律等。
v困难：一价金属的导电率比二价、三价金属高 ； 有些金属的Hall系数大于零； 电子的平均自由程远大于原子间距； 固体材料分为导体、半导体和绝缘体； 实际金属的费米面基本上都不是球面。
E = m时
fm
当E-m>几个kBT时 f E exp
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
能带理论
声子和 Bloch电 子在外场中的行 为及相互作用
合作解释 各个专题 各种性质
例如：
价电子的运动
提醒：两种理论的实验研究，不单是理论 的验证和应用，更是理论的有力补充。例 如色散关系、费米面和态密度的测量。
C Ce Cl
e l
第五章 金属自由电子论
5.1 经典自由电子论（Drude-Lorentz) 5.2 量子自由电子论（Sommerfeld ） 5.3 金属的热容和顺磁磁化率
a0
4 0
me2
2
0.529 1010 m=0.0529nm
大多数金属自由电子的 rs / a0 在 2 和 3 之间，
碱金属自由电子的 rs / a0 在 3 到 6 之间。
例如Cu的 n 8.47 1028 m3
rs ao
2.67, rs
0.141nm
～1.4 Å
注意：rs 不是电子自身大小！是它在晶体中可以占有的
电 等 等
金属及其电导理论
自由电子论
近自由电子模型
能带理论
金属导电理论 （输运理论）
金属的电导、热导、热电及热、磁和光 学性质，在电场、磁场中的各种现象。
其它专题：
半导体理论 电介质理论 磁性物理学
观点：固体（晶体）理论的两大支柱（核心理论）：
离子实的运动 晶格动力学理论 晶体周期性结构 绝热近似下分别考虑
自由电子模型是固体理论的最早尝试，一个非常简单的模型 竟然给出了意想不到的结果，它改变了我们对固体的认识， 也指出了理论上逐步逼近真实情况的途径。它的成功告诉我 们：只有抓住相关问题物理过程的本质，才能作出最恰当的 近似，最简单的模型也能解释很复杂的现象。
1897年Thomson发现电子，1900年Drude 就大胆地将当时 已经很成功的气体分子运动论用于金属，提出用自由电子气 模型来解释金属的导电性质，他假定：金属晶体内的价电子 可以自由运动，它们在晶体内的行为宛如理想气体中的粒子， 故称作自由电子模型，以此模型可以解释欧姆定律。几年之 后 Lorentz 又假定自由电子的运动速度服从 MaxwellBoltzman分布， 由此解释了 Wiedemann-Franz 定律。
半导体
金属
室温下
10-18 ~10-6 10-5 ~10+5
106 ~108
2. 等温条件下，服从欧姆定律： J E
3. 高热导率 。在足够高的温度下热导率与电导率之比等
于一个普适常数乘以温度。
Wiedemann-Franz 定律 ：LT
或：
L
T
2
3
kB e
2
4. 载流子浓度与温度无关； 5. 在可见光谱区有几乎不变的强的光学吸收；反射率大或
自由电子论在解释金属性质上获得了相当的成功，虽然之后 发展起来的能带论，适用范围更具有普遍性，理论说明更加 严格，定量计算的结果更符合实际，但由于自由电子论的简 明直观特点，直到今天依然常被人们所利用。
金属的性质：观察和实验得到的认识 1. 高电导率σ；在一定温度以上σ反比于温度 T。
(1 m1) 绝缘体
一百余个化学元素中，在正常情况下，约有75种元素晶体处 于金属态，人们经常使用的合金更是不计其数。
金属因具有良好的电导率、热导率和延展性等特异性质，最 早获得了广泛应用和理论上的关注。
尝试对金属特性的理解（自由电子论和能带论）既是现代固 体理论的起步，也是现代固体理论的核心内容，而且对金属 性质的理解也是对非金属性质理解的基础。
说有金属光泽。
6. 有良好的延展性，可以进行轧制和锻压。
关于金属的理论必须以全面和谐的解释上述性质为准。
高纯Cu的热导率和电导 率的温度依赖性：
温度 T ↑ 电导率 σ↓
热导率
Lorentz常数的变化
（在一定温区内是常数）
从理论上来解释固体的性质并不是一件容易的事情，因为任 何宏观固体都是由很多原子（~ 1023/cm3）组成的，而每个 原子又是由原子核和众多电子组成的，所以既便今天我们已 经掌握了微观粒子的运动规律，又有了大型计算机的帮助， 但对这样一个复杂的多体问题也仍然是无法完整求解的，所 以我们只能通过各种合理的近似去接近真实的情况，成功的 固体理论都是合理近似的结果。
要比理想气体的密度高上千倍。如果将每个电子平均占据的
体积等效成球体，其等效球半径 ：
1 n
4
3
rs3
rs
3
4n
1/ 3
~ 1010 m
如此高浓度的电子，仍然可以以自由粒子运动的方式来描 述，是量子力学出现后才得到解释的。
补充知识：微观粒子尺寸习惯上常用玻尔半径（Bohr radius）做单位：
5.4 金属的电导率和热导率
5.5 金属的热电子发射和接触电势
5.6 金属的交流电导率和光学性质
5.7 Hall效应和磁阻
5.8 自由电子模型的局限性
参考：阎守胜书 第一章 黄昆 书 6.1,6.2 p275 Kittel 8版第6章
5.1 经典自由电子论（Drude-Lorentz)
金属在固体性质的研究和应用中占据着重要位置：
这些成功使自由电子模型得到承认。虽然之后发现经典模型 并不能解释金属比热、顺磁磁化率等多种金属性质，不过这 些困难并不是自由电子模型本身造成的，而是采用经典气体 近似所造成的，改用量子理论矫正自由电子的行为后，上述 困难得到了圆满解决，因此自由电子模型成为固体理论研究 一个成功尝试，是理解金属、特别是简单金属物理性质的有 力工具。
平均空间。
· Drude 模型把金属简单地看成是由自由电子组成的理想气体， 因此可以套用处理理想气体的方法来处理金属的各种特性。
· Drude Model 中的唯一的参量：电子密度（浓度）
n
NA
Zm
A
6.022 1023
Zm
A
其中 NA是Avogadro常数，Z是每个原子贡献的价电子数目， m 是金属的质量密度（kg/m3），A 是元素的原子量。 我们要注意到：对于金属，n 的典型值为1029/m3。这个值
晶体结构
晶体对幅射波 的衍射现象
晶体结合
晶体结合能 和弹性性质
晶格振动
晶体热容热导与 热膨胀，与幅射 波的相互作用。 红外光学性质。
晶体缺陷
晶体范型形变 合金强度理论 原子扩散理论 色心 晶体生长
力
、
热
、
究晶体 磁
性质的基础
、 超
导
实际晶体是有 、
缺陷的处于热 介
振动状态下的 周期结构。
声子和 Bloch电 子在外场中的行 为及相互作用
合作解释 各个专题 各种性质
例如：
价电子的运动
提醒：两种理论的实验研究，不单是理论 的验证和应用，更是理论的有力补充。例 如色散关系、费米面和态密度的测量。
C Ce Cl
e l
第五章 金属自由电子论
5.1 经典自由电子论（Drude-Lorentz) 5.2 量子自由电子论（Sommerfeld ） 5.3 金属的热容和顺磁磁化率
a0
4 0
me2
2
0.529 1010 m=0.0529nm
大多数金属自由电子的 rs / a0 在 2 和 3 之间，
碱金属自由电子的 rs / a0 在 3 到 6 之间。
例如Cu的 n 8.47 1028 m3
rs ao
2.67, rs
0.141nm
～1.4 Å
注意：rs 不是电子自身大小！是它在晶体中可以占有的
电 等 等
金属及其电导理论
自由电子论
近自由电子模型
能带理论
金属导电理论 （输运理论）
金属的电导、热导、热电及热、磁和光 学性质，在电场、磁场中的各种现象。
其它专题：
半导体理论 电介质理论 磁性物理学
观点：固体（晶体）理论的两大支柱（核心理论）：
离子实的运动 晶格动力学理论 晶体周期性结构 绝热近似下分别考虑
自由电子模型是固体理论的最早尝试，一个非常简单的模型 竟然给出了意想不到的结果，它改变了我们对固体的认识， 也指出了理论上逐步逼近真实情况的途径。它的成功告诉我 们：只有抓住相关问题物理过程的本质，才能作出最恰当的 近似，最简单的模型也能解释很复杂的现象。
1897年Thomson发现电子，1900年Drude 就大胆地将当时 已经很成功的气体分子运动论用于金属，提出用自由电子气 模型来解释金属的导电性质，他假定：金属晶体内的价电子 可以自由运动，它们在晶体内的行为宛如理想气体中的粒子， 故称作自由电子模型，以此模型可以解释欧姆定律。几年之 后 Lorentz 又假定自由电子的运动速度服从 MaxwellBoltzman分布， 由此解释了 Wiedemann-Franz 定律。
半导体
金属
室温下
10-18 ~10-6 10-5 ~10+5
106 ~108
2. 等温条件下，服从欧姆定律： J E
3. 高热导率 。在足够高的温度下热导率与电导率之比等
于一个普适常数乘以温度。
Wiedemann-Franz 定律 ：LT
或：
L
T
2
3
kB e
2
4. 载流子浓度与温度无关； 5. 在可见光谱区有几乎不变的强的光学吸收；反射率大或
自由电子论在解释金属性质上获得了相当的成功，虽然之后 发展起来的能带论，适用范围更具有普遍性，理论说明更加 严格，定量计算的结果更符合实际，但由于自由电子论的简 明直观特点，直到今天依然常被人们所利用。
金属的性质：观察和实验得到的认识 1. 高电导率σ；在一定温度以上σ反比于温度 T。
(1 m1) 绝缘体
一百余个化学元素中，在正常情况下，约有75种元素晶体处 于金属态，人们经常使用的合金更是不计其数。
金属因具有良好的电导率、热导率和延展性等特异性质，最 早获得了广泛应用和理论上的关注。
尝试对金属特性的理解（自由电子论和能带论）既是现代固 体理论的起步，也是现代固体理论的核心内容，而且对金属 性质的理解也是对非金属性质理解的基础。
说有金属光泽。
6. 有良好的延展性，可以进行轧制和锻压。
关于金属的理论必须以全面和谐的解释上述性质为准。
高纯Cu的热导率和电导 率的温度依赖性：
温度 T ↑ 电导率 σ↓
热导率
Lorentz常数的变化
（在一定温区内是常数）
从理论上来解释固体的性质并不是一件容易的事情，因为任 何宏观固体都是由很多原子（~ 1023/cm3）组成的，而每个 原子又是由原子核和众多电子组成的，所以既便今天我们已 经掌握了微观粒子的运动规律，又有了大型计算机的帮助， 但对这样一个复杂的多体问题也仍然是无法完整求解的，所 以我们只能通过各种合理的近似去接近真实的情况，成功的 固体理论都是合理近似的结果。
要比理想气体的密度高上千倍。如果将每个电子平均占据的
体积等效成球体，其等效球半径 ：
1 n
4
3
rs3
rs
3
4n
1/ 3
~ 1010 m
如此高浓度的电子，仍然可以以自由粒子运动的方式来描 述，是量子力学出现后才得到解释的。
补充知识：微观粒子尺寸习惯上常用玻尔半径（Bohr radius）做单位：
5.4 金属的电导率和热导率
5.5 金属的热电子发射和接触电势
5.6 金属的交流电导率和光学性质
5.7 Hall效应和磁阻
5.8 自由电子模型的局限性
参考：阎守胜书 第一章 黄昆 书 6.1,6.2 p275 Kittel 8版第6章
5.1 经典自由电子论（Drude-Lorentz)
金属在固体性质的研究和应用中占据着重要位置：
这些成功使自由电子模型得到承认。虽然之后发现经典模型 并不能解释金属比热、顺磁磁化率等多种金属性质，不过这 些困难并不是自由电子模型本身造成的，而是采用经典气体 近似所造成的，改用量子理论矫正自由电子的行为后，上述 困难得到了圆满解决，因此自由电子模型成为固体理论研究 一个成功尝试，是理解金属、特别是简单金属物理性质的有 力工具。
平均空间。
· Drude 模型把金属简单地看成是由自由电子组成的理想气体， 因此可以套用处理理想气体的方法来处理金属的各种特性。
· Drude Model 中的唯一的参量：电子密度（浓度）
n
NA
Zm
A
6.022 1023
Zm
A
其中 NA是Avogadro常数，Z是每个原子贡献的价电子数目， m 是金属的质量密度（kg/m3），A 是元素的原子量。 我们要注意到：对于金属，n 的典型值为1029/m3。这个值
晶体结构
晶体对幅射波 的衍射现象
晶体结合
晶体结合能 和弹性性质
晶格振动
晶体热容热导与 热膨胀，与幅射 波的相互作用。 红外光学性质。
晶体缺陷
晶体范型形变 合金强度理论 原子扩散理论 色心 晶体生长
力
、
热
、
究晶体 磁
性质的基础
、 超
导
实际晶体是有 、
缺陷的处于热 介
振动状态下的 周期结构。