固体物理学6自由电子论

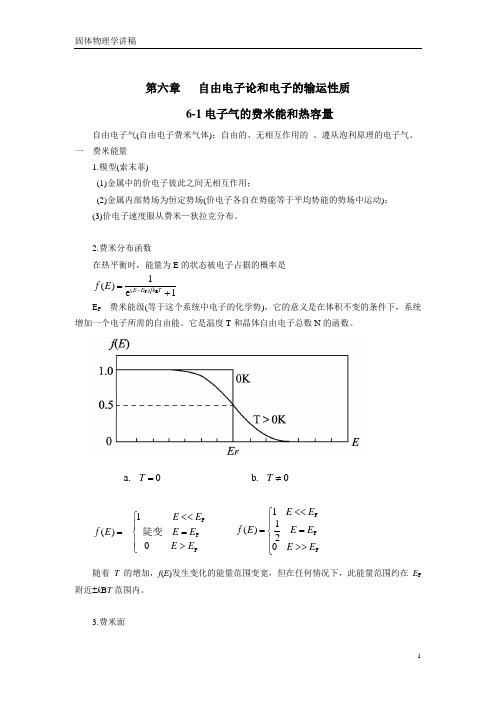
第六章 自由电子论和电子的输运性质6-1电子气的费米能和热容量自由电子气(自由电子费米气体)：自由的、无相互作用的 、遵从泡利原理的电子气。

一 费米能量1.模型(索末菲)(1)金属中的价电子彼此之间无相互作用；(2)金属内部势场为恒定势场(价电子各自在势能等于平均势能的势场中运动)； (3)价电子速度服从费米—狄拉克分布。

2.费米分布函数在热平衡时，能量为E 的状态被电子占据的概率是1e 1)(B F )(+=-T k E E E fE F ---费米能级(等于这个系统中电子的化学势)，它的意义是在体积不变的条件下，系统增加一个电子所需的自由能。

它是温度T 和晶体自由电子总数N的函数。

随着T 的增加，f (E )发生变化的能量范围变宽，但在任何情况下，此能量范围约在E F附近±k B T 范围内。

3.费米面0.a =T ⎪⎩⎪⎨⎧>=<<=F FF 01)(E E E E E E E f 陡变0.b ≠T ⎪⎩⎪⎨⎧>>=<<=FFF0211)(E E E E E E E fE=EF 的等能面称为费米面。

在绝对零度时，费米面以内的状态都被电子占据，球外没有电子。

T ≠0时，费米球面的半径k F 比绝对零度时费米面半径小，此时费米面以内能量离EF 约k B T 范围的能级上的电子被激发到EF 之上约k B T 范围的能级。

4.求EF 的表达式E~E+dE 间的电子状态数：E E N )d ( E~E+dE 间的电子数：E E N E f )d ()( 系统总的电子数：⎰∞=０E E N E f N )d ()(分两种情况讨论：(1)在T=0K 时，上式变成：⎰=0)d (FE E E N N ０将自由电子密度N(E)=CE 1/2代入得：()23021032d ⎰==FE FE C E CE N ０其中23222π2⎪⎭⎫⎝⎛= m V C c()23023222π232FE m V N ⎪⎭⎫ ⎝⎛=令n=N/V ，代表系统的价电子浓度()32220π32n mE F=金属中一般 n~1028m-3，电子质量m=9×10-31kg ， 自由电子气系统中每个电子的平均能量由下式计算NN E E ⎰d ＝０⎰=0023d FE E E NC053F E =由上式可以看出即使在绝对零度时电子仍有相当大的平均能量，这与经典的结果是截然不同的。

(1)在T ≠0K 时，)(Ef∂∂-函数的特点具有类似于δ(E -E F )函数的性质，仅在E F 附近k B T 的范围内才有显著的值，且是E -E F 的偶函数。

因此一方面，()E EfE g N d )(⎰∞∞-∂∂-=另一方面，将g(E)在E F 附近展开为泰勒级数：⋅⋅⋅+-''+-'+=2F F F F F )(21)()()(）（）（E E E g E E E g E g E g 只考虑到二次方项，略去三次方以上的高次项，可得到(分步积分得来)EEfE C E E Cf d 32)(32023023⎰∞∞∂∂-=EEfE C d 32023⎰∞∂∂-==0⎰∞=０EE f CE N )d (21,32)(23CE E g =若令则上式化简为()E Ef Eg N d )(0⎰∞∂∂-=)()()()d ()()(21)d )(()()d ()(F 2F 1F 02F F F F F E g I E g I E g I EEfE E E g EE f E E E g EE f E g N ''+'+=∂∂--''+∂∂--'+∂∂-≈⎰⎰⎰∞∞-∞∞-∞∞-T k E f B 1)1(e e 2+=∂∂-ηη2B 2)(6πT k I =２计算得定义电子气的费米温度，B 0F 0Fk E T =很显然，I 0等于１，由于为(E -E F )的偶函数，因此I 1=0。

)(E f ∂∂-1=I 令(E -E F )/k B T =η，则1e 1+=ηf E Ef E E I )d ()(212F 2⎰∞∞-∂∂--=⎰∞∞-+=ηηηηd )1(e e 2)(222B 2T k I 为偶函数，因此由于22)1(e e )1(e e +=+--ηηηη⎰∞+=０ηηηηd )1(e e )(222B 2T k I )()()(F 2F 1F 0E g I E g I E g I N ''+'+≈:=12B 2)(6πT k =02B F 2F ))((6π)(T k E g E g ''+=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+=2F B223F 8π132E T k CE当温度升高时，EF 降低。

在金属熔点以下,T <<0F T , E F 与0F E 差别不大。

二 金属中电子气的热容量1.每个电子的平均能量E~E+dE 间的电子数：E E N E f )d ()( E~E+dE 间电子的能量: E E N E Ef )d ()( 电子的总能量：⎰∞)d ()(E E N E Ef每个电子的平均能量：⎰⎰∞∞==230d )(1)d ()(E E E Cf NNEE N E Ef E利用k B T <<E F ，最后得⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-≈20F B20FF 12π1T T k E E 230F 2F B 223F )(328π132E C E T k CE N =⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+=230F 2F B223F 8π1E E T k E =⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+E Ef E N C E E f N C )d (52)(52025025∂∂-=⎰∞∞=0⎰⎰∞∞==230d )(1)d ()(EE E Cf NNEE N E Ef E )(6)(π)()d ()(F 2B F E g T k E g E E f E g I ''+≈∂∂-=⎰∞∞-21232523)(,)(,52)(E NC E g E N C E g E N C E g =''='=21F2B 25F 236)(π52E NC T k E N C E +=2.每个电子对热容量的贡献B 0F 20F B B 22π2πk T T E T k k T EC V V ⎪⎪⎭⎫⎝⎛==⎪⎪⎭⎫ ⎝⎛∂∂=在常温下晶格振动对热容量的贡献的量级为J/mol· k2而电子比热的量级为mJ/mol· k2 。

常温下电子对与热容量的贡献很小，如何解释呢?这是因为在常温下，费米球内部的电子从晶格振动获取的能量不足以使其跃迁到费米面附近或以外的空状态，只有费米面附近kBT 范围的电子才能受热激发而跃迁至较高的能级。

也就是说能量随温度发生变化的只是少数电子。

所以电子的热容量很小。

3.低温时金属热容量当温度很低时，晶格热容迅速减小，此时电子热容不可忽略 晶体的摩尔热容量可以表示为：3e bT T C C C aV V V +=+=γ3D4π512θR b = 2bT TC V+=γ6-2 接触电势差 热电子发射⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+=20F B 20F 12π5153E T k E 0F 2B 20F )(4π53E T k E +=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+≈20F B 2250F 12π51)(52E T k E NC E接触电势:两块不同的金属A 和Ｂ相接触，或用导线连接起来，两块金属就会彼此带电产生不同的电势V A 和VB ，这称为接触电势。

1.功函数电子在深度为E 0的势阱内，要使费米面上的电子逃离金属，至少使之获得 ψ=E 0－E Ｆ的能量，称为脱出功又称为功函数。

脱出功越小，电子脱离金属越容易。

2.热电子发射热电子发射：电子从外界获得热能逸出金属的现象称为热电子发射。

发射电流密度：Tk AT j B e 2ϕ-=---里查逊－杜师曼公式由上式可知，温度越高，脱出功越小，发射电流越大。

3 接触电势差设两块金属的温度都是T ，当他们接触时，每秒内从金属A 和金属B 的单位表面积所溢出的电子数分别为：若ψB>ψA ，则V A>0, VB<0，两块金属中的电子分别具有附加的静电势-eV A 和-eV Ｂ，这时两块金属发射的电子数分别为：当达到平衡时，接触电势差：)(1A B B A ϕϕ-=-eV V 上式说明两块金属的接触电势差来源于两块金属的脱出功不同，而脱出功表示真空能级T k eV T k h mI B A A )(2B 3Ae )(π4+-='ϕT k eV T k hmI B B B )(2B 3Be )(π4+-='ϕ,'B 'A I I =,B B A eV eV ＋＋Ａϕϕ=和金属费米能级之差，所以接触电势差来源于两块金属的费米能级不一样高。

两金属接触平衡后，价电子有费米能高的一方流向费米能低的一方，费米能差别大，接触电势差就大。

6-3 玻尔兹曼方程金属中的电子，在外场作用下会产生附加运动。

如在外加电场中，产生电流；在外加温度场中，产生热流。

这种由外场引起的电荷或能量从一个区域到另一个区域的迁移现象称为输运现象。

电流密度：E j σ= σ为金属的电导率。

k k k d ~+间的电子数 k V k f Cd π)2(2)(3取单位体积VC=1 k d中的电子对电流密度的贡献为：k k f k ev d π)2(2)()(3- ⎰-=k k f k ev j d π)2(2)()(3不同状态电子的分布函数不同，)(k f 是在外场下的非平衡分布函数。

如何确定非平衡状态下电子的分布函数呢？玻尔兹曼方程是用来研究非平衡状态下电子的分布函数的方程。

由于玻尔兹曼方程比较复杂，我们只限于讨论电子的等能面是球面，且在各向同性的弹性散射以及弱场的情况。

一 玻尔兹曼方程的微分积分方程漂移项=外场作用力引起的电子波矢的漂移+速度引起的电子位置的漂移漂tf ∂∂f k f r k r ∇-∇-=碰撞项：由于晶格原子的振动或杂质的存在等具体的原因，电子不断发生从'k k →态的跃迁，电子态的这种变化常称为散射只考虑相同自旋态之间的跃迁。

如果系统处于稳定状态，则0=∂∂t f 即0＝＋漂碰t ftf∂∂∂∂ a b f k f r k r -=∇+∇它是一个微分--积分方程。

由于难于求出此方程的解，因此常采用近似方法。

最常用的方法为弛豫时间近似方法。

二 弛豫时间近似有了外场和温度梯度，系统的分布才会偏离平衡，无休止的漂移；有了碰撞，就会使漂移受到遏制，被限制在一定程度而达到稳定分布。