《固体物理学答案》第一章晶体的结构
《固体物理学》房晓勇主编教材-习题解答参考01第一章 晶体的结构

(h
2 1
2 + k + l12 ) i( h22 + k22 + l2 ) 2 1 12
h1h2 + k1k2 + l1l2
12
பைடு நூலகம்
解:三个晶轴相互垂直且等于晶格常数 a,则晶胞基矢为
a1 = ai, a2 = a j, a3 = ak ,
其倒格子基矢为
b1 =
2π 2π 2π i, b2 = i, b3 = i a a a 2π ( hi + k j + lk ) a
a 2 +j a 0 − 2
a 2
a 2 +k a 0 2
0 a 2
=−
b 1=
a2 a2 a2 i+ j+ k 4 4 4
2π 2π a 2 ⎛ a 2 a2 a2 a 2 × a3 = 3 − i + j + ⎜ a Ω 2 ⎝ 4 4 4 4 2π 2π b 2= i − j + k ,b 3= i+ j−k a a
i = −( h + k )
得证 (2)由上可知,h,k,i 不是独立的, ( 001) , 133 , 110 , 323 , (100 ) , ( 010 ) , 213 . 中各 i 等于
( )( )( )
( )
i1 = −(h1 + k1 ) = −(0 + 0) = 0, i2 = 2 , i3 = 0 , i4 = 1 , i5 = 1 i6 = 1 , i7 = 3 即得
a1 ⋅ n = h1d , a2 ⋅ nh2 d , a3 ⋅ n = h3d ,
假定 h1 , h2 , h3 不是互质的数,则有公约数 p,且 p>1;设 k1 , k2 , k3 为互质的三个数,满足
黄昆版固体物理课后习题解答

《固体物理学》习题解答黄昆 原著 韩汝琦改编 (陈志远解答,仅供参考)第一章 晶体结构1.1、解:实验表明,很多元素的原子或离子都具有或接近于球形对称结构。
因此,可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。
这样,一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。
它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比,即:晶体原胞的空间利用率, VcnVx = (1)对于简立方结构:(见教材P2图1-1)a=2r , V=3r 34π,Vc=a 3,n=1 ∴52.06r 8r34a r 34x 3333=π=π=π= (2)对于体心立方:晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)r 334(r 342a r 342x 3333≈π=π⨯=π⨯=(3)对于面心立方:晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4,Vc=a 374.062)r 22(r 344a r 344x 3333≈π=π⨯=π⨯= (4)对于六角密排:a=2r 晶胞面积:S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233 晶胞的体积:V=332r 224a 23a 38a 233C S ==⨯=⨯ n=1232126112+⨯+⨯=6个 74.062r224r 346x 33≈π=π⨯= (5)对于金刚石结构,晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 334.063r 338r 348a r 348x 33333≈π=π⨯=π⨯=1.2、试证:六方密排堆积结构中633.1)38(a c 2/1≈=证明:在六角密堆积结构中,第一层硬球A 、B 、O 的中心联线形成一个边长a=2r 的正三角形,第二层硬球N 位于球ABO 所围间隙的正上方并与这三个球相切,于是: NA=NB=NO=a=2R.即图中NABO 构成一个正四面体。
黄昆版固体物理学课后答案解析答案

《固体物理学》习题解答黄昆 原著 韩汝琦改编 (陈志远解答,仅供参考)第一章 晶体结构1.1、解:实验表明,很多元素的原子或离子都具有或接近于球形对称结构。
因此,可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。
这样,一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。
它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比,即:晶体原胞的空间利用率, VcnVx = (1)对于简立方结构:(见教材P2图1-1)a=2r , V=3r 34π,Vc=a 3,n=1 ∴52.06r 8r34a r 34x 3333=π=π=π= (2)对于体心立方:晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)r 334(r 342a r 342x 3333≈π=π⨯=π⨯= (3)对于面心立方:晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4,Vc=a 374.062)r 22(r 344a r 344x 3333≈π=π⨯=π⨯= (4)对于六角密排:a=2r 晶胞面积:S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233 晶胞的体积:V=332r 224a 23a 38a 233C S ==⨯=⨯ n=1232126112+⨯+⨯=6个 74.062r224r 346x 33≈π=π⨯= (5)对于金刚石结构,晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 334.063r 338r 348a r 348x 33333≈π=π⨯=π⨯=1.2、试证:六方密排堆积结构中633.1)38(a c 2/1≈= 证明:在六角密堆积结构中,第一层硬球A 、B 、O 的中心联线形成一个边长a=2r 的正三角形,第二层硬球N 位于球ABO 所围间隙的正上方并与这三个球相切,于是: NA=NB=NO=a=2R.即图中NABO 构成一个正四面体。
固体物理答案第一章

bc
2π
b
c
2π
i
Ω
a bc a
同理
b
2π
j
b
c
2π
k
c
khkl
2π
h a
i
k b
j
l c
k
khkl
2π
h
2
k
2
l
2
a b c
d hkl
3π 16
32
a
图1.6 金刚石结构
1.7 证明:用半径不同的两种硬球构成下列稳定结构时小球半 径和大球半径之比值分别为
(1)体心立方(配位数为8):1 r / R 0.73 ; (2)简单立方(配位数为6):0.73 r / R 0.41 ; (3)正四面体结构(配位数为4):0.41 r / R 0.23 ; (4)层状结构(配位数为3):0.23 r / R 0.16 。
z
z
2 10
131
o
y
x
x
o
y
1.3 若基矢 a,b,c 构成简单正交系,试证明,晶面族(hkl)
的面间距为
dhkl
1 h 2 k 2 l 2 a b c
并说明面指数简单的晶面,其面密度比较大,容易解理。
证明:设
a,b,c
第一章 晶体结构和X射线衍射
1.1 指出立方晶格(111)面与(110)面的交线的晶向。
解: 立方晶格(111)面与(110)面的交线为AB,其等效
固体物理参考答案(前七章)

固体物理习题参考答案(部分)第一章 晶体结构1.氯化钠:复式格子,基元为Na +,Cl -金刚石:复式格子,基元为两个不等价的碳原子 氯化钠与金刚石的原胞基矢与晶胞基矢如下:原胞基矢)ˆˆ()ˆˆ()ˆˆ(213212211j i a a i k a a k j a a +=+=+= , 晶胞基矢 ka a j a a ia a ˆˆˆ321===2. 解:31A A O ':h:k;l;m==-11:211:11:111:1:-2:1 所以(1 1 2 1) 同样可得1331B B A A :(1 1 2 0); 5522A B B A :(1 1 0 0);654321A A A A A A :(0 0 0 1)3.简立方: 2r=a ,Z=1,()63434r 2r a r 3333πππ===F体心立方:()πππ833r4r 342a r 3422a 3r 4a r 4a 33333=⨯=⨯=∴===F Z ,,则面心立方:()πππ622r 4r 34434442r 4a r 4a 233ar 33=⨯=⨯=∴===F Z ,,则 六角密集:2r=a, 60sin 2c a V C = a c 362=,πππ622336234260sin 34223232=⨯⨯⨯=⨯=⎪⎭⎫ ⎝⎛a a c a r F a金刚石:()πππ163r 38r 348a r 3488Z r 8a 33333=⨯=⨯===F ,, 4. 解:'28109)31arccos(312323)ˆˆˆ()ˆˆˆ(cos )ˆˆˆ()ˆˆˆ(021*******12211=-=-=++-⋅+-=⋅=++-=+-=θθa a k j i a k j i a a a a a kj i a a kj i a a 5.解:对于(110)面:2a 2a a 2S =⋅=所包含的原子个数为2,所以面密度为22a2a22=对于(111)面:2a 2323a 22a 2S =⨯⨯= 所包含的原子个数为2,所以面密度为223a34a 232=8.证明:ABCD 是六角密堆积结构初基晶胞的菱形底面,AD=AB=a 。
固体物理学_答案

《固体物理学》习题解答黄昆 原著 韩汝琦改编第一章 晶体结构1.1、解:实验表明,很多元素的原子或离子都具有或接近于球形对称结构。
因此,可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。
这样,一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。
它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比,即:晶体原胞的空间利用率, VcnVx = (1)对于简立方结构:(见教材P2图1-1)a=2r , V=3r 34π,Vc=a 3,n=1 ∴52.06r 8r34a r 34x 3333=π=π=π= (2)对于体心立方:晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)r 334(r 342a r 342x 3333≈π=π⨯=π⨯=(3)对于面心立方:晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4,Vc=a 374.062)r 22(r 344a r 344x 3333≈π=π⨯=π⨯= (4)对于六角密排:a=2r 晶胞面积:S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233 晶胞的体积:V=332r 224a 23a 38a 233C S ==⨯=⨯ n=1232126112+⨯+⨯=6个 74.062r224r346x 33≈π=π⨯= (5)对于金刚石结构,晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 334.063r 338r 348a r 348x 33333≈π=π⨯=π⨯=1.2、试证:六方密排堆积结构中633.1)38(a c 2/1≈= 证明:在六角密堆积结构中,第一层硬球A 、B 、O 的中心联线形成一个边长a=2r 的正三角形,第二层硬球N 位于球ABO 所围间隙的正上方并与这三个球相切,于是: NA=NB=NO=a=2R.即图中NABO 构成一个正四面体。
黄昆版固体物理学课后答案解析答案

《固体物理学》习题解答黄昆 原著 韩汝琦改编 (陈志远解答,仅供参考)第一章 晶体结构1.1、解:实验表明,很多元素的原子或离子都具有或接近于球形对称结构。
因此,可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。
这样,一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。
它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比,即:晶体原胞的空间利用率, VcnVx = (1)对于简立方结构:(见教材P2图1-1)a=2r , V=3r 34π,Vc=a 3,n=1 ∴52.06r8r34a r 34x 3333=π=π=π= (2)对于体心立方:晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)r 334(r 342a r 342x 3333≈π=π⨯=π⨯= (3)对于面心立方:晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4,Vc=a 374.062)r 22(r 344a r 344x 3333≈π=π⨯=π⨯= (4)对于六角密排:a=2r 晶胞面积:S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233 晶胞的体积:V=332r 224a 23a 38a 233C S ==⨯=⨯ n=1232126112+⨯+⨯=6个 74.062r224r 346x 33≈π=π⨯= (5)对于金刚石结构,晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 334.063r 338r 348a r 348x 33333≈π=π⨯=π⨯=1.2、试证:六方密排堆积结构中633.1)38(a c 2/1≈= 证明:在六角密堆积结构中,第一层硬球A 、B 、O 的中心联线形成一个边长a=2r 的正三角形,第二层硬球N 位于球ABO 所围间隙的正上方并与这三个球相切,于是: NA=NB=NO=a=2R.即图中NABO 构成一个正四面体。
黄昆版固体物理学课后答案解析答案

黄昆版固体物理学课后答案解析答案Prepared on 24 November 2020《固体物理学》习题解答黄昆 原着 韩汝琦改编 (陈志远解答,仅供参考)第一章 晶体结构、解:实验表明,很多元素的原子或离子都具有或接近于球形对称结构。
因此,可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。
这样,一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。
它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比,即:晶体原胞的空间利用率, VcnV x =(1)对于简立方结构:(见教材P2图1-1) a=2r , V=3r 34π,Vc=a 3,n=1∴52.06r8r 34a r 34x 3333=π=π=π=(2)对于体心立方:晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)r 334(r 342a r 342x 3333≈π=π⨯=π⨯=(3)对于面心立方:晶胞面对角线BC=r 22a ,r 4a 2=⇒=n=4,Vc=a 3(4)对于六角密排:a=2r 晶胞面积:S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233晶胞的体积:V=332r 224a 23a 38a 233C S ==⨯=⨯ n=1232126112+⨯+⨯=6个(5)对于金刚石结构,晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 3、试证:六方密排堆积结构中633.1)38(ac 2/1≈=证明:在六角密堆积结构中,第一层硬球A 、B 、O 的中心联线形成一个边长a=2r 的正三角形,第二层硬球N 位于球ABO 所围间隙的正上方并与这三个球相切,于是: NA=NB=NO=a=2R.即图中NABO 构成一个正四面体。
…、证明:面心立方的倒格子是体心立方;体心立方的倒格子是面心立方。
固体物理学答案(朱建国版)

固体物理学·习题指导配合《固体物理学(朱建国等编著)》使用2019年11月20日第1章晶体结构 (1)第2章晶体的结合 (12)第3章晶格振动和晶体的热学性质 (20)第4章晶体缺陷 (33)第5章金属电子论 (37)第1章 晶体结构1.1 有许多金属即可形成体心立方结构,也可以形成面心立方结构。
从一种结构转变为另一种结构时体积变化很小.设体积的变化可以忽略,并以R f 和R b 代表面心立方和体心立方结构中最近邻原子间的距离,试问R f /R b 等于 多少?答:由题意已知,面心、体心立方结构同一棱边相邻原子的距离相等,都设为a : 对于面心立方,处于 面心的原子与顶角原子的距离为:R f =22a 对于体心立方,处于体心的原子与顶角原子的距离为:Rb =32a 那么,Rf Rb =23aa=631.2 晶面指数为(123)的晶面ABC 是离原点O 最近的晶面,OA 、OB 和OC 分别与基失a 1,a 2和a 3重合,除O 点外,OA ,OB 和OC 上是否有格点?若ABC 面的指数为(234),情况又如何?答:晶面族(123)截a 1,a 2,a 3分别为1,2,3等份,ABC 面是离原点O 最近的晶面,OA 的长度等于a 1的长度,OB 的长度等于a 2长度的1/2,OC 的长度等于a 3长度的1/3,所以只有A 点是格点。
若ABC 面的指数为(234)的晶面族,则A 、B 和C 都不是格点。
1.3 二维布拉维点阵只有5种,试列举并画图表示之。
答:二维布拉维点阵只有五种类型,两晶轴b a 、,夹角ϕ,如下表所示。
序号 晶系 基矢长度与夹角关系 布拉维晶胞类型 所属点群 1 斜方 任意2,πϕ≠b a 、简单斜方(图中1所示) 1,2 2 正方 2,πϕ==b a简单正方(图中2所示) 4,4mm 3 六角 32,πϕ==b a简单六角(图中3所示) 3,3m ,6,6mm 4长方2,πϕ=≠b a简单长方(图中4所示) 有心长方(图中5所示)1mm ,2mm1 简单斜方2 简单正方3 简单六角4 简单长方5 有心长方二维布拉维点阵1.4 在六方晶系中,晶面常用4个指数(hkil )来表示,如图所示,前3个指数表示晶面族中最靠近原点的晶面在互成120°的共平面轴a 1,a 2,a 3上的截距a 1/h ,a 2/k ,a 3/i ,第四个指数表示该晶面的六重轴c 上的截距c/l.证明:i=-(h+k ) 并将下列用(hkl )表示的晶面改用(hkil )表示:(001)(133)(110)(323)(100)(010)(213)答:证明设晶面族(hkil )的晶面间距为d ,晶面法线方向的单位矢量为n °。
黄昆版固体物理学课后答案解析答案 (3)

《固体物理学》习题解答黄昆 原着 韩汝琦改编 (陈志远解答,仅供参考)第一章 晶体结构、解:实验表明,很多元素的原子或离子都具有或接近于球形对称结构。
因此,可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。
这样,一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。
它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比,即:晶体原胞的空间利用率, VcnVx = (1)对于简立方结构:(见教材P2图1-1) a=2r , V=3r 34π,Vc=a 3,n=1∴52.06r8r34a r 34x 3333=π=π=π= (2)对于体心立方:晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)r 334(r 342a r 342x 3333≈π=π⨯=π⨯= (3)对于面心立方:晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4,Vc=a 3(4)对于六角密排:a=2r 晶胞面积:S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233 晶胞的体积:V=332r 224a 23a 38a 233C S ==⨯=⨯n=1232126112+⨯+⨯=6个(5)对于金刚石结构,晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 3、试证:六方密排堆积结构中633.1)38(ac 2/1≈=证明:在六角密堆积结构中,第一层硬球A 、B 、O 的中心联线形成一个边长a=2r 的正三角形,第二层硬球N 位于球ABO 所围间隙的正上方并与这三个球相切,于是:NA=NB=NO=a=2R.即图中NABO 构成一个正四面体。
…、证明:面心立方的倒格子是体心立方;体心立方的倒格子是面心立方。
证明:(1)面心立方的正格子基矢(固体物理学原胞基矢):123()2()2()2a a j k a a i k a a i j ⎧=+⎪⎪⎪=+⎨⎪⎪=+⎪⎩r r r r r rr r r由倒格子基矢的定义:1232()b a a π=⨯Ωr r r31230,,22(),0,224,,022a a a a a a a a a a Ω=⋅⨯==r r rQ ,223,,,0,()224,,022i j ka a a a a i j k a a ⨯==-++r rr r r r r r 同理可得:232()2()b i j k ab i j k aππ=-+=+-r rr r r r r r 即面心立方的倒格子基矢与体心立方的正格基矢相同。
《固体物理学》房晓勇主编教材-思考题解答参考01第一章 晶体的结构

第一章 晶体的结构习题
变化很小。设体积的变化可以忽略,并以 R f 和 Rb 代表面心立方和体心立方结构中最近邻原子间的距离, 试问 R f / Rd 等于多少? 解答:在面心立方晶胞结构的空间面对角线为 4 R f ,晶胞的边长 a f = 位体积中的原子数为 n f =
4R f 2
;一个晶胞包含 4 个原子,单
1.11 面心立方和体心立方晶格中原子线密度最大的是哪个方向? 解答:参考王矜奉 1.2.11 面间距最大的晶面上的格点 最密, 格点最密的线一定分布在 格点最密的面上。 根据《固体物理学》习题 1.12,面心立方晶格中格点面密 度最大的面是面指数为(111) 的晶面, 所以面心立方晶格中原 子线密度最大的方向是晶面 (111)内如图所示,最小的晶 列周期为 2a / 2 . 体心立方晶格中,面密度最大的面是面指数为(110)的晶面,所以面心立方晶格中原子线密度最大的 方向是晶面(110)内如图所示,最小的晶列周期为 3a / 2 . 1.12 二维布喇菲点阵只有五种,试列举并画图表示之。 解答:参考基泰尔 P6 有斜方晶格、正方晶格、长方晶格、六角晶格和有心长方晶格五种。
4
第一章 晶体的结构习题
解答:王矜奉 1.1.8 正格子与倒格子互为倒格子,正格子晶面 ( h 1 , h2 , h3 ) 与倒格式 K h = h1 b1 + h2 b 2 + h3 b3 垂直,则倒格晶面
( l1l2l3 ) 与正格矢 Rl = l1 a1 + l2 a2 + l3 a3 正交,即晶列 [l1l2l3 ] 与倒格面 ( l1l2l3 ) 垂直。
且 a1 ≠ a2 , ϕ = π / 2.
第一章 晶体的结构习题
1.13 具有 4 度象轴而没有 4 度旋转对称轴的晶体,有没有对称中心?举例说明。 解答: 1.14 如晶体中存在两个相互交角为Л/4 的对称面,试问这两个对称面的交线是几度旋转对称轴? 解答: 1.15 面心立方元素晶体中最小的晶列周期为多大?该晶列在那些晶面内? 解答:参考王矜奉 1.1.12 周期最小的晶列一定在原子面密度最大的晶面内。若以密堆积模型,则原子密度 最的晶面就是密排面。如《固体物理学》图 1-9 所示,可知密勒指数(111)[可以 证明原胞坐标系中的面指数也为(111)]是一个密排面晶面族,最小的晶列周期为
《固体物理学答案》第一章晶体的结构

第一章、 晶体的结构习 题1. 以刚性原子球堆积模型,计算以下各结构的致密度分别为: (1)简立方,6π; (2)体心立方, ;83π (3)面心立方,;62π (4)六角密积,;62π (5)金刚石结构,;163π [解答]设想晶体是由刚性原子球堆积而成,一个晶胞中刚性原子球占据的体积与晶胞体积的比值称为结构的致密度,设 n 为一个晶胞中的刚性原子球数,r 表示刚性原子球半径,V 表示晶胞体积,则致密度ρ=Vr n 334π(1) 对简立方晶体,任一个原子有6个最近邻,若原子以刚性球堆积,如图1.2所示,中心在1,2,3,4处的原子球将依次相切,因为,,433a V r a ==面1.2 简立方晶胞 晶胞内包含1个原子,所以ρ=6)(33234ππ=aa(2)对体心立方晶体,任一个原子有8个最近邻,若原子刚性球堆积,如图1.3所示,体心位置O 的原子8个角顶位置的原子球相切,因为晶胞空间对角线的长度为,,433a V r a ==晶胞内包含2个原子,所以ρ=ππ83)(*2334334=a a图1.3 体心立方晶胞(3)对面心立方晶体,任一个原子有12个最近邻,若原子以刚性球堆积,如图 1.4所示,中心位于角顶的原子与相邻的3个面心原子球相切,因为3,42a V r a ==,1个晶胞内包含4个原子,所以ρ=62)(*4334234ππ=a a .图1.4面心立方晶胞(4)对六角密积结构,任一个原子有12个最近邻,若原子以刚性球堆积,如图1。
5所示,中心在1的原子与中心在2,3,4的原子相切,中心在5的原子与中心在6,7,8的原子相切,图 1.5 六角晶胞 图 1.6 正四面体晶胞内的原子O 与中心在1,3,4,5,7,8处的原子相切,即O 点与中心在5,7,8处的原子分布在正四面体的四个顶上,因为四面体的高h =223232c r a == 晶胞体积 V = 222360sin ca ca =, 一个晶胞内包含两个原子,所以ρ=ππ62)(*22233234=ca a .(5)对金刚石结构,任一个原子有4个最近邻,若原子以刚性球堆积,如图1.7所示,中心在空间对角线四分之一处的O 原子与中心在1,2,3,4处的原子相切,因为,83r a =晶胞体积 3a V =,图1.7金刚石结构一个晶胞内包含8个原子,所以ρ=163)83(*83334ππ=aa . 2.在立方晶胞中,画出(102),(021),(122-),和(201-)晶面。
固体物理学答案(朱建国版)

固体物理学·习题指导配合《固体物理学(朱建国等编著)》使用2020年6月21日第1章晶体结构 0第2章晶体的结合 (13)第3章晶格振动和晶体的热学性质 (22)第4章晶体缺陷 (35)第5章金属电子论 (39)第1章晶体结构有许多金属即可形成体心立方结构,也可以形成面心立方结构。
从一种结构转变为另一种结构时体积变化很小.设体积的变化可以忽略,并以R f和R b代表面心立方和体心立方结构中最近邻原子间的距离,试问R f/R b等于多少答:由题意已知,面心、体心立方结构同一棱边相邻原子的距离相等,都设为a:对于面心立方,处于面心的原子与顶角原子的距离为:R f=2a对于体心立方,处于体心的原子与顶角原子的距离为:R b=2a那么,Rf Rb晶面指数为(123)的晶面ABC是离原点O最近的晶面,OA、OB和OC分别与基失a1,a2和a3重合,除O点外,OA,OB和OC上是否有格点若ABC面的指数为(234),情况又如何答:晶面族(123)截a1,a2,a3分别为1,2,3等份,ABC面是离原点O最近的晶面,OA的长度等于a1的长度,OB的长度等于a2长度的1/2,OC的长度等于a3长度的1/3,所以只有A 点是格点。
若ABC面的指数为(234)的晶面族,则A、B和C都不是格点。
二维布拉维点阵只有5种,试列举并画图表示之。
答:二维布拉维点阵只有五种类型,两晶轴ba、,夹角ϕ,如下表所示。
4长方2,πϕ=≠ba简单长方(图中4所示)有心长方(图中5所示)1mm,2mm1 简单斜方2 简单正方3 简单六角4 简单长方5 有心长方二维布拉维点阵在六方晶系中,晶面常用4个指数(hkil)来表示,如图所示,前3个指数表示晶面族中最靠近原点的晶面在互成120°的共平面轴a1,a2,a3上的截距a1/h,a2/k,a3/i,第四个指数表示该晶面的六重轴c上的截距c/l.证明:i=-(h+k)并将下列用(hkl)表示的晶面改用(hkil)表示:(001)(133)(110)(323)(100)(010)(213)答:证明设晶面族(hkil)的晶面间距为d,晶面法线方向的单位矢量为n°。
黄昆版固体物理学课后答案解析答案

《固体物理学》习题解答黄昆 原着 韩汝琦改编 (陈志远解答,仅供参考)第一章 晶体结构、解:实验表明,很多元素的原子或离子都具有或接近于球形对称结构。
因此,可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。
这样,一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。
它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比,即:晶体原胞的空间利用率, VcnVx = (1)对于简立方结构:(见教材P2图1-1) a=2r , V=3r 34π,Vc=a 3,n=1∴52.06r8r34a r 34x 3333=π=π=π= (2)对于体心立方:晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)r 334(r 342a r 342x 3333≈π=π⨯=π⨯= (3)对于面心立方:晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4,Vc=a 3(4)对于六角密排:a=2r 晶胞面积:S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233 晶胞的体积:V=332r 224a 23a 38a 233C S ==⨯=⨯n=1232126112+⨯+⨯=6个(5)对于金刚石结构,晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 3、试证:六方密排堆积结构中633.1)38(ac 2/1≈=证明:在六角密堆积结构中,第一层硬球A 、B 、O 的中心联线形成一个边长a=2r 的正三角形,第二层硬球N 位于球ABO 所围间隙的正上方并与这三个球相切,于是: NA=NB=NO=a=2R.即图中NABO 构成一个正四面体。
…、证明:面心立方的倒格子是体心立方;体心立方的倒格子是面心立方。
证明:(1)面心立方的正格子基矢(固体物理学原胞基矢):123()2()2()2a a j k a a i k a a i j ⎧=+⎪⎪⎪=+⎨⎪⎪=+⎪⎩由倒格子基矢的定义:1232()b a a π=⨯Ω31230,,22(),0,224,,022a aa a a a a a a a Ω=⋅⨯==,223,,,0,()224,,022i j ka a a a a i j k a a ⨯==-++ 同理可得:232()2()b i j k ab i j k aππ=-+=+-即面心立方的倒格子基矢与体心立方的正格基矢相同。
黄昆版固体物理学课后答案解析答案 (1)

《固体物理学》习题解答黄昆 原着 韩汝琦改编 (陈志远解答,仅供参考)第一章 晶体结构、解:实验表明,很多元素的原子或离子都具有或接近于球形对称结构。
因此,可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。
这样,一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。
它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比,即:晶体原胞的空间利用率, VcnVx = (1)对于简立方结构:(见教材P2图1-1)a=2r , V=3r 34π,Vc=a 3,n=1 ∴52.06r8r34a r 34x 3333=π=π=π= (2)对于体心立方:晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)r 334(r 342a r 342x 3333≈π=π⨯=π⨯= (3)对于面心立方:晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4,Vc=a 3(4)对于六角密排:a=2r 晶胞面积:S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233 晶胞的体积:V=332r 224a 23a 38a 233C S ==⨯=⨯ n=1232126112+⨯+⨯=6个 (5)对于金刚石结构,晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 3、试证:六方密排堆积结构中633.1)38(a c 2/1≈= 证明:在六角密堆积结构中,第一层硬球A 、B 、O 的中心联线形成一个边长a=2r 的正三角形,第二层硬球N 位于球ABO 所围间隙的正上方并与这三个球相切,于是: NA=NB=NO=a=2R.即图中NABO 构成一个正四面体。
…、证明:面心立方的倒格子是体心立方;体心立方的倒格子是面心立方。
证明:(1)面心立方的正格子基矢(固体物理学原胞基矢):123()2()2()2a a j k a a i k a a i j ⎧=+⎪⎪⎪=+⎨⎪⎪=+⎪⎩r r r r r rr r r由倒格子基矢的定义:1232()b a a π=⨯Ωr r r31230,,22(),0,224,,022a a a a a a a a a a Ω=⋅⨯==r r rQ ,223,,,0,()224,,022i j ka a a a a i j k a a ⨯==-++r rr r r r r r同理可得:232()2()b i j k ab i j k aππ=-+=+-r rr r r r r r 即面心立方的倒格子基矢与体心立方的正格基矢相同。
黄昆固体物理习题解答
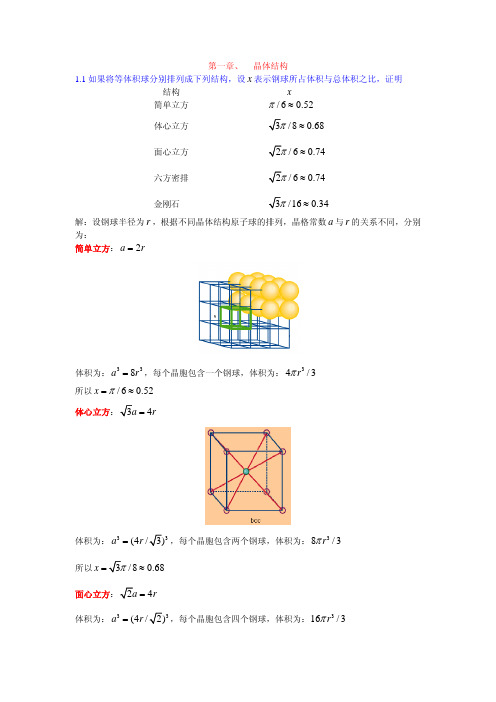
因此只要先求出倒格点 Ghkl ,求出其大小即可。
由正格子基矢 a = ai , b = bj , c = ck ,可以马上求出:
a∗ = 2π i , b ∗ = 2π j , c∗ = 2π k
a
b
c
因为倒格子基矢互相正交,因此其大小为
Ghkl =
(ha∗ )2 + (kb∗ )2 + (lc∗ )2 = 2π
(h)2 + (k )2 + ( l )2 abc
则带入前边的关系式,即得晶面族的面间距。 1.7 写出体心立方和面心立方晶格结构的金属中,最近邻和次近邻的原子数。若立方边长为
a ,写出最近邻和次近邻的原子间距。
答:体心立方晶格的最近邻原子数(配位数)为 8,最近邻原子间距等于 3 a ,次近邻原 2
=V0
∂2U ( ∂r2
)r0
=
N 2
[−
m(m +1)α r m+2
0
+
n(n +1)β r n+2
0
=
N 2
{−
1 r02
m2α [( r0m
−
n2β r0n
)
+
(
mα r0m
−
nβ r0n
)]}
=
N 2
[−
1 r02
m2α ( r0m
−
n2β r0n
)]
=
N 2
[−
1 r m+2
0
(m2α
−
n2β nβ
AB = a (i − j − k ) 2
c
B
b
C
O
a
OB ⋅ AB =| OB || AB | cosθ = a2 (−1) 4
中南大学版固体物理学习题及答案详解

第一章晶体结构1.试述晶态、非晶态、准晶、多晶和单晶的特征性质。
解:晶态固体材料中的原子有规律的周期性排列,或称为长程有序。
非晶态固体材料中的原子不是长程有序地排列,但在几个原子的范围内保持着有序性,或称为短程有序。
准晶态是介于晶态和非晶态之间的固体材料,其特点是原子有序排列,但不具有平移周期性。
另外,晶体又分为单晶体和多晶体:整块晶体内原子排列的规律完全一致的晶体称为单晶体;而多晶体则是由许多取向不同的单晶体颗粒无规则堆积而成的。
2.晶格点阵与实际晶体有何区别和联系?解:晶体点阵是一种数学抽象,其中的格点代表基元中某个原子的位置或基元质心的位置,也可以是基元中任意一个等价的点。
当晶格点阵中的格点被具体的基元代替后才形成实际的晶体结构。
晶格点阵与实际晶体结构的关系可总结为:晶格点阵+基元=实际晶体结构3.晶体结构可分为Bravais格子和复式格子吗?解:晶体结构可以分为Bravais格子和复式格子,当基元只含一个原子时,每个原子的周围情况完全相同,格点就代表该原子,这种晶体结构就称为简单格子或Bravais格子;当基元包含2个或2个以上的原子时,各基元中相应的原子组成与格点相同的网格,这些格子相互错开一定距离套构在一起,这类晶体结构叫做复式格子。
4.图1.34所示的点阵是布喇菲点阵(格子)吗?为什么?如果是,指明它属于那类布喇菲格子?如果不是,请说明这种复式格子的布喇菲格子属哪类?(a)(b)(c)(d)图 1.34(a)“面心+体心”立方;(b)“边心”立方;(c)“边心+体心”立方;(d)面心四方解:(a)“面心+体心”立方不是布喇菲格子。
从“面心+体心”立方体的任一顶角上的格点看,与它最邻近的有12个格点;从面心任一点看来,与它最邻近的也是12个格点;但是从体心那点来看,与它最邻近的有6个格点,所以顶角、面心的格点与体心的格点所处的几何环境不同,即不满足所有格点完全等价的条件,因此不是布喇菲格子,而是复式格子,此复式格子属于简立方布喇菲格子。
黄昆版固体物理学课后答案解析答案

《固体物理学》习题解答黄昆 原着 韩汝琦改编 (陈志远解答,仅供参考)第一章 晶体结构1.1、解:实验表明,很多元素的原子或离子都具有或接近于球形对称结构。
因此,可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。
这样,一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。
它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比,即:晶体原胞的空间利用率, VcnVx =(1)对于简立方结构:(见教材P2图1-1) a=2r , V=3r 34π,Vc=a 3,n=1∴52.06r8r 34a r 34x 3333=π=π=π=(2)对于体心立方:晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)r 334(r 342a r 342x 3333≈π=π⨯=π⨯=(3)对于面心立方:晶胞面对角线BC=r 22a ,r 4a 2=⇒=n=4,Vc=a 3(4)对于六角密排:a=2r 晶胞面积:S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233晶胞的体积:V=332r 224a 23a 38a 233C S ==⨯=⨯n=1232126112+⨯+⨯=6个(5)对于金刚石结构,晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8,Vc=a 31.2、试证:六方密排堆积结构中633.1)38(ac 2/1≈=证明:在六角密堆积结构中,第一层硬球A 、B 、O 的中心联线形成一个边长a=2r 的正三角形,第二层硬球N 位于球ABO 所围间隙的正上方并与这三个球相切,于是: NA=NB=NO=a=2R.即图中NABO 构成一个正四面体。
…1.3、证明:面心立方的倒格子是体心立方;体心立方的倒格子是面心立方。
证明:(1)面心立方的正格子基矢(固体物理学原胞基矢):123()2()2()2a a j k aa i k a a i j ⎧=+⎪⎪⎪=+⎨⎪⎪=+⎪⎩由倒格子基矢的定义:1232()b a a π=⨯Ω31230,,22(),0,224,,022a aa a a a a a a a Ω=⋅⨯==,223,,,0,()224,,022i j ka a a a a i j k a a ⨯==-++ 同理可得:232()2()b i j k ab i j k aππ=-+=+-即面心立方的倒格子基矢与体心立方的正格基矢相同。
固体物理答案陆栋.pdf

《固体物理学》习题解答( 仅供参考 )参加编辑学生柯宏伟(第一章),李琴(第二章),王雯(第三章),陈志心(第四章),朱燕(第五章),肖骁(第六章),秦丽丽(第七章)指导教师黄新堂华中师范大学物理科学与技术学院2003级2006 年 6 月第一章晶体结构1.氯化钠与金刚石型结构是复式格子还是布拉维格子,各自的基元为何?写出这两种结构的原胞与晶胞基矢,设晶格常数为 a。
解:氯化钠与金刚石型结构都是复式格子。
氯化钠的基元为一个 Na+和一个 Cl-组成的正负离子对。
金刚石的基元是一个面心立方上的C原子和一个体对角线上的C原子组成的C原子对。
由于 NaCl 和金刚石都由面心立方结构套构而成,所以,其元胞基矢都为:⎧⎪a1=a2( j + k)⎪⎪⎨a 2=a2( k + i)⎪⎪⎪a 3=a ( i +j)⎩ 2相应的晶胞基矢都为:⎧a =a i,⎪⎨b =a j,⎪⎩c =a k.2.六角密集结构可取四个原胞基矢a1, a 2,a 3与 a4,如图所示。
试写出O'A1A3、A1 A3 B3 B1、 A2 B2 B5 A5、 A1 A2 A3 A4 A5 A6这四个晶面所属晶面族的晶面指数(h k l m)。
解:(1).对于O'A1A3面,其在四个原胞基矢上的截矩分别为:1,1,- 1 ,1。
所以,其晶面2( )指数为。
(2).对于A1A3B3B1面,其在四个原胞基矢上的截矩分别为:1,1,-12,∞。
所以,其晶面指数为(1120)。
(3).对于A2B2B5A5面,其在四个原胞基矢上的截矩分别为:1,-1,∞,∞。
1所以,其晶面指数为 (1 100)。
(4).对于 A 1 A 2 A 3 A 4 A 5 A 6 面,其在四个原胞基矢上的截矩分别为:∞ ,∞ ,∞ ,1。
所以, 其晶面指数为 (0001) 。
3. 如将等体积的硬球堆成下列结构,求证球体可能占据的最大体积与总体积的比为:简立方: π6 ;体心立方: 83π;面心立方: 62π ;六角密集: 62π ;金刚石:3π 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章、 晶体的结构习 题1. 以刚性原子球堆积模型,计算以下各结构的致密度分别为: (1)简立方,6π; (2)体心立方, ;83π (3)面心立方,;62π (4)六角密积,;62π (5)金刚石结构,;163π [解答]设想晶体是由刚性原子球堆积而成,一个晶胞中刚性原子球占据的体积与晶胞体积的比值称为结构的致密度,设 n 为一个晶胞中的刚性原子球数,r 表示刚性原子球半径,V 表示晶胞体积,则致密度ρ=Vr n 334π(1) 对简立方晶体,任一个原子有6个最近邻,若原子以刚性球堆积,如图1.2所示,中心在1,2,3,4处的原子球将依次相切,因为,,433a V r a ==面1.2 简立方晶胞 晶胞内包含1个原子,所以ρ=6)(33234ππ=aa(2)对体心立方晶体,任一个原子有8个最近邻,若原子刚性球堆积,如图1.3所示,体心位置O 的原子8个角顶位置的原子球相切,因为晶胞空间对角线的长度为,,433a V r a ==晶胞内包含2个原子,所以ρ=ππ83)(*2334334=a a图1.3 体心立方晶胞(3)对面心立方晶体,任一个原子有12个最近邻,若原子以刚性球堆积,如图 1.4所示,中心位于角顶的原子与相邻的3个面心原子球相切,因为3,42a V r a ==,1个晶胞内包含4个原子,所以ρ=62)(*4334234ππ=a a .图1.4面心立方晶胞(4)对六角密积结构,任一个原子有12个最近邻,若原子以刚性球堆积,如图1。
5所示,中心在1的原子与中心在2,3,4的原子相切,中心在5的原子与中心在6,7,8的原子相切,图 1.5 六角晶胞 图 1.6 正四面体晶胞内的原子O 与中心在1,3,4,5,7,8处的原子相切,即O 点与中心在5,7,8处的原子分布在正四面体的四个顶上,因为四面体的高h =223232c r a == 晶胞体积 V = 222360sin ca ca =, 一个晶胞内包含两个原子,所以ρ=ππ62)(*22233234=ca a .(5)对金刚石结构,任一个原子有4个最近邻,若原子以刚性球堆积,如图1.7所示,中心在空间对角线四分之一处的O 原子与中心在1,2,3,4处的原子相切,因为,83r a =晶胞体积 3a V =,图1.7金刚石结构一个晶胞内包含8个原子,所以ρ=163)83(*83334ππ=aa . 2.在立方晶胞中,画出(102),(021),(122-),和(201-)晶面。
[解答]图1.8中虚线标出的面即是所求的晶面。
3.如图1.9所示,在六角晶系中,晶面指数常用(hkml )表示,它们代表一个晶面在基矢的截距分别为,,,321m a k a h a 在C 轴上的截距为 lc 证明:m k h -=+求出 O 5522133131,,,A B B A B B A A A A 和A 531A A 四个面的面指数。
图1.9六角晶胞对称画法[解答]设 d 是晶面族(hkml )的面间距, n 是晶面族的单位法矢量,晶面族(hklm )中最靠近原点的晶面在a c a a ,321 轴上的截距分别为 l c m a k a h a /,/,/,/321 所以有1a ·n =hd , 2a ·n =kd , 3a ·n =md .因为),(323a a a +-=所以3a ·)(32a a n +-=·n 。
由上式得到md =)(kd hd +-. 即),(k h m +-=由图可得到: 31'A A O 晶面的面指数为(11-21) 1331B B A A 面的面指数为(11-20)5522A B B A 晶面的面指数为(1-100)531A A A 晶面的面指数为(0001)4.设某一晶面族的面间距为 d , 三个基矢 321,,a a a 的末端分别落在离原点的距离为d h 1,d h d h 32,的晶面上,试用反证法证明:321,,h h h 是互质的。
[解答]设该晶面族的单位法量为 321,,a a a 由已知条件可得1a ·21,a d h n =·,2d h n =3a ·,3d h n =假定321,,h h h 不是互质数,且公约数 1≠p 即332211,,pk h pk h pk h ===321,,k k k 是互质的整数,则有1a ·21,a d pk n =·32,a d pk n =·d pk n 3=今取离原点最近的晶面上的一个格点,该格点的位置矢量为,332211a l a l a l r ++=由于 心定是整数,而且r ·11a l d n ==·22a l n +·33a l n +·n于是得到1332211=++l pk l pk l pk由上式可得pl k l k l k 1332211=++ 上式左端是整数,右端是分数,显然是不成立的。
矛盾的产生是 p 为不等于1的整数的假定。
也就是说,p 只能等于1,即321,,h h h 一定是互质数。
5.证明在立方晶体中,晶列[hkl ]与晶面(hkl )正交,并求晶面(111l k h ) 与晶面(222l k h )的夹角。
[解答]设d 是为晶面族(hkl )的面间距 ,n 为法向单位矢量,根据晶面族的定义,晶面族(hkl )将 a,b, c 分别截为l k h ,, 等份,即a•n =a cos(a,n )=hd, b•n =b cos(b,n )=kd,c•n =c cos(c,n )=ld 于是有n =a d h i +adk j +a d l k=ad(h i +k j +l k )其中,i ,j,k 分别为平行于a,b,c 三个坐标轴的单位矢量,而晶列[hkl ] 的方向矢量为R =ha i +ka j +la k =a(h i +k j +l k ) 由(1),(2)两式得n =2ad R 即n 与R 平行,因此晶列[hkl ]与晶面(hkl )正交。
对于立方晶系,晶面(111l k h ) 与晶面(222l k h ) 的夹角,就是晶列 R 1=1h a +1k b +1l c与晶列R 2=2h a +2k b +2l c的夹角,设晶面 (111l k h )与晶面 (122l k h ) 的夹角为 ϕ 由R 1∙R 2=ϕϕcos cos 222222221212121a l k h l k h R R ++++= =221221221a l l a k k a h h ++ 得})(({cos 2222222121212121211lk h l k h l l k k h h ++++++=-ϕ6.如图1.10所示,B,C 两点是面心立方晶胞上的两面心。
(1) 求 ABC 面的密勒指数;(2) 求 AC 晶列的指数,并求相应原胞坐标系中的指数。
图1.10 面心立方晶胞[解答](1) 矢量A B与矢量C B 的叉乘即是 ABC 面的法矢量A B =),2(21)(21)(c b a c b b a B O A O -+=+-+=-),(21)(21)](21[c a c b b a c B O C O C B +=+-++=-=A B ⨯).3(4)(21)2(21c b a ac a c b a C B --=+⨯-+=因为对立方晶系,晶列[hkl ]与晶面族(hkl )正交,所以ABC 面的密勒指数为(-131).(2)).2(21)()](21[c b a b a b a c A O C O C A -+-=+-++=-=可见 C A与晶列 (a+b-2c) 平行,因此 AC 晶列的晶列指数为[11-2]. 由《固体物理教程》(1•3)式可得面心立言结构晶胞基矢与原胞基矢的关系,321a a a a ++-= ,321a a a b +-= 321a a a c -+=晶列 (a+b-2c) 可化为 (a+b-2c)=-2(3212a a a -+) 由上式可知,AC 晶列在原胞坐标系中的指数为[11-2]7.试证面心立方的倒格子是体心立方;体心立方的倒格子是面心立方。
[解答]设与晶轴a,b,c 平行的单位矢量分别为i,j,k 面心立方正格子的原胞基矢可取为),(21k j aa +=).(2),(232j i aa j k aa +=+=由倒格矢公式Ω⨯=Ω⨯=Ω⨯=][2,][2,][2213132321a a b a a b a a b πππ, 可得其倒格矢为).(2),(2),(2321k j i a b k j i a b k j i a b -+=+-=++-=πππ设与晶轴a,b,c 平行的单位矢量分别为i,j,k ,体心立方正格子的原胞基矢可取为).(2),(2),(2321k j i aa k j i aa k j i aa -+=+-=++-=以上三式与面心立方的倒格基矢相比较,两者只相差一常数公因子, 这说明面心立方的倒格子是体心立方。
将体心立方正格子原胞基矢代入倒格矢公式 .][2,][2,][2213132321Ω⨯=Ω⨯=Ω⨯=a ab a a b a a b πππ 则得其倒格子基矢为).(2),(2),(2321j i ab i k a b k i a b +=+=+=πππ可见体心立方的倒格子是面心立方。
8.六角晶胞的基矢ck C j a ai b j a ai a =+-=+=,223,223求其倒格基矢。
[解答]晶胞体积为 ][c b a ⨯⋅=Ω.23)]()223([)223(2c a ck j a ai j a ai =⨯+-⋅+= 其倒格矢为k cca j a ai j a aib ac j i a c a j a ai ck a c b j i a c a ck j a ai c b a πππππππππ232)]223()223[(2][2).33(232)]223()[(2][2).33(232)]()223[(2][2222=⨯+-⨯+=Ω⨯=+-=⨯+⨯=Ω⨯=+=⨯⨯+-=Ω⨯=***9.证明以下结构晶面族的面间距:(1) 立方晶系:,][21222-++=l k h a d hkl(2) 正交晶系:21])()()[(222-++=c l b k a h d hkl(3) 六角晶系:21])()(34[2222-+++=c l ahk k h d hkl(4) 简单单斜:21])cos 2(sin 1[2222222-+-+=bk ac hl c l a h d hklββ.[解答](1)设沿立方晶系轴a,b,c 的单位矢量分别为i,j,k ,则正格子基矢为,,,ak c bj b ai a ===图1.11立方晶胞倒格子晶矢为.2,2,2k a c j a b i a a πππ===***与晶面族(hkl )正交的倒格为.***++=lc kb ha K hkl由晶面间距 hkl d 与倒格矢hkl K 的关系式得,.2222lk h a d K d hkl hklhkl ++==π(2)对于正交晶系,晶胞基矢c b a ,,相互垂直,但晶格常数.c b a ≠≠设沿晶轴c b a ,,的单位矢量分别为i,j,k 则正格子基矢为 ,,,ck c bj b ai a ===图1.12正交晶胞倒倒格子基矢为.2,2,2k c c j b b i a a πππ===***与晶面族 (hkl ) 正交的倒格为.***++=lc kb ha K hkl由晶面间距 hkl d 与倒格矢hkl K 的关系式hklhkl K d π2=得21])()()[(222-++=cl b k a h d hkl(2) 对于六角晶系,,120,90, ===≠=γβαc b a 晶面族 (hkl ) 的面间距图 1.13 六角晶胞.2222******++=++==lckb hk lckb ha K d hkl hkl πππ也即)].(2)(2)(2[41122222222*********⋅+⋅+⋅+++=c a hl c b kl b a hk c l b k a hd hklπ由图1.13可得六角晶胞的体积.23120sin sin )(222c a c a c a b a a c ===⨯⋅=Ω γ 倒格基矢的模()()().223sin 22,3423sin 22222cca ab ac c aca ac cb a b a πγπππαππ==Ω⨯====Ω⨯===*****倒格基矢的点积()()(){()()()()[]().38cos cos cos 44]}[4][4222222222222ac a c c a b a c c b c b a c a c c b b a πγβαππππ=-Ω=⋅⋅-⋅⋅Ω=⨯⨯⋅Ω=⨯⋅⨯Ω=⋅**其中利用了矢量混合的循环关系()()()B A C A C B C B A ⨯⋅=⋅⋅=⋅⋅及关系式()()().B A C C A B C B A ⋅-⋅=⨯⨯因为()b a ⨯ 矢量平行于 c 所以()()[]()()[].04,042222=⨯⋅⨯Ω=⋅=⨯⋅⨯Ω=⋅****b a ac c b b a c b c a ππ 将以上诸式代入(1)式得hkld ,3)(4222222cl a hk k h +++=- 即hkl d =212222])()(34[-+++c l ahk k h (4)单斜晶系晶胞基矢长度及晶胞基矢间的夹角分别满足c b a ≠≠ 和90==γα, 90≠β 晶胞体积 βsin )(abc a c b =⨯⋅=Ω 由a []Ω⨯=*c b π2b []Ω⨯=*ac π2 c []Ω⨯=*b a π2 得其倒格子基矢长度a ,sin 2sin 2βπβπa abc bc a ==*=*及 b bb π2==**c βπsin 2ac c =*=*倒格基矢间的点积()()c b b a a c ⨯⋅⨯Ω=⋅**224π=()()()()[]b b c a c b b a ⋅⋅-⋅⋅Ω224π=ββγαπ222sin )cos cos (cos 4abc c ab -因为)(a c ⨯矢量平行于b 所以()()[]0422=⨯⋅⨯=⋅**a c cb b a ππ()()[]b a a c c b ⨯⋅⨯Ω=⋅**224π将以上诸式代入()()()[]*********⋅+⋅+⋅+++=c a hl c b kl b a hk c l b k a h d a hkl 2224112222222π得到ββββ2222222222sin cos 2sin sin 1ac hl c l b k a h d hkl -++= =+⎪⎪⎭⎫ ⎝⎛++ac hl c l a h 2sin 122222β22b k 即 212222222cos 2sin 1-⎥⎦⎤⎢⎣⎡+⎪⎪⎭⎫ ⎝⎛-+=b k ac hl c l a h d hklββ10.求晶格常数为 a 的面心立方和体立方晶体晶面族()321h h h 的面间距 [解答]面心立方正格子的原胞基矢为a ()k j a+=21()i k aa +=22()j i aa +=23由 [][][],2,2,2213132321Ω⨯=Ω⨯=Ω⨯=a ab a a b a a b πππ可得其倒格基矢为 (),21k j i a b ++-=π(),22k j i a b +-=π(),23k j i ab -+=π倒格矢.332211b h b h b h K h ++= 根据《固体物理教程》(1。
