习题(弯曲变形) (1)

合集下载

弯曲变形例题

20
第20页/共65页
解：
解除B点约束以反力qa代替
vB
q(2a) 4 8EI
qa (2a ) 3 3EI
14qa 4 3EI
vD
vB 2
2qa (2a ) 3 48EI
8qa 4 3EI
21
第21页/共65页
例8：求图示梁 C、D两点的挠度 vC、 vD。
22
第22页/共65页
解：
可由载荷等效法求得弯矩和剪力的大小及方向
30
3)如图(d)所示，B端由于而引起的挠度为：
fD ，D
(a) A
P
I
I1=2I
C
D
B
fB2
fD
D
l 4
5 pl3 768 EI
3Pl 2 64 EI
l 4
l/4
13 pl3 768 EI
4)叠加 f B1和 fB2，可求出作为
自由端B处的挠度为：
f f f pl3 3pl3 3pl3 B B1 B2 384EI 768EI 256EI
f2 C
0
(表7.1.7)
叠加:
f
f1
f2
5q l 4 0
C
C
C
768EI
18
第18页/共65页
第七章
例6-2 试用叠加法求简支梁在图示载荷作用下跨度中
点C的挠度。
q2
q1-q2
+
q1
=
q2
C
C
C
(b)
(c)
(a)
解：图(a)分解为图(b)和图(c)之和
图(b)中点C的挠度为:
f1 C
5q2l 4 384EI

《材料力学》练习题 (弯曲变形)

《材料力学》练习题（弯曲变形）
院系：年级：专业：
姓名：学号：成绩：
1、试用积分法求如图所示梁：
（1）挠曲线方程，并绘出挠曲线的大致形状；
（2）截面A处的挠度和截面B处的转角。

（EI为已知）
2、用积分法求图所示各梁的挠曲线方程、转角方程和B截面的转角、挠度。

（设EI=常数）
3、试用积分法求图中截面A 处的挠度和转角。

4、外伸梁受力如图所示，试用积分法求A θ、B θ及D y 、C y 。

（设EI =常数）
6、试用叠加法求如图所示简支梁C截面的挠度和两端的转角。

8、如图所示梁AB 的右端由拉杆BC 支承。

已知：4kN/m q =，2m l =，3m h =，梁的截面为边长200mm b =的正方形，材料的弹性模量110GPa E =；拉杆的横截面面积2250mm A =，材料的弹性模量2200GPa E =。

试求拉杆的伸长l ∆，以及梁的中点在竖直方向的位移。

工程力学课后习题答案第10章题解g

( ) ∑ M B
= 0 ， FC
= − Me l
↓
77
CA 段
M
=
−
Me l
x1
⎜⎛ 0 ⎝
≤
x1
<
l 2
⎟⎞ ⎠
AB 段
M
=
−
Me l
x2
+
Me
⎜⎛ ⎝
l 2
<
x2
≤
l
⎟⎞ ⎠
CA
段 ⎜⎛ 0 ⎝
≤
x1
<
l 2
⎟⎞ ⎠
AB
段 ⎜⎛ ⎝
l 2
<
x2
≤
l ⎟⎞ ⎠
EIw1′′ =
−
Me l
x1
EIw1′
=
3d × (3d )3
12
=
81d 4 12
；设钢丝绳每股横截面为 d × d ，则 9 股钢丝绳的惯
性矩为 I 2
= 9× d ×d3 12
=
9d 4 12
=
1 9
I1
，故钢丝绳要柔软得多。
10-4 用叠加法求梁的位移时，应满足哪些条件？答小变形。
10-5 提高梁的弯曲刚度的主要措施有哪些？与提高梁强度的措施有何不同？答提高梁的弯曲刚度的主要措施有（1）调整加载方式，改善结构设计；（2）减小梁的跨度，增加支承约束；（3）增大梁的弯曲刚度 EI。
)
=
3 8
qlx2
−
ql 2
⎜⎛ ⎝
x2
−
l 4
⎟⎞ ⎠
⎜⎛ ⎝
l 2
≤
x2
≤
l ⎟⎞ ⎠

工程力学：弯曲变形习题与答案

一、单选题1、研究梁的变形的目的是（）。

A.进行梁的正应力计算B.进行梁的刚度计算C.进行梁的稳定性计算D.进行梁的剪应力计算正确答案：B2、图示圆截面悬臂梁，若直径d增大1倍(其它条件不变)，则梁的最大正应力、最大挠度分别降至原来的（）。

A.1/2 1/4B.1/4 1/8C.1/8 1/8D.1/8 1/16正确答案：D3、下面关于梁、挠度和转角的讨论中，正确的结论是（）。

A.挠度最大的截面转角为零B.挠度最大的截面转角最大C.转角为零的截面挠度最大D.挠度的一阶导数等于转角正确答案：D4、已知两悬臂梁的抗弯截面刚度EI相同，长度分别为l和2l，在自由端各作用F1和F2，若二者自由端的挠度相等，则F1/F2=（）。

A.2B.4C.6D.8正确答案：D5、梁上弯矩为零处（）。

A.梁的转角一定为零B.梁的挠度一定为零C.挠度一定为零，转角不一定为零D.梁的挠曲线的曲率一定为零正确答案：D6、已知等直梁在某段上的挠曲轴方程w(x)=–Cx4，C为常量，则在该段梁上（）。

A.分布载荷是x的一次函数B.分布载荷是x的二次函数C.无分布载荷作用D.有均匀分布载荷作用正确答案：D7、在等直梁弯曲变形中，挠曲线曲率最大值发生在（）。

A.剪力最大处B.转角最大处C.弯矩最大处D.挠度最大处正确答案：C8、材料相同的（a）悬臂梁和（b）悬臂梁，长度也相同，在自由端各作用2P和P，截面形状分别是b（宽）×2b（高）、b×b。

关于它们的最大挠度正确的是（）。

A.（a）梁最大挠度是（b）梁的1/4倍B.（a）梁最大挠度是（b）梁的1/2倍C.（a）梁最大挠度与（b）梁的相等D.（a）梁最大挠度是（b）梁的2倍正确答案：A9、已知简支梁的EI为常数，在梁的左端和右端分别作用一力偶m1和m2今欲使梁的挠曲线在x=l/3处出现一拐点，则比值m1/m2为（）。

A.2B.3C.1/2D.1/3正确答案：C10、两根梁尺寸，受力和支承情况完全相同，但材料不同，弹性模量分别为E1和E2，且E1=7E2，则两根梁的挠度之比y1/y2为（）。

弯曲应力、变形习题课

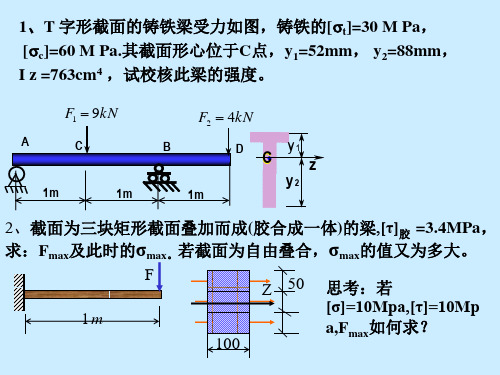
最大拉、压应力不在同一截面上
2、截面为三块矩形截面叠加而成(胶合成一体)的梁,[τ]胶 =3.4MPa，求：Fmax及此时的σmax。若截面为自由叠合，σmax的值又为多大。解：1、确定 Fmax F F S Z 50 胶 s z I zb 1m Fs -F*1 F x x
F (100 50 50)
wBFN l 3 FN ( ) 2 () 3EI
2
3
l/2
l/2
代入（1）：5 Fl 3 解得：
FN l 3 FN l 48 EI 24 EI EA
FN
A l/2 B l/2
F C
5F 1 FN 2 (1 24 I ) 2 Al 3、在基本静定梁上由叠加法求 wC 。
在F力单独作用下：在 FN 力单独作用下：
6 M C y2 2.5 8810 28.2MPa 4 763 10 Iz
M
C
y1 y2
A1
A3
27.3MPa
C
c max
M C y1 17.04 MPa Iz
z
A2 4 28.2MPa A
4 ) 强度校核
t max 28.2 t
46.2MPa
c max 46.2 c
解得： N
3 qa 28
—— ①
DB梁在D处的挠度为
Na 3 yD 3(2EI )
—— ②
变形协调条件为：
yC yD
即
qa4 Na 3 Na 3 8EI 3EI 3(2 EI )
1 N qa 可解出： 4
（二）CD杆刚度为EA时的内力
此时C、D处的挠度表达式仍为式①、②

材料力学弯曲变形

13
压杆稳定计算 1）根据压杆的约束条件确定长度系数）根据压杆的约束条件确定长度系数µ 2）计算杆件自身的柔度）计算杆件自身的柔度λ(10.7)，判断发生弯曲的平面，也可由惯性矩来判断最大、最小刚度平面）（也可由惯性矩来判断最大、最小刚度平面） 3）通过比较的大小，判断计算临界压力的公式的大小，）通过比较λ的大小
1. λ1与材料的性能有关，材料不同，λ1的数与材料的性能有关，材料不同，值也就不同；越大，杆件越容易弯曲。值也就不同；λ越大，杆件越容易弯曲。 2. 满足 1条件的杆件称为细长杆或大柔度杆；满足λ≥λ 条件的杆件称为细长杆大柔度杆；细长杆或也叫大柔度杆的分界条件。也叫大柔度杆的分界条件。其临界应力可用欧拉公式计算。拉公式计算。 3. λ越大杆件越容易弯曲。越大杆件越容易弯曲。越大杆件越容易弯曲解题步骤：解题步骤： 1）由截面形状确定最大、最小刚度平面）由截面形状确定最大、 2）计算柔度，判断欧拉公式是否适用）计算柔度， 3）计算临界压力和临界应力）
σ =
P ≤ [σ ] st A
14
图示结构中，为圆截面杆直径d=80 mm，A端固为圆截面杆，例10.4 图示结构中，AB为圆截面杆，直径，端固端铰支；是正方形截面杆边长a=70 mm，C端也为是正方形截面杆，定，B端铰支；BC是正方形截面杆，边长端铰支，端也为铰支；和杆可以独自发生弯曲变形而互不影响杆可以独自发生弯曲变形而互不影响；铰支；AB和BC杆可以独自发生弯曲变形而互不影响；两杆的材料是A3钢的材料是钢，其λp=104 ，l=3 m，稳定安全系数 st=2.5 ；，稳定安全系数n 求结构的许可载荷P。求结构的许可载荷。
π 2E Pcr = σ cr A = 2 ⋅ A = 269kN λ

工程力学习题库-弯曲变形

第8章弯曲变形本章要点【概念】平面弯曲，剪力、弯矩符号规定，纯弯曲，中性轴，曲率，挠度，转角。

剪力、弯矩与荷载集度的关系；弯曲正应力的适用条件；提高梁的弯曲强度的措施；运用叠加法求弯曲变形的前提条件；截面上正应力分布规律、切应力分布规律。

【公式】 1. 弯曲正应力变形几何关系：yερ=物理关系：Ey σρ=静力关系：0N AF dA σ==⎰，0y AM z dA σ==⎰，2zz AAEI EM y dA y dA σρρ===⎰⎰中性层曲率：1MEIρ=弯曲正应力应力：，My Iσ=，max max z M W σ=弯曲变形的正应力强度条件：[]maxmax zM W σσ=≤ 2. 弯曲切应力矩形截面梁弯曲切应力：bI S F y z z S ⋅⋅=*)(τ，A F bh F S S 2323max ==τ工字形梁弯曲切应力：dI S F y z z S ⋅⋅=*)(τ，A F dh F S S ==max τ圆形截面梁弯曲切应力：bI S F y z z S ⋅⋅=*)(τ，A F S 34max =τ弯曲切应力强度条件：[]ττ≤max3. 梁的弯曲变形梁的挠曲线近似微分方程：()''EIw M x =-梁的转角方程：1()dwM x dx C dx EIθ==-+⎰ 梁的挠度方程：12()Z M x w dx dx C x C EI ⎛⎫=-++ ⎪⎝⎭⎰⎰ 练习题一. 单选题1、建立平面弯曲正应力公式zI My /=σ,需要考虑的关系有（）。

查看答案A 、平衡关系,物理关系，变形几何关系B 、变形几何关系，物理关系，静力关系；C 、变形几何关系，平衡关系，静力关系D 、平衡关系, 物理关系，静力关系；2、利用积分法求梁的变形，不需要用到下面那类条件（）来确定积分常数。

查看答案A 、平衡条件B 、边界条件C 、连续性条件D 、光滑性条件3、在图1悬臂梁的AC 段上，各个截面上的（）。

02-弯曲变形-习题课

D1
(b)
在截面A， x1 0 ，故有 C1 A, D1 0 A w 0
将 C和1 D的1 值代入式(a)和式(b)，并令 x1 ，a 求得截面 C
的转角和挠度分别为
C
Fa2 EI
A
wC
Fa3 3EI
Aa
7-9 计算题
讨论
3F
EI
2EI
A
B
x1
C x2
a
2a
在CB段内积分时，把原点也放在这一段的左端，即放在截面C上。这时，
3l 4 l
4
qx2 6EI
(3l
x)dx
7ql 4 128EI
(↓)
d B
qdx 2EI
x2
B
dB
3l 4 l
4
qx2 2EI
dx
13ql3 192EI
(顺时针)
7-13 计算题
一悬臂梁如图所示，梁的弯曲刚度EI为常量。当受到集度为q的均布载荷作用时，其自由端的挠度
f
ql 4 8EI
。若欲使自由端的挠度等于零，试求在自由端应施加多大的向上集中力F？并求此时梁的最大转角。
2 max 2
max1
hb3 2b4 1
I2 12 12 4 ，I1
w 4w max 2
max1
7-8 选择题在等直梁的最大弯矩所在截面附近，局部加大横截面的尺寸。
A.仅对提高梁的强度是有效的 B.仅对提高梁的刚度是有效的 C.对提高梁的强度和刚度都有效 D.对提高梁的强度和刚度都无效
其他条件不变，则梁的最大挠度和最大正应力分别为原来的倍。
F
F
h
b
(a)
(b)
A. 2和2 B. 4和2 C. 4和4 D. 8和4

材料力学第八章-弯曲变形

q0 B x 等价 MA A EI f q0 B
L
A
L
解：建立静定基确定超静定次数用反力代替多余约束得新结构 —— 静定基
或
q0
A
B L RB
32
q0 A L B RB
几何方程——变形协调方程
f B f Bq f BRB 0
物理方程
=
A B RB q0 A B
qL RB L f Bq ; f BRB 8EI 3EI
A A 铰连接
P
C D
C
D
B
A点：f A 0, A 0
B点： f B左 f B右
C点： f C左 f C右 C左 C右
D点：f D 0
21
边界条件、连续条件应用举例
P
弯矩图分二段，
共积分常数需4个边界条件和连续条件
A B
C
(+)
A点： A 0 B点： f B左 f B右 , C点：f C 0
解：载荷分解如图
=
P A B
查梁的简单载荷变形表，
得到变形
Pa PA 4 EI
q B
2
Pa f PC 6 EI
3
+
A
qa qA 3EI
3
5qL f qC 24 EI24
4
P
A
C a a
q B
Pa PA 4 EI
qa 3 qA 3EI
2
Pa 3 f PC 6 EI
Differential Equation of beam deformation 1 M ( x) 已知曲率为 EI z x
M>0

(修订)第9章弯曲应力与弯曲变形-习题解答

第9章弯曲应力与弯曲变形习题解答题9 – 1 试计算下列各截面图形对z 轴的惯性矩I z （单位为mm ）。

解：（a ）mm 317400250500350200400250250500350≈⨯-⨯⨯⨯-⨯⨯=c y()()49323mm 107314002502003171240025050035025031712500350⨯≈⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯-⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯=.I Z （b ）mm 431550400800500375550400400800500≈⨯-⨯⨯⨯-⨯⨯=c y()()410323mm 1054615504003754311255040080050040043112800500⨯≈⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯-⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯=.I Z （c ）()mm 3060202060506020102060=⨯+⨯⨯⨯+⨯⨯=c y()()46323mm103616020503012602020601030122060⨯=⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯+⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯=.Z I(a)(b) (c)题9-1图题9–2 悬臂梁受力及截面尺寸如图所示。

设q = 60kN/m ，F = 100kN 。

试求（1）梁1– 1截面上A 、B 两点的正应力。

（2）整个梁横截面上的最大正应力和最大切应力。

解：（1）求支反力kN 220100260=+⨯=A F （↑）m kN 32021001260⋅=⨯+⨯⨯=A M （）（2）画F S 、M 图（3）求1-1截面上A 、B 两点的正应力 m kN 1305016011001⋅=⨯⨯+⨯=.MF MA 点：MPa 254Pa 1025412150100550101306331=⨯≈⨯⨯⨯==...I y M zA t σB 点：MPa 162Pa 107816112150100*********331=⨯≈⨯⨯⨯==....I y M σzB c （4）求最大正应力和最大切应力M P a 853Pa 10385361501010320623max max =⨯≈⨯⨯==...W M σzM P a 22Pa 10221501010220232363max =⨯≈⨯⨯⋅=⋅=..A F τS 题9 - 3 简支梁受力如图所示。

材料力学课件第六章1 弯曲变形

代入通解得方程组： F (0) 2 Fl (0) C 0
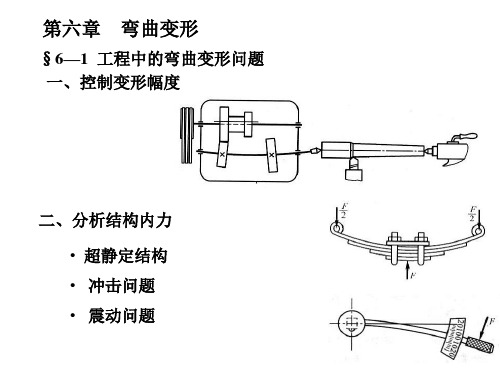
2 F 1 3 (0) Fl (0) 2 C (0) D 0 6 2 D0
解得： C 0, 6、确定挠曲线方程和转角方程: F EIw ' x 2 Flx 2 F Fl 2 EIw x 3 x 6 2 7、求截面位移
由方程所确定的曲率：

1 3 2 2 ( x) dw 1 dx
d w dx2 dw 1 dx
2 2
d 2w dx2
y

w x
x

3
F
因此有：
2

2
M ( x) EI
dw d 2 w M ( x) 又 1 得： 2 dx EI dx
二、画AB、DE受力图
三、变形协调条件三、建立补充方程
v AB中 vDE中
( P RC ) L RC L2 48EI1 48EI 2
3 1 3
D
E
3 I 2 L1 P 解得：RC 3 3 I 2 L1 I1 L2 I1 L3 P 2 AB梁负担：P RC 3 3 I 2 L1 I1 L2
ห้องสมุดไป่ตู้
水平位移 2、弯曲变形的度量：（1）截面位移及特点： •横截面形心的竖向线位移 •横截面绕中性轴的角位移。 •横截面形心的水平线位移，较竖向线位移小许多。
（2）度量变形的基本量： •挠度w：横截面形心的竖向线位移，向上为正。 •截面转角θ ：横截面绕中性轴的角位移，逆时针为正。
3、弯曲变形简化计算（1）简化：认为截面只有竖向位移。 y （2）简化后问题的特点： •挠曲线方程为挠度方程：

第06章弯曲变形题解

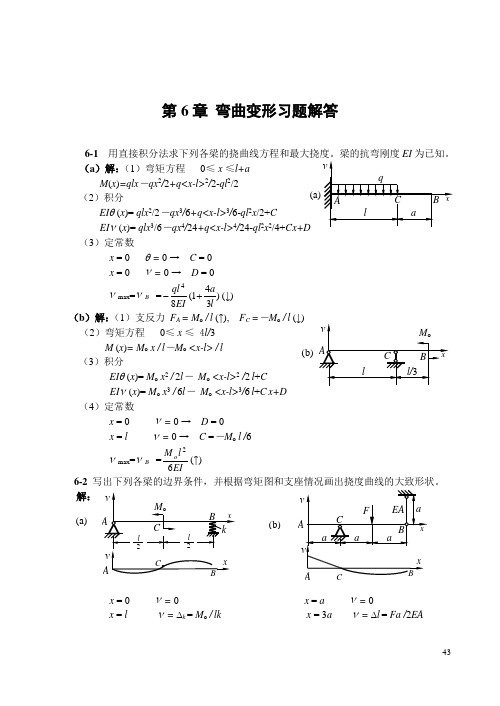
第6章弯曲变形习题解答6-1 用直接积分法求下列各梁的挠曲线方程和最大挠度。

梁的抗弯刚度EI 为已知。

（a ）解：（1）弯矩方程 0≤ x ≤l+aM (x )=qlx －qx 2/2+q<x-l>2/2-ql 2/2（2）积分 EI θ (x )= qlx 2/2－qx 3/6+q<x-l>3/6-ql 2x /2+CEI ν(x )= qlx 3/6－qx 4/24+q<x-l>4/24-ql 2x 2/4+Cx+D （3）定常数x = 0 θ = 0 → C = 0 x = 0 ν= 0 → D = 0νmax =ν B =)341(84laEI ql +-(↓)（b ）解：（1）支反力 F A = M o / l (↑), F C =－M o / l (↓) （2）弯矩方程 0≤ x ≤ 4l/3M (x )= M o x / l －M o <x-l> / l （3）积分EI θ (x )= M o x 2 / 2l － M o <x-l>2 /2 l +CEI ν(x )= M o x 3 / 6l － M o <x-l>3/6 l +C x+D （4）定常数x = 0 ν= 0 → D = 0x = l ν= 0 → C =－M o l /6νmax =ν B =EIl M o 62(↑)6-2 写出下列各梁的边界条件，并根据弯矩图和支座情况画出挠度曲线的大致形状。

解：x = 0 ν= 0 x = a ν= 0x = l ν= ∆k = M o / lk x = 3a ν= ∆l = Fa /2EA(b) ν(b) (a)x = 0 θ = 0 x = 0 ν= 0 x = 0 ν=0 x = 3a ν= 0x = 0 ν= 0 x = 0 ν= 0 , θ = 0x =2a ν=0 x = 2a ν= 06-3 用叠加法求下列各梁C 截面的挠度和B 截面的转角。

材料力学典型例题及解析 6.弯曲变形典型习题解析

弯曲变形典型习题解析1 试用积分法写出图示梁的挠曲轴方程，说明用什么条件决定方程中积分常数，画出挠曲轴大致形状。

图中C 为中间铰。

为已知。

I E解题分析：梁上中间铰处，左、右挠度相等，转角不相等。

解：设支反力为，如图示。

yB A yA FM F、、1、建立各段挠曲轴近似微分方程并积分将梁分为AC 、CB 、BD 段。

AC 段 a x ≤≤10挠曲轴近似微分方程 11x FM w I E yA A ⋅−=′′转角方程1211'12C x Fx Mw IE yA A+−= (a) 挠度方程1113121162D x C x F x M w I E y A A ++−=(b)CB 段 )(2b a x a +≤≤挠曲轴近似微分方程2"2x FMw I E yA A ⋅−=转角方程 222222C x F xM w I E yA A+−=′(c)挠度方程2223222262D x C xFx M w I E yA A++−= (d)BD 段 l x b a ≤≤+3)(挠曲轴近似微分方程[])(333b a x Fx FM w I E yB yA A+−+−=′′转角方程[]32323332)(2C b a x F x F x M w I E yB yA A++−+−=′ (e) 挠度方程[]33333332336)(62D x C b a x FxFxM w I E yB yA A+++−+−= (f)2、确定积分常数共有6个积分常数。

需要6个位移边界条件和光滑连续条件。

332211D C D C D C 、、、、、题1图M A边界条件：，代入(b)得 01=x 01=w 01=D (g)0'1=w 代入(a)得 01=C(h)b a x +=2，02=w (i)连续条件：， a x x ==2121w w =(j) b a x x +==32， 32w w ′=′ (k) 32w w =(l)联立(i)、(j)、(k)、(l)，可求出。

材料力学习题弯曲变形

弯曲变形基本概念题一、选择题1.梁的受力情况如图所示，该梁变形后的挠曲线如图（）所示(图中挠曲线的虚线部分表示直线，实线部分表示曲线)。

2. 如图所示悬臂梁，若分别采用两种坐标系，则由积分法求得的挠度和转角的正负号为（）。

题2图题1图A．两组结果的正负号完全一致B．两组结果的正负号完全相反C．挠度的正负号相反，转角正负号一致D．挠度正负号一致，转角的正负号相反3.已知挠曲线方程y = q0x(l3 - 3lx2 +2 x3)∕(48EI)，如图所示，则两端点的约束可能为下列约束中的（）。

题3图4. 等截面梁如图所示，若用积分法求解梁的转角、挠度，则以下结论中（）是错误的。

A．该梁应分为AB、BC两段进行积分B．挠度积分表达式中，会出现4个积分常数-26-题4图题5图 C ．积分常数由边界条件和连续条件来确定D ．边界条件和连续条件表达式为x = 0，y = 0；x = l ，0==右左y y ，0='y 5. 用积分法计算图所示梁的位移，边界条件和连续条件为( )A ．x = 0，y = 0；x = a + l ，y = 0；x = a ，右左y y =，右左y y '=' B ．x = 0，y = 0；x = a + l ，0='y ；x = a ，右左y y =，右左y y '=' C ．x = 0，y = 0；x = a + l ，y = 0，0='y ；x = a ，右左y y =D ．x = 0，y = 0；x = a + l ，y = 0，0='y ；x = a ，右左y y '=' 6. 材料相同的悬臂梁I 、Ⅱ，所受荷载及截面尺寸如图所示。

关于它们的最大挠度有如下结论，正确的是（）。

A ． I 梁最大挠度是Ⅱ梁的41倍 B ．I 梁最大挠度是Ⅱ梁的21倍 C ． I 梁最大挠度与Ⅱ梁的相等 D ．I 梁最大挠度是Ⅱ梁的2倍题6图题7图 7. 如图所示等截面梁，用叠加法求得外伸端C 截面的挠度为（）。

材料力学第四章弯曲变形

习题： 182页，5-11、13、15
第4章
弯曲变形
叠加法
§4-4 梁的刚度校核提高梁的刚度的措施
1、梁的刚度校核
保证梁的正常工作除要满足强度条件外，产生的变形也不能太大，应满足刚度条件，即有：
wmax w l l
w 其中，与 l
qmax q
第4章
弯曲变形
叠加法
2、提高刚度措施
除外加载荷外，梁的位移w、q还与梁的弯曲刚度EI成反比，与跨长l的n次方成正比，因此，提高刚度的措施有：
1）升高EI。各种钢材E相差不大，主要提高I，在截面面积 A不变时，尽可能使面积分布远离中性轴。如工字形、箱形等截面。
2）减少梁的跨度或增加支承。如下图所示结构：
从以上两例题知: 转角及挠度方程中的积分常数C,D的几何意义为: C EIw ' x 0 EIq 0
D EIw0
θ0和w0分别代表坐标原点处截面的转角和挠度。梁的刚度条件
wmax w
q max q
其中[q]称为许用转角；[w]称为许用挠度。
习题： 180页，5-2、3、5
Fl q B1 q C1 2 EI
2
（顺时针）
第4章
弯曲变形
叠加法
对图b，可得D截面的挠度和转角为：
F
·
(b)
wD2
直线
wD 2
wD2
F 2l 3EI
F 2l 2 EI
3
qD2
qD2 BD qB 2
wB2
2
qD2
同理可得此时B截面的挠度和转角为：
wB 2
8Fl3 4 Fl 2 14Fl3 wD 2 q D 2 BD l （向下） 3EI 2 EI 3EI

第8章梁的弯曲变形及其刚度计算(练习题)

第8章梁的弯曲变形及其刚度计算(练习题)
在自由端承受集中力P作用的悬臂梁AB长度为l，
EI为常数。试求其转角与挠度方程，以及最大的转角
θmax与挠度ymax。
第8章梁的弯曲变形及其刚度计算(练习题)
一、单项选择题
1、通常我们用（
A.挠度和转角答案：A
）度量梁的弯曲变形。
C.角应变 D.应变
B.单位长度扭转角
bh3 8b 4 I1 12 12
hb 2b 1 I2 I1 12 12 4
3 4
bh2 4b 3 W1 6 6
hb 2 2b 3 1 W2 W1 6 6 2
wmax 2 4wmax 1
max 2 2 max 1
第8章梁的弯曲变形及其刚度计算(练习题)
就能减小 max 。而梁的最大挠度和转角却与整个梁的 EI 都有关，局部加大
第8章梁的弯曲变形及其刚度计算(练习题)
2、如图所示，高宽比h/b=2的矩形截面梁，若将梁的横截面由竖放改为平放，其它条件不变，则梁的最大挠度和最大正
应力分别为原来的——倍。
A.2和2 B.4和2 F
F
C.4和4
D.8和4
c h
z
y b
第8章梁的弯曲变形及其刚度计算(练习题)
答案：B
wmax 与 EI 成反比， max 与 W 成反比。
一、单项选择题
3、在等直梁的最大弯矩所在截面附近，局部加大横截面的尺寸（）。
A.仅对提高梁的强度是有效的 C.对提高梁的强度和刚度都有效 B. 仅对提高梁的刚度是有效的 D. 对Wz
，式中 W z 是 M max 所在截面的抗弯截面系数，加大它并不能显著地减小变形。 I

材料力学第2版课后习题答案第7章弯曲变形

解：查自重得：
q = 587.02 N / m
J = 15760cm4 Pl 3 5ql 4 f =− − 48EJ 384EJ −176 × 103 × 113 = 48 × 210 × 109 × 15760 × 10−8 × 4 −587.02 × 5 × 114 + 385 × 210 × 109 × 15760 × 10−8 × 4 = 0.0377 m = 3.77cm
(d) 解：
D A P P E
' yC = y E + θ B ia + y C
C B P
− P ( 2a ) − Pa 3 − Pa3 = − − 3EJ 3EJ 3EJ 3 −10 Pa = 3EJ
3
252
7-5 门式起重机横梁由4根36a工字钢组成如图所示，梁的两端均可视为铰支，钢的弹性模量E=210Gpa。试计算当集中载荷P＝176 kN作用在跨中并考虑钢梁自重时，跨中截面 C的挠度yC。
x=l
∴y =−
'
∴D = 0
y=0
∴C =
− M 0l 6
M 0l 2 ⎛ x x 3 ⎞ ⎜ − ⎟ 6 EJ ⎝ l l 3 ⎠
M 0l 2 ⎛ 1 3 x 2 ⎞ ∴θ = y = − ⎜ − ⎟ 6 EJ ⎝ l l 3 ⎠
− M 0l 2 l ；此时挠度最大 f = 3 9 3EJ 2 ⎛ l ⎞ − M 0l 中点挠度 y ⎜ ⎟ = ⎝ 2 ⎠ 16 EJ − M 0l Ml θA = θB = 0 6 EJ 3EJ （b）解：设中点为C点，则分析CB段
''
C2 = −
D2 = −
a4 24