logistic回归分析
18[1].logistic回归分析
![18[1].logistic回归分析](https://img.taocdn.com/s3/m/0ebd87d226fff705cc170aa7.png)
?
P 0 1 x1 2 x2 8 x8 ?
4
多元线性回归模型要求:因变量为服从正 态分布的连续性变量… 但在病因学研究或疾病预后研究中,观察 结果常为两分类资料:
1 阳性结果 (发病、有效、死亡等) Y 0 阴性结果 (未发病、无效、存活等)
5
表2.冠心病危险因素的病例对照调查资料
腋下淋巴 结转移 无=0 有=1 合计 甲医院=1 病例 生存 生存率% 45 35 77.7 710 450 63.4 755 485 64.2
病例 300 83 383
乙医院=0 生存 生存率% 215 71.6 42 50.6 257 67.1
多因素分析作用: 1.可校正混杂因素,正确评价结果的效应。 2.回答哪个因素对事件(疾病)作用更大?
回顾性收集暴露情况 比较 人数 过去 现在
暴露
调查方向
疾病
a
a/(a+c)
+
病 人
c b
b/(b+d)
+
非 病 人
研究 人群
d
-
图1 病例对照研究的结构模式图
队列研究的概念
队列研究 (cohort study)
是将一个范围明确的人群按是否暴露于某可疑 因素及其暴露程度分为不同的亚组,追踪其各 自的结局,比较不同亚组之间结局的差异,从 而判定暴露因子与结局之间有无因果关联及关 联大小的一种观察性研究方法。
15
第一节 logistic回归
(非条件logistic回归)
16
一、基本概念
Logistic回归:属于概率型非线性回归, 是研究二分类或多分类观察结果与一些影响 因素之间关系的一种多变量分析方法。 它是以疾病发生概率为应变量,影响疾 病发生的因子为自变量,分析疾病与致病因 子之间联系的一种回归分析法。
LOGISTIC回归分析

LOGISTIC回归分析前⾯的博客有介绍过对连续的变量进⾏线性回归分析,从⽽达到对因变量的预测或者解释作⽤。
那么如果因变量是离散变量呢?在做⾏为预测的时候通常只有“做”与“不做的区别”、“0”与“1”的区别,这是我们就要⽤到logistic分析(逻辑回归分析,⾮线性模型)。
参数解释(对变量的评价)发⽣⽐(odds): ODDS=事件发⽣概率/事件不发⽣的概率=P/(1-P)发⽣⽐率(odds ratio):odds ratio=odds B/odds A (组B相对于组A更容易发⽣的⽐率)注:odds ratio⼤于1或者⼩于1都有意义,代表⾃变量的两个分组有差异性,对因变量的发⽣概率有作⽤。
若等于1的话,该组变量对事件发⽣概率没有任何作⽤。
参数估计⽅法线性回归中,主要是采⽤最⼩⼆乘法进⾏参数估计,使其残差平⽅和最⼩。
同时在线性回归中最⼤似然估计和最⼩⼆乘发估计结果是⼀致的,但不同的是极⼤似然法可以⽤于⾮线性模型,⼜因为逻辑回归是⾮线性模型,所以逻辑回归最常⽤的估计⽅法是极⼤似然法。
极⼤似然公式:L(Θ)=P(Y1)P(Y2)...p(Y N) P为事件发⽣概率P I=1/(1+E-(α+βX I))在样本较⼤时,极⼤似然估计满⾜相合性、渐进有效性、渐进正太性。
但是在样本观测少于100时,估计的风险会⽐较⼤,⼤于100可以介绍⼤于500则更加充分。
模型评价这⾥介绍拟合优度的评价的两个标准:AIC准则和SC准则,两统计量越⼩说明模型拟合的越好,越可信。
若事件发⽣的观测有n条,时间不发⽣的观测有M条,则称该数据有n*m个观测数据对,在⼀个观测数据对中,P>1-P,则为和谐对(concordant)。
P<1-P,则为不和谐对(discordant)。
P=1-P,则称为结。
在预测准确性有⼀个统计量C=(NC-0.5ND+0.5T)/T,其中NC为和谐对数,ND为不和谐对数,这⾥我们就可以根据C统计量来表明模型的区分度,例如C=0.68,则表⽰事件发⽣的概率⽐不发⽣的概率⼤的可能性为0.68。
logistic回归分析案例

logistic回归分析案例Logistic回归分析案例。
Logistic回归分析是一种常用的统计分析方法,主要用于预测二分类或多分类的结果。
在实际应用中,Logistic回归分析可以帮助我们理解影响某一事件发生的因素,以及对事件发生的概率进行预测。
本文将通过一个实际的案例来介绍Logistic回归分析的应用。
案例背景。
假设我们是一家电商公司的数据分析师,现在我们需要分析用户的购买行为,并预测用户是否会购买某一产品。
我们收集了一些用户的个人信息和他们最近一次购买的产品,希望通过这些数据来预测用户是否会购买新产品。
数据准备。
首先,我们需要收集用户的个人信息和购买行为数据。
个人信息包括年龄、性别、职业等;购买行为数据包括购买的产品类型、购买时间等。
在收集完数据后,我们需要对数据进行清洗和预处理,包括缺失值处理、异常值处理等。
模型建立。
在数据准备完成后,我们可以开始建立Logistic回归模型。
首先,我们需要将数据划分为训练集和测试集,以便对模型进行验证。
然后,我们可以利用训练集来拟合Logistic回归模型,并利用测试集来评估模型的预测效果。
模型评估。
在模型建立完成后,我们需要对模型进行评估。
常用的评估指标包括准确率、精确率、召回率等。
这些指标可以帮助我们判断模型的预测效果,并对模型进行调优。
模型应用。
最后,我们可以利用建立好的Logistic回归模型来预测用户是否会购买新产品。
通过输入用户的个人信息和购买行为数据,模型可以给出用户购买新产品的概率,从而帮助我们进行精准营销和推广。
结论。
通过以上实例,我们可以看到Logistic回归分析在预测用户购买行为方面具有很好的应用价值。
通过收集用户数据、建立模型、评估模型和应用模型,我们可以更好地理解用户行为,并做出更精准的预测和决策。
总结。
Logistic回归分析是一种强大的统计工具,可以帮助我们预测二分类或多分类的结果。
在实际应用中,我们可以根据具体情况收集数据、建立模型,并利用模型进行预测和决策。
数据分析知识:数据分析中的Logistic回归分析

数据分析知识:数据分析中的Logistic回归分析Logistic回归分析是数据分析中非常重要的一种统计分析方法,它主要用于研究变量之间的关系,并且可以预测某个变量的取值概率。
在实际应用中,Logistic回归分析广泛应用于医学疾病、市场营销、社会科学等领域。
一、Logistic回归分析的原理1、概念Logistic回归分析是一种分类分析方法,可以将一个或多个自变量与一个二分类的因变量进行分析,主要用于分析变量之间的关系,并确定自变量对因变量的影响。
Logistic回归分析使用的是逻辑回归模型,该模型是将自变量与因变量的概率映射到一个范围为0-1之间的变量上,即把一个从负无穷到正无穷的数映射到0-1的范围内。
这样,我们可以用这个数值来表示某个事件发生的概率。
当这个数值大于0.5时,我们就可以判定事件发生的概率比较高,而当这个数值小于0.5时,我们就可以判定事件发生的概率比较小。
2、方法Logistic回归分析的方法有两种:一是全局最优化方法,二是局部最优化方法。
其中全局最优化方法是使用最大似然估计方法,而局部最优化方法则是使用牛顿法或梯度下降算法。
在进行Logistic回归分析之前,我们首先要对数据进行预处理,将数据进行清洗、变量选择和变量转换等操作,以便进行回归分析。
在进行回归分析时,我们需要先建立逻辑回归模型,然后进行参数估计和模型拟合,最后进行模型评估和预测。
在进行参数估计时,我们通常使用最大似然估计方法,即在估计参数时,选择最能解释样本观测数据的参数值。
在进行模型拟合时,我们需要选取一个合适的评价指标,如准确率、召回率、F1得分等。
3、评价指标在Logistic回归分析中,评价指标包括拟合度、准确性、鲁棒性、可解释性等。
其中最常用的指标是拟合度,即模型对已知数据的拟合程度,通常使用准确率、召回率、F1得分等指标进行评价。
此外,还可以使用ROC曲线、AUC值等指标评估模型的性能。
二、Logistic回归分析的应用1、医学疾病预测在医学疾病预测中,Logistic回归分析可以用来预测患某种疾病的概率,如心脏病、肺癌等。
统计学中的Logistic回归分析

统计学中的Logistic回归分析Logistic回归是一种常用的统计学方法,用于建立并探索自变量与二分类因变量之间的关系。
它在医学、社会科学、市场营销等领域得到广泛应用,能够帮助研究者理解和预测特定事件发生的概率。
本文将介绍Logistic回归的基本原理、应用领域以及模型评估方法。
一、Logistic回归的基本原理Logistic回归是一种广义线性回归模型,通过对数据的处理,将线性回归模型的预测结果转化为概率值。
其基本原理在于将一个线性函数与一个非线性函数进行组合,以适应因变量概率为S形曲线的特性。
该非线性函数被称为logit函数,可以将概率转化为对数几率。
Logistic回归模型的表达式如下:\[P(Y=1|X) = \frac{1}{1+e^{-(\beta_0+\beta_1X_1+...+\beta_pX_p)}}\]其中,P(Y=1|X)表示在给定自变量X的条件下,因变量为1的概率。
而\(\beta_0\)、\(\beta_1\)、...\(\beta_p\)则是待估计的参数。
二、Logistic回归的应用领域1. 医学领域Logistic回归在医学领域中具有重要的应用。
例如,研究者可以使用Logistic回归分析,探索某种疾病与一系列潜在风险因素之间的关系。
通过对患病和非患病个体的数据进行回归分析,可以估计各个风险因素对疾病患病的影响程度,进而预测某个个体患病的概率。
2. 社会科学领域在社会科学研究中,研究者常常使用Logistic回归来探索特定变量对于某种行为、态度或事件发生的影响程度。
例如,研究者可能想要了解不同性别、教育程度、收入水平对于选民投票行为的影响。
通过Logistic回归分析,可以对不同自变量对于投票行为的作用进行量化,进而预测某个选民投票候选人的概率。
3. 市场营销领域在市场营销中,Logistic回归也被广泛应用于客户分类、市场细分以及产品销量预测等方面。
通过分析客户的个人特征、购买习惯和消费行为等因素,可以建立Logistic回归模型,预测不同客户购买某一产品的概率,以便制定个性化的市场营销策略。
logistic回归分析

Logistic回归分析
数学模型:
e p 1 e
1 X 1 2 X 2 m X m
1 X 1 2 X 2 m X m
Logistic回归分析
一、基本思想
用模型去描述实际资料时,须使 得理论结果与实际结果尽可能的一致。
资料整理格式
Logistic回归分析
1
消除xj量纲的影响
2.标准化偏回归系数j 的意义
果的发生,为“不利因素”;
xij
xij x j sj
(1)符号:取 “+”,xj 增大,则P增大,即促进阳性结
取 “-”,xj增大,则P减小,即抑制阳性结 果的发生,为“保护因素”。 (2)大小 :∣ j ∣越大,则xj 对结果的影响也就越大。
i 1 2 n
x1 x11 x21 xn1
x2
...
xm x1m x2m xnm
δ δ δ δ
1 2
x12 ... x22 ... …... xn2 ...
n
Logistic回归分析
二、基本原理
1.结果问题 : 对于第i个个体而言,其理论结果为pi , 而实际结果是i 。 2.一致问题: 对于第i个个体而言, i =1 pi i =0 qi
m
▲
OR e j 1
j ) ˆ j ( x*j x
(1)对多指标的共同效应进行评价:
若OR>1,则处于X*水平下的阳性结果发生风险要高于X 水平, 即“不利因素”占主导地位;
▲
▲
若OR<1,则处于X*水平下的阳性结果发生风险要低于X 水平, 即“保护因素”占主导地位;
▲
Logistic回归分析

注:因为p>a,所以认为样本实际值得到的分布与 预测值得到的分布无显著差异,模型拟合优度较好 。
33
注:模型整体的准确度不高,对不购买人群的准确 率极高,对购买人群的准确率很低。
34
注:预测类别图上可以看出,预测概率在0.4附近的 样本预测准确率相对最低。事实上,无论用什么分 类方法,这类样本身就是最难预测的。
Hosmer—Lemeshow检验:通过模型可以计算出给 定解释变量取值时被解释变量取1的概率预测。如 果模型拟合较好,则应给实际值为1的样本以较高 的概率,给实际值为0的样本以低的概率预测值。 于是对概率预测值进行分位数分组(通常为10分位 数,将样本分为10组),预测概率大小分得的10组 和实际观测值0/1类别分组形成了交叉列联表。由 观测频数和期望频数计算卡方统计量,即Hosmer— Lemeshow统计量,它服从自由度为n-2的卡方分布 ,n为组数。
39
模型拟合优度的评价与检验 目的:第一,回归方程能够解释被解释变量变差的 程度,即线性回归的部分能解释LogitP的程度,这 一点与一般线性回归分析是相同的;第二,由回归 方程得到的概率进行分别判别的准确率。 方法: 第一目的:Cox &Snell R2 统计量和 Nagel ker ke R2 统计量 第二目的:混淆矩阵(错判矩阵)和 Hosmer-Lemeshow检验
16
2 L0 N 1 ( ) 2 Cox & Snell R 统计量= L1
,N为样本容量。 该统计量类似于一般线性模型中的R方,统计量的值 越大表明模型的拟合优度越高。不足之处在于其取值 范围无法确定,不利于模型之间的比较。
Cox &Snell R 2
logistic回归分析

队列研究(cohort study):也称前瞻性研究、随访研究等。是一种由因及果的研
究,在研究开始时,根据以往有无暴露经历,将研究人群分为暴露人群和非暴 露人群,在一定时期内,随访观察和比较两组人群的发病率或死亡率。如果两 组人群发病率或死亡率差别有统计学意义,则认为暴露和疾病间存在联系。队 列研究验证的暴露因素在研究开始前已存在,研究者知道每个研究对象的暴露 情况。
调查方向:追踪收集资料 暴露 疾病 +
人数
比较
aபைடு நூலகம்
b c
+
研究人群
a/(a+b)
+ -
-
c/(c+d)
d
队列研究原理示意图
暴露组 非暴露组
病例 a c
非病例 b d
合计 n1=a+b n0=c+d
发病率 a/ n1 c/ n0
相对危险度(relative risk, RR)也称危险比(risk ratio) 或率比(rate ratio) RR I e a / n1 、 I e a / n1 、 I 0 c / n2 。
研究,先按疾病状态确定调查对象,分为病例(case)和对照 (control)两组,然后利用已有的记录、或采用询问、填写调查表 等方式,了解其发病前的暴露情况,并进行比较,推测疾病与 暴露间的关系。
调查方向:收集回顾性资料
比较 a/(a+b)
人数 a b c
暴露 +
疾病 病例
+ 对照 -
c/(c+d) d
二、 logistic回归模型的参数估计
logistic 回归模型的参数估计常采用最大似然估计。 其基本思想是先建立似然函数与对数似然函数, 求使对数似然函数最大时的参数值,其估计值即 为最大似然估计值。 建立样本似然函数:
Logistic回归分析

Logistic 回归分析Logistic 回归分析是与线性回归分析方法非常相似的一种多元统计方法。
适用于因变量的取值仅有两个(即二分类变量,一般用1和0表示)的情况,如发病与未发病、阳性与阴性、死亡与生存、治愈与未治愈、暴露与未暴露等,对于这类数据如果采用线性回归方法则效果很不理想,此时用Logistic 回归分析则可以很好的解决问题。
一、Logistic 回归模型设Y 是一个二分类变量,取值只可能为1和0,另外有影响Y 取值的n 个自变量12,,...,n X X X ,记12(1|,,...,)n P P Y X X X ==表示在n 个自变量的作用下Y 取值为1的概率,则Logistic 回归模型为:[]0112211exp (...)n n P X X X ββββ=+-++++它可以化成如下的线性形式:01122ln ...1n n P X X X P ββββ⎛⎫=++++ ⎪-⎝⎭通常用最大似然估计法估计模型中的参数。
二、Logistic 回归模型的检验与变量筛选根据R Square 的值评价模型的拟合效果。
变量筛选的原理与普通的回归分析方法是一样的,不再重复。
三、Logistic 回归的应用(1)可以进行危险因素分析计算结果各关于各变量系数的Wald 统计量和Sig 水平就直接反映了因素i X 对因变量Y 的危险性或重要性的大小。
(2)预测与判别Logistic回归是一个概率模型,可以利用它预测某事件发生的概率。
当然也可以进行判别分析,而且可以给出概率,并且对数据的要求不是很高。
四、SPSS操作方法1.选择菜单2.概率预测值和分类预测结果作为变量保存其它使用默认选项即可。
例:试对临床422名病人的资料进行分析,研究急性肾衰竭患者死亡的危险因素和统计规律。
Logistic回归分析.sav解:在SPSS中采用Logistic回归全变量方式分析得到:(1)模型的拟合优度为0.755。
Logistic回归分析(共53张PPT)

• 优势比
• 常把出现某种结果的概率与不出现的概率 之比称为比值(odds),即odds=p/1-p。两个
比值之比称为比值比(Odds Ratio),简称 OR。
• Logistic回归中的常数项(b0)表示,在不
接触任何潜在危险/保护因素条件下,效 应指标发生与不发生事件的概率之比的对 数值。
Forward: LR ( 向前逐步法:似然比 法 likelihood ratio,LR)→ 再击下 方的 Save 钮,将 Predicted values 、 Influence 与 Residuls 窗口中的 预选项全勾选 → Continue → 再击 下方的 Options 钮,将 Statistics and Plot 小窗口中的选项全勾选 → Continue → OK 。
三、参数检验
• 似然比检验(likehood ratio test)
通过比较包含与不包含某一个或几 个待检验观察因素的两个模型的对数似 然函数变化来进行,其统计量为G (又 称Deviance)。
G=-2(ln Lp-ln Lk) 样本量较大时, G近似服从自由度
为待检验因素个数的2分布。
• 比分检验(score test)
, Logistic回归系数的解释变得更为复杂 ,应特别小心。
根据Wald检验,可知Logistic回归系
数bi服从u分布。因此其可信区间为
病例与对照匹配---条件logistic回归 其中, 为常数项, 为偏回归系数。 应变量水平数大于2,且水平之间不存在等级递减或递增的关系时,对这种多分类变量通过拟合一种广义Logit模型方法。
u= bi s bi
u服从正态分布,即为标准正态离差。
(卫生统计学)第十九章 Logistic回归分析

结果解释
3个βi的估计值都是正数,表明这三个因素都是危险因素且都有统计学意 义。从优势比OR上可以看出,在因素x2和x3固定不变时,因素x1每增加一个 等级所引起的优势比为增加前的3.034倍;在因素X1和X3固定不变时,因素x2 每增加一个等级所引起的优势比为增加前的2.019倍 。在因素x1和x2固定不变 时,因素x3每增加一个等级所引起的优势比为增加前的2.651倍。同时在考察 因素相对贡献大小时,从标准系数看, β'1> β' 3 > β'2 ,故x1的相对贡献比x2和 x3大。
OR
P1 P0
/1 /1
P1 P0
e i
亦称比数比
反映某一个危险因素 xi在不同暴露水平下发病 与不发病的比。
当阳性率 P 1时, OR RR
二、参数估计
由于Logistic回归是一种概率模型,通常采用最大似然估计法(maximum likelihood estimate)求解模型中的参数βj的估计值 bj (j=0,1,2,….k)。
1. 相对危险度 RR( Re lative Risk ) RR P1 P0
反映某一个危险因素 xi两个不同暴露水平 1与 0的发病率的比
2. 优势 Odds
Odds P1 P1 1 P1 q1
亦称比数
反映某一个危险因素 xi在暴露水平 1下发病率与不发病率的 比
3. 优势比 OR ( Odds Ratio )
个例预测
设某AMI患者在症状5小时内送到医院(x3=0),未发生休克(x1=0), 已有心衰(x2=1),求抢救成功的概率。
logistic回归分析

表13-7 例13-2的logistic回归模型自变量筛选结果
模型
因素 X
第1步 常数项
回归系数 标准误
b
Sb
-2.528 0.238
Wald χ2 P值 112.433 <0.001
OR值
OR值95%可信区间 下限 上限
0.080
治疗11周
2.149 0.289 55.267 <0.001 8.578 4.867 15.117
因素 X 常数项
回归系数 标准误
Waldχ2 P值 OR值
b
Sb
-0.910 0.136 44.870 0.000 0.403
OR值95%可信区间
下限
上限
吸烟
0.886 0.150 34.862 0.000 2.424 1.807
3.253
饮酒
0.526 0.157 11.207 0.001 1.692 1.244
logistic回归分析
Logistic regression analysis
• 医学研究中应变量有时是二分类结果,如发病与不 发病、死亡与生存、有效与无效、复发与未复发等, 当需要研究二分类应变量的影响因素时,适合采用 logistic回归分析。
logistic回归属于概率型非线性回归,它是研究二 分类(可以扩展到多分类)反应变量与多个影响 因素之间关系的一种多变量分析方法。logistic回 归模型参数具有明确的实际意义。
OR值的可信区间:
exp(bj - zα/2 Sbj ) ORj exp(bj zα/2 Sb j )
• 例13-1 研究吸烟(X1)、饮酒(X2)与食道癌 (Y)关系的病例-对照资料,试作logistic回归 分析。
Logistic回归模型分析
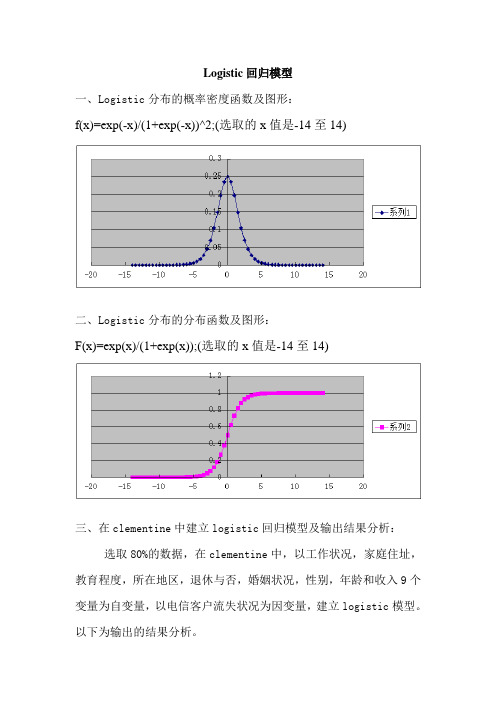
Logistic回归模型一、Logistic分布的概率密度函数及图形:f(x)=exp(-x)/(1+exp(-x))^2;(选取的x值是-14至14)二、Logistic分布的分布函数及图形:F(x)=exp(x)/(1+exp(x));(选取的x值是-14至14)三、在clementine中建立logistic回归模型及输出结果分析:选取80%的数据,在clementine中,以工作状况,家庭住址,教育程度,所在地区,退休与否,婚姻状况,性别,年龄和收入9个变量为自变量,以电信客户流失状况为因变量,建立logistic模型。
以下为输出的结果分析。
1、变量重要性分析:如下图所示,9个变量对客户流失的影响作用不一样,其中工作状况是影响最大的变量,其比重为0.376。
另外,教育程度(比重为0.225)和家庭地址(比重为0.223)的影响也比较明显。
而年龄几乎不是影响因素。
2、单个变量显著性及系数经济意义分析:下图中,B为自变量的回归系数,若B为负则代表该自变量与因变量呈反向变动的关系。
S.E.是标准差;Wald指的是Wald统计量;df是指自由度;sig.指的是显著性(其值越小说明自变量对因变量的影响越显著);Exp(B)代表着各自变量的回归系数的经济意义,即在保持其他条件不变时,特定自变量变动1单位时,所影响到发生率的变化率为B单位。
从图中可以看出,工作状况对因变量的影响是完全显著,其系数为-0.064,说明了工作状况与客户流失之间的反向变动关系,且当其他自变量保持不变的条件下,消费者的工作状态每变动1单位,所带来的客户流失的发生率的变化率为0.064个单位。
这与实际情况相符合。
其次,教育程度,家庭住址和婚姻状况对因变量的影响也较显著,这可能与电信的宣传策略和信号覆盖以及状况相关。
然而,其他变量的显著性水平就比较低。
其中收入的显著性最差,可能是因为各个通信公司的服务价格与质量区别不大,收入水平对客户流失情况影响很小。
logistic回归分析

它与自变量x1, x2,…,xp之间的Logistic回
归模型为:
p exp(0 1X1 2 X 2 ... m X m ) 1 exp(0 1X1 2 X 2 ... m X m )
1
1 p
1 exp( 0 1 X 1 p X p )
6
模 型
ln
P 1 P
=0
1
• 按照研究设计类型 –非条件logistic回归(研究对象未经匹配) –条件logistic回归(研究对象经过匹配)
5
Logistic回归模型
应变量Y
1 0
发生 未发生 ,
自变量X1, X 2 ,
, Xm
在m个自变量的作用下阳性结果发生的概率记作:
P P(Y 1| X1, X 2 ,, X m ) 0 P 1
X1
2
X
2
m X m log itP
参 数
常数项 0
表示暴露剂量为0时个体
的
发病与不发病概率之比的自然对数。
意 义
回归系数 j ( j 1,2,, m)
表示自变量 X j 改变一个单位时
logitP 的改变量。 7
优势比OR(odds ratio)
流行病学衡量危险因素作用大小的比数比例指标。 计算公式为:
OR j
P1 P0
/(1 /(1
P1 ) P0 )
式中 P1 和 P0 分别表示在 X j 取值为 c1 及 c0 时 的发病概率, OR j 称作多变量调整后的优势比, 表示扣除了其他自变量影响后危险因素的作用。
8
与 logisticP 的关系:
对比某一危险因素两个不同暴露水平 X j c1 与 X j c0 的发病 情况(假定其它因素的水平相同),其优势比的自然对数为:
统计学-logistic回归分析

研究问题可否用多元线性回归方法?
ˆ y a b x b x b x 1 1 2 2 m m 1.多元线性回归方法要求 Y 的取值为计量
的连续性随机变量。 2.多元线性回归方程要求Y与X间关系为线 性关系。 ˆ 不能回答“发生与 3.多元线性回归结果 Y 否” logistic回归方法补充多元线性回归的不足
第十六章 logistic回归分析
logistic回归为概率型非线性回归 模型,是研究分类观察结果(y)与 一些影响因素(x)之间关系的一种 多变量分析方法
问题提出:
医学研究中常研究某因素存在条件下某结果是否 发生?以及之间的关系如何? 因素(X) 疾病结果(Y) x1,x2,x3…XK 发生 Y=1 不发生 Y=0 例:暴露因素 冠心病结果 高血压史(x1):有 或无 有 或 无 高血脂史(x2): 有 或 无 吸烟(x3): 有或无
lnllnplnlikehoodratiotest通过比较包含与不包含某一个或几个待检验观察因素的两个模型的对数似然函数变化来进行其统计量为近似服从自由度为待检验因素个数的scoretest以未包含某个或几个变量的模型为基础保留模型中参数的估计值并假设新增加的参数为零计算似然函数的一价偏导数又称有效比分及信息距阵两者相乘便得比分检验的统计量分布
• 分析因素xi为等级变量时,如果每个等级的 作用相同,可按计量资料处理:如以最小或 最大等级作参考组,并按等级顺序依次取为 0,1,2,…。此时, e(bi) 表示xi增加一个等 级时的优势比, e(k* bi)表示xi增加k个等级时 的优势比。如果每个等级的作用不相同,则 应按多分类资料处理。 • 分析因素xi为连续性变量时, e(bi)表示xi增加 一个计量单位时的优势比。
Y 发病=1 不发病=0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
i 反映了在其他变量固定后,X=1与x=0相
比发生Y事件的对数优势比。
回归系数β与OiR
X与Y的关联
β=0,OR=1,
无关
β>1,OR>1 , 有关,危险因素
β<1,OR<1, 有关,保护因子
事件发生率很小,OR≈RR。
二、logistic回归模型的参数估计
1. 模型中的参数(βi)估计
, l n 1 P P =01 X 12 X 2 m X m
四、变量筛选
目的;将回归系数有显著意义的自变量选入 模型中,作用不显著的自变量则排除在外。
变量筛选算法有:前进法、后退法和
逐步法(stepwise)。 例:讲义例16-2,用逐步法 选入变量的显著水准为0.10,变量保留在方
程的水准为0.15 例:16-2讲义261-263页
表16-4 进入方程的自变量及参数估计
X8 1.ቤተ መጻሕፍቲ ባይዱ47 0.847 5.29 0.0215 0.523 7.01
bj'bjsj/(/ 3)
标准回归系数(b’) 比较各自变量对Y 的相对贡献
第二节 条件Logistic回归
概念: 用配对设计获得病例对照研究资料,计算的
Logistic回归模型为条件Logistic回归。
成组(未配对)设计的病例对照研究资料,计算的 Logistic回归模型为非条件Logistic回归。
三类研究计算的logistic 回归模型的β意义是一致。仅常 数项不同。(证明略)
Logistic回归的应用
2.校正混杂因素,对疗效做评价 在临床研究和疗效的评价,组间某些因素构
成不一致干扰疗效分析,通过该法可控制 非处理因素,正确评价疗效。
3.预测与判别 预测个体在某因素存在条件下,发生某事件
(发病)的概率,为进一步治疗提供依据。
Y 发病=1 不发病=0
Y 发病=1 不发病=0
危险因素
x= 1 x= 0
30(a) 10( b)
70(c) 90(d)
a+c
b+d
危险因素
x= 1 x= 0
p1 1-p1
p0 1-p0
p1
a
a
c
有暴露因素人群中发病的比例
多元回归模型的的 i概念
lo g it(p ) ln 1 P P =01 X 1 m X m
2.检验二:
检验模型中某β是否对Y有作用。
检验假设: H0:j 0 H1:j 0
检验统计量:主要为Wald检验(SAS软件)
2 ( bj )2
例;
Sbj
ν=1的χ2
公式16-13
在大样本时 ,2 三 方(法0.0 结8.8 1 果5 5一6)致2。33.86
例表16-1资料,对各x的β做检验(wald检验) 参数 β估计值 标准误 Chi-Squa Pr 常数-0.9099 0.1358 44.8699 .0001 吸烟 0.8856 0.1500 34.8625 .0001 饮酒 0.5261 0.1572 11.2069 .0008
第一节 logistic回归 一、基本概念
1.变量的取值 logistic回归要求应变量(Y)取值为分类变量
(两分类或多个分类)
1 Y0
出现阳性(发 结病 果、有效、死亡 出现阴性(未 结发 果病、无效) 、存
自变量(Xi)称为危险因素或暴露因素,可为连续变 量、等级变量、分类变量。 可有m个自变量X1, X2,… Xm
第十六章 logistic回归分析
logistic回归为概率型非线性 回归模型,是研究分类观察 结果(y)与一些影响因素(x) 之间关系的一种多变量分析 方法
问题提出:
医学研究中常研究某因素存在条件下某结果是否 发生?以及之间的关系如何?
因素(X)
疾病结果(Y)
x1,x2,x3…XK
发生
Y=1
不发生 Y=0
或
1 p (y 1 /x 1 ,x 2 x k ) 1 e ( 0 1 x k .... k x k )
2.模型中参数的意义
ln1 PP=01X1
Β0(常数项):暴露因素Xi=0时,个体发病 概率与不发病概率之比的自然对数比值。
ln 1 P P (y (y 1/0x/x 0)0)=0
i 的含义:某危险因素,暴露水平变化时,即
Xi=1与Xi=0相比,发生某结果(如发病)优势 比的对数值。
lnORlnPP01 //((11PP10)) logitP1 logitP0
P1(y=1/x=1)的概率 P0(y=1/x=0)的概率
(0 1x1)(0 x0) 1x1
ORe
OR P1/1 (P1)od1d P0/1 (P0) od0d
ln L 0 (X 1 ) 5 8 5 .3 2 6 lo g it(p )01 x 1
G 2 [lnL (X 1,X 2)lnL (X 1) 2 ( 5 7 9 .7 1 1( 5 8 5 .3 2 6 )] 1 1 .2 3
G >3.84,p<0.05,说明调整吸烟因素 后,饮酒与食管癌有关系。
方程如下:
线形 关系
y lo i(t p g )01 x 1 Y~(-∞至+∞)
截距(常数)
回归系数
在有多个危险因素(Xi)时
多个变量的logistic回归模型方程的线性表
达:
公式16-2
lo g l 1 n P iP t = (0 p 1 X 1 ) 2 X 2 m X m
通常用最大似然函数 (maximum likelihood estimate, MLE)估计β, 由统计软件包完成。(讲义259页)
ORe
如X=1,0两分类,则OR的1-α可信区间
估计公式
e(bj u/2Sbj )
S 为回归系数 b j 的标准误
(公式16-10)
例:讲义表16-1资料
一个研究吸烟、饮酒与食道癌关系的病例-对 照资料(886例),试作logistic回归分析。
乙疗法
治疗 原治 预期
原治 预期
人数 愈率 治愈数 愈率 治愈数
普通型 400 60.0 240
65.0 260
重型 400 35.0 140
41.7 167
合计 800
380
427
调整率(标准化率):
P 甲 ' N N iP ii 8 30 84 0 0.5 7% P乙'8402075.34%
X1疗法(甲=0,乙=1)X2病情(轻=1,重 =0) Y疗效(Y=1有效,Y=0无效)
e 0 x P (y 0 /x 1 ) 1 1 e 0 x 1 p 1
e0 p0P (y1/x0)e 0 1e0 P (y 0 /x 0 ) 1 1 e 0 1 p 0
logistic回归模型方程的线性表达
对logistic回归模型的概率(p)做logit变
换, logit(p)ln( p ) 1p
3.多元线性回归结果 Yˆ 不能回答“发生
与否” logistic回归方法补充多元线性回归的不足
Logistic回归方法
该法研究是 当 y 取某值(如y=1)发生的概率(p)与
某暴露因素(x)的关系。
p ( y 1 /x ) f( x ) ,即 p f( x )
P(概率)的取值波动0~1范围。 基本原理:用一组观察数据拟合Logistic模型, 揭示若干个x与一个因变量取值的关系,反映y 对x的依存关系。
变量 β
Sb Waldχ2 P 标准β’ OR
常数 -4.705 1.54 9.30 0.0023
年龄 0.924 0.477 3.76 0.0525 0.401 2.52
X5 1.496 0.744 4.04 4.46
0.0443 0.406
X6 3.136 1.249 6.30 0.0121 0.703 23.06
例1
例:
表5-4甲乙两疗法某病治愈率%比较
病型
愈
率 普通型
65.0 重型
41.7 合计
47.5
病人 数
300 100 400
甲疗法 治愈 治愈
数
率
180 60.0
35 35.0
215 53.8
乙疗法 病人 治愈 治
数
数
100
65
300
125
400
190
表5-5直接法计算标准化治愈率
病型 标准
甲疗法
变量的赋值
1 Y
0
食 管 癌 患 者 对 照 : 非 食 管 癌
1 X1 0
吸烟
1
不吸烟 X2 0
饮酒 不饮酒
经logistic回归计算后得 b0 =-0.9099, b1 =0.8856, b2
方程=表0.5达2:61,
ln (p) 0 .9 0 9 9 0 .8 8 5 6 x 1 0 .5 2 6 1 x 2 1 p
Odds Ratio Estimates Point 95% Wald
Effect Estimate Confidence Limits 吸烟x1 2.424 1.807 3.253 饮酒x2 1.692 1.244 2.303
似然比检验(讲义)
对某个β做检验,检验统计量(G)
G 2 (lnL 1lnL 0)
1.对建立的整个模型做检验。 ln (p) 0 .9 0 9 9 0 .8 8 5 6 x 1 0 .5 2 6 1 x 2 1 p
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr 似然比 68.5457 2 <.0001 计分检验 67.0712 2 <.0001 Wald检验 64.2784 2 <.0001
