基于weber能量法的直齿轮时变啮合刚度数值计算
一种考虑温度影响的直齿圆柱齿轮时变啮合刚度计算方法与流程

一种考虑温度影响的直齿圆柱齿轮时变啮合刚度计算方法与流程下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!并且,本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by theeditor.I hope that after you download them,they can help yousolve practical problems. The document can be customized andmodified after downloading,please adjust and use it according toactual needs, thank you!In addition, our shop provides you with various types ofpractical materials,such as educational essays, diaryappreciation,sentence excerpts,ancient poems,classic articles,topic composition,work summary,word parsing,copy excerpts,other materials and so on,want to know different data formats andwriting methods,please pay attention!考虑温度影响的直齿圆柱齿轮时变啮合刚度计算方法及流程一、引言在机械传动系统中,直齿圆柱齿轮是广泛应用的重要部件。
齿轮变位对啮合刚度影响的数值仿真

齿轮变位对啮合刚度影响的数值仿真王志钦王晓笋王施茹巫世晶(武汉大学动力与机械学院,湖北武汉430072)摘要为探究齿轮变位对啮合刚度的影响,采用两种不同方法计算齿轮啮合刚度:一是运用Pro/E二次开发对齿轮进行参数化建模,并将齿轮模型导入Abaqus软件进行有限元仿真计算,根据计算结果得出不同变位系数齿轮的时变啮合刚度曲线;二是基于能量法的解析法计算得出时变啮合刚度曲线。
结果表明,在一定范围内,齿轮啮合的重合度随齿轮变位系数的增大而减小,齿轮的平均啮合刚度随齿轮变位系数的增大而减小。
关键词齿轮变位啮合刚度参数化建模接触有限元能量法Numerical Simulation of the Influence of Gear Modification on the Meshing StiffnessWang Zhiqin Wang Xiaosun Wang Shiru Wu Shijing(School of Power and Mechanical Engineering,Wuhan University,Wuhan430072,China)Abstract In order to explore the influence of gear modification on the meshing stiffness,two different methods are used to calculate the gear meshing stiffness.First,the gear is parametrically modeled by Pro/E sec⁃ondary development,and the gear model is imported into Abaqus software for finite element simulation calcula⁃tion.The time-varying mesh stiffness curve is obtained through data processing.Second is based on the energy method of the analytical method to calculate the time-varying mesh stiffness curve.The results show that within a certain range,the coincidence degree of gear meshing decreases with the increase of gear displacement coeffi⁃cient and the average meshing stiffness of the gear decreases as the gear displacement coefficient increases.Key words Gear modification Meshing stiffness Parametric modeling Contact finite element Ener⁃gy method0引言齿轮传动系统具有承载能力强、传动效率高、工作可靠、寿命长和结构紧凑等特点,是机械传动装置中最重要、应用最广泛的一种传动形式[1]。
一种齿轮时变啮合刚度的通用计算方法

一种齿轮时变啮合刚度的通用计算方法李大磊; 李安民; 张二亮【期刊名称】《《重庆理工大学学报(自然科学版)》》【年(卷),期】2019(033)010【总页数】6页(P61-66)【关键词】时变啮合刚度; 势能法; 有限元法; 装配误差【作者】李大磊; 李安民; 张二亮【作者单位】郑州大学机械工程学院郑州450001【正文语种】中文【中图分类】TH132.4齿轮箱是现代机械传动系统中的重要部件之一,由于其恒定的传动比、大功率及高效率等特点,被广泛应用于各类工程机械。
振动与噪声是评价齿轮箱工作性能的主要指标,齿轮在传动过程中啮合刚度的时变特性是引起齿轮箱产生振动与噪声的主要原因[1]。
因此,齿轮时变啮合刚度的计算研究得到了国内外学者的广泛关注。
齿轮时变啮合刚度的计算方法主要分为3类:基于势能原理的解析法[2-7]、基于有限元的数值计算方法[8-11]和解析有限元法[12-15]。
势能解析法的基本思想是视轮齿为基圆上的变截面悬臂梁,并根据弹性力学理论,推导齿轮啮合过程中储存在轮齿中的应变能,进而计算齿轮啮合刚度。
Yang等[2]考虑了轮齿的弯曲势能、径向压缩势能以及轮齿接触赫兹能,计算了齿轮的啮合刚度;Wu等[3]进一步考虑了齿轮啮合时的剪切变形能,完善了解析算法;Wan和Xiang等[4-5]考虑了轮齿基体的应变能和齿轮基圆与齿根圆不重合的情况,提高了解析法的计算精度,但也增加了算法的复杂度。
随着有限元软件几何建模能力的日益增强,基于数值分析的齿轮啮合刚度计算也得到了重视和发展,其主要途径有:① 通过有限元方法分析计算轮齿接触部位沿啮合方向的位移量,提取啮合轮齿的法向载荷,根据刚度的定义计算齿轮的啮合刚度,如:唐进元等[8]应用有限元分析软件构建螺旋锥齿轮模型并计算出法向接触力和综合弹性变形量,得到单齿啮合刚度和多齿综合啮合刚度;Song等[9]利用有限元法研究了渐开线行星轮系的扭转刚度。
② 在准静态条件下(转速很低),通过计算齿轮副的传递误差,获得齿轮的啮合刚度。
浅论齿轮刚度的计算全文

浅论齿轮刚度的计算齿轮刚度计算首先要计算轮齿变形,计算轮齿变形的方法一般有3种,分别是材料力学,数学弹性力学和有限元法.在所有计算方法中,最早使用的是材料力学方法.根本方法是先将轮齿简化为弹性根底上的变截面悬臂梁,即轮齿任意啮合点处的方向力的作用下产生的法向弹性变形.这主要是由三局部组成:1〕齿部的弯曲剪切变形,2〕由齿根弹性引起的附加变形,3〕啮合点处的接触变形.主要就非常简便而且利于计算,只是需要先对轮齿模型进行简化,不同的轮齿模型需要有不同的方式进行计算.比拟常见的方法有Weber-Bnschek法,石川法和数值方法等.Weber-Bnschek方法的依据是轮齿在法向力Fn作用下,沿啮合线方向发生了变形,这时法向力所做的功应与变形能相等.石JI法是把齿轮简化为梯形和矩形模型进行计算.数学弹性力学方法的根本思想就是把齿轮轮齿的受载变形问题简化为一个半无限体的受载变形,利用保角映射函数把轮齿的曲线边界C映射为直边边界场.这样可以应用弹性力学中平面问题的复变函数解答求解集中力作用下的半无限体的位移场,再由此确定受载轮齿的位移场.康凝用有限元方法计算了渐开线直齿内齿轮的轮齿刚度,其最后得到的渐开线直齿内齿轮的载荷作用点的轮齿刚度的计算公式为[2-3]:1 C=(E/)(入x+1)B(x+1)CX10-9(3)式中:=0.0011Z2-0.1381Z+12.8587B=-0.0056Z+1.0483C=-0.0002Z+0.0376计算由轮齿任意啮合点k处的法向弹性变形6k以后,单个轮齿的啮合刚度即可求由kk=Fk6k,应该说明的是轮齿在不同的啮合点啮合时6k是不同的,因此轮齿的啮合刚度也是啮合点位置的函数.一对轮齿i啮合时,在啮合力的作用下,主从动轮齿都会发生弹性变形.假设将单个轮齿视为一个弹簧,那么相啮合的一对轮齿可视为一对串联的弹簧.设k1,k2分别为主、从动齿轮在啮合点处法线方向的啮合刚度,那么一对轮齿的综合啮合刚度kvi为kvi=k1k2k1+k2,由于k1,k2是啮合点位置的函数,因此齿对i的综合啮合刚度kvi也是齿对啮合刚度的函数,具有时变性.图1啮合刚度K(X)曲线为啮入点、B为啮由点、C为节点,重合度为£.由于在一般情况下,直齿轮的重合度1w£2,因此在一对齿啮合和两对齿啮合的交替,一对齿是一组串联的弹簧,两对齿就是两组这样串联的弹簧并联,那么kv=kv1+kv2o斜齿轮啮合刚度计算与直齿轮啮合刚度的计算不同,由于在斜齿轮传动中轮齿啮合的接触线是倾斜的,接触线上的载荷分布1是非均匀的,因此斜齿轮轮齿不能简化为二维平面问题,必须作为三维问题进行分析,因而其弹性变形的计算就更为复杂.梅泽清彦得由求斜齿轮刚度计算公式:k=[(-0.166XbH+0.08]X(B0-5)+44.5]Xexp[0.322X(B0-5)+(0.23XbH-23.26)Xx3](4)有限元法是现在计算斜齿轮轮齿最有效的方法.它主要有3类,一种是使用有限元法求在给定载荷作用下的轮齿变形,第二 种是通过对大量计算结果的回归分析得到变形计算公式,第三种 是采纳接触问题有限元法,考虑多对轮齿的同时啮合及轮齿的接 触变形,进行轮齿的啮合接触分析.一般在进行齿轮刚度计算时,可以采纳简化的方法来进行计 算.图2轮齿刚度曲线CQ=20.80-49.5/z1-38.8/z2+40(5)C=CE=13.83-31.5/z1-20.5/z2+40Ex/Ez(6)CD=CB=20.86-53.7/z1-44.7/z2+25a/Zz(7)式中:CCBCDCE 分另I 」代表图中 z1z2x1x2分别代表齿轮1,2的齿数和变位系数,Ex 、*分别为两齿轮变位系数之和与齿数之和.CD 代表平均双对齿啮合刚 度,Cr 代表整个啮合过程的综合啮合刚度,其计算式如下x1/z1+x2/z2)+60入/ (x1/z1+x2/z2)+45 (x1/z1+x2/z2)+45 BDE 点的啮合刚度,CD=C+CD=CB+CE=0.5 (C+CD+CB+CE)(8)Cr=CD(£优1)+0.5(CD+CQ)(2-£a)(9)利用上述公式进行计算得(变位系数均为0),通过上述公式,可以计算由齿轮对的啮合刚度.(郑州华信学院机电工程学院)。
基于Workbench的齿轮啮合振动分析

基于Workbench的齿轮啮合振动分析李添翼;武志斐;王铁;王道勇【摘要】齿轮的振动能快速、全面地反映其运转状态,有限元法能更为准确模拟轮齿啮合过程,求解啮合刚度进而研究其振动响应.联合利用Hypermesh 和Workbench对啮合齿轮模型进行有限元仿真,得出齿轮啮合时变刚度.利用MATLAB求解齿轮系统动力学模型得到动力学响应.通过机械式封闭功率流试验台对仿真结果进行试验验证.试验结果表明仿真分析得到的结果与试验结果基本相符.利用有限元方法求解啮合刚度进而研究振动响应有更高的可靠性和准确性,为齿轮振动的研究及改善提供方法参考.%The vibration of gear reflects its operating state quickly and comprehensively.The finite element method can be used to simulate the gear meshing process more accurately, and solve the meshing stiffness and study its vibration response.The finite element simulation of the meshing gear model is carried out by using Hypermesh and Workbench, and the time-varying meshing stiffness can be solved.The dynamic response of the gear meshing process is obtained by using MATLAB.Results of simulation agree well with those of experiments by mechanical test-bed of closed flow.The results of research turn out that the finite element method is reliable and accurate to solve the meshing stiffness and the result can be used to study the dynamic response, and the method is provided for the research and improvement of the gear vibration.【期刊名称】《科学技术与工程》【年(卷),期】2017(017)024【总页数】6页(P49-54)【关键词】有限元方法;时变啮合刚度;动力学模型;齿轮振动特性【作者】李添翼;武志斐;王铁;王道勇【作者单位】太原理工大学齿轮研究所,太原 030024;太原理工大学齿轮研究所,太原 030024;太原理工大学齿轮研究所,太原 030024;太原理工大学齿轮研究所,太原030024【正文语种】中文【中图分类】TH132.41齿轮系统是各种机器和机械装备中应用最为广泛的动力和运动传递装置,其力学行为和工作性能对整个机器有重要的影响[1]。
基于渐开线齿轮精确建模的啮合刚度的数值计算

{ 0 l t o o t h p r o i f l e mo d fc i ti a o n t o r e d u c e t h e v i b r a t i o n d u r i n g t h e ea g r m e s h i n g .
i s m a d e o n t h e n u me r i c a l i n t e g r lf a o r mu l a b se a d o n We b e r e n e r g y me t h o d, a n d t h e 0’ D o n n e l l c o e f ic f i e n t s i s i n t r o d u c e d w i t h
机 械 设 计 与 制 造
Ma c h i n e r y De s i g n & Ma n u f a c t u r e
ห้องสมุดไป่ตู้
第 2期 2 0 1 3年 2月
基 于渐开线齿轮精确建模 的啮合 刚度 的数值计算
张奎 晓 , 胡 鹏, 张 义民
1 1 0 8 1 9 ) ( 东北大学 机械工程与 自动化学院, 辽宁 沈阳
摘
要: 给 出 了基 于齿轮 加 工 工 艺的 渐 开线 齿轮 精 确建模 的方 程 , 对基 于 We b e r 能量 法 的数值 积 分公 式 进行 了详 细 的推
导, 基体变形量引入 了0’ D o n n e l l 的基体变形 因子, 并采用最大变形条件定义基点 M。 通过计算单对轮齿啮合的总变形量 来计算啮合 刚度。编制 了 M a t l a b计算程序 , 将得到的数值计算结果与 1 S 0 6 3 3 6 、 日本机械学会得到结果相 比较 , 该方法得 出的数据误 差小、 准确, 可以很好 的指导齿廓修形 , 以减少齿轮啮合过程 中的振动冲击。 关键词 : 渐开线齿轮 ; 精确建模 ; We b e r 能量法; 啮合刚度 ; I S O6 3 3 6
一种直齿圆柱齿轮内啮合齿轮副时变啮合刚度的计算方法[发明专利]
![一种直齿圆柱齿轮内啮合齿轮副时变啮合刚度的计算方法[发明专利]](https://img.taocdn.com/s3/m/e1edf2aa336c1eb91b375d83.png)
专利名称:一种直齿圆柱齿轮内啮合齿轮副时变啮合刚度的计算方法
专利类型:发明专利
发明人:孙亚林,何国林,丁康
申请号:CN201811449533.2
申请日:20181130
公开号:CN109783840A
公开日:
20190521
专利内容由知识产权出版社提供
摘要:本发明公开了一种直齿圆柱齿轮内啮合齿轮副时变啮合刚度的计算方法。
该方法包括以下步骤:S1、基于势能法分别计算直齿圆柱齿轮内啮合齿轮副中内齿轮、外齿轮的单齿啮合刚度;S2、由几何关系分别将内外齿轮单齿啮合刚度转变为关于外齿轮角位移的函数;S3、通过齿轮角位移判断出齿轮对啮合所处阶段是单啮合还是双啮合,并基于刚度串并联理论,计算直齿圆柱齿轮内啮合齿轮副时变啮合刚度值。
本发明一方面可弥补现阶段齿轮在内啮合下时变刚度计算方法的空缺,另一方面在发挥解析法高精度优势的基础上结合齿轮几何信息可简化求解提高计算效率。
申请人:华南理工大学
地址:510640 广东省广州市天河区五山路381号
国籍:CN
代理机构:广州粤高专利商标代理有限公司
更多信息请下载全文后查看。
基于改进能量法的行星齿轮时变啮合刚度求解

基于改进能量法的行星齿轮时变啮合刚度求解
张慧玲
【期刊名称】《机械传动》
【年(卷),期】2018(42)8
【摘要】时变啮合刚度是研究行星齿轮故障机理的重要参数。
在考虑基圆与齿根圆之间关系的情况下,以齿数为参量,建立了一个改进的悬臂梁模型。
对行星齿轮的各对齿轮啮合的时变啮合刚度进行分情况讨论,在考虑轮体刚度的基础上,应用能量法求解更加准确的轮齿时变啮合刚度。
在该方法的基础上,分别求解太阳轮、行星轮、内齿圈存在裂纹时各对轮齿啮合的时变啮合刚度,并分别探究裂纹深度和裂纹角度对时变啮合刚度的影响。
该研究为掌握行星齿轮故障机理提供了理论帮助。
【总页数】7页(P91-97)
【关键词】行星齿轮;啮合刚度;裂纹;故障激励
【作者】张慧玲
【作者单位】新乡职业技术学院汽车技术系
【正文语种】中文
【中图分类】TH132.41
【相关文献】
1.行星齿轮系统时变啮合刚度研究 [J], 李宽阳;陈彩凤;张亮;胡永安
2.基于改进能量法的直齿轮时变啮合刚度计算 [J], 马辉;逄旭;宋溶泽;杨健
3.基于全齿廓普遍方程的齿轮时变啮合刚度改进算法 [J], 黄金凤;张飞斌;崔玲丽;
陈雄飞
4.基于全齿廓的行星齿轮点蚀故障时变啮合刚度计算模型 [J], 蒋超阳;王衍学;赖俊杰
5.基于有限元法的疲劳点蚀斜齿轮时变啮合刚度分析与试验研究 [J], 李金锴;陈勇;臧立彬;毕旺洋;杨小朋
因版权原因,仅展示原文概要,查看原文内容请购买。
Weber能量法求裂纹齿轮轴的啮合刚度

第6期2021年6月机械设计与制造Machinery Design&Manufacture101W e ber能量法求裂纹齿轮轴的啮合刚度冯今昭,高鹏,刘畅(辽宁石油化工大学机械工程学院,辽宁抚顺113001)摘要:在进行齿轮相关的分析时常用有限元法和集中质量法,对集中质量法分析裂纹齿轮时需要的刚度参数进行计算。
不同于传统的梯形、矩形等齿型简化算法,Weber能量法可以直接加入裂纹因素进行不规则轮齿的刚度计算,避免了简化环节带来的计算误差。
下文以齿轮轴为研究对象,首先用Matlab对轴段进行有限元分析得出轴的变形状态,并结合有限元分析结果对产生齿根裂纹的轮齿用Weber法计算啮合刚度,将其结果与完整轮齿的啮合刚度比对,证明了该方法的可行性,解决了裂纹齿轮集中质量法分析中的刚度参数获取困难的问题。
关键词:Weber能量法;裂纹轮齿;轮齿刚度中图分类号:TH16;TH132.413文献标识码:A文章编号:1001-3997(2021)06-0101-04Calculation of Meshing Stiffness of Cracked Gear Shaftby Extended Weber Energy MethodFENG Jin-zhao,GAO Peng,Liu Chang(School of Mechanical Engineering,Liaoning Shihua University,Liaoning Fushun113001,China)Abstract:The f inite element method and the lumped mass method are commonly used in gear-related analysis,when using the lumped mass method to analyze cracked gears,it is necessary to calculate the gear tooth stiffness in advance,it is aim to calculate the stiffness of c rack tooth.Different f rom the simplified tooth profile algorithm like trapezoidal and rectangular9the Weber energy method can add crack f actors directly to calculate the stiffness of i rregular teeth.This method can avoid the calculation errors caused by simplification,it takes the gear shaft as the research object.Firstly use matlab to do f inite element analysis of t he shaft and f ind the deformation state of t he shaft9then calculate the meshing stiffness of g ear teeth by weber method.Finally,compare the result with the meshing stiffness of t he complete tooth,prove the f easibility of t his method.This method solves the problem that difficult to obtain stiffness in the analysis of c oncentrated mass method f or cracked gears.Key Words:Weber Energy Method;Crack Wheel Gear;Tooth Stiffness1引言在齿轮啮合的一系列研究中,行星轮系的研究占有很大比重。
计及摩擦影响的直齿轮时变啮合刚度计算方法

计及摩擦影响的直齿轮时变啮合刚度计算方法
黄康;汪涛;熊杨寿;赵韩;马加奇;吴其林
【期刊名称】《应用力学学报》
【年(卷),期】2017(34)3
【摘要】针对现有的齿轮时变啮合刚度计算模型不考虑时变摩擦影响的问题,以一种弹流润滑状态下的时变摩擦系数为基础,通过推导齿轮副的齿面速度、滚滑比、卷汲速度、赫兹应力,得到了弹流润滑状态下,考虑单双齿啮合情况下载荷变化的时变摩擦系数;并应用于势能法刚度计算模型,提出了计及齿面摩擦的时变啮合刚度计算方法。
计算结果表明:齿面摩擦对时变啮合刚度有很大的影响;在节点位置,不存在相对滑动,刚度和不考虑摩擦情况一致;在单双齿啮合区的临界点,单齿刚度存在突变的现象;随着载荷的增大,时变啮合刚度减小。
该方法同样适合于其它摩擦模型,从而为后续进行考虑摩擦影响的齿轮动力学分析提供新的时变啮合刚度理论基础。
【总页数】6页(P564-569)
【作者】黄康;汪涛;熊杨寿;赵韩;马加奇;吴其林
【作者单位】合肥工业大学机械工程学院
【正文语种】中文
【中图分类】TH123.3
【相关文献】
1.齿轮故障对直齿轮副时变啮合刚度的影响研究
2.基于几何学和势能法的直齿轮副时变啮合刚度精确建模及应用
3.考虑时变摩擦的直齿轮副啮合刚度计算及其影响
因素分析4.直齿圆柱齿轮齿根裂纹扩展仿真及齿轮时变啮合刚度分析5.基于Matlab的渐开线变位直齿轮时变啮合刚度计算分析
因版权原因,仅展示原文概要,查看原文内容请购买。
一种面齿轮传动时变啮合刚度数值计算方法
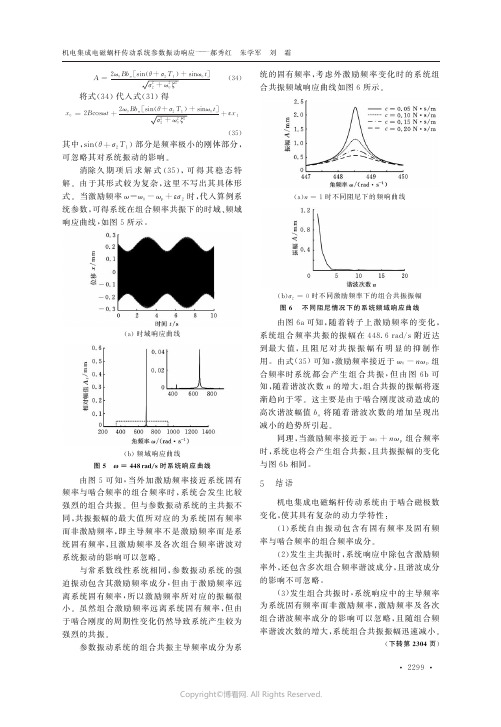
A =2ω0B b n [s i n (θ+σ2T 1)+s i n ω0t ]σ22+ω20ζ2(34)将式(34)代入式(31)得x 0=2B c o s ωt +2ω0B b n [s i n (θ+σ2T 1)+s i n ω0t ]σ22+ω20ζ2+εx 1(35)其中,s i n (θ+σ2T 1)部分是频率极小的刚体部分,可忽略其对系统振动的影响㊂消除久期项后求解式(35),可得其稳态特解㊂由于其形式较为复杂,这里不写出其具体形式㊂当激励频率ω=ω0-ωp +εσ2时,代入算例系统参数,可得系统在组合频率共振下的时域㊁频域响应曲线,如图5所示㊂(a)时域响应曲线(b)频域响应曲线图5 氊=448r a d /s 时系统响应曲线由图5可知,当外加激励频率接近系统固有频率与啮合频率的组合频率时,系统会发生比较强烈的组合共振㊂但与参数振动系统的主共振不同,共振振幅的最大值所对应的为系统固有频率而非激励频率,即主导频率不是激励频率而是系统固有频率,且激励频率及各次组合频率谐波对系统振动的影响可以忽略㊂与常系数线性系统相同,参数振动系统的强迫振动包含其激励频率成分,但由于激励频率远离系统固有频率,所以激励频率所对应的振幅很小㊂虽然组合激励频率远离系统固有频率,但由于啮合刚度的周期性变化仍然导致系统产生较为强烈的共振㊂参数振动系统的组合共振主导频率成分为系统的固有频率,考虑外激励频率变化时的系统组合共振频域响应曲线如图6所示㊂(a )n =1时不同阻尼下的频响曲线(b )σ2=0时不同激励频率下的组合共振振幅图6 不同阻尼情况下的系统频域响应曲线由图6a 可知,随着转子上激励频率的变化,系统组合频率共振的振幅在448.6r a d /s 附近达到最大值,且阻尼对共振振幅有明显的抑制作用㊂由式(35)可知,激励频率接近于ω0-n ωp 组合频率时系统都会产生组合共振,但由图6b 可知,随着谐波次数n 的增大,组合共振的振幅将逐渐趋向于零㊂这主要是由于啮合刚度波动造成的高次谐波幅值b n 将随着谐波次数的增加呈现出减小的趋势所引起㊂同理,当激励频率接近于ω0+nωp 组合频率时,系统也将会产生组合共振,且共振振幅的变化与图6b 相同㊂5 结语机电集成电磁蜗杆传动系统由于啮合磁极数变化,使其具有复杂的动力学特性:(1)系统自由振动包含有固有频率及固有频率与啮合频率的组合频率成分㊂(2)发生主共振时,系统响应中除包含激励频率外,还包含多次组合频率谐波成分,且谐波成分的影响不可忽略㊂(3)发生组合共振时,系统响应中的主导频率为系统固有频率而非激励频率,激励频率及各次组合谐波频率成分的影响可以忽略,且随组合频率谐波次数的增大,系统组合共振振幅迅速减小㊂(下转第2304页)机电集成电磁蜗杆传动系统参数振动响应郝秀红 朱学军 刘 霜一种面齿轮传动时变啮合刚度数值计算方法雷敦财 唐进元中南大学高性能复杂制造国家重点实验室,长沙,410083摘要:准确计算时变啮合刚度是齿轮动力学研究的基础㊂提出了一种面齿轮传动时变啮合刚度数值计算新方法㊂以直齿圆柱齿轮为例,建立合理的有限元模型,得到直齿圆柱齿轮的时变啮合刚度曲线,并将其与I S O 6336方法计算结果进行对比,验证了该啮合刚度计算方法的正确性及有限元模型的精确性㊂应用该数值计算方法,研究面齿轮传动时变啮合刚度变化规律,得到了精确的面齿轮传动时变啮合刚度曲线㊂研究结果为面齿轮传动的动力学分析及设计提供参考㊂关键词:啮合刚度;有限元;面齿轮;传动误差中图分类号:T H 132.4 D O I :10.3969/j.i s s n .1004-132X.2014.17.006AC a l c u l a t i o n M e t h o do fM e s hS t i f f n e s s f o rF a c eG e a rT r a n s m i s s i o nS ys t e m L e i D u n c a i T a n g J i n yu a n S t a t eK e y L a b o r a t o r y o fH i g h ‐p e r f o r m a n c eC o m p l e x M a n u f a c t u r i n g,C e n t r a l S o u t hU n i v e r s i t y ,C h a n gs h a ,H u n a n ,410083A b s t r a c t :An e w m e t h o d f o r c a l c u l a t i n g t h em e s h s t i f f n e s s o f g e a r t r a n s m i s s i o n s ys t e m w h i c hw a s t h e f o u n d a t i o no f g e a rd y n a m i c sa n a l y s i sw a s p r o po s e db a s e do nf i n i t ee l e m e n tm e t h o d .T ov a l i d a t e t h e c a l c u l a t i o nm e t h o d ,a s p u r g e a r p a i rw a s a d o pt e d t o c a l c u l a t e t h em e s h s t i f f n e s s .T h e r e s u l t s s h o w t h a t t h e m e s hs t i f f n e s s i s i d e n t i c a lw i t ht h a tf r o m I S O 6336m e t h o d .S u b s e q u e n t l y ,t h e p r o p o s e d m e t h o dw a s u s e d t o c a l c u l a t e t h em e s h s t i f f n e s s o f f a c e g e a r t r a n s m i s s i o n s y s t e m ,a n d t h e c h a n ge l a w of t h em e s h i ng s t i f f n e s s f o r th e f a c e g e a r t r a n s mi s s i o ns y s t e m w a s r e s e a r c h e d .T h e r e s e a r c hr e s u l t s p r o v i d e t h eb a s i c c o n d i t i o n f o r d y n a m i c s a n a l y s i s a n dd e s i gno f f a c e g e a r t r a n s m i s s i o n .K e yw o r d s :m e s hs t i f f n e s s ;f i n i t e e l e m e n t ;f a c e g e a r ;t r a n s m i s s i o ne r r o r 收稿日期:2013 03 11基金项目:国家重点基础研究发展计划(973计划)资助项目(2011C B 706800);中南大学学位论文创新项目(2011S S X T 095)0 引言作为机械装置中的一个重要零部件,齿轮传动被广泛应用于航空㊁风电㊁汽车等领域㊂随着工作转速的逐步提高,齿轮传动的动力学性能越来越受到设计㊁制造及使用者的重视[1]㊂相比较其他类型的传动系统,齿轮传动系统的主要不同之处在于:它不但会因为外部激励而产生动态响应,同时会因为传动过程中啮合齿对数的改变㊁轮齿的弹性变形及轮齿误差而导致啮合刚度发生变化,从而产生轮齿动态啮合力,且此种由于啮合综合刚度的时变性引起的动态激励是齿轮传动中最主要的动态激励形式之一㊂因此,确定齿轮传动的时变啮合刚度一直是齿轮动力学研究中的重要问题[2‐3]㊂对于圆柱齿轮的啮合刚度计算问题,已有较多的学者进行过深入研究,得到了一些比较成熟的计算方法[4‐5]㊂对于面齿轮及螺旋锥齿轮等结构相对复杂的齿轮传动形式的啮合刚度计算问题,由于其齿面为复杂曲面,要准确计算时变啮合刚度存在较大难度,因此相关研究文献较少㊂G o s s e l i n 等[6]基于有限条法给出了计算螺旋锥齿轮刚度的方法,但也只得到了沿齿高和齿长方向的位移曲线,并没有得到刚度曲线㊂M e n n e m等[7]使用有限单元法计算了不同载荷下轮齿接触柔度,获得了时变刚度㊂面齿轮传动是近二十年才真正发展起来的一种主要用于航空领域的齿轮传动形式[8‐12],针对其啮合刚度的计算方法,目前尚未见文献报道㊂在面齿轮的动力学研究中,齿轮啮合刚度都采用经过傅里叶变换后的一次正余弦函数来近似,与实际啮合刚度存在比较大的差异㊂有学者研究发现,采用近似时变啮合刚度得到的系统动态因子比采用实际啮合刚度时大,而且不能有效地得到系统在低频阶段的动态响应㊂因此,采用近似时变啮合刚度来拟合实际啮合刚度研究齿轮传动系统动力学行为,并不能正确反映齿轮系统的动态特性㊂本文提出了一种新的齿轮传动时变啮合刚度数值计算方法㊂首先以直齿圆柱齿轮为例,建立合理的有限元模型,得到直齿圆柱齿轮时变啮合刚度曲线,并与I S O 6336[13]方法计算结果进行对比,说明该啮合刚度计算方法的正确性及有限元模型的精确性;然后应用该啮合刚度计算方法,研究面齿轮传动时变啮合刚度变化规律,得到精确的面齿轮传动时变啮合刚度曲线㊂研究结果为面齿轮传动的动力学分析及设计提供参考㊂中国机械工程第25卷第17期2014年9月上半月1 齿轮传动啮合刚度计算方法在齿轮运转过程中,轮齿之间的啮合作用可以简化为一个在啮合线方向上的时变弹簧,弹簧刚度等于该时刻的啮合刚度,如图1所示㊂图中,图1 啮合刚度示意图ω为主动轮转速,R b p ㊁R b g 分别为主从动轮基圆半径,K m 为啮合刚度,T 为负载扭矩,L O A (l i n e o f a c t i o n )表示啮合线㊂齿轮啮合刚度的一般表达式为K n =F n /δn(1)其中,F n 为法向接触力;δn 为法向综合弹性变形,它应包括由于局部赫兹接触产生的接触弹性变形量δH ㊁轮齿弯曲产生的接触位置的位移δF ㊁轮毂变形产生的接触位置的位移δR ㊁轴和支撑结构变形对接触点位置的影响量δA ㊂由于考虑轴㊁轴承及支撑结构变形会使问题过于复杂,故本文暂只考虑δH ㊁δF 及δR ,因此可以得到δn =∑pi =1δH i+∑p i =1δF i +∑pi =1δR i(2)在齿轮传动过程中,由于轮齿受载变形及齿轮误差,从动轮转动位置会偏离其不考虑受载变形及齿轮误差时所应处的理想转动位置㊂齿轮传递误差e T在1958年被H a r r i s 定义为 从动轮实际转动位移与理想转动位移之差”[14],如图2所示,其一般表达式为e T =θg -z pz gθp (3)式中,θp ㊁θg 分别为主从动轮转角;z p ㊁z g 分别为主从动轮齿数㊂假设齿轮没有承受载荷,此时轮齿没有弹性变形,但是由于轮齿误差的存在,依旧会产生无负载传递误差e N L T㊂在齿轮传动的加载接触分析中,由于存在几何模型误差㊁有限元网格划分产生的几何误差以及网格划分产生的尺侧间隙,故无负载传递误差是不可避免的㊂无负载传递误差导致齿轮啮合过程中轮齿产生刚性位移,该位移在计算轮齿受载变形时必须减除㊂同时,为了方便理解,将传递误差转换成啮合线方向上的位移,因此可以得到齿轮副在一定负载下的受载传递误差e L T一般表达式:e L T (θp ,T )=R b g (θg -z pz gθp )(4)图2 传递误差计算示意图由此可以得到轮齿啮合过程中综合弹性变形δn =e L T (θp ,T )-e N L T(5)故而,齿轮啮合刚度计算的一般表达式为K m =TR b g δn(6)2 啮合刚度数值计算方法验证由于结构的复杂性,面齿轮传动啮合刚度计算方法目前尚未见相关文献报道㊂为了说明上述啮合刚度计算方法的正确性及有限元模型的精确性,本文先以直齿圆柱齿轮为例进行计算,并将其与I S O 6336:2006方法的计算结果进行对比㊂2.1 有限元建模基于唐进元等[15]提出的齿轮虚拟加工制造方法,采用表1所示齿轮传动参数,得到高精度的直齿圆柱齿轮三维几何装配模型㊂表1 直齿圆柱齿轮几何参数小轮齿数25大轮齿数33模数(mm )4.0压力角(°)25齿宽(mm )28齿顶高系数1.0齿根高系数1.25刀具齿顶圆角半径(mm )1.2为了节约计算成本,忽略轴及轴承等支撑结构的影响㊂鉴于静力学分析中质量分布不会影响分析结果,因此在模型中仅考虑可能产生啮合的5对轮齿,其他部分简化为一个轮缘圆柱,并分别在大小轮内孔面与其对应旋转轴线上的参考点之间建立刚性耦合约束,在大轮耦合节点施加负载扭矩,在小轮耦合节点施加转动位移,以此来模拟小轮通过与大轮啮合抵消大轮反抗扭矩带动大轮运转的实际工况,边界条件如图3所示㊂对可能发生接触的5对轮齿进行局部网格细化,齿厚方一种面齿轮传动时变啮合刚度数值计算方法雷敦财 唐进元向最小网格尺寸为0.037mm ,齿高方向最小网格尺寸为0.142mm ,总节点数为180462,总单元数为158592㊂网格模型如图4所示㊂图3圆柱齿轮模型边界条件示意图图4 圆柱齿轮模型网格划分将大轮及小轮的工作齿面定义为接触对,暂不考虑摩擦对啮合刚度的影响㊂采用隐式静力学分析算法,输出接触力及大小轮的绕自身旋转轴线的旋转位移历程曲线㊂2.2 直齿圆柱齿轮啮合刚度计算理论上,标准渐开线齿轮的静态传递误差为零,但考虑到有限元模型不可避免地存在网格划分带来的几何误差,且有限元分析时必须要有完整的边界约束条件,因此,本文近似以大轮负载为13.2N ㊃m 时的传递误差作为无负载传递误差,该负载与额定负载660N ㊃m 相比较小,产生的轮齿接触变形及弯曲变形可以忽略不计㊂基于上述齿轮传动啮合刚度计算方法,计算得到该齿轮副时变啮合刚度曲线,并与I S O 6336:2006给出的计算公式得到的结果进行对比,如图5所示㊂图5 啮合刚度对比图由图5可知,所提出的方法得到的时变啮合刚度曲线与I S O 6336:2006方法计算结果相比,平均值相对误差为5.86%㊂因此可以证明所提出的齿轮传动时变啮合刚度计算方法的正确性,同时说明有限元模型已足够精确㊂3 面齿轮传动啮合刚度数值计算3.1 有限元模型面齿轮传动几何参数如表2所示,其中面齿轮轮缘系数定义为面齿轮轮齿高度与面齿轮齿根平面到面齿轮齿底平面之间距离的比值㊂表2 面齿轮传动几何参数小轮齿数19面齿轮齿数73插齿刀齿数21模数(mm )4.5压力角(°)20面齿轮齿宽(mm )29.4小轮齿宽(mm )30.0刀具齿顶高系数1.25刀具齿根高系数1.0面齿轮轮缘系数3.14 采用上述有限元建模方法,将可能发生接触的5对轮齿之外的部分简化为一个阶梯圆柱,忽略轴及轴承等支撑结构变形对面齿轮传动接触位置的影响,在小轮内孔面与位于其旋转轴线上的参考节点之间建立刚性耦合约束,在面齿轮与位于其旋转轴线上的参考节点之间建立刚性耦合约束,即将轴及轴承简化为刚性支撑,在小轮参考节点施加旋转位移,在面齿轮参考节点施加负载扭矩,以模拟小轮通过与大轮啮合作用带动大轮抵消负载扭矩而运转的实际工况,边界条件设置如图6所示㊂图6 面齿轮模型边界条件示意图中国机械工程第25卷第17期2014年9月上半月对于未修形的直齿面齿轮传动而言,面齿轮由齿顶进入啮合,由齿根退出啮合,其理论接触轨迹在齿高方向大致呈一条竖直线㊂经齿轮接触分析得到,该对齿轮理论接触轨迹大致位于半径为164.4mm 处,因此对面齿轮靠近内端的一半轮齿及配对小轮对应啮合位置进行网格细化,其网格密度与上述直齿圆柱齿轮模型中细化部分网格密度基本一致,总节点数为242312,总单元数为201420,网格模型如图7所示㊂接触定义㊁材料参数及分析步设置与上述直齿圆柱齿轮有限元模型保持一致㊂此时对于单个面齿轮轮齿而言,约有54个计算点㊂图7 面齿轮模型网格模型3.2 面齿轮传动啮合刚度数值计算采用上述有限元模型,在大轮额定载荷为1536.8N ㊃m 条件下,取负载为38.42N ㊃m 时的传递误差为无负载传递误差㊂额定载荷作用下各齿对法向接触力历程曲线如图8所示㊂由图8可知,该对齿轮副存在双齿接触区(D T )及三齿接触区(T T ),并且,由于在三齿接触区时前一对轮齿即将退出啮合,后一对轮齿刚刚进入啮合,齿间载荷分布非常不均匀,因此该对轮齿法向接触力最大值出现在该啮合区域㊂图8 法向接触力历程曲线(T =1536.8N ㊃m )进一步根据式(6)计算得到面齿轮传动时变啮合刚度曲线,如图9所示㊂由图9可以看出,面齿轮传动时变啮合刚度曲线类似于一条正弦曲线,呈现明显的周期特征,其最小值大致出现在三齿接触区内前后两对轮齿受载相同的位置(图8中点A 处)㊂此时该两对轮齿约各承担总载荷的6.44%,中间一对轮齿约承担总载荷的87.15%,齿间载荷的分布非常不均匀,并且此时前后两对轮齿分别在靠近齿根及齿顶位置接触,因此该啮合位置齿轮副弹性综合变形最大,啮合刚度最小㊂啮合刚度最大值出现在双齿啮合区内参与啮合的两对轮齿受载相同的位置(图8中点B 处),此时该两对轮齿各承担总载荷的50%,载荷分布最为均匀,因此该啮合位置齿轮弹性综合变形最小,啮合刚度最大㊂图9 时变啮合刚度曲线(T =1536.8N ㊃m )4 结论(1)提出了一种新的齿轮传动时变啮合刚度数值计算方法,并给出了相应的加载接触分析有限元建模方法㊂(2)以直齿圆柱齿轮为例,采用该方法得到该齿轮副时变啮合刚度曲线,与I S O 6336方法计算结果相对比,验证了上述方法的正确性及所建有限元模型的精确性㊂(3)应用该啮合刚度数值计算方法得到了面齿轮传动载荷分布规律及时变啮合刚度曲线㊂参考文献:[1] F e r n a n d e zRA ,V i a d e r oF ,I gl e s i a sM ,e t a l .A M o d e l f o r t h e S t u d y o fM e s h i n g S t i f f n e s s i nS p u rG e a rT r a n s -m i s s i o n s [J ].M e c h a n i s ma n d M a c h i n eT h e o r y,2013,61:30‐58.[2] C h e nS i y u ,T a n g J i u y u a n ,L u oC a i w a n g.E f f e c t s o f t h eG e a rT o o t h M o d i f i c a t i o no nt h e N o n l i n e a rD y -n a m i c s o fG e a rT r a n s m i s s i o nS y s t e m [J ].A d v a n c e d M a t e r i a l sR e s e a r c h ,2010,97:2764‐2769.[3] C h e nS i y u ,T a n g J i u y u a n ,L u oC a i w a n g,e t a l .N o n l i n e a r D y n a m i cC h a r a c t e r i s t i c so fG e a r e dR o t o rB e a r i n g S y s -t e m sw i t hD y n a m i cB a c k l a s ha n dF r i c t i o n [J ].M e c h a -n i s ma n dM a c h i n eT h e o r y ,2011,46(4):466‐478.[4] Z h a n g J ,E s a t I ,S h iY.L o a d A n a l y s i sw i t h V a r -y i n g M e s hS t i f f n e s s [J ].C o m pu t e r s &S t r u c t u r e s ,1999,70(3):273‐80.[5] P i m s a r n M ,K a z e r o u n i a nK.E f f i c i e n tE v a l u a t i o no fS p u rG e a rT o o t hM e s hL o a dU s i n g P s e u d o ‐i n t e r f e r -e n c eS t if f n e s sE s t i m a t i o n M e t h o d [J ].M e c h a n i s m a n d M a c h i n eT h e o r y,2002,37(8):769‐786.一种面齿轮传动时变啮合刚度数值计算方法雷敦财 唐进元。
一种求解直齿圆柱齿轮啮合刚度的方法

一种求解直齿圆柱齿轮啮合刚度的方法
张建云;丘大谋
【期刊名称】《西安建筑科技大学学报:自然科学版》
【年(卷),期】1996(028)002
【摘要】在ISO标准计算啮合刚度的基础上,用抛物线拟合单齿副的啮合刚度,经过叠加求得直啮合刚度的数学表达式,并对刚度波动函数进行付立叶展开,使之在振动分析的应用中极为方便。
【总页数】4页(P134-137)
【作者】张建云;丘大谋
【作者单位】不详;不详
【正文语种】中文
【中图分类】TH132.417
【相关文献】
1.一种斜齿轮啮合刚度的简易求解方法 [J], 张强;刘晓宇;汪玉兰;何鸣
2.直齿圆柱齿轮啮合刚度计算方法研究 [J], 陈思宇;谭儒龙;郭晓东;阚磊
3.直齿圆柱齿轮啮合刚度计算方法研究 [J], 陈思宇;谭儒龙;郭晓东;阚磊
4.直齿圆柱齿轮齿根裂纹扩展仿真及齿轮时变啮合刚度分析 [J], 万志国;訾艳阳;曹宏瑞
5.直齿圆柱齿轮啮合刚度的影响因素及其规律性 [J], 王龙宝;王贵成;王志
因版权原因,仅展示原文概要,查看原文内容请购买。
一种斜齿圆柱齿轮时变啮合刚度解析计算方法[发明专利]
![一种斜齿圆柱齿轮时变啮合刚度解析计算方法[发明专利]](https://img.taocdn.com/s3/m/b0c622b96429647d27284b73f242336c1fb93050.png)
(10)申请公布号(43)申请公布日 (21)申请号 201410799904.5(22)申请日 2014.12.18G06F 17/50(2006.01)(71)申请人西安交通大学地址710049 陕西省西安市咸宁路28号(72)发明人訾艳阳 万志国 曹宏瑞 贺王鹏(74)专利代理机构西安通大专利代理有限责任公司 61200代理人陆万寿(54)发明名称一种斜齿圆柱齿轮时变啮合刚度解析计算方法(57)摘要本发明涉及一种斜齿圆柱齿轮时变啮合刚度解析计算方法。
该方法首先沿斜齿圆柱齿轮齿宽方向把斜齿圆柱齿轮划分成一系列交错排列的直齿轮,然后基于材料力学中的梁变形能理论,利用势能法计算其中任一直齿轮的啮合刚度,最后利用累计积分的思想沿斜齿圆柱齿轮齿宽方向进行积分,得到斜齿圆柱齿轮的啮合刚度。
本发明所述斜齿圆柱齿轮时变啮合刚度解析计算方法既能够显著提高斜齿圆柱齿轮时变啮合刚度的计算效率,又能够充分保证时变啮合刚度的计算精度。
利用本方法计算得到的时变啮合刚度可以有效用于斜齿轮传动系统的振动响应机理研究。
(51)Int.Cl.(19)中华人民共和国国家知识产权局(12)发明专利申请权利要求书3页 说明书10页 附图3页(10)申请公布号CN 104573196 A (43)申请公布日2015.04.29C N 104573196A1.一种斜齿圆柱齿轮时变啮合刚度解析计算方法,其特征在于:包括以下步骤:1)直齿轮啮合刚度计算:1-1)沿斜齿圆柱齿轮齿宽方向将斜齿圆柱齿轮划分成一系列交错排列的直齿轮;1-2)基于材料力学中的梁变形能理论,利用势能法计算任一直齿轮的啮合刚度;2)基于累计积分原理的斜齿圆柱齿轮啮合刚度计算:2-1)利用累计积分原理,沿斜齿圆柱齿轮齿宽方向对步骤1-2)得到的任一直齿轮的啮合刚度进行积分,然后计算得到斜齿圆柱齿轮啮合刚度。
2.根据权利要求1所述一种斜齿圆柱齿轮时变啮合刚度解析计算方法,其特征在于:所述步骤1-1)具体包括以下步骤:沿斜齿圆柱齿轮齿宽方向将斜齿圆柱齿轮划分成多个厚度为dy 的微段,从而使斜齿圆柱齿轮看作是由一系列交错排列的直齿轮组合而成。
齿轮时变啮合刚度计算研究 杨雄威 夏宗朝

齿轮时变啮合刚度计算研究杨雄威夏宗朝发表时间:2018-03-05T15:12:56.943Z 来源:《基层建设》2017年第33期作者:杨雄威夏宗朝[导读] 摘要:本文分析总结了齿轮啮合刚度的常见计算方法。
广东明阳风电产业集团有限公司广东中山 528437摘要:本文分析总结了齿轮啮合刚度的常见计算方法。
提出了一种接触有限元法计算时变啮合刚度且验证了其准确性,并分析了齿轮产生冲击振动的缘由。
关键词:齿轮;时变啮合刚度;接触有限元;冲击振动0.引言齿轮刚度的精确计算是轮齿修形、动态特性、故障诊断、寿命预测以及齿轮参数优化设计等研究的前提条件。
有必要对圆柱齿轮刚度的计算作进一步的探讨和研究。
日本机械学会[1]上齿轮的刚度定义为如下:齿轮刚度为使一对或几对同时啮合的精确齿轮在1mm齿宽上产生1um绕度所需的啮合线上的载荷。
设齿轮宽度为b(mm),齿轮所受的作用于齿廓的法向载荷为Fn(N),齿轮的总变形为δ(um),齿轮上的载荷集度,即齿轮单位齿宽的载荷ω为:ω=Fn/b;齿轮的柔度为:q=δ/ω; 则齿轮的刚度为:c=1/q= Fn/b/δ。
齿轮的单齿刚度的定义为单齿在外载荷的作用下,接触力与位移的比例系数,其表达式为:Kn=Fn/un;其中Fn为作用于轮齿齿廓曲面的接触力;un为齿轮的综合弹性变形量,其中包括了弯曲变形、剪切变形和接触变形等。
单齿对啮合刚度的定义为两个齿轮啮合过程中的综合刚度,两个齿轮以串联的方式耦合形成的单齿接触对,通过单齿刚度可以计算出啮合刚度为:K=K1*K2/(K1+ K2);其中1,2分别为小齿轮和大齿轮。
齿轮啮合综合刚度定义为多对齿轮接触时,各对齿轮间形成并联的耦合关系,所以齿轮啮合综合刚度的表达式为:Km=K1+K2+…+Kn 所以齿轮啮合综合刚度主要与单齿的弹性变形、单齿对齿轮的综合弹性变形以及齿轮重合度有关。
因此只要求得齿轮的弹性变形,即可确定齿轮啮合综合刚度。
1.几种常用齿轮刚度计算方法的比较目前关于齿轮轮齿啮合变形的计算方法大致有三种,即材料力学方法、弹性力学方法和数值方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于weber能量法的直齿轮时变啮合刚度数值计算
文章标题:基于Weber能量法的直齿轮时变啮合刚度数值计算
一、引言
在机械传动系统中,直齿轮是一种常见的机械元件,其传动效率和稳
定性对整个系统的性能起着至关重要的作用。
而直齿轮啮合刚度则是
评估其传动性能的重要参数之一。
本文将基于Weber能量法,探讨直齿轮时变啮合刚度的数值计算方法,以期为工程实践提供有益的参考。
二、Weber能量法概述
Weber能量法是一种广泛应用于机械系统分析的方法,其核心思想是通过对系统的能量变化进行分析,推导出系统的基本动力学方程。
在
直齿轮系统中,Weber能量法可以有效地描述啮合过程中的能量转换和传递关系,从而为计算啮合刚度提供了理论基础。
三、直齿轮啮合刚度的基本概念
啮合刚度是指在一定啮合几何条件下,轴向载荷改变时,啮合点处齿
轮轴向位移与载荷之比的物理量。
直齿轮啮合刚度是对直齿轮在啮合
过程中的刚度特性进行描述的重要参数,其大小和变化对于齿轮传动的动态特性具有重要影响。
四、基于Weber能量法的直齿轮时变啮合刚度数值计算
1. 通过Weber能量法建立直齿轮系统的动力学模型,考虑齿轮的轴向位移、载荷和啮合几何条件等因素。
2. 根据啮合接触几何关系和实际工况条件,确定直齿轮系统的能量变化规律。
3. 建立直齿轮系统的动力学方程,利用Weber能量法推导出直齿轮啮合刚度的数值计算公式。
4. 通过数值计算的方法,对直齿轮啮合刚度在不同工况下的变化规律进行分析和评估。
5. 结合实际工程案例,验证基于Weber能量法的直齿轮时变啮合刚度数值计算的有效性和准确性。
五、个人观点和总结
基于Weber能量法的直齿轮时变啮合刚度数值计算,是一种理论与实践相结合的方法,可以有效地描述直齿轮系统的动力学特性,为工程实践提供了有益的参考。
在实际工程中,我们可以根据该方法计算并优化直齿轮系统的传动性能,提高其工作效率和稳定性。
对于未来的研究方向,我认为可以进一步探讨基于Weber能量法的直齿轮系统动
态响应特性分析,为直齿轮传动系统的设计和优化提供更多的理论支
持和实用方法。
总结而言,基于Weber能量法的直齿轮时变啮合刚度数值计算是一个具有重要理论和实践意义的课题,其研究成果将有助于提高直齿轮传
动系统的设计水平和工作性能,促进机械传动技术的发展和应用。
以上是根据您的要求,撰写的关于“基于Weber能量法的直齿轮时变啮合刚度数值计算”的文章,希望能为您提供有益的帮助。
如果需要
进一步修改或补充其他内容,请随时告知。
六、直齿轮时变啮合刚度
数值计算的工程应用
基于Weber能量法的直齿轮时变啮合刚度数值计算方法在工程实践中具有广泛的应用价值。
该方法可以为直齿轮传动系统的设计优化提供
重要的理论支持。
通过对直齿轮系统的动力学特性进行分析和计算,
可以更准确地预测系统的传动性能,为工程师在设计阶段提供重要参考,从而优化传动系统的结构和工作参数,提高其工作效率和稳定性。
基于Weber能量法的直齿轮时变啮合刚度数值计算方法还可以为直齿轮传动系统的动态特性分析提供重要的数据支持。
在实际工程中,传
动系统的动态特性对系统的可靠性和稳定性具有重要影响。
通过对直
齿轮系统的啮合刚度进行数值计算和分析,可以更准确地描述系统的
动态响应特性,为工程师在系统设计和工作过程中提供科学依据,从
而确保传动系统的安全可靠运行。
基于Weber能量法的直齿轮时变啮合刚度数值计算方法还可以为直齿轮系统的故障诊断和故障预测提供重要的技术支持。
通过对系统的啮合刚度进行实时监测和分析,可以及时发现系统的异常情况,预测可能发生的故障,从而采取相应的维护和修复措施,确保传动系统的长期稳定运行。
七、进一步探讨
基于Weber能量法的直齿轮时变啮合刚度数值计算方法为直齿轮传动系统的设计、优化和故障诊断提供了重要的理论和实践支持。
然而,目前的研究主要集中在静态和定态情况下的啮合刚度计算,对于动态工况下的啮合刚度变化特性尚未深入研究。
未来的研究方向可以进一步探讨基于Weber能量法的直齿轮系统动态响应特性分析,以及在实际工程应用中的更多案例研究。
另外,随着工程技术的不断发展和进步,新材料、新工艺的应用也将对直齿轮传动系统的设计和性能提出新的挑战。
基于Weber能量法的直齿轮时变啮合刚度数值计算方法也需要不断进行更新和改进,以适应新材料、新工艺和新工程要求。
八、总结
基于Weber能量法的直齿轮时变啮合刚度数值计算方法是一个具有重要理论和实践意义的课题。
该方法不仅可以为直齿轮传动系统的设计和优化提供重要的理论支持,还可以为系统的动态特性分析和故障诊断提供重要的技术支持。
未来的研究方向应重点关注直齿轮系统动态响应特性分析和在实际工程应用中的更多案例研究,同时也需要不断更新和改进该方法,以适应新材料、新工艺和新工程要求。
相信通过持续的研究和改进,基于Weber能量法的直齿轮时变啮合刚度数值计算方法将为直齿轮传动技术的发展和应用做出重要贡献。
