高二数学下册暑假作业及答案(Word版)
高二下数学暑假作业答案(Word版)

高二下数学暑假作业答案(2021最新版)作者:______编写日期:2021年__月__日【一】1、已知点P是抛物线y2=4x上的动点,那么点P到点A(-1,1)的距离与点P到直线x=-1距离之和最小值是。
若B(3,2),则最小值是2、过抛物线y2=2px(p>0)的焦点F,做倾斜角为的直线与抛物线交于两点,若线段AB的长为8,则p=3、将两个顶点在抛物线上,另一个顶点是此抛物线焦点的正三角形个数记为n,则n=_________4、在抛物线y=x2+ax-5(a≠0)上取横坐标为x1=-4,x2=2的两点,经过两点引一条割线,有平行于该割线的一条直线同时与该抛物线和圆相切,则抛物线的顶点坐标是_______【二】1.(本题满分12分)有6名同学站成一排,求:(1)甲不站排头也不站排尾有多少种不同的排法:(2)甲不站排头,且乙不站排尾有多少种不同的排法:(3)甲、乙、丙不相邻有多少种不同的排法.2.(12分)甲、乙两人参加一次英语口语考试,已知在编号为1~10的10道试题中,甲能答对编号为1~6的6道题,乙能答对编号为3~10的8道题,规定每位考生都从备选题中抽出3道试题进行测试,至少答对2道才算合格,(1)求甲答对试题数的概率分布及数学期望;(2)求甲、乙两人至少有一人考试合格的概率.【三】1.直线与圆的位置关系为()A.相切B.相交但直线不过圆心C.直线过圆心D.相离2.方程x2+y2+2ax-by+c=0表示圆心为C(2,2),半径为2的圆,则a、b、c的值依次为()A.2、4、4;B.-2、4、4;C.2、-4、4;D.2、-4、-43圆心在轴上,半径为1,且过点(1,2)的圆的方程为()4.直线3x-4y-4=0被圆(x-3)2+y2=9截得的弦长为()5.M(x0,y0)为圆x2+y2=a2(a>0)内异于圆心的一点,则直线x0x+y0y=a2与该圆的位置关系是()A.相切B.相交C.相离D.相切或相交。
2021年高二下学期暑假作业数学文试题(20) 含答案

2021年高二下学期暑假作业数学文试题(20) 含答案一、选择题1.复数在复平面内对应的点在( )A.第一象限B.第二象限C.第三象限D.第四象限2、两个变量与的回归模型中,分别选择了4个不同模型,它们的相关指数如下 ,其中拟合效果最好的模型是( )A.模型1的相关指数为0.98B.模型2的相关指数为0.80C.模型3的相关指数为0.50D.模型4的相关指数为0.25 3、设)(,,,3.0log ,2,3.023.02的大小关系为则c b a c b a ===A .B .C .D . 4.如果,则实数( )A.2B.3C.4D.65.设随机变量的分布列为,则实数的值为( ) A.1 B. C. D. 二、填空题6.某市为增强市民的节约粮食意识,面向全市征召务宣传志愿者现从符合条件的志愿者中随机抽取100名按年龄分组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45],得到的频率分布直方图如图所示.若用分层抽样的方法从第3,4,5组中共抽取了12名志愿者参加l0月16日的“世界粮食日”宣传活动,则从第4组中抽取的人数为 .7.若点在以坐标原点为圆心的圆上,则该圆在点处的切线方程为 . 三、解答题 8. 已知函数(1)写出函数的递减区间; (2)求函数在区间上的最值.9.某校的教育教学水平不断提高,该校记录了xx年到xx年十年间每年考入清华大学、北京xx1xx2 (xx10)多于20人的概率;(Ⅱ)根据前5年的数据,利用最小二乘法求出y关于x的回归方程y=x+,并计算xx年的估计值和实际值之间的差的绝对值.=,=﹣.10.(本小题满分12分)已知是函数的一个极值点,其中,(1)求与的关系式;(2)求的单调区间;答案1-5 ACAAC 6、 4 7、8.解:解:令,得,,(1)由表可得函数的递减区间为.(2)由表可得,当时,函数有极大值;当时,函数有极小值9.解:(Ⅰ)设考入清华大学、北京大学的人数和至少有一年多于15人的事件为A 则P(A)=1﹣=;(Ⅱ)由已知数据得=3,=8,所以b==2.6,a=8﹣2.6×3=0.2所以:y=2.6x+0.2.则xx年的估计值与实际值之间的差的绝对值为|2.6×8+0.2﹣22|=1.10.(本小题满分12分)解(I)因为是函数的一个极值点,所以,即,所以(II)由(I)知,=当时,有,当变化时,与的变化如下故有上表知,当时,在单调递减,在单调递增,在上单调递减.o38674 9712 霒20899 51A3 冣33678 838E 莎^29744 7430 琰39483 9A3B 騻32423 7EA7 级N?Z36719 8F6F 软27150 6A0E 樎 G。
2021年高二下学期暑假作业数学文试题(35) 含答案

2021年高二下学期暑假作业数学文试题(35)含答案一、选择题:1.(xx秋•霍邱县校级期末)如果方程表示双曲线,那么实数m的取值范围是()A.m>2 B.m<1或m>2 C.﹣1<m<2 D.﹣1<m<1或m>22. 9.设曲线y=在点(3,2)处的切线与直线ax+y+3=0垂直,则a等于()A.2 B. C.—D.-23. 曲线y=x3﹣3x2+1在点(1,﹣1)处的切线与坐标轴围成的三角形的面积为()A.B.C.D.4.(xx•郴州二模)执行如图所示的程序框图,则输出的S值是()A.﹣1 B. C. D.45.(xx秋•霍邱县校级期末)过双曲线x2﹣y2=1的右焦点且与右支有两个交点的直线,其倾斜角范围是()A.[0,π)B.(,)C.(,)∪(,)D.(0,)∪(,π)二、填空题:6. 为净化水质,向一个游泳池加入某种化学药品,加药后池水中该药品的浓度C(单位:)随时间t(单位:h)的变化关系为,则经过______h后池水中药品浓度达到最大. 7.(xx•沙坪坝区校级一模)已知椭圆(a>b>0),A为左顶点,B为短轴一顶点,F为右焦点且AB⊥BF,则这个椭圆的离心率等于.三、解答题:.8.(12分)(xx•安徽)某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50],[50,60],…,[80,90],[90,100](1)求频率分布图中a的值;(2)估计该企业的职工对该部门评分不低于80的概率;(3)从评分在[40,60]的受访职工中,随机抽取2人,求此2人评分都在[40,50]的概率.9.已知函数.(Ⅰ)当a=3时,求函数f(x)的单调区间;(Ⅱ)若过点可作函数y=f(x)图象的三条不同切线,求实数a的取值范围.10.(12分)(xx•安徽)设椭圆E的方程为=1(a>b>0),点O为坐标原点,点A的坐标为(a,0),点B的坐标为(0,b),点M在线段AB上,满足|BM|=2|MA|,直线OM的斜率为.(1)求E的离心率e;(2)设点C的坐标为(0,﹣b),N为线段AC的中点,证明:MN⊥AB.答案1. D2. C3. C4. D5. B6.: 2 .7.:.8. 解:(1)因为(0.004+a+0.018+0.022×2+0.028)×10=1,解得a=0.006;(2)由已知的频率分布直方图可知,50名受访职工评分不低于80的频率为(0.022+0.018)×10=0.4,所以该企业职工对该部门评分不低于80的概率的估计值为0.4;(3)受访职工中评分在[50,60)的有:50×0.006×10=3(人),记为A1,A2,A3;受访职工评分在[40,50)的有:50×0.004×10=2(人),记为B1,B2.从这5名受访职工中随机抽取2人,所有可能的结果共有10种,分别是{A1,A2},{A1,A3},{A1,B1},{A1,B2},{A2,A3},{A2,B1},{A2,B2},{A3,B1},{A3,B2},{B1,B2},又因为所抽取2人的评分都在[40,50)的结果有1种,即{B1,B2},故所求的概率为P=.9.(1)当a=3时,f′(x)=﹣x2+3x﹣2=﹣(x﹣1)(x﹣2),当1<x<2时,f′(x)>0,函数f(x)单调递增;当x<1或x>2时,f′(x)<0,函数f(x)单调递减,所以函数f(x)的单调递增区间为(1,2),单调递减区间为(﹣∞,1)和(2,+∞);(2)设点A(t,﹣t3+t2﹣2t)是函数f(x)图象上的切点,则过点A的切线斜率k=﹣t2+at﹣2,所以过点A的切线方程为y+t3﹣t2+2t=(﹣t2+at﹣2)(x﹣t),因为点(0,﹣)在该切线上,所以﹣+t3﹣t2+2t=(﹣t2+at﹣2)(0﹣t),即t3﹣at2+=0,若过点(0,﹣)可作函数y=f(x)图象的三条不同切线,则方程t3﹣at2+=0三个不同的实数根,令g(t)=t3﹣at2+=0,则函数y=g(t)的图象与x轴有三个不同的交点,g′(t)=2t2﹣at=0,解得t=0或t=,因为g(0)=,g()=﹣a3+,所以令g()=﹣a3+<0,即a>2,所以实数a的取值范围是(2,+∞).10(1)解:设M(x,y),∵A(a,0)、B(0,b),点M在线段AB上且|BM|=2|MA|,∴=2,即(x﹣0,y﹣b)=2(a﹣x,0﹣y),解得x=a,y=b,即M(a,b),又∵直线OM的斜率为,∴=,∴a=b,c==2b,∴椭圆E的离心率e==;(2)证明:∵点C的坐标为(0,﹣b),N为线段AC的中点,∴N(,﹣),∴=(,﹣),又∵=(﹣a,b),∴•=(﹣a,b)•(,﹣)=﹣a2+=(5b2﹣a2),由(1)可知a2=5b2,故•=0,即MN⊥AB.V 30504 7728 眨036755 8F93 输28718 702E 瀮I21743 54EF 哯(26932 6934 椴b!38094 94CE 铎25146 623A 戺。
【最新推荐】201X年高二数学暑假作业答案-实用word文档 (4页)

本文部分内容来自网络整理,本司不为其真实性负责,如有异议或侵权请及时联系,本司将立即删除!== 本文为word格式,下载后可方便编辑和修改! ==201X年高二数学暑假作业答案亲爱的同学们,数学网小编给大家整理了201X年高二数学暑假作业答案,希望能给大家到来帮助。
祝大家暑假愉快!【快乐暑假】201X年高二数学暑假作业答案一.填空题1.A.2.3.3.(1)(4).π.5.212cm4.(1)(2)..6.(2)(4).7.300..8.90°.9.①与③.10.④.30.︒11.12.2:1.13.3.14.若②③④则①.二.解答题π=3148π-38π2;V=52π+4π15. S=60,垂足分别为,,OEF,连结,,OEOFOA,⊥⊥,,PEABPFAC⊥α16.证明:作PO,Θ⎩⊂⎨⊥⇒⎧⊥αα,POABPOAB⎩=⎪⎨=⇒∆≅∆⇒∠=∠⎪⎧⊥⊥∵,PEABPFACPAEPAFRtPAERtPAFAEAFPAPA,⊥又∵ABPE∴平面PEO,⊥AB∴⊥ABOE⊥.同理ACOF,==,,AEAFOAOA∆和RtAOF∆.在RtAOE∴,∆RtAOF≅∆RtAOE∴,∠=∠EAOFAO的平分线上.∠上的射影在BACα即点P在平面17.证明:(1)因为E,F分别是11AB,AC的中点,所以EF//BC,面ABC,⊂面ABC,BC⊄又EF,-所以EF∥ABC平面;(2)因为直三棱柱111ABCABC,⊥面,11BBAD⊥所以1111BBABC,⊥又11ADBC面B,⊥所以111ADBCC面,⊂又11ADAFD平面平面.⊥所以111AFDBBCC,=且11ACAC∏∴是平行四边形11ACAC∴是正方体11AACC-1111ABCDABCDΘ连结1AO,I=18.证明:(1)连结11AC,设11111ACBDO∴又1,OO分别是11,ACAC的中点,11OCAO。
2021年高二下学期暑假作业数学(理)试题(12) 含答案

2021年高二下学期暑假作业数学(理)试题(12)含答案姓名班级学号完成日期家长签字一、选择题1.已知向量,,若,则实数λ的值为()A.﹣4 B.﹣3 C.﹣2 D.﹣12.设复数(是虚数单位),则复数的虚部是()A. B. C. D.3.利用数学归纳法证明“22111(1)1nnaa a a a n Na++*-++++=≠∈-,”,在验证成立时,等号左边是()A. B. C. D.4.某中学为了研究学生的视力和座位(有关和无关)的关系,运用2×2列联表进行独立性研究,经计算K2=7.069,则至少有()的把握认为“学生的视力与座位有关”.附:P(K2≥k0)0.100 0.050 0.025 0.010 0.001k0 2.706 3.841 5.024 6.635 10.828A.95% B.99% C.97.5% D.90%5.由不等式组确定的平面区域记为Ω1,不等式组确定的平面区域记为Ω2,在Ω1中随机取一点,则该点恰好在Ω2内的概率为()A.B.C.D.二填空题6.函数f(x)=x3+ax2+bx+a2在x=1时有极值为10,则a+b的值为7.等于8.将序号分别为1,2,3,4,5的5张参观券全部分给4人,每人至少1张,如果分给同一人的2张参观券连号,那么不同的分法种数是.9.已知F1、F2为双曲线的两个焦点,P为双曲线右支上异于顶点的任意一点,O为坐标原点,下列四个命题:①△PF1F2的内切圆的圆心必在直线x=3上;②△PF1F2的内切圆的圆心必在直线x=2上;③△PF1F2的内切圆的圆心必在直线OP上;④△PF1F2的内切圆必过(3,0).其中真命题的序号是.三计算题10..已知函数f(x)=x3+ax2+bx+c,曲线y=f(x)在点x=0处的切线为l:4x+y﹣5=0,若x=﹣2时,y=f(x)有极值.(1)求a,b,c的值;(2)求y=f(x)在[﹣3,1]上的最大值和最小值.11. 已知各项均为正数的等比数列{a n}的首项a1=2,S n为其前n项和,若5S1,S3,3S2成等差数列.(1)求数列{a n}的通项公式;(2)设b n=log2a n,,记数列{c n}的前n项和T n.若对∀n∈N*,T n≤k(n+4)恒成立,求实数k的取值范围.12.如图,在直三棱柱ABC﹣A1B1C1中,底面△ABC是直角三角形,AB=AC=1,AA1=2,点P是棱BB1上一点,满足=λ(0≤λ≤1).(1)若,求直线PC与平面A1BC所成角的正弦值;(2)若二面角P﹣A1C﹣B的正弦值为,求λ的值.暑假作业12答案1. B2. A3. C4. B5. D6. -77.8. 1.9. 9610. 解:(1)由f(x)=x3+ax2+bx+c,得:f′(x)=3x2+2ax+b,当x=0时,切线l的斜率为﹣4,可得b=﹣4①,当x=﹣2时,y=f(x)有极值,得f′(﹣2)=0,∴12﹣4a+b=0②,由①②得:a=2,b=﹣4,由于切点的横坐标为x=0,∴f(0)=5,∴c=5,∴a=2,b=﹣4,c=5.(2)由(1)得f(x)=x3+2x2﹣4x+5,∴f′(x)=3x2+4x﹣4,令f′(x)=0,解得:x=﹣2或x=,当x变化时,y′,y的值及变化如下表:∴y=f(x)在[﹣3,1]上的最大值为13,最小值为.11. 11. 解:(1)∵5S1,S3,3S2成等差数列,∴2S3=5S1+3S2…即2(a1+a1q+a1q2)=5a1+3(a1+a1q),化简得2q2﹣q﹣6=0…解得:q=2或q=﹣…因为数列{a n}的各项均为正数,所以q=﹣不合题意…所以{a n}的通项公式为:a n=2n.…(2)由b n=log2a n得b n==n…∴c n===﹣…∴T n=1﹣+﹣+…+﹣==…∵≤k(n+4)∴k≥=…=…﹣∵n++5≥2+5=9,当且仅当n=,即n=2时等号成立﹣﹣﹣﹣﹣﹣∴≤…∴k的取值范围[,+∞).…12. 解:(1)如图所示,建立空间直角坐标系,A(0,0,0),B(1,0,0),C(0,1,0),A1(0,0,2),P.=(1,0,﹣2),=(﹣1,1,0),=.设平面A1BC的法向量为=(x,y,z),则,即,取=(2,2,1),设直线PC与平面A1BC所成角为θ,则sinθ====.(2)设二面角P﹣A1C﹣B的平面角为α,由图可知为锐角,∵sinα=,∴cosα==.∵=λ(0≤λ≤1),∴P(1,0,2λ).∴=(1,﹣1,2λ),=(1,0,2λ﹣2).设平面A1CP的法向量为=(x0,y0,z0),则,即,取=(2﹣2λ,2,1),∴===.∴=.化简解得:λ2+8λ﹣9=0,0≤λ≤1,解得λ=1.r38644 96F4 雴X33733 83C5 菅?"#28459 6F2B 漫34095 852F 蔯36774 8FA6 辦33817 8419 萙25165 624D 才。
2021年高二下学期暑假作业数学(理)试题(5) 含答案

2021年高二下学期暑假作业数学(理)试题(5) 含答案一、选择题:1.圆上有10个点,过每三个点画一个圆内接三角形,则一共可以画的三角形个数为( )A .720B .360C .240D .1202. 的展开式中的系数是( )A .42B .35C .28D .213.从甲、乙、丙、丁、戊5个人中选1名组长1名副组长,但甲不能当副组长,不同的选法种数是( )A .6B . 10C .16D .204.从0、2中选一个数字,从1、3、5中选两个数字,组成无重复数字的三位数,其中奇数的个数为( )A .24B .18C .12D .65.分别抛掷2枚质地均匀的硬币,设是事件“第一枚为正面”, 是事件“第二枚为正面”, 是事件“2枚结果相同”.则事件与,事件与,事件与中相互独立的有( )A .0个B .1个C .2个D .3个第Ⅱ卷(共90分)二、填空题(4小题,每小题5分,满分20分,将答案填在答题纸上)6.从黄瓜、白菜、油菜、扁豆4种蔬菜品种中,共选出3种,分别种在不同土质的三块土地上,其中黄瓜必须种植,不同的种植方法共有_________(用数字作答).7. 521(2)() 1x x x -+展开式中项的系数为 . 8.有4名优秀学生全部被保送到甲、乙、丙3所学校,每所学校至少去一名,则不同的报送方案共有________(用数字作答).9. 彩票公司每天开奖一次,从1,2,3,4四个号码中随机开出一个作为中奖号码,开奖时如果开出的号码与前一天相同,就要重开,直到开出与前一天不同的号码为止.如果第一天开出的号码是4,则第五天开出的号码也同样是4的概率为 .三、解答题(本大题共6小题,共70分.)10.如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=4,DC=3,E是PC的中点.(I)证明:PA∥平面BDE;(II)求△PAD以PA为轴旋转所围成的几何体体积.11.(本小题满分12分)已知二项式.(1)若展开式中第5项、第6项与第7项的二项式系数成等差数列,求展开式中二项式系数最大的项的系数;(2)若展开式前三项的二项式系数和等于79,求展开式中系数最大的项.12.(本小题满分12分)乒乓球单打比赛在甲、乙两名运动员间进行,比赛采用7局4胜制(即先胜4局者获胜,比赛结束),假设两人在每一局比赛中获胜的可能性相同.(1)求甲以4比1获胜的概率;(2)求乙获胜且比赛局数多于5局的概率;(3)求比赛局数的分布列.参考答案一、选择题1. D2. D3. C4. B5. D 二、 填空题6. 187.8. 369.三、解答题10.解:(I )连接AC 交BD 于O ,连接EO .∵ABCD 是正方形,∴O 为AC 中点,∵E 为PA 的中点,∴OE ∥PA .又∵OE ⊂平面BDE ,PA ⊄平面BDE ,∴PA ∥平面BDE .(II )过D 作PA 的垂线,垂足为H ,则△PAD 以以PA 为轴旋转所围成的几何体为DH 为半径,分别以PH ,AH 为高的两个圆锥的组合体∵侧棱PD ⊥底面ABCD ,AD ⊆底面ABCD∴PD ⊥AD ,∵PD=4,DA=DC=3,∴PA=5,所以,该几何体的体积为:===.11.(1),解得或,当时,展开式中二项式系数最大的项是和,()()43343344475713512,270222T C x x T C x x ⎛⎫⎛⎫==== ⎪ ⎪⎝⎭⎝⎭当时,展开式中二项式系数最大的项是,(2), 解得,设项系数最大,由于 ,,第11项最大.12.(1)由已知,甲、乙两名运动员在每一局比赛中获胜的概率都是,记“甲以4比1获胜”为事件,则;(2)记“乙获胜且比赛局数多于5局”为事件,因为,乙以4比2获胜的概率为,乙以4比3获胜的概率为,所以.(3)设比赛的局数为,则的可能值为4,5,6,7()()4343134411111142,52282224P X C P X C -⎛⎫⎛⎫⎛⎫====== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,()()35236333561115111562,722221622216P X C P X C --⎛⎫⎛⎫⎛⎫⎛⎫====== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭, 比赛局数的分布列为:229004 714C 煌n }28026 6D7A 浺U 33107 8153 腓,.j37934 942E 鐮。
2021年高二下学期暑假作业数学(理)试题(1) 含答案

2021年高二下学期暑假作业数学(理)试题(1) 含答案一、选择题:1.若复数是纯虚数,是虚数单位,则的值是( )A .2B .1C .-1D . -2 2.从一批产品中取出三件产品,设A 表示事件“三件产品全不是次品”,B 表示事件“三件产品全是次品”,C 表示事件“三件产品至少有一件是次品”,则下列结论正确的是( )A .事件A 与C 互斥B .任何两个事件均互斥C .事件B 与C 互斥D .任何两个事件均不互斥 3.某品牌空调在元旦期间举行促销活动,下面的茎叶图表示某专卖店记录的每天销售量情况(单位:台),则销售量的中位数是( ) A .13 B .14 C .15 D .164.下表提供了某厂节能降耗技术改造后在生产A 产品过程中记录的产量(吨)与相应的生产能耗(吨)的几组对应数据,根据下表提供的数据,求出关于的线性回归方程为,则下列结论错误的是( )A C .回归直线一定过点D .A 产品每多生产吨,则相应的生产能耗约增加吨5.在平面直角坐标系中,满足的点的集合对应的平面图形的面积为;类似的,在空间直角坐标系中,满足,的点的集合对应的空间几何体的体积为( ) A . B . C . D . 二、填空题:6.若复数满足 (为虚数单位),则= . 7.设的展开式的各项系数之和为,二项式系数之和为,若,则的值为________.8.已知{}{}(,)34,0,0,(,)Q x y x y x y A x y x y =+≤≥≥=≤若向区域Q 内随机投入一点P ,则点P 落入区域A 的概率为 . 9.在的展开式中,含项的系数是___________. 三、解答题:10.已知函数f (x )=﹣x 3+3x 2+9x+a . (Ⅰ)求f (x )的单调递减区间;(Ⅱ)若f(x)在区间[﹣2,2]上的最大值为20,求它在该区间上的最小值.11.(10分)某市政府为了确定一个较为合理的居民用电标准,必须先了解全市居民日常用电量的分布情况.现采用抽样调查的方式,获得了n位居民在xx年的月均用电量(单位:度)数据,样本统计结果如下图表:分组频数频率[0,10)0.05[10,20)0.10[20,30)30[30,40)0.25[40,50)0.15[50,60] 15合计n 1(1)求月均用电量的中位数与平均数估计值;(2)如果用分层抽样的方法从这n位居民中抽取8位居民,再从这8位居民中选2位居民,那么至少有1位居民月均用电量在30至40度的概率是多少?(3)用样本估计总体,把频率视为概率,从这个城市随机抽取3位居民(看作有放回的抽样),求月均用电量在30至40度的居民数X的分布列.12、(12分)在底面是矩形的四棱锥P-ABCD 中,PA⊥平面ABCD ,PA =AB =1,BC =2,E 是PD 的中点.(1)求证:平面PDC⊥平面PAD ;(2)求二面角E-AC-D 的余弦值;(3)求直线CP 与平面AEC 所成角的正弦值.高二数学(理科)答案一、选择题:本大题共10个小题,每小题3分,共30分.1-5、AACBB二、填空题:本大题共5小题,每小题4分,共20分.6.;7.14. 4;8.;9. 1139三、解答题:本大题共6小题,共50分.10.解:(I)f′(x)=﹣3x2+6x+9.令f′(x)<0,解得x<﹣1或x>3,所以函数f(x)的单调递减区间为(﹣∞,﹣1),(3,+∞).(II)因为f(﹣2)=8+12﹣18+a=2+a,f(2)=﹣8+12+18+a=22+a,所以f(2)>f(﹣2).因为在(﹣1,3)上f′(x)>0,所以f(x)在[﹣1,2]上单调递增,又由于f(x)在[﹣2,﹣1]上单调递减,因此f(2)和f(﹣1)分别是f(x)在区间[﹣2,2]上的最大值和最小值,于是有22+a=20,解得a=﹣2.故f(x)=﹣x3+3x2+9x﹣2,因此f(﹣1)=1+3﹣9﹣2=﹣7,即函数f(x)在区间[﹣2,2]上的最小值为﹣7.11. (10分)解析:中位数的估计值为;平均数的估计值为+++++= 0.005*10*50.010*10*150.030*10*250.025*10*350.015*10*450.015*10*553312. 【解析】(1) 证明: 略(2)以为原点,、、所在直线为、、轴,建立空间直角坐标系,P(0,0,1) D(0,2,0) C(1,2,0) ∴平面ACD法向量设平面ACE法向量由则取∴∴二面角E-AC-D的余弦值为(3) 设直线CP与平面AEC所成角为35889 8C31 谱27852 6CCC 泌:26428 673C 朼/(H24280 5ED8 廘l}21155 52A3 劣w。
2021年高二下学期暑假作业数学文试题(34) 含答案

2021年高二下学期暑假作业数学文试题(34) 含答案一.选择题1. 8.函数f (x )=x 3﹣3x 2﹣9x+4的单调递减区间是( )A. (﹣3,1) B .(﹣∞,﹣3) C .(﹣1,3) D .(3,+∞)2.在同一平面直角坐标系中,经过伸缩变换 后曲线C 变为曲线, 则曲线C 的方程为A . B. C . D.3. 已知椭圆的参数方程⎩⎪⎨⎪⎧x =2cos t y =4sin t (t 为参数),点M 在椭圆上,对应参数t =π3,点O 为原点,则直线OM 的斜率为 ( )A . B. C . D.4.若点P 是曲线上任意一点,则点P 到直线y=x-2的最小距离为( )A .B .1C .D .25. 12.已知函数,给出下列结论:①的单调递减区间;②当时,直线y=k 与y=f (x)的图象有两个不同交点;③函数y=f(x)的图象与的图象没有公共点.其中正确结论的序号是( )A .①③B .①C .①②D .②③二.填空题6.过抛物线错误!未找到引用源。
的焦点F 的直线交该抛物线于点A .若|AF|=3,则点A 的坐标为7. 若直线l 与曲线C 满足下列两个条件:(i )直线l 在点处与曲线C 相切;(ii )曲线C 在点P附近位于直线l 的两侧,则称直线l 在点P 处“切过”曲线C ,下列命题正确的是___ (写出所有正确命题的编号).①直线在点处“切过”曲线②直线在点处“切过”曲线③直线在点处“切过”曲线④直线在点入“切过”曲线三.解答题8.(本小题12分)为了保护环境,某工厂在政府部门的鼓励下,进行技术改进:把二氧化碳转化为某种化工产品,经测算,该处理总成本y (万元)与处理量x (吨)之间的函数关系可近似的表示为:,且每处理一吨二氧化碳可得价值为20万元的某种化工产品.(Ⅰ)当时,判断该技术改进能否获利?如果能获利,求出最大利润;如果不能获利,则国家至少需要补贴多少万元,该工厂才不会亏损?(1)证明:曲线y=f(x)在x=0处的切线过点(2,1);(2)若f(x)在x=x0处取得极小值, x0(1,3)求实数a的取值范围.10.已知函数(Ⅰ)若函数f(x)的图象在x=0处的切线方程为y=2x+b,求a,b的值;(Ⅱ)若函数在R上是增函数,求实数a取值范围;答案1. C2. B3. B4. C5. A6.7. ③④、8.9. (1)略(2)a10.解:(Ⅰ)∵f(x)=e x﹣x2﹣ax,∴f′(x)=e x﹣x﹣a,∴根据导数的几何意义可得,切线的斜率k=f'(0)=1﹣a,∵切线方程为y=2x+b,则k=2,∴1﹣a=2,解得a=﹣1,∴f(x)=e x﹣x2+x,∴f(0)=1,即切点(0,1),∴1=2×0+b,解得b=1;(Ⅱ)由题意f'(x)>0即e x﹣x﹣a≥0恒成立,∴a≤e x﹣x恒成立.设h(x)=e x﹣x,则h′(x)=e x﹣1.∴h(x)min=h(0)=1,∴a≤1;(Ⅲ)∵g(x)=f(x)﹣(a﹣)x2,∴g(x)=e x﹣x2﹣ax﹣ax2+x2=e x﹣ax2﹣ax,∴g′(x)=e x﹣2ax﹣a,∵x1,x2是函数g(x)的两个不同极值点(不妨设x1<x2),∴e x﹣2ax﹣a=0(*)有两个不同的实数根x1,x2当时,方程(*)不成立则,令,则由p′(x)=0得:当时,方程(*)若有两个解,则所以,.-M 37350 91E6 釦J a21276 531C 匜29759 743F 琿28058 6D9A 涚j26102 65F6 时25209 6279 批。
2021年高二下学期暑假作业数学文试题(6) 含答案
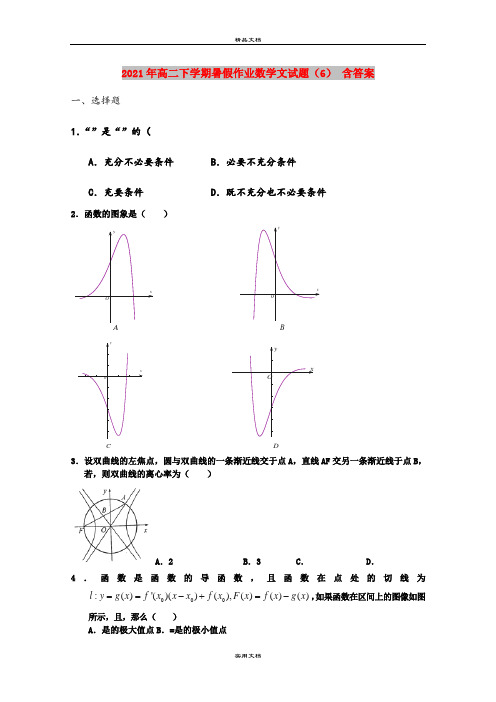
2021年高二下学期暑假作业数学文试题(6) 含答案一、选择题1.“”是“”的(A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 2.函数的图象是( )xy AO x yB Oxy C O xy DO3.设双曲线的左焦点,圆与双曲线的一条渐近线交于点A ,直线AF 交另一条渐近线于点B ,若,则双曲线的离心率为( ) A .2 B .3 C . D .4.函数是函数的导函数,且函数在点处的切线为000:()'()()(),()()()l y g x f x x x f x F x f x g x ==-+=-,如果函数在区间上的图像如图所示,且,那么( )A .是的极大值点B .=是的极小值点C.不是极值点D.是极值点5.若函数,若则( )A. a< b < cB. c < b < aC. c < a < bD. b < a < cB.C.D.二填空题6.已知曲线C:|x|+|y|=m(m>0).(1)若m=1,则由曲线C围成的图形的面积是;(2)曲线C与椭圆有四个不同的交点,则实数m的取值范围是.7.两个命题:“对任意实数都有恒成立”;:“关于的方程有两个不等的实数根”,如果为真命题,为假命题,则实数的取值范围是三解答题8.设命题p:实数x满足x2﹣(a+)x+1<0,其中a>1;命题q:实数x满足x2﹣4x+3≤0.(1)若a=2,且p∧q为真,求实数x的取值范围;(2)若p是q的必要不充分条件,求实数a的取值范围.9.(本小题满分14分)已知(为常数),曲线在点处的切线与直线垂直.(Ⅰ)求的值及函数的单调区间;(Ⅱ)证明:当时,;(Ⅲ)设,若在上单调递减,求实数的取值范围.10.选修4——5 不等式选讲已知函数.(Ⅰ)若,解不等式:;(Ⅱ)若恒成立,求的取值范围.参考答案1.A 2.D 3.A.4.B 5.B 6. (1)2;(2)2<m<3或7.x2=±16y8. 1)1≤x<2(2)3<a分析:(1)命题p:实数x满足x2﹣(a+)x+1<0,其中a>1,解得,由a=2,可得;命题q:实数x满足x2﹣4x+3≤0,解得x范围.利用p∧q为真即可得出.(2)p是q的必要不充分条件,可得q⇒p,且p推不出q,设A=,B=[1,3],则B⊊A,即可得出.解:(1)命题p:实数x满足x2﹣(a+)x+1<0,其中a>1,化为<0,解得,∵a=2,∴;命题q:实数x满足x2﹣4x+3≤0,解得1≤x≤3.∵p∧q为真,∴,解得1≤x<2.∴实数x的取值范围是1≤x<2.(2)p是q的必要不充分条件,∴q⇒p,且p推不出q,设A=,B=[1,3],则B⊊A,∴,解得3<a.∴实数a的取值范围是3<a.9. .(Ⅰ);的单调递增区间为,单调递减区间为;(Ⅱ)见解析;(Ⅲ).(Ⅰ)由题知曲线在点处的切线的斜率为-1,求出在x=0处导数,即可列出关于方程,即可解出值,代入导函数中,再利用导数与函数单调性关系即可求出函数的单调区间;(Ⅱ)构造函数,求出,根据(Ⅰ)知道的单调性,再利用函数性质即可证明所需证明的不等式;(Ⅲ)先求出,由在上单调递减得,≤0对1≤≤3恒成立,转化为二次函数在某个区间上恒成立问题,利用二次函数图像与性质及数形结合思想,列出关于m的不等式,即可求出实数m 的取值范围.试题解析:(Ⅰ)由题意知,曲线在点处的切线的斜率为-1.由,得,,得所以,令,得当时,,单调递减;当时,,单调递增;所以的单调递增区间为,单调递减区间为.(Ⅱ)令,则由(Ⅰ)知,的极小值即最小值,,故在上单调递增,因此,当时,,即;(Ⅲ)法一:由题意知,,因为在上单调递减在恒成立, 10分 图像过点,1(1)1220727(3)962066m F m m F m m ⎧≤⎪'=+-≤⎧⎪∴⇒⇒≤-⎨⎨'=+-≤⎩⎪≤-⎪⎩. 13分 所以满足实数的取值范围为. 14分法二:由题意知,,因为在上单调递减在恒成立, 10分在恒成立,令 只需 11分在上为减函数,所以满足实数的取值范围为. 14分考点:曲线的切线;导数与函数单调性的关系;导数的综合应用10.(Ⅰ);(Ⅱ) 或.【解析】试题分析:(Ⅰ)当时,写出不等式,运用零点分区间的方法,讨论时,当时,当时,去掉绝对值解不等式,然后取并集;(Ⅱ)因为,所以将转化就可以解出来.试题解析:(Ⅰ)当时,0)51)(42(5152)(≥---+⇔+≥-⇒+≥x x x x x x x f 解得:,所以原不等式解集为 (Ⅱ)5)5(5)(+=+--≥++-=a x a x x a x x f ,若恒成立,只需:解得:或考点:不等式求解,恒成立.(•34054 8506 蔆23953 5D91 嶑23507 5BD3 寓y25124 6224 戤e27803 6C9B 沛€31544 7B38 笸J26548 67B4 枴30204 75FC 痼=。
2021年高二数学暑期作业(套卷)(4) Word版含答案

2021年高二数学暑期作业(套卷)(4) Word版含答案一、填空题:本大题共14小题,每小题5分,共70分.请把答案直接填写在答.题卡相应位置上........1.设集合则▲.2.某学校共有师生2 400人,现用分层抽样的方法,从所有师生中抽取一个容量为160的样本,已知从学生中抽取的人数为150,那么该学校的教师人数是____▲____.3.计算复数=▲(为虚数单位).4. 连续抛掷一个骰子(一种各面上分别标有1,2,3,4,5,6个点的正方体玩具)两次,则出现向上点数之和大于9的概率是▲.Array 5.若,则的最小值是___▲______.6.已知直线平面,直线平面,给出下列命题:①若,则;②若,则;③若,则;④若,则.其中正确命题的序号是▲.7.已知满足约束条件,则的最大值为▲.8.程序框图如图(右)所示,其输出结果是____▲____.9.已知条件p:,条件q:,若p是q的充分不必要条件,则实数的取值范围是____▲____.10.若正四棱锥的底面边长为,体积为,则它的侧面积为▲.11.已知抛物线的焦点恰好是双曲线的右焦点,则双曲线的渐近线方程为▲. 12.已知函数的图像的对称中心为,函数的图像的对称中心为,函数的图像的对称中心为,……,由此推测函数的图像的对称中心为▲.13.在△ABC中,角A,B,C的对边分别是a,b,c.已知a=2,3b sin C-5c sin B cos A=0,则△ABC面积的最大值是▲.14.已知是锐角的外接圆圆心,,,则▲ .二、解答题:本大题共6小题,共计90分.请在答题卡指....定区域...内作答,解答时应写出文字说明、证明过程或演算步骤.15.(本题满分14分)如图,斜三棱柱中,侧面是菱形,与交于点,E是AB的中点.(I)求证:平面;(II)若,求证:.16.(本小题满分14分)已知函数的最小正周期为.(I)求.(II)在图中给定的平面直角坐标系中,画出函数在区间上的图象,并根据图象写出其在上的单调递减区间.EOC1 A1B1CBA17. (本小题满分14分)光在某处的照度与光的强度成正比,与光源距离的平方成反比,假设比例系数都为1。
2021年高二下学期暑假作业数学(理)试题(7) 含答案

2021年高二下学期暑假作业数学(理)试题(7)含答案一、选择题1.在(1﹣x3)(1+x)10展开式中,x5的系数是()A.﹣297 B.﹣252 C.297 D.2072.如果命题p(n)对n=k成立(n∈N*),则它对n=k+2也成立,若p(n)对n=2成立,则下列结论正确的是()A.p(n)对一切正整数n都成立B.p(n)对任何正偶数n都成立C.p(n)对任何正奇数n都成立D.p(n)对所有大于1的正整数n都成立3.若执行如图所示的程序框图后,输出的结果是﹣29,则判断框中的整数k的值是()A.3 B.4 C.5 D.64.如图,在正三棱柱ABC﹣A1B1C1中,AB=AA1=2,M、N分别是BB1和B1C1的中点,则实用文档直线AM与CN所成角的余弦值等于()A.B.C.D.5.函数有零点,则实数m的取值范围是()A.B.C.D.二、填空题6.要从已编号1~360的360件产品中随机抽取30件进行检验,用系统抽样的方法抽出样本.若在抽出的样本中有一个编号为105,则在抽出的样本中最小的编号为.7.航空母舰“辽宁舰”将进行一次编队配置科学实验,要求2艘攻击型核潜艇一前一后,2艘驱逐舰和2艘护卫舰分列左、右,同侧不能都是同种舰艇,则舰艇分配方案的方法数为.实用文档8.若(x﹣2)5=a5x5+a4x4+a3x3+a2x2+a1x+a,则a1+a2+a3+a4+a5= .(用数字作答)9.甲乙两人独立地对同一目标各射击一次,命中率分别为0.6和0.5,现已知目标被击中,则它是被甲击中的概率为.三.解答题10.已知三棱柱ABC﹣A′B′C′中,平面BCC′B′⊥底面ABC,BB′⊥A C,底面ABC是边长为2的等边三角形,AA′=3,E、F分别在棱AA′,CC′上,且AE=C′F=2.( 1)求证:BB′⊥底面ABC;(2)在棱A′B′上是否存在一点M,使得C′M∥平面BEF,若存在,求值,若不存在,说明理由;(3)求棱锥A′﹣BEF的体积.实用文档11.已知关于x,y的方程C:x2+y2﹣2x﹣4y+m=0.(1)当m为何值时,方程C表示圆.(2)若圆C与直线l:x+2y﹣4=0相交于M,N两点,且MN=,求m的值.实用文档12.已知圆M的圆心M在x轴上,半径为1,直线,被圆M所截的弦长为,且圆心M在直线l的下方.(I)求圆M的方程;(II)设A(0,t),B(0,t+6)(﹣5≤t≤﹣2),若圆M是△ABC的内切圆,求△ABC的面积S的最大值和最小值.实用文档实用文档答案1. A2. B3. D4. C5. C 6 . 9 7. 32 8. 31. 9. 0.75 10.(1)证明:取BC中点O,连接AO,因为三角形ABC是等边三角形,所以AO⊥BC,又因为平面BCC′B′⊥底面ABC,AO⊂平面ABC,平面BCC′B′∩平面ABC=BC,所以AO⊥平面BCC′B′,又BB′⊂平面BCC′B,所以AO⊥BB′.又BB′⊥AC,AO∩AC=A,AO⊂平面ABC,AC⊂平面ABC.所以BB′⊥底面ABC.…(2)解:显然M不是A′,B′,棱A′B′上若存在一点M,使得C′M∥平面BEF,过M作MN∥AA′交BE于N,连接FN,MC′,所以MN∥CF,即C′M和FN 共面,所以C′M∥FN,实用文档所以四边形C′MNF为平行四边形,所以MN=2,所以MN是梯形A′B′BE的中位线,M为A′B′的中点.即…(3)解:…11. 解:(1)方程C可化为:(x﹣1)2+(y﹣2)2=5﹣m,显然,当5﹣m>0时,即m<5时,方程C表示圆.(2)圆的方程化为(x﹣1)2+(y﹣2)2=5﹣m,圆心C(1,2),半径,则圆心C(1,2)到直线l:x+2y﹣4=0 的距离为,∵,有,∴,解得 m=4.12.解:(Ⅰ)设圆心M(a,0),由已知,得M到l:8x﹣6y﹣3=0的距离为,∴,又∵M在l的下方,∴8a﹣3>0,∴8a﹣3=5,a=1,故圆的方程为(x﹣1)2+y2=1.实用文档(Ⅱ)设AC斜率为k1,BC斜率为k2,则直线AC的方程为y=k1x+t,直线BC的方程为y=k2x+t+6.由方程组,得C点的横坐标为,∵|AB|=t+6﹣t=6,∴,由于圆M与AC相切,所以,∴;同理,,∴,∴,∵﹣5≤t≤﹣2,∴﹣2≤t+3≤1,∴﹣8≤t2+6t+1≤﹣4,∴,.34745 87B9 螹24114 5E32 帲38486 9656 陖33937 8491 蒑33490 82D2 苒29556 7374 獴31620 7B84 箄32235 7DEB 緫v20626 5092 傒V(CN实用文档。
2021年高二下学期暑假作业数学(理)试题(18) 含答案

2021年高二下学期暑假作业数学(理)试题(18)含答案一、选择题1.若f(x)=x2+2f(x)dx,则f(x)dx=()A.﹣1 B.﹣C.D.12.设复数(是虚数单位),则复数的虚部是()A. B. C. D.3.过抛物线y2=4x的焦点F作斜率为1的直线,交抛物线于A、B两点,若=λ(λ>1),则λ等于()A.+1 B.+1 C.+1 D.2+34.登山族为了了解某山高y(km)与气温x(°C)之间的关系,随机统计了4次山高与相应气温x(°C) 18 13 10 ﹣1山高y(km)24 34 38 6472(km)处气温的度数为()A.﹣10 B.﹣8 C.﹣4 D.﹣65.如图所示,在△ABC中,∠B=60°,∠C=45°,高AD=,在∠BAC内作射线AM交BC于点M,则BM<1的概率为()A.B.C.D.二、填空题6.某班有学生48人,现用系统抽样的方法,抽取一个容量为6的样本,已知座位号分别为6,x,22,y,38,46的同学都在样本中,则x+y=.7.命题:若a>0,则二元一次不等式x+ay-1≥0表示直线x+ay-1=0的右上方区域(包含边界)是________命题(“真”或“假”).8已知=(2,﹣1,2),=(﹣1,3,﹣3),=(13,6,λ),若向量,共面,则λ=.9.方程+=λ(λ<0)的曲线即为函数y=f(x)的图象,对于函数y=f(x),下列命题中正确的是.(请写出所有正确命题的序号)①函数y=f(x)在R上是单调递减函数;②函数y=f(x)的值域是R;③函数y=f(x)的图象不经过第一象限;④函数y=f(x)的图象关于直线y=x对称;⑤函数F(x)=4f(x)+3x至少存在一个零点.三、解答题10.已知命题P:方程+=1表示双曲线;命题q:1﹣m<t<1+m(m>0),若¬p是¬q的充分非必要条件,试求实数m的取值范围.11.已知抛物线C:y2=2px(p>0)的焦点为F(1,0),过F且斜率为1的直线l交抛物线C于A(x1,y1),B(x2,y2)两点.(Ⅰ)求抛物线C的标准方程;(Ⅱ)求△OAB的面积.12.在平面直角坐标系中,已知点A(1,0),点B在直线l:x=﹣1上运动,过点B与l垂直的直线和线段AB的垂直平分线相交于点M.(1)求动点M的轨迹E的方程;(2)过(1)中轨迹E上的点P (1,2)作两条直线分别与轨迹E相交于C(x1,y1),D(x2,y2)两点.试探究:当直线PC,PD的斜率存在且倾斜角互补时,直线CD的斜率是否为定值?若是,求出这个定值;若不是,说明理由.答案1. B2. A3. D4. D5. B.6.:44.7:真.8.:3.9.:①②③.10. 解:由命题P得(t+2)(t﹣10)<0,即﹣2<t<10,即t∈(﹣2,10),由命题q:1﹣m<t<1+m(m>0),即t∈(1﹣m,1+m)由题意及逆否命题的等价性可知q⇒p,即(1﹣m,1+m)⊂(﹣2,10),∴由1﹣m≥2,1+m≤10(不同时取等号)及m>0得0<m≤3,∴所求m的取值范围为(0,3].11. 解:(Ⅰ)由抛物线C:y2=2px(p>0)的焦点为F(1,0),即有=1,解得p=2.即有抛物线方程为y2=4x;(Ⅱ)直线方程为y=x﹣1,联立抛物线得x2﹣6x+1=0,故x1+x2=6,x1x2=1,即有|AB|=•=•=8.又原点到直线距离为d==.故△OAB的面积为••8=2.12. 解:(1)依题意,得|MA|=|MB|…∴动点M的轨迹E是以A(1,0)为焦点,直线l:x=﹣1为准线的抛物线,…∴动点M的轨迹E的方程为y2=4x.…(2)∵P (1,2),C(x1,y1),D(x2,y2)在抛物线y2=4x上,∴由①﹣②得,(y1+y2)(y1﹣y2)=4(x1﹣x2),∴直线CD的斜率为,…③…设直PC的斜率为k,则PD的斜率为﹣k,可设直线PC方程为y﹣2=k(x﹣1),由得:ky2﹣4y﹣4k+8=0,由,求得y1=﹣2,同理可求得y2=﹣﹣2…∴∴直线CD的斜率为定值﹣1.…30982 7906 礆20881 5191 冑20435 4FD3 俓)^39465 9A29 騩40081 9C91 鲑4A23476 5BB4 宴27132 69FC 槼l29280 7260 牠0。
2024-2025学年苏教版高二数学下册暑假练习试卷及答案

2024-2025学年苏教版高二数学下册暑假练习试卷一、单选题(每题3分)1.设函数(f(x)=x3−6x2+9x),则该函数的极小值点为:A.(x=1)B.(x=3)C.(x=0)D. 不存在答案解析:要找到极值点,我们首先求函数的一阶导数并解方程(f′(x)=0)。
[f′(x)=3x2−12x+9=0]解这个二次方程得到(x)的值。
方程的解为(x=1)和(x=3)。
这两个点是临界点,可能是极大值点、极小值点或拐点。
为了确定极值类型,我们需要计算二阶导数并在这些点上测试符号。
[f″(x)=6x−12]接下来,我们将计算二阶导数在(x=1)和(x=3)处的值,以确定极值点。
对于(x=1),二阶导数值为(−6),表明这是一个极大值点;对于(x=3),二阶导数值为(6),表明这是一个极小值点。
因此,正确答案是 B.(x=3)。
2.若(lim x→0sin(3x))存在,则此极限等于:xA. 0B. 1C. 3D. 不存在答案解析:利用洛必达法则或者直接利用(sinx/x)当(x→0)时极限为 1 的性质来解题。
[lim x→0sin(3x)x=lim x→03cos(3x)1=3]因此,正确答案是 C. 3。
3.曲线(y=ln(x))在点 (1, 0) 处的切线方程是:A.(y=x−1)B.(y=x+1)C.(y=−x+1)D.(y=−x−1)答案解析:首先求曲线的导数,然后使用点斜式方程。
[y′=ddxln(x)=1x]点 (1, 0) 处的斜率是(1),所以切线方程为(y−0=1(x−1)),即(y=x−1)。
因此,正确答案是 A.(y=x−1)。
4.下列函数中,既是偶函数又是周期函数的是:A.(f(x)=cos(x))B.(f(x)=sin(x))C.(f(x)=e x)D.(f(x)=x2)答案解析:偶函数满足(f(x)=f(−x)),周期函数满足(f(x)=f(x+T))对某个非零常数(T)。
2021年高二数学暑期作业(套卷)(6) Word版含答案

2021年高二数学暑期作业(套卷)(6) Word 版含答案参考公式:棱柱的体积公式:其中是棱柱的底面积,是高.一、填空题:本大题共14小题,每小题5分,共70分.请把答案直接填写在答.题卡相应位置上........ 1.已知集合则 ▲ .2.已知复数(其中是虚数单位,),若是纯虚数,则的值为 ▲ .3.从集合{1,2,3}中随机取一个元素,记为,从集合{2,3,4}中随机取一个元素,记为,则的概率为▲ .4.对一批产品的长度(单位:毫米)进行抽样检测,样本容量为400,右图为检测结果的频率分布直方图,根据产品标准,单件产品长度在区间的为一等品,在区间 和的为二等品,其余均为三等品,则样本中三等品的件数为 ▲ .5.右面是一个算法的伪代码,其输出的结果为▲ .6. 若函数在区间上单调递增,在区间单调递减,则的值为 ▲ .7.在平面直角坐标系中,若双曲线的离心率为,则双曲线的渐近线方程为S 0 11011(1)Pr int For i From To Step S S i i End For S←←++A BDE FG▲ .8.已知实数满足则当取得最小值时,的值为 ▲ .9.在平面直角坐标系中,是曲线上的一点,直线 经过点,且与曲线在点处的切线垂直,则实数的值为 ▲ .10.设向量若,则的最小值为 ▲ . 11.以知是定义在区间上的奇函数,当时,,则关于的不等式的解集为 ▲ . 12.设为数列的前项和,若,且,则的值为 ▲ .13.在中,已知sin 13sin sin ,cos 13cos cos ,A B C A B C ==则的值为 ▲ .14. 在平面直角坐标系中,设为函数的图象与轴的两个交点,为函数的图象上的两个动点,且在轴上方(不含轴),则的取值范围为 ▲ .二、解答题:本大题共6小题,共90分.请在答题卡指定区域.......内作答. 解答时应写出文字说明、证明过程或演算步骤. 15.(本小题满分14分)中,分别为角的所对边的长,若,,且。
2021年高二下学期暑假作业数学(理)试题(33) 含答案

2021年高二下学期暑假作业数学(理)试题(33)含答案一.选择题:1. 函数的导数是( )A. B. C. D.2.用1、2、3、4、5这5个数字,组成无重复数字的三位数,这样的三位数有( )A.12个B.48个C.60个D.125个3. 在二项式的展开式中,含的项的系数是()A.B.C.D.4. 已知椭圆的中心在原点,离心率,且它的一个焦点与抛物线的焦点重合,则此椭圆的方程为()A B C D5. 若函数y=x3-3bx+3b在(0,1)内有极小值,则A.0<b<1B.b<1C.b>0D.b<二、填空题6.若动点P在y=2x2+1上移动,则点P与点Q(0,-1)连线的中点的轨迹方程是________________.7.如图所示2×2方格,在每一个方格中填入一个数字,数字可以是1,2, 3,4中的任何一个,允许重复,则填入A方格的数字大于B方格的数字的概率为.AB8.若…,则= .9. 以下四个关于圆锥曲线的命题中:①设A、B为两个定点,k为非零常数,,则动点P的轨迹为双曲线;②平面内到两定点距离之和等于常数的点的轨迹是椭圆③方程的两根可分别作为椭圆和双曲线的离心率;④双曲线有相同的焦点.其中真命题的序号为(写出所有真命题的序号)三.解答题10.. 已知椭圆G的中心在坐标原点,长轴在轴上,离心率为,两个焦点分别为和,椭圆G上一点到和的距离之和为12.圆:的圆心为点.(1)求椭圆G的方程11.袋子中共有12个球,其中有5个黑球,4个白球,3个红球,从中任取2个球(假设取到每个球的可能性都相同)。
已知每取到一个黑球得0分,每取到一个白球得1分,每取到一个红球得2分,用ξ表示任取2个球的得分的差的绝对值.(I)求椭机变量ξ的分布列及ξ的数学期望Eξ;12.已知点A在圆C:上运动,点B在以为右焦点的椭圆上运动,求|AB|的最大值。
答案1. A2.C3. C4. A5. :A6. y =4x 2 7 . 8. ―448 9. ③④10..解: (1)设椭圆G 的方程为: ()半焦距为c;则 , 解得 , 所求椭圆G 的方程为:.(2)点的坐标为,1212112222K A F F SF F =⨯⨯=⨯= (3)若,由可知点(6,0)在圆外,若,由可知点(-6,0)在圆外; 不论K 为何值圆都不能包围椭圆G . 11. 解:(I )由已知可得ξ的取值为:0,1,2,)4(,6615)2(,6632)1(,6619)0(212131521213141415212232425分====+===++==C C C P C C C C C P C C C C P ξξξ∴ξ的概率分布列为:∴ξ的数学期望为Eξ=0×+1×+2×= (6分)(II)显然ξ=0时不等式成立;若ξ≠0,则有:)12(665166326619)1()0()(,222142分=+==+==∴<≤∴<<⇒⎪⎩⎪⎨⎧<⨯-=∆>ξξξξξξξPPAP12. 如图8-1所示∵∴k=4∴椭圆的方程为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高二数学下册暑假作业及答案
(2021最新版)
作者:______
编写日期:2021年__月__日
【一】
1.(09年重庆高考)直线与圆的位置关系为()
A.相切B.相交但直线不过圆心
C.直线过圆心D.相离
2.方程x2+y2+2ax-by+c=0表示圆心为C(2,2),半径为2的圆,则a、b、c的值
依次为()
A.2、4、4;B.-2、4、4;
C.2、-4、4;D.2、-4、-4
3(2021年重庆高考)圆心在轴上,半径为1,且过点(1,2)的圆的方程为()
A.B.
C.D.
4.直线3x-4y-4=0被圆(x-3)2+y2=9截得的弦长为()
A.B.4
C.D.2
5.M(x0,y0)为圆x2+y2=a2(a>0)内异于圆心的一点,则直线x0x+y0y=a2与该圆的位置关系是()
A.相切B.相交
C.相离D.相切或相交
6、圆关于直线对称的圆的方程是().
A.
B.
C.
D.
7、两圆x2+y2-4x+6y=0和x2+y2-6x=0的连心线方程为().
A.x+y+3=0B.2x-y-5=0
C.3x-y-9=0D.4x-3y+7=0
8.过点的直线中,被截得最长弦所在的直线方程为()
A.B.
C.D.
9.(2021年四川高考)圆的圆心坐标是
10.圆和
的公共弦所在直线方程为____.
11.(2021年天津高考)已知圆的圆心是直线与轴的交点,且圆与直线相切,则圆的方程为.
12(2010山东高考)已知圆过点,且圆心在轴的正半轴上,直线被该圆所截得的弦长为,则圆的标准方程为____________
13.求过点P(6,-4)且被圆截得长为的弦所在的直线方程.
14、已知圆C的方程为x2+y2=4.
(1)直线l过点P(1,2),且与圆C交于A、B两点,若|AB|=23,求直线l的方程;
(2)圆C上一动点M(x0,y0),ON→=(0,y0),若向量OQ→=OM→+ON→,求动点Q的轨迹方程
“人”的结构就是相互支撑,”众”人的事业需要每个人的参与。
【二】
1.点的内部,则的取值范围是()
A.B.
C.D.
2.(09年上海高考)点P(4,-2)与圆上任一点连续的中点轨迹方程是()
A.
B.
C.
D.
3.(09年陕西高考)过原点且倾斜角为的直线被圆所截得的弦长为
A.B.2C.D.2
4.已知方程x2+y2+4x-2y-4=0,则x2+y2的值是()
A.9B.14C.14-D.14+
5、(09年辽宁高考)已知圆C与直线x-y=0及x-y-4=0都相切,圆心在直线x+y=0上,则圆C的方程为()
A.
B.
C.
D.
6、两圆相交于两点(1,3)和(m,1),两圆的圆心都在直线x-y+c2=0上,则m+c的值是()
A.-1B.2C.3D.0
7.(2021安徽)若直线过圆的圆心,则a的值为()
A.1B.1C.3D.3
8.(09年广东高考)设圆C与圆x2+(y-3)2=1外切,与直线y=0相切,则C的圆心轨迹为()
A.抛物线B.双曲线
C.椭圆D.圆
9.(09年天津高考)若圆与圆的公共弦长为,则a=________.
10.(09年广东高考)以点(2,)为圆心且与直线相切的圆的方程是.
11.(09年陕西高考)过原点且倾斜角为的直线被圆所截得的弦长为.
12、过点P(-3,-32)且被圆x2+y2=25所截得的弦长为8的直线方程为__________.
13、已知圆C的圆心在直线l1:x-y-1=0上,与直线l2:4x +3y+14=0相切,且截得直线l3:3x+4y+10=0所得弦长为6,求圆C的方程.。
