利用Excel解多元一次方程组ppt2003
EXCEL解方程组

逆矩阵 行数等于列数的矩阵称为方阵。若一方 阵的主对角元素aii均为1,其他位置上的 元素均为0,则该矩阵称为单位矩阵I 。 设有一n阶方阵A和另一n阶方阵B,它 们的乘积为:AB=BA=I 则B为A的逆阵,可记为A-1。
3.1 Excel 矩阵运算
逆矩阵 Excel求逆矩阵的工作表函数为 MINVERSE(array) 例1. MINVERSE({4,-1;2,0}) 例2. MINVERSE({1,2,1;3,4,-1;0,2,0}) 例3. MINVERSE()为一矩阵,可参与其他 矩阵运算。
数组乘以一常数 数组乘以一常数,得到与原数组大小相同的 新数组,新数组的每个单元格的值等于原数 组单元格的值乘以此常数。
3.1 Excel 矩阵运算
4.
矩阵乘法 矩阵A(m×n)与B(n×p)相乘,得 一矩阵C(m×p)。仅当第一个矩阵的 列数等于第二个矩阵的行数时,两矩阵 才能相乘。 矩阵相乘时,各矩阵元素按一定规则相 乘再相加。Excel有矩阵相乘的工作表函 数MMULT(array1,array2)。
其中xi(x1, x2, x3,…) 是实验未知数,ci是实验测量值, aij是系数。这些方程必须是线性独立的,上式的矩 阵表示为: AX=C
3.2 解线性联立方程
A是系数矩阵:
a11 a21 A am1 a12 a22 am 2 a1n ... a2 n ... amn ...
5.
3.1 Excel 矩阵运算
行列式 行列式是在研究线性方程组的解法中产生 的概念。n阶行列式可表示为:
6.
a11 D a21 an1
a12 a22 an 2
...
a1n
... a2 n ... ann
excel三元一次方程

excel三元一次方程
要在Excel中解三元一次方程,请按照以下步骤操作:
1. 打开Excel并创建一个新的工作表。
2. 在A列中输入方程的各个系数。
假设你的方程是:ax + by + cz = d,那么在A列中,依次输入a,b,c,d。
3. 在B列中输入变量的值。
假设你的方程是:2x + 3y - 4z = 10,那么在B列中,依次输入2,3,-4,10。
4. 在C列中计算每个变量的乘积。
使用Excel的乘法函数,将第A列和第B列中的对应单元格相乘。
假设你的方程是:2x + 3y - 4z = 10,那么在C列中,分别输入"=A1*B1",
"=A2*B2","=A3*B3",然后拖动这些公式以填充整个C列。
5. 在D列中计算变量的乘积的总和。
使用Excel的求和函数,将C列中的所有单元格相加。
假设你的方程是:2x + 3y - 4z = 10,那么在D列中,输入"=SUM(C1:C3)"。
6. 在E列中计算每个变量的解。
将D列中的总和与方程的d
值相除,以得到每个变量的解。
假设你的方程是:2x + 3y - 4z = 10,那么在E列中,分别输入"=D1/A1","=D2/A2",
"=D3/A3",然后拖动这些公式以填充整个E列。
7. 最后,E列中的值就是该三元一次方程的解。
excel怎么解二元一次方程组

excel怎么解二元一次方程组
Excel可以通过求解器来解二元一次方程组,具体步骤如下:
1.打开Excel,在工具栏中选择“数据”-“分析”-“求解器”。
2.在弹出的“求解器参数”对话框中,选择“最小化/最大化”选项,根据需要选择“约束”选项。
3.在“单元格”框中分别输入两个未知数的单元格位置。
4.在“公式”框中输入方程组的两个方程,并用“=0”将其等于零。
5.点击“确定”按钮,Excel会自动计算得出方程组的未知数解。
例如,对于以下二元一次方程组:
2x + 3y = 5
3x - 4y = 2
可以在Excel中依次操作:
1.选择“数据”-“分析”-“求解器”。
2.在“求解器参数”对话框中选择“最小化/最大化”选项,约束项
选择“无约束”。
3.在“单元格”框中输入两个未知数的单元格位置,如A1和B1。
4.在“公式”框中输入方程组的两个方程,并用“=0”将其等于零,如“=2*A1+3*B1-5=0”和“=3*A1-4*B1-2=0”。
5.点击“确定”按钮,Excel会自动计算得出方程组的未知数解,如A1为1,B1为1。
excel解方程三元一次方程

excel解方程三元一次方程
一个三元一次方程是指一个包含三个未知数和仅具有一次项次的
方程式。
要通过Excel解决三元一次方程,可以按照以下步骤进行操作:
1.选定三列分别用于输入三个未知数,如x、y和z。
2.然后在单元格底部的空白单元格中输入方程式。
例如,对于
方程式 a*x + b*y + c*z = d,您可以再单元格中输入 a、b、c、d
的值,并使用乘法符号“*”表示乘号。
例如,a = 2,b = 3,c = 4,
d = 5,则输入式子为 2*x + 3*y + 4*z = 5。
3.单击单元格,然后选择“求解器”在“数据”中(如果这不在Excel中,则需要添加),在该对话框中,选择“线性规划”并填写未知数所在的单元格,约束为A = B。
4.然后单击“确定”,一旦Excel已解决方程,您将得到每个未
知数的答案。
通过这种方法,您就可以用Excel来解决三元一次方程式。
excel解方程三元一次方程

excel解方程三元一次方程在Excel中解三元一次方程可以通过使用矩阵运算的方法来实现。
下面我们将详细介绍如何在Excel中解三元一次方程。
首先,我们假设有以下的三元一次方程:```a1x + b1y + c1z = d1a2x + b2y + c2z = d2a3x + b3y + c3z = d3```其中,a1、b1、c1、d1、a2、b2、c2、d2、a3、b3、c3和d3都是已知的数值。
我们可以将方程写成矩阵形式:```| a1 b1 c1 | | x | | d1 || a2 b2 c2 | x | y | = | d2 || a3 b3 c3 | | z | | d3 |```现在我们将矩阵形式的三元一次方程输入到Excel的单元格中。
假设方程的系数矩阵在A1:C3范围内,常数矩阵在D1:D3范围内。
接下来,我们需要使用Excel中的逆矩阵函数(MINVERSE)来求解方程的解。
在Excel中,逆矩阵函数的语法如下:```MINVERSE(array)```其中,array表示要求逆的矩阵。
我们可以将逆矩阵函数应用于方程的系数矩阵,得到它的逆矩阵。
将逆矩阵与常数矩阵相乘,即可得到方程的解向量。
在Excel中,可以使用矩阵乘法函数(MMULT)来进行矩阵乘法运算。
矩阵乘法函数的语法如下:```MMULT(array1, array2)```其中,array1和array2表示要相乘的两个矩阵。
将逆矩阵与常数矩阵相乘,可以得到方程的解向量。
最后,我们将解向量的结果输出到Excel的单元格中,即可得到三元一次方程的解。
通过以上步骤,我们可以在Excel中解三元一次方程。
这种方法的优点是简单易行,只需使用Excel中的基本函数即可。
但是需要注意的是,当系数矩阵的逆矩阵不存在时,方程无解。
在使用Excel解方程时,需要对此进行判断和处理。
excel解多元方程组

excel解多元方程组Excel是一款功能强大的电子表格软件,除了可以进行简单的数据处理和计算外,还可以用来解决复杂的多元方程组。
在本文中,我将介绍如何使用Excel来解决多元方程组的问题。
首先,我们需要将多元方程组的方程转化为Excel中的表达式。
假设我们有一个包含n个未知数和m个方程的多元方程组。
我们可以将每个方程表示为一个Excel的单元格,并在每个单元格中输入相应的表达式。
例如,如果我们有一个方程为2x + 3y = 10,我们可以在一个单元格中输入“=2*x+3*y-10”。
接下来,我们需要在Excel中创建一个工作表来解决这个多元方程组。
我们可以使用Excel的“数据分析”功能来进行求解。
首先,我们需要打开Excel的“数据”选项卡,然后选择“数据分析”。
在弹出的对话框中,我们可以选择“线性回归”选项,并点击“确定”。
在“线性回归”对话框中,我们需要输入多元方程组的输入范围和输出范围。
输入范围是包含所有未知数的单元格区域,输出范围是包含所有方程结果的单元格区域。
然后,我们可以点击“确定”来进行求解。
Excel将自动计算出多元方程组的解,并将结果显示在输出范围中的相应单元格中。
我们可以通过查看这些单元格来获取多元方程组的解。
除了使用“线性回归”功能外,我们还可以使用Excel的“求解器”来解决多元方程组的问题。
首先,我们需要打开Excel的“数据”选项卡,然后选择“求解器”。
在弹出的对话框中,我们可以选择需要求解的目标单元格和约束条件。
然后,我们可以点击“确定”来进行求解。
Excel的“求解器”将自动计算出多元方程组的解,并将结果显示在目标单元格中。
我们可以通过查看这些单元格来获取多元方程组的解。
总之,Excel是一款非常实用的工具,可以用来解决复杂的多元方程组。
通过使用Excel的“数据分析”功能和“求解器”,我们可以轻松地求解多元方程组的问题。
无论是在学术研究还是实际应用中,Excel都是一个非常有用的工具。
excel解多元方程组

excel解多元方程组(实用版)目录1.引言:介绍 Excel 解多元方程组的方法和优势2.准备:需要了解的 Excel 功能和操作3.示例:用 Excel 解一个多元方程组4.总结:Excel 解多元方程组的步骤和注意事项5.展望:Excel 在其他数学领域的应用正文1.引言在数学中,解多元方程组是一个重要的课题。
而在现实生活中,我们也会遇到需要解决多元方程组的问题。
例如,在经济学中,我们需要分析多种因素对市场需求的影响;在物理学中,我们需要研究多个物理量之间的关系等。
在这种情况下,Excel 作为一种强大的数据处理工具,可以帮助我们快速解决多元方程组问题。
本文将介绍如何使用 Excel 解多元方程组,并阐述这种方法的优势。
2.准备在使用 Excel 解多元方程组之前,我们需要了解一些 Excel 的基本功能和操作。
首先,我们需要熟悉 Excel 的工作表,其中包括单元格、行和列。
在单元格中,我们可以输入数据和公式。
其次,我们需要掌握Excel 的一些基本函数,如 SUM(求和)、AVERAGE(平均值)、COUNT(计数)等。
此外,我们还需要了解如何使用 Excel 的数据表功能,如排序、筛选和透视表等。
3.示例下面,我们通过一个示例来说明如何使用 Excel 解多元方程组。
假设我们有如下多元方程组:x + y = 102x - 3y = 12我们首先将数据输入到 Excel 的工作表中,然后使用“数据”选项卡中的“排序”功能,对数据进行排序。
接着,我们使用“插入”选项卡中的“透视表”功能,创建一个透视表。
在透视表中,我们将两个方程组的值分别放入“行标签”和“值”区域。
然后,在“值字段设置”中,选择“计算字段”,并输入如下公式:=SUM(此行所有值)在“行标签”区域,我们选择“标签”选项,并输入公式:=GET.CELL(1,此行)最后,我们在透视表中添加一个新的行标签,命名为“解”。
在“解”行的“值”区域,我们输入以下公式:=IF(SUM(此行所有值)=0,0,SUM(此行所有值))这样,我们就可以得到多元方程组的解。
excel三元一次方程组

excel三元一次方程组
三元一次方程组是指包含三个未知数和每个未知数的次数都是1的一组方程,且方程数与未知数数相等的代数方程组。
2. 如何求解三元一次方程组?
求解三元一次方程组可以通过消元法或矩阵法来实现。
消元法是将方程组中某一变量的系数通过加减法消去,得到新的方程组,再重复该过程,直至得出最终的解。
矩阵法是将方程组表示为矩阵形式,并通过行变换将其化为行最简矩阵,再通过回代求解未知数。
3. 如何在Excel中求解三元一次方程组?
在Excel中,可以通过使用线性求解器来求解三元一次方程组。
首先将方程组表示为矩阵形式,并在Excel中输入该矩阵,然后选择“工具”-“数据分析”-“线性求解器”,设置求解参数,即可得到方程组的解。
4. 实际应用
三元一次方程组在实际问题中有广泛的应用,如在工程中的结构力学、电路分析、流体力学等领域,以及在经济、金融、物理等领域中也有应用。
在Excel中求解三元一次方程组,可以简化计算过程,提高工作效率。
- 1 -。
excel三元一次方程

excel三元一次方程
Excel可以通过使用求根函数,如“ROOT”、“SOLVE”或“GOAL SEEK”来求解三元一次方程。
以下是通过Excel求解三元一次方程的步骤:
1. 打开Excel并创建一个新的工作表。
2. 在单元格A1至A3中分别输入方程的系数。
3. 在单元格B1至B3中分别输入方程的常数。
4. 在单元格C1至E3中输入一个初始的猜测解。
5. 点击单元格F1,并输入以下公式:=A1*C1+A2*D1+A3*E1-B1
这个公式计算出方程的第一个变量的值。
6. 在单元格F2至F3中输入类似的公式,分别计算出方程的
其他两个变量的值。
7. 选择F1至F3的单元格,点击Excel菜单中的“数据”选项卡,然后选择“求根”。
8. 在弹出的对话框中,选择“三元多项式”选项,然后选择C1
至E3的单元格作为初始猜测解。
9. 点击“确定”按钮,Excel将计算出方程的解并将其显示在C1
至E1的单元格中。
注意:通过以上步骤,Excel可以通过求解方程的根来得到三元一次方程的解。
但是,偶尔可能会有多个解或无解的情况,这时需要根据具体的方程调整初始猜测解来获得正确的解。
Excel解一元二次方程和多元方程的几种方法

Excel解一元二次方程和多元方程的几种方法humphrey①一元二次方程形如ax2+bx+c=0 (a≠0)的方程称之为一元二次方程。
他有三种解/根:令Δ=b2−4ac•如果Δ<0,方程无实数根,有两个复数根:▪x1=−b±ⅈ√−(b 2−4ac)2a▪x2=−b±ⅈ√4ac−b 22a•如果Δ=0,方程有两个相等的实数根:▪x1=x2=−b2a•如果Δ>0,方程有两个不等实根(求根公式):▪x=−b±√b 2−4ac2a1.求根公式现在,我们使用求根公式在Excel中求一元二次方程的解:(Δ≥0)将输入系数的单元格重命名为a、b、cc(单独的c表示一列,因此用cc) 输入求根公式•=(-b+SQRT(b^2-4*a*cc))/2/a•或•=(-b-SQRT(b^2-4*a*cc))/2/a当a+b+c=0时,x1=12.模拟分析-单变量求解首先,重命名单变量单元格为x,其次,在单变量方程式单元格中输入公式:=a*x^2+b*x+cc点击【数据】-【模拟分析】-【单变量求解】•目标单元格为单变量方程式•目标值为0•可变单元格为xExcel将自动计算出一个,并显示在x单元格中。
3.韦达定理使用【模拟分析】-【单变量求解】只能得到一个解,求另一个解的简便计算的方法是韦达定理:x1+x2=−b ax1x2=c a当我们已经计算出或者试算出来一个解,那么通过韦达定理可以快速计算出另一个解。
另外,有些特殊情况下,x有已知的一个解(或者有明显规律的解可以试算),这时利用韦达定理可以快速得出另一个解。
▪a+b+c=0,x1=1▪a-b+c=0,x1=-1▪c=0时,x1=0▪ac+b+1=0,x1=c▪ac-b+1=0,x1=-c▪a=1,x1+x2=-b,x1x2=c▪a=b=1,x1+x2=-1,x1*x2=c▪a=1 & b=-1,x1+x2=1, x1*x2=c首先,重命名一个解的单元格为x_1或x_2在Excel中输入:••= -b/a-x_1或=cc/a/x_2当C=0时,x1=0②Excel规划求解三元、多元方程的方法1.单变量求解之前,我们使用单变量求解帮助解一元二次方程,实际上,单变量求解可以解决任何一元方程,而不仅限于一元二次方程。
如何利用EXCEL解方程

如何利用EXCEL 解方程?
一些简单的方程可以简单地通过普通的算法求出其解,但对于特殊和复杂的方程手算就无能为力了,用EXCEL 可以用迭代法轻松地求出方程的解。
下面就利用图示的方法简要介绍一下计算的全过程:
在EXCEL 中创建一个未知数单元格,一个方程单元格,用公式(也就是方程)使方程单元格等未知数格中的值作为未知数代入方程中计算所得的值。
比如:要解方程:3sin(x)+4e^x=0,可以先在未知数单元格(如A1)中输入任意值,然后在方程单元格(如B1)中输入”=3*sin(a1)+4*exp(a1)”. 在工具菜单下,选择单变量求解,
在目标单元格填入方程单元格,也就是刚才带公式的单元格的名称(如B1);目标值按你要解的方程填写你想求公式的值,如3sin(x)+4e^x=0这一方程中,目标值填为0,你如果你想求:3sin(x)+4e^x=2的解则目标值填为2,依此类。
可变单元格填入未知数单元格的名称(本例中为A1)。
按确定求解:
求出方程的一个解是-0.76885,这时的公式的值等于1.81×10-5 注意解显示在未知数单元格中。
此处为目标值。
使用Excel解多元一次方程组的三种方法
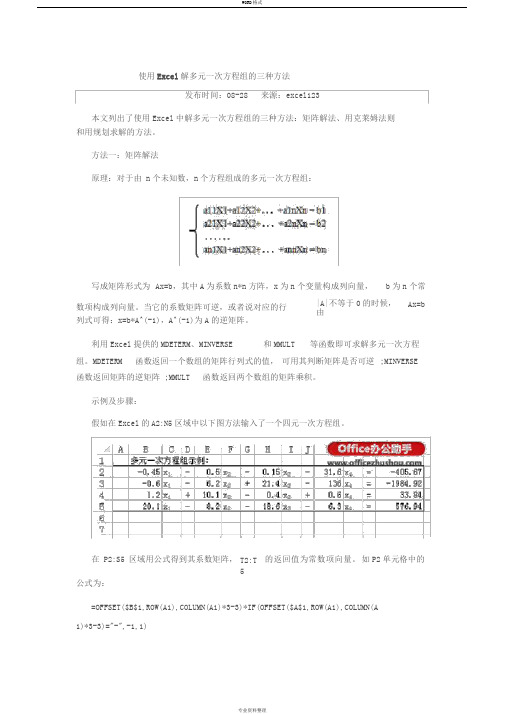
区域设置公式,即以Q8:Q11为未知数代入方程左侧。如S8中的公式:
在
S8:S11
=P2*$Q$8+Q2*$Q$9+R2*$Q$10+S2*$Q$11
3、设置“规划求解”参数。在“数据”选项卡的“分析”组中单击“规划求解”按钮,弹出“规
1)*3-3)="-",-1,1)
由于“=MDETERM(P2:S5)”的值不等于“0,”可知系数矩阵可逆。选择某列中的四个连续
单元格,如Q11:Q14,输入数组公式:
=MMULT(MINVERSE(P2:S5),T2:T5)
公式输入完毕按
Ctrl+Shift+En到方程组的解。
函数返回矩阵的逆矩阵;MMULT函数返回两个数组的矩阵乘积。
示例及步骤:
假如在Excel的A2:N5区域中以下图方法输入了一个四元一次方程组。
在P2:S5区域用公式得到其系数矩阵,
T2:T5
的返回值为常数项向量。
如P2单元格中的
公式为:
=OFFSET($B$1,ROW(A1),COLUMN(A1)*3-3)*IF(OFFSET($A$1,ROW(A1),COLUMN(A
方法二:用克莱姆法则
示例及步骤:
对于上述四元一次方程组,复制P2:S5区域,将其粘贴到其他区域,如本例有4个未知
数,用“选择性粘贴——粘贴链接”的方法将其粘贴到4个不同的区域。然后复制T2:T5常数
项的列向量,用“选择性粘贴——粘贴链接”的方法分别将其粘贴到上述四个区域中的各列,依次得到矩阵A1、A2、A3、A4,再用MDETERM函数计算各矩阵行列式的值,分别除以系数矩阵A的行列式的值,即可得到方程组的解。
EXCEL小妙用——运用矩阵运算解有n个方程的n元1次非齐次线形方程组

EXCEL小妙用——运用矩阵运算解有n个方程的n元1次非齐次线形方程组■-—●■■—■■■'■■■'■●■~.一■■■__lEXCEL妙用文/图徐方运用矩阵运算解有n个方程的n元1次非齐次线形方程组解方程组:2x+2y—z6x一2y+4z35x+7y+z28方程组的解为:x1;y3;z2下面一步一步教你解:第一步:将系数和常数分别填入A1至C3和E1至E3的单元格中第二步:选定A5至C7的单元格●●…-』-!●●■U■嚣?●?▲?:雹埔一∞一∞卧∞曩n∞-■一∞一■-■IO窖■墨●争I'■?n.●£?●'■.嘛?田:^5?●!互£.1~一2I吨'}5I箱'嘲量+城.~{雌i院甜厂~一一一t.…一…一……f_|ir:-_第三步:使用"插入"菜单中的"函数"第四步:选择"数学和三角函数"中的94电●2∞幺l2第五步:在弹出的对话框中填入"A1C3",按"确定".l^盯?q,.鼻t-I:1,.薯'?:-nntⅫⅢtO鼍■■■钾■嘲——-|.■t?矗■翻—■—■—啊■■?t■●泊■_H●?'哪H 计—●'■-O—■,口瑚柚_■■_岫厂_ii]■■I第六步:现在只在A5中出现一个数值,将光标确定在公式栏的=号和MINVEKSE之间,按下SHIFT键和CTRL键的同时按下ENTEK键.第七步:现在A5至C7单元格中都有数值了,这就是A1至C3的逆矩阵.第八步:选定E5至E7的单元格,同第三步做法.n-,n+●-l:●-▲?:捕哪一∞_∞瓯菌1黛脚工I∞_∞∞∞i::I_:D瞎■啦●争lc)?●l■l啦-回:髓?●?I帼I∞I::;三圜甲f1I:器II%9n102o.Is$8'5第九步:公式选MMULT■啊■∞:l曙,唧腿啊秘曩.I什'晡__!曼堕J嘲嘲■0:聃事舳_"-I■●酗∞:I二Jl器—lM■vⅢl∞二1w?,l.-r_t,骶膏__'_雕_l_'董划墨岫蛳I_l瞄I第十步:分别填A5:C7和E1:E3-r-I-_-口j一'■_-—_嘲-r_|m.日l.I:埘u嘲._-_mh.-一.茹==:=●"鬣■?恻'-r.I—嘲...计■■量-l毯_[墓==1-I第十一步:现在只在E5中出现~个数值,将光标确定在公式栏的=号和MMULT 之间,按下SHIFT键和CTRL键的同时按下ENTEK键.瓣?n?!-』ⅡI■la!●一▲?:噎捕∞一∞m姒∞工I∞_-∞!—-∞?●I'D瞎U啦●工■?■£?.{●I_?田:●=IⅡTC^5:cLEl:日)t^^'C,n______,.j?¨2-】5—_耋一1,I量5T128一oT6923l6g.ls3皓冒豳盏::lrfMr—lIJ二…jU■E5至E7将出现1,3,2,这就是方程组的解了.'瓣-n?-,Ⅱ●●l'●?▲?:漕捕∞一∞_∞姒∞∞工I∞_∞∞-∞.●I:DU亩啦:●争工■?■£?"●I啦-回:巧?●仁Ⅱ吐TC^5:CLEl:日)l^l:CD目_,:.226一圈一_嗣...i_i\_土"誊舔醴…l…一…一I!I广注:在EXCEL工作表任何位置的单元格中都可以操作,将本例中所填位置改变成相应位置即可.这个方法用于解元数特别多的方程组则更为方便,在经济统计工作中是很实用的群絮{l肇}《墨。
高中数学_人教A版2003课标版_必修5_信息技术应用 用Excel解线性规划问题举例(共30张PPT)

y
x
3x 2y
12
的解集.
y
0
x
x-2y=0
x y 0
例3:用平面区域表示不等式组
x
y
5
0
的解集.
y
x 3
x+y=0
x-y+5=0
o
x
x=3
3、画二元一次不等式(组)所表示平面区域的步骤:
画线(不等式中带等号,则画实线,否则,画虚线) 定侧(特殊点,同侧同号、异侧异号) 取“交”(各个不等式所表示平面区域的公共部分)
二、例题
例1:画出不等式 x + 4y < 4表示的平面区域 .
y
1
4
O
x
x+4y―4=0
三、当堂检测
1.画出不等式x-2y+6>0表示的平 面区域;
2.画出不等式3x+2y-6 ≤0表示的 平面区域;
3.画出不等式组 的平面区域。
表示
四、课堂小结:
⑴ 二元一次不等式(组)表示平面区域: 对应直线某一侧所有点组成的平面区域. 各个不等式所表示平面区域的公共部分.
高中数学>人教A版2003课标版>必修5>信息技术应用 用Excel解线性规划问题举例
3.3.1 二元一次不等 式(组)与平面区域
课前自主学习
二元一次不等式和二元一次不等式组的定义
(1)二元一次不等式: 含有两个未知数,并且未知数的最高次数是1的不等式.
(2)二元一次不等式组: 由几个二元一次不等式组成的不等式组.
果只会是永远装不满水桶的半桶水。和老师通完电话后,我调整了几天,也对自己手头上的事物做一些大改变。将目前摆在面前的计划一一列出来,挑出最重要的、最 排完手中所有的计划。对于那些不是很急的,对目前生活和工作不是特别重要的,先果断放弃。我现在最迫切的目标是什么?当然是七月份的转行新媒体咯,那么学习 媒体所需学习的技能又有很多,那怎么办呢?先挑自己有点底子的,有点基础的,把巩固持续加强。个人感觉自己写还是有点小基础的,所以就给自己一个小目标,每 案方面的训练。而另外PS也是做运营的必备条件之一,所以在训练文案的同时,还得练习PS,给自己的要求是每天练习PS半小时。还有别的吗?不敢有了,两样训练加 喜欢作家刘瑜的一段话:每当我一天什么也没干的时候,我就开始焦虑。每当我两天什么都没干的时候,我就开始烦躁。每当我三天什么都没干的时候,我就开始抓狂 没干啊,我寝食难安……这正是我三个月前的真实写照。多年来,我已经养成一种习惯,绝不让任何一分钟死有余辜:我在堵车的时候听日语,在等人的时候写文章, 事的衔接点那里扒出细缝,用来回邮件、回短信……我以为这就是所谓的勤奋,也心安理得地享受着同伴的钦佩。但我很快就发现,我的工作时间越来越长,我的休息 躁,只要有十分钟的无作为,我就会变得非常慌张!而我的社交时间也不得不尽量地缩短,我甚至不再有功夫交朋友。更可怕的是,我的工作量明明没有变化,可看起 始害怕夜幕降临的那一刻,因为那意味着这一天有更多的事情被贴上了“没完成”的标签。我责备那是自己“无能”的表现,直到我意识到问题的关键“没有效率的勤
浅谈用excel求解多元一次方程

当你在工作中遇到一个多元一次方程当你在工作中遇到一个多元一次方程,,是不是很头疼?不解吧,工作无法继续工作无法继续,,解吧解吧,,费神又上脑费神又上脑,,还有可能算错还有可能算错。
Excel 可以帮你解决这一难题,本文以例题详细说明其解答过程。
多元一次方程的求解可以看成是求矩阵的积,未知数的系数构成系数矩阵,等式左边的值则构成常数项矩阵,求解方程,分为两步:1、求解系数矩阵的逆矩阵2、求解系数矩阵与常数项矩阵的积。
对应的这两个过程,分别用到两个函数:1、MINVERSE MINVERSE,即返回数组的逆矩阵,在函数选择类别中,选择数学与,即返回数组的逆矩阵,在函数选择类别中,选择数学与三角函数三角函数,,则可以找到该函数则可以找到该函数,,它是用来求逆矩阵的它是用来求逆矩阵的,,下面有例题说明如何应用该函数。
2、MMULT MMULT,即返回两数组的矩阵积,也是在数学与三角函数类别中,即返回两数组的矩阵积,也是在数学与三角函数类别中,即返回两数组的矩阵积,也是在数学与三角函数类别中,,用它来求解两个矩阵的积。
下面,请先了解如何求解逆矩阵(类容来自百度文库)利用Excel进行矩阵求逆1、输入待求逆矩阵:2、在空白区选择一存放逆矩阵的区域,与待求逆矩阵大小相同:3、保持该区域为选中状态,在公式输入栏输入公式“Minverse(a1:c3)”,并按“Ctrl+Shift+EnterCtrl+Shift+Enter””,特别注意,不能直接回车键,必须在按住“Ctrl”“Shift”后再按回车键:4、逆矩阵为:了解了如何求解逆矩阵后,下面我们来求解一个二元一次方程。
方程:⎭⎬⎫⎩⎨⎧=−=+452y x y x 首先在首先在excel excel excel表格中输入系数行列式和常数项行列式表格中输入系数行列式和常数项行列式如下图所示现在求出系数矩阵的逆矩阵方法已在前文详述,这里不再赘述,其结果为下面求解两矩阵的积首先选择一个两行一列的矩阵首先选择一个两行一列的矩阵,,这里说明一下这里说明一下,,选择矩阵积得行数和列数很关键行数和列数很关键,,选错了选错了,,就得不到解答就得不到解答,,这里的行数就是未知数的个数,列数为未知数的个数,列数为1.1.1、选择一个两行一列的空白范围2、点击函数,找到点击函数,找到MMULT MMULT MMULT,会出现如下对话框,会出现如下对话框3、同时按下同时按下CTRL CTRL CTRL和和SHIFT SHIFT,,点击点击Array1Array1Array1后面的后面的,出现一下窗口,此过程,要按住程,要按住CTRL CTRL CTRL和和SHIFT SHIFT不放,点击不放,点击,选择系数矩阵的逆矩阵,完成后,再点击,出现,接着接着,,再点击再点击Array2Array2Array2后面的后面的,选择常数项矩阵选择常数项矩阵,,方法同上方法同上,,完成后,出现如下界面点击确定按钮,即可得到答案需要说明的是以上方法仅对需要说明的是以上方法仅对microsoft microsoft excel excel有作用,对有作用,对有作用,对wps wps wps则不行。
例用Excel回归工具进行多元线性回归PPT学习教案

第9页/共27页
用Excel回归工具 进行多元线性回归
例子 5.7 的多元线性回归方程: 年用电量 =760315.3-11232.1总人口
+0.02046GDP+0.08232全社会投资+0.1865消费品零售 总额 尽管判断系数R2=0.9836非常接近1,与样本数据拟合 很好,但这个回归方程还是有点问题。例如,假设检 验表明四个变量中只有一个变量全社会投资通过t-检验, 而且总人口的回归系数还是负数的,说明人口每增加1 万人,用电量反而会减少11232.1万度,有悖于常理。 造成上述问题的根本原因是四个变量中 有两个变量两 两相关的。。
用excelexcel回归工具进行多元线回归工具进行多元线性回归性回归excel例子选取用电量为因变量总人口gdp全社会投资消费品零售总额四个变量为自变量用19902006年17个样本数据进行多元线性回归
例用Excel回归工具进行多元线性回归
会计学
1
用Excel回归工具 进行多元线性回归
例子 选取用电量为因变量,总人口、GDP、 全社会投资、消费品零售总额四个变量为 自变量,用1990-2006年17个样本数据进行 多元线性回归。
第15页/共27页
第16页/共27页
第17页/共27页
第18页/共27页
用Excel回归工具 进行多元线性回归
在回归方程来看…总人口的系数仍 旧是负数,而且总人口的P值 依然 远大于显著性水平0.05.
重新相关系数分析 ,依然发现
第19页/共27页
第20页/共27页
第21页/共27页
第1页/共27页
用Excel回归工具 进行多元线性回归
例子 首先打开“例子5.1 散点图添加趋势线 进行简单线性回归”文件。单击菜单“工 具”|
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
将左边的系数矩阵与右边的系数向 量输入Excel表格的任意位置
3 1 −1 1 1 1 −1 1 2 1 −1 −1 3 2 1
2 1 1 1 1
1 x1 −2 1 x2 3 −2 x3 = 10 1 x4 −7 1 x5 7
利用Excel解多元一次方程组
例:5元一次方程的求解计算
3x1 + x2 − x3 + 2 x4 + x5 = −2 x + x + x + x + x = 3 1 2 3 4 5 − x1 + x2 + 2 x3 + x4 − 2 x5 = 10 x − x − x + x + x = −7 1 2 3 4 5 3x1 + 2 x2 + x3 + x4 + x5 = 7
作业:用Excel求解以下方程组
10 x1 + 2 x2 + 3x3 + 4 x4 + 5 x5 + 6 x6 = 110 2 x + 10 x + 4 x + 5 x + 6 x + 7 x = 112 2 3 4 5 6 1 3x1 + 4 x2 + 10 x3 + 6 x4 + 7 x5 + 8 x6 = 118 4 x1 + 5 x2 + 6 x3 + 10 x4 + 8 x5 + 9 x6 = 128 5 x1 + 6 x2 + 7 x3 + 8 x4 + 10 x5 + 10 x6 = 142 6 x1 + 7 x2 + 8 x3 + 9 x4 + 10 x5 + 10 x6 = 160
将上述方程用下式矩阵形式表示
3 1 −1 1 1 1 −1 1 2 1 −1 −1 3 2 1 2 1 1 1 1 1 x1 −2 x 3 1 2 −2 x3 = 10 −7 1 x4 1 x5 7
点击这里
点击第一空白栏的右侧
点击这里
选择逆矩阵范围后回车
选择这个范围
点击第二栏的右侧
点击这里
选择系数向量范围后回车
选择这个范围
先同时按住键盘的Shift和Ctrl键(不要放开),后按 回车Enter。此时在原先选择的范围内出现方程解
方程组的解为
x1 1 x 2 2 x3 = 3 x −1 4 x5 −2
窗口收缩后,选择对象范围后回车
选择这个范围
窗口被拉开后不要点击OK。先同时按住键盘的Shift 和Ctrl键(不要放开),后按回车Enter。此时在原先 选择的范围内出现了逆矩阵
在任意空白处选择5行1列后,点击fx
点击这里
选择5行 列 选择 行1列
输入mmult后回车,点击下方的OK
输入mmult后回车 后回车 输入
在任意空白处选择5行5列(必须与系数矩 阵的范围一样大),点击菜单栏的fx
点击这里
选择5行 列 选择 行5列
跳出一个窗口,将minverse输入第一 栏后回车(Enter),点击下方的OK
输入minverse后回车 后回车 输入
点击这里
跳出另一个窗口后,点击系数矩阵 位置(空白栏的右侧)Fra bibliotek点击这里
