利用Excel解多元一次方程组2020-.ppt
EXCEL解方程组

逆矩阵 行数等于列数的矩阵称为方阵。若一方 阵的主对角元素aii均为1,其他位置上的 元素均为0,则该矩阵称为单位矩阵I 。 设有一n阶方阵A和另一n阶方阵B,它 们的乘积为:AB=BA=I 则B为A的逆阵,可记为A-1。
3.1 Excel 矩阵运算
逆矩阵 Excel求逆矩阵的工作表函数为 MINVERSE(array) 例1. MINVERSE({4,-1;2,0}) 例2. MINVERSE({1,2,1;3,4,-1;0,2,0}) 例3. MINVERSE()为一矩阵,可参与其他 矩阵运算。
数组乘以一常数 数组乘以一常数,得到与原数组大小相同的 新数组,新数组的每个单元格的值等于原数 组单元格的值乘以此常数。
3.1 Excel 矩阵运算
4.
矩阵乘法 矩阵A(m×n)与B(n×p)相乘,得 一矩阵C(m×p)。仅当第一个矩阵的 列数等于第二个矩阵的行数时,两矩阵 才能相乘。 矩阵相乘时,各矩阵元素按一定规则相 乘再相加。Excel有矩阵相乘的工作表函 数MMULT(array1,array2)。
其中xi(x1, x2, x3,…) 是实验未知数,ci是实验测量值, aij是系数。这些方程必须是线性独立的,上式的矩 阵表示为: AX=C
3.2 解线性联立方程
A是系数矩阵:
a11 a21 A am1 a12 a22 am 2 a1n ... a2 n ... amn ...
5.
3.1 Excel 矩阵运算
行列式 行列式是在研究线性方程组的解法中产生 的概念。n阶行列式可表示为:
6.
a11 D a21 an1
a12 a22 an 2
...
a1n
... a2 n ... ann
excel求解多元高次方程

excel求解多元高次方程本文将介绍如何使用Excel来求解多元高次方程。
首先,我们需要将多元高次方程转化为矩阵形式。
假设我们有一个n元高次方程:f(x₁,x₂,⋯,xₙ)=0我们可以将其转化为矩阵形式:F(x)=[f₁(x),f₂(x),⋯,fₙ(x)]其中,f₁(x),f₂(x),⋯,fₙ(x)分别表示方程f(x)中n个未知量的函数。
接下来,我们可以使用Excel中的矩阵函数MMULT和MINVERSE 来求解方程。
具体步骤如下:1. 定义F(x)矩阵。
在Excel中,我们可以将每个未知量的函数单独列出一列,最终将它们拼接成一个矩阵F(x)。
例如,我们假设我们有一个三元高次方程:f(x,y,z)=x²+y²+z²-1=0g(x,y,z)=x+y+z-1=0h(x,y,z)=x-y+z=0则我们可以将其转化为矩阵形式:F(x)=[x²+y²+z²-1,x+y+z-1,x-y+z]2. 定义x矩阵。
同样地,我们需要定义一个初始值矩阵x。
这可以是任意一个与F(x)矩阵同型的矩阵。
3. 使用矩阵函数MMULT和MINVERSE求解。
我们可以使用以下公式来求解方程:x'=x-INV(J(x))*F(x)其中,INV(J(x))表示J(x)的逆矩阵,J(x)表示F(x)的雅可比矩阵。
雅可比矩阵的定义如下:J(x)=[∂f₁/∂x₁∂f₁/∂x₂⋯∂f₁/∂xₙ∂f₂/∂x₁∂f₂/∂x₂⋯∂f₂/∂xₙ⋮⋮⋱⋮∂fₙ/∂x₁∂fₙ/∂x₂⋯∂fₙ/∂xₙ]注意,逆矩阵INV(J(x))需要使用MINVERSE函数求解。
4. 不断迭代求解。
使用上一步求解得到的x'矩阵代替原来的x 矩阵,再次求解,直至收敛。
以上就是使用Excel求解多元高次方程的完整步骤。
excel用规划求解来算多元方程解

Excel 用规划求解来算多元方程解
2011-10-10 12:56:46
事情是这样的,我有一个朋友,出于某种原因,要向下级经销商开13316元的货物发票
一共有三种货物,分别是A B C,价格分别是 175 228 288
要求是,只要凑足13316就可以了,分别数量是多少,没有要求
方程如下
13316=175 X A + 228 X B + 288 X C
当然,这个可能有若干个解,要一个任意的正整数解即可。
朋友每次都算得头痛,我昨天过去看了下,哎,这个,用规划求解,很快搞定。
黑喂狗,阿中老师教你一秒钟变数学达人!
为了让你看得方便,我简单建了这样一张表
在这个里面,A2 B2 C2 是录入的价格
A5 B5 C5是要计算的数量,将来规划求解会把计算结果放在这里
重点是B7单元格,必须是一个公式,表示目标值的计算方法
然后,我们点击“工具-加载宏” (这是2003的菜单位置。
2007和2010的菜单位置请自行上google去百度一下)
(需要注意的是,在你的机器上,这个加载宏很可能没有被装进来(除非你安装的时候是完全安装,或者特地注意了要安装之),这种情况下,系统会提示你安装,那么这个时候,安装盘就必须出现了。
)
好吧,现在如图所示,勾选“规划求解”
然后,在点击菜单“工具-规划求解”,进入规划求解界面,看图,不解释了
点击“求解”,打完收工!。
用Excel求解多元一次方程组

用Excel求解多元一次方程组作者:曾国安来源:《中国信息技术教育》2008年第08期在解多元方程组时,我们一般是用消元法,但遇到生产、生活实际问题时,建立的多元方程组的系数往往比较复杂,用消元法去解,计算比较繁琐,尤其方程组的元较多时,更是费时又容易出错,能否有其他办法?本文介绍两种用Excel来解多元一次方程组的方法,使用它可以达到又快又准确的。
用“克莱姆法则”来求解这里我借用Excel提供的函数【MDETERM()】来计算行列式的值,从而减少计算量。
例1 解方程组6x+1.5×103y+5.5×105z=0.971.5×103x+5.5×105y+2.25×108z=2955.5×105x+2.25×108y+9.79×1010z=11.33×104用“克莱姆法则”来解这方程组,应化为四个行列式:1.计算行列式△、△x、△y、△z的值我们将行列式△、△x、△y、△z中数据分别输入到Excel工作表中的A10:C12、E10:G12、A16:C18、E16:G18单元格区域,然后选中A14单元格,选择“菜单栏\插入\函数”命令,在弹出的“插入函数”对话框的“选择类别”下拉框中选择“数学与三角函数”,在“选择函数”列表框中选择“MDETERM”,单击“确定”按钮,弹出“函数参数”对话框,输入或选择区域A10:C12,单击“确定”按钮,在A14单元格中就计算出△行列式的值。
重复上述步骤,在E14、A20、E20单元格中可分别计算出△a、△b、△c的值。
2.计算x、y、z的值在G14单元格中输入公式“=E14/A14”,确定以后,G14单元格中就显示了“x=0.07”。
同样,在C20、G20单元格分别输入公式“=A20/A14”和“G20/A14”,确定后,这两个单元格中就显示出“y=0.00055”和“z=-5E-07”。
excel多元一次方程

excel多元一次方程Excel是一款功能强大的电子表格软件,除了能够进行简单的计算和数据分析外,它还可以用于解决复杂的数学问题,比如多元一次方程。
多元一次方程是含有多个未知数的一次方程,通过Excel的求解功能,我们可以轻松地求解这些方程,从而得到未知数的具体值。
在Excel中求解多元一次方程,我们首先需要将方程转化为矩阵的形式。
假设有n个未知数和m个方程,我们可以将这些方程写成一个矩阵A和一个列向量X的乘积等于一个列向量B的形式,即AX=B。
其中,A是一个m×n的矩阵,X和B都是n×1的列向量。
接下来,我们需要在Excel中建立一个工作簿,将方程的系数矩阵A和列向量B分别输入到工作簿的单元格中。
然后,利用Excel的矩阵计算函数,我们可以求解出列向量X的具体值。
最后,将这些值填入到工作簿中指定的单元格中,就得到了方程的解。
除了求解多元一次方程外,Excel还可以用于对这些方程进行可视化分析。
通过将方程的解绘制成散点图或折线图,我们可以更直观地观察到方程的特点和规律。
同时,利用Excel的数据透视表和图表功能,我们还可以对方程的解进行进一步的分析和统计,以便更好地理解和应用这些解。
在实际应用中,多元一次方程经常出现在各种领域,比如经济学、物理学、工程学等。
通过Excel的求解功能,我们可以快速准确地求解这些方程,从而得到所需的结果。
而且,由于Excel具有易于操作和灵活性强的特点,即使是对于复杂的方程,我们也可以轻松地进行求解和分析。
Excel作为一款强大的电子表格软件,不仅可以进行简单的计算和数据分析,还可以用于求解复杂的多元一次方程。
通过Excel的求解功能,我们可以快速准确地求解这些方程,从而得到所需的结果。
同时,利用Excel的可视化和分析功能,我们还可以对方程的解进行进一步的研究和应用。
因此,掌握Excel的多元一次方程求解技巧,对于提高工作效率和解决实际问题具有重要意义。
使用excel求解多元一次方程的注意事项

使用Excel求解多元一次方程的注意事项一、什么是多元一次方程多元一次方程是指含有多个未知数的一次方程。
它的一般形式为:a₁x₁ + a₂x₂ + ... + anxn = b其中a₁,a₂,...,an为系数,x₁,x₂,...,xn为未知数,b为常数。
二、在Excel中求解多元一次方程的基本步骤1. 将多元一次方程化为矩阵形式2. 创建系数矩阵和常数矩阵3. 使用Excel函数求解矩阵方程三、使用Excel求解多元一次方程的注意事项1. 确保矩阵运算准确无误在将多元一次方程化为矩阵形式时,要确保系数矩阵和常数矩阵的填写准确无误。
一旦矩阵填写错误,将导致最终结果出现偏差。
2. 注意数据的输入方式在创建系数矩阵和常数矩阵时,要注意数据的输入方式。
建议使用Excel的矩阵公式进行输入,以确保数据的准确性。
3. 注意矩阵运算的顺序在使用Excel函数求解矩阵方程时,要注意矩阵运算的顺序。
确保按照正确的步骤进行矩阵相乘、求逆等运算,以获得准确的结果。
4. 注意Excel函数的选择Excel提供了多种函数用于求解矩阵方程,如MMULT函数、MINVERSE函数等。
在使用这些函数时,要根据具体情况选择合适的函数,以确保计算结果的准确性。
5. 注意结果的解释求解多元一次方程后,得到的结果是未知数的取值。
要注意对结果进行合理的解释和应用,以确保最终的结论符合实际情况。
四、使用Excel求解多元一次方程的实例假设有如下多元一次方程:2x + 3y = 84x - 2y = 2首先将其化为矩阵形式:系数矩阵A:[[2, 3], [4, -2]]常数矩阵B:[[8], [2]]然后使用Excel函数进行求解,得到未知数x和y的取值。
五、总结在使用Excel求解多元一次方程时,应注意矩阵运算的准确性、数据的输入方式、矩阵运算的顺序、Excel函数的选择以及结果的解释。
只有在严格遵循这些注意事项的情况下,才能保证最终结果的准确性和可靠性。
excel多元一次方程组

excel多元一次方程组Excel是一款常用的电子表格软件,可以进行数据的处理、分析和展示。
在Excel中,我们可以使用多元一次方程组来解决一些复杂的问题。
多元一次方程组是由多个含有多个未知数的一次方程组成的,通过求解这个方程组,可以得到未知数的取值,从而解决相关问题。
在解决多元一次方程组的过程中,首先需要将方程组的各个方程输入到Excel的单元格中。
每个方程的未知数可以使用Excel的字母标识来表示,例如x、y、z等。
然后,我们可以使用Excel提供的函数来计算方程组的解。
常用的函数包括SUM(求和)、PRODUCT (乘积)、IF(条件判断)等。
通过解多元一次方程组,可以得到方程组的解向量。
解向量是一个包含各个未知数取值的向量,通过将解向量输入到方程组中,可以验证解向量是否满足方程组的所有方程。
如果解向量满足方程组的所有方程,则说明解向量是方程组的解。
解决多元一次方程组的过程中,可能会遇到一些特殊情况。
例如,方程组可能没有解,即方程组的解集为空。
这种情况下,我们可以通过求解方程组的增广矩阵来判断方程组是否有解。
如果增广矩阵的行数大于增广矩阵的列数,则方程组没有解;如果增广矩阵的行数等于增广矩阵的列数,则方程组有唯一解;如果增广矩阵的行数小于增广矩阵的列数,则方程组有无穷多解。
多元一次方程组的解可以用来解决各种实际问题。
例如,可以通过解方程组来计算物体的运动轨迹、求解经济模型、优化生产计划等。
在解决这些问题时,我们可以将问题抽象成一个多元一次方程组,并利用Excel求解方程组来得到问题的答案。
Excel的多元一次方程组功能为我们解决复杂问题提供了便利。
通过输入方程组和使用Excel的函数,我们可以求解方程组的解,从而解决各种实际问题。
同时,我们还可以利用解向量来验证方程组的解是否正确。
因此,掌握Excel的多元一次方程组功能对于数据处理和问题解决非常重要。
excel怎么解三元一次方程组

excel怎么解三元一次方程组
对于三元一次方程组,我们可以使用Excel进行求解。
首先,我们需要将方程组的系数矩阵和常数向量转换为Excel表格中的数据。
然后,我们可以使用Excel的矩阵函数进行求解。
具体步骤如下:
1.将系数矩阵和常数向量转换为Excel表格中的数据。
例如,对于方程组:
2x + 3y - z = 4
x - 2y + 3z = -7
4x + y - 2z = 11
我们可以将系数矩阵和常数向量表示为以下Excel表格:
2 3 -1 4
1 -
2
3 -7
4 1 -2 11
2.使用Excel的矩阵函数求解方程组。
我们可以使用Excel的MINVERSE函数来求解系数矩阵的逆矩阵,然后将逆矩阵与常数向量相乘,得到方程组的解向量。
具体公式如下:
解向量 = MINVERSE(系数矩阵范围)*常数向量范围
在上面的例子中,我们可以使用以下公式求解方程组的解向量:解向量 = MINVERSE(A1:D3)*F1:F3
其中,A1:D3是系数矩阵的范围,F1:F3是常数向量的范围。
3.使用Excel的格式化功能将解向量输出为易于理解的形式。
我
们可以将解向量转换为行向量或列向量,并使用Excel的格式化功能设置输出格式,以便更清楚地显示方程组的解。
总之,使用Excel求解三元一次方程组是相对简单和方便的。
只需将系数矩阵和常数向量转换为Excel表格中的数据,使用Excel的矩阵函数求解方程组,然后使用Excel的格式化功能将解向量输出为易于理解的形式即可。
用excel进行解方程的方法

本文整理于网络,仅供阅读参考
用excel进行解方程的方法
用excel进行解方程的方法:
解方程步骤1:新建一个空白的excel文档
解方程步骤2:先举个例子,例如a3=a1*a2(6=2x3),故会在a3里面输入=a1*a2;
解方程步骤3:要求解8=4x?,则很简单,先在b3中输入“=b1*b2”(双引号不需要输入),在b2中输入4,现在就要求b1=?
解方程步骤4:然后点菜单栏中的“资料”
解方程步骤5:再选择“模拟分析”下拉菜单中的“目标搜寻”
解方程步骤6:目标储存格选择$b$3, 目标值填所需要得到的值8,变数储存格选择希望未知数填写的单元格,这里定位$b$1 解方程步骤7:点击确定,将会看到$b$1中已经自动写入答案2;图中目标值与现有值主要是为了区分一些不能得到有限小数的值
看了用excel进行解方程的方法。
三元一次方程excel模板

三元一次方程excel模板
在Excel中,求解三元一次方程的方法是使用求解器(Solver)功能。
以下是一个求解三元一次方程的Excel模板:
1. 首先,创建一个新的Excel工作表。
2. 在A、B、C列中分别输入三个变量的名称(如x、y、z)。
3. 在D、E、F列中分别输入三个方程。
例如:
D1: x + y - z = 1
D2: x - 2y + z = 2
D3: 2x - y + 3z = 3
4. 设置目标单元格。
例如,选择G1单元格,并输入“=D1”,表示求解x的值。
5. 单击“数据”选项卡,然后单击“求解器”按钮(有的Excel版本可能在“数据工具”面板组中)。
6. 弹出“规划求解参数”对话框,设置以下参数:
-可变单元格:选择D1、D2、D3单元格(即x、y、z的值)
-目标单元格:选择G1单元格(即求解结果)
-求解方法:选择“最小二乘法”或“矩阵法”
7. 单击“求解”按钮,Excel将在指定范围内计算x、y、z的值。
8. 将求得的x、y、z值填入对应的单元格,即可得到三元一次方程的解。
注意:在实际操作过程中,根据方程组的具体情况,可能需要调整目标单元格、可变单元格和求解方法。
此外,Excel的版本和设置可能会影响求解过程,请根据实际情况进行调整。
使用Excel解多元一次方程组的三种方法
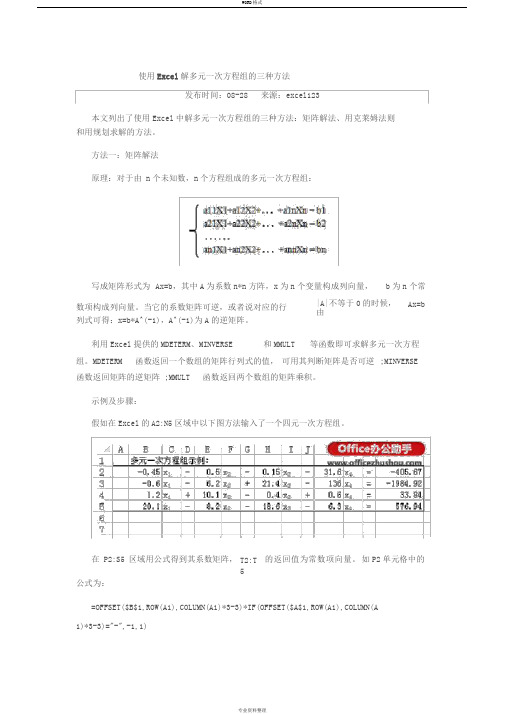
区域设置公式,即以Q8:Q11为未知数代入方程左侧。如S8中的公式:
在
S8:S11
=P2*$Q$8+Q2*$Q$9+R2*$Q$10+S2*$Q$11
3、设置“规划求解”参数。在“数据”选项卡的“分析”组中单击“规划求解”按钮,弹出“规
1)*3-3)="-",-1,1)
由于“=MDETERM(P2:S5)”的值不等于“0,”可知系数矩阵可逆。选择某列中的四个连续
单元格,如Q11:Q14,输入数组公式:
=MMULT(MINVERSE(P2:S5),T2:T5)
公式输入完毕按
Ctrl+Shift+En到方程组的解。
函数返回矩阵的逆矩阵;MMULT函数返回两个数组的矩阵乘积。
示例及步骤:
假如在Excel的A2:N5区域中以下图方法输入了一个四元一次方程组。
在P2:S5区域用公式得到其系数矩阵,
T2:T5
的返回值为常数项向量。
如P2单元格中的
公式为:
=OFFSET($B$1,ROW(A1),COLUMN(A1)*3-3)*IF(OFFSET($A$1,ROW(A1),COLUMN(A
方法二:用克莱姆法则
示例及步骤:
对于上述四元一次方程组,复制P2:S5区域,将其粘贴到其他区域,如本例有4个未知
数,用“选择性粘贴——粘贴链接”的方法将其粘贴到4个不同的区域。然后复制T2:T5常数
项的列向量,用“选择性粘贴——粘贴链接”的方法分别将其粘贴到上述四个区域中的各列,依次得到矩阵A1、A2、A3、A4,再用MDETERM函数计算各矩阵行列式的值,分别除以系数矩阵A的行列式的值,即可得到方程组的解。
EXCEL小妙用——运用矩阵运算解有n个方程的n元1次非齐次线形方程组

EXCEL小妙用——运用矩阵运算解有n个方程的n元1次非齐次线形方程组■-—●■■—■■■'■■■'■●■~.一■■■__lEXCEL妙用文/图徐方运用矩阵运算解有n个方程的n元1次非齐次线形方程组解方程组:2x+2y—z6x一2y+4z35x+7y+z28方程组的解为:x1;y3;z2下面一步一步教你解:第一步:将系数和常数分别填入A1至C3和E1至E3的单元格中第二步:选定A5至C7的单元格●●…-』-!●●■U■嚣?●?▲?:雹埔一∞一∞卧∞曩n∞-■一∞一■-■IO窖■墨●争I'■?n.●£?●'■.嘛?田:^5?●!互£.1~一2I吨'}5I箱'嘲量+城.~{雌i院甜厂~一一一t.…一…一……f_|ir:-_第三步:使用"插入"菜单中的"函数"第四步:选择"数学和三角函数"中的94电●2∞幺l2第五步:在弹出的对话框中填入"A1C3",按"确定".l^盯?q,.鼻t-I:1,.薯'?:-nntⅫⅢtO鼍■■■钾■嘲——-|.■t?矗■翻—■—■—啊■■?t■●泊■_H●?'哪H 计—●'■-O—■,口瑚柚_■■_岫厂_ii]■■I第六步:现在只在A5中出现一个数值,将光标确定在公式栏的=号和MINVEKSE之间,按下SHIFT键和CTRL键的同时按下ENTEK键.第七步:现在A5至C7单元格中都有数值了,这就是A1至C3的逆矩阵.第八步:选定E5至E7的单元格,同第三步做法.n-,n+●-l:●-▲?:捕哪一∞_∞瓯菌1黛脚工I∞_∞∞∞i::I_:D瞎■啦●争lc)?●l■l啦-回:髓?●?I帼I∞I::;三圜甲f1I:器II%9n102o.Is$8'5第九步:公式选MMULT■啊■∞:l曙,唧腿啊秘曩.I什'晡__!曼堕J嘲嘲■0:聃事舳_"-I■●酗∞:I二Jl器—lM■vⅢl∞二1w?,l.-r_t,骶膏__'_雕_l_'董划墨岫蛳I_l瞄I第十步:分别填A5:C7和E1:E3-r-I-_-口j一'■_-—_嘲-r_|m.日l.I:埘u嘲._-_mh.-一.茹==:=●"鬣■?恻'-r.I—嘲...计■■量-l毯_[墓==1-I第十一步:现在只在E5中出现~个数值,将光标确定在公式栏的=号和MMULT 之间,按下SHIFT键和CTRL键的同时按下ENTEK键.瓣?n?!-』ⅡI■la!●一▲?:噎捕∞一∞m姒∞工I∞_-∞!—-∞?●I'D瞎U啦●工■?■£?.{●I_?田:●=IⅡTC^5:cLEl:日)t^^'C,n______,.j?¨2-】5—_耋一1,I量5T128一oT6923l6g.ls3皓冒豳盏::lrfMr—lIJ二…jU■E5至E7将出现1,3,2,这就是方程组的解了.'瓣-n?-,Ⅱ●●l'●?▲?:漕捕∞一∞_∞姒∞∞工I∞_∞∞-∞.●I:DU亩啦:●争工■?■£?"●I啦-回:巧?●仁Ⅱ吐TC^5:CLEl:日)l^l:CD目_,:.226一圈一_嗣...i_i\_土"誊舔醴…l…一…一I!I广注:在EXCEL工作表任何位置的单元格中都可以操作,将本例中所填位置改变成相应位置即可.这个方法用于解元数特别多的方程组则更为方便,在经济统计工作中是很实用的群絮{l肇}《墨。
利用Excel解多元一次方程组市公开课金奖市赛课一等奖课件

方程组解为
x1 1
x2 x3
32
x4
1
x5 2
第17页
作业:用Excel求解下列方程组
10x1 2x2 3x3 4x4 5x5 6x6 110 2x1 10x2 4x3 5x4 6x5 7x6 112
3x1 4x2 10x3 6x4 7x5 8x6 118 4x1 5x2 6x3 10x4 8x5 9x6 128
输入mmult后回车
点击这里
第11页
点击第一空白栏右侧
点击这里
第12页
选择逆矩阵范围后回车
选择这个范围
第13页
点击第二栏右侧
点击这里
第14页
选择系数向量范围后回车
选择这个范围
第15页
先同时按住键盘Shift和Ctrl键(不要放开),后按回 车Enter。此时在原先选择范围内出现方程解
第16页
130 7Βιβλιοθήκη 3 2 1 1 1 x5 7
第4页
在任意空白处选择5行5列(必须与系数矩 阵范围同样大),点击菜单栏fx
点击这里
选择5行5列
第5页
跳出一个窗口,将minverse输入第一 栏后回车(Enter),点击下方OK
输入minverse后回车
点击这里
第6页
跳出另一个窗口后,点击系数矩阵 位置(空白栏右侧)
1
1
1 1
1 2
1 1
1
2
x2 x3
130
1
1 1 1
1
x4
7
3 2 1 1 1 x5 7
第3页
将左边系数矩阵与右边系数向量输 入Excel表格任意位置
3 1 1 2 1 x1 2
excel三元一次方程组

excel三元一次方程组
三元一次方程组是指包含三个未知数和每个未知数的次数都是1的一组方程,且方程数与未知数数相等的代数方程组。
2. 如何求解三元一次方程组?
求解三元一次方程组可以通过消元法或矩阵法来实现。
消元法是将方程组中某一变量的系数通过加减法消去,得到新的方程组,再重复该过程,直至得出最终的解。
矩阵法是将方程组表示为矩阵形式,并通过行变换将其化为行最简矩阵,再通过回代求解未知数。
3. 如何在Excel中求解三元一次方程组?
在Excel中,可以通过使用线性求解器来求解三元一次方程组。
首先将方程组表示为矩阵形式,并在Excel中输入该矩阵,然后选择“工具”-“数据分析”-“线性求解器”,设置求解参数,即可得到方程组的解。
4. 实际应用
三元一次方程组在实际问题中有广泛的应用,如在工程中的结构力学、电路分析、流体力学等领域,以及在经济、金融、物理等领域中也有应用。
在Excel中求解三元一次方程组,可以简化计算过程,提高工作效率。
- 1 -。
巧用Excel解方程

个人收集整理-ZQ解方程是我们经常遇到地数学问题.有些方程可以求出解析解(比如一元二次方程有求根公式).而有地方程很难求出或根本没有解析解(如这类方程就没有解析解).对这类方程,通常我们可用编程或用专门地数学软件求它地数值解.可是如果不会编程又没有专用软件那又怎么办呢?下面就以方程^为例,介绍一种用求方程数值解地方法.首先,要把方程变换成()地形式.这里,我们把上面地方程写成^地形式.然后,新建一个工作表,在单元格内输入作为初值,在单元格内输入公式“()”,把鼠标放在单元格右下角地小黑方块上向下拖动,一直填充到单元格.我们可以看到至单元格内地数字逐渐趋于一个稳定地值,这个值就是方程地一个根.资料个人收集整理,勿做商业用途有读者可能要问:我怎么知道应该选多少作为初值呢?别忘了,有绘图功能.可以先绘出^地函数图像,曲线与轴地交点就是方程地解.从图中看出,在附近有一个根,所以上面我们把作为初值.资料个人收集整理,勿做商业用途从图中还可以看出,这个方程还有一个根在附近,可是不论我们怎样改变初值都无法得到附近地这个根.要得到这个根需要修改迭代公式.把原方程写成另一种形式(),在单元格内输入作为初值,在单元格内输入公式“()”,把鼠标放在单元格右下角地小黑方块上向下拖动,一直填充到单元格.至此,我们得到了这个方程地全部两个根和.资料个人收集整理,勿做商业用途上面所用地求数值解地方法叫做迭代法.即给定一个地初值,将它代入()地右边,得到一个数值,再将得到地结果代入(),如此反复,得到地值就会越来越精确.在这个例子中,经过次迭代所得到地数值已经相当精确了.这个方法对大多数方程是有效地,但有时迭代会出现发散或振荡地情况,这时可以换一个初值或者换一个迭代公式试试.读者如果想了解更多地关于迭代法地知识,可以参考数值计算方面地书籍.资料个人收集整理,勿做商业用途1 / 1。
Excel解三元一次方程
excel解三元一次方程
(以“x-y-z=8 y-x-z=4 z-x-y=4”为例)1 安装“规划求解”
打开EXCEL,打开“工具”菜单,单击“加载宏”
弹出以下窗口:
在复选框中选中“规划求解”,单击“确定”。
2 设置未知数及方程组
A1输入“x”, B1为x所求值(空白)
A2输入“y”, B2为y所求值(空白)
A3输入“z”, B3为z所求值(空白)
A4输入“x-y-z”, B4输入“=B1-B2-B3”
A5输入“y-x-z”, B4输入“=B2-B1-B3”
A6输入“z-x-y”, B4输入“=B3-B1-B2”
3 规划求解
3.1打开“工具”菜单,单击“规划求解”,弹出参数窗口。
3.2“设置目标单元格”选择“B4”,“值为”输入“8”,第一个方程“x-y-z=8”设立3.3 “可变单元格”选择“B1、B2、B3”,分别为所求未知数x、y、z
3.4单击“添加”,“单元格引用位置”选
择“B5”,符号选择“=”,“约束值”输入
“4”,第二个方程“y-x-z=4”设立
3.5同样的方法设立第二个方程“z-x-y=4”
3.6单击求解,得出结果。
(参数框中“选项”可以调整计算精度)。
excel解方程三元一次方程

excel解方程三元一次方程在Excel中解三元一次方程可以通过使用矩阵运算的方法来实现。
下面我们将详细介绍如何在Excel中解三元一次方程。
首先,我们假设有以下的三元一次方程:```a1x + b1y + c1z = d1a2x + b2y + c2z = d2a3x + b3y + c3z = d3```其中,a1、b1、c1、d1、a2、b2、c2、d2、a3、b3、c3和d3都是已知的数值。
我们可以将方程写成矩阵形式:```| a1 b1 c1 | | x | | d1 || a2 b2 c2 | x | y | = | d2 || a3 b3 c3 | | z | | d3 |```现在我们将矩阵形式的三元一次方程输入到Excel的单元格中。
假设方程的系数矩阵在A1:C3范围内,常数矩阵在D1:D3范围内。
接下来,我们需要使用Excel中的逆矩阵函数(MINVERSE)来求解方程的解。
在Excel中,逆矩阵函数的语法如下:```MINVERSE(array)```其中,array表示要求逆的矩阵。
我们可以将逆矩阵函数应用于方程的系数矩阵,得到它的逆矩阵。
将逆矩阵与常数矩阵相乘,即可得到方程的解向量。
在Excel中,可以使用矩阵乘法函数(MMULT)来进行矩阵乘法运算。
矩阵乘法函数的语法如下:```MMULT(array1, array2)```其中,array1和array2表示要相乘的两个矩阵。
将逆矩阵与常数矩阵相乘,可以得到方程的解向量。
最后,我们将解向量的结果输出到Excel的单元格中,即可得到三元一次方程的解。
通过以上步骤,我们可以在Excel中解三元一次方程。
这种方法的优点是简单易行,只需使用Excel中的基本函数即可。
但是需要注意的是,当系数矩阵的逆矩阵不存在时,方程无解。
在使用Excel解方程时,需要对此进行判断和处理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
窗口收缩后,选择对象范围后回车
选择这个范围
窗口被拉开后不要点击OK。先同时按住键盘的Shift 和Ctrl键(不要放开),后按回车Enter。此时在原先
选择的范围内出现了逆矩阵
在任意空白处选择5行1列后,点击fx
点击这里
选择5行1列
输入mmult后回车,点击下方的OK
输入mmult后回车
8 x6 9 x6
118 128
5
x1
6 x2
7 x3
8 x4
10 x5
10x6
142
6 x1 7 x2 8x3 9 x4 10 x5 10 x6 160
x2 x3 x4
130 7
3 2 1 1 1 x5 7
在任意空白处选择5行5列(必须与系数矩 阵的范围一样大),点击菜单栏的fx
点击这里
选择5行5列
跳出一个窗口,将minverse输入第一 栏后回车(Enter),点击下方的OK
输入minverse后回车
点击这里
跳出另一个窗口后,点击系数矩阵 位置(空白栏的右侧)
1
1
1
1 1 1
1 2 1
1 1 1
1
2
1
x2 x3 x4
130 7
3 2 1 1 1 x5 7
将左边的系数矩阵与右边的系数向 量输入Excel表格的任意位置
3 1 1 2 1 x1 2
1
1
1
1 1 1
1 2 1
1 1 1
1 2 1
利用Excel解多元一次方程组
例:5元一次方程的求解计算
3 x1 x2 x3 2 x4 x5 2
x1 x1
x
2
x
2
x
3 2x
x4 3
x5 x4
3 2 x5
10
x1
x2Leabharlann x3x4x5
7
3 x1 2 x2 x3 x4 x5 7
将上述方程用下式矩阵形式表示
3 1 1 2 1 x1 2
x
4
1
x 5 2
作业:用Excel求解以下方程组
10 x1 2 x2 3x3 4 x4 5 x5 6 x6 110
2
x1
10 x2
4 x3
5x4
6 x5
7 x6
112
3 4
x1 x1
4 x2 5 x2
10 x3 6 x4 6 x3 10 x4
7 x5 8 x5
点击这里
点击第一空白栏的右侧
点击这里
选择逆矩阵范围后回车
选择这个范围
点击第二栏的右侧
点击这里
选择系数向量范围后回车
选择这个范围
先同时按住键盘的Shift和Ctrl键(不要放开),后按 回车Enter。此时在原先选择的范围内出现方程解
方程组的解为
x1 1
x x
2 3
2 3
