如何用EXCEL解方程组
excel解9元一次方程组

excel解9元一次方程组
以下是在Excel中解9元一次方程组的一般步骤:
1. 将方程组放入一个Excel表格中,确保每个方程都有正确的行、列和系数。
2. 在Excel中使用“求和”功能来计算每个方程的和。
假设方程组为“ax + by = c”和“dx +ey = f”,则可以使用以下公式:
```
=SUMIF(A:A,">=c",B:B)
```
该公式将返回“a”到“f”中所有大于等于“c”的行。
3. 使用“替换”功能来将方程组的系数替换为对应的值。
4. 使用Excel中的“VLOOKUP”函数或“ Siri”功能来查找和匹配方程组的值。
VLOOKUP函数可以查找指定值在指定列中的值, Siri 功能可以查找指定值在指定文本框中的值。
假设我们要查找“c”在“ax + by = c”和“dx +ey = f”中的值,则可以使用以下公式:
```
=Siri("请告诉我要找的值是什么?","ax + by = c")
```
如果使用 Siri 功能,则可能需要在“Siri”输入框中输入“请告诉我要找的值是什么?”,然后按下“Home”键。
系统将返回“ax +
by = c”和“dx +ey = f”中的“c”的值。
5. 如果找到了匹配的值,则使用Excel中的“=VLOOKUP(表达式,数组,范围,返回值)”公式将值应用于方程组中。
6. 最后,使用 Excel 中的“重排”功能将所有方程按顺序排列。
excel解复杂的二元一次方程组

excel解复杂的二元一次方程组Excel是一款功能强大的电子表格软件,在数字计算、数据分析、图表制作等方面有着广泛的应用。
今天,我们将着重介绍如何利用Excel解决复杂的二元一次方程组。
首先,我们需要了解什么是二元一次方程组。
简单来说,它就是由两个含有两个未知数的一次方程组成的方程组。
比如说,下面这个方程组:4x - 3y = 52x + 7y = 11其中,未知数为x和y。
我们需要找到它们的值,使得这两个方程同时成立。
接下来,我们就可以利用Excel中的“求解器”功能来解决这个方程组。
第一步,我们需要将方程组转化为标准形式。
标准形式指的是将未知数放在等号的左侧,常数放在等号的右侧,且系数为整数的形式。
对于上面的方程组,标准形式为:4x - 3y - 5 =02x + 7y - 11 = 0第二步,我们需要用Excel创建一个工作表。
在工作表中,我们需要输入上述标准形式的方程组。
具体来说,我们可以使用Excel的单元格来分别表示每个未知数的系数和常数项。
第三步,我们需要启用Excel内置的“求解器”功能。
求解器功能可以帮助我们找到方程组的解。
在Excel中,我们可以通过点击“数据”选项卡,然后选择“求解器”按钮来打开求解器功能。
然后选择“最小化误差”模型类型,并输入对应的目标函数和约束条件。
第四步,我们需要设置求解器的参数。
具体来说,我们需要选择求解器要解决的问题类型(线性或非线性)、选择求解方法(单纯形法、遗传算法等)、设置约束条件、设置目标函数等。
在Excel中,我们可以通过单击“求解”按钮,来启动求解器,并查看求解结果。
值得注意的是,求解器只能解决线性问题。
对于非线性问题,我们需要使用其他工具或方法来解决。
最后,通过分析Excel的求解结果,我们可以得到该方程组的解,即x和y的值。
这样,我们就成功地解决了这个复杂的二元一次方程组。
总之,利用Excel解决二元一次方程组是一项非常实用的技能。
EXCEL解方程组

逆矩阵 行数等于列数的矩阵称为方阵。若一方 阵的主对角元素aii均为1,其他位置上的 元素均为0,则该矩阵称为单位矩阵I 。 设有一n阶方阵A和另一n阶方阵B,它 们的乘积为:AB=BA=I 则B为A的逆阵,可记为A-1。
3.1 Excel 矩阵运算
逆矩阵 Excel求逆矩阵的工作表函数为 MINVERSE(array) 例1. MINVERSE({4,-1;2,0}) 例2. MINVERSE({1,2,1;3,4,-1;0,2,0}) 例3. MINVERSE()为一矩阵,可参与其他 矩阵运算。
数组乘以一常数 数组乘以一常数,得到与原数组大小相同的 新数组,新数组的每个单元格的值等于原数 组单元格的值乘以此常数。
3.1 Excel 矩阵运算
4.
矩阵乘法 矩阵A(m×n)与B(n×p)相乘,得 一矩阵C(m×p)。仅当第一个矩阵的 列数等于第二个矩阵的行数时,两矩阵 才能相乘。 矩阵相乘时,各矩阵元素按一定规则相 乘再相加。Excel有矩阵相乘的工作表函 数MMULT(array1,array2)。
其中xi(x1, x2, x3,…) 是实验未知数,ci是实验测量值, aij是系数。这些方程必须是线性独立的,上式的矩 阵表示为: AX=C
3.2 解线性联立方程
A是系数矩阵:
a11 a21 A am1 a12 a22 am 2 a1n ... a2 n ... amn ...
5.
3.1 Excel 矩阵运算
行列式 行列式是在研究线性方程组的解法中产生 的概念。n阶行列式可表示为:
6.
a11 D a21 an1
a12 a22 an 2
...
a1n
... a2 n ... ann
excel解方程

excel解方程在Excel中解方程可以通过使用“求解器”工具来实现。
求解器是一种用于求解多变量线性和非线性方程组的工具,能够帮助我们在Excel中快速准确地求解各种类型的方程。
步骤一:建立Excel工作表首先,在Excel中新建一个工作表,用于输入方程和变量的值。
通常情况下,我们将在某个单元格中输入一个方程,并在其他单元格中输入变量和参数的值。
步骤二:输入方程在Excel的某个单元格中输入要解的方程。
方程可以是线性的,也可以是非线性的。
例如,我们要解决以下方程:2x + 3y = 12,其中x和y是我们要求解的变量。
步骤三:输入变量和参数的值在其他的单元格中输入变量和参数的值。
我们需要给出至少两个变量的值,以确定方程的解。
在上述例子中,我们可以为x和y输入任意值。
步骤四:使用求解器工具1. 首先,点击工具菜单中的“数据分析”选项。
如果您没有找到“数据分析”,您可能需要先启用Excel的“加载项”选项。
2. 在弹出的“数据分析”对话框中,选择“求解器”并单击“确定”按钮。
3. 在打开的求解器对话框中,将目标单元格设置为方程等式的左边(在本例中为C1单元格)。
4. 在“约束”区域中,设置变量单元格(在本例中为A1和B1单元格)的约束条件。
我们可以通过选择“变量单元格”选项来指定每个变量的约束条件,例如是否限制为整数或是否具有上下限等。
5. 选择一个求解方法,例如“喇叭曲线平滑法”或“演化策略”。
通常情况下,您可以选择默认的求解方法。
6. 单击“确定”按钮进行求解。
步骤五:查看解的结果如果一切顺利,求解器将会找到方程的解并显示在相应的单元格中。
在本例中,求解器将计算并显示x和y的值。
总结:通过Excel的“求解器”工具,我们可以在Excel中方便地求解各种类型的方程。
无论是线性方程还是非线性方程,只要我们按照上述步骤进行操作,就能够快速准确地得到方程的解。
Excel的求解器功能使我们能够轻松地进行方程求解,为工程技术人员和数学爱好者提供了一个非常有用的工具。
excel解方程

excel解方程Excel是一款强大的电子表格软件,广泛应用于数据处理和数学计算。
它不仅可以进行基本的四则运算,还可以使用内置的函数和工具进行复杂的数学运算,如解方程。
在本文中,我们将介绍如何利用Excel解方程。
解一元一次方程:一元一次方程是最简单的方程形式,通常表示为ax + b = 0,其中a和b为已知数,x为未知数。
在Excel中,我们可以使用“数据分析”工具和求解器来求解这类方程。
首先,我们需要确保求解器已启用。
在Excel中,选择“文件”-“选项”-“加载项”-“Excel加载项”-“管理”中勾选“求解器”,然后点击“确认”。
接下来,我们需要在Excel的工作表中设置方程的参数。
假设我们以单元格A1和A2分别表示a和b的值,我们可以使用函数“=解方程(a*x+b, x)”来表示方程。
然后,在单元格A3中输入0,表示等式右边的常数项。
此时,我们需要选择某个单元格,例如A4,作为解的输出。
然后,点击“数据”-“数据分析”,在弹出的窗口中选择“求解器”,然后点击“确定”。
在求解器窗口中,我们需要设置参数。
在“目标单元格”中,选择解的输出的单元格,即A4。
在“调整单元格”中,选择变量的单元格,即A5。
在“条件”下方的“优化选项”中,选择“最小值”,并确保“最大迭代次数”为100。
最后,点击“确定”。
Excel会自动计算方程的解,并将结果显示在单元格A5中。
此时,A5中显示的就是方程的解。
解其他类型的方程:除了一元一次方程,Excel还可以解其他类型的方程,如二次方程、高次方程和多元方程组。
在这些情况下,我们可以使用Excel的数组公式来实现。
对于二次方程ax^2 + bx + c = 0,可以使用函数“=根据系数求解(a,b,c)”来计算方程的解。
该函数将返回一个数组,其中包含方程的两个实根。
我们可以将函数输入到多个单元格中,分别表示两个实根。
对于高次方程和多元方程组,Excel提供了多个函数和工具。
excel怎么解二元一次方程

excel怎么解二元一次方程
Excel可以通过计算函数的方法来解二元一次方程,具体步骤如下:
1. 在Excel中建立一个新的工作表,并在工作表中设置列名称和变量值。
2. 输入二元一次方程的常数项和系数,例如:ax + by = c、dx + ey = f。
3. 选择一个空白的单元格,输入一个函数来计算二元一次方程的解。
4. 通过一元二次方程公式求解得出变量值。
根据上述步骤,可以分为以下几个层面的详细操作:
1. 新建立工作表
在Excel中新建一个工作表,并设置好列名,可以设置为x、y、a、b、c、d、e、f等名称。
2. 设置变量值
在工作表中设置二元一次方程的系数和常数项的值,例如:a=2、b=3、c=4、d=5、e=6、f=7。
3. 计算方程的解
在一个新的单元格中输入公式:=解方程组(x的系数, y的系数, 常数项; x的系数, y的系数, 常数项)。
例如:=解方程组(2, 3, 4; 5, 6, 7)。
4. 解得变量值
通过解得的变量值,即可得出方程的解,例如:x=1,y=2。
总结:
Excel可以通过一些简单的计算函数来解方程组,让研究二元一次方程的学生更加方便快捷地计算出方程的解。
在进行这项工作时,请遵循上述步骤,在Excel工作表中设置相应的列名称和变量值,并使用公式求解得到方程组的解。
excel解多元方程组

excel解多元方程组在数学领域,多元方程组是指包含两个或更多个未知数的方程组。
解决多元方程组的方法有很多,如代入法、消元法、矩阵运算等。
在实际应用中,我们可以使用Excel这款强大的工具来求解多元方程组。
以下是使用Excel解决多元方程组的方法和步骤。
1.打开Excel,新建一个工作表。
2.假设我们有如下多元方程组:a * x +b * y = cd * x +e * y = f3.在第一行和第二行分别输入方程组的系数和常数项,如下所示:```A1:aB1:bC1:cD1:dE1:eF1:f```4.在第三行和第四行输入未知数的名称,例如:```A3:xB3:y```5.利用Excel的公式功能求解方程组。
在第五行输入以下公式:```= Solver(A1*A3+B1*B3=C1, A2*A3+B2*B3=D1, A3)```6.按下Enter键,Excel将显示一个对话框,要求我们设置求解参数。
在对话框中,设置以下参数:- 目标单元格:第五行的公式结果(如F5)- 约束条件:第二行和第四行的单元格(如B2和B4)- 变量范围:第一行和第三行的单元格(如A1:A3和B1:B3)7.点击“确定”按钮,Excel将自动计算出未知数的解。
解的单元格显示为公式结果,如F5。
8.检查计算结果,确保解符合实际意义。
需要注意的是,在实际操作中,我们可能需要根据方程组的实际情况调整输入方式和参数设置。
此外,Excel的求解能力受限于工作表的规模和计算复杂度,过于复杂的方程组可能无法得到准确结果。
在遇到此类情况时,我们可以考虑使用专业的数学软件或寻求其他解决方法。
总之,通过以上步骤,我们可以使用Excel轻松解决多元方程组。
excel三元一次方程组

excel三元一次方程组Excel三元一次方程组Excel是一款功能强大的电子表格软件,除了可以进行数据处理和分析外,还可以进行数学计算。
其中,Excel的求解器功能可以帮助我们解决复杂的数学问题,包括三元一次方程组。
三元一次方程组是指由三个未知数和三个方程组成的方程组。
在Excel中,我们可以使用求解器功能来求解三元一次方程组。
下面,我们将介绍如何使用Excel求解三元一次方程组。
我们需要在Excel中输入三个方程。
假设我们要求解以下三元一次方程组:2x + 3y + 4z = 103x + 4y + 5z = 154x + 5y + 6z = 20我们可以将这三个方程分别输入到Excel的三个单元格中,如下图所示:接下来,我们需要使用Excel的求解器功能来求解这个方程组。
首先,我们需要打开Excel的求解器功能。
在Excel 2010及以上版本中,求解器功能位于“数据”选项卡中的“分析”组中。
在Excel 2007及以下版本中,求解器功能位于“工具”菜单中的“插件”选项中。
打开求解器功能后,我们需要设置求解器的参数。
首先,我们需要选择要优化的单元格,也就是我们要求解的未知数。
在本例中,我们需要选择三个单元格,分别对应x、y和z的值。
接着,我们需要设置目标单元格,也就是我们要求解的方程组。
在本例中,我们需要选择三个单元格,分别对应三个方程。
设置好参数后,我们需要点击“确定”按钮,Excel会自动求解方程组,并将结果显示在我们选择的单元格中。
在本例中,我们可以得到以下结果:x = 1y = 2z = 3这就是我们所求解的三元一次方程组的解。
通过Excel的求解器功能,我们可以轻松地求解各种复杂的数学问题,包括三元一次方程组。
用Excel解方程(组)

用Excel解方程(组)准备工作本方法要用到"规划求解"这一功能,在"工具"菜单中若没有"规划求解…"命令,则单击菜单栏"工具"→"加载宏…",在"加载宏"对话框的"当前加载宏"的列表框中选中"规划求解加载宏",然后按"确定"钮,即可在"工具"菜单下出现"规划求解…"。
若"当前加载宏"的列表框中没有"规划求解加载宏"一行,则需重新安装Excel(自定义安装),具体过程本文从略。
求解步骤例如解方程组:1.运行Excel。
2.在A1~A3三个单元格中(也可在其他单元格中,最好是连续的,单元格个数由方程的个数决定。
我们暂称这个区为"方程区")依次输入"=2*b1-b2+2*b3"、"=-b1+3*b2-5*b3"、"=4*b1+2*b2+3*b 3"(不分大小写,引号不输入,下同。
b1、b2、b3分别表示三个未知数x、y、z的值,即B1~B3单元格将显示三个未知数的值,它决定第4(3)步中要输入的内容),分别回车后,三个单元格均显示"0"(因此时B 1~B3单元格均为空,当"0"处理,通过计算,刚输入的三个表达式的值也为0,故都显示0)。
3.单击菜单栏"工具"→"规划求解…"。
4.在"规划求解参数"对话框中进行下列设置:(1)在第一行"设置目标单元格"中输入"$A$1"(也可只输入"A1",还可用鼠标选取对应的单元格,下同);(2)在第二行"等于"中选取"值为"一项,并在其后的框中输入"-1"(即第一个方程右边的值);(3)在第三行"可变单元格"框中输入"$B$1:$B$3"(即B1~B3单元格,由第2步决定,这三个单元格用于显示三个未知数的值,暂称之为"解区");(4)在"约束"框中单击"添加"钮,出现"添加约束"对话框,在"单元格引用位置"中输入"$A$2",在中间的下拉列表框中选取"=",在"约束值"中输入"12"(即第二个方程右边的值)。
excel解多元方程组

excel解多元方程组(实用版)目录1.引言:介绍 Excel 解多元方程组的方法和优势2.准备:需要了解的 Excel 功能和操作3.示例:用 Excel 解一个多元方程组4.总结:Excel 解多元方程组的步骤和注意事项5.展望:Excel 在其他数学领域的应用正文1.引言在数学中,解多元方程组是一个重要的课题。
而在现实生活中,我们也会遇到需要解决多元方程组的问题。
例如,在经济学中,我们需要分析多种因素对市场需求的影响;在物理学中,我们需要研究多个物理量之间的关系等。
在这种情况下,Excel 作为一种强大的数据处理工具,可以帮助我们快速解决多元方程组问题。
本文将介绍如何使用 Excel 解多元方程组,并阐述这种方法的优势。
2.准备在使用 Excel 解多元方程组之前,我们需要了解一些 Excel 的基本功能和操作。
首先,我们需要熟悉 Excel 的工作表,其中包括单元格、行和列。
在单元格中,我们可以输入数据和公式。
其次,我们需要掌握Excel 的一些基本函数,如 SUM(求和)、AVERAGE(平均值)、COUNT(计数)等。
此外,我们还需要了解如何使用 Excel 的数据表功能,如排序、筛选和透视表等。
3.示例下面,我们通过一个示例来说明如何使用 Excel 解多元方程组。
假设我们有如下多元方程组:x + y = 102x - 3y = 12我们首先将数据输入到 Excel 的工作表中,然后使用“数据”选项卡中的“排序”功能,对数据进行排序。
接着,我们使用“插入”选项卡中的“透视表”功能,创建一个透视表。
在透视表中,我们将两个方程组的值分别放入“行标签”和“值”区域。
然后,在“值字段设置”中,选择“计算字段”,并输入如下公式:=SUM(此行所有值)在“行标签”区域,我们选择“标签”选项,并输入公式:=GET.CELL(1,此行)最后,我们在透视表中添加一个新的行标签,命名为“解”。
在“解”行的“值”区域,我们输入以下公式:=IF(SUM(此行所有值)=0,0,SUM(此行所有值))这样,我们就可以得到多元方程组的解。
excel解析方程

excel解析方程
Excel是一款强大的电子表格软件,除了常规的数据处理外,它还可以用来解析方程。
下面是一些使用Excel解析方程的方法:
1. 制作方程表格:在Excel中,可以通过表格的方式将方程转
换为数据,从而进行计算。
首先,在表格中添加一个列作为变量,再添加一个列作为方程运算的结果。
然后,将方程中每个变量的值输入到变量列中,再将方程输入到结果列中。
最后,通过Excel的函数功能计算出结果。
2. 使用 Excel 内置函数:Excel中内置了很多数学函数,如SUM、AVERAGE、PRODUCT、SQRT、POWER等,这些函数可以用来计算各种方程的解。
例如,如果需要计算方程y = x^2 + 2x + 1在x=2时的解,可以使用Excel的POWER函数和SUM函数进行计算,即
SUM(POWER(2,2),2*2,1)。
3. 使用插件:如果需要更高级的方程求解功能,可以使用Excel 的插件,如Solver插件、Data Analysis插件等。
这些插件可以解
决各种复杂的方程组和非线性方程。
使用Excel解析方程可以大大提高数学计算的效率,同时也可以帮助我们更好地理解数学知识。
- 1 -。
使用Excel解多元一次方程组的三种方法

使用Excel解多元一次方程组的三种方法本文列出了使用Excel中解多元一次方程组的三种方法:矩阵解法、用克莱姆法则和用规划求解的方法。
方法一:矩阵解法原理:对于由n个未知数,n个方程组成的多元一次方程组:写成矩阵形式为Ax=b,其中A为系数n*n方阵,x为n个变量构成列向量,b为n个常数项构成列向量。
当它的系数矩阵可逆,或者说对应的行列式|A|不等于0的时候,由Ax=b可得:x=b*A^(-1) ,A^(-1)为A的逆矩阵。
利用Excel提供的MDETERM、MINVERSE和MMULT等函数即可求解多元一次方程组。
MDETERM函数返回一个数组的矩阵行列式的值,可用其判断矩阵是否可逆;MINVERSE函数返回矩阵的逆矩阵;MMULT函数返回两个数组的矩阵乘积。
示例及步骤:假如在Excel的A2:N5区域中以下图方法输入了一个四元一次方程组。
在P2:S5区域用公式得到其系数矩阵,T2:T5的返回值为常数项向量。
如P2单元格中的公式为:=OFFSET($B$1,ROW(A1),COLUMN(A1)*3-3)*IF(OFFSET($A$1,ROW(A1),COLUMN(A1)*3-3)="-",-1,1)由于“=MDETERM(P2:S5)”的值不等于“0”,可知系数矩阵可逆。
选择某列中的四个连续单元格,如Q11:Q14,输入数组公式:=MMULT(MINVERSE(P2:S5),T2:T5)公式输入完毕按Ctrl+Shift+Enter结束,即可在Q11:Q14得到方程组的解。
方法二:用克莱姆法则示例及步骤:对于上述四元一次方程组,复制P2:S5区域,将其粘贴到其他区域,如本例有4个未知数,用“选择性粘贴——粘贴链接”的方法将其粘贴到4个不同的区域。
然后复制T2:T5常数项的列向量,用“选择性粘贴——粘贴链接”的方法分别将其粘贴到上述四个区域中的各列,依次得到矩阵A1、A2、A3、A4,再用MDETERM函数计算各矩阵行列式的值,分别除以系数矩阵A的行列式的值,即可得到方程组的解。
Excel解三元一次方程
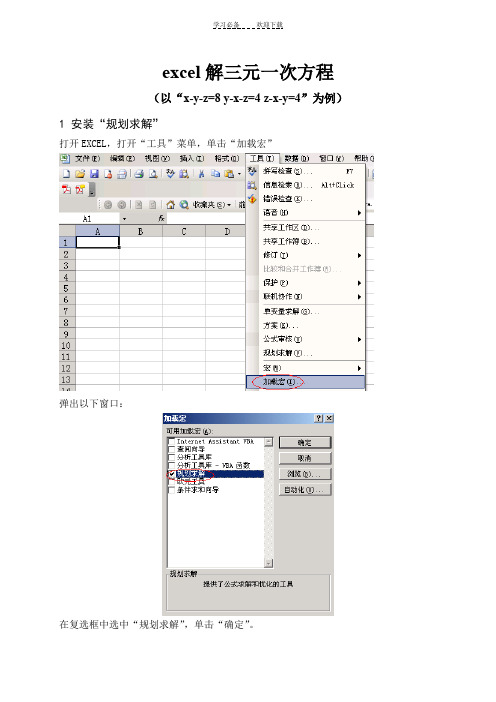
excel解三元一次方程
(以“x-y-z=8 y-x-z=4 z-x-y=4”为例)1 安装“规划求解”
打开EXCEL,打开“工具”菜单,单击“加载宏”
弹出以下窗口:
在复选框中选中“规划求解”,单击“确定”。
2 设置未知数及方程组
A1输入“x”, B1为x所求值(空白)
A2输入“y”, B2为y所求值(空白)
A3输入“z”, B3为z所求值(空白)
A4输入“x-y-z”, B4输入“=B1-B2-B3”
A5输入“y-x-z”, B4输入“=B2-B1-B3”
A6输入“z-x-y”, B4输入“=B3-B1-B2”
3 规划求解
3.1打开“工具”菜单,单击“规划求解”,弹出参数窗口。
3.2“设置目标单元格”选择“B4”,“值为”输入“8”,第一个方程“x-y-z=8”设立3.3 “可变单元格”选择“B1、B2、B3”,分别为所求未知数x、y、z
3.4单击“添加”,“单元格引用位置”选
择“B5”,符号选择“=”,“约束值”输入
“4”,第二个方程“y-x-z=4”设立
3.5同样的方法设立第二个方程“z-x-y=4”
3.6单击求解,得出结果。
(参数框中“选项”可以调整计算精度)。
利用Excel求解线性方程组

利用Excel求解线性方程组{x1+x2=7…① x1-x2=-5…②}实例
一、打开excel,点击菜单栏中的数据选项,如图1:
二、在单元格a1中输入x1,在单元格a2中输入x2,在单元格a3中输入x1+x2,在a4单元格中输入x1-x2,如下图:
三、在单元格b3输入公式”=b1+b2”,回车;在单元格b4输入公式”=b1-b2”,回车,如图:
四、将b3单元格设为活动单元格,再点击命令按钮“规划求解”,如图:
五、在规划求解参数对话框中,设置目标为b3单元格绝对地址,到目标值(选中)为7,通过更改可变单元格,用鼠标选中b1:b2单元格,遵守约束里点击添加按钮,在添加约束对话框中,单元格引用中选择b4单元格,点击下拉按钮选择”=”,在约束栏填-5,再点击确定,如图:
六、再点击求解,即可在b1和b2单元格中求出x1和x2的值,如图:
Δ若点击数据菜单项没有规划求解,怎么办呢?可在文件菜单项中的选项子菜单中点击加载项,选择规划求解加载项,然后点击确定即可,如图:。
excel解齐次方程组

excel解齐次方程组【原创实用版】目录1.引言2.什么是齐次方程组3.Excel 解齐次方程组的方法和步骤4.实际操作示例5.总结正文1.引言在数学中,方程组是常见的问题,特别是在实际生活和工作中。
解方程组是数学中的一个重要环节,也是计算机科学中的一个基本操作。
而在众多解方程组的工具中,Excel 是一个非常实用的工具。
本文将介绍如何使用 Excel 解齐次方程组。
2.什么是齐次方程组齐次方程组是指含有多个未知数的代数方程组,且所有方程的系数都是常数,且所有方程的指数都相同。
例如,下面这个方程组就是齐次方程组:```2x + 3y = 15x - 4y = 2```3.Excel 解齐次方程组的方法和步骤在 Excel 中,解齐次方程组主要通过使用“数据”菜单下的“求解”功能。
具体的操作步骤如下:1)首先,在 Excel 中输入方程组,将其放入一个工作表中。
例如,将上述方程组输入到一个工作表中。
2)然后,选择整个工作表,包括方程组和空白单元格。
3)接着,点击“数据”菜单,选择“求解”。
4)在弹出的对话框中,选择“线性”选项,然后点击“确定”。
5)Excel 会自动计算出方程组的解,将其显示在空白单元格中。
4.实际操作示例假设我们有如下齐次方程组:```2x + 3y = 15x - 4y = 2```我们可以按照上述步骤,在 Excel 中解这个方程组。
首先,将方程组输入到一个工作表中,然后选择整个工作表,点击“数据”菜单下的“求解”,在弹出的对话框中选择“线性”,最后点击“确定”。
Excel 会自动计算出方程组的解,将其显示在空白单元格中。
5.总结通过 Excel 解齐次方程组,我们可以更方便、更快捷地解决数学问题。
excel解10元1次方程组

excel解10元1次方程组
要解决一个包含10个一次方程的方程组,可以使用Excel的线性代数工具。
下面是一种基本的步骤:
1. 打开Excel并创建一个新的工作表。
2. 在工作表中选择一个区域,可以用来输入方程组的系数矩阵和常数向量。
例如,可以选择A1到K11的区域。
3. 在选定的区域中,按照方程组的形式输入系数矩阵和常数向量。
确保每个方程的系数和常数都在正确的位置上。
例如,如果方程组是:
2x + 3y = 10。
4x 2y = 5。
则在Excel中,可以在A1到K2的区域中输入系数矩阵:
2 3 10。
4 -2 5。
4. 在工作表中选择一个空白单元格,用于计算方程组的解。
例如,选择M1单元格。
5. 在M1单元格中输入以下公式:
=MINVERSE(A1:K10)A1:K10。
这个公式使用MINVERSE函数来计算系数矩阵的逆矩阵,并将其乘以系数矩阵本身。
这将得到一个新的矩阵,其中包含方程组的解。
6. 按下Enter键,Excel将计算并显示解矩阵。
7. 如果需要,可以将解矩阵的结果复制到其他单元格中进行格式化或进一步计算。
通过上述步骤,你可以使用Excel解决包含10个一次方程的方程组。
请注意,这种方法要求方程组有唯一解。
如果方程组没有解或有无穷多解,Excel可能会显示错误或不完整的结果。
excel解多元方程组

excel解多元方程组
在Excel中解多元方程组可以使用矩阵运算和线性代数函数来实现。
下面是一个示例:
假设有如下的多元方程组:
2x + y - z = 5
x - y + 3z = -1
3x + 2y + z = 3
将方程组的系数矩阵和常数向量分别输入到Excel的工作表中,如下所示:
| 2 1 -1 | | x | | 5 |
| 1 -1 3 | * | y | = | -1 |
| 3 2 1 | | z | | 3 |
然后,选中一个空白单元格,输入以下公式来计算方程组的解:
=MMULT(MINVERSE(A1:C3),E1:E3)
其中,A1:C3是系数矩阵的范围,E1:E3是常数向量的范围。
按下回车键后,Excel将自动计算出方程组的解并显示在该单元格中。
注意:在使用上述公式之前,请确保安装了Excel的Analysis ToolPak插件,该插件提供了MINVERSE和MMULT函数的支持。
如果你想要以矩阵形式显示方程组的解,可以使用数组公式。
选中一个3x1的单元格区域,输入以下公式:
{=MMULT(MINVERSE(A1:C3),E1:E3)}
注意:这是一个数组公式,需要在输入完公式后按下Ctrl + Shift + Enter键来确认。
Excel将自动将结果显示为一个3x1的矩阵。
excel解三元一次方程组

excel解三元一次方程组
一、 Excel解三元一次方程组
1、开辟空白Excel表格
第一步,打开Excel程序,开辟一个新的文件;
第二步,在右上角文件名一栏中,输入文件名;
第三步,在新的文件中,写入方程:
2x+3y+z=10
3x+2y+2z=13
2x+y+3z=11
接下来,双击Excel表格上右下角坐标点,将表格大小扩充至三行三列。
2、解三元一次方程组
第一步,建立矩阵关系,将三元一次方程写成一个方阵,在Excel 中建立如下矩阵关系:
A1:2 A2:3 A3:1 B1:3 B2:2 B3:2 C1:2 C2:1 C3:3 D1:10 D2:13 D3:11
第二步,计算行列式的值,输入如下公式:
D4:=DETERM(A1:C3)
按回车键,计算结果为:6
第三步,求解x、y、z,计算每个未知量的值,输入如下公式: D5:=DETERM(A2:C3|D2:D3)*1/D4
D6:=DETERM(A1:A2|D1:D2)*1/D4
D7:=DETERM(A1:C2|D1:D3)*1/D4
按回车键,计算结果分别为:D5:2 D6:4 D7:1
以上,就是Excel解三元一次方程组的步骤,得出最终结果:x=2, y=4, z=1。
使用Excel解多元一次方程组的三种方法
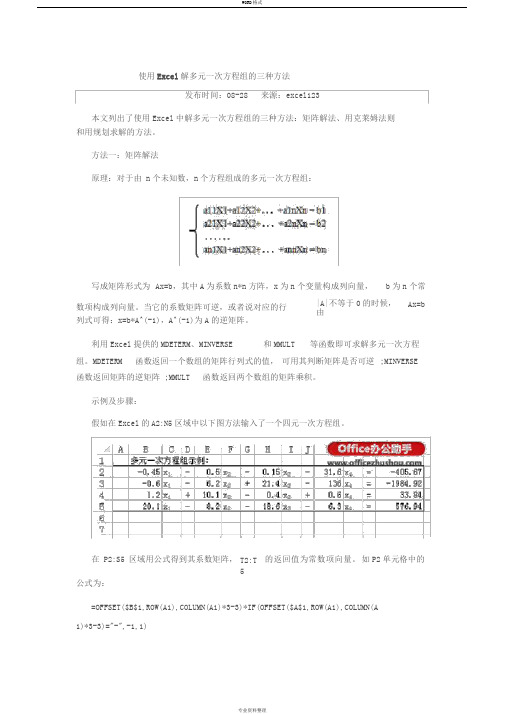
区域设置公式,即以Q8:Q11为未知数代入方程左侧。如S8中的公式:
在
S8:S11
=P2*$Q$8+Q2*$Q$9+R2*$Q$10+S2*$Q$11
3、设置“规划求解”参数。在“数据”选项卡的“分析”组中单击“规划求解”按钮,弹出“规
1)*3-3)="-",-1,1)
由于“=MDETERM(P2:S5)”的值不等于“0,”可知系数矩阵可逆。选择某列中的四个连续
单元格,如Q11:Q14,输入数组公式:
=MMULT(MINVERSE(P2:S5),T2:T5)
公式输入完毕按
Ctrl+Shift+En到方程组的解。
函数返回矩阵的逆矩阵;MMULT函数返回两个数组的矩阵乘积。
示例及步骤:
假如在Excel的A2:N5区域中以下图方法输入了一个四元一次方程组。
在P2:S5区域用公式得到其系数矩阵,
T2:T5
的返回值为常数项向量。
如P2单元格中的
公式为:
=OFFSET($B$1,ROW(A1),COLUMN(A1)*3-3)*IF(OFFSET($A$1,ROW(A1),COLUMN(A
方法二:用克莱姆法则
示例及步骤:
对于上述四元一次方程组,复制P2:S5区域,将其粘贴到其他区域,如本例有4个未知
数,用“选择性粘贴——粘贴链接”的方法将其粘贴到4个不同的区域。然后复制T2:T5常数
项的列向量,用“选择性粘贴——粘贴链接”的方法分别将其粘贴到上述四个区域中的各列,依次得到矩阵A1、A2、A3、A4,再用MDETERM函数计算各矩阵行列式的值,分别除以系数矩阵A的行列式的值,即可得到方程组的解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
11.对话框中最后一栏为:约束;首先点击添加按钮,屏幕出现添加约束对话框。
12.在添加约束对话框的单元格引用位置键入:B2;在中间的下拉式菜单中选取=;在约束值处键入:-4;然后按添加按钮,屏幕出现空白的添加约束对话框。
13.在添加约束对话框的单元格引用位置键入:B3;在中间的下拉式菜单中选取=;在约束值处键入:-6;然后按添加按钮,屏幕出现空白的添加约束对话框。
例如要解线性方程组
x1+x2+2x3+3x4=1
3x1-x2-x3-2x4=-4
2x1+3x2-x3-x4=-6
x1+2x2+3x3-x4=-4
可按如下的步骤来解这个方程组:
1.打开Excel。
2.由于在本方程组中未知数有4个,所以预留4个可变单元格的位置A1?A4。
14.在添加约束对话框的单元格引用位置键入:B4;在中间的下拉式菜单中选取=;在约束? 键入:-4;然后按确定键,返回规划求解参数对话框。特别注意在最后一个约束条件键入后,按确定键(而不是像前面一样按添加键)。
15.按求解键,出现求解结果对话框。此时在A1-A4的位置依次为:-1,-1,0,1;这就是说,原方程组的解为:X1=-1,X2=-1,X3=0,X4=1。这样我们就求出了方程组的解。
如何用EXCEL解方程组Finance 2007-06-28 01:21:43 阅读35广泛的应用。许多实际问题可以归结为一个线性方程组的解,因此线性方程组的解法已成为广大工程技术人员、经济工作者必须掌握的知识。在线性代数领域,Excel可以通过插入函数来直接求行列式的值,逆矩阵和矩阵的乘积。但Excel并没有直接求解线性方程组的功能,本人发现Excel的规划求解可用来解线性方程组,现把这种方法介绍给大家。
3.将活动单元格移至B1处,从键盘键入:=A1+A2+2*A3+3*A4:然后回车(此时B1显示0)。即在B1处输入方程组中第一个方程等号左边的表达式。
4.在B2处从键盘键入:=3*A1-A2-A3-2*A4;然后回车(此时B2显示0)。即在B2处输入方程组中第二个方程等号左边的表达式。
5.在B3处从键盘键入:=2*A1+3*A2-A3-A4;然后回车(此时B3显示0)。即在B3处输入方程组中第三个方程等号左边的表达式。
6.在B4处从键盘键入:=A1+2*A2+3*A3-A4;然后回车(此时B4显示0)。即在B4处输入方程组中第四个方程等号左边的表达式。
7.点击工具?规划求解,出现规划求解参数对话框。
8.对话框中第一栏为:设置目标单元格,在相应的框中填入$B$1。
9.对话框中第二栏为:等于;后有三个选项,依次为最大值,最小值,值为。根据题意B1表示方程组中第一个方程等号左边的表达式,它的值应为1,因此点击值为前的圆圈,输入1。
10.对话框中第三栏为:可变单元格;我们预留的可变单元格为A1?A4,所以在可变单元格框内键入 A 1: A 4。
