圆柱齿轮任意弧齿厚计算公式
齿轮各参数计算公式

模数齿轮计算公式:名称代号计算公式模数m m=p/π=d/z=da/(z+2) (d为分度圆直径,z为齿数)齿距p p=πm=πd/z齿数z z=d/m=πd/p分度圆直径d d=mz=da-2m齿顶圆直径da da=m(z+2)=d+2m=p(z+2)/π齿根圆直径df df=d-2.5m=m(z-2.5)=da-2h=da-4.5m齿顶高ha ha=m=p/π齿根高hf hf=1.25m齿高h h=2.25m齿厚s s=p/2=πm/2中心距a a=(z1+z2)m/2=(d1+d2)/2跨测齿数k k=z/9+0.5公法线长度w w=m[2.9521(k-0.5)+0.014z]13-1 什么是分度圆?标准齿轮的分度圆在什么位置上?13-2 一渐开线,其基圆半径r b=40 mm,试求此渐开线压力角?=20°处的半径r和曲率半径ρ的大小。
13-3 有一个标准渐开线直齿圆柱齿轮,测量其齿顶圆直径d a=106.40 mm,齿数z=25,问是哪一种齿制的齿轮,基本参数是多少?13-4 两个标准直齿圆柱齿轮,已测得齿数z l=22、z2=98,小齿轮齿顶圆直径d al =240 mm,大齿轮全齿高h=22.5 mm,试判断这两个齿轮能否正确啮合传动?13-5 有一对正常齿制渐开线标准直齿圆柱齿轮,它们的齿数为z1=19、z2=81,模数m=5 mm,压力角?=20°。
若将其安装成a′=250 mm的齿轮传动,问能否实现无侧隙啮合?为什么?此时的顶隙(径向间隙)C是多少?13-6 已知C6150车床主轴箱内一对外啮合标准直齿圆柱齿轮,其齿数z1=21、z2=66,模数m=3.5 mm,压力角?=20°,正常齿。
试确定这对齿轮的传动比、分度圆直径、齿顶圆直径、全齿高、中心距、分度圆齿厚和分度圆齿槽宽。
13-7 已知一标准渐开线直齿圆柱齿轮,其齿顶圆直径d al=77.5 mm,齿数z1=29。
齿轮各参数计算公式

模数齿轮计算公式:名称代号计算公式模数m m=p/π=d/z=da/(z+2) (d为分度圆直径,z为齿数)齿距p p=πm=πd/z齿数z z=d/m=πd/p分度圆直径 d d=mz=da-2m齿顶圆直径da da=m(z+2)=d+2m=p(z+2)/π齿根圆直径df df=d-2.5m=m(z-2.5)=da-2h=da-4.5m齿顶高ha ha=m=p/π齿根高hf hf=1.25m齿高h h=2.25m齿厚s s=p/2=πm/2中心距 a a=(z1+z2)m/2=(d1+d2)/2跨测齿数k k=z/9+0.5公法线长度w w=m[2.9521(k-0.5)+0.014z]13-1 什么是分度圆?标准齿轮的分度圆在什么位置上?13-2 一渐开线,其基圆半径r b=40 mm,试求此渐开线压力角α=20°处的半径r和曲率半径ρ的大小。
13-3 有一个标准渐开线直齿圆柱齿轮,测量其齿顶圆直径d a=106.40 mm,齿数z=25,问是哪一种齿制的齿轮,基本参数是多少?13-4 两个标准直齿圆柱齿轮,已测得齿数z l=22、z2=98,小齿轮齿顶圆直径d al=240 mm,大齿轮全齿高h =22.5 mm,试判断这两个齿轮能否正确啮合传动?13-5 有一对正常齿制渐开线标准直齿圆柱齿轮,它们的齿数为z1=19、z2=81,模数m=5 mm,压力角α=20°。
若将其安装成a′=250 mm的齿轮传动,问能否实现无侧隙啮合?为什么?此时的顶隙(径向间隙)C是多少?13-6 已知C6150车床主轴箱内一对外啮合标准直齿圆柱齿轮,其齿数z1=21、z2=66,模数m=3.5 mm,压力角α=20°,正常齿。
试确定这对齿轮的传动比、分度圆直径、齿顶圆直径、全齿高、中心距、分度圆齿厚和分度圆齿槽宽。
13-7 已知一标准渐开线直齿圆柱齿轮,其齿顶圆直径d al=77.5 mm,齿数z1=29。
齿轮各参数计算公式

模数齿轮计算公式:名称代号计算公式模数m m=p/π=d/z=da/(z+2) (d为分度圆直径,z为齿数)齿距p p=πm=πd/z齿数z z=d/m=πd/p分度圆直径d d=mz=da-2m齿顶圆直径da da=m(z+2)=d+2m=p(z+2)/π齿根圆直径df df==m=da-2h=齿顶高ha ha=m=p/π齿根高hf hf=齿高h h=齿厚s s=p/2=πm/2中心距a a=(z1+z2)m/2=(d1+d2)/2跨测齿数k k=z/9+公法线长度w w=m[+]13-1 什么是分度圆标准齿轮的分度圆在什么位置上13-2 一渐开线,其基圆半径r b=40 mm,试求此渐开线压力角=20°处的半径r和曲率半径ρ的大小。
13-3 有一个标准渐开线直齿圆柱齿轮,测量其齿顶圆直径d a=mm,齿数z=25,问是哪一种齿制的齿轮,基本参数是多少13-4 两个标准直齿圆柱齿轮,已测得齿数z l=22、z2=98,小齿轮齿顶圆直径d al=240 mm,大齿轮全齿高h =mm,试判断这两个齿轮能否正确啮合传动13-5 有一对正常齿制渐开线标准直齿圆柱齿轮,它们的齿数为z1=19、z2=81,模数m=5 mm,压力角=20°。
若将其安装成a′=250 mm的齿轮传动,问能否实现无侧隙啮合为什么此时的顶隙(径向间隙)C是多少13-6 已知C6150车床主轴箱内一对外啮合标准直齿圆柱齿轮,其齿数z1=21、z2=66,模数m=mm,压力角=20°,正常齿。
试确定这对齿轮的传动比、分度圆直径、齿顶圆直径、全齿高、中心距、分度圆齿厚和分度圆齿槽宽。
13-7 已知一标准渐开线直齿圆柱齿轮,其齿顶圆直径d al=mm,齿数z1=29。
现要求设计一个大齿轮与其相啮合,传动的安装中心距a=145 mm,试计算这对齿轮的主要参数及大齿轮的主要尺寸。
13-8 某标准直齿圆柱齿轮,已知齿距p=mm,齿数z=25,正常齿制。
齿厚计算
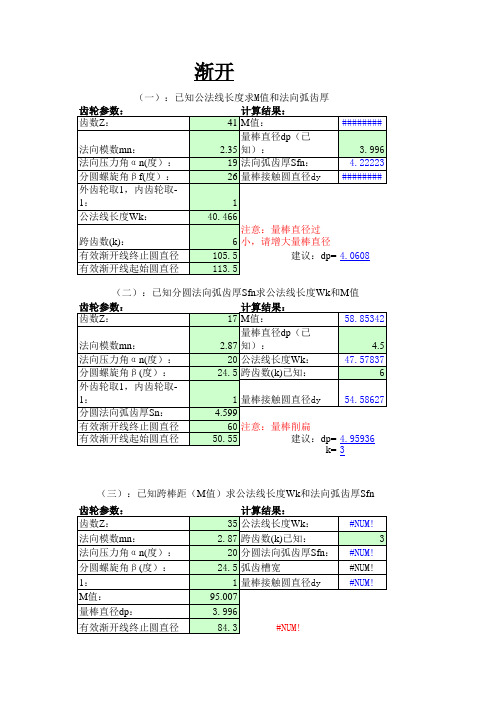
#NUM! #NUM!
M值:
95.007
量棒直径dp:
3.996
有效渐开线终止圆直径
84.3
#NUM!
有效渐开线起始圆直径
92.5
建议:k= #NUM!
(四):圆柱齿轮任意圆弧齿厚计算
法向模数mm
2.5 分圆端面弧齿厚Ss
齿数Z
75 分圆直径d
法向压力角αn
20 基圆直径db
分圆螺旋角β
0 任意圆端面压力角
Wn #NUM!
mt= 1.125043
Zk #NUM!
Xn 46.45145464
Kn #NUM!
= #NUM!
#NUM! #NUM!
#NUM!
分圆法向弧齿厚Sn
4.964 任意圆端面弧齿厚
外齿取1,内齿取-1
1 任意圆法向弧齿厚
任意圆直径
187.5 法向变位系数Xn Nhomakorabea端面压力角αs
20
4.964 187.5 176.1924 0.349066 4.964 4.964 0.569832
***注意:本计算法 中弧齿厚和变位系 数均为有材质部分
αfs= 1 端面模数 ms1 9 分圆直径 D1
渐开
(一):已知公法线长度求M值和法向弧齿厚
齿轮参数:
计算结果:
齿数Z:
41 M值:
########
量棒直径dp(已
法向模数mn:
2.35 知):
3.996
法向压力角αn(度):
19 法向弧齿厚Sfn:
4.22223
分圆螺旋角βf(度):
26 量棒接触圆直径dy ########
外齿轮取1,内齿轮取-
圆柱齿轮传动几何尺寸计算公式1

mz cos f
d f 1 153 .75 d f 2 256 .25
De1 163 .75 De2 266 .25 Di1 141 .25 Di2 243 .75
De
Di
De d f 2m fn
Di d f 2m( f n Cn )
ro
t
jn
ro
பைடு நூலகம்
一、直齿圆柱齿轮传动几何尺寸计数公式
名称 代号 公式 例 模数
m Z
m
tf
df z
m5
z1 30 z 2 50
齿数
z
cos
df
m
r0 rf
分度圆 压力角
f
df
De
f
f 20
d f 150
分度圆 直径 齿顶圆 直径 齿根圆 直径 基圆半 径 基节 周节
d f mz
fs
分 度 圆 螺旋角 分 度 圆 直径 齿 顶 圆 直径 齿 根 圆 直径 基 圆 半 径 法 向 基 节 端 面 基 节 法 向 周 节 端 面 周 节 齿顶高
f
df
cos f
zmn df
f 1 f 2 12 4049
d
f
d
f
mz cos
f1 f 2
153 .75 256 .25
d
De
De d f 2m(f n n )
Di d f 2m( f n n Cn )
De1 166 .75 De2 263 .25
Di
Di1 144 .25 Di2 240 .75
ro
齿轮各参数计算公式知识讲解

齿轮各参数计算公式13-1什么是分度圆?标准齿轮的分度圆在什么位置上? 13-2 一渐开线,其基圆半径r b = 40 mm ,试求此渐开线压力角 =20。
处的半径r 和曲率半径p的大小。
13-3有一个标准渐开线直齿圆柱齿轮,测量其齿顶圆直径 da = 106.40 mm ,齿数z=25,问是哪一种齿制的齿轮,基本参数是多少?13-4两个标准直齿圆柱齿轮,已测得齿数 z i = 22、z 2 = 98,小齿轮齿顶圆直径d ai = 240 mm ,大 齿轮全齿高h = 22.5 mm ,试判断这两个齿轮能否正确啮合传动 ?名称 代号 计算公式 模数 m m=p/n =d/z=da/(z+2)(d 为分度圆直径齿距 P p= n m=t d/z 齿数 z z=d/m=n d/p 分度圆直径 d d=mz=da-2m齿顶圆直径 da da=m(z+2)=d+2m=p(z+2)/ n 齿根圆直径 df df=d-2.5m=m(z-2.5)=da-2h=da-4.5m齿顶咼 ha ha=m=p/n 齿根高 hf hf=1.25m齿高 h h=2.25m 齿厚 s s=p/2= n m/2中心距 a a=(z1+z2)m/2=(d1+d2)/2跨测齿数 k k=z/9+0.5公法线长度ww=m[2.9521(k-0.5)+0.014z]模数齿轮计算公式 ,z 为齿数)13-5有一对正常齿制渐开线标准直齿圆柱齿轮,它们的齿数为z i = 19、Z2 = 81,模数m= 5 mm,压力角=20°若将其安装成a' = 250 mm的齿轮传动,问能否实现无侧隙啮合?为什么?此时的顶隙(径向间隙)C是多少?13-6已知C6150车床主轴箱内一对外啮合标准直齿圆柱齿轮,其齿数Z1 = 21、Z2 = 66,模数m =3.5 mm,压力角 =20°正常齿。
试确定这对齿轮的传动比、分度圆直径、齿顶圆直径、全齿高、中心距、分度圆齿厚和分度圆齿槽宽。
齿轮各参数计算公式

齿轮各参数计算公式模数齿轮计算公式:名称代号计算公式模数m m=p/π=d/z=da/(z+2) (d为分度圆直径,z为齿数)齿距p p=πm=πd/z齿数z z=d/m=πd/p分度圆直径 d d=mz=da-2m齿顶圆直径da da=m(z+2)=d+2m=p(z+2)/π齿根圆直径df df=d-2.5m=m(z-2.5)=da-2h=da-4.5m齿顶⾼ha ha=m=p/π齿根⾼hf hf=1.25m齿⾼h h=2.25m齿厚s s=p/2=πm/2中⼼距 a a=(z1+z2)m/2=(d1+d2)/2跨测齿数k k=z/9+0.5公法线长度w w=m[2.9521(k-0.5)+0.014z]13-1 什么是分度圆?标准齿轮的分度圆在什么位置上?13-2 ⼀渐开线,其基圆半径r b=40 mm,试求此渐开线压⼒⾓α=20°处的半径r和曲率半径ρ的⼤⼩。
13-3 有⼀个标准渐开线直齿圆柱齿轮,测量其齿顶圆直径d a=106.40 mm,齿数z=25,问是哪⼀种齿制的齿轮,基本参数是多少?13-4 两个标准直齿圆柱齿轮,已测得齿数z l=22、z2=98,⼩齿轮齿顶圆直径d al=240 mm,⼤齿轮全齿⾼h =22.5 mm,试判断这两个齿轮能否正确啮合传动?13-5 有⼀对正常齿制渐开线标准直齿圆柱齿轮,它们的齿数为z1=19、z2=81,模数m=5 mm,压⼒⾓α=20°。
若将其安装成a′=250 mm的齿轮传动,问能否实现⽆侧隙啮合?为什么?此时的顶隙(径向间隙)C是多少?13-6 已知C6150车床主轴箱内⼀对外啮合标准直齿圆柱齿轮,其齿数z1=21、z2=66,模数m=3.5 mm,压⼒⾓α=20°,正常齿。
试确定这对齿轮的传动⽐、分度圆直径、齿顶圆直径、全齿⾼、中⼼距、分度圆齿厚和分度圆齿槽宽。
13-7 已知⼀标准渐开线直齿圆柱齿轮,其齿顶圆直径d al=77.5 mm,齿数z1=29。
齿轮计算公式

齿轮计算公式节圆柱上的螺旋角:L d /tan 00⋅=πβ 基圆柱上的螺旋角:n g αββcos sin sin 0⋅= 齿厚中心车角:Z θ/90︒= 量棒直径:m 728.1dp ⋅=中心距离增加系数:)1cos /(cos )2/)((y b 021-⋅+=ααZ Z标准正齿轮的计算(小齿轮①,大齿轮②)1. 齿轮齿 标准 2. 工齿齿形 直齿 3. 模数 m 4. 压力角 c αα=0 5. 齿数 21,Z Z6. 有效齿深 m 2h e ⋅=7. 全齿深 c m h +=28. 齿顶隙 m 35.0,m 25.0,m 2.0c ⋅⋅⋅=9. 基础节圆直径 m d 0⋅=Z 10. 外径 m )2(d k ⋅+=Z 11. 齿底直径 c 2m )2(d r ⋅-⋅-=Z12. 基础圆直径 0g cos m d αZ ⋅⋅= 13. 周节 m t 0⋅=π 14. 法线节距 0e cos m t απ⋅⋅= 15. 圆弧齿厚2/m S 0⋅=π16. 弦齿厚)2sin(m S 1j Z πZ ⋅⋅⋅= 17. 齿轮油标尺齿高 m m h j +Z⋅-⨯⋅Z =)2cos1()2/(π18. 跨齿数5.0)180/(0m ⨯⋅=Z αZ19. 跨齿厚 ])5.0([cos 0o m inva m m S Z ⨯-⋅Z ⋅⋅=πα20. 销子直径 m 728.1d ⋅=21. 圆柱测量尺寸 d m d m +⋅Z =)cos /cos (0φα (偶数齿)d )]90(cos)cos /cos m [(d 0m +︒⨯⋅=ZφαZ (奇数齿)其中, 00)2cos (1απαφinv m d inv +-⋅Z 22. 齿隙f ?移位正齿轮计算公式(小齿轮①,大齿轮②)1. 齿轮齿形 转位 2. 工具齿形 直齿 3. 模数 m 4. 压力角 c αα=05. 齿数 Z6. 有效齿深 m 2h e ⋅=7. 全齿深 c m )]x x (y 2[h 21+⋅⋅-+= 或 c m 2h +⋅=8. 齿隙 c 9. 转位系数 x10. 中心距离 m y x ⋅+=αα11. 基准节圆直径m d 0⋅=Z12. 啮合压力角021210b inv )x x (tan 2inv αZ Z αα+++⋅=13. 啮合节圆直径)(x 2d 211b Z Z Z α+⋅⋅=14. 外径 m )x y (2m )2(d 21k ⋅-⋅+⋅+=Z15. 齿顶圆直径 h 2d d 1k r ⋅-=16. 基圆直径 0cos t g m d α⋅⋅Z = 17. 周节 m t 0⋅=π 18. 法线节距00cos m t απ⋅⋅=19. 圆弧齿厚 010tan m x 22mS απ⋅⋅⋅⋅⋅=20. 弦齿厚)tan x 2x 2sin(m S 1111j Z απZ ⋅⋅+⋅⋅⋅=21. 齿轮游标尺齿高2d d )]tan x 22cos(1[2mh 110k10111j -+⋅⋅+⋅-⋅⋅=Z αZ πZ 22. 跨齿数 5.0180x 1b m 1+⋅=αZ23. 跨齿厚 01m sin m x 2)(S 1α⋅⋅⋅+=标准齿轮的齿厚 24. 梢子直径m 728.1d 1⋅=25. 圆柱测量尺寸11cos cos 1d m d m +⋅⋅Z =φα (偶数齿)1110)90cos(cos cos 1d m d m +Z ︒⋅⋅⋅Z =φα (奇数齿)1010101i 1tan x 2)inv 2(cos m d inv Z ααZ παZ Φ⋅⋅+-⋅-⋅⋅=标准螺旋齿的计算公式(齿直角方式)(小齿轮①,大齿轮②)1. 齿轮齿形 标准2. 齿形基准断面 齿直角3. 工具齿形 螺旋齿4. 模数 n c m m =5. 压力角 n 0c ααα==6. 齿数 1Z7. 螺旋角方向 0β(左或右)8. 有效齿深 n e m 2h ⋅=9.全齿深c m 2h n +⋅=10. 正面压力角n1s cos m tan βZ α⋅=11. 中心距离n21cos 2m )(βZ Z α⋅⋅+=12. 基准节圆直径n10cos m d βZ ⋅=13. 外径 n 01k m 2d d ⋅+= 14. 齿底圆直径 )c m (2d d n 01r ++= 15. 基圆直径gnn 1g cos cos m d 1βαZ ⋅⋅=16. 基圆上的螺旋角 n 0g cos sin sin αββ⋅= 17. 导程1001cot d L 1βπ⋅⋅=18. 周节(齿直角)n n 0m t ⋅=π19. 法线节距(齿直角) n n en cos m t απ⋅⋅= 20. 圆弧齿厚(齿直角) 2m S nn 0⋅=π21. 相当正齿轮齿数101cos βZ Z =22. 弦齿厚)2sin(m S 1v n 1v j 1Z πZ ⋅⋅⋅=23. 齿轮游标尺齿深n 1v n1v 1j m )2cos 1(2m h +⋅-⋅⋅=Z πZ24. 跨齿数 5.01801v n m 1+⋅=Z αZ25. 跨齿厚]inv )5.0m ([cos m S s 11n n m 1αZ Z πα⋅+-⋅⋅⋅=26. 梢子直径)2(cos 1111n v n v n inv inv m d απφα-Z ⋅+⋅Z ⋅=其中,)(2tan 11Rad inv n v n απαφ-Z ⋅+=27. 圆柱测量尺寸11cos cos 1d m d m +⋅⋅Z =φα (偶数齿)1110)90cos(cos cos 1d m d m +Z ︒⋅⋅⋅Z =φα (奇数齿)10101011tan 2)2(cos Z ⋅⋅+-Z ⋅-⋅⋅Z =ααπαφx inv m d inv i 28. 齿隙f移位螺旋齿的计算公式(齿直角方式)(小齿轮①,大齿轮②)1. 齿轮齿形 移位2. 齿形基准断面 齿直角3. 工具齿形 螺旋齿4. 模数(齿直角) n c m m =5. 压力角(齿直角) 0a a a c n -=6. 齿数 1Z7. 螺旋方向 0β8. 有效齿深 n e m h 2= 9. 全齿深 c m h n +=2 10. 移位系数 1n x11. 中心距离n x ym a a +=12. 正面模数0cos βns m m =13. 正面压力角0cos tan βans m =14. 相当正齿轮齿数311βϑs z z v =15. 齿直角啮齿压力角an v v n n ann a inv z z x x b inv +++=2121t an 216. 基准节圆直径11cos βno m z d =17. 外径n n n nk m x m m z d 101122cos ++=β18. 啮齿节圆直径)(22111z z z a d x b +=19. 基圆直径gnn g a m z d βcos cos 11⋅=20. 基础圆柱上的螺旋角 n o g a cos sin sin ββ=21. 圆弧齿厚 n n n on m a x s ⋅⋅+=)tan 22(1π22. 弦齿厚 )t an 22sin(11111v on v n v j z a x z m z s ⋅+⋅⋅=π23. 齿轮游标尺齿高2)}t an 22cos(1{21111111o k v o n v n v d d z a x z m z hj -+⋅+-⋅=π24. 跨齿数 5.018011+=v n m z ab z25. 跨齿厚111sin 2n n n m a m x s ⋅⋅+=)(标准螺旋齿轮的齿厚 26. 销子直径 近似值=1d27. 圆柱测量尺寸/1111cos cos d a m z d ss m +⋅=φ(偶数齿)/1111190cos cos cos d z a m z d s s m +⋅= φ111111tan 2)2(cos z a x inva z a m z d in n n s n n ⋅+--='πφ 注:齿隙f=m 1.25以下 0.025-0.075m 1.25-2.5 0.05-0.10))*25.2((tan 2)2(cos 22111111m r r L z a x inva z a m z d in n n s n n ---⋅+--='πφ。
直齿圆柱齿轮变位系数、公法线长度、齿厚、最小法向侧隙的计算

外啮合直齿圆柱齿轮变位系数、公法线长度、齿厚、最小法向侧隙的计算1,直齿圆柱齿轮变位系数计算:Case1:a,此处例子仅计算用齿条型刀具加工时的情况(插齿刀加工见相关手册公式):小结:由此可知本例选取的齿数在不变位的情况也不会产生根切现象。
b,根据下图选择大小齿轮的变位系数和x∑。
本例在P6-P7区间取值。
即齿根及齿面承载能力较高区,进行选择。
因大小齿轮的齿数和为18+19=37。
所以本例选择的变位系数和x∑=0.8。
本例我们的两个齿轮在工作时属于减速运动,所以按减速运动的变位系数分配线图,进行2个齿轮的变位系数的选择。
先按(z1+z1)/2=18.5,作为横坐标,做一条垂线(图中蓝色的线),再按x∑/2=0.4,作为纵坐标,做一条水平线(图中橙色的线),接着沿着L线的趋势,穿过上面2条线的交点做一条射线(图中红色的线)最后按大小齿轮的齿数做相应的垂线(图中紫色的线),即得到需要的各自变位系数。
最后我们选择的变位系数即为:小齿轮x1=0.42,大齿轮x2=0.38。
【基本保障其和与之前x ∑一致,即可】。
c,验算变位后的齿顶厚度:注:一般要求齿顶厚Sa≥0.25m;对于表面淬火的齿轮要求Sa≥0.4m下表中的da的计算见后面的计算表格中的计算公式(因为当齿轮变位后,齿顶圆的计算和未变位齿轮的计算稍有差别-涉及到变位系数和中心距变位系数。
)。
分度圆直径db mm 73.8 77.9齿轮的齿顶圆直径da mm 83.027 86.799齿轮的齿顶压力角αa °27.27 26.17中间值invα0.0215 0.0215中间值invαa 0.0587 0.0347齿顶厚Sα 5.77 7.47判断值0.25m 1.025 1.025判断值0.4m 1.64 1.64小结:计算发现变位后的齿轮齿顶厚满足设计需求。
根据上面确定的变位系数,计算齿轮的中心距变位系数和节圆直径、齿根圆直径、齿顶圆直径。
齿轮计算公式和数学公式

圆的一般方程 x2+y2+dx+ey+f=0 注:d2+e2-4f>0
抛物线标准方程 y2=2px y2=-2px x2=2py x2=-2py
直棱柱侧面积 s=c*h 斜棱柱侧面积 s=c'*h
锥体体积公式 v=1/3*s*h 圆锥体体积公式 v=1/3*pi*r2h
斜棱柱体积 v=s'l 注:其中,s'是直截面面积, l是侧棱长
柱体体积公式 v=s*h 圆柱体 v=pi*r2h
公式分类 公式表达式
乘法与因式分解 a2-b2=(a+b)(a-b) a3+b3=(a+b)(a2-ab+b2) a3-b3=(a-b)(a2+ab+b2)
判别式 b2-4a=0 注:方程有相等的两实根
b2-4ac>0 注:方程有一个实根
b2-4ac<0 注:方程有共轭复数根
三角函数公式
两角和公式 sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosA
cos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinB
tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosB
ctgA+ctgBsin(A+B)/sinAsinB -ctgA+ctgBsin(A+B)/sinAsinB
4种齿轮计算公式
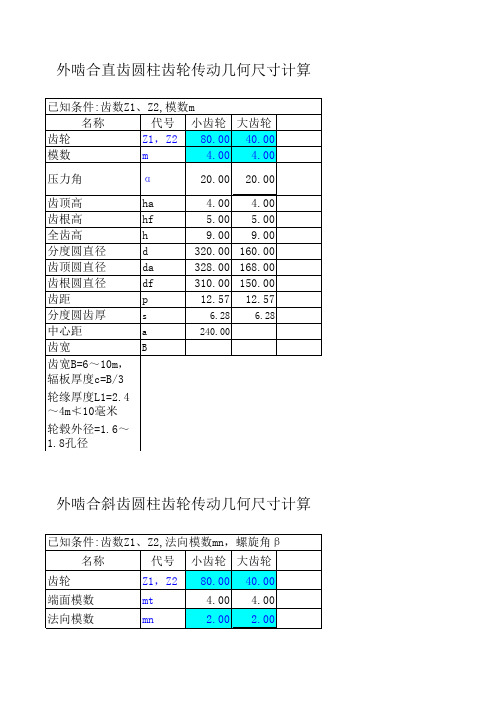
外啮合直齿圆柱齿轮传动几何尺寸计算外啮合斜齿圆柱齿轮传动几何尺寸计算压力角α20.0020.00齿顶高ha 2.00 2.00齿根高hf 2.50 2.50全齿高h 4.50 4.50分度圆直径d320.00160.00齿顶圆直径da324.00164.00齿根圆直径df315.00155.00分度圆齿厚s 6.28 6.28中心距a240.00齿宽计算m n=(da-df)/4.5计算螺旋角cosβ =m n z/(da-2mn)注注:☆蜗杆齿宽:当注:☆最大外圆直注:☆蜗轮齿宽:当注:模数为12,10注注:☆蜗杆螺纹长注:蜗杆在分度圆外啮合直齿锥齿轮传动几何尺齿顶高h a 齿根高hf 分度圆直径d1节圆直径dje1齿顶圆直径da1齿根圆直径df1分度圆螺旋导程角(弧度)γ法向模数m f 轴向齿距Px 分度圆柱螺旋导程P Z螺牙沿分度圆柱上的轴向齿厚S z1螺牙沿分度圆柱上的法向齿厚S f1齿厚测量高度h~齿数Z 2分度圆直径d2齿根圆直径df2齿顶圆直径da2最大外圆直径D2蜗轮宽度b2齿顶圆弧半径R a 齿根圆弧半径Rf注:☆磨削蜗杆需加长:m≤10时,加长25mm;10≤m≤16时,加长35mm;m>16时,加长40-50mm 注:☆蜗杆齿宽:当Z=1~2时取(13~16)m, 当Z=3~4时取(15~21)m注:☆最大外圆直径:当Z=1取≤da2+2m,当Z=2~3取≤da2+1.5m,当Z=4取≤da2+m注:☆蜗轮齿宽:当Z≤3时取≤0.75Ddi1, 当Z=4时取≤0.67Ddi1,包角2θ=45°~130°注:模数为12,10,8,6,5,4,3,2.5,2,1.5,1蜗 轮蜗 杆螺旋长度L☆注:蜗杆特性系数q为14,13,12,11,10,9,8注:☆蜗杆螺纹长度L:当Z=1~2时取大于(11+0.06Z2)m, 当Z=3~4时取大于(12.5+0.09Z2)m 注:蜗杆在分度圆上的轴向齿厚=1.498m,分度圆上的法向齿厚=1.498mcos γ齿齿齿轴向齿距轴向齿形齿齿分h高h 顶高h 根高 3:1a压力角齿根圆弧半d 顶圆直径L切制螺纹部分长度d 根圆直径d 度圆直径21f 1a 1P xa 1f 1(a )蜗杆(b几何尺寸计算mm;m>16时,加长40-50mm+1.5m,当Z=4取≤da2+m67Ddi1,包角2θ=45°~130°时取大于(12.5+0.09Z2)m向齿厚=1.498mcos γ齿顶圆弧半径R 齿根圆弧半径R a 2(b )蜗轮。
渐开线圆柱齿轮齿厚测量方法及其计算公式

渐开线直齿圆柱齿轮齿厚测量方法及其计公算式本文意欲回答读者在查阅设计手册时无从知晓而常常提出来的关于几个基本含义的问题:什么是公法线?什么是量柱距?什么是固定弦和分度圆弦?它们的计算公式是怎样推出来的等等。
渐开线圆柱齿轮常用的齿厚测量方法有公法线长度、量柱(或球)距、分度圆弦齿厚、固定弦齿厚四种方法。
后两种方法是测量单个齿,一般用于大型齿轮。
对于精度要求不太高的齿轮也常用分度圆弦测量法。
公法线长度测量在外齿轮上用得最多,内齿轮也可用;大齿轮测量因受量具限制很少用。
量柱距测量主要用于内齿轮和小模数齿轮。
1. 公法线长度测量(1)公法线及其长度计算式对于渐开线齿廓,根据渐开线的性质,其上任意点的法线总是和基圆相切,因此用两个平行的卡爪卡住几个齿时(见图1),两个卡爪接触点A 、B 的连线必定与基圆相切于某一点C ,这条AB 连线就叫公法线,一般用W k 表示;下标k 表示卡住的齿数。
图1中,根据渐开线的性质,A C =A C ');B C =B C '⌒;A B =A B ''⌒。
A B 是(k-1)个基圆齿距p b和一个基圆齿厚S b 之和,即:(1)(1)cos k b b b W k p S k m S πα=-+=-+……(1-1) 式中,k –跨测齿数;α–压力角(°); m –模数,mm ;分度圆和基圆上的齿厚具有如下关系:22b bs sinv invo r r α+=+ 由上等式可得:(2tan )22b b b r ms xm r inv r παα=++ 图1 公法线长度的测量计算 =1cos 2sin cos 2m xm zm inv παααα++…………(1-2) 将(1-2)式代入(1-1)式,经整理后可得公法线长度计算式为:cos [(0.5)2tan ]k W m zinv k x ααπα=+-+…………(1-3)式中,z –齿轮的齿数; inv α–渐开线函数;x –变位系数;若模数m=1,(1-3)式变为:cos [(0.5)2tan ]k W zinv k x ααπα=+-+cos [(0.5)2sin zinv k x ααπα=+-]+K k W W **=+∆…………(1-4)(1-4)式中第二行的前一项cos (0.5)k W k ααπ*=+-[zinv ]就是m=1的标准齿轮的公法线长度。
齿轮各参数计算公式知识讲解

齿轮各参数计算公式模数齿轮计算公式:名称代号计算公式模数m m=p/π=d/z=da/(z+2) (d为分度圆直径,z为齿数)齿距p p=πm=πd/z齿数z z=d/m=πd/p分度圆直径 d d=mz=da-2m齿顶圆直径da da=m(z+2)=d+2m=p(z+2)/π齿根圆直径df df=d-2.5m=m(z-2.5)=da-2h=da-4.5m齿顶高ha ha=m=p/π齿根高hf hf=1.25m齿高h h=2.25m齿厚s s=p/2=πm/2中心距 a a=(z1+z2)m/2=(d1+d2)/2跨测齿数k k=z/9+0.5公法线长度w w=m[2.9521(k-0.5)+0.014z]13-1 什么是分度圆?标准齿轮的分度圆在什么位置上?13-2 一渐开线,其基圆半径r b=40 mm,试求此渐开线压力角 =20°处的半径r和曲率半径ρ的大小。
13-3 有一个标准渐开线直齿圆柱齿轮,测量其齿顶圆直径d a=106.40 mm,齿数z=25,问是哪一种齿制的齿轮,基本参数是多少?13-4 两个标准直齿圆柱齿轮,已测得齿数z l=22、z2=98,小齿轮齿顶圆直径d al=240 mm,大齿轮全齿高h=22.5 mm,试判断这两个齿轮能否正确啮合传动?13-5 有一对正常齿制渐开线标准直齿圆柱齿轮,它们的齿数为z1=19、z2=81,模数m=5 mm,压力角α=20°。
若将其安装成a′=250 mm的齿轮传动,问能否实现无侧隙啮合?为什么?此时的顶隙(径向间隙)C是多少?13-6 已知C6150车床主轴箱内一对外啮合标准直齿圆柱齿轮,其齿数z1=21、z2=66,模数m =3.5 mm,压力角α=20°,正常齿。
试确定这对齿轮的传动比、分度圆直径、齿顶圆直径、全齿高、中心距、分度圆齿厚和分度圆齿槽宽。
13-7 已知一标准渐开线直齿圆柱齿轮,其齿顶圆直径d al=77.5 mm,齿数z1=29。
(整理)渐开线圆柱齿轮齿厚测量方法及其计算公式

渐开线直齿圆柱齿轮齿厚测量方法及其计公算式本文意欲回答读者在查阅设计手册时无从知晓而常常提出来的关于几个基本含义的问题:什么是公法线?什么是量柱距?什么是固定弦和分度圆弦?它们的计算公式是怎样推出来的等等。
渐开线圆柱齿轮常用的齿厚测量方法有公法线长度、量柱(或球)距、分度圆弦齿厚、固定弦齿厚四种方法。
后两种方法是测量单个齿,一般用于大型齿轮。
对于精度要求不太高的齿轮也常用分度圆弦测量法。
公法线长度测量在外齿轮上用得最多,内齿轮也可用;大齿轮测量因受量具限制很少用。
量柱距测量主要用于内齿轮和小模数齿轮。
1. 公法线长度测量(1)公法线及其长度计算式对于渐开线齿廓,根据渐开线的性质,其上任意点的法线总是和基圆相切,因此用两个平行的卡爪卡住几个齿时(见图1),两个卡爪接触点A 、B 的连线必定与基圆相切于某一点C ,这条AB 连线就叫公法线,一般用W k 表示;下标k 表示卡住的齿数。
图1中,根据渐开线的性质,A C =A C ');B C =B C '⌒;A B =A B ''⌒。
A B 是(k-1)个基圆齿距p b和一个基圆齿厚S b 之和,即:(1)(1)cos k b b b W k p S k m S πα=-+=-+……(1-1) 式中,k –跨测齿数;α–压力角(°);m –模数,mm ;分度圆和基圆上的齿厚具有如下关系:22b bs sinv invo r r α+=+ 由上等式可得:(2tan )22b b b r ms xm r inv r παα=++ 图1 公法线长度的测量计算 =1cos 2sin cos 2m xm zm inv παααα++…………(1-2) 将(1-2)式代入(1-1)式,经整理后可得公法线长度计算式为:cos [(0.5)2tan ]k W m zinv k x ααπα=+-+…………(1-3)式中,z –齿轮的齿数; inv α–渐开线函数;x –变位系数;若模数m=1,(1-3)式变为:cos [(0.5)2tan ]k W zinv k x ααπα=+-+cos [(0.5)2sin zinv k x ααπα=+-]+K k W W **=+∆…………(1-4)(1-4)式中第二行的前一项cos (0.5)k W k ααπ*=+-[zinv ]就是m=1的标准齿轮的公法线长度。
标准直齿圆柱齿轮的分度圆齿厚( )齿槽宽

标准直齿圆柱齿轮的分度圆齿厚( )齿槽宽标准直齿圆柱齿轮的分度圆齿厚和齿槽宽是齿轮设计和制造的关键参数。
分度圆齿厚是指齿轮轴上分度圆位置处的齿轮牙齿的厚度。
齿槽宽则是测量两相邻齿槽道顶部之间的距离。
在齿轮设计和制造过程中,这两个参数必须满足标准的规定和要求,以确保齿轮能够高效准确地传递动力和扭矩,同时一定程度上保证齿轮的耐久性和寿命。
标准直齿圆柱齿轮的分度圆齿厚要求严格,它的计算方法主要取决于齿轮的模数和齿数。
模数是齿轮设计过程中不可或缺的重要参数,它的定义是齿轮齿廓图的尺寸与模量的比率。
常用的模数有0.5、1、1.5、2、2.5和3等,其中1是最常用的模数。
分度圆齿厚计算公式为h = m,其中h为齿厚,m为模数。
根据这个公式,分度圆齿厚会随着模数的变化而变化,模数越大,分度圆齿厚也越大,反之亦然。
对于标准直齿圆柱齿轮,齿槽宽也有着严格的规定和要求。
齿槽宽通常由齿槽道顶到顶距离来决定。
在设计过程中,应该考虑到表面干涉等因素。
标准直齿圆柱齿轮的齿槽宽取决于模数和齿数,可以根据公式计算得出。
齿槽宽的计算公式为b = m * (Z + 2),其中b为齿槽宽,m为模数,Z为齿数。
除了以上两个重要参数,标准直齿圆柱齿轮的其他关键参数还包括法向齿向厚度、压力角、齿顶高和齿根径等。
这些关键参数都是齿轮设计和制造过程中需要优化的要素。
例如,法向齿向厚度是齿轮牙齿在法向方向之间的距离,它的大小直接影响到齿轮的强度和耐用性。
而压力角则是齿顶与齿廓交点处的夹角大小,它的大小与齿轮的传动效率有关。
在工业生产中,标准直齿圆柱齿轮被广泛应用于各种机械设备中。
为了确保齿轮能够顺畅高效地传递动力和扭矩,设计和制造过程中需要严格遵守标准的要求和规定。
只有在严格实施标准操作的情况下,齿轮才能够正确地满足各种动态负载的需求,并在工业生产中发挥最佳的效用。
