电子科技大学【一阶电路分析】精品教学ppt课件讲义
合集下载
大学物理电路分析基础第6章一阶电路分析.ppt

t
iC d 1(V)
1
其波形如图6-5(c)所示。
第6章 一阶电路分析
6.1.2
通常把由导线绕成的线圈称为电感器或电感线圈。 当 线圈通过电流时, 即在线圈内外建立磁场并产生磁通Φ, 如 图6-6所示。 各线匝磁通的总和称为磁链φ(若线圈匝数为N, 则φ=NΦ )。 可见, 电感器是一种能建立磁场、 储存磁场 能量的器件。
从本例可以看出: (1) 电容电流是可以跳变的。 (2) 电容的功率也是可以跳变的,这是由于电容电流跳 变的原因。 功率值可正可负: 功率为正值, 表示电容从电 源us(t)吸收功率; 功率为负值, 表示电容释放功率且交还 电源。 (3) wC(t)总是大于或等于零,储能值可升可降, 但为连 续函数。
第6章 一阶电路分析
图6-4 例6-1波形图
第6章 一阶电路分析
例 6-2 在图6-5(a)所示电路中, is(t)的波形如图6-5(b)所 示, 已知电容C=2 F, 初始电压uC(0)=0.5 V, 试求t≥0时的 电容电压, 并画出其波形。
第6章 一阶电路分析
图6-5 例6-2题图
第6章 一阶电路分析
dq dt
和电容的定义q(t)=Cu(t),
可得
i C du
(6-2)
dt
第6章 一阶电路分析
这就是电容元件微分形式的VCR。 若电容端电压u与电流i 参考方向不关联, 则上式右边应加负号, 即
du i C
(6-3)
dt
式(6-2)表明, 任一时刻通过电容的电流i取决于该时刻电容
两端的电压的变化率 du 。若电压恒定不变, 则虽有电压 dt
与电阻元件相类似, 若约束电容元件的q—u平面上的 曲线为通过原点的直线, 则称它为线性电容; 否则, 称为 非线性电容。 若曲线不随时间而变化, 则称为非时变电容; 否则, 称为时变电容。
第 一阶动态电路分析PPT课件

t
t
-
uC uC (0 )e U0e RC
1S 2
R
iC +
C -uC
第24页/共34页
放电电流
iC
C
duC dt
U0 R
t
e RC
t
iC (0 )e RC
放电过程的快慢是由时间常数τ决定。 uC,iC
τ越大,在电容电压的初始值U0一定 的情况下,C越大,电容存储的电
式中,f(0+)为待求电流或电压的初始值,f(∞)为待求电流 或电压的稳态值,τ为电路的时间常数。 对于RC电路,时间常数为:
RC
对于RL电路,时间常数为:
L
R
第15页/共34页
例:图示电路,IS=10mA,R1=20kΩ,R2=5kΩ,C=100μF。 开关S闭合之前电路已处于稳态,在t=0时开关S闭合。试用 三要素法求开关闭合后的uC。
第17页/共34页
例:图示电路,US1=9V,US2=6V ,R1=6Ω,R2=3Ω,L=1H。 开关S闭合之前电路已处于稳态,在t=0时开关S闭合。试用
三要素法求开关闭合后的iL和u2。
解:(1)求初始值。因为开关S闭合之前电路已处于稳态,
故在瞬间电感L可看作短路,因此:
iL (0 ) iL (0 )
R3
R1 R2
+
U
-
iC
+
C -uC
R0
iC +
+
C -uC
US
-
iC
IS
R0
+ C -uC
因此,对一阶电路的分析, 实际上可归结为对简单的RC 电路和RL电路的求解。一阶 动态电路的分析方法有经典 法和三要素法两种。
大学物理电路分析基础第6章一阶电路分析.ppt

第6章 一阶电路分析
动态电路在任一时刻的响应与激励的全部历史有关, 也就是说, 动态电路是有记忆的, 这是与电阻电路完全不 同的。 当动态电路的连接方式或元件参数发生突然变化时, 电路原有的工作状态需要经过一个过程逐步到达另一个新的 稳定工作状态, 这个过程称为电路的瞬态过程或过渡过程。 瞬态分析(或称动态电路分析)是指分析动态电路从电路结构 或参数突然变化时刻开始直至进入稳定工作状态的电压、 电流的变化规律。
t
iC d 1(V)
1
其波形如图6-5(c)所示。
第6章 一阶电路分析
6.1.2
通常把由导线绕成的线圈称为电感器或电感线圈。 当 线圈通过电流时, 即在线圈内外建立磁场并产生磁通Φ, 如 图6-6所示。 各线匝磁通的总和称为磁链φ(若线圈匝数为N, 则φ=NΦ )。 可见, 电感器是一种能建立磁场、 储存磁场 能量的器件。
第6章 一阶电路分析
事实上, 许多实际电路模型并不能只用电阻元件和电 源元件来构成。 电路中的电磁现象将不可避免地涉及到电 容元件和电感元件, 由于这两种元件的伏安关系都涉及对 电压或电流的微分或积分, 因此称这两种元件为动态元件。 含有动态元件的电路称为动态电路。 描述动态电路激励— 响应关系的数学方程称为微分方程, 在线性非时变条件下 为线性常系数微分方程。
第6章 一阶电路分析
6.1 电容元件和电感元件
6.1.1 电容元件
把两块金属极板用电介质隔开就可构成一个简单的电容 器。 由于理想介质是不导电的, 因此在外电源的作用下, 两块极板上能分别积聚等量的异性电荷, 在极板之间形成 电场。可见, 电容器是一种能积聚电荷、 储存电场能量的 器件。 电容器的种类很多, 按介质分有纸质电容器、 云母 电容器、 电解电容器等; 按极板形状分有平板电容器、 圆 柱形电容器等。
一阶电路课件PPT

其解为 s - 1 RC
(6 3)
称为电路的固有频率。
于是电容电压变为
t
uC (t) Ke RC
t 0
式中K是一个常量,由初始条件确定。当t=0+
时上式变为
t
uC (0 ) Ke RC K
根据初始条件 uC (0 ) uC (0 ) U 0
求 得 K U0
图6-3
最后得到图6-3(b)电路的零输入响应为
Rt
iL (t) Ke L
(t 0)
代入初始条件iL(0+)=I0求得
K I0
最后得到电感电流和电感电压的表达式为
Rt
t
iL (t) I0e L I0e τ
uL
(t
)
L
diL dt
RI0e
Rt L
RI0e
t τ
(t 0) (t 0)
(6 7a) (6 7b)
其波形如图所示。RL电路零输入响应也是按指数规
0.018U0
0.007U0
0
表6-1
图6-4 RC电路零输入响应的波形曲线
电阻在电容放电过程中消耗的全部能量为
WR=
i 2
0R
(t)Rdt
U (
0
0R
t
e RC
)2
Rdt
1 2
CU
2 0
计算结果证明了电容在放电过程中释放的能量的
确全部转换为电阻消耗的能量。
由于电容在放电过程中释放的能量全部转换为电阻 消耗的能量。电阻消耗能量的速率直接影响电容电压 衰减的快慢,我们可以从能量消耗的角度来说明放电 过程的快慢。
将连接到电感的电阻单口网络等效为一个的电阻,
一阶动态电路分析.pptx
t
t
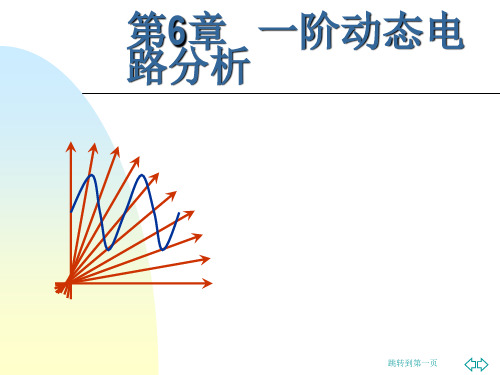
uC (U0 US )e (U0 US )e RC
只存在于暂态过程中, t→∞时uC''→0,称为暂态分量。
τ=RC称为时间常数,决定过渡过程的快慢。
波 形 图:
uC US
U0
0
U0<US
uC U0
U0>US
US
t
t
0
跳转到第一页
电路中的电流为:
iC
C duC dt
US R
t
e
US R
uC (0 ) uC (0 ) 10V
-
R1
+
iC t=0
i2
uC C
R2
-
由此可画出开关S闭合后瞬间即时的等
效电路,如图所示。由图得:
i1(0+)
i1(0 )
US
uC (0 ) R1
10 10 10
0A
i2 (0 )
uC (0 ) R2
10 5
2A
+
R1
+
iC(0+)
i2(0+)
US
uC(0+)
R3
R1 R2
+
U
-
iC
+
C -uC
R0
iC
+
+
C -uC
US
-
iC
IS
R0
+ C -uC
因此,对一阶电路的分析, 实际上可归结为对简单的RC 电路和RL电路的求解。一阶 动态电路的分析方法有经典 法和三要素法两种。
跳转到第一页
6.2.1 经典分析法
1.RC电路分析
第17讲一阶电路3-PPT精选文档

解得
8 图 (C)右边回路中有 u 10 ( 0 ) 6 i ( 0 ) 6 i ( 0 ) i ( 0 ) V L 电路分析的基础知识 L 1 L 第一章 3
(3) 求f(∞)。作t=∞电路如图(d),电感用短路线代 替。 根据图(d),容易求出
12 i1 () 2 6 6 3 66
重点
三要素分析法,瞬态和 稳态的概念
难点
正弦激励的过渡过程
第一章 电路分析的基础知识
4
§6.6 求解一阶电路三要素法
1、一阶电路响应的三要素通式
如用 y (t) 表示电路的响应,y(0+)表示该电压或电 流的初始值,y(∞) 表示响应的稳定值, 表示电路 的时间常数,则电路的响应可表示为:
t y ( t ) y ( ) y ( 0 ) y ( ) e 0
第 十七 讲
第一章 电路分析的基础知识
1
第六章
6-1 6-2 6-3 6-4 6-5 6-6 6-7 6-8
一阶电路
分解方法在动态电路分析中的运用 零输入响应 零状态响应 线性动态电路响应的叠加 阶跃响应 冲激响应 三要素法 瞬态和稳态 正弦激励的过渡过程和稳态
第一章 电路分析的基础知识 2
本章教学要求
1、稳态 稳态:电路的电压和电流保持恒定值(即常数), 或随时间周期变化的状态,此时电路的变量处于稳 定(确定)状态,故被称为稳态。 电流保持常数的电路,叫直流电路;电流随时间周 期变化的电路,叫交流电路。 电流按正弦规律变化的电路,叫正弦电流电路。
电流按非正弦规律周期变化的电路,叫非正弦周期 电流电路。 15
第一章 电路分析的基础知识
12
电路课件-一阶电路分析

電容元件的電壓電流關係
i(t) dq d(Cu) C du
dt dt
dt
1. 電容是動態元件
電容的電流與其電壓對時間的變化率 成正比。假如電容的電壓保持不變, 則電容的電流為零。電容元件相當於 開路(i=0)。
2. 電容是慣性元件
du
當i 有限時,電壓變化率 dt 必然有 限;電壓只能連續變化而不能跳變。
+u1 (0+)- iL(0+)
R3
+
R1
+uL
(0+)-
+
iC(0+) i2(0+)
uS -
uC (0+)
-
R i3(0+)
2
t=0+圖 (3)求初始值 i1(0 ) iL (0 ) 0.2A
+u1 (0+)- 0.2 A
電容器除了標明容量外,還須說明它的 工作電壓,電解電容還須標明極性。漏 電很小,工作電壓低時,可用一個電容 作為它的電路模型。當漏電不能忽略時 ,需用一個電阻與電容的並聯作為電路 模型。工作頻率很高時,還需要增加一 個電感來構成它的電路模型
電阻,電容和電感是三種最基本的電路元件。它們是用 兩個電路變數之間的關係來定義的:電壓和電流間存在 確定關係的元件是電阻元件;電荷和電壓間存在確定關 係的元件是電容元件;磁鏈和電流間存在確定關係的元 件是電感元件。這些關係從下圖可以清楚看到。
上式也可以理解為什麼電容電壓不 能輕易躍變,因為電壓的躍變要伴隨 儲能的躍變,在電流有界的情況下, 是不可能造成電場能發生躍變和電容 電壓發生躍變的。
例1 C =4F,其上電壓如圖(b),試求
iC(t), pC(t)和 wC(t),並畫出u波S 形。
一阶电路分析ppt

uR 2iL 4 e4t V t 0
uL
L d iL dt
8 e4t
V
t0
例7.1—2 电路如图7.1—5(a)所示,电路
已处于稳定,t 0 开关打开,
求 t 0 u1 的变化规律。 解:
1、求 uc (0 ),t 0 电路稳定C开路
uc (0 ) 1.5 V
2、求 u`1(0 ),画 t 0 等效电路如 图(b); 4 i (6 3) i 1.5 i 0.3A u1(0 ) 6i 1.8V
四、分析示例
例7.1—1 电路如图7.1—4(a)所示,电路已处于稳定,
t 0 时开关打开,求时 t 0,iL (t)、uR (t) 、uL (t)。
解:1、求 iL (0 ) ,t 0,
电路稳定 L看作短路,
i
(0
)
(2
8 // 2)
1
8 11
4A
iL
(0
)
2
2
2
4
2A
iL
(0
)
2、求 uR (0 ) 、uL (0 ) ,画 t 0 等效电路如图(b)有:
3、求 R 0 ,用外加激励法求的电路如图(c)所示,有: u
9 i 4 i u R0 i 5
R0 c 5 0.02 0.1s
∴
u1(t) 1.8 e10t V t 0
图7.1—5
第七章 一阶电路分析
用一阶微分方程描述的电路称为一阶电路, 一般含有一个动态元件的电路就是一阶电路。
§7.1 一阶电路的零输入响应
一、定义:外加激励为零,仅由初始储能所产生的响 应称为零输入响应,如图7.1—1所示。
我们以图7.1—2(a)的RC电路 为例,所得结论用对偶关系可 推广到RL电路。
电路第06章-一阶电路和二阶电路课件.ppt
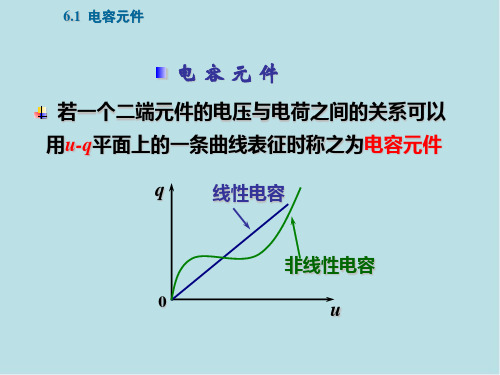
C — 电压源, L — 电流源
若uC(t0-) =0, iL(t0-) = 0, 则:
C — 短路, L — 断路 3. 利用电阻电路的计算方法求初始值
6.4 电路的初始条件
例:已知:t<0时,原电路已稳定,t=0时,打开开关S。
求: uR1(0+), uL(0+), iR2(0+), iC(0+)
6.1 电容元件
电容元件
若一个二端元件的电压与电荷之间的关系可以 用u-q平面上的一条曲线表征时称之为电容元件
q
线性电容
非线性电容
0
u
6.1 电容元件
6.1 电容元件
线性电容
q
Cq
.
.
u
0
u
量纲:F(法拉)
1μF 106 F, 1pF 106 μF 1012 F
6.1 电容元件
电容元件的伏安关系
+
uC(t)
.
_
t
iC ( )d
t
C
duC ( ) d
d
C[uC (t)
uC ()]
uC
()
0
uC
(t)
1 C
t
iC ( )d
取中间时间点:
uC
(t)
1 C
t0
iC
(
)d
1 C
t
t0 iC ( )d
uC (t0 )
1 C
t
t0 iC ( )d
t0: 初始时刻,uC(t0): 初始值
t=0+时:
1. 定性分析
+ uR(0-) _
+ uR(0+) _
若uC(t0-) =0, iL(t0-) = 0, 则:
C — 短路, L — 断路 3. 利用电阻电路的计算方法求初始值
6.4 电路的初始条件
例:已知:t<0时,原电路已稳定,t=0时,打开开关S。
求: uR1(0+), uL(0+), iR2(0+), iC(0+)
6.1 电容元件
电容元件
若一个二端元件的电压与电荷之间的关系可以 用u-q平面上的一条曲线表征时称之为电容元件
q
线性电容
非线性电容
0
u
6.1 电容元件
6.1 电容元件
线性电容
q
Cq
.
.
u
0
u
量纲:F(法拉)
1μF 106 F, 1pF 106 μF 1012 F
6.1 电容元件
电容元件的伏安关系
+
uC(t)
.
_
t
iC ( )d
t
C
duC ( ) d
d
C[uC (t)
uC ()]
uC
()
0
uC
(t)
1 C
t
iC ( )d
取中间时间点:
uC
(t)
1 C
t0
iC
(
)d
1 C
t
t0 iC ( )d
uC (t0 )
1 C
t
t0 iC ( )d
t0: 初始时刻,uC(t0): 初始值
t=0+时:
1. 定性分析
+ uR(0-) _
+ uR(0+) _
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
t
uC (t) U0e τ
iC (t)
C
duC dt
U0 R
t
eτ
iR (t) iC (t)
U0
t
eτ
R
(t 0) (t 0) (t 0)
(8 5a) (8 5b) (8 5c)
图8-4 RC电路零输入响应的波形曲线
下面以电容电压
uC (t)
t
U0e τ
为例,说明电压的变化与
时间常数的关系。
§8-1 零输入响应
一、RC电路的零输入响应
图8-3(a)所示电路中的开关原来连接在1端,电压源U0 通过电阻Ro对电容充电,假设在开关转换以前,电容电压 已经达到U0。在t=0时开关迅速由1端转换到2端。已经充电 的电容脱离电压源而与电阻R并联,如图(b)所示。
图8-3
我们先定性分析t>0后电容电压的变化过程。当开关倒
6
iC
(t)
1 3
0.6e 20t
mA
0.2e 20t
mA
二、RL电路的零输入响应
我们以图8-6(a)电路为例来说明RL电路零输入响应的 计算过程。
图8-6
电感电流原来等于电流I0,电感中储存一定的磁场能 量,在t=0时开关由1端倒向2端,换路后的电路如图(b)所示。
在开关转换瞬间,由于电感电流不能跃变,即iL(0+)= iL(0-)= I0 ,这个电感电流通过电阻R时引起能量的消耗,这 就造成电感电流的不断减少,直到电流变为零为止。
向2端的瞬间,电容电压不能跃变,即
uC (0 ) uC (0 ) U 0
由于电容与电阻并联,这使得电阻电压与电容电压相
同,即
uR (0 ) uC (0 ) U 0
电阻的电流为
iR (0 )
U0 R
该电流在电阻中引起的功率和能量为
p(t) RiR2 (t)
WR (t)=R
it 2
0R
( )d
3
6
根据式8-5得到
t
uC (t) U0e
6e20t V
iC (t) C
duC dt
U0 R
t
e
10
6 103
e20t mA
0.6e20tmA
(t 0) (t 0)
电阻中的电流iR(t)可以用与iC(t)同样数值的电流源代替 电容,用电阻并联的分流公式求得 iR(t)
iR
(t)
3
3
当t=0时,uC(0)=U0,当t=时,uC()=0.368U0。表8-1 列出t等于0,,2,3,4,5 时的电容电压值,由于波 形衰减很快,实际上只要经过4~5的时间就可以认为放电
过程基本结束。
t
0
2
3
4
5
uc(t)
U0
0.368U0 0.135U0 0.050U0 0.018U0 0.007U0
s - 1 RC
称为电路的固有频率。
(8 3)
于是电容电压变为
t
uC (t) Ke RC
t 0
式中K是一个常量,由初始条件确定。当t=0+时上式变
为
t
uC (0 ) Ke RC K
根据初始条件
uC (0 ) uC (0 ) U 0
求得
K U0
图8-3
最后得到图8-3(b)电路的零输入响应为
电容中的能量为
WC
(t)
1 2
Cu 2 (t)
随着时间的增长,电阻消耗的能量需要电容来提供, 这造成电容电压的下降。一直到电容上电压变为零和电容 放出全部存储的能量为止。也就是电容电压从初始值 uC(0+)=U0逐渐减小到零的变化过程。这一过程变化的快慢 取决于电阻消耗能量的速率。
Hale Waihona Puke 为建立图(b)所示电路的一阶微分方程,由KVL得到
我们的重点是讨论一个电压源与电阻及电容串联,或 一个电流源与电阻及电感并联的一阶电路。
与电阻电路的电压电流仅仅由独立电源所产生不同, 动态电路的完全响应则由独立电源和动态元件的储能共同 产生。
仅由动态元件初始条件引起的响应称为零输入响应。 仅由独立电源引起的响应称为零状态响应。 动态电路分析的基本方法是建立微分方程,然后用数 学方法求解微分方程,得到电压电流响应的表达式。
例如在电容电压初始值U0不变的条件下,增加电容C, 就增加电容的初始储能,使放电过程的时间加长;若增加 电阻R,电阻电流减小,电阻消耗能量减少,使放电过程 的时间加长。
这就可以解释当时间常数=RC变大,电容放电过程会
加长的原因。
例8-1 电路如图8-5(a)所示,已知电容电压uC(0-)=6V。 t=0闭合开关,求t > 0的电容电压和电容电流。
t
uC (t) U 0e RC
iC
(t
)
C
duC dt
U0 R
t
e RC
iR (t) iC (t)
U0
t
e RC
R
(t 0) (t 0) (t 0)
(8 4a) (8 4b) (8 4c)
从式8-4可见,各电压电流的变化快慢取决于R和C的
乘积。令 =RC,由于 具有时间的量纲,故称它为RC电 路的时间常数。引入 后,式8-4表示为
图8-5 例8-1
解:在开关闭合瞬间,电容电压不能跃变,由此得到
uC (0 ) uC (0 ) 6V
将连接于电容两端的电阻单口网络等效于一个电阻,其
电阻值为
Ro
(8
6 3)k 63
10k
得到图(b)所示电路,其时间常数为
5 10 s 0.05s 2
RC 10 10 5 10 s
uR uC 0
由KCL和电阻、电容的VCR方程得到
uR
RiR
RiC
RC duC dt
代入上式得到以下方程
RC
duC dt
uC
0
(t 0) (8 1)
这是一个常系数线性一阶齐次微分方程。其通解为
uC (t) Ke st
代入式(8-1)中,得到特征方程
RCs 1 0 (8 2)
其解为
第八章 一阶电路分析
由一阶微分方程描述的电路称为一阶电路。本章主要 讨论由直流电源驱动的含一个动态元件的线性一阶电路。 含一个电感或一个电容加上一些电阻元件和独立电源组成 的线性一阶电路,可以将连接到电容或电感的线性电阻单 口网络用戴维宁-诺顿等效电路来代替(如图8-1和8-2 所示)。
图8-1
图8-2
0
图8-4 RC电路零输入响应的波形曲线
电阻在电容放电过程中消耗的全部能量为
WR=
i 2
0R
(t)Rdt
(U 0 0R
t
e RC
)2 Rdt
1 2
CU
2 0
计算结果证明了电容在放电过程中释放的能量的确全 部转换为电阻消耗的能量。
由于电容在放电过程中释放的能量全部转换为电阻消 耗的能量。电阻消耗能量的速率直接影响电容电压衰减的 快慢,我们可以从能量消耗的角度来说明放电过程的快慢。
