勾股定理第1课时
《勾股定理》PPT(第1课时)

命题1 如果直角三角形的两条直角边长分别为a,b,斜边 长为c,那么a2+b2=c2.两直角边的平方和等于斜边的平方.
ac
b
课程讲授
1 勾股定理
下面让我们跟着以前的数学家们用拼图法来证明这一猜想.
c b a
b-a
证明:∵S大正方形=c2, S小正方形=(b-a)2,
∴S大正方形=4S三角形+S小正方形,
课程讲授 2 勾股定理与图形面积
归纳:与直角三角形三边相连的正方形、半圆及 正多边形、圆都具有相同的结论:两直角边上图 形面积的和等于斜边上图形的面积.本例考查了 勾股定理及半圆面积的求法,解答此类题目的关 键是仔细观察所给图形,面积与边长、直径有平 方关系,就很容易联想到勾股定理.
课程讲授Biblioteka 2 勾股定理与图形面积定有a2+b2=c2.
勾股定理:直角三角形两直角边的平方和等于斜边的平方.
课程讲授
1 勾股定理
几何语言: ∵在Rt△ABC中 ,∠C=90°,
B ac
∟
∴a2+b2=c2(勾股定理).
C
勾股定理揭示了直角三角形三边之间的关系.
bA
课程讲授 1 勾股定理
例 在Rt△ABC中,∠C=90°,AB=10 cm, BC=8 cm,求AC的长.
(1)正方形P的面积是 1 平方厘米; (2)正方形Q的面积是 1 平方厘米; (3)正方形R的面积是 2 平方厘米.
AR P
CQ B
上面三个正方形的面积之间有什么关系? SP+SQ=SR
(图中每一格代表一平方厘米)
课程讲授 1 勾股定理
直角三角形ABC三边长度之间存在什么关系吗? SP=AC2 SQ=BC2 SR=AB2 AC2+BC2=AB2
第一课时勾股定理优秀教学案例

1.布置巩固性作业:让学生运用勾股定理解决实际问题,如计算房屋建筑中的长度、设计直角三角形图案等。检查学生对勾股定理的理解和应用能力。
2.布置拓展性作业:让学生探索其他数学定理或公式,如平方根、立方根等。培养学生的探索精神和创新能力。
3.鼓励学生进行自我评价,反思自己在学习过程中的优点和不足。指导学生制定改进措施,提高学习效果。
此外,我还注重课堂评价的多元化,充分关注学生的个体差异,给予他们积极的评价和鼓励,使他们在课堂上充满自信,更好地投入到学习过程中。整个教学过程既注重知识的传授,又重视学生的全面发展,体现了新课程改革的理念和要求。
二、教学目标
(一)知识与技能
1.让学生掌握勾股定理的内容,理解直角三角形三边之间的关系,能够运用勾股定理解决实际问题。
(一)导入新课
1.故事导入:讲述毕达哥拉斯如何通过观察木匠修鞋匠的鞋子长度比例,发现了勾股定理。引导学生关注古代数学家的伟大发现,激发学生学习兴趣。
2.实物模型导入:展示古代的勾股定理证明雕塑,让学生直观地感受数学与艺术的完美结合。引发学生对勾股定理的好奇心,激发他们的探究欲望。
3.现实生活实例导入:分析房屋建筑、自行车轮胎等实例,让学生感受到勾股定理在实际应用中的重要性,引发学生思考。
2.鼓励学生提出问题,培养他们的问题意识和批判性思维。例如,在教学过程中,让学生大胆质疑,挑战古代数学家的证明方法。
3.创设循序渐进的问题序列,引导学生逐步深入探究勾股定理。例如,从简单的情形开始,让学生观察、实验、猜测,逐步引导学生得出勾股定理的结论。
(三)小组合作
1.组织学生进行小组讨论,培养他们的团队协作能力和沟通能力。例如,在探究勾股定理的过程中,让学生分组讨论,相互启发,共同解决问题。
2.1 勾股定理(第1课时)

古今中外,无数的数学家对勾 股定理进行了充分的研究,其 中也有很多的有趣的故事,下 面有一些勾股趣事,当然同 学们也可以通过上网去了解.
勾股故事1
最早对勾股定理进行证明的,是 三国时期吴国的数学家赵爽。赵 爽创制了一幅“勾股圆方图”, 用数形结合得到方法,给出了勾 股定理的详细证明。
如图,在边长为c的正方形中,有四 个斜边是c的全等直角三角形,已 知它们的直角边分别是a, b . 勾股圆方图
A c b C a B
41 1)已知:a=9,b=40, 则c=_____; 8 2)已知:a=6,c=10,则b=_____;
20 3)已知:b=15,c=25,则a=_____; n2-1 4)已知c=n2+1,b=2n,则a=____
C
B
4000
4000
A
想 一 想
小明的妈妈买了一部29英寸(74厘 米)的电视机。小明量了电视机的屏 幕后,发现屏幕只有58厘米长和46厘 米宽,他觉得一定是售货员搞错了。 你能解释这是为什么吗? 我们通常所说的29 英寸或74厘米的电视 机,是指其荧屏对角 线的长度
2 2 2 2
a b c
a
b
勾股定理
在西方又称毕达 哥拉斯定理耶!
直角三角形中,两直角边的
平方和等于斜边平方。
用数学式子表示:c2=a2+b2 A
c=
股
b C a 勾 B c 弦
a b
2
2
a= b=
c b
2
ቤተ መጻሕፍቲ ባይዱ2 2
c a
2
运用勾股定理
可解决直角三角形中边的计算或证明
A
B
D
C
《勾股定理》PPT优质课件(第1课时)

A. 3
B.3
C. 5
D.5
E
课堂检测
基础巩固题
1. 若一个直角三角形的两直角边长分别为9和12,则斜边的
长为( C)
A.13
B.17
C. 15
D.18
2.若一个直角三角形的斜边长为17,一条直角边长为15,则
另一直角边长为( A )
A.8
B.40
C.50
D.36
3.在Rt△ABC中,∠C=90°,若a︰b=3︰4,c=100,则 a= _6_0___,b = __8_0___.
课堂检测
4.如图,所有的四边形都是正方形,所有的三角形都是直角三角 形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面 积之和为_____4_9_____cm2 .
C D
B A
7cm
课堂检测
能力提升题
在Rt△ABC中,AB=4,AC=3,求BC的长.
解:本题斜边不确定,需分类讨论:
当AB为斜边时,如图,BC 42 32 7;
形,拼成一个新的正方形.
探究新知 剪、拼过程展示:
b
a ca
朱实
b 朱实 黄实朱实
c 〓b
ba
朱实
a
M a P bb
N
探究新知 “赵爽弦图”
c
朱实
b
朱实
黄实 朱实
a
朱实
证明:∵S大正方形=c2, S小正方形=(b-a)2,
∴S大正方形=4·S三角形+S小正方形,
探究新知
毕达哥拉斯证法:请先用手中的四个全等的直角三角形按图 示进行拼图,然后分析其面积关系后证明吧.
因此设a=x,c=2x,根据勾股定理建立方程得 (2x)2-x2=152,
1勾股定理(第1课时)(教学PPT课件(华师大版))28张
1955年希腊发行的一枚纪念邮票.
讲授新课
知识点一 直角三角形三边的关系
视察正方形瓷砖铺成的地面.
(1)正方形P的面积是
1
(2)正方形Q的面积是
1
平方厘米;
(3)正方形R的面积是
2
平方厘米.
平方厘米;
上面三个正方形的面积之间有什么关系?
等腰直角三角形ABC三边长度之间存在什么关系吗?
程.
b
a
b
a
c
c
b
c
c
a
a
b
讲授新课
证明:大正方形的面积=(a+b)2.
四个个全等的直角三角形和小正方形的面积
1
2
2
之和= 4 ab c 2ab c .
2
b
由题可知(a+b)2=2ab+c2,
a
c
化简可得a2+b2=c2.
我们利用拼图的方法,将形的问题
与数的问题结合起来,再进行整式
A的面积
B的面积
C的面积
左图
4
9
13
右图
16
9
25
结论:以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.
SA+SB=SC
讲授新课
猜想:两直角边a、b与斜边 c 之间的关系?
A
a
B b
c
a2+b2=c2
C
讲授新课
概念总结
由上面的探索可以发现:对于任意的直角三角形,如果它的两
数学(华东师大版)
八年级 上册
第14章 勾股定理
冀教版初中八年级数学上册17-3勾股定理第一课时勾股定理课件

11.(2024江苏扬州邗江期末,16,★★☆)如图,在Rt△ABC中,
AC=4,AB=5,∠C=90°,BD平分∠ABC交AC于点D,则DC的长
3
是2.
解析 在Rt△ABC中,AC=4,AB=5,∠C=90°,∴BC=
A=B2 =3A,C如2图,过52 D 作42 DE⊥AB于点E,∵BD平
分∠ABC,DC⊥BC,∴DC=DE,设DC=DE=x,∵S△BCD+S△ABD=S△ABC,
2
2ab+b2-2ab=a2+b2,∵中间小正方形的边长为c,∴小正方形的
面积为c2,∴a2+b2=c2,∴甲能利用面积验证勾股定理.乙中直
角梯形的面积为 (a =b)(aa2+b) b12+ab1,两个直角三角形
2
22
的面积和为2× 1 ab=ab,则中间等腰直角三角形的面积为1 a2+
2
2
1 b2+ab-ab=1 a12+ b2,∵中间等腰直角三角形的两条直角边
7.(2024四川成都龙泉驿期末)如图,△ABC中,AB=AC,BD⊥AC于 点D,∠BDF=∠BAF=∠C,BD=3,CD=1. (1)求证:∠CBD=∠EDA. (2)求AB的长.
解析 (1)证明:∵BD⊥AC, ∴∠C+∠CBD=∠EDA+∠BDF=90°, ∵∠BDF=∠C,∴∠CBD=∠EDA. (2)设AD=x,则AB=AC=AD+CD=x+1, ∵BD=3,AD2+BD2=AB2,∴x2+32=(x+1)2, 解得x=4,∴AB=x+1=5.
∴1 BC·DC+1 AB·DE1=222解33
17.1勾股定理(第1课时)课件(共23张PPT)

让我们一起再探究:等腰直角三角形三边关系
C A B 9 C A B 图2-2 4 9 4 18 8
图2-1
(图中每个小方格代表一个单位面积)
C A B 图2-1 A B
S正方形c
C
1 4 3318 2
图2-2
(图中每个小方格代表一个单位面积)
(单位面积)
分“割”成若干个直 角边为整数的三角形
弦 勾
股
图1-1
漂亮的勾股树
活动 2
相传2500年前,毕达哥拉斯有一次 在朋友家里做客时,发现朋友家用砖铺 成的地面中反映了直角三角形三边的某 种数量关系.
我们也来观察右 图中的地面,看看有 什么发现?
数学家毕达哥拉斯的发现:
A
B
C
A、B、C的面积有什么关系? SA+SB=SC 直角三角形三边有什么关系? 两直边的平方和等于斜边的平方
设:直角三角形的三边长分别是a、b、c
猜想:两直角边a、b与斜边c 之间的关系? A a B b
Sa+Sb=Sc
c
C
2 2 2 a +b =c
b
a
c b (a+b )2
证 明 二
a
c
c
1 = c 4 ab 2
2
a2 + b2 + 2ab = c2+2ab
b a
c
b
a
可得: a2 + b2 = c2
C A B 图2-1 A B
S正方形c
C
1 6 2
2
1 8(单位面积)
图2-2
(图中每个小方格代表一个单位面积)
把C“补” 成边长为6的 正方形面积的一半
第1课时勾股定理课件(湘教版)

由图②可以得到:若将大正方形的面积整体表示,可表示
为
c2
,若看成四个全等小三角形与一个小正方形面积之和,可表
2
示为 4×ab+(b-a) .
2
2
2
2
2
4
×
ab+
(
b-a
)
=c
根据面积相同得到等式:
. 整理得 a +b =c
.
综合(1)与(2)可得:直角三角形中,两条直角边的
第1课时
勾股定理
例3 [教材补充例题] 如图1-2-2,在Rt△ABC中,∠ACB=90°,CD⊥AB,
垂足为D,BC=6,AC=8,求AB与CD的长.
图1-2-2
第1课时
勾股定理
解:在 Rt△ABC 中,BC=6,AC=8.
∵AB2=BC2+AC2,
∴AB=10.
×
∵SABC=AB·CD=BC·AC=×6×8,∴CD= =4.8.
第1章 直角三角形
1.2
直角三角形的性质和判定(Ⅱ)
第1章 直角三角形
第1课时
勾股定理
目标突破
总结反思
第1课时
勾股定理
目标突破
目标一 会运用面积方法推理证明勾股定理
例 1 [教材习题 P17T7 改编题] 阅读下面的材料:先做四个全等
的直角三角形,设它们的两条直角边分别为 a,b,斜边为 c,然后按图
图 1-2-4
第1课时
勾股定理
总结反思
小结
知识点 勾股定理
勾股定理:直角三角形两直角边a,b的 平方和 ,等
八上-第一章勾股定理

第一章勾股定理第1课时认识勾股定理1 我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称弦·直角三角形三边之间的关系称为勾股定理。
2 勾股定理是指直角三角形两直角边的平方和等于边的平方.如果用a,b和c分别表示直角三角形的两直角边和斜边,那么 a2+b2=c2 。
预学感知在Rt△ABC中,∠B=90°,AC=10,AB=6,则则BC的长为。
知识点一勾股定理的认识【例1】在△ABC中,∠ACB=90°,∠A,∠B,∠C的对边分别为a,b,C.当a=9,c=41时,则b= 。
【名师点拔】由于∠ACB=90°,则有a2=c2,因而只需把已知数据代入相应字母,即可求出第三条线段的长。
知识点二勾股定理的简单运用【例2】如图,△ABC中,∠ACB=90°,AC=7,BC=24,CD⊥AB于点D。
求:(1)AB的长;(2)CD的长。
【名师点拔】由于△.ABC为直角三角形,就可先由匀股定理理求出AB,再根据面积求出CD的长。
1.已知直角三角形中两条边长,要弄清哪条是斜边,哪条是直角边,不能确定时,要分类讨论;2.在直角三角形中求斜边上的高,一般是借助面积这个中间量,21ab=21ch 。
1.在Rt △ABC 中,两直角边长分别为10和24,则斜边长等于 ( )A.25B.26C.27D.282.在Rt △ABC 中,斜边长BC =3,则AB 2+AC 2= 。
3. 如图,分别以直角三角形的三边为边向外作正方形,则正方形A 的面积是 ,B 的面积是 。
4. 要登上某建筑物,靠墙有一架梯子,底端离建筑物5m ,顶端离地面12m ,则梯子的长度为 。
5. 如图,有两棵树,一棵高12m ,另一棵高6m ,两树相距8m ,一只鸟从一棵树的树梢飞到另一棵树梢,则小鸟至少飞行 m 。
6. 某天我国海监船驶向钓鱼岛海域执法时,海监船甲以15海里/时的速度离开港口向北航行,海监船乙同时以20海里/时的速度离开港口向东航行,则它们离开港口2h 后相距 海里。
人教版勾股定理第一课时

பைடு நூலகம்
拼图证明
1、拿出准备好的四个全等的直角三角形 (设直角三角形的两条直角边分别为a,b, 斜边c);
2、你能用这四个直角三角形拼成一个正方
形
吗?拼一拼试试看
3、你拼的正方形中是否含有以斜边c为边长的正 方形?
4、你能否就你拼出的图说明a2+b2=c2?
c a
b
13
拼图证明
如何利用下图证明a2+b2=c2?
赵爽弦图
图1-1
图1-2
古往今来,下至平民百姓,上至帝王总统都愿意探讨、
研究它的证明,新证法不断出现。目前世界上共有500
多种证明“勾股定理”的方法。其中包括大画家达·芬奇
18
和美国总统加菲尔德的证法。
勾股定理运用1
已知S1=1,S2=3,S3=2,S4=4,求S5、S6、S7的值
S2 S1 S5
青 出
青 入
朱朱
朱 出出 方
朱朱入入 青入
以刘徽的“青朱 出入图”为代表, 证明不需用任何 数学符号和文字, 更不需进行运算, 隐含在图中的勾 股定理便清晰地 呈现,整个证明 单靠移动几块图 形而得出,被称 为“无字证明”.
青出
29
证法欣赏3
④
⑤
b
c
③
a
①②
以刘徽的“青朱 出入图”为代表, 证明不需用任何 数学符号和文字, 更不需进行运算, 隐含在图中的勾 股定理便清晰地 呈现,整个证明 单靠移动几块图 形而得出,被称 为“无字证明”.
长分别为a、b,斜边长为c,那么 a2 + b2 = c2
数学方法:1.观察—探索—猜想—验证—归纳—应用
2.“割补、拼接”法
18.1勾股定理(第1课时)

弦 勾
股
王
辉
2012年3月
菲尔兹奖
18.1 勾股定理(一) 勾股定理(
勾股定理!??? 勾股定理!???
探究一: 探究一:发现规律
相传2500年前,古希腊数学家毕达哥拉斯在朋友家做客时, 年前,古希腊数学家毕达哥拉斯在朋友家做客时, 相传 年前 发现朋友家用砖铺成的地面中反映了直角三角形三边之间的 某种数值关系.你发现了吗 你发现了吗? 某种数值关系 你发现了吗? A a c C b B
sA+sB=sC
两直角边的平方和 等于斜边的平方
命题1: 命题1 如果直角三角形的两直角边长分 别为a 斜边长为c 那么a 别为a、b,斜边长为c,那么a2+b2=c2。
论证命题
朱实 中黄实 c b a ( b- a) 2 - )
看左边的图案, 看左边的图案,这个图案是 公元 3 世纪我国汉代的赵爽在注 周髀算经》时给出的, 解《周髀算经》时给出的,人们 称它为“赵爽弦图” 称它为“赵爽弦图”.赵爽根据 此图指出: 此图指出:四个全等的直角三角 红色) 形(红色)可以如图围成一个大 正方形, 正方形,中间的部分是一个小正 黄色). 方形 (黄色).
赵爽弦图的证法
S大正方形 = S小正方形 + 4S直角三角形 ab c = (b − a) + 4 ⋅ 2
2 2
朱实 中黄实 c b a ( b- a) 2 - )
c2 = b2 -2ab+ a2+2ab
化简得: 化简得: c2 =a2+ b2.
类似的请同学利用探究材料中的图五和四 个全等的直角三角形按照提示拼一拼图,并列 出与面积有关的等式,然后化简你有什么发现? 比比看谁先完成!
八年级数学《勾股定理》第一课时课件

c a
=2ab+b2-2ab+a2
b
=a2+b2
∴a2+b2=c2
c a
b
c a
b
c a
b
我探索、我验证!
大正方形的面积可以表示为 (a+b)2 ;
也可以表示为
c2 +4• ab
2
c a
b
c a
b
c a
b
c a
b
∵
(a+b)2
=
c2
+4•
ab 2
a2+2ab+b2 = c2 +2ab
∴a2+b2=c2
这就是本届大会 会徽的图案.
这个图案被称为“赵爽弦 图”, 是我国汉代数学家赵 爽在证明勾股定理时用到的.
你听说过勾股定理吗?
我操作 ,我猜想!
请同学们以四人一小组合作完成下列问题,其中 每组选两名同学动手操作,另两名同学负责监督整个 操作过程确保准确无误,最后每组派一名同学代表本 组发言。
(1)分别在方格纸上作两个直角三角形,使其两直角 边分别是3厘米和4厘米,5厘米和12厘米。
勾股定理 (毕达哥拉斯定理)
直角三角形两直角边的平方 和等于斜边的平方.
弦c b股
┏
勾a
a2+b2=c2
走进勾股世界
两千两多千多年年前前,,古古希希腊有腊个有哥拉个毕达哥拉斯 学斯学派派,,他他们们首首先发先现发了勾现股了定勾理,股因定此 理,因此在 国在国外外人人们们通通常常称勾称股勾定理股为定毕理达哥为拉毕斯 达哥拉斯定 理定理。。为为了了纪纪念念毕达毕哥达拉斯哥学拉派斯,1学95派5 ,1955年 希年希腊腊曾曾经经发发行行了一了枚一纪念枚票纪。念邮票。
第1课时勾股定理微课ppt课件
赵爽指出:按弦图,又可以
勾股相乘为朱实二,倍之为
朱实四.以勾股之差自相乘为 中黄实.加差实,亦成弦实.
赵爽弦图
思考 你是如何理解的?你会证明吗?
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的
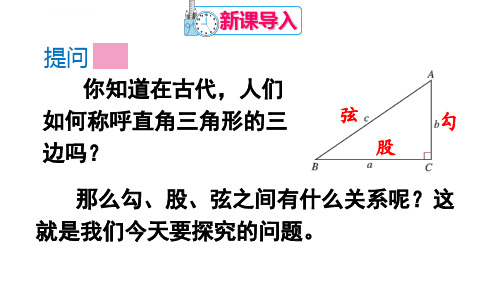
如何称呼直角三角形的三 边吗?
弦 股
勾
那么勾、股、弦之间有什么关系呢?这 就是我们今天要探究的问题。
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
C'
A面、积B/格、C的9面积有25什么关3系4 ? SA+SB=SC
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
思考
等腰直角三角形三条边长度 之间有怎样的特殊关系?
小结
等腰直角三角形斜边的平 方等于两直角边的平方和.
证明
赵爽弦图
小正方形的面积= (a-b)2
=c2-4×
1 2
ab
即c2=a2+b2.
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
人教版勾股定理(第1课时)

二、观察思考,探究新知
毕达哥拉斯(公元前572----前492年),古希 腊著名的哲学家、数学家、天文学家。
相传2500年前,毕达哥拉斯有 一次在朋友家做客时,发现朋友家 的用砖铺成的地面中反映了直角三 角形三边的某种数量关系.
1.问题:A、B、C的面积有什么关系?
A
B
C
AB C
SA+SB=SC 对于等腰直角三角形三边有这样的关系:
两条直边的平方和等于斜边的平方
2.问题:观察图甲、图乙,小方格的 边长为1.正方形A、B、C的面积有什么 关系?
C
A ac
B
b
B
图甲
A
图乙
a bc
C
49 4 16 8 25
SA+SB=SC
a2+b2=c2
3.探究总结,提出猜想
a
c
b
命题1:如果直角三角形的两直角边 长分别为a、b,斜边长为c,那么a2+b2=c2
新人教版八年级下册 17.1 勾股定理
(第1课时)
一、创设情境,复习引入
国际数学家大会是最高水平的全球性数学学科学术会议,被誉为 数学界的“奥运会”.2002年在北京召开了第24届国际数学家大会.
为什么选用这个图 案做为2002年国际数学
家大会的会徽呢?
它由哪些我们学过 的基本图形组成?这些 图形的边之间有哪些关 系,面积怎样计算?
2.编题目游戏,考一考你的同学
游戏要求:每一位同学画一个直角三角形, 给出任意两条边的长,求第三条边 x.然后小组 之间每两个同学交换解答,再交换回来批改, 看看你的同学是否会学会运用勾股定理,如果 他(她)不会,请你教教他(她).最后由各小 组长汇报游戏情况.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
看Байду номын сангаас看
毕达哥拉斯是2005年前古希腊 著名的数学家,一天发现朋友家的用砖 铺成的地面中反映了等腰直角三角形三 边的某种数量关系„„
A
B
C
方格中感悟
对于一般的直角三角形是否也有这样的性 质呢?
C A
B
拼图游戏
• 勾股定理的证明勾股定理是初等几何中的
一个基本定理。这个定理有十分悠久的 历史,两千多年来,人们对勾股定理的 证明颇感兴趣,因为这个定理太贴近人 们的生活实际,以至于古往今来,下至 平民百姓,上至帝王总统都愿意探讨和 研究它的证明.下面结合几种图形来进 行证明。
总统巧证勾股定理
D
a
C
c
b
c
b
A
E a B
美国第二十任 总统伽菲尔德
返回
向常春的证明方法
S梯形ABCD 1 1 1 (a b b )(a b ) a 2 ab 2 2 2
S梯形ABCD S四边形AECD S EBC 1 2 1 c (a b )b 2 2 1 2 1 1 2 c ab b 2 2 2
勾 股
在中国古代,人们 把弯曲成直角的手臂的 上半部分称为"勾",下 半部分称为"股"。我国 古代学者把直角三角形 较短的直角边称为 “勾”,较长的直角边 称为“股”,斜边称为 “弦”.
勾
股
知
识
•我国是最早了解勾股定理的 国家之一。早在三千多年前, 周朝数学家商高就提出,将一 根直尺折成一个直角,如果勾 等于三,股等于四,那么弦就 • 勾股定理在国外,尤其在 等于五,即“勾三、股四、弦 五”,它被记载于我国古代著 西方被称为毕达哥拉斯定 理或百牛定理.相传这个定 名的数学著作《周髀算经》中, 以后人们就简单 理是公元前500多年时古希 地把这个事实说 腊数学家毕达哥拉斯首先 成“勾三股四弦 发现的。他发现勾股定理 五” ,所以在我 后高兴异常,命令他的学 国人们就把这个 生宰了一百头牛来庆祝这 定理叫作 “商高 个伟大的发现,因此勾股 定理”。
I
令正方形ABCD为朱方,正方 形BEFG为青方.在BG间取一点H, 使AH=BG,裁下△ADH,移至 △CDI,裁下△HGF,移至△IEF,
D E C F
是为“出入相补,各从其类”,其
余不动,则形成弦方正方形 DHFI.勾股定理由此得证.
A
B
H
G
返回
总统巧证勾股定理
学过几何的人都知道勾股定理.它是几何中一个比较重要的定理,应用十分 广泛.迄今为止,关于勾股定理的证明方法已有500余种.其中,美国第二十任 总统伽菲尔德的证法在数学史上被传为佳话. 总统为什么会想到去证明勾股定理呢?难道他是数学家或数学爱好者?答案 是否定的.事情的经过是这样的: 1876年一个周末的傍晚,在美国首都华盛顿的郊外,有一位中年人正在散步, 欣赏黄昏的美景,他就是当时美国俄亥俄州共和党议员伽菲尔德.他走着走着, 突然发现附近的一个小石凳上,有两个小孩正在聚精会神地谈论着什么,时而大 声争论,时而小声探讨.由于好奇心驱使伽菲尔德循声向两个小孩走去,想搞清 楚两个小孩到底在干什么.只见一个小男孩正俯着身子用树枝在地上画着一个直 角三角形.于是伽菲尔德便问他们在干什么?只见那个小男孩头也不抬地说: “请问先生,如果直角三角形的两条直角边分别为3和4,那么斜边长为多少呢?” 伽菲尔德答到:“是5呀.”小男孩又问道:“如果两条直角边分别为5和7,那 么这个直角三角形的斜边长又是多少?”伽菲尔德不加思索地回答到:“那斜边 的平方一定等于5的平方加上7的平方.”小男孩又说道:“先生,你能说出其中 的道理吗?”伽菲尔德一时语塞,无法解释了,心理很不是滋味. 于是伽菲尔德不再散步,立即回家,潜心探讨小男孩给他留下的难题.他经 过反复的思考与演算,终于弄清楚了其中的道理,并给出了简洁的证明方法.
2
a
1 2 1 1 2 1 1 2 a ab c ab b 2 2 2 2 2
b
A
a c c
D
E
a-b
B
b
C
从而得到 : a 2 b2 c 2
注:这一方法是向常春 于1994年3月20日构想发 现的新法.
试
一
试
b a c c c a a b
我们用拼图的方法来说明 勾股定理是正确的.
在数学的天地里,重要的不是我 们知道什么,而是我们怎么知道什么。
——毕达哥拉斯
这个图形里蕴 涵着怎样博大 精深的知识呢 ?
弦图
拼一拼
现在我们一起来探 索“弦图”的奥妙吧!
试用两种不同的方法求出弦图的面积。
a
c
b
勾股定理:如果直角三角形的两直角边长 分别为a、b,斜边长为c,那么a2+b2=c2。
• 完成课本24页练习1、2 • 了解常见的勾股数: • 3、4、5及其整数倍 • 5、12、13 • 8、15、17 • 7、24、25
请 你 欣 赏
毕达哥拉斯树
1
1
美丽的毕达哥拉斯树
刘徽的证法
刘徽在《九章算术》中对勾股定理的证明: 勾自乘为朱方,股自乘为青方,令出入相补,各 从其类,因就其余不移动也.合成弦方之幂,开 方除之,即弦也.
•毕达哥拉斯(毕达 哥拉斯,前572~前 497),西方理性数 学创始人,古希腊数 学家,他是公元前五 世纪的人,比商高晚 出生五百多年.
定理又叫做“百牛定理”
• 著名网络科普作家培米姆.安萨利最近提出人 类最伟大的十大科学发现中,第一项就是勾股 定理,它在公元前一千多年西周的“周髀算经” 中就有记载,称为商高定理.在西方,称之为 毕达哥拉斯定理(公元前6世纪).而古巴比 伦人发现勾股数,其年代比商高和毕达哥拉斯 都更早,大约在公元前19⒁-1600年之 间.(其它9项科学发现依次是微生物的存在; 牛顿三大运动定律和微积分;物质结构;血液 循环;电流;物种进化;基因;热力学四大定 律;光的波粒二象性导致量子力学的诞生).
证明:上面的大正方形的面积为:c 2 4
1 ab 2
b
c b
a
1 下面大的正方形的面积为:a 2 b 2 4 ab 2
从右图中我们可以看出,这两个正方形的 边长都是a+b,所以面积相等,即
a
a a a b c b c
b a b b b
1 1 2 2 c 4 ab c b 4 ab 2 2 c 2 a 2 b2
