同方向不同频率两个简谐振动的合成共21页文档
合集下载
简谐振动的合成
0 < ∆ϕ < π
质点沿顺时针方向运动
π < ∆ϕ < 2π 质点沿逆时针方向运动
说明：任何一个直线简谐振动， 说明：任何一个直线简谐振动，椭圆运动或匀速 圆周运动都可分解为两个相互垂直的简谐振动. 圆周运动都可分解为两个相互垂直的简谐振动
上页 下页 返回 结束
第九章 振 动
用旋转矢量描绘振动合成图
(1) ϕ2 − ϕ1 = 0或2π
A2 y= x A1
y
A2
o
A1
x
时刻t 质点离开平衡位置的位移（合振动） 时刻 质点离开平衡位置的位移（合振动）
2 r = x2 + y 2 = A12 + A2 cos(ωt + ϕ )
2 2 A = A1 + A2
——合振动也是谐振动 合振动也是谐振动
上页 下页 返回 结束
上页 下页 返回 结束
第九章 振 动
Acosϕ = A1 cosϕ1 + A2 cosϕ2
令
Asinϕ = A1 sinϕ1 + A2 sinϕ2
A = A12 + A22 + 2A1 A2 cos( 2 −ϕ1 ) ϕ
A1 sin ϕ 1 + A2 sin ϕ 2 tan ϕ = A1 cos ϕ 1 + A2 cos ϕ 2
上页
下页
返回
结束
第九章 振 动
两相 互垂直同 频率不同 相位差简 谐运动的 合成图
上页
下页
返回
结束
第九章 振 动பைடு நூலகம்
§9.4.4 互相垂直不同频率简谐振动的合成·李萨如图形 互相垂直不同频率简谐振动的合成 李萨如图形
10.2 两个简谐振动的合成
2
2
频率都较大且频率差很小的两个同方向简谐
振动，在合成时会产生合振幅时强、时弱的现 象，这称为拍。
拍频 ：单位时间内振动加强或减弱的次数
振幅 2Acos (2 1)t 的频率
2 由于是绝对值，所以
2
2
1
2
2
1
拍频等于两个分振动的频率之差
10.2.3 互相垂直的同频率简谐振动的合成
质点按分振动的周 期作左旋正椭圆运动
A1=A2：左旋圆运动
（5）当 2 1 取其他值时，合振动的轨迹一
般为斜椭圆。 与上述合成过程相反，一个圆运动或椭圆运
动可以分解成两个互相垂直的同频率简谐振动 这在分析光的偏振时要经常用到
*10.2.4 互相垂直的不同频率简谐振动的合成
合振动的轨迹一般是不稳定的。但当两个分 振动的频率比恰好等于简单的整数比时，合振 动的轨迹是稳定的封闭曲线，称为李萨如图。
李萨如图
判定两种频率是否成整数比，据此可由已知 频率确定未知频率。
x1 A1 cos( t 1)
x2 A2 cos( t 2 )
合振动仍是一个角 频率为ω的简谐振动：
x x1 x2 Acos( t )
A A12 A22 2A1 A2 cos(2 1) tan A1 sin 1 A2 sin 2
A1 cos1 A2 cos2
（3）2
1
2
，y 比 x 超前
2
：
x2 y2 1 A12 A22
质点的运动轨迹是以
坐标轴为主轴的正椭圆 （或圆） 不是简谐振动!
第三节 简谐运动的合成
2 1 2k k 0,1,2,
A1
A A1 A2 合振动加强
A2
若两分振动反相:
2 1 (2k 1) k 0,1,2,
A A1 A2
合振动减弱
若 A1=A2 , 则 A=0
A2
A1
课堂练习：
两个同方向同频率的谐振动，振动方程分别为
x1
6102 cos(5t )m，
2
x2
2102 sin(
t
)
A
ω2t
O
ω2
2
ω1
ω1t
A
(ω 2
A1
ω1)
t
2
2
A
A2 1
A2 2
2A1A2cos(2
1)t
x2 x
x1x1
x2
x
当 (ω2 ω1) t时,2kπ
A 有最大值 A A1 A2
当 (ω2 ω1) t (时2k，1) π
A有最小值 A A1 A2
合振动振幅的频率为: (ω2 ω1) 2π
(2) 0, ,2 (或 )时,退化为直线;
(3) , 3 (或 ) 时,为正椭圆,若A1=A2,则退化
为圆.2 2
2
(4)椭圆轨迹内切于边长为2A1和2A2的矩形; (5)0 时,椭圆顺时针方向转;
0(或 2 ) 椭圆逆时针方向转.
四、相互垂直但频率不同的简谐振动的合成
5t)m
则其合振动的振幅为谐振动,振幅为：
（1）0 ；
（2）4cm；
（3）4 5cm ；
2
（4）8 cm。
二、同方向不同频率谐振动的合成
1. 分振动 : x1 A1 cosω1 t x2 A2 cosω2t
同方向、不同频率的简谐振动的合成
02 x
h cos
pt
• 共振
同方向、同频率的简谐振动的合成(干涉)
A A12 A22 2A1A2 cos2 1
tan A1 sin 1 A2 sin 2 A1 cos1 A2 cos2
同方向、不同频率的简谐振动的合成(拍) 21
垂直方向、同(不同)频率简谐振动的合成
李萨如图
23
mghsin I
O
mgh 0Iຫໍສະໝຸດ 2 0mgh IC
简谐振动的能量
mg
E
Ek
E p
1 4
kA2
1 4
kA2
1 2
kA2
* 任一简谐振动总能量 与振幅的平方成正比
22
• 谐振子的阻尼振动
mx kx x
令
2 0
k ;
m
；h
2m
H m
• 谐振子的受迫振动
d 2x dt 2
2
dx dt
2
2
cos cos 2 sin
sin
2
2
24
sin(
20
10 )
x2 A12
y2 A22
2 xy A1 A2
cos
sin2
上式是个椭圆方程，具体形状由
(20 10) 相位差决定。
质点的运动方向与 有关。当 0 时，
质点沿顺时针方向运动；当 2 时，
质点沿逆时针方向运动。
当 A1 A2 时，正椭圆退化为圆。13
x2 A12
用李萨如图形在 无线电技术中可 以测量频率：
Tx :Ty 1: 2
在示波器上，垂直方向与水平方向同时输入 两个振动，已知其中一个频率，则可根据所 成图形与已知标准的李萨如图形去比较，就 可得知另一个未知的频率。
谐振动的合成
简谐振动的合成
当一个物体同时参与几个谐振动时，就需 考虑振动的合成问题。
本节只讨论满足线性叠加的情况 本节所讨论的同频率的谐振动合成结果， 是波的干涉和偏振光干涉的重要基础。 本节所讨论的不同频率的谐振动合成结果， 可以给出重要的实际应用。
一、 两个同方向同频率简谐运动的合成
x1 A1 cos(t 1) x2 A2 cos(t 2 )
A
x2 A0 cos(t ) x3 A0 cos(t 2 )
o
A1
A2
A3
A4
A5
x
A Ai NA0
xN A0 cos[t (N 1) ]
1） 2kπ
讨
论
(k 0,1,2, )
2）N 2k 'π
(k' kN, k' 1,2, )
个N矢量依次相接构成
i A4
A3
x x1 x2
讨论 A1 A2 , 2 1 1 2 的情况
方法：旋转矢量合成法
(2 1)t (2 1)
2t 2
2 A2
1t 1 o
x2
A
1
A1
x1
2 1
x x
A
A2 1
A2 2
2A1 A2
cos
1 2 0
(2 1)t (2 1) 2π ( 2 1)t
A
A2 1
A2 2
y
A1
cos(t
1
2
)
质点沿椭圆的运动方向是顺时针的。
x2 A12
y2 A22
2 x A1
y A2
cos(2
1
)
sin2 ( 2
1 )
(4) 2
1
当一个物体同时参与几个谐振动时，就需 考虑振动的合成问题。
本节只讨论满足线性叠加的情况 本节所讨论的同频率的谐振动合成结果， 是波的干涉和偏振光干涉的重要基础。 本节所讨论的不同频率的谐振动合成结果， 可以给出重要的实际应用。
一、 两个同方向同频率简谐运动的合成
x1 A1 cos(t 1) x2 A2 cos(t 2 )
A
x2 A0 cos(t ) x3 A0 cos(t 2 )
o
A1
A2
A3
A4
A5
x
A Ai NA0
xN A0 cos[t (N 1) ]
1） 2kπ
讨
论
(k 0,1,2, )
2）N 2k 'π
(k' kN, k' 1,2, )
个N矢量依次相接构成
i A4
A3
x x1 x2
讨论 A1 A2 , 2 1 1 2 的情况
方法：旋转矢量合成法
(2 1)t (2 1)
2t 2
2 A2
1t 1 o
x2
A
1
A1
x1
2 1
x x
A
A2 1
A2 2
2A1 A2
cos
1 2 0
(2 1)t (2 1) 2π ( 2 1)t
A
A2 1
A2 2
y
A1
cos(t
1
2
)
质点沿椭圆的运动方向是顺时针的。
x2 A12
y2 A22
2 x A1
y A2
cos(2
1
)
sin2 ( 2
1 )
(4) 2
1
简谐振动的合成
π
3 π
0.104sin 5 π 6
0.104cos 5 π
2 3
π
3
6
所以，合振动的运动方程为：
x 0.12 cos π t 2 π 2 3
1.3 两个同方向、不同频率 简谐振动的合成
两个同方向、不同频率简谐振动的合成结果比较复杂，为了
便于理解，设两分振动的振幅和初相相同，则两分振动的运动方
上式表明，当两个分振动反相，即其相位差为π的奇数倍时， 合振动的振幅为两个分振动振幅之差的绝对值，合成结果为两 个振动相互减弱，此时合振幅最小。若两分振动的振幅相等， 则此时合振动振幅为零。
一般情况下，相位差Δφ并不是π的整数倍，此时，合振幅就 介于|A1－A2|和A1＋A2之间。
【例10-5】一质点同时参与两个同方向、同频率的简谐振动 周期都为4s，振幅分别为A1＝0.06m，A2＝0.104m，初相分别为
x＝x1＋x2＝A1cos（ωt＋φ1）＋A2cos（ωt＋φ2） 应用旋转矢量法可以更直观、更简洁的得出合振动的规律。
如下图所示，取坐标轴Ox，画出两个分振动的旋转矢量A1和 A2，它们在Ox轴上的投影x1和x2分别表示两个分振动的位移。根 据平行四边形法则，可作出合矢量A＝A1＋A2，它在Ox轴上的投 影x表示合振动的位移，可以看出，x＝x1＋x2。t＝0时，合矢量A 与Ox轴的夹角为φ。
的频率相近，且有|ω1－ω2|＜＜（ω1＋ω2）时，上式中，
cos 1 2 t 项随时间快速变化，而 cos1 2 t 项随时间缓慢
2
2
变化。因此，可以将此合振动看作是角频率为
1
2
2
1
2，振
幅为 2Acos 1 2 t 的简谐振动。这种振幅时大时小作缓慢周期性
简谐振动的合成
2、次谐频：
(1)振动的分解在大多数情况下都是按福里哀谐频分解，即这时分振动的频率都 是某个基频的整数倍。但在另外一定的条件下，其分振动的频率是某个分数基频 （例ν/2）的“谐频”──这种现象叫做次谐频。
(2)出现福里哀谐频和次谐频现象，都是一种非线性效应。但二者有区别；无论多 么弱的非线性都可产生福里哀谐频。但要产生次谐频，则对非线性有阈值限制。
2
由 1cos2 2 cos1
得
x A1
cos2
y A2
cos1
sint sin(2
1)
311Βιβλιοθήκη 由 1 sin2 2sin1
得
x A1
s in 2
y A2
s in 1
cost sin(2
1)
4
32 42 并整理可得
x2 A12
y2 A22
2xy A1 A2
cos(2
1)
sin2 (2
1)
Acos(t 0 )
两个同方向、同频率的谐振动的合振动仍然是一个同频率的谐振动。
其中 合振幅
A A12 A22 2 A1A2 cos(20 10 )
初位相
0
tg 1
A1 sin10 A1 cos10
A2 sin20 A2 cos20
2
2、旋转矢量合成法
两振动频率相同，则它们的旋转矢量以相同的角速度 旋转，故形成稳定的平 形四边形。
谐振动，这种分解叫做谐波分析，其中ω—基频，nω—泛频（倍频）或福里哀谐频。
15
16
一个任意的周期性复杂运动，分解后是一组包含一系列谐泛频振动的无穷级数。
一个随机的振动分解后只能用福里哀积分表示，即其频谱线不是分立的，而是 连续的，即
同方向、不同频率的简谐振动的合成
合振幅 Acos cost Asin sin t
的仍 简然 谐是 振同 动频 。率
Acos(t )
3
式中：
A A12 A22 2A1A2 cos(2 1)
arctg A1 sin1 A2 sin2 A1 cos1 A2 cos2
可见：
2 1 2k
k 0,1,2,
A A1 A2
2Acos (2 1）t cos[ (2 1)t ]
2
2
当1与2 都很大，且相差甚微时，可将
| 2Acos(2 1)t / 2 | 视为振幅变化部分，
合成振动是以 (2 1) / 2 为角频率的谐振动。
其振幅变化的周期是由振幅绝对值变化来决定， 即振动忽强忽弱，所以它是近似的谐振动.
这种合振动忽强忽弱的现象称为拍。 10
arctg A1 sin 1 A2 sin 2
讨论一：
A1 cos1 A2 cos2
2 1 2k k 0,1,2,
A A1 A2 合振幅最大。
当 A1 A2 称为干涉相长。
A A2
A 2A1
A1
6
讨论二：
2 1 (2k 1)
k 0,1,2,
A2
A | A1 A2 |
A
1动、的2相位1 差0在视缓为慢同地频变率化的，合所成以，质不点过运两动个的振轨
道将不断地从下图所示图形依次的循环变化。
当 0 2 1 时是顺时针转；
sin(
20
10 )
x2 A12
y2 A22
2 xy A1 A2
cos
sin2
上式是个椭圆方程，具体形状由
(20 10) 相位差决定。
质点的运动方向与 有关。当 0 时，
的仍 简然 谐是 振同 动频 。率
Acos(t )
3
式中：
A A12 A22 2A1A2 cos(2 1)
arctg A1 sin1 A2 sin2 A1 cos1 A2 cos2
可见：
2 1 2k
k 0,1,2,
A A1 A2
2Acos (2 1）t cos[ (2 1)t ]
2
2
当1与2 都很大，且相差甚微时，可将
| 2Acos(2 1)t / 2 | 视为振幅变化部分，
合成振动是以 (2 1) / 2 为角频率的谐振动。
其振幅变化的周期是由振幅绝对值变化来决定， 即振动忽强忽弱，所以它是近似的谐振动.
这种合振动忽强忽弱的现象称为拍。 10
arctg A1 sin 1 A2 sin 2
讨论一：
A1 cos1 A2 cos2
2 1 2k k 0,1,2,
A A1 A2 合振幅最大。
当 A1 A2 称为干涉相长。
A A2
A 2A1
A1
6
讨论二：
2 1 (2k 1)
k 0,1,2,
A2
A | A1 A2 |
A
1动、的2相位1 差0在视缓为慢同地频变率化的，合所成以，质不点过运两动个的振轨
道将不断地从下图所示图形依次的循环变化。
当 0 2 1 时是顺时针转；
sin(
20
10 )
x2 A12
y2 A22
2 xy A1 A2
cos
sin2
上式是个椭圆方程，具体形状由
(20 10) 相位差决定。
质点的运动方向与 有关。当 0 时，
《大学物理》同方向的简谐振动的合成
同方向的简谐振动的合成
§10-5 同方向的简谐振动的合成
1.同方向同频率的两个简谐振动的合成
设一质点同时参与沿同一方向的两个独立的 同频率的简谐振动，两个简谐振动的频率为 ω，
振动方向为 X 轴方向，以 x1和 x2 分别代表同一
个质点的两个运动位移：
x1 A1 cos(t 10) x2 A2 cos(t 20)
解：已知 A = 20 cm
A1 = 17.3 cm A2 =[A2 +A12 -2AA1cos( - １)]1/2
= 10 cm
o
A
A2
１ A1 x
∵A2 = A12 + A22 + 2A1A2 cos ( 1 - 2 ) ∴ cos (1 - 2 ) = [A2 - A12 - A22] / 2A1A2
同相迭加，合振幅最大。
(2)当D 2010(2k+1) (k=0及 正负整数), cos(20-10)=0, 有
O
A1
A A1 A2 A A1 A2
A2
O
X
反相迭加，合振幅最小。 当A1=A2 时，A=0。
(3)通常情况下，合振幅介于 和
之间。
A1 A2 A1 A2
补例1两个同方向同频率的简谐振动，其合 振动的振幅为 20 cm，与第一个简谐振动的 相位差为 - １= π/6，若第一个简谐动的振 幅为 17.3 cm，试求： 1、第二个简谐振动的振幅 A2 2、第一、二两个简谐振动的相位差 1 - 2
旋转矢量图示法
矢量沿X 轴之投影表征了合运动的规律。
A1
10
X
O
x2
x x1
A
同方向同频率的两个简谐振动的合成
§10-5 同方向的简谐振动的合成
1.同方向同频率的两个简谐振动的合成
设一质点同时参与沿同一方向的两个独立的 同频率的简谐振动，两个简谐振动的频率为 ω，
振动方向为 X 轴方向，以 x1和 x2 分别代表同一
个质点的两个运动位移：
x1 A1 cos(t 10) x2 A2 cos(t 20)
解：已知 A = 20 cm
A1 = 17.3 cm A2 =[A2 +A12 -2AA1cos( - １)]1/2
= 10 cm
o
A
A2
１ A1 x
∵A2 = A12 + A22 + 2A1A2 cos ( 1 - 2 ) ∴ cos (1 - 2 ) = [A2 - A12 - A22] / 2A1A2
同相迭加，合振幅最大。
(2)当D 2010(2k+1) (k=0及 正负整数), cos(20-10)=0, 有
O
A1
A A1 A2 A A1 A2
A2
O
X
反相迭加，合振幅最小。 当A1=A2 时，A=0。
(3)通常情况下，合振幅介于 和
之间。
A1 A2 A1 A2
补例1两个同方向同频率的简谐振动，其合 振动的振幅为 20 cm，与第一个简谐振动的 相位差为 - １= π/6，若第一个简谐动的振 幅为 17.3 cm，试求： 1、第二个简谐振动的振幅 A2 2、第一、二两个简谐振动的相位差 1 - 2
旋转矢量图示法
矢量沿X 轴之投影表征了合运动的规律。
A1
10
X
O
x2
x x1
A
同方向同频率的两个简谐振动的合成
5-3 、 5-4 简谐振动的合成
ϕ
A2
x
O C A1
N −1 ∆ϕ ϕ = 合振动表达式 2 x ( t ) = A cos( ω t + ϕ ) sin(N∆ϕ / 2) N −1 = A0 cos(ω t + ∆ϕ ) sin(∆ϕ / 2) 2
讨论1： 讨论 ： 当 δ
= ±2kπ k = 0,1,2,L sin(N∆ϕ / 2) A = lim A0 = NA0 sin(∆ϕ / 2)
四、两个相互垂直的同频率简谐振动的合成
某质点同时参与两个同频率的互相垂直方向的简谐运动
x = A1 cos(ω t + ϕ 1 ) y = A2 cos(ω t + ϕ 2 )
合振动的轨迹方程为
x y 2 xy 2 cos(ϕ 2 − ϕ 1 ) = sin (ϕ 2 − ϕ 1 ) + 2− 2 A1 A2 A1 A2
'
各分振动矢量依次相接， 各分振动矢量依次相接，构 成闭合的正多边形， 成闭合的正多边形，合振动 的振幅为零。 的振幅为零。
三、同方向不同频率的简谐振动的合成
某质点同时参与两个不同频率且在同一条直线上的简谐振动
x1 = A1 cos(ω 1 t + ϕ 1 )
x 2 = A2 cos(ω 2 t + ϕ 2 )
A2 y=− x A1
y
x2 y2 2 xy + 2+ =0 2 A1 A2 A1 A2
x
合振动的轨迹是一条通过原点的直线
讨论3 讨论
∆ϕ = ϕ 2 − ϕ 1 = π / 2 x2 y2 合振动的轨迹是的椭圆 合振动的轨迹是的椭圆 + 2 =1 2 A1 A2 方程， 方程，且顺时针旋转
同方向不同频率的简谐振动的合成
同方向不同频率的简谐振动的合成好，今天咱们就来聊聊同方向不同频率的简谐振动合成。
别急，听我慢慢说，保证你一听就明白。
你得知道，简谐振动就像是一个物体在做上下左右那种规律性的摆动，感觉就像小孩子在秋千上摇来荡去那样，一来一回，一直不带停的。
你看过钟摆摆动吧？就那种感觉，越来越平稳，越过越规律，跟着一个固定的节奏跑。
但是，今天我们不光是讲单一的那种振动，我们要聊的可是两种频率不同的振动合成，它们在一起会怎么样呢？想象一下，两个人在同一个舞池跳舞，他们的舞步却不完全一致。
一个跳得慢，一个跳得快，开始的时候，大家还好像能勉强跟上，但过了一会儿，慢的那个开始觉得有点跟不上节奏，快的那个又有点等不及了。
是不是有点儿这种意思？没错，这就像两种不同频率的简谐振动，如果它们方向相同，但频率不同，合成出来的效果就有点复杂了。
你可以这样想：其中一个振动快得像飞一样，另一种则慢得像老牛拉破车，结果它们俩在同一个方向上“跑”来跑去。
它们的振动轨迹会不断交错，甚至会出现“合成振动”的现象，你可以理解成两者互相“纠缠”的结果。
要是它们的频率差别特别大，你会看到，快的那个有时候走得远了，慢的还在原地打转，合成的波形看上去就有点像一张波浪形的图，忽高忽低，像是过山车一样的刺激。
但是，有趣的地方就在这了！你看，两个不同频率的振动合成之后，它们的频率不单单是快的和慢的，而是产生了一种新的频率，这个频率叫做“合成频率”。
它就像是你听到两首歌，分别有各自的节奏，但一旦合并在一起，突然间你听到了一个新的旋律，乍一听挺陌生，但又有点儿奇妙的和谐感。
这个合成频率一般是由两种原始振动的频率差所影响的，也就是说，快的那个和慢的那个在一起后，调皮地产生了一种“中间”频率，所有的节奏似乎变得更有韵律了。
再说到合成的幅度，那更是有趣！幅度就像是你跳舞时的力度和气势。
你跳得越用力，别人就能感受到你那个震撼。
而在这两种不同频率的振动合成中，幅度也不是那么简单的加和，而是依赖于它们之间的相对位置。
简谐振动的合成与分解(原创)
一、两个同方向同频率简谐运动的合成
讨论两个特例
(1)两个振动同相，则A=A1+A2。如图一
(2)两个振动反相，则A=|A1-A2|。如图二
图一
图二
上述结果说明两个振动的相位差对合振动起着重要作用。
二、两个同方向不同频率简谐运动的合成
频率较大而频率之差很小的两个同方向简谐运动的合成，其合振动的振幅时而加强时而减弱的现象叫拍。
简谐振动的合成与分解
学号：2901304019班级：29001020姓名：李晓林
在自然界和工程技术中，我们所遇到的振动大多不是简谐振动，而是复杂的振动，处理这类问题，往往把复杂振动看成由一系列不同性质（频率、方向等）的间谐振动组合而成，也就是把复杂振动分解为一系列不同性质（频率、方向等）的间谐振动。
下图给出了用傅里叶级数合成方波的公式及图像演示。
心得与体会：
用MATHCAD软件画出各种振动的图像过程，过程比较繁琐。进行分析，得出结论，虽然所做的研究比较简单，但在此过程中更好的了解振动的合成。
（3） 时， 。
（4） 为任意值时，合振动的轨迹一般为椭圆。
（5）不同频率垂直方向简谐振动的合成
一般轨迹曲线复杂，且不稳定。
而当两振动的频率成正数比时，合成轨迹稳定，称为李萨如图形。如右图：
四、例子
方波信号的频谱展开。
三角函数展开式：
拓展：傅里叶级数
傅立叶变换是数字信号处理领域一种很重要的算法。要知道傅立叶变换算法的意义，首先要了解傅立叶原理的意义。傅立叶原理表明：任何连续测量的时序或信号，都可以表示为不同频率的正弦波信号的无限叠加。而根据该原理创立的傅立叶变换算法利用直接测量到的原始信号，以累加方式来计算该信号中不同正弦波信号的频率、振幅和相位。
讨论两个特例
(1)两个振动同相，则A=A1+A2。如图一
(2)两个振动反相，则A=|A1-A2|。如图二
图一
图二
上述结果说明两个振动的相位差对合振动起着重要作用。
二、两个同方向不同频率简谐运动的合成
频率较大而频率之差很小的两个同方向简谐运动的合成，其合振动的振幅时而加强时而减弱的现象叫拍。
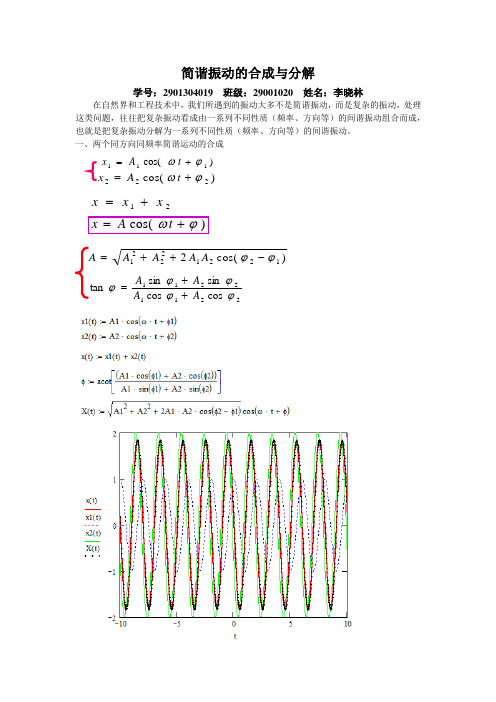
简谐振动的合成与分解
学号：2901304019班级：29001020姓名：李晓林
在自然界和工程技术中，我们所遇到的振动大多不是简谐振动，而是复杂的振动，处理这类问题，往往把复杂振动看成由一系列不同性质（频率、方向等）的间谐振动组合而成，也就是把复杂振动分解为一系列不同性质（频率、方向等）的间谐振动。
下图给出了用傅里叶级数合成方波的公式及图像演示。
心得与体会：
用MATHCAD软件画出各种振动的图像过程，过程比较繁琐。进行分析，得出结论，虽然所做的研究比较简单，但在此过程中更好的了解振动的合成。
（3） 时， 。
（4） 为任意值时，合振动的轨迹一般为椭圆。
（5）不同频率垂直方向简谐振动的合成
一般轨迹曲线复杂，且不稳定。
而当两振动的频率成正数比时，合成轨迹稳定，称为李萨如图形。如右图：
四、例子
方波信号的频谱展开。
三角函数展开式：
拓展：傅里叶级数
傅立叶变换是数字信号处理领域一种很重要的算法。要知道傅立叶变换算法的意义，首先要了解傅立叶原理的意义。傅立叶原理表明：任何连续测量的时序或信号，都可以表示为不同频率的正弦波信号的无限叠加。而根据该原理创立的傅立叶变换算法利用直接测量到的原始信号，以累加方式来计算该信号中不同正弦波信号的频率、振幅和相位。
同方向不同频率两个简谐振动的合成
A
x2 A2 cos(t 20 ) x x1 x2
x Acos(t 0 )
A2
A1
A2
A A12 A22 2 A1 A2 cos(20 10 )
tg0
A1 sin10 A2 sin20 A1 cos10 A2 cos20
2010
x20
0
x10
AM
A1
x0
t o .P x
同方向同频率两个简谐振动的合成仍为简谐振动。
例: 两个沿同一直线且具有相同振幅和周期的谐振动
合成后，产生一个具有相同振幅的谐振动，求原来两
个振动的相位差。
解：
A A1 A2
A2
A
A1 A2 A
O
2
1
2
3
A1
例: N个同方向，同频率的谐振动，若它们相位依次
为， 2，…,试求它们的合振幅;并证明当N=2k
时的合振幅为零。
解： 合振幅A
本讲主要内容： 一、同方向同频率两个简谐振动的合成
二、同方向不同频率两个简谐振动的合成
三、个互相垂直同频率简谐振动的合成
四、两个互相垂直不同频率简谐振动的合成
五、谐振分析和频谱 研究方法： 采用振动描述的三种方法来分析简谐 振动的合成。
一、同方向同频率两个简谐振动的合成
x1 A1 cos(t 10 )
2 2
x x x1 x2 x1 x2 o
| 振幅2变化缓慢1 |
2
一个强弱变化所需的时间
t
一个拍
合振幅变化的频率即拍频Βιβλιοθήκη 拍|2 1 2
|| 2
1
|
拍现象是一种很重要的物理现象。
▪手风琴的中音簧： 键盘式手风琴（Accordion)的两排中音簧的频率 大概相差6到8个赫兹，其作用就是产生“拍”频。 而俄罗斯的“巴扬”---纽扣式手风琴则是单簧片 的，因此没有拍频造成的颤音效果。
4.2振动的合成
(1 、振幅2)为2
合振动的振幅随时间作缓慢的周期性的变化，振动
出现时强时弱的拍现象。
拍频:振幅随时间缓慢变化的频率或单位时间内强弱 变化的次数。
221
2
21
拍22 1 21
3、相互垂直的简谐振动的合成
两个同频率的相互垂直的分运动位移表达式
x A 1 co t s 1)( 0 y A 2 co t s 2) ( 0
y A2 x A1
(3) A x 21 2 2 0 1A y 02 2 2 /22 ，A x 得1A y 2 Axc 122 o Ay2 222 0 s 11) ( 0 s2 i(2 n 01)0
这是坐标轴为主轴的椭圆，质点 的轨迹是顺时针旋转。
(4) 20103/2，仍然得
根据矢量合成法则，N个简谐振动对应的旋转矢量 的合成如下图所示：
O
a1
M
a5
A a4
a2
a
3
X
M
C
a5
O
A
a2
a
3
a4
a1
X
因各个振动的振幅相同且相差依次恒为 ，上图中
各个矢量的起点和终点都在以C为圆心的圆周上，
C
M
a5
O
A
a2
a
3
a4
OCM N
a1
X
在三角形DOCM中,OM 的长度就是和振动位移矢量
微 扬 读 ， 云 淡 风轻
立 世 ， 有 苦有 甜 泪 水 清 刷 过的 心空 一 定
碧 蓝 相 信 所 有 救赎 终 归 菩 提
三
心无芥蒂 始显事物
本 真 山 巍 峨 ， 水轻柔 花 儿 开 得 像云彩 般 灿 美
医用物理学教学两个简谐振动的合成
A0
cos 1
2
2
t
cos
1
2
2
t
可以看出，合振动x出现振幅时大时小、时强时弱的现象---拍
第15页/共31页
因为ω1和ω2差值很小，所以有：
2 1 2 1
cos 2 1 t
2
则有:
随时间变化比
cos 2 1 t
2
慢得多
可以将拍看成以
2 A0
cos
1
2
2
t
为振幅，
以 1 2 为圆频率的简谐振动。
同方向 1 2 拍 2 1
垂直方向
x m y n
李萨如图
x y
Y方向切点数 X方向切点数
第26页/共31页
作业一
• 两物体作简谐振动，它们的振幅和周期分别是10cm和2s。 当t=0时，它们的位移分别为10cm和-10cm，二者的位相 差是多少？是同相还是反相？当t=1s时，它们的位移各是
讨论
若 0
YBX A
同相，1、3象限振动
若 Y BX A
反相，2、4象限振动
第21页/共31页
2
X2 A2
Y2 B2
1
X A t1 0 Y 0
X 0 t2 2 Y B
t3
X A Y 0
3 X 0 t4 2 Y B
2
X2 A2
Y2 B2
1
X 0 t1 0 Y B
2
M2
M
A 1
A2
A1
M1
A0 2(1 cos)
2 A0
1 (1 cos )
2
2
A0
cos
2
O
X
2 A0
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
31、只有永远躺在泥坑里的人，才不会再掉进坑里。——黑格尔 32、希望的灯一旦熄灭，生活刹那间变成了一片黑暗。——普列姆昌德 33、希望是人生的乳母。——科策布 34、形成天才的决定因素应该是勤奋。——郭沫若 35、学到很多东西的诀窍，就是一下子不要学很多。—且只有两个……公平和实用。——伯克 7、有两种和平的暴力，那就是法律和礼节。——歌德
8、法律就是秩序，有好的法律才有好的秩序。——亚里士多德 9、上帝把法律和公平凑合在一起，可是人类却把它拆开。——查·科尔顿 10、一切法律都是无用的，因为好人用不着它们，而坏人又不会因为它们而变得规矩起来。——德谟耶克斯