2016高考数学全国1卷导数压轴题《极值点偏移问题》
极值点偏移问题的两种常见解法之比较演示教学

极值点偏移问题的两种常见解法之比较浅谈部分导数压轴题的解法在高考导数压轴题中,不断出现极值点偏移问题,那么,什么是极值点偏移问题?参考陈宽宏、邢友宝、赖淑明等老师的文章,极值点偏移问题的表述是:已知函数()y f x =是连续函数,在区间12(,)x x 内有且只有一个极值点0x ,且12()()f x f x =,若极值点左右的“增减速度”相同,常常有极值点1202x x x +=,我们称这种状态为极值点不偏移;若极值点左右的“增减速度”不同,函数的图象不具有对称性,常常有极值点1202x x x +≠的情况,我们称这种状态为“极值点偏移”. 极值点偏移问题常用两种方法证明:一是函数的单调性,若函数()f x 在区间(,)a b 内单调递增,则对区间(,)a b 内的任意两个变量12x x 、,1212()()f x f x x x <⇔<;若函数()f x 在区间(,)a b 内单调递减,则对区间(,)a b 内的任意两个变量12x x 、,1212()()f x f x x x <⇔>. 二是利用“对数平均不等式”证明,什么是“对数平均”?什么又是“对数平均不等式”?两个正数a 和b 的对数平均数定义:,,(,)ln ln ,,a ba b L a b a b a a b -⎧≠⎪=-⎨⎪=⎩对数平均数与算术平均数、(,)2a bL a b +≤≤,(此式记为对数平均不等式)下面给出对数平均不等式的证明: i )当0a b =>时,显然等号成立 ii )当0a b ≠>时,不妨设0a b >>, ①ln ln a b a b -<-,ln ln a ba b-<-,只须证:ln a b <,1x =>,只须证:12ln ,1x x x x≤-> 设1()2ln ,1f x x x x x=-+>,则22221(1)()10x f x x x x -'=--=-<,所以()f x在(1,)+∞内单调递减,所以()(1)0f x f <=,即12ln x x x<-,ln ln a ba b --②再证:ln ln 2a b a ba b -+<- 要证:ln ln 2a b a ba b -+<-,只须证:1ln21a ab b a b-<+令1a x b =>,则只须证:1ln 12x x x -<+,只须证2ln 1112x x x -<>+,设2ln ()112xg x x =--+,1x >,则22221(1)()0(1)22(1)x g x x x x x --'=-=<++ 所以()g x 在区间(1,)+∞内单调递减,所以()g(1)0g x <=,即2ln 112xx -<+, 故ln ln 2a b a ba b -+<- 综上述,当0,0a b >>(,)2a bL a b +≤≤例1 (2016年高考数学全国Ⅰ理科第21题)已知函数2)1()2()(-+-=x a e x x f x有两个零点.(Ⅰ)求a 的取值范围;(Ⅱ)设21,x x 是)(x f 的两个零点,证明:221<+x x . 解:(Ⅰ)函数()f x 的定义域为R ,当0a =时,()(2)0xf x x e =-=,得2x =,只有一个零点,不合题意; 当0a ≠时,()(1)[2]x f x x e a '=-+当0a >时,由()0f x '=得,1x =,由()0f x '>得,1x >,由()0f x '<得,1x <, 故,1x =是()f x 的极小值点,也是()f x 的最小值点,所以min ()(1)0f x f e ==-< 又(2)0f a =>,故在区间(1,2)内存在一个零点2x ,即212x << 由21lim (2)limlim 0,xx x x x x x x e e e--→-∞→-∞→-∞--===-又2(1)0a x ->,所以,()f x 在区间 (,1)-∞存在唯一零点1x ,即11x <, 故0a >时,()f x 存在两个零点;当0a <时,由()0f x '=得,1ln(2)x x a ==-或, 若ln(2)1a -=,即2ea =-时,()0f x '≥,故()f x 在R 上单调递增,与题意不符 若ln(2)1a ->,即02ea -<<时,易证()=(1)0f x f e =-<极大值故()f x 在R 上只有一 个零点,若ln(2)1a -<,即2ea <-时,易证()=(ln(2)f x f a -极大值2(ln (2)4ln(2)5)0a a a =---+<,故()f x 在R 上只有一个零点综上述,0a >(Ⅱ)解法一、根据函数的单调性证明 由(Ⅰ)知,0a >且1212x x <<<令2()()(2)(2),1xxh x f x f x x e xe x -=--=-+>,则2(1)2(1)(e 1)()x x x h x e ----'= 因为1x >,所以2(1)10,10x x e-->->,所以()0h x '>,所以()h x 在(1,)+∞内单调递增所以()(1)0h x h >=,即()(2)f x f x >-,所以22()(2)f x f x >-,所以12()(2)f x f x >-,因为121,21x x <-<,()f x 在区间(,1)-∞内单调递减,所以122x x <-,即122x x +< 解法二、利用对数平均不等式证明由(Ⅰ)知,0a >,又(0)2f a =- 所以, 当02a <≤时,10x ≤且212x <<,故122x x +<当2a >时,12012x x <<<<,又因为12122212(2)(2)(1)(1)x x x e x e a x x --=-=--- 即12122212(2)(2)(1)(1)x x x e x e x x --=--所以111222ln(2)2ln(1)ln(2)2ln(1)x x x x x x -+--=-+--所以12122112ln(2)ln(2)2(ln(1)ln(1))(2)(2)x x x x x x x x -------=-=---所以1212121212ln(1)ln(1)(2)(2)412ln(2)ln(2)ln(2)ln(2)2x x x x x x x x x x ---------=<------所以1212122ln(1)ln(1)22ln(2)ln(2)x x x x x x +----<--- ①下面用反证法证明不等式①成立因为12012x x <<<<,所以12220x x ->->,所以12ln(2)ln(2)0x x ---> 假设122x x +≥,当122x x +=,1212122ln(1)ln(1)02=02ln(2)ln(2)x x x x x x +----=---且,与①矛盾; 当122x x +>时1212122ln(1)ln(1)02<02ln(2)ln(2)x x x x x x +---->---且,与①矛盾,故假设不成立 所以122x x +<例2 (2011年高考数学辽宁卷理科第21题)已知函数2()ln (2)f x x ax a x =-+-(Ⅰ)讨论函数()f x 的单调性;(Ⅱ)若曲线()y f x =与x 轴交于A B 、两点,A B 、中点的横坐标为0x ,证明:0()0f x '<解:(Ⅰ)函数()f x 的定义域是(0,)+∞1(12)(1)()2(2)x ax f x ax a x x+-'=-+-=当0a ≤时,()0f x '>在区间(0,)+∞内恒成立,即()f x 在区间(0,)+∞内单调递增 当0a >时,由()f x '>0,得函数()f x 的递增区间1(0,)a, 由()f x '<0,得函数()f x 的递减区间1(,)a+∞ (Ⅱ)解法一、根据函数的单调性求解设点A B 、的横坐标分别为12x x 、,则1202x x x +=,且1210x x a<<< 由(Ⅰ)知,当0a >时,max 111[()]=[()]()ln 1f x f x f a a a ==+-极大值因为函数()f x 有两个不同的零点,所以max [()]0f x >,所以01a <<要证0000(12)(1)()0x ax f x x +-'=<,只须证01ax >,即证122x x a+>令2()()()h x f x f x a =--=21ln ln()22,0x x ax x a a ---+<<则212(1)()202(2)a ax h x a x ax x ax -'=+-=>--,所以()h x 在1(0,)a内单调递增 所以1()()0h x h a <=,即2()()f x f x a <- 因为1210x x a <<<,所以112()()f x f x a <-,所以212()()f x f x a <-又21121,x x a a a >->,且()f x 在区间1(,)a +∞内单调递减所以212x x a >-,即122x x a+>,故0()0f x '<解法二、利用对数平均不等式求解设点A B 、的坐标分别为12(,0)(,0)A x B x 、,则1202x x x += 由(Ⅰ)知,当0a >时,max111[()]=[()]()ln 1f x f x f a a a==+-极大值因为函数()f x 有两个不同的零点,所以max [()]0f x >,所以01a <<因为21112222ln (2)0ln (2)0x ax a x x ax a x ⎧-+-=⎪⎨-+-=⎪⎩,所以212121ln ln [()(2)]()x x a x x a x x -=+--- 所以211212211()(2)ln ln 2x x x x a x x a x x -+=<+---,即12121()(2)2x x a x x a +<+--所以21212()(2)()20a x x a x x ++-+-> ,所以1212[()2][()1]0a x x x x +-++>所以12102x x a+-<,所以121212012(1)(1)2()()022x x x x ax xf x f x x +++-+''==<+.例3 (2014年高考数学湖南卷文科第21题)已知函数21()1xx f x e x-=+ (Ⅰ)求函数()f x 的单调区间;(Ⅱ)当1212()(),f x f x x x =≠时,求证:120x x +< 解:(Ⅰ)函数()f x 的定义域为R()f x '=2222222(1)2(1)1[(1)2](1)1(1)x x xx x x x x x e e e x x x -+-----++=+++ 由()0f x '=,得0x =,由()0f x '>,得函数的递增区间(,0)-∞,由()0f x '<,得函数的递减区间(0,)+∞,所以max ()(0)1f x f ==(Ⅱ)解法一、利用函数的单调性求解令2211()()()11x xx x h x f x f x e e x x --+=--=-++ ,0x > 则22222(23)(23)()(1)x xx x e x x h x xx e -+-++'=-+令222()(23)(2+3),0xH x x x ex x x =-+-+>则22()2[(2)(1)],0xH x x x ex x '=-+-+>,则22()2[(23)1],0x H x x e x ''=+->由0x >得,()2(31)40H x ''>-=>,故()H x '在(0,)+∞内单调递增 故()(0)20H x H ''>=>,故()H x 在(0,)+∞内单调递增 故()(0)0H x H >=,故()0h x '<,故()h x 在(0,)+∞上单调递减 所以,()(0)0h x h <=由(1)及1212()(),f x f x x x =≠知,1201x x <<<,故222()()()0h x f x f x =--< 所以22()()f x f x <-,所以12()()f x f x <-,又()f x 在(,0)-∞上单调递增 所以,12x x <-,即120x x +< 解法二、利用对数平均不等式求解因为1x <时,()0f x >,1x >时,()0f x <,1212()(),f x f x x x =≠ 所以,1201x x <<<,121222121111x x x x e e x x --=++,所以,21111222121111x x x x e e x x ----=++ 所以,22121212ln(1)(1)ln(1)ln(1)(1)ln(1)x x x x x x -+--+=-+--+ 所以,22212112(1)(1)ln(1)ln(1)ln(1)ln(1)x x x x x x ---=---++-+所以,222112212121(1)(1)ln(1)ln(1)111ln(1)ln(1)ln(1)ln(1)2x x x x x x x x x x ---+-+-+-=+<------ 所以,22121212ln(1)ln(1)2ln(1)ln(1)x x x x x x ++-+<---① 因为1201x x <<<,所以12ln(1)ln(1)0x x ---> 下面用反证法证明120x x +<,假设120x x +≥当120x x +=时,22121212ln(1)ln(1)0,=02ln(1)ln(1)x x x x x x ++-+=---且,与不等式①矛盾当120x x +>时,210x x >->,所以120,2x x +>且221212ln(1)ln(1)0ln(1)ln(1)x x x x +-+<---,与不等式①矛盾.所以假设不成立,所以120x x +<例4 (2014年江苏省南通市二模第20题)设函数()(),xf x e ax a a R =-+∈其图象与x 轴交于12(,0),(,0)A x B x 两点,且12x x <. (Ⅰ)求实数a 的取值范围;(Ⅱ)证明:0(()f f x ''<为函数()f x 的导函数); (Ⅲ)略.解:(Ⅰ)()xf x e a '=-,x R ∈,当0a ≤时,()0f x '>在R 上恒成立,不合题意 当0a >时,易知,ln x a =为函数()f x 的极值点,且是唯一极值点, 故,min ()(ln )(2ln )f x f a a a ==-当min ()0f x ≥,即20a e <≤时,()f x 至多有一个零点,不合题意,故舍去;当min ()0f x <,即2a e >时,由(1)0f e =>,且()f x 在(,ln )a -∞内单调递减,故()f x 在(1,ln )a 有且只有一个零点;由22(ln )2ln (12ln ),f a a a a a a a a =-+=+- 令212ln ,y a a a e =+->,则210y a'=->,故2212ln 1430a a e e +->+-=-> 所以2(ln )0f a >,即在(ln ,2ln )a a 有且只有一个零点. (Ⅱ)解法一、根据函数的单调性求解由(Ⅰ)知,()f x 在(,ln )a -∞内递减,在(ln ,)a +∞内递增,且(1)0f e => 所以121ln 2ln x a x a <<<<,要证0f '<,只须证a <ln a <122x x +<,故只须证122ln x x a +<令2ln ()()(2ln )(2ln ),xa xh x f x f a x e ax a e a a x a -=--=-+-+--222ln xxe a e ax a a -=--+,1ln x a <<则2()220x x h x e a e a a -'=+-≥=,所以()h x 在区间(1,ln )a 内递增所以ln 2ln ()2ln 2ln 0aa h x e a e a a a a -<--+=,即()(2ln )f x f a x <-所以11()(2ln )f x f a x <-,所以21()(2ln )f x f a x <-因为21ln ,2ln ln x a a x a >->,且()f x 在区间(ln ,)a +∞内递增所以212ln x a x <-,即122ln x x a +<,故0f '< 解法二、利用对数平均不等式求解由(Ⅰ)知,()f x 在(,ln )a -∞内递减,在(ln ,)a +∞内递增,且(1)0f e =>所以121ln 2ln x a x a <<<<,因为111()0x f x e ax a =-+=,222()0x f x e ax a =-+=121211x x e e a x x ==--,即12111211x x e e x x --=--,所以1212(1)(1)1ln(1)ln(1)x x x x ---=>---所以1212()0x x x x -+<,要证:0f '<,只须证a <ln a <11ln(1)x x <--22ln(1)x x <--所以1212ln(1)(1)x x x x <+---,所以121212ln(()1)x x x x x x -++<+-因为1212()0x x x x -+<,所以1212ln(()1)ln10x x x x -++<=,而120x x +->所以121212ln(()1)x x x x x x -++<+-0f '<从以上四个例题可以看出,两种方法解决的问题相同,即若12,x x 是函数()f x 的两个零点,而0x x =是函数()f x 的极值点,证明1202x x x +<(或1202x x x +>),根据函数单调性求解的步骤是:一、构建函数0()()(2)h x f x f x x =--,二、判断函数()h x 的单调性,三、证明()0h x >(或()0h x <)即0()(2)f x f x x >-(或0()(2)f x f x x <-),四、故函数()f x 的单调性证1202x x x +<(或1202x x x +>).根据对数平均不等式求解的步骤是:一、通过等式两边同取自然对数或相减等配凑出1212ln ln x x x x --及,二、通过等式两边同除以12ln ln x x -构建对数平均数1212ln ln x x x x --,三、利用对数平均不等式将1212ln ln x x x x --转化为122x x +后再证明1202x x x +<(或1202x x x +>). 两种方法各有优劣,适用的题型也略有差异,考生若能灵活驾驭这两种方法,便能在考场上发挥自如,取得理想的成绩.。
完整版导数压轴题分类2 极值点偏移问题含答案

导数压轴题分类(2)---极值点偏移问题极值点偏移问题常见的处理方法有⑴构造一元差函数Fx f x f 2x 0 x 或者F x f x o x f x o x 。
其中x o 为函数y f x 的极值点。
⑵利用对数平均不等式。
•、ab-—b -—b 。
⑶变换主元等方法。
In a In b 2任务一、完成下面问题,总结极值点偏移问题的解决方法。
2 21 设函数 f(x) a In x x ax (a R)(1)试讨论函数f (x)的单调性;a 21nx x 2 ax 可知 2x 2 ax a 2 (2x a)(x a)x x① 若a 0时,当 x (0, a)时,f (x)0 ,函数f (x)单调递减,当 x (a, )时,f (x) 0,函数f (x)单调递增;② 若a 0时,当 f (X) 2x 0在x (0,)内恒成立,函数f (x)单调递增;③ 若a 0时,当 x (0,a)时,f (X )0 ,函数f (x)单调递减, 因为函数f(x)的定义域为(0,),所以2 f (x)0,函数f (x)单调递增;当)时,((2) f (x) m 有两解捲必(论x 2),求证:x-i x 2 2a .解析:(1)由f(x)a 2f (x)2x axa 2,(2)要证 X i X 2 2a , 只需证 a 22 a 2xg(x) f (x)为增函数。
只需证: f (X ^jX1) f (a)0,即证2- N +X 2 a 0 (*)x , x 2 a又 a 21n X i X i 2ax i2 2m, a In X 2 X 2 ax 2 m,两式相减整理得:2x a,则 g (x)g(x) (x)x2a 2x , +x 2 aln x 1 ln x 2 1 2(x 1ix x 2a)a0,把丄(x 1aX 2 a) ln x ( xlnX 2 代入(*) X 2式,即证:x 1 x 22ln x (lnx2o 化为2(竺1)=t 即证:2(t 1) lnt 0x2ln^10,令冬x-i x 2x X 2生1xx t 1x令(t ) 2(t 1) ln t(0 t1),则⑴4 1 (t 1)2卜ot 21t 1t t1 t所以⑴为减函数,⑴(1)综上得:原不等式得证。
导数高考题分析之2016年全国I理数:零点个数求参数、极值点偏移

导数高考题分析之2016年全国I理数:零点个数求参数、极值点偏移函数导数研究函数性质和证明不等式问题,一直都是以高考压轴题的地位出现,也是大家的噩梦,但其实这类问题最大的敌人是自己心中的畏惧,接下来如果看到一个导数题,不要说话,努力灭它.下面的专题以高考压轴题为例,一天一个的去消灭它们,希望能在解题的过程中再次学习,归纳总结,大家多多指点.今天的问题是:2016年全国I理数吐槽一下:函数导双变量不等式(极值点偏移)第一问研究由零点个数确定参数范围,注意化简变形,分类讨论,零点存在定理确定零点区间。
第二问考察极值点偏移.【小结】此题考查利用导数研究函数的零点问题,以及双变量不等式,即极值点偏移问题,考查学生的运算求解能力及化归与转化思想.第一问,是常规的通过函数单调性、极值点的性质来讨论函数零点分别情况,涉及到求导后分解因式、找到分类讨论的界点并分析清楚、利用零点存在定理估计零点所在区间,都是热点和难点.第二问是双变量不等式,常规方法是通过关系上消元解决,这里又是典型的极值点偏移问题,通过对称构造即可解决,比较套路化.学习时间的长短并不重要,重要的是效率高考得分策略:细节决定命运,细节改变命运(1)内紧外松(2)一慢一快,相得益彰,即审题慢,解题快(3)确保运算准确,立足一次成功(4)做快不等于做对,准确放第一位(5)书写规范(6)抓紧时间,不为难题纠缠(7)控制节奏(8)执过索因,逆向思考,正难则反(9)面对难题,讲究策略,争取得分(10)用好开考前5分钟教育就是当学的东西全都忘了的时候,仍保留下来的东西数学是研究现实中数量关系和空间形式的科学数学不仅是一种方法、一门艺术或一种语音,数学是一种精神,一种理性的精神教育是一个圆形概念,方方面面都要兼顾到每天都要加油哦作者简介:廖邦亮,男,中学一级教师,湖南师范大学计算数学研究生,现就职于广东河源市河源中学,任教高中数学。
极值点偏移问题的两种常见解法之比较(汇编)

极值点偏移问题的两种常见解法之比较浅谈部分导数压轴题的解法在高考导数压轴题中,不断出现极值点偏移问题,那么,什么是极值点偏移问题?参考陈宽宏、邢友宝、赖淑明等老师的文章,极值点偏移问题的表述是:已知函数()y f x =是连续函数,在区间12(,)x x 内有且只有一个极值点0x ,且12()()f x f x =,若极值点左右的“增减速度”相同,常常有极值点1202x x x +=,我们称这种状态为极值点不偏移;若极值点左右的“增减速度”不同,函数的图象不具有对称性,常常有极值点1202x x x +≠的情况,我们称这种状态为“极值点偏移”. 极值点偏移问题常用两种方法证明:一是函数的单调性,若函数()f x 在区间(,)a b 内单调递增,则对区间(,)a b 内的任意两个变量12x x 、,1212()()f x f x x x <⇔<;若函数()f x 在区间(,)a b 内单调递减,则对区间(,)a b 内的任意两个变量12x x 、,1212()()f x f x x x <⇔>. 二是利用“对数平均不等式”证明,什么是“对数平均”?什么又是“对数平均不等式”?两个正数a 和b 的对数平均数定义:,,(,)ln ln ,,a ba b L a b a b a a b -⎧≠⎪=-⎨⎪=⎩对数平均数与算术平均数、(,)2a bL a b +≤≤,(此式记为对数平均不等式)下面给出对数平均不等式的证明: i )当0a b =>时,显然等号成立 ii )当0a b ≠>时,不妨设0a b >>, ①ln ln a b a b -<-,ln ln a ba b-<-,只须证:ln a b <,1x =>,只须证:12ln ,1x x x x≤-> 设1()2ln ,1f x x x x x=-+>,则22221(1)()10x f x x x x -'=--=-<,所以()f x在(1,)+∞内单调递减,所以()(1)0f x f <=,即12ln x x x<-,ln ln a ba b --②再证:ln ln 2a b a ba b -+<- 要证:ln ln 2a b a ba b -+<-,只须证:1ln21a ab b a b-<+令1a x b =>,则只须证:1ln 12x x x -<+,只须证2ln 1112x x x -<>+,设2ln ()112xg x x =--+,1x >,则22221(1)()0(1)22(1)x g x x x x x --'=-=<++ 所以()g x 在区间(1,)+∞内单调递减,所以()g(1)0g x <=,即2l n 112xx -<+, 故ln ln 2a b a ba b -+<- 综上述,当0,0a b >>(,)2a bL a b +≤≤例1 (2016年高考数学全国Ⅰ理科第21题)已知函数2)1()2()(-+-=x a e x x f x有两个零点.(Ⅰ)求a 的取值范围;(Ⅱ)设21,x x 是)(x f 的两个零点,证明:221<+x x . 解:(Ⅰ)函数()f x 的定义域为R ,当0a =时,()(2)0xf x x e =-=,得2x =,只有一个零点,不合题意; 当0a ≠时,()(1)[2]x f x x e a '=-+当0a >时,由()0f x '=得,1x =,由()0f x '>得,1x >,由()0f x '<得,1x <, 故,1x =是()f x 的极小值点,也是()f x 的最小值点,所以min ()(1)0f x f e ==-< 又(2)0f a =>,故在区间(1,2)内存在一个零点2x ,即212x << 由21lim (2)limlim 0,xx x x x x x x e e e--→-∞→-∞→-∞--===-又2(1)0a x ->,所以,()f x 在区间 (,1)-∞存在唯一零点1x ,即11x <, 故0a >时,()f x 存在两个零点;当0a <时,由()0f x '=得,1ln(2)x x a ==-或, 若ln(2)1a -=,即2ea =-时,()0f x '≥,故()f x 在R 上单调递增,与题意不符 若ln(2)1a ->,即02ea -<<时,易证()=(1)0f x f e =-<极大值故()f x 在R 上只有一 个零点,若ln(2)1a -<,即2ea <-时,易证()=(l n (2f x f a -极大值2(l n (2)4l n (2)5)0a a a =---+<,故()f x 在R 上只有一个零点综上述,0a >(Ⅱ)解法一、根据函数的单调性证明 由(Ⅰ)知,0a >且1212x x <<<令2()()(2)(2),1xxh x f x f x x e xe x -=--=-+>,则2(1)2(1)(e 1)()x x x h x e ----'= 因为1x >,所以2(1)10,10x x e-->->,所以()0h x '>,所以()h x 在(1,)+∞内单调递增所以()(1)0h x h >=,即()(2)f x f x >-,所以22()(2)f x f x >-,所以12()(2)f x f x >-,因为121,21x x <-<,()f x 在区间(,1)-∞内单调递减,所以122x x <-,即122x x +< 解法二、利用对数平均不等式证明由(Ⅰ)知,0a >,又(0)2f a =- 所以, 当02a <≤时,10x ≤且212x <<,故122x x +<当2a >时,12012x x <<<<,又因为12122212(2)(2)(1)(1)x x x e x e a x x --=-=--- 即12122212(2)(2)(1)(1)x x x e x e x x --=--所以111222ln(2)2ln(1)ln(2)2ln(1)x x x x x x -+--=-+--所以12122112ln(2)ln(2)2(ln(1)ln(1))(2)(2)x x x x x x x x -------=-=---所以1212121212ln(1)ln(1)(2)(2)412ln(2)ln(2)ln(2)ln(2)2x x x x x x x x x x ---------=<------所以1212122ln(1)ln(1)22ln(2)ln(2)x x x x x x +----<--- ①下面用反证法证明不等式①成立因为12012x x <<<<,所以12220x x ->->,所以12ln(2)ln(2)0x x ---> 假设122x x +≥,当122x x +=,1212122ln(1)ln(1)02=02ln(2)ln(2)x x x x x x +----=---且,与①矛盾; 当122x x +>时1212122ln(1)ln(1)02<02ln(2)ln(2)x x x x x x +---->---且,与①矛盾,故假设不成立 所以122x x +<例2 (2011年高考数学辽宁卷理科第21题)已知函数2()ln (2)f x x ax a x =-+-(Ⅰ)讨论函数()f x 的单调性;(Ⅱ)若曲线()y f x =与x 轴交于A B 、两点,A B 、中点的横坐标为0x ,证明:0()0f x '<解:(Ⅰ)函数()f x 的定义域是(0,)+∞1(12)(1)()2(2)x a x f x a x a x x+-'=-+-= 当0a ≤时,()0f x '>在区间(0,)+∞内恒成立,即()f x 在区间(0,)+∞内单调递增 当0a >时,由()f x '>0,得函数()f x 的递增区间1(0,)a, 由()f x '<0,得函数()f x 的递减区间1(,)a+∞ (Ⅱ)解法一、根据函数的单调性求解设点A B 、的横坐标分别为12x x 、,则1202x x x +=,且1210x x a<<< 由(Ⅰ)知,当0a >时,max 111[()]=[()]()ln 1f x f x f a a a ==+-极大值因为函数()f x 有两个不同的零点,所以max [()]0f x >,所以01a <<要证0000(12)(1)()0x ax f x x +-'=<,只须证01ax >,即证122x x a+>令2()()()h x f x f x a =--=21ln ln()22,0x x ax x a a ---+<<则212(1)()202(2)a ax h x a x ax x ax -'=+-=>--,所以()h x 在1(0,)a内单调递增所以1()()0h x h a <=,即2()()f x f x a <- 因为1210x x a <<<,所以112()()f x f x a <-,所以212()()f x f x a <-又21121,x x a a a >->,且()f x 在区间1(,)a +∞内单调递减所以212x x a >-,即122x x a+>,故0()0f x '<解法二、利用对数平均不等式求解设点A B 、的坐标分别为12(,0)(,0)A x B x 、,则1202x x x += 由(Ⅰ)知,当0a >时,max111[()]=[()]()ln 1f x f x f a a a==+-极大值因为函数()f x 有两个不同的零点,所以max [()]0f x >,所以01a <<因为21112222ln (2)0ln (2)0x ax a x x ax a x ⎧-+-=⎪⎨-+-=⎪⎩,所以212121ln ln [()(2)]()x x a x x a x x -=+--- 所以211212211()(2)ln ln 2x x x x a x x a x x -+=<+---,即12121()(2)2x x a x x a +<+--所以21212()(2)()20a x x a x x ++-+-> ,所以1212[()2][()1]0a x x x x +-++>所以12102x x a+-<,所以121212012(1)(1)2()()022x x x x ax xf x f x x +++-+''==<+.例3 (2014年高考数学湖南卷文科第21题)已知函数21()1xx f x e x -=+(Ⅰ)求函数()f x 的单调区间;(Ⅱ)当1212()(),f x f x x x =≠时,求证:120x x +< 解:(Ⅰ)函数()f x 的定义域为R()f x '=2222222(1)2(1)1[(1)2](1)1(1)x x xx x x x x x e e e x x x -+-----++=+++ 由()0f x '=,得0x =,由()0f x '>,得函数的递增区间(,0)-∞,由()0f x '<,得函数的递减区间(0,)+∞,所以max ()(0)1f x f == (Ⅱ)解法一、利用函数的单调性求解令2211()()()11x xx x h x f x f x e e x x --+=--=-++ ,0x > 则22222(23)(23)()(1)x xx x e x x h x xx e -+-++'=-+令222()(23)(2+3),0xH x x x ex x x =-+-+>则22()2[(2)(1)],0xH x x x ex x '=-+-+>,则22()2[(23)1],0x H x x e x ''=+->由0x >得,()2(31)40H x ''>-=>,故()H x '在(0,)+∞内单调递增 故()(0)20H x H ''>=>,故()H x 在(0,)+∞内单调递增 故()(0)0H x H >=,故()0h x '<,故()h x 在(0,)+∞上单调递减 所以,()(0)0h x h <=由(1)及1212()(),f x f x x x =≠知,1201x x <<<,故222()()()0h x f x f x =--< 所以22()()f x f x <-,所以12()()f x f x <-,又()f x 在(,0)-∞上单调递增 所以,12x x <-,即120x x +< 解法二、利用对数平均不等式求解因为1x <时,()0f x >,1x >时,()0f x <,1212()(),f x f x x x =≠ 所以,1201x x <<<,121222121111x x x x e e x x --=++,所以,21111222121111x x x x e e x x ----=++ 所以,22121212ln(1)(1)ln(1)ln(1)(1)ln(1)x x x x x x -+--+=-+--+ 所以,22212112(1)(1)ln(1)ln(1)ln(1)ln(1)x x x x x x ---=---++-+所以,222112212121(1)(1)ln(1)ln(1)111ln(1)ln(1)ln(1)ln(1)2x x x x x x x x x x ---+-+-+-=+<------ 所以,22121212ln(1)ln(1)2ln(1)ln(1)x x x x x x ++-+<---① 因为1201x x <<<,所以12ln(1)ln(1)0x x ---> 下面用反证法证明120x x +<,假设120x x +≥当120x x +=时,22121212ln(1)ln(1)0,=02ln(1)ln(1)x x x x x x ++-+=---且,与不等式①矛盾当120x x +>时,210x x >->,所以120,2x x +>且221212ln(1)ln(1)0ln(1)ln(1)x x x x +-+<---,与不等式①矛盾.所以假设不成立,所以120x x +<例4 (2014年江苏省南通市二模第20题)设函数()(),xf x e ax a a R =-+∈其图象与x 轴交于12(,0),(,0)A x B x 两点,且12x x <. (Ⅰ)求实数a 的取值范围;(Ⅱ)证明:0(()f f x ''<为函数()f x 的导函数); (Ⅲ)略.解:(Ⅰ)()xf x e a '=-,x R ∈,当0a ≤时,()0f x '>在R 上恒成立,不合题意 当0a >时,易知,ln x a =为函数()f x 的极值点,且是唯一极值点, 故,min ()(ln )(2ln )f x f a a a ==-当min ()0f x ≥,即20a e <≤时,()f x 至多有一个零点,不合题意,故舍去;当min ()0f x <,即2a e >时,由(1)0f e =>,且()f x 在(,ln )a -∞内单调递减,故()f x 在(1,ln )a 有且只有一个零点;由22(ln )2ln (12ln ),f a a a a a a a a =-+=+- 令212ln ,y a a a e =+->,则210y a'=->,故2212ln 1430a a e e +->+-=-> 所以2(ln )0f a >,即在(ln ,2ln )a a 有且只有一个零点. (Ⅱ)解法一、根据函数的单调性求解由(Ⅰ)知,()f x 在(,ln )a -∞内递减,在(ln ,)a +∞内递增,且(1)0f e => 所以121ln 2ln x a x a <<<<,要证0f '<,只须证a <ln a <122x x +<,故只须证122ln x x a +< 令2ln ()()(2ln )(2ln ),xa xh x f x f a x e ax a e a a x a -=--=-+-+--222ln xxe a e ax a a -=--+,1ln x a <<则2()220x x h x e a e a a -'=+-≥=,所以()h x 在区间(1,ln )a 内递增所以ln 2ln ()2ln 2ln 0aa h x ea e a a a a -<--+=,即()(2ln )f x f a x <-所以11()(2ln )f x f a x <-,所以21()(2ln )f x f a x <-因为21ln ,2ln ln x a a x a >->,且()f x 在区间(ln ,)a +∞内递增 所以212ln x a x <-,即122ln x x a +<,故0f '<解法二、利用对数平均不等式求解由(Ⅰ)知,()f x 在(,ln )a -∞内递减,在(ln ,)a +∞内递增,且(1)0f e =>所以121ln 2ln x a x a <<<<,因为111()0xf x e ax a =-+=,222()0xf x e ax a =-+=121211x x e e a x x ==--,即12111211x x e e x x --=--,所以1212(1)(1)1ln(1)ln(1)x x x x ---=>---所以1212()0x x x x -+<,要证:0f '<,只须证a <ln a<11ln(1)x x <--22ln(1)x x <--所以1212ln(1)(1)x x x x <+---,所以121212ln(()1)x x x x x x -++<+-因为1212()0x x x x -+<,所以1212ln(()1)ln10x x x x -++<=,而120x x +->所以121212ln(()1)x x x x x x -++<+-0f '<从以上四个例题可以看出,两种方法解决的问题相同,即若12,x x 是函数()f x 的两个零点,而0x x =是函数()f x 的极值点,证明1202x x x +<(或1202x x x +>),根据函数单调性求解的步骤是:一、构建函数0()()(2)h x f x f x x =--,二、判断函数()h x 的单调性,三、证明()0h x >(或()0h x <)即0()(2)f x f x x >-(或0()(2)f x f x x <-),四、故函数()f x 的单调性证1202x x x +<(或1202x x x +>).根据对数平均不等式求解的步骤是:一、通过等式两边同取自然对数或相减等配凑出1212ln ln x x x x --及,二、通过等式两边同除以12ln ln x x -构建对数平均数1212ln ln x x x x --,三、利用对数平均不等式将1212ln ln x x x x --转化为122x x +后再证明1202x x x +<(或1202x x x +>). 两种方法各有优劣,适用的题型也略有差异,考生若能灵活驾驭这两种方法,便能在考场上发挥自如,取得理想的成绩.。
导数压轴题分类(2)---极值点偏移问题(含答案)

导数压轴题分类(2)---极值点偏移问题极值点偏移问题常见的处理方法有⑴构造一元差函数()()()x x f x f F --=02x 或者()()()x x f x x f x F --+=00。
其中0x 为函数()x f y =的极值点。
⑵利用对数平均不等式。
2ln ln ab ba b a b a +<--<。
⑶变换主元等方法。
任务一、完成下面问题,总结极值点偏移问题的解决方法。
1.设函数22()ln ()f x a x x ax a R =-+-∈ (1)试讨论函数()f x 的单调性;(2)()f x m =有两解12,x x (12x x <),求证:122x x a +>. 解析:(1)由22()ln f x a x x ax =-+-可知2222(2)()()2a x ax a x a x a f x x a x x x--+-'=-+-==因为函数()f x 的定义域为(0,)+∞,所以① 若0a >时,当(0,)x a ∈时,()0f x '<,函数()f x 单调递减,当(,)x a ∈+∞时,()0f x '>,函数()f x 单调递增;② 若0a =时,当()20f x x '=>在(0,)x ∈+∞内恒成立,函数()f x 单调递增; ③ 若0a <时,当(0,)2a x ∈-时,()0f x '<,函数()f x 单调递减,当(,)2ax ∈-+∞时,()0f x '>,函数()f x 单调递增; (2)要证122x x a +>,只需证122x x a +>,(x)g =222(x)2,g (x)20(x)(x)a a f x a g f x x'''=-+-=+>∴=则为增函数。
只需证:12x x ()()02f f a +''>=,即证()2121221212221+0+0a x x a x x a x x x x a-+->⇔-+->++(*) 又2222111222ln ,ln ,a x x ax m a x x ax m -+-=-+-=两式相减整理得:1212212ln ln 1(x x a)0x x x x a --++-=-,把1212212ln ln 1(x x a)x x a x x -+-=-代入(*)式,即证:121212ln ln 20x x x x x x --+>+-化为:121112222(1)2(1)ln 0,=,ln 011x x x x t t t x x x t x ---+>-+>++令即证: ()()2222(1)41(t 1)(t)ln (01),(t)0111t t t t t t t tϕϕ---'=-+<<=-+=<+++令则所以(t)ϕ为减函数,(t)(1)0ϕϕ<= 综上得:原不等式得证。
极值点偏移问题的求解策略课件(共29张PPT)——江西省会昌中学2022届高三数学二轮复习微专题

t
t
0,即ln t t 1 0; 对于左边不等式:1 1 ln t ln t 1 1 0,
t
t
令p(t) ln t 1 1,则p' (t) 1 1 t 1 0,
t
t t2 t2
p(t)在(1,+)上单调递增, p(t) p(1) 0.
综上所述,1 k 1 .
x2
x1
的中点
问题提出
x1 x2 2
x0
极值点居中
x1
x2 2
x0
极值点偏移
问题解决
【2016 全国课标Ⅰ卷理 21】
【题目】已知函数 f (x) (x 2)ex a(x 1)2 有两个零点.
(Ⅰ)求 a 的取值范围; (0, )
(Ⅱ)设 x1, x2 是 f (x) 的两个零点,证明:x1 x2 2 .
问题提出
【2016 全国课标Ⅰ卷理 21】
【题目】已知函数 f (x) (x 2)ex a(x 1)2 有两个零点.
(Ⅰ)求 a 的取值范围;
解法二:(分离参数)
f (x) (x 2)ex a(x 1)2 有两个零点
方程 a
(2 x)ex (x 1)2
有两根.
g(x) (2 x)ex (x 1)2
原始型差函数
构造
对称型差函数
F(x) f (x) f (2 x)
F(x) f (1 x) f (1 x)
准确定位
目标 +
落实
认真落实
Hale Waihona Puke 成功 +提升坚持不懈
典典例例分分析:析
题型1.对称构造函数+主元法
例1已知函数f (x) 1 x ex. 1 x2
导数压轴题分类(2)---极值点偏移问题(含答案)

导数压轴题分类(2)---极值点偏移问题(含答案)极值点偏移问题是在求解函数的极值点时,由于函数表达式的特殊性质,导致极值点位置发生偏移,需要采用特殊的解决方法。
常见的处理方法有以下几种:1.构造一元差函数F(x)=f(x)-f(2x-x)或F(x)=f(x+x)-f(x-x),其中x为函数y=f(x)的极值点。
2.利用对数平均不等式ab<a-b+a+b。
3.变换主元等方法lna-lnb^2<ln(a-b^2)。
接下来,我们以一个具体的例子来说明极值点偏移问题的解决方法。
题目:设函数f(x)=-alnx+x-ax(a∈R),试讨论函数f(x)的单调性;若f(x)=m有两解x1,x2(x12a。
解析:1.讨论函数f(x)的单调性由f(x)=-alnx+x-ax可知:f'(x)=-a/x+1-a=-(a/x+a-1)因为函数f(x)的定义域为(0,+∞),所以:①若a>0时,当x∈(0,a)时,f'(x)0,函数f(x)单调递增。
②若a=0时,当f'(x)=1/x>0在x∈(0,+∞)XXX成立,函数f(x)单调递增。
③若a0,函数f(x)单调递增。
2.求证x1+x2>2a因为f(x)=m有两解x1,x2(x1<x2),所以:alnx1+x1-ax=m,-alnx2+x2-ax=m将两式相减,整理得:lnx1-lnx2+ln(x1-x2)=a根据对数平均不等式,有:ln(x1-x2)<(lnx1-lnx2)/2代入上式得:a>-[(lnx1-lnx2)/2]化XXX:x1-x2<2e^-2a因为x1+x2>2x2>a,所以:x1+x2>2a综上所述,极值点偏移问题的解决方法包括构造一元差函数、利用对数平均不等式和变换主元等方法。
在具体求解中,需要根据函数表达式的特殊性质,选择合适的方法进行处理。
2(t-1)x2-1)/(4(t-1)2+1)为减函数,且在(1,∞)上递增,所以原不等式得证。
极值点偏移专题(一)

极值点偏移专题(一)1、极值点偏移以函数函数为例,极值点为0,如果直线与它的图像相交,2x y =1=y 交点的横坐标为和,我们简单计算:.也就是说极值点刚好位1-10211=+-于两个交点的中点处,此时我们称极值点相对中点不偏移.当然,更多的情况是极值点相对中点偏移,下面的图形能形象地解释这一点.那么,如何判断一道题是否属于“极值点偏移”问题呢?其具体特征就是:2、主元法破解极值点偏移问题2016年全国I 卷的第21题是一道导数应用问题,呈现的形式非常简洁,考查了函数的双零点的问题,也是典型的极值点偏移的问题, 是考生实力与潜力的综合演练场.所谓主元法就是在一个多元数学问题中以其中一个为“主元”,将问题化归为该主元的函数、方程或不等式等问题,其本质是函数与方程思想的应用.例1.(2016全国1-21)已知函数有两个零点.()()()221xf x x e a x =-+- (I)求a 的取值范围;(II)设x 1,x 2是的两个零点,证明:. ()f x 122x x +<(1)解析:详细解答⑴方法一:由已知得:()()()()()'12112x x f x x e a x x e a =-+-=-+①若,那么,只有唯一的零点,不合题意; 0a =()()0202x f x x e x =⇔-=⇔=()f x 2x =②若,那么,所以当时,,单调递增0a >20x x e a e +>>1x >()'0f x >()f x 当时,,单调递减,即:1x <()'0f x <()f xx(),1-∞1()1,+∞ ()'f x-+()f x ↓ 极小值 ↑故在上至多一个零点,在上至多一个零点()f x ()1,+∞(),1-∞由于,,则,()20f a =>()10f e =-<()()210f f <根据零点存在性定理,在上有且仅有一个零点. ()f x ()1,2而当时,,,1x <x e e <210x -<-<故()()()()()()()222212111x f x x e a x e x a x a x e x e =-+->-+-=-+--则的两根,, ,因为()0f x =11t =+21t =12t t <,故当或时,0a >1x t <2x t >()()2110a x e x e -+-->因此,当且时,1x <1x t <()0f x >又,根据零点存在性定理,在有且只有一个零点.()10f e =-<()f x (),1-∞此时,在上有且只有两个零点,满足题意.()f x R ③ 若,则,02ea -<<()ln 2ln 1a e -<=当时,,,()ln 2x a <-()1ln 210x a -<--<()ln 2220a x e a e a -+<+=即,单调递增;()()()'120x f x x e a =-+>()f x 当时,,,即()ln 21a x -<<10x -<()ln 2220a x e a e a -+>+=,单调递减;()()()'120x f x x e a =-+<()f x 当时,,,即,单调递增.1x >10x ->()ln 2220a x e a e a -+>+=()'0f x >()f x 即:x()(),ln 2a -∞- ()ln 2a -()()ln 2,1a -1()1,+∞ ()'f x +0 -+()f x ↑ 极大值 ↓ 极小值 ↑而极大值()()()(){}22ln 22ln 22ln 21ln 2210f a a a a a a a -=---+--=--+<⎡⎤⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦⎣⎦故当时,在处取到最大值,那么1x ≤()f x ()ln 2x a =-()ln 2f a -⎡⎤⎣⎦恒成立,即无解()()ln 20f x f a -<⎡⎤⎣⎦≤()0f x =而当时,单调递增,至多一个零点,此时在上至多一个零点,1x >()f x ()f x R 不合题意.④ 若,那么2ea =-()ln 21a -=当时,,,即,单()1ln 2x a <=-10x -<()ln 2220a x e a e a -+<+=()'0f x >()f x 调递增当时,,,即,单()1ln 2x a >=-10x ->()ln 2220a x e a e a -+>+=()'0f x >()f x 调递增又在处有意义,故在上单调递增,此时至多一个零点,不合题()f x 1x =()f x R 意.⑤ 若,则2ea <-()ln 21a ->当时,,,即,单1x <10x -<()ln 212220a x e a e a e a -+<+<+=()'0f x >()f x 调递增当时,,,即,单()1ln 2x a <<-10x ->()ln 2220a x e a e a -+<+=()'0f x <()f x 调递减当时,,,即,()ln 2x a >-()1ln 210x a ->-->()ln 2220a x e a ea -+>+=()'0f x >单调递增,即:()f xx(),1-∞1()()1,ln 2a - ()ln 2a -()()ln 2,a -+∞ ()'f x +0 -+()f x ↑ 极大值 ↓ 极小值 ↑故当时,在处取到最大值,那么()ln 2x a -≤()f x 1x =()1f e =-()0f x e -<≤恒成立,即无解()0f x =当时,单调递增,至多一个零点,此时在上至多一个零()ln 2x a >-()f x ()f x R 点,不合题意.综上所述,当且仅当时符合题意,即的取值范围为.0a >a ()0,+∞简要解析(Ⅰ)方法二:.'()(1)2(1)(1)(2)x xf x x e a x x e a =-+-=-+(i )设,则,只有一个零点.0a =()(2)xf x x e =-()f x (ii )设,则当时,;当时,.所以在0a >(,1)x ∈-∞'()0f x <(1,)x ∈+∞'()0f x >()f x 上单调递减,在上单调递增.(,1)-∞(1,)+∞又,,取满足且,则 (1)f e =-(2)f a =b 0b <ln2a b <, 223()(2)(1)()022a fb b a b a b b >-+-=->故存在两个零点.()f x (iii )设,由得或.0a <'()0f x =1x =ln(2)x a =-若,则,故当时,,因此在上单调递2ea ≥-ln(2)1a -≤(1,)x ∈+∞'()0f x >()f x (1,)+∞增.又当时,,所以不存在两个零点.1x ≤()0f x <()f x 若,则,故当时,;当时,2ea <-ln(2)1a ->(1,ln(2))x a ∈-'()0f x <(ln(2),)x a ∈-+∞.因此在单调递减,在单调递增.又当时,'()0f x >()f x (1,ln(2))a -(ln(2),)a -+∞1x ≤,所以不存在两个零点.综上,的取值范围为.()0f x <()f x a (0,)+∞⑵ 方法一:由已知得:,不难发现,,()()120f x f x ==11x ≠21x ≠故可整理得:()()()()121222122211xx x e x e a x x ---==--设,则,那么, ()()()221x x e g x x -=-()()12g x g x =()()()2321'1x x g x e x -+=-当时,,单调递减;当时,,单调递增. 1x <()'0g x <()g x 1x >()'0g x >()g x 设,构造代数式:0m > ()()111222*********m m m m m m m m g m g m e e e e m m m m +-----+-⎛⎫+--=-=+ ⎪+⎝⎭设, ()2111mm h m e m -=++0m >则,故单调递增,有.()()2222'01m m h m e m =>+()h m ()()00h m h >=因此,对于任意的,.0m >()()11g m g m +>-由可知、不可能在的同一个单调区间上,不妨设,则()()12g x g x =1x 2x ()g x 12x x <必有121x x <<令,则有110m x =->()()()()()1111211112g x g x g x g x g x +->--⇔->=⎡⎤⎡⎤⎣⎦⎣⎦而,,在上单调递增,因此:121x ->21x >()g x ()1,+∞()()121222g x g x x x ->⇔->整理得:.122x x +<(2)方法二:不妨设,由(1)知,12x x <,在上单调递减,()()()122,1,1,,2,1x x x ∈-∞∈+∞-∈-∞()f x (),1-∞所以等价于,即. 122x x +<()()122f x f x >-()()222f x f x >-由于,而,()()22222221x f x x ea x --=-+-()()()2222221x f x x e a x =-+-所以.()()()222222222x x f x f x x e x e ---=---令,则,()()22xx g x xex e -=---()()()21x x g x x e e -'=--所以当时,,而,1x >()0g x '<()10g =故当时,.从而,故. 1x >()()10g x g <=()()2220g x f x =-<122x x +<(二)对解析的分析本问待证是两个变量的不等式,官方解析的变形是,借助于函数的特性及其122x x <-单调性,构造以为主元的函数.由于两个变量的地位相同,当然也可调整主元变形为2x ,同理构造以为主元的函数来处理.此法与官方解析正是极值点偏移问题的处212x x <-1x 理的通法.不妨设,由(1)知,,在12x x <()()()121,1,1,,21,x x x ∈-∞∈+∞-∈+∞()f x 上单调递增,所以等价于,即. ()1,+∞122x x +<()()212f x f x <-()()1120f x f x --<令,则()()()()()2221xx u x f x f x xex e x -=--=--<,()()()210x x u x x e e -'=-->所以,即, ()()10u x u <=()()()21f x f x x <-<所以; ()()()1212f x f x f x =<-所以,即.212x x <-122x x +<变式、(2010年天津理科21题)已知函数()()xf x xe x R -=∈(Ⅰ)求函数的单调区间和极值;()f x (Ⅱ)已知函数的图象与函数的图象关于直线对称,证明当()y g x =()y f x =1x =时,1x >()()f x g x > (Ⅲ)如果,且,证明.12x x ≠12()()f x f x =122x x +>解:(21)本小题主要考查导数的应用,利用导数研究函数的单调性与极值等基础知识,考查运算能力及用函数思想分析解决问题的能力,满分14分 (Ⅰ)解:f ′,令f ′(x )=0,解得x =1()(1)xx x e-=-当x 变化时,f ′(x ),f (x )的变化情况如下表 X(),1-∞ 1()1,+∞f ’(x ) + 0 -f (x )极大值所以f (x )在()内是增函数,在()内是减函数。
极值点偏移问题1

作者的话(可作为编者按):极值点偏移,在近几年的数学圈里可谓是一个时髦的名词.特别地,它作为2016年高考新课标Ⅰ卷导数压轴题第(2)问出现,更是引起了人们的广泛关注和讨论.一时间,全国上下竞相效仿,各地的模拟题都呈现出大偏移状态.说起极值点偏移,必然要提到对称化构造的处理策略,这可一直追溯到7年前,2010年高考天津卷理数第21题,之后在高考中时有出现,如2011年辽宁卷理数第21题,2013年湖南卷文数第21题等.笔者决定发布极值点偏移问题的系列短文,一期一个解题方法或操作细节,敬请关注.希望对此已有所了解的朋友能认识得更加深入,还不甚了解的朋友能由此入门.极值点偏移问题(1)——对称化构造(解题方法)杨春波(高新区枫杨街 郑州外国语学校,河南 郑州 450001)三张图教你直观认识极值点偏移:xx 0=2(左右对称,无偏移,如二次函数;若()()12f x f x =,则1202x x x +=)x2(左陡右缓,极值点向左偏移;若()()12f x f x =,则1202x x x +>)2x(左缓右陡,极值点向右偏移;若()()12f x f x =,则1202x x x +<) 例1 (2010天津)已知函数()x f x xe -=. (1)求函数()f x 的单调区间和极值;(2)已知函数()g x 的图象与()f x 的图象关于直线1x =对称,证明:当1x >时,()()f x g x >;(3)如果12x x ≠,且()()12f x f x =,证明:122x x +>. 解:(1)()()1xf x e x -'=-,得()f x 在(),1-∞上递增,在()1,+∞上递减,()f x 有极大值()11f e=,无极小值; (2)由()g x 的图象与()f x 的图象关于直线1x =对称,得()g x 的解析式为()2y f x =-,构造辅助函数()()()()()2F x f x g x f x f x =-=--,()1,x ∈+∞,求导得()()()()()()()222111x x x x F x f x f x e x e x x e e ----'''=+-=-+-=--,当1x >时,10x ->,20x x ee --->,则()0F x '>,得()F x 在()1,+∞上单增,有()()10F x F >=,即()()f x g x >.(3)由()()12f x f x =,结合()f x 的单调性可设121x x <<,将2x 代入(2)中不等式得()()222f x f x >-,又()()12f x f x =,故()()122f x f x >-,又11x <,221x -<,()f x 在(),1-∞上单增,故122x x >-,122x x +>.点评:该题的三问由易到难,层层递进,完整展现了处理极值点偏移问题的一般方法——对称化构造的全过程,直观展示如下:x例1是这样一个极值点偏移问题:对于函数x f x xe -=,已知()12f x f x =,且21x x ≠,证明122x x +>.再次审视解题过程,发现以下三个关键点:(1)1x ,2x 的范围()1201x x <<<; (2)不等式()()()21f x f x x >->;(3)将2x 代入(2)中不等式,结合()f x 的单调性获证结论. 把握以上三个关键点,就可以轻松解决一些极值点偏移问题.例2 (2016新课标1卷)已知函数()()()221xf x x e a x =-+-有两个零点.(1)求a 的取值范围;(2)设1x ,2x 是()f x 的两个零点,证明:122x x +<.解:(1)()0,+∞,过程略;(2)由(1)知()f x 在(),1-∞上递减,在()1,+∞上递增,由()()120f x f x ==,可设121x x <<.构造辅助函数()()()2F x f x f x =--,求导得()()()()()()()2221(2)1(2)1x x x x F x f x f x x e a x e a x e e --'''=+-=-++-+=--,当1x <时,10x -<,20xxe e --<,则()0F x '>,得()F x 在(),1-∞上单增,又()10F =,故()()01F x x <<,即()()()21f x f x x <-<.将1x 代入上述不等式中,得()()()1212f x f x f x =<-,又21x >,121x ->,()f x 在()1,+∞递增,故212x x <-,122x x +<.通过以上两例,相信读者对极值点偏移问题以及对称化构造的一般步骤已有所了解.但极值点偏移问题的结论不一定总是()1202x x x +><,也可能是()2120x x x ><,借鉴前面的解题经验,我们就可以给出类似的过程.例 3 已知函数()ln f x x x =的图象与直线y m =交于不同的两点()11,A x y ,()22,B x y ,求证:1221x x e<. 证明:()ln 1f x x '=+,得()f x 在10,e ⎛⎫ ⎪⎝⎭上递减,在1,e⎛⎫+∞ ⎪⎝⎭上递增;当01x <<时,()0f x <;()10f =;当1x >时,()0f x >;当0x +→时,()0f x →(洛必达法则);当x →+∞时,()f x →+∞.于是()f x 的图象如下,得12101x x e<<<<. x构造函数()()21F x f x f e x ⎛⎫=-⎪⎝⎭,求导得 ()()()22222222111111ln 1ln 1ln 1F x f x f x x e x e x e x e x e x ⎛⎫⎛⎫⎛⎫'''=+=+++=+- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 当10x e <<时,1ln 0x +<,22110e x -<,则()0F x '>,得()F x 在10,e ⎛⎫⎪⎝⎭上递增,有()10F x F e ⎛⎫<= ⎪⎝⎭,即()2110f x f x e x e ⎛⎫⎛⎫<<< ⎪⎪⎝⎭⎝⎭.将1x 代入(2)中不等式得()1211f x f e x ⎛⎫<⎪⎝⎭,又()()12f x f x =,故()2211fx f e x ⎛⎫<⎪⎝⎭,又21x e >,2111e x e >,()f x 在1,e ⎛⎫+∞ ⎪⎝⎭上递增,故2211x e x <,1221x x e<. 小结:用对称化构造的方法解决极值点偏移问题大致分为以下三步:Step 1. 求导,获得()f x 的单调性,极值情况,作出()f x 的图象,由()()12f x f x =得1x ,2x 的取值范围(数形结合);Step 2. 构造辅助函数(对结论()1202x x x ><,构造()()()02F x f x f x x =--;对结论()2120x x x ><,构造()()20x F x f x f x ⎛⎫=- ⎪⎝⎭),求导,限定范围(1x 或2x 的范围),判定符号,获得不等式;Step 3. 代入1x (或2x ),利用()()12f x f x =及()f x 的单调性证明最终结论. 练习1 已知函数()ln f x x =和()g x ax =,若存在两个实数1x ,2x 且12x x ≠,满足()()11f x g x =,()()22f x g x =,求证:(1)122x x e +>;(2)212x x e >.。
高考全国I卷导数压轴大题

f
x
有两个零点.
(ii)设 a=0,则 f x x 2 ex 所以 f x 有一个零点.
(iii)设 a<0,若 a e ,则由(I)知, f x 在 1, 单调递增.
2
全国高考 I 卷文科数学导数压轴大题
又当 x 1时, f x <0,故 f x 不存在两个零点;若 a e ,则由(I)知, f x 在
2 f (x1 x2 ) f (x1 ) f (x2 ).
(Ⅰ)设 f (1) 2,求f (1 ), f (1 ); 24
(Ⅱ)证明 f (x) 是周期函数。
(Ⅰ)解:由
f (x1
x2 )
f (x1 )
f (x2 ), x1, x2
[0, 1 ] 知 2
f (x) f ( x ) f ( x ) 0, x [0,1]. 22
②若 a e ,则 ln(-2a)<1,故当 x , ln 2a 1, 时, f ' x 0 ; 2
当 x ln 2a,1 时, f ' x 0 ,所以 f x 在 ,ln 2a,1, 单调递增, 在 ln 2a,1 单调递减.
(II)(i)设 a 0 ,则由(I)知, f x 在 ,1 单调递减,在 1, 单调递增.
又 f 1 e,f 2 a ,取 b 满足 b<0 且 b ln a ,
22
则
f
b
a 2
b
2
ab
12
a
b3
3 2
b
0 ,所以
ln(
隐零点与极值点偏移问题 解析版

隐零点与极值点偏移问题【考试提醒】隐零点问题是指对函数的零点设而不求,通过一种整体代换和过渡,再结合题目条件最终解决问题;极值点偏移是指函数在极值点左右的增减速度不一样,导致函数图象不具有对称性,隐零点与极值点偏移问题常常出现在高考数学的压轴题中,这类题往往对思维要求较高,过程较为烦琐,计算量较大,难度大【核心题型】题型一 隐零点零点问题求解三步曲(1)用函数零点存在定理判定导函数零点的存在性,列出零点方程f ′(x 0)=0,并结合f ′(x )的单调性得到零点的取值范围.(2)以零点为分界点,说明导函数f ′(x )的正负,进而得到f (x )的最值表达式.(3)将零点方程适当变形,整体代入最值式子进行化简证明,有时(1)中的零点范围还可以适当缩小.1(2024·吉林长春·东北师大附中校联考模拟预测)已知f x =ae 2x -2xe x (其中e =2.71828⋯为自然对数的底数).(1)当a =0时,求曲线y =f x 在点1,f 1 处的切线方程,(2)当a =12时,判断f x 是否存在极值,并说明理由;(3)∀x ∈R ,f x +1a≤0,求实数a 的取值范围.【答案】(1)y =-4ex +2e ;(2)有一个极大值,一个极小值,理由见解析;(3)1-2 e 2,0 【解析】(1)当a =0时,f x =-2xe x ,可得f x =-2x +1 e x ,则f 1 =-4e ,f 1 =-2e ,所以曲线y =f x 在点1,f 1 处的切线方程为y +2e =-4e x -1 ,即y =-4ex +2e.(2)当a =12时,f x =12e 2x -2xe x ,定义域为R ,可得f x =e 2x -2x +1 e x =e x e x -2x -2 ,令F x =e x -2x -2,则F x =e x -2,当x ∈-∞,ln2 时,F x <0;当x ∈ln2,+∞ 时,F x >0,所以F x 在-∞,ln2 递减,在ln2,+∞ 上递增,所以F (x )min =F ln2 =2-2ln2-2=-2ln2<0,又由F -1 =1e>0,F 2 =e 2-6>0,存在x 1∈-1,ln2 使得F x 1 =0,存在x 2∈ln2,2 使得F x 2 =0,当x ∈-∞,x 1 时,F x >0,f x >0,f x 单调递增;当x ∈x 1,x 2 时,F x <0,f x <0,f x 单调递减;当x ∈x 2,+∞ 时,F x >0,f x >0,f x 单调递增;所以a =12时,f x 有一个极大值,一个极小值.(3)由f x =ae 2x -2xe x ,可得f x =2ae 2x -2x +1 e x =2e x ae x -x -1 ,由∀x ∈R ,f x +1a ≤0,因为f 0 +1a =a +1a =a 2+1a≤0,可得a <0,令g x =ae x -x -1,则g x 在R 上递减,当x <0时,可得e x ∈(0,1),则ae x ∈(a ,0),所以g x =ae x -x -1>a -x -1,则g a -1 >a -a -1 -1=0,又因为g -1 =ae -1<0,∃x 0∈a -1,-1 使得g x 0 =0,即g x 0 =ae x 0-x 0-1=0且当x ∈-∞,x 0 时,g x >0,即f x >0;当x 0∈x 0,+∞ 时,g x <0,即f x <0,所以f x 在-∞,x 0 递增,在x 0,+∞ 递减,所以f (x )max =f x 0 =ae 2x 0-2x 0e x 0,由g x 0 =ae x-x 0-1=0,可得a =x 0+1ex 0,由f (x )max +1a ≤0,可得x 0+1 e x 0-2x 0e x 0+exx 0+1≤0,即1-x 0 1+x 0 +1x 0+1≤0,由x 0+1<0,可得x 20-1≤1,所以-2≤x 0<-1,因为a =x 0+1ex 0,设h x =x +1e x(-2≤x <-1),则h x =-xe x >0,可知h x 在-2,1 上递增,h x ≥h -2 =1-2e-2=1-2 e 2且h x <h -1 =0,所以实数a 的取值范围是1-2 e 2,0 .2(23-24高三上·河南焦作·期末)(1)求函数f (x )=e x -1-x 的极值;(2)若a ∈(0,1],证明:当x >0时,(x -1)e x -a +1≥ln x +a .【答案】(1)极小值为0,无极大值;(2)证明见解析【分析】(1)求导,得到单调性,从而得到极值情况;(2)在(1)基础上得到x -1≥ln x ,构造函数h (x )=(x -1)e x -a -ln x +1-a (x >0),求导得到其单调性,结合隐零点得到函数的最小值h x 0 ≥0,证明出结论.【详解】(1)依题意,f (x )=e x -1-1,令f (x )=0,解得x =1,所以当x ∈(-∞,1)时,f (x )<0,当x ∈(1,+∞)时,f (x )>0,即f (x )在(-∞,1)上单调递减,在(1,+∞)上单调递增,而f (1)=0,故f (x )的极小值为0,无极大值.(2)由(1)可知,当x >0时,e x -1≥x ,则x -1≥ln x .令h (x )=(x -1)e x -a -ln x +1-a (x >0),则h (x )=xe x -a -1x,易知h (x )在(0,+∞)上单调递增.因为a ∈(0,1],所以h 12 =12e 12-a -2<0,h (1)=e 1-a -1≥0,故∃x 0∈12,1 ,使得hx 0 =0,即x 0e x 0-a =1x 0①.当x ∈0,x 0 时,h (x )<0,当x ∈x 0,+∞ 时,h (x )>0,所以h (x )在x ∈0,x 0 上单调递减,在x ∈x 0,+∞ 上单调递增,故h (x ) min =h x 0 =x 0-1 e x 0-a-ln x 0+1-a ②.由①可得e x 0-a =1x 20,x 0-a =-2ln x 0,代入②,得h x 0 =x 0-1x 20-3ln x 0-x 0+1≥x 0-1x 20-3x 0-1 -x 0+1=1-x 0 2x 0-1 2x 0+1x 20,而x 0∈12,1,故h x 0 ≥0,故h (x )≥0,即原命题得证.【点睛】方法点睛:隐零点的处理思路:第一步:用零点存在性定理判定导函数零点的存在性,其中难点是通过合理赋值,敏锐捕捉零点存在的区间,有时还需结合函数单调性明确零点的个数;第二步:虚设零点并确定取范围,抓住零点方程实施代换,如指数与对数互换,超越函数与简单函数的替换,利用同构思想等解决,需要注意的是,代换可能不止一次3(2024·浙江宁波·高三统考期末)已知函数f x =x ln x -ax +1,其中a ∈R .(1)当a =2时,求曲线f x 在x =1处的切线方程;(2)记f x 为f x 的导函数,若对∀x ∈1,3 ,都有f x +5x -1x +1≤f x ,求a 的取值范围.【答案】(1)y =-x ;(2)52,+∞【解析】(1)由题知,f x =ln x +1-a ,当a =2时,f 1 =-1,f 1 =-1,所以曲线f x 在x =1处的切线方程为y =-x ;(2)由题意,原不等式等价于x ln x -ax +1+5x -1x +1≤ln x +1-a ,即x -1 ln x +5x +1≤a x -1 ,当x =1时,对任意a ∈R ,不等式恒成立,当x ∈1,3 时,原不等式等价于ln x +5x +1≤a ,设g x =ln x +5x +1,则g x =1x -5(x +1)2=x 2-3x +1x (x +1)2,设h x =x 2-3x +1,因为h 1 0,h 3 0,h 32<0,所以存在唯一x 0∈32,3 ,使得h x 0 =0,即g x 0 =0,当x ∈1,x 0 时,g x <0,g x 单调递减,当x ∈x 0,3 时,g x >0,g x 单调递增,故g (x )max =max g 1 ,g 3 =g 1 =52,即a ≥52.综上所述,a 的取值范围为52,+∞ .4(2024·河北邢台·高三统考期末)已知函数f (x )=sin x +x 2.(1)求曲线y =f (x )在点π2,f π2 处的切线方程;(2)证明:f (x )>-516.【答案】(1)4πx -4y -π2+4=0;(2)证明见解析【解析】(1)f (x )=cos x +2x ,f π2 =π,f π2 =π24+1.故曲线y =f (x )在点π2,f π2 处的切线方程为y =πx -π24+1,即4πx -4y -π2+4=0.(2)由(1)得f(x )=cos x +2x .令函数u (x )=f (x ),则u (x )=-sin x +2>0,所以u (x )=f (x )是增函数.因为f (0)=1,f -12 =cos 12-1<0,所以存在x 0∈-12,0 ,使得f (x 0)=cos x 0+2x 0=0,即x 20=14cos 2x 0.所以当x ∈-∞,x 0 时,f (x )<0,当x ∈x 0,+∞ 时,f (x )>0,所以f (x )在-∞,x 0 上单调递减,在x 0,+∞ 上单调递增.f (x )≥f x 0 =sin x 0+x 20=sin x 0+14cos 2x 0=-14sin 2x 0+sin x 0+14.因为x 0∈-12,0 ,所以sin x 0>sin -12 >sin -π6 =-12,所以-14sin 2x 0+sin x 0+14>-14×-12 2-12+14=-516.故f (x )>-516.题型二 极值点偏移极值点偏移问题的解法(1)(对称化构造法)构造辅助函数:对结论x 1+x 2>(<)2x 0型,构造函数F (x )=f (x )-f (2x 0-x );对结论x 1x 2>(<)x 20型,构造函数F (x )=f (x )-f x 20x,通过研究F (x )的单调性获得不等式.(2)(比值代换法)通过代数变形将所证的双变量不等式通过代换t =x1x 2化为单变量的函数不等式,利用函数单调性证明.1(2023·全国·高三专题练习)已知函数f x =e xx-ln x +x -a .若f (x )有两个零点x 1,x 2,证明:x 1x 2<1.【答案】证明见解析【分析】利用构造函数法,从而只需证明x 1x 2<x 2-x 1ln x 2-ln x 1,即可求解.【详解】由题意得f x =e x x +ln e x x -a ,令t =e x x >1,则f t =t +ln t -a ,f t =1+1t>0,所以f t =t +ln t -a 在1,+∞ 上单调递增,故f t =0至多有1解;又因为f x 有两个零点x 1,x 2,所以,t =e xx有两个解x 1,x 2,令y =e x x ,y =e xx -1 x 2,易得y =e xx 在0,1 上递减,在1,+∞ 上递增,所以0<x 1<1<x 2.此时e x1=tx 1;e x 2=tx 2,两式相除,可得:e x 2-x 1=x 2x 1⇔x 2-x 1=ln x 2-ln x 1.于是,欲证x 1x 2<1只需证明:x 1x 2<x 2-x 1ln x 2-ln x 1,下证x 1x 2<x 2-x 1ln x 2-ln x 1:因为x 1x 2<x 2-x 1ln x 2-ln x 1⇔ln x 2-ln x 1<x 2-x 1x 1x 2⇔ln x 2x 1<x 2x 1-x 1x 2,不妨设s =x 2x 1>1,则只需证2ln s <s -1s,构造函数h s =2ln s -s +1s ,s >1,则h s =2s -1-1s2=-1-1s 2<0,故h s 在1,+∞ 上单调递减,故h s <h 1 =0,即2ln s <s -1s得证,综上所述:即证x 1x 2<1.【点睛】关键点睛:本题通过构造对数不等式证明极值点偏移问题.2(2022·全国·模拟预测)设函数f x =ln x -ax a ∈R .(1)若a =3,求函数f x 的最值;(2)若函数g x =xf x -x +a 有两个不同的极值点,记作x 1,x 2,且x 1<x 2,求证:ln x 1+2ln x 2>3.【答案】(1)无最小值,最大值为-ln3-1(2)证明见解析【分析】(1)对函数f x =ln x -3x 求导后得f x =1-3xx,x >0,分别求出f x >0和f x <0的解集,从而可求解.(2)由g x =xf x -x +a 有两个极值点x 1,x 2⇔ln x 1=2ax 1,ln x 2=2ax 2,从而要证ln x 1+2ln x 2>3⇔2ax 1+4ax 2>3⇔a >32x 1+4x 2⇔ln x2x 1x 2-x 1>3x 1+2x 2,令t =x 2x 1,t >1,构建函数h t =ln t -3t -1 1+2t,然后利用导数求解h t 的最值,从而可求解证明.【详解】(1)由题意得f x =ln x -3x ,则f x =1-3xx,x >0.令f x >0,解得0<x <13;令f x <0,解得x >13,∴f x 在0,13 上单调递增,在13,+∞ 上单调递减,∴f (x )max =f 13 =ln 13-3×13=-ln3-1,∴f x 无最小值,最大值为-ln3-1.(2)∵g x =xf x -x +a =x ln x -ax 2-x +a ,则g x =ln x -2ax ,又g x 有两个不同的极值点x 1,x 2,∴ln x 1=2ax 1,ln x 2=2ax 2,欲证ln x 1+2ln x 2>3,即证2ax 1+4ax 2>3,∵0<x 1<x 2,∴原式等价于证明a >32x 1+4x 2①.由ln x 1=2ax 1,ln x 2=2ax 2,得ln x 2x 1=2a x 2-x 1 ,则a =ln x2x 12x 2-x 1 ②.由①②可知原问题等价于求证ln x2x 1x 2-x 1>3x 1+2x 2,即证ln x 2x 1>3x 2-x 1 x 1+2x 2=3x2x 1-1 1+2x 2x1.令t =x 2x 1,则t >1,上式等价于求证ln t >3t -1 1+2t.令h t =ln t -3t -1 1+2t ,则h t =1t -31+2t -6t -1 (1+2t )2=t -1 4t -1 t (1+2t )2,∵t >1,∴h t >0恒成立,∴h t 在1,+∞ 上单调递增,∴当t >1时,h t >h 1 =0,即ln t >3t -11+2t,∴原不等式成立,即ln x 1+2ln x 2>3.【点睛】方法点睛:①对于极值点偏移问题,首先找到两极值点的相应关系,然后构造商数或加数关系t =x 2x 1,t =x 2+x 1;②通过要证明的不等式,将两极值点变形后构造相应的函数,③利用导数求解出构造函数的最值,从而证明不等式或等式成立.3(2024下·安徽宿州·高二安徽省泗县第一中学校考开学考试)已知函数f x =x-2e-x(其中e= 2.71828⋯为自然对数的底数).(1)求函数f x 的单调区间;(2)若a,b为两个不相等的实数,且满足ae b-be a=2e b-e a,求证:a+b>6.【答案】(1)增区间为-∞,3,减区间为3,+∞(2)证明见解析【分析】(1)求导,然后根据导函数的正负来判断f x 得单调性;(2)将ae b-be a=2e b-e a变形为a-2e a=b-2e b得到f a =f b ,然后构造函数g x =f x -f6-x,根据g x 得单调性和g x <0得到f a <f6-a,最后根据f a =f b 和f x 得单调性即可证明a+b >6.【详解】(1)f x =e-x+x-2⋅-1⋅e-x=3-xe-x,令f x >0,解得x<3,令f x <0,解得x>3,所以f x 的增区间为-∞,3,减区间为3,+∞.(2)证明:将ae b-be a=2e b-e a两边同时除以e a e b得ae a-be b=2e a-2e b,即a-2e a=b-2e b,所以f a =f b ,由(1)知f x 在-∞,3上单调递增,在3,+∞上单调递减,又f2 =0,f3 =1e3,当x∈2,+∞时,f x >0,设a<b,则2<a<3<b,令g x =f x -f6-x=x-2e x-4-xe6-x2<x<3,则g x =3-xe x-3-xe6-x=3-xe6-x-e xe6,由2<x<3得6-x>x,所以e6-x>e x,3-x>0,所以g x >0,g x 在2,3上单调递增,又g3 =f3 -f3 =0,所以g x <0,当2<x<3时,f x -f6-x<0,即f a -f6-a<0,即f a <f6-a,又f a =f b ,所以f b <f6-a,又6-a>3,b>3,f x 在3,+∞上单调递减,所以b>6-a,即a+b>6.【点睛】方法点睛:处理极值点偏移问题中的类似于x1+x2>a f x1=f x2的问题的基本步骤如下:①求导确定f x 的单调性,得到x1,x2的范围;②构造函数F x =f x -f a-x,求导可得F x 恒正或恒负;③得到f x1与f a-x1的大小关系后,将f x1置换为f x2;④根据x2与a-x1的范围,结合f x 的单调性,可得x2与a-x1的大小关系,由此证得结论.4(2024·辽宁·模拟预测)已知函数f x =e x-ax2(a>0).(1)当a=e24时,判断f x 在区间1,+∞内的单调性;(2)若f x 有三个零点x1,x2,x3,且x1<x2<x3.(i)求a的取值范围;(ii)证明:x1+x2+x3>3.【答案】(1)f x 在1,2上单调递减,在2,+∞上单调递增(2)(i)a∈e24,+∞;(ii)证明见解析【分析】(1)多次求导后,借助导数的单调性及正负即可判断原函数的单调区间;(2)(i)原条件可转化a=e xx2有三个不等实根,从而构造函数h x =e xx2,研究该函数即可得;(ii)借助的h x 单调性,得到x1>-1,从而将证明x1+x2+x3>3,转化为证明x2+x3>4,再设t=x3x2,从而将三个变量的问题转化为单变量问题,即可构造函数μx =ln x-2x-1x+1x>1,证明其在1,+∞上大于0即可.【详解】(1)当a=e24时,f x =ex-e24x2,f x =e x-e22x,令g x =f x =e x-e22x,g x =e x-e22,令g x =e x-e22=0,可得x=ln e22=2-ln2,则当x∈1,2-ln2时,g x <0,当x∈2-ln2,+∞时,g x >0,即g x 在1,2-ln2上单调递减,在2-ln2,+∞上单调递增,又g1 =f 1 =e-e22<0,g2 =f 2 =e2-e2=0,故当x∈1,2时,f x <0,当x∈2,+∞时,f x >0,故f x 在1,2上单调递减,在2,+∞上单调递增;(2)(i)f x 有三个零点,即e x-ax2=0有三个根,由x=0不是该方程的根,故a=e xx2有三个根x1,x2,x3,且x1<x2<x3,令h x =e xx2,h x =x-2e xx3,故当x∈-∞,0∪2,+∞时,h x >0,当x∈0,2时,h x <0,即h x 在-∞,0、2,+∞上单调递增,在0,2上单调递减,h2 =e222=e24,当x→-∞时,h x →0,x→0-时,h x →+∞,当x→0+时,h x →+∞,x→+∞时,h x →+∞,故a∈e24,+∞时,a=e xx2有三个根;(ii)由h x 在-∞,0上单调递增,h-1=e-1-22=14e<e24,故x1>-1,由(i)可得e x1x21=ex2x22=ex3x23=a,且-1<x1<0<x2<2<x3,即只需证x2+x3>4,设t=x3x2>1,则x3=x2t,则有e x2x22=ex2tx2t2,即有t2=e x2t-1 ,故2ln t=x2t-1,x2=2ln tt-1,则x3=2t ln tt-1,即x2+x3=2ln tt-1+2t ln tt-1=2t+1ln tt-1,即只需证2t+1ln tt-1>4⇔t+1ln tt-1>2⇔ln t-2t-1t+1>0,令μx =ln x-2x-1x+1x>1,则μx =1x -2x +1 -2x -1 x +12=x +1 2-4x x x +1 2=x -1 2x x +1 2>0恒成立,故μx 在1,+∞ 上单调递增,则μx >μ1 =ln1-0=0,即得证.【点睛】方法点睛:极值点偏移问题的一般题设形式:1.若函数f (x )存在两个零点x 1,x 2且x 1≠x 2,求证:x 1+x 2>2x 0(x 0为函数f (x )的极值点);2.若函数f (x )中存在x 1,x 2且x 1≠x 2满足f (x 1)=f (x 2),求证:x 1+x 2>2x 0(x 0为函数f (x )的极值点);3.若函数f (x )存在两个零点x 1,x 2且x 1≠x 2,令x 0=x 1+x22,求证:f x 0 >0;4.若函数f (x )中存在x 1,x 2且x 1≠x 2满足f (x 1)=f (x 2),令x 0=x 1+x22,求证:f x 0 >0.【课后强化】【基础保分练】一、单选题1(2022·四川成都·一模)已知a >b ,且e a -a =e b -b =1.01,则下列说法正确的有()①b <-1; ②0<a <12;③b +a <0; ④a -b <1.A.①②③B.②③④C.②④D.③④【答案】B【分析】令f x =e x -x ,利用导数讨论其单调性后可判断①②④正负,利用极值点偏移可判断③的正误.【详解】令f x =e x -x ,则f x =e x -1,当x <0时,f x <0;当x >0时,f x >0;故f x <0在0,+∞ 上为增函数,在-∞,0 上为减函数,而f a =f b ,a >b ,故b <0,a >0,而f -12 =12+1e >12+11.7=3734>1.02>1.01=f b ,故-12<b <0,故①错误.又f 12 =e -12> 2.56-12=1.6-0.5>1.01=f a ,故0<a <12,故②正确,此时a -b <1,故④正确.设h x =f x -f -x =e x -e -x -2x ,x ≥0,则h x =e x +e -x -2≥2e x ×e -x -2=0(不恒为零),故h x 在0,+∞ 上为增函数,故∀x >0,必有h x >h 0 =0即f x >f -x x >0 ,所以f a >f -a ,即f b >f -a ,由f x 的单调性可得b <-a 即a +b <0,故③成立.故选:B .【点睛】思路点睛:导数背景下不等关系的讨论,注意根据等式或不等式的关系构建新函数,并结合单调性来比较大小关系,在不等式关系的讨论中,注意利用极值点偏移来处理大小关系.2(2023·全国·模拟预测)若关于x 的方程e x =m ln x +x -1x 有两个解,则实数m 的取值范围为()A.e ,+∞B.e 2,+∞C.8,+∞D.4e ,+∞【答案】B【分析】首先变形构造函数f x =xe x -m ln x +x -1 ,讨论m ≤0和m >0两种情况,利用导数判断函数的单调性,再结合函数的最值,并结合零点存在性定理,求实数m 的取值范围.【详解】依题意,有xe x -m ln x +x -1 =0,令f x =xe x -m ln x +x -1 ,则f x =x +1 e x -mx.当m ≤0时,f x >0在0,+∞ 上恒成立,f x 在0,+∞ 上单调递增,故f x 至多只有1个零点;当m >0时,令e x -mx=0,设x 0为该方程的解,故当x ∈0,x 0 时,f x <0,f x 单调递减,当x ∈x 0,+∞ 时,f x >0,f x 单调递增,则函数f x 的最大值为f x 0 =x 0e x 0-m ln x 0+x 0-1 <0;而e x 0-m x 0=0,故x 0e x 0=m ,故ln x 0+x 0=ln m ,故f x 0 =m 2-ln m <0,解得m >e 2,可知x 0>1,故f 1 =e -m +m =e >0,所以f x 在0,x 0 上仅有1个零点,当x →+∞时,f x →+∞,故f x 在x 0,+∞ 上也有1个零点,故实数m 的取值范围为e 2,+∞ .故选:B .【点睛】本题考查利用导数研究函数的性质和零点问题,涉及构造函数,分类讨论,以及隐零点问题,本题的一个关键是根据x 0e x=m ,变形求f x 0 <0,再结合函数零点存在性定理说明存在两个零点.3(2023·四川南充·一模)已知函数f (x )=ln x -2x+2 -m (0<m <3)有两个不同的零点x 1,x 2(x 1<x 2),下列关于x 1,x 2的说法正确的有( )个①x 2x 1<e 2m ②x 1>2m +2 ③e m3<x 2<33-m ④x 1x 2>1A.1 B.2C.3D.4【答案】D【分析】函数f x =ln x -2x +2 -m 0<m <3 有两个不同零点x 1,x 2x 1<x 2 ,转化为ln x -2x+2 =m 有两个交点,构造函数g x =ln x -2x+2 ,判断单调性,利用数形结合,判断①,再根据①判断②,再根据零点,构造函数,判断选项③,根据零点判断④.【详解】由函数f x =ln x -2x+2 -m 0<m <3 有两个不同零点x 1,x 2x 1<x 2 ,转化为ln x -2x+2 =m 0<m <3 有两个交点x 1,x 2x 1<x 2 ,构造函数g x =ln x -2x +2,h x =ln x -2x +2 ,则g x =1x +2x 2,故g x >0,所以g x 在0,+∞ 单调递增,而g 1 =0,可得h x 图象如图所示故h x 在0,1 单调递减,在1,+∞ 单调递增,所以0<x 1<1<x 2,对于①,m =-ln x 1+2x 1-2=ln x 2-2x 2+2,所以2m =-ln x 1+ln x 2+2x 1-2x 2>ln x 2x 1,所以x2x 1<e 2m ,故①正确;对于②,由①可知m =-ln x 1+2x 1-2,故mx 1+2x 1-2=-x 1ln x 1>0,因此x 1>2m +2,故②正确;对于③,因为0<m <3,所以0<m 3<1,故1<e m3<e ,33-m >1,所以g 33-m =ln 33-m -23-m 3+2=ln 33-m +2m3,则g 33-m -m =-ln 3-m-m3+ln3,构造函数Q x =-ln 3-m -m3+ln3,则Q x =13-m -13=m33-m >0,而Q 0 =0,所以g 33-m >m =g x 2 ,所以x 2<33-m ,因为g e m 3 =m 3-2e m 3+2,所以m -g e m3 =2m 3-1e m 3+1,令m 3=t 0<t <1 ,构造I t =t -1et +1,显然I t 单调递增,且I 0 =0,所以m =g x 2 >g e m 3所以e m3<x 2<33-m,故③正确;对于④,由①可知,ln x 1x 2=2x 1+2x 2-4>4x 1x 2-4,所以ln x 1x 2-4x 1x 2+4>0,令x 1x 2=n ,W n =2ln n -4n+4,显然W n 单调递增,且W 1 =0,所以x 1x 2>1,故④正确.故选:D二、多选题4(2023·湖南永州·二模)已知a ln a =bln b =2.86,c ln c =d ln d =-0.35,a <b ,c <d ,则有()A.a +b <2eB.c +d >2eC.ad <1D.bc >1【答案】BCD【分析】令f x =xln xx >1 ,g x =x ln x ,求导可求得f x ,g x 的单调性,利用极值点偏移的求解方法可求得AB 正误;由f 1x =-1g x ,可确定f 1d <f a ,f 1c <f b ,结合f x 单调性可得CD 正误.【详解】令f x =xln xx >1 ,g x =x ln x ,∵f x =ln x -1ln 2x,∴当x ∈1,e 时,f x <0;当x ∈e ,+∞ 时,f x >0;∴f x 在1,e 上单调递减,在e ,+∞ 上单调递增,且f x min =f e =e ;若f a =f b =2.86,则1<a <e <b ,令F x =f x -f 2e -x ,1<x <e则Fx =ln x -1ln 2x +ln 2e -x -1ln 22e -x =ln x ⋅ln 22e -x +ln 2x ⋅ln 2e -x -ln 2x -ln 22e -x ln 2x ⋅ln 22e -x=ln x ln 2e -x ln 2e -x +ln x -ln 2x -ln 22e -xln 2x ⋅ln 22e -x=ln x ln 2e -x ⋅ln -x 2+2ex -ln 2x -ln 22e -xln 2x ⋅ln 22e -x,∵当x ∈1,e 时,-x 2+2ex <e 2,∴ln x ln 2e -x ⋅ln -x 2+2ex -ln 2x -ln 22e -x <2ln x ln 2e -x -ln 2x -ln 22e -x =-ln x -ln 2e -x 2,∴F x <0在1,e 上恒成立,∴F x 在1,e 上单调递减,∴F x >F e =0,即f x >f 2e -x ,又1<a <e ,∴f a >f 2e -a ,∵f a =f b ,∴f b >f 2e -a ,∵b >e ,2e -a >e ,f x 在e ,+∞ 上单调递增,∴b >2e -a ,即a +b >2e ,A 错误;∵g x =ln x +1,∴当x ∈0,1e 时,g x <0;当x ∈1e,+∞ 时,g x >0;∴g x 在0,1e 上单调递减,在1e ,+∞ 上单调递增,且g x min =g 1e =-1e;由c ln c =d ln d =-0.35得:0<c <1e<d <1;设G x =g x -g 2e -x ,0<x <1e,则G x =ln x +1+ln 2e -x +1=ln 2ex -x 2 +2;当0<x <1e 时,-x 2+2e x ∈0,1e 2,∴G x <0,∴G x 在0,1e 上单调递减,∴G x >G 1e =0,即g x >g 2e -x ,又0<c <1e ,∴g c >g 2e -c ,又g c =g d ,∴g d >g 2e -c ,∵d >1e ,2e -c >1e ,g x 在1e,+∞ 上单调递增,∴d >2e -c ,即c +d >2e,B 正确;∵1<a <e <b ,0<c <1e <d <1,f 1x =1xln 1x =-1x ln x =-1g x ,∴f 1d =-1g d=10.35≈2.857<2.86=f a ,又1<1d <e ,1<a <e ,f x 在1,e 上单调递减,∴1d >a ,则ad <1,C 正确;∵f 1c =-1g c ≈2.857<2.86=f b ,又1c >e ,b >e ,f x 在e ,+∞ 上单调递增,∴1c <b ,则bc >1,D 正确.故选:BCD .【点睛】方法点睛:本题考查了导数中的极值点偏移问题,处理极值点偏移问题中的类似于x 1+x 2>a f x 1 =f x 2 的问题的基本步骤如下:①求导确定f x 的单调性,得到x 1,x 2的范围;②构造函数F x =f x -f a -x ,求导后可得F x 恒正或恒负;③得到f x 1 与f a -x 1 的大小关系后,将f x 1 置换为f x 2 ;④根据x 2与a -x 1所处的范围,结合f x 的单调性,可得到x 2与a -x 1的大小关系,由此证得结论.5(2023·湖北襄阳·模拟预测)已知关于x 的方程xe x -a =0有两个不等的实根x 1,x 2,且x 1<x 2,则下列说法正确的有()A.-e -1<a <0B.x 1+x 2<-2C.x 2>aD.x 1+e x 1<0【答案】ABD【分析】由已知y =a 与y =xe x 有两个不同的交点,利用导数研究函数f (x )=xe x 性质,结合图象确定a 的范围,判断A ,要证明x 1+x 2<-2只需证明x 2<-2-x 1,结合函数f (x )单调性只需证明f x 1 <f -2-x 1 ,故构建函数F (x )=f x -f -2-x ,利用导数证明结论,判断B ,利用比差法比较x 2,a ,判断C ,利用x 1的范围,结合指数函数性质证明x 1+e x 1<0,判断D .【详解】方程xe x -a =0,可化为xe x =a ,因为方程xe x -a =0有两个不等的实根x 1,x 2,所以y =a 与y =xe x 有两个不同的交点,令f (x )=xe x ,则f (x )=e x +xe x =(1+x )e x ,令f (x )=0,可得x =-1,当x <-1时,f (x )<0,函数f (x )在-∞,-1 单调递减,当x >-1时,f (x )>0,函数f (x )在-1,+∞ 单调递增,f (x )min =f (-1)=-1e,当x <0时,f (x )<0,且f (0)=0,当x >0时,f (x )>0,当x →-∞时,与一次函数相比,指数函数y =e -x 呈爆炸性增长,故f x =--xe-x →0,当x →+∞时,f x →+∞,f x →+∞,根据以上信息,可得函数f x 的大致图象如下:∴-1e<a <0,且x 1<-1<x 2<0,故A 正确.因为x 1<-1<x 2<0,-2-x 1>-1构造F (x )=f x -f -2-x =xe x +(2+x )e -2-x ,x <-1,F (x )=(x +1)e x +(-1-x )e -2-x =(x +1)e x -e -2-x >0,∴F (x )在(-∞,-1)上单调递增,∴F x 1 <F (-1)=0,∴f x 1 <f -2-x 1 ,即f x 2 <f -2-x 1 ,由f x 在-1,+∞ 单调递增所以x 2<-2-x 1⇒x 1+x 2<-2,故B 正确.对于C ,由x 2=a ex 2,-1e <a <0,所以x 2-a =a e x 2-a =a 1ex 2-1,又-1<x 2<0,所以1e x 2>1,则1ex 2-1>0,所以x 2<a ,故C 错误.对于D ,由x 1<-1,可得0<e x1<e -1,所以x 1+e x 1<-1+e -1<0,D 正确.故选:ABD .【点睛】关键点点睛:导函数中常用的两种常用的转化方法:一是利用导数研究含参函数的单调性,常化为不等式恒成立问题.注意分类讨论与数形结合思想的应用;二是函数的零点、不等式证明常转化为函数的单调性、极(最)值问题处理.6(2023·福建宁德·二模)已知函数f (x )=ln xx,则()A.f (2)>f (3)B.若f (x )=m 有两个不相等的实根x 1,x 2,则x 1x 2>e 2C.ln2<2eD.若2x =3y,x ,y 均为正数,则2x >3y【答案】BCD【分析】A :代入2、3直接计算比较大小;B :求f x 的导函数,分析单调性,可得当f x =m 有两个不相等实根时x 1、x 2的范围,不妨设x 1<x 2,则有0<x 1<e <x 2,比较f x 1 ,f e 2x 1的大小关系,因为f x 1 =f x 2 ,可构造F x =f x -f e 2x(0<x <e ),求导求单调性,计算可得F x <0成立,可证x 1x 2>e 2;C :用f x 在0,e 上单调递增,构造ln22<ln e e 可证明;D :令2x =3y=t ,解出x =lg t lg2,y =lg t lg3,做差可证明2x >3y .【详解】对于A:f2 =ln22=ln2,f3 =ln33=ln33,又26=23=8,336=9,所以2<33,所以ln2<ln33,则f2 <f3 ,故A错误;对于B:函数f x =ln xx,定义域为0,+∞,则f x =1-ln xx2,当f x >0时,0<x<e;当f x <0时,x>e;所以f x 在0,e上单调递增,在e,+∞上单调递减,则f x max=1e且x>e时,有f x >0,所以若f x =m有两个不相等的实根x1、x2,有0<m<1e,不妨设x1<x2,有0<x1<e<x2,要证x1x2>e2,只需证x2>e2x1,且x2>e2x1>e,又f x1=f x2,所以只需证f x1<fe2x1 ,令F x =f x -fe2x(0<x<e),则有F x =f x +fe2x⋅1x2=1-ln x1x2-1e4,当0<x<e时,1-ln x>0,1x2-1e4>0,所以有F x >0,即F x 在(0,e)上单调递增,且F e =0,所以F x <0恒成立,即f x1<fe2x1,即f x2 <f e2x1,即x1x2>e2,故B正确.对于C:由B可知,f x 在0,e上单调递增,则有f2 <f e ,即ln22<ln ee,则有ln2<2e<2e,故C正确;对于D:令2x=3y=t,则t>1,x=log2t=lg tlg2,y=log3t=lg tlg3,∴2x-3y=2lg tlg2-3lg tlg3=lg t(lg9-lg8)lg2⋅lg3>0,∴2x>3y,故D正确;故选:BCD.【点睛】方法点睛:(1)给定函数比较大小的问题,需判断函数单调性,根据单调性以及需要比较的数值构造函数,利用函数的单调性可比较大小;(2)极值点偏移法证明不等式,先求函数的导数,找到极值点,分析两根相等时两根的范围,根据范围以及函数值相等构造新的函数,研究新函数的单调性及最值,判断新函数小于或大于零恒成立,即可证明不等式.三、解答题7(22-23高三上·河南洛阳·开学考试)(1)证明不等式:e x-2>ln x(第一问必须用隐零点解决,否则不给分);(2)已知函数f(x)=(x-2)e x+a(x-1)2有两个零点.求a的取值范围.(第二问必须用分段讨论解决,否则不给分)【答案】(1)证明见解析;(2)(0,+∞).【分析】(1)根据给定条件,构造函数g(x)=e x-2-ln x,借助导数探讨函数最小值为正即可推理作答.(2)求出函数f(x)的导数,利用导数分类讨论函数f(x)的单调性、零点情况作答.【详解】(1)令函数g x =e x-2-ln x,x>0,求导得:g x =e x-2-1x,显然函数g(x)在(0,+∞)上单调递增,而g (1)=e-1-1<0,g (2)=12>0,则存在x0∈(1,2),使得g (x0)=0,即e x0-2=1x0,有x0-2=-ln x0,当0<x<x0时,g (x)<0,当x>x0时,g (x)>0,函数g(x)在(0,x0)上单调递减,在(x0,+∞)上单调递增,g(x)min=g(x0)=e x0-2-ln x0=1x0+x0-2>21x⋅x0-2=0,所以e x-2>ln x.(2)函数f(x)=(x-2)e x+a(x-1)2定义域R,求导得f (x)=(x-1)e x+2a(x-1)=(x-1)(e x+2a),当a>0时,由f (x)<0得,x<1,由f (x)>0得,x>1,即函数f(x)在(-∞,1)上递减,在(1,+∞)上递增,f(x)min=f(1)=-e<0,而f(2)=a>0,即存在x1∈(1,2),使得f(x1)=0,则函数f(x)在(1,+∞)上有唯一零点,取b<0且b<ln a2,则f(b)=(b-2)eb+a(b-1)2>a2(b-2)+a(b-1)2=a b2-32b>0,即存在x2∈(b,1),使得f(x2)=0,则函数f(x)在(-∞,1)上有唯一零点,因此当a>0时,函数f(x)有两个零点,当a=0时,函数f(x)=(x-2)e x只有一个零点2,当a<0时,若-e2<a<0,当x<ln(-2a)或x>1时,f (x)>0,当ln(-2a)<x<1时,f (x)<0,即有f(x)在(-∞,ln(-2a)),(1,+∞)上单调递增,在(ln(-2a),1)上单调递减,又∀x<1,f(x)<0,因此函数f(x)在(-∞,1)上没有零点,在(1,+∞)上最多一个零点,即函数f(x)最多一个零点,若a=-e2,恒有f(x)≥0,即函数f(x)在R上单调递增,函数f(x)最多一个零点,若a<-e2,当x<1或x>ln(-2a)时,f(x)>0,当1<x<ln(-2a)时,f (x)<0,即有f(x)在(-∞,1),(ln(-2a),+∞)上单调递增,在(1,ln(-2a))上单调递减,又∀x<1,f(x)<0,当x∈1,ln-2a时,f x <0,因此函数f(x)在(-∞,ln(-2a))上没有零点,在(ln(-2a),+∞)上最多一个零点,即函数f(x)最多一个零点,综上得,当a>0时,函数f(x)有两个零点,当a≤0时,函数f(x)最多一个零点,所以a的取值范围是(0,+∞).8(2024·全国·模拟预测)已知函数f(x)=ln x+1x,g(x)=e xx.(1)若对任意的m,n∈(0,+∞)都有f(m)≤t≤g(n),求实数t的取值范围;(2)若x1,x2∈(0,+∞)且x1≠x2,e x2-x1=x x12x x21,证明:x31+x32>2.【答案】(1)[1,e] (2)证明见解析【分析】(1)分别计算f(x)=ln x+1x,g(x)=e xx的导函数,接着分析它们的单调性,求得在x=1时,f(x)的最大值为f(1)=1,g(x)的最小值为g(1)=e,问题得解;(2)先将e x2-x1=x x12x x11转化为f x1=f x2,再设x1<x2,数形结合得到1e<x1<1<x2,接着构造函数,利用函数的单调性得到x1+x2>2,最后利用放缩法证明不等式.【详解】(1)由f(x)=ln x+1x,g(x)=e xx,得f (x)=-ln xx2,g (x)=e x(x-1)x2,当0<x<1时,f (x)>0,f(x)在区间(0,1)上单调递增,当x>1时,f (x)<0,f(x)在区间(1,+∞)上单调递减,所以当x∈(0,+∞)时,f(x)的最大值为f(1)=1.当0<x<1时,g (x)<0,g(x)在区间(0,1)上单调递减,当x>1时,g (x)>0,g(x)在区间(1,+∞)上单调递增,所以当x∈(0,+∞)时,g(x)的最小值为g(1)=e.所以1≤t≤e,故实数t的取值范围为[1,e].(2)由e x1-x1=x x12x x11得e x1-x1⋅x x11=x x12,两边取对数并整理,得x2ln x1+1=x1ln x2+1,即ln x1+1x1=ln x2+1x2,即f x1=f x2.由(1)知,函数f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,f(x)max=f(1)=1,(技巧:注意对第(1)问结论的应用)而f1e=0,当x>1时,f(x)>0恒成立,不妨设x1<x2,则1e<x1<1<x2.记h(x)=f(x)-f(2-x),x∈1e,1 ,则h (x)=f (x)+f (2-x)=-ln xx2-ln(2-x)(2-x)2>-ln xx2-ln(2-x)x2=-ln-(x-1)2+1x2>0,所以函数h(x)在1e,1上单调递增,所以h(x)<f(1)-f(2-1)=0,即f(x)<f(2-x),x∈1e,1 ,于是f x2=f x1<f2-x1,2-x1∈1,2-1 e,又f(x)在(1,+∞)上单调递减,因此x2>2-x1,即x1+x2>2,所以x31+x32>x31+2-x13=8-12x1+6x21=6x1-12+2>2.【点睛】利用对称化构造的方法求解极值点偏移问题的“三步曲”:(1)求导,得到函数f(x)的单调性、极值情况,作出函数图象,由f x2=f x1得到x1,x2的大致范围.(2)构造辅助函数(若要证x1+x2>(<)2x0,则构造函数g(x)=f(x)-f2x0-x;若要证x1x2>(<)x20,则构造函数g(x)=f(x)-fx20x.),限定x1,x2的范围,求导,判定符号,获得不等式.(3)代入x1,x2,利用f x2=f x1及f(x)的单调性即得所证结论.9(2024·全国·模拟预测)已知函数f(x)=2ln x-ax2.(1)若x>0时,f(x)≤1恒成立,求实数a的取值范围;(2)当实数a取第(1)问中的最小值时,若方程f(x)=m有两个不相等的实数根x1,x2,请比较x21+x22,2x21 x22,2这三个数的大小,并说明理由.【答案】(1)a≥-1;(2)x21+x22>2x21x22>2.【分析】(1)根据给定条件,变形不等式,分离参数构造函数,并求出函数的最大值即得.(2)由(1)求出函数f(x)并变形,换元构造函数h(t)=t(1-ln t),利用导数结合极值点偏移推理即得.【详解】(1)当x>0时,不等式f(x)≤1⇔2ln x-ax2≤1⇔a≥2ln x-x2,令g(x)=2ln x-x2,x>0,依题意,∀x>0,a≥g(x)恒成立,求导得g (x)=2x-2x=2(1-x2)x,当0<x<1时,g(x)>0,当x>1时,g (x)<0,于是函数g(x)在(0,1)上单调递增,在(1,+∞)上单调递减,g(x)max=g(1)=-1,所以a ≥-1.(2)由(1)知,a min =-1,此时函数f (x )=2ln x +1x 2=1x 21-ln 1x2,令1x 2=t ,h (t )=t (1-ln t ),则f (x )=h (t ),由方程f (x )=m 有两个不相等的实数根x 1,x 2,得方程h (t )=m 有两个不相等的实数根t 1,t 2,t 1=1x 21,t 2=1x 22,要比较x 21+x 22,2x 21x 22,2这三个数的大小,只需比较1x 21+1x 22,2,2⋅1x 21⋅1x 22这三个数的大小,即比较t 1+t 2,2,2t 1t 2这三个数的大小,h (t )=-ln t ,当0<t <1时,h (t )>0,当t >1时,h (t )<0,则函数h (t )在(0,1)上单调递增,在(1,+∞)上单调递减,显然t ∈(0,1),h (t )>0,而h (e )=0,由方程h (t )=m 有两个不相等的实数根t 1,t 2,不妨设t 1<t 2,则0<t 1<1<t 2<e ,令函数φ(t )=h (t )-h (2-t ),0<t <1,显然2t -t 2=-(t -1)2+1∈(0,1),求导得φ (t )=h (t )+h (2-t )=-ln t -ln (2-t )=-ln (2t -t 2)>0,函数φ(t )在(0,1)上单调递增,于是φ(t 1)<φ(1)=0,即h (t 1)<h (2-t 1),而h (t 1)=h (t 2),t 2>1,2-t 1>1,h (t )在(1,+∞)上单调递减,因此h (t 2)<h (2-t 1),即有t 2>2-t 1,则t 1+t 2>2,令函数u (t )=h (t )-h 1t ,0<t <1,1t 2>1,ln t <0,求导得u (t )=h (t )+1t 2h 1t =-ln t -1t 2ln 1t =1t 2-1ln t <0,函数u (t )在(0,1)上单调递减,u (t 1)>u (1)=0,即h (t 1)>h 1t 1,而h (t 1)=h (t 2),t 2>1,1t 1>1,h (t )在(1,+∞)上单调递减,因此h (t 2)>h 1t 1,即有t 2<1t 1,则t 1t 2<1,有2t 1t 2<2,于是t 1+t 2>2>2t 1t 2,从而1x 21+1x 22>2>2⋅1x 21⋅1x 22,所以x 21+x 22>2x 21x 22>2.【点睛】思路点睛:涉及函数的双零点问题,不管待证的是两个变量的不等式,还是导函数的值的不等式,都是把双变量的等式或不等式转化为一元变量问题求解,途径都是构造一元函数.10(23-24高三上·云南昆明·阶段练习)设a ,b 为函数f x =x ⋅e x -m (m <0)的两个零点.(1)求实数m 的取值范围;(2)证明:e a +e b <1.【答案】(1)-1e ,0 (2)证明见解析【分析】(1)求出定义域,求导,得到f x 的单调性和极值情况,根据函数零点个数,得到f x min <0,求出m>-1e ,结合题目条件,得到当-1e <m <0时,f 1m >0,根据零点存在性定理得到f x 在-∞,-1 内存在唯一零点,同理得到f (x )在-1,0 内存在唯一零点,从而求出答案;(2)设a <-1<b <0,由a ⋅e a =b ⋅e b 可得e a -b =b a ,令b a =t ∈0,1 ,故a =ln t 1-t ,b =t ln t1-t,推出要证e a+e b <1,即证ln t +1 t <ln t t -1,构造g x =ln xx -1,x ≠1,求导,对分子再构造函数,证明出g x ≤0,g x 在定义域内单调递减,故g t +1 <g t ,即ln 1+t +t ln t1-t<0,证明出结论.【详解】(1)f x 的定义域为R ,f (x )=x +1 e x ,当x ∈-∞,-1 时,f x <0,当x ∈-1,+∞ 时,f x >0,故f x 在-∞,-1 内单调递减,在-1,+∞ 单调递增,故要使f x 有两个零点,则需f x min =f -1 =-e -1-m <0,故m >-1e,由题目条件m <0,可得-1e<m <0,当-1e <m <0时,因为f 1m =1m e 1m -m >m -m =0,又1m <-e <-1,故f x 在-∞,-1 内存在唯一零点,又f 0 =-m >0,故f (x )在-1,0 内存在唯一零点,则f x 在R 上存在两个零点,故满足题意的实数m 的取值范围为-1e,0 ;(2)证明:由(1)可设a <-1<b <0,由a ⋅e a =b ⋅e b 可得e a -b =ba,令b a =t ∈0,1 ,则b =at ,所以e a -at =t ,故a =ln t 1-t,所以b =at =t ln t1-t,要证e a +e b <1,即证e ln t1-t +e t ln t1-t <1⇒e t ln t1-t e ln t +1 <1⇒e t ln t1-t t +1 <1⇒e t ln t1-t e ln t +1<1⇒e t ln t 1-t+ln t +1<1,即证ln 1+t +t ln t1-t<0,因为t ∈0,1 ,即证ln 1+t t +ln t 1-t <0,即ln t +1 t <ln tt -1,令g x =ln x x -1,x ≠1,g x =x -1x -ln x x -1 2=1-1x +ln 1xx -12,令h u =u -1-ln u ,则h u =1-1u,当u ∈0,1 时,h u <0,当u ∈1,+∞ 时,h u >0,故h u 在0,1 内单调递减,在1,+∞ 单调递增,所以h u ≥h 1 =0,所以u -1-ln u ≥0,令u =1x 得1x -1-ln 1x≥0,故g x =1-1x +ln 1xx -12≤0,g x 在定义域内单调递减,故g t +1 <g t ,即ln t +1 t <ln t t -1,ln t +1 <t ln t t -1,ln 1+t +t ln t1-t<0,则e a +e b <1,证毕.【点睛】导函数处理零点个数问题,由于涉及多类问题特征(包括单调性,特殊位置的函数值符号,隐零点的探索、参数的分类讨论等),需要学生对多种基本方法,基本思想,基本既能进行整合,注意思路是通过极值的正负和函数的单调性判断函数的走势,从而判断零点个数,较为复杂和综合的函数零点个数问题,分类讨论是必不可少的步骤,在哪种情况下进行分类讨论,分类的标准,及分类是否全面,都是需要思考的地方【综合提升练】一、单选题1(22-23高二下·福建厦门·期末)已知函数f x =ln xx,0<x ≤e -1e2x +2e ,x >e,若a <b <c ,且f a =f b =f c ,则b ln aa ln b·c 的取值范围为()。
课堂教学中巧选典例 破解极值点偏移问题

构造新函数,极值点 偏 移 问 题 多 数 与 指 数 或 对 数 函
数有关,根据f(x1)=f(x2)建立指数式等式 进 行 运 算,化归到参数t有 关 的 不 等 式,构 造 函 数,推 证 不
等 式 成 立 ,从 而 转 化 到 x1+x2>2. 教师总结:两种 方 法 均 是 为 了 实 现 将 双 变 量 的
>1,x1+2x2
就
是
直
线
y=
f(x1)=f(x2)=t被 函 数 y=f(x)图 像 所 截 线 段 中 点 的横坐标,因此,问题本质是证明极值点的偏移.
第一个小组分 享 完 解 法 后,另 一 个 小 组 组 长 举
手 示 意 还 有 方 法 2,分 享 如 下 .
方法 2:不妨设 x2>x1,x1e-x1 =x2e-x2 ex2-x1
=a(ex+e1x )-2a>2a-2a=0,则 F(x)在(0,+∞) 单 调 递 增,F (x)> F (0)= 0,f (lna + x)> f(lna-x)(x>0).由 x1<lna<x2,f(x1)=f(x2) =f[lna+ (x2 -lna)]=f(2lna-x2 ),f(x)在 (-∞,lna)上单调 递 减,得 x1 <2lna-x2 <lna,因 此 x1 +x2 <2lna.
=xx21 ,设t=x2-x1(t>0),则 x2=t+x1.
ex2-x1 =xx21et=xx1+1tx1=ett-1,x2=t+x1
=t+ett-1,x1+x2=t+et2-t1,而 x1+x2>2t+
et2-t1>2 (t-2)(et-1)+2t>0,g(t)= (t-2)(et
-1)+2t(t>0),g′(t)= (t-1)et+1,g′′(t)=tet> 0,所 以 g′(t)在 (0,+ ∞ )单 调 递 增 ,g′(t)>g′(0)= 0,则 g(t)在 (0,+ ∞ )单 调 递 增 ,g(t)>g(0)=0,从 而 (t-2)(et-1)+2t>0,即 x1+x2>2.
导数压轴题之极值点偏移归纳总结
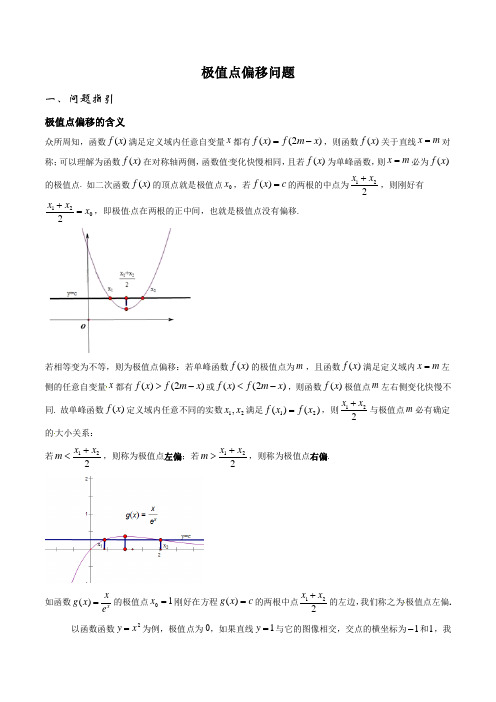
极值点偏移问题一、问题指引极值点偏移的含义众所周知,函数)(x f 满足定义域内任意自变量x 都有)2()(x m f x f -=,则函数)(x f 关于直线m x =对称;可以理解为函数)(x f 在对称轴两侧,函数值变化快慢相同,且若)(x f 为单峰函数,则m x =必为)(x f 的极值点. 如二次函数)(x f 的顶点就是极值点0x ,若c x f =)(的两根的中点为221x x +,则刚好有0212x x x =+,即极值点在两根的正中间,也就是极值点没有偏移.若相等变为不等,则为极值点偏移:若单峰函数)(x f 的极值点为m ,且函数)(x f 满足定义域内m x =左侧的任意自变量x 都有)2()(x m f x f ->或)2()(x m f x f -<,则函数)(x f 极值点m 左右侧变化快慢不同. 故单峰函数)(x f 定义域内任意不同的实数21,x x 满足)()(21x f x f =,则221x x +与极值点m 必有确定的大小关系: 若221x x m +<,则称为极值点左偏;若221x x m +>,则称为极值点右偏.如函数x e x x g =)(的极值点10=x 刚好在方程c x g =)(的两根中点221x x +的左边,我们称之为极值点左偏. 以函数函数2x y =为例,极值点为0,如果直线1=y 与它的图像相交,交点的横坐标为1-和1,我们简单计算:0211=+-.也就是说极值点刚好位于两个交点的中点处,此时我们称极值点相对中点不偏移.当然,更多的情况是极值点相对中点偏移,下面的图形能形象地解释这一点.二、极值点偏移问题的一般题设形式:1. 若函数)(x f 存在两个零点21,x x 且21x x ≠,求证:0212x x x >+(0x 为函数)(x f 的极值点);2. 若函数)(x f 中存在21,x x 且21x x ≠满足)()(21x f x f =,求证:0212x x x >+(0x 为函数)(x f 的极值点);3. 若函数)(x f 存在两个零点21,x x 且21x x ≠,令2210x x x +=,求证:0)('0>x f ; 4. 若函数)(x f 中存在21,x x 且21x x ≠满足)()(21x f x f =,令2210x x x +=,求证:0)('0>x f .二、方法详解(一)基本解法之对称化构造例1是这样一个极值点偏移问题:对于函数()e xf x x -=,已知()()12f x f x =,12x x ≠,证明122x x +>.再次审视解题过程,发现以下三个关键点: (1)1x ,2x 的范围()1201x x <<<; (2)不等式()()()21f x f x x >->;(3)将2x 代入(2)中不等式,结合()f x 的单调性获证结论. 小结:用对称化构造的方法解极佳点偏移问题大致分为以下三步:step1:求导,获得()f x 的单调性,极值情况,作出()f x 的图像,由()()12f x f x =得1x ,2x 的取值范围(数形结合);step2:构造辅助函数(对结论()1202x x x +><,构造()()()02F x f x f x x =--;对结论()2120x x x ><,构造()()20x F x f x f x ⎛⎫=- ⎪⎝⎭),求导,限定范围(1x 或2x 的范围),判定符号,获得不等式;step3:代入1x (或2x ),利用()()12f x f x =及()f x 的单调性证明最终结论. 下面给出第(3)问的不同解法【解析】法一:()(1)xf x x e -'=-,易得()f x 在(,1)-∞上单调递增,在(1,)+∞上单调递减,x →-∞时,()f x →-∞,(0)0f =,x →+∞时,()0f x →, 函数()f x 在1x =处取得极大值(1)f ,且1(1)f e=,如图所示.由1212()(),f x f x x x =≠,不妨设12x x <,则必有1201x x <<<, 构造函数()(1)(1),(0,1]F x f x f x x =+--∈, 则21()(1)(1)(1)0x x xF x f x f x e e+'''=++-=->,所以()F x 在(0,1]x ∈上单调递增,()(0)0F x F >=,也即(1)(1)f x f x +>-对(0,1]x ∈恒成立.由1201x x <<<,则11(0,1]x -∈,所以11112(1(1))(2)(1(1))()()f x f x f x f x f x +-=->--==, 即12(2)()f x f x ->,又因为122,(1,)x x -∈+∞,且()f x 在(1,)+∞上单调递减, 所以122x x -<,即证12 2.x x +>法二:欲证122x x +>,即证212x x >-,由法一知1201x x <<<,故122,(1,)x x -∈+∞,又因为()f x 在(1,)+∞上单调递减,故只需证21()(2)f x f x <-,又因为12()()f x f x =,故也即证11()(2)f x f x <-,构造函数()()(2),(0,1)H x f x f x x =--∈,则等价于证明()0H x <对(0,1)x ∈恒成立. 由221()()(2)(1)0x x x H x f x f x e e--'''=+-=->,则()H x 在(0,1)x ∈上单调递增,所以()(1)0H x H <=,即已证明()0H x <对(0,1)x ∈恒成立,故原不等式122x x +>亦成立.法三:由12()()f x f x =,得1212x xx e x e --=,化简得2121x x x ex -=…①, 不妨设21x x >,由法一知,121o x x <<<.令21t x x =-,则210,t x t x >=+,代入①式,得11tt x e x +=,反解出11t t x e =-,则121221t t x x x t t e +=+=+-,故要证:122x x +>,即证:221t tt e +>-,又因为10t e ->,等价于证明:2(2)(1)0t t t e +-->…②,构造函数()2(2)(1),(0)tG t t t e t =+-->,则()(1)1,()0ttG t t e G t te '''=-+=>,故()G t '在(0,)t ∈+∞上单调递增,()(0)0G t G ''>=,从而()G t 也在(0,)t ∈+∞上单调递增,()(0)0G t G >=,即证②式成立,也即原不等式122x x +>成立.法四:由法三中①式,两边同时取以e 为底的对数,得221211lnln ln x x x x x x -==-,也即2121ln ln 1x x x x -=-,从而221212121212221211111ln ln ()ln ln 1x x x x x x x xx x x x x x x x x x x x +-++=+==---, 令21(1)x t t x =>,则欲证:122x x +>,等价于证明:1ln 21t t t +>-…③, 构造(1)ln 2()(1)ln ,(1)11t t M t t t t t +==+>--,则2212ln ()(1)t t t M t t t --'=-, 又令2()12ln ,(1)t t t t t ϕ=-->,则()22(ln 1)2(1ln )t t t t t ϕ'=-+=--,由于1ln t t ->对(1,)t ∀∈+∞恒成立,故()0t ϕ'>,()t ϕ在(1,)t ∈+∞上单调递增,所以()(1)0t ϕϕ>=,从而()0M t '>,故()M t 在(1,)t ∈+∞上单调递增,由洛比塔法则知:1111(1)ln ((1)ln )1lim ()limlim lim(ln )21(1)x x x x t t t t t M t t t t t→→→→'+++===+='--,即证()2M t >,即证 式成立,也即原不等式122x x +>成立.【点评】以上四种方法均是为了实现将双变元的不等式转化为单变元不等式,方法一、二利用构造新的函数来达到消元的目的,方法三、四则是利用构造新的变元,将两个旧的变元都换成新变元来表示,从而达到消元的目的.【类题展示】已知函数2)1()2()(-+-=x a e x x f x 有两个零点21,x x .证明:122x x +<.法二:参变分离再构造差量函数,由已知得:()()120f x f x ==,不难发现11x ≠,21x ≠,故可整理得:()()()()121222122211xx x e x e a x x ---==--,设()()()221xx e g x x -=-,则()()12g x g x =那么()()()2321'1xx g x e x -+=-,当1x <时,()'0g x <,()g x 递减;当1x >时,()'0g x >,()g x 递增. 设0m >,构造代数式:()()111222*********m m m m m m m m g m g m e e e e m m m m +-----+-⎛⎫+--=-=+ ⎪+⎝⎭设()2111mm h m e m -=++,0m >则()()2222'01m m h m e m =>+,故()h m 单调递增,有()()00h m h >=. 因此,对于任意的0m >,()()11g m g m +>-.由()()12g x g x =可知1x 、2x 不可能在()g x 的同一个单调区间上,不妨设12x x <,则必有121x x <<令110m x =->,则有()()()()()1111211112g x g x g x g x g x +->--⇔->=⎡⎤⎡⎤⎣⎦⎣⎦,而121x ->,21x >,()g x 在()1,+∞上单调递增,因此:()()121222g x g x x x ->⇔->整理得:122x x +<. 法三:参变分离再构造对称函数由法二得()()()221x x e g x x -=-,构造()()(2),((,1))G x g x g x x =--∈-∞,利用单调性可证,此处略.法五:利用“对数平均”不等式参变分离得:222211)1()2()1()2(21--=--=x e x x e x a x x ,由0>a 得,2121<<<x x ,将上述等式两边取以e 为底的对数,得22221211)1()2(ln )1()2(lnx x x x x x +--=+--,化简得:21212221)]2ln()2[ln(])1ln()1[ln(x x x x x x -=-------,故2121212221)]2ln()2[ln(])1ln()1[ln(1x x x x x x x x ---------=)2()2()]2ln()2[ln()1()1(])1ln()1[ln()]1()1[(21212221222121x x x x x x x x x x ------+-------+-= 由对数平均不等式得:221222221212[ln(-1)-ln(-1)]2(1)(1)(1)(1)x x x x x x >----+-,121212[ln(2-)-ln(2-)]22222x x x x x x >----+-()()()(),从而122212122(2)21(1)(1)22x x x x x x +->+-+--+-()()1212122212122(2)[4()]2(1)(1)4()x x x x x x x x x x +--+++-=+-+--+12122212122(2)21(1)(1)4()x x x x x x x x +-+-=++-+--+等价于:12122212122(2)20(1)(1)4()x x x x x x x x +-+->+-+--+1222121221(2)[](1)(1)4()x x x x x x =+-+-+--+ 由221212(1)(1)0,4()0x x x x -+->-+>,故122x x +<,证毕.(二) 含参函数问题可考虑先消去参数【例2】已知函数()ln f x x ax =-,a 为常数,若函数()f x 有两个零点12,x x ,试证明:212.x x e ⋅>【解析】法一:消参转化成无参数问题:ln ()0ln ln x f x x ax x ae =⇔=⇔=,12,x x 是方程()0f x =的两根,也是方程ln ln x x ae =的两根,则12ln ,ln x x 是x x ae =,设1122ln ,ln u x u x ==,()xg x xe -=,则12()()g u g u =,从而2121212ln ln 22x x e x x u u >⇔+>⇔+>,此问题等价转化成为例1,下略.法二:利用参数a 作为媒介,换元后构造新函数: 不妨设12x x >,∵1122ln 0,ln 0x ax x ax -=-=,∴12121212ln ln (),ln ln ()x x a x x x x a x x +=+-=-,∴1212ln ln x x a x x -=-,欲证明212x x e >,即证12ln ln 2x x +>.∵1212ln ln ()x x a x x +=+,∴即证122a x x >+,∴原命题等价于证明121212ln ln 2x x x x x x ->-+,即证:1122122()ln x x x x x x ->+,令12,(1)x t t x =>,构造2(1)ln ,1)1(t t g t t t -=->+,此问题等价转化成为例2中思路二的解答,下略. 法三:直接换元构造新函数:12221211ln ln ln ,ln x x x x a x x x x ==⇔=设2121,,(1)x x x t t x <=>,则112111ln ln ln ,ln ln tx t x x tx t t x x +==⇔=, 反解出:1211ln ln ln ln ,ln ln ln ln ln 111t t t tx x tx t x t t t t ===+=+=---, 故212121ln ln 2ln 21t x x e x x t t +>⇔+>⇔>-,转化成法二,下同,略. 【点评】含参数的极值点偏移问题,在原有的两个变元12,x x 的基础上,又多了一个参数,故思路很自然的就会想到:想尽一切办法消去参数,从而转化成不含参数的问题去解决;或者以参数为媒介,构造出一个变元的新的函数。
导数处理极值点偏移问题

第二讲 导数应用-------极值点偏移问题的处理策略及探究所谓极值点偏移问题,是指对于单极值函数,由于函数极值点左右的增减速度不同,使得函数图像没有对称性。
若函数()f x 在0x x =处取得极值,且函数()y f x =与直线y b =交于1(,)A x b ,2(,)B x b 两点,则AB 的中点为12(,)2x x M b +,而往往1202x xx +≠.如下图所示.极值点没有偏移此类问题在近几年高考及各种模考,作为热点以压轴题的形式给出,很多学生对待此类问题经常是束手无策。
而且此类问题变化多样,有些题型是不含参数的,而更多的题型又是含有参数的。
不含参数的如何解决?含参数的又该如何解决,参数如何来处理?是否有更方便的方法来解决?其实,处理的手段有很多,方法也就有很多,我们先来看看此类问题的基本特征,再从几个典型问题来逐一探索! 【问题特征】2016年全国I 卷的第21题是一道导数应用问题,呈现的形式非常简洁,考查了函数的双零点的问题,也是典型的极值点偏移的问题, 是考生实力与潜力的综合演练场.虽然大多学生理解其题意,但对于极值点偏移的本质理解的深度欠佳,面对此类问题大多感到“似懂非懂”或“云里雾里”.一、试题再现及解析 (一)题目(2016年全国I 卷)已知函数()()()221xf x x e a x =-+-有两个零点.(1)求a 的取值范围;(2)设12,x x 是()f x 的两个零点,证明:122x x +<.本题第(1)小题含有参数的函数()f x 有两个零点,自然想到研究其单调性,结合零点存在性定理求得a 的取值范围是()0,+∞.第(2)小题是典型的极值点偏移的问题,如何证明呢?(二)官方解析(2)不妨设12x x <,由(1)知,()()()122,1,1,,2,1x x x ∈-∞∈+∞-∈-∞,()f x 在(),1-∞上单调递减,所以122x x +<等价于()()122f x f x >-,即()()222f x f x >-.由于()()22222221x f x x ea x --=-+-,而()()()2222221x f x x e a x =-+-,所以()()()222222222x x f x f x x e x e ---=---.令()()22x x g x xe x e -=---,则()()()21x x g x x e e -'=--,所以当1x >时,()0g x '<,而()10g =, 故当1x >时,()()10g x g <=.从而()()2220g x f x =-<,故122x x +<. 二、对解析的分析本问待证是两个变量的不等式,官方解析的变形是122x x <-,借助于函数的特性及其单调性,构造以2x 为主元的函数.由于两个变量的地位相同,当然也可调整主元变形为212x x <-,同理构造以1x 为主元的函数来处理.此法与官方解析正是极值点偏移问题的处理的通法.不妨设12x x <,由(1)知,()()()121,1,1,,21,x x x ∈-∞∈+∞-∈+∞,()f x 在()1,+∞上单调递增,所以122x x +<等价于()()212f x f x <-,即()()1120f x f x --<.令()()()()()2221xx u x f x f x xex e x -=--=--<,则()()()210x x u x x e e -'=-->,所以()()10u x u <=,即()()()21f x f x x <-<,所以()()()1212f x f x f x =<-;所以212x x <-,即122x x +<.极值点偏移问题的处理策略: 【处理策略一】主元法所谓主元法就是在一个多元数学问题中以其中一个为“主元”,将问题化归为该主元的函数、方程或不等式等问题,其本质是函数与方程思想的应用.作为一线的教育教学工作者,笔者尝试用主元法破解函数的极值点偏移问题,理性的对此类进行剖析、探究,旨在为今后的高考命题和高考复习教学提供一点参考.一般地,主元法破解极值点偏移问题思路是:第一步:根据()()()1212f x f x x x =≠建立等量关系,并结合()f x 的单调性,确定12,x x 的取值范围; 第二步:不妨设12x x <,将待证不等式进行变形,进而结合原函数或导函数的单调性等价转化. 第三步:构造关于1x (或2x )的一元函数()()()()21,2i i T x f x f a x i =--=,应用导数研究其单调性,并借助于单调性,达到待证不等式的证明.题型一:不含参数的问题.例1.(2010天津理)已知函数()()xf x xe x R -=∈ ,如果12x x ≠,且12()()f x f x = ,证明:12 2.x x +>【解析】法一:()(1)xf x x e -'=-,易得()f x 在(,1)-∞上单调递增,在(1,)+∞上单调递减,x →-∞时,()f x →-∞,(0)0f =,x →+∞时,()0f x →, 函数()f x 在1x =处取得极大值(1)f ,且1(1)f e=,如图所示. 由1212()(),f x f x x x =≠,不妨设12x x <,则必有1201x x <<<,欲证122x x +>,即证212x x >-,故122,(1,)x x -∈+∞,又因为()f x 在(1,)+∞上单调递减,故只需证21()(2)f x f x <-,又因为12()()f x f x =,故也即证11()(2)f x f x <-,构造函数()()(2),(0,1)H x f x f x x =--∈,则等价于证明()0H x <对(0,1)x ∈恒成立.由221()()(2)(1)0x x xH x f x f x e e--'''=+-=->,则()H x 在(0,1)x ∈上单调递增,所以()(1)0H x H <=,即已证明()0H x <对(0,1)x ∈恒成立,故原不等式122x x +>亦成立.法二:由12()()f x f x =,得1212x x x ex e --=,化简得2121x x x e x -=…①, 不妨设21x x >,由法一知,121o x x <<<.令21t x x =-,则210,t x t x >=+,代入①式,得11tt x e x +=,反解出11t t x e =-,则121221t t x x x t t e +=+=+-,故要证:122x x +>,即证:221t tt e +>-,又因为10te ->,等价于证明:2(2)(1)0tt t e +-->…②,构造函数()2(2)(1),(0)t G t t t e t =+-->,则()(1)1,()0t tG t t e G t te '''=-+=>,故()G t '在(0,)t ∈+∞上单调递增,()(0)0G t G ''>=,从而()G t 也在(0,)t ∈+∞上单调递增,()(0)0G t G >=,即证②式成立,也即原不等式122x x +>成立.法三:由法二中①式,两边同时取以e 为底的对数,得221211lnln ln x x x x x x -==-,也即2121ln ln 1x x x x -=-,从而221212121212221211111ln ln ()ln ln 1x x x x x x x xx x x x x x x x x x x x +-++=+==---, 令21(1)x t t x =>,则欲证:122x x +>,等价于证明:1ln 21t t t +>-…③, 构造(1)ln 2()(1)ln ,(1)11t t M t t t t t +==+>--,则2212ln ()(1)t t t M t t t --'=-, 又令2()12ln ,(1)t t t t t ϕ=-->,则()22(ln 1)2(1ln )t t t t t ϕ'=-+=--,由于1ln t t ->对(1,)t ∀∈+∞恒成立,故()0t ϕ'>,()t ϕ在(1,)t ∈+∞上单调递增,所以()(1)0t ϕϕ>=,从而()0M t '>,故()M t 在(1,)t ∈+∞上单调递增,由洛比塔法则知:1111(1)ln ((1)ln )1lim ()limlim lim(ln )21(1)x x x x t t t t t M t t t t t→→→→'+++===+='--,即证()2M t >,即证③式成立,也即原不等式122x x +>成立.【点评】以上三种方法均是为了实现将双变元的不等式转化为单变元不等式,方法一利用构造新的函数来达到消元的目的,方法二、三则是利用构造新的变元,将两个旧的变元都换成新变元来表示,从而达到消元的目的.例2.已知()ln f x x x =的图像上有,A B 两点,其横坐标为1201x x <<<,且12()()f x f x =.(1)证明:1221x x e <+<;(2)证明:1<<. 【解析】(1)证明:由()ln ,()ln 1f x x x f x x '==+,令()0f x '=,得1x e=, 故12101x x e <<<<,构造函数21()()(),(0),F x f x f x x e e=--<< 则2221()ln ln()2ln ()2ln 20F x x x x x e e e '=+-+=-+<+=,故()F x 在1(0,)e上单调递减,即1()()0F x F e >=,∴2()()f x f x e >-,令1x x =,则2112()()()f x f x f x e =>-,再由2121,(,1)x x e e -∈,且()f x 在1(,1)e 上单调递增,故212x x e >-,即证:122x x e+>. 又构造函数:1()()(1),(0)2g x f x f x x =--<<,则1112()ln ln(1)2,()01(1)x g x x x g x x x x x -'''=+-+=-=>--,故()g x '在1(0,)2上单调递增,由于0x →时,()g x '→-∞,且1()ln(1)0g e e '=->,故必存在01(0,)x e ∈,使得0()0g x '=,故()g x 在0(0,)x 上单调递减,在01(,)2x 上单调递增,又0x →时,()0g x →,且1()02g =,故()0g x <在1(0,)2x ∈上恒成立,也即()(1)f x f x <-在1(0,)2x ∈上恒成立,令1x x =,有121()()(1)f x f x f x =<-,再由211,1(,1)x x e -∈,且()f x 在1(,1)e 上单调递增,故211x x <-,即证:121x x +<成立.综上:即证1221x x e<+<成立.(2)令12t t =则22112212,,,(0,1)x t x t t t ==∈,且212()2ln ,()(),()2(2ln 1)h t t t h t h t h t t t '===+,令()0h t '=,得t =, 故1201t t <<<<.构造函数()()),(0H t h t h t t =-<<,则 ()()),()())H t h t h t H t h t h t'''''''''=+-=-,由于4()0h t t '''=>,则()h t ''在上单调递增,因为t t <-,故()0H t ''<,()H t '在上单调递减,故()0H t H ''>=,即()H t在上单调递增,即()0H t H <=,即())h t h t <-,同理得出:12t t +<; 再构造1()()(1),(0)2G x h t h t t =--<<,同样求导利用单调性可得出1()()02G t G >=,从而()(1)h t h t >-对1(0,)2t ∈恒成立,同理得出:121t t +>.综上:即证121t t <+<成立,也即原不等式1<<成立.练习1:已知函数2()ln f x x x x =++,正实数12,x x 满足1212()()0f x f x x x ++=,证明:12x x +≥. 【解析】由1212()()0f x f x x x ++=,得2211122212ln ln 0x x x x x x x x ++++++= 从而212121212()()ln()x x x x x x x x +++=-,令12t x x =,构造函数()ln t t t ϕ=-,得11()1t t t tϕ-'=-=,可知()t ϕ在(0,1)上单调递减,在(1,)+∞上单调递增,所以()(1)1t ϕϕ≥=,也即21212()()1x x x x +++≥,解得:12x x +≥.练习2(2013年湖南文科第21题)已知函数()211xx f x e x-=+. (1)求()f x 的单调区间;(2)证明:当()()()1212f x f x x x =≠时,120x x +<.解: (1) ()f x 在(),0-∞上单调递增,在()0,+∞上单调递减;(2)由(1)知当1x <时,()0f x >. 不妨设12x x <,因为()()12f x f x =,即121222121111x x x x e e x x --=++,则1201x x <<<, 要证明120x x +<,即120x x <-<,只需证明()()12f x f x <-,即()()22f x f x <-.而22()()f x f x <-等价于2222(1)10x x e x ---<,令()2()(1)10xg x x ex x =--->,则2'()(12)1x g x x e =--,令2()(12)1xh x x e=--,则2()40x h x xe '=-<,所以()h x 单调递减,()()00h x h <=,即()0g x '<,所以()g x 单调递减, 所以()()00g x g <=,得证.题型二:含参数的问题例3.已知函数x ae x x f -=)(有两个不同的零点12,x x ,求证:221>+x x . 【解析】思路1:函数()f x 的两个零点,等价于方程xxea -=的两个实根,从而这一问题与例1完全等价,例1的四种方法全都可以用;思路2:也可以利用参数a 这个媒介去构造出新的函数.解答如下:因为函数()f x 有两个零点12,x x , 所以⎩⎨⎧==)2()1(2121x x ae x ae x ,由)2()1(+得:)(2121xx e e a x x +=+,要证明122x x +>,只要证明12()2x x a e e +>,由)2()1(-得:1212()xxx x a e e -=-,即1212x x x x a e e -=-,即证:121212()2x x xx e e x x e e+->-211)(212121>-+-⇔--x x x x e e x x , 不妨设12x x >,记12t x x =-, 则0,1tt e >>, 因此只要证明:121t te t e +⋅>-01)1(2>+--⇔t t e e t , 再次换元令x t x e t ln ,1=>=,即证2(1)ln 0(1,)1x x x x -->∀∈+∞+ 构造新函数2(1)()ln 1x F x x x -=-+,0)1(=F求导2'2214(1)()0(1)(1)x F x x x x x -=-=>++,得)(x F 在),1(+∞递增, 所以0)(>x F ,因此原不等式122x x +>获证.【点评】含参数的极值点偏移问题,在原有的两个变元12,x x 的基础上,又多了一个参数,故思路很自然的就会想到:想尽一切办法消去参数,从而转化成不含参数的问题去解决;或者以参数为媒介,构造出一个变元的新的函数。
导数压轴大题之极值点偏移问题,把握本质与通用思路才能举一反三

导数压轴大题之极值点偏移问题,把握本质与通用思路才能举一反三极值点偏移题型是上一篇所讲述的双变量题型的一种重要分型。
2016年高考I卷的压轴大题就考了这种题型。
这类题型的特点鲜明,解题思路通用性强。
本文通过原创的一张图来直观、简明地揭示极值点偏移问题的基本原理(未见第二家如此系统地阐述它的原理)。
相信每一位同学学会后,再遇到此类题型就有底气而不会再发怵了,真正做到举一反三。
1. 导数(应用)压轴大题之不等式有关问题的极值点偏移题型及典型例题例1(2016国I) 已知函数f(x) = (x-2)e^x +a(x-1)^2有两个零点。
(1) 求a的取值范围;(2) 设x1, x2是f(x)的两个零点,证明:x1+x2<2。
(提示:这题在上一篇中已给出详细解答,这里不再赘述。
作为2016年的压轴题,第(2)问算是极值点偏移题型中的一个难度适中的题目,因此刚好可用来清晰地揭示极值点偏移题型的基本原理与通用解题思路。
不熟悉这类题型的同学应先把该题学透,再继续学习其它例题)例2 已知函数f(x) = xlnx,g(x) = 1/2×mx^2+x。
(1) 若函数f(x)与g(x)的图像上存在关于原点对称的点,求实数m 的取值范围;(2) 设F(x) = f(x) – g(x),已知F(x)在(0, +∞)上存在两个极值点x1、x2,且x1<x2,求证:x1x2 > e^2 (其中e为自然对数的底数)。
解:依题意,x>0,讲解:①从极值点偏移题型角度看,本题(2)问稍有变化(可视作常规题型的变式——出题人常以类似的方式改题或增加难度):(a) 分析的函数对象为‘导函数’及其两个零点——即两个等值点。
但这些变化对以极值点偏移的思路进行解题并无太大差别,仅仅是对象不同而已。
(b) 已知函数的定义域受限——x>0;处理时不要忘了其约束。
(c) 从所求证的‘x1x2 > e^2’看不出与极值点偏移问题相关,但只需利用已知推出可知条件“x1=lnx1/m和x2=lnx2/m”,即可把所求证问题转化为需知问题(或称需知条件)“x2+x1>2/m”——此为极值点偏移的标准形态。
