二次曲面的一般理论
二次曲面方程

二次曲面方程一、引言二次曲面方程是数学中非常重要的一类曲面方程。
它们具有丰富的几何性质和广泛的应用领域,如物理学、工程学和计算机科学等。
本文将从二次曲面的定义和性质、几何图形以及实际应用三个方面,生动全面地介绍二次曲面方程。
二、定义和性质二次曲面是由二次方程表示的曲面。
一般地,二次曲面方程可以写成Ax² + By² + Cz² + Dxy + Exz + Fyz + Gx + Hy + Iz + J = 0的形式。
其中A、B、C不全为零,D、E、F、G、H、I、J是常数。
这种方程描述了空间中的一个曲面,其形状和性质与方程的系数有关。
对于二次曲面方程,有一系列重要的性质。
首先,二次曲面在三维空间中通常表示一个曲面,形状可以是椭圆、双曲线或抛物面。
其次,二次曲面可能有中心或焦点等特殊点,这些点对于曲面的性质和几何特征具有重要意义。
最后,通过调整方程的系数,可以改变二次曲面的形状和方向,从而产生不同的几何图形。
三、几何图形根据二次曲面方程的不同形式,我们可以了解到不同的几何图形。
首先是椭球面,当A、B、C都为正数时,方程描述了一个椭球体。
椭球体在三维空间中呈现出类似于地球的形状,可以用来表示行星、人工卫星等球状物体。
其次是双曲面,当A、B、C中有一个为负数时,方程描述了一个双曲体。
双曲体的形状类似于双曲线,可以用来表示一些物理现象,如电场分布和透镜等。
最后是抛物面,当A或B为零,且C不为零时,方程描述了一个抛物体。
抛物体可以用来描述抛物运动,也可以用于建模天文、航空等领域的问题。
四、实际应用二次曲面方程在现实生活中有广泛的应用。
首先,它们在物理学中发挥着重要作用。
例如,抛物面方程可以用来描述物体的运动轨迹,从而对物体的运动进行预测和分析。
其次,二次曲面方程在工程学中也有重要应用。
通过使用椭球面方程,工程师可以设计出符合实际需求的复杂三维结构,如建筑物、车辆和飞机等。
此外,二次曲面方程还在计算机科学领域得到了广泛应用。
高等数学二次曲面

高等数学二次曲面引言在高等数学中,二次曲面是一类重要的曲面,它们在空间中具有特定的几何性质和数学定义。
本文将介绍二次曲面的定义、分类以及一些重要的性质和应用。
定义二次曲面是定义在三维空间中的曲面,它可以用一个二次方程的方程来表示。
二次曲面的方程一般具有以下形式:Ax^2 + By^2 + Cz^2 + Dxy + Exz + Fyz + Gx + Hy + Iz + J = 0其中,A、B、C、D、E、F、G、H、I和J是实数。
当方程中的系数满足一些条件时,可以得到不同种类的二次曲面。
分类根据方程中系数的特点,可以将二次曲面分为以下几类:1. 椭球面当A、B和C的系数都为正时,方程表示一个椭球面。
椭球面具有两个主轴,其中两个主轴的长度由A、B和C的值决定。
椭球面在物理学、天文学和工程学等领域有广泛的应用。
2. 单叶双曲面当A、B和C的系数分别为正、负和负时,方程表示一个单叶双曲面。
单叶双曲面有一个中心点,可以通过平移和旋转变换得到不同的形状。
3. 双叶双曲面当A、B和C的系数分别为负、负和正时,方程表示一个双叶双曲面。
双叶双曲面同样有一个中心点,可以通过平移和旋转变换得到不同的形状。
4. 椭圆抛物面当D、E和F的系数都为零时,方程表示一个椭圆抛物面。
椭圆抛物面具有一个焦点和一条对称轴,可以通过平移和旋转变换得到不同的形状。
5. 双曲抛物面当D、E和F的系数至少有一个不为零时,方程表示一个双曲抛物面。
双曲抛物面同样具有一个焦点和一条对称轴,可以通过平移和旋转变换得到不同的形状。
6. 椭圆锥面当A、B、C的系数满足一个特定的条件时,方程表示一个椭圆锥面。
椭圆锥面可以看作是椭球面在一个主轴的方向上无限延伸而成的曲面。
7. 双曲锥面当A、B、C的系数满足另一个特定的条件时,方程表示一个双曲锥面。
双曲锥面同样可以看作是椭球面在一个主轴的方向上无限延伸而成的曲面。
性质和应用二次曲面具有许多重要的性质和应用,以下是其中的一些:•二次曲面对称性:对于大多数二次曲面,它们都具有某种对称性,可以通过变换来描述这种对称性。
二次曲线和二次曲面的性质

二次曲线和二次曲面的性质二次曲线和二次曲面是数学中重要的概念,它们在几何学、代数学和物理学等领域中有着广泛的应用。
本文将就二次曲线和二次曲面的性质展开讨论。
一、二次曲线的性质1. 定义二次曲线是由二次方程所描述的曲线,其一般方程可以表示为Ax²+ Bxy + Cy² + Dx + Ey + F = 0,其中A、B、C、D、E和F为常数,并且A和C不同时为零。
2. 类型根据一般方程的系数,二次曲线可分为椭圆、双曲线和抛物线三种类型。
椭圆:当B² - 4AC < 0 时,方程描述的曲线为椭圆。
椭圆是一个闭合曲线,具有对称轴和离心率等性质。
双曲线:当B² - 4AC > 0 时,方程描述的曲线为双曲线。
双曲线有两个分离的曲线支,其特点是无界且具有两个渐近线。
抛物线:当B² - 4AC = 0 时,方程描述的曲线为抛物线。
抛物线具有轴对称性,分为开口向上和开口向下两种类型。
3. 几何性质不同类型的二次曲线具有不同的几何性质。
椭圆的主轴为长轴,副轴为短轴,其焦点在椭圆的长轴上。
椭圆的离心率介于0和1之间,且椭圆上的任意点到两个焦点的距离之和等于常数。
双曲线的主轴为虚轴,分别与两个焦点连线构成直角。
双曲线的离心率大于1,且双曲线上的任意点到两个焦点的距离之差等于常数。
抛物线的焦点位于曲线的顶点上方或下方,其离心率等于1。
抛物线具有镜像对称性,焦点和顶点关于准线对称。
二、二次曲面的性质1. 定义二次曲面是由二次方程所描述的曲面,其一般方程可以表示为Ax²+ By² + Cz² + Dxy + Exz + Fyz + Gx + Hy + Iz + J = 0,其中A、B、C、D、E、F、G、H、I和J为常数,并且A、B和C不同时为零。
2. 类型根据一般方程的系数,二次曲面可分为椭圆锥面、双曲面、抛物面和椭球面等类型。
椭圆锥面:当D² - 4AC < 0 时,方程描述的曲面为椭圆锥面。
2二次曲面分类简介

或
x cos1 cos 1 cos1 x y cos2 cos 2 cos 2 y
z cos3 cos 3 cos 3 z
空间直角坐标变换
一般的空间直角坐标 (点) 变换公式:
x y
x cos1 x cos2
y cos 1 z cos y cos 2 z cos
1
d1 2 d2
z x cos3 y cos 3 z cos 3 d3
或
x cos1 cos 1 cos1 x d1 y cos2 cos 2 cos 2 y d2 ,
z cos3 cos 3 cos 3 z d3
空间直角坐标变换
空间一般坐标变换公式, 还可以由新坐标系的 三个坐标面来确定.
x2 y2 a2 b2 1;
x2 y2 a2 b2 1;
x2 a2
y2 b2
0;
二次曲面的类型
[12] 双曲柱面: [13] 一对相交平面:
x2 y2 a2 b2 1;
x2 a2
y2 b2
0;
[14] 抛物柱面:
x2 2 py;
[15] 一对平行平面:
x2 a2 , a 0.
[16] 一对平行平面:
a13 a23 a33 z
x
x
y
z
A0
y
z
用不变量判断二次曲面类型
记 F1(x, y, z) = a11x + a12y + a13z + b1
F2(x, y, z) = a12x + a22y + a23z + b2
F3(x, y, z) = a13x + a23y + a33z + b3
I二次曲面介绍

对称性:对称于 xz , yz 对称性: 平面和 z轴. 用z = h截曲面得 截曲面得 x2 y2 到 − = h,
a2 b2 z = h.
z
用y = 0截曲面得到 截曲面得到
x 2 = a 2 z, y = 0.
x 0 y
用x = k截曲面得到 截曲面得到
2 k2 2 y = −b ( z − 2 ) a x = k
双曲抛物面可以看成是顶点在 一条抛物线上的抛物线运动产生。
椭圆抛物面,双曲抛物面没有对称中心, 椭圆抛物面,双曲抛物面没有对称中心,所以叫做 无心二次曲面
z z
x y 0 x
.
0 y
椭圆抛物面
双曲抛物面
§3 二次方程的化简 二次曲面:三元二次方程所表示的曲面. 二次曲面:三元二次方程所表示的曲面 二次方程所表示的曲面 三元二次方程的一般形状; 三元二次方程的一般形状;
这17种方程叫做二次曲面的标准方程。
我们可以根据方程的特点建立新的坐标系把方程化为17 种标准方程中的一种,从而可以得到方程所表示的曲面。
如(1) z = xy,(2) z 2 = xy,(3) x 2 + 2 xy + y 2 + z 2 = 1, (4) z = xy − x − y − 2.
(4) z = xy − x − y − 2
对称性:关于原点,坐标轴, (1) 对称性:关于原点,坐标轴,坐标 平面对称. 平面对称. 有界性: (2) 有界性:椭球面上点的坐标适合
| x |≤ a,| y |≤ b,| z |≤ c.
也就是说椭球面可以被包含在六个平面
x = ± a, y = ±b, z = ± c.
所围成的长方体里. 所围成的长方体里
二次曲面的一般理论

第六章 二次曲面的一般理论教学目的 : 本章讨论了一般二次曲面的渐近方向、中心、切线、切平面、径面 奇向、主径面与主方向等重要概念 ,从不同角度对二次曲面进行了分类 .研究了二次曲面的几何性质 , 并通过坐标变换和不变量、半不变量两种形式 化二次曲面的一般方程为规范方程 , 对二次曲面进行了分类和判定 , 是二次曲面理 论的推广和扩充 .教学重难点 : 通过坐标变换和运用不变量、半不变量化二次曲面的一般方程为 规范方程 , 既是重点又是难点 .基本概念二次曲面 : 在空间 , 由三元二次方程2 2 2a 11xa 22 y a 33z 2a 12 xy 2a 13 xz 2a 23 yz 2a 14 x 2a 24 y 2a 34z a 44 0 (1)所表示的曲面 .虚元素 :空间中,有序三复数组 (x,y,z) 叫做空间复点的坐标,如果三坐标全是 实数,那么它对应的点是 实点 ,否则叫做 虚点 二次曲面的一些记号F(x,y,z)F 1(x,y,z) a 11x a 12y a 13z a 14F 2(x,y,z) a 12x a 23y a 23z a 24 F 3( x, y, z) a 13x a 23y a 33z a 34 F 4 (x,y,z) a 14x a 24y a 34z a 442 2 2(x, y,z) a 11x 2a 22y 2 a 33z 2 2a 12 xy 2a 13 xz 2a 23 yz1(x,y,z) a 11x a 12 y a 13z 2(x,y,z) a 12 x a 22 y a 23z2a 11 x 22a 22 y a 33 z2a 12 xy 2a 13 xz 2a 23 yz 2a 14 x 2a 24 y 2a 34 z a 443(x, y,z) a 13x a 23 y a 33z 4(x,y,z) a 14 x a 24 y a 34 z即有恒等式成立 : F(x,y,z) xF 1 ( x, y,z) yF 2 (x, y, z) zF 3(x,y,z) F 4(x,y,z)(x,y,z) x 1(x,y,z) y 2(x, y,z) z 3(x,y,z)a 11 a 12 a 13 a 14 二次曲面 F(x,y,z) 的系数矩阵Aa 12a 22a 23a 24a 13 a 23 a 33 a 34a 14a 24 a 34 a 44a 11 a 12 a 13而由 (x, y,z) 的系数矩阵为Aa 12 a 22 a 23a 13a 23a 33二次曲面(1)的矩阵 A 的第一,第二,第三,与第四行的元素分别是 F 1 (x, y,z) ,a 11 a 12 a 13a 11 a 12 a 11 a 13a 22 a 231 a 11 a 22 a 33 I 2I 3a 12 a 22 a 23a 12 a 22a 13 a 33a 23 a 33a 13 a 23 a 33a 11 a 12 a 14a 11 a 13 a 14 a 22 a 23 a 24K 2a 12 a 22 a 24a 13 a 33 a 34 a 23 a 33 a 34a 14a 24a 44a 14a 34a 44a 24a 34a 44§6.1 二次曲面与直线的相关位置2 2 2 F(x, y,z) a 11x a 22 y a 33z 2a 12xy 2a 13xz2a 23 yz 2a 14 x 2a 24 y 2a 34 z a 44(1)x x 0 Xt与过点 (x 0, y 0, z 0 )的直线 y y 0 Yt (2)z z 0 Zt将(2)代入(1)得F 2(x,y,z), F 3(x, y, z) , F 4(x,y,z) 的系数。
第六章 二次曲面的一般理论

第六章 二次曲面的一般理论教学目的: 本章讨论了一般二次曲面的渐近方向、中心、切线、切平面、径面奇向、主径面与主方向等重要概念,从不同角度对二次曲面进行了分类.研究了二次曲面的几何性质,并通过坐标变换和不变量、半不变量两种形式,化二次曲面的一般方程为规范方程,对二次曲面进行了分类和判定,是二次曲面理论的推广和扩充.教学重难点: 通过坐标变换和运用不变量、半不变量化二次曲面的一般方程为规范方程,既是重点又是难点. 基本概念二次曲面: 在空间,由三元二次方程022222244342414231312233222211=+++++++++a z a y a x a yz a xz a xy a z a y a x a (1)所表示的曲面.虚元素:空间中,有序三复数组),,(z y x 叫做空间复点的坐标,如果三坐标全是实数,那么它对应的点是实点,否则叫做虚点二次曲面的一些记号≡),,(z y x F 44342414231312233222211222222a z a y a x a yz a xz a xy a z a y a x a +++++++++ 141312111),,(a z a y a x a z y x F +++≡242323122),,(a z a y a x a z y x F +++≡ 343323133),,(a z a y a x a z y x F +++≡ 443424144),,(a z a y a x a z y x F +++≡yz a xz a xy a z a y a x a z y x 231312233222211222),,(+++++≡Φz a y a x a z y x 1312111),,(++≡Φ z a y a x a z y x 2322122),,(++≡Φz a y a x a z y x 3323133),,(++≡Φ z a y a x a z y x 3424144),,(++≡Φ即有恒等式成立: ≡),,(z y x F ),,(),,(),,(),,(4321z y x F z y x zF z y x yF z y x xF +++),,(),,(),,(),,(321z y x z z y x y z y x x z y x Φ+Φ+Φ≡Φ二次曲面),,(z y x F 的系数矩阵: ⎪⎪⎪⎪⎪⎭⎫⎝⎛=44342414343323132423221214131211a a a a a a a a a a a a a a a a A 而由),,(z y x Φ的系数矩阵为 ⎪⎪⎪⎭⎫ ⎝⎛=*332313232212131211a a a a a a a a a A 二次曲面(1)的矩阵A 的第一,第二,第三,与第四行的元素分别是),,(1z y x F ,),,(2z y x F ,),,(3z y x F ,),,(4z y x F 的系数。
二次曲面一般式

二次曲面一般式摘要:一、二次曲面的定义二、二次曲面的分类1.椭圆曲面2.双曲线曲面3.抛物线曲面三、二次曲面的性质1.标准方程2.参数方程3.二次曲面的对称性四、二次曲面的应用1.数学领域2.物理领域3.工程领域正文:二次曲面是数学中的一种曲面,它的定义可以表示为二次方程的曲面。
在三维空间中,二次曲面是一个与二次方程相关的曲面。
根据二次方程的不同,二次曲面可以分为椭圆曲面、双曲线曲面和抛物线曲面三类。
1.椭圆曲面椭圆曲面是一种二次曲面,它的标准方程为:(x^2 / a^2) + (y^2 / b^2) = 1其中a和b分别表示椭圆的长短轴。
椭圆曲面在数学和物理领域中都有着广泛的应用,比如在光学和天文学中,椭圆曲面常用于描述光的传播和成像。
2.双曲线曲面双曲线曲面是另一种二次曲面,它的标准方程为:(x^2 / a^2) - (y^2 / b^2) = 1或(x^2 / b^2) - (y^2 / a^2) = 1其中a和b分别表示双曲线的长短轴。
双曲线曲面在数学和物理领域中也有广泛的应用,例如在电场和磁场的研究中,双曲线曲面可以用于描述电荷和电流分布。
3.抛物线曲面抛物线曲面是一种特殊的二次曲面,它的标准方程为:y = ax^2 + bx + c或x = ay^2 + by + c其中a、b和c是常数。
抛物线曲面在数学和工程领域中都有广泛的应用,例如在计算机图形学和机器人运动控制中,抛物线曲面可以用于描述物体的运动轨迹。
二次曲面不仅具有标准方程和参数方程,而且还具有丰富的性质和应用。
例如,二次曲面的对称性可以通过其标准方程或参数方程进行判断。
在数学领域,二次曲面是代数几何、微分几何和拓扑学等学科的重要研究对象。
二次曲面部分内容总结归纳

二次曲面部分内容总结归纳在数学中,二次曲面是一类重要的曲线图形,具有广泛的应用。
本文将对二次曲面的定义、性质以及常见的二次曲面进行总结归纳,以帮助读者更好地理解和应用这一内容。
一、二次曲面的定义和特点二次曲面是由二次方程定义的曲面,其一般方程可以表示为Ax² + By² + Cz² + Dxy + Exz + Fyz + Gx + Hy + Iz + J = 0,其中A、B、C、D、E、F、G、H、I、J为系数。
1. 定义:二次曲面是在三维空间中满足以上方程的点的集合。
它是由平面或曲线与另外一个平面所构成的立体。
2. 分类:根据系数之间的关系,二次曲面可以分为椭球面、双曲面、抛物面和圆锥曲面等。
3. 对称性:二次曲面通常具有一定的对称性,例如椭球面关于三个坐标轴对称,双曲面关于两个坐标轴对称,抛物面则关于一个坐标轴对称。
二、常见的二次曲面下面将介绍几种常见的二次曲面及其特点:1. 椭球面:椭球面是指A、B、C系数均为正数的二次曲面。
它可以是一个三维椭球,具有三个轴,其中有一个是最大的主轴。
2. 双曲面:双曲面是指A、B、C系数有正有负的二次曲面。
它可以是两个相交的曲面,呈现典型的双曲线形状。
3. 抛物面:抛物面是指A、B系数有一个为零的二次曲面。
它可以是开口向上或向下的形状,对称于坐标轴。
4. 圆锥曲面:圆锥曲面是指除了A、B、C系数外,D、E、F系数都为零的二次曲面。
它可以是圆锥的侧面,或者是圆锥的顶部和底部。
三、二次曲面的应用二次曲面具有广泛的应用,其中一些常见的领域包括:1. 几何学:二次曲面在几何学中的应用非常广泛,如描述平面、曲线和曲面之间的关系,解决几何问题等。
2. 物理学:在物理学中,二次曲面可以用来描述电磁场、电荷分布和光学等现象。
3. 工程学:二次曲面在工程学中常用于描述悬索桥、天线接收器的覆盖范围等。
4. 经济学:二次曲面可以用于描述经济模型中的供需曲线、成本函数等。
二次曲面形的性质及求法

二次曲面形的性质及求法二次曲面是一个重要的数学概念,它在图像处理、物理学、工程学等领域中都有重要的应用。
本文将介绍二次曲面的性质及其求法。
一、二次曲面的定义二次曲面是指具有二次项(或更高次项)的二元多项式所构成的曲面。
一般二次曲面的方程可以写为以下形式:$$ax^2+by^2+cz^2+2fxy+2gxz+2hyz+d=0$$其中,$a,b,c,f,g,h$和$d$均为实数,并且至少其中一项系数不为零。
二、二次曲面的性质1.对称性对于任意一个二次曲面,它都具有以下三种对称性:(1)关于$x$轴的对称性当$a=b$且$f=g=h=0$时,二次曲面具有关于$x$轴的对称性。
(2)关于$y$轴的对称性当$a=c$且$f=h=g=0$时,二次曲面具有关于$y$轴的对称性。
(3)关于$z$轴的对称性当$c=b$且$h=g=f=0$时,二次曲面具有关于$z$轴的对称性。
2.焦点和直线二次曲面的焦点是指使二次曲面上的所有点到其确定的两个固定点的距离之比等于一个定值的点对。
二次曲面的焦线是指对于二次曲面上的任一点,都满足其到焦点的距离与到焦线的距离之比等于一个定值。
3.标准形式通过线性代数的方法,可以将任意一个二次曲面通过坐标变换,化为以下标准形式:$$\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$$其中,$a,b,c$为正实数,分别代表$x,y,z$轴上的半轴长。
三、二次曲面的求法1.第一种方法:配方法配方法是求解二次曲面的一种基本方法。
通过将二次曲面的方程变形为一个平方差式,来实现对二次曲面的求解。
例如,对于方程$4x^2+y^2+z^2+4xy+4xz+2yz=1$,可以通过配方法将其变为以下形式:$$\bigg(2x+\frac{y}{2}+\frac{z}{2}\bigg)^2+\frac{3}{4}y^2+\frac{3} {4}z^2=1$$我们最终得到的形式就是一个椭球面的标准形式。
二次曲面的一般理论

第六章 二次曲面的一般理论教学目的: 本章讨论了一般二次曲面的渐近方向、中心、切线、切平面、径面奇向、主径面与主方向等重要概念,从不同角度对二次曲面进行了分类.研究了二次曲面的几何性质,并通过坐标变换和不变量、半不变量两种形式,化二次曲面的一般方程为规范方程,对二次曲面进行了分类和判定,是二次曲面理论的推广和扩充.教学重难点: 通过坐标变换和运用不变量、半不变量化二次曲面的一般方程为规范方程,既是重点又是难点. 基本概念二次曲面: 在空间,由三元二次方程022222244342414231312233222211=+++++++++a z a y a x a yz a xz a xy a z a y a x a (1)所表示的曲面.虚元素:空间中,有序三复数组),,(z y x 叫做空间复点的坐标,如果三坐标全是实数,那么它对应的点是实点,否则叫做虚点二次曲面的一些记号≡),,(z y x F 44342414231312233222211222222a z a y a x a yz a xz a xy a z a y a x a +++++++++ 141312111),,(a z a y a x a z y x F +++≡242323122),,(a z a y a x a z y x F +++≡ 343323133),,(a z a y a x a z y x F +++≡ 443424144),,(a z a y a x a z y x F +++≡yz a xz a xy a z a y a x a z y x 231312233222211222),,(+++++≡Φz a y a x a z y x 1312111),,(++≡Φ z a y a x a z y x 2322122),,(++≡Φz a y a x a z y x 3323133),,(++≡Φ z a y a x a z y x 3424144),,(++≡Φ即有恒等式成立: ≡),,(z y x F ),,(),,(),,(),,(4321z y x F z y x zF z y x yF z y x xF +++),,(),,(),,(),,(321z y x z z y x y z y x x z y x Φ+Φ+Φ≡Φ二次曲面),,(z y x F 的系数矩阵: ⎪⎪⎪⎪⎪⎭⎫⎝⎛=44342414343323132423221214131211a a a a a a a a a a a a a a a a A 而由),,(z y x Φ的系数矩阵为 ⎪⎪⎪⎭⎫ ⎝⎛=*332313232212131211a a a a a a a a a A 二次曲面(1)的矩阵A 的第一,第二,第三,与第四行的元素分别是),,(1z y x F ,),,(2z y x F ,),,(3z y x F ,),,(4z y x F 的系数。
第4章二次曲面的一般理论

c11 其中T c21 c 31
c12 c22 c3 c31 1, c11c12 c21c22 c31c32 0 2 2 2 c12 c22 c32 1, c12c13 c22c23 c32c33 0 2 2 2 c13 c23 c33 1, c11c13 c21c23 c31c33 0
四、转轴变换
设 {O; i , j , k }及 {O; i , j , k }两个直角坐标系 新坐标系可以看成原坐标系 绕原点O旋转, 使得i , j , k分别与i , j , k 重合得到的, 这种坐标变换叫旋转变 换,简称转轴
设i , j , k 在直角坐标系 Oxyz中的方向角分别为 i, i, i;i 1,2,3
六个关系式为正交的条件,则T也是正交矩阵 则T 1 T T
{O; i , j , k }及{O; i , j, k }都是右手系 ( i , j , k ) ( i , j , k ) 1
c11 det T c21 c31 c12 c22 c32 c13 c23 1 c33
y(c12 i c22 j c32 k ) z (c13 i c23 j c33 k ) ( x0 c11 x c12 y c13 z )i ( y0 c21 x c22 y c23 z ) j ( z0 c31 x c32 y c33 z )k
原方程可化为: 3x2
2 3z2 27 0 3y
例4、讨论曲面4 x 2 y 2 8z 2 8 yz 4 xz 4 xy 8 x 4 y 4 z 4 0的形状
解:把所给方程改写为:
4( x 1)2 y 2 8z 2 8 yz 4( x 1)z 4( x 1) y 0
二次曲面(2012)

解
表示圆柱面, x 2 + y 2 = 1 表示圆柱面, 表示平面, 2 x + 3 y + 3 z = 6 表示平面,
x2 + y2 = 1 2 x + 3 y + 3z = 6
交线为椭圆. 交线为椭圆
z = a2 − x2 − y2 表示怎样的曲线? 例2 方程组 a2 a2 表示怎样的曲线? 2 ( x − ) + y = 2 4
(一)椭球面
x2 y2 z2 1 2 + 2 + 2 = a b c
椭球面与 三个坐标面 的交线: 的交线:
2 z2 x2 + 2 = 1 , a c y = 0
2 y2 x2 + 2 = 1 , a b z = 0
2 y2 2 + z2 = 1 . b c x = 0
= z1 ( | z1 |< c)的交线为圆 的交线为圆.
2 a2 2 2 x + y 2 = 2 (c − z1 ) . 截面上圆的方程 c z = z 1
( 2) a = b = c ,
x2 y2 z2 1 球面 2 + 2 + 2 = a a a
方程可写为 x 2 + y 2 + z 2 = a 2 .
( x1 , y1 , z1 ),随着参数的变化可得到曲线上的全
部点. 部点
M 在圆柱面x2 + y2 = a2 上以 例 3 如果空间一点 ω z 轴旋转, v z 角速度 绕 轴旋转,同时又以线速度 沿平行于 ω v 都是常数), 轴的正方向上升( ),那么点 轴的正方向上升(其中 、 都是常数),那么点 M构成的图形叫做螺旋线.试建立其参数方程. 构成的图形叫做螺旋线 试建立其参数方程. 螺旋线. z 取时间t为参数 动点从 点出 为参数, 取时间 为参数, 动点从A点出 解 经过t时间 运动到M点 时间, 发,经过 时间,运动到 点 M 在 xoy 面的投影 M ′( x , y ,0)
6. 二 次 曲 面
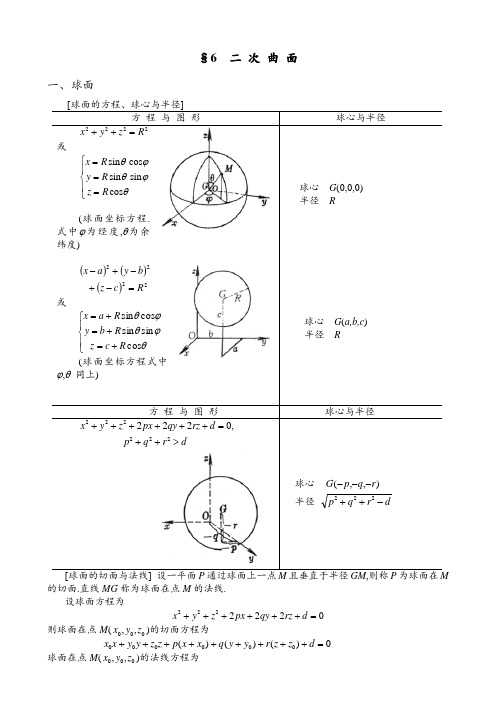
§6 二 次 曲 面一、 球面的切面.直线MG 称为球面在点M 的法线.设球面方程为x y z px qy rz d 2222220++++++=则球面在点M (x y z 000,,)的切面方程为x x y y z z p x x q y y r z z d 0000000+++++++++=()()() 球面在点M (x y z 000,,)的法线方程为x x x p y y y q z z z r-+=-+=-+000000 [两个球面的交角] 设两个球面S x y z p x q y r z d 12221111222++++++=0 S x y z p x q y r z d 22222222222++++++=0两个球面的交角是指它们在交点的两个切面的夹角,记作θ,则cos θ=++--++-++-22221212121212121212222222p p q q rr d d p q r d p q r d 因公式中不包含交点的坐标,所以在两个球面的交线上的各点的交角必相等.两个球面的正交条件为222012121212p p q q r r d d ++--=[球面束·两个球面的根面] 设S S S λλ120+=式中S 1和S 2如(1)式定义,λ为参数,则有)()(2)(2)(2))(1(21212121222=+++++++++++d d z r r y q q x p p z y x λλλλλ对λλ()≠-1的一个确定值,S λ表示一个球面,当λ取一切值()λ≠-1时,S λ所表示的球面的全体称为球面束.λ=-1时为一平面,称为两个球面S S 12,的根面,其方程为()()()222012121212()p p x q q y r r z d d -+-+-+-=根面与S 1和S 2的连心线垂直,束中任一球面λS 的中心在连心线上,且分连心线的比为λ.[球面汇·三个球面的根轴] 设S 1和S 2如(1)式定义,又设S x y z p x q y r z d 322233332220++++++=设 S S S S λμλμ1230++= 式中λμ,为二独立参数,则有()()()()()()12220222123123123123++++++++++++++++=λμλμλμλμλμx y z p p p x q q q y r r r z d d d对λμ,()λμ+≠-1的一对确定值,S λμ表示一个球面,当λμ,取一切值()λμ+≠-1时,S λμ所表示的球面的全体称为球面汇.三个球面中每对球面的根面分别为S S S S 122300-=-=,,和S S 210-=这三个平面交于一条直线,称为S S S 123,,的根轴.二、 椭球面三、双曲面a b c [双叶双曲面]x aybzc222222+-=-a=b时,为旋转双曲面]在Oxz平面上的曲线当a=b时,为旋转抛物面五、锥面与柱面当a=b时, 为圆锥面在Oxz平面上a b当a=b时,为圆柱面渐近锥面] 二次锥面 六、 一般二次曲面1. 二次曲面的一般性质上面所列举的椭球面、双曲面、抛物面等,它们的方程关于x,y,z 都是二次的.关于x,y,z 的一般二次方程的形式是ax by cz fyz gzx hxy px qy rz d 2222222220+++++++++= 它表示的曲面称为一般二次曲面.这里列举这些曲面的一些共同性质.[直线与二次曲面的交点] 一直线与一个二次曲面交于两点(实的,虚的,重合的).或者这直线全在曲面上,此时称它为二次曲面的直母线或母线.[平面与二次曲面的交线] 任一平面与一个二次曲面的交线为一个二次曲线.[二次曲面的直径平面与中心] 一个二次曲面的平行于已知方向的弦的中点在一个平面上,称为直径平面,它平分某一组平行弦.设已知方向的方向数为l ,m ,n ,则直径平面的方程为()()()()0=+++++++++++rn qm pl z cn fm gl y fn bm hl x gn hm al或改写为()()()ax hy gz p l hx by fz q m gx fy cz r n +++++++++++=0当l ,m ,n 变动时,这个方程表示一个平面把,由此二次曲面的直径平面组成一个平面把.把内任一平面都通过下列三个平面的交点:ax hy gz p hx by fz q gx fy cz r +++=+++=+++=000如果交点不在曲面上,则称它为二次曲面的中心,如果交点在曲面上,则称它为二次曲面的顶点.凡有中心的二次曲面称为有心二次曲面,其余的都称为无心二次曲面.[二次曲面的主平面与主轴] 如果直径平面垂直于被它所平分的弦,则称为主平面(对称平面),每个二次曲面至少有一个实主平面,非旋转二次曲面的任两主平面是互相垂直的,它们的交线为主轴.[二次曲面的切面与法线] 二次曲面在一点M (x y z 000,,)的切面方程为()()()()()()ax x by y cz z f y z z y g z x x z h x y y x p x x q y y r z z d 0000000000000+++++++++++++++=在点M 与二次曲面的切面垂直的直线称为曲面在点M 的法线,它的方程可写为x x ax hy gz p y y hx by fz q z z gx fy cz r-+++=-+++=-+++000000000000 [二次曲面的圆截面] 如果一个平面与一个二次曲面的交线为一个圆,则称该平面为曲面的圆截面.如果二次曲面不是球面,则通过空间中一点,二次曲面有六个圆截面;其中一般有两个实圆截面,四个虚圆截面;而且六个圆截面中有几个是重合的.2.二次曲面的不变量 由二次曲面的一般方程ax by cz fyz gzx hxy px qy rz d 2222222220+++++++++= (1)的系数组成的下列四个函数:222,,h g f ca bc ab J c b a I cf g f b h gh a D dr q p rc f g q f b h pg h a ---++=++===∆ 称为二次曲面的不变量,即经过坐标变换后,这些量是不变的.行列式∆称为二次方程(1)的判别式.。
《I二次曲面介绍》课件

二次曲面的切线和法平面
1
切线
切线方程式是确定点切线方向的关键工具,可以帮助我们理解二次曲面的基本特 征。
2
法平面
法平面相切于曲面上的点,并垂直于该点的切线,是描述曲面矢量值和方向的基 本方法。
3
应用
对于计算两个表面之间的夹角和反射光线,有着应用上的力量,也是了解曲面空 间特征的重要手段。
二次曲面的焦点和准线
《二次曲面介绍》PPT课 件
欢迎来到《二次曲面介绍》课程!二次曲面是数学中一个重要的概念,也具 有广泛应用。在此课程中,我们将深入了解二次曲面的分类、性质、公式和 应用,希望你享受这次学习!
什么是二次曲面?
定义
由二元二次方程$x^2+y^2+z^2+ax+by+cz+d=0$所确定的曲面称为一般二次曲面。
工程领域
2
对于数学知识结构的完备和优化起着重 要的推进作用。
在多种物理和工程应用中,二次曲面有
着广泛的实际用途。谷歌、苹果等大型IT
公司也在开发利用二次曲面技术的产品。
3
学术研究
二次曲面仍然是数学与物理学研究领域 的重要研究对象,对未来科学教育的贡 献巨大。
二次曲面的实践应用案例分析
医学成像
二次曲面在体绘制和定义了新 的医学成像方法。它可以为医 师提供三维数据,从而进行更 高质量的检查和诊断。
二次曲面的思考与总结
1 对数学的重要性
了解二次曲面的形式,有助于人们理解和应用数学知识,可以使数学这一抽象的学科更 加形象化、通透化。
2 对科学的启示
二次曲面的理论和应用研究有助于开拓科学领域的新思路,推动科学的不断发展和进步。
3 对未来的期许
二次曲面的标准方程

二次曲面的标准方程一、引言二次曲面是解析几何中的重要概念之一,广泛应用于物理学、工程学等学科中。
本文将探讨二次曲面的标准方程及其基本性质。
二、二次曲面的定义二次曲面是由二次函数所描述的曲面。
在三维空间中,一般可以表示为一个二次方程,即Ax^2 + By^2 + Cz^2 + Dxy + Exz + Fyz + Gx + Hy + Iz + J = 0三、二次曲面的分类二次曲面可以分为三类:椭圆面、抛物面和双曲面。
它们的标准方程分别为:1. 椭圆面椭圆面是一个封闭的曲面,其标准方程为(x/a)^2 + (y/b)^2 + (z/c)^2 = 1其中,a、b、c分别为椭圆长轴、长半轴和短半轴的长度。
2. 抛物面抛物面是一个开口朝上或朝下的曲面,其标准方程为z = Ax^2 + By^2其中,A和B为常数,决定了抛物面的形状和方向。
3. 双曲面双曲面有两个分支,其标准方程可以分为两种形式:(1)椭圆双曲面:(x/a)^2 + (y/b)^2 - (z/c)^2 = 1其中,a、b、c为常数,决定了椭圆双曲面的形状。
(2)双曲抛物面:z = (x/a)^2 + (y/b)^2其中,a和b为常数,决定了双曲抛物面的形状。
四、二次曲面的性质二次曲面具有多种有趣的性质,以下列举其中几个典型的性质:1. 对称性二次曲面通常具有一定的对称性,可以分为关于x轴、y轴、z轴、原点等不同的对称性。
2. 交点与切线二次曲面与坐标轴的交点,即截距,可以通过将某一坐标设为0求解得到。
而在交点处,二次曲面的切线与坐标轴平行。
3. 焦点与准线对于椭圆面和双曲面,其焦点和准线是重要的概念。
焦点是指到其上任意一点距离差的长度之和为常数,准线则是过焦点的直线。
4. 焦点和直径对于椭圆面,焦点和直径是有着紧密联系的。
直径是通过椭圆中心并且两端都在椭圆上的线段,它的中垂线过焦点。
五、应用示例二次曲面的标准方程在物理学和工程学中有着广泛的应用,下面以一个简单的实例来说明:一个椭圆形的太阳能反射镜可以通过椭圆面的标准方程来描述。
二次曲面类型

二次曲面类型
二次曲面是三维欧氏空间中,由三元二次方程所表示的曲面。
其一般方程为\(Ax^2+By^2+Cz^2+2Fxy+2Gxz+2Hyz=D\)。
二次曲面有很多类型,常见的包括:
1.平面:所有平面的方程都可以写成\(Ax+By+Cz=D\)的形式,其中\(A,B,C,D\)是常数。
2.球面:球面的方程可以写成\(x^2+y^2+z^2=R^2\)的形式,其中\(R\)是球的半径。
3.椭球面:椭球面的方程可以写成\(\frac{x^2}{a^2}+\frac{y ^2}{b^2}+\frac{z^2}{c^2}=1\)的形式,其中\(a,b,c\)是椭球的半轴长度。
4.抛物面:抛物面的方程可以写成\(x^2+y^2=2az\)或\(x^2+z^ 2=2ay\)的形式,其中\(a\)是抛物面的开口大小。
5.双曲面:双曲面的方程可以写成\(x^2+y^2-z^2=1\)或\(\fra c{x^2}{a^2}-\frac{y^2}{b^2}=1\)的形式,其中\(a,b\)是双曲面的半轴长度。
2.6二次曲面

二. 几种常见二次曲面. x2 y2 z2 (一) 椭球面 2 2 1 2 a b c 1 用平面z = 0去截割, 得椭圆
x2 y2 2 2 1 b a z 0
2 用平面z = k去截割(要求 |k | c), x2 y2 得椭圆 k2
2 2 1 2 b c a z k
2
2
( p 0)
旋转抛物面
(由 xoz 面上的抛物线 x 2 2 pz 绕它的轴旋转而成的) 与平面 z z1 ( z1 0) 的交线为圆. 当 z1 变动时,这种圆 2 2 x y 2 pz1 的中心都在 z 轴上.
z z1
(五). 双曲抛物面 (马鞍面)
§6
二次曲面的定义:
二次曲面
一个仿射坐标系中,x,y,z的一个三元二次方程的 图像称为二次曲面. 相应地平面被称为一次曲面. 讨论二次曲面形状的截线(截痕)法: 用坐标面和平行于坐标面的平面与曲面 相截,考察其交线(即截痕)的形状,然后 加以综合,从而了解曲面的全貌. 以下用截痕法讨论几种特殊的二次曲面.
x2 y2 2 z 2 p q
z
截痕法
用z = a截曲面
用y = 0截曲面 用x = b截曲面
y
x
0
(马鞍面) (五). 双曲抛 物面
x2 y2 2 z 2 p q
z
截痕法
用z = a截曲面
用y = 0截曲面 用x = b截曲面
y
x
0
.
(五)双曲抛物面
(马鞍面)
x2 y2 2 z 2 p q
(1 ) ( 2 )
2 y1 b 2 , 实轴与 x
轴平行,虚轴与 z 轴平行.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章 二次曲面的一般理论教学目的: 本章讨论了一般二次曲面的渐近方向、中心、切线、切平面、径面奇向、主径面与主方向等重要概念,从不同角度对二次曲面进行了分类.研究了二次曲面的几何性质,并通过坐标变换和不变量、半不变量两种形式,化二次曲面的一般方程为规范方程,对二次曲面进行了分类和判定,是二次曲面理论的推广和扩充.教学重难点: 通过坐标变换和运用不变量、半不变量化二次曲面的一般方程为规范方程,既是重点又是难点. 基本概念二次曲面: 在空间,由三元二次方程022222244342414231312233222211=+++++++++a z a y a x a yz a xz a xy a z a y a x a (1)所表示的曲面.虚元素:空间中,有序三复数组),,(z y x 叫做空间复点的坐标,如果三坐标全是实数,那么它对应的点是实点,否则叫做虚点二次曲面的一些记号≡),,(z y x F 44342414231312233222211222222a z a y a x a yz a xz a xy a z a y a x a +++++++++ 141312111),,(a z a y a x a z y x F +++≡242323122),,(a z a y a x a z y x F +++≡ 343323133),,(a z a y a x a z y x F +++≡ 443424144),,(a z a y a x a z y x F +++≡yz a xz a xy a z a y a x a z y x 231312233222211222),,(+++++≡Φz a y a x a z y x 1312111),,(++≡Φ z a y a x a z y x 2322122),,(++≡Φz a y a x a z y x 3323133),,(++≡Φ z a y a x a z y x 3424144),,(++≡Φ即有恒等式成立: ≡),,(z y x F ),,(),,(),,(),,(4321z y x F z y x zF z y x yF z y x xF +++),,(),,(),,(),,(321z y x z z y x y z y x x z y x Φ+Φ+Φ≡Φ二次曲面),,(z y x F 的系数矩阵: ⎪⎪⎪⎪⎪⎭⎫⎝⎛=44342414343323132423221214131211a a a a a a a a a a a a a a a a A 而由),,(z y x Φ的系数矩阵为 ⎪⎪⎪⎭⎫ ⎝⎛=*332313232212131211a a a a a a a a a A 二次曲面(1)的矩阵A 的第一,第二,第三,与第四行的元素分别是),,(1z y x F ,),,(2z y x F ,),,(3z y x F ,),,(4z y x F 的系数。
3322111a a a I ++= 3323232233131311221212112a a a a a a a a a a a a I ++=3323132322121312113a a a a a a a a a I = 443424143433231324232212141312114a a a a a a a a a a a a a a a a I =,4434343344242422441414111a a a a a a a a a a a a K ++=4434243433232423224434143433131413114424142422121412112a a a a a a a a a a a a a a a a a a a a a a a a a a a K ++=§6.1 二次曲面与直线的相关位置≡),,(z y x F xz a xy a z a y a x a 131223322221122++++44342414232222a z a y a x a yz a +++++ (1)与过点),,(000z y x 的直线⎪⎩⎪⎨⎧+=+=+=Ztz z Yt y y Xt x x 000 (2)将(2)代入(1)得[]0),,(),,(),,(),,(2),,(0000003000200012=++++Φz y x F t z y x ZF z y x YF z y x XF t Z Y X (3)现讨论直线(2)与二次曲面(1)相交的各种情况:1.0),,(≠ΦZ Y X ,这时方程(3)是一个关于t 的二次方程,它的判别式为:[]),,(),,(),,(),,(),,(0002000300020001z y x F Z Y X z y x ZF z y x YF z y x XF Φ-++=∆10 0>∆,有两不等实根,直线与二次曲面有两不同实交点; 20 0=∆,有两相等实根,直线与二次曲面有两相互重合实交点; 30 0<∆,有两共轭虚根,直线与二次曲面有两共轭虚交点 2.0),,(=ΦZ Y X10 0),,(),,(),,(000300020001≠++z y x ZF z y x YF z y x XF ,直线与二次曲面有唯一交点;20 0),,(),,(),,(000300020001=++z y x ZF z y x YF z y x XF ,但0),,(000≠z y x F 直线与二次曲面无交点30 0),,(),,(),,(000300020001=++z y x ZF z y x YF z y x XF ,且0),(00=y x F ,直线与二次曲面有无穷交点,直线在二次曲面上.§6.2 二次曲面的渐进方向与中心1. 二次曲面的渐进方向定义 5.2.1: 满足0),,(=ΦZ Y X 的方向Y X ::Z 称为二次曲面的渐进方向,否则称为非渐进方向.对于给定的二次曲面≡),,(z y x F xz a xy a z a y a x a 131223322221122++++44342414232222a z a y a x a yz a +++++ (1)和过点),,(000z y x 的直线⎪⎩⎪⎨⎧+=+=+=Ztz z Yt y y Xt x x 000 (2)当Y X ::Z 为曲面(1)的渐进方向时,直线(2)与曲面(1)总有两个交点;当Z Y X ::为曲面(1)的渐进方向时,直线(2)与(1)或者只有一个交点,或者没有交点,或者整条直线在曲面上。
2. 二次曲面的中心当Z Y X ::为二次曲面的非渐进方向时,即当02),(22212211≠++≡ΦY a XY a X a Y X以非渐进方向为方向的直线⎪⎩⎪⎨⎧+=+=+=Ztz z Yt y y Xt x x 000与二次曲面交于两个点,由这两点决定的线段叫二次曲面的弦.定义 6.2.2:若点C 是二次曲面的通过它的所有弦的中点,C 是二次曲面的对称中心,那么点C 叫做二次曲面的中心.定理6.2.1若点),,(000z y x C 是二次曲面的中心,其充要条件是:⎪⎩⎪⎨⎧=+++≡=+++≡=+++≡0),,(0),,(0),,(340330230130003240230230120002140130120110001a z a y a x a z y x F a z a y a x a z y x F a z a y a x a z y x F (6.2-1) 推论 坐标原点是二次曲面的中心,其充要条件是曲面的方程不含有z y x ,,的一次项。
二次曲面的中心坐标,由方程组⎪⎩⎪⎨⎧=+++≡=+++≡=+++≡0),,(0),,(0),,(343323133242323122141312111a z a y a x a z y x F a z a y a x a z y x F a z a y a x a z y x F (6.2-2)决定,方程组(6.2-2)叫做二次曲面(1)的中心方程组。
根据(6.2-2)的系数矩阵A 与增光矩阵B⎪⎪⎪⎭⎫ ⎝⎛=332313232212131211a a a a a a a a a A ,⎪⎪⎪⎭⎫⎝⎛=342414332313232212131211a a a a a a a a a a a a B 的秩r 与R ,有: 10 3==R r ,这时方程组的系数行列式03323132322121312113≠=a a a a a a a a a I ,方程组有惟一解,二次曲面(1)有惟一中心。
20 2==R r ,(6.2-2)有无数多解,这些解可用一个参数来线性表示。
曲面有无数个中心,这些中心构成一条直线。
30 1==R r ,(6.2-2)有无数多解,这些解可用两个参数来线性表示。
曲面有无数个中心,这些中心构成一个平面。
40R r ≠,(6.2-2)无解,这时二次曲面(1)无中心。
定义 6.2.3: 有唯一中心的二次曲面叫中心二次曲面,没有中心的二次曲面叫 无心二次曲面,有无数中心构成一条直线的二次曲面叫线心二次曲面, 有无数中心构成一平面的二次曲面叫面心二次曲面,二次曲面中的无心曲面、线心曲面与面心曲面统称为非中心二次曲面.推论 二次曲面(1)成为中心二次曲面的充要条件为03≠I ,成为非中心二次曲面的充要条件为03=I例1 椭球面1222222=++c z b y a x 与双曲面1222222±=-+cz b y a x 的3I 分别为0110010001222222≠=cb ac b a 与0110010001222222≠-=-cb ac b a 所以椭球面与双曲面都是中心曲面,他们的中心方程组分别为⎪⎪⎪⎩⎪⎪⎪⎨⎧=≡=≡=≡0),,(0),,(0),,(232221c z z y x F b y z y x F a x z y x F 与⎪⎪⎪⎩⎪⎪⎪⎨⎧=-≡=≡=≡0),,(0),,(0),,(232221c z z y x F b y z y x F a x z y x F 因此,它们的中心都是坐标原点(0,0,0)例2 抛物面z by a x 22222=±.其3I =000100122=±b a ,所以抛物面为非中心二次曲面,它的1),,(3-=z y x F ,中心方程组有矛盾,因此抛物面为无心二次曲面。
例3 对于曲面0222=-+c z y3I =010001000=,所以他是非中心二次曲面,但由于0),,(1≡z y x Fy z y x F ≡),,(2z z y x F ≡),,(3,所以曲面有一条中心直线⎩⎨⎧==0z y ,所给曲面为线心曲面。
