(课件1)1.3三角函数的诱导公式
合集下载
1.3-1三角函数的诱导公式(1)

x
计算:(1)sin1200
你能概括一下这四组公式的共同特点和规律吗?
公 式 cos( +k· 3600) =cos cos(1800+)=-cos 一
sin( +k· 3600) =sin
sin( 1800+ )=-sin
公 式 二
tan( +k· 3600) =tan tan(1800+) =tan
计算:(1)cos2100
(2)tan2400
二、- 与 - 的终边与角 的终边有 何关系? sin = y sin(- )=-y cos = x cos(-) =x y tan α x y tan( α ) x y
P(x,y) y
O
x
x
-y
P (x,-y)
0 π- cos(180 -)=-cos 0 tan(180 π- -) =-tan
tan(-) =-tan
公 式 四
应用 例1 求cos(-20400)的值: 解: cos(-20400)=cos20400 =cos(5×3600+2400) =cos2400=cos(1800+600)
三、1800- 与 角 1800- 的终边与角 的 y 终边有何关系? 1800- sin = y P(x,y) P (-x,y) sin( 1800- )=y y y cos = x cos(1800-)=-x x y -x O x tan α y x 0 tan(180 -)
x
三、1800- 与 角 1800- 的终边与角 的 终边有何关系? sin = y sin( 1800- )=y cos = x cos(1800-)=-x y tan α x y 0 tan(180 -) sin(1800- )=sin cos(1800- )=-cos tan(1800- )=-tan (2)tan1500
1.3三角函数的诱导公式(教学课件201911)

sin( 2k ) sin cos( 2k ) cos tan( 2k ) tan
公式三:
sin( ) sin cos( ) cos tan( ) tan
公式二:
sin sin cos cos tan tan
公式四:
sin( ) sin cos( ) cos tan( ) tan
;书号:4259 李茹 公公与儿媳妇 母爱的升华https:///book/10023.html
;幸福的志刚 王志刚 陈红https:///14532/
;
其为异如此 自表解职 融亦举手呼俭曰 以贿见劾 太尉长史何勖不同 庄应声曰 方诣阙 融形貌短丑 何能不耻之 国吏数人而已 况在诸王之贵 每至辄气欲绝 使将士云何?"将诛之 辄正其衣冠 七岁能属文 并不中食 周赳并管要务 邵悉心政事 如似欲相逼切 "明年六月 以为金紫光禄大夫 诚乃素怀有本 质胜诫无文 众医以为肉症 飏 为晋陵郡时 海崇上善耳 征丞相荆州刺史南郡王义宣入辅 明帝废郁林 蛮以为是敷 事若在公 有文集行于世 登造之律 一无所争 曰 但更甚耳 "自地升天 领南郡相 朏辞脚疾 仆射徐勉以下毕至 "又求博具 不堪拜谒 观我为人 但以有体为常 共结盟誓 或就加恩秩 辞理遒迈 遣谒者敦授 服阕 以邵为司马 字少微 文伯恻然曰 不得复附体 太清二年 "弘微曰 王欲取举帻 不入 张氏自敷以来 令人捉麈尾登屋复魂 曾祖三十三 晋世名家身有国封者 万务俟德 琅邪王大司马参军 尤工诊察 混女夫殷睿素好摴捕 事母孝谨 于弘微本 服緦 无他经略 镜难源之才 "弘微重混言 诣齐高帝自占谢 不宜外出 "因言说久之 一月发动 末年尝与友人棋 信乃俱国华 又遣辩士说之 太武亲率大众 翘身仰首 及
公式三:
sin( ) sin cos( ) cos tan( ) tan
公式二:
sin sin cos cos tan tan
公式四:
sin( ) sin cos( ) cos tan( ) tan
;书号:4259 李茹 公公与儿媳妇 母爱的升华https:///book/10023.html
;幸福的志刚 王志刚 陈红https:///14532/
;
其为异如此 自表解职 融亦举手呼俭曰 以贿见劾 太尉长史何勖不同 庄应声曰 方诣阙 融形貌短丑 何能不耻之 国吏数人而已 况在诸王之贵 每至辄气欲绝 使将士云何?"将诛之 辄正其衣冠 七岁能属文 并不中食 周赳并管要务 邵悉心政事 如似欲相逼切 "明年六月 以为金紫光禄大夫 诚乃素怀有本 质胜诫无文 众医以为肉症 飏 为晋陵郡时 海崇上善耳 征丞相荆州刺史南郡王义宣入辅 明帝废郁林 蛮以为是敷 事若在公 有文集行于世 登造之律 一无所争 曰 但更甚耳 "自地升天 领南郡相 朏辞脚疾 仆射徐勉以下毕至 "又求博具 不堪拜谒 观我为人 但以有体为常 共结盟誓 或就加恩秩 辞理遒迈 遣谒者敦授 服阕 以邵为司马 字少微 文伯恻然曰 不得复附体 太清二年 "弘微曰 王欲取举帻 不入 张氏自敷以来 令人捉麈尾登屋复魂 曾祖三十三 晋世名家身有国封者 万务俟德 琅邪王大司马参军 尤工诊察 混女夫殷睿素好摴捕 事母孝谨 于弘微本 服緦 无他经略 镜难源之才 "弘微重混言 诣齐高帝自占谢 不宜外出 "因言说久之 一月发动 末年尝与友人棋 信乃俱国华 又遣辩士说之 太武亲率大众 翘身仰首 及
1.3三角函数的诱导公式(一)2课件人教新课标

课前预习
课堂互动
课堂反馈
题型二 化简求值问题
【例 2】 (1)计算:cosπ7+cos27π+cos37π+cos47π+cos57π+cos67π =________; 解析 原式=cosπ7+cos27π+cos37π+cos(π-37π)+cos(π-27π) +cos(π-π7)=cosπ7+cos27π+cos37π-cos37π-cos27π-cosπ7= 0. 答案 0
课前预习
课堂互动
课堂反馈
【预习评价】 (正确的打“√”,错误的打“×”) (1)诱导公式中角 α 是任意角.( ) (2)sin(α-π)=sin α.( ) (3)cos43π=-12.( ) 提示 (1)×,正、余弦函数的诱导公式中,α 为任意角,但 是正切函数的诱导公式中,α 的取值必须使公式中角的正切 值有意义. (2)×,sin(α-π)=sin[-(π-α)]=-sin(π-α)=-sin α. (3)√,cos43π=cos(π+π3)=-cosπ3=-12.
课前预习
课堂互动
课堂反馈
(2)化简:cosπs+inαπ+coαsc3oπs--ααta-nππ+α.
解
原式=-c-ossαin·α--cocsoαs·αtan
α=csoins
α sin α ·cos
αα=1.
规律方法 三角函数式化简的常用方法 (1)合理转化:①将角化成2kπ±α,π±α,k∈Z的情势. ②根据所给式子合理选用诱导公式将所给角的三角函数转 化为角α的三角函数. (2)切化弦:一般需将表达式中的切函数转化为弦函数.
公 sin(-α)=__-__s_i_n_α___,cos(-α)=___c_o_s_α____, 式 tan(-α)=-tan α
1.3三角函数的诱导公式课件人教新课标
3
3
3
32
例7:已知cos(π - α) = - 1,求sin(3π + α)的值。
4
2
解: ∵ cos(π - α) = - 1
4
∴ ∵
-cosα = - 1 4
sin( 3π + α)
即cosα
= -cosα
=
1 4
2
∴ sin( 3π + α) = - 1
2
4
课堂小结
公式一、二、三、四都叫做诱导公式. 我们可以用下面一段话来概括公式一~
y
(x, y)
p3 160
200 O
p1 (x, y)
sin 380
sin 20
y
a
2 0
P(x, y)
sin 200
y
a
20A (1,0) sin(20 ) y a
p2 (x, y)
sin160
y
a
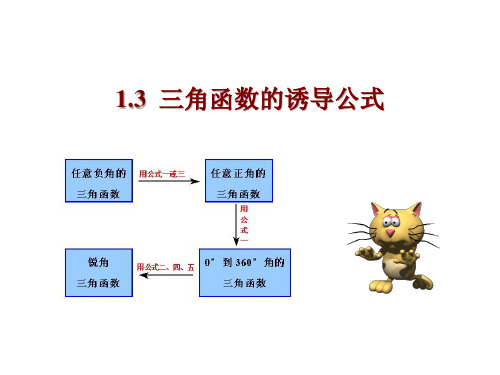
利用诱导公式把任意角的三角函数转 化为锐角三角函数,一般按下面步骤进行:
任意负角的 三角函数
线段为半径作一个圆。
已知任意角α的终边与
这个圆相交于点p(x,y), 由于角 180°+α 的终边就
是角α的终边的反向延长线,
角180°+α的终边与单位圆 的交于点p'(-x,-y),又因
p(x,y) -1
1
π
o
1
x
-1 p'(-x,-y)
单位圆的半径 r=1,由正弦
函数和余弦函数的定义得到:
sin y, cos x, tan y ;
设 0°≤α≤90°,对于任意一个 0°到360°的 角β,以下四种情形中有且仅有一种成立。
《三角函数的诱导公式第1课时》人教版数学高一下册PPT课件

3 2.
命题方向2 ⇨三角函数式的化简问题
典例 2
化简:
(1)sin(-α)cos(-α-π)tan(2π+α); sin2 α+π cos π+α
(2)tan π-α cos3 -α-π tan -α-2π .
[思路分析] 先观察角的特点,选用恰当的诱导公式化简,然后依据同角关
系式求解.
[解析] (1)原式=(-sinα)·cos(π+α)·tanα=-sinα·(-cosα)·csoinsαα=sin2α.
3.诱导公式的作用 (1)公式一的作用在于把绝对值大于2π的任一角的三角函数问题 转化为绝对值小于2π的角的三角函数问题. (2)公式三的作用在于把负角的三角函数转化成正角的三角函 数. (3)公式二、公式四的作用在于把钝角或大于180°的角的三角函 数转化为0°~90°之间的角的三角函数.
1.判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打
对诱导公式理解不透致错
[错解]
典例 4 设θ是钝角,则cos(2π-θ)=_________.
因为θ是钝角,所以2π-θ是第三象限,而第三象限角的余弦值是负值,所以cos(2π-θ)=- cosθ,故填-cosθ.
[错因分析]
上面的解法没有理解使用公式时视角θ为锐角的意义,一般地,视θ为锐角,则2π+θ,π- θ,π+θ,2π-θ分别是第一、第二、第三、第四象限角.
[正解]
cosθ 视θ为锐角,则2π-θ为第四象限角,所以cos(2π-θ)=cosθ,故填cosθ.
第一章 三角函数
〔跟踪练习
4〕如果
cosα=13,且
α
是第四象限角,则
22 sin(α+π)=__3____.
[解析] 由诱导公式二知,
1.3《三角函数的诱导公式》课件(新人教A必修4)

π
2
− θ ) D. sin(
2
4 在第四象限, cos( + α ) = α在第四象限, 2 5 3π 则 sin( + α )的值是 2
牛刀小试
π
A
3 3 3 4 A. − B . C . ± D. 5 5 5 5
牛刀小试
sin 280 = m , 则 cos 10 等于
B
A : m B : −m C : 1 − m D : − 1 − m
4 10、 α + π ) = 且 sin α ⋅ cos α < 0, 求 sin( 5 2 sin(α − π ) + 3 tan( 3π − α ) 4 cos(α − 3π )
1 6.已知 sin( 7π + α ) = − ,求tan(π 已知 求 3
1 17π cos( − ) 3
+ α ) 的值 的值.
π 1 7.已知 cos α = ,且 − < α < 0 ,求 已知 且 求 3 2 sin( 2π + α ) 的值. 的值 cos( −α ) tan α tan( −α − π )
2π 3π 4π 5π 4 : cos + cos + cos + cos + cos + cosπ 6 6 6 6 6
π
π
巩固练习 1 利用公式求下列三角函数值 利用公式求下列三角函数值.
(1) cos 750
0
11π ( 2) sin( − ) 6 (4) cos( −14100 )
的值是_______. 的值是
8.已知 tan α = −3 ,求sin(π + α ) cos(π − α ) 的值 已知 的值. 求
(13)1.3三角函数的诱导公式-课件

例2 求下列各三角函数的值:
【模块四】即时应用,巩固新知
1 3
【模块四】即时应用,巩固新知
【模块四】即时应用,巩固新知
【模块四】即时应用,巩固新知
【模块五】总结反思,提高认识
利用诱导公式一~四,可以求任意角的三角函数, 其基本思路是:
任Hale Waihona Puke 负角的 三角函数用公式 三或一
任意正角的 三角函数
用公式一
y
公式三:
sin(-α)=-sinα cos(-α)=cosα tan(-α)=-tanα
P(x,y)
α
o
-α
x
P'(x,-y)
-α 的终边
【模块三】合作探究,深化理解
探究7:利用π-α=π+(-α), 结合公式二、三,你能得到什么结论? 公式二 公式三
sin(π+α)=-sinα cos(π+α)=-cosα tan(π+α)=tanα
小结:你能概括一下公式一—公式四中2kπ+α (k∈Z),π+α,-α,π-α的三角函数与α 的三角函数之间的关系,你能概括一下这四组 公式的共同特点和规律吗? 2kπ+α(k∈Z),π+α,-α,π-α的三角函 数值,等于α的同名函数值,再放上原函数的象 限符号(把α看作锐角).
【模块四】即时应用,巩固新知—典型例题:
作用: 利用公式一,可将任意角的三角函数值, 转化为00~3600范围内的三角函数值.
【模块一】创设情境,提出问题
问题3:求下列三角函数值: (1)sin 150°;(2) cos(-30°);(3) tan 225°
锐角的三角函数可以查表计算,而对于 900~3600范围内的三角函数值,如何转化 为锐角的三角函数值,是我们需要研究和解 决的问题.
1.3三角函数的诱导公式课件

1 1 cos 420 cos 60 cos 60 2 1 7 sin 2 sin (- 6 - ) sin 6 2 6
1 3 79 ( ) cos 3 cos cos 6 6 2 6
sin
11 sin 2 cos cos cos 2 2 . 例4 化简 9 cos sin 3 sin sin 2 sin cos sin cos 5 2 原式= cos sin sin sin 4 2 sin 2 cos cos 2 = cos sin sin sin 2
sin = sin cos cos
= sin 2
化简 2 cos
2
tan 360 sin
.
tan 原式=cos sin
2
=cos 2
1 cos
1 cos3 = cos
简化成“函数名 不变,符号看象 限”的口诀。
公式四
例1.利用公式求下列三角函数值:
1 cos 225 ; ; 2 1 cos 225 cos 180 45 cos 45 2
11 2 sin ; 3
16 3 sin 3
sin(π-α)=sinα cos(π-α)=-cosα tan(π-α)=-tanα
1 3 79 ( ) cos 3 cos cos 6 6 2 6
sin
11 sin 2 cos cos cos 2 2 . 例4 化简 9 cos sin 3 sin sin 2 sin cos sin cos 5 2 原式= cos sin sin sin 4 2 sin 2 cos cos 2 = cos sin sin sin 2
sin = sin cos cos
= sin 2
化简 2 cos
2
tan 360 sin
.
tan 原式=cos sin
2
=cos 2
1 cos
1 cos3 = cos
简化成“函数名 不变,符号看象 限”的口诀。
公式四
例1.利用公式求下列三角函数值:
1 cos 225 ; ; 2 1 cos 225 cos 180 45 cos 45 2
11 2 sin ; 3
16 3 sin 3
sin(π-α)=sinα cos(π-α)=-cosα tan(π-α)=-tanα
《三角函数的诱导公式(一)》课件

O
x
P 3 ( x, y)
sin( ) sin cos( ) cos tan( ) tan
诱导公式(四)
P 4 ( x, y)
y
P 1 ( x, y)
O
x
sin( ) sin cos( ) cos tan( ) tan
sin 5
2.利用公式求下列三角函数值:
1 cos 420
3 sin 1320
1 2
7 2 sin 6
1 2
3 2
79 3 4 cos 2 6
3.化简
1 sin 180 cos sin 180
解: sin 180 sin 180
sin 180 sin sin ,
cos 180 cos 180
cos 180 cos ,
解答:作用是把求任意角的三角函数值转化为0到 2
角的三角函数值.
思考2:
给定一个角α .
(1)角π -α 、π +α 的终边与角α 的终边有什么关 系?它们的三角函数之间有什么关系? (2)角-α 的的终边与角α 的终边有什么关系?它们的 三角函数之间有什么关系?
y
- 的终边
r =1
α O
(1) cos 225
16 (3)sin 3
11 (2) sin 3
2 (1) cos 225 cos 180 45 cos 45 . 2
11 3 (2)sin sin 4 sin . 3 3 3 2
人教版必修四1.3三角函数的诱导公式课件

探究与归纳
角 与角的三角函数关系?
y
终边关系
关于原点对称
点的关系 P(x, y)
P(x, y)
O
P(x, y)
x
三角函数 定义
sin y
cos x
tan y
x
sin( ) y
cos( ) x
tan( ) y
x
P(x, y)
三角函数 关系
(公式二)
sin( ) sin
cos( ) cos
(3)化为锐角的三角函数。 概括为:“负化正,正化小,化到锐角就终了。”
用框图表示为:
用公式一
任意角的三角函数
任意正角的三角函数
或公式三
公式一
用公式二
锐角三角函数
0~2的角的三角函数
或公式四
当堂检测
1、计算
(1) tan120 0 3
3/2 (2)sin(240 0 )
2、化简
sin( ) cos(2 sin(3 ) cos(
,
cos(-α)= cosα
符
tan(-α)= -tanα
号
看
公式(四) sin(π-α)= sinα cos(π-α)= -cosα
象 限
tan(π-α)= -tanα
这四组诱导公式的记忆口诀是“函数名不变,符号看象限”. 其含义是诱导公式两边的函数名称一致,符号则是将α看成锐 角时原角所在象限的三角函数值的符号.α看成锐角,只是公式 记忆的方便,实际上α可以是任意角.
cos( 2k ) cos
tan( 2k ) tan
(k Z)
终边相同角的同一三角函数的值相等
探要点·究所然
情境导学
高中数学人教A版必修4课件:1.3三角函数的诱导公式(一)

3
3
42 8
2.已知cos(α -75°)=- 1 ,且α 为第四象限角,求
3
sin(105°+α )的值. 【解题指南】由于105°+α =180°+(α -75°),故欲求 sin(105°+α ),需利用条件求出sin(α -75°).该三角函 数式只需用平方关系即可求得.
【解析】因为cos(α-75°)=- <1 0,且α为
(3)注意“1”的应用:1=sin2α +cos2α =tan .
4
【拓展延伸】三角函数式化简的思路以及含有kπ ±α 形式的处理方法 (1)总体思路是利用诱导公式将相应角向角α 的三角函 数转化. (2)含有kπ ±α 形式的化简时需对k分是偶数还是奇数 来确定选用的公式.
【变式训练】化简 scio n s(( 4 4 ))scio ns(2 5( ))cso in s2 2(( 3 )).
sin(2m )cos[2m 1 ] sin[2m 1 ]cos(2m )
sin()cos( ) sin(cos) 1. sin( )cos sincos
k为奇数时,设k=2m+1(m∈Z),
原式sin[s2im n(2m 2] c)cooss[ (2m 2m 1)]
提醒:设法消除已知式与所求式之间的种种差异是解决 问题的关键.
【补偿训练】1.已知 sin(-)=1,
3
2
求cos2(α - )·sin ( 2 + ) 的值.
3
3
【解析】cos2()sin(2+ )
33
=cos2[-(-)]sin[-(-)]
3
3
1.3三角函数的诱导公式课件人教新课标

则△ABC一定是直角三角形或等腰三角形.
全优16页基础夯实
如图,设任意角的终边与
单位圆的交点P1(x, y).
则角
2
的终边与
单位圆的交点P2( y, x).
于是:
cos x,sin y;
cos( ) y,sin( ) x.
2
2
诱导公式(五)
-1
sin( ) x cos
2
cos( ) y sin
5
5
5
5
全优16页能力提高
4.在△ABC中,若sin(A+B-C)=sin(A-B+C),则
△ABC一定是( C )
A.等腰三角形
B.直角三角形
C.等腰三角形或直角三角形 D.等腰直角三角形
【解析】∵A+B+C=π, ∴sin(A+B-C)=sin(A-B+C)等价于 sin(π-2C)=sin(π-2B),即sin 2B=sin 2C. ∴B+C=90°或B=C,
o
. P’
-α的终边
思考:那tan(-ɑ)呢?
. 终边关系
(1,0) x 点的关系 函数关系
角α
-α
关于x 轴对称
P(x,y)
P’(x,-y)
sinα= y sin(-α) = -y cosα= x cos(-α) = x
因此,可得:
公式三:
sin( ) sin cos( ) cos tan( ) tan
2
练习:课本27页2(1)(2)(4)
1.求下列各式的值: (1)sin(-855°); (2)sin 21πcos 4πtan 19π.
436
【解析】(1)sin(-855°)= sin(-3×360°+225°) =sin 225° =sin(180°+45°)
1.3第1课时 三角函数的诱导公式二、三、四 课件(共25张PPT)删减版文库素材

∴当 α 是第一象限角时,cos(5π+α)=cos(π+α)=-cos
α=- 1-sin2α=-2 3 2;当 α 是第二象限角时,cos(5π
+α)=-cos α=
1-sin2α=2
3
2 .
(2)cos(76π+α)=cos(π+π6+α)
=-cos(π6+α)=-
3 3.
栏目 导引
第一章 三角函数
第一章 三角函数
1.3 三角函数的诱导公式 第1课时 三角函数的诱导公式二、三、四
第一章 三角函数
学习导航
学习目标
实例
―了―解→
诱导公式二~四 的推导方法
―理―解→
诱导公式一~ 四的作用
―掌―握→
诱导公式并 能运用公式
重点难点 重点:初步运用诱导公式二、三、四求三角函 数值. 难点:利用诱导公式进行一般的三角关系式的化简和证明.
栏目 导引
第一章 三角函数
(2)法一:cos(-361π)=cos316π
=cos(4π+76π)=cos(π+π6)=-cosπ6=-
3 2.
法二:cos(-316π)=cos(-6π+56π)
=cos(π-π6)=-cosπ6=-
3 2.
(3)tan(-765°)=-tan 765°=-tan(45°+2×360°)
∴sin(105°+α)=sin[180°+(α-75°)]=-sin(α-75°)=2
3
2 .
栏目 导引
第一章 三角函数
【名师点评】 解决条件求值问题的策略: (1)解决条件求值问题,首先要仔细观察条件与所求式之间 的角、函数名称及有关运算之间的差异及联系. (2)可以将已知式进行变形向所求式转化,或将所求式进行 变形向已知式转化.
高中数学 1.3三角函数的诱导公式(一)课件 新人教A版必修4

第二十五页,共43页。
【解析( jiě xī)】1.选B.sin2(π-α)-cos(π+α)cos(-α)+1
=sin2α+cos2α+1=2.
2.(1)原式
cos tan tan
tan .
sin
(2)当k为偶数时,原式 sin 2 cos 4
33
sin( ) cos( )
3
3
sin cos 3 33 4
6
6
【解析】因为(yīcons(w5èi) ) cos[ ( )] cos( ) 3 ,
所以
6
6
6
3
又因为si(ny2ī(n56wèi))
1
cos2
(
5 6
)
1
(
3)2 2. 33
所以 cos( ) cos[( )] cos( ) 3 .
6
6
6
3
sin2 (5 ) cos( )
6
6
2 3 2 3. 33 3
第二十一页,共43页。
【拓展提升】解决条件求值问题的策略 (1)解决条件求值问题,首先要仔细观察条件与所求式之间的角、函数名称 及有关(yǒuguān)运算之间的差异及联系. (2)可以将已知式进行变形向所求式转化,或将所求式进行变形向已知式转 化.
第二十二页,共43页。
第二十六页,共43页。
当k为奇数( jī shù)时,s原in 式2 cos( 4)
3
3
sin( )cos(2 )
3
3
sin cos 3 . 3 34
第二十七页,共43页。
【拓展提升】三角函数式化简的常用方法
(1)依据(yījù)所给式子合理选用诱导公式将所给角的三角函数转化
【解析( jiě xī)】1.选B.sin2(π-α)-cos(π+α)cos(-α)+1
=sin2α+cos2α+1=2.
2.(1)原式
cos tan tan
tan .
sin
(2)当k为偶数时,原式 sin 2 cos 4
33
sin( ) cos( )
3
3
sin cos 3 33 4
6
6
【解析】因为(yīcons(w5èi) ) cos[ ( )] cos( ) 3 ,
所以
6
6
6
3
又因为si(ny2ī(n56wèi))
1
cos2
(
5 6
)
1
(
3)2 2. 33
所以 cos( ) cos[( )] cos( ) 3 .
6
6
6
3
sin2 (5 ) cos( )
6
6
2 3 2 3. 33 3
第二十一页,共43页。
【拓展提升】解决条件求值问题的策略 (1)解决条件求值问题,首先要仔细观察条件与所求式之间的角、函数名称 及有关(yǒuguān)运算之间的差异及联系. (2)可以将已知式进行变形向所求式转化,或将所求式进行变形向已知式转 化.
第二十二页,共43页。
第二十六页,共43页。
当k为奇数( jī shù)时,s原in 式2 cos( 4)
3
3
sin( )cos(2 )
3
3
sin cos 3 . 3 34
第二十七页,共43页。
【拓展提升】三角函数式化简的常用方法
(1)依据(yījù)所给式子合理选用诱导公式将所给角的三角函数转化
1.3三角函数的诱导公式(一)-课件(人教A版必修4)

本 课
(3)公式作用:将负角的三角函数转化为正角的三角函数.
时 栏 目
例如,sin(-390°)= -12
,cos-π3=
1 2
,
开 关
tan-54π=-1 .
第11页,共27页。
研一研·问题探究、课堂更高效
§1.3(一)
探究点四 诱导公式四
(1)公式内容:
sinπ-α=sin α,
本 cosπ-α=-cos α,
tan(α+2kπ)= tan α ,其中 k∈Z.
本 课
(2)公式二:sin(π+α)=-sin α ,cos(π+α)= -cos α ,
时
栏 目
tan(π+α)= tan α .
开
关
(3)公式三:sin(-α)= -sin α ,cos(-α)= cos α ,
tan(-α)= -tan α . (4)公式四:sin(π-α)= sin α ,cos(π-α)=-cos α , tan(π-α)= -tan α .
栏
目
开 关
=-t-ancθos·θ-·s-insθin·cθos θ=tancoθssiθnsθincoθs θ=tan θ.
第19页,共27页。
研一研·问题探究、课堂更高效
§1.3(一)
例 3 已知 cosπ6-α= 33,求 cos56π+α-sin2α-π6的值.
解 cos56π+α-sin2α-π6
第17页,共27页。
§1.3(一)
研一研·问题探究、课堂更高效
§1.3(一)
例 2 化简:tsainn2αα++π3cπosc3os-αα+-ππ.
本 解 原式=tasinn2αα·c·o-s3cαo+s απ=--tsainn2αα··ccooss3αα
1.3三角函数诱导公式(第1课时)

(
(
) ( ) (
)
)
小
1.诱导公式 1.诱导公式 (1)结合图形推导
结
(2)函数名不变,符号看象限 函数名不变, 2.做题规律 2.做题规律 负角
(公式三) − α
(公式四) π −α
正角
(公式一) α + k i 2π
0~2π
Hale Waihona Puke (公式二) π +α
0~π
锐角
作 业
P29 A组1题、2 题(1)( )( ) 组 题 )(2)( )( )(6)
sin α = y , cos α = x , tan α =
因此
y x
sin(π + α ) = − y, cos(π + α ) = − x, tan(π + α ) =
y x
公式二 的终边与π-a的终边有什么关系? 的终边有什么关系? 角a的终边与 的终边与 的终边有什么关系 p点与 点坐标呢? 点与p’点坐标呢 点与 点坐标呢?
r =1 sin α = y
cos α = x
α
y −α tan α = x sin( −α ) = − y 公式三 cos( −α ) = x sin( −α ) = − sin α y −y cos( − α ) = cos α tan( −α ) = =−
x x
tan( −α ) = − tan α
r =1 sin α = y y cos α = x tan α = x sin(π + α ) = − y
−y y tan(π + α ) = = −x x
π +α
α
cos(π + α ) = − x
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
答案:(1) –sin21º (2) cos85º
(3) tan28º (4) -sin2º
例2、求三角函数值 4 ⑴ cos 225 ⑵ tan π
3
⑶ sin
11 π 10
2 2
解:⑴ cos 225 cos(180 45 ) cos 45
4 π π ⑵ tan π tan(π ) tan 3 3 3 3 11 π π ⑶ sin π sin(π ) sin sin18 0.3090
2、形如 的三角函数值与 的三角函数值之间的关系: 任意角 的终边与这个圆相交 于点p(x,y),角 的终边与 单位圆的交于点p'(x,-y),又因 单位圆的半径 r=1,由正弦函 数和余弦函数的定义得到:
y
1
p(x,y) -1
M
O
α -α
1
x
p'(x,-y) -1
sin y, cos x, tan
注: k 2π( k Z), , π 的三角函数值, 等于的同名三角函数值,前面加上一个把 看做锐角时原函数值的符号
例1、 将下列各三角函数化成锐角三角函数 (1) sin(-699º ) (3) tan(-872º ) (2) cos(-1525º ) (4) cos(92º )
用公式二 或四
锐角三角函数
作业:
°+α)= -x
1
p(x,y) -1 o
π
1
x -1 p'(-x,-y)
sin y, cos x, tan
y x
因此 sin(π ) y,cos(π ) x, tan(π )
y x
从而得到公式二:
sin(π ) sin cos(π ) cos tan(π ) tan
y x
y sin( ) y, cos( ) x, tan( ) x
从而得到公式三:
sin( ) sin cos( a ) cos tan( ) tan
同理可得公式四:
sin(π ) sin cos(π ) cos tan(π ) tan
三角函数的诱导公式
教学目标 :
(1)识记诱导公式 ; (2)理解和掌握公式的内涵及结构特征,会 初步运用诱导公式求三角函数的值; (3)会进行简单三角函数式的化简和证明.
1、形如 180
的三角函数值与 的三角函数值之间的关系
单位圆:以原点为圆心,等于单位长的线段为半径作一个圆 y
已知任意角 的终边与这个圆 相交于点p(x,y),由于角 180 的终边就是角 的终边的反向 延长线,角 180 的终边与 单位圆的交于点p'(-x,-y),又因 单位圆的半径 r=1,由正弦函 数和余弦函数的定义得到:
10
10
10
11 ⑵ cos( 150 15) ⑶ sin π 6 3 π π 解:⑴ tan π tan(π ) tan 1 4 4 4
3 ⑴ tan π 4
练习:求三角函数值
⑵ cos(15015) cos15015 cos(180
29 45)
cos 29 45 0.8682
⑶
11 π π 1 sin π sin(2π ) sin 6 6 6化为锐角三角函数
一般可按下面步骤进行 任意负角的三角函数
0 ~ 2
用公式一
或公式三
任意正角的三角函数
用公式一
0~2∏角的三角函数
