Excel 2000计算毒力回归线和卡方表
Excel中回归分析的方法

图8-10 “身高体重”工作表
图8-11 “身高体重”回归计算结果 返回本节
8.3 Excel回归分析工具
• 8.3.1 回归分析工具的主要内容 • 8.3.2 回归分析工具的应用 • 8.3.3 回归分析工具的输出解释
返回首页
8.3.1 回归分析工具的主要内容
• 回归分析工具是通过对一组观察值使用 “最小平方法”进行直线拟合,以分析一 个或多个自变量对单个因变量的影响方向 与影响程度的方法。它是Excel中数据分析 工具的一个内容。
8-20 “回归”工具获得的指数曲线模型拟合结果
• 3.
y axebx
返回本节
图8-13 “回归”对话框
图8-14 回归分析结果 返回本节
8.3.3 回归分析工具的输出解释
• Excel 回归分析工具的输出结果包括 3 个部 分: • 1.回归统计表 • 2.方差分析表 • 3.回归参数表
• • • •
回归统计表包括以下几部分内容: (1)Multiple R(复相关系数R): (2)R Square(复测定系数R2): (3)Adjusted R Square(调整复测定系 数R2): • (4)标准误差: • (5)观测值:
(1)截距函数。
• 其功能是利用现有的x值与y值计算直线与y 轴的截距。截距为穿过已知的 known_x's 和 known_y's 数据点的线性回归线与y轴的 交点。当自变量为 0 时,使用 INTERCEPT 函数可以决定因变量的值。例如,当所有 的数据点都是在室温或更高的温度下取得 的,可以用 INTERCEPT 函数预测在 0°C 时金属的电阻。 • 语 法 : INTERCEPT(known_y's,known_x's)
卡方检验excel操作步骤

卡方检验excel操作步骤
嘿,朋友们!今天咱就来唠唠卡方检验在 Excel 里咋操作。
咱先打开 Excel 表格,就像打开一扇通往知识宝库的门一样。
然后呢,把咱要分析的数据整整齐齐地填进去,这就好比给宝库里面摆上
宝贝。
接下来,咱得找到那个专门算卡方的工具。
这就好像在宝库里面找
一件特别趁手的兵器。
找到了,就可以开始大显身手啦!
咱把该填的数据都填进去,就跟给兵器装上弹药似的。
然后轻轻一点,嘿,结果就出来啦!这感觉,就像魔术师突然变出了神奇的东西。
你说这卡方检验有啥用啊?那用处可大了去了!它能帮咱看看两组
数据之间是不是有啥关联呀。
比如说,咱想知道男生和女生对某个东
西的喜好是不是不一样,卡方检验就能给出答案。
这就好像有个小侦
探在帮咱找线索一样。
咱再想想,要是没有 Excel 这么方便的工具,那得费多大劲去算这
个卡方啊!咱得一个数一个数地去摆弄,那多麻烦!现在可好啦,Excel 就像个智能小助手,几下就帮咱搞定了。
操作卡方检验的时候,可别粗心大意哦,就像走钢丝一样,得小心
翼翼的。
一个数据错了,那结果可能就全错啦!那可不行,咱得认真
对待,就像对待宝贝一样。
你说这 Excel 是不是很厉害?它能帮咱干好多事儿呢!卡方检验只
是其中之一。
咱学会了这个,以后再遇到类似的问题,就可以轻松解
决啦,就像有了一把万能钥匙。
总之呢,卡方检验在 Excel 里的操作其实不难,只要咱用心去学,
去练,肯定能掌握得牢牢的。
到时候,咱就能用它来解决各种问题啦,那感觉多棒啊!还等啥,赶紧去试试吧!。
毒力回归方程计算用表.xls
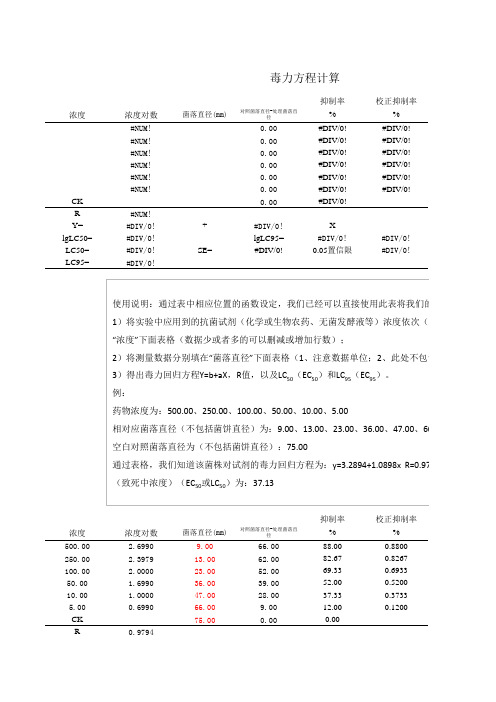
CK R Y= lgLC50= LC50= LC95=
浓度对数 #NUM! #NUM! #NUM! #NUM! #NUM! #NUM!
#NUM! #DIV/0! #DIV/0! #DIV/0! #DIV/0!
毒力方程计算
菌落直径(mm)
对照菌落直径-处理菌落直 径
0.00 0.00 0.00 0.00 0.00 0.00 0.00
66.00 62.00 52.00 39.00 28.00 9.00 0.00
抑制率 %
88.00 82.67 69.33 52.00 37.33 12.00 0.00
校正抑制率 %
0.8800 0.8267 0.6933 0.5200 0.3733 0.1200
Y=
3.2894
+
1.0898
X
lgLC50=
1.5697
lgLC95=
3.0790
1.57
LC50=
37.13
SE=
0.00
0.05置信限
37.13
LC95=
1199.56
#DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0!
校正死亡率
机率植
#DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0!
1.57 37.13
抑制率 %
#DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/
lgLC95=
#DIV/0!
SE=
#DIV/0!
0.05置信限
校正抑制率 %
#DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0!
用Excel进行相关性与回归分析分析

用Excel进行回归分析
Excel进行回归分析同样分函数和回归分析宏两种形 式,其提供了9个函数用于建立回归模型和预测,这 9个函数分别是:
1.INTERCEPT返回线性回归模型的截距 2.SLOPE返回线性回归模型的斜率 3.RSQ返回线性回归模型的判定系数 4.FORECAST返回一元线性回归模型的预测值 5.STEYX计算估计的标准误差 6.TREND计算线性回归线的趋势值 7.GROWTH返回指数曲线的趋势值 8.LINEST返回线性回归模型的参数 9.LOGEST返回指数曲线模型的参数
常用的统计量函数
由于公式执行后显示的是计算结果.按Ctrl+、键(位于键 盘左上角).可使公式在显示公式内容与显示公式结果之 间切换.
二、描述统计菜单项的使用
仍使用上面的例子 我们已经把数据输入到B2:B11单元格, 然后按以下步骤操作:
第一步:在工具菜单中选择数据分析选项,从其对话框中 选择描述统计,按确定后打开描述统计对话框。
用函数进行回归分析比较麻烦,这里介绍使用回归 分析宏进行回归分析。
用Excel进行回归分析
第一步:单击“工具”菜单,选择“数据分析”选项,出现 “数据分析”对话框,在分析工具中选择“回归”。
用Excel进行回归分析
第二步:单击“确定”按钮,弹出“回归”对话框,在“Y值输 入区域”输入$B$1:$B$11;在“X值输入区域”输入 $C$1:$C$11,在“输出选项”选择“$E$1”,如下图所示。
利用EXCEL计算相关系数
1.利用函数计算相关系数 2.用相关系数宏计算相关系数
1.利用函数计算相关系数
在Excel中,提供了两个计算两个变量之间相关系 数的方法,CORREL函数和PERSON函数,这两个 函数是等价的,这里我们介绍用CORREL函数计算 相关系数。
用Excel进行回归线分析操作

”
第4步:当对话框出现时
在“Y值输入区域”方框内键入Y的数据区域B3:B15 ,在“X值输入区域”方框内键入X的数据区域C3: C15。如果是多元线性回归,则X值的输入区就是除Y 变量以外的全部解释变量。 在“置信度”选项中给出所需的数值(这里我们使用 隐含值95%)。 在“输出选项”中选择输出区域(这里我们选择新工 作表组)。 在“残差”分析选项中选择所需的选项(这里我们暂 时未选)。 结果如下图所示。
下面给出利用Excel求线性回归方程的操作过程
首先,省94-2005年国内生产总值和固定资产 投资完成额资料到Excel工作表中的B3:C15单 元格。然后按下列步骤进行操作。 第1步:选择“工具”下拉菜单。 第2步:选择“数据分析”选项。
第3步:在分析工具中选择“回归”,然后选择“确定。
Excel输出的回归 分析结果回括以下几个部分
第一部分是“回归统计”,这部分主要是回归 分析中的一些常用统计量,包括相关系数( Multiple R)、判定系数(R Square)、调整 判定系数(Adjusted R Square)、估计标准误 差、观测值个数等。 第二部分是参数估计的内容。包括回归方程的 截距(Intercept)斜率(X Variabl)、截距和 斜率的标准误差、用于检验回归系数的统计量 (t Stat)和P-值(P-valu)以及截距和斜率的 置信区间(Lower 95%和Upper 95%)等。
卡方检验医学统计EXCEL模板

卡方检验医学统计EXCEL模板卡方检验是一种用来判断两个分类变量之间是否存在显著关联的统计方法,常应用于医学研究中,比如判断其中一种疾病是否与其中一种风险因素相关等。
在进行卡方检验时,我们需要计算一个卡方值,并根据卡方分布表得到相应的P值,进而判断两个变量之间的关联性。
下面我们介绍如何使用Excel来进行卡方检验,并给出一个模板供参考。
首先,我们需要准备两个分类变量的数据,假设我们研究其中一种疾病与性别的关系,将性别分为男和女两个分类。
假设我们有100个样本数据,其中男性有60人,女性有40人。
我们想要判断性别是否与患该种疾病的风险相关。
接下来,我们使用Excel来计算卡方值。
首先,将数据按照以下表格形式输入到Excel中:```疾病男性女性患病ab未患病cd```在Excel中,我们可以将上述数据输入到A1:D3单元格范围中。
然后,我们需要计算每个单元格的期望频数。
期望频数是指根据两个变量的边际分布计算得到的理论上的预期频数。
在E1单元格中输入以下公式:"=SUM($B$2:$B$3)*SUM($C$2:$D$2)/SUM($B$2:$D$3)",在F1单元格中输入公式:"=SUM($B$2:$B$3)*SUM($D$2:$D$3)/SUM($B$2:$D$3)",在E2单元格中输入公式:"=SUM($C$2:$D$3)*SUM($C$2:$D$2)/SUM($B$2:$D$3)",在F2单元格中输入公式:"=SUM($C$2:$D$3)*SUM($D$2:$D$3)/SUM($B$2:$D$3)"。
然后,我们需要计算每个单元格的卡方值。
在G2单元格中输入公式:"=((B2-E2)^2)/E2",在H2单元格中输入公式:"=((B2-F2)^2)/F2",在G3单元格中输入公式:"=((C3-E3)^2)/E3",在H3单元格中输入公式:"=((C3-F3)^2)/F3"。
利用Excel 进行快速回归分析
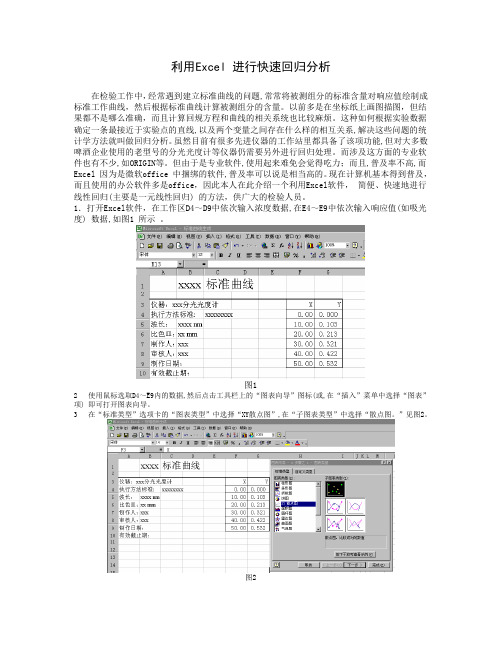
利用Excel 进行快速回归分析在检验工作中,经常遇到建立标准曲线的问题,常常将被测组分的标准含量对响应值绘制成标准工作曲线,然后根据标准曲线计算被测组分的含量。
以前多是在坐标纸上画图描图,但结果都不是哪么准确,而且计算回规方程和曲线的相关系统也比较麻烦。
这种如何根据实验数据确定一条最接近于实验点的直线,以及两个变量之间存在什么样的相互关系,解决这些问题的统计学方法就叫做回归分析。
虽然目前有很多先进仪器的工作站里都具备了该项功能,但对大多数啤酒企业使用的老型号的分光光度计等仪器仍需要另外进行回归处理。
而涉及这方面的专业软件也有不少,如ORIGIN等。
但由于是专业软件,使用起来难免会觉得吃力;而且,普及率不高,而Excel 因为是微软office 中捆绑的软件,普及率可以说是相当高的。
现在计算机基本得到普及,而且使用的办公软件多是office,因此本人在此介绍一个利用Excel软件,简便、快速地进行线性回归(主要是一元线性回归) 的方法,供广大的检验人员。
1.打开Excel软件,在工作区D4~D9中依次输入浓度数据,在E4~E9中依次输入响应值(如吸光度) 数据,如图1 所示。
图12 使用鼠标选取D4~E9内的数据,然后点击工具栏上的“图表向导”图标(或,在“插入”菜单中选择“图表”项) 即可打开图表向导。
3 在“标准类型”选项卡的“图表类型”中选择“XY散点图”,在“子图表类型”中选择“散点图。
”见图2。
图24 连点两次“下一步”,在“图表标题栏”和“X、Y轴”栏内填上相应的内容,点击“完成”键即出现散点图(其它如横、纵坐标、图表标题、网络线、线形的粗细等可根据需要添加、删除或修改) 。
5 在散点图中任一数据点上右击,在出现的浮动菜单中选择“添加趋势线”项则出现“添加趋势线”窗口。
6 在“添加趋势线”窗口的“类型”选项卡“趋势预测/ 回归分析类型”中选择“线性”;在“选项”选项卡中选中“显示公式”和“显示R 平方值”(即在其前面的复选框中打上“√”) ,按“确定”键后在绘图区即显示一元线性回归方程、曲线和相关系数R 的平方值,如图3 所示。
[精品WORD]教你用Excel做回归分析
![[精品WORD]教你用Excel做回归分析](https://img.taocdn.com/s3/m/433c51b9fbb069dc5022aaea998fcc22bcd143c4.png)
[精品WORD]教你用Excel做回归分析用Excel进行回归分析可以很方便地对数据进行分析和预测。
以下是使用Excel进行回归分析的步骤和解释:1.导入数据首先,将需要分析的数据导入Excel中。
可以在Excel的菜单栏中选择“数据”,然后选择“导入外部数据”或“从数据库导入数据”。
导入数据后,将数据放置在一个表格中。
2.选中数据在Excel表格中选中包含数据的区域。
确保包含需要分析的数据,以及任何其他相关的数据列。
3.插入图表在Excel的菜单栏中选择“插入”,然后选择“图表”。
在图表类型中选择适合的数据类型,例如线性图、散点图等。
在弹出的对话框中,选择需要分析的数据区域,并设置图表的其他选项。
4.添加趋势线在图表中单击鼠标右键,选择“添加趋势线”。
在弹出的对话框中,选择要添加趋势线的图表类型,例如线性、指数、对数等。
选择要添加趋势线的数据系列,并设置趋势线的其他选项。
5.显示回归分析结果在趋势线对话框中,选择“显示公式”和“显示R平方值”。
这将显示回归分析的结果,包括回归线的公式和R平方值。
R平方值越接近1,说明回归模型越精确。
6.分析回归结果根据回归分析的结果,可以得出以下结论:•斜率:回归线的斜率表示自变量对因变量的影响程度。
斜率越大,影响程度越大。
•截距:回归线的截距表示因变量在自变量为0时的值。
•R平方值:R平方值表示回归模型对数据的拟合程度。
如果R平方值接近1,说明模型拟合度较高。
•F值:F值是进行回归分析时的统计量,表示整个回归模型的显著性。
如果F值较大,说明模型显著性较高。
•P值:P值表示自变量对因变量的影响是否显著。
如果P值小于0.05,说明自变量对因变量的影响是显著的。
7.使用回归模型进行预测根据回归分析的结果,可以使用回归模型对未来数据进行预测。
将自变量的预测值代入回归模型中,即可得出因变量的预测值。
总之,使用Excel进行回归分析可以方便地得出数据的回归分析结果,以及对未来数据进行预测。
Excel中的数据分析工具回归分析和相关性计算

Excel中的数据分析工具回归分析和相关性计算Excel中的数据分析工具:回归分析和相关性计算在现代社会中,数据分析成为了各行各业中不可或缺的工作内容。
Excel作为一种广泛使用的数据处理工具,提供了许多强大的数据分析功能。
本文将重点介绍Excel中的两个重要数据分析工具:回归分析和相关性计算。
一、回归分析回归分析是一种用于探索变量之间关系的统计方法。
通过回归分析,我们可以确定一个或多个自变量与因变量之间的关系,并建立一个数学模型来预测因变量的值。
Excel中的回归分析工具可以帮助我们轻松地进行这一分析。
在Excel中进行回归分析,首先需要准备好需要分析的数据。
假设我们有一组数据:自变量X和因变量Y的取值。
我们可以按照以下步骤进行回归分析:1. 将数据输入Excel表格中的两列,一列用于自变量X,另一列用于因变量Y。
2. 选中数据区域,点击Excel的“数据”选项卡,然后点击“数据分析”。
3. 在弹出的对话框中,选择“回归”并点击“确定”。
4. 在回归分析对话框中,输入自变量和因变量的范围,并选择其他参数,比如是否需要常数项等。
5. 点击“确定”,Excel将为我们生成回归分析报告,其中包括相关系数、回归系数、显著性等统计结果。
通过回归分析,我们可以得到一组回归系数,用于描述自变量与因变量之间的关系。
这些回归系数可以帮助我们预测因变量的值,并进一步分析自变量的影响程度。
二、相关性计算相关性计算是一种用于衡量两个变量之间相关程度的方法。
在数据分析中,我们常常需要知道一个变量是否与另一个变量相关,以及它们之间的相关性强度。
Excel提供了相关性计算工具,可以方便地进行相关性分析。
要在Excel中进行相关性计算,我们可以按照以下步骤操作:1. 将需要进行相关性计算的数据输入Excel表格中的两列。
2. 选中数据区域,点击Excel的“数据”选项卡,然后点击“数据分析”。
3. 在弹出的对话框中,选择“相关性”并点击“确定”。
Excel中进行计算两个变量回归方程的操作技巧

Excel中进行计算两个变量回归方程的操作技巧
Excel是office办公软件中的一个重用要组成部分,怎么运用Excel计算两个变量的回归方程呢?今天,店铺就教大家在Excel中进行计算两个变量回归方程的操作技巧。
Excel中进行计算两个变量回归方程的操作步骤
首先打开Excel 2010。
新建一个Excel空白工作簿,分别在两列输入变量。
在“数据”选项卡中,选择“数据分析”,单击确定“回归分析”
选定“X”区域,单击鼠标选定目标区域。
选定“Y”区域。
同上。
选定输出区域。
分析结果。
第一列Conefficients对应模型的回归系数,包括截距a和斜率b,由回归此可以建立回归模型;第二列为回归系数的标准误差,误差值越小,表明的参数的精确度越高;第三列对应模型参数的检验,需要查表才能进行检验。
第四列对应参数P的值。
利用EXCEL快速进行毒力测定中的致死中量计算和卡方检验

利用EXCEL快速进行毒力测定中的致死中量计算和卡方检验黄剑;吴文君
【期刊名称】《昆虫知识》
【年(卷),期】2004(41)6
【摘要】根据机率值分析法和最小二乘法的原理 ,在Windows 98 Me 2 0 0 0 XP 系统中 ,利用EXCEL软件编制了 2个杀虫剂毒力测定中计算有关毒力回归方程、LD50 、相关系数、LD50 的 95 %置信限、标准误以及卡平方检验等计算程序模板。
计算时只需要输入试验浓度 (或剂量 )、试虫数和试虫死亡数 ,即可快速、简便、准确计算毒力测定的结果 ,并进行卡平方值的计算和适合性判断。
【总页数】5页(P594-598)
【关键词】毒力测定;死亡数;利用;致死中量;LD50;毒力回归方程;杀虫剂;适合性;剂量;卡方检验
【作者】黄剑;吴文君
【作者单位】西北农林科技大学农药研究所
【正文语种】中文
【中图分类】Q343.17;S114
【相关文献】
1.毒力测定中致死中量的简便计算方法 [J], 曹晓宇;黄春霞;倪珏萍
2.毒力测定中致死中量的简便计算方法 [J], 曹晓宇;黄春霞;等
3.毒力测定中致死中量的简便计算方法 [J], 曹晓宇;黄春霞
4.利用Excel快速计算化学分析测定结果 [J], 雷郑莉;钟红舰;胡京枝
5.采用Excel软件快速计算杀螺药药效试验中的半数致死量 [J], 周焕峰;金伟;朱磊;郭见多;汪敏
因版权原因,仅展示原文概要,查看原文内容请购买。
excel做回归分析的教程

excel做回归分析的教程Excel中经常需要对数据进行回归分析的一个操作,回归分析具体该如何进行操作呢?下面是由店铺分享的excel做回归分析的教程,以供大家阅读和学习。
excel做回归分析的教程(一)步骤1:首先将预处理的数据输到单元格里步骤2:“数据”里有一项“数据分析”,至于如何导入,详见我另外的经验步骤3:在一堆数据分析工具里找到回归这一项步骤4:对应框入Y值和X值,即可进行分析步骤5:点击确定后,即出现以下分析,常用的几个数据已圈出excel做回归分析的教程(二)步骤1:选择成对的数据列,将它们使用“X、Y散点图”制成散点图。
步骤2:在数据点上单击右键,选择“添加趋势线”-“线性”,并在选项标签中要求给出公式和相关系数等,可以得到拟合的直线。
步骤3:由图中可知,拟合的直线是y=15620x+6606.1,R2的值为0.9994。
步骤4:因为R2 >0.99,所以这是一个线性特征非常明显的实验模型,即说明拟合直线能够以大于99.99%地解释、涵盖了实测数据,具有很好的一般性,可以作为标准工作曲线用于其他未知浓度溶液的测量。
步骤5:为了进一步使用更多的指标来描述这一个模型,我们使用数据分析中的“回归”工具来详细分析这组数据。
步骤6:在选项卡中显然详细多了,注意选择X、Y对应的数据列。
“常数为零”就是指明该模型是严格的正比例模型,本例确实是这样,因为在浓度为零时相应峰面积肯定为零。
先前得出的回归方程虽然拟合程度相当高,但是在x=0时,仍然有对应的数值,这显然是一个可笑的结论。
所以我们选择“常数为零”。
步骤7:“回归”工具为我们提供了三张图,分别是残差图、线性拟合图和正态概率图。
重点来看残差图和线性拟合图。
步骤8:在线性拟合图中可以看到,不但有根据要求生成的数据点,而且还有经过拟和处理的预测数据点,拟合直线的参数会在数据表格中详细显示。
本实例旨在提供更多信息以起到抛砖引玉的作用,由于涉及到过多的专业术语,请各位读者根据实际,在具体使用中另行参考各项参数,此不再对更多细节作进一步解释。
excel数据回归方程

Excel 数据回归方程本文介绍了如何在 Excel 中制作数据回归方程,包括使用 WPS 表格和Excel 自带的数据分析工具两种方法。
同时,文章通过一个实例说明了如何使用回归方程来进行数据分析,并对拟合结果进行了评价。
下面是本店铺为大家精心编写的3篇《Excel 数据回归方程》,供大家借鉴与参考,希望对大家有所帮助。
《Excel 数据回归方程》篇1在数据分析中,回归分析是一种常用的方法,用于研究两个或多个变量之间的关系。
在 Excel 中,可以使用内置的数据分析工具来制作回归方程,从而对数据进行分析。
本文将介绍两种制作回归方程的方法:使用 WPS 表格和 Excel 自带的数据分析工具。
使用方法一:WPS 表格1.在 WPS 表格中输入数据,选择插入 - 图表。
2.选择散点图,然后选择好,填入自己需要的横纵坐标,标题之类。
3.完成插入图表,在界面上出现散点图。
4.对着散点右击,选择添加趋势线”。
5.可以选择线性,此时界面中会出现一天近拟的直线。
6.同时在选项”一栏中,还可添加方程和 R 平方值。
使用方法二:Excel 自带数据分析工具1.在 Excel 中选择数据区域,并选择“数据” - “数据分析”。
2.在数据分析工具中选择“回归”,并设置好需要的参数。
3.点击“确定”按钮,Excel 将自动生成回归方程和相关的统计数据。
实例:建立标准曲线已知 8 组对应数据,建立标准曲线,并且对此曲线进行评价,给出残差等分析数据。
首先,在 Excel 中输入数据,并选择“数据” - “数据分析”。
在数据分析工具中选择“回归”,并设置好需要的参数。
点击“确定”按钮,Excel 将自动生成回归方程和相关的统计数据。
根据得到的结果,可以计算出 R 平方值和残差等数据,从而对模型的拟合效果进行评价。
总之,Excel 提供了多种制作回归方程的方法,可以根据不同的情况选择适合的方法。
《Excel 数据回归方程》篇2Excel 是一种常用的电子表格软件,可以用来进行数据分析和绘制图表。
excel计算回归算法

excel计算回归算法Excel计算回归算法回归分析是一种常用的统计分析方法,它可以用来研究两个或多个变量之间的关系。
在实际应用中,回归分析可以用来预测未来的趋势,评估变量之间的相关性,以及探索变量之间的因果关系。
在Excel中,我们可以使用内置的回归分析工具来进行回归分析。
一、线性回归线性回归是回归分析中最常用的方法之一。
它假设变量之间存在线性关系,即一个变量的变化会导致另一个变量的相应变化。
在Excel中,我们可以使用内置的“数据分析”工具来进行线性回归分析。
首先,我们需要打开Excel并导入数据。
在Excel中,我们可以使用“数据”选项卡中的“数据分析”工具来进行回归分析。
在“数据分析”对话框中,选择“回归”选项,然后点击“确定”按钮。
在“回归”对话框中,我们需要指定自变量和因变量的数据范围。
自变量是我们用来预测因变量的变量,因变量是我们要预测的变量。
在本例中,我们将自变量指定为“X”列,因变量指定为“Y”列。
然后,我们需要勾选“置信水平”选项,并指定置信水平的值。
置信水平是指我们对回归系数的估计的置信程度。
通常情况下,我们会选择95%的置信水平。
点击“确定”按钮后,Excel会自动计算回归系数和拟合优度。
回归系数是指自变量对因变量的影响程度,拟合优度是指回归模型对数据的拟合程度。
我们可以使用这些值来评估回归模型的质量。
二、多元回归多元回归是一种回归分析方法,它可以用来研究多个自变量对因变量的影响。
在Excel中,我们可以使用内置的“数据分析”工具来进行多元回归分析。
首先,我们需要打开Excel并导入数据。
在Excel中,我们可以使用“数据”选项卡中的“数据分析”工具来进行回归分析。
在“数据分析”对话框中,选择“回归”选项,然后点击“确定”按钮。
在“回归”对话框中,我们需要指定自变量和因变量的数据范围。
在本例中,我们将自变量指定为“X1”列和“X2”列,因变量指定为“Y”列。
然后,我们需要勾选“置信水平”选项,并指定置信水平的值。
用Excel做回归分析的详细步骤

⽤Excel做回归分析的详细步骤⼀、什么是法“回归分析”是解析“注⽬变量”和“因于变量”并明确两者关系的统计⽅法。
此时,我们把因⼦变量称为“说明变量”,把注⽬变量称为“⽬标变量址(被说明变量)”。
清楚了回归分析的⽬的后,下⾯我们以回归分析预测法的步骤来说明什么是回归分析法: 回归分析是对具有因果关系的影响因素(⾃变量)和预测对象(因变量)所进⾏的数理统计分析处理。
只有当变量与因变量确实存在某种关系时,建⽴的回归⽅程才有意义。
因此,作为⾃变量的因素与作为因变量的预测对象是否有关,相关程度如何,以及判断这种相关程度的把握性多⼤,就成为进⾏回归分析必须要解决的问题。
进⾏相关分析,⼀般要求出相关关系,以相关系数的⼤⼩来判断⾃变量和因变量的相关的程度。
⼆、回归分析的⽬的回归分析的⽬的⼤致可分为两种:第⼀,“预测”。
预测⽬标变量,求解⽬标变量y和说明变量(x1,x2,…)的⽅程。
y=a0+b1x1+b2x2+…+bkxk+误差(⽅程A)把⽅程A叫做(多元)回归⽅程或者(多元)回归模型。
a0是y截距,b1,b2,…,bk是回归系数。
当k=l时,只有1个说明变量,叫做⼀元回归⽅程。
根据最⼩平⽅法求解最⼩误差平⽅和,⾮求出y截距和回归系数。
若求解回归⽅程.分別代⼊x1,x2,…xk的数值,预测y的值。
第⼆,“因⼦分析”。
因⼦分析是根据回归分析结果,得出各个⾃变量对⽬标变量产⽣的影响,因此,需要求出各个⾃变量的影响程度。
希望初学者在阅读接下来的⽂章之前,⾸先学习⼀元回归分析、相关分析、多元回归分析、数量化理论I等知识。
根据最⼩平⽅法,使⽤求解y=a+bx中的a和b。
那么什么是最⼩平⽅法?分别从散点图的各个数据标记点,做⼀条平⾏于y轴的平⾏线,相交于图中直线(如下图)平⾏线的长度在统计学中叫做“误差”或者‘残差”。
误差(残差)是指分析结果的运算值和实际值之间的差。
接这,求平⾏线长度曲平⽅值。
可以把平⽅值看做边长等于平⾏线长度的正⽅形⾯积(如下图)最后,求解所有正⽅形⾯积之和。
实验二用EXCEL进行相关与回归分析

实验二用EXCEL进行相关与回归分析引言:相关与回归分析是统计学中常用的分析方法,用于研究两个或多个变量之间的关系。
这些分析方法可以帮助我们了解变量之间的关联程度,并根据已有数据预测未来的值。
在本实验中,我们将使用EXCEL进行相关与回归分析的实践。
实验步骤:1.数据准备:在EXCEL中,我们需要准备好相关的数据。
假设我们有两个变量X和Y,每个变量有10个数据点。
我们可以将X值输入到A列,Y值输入到B 列。
2.相关分析:EXCEL提供了计算变量之间相关系数的函数CORREL(。
在C列,输入函数`=CORREL(A2:A11,B2:B11)`,然后拖动单元格填充其余的数据点。
这将计算出X和Y之间的相关系数。
3.回归分析:EXCEL也提供了计算回归方程的函数LINEST(。
在D列,输入函数`=LINEST(B2:B11,A2:A11)`。
这将计算出X和Y之间的回归方程。
回归方程的一般形式为:Y=aX+b,其中a称为斜率,b称为截距。
准确地说,这个方程通过最小化残差平方和来解释X和Y之间的关系。
LINEST(函数返回的数组会按如下顺序排列:斜率、截距、相关系数R,以及R的平方值R²。
即,在D2:D5中,分别获得斜率、截距、相关系数R和R²。
4.绘制散点图和回归线:在EXCEL中,我们可以很方便地绘制散点图和回归线。
选择A列和B 列的数据点,然后通过插入选项卡上的散点图功能绘制散点图。
接下来,我们需要添加回归线。
右键单击散点图上的数据点,选择添加趋势线。
在趋势线选项中,选择线性趋势线并勾选显示方程和R²值。
这将在散点图上显示回归线和回归方程。
实验结果分析:现在,我们已成功进行了相关与回归分析。
通过计算CORREL(函数,我们得到了X和Y之间的相关系数R。
相关系数的绝对值在0到1之间,可以反映变量之间的线性关系程度。
如果相关系数接近1,则两个变量之间存在强正相关;如果相关系数接近-1,则两个变量之间存在强负相关;如果相关系数接近0,则两个变量之间可能不存在线性关系。
EXCEL在毒力回归计算中的应用

技术与方法EXCE L 在毒力回归计算中的应用张志祥 徐汉虹(华南农业大学昆虫毒理研究室 广州 510642)程东美(仲恺农业技术学院植保系 广州 510225)C alculating toxicity regression with EXCE L .ZH ANG Zhi 2X iang ,X U Han 2H ong (Laboratory Insect Toxicity ,South China Agricultural Univer sity ,G uangzhou 510642,China );CHE NGD ong 2Mei (Department o f Plant Protection ,Zhongkai Agrotechnical College ,G uangzhou 510225,China ).Abstract The method of calculating toxicity regression ,LC 50,relation coefficient ,S E ,95%limited distance of LC 50and CT C with EXCE L was introduced.K ey w ords EXCE L ,toxicity regression摘 要 本文介绍了应用EXCE L 进行毒力回归分析、计算LC 50,a ,b ,相关系数,以及S E ,LC 50的95%置信区间和共毒系数的方法。
关键词 EXCE L ,毒力回归收稿日期:2000212229,修回日期:20012062181 前言EXCE L 是美国微软公司研制开发的用于个人财务分析与规划、公司营运管理与目标设定和薪水管理等的一套软件。
EXCE L 具有一个显著的特点,那就是它可以进行公式编辑和插入函数,并且具有连环计算的能力。
作者通过使用发现,在单元格中输入公式或插入函数后,EXCE L 可以将毒力回归中的所有结果计算出来,并且计算方法简单和快捷。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
nwx2 402.0684 360.1957 306.9780 221.8473 109.8897 1400.9790
nwxy 827.6345 795.5001 712.3112 548.0071 273.2810 3156.7339
X
2 0.05
(df=3)
3.5005
符合
当百分比浓度带入本程序时,应× 10000倍 ),在B3中输入250即可;药剂浓度为毫克/ 入。C3公式中的点滴器体积改为相应的体
供试真菌: 死亡虫数 79 71.5 56.5 41 19.5 5 m 2.1809 100 100 100 100 100 100 b 1.4449
Байду номын сангаас
日期: 0.7900 0.7150 0.5650 0.4100 0.1950 0.0500 LD50 151.6733
剂量对数 x 总试虫数
634.5 317.25 158.625 79.3125 39.65625
毒力测定与卡方检验计算表 编号 1 2 3 4 5 CK 求和 计算结果 X均值 2.2139 Y均值 5.0477 浓度(μ
g/ml)
药剂: 剂量 634.5000 317.2500 158.6250 79.3125 39.6563 2.8024 2.5014 2.2004 1.8993 1.5983 11.0019 a 1.8488
nwy 295.3273 318.0217 323.7231 288.5248 170.9811 1396.5780
nwy2 1703.6376 1756.8794 1652.8458 1353.6871 679.6134 7146.6634
理论机率值 理论死亡率 理论死虫数 校正死虫数 5.8980 5.4631 5.0281 4.5932 4.1582 0.8154 0.6783 0.5112 0.3421 0.2000 81.5415 67.8345 51.1217 34.2065 19.9953 77.8947 70.0000 54.2105 37.8947 15.2632
备注:B列中的浓度单位应为微克/毫升(ppm),如有不同,均应换算为该单位。当百分比浓度带入本程序时,应× 10000倍 后输入B列。例如,当浓度为0.025%时,应为0.025%× 1,000,000=250(微克/头),在B3中输入250即可;药剂浓度为毫克 毫升时,应×1000倍后输入B列,如0.0625(毫克/毫升)×1000=62.5(微克/毫升)输入。C3公式中的点滴器体积改为相应的体 积值。
日期: 校正死亡率 0.7789 0.7000 0.5421 0.3789 0.1526 观察机率值y 5.7686 5.5244 5.1057 4.6918 3.9748 25.0653 Sm 0.0417 LD50下限 125.6274 权重系数w 0.5120 0.5757 0.6340 0.6150 0.4302 2.7668 LD50上限 183.1193 nw 51.1953 57.5667 63.4038 61.4962 43.0164 276.6783 相关系数r 0.9830 nwx 143.4713 143.9975 139.5119 116.8022 68.7536 612.5365 X
