《弹性力学》第十三章 有限元简介
合集下载
弹性力学的有限元求法
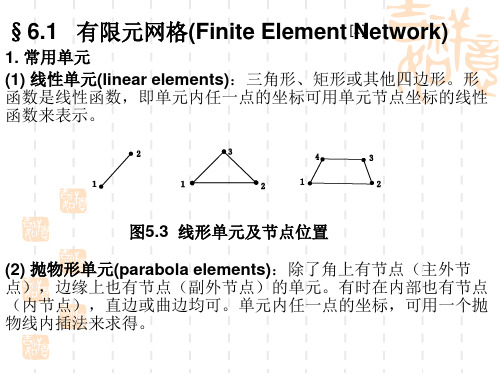
形态函数的几何意义
1 Ni 2A (ai bi x ci y)
1x y
Ni
11 2A
xj
yj
1 xm ym
Ni
SPJM SMIJ
Nj
SPMI SIJM
Nm
SPIJ SIJM
任意一点P的形态函数Ni是点P与结点I的对边所构 成的三角形面积与整个单元面积之比。
2.3单元载荷移置
有限元法的求解对象是单元的组合体，待求解 的未知变量都定义在单元的结点上，因此作用 在弹性体上的外力，需要移置到相应的单元结 点上成为结点载荷。
)T {P}
( xp, yp)
由于虚位移是任意的，
{R}e ([N ]
)T {P}
( xp, yp)
(2-16)
例2.3、在均质，等厚的三角形单元ijm的一点p （0.25a, 0.5a）上作用有集中载荷Px, Py。
Rxi Ni
Ryi
0
Rxj Ryj
Nj 0
Rxm
N
a1 a4
a2 a5
x x
a3 a6
y y
(2-6)
将3个结点上的坐标和位移分量代入公式（2-6） 就可以将六个待定系数用结点坐标和位移分量 表示出来。首先计算位移分量u的系数，
ui a1 a2 xi a3 yi u j a1 a2 x j a3 y j um a1 a2 xm a3 ym
图5.4 抛物线形单元及节点位置
2. 单元划分要注意的几个问题 (1) 相邻两个单元的节点要与节点重合（外节点与外节点、内节点 与内节点），不能与无节点边重合。
( ,)
(2) 单元不必是相同尺寸，应力有突变的地方，单元划分应较小。 (3) 任何一个单元必须只能在一种材料区，即它不能跨越两种材料
第一讲有限元绪论
考虑微段dx，内力 N=q (L-x)
dx的伸长为
Δ(dx) N(x)dx q(L x)dx
EA
x截面上的位移：
x N(x)dx x q(L x)dx q
x2
u 0 EA 0
EA
(Lx )
EA
2
根据几何方程求应变，物理方程求应力。这里
应变
du q ε x dX EA(L X)
实验方法的最大优点是结果真实可靠，通
常被当作产品最终定型的权威性依据。
实验方法也存在不足：
1）实验一定要在样品或样机试制之后才 能进行，成本高、周期长，并且只适合 批量生产的产品。
2）可以获得的数据量有限，无法对设计 提供更多的指导，更无法进行结构优化。
3）受实验手段的限制，有些参数无法测 准。
应力
σx
Eε x
q A
(L X)
有限单元法求解直杆拉伸：
1、离散化
2、外载荷集中到结点上，即把投 影部分的重量作用在结点i上
L1
1
L2
2
Li Li+1
i-1 i i+1
n-1 n
图 2-2
i-1
Li
i q (Li + Li+1)
Li+1
2
i+1
图 2-3
有限单元法求解直杆拉伸：
3、假设线单元上的位移为线性函数
五、数值分析与实验分析的比较
分析方法可分为理论计算和实验两大类。
1、基于实验的分析方法
指通过的实验测试获取需要的性能参数的 方法。这种方法获取不同的性能参数需要采用 不同的测试方法、仪器设备和辅助实验装置。 如：强度实验，可以采用电阻应变片及应变仪、 光弹涂膜或云纹栅、应变涂料等；扭转与弯曲 刚度实验则需要专门的实验台等等。
弹性力学及有限元法 ANSYS实例演示课件
有限元法是一种数值分析方法，通过 将连续的物理系统离散化为有限数量 的单元，利用这些单元的组合来逼近 真实系统的行为。
它广泛应用于工程领域，用于解决各 种复杂的力学、热学、电磁学等问题 。
有限元法的实现过程
01
离散化
将连续的物理系统划分为有限数量 的离散单元。
整体分析
将所有单元的数学模型组合起来， 形成整个系统的数学模型。
使用ANSYS的几何建模 功能，创建一个矩形薄 板模型。
选择适当的单位制，如 国际单位制（SI）。
为薄板指定弹性模量、 泊松比和密度等材料属 性。
通过与已知解进行比较 ，验证模型的正确性和 准确性。
材料属性设置与网格划分
01
02
03
材料属性
根据问题描述，为薄板设 置弹性模量、泊松比和密 度等材料属性。
局限性
ANSYS软件的学习曲线较陡峭，需要用户具备一定的专业背景和经验；同时，对于某些特殊问题，可 能需要结合其他软件或方法进行求解。
未来研究与发展的方向
多物理场耦合
进一步发展多物理场耦合的有限元分析方法 ，以模拟更复杂的工程问题。
智能化与自动化
研究有限元分析的智能化和自动化技术，提 高分析效率和精度。
网格划分
对薄板进行网格划分，选 择合适的网格密度以提高 求解精度。
网格质量检查
检查网格质量，确保网格 划分满足求解精度要求。
边界条件与载荷设置
边界条件
载荷与边界条件验证
根据实际情况，为薄板的边界设置约 束条件，如固定约束或简支约束。
通过有限元分析理论，验证所设置的 载荷和边界条件的正确性。
载荷设置
结构分析
有限元法能够模拟复杂结构的力学行为，为工程设计 和优化提供依据。
它广泛应用于工程领域，用于解决各 种复杂的力学、热学、电磁学等问题 。
有限元法的实现过程
01
离散化
将连续的物理系统划分为有限数量 的离散单元。
整体分析
将所有单元的数学模型组合起来， 形成整个系统的数学模型。
使用ANSYS的几何建模 功能，创建一个矩形薄 板模型。
选择适当的单位制，如 国际单位制（SI）。
为薄板指定弹性模量、 泊松比和密度等材料属 性。
通过与已知解进行比较 ，验证模型的正确性和 准确性。
材料属性设置与网格划分
01
02
03
材料属性
根据问题描述，为薄板设 置弹性模量、泊松比和密 度等材料属性。
局限性
ANSYS软件的学习曲线较陡峭，需要用户具备一定的专业背景和经验；同时，对于某些特殊问题，可 能需要结合其他软件或方法进行求解。
未来研究与发展的方向
多物理场耦合
进一步发展多物理场耦合的有限元分析方法 ，以模拟更复杂的工程问题。
智能化与自动化
研究有限元分析的智能化和自动化技术，提 高分析效率和精度。
网格划分
对薄板进行网格划分，选 择合适的网格密度以提高 求解精度。
网格质量检查
检查网格质量，确保网格 划分满足求解精度要求。
边界条件与载荷设置
边界条件
载荷与边界条件验证
根据实际情况，为薄板的边界设置约 束条件，如固定约束或简支约束。
通过有限元分析理论，验证所设置的 载荷和边界条件的正确性。
载荷设置
结构分析
有限元法能够模拟复杂结构的力学行为，为工程设计 和优化提供依据。
东南大学 有限元分析课程 弹性力学简介
0 ∂ ∂y 0 ∂ ∂x ∂ ∂z 0
0 0 ∂ ∂z 0 ∂ ∂y ∂ ∂x
u v w
16
3. 物理方程（应力－应变关系，描述了物质的一种特有的性质，称本构关系） 物理方程（应力－应变关系，描述了物质的一种特有的性质，
由材料力学知，胡克定律可表示为 简单拉压：ε = 纯剪切：γ =
σ
E
τ
G 一个方向拉伸引起的与垂直的方向的横向收缩应满足 ε ′=-µε E为拉压弹性模量，µ为横向变形系数（泊松比），G为剪切弹性模量， G= E 2(1 + µ )
设由σ x在x方向产生的拉伸正应变用ε x1表示,由σ y 和σ z 在x方向产生的 横向收缩正应变为ε x 2和ε x 3。则
σ x τ xy τ yx σ y τ zx τ zy 其中，τ xy
τ xz τ yz σz
= τ yx，
z
τ zx
τ zy
τ yz
σy
τ xz τ x τ xy τ yx σx
y x
6
τ yz = τ zy，τ zx = τ xz
记为σ ij 或 [σ ]
1.2.2 应变 1. 位移
8
同理可得：ε y =
∂v ∂y
γ xy =
π
2
− ∠B′A′D′ = α + β
∂v ∂v dx B′B′′ ∂v ∂u 式中，α ≈ tan α = = ∂x = ∂x = , β ≈ A′B′′ dx + ∂u dx 1 + ∂u ∂x ∂y ∂x ∂x ∂u ∂v ∂u ∂v 小变形条件下， =ε《1， =ε《1，可忽略，则γ xy = + x y ∂x ∂y ∂y ∂x
弹性有限元法及应用
Ty Tz
，所受的面积力
Tx Tx T y Ty T z T z
设应力边界的外法线为N，其方向余弦为 l m n ，则：
Tx l x s m xy n xz s s Ty l yx s m y s n yz s T l m n zx s zy s z s z
29
1 有限元法的基础
V wj
V wj
权函数
就可得到近似的积分形式
w A( Na )d w B( Na )d 0
T j T j j
T
w Rd w Rd 0
j
T
重庆大学材料学院
30
1 有限元法的基础
w A( Na )d w1 B( Na )d 0
28
1 有限元法的基础
（2）等效积分形式的近似：加权余量法
对于微分方程和边界条件所表达的物理问题，未知场函 数可以采用试探函数来表示，去求近似解。
u u N i ai Na
i 1
n
N是已知函数，a是待定系数
显然
A( Na ) R B( Na ) R
残差也称为余量
重庆大学材料学院
以矩阵形式表示为：
L σ f 0
T
应
力
外
力
重庆大学材料学院
18
1 有限元法的基础
其中，
x 0 0 L y 0 z 0 0 z 0 y x
力的平衡描述
方程：（针对微体dxdydz） 物理本构方程
力的平衡描述
有限元与弹性力学的基本原理
变εx，εy和剪应变 xy，而没有εz，γyz，γzx。
▪ 弹性力学的基本方程
弹性体在载荷作用下，体内任意一点的应力状态可由 六个应力分量：
x , y , z , xy , yz , zx
应力分量的正负号规定如下:如果
某一个面的外法线方向与坐标轴的
正方向一致，这个面上的应力分量
就以沿坐标轴正方向为正，与坐标
有限元分析的基本原理
有限元与弹性力学的基本原理
之所以介绍弹性力学的有限元法的主要是:它概念浅显， 易于掌握，既可以从直观的物理模型来理解，也可以按 严格的数学逻辑来研究; 不仅能成功地分析具有复杂边界 条件、非线性、非均质材料、动力学等难题，而且还可 以推广到解答数学方程的其它边值问题，如热传导、电 磁场、流体力学等问题。
区别:
▪ 平面应力： 只在平面内有应力，与该面垂直方向的应力可忽略，例如薄板拉压问题。
平面应变： 只在平面内有应变，与该面垂直方向的应变可忽略，例如水坝侧向水压问题。
▪ 具体说来： 平面应力是指所有的应力都在一个平面内，如果平面是OXY平面，那么只有正应力 σx，σy，剪应力τxy(它们都在一个平面内)，没有σz，τyz，τzx。 平面应变是指所有的应变都在一个平面内，同样如果平面是OXY平面，则只有正应
弹性力学所依据的基本规律有三个：变形连续规律、 应力-应变关系和运动(或平衡)规律，它们有时被称为弹性 力学三大基本规律。弹性力学中许多定理、公式和结论等， 都可以从三大基本规律推导出来。
弹性力学的基本假设
✓ 物体是连续的
✓ 物体是完全弹性的 ✓ 物体是均匀的
理想弹性体
✓ 物体是各向同性的
✓ 位移和形变是很小的
根据平衡应有 Tx TX ,Ty TY ,Tz TZ ,
▪ 弹性力学的基本方程
弹性体在载荷作用下，体内任意一点的应力状态可由 六个应力分量：
x , y , z , xy , yz , zx
应力分量的正负号规定如下:如果
某一个面的外法线方向与坐标轴的
正方向一致，这个面上的应力分量
就以沿坐标轴正方向为正，与坐标
有限元分析的基本原理
有限元与弹性力学的基本原理
之所以介绍弹性力学的有限元法的主要是:它概念浅显， 易于掌握，既可以从直观的物理模型来理解，也可以按 严格的数学逻辑来研究; 不仅能成功地分析具有复杂边界 条件、非线性、非均质材料、动力学等难题，而且还可 以推广到解答数学方程的其它边值问题，如热传导、电 磁场、流体力学等问题。
区别:
▪ 平面应力： 只在平面内有应力，与该面垂直方向的应力可忽略，例如薄板拉压问题。
平面应变： 只在平面内有应变，与该面垂直方向的应变可忽略，例如水坝侧向水压问题。
▪ 具体说来： 平面应力是指所有的应力都在一个平面内，如果平面是OXY平面，那么只有正应力 σx，σy，剪应力τxy(它们都在一个平面内)，没有σz，τyz，τzx。 平面应变是指所有的应变都在一个平面内，同样如果平面是OXY平面，则只有正应
弹性力学所依据的基本规律有三个：变形连续规律、 应力-应变关系和运动(或平衡)规律，它们有时被称为弹性 力学三大基本规律。弹性力学中许多定理、公式和结论等， 都可以从三大基本规律推导出来。
弹性力学的基本假设
✓ 物体是连续的
✓ 物体是完全弹性的 ✓ 物体是均匀的
理想弹性体
✓ 物体是各向同性的
✓ 位移和形变是很小的
根据平衡应有 Tx TX ,Ty TY ,Tz TZ ,
《有限元分析及应用》课件
受垂直载荷的托架
31
体单元
•线性单元 / 二次单元 –更高阶的单元模拟曲面的精度就越高。
低阶单元
更高阶单元
32
有限元分析的作用
复杂问题的建模简化与特征等效 软件的操作技巧（单元、网格、算法参数控制） 计算结果的评判 二次开发 工程问题的研究 误差控制
36
第二章 有限元分析的力学基础
(3) 研究的基本技巧
采用微小体积元dxdydz的分析方法（针对任意变
形体）
40
2.2 弹性体的基本假设
为突出所处理的问题的实质，并使问题简单化和抽 象化，在弹性力学中，特提出以下几个基本假定。
物质连续性假定: 物质无空隙，可用连续函数来描述 ；
物质均匀性假定: 物体内各个位置的物质具有相同特 性；
0.02 0.04 0.06 0.08
0.1
0.12
X
0.056
0.058
X
0.06
28
Y
Y
0 -0.02 -0.04 -0.06 -0.08
0
-0.001
-0.002
-0.003 0.054
-0.1 0
0.02 0.04 0.06 0.08
0.1
0.12
X
0.056
0.058
X
0.06
29
30
y
dy zy
1 2
zy
z
dz
0
略去微量项，得 yz zy
MY 0 zx xz
MZ 0
xy yx
剪切力互等定律
53
二维问题: 平衡微分方程
x yx X 0
x y xy y Y 0 x y
剪切力互等定律
弹性力学及有限元
热传导案例
总结词
热传导是有限元分析中用于模拟物体内部热量传递规律的应用之一。
详细描述
在电子、机械、化工和材料等领域，热传导分析用于研究材料的热性能、热应力和热变形等。通过有 限元方法，可以模拟物体内部的热量传递过程，预测温度分布和热应力分布，优化材料和系统的热设 计。
06
结论展望
结论
01
02
有限元分析
有限元分析是一种数值分析方法，通过将复杂的物体或系统离散 化为有限个小的单元（或称为元素），并分析这些单元的应力、 应变和位移，从而对整个物体或系统的行为进行预测和分析。
主题的重要性
工程应用
弹性力学和有限元分析在工程领域中具有广泛的应用，如结 构分析、机械设计、航空航天、土木工程等。通过这些方法 ，工程师可以更准确地预测和分析结构的性能，优化设计， 提高安全性。
03
04
研究意义
弹性力学及有限元分析在工程 领域具有广泛应用，为复杂结 构的分析提供了有效方法。
主要成果
本文系统地介绍了弹性力学的 基本原理和有限元分析的方法 ，并通过实例验证了其有效性 。
研究限制
由于时间和资源的限制，本研 究未能涵盖所有相关领域，未 来研究可进一步拓展。
对实践的指导意义
本文为实际工程中的结构分析 提供了理论依据和实践指导， 有助于提高结构的安全性和稳 定性。
优势
有限元方法具有广泛的适用性，可以用于求解各种复杂的物理问题；能够处理 复杂的几何形状和边界条件；可以通过增加单元数目来提高解的精度；可以方 便地处理非线性问题和材料非均质性问题等。
局限性
有限元方法需要较大的计算资源和时间，尤其对于大规模问题；对于某些特殊 问题（如高速冲击、爆炸等），需要采用特殊处理方法；对于多物理场耦合问 题，需要采用多场耦合有限元方法等。
有限元分析理论（弹性力学）
如果插值函数选得合适，单元分得越多、越细，得到的计算结果就越精确。当单元数趋于 无穷时，计算结果就收敛于精确解。但是，随着单元数、节点数的增加，计算工作量和存储信 息量就会迅速地增加，因此一般都是根据具体问题对精度的要求，只取一定数量(有限个)的单 元和节点进行分析。由于这种方法需要求解大型联立方程组，因此只是在解决了计算机的运算 速度和存储容量等问题后，这种方法才有实用意义并得到了迅速发展。
3)可以适应不连续的边界条件和载荷条件。 4)各单元的计算程式都相同，便于实现规范化和在计算机上统一编程，容易将程序编成模 块式结构。 5)有限元法最后得到的大型联立方程组的系数是一个稀疏矩阵，其中所有元素都分布在矩 阵的主对角线附近，且是对称的正定矩阵，方程间的联系较弱。这种方程计算工作量小，稳定 性好，便于求解，占用的计算机内存也少。 有限元法的这些特点，正好可以克服工程科学计算中所遇到的许多困难。对于已有方程的 物理问题，主要是因为集合形状复杂、边界条件复杂、本构关系复杂而解不出来。利用有限元 法离散化的手段，用各种小单元来适应这些复杂多变的因素，用分块近似插值函数来逼近全域 上的连续函数，问题就变得容易了。
目前，有限元法以远远超出了原有的应用范畴，已从弹性力学扩展到了弹塑性力学、岩石 力学、地质力学、流体力学、传热学、气动力学、计算物理学、海洋工程、大气污染等各种学 科和应用领域，取得了出人意料的成功。
在机械工程领域内，可以用有限元法解决的问题有： 1)包括杆、梁、板、壳、三维块体、二维平面、管道等各种单元的各种复杂结构的静力分 析。 2)各种复杂结构的动力分析，包括频率、振型和动力响应计算。 3)整机（如水压机、汽车、发电机、泵、机床）的静、动力分析。 4)工程结构和机械零部件的弹塑性应力分析及大变形分析。 5)工程结构和机械零件的热弹性蠕变、粘弹性、粘塑性分析。 6)大型工程机械轴承油膜计算等。
3)可以适应不连续的边界条件和载荷条件。 4)各单元的计算程式都相同，便于实现规范化和在计算机上统一编程，容易将程序编成模 块式结构。 5)有限元法最后得到的大型联立方程组的系数是一个稀疏矩阵，其中所有元素都分布在矩 阵的主对角线附近，且是对称的正定矩阵，方程间的联系较弱。这种方程计算工作量小，稳定 性好，便于求解，占用的计算机内存也少。 有限元法的这些特点，正好可以克服工程科学计算中所遇到的许多困难。对于已有方程的 物理问题，主要是因为集合形状复杂、边界条件复杂、本构关系复杂而解不出来。利用有限元 法离散化的手段，用各种小单元来适应这些复杂多变的因素，用分块近似插值函数来逼近全域 上的连续函数，问题就变得容易了。
目前，有限元法以远远超出了原有的应用范畴，已从弹性力学扩展到了弹塑性力学、岩石 力学、地质力学、流体力学、传热学、气动力学、计算物理学、海洋工程、大气污染等各种学 科和应用领域，取得了出人意料的成功。
在机械工程领域内，可以用有限元法解决的问题有： 1)包括杆、梁、板、壳、三维块体、二维平面、管道等各种单元的各种复杂结构的静力分 析。 2)各种复杂结构的动力分析，包括频率、振型和动力响应计算。 3)整机（如水压机、汽车、发电机、泵、机床）的静、动力分析。 4)工程结构和机械零部件的弹塑性应力分析及大变形分析。 5)工程结构和机械零件的热弹性蠕变、粘弹性、粘塑性分析。 6)大型工程机械轴承油膜计算等。
弹性力学与有限元分析.ppt
上式建立了单元中任意一点的位移与节点位移的关系，
即通过单元节点位移 e 插值求出单元中任一点位移
f (x, y)，把位移函数的这种描述形式称为插值函数形
式。 形函数具有以下两个性质： 1、形函数 N i在节点 i处的值为1，而在其余两个节点 处的值为0。
2、在单元中任意一点，3个形函数之和为1，即：
差太大，即单元划分中不应出现过大的钝角或过 小的锐角，否则，计算误差较大。 在应力较大和应力集中的区域，单元应划分细一 些，以提高精度。 如果边界上有集中力作用，则该点应被划分为点。
单元的大小和数目应根据精度要求来确定，在保证
精度的前提下，力求采用较少的单元。
当物体的厚度有突变或物体由不同材料组成时，不 要把厚度不同或材料不同的区域划分在统一单元。
x y xy
且它们只是
x, y 的函数，与 z 无关。工程实际中，炮
筒、桥梁支座的柱形辊轴等都可简化为平面应变问题。
所以无论是平面应力问题还是平面应变问题，都只 需研究3个应力分量 x ,y ,xy，3个应变分量 x , y , xy
2个位移分量 U和 V。
四、单元划分
单元划分是有限元分析的基本前提，也是有限元 法解题的重要步骤。常用的单元类型有： 杆单元 平面单元 轴对称单元
空间单元 对平面问题，一般采用三角形单元，此时单元划
分应注意以下问题：
任一三角形单元的顶点必须同时也是其相邻三角
形单元的顶点，而不能是其内点。
三角形单元的3条边长（或3个顶角）之间不应相
x y xy
x y xy
弹性力学有限元位移法原理
一、课程论文：弹性力学有限元位移法原理（30分）主要针对一维（直杆）问题，撰写一篇论文，对有限元位移法的原理作一般性概括和论述。
要求论文论及但不限于下列内容：1）弹性力学有限元位移法的数学、力学基础和基本思想；2）有限元法求解的原理和过程，推导所有计算列式；对基本概念和符号进行解释和讨论；3）收敛性、收敛准则及其数学、力学意义的讨论。
弹性力学有限元位移法原理一、有限单元法的起源有限单元法的形成可以追溯到20世纪50年代甚至更早些时间，基本思路来源于固体力学中矩阵位移法的发展和工程师对结构相似性的直觉判断。
对不同结构的杆系、不同的载荷，用矩阵位移法求解都可以得到统一的公式。
在1952-1953年期间，R·W·Clough和M·J·Turner在分析飞机三角翼振动问题时，提出了把平面应力三角形或矩形板组合起来表达机翼刚度的方法，当时被称为直接刚度法。
1956年M·J·Turner，R·W·Clough，H·C·Martin，L·J·Topp在纽约举行的航空学会年会上发表论文《Stiffness and deflection analysis of complex structures》(复杂结构的刚度和变形分析)介绍了这种新的计算方法，从而将矩阵位移法推广推广到求解弹性力学平面应力问题。
它们把平面板壳结构划分为一个个三角形和矩形的“单元”，利用单元中近似位移函数，求得单元节点力与结点位移关系的单元刚度矩阵。
1960年，R·W·Clough在论文《The finite element in plane stress analysis》(平面应力分析的有限元法)中首次提出了有限单元（Finite Element）这一术语，他也因此被称为“有限单元之父”二、有限元法的基本思想有限元法是一种结构分析的方法，正如O·C·Zienkiewicz所说的：“人类思维的限制在于不能通过一步运算就掌握复杂环境和事物的行为。
弹性力学平面问题有限元法
度之间相关的是应力在其作用截面的法线方向和
z
C
τ zx +
∂τ zx dz ∂z ∂τ yz σx ∂τ xz dy τ yz + τ xz + dx ∂y ∂x fz τxy τyx ∂σ y fy fx σy + dy ∂τ xy τxz σy ∂y τ xy + dx ∂τ yx ∂x ∂σ x τ yx + dy σx + dx ∂y ∂x τ B
yz
σz +
∂σz dz ∂z ∂τ zy dz τ zy + ∂z
P
τzy
τzx
A
σz
o
y
x
正六面单元体的取法
经过物体内任一点如P 经过物体内任一点如P点取出一个微小的正六面 体，它的棱边分别平行于三个坐标轴而长度分别 为： PA = ∆x, PB = ∆y, PC = ∆z。将每个面上的应力分 解为一个正应力和两个切应力。 解为一个正应力和两个切应力。正应力用 σ 表 表示。 示，切应力用 τ 表示。 应力下标的含意： 应力下标的含意：
物理方程的表达形式
以应力表示应变
以应变表示应力
τxy 1 εx = σx −v(σy +σz ) γ xy = E G τ yz 1 ε y = σy − v(σx +σz γ yz = E G τxz 1 εz = σz −v(σx +σy ) γ xz = E G
σx =λθ +2Gεx τxy =Gγxy σy =λθ +2Gεy τyz =Gγ yz σz =λθ +2Gεz τxz =Gγxz
θ = εx + ε y + εz
有限元第一讲 绪论、弹簧单元
五、本课程目标
本课程主要涉及弹性力学有限元法的基本原理。
通过本课程学习，为应用大型通用有限元软件解决工 程中的力学问题和产品设计问题提供一个初步基础， 以及作为进一步学习的入门。
六、引例——弹簧单元
弹簧是宏观上最简单的弹性元件。 1、一个弹簧单元的分析
2个节点： 节点位移： 节点力： 弹簧刚度：
单元特性
KD F
系统平衡方程
2）单元方程扩大相加法 单元特性
相加
F1 f11
F2
f
1 2
f12
F3
f
2 2
系统节点 平衡条件
KD F
系统平衡方程
或 KD F （的结构总刚度矩阵
D —— 系统节点位移列阵
F —— 系统节点载荷列阵
讨论：（1） K 有那些特点和性质？
（2）上述方程能求解吗？
方法2： 将单元刚度方程扩大到整体规模：
将上面的矩阵方程叠加，得到：
代入前面节点平衡条件，得系统节点平衡方程：
3）给定载荷和约束条件下的求解 设边界条件为：
k k
kui
k
u
j
矩阵符号形式：
f kd ——弹簧单元刚度方程
上式中：
k 弹簧单元的刚度矩阵 d 单元节点位移向量 f 单元节点力向量
刚度方程讨论：
1） k 有什么特点？ 2） k 中元素代表什么含义？
3）上面方程可以求解吗？为什么？
2、弹簧系统
各单元的特性分别为： 单元1： 单元2：
应用前面的叠加方法，直接得到弹簧系统的总刚度矩阵： 或 总刚度矩阵特征：对称，奇异、带状、稀疏
由前面的做法，可得到弹簧系统的节点平衡方程：
（b）：先施加位移边界条件
弹性力学平面问题有限元法
弹性：（塑性） 结构在外力拆除后能够完全恢复原有形状的特性。
静力分析： （动态分析） 结构所受外力是不随时间变化的恒力。
一、弹性力学中的物理量
载荷、应力、应变、位移
1.载荷
载荷是外界作用在弹性体上的力，又称为外力。它包括体力、面力和 集中力三内任一点，单位体积的体力用 Pv 表示，它可分解为给定坐标系x、y和z 三个坐标轴上的投影 P v x 、P v y 、P v z ，称为体力分量。
3 弹性力学平面问题有限元法
材料力学主要研究杆、梁、柱 结构力学主要研究杆系（或梁系） 弹性力学主要研究实体和板得受力和变形
弹性力学假设所研究的物体：连续的、完全弹性的 均匀的、各向同性的、微小变形的和无初应力的
在这假设基础上研究受力物体一点上的应力、应变、 变形和平衡关系。
线性： （非线性） 结构的应力与应变的关系（本构关系）呈线性变化。
➢除了在推导公式过程中沿坐标轴分解外，通常
采用沿截面法向和切向分解的方式，即分解为正
应力 和切应力 ， 因为与物体形变和材料强
度之间相关的是应力在其作用截面的法线方向和 切线方向的分量。
C
z
y
zx
yx yz
zx dz
z
z
z dz
zy
z
zy
z
dz
xz x
xz
x f
fx
x
x
dx
z
xy
vu4125xx36yy
1 2
x,yuv10
x 0
y 0
0 1
0 x
0y43fx,y
65
（4－9）
第三步： 求单元中任一点位移 x,y与节点位移 e 的关系
这一步的目的是求出待定系数。
静力分析： （动态分析） 结构所受外力是不随时间变化的恒力。
一、弹性力学中的物理量
载荷、应力、应变、位移
1.载荷
载荷是外界作用在弹性体上的力，又称为外力。它包括体力、面力和 集中力三内任一点，单位体积的体力用 Pv 表示，它可分解为给定坐标系x、y和z 三个坐标轴上的投影 P v x 、P v y 、P v z ，称为体力分量。
3 弹性力学平面问题有限元法
材料力学主要研究杆、梁、柱 结构力学主要研究杆系（或梁系） 弹性力学主要研究实体和板得受力和变形
弹性力学假设所研究的物体：连续的、完全弹性的 均匀的、各向同性的、微小变形的和无初应力的
在这假设基础上研究受力物体一点上的应力、应变、 变形和平衡关系。
线性： （非线性） 结构的应力与应变的关系（本构关系）呈线性变化。
➢除了在推导公式过程中沿坐标轴分解外，通常
采用沿截面法向和切向分解的方式，即分解为正
应力 和切应力 ， 因为与物体形变和材料强
度之间相关的是应力在其作用截面的法线方向和 切线方向的分量。
C
z
y
zx
yx yz
zx dz
z
z
z dz
zy
z
zy
z
dz
xz x
xz
x f
fx
x
x
dx
z
xy
vu4125xx36yy
1 2
x,yuv10
x 0
y 0
0 1
0 x
0y43fx,y
65
（4－9）
第三步： 求单元中任一点位移 x,y与节点位移 e 的关系
这一步的目的是求出待定系数。
弹性力学与有限元法分析及实例讲解
弹性力学与有限元法分析弹性力学是固体力学的一个重要分支，是研究弹性固体在受外力作用、温度改变、边界约束或其他外界因素作用下而发生的应力、形变和位移状态的科学。
有限单元法是力学、数学、物理学、计算方法、计算机技术等多种学科综合发展和结合的产物，是随着计算机技术的广泛应用而迅速发展起来的一种数值分析方法。
有限元法的基本思想就是化整为零，分散分析，再集零为整。
即用结构力学方法求解弹性力学问题，实质是将复杂的连续体划分为有限多个简单的单元体，单元体之间仅仅通过结点相连，实现化无限自由度问题为有限稀有度问题，将连续场函数的（偏）微分方程的求解问题转化为有限个参数的代数方程组的求解问题。
有限元方法经过近半个世纪的发展，目前已经成为各种工程问题特别是结构分析问题的标准分析方法，而有限元软件也已成为现代结构设计中不可缺少的工具。
有限元软件是有限元理论通向实际工程应用的桥梁，它的应用极大地提高了力学学科解决自然科学和工程实际问题的能力，进一步促进了有限元方法的发展。
ANSYS 软件是融结构、流体、电场、磁场、声场分析于一体的大型通用有限元分析软件，广泛用于机械制造、石油化工、航空航天、汽车交通、土木工程、造船、水利等一般工业及科学研究。
ANSYS 软件的组成：（一）前处理模块该模块为用户提供了一个强大的实体建模及网格划分工具，可以方便的构造有限元模型，软件提高了100种以上的单元类型，用来模拟工程中的各种结构和材料。
包括：1.实体建模：参数化建模，布尔运算及体素库，拖拉、旋转、拷贝、蒙皮、倒角等。
2.自动网格划分，自动进行单元形态、求解精度检查及修正。
3.在集合模型上加载：点加载、分布载荷、体载荷、函数载荷。
4.可扩展的标准梁截面形状库。
（二）分析计算模块该模块包括结构分析（可进行线性分析、非线性分析和高度非线性分析）、流体动力学分析、电磁场分析、声场分析、压电分析以及多物理场的耦合分析，可模拟多种物理介质的相互作用，具有灵敏度分析及优化分析能力。